平行线中的题型解析
平行线动点问题的解题技巧

平行线动点问题的解题技巧平行线动点问题是初中数学中常见的一种几何题型,也是高中数学中的重要考点之一。
这类问题常涉及到平行四边形、三角形等图形,需要运用多种定理和方法进行解题。
本文将从以下几个方面详细介绍平行线动点问题的解题技巧。
一、基本概念在介绍解题技巧之前,我们首先需要了解一些基本概念。
平行线指在同一个平面内不相交的两条直线,它们的斜率相等;动点指随着某种规律不断运动的点。
在平行线动点问题中,我们通常需要确定某个动点在运动过程中所处的位置或满足什么条件时两直线之间的距离最短等。
二、解题思路对于平行线动点问题,我们可以采用以下步骤进行分析和求解:1.画图:根据题目所给条件画出图形,并标出所需求的点或长度。
2.列出已知和未知量:根据图形标注出已知量和未知量,并列出方程或条件式。
3.确定关系式:利用几何定理或代数方法推导出各个量之间的关系式。
4.代入求解:将已知量代入关系式中,求解未知量。
三、常用定理和方法1.平行线的性质:平行线在同一平面内,它们的斜率相等。
2.三角形内角和定理:任何一个三角形的三个内角之和等于180度。
3.全等三角形的性质:两个全等的三角形对应边长相等,对应角度相等。
4.相似三角形的性质:两个相似的三角形对应边长成比例,对应角度相等。
5.勾股定理:直角三角形斜边上的正方形面积等于两腰上各自正方形面积之和。
6.垂线定理:在平面直角坐标系中,点(x,y)到直线Ax+By+C=0的距离为|Ax+By+C|/√(A²+B²)。
7.向量法求解:通过向量法求解可以简化计算过程。
利用向量叉积可判断两条线段是否相交,在一些特殊情况下可以极大地减少计算时间。
四、实例分析下面我们以一个具体例子来说明平行线动点问题的解题技巧:已知ABCD为矩形,P、Q分别在AB、CD上滑动,并且AP=PQ=QB。
若M为AC与QP交点,求证:BM=2AM。
解题思路:1.画图:如图所示,画出矩形ABCD和动点P、Q的运动轨迹。
平行线中的四大基本模型(4大题型+20道拓展培优)—2023-2024七年级下册(浙教版)(解析版)
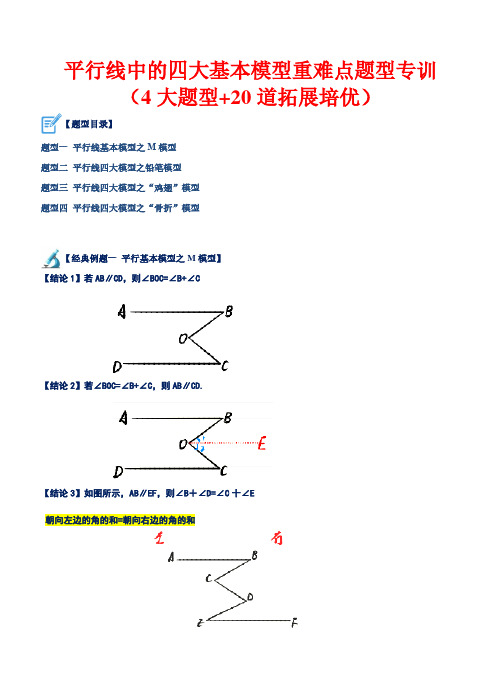
平行线中的四大基本模型重难点题型专训(4大题型+20道拓展培优)【题型目录】题型一平行线基本模型之M模型题型二平行线四大模型之铅笔模型题型三平行线四大模型之“鸡翅”模型题型四平行线四大模型之“骨折”模型【经典例题一平行基本模型之M模型】【结论1】若AB∥CD,则∠B0C=∠B+∠C【结论2】若∠BOC=∠B+∠C,则AB∥CD.【结论3】如图所示,AB∥EF,则∠B+∠D=∠C十∠E朝向左边的角的和=朝向右边的角的和结论3的模型也称为锯齿模型;锯齿模型的变换解题思路拆分成猪蹄模型和内错角拆分成2个猪蹄模型【例1】(2023春·山东济宁·七年级统考阶段练习)如图所示,如果AB ∥ CD ,则∠α、∠β、∠γ之间的关系为()A.∠α+∠β+∠γ=180°B.∠α-∠β+∠γ=180°C.∠α+∠β-∠γ=180°D.∠α-∠β-∠γ=180°[【答案】C【分析】过E作EF∥AB,由平行线的质可得EF∥CD,∠α+∠AEF=180°,∠FED=∠γ,由∠β=∠AEF+∠FED即可得∠α、∠β、∠γ之间的关系.【详解】解:过点E作EF∥AB,∴∠α+∠AEF=180°(两直线平行,同旁内角互补),∵AB∥CD,∴EF∥CD,∴∠FED=∠EDC(两直线平行,内错角相等),∵∠β=∠AEF+∠FED,又∵∠γ=∠EDC,∴∠α+∠β-∠γ=180°,故选:C.【点睛】本题主要考查了平行线的性质,正确作出辅助线是解答此题的关键.【变式训练】 1.(2023上·黑龙江哈尔滨·七年级校考期中)已知:直线AB 与直线CD 内部有一个点P ,连接BP .(1)如图1,当点E 在直线CD 上,连接PE ,若B PEC P ∠+∠=∠,求证:AB CD ;(2)如图2,当点E 在直线AB 与直线CD 的内部,点H 在直线CD 上,连接EH ,若ABP PEH P EHD ∠+∠=∠+∠,求证:AB CD ;(3)如图3,在(2)的条件下,BG 、EF 分别是ABP ∠、PEH ∠的角平分线,BG 和EF 相交于点G ,EF 和直线AB 相交于点F ,当BP PE ⊥时,若10BFG EHD ∠=∠+︒,36BGE ∠=︒,求EHD ∠的度数.【答案】(1)证明见解析;(2)证明见解析;(3)18︒.【分析】(1)过点P 作PF AB ∥,推出PEC EPF ∠=∠,进而得PF CD ∥,根据平行公理的推论即可得证; (2)分别过点P 和点E 作PF AB ∥,EM CD ,推出PEM FPE ∠=∠,进而得PF EM ∥,根据平行公理的推论即可得证;(3)过点E 作EN AB ∥,同(1)(2)理证明FEH FEN NEH BFE EHD ∠=∠+∠=∠+∠,设EHD α∠=,PBG β∠=,PEG γ∠=,则10BFG α∠=+︒,结合角平分线得2290βγα+=︒+,用含α的式子代替β,γ,代入2290βγα+=︒+即可求解.【详解】(1)证明:如图,过点P 作PF AB ∥,∴B BPF Ð=Ð,∵B PEC BPE BPF EPF ∠+∠=∠=∠+∠,∴PEC EPF ∠=∠,∴PF CD ∥,∴AB CD ∥;(2)证明:如图,分别过点P 和点E 作PF AB ∥,EM CD ,∴ABP BPF ∠=∠,MEH EHD ∠=∠,∵ABP PEH P EHD ∠+∠=∠+∠, 即ABP PEM MEH BPF FPE EHD ∠+∠+∠=∠+∠+∠,∴PEM FPE ∠=∠,∴PF EM ∥,∴EM AB ∥,∴AB CD ∥;(3)如图,过点E 作EN AB ∥,由 (2) 得AB CD ∥,∴EN CD ∥,BFE FEN ∠=∠,NEH EHD ∠=∠,∴FEH FEN NEH BFE EHD ∠=∠+∠=∠+∠,设EHD α∠=,PBG β∠=,PEG γ∠=,则10BFG α∠=+︒,∵ BG 、EF 分别是ABP ∠、PEH ∠的角平分线,∴2ABP β∠=,2PEH γ∠=∵BP PE ⊥,∴90P ∠=︒,由 (2) 得ABP PEH P EHD ∠+∠=∠+∠,∴2290βγα+=︒+,∵FEH FEN NEH BFE EHD ∠=∠+∠=∠+∠,∴10210γααα=+︒+=+︒,∵36BGE ∠=︒,()180FGB BFG FBG ∠=︒−∠+∠,180FGB BGE ∠=︒−∠,∴36BFG FBG BGE ∠+∠=∠=︒,∴1036αβ+︒+=︒,∴26βα=︒−∴()()226221090ααα︒−++︒=︒+,∴18α=︒,即EHD ∠的度数为18︒.【点睛】本题考查平行线的判定与性质,角平分线的定义,三角形的内角和,平角定义等知识,添加辅助线,灵活运用平行公理的推论是解题的关键. 2.(2021下·广东河源·七年级河源市第二中学校考期中)已知直线12l l ∥, A 是l1上的一点,B 是l2上的一点,直线l3和直线l1,l2交于C 和D ,直线CD 上有一点P .(1)如果P 点在C ,D 之间运动时,问PAC ∠,APB ∠,PBD ∠有怎样的数量关系?请说明理由.(2)若点P 在C ,D 两点的外侧运动时(P 点与C ,D 不重合),试探索PAC ∠,APB ∠,PBD ∠之间的关系又是如何?(请直接写出答案,不需要证明)【答案】(1)PAC PBD APB ∠+∠=∠(2)当点P 在直线1l 上方时,∠−∠=∠PBD PAC APB ;当点P 在直线2l 下方时,∠−∠=∠PAC PBD APB .【分析】(1)过点P 作1PE l ∥,由“平行于同一条直线的两直线平行”可得出12PE l l ∥∥,再由“两直线平行,内错角相等”得出PAC APE ∠=∠、PBD BPE ∠=∠,再根据角与角的关系即可得出结论;(2)按点P 的两种情况分类讨论:①当点P 在直线1l 上方时;②当点P 在直线2l 下方时,同理(1)可得PAC APE ∠=∠、PBD BPE ∠=∠,再根据角与角的关系即可得出结论.【详解】(1)解:PAC PBD APB ∠+∠=∠.过点P 作1PE l ∥,如图1所示.1PE l ∥,12l l ∥,∴12PE l l ∥∥,PAC APE ∴∠=∠,PBD BPE ∠=∠,APB APE BPE ∠=∠+∠,PAC PBD APB ∴∠+∠=∠.(2)解:结论:当点P 在直线1l 上方时,∠−∠=∠PBD PAC APB ;当点P 在直线2l 下方时,∠−∠=∠PAC PBD APB .①当点P 在直线1l 上方时,如图2所示.过点P 作1PE l ∥.1PE l ∥,12l l ∥,∴12PE l l ∥∥,PAC APE ∴∠=∠,PBD BPE ∠=∠,APB BPE APE ∠=∠−∠,PBD PAC APB ∴∠−∠=∠.②当点P 在直线2l 下方时,如图3所示.过点P 作1PE l ∥.1PE l ∥,12l l ∥,∴12PE l l ∥∥,PAC APE ∴∠=∠,PBD BPE ∠=∠,APB APE BPE ∠=∠−∠,PAC PBD APB ∴∠−∠=∠.【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据“两直线平行,内错角相等”找到相等的角.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质得出相等(或互补)的角是关键.3.(2022下·广东东莞·七年级东莞市光明中学校考期中)阅读下面内容,并解答问题.已知:如图1, AB CD ∥,直线EF 分别交AB ,CD 于点E ,F .BEF ∠的平分线与DFE ∠的平分线交于点G .(1)求证:EG FG ⊥;(2)填空,并从下列①、②两题中任选一题说明理由.我选择 题.①在图1的基础上,分别作BEG ∠的平分线与DFG ∠的平分线交于点M ,得到图2,则EMF ∠的度数为 . ②如图3,AB CD ∥,直线EF 分别交AB ,CD 于点E ,F .点O 在直线AB ,CD 之间,且在直线EF 右侧,BEO ∠的平分线与DFO ∠的平分线交于点P ,则EOF ∠与EPF ∠满足的数量关系为 .【答案】(1)见解析(2)①45︒;②结论:2EOF EPF ∠=∠【分析】(1)利用平行线的性质解决问题即可;(2)①利用基本结论EMF BEM MFD ∠=∠+∠求解即可;②利用基本结论EOF BEO DFO ∠=∠+∠,EPF BEP DFP ∠=∠+∠,求解即可.【详解】(1)证明:如图,过G 作GH AB ∥,∥AB CD ,AB GH CD ∴∥∥,BEG EGH DFG FGH ∠∠∠∠∴==,,//AB CD ,180BEF DFE ∴∠+∠=︒, EG 平分BEF ∠,FG 平分DFE ∠,12GEB BEF ∴∠=∠,12GFD DFE ∠=∠,111()90222GEB GFD BEF DFE BEF DFE ∴∠+∠=∠+∠=∠+∠=︒, 90EGF GEB GFD ∴∠=∠+∠=︒,EG FG ∴⊥;(2)解:①如图2中,由题意,90BEG DFG ∠+∠=︒, EM 平分BEG ∠,MF 平分DFG ∠,1()452BEM MFD BEG DFG ∴∠+∠=∠+∠=︒,45EMF BEM MFD ∴∠=∠+∠=︒,故答案为:45︒;②结论:2EOF EPF ∠=∠.理由:如图3中,由题意,EOF BEO DFO ∠=∠+∠,EPF BEP DFP ∠=∠+∠, PE 平分BEO ∠,PF 平分DFO ∠,2BEO BEP ∴∠=∠,2DFO DFP ∠=∠,2EOF EPF ∴∠=∠,故答案为:2EOF EPF ∠=∠.【点睛】本题考查平行线的性质和判定,角平分线的定义,垂直的定义,解题的关键是熟练掌握相关的性质. 4.(2020下·北京西城·七年级北京师大附中校考阶段练习)请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型“猪蹄模型”.即已知:如图1,AB CD ∥,E 为AB 、CD 之间一点,连接AE ,CE 得到AEC ∠.求证:AEC A C ∠=∠+∠小明笔记上写出的证明过程如下:证明:过点E 作EF AB ∥∵1A ∠=∠∵AB CD ∥,EF AB ∥∴EF CD ∥∴2C ∠=∠∴12AEC ∠=∠+∠∴AEC A C ∠=∠+∠请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.(1)如图,若AB CD ∥,60E ∠=o ,求B C F ∠+∠+∠;(2)如图,AB CD ∥, BE 平分ABG ∠, CF 平分DCG ∠,27G H ∠=∠+,求H ∠.【答案】(1)240(2)51【分析】(1)作EM AB ∥,FN CD ∥,如图,根据平行线的性质得EM AB FN CD ∥∥∥,所以1B ∠=∠,23∠∠=,4180C ∠+∠=,然后利用等量代换计算240B F C ∠+∠+∠=;(2)分别过G 、H 作AB 的平行线MN 和RS ,根据平行线的性质和角平分线的性质可用ABG ∠和DCG ∠分别表示出H ∠和G ∠,从而可找到H ∠和G ∠的关系,结合条件可求得51H ∠=.【详解】(1)作EM AB ∥,FN CD ∥,如图,且AB CD ∥∴EM AB FN CD ∥∥∥∴1B ∠=∠,23∠∠=,4180C ∠+∠=∴1344180B CFE C C BEF C BEF ∠+∠+∠=∠+∠+∠+∠=∠+∠+∠=∠+,∵60BEF ∠=,∴60180240B CFE C ∠+∠+∠=+=;(2)如图,分别过G 、H 作AB 的平行线MN 和RS ,∵BE 平分ABG ∠,CF 平分DCG ∠,∴12ABE ABG ∠=∠,12SHC DCF DCG ∠=∠=∠,∵AB CD ∥∴AB CD RS MN ∥∥∥ ∴12RHB ABE ABG ∠=∠=∠,12SHC DCF DCG ∠=∠=∠,∴180NGB ABG MGC DCG ∠+∠=∠+∠=, ∴()11801802BHC RHB SHC ABG DCG ∠=−∠−∠=−∠+∠, ()()180180180180180BGC NGB MGC ABG DCG ABG DCG ∠=−∠−∠=−−∠−−∠=∠+∠−∴36021801802BGC BHC BHC ∠=−∠−=−∠,∵27BGC BHC ∠=∠+,∴180227BHC BHC −∠=∠+,∴51BHC ∠=.【点睛】本题考查了平行线的性质和判定的应用,能运用平行线的性质和判定进行推理是解此题的关键,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.【经典例题二 平行基本模型之铅笔模型】【结论1】如图所示,AB ∥CD ,则∠B+∠BOC+∠C=360°【结论2】如图所示,∠B+∠BOC+∠C=360°,则AB ∥CD.变异的铅笔头:拐点数n,∠A+...+∠C=180°×(n+1)拐点数:1 拐点数:2 拐点数:n 【例2】(2023下·山东德州·七年级统考期中)如图,AB DE ∥,则下列说法中一定正确的是( )A .123∠=∠+∠B .123180∠+∠−∠=︒C .123270∠+∠+∠=︒D .12390∠−∠+∠=︒【答案】B 【分析】此题要作辅助线,过点C 作CM AB ∥,则根据平行线的传递性,得CM DE ∥.先利用AB CM ∥,可得1180BCM ∠+∠=︒,即1801BCM ∠=︒−∠,再利用CM DE ∥,可得3DCM ∠=∠,而23BCM ∠−∠=∠,整理可得:123180∠+∠−∠=︒.【详解】解:过点C 作CM AB ∥,AB DE ,CM DE ∴∥,1180BCM ∴∠+∠=︒,3MCD ∠=∠,又BCM BCD MCD ∠=∠−∠,180123∴︒−∠=∠−∠,123180∴∠+∠−∠=︒.故选:B .【点睛】注意此类题要作的辅助线:构造平行线.根据平行线的性质即可找到三个角之间的关系.【变式训练】 【变式1】(2023下·甘肃白银·七年级校考期中)如图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架,其主要作用是动力传输.如图2是手动变速箱托架工作时某一时刻的示意图,已知AB CD ,∥CG EF ,150BAG ∠=︒,80AGC ∠=︒,则DEF ∠的度数为( )A .110︒B .120︒C .130︒D .140︒【答案】C 【分析】过点F 作FM CD ∥,则AB CD FM ∥∥,再根据平行线的性质可以求出MFA ∠、EFA Ð,进而可求出EFM ∠,再根据平行线的性质即可求得DEF ∠.【详解】解:如图,过点F 作FM CD ∥,∥AB CD ,AB CD FM ∴∥∥,180DEF EFM ∴∠+∠=︒,180MFA BAG ∠+∠=︒,180********MFA BAG ∴∠=︒−∠=︒−︒=︒.CG EF ∥,80EFA AGC ∴∠=∠=︒.803050EFM EFA MFA ∴∠=∠−∠=︒−︒=︒.180********DEF EFM ∴∠=︒−∠=︒−︒=︒.故选:C .【点睛】本题考查平行线的性质,结合图形利用平行线的性质进行角的转化和计算是解题关键. 【变式2】(2023下·浙江杭州·七年级统考期末)如图,AB CD ∥,射线FE ,FG 分别与AB ,CD 交于点M ,N ,若3F FND EMB ∠=∠=∠,则F ∠的度数是 .【答案】108︒/108度【分析】过点F 作FH AB ∥,可得AB FH CD ∥∥,根据平行线的性质结合已知求出23HFN EFN ∠=∠,可得21803EFN EFN ∠+∠=︒,即可求出EFN ∠的度数.【详解】解:如图,过点F 作FH AB ∥,∵AB CD ∥,∴AB FH CD ∥∥,∴EMB EFH ∠=∠,180HFN FND ∠+∠=︒,∵3EFN FND EMB ∠=∠=∠,∴13EFH EFN ∠=∠,∴23HFN EFN ∠=∠, ∴21803EFN EFN ∠+∠=︒,∴108EFN ∠=︒,故答案为:108︒.【点睛】此题考查了平行线的判定与性质,熟记:①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补是解题的关键. 【变式3】(2023下·内蒙古鄂尔多斯·七年级统考期中)探究题 (1)如下图,AB CD ∥,130PAB ∠=︒,120PCD ∠=︒.求APC ∠度数;(2)如下图,AD BC ∥,点P 在射线OM 上运动,ADP α∠=∠,BCP β∠=∠.①当点P 在A ,B 两点之间运动时,CPD ∠,α∠,∠β之间的数量关系为__________②当点P 在A ,B 两点外侧运动时(点P 与点A ,B ,O 三点不重合),请写出CPD ∠,α∠,∠β之间的数量关系,并说明理由.【答案】(1)110APC ∠=︒;(2)①CPD αβ∠=∠+∠;②CPD βα∠=∠−∠或CPD αβ∠=∠−∠.【分析】本题考查了平行线的性质和判定的应用,解决问题的关键是作辅助线构造内错角以及同旁内角.(1)过P 作PE AB ∥,构造同旁内角,利用平行线性质,可得110APC ∠=︒;(2)①过P 作PE AD ∥交CD 于E ,推出AD PE BC ∥∥,根据平行线的性质得出DPE α∠=∠,CPE β∠=∠,即可得出答案;②画出图形(分两种情况:点P 在BA 的延长线上,点P 在AB 的延长线上),根据平行线的性质得出DPE α∠=∠,CPE β∠=∠,即可得出答案.【详解】(1)解:过P 作PE AB ∥,∵AB CD ∥,∴PE AB CD ∥∥,∵130PAB ∠=︒,120PCD ∠=︒.∴18050APE PAB ∠=︒−∠=︒,18060CPE PCD ∠=︒−∠=︒,∴5060110APC ∠=︒+︒=︒;(2)解:①CPD αβ∠=∠+∠:如图3,过P 作PE AD ∥交CD 于E ,∵AD BC ∥,∴AD PE BC ∥∥,∴DPE α∠=∠,CPE β∠=∠,∴CPD DPE CPE αβ∠=∠+∠=∠+∠;故答案为:CPD αβ∠=∠+∠;②当P 在AB 延长线时,CPD βα∠=∠−∠;理由:如图4,过P 作PE AD ∥交CD 于E ,∵AD BC ∥,∴AD PE BC ∥∥,∴DPE α∠=∠,CPE β∠=∠,∴CPD CPE DPE βα∠=∠−∠=∠−∠;当P 在BO 之间时,CPD αβ∠=∠−∠.理由:如图5,过P 作PE AD ∥交CD 于E ,∵AD BC ∥,∴AD PE BC ∥∥,∴DPE α∠=∠,CPE β∠=∠,∴CPD DPE CPE αβ∠=∠−∠=∠−∠.CPD αβ∴∠=∠−∠综上所述,CPD ∠,α∠,∠β之间的数量关系为CPD βα∠=∠−∠或CPD αβ∠=∠−∠.【经典例题三 平行基本模型之“鸡翅”模型】【例3】(2023秋·全国·八年级专题练习)①如图1,AB ∥CD ,则360A E C ∠+∠+∠=︒;②如图2,AB ∥CD ,则P A C ∠=∠−∠;③如图3,AB ∥CD ,则1E A ∠=∠+∠;④如图4,直线AB ∥CD ∥ EF ,点O 在直线EF 上,则180αβγ∠−∠+∠=︒.以上结论正确的个数是( )A .1个B .2个C .3个D .4个【答案】B【分析】①过点E 作直线EF ∥AB ,由平行线的性质:两直线平行,同旁内角互补,即可得出结论; ②如图2,先根据三角形外角的性质得出∠1=∠C+∠P ,再根据两直线平行,内错角相等即可作出判断; ③如图3,过点E 作直线EF ∥AB ,由平行线的性质可得出∠A+∠AEC ﹣∠1=180°,即得∠AEC =180°+∠1﹣∠A ; ④如图4,根据平行线的性质得出∠α=∠BOF ,∠γ+∠COF =180°,再利用角的关系解答即可.【详解】解:①如图1,过点E 作直线EF ∥AB ,∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠1=180°,∠2+∠C=180°,∴∠A+∠B+∠AEC=360°,故①错误;②如图2,∵∠1是△CEP的外角,∴∠1=∠C+∠P,∵AB∥CD,∴∠A=∠1,即∠P=∠A﹣∠C,故②正确;③如图3,过点E作直线EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠3=180°,∠1=∠2,∴∠A+∠AEC﹣∠1=180°,即∠AEC=180°+∠1﹣∠A,故③错误;④如图4,∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠COF=∠α﹣∠β,∴∠γ+∠α﹣∠β=180°,故④正确;综上结论正确的个数为2,故选:B.【点睛】本题考查的是平行线的性质及三角形外角的性质,熟练掌握平行线的性质,根据题意作出辅助线是解答此题的关键.【变式训练】 1、(2021下·广东东莞·七年级东莞市光明中学校考期中)(1)如图(1)ABCD ,猜想BPD ∠与B D ∠∠、的关系,说出理由.(2)观察图(2),已知AB CD ,猜想图中的BPD ∠与B D ∠∠、的关系,并说明理由.(3)观察图(3)和(4),已知ABCD ,猜想图中的BPD ∠与B D ∠∠、的关系,不需要说明理由.【答案】(1)360B BPD D ∠+∠+∠=︒,理由见解析;(2)BPD B D ∠=∠+∠,理由见解析;(3)图(3)BPD D B ∠=∠−∠,图(4)BPD B D ∠=∠−∠【分析】(1)过点P 作EF AB ∥,得到180B BPE ∠+∠=︒,由ABCD ,EF AB ∥,得到EF CD ,得到180EPD D ∠+∠=︒,由此得到360B BPD D ∠+∠+∠=︒; (2)过点P 作PE AB ,由PE AB CD ∥∥,得到12B D ∠=∠∠=∠,,从而得到结论12BPD B D ∠=∠+∠=∠+∠;(3)由ABCD ,根据两直线平行,内错角相等与三角形外角的性质,即可求得BPD ∠与B D ∠∠、的关系. 【详解】(1)解:猜想360B BPD D ∠+∠+∠=︒.理由:过点P 作EF AB ∥,∴180B BPE ∠+∠=︒,∵AB CD ,EF AB ∥,∴EF CD ,∴180EPD D ∠+∠=︒,∴360B BPE EPD D ∠+∠+∠+∠=︒,∴360B BPD D ∠+∠+∠=︒;(2)BPD B D ∠=∠+∠.理由:如图,过点P 作PEAB ,∵AB CD ,∴PE AB CD ∥∥,∴12B D ∠=∠∠=∠,,∴12BPD B D ∠=∠+∠=∠+∠;(3)如图(3):BPD D B ∠=∠−∠.理由:∵AB CD ,∴1D ∠=∠,∵1B P ∠=∠+∠,∴D B P ∠=∠+∠,即BPD D B ∠=∠−∠;如图(4):BPD B D ∠=∠−∠.理由:∵AB CD ,∴1B ∠=∠,∵1D P ∠=∠+∠,∴B D P ∠=∠+∠,即BPD B D ∠=∠−∠.【点睛】此题考查了平行线的性质,平行公理的推论,三角形的外角的性质定理,熟记平行线的性质是解题的关键. 2.(2020下·湖北武汉·七年级校考期中)如图,已知:点A 、C 、B 不在同一条直线,AD BE ∥(1)求证:180B C A ∠+∠−∠=︒:(2)如图②,AQ BQ 、分别为DAC EBC ∠∠、的平分线所在直线,试探究C ∠与AQB ∠的数量关系;(3)如图③,在(2)的前提下,且有AC QB ∥,直线AQ BC 、交于点P ,QP PB ⊥,直接写出=DAC ACB CBE ∠∠∠:: .【答案】(1)见解析(2)2=180AQB C ∠+∠︒,理由见解析(3)122::【分析】(1)过点C 作CF AD ∥,则CF BE ∥,根据平行线的性质可得出ACF A ∠=∠、180BCF B ∠=︒−∠,据此可得;(2)过点Q 作QM AD ∥,则QM BE ∥,根据平行线的性质、角平分线的定义可得出1()2AQB CBE CAD ∠=∠−∠,结合(1)的结论可得出2180AQB C ∠+∠=︒;(3)由(2)的结论可得出12CAD CBE ∠=∠①,由QP PB ⊥可得出180CAD CBE ∠+∠=︒②,联立①②可求出CAD CBE ∠∠、的度数,再结合( 1)的结论可得出ACB ∠的度数,将其代入DAC ACB CBE ∠∠∠::中可求出结论.【详解】(1)在图①中,过点C 作CF AD ∥,则CF BE ∥.∵CF AD BE ∥∥,∴180ACF A BCF B ∠=∠∠+∠=︒,,∴180180ACB B A ACF BCF B A A A ∠+∠−∠=∠+∠+∠−∠=∠+︒−∠=︒.(2)在图2中,过点Q 作QM AD ∥,则QM BE ∥.∵QM AD QM BE ∥,∥,∴AQM NAD BQM EBQ ∠=∠∠=∠,.∵AQ 平分CAD ∠,BQ 平分CBE ∠, ∴11,22NAD CAD EBQ CBE ∠=∠∠=∠, ∴1()2AQB BQM AQM CBE CAD ∠=∠−∠=∠−∠. ∵180()1802C CBE CAD AQB ︒︒∠=−∠−∠=−∠,∴2180AQB C ∠+∠=︒.(3)∵AC QB ∥, ∴11,22AQB CAP CAD ACP PBQ CBE ∠=∠=∠∠=∠=∠, ∴11801802ACB ACP CBE ∠=︒−∠=︒−∠.∵2180AQB ACB ∠+∠=︒, ∴1.2CAD CBE ∠=∠.又∵QP PB ⊥,∴90CAP ACP ∠+∠=︒,即180CAD CBE ∠+∠=︒,∴60120CAD CBE ∠=︒∠=︒,,∴180120()ACB CBE CAD ∠=︒−∠−∠=︒,∴60120120122DAC ACB CBE ∠∠∠=︒︒︒=::::::, 故答案为:122::. 【点睛】本题主要考查平行线的的判定与性质,解题的关键是熟练掌握平行线的性质、添加辅助线构建平行线. 3.(2021上·八年级课时练习)(1)已知:如图(a ),直线DE AB ∥.求证:ABC CDE BCD ∠+∠=∠; (2)如图(b ),如果点C 在AB 与ED 之外,其他条件不变,那么会有什么结果?你还能就本题作出什么新的猜想? 【答案】(1)见解析;(2)当点C 在AB 与ED 之外时,ABC CDE BCD ∠−∠=∠,见解析【分析】(1)由题意首先过点C 作CF ∥AB ,由直线AB ∥ED ,可得AB ∥CF ∥DE ,然后由两直线平行,内错角相等,即可证得∠ABC+∠CDE=∠BCD ;(2)根据题意首先由两直线平行,内错角相等,可得∠ABC=∠BFD ,然后根据三角形外角的性质即可证得∠ABC -∠CDE=∠BCD .【详解】解:(1)证明:过点C 作CF ∥AB ,∵AB ∥ED ,∴AB ∥ED ∥CF ,∴∠BCF=∠ABC ,∠DCF=∠EDC ,∴∠ABC+∠CDE=∠BCD ;(2)结论:∠ABC -∠CDE=∠BCD ,证明:如图:∵AB ∥ED ,∴∠ABC=∠BFD ,在△DFC 中,∠BFD=∠BCD+∠CDE ,∴∠ABC=∠BCD+∠CDE ,∴∠ABC -∠CDE=∠BCD .若点C 在直线AB 与DE 之间,猜想360ABC BCD CDE ︒∠+∠+∠=,∵AB ∥ED ∥CF ,∴180,180,ABC BCF CDE DCF ︒︒∠+∠=∠+∠=∴360ABC BCD CDE ABC BCF DCF CDE ︒∠+∠+∠=∠+∠+∠+∠=.【点睛】本题考查的是平行线的性质及三角形外角的性质,熟练掌握平行线的性质是解答本题的关键,注意掌握辅助线的作法.4.(2021下·浙江·七年级期末)已知//AM CN ,点B 为平面内一点,AB BC ⊥于B .(1)如图1,点B 在两条平行线外,则A ∠与C ∠之间的数量关系为______;(2)点B 在两条平行线之间,过点B 作BD AM ⊥于点D .①如图2,说明ABD C ∠=∠成立的理由;②如图3,BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E .若180,3FCB NCF BFC DBE ∠∠∠∠+=︒=,求EBC ∠的度数.【答案】(1)∠A+∠C=90°;(2)①见解析;②105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)①过点B 作BG ∥DM ,根据平行线找角的联系即可求解;②先过点B 作BG ∥DM ,根据角平分线的定义,得出∠ABF=∠GBF ,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得2α+β+3α+3α+β=180°,根据AB ⊥BC ,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.【详解】解:(1)如图1,AM 与BC 的交点记作点O ,∵AM ∥CN ,∴∠C=∠AOB ,∵AB ⊥BC ,∴∠A+∠AOB=90°,∴∠A+∠C=90°;(2)①如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,∴∠DBG=90°,∴∠ABD+∠ABG=90°,∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥DM,//,BG CN∴∠C=∠CBG,∠ABD=∠C;②如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)知∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=∠AFB=β,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°得:2α+β+3α+3α+β=180°,∵AB⊥BC,∴β+β+2α=90°,∴α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点睛】本题主要考查了平行线的性质的运用,解决问题的关键是作平行线构造内错角,运用等角的余角(补角)相等进行推导.余角和补角计算的应用,常常与等式的性质、等量代换相关联.解题时注意方程思想的运用.【经典例题四平行基本模型之“骨折”模型】【例4】(2023·全国·九年级专题练习)如图所示,AB∥CD,∠E=37°,∠C=20°,则∠EAB的度数为__________.【答案】57°【分析】根据三角形内角和180°以及平行线的性质:1、如果两直线平行,那么它们的同位角相等;2、如果两直线平行,那么它们的同旁内角互补;3、如果两直线平行,那么它们的内错角相等,据此计算即可.【详解】解:设AE、CD交于点F,∵∠E =37°,∠C = 20°,∴∠CFE=180°-37°-20°=123°,∴∠AFD=123°,∵AB ∥CD ,∴∠AFD+∠EAB=180°,∴∠EAB=180°-123°=57°,故答案为:57°.【点睛】本题主要考查三角形内角和定理以及平行线的性质,熟知平行的性质是解题的关键.【变式训练】【变式1】(2023春·湖北黄冈·七年级校考期中)如图,已知//AB DE ,∠ABC =80°,∠CDE =140°,则∠BCD =_____.【答案】40︒【分析】延长ED 交BC 于M ,根据两直线平行,内错角相等证明∠BMD=∠ABC ,再求解CMD ∠,再利用三角形的外角的性质可得答案.【详解】解:延长ED 交BC 于M ,∵//AB DE ,∴∠BMD=∠ABC=80°,∴180100CMD BMD ∠=︒−∠=︒;又∵∠CDE=∠CMD+∠C ,∴14010040BCD CDE CMD ∠=∠−∠=︒−︒=︒.故答案是:40°【点睛】本题考查了平行线的性质.三角形的外角的性质,邻补角的定义,掌握以上知识是解题的关键.【变式2】(2023春·江苏盐城·七年级景山中学校考阶段练习)如图,若//AB CD ,则∠1+∠3-∠2的度数为______【答案】180°【分析】延长EA 交CD 于点F ,则有∠2+∠EFC=∠3,然后根据//AB CD 可得∠1=∠EFD ,最后根据领补角及等量代换可求解.【详解】解:延长EA 交CD 于点F ,如图所示://AB CD ,∴∠1=∠EFD ,∠2+∠EFC=∠3,∴32EFC ∠=∠−∠,+180EFC EFD ∠∠=︒,∴132180∠+∠−∠=︒;故答案为180°.【点睛】本题主要考查三角形外角的性质及平行线的性质,熟练掌握三角形外角的性质及平行线的性质是解题的关键.【变式3】(2023春·全国·七年级专题练习)(1)如图,AB //CD ,CF 平分∠DCE ,若∠DCF =30°,∠E =20°,求∠ABE 的度数;(2)如图,AB//CD,∠EBF=2∠ABF,CF平分∠DCE,若∠F的2倍与∠E的补角的和为190°,求∠ABE的度数.(3)如图,P为(2)中射线BE上一点,G是CD上任一点,PQ平分∠BPG,GN//PQ,GM平分∠DGP,若∠B=30°,求∠MGN的度数.【答案】(1)∠ABE=40°;(2)∠ABE=30°;(3)∠MGN=15°.【分析】(1)过E作EM∥AB,根据平行线的判定与性质和角平分线的定义解答即可;(2)过E作EM∥AB,过F作FN∥AB,根据平行线的判定与性质,角平分线的定义以及解一元一次方程解答即可;(3)过P作PL∥AB,根据平行线的判定与性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义解答即可.【详解】解:(1)过E作EM∥AB,∵AB∥CD,∴CD∥EM∥AB,∴∠ABE=∠BEM,∠DCE=∠CEM,∵CF平分∠DCE,∴∠DCE=2∠DCF,∵∠DCF=30°,∴∠DCE=60°,∴∠CEM=60°,又∵∠CEB=20°,∴∠BEM=∠CEM﹣∠CEB=40°,∴∠ABE=40°;(2)过E作EM∥AB,过F作FN∥AB,∵∠EBF=2∠ABF,∴设∠ABF=x,∠EBF=2x,则∠ABE=3x,∵CF平分∠DCE,∴设∠DCF=∠ECF=y,则∠DCE=2y,∵AB∥CD,∴EM∥AB∥CD,∴∠DCE=∠CEM=2y,∠BEM=∠ABE=3x,∴∠CEB=∠CEM﹣∠BEM=2y﹣3x,同理∠CFB=y﹣x,∵2∠CFB+(180°﹣∠CEB)=190°,∴2(y﹣x)+180°﹣(2y﹣3x)=190°,∴x=10°,∴∠ABE=3x=30°;(3)过P作PL∥AB,∵GM平分∠DGP,∴设∠DGM=∠PGM=y,则∠DGP=2y,∵PQ平分∠BPG,∴设∠BPQ=∠GPQ=x,则∠BPG=2x,∵PQ∥GN,∴∠PGN=∠GPQ=x,∵AB∥CD,∴PL∥AB∥CD,∴∠GPL=∠DGP=2y,∠BPL=∠ABP=30°,∵∠BPL=∠GPL﹣∠BPG,∴30°=2y﹣2x,∴y﹣x=15°,∵∠MGN=∠PGM﹣∠PGN=y﹣x,∴∠MGN=15°.【点睛】此题考查平行线的判定与性质,角平分线的定义,三角形的内角和定理,解题关键在于作辅助线和掌握判定定理.【拓展培优】1.(2023下·安徽·九年级专题练习)如图,已知:AB EF∥.在证明该结论∥,B E∠=∠,求证:BC DE时,需添加辅助线,则以下关于辅助线的作法不正确的是()A .延长BC 交FE 的延长线于点GB .连接BEC .分别作BCD ∠,CDE ∠的平分线CG ,DHD .过点C 作CG AB ∥(点G 在点C 左侧),过点D 作DH EF ∥(点H 在点D 左侧)【答案】C【分析】根据平行线的性质与判定逐一判断即可.【详解】解:A 、如图,∵AB EF ∥,∴B G ∠=∠,∵B DEF ∠=∠,∴G DEF =∠∠,∴BC DE ∥,故此选项不符合题意;B 、如图,∵AB EF ∥,∴ABE FEB ∠=∠,∵ABC FED ∠=∠,∴CBE DEB ∠=∠,∴BC DE ∥,故此选项不符合题意;C 、如图,由CG 平分BCD ∠,DH 平分CDE ∠,没有条件说明BCD ∠与CDE ∠相等,也没有条件说明CG 与DH 平行,∴此辅助线的作法不能说明BC 与DE 平行,故此选项符合题意;D 、如图,延长BC 交DH 于点M ,∵AB EF ∥,CG AB ∥,DH EF ∥,∴AB CG DH EF ∥∥∥,∴B BMD ∠=∠,MDE E ∠=∠,∵B E ∠=∠,∴BMD MDE ∠=∠,∴BC DE ∥,故此选项不符合题意.故选:C .【点睛】本题考查平行线的判定和性质,角平分线的定义,平行公理的推论.掌握平行线的判定和性质是解题的关键. 2.(2023下·山东菏泽·七年级统考期末)图1是男子竞技体操项目双杠的静止动作,图2是其俯视示意图,已知a b ∥,若AB 与BC 的夹角为100︒,150∠=︒,则2∠的度数为( )A .100︒B .120︒C .125︒D .130︒【答案】D 【分析】过点B 作BD a ∥,则BD b ∥,利用平行线的性质,进行求解即可.【详解】解:如图,过点B 作BD a ∥,∵a b ,∴BD b ∥,∴150ABD ∠=∠=︒,2180CBD ∠+∠=︒,∵100ABC ∠=︒,∴1005050CBD ∠=︒−︒=︒,∴218050130︒︒=∠=−︒.故选:D .【点睛】本题考查平行线的判定和性质.解题的关键是构造平行线.3.(2021下·湖北武汉·七年级武汉外国语学校(武汉实验外国语学校)校考期中)如图,直线AB CD EF ∥∥,且40B ∠=︒,125C ∠=︒,则(CGB ∠= )A .10︒B .15︒C .20︒D .25︒【答案】B【分析】根据平行线的性质得出40BGF B ∠=∠=︒,180C CGF ∠+∠=︒,求出55CGF ∠=︒,即可得出答案.【详解】解:∵AB CD EF ∥∥,40B ∠=︒,125C ∠=︒,40BGF B ∴∠=∠=︒,18055CGF C ∠=︒−∠=︒,15CGB CGF BGF ∴∠=∠−∠=︒.故选:B .【点睛】本题考查了平行线的性质的应用,主要考查学生的推理能力和计算能力. 4.(2023下·甘肃白银·八年级统考期末)如图,ABC 为等边三角形,AP CQ ∥.若20BAP ∠=︒,则1∠=()A .80︒B .40︒C .60︒D .70︒【答案】B【分析】过点B 作BE CQ ,可得AP CQ BE ,用平行线性质求解即可.【详解】解:过点B 作BE CQ ,如图,∵AP CQ ∥,∴AP CQ BE ,∴20BAP ABE ∠=∠=︒,∵ABC 为等边三角形,∴60ABC ∠=︒,∴40CBE ABC ABE ∠∠=−∠=︒,∵BE CQ ,∴140CBE ∠=∠=︒,故选:B .【点睛】本题考查平行线的判定与性质,正确作出辅助线是关键. 5.(2023下·浙江绍兴·七年级统考期末)如图,AB CD ∥,AE 平分BAN ∠,AE 的反向延长线交CDN ∠的平分线于点M ,则M ∠与N ∠的数量关系是( )A .2M N ∠=∠B .3M N ∠=∠C .180M N ∠+∠=︒D .2180M N ∠+∠=︒【答案】D 【分析】先利用角平分线的定义得到12BAE BAN ∠=∠,12CDM CDN ∠=∠,过M 作MF AB ∥,过N 作NH AB ∥,再利用平行线的判定与性质得到12FME BAE BAN ∠=∠=∠,BAN ANH ∠=∠,12FMD CDM CDN ∠=∠=∠,180CDN HND ∠+∠=︒,经过角度之间的运算得到180CDN BAN AND ∠−∠=︒−∠,()11802DMA AND ∠=︒−∠,即2180DMA AND ∠+∠=︒可求解.【详解】解:∵AE 平分BAN ∠,DM 平分CDN ∠,∴12BAE BAN ∠=∠,12CDM CDN ∠=∠,过M 作MF AB ∥,过N 作NH AB ∥,则12FME BAE BAN ∠=∠=∠,BAN ANH ∠=∠,∵AB CD ∥,∴MF CD ∥,NH CD ∥,∴12FMD CDM CDN ∠=∠=∠,180CDN HND ∠+∠=︒, ∴180AND ANH HND BAN CDN ∠=∠+∠=∠+︒−∠,即180CDN BAN AND ∠−∠=︒−∠,又∵DMA FMD FME ∠=∠−∠()12CDN BAN =∠−∠()11802AND =︒−∠,∴2180DMA AND ∠+∠=︒,即2180M N ∠+∠=︒,故选:D .【点睛】本题考查角平分线的定义、平行线的判定与性质、角的运算,添加平行线,利用平行线的性质探究角之间的关系是解答的关键. 6.(2023下·辽宁沈阳·七年级统考期中)如图,AD BC ∥,CAD ∠和CBD ∠的平分线相交于点P .请写出C ∠、D ∠、P ∠的数量关系 .【答案】2P C D ∠=∠+∠【分析】作PG AD ∥,则PG AD BC ∥∥,根据平行线的性质可得APB DAP CBP ∠=∠+∠,结合角平分线定义可得1122APB DAC CBD ∠=∠+,再根据AD BC ∥推出DAC C ∠=∠,D CBD ∠=∠,即可得出2P C D ∠=∠+∠.【详解】解:如图,作PG AD ∥,AD BC ∥,∴PG AD BC ∥∥,PG AD ∥,∴DAP APG ∠=∠,PG BC ∥,∴CBP BPG ∠=∠,∴APB APG BPG DAP CBP ∠=∠+∠=∠+∠,CAD ∠和CBD ∠的平分线相交于点P .∴12DAP DAC ∠=∠,12CBP CBD ∠=∠, ∴1122APB DAC CBD ∠=∠+,∴2APB DAC CBD ∠=∠+∠,AD BC ∥,∴DAC C ∠=∠,D CBD ∠=∠,∴2APB C D ∠=∠+∠,即2P C D ∠=∠+∠.故答案为:2P C D ∠=∠+∠.【点睛】本题考查平行线的判定与性质,角平分线的定义,角的和差关系等,解题的关键是熟练掌握平行线的性质. 7.(2023下·浙江·七年级校联考期中)如图,图1是一盏可折叠台灯,图2为其平面示意图,底座AO OE ⊥点O ,支架AB ,BC 为固定支撑杆,BAO ∠是CBA ∠的两倍,灯体CD 可绕点C 旋转调节,现把灯体CD 从水平位置旋转到CD '位置(如图 2中虚线所示),此时,灯体CD '所在的直线恰好垂直支架AB ,且120BCD DCD '∠−∠=︒,则DCD '∠= .【答案】40︒/40度【分析】延长OA 交CD 于点F ,延长D C '交AB 于G ,可得90AGC AFC ∠=∠=︒,可得DCD GAF '∠=∠,在四边形ABCF 中,利用四边形内角和为360︒列出等式计算即可.【详解】解:延长OA 交CD 于点F ,延长D C '交AB 于G ,如图.CD OE ∥,AO OE ⊥,OA CD ∴⊥,AO OE ⊥Q ,D C AB '⊥,90AGC AFC ∴∠=∠=︒,180GCF GAF ∴∠+∠=︒,180DCD GCF '∠+∠=︒Q ,DCD GAF '∴∠=∠,180180BAO GAF DCD '∴∠=︒−∠=︒−∠,∵BAO ∠是CBA ∠的两倍,()11802CBA DCD '∴∠=︒−∠∵120BCD DCD '∠−∠=︒,120BCD DCD '∴∠=∠+︒,在四边形ABCF 中,360GAF CBA BCD AFC ∠+∠+∠+∠=︒,()1180120903602DCD DCD DCD '∴∠'+︒−∠+∠'+︒+︒=︒,解得40DCD '∠=︒.故答案为:40︒.【点睛】此题考查平行线的性质,四边形的内角和定理,一元一次方程的应用,利用图形性质建立方程求解是解题关键.8.(2023下·湖北·七年级黄石市有色中学校联考期末)如图,直线AB CD ∥,直线EF 与AB ,CD 分别交于点E ,F ,AEF ∠与CFE ∠的角平分线交于点P ,延长FP 交AB 于点G ,过点G 作GQ FG ⊥交直线EF 于点Q ,连接PQ ,点M 是QG 延长线上的一点,且PQM QPM ∠=∠,若PN 平分FPM ∠交CD 于点N ,则NPQ ∠的度数为 .【答案】135︒/135度【分析】根据平行线的性质求出180AEF CFE ∠+∠=︒,根据角平分线定义求出90PEF PFE ∠+∠=︒,求出90EPF ∠=︒,求出GQ EP ∥,根据平行线的性质求出PQM QPE ∠=∠,再求出答案即可.【详解】设PQM QPM x ∠=∠=︒,∵PN 平分MPF ∠,∴MPN FPN ∠=∠,设MPN FPN y ∠=∠=︒,∵AEF ∠与CFE ∠的角平分线交于点P ,∴12PEF AEF ∠=∠,12EFP CFE ∠=∠,∵AB CD ∥,∴180AEF CFE ∠+∠=︒,∴1180902PEF PFE ∠+∠=⨯︒=︒,∴()1801809090EPF PEF PFE ∠=︒−∠+∠=︒−︒=︒,∵GQ PF ⊥,∴90QGP =︒∠,∴QGP EPF ∠=∠,∴GQ EP ∥,∴PQM QPE x ∠=∠=︒,∵360QPE QPM FPN NPM EPF ∠+∠+∠+∠+∠=︒,∴90360x x y y ++++=,∴135x y +=,即135QPM NPM ∠+∠=︒,∴135NPQ QPM NPM ∠=∠+∠=︒.故答案为:135︒.【点睛】本题考查了平行线的性质,角平分线的定义,三角形的内角和定理等知识点,能综合运用知识点进行推理是解此题的关键. 9.(2023下·四川成都·七年级统考期末)如图,直线AE CF ,ABC ∠ 的平分线BD 交直线CF 于点D ,若2260A BCF ∠=︒∠=︒,,则D ∠的度数为 . 【答案】19︒/19度【分析】过点B 作B G C F ∥,利用平行线的性质求得22,60ABG CBG ∠=︒∠=︒,从而得到82ABC ∠=︒,再运用角平分线的性质得到1412CBD ABC ∠=∠=︒,继而求出19DBG ∠=︒,最后利用平行线的性质得到19D DBG ∠=∠=︒.【详解】过点B 作B G C F ∥,∵B G C F ∥,AE CF ,∴BG CF AE ∥∥∴,A ABG CBG BCF ∠=∠∠=∠,又∵2260A BCF ∠=︒∠=︒,,∴22,60A ABG CBG BCF ∠=∠=︒∠=∠=︒,∴82ABC ABG CBG ∠=∠+∠=︒,又∵BD 是ABC ∠ 的平分线, ∴1412CBD ABC ∠=∠=︒, ∴19DBG CBG CBD ∠=∠−∠=︒,又∵B G C F ∥,∴19D DBG ∠=∠=︒.【点睛】本题考查角平分线的定义,平分线的性质等知识,掌握平行线的性质是解题的关键. 10.(2023下·湖北武汉·七年级统考期末)如图,80AEC ∠=︒,在AEC ∠的两边上分别过点A 和点C 向同方向作射线AB 和CD ,且ABCD ,若EAB ∠和ECD ∠的角平分线所在的直线交于点P (P 与C 不重合),则APC ∠的大小为 . 【答案】40︒【分析】根据题意作图,过点E 作EF AB ∥,过点P 作PQ AB ∥,利用平行线的性质可得80ECD EAB AEC ∠−∠=∠=︒,PCD PAB APC ∠−∠=∠,再结合角平分线即可求得答案.【详解】解:根据题意作图,过点E 作EF AB ∥,过点P 作PQ AB ∥,∵AB CD ,∴AB CD EF PQ ∥∥∥,∵EF AB ∥,EF CD ,∴180EAB AEC CEF ∠+∠+∠=︒,180CEF ECD ∠+∠=︒,∴EAB AEC ECD ∠+∠=∠,即80ECD EAB AEC ∠−∠=∠=︒,∵PQ AB ∥,PQ CD ∥,∴180PAB APC CPQ ∠+∠+∠=︒,180CPQ PCD ∠+∠=︒,∴PAB APC PCD ∠+∠=∠,即PCD PAB APC ∠−∠=∠,又∵点P 为EAB ∠和ECD ∠的角平分线所在的直线的交点, ∴12PAB EAB ∠=∠,12PCD ECD ∠=∠, ∴11140222APC PCD PAB ECD EAB AEC ∠=∠−∠=∠−∠=∠=︒,故答案案为:40︒.【点睛】本题考查平行线的性质,角平分线的定义,掌握平行线的性质是解决问题的关键. 11.(2023下·七年级课时练习)如图,AB ∥CD ,ME 平分∠AMF ,NF 平分∠CNE ,EN ,MF 交于点O . (1)若∠AMF =50°,∠CNE =40°,分别求∠MEN ,∠MFN 的度数;(2)若图中∠MEN +60°=2∠MFN ,求∠AMF 的度数;(3)探究∠MEN ,∠MFN 与∠MON 之间的数量关系.【答案】(1)∠MEN =65°,∠MFN =70°(2)∠AMF =40°(3)32MEN MFN MON ∠+∠=∠,理由见解析【详解】(1)分别过点E ,F 作AB 的平行线,则它们同时也与CD 平行,则有∠MEN =∠AME +∠CNE ,∠MFN =∠AMF +∠CNF .由∠AMF =50°,∠CNE =40°,ME 平分∠AMF ,NF 平分∠CNE ,得∠AME =25°,∠CNF =20°,∴∠MEN =65°,∠MFN =70°.(2)由(1)可知,∠MEN =∠AME +∠CNE ,∠MFN =∠AMF +∠CNF ,则有∠AME +∠CNE +60°=2∠AMF +2∠CNF .又2∠CNF =∠CNE ,2∠AME =∠AMF . ∴3602AMF ∠=︒,故∠AMF =40°.(3)过点O 作AB 的平行线,则它同时也与CD 平行,易证∠MON =∠AMF +∠CNE .∵∠MEN =∠AME +∠CNE ,∠MFN =∠AMF +∠CNF , ∴32MEN MFN ∠+∠=(∠AMF +∠CNE ). ∴32MEN MFN MON ∠+∠=∠. 12.(2023上·浙江·八年级专题练习)已知,如图,AB 与CD 交于点O (1)如图1,若A B ∠∠=,求证:A C B D ∠+∠∠+∠=(2)如图2,若A B ∠≠∠,(1)中的结论是否仍然成立?请判断并证明你的结论(注:不能用三角形内角和定理)(3)如图3,若65B ∠︒=,25C ∠︒=,AP 平分BAC ∠,DP 平分BDC ∠,请你(2)中结论求出P ∠的度数,请直接写出结果P ∠= .【答案】(1)见解析(2)仍然成立,证明见解析(3)45︒【分析】本题考查了平行线的性质、三角形内角和定理的综合运用,掌握三角形内角和180︒是解题的关键.(1)依据平行线的性质,即可得到C D ∠∠=,依据等式基本性质得到A C B D ∠+∠∠+∠=;。
平行线拐点问题六种模型题型

平行线常见四种易错题型分析七年级下学期,平行线常见四种易错题型分析:过拐点作已知直线的平行线。
本篇内容,我们接着介绍平行线中常见的六种易错题型,早掌握避免遇到时出错。
平行线间拐点问题基本模型有三种: 第一种铅笔模型;第二种M型;第三种猪手模型。
我们还介绍了平行线四大拐点模型:“铅笔”模型、“猪蹄”模型、“臭脚”模型、“骨折”模型,这四类模型的共通点是需要做辅助线,做辅助线的方法比较多,通用的方法为:过拐点作已知直线的平行线。
一、性质定理与判定定理的区分要分清它们,只要注意:(1)由角得到直线平行,是判定定理,选择①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行,这三个定理之一。
(2)由平行的直线得到角的关系,是性质定理,选择①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补,这三个定理之一。
【分析】先由垂直的定义得到:∠2=∠3,然后由同位角相等,两直线平行得到:EF∥BD,再由两直线平行,同位角相等得到:∠4=∠5,然后根据等量代换得到:∠1=∠5,再根据内错角相等,两直线平行得到:DG∥BC,最后由两直线平行,同位角相等即可证∠ADG=∠C.二、三线八角理解不透彻很多学生遇到两条平行线被第三条直线所截时,会找同位角、内错角、同旁内角,但是遇到两条相交线被第三条直线所截时,却不会找了,主要原因就是对“三线八角”理解不透彻。
要想准确地解决这类问题,首先要明确三种角的位置特点,在前一篇文章中我们特地介绍过,七年级下学期,三线八角、平行线的性质与判定定理,掌握解题诀窍其次要搞清楚被哪条直线所截。
【分析】∠A与∠B的共边线为直线AB,那么直线AB为截线,即直线AC与直线BC被第三条直线AB所截,那么∠A与∠B是同旁内角,正确;∠1与∠2是邻补角,错误;∠2与∠A的共边线为直线AC,是同位角,错误;∠2与∠3是内错角,错误。
三、对平行线的概念理解不透彻例题3:判断题:同一平面内不相交的两条线,叫做平行线.【分析】这句话,乍看没有问题,但是细看的话,与定义有出入。
七年级数学下册 5.2平行线及其判定(十大题型)(解析版 )

七级下册数学《第五章相交线与平行线》5.2平行线及其判定平行线及其表示方法★1、平行线定义:在同一个平面内,不相交的两条直线叫做平行线.记作:AB∥CD;记作:a∥b;读作:直线AB平行于直线CD.读作:直线a平行于直线b.【注意】1、在同一平面内,不重合的两条直线只有两种位置关系:相交和平行.(重合的直线视为一条直线)2、.线段或射线平行是指它们所在的直线平行.平行线的画法◆过直线外一点画已知直线的平行线的方法:一“落”把三角尺一边落在已知直线上;二“靠”把直尺紧靠三角尺的另一边;三“移”沿直尺移动三角尺,使三角尺与已知直线重合的边过已知点;四“画”沿三角尺过已知点的边画直线.【注意】1.经过直线上一点不能作已知直线的平行线.2.画线段或射线的平行线是指画它们所在直线的平行线.3.借助三角尺画平行线时,必须保持紧靠,否则画出的直线不平行.平行公理及其推论★1、平行公理:经过直线外一点,有且只有一条直线与这条直线平行.★2、平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.也就是说:如图,如果b∥a,c∥a,那么b∥c.几何语言:∵b∥a,c∥a,∴b∥c.【注意】1、平行公理的推论中,三条直线可以不在同一个平面内.2、平行公理中强调“直线外一点”,因为若点在直线上,不可能有平行线;“有且只有”强调这样的直线是存在的,也是唯一的.平行线的判定方法★1、平行线的判定:判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.几何语言表示:∵∠2=∠3(已知),∴a∥b(同位角相等,两直线平行).判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.几何语言表示:∵∠2=∠4(已知),∴a∥b.(内错角相等,两直线平行).判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.几何语言表示:∵∠1+∠2=180°(已知),∴a∥b(同旁内角互补,两直线平行).★2、在同一平面内,垂直于同一条直线的两直线垂直.几何语言表示:直线a,b,c在同一平面内,∵a⊥c,b⊥c,∴a∥b.【注意】三条直线在“同一平面内”是前提,没有这个条件结论不一定成立.★3、判定两直线平行的方法(1)平行线的定义;(2)平行公理的推论(如果两条直线都与第三条直线平行,那么这两条直线也互相平行);(3利用同位角相等说明两直线平行;(4)利用内错角相等说明两直线平行;(5)利用同旁内角互补说明两直线平行;(6)同一平面内,垂直于同一直线的两直线平行.【例题1】(2023秋•埇桥区期中)在同一平面内,两条直线的位置关系可能是()A.相交或垂直B.垂直或平行C.平行或相交D.相交或垂直或平行【分析】根据两条直线有一个交点的直线是相交线,没有交点的直线是平行线,可得答案.【解答】解:在同一平面内,两条直线有一个交点,两条直线相交;在同一平面内,两条直线没有交点,两条直线平行,故C正确;故选:C.【点评】本题考查了平行线,两条直线有一个交点的直线是相交线,没有交点的直线是平行线.解题技巧提炼解题的关键是准确把握平行线的概念,牢记平行线的三个条件:①在同一平面内;②不相交;③都是直线,通过与定义进行对比来进行判断.【变式1-1】如图所示,能相交的是,平行的是.(填序号)【分析】根据平行线、相交线的定义,逐项进行判断,即可正确得出结果.【解答】解:①中一条直线,一条射线,不可相交,也不会平行;②中一条直线,一条线段,不可相交,也不会平行;③中一条直线,一条线段,可相交;④中都是线段,不可延长,不可相交,也不平行,⑤中都是直线,延长后不相交,是平行.故答案为:③,⑤.【点评】本题考查平行线和相交线,解题的关键是掌握直线可以沿两个方向延伸,射线可以沿一个方向延伸,线段不能延伸.【变式1-2】下列说法正确的是()A.同一平面内,如果两条直线不平行,那么它们互相垂直B.同一平面内,如果两条直线不相交,那么它们互相垂直C.同一平面内,如果两条直线不相交,那么它们互相平行D.同一平面内,如果两条直线不垂直,那么它们互相平行【分析】根据平行线的判定及垂直、相交的定义判断求解即可.【解答】解:在同一平面内,如果两条直线不平行,那么这两条直线相交,故A不符合题意;在同一平面内,两条直线不相交,那么这两条直线平行,故B不符合题意;同一平面内,如果两条直线不相交,那么这两条直线平行,故C符合题意;同一平面内,如果两条直线不垂直,它们不一定平行,故D不符合题意;故选:C.【点评】此题考查了平行线的判定、垂直、相交等知识,熟练掌握有关定理、定义是解题的关键.【变式1-3】(2022春•莱芜区校级期末)下列说法中,正确的是()A.两条不相交的直线叫做平行线B.一条直线的平行线有且只有一条C.在同一平面内,若直线a∥b,a∥c,则b∥cD.若两条线段不相交,则它们互相平行【分析】根据平行线的定义、性质、判定方法判断,排除错误答案.【解答】解:A、平行线的定义:在同一平面内,两条不相交的直线叫做平行线.故错误;B、过直线外一点,有且只有一条直线与已知直线平行.一条直线的平行线有无数条,故错误;C、在同一平面内,平行于同一直线的两条直线平行.故正确;D、根据平行线的定义知是错误的.故选:C.【点评】本题考查平行线的定义、性质及平行公理,熟练掌握公理和概念是解决本题的关键.【变式1-4】(2022秋•乌鲁木齐期末)如图,在长方体AB CD-EFGH中,与棱EF异面且与平面EFGH 平行的棱是.【分析】与棱EF异面且与平面EFGH平行的棱是:棱AD和棱BC.【解答】解:与棱EF异面且与平面EFGH平行的棱是:棱AD和棱BC.故答案为:棱AD和棱BC.【点评】本题主要考查了平行线与立体图形,熟练掌握平行线与立体图形的特征进行求解是解决本题的关键.【变式1-5】(2022春•沙河市期末)观察如图所示的长方体,与棱AB平行的棱有几条()A.4B.3C.2D.1【分析】根据长方体即平行线的性质解答.【解答】解:图中与AB平行的棱有:EF、CD、GH.共有3条.故选:B.【点评】本题考查了平行线的定义、长方体的性质.一个长方形的两条对边平行.【变式1-6】在同一平面内,直线l1与l2满足下列关系,写出其对应的位置关系:(1)若l1与l2没有公共点,则l1和l2;(2)若l1与l2只有一个公共点,则l1和l2;(3)若l1与l2有两个公共点,则l1和l2.【分析】(1)结合平行线的定义进行解答即可;(2)结合相交的定义进行解答即可;(3)结合重合的定义进行解答即可.【解答】解:(1)由于l1和l2没有公共点,所以l1和l2平行;(2)由于l1和l2有且只有一个公共点,所以l1和l2相交;(3)由于l1和l2有两个公共点,所以l1和l2重合;故答案为:(1)平行;(2)相交;(3)重合.【点评】本题侧重考查两直线的位置关系,掌握平行定义是解题关键.【变式1-7】(2022春•赵县月考)在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是.【分析】根据同一平面内,一条直线与两条平行线中的一条相交,则必与另一条直线也相交.解答即可.【解答】解:因为a∥c,直线a,b相交,所以直线b与c也有交点;故答案为:相交.【点评】本题主要考查了平行线和相交线,同一平面内,一条直线与两条平行线中的一条相交,则必与另一条直线也相交.【例题2】(2022春•梁山县期中)若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有()A.1个或2个或3个B.0个或1个或2个或3个C.1个或2个D.以上都不对【分析】根据平行线的定义,相交线的定义,可得答案.【解答】解:当三条直线互相平行,交点是个0;当两条直线平行,与第三条直线相交,交点是2个;当三条直线两两相交交于同一点,交点个数是1个;当三条直线两两相交且不交于同一点,交点个数是3个;故选:B.【点评】本题考查了平行线,分类讨论是解题关键.解题技巧提炼用分类讨论的思想根据平面内两条直线的位置关系去讨论求解.【变式2-1】在同一平面内,两条不重合直线的位置关系可能是()A.垂直或平行B.垂直或相交C.平行或相交D.平行、垂直或相交【分析】同一平面内,直线的位置关系通常有两种:平行或相交;垂直不属于直线的位置关系,它是特殊的相交.【解答】解:平面内的直线有平行或相交两种位置关系.故选:C.【点评】本题主要考查了在同一平面内的两条直线的位置关系.【变式2-2】在同一平面内有三条直线,如果使其中有且只有两条直线平行,那么这三条直线有且只有个交点.【分析】根据同一平面内直线的位置关系得到第三条直线与另两平行直线相交,再根据直线平行和直线相交的定义即可得到交点的个数.【解答】解:∵在同一平面内有三条直线,如果其中有两条且只有两条相互平行,∴第三条直线与另两平行直线相交,∴它们共有2个交点.故答案为2.【点评】本题考查了直线平行的定义:没有公共点的两条直线是平行直线.也考查了同一平面内两直线的位置关系有:平行,相交.【变式2-3】平面内四条直线共有三个交点,则这四条直线中最多有条平行线.【分析】根据同一平面内两条直线的位置关系有两种:相交或平行,及一条直线的平行线有无数条,由四条直线相互平行,其交点为0个开始分析,然后依次变为三条直线相互平行、两条直线相互平行即可求解.【解答】解:若四条直线相互平行,则没有交点;若四条直线中有三条直线相互平行,则此时恰好有三个交点;若四条直线中有两条直线相互平行,另两条不平行,则此时有三个交点或五个交点;若四条直线中有两条直线相互平行,另两条也平行,但它们之间相互不平行,则此时有四个交点;若四条直线中没有平行线,则此时的交点是一个或四个或六个.综上可知,平面内四条直线共有三个交点,则这四条直线中最多有三条平行线.故答案是:三.【点评】本题考查了平行线,题目没有明确平面上四条不重合直线的位置关系,需要运用分类讨论思想,从四条直线都是平行线,然后数量上依次递减,直至都不平行,这样可以做到不重不漏,准确找出答案.【变式2-4】平面上不重合的四条直线,可能产生交点的个数为个.【分析】从平行线的角度考虑,先考虑四条直线都平行,再考虑三条、两条直至都不平行,作出草图即可看出.【解答】解:(1)当四条直线平行时,无交点;(2)当三条平行,另一条与这三条不平行时,有三个交点;(3)当两两直线平行时,有4个交点;(4)当有两条直线平行,而另两条不平行时,有5个交点;(5)当四条直线同交于一点时,只有一个交点;(6)当四条直线两两相交,且不过同一点时,有6个交点;(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点.故答案为:0,1,3,4,5,6.【点评】本题没有明确平面上四条不重合直线的位置关系,需要运用分类讨论思想,从四条直线都平行线,然后数量上依次递减,直至都不平行,这样可以做到不重不漏,准确找出所有答案;本题对学生要求较高.【例题3】如图,直线a,点B,点C.(1)过点B画直线a的平行线,能画几条?(2)过点C画直线a的平行线,它与过点B的平行线平行吗?【分析】根据平行公理及推论进行解答.【解答】解:(1)如图,过直线a外的一点画直线a的平行线,有且只有一条直线与直线a平行;(2)过点C画直线a的平行线,它与过点B的平行线平行.理由如下:如图,∵b∥a,c∥a,∴c∥b.【点评】本题考查了平行公理及推论.平行公理:经过直线外一点,有且只有一条直线与这条直线平行(平行公理中要准确理解“有且只有”的含义.从作图的角度说,它是“能但只能画出一条”的意思);推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.【变式3-1】如图中完成下列各题.(1)用直尺在网格中完成:①画出直线AB的一条平行线;②经过C点画直线垂直于CD.(2)用符号表示上面①、②中的平行、垂直关系.【分析】(1)根据AB所在直线,利用AB所在直角三角形得出EF,以及MD⊥CD即可;(2)根据图形得出EF,MD⊥CD,标出字母即可.【解答】解:(1)如图所示:(2)EF∥AB,MC⊥CD.【点评】此题考查了基本作图以及直角三角形的性质,利用直角三角形的性质得出平行线以及垂线是解答此题的关键.【变式3-2】如图,已知直线a和直线a外一点A.(1)完成下列画图:过点A画AB⊥a,垂足为点B,画AC∥a;(2)过点A你能画几条直线和a垂直?为什么?过点A你能画几条直线和a平行?为什么?(3)说出直线AC与直线AB的位置关系.【分析】(1)根据要求画出图形即可;(2)过点A有一条直线和直线a垂直,过点A可以画一条直线和a平行.(3)结论:AC⊥AB.【解答】解:(1)直线AB、AC如图所示;(2)过点A有一条直线和直线a垂直,理由:过直线外一点有且只有一条直线和已知直线垂直.过点A可以画一条直线和a平行.理由:过直线外一点有且只有一条直线和已知直线平行.(3)结论:AC⊥AB.【点评】本题考查复杂作图、垂线、平行线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.【变式3-3】作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:(1)过点A作BC的平行线;(2)过点C作AB的平行线,与(1)中的平行线交于点D;(3)过点B作AB的垂线.【分析】(1)A所在的横线就是满足条件的直线;(2)在直线AD上到A得等于BC的点D,则直线CD即为所求;(3)取AE上D右边的点F,过B,F的直线即为所求.【解答】解:如图,(1)A所在的横线就是满足条件的直线,即AE就是所求;(2)在直线AE上,到A距离是5个格长的点就是D,则CD就是所求与AB平行的直线;(3)取AE上D右边的点F,过B,F作直线,就是所求.【点评】本题考查复杂作图、垂线、平行线的定义等知识,解题的关键是灵活运用所学知识解决问题,【变式3-4】(2022秋•内乡县期末)如图所示,在∠AOB内有一点P.(1)过P画l1∥OA;(2)过P画l2∥OB;(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样关系?【分析】用两个三角板,根据同位角相等,两直线平行来画平行线,然后用量角器量一量l1与l2相交的角与∠O的关系为:相等或互补.【解答】解:(1)(2)如图所示,(3)l1与l2夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补.【点评】注意∠2与∠O是互补关系,容易漏掉.【例题4】(2022•寻乌县模拟)下面推理正确的是()A.∵a∥b,b∥c,∴c∥d B.∵a∥c,b∥d,∴c∥dC.∵a∥b,a∥c,∴b∥c D.∵a∥b,c∥d,∴a∥c【分析】根据平行公理的推论“如果两条直线都和第三条直线平行,那么这两条直线平行“进行分析,得出正确答案.【解答】解:A、a、c都和b平行,应该推出的是a∥c,而非c∥d,故错误;B、没有两条直线都和第三条直线平行,推不出平行,故错误;C、b、c都和a平行,可推出是b∥c,故正确;D、a、c与不同的直线平行,无法推出两者也平行.故选:C.【点评】本题考查的重点是平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线平行.【变式4-1】(2022春•丛台区校级期中)如图,过点A画直线l的平行线,能画()A.两条以上B.2条C.1条D.0条【分析】经过直线外一点,有且只有一条直线与这条直线平行.【解答】解:因为经过直线外一点,有且只有一条直线与这条直线平行.所以如图,过点A画直线l的平行线,能画1条.故选:C.【点评】本题考查了平行公理及推论.平行公理中要准确理解“有且只有”的含义.从作图的角度说,它是“能但只能画出一条”的意思.【变式4-2】(2023春•萨尔图区期中)下面说法正确的个数为()(1)在同一平面内,过直线外一点有一条直线与已知直线平行;(2)过一点有且只有一条直线与已知直线垂直;(3)两角之和为180°,这两个角一定邻补角;(4)同一平面内不平行的两条直线一定相交.A.1个B.2个C.3个D.4个【分析】根据同一平面内,过直线外一点有一条直线和已知直线平行即可判断(1);在同一平面内,过一点有且只有一条直线和已知直线垂直即可判断(2);举出反例即可判断(3);根据在同一平面内,两直线的位置关系是平行或相交,即可判断(4).【解答】解:在同一平面内,过直线外一点有一条直线和已知直线平行,故(1)正确;只有在同一平面内,过一点有且只有一条直线和已知直线垂直,故(2)错误;如图:∠ABC=∠DEF=90°,且∠ABC+∠DEF=180°,但是两角不是邻补角,故(3)错误;同一平面内不平行的两条直线一定相交正确,因为不特别指出时,一般认为,两条直线重合就是同一条直线,所以所提出的命题是正确的,故(4)正确.即正确的个数是2个.故选:B.【点评】本题考查了平行公理和推论,邻补角,垂线,平行线等知识点,此题比较典型,但是一道比较容易出错的题目.【变式4-3】(2023春•泸县校级期中)下列说法正确的是()A.经过一点有一条直线与已知直线平行B.经过一点有无数条直线与已知直线平行C.经过一点有且只有一条直线与已知直线平行D.经过直线外一点有且只有一条直线与已知直线平行【分析】平行线公理:经过直线外一点有且只有一条直线与已知直线平行.【解答】解:根据平行线公理:经过直线外一点有且只有一条直线与已知直线平行,可判断只有D选项正确.【点评】本题考查了平行公理,要熟练掌握.【变式4-4】(2023春•新民市期中)已知a∥b,c∥d,若由此得出b∥d,则直线a和c应满足的位置关系是()A.在同一个平面内B.不相交C.平行或重合D.不在同一个平面内【分析】根据平行推论:平行于同一条直线的两条直线互相平行,可得答案.【解答】解:当a∥c时,a∥b,c∥d,得b∥d;当a、c重合时,a∥b,c∥d,得b∥d,故C正确;故选:C.【点评】本题考查了平行公理及推论,利用了平行推论:平行于同一条直线的两条直线互相平行.【变式4-5】(2022春•和平区校级月考)下列语句正确的有()个①任意两条直线的位置关系不是相交就是平行②过一点有且只有一条直线和已知直线平行③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b④若直线a∥b,b∥c,则c∥a.A.4B.3C.2D.1【分析】根据同一平面内,任意两条直线的位置关系是相交、平行;过直线外一点有且只有一条直线和已知直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行进行分析即可.【解答】解:①任意两条直线的位置关系不是相交就是平行,说法错误,应为根据同一平面内,任意两条直线的位置关系不是相交就是平行;②过一点有且只有一条直线和已知直线平行,说法错误,应为过直线外一点有且只有一条直线和已知直线平行;③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b,说法错误;④若直线a∥b,b∥c,则c∥a,说法正确;【点评】此题主要考查了平行线,关键是掌握平行公理:过直线外一点有且只有一条直线和已知直线平行;推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.【变式4-6】(2022春•大荔县期末)如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由是.【分析】利用平行公理:经过直线外一点,有且只有一条直线与这条直线平行,进而得出答案.【解答】解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.故答案为:经过直线外一点,有且只有一条直线与这条直线平行.【点评】此题主要考查了平行公理,正确掌握平行公理是解题关键.【变式4-7】(2022春•海阳市期末)若P,Q是直线AB外不重合的两点,则下列说法不正确的是()A.直线PQ可能与直线AB垂直B.直线PQ可能与直线AB平行C.过点P的直线一定与直线AB相交D.过点Q只能画出一条直线与直线AB平行【分析】根据过直线外一点有且只有一条直线与已知直线平行以及两直线的位置关系即可回答.【解答】解:PQ与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、D均正确,故C错误;故选:C.【点评】本题考查了平行线、相交线、垂线的性质,掌握相关定义和性质是解题的关键.【变式4-8】如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是()A.平行B.垂直C.平行或垂直D.无法确定【分析】根据平行公理和垂直的定义解答.【解答】解:∵长方形对边平行,∴根据平行公理,前两次折痕互相平行,∵第三次折叠,是把平角折成两个相等的角,∴是90°,与前两次折痕垂直.∴折痕与折痕之间平行或垂直.故选:C.【点评】本题利用平行公理和垂直定义求解,需要熟练掌握.【例题5】(2022春•昭阳区校级月考)如图,把三角尺的直角顶点放在直线b上.若∠1=50°,则当∠2=时,a∥b.【分析】由直角三角板的性质可知∠3=180°﹣∠1﹣90°=40°,当∠2=40°时,∠2=∠3,得出a∥b即可.【解答】解:当∠2=40°时,a∥b;理由如下:如图所示:∵∠1=50°,∴∠3=180°﹣90°﹣50°=40°,当∠2=40°时,∠2=∠3,∴a∥b.故答案为:40°.【点评】本题考查了平行线的判定方法、平角的定义;熟记同位角相等,两直线平行是解决问题的关键.【变式5-1】(2022春•洞头区期中)如图,在下列给出的条件中,能判定DF∥BC的是()A.∠B=∠3B.∠1=∠4C.∠1=∠B D.∠B+∠2=180°【分析】根据平行线的判定定理求解即可.【解答】解:∵∠B=∠3,∴AB∥EF,故A不符合题意;∵∠1=∠4,∴AB∥EF,故B不符合题意;∵∠1=∠B,∴DF∥BC,故C符合题意;∵∠B+∠2=180°,∴AB∥EF,故D不符合题意;故选:C.【点评】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.【变式5-2】(2023秋•淮阳区校级期末)如图,木条a,b,c在同一平面内,经测量∠1=115°,要使木条a∥b,则∠2的度数应为()A.65°B.75°C.115°D.165°【分析】根据邻补角互补和平行线的判定定理求解即可.【解答】解:∠2的度数应为65°.证明:如图,∵∠1=115°,∴∠3=180°﹣115°=65°,∵∠2=65°,∴∠2=∠3,∴a∥b.故选:A.【点评】本题考查邻补角互补,平行线的判定.熟练掌握平行线的判定定理是解题关键.【变式5-3】(2023秋•泾阳县期末)如图,直线AB、CD分别与EF相交于点G、H,已知∠1=70°,∠2=70°,试说明:AB∥CD.【分析】根据对顶角相等得出∠1=∠AGH,进而根据∠2=∠AGH,即可得证.【解答】解:∵∠1=∠AGH,∠1=∠2=70°,∴∠2=∠AGH,∴AB∥CD.【点评】本题考查了对顶角相等,同位角相等两直线平行,熟练掌握平行线的判定定理是解题的关键.【变式5-4】(2023秋•泰和县期末)如图,CE平分∠ACD,若∠1=30°,∠2=60°,求证:AB∥CD.【分析】根据平行线的判定,依据角平分线的定义即可解决问题.【解答】证明:∵CE平分∠ACD,∠1=30°,∴∠ACD=2∠1=60°(角平分线定义),∵∠2=60°,(已知),∴∠2=∠ACD(等量代换),∴AB∥CD(同位角相等两直线平行).【点评】本题主要考查平行线的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.【变式5-5】(2023春•樟树市期中)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.求证:CF∥AB.【分析】根据CF平分∠DCE以及∠DCE=90°即可得出∠FCE=45°,再根据三角形ABC为等腰直角三角形,即可得出∠ABC=∠FCE=45°,利用“同位角相等,两直线平行”即可证出结论.【解答】证明:∵CF平分∠DCE,∠DCE=90°,∴∠FCE=12∠DCE=45°.∵△ABC为等腰直角三角形,∴∠ABC=45°,∴∠ABC=∠FCE,∴CF∥AB.【点评】本题考查了平行线的判定,解题的关键是找出∠ABC=∠FCE=45°.本题属于基础题,难度不大,解决该题型题目时,找出相等(或互补)的角的关键.【变式5-6】(2023秋•靖边县期末)如图,AF与BD相交于点C,∠B=∠ACB,且CD平分∠ECF.试说明:AB∥CE.【分析】根据角平分线的定义结合对顶角得到∠ECD=∠ACB,则可证明∠B=∠ECD,根据平行线的判定即可证明AB∥CE.【解答】证明:因为CD平分∠ECF,所以∠ECD=∠FCD(角平分线的定义).因为∠ACB=∠FCD(对顶角相等),所以∠ECD=∠ACB(等量代换).因为∠B=∠ACB,。
七年级数学下册平行线的性质【十大题型】(举一反三)(人教版)

专题5.2 平行线的性质【十大题型】【人教版】【题型1 平行线的判定与性质的运用(计算与证明)】 (1)【题型2 平行线的判定与性质(书写过程)】 (5)【题型3 平行线与三角尺(直角顶点在平行线上)】 (9)【题型4 平行线与三角尺(直角顶点不在平行线上)】 (11)【题型5 平行线的判定与性质综合(角度之间的数量关系)】 (16)【题型6 平行线的判定与性质综合(求定值)】 (21)【题型7 平行线的判定与性质综合(规律问题)】 (31)【题型8 平行线的性质(折叠问题)】 (36)【题型9 平行线的应用(转角问题)】 (41)【题型10 平行线的判定与性质综合(旋转)】 (46)【知识点平行线的性质】【例1】(2022·西藏·林芝市广东实验中学七年级期中)如图,点D,E在AC上,点F,G分别在BC,AB上,且DG∥BC,∠1=∠2.(1)求证:DB∥EF;(2)若EF∠AC,∠1=50°,求∠ADG的度数.【答案】(1)见解析(2)∠ADG=40°【分析】(1)利用两直线平行,内错角相等,再根据同位角相等,两直线平行即可得证;(2)先求出∠C,再根据两直线平行,同位角相等,即可得解.(1)证明:∠DG∥BC,∠∠1=∠DBC.又∠∠1=∠2,∠∠2=∠DBC,∠DB∥EF.(2)∠EF∠AC,∠∠CEF=90°.∠∠2=∠1=50°,∠∠C=90°-50°=40°.∠DG∥BC,∠∠ADG=∠C=40°.【点睛】本题考查平行线的判定和性质.熟练掌握平行线的性质和判定是解题的关键.【变式1-1】(2022·湖北·五峰土家族自治县中小学教研培训中心七年级期末)已知:如图,AE⊥BC,FG⊥BC,∠CEA=∠FGB,∠D=∠ABC+50°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.【答案】(1)证明见解析(2)∠C=30°【分析】(1)先证明AE∥GF,可得∠EAB=∠FGB,再证明∠CEA=∠EAB,从而可得答案;(2)由AB∥CD,可得∠D+∠CBD+∠ABC=180°,再把∠D=∠ABC+50°,∠CBD=70°代入进行计算即可.(1)证明:∵AE⊥BC,FG⊥BC,∠AE∥GF,∴∠EAB=∠FGB,∵∠CEA=∠FGB,∴∠CEA=∠EAB,∠AB∥CD;(2)解:由(1)得,AB∥CD,∴∠D+∠CBD+∠ABC=180°,∵∠D=∠ABC+50°,∠CBD=70°,∠∠ABC+70°+∠ABC+50°=180°∴∠ABC=30°,∴∠C=∠ABC=30°.【点睛】本题考查的是平行线的判定与性质,方程思想的应用,掌握“平行线的判定与性质”是解本题的关键.【变式1-2】(2022·重庆·巴川初级中学校七年级期中)如图,∠ABC中,∠BAC的角平分线交BC于D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,且∠BDA+∠CEG=180°.(1)求证:AD∥EF;(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗?请说明理由.【答案】(1)见详解(2)∠F=∠H,说明见详解【分析】(1)根据∠BDA+∠CEG=180°,∠DEF+∠CEG=180°,可得∠BDA=∠DEF,根据同位角相等,两直线平行可判定AD∥EF;(2)根据∠EDH=∠C,可得DH∥AC,继而得到∠H=∠EGC,由对顶角∠AGF=∠EGC,可得∠H=∠AGF,由(1)AD∥EF可得∠DAG=∠AGF,∠BAD=∠F,再因为AD是∠BAC的角平分线,有∠DAG=∠BAD,即可证明∠F=∠H.(1)证明:∠∠BDA+∠CEG=180°,∠DEF+∠CEG=180°,∠∠BDA=∠DEF,∠AD∥EF.(2)解:∠F=∠H,理由如下:∠∠EDH=∠C,∠DH∥AC,∠∠H=∠EGC,∠∠AGF=∠EGC,∠∠H=∠AGF,∠AD∥EF,∠∠DAG=∠AGF,∠BAD=∠F,又∠AD是∠BAC的角平分线,∠∠DAG=∠BAD,∠∠F=∠H.【点睛】本题考查了平行线的判定与性质,角平分线的定义,熟练掌握并应用平行线的判定与性质是解答本题的关键.【变式1-3】(2022·湖北·武汉市新洲区阳逻街第一初级中学三模)如图,已知AD⊥BC,EF⊥BC,∠1=∠2.(1)求证:EF∥AD;(2)求证:∠BAC+∠AGD=180°.【答案】(1)见解析(2)见解析【分析】(1)根据垂直得出∠EFB=∠ADB=90°,根据平行线的判定得出EF∥AD;(2)根据平行线的性质得出∠1=∠BAD,由∠1=∠2得出∠2=∠BAD,根据平行线的判定得出DG∥BA,再根据平行线的性质即可得解.【详解】(1)证明:∠AD⊥BC,EF⊥BC,∠∠EFB=90°,∠ADB=90°(垂直的定义),∠∠EFB=∠ADB(等量代换),∠EF∥AD(同位角相等,两直线平行);(2)证明:∠EF∥AD,∠∠1=∠BAD(两直线平行,同位角相等),又∵∠1=∠2(已知),∠∠2=∠BAD(等量代换),∠DG∥BA(内错角相等,两直线平行),∠∠BAC+∠AGD=180°(两直线平行,同旁内角互补).【点睛】本题主要考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.【题型2 平行线的判定与性质(书写过程)】【例2】(2022·黑龙江·哈尔滨市风华中学校七年级期中)如图,∠1=∠2,∠A=∠D.求证:∠B=∠C.(请把下面证明过程补充完整)证明:∵1=∠2(已知)又∵∠1=∠3(____________)∴∠2=∠3(____________)∴AE∥FD(_____________)∴∠A=∠_____(______________)∵∠A=∠D(已知)∴∠D=∠BFD(等量代换)∠_____∥CD(__________________)∴∠B=∠C(____________)【答案】对顶角相等;等量代换;内错角相等,两直线平行;BFD;两直线平行,内错角相等;AB;内错角相等,两直线平行;两直线平行,内错角相等.【分析】先利用对顶角的性质证明∠2=∠3,再证明AE∥FD,可证明∠A=∠BFD,可得∠D=∠BFD,再证明AB∥CD,从而可得答案.【详解】证明:∵1=∠2(已知)又∵∠1=∠3(对顶角相等)∴∠2=∠3(等量代换)∴AE∥FD(内错角相等,两直线平行)∴∠A=∠BFD(两直线平行,内错角相等)∵∠A=∠D(已知)∴∠D=∠BFD(等量代换)∠AB∥CD(内错角相等,两直线平行)∴∠B=∠C(两直线平行,内错角相等)【点睛】本题考查的是对顶角的性质,平行线的判定与性质,熟练的利用平行线的判定与性质进行证明是解本题的关键.【变式2-1】(2022·黑龙江·哈尔滨市萧红中学校七年级阶段练习)阅读并完成下面的证明过程:已知:如图,AB∥EF,∠1=∠2,BE、CE分别平分∠ABC和∠BCD,求证:BE⊥CE.证明:∠BE、CE分别平分∠ABC和∠BCD.∠ABC∠∠ABE=∠EBC=12∠2=________=1∠BCD(角平分线定义)2又∠∠1=∠2,∠∠1=∠ECD()∠EF∥CD()又∠AB∥EF(已知)∠________________()∠∠ABC+∠BCD=180°()(∠ABC+∠BCD)=90°,∠∠ABE+∠2=12又∠AB∥EF,∠∠ABE=∠BEF()∠∠BEF+∠1=90°,∠∠BEC=90°,∠BE⊥CE()【答案】∠ECD;等量代换;内错角相等,两直线平行;AB∥CD;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,同旁内角互补;两直线平行,内错角相等;垂直定义.【分析】根据平行线的性质、平行线的判定以及垂直的定义进行分析即可解答.【详解】证明:∠BE、CE分别平分∠ABC和∠BCD.∠ABC∠∠ABE=∠EBC=12∠BCD(角平分线定义)∠2=∠ECD=12又∠∠1=∠2,∠∠1=∠ECD(等量代换)∠EF∥CD(内错角相等,两直线平行)又∠AB∥EF(已知)∠AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行)∠∠ABC+∠BCD=180°(两直线平行,同旁内角互补)(∠ABC+∠BCD)=90°,∠∠ABE+∠2=12又∠AB∥EF,∠∠ABE=∠BEF(两直线平行,内错角相等)∠∠BEF+∠1=90°,∠∠BEC=90°,∠BE⊥CE(垂直定义).故答案为:∠ECD;等量代换;内错角相等,两直线平行;AB∥CD;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,同旁内角互补;两直线平行,内错角相等;垂直定义.【点睛】本题主要考查了平行线的判定与性质、垂直的定义等知识点,灵活运用平行线的判定与性质是解答本题的关键.【变式2-2】(2022·湖南·株洲景炎学校七年级期中)完成下面证明过程并写出推理根据:已知:如图所示,∠BAP与∠APD互补,∠1=∠2.求证:∠E=∠F.证明:∠∠BAP与∠APD互补(已知),即∠BAP+∠APD=180°,∠____________∥_____________(_____________________),∠∠BAP=∠APC(_____________________).又∠∠1=∠2,∠∠BAP-∠1=∠APC-∠2(等式的性质),即∠3=∠4,∠____________∥_____________(_____________________),∠∠E=∠F(_____________________).【答案】AB;CD;同旁内角互补,两直线平行;两直线平行,内错角相等;AE;FP;内错角相等,两直线平行;两直线平行,内错角相等【分析】根据平行线的判定与性质,结合图形完成填空即可求解.【详解】∠∠BAP与∠APD互补(已知),即∠BAP+∠APD=180°,∠AB∥CD(同旁内角互补,两直线平行),∠∠BAP=∠APC(两直线平行,内错角相等).又∠∠1=∠2,∠∠BAP-∠1=∠APC-∠2(等式的性质),即∠3=∠4,∠AE∥FP(内错角相等,两直线平行),∠∠E=∠F(两直线平行,内错角相等)故答案为:AB;CD;同旁内角互补,两直线平行;两直线平行,内错角相等;AE;FP;内错角相等,两直线平行;两直线平行,内错角相等.【点睛】本题考查了平行线的性质与判定进行证明,掌握平行线的性质与判定是解题的关键.【变式2-3】(2022·重庆·巴川初级中学校七年级期中)推理填空:完成下面的证明过程.如图,已知∠1+∠2=180°,∠B=∠DEF,求证:.DE∠BC证明:∠∠1+∠2=180°()∠2=∠3(_______________________________)∠∠1+∠3=180°∠______∥______(_____________________________)∠∠B=______(________________________________)∠∠B=∠DEF(已知)∠∠DEF=_______ (_______________________)∠DE∠BC()【答案】已知;对顶角相等;AB;EF;同旁内角互补,两直线平行;∠EFC;两直线平行,同位角相等;∠EFC;等量代换;内错角相等,两直线平行【分析】由于∠1+∠2=180°,∠2=∠3,则∠1+∠3=180°,根据同旁内角互补,两直线平行得到AB∥EF,则利用平行线的性质得∠B=∠CFE,由于∠B=∠DEF,所以∠DEF=∠CFE,于是根据平行线的判定得到DE∥BC.【详解】证明:∠∠1+∠2=180°(已知)∠2=∠3(对顶角相等)∠∠1+∠3=180°∠AB∥EF(同旁内角互补,两直线平行)∠∠B=∠EFC(两直线平行,同位角相等)∠∠B=∠DEF(已知)∠∠DEF=∠EFC(等量代换)∠DE∥BC(内错角相等,两直线平行)【点睛】本题考查了平行线的判定与性质:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等.掌握平行线的判定与性质是解题的关键.【题型3 平行线与三角尺(直角顶点在平行线上)】【例3】(2022·辽宁·阜新实验中学七年级期末)如图,含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是()A.100°B.105°C.115°D.120°【答案】C【分析】根据直角三角形两锐角互余得到∠1=25°,根据平角的定义得到∠AEF=90°-∠1=65°,根据平行线的性质即可得到结论.【详解】解:∠∠D=90°,∠3=65°,∠∠1=25°,∠∠FEG=90°,∠∠AEF=90°-∠1=65°,∠AD∥BC,∠∠2=180°-∠AEF=115°,故选:C.【点睛】本题考查了直角三角形两锐角互余和平行线的性质,关键是得出∠AEF与∠2互补.【变式3-1】(2022·浙江·金华市第四中学九年级阶段练习)将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠2;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是()A.1B.2C.3D.4【答案】D【分析】根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.【详解】解:∠纸条的两边平行,∠(1)∠1=∠2(两直线平行,同位角相等);(2)∠3=∠4(两直线平行,内错角相等);(4)∠4+∠5=180°(两直线平行,同旁内角互补)均正确;又∠直角三角板与纸条下线相交的角为90°,∠(3)∠2+∠4=90°,正确.故选:D.【点睛】本题考查平行线的性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.【变式3-2】(2022·山东青岛·七年级期中)将一块直角三角板ABC按如图方式放置,其中∠ABC=30°,A,B两点分别落在直线m、n上,∠1=20°,添加下列哪一个条件可使直线m∥n ()A.∠2=20°B.∠2=30°C.∠2=45°D.∠2=50°【答案】D【分析】根据平行线的判定定理求解即可.【详解】解:由平行线的判定可知,当∠2=∠ABC+∠1时,m∥n,即∠2=∠ABC+∠1=30°+20°=50°,故选:D.【点睛】本题考查了平行线的判定,熟练掌握平行线的判定定理是解题的关键.【变式3-3】(2022·河南南阳·二模)小明把一副三角板按如图所示方式摆放,直角边CD与直角边AB相交于点F,斜边DE∥BC,∠B=30°,∠E=45°,则∠CFB的度数是()A.95°B.115°C.105°D.125°【例4】(2022·全国·八年级专题练习)如图,a∥b,一块含45°的直角三角板的一个顶点落在直线b上,若∠1=58°54′,则∠2的度数为()A.103°6′B.104°6′C.103°54′D.104°54′【答案】C【分析】设∠2的同位角为∠3,∠3的邻补角为∠5,三角板的一个锐角为∠4,根据等腰三角板的特点可求出∠4,根据三角形内角和即可求出∠5,再根据平角的性质即可求出∠3,进而根据两直线平行同位角相等即可求出∠2.【详解】设∠2的同位角为∠3,∠3的邻补角为∠5,三角板的一个锐角为∠4,如图,∠直角三角板含一个45°的锐角,∠该三角板为等腰三角形,∠∠4=45°,∠∠1=58°54′,又∠在三角形中有∠1+∠4+∠5=180°,∠∠5=180°-(∠1+∠4)=180°-(58°54′+45°)=180°-103°54′=76°6′,∠∠3+∠5=180°,∠∠3=180°-∠5=180°-76°6′=103°54′,∠a∥b,∠∠2=∠3,∠∠2=103°54′,故选:C.【点睛】本题主要考查了平行线的性质以及三角形的内角和等知识,掌握两直线平行同位角相等是解答本题的关键.【变式4-1】(2022·山西晋中·七年级期末)用一块含60°角的直角三角板和一把直尺按图中所示的方式放置,其中直尺的直角顶点与三角板的60°角顶点重合,直尺两边分别与三角板的两条直角边相交,若∠1=50°,则∠2的度数为()A.25°B.22.5°C.20°D.15°【答案】C【分析】如图,根据题意得到∠C=90°,AB∠DE,∠CDF=60°.先根据三角形内角和求出∠ABC=40°,再根据平行的性质求出∠CDE=40°,即可求出∠2=20°.【详解】解:如图,由题意得∠C=90°,AB∠DE,∠CDF=60°.∠∠C=90°,∠1=50°,∠∠ABC=180°-∠C-∠1=40°,∠AB∠DE,∠∠CDE=∠CBA=40°,∠∠CDF=60°∠∠2=∠CDF-∠CDE=20°.故选:C【点睛】本题考查了三角形的内角和定理,平行线的性质,熟知两个定理并理解题意得到已知条件是解题的关键.【变式4-2】(2022·福建·莆田市城厢区南门学校七年级阶段练习)如图,AB∥CD,将一副直角三角板作如下摆放,∠GEF=60°,∠MNP=45°.下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=75°;④∠AEG=∠PMN.其中正确的是_______.【答案】①②③④【分析】①由题意得∠G=∠MPN=∠MPG=90°,利用内错角相等,两直线平行即可判定GE∥MP;②由题意得∠EFG=30°,利用邻补角即可求出∠EFN的度数;③过点F作FH⊥AB,可得FH∥CD,从而得到∠HFN=∠MNP=45°,可求得∠EFN=105°,再利用平行线的性质即可求出∠BEF;④利用角的计算可求出∠AEG=45°,从而可判断.【详解】解:①∵∠G=∠MPN=∠MPG=90°,∴GE∥MP,故①正确;②∵∠EFG=30°,∴∠EFN=180°−30°=150°,故②正确;③过点F作EH∥AB,如图,∵AB∥CD,∴FH∥CD,∴∠HFN=∠MNP=45°,∴∠EFN=150°−45°=105°,∵FH∥AB,∴∠BEF=180°−105°=75°;故③正确;④∵∠GEF=60°,∠BEF=75°,∴∠AEG=180°−60°−75°=45°,∴∠AEG=∠PMN=45°,故④正确.故答案为:①②③④.【点睛】本题考查平行线的性质与判定,解题的关键是熟记平行线的判定条件与性质并灵活运用.【变式4-3】(2022·山东淄博·期末)如图所示,将一直角三角板放在AB,CD两条平行线之间:(1)图甲中,容易求得∠1+∠2=90°,请直接写出图乙中∠1,∠2的数量关系;(2)请问图丙中∠1,∠2的数量关系是什么?并加以说明;(3)请直接写出图丁中∠1,∠2的数量关系.【答案】(1)∠1+∠2=270°(2)∠2-∠1=90°;见解析(3)∠1=∠2+90°【分析】(1)过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD.根据两直线平行,同旁内角互补,即可得∠1,∠2的关系.(2)过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD.根据两直线平行,内错角相等,平角互补,即可得∠1,∠2的关系.(3)过点O作AB的平行线MN,得AB∥MN∥CD,据两直线平行,内错角相等,即可得∠1,∠2的关系.(1)如图,过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD∠∠1+∠3=180°,∠2+∠4=180°又∠∠3+∠4=90°∠∠1+∠3+∠2+∠4=180°+180°∠∠1+∠2=360°−90°=270°∠∠1+∠2=270°.(2)如图,过三角板的直角顶点作AB的平行线MN,得AB∥MN∥CD∠∠1=∠3,∠2+∠4=180°又∠∠3+∠4=90°∠∠1+180°−∠2=90°∠∠2−∠1=90°.(3)如图,过点O作AB的平行线MN,得AB∥MN∥CD∠∠MOC=∠2∠∠1=90°+∠MOC∠∠1=90°+∠2.【点睛】本题考查平行线的性质,解题的关键是掌握两直线平行,内错角相等,同旁内角互补;平角互补.【题型5 平行线的判定与性质综合(角度之间的数量关系)】【例5】(2022·黑龙江鹤岗·七年级期末)如图①,AB∥CD,M为平面内一点,若BM∠MC,则易证∠ABM与∠DCM互余.(1)如图②,AB∥CD.点M在射线EA上运动,猜想点M在点A和D之间时,∠BMC与∠ABM、∠DCM之间的数量关系,并证明.(2)在(1)的条件下,当点M在射线EA的其它位置上时(不与点E,A,D重合)请直接写出∠BMC与∠ABM、∠DCM之间的数量关系.又∠AB∥CD,∠MF∥CD,∠∠DCM=∠FMC,∠∠ABM+∠DCM=∠BMF+∠CMF=∠BMC;(2)解:当点M在E、A两点之间时,如图3,∠BMC=∠DCM-∠ABM;过M作MF∥AB,交EC于F,则∠ABM=∠BMF,又∠AB∥CD,∠MF∥CD,∠∠DCM=∠FMC,∠∠BMC=∠CMF-∠BMF=∠DCM-∠ABM;当点M在AD的延长线上时,如图4,∠BMC=∠ABM-∠DCM.过M作MF∥AB,交EC于F,则∠ABM=∠BMF,又∠AB∥CD,∠MF∥CD,∠∠DCM=∠FMC,∠∠BMC=∠BMF-∠CMF=∠ABM-∠DCM.【点睛】本题考查了平行线的判定和性质,关键是构建平行线,利用平行线的性质进行解答.解题时注意分类思想的运用.【变式5-1】(2022·辽宁·兴城市第二初级中学七年级阶段练习)已知,点A,点B分别在线段MN,PQ上,且∠ACB-∠MAC=∠CBP.(1)如图1,求证:MN∥PQ;(2)分别过点A和点C作直线AG、CH使AG∥CH,以点B为顶点的直角∠DBI的两边分别与直线CH,AG交于点F和点E,如图2,试判断∠CFB、∠BEG之间的数量关系,并证明;(3)在(2)的条件下,若BD和AE恰好分别平分∠CBP和∠CAN,并且∠ACB=80°,求∠CFB 的度数.(直接写出答案)【答案】(1)见解析(2)∠CFB−∠BEG=90°,证明见解析(3)∠CFB=130°【分析】(1)过C作CE∥MN,根据平行线的判定和性质即可得到结论;(2)过B作BR∥AG,根据平行线的性质得到∠BEG=∠EBR,∠RBF+∠CFB=180°,等量代换即可得到结论;(3)过E作ES∥MN,根据平行线的性质得到∠NAE=∠AES,∠QBE=∠BES,根据角平分线的定义得到∠NAE=∠EAC,∠CBD=∠DBP,根据四边形的内角和即可得到结论.(1)解:如图,过C作CE∥MN,∠∠1=∠MAC,∠∠2=∠ACB-∠1,∠∠2=∠ACB-∠MAC,∠∠ACB-∠MAC=∠CBP,∠∠2=∠CBP,∠CE∥PQ,∠MN∥PQ;(2)如图,过B作BR∥AG,∠AG∥CH,∠BR∥HF,∠∠BEG=∠EBR,∠RBF+∠CFB=180°,∠∠EBF=90°,∠∠BEG=∠EBR=90°-∠RBF,∠∠BEG=90°-∠RBF=90°-(180°-∠CFB),∠∠CFB-∠BEG=90°;(3)如图,过E作ES∥MN,∠MN∥PQ,∠ES∥PQ,∠∠NAE=∠AES,∠QBE=∠BES,∠BD和AE分别平分∠CBP和∠CAN,∠∠NAE=∠EAC,∠CBD=∠DBP,∠∠CAE=∠AES,∠∠EBD=90°,∠∠EBQ+∠PBD=∠EBC+∠CBD=90°,∠∠QBE=∠EBC,∠∠EBC=∠BES,(360°−∠ACB),∠∠AEB=∠AES+∠BES=∠CAE+∠EBC=12∠∠ACB=80°,∠∠AEB=140°,∠∠BEG=40°,∠∠CFB-∠BEG=90°,∠∠CFB=130°.【点睛】本题考查了平行线的判定和性质,余角的性质,四边形的内角和,正确的作出辅助线是解题的关键.【变式5-2】(2022·湖北·宜昌市第九中学七年级期中)如图,∠1=∠2,∠D=∠CMG.(1)求证:AD∥NG;(2)若∠A+∠DHG=180°,试探索:∠ANB,∠NBG,∠1的数量关系;(3)在(2)的条件下,若∠ANB:∠BNG=2:1,∠1=100°,∠NBG=130°,求∠A的度数.【答案】(1)见解析(2)∠NBG+∠1−∠ANB=180°(3)∠A=105°【分析】(1)由∠1=∠2,∠1=∠GFC,得到∠2=∠CFG,于是得到CM∥DE,根据平行线的性质得到∠D=∠ACM,等量代换得到∠CMG=∠ACM,于是得到结论.(2)过B作BP∥AN交NG于P,由于AD∥NG,于是得到∠D=∠DHG,等量代换得到∠A+∠D=180°,得到AN∥DH,根据平行线的判定得到BP∥CM,由平行线的性质得到∠PBG+∠1=180°,等量代换即可得到结论;(3)由∠1+∠PBG=180°,∠1=100°,得到∠PBG=80°,由于∠NBG=130°,于是得到∠ANB=∠NBP=50°,根据已知条件得到∠ANB:∠BNG=2:1,即可得到结论.(1)证明:∠∠1=∠2,∠1=∠GFC,∠∠2=∠CFG,∠CM∥DE,∠∠D=∠ACM,∠∠D=∠CMG,∠∠CMG=∠ACM,∠AD∥NG;(2)解:∠NBG−∠ANB+∠1=180°;理由如下:过B作BP∥AN交NG于P,∠∠ANB=∠NBP,∠AD∥NG,∠∠D=∠DHG,∠∠A+∠DHG=180°,∠∠A+∠D=180°,∠AN∥DH,又∠CM∠DH,∠BP∥CM,∠∠PBG+∠1=180°,∠∠PBG=∠NBG−∠NBP=∠NBG−∠ANB,∠∠NBG−∠ANB+∠1=180°;(3)解:∠∠1+∠PBG=180°,∠1=100°,∠∠PBG=80°,∠∠NBG=130°,∠∠ANB=∠NBP=50°,∠∠ANB:∠BNG=2:1,∠∠BNP=25°,∠∠ANG=75°,∠∠A=105°.【点睛】本题考查了平行线的判定和性质,对顶角的性质,正确的作出辅助线是解题的关键.【变式5-3】(2022·湖北·潜江市高石碑镇第一初级中学七年级期中)如图1,AB∥CD,直线AE分别交AB、CD于点A、E.点F是直线AE上一点,连结BF,BP平分∠ABF,EP平分∠AEC,BP与EP交于点P.(1)若点F是线段AE上一点,且BF∠AE,求∠P的度数;(2)若点F 是直线AE 上一动点(点F 与点A 不重合),请写出∠P 与∠AFB 之间的数量关系并证明. 【答案】(1)45°(2)当F 点在A 点上方时,∠BPE =12∠AFB ,当F 点在A 点下方时,∠BPE =90°﹣12∠AFB【分析】(1)过点P 作PQ ∥AB ,过点F 作FH ∥AB ,由平行线的性质得∠ABP +∠CEP =∠BPE ,∠ABF +∠CEF =∠BFE ,再由垂直定义和角平分线定义求得结果;(2)分三种情况:点F 在EA 的延长线上时,点F 在线段AE 上时,点F 在AE 的延长线上时,分别进行探究便可.(1)解:过点P 作PQ ∥AB ,过点F 作FH ∥AB ,∠AB ∥CD ,∠AB ∥CD ∥PQ ∥FH ,∠∠ABP =∠BPQ ,∠CEP =∠EPQ ,∠ABF =∠BFH ,∠CEF =∠EFH ,∠∠ABP +∠CEP =∠BPQ +∠EPQ =∠BPE ,∠ABF +∠CEF =∠BFH +∠EFH =∠BFE ,∠BF ∠AE ,∠∠ABF +∠CEF =∠BFE =90°,∠BP 平分∠ABF ,EP 平分∠AEC ,∠∠ABP +∠CEP =12(∠ABF +∠CEF )=45°, ∠∠BPE =45°;(2)①当点F 在EA 的延长线上时,∠BPE =12∠AFB ,理由如下:如备用图1,过点P作PQ∥AB,过点F作FH∥AB,过点P作PQ∥AB,过点F作FH∥AB,过点P 作PQ ∥AB ,过点F 作FH ∥AB ,∠AB ∥CD ,∠AB ∥CD ∥PQ ∥FH ,∠∠ABP =∠BPQ ,∠CEP =∠EPQ ,180°﹣∠ABF =∠BFH ,∠AEC =∠EFH ,∠∠CEP +∠ABP =∠EPQ +∠BPQ =∠BPE ,∠BFH ﹣∠EFH =180°﹣∠ABF ﹣∠AEC =∠AFB , ∠BP 平分∠ABF ,EP 平分∠AEC ,∠∠CEP +∠ABP =12(∠AEC +∠ABF )=12(180°﹣∠AFB ), ∠∠BPE =90°﹣12∠AFB ;综上,当E 点在A 点上方时,∠BPE =12∠AFB ,当E 点在A 点下方时,∠BPE =90°﹣12∠AFB . 【点睛】此题考查平行线的性质:两直线平行内错角相等,两直线平行同位角相等,两直线平行同旁内角互补,以及角平分线的性质,在相交线问题中通常作平行线利用平行线的性质解答,将角度转化由此求出答案.解题中运用分类思想解答问题.【题型6 平行线的判定与性质综合(求定值)】【例6】(2022·湖南·株洲二中七年级期末)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线m 射到平面镜a 上,被a 反射后的光线为n ,则入射光线m 、反射光线n 与平面镜a 所夹的锐角∠1=∠2.(1)如图2,一束光线m 射到平面镜a 上,被a 反射到平面镜b 上,又被b 反射.若被b 反射出的光线n 与光线m 平行,且∠1=50°,则∠2= °,∠3= °.(2)请你猜想:当射到平面镜a 上的光线m ,经过平面镜a 、b 的两次反射后,入射光线m 与反射光线n 平行时,两平面镜a 、b 间的夹角∠3的大小是否为定值?若是定值,请求出∠3,若不是定值,请说明理由.(3)如图3,两面镜子的夹角为α°(0<α<90),进入光线与离开光线的夹角为β°(0<β<90).试探索α与β的数量关系,并说明理由.【答案】(1)100;90;(2)90°(3)2α+β=180°【分析】(1)根据平面镜反射光线的规律得∠1=∠4=50°,再利用平角的定义得∠5=80°,然后利用平行线的性质计算出∠2=100°,则∠6=40°,再利用三角形内角和定理计算∠3;(2)当∠3=90°时,根据三角形内角和定理得∠4+∠6=90°,则2∠4+2∠6=180°,利用平角的定义得到∠2+∠5=180°,然后根据平行线的判定得到m∥n;(3)由(1)可得,∠5=180°-2∠2,∠6=180°-2∠3,再根据∠2+∠3=180°-∠α,即可得出∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α.(1)解:如图:∠∠1=∠4=50°,∠∠5=180°-2×50°=80°,∠m∥n∠∠2+∠5=180°,∠∠2=100°,(180°-∠2)=40°,∠∠6=12∠∠3=180°-∠4-∠6=90°;故答案为:100,90;(2)当∠3=90°时,m∥n理由如下:∠∠3=90°,∠∠4+∠6=90°,∠2∠4+2∠6=180°,∠∠2+∠5=180°,∠m∥n;(3)解:如图3,由(1)可得,∠5=180°-2∠2,∠6=180°-2∠3,∠∠2+∠3=180°-∠α,∠∠β=180°-∠5-∠6=2(∠2+∠3)-180°=2(180°-∠α)-180°=180°-2∠α,∠α与β的数量关系为:2α+β=180°,故答案为:2α+β=180°.【点睛】本题考查了平行线的判定与性质以及三角形内角和定理,解题时注意:同旁内角互补,两直线平行;两直线平行,同旁内角互补.【变式6-1】(2022·河北保定·七年级阶段练习)如图,直线AB∠CD,点M,N分别在直线AB,CD 上,H为直线CD下方一点.(1)如图1,MH和NH相交于点H,求证:∠MHN=∠AMH−∠CNH.(温馨提示:可过点H 作AB的平行线)(2)延长HN至点G,∠BMH的平分线ME和∠GND的平分线NE相交于点E,HM与CD相交于点F.①如图2,若∠BME=50°,∠END=30°,求∠MHN的度数;②如图2,当点F在点N左侧时,若∠BME的度数为x°,∠END的度数为y°,且x+y的值是一个定值,请问∠MHN的度数是否会随x的变化而发生改变?若不变,求出∠MHN的度数;若变化,请说明理由.③如图3,当点N在点F左侧时,②中其他条件不变,请问∠MHN的度数是否会随x的变化而发生改变?若不变,直接写出....∠MHN的度数;若变化,请说明理由.【答案】(1)见解析(2)①20°;②不变,180°−2(x°+y°);③不变,2(x°+y°)−180°【分析】(1)过点H作HQ∥AB.可得HQ∥CD,从而得到∠AMH=∠MHQ,∠CNH=∠NHQ,即可求证;(2)①根据∠BME=50°,∠END=30°,可得∠BMH=100°,∠GND=60°,从而得到∠AMH=180°−∠BMH=80°,∠CNH=60°.再由∠MHN=∠AMH−∠CNH,即可求解;②根据题意可得∠AMH=180°−2x°,∠CNH=2y°,再由∠MHN=∠AMH−∠CNH,即可求解;③过点H作OH∠AB,根据平行线的性质,可证得∠MHN=∠OHM−∠OHN=∠BMH−∠DNH.从而得到∠MHN=2x°+2y°−180°=2(x°+y°)−180°,即可求解.(1)证明:如图,过点H作HQ∥AB.∠HQ∥AB且AB∥CD,∠HQ∥CD,∠∠AMH=∠MHQ,∠CNH=∠NHQ,∠∠MHN=∠MHQ−∠NHQ=∠AMH−∠CNH;(2)解:①ME平分∠BMH,∠BME=50°,∠∠BMH=100°,∠NE平分∠DNG,∠DNE=30°,∠∠GND=60°,∠∠AMH=180°−∠BMH=80°,∠CNH=60°.由(1)可知:∠MHN=∠AMH−∠CNH=80°−60°=20°.∠∠MHN=20°;②∠ME平分∠BMH,∠BME=x°,∠∠BMH=2x°,∠NE平分∠DNG,∠DNE=y°,∠∠GND=2y°,∠∠AMH=180°−2x°,∠CNH=2y°,∠∠MHN=180°−2x°−2y°=180°−2(x°+y°).∠x+y为一个定值,∠∠MHN不会随x的变化而发生改变,度数为180°−2(x°+y°);③不变,∠MHN的度数为2(x°+y°)−180°.理由如下:如图,过点H作OH∥AB,∠∠BMH=∠OHM,∠AB∥CD,∠OH∥CD,∠∠DNH=∠OHN,∠∠MHN=∠OHM−∠OHN=∠BMH−∠DNH.∠ME平分∠BMH,∠BME=x°,∠∠BMH=2x°∠NE平分∠DNG,∠DNE=y°,∠∠GND=2y°,∠∠DNH=180°−2y°,∠∠MHN=2x°−(180°−2y°),∠∠MHN=2x°+2y°−180°=2(x°+y°)−180°.∠x+y为一个定值,∠∠MHN不会随x的变化而改变.【点睛】本题主要考查了平行线的性质和判定,有关角平分线的计算,熟练掌握平行线的性质和判定,利用类比思想解答是解题的关键.【变式6-2】(2022·福建龙岩·七年级期末)如图1,点A、D分别在射线BM、CN线上,BM∥CN,BM∠BC于点B,AE平分∠BAD交BC于点E,连接DE,∠1+∠2=90°.(1)求证:AE∠ED;(2)求证:DE平分∠ADC;(3)如图2,∠EAM和∠EDN的平分线交于点F,试猜想∠F的值是否为定值,若是,请予以证明;若不是,请说明理由.【答案】(1)见解析(1)证明:如图1,过点E作EG∥BM,则∠1=∠3,∠BM∥CN,∠EG∥CN,∠∠4=∠2,∠∠3+∠4=∠1+∠2=90°,∠∠AED=90°,∠AE∠ED.(2)证明:∠ AE平分∠BAD,∠∠BAD=2∠1,∠BM∥CN,∠∠BAD+∠CDA=180°,∠2∠1+∠CDA,(3)∠F为定值.证明:如图2,过点F作FH∥BM,设∠AFH=α,∠DFH=β,∠BM∥CN,∠FH∥CN,∠∠α+∠β=∠6+∠7,∠∠EAM和∠EDN的平分线交于点F,∠∠α+∠β=12(180°−∠1)+12(180°−∠2)=180°−12(∠1+∠2)=180°−45°=135°,∠∠F=∠α+∠β=135°,∠∠F为定值,∠F=135°,故答案为:∠F=135°.【点睛】本题主要考查垂线、角平分线的性质,解题的关键是掌握垂垂线的概念和角平分线与∠CFM互补(1)如图1,试判断直线AB与直线CD的位置关系,并说明理由.(2)如图2,∠BEF与∠EFD的平分线交于点P,EP的延长线与CD交于点G,H是MN上一点,且GH⊥EG,求证:PF∥GH.(3)如图3,在(2)的条件下,连接PH,K是GH上一点,使∠PHK=∠HPK,作PQ平分∠EPK,求证:∠HPQ的大小是定值.【答案】(1)平行;理由见解析(2)见解析(3)见解析【分析】(1)根据同旁内角互补,两条直线平行,即可判断直线AB与直线CD平行;(2)先根据两条直线平行,同旁内角互补,再根据∠BEF与∠EFD的角平分线交于点P,可得∠EPF=90°,进而证明PF∥GH;(3)根据角平分线定义,及角的和差计算即可求得∠HPQ的度数.(1)解:结论:AB∥CD;理由如下:∠∠MEB与∠CFM互补,∠MEB=∠AEF,∠∠AEF与∠CFM互补,∠AB∥CD.(2)∠EG平分∠BEF,∠∠PEF=1∠BEF,2又∠FP平分∠EFD,∠∠EFP=1∠EFD,2由(1)知AB∥CD,∠∠BEF+∠EFD=180°,∠∠PEF+∠EFP=90°,∠∠EPF=90°,【例7】(2022·辽宁·鞍山市第十四中学七年级阶段练习)如图,已知AB//CD,若按图中规律继续划分下去,则∠1+∠2+⋯+∠n等于()A.n•1800B.2n•1800C.(n−1)•1800D.(n−1)2•1800【答案】C【分析】根据第1个图形∠1+∠2=180°,第2个图形∠1+∠2+∠3=2×180°,第,3个图形∠1+∠2+∠3+∠4=3×180°…,进而得出答案.【详解】(1)∠AB∠CD,∠∠1+∠2=180°(两直线平行,同旁内角互补);(2)过点E作一条直线EF平行于AB,∠AB∠CD,∠AB∠EF,CD∠EF,∠∠1+∠AEF=180°,∠FEC+∠3=180°,∠∠1+∠2+∠3=360°;(3)过点E、F作EM、FN平行于AB,∠AB∠CD,∠AB∠EM∠FN∠CD,∠∠1+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠4=180°;∠∠1+∠2+3+∠4=540°;(4)中,根据上述规律,显然作(n-1)条辅助线,运用(n-1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n-1).故选:C.【点睛】此题主要考查了平行线的性质,正确得出图中变化规律是解题关键.【变式7-1】(2022·湖南·邵阳市第六中学八年级阶段练习)如图,已知直线AE,BF被直线AB所截,且AE//BF,AC1,BC1分别平分∠EAB,∠FBA;AC2,BC2分别平分∠BAC1和∠ABC1;AC3,BC3分别平分∠BAC2,∠ABC2…依次规律,得点C n,则∠C n的度数为()A.90−902n B.180−902n−1C.902n−1D.1802nAB∠CD.试求:(1)图(1)中∠A+∠C的度数,并说明理由.(2)图(2)中∠A+∠APC+∠C的度数,并说明理由.(3)图(3)中∠A+∠AEF+∠EFC+∠C的度数,并简要说明理由.(4)按上述规律,∠A+……+∠C(共有n个角相加)的和为【答案】(1)180°,理由见解析;(2)360°,理由见解析;(3)540°,理由见解析;(4)180°(n-1)【分析】(1)据两直线平行,同旁内角互补可得∠A+∠C=180°;(2)沿P作一条平行A B、CD的平行线PM,由两直线平行,同旁内角互补可得∠A+∠APM=180°,∠MPC+∠C=180°,故∠A+∠APC+∠C=360°;(3)根据第二题,同理可得∠A+∠AEF+∠EFC+∠C=540°;(4)由以上规律,有两个角时,和为180°;有三个角时和为360°;有四个角时和为540°…故可得有n个角时,和为180°(n-1).【详解】解:(1)∠AB∠CD,∠∠A+∠C=180°(两直线平行,同旁内角互补);(2)过点P作一条直线PM平行于AB,∠AB∠CD,∠AB∠PM,∠CD∠PM∠AB,∠∠A+∠APM=180°,∠MPC+∠C=180°,∠∠A+∠APC+∠C=360°;(3)分别过点E、F作EM、FN平行于AB,∠AB∠CD,∠AB∠EM∠FN∠CD,∠∠A+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠C=180°;∠∠A+∠AEF+∠EFC+∠C=540°;(4)由以上规律,有两个角时,和为180°;有三个角时和为360°;有四个角时和为540°…故可得有n个角时,和为180°(n-1).【点睛】本题主要考查两直线平行,同旁内角互补的性质,并考查学生通过计算总结规律的能力,是一道好题.【变式7-3】(2022·浙江·七年级阶段练习)阅读并探究下列问题.(1)如图①,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?请进行证明.(2)如图②,将长方形纸片剪四刀,其中AB∥CD,则∠1、∠2、∠3、∠4、∠5的关系为.(3)如图③,将长方形纸片剪2016刀,其中AB∥CD,则共剪出个角.若将剪出的角(∠A、∠C除外)分别用∠E1、∠E2、∠E3…表示,则被剪出的这些角的关系为.(4)如图④,直线AB∥CD,∠EF A=∠HMN=x°,∠FGH=3x°,∠CNP=y°|2x+y−102|+√x+y−72=0由上述结论求∠GHM的度数.【答案】(1)∠1+∠3=∠2,证明见解析;(2)∠1+∠3+∠5=∠2+∠4;(3)2017,∠A+∠C+∠E2+∠E4+…+∠E2014=∠E1+∠E3+…+∠E2015.(4)48°.【分析】(1)过E点作EF∠AB,则EF∠CD,根据两直线平行,内错角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3;(2)分别过E、G、F分别作EM∠AB,GN∠AB,FP∠AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5;(3)综合(1)(2)易得开口向左的角的度数的和等于开口向右的角的度数的和.(4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM.。
(完整)七年级上册平行线经典题型及答案解析(经典)

1、如图,∠1=∠2,∠3=110°,求∠4.2、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A=37°,求∠D 的度数.3、如图,AB ,CD 是两根钉在木板上的平行木条,将一根橡皮筋固定在A ,C 两点,点E 是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A ,∠AEC ,∠C 之间具有怎样的关系并说明理由。
(提示:先画出示意图,再说明理由)提示:这是一道结论开放的探究性问题,由于E 点位置的不确定性,可引起对E 点不同位置的分类讨论。
本题可分为AB ,CD 之间或之外。
结论:①∠AEC =∠A +∠C ②∠AEC +∠A +∠C =360°③∠AEC =∠C -∠A④∠AEC =∠A -∠C ⑤∠AEC =∠A -∠C ⑥∠AEC =∠C -∠A .4、如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )A 、80B 、50C 、30D 、205、将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )A 、43°B 、47°C 、30°D 、60°6、如图,点A 、B 分别在直线CM 、DN 上,CM ∥DN .(1)如图1,连结AB ,则∠CAB +∠ABD = ;(2)如图2,点错误!未找到引用源。
是直线CM 、DN 内部的一个点,连结错误!未找到引用源。
、错误!未找到引用源。
.求证:错误!未找到引用源。
=360°;(3)如图3,点错误!未找到引用源。
、错误!未找到引用源。
是直线CM 、DN 内部的一个点,连结错误!未找到引用源。
、错误!未找到引用源。
、错误!未找到引用源。
.试求错误!未找到引用源。
的度数;(4)若按以上规律,猜想并直接写出错误!未找到引用源。
…错误!未找到引用源。
平行线的判定例题与讲解

3 平行线的判定1.平行线的判定公理(1)平行线的判定公理:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单记为:同位角相等,两直线平行.如图,推理符号表示为:∵∠1=∠2,∴AB∥CD.谈重点同位角相等,两直线平行①平行线的判定公理是证明两直线平行的原始依据;②应用时,应先确定同位角及形成同位角的是哪两条直线;③本判定方法是由两同位角相等(数量关系)来确定两条直线平行(位置关系),所以在推理过程中要先写“两角相等”,然后再写“两线平行”.(2)平行公理的推论:①垂直于同一条直线的两条直线平行.若a⊥b,c⊥b,则a∥c;②平行于同一条直线的两条直线平行.若a∥b,c∥b,则a∥c.【例1】工人师傅想知道砌好的墙壁的上下边缘AB和CD是否平行,于是找来一根笔直的木棍,如图所示将其放在墙面上,那么,他通过测量∠EGB和∠GFD的度数,就知道墙壁的上下边缘是否平行了.请问:∠EGB和∠GFD满足怎样的条件时,墙壁的上下边缘才会平行?你的依据是什么?解析:判定两条直线是否平行,常根据两条直线被第三条直线所截而构成的角来判断.题中∠EGB和∠GFD是直线AB和直线CD(墙的上下边缘)被直线EF所截时形成的同位角,根据“同位角相等,两直线平行”,可知只有∠EGB和∠GFD相等时,墙壁的上下边缘才会平行.答案:∠EGB和∠GFD相等时,墙壁的上下边缘才会平行.其依据是同位角相等,两直线平行.2.平行线的判定定理(1)判定定理1两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单记为:同旁内角互补,两直线平行.符号表示:如下图,∵∠2+∠3=180°,∴AB∥CD.谈重点同旁内角互补,两直线平行①定理是根据公理推理得出的真命题,可直接应用;②应用时,找准哪两个角是同旁内角,使哪两条直线平行.(2)判定定理2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单记为:内错角相等,两直线平行.符号表示:如上图,∵∠2=∠4,∴AB∥CD.【例2-1】如图,小明利用两块相同的三角板,分别在三角板的边缘画直线AB和CD,这是根据________,两直线平行.解析:由题图可看出,直线AB和CD被直线BC所截,此时两块相同的三角板的两个最小角的位置关系正好是内错角,所以这是根据内错角相等,来判定两直线平行的.答案:内错角相等【例2-2】如图,下列说法中,正确的是().A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD .因为∠A+∠C=180°,所以AB∥CD错解:A或B或D错解分析:判定直线平行所需要的内错角或同旁内角找不准.条件不能推出结论.正解:C正解思路:∠A与∠D是直线AB和CD被直线AD所截得到的同旁内角.因为∠A+∠D =180°,所以AB∥CD.3.平行线的判断方法平行线的判定方法主要有以下六种:(1)平行线的定义(一般很少用).(2)同位角相等,两直线平行.(3)同旁内角互补,两直线平行.(4)内错角相等,两直线平行.(5)同一平面内,垂直于同一条直线的两条直线相互平行.(6)如果两条直线都和第三条直线平行,那么这两条直线平行.析规律如何选择判定两直线平行的方法①在利用平行线的公理或定理判定两条直线是否平行时,要分清同位角、内错角以及同旁内角是由哪两条直线被第三条直线所截而构成的;②证明两条直线平行,关键是看与待证结论相关的同位角或内错角是否相等,同旁内角是否互补.【例3】如图,直线a,b与直线c相交,形成∠1,∠2,…,∠8共八个角,请你填上你认为适当的一个条件:__________,使a∥b.解析:本题主要是考查平行线的三种判定方法.若从“同位角相等,两直线平行”考虑,可填∠1=∠5,∠2=∠6,∠3=∠7,∠4=∠8中的任意一个条件;若从“内错角相等,两直线平行”考虑,可填∠3=∠6,∠4=∠5中的任意一个;若从“同旁内角互补,两直线平行”考虑,可填∠3+∠5=180°,∠4+∠6=180°中的一个条件;从其他方面考虑,还可以填∠1=∠8,∠2=∠7,∠1+∠7=180°,∠2+∠8=180°,∠4+∠7=180°,∠3+∠8=180°,∠2+∠5=180°,∠1+∠6=180°中的任意一个条件.答案:答案不唯一,如可填下列之一:∠1=∠5或∠4=∠5或∠3+∠5=180°…4.平行线判定的应用(1)平行线的生活应用数学来源于生活,同样生活中也有大量的平行线,其判定平行的方法也常在生活中遇到.如木工师傅判定所截得的木板的对边是否平行,工人师傅判定所制造的机器零件是否符合平行的要求……对于生活中的平行线判断,关键是利用工具确定与平行有关的角是否相等,比较常用的是利用直角尺判断同位角是否相等,从而判定两直线是否平行.(2)平行线在数学中的运用平行线判定方法在数学中的运用主要通过角之间的关系判定两条直线平行,进一步解决其他有关的问题.常见的条件探索题就是其应用之一.探索题是培养发散思维能力的题型,它具有开放性,所要求的答案一般不具有唯一性.解决探索性问题,不仅能提高分析问题的能力,而且能开阔视野,增加对知识的理解和掌握.释疑点判定平行的关键判定两直线平行,关键是确定角的位置关系及大小关系.【例4-1】如图,一个零件ABCD需要AB边与CD边平行,现只有一个量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?__________(填“合格”或“不合格”).解析:要判断AB边与CD边平行,则需满足同旁内角互补的条件.∵∠ABC=120°,∠BCD=60°,∴∠ABC+∠BCD=120°+60°=180°.∴AB∥CD.∴这个零件合格.答案:合格【例4-2】已知:如图在四边形ABCD中,∠A=∠D,∠B=∠C,试判断AD与BC的位置关系,并说明理由.分析:根据四边形ABCD的内角和是360°,结合已知条件得到∠A+∠B=180°,根据同旁内角互补,两直线平行得AD∥BC.解:AD与BC的位置关系是平行.理由:∵四边形ABCD的内角和是360°,∴∠A+∠B+∠C+∠D=360°.∵∠A=∠D,∠B=∠C,∴∠A+∠B=180°.∴AD∥BC(同旁内角互补,两直线平行).点评:本题考查四边形的内角和以及利用同旁内角互补,来判定两直线平行.。
专题 与平行线有关的角度计算(四大题型)(解析版 )

(人教版)七年级下册数学《第五章相交线与平行线》专题与平行线有关的角度计算1.(2023秋•惠安县期末)如图,直线l1和l2被l3所截,若l1∥l2,∠1+∠2=232°,则∠3的度数为()A.64°B.66°C.84°D.86°【分析】根据对顶角相等结合已知可求出∠1的度数,再根据两直线平行,同旁内角互补即可求出∠4的度数,再根据对顶角相等即可得出∠3的度数.【解答】解:如图,∵∠1+∠2=232°,又∵∠1=∠2,∴∠1=116°,∵l1∥l2,∴∠1+∠4=180°,∴∠4=64°,∵∠3=∠4,∴∠3=64°,故选:A.【点评】本题考查了平行线的性质,对顶角的性质,熟练掌握平行线的性质及对顶角的性质是解题的关键.2.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是()A.154°B.144°C.134°D.124°【分析】根据平行线的判定和性质定理即可得到结论.【解答】解:∵DA⊥AB,CD⊥DA,∴∠A=∠D=90°,∴∠A+∠D=180°,∴AB∥CD,∴∠B+∠C=180°,∵∠B=56°,∴∠C=180°﹣∠B=124°,故选:D.【点评】本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质定理是解题的关键.3.(2023秋•遂平县期末)如图.直线a∥b,直线L与a、b分别交于点A、B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为()A.130°B.50°C.40°D.25°【分析】直接利用垂直的定义得出∠ACB=90°,再利用平行线的性质得出答案.【解答】解:∵AC⊥b,∴∠ACB=90°,∵∠1=50°,∴∠ABC=40°,∵a∥b,∴∠ABC=∠2=40°.故选:C.【点评】此题主要考查了垂线以及平行线的性质,正确得出∠ABC的度数是解题关键.4.如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为()A.30°B.44°C.46°D.56°【分析】根据直角三角形的两个锐角互余,可以得到∠CBD的度数,再根据直线l1∥l2,可以得到∠CBD =∠2,从而可以得到∠2的度数,本题得以解决.【解答】解:∵CD⊥AB于点D,∠1=44°,∴∠CBD=46°,∵直线l1∥l2,∴∠CBD=∠2,∴∠2=46°,故选:C.【点评】本题考查平行线的性质、垂线,解答本题的关键是明确题意,利用数形结合的思想解答.5.如图,一个由4条线段a,b,c,d组成的“鱼”形图案,若∠1=45°,∠2=45°,∠3=140°,则∠4的度数为()A.35°B.40°C.45°D.50°【分析】先由∠1、∠2的关系得到b与c的关系,再利用平行线的性质求出∠4.【解答】解:∵∠1=45°,∠2=45°,∴∠1=∠2.∴b∥c.∴∠3+∠4=180°.∵∠3=140°,∴∠4=180°﹣140°=40°.故选:B.【点评】本题考查了平行线的判定与性质,解决本题的关键是注意平行线的性质和判定定理的综合运用.6.(2023秋•泰兴市期末)如图,AB∥CD,直线EF和AB、CD分别交于点G、H,若∠EGB=(2x+30)°,∠CHF=(80﹣3x)°,则x的值为()A.10B.20C.100D.110【分析】根据平行线的性质和对顶角的性质,可以得到∠EGB和∠CHF的关系,然后即可求得x的值.【解答】解:∵AB∥CD,∴∠EGB=∠EHD,∵∠EHD=∠CHF,∴∠EGB=∠CHF,∵∠EGB=(2x+30)°,∠CHF=(80﹣3x)°,∴2x+30=80﹣3x,解得x=10,故选:A.【点评】本题考查平行线的性质、对顶角的性质,解答本题的关键是明确题意,利用数形结合的思想解答.7.如图,DE∥BC,点A在直线DE上,∠DAB=78°,∠ACF=135°,∠BAC=度.【分析】由DE∥BC可知∠DAC=∠ACF=135°,再利用角的差求∠BAC即可.【解答】解:∵DE∥BC,∴∠DAC=∠ACF=135°,∵∠DAB=78°,∴∠BAC=∠DAC﹣∠DAB=57°.故答案为:57.【点评】本题考查平行线的性质,解题关键是结合图形利用平行线的性质进行角的转化和计算.8.(2023秋•东坡区期末)如图,AB∥CD,∠ACD=155°,∠AFE=26°,则∠CEF的度数为.【分析】先利用平行线的性质可得∠A=25°,然后利用三角形的外角性质进行计算,即可解答.【解答】解:∵AB∥CD,∠ACD=155°,∴∠A=180°﹣∠ACD=25°,∵∠CEF是△AEF的一个外角,∠AFE=26°,∴∠CEF=∠A+∠AFE=51°,故答案为:51°.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.9.如图,直线AB∥EF,直线AG,BD分别交直线EF于点C,D.若∠A=2∠B,∠ECG=108°,则∠BDF的度数为°.【分析】由∠ECG=108°,AB∥EF,可得∠A=72°,而∠A=2∠B,知∠B=12∠A=36°;故∠BDF=∠B=36°.【解答】解:∵∠ECG=108°,∴∠ACD=108°,∵AB∥EF,∴∠A=180°﹣∠ACD=72°,∵∠A=2∠B,∴∠B=12∠A=36°;∵AB∥EF,∴∠BDF=∠B=36°;故答案为:36.【点评】本题考查平行线的性质,掌握两直线平行,内错角相等,同旁内角互补是解题的关键.10.(2022春•五莲县期末)如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数为.【分析】由AB∥CF,∠ABC=70°,易求∠BCF,又DE∥CF,∠CDE=130°,那么易求∠DCF,于是∠BCD=∠BCF﹣∠DCF可求.【解答】解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,又∵DE∥CF,∴∠DCF+∠CDE=180°,∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.故答案为:20°.【点评】本题主要考查了平行线的性质,两直线平行,内错角相等;两直线平行,同旁内角互补.11.(2023秋•商水县期末)如图,已知DE∥CB,∠B=∠D.(1)判断AB、CD是否平行,并说明理由.(2)若∠B+∠F=102°,求∠DEF的度数.【分析】(1)由平行线的性质可得∠D=∠BCF,从而可求得∠BCF=∠B,即可判定AB∥CD;(2)由平行线的性质可得∠B+∠BED=180°,∠F=∠BEF,结合条件即可求解.【解答】解:(1)AB∥CD,理由如下:∵DE∥CB,∴∠D=∠BCF,∵∠B=∠D,∴∠BCF=∠B,∴AB∥CD;(2)∵DE∥CB,∴∠B+∠BED=180°,∴∠B+∠BEF+∠DEF=180°,∵AB∥CD,∴∠F=∠BEF,∴∠B+∠F+∠DEF=180°,∵∠B+∠F=102°,∴∠DEF=78°.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的判定定理与性质并灵活运用.12.(2023秋•长沙期末)如图,直线EF与CD交于点O,OA平分∠COE交直线l于点A,OB平分∠DOE交直线l于点B,且∠1+∠2=90°.(1)求∠AOB的度数;(2)求证:AB∥CD;(3)若∠2:∠3=2:5,求∠AOF的度数.【分析】(1)利用角平分线的定义可得∠A=12∠A,∠A=12∠A,然后利用平角定义,以及角的和差关系进行计算,即可解答;(2)利用(1)的结论可得:∠AOB=90°,从而利用平角定义可得:∠AOC+∠2=90°,然后利用同角的余角相等可得∠AOC=∠1,从而利用内错角相等,两直线平行可得AB∥CD,即可解答;(3)利用角平分线的定义可得∠2=12∠DOE,从而可得∠DOE:∠3=4:5,然后利用平角定义可得∠DOE+∠3=180°,从而可得∠3=100°,进而可得∠COE=∠3=100°,最后利用角平分线的定义可得∠AOE =50°,从而利用平角定义进行计算,即可解答.【解答】(1)解:∵OA,OB分别平分∠COE和∠DOE,∴∠A=12∠A,∠A=12∠A,∴∠AOE+∠BOE=12∠COE+12∠DOE=12(∠COE+∠DOE)=12×180°=90°,∴∠AOB=90°,∴∠AOB的度数为90°;(2)证明:由(1)得:∠AOB=90°,∴∠AOC+∠2=180°﹣∠AOB=180°﹣90°=90°,∵∠1+∠2=90°,∴∠AOC=∠1,∴AB∥CD;(3)解:∵OB平分∠DOE,∴∠2=12∠DOE,∵∠2:∠3=2:5,∴∠DOE:∠3=4:5,∵∠DOE+∠3=180°,∴∠3=180°×59=100°,∴∠COE=∠3=100°,∵OA平分∠COE,∠A=12∠A=50°,∴∠AOF=180°﹣∠AOE=130°,∴∠AOF的度数为130°.【点评】本题考查了平行线的性质,三角形的外角性质,根据题目的已知条件并结合图形进行分析是解题的关键.1.(2023秋•南关区校级期末)如图,一把长方形直尺沿直线断开并错位摆放,点E、D、B、F在同一条直线上,若∠ADE=131°,则∠DBC的度数为.【分析】由平行线是的性质推出∠GED=∠ADE=131°,∠DBC+∠GED=180°,即可求出∠DBC的度数.【解答】解:∵AD∥EG,∴∠GED=∠ADE=131°,∵EG∥BC,∴∠DBC+∠GED=180°,∴∠DBC=49°.故答案为:49°.【点评】本题考查平行线的性质,关键是由平行线的性质得到∠GED=∠ADE,∠DBC+∠GED=180°.2.(2023秋•威宁县期末)一把直尺按如图所示摆放,AB∥CD,且∠1=70°,则∠2的度数是()A.70°B.60°C.30°D.80°【分析】根据题意可得:EF∥HG,从而利用平行线的性质可得∠1=∠3=70°,然后再利用平行线的性质可得∠3=∠2=70°,即可解答.【解答】解:如图:由题意得:EF∥HG,∴∠1=∠3=70°,∵AB∥CD,∴∠3=∠2=70°,故选:A.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.3.(2023秋•海安市期末)将一直尺和一块含30°角的三角尺按如图放置,若∠CDE=40°,则∠BF A 的度数为()A.40°B.50°C.130°D.140°【分析】先求∠CFA的度数,再求∠BFA的度数.【解答】解:∵DE∥AF,∴∠CDE=∠CFA,∵∠CDE=40°,∴∠CFA=40°,∴∠BFA=180°﹣∠CFA=140°.故选:D.【点评】本题主要考查平行线的性质,解决本题的关键是熟练运用平行线的性质.4.(2023秋•铜官区期末)如图,将一块含有45°角的三角板的两个顶点放在直尺的一组对边上.如果∠2=65°,那么∠1的度数为()A.15°B.20°C.25°D.30°【分析】根据题意∠2=65°即可算出∠3度数,再利用平行性质即可算出本题答案.【解答】解:如下图所示:∵∠2=65°,一块含有45°角的三角板,∴∠3=90°﹣65°=25°,∵两个顶点放在直尺的一组对边上,∴∠3=∠4=25°,∴∠1=45°﹣25°=20°,故选:B.【点评】本题考查平行线性质,关键是余角定义,角度计算.5.(2023秋•锦江区校级期末)一块含30°角的直角三角板,按如图所示方式放置,顶点A,C分别落在直线a,b上,若直线a∥b,∠1=35°,则∠2的度数是()A.45°B.35°C.30°D.25°【分析】先根据题意得出∠1+∠BAC的度数,再由平行线的性质即可得出结论.【解答】解:∵∠1=35°,∴∠1+∠BAC=35°+30°=65°,∵a∥b,∴∠2+∠ACB+∠1+∠BAC=180°,即∠2+90°+35°+30°=180°,∴∠2=25°.故选:D.【点评】本题考查的是平行线的性质,熟知两直线平行,同旁内角互补是解题的关键.6.如图,将一副三角尺按如图所示的位置在同一平面内摆放,其中∠ACB=∠CED=90°,∠B=30°,∠ECD=45°.若AB∥CE,CB与DE相交于点F,则∠BCD的度数为()A.15°B.20°C.25°D.30°【分析】根据平行线的性质得出∠ECA=120°,进而利用角的关系解答即可.【解答】解:∵AB∥CE,∴∠ECA=180°﹣∠A=180°﹣60°=120°,∵∠ECD=45°,∴∠DCA=120°﹣45°=75°,∵∠BCA=90°,∴∠BCD=90°﹣75°=15°,故选:A.【点评】此题考查平行线的性质,关键是根据两直线平行,同旁内角互补解答.7.(2023秋•新都区期末)如图,将含有30°的直角三角尺CAB(∠C=60°)直角顶点A放到矩形DEFH 的边DE上,若∠EAB=15°,则∠FQG的度数是()A.25°B.30°C.35°D.45°【分析】先根据∠EAB=15°,∠CAB=90°得出∠CAE的度数,再由HF∥DE得出∠CMF的度数,由三角形内角和定理得出∠CQM的度数,进而可得出结论.【解答】解:∵∠EAB=15°,∠CAB=90°,∴∠CAE=90°﹣15°=75°,∵HF∥DE,∴∠CMF=∠CAE=75°,∵∠C=60°,∴∠CQM=180°﹣60°﹣75°=45°,∴∠FQG=∠CQM=45°.故选:D.【点评】本题考查的是平行线的性质,熟知两直线平行,同位角相等是解题的关键.8.将一副三角尺如图放置,其中∠D=∠BAC=90°,∠F=30°,∠B=45°,则∠BCF的度数为()A.105°B.120°C.150°D.165°【分析】由∠D=∠BAC,利用“同位角相等,两直线平行”,可得出AC∥DF,利用“两直线平行,同位角相等”,可求出∠ACE的度数,结合∠BCE=∠ACB﹣∠ACE,可求出∠BCE的度数,再利用邻补角互补,即可求出∠BCF的度数.【解答】解:∵∠D=∠BAC=90°,∴AC∥DF,∴∠ACE=∠F=30°,∴∠BCE=∠ACB﹣∠ACE=45°﹣30°=15°.又∵∠BCE+∠BCF=180°,∴∠BCF﹣180°﹣∠BCE=180°﹣15°=165°.故选:D.【点评】本题考查了平行线的判定与性质以及邻补角,根据各角之间的关系,求出∠BCE的度数是解题的关键.9.一副三角形板如图放置,DE∥BC,∠C=∠DBE=90°,∠E=45°,∠A=30°,则∠ABD的度数为()A.5°B.15°C.20°D.25°【分析】根据三角形内角和定理以及平行线的性质,即可得到∠DC=45°,∠AB=60据此可得∠ABD的度数.【解答】解:Rt△ABC中,∠A=30°,∴∠ABC=60,∵BC∥DE,∠EDB=∠E=45°,∴∠DBC=45°,∴∠ABD=60°﹣45°=15°,故选:B.【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等.10.如图,将一副三角尺按图中所示位置摆放,点F在AC上,∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE.则∠AFD的度数是()A.25°B.20°C.15°D.10°【分析】利用三角板的度数可得∠A=30°,∠D=45°,由平行线的性质定理可得∠1=∠D=45°,利用三角形外角的性质可得结果.【解答】解:如图,∵∠ACB=90°,∠ABC=60°,∴∠A=180°﹣∠ACB﹣∠ABC=180°﹣90°﹣60°=30°,∵∠EFD=90°,∠DEF=45°,∴∠D=180°﹣∠EFD﹣∠DEF=180°﹣90°﹣45°=45°,∵AB∥DE,∴∠1=∠D=45°,∴∠AFD=∠1﹣∠A=45°﹣30°=15°,故选:C.【点评】本题主要考查了平行线的性质定理和外角的性质,求出∠A,∠D的度数是解本题的关键.11.(2023秋•莲湖区期末)如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠2=55°,求∠1的度数.【分析】先根据两直线平行的性质,得到∠3=∠2,再根据平角的定义,即可得出∠1的度数.【解答】解:∵AB∥CD,∴∠2=∠3.∵∠2=55°,∴∠3=55°.∵∠1+60°+∠3=180°,∴∠1=65°.【点评】本题主要考查了平行的性质,解题的关键是掌握:两直线平行,同位角相等.12.将一副直角三角板如图1摆放在直线MN上(直角三角板ABC和直角三角板EDC,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°),保持三角板EDC不动,将三角板ABC绕点C以每秒5°的速度顺时针旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.(1)如图2,当AC为∠DCE的角平分线时,t=.(2)当t=18时,求∠BCD的度数?(3)在旋转过程中,当三角板ABC的AB边平行于三角板EDC的某一边时(不包含重合的情形),求此时t的值为.(直接写出答案即可)【分析】(1)当AC为∠DCE的角平分线时,可以求出旋转角,再根据旋转的速度即可求解.(2)当t=18时,旋转角为90°,可求出∠ACD,即可求出∠BCD.(3)数形结合,分情况进行讨论即可.【解答】解:(1)当AC为∠DCE的角平分线时,旋转角为15°,∴t=155=3,故答案为3.(2)当t=18时,旋转角为90°,如图:∵∠DCE=30°,∠ACB=45°,∴∠ACD=60°,∠BCD=60°﹣45°=15°.(3)当三角板ABC的AB边平行于三角板EDC的某一边时,有3种情况:①当AB∥DE时,如图:此时,BC与CD重合,t=(30+40)÷5=15,②当AB∥CE时,如图:∵AB∥CE,∴∠BCE=∠B=90°,∴∠ACE=90°+45°=135°,∴t=135÷5=27,③当AB∥CD时,如图:∵AB∥CD,∴∠BCD=∠D=90°,∴∠ACE=30°+90°+45°=165°,∴t=165÷3=33.综上所述,t=15或27或33.【点评】本题考查旋转的性质,角平分线的性质,平行线的性质,关键在于数形结合,分类讨论.1.如图,在弯形管道ABCD中,若AB∥CD,拐角∠ABC=122°,则∠BCD的大小为()A.58°B.68°C.78°D.122°【分析】根据平行线的性质得出∠ABC+∠BCD=180°,代入求出即可.【解答】解:∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABC=122°,∴∠BCD=180°﹣122°=58°,故选:A.【点评】本题考查了平行线的性质,能熟练地运用平行线的性质定理进行推理是解此题的关键,注意:两直线平行,同旁内角互补.2.如图,万岁山大宋武侠城的两条小路AB∥CD,则∠BAE+∠AEC+∠ECD=()A.180°B.270°C.360°D.540°【分析】作辅助线EF∥AB,然后根据平行线的性质,可以得到∠BAE+∠AEC+∠ECD的度数.【解答】解:过点E作EF∥AB,如图:∵AB∥CD,∴AB∥CD∥EF,∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,∵∠AEF+∠FEC=∠AEC,∴∠BAE+∠AEC+∠ECD=360°,故选:C.【点评】本题考查平行线的性质,解答本题的关键是熟练掌握平行线的性质,明确题意,利用数形结合的思想解答.3.(2023秋•海门区期末)如图,两面镜子AB,BC的夹角为∠α,入射光线OM经过镜子两次反射后的出射光线NO平行于AB,图中∠1=∠2,∠3=∠4.当OM∥BC时,∠α的度数是()A.30°B.45°C.60°D.75°【分析】由平行线的性质推出∠4=∠α,∠1=∠α,又∠3=∠4,∠2=∠1,得到∠1=∠2=∠α,判定△MNB是等边三角形,得到∠α=60°.【解答】解:∵ON∥AB,∴∠4=∠α,∵∠3=∠4,∴∠3=∠α,∵OM∥BN,∴∠1=∠α,∵∠2=∠1,∴∠2=∠α,∴∠3=∠2=∠α,∴△MNB是等边三角形,∴∠α=60°.故选:C.【点评】本题考查平行线的性质,关键是由平行线的性质推出∠3=∠2=∠α.4.(2023秋•即墨区期末)生活中的椅子一般依据人体工学原理设计,如图为生活中一把椅子的侧面图,从人体脊柱的形势而言,当靠背角度∠DEF=115°时,能产生较为接近自然腰部的形状,此时最舒适.已知DE与地面平行,支撑杆BD与地面夹角∠ABD=50°,则制作时用螺丝固定时支撑杆BD和AF需构成夹角∠ACB为()A.70°B.65°C.60°D.50°【分析】先求出∠DEC的度数,再求出∠CAB的度数,最后求出∠ACB的度数.【解答】解:∵∠DEF=115°,∴∠DEC=180°﹣∠DEF=65°,∵DE∥AB,∴∠CAB=∠DEC=65°,∵∠ABD=50°,∴∠ACB=180°﹣∠ABD﹣∠CAB=65°.故选:B.【点评】本题主要考查了平行线的性质,解题的关键是熟练运用平行线的性质.5.当光从一种介质射向另一种介质时,光线会发生折射,不同介质的折射率不同.如图,水平放置的水槽中装有适量水,空气中两条平行光线射入水中,两条折射光线也互相平行.若∠1=110°,则∠2的度数为()A.70°B.60°C.50°D.40°【分析】根据题意可得:AB∥CE,然后利用平行线的性质可得∠ACE=70°,再利用两直线平行,内错角相等可得∠2=∠ACE=70°,即可解答.【解答】解:如图:由题意得:AB∥CE,∴∠1+∠ACE=180°,∴∠ACE=180°﹣∠1=70°,∵AC∥BE,∴∠2=∠ACE=70°,故选:A.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.6.(2023秋•鹿寨县期末)如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD=.【分析】过点B作BF∥AE,如图,由于CD∥AE,则BF∥CD,根据两直线平行,同旁内角互补得∠BCD+∠CBF=180°,由AB⊥AE得AB⊥BF,所以∠ABF=90°,于是有∠ABC+∠BCD=∠ABF+∠CBF+∠BCD =270°.【解答】解:过点B作BF∥AE,如图:∵CD∥AE,∴BF∥CD,∴∠BCD+∠CBF=180°,∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,∴∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=90°+180°=270°.故答案为:270°.【点评】本题主要考查了平行线的性质,正确作出辅助线,并熟记两直线平行,同旁内角互补是解决问题的关键.7.(2023秋•鼓楼区校级期末)如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,则∠2+∠3的度数为.【分析】过∠2顶点做直线l∥支撑平台,直线l将∠2分成两个角,根据平行的性质即可求解.【解答】解:过∠2顶点做直线l∥支撑平台,∴l∥支撑平台∥工作篮底部,∴∠1=∠4=30°、∠5+∠3=180°,∴∠4+∠5+∠3=30°+180°=210°,∵∠4+∠5=∠2,∴∠2+∠3=210°.故答案为:210°.【点评】本题考查平行线的性质,熟练掌握平行线的性质是解题的关键.8.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB∥DE,∠D=70°,则∠ACD=.【分析】过点C作CF∥AB,先证明CF∥DE,然后根据平行线的性质求出∠ACF=130°,∠DCF=110°,最后利用角的和差关系求解即可.【解答】解:过点C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠ACF=∠BAC,∠D+∠DCF=180°,又∠BAC=130°,∠D=70°,∴∠ACF=130°,∠DCF=110°,∴∠ACD=∠ACF﹣∠DCF=20°.故答案为:20°.【点评】本题考查了平行线的判定与性质,添加合适的辅助线是解题的关键.9.乐乐观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC的度数是()A.30°B.29°C.28°D.27°【分析】延长DC交AE于F,依据AB∥CD,∠BAE=92°,可得∠CFE=92°,再根据三角形外角性质,即可得到∠AEC=∠DCE﹣∠CFE.【解答】解:如图,延长DC交AE于F,∵AB∥CD,∠BAE=92°,∴∠CFE=92°,又∵∠DCE=121°,∴∠AEC=∠DCE﹣∠CFE=121°﹣92°=29°.故选:B.【点评】本题主要考查了平行线的性质,解决问题的关键是掌握:两直线平行,同位角相等.10.(2023秋•鹰潭期末)生活现象如图1,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.数学模型如图2,是杆秤的示意图,AC∥BD,经测量发现∠A=104°,∠BOE=76°,请判断OE与BD的位置关系,并说明理由.【分析】由AC∥BD可得∠A+∠ABD=180°,进而得出∠ABD=76°,再根据内错角相等,两直线平行可得答案.【解答】解:OE∥BD,理由如下:∵AC∥BD,∴∠A+∠ABD=180°,∴∠ABD=180°﹣104°=76°,∴∠ABD=∠BOE,∴OE∥BD.【点评】本题考查了平行线的判定和性质,熟练掌握这些判定和性质解题的关键.11.如图所示①是一种网红弹弓的示意图,在两头系上皮筋,拉动皮筋可形成如图②所示的平面示意图,弹弓的两边可看成平行的,即AB∥CD.活动小组在探索∠APD与∠A,∠D的数量关系时,有如下发现:当拉起皮筋使∠A=∠D时,瞄准最准确.现测得∠A=160°,∠APD=40°,判断此时瞄准是否最准确,请说明理由.【分析】如图所示,过点P作PQ∥AB,利用平行线的性质得到∠APQ=180°﹣∠A=20°,∠D=180°﹣∠DPQ,在求出∠DPQ的度数即可得到答案.【解答】解:此时瞄准最准确.如图所示,过点P作PQ∥AB,∵AB∥CD,∴AB∥PQ∥CD,∴∠APQ=180°﹣∠A=20°,∠D=180°﹣∠DPQ,∵∠APD=40°,∴∠DPQ=∠APD﹣∠APQ=20°∴∠D=160°,此时瞄准最准确.【点评】本题主要考查了平行线的性质,正确作出辅助线是解题的关键.1.(2023秋•天元区期末)如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFC=125°,则∠1=()A.35°B.55°C.70°D.65°【分析】根据两直线平行,同旁内角互补可得∠DEF+∠EFC=180°,再根据翻折的性质和平角的定义列式计算,即可求出∠1.【解答】解:∵长方形对边AD∥BC,∴∠DEF+∠EFC=180°,∴∠DEF=180°﹣∠EFC=180°﹣125°=55°,由翻折的性质得:∠DEF=∠MEF=55°,∴∠1=180°﹣55°×2=70°,故选:C.【点评】本题主要考查平行线的性质,折叠的性质,熟练掌握平行线的性质和折叠的性质是解题的关键.2.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=30°,则∠EFC′的度数为()A.120°B.100°C.150°D.90°【分析】根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,根据平角定义可求出∠BED的度数,即得∠BEF的度数,再根据平行线的性质即可得解.【解答】解:Rt△ABE中,∠ABE=30°,∴∠AEB=60°,由折叠的性质知:∠BEF=∠DEF=12∠BED,∵∠BED=180°﹣∠AEB=120°,∴∠BEF=60°,∵BE∥C′F,∴∠BEF+∠EFC′=180°,∴∠EFC′=180°﹣∠BEF=120°.故选:A.【点评】本题考查平行线的性质,熟记折叠的性质及“两直线平行,同旁内角互补”是解题的关键.2.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为()A.40°B.45°C.50°D.60°【分析】由邻补角概念和翻折变换性质得出∠EFB′=∠1=115°,∠EFC=65°,据此知∠CFB′=50°,结合∠B=∠B′=90°知∠2=90°﹣∠CFB′,从而得出答案.【解答】解:∵∠1=115°,∴∠EFB′=∠1=115°,∠EFC=65°,∴∠CFB′=50°,又∵∠B=∠B′=90°,∴∠2=90°﹣∠CFB′=40°,故选:A.【点评】本题主要考查翻折变换的性质,解题的关键是掌握翻折变换的对应边、对应角相等的性质及直角三角形两锐角互余、对顶角相等的性质.3.(2022•南京模拟)如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为()A.90°﹣αB.45°+αC.45°+2D.90°−2【分析】根据平行线的性质即可求解.【解答】解:如图,作过点B的射线AF',∵AB∥CD,∴∠1+∠FBC+∠2=180°,∠F'BC=∠2∵纸条是对折,∴∠FBC=∠F'BC=∠2,∴2∠2+∠1=180°,∵∠1=α,∴∠2=12×(180°﹣α),∴∠2=90°−12α,故选:D.【点评】本题考查了平行线的性质,本题的解题关键找出是纸条对折后的角度关系.4.(2022秋•宛城区校级期末)如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO=度.【分析】设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x,根据平角的定义解出x,由矩形的性质进而可以得出∠BGO的度数.【解答】解:∵∠AOD':∠D'OG=4:3,设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,即10x=180°,解得x=18°,∵AD∥BC,∴∠BGO=∠DOG=3x=54°,故答案为:54.【点评】本题考查了折叠的性质和平角的等于180°,解题关键是发现图中折叠前后重合的角相等.5.(2023秋•北林区校级期末)将长方形ABCD纸片沿AE折叠得到如图所示的图形,已知∠CED′=68°,则∠EAB的度数是.【分析】由折叠可得∠DEA=∠D'EA,再由已知的条件可求得∠DEA的度数,从长方形可得AB∥CD,从而可求∠EAB的度数.【解答】解:由折叠得:∠DEA=∠D'EA,∵∠CED′=68°,∴∠DED'=180°﹣∠CED'=112°,∴∠DEA=12∠DED'=56°,∵四边形ABCD是长方形,∴AB∥CD,∴∠EAB=∠DEA=56°.故答案为:56°.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.6.(2023秋•萍乡期末)如图,△ABC中,∠B=40°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为°.【分析】根据平行线的性质得到∠BDE=∠B=40°,根据折叠的性质得到∠ADE=∠ADC,根据平角的定义可得∠ADB+∠ADC=180°,由此可以求出∠ADC的度数即可得到答案.【解答】解:∵DE∥AB,∠B=40°,∴∠BDE=40°,由折叠的性质得∠ADE=∠ADC,∵∠ADB+∠ADC=180°,∠ADB=∠ADE﹣∠BDE=∠ADC﹣40°,∴∠ADC﹣40°+∠ADC=180°,∴∠ADC=110°,∴∠ADE=∠ADC=110°.故答案为:110.【点评】本题考查了折叠的性质,平行线的性质,熟练掌握平行线的性质、折叠的性质是解题的关键.7.(2023秋•淮南期末)如图,在Rt△ABC中,∠C=90°,∠1=76°,D、E分别在AB、AC上,将△ADE沿DE折叠得△FDE,且满足EF∥AB,则∠B的度数为.【分析】由折叠的性质得∠FED=∠1,∠A=∠F,根据平角的定义求出∠FEC的度数,再根据平行线的性质求出∠F的度数,即可得出∠A的度数,从而求出∠B的度数.【解答】解:由折叠的性质得∠FED=∠1,∠A=∠F,∵∠1=76°,∴∠FED=76°,∴∠FEC=180°﹣∠FED﹣∠1=180°﹣76°﹣76°=28°,∵EF∥AB,∴∠F=∠FEC=28°,∴∠A=28°,∵∠C=90°,∴∠B=90°﹣∠A=90°﹣28°=62°,故答案为:62°.【点评】本题考查了平行线的性质,折叠的性质,平角的定义,三角形内角和定理,熟练掌握这些知识点是解题的关键.8.(2023秋•丹徒区期末)如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠EFC =30°,则∠DAE等于.【分析】由长方形的性质得出∠D=90°,AD∥BC,再由折叠的性质得出∠DAE=∠FAE,∠AFE=∠D =90°,结合已知∠EFC=30°即可求出∠AFB的度数,从而求出∠DAE的度数.【解答】解:∵四边形ABCD为长方形,∴∠D=90°,AD∥BC,由折叠得,∠DAE=∠FAE,∠AFE=∠D=90°,∵∠EFC=30°,∴∠AFB=180°﹣∠AFE﹣∠EFC=180°﹣90°﹣30°=60°,∵AD∥BC,∴∠AFB=∠DAF,即60°=2∠DAE,∴∠DAE=30°,故答案为:30°.【点评】本题考查了平行线的性质,长方形的性质,折叠的性质,熟练掌握这些图形的性质是解题的关键.9.(2022•郑州模拟)如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF =α,用含α的式子可以将∠C'FG表示为()A.2αB.90°+αC.180°﹣αD.180°﹣2α【分析】由折叠的性质可得:∠DEG=2α,C'F∥D'E,由AD∥BC可得∠D'GF=∠DEG=2α,从而有∠C'FG=180°﹣∠D'GF,即可得出结果.【解答】解:由长方形纸带ABCD及折叠性质可得:∠D'EF=∠DEF=α,C'F∥D'E,∴∠DEG=2∠DEF=2α,∠C'FG=180°﹣∠D'GF,∵AD∥BC,∴∠D'GF=∠DEG=2α,∴∠C'FG=180°﹣2α.故选:D.【点评】本题主要考查平行线的性质,折叠的性质,解答的关键是熟记折叠的性质.10.(2023秋•泉州期末)如图,四边形ABCD是一条两边互相平行的纸带,将其沿着EG折叠,使得点B,C分别落在点H,I处,EH与DG相交于点F,若∠EGF=56°,求∠EFD的度数.【分析】利用平行线的性质可得∠BEG=∠EGD=56°,再利用折叠的性质可得:∠BEF=2∠BEG=112°,然后利用平行线的性质可得∠BEF=∠EFD=112°,即可解答.【解答】解:∵AB∥CD,∴∠BEG=∠EGD=56°,由折叠得:∠BEF=2∠BEG=112°,∵AB∥CD,∴∠BEF=∠EFD=112°,∴∠EFD的度数为112°.【点评】本题考查了平行线的性质,根据题目的已知条件并结合图形进行分析是解题的关键.11.在图中,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3.(1)若在图1中,∠DEF=20°,则图3中∠C2FE的度数是多少?(2)若∠DEF=α,请用α表示图3中的∠C2FE的度数.【分析】(1)根据两直线平行,同旁内角互补可得∠CFE=160°,根据两直线平行,内错角相等可得∠BFE=∠DEF,然后求出∠BFC1,再根据翻折的性质可得∠CFE=∠EFC1,∠C2FB+∠BFC1,即可得解;(2)同(1)的方法求解即可.【解答】解:(1)∵矩形对边AD∥BC,∴CF∥DE,∴∠CFE=180°﹣∠DEF=180°﹣20°=160°,∵AD∥BC,∴∠BFE=∠DEF=20°,由翻折的性质得,∠CFE=∠EFC1,∴∠BFC1=160°﹣20°=140°,由翻折的性质得,∠C2FB+∠BFC1,所以,∠C2FE=140°﹣20°=120°;(2)∵矩形对边AD∥BC,∴CF∥DE,∴∠CFE=180°﹣∠DEF=180°﹣α,∵AD∥BC,∴∠BFE=∠DEF=α,由翻折的性质得,∠CFE=∠EFC1,∴∠BFC1=180°﹣α﹣α=180°﹣2α,由翻折的性质得,∠C2FB+∠BFC1,所以,∠C2FE=180°﹣2α﹣α=180°﹣3α.【点评】本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图,理清翻折前后重叠的角是解题的关键.12.(2022秋•东阳市期末)如图,长方形纸片ABCD中,G、H分别是AB、CD边上的动点,连GH,将长方形纸片ABCD沿着GH翻折,使得点B,C分别落在点E,F位置.(1)若∠BGH=110°,求∠AGE的度数.(2)若∠FHD=20°,求∠CHG的度数.(3)已知∠BGH和∠CHG始终互补,若∠BGH=α,请直接写出∠FHC的度数(含α的代数式).【分析】(1)根据折叠得到∠BGH=∠EGH=110°,再根据平角的定义,利用∠AGE=∠BGH+∠EGH ﹣180°计算可得;(2)根据折叠得到∠CHG=∠FHG,再根据平角的定义计算即可;(3)根据互补得到∠BGH+∠CHG=180°,从而求出∠CHG=∠FHG=180°﹣α,分情况继而可得结果.【解答】解:(1)由折叠可得:∠BGH=∠EGH=110°,∵∠BGH+∠AGH=180°,∴∠AGE=∠BGH+∠EGH﹣180°=40°;(2)由折叠可得:∠CHG=∠FHG,∴∠C=12(180°−∠Cp=80°;(3)情况一:∵∠BGH和∠CHG始终互补,∴∠BGH+∠CHG=180°,∵∠BGH=α,∴∠CHG=180°﹣α,∴∠FHG=180°﹣α,∴∠FHC=∠FHG+∠CHG=360°﹣2α.情况二:由第一种情况可知:∠1=360°﹣2α,∴∠FHC=360°﹣(360°﹣2α)=2α.【点评】本题考查了折叠的性质,平角的定义,解题的关键是掌握折叠前后对应角相等.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线中的题型解析
平行线是是平面几何的基础内容,在简单的背景下,富有新意的题型也层出不穷,可谓生动活泼,奥妙无穷,下面选择几例希望对同学们有所帮助.
一、操作型
例1 如图1,给出了过直线外一点作已知直线的平行线的方法,其依据是 析解:从图中可以看出,三角板平移的过程中,角的
大小不变,因此根据的依据是同位角相等,两直线平行.
评注:平行线的条件和特征是互逆的,我们在运用时,
要搞清条件和结论,不要混淆,象本题中,不能写成两直
线平行,同位角相等.
二、网格判断型
例2 如图2,在正方形网格中,∠1、∠2、∠3的大
小关系是( )
A .∠1=∠2>∠3
B .∠1<∠2<∠3
C .∠1>∠2>∠3
D .∠1=∠2=∠3 析解:观察网格,AB 、CD 都是“1×3”的长方形的对角线,有AB ∥CD ,根据“两直线平行,内错角相等”,得到∠1=∠2,用类似的方法可以得出∠2>∠3,故选A . 评注:我们常用网格研究线段的平行、垂直问题,一般的方法就是通过线段放在网格中的长方形中,作为长方形的对角线研究.
三、结论探索型
例3 将直尺与三角板按如图4所示的方式叠放在一起,在
图中标示的角中,写出所有与∠1互余的角. 析解:因为∠AEB=90°,所以∠1+∠2=90°,因为AB ∥CD ,所以∠2=∠3,∠2=∠4,所以∠1+∠3=90°,∠1+∠4=90°,故与∠1互余的角有三个,分别是∠2,∠3,∠4. 评注:解决这类问题,同学们需要熟练掌握余角、对顶角
及直线平行的条件.
四、条件、结论探索型
例4 对于同一平面内的三条直线a 、b 、c ,给出下列五个论断:①a ∥b ;②b ∥c ;③a ⊥b ;④a ∥c ;⑤a ⊥c ,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的判断,并以其中一个为例画出图形,简要说明理由.
解析:该题要求在五个论断中选取两个论断为条件,再从剩下的论断中选取一个为结论,组成一个正确的判断,则可以有:①②→④;②③→⑤;③⑤→②.
以②③→⑤为例,如图5所示,理由如下:
因为a ⊥b 所以∠1=90° 因为b ∥c
所以∠2=∠190° 所以a ⊥c
评注:这类开放性问题具有较强的灵活性,解决这类问题的关建是先确定可能有哪些判断,再确定其是否正确.
D C B A 654321
21a c b
321E D
C B A。
