理论力学第5章点的复合运动
理论力学答案第5章点的复合运动分析
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
理论力学答案

1、加减平衡力系公理不但适用于刚体,还适用于变形体。
(×)2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
(×)3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
(√)4、凡是受两个力作用的刚体都是二力构件。
(×)5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
(×)6、若作用于刚体上的三个力组成平衡力系,那么此三力一定共面,但不一定交于一点。
(√)7、如果所作的受力图是一个显然不平衡的力系,那么受力图一定有错。
(×)8、如果作用在一个刚体上的力系对任何点主矩均不为零,该力系可以等效为一个力偶。
(×)9、作用在一个刚体上的任意两个力平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
(√)10、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
(×)11、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
(×)12、力偶永远不能与一个力等效,共面的一个力与一个力偶总可以合成为一个力。
(√)13、力偶的作用效应用力偶矩来度量。
(√)14、力对于一点的矩不因力沿其作用线移动而改变。
(√)15、只要平面力偶的力偶矩保持不变,可将力偶的力和臂作相应的改变,而不影响其对刚体的效应。
(√)16、当力与轴共面时,力对该轴之矩等于零(√)17、在保持力偶矩不变的情况下,可任意改变力和力偶臂的大小,并可以在作用面内任意搬移(√)18、在任意力系中,若其力多边形自行封闭,则该任意力系的主矢为零。
(√)19、当平面一般力系向某点简化为力偶时,如果向另一点简化,则其结果是一样的。
(×)20、首尾相接构成一封闭力多边形的平面力系是平衡力系。
(×)21、若一平面力系对某点之主矩为零,且主矢亦为零,则该力系为一平衡力系。
(√)22、如果某平面力系由多个力偶和一个力组成,则该力系一定不是平衡力系(√)23、任一力系如果向A、B两点简化的主矩均等于零,则力系的主矢向与AB连线垂直的轴的投影一定为零(√)24、力系的主矢与简化中心的位置有关,而力系的主矩与简化中心的位置无关(√)25、在空间问题中,力对轴之矩是代数量,而力对点之矩是矢量。
论点的复合运动中动点、动系的选择原则和方法

论点的复合运动中动点、动系的选择原则和方法1引言理论力学是机械、土木类专业的专业基础课。
包括静力学、运动学和动力学三大部分。
运动学是从几何角度研究物体运动轨迹、运动方程、速度和加速度,而不考虑引起物体运动的物理原因。
其中点的合成运动是运动学的重点内容。
此部分内容题目多样,解题方法灵活,并且具有趣味性,完成一道题目时很有成就感。
当然也是让学生感到没有思路、无从下手的部分,普遍反映难度较大,也是测验、考核过程中丢分比较多的部分,问题的关键是无法正确的选取动点和动系。
本文从典型例题出发,介绍了点的合成运动中动点和动系的选取原则,可以帮助学生理清思路,提高点的合成运动的解题能力。
2点的合成运动概述在日常生活中,会经常遇到这样的情况。
当我们站在不同的参考物上,观察同一个物体的运动,发现物体所呈现的运动形式是不一样的。
举个最常见的例子,如图1。
人站在一辆沿直线匀速行驶的公共汽车上,以地面为参考物,观察人的运动,人在作匀速直线运动。
而以公共汽车为参考物,则人静止的。
可见,人的运动形式依选取的参考物不同而不同。
再引申一个例子,如图2。
沿直线轨道滚动的车轮,研究其轮缘上任意一点M的运动。
对于地面来说,点M的轨迹是旋轮线,而对于车厢来说,点M的轨迹则是一个圆。
车轮上的点M是沿旋轮线运动,是一种比较复杂复杂的运动形式,但是以车厢作为参考体,则点M相对于车厢的运动是简单的定轴转动,车厢相对于地面的运动是简单的平移。
轮缘上一点M的运动就可以看成为两个简单运动的合成,即点M相对于车厢作圆周运动,同时车厢相对地面作平移。
于是得到了合成运动的定义,即相对于某一参考体的运动可由相对于其他参考体的几个运动组合而成,称这种运动为合成运动。
3一点二系三运动研究点的合成运动,确定一个动点,选择定参考系和动参考系两个坐标系,分析动点的绝对运动、相对运动和牵连运动是首要任务。
3.1两个参考坐标系研究点的合成运动,总要涉及两个参考坐标系。
(1)定参考系建立在固定参考物上的坐标系,简称定系。
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
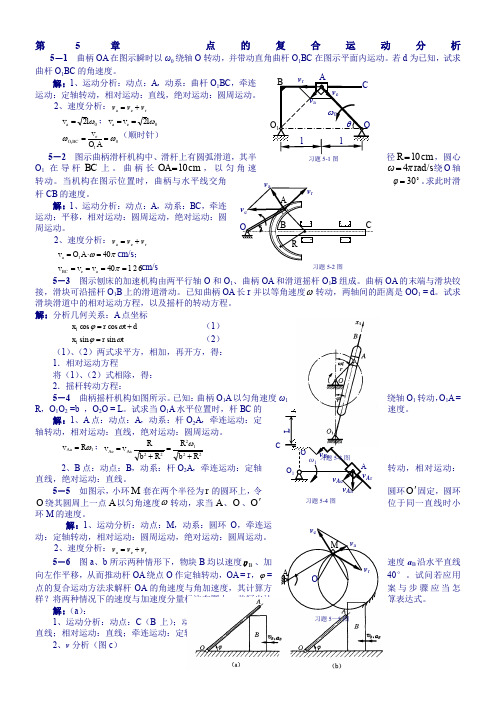
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
理论力学点的合成运动

例 8-4 曲柄OA以匀角速度 w绕O轴转动,其上
套有小环 M,而小环 M又在固定的大圆环上运动,大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时,小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解:(1)选择动点及 动系: 小环M为动点,动系固连在 OA上。
(2)分析三种运动:绝 对运动为圆周运动,相对运 动为沿OA的直线运动,牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中,设 Oxyz为定系,Oxyz为动系且作平
动,M为动点。动点M在动系中的坐标为 x、y 、z, 动系单位矢量为 i、 j、k。动系平动,i、j、k 的
Oxyz 作某种运动,在瞬时t,动系连同相对轨迹AB在
定系中的I位置,动点则在曲线 AB
上的 M 点。经过时间间 隔 t ,动系运动到定系 中的II位置,动点运动到
点 M。 如果在动系上观
察点M 的运动,则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶,雨滴 以速度 v2 铅直下落,试求雨滴相对于汽车的速度。
v1
解: 因为雨滴相对运动的汽车有运动,所以本题 为点的合成运动问题,可应用点的速度合成定理求解。
理论力学选择判断自测题

动量距定理1.如果作用于质点系上的外力对固定点O的主矩不为零,那末质点系的动量矩一定不守恒。
正确答案:错对错2.如果质点系对于某点或某轴的动量矩很大,则质点系的动量也很大正确答案:错对错3.系统的动量矩守恒,则每一质点的动量矩都一定保持不变。
正确答案:错对错4.系统的动量守恒,动量矩也必定守恒。
正确答案:错对错5.质点系的质心位置保持不变的条件是作用于质点系的所有外力主矢恒为零及质心的初速度为零。
正确答案:对对错6.均质杆长为l,质量为m,在图6所示位置质心速度为vC,则此杆对O轴的动量矩为()。
正确答案:B(A)lm vC/2 (B)2lm vC/3 (C)lmvC/3 (D)lmvC /67.质量为m,长为l的均质杆OA,一端可绕O轴转动,另一端与半径为R,质量为m的均质圆盘(1)固接;(2)光滑铰接于轮心A.系统从水平位置由静止开始运动,哪种情况下OA杆先到达铅垂位置()。
正确答案:B(A)情况(1)先到(B)情况(2)先到(C)两种情况同时达到8.如果把图8(a)中重为的物体换为图8(b)所示的力,在这两种情况下,若把匀质滑轮的角加速度和的大小比较,则有()。
正确答案:A9.质量为m的小球,放在绕铅垂轴转动的套管内,球用绳ABC拉住(图9),当拉力为F时,套管以匀角速度ω转动,小球相对套管静止.若突然释放绳子,则()。
正确答案:C(A)系统动能增加,动量矩增加。
(B)系统动能增加,动量矩减少。
(C)系统动能不变,动量矩不变。
(D)系统动能减少,动量矩不变。
10.两个相同的均质圆盘放在光滑的水平面上(图10),分别受力F、F′的作用,由静止开始运动。
若F=F′,则在运动开始后的任一瞬时,两盘各自对质心的动量矩比较是()。
正确答案:A(A)LA < LB (B)LA>LB (C)LA=LB (D)不能确定动量定理1.质点系中各个质点的动量均不为零时,则质点系的动量一定不为零。
正确答案:错对错2.质点系的动量不一定大于该质点系中单个质点或部分质点的动量。
点的合成运动

点的合成运动
在此之前,我们研究点的运动时,都是相对于某 一个参考系(定系)而言。但在有些问题中,往往需 要同时在两个不同的参考系中来描述同一点的运动, 而其中一个参考系相对于另一参考系也在运动。
为此,引入动点,动系,定系。并研究同一动点 相对 于两个不同参考系的运动之间的关系。
2013年8月6日
计算有何影响?
2013年8月6日
理论力学CAI
20
选择方法一
动系
动点
2013年8月6日
理论力学CAI
21
选择方法二
动系
动点
2013年8月6日
理论力学CAI
22
动点、动系和定系的选择原则
1. 动点是个确定的点。
2. 动点与动系必须分别选在两个不同的物体上,动点
与动系间有相对运动。
3. 动点相对动系的相对运动轨迹易于直观判断。
例题
已知:AB匀角速度转动。 求:M在导槽EF及BC中运动的速度与加速度。
E
B
C M
A
l F D
2013年8月6日
理论力学CAI
35
y
vB
B
ve
M
E
vM
C
速度分析:
x 动点—M点 动系—BC杆
A
vr
D
l
F
ve = vB = l
v M = ve v r
y : vM = ve sin = l sin x : 0 = vr ve cos
相对轨迹,相对速度vr,相对加速度ar。
2013年8月6日 理论力学CAI
7
牵连运动(entangled motion) :
[工学]理论力学习题及解答1
![[工学]理论力学习题及解答1](https://img.taocdn.com/s3/m/20bdb204cd7931b765ce0508763231126edb7788.png)
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
谢传峰《理论力学》课后习题及详解
1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lk lk l y v ====θθθ938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以质点的加速度为:n t a a a +=,设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n va =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10 解:设初始时,绳索AB 的长度为L ,时刻t 时的长度为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= ,x x s s 22= xyoan avy vθθtayzoan aθxovovF N Fg myθ由此解得:xsv x 0-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得:2002v v s x x x=-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-== (负号说明滑块A 的加速度向上)取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的运动微分方程:N F F ym F mg xm +-=-=θθsin cos其中:2222sin ,cos l x l lx x +=+=θθ0,3220=-=yx l v x将其代入直角坐标形式的运动微分方程可得:23220)(1)(x lxl v g m F ++=1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即:θcos A B v v = (a ) 因为x R x 22cos -=θ (b )将上式代入(a )式得到A 点速度的大小为:22R x xRv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x x ω=--22 ,将该式两边平方可得:222222)(x R R x xω=-将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=--将上式消去x 2后,可求得:22242)(R x xR x--=ω (d)由上式可知滑块A 的加速度方向向左,其大小为 22242)(R x xR a A -=ω取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:g F F a m m N ++=将该式在y x ,轴上投影可得直角坐标形式的 运动微分方程:mg F F ym F xm N -+=-=θθsin cos其中:x R x xR22cos ,sin -==θθ, 0,)(22242=--=y R x x R x ω将其代入直角坐标形式的运动微分方程可得2525)(,)(225222242R x x R m mg F R x x R m F N --=-=ωω1-13解:动点:套筒A ;动系:OC 杆;定系:机座;xθ AvAω ONF BRg mFyavevr v运动分析:绝对运动:直线运动;相对运动:直线运动;牵连运动:定轴转动。
理论力学运动学部分

一、判断题:1. 在自然坐标系中,如果速度v = 常数,则加速度a = 0。
( ) 2、在分析点的合成运动时,动点的绝对速度一定不能恒等于零。
( ) 3、对于平动刚体,任一瞬时,各点速度大小相等而方向可以不同。
( )4、在刚体运动过程中,若刚体内任一平面始终与某固定平面平行,则这种运动就是刚体的平面运动。
( )5、加速度d d v t 的大小为d d vt。
( ) 6、点的法向加速度与速度大小的改变率无关。
( ) 7、速度瞬心的速度为零,加速度也为零。
( )8、火车在北半球上自东向西行驶,两条铁轨的磨损程度是相同的。
( ) 9、平动刚体上各点运动状态完全相同。
( )10、某瞬时动点的加速度等于零,则其速度可能为零。
( ) 11、不论点作什么运动,点的位移始终是一个矢量。
( )12、某动点如果在某瞬时法向加速度为零,而切向加速度不为零,则该点一定做直线运动。
( )13、在研究点的合成运动时,所选动点必须相对地球有运动( )14、已知自然法描述的点的运动方程为S=f(t),则任意瞬时点的速度、加速度即可确定。
( )15、科氏加速度的大小等于相对速度与牵连角速度之大小的乘积的两倍。
( ) 16、作平面运动的平面图形可以同时存在两个或两个以上的速度瞬时中心。
( ) 17、在自然坐标系中,如果速度v = 常数,则加速度0a 。
( ) 18、在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
( ) 19、在分析点的合成运动时,动点的绝对速度一定不能恒等于零。
( ) 20、若动系的牵连运动为定轴转动,则肯定存在哥氏加速度C a。
( )21、在直角坐标系中,如果一点的速度v 在三个坐标上的投影均为常数,其加速度a 必然为零。
( )22、刚体平行移动时,其上各点的轨迹一定是相互平行的直线。
二.填空题1.点M 沿螺旋线自外向内运动,如图所示。
它走过的弧长与时间的一次方成正比。
试分析它的加速度越来越__________ (填大或小)2.图所示平板绕AB 轴以匀角速度ω定轴转动,动点M 在板上沿圆槽顺时针运动,运动方程为t v s ⋅=0。
工程力学学习资料 点的复合运动2

aa ae ar ak
点的合成运动2种类型的问题: 1、带有滑套的机构。
2、运动中,物体相互接触 的机构,接触点不变。
例题:已知:OA杆匀速转动 w,OA=r,该 瞬时已知,求:BC杆的加速度。
解: 动点:滑块A 动系:杆BCDE
绝对运动-
O
D w B C A
以O为圆心的圆周运动
v v v
a e
vr
va
r
ve
即在任一瞬时点的绝对速度等于其牵连速度与相对 速度的矢量和,这就是点的速度合成定理。
选择动点、动系的原则: 动点对动系有相对运动,且相对运动的轨迹是 已知的,或者能直接看出的。
(相对轨迹、
动 点
速度与加速度)
(绝对轨迹、
速度与加速度)
动 系
牵连运动 (刚体运动)
定 系 (牵连速度与加速度)
E
相对运动- 沿DE的直线运动
牵连运动-
水平直线平移
aa ae ar
大小: 方向: ?
2
?
D
ae
O
w
A
aa rw
aa
ar B
E
C
加速度向水平方向投影
aa cos=ae
ae rw cos
2
aBC w r cos()
2
作业:17-7,8
12(a)
ve v0
0=ve vr sin
v0 2 vr v0 o sin 60 3
4v v a R 3R
n r
2 r
2 0
aa ae a r ar
加速度向AC方向投影
0 0
理论力学运动学习题及详解
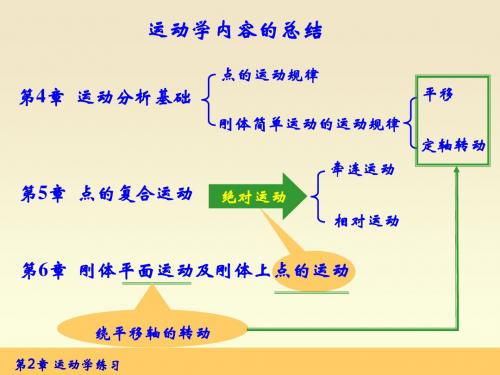
y f 2 (t ) z f 3 (t )
2 2
a x x a y y a z z
2 2 2
v vx v y vz
2
a ax a y az
方向均由相应的方向余弦确定。
第2章 运动学练习
二.基本公式 自然法(轨迹已知时)
运动方程 速度
ae 5 2 0 r 4
5 2a r0 4
B
aC 0
O2
3销钉C固定在AB杆,在滑槽O2D中运动,该瞬时O1A与AB水平,O2D
铅直,且O1A=AC=CB=O2C=r,ω0=常数,求
AB、O2 D、 AB、O2 D .
D
n aCA
(2)加速度分析
AB 0
a 常量, an 0
,点做何种运动( B)。
B.匀变速曲线运动 D.匀变速直线运动
(3)已知点的运动方程为 x 2t 2 4, y 3t 2 3 ,其轨迹方程为(
B)
A.3x 4 y 36 0, C.2 x 2 y 24 0,
第2章 运动学练习
B.3x 2 y 18 0 D.2 x 4 y 36 0
1.选择题:
【练习题】
(4). 如图所示平面机构中,O1A=O2B= r, O1O2 =AB, O1A以匀角速度绕垂直于图 面的O1轴转动,图示瞬时,C点的速度为:( D )
A.
B. C.
Vc 0
Vc r a
2 2
水平向右
O1 A
O2
Vc r0 D. Vc r0
铅直向上 水平向右
2.刚体运动学
基本运动 平面运动
清华大学理论力学lecture05A
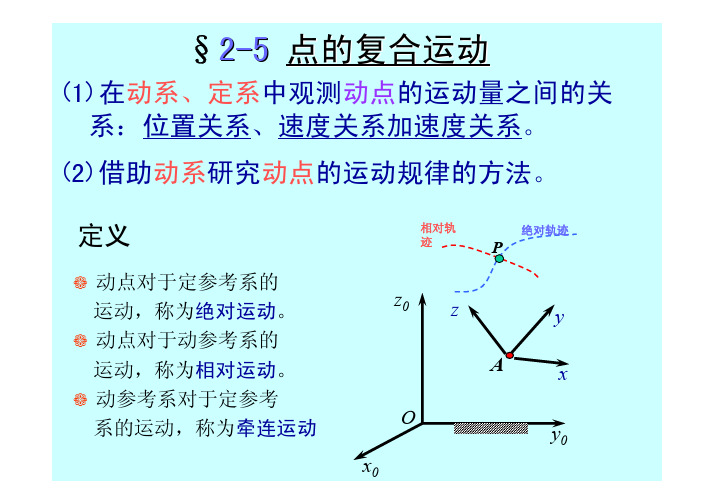
§2-5 点的复合运动(1)在动系、定系中观测动点的运动量之间的关 系:位置关系、速度关系加速度关系。
(2)借助动系研究动点的运动规律的方法。
定义动点对于定参考系的 运动,称为绝对运动。
动点对于动参考系的 运动,称为相对运动。
动参考系对于定参考 系的运动,称为牵连运动 x0 z0相对轨 迹 绝对轨迹Pz Ay x y0O绝对运动、相对运动与牵连运动 例1 动点:滑块P;定系:圆板;动系:杆 OA 绝对运动:螺旋线相对运动:沿杆直线 牵连运动:定轴转动 牵连点Pe: 动系上与动点P位置重 合的点(杆上的点) 牵连点的位置随动点的相对运动而改变。
牵连速度:牵连点的绝对速度,记为ve 。
点的复合运动公式动点的绝对速度 v a 等于动点相 对动系的相对速度 v r 与其牵连点 的速度 ve 之和。
该动系上瞬时与 动点的几何位置重合的点称为动点 的牵连点。
相对 轨迹P绝对轨迹z0z Ay x y0v a = ve + v r动点的绝对加速度 aa 等于 动点相对动系的相对加速度 ar 与其牵连点的加速度 ae 以及哥 氏加速度 aC 之和。
O x0a a = ae + a r + ac哥氏加速度 ac = 2ω × vrω动系的绝对角速度例:速度合成定理的一个启发性证明Oxyz 为定系;刚性金属丝为动系,作刚体一般运动;丝上套小环P为动点。
绝对 轨迹 相对 轨迹e e前时刻动系上与动点重合的点的绝对轨迹速度合成定理:动点的绝对速度等于其牵连速度与相对 速度的矢量和: v a = ve + v r∆r = ∆rr + ∆re⎛ ∆r ∆rr ∆re ⎞ = + lim ⎜ ⎟ t →0 ⎝ ∆t ∆t ∆t ⎠绝对 速度v a = ve + v rP的绝 对位移牵连 速度相对 速度∆rr相对 位移e牵连点的 绝对位移ee定义:在t 瞬时,动系上与动点相重合之点(牵连点) 的绝对速度称为牵连速度,记为 v e 。
理论力学-5-点的复合运动分析

5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动点相对于动系的运动,称为 动点的相对运动(relative)。动 点刀尖上P点的相对运动是在工件 圆柱面上的螺旋线(相对轨迹)运 动。 动点相对于动系的运动速度和 加速度,分别称为动点的相对速度 和相对加速度,分别用符号vr和ar 表示。
具体方法:在有的机构中,一个构件上总有一个点被另一个构件所约束。 这时,以被约束的点作为动点,在约束动点的构件上建立动系,相对运动 轨迹便是约束构件的轮廓线或者约束动点的轨道。
(3) 应用速度合成定理时,可利用速度平行四边形中的几何关系解出 未知数。也可以采用投影法:即等式左右两边同时对某一轴进行投 影,投影的结果相等。
5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动系相对于定系的运动, 称为牵连运动。图中,牵连 运动为绕Oy ' 轴的定轴转动。
5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动系上每一瞬时与动点相重 合的那一点,称为瞬时重合点,又 称为牵连点。由于动点相对于动 系是运动的,因此,在不同的瞬 时,牵连点是动系上的不同点。 动系上牵连点相对定系的运 动速度和加速度,分别称为为动 点的牵连速度和牵连加速度,分 别用符号ve和ae表示。
第5章 点的复合运动分析 5.1 点的合成运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论
第5章 点的复合运动分析
5.1 点的合成运动的基本概念
5.1 点的合成运动的基本概念
vr
q
ve OA
3 2 3e va ve tan q OA 3 3
第五章 点的复合运动

aa ae a r ar
n
n
将上式向n轴投影,得
j
n
aa sinj ae cosj a r
4v 0 2 aa (ae cosj ar n )/sinj (a0 cos60 )/sin60 3R
得
3 8 v0 a A B aa ( a0 ) 3 3 R
dx' dy ' dz ' vr i ' j ' k' dt dt dt d 2 x' d 2 y' d 2 z' ar 2 i ' 2 j ' 2 k ' dt dt dt
②动系绕z轴转动,动系上与动点重合的点的速度、加速度即 牵连速度、牵连加速度:由公式(4-2-13)(4-2-14)
va ve v r wR v r 常数
即绝对运动也为匀速圆周运动,所以 2 va 2 ( Rw vr ) 2 vr 2 aa Rw 2wvr ae ar 2wvr R R R 方向指向圆心O点。
34
可见,当牵连运动为转动时,动点的绝对加速度 等于牵连加速度
速度合成定理 将建立动点的绝对 速度,相对速度和 牵连速度之间的关 系。
t→t+△t
M →M′ 也可看成:
M →M1 →M′
MM′ — 绝对轨迹 M M′ — 绝对位移 — M1M′ 相对轨迹
请看动画
M1M′ 相对位移 M M1— 牵连位移17 —
由图:
MM ' = MM1 + M 1M '
MM1 M1 M MM lim lim lim t t 0 t t 0 t t 0
解:取杆AB上的A点为动点,
理论力学课件:5-3 点的复合运动

• 平行于转轴的直线MP上的所
z
有点的运动与 P 点的运动相同
• 除转轴上的点以外,所有点 均作为圆周运动。
y
M
y
o
x
P
S
ϕ
P
o
x
2012-11-7
12
理论力学
§5-3 点的复合运动
定轴转动刚体上点的速度和加速度
1、点的速度
速度的大小: v = OPϕ& = Rω
速度的分布规律: v ⊥ OP,v与R成正比
2012-11-7
§5-3 点的复合运动
问题:小球相对管子匀速运动, 管子绕固定轴 O 匀速转动,如
何求小球相对地面的速度?
M2
y' y M′
x'
vr
v M 1 r
ω
x
相对位移:M'M2 绝对位移:M1M2
问题:M1 M’是什么位移?
19
理论力学
§5-3 点的复合运动
•瞬时重合点: 在某瞬时 动系上与动点重合的点
速度分析: va = ve + vr
va = ve tanθ = u tanθ
vr
=
ve
cosθ
=
u
cosθ
23
理论力学
§5-3 点的复合运动
加速度分析: aa = ae + ar aa = ae + art + arn
?
?
B
arn : aa cosθ = −ae sinθ + arn
u
a
t r
aa
相对轨迹越简单越好
2012-11-7
26
理论力学
理论力学(30-6) 2-5 刚体的复合运动

ε = ω e ×ω r
解 第 2章
例4 第 2章
解法1 解法 1
r =
刚 体 运 动 与 复 合 运 动
动系:轮轴OE 相对运动:车轮绕OE轴的定轴转动 牵连运动 :动系绕着竖直轴 OD的定轴转动
刚 体 运 动 与 复 合 运 动
ωe = u / R
D
O
已知:差动轮系如图,其中 R = 7cm, 2cm, ω1 = 5rad/s, ω2 = 3rad/s; 求: ω3 , ω4
v = ve + vr
ω × r = (ω e + ω r ) × r
X
?e
r P ?
r
y
O
Y
ω = ωe + ω r
x
上式可推广到多个定点运动合成 和牵连运动 和相对运动都是一般运动的情况.
ω30
动轮 2 定轮 0 惰轮 1
ω = ∑ ωi
i=1
n
解法1 解法 1 第 2章
刚体复合运动 第 2章
解法2 解法 2
工程实例 第 2章
角速度合成 第 2章
例1 第 2章
?
Z
齿轮系统
刚 体 运 动 与 复 合 运 动
刚 体 运 动 与 复 合 运 动
取刚体上任意一点P为动点 vr = ω r × r ve = ω e × r z v =ω ×r
刚 体 运 动 与 复 合 运 动
一个机构有三个齿轮互相啮合,并用一曲柄 相连,轮子中心在同一直线上. 已知:定轮0与动轮2的半径相等,曲柄的绝 对角速度ω30 求:动轮2的绝对角速度 ω20 .
ε = ω1 × ω 2 = ω 1ω 2 cosα j
v o ' = a ω1 i, a o ' = a ω12 j
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
vr
va
ve
va ve vr
即在任一瞬时动点的绝对速度等于其牵连速度与相对速度的 矢量和,这就是点的速度合成定理。
47
①点的速度合成定理是瞬时矢量式,共包括大小‚方向 六个元
素,已知任意四个元素,就能求出其他两个。 ②在速度平行四边形中,va 一定夹在ve 与
vr 之间。
③无论牵连运动为何种运动,此定理都成立。
将上式向h轴投影,得
aa cos2j ae cosj ar
n
aa
即:Rw 2 cos2j ae cosj Rw 2 2 Rw (cos2j 1) ae cosj 2Rw 2 cosj aCD
62
二、牵连运动为转动时点的加速度合成定理
1.牵连运动为转动时的加速度合成定理与牵连运动为平动时 有何不同? 前面我们证明了牵连运动为平动时的点的加速度合成定理, 那么当牵连运动为转动时,上述的加速度合成定理是否还 适用呢?下面我们来分析一特例。 设一圆盘以匀角速度w 绕定轴O顺 时针转动,盘上圆槽内有一点M以大
31
练习题 5
32
动点:套筒A
动系:OC
33
动点: OC上的A点 动系:O1B
34
练习题 6
动
点?
动参考系?
绝对运动? 相对运动? 牵连运动?
35
动点:滑块A 动系:BC
36
动点: BC上的A'点 动系:OA'
37
练习题 7
动
点?
动参考系? 绝对运动?
相对运动? 牵连运动?
51
(其中 i ' , j' , k ' 为动系坐标的单位矢量,因为动系为平动,故它 di ' dj ' dk ' 们的方向不变,是常矢量,所以 0, 0, 0 ) dt dt dt
dvO ' d 2 x' d 2 y' d 2 z' 又 aO ' ae , ar 2 i ' 2 j ' 2 k ' dt dt dt dt
vr :vr = ? , 方位O1A;
由 va ve vr , 作速度□:
60
由图知:∠ABE=∠BAE =90°-j vr va wR, ve 2va cos(90 j ) 2wR sin j (0 j 90) (2)求 aCD ae
va
方向:A→O
ve
aa :aa=aa
n=Rw2,
E
vr
ae :ae=? ,
B
方位:水平,指向:假设
ae
aa
61
ar : arτ =? 方位O1A,指向:假设
2 v 2 r an R w r R
方向:A→O1
由牵连运动为平动的加速度合成定理:
aa ae ar ar
h j ae j
n
a r a rn
练习题 2
动Leabharlann 点?动参考系?绝对运动?
相对运动?
牵连运动?
练习题
21
22
23
练习题 3
动
点?
动参考系?
绝对运动?
相对运动?
牵连运动?
24
25
26
27
28
练习题 4
动
点?
动参考系?
绝对运动? 相对运动? 牵连运动?
29
动点:套筒A
动系:O1B
30
动点: O1B上的A点 动系:OA
1
第五章 点的复合运动
(或称点的合成运动)
§5–1 绝对运动、相对运动和牵连运动
§5–2 点的速度合成定理 §5–3 点的加速度合成定理
2
本章重点:
运动的分解,点的速度合成定理和加速度合成定 理及其应用。 本章难点: 点的牵连速度和牵连加速度的概念和计算,动点 动系的选择,点的加速度合成定理的应用。
z′ 水平直线飞行: 螺旋桨端点P的 x′ y′ 运动:以机舱和 以地面为参考系 观察到的P点的 运动是不同的。
z
x
y
请看动画
一.坐标系: 1.静坐标系(静系):固结于地面上的坐标系。 2.动坐标系(动系):固结于相对于地面运动物体上的坐标系。
9
二.动点:所研究的点(运动着的点)。 三.三种运动
1.绝对运动:动点相对于静系的运动。
情况为圆心。
[注] 要指明动点在哪个物体上。
18
练习题 1
动点:圆盘上的销钉A,动系:摆杆O'A, 静系:机架 绝对运动:曲线(圆周),相对运动:直线 牵连运动:定轴转动
19
动点:A1(在O'A1 摆杆上),动系:圆盘,静系:机架 绝对运动:曲线(圆弧),相对运动:曲线 牵连运动:定轴转动
20
59
[例3] 图示具有圆弧形滑道的曲柄滑道机构。已知圆弧半径为
R,曲柄OA以匀w绕水平轴O转动,OA=R。求当曲柄与水平成
j 角时滑道CD的速度和加速度。 v a
解:取曲柄上的滑块A为动点, 动系固连在滑道CD上。 (1)求 vCD ve
ve
vr
va :va = w· OA= w·R,
方向:⊥OA 与w一致 ve :ve=? , 方位 :水平。
例如: P点相对于地面的运动。 2.相对运动:动点相对于动系的运动。 点的运动
例如:P点相对于飞机机身的运动。
3.牵连运动:动系相对于静系的运动。 例如:飞机相对于地面的运动。 可见(1)没有牵连运动,相对运动和绝对运动是相同的。 (2)绝对运动是相对运动和牵连运动的合成。
11
刚体的运动
例如:车刀的运动分析
38
动点:AB杆的A点 动系:轮C
39
动点:轮上的A'点 动系:顶杆AB
40
练习题 8
动
点?
动参考系?
绝对运动?
相对运动?
牵连运动?
思考
41
动点:BD杆的B点 动系:OA
42
动点:OA杆上的M点 动系:CD
43
§5-2点的速度合成定理
速度合成定理 将建立动点的绝对 速度,相对速度和 牵连速度之间的关 系。
动点:车刀刀尖
绝对运动:直线运动 牵连运动:定轴转动 相对运动:曲线运动(螺旋运动)
动系:工件
12
四.三种速度、加速度的定义
1.动点相对于静系的速度与加速度称为绝对速度 va 与绝对加
速度 aa 2.动点相对于动系的速度和加速度称为相对速度 v r 与相对加 速度 ar 3.牵连运动中,牵连点的速度和加速度称为牵连速度 v e 与牵连 加速度 ae 牵连点:在某瞬时,动系上与动点相重合的点。 注意:① ve , ae 是动系上某点的速度、加速度;
3
前一章我们研究点的运动,一般都是以地面为参考系的, 即:是研究点对一个坐标系(参考系)的运动。然而在实际问 题中,还常常要在相对于地面运动着的参考系上观察和研究物 体的运动,即:点的运动涉及到两个坐标系, 例如,无风下 雨时从行驶的汽车上看下雨的雨点是向后斜落的。根据这种关
系可以把点的复杂运动分解为两种简单运动来研究。
t→t+△t
M →M′ 也可看成:
M →M1 →M′
MM′ — 绝对轨迹 M M′ — 绝对位移 M1M— ′ 相对轨迹
请看动画
M1M— ′ 相对位移 M M1— 牵连位移44
由图:
MM ' = MM 1 + M1M '
将两边同除以△t,并取△t →0时的极限:
MM 1 M1 M MM lim lim lim t t 0 t t 0 t t 0
由速度合成定理 va ve vr作出速度□ ,得 ve lw va 方向:↑ 2 cosj cos j
49
解题步骤: (1)选取动点、动系 动系可以用文字说明,也可以在所选物体上画出x'o'y', 静系可以不叙述。 (2)分析三种运动
(3)分析三种速度 (4)由 va ve vr 作速度平行四边形
va 要位于ve 与 vr之间 注意:
(5)由速度平行四边形求解
50
§5-3 点的加速度合成定理 一、牵连运动为平动时点的加速度合成定理
设有一动点M按一定规律沿着固连于动系O'x'y'z' 的曲线AB 运动, 而曲线AB同时又随同动系O'x'y'z' 相对静系Oxyz平动。 由于牵连运动为平动,故
方向:A→C
注意:①不同于速度, 加速度的指向一般为假 设;②加速度图要与速 度图分开画
j
58
因牵连运动为平动,故有
aa ae a r ar
n
n
将上式向n轴投影,得
j
n
aa sinj ae cosj ar
得
3 8 v0 a AB a a ( a0 ) 3 3 R
2
[注意]加速度矢量方程的投影是等式两端的投影,与静平 衡方程的投影关系不同.
aa ae ar —牵连运动为平动时点的加速度合成定理
即当牵连运动为平动时,动点的绝对加速度等于牵连加速度
与相对加速度的矢量和。
a a a n
∴一般式可写为:
a
n a a a
a
n e ae ar
ar
n
52
[例2] 已知:凸轮半径 R,vo ,ao
求:j =60o时, 顶杆AB的加速度。
ve vO ' , ae aO '
由速度合成定理
va ve vr
dx ' dy ' dz ' 而 vr i' j' k' dt dt dt
