第六章相平衡与相图第五讲
第六章 相平衡与相图

• 无气相或虽有气相但其影响可忽略不计的系统称
为凝聚系统:如合金、硅酸盐系统
•
对于某些硅酸盐系统,气相不可忽略,则不能按
一般凝聚系统对待。
• (三)相 • 系统中物理与化学性质相同且完全均匀部分的总和。
•
1.特点
质突变;
• (1)相之间有界面,可用机械方法分离,越过界面时性
• (2)一个相在物理和化学性质上都是微观尺度的均匀,
4.形成固溶体的二元系统相图
• ⑴ 连续(或完全互溶、无限 互溶)固溶体:溶质和溶剂 能以任意比例相互溶解的固 溶体。 • 特点:无二元无变量点。 • 液相线:aL2b , • P=2,F=1。 • 固相线:aS2b , • P=2,F=1。 • 此系统内只有液相和固溶 体两相,不会出现三相平衡 状态 。
•
•
b .转变速度慢,由表面开始逐渐向内部进行
c .体积变化对生产影响不大
•
由于转变速度缓慢,则高温型SiO2变体常以介
稳状态在常温下存在,而不发生转变。
2.相图分析
• ⑴ 常温下SiO2稳定态是什么?其稳定的温度范围是多少? • β-石英,573℃以下。 • ⑵ β-石英加热过程中如何变化?(快热,慢热) • β-石英 转变为α-石英(慢热)
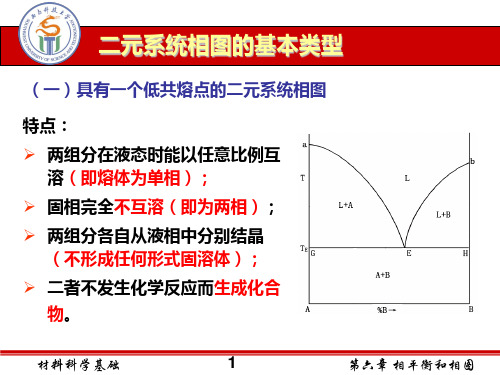
• 但在固态时则完全不互溶, 两个组分各自从液相中分 别析晶; • 组分间不生成新化合物。
• • • • • • • • • •
(1)相图分析 液相线aE、bE:P=2,F=1 固相线GH 相区:液相单相区L:P=1, F=2 固液共存区(L+A),(L+B) 固相区(A+B):P=2,F=1 低共熔点E:LE A+ B P=3,F=0 (2)熔体的冷却析晶过程 指将一定组成的二元混合 物加热熔化后再将其平衡冷却 而折晶的过程。
材料物理化学-第六章 相平衡与相图

湖南工学院
料。⑤碳纤维、石墨、金刚石与C6 。⑥计算机模拟与材料设计。⑦用新材料科 学技术武装改造传统材料产业。 GRM—巨磁电阻(Giant Magnetoresistance),通常作传感器使用,主要应 用于探测磁场、电流、位移、角速度等领域。探测微弱磁场的GM R 传感器最早 被商业化应用在磁记录领域, 作为硬盘的读出磁头。 薄膜集成的GMR磁头体积变 小, 磁记录介质的存储单元也随之变小, 这样存储密度就大大提高了。 至2000年, 存储密度为56. 3Gb/in2 的GMR 的磁头已经在日本的富士通制作所研制出来。 在21世纪初,我国的水泥产量就已跃居世界第一,但是,水泥工业的结构优 化和产品升级是当前要务。大量利用废弃的粉煤灰、矿渣、钢渣、硫酸铁渣、废 石膏、污泥等作为水泥的原料和掺合料是我国的特色,几乎占水泥产量的1/3, 这是“资源循环利用”的重大举措。研制的抗氯盐腐蚀、水化热低、抗微收缩和 后期强度高的水泥,已成功应用于我国几个超大型的海工工程中。在混凝土中, 除水泥、黄沙、石子、水和添加剂(如减水剂)的5组分外,为获得更为优异的 性能,第六组分的研究也是一个研究热点。 黄伯云:粉末冶金专家,中南大学校长,中国工程院院士。1945年11月生于 湖南益阳南县, 1969年毕业于中南矿冶学院特种冶金系,1980年至1986年在美国 依阿华州立大学获硕士、 博士学位,随后进入美国田纳西大学和橡树岭国家实验 室从事博士后研究工作。1988年回国,1997年任中南工业大学校长,2001年任中 南大学校长, 1999年当选为中国工程院院士。黄伯云是我国材料科学领域的战略 科学家,他率领团队历时20年研制出的“高性能碳/碳航空制动材料的制备技 术”,打破了国外的技术垄断,使我国成为世界上有能力生产碳/碳复合材料飞 机刹车片的四个国家之一。也正是这项技术,在2005年荣获了已连续空缺6年的 国家技术发明一等奖。 C/C复合材料的密度仅为钢的1/4在波音747——400飞机上使用了C/C复合材 料刹车盘后, 使飞机机身大约减重816.5Kg。
第六章相平衡和相图解析

6/156
第六章 相平衡和相图
(3)相(P):系统中具有相同物理性质和化学性质的完 全均匀部分的总和 NOTES: (a)均匀是指微观尺度的均匀,并非要求每一相均为纯净物, 一相中可以含有多种物质,如乙醇和水溶液; (b)一种物质可以有几种相,与物质的数量多少无关,与物质 是否连续也无关,如水、冰,水蒸汽等; (c)所有气体视为一个相; (d)对于液体而言,纯液体视为一个相,如果是混合液体则视 其互溶程度而定; (e)对于固体来说较为复杂,可以分为以下几种情况。
要的最少 的化学纯物质的数目; 自由度F等于零时,相数P最大;
P----相的数目; 相数P最小时,自由度F最大。
n----温度、压力等能影响系统平衡状态的外界因素
材料科学基础
10/156
第六章 相平衡和相图
相律是检验、分析和使用相图的重要工具。利用它可分析和确
定系统中可能存在的相数,检验和研究相图。
第六章 相平衡和相图
第一节 相平衡及研究方法 第二节 单元系统
第三节 二元系统 第四节 三元系统
1/156
材料科学基础
第六章 相平衡和相图
概 述
能否用一个较为直观的方式建立材料科 学四要素之间的联系 , 且能够用于指导 生产? 相平衡
Properties: Mechanical and Functional
第六章 相平衡和相图
材料科学基础
(4)自由度(F) 在一定范围内可以任意改变而不会引起旧相消失或新相 产生的最大变量数,又称独立变量数
F=2 变量:浓度、温 双变量 度、压力等。 系统
对于给定的相平衡系统, 在保持系统中相的数目 F=1 单变量 和相的状态不发生变化 系统 的条件下,并不是所有 的变量都可以任意改变
相平衡及相图

第六章 相平衡与相图1、什么是平衡状态?影响平衡的因素有哪些?解:平衡态:不随时间而发生变化的状态称为平衡状态。
影响平衡的因素有:温度、压力、组分浓度等。
2、什么是凝聚系统?什么是介稳平衡?解:凝聚系统:不含气相或气相可以忽略的系统。
介稳平衡:即热力学非平衡态,能量处于较高状态,经常出现于硅酸盐系统中。
3、简述一致熔化合物与不一致熔化合物各自的特点。
解:一致熔化合物是指一种稳定的化合物。
它与正常的纯物质一样具有固定的熔点,熔化时,所产生的液相与化合物组成相同,故称一致熔融。
不一致熔化合物是指一种不稳定的化合物。
加热这种化合物某一温度便发生分解,分解产物是一种液相和一种晶相,二者组成与化合物组成皆不相同,故称不一致熔融。
4、比较各种三元无变量点(低共熔点、双升点、双降点、过渡点和多晶转变点)的特点,写出它们的相平衡关系。
解:低共熔点:是一种无变量点,系统冷却时几种晶相同时从熔液中析出,或加热时同时融化。
E L A S C →++双升点:处于其相应的副三角形的交叉位的单转熔点。
PL A B S +→+ 双降点:处于其相应的副三角形的共轭位的双转熔点。
RL A B S++→ 5、简述SiO2的多晶转变现象,说明为什么在硅酸盐产品中SiO2经常以介稳状态存在?解:在573℃以下的低温,SiO2的稳定晶型为b -石英,加热至573℃转变为高温型的 a -石英,这种转变较快;冷却时在同一温度下以同样的速度发生逆转变。
如果加热速度过快,则a -石英过热而在1600℃时熔融。
如果加热速度很慢,则在870℃转变为a -鳞石英。
a -鳞石英在加热较快时,过热到1670℃时熔融。
当缓慢冷却时,在870℃仍可逆地转变为a -石英;当迅速冷却时,沿虚线过冷,在163℃转变为介稳态的b -鳞石英,在117℃转变为介稳态的g -鳞石英。
加热时g -鳞石英仍在原转变温度以同样的速度先后转变为b -鳞石英和a -鳞石英。
a -鳞石英缓慢加热,在1470℃时转变为a -方石英,继续加热到1713℃熔融。
6相平衡与相图

转变点。 ③在同一温度下,蒸气压低的相更加稳定。所以,
介稳平衡的虚线,总是在稳定平衡的实线上方 。
④交汇于三相点的三条平衡曲线互相之间 的位置遵循下面两条准则:
a、每条曲线越过三相点的延长线必定在另 外两条曲线之间。
b、同一温度时,在三相点附近比容差最大 的两相之间的单变量曲线或其介稳延长 线居中间位置。
晶型的升华曲线; CF线:是α-晶型和液相两相平衡共存线,即α-
晶型的熔融曲线;
BE线:是α-晶型和β-晶型两相平衡共存线,即 两种晶型之间的多晶转变曲线。
特性点: B点:是α-晶型、β-晶型和气相三相平衡共存
点,也叫多晶转变点; C点:是α-晶型、液相和气相三相平衡共存点,
也是α-晶型的熔点。
(2)介稳相平衡部分(虚线部分) 相区: FCGH:是过冷液体的介稳状态区; EBGH:是过热β-晶型的介稳相区; EBK:是过冷α-晶型的介稳相区。
C=1,代入公式,则f=0,∴温度不能改变。 而二元合金凝固时,也是二相共存,P=2,
C=2,则 f=C-P+1=1,即存在一个变量。对 于给定成分的合金,其温度可以变化。
三、相平衡的研究方法 1、动态法
最普通的动态法是热分析法。这种方法主 要是观察系统中的物质在加热和冷却过程中所 发生的热效应。
一个系统中所含相的数目,叫做相 数,以符号P表示。
按照相数的不同,系统可以分为: 单相系统(P=1),二相系统(P=2), 三相系统(P=3)等等。
含有两个相以上的系统,统称为多 相系统。
几点规律: (1)一种物质可以有几个相。 (2)相是一个抽象的概念,它一般不涉及
第六章相平衡和相图

(4)自由度(F) 在一定范围内可以任意改变而不会引起旧相消失或新相产
生(chǎnshēng)的最大变量数,又称独立变量数
变量:浓度、温 度(wēndù)、压力 等。
F=2
双变量 系统
对于给定的相平衡系统
F = 1,在保持系统中相的数 单变量目和相的状态不发生变
系统化的条件下,并不是所
第十九页,共154页。
一、具有多晶转变的单元系统(xìtǒng)相图
关键:明确(míngquè)各分相区、各线(实线和虚线)、 多晶转变曲线 各点意义
熔融曲线
p1
F=1
F=2
F=0
F=2 蒸发曲线
升华(shēnghuá)曲线
t1
第二十页,共154页。
过热(ɡuò rè)β-晶型的介稳相区
过冷液体(yètǐ)的介稳状态区
多晶转变(zhuǎnbiàn)温度低 于两种晶型熔点
晶 型 I 晶 型 I I 熔 体
低于T3温度(wēndù),晶型I稳定, 而晶型II介稳
而高于T3温度(wēndù),晶型I介稳 ,晶型II稳定
第二十五页,共154页。
多晶转变温度(wēndù)高于两 种晶型熔点
晶型I
熔体
晶型II 晶型II的蒸气压不论在高温还是低 温(dīwēn)阶段都比晶型I的蒸气压 高,因此晶型II始终处于介稳状态
F=2
过冷液体的蒸化曲线
F=1
过热β-晶型的熔融曲线
过热β-晶型的升华曲线 过冷α-晶型的介稳相区
过冷α-晶型的升华
(shēnghuá)曲线
过热β-晶型的熔点
第二十一页,共154页。
二、单元系统(xìtǒng)相图的特点:
6相平衡和相图分析

引言
材料的性质除了与化学成分有关还取决与 起显微结构
研究材料的显微结构,需要综合考虑热力 学和动力学两方面因素
相平衡为我们从热力学平衡角度判断系统 在一定热力学条件下所趋向的最终状态提 供依据
相平衡是研究一个或者多个组分,多相体 系的平衡状态如何随影响因素(温度、压 力、组分浓度)变化而改变的规律源自2.相图的应用及相图的重要性
冶金工业中控制金属的冶炼过程、对物质的
高度提纯、分析金属组成和性能的关系研究 试制具有优良性能的新合金以及探讨稀土元 素对改善钢的性能的影响等都与相图有密切 的关系。在硅酸盐工业中,确定某种材料的 配方,选择烧成制度、预测产品性能等也离 不开相图。在开发新材料过程中,往往要研 究用什么原料在什么条件下可以形成什么相, 预计可以获得什么性能。
6.1 相平衡及其研究方法
研究内容:在一定外界条件下(温度、压 力等)热力学平衡下,一个体系或系统所 处的状态。
研究对象称为系统 系统外的一切称为环境 外界条件不变时,如果系统的各种系统不
随时间变化,则系统处于平衡状态
6.1.1 相平衡的基本概念 6.1.1.1 系统
选择的研究对象称为系统。系统以外的一 切物质都称为环境。例如,在硅碳棒炉中炼 制压电陶瓷PZT,那么PZT就是研究对象, 即PZT为系统。炉壁、垫板和炉内的气氛均 为环境。如果研究PZT和气氛的关系,则 PZT和气氛为系统,其它为环境。所以系统 是人们根据实际情况而确定的。
其优点是不需要把体系中的化学物质或相 加以分离来分别单独研究,综合考虑系统 中组分间发生的各种物理、化学变化,因 而具有极大的普遍意义和使用价值
材料工作者能必须熟练判读相图
1 什么是相图
在一个多相体系中,随温度、压力和浓度
相图与相平衡基础知识

推导过程
假设一个平衡系统中有C个组分,P个相, 如果C个组分在每个相中都存在,那么对每 一个相来讲,只要任意指定(C-1)个组分 的浓度就可以表示出该相中所有组分的浓度, 因为余下的一个组分的浓度可以从100中减去 (C-1)个组分的浓度之和求得。由于系统 有P个相,所以需要指定的浓度数总共有P (C-1)个,只要才能确定体系中各相浓度。
相律 吉布斯根据前人的实验素材,用严谨的热力学作 为工具,于1876年导出了多相平衡系统中,系统的 自由度数(F),独立组元数(C),相数(P)和 对系统的平衡状态能够发生影响的外界影响因素 (n)之间的关系,相律的数学表达式为: F=C-P+n 一般情况下,只考虑温度和压力对系统的平衡状态的 影响,即n=2,则相律表达式为 F=C-P+2
总之,气相只能一个相,无论多少种气体混在一起 都一样,形成一个气相,液体可以是一个相,也可 以是两个相(互溶程度有限时)。固体如果是连续 固溶体为一相;其他情况下,一种固体物质是一个 相。
一个系统中所含有相的数目,叫做相数,以符号P 表示,按照相数的不同,系统可分为单相系统 (P=1),二相系统(P=2),三相系统(P=3)等。 含有两个相以上的系统,统称为多相系统。
第六章 相平衡和相图
什么是相图
相图的研究方法有哪些 相图的应用
相图的定义
在一个多相体系中,随温度、压力和浓度的
变化,相的种类、数量及含量都要相应地发 生变化,对于变化情况可用几何图形来描绘, 这个图形就可以反映出该系统在一定组成、 温度和压力下,达到平衡时所处的状态,这 个几何图形就是相图,也叫相平衡图、状态 图。
相平衡研究方法
动态法 热分析法 差热分析法(DTA) 溶解度法 静态法(淬冷法)
相平衡和相图
30
第六章 相平衡和相图
C 例:根据下列相图 (1) 用连线规则划分副三角形。 (2) 用箭头标出界线上温度变化方向及界线性质。 C (3) 判断S、S1、S2化合物的性质。 (4) 写出各无变量点的性质及反应式。 (5)在相图下侧画出A-B二元系统相图。 u v (6) 分析熔体M1、M2的析晶路程。 S (M1在SO连线上)
第六章 相平衡和相图
13
3、背向线规则
在浓度三角形中,一个三元系统的组成点愈靠近某个顶点,
该顶点所代表的组分的含量就愈高;反之,愈少。
C 若熔体在冷却时析出某一
顶点所代表的组元,则液
相中组成点必定沿着该顶 点与熔体组成点的连线向 背离该顶点的方向 A
材料科学基础
D
B
第六章 相平衡和相图
14
4、杠杆规则
C C
b L .2 N
a
e2
K
1
.
B
x B
z y
熔体1
L LB 1[B,(B)] a[B,B+(A)] f=3 f=2
L B+N f=1
L B+A K[x,B+A+(N)] f=1
e1
L+AB+N f=0
K[y(A消失),N+B]
LN+B+C L[z,N+B+(C)] f=0
L(液相消失)[1,N+B+C]
所谓一致熔融化合物是一种稳定 的化合物。它与正常的纯物质一 样具有固定的熔点,融化时,所
产生的液相与固相的化合物组成 相同,故称一致熔融
材料科学基础
2
第六章 相平衡和相图
2、不一致熔融化合物: 一种不稳定的化合物,加热这种 化合物到某一温度便发生分解, 分解产物是一种液相和一种晶相, 二者组成与原来化合物组成完全 不同。 点:纯物质熔点;低共熔点; 转熔点等 线:液相线(3条)固相线等;
材料科学基础---第六章 相平衡

组分:组成系统的物质。必须具有相同的化学性质,
能用机械方法从系统中分离出来且能长期独立存在的
化学纯物质。组分的数目叫组分数(S)。
独立组分:构成平衡物系所有各相组成所需要的最
少数目的化学纯物质。 独立组分数:以C表示
注:只有在特殊情况下,独立组分和组分的含义才相同。
·若系统中不发生化学反应,则独立组分数=组分数; ·若系统中存在化学反应和浓度关系,则:
不一致熔融化合物:不稳定化合物,加热该化合物到
某一温度便分解,分解为一种液相和一种晶相,二者
组成与化合物组成皆不相同。
特点:化合物组成点不在其液相线范围内
1.相图分析: 点: p=3
E:
f =0
低共熔点
△
LE 冷却 A Am Bn P: 转熔点
冷却
△
LP B
Am Bn
2.
熔 体 的 冷 却 析 晶 过 程
液相点: 2 L f=2 B
K
M
H E
J
K L→B P (LP +B→C) L→C E (LE →A+C) f=1 f=1
f=0 f=0
固相点: M
F B+C D
C
J C+A
H
Q
S
液相点: 3 固相点: b
L f=2 B
Q L→B P (LP +B→C) f=1
f=0
F B+C
S
⑶固相中有化合物生成和分解的二元系统相图
七种晶型分为三个系列:石英-鳞石英-方石英
(1)重建型转变(一级变体间的转变):横向,转变 速度慢,石英-鳞石英-方石英。 (2)位移型转变(二级变体间的转变):纵向,速度 快,α -β -γ ,同一系列转变。
化工热力学 第六章 相平衡.

5
2019/9/8
2 相律
F N 2
相律是各种平衡系统都必须遵守的规律。
相数π讨论:
(1)甲醇-水二元汽液平衡 甲醇-水全浓度下互溶, 仅存在一个液相, 和一个与
之平衡的汽相. π = 2
(2)戊醇-水二元汽液平衡 戊醇-水不能在全浓度下互溶, 存在两个液相, 和一
个汽相. π = 3 在有限浓度范围内, 戊醇-水能够互溶, 仅存在一个
fˆil
fi
l i
xi
(i
1,2,, N )
分析:
v难于
i
计算,
l i
重点计算
2019/9/8
8
1 状态方程法 (Equitions of States)
汽、液相逸度均用逸度系数表示
pyi iv pxi il yi iv xi il
ln i
fi是i组元标准态下的逸度(L R) fi fil (i 1,2,, N )
2019/9/8
10
fi fil (i 1,2,, N )
fi1
fis
exp[ Vil ( p RT
pis )]
Pi sis
exp[ Vil ( p RT
pis )]
pyiˆiv
pyi pis i xi (i 1,2,, N )
对于低压的二元汽液平衡:
p1 py1 p1s1x1
p2 py2 p2s 2 x2
p p1 p2 p1s1x1 p2s 2 x2
2019/9/8
y1
p1s 1x1 p1s 1x1 p2s 2 x2
材料科学基础课件第六章--相平衡与相图(2024版)

FCD 液相
AB 气相,β-晶型
BC 气相,α-晶型
CD 相线
BE
气相,液相 β-晶型,α-晶型
FC α-晶型,液相
B 相点 C
β-晶型,α-晶型,气相 α-晶型,气相,液相
单元系统相图中各介稳相
P E H F F=2
F =2
液相
F=2
D
α-晶型
β-晶型
G C F=0
K
B F=0 气相
A
F=2
T
图 6-3 具有多晶转变的单元系 统相图
6.3.1 二元系统相图的表示
方法及杠杆规则
一、相图表示方法
相图中组成可以用质量百分
T
数(ω)表示,也可以用摩
T1
M
尔百分数或摩尔分数(x)
●
表示,其图形有明显差别。
B含量
A含量
A
m B%
B
图6-10 二一点既代表一 定的组成又代表系统所处的 温度,即每一点都和系统的 一个状态相对应,即为状态 点。
二、杠杆规则
杠杆规则
G1 MM 2 G2 MM1
b2 b b1
●
●
A
M1
M
●
M2
B
图6-11 杠杆规则示意图
M:G,M1:G1,M2:G2
G1 MM 2 G M1M 2
G2 MM1 G M1M 2
系统中平衡共存的两相的含量 与两相状态点到系统总状态点 的距离成反比。
关键:分清系统的总状态点, 成平衡的两相的状态点,找准 在某一温度下,它们各自在相 图中的位置。
2 两种晶型的升华曲线的交点 是多晶转变点,B点;
3 在同一温度下,蒸气压低的 相较稳定,KB、BA线;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
液相L:M a R
L A F 2
L A B F 1
(
L A BS
F 0,B消失
LS L AS e d F 2 ) F 1
E1 (
L S C F 1
L S C B
F 0,L消失
)
f=0
S p
S
B
LE → A+S+C LP+B→S+C
p1
S1 B1
熔体1
LP+B→S+C
液相: 1 a ( P F =0,L消失) F 2
F 1
B B C B C S 固相:B B b 1
LB
L B C
LP B S C
固相S:
M 熔体的冷却析晶过程: 液相L: L S A B L A B C L S L A S L A B m n ( P F 0,S消失) ( E F 0,L消失) F=2 F=1 F=1
S S r r i m
S
A S
A B S
A B
A B C
(六)具有一个一致熔融三元化合物的三元系统相图 1.相图特点:
•S的组成点在三角形内部 且在其初晶区内,
•能划分三个副三角形 2.相图分析: •四个初晶区, •六条界线, •三个三无变量点。
(七)具有一个不一致熔融三元化合物的三元系统相图 1、分析相图:
e2 e1
E2 m S E1 B A S
降温 S LR A B 升温
C
C
C
C
有单转熔点的形 成不一致熔三元 化合物的三元系 统相图
思考题: E1R界线性 质的分析?
e1
E1
m2 S
E2
e2
A S
R
P
e3
B 18 B
A
e3
B
A
3、冷却析晶过程
设:组成点M在副三角形CSB内,离S点较近。
3、M的析晶路程
分析:
A B S
L
•析晶终点为E点, 析出晶相B、C、S
M
A A B B S M L L L R( LR A B S ) L E( LE B S C)
液相:M L ( R F 0,A消失
3、结晶路程分析
① 划分副三角形,确定组成点的位臵
② 判定界线及无变量点的性质
③ 分析析晶产物和析晶终点;
④ 分析析晶路线,正确书写其结晶路程;
⑤ 利用规则检验其正确性。
C
① 划分副三角形
C e3 e2
② 判定界线及无变量点 的性质 ③ 分析产物和终点 ④ 书写路程
B
E
P
A A e1 e11 A1
LS
L S C
LE S C A
F 1
F 2
F 1
B B S S S C S C A 固相:B B S S q 3
熔体4
冷 却
液相: 4 v ( E F =0,L消失) F 1 固相:S S w 4
(1)转熔点不一定是析晶的结束点
单转熔点P上的相平衡关系: L B DC 可能产生三种结果: •一是液相先消失,固相B有剩余,析晶在P点结束;如熔体1 •二是固相B先消失,液相有剩余,回吸结果液相与固相D和C 建立三相平衡,继续冷却,沿PE界线变化。如熔体2 •三是液相与固相B同时消失,析晶也在P点结束,析晶产物是 C、S两种固相,在CS连线上的组成点,其冷却析晶属于这种 情况。 (2)在转熔线上的析晶过程,有时会出现液相组成点离开界线 进入初晶区的现象,称为“穿相区”现象。
熔体2
LP+B→S+C LE → A+S+C
液相: 2 a p ( E F =0,L消失) F 2 F 1 (B消失,转熔结束 )
F 1
LB
L B C
LP B C S,F 0
L S C
LE S C A
固相:B B n d h 2
F 2
F 1
L A
L A B
L mA nB S
( E ) F 1
LB S
LE B S C F 0,L消失
)
固相:
A A B A S B BS B S C A A D D G M
首先要解决的2个问题
三角形规则
(1)确定析晶结束点和最终的结晶产物
M熔体的结晶产物是C、S、B,在 E1点结束析晶;
C
(2)确定冷却过程析出的初晶相
M熔体在A的初晶区内,冷却析晶 过程首先析出A晶相;
e2 E2 S A A S A e3
C e1 E1 B
R
MM M
B
熔体M的冷却析晶过程:
至B相消失,转熔结束
B
BC
B C S
C S
C S A
LP+B→S+C
Байду номын сангаас LP+B→S+C
熔体3
LE → A+S+C LpP+B→S
组成点在SPp 范围内内, “穿区”现 象
液相: 3 e ( f B消失) g ( E F=0,L消失 )
F 2
L B
L BS
S
A S L S L 液相:E( A S C LE ) V 4
L S F 2
LS A
LE S C A
S A
S C A
加 F 1 F 0 A S C A S 热 固相: 4 w S
F 2
小结:
(五)形成一个高温稳定,低温分解的二元化合物的三元相图 化合物S由A、B二组分高温下固相反应得到。
E点:在三角形ABC内,
L
A+B+C;
P点:没有相应的副三角形,为双
升点形式的过渡点。 在P点 :S(AmBn)
L
S的初晶区在 高温区
mA+nB
(P=4,F=0)
温度升高形成化合物S,降温则化
合物分解。在该点上,液相量不 变,温度不变,液相组成不变。
m2 S S
E2
e2
F
A
m1 S
P
B B
e3
(3)无变量点 E1、E2是低共熔点;根据图上转熔点性质,可再分为二种类型。
①P点:交叉位——双升点或单转熔点
降温 平衡过程: LP A S B 升温
②R点: 共轭位——双降点或双转熔点
平衡过程:
有双转熔点的形 成不一致熔三元 化合物的三元系 统相图
S的初晶区在 低温区
S在A-B二元系统中不能由熔 体直接结晶析出,但在三元
系统中,其初晶区的液相面 S的分解
可以降到TR温度以下,可从 三元熔体中直接析出S晶体。
温度TR
相图特点:
图中有三个无变点P、E、R,但只能划出与P、E点相应的副三 角形;R点没有对应的副三角形;
三角形内任一组成的熔体,冷却结晶只能在P点或E点结束, 不能在R点结束结晶过程。
(1)连线与界线 连线:SA、SB、SC,分别代表三个独立的二元系统S-A、S-B、 S-C; 注意:延长连 界线E1P? 是一条转熔和共熔性质 共存的界线。 界线E2P? 是一条共熔界线。 (2)分三元系统 A-B-S、B-S-C、A-S-C;
A
线并由切线规 则分段判断
C
C
延长界线 后再判断
e1
E1
与R点液相平衡的三晶 相A、S、B组成点在 同一直线上。
2、相图分析
四个初晶区
•六条界线 PR界线 L A S •三个无变量点 P 单转熔点 L A C S E 低共熔点 L S B C R 过渡点(化合物分解或形成点)
L A B S (L起介质作用)
判断方法:周围三个初晶区所对应 的晶相组成点在一条直线上,没有 对应副三角形
总结 1、无变量点性质 P点:Lp+B S+C E点: LE A+S+C 2、界线性质PQ是转熔线 L+B S
C
C
e4 E P m
e3
其它为共熔线。
3、组成点 在 ASC内,E点是析晶终点, 在 BSC内,P点是析晶终点。 在连线SC上,P点是析晶终点。 A
A
e1
S
Q S
B
B
4 、 P点 :
B
A
b
20
B
f=0
思考题1:如图M点 (RM延长线与SB相交) ,冷却析晶过程如何?
E2
C e1 m e S d A
M
思考题2:R点是否为析晶 结束点?若熔体在R点结束 析晶,原始配料组成在何
E1
范围?
aR g f
B
S
e3 21 B
A
b
在连线SC上,B和液相同时消失。 在 SCP范围内,经过P点时发生转熔,晶相B先消失, 液相在E点消失; 在 BSC内,在P点液相先消失; 在 SPQ内存在穿晶区, 液相在E点消失
(四)形成一个高温分解,低温稳定二元化合物的三元系统相图
化合物S由A、B二组分低温
下固相反应得到,在三元相
图上所处的初晶区在低温区。
固相S:
B消失,f点在AS连线上
C
A B S A S A A B f S A A b
e1
C S S C S B g S M
E2
m e S
E1
液相刚到E1点,g点在 E1M延长线与SC连线 的交点上
