平行四边形最值问题
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
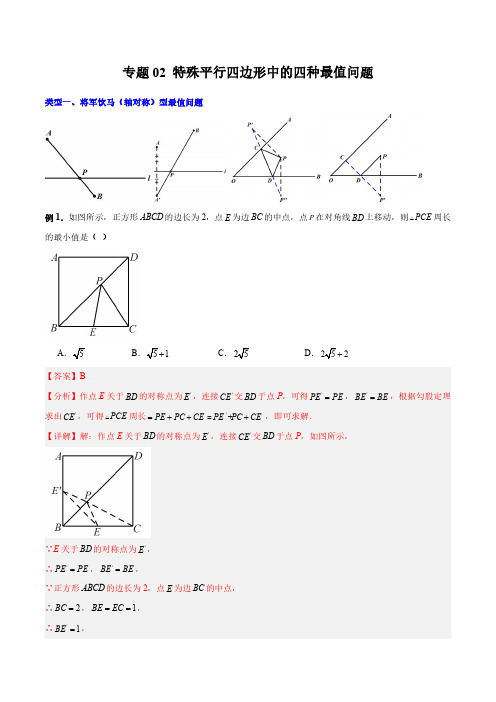
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
四边形最值问题解题技巧

四边形最值问题解题技巧介绍四边形是几何图形中最常见的形状之一。
对于给定的四边形,我们常常需要解决最值问题,即找出四边形的最大或最小值。
本文将介绍一些解决四边形最值问题的技巧和方法。
一、四边形的基本概念在开始讨论解题技巧之前,我们首先需要了解一些关于四边形的基本概念。
一个四边形由四条线段组成,相邻的两个线段之间有一个角。
四边形的内角和为360度。
常见的四边形类型包括矩形、正方形、平行四边形、菱形等。
二、解决四边形最值问题的一般步骤解决四边形最值问题的一般步骤可以分为以下几步:1. 确定四边形的类型根据给定的条件,确定四边形的类型。
不同类型的四边形具有不同的属性和特点,需要根据具体的情况选择相应的解题技巧。
2. 利用基本几何性质寻找约束条件根据四边形的性质和已知条件,寻找约束条件。
这些约束条件将帮助我们确定四边形的其他属性,从而解决最值问题。
3. 应用数学方法求解最值根据已知条件,利用数学方法求解四边形的最值。
这些方法可能包括求导、代数运算、三角函数等。
4. 检验结果求解完最值问题后,需要检验结果是否合理。
检验过程包括验证数学计算的正确性和对结果的合理性进行分析。
三、解决不同类型四边形最值问题的技巧下面将介绍一些常见的四边形类型及其对应的最值问题解题技巧。
1. 矩形和正方形矩形和正方形是最常见的四边形类型。
对于矩形和正方形的最值问题,常用的解题技巧包括:(1)对角线长度最值问题对角线长度最值问题是指在给定矩形或正方形的周长不变的情况下,找出对角线长度的最大或最小值。
解决该问题的技巧是使用两个对角线的长度表示矩形或正方形的面积,并应用数学方法求解。
(2)面积最值问题面积最值问题是指在给定矩形或正方形的周长不变的情况下,找出面积的最大或最小值。
解决该问题的技巧是使用两个相等的邻边的长度表示矩形或正方形的面积,并应用数学方法求解。
2. 平行四边形和菱形平行四边形和菱形也是常见的四边形类型。
对于平行四边形和菱形的最值问题,常用的解题技巧包括:(1)对角线长度最值问题对角线长度最值问题是指在给定平行四边形或菱形的周长不变的情况下,找出对角线长度的最大或最小值。
平行四边形的最值问题方法技巧

平行四边形的最值问题方法技巧平行四边形,这个名字听起来是不是有点高大上?但其实它就是我们日常生活中随处可见的形状,比如你窗户的形状、桌子上摆放的书本,甚至是你最爱的披萨切成的片儿,嘿,不小心又饿了!今天我们就来聊聊如何通过平行四边形的最值问题,找到那些“藏在角落里的小秘密”。
我们先来搞清楚几个基本概念,之后再深入挖掘其中的技巧,保证让你一边学一边乐,像是在吃冰淇淋那样爽!1. 平行四边形的基本知识1.1 什么是平行四边形?简单来说,平行四边形就是两组对边平行且相等的四边形。
听起来像是在说数学咒语,其实你看看书本、课桌,都是这些家伙的身影。
它的对角线虽然不一定相等,但相交时却恰好把彼此分成两个相等的部分,真是个小聪明啊。
1.2 平行四边形的面积和周长说到平行四边形,咱们不能不提面积和周长。
这俩小子就像是平行四边形的“身份证”,一个告诉你这个形状有多大,另一个则告诉你它的边界有多长。
面积的计算其实很简单,底边乘以高就能搞定,记住了么?周长嘛,就是把四条边加起来,简简单单,就像数钱一样。
2. 最值问题的引入2.1 什么是最值问题?最值问题,顾名思义,就是找出某个数值的最大或最小值。
就像你想知道,哪种披萨的切片最大,或者今天你吃的那一碗面条,能不能多来几块肉?在平行四边形中,最值问题经常会出现,比如找最大面积、最小周长等等。
这种问题其实蛮有趣的,像是一场智力的较量。
2.2 如何求解最值问题?这儿就需要用到一些小技巧了。
首先,得明确你要找的是什么最值,是面积、周长还是其他?比如,面积最大的时候,底边和高得是完美的搭档,想象一下,正方形就是平行四边形中面积最大的,真是个“勤奋”的小家伙。
而要找最小周长时,注意这家伙的两边得保持比例,得心应手,才能事半功倍。
3. 实际应用与技巧3.1 实际应用平行四边形的最值问题不仅仅是在课本上跳舞,它在生活中也很常见。
例如,在建筑设计中,工程师们常常要计算出某个区域的最大利用面积,来规划更合理的空间布局。
18.2 拓展专题 特殊平行四边形中的最值问题-2022-2023学年八年级下册初二数学(人教版)

18.2 拓展专题特殊平行四边形中的最值问题•作者:初二数学(人教版)编写组•发布日期:2022年引言本文将介绍拓展专题中的一个重要主题:特殊平行四边形中的最值问题。
我们将通过解析具体的例题,帮助读者理解并掌握该问题的解题方法和技巧。
1. 特殊平行四边形简介特殊平行四边形是指具有一些特殊性质的平行四边形,如矩形、正方形和菱形等。
这些特殊平行四边形在几何学中经常出现,具有重要的几何性质。
2. 特殊平行四边形中的最值问题特殊平行四边形中的最值问题是指在特殊平行四边形中寻找某些属性的最大值或最小值。
这种问题通常需要我们利用特殊平行四边形的某些性质来进行求解。
在解决这类问题时,我们通常需要先了解特殊平行四边形的性质,然后确定所要求的属性,并根据特殊平行四边形的性质来推导解决方法。
3. 解题方法和技巧3.1 矩形中的最值问题矩形是一种特殊的平行四边形,具有相等的对边和相等的内角。
因为矩形具有对角线相等、对角线互相平分以及对边相等的性质,所以在矩形中寻找某些属性的最值问题,我们可以运用这些性质来解决。
例如,我们要在一个给定周长的矩形中求解最大的面积。
由于矩形的周长等于两倍的长加两倍的宽,我们可以设矩形的长为x,宽为y,得出周长等式:2x + 2y= 周长。
然后,我们利用矩形的面积公式S = xy,将x用y的表达式代入,从而得到关于y的函数,然后求这个函数的最大值,即可得到最大面积。
3.2 正方形中的最值问题正方形是边长相等的矩形,具有特殊的性质。
在正方形中寻找某些属性的最值问题,常常可以通过利用其对称性来解决。
例如,我们要在一个给定周长的正方形中求解最大的面积。
由于正方形的周长等于四倍的边长,我们可以设正方形的边长为x,得出周长等式:4x = 周长。
然后,我们利用正方形的面积公式S = x²,将x代入,从而得到关于x的函数,然后求这个函数的最大值,即可得到最大面积。
3.3 菱形中的最值问题菱形是具有对边相等、对角线互相垂直的平行四边形。
初二平行四边形最值问题(一)

初二平行四边形最值问题(一)初二平行四边形最值问题有以下相关问题:1.初二平行四边形面积最大值问题–解释:在给定周长的条件下,如何确定平行四边形的面积达到最大值。
–解决方法:使用优化理论中的求极值方法,将平行四边形的面积表示为一个关于某个变量的函数,然后求导找到函数的极值点。
2.初二平行四边形周长最小值问题–解释:在给定面积的条件下,如何确定平行四边形的周长达到最小值。
–解决方法:同样使用优化理论中的求极值方法,将平行四边形的周长表示为一个关于某个变量的函数,然后求导找到函数的极值点。
3.初二平行四边形对角线长度最小值问题–解释:在给定面积或周长的条件下,如何确定平行四边形的对角线长度达到最小值。
–解决方法:可以通过将平行四边形的对角线长度表示为一个关于某个变量的函数,然后利用求导的方法找到函数的极值点。
4.初二平行四边形不等边问题–解释:当平行四边形的两对边不相等时,如何确定平行四边形的面积和周长。
–解决方法:根据已知的条件,可以利用平行四边形的性质和几何关系,建立方程并求解。
5.初二平行四边形不等角问题–解释:当平行四边形的两对角不相等时,如何确定平行四边形的面积和周长。
–解决方法:同样根据已知的条件,利用平行四边形的性质和几何关系,建立方程并求解。
6.初二平行四边形面积、周长同时最大最小值问题–解释:在给定的条件下,如何确定平行四边形的面积和周长同时达到最大或最小值。
–解决方法:通过对面积和周长进行约束条件的建立,并利用优化理论中的求多元函数的极值方法。
以上是初二平行四边形最值问题的一些相关问题及解释说明。
通过研究这些问题,可以帮助学生更好地掌握平行四边形的性质和应用,同时提升解决数学问题的能力。
人教版初二数学8年级下册 第18章(平行四边形)最值问题专项训练(含答案)

人教版数学八年级下期第十八章平行四边形最值问题训练一、选择题1.如图,在菱形ABCD中,∠ABC=60∘,E为BC边的中点,M为对角线BD上的一BM最小值的是()个动点.则下列线段的长等于AM+12A. ADB. AEC. BDD. BES矩形2.如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P,满足S△PAB=13,则点P到A、B两点的距离之和PA+PB的最小值( )ABCDA. 4B. 42C. 22D. 23.如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为( )A. 4B. 4.8C. 5D. 5.54.如图,正方形ABCD的边长为4,E点是BC上一点,F是AB上一点,P是AC上一动点,且BE=1,AF=2,则PE+PF的最小值是( )A. 4B. 15C. 5D. 175.如图,矩形ABCD中,AB=8,BC=6,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )A. 10B. 43C. 20D. 876.如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为()A. 3B. 4C. 5D. 6二、填空题7.如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是____.8.如图,在边长为6的菱形ABCD中, ∠ DAB=120°,E,F分别为边CD、CB上的动点,且CE+CF= 6,则线段EF长的最小值是 .9.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为______.10.填空如图,在菱形ABCD中,∠B=45°,BC=23,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH,则GH的最小值为____.11.如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′B,则线段A′B 长度的最小值是_____________.12.如图,将边长为4的正方形ABCD纸片沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则▵GPQ的周长最小值是_________.三、解答题13.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)四边形EDFG面积的最小值为________.14.如图,点O为▱ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.(1)求线段EF的长;(2)若△OAE的面积为S1,△OCF的面积为S2,S1+S2的值是否发生变化?若不变,求出这个不变的值;若变化,请说明随着DE的增大,S1+S2的值是如何发生变化的?(3)求AE+CF的最小值.15.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.(1)求证:四边形AGPH是矩形;(2)是否存在点P,使得GH最短?若存在,请求出最小值,若不存在,请说明理由.16.如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.(3)若正方形ABCD的边长为4,取DH的中点M,请直接写出线段BM长的最小值.17.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).(1)证明无论动点P在何处,四边形PMCN的面积总是固定值,这个固定值是多少?(2)试探究动点P在何处时,四边形PMCN的周长最小,最小值是多少?18.如图,正方形ABCD中,以B为顶点的交AD于E,交CD于F,延长DC使得CG=AE.(1)证明:△ABE≌△CBG;(2)若EF=5,AE=2,求AB的长度.(3)在(2)条件下,若P为线段BF上一动点,求PG+PC最小值.参考答案1.B2.B3.B4.D5.C6.A7.38.339.310.6211.23−212.2+2513.解:(1)连接DC,∵O是EF的中点,GO=OD,∴四边形EDFG是平行四边形,∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,∴∠A=∠DCF=45°,AD=CD,在△ADE和△CDF中,AE=CF,∠A=∠DCFAD=CD∴△ADE≌△CDF,∴DE=DF,∠ADE=∠CDF,∴四边形EDFG是菱形,∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴四边形EDFG是正方形;(2)4.14.解:(1)∵四边形ABCD是平行四边形,∴OD=OB,∵DE=OF,BD=4;∴EF=OD=12(2)S1+S2的值不变,理由如下:如图所示,连结AF,∵四边形ABCD是平行四边形,∴AO=OC,∴S△AOF=S△COF,∵DE=OF,∴S △ADE =S △COF ,∴S 1+S 2=S △AEF =S △AOD ,∵∠BCO =90°,∠BOC =60°,∴∠DAC =90°,∠AOD =60°,∴AO =12OD =2,在Rt △AOD 中,AD =3AO =23,∴S 1+S 2=S △AOD =12AD •OA =12×23×2=23;(3)当DE =OE 时,AE +CF 的值最小,此时E 为OD 的中点,∵∠OAD =90°,∴AE =12OD =2,同理CF =2,∴AE +CF 的最小值=4.15.(1)证明∵AC =9 AB =12 BC =15,∴AC 2=81,AB 2=144,BC 2=225,∴AC 2+AB 2=BC 2,∴∠A =90°.∵PG ⊥AC ,PH ⊥AB ,∴∠AGP =∠AHP =90°,∴四边形AGPH 是矩形;(2)存在.理由如下:连结AP .∵四边形AGPH 是矩形,∴GH =AP .∵当AP ⊥BC 时AP 最短.根据三角形面积有12×9×12=12×15•AP .∴AP =365,.∴GH=36516.证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点A关于直线DE的对称点为F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°,在Rt△DFG和Rt△DCG中,∵DF=DCDG=DG,∴Rt△DFG≌Rt△DCG(HL),∴GF=GC;(2)BH=2AE,理由是:证法一:如图2,在线段AD上截取AM,使AM=AE,∵AD=AB,∴DM=BE,由(1)知:∠1=∠2,∠3=∠4,∵∠ADC=90°,∴∠1+∠2+∠3+∠4=90°,∴2∠2+2∠3=90°,∴∠2+∠3=45°,即∠EDG=45°,∵EH⊥DE,∴∠DEH=90°,△DEH是等腰直角三角形,∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,∴∠1=∠BEH,在△DME和△EBH中,∵DM=BE∠1=∠BEH DE=EH,∴△DME≌△EBH,∴EM=BH,Rt△AEM中,∠A=90°,AM=AE,∴EM=2AE,∴BH=2AE;证法二:如图3,过点H作HN⊥AB于N,∴∠ENH=90°,由方法一可知:DE=EH,∠1=∠NEH,在△DAE和△ENH中,∵∠A=∠ENH ∠1=∠NEH DE=EH,∴△DAE≌△ENH,∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=2HN=2AE.(3)22.17.解:(1)如图所示:∵M、N分别是边BC、CD的中点,∴MN∥BD.∴△PMN的面积=△BMN的面积=△CMN的面积,∴四边形PMCN的面积=1菱形ABCD的面积=6;4(2)如图所示:作M关于BD的对称点Q,连接NQ交BD于P,连接MP,此时MP+NP的值最小,∵四边形ABCD是菱形,∴AC⊥BD,∠QBP=∠MBP,即Q在AB上,∵MQ⊥BD,∴AC∥MQ,∵M为BC中点,∴Q为AB中点,∵N为CD中点,四边形ABCD是菱形,∴BQ∥CD,BQ=CN,∴四边形BQNC是平行四边形,∴NQ=BC,∵四边形ABCD是菱形,∴CP=AP=3,BP=PD=4,在Rt△BPC中,由勾股定理得:BC=5,即NQ=5,∴MP+NP=QP+NP=QN=5,∴四边形PMCN周长最小值是10.18.证明:(1)∵四边形ABCD是正方形,∴AB=BC,∠A=∠BCD=90°,∴∠A=∠BCG=90°,∵AE=CG,∴△ABE≌△CBG;(2)设AB=x,∵四边形ABCD是正方形,∴AB=AD=CD=x,∵AE=2,AE=CG,∴DE=x-2,CG=2,由(1)知△ABE≌△CBG,∴BE=BG,∠ABE=∠CBG,∵∠EBF=45°,∴∠ABE+∠CBF=45°,∴∠ABE+∠CBG=45°,即∠GBF=45°,∴∠EBF=∠GBF,∵BF=BF,∴△EBF≌△GBF,∴EF=GF=5,∴FC=GF-CG=5-2=3,∴DF=x-3,在RT△DEF中,由勾股定理得,DE2+DF2=EF2,∴(x-2)2+(x-3)2=52,解得x=6或-1(舍去),即AB的长度是6;(3)连接EG,EC,如图,由(2)知△EBF≌△GBF,∴点E与点G关于BF对称,连接EC,则EC与BF的交点即为点P,此时PG+PC最小,且最小值是PG+PC=PE+PC=EC,在Rt△CDE中,由勾股定理得:CD2+DE2=EC2,由(2)知CD=AB=6,DE=6-2=4,∴EC2=62+42=52,∴EC=213,即PG+PC的最小值是213.。
人教版初中数学讲义八年级下册第09讲 专题4 平行四边形(特殊的平行四边形)中的最值问题(解析版)

第09讲专题4平行(特殊)四边形中的最值问题1.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是()A.2B.C.3D.【解答】解:连接CM,当CM⊥AB时,CM的值最小(垂线段最短),此时DE有最小值,理由是:∵∠C=90°,AC=6,BC=8,∴AB===10,∴AC•BC=,∴=,∴CM=,∵点D、E分别为CN,MN的中点,∴DE=CM==,即DE的最小值是,故选:B.2.如图,在▱ABCD中,∠C=120°,AD=2AB=8,点H,G分别是边CD,BC上的动点,连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最大值与最小值的差为.【解答】解:如图:取AD的中点M,连接CM、AG、AC,过点A作AN⊥BC于点N,∴AM=DM=AD=×8=4,∵四边形ABCD是平行四边形,∠BCD=120°,AD=2AB=8,∴∠D=180°﹣∠BCD=60°,AB=CD=AD=×8=4,∴AM=DM=DC=4,∴△CDM是等边三角形,∴∠DMC=∠MCD=60°,AM=MC,∴∠MAC=∠MCA=∠DMC=×60°=30°,∴∠ACD=∠MCA+∠MCD=30°+60°=90°,在Rt△ACD中,由勾股定理得:AC===4,在Rt△ACN中,∠ACN=∠BCD﹣∠ACD=120°﹣90°=30°,∴AN=AC=×4=2,∵AE=EH,GF=FH,∴EF是△AHG的中位线,∴EF=AG,∵AG的最大值为AC的长,最小值为AN的长,∴AG的最大值为4,最小值为2,∴EF的最大值为2,最小值为,∴EF的最大值与最小值的差为2﹣=,故答案为:.3.如图,在▱ABCD中,已知AB=4,BC=6,∠ABC=60°,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点Q,则线段QC的最小值为2﹣4.【解答】解:如图,过点A作AH⊥BC于H,连接AC,∵AB=4,BC=6,∠ABC=60°,则AH=AB•sin∠ABC=4sin60°=2,BH=AB•cos∠ABC=4cos60°=2,∴CH=BC﹣BH=6﹣2=4,在Rt△ACH中,AC===2,∵点B与点Q关于直线AP对称,∴AQ=AB=4,∴点Q在以A为圆心AB为半径的⊙A上,∴当C、Q、A三点共线时QC最小,QC的最小值=AC﹣AQ=2﹣4,故答案为:2﹣4.4.如图,在△ABC中,∠BAC=30°,AB=AC=12,P为AB边上一动点,以PA,PC为边作平行四边形PAQC,则对角线PQ的长度的最小值为6.【解答】解:如图所示:∵四边形PAQC是平行四边形,∴AO=CO,OP=OQ,∵PQ最短也就是PO最短,过点O作OE⊥AB,当点P与E重合时,OP最短,OE即为所求,∵∠BAC=30°,∴OE=OA,∵AB=AC=12,∵AO=AC=×12=6,∴OE=3,∴PQ的最小值=2OE=6,故答案为:6.5.如图,在△ABC中,AB=BC=10,AC=12,点D,E分别是AB,BC边上的动点,连结DE,F,M分别是AD,DE的中点,则FM的最小值为()A.12B.10C.9.6D.4.8【解答】解:如图,过点B作BH⊥AC于H,∵F,M分别是AD,DE的中点,∴FM=,∴当AE取最小值时,FM的值最小,由垂线段最短可知,当AE⊥BC于点E时,AE的值最小,在△ABC中,AB=BC=10,AC=12,∴CH=,∴BH===8,∴=48,又∵,∴,∴AE=9.6,∴FM=4.8,故选:D.6.如图,在△ABC中,∠BAC=30°,AB=AC=4,P为AB边上一动点,以PA,PC为邻边作平行四边形PAQC,则对角线PQ的最小值为()A.2cm B.2.5cm C.3cm D.4cm【解答】解:如图,过点C作CD⊥AB于点D,∵在Rt△ACD中,∠ADC=90°,∠BAC=30°,AC=4cm,∴,∵四边形PAQC是平行四边形,∴AB∥CQ,∴当PQ⊥AB时,PQ取得最小值,此时PQ=CD=2cm,故选:A.7.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为()A.4B.5C.6D.10【解答】解:∵点E,F分别为DM,MN的中点,∴EF是△MND的中位线,∴EF=DN,当点N与点B重合时,DN最大,此时DN==10,∴EF长度的最大值为5,故选:B.8.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD 的最小值是()A.B.3+3C.6+D.【解答】解:如图,过点D作DE⊥AB于点E,连接BD,∵菱形ABCD中,∠ABC=120°,∴∠DAB=60°,AD=AB=DC=BC,∴△ADB是等边三角形,∴∠MAE=30°,∴AM=2ME,∵MD=MB,∴MA+MB+MD=2ME+2DM=2DE,根据垂线段最短,此时DE最短,即MA+MB+MD最小,∵菱形ABCD的边长为6,∴DE===3,∴2DE=6.∴MA+MB+MD的最小值是6.故选:D.9.如图,在矩形ABCD中,AB=6,BC=8,点E是AD边上的动点,点M是点A关于直线BE的对称点,连接MD,则MD的最小值是()A.6B.5C.4D.3【解答】解:连接BD,以点B为圆心,BA为半径作圆,交BD于点M,∵四边形ABCD为矩形,∴∠A=90°,∴BD==10,∵点A和点M关于BE对称,∴AB=BM=6,∴DM=BD﹣BM=10﹣6=4.故DM的最小值为4.故选:C.G,H为垂足,连接GH.若AB=8,AD=6,EF=5,则GH的最小值是7.5.【解答】解:连接AC、AP、CP,如图所示:∵四边形ABCD是矩形,∴BC=AD=6,∠BAD=∠B=∠C=90°,∴AC===10,∵P是线段EF的中点,∴AP=EF=2.5,∵PG⊥BC,PH⊥CD,∴∠PGC=∠PHC=90°,∴四边形PGCH是矩形,∴GH=CP,当A、P、C三点共线时,CP最小=AC﹣AP=10﹣2.5=7.5,∴GH的最小值是7.5,故答案为:7.5.11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为.【解答】解:如图,连接AC、AE、CF、CG,在正方形ABCD和正方形DEFG中,AD=CD,DE=DG=EF,∠ADC=∠EDG=90°,∴∠ADC﹣∠EDC=∠EDG﹣∠EDC,∴∠ADE=∠CDG,∴△ADE≌△CDG,∴AE=CG,∴d1+d2+d3=DE+CF+CG=EF+CF+AE,∴当点A、E、F、C在同一直线上时(此时点F与点C重合),DE+CF+AE最小,最小值为线段AC长,在Rt△ABC中,AC=,∴d1+d2+d3的最小值为.12.如图所示,在边长为2的菱形ABCD中,∠DAB=60°,点E为AB中点,点F是AC上一动点,则EF+BF的最小值为.(提示:根据轴对称的性质)【解答】解:连接DB,DE,设DE交AC于M,连接MB,DF,∵四边形ABCD是菱形,∴AC,BD互相垂直平分,∴点B关于AC的对称点为D,∴FD=FB,∴FE+FB=FE+FD≥DE.只有当点F运动到点M时,取等号(两点之间线段最短),△ABD中,AD=AB,∠DAB=60°,∴△ABD是等边三角形.∵E为AB的中点,∴DE⊥AB,∴AE=AD=1,DE==,∴EF+BF的最小值为.13.如图,P是Rt△ABC的斜边AC(不与点A、C重合)上一动点,分别作PM⊥AB于点M,PN⊥BC于点N,O是MN的中点,若AB=5,BC=12,当点P在AC上运动时,BO的最小值是.【解答】解:连接BP,如图所示:∵∠ABC=90°,PM⊥AB于点M,PN⊥BC于点N,∴∠ABC=∠PMB=∠PNB=90°,∴四边形BMPN是矩形,AC===13,∴BP=MN,BP与MN互相平分,∵点O是MN的中点,∴点O是BP的中点,∴BO=BP=MN,当BP⊥AC时,BP最小===,∴MN=,∴BO的最小值=MN=,故答案为:.14.如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是菱形内一动点,且满足MN=1,连接CN,则CN的最小值为﹣1.【解答】解:过点M作MH⊥CD,交CD的延长线于点H,如图所示:在边长为2的菱形ABCD中,∠A=60°,AB∥CD,∴∠HDM=∠A=60°,∴∠HMD=30°,∵点M是AD边的中点,∴DM=1,∴DH=,根据勾股定理,得HM=,∵CD=2,∴CH=,根据勾股定理,得CM=,∵MN=1,当点N运动到线段CM上的点N′时,CN取得最小值,CN′=CM﹣MN=﹣1,∴CN的最小值为﹣1,故答案为:﹣1.15.如图,在菱形ABCD中,AC=24,BD=10.E是CD边上一动点,过点E分别作EF⊥OC于点F,EG⊥OD于点G,连接FG,则FG的最小值为.【解答】解:连接OE,作OH⊥CD于点H,∵四边形ABCD是菱形,AC=24,BD=10,∴AC⊥BD,OC=OA=AC=12,OD=OB=BD=5,∴∠COD=90°,∴CD===13,,∵CD•OH=OC•OD=S△COD∴×13OH=×12×5,解得OH=,∵EF⊥OC于点F,EG⊥OD于点G,∴∠OFE=∠OGE=∠FOG=90°,∴四边形OGEF是矩形,∴OE=FG,∴OE≥OH,∵FG≥,∴FG的最小值为,故答案为:.16.如图,矩形ABCD中,AB=6,AD=4,点E,F分别是AB,DC上的动点,EF∥BC,则BF+DE最小值是()A.13B.10C.12D.5【解答】解:延长AD,取点M,使得AD=DM,连接MP,如图,∵EF∥BC,四边形ABCD是矩形,∴四边形AEFD和四边形EBCF是矩形,∵AD=DM,AE=DF,∠EAD=∠FDM=90°,∴△ADE≌△DMF(SAS),∴DE=MF,∴BF+DE=BF+FM,∵点E,F分别是AB,DC上的动点,故当B,F,M三点共线时,BF+DE的值最小,且BF+DE的值等于BM的值,在Rt△BAM中,,故选:B.17.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点.且BE=CF,连接BF、DE,则BF+DE的最小值为()A.B.C.D.【解答】解:连接AE,如图1,∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°.又BE=CF,∴△ABE≌△BCF(SAS).∴AE=BF.所以BF+DE最小值等于AE+DE最小值.作点A关于BC的对称点H点,如图2,连接BH,则A、B、H三点共线,连接DH,DH与BC的交点即为所求的E点.根据对称性可知AE=HE,HA=4+4=8,所以AE+DE=DH.在Rt△ADH中,DH=∴BF+DE最小值为4.故选:C.18.如图,在Rt△ABC中,∠BAC=90°,且AB=6,AC=8,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,点O为MN的中点,则线段AO的最小值为()A.4.8B.5C.2.4D.3.6【解答】解:如图,连接AD,∵∠BAC=90°,且AB=6,AC=8,∴,∵DM⊥AB,DN⊥AC,∴∠DMA=∠DNA=∠BAC=90°,∴四边形DMAN是矩形,∴MN=AD,,∴当AD⊥BC时,AD的值最小,此时,,∴,∴AO的最小值为2.4,故选:C.19.如图,在△ABC中,∠C=90°,点D在斜边AB上,E、F分别在直角边CA、BC上,且DE⊥AC,DF∥AC.(1)求证:四边形CEDF是矩形;(2)连接EF,若C到AB的距离是5,求EF的最小值.【解答】(1)证明:∵DF∥AC,∠C=90°,∴∠DFB=∠C=90°,∴∠DFC=90°=∠C,∵DE⊥AC,∴∠DEC=90°=∠DFC=∠C,∴四边形CEDF是矩形;(2)解:连接CD,如图所示:由(1)可知,四边形CEDF是矩形,∴CD=EF,∴当CD有最小值时,EF的值最小,∵当CD⊥AB时,CD有最小值,∴CD⊥AB时,EF有最小值,∵C到AB的距离是5,即点C到AB的垂直距离为5,∴CD的最小值为5,∴EF的最小值为5.20.如图所示,在菱形ABCD中,AB=8,∠BAD=120°,△AEF为等边三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF.(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.【解答】(1)证明:连接AC,如图所示:∵四边形ABCD为菱形,∠BAD=120°,∴∠BAC=60°,∵△AEF是等边三角形,∴∠EAF=60°,∴∠BAE+∠EAC=60°,∠CAF+∠EAC=60°,∴∠BAE=∠CAF,∵四边形ABCD为菱形,∴AD∥BC,∴∠ABC+∠BAD=180°,∵∠BAD=120°,∴∠ABC=60°,∴△ABC和△ACD为等边三角形,∴∠ACF=60°,AC=AB,在△ABE和△ACF中,,∴△ABE≌△ACF(ASA).∴BE=CF.(2)解:四边形AECF的面积不变.理由:由(1)得△ABE≌△ACF,=S△ACF,则S△ABE=S△AEC+S△ACF=S△故S四边形AECFAEC+S△ABE=S△ABC,是定值;作AH⊥BC于H点,如图所示:∵∠AHB=90°,∠ABC=60°,∴∠BAH=90°﹣60°=30°,∴,在Rt△ABH中,根据勾股定理得:,=S△ABC=.∴S四边形AECF=S四边形AECF﹣S△AEF=S菱形ABCD﹣S△AEF,∵S△CEF∴△CEF的面积随△AEF面积的变化而变化,∵△AEF为等边三角形,∴当AE最短时,△AEF的面积最小,则△CEF的面积有最大值,∵当AE⊥BC时,AE最小,∴AE的最小值为AH的长,过点A作AM⊥EF,垂足为M,如图所示:∵△AEF为等边三角形,∴,∠AEF=60°,∴,∴,∴,=S四边形AECF﹣S△AEF=16,∴S△CEF即△CEF的面积的最大值为.21.如图①,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)连接MN,△BMN是等边三角形吗?为什么?(2)求证:△AMB≌△ENB;(3)①当M点在何处时,AM+CM的值最小;②如图②,当M点在何处时,AM+BM+CM的值最小,请你画出图形,并说明理由.【解答】(1)解:△BMN是等边三角形.理由如下:如图①,∵BM绕点B逆时针旋转60°得到BN,∴BM=BN,∠MBN=60°,∴△BMN是等边三角形;(2)证明:∵△ABE和△BMN都是等边三角形,∴AB=EB,BM=BN,∠ABE=∠MBN=60°,∴∠ABE﹣∠ABN=∠MBN﹣∠ABN,即∠ABM=∠EBN,在△AMB和△ENB中,,∴△AMB≌△ENB(SAS);(3)①由两点之间线段最短可知A、M、C三点共线时,AM+CM的值最小,∵四边形ABCD是正方形,∴点M为BD的中点;②当点M在CE与BD的交点时,AM+BM+CM的值最小,理由如下:如图②,∵△AMB≌△ENB,∴AM=EN,∵△BMN是等边三角形,∴BM=MN,∴AM+BM+CM=EN+MN+CM,由两点之间线段最短可知,点E、N、M、C在同一直线上时,EN+MN+CM,故,点M在CE与BD的交点时,AM+BM+CM的值最小.。
特殊的平行四边形中的最值模型之将军饮马、遛马、造桥模型(解析版)

特殊的平行四边形中的最值模型之将军饮马、遛马、造桥模型“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗,由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
将军饮马问题从本质上来看是由轴对称衍生而来,同时还需掌握平移型将军饮马(即将军遛马、造桥或过桥),主要考查转化与化归等的数学思想。
在各类考试中都以中高档题为主,本专题就特殊的平行四边形背景下的将军饮马问题进行梳理及对应试题分析,方便掌握。
模型1.将军饮马模型(双线段和的最小值)模型2.将军饮马模型(双线段差的最大值)模型3.将军饮马(多线段和的最值模型)模型4.将军遛马、造桥(过桥)模型模型1.将军饮马模型(双线段和的最小值)条件:A,B为定点,m为定直线,P为直线m上的一个动点,求AP+BP的最小值。
模型(1)点A、B在直线m两侧:模型(2)点A、B在直线同侧:模型(1)点A、B在直线m两侧:模型(2)点A、B在直线同侧:图(1)图(2)模型(1):如图(1),连结AB ,根据两点之间线段最短,AP +BP 的最小值即为:线段AB 的长度。
模型(2):如图(2),作点A 关于定直线m 的对称点A ',连结A 'B ,根据对称得到:P A =P A ',故AP +BP =A 'P +BP ,再利用“两点之间线段最短”,得到AP +BP 的最小值即为:线段A 'B 的长度。
1.(2024·四川广安·中考真题)如图,在▱ABCD 中,AB =4,AD =5,∠ABC =30°,点M 为直线BC 上一动点,则MA +MD 的最小值为.【答案】41【分析】如图,作A 关于直线BC 的对称点A ,连接A D 交BC 于M ,则AH =A H ,AH ⊥BC ,AM =A M ,当M ,M 重合时,MA +MD 最小,最小值为A D ,再进一步结合勾股定理求解即可.【详解】解:如图,作A 关于直线BC 的对称点A ,连接A D 交BC 于M ,则AH =A H ,AH ⊥BC ,AM =A M ,∴当M ,M 重合时,MA +MD 最小,最小值为A D ,∵AB =4,∠ABC =30°,在▱ABCD 中,∴AH =12AB =2,AD ∥BC ,∴AA =2AH =4,AA ⊥AD ,∵AD =5,∴A D =42+52=41,故答案为:41【点睛】此题考查了平行四边形的性质,勾股定理,轴对称的性质,求最小值问题,正确理解各性质及掌握各知识点是解题的关键.2.(23-24八年级下·广东广州·期中)如图,在矩形ABCD 中,AB =5,AD =3,点P 满足S △P AB =13S 矩形ABCD,则点P 到A ,B 两点距离之和P A +PB 的最小值为()A.29B.34C.52D.41【答案】D【分析】首先由S△P AB=13S矩形ABCD,得出动点在与平行且与的距离是2的直线上,作点A关于直线l的对称点E,连结AE,BE,则BE的长就是所求的最短距离,然后勾股定理求得BE的长,即得答案.【详解】设AB边上的高是h,∵S△P AB=13S矩形ABCD,∴12AB⋅h=13AB⋅AD,∴h=23AD=2,∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作点A关于直线l的对称点E,连结AE,BE,则BE的长就是所求的最短距离,在Rt△ABE中,∵AB=5,AE=2+2=4,∴BE=AB2+AE2=52+42=41,即P A+PB的最小值为41.故选D.【点睛】本题考查了最短路线问题,轴对称的性质,矩形的性质,勾股定理,两点之间线段最短的性质,作点A 关于直线l的对称点E,并得到BE的长就是所求的最短距离是解题的关键.3.(23-24八年级下·重庆沙坪坝·期中)如图,菱形ABCD的周长为8,∠DAC=30°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是.【答案】3【分析】此题考查轴对称确定最短路线问题,菱形的性质,等边三角形的判定与性质。
2022-2023学年初二数学第二学期培优专题06 平行四边形中的最值问题

2022-2023学年初二数学第二学期培优专题06 平行四边形中的最值问题【例题讲解】如图,在平行四边形ABCD 中,30BCD ∠=︒,6BC =,33CD =,(1)平行四边形ABCD 的面积为________.(2)若M 是AD 边的中点,N 是AB 边上的一个动点,将AMN 沿MN 所在直线翻折得到A MN '△,连接A C ',则A C '长度的最小值是________.解:(1)过点C 作CF ⊥AB ,交AB 延长线于F ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,BC =6,AB =CD =33,∵∠BCD =30°=∠CBF ,∴CF =12BC =3, ∴四边形ABCD 的面积=AB CF ⨯=333⨯=93;(2)连接MC ,过点M 作ME ⊥CD 于E ,交CD 的延长线于点E ;∵四边形ABCD 为平行四边形,∴AD ∥BC ,AD =BC =6,∵点M 为AD 的中点,∠BCD =30°,∴DM =MA =3,∠MDE =∠BCD =30°,∴ME =12DM =32,DE =332,∴CE =CD +DE =33332+=932,由勾股定理得:CM 2=ME 2+CE 2, ∴CM=2239322⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭=37,由翻折变换的性质得:MA ′=MA =3,∵MA ′+A ′C ≥MC , ∴A ′C ≥MC- MA ′= MC -3,显然,当折线MA ′C 与线段MC 重合时,线段A ′C 的长度最短,此时A ′C =373-,故答案为:(1)93;(2)373-.【综合演练】1.如图 ,在平行四边形ABCD 中 ,120C ∠=︒ ,AB =4 ,AD =8 , 点H 、G 分别是边CD 、BC 上的动点.连接AH 、HG ,点E 为AH 的中点 ,点F 为GH 的中点 ,连接EF .则EF 的最大值与最小值的差为( )A .2B .232-C .3D .43-2.如图,在△ABC 中,∠ACB =60°,∠CAB =45°,BC =4,点D 为AB 边上一个动点,连接CD ,以DA 、DC 为一组邻边作平行四边形ADCE ,则对角线DE 的最小值是( )A .2+6B .1+3C .4D .2+23第II 卷(非选择题)二、填空题(共0分)3.如图,在Rt ABC 中,90,3,4B AB BC ∠=︒==,点D 为BC 上一动点(不与点C 重合),以AD ,CD 为一组邻边作平行四边形ADCE ,当DE 的值最小时,平行四边形ADCE 的周长..为_____. 4.如图,在ABCD 中,=60B ∠︒,10AB =,8BC =,点E 为边AB 上的一个动点,连接ED ,EC , 以ED 、CE 为邻边构造EDGC ,连接EG ,则EG 的最小值为__________.5.如图,平行四边形ABCD 中,AB =2,AD =1,∠ADC =60°,将平行四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D 处,折痕交CD 边于点E .若点P 是直线l 上的一个动点,则PD '+PB 的最小值_______.6.如图,平行四边形ABCD中,8∠=︒,E是边AD上且2AAB=,6AD=,60=,F是边AB上AE DE+的最小值__________.的一个动点,将线段EF绕点E逆时针旋转60︒,得到EG,连接BG、CG,则BG CG7.如图,CD是直线x=1上长度固定为1的一条动线段.已知A(﹣1,0),B(0,4),则四边形ABCD 周长的最小值为_________________.8.如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC 为边作平行四边形PCQD,则对角线PQ的长的最小值是_____.9.如图,四边形ABCD中,∠B=∠D=90°,∠C=50°,在BC、CD边上分别找到点M、N,当△AMN 周长最小时,∠AMN+∠ANM的度数为______.10.如图,在ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是边AD 、AB 上的点,连结OE 、OF 、EF .若7AB =,52BC =,45DAB ∠=︒,则OEF 周长的最小值是_______.11.如图,点(1,3),(6,1),(,0),(2,0)A B P a N a --+为四边形的四个顶点,当四边形PABN 的周长最小时,=a ________.12.如图,在四边形ABCD 中,90,5,4,A D AB AD ∠=∠=︒==3,CD =点P 是边AD 上的动点,则PBC 周长的最小值为( )A .8B .45C .12D .65三、解答题(共0分)13.如图,四边形ABCD 为平行四边形,延长AD 到点E ,使DE AD =,且BE DC ⊥.(1)求证:四边形DBCE 为菱形;(2)若DBC △是边长为2的等边三角形,点P 、M 、N 分别在线段BE 、BC 、CE 上运动,求PM PN +的最小值.14.如图,在平行四边形ABCD 中,2,1,60AB AD B ==∠=︒,将平行四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点'D 处,折痕交CD 边于点E .(1)求证:四边形'BCED 是菱形;(2)若点P 是直线l 上的一个动点,请作出使'PD PB +为最小值的点P ,并计算'PD PB +.15.如图,在平行四边形ABCD 中,30BCD ∠=︒,6BC =,33CD =,(1)平行四边形ABCD 的面积为________.(2)若M 是AD 边的中点,N 是AB 边上的一个动点,将AMN 沿MN 所在直线翻折得到A MN '△,连接A C ',则A C '长度的最小值是________.答案与解析【例题讲解】如图,在平行四边形ABCD 中,30BCD ∠=︒,6BC =,33CD =,(1)平行四边形ABCD 的面积为________.(2)若M 是AD 边的中点,N 是AB 边上的一个动点,将AMN 沿MN 所在直线翻折得到A MN '△,连接A C ',则A C '长度的最小值是________.解:(1)过点C 作CF ⊥AB ,交AB 延长线于F ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,BC =6,AB =CD =33,∵∠BCD =30°=∠CBF ,∴CF =12BC =3, ∴四边形ABCD 的面积=AB CF ⨯=333⨯=93;(2)连接MC ,过点M 作ME ⊥CD 于E ,交CD 的延长线于点E ;∵四边形ABCD 为平行四边形,∴AD ∥BC ,AD =BC =6,∵点M 为AD 的中点,∠BCD =30°,∴DM =MA =3,∠MDE =∠BCD =30°,∴ME =12DM =32,DE =332,∴CE =CD +DE =33332+=932,由勾股定理得:CM 2=ME 2+CE 2, ∴CM=2239322⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭=37,由翻折变换的性质得:MA ′=MA =3,∵MA ′+A ′C ≥MC , ∴A ′C ≥MC- MA ′= MC -3,显然,当折线MA ′C 与线段MC 重合时,线段A ′C 的长度最短,此时A ′C =373-,故答案为:(1)93;(2)373-.【综合演练】1.如图 ,在平行四边形ABCD 中 ,120C ∠=︒ ,AB =4 ,AD =8 , 点H 、G 分别是边CD 、BC 上的动点.连接AH 、HG ,点E 为AH 的中点 ,点F 为GH 的中点 ,连接EF .则EF 的最大值与最小值的差为( ) A .2 B .232- C .3 D .43- 【答案】C【分析】如图,取AD 的中点M ,连接CM 、AG 、AC ,作AN ⊥BC 于N .首先证明∠ACD =90°,求出AC ,AN ,利用三角形中位线定理,可知EF =12AG ,求出AG 的最大值以及最小值即可解决问题. 【解答】解:如图,取AD 的中点M ,连接CM 、AG 、AC ,作AN ⊥BC 于N .∵四边形ABCD 是平行四边形,∠BCD =120°,28AD AB ==∴∠D =180°−∠BCD =60°,AB =CD =4,∵AM =DM =DC =4,∴△CDM 是等边三角形,∴∠DMC =∠MCD =60°,AM =MC ,∴∠MAC =∠MCA =30°,∴∠ACD =90°,∴AC =43在Rt △ACN 中,∵AC =43,∠ACN =∠DAC =30°,∴AN =12AC =23∵AE =EH ,GF =FH ,∴EF =12AG ,∵点G 在BC 上,∴AG 的最大值为AC 的长,最小值为AN 的长,∴AG 的最大值为43,最小值为23,∴EF 的最大值为23,最小值为3,∴EF的最大值与最小值的差为:3故选C.【点评】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明∠ACD=90°,属于中考选择题中的压轴题.2.如图,在△ABC中,∠ACB=60°,∠CAB=45°,BC=4,点D为AB边上一个动点,连接CD,以DA、DC为一组邻边作平行四边形ADCE,则对角线DE的最小值是()A.2+6B.1+3C.4 D.2+23【答案】ABC=2,AF=BF=3CF 【分析】设DE交AC于O,作BF⊥AC于F,由直角三角形的性质得出CF=12AC=1+3,DO=EO,当OD⊥AB =23,求出AC=CF+AF=2+23,由平行四边形性质得出AO=CO=12时,DO的值最小,即DE的值最小,则△AOD是等腰直角三角形,即可得出结果.【解答】解:设DE交AC于O,作BF⊥AC于F,如图所示:则∠BFC=∠BF A=90°,∵∠ACB=60°,∠CAB=45°,∴∠CBF=30°,∠ABF=45°=∠CAB,BC=2,AF=BF=3CF=23,∴CF=12∴AC=CF+AF=2+23,∵四边形ADCE是平行四边形,AC=1+3,DO=EO,∴AO=CO=12∴当OD ⊥AB 时,DO 的值最小,即DE 的值最小,则△AOD 是等腰直角三角形,∴OD =22AO =622+, ∴DE =2OD =26+.故选:A .【点评】本题主要考查解直角三角形,平行四边形的性质,掌握平行四边形的性质和特殊角的三角函数值是解题的关键.3.如图,在Rt ABC 中,90,3,4B AB BC ∠=︒==,点D 为BC 上一动点(不与点C 重合),以AD ,CD 为一组邻边作平行四边形ADCE ,当DE 的值最小时,平行四边形ADCE 的周长..为_____. 【答案】4+213【分析】根据题意,可知当DE ⊥AE 时,DE 取得最小值,然后根据题目中的数据,即可得到A D 、CD 的长,从而可以得到当DE 的值最小时,平行四边形ADCE 周长.【解答】解:当DE ⊥AE 时,DE 取得最小值,设此时CD =x ,∵四边形ADCE 是平行四边形,∴CD =AE ,AD =CE ,BC ∥AE ,∵∠B =90°,DE ⊥AE ,∴四边形BAED 是矩形,∴BD =AE ,∴BD =CD =x ,∵BC =BD +CD ,BC =4,∴BD =CD =2,∵AB =3,∠B =90°,∴AD =22222313BD AB +=+=,∴当DE 的值最小时,平行四边形ADCE 周长为:2+13+2+13=4+213,故答案为:4+213.【点评】本题考查平行四边形的性质、矩形的判定与性质、垂线段最短,解答本题的关键是明确题意,利用数形结合的思想解答. 4.如图,在ABCD 中,=60B ∠︒,10AB =,8BC =,点E 为边AB 上的一个动点,连接ED ,EC , 以ED 、CE 为邻边构造EDGC ,连接EG ,则EG 的最小值为__________.【答案】83【分析】根据平行四边形的性质得到EG ,FG ,根据垂线段最短得到EG ⊥CD 时取最小值,过点C 作CH ⊥AB 于点H ,求出CH 的长度,从而得到结果.【解答】解:∵四边形EDGC 是平行四边形,∴EF =FG ,∴当EF ⊥CD 时,EF 最小,此时EG 最小,过点C 作CH ⊥AB 于点H ,则CH =EF ,∵∠B =60°,∴∠BCH =30°,∵BC =8,∴BH =4,∴CH =2284-=43,∴EF 的最小值为43,∴EG 的最小值为83,故答案为:83.【点评】本题考查了平行四边形的性质,垂线段最短,直角三角形的性质,勾股定理,解题的关键是理解题意,找到EG最短时满足的条件.5.如图,平行四边形ABCD中,AB=2,AD=1,∠ADC=60°,将平行四边形ABCD沿过点A的直线l 折叠,使点D落到AB边上的点D处,折痕交CD边于点E.若点P是直线l上的一个动点,则PD +PB 的最小值_______.【答案】7【分析】不管P点在l上哪个位置,PD始终等于PD',故求PD'+PB可以转化成求PD+PB,显然当D、P、D'共线时PD+ PB最短.【解答】过点D作DM⊥AB交BA的延长线于点M,∵四边形ABCD是平行四边形,AD=1,AB=2,∠ADC=60°,∴∠DAM=60°,由翻折变换可得,AD=AD′=1,DE=D′E,∠ADC=∠AD′E=60°,∴∠DAM=∠AD′E=60°,∴AD∥D′E,又∵DE∥AB,∴四边形ADED′是菱形,∴点D与点D′关于直线l对称,连接BD交直线l于点P,此时PD′+PB最小,PD′+PB=BD,在Rt△DAM中,AD=1,∠DAM=60°,∴AM=12AD=12,DM=32AD=32,在Rt△DBM中,DM=32,MB=AB+AM=52,∴BD=DM2+MB2=322+522=7,即PD′+PB最小值为7,故答案为:7.【点评】本题考查平行四边形性质和菱形性质,掌握这些是本题解题关键.6.如图,平行四边形ABCD中,8∠=︒,E是边AD上且2AAD=,60AB=,6=,F是边AB上AE DE+的最小值__________.的一个动点,将线段EF绕点E逆时针旋转60︒,得到EG,连接BG、CG,则BG CG【答案】221【分析】如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H.利用全等三角形的性质证明∠GNB=60°,点G的运动轨迹是射线NG,由“SAS”可证△EGN≌△BGN,可得GB=GE,推出GB+GC=GE+GC≥EC,求出EC即可解决问题.【解答】解:如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H,∵AE=2DE,∴AE=4,DE=2,∵点N是AB的中点,∴AN=NB=4,∴AE=AN,∵∠A=60°,∴△AEN是等边三角形,∴∠AEN=∠FEG=60°,∴∠AEF=∠NEG,∵EA=EN,EF=EG,∴△AEF≌△NEG(SAS),∴∠ENG=∠A=60°,∵∠ANE=60°,∴∠GNB=180°-60°-60°=60°,∴点G的运动轨迹是射线NG,∵BN=EN,∠BNG=∠ENG=60°,NG=NG∴△EGN≌△BGN(SAS),∴GB=GE,∴GB+GC=GE+GC≥EC,在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,DE=1,EH=3,∴DH=12在Rt△ECH中,EC=22221+=,EH CH∴GB+GC≥221,∴GB+GC的最小值为221,故答案为:221.【点评】本题考查旋转变换,轨迹,平行四边形的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.7.如图,CD是直线x=1上长度固定为1的一条动线段.已知A(﹣1,0),B(0,4),则四边形ABCD 周长的最小值为_________________.【答案】17132++【分析】在y轴上取点E,使BE=CD=1,则四边形BCDE为平行四边形,根据勾股定理得到AB,作点A关于直线x=1的对称点A',得到A'、E、D三点共线时,AD+DE最小值为A'E的长,根据勾股定理求出A'E,即可得解;【解答】解:如图,在y轴上取点E,使BE=CD=1,则四边形BCDE为平行四边形,∵B(0,4),A(﹣1,0),∴OB=4,OA=1,∴OE=3,AB=22+=,1417作点A关于直线x=1的对称点A',∴A'(3,0),AD=A'D,∴AD+DE=A'D+DE,即A'、E、D三点共线时,AD+DE最小值为A'E的长,在Rt△A'OE中,由勾股定理得A'E=22+=,3332∴C四边形ABCD最小值=AB+CD+BC+AD=AB+CD+A'E=17+1+32.故答案为:17132++.【点评】本题主要考查了轴对称最短路线问题、勾股定理、位置与坐标,准确分析作图计算是解题的关键.8.如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC 为边作平行四边形PCQD,则对角线PQ的长的最小值是_____.【答案】4【分析】根据题意在平行四边形PCQD中,设对角线PQ与DC相交于点O,可得O是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,易证得Rt△ADP≌Rt△HCQ,即可求得BH=4,则可得当PQ⊥AB 时,PQ的长最小,即为4.【解答】解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,则O是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,∵AD ∥BC ,∴∠ADC=∠DCH ,即∠ADP+∠PDC=∠DCQ+∠QCH ,∵PD ∥CQ ,∴∠PDC=∠DCQ ,∴∠ADP=∠QCH ,又∵PD=CQ ,在Rt △ADP 与Rt △HCQ 中,ADP QCH A QHCPD CQ ⎧⎪⎨⎪∠∠⎩∠∠=== ∴Rt △ADP ≌Rt △HCQ (AAS ),∴AD=HC ,∵AD=1,BC=3,∴BH=4,∴当PQ ⊥AB 时,PQ 的长最小,即为4.故答案为:4.【点评】本题考查梯形的中位线的性质,注意掌握梯形的中位线等于两底和的一半且平行于两底.9.如图,四边形ABCD 中,∠B =∠D =90°,∠C =50°,在BC 、CD 边上分别找到点M 、N ,当△AMN 周长最小时,∠AMN +∠ANM 的度数为______.【答案】100°【分析】根据要使△AMN 的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A 关于BC和CD 的对称点A′,A″,即可得出∠AA′M+∠A″=180°-∠DAB =∠C=50°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.【解答】解:作A 关于BC 和CD 的对称点A′,A″,连接A′A″,交BC 于M ,交CD 于N ,则A′A″即为△AMN 的周长最小值.∵∠B =∠D =90°,∠C =50°,∵∠DAB=130°,∴∠AA′M+∠A″=180°-130°=50°,由对称性可知:∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN ,∠NAD+∠A″=∠ANM ,∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,故答案为:100°.【点评】此题主要考查了平面内最短路线问题求法以及三角形的内角和定理及外角的性质和轴对称的性质等知识,根据已知得出M ,N 的位置是解题关键.10.如图,在ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是边AD 、AB 上的点,连结OE 、OF 、EF .若7AB =,52BC =,45DAB ∠=︒,则OEF 周长的最小值是_______.【答案】1322【分析】作点O 关于AB 的对称点M ,点O 关于AD 的对称点N ,连接MN 交AB 于F ,交AD 于E ,此时△OEF 的周长最小,周长的最小值=MN ,由作图得AN =AO =AM ,∠NAD =∠DAO ,∠MAB =∠BAO ,于是得到∠MAN =90°,过D 作DP ⊥AB 于P ,则△ADP 是等腰直角三角形,根据等腰直角三角形的性质得到AP =DP =22AD ,求得AP =DP =5,根据三角形的中位线的性质得到OQ =12DP =52,BQ =12BP=12(AB−AP )=1,根据勾股定理求出AO =132,然后根据等腰直角三角形的性质即可得到结论. 【解答】解:作点O 关于AB 的对称点M ,点O 关于AD 的对称点N ,连接MN 交AB 于F ,交AD 于E ,此时△OEF 的周长最小,周长的最小值=MN ,∴AN =AO =AM ,∠NAD =∠DAO ,∠MAB =∠BAO ,∵∠DAB =45°,∴∠MAN =90°,过D 作DP ⊥AB 于P ,则△ADP 是等腰直角三角形,∴AP =DP =22AD , ∵AD =BC =52,∴AP =DP =5,设OM ⊥AB 于Q ,则OQ ∥DP ,∵OD =OB ,∴OQ =12DP =52,BQ =12BP =12(AB−AP )=1, ∴AQ =6,∴AO =2222513622AQ OQ , ∴AM =AN =AO =132, ∴MN =2AM =1322, ∴△OEF 周长的最小值是1322. 故答案为:1322. 【点评】此题主要考查轴对称−−最短路线问题,平行四边形的性质,等腰直角三角形的性质,勾股定理以及三角形中位线定理等,正确的作出辅助线是解题的关键.11.如图,点(1,3),(6,1),(,0),(2,0)A B P a N a --+为四边形的四个顶点,当四边形PABN 的周长最小时,=a ________.【答案】13 4【分析】作点A关于x轴的对称点A′,则A′(1,3),将A′向右平移2个单位,即A″(3,3),连接A″B,与x轴交于点N,可判断出AP+BN=A″N+BN≥A″B,即此时四边形ABNP的周长最小,求出A″B的表达式,得到与x轴的交点,即为点N,从而可得a值.【解答】解:如图,作点A关于x轴的对称点A′,则A′(1,3),将A′向右平移2个单位,即A″(3,3),连接A″B,与x轴交于点N,则此时AP=A′P=A″N,则AP+BN=A″N+BN≥A″B,在四边形ABNP中,PN和AB均为定值,∴此时四边形ABNP的周长最小,设A″B的表达式为y=kx+b,则3361k bk b+=⎧⎨+=-⎩,解得:437kb⎧=-⎪⎨⎪=⎩,∴直线A″B的表达式为473y x=-+,令y=0,则214x=,即此时N(214,0),2124a+=,解得:a=134,故答案为:134. 【点评】本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.12.如图,在四边形ABCD 中,90,5,4,A D AB AD ∠=∠=︒==3,CD =点P 是边AD 上的动点,则PBC 周长的最小值为( )A .8B .45C .12D .65【答案】D【分析】根据勾股定理可求BC 的长,所以要使△PBC 的周长最小,即BP+PC 最短,利用对称性,作点C 关于AD 的对称点E ,即可得出最短路线,从而求解可.【解答】解:过点C 作CG ⊥AB ,由题意可知四边形DAGC 是矩形∴CG=AD=4,BG=AB-AG=AB-CD=2∴在Rt △BCG 中,222425BC =+=作点C 关于AD 的对称点E ,连接BE ,交AD 于点P',连接'CP此时'P BC 的周长为最小值,即''''BP CP BC BP EP BC BE BC ++=++=+过点E 作EF ⊥BA ,交BA 的延长线于点F由题意可知四边形EFAD 为矩形∴EF=AD=4,DE=CD=AF=3∴在Rt △EBF 中,224(35)45BE =++=∴此时'P BC 的周长为:65BE BC +=故选:D .【点评】本题考查勾股定理解直角三角形及应用对称的性质求最短路线,掌握相关性质定理正确添加辅助线进行推理计算是解题关键.13.如图,四边形ABCD 为平行四边形,延长AD 到点E ,使DE AD =,且BE DC ⊥.(1)求证:四边形DBCE 为菱形;(2)若DBC △是边长为2的等边三角形,点P 、M 、N 分别在线段BE 、BC 、CE 上运动,求PM PN +的最小值. 【答案】(1)证明见解析(2)3【分析】(1)先根据四边形ABCD 为平行四边形的性质和DE AD =证明四边形DBCE 为平行四边形,再根据BE DC ⊥,即可得证;(2)先根据菱形对称性得,得到'PM PN PM PN +=+,进一步说明PM PN +的最小值即为菱形的高,再利用三角函数即可求解.(1)证明:∵四边形ABCD 是平行四边形,∴AD BC ∥,AD BC =,∵DE AD =,∴DE BC =,又∵点E 在AD 的延长线上,∴DE BC ∥,∴四边形DBCE 为平行四边形,又∵BE DC ⊥,∴四边形DBCE 为菱形.(2)解:如图,由菱形对称性得,点N 关于BE 的对称点'N 在DE 上,∴'PM PN PM PN +=+,当P 、M 、'N 共线时,''PM PN PM PN MN +=+=,过点D 作DH BC ⊥,垂足为H ,∵DE BC ∥,∴'MN 的最小值即为平行线间的距离DH 的长,∵DBC △是边长为2的等边三角形,∴在Rt DBH 中,60DBC ∠=︒,2DB =,sin DH DBC DB ∠=, ∴3sin 232DH DB DBC =∠=⨯=, ∴PM PN +的最小值为3.【点评】本题考查了最值问题,考查了菱形的判定和性质,平行四边形的判定和性质,三角函数等知识,运用了转化的思想方法.将最值问题转化为求菱形的高是解答本题的关键.14.如图,在平行四边形ABCD 中,2,1,60AB AD B ==∠=︒,将平行四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点'D 处,折痕交CD 边于点E .(1)求证:四边形'BCED 是菱形;(2)若点P 是直线l 上的一个动点,请作出使'PD PB +为最小值的点P ,并计算'PD PB +.【答案】(1)见解析;(2)作图见解析,7得到DAD E'是菱形,作DG BA⊥)将ABCD沿过点A的直线∠=EA,D//DE AD∴∠=DEA∴∠=,DAE EA∴∠'DAD∴四边形=AD ADAB=,2∴=AD AD∴'是菱形;BCED(2)四边形∴与D'D连接BD交CD AB//∴∠=DAGAD=,112AG ∴=,32DG =, 52BG ∴=, 227BD DG BG ∴=+=,PD PB ∴'+的最小值为7.【点评】本题考查了平行四边形的性质,最短距离问题,勾股定理,菱形的判定和性质,正确的作出辅助线是解题的关键.。
部编数学八年级下册专题15特殊平行四边形中的最值问题(解析版)含答案

专题15 特殊平行四边形中的最值问题(解析版)类型一特殊四边形中求一条线段的最小值1.(2021春•叶集区期末)如图,在矩形ABCD中,AB=2,AD=3,E是BC边上一点,将△ABE沿AE折叠,使点B落在点B′处,连接CB′,则CB′的最小值是( )A2B2C―3D.1思路引领:由矩形的性质得出∠B=90°,BC=AD=3,由折叠的性质得:AB'=AB=2,当A、B'、C三点共线时,CB'的值最小,由勾股定理得出AC=CB'=AC﹣AB'2.解:∵四边形ABCD是矩形,∴∠B=90°,BC=AD=3,由折叠的性质得:AB'=AB=2,当A、B'、C三点共线时,CB'的值最小,此时AC∴CB'=AC﹣AB'=2;故选:A.总结提升:本题考查了翻折变换的性质、矩形的性质、勾股定理等知识;熟练掌握翻折变换的性质和勾股定理是解题的关键.类型二特殊四边形中求一条线段的最大值2.(2020•洪山区校级自主招生)如图,在菱形ABCD中,AB=4,∠BAD=120°,点E,F分别是边AB,BC边上的动点,沿EF折叠△BEF,使点B的对应点B′始终落在边CD上,则A、E两点之间的最大距离为 .思路引领:作AH ⊥CD 于H ,由B ,B '关于EF 对称,推出BE =EB ',当BE 最小时,AE 最大,根据垂线段最短即可解决问题.解:作AH ⊥CD 于H ,∵四边形ABCD 是菱形,∠BAD =120°,∴AB ∥CD ,∠D =180°﹣∠BAD =60°,∵AD =AB =4,∴AH =AD •sin60°=∵B ,B '关于EF 对称,∴BE =B 'E ,∴当BE 最小时,AE 最大,根据垂线段最短可知,当EB '=AH =BE 的值最小,∴AE 的最大值为4﹣故答案为:4﹣总结提升:本题主要考查图形的翻折,熟练掌握菱形的性质,垂线段最短等知识是解题的关键.类型三 特殊四边形中求线段和的最小值3.(2019•红桥区二模)如图,在矩形ABCD 中,E 为BC 的中点,P 为对角线AC 上的一个动点,若AB =2,BC =PE +PB 的最小值为( )A B .3C .D .6思路引领:作E 关于AC 的对称点E ',连接BE ',则PE +PB 的最小值即为BE '的长;由已知可求E 'C =ECE '=60°;过点E '作E 'G ⊥BC ,在Rt △E 'CG 中,E 'G =32,CG Rt △BE 'G 中,BG =BE '=3;解:作E 关于AC 的对称点E ',连接BE ',则PE +PB 的最小值即为BE '的长;∵AB =2,BC =E 为BC 的中点,∴∠ACB =30°,∴∠ECE '=60°,∵EC =CE ',∴E 'C 过点E '作E 'G ⊥BC ,在Rt △E 'CG 中,E 'G =32,CG =在Rt △BE 'G 中,BG =∴BE '=3;∴PE +PB 的最小值为3;故选:B .总结提升:本题考查矩形的性质,轴对称求最短距离;通过轴对称将PE +PB 转化为线段BE '的长是解题的关键.4.(2018春•铜山区期中)如图,在菱形ABCD 中,AD =2,∠ABC =120°,E 是BC 的中点,P 为对角线AC 上的一个动点,则PE +PB 的最小值为( )A B .2C .1D .5思路引领:连接BD ,DE ,则DE 的长即为PE +PB 的最小值,再根据菱形ABCD 中,∠ABC =120°得出∠BCD 的度数,进而判断出△BCD 是等边三角形,故△CDE 是直角三角形,根据勾股定理即可得出DE 的长.解:连接BD,DE,∵四边形ABCD是菱形,∴B、D关于直线AC对称,∴DE的长即为PE+PB的最小值,∵∠ABC=120°,∴∠BCD=60°,∴△BCD是等边三角形,∵E是BC的中点,∴DE⊥BC,CE=12BC=12×2=1,∴DE故选:A.总结提升:本题考查的是轴对称﹣最短路线问题,熟知菱形的性质及两点之间线段最短是解答此题的关键.5.(2022秋•龙华区期中)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=BD=2,点P是AC上一动点,点E是AB的中点,则PD+PE的最小值为 .思路引领:由两点之间线段最短,可得当点P在DE上时,PD+PE的值最小,最小值为DE的长,由菱形的性质可得AO=CO=BO=DO=1,AC⊥BD,AB=AD,由锐角三角函数可求∠ABO=60°,可证△ABD是等边三角形,由等边三角形的性质可得DE⊥AB,即可求解.解:如图,连接DE,交AC于点P,此时PD+PE的最小值为DE的长,∵四边形ABCD 是菱形,∴AO =CO =BO =DO =1,AC ⊥BD ,AB =AD ,∴AO BO ∴∠ABO =60°,∴△ABD 是等边三角形,∵点E 是AB 的中点,∴DE ⊥AB ,∴DE 2=∴DE总结提升:本题考查了轴对称﹣最短路线问题,菱形的性质,两点之间线段最短,等边三角形的判定和性质,锐角三角函数等知识,利用锐角三角函数求出∠ABD 的度数是解题的关键.6.(2022秋•桐柏县期末)如图,在边长为4的正方形ABCD 中,将△ABD 沿射线BD 平移,连接EC 、GC .求EC +GC 的最小值为 .思路引领:如图,连接AC 与BD 交于点O ,过点C 作l ∥BD ,点E 关于l 对称的对称点为M ,连接CM ,GM ,EM ,EM 与l 的交点为N ,与BD 交点为P ,则EM ⊥l ,EM ⊥BD ,CE =CM ,EN =MN ,求出AC ,NP ,GP ,PE ,MN ,PM 的值,当G 、C 、M 三点不共线时,有GC +CM >GM ;当G 、C 、M 三点共线时,有GC +CM =GM ;有EC +GC =GC +CM ≥GM ,可知G 、C 、M 三点共线时,EC +GC 值最小,在Rt △PGM 中,由勾股定理得GM EC +GC =GM 可得EC +GC 的最小值.解:如图,连接AC 与BD 交于点O ,过点C 作l ∥BD ,点E 关于l 对称的对称点为M ,连接CM ,GM ,EM ,EM 与l 的交点为N ,与BD 交点为P则EM ⊥l ,EM ⊥BD ,CE =CM ,EN =MN ,∵AC =AB sin 45°=∴两平行线的距离NP =12AC =∵EM ⊥BD ,∴∠GEP =45°,∴GP =PE =EG ×sin 45°=∴EN =EP +NP =∴MN =EN =∴PM =PN +MN =当G 、C 、M 三点不共线时,有GC +CM >GM ,当G 、C 、M 三点共线时,有GC +CM =GM ,∴EC +GC =GC +CM ≥GM ,∴G 、C 、M 三点共线时,EC +GC 值最小,在Rt △PGM 中,由勾股定理得GM =∴EC +GC 的最小值为故答案为:总结提升:本题考查了正方形的性质,垂直平分线的性质,三角形的三边关系,勾股定理,正弦值等知识,对知识的灵活运用是解题的关键.7.(2022•朝阳区二模)如图,在矩形ABCD 中,AD =2AB ,E 是边AD 的中点,F 是边AB 上的一个动点,连接EF ,过点E 作EG ⊥EF 交BC 于点G .(1)求证:EF =GE ;(2)若AB =1,则AF +EF +CG 的最小值为 .思路引领:(1)过点E作EH⊥BC于点H,可证△AEF≌△EGH,结论可得.(2)根据△AEF≌△EGH可得AF=HG,EF=EG,则CG+AF=CH=1,所以当EG值最小时,AF+EF+CG 值最小.即EG⊥BC时,AF+EF+CG值最小,即可求其值.解:(1)如图,过点E作EH⊥BC于点H.∵四边形ABCD是矩形,∴AB∥BC,∠A=90°.∴AB=EH,∠A=∠EHG=∠AEH=90°.∴∠FEH+∠AEF=90°.∵EG⊥EF,∴∠FEH+∠HEG=90°.∴∠AEF=∠HEG.∵AD=2AB,AD=2AE,∴AE=AB.∴AE=HE且∠AEF=∠HEG,∠A=∠EHG∴△AEF≌△HEG.∴EF=GE.(2)∵在矩形ABCD中,AD=2AB,AB=1∴AD=2,∴AE=DE=1∵∠D=∠C=90°,EH⊥BC∴DCHE是矩形∴DE=CH=1∵△AEF≌△EHG∴AF=HG,EF=EG,EH=AE=1∴AF+EF+CG=HG+CG+EG=CH+EG=1+EG由两平行线之间垂线段最短,当EG⊥BC时,AF+EF+CG的值最小即EG=1时,AF+EF+CG的最小值为2总结提升:本题考查的是最短距离问题,全等三角形,矩形的性质,关键是灵活运用各个性质解决问题.类型四特殊四边形中求周长面积的最小值8.(2022•雁塔区校级模拟)如图,在矩形ABCD中,AB=5,BC=4,E、F分别是AD、BC的中点,点P、Q在EF上.且满足PQ=2,则四边形APQB周长的最小值为 .思路引领:由于四边形APQB的周长可表示为AP+BQ+7,则要使其最小,只要AP+BQ最小即可.在AB 边上截取AM=PQ,因为点F是BC的中点,所以点B关于EF的对称点为点C,连接CM,交EF于点Q,则CM即为AP+BQ的最小值.在Rt△BCM中,利用勾股定理可求出MC的值,进而可得出答案.解:∵AB=5,PQ=2,∴四边形APQB的周长为AP+PQ+BQ+AB=AP+BQ+7,则要使四边形APQB的周长最小,只要AP+BQ最小即可.在AB边上截取AM=PQ,∵点F是BC的中点,∴点B关于EF的对称点为点C,连接CM,交EF于点Q,则CM即为AP+BQ的最小值.在Rt△BCM中,MB=AB﹣AM=5﹣2=3,BC=4,∴CM==5,∴四边形APQB的周长最小值为5+7=12.故答案为:12.总结提升:本题考查轴对称﹣最短路线问题、矩形的性质,能够将所求四边形的周长转化为求AP+BQ 的最小值是解题的关键.9.(2022春•姑苏区校级月考)如图,矩形ABCD中,AB=3,BC=6,点E、F、G、H分别在矩形的各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )A.B.C.D.思路引领:作点E关于BC的对称点E′,连接E′G交BC于点F,此时四边形EFGH周长取最小值,过点G作GG′⊥AB于点G′,由对称结合矩形的性质可知:E′G′=AB,GG′=AD,利用勾股定理即可求出E′G的长度,进而可得出四边形EFGH周长的最小值.解:作点E关于BC的对称点E′,连接E′G交BC于点F,此时四边形EFGH周长取最小值,EF=E'F,过点G作GG′⊥AB于点G′,如图所示.∵AE=CG,BE=BE′,∴E′G′=AB=3,∵GG′=AD=6,∴E′G=∴C=2(GF+EF)=2E′G=四边形EFGH故选:C.总结提升:本题考查了轴对称中的最短路线问题以及矩形的性质,找出四边形EFGH周长取最小值时点E、F、G之间的位置关系是解题的关键.10.(2022秋•沙坪坝区校级期末)如图,在平面直角坐标系中,点A(﹣2,2),B(﹣5,5)是第二象限角平分线上的两点,点C的纵坐标为2,且CA=CB,在y轴上取一点D,连接AC,BC,AD,BD,使得四边形ACBD的周长最小,则周长的最小值为 .思路引领:根据平行线的性质得到∠BAC=45°,得到∠C=90°,求得AC=BC=3,作点A关于y轴的对称点A′,连接A′B交y轴于D′,则此时,四边形ACBD的周长最小,这个最小周长的值=AC+BC+A′B,然后根据勾股定理即可得到结论.解:∵点A(﹣2,2),点C的纵坐标为2,∴AC∥x轴,∴∠BAC=45°,∵CA=CB,∴∠ABC=∠BAC=45°,∴∠C=90°,∵B(﹣5,5),∴C(﹣5,2),∴AC=BC=3,如图,作点A关于y轴的对称点A′,连接A′B交y轴于D′,此时,四边形ACBD的周长最小,这个最小周长的值=AC+BC+A′B,∵AC=BC=3,AA′=4,∴A′C=3+4=7,∴A′B=∴最小周长的值=AC+BC+A′B=6故答案为:6总结提升:本题考查了轴对称﹣最短路线问题,坐标与图形的性质,勾股定理,正确的作出辅助线是解题的关键.11.(2019春•仙游县期中)菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°(1)试判断△AEF的形状并说明理由;(2)若菱形的边长为2,求△ECF周长的最小值.思路引领:(1)先根据四边形ABCD是菱形判断出△ABC的形状,在AB上截取BG=BE,则△BGE是等边三角形.再由ASA定理得出△AGE≌△ECF,故可得出AE=AF,由此可得出结论;(2)根据垂线段最短可知当AE⊥BC时△ECF周长最小,由直角三角形的性质求出CE的长,故可得出结论.解:(1)△AEF是等边三角形,理由是:∵四边形ABCD是菱形,∴AB=BC.∵∠B=60°.∴△ABC是等边三角形,在AB上截取BG=BE,则△BGE是等边三角形∴AG=AB﹣BG=BC﹣BE=EC,∵∠AEC=∠BAE+∠B=∠AEF+∠FEC,又因为∠B=∠AEF=60°∴∠BAE=∠CEF.在△AGE与△ECF中,∠AGE=∠ECF=120°AG=EC.∠GAE=∠CEF∴△AGE≌△ECF(ASA),∴AE=AF.∵∠AEF=60°,∴△AEF是等边三角形.(2)由(1)知△AEF是等边三角形,△AGE≌△ECF∴CF=GE=BE,CF+EC=BC=2(定值)∵垂线段最短,∴当AE⊥BC时,AE=EF最小,此时△ECF周长最小、∵BC=2,∠B=60°,∴AE=∴△ECF周长的最小值=2+总结提升:本题考查的是菱形的性质,熟知四条边都相等的平行四边形是菱形是解答此题的关键.。
人教版初二数学8年级下册 第18章(平行四边形)最值问题专题训练(含答案)

人教版数学八年级下期第十八章平行四边形最值问题训练一、选择题1.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是()A. 1B. 1C. 2D. 222.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是( )A. 33B. 3+33C. 6+3D. 633.如图,在矩形ABCD中,AB=3,BC=4,在矩形内部有一动点P满足S△PAB=3S△PDC,则动点P到点A,B两点距离之和PA+PB的最小值为()A. 5B. 35C. 3+32D. 2134.如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.则EF的最大值与最小值分别为()A. 4,2B. 4,23C. 5,3D. 5,325.如图,点P是正方形ABCD的边AD上的一动点,正方形的边长为4,点P到正方形的两条对角线AC和BD的距离分别为PM,PN,则PM2+PN2的最小值为()A. 2B. 4C. 9D. 126.如图,四边形ABCD是菱形,AB=8,且∠ABC=60°,M为对角线BD(不含B点)BM的最小值为( )上任意一点,则AM+12A. 43B. 33C. 42D. 32二、填空题7.如图,P为菱形ABCD的对角线上一点,PF⊥AD于F,PF=3cm,点E为AB边上一动点,则PE的最小值为______cm.8.如图,在边长为4的菱形ABCD中,∠A=60°,若M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则A′C的最小值为 .9.如图,在菱形ABCD中,∠ABC=60°,AB=8,点M、N分别在边AB、CD上,且AM=2,DN=4,点P、Q分别为BC、AD上的动点,连接PM、PN、PQ,则PM+PN+PQ 的最小值为______.10.如图,长方形ABCD中,AB=6,BC=4,在长方形的内部以CD边为斜边任意作Rt△CDE,连接AE,则线段AE长的最小值是_____.11.如图,在矩形ABCD中,AB=3,AD=10,点E在AD上且DE=2.点G为AE的中点,点P为BC边上的一个动点,F为EP的中点,则GF+EF的最小值为________.12.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为4,则线段DH长度的最小值是____.三、解答题13.如图,在边长为m的菱形ABCD中,∠DAB=60°,E是AD上不同于A,D两点的一动点,F是CD上一动点,且AE+CF=m.(1)证明:无论E,F怎样移动,△BEF总是等边三角形;(2)求△BEF面积的最小值.14.如图,在菱形ABCD中,AB=6,∠ADC=120°,P为对角线AC上的一点,过P作PE∥AB交AD与E,PF∥AD交CD于F,连接BE、BF、EF(1)求AC的长;(2)求证:△BEF为等边三角形;(3)四边形BEPF面积的最小值为______15.如图1,四边形ABCD是矩形,点O位于对角线BD上,将△ADE,△CBF分别沿DE、BF翻折,点A,点C都恰好落在点O处.(1)求证:∠EDO=∠FBO;(2)求证:四边形DEBF是菱形:(3)如图2,若AD=2,点P是线段ED上的动点,求2AP+DP的最小值.16.如图,在矩形ABCD中,AD=2AB,E是边AD的中点,F是边AB上的一个动点,连结EF,过点E作EG⊥EF交BC于点G.(1)求证:EF=GE;(2)若AB=1,则AF+EF+CG的最小值为______.17.如图,正方形ABCD的边长为25,O是BC边的中点,P是正方形内一动点,且OP=2,连接DP,将线段DP绕点D逆时针旋转90°到DQ,连接AP,CQ.(1)直接写出线段AP和CQ的关系.(2)当A,O,P三点共线时,求线段DP的长.(3)连接PQ,求线段PQ的最小值.18.如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形;(3)在(2)的条件下,如果AB=10,那么△AEF的周长是否存在最小值?如果存在,请求出来.参考答案1.B2.D3.B4.B5.B6.A7.38.27-29.231+4310.211.512.25-213.解:(1)连接BD,∵∠DAB=60°,∴△ABD是等边三角形,∴AB=DB,又∵AE+CF=m,∴AE=DF,在△ABE 和△DBF 中AB =DB ∠A =∠BDF =60°AE =DF,∴△ABE ≌△DBF (SAS ),∴BE =BF ∴∠EBF =∠ABD =60°,∴△BEF 是等边三角形.(2)当BE ⊥AD 时面积最小,此时BE =m 2−(12m )2=32m ,△BEF 的EF 边上的高=(32m )2−(34m )2=34m ,S △BEF =12×32m ×34m =3163m 2.14.解:(1)连接BD ,交AC 于G ,∵菱形ABCD 中,AC 和BD 是对角线,∴BD ⊥AC ,AG =CG =12AC ,∵AB =6,∠ADC =120°,∴∠BAC =∠BCA =30°,在Rt △ABG 中,AG =AB •cos ∠BAC =6×32=33,∴AC =2AG =63;(2)证明:∵在菱形ABCD 中,AB =6,∠ADC =120°,∴∠BAD =∠BCD =60°,∠ABD =∠CBD =∠ADB =∠CDB =60°,∴△ABD 是等边三角形,∴BD =AB =BC =6,∵PE ∥AB ,PF ∥AD ,∴∠CPF =∠CAD ,四边形DEPF 是平行四边形,∴ED =PF ,∵AD =DC ,∴∠CAD =∠ACD ,∴∠CPF =∠ACD ,∴PF =FC ,∴ED =FC ,在△BED 和△BFC 中ED =FC ∠EDB =∠FCB =60°BD =BC∴△BED ≌△BFC (SAS ),∴BE =BF ,∠EBD =∠FBC ,∵∠FBC +∠FBD =∠CBD =60°,∴∠EBD +∠FBD =∠EBF =60°,∴△BEF 是等边三角形;(3)93215.(1)证明:∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠ADB =∠CBD ,∵将△ADE ,△CBF 分别沿DE 、BF 翻折,点A ,点C 都恰好落在点O 处.∴△ADE ≌△ODE ,∴△CFB ≌△OFB ,∴∠ADE =∠ODE =12∠ADB ,∠CBF =∠OBF =12∠CBD ,∴∠EDO =∠FBO ;(2)证明:∵∠EDO =∠FBO ,∴DE ∥BF ,∵四边形ABCD 是矩形,∴AB ∥CD ,AD =BC ,∠A =90°,∵DE ∥BF ,AB ∥CD ,∴四边形DEBF 是平行四边形,又∵△ADE △≌△ODE ,∴∠A =∠DOE =90°,∴EF ⊥BD ,∴四边形DEBF 是菱形;(3)解:过点P 作PH ⊥AD 于点H ,∵四边形DEBF是菱形,△ADE≌△ODE,∴∠ADE=∠ODE=∠ODF=30°,∴在Rt△DPH中,2PH=PD,∴2AP+PD=2PA+2PH=2(AP+PH),过点O作OM⊥AD,与DE的交点即是2AP+PD的值最小的点P的位置.而此时(2AP+PD)的最小值=2OM,∵△ADE≌△ODE,AD=2,∴AD=DO=2,在Rt△OMD中,∵∠ODA=2∠ADE=60°,∴∠DOM=30°,∴DM=12DO=1,∵DM2+OM2=DO2,∴12+OM2=22,∴OM=3,∴(2PA+PD)的最小值为2OM=23.16.217.解:(1)AP=CQ,AP⊥CQ;理由如下:延长QC、AP交于点E,AP的延长线交BC于F,如图1所示:∵四边形ABCD是正方形,∴AD=CD,∠ADC=∠BCD=90°,AD∥BC,由旋转的性质得:∠PDQ=90°,DP=DQ,∴∠ADP=∠CDQ,在△ADP和△CDQ中,AD=CD∠ADP=∠CDQDP=DQ,∴△ADP≌△CDQ(SAS),∴AP=CQ,∠DAP=∠DCQ,∵∠BCD=90°,∴∠DCQ+∠ECF=90°,∵AD∥BC,∴∠DAP=∠CFE,∴∠CFE+∠ECF=90°,∴∠CEF=90°,∴AE⊥QE,∴AP⊥CQ;(2)作DH⊥AP于H,如图2所示:∵O是BC边的中点,∴OB=12BC=5,当A,O,P三点共线时,由勾股定理得:AO=AB2+OB2=(25)2+(5)2=5,∵四边形ABCD是正方形,∴∠B=90°,AD∥BC,∴∠DAH=∠BOA,∴sin∠DAH=sin∠BOA=ABAO =255,cos∠DAH=cos∠BOA=OBAO=55,∴DH=AD×sin∠DAH=25×255=4,AH=AD×cos∠DAH=25×55=2,∴PH=AO-AH-OP=5-2-2=1,∴DP=42+12=17;(3)连接OD,如图3所示:∵DQ=DP,∠PDQ=90°,∴PQ=2DP,OD=DC2+OC2=(25)2+(5)2=5,∵OP+DP≥OD,∴DP≥OD-OP=5-2=3,∴PQ≥32,∴线段PQ的最小值为32.18.证明:(1)如图1,连接AC,∵在菱形ABCD中,∠B=60°,∴AB=BC=CD,∠C=180°-∠B=120°,∴△ABC是等边三角形,∵E是BC的中点,∴AE⊥BC,∵∠AEF=60°,∴∠FEC=90°-∠AEF=30°,∴∠CFE=180°-∠FEC-∠ECF=180°-30°-120°=30°,∴∠FEC=∠CFE,∴EC=CF,∴BE=DF;(2)如图2,连接AC,∵△ABC是等边三角形,∴AB=AC,∠ACB=60°,∴∠B=∠ACF=60°,∵AD∥BC,∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD,∴∠AEB=∠AFC,在△ABE和△ACF中,∠B=∠ACF∠AEB=∠AFC,AB=AC∴△ABE≌△ACF(AAS),∴AE=AF,∵∠EAF=60°,∴△AEF是等边三角形.(3)由垂线段最短可知:当AE⊥BC时,AE有最小值.∵AE⊥BC,∠B=60°,∴AE AB =32.∴AE=10×32=53.∴△AEF周长的最小值为3×53=153.。
第十八章+平行四边形平行四边形中的最值问题+讲练课件+++2023—2024学年人教版数学八年级下册

如图2,过点O作OM⊥AD于点M,与DE的交点即是
2AP+PD的值最小的点P的位置. 而此时(2AP+PD)的
最小值=2OM,
∵△ADE≌△ODE,AD=2, ∴AD=DO=2.
在Rt△OMD中,∵∠ODA=2∠ADE=60°, ∴∠DOM=30°. ∴DM= 12 DO=1. ∵DM2+OM2=DO2, ∴12+OM2=22. ∴OM= 3 . ∴(2PA+PD)的最小值为2OM=2 3 .
6. 如图,∠MON=90°,长方形ABCD的顶点B,C分别 在边OM,ON上,当点B在边OM上运动时,点C随之 在边ON上运动,若CD=5,BC=24,运动过程中, 点D到点O的最大距离为_2_5__.
利用线段转化求最值 7. 如图,以边长为2的正方形的对角线的交点O为端点,
引两条相互垂直的射线,分别与正方形的边交于A,B 两点,求线段AB的最小值.
∴△AOB是等腰直角三角形. ∴AB= 2 OA. ∴当OA最小时,AB最小. ∵OA⊥CD时,OA最小, ∴A为CD的中点,∴OA= 12CD=1. ∴AB= 2 OA= 2 . ∴线段AB的最小值为 2 .
8. 如图1所示,四边形ABCD是矩形,点O位于对角线BD 上,将△ADE,△CBF分别沿DE,BF翻折,使点A、 点C都恰好落在点O处. (1)求证:∠EDO=∠FBO;平行四边形
专题:平行四边形中的最值问题
利用轴对称求最值
1. 如图,正方形ABCD的边长为3,点E在BC上,且BE =2,点P在对角线BD上,则PE+PC的最小值为 ( B )
2. 如图,菱形ABCD的边长为2,∠DAB=60°,点E为 BC边的中点,点P为对角线AC上一动点,则PB+PE 的最小值为__3__.
专题 平行四边形中的最值问题(原卷版)

八年级下册数学《第十八章 平行四边形》专题 平行四边形中的最值问题【例题1】(2022秋•榆树市期末)如图,在Rt △ABC 中,∠BAC =90°,∠ACB =45°,AB =8√2,点P 为BC 上任意一点,连结P A ,以P A ,PC 为邻边作平行四边形P AQC ,连结PQ ,则PQ 的最小值为( )A .4B .8C .4√2D .8√2【变式1-1】(2022春•溧水区期中)如图,∠AOB =30°,OB =4,点P 为射线OA 上任意一点,连接PB .以PO 、PB 为邻边作平行四边形POQB ,连接PQ ,则线段PQ 的最小值为 .【变式1-2】(2021秋•泰山区期末)如图,四边形ABCD 是平行四边形,∠BCD =120°,AB =2,BC =4,点E 是直线BC 上的点,点F 是直线CD 上的点,连接AF ,AE ,EF ,点M ,N 分别是AF ,EF 的中点.连接MN ,则MN 的最小值为( )A .1B .√3−1C .√32D .2−√3【变式1-3】(2021春•雁塔区校级月考)在平行四边形ABCD 中,BC =4,∠B =60°,过点A 分别作BC ,CD 的垂线,垂足分别为M 、N ,连接MN ,则MN 的最小值为( )A .√3B .3C .2√3D .2【变式1-4】(2022•瑶海区校级一模)如图,在平行四边形ABCD中,BD⊥AD,AB=√2AD,E是AB的中点,P是边AD上的一动点,若AD=2,则PE+PB的最小值为()A.2√2B.2√3C.√10D.2√10【变式1-5】(2021秋•海州区校级期末)如图,在平行四边形ABCD中,AD=12,AB=6,以AD为底边向右作腰长为10的等腰△ADP,Q为边BC上一点,BQ=4,连接PQ,则PQ的最小值为.【变式1-6】(2022•榆林模拟)如图,在Rt△ABC中,AC=2√3,BC=2.点P是斜边AB上任意一点,D是AC的中点.连接PD并延长,使DE=PD.以PE,PC为边构造平行四边形PCQE,则对角线PQ 的最小值.【变式1-7】(2021•沂水县一模)如图,在△ABC中,∠BAC=30°,AB=AC=3,P为AB边上一动点,以P A,PC为邻边作平行四边形P AQC,则对角线PQ的最小值为.【变式1-8】(2021•房县模拟)如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G 分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最大值与最小值的差为.【变式1-9】如图,在▱ABCD中,AB=2,BC=4,∠D=60°,点P,Q分别是AC,BC上的动点,在P,Q运动过程中,PB+PQ的最小值是.【例题2】(2021•内江模拟)如图,矩形ABCD中,∠BOC=120°,BD=12,点P是AD边上一动点,则OP的最小值为()A.3B.4C.5D.6【变式2-1】(2022春•永春县期末)如图,∠MON =90°,矩形ABCD 的顶点A 、B 分别在边OM 、ON 上,AB =6,BC =2.当B 在边ON 上运动时(点B 与O 不重合),A 随之在OM 上运动.点E 在AB 边上,AE =2EB ,四边形OADE 的面积为263,则OA +OB 的值等于( )A .7B .√50C .8D .8.5【变式2-2】(2022秋•南安市期末)如图,点P 是长方形ABCD 内部的一个动点,已知AB =7,BC =15,若△PBC 的面积等于30,则点P 到B 、C 两点距离之和PB +PC 的最小值是 .【变式2-3】(2021•阜新)如图,折叠矩形纸片ABCD ,使点B 的对应点E 落在CD 边上,GH 为折痕,已知AB =6,BC =10.当折痕GH 最长时,线段BH 的长为 .【变式2-4】(2021春•沭阳县期末)如图,在矩形ABCD 中,AB =6,AD =8,以BC 为斜边在矩形的外部作直角三角形BEC ,点F 是CD 的中点,则EF 的最大值为( )A .8B .9C .10D .2√41【变式2-5】(2022春•仪征市期中)如图,矩形ABCD的边AB=7,BC=3,点E在边AB上,且AE=1,F为AD边上的一个动点,连接EF,将线段EF绕点E顺时针旋转90°得到EG,连接CG,则CG的最小值为()A.2B.3C.√10D.√13【变式2-6】(2022春•晋安区期末)如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为()A.8B.10C.12D.20【变式2-7】(2022春•瑶海区期末)如图,在矩形ABCD中,点N、O、P.M分别是边AB、BC、CD、DA上的点(不与端点重合),若AN=CP、BO=DM,且AB=2BC=2,则四边形MNOP周长的最小值等于()A.2√5B.2√3C.√5D.√3【变式2-8】(2021秋•松山区期末)如图,矩形ABCD中,AB=√3,BC=3,P 为矩形内一点,连接P A,PB,PC,则P A+PB+PC的最小值是()A.2√3+3B.2√5C.2√3D.√21【例题3】(2021春•玉州区期中)如图,在菱形ABCD中,∠D=135°,AD=6√2,CE=4,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值()A.4√2B.6C.2√10D.4√5【变式3-1】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是()A.8B.10C.10.4D.12【变式3-2】(2022•花都区二模)如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,点P为边AB上一点,且点P不与点A,B重合.过点P作PE⊥AC于点E,PF⊥BD于点F,连接EF,则EF的最小值为()A.2B.2.4C.2.5D.3【变式3-3】(2022春•鼓楼区校级期中)如图,菱形ABCD的边长为3,且∠ABC=60°,E、F是对角线BD上的两个动点,且EF=2,连接AE、AF,则AE+AF的最小值为()A.2√3B.√6C.3√2D.√13【变式3-4】(2022春•兴宁区校级期中)如图,已知菱形ABCD的边长为8,点M是对角线AC上的一动点,且∠ADC=120°,则MA+MB+MD的最小值是()A.4√3B.8√3C.8+√3D.4+4√3【变式3-5】(2022春•惠民县期末)如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为()A.2+2√3B.4C.4√3D.6【变式3-6】(2022•安徽一模)如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是()A.√7B.√7−1C.√3D.2【变式3-7】如图,在菱形ABCD中,对角线AC=6,BD=8,点E为AB边的中点,点P为对角线BD 上一动点,连接PC,PE,求|PC﹣PE|的最大值.【变式3-8】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是边AD、CD上的动点,且AE+CF =4,连接BE、EF、FB.(1)证明:BE=BF;(2)求△BEF面积的最小值.【例题4】(2022春•海州区校级期末)如图,在边长为6的正方形ABCD 中,点M 为对角线BD 上一动点,ME ⊥BC 于E ,MF ⊥CD 于F ,则EF 的最小值为( )A .3√2 B .6√2 C .3 D .2【变式4-1】(2022春•潼南区期末)如图,正方形ABCD 的对角线AC ,BD 相交于点O ,点P 是BC 上任意一点,PE ⊥BD 于点E ,PF ⊥AC 于点F ,若AC =2√2,则EF 的长的最小值为( )A .2B .1C .√2D .√22【变式4-2】(2021春•莱州市期末)如图,正方形ABCD 的边长为4,点E 在AB 上,且BE =1,F 为对角线AC 上一动点,则△BFE 周长的最小值为 .【变式4-3】(2021春•惠山区期中)如图,平面内三点A 、B 、C ,AB =5,AC =4,以BC 为对角线作正方形BDCE ,连接AD ,则AD 的最大值是( )A .5B .9C .9√2D .92√2【变式4-4】(2022•扬州三模)如图,已知正方形ABCD 的边长为3,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90°到EF ,连接DF ,CF ,则DF +CF 的最小值是( )A .3√5B .4√3C .5√2D .2√13【变式4-5】如图,在矩形ABCD 中,AB =5,BC =6,点E 在BC 边上,且BE =2,F 为AB 边上的一个动点,连接EF ,以EF 为边作等边△EFG ,且点G 在矩形ABCD 内,连接CG ,则CG 的最小值为( )A .3B .2.5C .4D .2√3【变式4-6】如图,正方形ABCD中,AB=3,点E为对角线AC上的动点,以DE为边作正方形DEFG.点H是CD上一点,且DH=23CD,连接GH,CG,则∠DCG=度,运动变化过程中,GH的最小值为.【变式4-7】如图,正方形ABCD的边长为1,点P为BC上任意一点(可与点B或C重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是()A.1B.√2C.√3D.√5【变式4-8】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为2,则线段CF的最小值是()A.2B.1C.√5−1D.√5−2。
专题二 特殊平行四边形中的最值问题

∴∠FEG=∠AEB=90°,∴∠AEF=∠BEG.
又∵∠EFA=∠G=90°,EA=EB,
∴△AEF≌△BEG(AAS),∴PB=PF+AF+PG-BG=2PF=2EF.
∵EF≤AE,∴EF的最大值为AE=2 ,∴△APB周长的最大值为4+4 .
A. 6
B.2 3
C.3
D.2 6
第7题图
8.如图所示,平面内三点A,B,C,AB=4,AC=3,以BC为对角线作正方形
BDCE,连接AD,则AD的最大值是( D )
第8题图
A.5
B.7
C.7 2
D.
7 2
2
9.(2022·江苏泰州中考)如图所示,正方形ABCD的边长为2,E为与点D不重合
的动点,以DE为一边作正方形DEFG.设DE=d1,点F,G与点C的距离分别为
∴∠APB=90°,∴AM⊥BN.
(2)如图②所示,已知正方形ABCD的边长为4.点M,N分别从点B,C同时出
发,以相同的速度沿BC,CD方向向终点C和D运动,连接AM和BN,交于点P.求
△APB周长的最大值.
解:(2)如图所示,以AB为斜边向外作等腰直角三角形AEB,∠AEB=90°,
作EF⊥PA于点F,作EG⊥PB交PB的延长线于点G,连接EP.∵∠EFP=∠FPG=
一动点,PE⊥AB于点E,PF⊥AC于点F,点M为EF的中点,则AM的最小
值是( B )
第4题图
A.2.5
B.2.4
C.2
D.3
5.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是
,
OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为
第十八章全国通用版中考数学:《平行四边形》最值问题(一)—解析版

第十八章专题:《平行四边形》最值问题(一)1.如图,∠MON=90°,矩形ABCD在∠MON的内部,顶点A,B分别在射线OM,ON上,AB=4,BC=2,则点D到点O的最大距离是()A.222+C.252-D.22-B.222+【答案】B【解析】取AB中点E,连接OE、DE、OD,∵∠MON=90°,∴OE=AB=2.在Rt△DAE中,利用勾股定理可得DE=2.在△ODE中,根据三角形三边关系可知DE+OE>OD,∴当O、E、D三点共线时,OD最大为OE+DE=2+2.2.如图,矩形ABCD中,AB=2,BC=6,P为矩形内一点,连接P A,PB,PC,则P A+PB+PC的最小值是()A.433+B.221C.236+D.45【答案】B【解析】将△BPC绕点C逆时针旋转60°,得到△EFC,连接PF、AE、AC,则AE的长即为所求.由旋转的性质可知:△PFC是等边三角形,∴PC=PF,∵PB=EF,∴P A+PB+PC=P A+PF+EF,∴当A、P、F、E共线时,P A+PB+PC的值最小,∵四边形ABCD是矩形,∴∠ABC=90°,∴∠ACB=30°,AC=2AB=4,∵∠BCE=60°,∴∠ACE=90°,∴AE==2,3.如图,已知∠XOY=60°,点A在边OX上,OA=2,过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边△ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY 交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b最大值是.【答案】5【解析】如图1,过P作PH⊥OY交于点H,∵PD∥OY,PE∥OX,∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,∴EP=OD=a,Rt△HEP中,∠EPH=30°,∴EH=EP=a,∴a+2b=2(a+b)=2(EH+EO)=2OH,当P在点B时,如图2,OC=1,AC=BC=,Rt△CHP中,∠HCP=30°,∴PH=,CH =,则OH的最大值是:OC+CH=1+=,即(a+2b)的最大值是5,4.如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为()A.B.2C.22D.32【答案】A【解析】如图,作EH⊥x轴于H,连接CE.∵∠AOD=∠ADE=∠EHD=90°,∴∠ADO+∠EDH=90°,∠EDH+∠DEH=90°,∴∠ADO=∠DEH,∵AD=DE,∴△ADO≌△DEH(AAS),∴OA=DH=OC,OD=EH,∴OD=CH=EH,∴∠ECH=45°,∴点E在直线y=x﹣3上运动,作OE′⊥CE,则△OCE′是等腰直角三角形,∵OC=3,∴OE′=,∴OE的最小值为.5.如图,四边形ABCD中,AB∥CD,AB=BC=2,∠BCD=30°,∠E=45°,点D在CE上,且CD=BC,点H是AC上的一个动点,则HD+HE最小值为.【答案】【解析】∵AB∥CD,CD=BC=AB,∴四边形ABCD是平行四边形,∵AB=BC,∴四边形ABCD是菱形,∴B、D关于AC对称,连接BE交AC于H′,连接DH′,此时DH′+EH′的值最小,最小值=BE,作AM⊥EC于M,EN⊥BA交BA的延长线于N.∵四边形ABCD是菱形,∴AD∥BC,∴∠ADM=∠BCD=30°,∵AD=2,∴AM=AD=1,∵∠AEC=45°,∴AM=EM=1,∵AM⊥CE,EN⊥BN,CE∥NB,∴∠AME=∠N=∠MAN=90°,∴四边形AMEN是矩形,∵AM=EM=1,∴四边形AMEN是正方形,∴AN=EM=AM=EN=1,在Rt△BNE中,BE===,6.如图,正方形ABCD的边长为4,点E为AD的延长线上一点,且DE=DC,点P为边AD上一动点,且PC⊥PG,PG=PC,点F为EG的中点.当点P从D点运动到A点时,则CF的最小值为.【答案】22【解析】∵正方形ABCD的边长为4,∴AB=BC=4,∠B=90°,∴AC=42,当P与D重合时,PC=ED=P A,即G与A重合,∴EG 的中点为D ,即F 与D 重合,当点P 从D 点运动到A 点时,则点F 运动的轨迹为DF ,∵D 是AE 的中点,F 是EG 的中点,∴DF 是△EAG 的中位线,∴DF ∥AG ,∵∠CAG =90°,∠CAB =45°,∴∠BAG =45°,∴∠EAG =135°,∴∠EDF =135°,∴∠FDA =45°,∴F 为正方形ABCD 的对角线的交点,CF ⊥DF ,此时CF 最小,此时CF =AG =AC =22,7. 如图,在Rt △ABC 中,∠BAC=90°,∠B=60°,AB=1,点P 为BC 上任意一点,连接PA ,以PA 、PC 为邻边作▱PAQC ,连接PQ ,则PQ 的最小值为 __________。
第十八章全国通用版中考数学:《平行四边形》最值问题(四)—解析版

第十八章专题:《平行四边形》最值问题(四)1.如图,菱形ABCD中,AB=4,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°,则△BEF周长的最小值是()A.6 B.43C.4+3D.4+23【答案】D【解析】连接BD,∵菱形ABCD中,∠A=60°,∴△ADB与△CDB是等边三角形,∴∠DBE=∠C=∠60°,BD=DC,∵∠EDF=60°,∴∠BDE=∠CDF,在△BDE和△CDF中,∠DBE=∠C,∠BDE=∠CDF,BD=CD,∴△DBE≌△DCF,∴DE=DF,∠BDE=∠CDF,BE=CF,∴∠EDF=∠BDC=60°,∴△DEF是等边三角形,∵△BEF的周长=BE+BF+EF=BF+CF+EF=BC+EF=4+EF,∴等边三角形△DEF的边长最小时,△BEF的周长最小,当DE⊥AB时,DE最小=23,∴△BEF的周长最小值为4+23,2.如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,G为对角线BD(不含B点)上任意一点,将△ABG绕点B逆时针旋转60°得到△EBF,当AG+BG+CG取最小值时EF的长___________。
【答案】3 4【解析】如图,∵将△ABG绕点B逆时针旋转60°得到△EBF,∴BE=AB=BC,BF=BG,EF=AG,∴△BFG是等边三角形.∴BF=BG=F,.∴AM+BM+CM=EN+MN+CM.根据“两点之间线段最短”,∴当G点位于BD与CE的交点处时,AG+BG+CG的值最小,即等于EC的长,过E点作EF⊥BC交CB的延长线于F,∴∠EBF=180°-120°=60°,∵BC=4,∴BF=2,EF=23,在Rt△EFC中,∵EF2+FC2=EC2,∴EC=43.∵∠CBE=120°,∴∠BEF=30°,∵∠EBF=∠ABG=30°,∴EF=BF=FG ,∴EF=31CE=334,3. 如图,正方形ABCD 的边长为2,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC上有一点P ,使PD+PE 的和最小,则这个最小值为( )A .2B .22C .2D .6【答案】A【解析】连接BD ,与AC 交于点F .∵点B 与D 关于AC 对称,∴PD=PB ,∴PD+PE=PB+PE=BE 最小.∵正方形ABCD 的边长为2,∴AB=2.又∵△ABE 是等边三角形,∴BE=AB=2.∴所求最小值为24. 如图,正方形ABCD 的边长为6,EF 为正方形ABCD 的对称轴,交BC 于F 点,点G 是对称轴EF 上的一个动点,连接GC ,将线段GC 绕点C 逆时针旋转90°得到HC ,连接HF ,则在点G 运动过程中,HF 的最小值是( )A .21 B .22 C .23 D .3 【答案】D【解析】如图所示,取CD 的中点P ,连接GP ,∵正方形ABCD 的边长为6,EF 为正方形ABCD 的对称轴,∴CP=CF=3,∠FCP=90°,∵将线段GC 绕点C 逆时针旋转90°得到HC ,∴CG=CH ,∠HCG=90°,∴∠PCG+∠GCF=∠FCH+∠GCF=90°,∴∠PCG=∠FCH ,在△PCG 和△FCH 中,CP =CF,∠PCG =∠FCH,CG =CH ,∴△PCG ≌△FCH (SAS ),∴FH=PG ,∵点P到EF的距离为3,∴当GP⊥CD时,GP最短为3,此时,FH最短为3,5.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.EF的最小值为___________。
微讲座—利用平行四边形对角线关系解决最值问题

微讲座—利用平行四边形对角线关系解决最值问题引言本文将介绍如何利用平行四边形的对角线关系,解决数学中的最值问题。
通过理解对角线的性质以及最值的定义,在解决问题时可以更加高效和简便。
本文主要包括以下几个方面的内容:对角线的定义、平行四边形的性质、利用对角线关系解决最值问题的步骤以及一些应用示例。
---1. 对角线的定义平行四边形是指具有两对平行的边的四边形。
对角线是连接非相邻顶点的线段,分为两条。
我们用AC和BD分别表示平行四边形ABCD的两条对角线。
---2. 平行四边形的性质平行四边形的对角线具有以下性质:- 对角线相等:即AC = BD。
- 对角线互相平分:即AC和BD互相平分彼此的交点。
这些性质是平行四边形独有的,利用这些性质可以简化解决问题的过程。
---3. 利用对角线关系解决最值问题的步骤对于求解最值问题,我们可以利用平行四边形的对角线关系来简化计算。
步骤如下:1. 首先,根据题目给出的条件,构造一个平行四边形,并标记出对角线AC和BD。
2. 利用对角线的相等性质,得出AC = BD的等式。
3. 根据对角线相互平分的性质,可得到AC和BD互相平分的交点E。
4. 根据最值问题的要求,利用平行四边形中对角线长度相等的关系,将问题转化为AC和BD的长度问题。
5. 利用所学的数学知识,解决出AC和BD的长度,并据此得到最终结果。
通过以上步骤,我们可以利用平行四边形的对角线关系解决最值问题,简化计算过程,提高解题效率。
---4. 应用示例下面举一个应用示例来说明如何利用平行四边形的对角线关系解决最值问题。
示例:求解平行四边形的最大面积问题描述:已知平行四边形ABCD的两边长分别为5cm和8cm,求平行四边形的最大面积。
解题步骤:1. 构造平行四边形ABCD,并标记出对角线AC和BD。
2. 利用对角线的相等性质,得出AC = BD的等式。
3. 根据对角线相互平分的性质,可得到AC和BD互相平分的交点E。
四边形中的最值问题

四边形中的最值问题1.引言四边形是平面几何中的一个基本概念,它具有四个边和四个角的特征。
在四边形的研究中,我们常常遇到一些最值问题,即求解四边形中某个特征的最大值或最小值。
本文将探讨四边形中的最值问题,介绍不同类型的四边形及其特点,并通过具体例子进行分析和求解,帮助读者更好理解和应用相关知识。
2.四边形的分类四边形可以根据边的性质和角的性质进行分类,常见的四边形包括矩形、正方形、平行四边形、菱形、梯形等。
接下来我们将分别介绍这些四边形的特点和性质。
2.1 矩形矩形是一种特殊的平行四边形,其特点是拥有四个直角,对边相等且平行。
在矩形中,我们常常需要求解最大或最小的周长、面积或对角线长度。
2.2 正方形正方形是一种特殊的矩形,其特点是拥有四个相等的边和四个直角。
在正方形中,周长、面积和对角线长度都是最值问题的重点。
2.3 平行四边形平行四边形是指具有两组相等且平行的对边的四边形。
在平行四边形中,我们需要考虑最值问题时,常常涉及到边长、角度、面积等的求解。
2.4 菱形菱形是一种特殊的平行四边形,其特点是拥有四个相等的边和两组相互垂直的对角线。
在菱形中,最值问题常常涉及到边长、角度和面积等的求解。
2.5 梯形梯形是一种至少有一对平行边的四边形。
在梯形中,需要考虑最值问题时,我们常常需要求解最大或最小的面积、周长或某个角度的大小。
3.求解最值问题的方法在四边形中求解最值问题,我们可以采用不同的方法和技巧。
下面将介绍一些常用的方法,以帮助读者更好地解决类似问题。
3.1 几何方法在几何方法中,我们通过观察四边形的形状和特征,利用几何定理进行推导和证明,从而得出最值问题的结果。
例如,在矩形中求解最大面积,我们可以利用矩形的对称性和面积公式进行推导。
3.2 代数方法在代数方法中,我们通过引入代数变量,建立方程或不等式,利用数学运算和求解技巧,求解最值问题。
例如,在平行四边形中求解最大周长,我们可以表示边长为变量,建立周长的表达式,通过求导等方法求解最值。
平行四边形动点最值问题

平行四边形动点最值问题在平面直角坐标系中,给定平行四边形ABCD,其中AB与CD平行,AB=a,BC=h。
设点P在平行四边形内部运动,且其横坐标为x,纵坐标为y。
若定义函数f(x)=PA+PB-PC-PD,求f(x)的最大值和最小值。
解题思路:首先得出点P的坐标为(x,y),则点A的坐标为(0,h),点B的坐标为(a,h),点C的坐标为(a,-h),点D的坐标为(0,-h)。
接下来考虑如何求出PA、PB、PC、PD的值。
根据勾股定理,PA = (x-0) + (y-h) = x + y - 2hy + h,同理可得PB = (x-a) + (y-h) = x - 2ax + a + y - 2hy + h,PC = (x-a) + (y+h) = x - 2ax + a + y + 2hy + h,PD = (x-0) + (y+h) = x + y + 2hy + h。
将PA、PB、PC、PD的值代入f(x)的公式中,得到f(x) = 2x + 2y - 2ax - 2hy。
我们知道,对于给定的平行四边形ABCD,点P在平行四边形内部运动,所以点P的坐标(x,y)必须满足以下条件:1. 0 < x < a2. -h < y < h根据这个条件,我们可以得到f(x)的最大值和最小值。
当y=h时,f(x)的最小值为f(0) = -2ah + 2h。
当y=-h时,f(x)的最大值为f(0) = 2ah + 2h。
当y=0时,f(x)为一个抛物线开口朝上的二次函数,其顶点坐标为(x,y) = (a/2,h/2),最小值为f(a/2) = h - a/2。
综上所述,f(x)的最大值为2ah+2h,最小值为-2ah+2h,最小值出现在y=h时,最大值出现在y=-h时,当y=0时,f(x)的最小值为h-a/2。
