五大定理加立体几何
立体几何所有的定理大总结(绝对全)

⽴体⼏何所有的定理⼤总结(绝对全)(⼆)异⾯直线所成⾓1.定义:不同在任何⼀个平⾯内的两条直线或既不平⾏也不相交的两条直线叫异⾯直线。
2.画法:借助辅助平⾯。
1.定义:对于异⾯直线a 和b ,在空间任取⼀点P ,过P 分别作a 和b 的平⾏线1a 和1b ,我们把1a 和1b 所成的锐⾓或者叫做异⾯直线a 和b 所成的⾓。
2.范围:(0°,90°】(★空间两条直线所成⾓范围:【0°,90°】)(三)线⾯⾓1.定义:当直线l 与平⾯α相交且不垂直时,叫做直线l 与平⾯α斜交,直线l 叫做平⾯α的斜线。
设直线l 与平⾯α斜交与点M ,过l 上任意点A ,做平⾯α的垂线,垂⾜为O ,把点O 叫做点A 在平⾯α上的射影,直线OM 叫做直线l 在平⾯α上的射影。
1.定义:把直线l 与其在平⾯α上的射影所成的锐⾓叫做直线l 和平⾯α所成的⾓。
2.范围【0°,90°】(★斜线与平⾯所成⾓范围:【0°,90°】)(三)⼆⾯⾓1.定义:(1)半平⾯:平⾯内的⼀条直线把这个平⾯分成两个部分,其中每⼀个部分叫做半平⾯。
(3)⼆⾯⾓的棱:这⼀条直线叫做⼆⾯⾓的棱。
(4)⼆⾯⾓的⾯:这两个半平⾯叫做⼆⾯⾓的⾯。
(5)⼆⾯⾓的平⾯⾓:以⼆⾯⾓的棱上任意⼀点为端点,在两个⾯内分别作垂直于棱的两条射线,这两条射线所成的⾓叫做⼆⾯⾓的平⾯⾓。
(6)直⼆⾯⾓:平⾯⾓是直⾓的⼆⾯⾓叫做直⼆⾯⾓。
1.定义:从⼀条直线出发的两个半平⾯所组成的图形叫做⼆⾯⾓。
2.表⽰:如下图,可记作α-AB-β或P-AB-Q3.范围为【0°,180°】(五)六种距离1.点到点的距离:两点之间的线段PQ 的长。
2.点到线的距离:过P 点作1PP ⊥l ,交l 于1P ,线段1PP 的长。
3.点到⾯的距离:过P 点作1PP ⊥α,交α于1P ,线段1PP 的长。
立体几何所有的定理大总结绝对全

(二)异面直线所成角1.定义:不同在任何一个平面内的两条直线或既不平行也不相交的两条直线叫异面直线。
2.画法:借助辅助平面。
1.定义:对于异面直线a和b,在空间任取一点P,过P分别作a和b的平行线1a和1b,我们把1a和1b所成的锐角或者叫做异面直线a和b所成的角。
2.范围:(0°,90°】(★空间两条直线所成角范围:【0°,90°】)(三)线面角1.定义:当直线l与平面α相交且不垂直时,叫做直线l与平面α斜交,直线l叫做平面α的斜线。
设直线l与平面α斜交与点M,过l上任意点A,做平面α的垂线,垂足为O,把点O叫做点A在平面α上的射影,直线OM叫做直线l在平面α上的射影。
1.定义:把直线l与其在平面α上的射影所成的锐角叫做直线l和平面α所成的角。
2.范围【0°,90°】(★斜线与平面所成角范围:【0°,90°】)(三)二面角1.定义:(1)半平面:平面内的一条直线把这个平面分成两个部分,其中每一个部分叫做半平面。
(3)二面角的棱:这一条直线叫做二面角的棱。
(4)二面角的面:这两个半平面叫做二面角的面。
(5) 二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
(6) 直二面角:平面角是直角的二面角叫做直二面角。
1.定义:从一条直线出发的两个半平面所组成的图形叫做二面角。
2.表示:如下图,可记作α-AB-β或P-AB-Q3.范围为【0°,180°】(五)六种距离1.点到点的距离:两点之间的线段PQ 的长。
2.点到线的距离:过P 点作1PP ⊥l ,交l 于1P ,线段1PP 的长。
3.点到面的距离:过P 点作1PP ⊥α,交α于1P ,线段1PP 的长。
两条平行线的距离4.线到线的距离:异面直线的距离:公垂线段PQ ⊥1l , PQ ⊥2l ,则线段PQ 的长。
立体几何八大定理
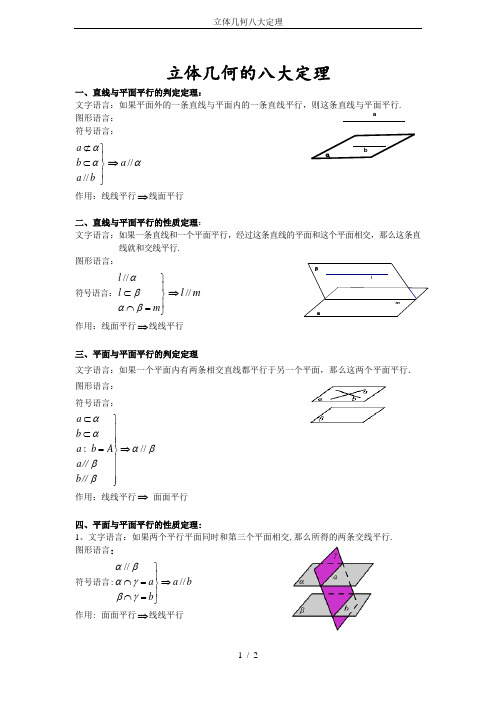
l m βααba 立体几何的八大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行.图形语言:符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行三、平面与平面平行的判定定理 文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言:符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 作用:线线平行⇒ 面面平行四、平面与平面平行的性质定理:1、文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行. 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行nm A αaB A l βαaβα2、如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒作用: 面面平行⇒线面平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面. 图形语言:符号语言: ,a m a n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理: 文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意一条直线. 图形语言:符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭ 作用:线面垂直⇒面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面.图形语言:符号语言:l AB AB AB l αβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直。
立体几何定理大全

立体几何公式大全基本概念公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
空间两直线的位置关系:空间两条直线只有三种位置关系:平行、相交、异面1、按是否共面可分为两类:〔1〕共面:平行、相交〔2〕异面:异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线间距离: 公垂线段(有且只有一条)2、假设从有无公共点的角度看可分为两类:〔1〕有且仅有一个公共点——相交直线;〔2〕没有公共点——平行或异面直线和平面的位置关系:直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为 [0°,90°]最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直直线和平面垂直的定义:如果一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直.直线a叫做平面的垂线,平面叫做直线a的垂面。
立体几何定理大全

立体几何公式大全基本概念公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
空间两直线的位置关系:空间两条直线只有三种位置关系:平行、相交、异面1、按是否共面可分为两类:〔1〕共面:平行、相交〔2〕异面:异面直线的定义:不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线间距离: 公垂线段(有且只有一条)2、假设从有无公共点的角度看可分为两类:〔1〕有且仅有一个公共点——相交直线;〔2〕没有公共点——平行或异面直线和平面的位置关系:直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为 [0°,90°]最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直直线和平面垂直的定义:如果一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直.直线a叫做平面的垂线,平面叫做直线a的垂面。
立体几何证明8条定理

立体几何证明8条定理立体几何是几何学的一个分支,研究的是在三维空间中的图形和体的性质。
在立体几何中有许多定理,其中一些重要的定理包括平行线定理、垂直线定理、欧拉定理、等角定理、切线定理、割线定理、同位角定理和三角形内角和定理等。
下面将详细讨论这些定理:1.平行线定理:如果两条平行线被一组平行线截断,那么它们的对应线段成比例。
这个定理可以用于证明两条线平行。
2.垂直线定理:如果两条直线相交,且其中一条直线垂直于另一条直线,那么相交处的四个角都是直角。
这个定理可以用于证明两条线垂直。
3.欧拉定理:在任意一个凸多面体中,顶点数、棱数和面数之间存在一个关系:顶点数加上面数等于棱数加上2、这个定理被应用于立体几何中的多面体的计算。
4.等角定理:如果两条线分别与一条平行线相交,且其中一对内错角(相对于平行线的两条线之间的两个角)或一个内错角和一个外错角(与平行线的两条线相交形成的一对内角和一对外角)相等,那么这两条线是平行线。
这个定理可以用于证明平行线。
5.切线定理:给定一个圆和一个与圆相切且通过切点的直线,那么切线的切点与切线所跨越的弦的两个端点之间的角是直角。
这个定理可以用于证明圆的性质。
6.割线定理:给定一个圆和一个与圆相交的直线,那么直线与圆的切线所跨越的弦的两个端点之间的角相等。
这个定理也可以用于证明圆的性质。
7.同位角定理:如果两条平行线被一条截线截断,那么同位角(相对于平行线的两条线的每一对内角)相等。
这个定理可以用于证明平行线。
8.三角形内角和定理:三角形的三个内角的度数之和等于180度。
这个定理是三角形的基本性质,可以用于证明其他三角形的性质。
这些定理是立体几何中的一些基本定理,通过运用它们可以推导出其他一些更复杂的定理。
这些定理不仅在几何学中有重要的应用,而且在物理学、工程学等其他学科中也有广泛的应用。
立体几何常考定理的总结(八大定理)
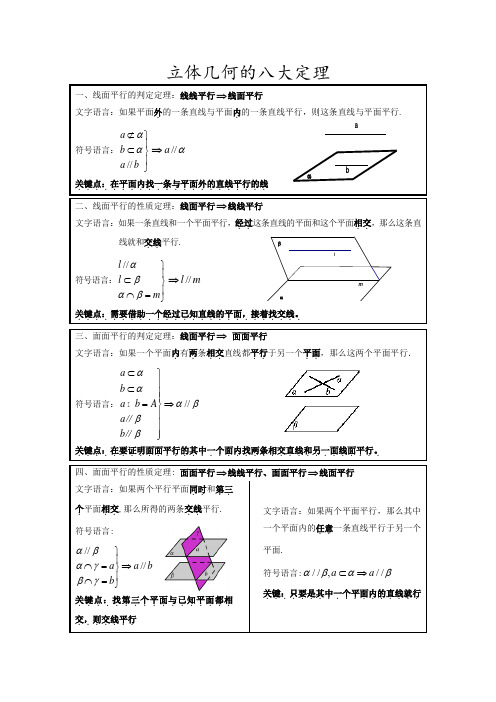
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
立体几何 重要定理 重要性质结论

立体几何重要定理重要性质结论㈠立体几何的基础(公理)公理1:一条直线上有不同的两点在一个平面内,那么称这条直线在这个平面内;(一条直线上有不同的两点在一个平面内,那么这条直线上所有的点都在这个平面内)公理2:不在一条直线上的三点可确定一个平面;(在一条直线上的三点不能可确定一个平面)公理3:如果不同的两个平面有一个公共点,那么这两个平面一定相交于过这一点的一条直线;(如果两个平面有一个公共点,那么这两个平面一定存在过这一点的一条直线)公理4:平行于同一条直线的两条直线平行;(平行于同一条直线的直线平行,平行直线有传递性)注意:‘可确定一个平面’‘存在唯一的一个平面’‘有且只有一个平面’是等价的说法。
㈡公理的进一步升华(推论)推论1:一条直线与直线外一点可确定一个平面;推论2:两条相交直线可确定一个平面;推论1:两条平行直线可确定一个平面;㈢两条直线的位置关系:1.一个平面内的两条直线的位置关系:相交于一点或相互平行。
2.空间的不同的两条直线的位置关系:相交于一点,相互平行,异面直线。
3.空间的不同的两条直线的位置关系:相交于一点(有公共点);相互平行或异面直线(没有公共点)。
㈣立体几何-----点----线-----面-----关系的证明分析方法有三种:1.由已知条件,定理,恒成立的结论为依据直接证明问题的真假;2.用反证法证明问题的真假,从“假设问题结论的否定成立”开始证明,综合已知条件,定理,问题结论的反面,恒成立的结论为依据,来证明假设的不正确,或证明出显然的矛盾结论。
3.用特殊的情况,特殊的实际例子,来推翻结论的对立面。
(特殊法)。
㈤两条异面直线所成的角:过空间任意一点分别作两条异面直线的平行直线,相交所成的锐角或直角叫两条异面直线所成的角。
(过空间任意一点,这一点可在其中一条直线上)。
注意:两条异面直线垂直是指两条异面直线所成的角为900称为两条异面直线垂直。
㈥直线与平面的位置关系:相交或平行。
立体几何证明定理归纳

立体几何证明定理归纳
公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]
立体几何证明定理归纳
(1)线线平行线面平行
定理内容:
图示:
符号语言:
(2)线面平行线线平行
定理内容:
图示:符号语言:
(3)线面平行面面平行
定理内容:
图示:符号语言:
(4)面面平行线面平行
定理内容:
图示:符号语言:
(5)面面平行线线平行
定理内容:
图示:符号语言:
(6)线线垂直线面垂直
定理内容:
图示:符号语言:
(7)线面垂直线线垂直
定理内容:
图示:符号语言:
(8)线面垂直面面垂直
定理内容:
图示:符号语言:
(9)面面垂直线面垂直
定理内容:
图示:符号语言:
(10)线面垂直线线平行
定理内容:
图示:符号语言:。
立体几何常考定理总结(八大定理)

南京大学附属中学立体几何主要定理复习立体几何的八大定理一、线面平行的判定定理:线线平行线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行.a ab符号语言:a//a// bb 关.键.点.:.在.平.面.内.找.一.条.与.平.面.外.的.直.线.平.行.的.线.二、线面平行的性质定理:线面平行线线平行文字语言:如果一条直线和一个平面平行,经.过.这条直线的平面和这个平面相.交.,那么这条直线就和交.线.平行.ll //l符号语言:l // mmm 关.键.点.:.需.要.借.助.一.个.经.过.已.知.直.线.的.平.面.,.接.着.找.交.线.。
.三、面面平行的判定定理:线面平行面面平行文字语言:如果一个平面内.有两.条相.交.直线都平.行.于另一个平.面.,那么这两个平面平行.ab符号语言:a b A //a∥b∥关.键.点.:.在.要.证.明.面.面.平.行.的.其.中.一.个.面.内.找.两.条.相.交.直.线.和.另.一.面.线.面.平.行.。
.四、面面平行的性质定理: 面面平行线线平行、面面平行线面平行文字语言:如果两个平行平面同.时.和第.三.个.平面相.交., 那么所得的两条交.线.平行. 文字语言:如果两个平面平行,那么其中符号语言: 一个平面内的任.意.一条直线平行于另一个//平面.a a // bb符号语言: / / , a a / /关.键.点.:.找.第.三.个.平.面.与.已.知.平.面.都.相.关.键.:.只.要.是.其.中.一.个.平.面.内.的.直.线.就.行.交.,.则.交.线.平.行.1南京大学附属中学立体几何主要定理复习五、线面垂直的判定定理:线线垂直线面垂直文字语言:如果一条直线和一个平面内.的两.条相.交.直线垂.直.,那么这条直线垂直于这个平面.a ma符号语言:a nm n AaAm ,nn m 关.键.点.:.在.平.面.内.找.两.条.相.交.直.线.与.所.要.证.的.直.线.垂.直.六、线面垂直的性质定理:线面垂直线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任.意.一条直线.符号语言:lal a关.键.点.:.往.往.线.面.垂.直.中.的.线.线.垂.直.需.要.用.这.个.定.理.推.出.七、平面与平面垂直的判定定理:线面垂直面面垂直文字语言:如果一个平面经.过.另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:aaa关.键.点.:.在.需.要.证.明.的.两.个.平.面.中.找.线.面.垂.直.八、平面与平面垂直的性质定理:面面垂直线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂.直.于它们的交.线.的直线垂直于另一个平面.l符号语言:ABAABAB ll 关.键.点.:.先.找.交.线.,.再.在.其.中.一.个.面.内.找.与.交.线.垂.直.的.线.。
立体几何公式定理大全

立体几何公式定理大全立体几何是研究空间中各种图形的性质和关系的分支学科,其主要研究对象是立体图形的特征、构造和性质。
在立体几何的学习过程中,我们需要掌握一些重要的公式和定理,以便解决与立体图形相关的问题。
下面是一些常用的立体几何公式和定理的详细介绍:1.体积公式:-直角三棱柱的体积公式:体积=底面积×高-正方体的体积公式:体积=边长^3-直角三角柱的体积公式:体积=面积×高-圆柱的体积公式:体积=底面积×高-锥体的体积公式:体积=1/3×底面积×高-球体的体积公式:体积=4/3×π×半径^32.表面积公式:-正方体的表面积公式:表面积=6×边长^2-正方体的棱长公式:棱长=根号下(表面积/6)-正方体的对角线长度:对角线长度=边长×根号下(3)-直角三角柱的表面积公式:表面积=(底面积+两倍底面积的开方)+2×底面积-圆柱的表面积公式:表面积=2×π×半径×高+2×π×半径^2-锥体的表面积公式:表面积=π×半径×斜高+π×半径^2-球体的表面积公式:表面积=4×π×半径^23.空间几何定理:-平行线截立体的定理:如果两组平行线截取同一直线的长度成比例,那么这两组平行线截取的其他直线的长度也成比例。
-空间角平分线的定理:空间中的角可由角平分线平分为两个等角。
-立体的等分线定理:平面将一个立体分为两个等体积的立体时,它将该立体的底面分为两个等面积的底面,并且过底面上的任意一点,以该点为顶点作平行于底面的面将该立体分为两个等体积的立体。
-线与面的关系定理:一条不等于底面的直线与底面所围的锥交于一点,但与底面围成的锥不是等体积的。
-垂直平分面定理:垂直与一条直线的平面把这条直线平分为两段,它把这条直线的平面所围的任一立体分为两个等体积的立体。
立体几何公理、定理推论汇总
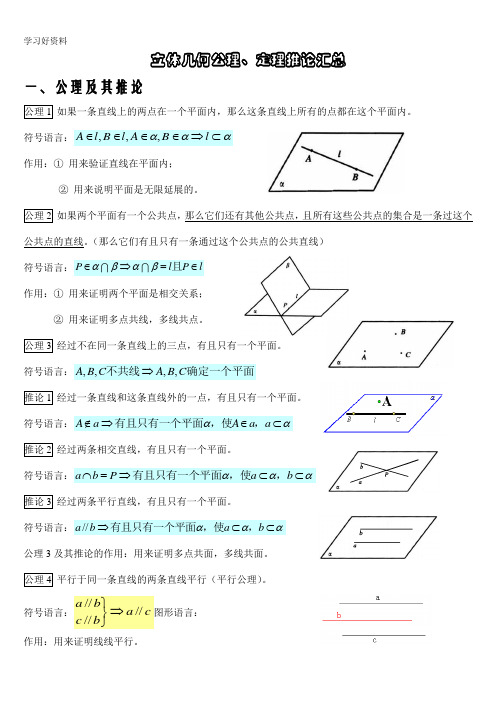
立体几何公理、定理推论汇总一、公理及其推论 公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
符号语言:,,,A l B l A B l ααα∈∈∈∈⇒⊂作用:① 用来验证直线在平面内;② 用来说明平面是无限延展的。
公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)符号语言:P l P l αβαβ∈⇒=∈且作用:① 用来证明两个平面是相交关系;② 用来证明多点共线,多线共点。
公理3 经过不在同一条直线上的三点,有且只有一个平面。
符号语言:,,,,A B C A B C ⇒不共线确定一个平面推论1 经过一条直线和这条直线外的一点,有且只有一个平面。
符号语言:A a A a a αα∉⇒∈⊂有且只有一个平面,使,推论2 经过两条相交直线,有且只有一个平面。
符号语言:a b P a b ααα⋂=⇒⊂⊂有且只有一个平面,使,推论3 经过两条平行直线,有且只有一个平面。
符号语言://a b a b ααα⇒⊂⊂有且只有一个平面,使,公理3及其推论的作用:用来证明多点共面,多线共面。
公理4 平行于同一条直线的两条直线平行(平行公理)。
符号语言://////a b a c c b ⎫⇒⎬⎭图形语言: 作用:用来证明线线平行。
二、平行关系 公理4 平行于同一条直线的两条直线平行(平行公理)。
(1)符号语言://////a b a c c b ⎫⇒⎬⎭图形语言: 线面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
(2)符号语言:////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭图形语言:线面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
(3)符号语言:////a b a a b βαβα⎫⎪⊂⇒⎬⎪=⎭图形语言:面面平行的判定定理 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(4) 符号语言://(/,///),a b b b O a a ββαααβ⊂⊂=⎫⎪⇒⎬⎪⎭图形语言: 面面平行的判定 如果两个平面垂直于同一条直线,那么这两个平面平行。
立体几何所有的定理大总结绝对全

(二)异面直线所成角1.定义:不一样在任何一个平面内的两条直线或既不平行也不订交的两条直线叫异面直线。
2.画法:借助协助平面。
1.定义:关于异面直线 a 和 b,在空间任取一点 P,过 P 分别作 a 和 b 的平行线a1和b1,我们把 a1和b1所成的锐角或许叫做异面直线 a 和 b 所成的角。
2.范围: (0 °, 90°】( ★空间两条直线所成角范围:【0°, 90°】 )(三)线面角1. 定义:当直线 l 与平面α订交且不垂直时,叫做直线 l 与平面α斜交,直线 l 叫做平面α的斜线。
设直线 l 与平面α斜交与点 M,过 l 上随意点 A,做平面α的垂线,垂足为O,把点 O叫做点 A 在平面α上的射影,直线 OM叫做直线 l 在平面α上的射影。
1.定义:把直线 l 与其在平面α上的射影所成的锐角叫做直线 l 和平面α所成的角。
2.范围【 0°, 90°】(★斜线与平面所成角范围:【0°, 90°】)(三)二面角1.定义:(1)半平面:平面内的一条直线把这个平面分红两个部分,此中每一个部分叫做半平面。
(3)二面角的棱:这一条直线叫做二面角的棱。
(4)二面角的面:这两个半平面叫做二面角的面。
(5)二面角的平面角:以二面角的棱上随意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
(6)直二面角:平面角是直角的二面角叫做直二面角。
1.定义:从一条直线出发的两个半平面所构成的图形叫做二面角。
2. 表示:以下列图,可记作 α-AB- β或 P-AB-Q3. 范围为【 0°, 180°】(五)六种距离1. 点到点的距离:两点之间的线段 PQ 的长。
2. 点到线的距离:过 P 点作 PPl ,交 l 于 P ,线段 PP 的长。
1 1 13. 点到面的距离:过 P 点作 PP 1,交 于 P 1 ,线段 PP 1 的长。
立体几何的计算定理

立体几何的计算定理立体几何是研究空间物体的形状、大小、位置和运动等性质的一门数学学科。
在立体几何中,存在着一些重要的计算定理,它们能够帮助我们准确计算立体图形的各种参数和性质。
本文将介绍一些常用的立体几何计算定理。
一、体积计算定理体积是描述立体图形容积大小的量。
在立体几何中,我们常用以下定理来计算体积。
1. 平行四边形棱柱的体积计算定理:平行四边形棱柱的体积等于底面积与高的乘积。
2. 直方体的体积计算定理:直方体的体积等于底面积与高的乘积。
3. 圆柱体的体积计算定理:圆柱体的体积等于底面积与高的乘积。
4. 锥体的体积计算定理:锥体的体积等于底面积与高的乘积的三分之一。
5. 球体的体积计算定理:球体的体积等于四分之三乘以半径的立方。
二、表面积计算定理表面积是描述立体图形外部覆盖的面积的量。
在立体几何中,我们常用以下定理来计算表面积。
1. 正方体的表面积计算定理:正方体的表面积等于底面积的六倍。
2. 矩形长方体的表面积计算定理:矩形长方体的表面积等于底面积的两倍加上底面积形成的四个侧面的面积。
3. 圆柱体的表面积计算定理:圆柱体的表面积等于底面积的两倍加上底面积与高的乘积的两倍。
4. 球体的表面积计算定理:球体的表面积等于四乘以半径的平方。
三、欧拉定理欧拉定理是立体几何中的一个重要定理,它描述了一个立体图形的顶点、棱边和面的关系。
欧拉定理可以表述为:一个立体图形的顶点数加上面的数目,再减去边的数目等于2。
欧拉定理在立体几何的计算中具有重要的作用,可以用来检验计算结果的准确性,或者通过已知的参数来计算未知的参数。
四、平行四边形定理平行四边形定理是立体几何中关于平行四边形的性质和关系的定理。
其中一条重要的定理是平行四边形的对角线等分的定理,即平行四边形的对角线相交于一个点,且该点把对角线分成两段,两段长度相等。
平行四边形定理可以用来证明或计算平行四边形的各种性质,例如四边形的面积、周长、对角线长等。
五、球面上的计算定理在球面上,也存在一些与计算相关的定理。
立体几何所有定理和判定

立体几何所有定理和判定立体几何是数学中的一个重要分支,研究的是三维空间中的图形和物体的性质。
在立体几何中,有许多重要的定理和判定,它们帮助我们理解和解决与立体图形相关的问题。
本文将介绍一些主要的定理和判定。
一、平行线与平面的关系1. 平行线定理:如果两条线与第三条线平行,则这两条线也互相平行。
2. 平行线截割定理:如果一对平行线被一组截线截割,则所得的对应线段成比例。
3. 平行线的垂直定理:如果两条平行线被一条截线垂直截断,则所得的对应线段也相互垂直。
二、线段与角的关系1. 点到直线的距离定理:一个点到一条直线的距离等于这条直线上任意一点到该点的距离。
2. 线段相等定理:如果两个线段的长度相等,则它们是相等的。
3. 角的平分线定理:如果一条直线将一个角分成两个相等的角,则这条直线是该角的平分线。
三、平面图形的性质1. 三角形内角和定理:三角形的三个内角的和等于180度。
2. 直角三角形定理:如果一个三角形的一个角是直角,则它是直角三角形。
3. 等腰三角形定理:如果一个三角形的两边相等,则它是等腰三角形。
4. 等边三角形定理:如果一个三角形的三边都相等,则它是等边三角形。
四、立体图形的性质1. 正方体的性质:正方体是一种六个面都是正方形的立体图形。
2. 立方体的性质:立方体是一种六个面都是正方形且相互平行的立体图形。
3. 正四面体的性质:正四面体是一种四个面都是等边三角形的立体图形。
五、空间图形的判定1. 平行四边形的判定:如果四边形的对边平行,则它是平行四边形。
2. 正多面体的判定:如果一个多面体的每个面都是正多边形且每个顶点的相邻边相等,则它是正多面体。
3. 立体图形的对称性判定:如果一个立体图形可以通过某种变换与自身完全重合,则它具有对称性。
以上只是立体几何中的一部分定理和判定,它们是我们理解和解决立体图形问题的基础。
通过运用这些定理和判定,我们可以更好地分析和推导立体图形的性质,从而解决各种与立体图形相关的问题。
立体几何五大定理

αbaNM C BAD A 1B 1C 1D 1B1A线面位置关系的五大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行图形语言: 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α 作用:线线平行⇒线面平行典例:在正方体1111ABCD A BC D -中,,M N 分别是11,AB CC 的中点, 求证://MN ABCD 平面二、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥作用:线线平行⇒ 面面平行典例:如图,在三棱柱111ABC A B C -中,点,DE 分别是BC 与11B C 的中点,求证:平面1//A EB 平面1ADCnmAαaFEPD CBA aβαC三、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言: 符号语言: ,a m a n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用:线线垂直⇒线面垂直典例:已知四棱锥,P ABCD PD -⊥底面ABCD ,底面ABCD 为正方形,且PD CD =,,E F 分别为,PB PC 的中点,求证:(1)AC ⊥平面PBD (2)PA AB ⊥(3)PC ⊥平面ADFE四、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直典例:如图,在四面体S ABC -中,SA SB SC a ===0090,60ASC ASB BSC ∠=∠=∠=求证:平面ASC ⊥平面ABCBA l βαCBAP五、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面 图形语言:符号语言:l AB AB AB l αβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直典例:如图,PA ABC ⊥平面,PAB PBC ⊥平面平面,求证:BC PAB ⊥平面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
E
?
8
5
2
O A B
C
D
E
F B C
E
蝴蝶定理、如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.
风筝定理、正方形ADEB 和正方形ECFG 底边对齐,两个正方形边长分别为6厘米和4厘米,三角形BDF 的面积是多少平方厘米?
鸟头定理、如图,在三角形ABC 中,BC 等于10厘米,BC 边上的高等于6厘米,
D 在AC 上,并且DC=DA ,
E 是BD 上一点,BD=3 BE ,求三角形BEC 的面积。
燕尾定理、(2009年清华附中入学测试题)如图,四边形ABCD 是矩形,E 、F 分别是AB 、BC 上的点,且1
3AE AB =,14
CF BC =,AF 与CE 相交于G ,若矩形
ABCD 的面积为120,则AEG ∆与CGF ∆的面积之和为 .
沙漏定理、点E 、M 分别为直角梯形ABCD 两边上的点,且DQ 、CP 、ME 彼此平行,若5AD =,7BC =,5AE =,3EB =.求阴影部分的面积.
立体几何
1、一个会议大厅有6根同样的圆柱形木柱,每根高4米,底面周长1.5分米,如果每千克油漆能够刷4.5平方米,把这些木柱刷上漆需要多少千克油漆。
2、一个铁皮圆柱体形的油桶,底面直径是6分米,高8分米,这个油桶能装油多少
千克?(每立方分米油重0.82千克,得数保留整数)
3、挖一个圆柱体形的蓄水池,从里面量底面周长31.4米,深2.4米。
在它的内壁
与底面抹上水泥,抹水泥部分的面积是多少平方米?蓄水池能蓄水多少吨?
(每立方米水重1吨)
4、一只玻璃缸,底面积15平方分米,水深15厘米,放进一块石头后水面升到18
厘米,这块石头体积是多少?
5、一座装满玉米的圆柱体形的粮仓,从里面量底面周长31.4米,高6米.玉米每
立方米重740千克,用车运走玉米的1/3,还剩下多少吨?
蝴蝶定理答案、连接DE 、CF .四边形EDCF 为梯形,所以EOD FOC S S ∆= ,又根据蝴蝶定
理,EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅,所以2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=,所以4EOD S ∆=(平方厘米),4812ECD S ∆=+=(平方厘米).那么长方形ABCD 的面积为12224⨯=平方厘米,四边形OFBC 的面积为245289---=(平方厘米).
?
8
5
2O A B
C
D
E
F
沙漏定理答案:连接CE 、DE .由于DQ 、CP 、ME 彼此平行,所以四边形CDQP 是梯形,且ME 与该梯形的两个底平行,那么三角形QME 与DEM 、三角形PME 与CEM 的面积分别相等,所以三角形PQM 的面积与三角形CDE 的面积相等.而三角形CDE 的面积根据已知条件很容易求出来.
由于ABCD 为直角梯形,且5AD =,7BC =,5AE =,3EB =,所以三角形CDE 的面积的
面积为:()()111
5753553725222
+⨯+⨯-⨯⨯-⨯⨯=.所以三角形PQM 的面积为25.
B C
E。
