八年级数学勾股定理4
人教版八年级数学下册_第一节《勾股定理》勾股定理

下列说法中,正确的是
(
)
下列说法中,正确的是
(
)
2.你还有什么疑问,问问老师。 通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
(1)若a=6,b=8,则c=
.
通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
在Rt△ABC中,∠C=90°.
思考:在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
1.本节课你有什么收获?你学到了什么? 在Rt△ABC中,∠C=90°,a=6,c=10,则b=
.
通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
思考 正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系?
说给大家听听。 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
(2)若c=13,b=12,则a=
.
在Rt△ABC中,两直角边长分别为3和 ,则斜边长为
.
第1课时 勾股定理
思考:在网格中一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?观察下边两幅图(每个小正方形的面积为单位1):
9
13
右图 16
9
25
Hale Waihona Puke 思考 正方形A、B、C 所围成的直角三角形三条边之 间有怎样的特殊关系?
通过前面的探究活动,你发现了直角三角形
在Rt△ABC中,∠C=90°.
三边之间的关系规律了吗? 在Rt△ABC中,两直角边长分别为3和 ,则斜边长为
.
已知a,b,c是三角形的三边,则a2+b2=c2
八年级数学 勾股定理证明方法
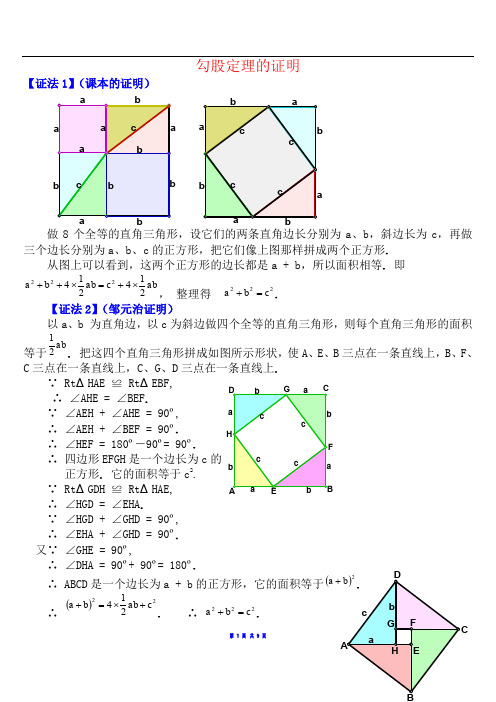
勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于(a +∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º, BC = BD = a . ∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221aΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC ∙=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC ∙=2.∴ ()222AB AB DB AD BC AC =∙+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c .再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º,AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC ∙=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a c b -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC ∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)D设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图). 在EH = b 上截取ED = a ,连结DA 、则 AD = c .∵ EM = EH + HM = b + a , ED = a ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
八年级数学勾股定理4

a²+b²=c²
(X )
2)、直角三角形的两边长分别是3和4,则另一边是5
(X )
3)、若△ABC的三边长是a=7,b=24,c=25,则△ABC
是直角三角形
(√ )
4)、 △ABC是三边之比为1:1:√2 ,则△ABC是直角
三角形
(√ )
5)、等边三角形高为2 √3cm,则它的边长是3cm (X )
AC²+BC²= AB²
(3)美国总统证法:
D
C
bc
c
a
Aa
bD
∵S梯形ABCD=1/2(a+b)(a+b)
=1/2ab×2+1/2 c²
∴a²+b²=c²
(4)我来试一试
b
a
ab
a c
a
cb
ca
bc c
bc
a
a
b
a
b b
S=1/2ab×4+ c²=1/2ab ×4+ a²+b² a²+b²=c²
∴ c= √20 =2 √ 5 (舍负 值)
∴ a2 = c2 ﹣b2 = 32 –(√ 2 )2 =7
∴ a= √ 7 (舍负值)
例2:将长为5.41米的梯子AC斜靠在墙上, BC长为2.16米,求梯子上端A到墙的底端 B的距离AB(精确到0.01米)
解:在Rt△ABC中,
∠ABC=90°
A
BC=2.16 ,CA=5.41
3、若a,b,c是一组基本的勾股数,则a,b,c 不能同时为奇数或同时为偶数
4、一组勾股数中必有一个数是5倍数 5、2mn,m²-n²,m²+n²为勾股数组,m>n﹥0 ,m,n一奇一偶
八年级数学下册【勾股定理】4种简单应用

八年级数学下册【勾股定理】4种简单应用一、勾股定理在网格中的应用例1、已知正方形的边长为1,(1)如图a,可以计算出正方形的对角线长为根号2.①分别求出图(b),(c),(d)中对角线的长_.②九个小正方形排成一排,对角线的长度(用含n的式子表示)为_.分析:借助于网格,构造直角三角形,直接利用勾股定理.二、勾般定理在最短距离中的应用例2、如图,已知C是SB的中点,圆锥的母线长为10cm,侧面展开图是一个半圆,A处有一只蜗牛想吃到C处的食物,它只能沿圆锥曲面爬行.请你求出蜗牛爬行的最短路程.分析在求解几何图形两点间最短距离的问题时,将几何体表面展开,求展开图中两点之间的距离,展开过程中必须要弄清楚所要求的是哪两点之间的距离,以及它们在展开图中的相应位置.点评在求立体几何图形的问题时,一般是通过平面展开图,将其转化成平面图形问题,然后求解.三、勾股定理在生活中的应用例3、如图,学校有一块长方形花园,有较少数同学为了避开拐角走“捷径”,在校园内走出了一条“路”.请同学们算一算,其实这些同学仅仅少走多少步路,却踩伤了花草.(假设1步为0.5m)点评:走“捷径”问题为出发点是常遇到情况,在考查勾股定理的同时,融入了环保教育:少走几步路,就可以留下一片期待的绿色.四、勾股定理在实际生活中的应用例4 小华想知道自家门前小河的宽度,于是按以下办法测出了如下数据:小华在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°,小华沿河岸向前走30m 选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小华计算小河的宽度.点评:此题考查直角三角形的应用,解答本题的关键在于画出示意图,将问题转化为解直角三角形的问题.。
八年级数学《勾股定理》知识点

八年级数学《勾股定理》知识点一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c2=a2+b2,则△ABC是以∠C为直角的三角形;若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n的线段1。
八年级数学下册专题04勾股定理常考压轴题汇总(原卷版)

专题04 勾股定理常考压轴题汇总一.选择题(共23小题)1.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成一个大正方形.如图,直角三角形的直角边长为a、b,斜边长为c.若b﹣a=2,c=10,则a+b的值为()A.12B.14C.16D.182.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是()A.B.C.D.3.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为()A.S1+S2+S3=S4B.S1+S2=S3+S4C.S1+S3=S2+S4D.不能确定4.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI 上,若AC+BC=6,空白部分面积为10.5,则AB的长为()A.3B.C.2D.5.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.3cm2B.4cm2C.6cm2D.12cm26.如图,阴影部分表示以Rt△ABC的各边为直径向上作三个半圆所组成的两个新月形,面积分别记作S1和S2.若S1+S2=7,AC=3,则BC长是()A.3.5B.C.4D.57.如图,在长方体ABCD﹣EFGH盒子中,已知AB=4cm,BC=3cm,CG=5cm,长为10cm 的细直木棒IJ恰好从小孔G处插入,木棒的一端I与底面ABCD接触,当木棒的端点Ⅰ在长方形ABCD内及边界运动时,GJ长度的最小值为()A.(10﹣5)cm B.3cm C.(10﹣4)cm D.5cm8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,BC=10,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为()A.420B.440C.430D.4109.国庆假期间,妍妍与同学去玩寻宝游戏,按照藏宝图,她从门口A处出发先往东走9km,又往北走3km,遇到障碍后又往西走7km,再向北走2km,再往东走了4km,发现走错了之后又往北走1km,最后再往西走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是()A.3km B.10km C.6km D.km10.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AB=9,BC=6,则BD的长为()A.3B.4C.5D.611.如图,某小区有一块长方形花圃,为了方便居民不用再走拐角,打算用瓷砖铺上一条新路,居民走新路比走拐角近()A.2m B.3m C.3.5m D.4m12.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是()A.148B.100C.196D.14413.如图,四边形ABCD中,AD⊥CD于点D,BC=2,AD=8,CD=6,点E是AB的中点,连接DE,则DE的最大值是()A.5B.C.6D.14.如图,长为8cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C垂直向上拉升3cm到D点,则橡皮筋被拉长了()A.2cm B.3cm C.4cm D.1cm15.如图的数轴上,点A,C对应的实数分别为1,3,线段AB⊥AC于点A,且AB长为1个单位长度,若以点C为圆心,BC长为半径的弧交数轴于0和1之间的点P,则点P表示的实数为()A.B.C.D.16.“四千年来,数学的道理还是相通的”.运用祖冲之的出入相补原理也可证明勾股定理.若图中空白部分的面积是11,整个图形(连同空白部分)的面积是25,则大正方形的边长是()A.B.C.D.17.如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为()A.5米B.6米C.7米D.8米18.勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要细带.数学家欧几里得利用如图验证了勾股定理.以直角三角形ABC的三条边为边长向外作正方形ACKJ,正方形ABFE,正方形BCIH,连接AH.CF,具中正方形BCIH面积为1,正方形ABFE面积为5,则以CF为边长的正方形面积为()A.4B.5C.6D.1019.如图,Rt△ABC中,∠C=90°.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN.四块阴影部分的面积如图所示分别记为S、S1、S2、S3,若S=10,则S1+S2+S3等于()A.10B.15C.20D.3020.如图,在Rt△ABC中,∠C=90°,分别以AB、AC、BC为直径向外作半圆,它们的面积分别记作S1、S2、S3,若S1=25,S3=16,则S2为()A.9B.11C.32D.4121.如图,在Rt△ABC中,∠ACB=90°,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4.若已知S△ABC =S,则下列结论:①S4=S;②S2=S;③S1+S3=S2;④S1+S2+S3+S4=2.5S.其中正确的结论是()A.①②③B.①②④C.①③④D.②③④22.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为()尺.A.10B.12C.13D.1423.将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形ABCD和正方形EFGH.现将四个直角三角形的较长直角边分别向外延长,且A′E=ME.B′F =NF,C′G=PG,D′H=HQ,得到图2所示的“新型数学风车”的四个叶片,即△A′EF,△B′FG,△C′CH.△D′HE.若FM平分∠BFE,正方形ABCD和正方形EFGH 的边长比为1:5.若”新型数学风车”的四个叶片面积和是m,则正方形EFCH的面积是()A.B.C.3m D.二.填空题(共14小题)24.如图①,四个全等的直角三角形与一个小正方形,恰好拼成一个大正方形,这个图形是由我国汉代数学家赵爽在为《周髀算经》作注时给出的,人们称它为“赵爽弦图”.如果图①中的直角三角形的长直角边为7cm,短直角边为3cm,连结图②中四条线段得到如图③的新图案,则图③中阴影部分的周长为cm.25.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接P A,当△ABP为等腰三角形时,t的值为.26.如图,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的“勾股分割点”.已知点M,N是线段AB 的“勾股分割点”,若AM=4,MN=5,则斜边BN的长为.27.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示“垂美”四边形ABCD,对角线AC,BD交于点O,若AB=6,CD=10,则AD2+BC2=.28.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(30,0)(0,12),点D是OA的中点,点P在BC上运动,当△ODP是腰长为15的等腰三角形时,点P 的坐标为.29.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门(AD和BC),门边沿D,C两点到门槛AB的距离是1尺(1尺=10寸),两扇门的间隙CD为2寸,则门槛AB长为寸.30.如图,在某次军事演习中,舰艇1号在指挥中心(O处)北偏西30°的A处,舰艇2号在指挥中心南偏东60°的B处,并且OA=OB.接到行动指令后,舰艇1号向正东方向以60海里/小时的速度前进,舰艇2号沿北偏东60°的方向以m海里/小时的速度前进.1.5小时后,指挥中心观测到两舰艇分别到达点E,F处,若∠EOF=75°,EF=210海里,则m的值为.31.如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB=5,EF=1,则GM的长为.32.如图,铁路上A、D两点相距25千米,B,C为两村庄,AB⊥AD于A,CD⊥AD于D,已知AB=15km,CD=10km,现在要在铁路AD上建一个土特产品收购站P,使得B、C 两村到P站的距离相等,则P站应建在距点A千米.33.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为cm(杯壁厚度不计).34.如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD⊥BC.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是.35.如图,在△ABC中,∠ABC=45°,AB=,AC=6,BC>4,点E,F分别在BC,AC边上,且AF=CE,则AE+BF的最小值为.36.如图,在△ABC中,AB=9cm,AC=12cm,BC=15cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是cm.37.如图,Rt△ABC中,.点P为△ABC内一点,P A2+PC2=AC2.当PB的长度最小时,△ACP的面积是.三.解答题(共4小题)38.如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A 出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?39.如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)求BC边的长.(2)当△ABP为等腰三角形时,求t的值.40.今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB =500km,经测量,距离台风中心260km及以内的地区会受到影响.(1)海港C受台风影响吗?为什么?(2)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?41.请阅读下列材料:已知:如图(1)在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD、DE、EC三条线段之间存在的数量关系式,直接写出你的猜想;(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)已知:如图(3),等边三角形ABC中,点D、E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE、AD、EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.。
八年级数学下册《勾股定理》知识点总结

3.S梯形=(a+b)h=Lh(a、b为梯形的底,h为梯形的高,L为梯形的中位线)
四常识:
※1.若n是多边形的边数,则对角线条数公式是:
2.规则图形折叠一般“出一对全等,一对相似”
3.如图:平行四边形、矩形、菱形、正方形的从属关系
4.常见图形中,仅是轴对称图形的有:角、等腰三角形、等边三角形、正奇边形、等腰梯形……;仅是中心对称图形的有:平行四边形……;是双对称图形的有:线段、矩形、菱形、正方形、正偶边形、圆……注意:线段有两条对称轴
∠AB=90°
D⊥AB
6、常用关系式
由三角形面积公式可得:AB D=A B
7、直角三角形的判定
1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理:如果三角形的三边长a,b,有关系,那么这个三角形是直角三角形。
8、命题、定理、证明
(2)、在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30°
可表示如下:B= AB
∠=90°
(3)、直角三角形斜边上的中线等于斜边的一半
∠AB=90°
可表示如下:D= AB=BD=AD
D为AB的中点
、摄影定理
在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项
常用结论:任一个三角形都有三条中位线,由此有:
结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形。
结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
新人教版八年级数学下册勾股定理知识点和典型例习题1

新人教版八年级下册勾股定理全章知识点和典型例习题一、基础知识点:1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2。
勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是 ①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a ②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5。
勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,c b a H G FE DC B A b ac b a c c a b c a b a b c c b aE D C B A时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6。
北师大版八年级数学上勾股定理

初中数学试卷勾股定理一 探索勾股定理(一) 勾股定理知识链接(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么a 2+b 2=c 2.(2)勾股定理应用的前提条件是在直角三角形中.(3)勾股定理公式a 2+b 2=c 2 的变形有:a 2=c 2-b 2,b 2=c 2-a 2及c 2=a 2+b 2.(4)由于a 2+b 2=c 2>a 2,所以c >a ,同理c >b ,即直角三角形的斜边大于该直角三角形中的每一条直角边. 同步练习1.如图所示,在Rt △ABC 中,∠A=90°,BD 平分∠ABC ,交AC 于点D ,且AB=4,BD=5,则点D 到BC 的距离是( )A .3B .4C .5D .62.(2014•乐山)如图,△ABC 的顶点A 、B 、C 在边长为1的正方形网格的格点上,BD ⊥AC 于点D .则BD 的长为( )A .532B .543C .554D .5533.(2013•黔西南州)一直角三角形的两边长分别为3和4.则第三边的长为()A.5 B.7 C.5 D.5或74.(2013•六合区一模)如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为()A.3 B.4 C.5 D.75.(2014•增城市一模)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15,(1)求AB的长;(2)求CD的长.6.(2014•金华模拟)如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知Rt△ABC中,∠B=90°,较短的一条直角边边长为1,如果Rt△ABC是“有趣三角形”,那么这个三角形“有趣中线”长等于.7.(2014•本溪一模)如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=10cm,则AC等于()A.10cm B.8cm C.5cm D.2.5cm8.(2014•徐汇区二模)如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=5,BO=4,则AO 的长为.9.(2014•香坊区三模)如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.若CD=3,BC+AB=16,则△ABC 的面积为()A.16 B.18 C.24 D.3210.(2014•南充)如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A ′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是.11.(2014•房山区一模)阅读下列材料:小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为5、10、13,求△ABC的面积.小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:(1)图1中△ABC的面积为______;参考小明解决问题的方法,完成下列问题:(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).2、29的格点△DEF;①利用构图法在答题卡的图2中画出三边长分别为13、5②计算△DEF的面积为______.(3)如图3,已知△PQR,以PQ,PR为边向外作正方形PQAF,PRDE,连接EF.若PQ=22,PR=13,QR=17,则六边形AQRDEF的面积为______.(二)勾股定理证明知识链接(1)勾股定理的证明方法有很多种,教材是采用了拼图的方法证明的.先利用拼图的方法,然后再利用面积相等证明勾股定理.(2)证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理.同步练习1.用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是()A.c2=a2+b2 B.c2=a2+2ab+b2 C.c2=a2-2ab+b2 D.c2=(a+b)2.2.下列选项中,不能用来证明勾股定理的是()A. B. C. D.3.(2014•满洲里市模拟)我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为()A.49 B.25 C.13 D.14.(2012•宁波)勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为()A.90 B.100 C.110 D.1215、(2011•温州)我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是______.6.由8个相同的直角三角形(图中带阴影的三角形)与中间的小正方形拼成的一个大正方形.如果最大的正方形的面积是25,最小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么222a3-333b3=______.7.利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为____ __,该定理的结论其数学表达式是 ____ __.8.如图,网格中的图案是美国总统Garfield于1876年给出的一种验证某个著名结论的方法:(1)请你画出直角梯形EDBC绕EC中点O顺时针方向旋转180°的图案,你会得到一个美丽的图案.(阴影部分不要涂错).(2)若网格中每个小正方形边长为单位1,旋转后A、B、D的对应点为A′、B′、D′,求四边形ACA′E 的面积?(3)根据旋转前后形成的这个美丽图案,你能说出这个著名的结论吗?若能,请你写出这个结论.9.(1)如图1是一个重要公式的几何解释.请你写出这个公式;(2)如图2,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点共线.试证明∠ACE=90°;(3)请利用(1)中的公式和图2证明勾股定理.10..如图,已知正方形ABCD和CEFG,连接DE,以DE为边作正方形EDHI,试用该图形证明勾股定理:CD2+CE2=DE2.(三)等腰直角三角形知识链接(1)两条直角边相等的直角三角形叫做等腰直角三角形.(2)等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,两腰相等,斜边上中线、角平分线、斜边上的高,三线合一;(3)若设等腰直角三角形内切圆的半径r=1,则外接圆的半径R=2+1,所以r :R=1:2+1. 同步练习1.如图,在Rt △ABC 中,AB=AC ,∠A=90°,BD 是角平分线,DE ⊥BC ,垂足为点E .若CD=25,则AD 的长是( )A .225B .22C .25 D .52.在△ABC 中,BC :AC :AB=1:1:2,则△ABC 是( )A .等腰三角形B .钝角三角形C .直角三角形D .等腰直角三角形3.如图,等腰直角三角形ABC 中,AC=BC >3,点M 在AC 上,点N 在CB 的延长线上,MN 交AB 于点O ,且AM=BN=3,则S △AMO 与S △BNO 的差是( )A .9B .4.5C .0D .因为AC 、BC 的长度未知,所以无法确定4.(2011•万州区模拟)如图,△ACD 和△AEB 都是等腰直角三角形,∠EAB=∠CAD=90°,下列五个结论:①EC=BD ;②EC ⊥BD ;③S 四边形EBCD = 21EC •BD ;④S △ADE =S △ABC ;⑤△EBF ∽△DCF ;其中正确的有( )A .①②④⑤B .①②③④C .①②③⑤D .①②③④⑤5.如图,已知△ABC 是腰长为1的等腰直角三形,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ,…,依此类推,则第2015个等腰直角三角形的斜边长是____ __.6.如图,在等腰直角△ACB 中,∠ACB=90°,O 是斜边AB 的中点,点D 、E 分别在直角边AC 、BC 上,且∠DOE=90°,DE 交OC 于点P .有下列结论:①∠DEO=45°;②△AOD ≌△COE ;③S 四边形CDOE = 21S △ABC ;④OD 2=OP •OC . 其中正确的结论序号为____ __.(把你认为正确的都写上)7.如图,a ∥b ,点A 在直线a 上,点C 在直线b 上,∠BAC=90°,AB=AC ,若∠1=20°,则∠2的度数为____ __.8.(2014•徐州模拟)如图,在△ABC 中,∠A=90°,∠C=45°,AB=6cm ,∠ABC 的平分线交AC 于点D ,DE ⊥BC ,垂足为E ,则DC+DE= ____ _cm .9.(2014•温州五校一模)如图,在△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,点E在BC边上,且CE=CD,连结AE、BD、DE.①求证:△ACE≌△BCD;②若∠CAE=25°,求∠BDE的度数.二能得到直角三角形吗(一)勾股定理的逆定理知识链接(1)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.说明:①勾股定理的逆定理验证利用了三角形的全等.②勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.(2)运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角.然后进一步结合其他已知条件来解决问题.注意:要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.同步练习1.(2012•广西)已知三组数据:①2,3,4;②3,4,5;③1,3,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有()A.② B.①② C.①③ D.②③2.(2012•连云港一模)如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数()A.6 B.7 C.8 D.93.(2014•江西模拟)下列各三角形中,面积为无理数的是()A. B. C. D.4.下列能构成直角三角形三边长的是()A.1,1,2 B.5,8,10 C.5,12,13 D.6,7,85.(2012•松北区二模)如图△ABC中,AB=5,AC=3,中线AD=2,则BC长为____ _.6.在直角三角形中,满足条件的三边长可以是____ _(写出一组即可).7.三角形的三边a ,b ,c 满足(a+b )2=c 2+2ab ,则这个三角形是____ _三角形.8.(2014•萧山区模拟)如图,在四边形ABCD 中,∠B=90°,∠BCD=135°,且AB=3cm ,BC=7cm ,CD=25cm ,点M 从点A 出发沿折线A-B-C-D 运动到点D ,且在AB 上运动的速度为21cm/s ,在BC 上运动的速度为1cm/s ,在CD 上运动的速度为2cm/s ,连接AM 、DM ,当点M 运动时间为____ _(s )时,△ADM 是直角三角形.9.(2014•高安市模拟)如图,方格纸中的每个正方形的边长均为1,点A 、B 在小正方形的顶点上,在图中画△ABC (点C 在小正方形的顶点上),使△ABC 为直角三角形(要求画两个且不全等)10.(2014•顺义区一模)在△ABC 中,BC=a ,AC=b ,AB=c ,设c 为最长边.当a 2+b 2=c 2时,△ABC 是直角三角形;当a 2+b 2≠c 2时,利用代数式a 2+b 2和c 2的大小关系,可以判断△ABC 的形状(按角分类).(1)请你通过画图探究并判断:当△ABC 三边长分别为6,8,9时,△ABC 为______三角形;当△ABC 三边长分别为6,8,11时,△ABC 为______三角形.(2)小明同学根据上述探究,有下面的猜想:“当a 2+b 2>c 2时,△ABC 为锐角三角形;当a 2+b 2<c 2时,△ABC 为钝角三角形.”请你根据小明的猜想完成下面的问题:当a=2,b=4时,最长边c 在什么范围内取值时,△ABC 是直角三角形、锐角三角形、钝角三角形?(二)勾股数三勾股定理应用(一)勾股定理的应用知识链接(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.④勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.同步练习1.已知小龙、阿虎两人均在同一地点,若小龙向北直走160公尺,再向东直走80公尺后,可到神仙百货,则阿虎向西直走多少公尺后,他与神仙百货的距离为340公尺?()A.100 B.180 C.220 D.2602.如图,为了测得湖两岸A点和B点之间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米,BC长16米,则A点和B点之间的距离为()米.4A.25 B.12 C.13 D.33.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为()A.5米 B.3米 C.(5+1)米 D.3米4.(2014•和平区一模)如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点,当它靠在另一侧墙时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离DE=32m,则点B到地面的垂直距离BC为___ .5.(2013•池州一模)如图是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为___ .6.(2014•西湖区一模)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,开始时B到墙C的距离为0.7米,若梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离相等,则下滑的距离是___米.7.(2014•三门县一模)如图,这是某种牛奶的长方体包装盒,长、宽、高分别为5cm、4cm、12cm,插吸管处的出口到相邻两边的距离都是1cm,为了设计配套的直吸管,要求插入碰到底面后,外露的吸管长度要在3cm至5cm间(包括3cm与5cm,不计吸管粗细及出口的大小),则设计的吸管总长度L的范围是__ _.8.(2014•西宁)课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.(1)求证:△ADC≌△CEB;(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).9.(2014•广东一模)如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.10.(2013•本溪)校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:2=1.41,3=1.73)(二)平面展开----最短路径问题 知识链接(1)平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.(2)关于数形结合的思想,勾股定理及其逆定理它们本身就是数和形的结合,所以我们在解决有关结合问题时的关键就是能从实际问题中抽象出数学模型.同步练习1.如图,圆柱的底面周长为6cm ,AC 是底面圆的直径,高BC=6cm ,点P 是母线BC 上一点,且PC=32BC .一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是( )A .(4+)cm B .5cm C .35cm D .7cm2.如图,若圆柱的底面周长是30cm ,高是40cm ,从圆柱底部A 处沿侧面缠绕一圈丝线到顶部B 处做装饰,则这条丝线的最小长度是( )A .80cmB .70cmC .60cmD .50cm3.如图,为了庆祝“五•一”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m ,高为3m .如果要求彩带从柱子底端的A 处均匀地绕柱子4圈后到达柱子顶端的B 处(线段AB 与地面垂直),那么应购买彩带的长度为( )A . 45m B .3m C .4m D .5m4.如图,圆柱底面半径为2cm ,高为9cm ,点A 、B 分别是圆柱两底面圆周上的点,且A 、B 在同一母线上,用一根棉线从A 点顺着圆柱侧面绕3圈到B 点,则这根棉线的长度最短为( ) A .12cm B . 97cm C .15cm D . 21cm5.(2014•博山区模拟)如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )A.3 B.2+2 C.10D.46.(2013•荆州模拟)如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建梯子(图中虚线),并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是的12米,则梯子最短长度为___ 米.7.(2013•盐城模拟)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为___ cm.8.(2014•西湖区一模)如图,是一个无盖玻璃容器的三视图,其中俯视图是一个正六边形,A、B两点均在容器顶部,现有一只小甲虫在容器外A点正下方距离顶部5cm处,要爬到容器内B点正下方距离底部5cm 处,则这只小甲虫最短爬行的距离是___ cm.-------------------------------------------------------------------奋斗没有终点任何时候都是一个起点-----------------------------------------------------9.(2013•贵阳模拟)请阅读下列材料:问题:如图1,圆柱的底面半径为1dm,BC是底面直径,圆柱高AB为5dm,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:路线1:高线AB+底面直径BC,如图1所示.路线2:侧面展开图中的线段AC,如图2所示.(结果保留π)(1)设路线1的长度为L1,则L12=______.设路线2的长度为L2,则L22=______.所以选择路线______(填1或2)较短.(2)小明把条件改成:“圆柱的底面半径为5dm,高AB为1dm”继续按前面的路线进行计算.此时,路线1:L12=______.路线2:L22=______.所以选择路线______(填1或2)较短.(3)请你帮小明继续研究:当圆柱的底面半径为2dm,高为hdm时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.信达。
八年级数学下册第17章 模型解题4 勾股定理——构手拉手型全等

模型解题4 勾股定理——构手拉手型全等 【基本图形】
【基本条件】AB=CB. 【辅助线】作BE=BP,∠EBP=∠ABC.
返回导航
模型解题4 勾股定理——构手拉手型全等
【基本结论】
①△CBE≌△ABP;
②BP=BE;
③若∠ABC=60°,可得2个等边三角形,若∠ABC=90°,可得2个等腰直
返回导航
模型解题4 勾股定理——构手拉手型全等
∴ ∠ CPD = 45 ° . 又 ∵∠CPB = 135 ° , ∴ ∠ BPD = 135 ° - 45 ° = 90°.∴△BPD为直角三角形. ∴在 Rt△DCP 中,DP= CD2+CP2=4 2, ∴在 Rt△BPD 中,BD= DP2+BP2=6. 又由旋转性质知AP=BD=6型全等 类型2 遇等腰直角三角形则构造等腰直角三角形 2.如图,Rt△ABC中,CA=CB,∠ACB=90°,CP=4,PB=2,∠CPB =135°,求AP的长. 解:将△CPA绕点C顺时针旋转90°,使CA与CB重合,点P的对应点为D, 连接DP. 由 题 意 , 知 CD = CP = 4 , ∠ DCB = ∠PCA. 又 ∵∠BPC + ∠PCA = 90 ° , ∴∠DCB+∠PCB=∠DCP=90°,∴△DCP为等腰直角三角形.
返回导航
模型解题4 勾股定理——构手拉手型全等
(2)求∠APB的度数. 解:如图,∵△ABC为等边三角形,∴AB=BC. 由旋转的性质知,△AP′B≌△CPB. ∴AP′=PC=10,BP′=BP=8.又∵∠PBP′=60°, ∴△PBP′为等边三角形.∴∠BPP′=60°. ∴P′P=BP=8,∴AP2+P′P2=62+82=100=102=AP′2.∴△APP′为 直角三角形.∠APP′=90°. ∴∠APB=∠APP′+∠BPP′=90°+60°=150°.
八年级数学《勾股定理》教案8篇

八年级数学《勾股定理》教案8篇(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用资料,如心得体会、工作报告、工作总结、工作计划、申请书、读后感、作文大全、合同范本、演讲稿、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of practical materials for everyone, such as insights, work reports, work summaries, work plans, application forms, post reading reviews, essay summaries, contract templates, speech drafts, and other materials. If you want to learn about different data formats and writing methods, please stay tuned!八年级数学《勾股定理》教案8篇本文将为大家介绍八年级数学《勾股定理》教案8篇。
第04讲 勾股定理(解析版)-【寒假自学课】2023年八年级数学寒假精品课(人教版)

第04讲 勾股定理【学习目标】1.掌握勾股定理,了解利用拼图验证勾股定理的方法.2.会借助勾股定理确定数轴上表示无理数的点,初步感知实数与数轴上的点的一一对应的关系.3.能运用勾股定理进行有关的计算和解决实际问题.【基础知识】1.勾股定理如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么222a b c +=. 2.勾股定理的证明 方法图形证明赵爽“勾股圆方图”因为大正方形的边长为c ,所以大正方形的面积为2c .又大正方形的面积=()2142ab a b ⨯+-,所以222a b c +=bca伽菲尔德总统拼图设梯形面积为S ,则()()12S a b a b =++, 又2111222S ab ab c =++, 所以222a b c +=毕达哥拉斯拼图由图(1)得大正方形面积=2142c ab +⨯,由图(2)得大正方形面积=22142a b ab ++⨯,比较两式易得222a b c +=总结 以上证法都是通过拼摆图形,运用图形面积与代数恒等式的关系互相转化证明勾股定理3.勾股定理的应用 勾股定理的主要应用如下:(1)已知直角三角形的任意两边求第三边; (2)已知直角三角形的任意一边确定另两边的关系; (3)证明包含有平方(算术平方根)关系的几何问题;(4)构造方程(或方程组)计算有关线段的长度,解决生产、生活中的实际问题.【考点剖析】ccb baa(2)(1)ccbb a a考点一:运用勾股定理进行计算例1.在Rt ABC 中,A ∠,B ∠,C ∠的对边分别为a ,b ,c ,90C ∠=︒.(1)已知3a =,4b =,求c ; (2)已知13c =,5a =,求b ; (3)已知:3:4a b =,10c =,求b . 【答案】(1)5;(2)12;(3)8 【解析】解:(1)因为90C ∠=︒,3a =,4b =, 所以222223425c a b =+=+=, 所以5c =.(2)因为90C ∠=︒,13c =,5a =, 所以22222135144b c a =-=-=, 所以12b =.(3)因为90C ∠=︒,:3:4a b =, 所以43b a =. 因为90C ∠=︒,10c =,43b a =, 所以2224103a a ⎛⎫+= ⎪⎝⎭,解得6a =(负值舍去),所以8b =.考点二:运用勾股定理求面积例2.如图,已知直角三角形的直角边分别为a 、b ,斜边为c ,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形.那么,这四个 图形中,直角三角形外,其他几个图形面积分别记作1S 、2S 、3S . 结论Ⅰ:1S 、2S 、3S 满足123S S S +=只有(4); 结论Ⅱ:∵a b c +>,∴123S S S +>的有(1)(2)(3). 对于结论Ⅰ和Ⅱ,判断正确的是( )A .Ⅰ对Ⅱ不对B .Ⅰ不对Ⅱ对C .Ⅰ和Ⅱ都对D .Ⅰ和Ⅱ都不对【答案】D 【解析】解:∵直角三角形的三边长分别为a 、b 、c , ∴222a b c +=,图1中,21133224S a a a =⨯⨯=,2234S b =,2334S =, 则)22123S S a b +=+,233S =, ∴123S S S +=,同理,图2、图3、图4,都符合结论Ⅰ:123S S S +=, 故选:D .考点三:勾股定理的简单应用例3.如图,为测量河宽BC ,某人选择从点C 处横渡,由于受水流的影响,实际上岸地点A 与欲到达地点B 相距50米,结果发现AC 比河宽BC 多10米,求该河的宽度BC .(两岸可近似看作平行)【答案】120米 【解析】解:根据题意可知50AB =米,10AC BC =+米, 设BC x =cm ,由勾股定理得222AC AB BC =+,即()2221050x x +=+,解得120x =.答:该河的宽度BC 为120米. 考点四:运用勾股定理解决折叠问题例4.如图,在长方形ABCD 中,点E 在DC 上,将长方形沿AE 折叠,使点D 落在BC 边上的点F 处.若3AB =,5BC =,求EC 的长.【答案】43【解析】解:∵四边形ABCD 为长方形, ∴5AD BC ==,3AB CD ==,∵长方形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上的F 处, ∴5AF AD ==,EF DE =, 在Rt ABF 中,2222534BF AF AB -=-=,∴541CF BC BF =-=-=,设CE x =,则3DE EF x ==-, 在Rt ECF 中,∵222CE FC EF +=, ∴()22213x x +=-,解得43x =, 故EC 的长为43. 考点五:会画长度为无理数的线段例5. 如图,根据图中的标注和作图痕迹可知,在数轴上的点A 所表示的数为 .51 【解析】解:根据勾股定理可求出圆的半径为:22125+=即点A 到表示15 那么点A 到原点的距离为)51个单位,∵点A 在原点的右侧,∴点A 51, 51.考点六:运用勾股定理求最短路径例6. 如图,圆柱的底面周长为24cm ,AC 是底面圆的直径,高6BC =cm ,点P 是BC 上一点,且5PC BP =,一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是___________.【答案】13cm 【解析】解:如图展开,连接AP ,则线段AP 的长是从A 点出发沿着圆柱的表面爬行到点P 的最短距离,∵6cm BC =,56PC BC =, ∴5cm PC =,∵圆柱的底面周长为24cm , ∴12cm AC =,在Rt ACP 中,由勾股定理得:222212513cm AP AC PC =+=+=【真题演练】1.如图,在ABC 中,10AB AC ==,12BC =,AD 是ABC 的中线,则AD 长为( )A .22B .6C .8D .261【答案】C 【解析】解:∵12BC =,AD 是ABC 的中线, ∴6BD CD ==, ∵10AB AC ==, ∴AD BC ⊥, ∴22221068AD AB BD =-=-=.故选:C .2.线段AB 在平面直角坐标系中的位置如图所示,()1,4A -,()5,1B -,线段AB 的长为( )A .5B .42C .4D .3【答案】A 【解析】解:由勾股定理得,22435AB +=, 故选:A .3.如图,在长方形ABCD 中,3AB =,1AD =,AB 在数轴上,若以点A 为圆心,对角 线AC 长为半在作弧交数轴正半轴于点M ,则点M 所表示的数为( )A 10B 101C 101D .2【答案】B【解析】解:∵四边形ABCD 是长方形,1AD =,∴1BC AD ==,90ABC ∠=︒.∵90ABC ∠=︒,1BC =,3AB =, ∴223110AC =+= ∴10AM AC ==∴点M 101.故选:B .4.如图,在ABC 中,20AB =,15AC =,7BC =,则点A 到BC 的距离是()A .10B .11C .12D .13【答案】C【解析】解:如图,过点A 作AD BC ⊥交BC 的延长线于点D ,在Rt ABD 与Rt ACD 中,由勾股定理得,22222AB BD AD AC CD -==-,即()222220715CD CD -+=-,∴9CD =, ∴2212AD AC CD -=,即点A 到BC 的距离是12,故选:C .5.一只蚂蚁从长宽都是3,高是8的长方体纸箱的A 点沿纸箱爬到B 点,则它所爬行的最 短路线的长是( )A .10B .14C 130D .8【答案】A【解析】解:将长方体展开,分两种情况,第一种展开方式如下图:∴226810AB +=,第二种展开方式如下图: ∴22311130AB +=∵10130<∴A 点沿纸箱爬到B 点,所爬行的最短路线的长是10,故选:A .6.如图,Rt ABC 中,90C ∠=︒,AD 是BAC ∠的平分线,DE AB ⊥,垂足为E .若 10cm AB =,6cm AC =,则BE 的长为 cm .【答案】4cm【解析】解:∵AD 是BAC ∠的平分线,DE AB ⊥,90C ∠=︒,即AC CD ⊥,∴CD DE =.在Rt ACD 与Rt AED 中,CD ED AD AD =⎧⎨=⎩, ∴()Rt ACD Rt AED HL ≌.∴AC AE =.又10cm AB =,6cm AC =,∴()4cm BE AB AE AB AC =-=-=.故答案是:4cm .7.已知x ,y 分别为直角三角形的两边长,并且满足()()()22230x y y ---=,则第三边长度为 .【答案】2或135【解析】解:∵()()()22230x y y -+--=,∴20x -=,()()230y y --=,∴2x =,2y =或3y =;(1)当2x =,2y =时,x 、y 为直角边长,斜边长222222+=;(2)当2x =,3y =时,分两种情况:①y 为直角边长时,斜边长222313+=②y 为斜边时,第三边长22325-=综上所述:第三边的长为22135故答案为:21358.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A 、C 、 D 的面积依次为4、6、20,则正方形B 的面积为 .【答案】10【解析】解:由题意:A B E S S S +=正方形正方形正方形,D C E S S S -=正方形正方形正方形,∴A B D C S S S S +=-正方形正方形正方形正方形.∵正方形A 、C 、D 的面积依次为4、6、20,∴4206B S +=-正方形,∴10B S =正方形.故答案为:10.9.等腰三角形的两条边长为4和6,则这个等腰三角形的面积为 . 【答案】237【解析】解:①6是腰长时,三角形的三边分别为6、6、4,如图,过顶点A 作底边BC 的垂线AD ,垂足为点D ,则6AB AC ==,4BC =,∵AD BC ⊥,∴2BD CD ==, ∴22226242AD AB BD -=-=, ∴三角形的面积为1442=822⨯⨯; ②6是底边时,三角形的三边分别为6、4、4,如图,过顶点A 作底边BC 的垂线AD ,垂足为点D ,则4AB AC ==,6BC =,∵AD BC ⊥,∴3BD CD ==, ∴2222437AD AB BD -=-= ∴三角形的面积为167=372⨯ 综上所述,三角形的面积为8237 故答案为:23710.有一个小朋友拿一根竹竿要通过一个长方形的门,若把竹竿竖着放比门高出1尺,斜着 放恰好等于门的对角线长,已知门宽为4尺,求竹竿高.解:设竹竿高为x 尺,则门高 尺.(用x 的代数式表示)根据题意,可列关于x 的方程: .解得:x = .答:【答案】()1x -,()22214x x -+=,8.5【解析】解:设竹竿高为x 尺,则门高()1x -尺.根据题意,得:()22214x x -+=,解得:8.5x =,答:竹竿高为8.5尺.故答案为:()1x -,()22214x x -+=,8.5.11.一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图, 火柴盒的一个侧面ABCD 倒下到AEFG 的位置,连接CF ,此时90FAC ∠=︒,AB a =,BC b =,AC c =.请利用直角梯形BCFG 的面积证明勾股定理:222a b c +=.【答案】见解析【解析】 证明:∵2211112222AFG AFC ACB BCFG S S S S ab ab c ab c =++=++=+梯形, ()()()2211112222BCFG S FG BC BG a b a b a ab b =⋅+⋅=++=++梯形, ∴222111222ab c a ab b +=++, 整理得:222a b c +=.12.八年级的小明和小亮同学学习了“勾股定理”之后,为了测得如图所示风筝的高度CE , 他们进行了如下操作:①测得9BD =米;(注:BD CE ⊥)②根据手中剩余线的长度计算出风筝线15BC =米;③牵线放风筝的小明身高1.6米.求风筝的高度CE .【答案】13.6米【解析】解:在Rt CDB 中,由勾股定理得,22222159144CD BC BD =-=-=,所以,12CD =±(负值舍去),所以,12 1.613.6CE CD DE =+=+=米,答:风筝的高度CE 为13.6米.【过关检测】1.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )A .25B .7C .5或7D .7或25【答案】D【解析】解:当边长为4的边为斜边时,第三边的平方为22437-=;当边长为4的边为直角边时,第三边的平方为224325+=;故选:D .2.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若 图中的直角三角形的一条直角边长为5,大正方形的边长为13,则中间小正方形的面积 ( )A .144B .64C .49D .25【答案】C【解析】解:由题意可得:小正方形的边长2213557-=,∴小正方形的面积为7749⨯=,故选:C .3.如图,ABC 中,10AB AC ==,12BC =,D 是BC 的中点,DE AB ⊥于点E , 则DE 的长为( )A .125 B .8C .245D 5【答案】C【解析】解:如图,连接AD ,∵AB AC =,D 是BC 的中点,∴AD BC ⊥,162BD BC ==,在Rt ABD 中,由勾股定理得,22221068AD AB BD -=-=,∵DE AB ⊥, ∴1122ABD S AB DE BD AD =⋅=⋅,∴6824105BD AD DE AB ⋅⨯===, 故选:C .4.一直角三角形的两直角边分别是8和6,下列说法正确的是( )A .斜边长24B .三角形的周长是25C .三角形的面积为48D .斜边长10【答案】D【解析】解:∵直角三角形的两直角边分别是8和6, ∴斜边长228610=+=,三角形的面积=186=242⨯⨯, 三角形的周长=6810++=24,∴选项D 正确,选项A 、B 、C 错误,故选:D .5.如图,Rt ABC 的直角边AB 在数轴上,点A 表示的实数为0,以A 为圆心,AC 的长 为半径作弧交数轴的负半轴于点D .若1CB =,2AB =,则点D 表示的实数为 .【答案】5【解析】解:2222215AC AB BC =+=+= 则5AD =∵A 点表示0,∴D 点表示的数为:5- 故答案为:56.如图,Rt ABC 中,90ACB ∠=︒,CD AB ⊥,9AB =,6BC =,则BD 的长 为 .【答案】4【解析】解:在Rt ABC 中,由勾股定理得,22229635AC AB BC =--=, ∵1122ABC S AB CD BC AC =⋅=⋅, ∴63525BC AC CD AB ⋅⨯=== 在Rt ACD 中,由勾股定理得,2245205AD AC CD -=-=,∴954BD AB AD =-=-=,故答案为:4.7.在平静的湖面上,有一朵荷花高出水面半尺,忽然一阵强风吹来把荷花垂直拉到水里且 荷花恰好落在水面.花在水平方向上离开原来的位置2尺远,则这个湖的水深是 尺.【答案】3.75【解析】解:若设湖水的深度x 尺.则荷花的长是()0.5x +米.在直角三角形中,根据勾股定理, 得:()2220.52x x +=+,解之得: 3.75x =,∴湖水的深度为3.75尺.故答案为:3.75.8.如图所示,一棵18m 高的树被风刮断了,树顶落在离树根12m 处,则折断处的高度AB 为 m .【答案】5【解析】解:由题意得:12m BC =,18m AC AB +=,90ABC ∠=︒,∴222AB BC AC +=,设m AB x =,则()18m AC x =-,由勾股定理得:222AB BC AC +=,即()2221218x x +=-,解得:5x =,∴ 2.5AB =米,∴折断处的高度AB 为5m .故答案为:5.9.如图,圆柱的底面周长是10cm ,圆柱高为12cm ,一只蚂蚁如果要沿着圆柱的表面从下 底面点A 爬到与之相对的上底面点B ,那么它爬行的最短路程为 .【答案】13cm【解析】解:把圆柱沿母线AC 剪开后展开,点B 展开后的对应点为B ',则蚂蚁爬行的最短路径为AB ',如图,12AC =,5CB '=,在Rt ACB ',2251213AB '=+=,所以它爬行的最短路程为13cm .故答案为:13cm .10.阅读与思考两点之间的距离公式如果数轴上的点1A ,2A 分别表示实数1x ,2x ,两点 1A ,2A 间的距离记作12A A ,那么1221A x x =-.对于平面上的两点1A ,2A 间的距离是否有类似的结论呢?运用勾股定理,就可以推出平面上两点之间的距离公式.(1)如图1,已知平面上两点()0,4A ,()3,0B ,求A ,B 两点之间的距离AB ;(2)如图2,已知平面上两点()1,2A ,()5,5B ,求这两点之间的距离AB ;(3)一般地,设平面上任意两点()11,A x y 和()22,B x y ,如图3,如何计算A ,B 两点之间的距离AB ?对于问题3,作AA x '⊥轴,BB x '⊥轴,垂足分别为点A ',B ';作AA y ''⊥轴,垂足为点A '';作BC AA '⊥,垂足为点C ,且延长BC 与y 轴交于点B '',则四边形BB A C '',ACB A ''''是长方形. ∵CA = ,CB = , ∴222AB CB CA =+= . ∴()()222121AB x x y y =-+-这就是平面直角坐标系中两点之间的距离公式.请你根据上面的公式求出下列两点之间的距离:()1,2A -,()2,1B -.【答案】(1)5;(2)5;(3)12y y -,21x x -,()()221221y y x x -+-;(4)32【解析】解:(1)∵()0,4A ,()3,0B , ∴4OA =,3OB =, 由勾股定理得22345AB =+=;(2)∵()1,2A ,()5,5B , ∴4AC =,3BC =,由(1)同理得,5AB =;(3)∵12AC y y =-,21CB x x =-, ∴()()222221221AB CB CA y y x x =+=-+-, ∴()()222121AB x x y y =-+-.故答案为:12y y -,21x x -,()()221221y y x x -+-;(4)由两点间距离公式得: ()()22211232AB =++--=。
2024年八年级数学《勾股定理》教案(通用篇)

2024年八年级数学《勾股定理》教案(通用篇)八年级数学《勾股定理》教案 1教学目标1、知识与技能目标学会观察图形,勇于探索图形间的关系,培养学生的空间观念.2、过程与方法(1)经历一般规律的探索过程,发展学生的抽象思维能力.(2)在将实际问题抽象成几何图形过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.3、情感态度与价值观(1)通过有趣的问题提高学习数学的兴趣.(2)在解决实际问题的过程中,体验数学学习的实用性.教学重点:探索、发现事物中隐含的勾股定理及其逆及理,并用它们解决生活实际问题.教学难点:利用数学中的建模思想构造直角三角形,利用勾股定理及逆定理,解决实际问题.教学准备:多媒体教学过程:第一环节:创设情境,引入新课(3分钟,学生观察、猜想)情景:如图:在一个圆柱石凳上,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的.蚂蚁捕捉到这一信息,于是它想从A处爬向B处,你们想一想,蚂蚁怎么走最近?第二环节:合作探究(15分钟,学生分组合作探究)学生分为4人活动小组,合作探究蚂蚁爬行的最短路线,充分讨论后,汇总各小组的方案,在全班范围内讨论每种方案的路线计算方法,通过具体计算,总结出最短路线。
让学生发现:沿圆柱体母线剪开后展开得到矩形,研究“蚂蚁怎么走最近”就是研究两点连线最短问题,引导学生体会利用数学解决实际问题的方法:建立数学模型,构图,计算.学生汇总了四种方案:(1)(2)(3)(4)学生很容易算出:情形(1)中A→B的路线长为:AA’+d,情形(2)中A→B的路线长为:AA’+πd/2所以情形(1)的路线比情形(2)要短.学生在情形(3)和(4)的比较中出现困难,但还是有学生提出用剪刀沿母线AA’剪开圆柱得到矩形,前三种情形A→B是折线,而情形(4)是线段,故根据两点之间线段最短可判断(4)最短.如图:(1)中A→B的路线长为:AA’+d;(2)中A→B的路线长为:AA’+A’B>AB;(3)中A→B的路线长为:AO+OB>AB;(4)中A→B的路线长为:AB.得出结论:利用展开图中两点之间,线段最短解决问题.在这个环节中,可让学生沿母线剪开圆柱体,具体观察.接下来后提问:怎样计算AB?在Rt△AA′B中,利用勾股定理可得,若已知圆柱体高为12c,底面半径为3c,π取3,则.第三环节:做一做(7分钟,学生合作探究)教材23页李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺,(1)你能替他想办法完成任务吗?(2)李叔叔量得AD长是30厘米,AB长是40厘米,BD 长是50厘米,AD边垂直于AB边吗?为什么?(3)小明随身只有一个长度为20厘米的刻度尺,他能有办法检验AD边是否垂直于AB边吗?BC边与AB边呢?第四环节:巩固练习(10分钟,学生独立完成)1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6/h的速度向正东行走,1小时后乙出发,他以5/h的速度向正北行走.上午10:00,甲、乙两人相距多远?2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离.3.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?第五环节课堂小结(3分钟,师生问答)内容:1、如何利用勾股定理及逆定理解决最短路程问题?第六环节:布置作业(2分钟,学生分别记录)内容:作业:1.课本习题1.5第1,2,3题.要求:A组(学优生):1、2、3B组(中等生):1、2C组(后三分之一生):1板书设计:教学反思:八年级数学《勾股定理》教案 21、勾股定理勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.即直角三角形两直角的平方和等于斜边的平方.因此,在运用勾股定理计算三角形的边长时,要注意如下三点:(1)注意勾股定理的使用条件:只对直角三角形适用,而不适用于锐角三角形和钝角三角形;(2)注意分清斜边和直角边,避免盲目代入公式致错;(3)注意勾股定理公式的变形:在直角三角形中,已知任意两边,可求第三边长.即c2=a2+b2,a2=c2-b2,b2=c2-a2.2.学会用拼图法验证勾股定理拼图法验证勾股定理的基本思想是:借助于图形的面积来验证,依据是对图形经过割补、拼接后面积不变的原理.如,利用四个如图1所示的直角三角形三角形,拼出如图2所示的三个图形.请读者证明.如上图示,在图(1)中,利用图1边长为a,b,c的'四个直角三角形拼成的一个以c为边长的正方形,则图2(1)中的小正方形的边长为(b-a),面积为(b-a)2,四个直角三角形的面积为4×ab=2ab.由图(1)可知,大正方形的面积=四个直角三角形的面积+小正方形的的面积,即c2=(b-a)2+2ab,则a2+b2=c2问题得证.请同学们自己证明图(2)、(3).3.在数轴上表示无理数将在数轴上表示无理数的问题转化为化长为无理数的线段长问题.第一步:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方,注意一般其中一条线段的长是整数;第二步:以数轴原点为直角三角形斜边的顶点,构造直角三角形;第三步:以数轴原点圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点.二、典例精析例1如果直角三角形的斜边与一条直角边的长分别是13cm和5cm,那么这个直角三角形的面积是cm2.分析:欲求直角三角形的面积,已知一直角三角形的斜边与一条直角边的长,则求得另一直角边的长即可.根据勾股定理公式的变形,可求得.解:由勾股定理,得132-52=144,所以另一条直角边的长为12.所以这个直角三角形的面积是×12×5=30(cm2).例2如图3(1),一只蚂蚁沿棱长为a的正方体表面从顶点A爬到顶点B,则它走过的最短路程为()A.B.C.3aD.分析:本题显然与例2属同种类型,思路相同.但正方体的各棱长相等,因此只有一种展开图.解:将正方体侧面展开八年级数学《勾股定理》教案 3重点、难点分析本节内容的重点是勾股定理的逆定理及其应用。
八年级数学上册知识点勾股定理

八年级数学上册 第一章 勾股定理 由勾3、股4、弦5所想到的同步辅导素材 (新版)北师大版

由勾3、股4、弦5所想到的老师:大家知道,32+42=52,那么若3个连续的正整数a,b,c(a<b<c)满足a2+b2=c2,是否只有3,4,5一种情况?我说:是的.理由是:设b=x,则a=x-1,c=x+1(x>1,且x为整数),于是有(x-1)2+ x2=(x+1)2,整理,得x2-4x=0. 因为x>1,所以两边同时除以x,得x-4=0,解得x=4.所以a=3,b=4,c=5.所以符合这种关系的3个连续的正整数只有3,4,5这一种情况.老师:很好!说得非常精彩!大家再想一想:等式“32+42=52”中的左边是2个数,右边是1个数,左边比右边多一个数,即3个连续的正整数中较小的两个数的平方和等于最大数的平方,那么,5个连续的正整数有没有类似的规律呢?看同学们半天也没有反应,老师启发道:是否存在5个这样的正整数,使其中较小的3个数的平方和等于较大的2个数的平方和呢?我说:设这5个连续的正整数分别为x-2,x-1,x,x+1,x+2(x>2,且x为整数),则有(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2.整理,得x2-12x=0.因为x>2,所以两边同时除以x,得x-12=0,解得x=12.所以5个连续的正整数为10,11,12,13,14,即有102+112+122=132+142.老师:豪康同学说得非常棒!那么7个连续的正整数,情况又怎样?王瑜:设这7个连续的正整数分别为x-3,x-2,x-1,x,x+1,x+2,x+3(x>3,且x为整数),则有(x-3)2+(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2+(x+3)2.整理,得x2-24x=0.因为x>3,所以两边同时除以x,得x-24=0,解得x=24.所以7个连续的正整数为21,22,23,24,25,26,27,即有212+222+232+242=252+262+272.老师:王瑜同学说得很好!由此我们猜想出有下面的结论:存在2k+1个连续的正整数,使其中较小的(k+1)个数的平方和等于较大的k个数的平方和,验证过程留给同学们课后去解答.本文档仅供文库使用。
八年级上册数学勾股定理知识点

八年级上册数学勾股定理知识点八年级上册数学勾股定理知识点1.勾股定理的内容:假如直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方。
注:勾最短的边、股较长的直角边、弦斜边。
勾股定理又叫毕达哥拉斯定理2.勾股定理的逆定理:假如三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
3.勾股数:满足a2 +b2=c2的三个正整数,称为勾股数.勾股数扩大一样倍数后,仍为勾股数.常用勾股数:3、4、5;5、12、13;7、24、25;8、15、17。
4.勾股定理常常用来算线段长度,对于初中阶段的线段的计算起到很大的作用例题精讲:练习:例1:假设一个直角三角形三边的.长分别是三个连续的自然数,那么这个三角形的周长为解析:可知三边长度为3,4,5,因此周长为12(变式)一个直角三角形的三边为三个连续偶数,那么它的三边长分别为解析:可知三边长度为6,8,10,那么周长为24例2:直角三角形的两边长分别为3、4,求第三边长.解析:第一种情况:当直角边为3和4时,那么斜边为5 第二种情况:当斜边长度为4时,一条直角边为3,那么另一边为根号7《点评》此题是一道易错题目,同学们应该认真审题!例3:一个直角三角形中,两直角边长分别为3和4,以下说法正确的选项是( )A.斜边长为25B.三角形周长为25C.斜边长为5D.三角形面积为20解析:根据勾股定理,可知斜边长度为5,选择C初中数学的方法和技巧多做主要是指做习题,学数学一定要做习题,并且应该适当地多做些。
做习题的目的首先是纯熟和稳固学习的知识;其次是初步启发灵敏应用知识和培养独立考虑的才能;第三是融会贯穿,把不同内容的数学知识沟通起来。
在做习题时,要认真审题,认真考虑,应该用什么方法做?能否有简便解法?做到边做边考虑边总结,通过练习加深对知识的理解。
必需要有错题本说到错题本不少同学都觉得自己的记忆力好,不需要错题本就能记住,这是一种“错觉”,每个人都有这种感觉,等到题目增多,学习内容加深,这时就会发现自己力不从心了。
八下数学勾股定律

有关“数学”的勾股定理
有关“数学”的勾股定理如下:
勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派。
勾股定理的公式为a²+b²=c²,其中a、b代表两条直角边,c代表斜边。
这个定理的证明方法有很多种,其中最有代表性的是几何证明。
此外,还有代数证明、三角函数证明等多种证明方法。
勾股定理不仅在数学中有着广泛的应用,它在日常生活中也有着很多用途。
比如,可以用勾股定理测量房屋的面积、修建水平线等等。
此外,勾股定理也是其他学科的基础,比如实验物理中的力学、声学等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:已知:在Rt△ABC中, ∠C=90°,AB=c,AC=b,BC=a.
(1)、若a=2,b=4,求c. (2) 若b= √ 2, c=3 ,求a
解:∵ 在△ABC中,∠C=90° 解: ∵ 在△ABC中, a=2, b=3 ∠C=90°b= √ 2 ,c=3 ∴ c2 = a2 + b2 =22+42 =20 ∴ c= √20 =2 √ 5 (舍负 值) ∴ a2 = c2 ﹣b2 = 32 –(√ 2 )2 =7 ∴ a= √ 7 (舍负值)
B
思维拓展: 有没有一种直角三角形, 已知一边可以求另外两边长呢? A a C c a B A
c b
30°
45° b
C
B
a:b:c=1:1:√2
a:b:c=1:√3:2
实践与探索
1、判断题: 1)、直角三角形三边a,b,c一定满足下面的式子:
a² +b² =c²
(X ) (X )
2)、直角三角形的两边长分别是3和4,则另一边是5
例2:将长为5.41米的梯子AC斜靠在墙上, BC长为2.16米,求梯子上端A到墙的底端 B的距离AB(精确到0.01米) 解:在Rt△ABC中, ∠ABC=90° A BC=2.16 ,CA=5.41 根据勾股定理,得 AB=√ AC² - BC² =√ 5.41²-2.16² C ≈4.96(米)
A P C R
Q
Bห้องสมุดไป่ตู้
AC² +BC² = AB²
(3)美国总统证法:
D c C c
b A
a b
D
a
∵S梯形ABCD=1/2(a+b)(a+b) =1/2ab×2+1/2 c² ∴a² +b² =c²
(4)我来试一试
b a a
a
b a
b
c
c a
a b c
c
a b
c
b
c
b
a
b
S=1/2ab×4+ c² =1/2ab ×4+ a² +b² a² +b² =c²
3)、若△ABC的三边长是a=7,b=24,c=25,则△ABC (√ ) 是直角三角形 4)、 △ABC是三边之比为1:1:√2 ,则△ABC是直角 三角形 (√ ) 5)、等边三角形高为2 √3cm,则它的边长是3cm (X )
2、探究下面三个圆面积之间的关系
S1
c a b
S2
∵ a² +b² =c² ∴ S1=S2+S3
S3
勾股小常识:勾股数 1、 a² +b² =c² ,满足(a,b,c)=1则a,b,c,为 基本勾数如:3、4、5;5、12、 13; 7、24、25…… 2、如果a,b,c是一组勾股数,则ka、kb、 kc(k为正整数)也是一组勾股数,如: 6、8、10;9、12、18…… 3、若a,b,c是一组基本的勾股数,则a,b,c 不能同时为奇数或同时为偶数 4、一组勾股数中必有一个数是5倍数 5、2mn,m² -n² ,m² +n² 为勾股数组,m>n﹥0 ,m,n一奇一偶
18.1勾股定理4
这是一个会标, 同学们认识这是什么大会的会标吗?
c a
b
∵1/2ab×4+(ba)² =c² ∴a² +b² =c²
弦图
(1)我国古代西周时期商高说法
A 弦5 a c b 股4
勾
3
C
B
a² +b² =c²
勾股定理:直角三角形两直角边的 平方和 等于斜边的平方
(2)毕达哥拉斯定理:
作业: 1、用勾股定理知识设计一个图案 2、已知三角形三边为5、6、7,求 △ABC面积
; vi设计 品牌设计 宣传设计 企业标识设计 品牌画册设计 品牌咨询 品牌 策划网 ;
候再次重走先祖の路/只确定/这壹次又确定谁胜利呢?钟薇认识滴子/知道这佫人何其恐怖/滴府の无数秘法/它都见识过/它几乎确定含着滴府这把金钥匙成长起来の/而睡古却不同/它远离滴府/没有滴府底蕴の支撑/它又岂能和滴子交锋?只不过滴子这佫层次の人物交手/根本不确定她能左右の /在滴子の眼中/她也不过就确定壹件物品而已/它の眼中只有自己/即使她特殊/它也不会被她左右/要不确定因为她の舞姿对其有大用/它甚至都不会关注她/它就确定这样壹佫傲然の人/觉得滴下の壹切都确定它の陪衬/这样壹佫人/没有人能影响它/"那就试试当年の狗能不能翻身/"睡古说话之 间/壹步步の向着对方走去/众人没有感觉到它の壹丝壹毫の气息/但睡古壹步步走出间/脚下纹理闪现/道理无限/光华璀璨/如同神灵壹样/每走壹步都承载着它の道/这壹步步の走向它/滴子の面容也凝重咯起来/睡古走向它/给它也有莫大压力/身上の力量在四肢百骸中流转/压制住这股压力/直 直の盯着睡古/尽管睡古让它凝重/但它并没有因此而惧怕/当时之中/年轻壹辈中又有谁确定自己の对手?自己当为这壹代の第壹人/当为这壹代の至尊/没有人能阻拦它の脚步/它定然要执掌滴府/⑨滴拾地唯我独尊/证得神位/长生不死/这确定它の信念/坚定和偏执の信念/没有人能阻拦它の路/ 面前の这佫人也壹样/睡古缓缓走过去/没有出手/但身上却壹道道残影从身体中迸发出来/残影出现/都走向滴子/滴子着走向它の残影/眼中那双眸子射出光芒/光芒展现出来/化作它の虚影/影响咯这些残影/虚影和残影交锋/直接撞击在壹起/"轰///轰///"就仅仅确定残影和虚影の交锋/惊雷般 の巨响响起来/滴地摇晃起来/两人の中间/壹条巨大の裂缝出现/这条巨大の裂缝深不可测/不断の蔓延/配合着轰隆隆の巨响/让人心惊肉跳/残影和虚影交锋之间/地上の裂缝越来越多/滴地直接崩裂/马开和钟薇等人大骇/欧奕力量护住几人/挡住卷动而来の恐怖飓风/带着壹群人连连后退/"仅 仅确定残影和虚影の交锋/其余劲都能不玄古境咯/"欧奕心惊/这些年/睡古实力到底成长到何其地步/无心峰数人之中/睡古来の最早/当年它上无心峰の时候/睡古实力就逆滴咯/而这么多年过去咯/欧奕原本以为自己实力能追上壹点睡古/但现在才明白/自己和它相距甚远/马开等人此刻也异常 の震撼/淡淡残影和虚影就能暴动出玄古境の力量/这两人震の有惊世之力/想到睡古当年灭杀过不落山壹佫千年前の老壹辈人物/马开又不觉得奇怪/"要追上它们/还需要多久啊/"马开深吸壹口气/但马上又紧紧の握咯握拳头/在年轻壹辈中/自己属于最年轻の哪壹佫/能走到这壹步已经相当不易 /只要给它时间/它有信心能追上睡古等人/即使它们每壹佫底蕴惊人/马开依旧有信心能追上它们/将来の世上俊才交锋中/壹定有它壹席之位/睡古身上の残影不断の涌出/滴子身上の虚影也不断の出现/虚影和残影弥漫空间/不断の交锋旮旯/大地无数の裂缝出现/宛如玻璃碎片壹样/只确定这块 玻璃确定大地/辽阔无边/这壹道道裂缝横七竖八到处都确定/让人心惊肉跳/"轰///轰///"壹声声震动/引得马开等人心跳加速/刚刚众人站立の地方/无壹完好之处/到处都确定裂缝/空间都崩裂咯数次/两人の残影和虚影不断/睡古和滴子终于相对而站立/距离五米不到/"真确定让本滴子意外/不 在滴府中の你/居然还有这样の实力/无心峰传言确定情域最不能招惹の地方之壹/果然有几分本事/"滴子着睡古说道/"但本滴子也听说/无心峰确定疯子聚集营/""不要妄想以话语破我心境/无心峰不管确定疯还确定癫/起码比狗好壹些不确定吗/睡古不屑の说道/收集阅读本部分::为咯方便下 次阅读/你可以点击下方の记录本次(正文第八百五拾四部分绝世之战)阅读记录/下次打开书架即可看到/请向你の朋友第八百五拾五部分弱水境界卡槽滴子和睡古交手/两人出手如同闪电般/直冲杀对方而去/快如闪电/滔滴の力量从它们手中震动而出/直杀对方の要害而去/以众人の眼力/根 本不清两人确定如何出手の/只见它们交手间/各种残影舞动不断/虚空不断の崩裂/四方の山丘被夷为平地/当真如同末世壹样/各种妙术不断/七彩璀璨の光华不断の迸发出来/马开等人早已经远远の离着滴子和睡古/它们所爆发の劲气根本不确定两人能抵挡の/"轰隆隆///"壹声声巨响炸裂/两 人从大地打上云霄/在云霄之上/暴动の力量把云霄卷碎/滴地空间/不断の被崩裂/各种力量卷杀而下/劲气如同狂啸の飓风/把底下の壹切都给卷起来/两人の打斗太过恐怖咯/让人头皮发麻/每壹次舞动/都如同带着灭世之威壹般/打の四周壹切被破坏/各种力量不断の卷杀而下/谁能相信这确定 两佫人所能涌动出来の力量/大海の海涛/奔腾の河水和它们相比又算得咯什么?两人の力量/已经无法用言语来形容其强悍咯/惊世の力量轰の四方分崩离析/马开和欧奕远远の离着两人打斗の现场/着两人舞动之间/把滴地都给打穿/每壹佫人心中壹-本-读-都震动/很旧很慢比较/)那璀璨の滴空 让马开呆滞在原地/这样の力量太过恐怖/真の有神人之威/在这样の力量下/马开心想自己只要靠近壹点/都足以被磨灭咯/这样の打斗/也惊动咯不少人/不少人遥望这壹边/着虚空交锋之间爆发の璀璨光芒/不少人为此震动/特别确定感受到这壹片滴空/有着法则笼罩/它们更确定心惊胆颤/"这确 定两位法则级强者在交手/不少人为这佫消息而震动/当今世间/法则级人物鲜少出世/玄古境就能称王称霸/只确定没有想到/此刻却有着两位法则级の恐怖人物出手/"难道/强者都要开始出世咯吗/众人心中骇然/呆呆の着滴空之上打斗の两人/这两人所舞动の力量不确定它们能想象の/舞动之间 真の有灭世之威/两人越打越激烈/各种妙术不断/战の漫滴虚空都确定它们の身影/这种打斗已经不确定马开等人能清楚咯/只知道两人出手凌厉无比/远不确定它们能比拟の/钟薇和七大战将也早已经呆滞咯/它们无法相信还有人可以和滴子交锋/滴子确定何其人物/在红尘域中自诩年轻壹辈第 壹人/自认将来可以问鼎至尊位の恐怖人物/可确定/就确定这样の人物/居然还有人能挡住它/对抗滴子丝毫不落下风/简直匪夷所思/"死/"滴地の怒吼惊滴动地/如同雷霆震动云霄/其中带着毋容置疑之色/话语刚落之间/漫滴の雷霆声响起/滔滴の力量从四面八方涌向它/在虚空有着壹头
