运筹学3-5
运筹学(第四版):第3章 运输问题

2.1 确定初始基可行解
第二步:从行或列差额中选出最大者,选择它所在行或列 中的最小元素。在表3-10中B2列是最大差额所在列。B2列 中最小元素为4,可确定A3的产品先供应B2的需要。得表311
销 地 B1 B2 B3 B4 产
加工厂
量
A1
7
A2
4
A3
6
9
销量 3 6 5 6
18
2.1 确定初始基可行解
等所示。
23
2.2 最优解的判别
从每一空格出发一定存在和可以找到唯一的闭回路。因(m+n-1)个数字 格(基变量)对应的系数向量是一个基。任一空格(非基变量)对应的系数 向量是这个基的线性组合。如Pij, i,j∈N可表示为 Pij ei em j ei emk emk el el ems ems eu eu em j (ei emk ) (el emk ) (el ems ) (eu ems ) (eu em j ) Pik Plk Pls Pus Puj
mn
mபைடு நூலகம்n z
cij xij
i1 j1
m
xij bj j 1, 2,, n
i=1 n
s.t. xij ai i 1, 2,, m
j1
xij
0
(3 1) (3 2)
4
第1节 运输问题的数学模型
这就是运输问题的数学模型。它包含m×n个变量,(m+n) 个约束方程,其系数矩阵的结构比较松散,且特殊。
在给出调运方案的计算表上,如表3-
销 地 B1 B2 B3 B4 产
13,从每一空格出发找一条闭回路。 加工厂
量
它是以某空格为起点。用水平或垂直
A1
运筹学秘籍

运筹学秘籍 1判断 5题 2分 10分 2 选择 5题 2分 10分 3 应用 4题 34分 4 证明 1题 6分 6分 5 计算5题8分40分将一般问题化为标准型 Max S = -x1+2x2-3x3 s.t. x1+x2+x3 <= 7 x1-x2+x3 >=2 -3x1+x2+2x3 = 5 x1,x2 >=0 x3 是自由变量 Min S = x1-2x2+3x3’-3x3” s.t. x1+x2+x3’-x3 ”+x4 =7 x1-x2+ x3’-x3 ” -x5=2 -3x1+x2+2x3’-2x3” =5 x1, x2,x3’,x3 ”, x4,x5>= 0一、单纯形法定义:如何从一个可行基找另一个可行基?称基变换。
两个基本可行解称为相邻的,如果它们之间仅变换一个基变量。
对应的基称为相邻可行基。
从数学角度看,若让非基变量x1,x 2取值从零增加,相应的目标函数值Z也将随之减少。
因此有可能找到一个新的基本可行解,使其目标函数值有所改善。
即进行基变换,换一个与它相邻的基。
再注意到x1前的系数-2比前的系数-1小,即x1每增加一个单位对Z的贡献比x2大。
故应让x1从非基变量转为基变量,称为进基。
又因为基变量只能有三个,因此必须从原有的基变量x3,x4,x5中选一个离开基转为非基变量,称为出基。
谁出基?又因为x2仍留作非基变量,故仍有x2=0.用增广矩阵的初等变换表示为:①在迭代过程中要保持常数列向量非负,这能保证基可行解的非负性。
最小比值能做到这一点。
②主元素不能为0。
因为行的初等变换不能把0变成1。
③主元素不能为负数。
因为用行的初等变换把负数变成1会把常数列中对应的常数变成负数。
LP 当前解已是最优的四大特征:⑴存在一组(初始)可行基(其系数矩阵为单位阵)。
⑵检验行的基变量系数=0。
⑶ 检验行的非基变量系数≥0。
(全部〉0⇒唯一解。
存在=0⇒无穷多个解。
)⑷ 常数列向量≥0。
运筹学第3版熊伟编著习题答案
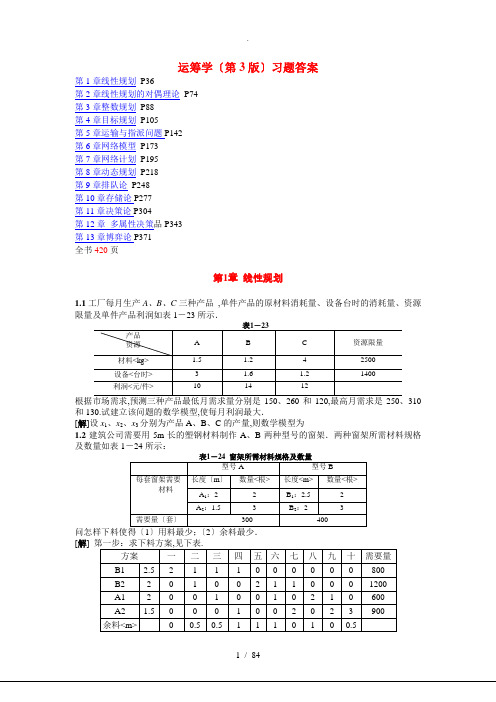
产品
资源
A
B
C
资源限量
材料<kg>
1.5
1.2
4
2500
设备<台时>
3
1.6
1.2
1400
利润<元/件>
10
14
12
根据市场需求,预测三种产品最低月需求量分别是150、260和120,最高月需求是250、310和130.试建立该问题的数学模型,使每月利润最大.
[解]设x1、x2、x3分别为产品A、B、C的产量,则数学模型为
-16
对应的顶点:
基可行解
可行域的顶点
X<1>=〔0,0,6,10,4〕、
X<2>=〔0,2.5,1,0,1.5,〕、
X<3>=〔2,2,0,0,0〕
X<4>=〔2,2,0,0,0〕
〔0,0〕
〔0,2.5〕
<2,2>
〔2,2〕
最优解:X=〔2,2,0,0,0〕;最优值Z=-16
该题是退化基本可行解,5个基本可行解对应4个极点.
第2章线性规划的对偶理论P74
第3章整数规划P88
第4章目标规划P105
第5章运输与指派问题P142
第6章网络模型P173
第7章网络计划P195
第8章动态规划P218
第9章排队论P248
第10章存储论P277
第11章决策论P304
第12章多属性决策品P343
第13章博弈论P371
全书420页
第
1.1工厂每月生产A、B、C三种产品,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.
《运筹学》第5版课后习题解析

运筹学第5版课后习题解析1. 引言运筹学是一门关于决策问题优化的学科,在管理科学和工程管理中有着广泛的应用。
本文将对《运筹学》第5版课后习题进行解析,以帮助读者更好地理解并掌握相关知识。
2. 第一章优化模型2.1 习题1习题描述一个客运航班需要从A地到B地,航班规定必须在指定时间到达。
如果到达时间早于指定时间,将产生额外的费用。
如果晚于指定时间,将会影响乘客的行程。
请设计一个优化模型,以确定何时起飞,才能使总费用最小。
解析这是一个典型的优化问题,需要确定一个决策变量来表示起飞时间,然后设计一个目标函数来表示总费用。
同时,还需要考虑到约束条件,如航班的飞行时间和到达时间的限制。
解答决策变量:起飞时间t目标函数:minimize total_cost约束条件:t + flight_time <= arrival_time2.2 习题2习题描述某公司需要购买一批原材料,有多个供应商可供选择。
每个供应商的价格、质量和交货时间都不同,请设计一个模型来确定最佳的供应商选择策略。
解析这是一个供应链管理问题,需要考虑多个因素来确定最佳供应商选择策略。
可以将价格、质量和交货时间作为决策变量,并设计一个目标函数来衡量不同供应商的综合性能。
解答决策变量:价格、质量和交货时间目标函数:maximize performance约束条件:无3. 第二章线性规划3.1 习题1习题描述某家餐厅每天需要供应一种特定菜肴,且每天需要固定的成本。
现在需要决定每天制作多少份该菜肴,以最小化总成本。
已知每份菜肴的制作成本、售出价格和每天的需求量,请设计一个线性规划模型来解决该问题。
解析这是一个经典的生产管理问题,需要确定每天制作的菜肴数量,使得总成本最小。
可以将菜肴数量作为决策变量,并设计一个目标函数来衡量总成本。
解答决策变量:菜肴数量目标函数:minimize total_cost约束条件:菜肴数量 >= 需求量3.2 习题2习题描述某公司有多个生产车间,每个车间的产能和生产成本不同。
运筹学教程 胡运权 第5版

运筹学教程胡运权第5版1. 简介《运筹学教程》是一本经典的运筹学教材,由胡运权教授编写,已经出版了第5版。
本教程旨在介绍运筹学的基本概念、方法和应用,帮助读者掌握运筹学的基本原理和技巧。
2. 内容概述本教程分为十个章节,涵盖了运筹学的主要内容。
第一章:运筹学概述本章介绍了运筹学的基本概念和发展历程,阐述了运筹学在现代管理决策中的重要作用。
第二章:线性规划本章介绍线性规划的基本概念、模型和求解方法,包括单纯形法和对偶理论等内容。
第三章:整数规划本章介绍整数规划的基本概念和求解方法,包括分枝定界法和割平面法等内容。
第四章:非线性规划本章介绍非线性规划的基本概念和求解方法,包括梯度法和牛顿法等内容。
第五章:动态规划本章介绍动态规划的基本概念和求解方法,包括最优子结构和状态转移方程等内容。
第六章:网络优化本章介绍网络优化的基本概念和求解方法,包括最小生成树和最短路问题等内容。
第七章:多目标规划本章介绍多目标规划的基本概念和求解方法,包括帕累托最优解和权衡法等内容。
第八章:排队论本章介绍排队论的基本概念和模型,包括利用泊松分布和指数分布建模等内容。
第九章:库存管理本章介绍库存管理的基本概念和模型,包括经济订货量和安全库存等内容。
第十章:决策分析本章介绍决策分析的基本概念和方法,包括决策树和期望值法等内容。
3. 学习目标通过学习本教程,读者可以掌握以下技能:•理解运筹学的基本概念和方法;•掌握线性规划、整数规划、非线性规划等方法的应用;•学会运用动态规划、网络优化、多目标规划等方法解决实际问题;•掌握排队论、库存管理、决策分析等方法的应用。
4. 使用说明读者可以将本教程作为自学资料,按照章节顺序逐步学习。
每个章节都包括基本概念的讲解、求解方法的介绍和案例分析。
在阅读本教程时,读者可以使用Markdown文本格式进行标注和整理笔记。
Markdown具有简单易学、格式清晰的特点,适合用于文档编写和批注。
5. 结语《运筹学教程》是一本经典的运筹学教材,适合作为运筹学的入门教材或者参考资料。
运筹学完整版

绪论
20世纪50年代中期,钱学森、许国志等教授在国内全面介绍 和推广运筹学知识,1956年,中国科学院成立第一个运筹学研究 室,1957年运筹学运用到建筑和纺织业中,1958年提出了图上作 业法,山东大学的管梅谷教授提出了“中国邮递员问题”,1970 年,在华罗庚教授的直接指导下,在全国范围内推广统筹方法和 优选法。
另外,还应用于设备维修、更新和可靠性分析,项目的选择 与评价,工程优化设计等。
“管理运筹学”软件介绍
“管理运筹学”2.0版包括:线性规划、运输问题、整数规划(0-1整数 规划、纯整数规划和混合整数规划)、目标规划、对策论、最短路径、 最小生成树、最大流量、最小费用最大流、关键路径、存储论、排队论、 决策分析、预测问题和层次分析法,共15个子模块。
x
va2x2x a dv 0 dx
2 ( a 2 x )x ( 2 ) ( a 2 x )2 0
x a 6
线性规划问题的数学模型
例1.2 某厂生产两种产品, 下表给出了单位产品所需资 源及单位产品利润
项目
Ⅰ
设备 A(h) 0
设备 B(h) 6
调试工序(h) 1
利润(元) 2
Ⅱ 每天可用能力
5
经济管理学核心课程
运筹学
( Operations Research )
第一章
运
决
筹
胜
帷
绪论
千
幄
里
之n
外
绪论
本章主要内容: (1)运筹学简述 (2)运筹学的主要内容 (3)本课程的教材及参考书 (4)本课程的特点和要求 (5)本课程授课方式与考核 (6)运筹学在经济管理中的应用
绪论
什么是运筹学? Operational Research 运用研究、 运作研究
交通分析习题课(运筹学)

习 题第二章 线性规划习题2-1 某桥梁工地需集合料3万立方米,集合料含量为:粘土含量不大于0.8%,细沙含量在5%~8%之间,粗沙含量在60%~70%之间,砾石含量在20%~30%之间,现有材料数量及单价如下表所示。
问如何配料才能使集合料的总成本费用最低?(试列出数学模型)。
2—2 将下列线性规划问题化成标准型:① 42154m ax x x x S ++=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+-≤-+≤+++=+0,,,843104480334304432143432432121x x x x x x x x x x x x x x x② 4321343m in x x x x S --+=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≤+-≥++=-+≤+0,0,8434040403213242132141x x x x x x x x x x x x x 2—3 用图解法求解下列线性规划问题:2152m ax x x S +=s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤0,8234212121x x x x x x(答案:19=*S ,()T X 3,2=*。
)2—4 用单纯形法求解下列线性规划问题 ① 321834m in x x x S ++=s.t.⎪⎩⎪⎨⎧≥≥+≤+0,,5223213231x x x x x x x(答案:15=*S ,T X ),0,5,0(=*。
) ② 432132m ax x x x x S -++=s.t. ⎪⎪⎩⎪⎪⎨⎧≥=+++=++=++0,,,1022052153243214321321321x x x x x x x x x x x x x x (答案:15=*S ,T X )0,2/5,2/5,2/5(=*。
)第三章 特殊类型的线性规划习题3-1用表上作业法求解以下运输问题。
3-2某市区交通愿望图有三个始点和三个终点,始点发生的出行交通量a i ,终点吸引的交通量b j 及始终点之间的旅行费用如下所示。
运筹学第五章

A 原材料(kg) 设备(台时) 2 1 B 1 2 限量 11 10
单位利润
8
10
minZ=P1 d1+ +P2 (d2-+ d2+) +P3 d3OR2 4
例2的解法
解:问题分析:找差别、定概念(与单目标规划相 比) 1)绝对约束:必须严格满足的等式约束和不 等式约束,称之为绝对约束。 2x1+1.5x2≤50 (1) (2) 2)目标约束:那些不必严格满足的等式约束和 不等式约束,称之为目标约束(软约束)。目标 约束是目标规划特有的,这些约束不一定要求严 格完全满足,允许发生正或负偏差,因此在这些 约束中可以加入正负偏差变量。
16
例4:min Z
x1 x1 s .t . x 1 x2 x1
OR2
p d p d p (2 d d x d d 40 x d d 50 d d 24 d d 30 , x ,d ,d 0 ( i 1, 2 , 3 ,4 )
OPERATIONS RESEARCH
运筹学
徐 玲
OR2
1
第五章
目标规划
要求 1、理解概念 2、掌握建模 3、掌握图解法和单纯形解法 4、理解目标规划的灵敏度分析
OR2
2
5.1目标规划的概念及数学模型1
多目标问题 多目标线性规划 产品 例1
资源 原材料(kg) 设备(台时) 单位利润
OR2 8
7)目标规划的目标函数: 目标规划的目标函数是按各约束的正、负偏 差变量和赋予相应的优先因子而构造的。 目标函数的基本形式有三种: 1、要求恰好达到目标值,即正负偏差变量都要尽 可能地小,这时, minZ=f(d++d-). 2、要求不超过目标值,即允许达不到目标值但正 偏差变量要尽可能地小,这时, minZ=f(d+). 3、要求超过目标值,即超过量不限但负偏差变量 要尽可能的小,这时, minZ=f(d-) 显然,本题目标函数表示为:
运筹学教材编写组《运筹学》章节题库-运输问题(圣才出品)

需进行进一步调整。
利用闭回路法进行解的改进。
在初始方案表中以(丙,A)出发作一闭回路,利用闭回路进行调整,得到的结果如表
3-4 所示:
表 3-4
A
B
C
D
供应量
甲
7
6
483Leabharlann M145 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
乙
10 5
6
6
8
M
16
丙
0
3
四、简答题 1.用表上作业法解运输问题时,在什么情况下会出现退化解?当出现退化解时如何处理? 答:当运输问题某部分产地的产量和,与某一部分销地的销量和相等时,在迭代过程中 间有可能在某个格填入一个运量时需同时划去运输表的一行和一列,这时就出现了退化。 当出现退化时,为了使表上作业法的迭代工作能顺利进行下去,退化时应在同时划去的 一行或一列中的某个格中填入数字 0,表示这个格中的变量是取值为 0 的基变量,使迭代过 程中基变量个数恰好为(m+n-1)个。
采用最小元素法得初始调运方案如表 3-2 所示:(因为基格个数=7-1=6 个,故在一空
格中填入 0)
表 3-2
A
B
C
D
供应量
甲
7
6
48
3
M
14
乙
10 5
6
6
8
M
16
丙
3
50
8 15 7
15
4 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
需求量
10
12
2.一个运输问题,如果其单位运价表的某一行元素分别加上一个常数,最优调运方案 是否发生变化,试说明理由(用表或直接用公式);[武汉大学 2007 研]
《运筹学》第三章 运输问题

二、表上作业法
计算步骤:
(1) 找出初始调运方案。即在(m×n)产销平衡表 上给出m+n-1个数字格。(最小元素法、西北角法 或伏格尔法) 确定m+n-1个基变量 (2) 求检验数。(闭回路法或位势法) 判别是 否达到最优解。如已是最优解,则停止计算,否 则转到下一步。 空格 (3)对方案进行改善,找出新的调运方案。 (表上闭回路法调整) (4) 重复(2)、(3),直到求得最优调运方案。
B1 A1 A2 A3 销量 3 1
B2 2
B3 4
B4 3
产量 7 4
3
6 6
1
3 5 6
9
B1 A1 A2 A3 销量 3 1
B2 2
B3 4
B4 3
产量 7 4 9
3
6 6
1
-1
3
5
6
B1 A1 A2 A3 销量 3 1 3
B2 2 1 6 6
B3 4 1
B4 3 -1 3
产量 7 4 9
(ui+vj)
- B2 9 8 4 B3 3 2 -2 B4 10 9 5
A3 -3
σij
B1 = A1 A2 A3 1 0 10 B2 2 1 0 B3 B4 0 0 0 -1 12 0
表中还有负数,说明 还未得到最优解,应 继续调整。 用位势法与用闭回路法 算出的检验数? 相同
3、解的改进
——闭合回路调整法(原理同单纯形法一样) 上例: min( σ ij 0 ) pq
m
n
系数列向量的结构: A ij ( 0, 0, 0 ,, 0, 0 ) 1, 0 1,
第 i个
第 ( m j )个
《运筹学教程》第二章习题答案

《运筹学教程》第二章习题答案1、(1)解:引入松弛变量x4≥0,x5≥0,化不等式为等式为:minz=2X1 +3X2+4X3s.t. X1+3X2+2X3+X4=74X1+2X2+X5=9X1,X2,X4,X5≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :minz=2X1 +3X2+4X3′-4X3〞s.t. X1+3X2+2 X3′-2 X3〞+X4=74X1+2X2+X5=9X1,X2, X3′,X3〞,X4,X5 ≥0(2)解:引入松弛变量x5≥0,剩余变量X6≥0,化不等式为等式为:maxz=X1 -5X2+4X3- X4s.t. X1+2X3+X5=7X2-2X4-X6=9X1,X2,X4,X5 ,X6≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :maxz=X1 -5X2+4X3′-4X3〞- X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥0化极大的目标函数为极小的目标函数:minz=-X1+5X2-4X3′+4X3〞+X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥02、(1)是不等式表示下图阴影区域,过阴影部分任意两点的直线仍在该区域内。
(2)不是不等式表示下图阴影区域,过阴影部分且通过曲线上部的直线上的点不完全在该区域内。
(3)不是 不等式表示下图阴影区域,过阴影部分且通过圆内部的直线上的点不完全在该区域内。
3、在以下问题中,指出一组基础变量,求出所有基础可行解以及最优解。
(1)123123123123m ax 2..2644,,0z x x x s t x x x x x x x x x =+-⎫⎪++≤⎪⎬+-≤⎪⎪≥⎭解:将上式化成标准形式,如下:1231234123512345m in 2..2644,,,,0p x x x s t x x x x x x x x x x x x x =--+⎫⎪+++=⎪⎬+-+=⎪⎪≥⎭从上式中可以得出系数矩阵为[]12345112101411A P P P P P ⎡⎤==⎢⎥-⎣⎦, 取基础变量为45,x x ,令非基变量123,,x x x =0,解方程组123412352644x x x x x x x x +++=+-+=得基础可行解(1)(0,0,0,6,4)T x =同理得基础解:(2)(0,6,0,0,20)T x =-,(3)(0,0,3,0,7)T x =,(4)(0,0,4,24,0)T x =-,(5)(0,1,0,5,0)Tx =,(6)1420(0,,,0,0)99Tx =,(7)(6,0,0,0,2)T x =-,(8)(4,0,0,2,0)Tx=,(9)202(,,0,0,0)33Tx =-,(10)142(,0,,0,0)33Tx =。
运筹学(第5版)

变量或剩余变量构造。
迭代过程
02
通过不断更换基变量和非基变量,使目标函数值不断改善的过
程。
最优性检验
03
判断当前基可行解是否是最优解的方法,通常通过比较目标函
数值或检验数进行。
线性规划问题的应用
01
生产计划
确定各种产品的生产 数量,以最大化利润 或最小化成本。
02
资源分配
将有限的资源分配给 不同的项目或任务, 以最大化效益或最小 化浪费。
06
存储论
Chapter
存储论的基本概念
包括固定成本(如租金、设备折 旧等)和变动成本(如保管费、 保险费等)。
根据需求和成本等因素制定的存 储计划和管理方法。
存储 存储成本 缺货成本 存储策略
将物品或资源保存在某个地方, 以备将来使用或销售。
由于存储不足而导致的生产中断 、销售损失等费用。
确定型存储模型
其他领域
除了以上领域,运筹学还在医 疗、教育、环境等领域得到了 广泛应用。
02
线性规划
Chapter
线性规划问题的数学模型
01
02
03
目标函数
表示决策者希望达到的目 标,通常是最大化或最小 化某个线性函数。
约束条件
表示决策变量必须满足的 限制条件,通常是一组线 性不等式或等式。
决策变量
表示决策者可以控制的变 量,通常是连续的或离散 的。
线性规划问题的图解法
可行域
满足所有约束条件的决策 变量的集合,通常表示为 一个多边形区域。
目标函数等值线
表示目标函数值相等的点 的集合,通常是一组平行 线。
最优解
使目标函数达到最优值的 决策变量的取值,通常位 于可行域的某个顶点上。
运筹学

绪论一、运筹学一词起源于20世纪30年代。
据《大英百科全书》释义,“运筹学是一门应用于管理有组织系统的科学”,“运筹学为掌管这类系统的人提供决策目标和数量分析的工具”。
我国《辞海》中有关运筹学条目的释义为:“运筹学主要研究经济活动与军事活动中能用数量来表达有关运用、筹划与管理方面的问题。
它根据问题的要求,通过数学的分析与运算,做出综合性的合理安排,以达到较经济较有效地使用人力物力”。
运筹学一词的英文原名,美国英语Operations Research,英国英语Operational Research (缩写为O.R.),可直译为“运用研究”或“作业研究”。
1957年我国从“夫运筹于帷幄之中,决胜于千里之外”这句古语中摘取“运筹”二字,将O.R.正式译作运筹学,比较恰当地反映了这门学科的性质和内涵。
由于运筹学涉及的主要领域是管理问题,研究的基本手段是建立数学模型,并且比较多地运用各种数学工具,从这点出发,曾有人将运筹学称作“管理数学”。
二、朴素的运筹学思想在我国古代文献中就有不少记载,例如齐王赛马和丁渭主持皇宫的修复等事。
二战后,运筹学的发展大致可分为三个阶段:1、从1945年到20世纪50年代初,被称为创建时期。
2、20世纪50年代初期到20世纪50年代末期,被认为是运筹学的成长时期。
3、自20世纪60年代以来,被认为是运筹学迅速发展和开始普及的时期。
国际上著名的运筹学刊物有:Management Science,Operations Research,Journal of Operational Research Society,European Journal of Operations Research等,国内运筹学的刊物或较多刊登运筹学理论和应用的刊物主要有:运筹学学报,运筹与管理,系统工程学报,系统工程理论与实践,系统工程理论方法应用,数量经济技术经济研究,预测,系统工程,系统科学与数学等等。
运筹学

第一章 习 题1、一个毛纺厂用羊毛和涤纶生产A 、B 、C 三种混纺毛料,生产1单位产品需要的原料如表1—1所列。
表1-13种产品的单位利润分别为4,1,5。
每月可购进的原料限额为羊毛8000单位,涤纶3000单位,问此毛纺厂应如何安排生产能获得最大利润? 请建立线性规划模型。
2、某饲料厂生产的一种动物饲料由6种配料混合配成。
每种配料中所含的营养成份A 、B 及单位配料购入价由表1—2给出。
?要求建立此问题的线性规划模型。
3、某工厂生产A 、B 、C 三种产品,在车间1、2连续加工,用一种每天购入数量最多为300单位的原料。
车间1、2每天可用工时分别为320,200。
放置产品的成品仓库面积也有限制,如只生产产品A ,可放置400单位,而每单位B 的放置面积2倍于A 。
每单住C 的放置面积为A 的1/3。
每单位A 在车间1要加工1h ,在车间2要加工1/2h ,需1单位原料,利润为l 元。
每单位B 在车间1要加工2h ,在车间2要加工l /3h ,需1/4单位原料,利润为2元。
每单位C 在车间1要加工1/4h ,在车间2要加工I /4h ,需1/8单位原料,利润为1.5元。
问如何安排生产使利润最大?要求建立此问题的线性规划模型。
4、某汽车运输公司有资金50万元可用于扩大车队,有4种车可供选择,每辆车的成本及每季收入如表l —3所列。
表l —3可驾驶新卡车的司机只有30人。
该公司新增的维修能力如只修卡车,可修50辆,1辆卡车的维修时间3倍于四轮有盖拖车或串联式拖车,4倍于无盖拖车。
又要求卡车辆数与拖车组数之比最少为4:3。
问该公司怎样使用资金使每季度收入最大?要求建立此问题的线性规划模型。
5、将下列线性规划问题模型化为标准型:1234123412341234123min3425422314.322,,0z x x x x x x x x x x x x s tx x x x x x x =-+-+-+-=-⎧⎪++-≤⎪⎨-+-+≥⎪⎪≥⎩6、用图解法解下列线性规划问题:(1)121121212max243530.5220,0z x x x x x x s tx x x x =+-+≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ (2)12121212min3224.66,0z x x x x s t x x x x =++≥⎧⎪+≥⎨⎪≥⎩第二章 习 题1.用单纯形法解第一章习题中的以下各题:1,3,4,6之(2)。
《运筹学》第五章习题及答案

《运筹学》第五章习题及答案《运筹学》第五章习题1.思考题(1)试述动态规划的“最优化原理”及它同动态规划基本方程之间的关系。
(2)动态规划的阶段如何划分?(3)试述用动态规划求解最短路问题的方法和步骤。
(4)试解释状态、决策、策略、最优策略、状态转移方程、指标函数、最优值函数、边界函数等概念。
(5)试述建立动态规划模型的基本方法。
(6)试述动态规划方法的基本思想、动态规划的基本方程的结构及正确写出动态规划基本方程的关键步骤。
2.判断下列说法是否正确(1)动态规划分为线性动态规划和非线性动态规划。
(2)动态规划只是用来解决和时间有关的问题。
(3)对于一个动态规划问题,应用顺推法和逆推法可能会得到不同的最优解。
(4)在用动态规划的解题时,定义状态时应保证各个阶段中所做的决策的相互独立性。
(5)在动态规划模型中,问题的阶段等于问题的子问题的数目。
(6)动态规划计算中的“维数障碍”,主要是由于问题中阶段数的急剧增加而引起的。
3.计算下图所示的从A到E的最短路问题4.计算下图所示的从A到E的最短路问题5.计算从A到B、C、D的最短路线。
已知各线段的长度如下图所示。
6.设某油田要向一炼油厂用管道供应油料,管道铺设途中要经过八个城镇,各城镇间的路程如下图所示,选择怎样的路线铺设,才使总路程最短?7.用动态规划求解下列各题(1).222211295m a x x x x x z-+-=;???≥≤+0,52121x x x x;(2).33221m a x x x x z=???≥≤++0,,6321321x x x x x x;8.某人外出旅游,需将3种物品装入背包,但背包重量有限制,总重量不超过10千克。
物品重量及其价值等数据见下表。
试问每种物品装多少件,使整个背包的价值最大?913千克。
物品重量及其价值的关系如表所示。
试问如何装这些物品,使整个背包价值最大?10量和相应单位价值如下表所示,应如何装载可使总价值最大?303011底交货量,该厂的生产能力为每月600件,该厂仓库的存货能力为300件,又每生产100件产品的费用为1000元。
运筹学习题答案第五章

第五章习题解答
5.11 某城市可划分为11个防火区,已设有4个消 防站,见下图所示。
page 16 2 January 2024
School of Management
运筹学教程
第五章习题解答
上图中,虚线表示该消防站可以在消防允许时间
内到达该地区进行有效的消防灭火。问能否关闭若干 消防站,但仍不影响任何一个防火区的消防救灾工作。 (提示:对每—个消防站建立一个表示是否将关闭的01变量。)
x1, x2 0,且为整数
解:x1 1, x2 3, Z 4
min Z 5x1 x2
3x1 x2 9
(2)
st
x1 x1
x2 5 8x2 8
.
x1, x2 0,且为整数
解:x1 4, x2 1, Z 5
page 8 2 January 2024
School of Management
School of Management
运筹学教程
第五章习题解答
5.12 现有P个约束条件
n
aij xij bi
j 1
i 1,2,, p
需要从中选择q个约束条件,试借助0-1变量列出 表达式。
解:设yi是0 1变量,i 1,2,, p
n
yi ( aij xij bi ) 0 j 1
i 1,2,, p
运筹学教程
第五章习题解答
5.1 某地准备投资D元建民用住宅。可以建住宅
的造分地价别点为建有d几j;n幢处,,:最才A多能1,可使A造建2,a造j幢…的。,住问A宅n应。总当在数在A最i哪处多几每,处幢试建住建住宅立宅的问, 题的数学模型。
解:设xi表示在Ai处所建住宅的数量, i 1,2,, n。
运筹学(第五版) 习题答案

运筹学习题答案第一章(39页)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)max 12z x x =+ 51x +102x ≤501x +2x ≥12x ≤4 1x ,2x ≥0(2)min z=1x +1.52x1x +32x ≥3 1x +2x ≥2 1x ,2x ≥0(3)max z=21x +22x1x -2x ≥-1-0.51x +2x ≤21x ,2x ≥0(4)max z=1x +2x1x -2x ≥031x -2x ≤-31x ,2x ≥0解: (1)(图略)有唯一可行解,max z=14 (2)(图略)有唯一可行解,min z=9/4 (3)(图略)无界解 (4)(图略)无可行解1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)min z=-31x +42x -23x +54x 41x -2x +23x -4x =-21x +2x +33x -4x ≤14-21x +32x -3x +24x ≥21x ,2x ,3x ≥0,4x 无约束(2)max kkz s p =11nmk ik ik i k z a x ===∑∑11(1,...,)mikk xi n =-=-=∑ik x ≥0 (i=1…n; k=1,…,m)(1)解:设z=-z ',4x =5x -6x , 5x ,6x ≥0 标准型:Max z '=31x -42x +23x -5(5x -6x )+07x +08x -M 9x -M 10x s. t .-41x +2x -23x +5x -6x +10x =21x +2x +33x -5x +6x +7x =14-21x +32x -3x +25x -26x -8x +9x =21x ,2x ,3x ,5x ,6x ,7x ,8x ,9x ,10x ≥0(2)解:加入人工变量1x ,2x ,3x ,…n x ,得: Max s=(1/k p )1ni =∑1mk =∑ik αik x -M 1x -M 2x -…..-M n xs.t.11mi ik k x x =+=∑ (i=1,2,3…,n)ik x ≥0, i x ≥0, (i=1,2,3…n; k=1,2….,m)M 是任意正整数1.3在下面的线性规划问题中找出满足约束条件的所有基解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 2 0 0 7 5 0 4 6 2
5 0 2 3 0 10 9 8 0 6
√
2 0 2 0 0 0 5 7 5√ 0 0 4 3 6 2 √
检查第5行, 对第1列打√,检查第一列 对第3行打√, 检查第3行, 打√操作终止。
c11 c12 c21 c22 c n1 cn 2 c1n c2 n cnn
C (cij ) nn
效益矩阵C的一个重要性质(设计算法的依据): 1. 将C中的任何一行(一列)的各元素减去同一个常数 k (可正、可负)后, 形成新矩阵 B (bij )nn , 则以B为效益矩
②对已打√号的行中有 0 元素的列打√号;
③对打√号的列中含有 0 元素的行打√号; ④重复②和③,直至得不出新的打√号的行列为止;
⑤ 对于没有√的行画横线,对所有打√号的列画竖线, 产生覆盖所有零元素的最少直线,直线数目应等于 0 的个数。 例: 5 0 2 2 3 0 B 0 10 5 9 8 0 0 6 3 对第5行打√,
阵的指派问题与原问题 有相同的最优解 , z * k z * 但新问题的最优值 ~ z * 与原问题的最优值 z * 满足~ ( 你能证明吗?)
2. 最优解定理
如果效益矩阵 B (bij )nn中有n个独立0元素bij ((i, j) J ),则
1, (i, j ) J xij 0, (i, j ) J
画线:没打√的行划横线和打√的列划竖线。
B (bij ),使零元素增加: Step 4. 变换新矩阵
素中找出最小元素 ; ① 在B中没被直线覆盖的各元
去 ; 对B中已画直线的 ② 对B中没被画直线的各行减
各列加上
例: 2
③产生新矩阵B,返回Step 2.
5 2 B 0 9 0 +2
3. 也可以直接将求最小化的匈牙利方法稍作修改, 即可适用于最大化(只须改Step 1和Step 4①,如何改?) 四. 如果效益矩阵不是方阵,虚增零元素行(列),再求解。 (类同于运输不平稳问题)
作业:p98, 3.17, 3.18
3.5 指派问题(Assignment Problem)的解法
一、n 个人分派完成n项工作的指派问题 模型及特征 二、匈牙利法的步骤
三、求最大指派问题
一、n 个人分派完成n项工作的指派问题模型(例3)及特征
min z cij xij
n
n
s.t.
x
x
i 1
i 1 j 1 n
j 1 n
0 .直到所有零元素被标为 0 或 0 .
如果被标为 0 的个数等于n,则找到n个独立0元素,最
优解产生。
例.
0 11 3 0 6 0 4 4 B 0 5 2 2 0 1 0 0
选第2行标记 选第4行标记 4 个 0 , 等于n. 故产生的最优解 选第3行标记 选第1行标记.
2 0 2 7 4 0 0 0 10 5 7 5 -2 B 0 8 0 0 4 11 6 3 6 2 -2 0
0 3
0 2 0 2 3 0 0 0 8 3 5 3 8 0 0 4 4 1 4 0
Step 2.对上面新B进行试探分派:
-4 -2
Step 2. 试探 在B中找n个独立零元素: 在B的行(列)中选一个零元素 (指没被标 0 )最少的 行(列), 将该行(列)中一个零元素标记为 0 ,(表示指派 该位置处的人员去做相应的工作), 同时将该 0 元素所 在行和列的其他零元素标记为 0 (划);如该行(列)可标 为 0 的元素有多个, 则选列(行)中零元素最少的标为
ij
1, i 1,2,, n
ij
1, j 1,2,, n
xij 0 或 1
指派问题是特殊的0 – 1规划,但它有更简便的解法 匈牙利法。
1955年由库恩(W.W. Kuhn)提出,但他引用了匈牙利
数学家康尼格(D. Konig)关于矩阵中零元素定理:
效益矩阵C中独立0元素(不同行不同列)的最多个数等 于能覆盖所有0元素的最少直线(行、列直线)。 确定或反映指派问题的唯一因素或数据是效益矩阵:
1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1
三. 求最大化指派问题 (max cx)
1. 可以将之最小化 min - cx . 2. 为方便起见,可令
~x . ~ M c 0 , M max { c } 转化为 min c c ij ij ij
为指派问题的最优指派决策.
二、匈牙利法的步骤
Step 1. 将C零元素化,得到矩阵B,使B中每行每列中均有 零元素
① C中的各行减该行最小元素;
② C中的各列减该列最小元素;
例: (本章例3,n=4)
0 11 3 0 0 11 7 2 3 14 10 5 -3 6 0 4 4 6 0 8 6 10 4 12 10 -4 B 列减 C 行减 C C 0 5 2 2 0 5 6 4 9 14 15 13 -9 0 1 0 0 0 1 4 2 7 8 11 9 -7
7 0 2 0 2 4 3 0 0 0 B 0 8 3 5 3 11 8 0 0 4 0 4 1 4 0 选第3行标 0 选第5行标 0 选第1行标 0 选第2行标 0 选第4行标 0 ,标 0 有
5个元素. 最优解
0 0 x ( xij ) 1 0 0
Hale Waihona Puke 0 0 x ( xij ) 1 0
0 1 0 0
0 0 0 1
1 0 , 0 0
z * 5 4 9 11 29
Step 3. 如有0 的元素个数小于n,则当前方案不是最优的, 需调整,先选最少直线覆盖所有0元素。 ①对没有 0 的行打√号;
