湖北省荆州市2013届高中毕业班3月质量检查(II)数学文试题
湖北省荆州市2013届高中毕业班3月质量检测(II)文科综合试题
荆州市2013届高中毕业班质量检查(II)文科综合能力测试本科目考试时间:2013年3月13日上午9 : 00——11 : 30 编辑人:丁济亮本试卷分第1卷(选择题)和第II卷(非选择题)两部分,满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡密封线内相应的地方。
2 第I卷每小题选出答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净,再选涂其它答案标号。
第II卷用0.5毫米黑色签字笔在答题卡上作答,答在试题上无效。
3.考试结束,监考人员将答题卡收回,试题由学生保存。
第I卷(选择题,共140分)一、选择题(本卷共35小题,每小题4分,共计140分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
)读东亚地区2012年某季节海平面等压线(单位:百帕)分布图,回答1 .3题。
1. 图中气压差的最大差值最接近A 30百帕 B. 35百帕C 40百帕 D. 45百帕2. 该日中和乙网地日较差相比A.甲小于乙B.甲大于乙C.两地一样D.不能确定3. 目前北京的天气状况是A. 气温较高,气压较低,天气晴好B.气温较低,气压较高,天气晴好C.大风、雨雪、降温D.连续性降水《2012年社会蓝皮书》指出,2011年中国城镇人口占总人口的比重,数千年来首次超过农业人口,达到51. 27%。
结合下表回答4.5题。
表:我国某省(市、区)城乡人口统计表4.近30年来,我国快速城市化的主要原因是A.农业播种面积的减少B.人口总量的不断增长C.产业结构调整和工业化进程加快D.城市生活方式和价值观念的吸引5.表格数据所代表的省(市、区)最可能是A.天津市B.四川省C江苏省D.湖北省读“我国南、北方水资源、人口及耕地分布对照图”,回答6.7题。
6.下列有关图中内容的说法止确的是A.我国人口重心在北方地区B. 北方资源优势明显优于南方C.人均水资源南方多于北方D.人均耕地面积南方多于北方7.造成我国南方和北方地区水资源总量差异大的主要原因是A.地形差异导致地表储水差异较大B.雨季长短导致降水量差异较大C.人口数量差异导致用水差异较大D.纬度差异导致蒸发量差异较大下图为四个国家某年粮食作物生产状况示意图。
湖北省八市2013年高三年级三月调考数学(文科)试题

湖北省八市2013年高三年级三月调考数学(文科)试题本试卷共4页。
全卷满分150分,考试时间120分钟。
★ 祝考试顺利 ★注意事项:1.23A . ππ()4k k Z +∈ B .π2 C .3ππ()4k k Z +∈ D .3π44.平面向量a 与b 的夹角为60,(2,0)a =,1b =,则2a b +=A B . C .4 D .125.不等式组(3)()004x y x y x -++⎧⎨⎩≥≤≤表示的平面区域是A .矩形B .三角形C .直角梯形D .等腰梯形6.设a R ∈,函数()x x f x e ae -=+的导函数是()f x ',且()f x '是奇函数,则a 的值为A .1-B .12-C .1781009A .4 B .3 C . 2 D .1二、填空题(本大题共5小题,每小题7分,共35分,请将答案填在答题卡对应题号的位置上)11.已知集合{1,2,3,4,5,6}U =,}6,4,2,1{=M ,则U M =ð ▲ . 12.已知4cos 5θ=-,且tan 0θ<,则sin θ= ▲ .13.某高三年级有500名同学,将他们的身高(单位:cm )数据绘制成频率分布直方图(如图),若用分层抽样的方法选取30人参加一项活动,则从身高在[160,170)内的学生中选取的人数应为 ▲ .14.某地区恩格尔系数(%)y 与年份x 的统计数据如下表:从散点图可以看出y 与x 线性相关,且可得回归直线方程为ˆˆ4055.25ybx =+,据此模型可预测(1,cos )(3sin C C m n ==与求四棱锥P ABCD -的体积.21.(本大题满分14分)x =2x +1n =1第20题图已知△ABC 的两个顶点,A B 的坐标分别是(0,1)-,(0,1),且,AC BC 所在直线的斜率之积等于(0)m m ≠.(Ⅰ)求顶点C 的轨迹E 的方程,并判断轨迹E 为何种圆锥曲线;(Ⅱ)当12m =-时,过点(1,0)F 的直线l 交曲线E 于,M N 两点,设点N 关于x 轴的对称点为Q (,M Q 不重合).求证直线MQ 与x 轴的交点为定点,并求出该定点的坐标.上是否存在两点本大题共5小题, 共65(Ⅰ)∵m 与n 共线 21π1(1cos )sin()262C C C =++=++ …………………………3分 得πsin()16C += …………………………4分∴C=3π……………………………6分 (Ⅱ)方法1:由已知2a c b += (1)根据余弦定理可得:222c a b ab =+- (2)……………………8分(1)、(2)联立解得:()0b b a -=……………………………10分0,,C=3b b a ABC π>∴=∴∆又,为等边三角形,……………………………12分方法2:由正弦定理得:2sin cos sin 2sin 2sin()2sin cos sin 2sin cos 2cos sin A C C B A C A C C A C A C+==++=+ ……………………8分∴21cos =A , ∴在△ABC 中 ∠π3A = . ……………………………10分21(1)n c c c -+++++. ……………… 从而当1=c 时,2(31)322n n n n nS n -+=+=; ………………11分 当1≠c 时,(31)121n n n n c S c--=+-. ………………12分 20.(Ⅰ)证明:连结AC ,交BD 于O .因为底面ABCD 为菱形, 所以O 为AC 的中点.P因为 Q 是PA 的中点,所以PC OQ // , 因为⊂OQ 平面BDQ ,⊄PC 平面BDQ , 所以//PC 平面BDQ . …………………4分 (Ⅱ)证明:因为底面ABCD 为菱形,所以BD AC ⊥,O 为BD 的中点.(Ⅱ)设112222(,),(,),(,)M x y N x y Q x y -12(0)x x ⋅≠依题直线l 的斜率存在且不为零,则可设l :1x ty =+,代入221(0)2x y x +=≠整理得22(2)210t y ty ++-= 12222t y y t -+=+,12212y y t -=+, ………………………………9分又因为M Q 、不重合,则1212,x x y y ≠≠-Q MQ 的方程为121112()y y y y x x x x +-=-- 令0y =,得1211211211121212()()2112y x x ty y y ty y x x ty y y y y y y --=+=++=+=+++故直线MQ 过定点(2,0). ……………………………13分解二:设112222(,),(,),(,)M x y N x y Q x y -12(0)x x ⋅≠ 依题直线l 的斜率存在且不为零,可设l :(1)y k x =-代入221(0)x y x +=≠整理得:2222(12)4220k x k x k +-+-= 只为直角顶点的直角三角形,所以0OP OQ ⋅=,有解,即方程(。
湖北省荆州市2013届高三语文毕业班质量检查(Ⅰ)试题新人教版

荆州市2013届高中毕业班质量检查(Ⅰ)语文本试卷共8页。
全卷共150分。
考试时间150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上。
2.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试题卷上无效。
3.非选择题用0.5毫米黑色的签字笔直接答在答题卡上。
答在试题卷上无效。
4.考试结束,监考人员将答题卡收回,试题由学生保存。
本科目考试时间:2012年12月1日上午9∶00———11∶30一、语文基础知识(共15分,共5小题,每小题3分)1.下列各组词语中加点的字,读音全都相同的一组是A.劲.敌靓.妆噤.若寒蝉曲径.通幽B.蒲.草菩.提惊魂甫.定璞.玉浑金C 渗漉.戮.力绿.林起义风餐露.宿D.迤.逦蚁.群倚.老卖老颐.养天年2.下列词语中,没有错别字的一项是A.濡染猗郁贻笑大方铩羽而归B.熨帖慰藉沸返盈天通衢大道C.疏浚赊帐残羹冷炙冠冕堂皇D.班师谂知蝇头微利祸起箫墙3.依次填入下列横线处的词语,最恰当的一项是观山如读史。
驰车荆楚大地,_______那笼罩南山的一派空濛_______,能谛听到自然、社会、历史的无声倾诉。
一种_______的历史的激动和沉甸甸的时间感被呼唤出来,觉得有许多世事已经倏然远_______,又有多少天涯过客正在匆匆走来。
A.凝视依稀千秋万代走B.眺望仿佛源远流长逝C.遥望好像经久不息去D.鸟瞰隐约天长地久离4.下列各项中,没有语病的是A.在中日邦交正常化40周年之际,由于日本政府和右翼势力置中日友好大局于不顾,罔顾历史事实,强行实施所谓的“购岛”行动,引发我国民众的愤怒和不满。
B.为了避免地方电视台娱乐节目的不再泛滥,国家广电总局多次发文干预,但收效甚微,毕竟,这些节目迎合了部分观众的媚俗需求。
C.实体书店犹如一个不可或缺的文化沙龙,它所承载的文化滋养和文化气息,会让城市显得更安详,而没有实体书店的城市,则无异于文化沙漠。
湖北省荆州市2013届高中毕业班3月质量检测(II)语文试题

荆州市2013届高中毕业班第二次质量检查语文试题考试时间:150分钟试卷满分:150分编辑人:丁济亮祝考试顺利!一、语文基础知识(共15分,共5小题,每小题3分)1.下列词语中加点的字,每组读音都不相同的一项是A.伺.候/窥伺.体.己/剔.除得心应.手/一应.俱全B.薄.饼/薄.面打烊./佯.装笑语朗朗..../书声琅琅C.背.篓/背.阴瑰.丽/皈.依毁家纾.难/自出机杼.D.辟.邪/复辟.荠.菜/同侪.不卑不亢./引吭.高歌2.下列各组词语中,没有错别字的一组是A.嘻游蜕变信誓旦旦义愤填膺B.蓬松搅绊攻城略地短小精悍C.敕造隐遁运筹帷幄三缄其口D.厮守希翼色彩斑斓摩肩接踵3.依次填入下列横线处的词语,最恰当的一组是放眼荆州,过度拥挤的古城内居民正在迁出,沙市的旧城改造也在有序进行,沙北新区、荆北新区等新城建设,城市主干道快速延伸,城市空间不断,配套设施逐步。
荆州,这座古老的历史名城,焕发出青春,越来越美。
A.持续紧锣密鼓伸展完美B.陆续如火如荼拓展完善C.连续方兴未艾施展完备D.继续有条不紊延展完整4.下列各项中,没有语病的一项是A.“辽宁舰”指挥员的“起飞手势”成为亮点,经过报刊、网络和媒体的转载与报道,受到了国人的热情追捧和模仿。
B.记者获悉,荆州市总工会将开展农民工“顺利平安返乡返岗”系列服务活动,为农民工提供订票服务。
截至发稿时,市总工会已为返乡农民工集中购票近一万余张。
C.1月23日,旨在致力于战国秦汉简牍研究、整理、保护的荆州市简牍研究所在市博物馆成立,这必定为更好地诠释、传承优秀文明作出应有贡献。
D.一些作家急于求成,缺乏“坐冷板凳”的精神,以出版发行为目的,过于注重商业利益,其作品缺乏对人性的深度和广度的反映。
5.下列有关文学常识的表述,正确的一项是A.张衡“通五经,贯六艺”,“五经”指《诗经》《尚书》《礼记》《易经》《论语》等五部儒家经典著作。
B.我国第一部国别体史书是左丘明的《国语》,第一部叙事详细完整的编年体史书是左丘明的《左传》,第一部纪传体通史是司马迁的《史记》,第一部断代史是范晔的《后汉书》。
湖北荆州市2013届高中毕业班质量检查(Ⅰ)数学文-含答案

湖北荆州市2013届高中毕业班质量检查(Ⅰ)数学(文)试题注意事项:1.答卷前,考生务必将自己的学校、班级、姓名、考号填在试卷答题卡上。
2.第1至10小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
第11至22题用钢笔或圆珠笔在答题卡上作答,答在试题卷上的无效。
3.考试结束,只交答题卡。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,多涂、不涂或涂错均得0分.1.设集合A ={x|-1≤x ≤2},B ={x|x 2-4x >0,x∈R},则A ∩(C R B )= A .[1,2] B .[0,2] C .[1,4] D .[0,4] 2.已知{n a }是等比数列,4714,2a a ==,则公比q=A .-12B .-2C .2D .123.已知函数2log (1)y ax =-在(1,2)上单调递增,则实数a的取值范围是A .(0,1]B .[1,2]C .[1,+∞)D .[2,+∞)4.设变量x,y满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩,则目标函数z =2y -3x 的最大值为A .-3B .2C .4D .55.函数f (x )=ln (x +1)-2x的零点所在的大致区间是A .(3,4)B .(2,e)C .(1,2)D .(0,1)6.设a为实数,函数32()(2)(),()f x x ax a x f x f x ''=++-的导数是且是偶函数,则曲线()y f x =在原点处的切线方程为A .y=-2xB .y=3xC .y=-3xD .y=4x7.将函数sin(2)4y x π=+的图象向左平移4π个单位,再向上平移2个单位,则所得图象的一个对称中心是A .(,2)4πB .(,2)3πC .(,2)8πD .(,2)2π8.在△ABC 中,AB =2,AC =4,若点P 为△ABC 的外心,则AP BC ⋅的值为A .2B .4C .6D .89.设函数(2)(2)()1()1(2)2x a x x f x x -≥⎧⎪=⎨-<⎪⎩是R 上的单调递减函数,则实数a 的取值范围为A .(-∞,13]8B .(-∞,2]C .(0,2)D .[13,2]10.函数f(x)的定义域为D ,若存在闭区间[m ,n ]⊆D ,使得函数f(x)满足:①f(x)在[m,n]上是单调函数;②f(x)在[m,n]上的值域为[2m,2n],则称区间[m,n]为y=f(x)的“倍值区间”,以下函数:①2()(0)f x x x =≥;②()()xf x e x R =∈;③24()(0)1xf x x x =≥+;④1()l o g ()8xa f x a=-(a >0,a ≠1),其中存在“倍值区间”的是 A .①② B .②④ C .①③④ D .②③④二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中相应的横线上. 11.已知1sin(),23πθ+=则cos2θ= 。
2013年高考湖北文科数学试题及答案(word解析版)

2013年普通高等学校招生全国统一考试(湖北卷)数学(文科)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项符合题目要求. (1)【2013年湖北,文1,5分】已知全集{1,2,3,4,5}U =,集合{1,2}A =,{2,3,4}B =,则U B A =ð( )(A ){2} (B ){3,4} (C ){1,4,5} (D ){2,3,4,5} 【答案】B 【解析】U B A =ð{2,3,4}{3,4,5}{3,4}=,故选B .(2)【2013年湖北,文2,5分】已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的( ) (A )实轴长相等 (B )虚轴长相等 (C )离心率相等 (D )焦距相等 【答案】D【解析】在双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=中,都有222sin cos 1c θθ=+=,即焦距相等,故选D .(3)【2013年湖北,文3,5分】在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( ) (A )()p ⌝∨()q ⌝ (B )p ∨()q ⌝ (C )()p ⌝∧()q ⌝ (D )p ∨q【答案】A【解析】因为p 是“甲降落在指定范围”,q 是“乙降落在指定范围”,则p -是“没有降落在指定范围”,q -是“乙没有降落在指定范围”,所以命题“至少有一位学员没有降落在指定范围”可表示为()p ⌝∨()q ⌝,故选A .(4)【2013年湖北,文4,5分】四名同学根据各自的样本数据研究变量,x y 之间的相关关系,并求得回归直线方程,分别得到以下四个结论:① y 与x 负相关且 2.347 6.423y x =-;② y 与x 负相关且 3.476 5.648y x =-+; ③ y 与x 正相关且 5.4378.493y x =+;④ y 与x 正相关且 4.326 4.578y x =--.其中一定不正确...的结论的序 号是( )(A )①② (B )②③ (C )③④ (D )①④ 【答案】D【解析】在①中,y 与x 不是负相关;①一定不正确;同理④也一定不正确,故选D . (5)【2013年湖北,文5,5分】小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶,与以上事件吻合得最好的图像是( )(A ) (B ) (C ) (D )【答案】C【解析】可以将小明骑车上学的行程分为三段,第一段是匀速行驶,运动方程是一次函数,即小明距学校的距离是他骑行时间的一次函数,所对应的函数图象是一条直线段,由此可以判断A 是错误的;第二段因交通拥堵停留了一段时间,这段时间内小明距学校的距离没有改变,即小明距学校的距离是行驶时间的常值函数,所对应的函数图象是平行于x 轴的一条线段,由此可以排除D ;第三段小明为了赶时间加快速度行驶,即小明在第三段的行驶速度大于第一段的行驶速度,所以第三段所对应的函数图象不与第一段的平行,从而排除B ,故选C .(6)【2013年湖北,文6,5分】将函数sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )(A )π12 (B )π6 (C )π3 (D )5π6【答案】B【解析】因为sin ()y x x x =+∈R 可化为2cos()6y x π=-(x ∈R ),将它向左平移π6个单位得x x y cos 26)6(cos 2=⎥⎦⎤⎢⎣⎡-+=ππ,其图像关于y 轴对称,故选B .(7)【2013年湖北,文7,5分】已知点(1,1)A -、(1,2)B 、(2,1)C --、(3,4)D ,则向量AB 在CD 方向上的投影为( )(A(B(C) (D) 【答案】A【解析】2,1AB =(),5,5CD =(),则向量AB 在向量CD方向上的射影为cos AB CDAB CDθ⋅====,故选A . (8)【2013年湖北,文8,5分】x 为实数,[]x 表示不超过x 的最大整数,则函数()[]f x x x =-在R 上为( )(A )奇函数 (B )偶函数 (C )增函数 (D )周期函数 【答案】D【解析】函数()[]f x x x =-表示实数x 的小数部分,有(1)1[1][]()f x x x x x f x +=+-+=-=,所以函数()[]f x x x =-是以1为周期的周期函数,故选D .(9)【2013年湖北,文9,5分】某旅行社租用A 、B 两种型号的客车安排900名客人旅行,A 、B 两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆.则租金最少为( )(A )31200元 (B )36000元 (C )36800元 (D )38400元 【答案】C【解析】根据已知,设需要A 型车x 辆,B 型车y 辆,则根据题设,有2170,03660900x y y x x y x y +≤⎧⎪-≤⎪⎨>>⎪⎪+=⎩, 画出可行域,求出三个顶点的坐标分别为4(7)1A ,,2(5)1B ,,6(15C ,),目标函数 (租金)为16002400k x y =+,如图所示.将点B 的坐标代入其中,即得租金的最小值为:1600524001236800k =⨯+⨯=(元),故选C . (10)【2013年湖北,文10,5分】已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围是( )(A )(,0)-∞ (B )1(0,)2(C )(0,1) (D )(0,)+∞【答案】B【解析】'()ln 12f x x ax =+-,由()(ln )f x x x ax =-由两个极值点,得'()0f x =有两个不等的实数解,即ln 21x ax =-有两个实数解,从而直线21y ax =-与曲线ln y x =有两个交点. 过点01(,-)作ln y x =的切线,设切点为00x y (,),则切线的斜率01k x =,切线方程为011y x x =-. 切点在切线上,则00010x y x =-=,又切点在曲线ln y x =上,则00ln 01x x =⇒=,即切点为10(,).切线方程为1y x =-. 再由直线21y ax =-与曲线ln y x =有两个交点,知直线21y ax =-位于两直线0y =和1y x =-之间,如图所示,其斜率2a 满足:021a <<,解得102a <<,故选B .二、填空题:共7小题,每小题5分,共35分.请将答案填在答题卡对应题号.......的位置上....答错位置,书写不清,模棱两可均不得分.(11)【2013年湖北,文11,5分】i 为虚数单位,设复数1z ,2z 在复平面内对应的点关于原点对称,若123i z =-,则2z = . 【答案】23i -+【解析】复数123i z =-在复平面内的对应点123Z -(,),它关于原点的对称点2Z 为2,3-(),所对应的复数为223i z =-+.(12)【2013年湖北,文12,5分】某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4则(1)平均命中环数为;(2)命中环数的标准差为 .【答案】(1)7;(2)2【解析】(1)()178795491074710+++++++++=;(2)2s =. (13)【2013年湖北,文13,5分】阅读如图所示的程序框图,运行相应的程序.若输入m 的值为2,则输出的结果i = . 【答案】4【解析】初始值2110m A B i ====,,,,第一次执行程序,得121i A B ===,,,因为A B <不成立,则第二次执行程序,得2224122i A B ==⨯==⨯=,,,还是A B <不成立,第三次执行程序,得3428236i A B ==⨯==⨯=,,,仍是A B <不成立,第四次执行程序,得48216i A ==⨯=,,424B =⨯=,有A B <成立,输出4i =.(14)【2013年湖北,文14,5分】已知圆O :225x y +=,直线l :cos sin 1x y θθ+=(π02θ<<).设圆O 上 到直线l 的距离等于1的点的个数为k ,则k =_________. 【答案】4【解析】这圆的圆心在原点,半径为5,圆心到直线l 1=,所以圆O 上到直线l 的距离等于1的点有4个,如图A 、B 、C 、D 所示.(15)【2013年湖北,文15,5分】在区间[2,4]-上随机地取一个数x ,若x 满足||x m ≤的概率为56,则m = . 【答案】3 【解析】因为区间[2,4]-的长度为6,不等式||x m ≤的解区间为[-m ,m ] ,其区间长度为2m . 那么在区间[2,4]-上随机地取一个数x ,要使x 满足||x m ≤的概率为56,m 将区间[2,4]-分为[]2m -,和[m ,4],且两区间的长度比为5:1,所以3m =.(16)【2013年湖北,文16,5分】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是 寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸) 【答案】3【解析】如图示天池盆的半轴截面,那么盆中积水的体积为()22961061031963V ππ=⨯++⨯=⨯(立方寸),盆口面积S =196π(平方寸),所以,平地降雨量为323196()3196⨯=寸(寸)(寸). (17)【2013年湖北,文17,5分】在平面直角坐标系中,若点(,)P x y 的坐标x ,y 均为整数,则称点P 为格点. 若一个多边形的顶点全是格点,则称该多边形为格点多边形. 格点多边形的面积记为S ,其内部的格点数记为N ,边界上的格点数记为L . 例如图中△ABC 是格点三角形,对应的1S =,0N =,4L =.(1)图中格点四边形DEFG 对应的,,S N L 分别是 ;(2)已知格点多边形的面积可表示为S aN bL c =++,其中a ,b ,c 为常数. 若某格点多边形对应的71N =,18L =, 则S = (用数值作答). 【答案】(1)3, 1, 6;(2)79 【解析】(1)S=S △DFG +S △DEF =1+2=3 ,N=1,L =6.(2)根据题设△ABC 是格点三角形,对应的1S =,0N =,4L =,有 41b c += ①由(1)有63a b c ++= ② 再由格点DEF ∆中,S=2,N=0,L=6,得62b c += ③联立①②③,解得1,1, 1.2b c a ==-=所以当71N =,18L =时,171181792S =+⨯-=.三、解答题:共5题,共65分.解答应写出文字说明,演算步骤或证明过程.(18)【2013年湖北,文18,12分】在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c . 已知cos23cos()1A B C -+=. (1)求角A 的大小;(2)若△ABC 的面积S =5b =,求sin sin B C 的值.解:(1)由cos23cos()1A B C -+=,得22cos 3cos 20A A +-=,即(2cos 1)(cos 2)0A A -+=,解得1cos 2A =或cos 2A =-(舍去).因为0πA <<,所以π3A =.(2)由11sin 22S bc A bc ====得20bc =. 又5b =,知4c =.由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故a =.又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.(19)【2013年湖北,文19,13分】已知n S 是等比数列{}n a 的前n 项和,4S ,2S ,3S 成等差数列,且23418a a a ++=-.(1)求数列{}n a 的通项公式;(2)是否存在正整数n ,使得2013n S ≥?若存在,求出符合条件的所有n 的集合;若不存在,说明理由. 解:(1)设数列{}n a 的公比为q ,则10a ≠,0q ≠.由题意得243223418S S S S a a a -=-⎧⎨++=-⎩,即23211121(1)18a q a q a q a q q q ⎧--=⎪⎨++=-⎪⎩, 解得132a q =⎧⎨=-⎩,故数列{}n a 的通项公式为13(2)n n a -=-.(2)由(1)有3[1(2)]1(2)1(2)n n n S ⋅--==----.若存在n ,使得2013n S ≥,则1(2)2013n --≥,即(2)2012.n -≤-当n 为偶数时,(2)0n ->, 上式不成立;当n 为奇数时,(2)22012n n -=-≤-,即22012n ≥,则11n ≥. 综上,存在符合条件的正整数n ,且所有这样的n 的集合为{21,,5}n n k k k =+∈≥N .(20)【2013年湖北,文20,13分】如图,某地质队自水平地面A ,B ,C 三处垂直向地下钻探,自A 点向下钻到A 1处发现矿藏,再继续下钻到A 2处后下面已无矿,从而得到在A 处正下方的矿层厚度为121A A d =.同样可得在B ,C 处正下方的矿层厚度分别为122B B d =,123C C d =,且123d d d <<. 过AB ,AC 的中点M ,N 且与直线2AA 平行的平面截多面体111222A B C A B C -所得的截面DEFG 为该多面体的一个中截面,其面积记为S 中. (1)证明:中截面DEFG 是梯形;(2)在△ABC 中,记BC a =,BC 边上的高为h ,面积为S . 在估测三角形ABC 区域内正下方的矿藏储量(即多面体111222A B C A B C -的体积V )时,可用近似公式V S h =⋅估中来估算.已知1231()3V d d d S =++,试判断V 估与V 的大小关系,并加以证明.解:(1)依题意12A A ⊥平面ABC ,12B B ⊥平面ABC ,12C C ⊥平面ABC ,所以A 1A 2∥B 1B 2∥C 1C 2.又121A A d =, 122B B d =,123C C d =,且123d d d <<.因此四边形1221A A B B 、1221A A C C 均是梯形.由2AA ∥平面MEFN ,2AA ⊂平面22AA B B ,且平面22AA B B平面MEFN ME =,可得AA 2∥ME ,即A 1A 2∥DE .同理可证A 1A 2∥FG ,所以DE ∥FG .又M 、N 分别为AB 、AC 的中点,则D 、E 、F 、G 分别为11A B 、22A B 、22A C 、11A C 的中点,即DE 、FG 分别为梯形1221A A B B 、1221A A C C 的中位线.因此 12121211()()22DE A A B B d d =+=+,12121311()()22FG A A C C d d =+=+,而123d d d <<,故DE FG <,所以中截面DEFG 是梯形. (2)V V <估. 证明如下:由12A A ⊥平面ABC ,MN ⊂平面ABC ,可得12A A MN ⊥.而EM ∥A 1A 2,所以EM MN ⊥,同理可得FN MN ⊥.由MN 是△ABC 的中位线,可得1122MN BC a ==即为梯形DEFG 的高,因此13121231()(2)22228DEFG d d d d a a S S d d d ++==+⋅=++中梯形,即123(2)8ahV S h d d d =⋅=++估中.又12S ah =,所以1231231()()36ahV d d d S d d d =++=++.于是1231232131()(2)[()()]6824ah ah ahV V d d d d d d d d d d -=++-++=-+-估.由123d d d <<,得210d d ->,310d d ->,故V V <估.(21)【2013年湖北,文21,13分】设0a >,0b >,已知函数()1ax bf x x +=+. (1)当a b ≠时,讨论函数()f x 的单调性;(2)当0x >时,称()f x 为a 、b 关于x 的加权平均数.(i )判断(1)f, f ,()bf a是否成等比数列,并证明()b f f a ≤; (ii )a 、b 的几何平均数记为G . 称2aba b+为a 、b 的调和平均数,记为H . 若()H f x G ≤≤,求x的取值范围.解:(1)()f x 的定义域为(,1)(1,)-∞--+∞,22(1)()()(1)(1)a x ax b a bf x x x +-+-'==++. 当a b >时,()0f x '>,函数()f x 在(,1)-∞-,(1,)-+∞上单调递增; 当a b <时,()0f x '<,函数()f x 在(,1)-∞-,(1,)-+∞上单调递减.(2)(i )(1)02a b f +=>,2()0b abf a a b=>+,0f =>.故22(1)()[2b a b ab f f ab f a a b +=⋅==+,即2(1)()[b f f f a =.①所以(1),()bf f f a 成等比数列.因2a b +≥,即(1)f f ≥.由①得()b f f a ≤. (ii )由(i )知()bf H a=,f G =.故由()H f x G ≤≤,得()()(b f f xf a ≤≤.② 当a b =时,()()b f f x f a a ===.这时,x 的取值范围为(0,)+∞;当a b >时,01ba<<,从而b a <,由()f x 在(0,)+∞上单调递增与②式,得b x a ≤≤即x的取值范围为,b a ⎡⎢⎣;当a b <时,1ba>,从而b a >由()f x 在(0,)+∞上单调递减与②式,bx a ≤,即x的取值范围为b a ⎤⎥⎦. (22)【2013年湖北,文22,14分】如图,已知椭圆1C 与2C 的中心在坐标原点O ,长轴均为MN且在x 轴上,短轴长分别为2m ,2()n m n >,过原点且不与x 轴重合的直线l 与1C ,2C 的四个交点按纵坐标从大到小依次为A ,B ,C ,D .记mnλ=,△BDM 和△ABN 的面积分别为1S 和2S .(1)当直线l 与y 轴重合时,若12S S λ=,求λ的值;(2)当λ变化时,是否存在与坐标轴不重合的直线l ,使得12S S λ=?并说明理由.解:依题意可设椭圆1C 和2C 的方程分别为1C :22221x y a m +=,2C :22221x y a n +=. 其中0a m n >>>, 1.mnλ=>(1)解法一:如图1,若直线l 与y 轴重合,即直线l 的方程为0x =,则111||||||22S BD OM a BD =⋅=,211||||||22S AB ON a AB =⋅=,所以12||||S BD S AB =. 在C 1和C 2的方程中分别令0x =,可得A y m =,B y n =,D y m =-,于是||||1||||1B D A B y y BD m n AB y y m n λλ-++===---.若12S S λ=,则11λλλ+=-,化简得2210λλ--=. 由1λ>,可解得1λ=.故当直线l 与y 轴重合时,若12S S λ=,则1λ.解法二:如图1,若直线l 与y 轴重合,则||||||BD OB OD m n =+=+,||||||AB OA OB m n =-=-;111||||||22S BD OM a BD =⋅=,211||||||22S AB ON a AB =⋅=.所以12||1||1S BD m n S AB m n λλ++===--. 若12S S λ=,则11λλλ+=-,化简得2210λλ--=. 由1λ>,可解得1λ=. 故当直线l 与y 轴重合时,若12S S λ=,则1λ=.(2)解法一:如图2,若存在与坐标轴不重合的直线l ,使得12S S λ=. 根据对称性,不妨设直线l :(0)y kx k =>,点(,0)M a -,(,0)N a 到直线l 的距离分别为1d ,2d ,则因为1d ==2d ==,所以12d d =. 又111||2S BD d =,221||2S AB d =,所以12||||S BD S AB λ==,即||||BD AB λ=.由对称性可知||||AB CD =,所以||||||(1)||BC BD AB AB λ=-=-,||||||(1)||AD BD AB AB λ=+=+,于是||1||1AD BC λλ+=-.① 将l 的方程分别与C 1,C 2的方程联立,可求得A x =B x = 根据对称性可知C B x x =-,D A x x =-,于是2||||2A B x AD BC x = ②1(1)λλλ+=-.③令1(1)t λλλ+=-,则由m n >,可得1t ≠,于是由③可解 得222222(1)(1)n t k a t λ-=-.因为0k ≠,所以20k >. 于是③式关于k 有解,当且仅当22222(1)0(1)n t a t λ->-, 等价于2221(1)()0t t λ--<. 由1λ>,可解得11t λ<<,即111(1)λλλλ+<<-,由1λ>,解得1λ>+所以当11λ<≤+l ,使得12S S λ=;当1λ> 轴不重合的直线l 使得12S S λ=.解法二:如图2,若存在与坐标轴不重合的直线l ,使得12S S λ=. 根据对称性,不妨设直线l :(0)y kx k =>,点(,0)M a -,(,0)N a 到直线l 的距离分别为1d ,2d ,则因为1d ==,2d =12d d =. 又111||2S BD d =,221||2S AB d =,所以12||||S BD S AB λ==.因为||||A B A B x x BD AB x x λ+==-,所以11A B x x λλ+=-.由点(,)A A A x kx ,(,)B B B x kx 分别在C 1, C 2上,可得222221A A x k x a m +=,222221B B x k x a n +=,两式相减可得22222222()0A B A B x x k x x a mλ--+=, 依题意0A B x x >>,所以22A B x x >. 所以由上式解得22222222()()A B B A m x x k a x x λ-=-.因为20k >,所以由2222222()0()A B B A m x x a x x λ->-,可解得1A B x x λ<<.从而111λλλ+<<-,解得1λ>+所以当11λ<≤+l ,使得12S S λ=;当1λ>+l 使得12S S λ=.。
荆州市2013届高中毕业班质量检查(Ⅰ)数学(文史类)

荆州市2013届高中毕业班质量检查(Ⅰ)数学(文史类)本试卷共三大题22道小题,满分150分,考试用时120分钟。
注意事项:1·答卷前,考生务必将自己的学校、班级、姓名、考号填在试题答题卡上。
2·第1至10小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.第11至22题用钢笔或者圆珠笔在答题卡上作答,答在试题卷上无效。
3·考试结束,只交答题卡。
本科目考试时间:2012年12月1日下午3:00—5:00一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,多涂、不涂或涂错均得0分.1、 设集合{12}A x x =-≤≤,{}240,B x x x x R =->∈,则()R A B = ðA []1,2B []0,2C []1,4D []0,42 已知数列{}n a 是等比数列,4714,2a a ==,则公比q =A 12-B 2-C 2D 123已知函数2log (1)y ax =-在(1,2)上单调递增,则实数a 的取值范围是A (]0,1B []1,2C [)1,+∞D [)2,+∞4 设变量,x y 满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩,则目标函数23z x y =-的最大值为A 3-B 2C 4D 55 函数2()ln(1)f x x x=+-的零点所在的大致区间是A ()3,4B ()2,eC ()1,2D ()0,16 设a 为实数,函数32()(2)f x x ax a x =++-的导数是()f x ',且()f x '是偶函数,则曲线()y f x =在原点处的切线方程为A 2y x =-B 3y x =C 3y x =-D 4y x =7将函数sin(2)4y x π=+的图像向左平移4π个单位,再向上平移2个单位,则所得图像的一个对称中心是A (,2)4πB (,2)3πC (,2)8πD (,2)2π8 在A B C ∆中,2,4AB AC ==,若点P 为A B C ∆的外心,则AP BC的值为A 2B 4C 6D 89设函数(2),(2)()1()1,(2)2x a x x f x x -≥⎧⎪=⎨-<⎪⎩是R 上的单调递减函数,则实数a 的取值范围为A 13,8⎛⎤-∞ ⎥⎝⎦B (],2-∞C (0,2)D 13,28⎡⎤⎢⎥⎣⎦10 函数()f x 的定义域为D ,若存在闭区间[],m n D ⊆,使得函数()f x 满足:①()f x 在[],m n 上是单调函数,②()f x 在[],m n 上的值域为[]2,2m n ,则称区间[],m n 为()y f x =的“倍值区间”,以下函数:①2(),(0)f x x x =≥;②()()x f x e x R =∈;③24()(0)1x f x x x =≥+;④1()log ()(0,1)8xa f x a a a =->≠。
湖北省荆州中学高三第三次质量检查(数学文).pdf

第2课时 实数的运算 一、选择题 1.某市今年1月份某一天的最高气温是3℃,最低气温是4℃,那么这一天的最高气温比最低气温高( ) A.7℃ B.7℃ C.1℃ D.1℃ 2.450克)为基数,超过的克数记作正数, 不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接 近标准克数的是( )A.+2 B.-3 C.+3 D.+4 3. 下列计算不正确的是( ) B. C. D. 4.在下列实数中,无理数是( ) A.B.C.D. 5.小明和小莉出生于1998年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是22,那么小莉的出生日期是( ) A.15号B.16号C.17号D.18号 6.运算的结果是( ) A.-6B.6C.-9D.9 7.(2009年武汉)二次根式的值是( ) A.B.或C.D. 8.估计的值 ( ) A.在3到4之间 B.在4到5之间 C.在5到6之间 D.在6到7之间 9.( ) (C) (D) 二、填空题: 10.)=______;=______;=______;=_______. 11.已知点位于第二象限,并且,为整数,写出一个符合上述条件的点的坐标: 12.如图,在数轴上表示到原点的距离为3个单位的点有 13.已知:, ,观察前面的计算过程,寻找计算规律计算 (直接写出计算结果),并比较 (填“”或“”或“=”) 14. 15.计算: ; . 16.若则 . 17.在函数中,自变量的取值范围是____________. 甲、乙、丙、丁四位同学围成一圈依序循环报数,规定: ①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5、乙报6……按此规律,后一位同学报出的数比前一位同学报出的数大1,当报到的数是50时,报数结束;②若报出的数为3的倍数,则报该数的同学需拍手一次,在此过程中,甲同学需要拍手的次数为____________. 三、计算: (1)°+ (2) (3) (4) (5) (6); (7) (8) 四、解答题 (1)观察下面的变形规律: =1-; =-;=-;…… 解答下面的问题: (1)若n为正整数,请你猜想= ; (2)证明你猜想的结论; (3)求和:+++…+ . (2)同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道0×1+1×2+2×3+…+(n—1)×n=n(n+1)(n—1)时,我们可以这样做: (1)观察并猜想: 12+22=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2) 12+22+32=(1+0)×1+(1+1)×2+(1+2)×3=1+0×1+2+1×2+3+2×3=(1+2+3)+(0×1+1×2+2×3) 12+22+32+42=(1+0)×1+(1+1)×2+(1+2)×3+ =1+0×1+2+1×2+3+2×3+ =(1+2+3+4)+( ) …… (2)归纳结论: 12+22+32+…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…+n=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n=() += + =× (3)实践应用: 通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 . 初中学习网,资料共分享!我们负责传递知识! 反思与提高 反思与提高 第12题图。
湖北省荆州市2013届高中毕业班质量检查(II)试题(word版)理综

荆州市2013届高中毕业班质量检查(II)理科综合能力测试本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
满分300分。
考试用时150分钟。
可能用到的相对原子质量:H―1 0—16 Na—23 S-32 K-39 Ca-40 Fe-56本科目考试时间:2013年3月13日上午9: OO-11:30第I卷 (选择题,本卷共21题,共126分)注意事项:1. 备卷前,考生务必将自己的学校、班级、姓名、考号填在试卷答题卡上。
2. 每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷上的无效。
一、选择题(本题包括13小题,每小题只有一个选项符合题意)1.2012年10月10日讯,2012年度诺贝尔化学奖授予美国科学家罗伯特•莱夫科维茨和布莱恩•科比尔卡,以表彰他们破解了细胞感觉的“门锁”——G蛋白偶联受体的工作原理(当细胞膜受体与激素结合时,会引发细胞内一系列反应,改变细胞内的新陈代谢)。
下列有关叙述中,不正确的是A. 与受体偶联的G蛋白在细胞膜中存在的状态是横跨或贯穿磷脂双分子层B. 克隆G蛋白偶联受体基因,需运用限制性核酸内切酶和DNA聚合酶C. 当G蛋白偶联受体与激素结合时,受体的空间结构会发生改变D. 通过G蛋白偶联受体的作用,实现了细胞间的信息交流2. 麻疹病毒减活疫苗的广泛接种,显著降低了麻疹的发病率,世界卫生组织已将麻疹列为优先消灭的目标。
下列相关叙述中,不正确的是A. 该疫苗不具有细胞结构,其表面特有的抗原可被免疫细胞识别B. 初次接种该疫苗后,刺激机体免疫系统,可产生效应T细胞、浆细胞和记忆细胞C. 与麻疹病毒在循环系统中“作战”的免疫细胞,构成人体免疫的第三道防线D. 再次感染该疫苗后,记忆细胞分化形成的浆细胞产生抗体,并与麻疹病毒结合,进而被吞噬细胞吞噬消化3. 草甘膦是一种广泛应用的除草剂,能不加选择地杀死各种杂草和农作物。
湖北省荆州市2013高三数学3月第二次质量检查试题 文 A版

湖北省荆州市2013届高中毕业班质量检查(II)数学(文)试题本试卷共三大题22道小题,满分150分,考试用时120分钟。
注意事项:1答卷前,考生务必将自己的学校、班级、姓名、考号填在试卷答题卡上。
2第1至10小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
第11至22题用0.5毫米黑色签字笔在答题卡上作答,答在试题卷上的无效。
3.考试结束,只交答题卡。
本科目考试时间:2013年3月12日下午15∶00———17∶00一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,多涂、不涂或涂错均得0分.1.已知复数z满足zi=1+i,则z=A.1+iB.iC.-iD.1-i2.某班有54名同学,准备派6名同学参加某高校组织的夏令营活动。
现将54名同学编号(1~54),用系统抽样的方法抽取,已知5号在样本中,则样本中最大的号码是A.50B.51C.52D.533.已知集合A={x│≥0},集合B={y│y=sinx,x∈R},则B∩CRA=A.ΦB.{-1}C.{1}D.{-1,1}4.已知变量x,y满足约束条件,则目标函数z=3x+y的最小值为A.12B.11C.8D.-15.设l,m,n为不重合的三条直线,其中直线m,n在平面α内,则“l⊥α”是“l ⊥m且l⊥n”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件6.某程序的流程图如图所示,若使输出的结果不大于38,则输入的整数i的最大值为A.4B.5C.6D.77.在△ABC中,O是中线AM上一个动点,若AM=4,则的最小值是A.-4B.-8C.-10D.-128.设一个四面体的体积为V1,且它的各条棱的中点构成一个凸多面体,其体积为V2,则V2/V1为A.1/2B.2/3C.3/4D.5/69.以下四个命题(1)在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=acosB,则B=π/4;(2)设a,b是两个非零向量且│a·b│=│a│·│b│,则存在实数λ,使得b=λa;(3)函数f(x)=sin-x在R上的零点有且仅有一个;(4)a,b∈R且,则a>b.其中正确的个数有A.1个B.2个C.3个D.4个10.已知函数f(x)在R上可导,下列四个选项中正确的是A.若f(x)>f'(x)对x∈R恒成立,则ef(1)<f(2)B.若f(x)<f'(x)对x∈R恒成立,则f(-1)>f(1)C.若f(x)+f'(x)>0对x∈R恒成立,则ef(2)<f(1)D.若f(x)+f'(x)<0对x∈R恒成立,则f(-1)>f(1)二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中相应的横线上.11.若函数f(x)=为奇函数,则实数m=.12.已知{an}是等比数列,a4=4,a7=1/2,则其公比q=.13.一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为.14.已知α为第三象限的角,cos2α=-3/5,则tan(π/4+2α)=.15.若函数f(x)=,则函数f(f(x))的值域是.16.已知椭圆=1的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆于点P、Q,则(1)△F1PQ的周长是;(2)△F1PQ内切圆面积的最大值是.17.点O是等腰Rt△ABC底边BC的中点,AB=1,过点O的动直线与两腰或其延长线的交点为Q、R,则有S△AQR=S△AOQ+S△AOR,所以=;类比平面结论,拓展到空间有:设O是正三棱锥P-ABC的面ABC的中心,PA,PB,PC两两垂直且PA=1,过点O的动平面与三棱锥的三条侧棱或其延长线的交点分别为Q、R、S,则有.三、解答题:本大题共5小题,共65分,解答题应写出文字说明、证明过程或演算步骤.18.(本小题满分12分)已知函数f(x)=.(1)求函数f(x)图像的对称轴方程及最小值;(2)已知f(α-π/8)=,α∈(0,π/4),求f(α/2)的值.19.(本小题满分12分)在等差数列{}中,=3,其前n项和为Sn;在各项均为正数的等比数列{bn}中,b1=1,且b2+S2=12,S5=5b3.(1)求{}与{bn}的通项公式;(2)设数列{cn}满足cn=,求数列{cn}前n项和Tn,并证明Tn<0(n∈).20.(本小题满分13分)2013年6月6日是第18个全国“爱眼日”.某校为了解学生近视情况,决定按10%的比例对高一、高二近视在100度以上的700名学生按年级进行抽样检查,测得近视度的频数分布表如下表1、表2.表1:高二年级学生近视度频数分布表表2:高一年级学生近视度频数分布表(1)求该校高二年级近视在100度以上的人数并完成下面频率分布直方图;(2)估计高一年级学生近视度的平均值;(3)从样本中近视度在[500,700)之间的学生中任选2人,求至少有1人近视度在[600,700)之间的概率.21.(本小题满分14分)已知圆C:=8及点F(1,0),P为圆C上一动点,在同一坐标平面内的动点M满足:,││=││.(1)求动点M的轨迹E的方程;(2)过点F作直线l与(1)中轨迹E交于不同两点R,S,设=λ,λ∈[-2,-1),求直线l的纵截距的取值范围.22.(本小题满分14分)已知f(x)=.(1)当a>0时,求函数f(x)的最小值;(2)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图像相切?若存在,有多少条?若不存在,说明理由;(3)求证:对任意正整数n均有.。
2013届湖北省襄阳市高三3月调研考试文科数学试题及答案

机密★启用前试卷类型:A湖北省襄阳市2013届高三3月普通高中调研统一测试高三数学(文科)★祝考试顺利★注意事项:1.答题前,请考生认真阅读答题卡上的注意事项。
非网评考生务必将自己的学校、班级、姓名、考号填写在答题卡密封线内,将考号最后两位填在登分栏的座位号内。
网评考生务必将自己的姓名、考号填写在答题卡上指定位置,贴好条形码或将考号对应数字涂黑。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B铅笔把对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.非选择答题用0.5毫米黑色墨水签字笔直接答在答题卡上每题对应的答题区域内,答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的清洁。
考试结束后,监考人员将答题卡收回,按小号在上,大号在下的顺序封装。
一、选择题(本大题10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知集合A={x|0< x<3},B={x|x2≥4},则A∩B=A.{ x|-2<x<0} B.{x|2<x<3} C.{ x|2≤x<3} D.{ x|x ≤-2或2≤x<3}2.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为A.100 B.1000 C.90 D.9003.设向量a =(1,0),b =(1,1),则下列结论正确的是 A .|a |=| b | B .a ·b =22C. a -b 与a 垂直 D .a ∥b4.若变量x 、y 满足约束条件⎪⎩⎪⎨⎧≤--≥+≤0201y x y x y ,则z =x -2y 的最大值为A .4B .3C .2 D.15.已知条件p :k =3;条件q :直线y = kx +2与x 2+y 2=1相切,则p 是q 的A .充分必要条件B .既不充分也不必要条件C .充分不必要条件D .必要不充分条件6.在等差数列{a n }中,若a 4+ a 6+ a 8+ a 10+ a 12=90,则a 10-31a 14的值为 A.12 B .14 C.16 D .187.若某一几何体的正视图与侧视图均为边长是1的正方形,且其体积为21,则该几何体的俯视图可以是8.若F 1、F 2为双曲线C :42x -y 2=1的左、右焦点,点P 在双曲线C 上∠F 1P F 2=60°,则P 到x 轴的距离为 A .55 B .515 C .5152 D .2015 9.设不等式组⎩⎨⎧≤≤≤≤2020y x 表示的平面区域为D ,在区域D 内随机取一点,则此点到坐标原点的距离大于1的概率为A .21 B .1-4π C .41 D .1-16π 10.已知定义在R 上的偶函数,f (x )满足f (x+1)=- f (x ),且当x ∈[0,1]时f (x )= x ,则函数y = f (x )-㏒3|x |的零点个数是 A .多于4个 B .4个 C.3个 D .2个二、填空题(本大题共7小题,每小题5分,共35分。
2013届荆州市高中毕业班第二次质量检查理科数学试题及答案

2013届荆州市高中毕业班第二次质量检查理科数学试题及答案一、选择题1.(2012•日照)已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是()A.k>且k≠2 B.k≥且k≠2 C.k>且k≠2 D.k≥且k≠21.C1.解:∵方程为一元二次方程,∴k-2≠0,即k≠2,∵方程有两个不相等的实数根,∴△>0,∴(2k+1)2-4(k-2)2>0,∴(2k+1-2k+4)(2k+1+2k-4)>0,∴5(4k-3)>0,k>,故k>且k≠2.故选C.3.(2012•潍坊)如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为()A.32 B.126 C.135 D.1443.D3.解:根据图象可以得出,圈出的9个数,最大数与最小数的差为16,设最小数为:x,则最大数为x+16,根据题意得出:x(x+16)=192,解得:x1=8,x2=-24,(不合题意舍去),故最小的三个数为:8,9,10,下面一行的数字分别比上面三个数大7,即为:15,16,17,第3行三个数,比上一行三个数分别大7,即为:22,23,24,故这9个数的和为:8+9+10+15+16+17+22+23+24=144.故选:D.5.(2012•日照)已知关于x的一元二次方程(k﹣2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是()A.k>且k≠2 B. k≥且k≠2 C. k>且k≠2 D. k≥且k≠2考点:根的判别式;一元二次方程的定义。
专题:计算题。
分析:根据方程有两个不相等的实数根,可知△>0,据此列出关于k的不等式,解答即可.解答:解:∵方程为一元二次方程,∴k﹣2≠0,即k≠2,∵方程有两个不相等的实数根,∴△>0,∴(2k+1)2﹣4(k﹣2)2>0,∴(2k+1﹣2k+4)(2k+1+2k﹣4)>0,∴5(4k﹣3)>0,k>,故k>且k≠2.故选C.点评:本题考查了根的判别式和一元二次方程的定义,根据一元二次方程的定义判断出二次项系数不为0是解题的关键.6.(2012•烟台)下列一元二次方程两实数根和为﹣4的是()A.x2+2x﹣4=0 B. x2﹣4x+4=0 C. x2+4x+10=0 D. x2+4x﹣5=0考点:根与系数的关系。
荆州中学2013年秋高二上学期期末考试数学文试题Word版含答案

荆州中学2013~2014学年度上学期期 末 试 卷年级:高二 科目:数学(文科)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.采用系统抽样方法从960人中抽取32人做调查,为此将他们编号为1,2,……,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9,抽到的32人中,编号落入区间[1,450]的人数为( ) A .10 B .14 C .15 D .16 2.抛掷一枚质地均匀的骰子,落地后记事件A 为“奇数点向上”,事件B 为“偶数点向上”,事件C 为“3点或6点向上”,事件 D 为“4点或6点向上”.则下列各对事件中是互斥但不对立的是( )A .A 与B B .B 与C C .C 与D D .A 与D 3.下列说法中,正确的是( )A .命题“若a b <,则22am bm <”的逆命题是真命题B . “∧⌝p q 为真命题”是 “q 为假命题” 成立的充分不必要条件C .命题“存在2,0x R x x ∈->”的否定是“对任意2,0x R x x ∈-<”D .已知x R ∈,则“1x >”是“2x >”的充分不必要条件4.设1234518,19,20,21,22x x x x x =====,将这五个数据依次输入下面程序框进行计算,则输出的S 值及其统计意义分别是( )A .2S =,即5个数据的方差为2 B. 2S =,即5个数据的标准差为2 C. 10S =,即5个数据的方差为10 D. 10S =,即5个数据的标准差为105. 双曲线221169x y -=上的点P 到点(5, 0)的距离是15, 则点P 到点(-5, 0)的距离是( ) A .7 B .23 C .11或19 D .7或236. 从集合{1,1,2}A =-中随机选取一个数记为k ,从集合{2,1,2}B =-中随机选取一个数记为b ,则直线y kx b =+不经过第三象限的概率为 ( )A.29B.13C.49D.597.函数()cos sinf x x x x=⋅-的导函数的部分图象为()A B C D8.设双曲线2222:1(,0)x yC a ba b-=>的一条渐近线与抛物线2y x=的一个交点的横坐标为0x,若12x>,则双曲线C的离心率的取值范围是()A.B.C.)+∞D.)+∞9.设椭圆22221x ya b+=(0a b>>)的离心率12e=,右焦点(,0)F c,方程20ax bx c+-=的两个根分别为1x,2x,则点12(,)P x x在( )A.圆222x y+=内B.圆222x y+=上C.圆222x y+=外D.以上都有可能10. 对于三次函数32()f x ax bx cx d=+++(0)a≠,给出定义:设()'f x是函数()y f x=的导数,()''f x是函数()'f x的导数,若方程()0''=f x有实数解x,则称点00(,())x f x为函数()y f x=的“拐点”.某同学经过探究发现:任何一个一元三次函数都有“拐点”;且该“拐点”也为该函数的对称中心.若3231()122f x x x x=-++,则122013()()()201420142014f f f+++=( )A. 1B. 2012C. 2013D. 2014二、填空题(本大题共7小题,每小题5分,共35分)11.已知复数122,3z i z i=+=-(i是虚数单位),则复数12zz的实部为 . 12.若椭圆2222+1x ya b=过抛物线28y x=的焦点,且与双曲线221x y-=有相同的焦点,则该椭圆的方程为.13.已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均与圆22:650C x y x +-+=相切,则该双曲线离心率等于 . 14.函数322=+++y x ax bx a ,在1=x 时,有极值10,则a = ,b = .15. 已知函数()f x 的定义域为[1,)+∞,且(2)(4)1f f ==,()'f x 是()f x 的导函数,函数()y f x '=的图象如图所示,则不等式组00(2)1x y f x y ≥⎧⎪≥⎨⎪+≤⎩所表示的平面区域的面积是.16. 从一块短轴长为2b 的椭圆形玻璃镜中划出一块面积最大的矩形,其面积的取值范围是22[3,4]b b ,则该椭圆离心率e 的取值范围是 .17.以下四个关于圆锥曲线的命题中真命题的序号为 .①设A 、B 为两个定点,k 为正常数,||||PA PB k +=,则动点P 的轨迹为椭圆; ②双曲线221259-=x y 与椭圆22135x y +=有相同的焦点; ③若方程22520x x -+=的两根可分别作为椭圆和双曲线的离心率;④到定点)0,5(A 及定直线25:4l x =的距离之比为54的点的轨迹方程为221169x y -=. 三、解答题(本大题共5小题,其中第18、19小题各12分,第20题13分,第21、22题各14分,共65分,解答应写出文字说明、证明过程或演算步骤)18.已知p :方程222121+=--x y a a 表示焦点在x 轴上的双曲线,q :方程2y =(2a 一a )x 表示开口向右的抛物线.若“p ∨q ”为真命题,“p ∧q ”为假命题,求实数a 的取值范围.19.根据2012年初发布的《环境空气质量指数AQI 技术规定(试行)》,AQI 共分为六级,其中:0到50为一级优,51到100为二级良,101到150为三级轻度污染,151到200为四级中度污染,201到300为五级重度污染,300以上为六级严重污染.自2013年11月中旬北方启动集中供暖后北京市雾霾天气明显增多,有人质疑集中供暖加重了环境污染,以下数据是北京市环保局随机抽取的供暖前15天和供暖后15天的AQI 数据:1月份的31天中出现五级重度污染的天数;(保留到整数位)(2)分别求出样本数据中供暖前和供暖后AQI 的平均值,由此你能得出什么结论.20.已知函数323()1()2f x ax x x R =-+∈,其中0a >. (1)若1a =,求曲线()y f x =在点(2,(2))f 处的切线方程;(2)求函数的极大值和极小值,若函数()f x 有三个零点,求a 的取值范围.21.抛物线22(0)y px p =>与直线1y x =+相切,112212(,),(,)()A x y B x y x x ≠是抛物线上两个动点,F 为抛物线的焦点. (1)求p 的值;(2)若直线AB 与x 轴交于点(1,0)-Q ,且 ||2||=QA QB ,求直线AB 的斜率; (3)若AB 的垂直平分线l 与x 轴交于点C ,且 ||||8AF BF +=,求点C 的坐标.22.已知函数21()(21)2ln ()2f x ax a x x a =-++∈R . (1) 若曲线()y f x =在1x =和3x =处的切线互相平行,求a 的值; (2) 当0>a 时,讨论()f x 的单调区间;(3) 设2()2g x x x =-,若对任意1(0,2]x ∈,均存在2(0,2]x ∈,使得12()()f x g x <,求a 的取值范围.荆州中学2013~2014学年度上学期期 末 考 试 卷 答 案年级:高二 科目:数学(文科)一、选择题 CDBAB ADBAC 二、填空题11. 12 12.22142x y +=13. 14. 4,11- 15. 316. [,]3217.②③ 三、解答题18.由题意,p 与q 一真一假 ································································································ 1分若p 真,则22010a a ⎧->⎨-<⎩,求得a <············································································· 3分若q 真,则20a a ->,求得10a a ><或 ········································································· 5分当p 真q假时,01a a ⎧<⎪⎨≤≤⎪⎩当p 假q真时,10a a a ⎧≥⎪⎨><⎪⎩或,求得01a a ≤<>或综上:01a a ≤<>或. ································································································ 12分19.(1)概率415P = ·············································································································· 3分 预测1月份出现五级重度污染的天数为431815⨯≈天 ························································ 6分(2)供暖前AQI 的平均值 1252755125417522752365122153x ⨯+⨯+⨯+⨯+⨯==≈ 供暖后AQI 的平均值27561254225327513251445148153x ⨯+⨯+⨯+⨯+⨯==≈ 21x x >,故供暖后加重了环境污染. ················································································· 12分20.解:(1)当1a =时,3223()1,()332f x x x f x x x '=-+=- 此时(2)3,(2)6f f '==,切线方程为69y x =- ······························································ 6分a可求出()f x 在1(,0)(,)a -∞+∞和上单调递增,在1(0,)a上单调递减 极大值为(0)1f =,极小值为211()12f aa =-+ ·································································································· 10分 若函数()f x 有三个零点,则21102a -+<,解得0a << ······································ 13分21.解:(1)由22(0)1y px p y x ⎧=>⎨=+⎩ 得:2220(0)y py p p -+=>有两个相等实根即2484(2)0p p p p ∆=-=-= 得:2p =为所求 ···················································· 4分 (2)设直线AB 的方程为1x my =-由241y x x my ⎧=⎨=-⎩得2440y my -+=,设1122(,),(,)A x y B x y , 由||2||=QA QB 得122y y =,又121244y y m y y +=⎧⎨=⎩,联立解出m =故直线AB的斜率1k m ==····················································································· 9分 (3)抛物线24y x =的准线1x =-且||||8AF BF +=,由定义得1228x x ++=,则126x x += ···························· 10分设(,0)C m ,由C 在AB 的垂直平分线上,从而||||AC BC =则22221122()()x m y x m y -+=-+ 22221212()()x m x m y y ---=-+ 121212(2)()4()x x m x x x x +--=-- 因为12x x ≠,所以1224x x m +-=-又因为126x x +=,所以5m =,则点C 的坐标为(5,0) ··············································· 14分22.解:(1)2()(21)f x ax a x'=-++(0)x >. 由(1)(3)f f ''=,解得23a =. …………………………3分x ①当102a <<时,12a >,增区间是(0,2)和1(,)a +∞,减区间是1(2,)a . ………5分②当12a =时,2(2)()2x f x x -'=, 故()f x 的单调递增区间是(0,)+∞. ………7分③当12a >时,102a <<,增区间是1(0,)a 和(2,)+∞,减区间是1(,2)a. ………9分(3)由已知,在(0,2]上有max max ()()f x g x <. ………………10分由已知,max ()0g x =,由(Ⅱ)可知,当0a ≤时,0x >,10ax -<, 在区间(0,2)上,()0f x '>;结合(2)可知: ① 当12a ≤时,()f x 在(0,2]上单调递增, 故max ()(2)22(21)2ln 2222ln 2f x f a a a ==-++=--+,所以,222ln 20a --+<,解得ln 21a >-,故1ln 212a -<≤. ……………12分②当12a >时,()f x 在1(0,]a 上单调递增,在1[,2]a上单调递减,故max 11()()22ln 2f x f a a a==---. 由12a >可知11ln ln ln 12ea >>=-,2ln 2a >-,2ln 2a -<,所以,22ln 0a --<,max ()0f x <, 综上所述,ln 21a >-. …………………14分。
湖北省荆州市2013届高中毕业班质量检查(II)试题(word版)英语(含听力)

荆州市2013届高中毕业班质量检查(II)英语注意事项:1. 本试卷共12页,总分150分,考试时间120分钟。
2. 答卷前,考生务必将自己的学校、班级、姓名、学号填在试卷答题卡上。
3. 客观题部分答案选出后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
第四部分第一节完成句子和第二节短文写作的答案用0.5毫米黑色签字笔直接填写到答题卡上对应的空白处。
答在试题卷上的无效。
本科目考试时间:2013年3月13日下午3: 00 -5: 00第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. When will Susan come?A. At 4:45.B. At 5 :00.C. At 5 :15.2. What is the woman doing?A. Apologizing.B. Asking for directions.C. Asking for advice.3. What is the relationship between the speakers?A. Student and teacher.B. Bookseller and customer.C. Reader and librarian.4. What does the man mean?A. He agrees with the woman.B. He enjoys the whole lecture.C. The lecture was more than an hour long.5.What are the two speakers talking about?A.Their school life.B. The hot weather.C.The air conditioner.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
高三数学试题湖北省荆州中学2013届高三第二次质量检测(文)试题

2x a, x 1 ,若 f (1 a)
x 2a ,x 1
f (1 a) , 则 a 的 值
为
.
15.已知函数 f ( x) 3sin x cosx, x R ,若 f ( x) 1 ,则 x 的取值范围为
.
16 .设 f ( x) 是定义在 R 上的偶函数,对任意的 x R ,都有 f ( 2 x) f ( x 2) ,且当
2 sin[4( x ) ] 84
因为 0 x
,所以
4x
3 .
4
4
44
当 4x
, 即 x 3 时, g( x) 取最大值 3
42
16
2 sin(4 x 2;
) 3. 4
当 4x 4
,即 x 0, g(x) 取 最小值 2. 4
故所求值域为 [2,3+ 2] ………………………………………………………………………
] max 1
5x
而
x2 1
5 1
x
5 ,当且仅当 x 1 时取等号,所以 a
2
5
……………………………
2
8
x
12
( 2)依题意, x0 2k
3 ( x Z ) ,由周期性,
4
f (x0) f (2 x0) f (3x0 )
3 (sin
4
…………… 8
3
3
cos ) (sin
4
2
3
9
cos ) (sin
2
4
9 cos )
4
2 1; …………
22.解:( 1) f ( x) 的定义域为 (0,
…… 3
x1 ) ,且 f (x) x2 0 ,所以 f ( x) 为 (0,
湖北省荆州市2013届高中毕业班3月质量检测(II)文科综合试题

荆州市2013届高中毕业班质量检查(II)文科综合能力测试本科目考试时间:2013年3月13日上午9 : 00——11 : 30 编辑人:丁济亮本试卷分第1卷(选择题)和第II卷(非选择题)两部分,满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡密封线内相应的地方。
2 第I卷每小题选出答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净,再选涂其它答案标号。
第II卷用0.5毫米黑色签字笔在答题卡上作答,答在试题上无效。
3.考试结束,监考人员将答题卡收回,试题由学生保存。
第I卷(选择题,共140分)一、选择题(本卷共35小题,每小题4分,共计140分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
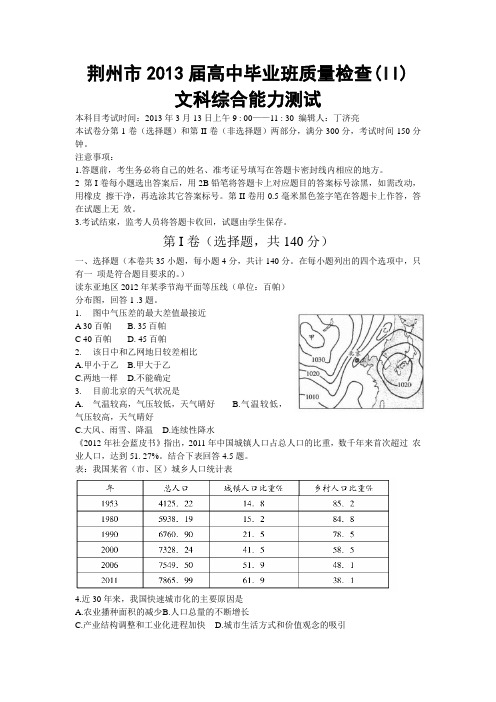
)读东亚地区2012年某季节海平面等压线(单位:百帕)分布图,回答1 .3题。
1. 图中气压差的最大差值最接近A 30百帕 B. 35百帕C 40百帕 D. 45百帕2. 该日中和乙网地日较差相比A.甲小于乙B.甲大于乙C.两地一样D.不能确定3. 目前北京的天气状况是A. 气温较高,气压较低,天气晴好B.气温较低,气压较高,天气晴好C.大风、雨雪、降温D.连续性降水《2012年社会蓝皮书》指出,2011年中国城镇人口占总人口的比重,数千年来首次超过农业人口,达到51. 27%。
结合下表回答4.5题。
表:我国某省(市、区)城乡人口统计表4.近30年来,我国快速城市化的主要原因是A.农业播种面积的减少B.人口总量的不断增长C.产业结构调整和工业化进程加快D.城市生活方式和价值观念的吸引5.表格数据所代表的省(市、区)最可能是A.天津市B.四川省C江苏省D.湖北省读“我国南、北方水资源、人口及耕地分布对照图”,回答6.7题。
6.下列有关图中内容的说法止确的是A.我国人口重心在北方地区B. 北方资源优势明显优于南方C.人均水资源南方多于北方D.人均耕地面积南方多于北方7.造成我国南方和北方地区水资源总量差异大的主要原因是A.地形差异导致地表储水差异较大B.雨季长短导致降水量差异较大C.人口数量差异导致用水差异较大D.纬度差异导致蒸发量差异较大下图为四个国家某年粮食作物生产状况示意图。
湖北省八市2013届高三3月联考试题数学文 含答案

湖北省八市2013年高三年级三月调考数学(文科)试题本试卷共4页.全卷满分150分,考试时间120分钟。
★ 祝考试顺利 ★注意事项:1.考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上。
2。
选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3.填空题和解答题用0。
5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内.答在试题卷上无效。
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1。
若,a b R ∈,i 是虚数单位,且(2)1a b i i +-=+,则a b +的值为A .1B .2C . 3D .42。
已知命题:,2xp x R ∀∈>,那么命题p ⌝为A .,20xx R ∃∈< B .20xx R ∀∈<,C .,20xx R ∃∈≤ D .20xx R ∀∈,≤3。
已知直线1:l y x =,若直线12l l⊥,则直线2l 的倾斜角为A.ππ()4k k Z +∈ B 。
π2C 。
3ππ()4k k Z +∈ D.3π44。
平面向量a 与b 的夹角为60,(2,0)a =,1b =,则2a b+=AB. C .4 D .125.不等式组(3)()004x y x y x -++⎧⎨⎩≥≤≤表示的平面区域是 A .矩形 B .三角形 C .直角梯形 D .等腰梯形 6.设a R ∈,函数()xxf x e ae -=+的导函数是()f x ',且()f x '是奇函数,则a 的值为A .1-B .12- C .1 D .127.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如右图,其中甲班学生成绩的平均分是85, 乙班学生成绩的中位数是83,则x +y 的值为A .7B .8C .9D .1688.《莱因德纸草书》(Rhind Papyrus )是世界上最古老的数学著作之一,书中有这样的一道题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的17是较小的两份之和,则最小的1份为A .53B .116C .56D .1039。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省荆州市2013届高中毕业班质量检查(II)
数学(文)试题
本试卷共三大题22道小题,满分150分,考试用时120分钟。
注意事项:
1 答卷前,考生务必将自己的学校、班级、姓名、考号填在试卷答题卡上。
2 第1至10小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
第11至22题用0.5毫米黑色签字笔在答题卡上作答,答在试题卷上的无效。
3.考试结束,只交答题卡。
编辑人:丁济亮
本科目考试时间:2013年3月12日下午15∶00———17∶00
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项正确,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,多涂、不涂或涂错均得0分.
1.已知复数z满足zi=1+i,则z=
A.1+iB.iC.-iD.1-i
2.某班有54名同学,准备派6名同学参加某高校组织的夏令营活动。
现将54名同学编号(1~54),用系统抽样的方法抽取,已知5号在样本中,则样本中最大的号码是A.50B.51C.52D.53
3.已知集合A={x│≥0},集合B={y│y=sinx,x∈R},则B∩CRA=
A.ΦB.{-1}C.{1}D.{-1,1}
4.已知变量x,y满足约束条件,则目标函数z=3x+y的最小值为
A.12B.11C.8D.-1
5.设l,m,n为不重合的三条直线,其中直线m,n在平面α内,则“l⊥α”是“l ⊥m且l⊥n”的
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
6.某程序的流程图如图所示,若使输出的结果不大于38,则输入的整数i的最大值为
A.4B.5C.6D.7
7.在△ABC中,O是中线AM上一个动点,若AM=4,则的最小值是
A.-4B.-8C.-10D.-12
8.设一个四面体的体积为V1,且它的各条棱的中点构成一个凸多面体,其体积为V2,则V2/V1为
A.1/2B.2/3C.3/4D.5/6
9.以下四个命题
(1)在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=
acosB,则B=π/4;
(2)设a,b是两个非零向量且│a·b│=│a│·│b│,则存在实数λ,使得b=λa;
(3)函数f(x)=sin-x在R上的零点有且仅有一个;
(4)a,b∈R且,则a>b.
其中正确的个数有
A.1个B.2个C.3个D.4个
10.已知函数f(x)在R上可导,下列四个选项中正确的是
A.若f(x)>f'(x)对x∈R恒成立,则ef(1)<f(2)
B.若f(x)<f'(x)对x∈R恒成立,则f(-1)>f(1)
C.若f(x)+f'(x)>0对x∈R恒成立,则ef(2)<f(1)
D.若f(x)+f'(x)<0对x∈R恒成立,则f(-1)>f(1)
二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答题卡中相应的横线上.
11.若函数f(x)=为奇函数,则实数m=.
12.已知{an}是等比数列,a4=4,a7=1/2,则其公比q=.
13.一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为.
14.已知α为第三象限的角,cos2α=-3/5,则tan(π/4+2α)=.
15.若函数f(x)=,则函数f(f(x))的值域是.
16.已知椭圆=1的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直
线l交椭圆于点P、Q,则(1)△F1PQ的周长是;(2)△F1PQ内切圆面积的最大值是.
17.点O是等腰Rt△ABC底边BC的中点,AB=1,过点O的动直线与两腰或其延
长线的交点为Q、R,则有S△AQR=S△AOQ+S△AOR,所以=;类比平面结论,拓展到空间有:
设O是正三棱锥P-ABC的面ABC的中心,PA,PB,PC两两垂直且PA=1,过点O的动平面与三棱锥的三条侧棱或其延长线的交点分别为Q、R、S,则有.
三、解答题:本大题共5小题,共65分,解答题应写出文字说明、证明过程或演算步骤.
18.(本小题满分12分)已知函数f(x)=.
(1)求函数f(x)图像的对称轴方程及最小值;
(2)已知f(α-π/8)=,α∈(0,π/4),求f(α/2)的值.
19.(本小题满分12分)在等差数列{}中,=3,其前n项和为Sn;在各项均为正数的等比数列{bn}中,b1=1,且b2+S2=12,S5=5b3.
(1)求{}与{bn}的通项公式;
(2)设数列{cn}满足cn=,求数列{cn}前n项和Tn,并证明Tn<0(n∈).
20.(本小题满分13分)2013年6月6日是第18个全国“爱眼日”.某校为了解学生近视情况,决定按10%的比例对高一、高二近视在100度以上的700名学生按年级进行抽样检查,测得近视度的频数分布表如下表1、表2.
表1:高二年级学生近视度频数分布表
表2:高一年级学生近视度频数分布表
(1)求该校高二年级近视在100度以上的人数并完成下面频率分布直方图;
(2)估计高一年级学生近视度的平均值;
(3)从样本中近视度在[500,700)之间的学生中任选2人,求至少有1人近视度在[600,700)之间的概率.
21.(本小题满分14分)已知圆C:=8及点F(1,0),P为圆C上一
动点,在同一坐标平面内的动点M满足:,││=││.
(1)求动点M的轨迹E的方程;
(2)过点F作直线l与(1)中轨迹E交于不同两点R,S,设=λ,λ∈[-2,-1),求直线l的纵截距的取值范围.
22.(本小题满分14分)已知f(x)=.
(1)当a>0时,求函数f(x)的最小值;
(2)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图像相切?若存在,有多少条?若不存在,说明理由;
(3)求证:对任意正整数n均有
.。
