高中椭圆基础知识专题练习题(有答案!)
高二数学--椭圆训练试卷(含答案)

高二数学椭圆一.选择题1.椭圆ax2+by2=1与直线y=1﹣x交于A、B两点,过原点与线段AB中点的直线的斜率为,则的值为()A.B.C.D.2.已知方程表示焦点在y轴上的椭圆,则实数k的取值范围是()A.B.(1,+∞)C.(1,2)D.3.椭圆x2+4y2=1的离心率为()A.B.C.D.4.椭圆+=1的右焦点到直线y=x的距离是()A.B.C.1D.5.以两条坐标轴为对称轴的椭圆过点P(,﹣4)和Q(﹣,3),则此椭圆的方程是()A.+y2=1 B.x2+=1C.+y2=1或x2+=1D.以上均不对6.已知P为椭圆+=1上的点,F1、F2为其两焦点,则使∠F1PF2=90°的点P有()A.4个B.2个C.1个D.0个7.椭圆4x2+9y2=1的焦点坐标是()A.(±,0)B.(0,±)C.(±,0)D.(±,0)8.若椭圆2kx2+ky2=1的一个焦点坐标是(0,4),则实数k的值为()A.B.﹣C.D.﹣9.已知椭圆上的一点P到椭圆一个焦点的距离为3,则P到另一焦点距离为()A.9B.7C.5D.3二.填空题(共6小题)10.(2009•湖北模拟)如图Rt△ABC中,AB=AC=1,以点C为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AB边上,且这个椭圆过A、B两点,则这个椭圆的焦距长为_________.11.若P是椭圆+=1上任意一点,F1、F2是焦点,则∠F1PF2的最大值为_________.12.F1、F2是椭圆+=1的两个焦点,P是椭圆上一点,则|PF1|•|PF2|有最_________值为_________.13.经过两点P1(),P2(0,)的椭圆的标准方程_________.14.已知焦距为8,离心率为0.8,则椭圆的标准方程为_________.15.点P在椭圆+=1上,F1,F2是椭圆的焦点,若PF1⊥PF2,则点P的坐标是_________.三.解答题(共5小题)16.已知椭圆的中心在坐标原点,焦点在x轴上,离心率为,且过点(1,2),求椭圆的标准方程.17.已知中心在原点,长轴在x轴上的椭圆的两焦点间的距离为,若椭圆被直线x+y+1=0截得的弦的中点的横坐标为﹣,求椭圆的方程.18.已知椭圆的焦点在x轴上,离心率为,且过点P(1,),求该椭圆的方程.19.求适合下列条件的椭圆的标准方程:(1)焦点在x轴上,a=6,e=;(2)焦点在y轴上,c=3,e=.20.已知椭圆两焦点的坐标分别是(﹣2,0),(2,0),并且经过点(2,),求椭圆方程.21.已知:△ABC的一边长BC=6,周长为16,求顶点A的轨迹方程.参考答案与试题解析一.选择题(共9小题)1.(2015•兴国县一模)椭圆ax2+by2=1与直线y=1﹣x交于A、B两点,过原点与线段AB中点的直线的斜率为,则的值为()A.B.C.D.考点:椭圆的简单性质.专题:综合题.分析:联立椭圆方程与直线方程,得ax2+b(1﹣x)2=1,(a+b)x2﹣2bx+b﹣1=0,A(x1,y1),B(x2,y2),由韦达定理得AB中点坐标:(),AB中点与原点连线的斜率k===.解答:解:联立椭圆方程与直线方程,得ax2+b(1﹣x)2=1,(a+b)x2﹣2bx+b﹣1=0,A(x1,y1),B(x2,y2),,y1+y2=1﹣x1+1﹣x2=2﹣=,AB中点坐标:(),AB中点与原点连线的斜率k===.故选A.点评:本题考查直线和圆锥曲线的经综合运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.2.(2012•香洲区模拟)已知方程表示焦点在y轴上的椭圆,则实数k的取值范围是()A.B.(1,+∞)C.(1,2)D.考点:椭圆的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:根据椭圆的标准方程,得焦点在y轴上的椭圆方程中,x2、y2的分母均为正数,且y2的分母较大,由此建立关于k的不等式组,解之即得实数k的取值范围.解答:解:∵方程表示焦点在y轴上的椭圆,∴,解之得1<k<2实数k的取值范围是(1,2)故选:C点评:本题给出标准方程表示焦点在y轴上的椭圆,求参数k的取值范围,着重考查了椭圆的标准方程的概念,属于基础题.3.(2007•安徽)椭圆x2+4y2=1的离心率为()A.B.C.D.考点:椭圆的简单性质.专题:综合题.分析:把椭圆的方程化为标准方程后,找出a与b的值,然后根据a2=b2+c2求出c的值,利用离心率公式e=,把a与c的值代入即可求出值.解答:解:把椭圆方程化为标准方程得:x2+=1,得到a=1,b=,则c==,所以椭圆的离心率e==.故选A点评:此题考查学生掌握椭圆的离心率的求法,灵活运用椭圆的简单性质化简求值,是一道综合题.4.(2006•东城区二模)椭圆+=1的右焦点到直线y=x的距离是()A.B.C.1D.考点:椭圆的简单性质;点到直线的距离公式.专题:计算题.分析:根据题意,可得右焦点F(1,0),由点到直线的距离公式,计算可得答案.解答:解:根据题意,可得右焦点F(1,0),y=x可化为y﹣x=0,则d==,故选B.点评:本题考查椭圆的性质以及点到直线的距离的计算,注意公式的准确记忆.5.以两条坐标轴为对称轴的椭圆过点P(,﹣4)和Q(﹣,3),则此椭圆的方程是()A.+y2=1 B.x2+=1C.+y2=1或x2+=1D.以上均不对考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:设经过两点P(,﹣4)和Q(﹣,3),的椭圆标准方程为mx2+ny2=1(m>0,n>0,m≠n),利用待定系数法能求出椭圆方程.解答:解:设经过两点P(,﹣4)和Q(﹣,3),的椭圆标准方程为mx2+ny2=1(m>0,n>0,m≠n),代入A、B得,,解得m=1,n=,∴所求椭圆方程为x2+=1.故选:B.点评:本题考查椭圆标准方程的求法,是中档题,解题时要认真审题,注意椭圆简单性质的合理运用.6.已知P为椭圆+=1上的点,F1、F2为其两焦点,则使∠F1PF2=90°的点P有()A.4个B.2个C.1个D.0个考点:椭圆的简单性质.专题:直线与圆;圆锥曲线的定义、性质与方程.分析:根据椭圆的标准方程,得出a、b、c的值,由∠F1PF2=90°得出点P在以F1F2为直径的圆(除F1、F2),且r<b,得出圆在椭圆内,点P不存在.解答:解:∵椭圆+=1中,a=4,b=2,∴c==2;∴焦点F1(﹣2,0),F2(2,0);又∵∠F1PF2=90°,∴点P在以F1F2为直径的圆x2+y2=4上(除F1、F2),又∵r=2<2=b,∴圆被椭圆内含,点P不存在.点评:本题考查了椭圆的标准方程与圆的标准方程的应用问题,解题时应灵活利用∠F1PF2=90°,是基础题.7.椭圆4x2+9y2=1的焦点坐标是()A.(±,0)B.(0,±)C.(±,0)D.(±,0)考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:把椭圆方程化为标准方程,再利用c=即可得出.解答:解:椭圆4x2+9y2=1化为,∴a2=,b2=,∴c==∴椭圆的焦点坐标为(±,0).故选:C.点评:熟练掌握椭圆的标准方程及其性质是解题的关键.8.若椭圆2kx2+ky2=1的一个焦点坐标是(0,4),则实数k的值为()A.B.﹣C.D.﹣考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:由椭圆的焦点坐标为(0,4)可得k>0,化椭圆方程为标准式,求出c,再由c=4得答案.解答:解:由2kx2+ky2=1,得,∵椭圆2kx2+ky2=1的一个焦点坐标是(0,4),∴,,则,.∴,解得.故选:C.点评:本题考查了椭圆的简单几何性质,考查了椭圆的标准方程,是基础题.9.已知椭圆上的一点P到椭圆一个焦点的距离为3,则P到另一焦点距离为()A.9B.7C.5D.3考点:椭圆的简单性质;椭圆的定义.专题:综合题.分析:由椭圆方程找出a的值,根据椭圆的定义可知椭圆上的点到两焦点的距离之和为常数2a,把a的值代入即可求出常数的值得到P到两焦点的距离之和,由P到一个焦点的距离为3,求出P到另一焦点的距离即可.解答:解:由椭圆,得a=5,则2a=10,且点P到椭圆一焦点的距离为3,由定义得点P到另一焦点的距离为2a﹣3=10﹣3=7.故选B点评:此题考查学生掌握椭圆的定义及简单的性质,是一道中档题.二.填空题(共6小题)10.(2009•湖北模拟)如图Rt△ABC中,AB=AC=1,以点C为一个焦点作一个椭圆,使这个椭圆的另一个焦点在AB边上,且这个椭圆过A、B两点,则这个椭圆的焦距长为.考点:椭圆的简单性质.专题:计算题.分析:设另一焦点为D,则可再Rt△ABC中,根据勾股定理求得BC,进而根据椭圆的定义知AC+AB+BC=4a求得a.再利用AC+AD=2a求得AD最后在Rt△ACD中根据勾股定理求得CD,得到答案.解答:解析:设另一焦点为D,∵Rt△ABC中,AB=AC=1,∴BC=∵AC+AD=2a,AC+AB+BC=1+1+=4a,∴a=又∵AC=1,∴AD=.在Rt△ACD中焦距CD==.故答案为:.点评:本题主要考查了椭圆的简单性质和解三角形的应用.要理解好椭圆的定义和椭圆中短轴,长轴和焦距的关系.11.若P是椭圆+=1上任意一点,F1、F2是焦点,则∠F1PF2的最大值为.考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:先根据椭圆方程求得a和b的大小,进而利用椭圆的基本性质,确定最大角的位置,求出∠F1PF2的最大值.解答:解:根据椭圆的方程可知:+=1,∴a=2,b=,c=1,由椭圆的对称性可知,∠F1PF2的最大时,P在短轴端点,此时△F1PF2是正三角形,∴∠F1PF2的最大值为.故答案为:.点评:本题主要考查了椭圆的应用.当P点在短轴的端点时∠F1PF2值最大,这个结论可以记住它.在做选择题和填空题的时候直接拿来解决这一类的问题.12.F1、F2是椭圆+=1的两个焦点,P是椭圆上一点,则|PF1|•|PF2|有最大值为16.考点:椭圆的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:运用椭圆的定义,可得|PF1|+|PF2|=2a=8,再由基本不等式,即可求得|PF1|•|PF2|的最大值.解答:解:椭圆+=1的a=4,则|PF1|+|PF2|=2a=8,则|PF1|•|PF2|≤()2=16,当且仅当|PF1|=|PF2|=4,则|PF1|•|PF2|有最大值,且为16.故答案为:大,16点评:本题考查椭圆的定义和性质,考查基本不等式的运用:求最值,考查运算能力,属于基础题.13.经过两点P1(),P2(0,)的椭圆的标准方程=1.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n),把两点P1(),P2(0,)代入,能求出结果.解答:解L:设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n)把两点P1(),P2(0,)代入,得:,解得m=5,n=4,∴椭圆方程为5x2+4y2=1,即=1.故答案为:=1.点评:本题考查椭圆的标准方程的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.14.已知焦距为8,离心率为0.8,则椭圆的标准方程为,或.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:由椭圆的焦距是8,离心率0.8,先求出a=5,c=4,b,由此能求出椭圆的标准方程.解答:解:∵椭圆的焦距是8,离心率0.6,∴,解得a=5,c=4,b2=25﹣16=9,∴椭圆的标准方程为,或.故答案为:,或.点评:本题考查椭圆的标准方程的求法,是基础题,解题时要避免丢解.15.点P在椭圆+=1上,F1,F2是椭圆的焦点,若PF1⊥PF2,则点P的坐标是(3,4),(3,﹣4),(﹣3,4),(﹣3,﹣4).考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:由椭圆方程求出椭圆的焦点坐标,根据PF1⊥PF2得=0,与椭圆方程联立解得即可.解答:解:由椭圆+=1,得F1(﹣5,0),F2(5,0)设P(x,y),=0,①即(x+5)(x﹣5)+y2=0因为P在椭圆上,所以+=1,②两式联立可得x=±3,∴P(3,4),P(3,﹣4),P(﹣3,4),P(﹣3,﹣4)故答案为:P(3,4),P(3,﹣4),P(﹣3,4),P(﹣3,﹣4).点评:本题主要考查了椭圆的几何性质,向量的应用.三.解答题(共5小题)16.已知椭圆的中心在坐标原点,焦点在x轴上,离心率为,且过点(1,2),求椭圆的标准方程.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:先假设椭圆的方程,再利用的椭圆C的离心率为,且过点(1,2),即可求得椭圆C的方程.解答:解:设椭圆方程为,椭圆的半焦距为c,∵椭圆C的离心率为,∴,∴,①∵椭圆过点(1,2),∴②由①②解得:b2=,a2=49∴椭圆C的方程为.点评:本题重点考查椭圆的标准方程,考查椭圆的性质,解题的关键是待定系数法.17.已知中心在原点,长轴在x轴上的椭圆的两焦点间的距离为,若椭圆被直线x+y+1=0截得的弦的中点的横坐标为﹣,求椭圆的方程.考点:椭圆的标准方程.分析:首先,设椭圆的标准方程为:=1 (a>b>0),然后,设出直线与椭圆的两个交点坐标,然后,将这两个交点坐标代入椭圆方程,两个方程相减,得到关于a,b的一个方程,再结合给定的a,c的关系式,求解即可.解答:解:设椭圆的标准方程为:=1(a>b>0),∵椭圆被直线x+y+1=0截得的弦的中点的横坐标是﹣,∴弦的中点的纵坐标是﹣,设椭圆与直线x+y+1=0的两个交点为P(x1,y1),Q(x2,y2).则有+=1 ①+=1 ②①﹣②,化简得+=0 ③x1+x2=2×(﹣)=﹣,y1+y2=2×()=﹣,且=﹣1,∴由③得a2=2b2,又由题意2c=,有c=,则可求得c2==b2,a2=,∴椭圆的标准方程为:+=1.点评:本题重点考查了椭圆的几何性质、标准方程、直线与椭圆的位置关系等知识,属于中档题,涉及到弦的中点问题,处理思路是“设而不求”的思想.18.已知椭圆的焦点在x轴上,离心率为,且过点P(1,),求该椭圆的方程.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:设椭圆方程为(a>b>0),由已知得,由此能求出椭圆方程.解答:解:设椭圆方程为(a>b>0),由已知得,解得,b2=1,∴椭圆方程为.点评:本题考查椭圆方程的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.19.求适合下列条件的椭圆的标准方程:(1)焦点在x轴上,a=6,e=;(2)焦点在y轴上,c=3,e=.考点:椭圆的标准方程.专题:计算题;圆锥曲线的定义、性质与方程.分析:(1)由离心率公式,求得c,再由a,b,c的关系,求得b,即可得到椭圆方程;(2)由离心率公式,求得a,再由a,b,c的关系,求得b,即可得到椭圆方程.解答:解:(1)a=6,e=,即,解得c=2,b2=a2﹣c2=32,则椭圆的标准方程为:=1;(2)c=3,e=,即,解得,a=5,b2=a2﹣c2=25﹣9=16.则椭圆的标准方程为:=1.点评:本题考查椭圆的性质和方程,考查运算能力,属于基础题.20.已知椭圆两焦点的坐标分别是(﹣2,0),(2,0),并且经过点(2,),求椭圆方程.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析: 直接根据焦点的坐标设出椭圆的方程,再根据点的坐标求出结果. 解答: 解:椭圆两焦点的坐标分别是(﹣2,0),(2,0), 所以:设椭圆的方程为:由于:椭圆经过点(2,), 则:, 且a 2=b 2+4, 则:, 解得:. 椭圆方程为:.点评: 本题考查的知识要点:椭圆方程的求法,属于基础题型.21. 以BC 边为x 轴,BC 线段的中垂线为y 轴建立直角坐标系,则A 点的轨迹是椭圆,其方程为:116y 25x 22=+。
高二数学椭圆专项练习题及参考答案

高二数学椭圆专项练习题及参考答案训练指要熟练掌握椭圆的定义、标准方程、几何性质;会用待定系数法求椭圆方程. 一、选择题.椭圆中心在坐标原点,对称轴为坐标轴,离心率为,长、短轴之和为,则椭圆方程为.16410022=+y x .11006422=+y x .1100641641002222=+=+y x y x 或 .110818102222=+=+y x y x 或 .若方程+=,表示焦点在轴上的椭圆,那么实数的取值范围是 .(,+∞) .(,) .(,+∞) .(,).已知圆+=,又(3,),为圆上任一点,则的中垂线与之交点轨迹为(为原点) .直线.圆.椭圆.双曲线二、填空题.设椭圆1204522=+y x 的两个焦点为、,为椭圆上一点,且⊥,则-=. .(年全国高考题)椭圆的一个焦点是(,),那么. 三、解答题.椭圆2222by a x +(>>)()、′()()为椭圆的右焦点,若直线⊥′,求椭圆的离心率..在面积为的△中,21,建立适当的坐标系,求以、为焦点且过点的椭圆方程..如图,从椭圆2222by a x +=(>>)上一点向轴作垂线,恰好通过椭圆的左焦点,且它的长轴端点及短轴的端点的连线∥.()求椭圆的离心率;()设是椭圆上任意一点,是右焦点,求∠的取值范围;()设是椭圆上一点,当⊥时,延长与椭圆交于另一点,若△的面积为3,求此时椭圆的方程.参考答案一、 二、5,40||||100)2(||||562|||:|212222121=⋅⇒⎪⎭⎪⎬⎫==+==+PF PF c PF PF a PF PF 提示 ∴(-)-×. -5. 三、.215- .以所在直线为轴,线段的中垂线为轴建立坐标系,可得椭圆方程为.1315422=+y x .()22 ()[,2π] ()1255022=+y x 提示:()∵⊥轴,∴-,代入椭圆方程求得a b 2,∴-,,2ab k ac b AB -= ∵∥,∴-c b abac b =⇒-=2 从而22. ()设,∠θ,则2a 1F 2c.由余弦定理,得θ212222124r r c r r -+1242)(21221221221-=--+=r r a r r c r r r r≥,01)2(2212=-+r r a 当且仅当时,上式取等号.∴≤θ≤,θ∈[,2π]. ()椭圆方程可化为122222=+cy c x ,又⊥,∴-.21==bak AB2(-)代入椭圆方程,得-2c .求得,526c 到的距离为,362c ∴.25320||2121=⇒=⋅=∆c d PQ S PQ F ∴椭圆方程为.1255022=+y x椭圆训练题:1. 椭圆19822=++y m x 的离心率21=e ,则2. 椭圆的准线方程是3. 已知、为椭圆192522=+y x 的两个焦点,、为过的直线与椭圆的两个交点,则△的周长是 4. 椭圆12222=+by a x ()0>>b a 上有一点到其右焦点的距离是长轴两端点到右焦点的距离的等差中项,则点的坐标是5. 椭圆12222=+b y a x 焦点为、,是椭圆上的任一点,为 的中点,若 的长为,那么的长等于6. 过椭圆1273622=+y x 的一个焦点作与椭圆轴不垂直的弦,的垂直平分线交于,交轴于,则FN :AB7. 已知椭圆的对称轴是坐标轴,离心率32=e ,长轴长是,则椭圆的方程是 8. 方程1162522=++-my m x 表示焦点在轴上的椭圆,则的值是 9. 椭圆的两焦点把准线间的距离三等分,则这椭圆的离心率是10. 椭圆142222=+by b x 上一点到右焦点的距离为,则点到左准线的距离是11. 椭圆⎪⎭⎫⎝⎛∈=+2,4,1csc sec 2222ππt t y t x ,这个椭圆的焦点坐标是 12. 曲线()023122=+--+m my y m x 表示椭圆,那么的取值是13. 椭圆13422=+y x 上的一点()11,y x A ,点到左焦点的距离为25,则 14. 椭圆()()19216122=-+-y x 的两个焦点坐标是15. 椭圆中心在原点,焦点在轴上,两准线的距离是5518,焦距为52,其方程为 16. 椭圆上一点与两个焦点、所成的∆1F 中,βα=∠=∠1221,F PF F PF ,则它的离心率17. 方程142sin 322=⎪⎭⎫ ⎝⎛+-παy x 表示椭圆,则α的取值是18. 若()()065562222=--+-λλλλy x 表示焦点在轴上的椭圆,则λ的值是19. 椭圆192522=+y x 上不同的三点()()2211,,59,4,,y x C B y x A ⎪⎭⎫ ⎝⎛与焦点()0,4F 的距离成等差数列,则=+21x x20. 是椭圆192522=+y x 上一点,它到左焦点的距离是它到右焦点的距离的倍,则点的坐标是21. 中心在原点,对称轴在坐标轴上,长轴为短轴的倍,且过()6,2-的椭圆方程是 22. 在面积为的△中,2tan ,21tan -==N M ,那么以、为焦点且过的椭圆方程是 23. 已知△,()()0,3,0,3-B A 且三边、、的长成等差数列,则顶点的轨迹方程是24. 椭圆1422=+y m x 的焦距为,则的值是 25. 椭圆14922=+y x 的焦点到准线的距离是 26. 椭圆()112222=-+m y m x 的准线平行于轴,则的值是 27. 中心在原点,准线方程为4±=x ,离心率为21的椭圆方程是 28. 椭圆的焦距等于长轴长与短轴长的比例中顶,则离心率等于29. 中心在原点,一焦点为()50,01F 的椭圆被直线23-=x y 截得的弦的中点横坐标为21,则此椭圆方程是 30. 椭圆的中心为()0,0,对称轴是坐标轴,短轴的一个端点与两个焦点构成面积为的三角形,两准线间的距离是225,则此椭圆方程是 31. 过点()2,3-且与椭圆369422=+y x 有相同焦点的椭圆方程是32. 将椭圆192522=+y x 绕其左焦点逆时针方向旋转︒,所得椭圆方程是 33. 椭圆192522=+y x 上一点到右准线的距离是,那么点右焦半径是34. 是椭圆14322=+y x 的长轴,是一个焦点,过的每一个十等分点作的垂线,交椭圆同一侧于点,,,⋅⋅⋅⋅⋅⋅,,则11912111BF F P F P F P AF ++⋅⋅⋅+++的值是 35. 中心在原点,一焦点为(,),长短轴长度比为,则此椭圆方程是 36. 若方程222x ky +=表示焦点在轴的椭圆,则的取值是37. 椭圆221123x y +=的焦点为、,点为椭圆上一点,若线段的中点在轴上,那么1PF :2PF38. 经过)()122,M M --两点的椭圆方程是39. 以椭圆的右焦点(为左焦点)为圆心作一圆,使此圆过椭圆中心并交椭圆于、,若直线是圆的切线,则椭圆的离心率是40. 椭圆的两个焦点、及中心将两准线间的距离四等分,则一焦点与短轴两个端点连线的夹角是41. 点(),0a 到椭圆2212x y +=上的点之间的最短距离是 42. 椭圆2214x y +=与圆()2221x y r -+=有公共点,则的取值是 43. 若k R ∈,直线1y kx =+与椭圆2215x y m+=总有公共点,则的值是 44. 设是椭圆上一点,两个焦点、,如果00211275,15PF F PF F ∠=∠=,则离心率等于45. 是椭圆22143x y +=上任一点,两个焦点、,那么12F PF ∠的最大值是 46. 椭圆2244x y +=长轴上一个顶点为,以为直角顶点作一个内接于椭圆的等腰直角三角形,则此直角三角形的面积是47. 椭圆长轴长为,焦距,过焦点作一倾角为α的直线交椭圆于、两点,当MN 等于短轴长时,α的值是48. 设椭圆22143x y +=的长轴两端点、,点在椭圆上,那么直线与的斜率之积是 49. 倾斜角为4π的直线与椭圆2214x y +=交于、两点,则线段的中点的轨迹方程是 50. 已知点(,)是椭圆上的一点,是椭圆上任一点,当弦长取最大值时,点的坐标是椭圆训练题答案. 544-或 . 1y =± . 20 . ()()0,0,b b -或 . 2sa - . 1:4 . 2222119559x y x y +=+=或 .9252m <<. 3.. (0, . ()1,+∞ . 1. ()()1,1.22194x y+= . cos2cos2αβαβ+- .()37,,88k k k Z ππππ⎛⎫++∈ ⎪⎝⎭.). 8. 1515,44⎛⎛ ⎝⎭⎝⎭或.222211148371352x y x y +=+=或 . 2241153x y += . 2213627x y += . 53或. . 102m m <≠且 . 22143x y +=. .2212575x y += . 222211259925x y x y +=+=或 .2211510x y += . ()()22441925x y +-+= . 6. 20.222221111x y t t t +=-- . ()0,1 . 7 . 221155x y +=.1 .2π. a a +. 3⎤⎥⎣⎦. ≥且≠.3 . ︒ . 1625 . 566ππ或 . 34-. 1,4y x x ⎛⎫⎛=-∈ ⎪⎝⎝⎭.13⎛⎫- ⎪ ⎪⎝⎭椭圆训练试卷一、选择题:本大题共小题,每小题分,共分.请将唯一正确结论的代号填入题后的括号内..椭圆3m 2y mx 222++=1的准线平行于轴,则实数的取值范围是 ( ).-1<<3 .-23<<且≠.-1<<3且≠.<-且≠. 、、、分别表示椭圆的半长轴、半短轴、半焦距、焦点到相应准线的距离,则它们的关系是 ( ).22a b.ba 2.ca 2.cb 2.短轴长为5,离心率为32的椭圆的两个焦点分别为、,过作直线交椭圆于、两点,则Δ的周长为 ( ). . . ..下列命题是真命题的是( ).到两定点距离之和为常数的点的轨迹是椭圆.到定直线ca 2和定(,)的距离之比为ac 的点的轨迹是椭圆.到定点(,)和定直线ca 2的距离之比为ac(>>)的点的轨迹 是左半个椭圆.到定直线ca 2和定点(,)的距离之比为ca (>>)的点的轨迹是椭圆.是椭圆4x 23y 2上任意一点,、是焦点,那么∠的最大值是( )..300...椭圆22b 4x 22b y 上一点到右准线的距离是3,则该点到椭圆左焦点的距离是( )..23.3 ..椭圆12x 23y 2的焦点为和,点在椭圆上,如果线段的中点在轴上,那么是的( ).倍.倍.倍.倍.设椭圆22ax 22b y (>>)的两个焦点是和,长轴是1A ,是椭圆上异于、的点,考虑如下四个命题: ①1F 1F ; ②<<;③若越接近于,则离心率越接近于; ④直线与的斜率之积等于22a b .其中正确的命题是 ( ) .①②④ .①②③ .②③④ .①④.过点M(-2,0)的直线与椭圆+=交于P1、P2两点,线段P1P2的中点为P,设直线的斜率为(≠),直线OP的斜率为,则的值为 ( ) .2.-2.21.-21 .已知椭圆22a x 22by (>>)的两顶点(,)、(,),右焦点为,且到直线的距离等于到原点的距离,则椭圆的离心率满足 ( ).<<22.22<<. <<2.2<<.设F1、F2是椭圆2222b y ax=1(>>)的两个焦点,以F1为圆心,且过椭圆中心的圆与椭圆的一个交点为M,若直线F2M与圆F1相切,则该椭圆的离心率是( ).2-3.3-1.23 .22.在椭圆4x 23y 2内有一点(,),为椭圆右焦点,在椭圆上有一点,使的值最小,则这一最小值是` ( ).25.27 . .二、填空题:本大题共小题,每小题分,共分.请将最简结果填入题中的横线上..椭圆3x 2ky 2的离心率是的根,则 ..如图,∠OFB=6π,SΔABF=2-3,则以OA为长半轴,OB 为短半轴,F为一个焦点的椭圆的标准方程为 ..过椭圆3y 2x 22+=1的下焦点,且与圆+-++23=相切的直线的斜率是 . .过椭圆9x25y 2的左焦点作一条长为12的弦,将椭圆绕其左准线旋转一周,则弦扫过的面积为 .三、解答题:本大题共小题,共分.解答题应写出必要的计算步骤或推理过程. .(本小题满分分)已知、为椭圆22a x 22a 9y 25上两点,为椭圆的右焦点,若58,中点到椭圆左准线的距离为23,求该椭圆方程. .(本小题满分分)设中心在原点,焦点在轴上的椭圆的离心率为23,并且椭圆与圆25交于、两点,若线段的长等于圆的直径. (1) 求直线的方程; (2) 求椭圆的方程. .(本小题满分分)已知9x 25y 2的焦点、,在直线:上找一点,求以、为焦点,通过点且长轴最短的椭圆方程..(本小题满分分)一条变动的直线与椭圆4x 22y 2交于、两点,是上的动点,满足关系·.若直线在变动过程中始终保持其斜率等于.求动点的轨迹方程,并说明曲线的形状. .(本小题满分分)设椭圆22a x 22by 的两焦点为、,长轴两端点为、.(1) 是椭圆上一点,且∠,求Δ的面积;(2) 若椭圆上存在一点,使∠,求椭圆离心率的取值范围..(本小题满分分)已知椭圆的一个顶点为A(0,-1),焦点在轴上,若右焦点到直线-+2=的距离为3. ()求椭圆的方程;()设椭圆与直线=+(≠)相交于不同的两点M、N,当|AM|=|AN|时,求的取值范围.椭圆训练试卷参考答案一、 D 二、.或49.12y 8x 22=+.5623±.π三、.解:设(,),(,),由焦点半径公式有58,∴21(∵54),即中点横坐标为41,又左准线方程为45,∴414523,即,∴椭圆方程为925..解:()直线的方程为21; ()所求椭圆的方程为12x 23y 2..解:由9x25y 2,得(,),(,),关于直线的对称点(,),连交于一点,即为所求的点,∴2a 5,∴5,又,∴,故所求椭圆方程为20x 216y 2..解:设动点(,),动直线:,并设(,),(,)是方程组⎩⎨⎧=-++=04y 2x ,m x y 22的解,消去,得2m 2,其Δ16m 2(2m 2)>,∴6<<6,3m4, 34m 22-,故2,2.由,得,也即(),于是有3mx434m 22-.∵,∴.由,得椭圆7x 27y 22夹在直线±6间两段弧,且不包含端点.由,得椭圆..解:()设,,则21F PF ∆21∠,由2a , 4c∠,得212PF F cos 1b 2∠+.代入面积公式,得 21F PF ∆2121PF F cos 1PF F sin ∠+∠∠2PF F 2133.()设∠α,∠β,点(,)(<<).θ(αβ)βα-β+αtg tg 1tg tg22020000y x a 1y x a y x a --++-220200a y x ay 2-+.∵220a x 220b y ,∴22b a .∴θ202220y b b a ay 2-- 022y c ab 2-3.∴≤3≤3, 即3c4a 2c-4a≥,∴≥,解之得≥32,∴36≤<为所求. .解:()用待定系数法.椭圆方程为22y 3x +=1.()设P为弦MN的中点.由⎪⎩⎪⎨⎧=++=,1y 3x ,m kx y 22得(+)++(-)=.由Δ>0,得<+ ①,∴=1k 3mk 32x x 2N M +-=+,从而,=+=1k 3m 2+.∴=km 31k 3m 2++-.由MN⊥AP,得 km 31k 3m 2++-=-k 1,即2m =+ ②.将②代入①,得2m >,解得0<<.由②得=31m 2->0.解得>21.故所求的取值范围为(21,2).。
高中椭圆基础练习题答案

、选择题:1•下列方程表示椭圆的是()2 26.如果x ^ ― 1表示焦点在x 轴上的椭圆,则实数 a 的取值范围为()a 2 a +2A.(-2, ::)B. -2,-1 一 2, ::C.(」:,-1)_. (2, ::)D.任意实数 R7. “m>n>0”是“方程 mx 2 • ny 2 =1表示焦点在y 轴上的椭圆的”() A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件38.椭圆的短轴长是 4,长轴长是短轴长的 倍,则椭圆的焦距是() 2A. .5B. 4C.6D. 2 59.关于曲线的对称性的论述正确的是()D .方程x 3_y 3=8的曲 2 2A. 方程x xy y =0的曲线关于X 轴对称 线关于原点对称B. 方程x 3 y 3 =0的曲线关于Y 轴对称2 2 2^2小B. -x -2y 8 2 xC.— 25 2 2D.(x-2) y =12.动点P 到两个定点F 1 (- 4 , 0) . F 2 (4, 0)的距离之和为 8,贝U P 点的轨迹为()A.椭圆B.线段F 1F 2C.直线F 1F 2 D .不能确定 23.已知椭圆的标准方程x 2±“,则椭圆的焦点坐标为()A. (_ 而0)B. (0, _ 而C.(0, _3)D. ( -3,0) 4椭圆 2 2 x_丄 a 2 b 2 2 2=1和-2 2 =1(a 2 b 2 k 2)的关系是 a …k b …k A •有相同的长 短轴B •有相同的离心率 C .有相同的准线D •有相同的焦点 2 25.已知椭圆'計1上一点P 到椭圆的一焦点的距离为3,则P到另一焦点的距离是() A. 2.5 -3B.2C.3D.6C.方程x2 - xy • y2 =10的曲线关于原点对称2 2x y22 =1( a > b > 0)表示的椭圆(a bA.有相同的离心率;B.有共同的焦点;C.有等长的短轴 长轴; D .有相同的顶点二填空题: (本大题共4小题,共20分.)2 2x y11. (6分)已知椭圆的方程为:1,则a=64 100___________ ,焦距等于 ______ ;若CD 为过左焦点 F1的弦,(如图)则? F 2CD 的周长为12. ( 6分)椭圆16x 2 25y 2二400的长轴长为 _______ ,短轴长为 ______ ,焦点坐标为四个顶点坐标分别为 ___________________ ,离心率为 ____ ;椭圆的左准线方程为 ___________ 13. ( 4分)比较下列每组中的椭圆:2 2(2 [①— y 1与②9x 2 • y 2 =36,哪一个更扁 ______________6 1014. (4分)若一个椭圆长轴的长度•短轴的长度和焦距成等差数列,则该椭圆的离心率是 三、解答题:本大题共 6小题,共80分•解答应写出文字说明,证明过程或演算步骤. 15. (30分)求满足下列条件的椭圆的标准方程:(1)两个焦点的坐标分别为(0, -3) , (0,3),椭圆的短轴长为 8;(2)两个焦点的坐标分别为(-.5 ,0), (、- 5,0),并且椭圆经过点(2、2 -)3(3)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点R (J6,I )、第11题,b= ____ ,c= ___ ,焦点坐标为:(1 [① 9x 2 4y 2 =36 与②12 16,哪一个更圆 ______2 2x2y2、、、' 16. (12分)已知点M在椭圆1上,M P垂直于椭圆焦点所在的直线,垂直为P,25 9并且M为线段P p'的中点,求P点的轨迹方程17.(12分)设点A,B的坐标为(-a,0),( a,O)(a 0),直线AM,BM相交于点M,且它们的斜率之积为-k(k・0且k -1)求点M的轨迹方程,并讨论k值与焦点的关系.2 218.(12分)当m取何值时,直线I :科=x m与椭圆9x 16y =144相切,相交,相离?2 2x y19.(14分)椭圆1(0 :::m : 45)的焦点分别是F i和F2,已知椭圆的离心率e二45 m过中心O作直线与椭圆交于A, B两点,O为原点,若L ABF2的面积是20,求:(1)m的值(2)直线AB的方程参考答案1.选择题:题号 1 2 3 4 5 6 7 8 9 10 答案BBCDCBCDCA.填空题:三.解答题:15. (1)解:由题意,椭圆的焦点在 y 轴上,设椭圆的标准方程为由焦点坐标可得c=3,短轴长为8,即2b=8,b=4,所以a^ b 2 c^ 252 2椭圆的标准方程为- 125 162 2(2)由题意,椭圆的焦点在 x 轴上,设椭圆的标准方程为 笃 -y 2 =1(a b 0) a b2 2所以b 2 = a 2 - c 2 =9-5=4,所以椭圆的标准方程为 x y 19 4设椭圆的方程为mx 2 • ny 2 =1( m 0, n • 0),P (j6,1)、P 2(-73,-妁p(x, y), m 点的坐标为(X 0,y °),由题意可知2 2因为点m 在椭圆——=1上,所以有25 922 2 2X o-1 ②,把①代入②得 — --1,所以P 点的轨迹是焦点在 y 轴上,标25 925 3611 10,8, 6, (0, ±6) , 12, 40 1210, 8, ( _0 ),(-5,0) . ( 5,0) . ( 0, -4) (0,4),25X 二313142 2笃二=1(a - b - 0)a b(2、、2- . 5)2因为椭圆过解得1m =91 n =3所以椭圆的标准方程为: 16•解:设p 点的坐标为6 m ■ n = 1 3 m 2 n = 12 2①2 2准方程为x y 1的椭圆.25 3617. 解:设点M的坐标为(x, y),因为点A的坐标是(-a,0),所以,直线AM的斜率k AM二一-(x = -a),同理直线BM的斜率k BM二—(x = a) •由已知有x +a x — a2 2—y y k(x =二a )化简得点M的轨迹方程为笃与=1(x=二a)x a x - a a ka当0 ::: k :::1时,表示焦点在x轴上的椭圆;当k 1时,表示焦点在y轴上的椭圆{ y =x 4m ....................... ①18•解:L 9x216 y2=144 …②①代入②得9x2 16(x m)2=144化简得25x232mx 16m2-144 =02 2 2:=(32m) -4 25(16m -144^ -576m 14400当,;",即m = 5时,直线l与椭圆相切;当U,即-5 ::: m ::: 5时,直线与椭圆相交;当:: 0,即m ::: -5或m .5时,直线与椭圆相离•19.解:(1)由已知e=C 5, a =、、45=3、-5 ,得c = 5 ,a 3所以m = b2 = a2—c2二45 —25 二20(2)根据题意SABF^ "SFf B " 20,设B( X, y),则S F^B二2^F1F j|y ,2 2=2c=10,所以y = 14,把y = ±4代入椭圆的方程=1,得x = =3,所以45 204 4B点的坐标为(土3, 士4),所以直线AB的方程为y= — x或y =-一x3 3。
高中椭圆基础知识专题练习题(有答案!)

高中椭圆基础知识专题练习题(有答案!)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、选择题:1.下列方程表示椭圆的是()A.22199x y += B.2228x y --=- C.221259x y -= D.22(2)1x y -+= 2.动点P 到两个定点1F (- 4,0).2F (4,0)的距离之和为8,则P 点的轨迹为() A.椭圆B.线段12F FC.直线12F FD.不能确定3.已知椭圆的标准方程22110y x +=,则椭圆的焦点坐标为()A.(B.(0,C.(0,3)±D.(3,0)±4.椭圆222222222222211()x y x y a b k a b a k b k+=+=>>--和的关系是 A .有相同的长.短轴B .有相同的离心率 C .有相同的准线 D .有相同的焦点5.已知椭圆22159x y +=上一点P 到椭圆的一焦点的距离为3,则P 到另一焦点的距离是()A.3B.2C.3D.66.如果22212x y a a +=+表示焦点在x 轴上的椭圆,则实数a 的取值范围为() A.(2,)-+∞ B.()()2,12,--⋃+∞ C.(,1)(2,)-∞-⋃+∞ D.任意实数R 7.“m>n>0”是“方程221mx ny +=表示焦点在y 轴上的椭圆的”()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件8.椭圆的短轴长是4,长轴长是短轴长的32倍,则椭圆的焦距是()4 C.6D.9.关于曲线的对称性的论述正确的是() A.方程220x xy y ++=的曲线关于X 轴对称B.方程330x y +=的曲线关于Y 轴对称C.方程2210x xy y -+=的曲线关于原点对称D.方程338x y -=的曲线关于原点对称第11题10.方程 22221x y ka kb +=(a >b >0,k >0且k ≠1)与方程22221x y a b+=(a >b >0)表示的椭圆( ).A.有相同的离心率;B.有共同的焦点;C.有等长的短轴.长轴;D.有相同的顶点.二、填空题:(本大题共4小题,共20分.)11.(6分)已知椭圆的方程为:22164100x y +=,则a=___,b=____,c=____,焦点坐标为:___ __,焦距等于______;若CD 为过左焦点F1的弦,(如图)则∆2F CD 的周长为________.12.(6分)椭圆221625400x y +=的长轴长为____,短轴长为____,焦点坐标为 四个顶点坐标分别为___ ,离心率为 ;椭圆的左准线方程为 13.(4分)比较下列每组中的椭圆:(1)①229436x y += 与②2211216x y += ,哪一个更圆 (2)①221610x y +=与②22936x y +=,哪一个更扁 14.(4分)若一个椭圆长轴的长度.短轴的长度和焦距成等差数列,则该椭圆的离心率是2F CcD1F三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(30分)求满足下列条件的椭圆的标准方程:(1)两个焦点的坐标分别为(0,-3),(0,3),椭圆的短轴长为8;(2)两个焦点的坐标分别为(,0),并且椭圆经过点2)3(3)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点12P P 、16.(12分)已知点M 在椭圆221259x y +=上,M 'P 垂直于椭圆焦点所在的直线,垂直为'P ,并且M 为线段P 'P 的中点,求P 点的轨迹方程17.(12分)设点A ,B 的坐标为(,0),(,0)(0)a a a ->,直线AM,BM 相交于点M ,且它们的斜率之积为(01)k k k ->≠且求点M 的轨迹方程,并讨论k 值与焦点的关系.18.(12分)当m 取何值时,直线l :y x m =+与椭圆22916144x y +=相切,相交,相离19.(14分)椭圆221(045)45x y m m +=<<的焦点分别是1F 和2F ,已知椭圆的离心率3e =过中心O 作直线与椭圆交于A ,B 两点,O 为原点,若2ABF 的面积是20,求:(1)m 的值(2)直线AB 的方程参考答案1.选择题:二.填空题:11 10,8,6,(0,6±),12,40 12 10,8,(3,0±),(-5,0).(5,0).(0,-4).(0,4),35,253x =- 13 ②,② 14 35三.解答题:15.(1)解:由题意,椭圆的焦点在y 轴上,设椭圆的标准方程为22221(0)y x a b a b+=>> 由焦点坐标可得3c =,短轴长为8,即28,4b b ==,所以22225a b c =+=∴椭圆的标准方程为2212516y x +=(2)由题意,椭圆的焦点在x 轴上,设椭圆的标准方程为22221(0)x y a b a b +=>> 由焦点坐标可得c=2a ==6所以2b =22a c -=9-5=4,所以椭圆的标准方程为22194x y += (3)设椭圆的方程为221mx ny +=(0,0m n >>),因为椭圆过12P P 、61321m n m n +=+=⎧∴⎨⎩解得1913m n ==⎧⎨⎩所以椭圆的标准方程为:22193x y += 16.解:设p 点的坐标为(,)p x y ,m 点的坐标为00(,)x y ,由题意可知000022y y x x x x y y ====⎧⎧⇒⎨⎨⎩⎩ ① 因为点m 在椭圆221259x y +=上,所以有22001259x y += ② , 把①代入②得2212536x y +=,所以P 点的轨迹是焦点在y 轴上,标准方程为2212536x y +=的椭圆. 17.解:设点M 的坐标为(,)x y ,因为点A 的坐标是(,0)a -,所以,直线AM 的斜率()AM y k x a x a =≠-+,同理直线BM 的斜率()BM y k x a x a=≠-.由已知有(),y yk x a x a x a=-≠±+-化简得点M 的轨迹方程为22221()x y x a a ka +=≠±当01k <<时,表示焦点在x 轴上的椭圆;当1k >时,表示焦点在y 轴上的椭圆. 18.解:{22916144y x m x y =++=…… … … ①②①代入②得22916()144x x m ++=化简得222532161440x mx m ++-=222(32)425(16144)57614400m m m ∆=-⨯-=-+当0,∆=即5m =±时,直线l 与椭圆相切; 当0∆>,即55m -<<时,直线与椭圆相交; 当0∆<,即5m <-或5m >时,直线与椭圆相离.19.解:(1)由已知3c e a ==,a ==5c =, 所以222452520m b a c ==-=-=(2)根据题意21220ABF F F BSS==,设(,)B x y ,则121212F F B S F F y =,12210F F c ==,所以4y =±,把4y =±代入椭圆的方程2214520x y +=,得3x =±,所以B 点的坐标为34±±(,),所以直线AB 的方程为4433y x y x ==-或。
椭圆专题训练卷(含解析)

椭圆专题训练卷一、单选题1.(2019·宁波市第四中学高二期中)设p 是椭圆2212516x y +=上的点.若12F F ,是椭圆的两个焦点,则12PF PF +等于( )A .4B .5C .8D .102.(2020·全国高三课时练习(理))设x 、y ∈R ,则“|x |≤4且|y |≤3”是“216x +29y ≤1”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件3.(2019·浙江省春晖中学高二月考)已知椭圆221102x y m m +=--的焦点在y 轴上,且焦距为4,则m 等于( ) A .4B .5C .7D .84.(2020·雅安市教育科学研究所高三一模(理))已知椭圆()222210x y a b a b+=>>的左顶点为A ,上顶点为B ,且OA (O 为坐标原点),则该椭圆的离心率为( )A B C D5.(2020·四川资阳 高三其他(理))已知椭圆C :()222210x y a b a b +=>>经过点),且C 的离心率为12,则C 的方程是( ) A .22143x y +=B .22186x y +C .22142x y +=D .22184x y +=6.(2020·全国高三课时练习(理))已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,A ,B 分别为C 的左,右顶点.P 为C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为( ) A .13B .12C .23D .347.(2020·河北枣强中学高三月考(文))已知椭圆C 的方程为()222210x y a b a b +=>>,焦距为2c ,直线:4l y x =与椭圆C 相交于A ,B 两点,若2AB c =,则椭圆C 的离心率为( )A .2B .34C .12D .148.(2020·甘肃城关 兰大附中高三月考(理))已知1F ,2F 分别为椭圆221168x y +=的左、右焦点,M 是椭圆上的一点,且在y 轴的左侧过点2F 作12F MF ∠的角平分线的垂线,垂足为N ,若2ON =(O 为坐标原点)则21MF MF -等于( )A .4B .2C D 9.(2020·黑龙江南岗 哈师大附中高三其他(文))已知1F 、2F 是椭圆22143x y +=的左、右焦点,点P 是椭圆上任意一点,以1PF 为直径作圆N ,直线ON 与圆N 交于点Q (点Q 不在椭圆内部),则12QF QF ⋅=( )A .B .4C .3D .110.(2019·宁波市第四中学高二期中)设椭圆22221x y a b+=0)a b >>(的左、右焦点分别为12(,0)(,0)F c F c -,,点(,)2aN c 在椭圆的外部,点M 是椭圆上的动点,满足11232MF MN F F +<恒成立,则椭圆离心率e 的取值范围是( )A .(0B .1)C .5)6, D .5(,1)6二、多选题11.(2019·江苏省苏州实验中学高二月考)已知椭圆22221(0)x y a b a b+=>>的左焦点F ,焦距为2,过点F的弦长最小值不小于2,则该椭圆的离心率可以是( ) A .45B .23C .12D .1312.(2019·辽宁葫芦岛 高二月考)椭圆C :2211612x y +=的右焦点为F ,点P 是椭圆C 上的动点,则||PF 的值可能是( ) A .1B .3C .4D .813.(2020·岳麓 湖南师大附中高二期末)设椭圆22:143x y C +=的左、右焦点分别为12,F F ,点P 为椭圆C上一动点,则下列说法中正确的是( ) A .当点P 不在x 轴上时,12PF F ∆的周长是6 B .当点P 不在x 轴上时,12PF F ∆面积的最大值为3 C .存在点P ,使12PF PF ⊥ D .1PF 的取值范围是[1,3]14.(2020·山东中区 济南外国语学校高三月考)我们通常称离心率为512-的椭圆为“黄金椭圆”.如图,已知椭圆2222:1(0)x y C a b a b+=>>,1212,,,A A B B 为顶点,12,F F 为焦点,P 为椭圆上一点,满足下列条件能使椭圆C 为“黄金椭圆”的有( )A .111222||,||,||A F F F F A 为等比数列B .11290F B A ∠=︒C .1PF x ⊥ 轴,且21//PO A BD .四边形1221A B A B 的内切圆过焦点12,F F 三、单空题15.(2020·商丘市回民中学高二期末(理))若椭圆的方程为221102x y a a +=--,且此椭圆的焦距为4,则实数a =________.16.(2020·河北桃城 衡水中学高三其他(文))已知椭圆C 的中心在原点,焦点在x 轴上,若C 的短轴长为2个相邻的五等分点,则此椭圆的标准方程为________.17.(2020·河南中原 郑州一中高三其他(文))已知A 、F 分别是椭圆C :22221x y a b+=()0a b >>的下顶点和左焦点,过A 且倾斜角为60︒的直线l 分别交x 轴和椭圆C 于M ,N 两点,且N 点的纵坐标为35b ,若FMN 的周长为6,则FAN 的面积为_____.四、双空题18.(2019·浙江高二学业考试)椭圆2214x y +=的离心率是___________,焦距长是________.19.(2020·上海高二课时练习)椭圆22192x y +=的焦点为F 1,F 2,点P 在椭圆上,若14PF =,2PF =_______;12F PF ∠的小大为__________.20.(2019·浙江高二期中)若方程22121x y m m+=+-表示椭圆,则实数m 的取值范围是______;当1m =-时,椭圆的焦点坐标为______.21.(2020·福建高三其他(理))已知椭圆22:143x y C +=的焦点是12,F F ,,A B 是C 上(不在长轴上)的两点,且1//2F A F B .M 为1F B 与2F A 的交点,则M 的轨迹所在的曲线是______;离心率为_____. 五、解答题22.(2020·上海高二课时练习)已知椭圆的中心在原点,焦距为6,且经过点(0,4).求它的标准方程.23.(2019·于都县第二中学高二月考(文))焦点在x 轴上的椭圆的方程为2214x ym+=,点(2,1)P 在椭圆上.(1)求m 的值.(2)依次求出这个椭圆的长轴长、短轴长、焦距、离心率. 24.(2019·永济市涑北中学校高二月考(理))设点是椭圆上一动点,椭圆的长轴长为,离心率为.(1)求椭圆的方程; (2)求点到直线距离的最大值.25.(2019·河南宛城 南阳中学高二月考(理))已知椭圆的两焦点为12(1,0),(1,0)F F -,P 为椭圆上一点,且12F F 是1PF 与2PF 的等差中项. (1)求此椭圆方程;(2)若点P 满足1260F PF ︒∠=,求12PF F ∆的面积.26.(2019·牡丹江市第三高级中学高二期末(文))已知点(2,1)P -在椭圆()222:102x yC a a +=>上,动点,A B 都在椭圆上,且直线AB 不经过原点O ,直线OP 经过弦AB 的中点. (1)求椭圆C 的方程; (2)求直线AB 的斜率.27.(2018·西藏拉萨中学高二期末(理))椭圆C 的中心在坐标原点,焦点在x 轴上,右焦点F 的坐标为(2,0),且点F 6. (1)求椭圆C 的方程;(2)过点F 作斜率为k 的直线l ,与椭圆C 交于A 、B 两点,若43OA OB ⋅>-,求k 的取值范围.一、单选题1.(2019·宁波市第四中学高二期中)设p 是椭圆2212516x y +=上的点.若12F F ,是椭圆的两个焦点,则12PF PF +等于( )A .4B .5C .8D .10【答案】D 【解析】因为椭圆的方程为2251162x y +=,所以225a =,由椭圆的的定义知12=210PF PF a +=,故选D .2.(2020·全国高三课时练习(理))设x 、y ∈R ,则“|x |≤4且|y |≤3”是“216x +29y ≤1”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】B 【解析】“|x |≤4且|y |≤3”表示的平面区域M 为矩形区域,“216x +29y ≤1”表示的平面区域N 为椭圆216x +29y ≤1及其内部, 则如图显然N 在M 内, 故选:B .3.(2019·浙江省春晖中学高二月考)已知椭圆221102x y m m +=--的焦点在y 轴上,且焦距为4,则m 等于( ) A .4 B .5C .7D .8【答案】D 【解析】∵ 椭圆221102x y m m +=--的焦点在y 轴上,∴ 22a m =-,210b m =-, ∵ 焦距为4, ∴ 24c =即24c =,在椭圆中:222a b c =+即2(10)4m m -=-+,解得:8m =, 故选:D4.(2020·雅安市教育科学研究所高三一模(理))已知椭圆()222210x y a b a b+=>>的左顶点为A ,上顶点为B ,且OA (O 为坐标原点),则该椭圆的离心率为( )A .3B .3C .2D .3【答案】B 【解析】依题意可知3ab ,即3b =,又c ===,所以该椭圆的离心率3c e a ==. 故选:B5.(2020·四川资阳 高三其他(理))已知椭圆C :()222210x y a b a b +=>>经过点),且C 的离心率为12,则C 的方程是( ) A .22143x y +=B .22186x y +C .22142x y +=D .22184x y +=【答案】A 【解析】依题意,可得2131412a ⎧+=⎪=,解得2243a b ⎧=⎨=⎩,故C 的方程是22143x y +=. 故选:A 点睛:求椭圆标准方程的两种思路方法(1)定义法:根据椭圆的定义,确定22a b ,的值,结合焦点位置可写出椭圆方程.(2)待定系数法:这种方法是求椭圆方程的常用方法,具体思路是先定形,再定量,即首先确定焦点所在位置,然后再根据条件建立关于a b ,的方程组.如果焦点位置不确定,也可把椭圆方程设22100()mx ny m n m n >>≠+=,,的形式.6.(2020·全国高三课时练习(理))已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,A ,B 分别为C 的左,右顶点.P 为C 上一点,且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为 A .13B .12C .23D .34【答案】A 【解析】试题分析:如图取P 与M 重合,则由2(,0),(,)b A a M c a--⇒直线22:()(0,)bb a AM y x a Ec a a c=+⇒-+-同理由222221(,0),(,)(0,)33b b b b B a Mc G a c e a a c a c a c -⇒⇒=⇒=⇒=+-+,故选A.7.(2020·河北枣强中学高三月考(文))已知椭圆C 的方程为()222210x y a b a b +=>>,焦距为2c ,直线2:4l y x =与椭圆C 相交于A ,B 两点,若2AB c =,则椭圆C 的离心率为( ) A .32B .34C .12D .14【答案】A 【解析】设直线与椭圆在第一象限内的交点为()x,y A ,则24y x =由2AB c =,可知22OA x y c =+=2224x x c ⎛⎫+= ⎪ ⎪⎝⎭,解得22x =, 所以221,33A c ⎛⎫ ⎪ ⎪⎝⎭把点A 代入椭圆方程得到222222131c a b ⎫⎛⎫⎪ ⎪⎝⎭⎝⎭+=,整理得4281890e e -+=,即()()2243230e e --=,因01e <<,所以可得3e =故选A 项.8.(2020·甘肃城关 兰大附中高三月考(理))已知1F ,2F 分别为椭圆221168x y +=的左、右焦点,M 是椭圆上的一点,且在y 轴的左侧过点2F 作12F MF ∠的角平分线的垂线,垂足为N ,若2ON =(O 为坐标原点)则21MF MF -等于( ) A .4 B .2C .32D .332【答案】A 【解析】延长2F N 交1MF 的延长线于点P ,作图如下:因为MN 为12F MF ∠的角平分线,且2F N MN ⊥, 所以2MF MP =,所以2111MF MF MP MF F P -=-=, 因为,O N 分别为122,F F F P 的中点, 所以ON 为12PF F ∆的中位线, 所以1122ON F P ==, 所以21124MF MF F P ON -===. 故选:A9.(2020·黑龙江南岗 哈师大附中高三其他(文))已知1F 、2F 是椭圆22143x y +=的左、右焦点,点P 是椭圆上任意一点,以1PF 为直径作圆N ,直线ON 与圆N 交于点Q (点Q 不在椭圆内部),则12QF QF ⋅=( )A .23B .4C .3D .1【答案】C 【解析】连接2PF ,设椭圆的基本量为,,a b c ,()()()()2212121QF QF QO OF QO OF QO QF ⋅=+⋅+=-,()221222222322PF PF QN NO c c a c b ⎛⎫=+-=+-=-== ⎪⎝⎭故答案为:C10.(2019·宁波市第四中学高二期中)设椭圆22221x y a b+=0)a b >>(的左、右焦点分别为12(,0)(,0)F c F c -,,点(,)2aN c 在椭圆的外部,点M 是椭圆上的动点,满足11232MF MN F F +<恒成立,则椭圆离心率e 的取值范围是( ) A .2(0, B .21) C .25)6, D .5(,1)6【答案】D 【解析】∵点,2a N c ⎛⎫ ⎪⎝⎭在椭圆的外部,∴222214c a a b +>,2212b a < ,由椭圆的离心率22121122c b e a a ==--=> ,122MF MN a MF MN +=-+, 又因为2MF MN -+≤2NF ,且22aNF =,要11232MF MN F F +<恒成立,即22a MF MN -+≤32222a a c +<⨯,则椭圆离心率的取值范围是5,16⎛⎫⎪⎝⎭.故选D . 二、多选题11.(2019·江苏省苏州实验中学高二月考)已知椭圆22221(0)x y a b a b+=>>的左焦点F ,焦距为2,过点F的弦长最小值不小于2,则该椭圆的离心率可以是( ) A .45B .23C .12D .13【答案】CD 【解析】由22c =,则1c =.过点F 的弦长最小值为222b a≥,即22b a ≥即有222a c a -≥,即2210a a --≥,解得:a ≥或152a(舍),122c e a=≤=. 故选: CD.12.(2019·辽宁葫芦岛 高二月考)椭圆C :2211612x y +=的右焦点为F ,点P 是椭圆C 上的动点,则||PF 的值可能是( ) A .1 B .3C .4D .8【答案】BC 【解析】由题意可得4a =,16122c ,则26a cPF a c .故选:BC .13.(2020·岳麓 湖南师大附中高二期末)设椭圆22:143x y C +=的左、右焦点分别为12,F F ,点P 为椭圆C上一动点,则下列说法中正确的是( )A .当点P 不在x 轴上时,12PF F ∆的周长是6B .当点P 不在x 轴上时,12PF F ∆C .存在点P ,使12PF PF ⊥D .1PF 的取值范围是[1,3] 【答案】ABD 【解析】由椭圆方程可知,2,a b ==,从而1c ==. 据椭圆定义,1224PF PF a +==,又1222F F c ==, 所以12PF F ∆的周长是6,A 项正确. 设点()()000,0P x y y ≠,因为122F F =, 则12120012PF F S F F y y ∆⋅==.因为003y b <=,则12PF F ∆项正确. 由椭圆性质可知,当点P 为椭圆C 短轴的一个端点时,12F PF ∠为最大. 此时,122PF PF a ===,又122F F =,则12PF F ∆为正三角形,1260F PF ︒∠=,所以不存在点P ,使12PF PF ⊥,C 项错误.由图可知,当点P 为椭圆C 的右顶点时,1PF 取最大值,此时13PF a c =+=; 当点P 为椭圆C 的左顶点时,1PF 取最小值,此时11PF a c =-=, 所以1[1,3]PF ∈,D 项正确, 故选:ABD .14.(2020·山东中区 济南外国语学校高三月考)我们通常称离心率为12的椭圆为“黄金椭圆”.如图,已知椭圆2222:1(0)x y C a b a b+=>>,1212,,,A A B B 为顶点,12,F F 为焦点,P 为椭圆上一点,满足下列条件能使椭圆C 为“黄金椭圆”的有( )A .111222||,||,||A F F F F A 为等比数列B .11290F B A ∠=︒C .1PF x ⊥ 轴,且21//PO A BD .四边形1221A B A B 的内切圆过焦点12,F F 【答案】BD 【解析】2222:1(0)x y C a b a b+=>>()()()()1212,0,,0,0,,0,A a A a B b B b ∴--,()()12,0,,0F c F c -对于A :111222||,||,||A F F F F A 为等比数列则2112212||||||A F F A F F ⋅=()()222a c c ∴-=2a c c ∴-=13e ∴=不满足条件,故A 错误; 对于B :11290F B A ∠=︒222211112A F B F B A ∴=+ ()2222a c a a b ∴+=++220c ac a ∴+-=即210e e ∴+-=解得e =或e = 故B 正确;对于C :1PF x ⊥ 轴,且21//PO A B2,b P c a ⎛⎫∴- ⎪⎝⎭21POA B k k =即2b c ab a =--解得bc =222a b c =+2c e a ∴===不满足题意,故C 错误; 对于D :四边形1221A B A B 的内切圆过焦点12,F F 即四边形1221A B A B 的内切圆的半径为c ,ab ∴=422430c a c a ∴-+=42310e e ∴-+=解得232e +=(舍去)或232e =e ∴=故D 正确 故选:BD 三、单空题15.(2020·商丘市回民中学高二期末(理))若椭圆的方程为221102x y a a +=--,且此椭圆的焦距为4,则实数a =________. 【答案】4或8 【解析】因为221102x y a a +=--是椭圆的方程,所以100a ->且a 20->,所以210a <<,由椭圆的方程可得()2c 102122a a a =---=-,又2c 4=,所以1224a -=,解得4a =或8a =. 故答案为4或816.(2020·河北桃城 衡水中学高三其他(文))已知椭圆C 的中心在原点,焦点在x 轴上,若C 的短轴长为2个相邻的五等分点,则此椭圆的标准方程为________.【答案】2212524x y +=【解析】椭圆的短轴长为,即2b =,∴b = .∵两个焦点恰好为长轴的2个相邻的五等分点,∴1225c a =⨯,得5a c =, 又因为222a b c =+,故可解得1c =,5a =,故该椭圆的标准方程为2212524x y +=.故答案为:2212524x y +=.17.(2020·河南中原 郑州一中高三其他(文))已知A 、F 分别是椭圆C :22221x y a b+=()0a b >>的下顶点和左焦点,过A 且倾斜角为60︒的直线l 分别交x 轴和椭圆C 于M ,N 两点,且N 点的纵坐标为35b ,若FMN 的周长为6,则FAN 的面积为_____.【解析】 如图所示,由题意得,()0,A b -,(),0F c -,直线MN 的方程为3y x b =-,把35y b =代入椭圆方程解得45x a =,∴4355N a b ⎛⎫ ⎪⎝⎭,, ∵N 在直线MN 上,∴34355b a b =-,解得3b a =又222a b c =+,∴222)3b c =+,解得3b c =, 令3y x b =-=0,则3M ⎫⎪⎭,即(),0M c ,∴M 为椭圆的右焦点,∴2FM c =, 由椭圆的定义可知,2NF NM a +=, ∵FMN 的周长为6,∴226a c +=, ∵3b a =2a c =,∴1,2,3c a b === ∴()13883255FANSFM b b c b ⎡⎤=⋅⋅--=⋅=⎢⎥⎣⎦故答案为:35. 四、双空题18.(2019·浙江高二学业考试)椭圆2214x y +=的离心率是___________,焦距长是________.323【解析】椭圆2214x y +=得:2,1,a b c ===2214x y +=椭圆的焦距长为:19.(2020·上海高二课时练习)椭圆22192x y +=的焦点为F 1,F 2,点P 在椭圆上,若14PF =,2PF =_______;12F PF ∠的小大为__________.【答案】2 ;23π; 【解解:因为由椭圆的定义,我们可知1221222121212121222||||cos 21642812422PF PF a PF a PF PF PF F F PF F F PF PF PF +=∴=-+-∆∠=⨯+-==-⨯⨯中,20.(2019·浙江高二期中)若方程22121x y m m+=+-表示椭圆,则实数m 的取值范围是______;当1m =-时,椭圆的焦点坐标为______. 【答案】11(2,)(,1)22---; (0,1),(0,1)-. 【解析】①根据椭圆的方程特征,方程22121x y m m+=+-表示椭圆,则201021m m m m+>⎧⎪->⎨⎪+≠-⎩解得:11(2,)(,1)22m ∈---; ②1m =-时,椭圆的方程2212y x +=,焦点在y 轴,其坐标分别为(0,1),(0,1)-故答案为:①11(2,)(,1)22m ∈---;②(0,1),(0,1)- 21.(2020·福建高三其他(理))已知椭圆22:143x y C +=的焦点是12,F F ,,A B 是C 上(不在长轴上)的两点,且1//2F A F B .M 为1F B 与2F A 的交点,则M 的轨迹所在的曲线是______;离心率为_____. 【答案】椭圆 45【解析】设()11,A x y ,()22,C x y 则()22,B x y --,1AF 的斜率不为0,可设1:1AF l x my =- 则122:11BF y y l x x =+-①,211:11AF y y l x x =--② 所以()12121221212121211112224y y y y y y y y x x x x my my m y y m y y ⋅=⋅=⋅=+------++ 联立221143x my x y =-⎧⎪⎨+=⎪⎩得2242303m y my ⎛⎫+--= ⎪⎝⎭,得122243m y y m +=+,122343y y m -=+ 所以222316133y x m -=--+由①②得()12122112y y x x m y y y y ++-+=-,所以35x m y = 所以22231316353y x x y -=-⎛⎫-+⎪⎝⎭整理得222215344x x +=⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,所以M 的轨迹所在的曲线是椭圆,14554e == 故答案为:椭圆;45.五、解答题22.(2020·上海高二课时练习)已知椭圆的中心在原点,焦距为6,且经过点(0,4).求它的标准方程.【答案】2212516x y +=或221167y x +=【解析】(1)若椭圆的焦点在x 轴上,设椭圆的标准方程为22221(0)x ya b a b+=>>.将点(0,4)代入,得4b =.由26c =,解得3c =.22225∴=+=a b c ,从而椭圆方程为2212516x y +=; (2)若椭圆的焦点在y 轴上,设椭圆的标准方程为22221(0)y xa b a b+=>>.将点(0,4)代入,得4a =.由26c =,解得3c =,2227b a c =-=,从而椭圆方程为221167y x +=. 综上所述,椭圆的标准方程为2212516x y +=或221167y x +=.23.(2019·于都县第二中学高二月考(文))焦点在x 轴上的椭圆的方程为2214x ym+=,点2,1)P 在椭圆上.(1)求m的值.(2)依次求出这个椭圆的长轴长、短轴长、焦距、离心率.【答案】(1)2(2)长轴长4、短轴长22、焦距22、离心率2 2【解析】(1)由题意,点(2,1)P在椭圆上,代入,得222114m+=,解得2m=(2)由(1)知,椭圆方程为22142x y+=,则2,2,2a b c===椭圆的长轴长24a=;’短轴长222b=;焦距222c=;离心率22cea==.24.(2019·永济市涑北中学校高二月考(理))设点是椭圆上一动点,椭圆的长轴长为,离心率为.(1)求椭圆的方程;(2)求点到直线距离的最大值.【答案】(1);(2)【解析】(1)由已知得,得椭圆(2)设,则当时,.25.(2019·河南宛城 南阳中学高二月考(理))已知椭圆的两焦点为12(1,0),(1,0)F F -,P 为椭圆上一点,且12F F 是1PF 与2PF 的等差中项.(1)求此椭圆方程;(2)若点P 满足1260F PF ︒∠=,求12PF F ∆的面积.【答案】(1) 22143x y +=;(2) 3【解析】(1)设所求椭圆方程为22221(0,0)x y a b a b+=>>, 根据已知可得2221212242,2,413F F PF PF a a b a c =∴+==∴==-=-=, 所以此椭圆方程为22143x y +=; (2)在12PF F ∆中,设12,PF m PF n ==,由余弦定理得:22242cos604()22cos60163m n mn m n mn mn mn︒︒=+-⋅∴=+--⋅=- 121134sin 6004322PF F mn S mn ︒∆=∴=⋅=⨯=26.(2019·牡丹江市第三高级中学高二期末(文))已知点(2,1)P -在椭圆()222:102x y C a a +=>上,动点,A B 都在椭圆上,且直线AB 不经过原点O ,直线OP 经过弦AB 的中点.(1)求椭圆C 的方程;(2)求直线AB 的斜率.【答案】(1)22182x y +=;(2)12. 【解析】(1)将(2,1)P -代入22212x y a +=, 得()2222112a -+=,28a =. 故椭圆方程为22182x y +=. (2)当直线AB 斜率不存在时不合题意,故设直线:AB y kx m =+,1122(,),(,)A x y B x y ,AB 的中点为00(,)M x y ,由22182y kx m x y =+⎧⎪⎨+=⎪⎩得222()148480k x kmx m +++-=, 0122()14214km x x x k +=-=+,00214m y kx m k =+=+, 直线OP 经过弦AB 的中点,则OM OP k k =,0012y x =-, 142m km =--,12k ∴=,即直线AB 的斜率为12. 27.(2018·西藏拉萨中学高二期末(理))椭圆C 的中心在坐标原点,焦点在x 轴上,右焦点F 的坐标为(2,0),且点F 到短轴的一个端点的距离是6.(1)求椭圆C 的方程;(2)过点F 作斜率为k 的直线l ,与椭圆C 交于A 、B 两点,若43OA OB ⋅>-,求k 的取值范围. 【答案】解(I )(II ) 【解析】(I )由已知,;,故椭圆C 的方程为………………4分(II )设则A、B坐标是方程组的解.消去,则,………………7分所以k的取值范围是………………12分。
椭圆练习题大题含详细答案

高中椭圆练习题一、选择题:1.下列方程表示椭圆的是()A.22199x y += B.2228x y --=- C.221259x y -= D.22(2)1x y -+= 2.动点P 到两个定点1F (- 4,0).2F (4,0)的距离之和为8,则P 点的轨迹为() A.椭圆 B.线段12F F C.直线12F F D.不能确定3.已知椭圆的标准方程22110y x +=,则椭圆的焦点坐标为()A.(B.(0,C.(0,3)±D.(3,0)±4.椭圆222222222222211()x y x y a b k a b a k b k+=+=>>--和的关系是 A .有相同的长.短轴B .有相同的离心率 C .有相同的准线D .有相同的焦点5.已知椭圆22159x y +=上一点P 到椭圆的一焦点的距离为3,则P 到另一焦点的距离是()A.3-6.如果22212x y a a +=+表示焦点在x 轴上的椭圆,则实数a 的取值范围为() A.(2,)-+∞ B.()()2,12,--⋃+∞ C.(,1)(2,)-∞-⋃+∞ D.任意实数R 7.“m>n>0”是“方程221mx ny +=表示焦点在y 轴上的椭圆的”()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件 8.椭圆的短轴长是4,长轴长是短轴长的32倍,则椭圆的焦距是()B.4C.6D.2F CcD1F9.关于曲线的对称性的论述正确的是() A.方程220x xy y ++=的曲线关于X 轴对称 B.方程330x y +=的曲线关于Y 轴对称 C.方程2210x xy y -+=的曲线关于原点对称 D.方程338x y -=的曲线关于原点对称10.方程22221x y ka kb +=(a >b >0,k >0且k ≠1)与方程22221x y a b+=(a >b >0)表示的椭圆( ). A.有相同的离心率;B.有共同的焦点; C.有等长的短轴.长轴; D.有相同的顶点.第11题二、填空题:(本大题共4小题,共20分.)11.(6分)已知椭圆的方程为:22164100x y +=,则a=___,b=____,c=____, 焦点坐标为:___ __,焦距等于______;若CD 为过左焦点F1的弦, (如图)则2F CD 的周长为________.12.(6分)椭圆221625400x y +=的长轴长为____,短轴长为____, 焦点坐标为 四个顶点坐标分别为___ , 离心率为 ;椭圆的左准线方程为 13.(4分)比较下列每组中的椭圆: (1)①229436x y += 与②2211216x y += ,哪一个更圆 (2)①221610x y +=与②22936x y +=,哪一个更扁 14.(4分)若一个椭圆长轴的长度.短轴的长度和焦距成等差数列, 则该椭圆的离心率是三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(30分)求满足下列条件的椭圆的标准方程:(1)两个焦点的坐标分别为(0,-3),(0,3),椭圆的短轴长为8;(2)两个焦点的坐标分别为(),,0),并且椭圆经过点2)3(3)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点12P P 、16.(12分)已知点M 在椭圆2211625x y +=上,M 'P 垂直于椭圆焦点所在的直线,垂足为'P ,并且M 为线段P 'P 的中点,求P 点的轨迹及其轨迹方程17.(12分)设点A ,B 的坐标为(,0),(,0)(0)a a a ->,直线AM,BM 相交于点M ,且它们的斜率之积为(01)k k k ->≠且求点M 的轨迹方程,并讨论k 值与焦点的关系.18.(12分)当m 取何值时,直线l :y x m =+与椭圆22916144x y +=相切,相交,相离19.(14分)椭圆221(045)45x y m m+=<<的焦点分别是1F 和2F ,已知椭圆的离心率e =过中心O 作直线与椭圆交于A ,B 两点,O 为原点,若2ABF V 的面积是20, 求:(1)m 的值(2)直线AB 的方程参考答案1.选择题:二.填空题:11 10,8,6,(0,6±),12,40 12 10,8,(3,0±),(-5,0).(5,0).(0,-4).(0,4),35,253x =-13 ②,② 1435三.解答题:15.(1)解:由题意,椭圆的焦点在y轴上,设椭圆的标准方程为22221(0)y x a b a b+=>>由焦点坐标可得3c =,短轴长为8,即28,4b b ==,所以22225a b c =+=∴椭圆的标准方程为2212516y x += (2)由题意,椭圆的焦点在x 轴上,设椭圆的标准方程为22221(0)x y a b a b+=>>由焦点坐标可得c =2a ==6所以2b =22a c -=9-5=4,所以椭圆的标准方程为22194x y += (3)设椭圆的方程为221mx ny +=(0,0m n >>),因为椭圆过12P P 、61321m n m n +=+=⎧∴⎨⎩解得1913m n ==⎧⎨⎩所以椭圆的标准方程为:22193x y += 16.解:设p 点的坐标为(,)p x y ,m 点的坐标为00(,)x y ,由题意可知000022y y x x x x y y ====⎧⎧⇒⎨⎨⎩⎩ ① 因为点m 在椭圆221259x y +=上,所以有 22001259x y += ② , 把①代入②得2212536x y +=,所以P 点的轨迹是焦点在y 轴上,标准方程为2212536x y +=的椭圆. 17.解:设点M 的坐标为(,)x y ,因为点A 的坐标是(,0)a -,所以,直线AM 的斜率()AM y k x a x a =≠-+,同理直线BM 的斜率()BM y k x a x a=≠-.由已知有(),y y k x a x a x a=-≠±+-g 化简得点M 的轨迹方程为22221()x y x a a ka +=≠±当01k <<时,表示焦点在x 轴上的椭圆;当1k >时,表示焦点在y 轴上的椭圆.18.解:{22916144y x m x y =++=…… … … ①②①代入②得22916()144x x m ++=化简得222532161440x mx m ++-=222(32)425(16144)57614400m m m ∆=-⨯-=-+当0,∆=即5m =±时,直线l 与椭圆相切; 当0∆>,即55m -<<时,直线与椭圆相交; 当0∆<,即5m <-或5m >时,直线与椭圆相离. 19.解:(1)由已知c e a ==,a ==5c =, 所以222452520m b a c ==-=-=(2)根据题意21220ABF F F B S S ==V V ,设(,)B x y ,则121212F F B S F F y =V g ,12210F F c ==,所以4y =±,把4y =±代入椭圆的方程2214520x y +=,得3x =±,所以B 点的坐标为34±±(,),所以直线AB 的方程为4433y x y x ==-或。
椭圆练习题及答案

椭圆练习题及答案
椭圆练习题及答案
椭圆是数学中的一个重要概念,它在几何学、物理学和工程学等领域都有着重要的应用。
为了帮助大家更好地理解和掌握椭圆的相关知识,我们准备了一些椭圆的练习题及答案,希望能够帮助大家更好地学习和理解椭圆。
1. 椭圆的定义是什么?
答:椭圆是一个平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。
2. 椭圆的离心率是多少?
答:椭圆的离心率e满足0<e<1。
3. 椭圆的焦点在坐标系中的位置是怎样的?
答:椭圆的焦点位于椭圆的长轴上。
4. 椭圆的长轴和短轴之间有什么关系?
答:椭圆的长轴是短轴的两倍。
5. 椭圆的面积公式是什么?
答:椭圆的面积为πab,其中a为长轴的一半,b为短轴的一半。
通过以上的练习题及答案,我们可以更好地理解和掌握椭圆的相关知识。
希望大家能够通过不断地练习和思考,更好地理解和应用椭圆的知识,为将来的学习和工作打下坚实的基础。
完整版)椭圆经典练习题两套(带答案)

完整版)椭圆经典练习题两套(带答案)A组基础过关1.选择题1.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于多少?A。
2B。
2/3C。
1/2D。
1/3解析:由题意得2a=2b,所以a=b,又a²=b²+c²,所以b=c,所以a=2c,e=c/a=1/2,答案为C。
2.中心在原点,焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是什么?A。
(x²/81)+(y²/72)=1B。
(x²/81)+(y²/9)=1C。
(x²/81)+(y²/45)=1D。
(x²/81)+(y²/36)=1解析:依题意知2a=18,所以a=9,2c=3×2a,所以c=3,所以b=a-c=81-9=72,所以椭圆方程为(x²/81)+(y²/72)=1,答案为A。
3.椭圆x²+4y²=1的离心率是多少?A。
2/3B。
2C。
1/2D。
3解析:先将x²+4y²=1化为标准方程,得(x/1)²+(y/(1/2))²=1,所以a=1,b=1/2,所以c=√(a²-b²)=√(3)/2,所以e=c/a=√(3)/2,答案为A。
2.解答题1.设F₁、F₂分别是椭圆4x²+y²=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF₁⊥PF₂,则点P的横坐标为多少?解析:由题意知,点P即为圆x²+y²=3与椭圆4x²+y²=1在第一象限的交点,解方程组x²+y²=3和4x²+y²=1,得点P的横坐标为√(2/3),答案为√(2/3)。
2.已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为2,且椭圆G上一点到其两个焦点的距离之和为12,则椭圆G的方程是什么?解析:依题意设椭圆G的方程为a²x²+b²y²=1(a>b>0),因为椭圆上一点到其两个焦点的距离之和为12,所以2a=12,所以a=6,又因为椭圆的离心率为2,所以c=a/2=3,所以b=√(a²-c²)=3√5,所以椭圆G的方程为36x²+45y²=1,答案为C。
高中数学 椭圆专题(经典例题 考题 练习)附答案
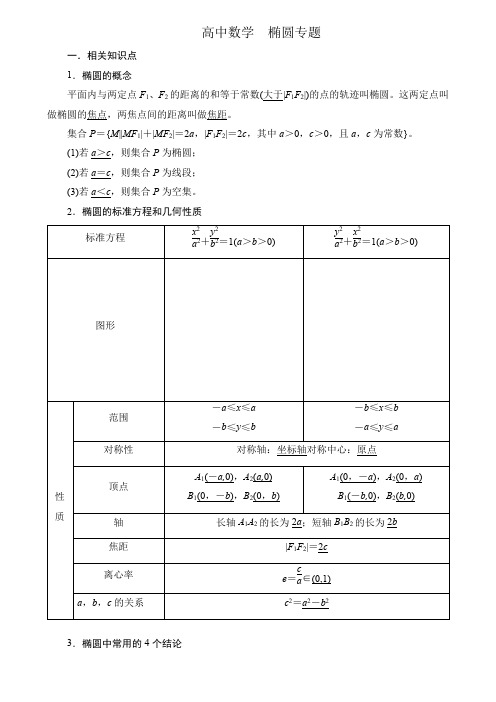
高中数学椭圆专题一.相关知识点1.椭圆的概念平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆。
这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
集合P={M||MF1|+|MF2|=2a,|F1F2|=2c,其中a>0,c>0,且a,c为常数}。
(1)若a>c,则集合P为椭圆;(2)若a=c,则集合P为线段;(3)若a<c,则集合P为空集。
2.椭圆的标准方程和几何性质3.椭圆中常用的4个结论(1)设椭圆x2a2+y2b2=1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最小值b,这时P在短轴端点处;当x=±a时,|OP|有最大值a,这时P在长轴端点处。
(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a是斜边长,a2=b2+c2。
(3)已知过焦点F1的弦AB,则△ABF2的周长为4a。
(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c。
一、细品教材1.(选修1-1P34例1改编)若F1(3,0),F2(-3,0),点P到F1,F2距离之和为10,则P点的轨迹方程是()A.x225+y216=1 B.x2100+y29=1 C.y225+x216=1 D.x225+y216=1或y225+x216=12.(选修1-1P42A组T6改编)设椭圆的两个焦点分别为F1,F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是()A.22 B.2-12C.2- 2 D.2-1走进教材答案1.A; 2.D 二、双基查验1.设P是椭圆x24+y29=1上的点,若F1,F2是椭圆的两个焦点,则|PF1|+|PF2|等于()A.4B.8 C.6 D.182.方程x25-m+y2m+3=1表示椭圆,则m的范围是()A.(-3,5) B.(-5,3) C.(-3,1)∪(1,5) D.(-5,1)∪(1,3)3.椭圆x 29+y 24+k =1的离心率为45,则k 的值为( )A .-21B .21C .-1925或21 D.1925或214.已知椭圆的一个焦点为F (1,0),离心率为12,则椭圆的标准方程为________。
高中数学-椭圆经典练习题-配答案

椭圆练习题一.选择题:1.已知椭圆上的一点P ,到椭圆一个焦点的距离为3,则P 到另一焦点距离为( D ) A .2 B .3 C .5 D .72.中心在原点,焦点在横轴上,长轴长为4,短轴长为2,则椭圆方程是( C )A. B. C. D. 3.与椭圆9x 2+4y 2=36有相同焦点,且短轴长为4的椭圆方程是( B )A4.椭圆的一个焦点是,那么等于( A )A. B.C.D.5.若椭圆短轴上的两顶点与一焦点的连线互相垂直,则离心率等于( B ) A.B.C.D.6.椭圆两焦点为 , ,P 在椭圆上,若 △的面积的最大值为12,则椭圆方程为( B )A.B .C .D . 7.椭圆的两个焦点是F 1(-1, 0), F 2(1, 0),P 为椭圆上一点,且|F 1F 2|是|PF 1|与|PF 2|的等差中项,则该椭圆方程是( C )。
A +=1B +=1C +=1D +=18.椭圆的两个焦点和中心,将两准线间的距离四等分,则它的焦点与短轴端点连线的夹角为( C )(A)450 (B)600 (C)900 (D)1209.椭圆上的点M 到焦点F 1的距离是2,N 是MF 1的中点,则|ON |为( A ) A. 4 B . 2 C. 8 D .10.已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是 ( C )(A )2 3 (B )6 (C )4 3 (D )12 二、填空题:1162522=+y x 22143x y +=22134x y +=2214x y +=2214y x +=51858014520125201202522222222=+=+=+=+y x D y x C y x B y x 2255x ky -=(0,2)k 1-1512221(4,0)F -2(4,0)F 12PF F 221169x y +=221259x y +=2212516x y +=221254x y +=16x 29y 216x 212y 24x 23y 23x 24y 2221259x y +=2311.方程表示焦点在轴的椭圆时,实数的取值范围_____12.过点且与椭圆有共同的焦点的椭圆的标准方程为_13.设,,△的周长是,则的顶点的轨迹方程为14.如图:从椭圆上一点向轴作垂线,恰好通过椭圆的左焦点,且它的长轴端点及短轴的端点的连线∥,则该椭圆的离心率等于_____________三、解答题:15.已知椭圆的对称轴为坐标轴,离心率,短轴长为,求椭圆的方程。
高中数学椭圆练习题(含答案)

椭圆练习题一、 选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中有只有一项是符合题目要求的.) 1.椭圆63222=+y x 的焦距是( )A .2B .)23(2-C .52D .)23(2+2.F 1、F 2是定点,|F 1F 2|=6,动点M 满足|MF 1|+|MF 2|=6,则点M 的轨迹是( ) A .椭圆 B .直线 C .线段 D .圆 3.若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点)23,25(-,则椭圆方程是 ( )A .14822=+x yB .161022=+x yC .18422=+x yD .161022=+y x4.方程222=+ky x 表示焦点在y 轴上的椭圆,则k 的取值范围是( )A .),0(+∞B .(0,2)C .(1,+∞)D .(0,1)5. 过椭圆12422=+y x 的一个焦点1F 的直线与椭圆交于A 、B 两点,则A 、B 与椭圆的另一焦点2F 构成2ABF ∆,那么2ABF ∆的周长是( )A . 22B . 2C . 2D . 16.已知椭圆的对称轴是坐标轴,离心率为31,长轴长为12,则椭圆方程为( ) A .112814422=+y x 或114412822=+y x B . 14622=+y x C .1323622=+y x 或1363222=+y x D . 16422=+y x 或14622=+y x 7. 已知k <4,则曲线14922=+y x 和14922=-+-k y k x 有( ) A . 相同的短轴 B . 相同的焦点 C . 相同的离心率 D . 相同的长轴8.椭圆192522=+yx 的焦点1F 、2F ,P 为椭圆上的一点,已知21PF PF ⊥,则△21PF F 的面积为( ) A .9 B .12 C .10 D .89.椭圆131222=+y x 的焦点为1F 和2F ,点P 在椭圆上,若线段1PF 的中点在y 轴上,那么1PF 是2PF 的( )A .4倍B .5倍C .7倍D .3倍10.椭圆1449422=+y x 内有一点P (3,2)过点P 的弦恰好以P 为中点,那么这弦所在直线的方程为( ) A .01223=-+y x B .01232=-+y xC .014494=-+y xD . 014449=-+y x11.椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是( )A .3B .11C .22D .1012.过点M (-2,0)的直线M 与椭圆1222=+y x 交于P 1,P 2,线段P 1P 2的中点为P ,设直线M 的斜率为k 1(01≠k ),直线OP 的斜率为k 2,则k 1k 2的值为( ) A .2 B .-2C .21 D .-21 二、 填空题:(本大题共4小题,每小题4分,共16分,把答案填在题中横线上.)13.椭圆2214x y m +=的离心率为12,则m = . 14.设P 是椭圆2214x y +=上的一点,12,F F 是椭圆的两个焦点,则12PF PF 的最大值为 ;最小值为 .15.直线y =x -21被椭圆x 2+4y 2=4截得的弦长为 .16.已知圆Q A y x C ),0,1(25)1(:22及点=++为圆上一点,AQ 的垂直平分线交CQ 于M ,则点M 的轨迹方程为 .三、解答题:(本大题共6小题,共74分,解答应写出文字说明.证明过程或演算步骤.) 17.已知三角形ABC 的两顶点为(2,0),(2,0)B C -,它的周长为10,求顶点A 轨迹方程.18.椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.19.点P到定点F(2,0)的距离和它到定直线x=8的距离的比为1:2,求点P的轨迹方程,并指出轨迹是什么图形.20.中心在原点,一焦点为F1(0,52)的椭圆被直线y=3x-2截得的弦的中点横坐标是21,求此椭圆的方程.21.已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与椭圆交于P和Q,且OP⊥OQ,|PQ|=210,求椭圆方程22.椭圆12222=+byax(a>b>)0与直线1=+yx交于P、Q两点,且OQOP⊥,其中O为坐标原点.(1)求2211ba+的值;(2)若椭圆的离心率e满足33≤e≤22,求椭圆长轴的取值范围.椭圆练习题参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案ACDDABD13、3或316 14、 4 , 1 15、5382 16、121425422=+yx17、3)(x 15922±≠=+y x 18、解:(1)当A (2,0)为长轴端点时,a =2 , b =1,椭圆的标准方程为: ;(2)当为短轴端点时,,,椭圆的标准方程为: ;19.解:设P (x ,y ),根据题意,|PF|=(x-2)2-y 2,d=|x-8|,因为|PF|d =12 ,所以 (x-2)2-y 2 |x-8| = 12.化简,得3x 2+4y 2=48,整理,得x 216 +y 212=1,所以,点P 的轨迹是椭圆。
高考数学专题《椭圆》习题含答案解析

专题9.3 椭圆1.(浙江高考真题)椭圆的离心率是( )ABC .D .【答案】B 【解析】,选B .2.(2019·北京高考真题)已知椭圆22221x y a b+=(a >b >0)的离心率为12,则( )A .a 2=2b 2B .3a 2=4b 2C .a =2bD .3a =4b【答案】B 【解析】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =,故选B.3.(上海高考真题)设p 是椭圆2212516x y+=上的点.若12F F ,是椭圆的两个焦点,则12PF PF +等于( )A.4B.5C.8D.10【答案】D 【解析】因为椭圆的方程为2251162x y +=,所以225a =,由椭圆的的定义知12=210PF PF a +=,故选D .4.(2020·四川资阳�高三其他(理))已知椭圆C :()222210x y a b a b +=>>经过点),且C 的离心率为12,则C 的方程是( )A .22143x y +=B .22186x y +=C .22142x y +=D .22184x y +=22194x y +=2359e ==练基础【答案】A 【解析】依题意,可得2131412a ⎧+=⎪⎪=,解得2243a b ⎧=⎨=⎩,故C 的方程是22143x y +=.故选:A5.(2020·河北枣强中学高三月考(文))已知椭圆C 的方程为()222210x y a b a b+=>>,焦距为2c,直线:l y x =与椭圆C 相交于A ,B 两点,若2AB c =,则椭圆C 的离心率为( )AB .34C .12D .14【答案】A 【解析】设直线与椭圆在第一象限内的交点为()x,y A,则y x =由2AB c =,可知OA c ==c =,解得x =,所以1,3A c ⎫⎪⎪⎭把点A 代入椭圆方程得到22221331c a b ⎫⎛⎫⎪ ⎪⎝⎭⎝⎭+=,整理得4281890e e -+=,即()()2243230e e --=,因01e <<,所以可得e =故选A 项.6.(2021·全国高三专题练习)已知1F ,2F 分别是椭圆2211615y x+=的上、下焦点,在椭圆上是否存在点P ,使11PF ,121F F ,21PF 成等差数列?若存在求出1PF 和2PF 的值;若不存在,请说明理由.【答案】不存在;理由见解析.【分析】假设存在点P 满足题设,解方程组1212121282112PF PF F F PF PF F F ⎧⎪+=⎪⎪=⎨⎪⎪+=⎪⎩得1PF 和2PF 的值,再检验即得解.【详解】解:假设存在点P 满足题设,则由2211615y x +=及题设条件有1212121282112PF PF F F PF PF F F ⎧⎪+=⎪⎪=⎨⎪⎪+=⎪⎩,即121288PF PF PF PF ⎧+=⎪⎨=⎪⎩,解得1244PF PF ⎧=+⎪⎨=-⎪⎩,或1244PF PF ⎧=-⎪⎨=+⎪⎩由2211615y x +=,得4a =,1c =.则135a c PF a c -=≤≤+=,235a c PF a c -=≤≤+=.∵45+>,43-,∴不存在满足题设要求的点P .7.(2021·全国高三专题练习)设F 是椭圆22176x y +=的右焦点,且椭圆上至少有21个不同的点i P (1i =,2,…),使1FP ,2FP ,3FP ,…组成公差为d 的等差数列,求a 的取值范围.【答案】11,00,1010⎡⎫⎛⎤-⎪ ⎢⎥⎣⎭⎝⎦ 【分析】分情况讨论等差数列是递增,还是递减,分别列出不等式求解范围.【详解】解:注意到椭圆的对称性及i FP 最多只能两两相等,可知题中的等差数列可能是递增的,也可能是递减的,但不可能为常数列,即0d ≠.先考虑一般情形,由等差数列的通项公式有()11n FP FP n d =+-,(n *∈N ),因此11n FP FP n d-=+.对于椭圆2222x y a b+(0a b >>),其焦半径的最大值是a c +,最小值是a c -(其中c =.当等差数列递增时,有n FP a c ≤+,1FP a c ≥-.从而()12n FP FP a c a c c -≤+--=.再由题设知1c =,且21n ≥,故2211d ≤+,因此1010d <≤.同理,当等差数列递减时,可解得1010d -≤<,故所求d 的取值范围为11,00,1010⎡⎫⎛⎤-⎪ ⎢⎥⎣⎭⎝⎦.8.(2021·全国高三专题练习)已知定点()2,2A -,点2F 为椭圆2212516x y +=的右焦点,点M 在椭圆上移动时,求2AM MF +的最大值;【答案】10+【分析】由椭圆定义,转化1121010A MF M MF AM AF ≤+=-++,即得解【详解】如图所示,设1F 是左焦点,则()13,0F -,1121010A MF M MF AM AF ≤+=-++,=∴10AM MF +≤+当点F 1在线段AM 上时,等号成立,即AM MF +的最大值为10.9.(2021·云南师大附中高三月考(理))椭圆C : 22221(0)x y a b a b +=>>,且点A (2,1)在椭圆C 上,O 是坐标原点.(1)求椭圆C 的方程;(2)直线l 过原点,且l ⊥OA ,若l 与椭圆C 交于B , D 两点,求弦BD 的长度.【答案】(1)22182x y C +=:;(2【分析】(1)利用离心率和点在椭圆上可求出椭圆的标准方程;(2)先利用直线垂直的判定得到直线l 的斜率和方程,联立直线和椭圆的方程,消元得到关于x 的一元二次方程,进而求出交点坐标,再利用两点间的距离公式进行求解.【详解】(1)由e =得:12c b a ==,,又点(21)A ,在椭圆上,所以224114a a +=,得a =b =所以椭圆的方程是22182x y C +=:.(2)直线OA 的方程是12y x =,因为l OA ⊥,且l 过点O ,所以直线l 的方程是2y x =-,与椭圆联立,得:2178x =,即x =所以B D ⎛ ⎝,,则||BD =10.(2021·南昌大学附属中学高二月考)已知()()122,0,2,0F F -是椭圆()222210x y a b a b+=>>两个焦点,且2259a b =.(1)求此椭圆的方程;(2)设点P 在椭圆上,且123F PF π∠=,求12F PF △的面积.【答案】(1)此椭圆的方程为22195x y +=;(2)12F PF △【分析】(1)由已知条件求出椭圆中229,5a b ==即可得到椭圆方程;(2)结合椭圆的定义以及余弦定理的知识求出12PF PF ⋅的值,运用三角形面积公式即可求解.【详解】(1)因为()()122,0,2,0F F -是椭圆()222210x y a b a b+=>>两个焦点,所以2224c a b =-=,①又因为2259a b =,②所以由①②可得229,5a b ==,所以此椭圆的方程为22195x y +=.(2)设()12,,,0PF m PF n m n ==>,由椭圆定义可知26m n a +==,③在12F PF △中,由余弦定理得()2222cos23m n mn c π+-=,即2216m n mn +-=,④由③④式可得,203mn =,所以121120sin 2323F PF S mn π==⨯=△即12F PF △1.(2021·全国高二课时练习)已知椭圆()22122:10x y C a b a b+=>>与圆2222:C x y b +=,若在椭圆1C 上存在点P ,使得过点P 所作的圆2C 的两条切线互相垂直,则椭圆1C 的离心率的取值范围是()A .1,12⎡⎫⎪⎢⎣⎭B.C.⎫⎪⎪⎭D.⎫⎪⎭【答案】C练提升【分析】若长轴端点P ',由椭圆性质:过P 的两条切线互相垂直可得45AP O α'=∠≤︒,结合sin b aα=求椭圆离心率的范围.【详解】在椭圆1C 的长轴端点P '处向圆2C 引两条切线P A ',P B ',若椭圆1C 上存在点P ,使过P 的两条切线互相垂直,则只需90AP B '∠≤︒,即45AP O α'=∠≤︒,∴sin sin 45b a α=≤︒=222a c ≤,∴212e ≥,又01e <<,1e ≤<,即e ⎫∈⎪⎪⎭.故选:C2.(2020·湖北黄州�黄冈中学高三其他(文))已知椭圆C :22221x y a b+=(0a b >>)的左焦点为F ,经过原点的直线与C 交于A ,B 两点,总有120AFB ∠≥︒,则椭圆C 离心率的取值范围为______.【答案】10,2⎛⎤ ⎥⎝⎦【解析】如图,设椭圆右焦点为2F ,由对称性知2AFBF 是平行四边形,22AF F BFF ∠=∠,∵120FB ∠≥︒,∴260FAF ∠≤︒,设AF m =,2AF n =,由椭圆定义知2m n a +=,则22()4m n mn a +≤=,当且仅当m n =时等号成立,在2AFF V 中,由余弦定理得2222222222222()244444cos 11122222m n FF m n mn c a c a c FAF emn mn mn a +-+----∠===-≥-=-,又260FAF ∠≤︒,21cos 2FAF ∠≥,∴21122e -≥,解得102e <≤.故答案为:10,2⎛⎤ ⎥⎝⎦.3.(2019·浙江高三月考)已知1F 、2F 分别为椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,点2F 关于直线y x =对称的点Q 在椭圆上,则椭圆的离心率为______;若过1F 且斜率为(0)k k >的直线与椭圆相交于AB 两点,且113AF F B =,则k =___.1 【解析】由于点2F 关于直线y x =对称的点Q 在椭圆上,由于y x =的倾斜角为π4,画出图像如下图所示,由于O 是坐标原点,根据对称性和中位线的知识可知12QF F ∆为等腰直角三角形,且Q为短轴的端点,故离心率πcos 4c a ==.不妨设,a b c t ===,则椭圆方程化为222220x y t +-=,设直线AB 的方程为10x my t m k ⎛⎫=-=> ⎪⎝⎭,代入椭圆方程并化简得()222220my mty t +--=.设()()1122,,,A x y B x y ,则12222mty y m +=+①,21222t y y m -⋅=+②.由于113AF F B = ,故123y y =-③.解由①②③组成的方程组得1m =,即11,1k k==.故填:(1;(2)1.4.(2019·浙江温州中学高三月考)已知点P 在圆22680x y y +-+=上,点Q 在椭圆()22211x y a a+=>上,且PQ 的最大值等于5,则椭圆的离心率的最大值等于__________,当椭圆的离心率取到最大值时,记椭圆的右焦点为F ,则PQ QF +的最大值等于__________.5+【解析】22680x y y +-+=化简为22(3)1x y +-=,圆心(0,3)A .PQ 的最大值为5等价于AQ 的最大值为4设(,)Q x y ,即22(3)16x y +-≤,又()22211xy a a+=>化简得到222(1)670(11)a y y a y --+-≤-≤≤ 当1y =-时,验证等号成立对称轴为231x a =-满足231,21x a a =≤-≤-故12a <≤22222211314c a e e a a a -===-≤∴≤当2a =时,离心率有最大值,此时椭圆方程为2214x y +=,设左焦点为1F11141455PQ QF PQ QF AQ QF AF +=+-≤++-≤+=+当1,,,A F P Q 共线时取等号.和5+5.(2020·浙江高三月考)已知P 是椭圆2222111x y a b +=(110>>a b )和双曲线2222221x y a b -=(220,0a b >>)的一个交点,12,F F 是椭圆和双曲线的公共焦点,12,e e 分别为椭圆和双曲线的离心率,若123F PF π∠=,则12e e ⋅的最小值为________..【解析】根据椭圆与双曲线的对称性,不妨设点P 在第一象限,那么12PF PF >,因为椭圆与双曲线有公共焦点,设椭圆与双曲线的半焦距为c ,根据椭圆与双曲线的定义,有:1212+=PF PF a ,1222-=PF PF a ,解得112=+PF a a ,212=-PF a a ,在12F PF ∆中,由余弦定理,可得:2221212122cos3π=+-F F PF PF PF PF ,即222121212124()()()()=++--+-c a a a a a a a a ,整理得2221243=+c a a ,所以22121134+=e e ,又2212113+≥e e ,所以12≥e e .6.(2020·浙江高三其他)已知当动点P 到定点F (焦点)和到定直线0x x =的距离之比为离心率时,该直线便是椭圆的准线.过椭圆2214x y +=上任意一点P ,做椭圆的右准线的垂线PH(H 为垂足),并延长PH 到Q ,使得HQ =λPH (λ≥1).当点P 在椭圆上运动时,点Q 的轨迹的离心率的取值范围是___.【答案】⎫⎪⎪⎭【解析】由题可知:椭圆2214x y +=的右准线方程为x =设()()00,,,P x y Q x y,所以点0⎫⎪⎭H y 由λ=HQ PH ,所以λ=HQPH0⎛⎫=-- ⎪⎝⎭ HQ x y y,0,0⎫=⎪⎭PH x 又λ= HQ PH,所以00,0λ⎛⎫⎫-=- ⎪⎪⎝⎭⎭x y y x所以00x y y==由220014x y +=221=y 则点Q221+=y 设点Q 的轨迹的离心率e则2222411144λλλ-==-e 由1λ≥,所以213144λ-≥所以234e ≥,则e ≥,又1e <所以⎫∈⎪⎪⎭e故答案为:⎫⎪⎪⎭7.(2021·全国高三专题练习)设椭圆的中心在坐标原点.长轴在z 轴上,离心率e =知点30,2P ⎛⎫⎪⎝⎭,求椭圆方程,并求椭圆上到点O 的距离的点的坐标.【答案】2214x y +=;12⎫-⎪⎭,12⎛⎫- ⎪⎝⎭.【分析】设以P 点为圆心的圆与椭圆相切,结合判别式等于零,参数值可确定,符合条件的两个点的坐标也可求得.【详解】∵e =c a =2234c a =.∵222a c b -=,∴2214a b =,224a b =,∴设椭圆方程为222214x y b b+=①又∵30,2P ⎛⎫⎪⎝⎭,则可构造圆22372x y ⎛⎫+-= ⎪⎝⎭. ②此圆必与椭圆相切,如图所示,由①②整理得221933404y y b ++-=.∵椭圆与圆相切,∴219912404b ⎛⎫∆=--= ⎪⎝⎭,③ ∴1b =,则2a =.则所求椭圆方程为2214x y +=. ④把1b =代入方程③可得12y =-,把12y =-代入④得x =∴椭圆上到点P的点的坐标为12⎫-⎪⎭,12⎛⎫- ⎪⎝⎭.8.(2021·全国高三专题练习)椭圆22194x y +=的焦点为1F 、2F ,点P 为其上动点,当12F PF ∠为钝角时,求点P 横坐标的取值范围.【答案】⎛ ⎝【分析】当12F PF ∠为直角时,作以原点为圆心,2OF 为半径的圆,若该圆与已知椭圆相交,则圆内的椭圆弧所对应的x 的取值范围即为所求点P 横坐标的取值范围.【详解】22194x y +=的焦点为1(F、2F ,如图所示:A 、B 、C 、D 四点,此时12F AF ∠、12F BF ∠、12F CF ∠、12F DF ∠都为直角,所以当角的顶点P 在圆内部的椭圆弧上时,12F PF ∠为钝角,由22221945x y x y ⎧+=⎪⎨⎪+=⎩,解得x x ==.因为椭圆和圆都关于坐标轴对称,所以点P横坐标的取值范围是⎛ ⎝.9.(2021·全国)(1)已知1F ,2F 是椭圆22110064x y+=的两个焦点,P是椭圆上一点,求12PF PF ⋅的最大值;(2)已知()1,1A ,1F 是椭圆225945x y +=的左焦点,点P 是椭圆上的动点,求1PA PF +的最大值和最小值.【答案】(1)100;(2)1||||PA PF +的最大值为66【分析】(1)利用椭圆定义和基本不等式求12||||PF PF ⋅的最值;(2)求1||||PA PF +的最值时,利用椭圆的定义将其转化为求2||||PF PA -的最值,显然当P ,A ,2F 三点共线时取得最值.【详解】(1)∵10a =,1220||||PF PF =+≥,当且仅当12||||PF PF =时取等号,∴12||||100PF PF ⋅≤,当且仅当12||||PF PF =时取等号,∴12||||PF PF ⋅的最大值为100.(2)设2F 为椭圆的右焦点,225945x y +=可化为22195x y +=,由已知,得12||||26PF PF a +==,∴12||6||PF PF =-,∴()12||||6||||PA PF PF PA +=--.①当2||||PA PF >时,有220||||||PA PF AF <-≤,等号成立时,1||||PA PF +最大,此时点P 是射线2AF 与椭圆的交点,1||||PA PF +的最大值是6+②当2||||PA PF <时,有220||||||PF PA AF <-≤,等号成立时,1||||PA PF +最小,此时点P 是射线2F A 与椭圆的交点,1||||PA PF +的最小值是6综上,可知1||||PA PF +的最大值为6610.(2021·贵州高三月考(文))已知椭圆C :22221(0)x y a b a b +=>>,直线l经过椭圆C 的右焦点F 与上顶点,原点O 到直线l (1)求椭圆C 的方程;(2)斜率不为0的直线n 过点F ,与椭圆C 交于M ,N 两点,若椭圆C 上一点P 满足MN = ,求直线n 的斜率.【答案】(1)2212x y +=;(2)±1.【分析】(1)由已知条件可得c a bc a⎧=⎪⎪⎨⎪=⎪⎩再结合222a b c =+,可求出,a b ,从而可求得椭圆方程,(2)设直线n 的方程为1x my =+,设点()()1122,,,M x y N x y ,将直线方程与椭圆方程联立方程组,消去x,利用根与系数的关系,结合MN =表示出点P 的坐标,再将其坐标代入椭圆方程中可求得直线n 的斜率【详解】(1)由题意可得椭圆C 的右焦点(c,0)F 与上顶点(0,)b ,所以直线l 为1x yc b+=,即0bx cy bc +-=,因为椭圆C,原点O 到直线0bx cy bc +-=,所以c a bc a⎧=⎪⎪⎨⎪=⎪⎩且222a b c =+,解得1b c ==,a =所以椭圆C 的方程为2212x y +=.(2)因为直线n 的斜率不为0,所以可设直线n 的方程为1x my =+.设点()()1122,,,M x y N x y ,联立方程22220,1,x y x my ⎧+-=⎨=+⎩得()222210my my ++-=,则12122221,22m y y y y m m +=-=-++.因为MN =,所以))2121P x x y y ⎫--⎪⎪⎭, 将点P 的坐标代入椭圆方程得1212223x x y y +=-,即()()121221123my my y y +++=-,解得21m =, 故直线n 的斜率为±1.练真题1.(2021·全国高考真题(理))设B 是椭圆2222:1(0)x y C a b a b+=>>的上顶点,若C 上的任意一点P 都满足||2PB b ≤,则C 的离心率的取值范围是( )A.⎫⎪⎪⎭B .1,12⎡⎫⎪⎢⎣⎭C.⎛ ⎝D .10,2⎛⎤ ⎥⎝⎦【答案】C 【分析】设()00,P x y ,由()0,B b ,根据两点间的距离公式表示出 PB ,分类讨论求出PB 的最大值,再构建齐次不等式,解出即可.【详解】设()00,P x y ,由()0,B b ,因为 2200221x y a b+=,222a b c =+,所以()()2223422222220000022221y c b b PB x y b a y b y a b b b c c ⎛⎫⎛⎫=+-=-+-=-++++ ⎪ ⎪⎝⎭⎝⎭,因为0b y b -≤≤,当32bb c-≤-,即 22b c ≥时,22max 4PB b =,即 max 2PB b =,符合题意,由22b c ≥可得222a c ≥,即0e <≤当32b b c ->-,即22b c <时, 42222max b PB a b c=++,即422224b a b b c ++≤,化简得,()2220c b -≤,显然该不等式不成立.故选:C .2.(2018·全国高考真题(理))已知,是椭圆的左,右焦点,是的左顶点,点在过的直线上,为等腰三角形,,则的离心率为( )A .B .C .D .【答案】D 【解析】因为为等腰三角形,,所以PF 2=F 1F 2=2c,由得,,1F 2F 22221(0)x y C a b a b+=>>:A C P A 12PF F △12120F F P ∠=︒C 2312131412PF F △12120F F P ∠=︒AP 222tan sin cos PAF PAF PAF ∠=∴∠=∠=由正弦定理得,所以,故选D.3.(2019·全国高考真题(文))已知椭圆C 的焦点为,过F 2的直线与C 交于A ,B 两点.若,,则C 的方程为( )A. B. C. D.【答案】B 【解析】法一:如图,由已知可设,则,由椭圆的定义有.在中,由余弦定理推论得.在中,由余弦定理得,解得.所求椭圆方程为,故选B .法二:由已知可设,则,由椭圆的定义有.在和中,由余弦定理得,又互补,,两式消去,得,解得.所求椭圆方程为,故选B .4.(2019·全国高考真题(文))设为椭圆的两个焦点,为上2222sin sin PF PAF AF APF ∠=∠22214,π54sin(3c a c e a c =∴==+121,01,0F F -(),()222AF F B =││││1AB BF =││││2212x y +=22132x y +=22143x y +=22154x y +=2F B n =212,3AF n BF AB n ===121224,22a BF BF n AF a AF n =+=∴=-=1AF B △22214991cos 2233n n n F AB n n +-∠==⋅⋅12AF F △2214422243n n n n +-⋅⋅⋅=n =22224,,312,a n a b a c ∴==∴=∴=-=-=∴22132x y +=2F B n =212,3AF n BF AB n ===121224,22a BF BF n AF a AF n =+=∴=-=12AF F △12BF F △2221222144222cos 4,422cos 9n n AF F n n n BF F n⎧+-⋅⋅⋅∠=⎨+-⋅⋅⋅∠=⎩2121,AF F BF F ∠∠2121cos cos 0AF F BF F ∴∠+∠=2121cos cos AF F BF F ∠∠,223611n n +=n =22224,,312,a n a b a c ∴==∴=∴=-=-=∴22132x y +=12F F ,22:+13620x y C =M C一点且在第一象限.若为等腰三角形,则的坐标为___________.【答案】【解析】由已知可得,.∴.设点的坐标为,则,又,解得,,解得(舍去),的坐标为.5.(2021·江苏高考真题)已知椭圆()2222:10x y C a b a b +=>>(1)证明:a;(2)若点9,10M ⎛ ⎝在椭圆C 的内部,过点M 的直线l 交椭圆C 于P 、Q 两点,M 为线段PQ 的中点,且OP OQ ⊥.①求直线l 的方程;②求椭圆C 的标准方程.【答案】(1)证明见解析;(20y -=;②2213x y +=.【分析】(1)由ba=可证得结论成立;(2)①设点()11,P x y 、()22,Q x y ,利用点差法可求得直线l 的斜率,利用点斜式可得出所求直线的方程;②将直线l 的方程与椭圆C 的方程联立,列出韦达定理,由OP OQ ⊥可得出0OP OQ ⋅=,利用平面向量数量积的坐标运算可得出关于2b 的等式,可求出2b 的值,即可得出椭圆C 的方程.【详解】12MF F △M (2222236,20,16,4a b c a b c ==∴=-=∴=11228MF F F c ∴===24MF =M ()()0000,0,0x y x y >>121200142MF F S F F y y =⋅⋅=△12014,42MF F S y =⨯=∴=△0y =20136x ∴=03x =03x =-M \((1)c e a =====b a ∴=a ;(2)①由(1)知,椭圆C 的方程为222213x y b b+=,即22233x y b +=,当9,10⎛ ⎝在椭圆C的内部时,22293310b ⎛⎛⎫+⋅< ⎪ ⎝⎭⎝,可得b >设点()11,P x y 、()22,Q x y,则121292102x x y y +⎧=⎪⎪⎨+⎪=⎪⎩,所以,1212y y x x +=+由已知可得22211222223333x y b x y b ⎧+=⎨+=⎩,两式作差得()()()()1212121230x x x x y y y y +-++-=,所以()12121212133y y x x x x y y -+⎛=-=-⨯= -+⎝,所以,直线l方程为910y x ⎛⎫-=- ⎪ ⎭⎝,即y =所以,直线l0y -=;②联立)222331x y by x ⎧+=⎪⎨=-⎪⎩,消去y 可得221018930x x b -+-=.()222184093120360b b ∆=--=->,由韦达定理可得1295x x +=,2129310b x x -=,又OP OQ ⊥ ,而()11,OP x y = ,()22,OQ x y =,))()12121212121211433OP OQ x x y y x x x x x x x x ∴⋅=+=--=-++()22293271566055b b --+-===,解得21b =合乎题意,故2233a b ==,因此,椭圆C 的方程为2213x y +=.6. (2020·天津高考真题)已知椭圆22221(0)x y a b a b+=>>的一个顶点为(0,3)A -,右焦点为F ,且||||OA OF =,其中O 为原点.(Ⅰ)求椭圆的方程;(Ⅱ)已知点C 满足3OC OF =,点B 在椭圆上(B 异于椭圆的顶点),直线AB 与以C为圆心的圆相切于点P ,且P 为线段AB 的中点.求直线AB 的方程.【答案】(Ⅰ)221189x y +=;(Ⅱ)132y x =-,或3y x =-.【解析】(Ⅰ) 椭圆()222210x ya b a b+=>>的一个顶点为()0,3A -,∴3b =,由OA OF =,得3c b ==,又由222a b c =+,得2228313a =+=,所以,椭圆的方程为221189x y +=;(Ⅱ) 直线AB 与以C 为圆心的圆相切于点P ,所以CP AB ⊥,根据题意可知,直线AB 和直线CP 的斜率均存在,设直线AB 的斜率为k ,则直线AB 的方程为3y kx +=,即3y kx =-,2231189y kx x y =-⎧⎪⎨+=⎪⎩,消去y ,可得()2221120k x kx +-=,解得0x =或21221k x k =+.将21221k x k =+代入3y kx =-,得222126321213k y k k k k =⋅--=++,所以,点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭,因为P 为线段AB 的中点,点A 的坐标为()0,3-,所以点P 的坐标为2263,2121k k k -⎛⎫⎪++⎝⎭,由3OC OF =,得点C 的坐标为()1,0,所以,直线CP 的斜率为222303216261121CPk kk k k k --+=-+-+=,又因为CP AB ⊥,所以231261k k k ⋅=--+,整理得22310k k -+=,解得12k =或1k =.所以,直线AB 的方程为132y x =-或3y x =-.。
高二数学椭圆测试题带答案

高二数学圆锥曲线椭圆测试题带答案一、选择题(每小题5分,共12小题60分)1、在平面直角坐标xoy 中,椭圆C 的中心为原点,焦点1F ,2F 在x 轴上,离心率为22,过1F 的直线l交C 于A ,B 两点,且2ABF ∆的周长为16,那么C 的方程为()A.181622=+y x B.12422=+y x C. 1182422=+y x D. 191622=+y x 2、已知椭圆C :)0(12222>>=+b a b y a x 的左右焦点为1F ,2F ,离心率为33,过2F 的直线l 交C 与A ,B 两点,若B AF 1∆的周长为34,则C 的方程为( )A.12322=+y x B.1322=+y xC.181222=+y x D.141222=+y x 3、曲线192522=+y x 与曲线)9(192522<=-+-k ky k x 的 ( ) A.长轴长相等B.短轴长相等C.焦距相等D.离心率相等4、图,1F ,2F 是椭圆1C :1422=+y x 与双曲线2C 的公共焦点,A ,B 分别是1C ,2C 在第二、四象限的公共点,若四边形21BF AF 为矩形,则2C 的离心率是( )A.2B.3C.23D.265、已知椭圆110222=-+-m y m x 的长轴在x 轴上,焦距为4,则m 等于( ) A.8B.7C.6D.56、已知()2,4是直线l 被椭圆193622=+y x 所截得的线段的中点,则直线l 的方程是( ) A.02=-y xB.042=-+y xC.0432=++y xD.082=-+y x7、设1F ,2F 分别是椭圆)0(12222>>=+b a b y a x 的左、右焦点,与直线b y =相切的⊙2F 交椭圆于点E ,E 恰好是直线1EF 与⊙2F 的切点,则椭圆的离心率为( )A.23B .33 C.35D.458、已知椭圆191622=+y x 及以下3个函数:①x x f =)(;②x x f sin )(=;③x x x f sin )(=,其中函数图像能等分该椭圆面积的函数个数有( ) A.0个 B.1个C.2个D.3个9、椭圆C :)0(12222>>=+b a by a x 的左、右焦点为1F ,2F ,过1F 作直线l 交C 于A ,B 两点,若2ABF ∆是等腰直角三角形,且︒=∠902B AF ,则椭圆C 的离心率为( ) B.221-C.12-D.2210、设椭圆C :)0(12222>>=+b a b y a x 的左、右焦点分别为1F ,2F ,P 是C 上的点,212F F PF ⊥,︒=∠3021F PF ,则C 的离心率为( ) A.63B.31C.21D.3311、椭圆)0(12222>>=+b a by a x 的一个焦点为1F ,若椭圆上存在一个点P ,满足以椭圆短轴为直径的圆与线段1PF 相切于该线段的中点,则椭圆的离心率为( )A.22 B.32C.95D.3512、已知1A ,2A 分别为椭圆C :)0(12222>>=+b a by a x 的左右顶点,椭圆C 上异于1A ,2A 的点P 恒满足9421-=⋅PA PA k k ,则椭圆C 的离心率为( )A.94B.32C.95D.35二、填空题(每小题5分,共4小题20分)13、已知1F ,2F 是椭圆11222=+++k y k x 的左、右焦点,过1F 的直线交椭圆于A ,B 两点,若2ABF ∆的周长为8,则k 的值为__________ 14、短轴长为52,离心率32=e 的椭圆两焦点为1F ,2F ,过1F 作直线交椭圆于A ,B 两点,则2ABF ∆的周长为__________15、直线01=-+y x 交椭圆122=+ny mx 于A ,B 两点,过原点与线段,AB 中点直线的斜率为22,则=n m__________16、在平面直角坐标系xOy 中,经过点()2,0且斜率为的直线l 与椭圆1222=+y x 有两个不同的交点P 和Q .则k 的取值范围为__________.三、解答题(每小题10分,共2小题20分) 17、已知椭圆1422=+y x 与直线l :0=+-λy x 相切.(1)求λ的值;(2)设直线:m 054=+-y x ,求椭圆上的点到直线m 的最短距离.18、已知椭圆4422=+y x 与斜率为1的直线l 交椭圆于A ,B 两点.(1)求弦AB 长的最大值;(2)求ABO ∆面积的最大值及此时直线l 的方程(O 为坐标原点)高二数学椭圆测试题答案解析第4题答案D第4题解析解答:第5题答案A第6题答案D第6题解析第7题答案C第7题解析第8题答案C第8题解析第9题答案C第10题答案D第10题解析第11题答案D第11题解析第12题答案D第12题解析第13题答案2第13题解析第14题答案12第14题解析第15题答案22第17题答案第18题答案。
高二数学椭圆专项练习题及参考答案

高二数学椭圆专项练习题及参考答案代入e=a/c=a/(a/2)=2,即椭圆的离心率为2。
5. 椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的焦点为$F_1$、$F_2$,$P$是椭圆上的任一点,$M$为$PF_1$的中点,若$PF_1$的长度为$s$,那么$OM$的长度等于$\sqrt{a^2-s^2}$。
1. 在椭圆上,焦点F和弦AB的垂直平分线交于M,AB交x轴于N。
求2. 已知椭圆的对称轴为坐标轴,离心率为2/3,长轴长为6。
求椭圆的方程。
3. 若x²/y² + 1 = 1表示焦点在y轴上的椭圆,则m的值是多少?4. 已知方程25-m/16+m = 1表示椭圆。
求m的值。
5. 椭圆的两焦点将准线间的距离分成三等分。
求该椭圆的离心率。
6. 椭圆x²/4 + y²/9 = 1上一点P到右焦点F₁的距离为b,则P点到左准线的距离是多少?7. 椭圆x²/4 + y²/9 = 1在t ∈ [0, 2π)时,x = sec t,y = ___。
求该椭圆的焦点坐标。
8. 曲线x + (m-1)y - 3my + 2m = 0表示椭圆。
求m的取值。
9. 椭圆432x² + 169y² = 上的一点A到左焦点的距离为多少?10. 椭圆x²/16 + y²/25 = 1上一点P到焦点F₂的距离为b。
求P点到左准线的距离。
11. 方程-3x² + y²sin²(2α + π/2) = 1表示椭圆。
求sin²α的取值。
12. 若λ-6x+5λy-5λλ-6 = 0表示焦点在x轴上的椭圆,则λ的值为多少?13. 椭圆259x² + 432y² = 上的一点到左焦点的距离是到右焦点的距离的4倍。
求该点的坐标。
14. 椭圆中心在原点,焦点在x轴上,两准线的距离为5。
椭圆专题习题含答案

椭圆专题一.椭圆的定义与性质1.设F 1(﹣4,0)、F 2(4,0)为定点,动点M 满足|MF 1|+|MF 2|=8,则动点M 的轨迹是( ) A .椭圆 B .直线C .圆D .线段2.如果方程表示焦点在y 轴上的椭圆,则m 的取值范围是( ) A .3<m <4B .C .D .3.椭圆C :4x 2+y 2=16的长轴长,短轴长,焦点坐标依次为( ) A . B .C .D .4.已知焦点在y 轴上的椭圆的焦距为,则a=( )A .8B .12C .16D .525.椭圆的焦距是2,则m 的值是( )A .9B .12或4C .9或7D .206.已知焦点在y 轴上的椭圆的离心率为,则实数m 等于( )A .3B .C .5D .7.方程+=1表示椭圆,则k 的取值范围是 .二.椭圆的标准方程(待定系数法):定位(确定焦点的位置),定量(求出a,b )焦点在x 轴 焦点在y 轴 知椭圆过两点求椭圆方程:设 、代点,解方程组。
知焦点(焦距)和椭圆经过某一点求椭圆方程:待定系数法、定义法。
)0(12222>>=+b a by a x )0(12222>>=+b a b x a y )0,0,(122>>≠=+n m n m ny mx1.椭圆(a >b >0)的一个焦点为(3,0),点(﹣3,2)在椭圆上,则该椭圆的方程为( )A .B .C .D .2.已知椭圆C :=1(a >b >0)的离心率为,且椭圆C 的长轴长与焦距之和为6,则椭圆C 的标准方程为( ) A .=1 B .C .=1 D .3.求符合下列条件的椭圆的标准方程:(1)过点的椭圆 (2)过点(-3,2)且与有相同的焦点;(3)焦点在轴上,,且过点;(4)焦距为6,.三.求离心率:直接法,方程法1)c e e a ==<< 1.椭圆的离心率为( )A. B. C.2 D.42.椭圆6x 2+y 2=6的离心率为( )A.B.C.D.3. 过椭圆+=1(a >b >0)的左焦点F 1作x 轴的垂线交椭圆于点P ,F 2为右焦点,若 ∠F 1PF 2=60°,则椭圆的离心率为 ( )A.B.C.D.4.已知椭圆+=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P .若=2,则椭圆的离心率是 ( )A.B.C.D.5.若一个椭圆的长轴长、短轴长、焦距成等比数列,则椭圆的离心率为 .6.已知F 1(-c ,0),F 2(c ,0)为椭圆+=1(a >b >0)的两个焦点,P 为椭圆上一点,且满足·=c 2,则此椭圆的离心率的取值范围是( )A.[,1)B.[,]C.[,]D.(0,]四.焦点三角形:以椭圆上的点、两焦点为顶点的三角形。
高中数学_椭圆经典练习题_配答案解析

椭圆练习题一.选择题:1.已知椭圆上的一点P ,到椭圆一个焦点的距离为3,则P 到另一焦点距离为( D )A .2B .3C .5D .72.中心在原点,焦点在横轴上,长轴长为4,短轴长为2,则椭圆方程是( C )A. B. C. D. 3.与椭圆9x 2+4y 2=36有相同焦点,且短轴长为4的椭圆方程是( B )A4.椭圆的一个焦点是,那么等于( A )A. B.C.D.5.若椭圆短轴上的两顶点与一焦点的连线互相垂直,则离心率等于( B ) A.B.C.D.6.椭圆两焦点为 , ,P 在椭圆上,若 △的面积的最大值为12,则椭圆方程为( B )A.B .C .D . 7.椭圆的两个焦点是F 1(-1, 0), F 2(1, 0),P 为椭圆上一点,且|F 1F 2|是|PF 1|与|PF 2|的等差中项,则该椭圆方程是( C )。
A +=1B +=1C +=1D +=18.椭圆的两个焦点和中心,将两准线间的距离四等分,则它的焦点与短轴端点连线的夹角为( C )(A)450 (B)600 (C)900 (D)1209.椭圆上的点M 到焦点F 1的距离是2,N 是MF 1的中点,则|ON |为( A ) A. 4 B . 2 C. 8 D .1162522=+y x 22143x y +=22134x y +=2214x y +=2214y x +=51858014520125201202522222222=+=+=+=+y x D y x C y x B y x 2255x ky -=(0,2)k 1-1512221(4,0)F -2(4,0)F 12PF F 221169x y +=221259x y +=2212516x y +=221254x y +=16x 29y 216x 212y 24x 23y 23x 24y 2221259x y +=2310.已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是 ( C )(A )2 3 (B )6 (C )4 3 (D )12二、填空题:11.方程表示焦点在轴的椭圆时,实数的取值范围_____12.过点且与椭圆有共同的焦点的椭圆的标准方程为_13.设,,△的周长是,则的顶点的轨迹方程为14.如图:从椭圆上一点向轴作垂线,恰好通过椭圆的左焦点,且它的长轴端点及短轴的端点的连线∥,则该椭圆的离心率等于_____________三、解答题:15.已知椭圆的对称轴为坐标轴,离心率,短轴长为,求椭圆的方程。
椭圆基础练习题及其完整答案

解析几何——椭圆精炼专题一、 选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中有只有一项是符合题目要求的.) 1.椭圆63222=+y x 的焦距是( )A .2B .)23(2-C .52D .)23(2+2.F 1、F 2是定点,|F 1F 2|=6,动点M 满足|MF 1|+|MF 2|=6,则点M 的轨迹是( ) A .椭圆 B .直线 C .线段 D .圆 3.若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点)23,25(-,则椭圆方程是 ( )A .14822=+x y B .161022=+x y C .18422=+x y D .161022=+y x4.方程222=+ky x 表示焦点在y 轴上的椭圆,则k 的取值范围是( )A .),0(+∞B .(0,2)C .(1,+∞)D .(0,1)5. 过椭圆12422=+y x 的一个焦点1F 的直线与椭圆交于A 、B 两点,则A 、B 与椭圆的另一焦点2F 构成2ABF ∆,那么2ABF ∆的周长是( ) A . 22 B . 2 C . 2 D . 16.已知椭圆的对称轴是坐标轴,离心率为31,长轴长为12,则椭圆方程为( ) A .112814422=+y x 或114412822=+y x B . 14622=+y x C .1323622=+y x 或1363222=+y x D . 16422=+y x 或14622=+y x 7. 已知k <4,则曲线14922=+y x 和14922=-+-k y k x 有( ) A . 相同的短轴 B . 相同的焦点 C . 相同的离心率 D . 相同的长轴8.椭圆192522=+y x 的焦点1F 、2F ,P 为椭圆上的一点,已知21PF PF ⊥,则△21PF F 的面积为( )A .9B .12C .10D .89.椭圆131222=+y x 的焦点为1F 和2F ,点P 在椭圆上,若线段1PF 的中点在y 轴上,那么1PF 是2PF 的( )A .4倍B .5倍C .7倍D .3倍 10.椭圆1449422=+y x 内有一点P (3,2)过点P 的弦恰好以P 为中点,那么这弦所在直线的方程为( )A .01223=-+y xB .01232=-+y xC .014494=-+y xD . 014449=-+y x11.椭圆141622=+y x 上的点到直线022=-+y x 的最大距离是( )A .3B .11C .22D .1012.过点M (-2,0)的直线M 与椭圆1222=+y x 交于P 1,P 2,线段P 1P 2的中点为P ,设直线M 的斜率为k 1(01≠k ),直线OP 的斜率为k 2,则k 1k 2的值为( )A .2B .-2C .21 D .-21二、 填空题:(本大题共4小题,每小题4分,共16分,把答案填在题中横线上.)13.椭圆2214x y m +=的离心率为12,则m = . 14.设P 是椭圆2214x y +=上的一点,12,F F 是椭圆的两个焦点,则12PF PF 的最大值为 ;最小值为 .15.直线y =x -21被椭圆x 2+4y 2=4截得的弦长为 .16.已知圆Q A y x C ),0,1(25)1(:22及点=++为圆上一点,AQ 的垂直平分线交CQ 于M ,则点M 的轨迹方程为 . 三、解答题:(本大题共6小题,共74分,解答应写出文字说明.证明过程或演算步骤.) 17.已知三角形ABC 的两顶点为(2,0),(2,0)B C -,它的周长为10,求顶点A 轨迹方程. 18.椭圆的一个顶点为A (2,0),其长轴长是短轴长的2倍,求椭圆的标准方程. 19.点P 到定点F (2,0)的距离和它到定直线x =8的距离的比为1:2,求点P 的轨迹方程,并指出轨迹是什么图形. 20.中心在原点,一焦点为F 1(0,52)的椭圆被直线y =3x -2截得的弦的中点横坐标是21,求此椭圆的方程.21.已知椭圆的中心在坐标原点O ,焦点在坐标轴上,直线y =x +1与椭圆交于P 和Q ,且OP ⊥OQ ,|PQ |=210,求椭圆方程 22.椭圆12222=+by a x (a >b >)0与直线1=+y x 交于P 、Q 两点,且OQ OP ⊥,其中O 为坐标原点. (1)求2211ba +的值; (2)若椭圆的离心率e 满足33≤e ≤22,求椭圆长轴的取值范围.椭圆练习题参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A CDDABD13、3或316 14、 4 , 1 15、5382 16、121425422=+y x 17、3)(x 15922±≠=+y x 18、解:(1)当A (2,0)为长轴端点时,a =2 , b =1,椭圆的标准方程为: ;(2)当为短轴端点时,,,椭圆的标准方程为: ;19.解:设P (x ,y ),根据题意,|PF|=(x-2)2-y 2,d=|x-8|,因为|PF|d =12 ,所以 (x-2)2-y 2 |x-8| = 12.化简,得3x 2+4y 2=48,整理,得x 216 +y 212=1,所以,点P 的轨迹是椭圆。
高中椭圆必会基础题(含答案)

一、选择题:1.下列方程表示椭圆的是()A.22199x y += B.2228x y --=- C.221259x y -= D.22(2)1x y -+=2.动点P 到两个定点1F (-4,0).2F (4,0)的距离之和为8,则P 点的轨迹为()A.椭圆B.线段12F F C.直线12F F D .不能确定3.已知椭圆的标准方程22110y x +=,则椭圆的焦点坐标为()A.(B.(0,C.(0,3)±D.(3,0)±4.椭圆222222222222211()x y x y a b k a b a k b k+=+=>>--和的关系是A .有相同的长.短轴B .有相同的离心率C .有相同的准线D .有相同的焦点5.已知椭圆22159x y +=上一点P 到椭圆的一焦点的距离为3,则P 到另一焦点的距离是()A.3B.2C.3D.66.如果22212x y a a +=+表示焦点在x 轴上的椭圆,则实数a 的取值范围为()A.(2,)-+∞ B.()()2,12,--⋃+∞ C.(,1)(2,)-∞-⋃+∞ D.任意实数R 7.“m>n>0”是“方程221mx ny +=表示焦点在y 轴上的椭圆的”()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件8.椭圆的短轴长是4,长轴长是短轴长的32倍,则椭圆的焦距是()B.4C.6D.9.关于曲线的对称性的论述正确的是()A.方程220x xy y ++=的曲线关于X 轴对称 B.方程330x y +=的曲线关于Y 轴对称C.方程2210x xy y -+=的曲线关于原点对称D.方程338x y -=的曲线关于原点对称2F C c D1F 第11题10.方程22221x y ka kb +=(a >b >0,k >0且k ≠1)与方程22221x y ab +=(a >b >0)表示的椭圆().A.有相同的离心率;B.有共同的焦点;C.有等长的短轴.长轴;D.有相同的顶点.二、填空题:(本大题共4小题,共20分.)11.(6分)已知椭圆的方程为:22164100x y +=,则a=___,b=____,c=____,焦点坐标为:_____,焦距等于______;若CD 为过左焦点F1的弦,(如图)则∆2F CD 的周长为________.12.(6分)椭圆221625400x y +=的长轴长为____,短轴长为____,焦点坐标为四个顶点坐标分别为___,离心率为;椭圆的左准线方程为13.(4分)比较下列每组中的椭圆:(1)①229436x y +=与②2211216x y +=,哪一个更圆(2)①221610x y +=与②22936x y +=,哪一个更扁14.(4分)若一个椭圆长轴的长度.短轴的长度和焦距成等差数列,则该椭圆的离心率是三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(30分)求满足下列条件的椭圆的标准方程:(1)两个焦点的坐标分别为(0,-3),(0,3),椭圆的短轴长为8;(2)两个焦点的坐标分别为(),并且椭圆经过点2)3(3)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点12P P 、16.(12分)已知点M 在椭圆221259x y +=上,M 'P 垂直于椭圆焦点所在的直线,垂直为'P ,并且M 为线段P 'P 的中点,求P 点的轨迹方程17.(12分)设点A ,B 的坐标为(,0),(,0)(0)a a a ->,直线AM,BM 相交于点M ,且它们的斜率之积为(01)k k k ->≠且求点M 的轨迹方程,并讨论k 值与焦点的关系.18.(12分)当m 取何值时,直线l :y x m =+与椭圆22916144x y +=相切,相交,相离?19.(14分)椭圆221(045)45x y m m+=<<的焦点分别是1F 和2F ,已知椭圆的离心率3e =过中心O 作直线与椭圆交于A ,B 两点,O 为原点,若2ABF 的面积是20,求:(1)m 的值(2)直线AB 的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题:
1.下列方程表示椭圆的是()
A. B. C. D.22199x y +=22
28x y --=-221259
x y -=22(2)1x y -+=2.动点P 到两个定点(- 4,0).(4,0)的距离之和为8,则P 点的轨迹为() 1F 2F A.椭圆
B.线段
C.直线 D .不能确定
12F F 12F
F 3.已知椭圆的标准方程,则椭圆的焦点坐标为()
2
2
1
10
y x +=A.
B.
C.
D.((0,(0,3)±(3,0)
±4.椭圆的关系是2222
222222222
11()x y x y a b k a b a k b k
+=+=>>--和A .有相同的长.短轴B .有相同的离心率 C .有相同的准线
D .有相同的焦点
5.已知椭圆上一点P 到椭圆的一焦点的距离为
3,则P 到另一焦点的距离是()
22
159
x y +=A.
B.2
C.3
D.6
36.如果表示焦点在x 轴上的椭圆,则实数a 的取值范围为()
22
212
x y a a +=+A. B. C. D.任意实数R
(2,)-+∞()()2,12,--⋃+∞(,1)(2,)-∞-⋃+∞7.“m>n>0”是“方程表示焦点在y 轴上的椭圆的”()
2
2
1mx ny +=A.充分而不必要条件 B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
8.椭圆的短轴长是
4,长轴长是短轴长的倍,则椭圆的焦距是()3
2
B.
C.
D.469.关于曲线的对称性的论述正确的是()
A.方程的曲线关于X 轴对称 22
0x xy y ++=B.方程的曲线关于Y 轴对称3
3
0x y +=C.方程的曲线关于原点对称
2
2
10x xy y -+= D.方程的曲3
3
8x y -=线关于原点对称
2
F F
2
C
c
D
1
F 第11题
10.方程 (a >b >0,k >0且k ≠1)与方程
(a >b >0)表示的椭圆2
2
22
1x y ka kb +=22
2
21x
y a b
+=( ).
A.有相同的离心率;
B.有共同的焦点;
C.有等长的短轴.长轴;
D.有相同的顶点.
二、填空题:(本大题共4小题,共20分.)
11.(6分)已知椭圆的方程为:,则a=___,b=____,c=____,焦点坐标为:
22
164100
x y +=___
__,焦距等于______;若CD 为过左焦点F1的弦,(如图)则∆CD 的周长为
2F ________.
12.(6分)椭圆的长轴长为____,短轴长为____,焦点坐标为 2
2
1625400x y +=四个顶点坐标分别为___ ,离心率为 ;椭圆的左准线方程为
13.(4分)比较下列每组中的椭圆:
(1)① 与② ,哪一个更圆
2
2
9436x y +=22
11216
x y +=(2)①与②,哪一个更扁
22
1610
x y +=22936x y +=14.(4分)若一个椭圆长轴的长度.短轴的长度和焦距成等差数列,则该椭圆的离心率是 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(30分)求满足下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别为(0,-3),(0,3),椭圆的短轴长为8;
(2)两个焦点的坐标分别为(),,0),并且椭圆经过点2
)
3
(3)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点12P P 、16.(12分)已知点M 在椭圆上,M 垂直于椭圆焦点所在的直线,垂直为
22
1259
x y +='P ,并且M 为线段的中点,求点的轨迹方程
'P P 'P P 17.(12分)设点A ,B 的坐标为,直线AM,BM 相交于点M ,且它
(,0),(,0)(0)a a a ->们的斜率之积为求点M 的轨迹方程,并讨论值与焦点的关系.
(01)k k k ->≠、k
18.(12分)当取何值时,直线:与椭圆相切,相交,相m l y x m =+22
916144x y +=离?
19.(14分)椭圆的焦点分别是和,已知椭圆的离心率
22
1(045)45x y m m
+=<<1F 2F
作直线与椭圆交于A ,B 两点,为原点,若的面积是20,e =
O O 2ABF A 求:(1)的值(2)直线AB 的方程
m
参考答案
1.选择题:
题号12345678910答案B B C D C B C D C A
二.填空题:
11 10,8,6,(0,),12,40 12 10,8,(),(-5,0).(5,0).(0,-4).
6±3,0
±
(0,4),,13 ②,② 14
3
5
25
3
x=-
3
5
三.解答题:
15.(1)解:由题意,椭圆的焦点在轴上,设椭圆的标准方程为
y
22
22
1(0)
y x
a b
a b
+=>>
由焦点坐标可得,短轴长为8,即,所以
3
c=28,4
b b
==22225
a b c
=+=椭圆的标准方程为
∴221
2516
y x
+=
(2)由题意,椭圆的焦点在轴上,设椭圆的标准方程为
x
22
22
1(0)
x y
a b
a b
+=>>由焦点坐标可得6
c=2a==
所以==9-5=4,所以椭圆的标准方程为
2
b22
a c
-
22
1
94
x y
+=
(3)设椭圆的方程为(),因为椭圆过
221
mx ny
+=0,0
m n
>>
12
P P
、
解得所以椭圆的标准方程为:61321
m n m n +=+=⎧∴⎨⎩
1
9
1
3
m n ==⎧⎨⎩22
193
x y +=16.解:设点的坐标为,点的坐标为,由题意可知
p (,)p x y m 00(,)x y ① 因为点在椭圆
上,所以有00
002
2y y x x x x y y ====⎧⎧⇒⎨⎨⎩⎩m 22
1259
x y += ② , 把①代入②得,所以P 点的轨迹是焦点在轴上,22
001
259x y +=22
125
36
x y +=
y 标准方程为的椭圆.
22
12536
x y +=17.解:设点M 的坐标为,因为点A 的坐标是,所以,直线AM 的斜率
(,)x y (,0)a -,同理直线BM 的斜率.由已知有()AM y k x a x a =
≠-+()BM y
k x a x a
=≠-化简得点M 的轨迹方程为(),y y
k x a x a x a
=-≠±+-A 22221()
x y x a a ka +=≠±当时,表示焦点在轴上的椭圆;当时,表示焦点在y 轴上的椭圆.
01k <<x 1k >18.解:
{
22916144y x m x y =++=…… …
…
①②
①代入②得化简得2
2916()144x x m ++=2
2
2532161440
x mx m ++-=222(32)425(16144)57614400
m m m ∆=-⨯-=-+当即时,直线与椭圆相切;
0,∆=5m =±l 当,即时,直线与椭圆相交;
0∆>55m -<<当,即或时,直线与椭圆相离.
0∆<5m <-5m >19.解:(1)由已知,,c e a =
=
a ==5c =所以2
2
2
452520
m b a c ==-=-= (2)根据题意,设,则,
2
1220ABF F F B S S ==A A (,)B x y 12
12
12
F F B S F F y =A A
,所以,把代入椭圆的方程,得,所12210F F c ==4y =±4y =±22
14520
x y +
=3x =±以点的坐标为,所以直线AB 的方程为B 34±±、、、4433
y x y x =
=-、。
