2019学年高一人教版数学必修一练习:第一章 单元质量测评1 Word版含解析
(word版)高一数学必修一第一章测试题及答案[1],文档
![(word版)高一数学必修一第一章测试题及答案[1],文档](https://img.taocdn.com/s3/m/dcc16befb52acfc789ebc9f3.png)
高中数学必修1检测题一、选择题:1.全集U {1,2,3,4,5,6.7},A {2,4,6},B {1,3,5,7}.那么A (C U B〕等于〔〕A.{2,4,6} B.{1,3,5} C.{2,4,5} D.{2,5}2.集合 A {x|x2 1 0},那么以下式子表示正确的有〔〕①1 A ②{ 1} A ③ A ④{1, 1} AA.1个B.2个C.3个D.4个3.假设 f:A B能构成映射,以下说法正确的有〔〕1〕A中的任一元素在B中必须有像且唯一;2〕A中的多个元素可以在B中有相同的像;3〕B中的多个元素可以在A中有相同的原像;4〕像的集合就是集合B.A、1个B、2个C 、3个D、4个4、如果函数f(x)x22(a1)x 2在区间,4上单调递减,那么实数a的取值范围是〔〕A、a≤3B、a≥3C、a≤5D、a≥55、以下各组函数是同一函数的是〔〕①f(x)2x3与g(x)x2x;②f(x)x与g(x)x2;③f(x)x0与g(x)1;④f(x)x22x1与g(t)t22t1。
x0A、①②B、①③C 、③④D、①④6.根据表格中的数据,可以断定方程e x x20的一个根所在的区间是〔〕x-10123 e x1x212345A.〔-1,0〕B.〔0,1〕C.〔1,2〕D.〔2,3〕7.假设lgx lgy a,那么lg(x)3lg(y)3〔〕22A.3a B.3a C.a D.a22-1-8、假设定义运算ab a bx log2x log1x的值域是〔ba,那么函数f〕a b2A0,B0,1C 1,D R9.函数y a x在[0,1]上的最大值与最小值的和为3,那么a〔〕1B.2C.41A.D.2410 .以下函数中,在0,2上为增函数的是〔〕A、ylog1(x1)B、y log2x21C、y log21D、y log1(x24x5) 2x211.下表显示出函数值y随自变量x变化的一组数据,判断它最可能的函数模型是〔〕x45678910 y15171921232527A.一次函数模型B.二次函数模型C.指数函数模型D.对数函数模型12、以下所给4个图象中,与所给3件事吻合最好的顺序为〔〕1〕我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;2〕我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;3〕我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
高一数学必修1《第一章》单元测试题(含答案).doc

班级:_______ 姓名:____________ 成绩: ____________一.选择题(本大题共12小题,第小题5分,共60分.1.设集合A = {xeQ\x>-l\,贝U ()A. 0^ AB.近冬AC. yf2e AD. |V2j c A2.已知集合A到B的映射f:x->y=2x+l,那么集合A中元素2在B中対应的元素是:A、2B、5C、6D、83.设集合A = {x\\< x <2} .B = {x\x < a}.若Au 3,则Q 的范围是( )A. a >2B. « < 1C. a > 1D. a <24.函数),=卮口的定义域是()A G'Z)B・[gg C.(列) D.(列]5.全集U= {0丄3,5,6,8},集合A={ 1, 5, 8}, B={2},则集合(qTl)UB:二()A. {0,2,3,6}B. {0,3,6}C. {2,1,5,8}D. 06.已知集合A = [x\-l<x<3},B = {x\2<x<5],则AljB=()A. (2,3)B. [-1,5]C. (-1,5)D. (-1,5]7.下列函数是奇函数的是()A. y = xB. y = 2x2 -3C. y =D. y = x2[0,1]8.化简:yl(7r-4)2 + 7T =()A. 4B. 2兀 _ 4C. 2兀一4 或4D. 4 — 2龙9.设集合M={x|-2<x<2), N={y\0<y<2},给出卜-列四个图形,其屮能表示以集合M为定义域,N为值域的函数关系的是()10.________________________________________________________________ 已知f (x) =g (.x) +2, •且g(x)为奇函数,若f (2) =3,则f (・2) = _______________________A 0 B・・3 C・1 D. 3x2x>011.己知f (x)=<71 % = 0,则f[f(-3)]等于0兀vOA> 0 Bx 7i C、d D> 912.已知函数/&)是人上的增函数,・A(O,—1), B(3,l)是其图像上的两点,那么|/(%)|<1 的解集是()A. (-3,0)B. (0,3)C.(一汽―l]u[3,+g)D. (―oo,0]u[l,-H«)二.填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上・)[x + 5(x>l) ,13.已知f(x) = \ .,则/T f (1)1 = .[2X2+1(X<1) ---------------------------------14 .已知/(兀一1) = /,贝|J于(兀)= __________15・定义在R上的奇函数/(%),当x>0时,/(%) = 2 ;则奇函数/(%)的值域是.16.关于下列命题:①若函数y = 2”的定义域是{x|x<0},则它的值域是{y | y <1};②若函数y=l-的定义域是{兀|兀>2},贝怕的值域是{y|y<-};x 2③若函数y = x2的值域是{y | 0 < > < 4},则它的定义域一定是{x|-2<x<2};④若函数=2r的定义域是{y | y < 4},则它的值域是{x|0<x<8}.其中不止确的命题的序号是___________ (注:把你认为不正确的命题的序号都填上).班级:_______ 姓名:____________ 成绩:____________一、选择题答案表:木人题共12题,每小题5分,共60分二、填空题答案:本人题共有4小题,每小题5分,满分20分13> __________ 14. _____________________________15> ____________ 16> ________________________三、解答题:本大题共5小题,共70分.题解答应写出文字说明,证明过程或演算步骤.17.设A = {% | x2 + 4% = 0} , A = {x\x2 +2(a + l)x + / -1 = 0},其中xe R ,如果 =求实数Q的取值范围.18.己知全集[/= {1,2,3,4,5,6,7,8}, A = {x | x2-3x4-2 = 0}, B = {x\\< x<5,xe Z} fC = {x\2<x<9,xeZ}. (1)求/lU(fiAC);(2)求(Q,B)U(Q,C).19.已知函数y=x2~2x+9分别求下列条件下的值域,(1)定义域是{x|3<x<8} (2)定义域是{% | -3 < x < 2}20.已知函数/(x) = x + -.兀(1)判断函数的奇偶性,并加以证明;⑵用定义证明f(x)在(0,1)上是减函数;(3)函数/(x)在(-1,0)上是单调增函数还是单调减函数?(直接写岀答案,不要求写证明过程).21.已知函数/(x)是定义在R上的偶函数,且当xWO吋,/⑴=F+2兀. ⑴现已应出函数/⑴在y轴左侧的图像,如图所示,请补出完整函数/*(兀)的图像,并根据图像写出函数/(%)的增区间;(2)写出函数/(%)的解析式和值域.1、B2、B3、A 4. B.提示:2x-l>0. 5. A.6. B.提示:运用数轴.7. A.提示:B为偶函数,C、D为非奇非偶函数.8. A.提示:+龙二”一4| + 兀=龙一4 + 龙二2龙一4 .9. B.捉刀P:10. c 11 B 12. B .提zjx: *•* —1 v /(兀)v 1,而y*(o)=—1,y*(3) = ], /(0)</(x)</(3), .\0<x<3.13.8.提示:/⑴=3, f(3) =8.14./(x) = (x + 1)2.提示:V/(x-l) = x2 =[(x —1) + 1 2, /. f(x) = (x + l)215.{-2, 0, 2 }.提示:因为/(0) = 0;x <0 时,f(x) = -2 ,所以f(x)的值域是{-2, 0, 2 }.16 .①②④.提示:若函数y = 2r的定义域是{ x | x < 0},则它的值域是{y\O<y<\};若函数v = 1的定义域是01 x > 2},则它的值域是{y\O<y<-}.x 2三.17、解A={0, —4} ........................................................A O B=B ・\BeA .........................................................由x2 + 2(a+ l)x + a2—1=0 得A =4 (a+1) 2—4 (a2—1) =8 (a+1) .....................................................................(1)当a<-l 时△<() B=4)CA ...........................................................(2)当a=・l 吋△=() B={O}cA ......................................................(3)当a>-l 时△>()要使BoA,则A=BVO, -4是方程x2+2(a+l)x+『・l=0的两根.J_2(d + 1) = -41 = 0解Z得a=l综上可得aW・l或a=l .....................................................1&解:(1)依题意有:A = {1,2},B = {1,2,3,4,5},C = {3,4,5,6,7,8}・・・MC = {3,4,5},故有AU(BAC) = {1,2}U{3,4,5} = {1,2,3,4,5}.由C"3二{6,7,8},C〃C二{1,2}(籾)U ( 〃C) = {6,7,8} u (1,2) = {1,2,6,7,8}.仃T)设x^x2 G(0」)冃・兀1 <x2••/ 0 < Xj < x2 < 1,/-兀]兀2 V 1,兀1尤2 一1 V 0T x2 > x A x2 -Xj > 0 .・• J&2)- / (“) V 0,/(x2) < /(xj因此函数/(兀)在(0,1)上是减函数(111) .f(x)在(-1,0)上是减函数.21. (1)函数图像如右图所示:/(兀)的递增区间是(-1,0) , (l,+oo).(2)解析式为:f(x) = [X +2x,x_0 值域为:[x-2x,x>0{y|y»-1}.20.解:y = 2x+2 -3-4' =-3-(2x)2 +4-2S令t = 2\则y = -3t2+4t= -3(t一 -)2 + -1 12 1V -1 < X < 0 , /.-<2X <lBPre[-,l],又・.•对称轴r = -e[-?l],32 2 4・••当t = -f即x = log2-时人ax=j ;当21 即x=o 时,y min =1.20•证明:仃)函数为奇函数f(-x)1=-x ——= =-/w一兀1 =(x2-Xj) 1-(兀2 —舛)(兀]兀2—1)第一章《集合与函数概念》单元测试题姓名:_______ 班别: _________ 成绩: _____________一、选择题:每小题4分,共40分1、在“①高一数学课本中的难题;②所有的正三角形;③方程午+2 = 0的实数解”中,能够表示成集合的是( )(A)②(B)③(C)②③(D)①②③2、若A=|x|0<x< V2 ={x11 < x < 2},则A^J B =( )(A) {x|x<0} (B) [x\x>2](C) {0<x<V2)(D) {x\0<x<2}3、若A={0丄2,3},B ={兀|兀=3a,dw 4},则Ar>B =( )(A) {1,2} (B) {0,1}(C) {0,3} (D) {3}4、在映射f : A T B中,A = B = {(x, y) \ x, ye R}, K / : (x, y) (x- >\x+ y),则与A中的元素(-1,2)对应的B屮的元素为( )(A) (—3,1) (B) (1,3) (C) (-1-3) (D) (3,1)5、下列各组函数.f⑴与g(x)的图象相同的是( )(A) /(x) = x,g(x) = (Vx)2(B) /(x) = x2)4g(x) = (x + l)2[x(X > 0)(C) f(x) = l,g(x) =兀(D) /(x)=|x|,g(x) = 2 / °、6、/⑴是定义在㈣上的增函数,则不等式的解集是()(A) (0 , +8) (B) (0 , 2) (C) (2 ,+8) (D) (2 ,—)77、若奇函数/(兀)在[1,3]上为增函数,且有最小值0,贝陀在[-3,-1]上()(C) (D)9、 若{1,4,牛{0,"+»,则严+严的值为()(A) 0 (B) 1 (C) -1(D) 1 或一 110、 奇函数f(x)在区间[・b,上单调递减,且f (x)>0,(0<a<b),那么I f (x)l 在区间[a, b ]上是 ( )A 单调递增B 单调递减C 不增也不减D 无法判断 二、填空题:每小题4分,共20分11、 ________________________________________________________________ 若A={0^2,},B = {1,2,3},C = {2,3,4},贝iJ(AnB)u(BnC) = ________________________12、 已知y = /(x)为奇函数,当%>0时/(x) = x(l — x),则当兀S0时,A.是减函数,有最小值0B.是增函数,有最小值0C.是减函数,有最大值0D.是增函数,有最大值0 (A)(B)则/(兀)= _______________________________________13、已知(兀)都是定义域内的非奇非偶函数,而f(x)-g(x)是偶函数,写出满足条件的一组隊I 数,/(%) = ____________ : g (x) = _________________ ;14、/(X)= X2+2X +1, XG[-2,2]的最大值是__________________15、奇函数/(兀)满足:①/⑴在(0,+oo)内单调递增;®/(1) = 0 ;则不等式(x-l)/(x)> 0 的解集为:________________________________ ;三、解答题:每小题12分,共60分16、设A = {xeZ\\x\< 6}, 3 二{1,2,3},C 二{3,4,5,6},求:(1) Au(BnC): (2) AnQ(fiuC)17、已知函数几兀) xe{x\x = 2nU9neZ}画出它的图象,并求心(_3))的值11,{x\x = 2n,ne Z}18、已知函数f (x)=兀+ —.x(1)判断f(X)在(0, +8)上的单调性并加以证明;(2)求f (x)的定义域、值域;19、中山市的一家报刊摊点,从报社买进《南方都市报》的价格是每份0.90元,卖出的价格是每份1.0元,卖不掉的报纸可以以每份0.10元的价格退冋报社。
人教A版数学必修一2019必修1第一章检测卷.docx

高中数学学习材料鼎尚图文*整理制作2019届必修1第一章检测卷班级: 姓名: 得分:第I 卷 选择题 共60分一、选择题(单选题,每小题5分,共60分。
)1、若集合},4,3,1{},3,2,1{==B A 则B A 的子集个数为…………………………………… ( ) A. 2 B. 3 C. 4 D. 162、满足条件}5,4,3,2,1{}2,1{⊆⊆M 的所有集合M 的个数是( )A 9B 8C 7D 63、已知函数()f x 为奇函数,且当0x >时,21()f x x x=+,则(1)f -=………… ( ) (A) 2- (B) 0 (C) 1 (D) 24、下列函数中,是同一函数的是………………………………………………………………… ( ) A 2x y x y ==与 B ||2x x y x y ==与C 31)3)(1(+=-+-=x y x x x y 与 D 1122+=+=t y x y 与5、设},,6|{},,15|{Q x x x B N k k x x A ∈≤=∈+==则B A 等于( )A }4,1{B }6,1{C }6,4{D }6,4,1{6、设全集为R , 函数11)(+⋅-=x x x f 的定义域为M , 则C M R 为………………………… ( )(A) (-∞,1) (B) ),1[+∞(C) ,1][1,)(∞-⋃+∞- (D) ,1)(1,)(∞-⋃+∞-7、下列函数中,在区间(0,+∞)上是增函数的是……………………………………………… …( )A .y =|x |B .y =3-xC .y =1xD .y =-x 2+48、函数1y x x =-+的定义域是………………………………………………… ( )A (,1]-∞B [0,)+∞C []0,1D ),1[]0,(+∞-∞9、设函数f (x )=200.x x x x ≤⎧⎨>⎩-,,,若f (α)=4,则实数α=……………………………………………… ( )A .-4或-2B .-4或2C .-2或4D .-2或210、函数||x x y =的图象大致是…………………………………………………………………… ( )11、已知,},01|{},065|{2B B A mx x B x x x A ==-==+-= 则m 的值为………………( ) A .21或31 B. 21 C. 31 D. 21,0,或31 12、某学校要招开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于..6.时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为……………………………………………………( )(A )y =[10x] (B )y =[310x +] (C )y =[410x +] (D )y =[510x +]第II 卷 非选择题 共90分二、填空题(每小题5分,共20分)13、用适当的符号填空:①},,__{c b a a ;②};01|___{2=+Φx x ③;__}1,0{N ④}8|__{}4,2,1{的约数是x x ;⑤Φ____0 ;⑥Φ___}0{。
人教版2019年高一数学必修一-第一章练习题与配套参考答案

集合与函数基础测试一、选择题(共12小题,每题5分,四个选项中只有一个符合要求)1.函数y ==x 2-6x +10在区间(2,4)上是( )A .递减函数B .递增函数C .先递减再递增D .选递增再递减.2.方程组20{=+=-y x y x 的解构成的集合是 ( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{3.已知集合A ={a ,b ,c },下列可以作为集合A 的子集的是 ( )A. aB. {a ,c }C. {a ,e }D.{a ,b ,c ,d }4.下列图形中,表示N M ⊆的是 ( )5.下列表述正确的是 ( )A.}0{=∅B. }0{⊆∅C. }0{⊇∅D. }0{∈∅6、设集合A ={x|x 参加自由泳的运动员},B ={x|x 参加蛙泳的运动员},对于“既参加自由泳又参加蛙泳的运动员”用集合运算表示为 ( )A.A∩BB.A ⊇BC.A ∪BD.A ⊆B7.集合A={x Z k k x ∈=,2} ,B={Z k k x x ∈+=,12} ,C={Z k k x x ∈+=,14}又,,B b A a ∈∈则有( )A.(a+b )∈ AB. (a+b) ∈BC.(a+b) ∈ CD. (a+b) ∈ A 、B 、C 任一个8.函数f (x )=-x 2+2(a -1)x +2在(-∞,4)上是增函数,则a 的范围是( )A .a ≥5B .a ≥3C .a ≤3D .a ≤-59.满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是 ( )A. 8B. 7C. 6D. 510.全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },那么集合 { 2 ,7 ,8}是 ( )A. A BB. B AC. B C A C U UD. B C A C U U11.下列函数中为偶函数的是( )A .x y =B .x y =C .2x y =D .13+=x y12. 如果集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ( )A .0B .0 或1C .1D .不能确定二、填空题(共4小题,每题4分,把答案填在题中横线上)13.函数f (x )=2×2-3|x |的单调减区间是___________.14.函数y =11+x 的单调区间为___________. 15.含有三个实数的集合既可表示成}1,,{ab a ,又可表示成}0,,{2b a a +,则=+20042003b a .16.已知集合}33|{≤≤-=x x U ,}11|{<<-=x x M ,}20|{<<=x x N C U 那么集合M N A M N B N M C M N D=N ,=⋂)(N C M U ,=⋃N M .三、解答题(共4小题,共44分)17. 已知集合}04{2=-=x x A ,集合}02{=-=ax x B ,若A B ⊆,求实数a 的取值集合.18. 设f (x )是定义在R 上的增函数,f (xy )=f (x )+f (y ),f (3)=1,求解不等式f (x )+f (x -2)>1.19. 已知函数f (x )是奇函数,且当x >0时,f (x )=x 3+2x 2—1,求f (x )在R 上的表达式.20. 已知二次函数222)1(2)(m m x m x x f -+-+-=的图象关于y 轴对称,写出函数的解析表达式,并求出函数)(x f 的单调递增区间.必修1 第一章 集合测试集合测试参考答案:一、1~5 CABCB 6~10 ABACC 11~12 cB二、13 [0,43],(-∞,-43) 14 (-∞,-1),(-1,+∞) 15 -1 16 03|{≤≤-=x x N 或}32≤≤x ;}10|{)(<<=⋂x x N C M U ;13|{<≤-=⋃x x N M 或}32≤≤x .三、17 .{0.-1,1}; 18. 解:由条件可得f (x )+f (x -2)=f [x (x -2)],1=f (3). 所以f [x (x -2)]>f (3),又f (x )是定义在R 上的增函数,所以有x (x -2)>3,可解得x >3或x <-1.答案:x >3或x <-1.19. .解析:本题主要是培养学生理解概念的能力.f (x )=x 3+2x 2-1.因f (x )为奇函数,∴f (0)=-1.当x <0时,-x >0,f (-x )=(-x )3+2(-x )2-1=-x 3+2x 2-1,∴f (x )=x 3-2x 2+1.20. 二次函数222)1(2)(m m x m x x f -+-+-=的图象关于y 轴对称,∴1=m ,则1)(2+-=x x f ,函数)(x f 的单调递增区间为(]0,∞-..。
人教新课标版数学高一-必修一练习第一章质量检测

(时间90分钟,满分120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题所给的四个选项中,只有一项是符合题目要求的)1.已知集合U ={1,2,3,4,5,6,7},A ={2,4,5,7},B ={3,4,5},则(∁U A )∪(∁U B )=( )A .{1,6}B .{4,5}C .{2,3,4}D .{1,2,3,6,7}解析:∵∁U A ={1,3,6},∁U B ={1,2,6,7},∴(∁U A )∪(∁U B )={1,2,3,6,7}.答案:D2.设全集U ={x ∈Z|-1≤x ≤5},A ={1,2,5},B ={x ∈N|-1<x <4},则B ∩(∁U A )=() A .{3} B .{0,3}C .{0,4}D .{0,3,4}解析:∵U ={-1,0,1,2,3,4,5},B ={0,1,2,3},∴∁U A =(-1,0,3,4}.∴B ∩(∁U A )={0,3}.答案:B 3.函数y =2x +1+3-4x 的定义域为( )A .(-12,34) B .[-12,34]C .(-∞,12] D .(-12,0)∪(0,+∞)解析:由⎩⎪⎨⎪⎧ 2x +1≥0,3-4x ≥0得⎩⎨⎧ x ≥-12,x ≤34,即-12≤x ≤34, 所以函数的定义域为[-12,34].答案:B4.若函数y =f (x )的定义域是[0,2],则函数g (x )=f (2x )x -1的定义域为( )A .[0,1]B .[0,1)C .[0,1)∪(1,4]D .(0,1) 解析:∵f (x )定义域为[0,2],∴对于g (x ),有⎩⎪⎨⎪⎧0≤2x ≤2,x -1≠0,∴x ∈[0,1).答案:B5.函数y =x |x |,x ∈R ,满足( )A .既是奇函数又是减函数B .既是偶函数又是增函数C .既是奇函数又是增函数D .既是偶函数又是减函数 解析:由f (-x )=-f (x )可知,y =x |x |为奇函数.当x >0时,y =x 2为增函数,而奇函数在对称区间上单调性相同.答案:C6.已知f (x )=x 5-ax 3+bx +2,且f (5)=17,则f (-5)的值为( )A .-13B .13C .-19D .19解析:设g (x )=x 5-ax 3+bx ,则g (x )为奇函数.f (x )=g (x )+2,f (5)=g (5)+2=17.∴g (5)=15.故g (-5)=-15.∴f (-5)=g (-5)+2=-15+2=-13.答案:A7.若函数f (x )为奇函数,且当x >0时,f (x )=x -1,则当x <0时,有( )A .f (x )>0B .f (x )<0C .f (x )·f (-x )≤0D .f (x )-f (-x )>0 解析:f (x )为奇函数,当x <0,-x >0时,f (x )=-f (-x )=-(-x -1)=x +1,f (x )·f (-x )=-(x +1)2≤0.答案:C8.函数f (x )=|x +1|+|x -1|的奇偶性是( )A .奇函数B .偶函数C .既是奇函数也是偶函数D .既不是奇函数也不是偶函数解析:f (x )=|x +1|+|x -1|的定义域是R,且f (-x )=|-x +1|+|-x -1|=|x -1|+|x +1|=f (x ),所以f (x )是偶函数.答案:B9.已知函数f (x )=⎩⎪⎨⎪⎧ 3x +2, x <1,x 2+ax , x ≥1.若f [f (0)]=4a ,则实数a 等于( )A .0B .1C.32 D .2解析:∵f (x )=⎩⎪⎨⎪⎧3x +2, x <1,x 2+ax , x ≥1.∴f (0)=2.∴f [f (0)]=f (2)=4+2a .∴4+2a =4a .∴a =2.答案:D10.设f (x )是R 上的偶函数,且在(-∞,0)上为减函数,若x 1<0,且x 1+x 2>0,则() A .f (x 1)>f (x 2)B .f (x 1)=f (x 2)C .f (x 1)<f (x 2)D .无法比较f (x 1)与f (x 2)的大小解析:∵x 1<0且x 1+x 2>0,∴-x 2<x 1<0.又f (x )在(-∞,0)上为减函数,∴f (-x 2)>f (x 1).而f (x )又是偶函数,∴f (-x 2)=f (x 2).∴f (x 1)<f (x 2).答案:C二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)11.用列举法表示集合:A ={x |2x +1∈Z ,x ∈Z}=____________.解析:∵2x +1∈Z ,∴-2≤x +1≤2,且x +1≠0,即-3≤x ≤1,且x ≠1. 当x =-3时,有-1∈Z ;当x =-2时,有-2∈Z ;当x =0时,有2∈Z ;当x =1时,有1∈Z.∴A ={-3,-2,0,1}.答案:{-3,-2,0,1}12.函数f (x )对于任意实数x 满足条件f (x +2)=1f (x ),若f (1)=-5,则f [f (5)]=________. 解析:由f (x +2)=1f (x )可得 f (x +4)=f (x ),f (5)=f (1)=-5,所以f [f (5)]=f (-5)=f (-1)=f (3)=1f (1)=-15, ∴f [f (5)]=-15. 答案:-1513.若函数f (x )=kx 2+(k -1)x +2是偶函数,则f (x )的递减区间是________.解析:∵f (x )是偶函数,∴f (-x )=kx 2-(k -1)x +2=kx 2+(k -1)x +2=f (x ).∴k =1.∴f (x )=x 2+2,其递减区间为(-∞,0].答案:(-∞,0]14.已知集合A ={x |0≤x ≤4},集合B ={y |0≤y ≤2},从A 到B 的对应关系f 分别为:①f :x →y =12x ;②f :x →y =x -2; ③f :x →y =x ;④f :x →y =|x -2|.其中,是函数关系的是________(将所有正确答案的序号均填在横线上).解析:由函数的定义可判定①③④正确.对于②,由于当0≤x ≤4时,-2≤x -2≤2,显然不满足存在性.答案:①③④三、解答题(本大题共4小题,共50分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R.(1)求A ∪B ,(∁U A )∩B ;(2)若A ∩C ≠∅,求a 的取值范围.解:(1)A ∪B ={x |2≤x ≤8}∪{x |1<x <6}={x |1<x ≤8}.∁U A ={x |x <2或x >8},∴(∁U A )∩B ={x |1<x <2}.(2)∵A ∩C ≠∅,∴a <8,即a 的取值范围为(-∞,8).16.(本小题满分12分)若f (x )是定义在(0,+∞)上的增函数,且对一切x ,y >0,满足f (x y)=f (x )-f (y ). (1)求f (1)的值;(2)若f (6)=1,解不等式f (x +3)-f (13)<2. 解:(1)在f (x y )=f (x )-f (y )中,令x =y =1,则有f (1)=f (1)-f (1),∴f (1)=0.(2)∵f (6)=1,∴f (x +3)-f (13)<2=f (6)+f (6), ∴f (3x +9)-f (6)<f (6).即f (x +32)<f (6). ∵f (x )是定义在(0,+∞)上的增函数,∴⎩⎨⎧ x +3>0,x +32<6.解得-3<x <9,即不等式的解集为(-3,9).17.(本小题满分12分)某市规定出租车收费标准:起步价(不超过2 km)为5元;超过2 km 时,前2 km 依然按5元收费,超过2 km 的部分,每千米收1.5元.(1)写出打车费用关于路程的函数解析式;(2)规定:若遇堵车,每等待5分钟(不足5分钟按5分钟计时),乘客需交费1元.某乘客打车共行了20 km ,中途遇到了两次堵车,第一次等待7分钟,第二次等待13分钟.该乘客到达目的地时,该付多少车钱?解:(1)设乘车x km ,乘客需付费y 元,则当0<x ≤2时,y =5;当x >2时,y =5+(x -2)×1.5=1.5x +2.∴y =⎩⎪⎨⎪⎧5, 0<x ≤2,1.5x +2, x >2为所求函数解析式. (2)当x =20时,应付费y =1.5×20+2=32(元).另外,第一次堵车等待7分钟=5分钟+2分钟,需付费2元;第二次堵车等待13分钟=2×5分钟+3分钟,需付费3元.所以该乘客到达目的地后应付费32+2+3=37(元).18.(本小题满分14分)已知函数f (x )=x +m x,且此函数的图象过点(1,5). (1)求实数m 的值;(2)判断f (x )的奇偶性;(3)讨论函数f (x )在[2,+∞)上的单调性?证明你的结论.解:(1)∵f (x )过点(1,5),∴1+m =5⇒m =4.(2)对于f (x )=x +4x ,∵x ≠0,∴f (x )的定义域为(-∞,0)∪(0,+∞),关于原点对称.∴f (-x )=-x +4-x =-f (x ).∴f (x )为奇函数.(3)设x 1,x 2∈[2,+∞)且x 1<x 2, f (x 1)-f (x 2)=x 1+4x 1-x 2-4x 2=(x 1-x 2)+4(x 2-x 1)x 1x 2=(x 1-x 2)(x 1x 2-4)x 1x 2,∵x 1,x 2∈[2,+∞)且x 1<x 2, ∴x 1-x 2<0,x 1x 2>4,x 1x 2>0. ∴f (x 1)-f (x 2)<0.∴f (x )在[2,+∞)上单调递增.。
2019年人教A版必修一高中数学单元质量评估(一)及答案

单元质量评估(一)(第一章)(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={0,1,2},B={x|-1<x<2},则A∩B=( )A.{0}B.{1}C.{0,1}D.{0,1,2}【解析】选C.因为A={0,1,2},B={x|-1<x<2},所以A∩B={0,1}.2.(2015·天津高一检测)设集合M={2,0,x},集合N={0,1},若N⊆M,则x的值为( ) A.2 B.0C.1D.不确定【解析】选C.因为N⊆M,所以集合N中元素均在集合M中,所以x=1.3.在下列由M到N的对应中构成映射的是( )【解析】选C.选项A中,集合M中的数3在集合N中没有数与之对应,不满足映射的定义;选项B中,集合M中的数3在集合N中有两个数a,b与之对应;选项D中,集合M中的数a在集合N中有两个数1,3与之对应,不满足映射的定义.4.已知函数f(x)=ax3+bx(a≠0),满足f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【解析】选 C.方法一:f(-3)=a(-3)3+b(-3)=-33a-3b=-(33a+3b)=3,所以33a+3b=-3.f(3)=33a+3b=-3.方法二:显然函数f(x)=ax3+bx为奇函数,故f(3)=-f(-3)=-3.【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( ) A.5 B.10C.8D.不确定【解析】选B.因为f(x)是偶函数,所以f(-4)=f(4)=5,所以f(4)+f(-4)=10. 5.已知一次函数y=kx+b为减函数,且kb<0,则在直角坐标系内它的大致图象是( )【解析】选A.选项A图象为减函数,k<0,且在y轴上的截距为正,故b>0,满足条件,而B,C,D均不满足条件.6.若f(x)=则f的值为( )A.-B.C.D.【解析】选C.因为<1,所以应代入f(x)=1-x2,即f=1-=.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+1【解析】选B.由f(g(x))=f(2x+1)=6x+3=3(2x+1),知f(x)=3x.8.(2015·西城区高一检测)下列四个图形中,不是以x为自变量的函数的图象是( )【解析】选 C.由函数定义知,定义域内的每一个x都有唯一函数值与之对应,A,B,D选项中的图象都符合;C项中对于大于零的x而言,有两个不同的值与之对应,不符合函数定义.9.已知集合A={x|x2+x+1=0},若A∩R=∅,则实数m的取值范围是( )A.m<4B.m>4C.0<m<4D.0≤m<4【解析】选D.因为A∩R=∅,所以A=∅,即方程x2+x+1=0无解,所以Δ=()2-4<0,所以m<4.又因为m≥0,所以0≤m<4.10.(2015·赣州高一检测)函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( ) A.(-∞,0]和(-∞,1] B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)【解析】选 C.函数f(x)=|x|的单调递增区间为[0,+∞),函数g(x)=x(2-x)=-(x-1)2+1的单调递增区间为(-∞,1].11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个【解析】选B.若a,b同奇偶,有12=1+11=2+10=3+9=4+8=5+7=6+6,前面的每种可以交换位置,最后一种只有1个点(6,6),这时有2×5+1=11;若a,b一奇一偶,有12=1×12=3×4,每种可以交换位置,这时有2×2=4,所以共有11+4=15个.12.(2015·西安高一检测)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)【解析】选 D.由f(x)为奇函数,可知=<0.而f(1)=0,则f(-1)=-f(1)=0.又f(x)在(0,+∞)上为增函数,所以当0<x<1时,f(x)<0=f(1),此时<0;又因为f(x)为奇函数,所以f(x)在(-∞,0)上为增函数,所以当-1<x<0时,f(x)>0=f(-1),此时<0,即所求x的取值范围为(-1,0)∪(0,1).二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.(2015·开封高一检测)已知集合A={x|1≤x<2},B={x|x<a},若A∩B=A,则实数a的取值范围是.【解析】因为A∩B=A,所以A B,所以a≥2.答案:a≥214.已知a是实数,若集合{x|ax=1}是任何集合的子集,则a的值是.【解析】若集合{x|ax=1}是任何集合的子集,则它是空集,即方程ax=1无解,所以a=0.答案:015.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-⎧⎨⎩≤≤≤≤【解析】当x∈[0,1]时,-x∈[-1,0],f(-x)=-x+1,又因为f(x)为偶函数,所以f(x)=f(-x)=1-x.答案:1-x16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).【解析】若a+b≤0,则a≤-b,b≤-a,又因为f(x)为R上递减的奇函数,所以f(a)≥f(-b),f(b)≥f(-a),所以f(a)+f(b)≥f(-a)+ f(-b),④正确;又因为f(-b)=-f(b),所以f(b)f(-b)=-f(b)f(b)≤0,③正确.其余错误.答案:③④三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.(1)分别求A∩B,(RðB)∪A.(2)已知C={x|a<x<a+1},若C⊆B,求实数a取值构成的集合.【解析】(1)A∩B={x|3≤x<6}.因为ðB={x|x≤2或x≥9},R所以(ðB)∪A={x|x≤2或3≤x<6或x≥9}.R(2)因为C⊆B,如图所示:所以解得2≤a≤8,所以所求集合为{a|2≤a≤8}.18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.【解析】(1)因为f(x)=,所以f(3)==-,所以点(3,14)不在f(x)的图象上.(2)f(4)==-3.(3)令=2,即x+2=2x-12,解得x=14.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b 的值.【解析】因为函数f(x)的对称轴方程为x=-2,所以函数f(x)在定义域[-2,b](b>-2)上单调递增,所以函数f(x)的最小值为f(-2)=a-4=-2,所以a=2.函数f(x)的最大值为f(b)=b2+4b+2=b.所以b2+3b+2=0,解得b=-1或b=-2(舍去),所以b=-1.20.(12分)(2015·烟台高一检测)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并用定义证明.【解析】(1)由f(1)=2,f(2)=-1,得a+b=2,2a+b=-1,即a=-3,b=5,故f(x)=-3x+5,f(m+1)=-3(m+1)+5=-3m+2.(2)函数f(x)在R上单调递减,证明如下:任取x1<x2(x1,x2∈R),则f(x2)-f(x1)=(-3x2+5)-(-3x1+5)=3x1-3x2=3(x1-x2),因为x1<x2,所以f(x2)-f(x1)<0,即f(x2)<f(x1),所以函数f(x)在R上单调递减.【拓展延伸】定义法证明函数单调性时常用变形技巧(1)因式分解:当原函数是多项式函数时,作差后的变形通常进行因式分解.(2)通分:当原函数是分式函数时,作差后往往进行通分,然后对分子进行因式分解.(3)配方:当原函数是二次函数时,作差后可考虑配方,便于判断符号.21.(12分)(2015·葫芦岛高一检测)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.【解析】(1)取x=y=0,则f(0+0)=2f(0),所以f(0)=0.取y=-x,则f(x-x)=f(x)+f(-x),所以f(-x)=-f(x)对任意x∈R恒成立,所以f(x)为奇函数.(2)任取x1,x2∈(-∞,+∞),且x1<x2,则x2-x1>0,f(x2)+f(-x1)=f(x2-x1)<0,所以f(x2)<-f(-x1),又f(x)为奇函数,所以f(x1)>f(x2),所以f(x)是R上的减函数.(3)由(2)知f(x)在R上为减函数,所以对任意x∈[-3,3],恒有f(3)≤f(x)≤f(-3),因为f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=-2×3=-6,所以f(-3)=-f(3)=6,所以f(x)在[-3,3]上的值域为[-6,6].22.(12分)定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.【解题指南】(1)结合已知等式利用赋值法求解.(2)利用赋值法并结合奇偶性定义判断.(3)结合(2)的结论及已知条件得f=1,再利用奇偶性和单调性脱去符号“f”,转化为一次不等式求解.【解析】(1)令x=y=0,得2f(0)=f(0),所以f(0)=0.(2)令y=-x,得f(x)+f(-x)=f(0)=0,即f(x)=-f(-x),所以f(x)为奇函数.(3)因为f=-1,f(x)为奇函数,所以f=1,所以不等式f(2x-1)<1等价于f(2x-1)<f,又因为f(x)在(-1,1)上是减函数,所以2x-1>-,-1<2x-1<1,解得<x<1.所以不等式的解集为.【误区警示】解答本题(3)时易忽视函数定义域而得出解集为的错误.。
2019-2020学年数学人教A版必修1作业与测评:第一章 单元质量测评(一) Word版含解析

第一章单元质量测评(一)对应学生用书P83 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.已知集合A含有三个元素2,4,6,且当a∈A,有6-a∈A,则a为( )A.2 B.2或4 C.4 D.0答案 B解析6-2=4∈A,6-4=2∈A.选B.2.若集合P,Q满足P={x∈Z|x<3},Q⊆N,则P∩Q不可能是( ) A.{0,1,2} B.{1,2}C.{-1} D.∅答案 C解析依题意,知P∩Q中的元素可能是0,1,2,也可能没有元素,所以P∩Q不可能是{-1}.故选C.3.50名同学参加跳远和铅球测验,跳远和铅球测验成绩及格分别为40人和31人,2项测验成绩均不及格的有4人,2项测验成绩都及格的人数是( )A.35 B.25 C.28 D.15答案 B解析全班分4类人:设两项测验成绩都及格的人数为x人;仅跳远及格的人数为(40-x)人;仅铅球及格的人数为(31-x)人;两项都不及格的人数为4人,∴40-x+31-x+x+4=50,∴x=25.4.如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,则A*B=( )A.∁U(A∪B)B.A∪(∁U B)C.(∁U A)∪(∁U B)D.(A∪B)∩∁U(A∩B)答案 D解析阴影部分为A∪B去掉A∩B后的部分,为(A∪B)∩∁(A∩B).选D.U5.设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B =( )A.∅ B.{1} C.∅或{2} D.∅或{1}答案 D解析集合A中的元素可以由-1,-2,1,2中的一个或多个数构成,故A∩B=∅或A∩B={1}.6.已知集合M={x|-1<x<3},N={x|-2<x<1},则M∩N=( ) A.{x|-2<x<1} B.{x|-1<x<1}C.{x|1<x<3} D.{x|-2<x<3}答案 B解析在数轴上表示出集合,如图所示,由图知M ∩N ={x |-1<x <1}.7.若函数f (x )=x -4mx 2+4x +3的定义域为R ,则实数m 的取值范围是( )A .(-∞,+∞) B.⎝ ⎛⎭⎪⎫0,43C.⎝ ⎛⎭⎪⎫43,+∞D.⎣⎢⎡⎭⎪⎫0,43答案 C解析 ∵mx 2+4x +3≠0,∴⎩⎪⎨⎪⎧m ≠0,Δ=16-12m <0,∴m >43.选C.8.已知函数y =f (x +1)定义域是[-2,3],则y =f (x -1)的定义域是( )A .[0,5]B .[-1,4]C .[-3,2]D .[-2,3] 答案 A解析 由题意知,-2≤x ≤3,∴-1≤x +1≤4.∴-1≤x -1≤4,得0≤x ≤5,即y =f (x -1)的定义域为[0,5]. 9.若y =f (x )是R 上的减函数,对于x 1>0,x 2<0,则( ) A .f (-x 2)>f (-x 1) B .f (-x 2)<f (-x 1) C .f (-x 2)=f (-x 1) D .无法确定 答案 B解析 因为x 1>0,x 2<0,所以-x 2>-x 1,又y =f (x )是R 上的减函数,所以f (-x 2)<f (-x 1).10.设f (x )=⎩⎪⎨⎪⎧x +3,x >10,f [f x +],x ≤10,则f (5)的值是( )A .24B .21C .18D .16 答案 A解析 f (5)=f [f (10)],∵f (10)=f [f (15)]=f (18)=21,∴f (5)=f (21)=24.选A.11.已知函数f (x )是(-∞,0)∪(0,+∞)上的奇函数,且当x <0时,函数的图象如图所示,则不等式xf (x )<0的解集是( )A .(-2,-1)∪(1,2)B .(-2,-1)∪(0,1)∪(2,+∞)C .(-∞,-2)∪(-1,0)∪(1,2)D .(-∞,-2)∪(-1,0)∪(0,1)∪(2,+∞) 答案 D解析 当x >0时,f (x )<0由图象关于原点对称, ∴x ∈(0,1)∪(2,+∞);当x <0时,f (x )>0, ∴x ∈(-∞,-2)∪(-1,0).∴选D.12.已知奇函数f (x )、偶函数g (x )的图象分别如图1,2所示,方程f [g (x )]=0,g [f (x )]=0的实根个数分别为a ,b ,则a +b =( )A .14B .10C .7D .3 答案 B解析 如图,可知m ∈(-2,-1),n ∈(1,2).由方程f [g (x )]=0,可得g (x )=-1或g (x )=0或g (x )=1,∴x =-1,1,m,0,n ,-2,2,∴方程f [g (x )]=0有7个实根,即a =7;由方程g [f (x )]=0,可得f (x )=m (舍去)或f (x )=0或f (x )=n (舍去),∴x =-1,0,1,∴方程g [f (x )]=0有3个实根,即b =3,∴a +b =10,故选B.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.函数y =x +1+12-x 的定义域为________.答案 [-1,2)∪(2,+∞)解析 由题意知⎩⎪⎨⎪⎧x +1≥0,2-x ≠0,∴x ≥-1且x ≠2.14.如图所示为函数y =f (x ),x ∈[-4,7]的图象,则函数f (x )的单调递增区间是________.答案 [-1.6,3],[5,6]解析 结合函数单调递增的概念及单调区间的概念可知,此函数的单调递增区间是[-1.6,3],[5,6].15.函数f (x )在闭区间[-1,2]上的图象如图所示,则f -12=________,f (1)=________.答案 12 -12解析由题中图象,知y =⎩⎪⎨⎪⎧x +1,-1≤x <0,-12x ,0≤x ≤2,所以f -12=-12+1=12,f (1)=-12×1=-12.16.函数f (x )=2x 2-3|x |的单调减区间是________.答案 ⎝⎛⎭⎪⎫-∞,-34,⎝ ⎛⎭⎪⎫0,34解析 f (x )=⎩⎪⎨⎪⎧2x 2-3x ,x ≥0,2x 2+3x ,x <0,图象如下图所示,f (x )减区间为⎝⎛⎭⎪⎫-∞,-34,⎝ ⎛⎭⎪⎫0,34.三、解答题(本大题共6小题,满分70分)17.(本小题满分10分)全集U =R ,若集合A ={x |3≤x <10},B ={x |2<x ≤7}.(1)求A ∩B ,A ∪B ,(∁U A )∩(∁U B );(2)若集合C ={x |x >a },A ⊆C ,求a 的取值范围. 解 (1)A ∩B ={x |3≤x <10}∩{x |2<x ≤7}={x |3≤x ≤7};A ∪B ={x |3≤x <10}∪{x |2<x ≤7}={x |2<x <10};(∁U A )∩(∁U B )={x |x ≤2或x ≥10}.(2)A ={x |3≤x <10},C ={x |x >a },要使A ⊆C ,结合数轴分析可知a <3,即a 的取值范围是{a |a <3}.18.(本小题满分12分)设A ={x |2x 2+ax +2=0},B ={x |x 2+3x +2a =0},且A ∩B ={2}.(1)求a 的值及集合A ,B ;(2)设全集U =A ∪B ,求(∁U A )∪(∁U B ); (3)写出(∁U A )∪(∁U B )的所有子集.解 (1)由交集的概念易得2是方程2x 2+ax +2=0和x 2+3x +2a=0的公共解,则a =-5,此时A =⎩⎨⎧⎭⎬⎫12,2,B ={-5,2}.(2)由并集的概念易得U =A ∪B =⎩⎨⎧⎭⎬⎫-5,12,2.由补集的概念易得∁U A ={-5},∁U B =⎩⎨⎧⎭⎬⎫12.所以(∁U A )∪(∁U B )=⎩⎨⎧⎭⎬⎫-5,12.(3)(∁U A )∪(∁U B )的所有子集即为集合-5,12的所有子集:∅,⎩⎨⎧⎭⎬⎫12,{-5},⎩⎨⎧⎭⎬⎫-5,12.19.(本小题满分12分)设集合A ={a ,a 2,b +1},B ={0,|a |,b }且A =B .(1)求a ,b 的值;(2)判断函数f (x )=-bx -ax在[1,+∞)的单调性,并用定义加以证明.解 (1)由集合A =B 知,a ≠0,∴b +1=0, 即b =-1.此时A ={a ,a 2,0},B ={0,|a |,-1}, ∴a =-1,∴A ={-1,1,0},B ={0,1,-1},满足集合的互异性, ∴a =-1,b =-1.(2)由(1)知f (x )=x +1x ,f (x )=x +1x在[1,+∞)上单调递增.证明:任取x 1,x 2∈[1,+∞)且x 1<x 2,f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+1x 1-⎝ ⎛⎭⎪⎫x 2+1x 2=(x 1-x 2)+x 2-x 1x 1·x 2=(x 1-x 2)⎝⎛⎭⎪⎫1-1x 1·x 2 =(x 1-x 2)x 1·x 2-1x 1·x 2,∵x 1,x 2∈[1,+∞)且x 1<x 2, ∴x 1-x 2<0,x 1·x 2-1>0,x 1·x 2>0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )=x +1x在[1,+∞)上单调递增.20.(本小题满分12分)设f (x )为定义在R 上的偶函数,当x ≥0时,f (x )=-(x -2)2+2.(1)求函数f (x )在R 上的解析式; (2)在直角坐标系中画出函数f (x )的图象;(3)若方程f (x )-k =0有四个解,求实数k 的取值范围. 解 (1)若x <0,则-x >0,f (x )=f (-x )=-(-x -2)2+2=-(x +2)2+2,则f (x )=⎩⎪⎨⎪⎧-x -2+2,x ≥0,-x +2+2,x <0.(2)图象如图所示.(3)由于方程f (x )-k =0的解就是函数y =f (x )的图象与直线y =k 的交点的横坐标,观察函数y =f (x )图象与直线y =k 的交点情况可知,当-2<k <2时,函数y =f (x )图象与直线y =k 有四个交点,即方程f (x )-k =0有四个解.故k 的取值范围是-2<k <2.21.(本小题满分12分)已知二次函数f (x )的最小值为1,且f (0)=f (2)=3.(1)求f (x )的解析式;(2)若f (x )在区间[2a ,a +1]上不单调,求实数a 的取值范围; (3)在区间[-1,1]上,y =f (x )的图象恒在y =2x +2m +1图象的上方,试确定实数m 的取值范围.解 (1)由题意设f (x )=a (x -1)2+1, 将点(0,3)的坐标代入得a =2, 所以f (x )=2(x -1)2+1=2x 2-4x +3. (2)由(1)知f (x )的对称轴为直线x =1, 所以2a <1<a +1,所以0<a <12.即实数a 的取值范围为⎝⎛⎭⎪⎫0,12.(3)f (x )-2x -2m -1=2x 2-6x -2m +2,由题意得2x 2-6x -2m +2>0对于任意x ∈[-1,1]恒成立, 所以x 2-3x +1>m 对于任意x ∈[-1,1]恒成立, 令g (x )=x 2-3x +1,x ∈[-1,1], 则g (x )min =g (1)=-1,所以m <-1,故实数m 的取值范围为(-∞,-1).22.(本小题满分12分)已知全集U =R ,集合P ={x ∈R |x 2-3x +b =0},Q ={x ∈R |(x -2)(x 2+3x -4)=0}.(1)若b =4时,存在集合M 使得PM ⊆Q ,求出这样的集合M ;(2)集合P ,Q 是否能满足(∁U Q )∩P =∅?若能,求出实数b 的取值范围;若不能,请说明理由.解 (1)b =4时,P ={x ∈R |x 2-3x +4=0}=∅,Q ={x ∈R |(x -2)(x 2+3x -4)=0}={-4,1,2}.由PM ⊆Q ,知M 是一个非空集合,且是Q 的一个子集,所以用列举法可得这样的集合M 共有7个:{-4},{1},{2},{-4,1},{-4,2},{1,2},{-4,1,2}.(2)集合P ,Q 可以满足(∁U Q )∩P =∅. 由(∁U Q )∩P =∅,得P ⊆Q .当P =∅时,满足P ⊆Q ,此时Δ=9-4b <0, 解得b >94.当P ≠∅时,因为Q ={-4,1,2},若-4∈P ,则b =-28,此时P ={-4,7},不满足P ⊆Q ; 若1∈P ,则b =2,此时P ={1,2},满足P ⊆Q ;若2∈P ,则b =2,此时P ={1,2},满足P ⊆Q . 综上,可知当P =∅或P ={1,2}时,满足(∁U Q )∩P =∅,实数b 的取值范围是bb >94或b =2.。
2019-2020学年高一数学人教A版必修1练习:第一章单元检测Word版含解析

第一章单元检测时间:120分钟分值:150分一、选择题:本大题共12题,每题5分,共60分.在下列各题的四个选项中,只有一个选项是符合题目要求的.1.下列各图中,可表示函数y=f(x)的图象的只可能是( )答案:A解析:由函数概念,只有“一对一”或“多对一”对应,才能构成函数关系.2.下列函数中图象相同的是( )A.y=x与y=x2B.y=x-1与y=x2-1 x+1C.y=x2与y=2x2D.y=x2-4x+6与y=(x-2)2+2答案:D3.设全集U={1,2,3,4,5},A∩B={1,2},(?U A)∩B={3},A∩(?U B)={5},则A∪B是( ) A.{1,2,3} B.{1,2,5}C.{1,2,3,4} D.{1,2,3,5}答案:D解析:A∪B=(A∩B)∪[(?U A)∩B]∪[A∩(?U B)]={1,2,3,5}.4.已知f(x)=错误!则f(3)等于( )A.2 B.3C.4 D.5答案:A解析:f(3)=f(5)=f(7)=7-5=2.故选A.5.函数y=1-x+1x+1的定义域是( )A.(-∞,-1)∪(1,+∞)B.(-1,1)C.(-∞,-1)∪(-1,1]D.(-∞,-1)∪(-1,1)答案:C解析:1-x≥0且x+1≠0,∴x<-1或-1<x≤1.6.已知f(x)=2x+3,g(x+2)=f(x),则g(x)的解析式为( )A.g(x)=2x+1 B.g(x)=2x-1C.g(x)=2x-3 D.g(x)=2x+3答案:B解析:令t=x+2,则x=t-2,∴g(x+2)=g(t)=f(t-2),∴g(x)=f(x-2)=2(x-2)+3=2x-1. 7.已知集合M满足{1,2}?M?{1,2,3,4,5},那么这样的集合M的个数为( )A.5 B.6C.7 D.8答案:C解析:根据题意,M集合一定含有元素1,2,且为集合{1,2,3,4,5}的真子集,所以集合M的个数为23-1=7个。
2019学年人教版高中数学必修一:第一章单元质量评估1 Word版含答案

(人教版)精品数学教学资料第一章单元质量评估(一)时限:120分钟 满分:150分一、选择题(每小题5分,共60分)1.已知全集U ={0,1,2,3,4},集合A ={1,2,3},B ={2,4},则(∁U A )∪B 为( )A .{1,2,4}B .{2,3,4}C .{0,2,4}D .{0,2,3,4}2.如图可作为函数y =f (x )的图象的是( )3.已知集合M ={y |y =x 2-1,x ∈R },N ={x |y =2-x 2},则M ∩N =( )A .[-1,+∞)B .[-1,2]C .[2,+∞)D .∅4.已知集合A ={1,3,m },B ={1,m },A ∪B =A ,则m =( ) A .0或 3 B .0或3 C .1或 3D .1或35.设函数f (x )=⎩⎨⎧x 2+1,x ≤1,2x ,x >1,则f (f (3))=( )A.15 B .3 C.23D.1396.下列函数中,不满足f (2x )=2f (x )的是( ) A .f (x )=|x | B .f (x )=x -|x | C .f (x )=x +1D .f (x )=-x7.已知A ={0,1},B ={-1,0,1},f 是从A 到B 映射的对应关系,则满足f (0)>f (1)的映射有( )A .3个B .4个C .5个D .6个8.若函数y =f (x )的定义域是[-2,4],则函数g (x )=f (x )+f (-x )的定义域是( )A .[-4,4]B .[-2,2]C .[-4,-2]D .[2,4]9.向高为H 的水瓶中注水,注满为止,如果注水量V 与水深h 的函数关系的图象如图所示,那么水瓶的形状是( )10.已知函数f (x )=12x 2-kx -8在区间[2,8]上具有单调性,则实数k 的取值范围是( )A .(-∞,2]B .[8,+∞)C .(-∞,2]∪[8,+∞)D .∅11.已知某种产品的购买量y (单位:吨)与单价x (单位:元)之间满足一次函数关系.如果购买1 000吨,每吨为800元;购买2 000吨,每吨为700元,若一客户购买400吨,则单价应该是( )A .820元B .840元C .860元D .880元12.对于任意两个正整数m ,n 定义某种运算“※”如下:当m ,n 都为正偶数或正奇数时,m ※n =m +n ;当m ,n 中一个为正偶数,另一个为正奇数时,m ※n =mn .则在此定义下,集合M ={(a ,b )|a ※b =12,a ∈N *,b ∈N *}中的元素个数是( )A .10B .15C .16D .18二、填空题(每小题5分,共20分) 13.函数y =x +1x 的定义域为________.14.若函数f (x )=⎩⎪⎨⎪⎧x +1,x ≥0,f (x +2),x <0,则f (-3)=________.15.已知二次函数f (x )=ax 2+2ax +1在区间[-3,2]上的最大值为4,则a 的值为________.答案1.C 先求集合A 关于全集U 的补集,再求它与集合B 的并集即可.(∁U A )∪B ={0,4}∪{2,4}={0,2,4}.2.D 只有选项D 中对定义域内任意x 都有唯一的y 值与之对应. 3.B 根据题意知集合M 是函数y =x 2-1,x ∈R 的值域[-1,+∞),集合N 是函数y =2-x 2的定义域[-2,2],所以M ∩N =[-1,2].4.B 依据并集的概念及A ∪B =A 可知,m =3或m =m ,由m =m 解得m =0或m =1.当m =0或m =3时,符合题意;当m =1时,不满足集合中元素的互异性,因此应舍去.综上可知m =0或m =3.5.D 由题意得f (3)=23,从而f (f (3))=f (23)=(23)2+1=139. 6.C 将选项中的函数逐个代入f (2x )=2f (x )去验证.f (x )=kx 与f (x )=k |x |均满足:f (2x )=2f (x ),故A ,B ,D 满足条件.7.A 当f (0)=1时,f (1)的值为0或-1都能满足f (0)>f (1);当f (0)=0时,只有f (1)=-1满足f (0)>f (1);当f (0)=-1时,没有f (1)的值满足f (0)>f (1),故有3个.8.B 由⎩⎪⎨⎪⎧-2≤x ≤4,-2≤-x ≤4,得-2≤x ≤2.9.B 取h =H 2,由图象可知,此时注水量V 大于容器容积的12,故选B.10.C f (x )=12x 2-kx -8的单调增区间是[k ,+∞),单调减区间是(-∞,k ],由f (x )在区间[2,8]上具有单调性可知[2,8]⊆[k ,+∞)或[2,8]⊆(-∞,k ],所以k ≤2或k ≥8.11.C 设y =kx +b (k ≠0),由题意得⎩⎪⎨⎪⎧1 000=800k +b ,2 000=700k +b ,解得k =-10,b =9 000. ∴y =-10x +9 000,当y =400时,得x =860.12.B 当m ,n 都为正偶数或正奇数时,m +n =12,故对应的元素为(1,11),(2,10),(3,9),(4,8),…,(10,2),(11,1),共11个;当m ,n 中一个为正偶数,另一个为正奇数时,mn =12,故对应的元素为(1,12),(3,4),(4,3),(12,1),共4个.故集合M 中的元素共15个.13.{x |x ≥-1,且x ≠0}解析:求函数的定义域就是求使解析式有意义的自变量的取值集合,本小题涉及分式,要注意分母不能等于0,偶次根式被开方数是非负数.由⎩⎪⎨⎪⎧x +1≥0,x ≠0得函数的定义域为{x |x ≥-1,且x ≠0}.14.2解析:f (-3)=f (-3+2)=f (-1)=f (-1+2)=f (1)=1+1=2. 15.-3或38解析:f (x )的对称轴为x =-1,当a >0时, f (x )max =f (2)=4,解得a =38;当a <0时,f (x )max =f (-1)=4,解得a =-3.———————————————————————————— 16.若函数f (x )同时满足①对于定义域上的任意x ,恒有f (x )+f (-x )=0;②对于定义域上的任意x 1,x 2,当x 1≠x 2时,恒有f (x 1)-f (x 2)x 1-x 2<0,则称函数f (x )为“理想函数”.给出下列三个函数中:(1)f (x )=1x .(2)f (x )=x 2.(3)f (x )=⎩⎪⎨⎪⎧-x 2,x ≥0,x 2,x <0.能被称为“理想函数”的有________(填相应的序号).三、解答题(写出必要的计算步骤、解答过程,只写最后结果的不得分,共70分)17.(10分)已知全集U=R,集合A={y|y=3-x2,x∈R,且x≠0},集合B是函数y=x-2+25-x的定义域,集合C={x|5-a<x<a}.(1)求集合A∪(∁U B)(结果用区间表示);(2)若C⊆(A∩B),求实数a的取值范围.(12分)已知函数f(x)=|x-1|.(1)用分段函数的形式表示该函数;(2)在平面直角坐标系中画出该函数的图象;(3)写出该函数的定义域、值域、奇偶性和单调区间(不要求证明).答案16.(3)解析:①要求函数f (x )为奇函数,②要求函数f (x )为减函数,(1)是奇函数但不是定义域上的减函数,(2)是偶函数而且也不是定义域上的减函数,只有(3)既是奇函数又是定义域上的减函数.17.解:(1)由已知得 A ={x |x <3},B ={x |2≤x <5}, ∴∁U B ={x |x <2,或x ≥5},∴A ∪(∁U B )={x |x <3,或x ≥5}=(-∞,3)∪[5,+∞). (2)由(1)知A ∩B ={x |2≤x <3},当C =∅时,满足C ⊆(A ∩B ),此时5-a ≥a ,解得a ≤52; 当C ≠∅时,要满足C ⊆(A ∩B ), 则⎩⎪⎨⎪⎧5-a <a ,5-a ≥2,a ≤3,解得52<a ≤3.综上可得a ≤3.18.解:(1)f (x )=⎩⎪⎨⎪⎧x -1,x ≥1,1-x ,x <1.(2)图象如图所示:(3)函数f (x )的定义域为R ,值域为[0,+∞),它既不是奇函数也不是偶函数,单调减区间为(-∞,1),单调增区间为[1,+∞).————————————————————————————19.(12分)已知函数f (x )=2x +1x +1,(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论; (2)求该函数在区间[1,4]上的最大值与最小值.20. (12分)已知奇函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0.(1)求实数m 的值;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.答案19.解:(1)函数f (x )在[1,+∞)上是增函数. 任取x 1,x 2∈[1,+∞),且x 1<x 2,f (x 1)-f (x 2)=2x 1+1x 1+1-2x 2+1x 2+1=x 1-x 2(x 1+1)(x 2+1),∵x 1-x 2<0,(x 1+1)(x 2+1)>0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以函数f (x )在[1,+∞)上是增函数.(2)由(1)知函数f (x )在[1,4]上是增函数,最大值f (4)=95,最小值f (1)=32.20.解:(1)当x <0时,-x >0,∴f (-x )=-(-x )2+2(-x )=-x 2-2x ,又f (x )是奇函数,∴f (-x )=-f (x ),于是当x <0时,f (x )=x 2+2x =x 2+mx ,∴m =2.(2)结合f (x )的图象(图略)可知,要使f (x )在[-1,a -2]上单调递增,需⎩⎪⎨⎪⎧a -2>-1,a -2≤1,解得1<a ≤3. 故实数a 的取值范围为(1,3].————————————————————————————21.(12分)设f(x)是定义在R上的函数,对任意x,y∈R,恒有f(x+y)=f(x)+f(y).(1)求f(0)的值;(2)求证:f(x)为奇函数;(3)若函数f(x)是R上的增函数,已知f(1)=1,且f(2a)>f(a-1)+2,求a的取值范围.22. (12分)已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.(1)求f(x)的解析式;(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.答案21.解:(1)令x=y=0,则f(0)=f(0)+f(0)⇒f(0)=0.(2)证明:令y=-x,则f(0)=f(x)+f(-x)⇒f(-x)=-f(x),所以f(x)为R上的奇函数.(3)令x=y=1,则f(1+1)=f(2)=f(1)+f(1)=2,∴f(2a)>f(a-1)+2⇔f(2a)>f(a-1)+f(2)⇒f(2a)>f(a+1).又因为f(x)是R上的增函数,所以2a>a+1⇒a>1,所以a的取值范围是(1,+∞).22.解:(1)由题意设f(x)=a(x-1)2+1,代入(2,3)得a=2,所以f(x)=2(x-1)2+1=2x2-4x+3.(2)对称轴为x =1,所以2a <1<a +1,所以0<a <12.(3)f (x )-2x -2m -1=2x 2-6x -2m +2,由题意得2x 2-6x -2m +2>0对于任意x ∈[-1,1]恒成立, 所以x 2-3x +1>m 对于任意x ∈[-1,1]恒成立, 令g (x )=x 2-3x +1,x ∈[-1,1],则g (x )min =-1,所以m <-1.。
(完整word版)人教版高中数学必修一第一章单元测试(含

第3题图高中数学《必修一》第一章教学质量检测卷一、选择题(将选择题的答案填入下面的表格.本大题共10小题,每小题5分,共50分。
)题号12345678910答案1、下列各组对象中不能构成集合的是( )A、佛冈中学高一(20)班的全体男生B、佛冈中学全校学生家长的全体C、李明的所有家人D、王明的所有好朋友( )A.{1,2,3,4,5} B.{2,3,4,5}C.{2,3,4},则图中的阴影部分表示的集合为( )的值是 ( )A、3B、1 C. 0 D。
-18、下列四个图像中,不可能是函数图像的是 ( )9、设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(—2),f题号一二151617181920总分得分10、在集合{a,b,c,d}上定义两种运算和如下:A.a B.b C.c D.d二、填空题(本大题共4小题,每小题5分,共20分)的定义域为在区间[0,4]的最大值是B是 .16上是减函数。
其中真命题的序号是 (把你认为正确的命题的序号都填上)。
三、解答题(本大题6小题,共80分。
解答时应写出文字说明、证明过程或演算步骤).15、(本题满分12分)已知集合a的取值范围.16、(本题满分1217、(本题满分1418、 (本题满分14分)已知函(1)用分段函数的形式表示该函数;(2)画出该函数的图象;(3)写出该函数的值域.19、(本题满分1420、 (本题满分14高中数学《必修一》第一章教学质量检测卷参考答案一、选择题题号12345678910答案D D B C C A A B A C二、填空题12、-1 13、 14、①②三、解答题15、解:(1)A∪B={x∣2<x<10}……………..4分(2)(C R A)∩B={ x∣2〈x〈3或7≤x<10}...。
..。
.。
.。
.。
..。
...。
8分(3)a≥7.。
..。
.。
.。
..。
12分16.解:.2分证明:的定义域是,定义域关于原点对称…………….4分内任取一个x,则有。
2019-2020人教版高中数学必修一第一章单元测试(一)--Word版含答案
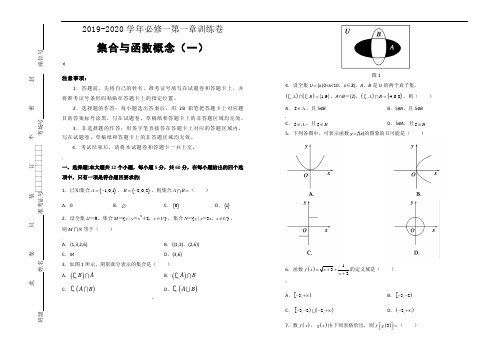
2019-2020学年必修一第一章训练卷 集合与函数概念(一) (注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
'一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}1,0,1A =-,{}2,0,2B =-,则集合A B =( )A .0B .∅C .{}0D .{}1 2.设全集U =R ,集合22{|}M y y x x U ∈==+,,集合3{|}N y y x x U ∈==,,则M N 等于( );A .{1,3,2,6}B .{(1,3),(2,6)}C .MD .{3,6}3.如图1所示,阴影部分表示的集合是( )A .()U B A B .()U A B C .()U A B D .()U A B*图1 4.设全集U ={x |0<x <10,x ∈Z },A ,B 是U 的两个真子集, ()(){}1,9U U A B =,A ∩B ={2},(){}4,6,8U A B =,则( ) A .5A ∈,且5∉B B .5∉A ,且5∉B : C .5A ∈,且5B ∈ D .5∉A ,且5B ∈ 5.下列各图中,可表示函数y =f (x )的图象的只可能是( )6.函数()132f x x x =+++的定义域是( ) ^ A .[)3,-+∞ B .[)3,2-- C .[)()3,22,---+∞ D .()2,-+∞ 7.数()f x ,()g x 由下列表格给出,则()3f g =⎡⎤⎣⎦( ) 此卷只装订不密封 班级姓名准考证号考场号座位号A .4B .3C .2D .1 ;8.已知函数()2,0,0x x f x x x ≥⎧⎪⎨<⎪⎩=,则2[()]f f -的值是( )A .2B .2-C .4D .4-9.函数223y x x -=+,12x -≤≤的值域是( )A .RB .[3,6]C .[2,6]D .[2,)+∞10.已知函数f (x )()()00,∞∞-,+上的奇函数,且当x <0时,函数的部分图象如图4所示,则不等式xf (x )<0的解集是( ) !图4A .()2,112(),--B .()2,10,)(2,(1)--+∞C .()(),21,01(,2)--∞-D .(),21,00,12,()()()∞-+∞--11.定义在R 上的偶函数f (x )在[0,7]上是增函数,在[7,)+∞上是减函数,f (7)=6,则f (x )( )/A .在[]7,0-上是增函数,且最大值是6B .在[]7,0-上是减函数,且最大值是6C .在[]7,0-上是增函数,且最小值是6D .在[]7,0-上是减函数,且最小值是612.定义在R 上的偶函数f (x )满足:对任意12(,]0x x -∈∞, (x 1≠x 2),都有2121>0x x f x f x -()-(),则( ) - A .5()f -<f (4)<f (6) B .f (4)<5()f - <f (6) C .f (6)<5()f -<f (4) D .f (6)<f (4)<5()f - 二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.设P 和Q 是两个集合,定义集合{|}P Q x x P x Q -=∈∉,且,若P ={1,2,3,4},1Q=<2,2x x ⎧⎫⎪⎪+∈⎨⎬⎪⎪⎩⎭R ,则P Q -=________. $ 14.函数223y x x +-的单调递减区间是________. 15.若函数()2(12)f x kx k x -=++是偶函数,则f (x )的递减区间是________. 16.设函数()1,0221,02x x x x f x x ⎧-<<⎪=⎨--≤≥⎪⎩或,则函数y =f (x ),y =12的图象的交点个数是________. 三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤) ] 17.(10分)已知集合A ={x |2≤x ≤8},B ={x |1<x <6},C ={x |x >a },U =R . (1)求A ∪B ,()U A B ; (2)若A C ≠∅,求a 的取值范围. ~【《|18.(12分)设A ={x |x 2+2(a +1)x +a 2-1=0},{|(02)14B x x x x ⎛⎫⎪⎝-⎭=+=,x ∈Z}.若A ∩B =A ,求a 的取值范围.)》*19.(12分)已知函数f (x )=-2x +m ,其中m 为常数.(1)求证:函数f (x )在R 上是减函数;(2)当函数f (x )是奇函数时,求实数m 的值.'[ ] 、 20.(12分)某公司生产的水笔上年度销售单价为08.元,年销售量为1亿支.本年度计划将销售单价调至055075.~.元(含端点值),经调查,若销售单价调至x 元,则本年度新增销售量y (亿支)与04x -.成反比,且当065x =.时,08y =.. (1)求y 与x 的函数关系式; (2)若每支水笔的成本价为03.元,则水笔销售单价调至多少时,本年度该公司的收益比上年度增加20% · %,`【21.(12分)已知函数f(x)是正比例函数,函数g(x)是反比例函数,且f(1)=1,g(1)=2,(1)求函数f(x)和g(x);(2)判断函数f(x)+g(x)的奇偶性.(3)求函数f(x)+g(x)在(上的最小值.- ) 。
人教版2019年高一数学必修一-第一章练习题与配套参考答案(解析版)

集合与函数基础测试一、选择题(共12小题,每题5分,四个选项中只有一个符合要求)1.函数y ==x 2-6x +10在区间(2,4)上是( )A .递减函数B .递增函数C .先递减再递增D .选递增再递减.2.方程组20{=+=-y x y x 的解构成的集合是 ( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{3.已知集合A ={a ,b ,c },下列可以作为集合A 的子集的是 ( )A. aB. {a ,c }C. {a ,e }D.{a ,b ,c ,d }4.下列图形中,表示N M ⊆的是 ( )5.下列表述正确的是 ( )A.}0{=∅B. }0{⊆∅C. }0{⊇∅D. }0{∈∅6、设集合A ={x|x 参加自由泳的运动员},B ={x|x 参加蛙泳的运动员},对于“既参加自由泳又参加蛙泳的运动员”用集合运算表示为 ( )A.A∩BB.A ⊇BC.A ∪BD.A ⊆B7.集合A={x Z k k x ∈=,2} ,B={Z k k x x ∈+=,12} ,C={Z k k x x ∈+=,14}又,,B b A a ∈∈则有( )A.(a+b )∈ AB. (a+b) ∈BC.(a+b) ∈ CD. (a+b) ∈ A 、B 、C 任一个8.函数f (x )=-x 2+2(a -1)x +2在(-∞,4)上是增函数,则a 的范围是( )A .a ≥5B .a ≥3C .a ≤3D .a ≤-59.满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是( ) A. 8 B. 7 C. 6 D. 510.全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },那么集合 { 2 ,7 ,8}是 ( )A. A B YB. B A IC. B C A C U U ID. B C A C U U Y11.下列函数中为偶函数的是( )A .x y =B .x y =C .2x y =D .13+=x y12. 如果集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ( )A .0B .0 或1C .1D .不能确定二、填空题(共4小题,每题4分,把答案填在题中横线上)13.函数f (x )=2×2-3|x |的单调减区间是___________.14.函数y =11+x 的单调区间为___________. 15.含有三个实数的集合既可表示成}1,,{ab a ,又可表示成}0,,{2b a a +,则=+20042003b a M N A M N B N M C M N D=N ,=⋂)(N C M U ,=⋃N M .三、解答题(共4小题,共44分)17. 已知集合}04{2=-=x x A ,集合}02{=-=ax x B ,若A B ⊆,求实数a 的取值集合.18. 设f (x )是定义在R 上的增函数,f (xy )=f (x )+f (y ),f (3)=1,求解不等式f (x )+f (x -2)>1.19. 已知函数f (x )是奇函数,且当x >0时,f (x )=x 3+2x 2—1,求f (x )在R 上的表达式.20. 已知二次函数222)1(2)(m m x m x x f -+-+-=的图象关于y 轴对称,写出函数的解析表达式,并求出函数)(x f 的单调递增区间.必修1 第一章 集合测试集合测试参考答案:一、1~5 CABCB 6~10 ABACC 11~12 cB二、13 [0,43],(-∞,-43) 14 (-∞,-1),(-1,+∞) 15 -1 16 03|{≤≤-=x x N 或}32≤≤x ;}10|{)(<<=⋂x x N C M U ;13|{<≤-=⋃x x N M 或}32≤≤x .三、17 .{0.-1,1}; 18. 解:由条件可得f (x )+f (x -2)=f [x (x -2)],1=f (3). 所以f [x (x -2)]>f (3),又f (x )是定义在R 上的增函数,所以有x (x -2)>3,可解得x >3或x <-1.答案:x >3或x <-1.19. .解析:本题主要是培养学生理解概念的能力.f (x )=x 3+2x 2-1.因f (x )为奇函数,∴f (0)=-1.当x <0时,-x >0,f (-x )=(-x )3+2(-x )2-1=-x 3+2x 2-1,∴f (x )=x 3-2x 2+1.20. Θ二次函数222)1(2)(m m x m x x f -+-+-=的图象关于y 轴对称,∴1=m ,则1)(2+-=x x f ,函数)(x f 的单调递增区间为(]0,∞-..。
新教材人教版高中数学必修1 第一章 单元质量测评

第一章单元质量测评本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列语句是命题的是()A.2x2+3x-1>0 B.比较两数大小C.撸起袖子加油干!D.cos45°=2 2答案 D解析A项不能判断真假,不是命题;B,C两项不是陈述句,不是命题;D 项是命题.2.下面所给三个命题中真命题的个数是()①若ac2>bc2,则a>b;②若四边形的对角互补,则该四边形是圆的内接四边形;③若二次函数y=ax2+bx+c中,b2-4ac<0,则该二次函数的图象与x轴有公共点.A.0 B.1C.2 D.3答案 C解析①该命题为真命题,由ac2>bc2,得c2>0,则有a>b.②该命题为真命题,根据圆内接四边形的定义可进行判定.③该命题为假命题,因为当b2-4ac<0时,一元二次方程ax2+bx+c=0没有实数根,因此二次函数的图象与x轴无公共点.综上所述,故选C.3.命题“∀x∈R,|x|+x2≥0”的否定是()A.∀x∈R,|x|+x2<0B.∀x∈R,|x|+x2≤0C.∃x∈R,|x|+x2<0D.∃x∈R,|x|+x2≥0答案 C解析“∀x∈R,|x|+x2≥0”的否定是“∃x∈R,|x|+x2<0”.4.已知x 1,x 2∈R ,则“x 1>1且x 2>1”是“x 1+x 2>2且x 1x 2>1”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件 答案 A解析 由x 1>1且x 2>1得x 1+x 2>1+1=2,x 1x 2>1×1=1,所以“x 1>1且x 2>1”是“x 1+x 2>2且x 1x 2>1”的充分条件;设x 1=3,x 2=12,则x 1+x 2=72>2且x 1x 2=32>1,但x 2<1,所以不满足必要性.故选A.5.下列命题中,真命题有( )①mx 2+2x -1=0是关于x 的一元二次方程;②抛物线y =ax 2+2x -1与x 轴至少有一个交点;③互相包含的两个集合相等;④空集是任何集合的真子集.A .1个B .2个C .3个D .4个答案 A解析 对于①来说,当m =0时,mx 2+2x -1=0是一元一次方程;对于②来说,抛物线y =ax 2+2x -1对应的一元二次方程的判别式Δ=4+4a ,当a <-1时,方程无实数根,此时抛物线与x 轴无交点;③正确,A ⊆B ,B ⊆A ⇔A =B ;空集是任何集合的子集,是任何非空集合的真子集,故④错误.6.“a 2+(b -1)2=0”是“a (b -1)=0”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件 答案 A解析 a 2+(b -1)2=0⇒a =0且b =1,而a (b -1)=0⇒a =0或b =1,故“a 2+(b -1)2=0”是“a (b -1)=0”的充分不必要条件.7.已知集合A ={1,2,3,4,5},B ={(x ,y )|x ∈A ,y ∈A ,x -y ∈A },则B 中所含元素的个数为( )A .3B .6C .8D .10 答案 D解析 当x =5时,y =1,2,3,4;当x =4时,y =1,2,3;当x =3时,y =1,2;当x =2时,y =1,共10个.故选D.8.在下列命题中,真命题的个数是( ) ①∀x ∈R ,x 2+x +3>0; ②∀x ∈Q ,13x 2+1是有理数;③关于x 的方程x 2+|x |-6=0有四个实数根; ④∃x ,y ∈Z,3x -2y =10. A .1 B .2 C .3 D .4答案 C解析 ①中,x 2+x +3=⎝ ⎛⎭⎪⎫x +122+114>0,故①是真命题;②中,∵x ∈Q ,∴13x 2+1是有理数,故②是真命题;③中,由x 2+|x |-6=0,得|x |=2,∴x =±2,方程有两个实数根,故③是假命题;④中,当x =4,y =1时,结论成立,故④是真命题.由以上可知,正确选项为9.给出下列四个命题:①设集合X ={x ②空集是任何集合的真子集;③集合A ={y |y =表示同一集合; ④集合P ={a ,其中正确的命题是A .①② B .①③ C .③④ D .④ 答案 D解析 ①中{0}与X 均表示集合,不能用∈来表示集合与集合之间的关系,①不正确;②中空集是任何非空集合的真子集,②不正确;③中A ={y |y ≥0},B ={x |x ≥1或x ≤-1},故不是同一集合,③不正确;④中根据集合中元素的无序性知④正确.故选D.10.下列命题中,是全称量词命题且是真命题的是( ) A .对任意的a ,b ∈R ,都有a 2+b 2-2a -2b +2<0 B .菱形的两条对角线相等 C .∀x ∈R ,x 2=x D .正方形是矩形 答案 D解析A中的命题是全称量词命题,但a2+b2-2a-2b+2=(a-1)2+(b-1)2≥0,故是假命题;B中的命题是全称量词命题,但是假命题;C中的命题是全称量词命题,但x2=|x|,故是假命题;D中的命题是全称量词命题且是真命题,故选D.11.设U为全集,A,B是集合,则“存在集合C使得A⊆C,B⊆∁U C”是“A∩B=∅”的()A.充分而不必要的条件B.必要而不充分的条件C.充要条件D.既不充分也不必要的条件答案 C解析若存在集合C使得A⊆C,B⊆∁U C,则可以推出A∩B=∅;若A∩B=∅,由Venn图可知,存在A=C,同时满足A⊆C,B⊆∁U C.故“存在集合C使得A⊆C,B⊆∁U C”是“A∩B=∅”的充要条件.12.已知△ABC的边长为a,b,c,定义它的等腰判别式为D=max{a-b,b-c,c-a}+min{a-b,b-c,c-a},则“D=0”是“△ABC为等腰三角形”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 C解析充分性:若“D=0”,设c≥b≥a,则D=max{a-b,b-c,c-a}+min{a-b,b-c,c-a}=c-a+b-c=0或c-a+a-b=0,∴a=b或b=c,则△ABC一定为等腰三角形,所以充分性成立.必要性:若△ABC为等腰三角形,设a=b,当c≠a时,则b-c与c-a中必然有一个为最大值,另一个为最小值,则D=b-c+c-a=b-a=0;当c=a 时,D=0+0=0,所以必要性成立.故选C.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横线上)13.“红豆生南国,春来发几枝?愿君多采撷,此物最相思.”这是唐代诗人王维的《相思》诗,在这四句诗中,可作为命题的是________________.答案红豆生南国解析“红豆生南国”是陈述句,意思是“红豆生长在中国南方”,这在唐代是事实,故本语句是命题,且是真命题;“春来发几枝”是疑问句,“愿君多采撷”是祈使句,“此物最相思”是感叹句,都不是命题.14.设x∈R,则“x>1”是“x3>1”的________条件.答案充要解析因为x∈R,“x>1”⇔“x3>1”,所以“x>1”是“x3>1”的充要条件.15.命题p:∀x∈R,x2+x+1≠0,则命题綈p为________________.答案∃x∈R,x2+x+1=0解析命题p是全称量词命题,根据全称量词命题的否定是改量词,否结论,则是∃x∈R,x2+x+1=0.16.由命题“∃x∈R,x2+2x+m=0”是假命题,求得实数m的取值范围是m>a,则实数a=________.答案 1解析因为命题“∃x∈R,x2+2x+m=0”是假命题,所以其否定“∀x∈R,x2+2x+m≠0”是真命题,等价于方程x2+2x+m=0无实根,所以Δ=4-4m<0,解得m>1,又因为m的取值范围是(a,+∞),所以实数a=1.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)写出下列命题的否定,并判断真假.(1)p1:∃x∈R,x2-x+1≤0;(2)p2:所有的菱形都是平行四边形;(3)p3:有的梯形是等腰梯形;(4)p4:任意x∈Z,x2的个位数字不等于3;(5)p5:有一个素数含三个正因数.解(1)綈p1:∀x∈R,x2-x+1>0;真命题.(2)綈p2:存在一个菱形,它不是平行四边形;假命题.(3)綈p3:所有的梯形都不是等腰梯形;假命题.(4)綈p4:存在x∈Z,使x2的个位数字等于3;假命题.(5)綈p 5:所有的素数都不含三个正因数;真命题.18.(本小题满分12分)已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},且B ≠∅.(1)若“命题p :∀x ∈B ,x ∈A ”是真命题,求m 的取值范围; (2)若“命题q :∃x ∈A ,x ∈B ”是真命题,求m 的取值范围.解 (1)∵A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},且B ≠∅,“命题p :∀x ∈B ,x ∈A ”是真命题,∴B ⊆A ,B ≠∅,∴⎩⎨⎧m +1≤2m -1,m +1≥-2,2m -1≤5,解得2≤m ≤3. (2)q 为真,则A ∩B ≠∅. ∵B ≠∅,∴m ≥2,∴⎩⎨⎧-2≤m +1≤5,m ≥2,∴2≤m ≤4. 19.(本小题满分12分)已知集合A ={x |-1<x <3},B ={x |x ≤m -1或x ≥m +1}.(1)当m =0时,求A ∩B ;(2)若p :-1<x <3,q :x ≤m -1或x ≥m +1,且q 是p 的必要不充分条件,求实数m 的取值范围.解 (1)当m =0时,B ={x |x ≤-1或x ≥1}, 又A ={x |-1<x <3},所以A ∩B ={x |1≤x <3}. (2)因为p :-1<x <3,q :x ≤m -1或x ≥m +1.q 是p 的必要不充分条件,所以m -1≥3或m +1≤-1,所以m ≤-2或m ≥4. 20.(本小题满分12分)求关于x 的方程ax 2+2x +1=0的实数根中有且只有一个负实数根的充要条件.解 若方程ax 2+2x +1=0有且仅有一个负实数根,则:当a =0时,x =-12,符合题意.当a ≠0时,方程ax 2+2x +1=0有实数根,则Δ=4-4a ≥0,解得a ≤1, 当a =1时,方程有且仅有一个负实数根x =-1,当a <1且a ≠0时,若方程有且仅有一个负实数根,则1a <0,即a <0.又以上过程均可逆,所以方程ax 2+2x +1=0有且仅有一个负实数根”的充要条件为“a ≤0或a =1”.21.(本小题满分12分)设a ,b ,c 为△ABC 的三边,求证:方程x 2+2ax +b 2=0与x 2+2cx -b 2=0有公共根的充要条件是∠A =90°.证明 必要性:方程x 2+2ax +b 2=0与x 2+2cx -b 2=0有公共根ξ, 则⎩⎨⎧ξ2+2aξ+b 2=0,ξ2+2cξ-b 2=0⇒ξ=-b 2a -c =b 2c -a .∴⎝ ⎛⎭⎪⎫b 2c -a 2+2c ·b 2c -a -b 2=0⇒a 2=b 2+c 2,∴∠A =90°.充分性:若∠A =90°,则a 2=b 2+c 2,解方程x 2+2ax +b 2=0得x =-2a ±4a 2-4b 22=-a ±c ,解方程x 2+2cx -b 2=0得x =-2c ±4c 2+4b 22=-c ±a ,得x 0=-a -c 是方程的公共根.综上可知,方程x 2+2ax +b 2=0与x 2+2cx -b 2=0有公共根的充要条件是∠A =90°.22.(本小题满分12分)已知两个关于x 的一元二次方程mx 2-4x +4=0和x 2-4mx +4m 2-4m -5=0,其中m ∈Z ,求这两个方程的根均为整数的充要条件.解 ∵mx 2-4x +4=0是一元二次方程,∴m ≠0.又另一方程为x 2-4mx +4m 2-4m -5=0,且两方程都有实根, ∴⎩⎨⎧Δ1=16-16m ≥0,Δ2=16m 2-4(4m 2-4m -5)≥0, 解得-54≤m ≤1.∵两方程的根都是整数,故其根的和与积也是整数, ∴⎩⎪⎨⎪⎧4m ∈Z ,4m ∈Z ,4m 2-4m -5∈Z ,∴m 为4的约数.又-54≤m ≤1,m ≠0,m ∈Z ,∴m =-1或1.当m =-1时,第一个方程x 2+4x -4=0的根不是整数;当m =1时,两方程的根均为整数.又以上过程均可逆,∴这两个方程的根均为整数的充要条件是m =1.。
最新高一人教版数学必修一练习:第一章 单元质量测评1 Word版含解析

最新人教版数学精品教学资料第一章单元质量测评(一) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.[2015·广东高考]已知集合M={-1,0,1},N={0,1,2},则M ∪N=()A.{0,1} B.{-1,0,2}C.{-1,0,1,2} D.{-1,0,1}答案 C解析依题意得M∪N={-1,0,1,2},故选C.2.[2015·天津高考]已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁U B=()A.{2,5} B.{3,6}C.{2,5,6} D.{2,3,5,6,8}答案 A解析因为∁U B={2,5,8},又A={2,3,5,6},所以A∩∁U B={2,5},故选A.3.50名同学参加跳远和铅球测验,跳远和铅球测验成绩分别为及格40人和31人,2项测验成绩均不及格的有4人,2项测验成绩都及格的人数是()A.35 B.25C.28 D.15答案 B解析全班分4类人:设两项测验成绩都及格的人数为x人;仅跳远及格的人数为(40-x)人;仅铅球及格的人数为(31-x)人;两项都不及格的人数为4人,∴40-x +31-x +x +4=50,∴x =25.4.[2015·陕西工大附中高一质检]如图所示的韦恩图中A ,B 是非空集合,定义集合A *B 为阴影部分表示的集合,则A *B =( )A .∁U (A ∪B ) B .A ∪(∁U B )C .(∁U A )∪(∁U B )D .(A ∪B )∩∁U (A ∩B )答案 D解析 阴影部分为A ∪B 去掉A ∩B 后的部分,为(A ∪B )∩∁U (A ∩B ).选D.5.函数f (x )是定义在[0,+∞)上的增函数,则满足f (2x -1)<f ⎝ ⎛⎭⎪⎫13的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13,23B.⎣⎢⎡⎭⎪⎫13,23 C.⎝ ⎛⎭⎪⎫12,23 D.⎣⎢⎡⎭⎪⎫12,23 答案 D 解析根据题意,得⎩⎨⎧2x -1≥0,2x -1<13,解得12≤x <23,选D.6.[2015·攀枝花米易中学月考]已知函数f (x )的定义域为(3-2a ,a +1),且f (x +1)为偶函数,则实数a 的值可以是( )A .2 B.23 C .4 D .6答案 A解析 因为函数f (x )的定义域为(3-2a ,a +1),所以在函数f (x+1)中,3-2a <x +1<a +1,则函数f (x +1)的定义域为(2-2a ,a ),又因为f (x +1)为偶函数,所以2-2a =-a ,a =2,故选A.7.[2015·衡水高一调研]已知函数y =f (x +1)定义域是[-2,3],则y =f (x -1)的定义域是( )A .[0,5]B .[-1,4]C .[-3,2]D .[-2,3]答案 A解析 由题意知,-2≤x ≤3,∴-1≤x +1≤4.∴-1≤x -1≤4,得0≤x ≤5,即y =f (x -1)的定义域为[0,5]. 8.[2016·湖南浏阳一中期中]若函数f (x )(f (x )≠0)为奇函数,则必有( )A .f (x )f (-x )>0B .f (x )f (-x )<0C .f (x )<f (-x )D .f (x )>f (-x ) 答案 B解析 ∵f (x )为奇函数,∴f (-x )=-f (x ),又f (x )≠0,∴f (x )f (-x )=-[f (x )]2<0.9.函数f (x )的定义域为R ,若f (x +y )=f (x )+f (y ),f (8)=3,则f (2)=( )A.54B.34 C.12 D.14答案 B解析 依题意得f (x +y +z +w )=f (x +y )+f (z +w )=f (x )+f (y )+f (z )+f (w ),令x =y =z =w =2可得f (8)=4f (2),因此代入f (8)=3可解得f (2)=34,选B.10.下图所给4个图象中,与所给3件事吻合最好的顺序为( ) (1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)小明骑着车一路以匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A .(1)(2)(4)B .(4)(2)(3)C .(4)(1)(3)D .(4)(1)(2)答案 D解析 事件(1)中因为返回,故回家后距离应该为0,应该选图象(4);事件(2)中交通堵塞,就是说离开家的距离停顿下来,故应该选图象(1);事件(3)说明速度先慢后快,故选图象(2).11.[2016·南安高一检测]已知函数f (x )=ax 2-x +1在(-∞,2)上是单调递减的,则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0,14B.⎣⎢⎡⎦⎥⎤0,14 C .[2,+∞) D .(0,4] 答案 B解析 当a =0时,f (x )=-x +1在(-∞,2)上是单调递减的;当a ≠0时,要使f (x )在(-∞,2)上单调递减.则⎩⎨⎧a >0,--12a ≥2,所以0<a ≤14.综上可得a 的取值范围为a ∈⎣⎢⎡⎦⎥⎤0,14.12.已知函数f (x )=4x 2-mx +5在区间[-2,+∞)上是增函数,则f (1)的取值范围是( )A .f (1)≥25B .f (1)=25C .f (1)≤25D .f (1)>25答案 A解析 ∵函数f (x )=4x 2-mx +5的图象对称轴为x =m 8,则有m8≤-2,∴m ≤-16,而f (1)=4-m +5=9-m ,∴f (1)≥25.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.函数y =x +1+12-x 的定义域为________.答案 [-1,2)∪(2,+∞)解析 由题意知⎩⎪⎨⎪⎧x +1≥0,2-x ≠0,∴x ≥-1且x ≠2.14.[2016·江苏盐城中学月考]设函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤1x 2+x -2,x >1,则f [f (-1)]的值为________.答案 4解析 ∵f (-1)=(-1)2+1=2, ∴f [f (-1)]=f (2)=22+2-2=4.15.[2016·荆州市中学期中]已知A 是有限集合,x ∉A ,B =A ∪{x },若A ,B 的子集个数分别为a ,b ,且b =ka ,则k =________.答案 2解析 不妨设集合A 中的元素个数为n ,则集合B 中的元素个数有n +1,所以a =2n ,b =2n +1,因此b =2a ,故所求k 的值为2.16.函数f (x )=2x 2-3|x |的单调减区间是________. 答案 ⎝ ⎛⎭⎪⎫-∞,-34,⎝ ⎛⎭⎪⎫0,34解析 f (x )=⎩⎪⎨⎪⎧2x 2-3x (x ≥0)2x 2+3x (x <0),图象如下图所示f (x )减区间为⎝⎛⎭⎪⎫-∞,-34,⎝ ⎛⎭⎪⎫0,34.三、解答题(本大题共6小题,满分70分)17.[2016·郑州高一检测](本小题满分10分)全集U =R ,若集合A ={x |3≤x <10},B ={x |2<x ≤7}.(1)求A ∩B ,A ∪B ,(∁U A )∩(∁U B );(2)若集合C ={x |x >a },A ⊆C ,求a 的取值范围. 解 (1)A ∩B ={x |3≤x <10}∩{x |2<x ≤7}={x |3≤x ≤7}; A ∪B ={x |3≤x <10}∪{x |2<x ≤7}={x |2<x <10}; (∁U A )∩(∁U B )={x |x ≤2,或x ≥10}.(2)A ={x |3≤x <10},C ={x |x >a },要使A ⊆C ,结合数轴分析可知a <3,即a 的取值范围是{a |a <3}.18.[2016·云南玉溪一中高一期中](本小题满分12分)设集合A ={a ,a 2,b +1},B ={0,|a |,b }且A =B .(1)求a ,b 的值;(2)判断函数f (x )=-bx -ax 在[1,+∞)的单调性,并用定义加以证明.解 (1)由集合A =B 知,a ≠0,∴b +1=0,即b =-1.此时A ={a ,a 2,0},B ={0,|a |,-1},∴a =-1,∴A ={-1,1,0},B ={0,1,-1}.满足集合的互异性, ∴a =-1,b =-1.(2)由(1)知f (x )=x +1x ,f (x )=x +1x 在[1,+∞)上单调递增. 任取x 1,x 2∈[1,+∞)且x 1<x 2,f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+1x 1-⎝ ⎛⎭⎪⎫x 2+1x 2=(x 1-x 2)+x 2-x 1x 1·x 2=(x 1-x 2)⎝ ⎛⎭⎪⎫1-1x 1·x 2=(x 1-x 2)x 1·x 2-1x 1·x 2, ∵x 1,x 2∈[1,+∞)且x 1<x 2, ∴x 1-x 2<0,x 1·x 2-1>0,x 1·x 2>0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )=x +1x 在[1,+∞)上单调递增.19.[2016·淄博高一检测](本小题满分12分)设函数f (x )是定义在R 上的奇函数,若当x ∈(0,+∞)时,f (x )=3x ·(1+x ).(1)求f (27)与f (-27)的值; (2)求f (x )的解析式.解 (1)由题意知f (27)=327×(1+27)=84,f (-27)=-f (27)=-84,所以f (27)=84,f (-27)=-84.(2)因为f (x )是定义在R 上的奇函数,所以f (0)=0. 设x <0,则-x >0,则f (-x )=3-x ·[1+(-x )]=-3x ·(1-x ). 又f (-x )=-f (x ), 所以f (x )=3x (1-x ), 所以f (x )=⎩⎪⎨⎪⎧3x (1+x ),x >0,0,x =0,3x (1-x ),x <0.20.(本小题满分12分)已知函数f (x )=x 2+2x +ax ,x ∈[1,+∞). (1)当a =12时,判断并证明f (x )的单调性; (2)当a =-1时,求函数f (x )的最小值.解 (1)当a =12时,f (x )=x 2+2x +a x =x +2+12x =x +12x +2. 设x 1,x 2是[1,+∞)上的任意两个实数,且x 1<x 2, 则f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+12x 1-⎝ ⎛⎭⎪⎫x 2+12x 2=(x 1-x 2)+⎝ ⎛⎭⎪⎫12x 1-12x 2=(x 1-x 2)+x 2-x 12x 1x 2=(x 1-x 2)⎝ ⎛⎭⎪⎫1-12x 1x 2=(x 1-x 2)·x 1x 2-12x 1x 2. 因为1≤x 1<x 2,所以x 1-x 2<0,x 1·x 2>1, x 1x 2-12>0,所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). 所以函数f (x )在[1,+∞)上是增函数. (2)当a =-1时,f (x )=x -1x +2.因为函数y 1=x 和y 2=-1x 在[1,+∞)上都是增函数,所以f (x )=x -1x +2在[1,+∞)上是增函数.当x =1时,f (x )取得最小值f (1)=1-11+2=2, 即函数f (x )的最小值为2.21.(本小题满分12分)定义在实数集R 上的函数y =f (x )是偶函数,当x ≥0时,f (x )=-4x 2+8x -3.(1)求f (x )在R 上的表达式;(2)求y =f (x )的最大值,并写出f (x )在R 上的单调区间(不必证明). 解 (1)设x <0,则-x >0.f (-x )=-4(-x )2+8(-x )-3=-4x 2-8x -3. ∵f (x )是R 上的偶函数,∴f (-x )=f (x ). ∴当x <0时,f (x )=-4x 2-8x -3.∴f (x )=⎩⎪⎨⎪⎧-4x 2+8x -3 (x ≥0),-4x 2-8x -3 (x <0), 即f (x )=⎩⎪⎨⎪⎧-4(x -1)2+1 (x ≥0)-4(x +1)2+1 (x <0). (2)∵y =f (x )开口向下,∴y =f (x )有最大值,f (x )max =f (-1)=f (1)=1. 函数y =f (x )的单调递增区间是(-∞,-1]和[0,1], 单调递减区间是[-1,0]和[1,+∞).22.[2015·许昌高一五校联考](本小题满分12分)已知函数f (x )的定义域为R ,对于任意的x ,y ∈R ,都有f (x +y )=f (x )+f (y ),且当x >0时,f (x )<0,若f (-1)=2.(1)求证:f (x )为奇函数; (2)求证:f (x )是R 上的减函数; (3)求函数f (x )在区间[-2,4]上的值域.解 (1)证明:∵f (x )的定义域为R ,令x =y =0, 则f (0+0)=f (0)+f (0)=2f (0),∴f (0)=0. 令y =-x ,则f (x -x )=f (x )+f (-x ),即f(0)=f(x)+f(-x)=0.∴f(-x)=-f(x),故f(x)为奇函数.(2)证明:任取x1,x2∈R,且x1<x2,则f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1).又∵x2-x1>0,∴f(x2-x1)<0,∴f(x2)-f(x1)<0,即f(x1)>f(x2).故f(x)是R上的减函数.(3)∵f(-1)=2,∴f(-2)=f(-1)+f(-1)=4.又f(x)为奇函数,∴f(2)=-f(-2)=-4,∴f(4)=f(2)+f(2)=-8.由(2)知f(x)是R上的减函数,所以当x=-2时,f(x)取得最大值,最大值为f(-2)=4;当x=4时,f(x)取得最小值,最小值为f(4)=-8.所以函数f(x)在区间[-2,4]上的值域为[-8,4].。
2019秋人教版高中数学选修1-1单元质量评估(一) Word版含解析

姓名,年级:时间:温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
单元质量评估(一)(第一章)(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面所给三个命题中真命题个数有( )(1)若ac2〉bc2,则a〉b;(2)若四边形的对角互补,则该四边形是圆的内接四边形;(3)若在二次函数y=ax2+bx+c中,b2—4ac<0,则该二次函数图象与x轴有公共点.A.0 B。
1 C。
2 D.3【解析】选C。
(1)该命题为真命题,因为当c=0时,ac2=bc2,而ac2>bc2说明c≠0,所以a〉b成立。
(2)该命题为真命题,根据圆内接四边形的定义可进行判定。
(3)该命题为假命题,因为当b2—4ac<0时,二次方程ax2+bx+c=0没有实数根,因此二次函数的图象与x轴无公共点。
2。
下列命题中的假命题是()A。
∀x=R,21-x〉0B.∃a0∈R,使函数y=的图象关于y轴对称C.函数y=x a的图象经过第四象限D. ∀x∈(-∞,+∞),有2x〉x【解析】选C.对于A,由指数函数性质可知是真命题.对于B, 当a=2时,y=x2的图象关于y轴对称,所以B是真命题,对C,当x〉0时,y=x a>0恒成立,从而图象不过第四象限,所以C为假命题。
对于D,由指数函数y= 2x 及函数y=x可知2x>x,所以是真命题。
3.设命题p:∃x0<0,≥1,则p为( )A。
∀x≥0,x2<1 B。
∀x〈0,x2〈1C.∃x0≥0,<1D.∃x0<0,〈1【解析】选B。
因为特称命题的否定是全称命题,且先将存在量词改成全称量词,然后否定结论,所以命题p:∃x0〈0,≥1的否定是p为∀x<0,x2〈1.【补偿训练】已知p:α≠β,q:cos α≠cos β,则p是q的( )A。
2019版高中数学人教A版必修1:第一章检测(A) 含解析

第一章检测(A)(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={1,2},B={2,4},则A∪B等于()A.{2}B.{1,2,2,4}C.{1,2,4}D.⌀答案:C2.下列给出函数y=f(x)的部分对应值,则f(f(8))等于 ()x-101478y0π1-31A.πB.4C.8D.0解析:∵f(8)=1,f(1)=π,∴f(f(8))=f(1)=π.答案:A3.已知集合A={-1,0,1},B={1,m}.若B⊆A,则实数m的值为()A.0B.-1C.0或-1D.-1或0或1解析:∵B⊆A,∴m∈A,且m≠1,∴m=0或-1.答案:C4.已知f(x)为R上的奇函数,且当x≥0时,f(x)=x2-2x,则f(-1)等于()A.3B.-1C.-3D.1解析:∵f(x)为奇函数,∴f(-1)=-f(1)=-(1-2)=1.答案:D5.下列图象能作为函数的图象的是()解析:A,B,C中都存在当x=a时,对应的y有2个值,不符合函数的定义,故选D.答案:D6.函数y的定义域是-A.[-1,1)∪(1,+∞)B.(-1,1)∪(1,+∞)C.(-1,1)D.(1,+∞)解得x>-1,且x≠1,故函数的定义域为(-1,1)∪(1,+∞).解析:当函数有意义时,需满足-答案:B7.函数y在∈[-1,1]上的最小值为()A解析:易知函数y在x∈[-1,1]上递减,故当x=1时,y取最小值答案:B8.设函数f(x)是定义在(-∞,0)∪(0,+∞)内的奇函数,且在区间(-∞,0)内是减函数.若f(-2)=0,则x2f(x)<0的解集为()A.(-2,0)∪(2,+∞)B.(-∞,-2)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-2,0)∪(0,2)解析:由x2f(x)<0,得f(x)<0.由f(x)为奇函数,且f(-2)=0,得f(2)=0.又f(x)在区间(-∞,0)内是减函数,所以f(x)在区间(0,+∞)内也是减函数,所以由f(x)<0,可得-2<x<0或x>2.故选A.答案:A9.设函数f(x)(x∈R)为奇函数,f(1)则等于A解析:由f(x+2)=f(x)+f(2),得当x=-1时,f(1)=f(-1)+f(2).又f(x)为奇函数,且f(-1)=-f(1)=∴f(2)=2f(1)=1.∴f(5)=f(3)+f(2)=2f(2)+f(1)答案:A10.已知奇函数f(x)、偶函数g(x)的图象分别如图1,2所示,方程f(g(x))=0,g(f(x))=0的实根个数分别为a,b,则a+b=()A.14B.10C.7D.3解析:设函数g(x)的图象在y轴两侧与x轴的交点的横坐标分别为m,n,如图所示,则可知m∈(-2,-1),n∈(1,2).由方程f(g(x))=0,可得g(x)=-1或g(x)=0或g(x)=1,∴x=-1,1,m,0,n,-2,2,∴方程f(g(x))=0有7个实根,即a=7;由方程g(f(x))=0,可得f(x)=m(舍去)或f(x)=0或f(x)=n(舍去),∴x=-1,0,1,∴方程g(f(x))=0有3个实根,即b=3,∴a+b=10,故选B.答案:B二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11.设集合A={-1,1,3},B={a+2,a2+4},若A∩B={3},则实数a=.解析:∵A∩B={3},∴3∈B,∴a+2=3,∴a=1.答案:1的最大值是12.函数y-解析:当x<1时,函数y=x+3单调递增,所以y<4,此时无最大值;当x≥1时,函数y=-x+6单调递减,所以在x=1处取得最大值为5.故在整个定义域内函数的最大值是5.答案:513.若函数f(x)是奇函数则解析:∵f(x)是奇函数,∴f(-1)=-f(1),即-1+a=-(1+a),∴a=0.∴f(x)≠0),∴f(2)=2.答案:214.已知集合A={-1,3,2m-1},集合B={3,m2}.若A∩B=B,则实数m的值是.解析:∵A∩B=B,∴B⊆A.∴m2=2m-1,解得m=1.答案:115.已知函数f(x)=ax2-2x-1在区间(-1,+∞)内单调递减,则a的取值范围是.解析:当a=0时,f(x)=-2x-1,满足题意;当a≠0时,f(x)在区间(-1,+∞)内递减,可得-解得-1≤a<0.综上所述,a的取值范围是-1≤a≤0.答案:-1≤a≤0三、解答题(本大题共5小题,共45分.解答时应写出文字说明、证明过程或演算步骤)16.(8分)设集合A={x∈Z|-6≤x≤6},B={1,2,3},C={3,4,5,6}.求:(1)A∪(B∩C);(2)A∩[∁A(B∪C)].解:由题意知A={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}.(1)易知B∩C={3},故A∪(B∩C)={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}.(2)∵B∪C={1,2,3,4,5,6},∴∁A(B∪C)={-6,-5,-4,-3,-2,-1,0},∴A∩[∁A(B∪C)]={-6,-5,-4,-3,-2,-1,0}.17.(8分)已知函数f(x)-(1)求f(f(-1));(2)若f(x0)>2,求x0的取值范围.解:(1)因为f(-1)=-(-1)+3=4,所以f(f(-1))=f(4)=4×4=16.(2)当x0≤0时,由2<-x0+3,得x0<1,得x0≤0;当x0>0时,由2<4x0,得x0所以x0的取值范围是x0≤0或x018.(9分)已知二次函数y=f(x)满足f(-2)=f(4)=-16,且f(x)的最大值为2.(1)求函数y=f(x)的解析式;(2)求函数y=f(x)在区间[t,t+1](t≥1)上的最大值.解:(1)因为已知二次函数y=f(x)满足f(-2)=f(4)=-16,且f(x)的最大值为2,所以函数y=f(x)的图象的对称轴为x=1.可设函数f(x)=a(x-1)2+2,a<0.根据f(-2)=9a+2=-16,解得a=-2,故f(x)=-2(x-1)2+2=-2x2+4x.(2)当t≥1时,函数f(x)在区间[t,t+1]上是减函数,故函数f(x)的最大值为f(t)=-2t2+4t.19.(10分)若f(x)是定义在区间(0,+∞)内的增函数,且对一切x,y>0,满足(1)求f(1)的值;(2)若f(6)=1,解不等式f(x+3)-解:(1)∵令x=y=1得f(1)=f(1)-f(1),∴f(1)=0.(2)∵f(6)=1,∴f(x+3)-可化为f(x+3)-又f(x)是定义在(0,+∞)内的增函数,解得-3<x<9.故原不等式的解集为{x|-3<x<9}.20.(10分)已知f(x)是奇函数且(1)求实数a,b的值;(2)判断函数f(x)在区间(-∞,-1]上的单调性,并加以证明.解:(1)∵f(x)为奇函数,∴f(-x)=-f(x),解得b=0.即-又f(2)(2)由(1)知f(x)则f(x)在区间(-∞,-1]上为增函数.证明:设x1<x2≤-1,则f(x1)-f(x2)-∵x1<x2≤-1,∴x1-x2<0,x1x2>1,1∴f(x1)-f(x2)<0,即f(x1)<f(x2),故f(x)在区间(-∞,-1]上为增函数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(人教版)精品数学教学资料第一章单元质量测评(一) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.[2015·广东高考]已知集合M={-1,0,1},N={0,1,2},则M ∪N=()A.{0,1} B.{-1,0,2}C.{-1,0,1,2} D.{-1,0,1}答案 C解析依题意得M∪N={-1,0,1,2},故选C.2.[2015·天津高考]已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁U B=()A.{2,5} B.{3,6}C.{2,5,6} D.{2,3,5,6,8}答案 A解析因为∁U B={2,5,8},又A={2,3,5,6},所以A∩∁U B={2,5},故选A.3.50名同学参加跳远和铅球测验,跳远和铅球测验成绩分别为及格40人和31人,2项测验成绩均不及格的有4人,2项测验成绩都及格的人数是()A.35 B.25C.28 D.15答案 B解析全班分4类人:设两项测验成绩都及格的人数为x人;仅跳远及格的人数为(40-x)人;仅铅球及格的人数为(31-x)人;两项都不及格的人数为4人,∴40-x +31-x +x +4=50,∴x =25.4.[2015·陕西工大附中高一质检]如图所示的韦恩图中A ,B 是非空集合,定义集合A *B 为阴影部分表示的集合,则A *B =( )A .∁U (A ∪B ) B .A ∪(∁U B )C .(∁U A )∪(∁U B )D .(A ∪B )∩∁U (A ∩B )答案 D解析 阴影部分为A ∪B 去掉A ∩B 后的部分,为(A ∪B )∩∁U (A ∩B ).选D.5.函数f (x )是定义在[0,+∞)上的增函数,则满足f (2x -1)<f ⎝ ⎛⎭⎪⎫13的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13,23B.⎣⎢⎡⎭⎪⎫13,23 C.⎝ ⎛⎭⎪⎫12,23 D.⎣⎢⎡⎭⎪⎫12,23 答案 D 解析根据题意,得⎩⎨⎧2x -1≥0,2x -1<13,解得12≤x <23,选D.6.[2015·攀枝花米易中学月考]已知函数f (x )的定义域为(3-2a ,a +1),且f (x +1)为偶函数,则实数a 的值可以是( )A .2 B.23 C .4 D .6答案 A解析 因为函数f (x )的定义域为(3-2a ,a +1),所以在函数f (x+1)中,3-2a <x +1<a +1,则函数f (x +1)的定义域为(2-2a ,a ),又因为f (x +1)为偶函数,所以2-2a =-a ,a =2,故选A.7.[2015·衡水高一调研]已知函数y =f (x +1)定义域是[-2,3],则y =f (x -1)的定义域是( )A .[0,5]B .[-1,4]C .[-3,2]D .[-2,3]答案 A解析 由题意知,-2≤x ≤3,∴-1≤x +1≤4.∴-1≤x -1≤4,得0≤x ≤5,即y =f (x -1)的定义域为[0,5]. 8.[2016·湖南浏阳一中期中]若函数f (x )(f (x )≠0)为奇函数,则必有( )A .f (x )f (-x )>0B .f (x )f (-x )<0C .f (x )<f (-x )D .f (x )>f (-x ) 答案 B解析 ∵f (x )为奇函数,∴f (-x )=-f (x ),又f (x )≠0,∴f (x )f (-x )=-[f (x )]2<0.9.函数f (x )的定义域为R ,若f (x +y )=f (x )+f (y ),f (8)=3,则f (2)=( )A.54B.34 C.12 D.14答案 B解析 依题意得f (x +y +z +w )=f (x +y )+f (z +w )=f (x )+f (y )+f (z )+f (w ),令x =y =z =w =2可得f (8)=4f (2),因此代入f (8)=3可解得f (2)=34,选B.10.下图所给4个图象中,与所给3件事吻合最好的顺序为( ) (1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)小明骑着车一路以匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A .(1)(2)(4)B .(4)(2)(3)C .(4)(1)(3)D .(4)(1)(2)答案 D解析 事件(1)中因为返回,故回家后距离应该为0,应该选图象(4);事件(2)中交通堵塞,就是说离开家的距离停顿下来,故应该选图象(1);事件(3)说明速度先慢后快,故选图象(2).11.[2016·南安高一检测]已知函数f (x )=ax 2-x +1在(-∞,2)上是单调递减的,则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0,14B.⎣⎢⎡⎦⎥⎤0,14 C .[2,+∞) D .(0,4] 答案 B解析 当a =0时,f (x )=-x +1在(-∞,2)上是单调递减的;当a ≠0时,要使f (x )在(-∞,2)上单调递减.则⎩⎨⎧a >0,--12a ≥2,所以0<a ≤14.综上可得a 的取值范围为a ∈⎣⎢⎡⎦⎥⎤0,14.12.已知函数f (x )=4x 2-mx +5在区间[-2,+∞)上是增函数,则f (1)的取值范围是( )A .f (1)≥25B .f (1)=25C .f (1)≤25D .f (1)>25答案 A解析 ∵函数f (x )=4x 2-mx +5的图象对称轴为x =m 8,则有m8≤-2,∴m ≤-16,而f (1)=4-m +5=9-m ,∴f (1)≥25.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分) 13.函数y =x +1+12-x 的定义域为________.答案 [-1,2)∪(2,+∞)解析 由题意知⎩⎪⎨⎪⎧x +1≥0,2-x ≠0,∴x ≥-1且x ≠2.14.[2016·江苏盐城中学月考]设函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤1x 2+x -2,x >1,则f [f (-1)]的值为________.答案 4解析 ∵f (-1)=(-1)2+1=2, ∴f [f (-1)]=f (2)=22+2-2=4.15.[2016·荆州市中学期中]已知A 是有限集合,x ∉A ,B =A ∪{x },若A ,B 的子集个数分别为a ,b ,且b =ka ,则k =________.答案 2解析 不妨设集合A 中的元素个数为n ,则集合B 中的元素个数有n +1,所以a =2n ,b =2n +1,因此b =2a ,故所求k 的值为2.16.函数f (x )=2x 2-3|x |的单调减区间是________. 答案 ⎝ ⎛⎭⎪⎫-∞,-34,⎝ ⎛⎭⎪⎫0,34解析 f (x )=⎩⎪⎨⎪⎧2x 2-3x (x ≥0)2x 2+3x (x <0),图象如下图所示f (x )减区间为⎝⎛⎭⎪⎫-∞,-34,⎝ ⎛⎭⎪⎫0,34.三、解答题(本大题共6小题,满分70分)17.[2016·郑州高一检测](本小题满分10分)全集U =R ,若集合A ={x |3≤x <10},B ={x |2<x ≤7}.(1)求A ∩B ,A ∪B ,(∁U A )∩(∁U B );(2)若集合C ={x |x >a },A ⊆C ,求a 的取值范围. 解 (1)A ∩B ={x |3≤x <10}∩{x |2<x ≤7}={x |3≤x ≤7}; A ∪B ={x |3≤x <10}∪{x |2<x ≤7}={x |2<x <10}; (∁U A )∩(∁U B )={x |x ≤2,或x ≥10}.(2)A ={x |3≤x <10},C ={x |x >a },要使A ⊆C ,结合数轴分析可知a <3,即a 的取值范围是{a |a <3}.18.[2016·云南玉溪一中高一期中](本小题满分12分)设集合A ={a ,a 2,b +1},B ={0,|a |,b }且A =B .(1)求a ,b 的值;(2)判断函数f (x )=-bx -ax 在[1,+∞)的单调性,并用定义加以证明.解 (1)由集合A =B 知,a ≠0,∴b +1=0,即b =-1.此时A ={a ,a 2,0},B ={0,|a |,-1},∴a =-1,∴A ={-1,1,0},B ={0,1,-1}.满足集合的互异性, ∴a =-1,b =-1.(2)由(1)知f (x )=x +1x ,f (x )=x +1x 在[1,+∞)上单调递增. 任取x 1,x 2∈[1,+∞)且x 1<x 2,f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+1x 1-⎝ ⎛⎭⎪⎫x 2+1x 2=(x 1-x 2)+x 2-x 1x 1·x 2=(x 1-x 2)⎝ ⎛⎭⎪⎫1-1x 1·x 2=(x 1-x 2)x 1·x 2-1x 1·x 2, ∵x 1,x 2∈[1,+∞)且x 1<x 2, ∴x 1-x 2<0,x 1·x 2-1>0,x 1·x 2>0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )=x +1x 在[1,+∞)上单调递增.19.[2016·淄博高一检测](本小题满分12分)设函数f (x )是定义在R 上的奇函数,若当x ∈(0,+∞)时,f (x )=3x ·(1+x ).(1)求f (27)与f (-27)的值; (2)求f (x )的解析式.解 (1)由题意知f (27)=327×(1+27)=84,f (-27)=-f (27)=-84,所以f (27)=84,f (-27)=-84.(2)因为f (x )是定义在R 上的奇函数,所以f (0)=0. 设x <0,则-x >0,则f (-x )=3-x ·[1+(-x )]=-3x ·(1-x ). 又f (-x )=-f (x ), 所以f (x )=3x (1-x ), 所以f (x )=⎩⎪⎨⎪⎧3x (1+x ),x >0,0,x =0,3x (1-x ),x <0.20.(本小题满分12分)已知函数f (x )=x 2+2x +ax ,x ∈[1,+∞). (1)当a =12时,判断并证明f (x )的单调性; (2)当a =-1时,求函数f (x )的最小值.解 (1)当a =12时,f (x )=x 2+2x +a x =x +2+12x =x +12x +2. 设x 1,x 2是[1,+∞)上的任意两个实数,且x 1<x 2, 则f (x 1)-f (x 2)=⎝ ⎛⎭⎪⎫x 1+12x 1-⎝ ⎛⎭⎪⎫x 2+12x 2=(x 1-x 2)+⎝ ⎛⎭⎪⎫12x 1-12x 2=(x 1-x 2)+x 2-x 12x 1x 2=(x 1-x 2)⎝ ⎛⎭⎪⎫1-12x 1x 2=(x 1-x 2)·x 1x 2-12x 1x 2. 因为1≤x 1<x 2,所以x 1-x 2<0,x 1·x 2>1, x 1x 2-12>0,所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). 所以函数f (x )在[1,+∞)上是增函数. (2)当a =-1时,f (x )=x -1x +2.因为函数y 1=x 和y 2=-1x 在[1,+∞)上都是增函数,所以f (x )=x -1x +2在[1,+∞)上是增函数.当x =1时,f (x )取得最小值f (1)=1-11+2=2, 即函数f (x )的最小值为2.21.(本小题满分12分)定义在实数集R 上的函数y =f (x )是偶函数,当x ≥0时,f (x )=-4x 2+8x -3.(1)求f (x )在R 上的表达式;(2)求y =f (x )的最大值,并写出f (x )在R 上的单调区间(不必证明). 解 (1)设x <0,则-x >0.f (-x )=-4(-x )2+8(-x )-3=-4x 2-8x -3. ∵f (x )是R 上的偶函数,∴f (-x )=f (x ). ∴当x <0时,f (x )=-4x 2-8x -3.∴f (x )=⎩⎪⎨⎪⎧-4x 2+8x -3 (x ≥0),-4x 2-8x -3 (x <0), 即f (x )=⎩⎪⎨⎪⎧-4(x -1)2+1 (x ≥0)-4(x +1)2+1 (x <0). (2)∵y =f (x )开口向下,∴y =f (x )有最大值,f (x )max =f (-1)=f (1)=1. 函数y =f (x )的单调递增区间是(-∞,-1]和[0,1], 单调递减区间是[-1,0]和[1,+∞).22.[2015·许昌高一五校联考](本小题满分12分)已知函数f (x )的定义域为R ,对于任意的x ,y ∈R ,都有f (x +y )=f (x )+f (y ),且当x >0时,f (x )<0,若f (-1)=2.(1)求证:f (x )为奇函数; (2)求证:f (x )是R 上的减函数; (3)求函数f (x )在区间[-2,4]上的值域.解 (1)证明:∵f (x )的定义域为R ,令x =y =0, 则f (0+0)=f (0)+f (0)=2f (0),∴f (0)=0. 令y =-x ,则f (x -x )=f (x )+f (-x ),即f(0)=f(x)+f(-x)=0.∴f(-x)=-f(x),故f(x)为奇函数.(2)证明:任取x1,x2∈R,且x1<x2,则f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1).又∵x2-x1>0,∴f(x2-x1)<0,∴f(x2)-f(x1)<0,即f(x1)>f(x2).故f(x)是R上的减函数.(3)∵f(-1)=2,∴f(-2)=f(-1)+f(-1)=4.又f(x)为奇函数,∴f(2)=-f(-2)=-4,∴f(4)=f(2)+f(2)=-8.由(2)知f(x)是R上的减函数,所以当x=-2时,f(x)取得最大值,最大值为f(-2)=4;当x=4时,f(x)取得最小值,最小值为f(4)=-8.所以函数f(x)在区间[-2,4]上的值域为[-8,4].。
