第二次算法分析实验 重邮
重庆邮电大学PB实验2

用户界面设计(一)实验日志指导教师刘伯红实验时间:2010年10月19日学院计算机科学与技术专业计算机科学与技术班级3110903学号2009214458姓名骆潇龙实验室S312实验题目:用户界面设计(一)实验目的:1、熟练掌握窗口画板的使用2、熟练使用基本控件设计用户界面3、掌握菜单和工具条的设计方法4、掌握SDI风格用户界面的设计方法实验要求:1、窗口及基本控件使用2、菜单和工具条设计3、设计SDI风格的程序实验主要步骤:1、创建一个工作区2、应用程序的创建3、窗体的创建4、了解窗口画板的简介和基本控件的简介和使用5、窗口画板的控件增加6、基本的属性设置和对象设置7、运用程序的open事件8、参数设置实验重点:窗口画板简介根据图形界面讲解(如图),重点介绍位于界面上方的菜单栏、工具栏、界面中间的视图区以及界面右方的属性区,参照教材P179-181页内容✧基本控件的简介和使用参照教材P222页表8-1介绍PowerBuilder的功能性控件,重点介绍常用的功能性控件,包括:CommandButton、PictureButton、CheckBox、RadioButton、StaticText、SingleLineEdit、MultiLineEdit等,简单介绍其具有的重要属性及实现功能,并演示控件的显示效果。
✧菜单和工具栏设计新建一菜单Object,在菜单根结点上单击鼠标右键,选择“Insert SubmenuItem”创建子菜单项目如图:在“Properties”的“General”里设置“Name”、“Text”、快捷键等属性。
在“Toolbar”里有选择的设置“ToolbarItemText”和“ToolbarItemName”等属性,观察菜单视图栏的变化。
继续进行类似操作设置菜单各项目。
实验结果:心得体会:通过这次试验我了解了窗口画板的使用,使用基本控件设计用户界面,菜单和工具条的设计方法,SDI风格用户界面的设计方法,窗口及基本控件使用,菜单和工具条设计,设计SDI风格的程序。
重庆邮电大学-软件技术基础--实验报告(耿道渠)

《软件技术基础》实验报告实验名称:顺序表的操作班级学号姓名第9 周星期 2 、5,6 节成绩一、实验目的:1、掌握顺序表结构的实现方式;2、掌握顺序表常用算法的实现;3、熟悉利用顺序表解决问题的一般思路;4、参照给定的顺序表的程序样例,验证给出的顺序表的常见算法,领会顺序表结构的优点和不足。
二、实验内容:1、设计一个静态数组存储结构的顺序表,要求编程实现如下任务:(1)建立一个顺序表,首先依次输人整数数据元素(个数根据需要键盘给定)。
(2)删除指定位置的数据元素(指定元素位置通过键盘输入),再依次显示删除后的顺序表中的数据元素。
(3)查找指定数据的数据元素(指定数据由键盘输入),若找到则显示位置,若没有找到则显示0。
2、使用顺序表实现一个电话本的管理程序,电话本中的每条记录包括学号、姓名、手机号码和固定电话四项。
要求实现菜单、初始化、添加、删除和显示等功能。
三、实验结果:四、实验中遇到的问题及解决方法:第一次编写C++,感觉力不从心,回去多看看PPT。
五、实验心得体会:对顺序表的一些常用语句不熟悉,对顺序表的整体思路理解不深刻以后要加强练习附:源程序(自行编写或修改的程序。
若为修改程序请注明修改部分的功能,若为书上实例则可不附。
)#include <iostream>#include <string>#include <stdlib.h>#include <iomanip>#define MAXSIZE 20using namespace std;int num;typedef struct{string student_number;string name;string tel;string home_phone;int id;} TEL;void shuaxin(TEL *);void delet(TEL *);void find(TEL *);void show(TEL *);int main(void){int choose;TEL List[MAXSIZE];while(1){cout << "***************************欢迎来到XXX电话本系统*********************" << endl;cout << "1.初始化并建立" <<endl;cout << "2.删除" <<endl;cout << "3.查找" <<endl;cout << "4.显示全部" << endl <<endl;cin >> choose;system("cls");while( choose < 1 || choose > 4){cout << "输入错误,数字1-4,请重新输入!" << endl;cin >> choose;system("cls");}switch(choose){case 1: shuaxin(List); break;case 2: delet(List); break;case 3: find(List); break;case 4: show(List); break;}//system("cls");}return 0;}void shuaxin(TEL * list){int i,j;for(i = 0; i < MAXSIZE; i++){list[i].id = i + 1;list[i].home_phone = "none";list[i].name = "none";list[i].student_number = "none";list[i].tel = "none";system("cls");cout << "初始化成功,现在开始建表:" << endl;cout << "请输入需要建立的电话个数:(小于" << MAXSIZE << ")"<<endl;cin >> num;while( num < 1 || num > MAXSIZE ){system("cls");cout << "输入错误,请重新输入" << endl;cin >> num;}system("cls");cout << "请依次输入学生的学号,姓名,移动电话,家庭电话" << endl;for(j = 1; j <= num; j++){cout << j << '.';cin >> list[j - 1].student_number;cin >> list[j - 1].name;cin >> list[j - 1].tel;cin >> list[j - 1].home_phone;cout << endl;if(num == (j - 1) ){system("cls");cout << "建立表完毕!" << endl;}}void delet(TEL * list){int j,i = 0;cout << "请输入你需要删除的序号" << endl;cin >> j;while( j < 0 || j > num){cout << "输入错误,请重新输入" << endl;cin >> j;}while(list[i].id != j)i++;for(j = i; j < num - 1; j++){list[j].name = list[j + 1].name;list[j].tel = list[j + 1].tel;list[j].student_number = list[j + 1].student_number;list[j].home_phone = list[j + 1].home_phone;}list[j].home_phone = "none";list[j].name = "none";list[j].student_number = "none";list[j].tel = "none";num--;system("cls");cout << "删除完毕" << endl;}void find(TEL * list){string telnum;int i,key = 0;cout << "请输入你需要查找的电话号码" << endl;cin >> telnum;system("cls");for(i = 0; i < MAXSIZE; i++){if(telnum == list[i].tel || telnum == list[i].home_phone){if(key == 0)cout << "依次学号姓名移动电话家庭电话" << endl;cout << list[i].id << '.';cout << setw(12) << list[i].student_number;cout << setw(10) << list[i].name;cout << setw(14) << list[i].tel;cout << setw(10) << list[i].home_phone;cout << endl;key = 1;}}if( key == 0)cout << "未找到此电话号码" << endl;}void show(TEL * list){int i;cout << "现在有" << num << "个电话号码" << endl;cout << "依次学号姓名移动电话家庭电话" << endl;for(i = 0; i < num; i++){cout << list[i].id << '.';cout << setw(12) << list[i].student_number;cout << setw(10) << list[i].name;cout << setw(14) << list[i].tel;cout << setw(10) << list[i].home_phone;cout << endl;}cout << "输出完毕" << endl;}《软件技术基础》实验报告实验名称:链表的操作(一)班级学号姓名第10 周星期 2 、5,6 节成绩一、实验目的:1、掌握单链表结构的实现方式;2、掌握单链表常用算法的实现。
算法设计与分析实验报告三篇

算法设计与分析实验报告一实验名称统计数字问题评分实验日期2014 年11 月15 日指导教师姓名专业班级学号一.实验要求1、掌握算法的计算复杂性概念。
2、掌握算法渐近复杂性的数学表述。
3、掌握用C++语言描述算法的方法。
4.实现具体的编程与上机实验,验证算法的时间复杂性函数。
二.实验内容统计数字问题1、问题描述一本书的页码从自然数1 开始顺序编码直到自然数n。
书的页码按照通常的习惯编排,每个页码都不含多余的前导数字0。
例如,第6 页用数字6 表示,而不是06 或006 等。
数字计数问题要求对给定书的总页码n,计算出书的全部页码中分别用到多少次数字0,1,2, (9)2、编程任务给定表示书的总页码的10 进制整数n (1≤n≤109) 。
编程计算书的全部页码中分别用到多少次数字0,1,2, (9)三.程序算法将页码数除以10,得到一个整数商和余数,商就代表页码数减余数外有多少个1—9作为个位数,余数代表有1—余数本身这么多个数作为剩余的个位数,此外,商还代表1—商本身这些数出现了10次,余数还代表剩余的没有计算的商的大小的数的个数。
把这些结果统计起来即可。
四.程序代码#include<iostream.h>int s[10]; //记录0~9出现的次数int a[10]; //a[i]记录n位数的规律void sum(int n,int l,int m){ if(m==1){int zero=1;for(int i=0;i<=l;i++) //去除前缀0{ s[0]-=zero;zero*=10;} }if(n<10){for(int i=0;i<=n;i++){ s[i]+=1; }return;}//位数为1位时,出现次数加1//位数大于1时的出现次数for(int t=1;t<=l;t++)//计算规律f(n)=n*10^(n-1){m=1;int i;for(i=1;i<t;i++)m=m*10;a[t]=t*m;}int zero=1;for(int i=0;i<l;i++){ zero*= 10;} //求出输入数为10的n次方int yushu=n%zero; //求出最高位以后的数int zuigao=n/zero; //求出最高位zuigaofor(i=0;i<zuigao;i++){ s[i]+=zero;} //求出0~zuigao-1位的数的出现次数for(i=0;i<10;i++){ s[i]+=zuigao*a[l];} //求出与余数位数相同的0~zuigao-1位中0~9出现的次数//如果余数是0,则程序可结束,不为0则补上所缺的0数,和最高位对应所缺的数if(yushu==0) //补上所缺的0数,并且最高位加1{ s[zuigao]++;s[0]+=l; }else{ i=0;while((zero/=10)>yushu){ i++; }s[0]+=i*(yushu+1);//补回因作模操作丢失的0s[zuigao]+=(yushu+1);//补回最高位丢失的数目sum(yushu,l-i-1,m+1);//处理余位数}}void main(){ int i,m,n,N,l;cout<<"输入数字要查询的数字:";cin>>N;cout<<'\n';n = N;for(i=0;n>=10;i++){ n/=10; } //求出N的位数n-1l=i;sum(N,l,1);for(i=0; i<10;i++){ cout<< "数字"<<i<<"出现了:"<<s[i]<<"次"<<'\n'; }}五.程序调试中的问题调试过程,页码出现报错。
西电软件学院算法实验报告模板2份

第二次试验一、问题:Matrix-chain product分析:本题是矩阵链乘问题,需要求出最优括号化方案。
即在矩阵的乘法链上添加括号来改变运算顺序以使矩阵链乘法的代价降低。
可以分析该链乘的一个子段总结一些结论。
假设m[i,j]表示Ai *…*Aj的链成需要进行的乘法次数(假设j-i足够大),我们可以将Ai *…*Aj分为两段进行计算:(Ai *…*Ak)*(Ak+1*…*Aj)可以得出m[i,j]的递推公式可以得出,当i=j的时候,m[i,j]=0。
当i<j的时候。
k的取值范围是i到j-1,对于k的每一个取值都可以得到一个m[i,j]的值,取出最小值即时m[i,j]的最优化方案。
递推公式如下:可以根据上式得到一个递归算法。
本题即是求m[1,n]的值。
用二维数组m存储m[i,j]的值,用二维数组s来储存应当分割的位置。
以本题中第一个矩阵a) <3, 5, 2, 1,10>为例,可以得出如下矩阵:通过m数组可以得出最少的乘法次数,通过s数组可以输出最优方案。
遇到的问题:在输出s数组的结果的时候仍然需要递归调用,需要合适的控制递归的条件。
总结:在矩阵链乘问题中可以看出,动态规划结合递归的思想可以快捷的解决很多问题。
本题中,重点是归纳出m[i,j]的递推公式。
二、问题:Longest Common Subsequence分析:本题即是最长公共子序列问题。
假设有序列A[m]和序列B[n],显然,对于每一个[i,j],都对应着一个公共子序列的长度。
假设长度为c,就可以得到一个二维数组c[m,n]。
对于c[i,j],当Ai=Bj的时候,问题就转变为求A[1..i-1]和B[1..j-1]的公共子序列长度的问题,所以c[i,j]的长度就是c[i-1,j-1] + 1;同理,当Ai != Bj的时候,c[i,j]应该在c[i-1,j]与c[i,j-1]中取最大值。
另外,当i或者j等于0的时候,显然c的值为0。
算法分析 重庆邮电大学第一次实验

实验四贪心算法求解最短路径问题实验目的:1)以解决最短路径问题为例,掌握贪心算法的基本设计策略;2)掌握Dijkstra贪心法求解单源点最短路径问题并实现;3)分析实验结果。
实验环境计算机、C语言程序设计环境实验学时2学时实验内容与步骤1.准备实验数据假设算法要处理下图,需要把图数据组织存放到相应的数据结构中,如:权值矩阵float graph[maxsize][maxsize]。
2.实现Dijkstra算法代码:#include <iostream>#include <fstream>#include <string>using namespace std;const int N = 6;const int M = 1000;ifstream fin("e://4d5.txt");ofstream fout("e://dijkstra-output1.txt");template<class Type>void Dijkstra(int n,int v,Type dist[],int prev[],Type c[][N+1]);void Traceback(int v,int i,int prev[]);//输出最短路径v源点,i终点int main(){int v = 1;//源点为1int dist[N+1],prev[N+1],c[N+1][N+1];cout<<"有向图权的矩阵为:"<<endl;for(int i=1; i<=N; i++){for(int j=1; j<=N; j++){fin>>c[i][j];cout<<c[i][j]<<" ";}cout<<endl;}Dijkstra(N,v,dist,prev,c);for(int i1=2; i1<=N; i1++){fout<<"源点1到点"<<i1<<"的最短路径长度为:"<<dist[i1]<<",其路径为";cout<<"源点1到点"<<i1<<"的最短路径长度为:"<<dist[i1]<<",其路径为";Traceback(1,i1,prev);cout<<endl;fout<<endl;}return 0;}template<class Type>void Dijkstra(int n,int v,Type dist[],int prev[],Type c[][N+1]){bool s[N+1];for(int i=1; i<=n; i++){dist[i] = c[v][i];//dist[i]表示当前从源到顶点i的最短特殊路径长度s[i] = false;if(dist[i] == M){prev[i] = 0;//记录从源到顶点i的最短路径i的前一个顶点}else{prev[i] = v;}}dist[v] = 0;s[v] = true;for(int i1=1; i1<n; i1++){int temp = M;int u = v;//上一顶点//取出V-S中具有最短特殊路径长度的顶点ufor(int j=1; j<=n; j++){if((!s[j]) && (dist[j]<temp)){u = j ;temp = dist[j];}}s[u] = true;//根据作出的贪心选择更新Dist值for(int j1=1; j1<=n; j1++){if((!s[j1]) && (c[u][j1]<M)){Type newdist = dist[u] + c[u][j1];if(newdist < dist[j1]){dist[j1] = newdist;prev[j1] = u;}}}}}//输出最短路径v源点,i终点void Traceback(int v,int i,int prev[]){if(v == i){cout<<i;fout<<i;return;}Traceback(v,prev[i],prev);cout<<"->"<<i;fout<<"->"<<i;}结果:#include <iostream>#include <limits>#include <fstream>#include <string>using namespace std;ofstream fout("e://dijkstra-output2.txt");struct Node { //定义表结点int adjvex; //该边所指向的顶点的位置int weight;// 边的权值Node *next; //下一条边的指针};struct HeadNode{ // 定义头结点int nodeName; // 顶点信息int inDegree; // 入度int d; //表示当前情况下起始顶点至该顶点的最短路径,初始化为无穷大bool isKnown; //表示起始顶点至该顶点的最短路径是否已知,true表示已知,false表示未知int parent; //表示最短路径的上一个顶点Node *link; //指向第一条依附该顶点的边的指针};//G表示指向头结点数组的第一个结点的指针//nodeNum表示结点个数//arcNum表示边的个数void createGraph(HeadNode *G, int nodeNum, int arcNum) {cout << "开始创建图(" << nodeNum << ", " << arcNum << ")" << endl; //初始化头结点for (int i = 0; i < nodeNum; i++) {G[i].nodeName = i+1; //位置0上面存储的是结点v1,依次类推G[i].inDegree = 0; //入度为0G[i].link = NULL;}inta[6][6]={{0,999,15,999,999,999},{2,999,999,999,10,30},{999,4,0,999,99 9,10},{999,999,999,0,999,999},{999,999,999,15,0,999},{999,999,999,4,1 0,0}};for (int j = 0;j<6;j++) {for(int k=0;k<6;k++){int begin, end, weight;begin = j+1;end=k+1;weight= a[j][k];// 创建新的结点插入链接表Node *node = new Node;node->adjvex = end - 1;node->weight = weight;++G[end-1].inDegree; //入度加1//插入链接表的第一个位置node->next = G[begin-1].link;G[begin-1].link = node;}}}void printGraph(HeadNode *G, int nodeNum) {for (int i = 0; i < nodeNum; i++) {cout << "结点v" << G[i].nodeName << "的入度为";cout << G[i].inDegree << ", 以它为起始顶点的边为: ";Node *node = G[i].link;while (node != NULL) {cout << "v" << G[node->adjvex].nodeName << "(权:" << node->weight << ")" << " ";node = node->next;}cout << endl;}}//得到begin->end权重int getWeight(HeadNode *G, int begin, int end) {Node *node = G[begin-1].link;while (node) {if (node->adjvex == end - 1) {return node->weight;}node = node->next;}}//从start开始,计算其到每一个顶点的最短路径void Dijkstra(HeadNode *G, int nodeNum, int start) {//初始化所有结点for (int i = 0; i < nodeNum; i++) {G[i].d = INT_MAX; //到每一个顶点的距离初始化为无穷大G[i].isKnown = false; // 到每一个顶点的距离为未知数}G[start-1].d = 0; //到其本身的距离为0G[start-1].parent = -1; //表示该结点是起始结点while(true) {//==== 如果所有的结点的最短距离都已知, 那么就跳出循环int k;bool ok = true; //表示是否全部okfor (k = 0; k < nodeNum; k++) {//只要有一个顶点的最短路径未知,ok就设置为falseif (!G[k].isKnown) {ok = false;break;}}if (ok) return;//==========================================//==== 搜索未知结点中d最小的,将其变为known//==== 这里其实可以用最小堆来实现int i;int minIndex = -1;for (i = 0; i < nodeNum; i++) {if (!G[i].isKnown) {if (minIndex == -1)minIndex = i;else if (G[minIndex].d > G[i].d)minIndex = i;}}//===========================================cout << "当前选中的结点为: v" << (minIndex+1) << endl;G[minIndex].isKnown = true; //将其加入最短路径已知的顶点集// 将以minIndex为起始顶点的所有的d更新Node *node = G[minIndex].link;while (node != NULL) {int begin = minIndex + 1;int end = node->adjvex + 1;int weight = getWeight(G, begin, end);if (G[minIndex].d + weight < G[end-1].d) {G[end-1].d = G[minIndex].d + weight;G[end-1].parent = minIndex; //记录最短路径的上一个结点}node = node->next;}}}//打印到end-1的最短路径void printPath(HeadNode *G, int end) {if (G[end-1].parent == -1) {cout << "v" << end;fout << "v" << end;} else if (end != 0) {printPath(G, G[end-1].parent + 1); // 因为这里的parent表示的是下标,从0开始,所以要加1cout << " -> v" << end;fout << " -> v" << end;}}int main() {HeadNode *G;int nodeNum, arcNum;nodeNum=6;arcNum=36;G = new HeadNode[nodeNum];createGraph(G, nodeNum, arcNum);cout << "=============================" << endl;cout << "下面开始打印图信息..." << endl;printGraph(G, nodeNum);cout << "=============================" << endl;cout << "下面开始运行dijkstra算法..." << endl;for (int i=1;i<=6;i++){Dijkstra(G, nodeNum, i);cout << "=============================" << endl;cout << "打印从v"<<i<<"开始所有的最短路径" << endl;fout << "打印从v"<<i<<"开始所有的最短路径" << endl;for (int k = 1; k <= nodeNum; k++) {if(k!=i){if(G[k-1].d>=150){cout<<"v"<<i<<"到v" << k << "无法到达!";fout<<"v"<<i<<"到v" << k << "无法到达!";}else{cout << "v"<<i<<"到v" << k << "的最短路径为" << G[k-1].d << ": "; fout << "v"<<i<<"到v" << k << "的最短路径为" << G[k-1].d << ": "; printPath(G, k);}cout << endl;fout << endl;}}}}算法分析:图中应用Dijkstra算法更好地实现最短路问题,效率提高很多。
重邮,王利,c语言实验课

C语言程序设计实验报告学号:姓名:班级:0801406任课教师:王利学期:2014-2015(2)第一次实验日志实验题目:1.改正错误,并让程序正确运行#include<stdio.h>void main(){printf(“these values are:\n”);int x=y=2.5;printf(“x=%d\n”,x);printf(“x=%d\n”,y);pri ntf(“x=%d\n”,z);}2.在屏幕上输出如下图形:*********3.已知三角形的底和高,求三角形的面积。
实验目的:掌握C程序的建立,和使用。
实验要求:独立完成实验题目实验主要步骤:1.打开C++;2.建立工作区和文件;3.根据题目要求,完成作业。
实验结果:#include <stdio.h>void main(){float x,y,z;x=y=z=2.5;printf("x=%f\n",x);printf("y=%f\n",y);printf("z=%f\n",z);printf("these values are:\n");printf(" *\n ***\n*****\n");float a,b,s;scanf("%f,%f",&a,&b);s=1/2*a*b;printf("三角形的面积:%f\n",(float)s);}心得体会:注意变量的精度问题,高精度不能赋值给低精度,可以通过(float)+变量名的方式改变变量精度。
第二次实验日志实验题目:1)某航空公司规定:在旅游旺季7~9月份,如果订票20张及其以上,优惠票价的10%;20张以下,优惠5%;在旅游淡季1~6月份、10~12月份,订票20张及其以上,优惠20%,20张以下,优惠10%。
数据结构实验报告(重邮)5个

数据结构实验报告学院:班级:姓名:学号:实验一线性链表的实现与操作题目:设计一个100位以内的长整数加减运算的程序班级:姓名:学号:完成日期:一、需求分析1、本实验中,100位长整数的每位上的数字必须为数字[0——9]之间,长整数的位数并要求100位以内。
测试的时候输入数据,当输入回车键的时候结束输入,如果输入的字符不符合题目要求,则程序能过滤这些不符合要求的字符。
2、演示程序以用户和计算机的对话方式执行,即在计算机显示“提示信息”后之后,由用户在键盘上输入演示程序中规定的运算命令;相应的输入数据(滤去输入中不符合要求的字符)和运算结果显示在其后。
3、程序执行的命令包括:(1)创建第一个整数(100以内);(2)执行加法或者减法;(3)创建第二个整数(100以内);(4)结束。
二、概要设计为实现上述程序功能,可以用链表或者长数组表示长整数,如果用数组表示长整数有个缺点就是长整数不能无限长,而链表能动态开辟空间,它克服了这个缺点,所以次试验用链表来表示长整数。
1、链表的抽象数据类型定义为:ADT Number{数据对象:D={a i| a i∈(0,1,…,9),i=0,1,2,…,n,n≥0}数据关系:R={< a i-1, a i>| a i-1, a i∈D,i=1,2,…,n}基本操作:CreateList(&L)操作结果:创建一个链表L。
PrintList(L)初始条件:链表L已存在。
操作结果:在屏幕上输出链表的值。
PlusList(L1,L2,a)初始条件:链表L1,L2已存在,a为+ or –表示加减。
操作结果:将两链表的值相加然后在屏幕上输出。
DestroyList(&L)初始条件:链表L已存在。
操作结果:销毁链表L。
} ADT Number2、本程序包含五个模块:int main(){定义变量;接受命令;处理命令;return 0;}各模块之间的调用关系如下:+or - :+or -三、详细设计1、定义头文件#include<stdio.h>#include<stdlib.h>#define LEN sizeof(Number)typedef struct number Number;struct number{int data;Number *next;Number *prior;};/////////////////////////////////////////////////////////////////////////////////////////////// ////////void main(){void DestoryList(Number *); //释放链表void PutNumber(Number *); //将求得的结果输出Number *GetNumber(); //创建链表,放被加数与加数Number *JiaFa(Number *num_1,Number *num_2);//加法函数Number *JianFa(Number *num_1,Number *num_2);//减法函数Number *number_1,*number_2,*number;char ch; //存放运算符号printf("Enter the first long number:");number_1=GetNumber();printf("put +or-:");ch=getchar();fflush(stdin); //吸收不相关的字符printf("Enter the second long number:");number_2=GetNumber();if(ch=='+')number=JiaFa(number_1,number_2);elseif(ch=='-')number=JianFa(number_1,number_2);printf("\n=\n");PutNumber(number);DestoryList(number);DestoryList(number_1);DestoryList(number_2);printf("链表释放完成。
算法分析与复杂性理论-实验报告-求最近点对的问题

深圳大学实验报告教务部制1.对于平面上给定的N个点,给出所有点对的最短距离,即,输入是平面上的N个点,输出是N点中具有最短距离的两点。
2.要求随机生成N个点的平面坐标,应用蛮力法编程计算出所有点对的最短距离。
3.要求随机生成N个点的平面坐标,应用分治法编程计算出所有点对的最短距离。
4.分别对N=100,1000,10000,100000 ,统计算法运行时间,比较理论效率与实测效率的差异,同时对蛮力法和分治法的算法效率进行分析和比较。
5.利用Unity3D输出分治算法中间每个步骤的计算结果,并增设help按钮,详细解释算法思想。
算法思想提示1.预处理:根据输入点集S中的x轴和y轴坐标进行排序,得到X和Y,很显然此时X和Y 中的点就是S中的点。
2.点数较少时的情形直接计菊只有三个疽3.点数|S|>3时,将平面点集S分割成为大小大致相等的两个子集S L和S R,选取一个垂直线L作为分割直线,考虑X L和X R,Y L和Y R,这里还需要排序吗?4.两个递归调用,分别求出S L和S R中的最短距离为d i和d r。
5.取d=min(dl, dr),在直线L两边分别扩展d,得到边界区域Y, Y'是区域Y中的点按照y坐标值排序后得到的点集,Y'又可分为左右两个集合Y 'L和Y 'RL.一L<dL+d6.对于Y'L中的每一点,检查Y'R中的点与它的距离,更新所获得的最近距离实验过程及内容:(实验代码已作为附件提交,名为“算法实验二.cpp)当点的数量小丁3时,直接计算,当点的个数大丁3时,采用分治法当N=1时当N=2时只有两个点,最近点对就是这两个点测试数据为(1,1 ) (2,2)预期结果为d=1.414使用蛮力法求最近点对,核心代码如下〃求距离平方的函数double Distinyuish2(Node a t Node b)return ((d.x-b.x)*(a.x-b.x)) + ((a.y-tj.y)*(a.y-b.y));〃蛮力法求最近对uoid BriiteForce(const HList & L,CloseHode & cnode,int begin v int end)For(int i=t)egin;i<=end;i*+)Forfinit j<-end;j + + )double space = Di stinguish2(L.data[i],L.data[j]); iF<sp^ce<cnode.5pact)cnode_a=L.data[l]; cnade.b=L.data[j]; cnode .space=space;(计算两点之间的距离,分别将每个点与其它点的距离求出来,找出最近点距离)当N>3时,使用分治法的情况核心代码如下:;15E 〃当n》3时进行分治<APOIHT *SL-nev fi_POINT[(high-low)/2+1];■[POINT *SR-nev A>0IHT[ (hi^i-low)/2];n)= (high-low)/2; /成曦(组以缺)界划分为茜半j=k=t);for(i=B;i<=high-lou;i*+)if(V[i]*indeK<=n){SL[ ji ] T [i];〃收集左边子集中的最近点对pise{SR[kt+]=Y[i];〃收集右边子集中的最近点对>)closest (K.SL,low,■,al,bl,dl);//i+ 算左边子集的最近点对closes t (X,Sft,m+1,tiigh,ar.br,dr 算右边子靠的最近点对if(dl<dr);b=bl;d=dl;}else(a=ar;b=tjr ;d=dr;POIlfT *2=new POI NT[higti-low+1 ];k=o;For(i=B;i<=t*igh-lcw;i*+)//收集距离中线?寤小于U的元素,保存S懒组?中(iF(f=abstX[n] .x-V[l] .x)<d>2(k].x=V[i],x;£[k^+].y=V[i]^:for(i-l;l<k;l++)< far(j=i>1;(-y-Z[i] j++)dl=aist(Z[i]^[j]);{a = 2[iJ;b - Z[j];ri = d) ■当N=6时,给定一组测试数据下面随机生成N个点的平面坐标,求解最近点对。
重庆邮电2015--2016研究生课表
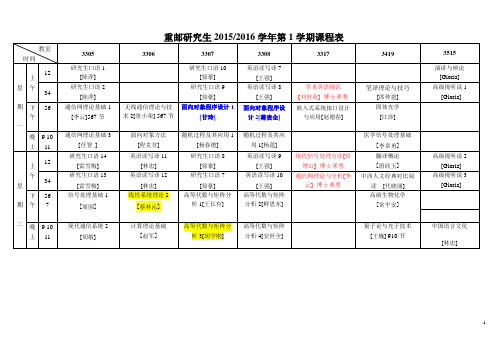
9 10
11
高级通信原理1
[雷维嘉]
优化理论与最优控制2
[李永福]
高等代数与矩阵分析6
[孙凤兰]
图论及其应用3
[陈六新]
光电子学
[王小发]
分子细胞生物学
[梁亦龙]910节
重邮研究生2015/2016学年第1学期课程表(续)
教室
时间
4214
4215
4216
4217
星
期三Biblioteka 上午12读写互动英语7
[刘雪琴]
自然辩证法概论(7)[马理]单周
自然辩证法概论(8)[马理]双周
信息安全理论
[陈龙罗文俊刘宴兵]博士课程
下
午
56
7
信号处理基础2
[张天骐]
运筹学
[卢安文]
随机过程及其应用2
[游晓黔]
图论及其应用4
[徐阳栋]
大数据分析与挖掘博士课程
[王国胤刘群]56节
高等量子力学
[朱家骥]
稳定性理论、方法和应用
[胡晓红]
[罗志勇]
马克思主义思想发展史
[郑洁]
晚上
9 10
11
现代电路理论及技术
[何丰管春]
刑事诉讼法专题研究
[熊志海]
中间件技术
[肖云鹏]910节
网络化控制技术
[谢昊飞]910节
星
期
四
上午
12
34
刑法专题研究
[赵长江]
下
午
56
7
民事诉讼法专题研究
[黄良友]
现代通信系统1
[余翔(通)]
通信网理论基础2
[刘焕淋]
56
重邮计算机专硕学制

重邮计算机专硕学制随着信息化时代的发展,计算机专业硕士(简称“专硕”)成为了热门的研究生教育形式。
重庆邮电大学(以下简称“重邮”)计算机专硕学制是在国家教育部的指导下,依据自身实际情况制定的。
本文将从以下几个方面介绍重邮计算机专硕学制。
一、学制概述重邮计算机专硕学制属于全日制研究生教育,学制为2年。
学制内,第一学年为课程学习阶段,第二学年为实践与论文阶段。
学生需完成指定的课程学习和实践任务,并完成硕士论文的撰写和答辩。
二、培养目标本专业旨在培养具备扎实的计算机基础知识和较强的问题解决能力,具备创新思维和实践能力,能够在计算机科学与技术领域的研究、开发和应用中发挥领导和推动作用的高层次计算机专业人才。
三、课程设置重邮计算机专硕学制的课程设置包括学科基础课程、专业方向课程和实践课程三部分。
学科基础课程包括计算机组成原理、操作系统、数据结构与算法分析、计算机网络、数据库系统等;专业方向课程包括人工智能、分布式系统、网络安全等;实践课程包括计算机系统设计、软件工程实践、课程设计等。
学生需根据自身学习计划和导师的要求,选修相应的课程。
四、实践与论文重邮计算机专硕学制的实践环节包括实验、课程设计和实习。
学生需在实习单位、学校实验室等实践场所,完成相应的实践任务,掌握实际工作中的计算机应用技能和解决问题的能力。
硕士论文是研究生培养的重要环节,也是考核学生综合能力的重要手段。
学生需选择合适的研究方向和题目,按照学校规定的格式和要求,撰写硕士论文。
论文答辩前,学生需进行答辩前的工作,包括论文修改、论文发表等。
五、研究生导师研究生导师是研究生教育中的重要人物,他们是学生学习和成长的引路人。
重邮计算机专硕学制的导师队伍由学校计算机学院的教授、副教授和高级工程师组成。
学生在入学后,需选择一名导师,导师将指导学生的学习、实践和论文撰写等工作。
六、招生要求重邮计算机专硕学制的招生对象为具有本科学位或同等学历的计算机相关专业毕业生。
重庆邮电大学计算机学院C++上机试验报告

C++集中上机实验日志实验6—1一、问题描述定义一个字符串类String,其数据成员有指向字符串的指针elems,成员函数包括构造函数、析构函数、判断字符串是否为空的operator!()。
编程测试类String的功能。
二、实验输出如图所示:三、实验思路以及方法判断字符串是否为空即是对字符串进行非运算,即重载operator!()。
逻辑非运算是单目运算符,按照运算符重载方针,应该重载为类的成员函数。
由于逻辑非运算结果只有两种:真、假,因此operator!()的返回值类型为bool型。
四心得体会开始没有判断elems的空指针问题,遇到一点麻烦,改过之后就ok了,本实验让我们学习了“运算符重载类的成员函数”,对以后的学习C++有了很大了帮助。
代码实现#include<iostream>#include<string>using namespace std;class String{public:String(const char *e=NULL);~String();bool operator!()const;private:char *elems;};String::String (const char *e){if(e==NULL){elems=NULL;return;}else{elems=new char[strlen(e)];strcpy(elems,e);return;}}bool String::operator !()const{if(elems==NULL)return true;else return false;}String::~String (){if(elems!=NULL)delete[]elems;}int main(){String str;if(!str)cout<<"这是一个空字符串!"<<endl;return 0;}实验6-3一、问题重述对于具有相同行列数的矩阵进行加、减、乘、转置、赋值运算。
南邮算法实验报告

一、实验目的本次实验旨在通过实际操作,加深对算法理论知识的理解,提高算法设计与分析能力,培养解决实际问题的能力。
通过实验,使学生掌握以下内容:1. 理解常见算法的基本原理和实现方法;2. 掌握算法设计与分析的常用方法;3. 能够运用算法解决实际问题。
二、实验内容本次实验选择了以下两个算法进行实现和分析:1. 冒泡排序算法;2. 快速排序算法。
三、实验过程1. 冒泡排序算法(1)算法原理冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
遍历数列的工作是重复地进行,直到没有再需要交换,也就是说该数列已经排序完成。
(2)实现步骤① 初始化一个布尔变量 swapped,用于判断是否发生交换;② 遍历数组,比较相邻的两个元素,如果前者大于后者,则交换它们的位置;③ 如果在一轮遍历中没有发生交换,则说明数组已经排序完成,退出循环;④ 重复步骤②和③,直到数组排序完成。
(3)代码实现```pythondef bubble_sort(arr):n = len(arr)for i in range(n):swapped = Falsefor j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]swapped = Trueif not swapped:breakreturn arr```2. 快速排序算法(1)算法原理快速排序是一种分而治之的排序算法。
基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
(2)实现步骤① 选择一个基准值(pivot),可以是数组的第一个元素、最后一个元素或中间元素;② 将数组分为两部分,一部分是小于基准值的元素,另一部分是大于基准值的元素;③ 对这两部分数据分别进行快速排序;④ 递归执行步骤①至③,直到数组排序完成。
重邮课程实验报告

一、实验名称数字信号处理实验二、实验目的1. 理解数字信号处理的基本概念和原理。
2. 掌握数字滤波器的设计方法及其应用。
3. 熟悉数字信号处理软件的使用,提高实验技能。
三、实验原理数字信号处理(Digital Signal Processing,DSP)是研究数字信号的产生、处理、分析和应用的科学。
本实验主要涉及以下几个方面:1. 数字滤波器的基本概念:数字滤波器是一种对数字信号进行频率选择的装置,可以用于信号的滤波、增强、抑制等。
2. 滤波器的设计方法:主要包括有限脉冲响应(FIR)滤波器和无限脉冲响应(IIR)滤波器的设计方法。
3. 数字信号处理软件的使用:利用MATLAB等软件进行数字信号处理实验,提高实验效率。
四、实验器材1. 实验计算机2. MATLAB软件3. 实验指导书五、实验步骤1. 实验一:FIR滤波器设计(1)打开MATLAB软件,创建一个新的脚本文件。
(2)根据实验指导书的要求,输入FIR滤波器的参数,如滤波器的阶数、截止频率等。
(3)运行脚本文件,观察滤波器的频率响应曲线。
(4)根据实验结果,分析滤波器的性能。
2. 实验二:IIR滤波器设计(1)打开MATLAB软件,创建一个新的脚本文件。
(2)根据实验指导书的要求,输入IIR滤波器的参数,如滤波器的阶数、截止频率等。
(3)运行脚本文件,观察滤波器的频率响应曲线。
(4)根据实验结果,分析滤波器的性能。
3. 实验三:数字信号处理软件的使用(1)打开MATLAB软件,创建一个新的脚本文件。
(2)根据实验指导书的要求,输入信号处理的参数,如采样频率、滤波器类型等。
(3)运行脚本文件,观察信号处理的结果。
(4)根据实验结果,分析数字信号处理软件的应用。
六、实验结果与分析1. 实验一:FIR滤波器设计实验结果表明,所设计的FIR滤波器具有较好的频率选择性,滤波效果符合预期。
2. 实验二:IIR滤波器设计实验结果表明,所设计的IIR滤波器具有较好的频率选择性,滤波效果符合预期。
重庆邮电大学算法分析复习

定义:如果存在正常数c1 ,c2 和n0 ,对于所 有的n≥n0,有 c1|g(n)| ≤|f(n)| ≤ c2|g(n)| 则记作:f (n) ( g (n)) 表示:算法在最好和最坏情况下的计算时间 就一个常数因子范围内而言是相同的。
多项式时间算法:可用多项式(函数)对其计算时 间限界的算法。常见的多项式限界函数有: Ο(1) < Ο(logn) < Ο(n) < Ο(nlogn) < Ο(n2) < Ο(n3) 指数时间算法:计算时间用指数函数限界的算法, 常见的指数时间限界函数: Ο(2n) < Ο(n!) < Ο(nn) 说明:当n取值较大时,指数时间算法和多项式时 间算法在计算时间上非常悬殊。
按增长率由小至大的顺序排列下列各 复杂度函数: 2^100, (2/3)^n,(3/2)^n, n^n , 根号n, n! ,2^n ,lgn ,n^lgn, n^(3/2)
分 析 如 下 : 2^100 是 常 数 阶 ; (2/3)^n 和 (3/2)^n是指数阶,其中前者是随n的增大而减 小的; n^n是指数方阶; √n 是方根阶, n! 就 是n(n-1)(n-2)... 就相当于n次方阶;2^n 是指 数阶,lgn是对数阶 ,n^lgn是对数方阶, n^(3/2) 是3/2次方阶。根据以上分析按增长率由小至 大的顺序可排列如下: (2/3)^n < 2^100 < lgn < √n < n^(3/2) < n^lgn < (3/2)^n < 2^n < n! < n^n
算法的5条特性及含义
确定性:算法的每一种运算必须要有确切的定义,即 每一种运算应该执行何种动作必须是相当清楚的、无 二义性。 可行性:一个算法是可行的指的是算法中有待实现的 运算都是基本的运算,每种运算至少在原理上能由人 用纸和笔在有限的时间内完成。 输入:一个算法有0个或多个输入,这些输入是算法开 始之前给出的量,这些输入取自特定的对象集合。 输出:一个算法产生一个或多个输出,这些输出是同 输入有某种特定关系的量。 有穷性:一个算法总是在执行了有穷步的运算之后终 止。 凡是算法,都必须满足以上5条特性。只满足前4条特性 的一组规则不能称为算法,只能叫做计算过程。
重邮【2009】26号大学生创新性实验计划项目管理办法

重庆邮电大学文件重邮〔2009〕26号关于印发《重庆邮电大学大学生创新性实验计划项目管理办法》的通知各学院、各相关单位:现将《重庆邮电大学大学生创新性实验计划项目管理办法》印发给你们,请遵照实施。
二○○九年一月十七日—1 —重庆邮电大学大学生创新性实验计划项目管理办法第一章总则第一条重庆邮电大学大学生创新性实验计划(以下均简称创新实验计划)旨在鼓励和支持大学生尽早开展科学研究、技术开发和社会实践等活动,探索并建立以问题和课题为核心的教学模式,促进以本科学生为主体的创新性实验改革,调动学生的主动性、积极性和创造性,激发学生的创新思维和创新意识,掌握思考问题、解决问题的方法,提高实践创新能力。
为保证该计划的顺利实施,特制定本办法.第二条创新实验计划严格遵循“立足兴趣、突出重点、鼓励创新、交叉联合、注重过程”的原则,按照“自主选题、自主设计、自主实验、自主管理”的要求,通过“自由申请、公开立项、择优资助、规范管理”的程序,以项目为载体,在导师指导下,注重学生自主实验和过程训练。
第二章组织机构第三条创新实验计划在分管校长领导下,由教务处牵头,汇同相关部门组成领导小组,负责制定和完善有关规章制度,统筹规划各项工作;领导小组下设项目管理办公室,挂靠教务处,具体负责日常工作的开展。
第四条学校分科类聘请相关专家组成创新实验计划指导委—2 —员会,负责项目的申报评审、中期检查、结题验收、专利申请及奖励建议.第五条各学院成立创新实验计划工作小组,具体负责本院系大学生创新性实验计划实施细则的制订和组织实施。
第三章申报与评审第六条项目申报范围为一至三年级本科生。
申请者要学有余力,善于独立思考,实践动手能力较强,具有一定的创新意识和研究探索精神,对科学研究、科技活动或社会实践有浓厚的兴趣。
对确有特长的学生,经学院工作小组考核,可适当放宽申报条件。
申报者可以是个人,也可以是两至三人组成的团队,鼓励学科交叉和年级交叉,个人不得一次同时申报两个项目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法分析与设计实验报告实验二减治策略查找顺序表实验目的1)以顺序表查找问题为例,掌握减治法的基本设计策略;2)熟练掌握折半查找算法的实现;3)掌握插值查找算法的实现;4) 分析实验结果。
实验环境计算机、C语言程序设计环境实验内容与步骤1.准备实验数据通过实验一获得的排好序的resultsMS.txt数据可作为本算法实验的输入数据。
要求:实现binary_search算法。
输入:已排序数据序列A、待查找的数据元素key;输出:数据元素key在数据序列A中的位置。
2.折半查找算法思想:二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。
因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。
重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
程序代码:#include <stdio.h>#include<stdlib.h>#include<time.h>int BSearch2(int a[],int x,int l,int h) {int m;while(l <= h){m = (l + h) / 2;if(a[m] == x) return m;if(a[m] < x)l= m + 1;elseh= m - 1;}return -1;}void main(){FILE *fp;int i,x,m;int A[2000];/* for(i=0;i<2000;i++)a[i]= rand()%10000;sort(a,10000);*/if( (fp=fopen("resultsMS.txt","r")) == NULL )printf("Error!");printf("请输入要查找数据:");scanf("%d",&m);for(i=0;i<2000;i++)fscanf(fp,"%d",&A[i]);fclose(fp);x=BSearch2(A,m,0,1999);if(x==-1)printf("查找失败,该数据不存在!\n");elseprintf("查找成功,下标为%d\n",x);}运行结果截图:复杂度分析:假设对n个元素的折半查找需要消耗的时间为t(n)。
容易知道:如果n = 1,则t(n) = c1如果n > 1,则t(n) = t(n/2) + c2其中n/2需要取整,c1、c2都是常数对于正整数n,可以有:t(n) = t(n/2) + c2= t(n/4) + 2*c2= t(n/8) + 4*c2= ...= t(n/(2的k次方)) + k*c2一直推演下去,直到n/(2的k次方)等于1,也就是k = log2(n),此时等式变为:t(n) = t(1) + k*c2= c1 + log2(n)*c2于是时间复杂度为log2(n)。
注意log2(n)和log(n)其实是同样的复杂度,因为它们之间仅仅差了一个常量系数而已。
插值查找算法1插值查找基本思想:(1)插值查找算法基本思想:比如要在取值范围1 ~ 10000 之间100 个元素从小到大均匀分布的数组中查找5,我们自然会考虑从数组下标较小的开始查找。
经过以上分析,折半查找这种查找方式,还是有改进空间的,并不一定是折半的!mid = (low+high)/ 2, 即mid = low + 1/2 * (high - low);改进为下面的计算机方案(不知道具体过程):mid = low + (key - a[low]) / (a[high] - a[low]) * (high - low),也就是将上述的比例参数1/2改进了,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
要求:实现interp_search算法。
输入:已排序数据序列A、待查找的数据元素key;输出:数据元素key在数据序列A中的位置。
程序#include<stdio.h>#include<string.h>#include<math.h>#include<ctype.h>#include<stdlib.h>#include<time.h>int interp_search(int key){int A[2100]={0},n=2000, i;int size=n-1;FILE *fp;fp=fopen("e:\\resultsMs.txt","r");for (i = 0; i < 2000; i++){fscanf(fp,"%d",&A[i]); } fclose(fp);int low = 0;int high = size - 1 ;int mid ;while (A[high] != A[low] && key >= A[low] && key <= A[high ]) {mid = low + (high - low) * ((key - A[low]) / ( A[high] - A[low])) ;if (A[mid] < key)low = mid + 1 ;else if (key < A[mid])high = mid - 1;elsereturn mid;}if (key == A[low])return low ;elsereturn -1;}void main(){int key,a,b;printf("请输入查找元素key:\n");scanf("%d",&key);b=interp_search(key);if(b==-1) printf("没有查找的元素\n");else printf("该元素的下标为:%d\n",b);}#include<stdio.h>#include<string.h>#include<math.h>#include<ctype.h>#include<stdlib.h>#include<time.h>int interp_search(int key){int A[2100]={0},n=2000, i;int size=n-1;FILE *fp;fp=fopen("e:\\resultsMs.txt","r");for (i = 0; i < 2000; i++){fscanf(fp,"%d",&A[i]); } fclose(fp);int low = 0;int high = size - 1 ;int mid ;while (A[high] != A[low] && key >= A[low] && key <= A[high ]) {mid = low + (high - low) * ((key - A[low]) / ( A[high] - A[low])) ;if (A[mid] < key)low = mid + 1 ;else if (key < A[mid])high = mid - 1;elsereturn mid;}if (key == A[low])return low ;elsereturn -1;}void main(){int key,a,b;printf("请输入查找元素key:\n");scanf("%d",&key);b=interp_search(key);if(b==-1) printf("没有查找的元素\n");else printf("该元素的下标为:%d\n",b);}实验结果:时间复杂度:时间复杂度是O(1)。
时间复杂度指的是当问题规模增大时候,运算量以什么规律增长。
对于计算一个插值点这个问题,无论数据点怎么增多,三个算法都不会发生运算量增长,每次插值都只在局部取固定数量的几个点而已,只不过有的简单有的复杂。
心得体会:本次实验所用到的基础知识与实验一很类似,只是算法有所不同,而实验报告中又给出了折半查找和插值查找算法的代码,所以相对实验一的基础上,本次实验所用时间可以减少很多。
基本按照实验一的步骤可以相对顺利的完成实验。
但是,在具体实施的过程中出现了文件调用的问题,经过自己的修改和向同学的请教终于顺利的解决了问题。
收获很多.。
