分子光谱基础
第九章分子光谱基础教程

这里R,r 分别是核运动和电子运动的坐标。 在忽略自旋和轨道相互作用后,分子哈密顿 算符的具体形式是
Hˆ
N
2 2MN
2 N
e
2 2me
2 e
VNN
Vee
VeN
核动能 电子动能
势能
采用B.O.(玻恩-奥本海默)近似后,分子的全波函数可以写
成核波函数和电子波函数的乘积:
玻恩-奥本海默近似(简称BO近似,又称绝热近似)认为由于原子 核的质量要比电子大很多,一般要大3-4个数量级,因而在同样的 相互作用下,原子核的动能比电子小得多,可以忽略不计。所以出 现在各粒子相互作用的势能项中的原子核坐标就可以视为常数,这 样,核与核之间的排斥能就应当看作是常数。在BO近似下,研究 一个分子内部核与电子运动的问题,就变为N个电子在固定的原子 核电场中运动的问题。而电子又都是电荷、质量、自旋等特征完全 相同的粒子,因此,分子结构问题的研究就化为N个全同粒子体系 的研究。这就大大简化了原来多粒子体系的复杂度。主要应用于分 子结构研究、凝聚态物理、量子化学、化学反应动力学等领域。
定通 过吸收或发射光的形式发生
mn
x
mn
y
mn
z
mn
显然,只有当 x mn 、 y mn和 z mn 不全为零时,跃迁才可
能发生,称为跃迁允许,反之,称为跃迁禁阻。
使 x mn 、 y mn 和 z mn 不全为零的条件,称为光谱选律。
光谱选律的确定,还可以借助群论作为工具
* n
Hˆ
'
(
t
)
md
* n
akm (t) kd
akm (t ) nk anm (t )
k
k
谱学导论 1-5分子光谱基础_2009

2009-9-30
谱学导论
3
§1.6 拉曼光谱
STOKES RaylHale Waihona Puke ighANTI-STOKES
0 -
0
0 +
和吸收光谱的差异:吸收光谱中光子的能量必须等于分子的某两个能 级之间的能量差,而拉曼光谱中入射光子的频率和分子跃迁所涉及的能 量差之间并没有确定的关系。拉曼光谱是通过测定散射光相对于入射光 频率的变化来获取分子内部结构信息
Anti-stokes 统一公式
4 B( J 3 / 2)
小拉曼位移
2009-9-30
谱学导论
7
§1.6 拉曼光谱
1.6.4
双原子分子振动拉曼光谱
0 (r r0 )
振动时的极化率变化
振动能级(谱项)
G (v) (v 1/ 2)
简谐振子
v 1
2009-9-30
谱学导论
1
§1.6 拉曼光谱
1.6.1
拉曼散射效应
弹性碰撞
散射 入射
瑞利(Rayleigh)散射
散射 入射
非弹性碰撞
斯托克斯(Stokes)线
散射 入射
散射 入射 反斯托克斯(Anti-Stokes)线
2009-9-30
谱学导论
2
§1.6 拉曼光谱
2009-9-30
谱学导论
14
§1.6 拉曼光谱
课后作业: 第一章 10, 11, 12
2009-9-30
谱学导论
15
§1.6 拉曼光谱
周鸣飞(分子反应机理) 蔡文斌(电化学,表面) 拉曼光谱: 曹勇(催化,表面) 核磁共振: 贺鹤勇(固体,催化) 王文宁(液体,蛋白质) 质谱: 杨芃原,陆豪杰(蛋白质组学) 丁传凡(质谱方法) X-射线衍射:翁林红(单晶,小分子) 朱元龙(多晶) 王文宁(单晶,蛋白质) 能谱: 戴维林(催化)
群论 分子光谱

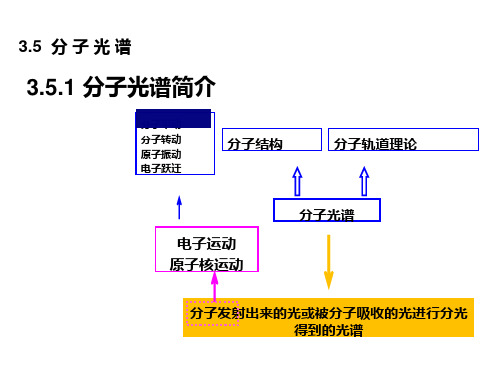
分子光谱的介绍
分子光谱是指物质中分子内部电子、振动和转动能级跃迁所产生的光谱。
它是一种非常重要的分析工具,可以用来研究分子结构、分子间的相互作用以及分子在外部环境中的行为。
分子光谱学的研究对象是分子中的电子、振动和转动能级跃迁。
电子能级跃迁产生的是电子光谱,主要包括紫外可见光谱、红外光谱、电子光谱等。
振动能级跃迁产生的是红外光谱,而转动能级跃迁则产生的是微波谱。
分子光谱在许多领域都有广泛的应用,例如化学、物理、生物和环境科学等。
通过分子光谱技术,我们可以了解分子的结构、化学键的种类和数量、分子中的电荷分布等信息。
这些信息有助于我们理解分子在化学反应、材料合成、生物过程和环境中的作用。
此外,分子光谱技术还可以用于医疗诊断和生物分析。
例如,红外光谱技术可以用于检测生物组织中的病变部位,而荧光光谱技术则可以用于检测生物样品中的某些生物分子。
这些技术的应用有助于提高我们对疾病的认识和治疗水平。
总之,分子光谱是一种非常重要的分析工具,它可以提供关于分子结构和行为的大量信息。
随着科技的发展,分子光谱技术的应用领域越来越广泛,它已经成为化学、物理、
生物和环境科学等领域中不可或缺的工具之一。
分子光谱解析知识点

分子光谱解析知识点分子光谱解析是一种用于研究分子结构和分子间相互作用的重要方法。
通过对分子在光照射下的吸收、散射或发射光谱进行测定和分析,可以获得关于分子结构、构型、光学性质等信息。
本文将介绍分子光谱解析的主要方法和相关知识点。
一、紫外-可见吸收光谱紫外-可见吸收光谱是一种常用的分子光谱解析方法,能够提供关于分子电子结构和电子能级的信息。
在紫外-可见区域(200-800纳米波长范围),分子发生电子跃迁的吸收峰可用于确定分子中的共轭结构、取代基团等。
例如,苯分子的紫外-可见吸收光谱显示了两个主要的吸收峰,大约在200-300纳米和240-300纳米波长范围内。
这些吸收峰对应于苯分子中的π-π*跃迁,提供了苯分子中芳香性的证据。
二、红外光谱红外光谱是一种常用的分子光谱解析方法,用于研究分子内部的振动和转动。
在红外光谱中,分子会吸收特定波长的红外辐射,这些波长与分子的振动或转动频率相对应。
红外光谱的峰位和强度可以提供关于分子的功能基团、键合和分子对称性的信息。
以甲醛为例,红外光谱显示了一个强烈的吸收峰,大约在1700-1750厘米⁻¹波数范围内。
这个吸收峰对应于甲醛中的羰基振动,表明甲醛分子中存在一个羰基功能基团。
三、拉曼光谱拉曼光谱是一种通过分子散射光谱和光子-分子相互作用的方法。
与红外光谱不同,拉曼光谱测定的是散射光的频率变化。
当分子受到激发和振动时,光子会发生散射,并且经历不同的频率变化。
通过测定散射光中的频率差异,可以获得关于分子振动和分子结构的信息。
举个例子,拉曼光谱可以用于鉴定和研究碳纳米管结构。
不同类型的碳纳米管在拉曼光谱中展现出不同的峰位和强度,这些特征可以帮助确定碳纳米管的外径、内径、手性等信息。
四、核磁共振光谱核磁共振光谱是一种通过测定核自旋与外磁场间相互作用的方法。
分子中的核自旋可以根据其不同的环境和化学键相互作用而发生不同的共振频率。
核磁共振光谱可以提供关于分子结构、构型、取代基团等信息。
13光谱的物理基础

本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不
第一节当原之处子,光请联谱系本人或网站删除。
一、原子光谱
1. 光谱 电磁辐射(不论在可见区或在可见区以外)的波长成 分和强度分布的记录,有时只是波长成分的记录。 光谱的类别从形状区分可分为三类:
明线光谱 、带状光谱 、连续光谱
2. 原子光谱(atomic spectrum),是由原子中的电子受激发在 不同能级间跃迁所产生的光谱。原子光谱的不连续表明了电子 的能量是量子化的。
原子光谱的特征:分立的线状光谱,发射谱是一些明亮的细线, 吸收谱是一些暗线。
本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不
第一节 原当子之光处谱,请联系本人或网站删除。
二、标识X射线谱
原子的光学光谱是最外层电子受激后辐射的,能级间的能量 差小,光子的频率较低;原子的标识X射线谱(详见本章第 五节)是内层电子电离后辐射的,能级间的能量差较大,光 子的频率很高。
2. 分子的纯转动光谱由分子转动能级之间的跃迁产生,分布在 远红外波段,波长是毫米或厘米的数量级,通常主要观测吸收 光谱。
本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不
第二节 分当子之光处谱,请联系本人或网站删除。
三、分子的振动光谱
1. 构成分子的诸原子之间的振动,形成振动能级。如双原子分 子沿着轴线振动。多原子分子的振动比较复杂,是多种振动方 式的叠加,振动的能量是量子化的。振动能级的间隔比电子能 级的间隔小。 2. 分布在近红外波段,波长是几个微米的数量级,通常主要观 测吸收光谱。
i表示X射线光子的频率,Ni为频率为vi的X射线的光子数,h
为普朗克常量。
分子光谱基础

谐振子的动能同样可以简化成单粒子体系处理。取分 子的质心作为坐标的原点,两原子的动能分别为
1 dr1 2 T1 = m1 ( ) 2 dt
由于
1 dr2 2 T2 = m2 ( ) 2 dt
m2 r1 = r m1 + m2
m1 r2 = r m1 + m2
所以总动能
以q = r- re代入,得
1 dr 2 T = T1 + T2 = µ ( ) 2 dt
e
x = 0.0174 k ) µ
0
(3)双原子分子的振动— 转动光谱
如在室温下(300K),若分子的折合质量为10-28 kg, 原子核间距为 10 - 7 cm,相邻两能级上的分子数之比为 0.996,这说明分子出现在个能级上的概率很接近。
利用远红外光谱测定异核双原子分子的键长 例 3.5.1 H35Cl 的远红外光谱线 ν =21.18, 42.38, 63.54, 84.72, 105.91 cm-1, 试求算转动惯量及核间距。 解: 相邻谱线的间隔
J = 0, 1, 2,· · ·
h2 E r = J ( J + 1) 2 8π I
J — 转动量子数
异核双原子分子转动光谱的具体选律为:
∆J = ±1
从J
J+1跃迁时吸收光的波数为:
~ = ∆E = E ( J + 1) − E ( J ) ν ch ch
h [( J + 2 )( J + 1) − ( J + 1) J ] = 2 8π Ic h = 2 × 2 ( J + 1) 8π Ic
Байду номын сангаас
分子运动的ΔE大致范围 ΔE/ eV
分子光谱

分子光谱:紫外、可见、红外等吸收光谱 带状光谱 I
黑体辐射:白炽灯、液、固灼热发光 连续光谱
分子对光的吸收与吸收光谱
不同颜色的可见光波长及其互补光
/nm 400 ~ 450 450 ~ 480 480 ~ 490 颜色 紫 蓝 绿蓝 互补光 黄绿 黄 橙
490 ~ 500 500 ~ 560 560 ~ 580 580 ~ 610 610 ~ 650
动能为: A
1 2 2 mAv A
Req
B A
B mB v
1 2
2 B
C
故分子的总转动能为:
1 2 2 R 1 m v m v 2 2 A A B B
同时有:
RCA MB Req MA MB
M B Req M
A
即
RCA
MB
同理:
RCB
M A Req MA MB
3. 多原子分子的SchrÖdinger方程
(1)核运动和电子运动的分离
包含核和电子的分子总Schrö dinger方程是
ˆ ( R, r ) E( R, r ) H
这里R,r 分别是核运动和电子运动的坐标。 在忽略自旋和轨道相互作用后,分子哈密顿 算符的具体形式是
2 2 2 2 ˆ H N e VNN Vee VeN N 2M N e 2m e
由此可以得到:
R A B
M A Req M B Req 1 1 2 )2 M A( ) M B ( 2 MA MB 2 MA MB
1 M AM B 2 Req 2 2 MA MB
记为
1 1 1 2 2 2 Req I ( I ) 2 2 2 2I
分子光谱
振动能级
注意区别振动量子数 v (英文)
和经典振动频率ν (希文). 以
下不再用颜色区分
振动跃迁选律: 整体选律:只有能够引起分子固有偶极矩变 化的振动方式才可能观察到红外光谱. 这对多原子 分子也是适用的. 具体选律:才有Δv=±1的跃迁是允许的.
对于非极性双原子分子(同核),没有振动光谱。但对 于非极性的多原子分子不受此限制,因为非极性的多原 子分子在振动过程中,其几何构型改变,偶极矩不恒等 于零。
动频率, 连接较轻的原子(如H)的化学键振动频 率较高.
频率较高的振动不易受其他因素影响. 经验表明:同一种官能团的振动频率在不同化合物中大 致相同, 据此可鉴别不同类型的化合物. 频率较低的振动则易随环境而变, 反映每一种具体分 子的结构信息, 出现的区域称为“指纹区”. IR谱的扫描范围通常在4000~650 cm-1, 特征频率区与
从可见区可延伸到毫米区,实现远红外光谱测定.
傅里叶变换红外光谱仪框图
化学键的振动研究对光纤通讯材料也具有实际意义。光在 光纤中传输时的损耗与光纤的总体性质和原子尺度上的性质有 关. 由玻璃密度、组成的随机涨落所引起的 Rayleigh 散射光强 与波长的四次方成反比,所以,与可见光和紫外光相比,使用 红外光可以显著降低损耗。 从另一方面看,红外光可以激发玻璃中Si、O和杂质原子 之间化学键的振动跃迁. 尽管目前大量使用的高透明度SiO2玻 璃已能满足远距离通信的要求,但若要进一步降低光损耗,还 需要减少振动激发. 使用原子量大于Si而化学键更弱的材料, 可以在更长的波长范围内实现红外透明,Rayleigh散射、振动 激发和电子激发都可以降至极低. 所以,近年来发展了性能更 加优越的ZrF4、LaF4和BaF2三元混合体氟玻璃,传输光信号 上万千米不需任何中继站.
分子光谱基础

(3) 若在稍高于 3000 cm?1有吸收, 则应在 2250 ~ 1450 cm?1 频区 分析不饱和碳碳键的伸缩振动吸收特征峰
3)1710 cm?1,C=O, 2820,2720 cm?1,醛基
4)结合化合物的分子式 此化合物为间甲基苯甲醛
例2 C3H4O
1)不饱和度: (3?2?2?4)?2=2 可能为烯,炔及含有羰基的化合物
2)3300 cm?1 处宽带,羟基
结合 1040 cm?1 处的吸收,可推测含有O-H,
4-4-3磁共振谱4
第一章 分子光谱基础
1.分子光谱,包括紫外可见光谱,红外光谱,荧光光谱和拉曼光谱等。光和物质之间的相互作用,使分子对光产生了吸收、发射或散射。将物质吸收、发射或散射光的强度对频率作图所形成的演变关系,称为分子光谱。
8.造成线宽的原因:1.自然致宽2. Doppler致宽
9.所有分子都有电子光谱
10.电子能级之间的跃迁伴随着振动能级和转动能级的跃迁,所以电子光谱是由许多振动谱带组成的谱带系谱项能量
第二章 红外和拉曼光谱
A 3355 C 1373,1355 偕二甲基
电子运动方程决定了分子的电子光谱。
4.分子的总能量主要由以下三项组成
5.转动光谱:同一振动态内不同转动能级之间跃迁所产生的光谱。转动能级的能量差在10-3~10-6eV,故转动频率在远红外到微波区,特征是线光谱。
6.振动光谱:同一电子态内不同振动能级之间跃迁所产生的光谱。振动能级的能量差在10-2-1eV,光谱在近红外到中红外区。由于振动跃迁的同时会带动转动跃迁,所以振动光谱呈现出谱带特征。
10.电子能级之间的跃迁伴随着振动能级和转动能级的跃迁,所以电子光谱是由许多振动谱带组成的谱带系谱项能量
结构化学基础-3分子光谱
1 d V 3! dr
3 re
3
( r re )
3
2、非谐振子模型
以平衡键长处为势能零点,将Taylor级数从三阶处 截断
V (r )
1 2
k ( r re ) k ( r re )
2
3
k
1 d V 6 dr
3 re
3
k 的值可以通过Morse函数来求算
将此势能项代入Schrödinger方程,解得分子振动能级
h 4 c I1
2
( J 1)
2 2 B 2 ( J 1)
h 4 c I 2
2
( J 1)
2 1 2 1 1 1 I1 1 1 1 1 1 I2 2
J=3
8B
2
( J 1) h 8 Ic
2
2 ( J 1) B
J=2
6B 4B
B
h 8 Ic
2
转动光谱谱线间隔 取决于原子质量和 键长
J=1
J=0
2B
2 ( J 1) B
红外光谱的应用
测定异核双原分子的键长
B I r
2 B ( J 1 ), B
J 1
5
4 3 2 1 0
Ev
5 4 3 2 1 0
P 支(△J = - 1)
o
R 支(△J = + 1)
3, 多原子分子的振动光谱
1) 多原子分子的振动光谱可以通过解原子核的薛定谔 方程得到;
2) Schrödinger方程中的势能项可以近似采用谐振势来 描述;
分子光谱概述

08:14:14
-胡罗卜素
咖啡因 阿斯匹林
几种有机化合物的 分子吸收光谱图。
丙酮
吸收光谱的获得
Absorption Spectra (Spectrum) 表征某物质对不同波长单色光的吸收程度。以波长()为横 坐标,吸光度(A)为纵坐标,即吸光度随波长变化的曲线, 即为吸收光谱。
08:14:14
吸光光度法定性与定量分析的基础
分子光谱概述
08:14:14
电子光谱-Uv-vis 振动光谱
分子吸收光谱 转动光谱 IR
分子光谱
分子荧光
分子发射光谱 分子磷光
化学发光光谱
拉曼光谱 (分子散射)
08:14:14
电子跃迁与分子吸收光谱
物质分子内部三种运动形式: (1)电子相对于原子核的运动--电子能级,Ee electron (2)原子核在其平衡位置附近的相对振动--振动能级, Ev
入射光 I0
透射光 It
T It I0
0.0 % ~ 100.0 % 全部吸收 T = 0.0 %
全部透射 T = 100.0 %
T越大,说明对光的吸收越弱; 相反,T越小,对光的吸收越强
08:14:15
吸收定律-------朗伯-比尔定律
Lambert – Beer Law
I
I-dI
I0
It
ln It kcb
B
定性分析基础
A
A
物质对光的选择 吸收
max (A) max (B)
定量分析基础
A
在一定实验条件 下,物质对光的 吸收与物质的浓 度成正比。
08:14:14
增 大 C
吸收曲线的讨论:
①吸光度最大处对应的波长称为最大
化学中的分子光谱学

化学中的分子光谱学化学中的分子光谱学是研究分子的结构、运动与反应等方面的一门重要分析技术。
它通过分析分子的吸收、散射、发射等光谱特性,得到有关分子的信息,从而揭示物质的本质和特性。
本文将介绍分子光谱学的基本概念、原理与应用,以及近年来在化学研究中的重要进展。
一、红外光谱红外光谱是最广泛应用的分子光谱学技术之一。
它利用红外辐射能够激发分子振动、弯曲和转动等模式的特性,来探测分子内部的结构和键合情况。
红外光谱图谱通常由波数(单位为cm-1)和吸收率(transmittance)组成。
波数是指辐射能量与光速之比,是研究红外光谱的基本量,可以指示分子中各种振动和转动模式的频率。
吸收率则是光线穿过样品后被吸收的比例,与样品的透光度相反。
由于不同的化学键在吸收特定波数的红外光时会产生不同的振动模式,因此红外光谱图谱可以指示分子中的化学键类型和数量,从而确定分子的结构和化学组成。
例如,C=O键的振动会导致位于1650-1750 cm-1的特征峰出现,C-H键的振动则可以在2900-3100 cm-1范围内检测到。
红外光谱在化学、材料、生命科学等领域中都具有广泛的应用价值,如在食品检测、环境监测、药品质量控制、生物样品分析等方面均得到广泛的应用。
二、紫外-可见光谱紫外-可见光谱是另一种常用的分子光谱学技术。
与红外光谱不同,紫外-可见光谱是针对分子中的电子转移、激发和跃迁等能级变化进行分析的。
它通常使用在紫外光波段和可见光波段(200-800 nm),即我们肉眼可见的范围内。
同样,紫外-可见光谱图谱是由波长和吸收率或透光度组成。
吸收率表示样品吸收辐射的能力与辐射强度之比,透光度则是指光线通过样品后被吸收的比例。
在紫外-可见光谱中,吸收特定波长的光子可以导致分子中的电子从低能级跃迁到高能级,从而在光谱图谱中生成特征吸收峰。
由于不同的有机分子和无机离子对光的吸收响应不同,因此紫外-可见光谱可以用于分子识别、定量和质量控制等方面。
分子光谱概述范文

分子光谱概述范文分子光谱是研究分子的光谱学方法之一,通过测量分子与电磁辐射相互作用而导致的光谱现象,可以获得有关分子结构、特性和相互作用的重要信息。
分子光谱的发展使得科学家能够探索分子的能级结构、转动-振动-电子能量级的分布,从而深入理解分子的物理和化学性质。
本文将对分子光谱的基本原理、种类和应用进行概述。
分子光谱的基本原理是根据分子在电磁辐射下的吸收、发射和散射的行为来研究和分析分子的结构和活性。
分子与电磁辐射相互作用的方式主要包括电子吸收、红外吸收、拉曼散射和核磁共振等。
其中,电子吸收和红外吸收是最常用的两种分子光谱方法。
电子吸收光谱是通过分子中的一些电子从低能量态跃迁到高能量态而产生吸收现象。
这种吸收可以是有机分子的紫外-可见吸收,也可以是过渡金属化合物的红外吸收。
通过测量吸收的波长和强度,可以得到分子的电子结构和电子态的能级分布信息。
红外吸收光谱是分子在红外辐射下发生振动或转动振动相互作用而产生的光谱现象。
不同分子结构和键的振动模式具有特定的红外吸收峰,通过观察和分析红外吸收谱图,可以识别出不同化合物的分子结构和功能基团的存在。
拉曼散射是当分子处于激发态时,散射入射光而产生的光谱现象。
拉曼光谱是通过测量散射光的频率和强度来研究分子的转动和振动信息。
由于拉曼光谱具有高分辨率和非侵入性的特点,因此在化学和生物分子的研究中得到了广泛应用。
核磁共振是基于原子核在磁场中的行为而产生的光谱现象。
通过测量核磁共振谱图,可以推断出分子中各个原子核的化学环境和相互作用。
核磁共振也是现代有机化学和生物化学中常用的结构分析方法之一分子光谱在理论研究和应用领域都具有重要意义。
在理论研究方面,通过分析光谱数据,可以精确计算分子的能级结构、键长和键角等参数,从而更深入地理解分子的电子和振动性质。
在应用方面,分子光谱被广泛应用于化学和生物领域。
例如,在有机化学中,红外吸收光谱可以用于分析和鉴定有机化合物的结构和纯度。
分子物理学中的分子光谱学

分子物理学中的分子光谱学在分子物理学领域中,分子光谱学是一门关于分子的光谱特性研究的学科。
通过研究分子在不同光谱区域的相互作用及其与分子结构之间的关系,我们可以揭示分子内部的结构、动力学过程以及分子与外界相互作用的规律。
它不仅在理论研究中起着重要作用,而且在实际应用中也有广泛的用途。
一、分子光谱学的基本原理分子光谱学基于分子与辐射之间的相互作用,研究分子在不同频率范围内的光谱特性。
它涉及几个主要的光谱学分支,包括紫外-可见光谱、红外光谱和拉曼光谱等。
紫外-可见光谱是通过测量分子在紫外和可见光波段的吸收和发射光谱来研究分子的能级结构和电子跃迁过程。
这种光谱可以提供分子的电子结构信息,比如能级分布和激发态产生的原因。
红外光谱是通过测量分子在红外波段的吸收和发射光谱来研究分子振动和转动能级结构。
不同的化学键和官能团在红外光谱中表现出特有的吸收峰,因此可以通过红外光谱鉴定分子结构的特征。
拉曼光谱是通过测量分子在激光照射下散射光的光谱来研究分子的振动和转动谱线。
拉曼光谱比红外光谱更为灵敏,因为它可以测量散射光的频率差异,提供了有关分子谐振子的信息。
二、分子光谱学的应用1. 分子结构鉴定和定量分析:分子光谱学可以通过分析光谱特征,准确地鉴定未知物质的组成和结构。
通过与已知光谱进行对比,我们可以确定物质的成分和相对含量,从而实现物质的定量分析。
2. 分子动力学过程研究:通过分析分子在不同频率下的光谱特性,我们可以了解分子的振动和转动能级结构,揭示分子内部的动力学过程。
这对于研究分子反应、分子间相互作用以及材料表面的吸附现象等具有重要意义。
3. 分子能级改变研究:分子光谱学可以研究分子在不同能级之间的跃迁过程,揭示分子激发态产生的机制和能级分布情况。
这对于理解分子能级改变的原因和规律,以及开发相关领域的应用有重要意义。
4. 分子光谱成像:分子光谱学可以结合成像技术,实现对样品的高分辨率成像。
这种技术在生物医学、环境监测和材料科学等领域中有广泛的应用,可以提供对样品内部结构和成分的详细信息。
分子光谱知识介绍
2. 振动跃迁选律: 整体选律:只有能够引起分子固有偶极矩变化的振动
方式才可能观察到红外光谱. 具体选律:才有Δv=±1的跃迁是允许的.
3. 双原子振动光谱的应用
(1)由实验得到的振动光谱数据 v0 ,可求得力常数k,
进而讨论化学键的强弱。
例1:HI的基本振动频率为2309.5 cm-1, 求弹力常数。
对称伸缩
反对称伸缩
偶极距不变无红外活性 偶极距变有红外活性
极化率变有拉曼活性 极化率不变无拉曼活性
互排法则:有对称中心的分子其分子振动
对红外和拉曼之一有活性,则另一非活性
互允法则:无对称中心的分子其分子振动
对红外和拉曼都是活性的。
3.5.5 电子光谱
分子中价电子在分子轨道 之间跃迁,产生的吸收光谱称 为电子光谱。
.5.4 Roman光谱
分子振动也可能引起分子极化率的变化,产生拉曼 光谱.
拉曼光谱不是观察光的吸收, 而是观察光的非弹性散 射.
非弹性散射光很弱,过去较难观测. 激光拉曼光谱的 出现使灵敏度和分辨力大大提高,应用日益广泛.
激光拉曼光谱仪 (示意图)
拉曼光谱与红外光谱的关系
O=C=O
O=C=O
例3:实验测得12CO的转动光谱第一条谱线的波数是3.84235cm-1,若取 12C=12.0000,O=15.9949,13C=13.0007,则13CO转动光谱第一条谱线的 波数是多少?
3.5.3 双原子分子振动光谱
1.谐振子模型
f ke (r re )
当AB间距偏离时, A和B都受到一个回复 力的作用,大小相等, 方向相反。
质谱(MS)
(Mass Spectrometry)
分子光谱

第九章分子光谱和分子结构前面我们从原子光谱、原子磁性了解了原子的结构,但在生产实践和生活中接触的物体极少是孤立的原子,往往是由原子结合而成的分子或分子集团,它是物质结构的一个重要层次.本章将简要介绍分子光谱和分子结构.§9.1 分子光谱和分子能级一、分子与化学键分子由原子组成,原子通过它们间的相互作用而结合在一起.而分子中相邻原子间存在的各种不同形式的相互作用称为化学键.化学键的力是电性质的,它只与原子的外层电子有关,与原子的内层电子关系较少.这是因为各元素的物理、化学性质的周期性由最外层电子的运动决定;而且较重元素的标识X射线不因该元素所在化合物而不同.内层电子在分子中和孤立原子中几乎一样,但价电子则大不相同.原子价电子间不同的结合会形成不同的化学键,常见的二类化学键是离子键和共价键,一般还有金属键和Van der Waals键. 1.离子键当电离能很小的金属原子(如碱金属和碱土金属原子价电子易脱落)和电子亲合能很大的非金属原子(如卤族原子和氧族非金属原子容易吸往电子)非常接近时,前者失去价电子而成为正离子,后者获得前者失去的电子而成为负离子,正负离子由于Coulomb力相互吸引结合成分子;但当二离子由于运动惯性而过分接近时,它们的外层电子相互排斥的力变得显著,表现为离子间的互斥力.当引力和斥力相等时,就形成稳定的分子.这种化学键称为离子键.如NaCl分子是由Na+离子与Cl-离子组成的离子键分子.Na是碱金属元素,具有较小的电离能5.14eV,电离过程为Na + 5.14eV →Na+ + e-Cl是卤族元素,Cl原子最外层在3p上有5个电子,再得到一个就构成稳定的闭合壳层,所以吸收一个电子形成Cl -离子是放能过程,这个能量称为亲合能,Cl-的亲合能为3.72eV ,此过程为Cl + e - →Cl - + 3.72eV上述两过程共增能5.14eV -3.72eV =1.42eV .虽然Na 、Cl 原子形成Na +、Cl -离子后能量增加了,但当它们相互接近时,由于正负离子的电荷将引起Coulomb 吸引位能,因此Na +、Cl -离子体系能量有可能小于Na 、Cl 原子体系的能量.ٛ 图9-1中的两条曲线分别表示离子和原子体系的位能变化.选Na 原子和Cl 原子相距无穷远时的位能为零点能,横坐标表示两离子或原子间距离,可以看到当距离小于某一数值后,离子间的位能将小于原子间的位能.ٛNa +、Cl -离子体系的位能曲线有一极小值,这是由于距离小到一定值后,两带正电原子核的Coulomb 斥力位能迅速增加,距离越小,此能量越大.位能曲线最低点对应的距离以r 0表示,称平衡距离.如NaCl 分子的r 0=2.51Å,其位能为-3.58eV .作用力方向总是指向位能减小的方向.当r >r 0时,位能曲线斜率为正,作用力使离子间距离减小,为吸引力;当r <r 0时,位能曲线斜率为负,作用力使距离增加,为斥力;当r = r 0时,位能曲线斜率为零,作用力亦为零,所以Na+、Cl-离子有可能在r 0附近振动,形成稳定的NaCl 分子.图9-1 NaCl分子的位能曲线2.共价键许多由两个相同原子组成的双原子分子和绝大多数有机化合物的分子不是由离子组成的,它们的化学键不再是离子键.它们有一对或多对电子为两个原子共有,内层电子仍然属于原来的原子.这类分子称为共价键分子或称原子键,同极键分子.如两个氢原子靠近时,每个氢原子中电子的状态都将重新分布,使系统处于能量最低的状态,这时两个电子起着连结两个原子的作用,为两个核所共有.从量子力学分析而知这一对组成共价键的电子自旋必是反平行的.一般地说,原子外层电子中,有未组成自旋相反的电子对的电子,就有可能与其它原子中未组成电子对的电子结合成共价键.如氢原子只有一个外层电子,显然在原子中不可能与其它电子组成自旋相反的电子对,这个电子就有可能与另一氢原子中同样的电子结合成共价键.锂原子有3个电子,而2s 态的外层电子未能与其它电子组成自旋相反的电子对,因此能与另一锂原子中的2s 电子组成共价单键,成为锂的双原子分子.如果两个原子各有两个或三个未成对的电子,则俩俩配对可构成共价双键或三键.共价键构成的分子可分为两类.第一类是无极分子,它由同类原子构成.如H 2、O 2等,分子内键电子分布对称,正负电荷“重心”重合,因而分子不具有电偶极矩.另一类是有极分子,由不同类原子组成.如HCl ,两种原子对电子的亲合力不同,分子内键电子的分布不对称,正负电荷“重心”不重合,分子具有电偶极矩. 图9-2 分子带光谱二、分子光谱原子光谱的特征是线状光谱,一个线系中各谱线间隔都较大,只在接近线系极限处越来越密,该处强度也较弱;若原子外层电子数目较少,谱线系也为数不多.分子光谱的一般分布如图9-2所示.许多谱线形成一段一段的密集区域成为连续带状,称为光谱带.所以分子光谱的特征是带光谱.它的波长分布范围很广,可出现在远红外区(波长是cm 或mm 数量级)、近红外区(波长是μm 数量级)、可见区和紫外区(波长约在10-1μm 数量级).分子光谱一般具有如下规律:(1)由光谱线组成光谱带;(2)几个光谱带组成一个光谱带组;(3)几个光谱带组组成分子光谱.ٛ三、分子能级据实验观察,分子光谱是由远红外光谱、近红外光谱、可见光和紫外光谱交织在一起的光谱.而远红外光谱是由于分子转动能级的变化引起的;近红外光谱是分子既有振动能级又有转动能级改变时产生的;而可见光和紫外光谱是分子既有电子能级又有振动和转动能级变化时产生的.所以分子内部既有分子转动,又有分子的振动,还有分子中电子的运动.ٛ1.分子的转动和转动能级即将分子看作一个整体绕某轴而转动.对于双原子分子,其转动轴通过分子的质心并垂直于分子轴(原子核间的联线).转动能量是量子化的,因而形成转动能级.转动能级的间隔约10-4~10-2eV.ٛ2.分子的振动和振动能级即组成分子的各原子在其平衡位置附近所做的微小振动.如双原子分子沿着轴线振动.与振动相联系的能量称为分子的振动能.振动能量也是量子化的,因而形成振动能级.振动能级间隔约10-1eV.3.分子中的电子运动和电子能级ٛ分子中外层电子的运动形成一些定态,电子在定态间跃迁运动.这些定态各具有一定能量,也就形成了电子的能级.当分子的电子能级间产生跃迁就产生光谱.电子能级间隔约为eV量级.ٛ若用E转、E振、E电分别代表上述三种运动状态的能量,分子能量可表示为E = E转 + E振 + E电(9-1)这三种能量的变化满足Δ>Δ>ΔE E E(9-2)振电转这样,在电子能级之上可以有较小间隔的振动能级;在振动能级之上又可以有更小间隔的转动能级.这些关系如图9-3所示,图中表示了振动能级和转动能级的特点,一组振动能级的间隔随能级的上升而减小;一组转动能级的间隔随着能级的上升而增加.由于分子能级的复杂结构,从而使分子光谱比原子光谱更复杂.图9-3 双原子分子能级示意图§9.2 分子的转动能级和转动光谱在辐射过程中,分子的电子状态和振动状态都没有改变,则辐射仅由分子的转动状态的改变而引起.由于△E 转ٛ最小,相应光子的能量很小,所产生的光谱一般在远红外区域.一、分子的转动能级假设分子是刚性分子.由于刚性分子不改变原子核间相对距离,所以它的转动是一个纯粹的转动,此简化模型忽略了振动对转动的影响.对双原子分子,其转动轴是通过质心而垂直于联接二原子核的直线的.分子的转动惯量ٛ (9-3) 2r I μ=其中1212m m m m μ=+是折合质量,r 是两原子核间的距离,如图9-4所示.对刚性分子r 是常数.若分子的转动角动量为P J .据经典力学,分子的转动动能IP I E J J 22122==ω (9-4) 其中P J =I ω,因为转动是自由的,所以势能为零,而体系总能量就等于转动动能.分子是微观粒子,它的角动量是量子化的,即=)1(+=J J P J ⋅⋅⋅=,,,,3210J (9-5)图9-4 刚性双原子分子的转动 J 称为转动量子数.代入(9-4) 式可得转动能级)1(22+=J J I E J = (9-6)由此所得能级图如图9-5所示.相邻二转动能级的间距ٛ)1(21+=−=Δ+J J IE E E J J J = (9-7)图9-5 双原子分子转动能级 可见转动能级的分布不是等间距的,J 越大,间隔也越大.ٛٛ二、分子的转动光谱实验和理论都证明转动能级间的跃迁须服从电偶极跃迁选择定则ٛ 1±=ΔJ (9-8)ΔJ =+1相当于吸收过程,ΔJ =-1相当于发射过程.当从能级J +1跃迁到能级J 的辐射频率12(1)2(14J J J J E E E h v J h h Iπ+)B J Δ−===+=+ (9-9)其中I hB 28π=称为转动常数.以波数表示2(1)Jv B J =+ B (9-10) 相邻二谱线间的波数差。
分子光谱基础知识

分光光度计的原理分光光度法测量的理论依据是伯郎—比耳定律:当容液中的物质在光的照射和激发下,产生了对光吸收的效应。
但物质对光的吸收是有选择性的,各种不同的物质都有其各自的吸收光谱。
所以根据定律当一束单色光通过一定浓度范围的稀有色溶液时,溶液对光的吸收程度A与溶液的浓度c(g/l)或液层厚度b(cm)成正比。
其定律表达式A=abc荧光分光光度计原理:在溶液中,当荧光物质的浓度较低时,其荧光强度与该物质的浓度通常有良好的正比关系,即IF=KC,利用这种关系可以进行荧光物质的定量分析,与紫外-可见分光光度法类似,荧光分析通常也采用标准曲线法进行。
由高压汞灯或氙灯发出的紫外光和蓝紫光经滤光片照射到样品池中,激发样品中的荧光物质发出荧光,荧光经过滤过和反射后,被光电倍增管所接受,然后以图或数字的形式显示出来。
物质荧光的产生是由在通常状况下处于基态的物质分子吸收激发光后变为激发态, 这些处于激发态的分子是不稳定的,在返回基态的过程中将一部分的能量又以光的形式放出,从而产生荧光.三. 荧光与分子结构的关系1. 分子结构与荧光具有p、p及n、p电子共轭结构的分子能吸收紫外和可见辐射而发生p -p* 或n - p* 跃迁,然后在受激分子的去活化过程中发生p*- p 或p*- n 跃迁而发射荧光。
发生p - p* 跃迁分子,其摩尔吸光系数(å)比n - p* 跃迁分子的大100—1000倍,它的激发单线态与三线态间的能量差别比n - p* 的大的多,电子不易形成自旋反转,体系间跨越几率很小,因此,p - p* 跃迁的分子,发生荧光的量子效率高,速率常数大,荧光也强。
所以——只有那些具有p- p共轭双键的分子才能发射较强的荧光;p电子共轭程度越大,荧光强度就越大(lex与lem长移)大多数含芳香环、杂环的化合物能发出荧光,且p电子共轭越长,F越大。
2. 取代基对分子发射荧光的影响(1)(苯环上)取代给电子基团,使p共轭程度升高à荧光强度增加:如–CH3,–NH2 ,–OH ,–OR等(2)(苯环上)取代吸电子基团,时荧光强度减弱甚至熄灭:如:–COOH ,–CHO,–NO2 ,–N=N–(3)高原子序数原子,增加体系间跨越的发生,使荧光减弱甚至熄灭。
4.分子光谱概述

能级跃迁示意图
第一电子激发态 电子能级跃迁
电子基态
转动能极跃迁 振动能级跃迁
电子能级上有许多振动能级,而振动能级 上有许多能量不同的转动能级
6
E E2 E1 h
(1) rotation:ΔΕr:0.005~0.050eV,248 - 25 m
hc
(2) vibration:ΔΕv:0.05~1eV, 25 - 1.2 m
3
分子的运动:
分子平动—整个分子的平动,不产生光谱;连续的 分子转动—分子围绕重心的转动 不连续、 分子振动—原子在平衡位置附近的振动 量子化 电子运动—分子中电子相对于原子核运动
每一种运动形式都有一定的能量,对应相应的能级,
用E转、E振、E电表示
每一种能量都是量子化的,是不连续的
4
分子的总能量:E分子= E电子+ E振动+ E转动
能级差:
△E电子1~20ev; △ E振动 0.025~1ev; △E转动<0.025ev
因这些能量都是量子化的,当一束具有特定能量的光照 射该分子时,若该分子上、下两能级差△E恰好等于该 光束的能量时,则光将被吸收,而分子被激发。 即△E = hc/λ 电子能级跃迁时伴随振动和转动能级的跃迁
5
△E电子> △E振动>△E转动1分子光谱分析来自电子能级振动能级
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.3 群表示及其性质
在数学上,图形可以用代数方法表示,所以代数方程是图形的数学表示。图形经过对称操作后,其数学表示就演变成另外一个代数方程。而两个代数方程之间可以通过矩阵运算得以转换。所以对称操作可以用代数方法的矩阵 来表示。
设 是另外一个矩阵,则矩阵运算
(1.1.1)
叫相似变换。对一个分子,如果其所有对称操作的表示矩阵经过相似变换后都具有下列准对角形式
(1.1.2)
O
H1 H2
A1 1 1 1 z
A2 1 1 -1
E 2 -1 0 (x,y)
若有两个状态 和 ,且从上表中知 ,则
C3v E 2C3 3
4 1 0
对直积进行分解,得到 = ,其中包含了全对称不可约表示 ,所以积分 可能有非零值。
常见的分子点群有以下几类:
1) 群:它只包含一根 旋转轴;
2) 群:在 群的基础上再增加一个垂直于 轴的 反映面;
3) 群:在 群的基础上,增加1个通过 轴的反映面;根据对称操作的组合规则,一定存在 个通过 轴的反映面;
4) 群:只包含一根 轴的点群;
5) 群:在 群中加入1根垂直于 轴的 轴( 轴是轴次最高旋转轴,被称为主轴),根据对称操作的组合规则,一定存在 根垂直于 轴的 轴;
分子可看成是一个有限图形,所以它的对称元素有旋转轴 、反映面 、对称中心 以及象转(旋转反映)轴 四种。与之相对应的对称操作是旋转 、反映 、反演 以及象转 。此外为了数学上自洽的需要,还要加上一个恒等操作 。这些操作的具体内容是:
1) 恒等操作 :维持分子中任何一点都保留在原来位置上不动的操作;
2) 旋转操作 :使分子旋转 角度后复原的操作。其中 和 都是整数, 称为轴次, 的旋转轴被为高次旋转轴。当分子中含有多于一根旋转轴时,轴次最高的旋转轴为分子的主轴,其它是副轴。
3) 反映操作 :将分子对某一平面进行反映后进入其等价构型,称该平面为分子的镜面,上述操作叫反映。与主轴垂直的镜面以 表示,包含主轴的镜面以 表示,平分两个相邻副轴的镜面以 表示。
6) 群:在 群的基础上再加一个垂直于主轴的 反映面;
7) 群:在 群的基础上再加上 个 面,形成 群;
8) 群:具有正四面体构型的分子属于 点群。
N
H3 H1
H2
9) 群:正八面体和立方体构型的分子属于 点群。
若定义两个对称操作之间的运算是两个操作的连续作用,容易验证,由分子全部对称操作所组成的集合构成了数学上的群。由于分子是一个有限图形,其所有对称元素都通过分子的质心,所以分子对称操作所构成的群被称为分子点群。按照分子中所包含对称元素的多少,可以将分子划归到一定的点群中。分子点群是对分子对称性高低的定量描述。
符号 叫直和。
在分子光谱中,经常需要计算诸如 形式的跃迁矩阵元的大小。由于这是一个多中心积分,计算通常是非常困难的。但是,在许多情况下,跃迁矩阵元的数值是零。依靠群论,我们往往不必通过计算就直接能对这一点作出判断。具体方法是:设跃迁前后分子的波函数分别是 和 ,它们分别属于分子点群的不可约表示 和 ,而偶极矩 属于 不可约表示。则跃迁矩阵元 所属的表示可以写成:
1.1.1 对称元素和对称操作
显然,诸如苯、甲烷、氨这样的分子都有对称性,但是怎样定量地描述分子的这种对称性高低呢?首先需要给出一个对分子对称性进行分类和描述的方法。以氨分子为例,它是正三角锥形状,N原子在正三角锥的顶点上,三个H原子位于三角锥基底正三角形的三个顶点上。设想,三个H原子构成的正三角形中心和N原子之间连成一条线,则当整个分子围绕这根线旋转120度后,我们不能分辨这个分子和它在旋转前有什么不同。这种在不改变分子中任何两个原子之间距离的前提下使分子复原的操作称为对称操作。对称操作赖以进行的几何元素称为对称元素。
C2v E C2
1 1 1 1
1 1 -1 -1
1 -1 1 -1
1 -1 -1 1
这样, 中包含不可约 的个数是
同样,包含 、 和 的个数分别是0、0和1。于是我们知道可约表示 是由一个 和一个 组成的,写成
, (1.1.3)
§1.1 多原子分子的结构和对称性
量子力学的基本原理告诉我们,只要知道了分子体系的波函数,就可以得到关于分子体系的任何信息。尽管写出一个分子的薛定鄂(Schr?dinger)方程并不困难,但是能够精确求解的微观体系却为数很少,绝大部分分子体系薛定鄂方程的求解都依赖于近似方法。因此,利用分子的某些特殊性质对繁复的量子化学计算过程进行简化,就非常有必要了。其中,分子的对称性是可供利用的最重要的性质之一。下面简单介绍一些分子对称性及其数学表示的最基本知识,有关详细内容可参阅相关的参考书。
称该表示是可约的,其中再不能约化的二个更小的矩阵表示(1个二维和1个一维)称为不可约表示。将可约表示分解为不可约表示的过程叫约化。
但是对称操作矩阵表示的具体形式和对称操作的具体对象有关。为了避免由此带来的复杂性(而且事实上也没有必要去求解具体的矩阵),我们只需要知道表示的特征标。特征标是对称操作表示矩阵的对角元之和。它的物理含义是,在所指定的对称操作下,操作对象保持不变的成分。以水分子为例,O原子到两个H连线的中点是 轴, H1-O-H2构成了一个 面,通过O原子到两个H连线的中点并垂直于纸平面的是另外一个 面。所以H2O是 点群。以两个H-O键为操作对象(被称为基),经过 操作后, H1-O和H2-O对换,即它们在各自原来的位置上都没有留下任何痕迹,所以特征标为零。同样对于垂直于纸面的 反映操作,H1-O和H2-O也是对换位置,所以特征标也是零。而对于纸平面内的 反映,H1-O和H2-O都保留在各自原来的位置上,所以特征标是2。综上所述, H2O分子以两个H-O键为基,在C2v点群各对称操作作用下的特征标是
第一章 分子光谱基础
很早人们就知道,物质的特殊颜色可以用于测定物质的含量,这就是比色分析法的基础。在量子力学诞生以后,人们对于光和物质之间相互作用的认识有了本质的飞跃,光谱技术不仅在定性定量分析上得到了很大发展,同时也演变成了人们了解物质结构信息的主要工具之一。本章主要介绍分子光谱的理论基础。物质对光产生的吸收、发射或散射,其本质是光和物质分子的相互作用,将物质吸收、发射或散射光的强度对频率作图所形成的演变关系,就是分子光谱。根据光辐射的波长范围和作用形式的不同,分子光谱又包括紫外可见光谱,红外光谱,吸收光谱、荧光光谱和拉曼光谱等。不同的光谱可提供物质分子内部不同运动的信息,由分子光谱了解物质的结构,这就是学习分子光谱的目的。
(1.1.4)
称为直积。直积的特征标等于单个表示特征标的乘积。直积一般是分子点群的可约表示,可以按照前面所讲的方法进行约化。经过约化后,如果直积中包含了全对称不可约表示,积分 才可能有非零值。例如,对C3v点群,特征标表是
C3v E 2C3 3
C2v E C2
2 0 0 2
这是一个可约表示。利用特征标表,利用公式我们可以对该可约表示 进行约化:
其中 是 中包含第 个不可约表示的数目, 是群的阶数(群元素的个数), 是对称操作 是第 个不可约表示的特征标。群论的有关书籍上提供了常见点群的特征标表,从中可以查阅到,C2v点群的特征标表是:
4) 反演操作 :将对称中心设在坐标原点,把分子中原来位于 的原子移到 而使分子复原的操作称为反演。
5) 象转操作 :将分子先旋转 ,然后再对垂直于旋转轴的镜面进行反映,使分子进入等价构型的操作。
1.1.2 群和分子点群
对一组元素 的集合,定义一种运算法则。集合中任何两个元素 和 ,按照这种法则运算,所得到的结果 ( ),满足封闭性、恒等元素、逆元素和结合律,称上述集合构成群(group)。这里所说的封闭性,指的是 一定是集合 中的一个元素。恒等元素指集合 中一定存在一个元素 ,它和其他任何元素 的运算结果始终满足 。对集合 中的任何一个元素 ,总存在另一个与之对应的元素 ( ),使得 , 就是 的逆元素。集合中任何三个元素之间的运算满足结合律,即 。
