【原子物理】第9章 分子结构与分子光谱
原子物理学教学大纲

原子物理学教学大纲
一、课程简介
本课程是一门针对大学物理专业的高级选修课,主要介绍原子物理
学的基础知识,包括原子结构、原子能级、原子核模型、原子光谱学
等内容。
通过学习本课程能够掌握原子物理学的基本理论和实验方法,为后续相关课程的学习和科研工作打下坚实的基础。
二、课程目标
本课程的主要目标在于:
1.着重掌握原子结构、原子能级、原子核模型、原子光谱学
等基础概念;
2.简要介绍原子物理学的历史发展和现状;
3.探讨原子物理学理论与实验的关系;
4.培养学生分析和解决有关原子物理学问题的能力;
5.激发学生对原子物理学科研工作的兴趣,为今后做好科研
工作奠定基础。
三、教学内容与教学时长
本课程共分为四个章节,具体内容如下:
第一章原子结构
•真空管和阴极射线实验
•半经验模型。
第9章羰基化合物

第9章 羰基化合物大体要求:1. 把握醛和酮的命名(系统命名法,一般命名法)2. 把握醛和酮的结构及对化学性质的阻碍。
3. 了解醛和酮的物理性质和光谱特点。
4. 把握亲核加成的反映类型、机理、应用。
5. α—H 的酸性,α—H 的卤代反映及缩合反映(羟醛缩合)6. 氧化、还原反映及其在有机合成中的应用。
7. α,β—不饱和醛、酮的反映特点。
醛(aldehydes )和酮(ketones )都是分子中含有羰基(碳氧双键)的化合物,因此又统称为羰基化合物。
羰基与一个烃基相连的化合物称为醛,与两个烃基相连的称为酮。
CO R'C RO HC R(H)O羰基 醛 酮醛能够简写为RCHO ,基团—CHO 为醛的官能团,称为醛基,酮能够简写为RCOR ’, 基团—CO —为酮的官能团,称为酮基。
醛和酮是一类超级重要的化合物,这不仅是因为学多化学产品和药物含有醛、酮结构,更重要的是醛、酮能发生许多化学反映,是进行有机合成的重要原料和中间体。
醌(quinone )类是一类特殊的环状不饱和二酮类化合物。
第一节 醛和酮一、羰基的结构羰基是醛、酮的官能团,它与醛、酮的物理化学性质紧密相关。
依照醛、酮分子的结构参数(见表10-1),能够以为羰基碳原子以sp 2杂化状态参与成键,即碳原子以三个sp 2轨道与其它三个原子的轨道重叠形成三个σ键,碳原子上未参加杂化的p 轨道与氧原子上的p 轨道在侧面彼此重叠形成一个π键(见图10-1)。
(请在图左侧第一幅图中,下半个轨道中着淡灰色,如中间那幅图轨道的颜色)表10-1 醛、酮分子的结构参数醛、酮分子 键长(pm ) 键角(0) HCHO C — ∠ ∠ CH 3CHOC — C —∠ ∠ ∠ CH 3COCH 3 C =O 121.4 C —∠ ∠δ-+图10-1 羰基的结构由于氧原子的电负性比碳原子大,因此成键处的电子云就不均匀地散布在碳氧原子之间,氧原子处电子云密度较高,带有部份负电荷,而碳原子处的电子云密度较低,带有部份正电荷。
原子光谱与分子光谱ppt课件

“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
一、 原子光谱
1.光谱项符号
原子外层有一个电子时,其能级可由四个量子数决定: 主量子数 n;角量子数 l;磁量子数 m;自旋量子数 s; 原子外层有多个电子时,其运动状态用总角量子数L;总 自旋量子数S;内量子数J 描述;
例:钠原子,一个外层电子, S =1/2;因此: M =2( S ) +1 = 2;双重线; 碱土金属:两个外层电子, 自旋方向相同时, S =1/2 + 1/2 =1, M = 3;三重线; 自旋方向相反时, S =1/2 - 1/2 =0, M = 1;单重线;
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
元素由基态到第一激发 态的跃迁最易发生,需要的 能量最低,产生的谱线也最 强,该谱线称为共振线 ,也 称为该元素的特征谱线;
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
2024/7/28
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
第2节 原子光谱与分子光谱

16:53:07
表征谱线轮廓(峰)的参数: 中心频率0 (峰值频率) :最大吸收系数对应的频率; 中心波长0 (nm):最大吸收系数对应的波长; 半宽度 :峰值强度一半处所对应的频率范围。 I
16:53:07
引起谱线变宽的原因
(1)自然变宽N 与原子处在激发态时的有限寿命有关,寿命越短,谱线越
16:53:07
同样,在原子吸收光谱法中,原子吸收强弱与
受激吸收跃迁几率Bij有关,即吸收光的强度为
Ia=BijUhνni 式中U为照射光的能量密度,即单位体积中的辐 射能量;ni为处于能态i的原子密度。
16:53:07
5. 谱线的形状与变宽
原子结构较分子简单,理论上应产生几何线状光谱线。
但实际上光谱线具有一定的宽度和轮廓。所谓谱线轮廓是
是对较宽波长范围的电磁辐射吸收或发射,即光谱呈现
为连续的带状光谱。 分子光谱也分为发射光谱和吸收光谱。
16:53:07
线光谱
16:53:07
带光谱
分子间作用力对吸收光谱形状的影响
稀薄气体,振动、转动结构 均存在 中等气体压力,转动结构消 失了,振动结构存在。 分子间作用力小的液体,转动 结构消失,振动结构存在,但 不明显。 分子间作用力大的液体,振 动结构均消失
自吸时,谱线中心吸收比边缘吸收严重,这是由于火 焰中心温度高,火焰边缘温度低,Doppler变宽中心比边缘 严重,故火焰中心的发射线宽,而火焰边缘的吸收线窄。
16:53:07
(5)场致变宽
外界电场、带电粒子、离子形成的电场及
磁场的作用使谱线变宽的现象,影响较小。
总结
谱线半宽度 = N + D + P
J = (L+S), (L+S-1),· · · · · · , |L-S|
第九章分子光谱基础教程

这里R,r 分别是核运动和电子运动的坐标。 在忽略自旋和轨道相互作用后,分子哈密顿 算符的具体形式是
Hˆ
N
2 2MN
2 N
e
2 2me
2 e
VNN
Vee
VeN
核动能 电子动能
势能
采用B.O.(玻恩-奥本海默)近似后,分子的全波函数可以写
成核波函数和电子波函数的乘积:
玻恩-奥本海默近似(简称BO近似,又称绝热近似)认为由于原子 核的质量要比电子大很多,一般要大3-4个数量级,因而在同样的 相互作用下,原子核的动能比电子小得多,可以忽略不计。所以出 现在各粒子相互作用的势能项中的原子核坐标就可以视为常数,这 样,核与核之间的排斥能就应当看作是常数。在BO近似下,研究 一个分子内部核与电子运动的问题,就变为N个电子在固定的原子 核电场中运动的问题。而电子又都是电荷、质量、自旋等特征完全 相同的粒子,因此,分子结构问题的研究就化为N个全同粒子体系 的研究。这就大大简化了原来多粒子体系的复杂度。主要应用于分 子结构研究、凝聚态物理、量子化学、化学反应动力学等领域。
定通 过吸收或发射光的形式发生
mn
x
mn
y
mn
z
mn
显然,只有当 x mn 、 y mn和 z mn 不全为零时,跃迁才可
能发生,称为跃迁允许,反之,称为跃迁禁阻。
使 x mn 、 y mn 和 z mn 不全为零的条件,称为光谱选律。
光谱选律的确定,还可以借助群论作为工具
* n
Hˆ
'
(
t
)
md
* n
akm (t) kd
akm (t ) nk anm (t )
k
k
原子光谱项与分子的电子光谱项

:
①一维表示标记为 A 或 B , 用 E、 T、 U 和 W 分别标记二、 三、 四、 五维不可约表示 。 π 2 ②对于绕主轴 Cn转动 ,对称的一维表示用 A 标记 , 反对称的用 B 标记 。
n
③如果有对称中心 ,则用“u ” 或“g ” 标记反演是对称或反对称的 。 ④如果有水平镜面 σh ,则用“′ ” 或“″ ” 表示对于 σh的反映为对称或反对称的。 ⑤如果上述标记还不足以区分全部表示时 ,再加上下标 1, 2, …。对于一维表示 A 或 B ,下 标 1 和 2 分别标记对垂直于主轴的 C2轴是对称的或反对称的 ; 如果没有 C2轴 ,则标记对垂直镜 π 2p 面的反映是对称的或是反对称的。对于二维表示 ,下标 1和 2标记绕主轴 Cn转动 角度中 p的
类似 ,双原子分子的光谱支项为 : 2S + 1 Λ + S,Λ + S - 1, …,Λ2 ( 7) Λ S Ω ,Ω = 如果分子有对称中心 ,分子谱项右下角也会有宇称符号 g 与 u。此外 , 对于 Σ谱项 (Λ = 0 ) , 右上角若有 + 、- 号 ,则代表其对包含键轴的平面的对称性 。 对于线性分子的电子光谱项 ,可根据该分子的最高占据轨道 ( HOMO )的电子排布来定 。线 p 性分子的基态光谱项见表 2。同原子体系一样 ,在分子中也存在互补定理 ,即开壳层组态 (λ) 与 p- 1 ( p为该壳层容纳的最大电子数 )具有相同的谱项 。 它的互补组态 (λ)
描述原子中单个电子的运动状态可以采用 n、 l、 m、 m s这 4 个量子数 。原则上讲 ,无论是原子 体系还是分子体系 ,其整体状态均取决于原子核外所有电子的运动状态 。在每一个原子中 ,由主 [1] 量子数 n、 角量子数 l描述的原子中的电子排布方式称为组态 ,例如基态碳原子的电子组态为 2 2 2 σg ) 2 ( 1 σu ) 2 1 s 2 s 2p 。电子组态也可以用于表示分子的电子排布 , 例如 L i2的电子组态为 ( 1
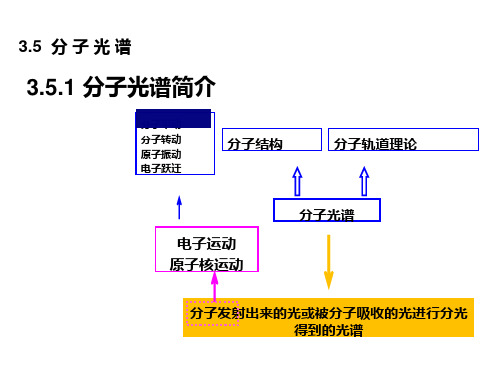
分子结构和分子光谱

第九章 分子结构和分子光谱一、内容提要E=E 电+E 振+E 转=E e +E v +E r 其中E e -∽1ev 量级,与原子的激发态能量同数量级;E v ∽0.01ev 量级; E r ∽0.001ev 量级分子光谱:远红外谱,近红外谱,可见和紫外谱2.双原子分子的状态(1)分子中单个电子的轨道角动量,用量子数λ来描述,即λ=0, 1, 2, 3,…电子态σ,π, δ, ϕ, …(2)分子的总轨道角动量为 Λ,∑=i i Λλ是代表分子的电子态的重要量子数 .对于不同Λ值的分子电子态,可用大写希腊字母正体表示,即:Λ= 0, 1, 2, 3, …分子态(正体)∑, ∏, ∆, Φ,…(3)对Λ≠0的诸态,分子总自旋角动量在分子轴向上的量子化分量为 Σ,Σ=S,S-1,…,-S ,一共取2S +1个值,S 是自旋量子数(4)分子的总角动量为 Ω,而ΣΛ+=Ω,ΣΛ+=S ΛS ΛS Λ-⋅⋅⋅-++,,1,双原子分子状态的多重性,由分子的总自旋量子数S 决定 .对一个Λ值,谱项分裂为2S +1个3.双原子分子的振动能量和振动光谱(1)双原子分子的谐振子模型:势能曲线视为抛物线, 2121m m m m +=μ,准弹性力:()c r r k F --=,振幅12r r r r A e e -=-=,固有频率μπkf 21=, a v E E v ⎪⎭⎫ ⎝⎛+==21振,hf a =,v =0,1,2,…是振动量子数 说明: (A)分子作谐振动时,能级是等间距的 .(B)v =0时 E 振=a /2=hf /2称零点能,振子永不会停止 .(C)选择定则:只有1±=∆v 时的跃迁才是允许的 .(D)分子从v →v +1的能级跃迁时,所吸收的光子波数为cf hc E v =∆=ν~. 说明在谐振子模型下,所有振动光谱的频率一样,只能观测到一条谱线. 这条谱线只不过是其中最强的一条.(E)谐振子模型无法解释较弱振动光谱线的产生 .(2)双原子的非谐振子势模型势能 32)()(21)(e e r r C r r k r U ---= 分子振动能量:E 振=E v =(v +1/2)hf -(v +1/2)2xhf =(v +1/2)a -(v +1/2)2b说明:①x 是非谐性常数,其值很小,x=a/b <1②能级不等间距,随v 的增大能级间隔逐渐减小③遵从选择定则,3,2,1±±±=∆v …(3)纯振动光谱在同一电子态中,v →v’ (v’>v )振动能级跃迁中吸收光子的波数()()()ωωλνx v v v v v v hcE E v v 11~++'-'--'=-==' 式中ω=a/hc=f/c , x=f/a . 忽略第二项得()ωωνv v v ∆=-'=~, ⋅⋅⋅=∆,3,2,1v 所以有ν~=ω,2ω,3ω,… 说明:只有有极分子才有纯振动光谱由相同原子组成的双原子分子是无极分子,无纯振动光谱振动能级间距的数量级仅为10-1eV振动光谱在近红外光区,λ是μm 量级由振动光谱可测分子的力常数k双原子分子中的一种原子有两种同位素,则相应吸收光谱中所得两同位素的 两种谱线的波数之比为μμμμνν'='='k k ~~ 4.有电子跃迁的振动光谱()ωωωωννx v v x v v E E E E hce v e v e 2221212121~ ])[(1~⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-''⎪⎭⎫ ⎝⎛+'-'⎪⎭⎫ ⎝⎛+'+=+-'+'=说明: (1)v ’=0→v =0为光谱带基线跃迁,其波数为()()ωωωωννx x e -''--'+=4121~~00 (2)两电子之间的振动能级跃迁产生一个光谱带系,在可见和紫外光区 .(3)当1=∆v 时,mk c c f πων21~===. 由此可求出力常数k , k 的大小可反映分子键的强弱5.双原子分子的转动能量和转动能量(1)双原子分子的刚性转子模型:双原子分子转轴过职心切垂直于二原子核链线 .(2)转动惯量 I =m 1r 12+m 2r 22=222121r r m m m m μ=+ 转动角动量P = )1(+J J ,J =0,1,2,……转动量子数转动态能量 E =()()1218222+=+J J I J J I h π说明:①随J 增加,相邻能级间隔增大. 相邻转动能级差为10-4eV 量级 ②()()[]1122+-+''=-'=∆J J J J I E E E r r ③跃迁选择定则=∆j J 末-J 初=±1(+表示吸收 .-表示发射)④分子从J →J’=J +1吸收光子的波数()J B J B hc E '=+=∆=212~ν, Ic hB 28π=称转动常数谱线波数的间隔是相等的,皆为B JJ 2~~~1=-=∆+ννν ⑤纯转动谱波长在cm 或mm 量级,在远红外区. 由转动光谱波长可求出两核之距r . ⑥非极性分子观察不到纯转动光谱,极性分子观察到纯转动光谱⑦基本与实验符合,但不能说明J 较大时谱线间距变小的现象.(2)非刚性转子模型:分子转动时,两核间距r 发生变化,设两核体积忽略不计,且两核之距r 比无转动时两核平均之距r e 略大 .E 转=E r =hc [BJ (J +1)-DJ 2(J +1)2], D=kc r h e 624332μπ, D<<B选择定则:1±=∆J分子从J →J +1吸收光子的波数()()21412~+-+=J D J B ν 6.振―转谱带结构(1)任一个振动能级上都有一组转动能级,振动能级能量和转动能量同时改变而产生的光谱称振―转光谱.(2)跃迁选择定则1±=∆v ,J ∆=±1;(3)谱线波数 ()()[]()()11~1~0+-+'''+=+-'+'=J BJ J J B E E E E hc r v r v νν 若B’=B,则0~~νν=+B[J’(J’+1)-J(J+1)] R支:当J’=J+1时,1+=∆J , 0~~νν=+2B(J+1)=ν~0+2BJ’,J’=1,2,... P支:当J’=J-1时,1-=∆J ,()BJ J B 2~12~~00-=+'-=ννν,J=1,2,3,... 说明:①在纯转动谱中,J’与J属于同一振动能级,∆J=+1表吸收,∆J=-1表发射 ②在振―转谱中,J’与分J属于不同振动能级,1±=∆J 皆表吸收(或发射) ③忽略转动,从10=→=v v 是一条振动吸收谱线;忽略振动,从10=→=v v 是一系列振―转谱线,即光谱带 . 00=→='J J 的谱线是基线. 基线跃迁不服从1±=∆J ,故观察不到 .④R支波数大于0~ν;P支波数小于0~ν . 相邻谱线的间隔为2B,两分支的间距为4B .7.电子谱带的转动结构(1)电子能量、振动能量和转动能量都变动,形成电子振动转动谱带 .在可见和紫外区(2)J 的跃迁选择定则0,1±=∆J (J ’=0到J =0的除外)(3)谱带的波数ν~=0~ν+B ‘J ’(J ‘+1)-BJ (J +1) P 支:当1-=∆J 时,1-='J J ,0~~νν=-(B ‘+B )J +(B ‘—B )J 2,J =1,2,…… Q 支:当0=∆J 时,J ‘=J ,0~~νν=+(B’+B )J +(B ’-B )J 2, J =1,2,…… R 支:当1+=∆J 时,J ‘=J +1,0~~νν=+(B ’+B )J ‘+(B ’—B )J 2,J =1,2,…… 说明:(1)若两电子态都属于∑态,则J ∆=1;若两电子态中有一个不是∑态,则J ∆=0,1; (2)当B’>B 时,对于R 支和 Q 支,ν~随 J (或J’)的增加而单调的增加;对P 支,ν~随J 增加而减小,然后当J 到达某一数值时,又随J 增加而增加 (3)当B’<B 时,对于P 支和 Q 支,ν~随 J 的增加而单调减小; 对R 支,ν~先是随J’增加而增加,然后当J’到达某一数值时,又随J’增加而逐渐减少 .8.拉曼效应(组合散射):1928年发现(1)以强的单色光照射某一种物质样品时,在与入射光线垂直方向观察到一条波数与入射光波数0~ν相同的谱线外,还有两条对称分布在0~ν两侧,波数分别为0~ν±ν~1,称为组合散射(或拉曼效应)(2)进一步发现:(a) 0~ν-ν~1的谱线强度比0~ν+ν~1强; (b) ν~1与散射物质有关与0~ν无关;(c) 0~ν和0~ν±ν~1附近还存在间隔很小的谱线 .(3)拉曼效应实际上是一种光的散射过程,和分子的振动和转动相联系.二、基本练习 :楮书P 284 习题。
原子光谱与分子光谱

原子光谱和分子光谱
原子光谱反映原子或离子的性质而与原 子或离子来源的分子状态无关。确定试 样物质的元素组成和含量。不能给出物 质分子结构的信息。
原子光谱为线状光谱
原子光谱和分子光谱
一、原子光谱
(一)核外电子运动状态
原子核外电子的运动状态可以用主量子数、角量子数、磁量 子数、自旋量子数来描述。
1、n决定电子的能量和电子离核的远近。
取值:K、L、M、N。。。。
2、L决定角动量的大小及电子轨道的形状。
符号: s, p, d, f
L=0,1,2,3…..,(n-1)
3、磁量子数m决定磁场中电子轨道在空间的伸展的方向。
4、自旋量子数ms决定电子自旋的方向,顺磁场和逆磁场
ms=1/2,-1/2
原子光谱和分子光谱
➢拉曼光谱法 (RS) Raman Spectroscopy
➢*核磁共振波谱法(NMR) Nuclear Magnetic Resonance
Spectroscopy ➢*质谱法 (MS)
Mass Spectroscopy
联用技术发展很电子相对于原子核的运动--电子能级; (△E=1~20eV,紫外、可见、近红外) 2.原子核在其平衡位置附近的相对振动--振动能级;
第二节 原子光谱和分子光谱
(二)光谱项 原子的能量状态需要用光谱项来表征。
N2s+1LJ 其中n为主量子数,L为总角量子数
L=∑Li S为总自旋量子数,S=Σms , I J内量子数,是由于轨道运动和自旋运动的相互作 用,即轨道磁距与自旋磁距的相互影响而得出的。
第二节 原子光谱和分子光谱
J=L+S
➢*红外吸收光谱法(IR) Infrared Spectroscopy
分子光谱

第九章分子光谱和分子结构前面我们从原子光谱、原子磁性了解了原子的结构,但在生产实践和生活中接触的物体极少是孤立的原子,往往是由原子结合而成的分子或分子集团,它是物质结构的一个重要层次.本章将简要介绍分子光谱和分子结构.§9.1 分子光谱和分子能级一、分子与化学键分子由原子组成,原子通过它们间的相互作用而结合在一起.而分子中相邻原子间存在的各种不同形式的相互作用称为化学键.化学键的力是电性质的,它只与原子的外层电子有关,与原子的内层电子关系较少.这是因为各元素的物理、化学性质的周期性由最外层电子的运动决定;而且较重元素的标识X射线不因该元素所在化合物而不同.内层电子在分子中和孤立原子中几乎一样,但价电子则大不相同.原子价电子间不同的结合会形成不同的化学键,常见的二类化学键是离子键和共价键,一般还有金属键和Van der Waals键. 1.离子键当电离能很小的金属原子(如碱金属和碱土金属原子价电子易脱落)和电子亲合能很大的非金属原子(如卤族原子和氧族非金属原子容易吸往电子)非常接近时,前者失去价电子而成为正离子,后者获得前者失去的电子而成为负离子,正负离子由于Coulomb力相互吸引结合成分子;但当二离子由于运动惯性而过分接近时,它们的外层电子相互排斥的力变得显著,表现为离子间的互斥力.当引力和斥力相等时,就形成稳定的分子.这种化学键称为离子键.如NaCl分子是由Na+离子与Cl-离子组成的离子键分子.Na是碱金属元素,具有较小的电离能5.14eV,电离过程为Na + 5.14eV →Na+ + e-Cl是卤族元素,Cl原子最外层在3p上有5个电子,再得到一个就构成稳定的闭合壳层,所以吸收一个电子形成Cl -离子是放能过程,这个能量称为亲合能,Cl-的亲合能为3.72eV ,此过程为Cl + e - →Cl - + 3.72eV上述两过程共增能5.14eV -3.72eV =1.42eV .虽然Na 、Cl 原子形成Na +、Cl -离子后能量增加了,但当它们相互接近时,由于正负离子的电荷将引起Coulomb 吸引位能,因此Na +、Cl -离子体系能量有可能小于Na 、Cl 原子体系的能量.ٛ 图9-1中的两条曲线分别表示离子和原子体系的位能变化.选Na 原子和Cl 原子相距无穷远时的位能为零点能,横坐标表示两离子或原子间距离,可以看到当距离小于某一数值后,离子间的位能将小于原子间的位能.ٛNa +、Cl -离子体系的位能曲线有一极小值,这是由于距离小到一定值后,两带正电原子核的Coulomb 斥力位能迅速增加,距离越小,此能量越大.位能曲线最低点对应的距离以r 0表示,称平衡距离.如NaCl 分子的r 0=2.51Å,其位能为-3.58eV .作用力方向总是指向位能减小的方向.当r >r 0时,位能曲线斜率为正,作用力使离子间距离减小,为吸引力;当r <r 0时,位能曲线斜率为负,作用力使距离增加,为斥力;当r = r 0时,位能曲线斜率为零,作用力亦为零,所以Na+、Cl-离子有可能在r 0附近振动,形成稳定的NaCl 分子.图9-1 NaCl分子的位能曲线2.共价键许多由两个相同原子组成的双原子分子和绝大多数有机化合物的分子不是由离子组成的,它们的化学键不再是离子键.它们有一对或多对电子为两个原子共有,内层电子仍然属于原来的原子.这类分子称为共价键分子或称原子键,同极键分子.如两个氢原子靠近时,每个氢原子中电子的状态都将重新分布,使系统处于能量最低的状态,这时两个电子起着连结两个原子的作用,为两个核所共有.从量子力学分析而知这一对组成共价键的电子自旋必是反平行的.一般地说,原子外层电子中,有未组成自旋相反的电子对的电子,就有可能与其它原子中未组成电子对的电子结合成共价键.如氢原子只有一个外层电子,显然在原子中不可能与其它电子组成自旋相反的电子对,这个电子就有可能与另一氢原子中同样的电子结合成共价键.锂原子有3个电子,而2s 态的外层电子未能与其它电子组成自旋相反的电子对,因此能与另一锂原子中的2s 电子组成共价单键,成为锂的双原子分子.如果两个原子各有两个或三个未成对的电子,则俩俩配对可构成共价双键或三键.共价键构成的分子可分为两类.第一类是无极分子,它由同类原子构成.如H 2、O 2等,分子内键电子分布对称,正负电荷“重心”重合,因而分子不具有电偶极矩.另一类是有极分子,由不同类原子组成.如HCl ,两种原子对电子的亲合力不同,分子内键电子的分布不对称,正负电荷“重心”不重合,分子具有电偶极矩. 图9-2 分子带光谱二、分子光谱原子光谱的特征是线状光谱,一个线系中各谱线间隔都较大,只在接近线系极限处越来越密,该处强度也较弱;若原子外层电子数目较少,谱线系也为数不多.分子光谱的一般分布如图9-2所示.许多谱线形成一段一段的密集区域成为连续带状,称为光谱带.所以分子光谱的特征是带光谱.它的波长分布范围很广,可出现在远红外区(波长是cm 或mm 数量级)、近红外区(波长是μm 数量级)、可见区和紫外区(波长约在10-1μm 数量级).分子光谱一般具有如下规律:(1)由光谱线组成光谱带;(2)几个光谱带组成一个光谱带组;(3)几个光谱带组组成分子光谱.ٛ三、分子能级据实验观察,分子光谱是由远红外光谱、近红外光谱、可见光和紫外光谱交织在一起的光谱.而远红外光谱是由于分子转动能级的变化引起的;近红外光谱是分子既有振动能级又有转动能级改变时产生的;而可见光和紫外光谱是分子既有电子能级又有振动和转动能级变化时产生的.所以分子内部既有分子转动,又有分子的振动,还有分子中电子的运动.ٛ1.分子的转动和转动能级即将分子看作一个整体绕某轴而转动.对于双原子分子,其转动轴通过分子的质心并垂直于分子轴(原子核间的联线).转动能量是量子化的,因而形成转动能级.转动能级的间隔约10-4~10-2eV.ٛ2.分子的振动和振动能级即组成分子的各原子在其平衡位置附近所做的微小振动.如双原子分子沿着轴线振动.与振动相联系的能量称为分子的振动能.振动能量也是量子化的,因而形成振动能级.振动能级间隔约10-1eV.3.分子中的电子运动和电子能级ٛ分子中外层电子的运动形成一些定态,电子在定态间跃迁运动.这些定态各具有一定能量,也就形成了电子的能级.当分子的电子能级间产生跃迁就产生光谱.电子能级间隔约为eV量级.ٛ若用E转、E振、E电分别代表上述三种运动状态的能量,分子能量可表示为E = E转 + E振 + E电(9-1)这三种能量的变化满足Δ>Δ>ΔE E E(9-2)振电转这样,在电子能级之上可以有较小间隔的振动能级;在振动能级之上又可以有更小间隔的转动能级.这些关系如图9-3所示,图中表示了振动能级和转动能级的特点,一组振动能级的间隔随能级的上升而减小;一组转动能级的间隔随着能级的上升而增加.由于分子能级的复杂结构,从而使分子光谱比原子光谱更复杂.图9-3 双原子分子能级示意图§9.2 分子的转动能级和转动光谱在辐射过程中,分子的电子状态和振动状态都没有改变,则辐射仅由分子的转动状态的改变而引起.由于△E 转ٛ最小,相应光子的能量很小,所产生的光谱一般在远红外区域.一、分子的转动能级假设分子是刚性分子.由于刚性分子不改变原子核间相对距离,所以它的转动是一个纯粹的转动,此简化模型忽略了振动对转动的影响.对双原子分子,其转动轴是通过质心而垂直于联接二原子核的直线的.分子的转动惯量ٛ (9-3) 2r I μ=其中1212m m m m μ=+是折合质量,r 是两原子核间的距离,如图9-4所示.对刚性分子r 是常数.若分子的转动角动量为P J .据经典力学,分子的转动动能IP I E J J 22122==ω (9-4) 其中P J =I ω,因为转动是自由的,所以势能为零,而体系总能量就等于转动动能.分子是微观粒子,它的角动量是量子化的,即=)1(+=J J P J ⋅⋅⋅=,,,,3210J (9-5)图9-4 刚性双原子分子的转动 J 称为转动量子数.代入(9-4) 式可得转动能级)1(22+=J J I E J = (9-6)由此所得能级图如图9-5所示.相邻二转动能级的间距ٛ)1(21+=−=Δ+J J IE E E J J J = (9-7)图9-5 双原子分子转动能级 可见转动能级的分布不是等间距的,J 越大,间隔也越大.ٛٛ二、分子的转动光谱实验和理论都证明转动能级间的跃迁须服从电偶极跃迁选择定则ٛ 1±=ΔJ (9-8)ΔJ =+1相当于吸收过程,ΔJ =-1相当于发射过程.当从能级J +1跃迁到能级J 的辐射频率12(1)2(14J J J J E E E h v J h h Iπ+)B J Δ−===+=+ (9-9)其中I hB 28π=称为转动常数.以波数表示2(1)Jv B J =+ B (9-10) 相邻二谱线间的波数差。
原子与分子物理专业介绍

原子与分子物理专业介绍原子与分子物理专业是物理学的分支领域之一,关注的是原子和分子的结构、性质、相互作用及其在物质世界中的应用。
原子和分子是物质的基本构成单位,从微观层面研究它们的行为和相互作用,可以深入了解物质的宏观特性,同时也对解决许多实际问题有很大的帮助。
原子与分子物理专业的学习内容包括原子结构、原子能级、化学键的形成和断裂、分子集体运动、原子和分子的光谱学、相互作用和反应等。
同时,也涉及到量子力学、量子场论、原子物理学和分子物理学的理论基础和实验技术等方面的知识。
在学习过程中,学生需要掌握基本的物理学和数学知识,如热力学、电磁学、微积分和线性代数等。
在实际应用中,原子与分子物理专业的毕业生可以在化学、材料科学、生物学、能源等领域中找到就业机会。
他们可以从事纳米技术、新材料研发、光电子设备设计、药物开发等方面的工作。
此外,原子与分子物理专业的毕业生还可以选择继续深入研究,攻读硕士和博士学位,成为研究人员或教师。
在学习原子与分子物理专业时,需要掌握的一些核心知识包括:1. 原子结构与能级原子由电子、质子和中子组成,其中质子和中子组成原子核,而电子以一定的能级分布在原子核周围。
了解原子结构和能级分布可以帮助我们理解化学键的形成和化学反应的机理,以及在光谱学中的应用。
2. 分子结构和化学键分子是由两个或多个原子组成的结构单元,它们通过化学键相互连接。
了解化学键的形成和断裂可以帮助我们理解材料的性质和化学反应的机理,对于研究新材料和制药等领域有着很重要的作用。
3. 原子和分子光谱学原子和分子在吸收和发射光辐射时会产生特定的光谱线,光谱学研究这些现象,可以帮助我们分析物质的结构和成分,同时也在光电子应用中有着广泛的应用。
原子和分子之间的相互作用是物质世界中重要的现象之一,包括分子间的静电作用力、分子间的范德华力、原子间的核力等。
了解原子和分子相互作用的机制和特点可以为物质科学和化学工程领域提供科学依据。
原子物理和分子物理

原子物理和分子物理原子物理和分子物理是研究物质微观结构和性质的两个重要学科。
本文将分别介绍原子物理和分子物理的基本概念、研究内容和应用领域。
一、原子物理原子物理是研究原子及其内部结构、性质和相互作用的学科。
原子是物质的基本组成单位,由原子核和围绕核运动的电子组成。
原子物理主要研究原子的结构、能级、光谱和原子核的性质。
1. 原子结构:原子由质子、中子和电子组成。
质子和中子集中在原子核中,而电子以轨道形式围绕原子核运动。
原子的质量主要由原子核决定,而化学性质则主要由电子决定。
2. 原子能级:原子中的电子分布在不同的能级上。
每个能级对应一定的能量,电子可以在不同的能级之间跃迁,吸收或发射能量。
这种能量转移常常以光的形式表现,形成了原子的光谱。
3. 光谱:原子吸收或发射的光具有特定的波长和频率,形成了原子的光谱。
通过观察和分析光谱,可以研究原子的能级结构和性质。
光谱在天文学、化学分析和材料研究等领域有广泛应用。
4. 原子核物理:原子核是原子的中心部分,由质子和中子组成。
原子核物理研究原子核的结构、衰变和相互作用。
核反应在能源产生、核技术和医学诊断等方面具有重要应用。
二、分子物理分子物理是研究分子结构、性质和相互作用的学科。
分子是由两个或多个原子通过化学键相互连接而成的。
分子物理主要研究分子的结构、振动、旋转和光谱。
1. 分子结构:分子的结构由原子之间的键长、键角和键的旋转自由度等决定。
分子的结构对其性质和反应具有重要影响。
分子结构研究是有机化学和生物化学的基础。
2. 分子振动:分子内部原子的振动是分子物理的重要研究内容。
分子振动可以通过红外光谱等技术进行观测和分析,对分子的结构和性质进行表征。
3. 分子旋转:分子的旋转是分子物理中的另一个重要研究内容。
分子的旋转行为可以通过微波光谱等方法进行研究,对分子的结构和动力学性质有深入了解。
4. 分子光谱:分子吸收或发射的光谱与分子的能级结构和振动旋转有关。
通过研究分子的光谱,可以了解分子的结构和性质。
第二-章-原子光谱项和分子光谱项

2、 S1P1能级示意图
组态
谱项 1P
支项 1P1
态 MJ
+1 0
-1
(np)1[(n+1)s]1 3P
中心场近似
真实的电 子排斥能
3P2
3P1 3P0 自旋-轨道 相互作用
MJ
+2 +1 0 -1 -2
+1 0 -1 0
外加磁场
3、光谱基项 组态中,能量最低旳谱项。
4、光谱基项旳得到 (1)得到组态下全部谱项,再利用洪特规则
2、光谱项符号 给定电子组态下,只有当两个定态旳量子数L
和S都相同,能量才相同。
我们将同一组态给出旳具有相同L和S值旳一 组状态称为一种光谱项(或简称谱项),并用符号 2S+1L标识 (n 2S+1L标识)。 (2S+1称为多重度)
这么,当考虑真实旳电子静电排斥能时,原 本在中心场近似下一种电子组态分裂成若干光谱 项,不同光谱项旳能量不同,各能级用电子组态 和光谱项符号共同标识。
所以,一种p2组态产生旳谱项是1S、3P、1D。
****阐明**** (1)比较p1p1 和p2 旳谱项。
(2)一种技巧: 2个等价电子旳L+S=偶数规则。
(3)取得等价电子组态旳谱项比不等价电子 组态旳谱项难。
(4)P4(如O)与P2谱项相同。
四、光谱支项(level)和光谱支项旳推求
1、光谱支项旳定义和意义 原子中旳静电相互作用。原子中还存在
光谱支项 3P0、3P1、3P2。
例2:3S谱项 有L=0, S=1,所以J可为1,从而给出1个光谱支
项 3S1
例 3:钠D线(3p3s旳跃迁)旳精细构造,两 条谱线波长相差6Ǻ。
分子结构与分子光谱

分子结构与分子光谱1. 分子结构两个原子A 、B 的结合,构成双原子分子(离子)。
分子(离子)内原子间的强相互作用称为化学键。
化学键可初分为共价键、离子键和金属键三种基本类型。
分子间的(氢键、分子键Van de Waals 力)1.1分子轨道理论1.1.1 H 2+的结构与H 2+的基态(单电子分子(离子)) 一、定核近似下的Schrödinger 方程),,(),,(111183611836121222b a e T T b a e T b a e b a R R r E R R r R r r ψ=ψ⎥⎦⎤⎢⎣⎡+--⎪⎭⎫⎝⎛∇+∇+∇- 定核近似ψψE R r r b a e =⎥⎦⎤⎢⎣⎡+--∇-111212二、线性变分法 (1). 变分原理**ˆE d d H E ≥=⎰⎰τϕϕτϕϕ(2). 线性变分法已知的},,2,1{m i i ⋅⋅⋅=φ变分函数,∑==+⋅⋅⋅++=mi ii m m c c c c 12211φφφφϕ01*11*1**)(ˆE c E d c c d c H c d d H E i m i i i m i i i m i i i m i i i ≥=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛==⎰∑∑⎰∑∑⎰⎰====τφφτφφτϕϕτϕϕ )(i c E 在极小值点有 021=∂∂=⋅⋅⋅=∂∂=∂∂mc Ec E c E得到联立方程,称为久期方程。
三、H 2+线性变分法求解b ac c φφϕ21+= )(1s a H φφ=,)(1s b H φφ=ϕ是描述分子中单电子的运动状态,称为分子轨道MO (molecular orbit )。
它是由原子轨道的线性组合。
(linear combination of atomic orbit ,LCAO-MO )代入变分法公式求解()()()()02,121212121**)(ˆE c c E d c c c c d c c H c c d d H E babababa≥=++++==⎰⎰⎰⎰τφφφφτφφφφτϕϕτϕϕ基态能量,E E =,所以⎰⎰⎰⎰⎰⎰⎰+++++=τφφτφφτφφτφφτφφτφφτφφd c d c c d cd H c d H c c d H c c d H c E bb ba aa b b a b b a a a 222121222121212ˆˆˆˆ⎰=τφφd H H a a aa ˆ,⎰=τφφd H H b b bb ˆ,ba b a ab H d H H ==⎰τφφˆ ⎰=τφφd S a a aa ,⎰=τφφd S b b bb ,ba b a ab S d S ==⎰τφφbbab aa bbab aaS c S c c S c H c H c c H c E 22212122212122+++++= 极值条件,有021=∂∂=∂∂c E c E ,得久期方程 0)()(21=-+-ab ab aa aa ES H c ES H c 0)()(21=-+-bb bb ab ab ES H c ES H c要有非零解,系数行列式等于00=----bbbb abab abab aa aa ES H ES H ES H ES H展开行列式,得0)()22()1(2222=-+-+-ab aa aa ab ab ab H H H S H E S E解二次方程,得1221,11E E S H H E S H H E ab abaa abab aa >--=++=其同时可以求得1c 和2c 及相应的MO 1ϕ和2ϕ)(221)(22121b a abb a abS S φφϕφφϕ--=++=讨论:(a )轨道能量随R 的变化曲线(b )轨道能级:1ϕ对应1E ,能量较低,成键轨道;2ϕ对应2E ,能量较高,反键轨道。
结构化学基础-3分子光谱
1 d V 3! dr
3 re
3
( r re )
3
2、非谐振子模型
以平衡键长处为势能零点,将Taylor级数从三阶处 截断
V (r )
1 2
k ( r re ) k ( r re )
2
3
k
1 d V 6 dr
3 re
3
k 的值可以通过Morse函数来求算
将此势能项代入Schrödinger方程,解得分子振动能级
h 4 c I1
2
( J 1)
2 2 B 2 ( J 1)
h 4 c I 2
2
( J 1)
2 1 2 1 1 1 I1 1 1 1 1 1 I2 2
J=3
8B
2
( J 1) h 8 Ic
2
2 ( J 1) B
J=2
6B 4B
B
h 8 Ic
2
转动光谱谱线间隔 取决于原子质量和 键长
J=1
J=0
2B
2 ( J 1) B
红外光谱的应用
测定异核双原分子的键长
B I r
2 B ( J 1 ), B
J 1
5
4 3 2 1 0
Ev
5 4 3 2 1 0
P 支(△J = - 1)
o
R 支(△J = + 1)
3, 多原子分子的振动光谱
1) 多原子分子的振动光谱可以通过解原子核的薛定谔 方程得到;
2) Schrödinger方程中的势能项可以近似采用谐振势来 描述;
原子光谱与分子光谱ppt实用资料

2021/7/23
电子能级跃迁的选择定则
一条谱线是原子的外层电子在两个能级之间的跃迁产 生的,可用两个光谱项符号表示这种跃迁或跃迁谱线:
例 钠原子的双重线 Na 5889.96 ; 32S1/ 2 — 32P3/ 2; Na 5895.93 ; 32S1/ 2 — 32P1/ 2;
2021/7/23
第七章 原子发射光谱
分析
Atomic emission spectrometry,AES
第二节 原子光谱与分子光谱
一、原子光谱 atom spectrum 二、分子光谱 molecular spectrum
atom spectrum and molecular spectrum
2021/7/23
一、 原子光谱
例:碳原子,基态的电子层结构(1s)2(2s) 2(2p) 2 , 两个外层2p电子: S =0 , ±1 ; 3个不同值; L与S之间存在相互作用;可裂分产生(2 S +1)个能级; 这就是原子光谱产生光谱多重线的原因,用 M 表示, 称为谱线的多重性;
2021/7/23
例:钠原子,一个外层电子, S =1/2;因此: M =2( S ) +1 = 2;双重线; 碱土金属:两个外层电子, 自旋方向相同时, S =1/2 + 1/2 =1, M = 3;三重线; 自旋方向相反时, S =1/2 - 1/2 =0, M = 1;单重线;
2021/7/23
内量子数 :
内量子数J取决于总角量子数L和总自旋量子数S的矢量和 :
J = (L + S), (L + S - 1),······, (L - S) 若 L ≥ S ; 其数值共(2 S +1)个; 若 L < S ; 其数值共(2 L +1)个; 例:L=2,S=1,则 J 有三个值,J = 3,2,1; L=0,S=1/2;则 J 仅有一个值 1/2; J 值称光谱支项;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若两电子自旋态相同,则自旋波函数 对称,空间波函数反对称,不能形成
共价键—两个核共同拥有一对自旋反平行的电子
对
原子,三态(S=1)的能量低为什么对
:一个核,只考虑两电子的排斥作用,
时两电子靠近的概率小,排斥作用弱,所以能量低
例如,汞光
射入Hcl, 散射光中偏红伴线
Hcl的红外振动谱线有2885.9
室温下
强,
弱,
解释 使分子从基态
使处于激发态
激发至虚能级再跃迁至激发态 的分子跃迁至虚能级再跃迁到基态
处于
的分子数
拉曼散射可激发用一般方法不能激发的纯振动谱或纯转动谱, 有利于研究分子结构或材料特性。
本节内容结束
选择定则:
谱线在
,
左右分为两支,间隔为4B,因
谱线不存在,其它相邻谱线的距离为2B
§9.5 电子—振—转光谱 电子能量、振动能量、转动能量都有变化,形成谱带
很大,在可见和紫外光区域,
的选择定则
除外
和
属于不同的电子能级
可相差很大
这时光子带走的角动量可由电子轨道角动量的变化来补偿,因而
是容许的,由
不同,谱线分为三支
支:
支
支
或
随
变化的规律是抛物线,设
对
和
支:
对
支:
先后
§9.6 拉曼散射
拉曼(C.V.Raman)1928年发现光的组合散射, 1930年获诺贝尔物理奖
实验
单色光
射入透明介质,测散射光的频率和强度,发现除
外有:
称偏红伴线,Stokes线
称偏紫伴线,反Stokes线
和 无关,只和散射物质有关,与散射物质的一些红外光的频率相同,
即
对
是对称或反对称的
在中点处为零,
可不为零(图2.2.3)。
描述的电子才有较大的概率出现在两核中间, 把两个核吸引在一起形成束缚态。
看一个氢原子和一个质子怎样形成
和 和 在二
相距∞时 无作用 接近时若为 之间 吸引
很小时 排斥
进入H的电子云内
再看氢分子
两电子的空间波函数必须是对称的才能出现在两质子中间
附近可看作简谐振子势
按普郎克理论振动能量是量子化的
量子力学得出
时,
, 零点能ຫໍສະໝຸດ 实际上,双原子分子势不是抛物线,振动能的表达式为
大时能级不等距 选择定则为
1.纯振动跃迁(有极分子)
低能级跃迁,近似有 了解分子键和结构
2.振—转光谱
和
同时改变产生的光谱,近红外
和
相应的
不同,因而
和
不同,
但相差不远,可认为相等
:希望两个电子都在两个核中间,这时它们对核的吸引作用 占优势,所以要求自旋反平行。
分子则相反?
原子最外层的电子凡未按自旋相反配成对的都可和其它原子 类似的电子组成共价键,例如
原子
电子是单独的可与另一
电子构成共价键形成 原子,有两个未成对的电子,可形成
也可形成双键的
原子的
§9.2 分子的光谱和能级
分子光谱的特点:带光谱、谱带组, 光谱的特点反映了分子的三种运动
按经典力学,转动能为
平动 按量子力学
特点:能级间隔为2, 4, 6, 8,…纯转动跃迁(电子和振动态都不变)
选择定则: 代表发射;
代表吸收
谱线波数的间隔是等距的为
由间隔
和理论比较说明:
1)分子不是刚体,转得快时
要变大
能量比公式给出的小,应加修正项
2)只有有极分子才有纯转动光谱
§9.4 双原子分子的振动光谱 势能曲线在平衡位置
(1)电子运动
分子大小为
电子在大小为
的范围内运动,由不确定关系
~
~
~
~
可算出
~几个
与原子中电子的束缚能相近,跃迁时发出 可见光、紫外光 (2)分子转动 双原子分子的转动惯量为(设A、B相同)
转动能
较低的转动能级
~
~
光谱波长:
(3)分子振动
振动能
~
量级,远红外区
光谱波长是
量级,近红外区
§9.3 双原子分子的转动光谱 可绕通过质心且垂直于对称轴的轴线转动, 看作刚体,转动惯量为
, 两者相互吸引
很小,原子核互相排斥 离子键:分子由正负离子组成,有电偶极矩—有极分子
(2)共价键
两相同原子组成的分子,如
等以及大多数有机化合物的分子 一部分价电子是两个原子所共有形成共价键
以
为例,电子在一个核场中的库仑势为
中电子在两质子的联线上的库能势, 它对过联线中点且与联线垂直的平面.
是对称的,电子波函数也应有对称性,即要求
第九章 分子结构与分子光谱
§9.1 分子的形成
1.分子的形成
原子
分子
一定的相互作用方式称为化学键, 常见的有两种:离子键和共价键 结合后体系的能量应较结合前低
(1)离子键(以NaCl为例)
碱金属、碱土金属原子和卤族、氧族原子的结合 碱金属原子电离能小易失去电子
原子
,再加一个电子壳层闭合放能
两过程共需能量 可发生电子转移形成
