空间立体几何测试题8套
立体测试题及答案

立体测试题及答案一、单项选择题(每题2分,共10题)1. 下列哪个选项是立体几何中的基本元素?A. 点B. 线C. 面D. 体答案:D2. 空间中两条直线的位置关系有几种?A. 1种B. 2种C. 3种D. 4种答案:C3. 一个立方体有多少个顶点?A. 6B. 8C. 12D. 14答案:B4. 一个正四面体有多少条棱?A. 6B. 8C. 12D. 16答案:A5. 空间直角坐标系中,点(1,2,3)到原点的距离是多少?A. 1B. 2C. 3D. √14答案:D6. 一个球体的表面积公式是?A. 4πr²B. 2πr²C. πr²D. 4πr³答案:A7. 空间中两个平面的位置关系有哪些?A. 平行B. 相交C. 重合D. 以上都是答案:D8. 一个圆柱体的体积公式是?A. πr²hB. 2πrhC. πr²D. πr³答案:A9. 空间中一个点到一个平面的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |Ax + By + Cz + D| / √(A² + B²)D. |Ax + By + Cz - D| / √(A² + B²)答案:B10. 空间中一个点到一条直线的距离公式是?A. |Ax + By + Cz + D| / √(A² + B² + C²)B. |Ax + By + Cz - D| / √(A² + B² + C²)C. |(Ax + By + Cz + D) / (A² + B² + C²)| * √(A² + B²)D. |(Ax + By + Cz - D) / (A² + B² + C²)| * √(A² + B²)答案:D二、多项选择题(每题3分,共5题)1. 空间中两个平面相交,它们的交线是?A. 直线B. 曲线C. 点D. 面答案:A2. 空间中一个点到一个平面的距离公式中,A、B、C、D分别代表什么?A. 平面方程的系数B. 平面方程的常数项C. 点的坐标D. 点到平面的距离答案:A, B3. 空间直角坐标系中,点(1,2,3)到点(4,5,6)的距离公式是?A. √((4-1)² + (5-2)² + (6-3)²)B. √((1-4)² + (2-5)² + (3-6)²)C. √((4-1)² + (5-2)² + (6-3)²)D. √((1-4)² + (2-5)² + (3-6)²)答案:A, B4. 空间中一个点到一条直线的距离公式中,A、B、C、D分别代表什么?A. 直线方程的系数B. 直线方程的常数项C. 点的坐标D. 点到直线的距离答案:A, C5. 空间中一个平面的方程可以表示为?A. Ax + By + Cz + D = 0B. Ax + By + Cz = DC. Ax + By + Cz + D = ED. Ax + By + Cz = 0答案:A, D结束语:以上是立体测试题及答案的全部内容,希望对你有所帮助。
(完整版)空间几何体练习题含答案
空间几何体练习题1.空间几何体的三视图如图所示,则此空间几何体的直观图为 ( )A. B. C. D.2.一个水平放置的平面图形的斜二测直观图是一个底角为45︒,腰长为1的等腰直角三角形,则这个平面图形的面积是( ) A. 2 B. 22 C. 28 D. 243.已知某几何体的三视图如图所示,则它的体积为( )A. 12πB. 45πC. 57πD. 81π4.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是 ( )A. 2π+1B. 2π+3C. 32π+1D. 32π+35.某几何体的三视图如图所示,则它的体积为( )A. 283π- B. 83π- C. 82π- D. 23π6.某几何体的三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )A. 163B. 8C. 203D. 127.某空间几何体的三视图如图所示,则该几何体的体积为()A. 16+2πB. 16+πC. 8+πD. 8+2π8.某空间几何体的三视图如图所示,则该几何体的体积为()A. 4B. 6C. 8D. 169.将棱长为2的正方体削成一个体积最大的球,则这个球的体积为( )A. 163π B.43πC.323π D. 4π10.如图是三棱锥D ABC-的三视图,则该三棱锥的外接球体积为( )A. 92πB.33πC. 62πD.23π11.某空间几何体的正视图是三角形,则该几何体不可能是( )A. 圆锥B. 圆柱C. 四面体D. 三棱锥12.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为().A. 2,22B. 2,4C. 23,2D. 4,313.某几何体的三视图如图所示,则该几何体的表面积是()A.322++ B.5322++ C.332++ D.7322++14.一个球的内接正方体的表面积为54,则球的表面积为( )A. 27πB. 18πC. 19πD. 54π15.将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为( )A. 4πB. 22πC. 2πD. 2π16.把球的表面积扩大到原来的2倍,那么体积扩大到原来的( )A. 2倍B. 22倍C. 2倍D. 32倍17.如果一个几何体的主视图与左视图是全等的长方形,边长分别是4,2,如图所示,俯视图是一个边长为4的正方形.(1)求该几何体的表面积;(2)求该几何体的外接球的体积.18.如图是一建筑物的三视图(单位:m),现需将其外壁用油漆粉刷一遍,已知每平方米用漆0.2kg,问需要油漆多少千克?(无需求近似值)cm. 19.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6cm,4cm,则该棱柱的侧面积为________2 20.一个几何体的三视图如图所示,则该几何体的体积为______.21.一个几何体的三视图如图所示,则该几何体的表面积为_______.22.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是________.23.已知正三棱锥的高为1,底面边长为26,则该三棱锥的表面积为________.-的所有棱长都为2,则该三棱锥的外接球的表面积为________.24.已知三棱锥A BCD25.若正三棱锥的底面边长为3,侧棱长为2,则其外接球的表面积为__________.26.已知高与底面直径之比为2:1的圆柱内接于球,且圆柱的体积为500π,则球的体积为________.cm).27.某几何体的三视图如图所示(单位:cm),则该几何体的体积是_____(单位:3参考答案1.A2.A3.C4.A5.A6.C7.D8.C9.B10.A11.B12.B13.D14.A15.C16.B17.(1)64;(2)36π.18.()()4.87.8kg π+19.7220.2π321.5π22.5423.24.3π25.4π26π+27.12。
空间几何体的综合计算测试题

空间几何体的综合计算测试题1. 综合计算题求以下空间几何体的表面积和体积:1.1 直方体已知直方体的长、宽、高分别为10 cm、6 cm、8 cm,求其表面积和体积。
解答:该直方体的表面积可通过公式2*(长×宽 + 长×高 + 宽×高)计算,代入数值计算得:表面积 = 2*(10 × 6 + 10 × 8 + 6 × 8) = 2*(60 + 80 + 48) = 376 cm²。
该直方体的体积可通过公式长×宽×高计算,代入数值计算得:体积 = 10 × 6 × 8 = 480 cm³。
1.2 正方体已知正方体的边长为5 cm,求其表面积和体积。
解答:该正方体的表面积可通过公式6×边长²计算,代入数值计算得:表面积 = 6×5² = 6×25 = 150 cm²。
该正方体的体积可通过公式边长³计算,代入数值计算得:体积 = 5³ = 125 cm³。
1.3 圆柱体已知圆柱体的底面半径为4 cm,高为10 cm,求其表面积和体积(π取3.14)。
解答:该圆柱体的表面积可分为两部分计算:侧面积和底面积。
侧面积可通过公式2×π×半径×高计算,代入数值计算得:侧面积 = 2×3.14×4×10 = 251.2 cm²。
底面积为圆的面积,可通过公式π×半径²计算,代入数值计算得:底面积 = 3.14×4² = 50.24 cm²。
因此,该圆柱体的表面积为251.2 + 50.24 = 301.44 cm²。
该圆柱体的体积可通过公式π×半径²×高计算,代入数值计算得:体积 = 3.14×4²×10 = 502.4 cm³。
高中空间立体几何经典例题精选全文完整版

可编辑修改精选全文完整版立体几何一、选择题1.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D2 2.(20XX 年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C 【答案】A3 3.(20XX 年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A4 4.(20XX 年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B .2C .2-12D .2+12【答案】C5.(20XX 年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,底面是边长为3.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A.512πB .3πC.4πD.6π【答案】B6.(20XX年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为()A.5603B.5803C.200D.240【答案】C7.(20XX年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为,m n,那么m n+=()A.8 B.9 C.10 D.11【答案】A二、填空题8.(20XX年高考北京卷(理))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________.1D1BPD1CCEBA1A【答案】2559.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2410.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-11.(20XX 年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π12.(20XX 年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______AB C1A D EF1B 1C【答案】3π三、解答题13.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值D 1 C 1 B 1A 1D C AB14.(20XX 年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,113tan 6233BC CC BC C =⋅∠==从而2333ABC S BC ∆==因此该三棱柱的体积为1336183ABC V S AA ∆=⋅==15.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))B 1 A 1C 1ACB如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF ∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF ∥平面ABC 同理:FG ∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC ∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SAB AF ⊥SB∴AF ⊥平面SBC 又∵BC ⊆平面SBC ∴AF ⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC ⊥平面SAB 又∵SA ⊆平面SAB ∴BC ⊥SA16.(20XX 年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯=而1AD C ∆中,11AC DC AD ==故132AD C S ∆= AB CSGFE所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.17.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE,在OCD ∆中,由余弦定理可得OD=由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O =,所以A O '⊥平面BCDE . (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos OH A HO A H '∠=='所以二面角ACD B '--向量法:以O 点为原点,建立空间直角坐标系O -.CO BDEA CDOBE'A图1图2C DO BE'AH则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,1,n =- 由(Ⅰ)知,(OA '=为平面CDB 的一个法向量,所以3cos ,3n OA n OA n OA'⋅'===',即二面角A CD B '--的平面角的余弦值为5.18.(20XX年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为2, 求线段AM的长.6【答案】19.(20XX年高考陕西卷(理))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,12AB AA==(Ⅰ) 证明: A1C⊥平面BB1D1D;(Ⅱ) 求平面OCB1与平面BB1D1D的夹角θ的大小.1A【答案】解:(Ⅰ) BDOAABCDBDABCDOA⊥∴⊂⊥11,,面且面;又因为,在正方形AB CD 中,BDCAACACAACABDAACOABDAC⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD中,AO = 1 . .111=∆OAOAART中,在OECAOCEAEDB1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又OOBDDDBBODDBBBD=⋂⊂⊂111111E.E,DDBBCA111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O为原点,以OC为X轴正方向,以OB为Y轴正方向.则)1,0,1()1,1,1(),10(),1(,0,1,0111-=⇒CABACB,,,,)(.由(Ⅰ)知, 平面BB1D1D的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OCOBCAn设平面OCB1的法向量为,则0,0,2122=⋅=⋅OCnOBnn).1-,1,0(法向量2=n为解得其中一个21221||||||,cos|cos212111=⋅=⋅=><=nnnnnnθ.所以,平面OCB1与平面BB1D1D的夹角θ为3π1A。
(完整版)空间几何体测试题及答案,推荐文档

而 l12 l22 4a2 , 即152 52 92 52 4a2 , a 8, S侧面积 ch 4 8 5 160
7.D
V1
: V2
(Sh) : (1 3
Sh)
3:1
8.C
V1 :V2 8 : 27, r1 : r2 2 : 3, S1 : S2 4 : 9
9.A
二、10、 3 R3
、
、
的几何体构成的组合体.
13.正方体 ABCD A1B1C1D1 中, O 是上底面 ABCD 中心,若正方体的棱长为 a ,
则三棱锥 O AB1D1 的体积为____________ 三、解答题(每小题 13 分,共 26 分) 14.将圆心角为1200 ,面积为 3 的扇形,作为圆锥的侧面,求圆锥的表面积和体积
空间几何体测试题
(满分 100 分)
一、选择题(每小题 6 分,共 54 分)
1.有一个几何体的三视图如下图所示,这个几何体应是一个( )
A.棱台
B.棱锥
C.棱柱
D.都不对
主视图
左视图
俯视图
3.对于一个底边在 x 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三
角形面积的( )
A. 2 倍
C.1: 2
D.1:4
二、填空题(每小题 5 分,共 20 分) 10.半径为 R 的半圆卷成一个圆锥,则它的体积为________.
11.右面三视图所表示的几何体是
.
正视图
侧视图
俯视图
12.已知,ABCD 为等腰梯形,两底边为 AB,CD 且 AB>CD,绕 AB 所在的直线旋转一周
所得的几何体中是由
11、 2 :1 12、 六棱锥
空间向量与立体几何测试试卷

空间向量与立体几何测试试卷空间向量与立体几何测试试卷一、选择题(每题2分,共20分)1.设向量a=(1,2,3),向量b=(4,5,6),则a·b的结果为:A. 4B. 14C. 32D. 562.设向量a=(1,2,3),向量b=(4,5,6),则a×b的结果为:A. (1,-2,1)B. (-1,2,-1)C. (1,2,1)D. (-1,-2,-1)3.已知向量a=(1,2,3),向量b=(4,5,6),则向量a+b的结果为:A. (5,7,9)B. (5,6,7)C. (4,7,9)D. (4,6,8)4.已知向量a=(1,2,3),向量b=(4,5,6),则向量a-b的结果为:A. (3,3,3)B. (-3,-3,-3)C. (-3,-1,1)D. (3,1,-1)5.已知向量a=(1,2,3),向量b=(4,5,6),则向量a·(a+b)的结果为:A. 42B. 56C. 70D. 846.设向量a=(1,2,3),向量b=(4,5,6),则向量a×(a+b)的结果为:A. (14,-28,14)B. (-14,28,-14)C. (14,28,14)D. (-14,-28,-14)7.设向量a=(1,2,3),向量b=(4,5,6),则向量|a|的结果为:A. √6B. √14C. √26D. √468.设向量a=(1,2,3),向量b=(4,5,6),则向量|b|的结果为:A. √14B. √26C. √38D. √509.设向量a=(1,2,3),向量b=(4,5,6),则向量a×b的模长为:A. √6B. √14C. √26D. √3810.设向量a=(1,2,3),向量b=(4,5,6),则向量a·b的模长为:A. 14B. 26C. 38D. 50二、填空题(每题3分,共30分)1.向量(2,3,4)与向量(-1,2,-3)的夹角为______度。
中班立体几何认知考试试题

中班立体几何认知考试试题
题一:辨识图形
请观察以下图中所示的立体图形,并回答相关问题:
1. 图形A是哪种立体图形?
2. 图形B有几个面?
3. 图形C有几条棱?
题二:比较大小
请比较以下两个立体图形的大小,并回答相关问题:
1. 图形D和图形E哪个更大?
2. 图形F和图形G哪个体积更小?
题三:图形拼凑
请根据以下提示,找出合适的立体图形来拼凑,并回答相关问题:提示:使用一个圆柱体和一个长方体组合成一个新的立体图形。
1. 你用了哪两个图形进行拼凑?
2. 拼凑后的图形有几个面?
3. 拼凑后的图形有几个顶点?
题四:图案识别
请观察以下图案,并回答相关问题:
1. 图案H与图案I有何不同?
2. 你能发现图案J中的几何形状?
题五:立体图形描绘
请根据以下描述,画出相应的立体图形:
1. 描述:这个立体图形有六个面,每个面都是正方形。
2. 描述:这个立体图形有三个面,两个面是圆形,一个面是矩形。
以上就是中班立体几何认知考试的试题。
请根据题目要求回答问题,并在各题下方绘制对应的图形。
确保回答准确无误,并将试卷交给监
考老师。
祝你好运!。
数学立体几何测试题

数学立体几何测试题测试题一:立体图形的表示1. 画出一个正方体,并标注出各个面、边和顶点。
测试题二:计算立体图形的性质2. 一个立方体的棱长为10cm,求它的表面积和体积。
3. 一个正方体的对角线长为12cm,求它的棱长。
4. 一个正方体的棱长为8cm,求它的对角线长。
测试题三:计算截面图形的面积5. 一个圆柱体的底面半径为6cm,高为10cm,求它的体积。
6. 一个球的半径为5cm,求它的表面积。
7. 一个锥体的高为12cm,底面半径为8cm,求它的体积。
测试题四:判断立体图形的性质8. 判断以下说法是否正确:a) 一个正方体的每个面都是正方形。
b) 一个棱柱的底面和顶面都是正多边形。
9. 判断以下说法是否正确:a) 一个正方体的对角线长度等于它的体对角线的两倍。
b) 一个圆柱的高等于它的侧面积除以底面积。
10. 判断以下说法是否正确:a) 一个棱锥的底面是一个正多边形。
b) 一个正球的体积等于它的表面积乘以π倍。
测试题五:运用立体几何解决实际问题11. 一张纸片的形状是一个以边长为6cm的正方形,若将这张纸片折叠成一个正立方体,则每个小正方体的体积是多少?12. 一个长方体箱子的长、宽、高分别为8cm、6cm、10cm,请问这个箱子的体积是多少立方厘米?13. 一个蜡烛用圆柱体塑料包装,如果塑料包装的高度是12cm,底面直径为4cm,蜡烛的高度为10cm,并且蜡烛剩余部分的直径与底面直径相等,求蜡烛的剩余部分的高度。
测试题六:解答题14. 已知一个棱长为a的正方体,将它的每个面都截去边长为b的正方形,最后剩下的多面体的体积是多少?15. 一个高度为h的圆锥的底面半径为r,切一个与底面平行的截面得到一个半径为R的圆,若R>r,则这个圆锥的高度能使得截面圆的面积最大吗?为什么?答案测试题一:立体图形的表示1. 略。
测试题二:计算立体图形的性质2. 表面积 = 6 * 边长² = 6 * 10² = 600 cm²体积 = 边长³ = 10³ = 1000 cm³3. 对角线长 = 边长* √3 = 10 * √3 cm4. 对角线长 = 边长* √3 = 8 * √3 cm测试题三:计算截面图形的面积5. 体积= π * 半径² * 高度= π * 6² * 10 = 360π cm³6. 表面积= 4π * 半径² = 4π * 5² = 100π cm²7. 体积= (1/3) * π * 半径² * 高度= (1/3) * π * 8² * 12 = 256π cm³测试题四:判断立体图形的性质8. a) 正确b) 正确9. a) 错误,它们相等。
空间立体几何练习题(含答案)
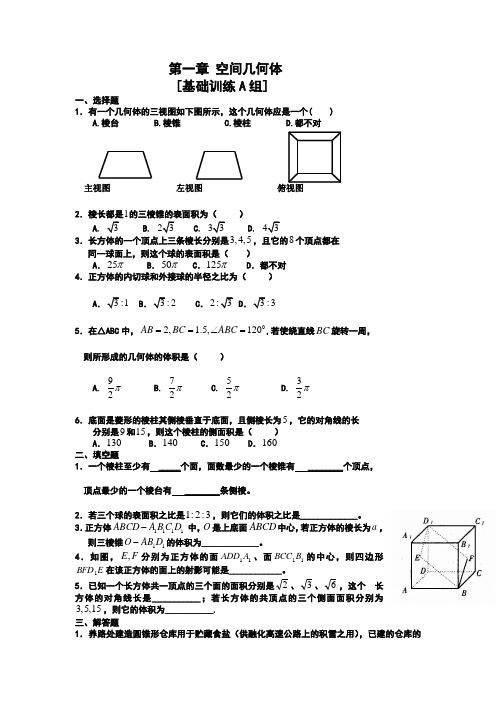
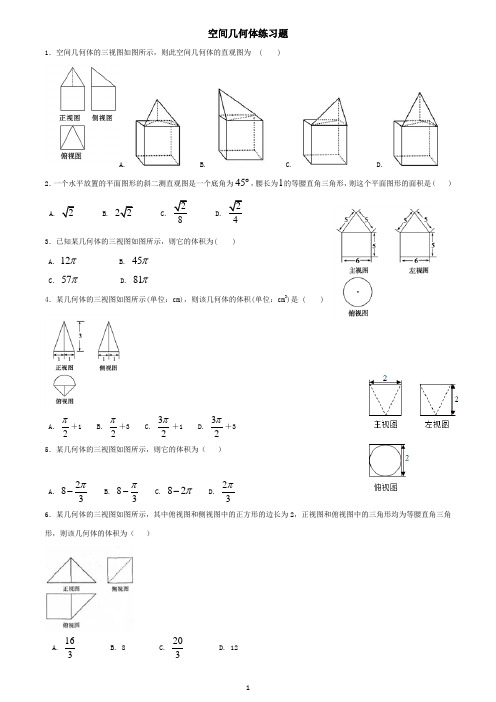
第一章 空间几何体 [基础训练A 组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对2.棱长都是1的三棱锥的表面积为( )3.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在 同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对 4.正方体的内切球和外接球的半径之比为( )AB2 C.5.在△ABC 中,02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周, 则所形成的几何体的体积是( )A.92π B. 72π C. 52π D. 32π 6.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长 分别是9和15,则这个棱柱的侧面积是( ) A .130 B .140 C .150 D .160 二、填空题1.一个棱柱至少有 _____个面,面数最少的一个棱锥有 ________个顶点, 顶点最少的一个棱台有 ________条侧棱。
2.若三个球的表面积之比是1:2:3,则它们的体积之比是_____________。
3.正方体1111ABCD A BC D - 中,O 是上底面ABCD 中心,若正方体的棱长为a , 则三棱锥11O AB D -的体积为_____________。
4.如图,,E F 分别为正方体的面11A ADD 、面11B BCC 的中心,则四边形E BFD 1在该正方体的面上的射影可能是____________。
5.已知一个长方体共一顶点的三个面的面积分别是2、3、6,这个 长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为___________. 三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的主视图 左视图 俯视图C 底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
空间几何体测试题及答案
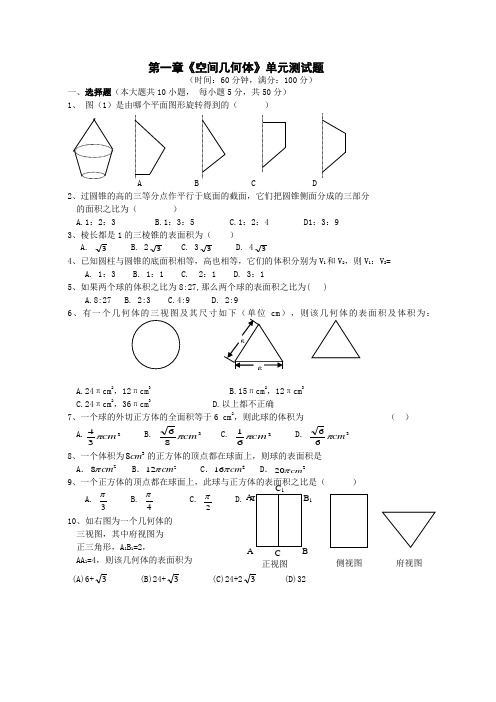
第一章《空间几何体》单元测试题(时间:60分钟,满分:100分)一、选择题(本大题共10小题,每小题5分,共50分)1、图(1)是由哪个平面图形旋转得到的()A B C D2、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A.1:2:3B.1:3:5C.1:2:4 D1:3:93、棱长都是1的三棱锥的表面积为()A. 3B. 23C. 33D. 434、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2=A. 1:3B. 1:1C. 2:1D. 3:15、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96A.24πcm2,12πcm3B.15πcm2,12πcm3C.24πcm2,36πcm3D.以上都不正确7、一个球的外切正方体的全面积等于6 cm2,则此球的体积为()A.334cmπ B. 386cmπ C. 361cmπ D. 366cmπ8、一个体积为38cm的正方体的顶点都在球面上,则球的表面积是A.28cmπ B.212cmπ C.216cmπ D.220cmπ9、一个正方体的顶点都在球面上,此球与正方体的表面积之比是()A.3π B.4π C.2π D. π10、如右图为一个几何体的三视图,其中府视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为(A)6+3 (B)24+3 (C)24+23 (D)32A B1C正视图侧视图府视图二、填空题(本大题共4小题,每小题5分,共20分)11. 长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为12.一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是______.13、球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题(本大题共3小题,每小题10分,共30分)15.将圆心角为1200,面积为3 的扇形, 16. (如图)在底半径为2母线长为4的作为圆锥的侧面,求圆锥的表面积和体积. 圆锥中内接一个高为3的圆柱,求圆柱的表面积*16、如图,在四边形ABCD中,,,,,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.参考答案:1.A ;2.B ;3.A ;4.D ;5.C ;6.A ;7.C ;8.B ;9.C ;10.C.11.15;12.910Q;13.8;14.2:1 15.解:l=3,R=1;S=4π;V=322π.16.R=1,h=3,S=2π+2π3.17.S=60π+4π2;V=52π-38π=3148π.。
空间几何体单元测试卷

空间几何体单元测试卷(时间:50分钟,满分:100分)一、选择题(每小题5分,共30分)1.在一个棱柱中,下列说法正确的是()A.只有两个面平行B.所有的棱都平行C.所有的面都是平行四边形D.两底面平行,且各侧棱也互相平行2.将图1所示的三角形绕直线l旋转一周,可以得到如图2所示的几何体的是哪一个三角形()3.如右图,能推断这个几何体可能是三棱台的条件是()A.A1B1=2,AB=3,B1C1=3,BC=4B.A1B l=1,AB=2,B l C l=1.5,BC=3,A1C1=2,AC=3C.A l B l=1,AB=2,B1C l=1.5,BC=3,A l C l=2,AC=4D.AB=A1B1,BC=B1C1,CA=C1A14.下列命题中错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.圆锥的轴截面是所有过顶点的截面中面积最大的一个C.圆台的所有平行于底面的截面都是圆D.圆锥所有的轴截面是全等的等腰三角形5.下面几何体正视图和左视图类似的一个是()6.如下图,一个封闭的立方体,它6个表面各标出1、2、3、4、5、6这6个数字,现放成下面3个不同的位置,则数字l、2、3对面的数字是()A.4、5、6 B.6、4、5 C.5、4、6 D.5、6、4二、填空题(每小题5分,共20分)7.一个几何体,无论我们从哪个方向看,看到的结果都是一样的,则该几何体必定为_____ _.8.将半径为R的圆分割成面积之比为1∶2∶3的三个扇形作为三个圆锥的侧面,设这三个圆锥的底面半径依次为r l,r2,r3,则r1+r2+r3=___ _.9.如图,在三棱锥S—ABC中,SA=SB=SC=1,∠ASB=∠ASC=∠BSC=30°,一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点,则蚂蚁爬过的最短路程为___ __.10.如图所示的积木是由16块棱长为1cm的正方体堆积而成的,则它表面积为_______ .第9题图第10题图三、解答题(共3小题,共50分)11.(本小题16分)正四棱柱的表面积是144cm2,对角线长是9cm.(1)试问满足这些条件的正四棱柱有多少个?请证明你的结论.(2)求所有满足条件的正四棱柱的体积.12.(本小题16分)圆锥的底面半径为5cm,高为12cm,当它的内接圆柱的底面半径为何值时,圆锥的内接圆柱表面积有最大值?最大值是多少?13. (本小题18分)一试管的上部为圆柱形,底部为与圆柱底面半径相同的半球形. 圆柱形部分的高为h cm ,半径为r cm ,试管的容量为108πcm 3,半球部分容量为全试管容量的61. (1)求r 和h ;(2)若将试管垂直放置,并注水至水面离管口4cm 处,求水的体积.。
立体几何经典习题集(含答案)

立体几何基础A 组题一、选择题:1.下列命题中正确命题的个数是 ( ) ⑴ 三点确定一个平面⑵ 若点P 不在平面α内,A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案:A2.已知异面直线a 和b 所成的角为︒50,P 为空间一定点,则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 ( ) A.1条 B.2条 C.3条 D.4条答案:B 3.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是 ( ) (1) 若βα//,则m l ⊥ (2) 若βα⊥,则m l // (3) 若m l //,则βα⊥ (4) 若 m l ⊥,则βα//A.(3)与(4)B.(1)与(3)C.(2)与(4)D.(1)与(2)答案:B4.已知m 、n 为异面直线,⊂m 平面α,⊂n 平面β,l =βα ,则l ( ) A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案:B5.设集合A={直线},B={平面},B A C =,若A a ∈,B b ∈,C c ∈,则下列命题中的真命题是 ( )A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案:A6.已知a 、b 为异面直线,点A 、B 在直线a 上,点C 、D 在直线b 上,且AC=AD ,BC=BD ,则直线a 、b 所成的角为 ( ) A. ︒90 B. ︒60 C. ︒45 D. ︒30答案:A7.下列四个命题中正确命题的个数是 ( ) 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案:D8.设M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},则这些集合之间关系是 ( ) A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案:B9.正四棱锥P —ABCD 中,高PO 的长是底面长的21,且它的体积等于334cm ,则棱AB 与侧面PCD 之间的距离是 ( ) A.cm 2 B. cm 2 C. cm 1 D.cm 22答案:A10.纬度为α的纬圈上有A 、B 两点,弧在纬圈上,弧AB 的长为απcos R (R 为球半径),则A 、B 两点间的球面距离为 ( )A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案:D11.长方体三边的和为14,对角线长为8,那么 ( ) A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案:D12.正四棱锥P —ABCD 的所有棱长都相等,E 为PC 的中点,那么异面直线BE 与PA 所成角的余弦值等于( )A.21B. 22C. 32D. 33答案:D13.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是 ( )A.正方形B.矩形C.菱形D.一般平行四边形答案:B二、填空题:14.正方体1111D C B A ABCD -中,E 、F 、G 分别为AB 、BC 、CC 1的重点,则EF 与BG 所成角的余弦值为________________________答案:510 15.二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4,到棱a 的距离为24,则这个二面角的大小为__________________答案:︒︒16575或16.四边形ABCD 是边长为a 的菱形,︒=∠60BAD ,沿对角线BD 折成︒120的二面角A —BD —C 后,AC 与BD 的距离为_________________________答案:a 43 17.P 为︒120的二面角βα--a 内一点,P 到α、β的距离为10,则P 到棱a 的距离是_________________答案:3320 18.如图:正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角,则异面直线AD 与BF 所成角的余弦值是______________________答案:4219.已知三棱锥P —ABC 中,三侧棱PA 、PB 、PC 两两互相垂直,三侧面与底面所成二面角的大小分别为γβα,,,则=++γβα222cos cos cos _______________答案:1 20.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值)。
立体几何大题(解析版)

立体几何大题1.空间中的平行关系(1)线线平行(2)线面平行的判定定理:平面外一直线与平面内一直线平行,则线面平行(3)线面平行的性质定理若线面平行,经过直线的平面与该平面相交,则直线与交线平行(4)面面平行的判定定理判定定理1:一个平面内有两条相交直线分别平行于另一个平面,则面面平行判定定理2:一个平面内有两条相交直线分别于另一个平面内两条相交直线平行,则面面平行(5)面面平行的性质定理性质定理1:两平面互相平行,一个平面内任意一条直线平行于另一个平面性质定理2:两平面互相平行,一平面与两平面相交,则交线互相平行6.空间中的垂直关系(1)线线垂直(2)线面垂直的判定定理一直线与平面内两条相交直线垂直,则线面垂直(3)线面垂直的性质定理性质定理1:一直线与平面垂直,则这条直线垂直于平面内的任意一条直线性质定理2:垂直于同一个平面的两条直线平行(4)面面垂直的判定定理一个平面内有一条直线垂直于另一个平面,则两个平面垂直(或:一个平面经过另一个平面的垂线,则面面垂直)(5)面面垂直的性质定理两平面垂直,其中一个平面内有一条直线与交线垂直,则这条直线垂直于另一个平面6.异面直线所成角cos θ=cos a ,b =|a ⋅b ||a |⋅|b |=|x 1x 2+y 1y 2+z 1z 2|x 12+y 12+z 12⋅x 22+y 22+z 22(其中θ(0°<θ≤90°)为异面直线a ,b 所成角,a ,b 分别表示异面直线a ,b 的方向向量)7.直线AB 与平面所成角,sin β=AB ⋅m |AB ||m |(m 为平面α的法向量).8.二面角α-l -β的平面角cos θ=m ⋅n |m ||n |(m ,n 为平面α,β的法向量).9.点B 到平面α的距离d =|AB ⋅n | |n |(n 为平面α的法向量,AB 是经过面α的一条斜线,A ∈α).模拟训练一、解答题1(22·23下·湖南·二模)如图,在直三棱柱ABC -A B C 中,∠ABC =120°,AB =BC =2,AC =BB ,点D 为棱BB 的中点,AE =13AC .(1)求DE 的长度;(2)求平面CDE 与平面BDE 夹角的余弦值.【答案】(1)393(2)34【分析】(1)在△ABC 中,用余弦定理可得到AC =23,在△ABE 中,用余弦定理可得BE =233,即可求得DE =DB 2+BE 2=393;(2)以B 为原点,分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立空间直角坐标系,求出平面CDE 与平面BDE 的法向量,即可求解【详解】(1)因为在直三棱柱ABC -A B C 中,∠ABC =120°,AB =BC =2,在△ABC 中,由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC=22+22-AC 22×2×2=-12,解得AC =23,则AE =13AC =233,在△ABE 中,由余弦定理得cos ∠BAE =AB 2+AE 2-BE 22AB ⋅AE =22+233 2-BE 22×2×233=32,解得BE =233,又AC =BB =23,所以BD =12BB =3,因为BB ⊥平面ABC ,BE ⊂平面ABC ,所以BB ⊥BE ,在直角三角形DBE 中,DE =DB 2+BE 2=(3)2+233 2=393;(2)因为AE =BE =233,所以∠ABE =∠BAE =30°,则∠CBE =∠ABC -∠ABE =120°-30°=90°,则BE ,BC ,BB 两两互相垂直,以B 为原点,分别以BE ,BC ,BB 所在的直线为x ,y ,z 轴建立如下图所示的空间直角坐标系:则点C 0,2,0 ,D 0,0,3 ,E 233,0,0 ,则CD =0,-2,3 ,CE =233,-2,0 ,设平面CDE 的法向量为n =x ,y ,z ,由n ⋅CD =x ,y ,z ⋅0,-2,3 =-2y +3z =0n ⋅CE =x ,y ,z ⋅233,-2,0 =233x -2y =0 ,得z =233y x =3y,令y =3,得平面CDE 的一个法向量为n =3,3,2 ;平面BDE 的一个法向量为m =0,1,0 .设平面CDE 与平面BDE 夹角的大小为θ,则cos θ=m ⋅n m n =0,1,0 ⋅3,3,2 1×4=34,故平面CDE 与平面BDE 夹角的余弦值为34.2(22·23下·绍兴·二模)如图,在多面体ABCDE 中,DE ⊥平面BCD ,△ABC 为正三角形,△BCD 为等腰Rt △,∠BDC =90°,AB =2,DE =2.(1)求证:AE ⊥BC ;(2)若AE ⎳平面BCD ,求直线BE 与平面ABC 所成的线面角的正弦值.【答案】(1)证明见解析(2)63【分析】(1)由线面垂直的性质定理和判定定理即可证明;(2)法一:由分析可知,∠EBH 就是直线BE 与平面ABC 所成的线面角,设∠AFD =α,当α<90°时,O 与D 重合,可得A ,E 两点重合,不符合题意,当α>90°时,求出EH ,BE ,即可得出答案;法二:建立空间直角坐标系,求出直线BE 的方向向量与平面ABC 的法向量,由线面角的向量公式代入即可得出答案.【详解】(1)设F 为BC 中点,连接AF ,EF ,则由△ABC 为正三角形,得AF ⊥BC ;DE ⊥平面BCD ,且△BCD 为等腰直角三角形,计算可得:BE =CE =2,∴EF ⊥BC .EF ∩AF =F ,EF ,AF ⊂面AEF ,于是BC ⊥面AEF ,AE ⊂面AEF ,从而BC ⊥AE .(2)法一:由(1)可知,过点E 作EH ⊥AF ,垂足为H ,则∠EBH 就是直线BE 与平面ABC 所成的线面角.当AE ⎳平面BCD 时,可得A 到平面BCD 的距离为 2.设∠AFD =α,所以AF ⋅sin α=2,可得sin α=63,当α<90°时,cos α=33,不妨设A 在底面BCD 射影为O ,则FO =1,此时O 与D 重合,可得A ,E 两点重合,不符合题意,舍去;当α>90°时,FO =1,此时O 在DF 的延长线上,作EH ⊥AF ,由于AODE 为矩形,可得AE =DO =2,AE ∥OD ,可得sin ∠EAH =63,可得EH =263.于是sin ∠EBH =EH BE=63.法二:建立如图坐标系,可得F 0,0,0 ,B 1,0,0 ,C -1,0,0 ,D 0,1,0 ,E 0,1,2 ,A 0,a ,b由AF =3,解得a 2+b 2=3,又∵AE ⎳平面BCD ,令n =0,0,1 ,可得AB ⋅n =0,解得b =2,a =±1.当a =1时A ,E 重合,所以a =-1,此时A 0,-1,2 .不妨设平面ABC 的法向量为m =x ,y ,z ,则CB ⋅m =0CA ⋅m =0代入得x -y +2z =02x =0 ,令z =1,则y =2,所以m =0,2,1 .由于BE =-1,1,2 ,不妨设所成角为θ,则sin θ=∣cos BE ,m |=63.3(22·23·张家口·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C 为菱形,∠CBB 1=60°,AB =BC =2,AC =AB 1=2.(1)证明:平面ACB 1⊥平面BB 1C 1C ;(2)求平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值.【答案】(1)证明见解析;(2)57.【分析】(1)利用面面垂直的判定定理进行证明;(2)利用垂直关系建立空间直角坐标系,用向量法进行求解.【详解】(1)如图,连接BC 1,交B 1C 于O ,连接AO .因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为BC 1的中点.又AC =AB 1=2,故AO ⊥B 1C .又AB =BC =2,且∠CBB 1=60°,所以CO =1,BO =3,所以AO =AC 2-CO 2=1.又AB =2,所以AB 2=BO 2+AO 2,所以AO ⊥BO .因为BO ,CB 1⊂平面BB 1C 1C ,BO ∩CB 1=O ,所以AO ⊥平面BB 1C 1C .又AO ⊂平面ACB 1,所以平面ACB 1⊥平面BB 1C 1C .(2)由(1)知,OA ,OB ,OB 1两两互相垂直,因此以O 为坐标原点,OB ,OB 1,OA 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系O -xyz ,则A (0,0,1),B (3,0,0),C (0,-1,0),C 1(-3,0,0).故CC 1 =(-3,1,0),CA =(0,1,1),CB =(3,1,0).设n =(x 1,y 1,z 1)为平面ACC 1A 1的一个法向量,则有n ⋅CC 1 =0n ⋅CA =0 ,即-3x 1+y 1=0y 1+z 1=0 ,令x 1=1,则n =(1,3,-3).设m =(x 2,y 2,z 2)为平面ABC 的一个法向量,则有m ⋅CA =0m ⋅CB =0,即y 2+z 2=03x 2+y 2=0 ,令x 2=1,则m =(1,-3,3).因为平面A 1B 1C 1∥平面ABC ,所以m =(1,-3,3)也是平面A 1B 1C 1的一个法向量.所以cos <n ,m > =n ⋅m n m=1-3-3 7×7=57.所以平面ACC 1A 1与平面A 1B 1C 1夹角的余弦值57. 4(22·23·湛江·二模)如图1,在五边形ABCDE 中,四边形ABCE 为正方形,CD ⊥DE ,CD =DE ,如图2,将△ABE 沿BE 折起,使得A 至A 1处,且A 1B ⊥A 1D .(1)证明:DE ⊥平面A 1BE ;(2)求二面角C -A 1E -D 的余弦值.【答案】(1)证明见解析(2)63【分析】(1)由已知易得DE ⊥BE ,即可证明线面垂直;(2)建立空间直角坐标系,用坐标公式法求解即可.【详解】(1)由题意得∠BEC =∠CED =π4,∠BED =π2,DE ⊥BE ,因为AB ⊥AE ,则A 1B ⊥A 1E ,又A 1B ⊥A 1D ,A 1E ∩A 1D =A 1,A 1E ,A 1D ⊂面A 1ED ,所以A 1B ⊥面A 1ED ,又DE ⊂面A 1ED ,则DE ⊥A 1B ,又DE ⊥BE ,A 1B ∩BE =B ,A 1B ⊂平面A 1BE ,BE ⊂平面A 1BE ,所以DE ⊥平面A 1BE .(2)取BE 的中点O ,可知BE =2CD ,OE =CD ,由DE ⊥BE ,且CD ⊥DE 可得OE ⎳CD ,所以四边形OCDE 是平行四边形,所以CO ∥DE ,则CO ⊥平面A 1BE ,设BE =2,以点O 为坐标原点,OB ,OC ,OA 1所在直线为坐标轴建立空间直角坐标系,如图,则A 1(0,0,1),E (-1,0,0),B (1,0,0),C (0,1,0),D (-1,1,0),EA 1 =(1,0,1),EC =(1,1,0),ED =(0,1,0),设平面A 1EC 的一个法向量为n 1 =(x 1,y 1,z 1),则n 1 ⋅EA 1 =0n 1 ⋅EC =0 ,即x 1+z 1=0x 1+y 1=0 ,取x 1=1,则n 1 =(1,-1,-1),设平面A 1ED 的一个法向量为n 2 =(x 2,y 2,z 2),则n 2 ⋅E 1A =0n 2 ⋅ED =0 ,即x 2+z 2=0y 2=0 ,取x 2=1,则n 2 =(1,0,-1),所以cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2=63,由图可知,二面角C -A 1E -D 为锐角,所以面角C -A 1E -D 的余弦值为63.5(22·23下·长沙·三模)如图,在多面体ABCDE 中,平面ACD ⊥平面ABC ,BE ⊥平面ABC ,△ABC 和△ACD 均为正三角形,AC =4,BE =3,点F 在AC 上.(1)若BF ⎳平面CDE ,求CF ;(2)若F 是AC 的中点,求二面角F -DE -C 的正弦值.【答案】(1)CF =1(2)8517【分析】(1)记AC 中点为M ,连接DM 、BM ,依题意可得DM ⊥AC ,根据面面垂直的性质得到DM ⊥平面ABC ,如图建立空间直角坐标系,求出平面CDE 的法向量,设F a ,0,0 ,a ∈2,-2 ,依题意可得BF ⋅n =0求出a 的值,即可得解;(2)依题意点F 与点M 重合,利用空间向量法计算可得.【详解】(1)记AC 中点为M ,连接DM 、BM ,△ACD 为正三角形,AC =4,则DM ⊥AC ,且DM =2 3.因为平面ACD ⊥平面ABC ,平面ACD ∩平面ABC =AC ,DM ⊂平面ACD ,所以DM ⊥平面ABC ,又△ABC 为正三角形,所以BM ⊥AC ,所以BM =23,如图建立空间直角坐标系,则B 0,23,0 ,C -2,0,0 ,D 0,0,23 ,E 0,23,3 ,所以CD =2,0,23 ,CE =2,23,3 ,设平面CDE 的法向量为n =x ,y ,z ,则n ⋅CD =2x +23z =0n ⋅CE =2x +23y +3z =0,令x =3,则z =-3,y =-32,则n =3,-32,-3 ,设F a ,0,0 ,a ∈-2,2 ,则BF =a ,-23,0 ,因为BF ⎳平面CDE ,所以BF ⋅n =3a +-23 ×-32+0×-3 =0,解得a =-1,所以F 为CM 的中点,此时CF =1.(2)若F 是AC 的中点,则点F 与点M 重合,则平面FDE 的一个法向量可以为m =1,0,0 ,设二面角F -DE -C 为θ,显然二面角为锐角,则cos θ=m ⋅n m ⋅n=332+-32 2+-3 2=651,所以sin θ=1-cos 2θ=1-651 2=8517,所以二面角F -DE -C 的正弦值为8517.6(22·23下·湖北·二模)如图,S 为圆锥的顶点,O 是圆锥底面的圆心,△ABC 内接于⊙O ,AC ⊥BC ,AC =BC =322,AM =2MS ,AS =3,PQ 为⊙O 的一条弦,且SB ⎳平面PMQ .(1)求PQ 的最小值;(2)若SA ⊥PQ ,求直线PQ 与平面BCM 所成角的正弦值.【答案】(1)22(2)3010【分析】(1)作出辅助线,找到符合要求的PQ ,并利用垂径定理得到最小值;(2)在第一问基础上,得到当PQ 取得最小值时,SA ⊥PQ ,并建立空间直角坐标系,利用空间向量求解线面角.【详解】(1)过点M 作MH ⎳SB 交AB 于点H ,过点H 作PQ ⊥AB ,此时满足SB ⎳平面PMQ ,由平面几何知识易知,PQ =2r 2-d 2,当弦心距d 最大时,d =OH ,弦长最短,即PQ 取得最小值,因为AM =2MS ,AS =3,所以AH =2HB ,因为AC ⊥BC ,AC =BC =322,由勾股定理得AB =322⋅2=3,故AH =2,HB =1,连接OQ ,则OQ =32,由勾股定理得HQ =OQ 2-OH 2=94-14=2,所以PQ =2HQ =22;(2)连接OS ,则OS ⊥平面ACB ,因为PQ ⊂平面ACB ,故OS ⊥PQ ,而SA ⊥PQ ,OS ∩SA =S ,所以PQ ⊥平面AOS ,即有PQ ⊥AB .以O 为坐标原点,过点O 且平行PQ 的直线为x 轴,OB 所在直线为y 轴,OS 所在直线为z 轴,建立空间直角坐标系,则P -2,12,0 ,Q 2,12,0 ,B 0,32,0 ,C 32,0,0 ,M 0,-12,3 ,设平面BCM 的法向量为m =x ,y ,z ,则m ⋅CB =x ,y ,z ⋅-32,32,0 =-32x +32y =0m ⋅MB =x ,y ,z ⋅0,2,-3 =2y -3z =0,令x =1,则y =1,z =233,故m =1,1,233,设直线PQ 与平面BCM 所成角的大小为θ,则sin θ=cos PQ ,m =PQ ⋅m PQ ⋅m =22,0,0 ⋅1,1,233 22×1+1+43=3010.故直线PQ与平面BCM所成角的正弦值为30 10.7(22·23·深圳·二模)如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA= AD=2AB,点M是PD的中点.(1)证明:AM⊥PC;(2)设AC的中点为O,点N在棱PC上(异于点P,C),且ON=OA,求直线AN与平面ACM所成角的正弦值.【答案】(1)证明见解析(2)1510【分析】(1)由等腰三角形的性质可得AM⊥PD,由面面垂直的性质可得CD⊥平面PAD,则CD⊥AM,所以由线面垂直的判定可得AM⊥平面PCD,从而可得结论;(2)以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,利用空间向量求解即可.【详解】(1)证明:因为PA=AD,点M是PD的中点,所以AM⊥PD.因为PA⊥平面ABCD,PA⊂平面PAD,所以平面PAD⊥平面ABCD,因为四边形ABCD为矩形,所以CD⊥AD,因为平面PAD∩平面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面PAD,所以CD⊥AM,因为PD∩CD=D,PD,CD⊂平面PCD,所以AM⊥平面PCD,因为PC⊂平面PCD,所以AM⊥PC.(2)解:由题意可得AB,AD,AP两两垂直,设AB=1,如图,以AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2),因为点M是PD的中点,所以M0,22,22,所以AM =0,22,22 ,AC =1,2,0 ,设平面ACM 的法向量为n =x ,y ,z ,则AM ⋅n =22y +22z =0AC ⋅n =x +2y =0,令y =-1可得x =2,z =1,所以平面ACM 的一个法向量n =2,-1,1 .PC =1,2,-2 ,设N x N ,y N ,z N ,PN =λPC =λ,2λ,-2λ (0<λ<1),即x N ,y N ,z N -2 =λ,2λ,-2λ ,所以N λ,2λ,2-2λ .又O 12,22,0 ,ON =OA =32,所以λ-12 2+2λ-22 2+(2-2λ)2=34,化简得5λ2-7λ+2=0,解得λ=25或λ=1(舍去).所以AN =25,225,325,设直线AN 与平面ACM 所成的角为θ,则sin θ=n ⋅AN n ⋅AN=3252+1+1×425+825+1825=1510,所以直线AN 与平面ACM 所成角的正弦值为1510.8(22·23下·温州·二模)已知三棱锥D -ABC 中,△BCD 是边长为3的正三角形,AB =AC =AD ,AD 与平面BCD 所成角的余弦值为33.(1)求证:AD ⊥BC ;(2)求二面角D -AC -B 的平面角的正弦值.【答案】(1)证明见解析(2)223【分析】(1)取BC 的中点E ,连接AE ,DE ,证明BC ⊥平面ADE ,即可得证;(2)取正三角形BCD 的中心O ,连接OA ,从而可得OA ⊥平面BCD ,则∠ODA 即为AD 与平面BCD 所成角的平面角,进而可得AB =AC =AD =3,取AC 中点为H ,连接DH ,BH ,则DH ⊥AC ,BH ⊥AC ,故∠BHD 即为二面角D -AC -B 的平面角,解△BDH 即可得解.【详解】(1)取BC 的中点E ,连接AE ,DE ,因为AB =AC ,所以AE ⊥BC ,因为△BCD 是边长为3的正三角形,所以DE ⊥BC ,又AE ∩DE =E ,AE ,DE ⊂平面ADE ,所以BC ⊥平面ADE ,因为AD ⊂平面ADE ,所以AD ⊥BC ;(2)取正三角形BCD 的中心O ,连接OA ,则点O 在DE 上,且OD =23DE ,由AB =AC =AD ,△BCD 是正三角形,得三棱锥A -BCD 为正三棱锥,则OA ⊥平面BCD ,故∠ODA 即为AD 与平面BCD 所成角的平面角,又AD 与平面BCD 所成角的余弦值为33,所以OD AD =3×32×23AD=33,即AB =AC =AD =3,即三棱锥A -BCD 是正四面体,取AC 中点为H ,连接DH ,BH ,则DH ⊥AC ,BH ⊥AC ,故∠BHD 即为二面角D -AC -B 的平面角,在△BDH 中,BH =DH =332,BD =3,则cos ∠BHD =BH 2+DH 2-BD 22⋅BH ⋅DH =274+274-92×332×332=13,所以sin ∠BHD =1-cos 2∠BHD =223,所以二面角D -AC -B 的平面角的正弦值223.9(22·23下·浙江·二模)如图,四面体ABCD ,AD ⊥CD ,AD =CD ,AC =2,AB =3,∠CAB =60°,E 为AB 上的点,且AC ⊥DE ,DE 与平面ABC 所成角为30°,(1)求三棱锥D -BCE 的体积;(2)求二面角B -CD -E 的余弦值.【答案】(1)答案见解析;(2)答案见解析.【分析】(1)取AC 中点F ,可证明AC ⊥平面DEF ,得平面ABC ⊥平面DEF ,DE 在平面ABC 内的射影就是直线EF ,∠DEF 是DE 与平面ABC 所成的角,即∠DEF =30°,由正弦定理求得∠FDE ,有两个解,在∠FDE =60°时可证DF ⊥平面ABC ,在∠FDE =120°时,取FE 中点H 证明DH ⊥平面ABC ,然后由棱锥体积公式计算体积;(2)建立如图所示的空间直角坐标系,用空间向量法求二面角.【详解】(1)取AC 中点F ,连接FE ,FD ,因为AD =CD ,所以DF ⊥AC ,又AC ⊥DE ,DE ∩DF =D ,DE ,DF ⊂平面DEF ,所以AC ⊥平面DEF ,而FE ⊂平面DEF ,所以AC ⊥FE ,由已知AF =1,∠BAC =60°,所以EF =3,AE =2,BE =1,由AC ⊥平面DEF ,AC ⊂平面ABC 得平面ABC ⊥平面DEF ,因此DE 在平面ABC 内的射影就是直线EF ,所以∠DEF 是DE 与平面ABC 所成的角,即∠DEF =30°,AD =CD ,AC =2,因此DF =12AC =1,在△DEF 中,由正弦定理EF sin ∠FDE =DF sin ∠DEF 得1sin30°=3sin ∠FDE ,sin ∠FDE =32,∠FDE 为△DEF 内角,所以∠FDE =60°或120°,S △ABC =12AB ×AC ×sin ∠BAC =12×3×2×sin60°=333,S △CBE =BE BAS △ABC =3-23×332=32,若∠FDE =60°,则∠DFE =90°,即DF ⊥FE ,AC ∩FE =F ,AC ,FE ⊂平面ABC ,所以DF ⊥平面ABC ,V D -BCE =13S △BCE ⋅DF =13×32×1=36;若∠FDE =120°,则∠DFE =30°,DF =DE =1,取EF 中点H ,连接DH ,则DH ⊥EF ,因为平面ABC ⊥平面DEF ,平面ABC ∩平面DEF =EF ,而DH ⊂平面DEF ,所以DH ⊥平面ABC ,DH =DF sin ∠DFE =1×sin30°=12,所以V D -BCE =13S △BCE ⋅DF =13×32×12=312;(2)若∠FDE =60°,以FA ,FE ,FD 为x ,y ,z 轴建立如图所示的空间直角坐标系F -xyz ,则D (0,0,1),C (-1,0,0),A (1,0,0),E (0,3,0),AE =(-1,3,0),EB =12AE =-12,32,0 ,所以B 点坐标为-12,332,0 ,CD =(1,0,1),CB =12,332,0 ,CE =(1,3,0),设平面DBC 的一个法向量是m =(x 1,y 1,z 1),则m ⋅CD =x 1+z 1=0m ⋅CB =12x 1+332y 1=0,取y 1=-1,则x 1=33,z 1=-33,即m =(33,-1,-33),设平面DEC 的一个法向量是n =(x 2,y 2,z 2),则n ⋅CD =x 2+z 2=0n ⋅CE =x 2+3y 2=0,取y 2=-1,则x 2=3,z 2=-3,即m =(3,-1,-3),cos m ,n =m ⋅n m n =9+1+955×7=19385385,所以二面角B -CD -E 的余弦值是19385385;若∠FDE =120°,以FA 为x 轴,FE 为y 轴,过F 且平行于HD 的直线为z 轴建立如图所示的空间直角坐标系F -xyz ,FH =12FE =32,则D 0,32,12 ,C (-1,0,0),A (1,0,0),E (0,3,0),AE =(-1,3,0),EB =12AE =-12,32,0 ,所以B 点坐标为-12,332,0 ,CD =1,32,12 ,CB =12,332,0 ,CE =(1,3,0),设平面DBC 的一个法向量是m =(x 1,y 1,z 1),则m ⋅CD =x 1+32y 1+12z 1=0m ⋅CB =12x 1+332y 1=0,取y 1=-1,则x 1=33,z 1=-53,即m =(33,-1,-53),设平面DEC 的一个法向量是n =(x 2,y 2,z 2),则n ⋅CD =x 2+32y 2+12z 2=0n ⋅CE =x 2+3y 2=0,取y 2=-1,则x 2=3,z 2=-3,即m =(3,-1,-3),cos m ,n =m ⋅n m n =9+1+15103×7=25721721,所以二面角B -CD -E 的余弦值是25721721.10(22·23下·襄阳·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面BB 1C 1C 为矩形,∠BAC =90°,AB =AC =2,AA 1=4,A 1在底面ABC 的射影为BC 的中点N ,M 为B 1C 1的中点.(1)求证:平面A 1MNA ⊥平面A 1BC ;(2)求平面A 1B 1BA 与平面BB 1C 1C 夹角的余弦值.【答案】(1)证明见解析(2)23015【分析】(1)利用线面垂直和面面垂直的判定定理证明;(2)利用空间向量的坐标运算求面面夹角的余弦值.【详解】(1)如图,∵A 1N ⊥面ABC ,连AN ,则AN ⊥A 1N ,又AB =AC =2,∴AN ⊥BC ,又AN ∩BC =N ,A 1N ⊂面A 1BC ,BC ⊂面A 1BC ,于是AN ⊥面A 1BC ,又AN ⊂面A 1MN ,,所以面A 1BC ⊥面A 1MNA .(2)由(1)可得,以NA ,NB ,NA 1 为x ,y ,z 轴,建系如图,∠BAC =90°,AB =AC =2,BC =22则A (2,0,0),B (0,2,0),C (0,-2,0),因为AA 1=4,AN =2,所以A 1N =14,则A 1(0,0,14),因为NB 1 =NB +BB 1 =NB +AA 1 =0,2,0 +-2,0,14 =-2,2,14 ,所以B 1-2,2,14 ,设平面A 1BB 1的一个法向量为m =(x ,y ,z ),因为A 1B =(0,2,-14),B 1B =(2,0,-14),所以A 1B ⋅m =2y -14z =0B 1B ⋅m =2x -14z =0 ,令y =7,则x =7,z =1,所以m =(7,7,1),设平面BCC 1B 1的一个法向量为n =(a ,b ,c ),因为BC =(0,-22,0),BB 1 =(-2,0,14),所以BC ⋅n =-22b =0BB 1 ⋅n =-2a +14c =0,令a =7,则b =0,c =1,所以n =(7,0,1),设平面A 1BB 1与平面BCC 1B 1夹角为θ,则cos θ=cos <m ,n >=m ⋅n m n=7+0+17+7+1×7+0+1=23015,所以平面A 1BB 1与平面BCC 1B 1夹角的余弦值为23015.11(22·23·唐山·二模)如图,在三棱柱ABC -A 1B 1C 1中,△ABC 是等边三角形,侧面ACC 1A 1⊥底面ABC ,且AA 1=AC ,∠AA 1C 1=120°,M 是CC 1的中点.(1)证明:A 1C ⊥BM .(2)求二面角A 1-BC -M 的正弦值.【答案】(1)证明见解析(2)45【分析】(1)根据菱形的性质、结合面面垂直的性质,线面垂直的判定定理进行证明即可;(2)建立空间直角坐标系,运用空间向量夹角公式进行求解即sk .【详解】(1)取AC 的中点O ,连接OM ,OB ,AC 1.在三棱柱ABC -A 1B 1C 1中,由AA 1=AC ,得四边形ACC 1A 1为菱形,所以A 1C ⊥AC 1,易知OM ∥AC 1,则A 1C ⊥OM .由△ABC 是等边三角形,知OB ⊥AC ,又平面ACC 1A 1⊥平面ABC ,平面ACC 1A 1∩平面ABC =AC ,OB ⊂平面ABC ,知OB ⊥平面ACC 1A 1,则OB ⊥A 1C ,又OB ∩OM =O ,OB ,OM ⊂平面OBM ,得A 1C ⊥平面OBM ,又BM ⊂平面OBM ,故A 1C ⊥BM ..(2)连接OA 1,因为侧面ACC 1A 1为菱形,∠AA 1C 1=120°,则∠A 1AC =60°,则△A 1AC 为等边三角形,所以A 1O ⊥AC ,又由(1)易知OA 1,OB ,AC 两两垂直,故以O 为坐标原点,分别以OB ,OC ,OA 1 的方向为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系.不妨设AB =2,则O 0,0,0 ,B 3,0,0 ,C 0,1,0 ,A 10,0,3 ,C 10,2,3 ,BA 1 =-3,0,3 ,BC =-3,1,0 ,CC 1 =0,1,3 ,设平面A 1BC 的法向量为n =x ,y ,z ,则n ⋅BC =-3x +y =0n ⋅BA 1 =-3x +3z =0 ,令x =1,得n =1,3,1 ,设平面BCC 1的法向量为m =a ,b ,c ,则m ⋅BC =-3a +b =0m ⋅CC 1 =b +3c =0,令a =1,得m =1,3,-1 ,所以cos n ,m =n ⋅m n ⋅m=35⋅5=35,即二面角A 1-BC -M 的正弦值为45.12(22·23下·盐城·三模)如图,该几何体是由等高的半个圆柱和14个圆柱拼接而成,点G 为弧CD 的中点,且C ,E ,D ,G 四点共面.(1)证明:平面BDF ⊥平面BCG ;(2)若平面BDF 与平面ABG 所成二面角的余弦值为155,且线段AB 长度为2,求点G 到直线DF 的距离.【答案】(1)证明见解析(2)62【分析】(1)过G 作GH ⎳CB ,交底面弧于H ,连接HB ,有HBCG 为平行四边形,根据题设可得FB ⊥HB ,即FB ⊥CG ,再由线面垂直的性质可得CB ⊥FB ,最后根据线面、面面垂直的判定即可证结论.(2)构建如下图示空间直角坐标系A -xyz ,令半圆柱半径为r ,高为h ,确定相关点坐标,进而求平面BDF 、平面ABG 的法向量,利用空间向量夹角的坐标表示及已知条件可得h =2r ,即可求出点G 到直线DF 的距离.【详解】(1)过G 作GH ⎳CB ,交底面弧于H ,连接HB ,易知:HBCG 为平行四边形,所以HB ⎳CG ,又G 为弧CD 的中点,则H 是弧AB 的中点,所以∠HBA =45°,而由题设知:∠ABF =45°,则∠HBF =∠HBA +∠ABF =90°,所以FB ⊥HB ,即FB ⊥CG ,由CB ⊥底面ABF ,FB ⊂平面ABF ,则CB ⊥FB ,又CB ∩CG =C ,CB ,CG ⊂平面BCG ,所以FB ⊥平面BCG ,又FB ⊂平面BDF ,所以平面BDF ⊥平面BCG .(2)由题意,构建如下图示空间直角坐标系A -xyz ,令半圆柱半径为r ,高为h ,则B 0,2r ,0 ,F 2r ,0,0 ,D 0,0,h ,G -r ,r ,h ,所以FD =-2r ,0,h ,BD =0,-2r ,h ,AB =0,2r ,0 ,AG =-r ,r ,h ,若m =x ,y ,z 是面BDF 的一个法向量,则m ⋅FD =-2rx +hz =0m ⋅BD =-2ry +hz =0 ,令z =2r ,则m =h ,h ,2r ,若n =a ,b ,c 是面ABG 的一个法向量,则n ⋅AB =2rb =0n ⋅AG =-ra +rb +hc =0 ,令c =r ,则n =h ,0,r ,所以cos m ,n =m ⋅n m n=h 2+2r 22h 2+4r 2×h 2+r 2=155,整理可得h 2-4r 2 h 2+2r 2 =0,则h =2r ,又AB =2,由题设可知,此时点G -1,1,2 ,D 0,0,2 ,F 2,0,0 ,则DF =2,0,-2 ,DG =-1,1,0 ,所以点G 到直线DF 的距离d =DG 2-DG ⋅DF 2DF2=62.13(22·23下·江苏·三模)如图,圆锥DO 中,AE 为底面圆O 的直径,AE =AD ,△ABC 为底面圆O 的内接正三角形,圆锥的高DO =18,点P 为线段DO 上一个动点.(1)当PO =36时,证明:PA ⊥平面PBC ;(2)当P 点在什么位置时,直线PE 和平面PBC 所成角的正弦值最大.【答案】(1)证明见解析;(2)P 点在距离O 点36处【分析】(1)利用勾股定理证明出AP ⊥BP 和AP ⊥CP ,再用线面垂直的判定定理证明出PA ⊥平面PBC ;(2)建立空间直角坐标系,利用向量法求解.【详解】(1)因为AE =AD ,AD =DE ,所以△ADE 是正三角形,则∠DAO =π3,又DO ⊥底面圆O ,AE ⊂底面圆O ,所以DO ⊥AE ,在Rt △AOD 中,DO =18,所以AO =DO 3=63,因为△ABC 是正三角形,所以AB =AO ×32×2=63×3=18,AP =AO 2+PO 2=92,BP =AP ,所以AP 2+BP 2=AB 2,AP ⊥BP ,同理可证AP ⊥CP ,又BP ∩PC =P ,BP ,PC ⊂平面PBC ,所以PA ⊥平面PBC .(2)如图,建立以O 为原点的空间直角坐标系O -xyz .设PO =x ,(0≤x ≤18),所以P 0,0,x ,E -33,9,0 ,B 33,9,0 ,C -63,0,0 ,所以EP =33,-9,x ,PB =33,9,-x ,PC =-63,0,-x ,设平面PBC 的法向量为n =a ,b ,c ,则n ⋅PB =33a +9b -cx =0n ⋅PC =-63a -cx =0,令a =x ,则b =-3x ,c =-63,故n =x ,-3x ,-63 ,设直线PE 和平面PBC 所成的角为θ,则sin θ=cos EP ,n =33x +93x -63x 108+x 2⋅x 2+3x 2+108=63x 108+x 2⋅4x 2+108=634x 2+1082x 2+540≤6324x 2⋅1082x 2+540=13,当且仅当4x 2=1082x 2,即PO =x =36时,直线PE 和平面PBC 所成角的正弦值最大,故P 点在距离O 点36处.14(22·23下·镇江·三模)如图,四边形ABCD 是边长为2的菱形,∠ABC =60°,四边形PACQ 为矩形,PA =1,从下列三个条件中任选一个作为已知条件,并解答问题(如果选择多个条件分别解答,按第一个解答计分).①BP ,DP 与平面ABCD 所成角相等;②三棱锥P -ABD 体积为33;③cos ∠BPA =55(1)平面PACQ ⊥平面ABCD ;(2)求二面角B -PQ -D 的大小;(3)求点C 到平面BPQ 的距离.【答案】(1)证明见解析(2)2π3(3)32【分析】(1)若选①,则作PA ⊥面ABCD ,证明A 和A 重合从而得到PA ⊥面ABCD ,从而得到面面垂直;若选②,计算得到P 到面ABD 的距离h =1=PA ,得到PA ⊥面ABCD ,从而得到面面垂直;若选③,通过余弦定理计算得到PA ⊥AB ,再通过PA ⊥面ABCD ,从而得到面面垂直;(2)通过建立空间直角坐标系,求出两个平面的法向量,结合二面角计算公式计算即可;(3)通过点面距离的计算公式直接计算即可.【详解】(1)选①,连接BD ,作PA ⊥面ABCD ,垂足为A .∵BP ,DP 与平面ABCD 所成角相等,∴A B =A D ,∴A 在BD 的中垂线AC 上,∵在平面PACQ 内,PA ⊥AC ,PA ⊥AC ,∴A 和A 重合,∴PA ⊥面ABCD ,又PA ⊂面PACQ ,∴面PACQ ⊥面ABCD若选②,设P 到面ABD 的距离为h ,∵V P -ABD =13S △ABD ⋅h =13×3⋅h =33,得h =1=PA ,∴PA 即为P 到面ABD 的距离,即PA ⊥面ABCD ,又PA ⊂面PACQ ,∴面PACQ ⊥面ABCD .若选③,由余弦定理得,cos ∠BPA =PB 2+PA 2-AB 22PB ⋅PA =55,∴BP =5,∴BP 2=AP 2+AB 2∴PA ⊥AB ,又PA ⊥AC ,AC ∩AB =A ,AC ,AB ⊂面ABCD∴PA ⊥面ABCD ,又PA ⊂面PACQ∴面PACQ ⊥面ABCD(2)因为PA ⊥面ABCD ,OB ,OC ⊂面ABCD ,所以PA ⊥OB ,PA ⊥OC ,取PQ 中点G ,则OG ⎳PA ,所以OG ⊥OB ,OG ⊥OC ,又因为OB ⊥OC ,所以建立如下图所示空间直角坐标系,∵B 3,0,0 ,P 0,-1,1 ,D -3,0,0 ,Q 0,1,1 ,∴BQ =-3,1,1 ,DQ =3,1,1 ,DP =3,-1,1 ,设平面BPQ 的一个法向量为m =x ,y ,z ,则m⋅BP =0m ⋅BQ =0 ,即-3x -y +z =0-3x +y +z =0 ,令x =3,则y =0,z =3,∴m =3,0,3 ,设平面DPQ 的一个法向量为n =x 1,y1,z 1 ,则n ⋅DP=0n ⋅DQ =0 ,即3x 1-y 1+z 1=3x 1+y 1+z 1=0,令x1=3,则y 1=0,z 1=-3,∴n =3,0,-3 ,∴cos m ,n =m ⋅n m ⋅ n =-623×23=-12,∵m ,n ∈0,π ,∴m ,n =2π3,由图可知二面角B -PQ -D 是钝角,所以二面角B -PQ -D 的大小为2π3.(3)∵C 0,1,0 ,Q 0,1,1 ,∴CQ =0,0,1 ,∵平面BPQ 的一个法向量为m =3,0,3 ,∴点C 到平面BPQ 的距离d =CQ ⋅m m=323=32.15(22·23下·江苏·一模)在三棱柱ABC -A 1B 1C 1中,平面A 1B 1BA ⊥平面ABC ,侧面A 1B 1BA 为菱形,∠ABB 1=π3,AB 1⊥AC ,AB =AC =2,E 是AC 的中点.(1)求证:A 1B ⊥平面AB 1C ;(2)点P 在线段A 1E 上(异于点A 1,E ),AP 与平面A 1BE 所成角为π4,求EP EA 1的值.【答案】(1)证明见解析(2)EP EA 1=25【分析】(1)作B 1O ⊥AB 交AB 于O 点,由面面垂直的性质可得B 1O ⊥平面ABC ,可得B 1O ⊥AC ,再由线面垂直的判定定理得AC ⊥平面A 1B 1BA ,从而得到AC ⊥A 1B ,再由线面垂直的判定定理可得答案;(2)以A 为原点,AB 、AC 、AO 1所在的直线分别为x 、y 、z 轴,建立空间直角坐标系,设EP =λEA 1 ,可得AP =-λ,1-λ,3λ ,求出平面A 1BE 的一个法向量,由线面角的向量求法可得答案.【详解】(1)因为侧面A 1B 1BA 为菱形,∠ABB 1=π3,AB =AC =2,所以△ABB 1、△AA 1B 1为边长为2的等边三角形,作B 1O ⊥AB 交AB 于O 点,则O 点为AB 的中点,因为平面A 1B 1BA ⊥平面ABC ,平面A 1B 1BA ∩平面ABC =AB ,B 1O ⊂平面A 1B 1BA ,所以B 1O ⊥平面ABC ,AC ⊂平面ABC ,可得B 1O ⊥AC ,又AB 1⊥AC ,B 1O ∩AB 1=B 1,B 1O 、AB 1⊂平面A 1B 1BA ,可得AC ⊥平面A 1B 1BA ,因为A 1B ⊂平面A 1B 1BA ,所以AC ⊥A 1B ,因为侧面A 1B 1BA 为菱形,所以B 1A ⊥A 1B ,AB 1∩AC =A ,AB 1、AC ⊂平面AB 1C ,所以A 1B ⊥平面AB 1C ;(2)由(1)知,AC ⊥平面A 1B 1BA ,∠BAC =π2,取做A 1B 1的中点O 1,连接AO 1,则B1O ⎳AO 1,所以AO 1⊥平面ABC ,以A 为原点,AB 、AC 、AO 1所在的直线分别为x 、y 、z 轴,建立空间直角坐标系,则A 0,0,0 ,A 1-1,0,3 ,B 2,0,0 ,E 0,1,0 ,A 1B =3,0,-3 ,EA 1 =-1,-1,3 ,设EP =λEA 1 ,可得P -λ,1-λ,3λ ,所以AP =-λ,1-λ,3λ ,设平面A 1BE 的一个法向量为n=x ,y ,z ,则A 1B ⋅n=0EA 1 ⋅n =0,即3x -3z =0-x -y +3z =0 ,令z =3,可得n =1,2,3 ,可得sin π4=cos n ,AP =n ⋅AP n AP=-λ+2-2λ+3λ 1+4+3λ2+1-λ 2+3λ2,解得λ=0舍去,或λ=25,所以EP EA 1=25.16(22·23下·河北·三模)如图,四棱锥P -ABCD 的底面ABCD 是菱形,其对角线AC ,BD 交于点O ,且PO ⊥平面ABCD ,OC =1,OD =OP =2,M 是PD 的中点,N 是线段CD 上一动点.(1)当平面OMN ⎳平面PBC 时,试确定点N 的位置,并说明理由;(2)在(1)的前提下,点Q 在直线MN 上,以PQ 为直径的球的表面积为214π.以O 为原点,OC ,OD ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系O -xyz ,求点Q 的坐标.【答案】(1)N 是CD 的中点(2)12,1,0 ,-1310,1,185 【分析】(1)根据面面平行的性质证明MN ⎳PC ,即可得解;(2)先根据球的体积求出PQ ,然后根据空间中两点间的距离公式即可得解.【详解】(1)因为平面OMN ⎳平面PBC ,平面OMN ∩平面PCD =MN ,平面PBC ∩平面PCD =PC ,所以MN ⎳PC ,因为M 是PD 的中点,所以N 是CD 的中点;(2)由题意4π×PQ 22=214π,解得PQ =212,设MQ =λMN,λ∈R ,由题意,P 0,0,2 ,M 0,1,1 ,N 12,1,0 ,则PM =0,1,-1 ,MN =12,0,-1 ,则PQ =PM +MQ =0,1,-1 +λ12,0,-1 =λ2,1,-λ-1 ,则λ24+1+-λ-1 2=212,解得λ=1或λ=-135,当λ=1时,MQ =MN ,则Q 12,1,0 ,当λ=-135时,MQ =-135MN =-1310,0,135,设Q x ,y ,z ,则MQ =x ,y -1,z -1 =-1310,0,135,所以x =-1310y -1=0z -1=135 ,解得x =-1310y =1z =185 ,则Q -1310,1,185 ,综上所述点Q 的坐标为12,1,0,-1310,1,185 .17(22·23·汕头·三模)如图,圆台O 1O 2的轴截面为等腰梯形A 1ACC 1,AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点.(1)在平面BCC 1内,过C 1作一条直线与平面A 1AB 平行,并说明理由;(2)若四棱锥B -A 1ACC 1的体积为23,设平面A 1AB ∩平面C 1CB =l ,Q ∈l ,求CQ 的最小值.【答案】(1)作图见解析,理由见解析(2)7【分析】(1)根据线面平行的判定和中位线定理即可求解;(2)根据几何关系或空间向量方法即可求解.【详解】(1)取BC 中点P ,作直线C 1P 即为所求,取AB 中点H ,连接A 2H ,PH ,则有PH ∥AC ,PH =12AC ,如图,在等腰梯形A 1ACC 1中,A 1C 1=12AC ,有HP ∥A 1C 1,HP =A 1C 1,则四边形A 1C 1PH 为平行四边形,即有C 1P ∥A 1H ,又A 1H ⊂平面A 1AB ,C 1P⊄平面A 1AB ,所以C 1P ∥平面A 1AB .(2)法一:延长AA 1,CC 1交于点O ,故O ∈AA 1⊂平面ABA 1,O ∈CC 1⊂平面CC 1B故平面A 1AB ∩平面C 1CB =BO ,BO 即l ,在△OBC 中,OC ,OB 均为圆锥母线.过点B 作BO ⊥AC 于O .在等腰梯形A 1ACC 1中,AC =2AA 1=2A 1C 1=4,此梯形的高h =AA 21-AC -A 1C 122=3,∴等腰梯形A 1ACC 1的面积为S =122+4 3=33,所以四棱锥B -A 1ACC 1的体积V =13S ×BO =13×33×BO =23,解得BO =2,故点O 与O 2重合,BC =22由AC =2AA 1=2A 1C 1,得OC =2CC 1,且∠C 1CA =60°,故OC =AC =4=OB .△OBC 中,O 到BC 距离h 1=OB 2-BC 22=14.则△OBC 面积=12OB ⋅CQ min =12BC ⋅h 1,得:CQ 的最小值为:CQ min =22⋅144=7.法二:同法一求出B 的位置.以O 2为原点,OB ,OC ,O 2O 1方向为x ,y ,z 轴正向建立空间直角坐标系,C 0,2,0 ,B 2,0,0 ,AA 1 =0,1,3 ,AB =2,2,0 ,CC 1 =0,-1,3 ,BC=-2,2,0设面A 1AB 的法向量为a=x 1,y 1,z 1a ⋅AA 1=y 1+3z 1=0a ⋅AB=2x 1+2y 1=0,取z 1=1,有a=3,-3,1 ;同理可得面C 1CB 的法向量为β=3,3,1 ,由l =面C 1CB ∩面A 1AB ,可知B ∈l ,设l 的方向向量为l=x ,y ,z ,故l ⋅a =3x -3y +z =0,l ⋅β=3x +3y +z =0取l=1,0,3 ,下面分2个方法求|CQ |min求|CQ |min 方法1:BQ =l=t ,0,3t ,,∵B 2,0,0 ,∴Q t -2,0,3t∴CQ =(t -2)2+22+(3t )2=4t 2-4t +8,当t =12时,CQ 取最小值为7.求CQ min 方法2:BC 在l 上的投影向量的模为BC ⋅l l =-2×1+2×0+0×32=1故CQ 的最小值即C 到l 的距离为BC 2-12=7.法三:在三角形△BCO 中,BO =CO =4,BC =22,cos ∠CBO =42+(22)2-422×4×22=122⋅sin ∠CBO =1-1222=722,所以CQ ≥CB sin ∠CBO =722×22=7.18(19·20下·临沂·二模)如图①,在Rt △ABC 中,B 为直角,AB =BC =6,EF ∥BC ,AE =2,沿EF 将△AEF 折起,使∠AEB =π3,得到如图②的几何体,点D 在线段AC 上.(1)求证:平面AEF ⊥平面ABC ;(2)若AE ⎳平面BDF ,求直线AF 与平面BDF 所成角的正弦值.【答案】(1)证明见解析;(2)64.【分析】(1)由余弦定理计算证明EA ⊥AB ,再利用线面垂直的判定、性质,面面垂直的判定推理作答.(2)以A 为原点,建立空间直角坐标系,利用空间向量求线面角的正弦作答.【详解】(1)在△ABE 中,AE =2,BE =4,∠AEB =π3,由余弦定理得:AB 2=AE 2+BE 2-2AE ⋅BE cos ∠AEB =4+16-2×2×4×12=12,则AB =23,有EB 2=EA 2+AB 2,于是∠EAB =π2,即有EA ⊥AB ,又EF ⊥EB ,EF ⊥EA ,EA ∩EB =E ,EA ,EB ⊂平面ABE ,因此EF ⊥平面ABE ,而AB ⊂平面ABE ,则EF ⊥AB ,又因为EA ∩EF =E ,EA ,EF ⊂平面AEF ,从而AB ⊥平面AEF ,而AB ⊂平面ABC ,所以平面AEF ⊥平面ABC .(2)以A 为原点,以AB ,AE 分别为x ,y 轴,过点A 垂直于平面ABE 的直线为z 轴,建立空间直角坐标系,如图,由(1)知,EF ⊥平面ABE ,而EF ⎳BC ,则有BC ⊥平面ABE ,则A (0,0,0),B (23,0,0),E (0,2,0),F (0,2,2),C (23,0,6),AF =(0,2,2),FB =(23,-2,-2),AC=(23,0,6),连接EC 与FB 交于点G ,连接DG ,因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =DG ,则AE ⎳GD ,有GC GE =DCDA,在四边形BCFE 中,由EF ⎳BC ,得GC GE =BC EF =3,即DC DA=3,AD =14AC =32,0,32 ,FD =AD -AF =32,-2,-12,设平面BDF 的法向量为n =(x ,y ,z ),则n ⋅FD =32x -2y -12z =0n ⋅FB =23x -2y -2z =0,令x =1,得n =(1,0,3),设直线AF 与平面BDF 所成角为θ,于是sin θ=|cos ‹n ,AF ›|=|n ⋅AF ||n ||AF |=2322×2=64,所以直线AF 与平面BDF 所成角的正弦值为64.19(22·23下·广州·三模)如图,四棱锥P -ABCD 的底面为正方形,AB =AP =2,PA ⊥平面ABCD ,E ,F 分别是线段PB ,PD 的中点,G 是线段PC 上的一点.(1)求证:平面EFG ⊥平面PAC ;(2)若直线AG 与平面AEF 所成角的正弦值为13,且G 点不是线段PC 的中点,求三棱锥E -ABG 体积.【答案】(1)证明见解析(2)19【分析】(1)由线面垂直判定可证得BD ⊥平面PAC ,由中位线性质知EF ⎳BD ,从而得到EF ⊥平面PAC ,由面面垂直判定可得结论;(2)以A 为坐标原点可建立空间直角坐标系,设PG =λPC ,λ∈0,12 ∪12,1 ,由线面角的向量求法可构造方程求得λ,结合垂直关系可得G 平面PAB 的距离为16BC =13,利用棱锥体积公式可求得结果.【详解】(1)连接BD ,∵E ,F 分别是线段PB ,PD 的中点,∴EF ⎳BD ,∵底面四边形ABCD 为正方形,∴BD ⊥AC ,∵PA ⊥平面ABCD ,BD ⊂平面ABCD ,∴PA ⊥BD ,又PA ∩AC =A ,PA ,AC ⊂平面PAC ,∴BD ⊥平面PAC ,∵EF ⎳BD ,∴EF ⊥平面PAC ,又EF ⊂平面EFG ,∴平面EFG ⊥平面PAC .(2)以A 为坐标原点,分别以AB ,AD ,AP 所在直线为x ,y ,z 轴建立空间直角坐标系,则A 0,0,0 ,E 1,0,1 ,F 0,1,1 ,P 0,0,2 ,C 2,2,0 ,设PG =λPC ,λ∈0,12 ∪12,1 ,则AG =AP +PG =0,0,2 +2λ,2λ,-2λ =2λ,2λ,2-2λ ,AE =1,0,1 ,AF =0,1,1 ,设平面AEF 的一个法向量为n=x ,y ,z ,则n ⋅AE=x +z =0n ⋅AF=y +z =0,令z =-1,解得:x =1,y =1,∴n =1,1,-1 ;设直线AG 与平面AEF 所成角为θ,sin θ=cos n ,AG =n ⋅AGn ⋅AG=6λ-2 3⋅4λ2+4λ2+2-2λ 2=13,解得:λ=16或λ=12(舍),∴PG =16PC ,∵PA ⊥平面ABCD ,BC ⊂平面ABCD ,∴PA ⊥BC ;∵BC ⊥AB ,PA ∩AB =A ,PA ,AB ⊂平面PAB ,∴BC ⊥平面PAB ,∴G 到平面PAB 的距离为16BC =13,∴V E -ABG =V G -ABE =13S △ABE ⋅16BC =13×12×12×2×2×13=19.20(22·23下·长沙·一模)斜三棱柱ABC -A 1B 1C 1的各棱长都为2,∠A 1AB =60°,点A 1在下底面ABC 的投影为AB 的中点O .(1)在棱BB 1(含端点)上是否存在一点D 使A 1D ⊥AC 1若存在,求出BD 的长;若不存在,请说明理由;(2)求点A 1到平面BCC 1B 1的距离.【答案】(1)存在,BD =25(2)2155【分析】(1)连接OC ,以O 点为原点,如图建立空间直角坐标系,设BD =tBB 1 ,t ∈0,1 ,根据AC 1 ⋅A 1D=0,求出t 即可;(2)利用向量法求解即可.【详解】(1)连接OC ,因为AC =BC ,O 为AB 的中点,所以OC ⊥AB ,由题意知A 1O ⊥平面ABC ,又AA 1=2,∠A 1AO =60°,所以A 1O =3,以O 点为原点,如图建立空间直角坐标系,则A 10,0,3 ,A 1,0,0 ,B -1,0,0 ,C 0,3,0 ,由AB =A 1B 1得B 1-2,0,3 ,同理得C 1-1,3,3 ,设BD =tBB 1,t ∈0,1 ,得D -1-t ,0,3t ,又AC 1 =-2,3,3 ,A 1D =-1-t ,0,3t -3 ,由AC 1 ⋅A 1D=0,得-2-1-t +33t -3 =0,得t =15,又BB 1=2,∴BD =25,∴存在点D 且BD =25满足条件;(2)设平面BCC 1B 1的法向量为n=x ,y ,z ,BC =1,3,0 ,CC 1 =-1,0,3 ,则有n ⋅BC=x +3y =0n ⋅CC 1=-x +3z =0,可取n =3,-1,1 ,又BA 1=1,0,3 ,∴点A 1到平面BCC 1B 1的距离为d =BA 1 cos BA 1 ,n =BA 1 ×3+0+3BA 1×5=2155,∴所求距离为2155.21(22·23下·长沙·三模)如图,三棱台ABC -A 1B 1C 1,AB ⊥BC ,AC ⊥BB 1,平面ABB 1A 1⊥平面ABC ,AB =6,BC =4,BB 1=2,AC 1与A 1C 相交于点D ,AE =2EB,且DE ∥平面BCC 1B 1.(1)求三棱锥C -A 1B 1C 1的体积;(2)平面A 1B 1C 与平面ABC 所成角为α,CC 1与平面A 1B 1C 所成角为β,求证:α+β=π4.【答案】(1)2(2)证明见解析【分析】(1)通过证明线线和线面垂直,并结合已知条件即可得出三棱锥C -A 1B 1C 1的体积;(2)建立空间直角坐标系,表达出各点的坐标,求出所成角为α与β的正余弦值,即可证明结论.【详解】(1)由题意,∵平面ABB 1A 1⊥平面ABC ,且平面ABB 1A 1∩平面ABC =AB ,AB ⊥BC ,BC ⊂平面ABC ∴BC ⊥平面ABB 1A 1,∵BB 1⊂平面ABB 1A 1,∴BC ⊥BB 1,又AC ⊥BB 1,BC ∩AC =C ,BC ,AC ⊂平面ABC ∴BB 1⊥平面ABC ,连接C 1B ,∵DE ⎳平面BCC 1B 1,DE ⊂平面ABC 1,平面ABC 1∩平面BCC 1B 1=C 1B ,∴DE ∥C 1B ,∵AE =2EB ,∴AD =2DC 1 ,∴A 1C 1=12AC .∴三棱锥C -A 1B 1C 1底面A 1B 1C 1的面积S 1=12×2×3=3,高h =BB 1=2,。
立体几何测试题(共10篇)

立体几何测试题(共10篇)立体几何测试题(一): 立体几何问题立体几何试题已知正方体ABCD-A1B1C1D1中,E、F分别为D1C1、C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D、B、F、E四点共面;(2)若A1C交平面DBFE于R点,则P、Q、R三点共线.1.EF平行于B1D1,B1D1平行于BD,所以EF平行于BD,EFBD四点共面2.F,D,A,C1属于平面A1ACC1,且AC1与PQ不平行,所以AC1与PQ相交A1C交平面DBFE于R点,又因为PQ属于平面DBFE,所以AC1与PQ相交于R 所以R属于PQ,PQR共线立体几何测试题(二): 几个书后练习题立体几何1.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.是否正确2.如果a、b是两条直线,且a‖b,那么a平行于经过b的任何平面.为什么不对谢不对,因为a有可能在经过b的面上,不是平行关系立体几何测试题(三): 一道数学基本的立体几何的题目~在正方形ABCD-A"B"C"D"中,P、Q分别为A"B"、BB"的中点.(1)求直线AP与CQ所成的角的大小(2)求直线AP与BD所成的角的大小我还没学过空间向量,1.取DC中点E,连EC,证明EC平行AP,用余弦定理算2.取AB中点F,连接FB,用余弦定理算【立体几何测试题】立体几何测试题(四): 求大量立体几何难题!立体几何综合试题(自己画图)1、已知正三棱柱ABC—A1B1C1中,各棱长都相等,D、E分别为AC1,BB1的中点.(1)求证:DE‖平面A1B1C1;(2)求二面角A1—DE—B1的大小.2、已知直三棱柱ABC—A1B1C1,AB=AC,F为棱BB1上一点,BF∶FB1=2∶1,BF =BC=2a.(I)若D为BC的中点,E为AD上不同于A、D的任意一点,证明EF⊥FC1;(II)试问:若AB=2a,在线段AD上的E点能否使EF与平面BB1C1C成60°角,为什么证明你的结论3、在底面是直角梯形的四棱锥中,AD‖BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a.(I)求二面角P—CD—A的正切值;(II)求点A到平面PBC的距离.4、在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.(Ⅰ)确定点G的位置;(Ⅱ)求直线AC1与平面EFG所成角θ的大小.5、已知四棱锥P—ABCD,底面ABCD是菱形,平面ABCD,PD=AD,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值6.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P 在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;(Ⅲ)求点P到平面ABD1的距离.7、在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.(I)证明平面;(II)证明平面EFD;(III)求二面角的大小.8、已知在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.(I)试确定点F的位置,使得D1E⊥平面AB1F;(II)当D 1E⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).9、直四棱柱ABCD-A1B1C1D1的底面是梯形,AB‖CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点.点P到直线AD1的距离为⑴求证:AC‖平面BPQ⑵求二面角B-PQ-D的大小10、已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心.(Ⅰ)证明:AF⊥平面FD1B1;(Ⅱ)求异面直线EB与O1F所成角的余弦值;这些题应该还可以!你来试试吧!题不要求多就精就可以了!不懂的或不会做的,我来帮你解答!立体几何测试题(五): 立体几何初步练习题已知正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱B1C1,C1D1,A1B1,D1A1的中点,求证(1)MN平行于DEF,(2)平面AMN平行于平面CEF(1)连接B1D1因为MN、EF为三角形A1B1D1、B1C1D1的中位线,所以MN平行于EF因为MN不属于面DEF,EF属于面DEF所以MN平行于面DEF(2)这题题目错了吧,应该是DEF吧立体几何测试题(六): 解析几何基础知识练习题靠!一楼的那么多废话那么多选择题:集合,函数(图像),立体几何,圆锥一、数学命题原则 1.普通高等学校招生数学科的考试,按照“考查基础知识的【立体几何测试题】立体几何测试题(七): 高一必修二立体几何习题1-7的题仓库的房顶呈正四棱锥形,量的地面的边长为2.6m,侧棱长2.1m,先要在房顶上铺一层油毡纸,问:需要油毡纸的面积多少运用海伦公式房顶为4个相同的三角形海伦公式a=2.6 b=2.1 c=2.1 p=a+b+c/2=3.4S=根号下p*(p-a)*(p-b)*(p-c)=2.1444S=2.144*4=8.576平方米立体几何测试题(八): 怎么根据题目画数学的立体几何图形搞懂了题目的要求,就照那意思去画,立体几何记住透视很重要.立体几何测试题(九): 求立体几何判断题的解题方法.①过平面外一点有且仅有一个平面与已知平面垂直②过直线外一点有且仅有一个平面与已知直线平行③过直线外一点有且仅有一条直线与已知直线垂直④过平面外一点有且仅有一条直线与已知平面垂直⑤……等等,诸如此类.见到很多这样的题目,但是却总找不到解题的方法,概念定理也经常记混.本人感激不尽!记一些模型,例如墙角模型什么的这个很重要.遇见不熟悉的题,用书本和笔(手指也可以)比划一下.这种题目主要是找反例!想象力也很重要啦……立体几何测试题(十): 一道高中立体几何的题目.已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,O1是底面A1B1C1D1的中心.E 是CO1上的点,设CE等于X,四棱锥E-ABCD的体积为y,求y关于X的函数关系式..图只有自己画一下了,做EF垂直于平面ABCD 垂足为F易得出CEF相似于O1CC1因为C1O1=根号2 CC1=4 得CO1=3根号2CE/CO1=EF/CC1 得出EF=4X/3根号2Y=底面积*EF/3=4*4X/9根号2Y=8根号2*X/9职高立体几何测试题空间立体几何测试题。
空间几何体测试题及答案.doc

空间几何体测试题(满分100分)一、选择题(每小题6分,共54分)1.柯一个几何体的三视阁如下阁所示,这个几何体应是一个(A.棱台B.棱锥C.棱柱D.都不对3. 对于一个底边在X 轴上的三角形,采用斜二测凼法作出观图,其直观图血积是原三角 形面积的()3. 棱长都是1的三棱锥的表凼积为()A. V3B. 2^3C. 3^3D. 4^34. 长方体的一个顶点上三条棱长分别是3,4,5,且仑的8个顶点都在同一球面上,则这个球的表曲'积是()A. 25TTB. 507TC. 125兀D.都不对 5. 正方体的内切球和外接球的半径之比为()A. 73:1B. 73:2C. 2:^3D. ^3:36. 底面是菱形的棱柱其侧棱乘直于底面,且侧棱长为5,它的对角线的K:分别是9和15,则这个棱柱的侧而积是()A. 130B. 140C. 150D. 1607. 已知岡柱与圆锥的底側积相等,高也相等,它们的体积分别为V 和V 2,则()A. 1:3B. 1:1C. 2:1D. 3:18. 如果两个球的体积之比为8:27,那么两个球的表面积之比为() A. 8:27 B. 2:3 C. 4:9 D. 2:99. 圆锥平行于底而的截而而积是底面积的一半,则此截面分圆锥的高为上、卜‘两段的比为 ()A.-1) B. 1:2C. 1: y/2D. 1:4二、填空题(每小题5分,共20分)10. 半径为/?的半圆卷成一个岡锥,则它的体积为 _________ .俯视图A. 2倍主视图 左视图俯视阁12. 己知,ABCD 为等腰梯形,两底边为AB ,CD 且AB 〉CD,绕AB 所在的直线旋转一周所 13. H •:方体—屮,0是上底面中心,若正方体的棱为《,则三棱锥O - AB,D X 的体积为 ______________三、解答题(每小题13分,共26分)14. 将圆心角为120(),而积为3兀的扇形,作为圆锥的侧而,求圆锥的表而积和体积15. (如阳在欣半径为2,时线长为4的圆锥中内接一个高为人的圆柱, 求岡柱农面积。
空间立体几何测试题8套

立体几何测试1一、选择题1、点P在直线a上,直线a在平面a内可记为()A、P€ a, a a B P a, a a C P a, a€ a D P€ a, a€a2、直线l是平面a外的一条直线,下列条件中可推出I //a的是()A、I与a内的一条直线不相交 B 、丨与a内的两条直线不相交C、I与a内的无数条直线不相交 D 、I与a内的任意一条直线不相交3、空间四点A B、C、D共面,但不共线,则下面结论成立的是()A、四点中必有三点共线B、四点中必有三点不共线C、直线AB与CD必相交D AB// CD或BC// DA4、已知正方形ABCD中, S是所在平面外一点,连接SA, SB SC SD AC BD在所有的10条直线中,其中异面直线共有()A、8 对B、10 对C 12 对D 、16 对5、在空间中,I , m n , a , b表示直线,a表示平面,则下列命题正确的是()A、若I / a , mL I ,贝U mL aB、若I 丄m mL n ,贝U m/ nC、若a 丄a, a 丄b,贝U b//aD、若I 丄a, I // a,贝U a丄a6、在四面体ABCD中, AB=BC=CD=DA=AC=BD, F分别为AB, CD的中点,贝U EF与AC所成角为()A、90°B、60°C、45° D 30°7、在长方体ABCD-A'B'C'D'中,/ AB'B=45°,Z CB'C'=60°,则/ AB'C 的余弦值为()B& A,B,C,D四点不共面,且A,B,C,D到平面a的距离相等,则这样的平面有()A、1个B、4个C、7个D、无数个、填空题9、在空间四边形ABCD中, E, H分别是ABAD的中点,F,G为CB CD上的点,且CF: CB=CG CD=2:3,2若BD=6cm梯形EFGH勺面积28cm,贝U EH与FG间的距离为____________________ 。
《空间几何体》基础达标测试(有详细答案)
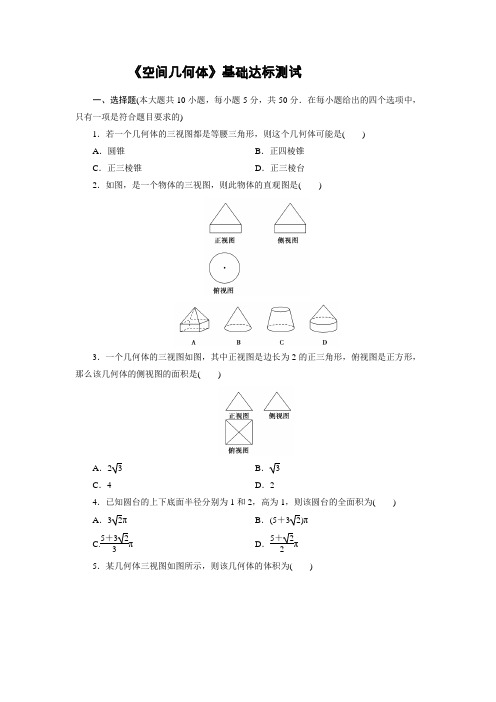
《空间几何体》基础达标测试一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是( ) A .圆锥 B .正四棱锥 C .正三棱锥D .正三棱台2.如图,是一个物体的三视图,则此物体的直观图是( )3.一个几何体的三视图如图,其中正视图是边长为2的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是( )A .23B .3C .4D .24.已知圆台的上下底面半径分别为1和2,高为1,则该圆台的全面积为( ) A .32π B .(5+32)π C.5+323πD .5+22π5.某几何体三视图如图所示,则该几何体的体积为( )A.13+2π B .13π6C.7π3D .5π26.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( ) A .120° B .150° C .180°D .240°7.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18 B .17C.16D .158.一个圆台的上、下底面面积分别为1,49,一个平行于底面的截面面积为25,则这个截面与上、下两个底面的距离之比为( )A .2∶1B .3∶1 C.2∶1D .3∶19.长方体ABCD -A 1B 1C 1D 1的三条棱长分别是AA 1=1,AB =2,AD =4,则从A 点出发,沿长方体的表面到C 1的最短距离是( )A .5B .7 C.29D.3710.如图所示,在三棱柱ABC -A 1B 1C 1中,侧棱垂直于底面,AB =AC =13,BB 1=BC =6,E ,F 为侧棱AA 1上的两点,且EF =3,则多面体BB 1C 1CEF 的体积为( )A.30 B.18C.15 D.12二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)11.底面直径和高都是4 cm的圆柱的侧面面积为______ cm2.12.如果圆锥的侧面展开图是半圆,那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是________.13.一个棱锥的三视图如图,则该棱锥的全面积为______________cm2.14.一个底面直径是32 cm的圆柱形水桶装入一些水,将一个球放入桶内完全淹没,水面上升了9 cm,则这个球的表面积是________ cm2.三、解答题(本大题共2小题,共20分.解答应写出文字说明、证明过程或演算步骤)15.(本小题12分)如图所示,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所形成几何体的表面积和体积.16.(本小题满分18分)如图,如果一个几何体的正视图与侧视图都是全等的长方形,边长分别是4 cm与2 cm,俯视图是一个边长为4 cm的正方形.(1)求该几何体的全面积;(2)求该几何体的外接球的体积.详细参考答案:一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.解析:圆锥的俯视图是一个圆,正四棱锥的俯视图是正方形和它的两条对角线,三棱台的正视图与侧视图是梯形,故只有C 正确.答案:C2.解析:由三视图知几何体为圆锥与圆柱的组合体如图.故选D.答案:D3.解析:由题意可知侧视图与正视图形状完全一样,是正三角形,面积S =34×22= 3. 答案:B4.解析:由已知可求得,圆台的母线长为2,∴圆台的全面积为π×(12+22)+π·2×(1+2)=(5+32)π.故选B. 答案:B5.解析:由三视图可知:原几何体左侧是半圆锥,右侧是圆柱,∴V =V 半圆锥+V 圆柱=12×13·π(1)2×1+π(1)2×1=136π. 答案:B6.解析:设圆锥底面半径为r ,母线为l ,则πrl +πr 2=3πr 2,得l =2r ,∴展开图扇形半径为2r ,弧长为2πr .∴展开图是半圆.∴扇形的圆心角为180°.故选C. 答案:C7.解析:如图所示,在正方体ABCD -A 1B 1C 1D 1中,截掉三棱锥A 1-AB 1D 1.设正方体的棱长为a ,则VA 1-AB 1D 1=13×12a 3=16a 3,故剩余几何体的体积为a 3-16a 3=56a 3,所以比值为15,故选D.答案:D8.解析:如图,设上底面、下底面、平行平面的半径分别为r ,R ,r 0,从圆台轴截面计算,还原为圆锥, 则有r R =17,r r 0=15,所以SO 1SO 2=15,SO 1SO =17.所以SO 1O 1O 2=14,SO 1O 2O =12.所以O 1O 2O 2O =21.答案:A9.解析:两点之间线段最短,在长方体展开图中,由A 到C 1的路线有三条,如下图,三条路线长分别为l 1=12+(2+4)2=37,l 2=42+(1+2)2=5, l 3=22+(1+4)2=29.所以最短距离为5. 答案:A10.解析:VBB 1C 1CEF =VABC -A 1B 1C 1-VF -A 1B 1C 1-V E -ABC =S △ABC ·6-13S △ABC ·A 1F -13S △ABC ·AE=S △ABC ·⎣⎡⎦⎤6-13(A 1F +AE )=5S △ABC , ∵AC =AB =13,BC =6, ∴S △ABC =12×6×(13)2-32=6.所以VBB 1C 1CEF =5×6=30. 答案:A二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 11.解析:圆柱的底面半径为r =12×4=2 cm ,故S 侧=2π·2×4=16π cm 2. 答案:16π12.解析:如图,∵半圆弧长为πl ,圆锥的底面圆周长为2πr ,∴πl =2πr .∴r =12l .∴在Rt △PBO 中,∠BPO =30°.∴∠APB =60°. 答案:60°13.解析:如图所示三棱锥.AO ⊥底面BCD ,O 是BD 中点,BC =CD =6,BC ⊥CD ,AO =4,AB =AD . S △BCD =12×6×6=18,S △ABD =12×62×4=12 2.取BC 中点E ,连接AE ,OE . 可得BC ⊥AE ,AE =AO 2+OE 2=5,∴S △ABC =S △ACD =12×6×5=15.∴S 全=18+122+15+15=48+12 2. 答案:48+12 214.解析:球的体积等于底面半径为16 cm ,高为9 cm 的圆柱的体积,设球的半径为R cm ,所以43πR 3=π·162×9,解得R =12.所以S 球=4πR 2=576π cm 2. 答案:576π三、解答题(本大题共2小题,共30分.解答应写出文字说明、证明过程或演算步骤) 15.解:S 表面=S 圆台底面+S 圆台侧面+S 圆锥侧面 =π·52+π·(2+5)×5+π·2×22=60π+42π. V =V 圆台-V 圆锥=13π(r 21+r 1r 2+r 22)h 圆台-13πr 21h 圆锥=1483π. 16. 解:(1)由题意可知,该几何体是长方体, 底面是正方形,边长是4 cm ,高是2 cm ,因此该几何体的全面积是2×4×4+4×4×2=64 (cm 2),即该几何体的全面积是64 cm 2.(2)由长方体与球的性质可得,长方体的体对角线是其外接球的直径,设长方体的体对角线为d cm ,外接球的半径为r cm ,则d =16+16+4=36=6 (cm),所以外接球的半径为r =3 (cm).所以外接球的体积V =43πr 3=43×27π=36π(cm 3).。
空间几何体练习试题及参考含答案

空间几何体部分1、假如一个水平搁置的图形的斜二测直观图是一个底面为45o,腰和上底均为1的等腰梯形,那么原平面图形的面积是()A. 2 2B. 1 2C. 2 2D. 1 22 22、半径为 R的半圆卷成一个圆锥,则它的体积为()A. 3 R3B. 3 R3C. 5 R3D. 5 R324 8 24 83、一个棱柱是正四棱柱的条件是A 、底面是正方形,有两个侧面是矩形B 、底面是正方形,有两个侧面垂直于底面C、底面是菱形,且有一个极点处的三条棱两两垂直D、每个侧面都是全等矩形的四棱柱4.有一个几何体的三视图以下列图所示,这个几何体应是一个A、棱台 B 、棱锥 C 、棱柱 D 、都不对5.在棱长为 1 的正方体上,分别用过共极点的三条棱中点的平面截该正方形,则截去8 个三棱锥后,剩下的几何体的体积是()A. 2B. 7C. 4D. 53 6 5 66.长方体的一个极点上三条棱长分别是 3、4、5,且它的 8 个极点都在同一球面上,则这个球的表面积是A、25 B 、 50 C 、125 D、都不对7. 正方体的内切球和外接球的半径之比为()A. 3 :1B. 3 : 2C. 2 : 3D. 3 : 3o8. 在△ ABC中,AB=2,BC=,∠ABC=120, 若使绕直线 BC旋转一周,则所形成的几何体的体积是A. 9B. 7C. 5D. 322 2 29、圆台的一个底面周长是另一个底面周长的 3 倍,母线长C 为 3,圆台的侧面积为84,则圆台较小底面的半径为A、7 B 、6 C、5 D、310. 直三棱柱 ABC—A1B1C1的体积为 V,点 P、Q分别在V侧棱 AA 和 CC上, AP=CQ,则四棱锥 B—APQC的体积 ED1 1 1FA CPB为A 、VB 、 VC 、 VD 、V234511、如图,在多面体 ABCDEF 中, 已知平面 ABCD 是边长为 3 的正方形 ,EF ∥AB, EF 3 ,且 EF 与平面 的距离为 2, 则该多面体的体2 ABCD积为 ( )A 、9、5 C 、6 D 、152212、如右图所示,正三棱锥V-ABC中,D,E,F分别是 VC ,VA,AC 的中点,P为VB上随意一点,则直线DE与P F 所成的角的大小是()ABCD 随P点的变化而623变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.相交的两直线都是平面 的斜线,那么这两斜线在平面 的设影是( (A)同一直线 (C)两条平行直线 (B)相交的两直线 (D)一直线或两相交直线
6.若三个平面把空间分成6个部分,那么这三个平面的位置关系是( (A)三个平面共线 (B)有两个平面平行且都与第三个平面相交 (C)三个平面共线或两个平面平行且都与第三个平面相交 (D)三个平面两两相交
7
德圣数学 培优拔高 决战高考
立体几何专项练习二 参考答案
一、选择题 1.D 7.C 2.C 8.D 3.C 9.B 4.B 10.C 5.D 11.D 6.D 12.D
二、填空题 13.(1)90º (2)45º (3)60º (4)90º 14.(1)30º (2)45º (3)90º (4)60º 15.arccos
三、解答题(共 45 分,14、14、17) 12、已知正方体 ABCD-A`B`C`D`中,E,F 分别是 A`B`,B`C`的中点。 求证:EF∥面 AD`C。 证明:连 A`C`,由 E,F 分别为 A`B`,B`C`的中点 则 EF∥A`C`, 又∵A`C`∥AC, ∴EF∥AC ∵AC 面 AD`C ∴EF∥面 AD`C A D B C A` D` F E B` C`
}
CE ⊥ PAM
面
A O D F N C
H
3
德圣数学 培优拔高 决战高考
AB 2 5 CM = AM 5
∴CE=
∴C 到平面 PAM 的距离为
2 5 5
连 AC 交 BD 于 O,交 MN 于 F,连 PF,过 O 作 OH⊥PF ∵M,N 为 BC,CD 中点, ∴MN∥BD ∴BD∥平面 PMN, ∴O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。 ∵BD⊥AC,MN∥BD ∴MN⊥AC, ∴MN⊥平面 PAC ∴MN⊥OH ∵OH⊥PF ∵PA=2,AC=2 2 ,AF= ∵PA⊥面 ABCD ∴PA⊥MN
7.在正方体 ABCD-A1B1C1D1 中,12 条棱互成异面直线的对数有 (A) 48 对 (B) 36 对 (C) 24 对 (D) 12 对
5
德圣数学 培优拔高 决战高考
8.分别平行于两条异面直线的两条直线的位置关系是 (A) 异面直线 (C) 相交直线 9.若θ 是两条异面直线所成的角,则 (A) (0, ] (C) [0, (B) (0, (D) (0, (B) 平行直线 (D) 异面直线或相交直线 ( ) ( )
D A B
C
13、已知 PA⊥正方形 ABCD,PA=AB=2,M,N 为 BC,CD 中点, ⑴求 C 到面 PAM 的距离,⑵求 BD 到面 PMN 的距离。 P
A B O M
H F N C
D
2
德圣数学 培优拔高 决战高考
立体几何专项练习一 参考答案 一、选择题 ADBCDCDC 二、填空题(每小题 5 分,共 15 分) 9、 在空间四边形 ABCD 中, E, H 分别是 AB, AD 的中点, F, G 为 CB, CD 上的点, 且 CF∶CB=CG∶CD=2∶3, 若 BD=6cm,梯形 EFGH 的面积 28cm ,则 EH 与 FG 间的距离为
(
)
(
)
(C) 一条直线和两条平行直线中的任何一条直线无公共点,那么这三条直线互相平行 (D) 一条直线和两条平行直线中的一条直线是异面直线,且与另一条直线无公共点,则必与另一条 直线也是异面直线 6.和两条异面直线都相交的两条直线是 (A) 平行直线 (B) 异面直线 (C) 相交直线(D) 异面直线或相交直线 ( ) ( )
2
]
2
]
2
)
10.已知 a 和 b 是成 60 º角的两条异面直线,则过空间一点且与 a、 b 都成 60º角的直线共有 ( ) (B) 2 条 (C) 3 条 (D) 4 条
(A) 1 条
11.在正方体 ABCD-A 1 B (A) 1 条
1 C 1 D 1 的所有面对角线中,与
AB
1 成异面直线且与
2.直线a和平面 都与同一直线平行,那么直线a和平面 的位置关系是( (A) 平行 (B)线在面内 (C)线在面内或平行 (D)线面相交 )。
3.直线L//平面 , ,那么L和平面 的位置关系是(
(A) 线在面内 (B)平行 (C)相交 (D) (A),(B),(C)中的情况都有可能 4.若a,b是两条平行直线,且都不垂直与平面 ,那么a,b在平面 内的射影为( (A)两条平行线 (C)两条平行线或同一直线 (B)相交的两直线 (D)相交的两直线或同一直线 )。 )。
2
。
10 、三个平面 α , β , γ 将空间分成七部分,且 α ∩ β =a , β ∩ γ =b ,则 a 与 b 的位置关系 为 。
11、a,b 为异面直线,且 a,b 所成角为 40°,直线 c 与 a,b 均异面,且所成角均为 θ ,若这样的 c
1
德圣数学 培优拔高 决战高考
共有四条,则 θ 的范围为 三、解答题 12、已知正方体 ABCD-A`B`C`D`中,E,F 分别是 A`B`,B`C`的中点。 求证:EF∥面 AD`C。 A` D` E B` F C` 。
3.已知 a、b、c 均是直线,则下列命题中,必成立的是 (A) 若 a⊥b,b⊥c,则 a⊥c (B) 若 a 与 b 相交,b 与 c 相交,则 a 与 c 也相交 (C) 若 a//b,b//c,则 a//c (D) 若 a 与 b 异面,b 与 c 异面,则 a 与 c 也是异面直线 4.已知异面直线 a、b 分别在平面α 、β 内,且α ∩β =c,那么直线 c (A) 一定与 a、b 交于同一点 (B) 至少与 a、b 中的一条相交 (C) 至多与 a、b 中的一条相交 (D) 一定与 a、b 中的一条平行,而与另一条相交 5.下列命题中,正确的是 (A) 一条直线和两条平行直线中的一条直线相交,则必与另一条直线相交 (B) 一条直线和两条平行直线中的一条直线能确定一个平面
)。
7.有下面几个问题:(1)若a//平面 ,b a,则平面 b.(2)若a//平面 ,平面 平面 , 则a 平面 .(3)若a,b是两平行线, b 平面 ,则a// .(4)若平面 平面 , 平面 平面 ,则平 面 //平面 。其中不正确的命题个数是( (A) 4 (B) 3 (C) 2 )。
(B)
60, d 90, d
2 a 2 2 a 2
(C) 90 , d 二、填空题
(D)
13.在正方体 ABCD-A 1 B (1) A 1 A 和 B (2) A 1 C
1和
1 C 1 D 1 中,下列两直线成角的大小是:
1 C 1 成角_________.A 1 C 1 和
AB 成角__________. BD 成角__________.
D
1C
成角_________.A 1 C
1和
14.在长方体 ABCD- A 1 B 1 C 1 D 1 中,∠BAB 1 =∠B 1 A 1 C 1 =30º,则 (1) AB 与 A 1 C 1 成角________.AA 1 与 B 1 C 成角_______. (2) AD 1 与 B 1 C 成角_________.AB 1 与 D 1 C 成角________. 15.在正方体 ABCD-A 1 B 1 C 1 D 1 中,E、F 分别为棱 AB、CC 1 的中点,则异面直线 EF 与 A 1 C 所成角的大 小是_______________.
13、已知 PA⊥正方形 ABCD,PA=AB=2,M,N 为 BC,CD 中点, ⑴求 C 到面 PAM 的距离,⑵求 BD 到面 PMN 的距离。 解:延长 AM,作 CE⊥AM 于 E ∵PA⊥正方形 ABCD, ∴PA⊥CE ∵CE⊥AM ∵AB=2,BM=1,CM=1 ∴AM= 5 , B M P
3 6
B、
2 6
C、
6 3
D、
6 4
)
8、A,B,C,D 四点不共面,且 A,B,C,D 到平面 α 的距离相等,则这样的平面有( A、1 个 B、4 个 C、7 个 D、无数个
二、填空题 9、 在空间四边形 ABCD 中, E, H 分别是 AB, AD 的中点, F, G 为 CB, CD 上的点, 且 CF∶CB=CG∶CD=2∶3, 若 BD=6cm,梯形 EFGH 的面积 28cm ,则 EH 与 FG 间的距离为
德圣数学 培优拔高 决战高考
2013 高考立体几何专项练习 立体几何专项练习一 一、选择题 1、点 P 在直线 a 上,直线 a 在平面 α 内可记为( A、P∈a,a α B、P a,a α ) D、P∈a,a∈α )
C、P a,a∈α
2、直线 l 是平面 α 外的一条直线,下列条件中可推出 l∥α 的是( A、l 与 α 内的一条直线不相交 C、l 与 α 内的无数条直线不相交 B、l 与 α 内的两条直线不相交
AB 1 成 60º的有 (
)
(B) 2 条
(C) 3 条
(D) 4 条
12.已知点 A 是△BCD 所在平面外的一点,且△ABC,△ACD,△BCD 均是边长为 a 的正三角形,若记 异面直线 AD,BC 间的成角为θ ,距离为 d,则 (A) 60 , d ( )
1 a 2 1 a 2
5、在空间中,l,m,n,a,b 表示直线,α 表示平面,则下列命题正确的是( A、若 l∥α ,m⊥l,则 m⊥α C、若 a⊥α ,a⊥b,则 b∥α B、若 l⊥m,m⊥n,则 m∥n D、若 l⊥α ,l∥a,则 a⊥α
6、在四面体 ABCD 中,AB=BC=CD=DA=AC=BD,E,F 分别为 AB,CD 的中点,则 EF 与 AC 所成角为( ) A、90°B、60°C、45°D、30° 7、在长方体 ABCD-A`B`C`D`中,∠AB`B=45°,∠CB`C`=60°,则∠AB`C 的余弦值为( A、 )
