2015届高三第一次月考分析

合集下载

2015届高三第一次月考试卷及答案

2015届高三政治月考试题及答案第I卷选择题（共48分）一、选择题（本大题共12小题，每小题4分，共48分）1.2013年，A国甲企业生产M商品的劳动生产率处于全国平均水平，M商品的价值量用货币表示为96元，甲企业的年产量为10万件， A国与B国的汇率比为1：8。

进入2014年，甲企业生产M商品的劳动生产率提高25%，M商品的社会劳动生产率提高20%，同时B国货币对A国货币贬值20%，不考虑其他因素，则2014年甲企业生产M商品的价值总量用B国货币单位表示为：（）A.12500万元B.9600万元C.8000万元D.10000万元.2.下图反映，价格的变动会对商品的需求量产生一定的影响。

在一般条件下，能表示汽车的价格和需求量关系的曲线是：（）A.曲线aB.曲线bC.曲线cD.曲线d3.经济生活是复杂的，同一现象或措施，有时会产生截然不同的两种效果。

下列表述中，正确体现了经济生活中“双刃剑”（一分为二）现象的是：（）A.国家财政集中的财富多，必然会减少企业和个人的收入B.合理的收入差距有利于调动人们的积极性，但违背了公平原则C.纸币发行量过多易引起通货膨胀，纸币发行不足可能导致通货紧缩D.劳动力价格上升导致企业的成本增加，但迫使企业转变经济发展方式4.“闪付”（QuickPass)作为一种消费新时尚，是针对单笔金额不超过1000元的消费，无需输入密码和签名，只需要在POS机上轻松一挥便可快速支付的方式。

它满足了人们对快捷、高效支付的需求,有利于刺激消费，更好地满足百姓生活所需。

这说明：（）A.“闪付”是一种钱货两清的消费B.收入水平影响人们的购买能力C.“闪付”是一种非信用消费方式D.新的消费方式可以创造消费动力5.2013年12月4日，工信部向中国移动、联通、电信三大电信运营商发放了4 G牌照，在 4G时代，边逛街边下单或将成为年轻一代的主流消费方式。

这表明：（）A.消费方式决定生产方式B.生产决定消费C.消费热点引导生产D.消费是生产的动力6.2014年3月27日，上港集团作为上海国有资产改革试点的代表，宣布向国际资本和民营企业在内的投资者开放，吸引战略投资者。

【名师解析】重庆市重庆一中2015届高三上学期第一次月考物理试题 Word版含解析

【名师解析】重庆市重庆一中2015届高三上学期第一次月考物理试题Word版含解析卷2014.9说明：①选择题答案按题号用2B铅笔填涂在机读卡上②非选择题按要求答写在答题卷指定位置处一、选择题（本题共5小题，每小题6分, 共30分，每小题只有一个选项符合题目要求）14、在物理学发展史上，伽利略、牛顿等许许多多科学家为物理学的发展做出了巨大贡献。

以下选项中符合伽利略和牛顿的观点的是()A．两物体从同一高度做自由落体运动，较轻的物体下落较慢B．两匹马拉车比一匹马拉车跑得快，这说明：物体受的力越大则速度就越大C．人在沿直线加速前进的车厢内，竖直向上跳起后，将落在起跳点的后方D．一个运动的物体，如果不再受力了，它总会逐渐停下来，这说明：静止状态才是物体不受力时的“自然状态”【知识点】物理学史．【答案解析】C 解析：A、伽利略、牛顿认为重物与轻物下落一样快，所以此选项不符合他们的观点．故A错误．B、力越大，物体运动的速度越大，不是伽利略、牛顿的观点．故B错误．C、人在沿直线加速前进的车厢内，竖直向上跳起后，人保持起跳时车子的速度，水平速度将车子的速度，所以将落在起跳点的后方．符合伽利略、牛顿的惯性理论．故C正确．D、此选项说明力是维持物体运动的原因，是亚里士多德的观点，不是伽利略、牛顿的观点．故D错误．故选C【思路点拨】人在沿直线加速前进的车厢内，竖直向上跳起后，将落在起跳点的后方，符合伽利略、牛顿的惯性理论．两匹马拉车比一匹马拉车跑得快，这说明：物体受的力越大速度就越大，不符合伽利略、牛顿的观点．伽利略、牛顿认为重物与轻物下落一样快、力不是维持物体运动的原因．根据伽利略、牛顿的观点判断选项的正误．本题要对亚里士多德的观点和伽利略、牛顿的观点关于力和运动关系的观点有了解．可以根据牛顿的三大定律进行分析．【题文】15、如题15图所示，竖直放置的轻弹簧一端固定在地面上，另一端与斜面体P连接，P与斜放的固定挡板MN接触且处于静止状态，则（）A．斜面体P此刻所受到的外力个数有可能为2个B．斜面体P此刻所受到的外力个数有可能为3个C．若迅速撤去挡板MN后瞬间，斜面体P可能有斜向左上的加速度D．若迅速撤去挡板MN后瞬间，斜面体P可能有竖直向下的加速度【知识点】物体的弹性和弹力．牛顿第二定律B2 C2【答案解析】A 解析：A、B对物体受分析如图：如果：（1）N=G的话，物体受力可以平衡，故P可能受2个力的作用．（2）N＜G的话，P不可能平衡（3）如果：N＞G，物体会受到挡板MN的弹力F和摩擦力f，受力分析如图：故P可能受4个力的作用．综上所述：P可能的受力个数是2个或4个，故A正确、B错误；C、D撤去MN，则物体受合力可能向上，也可能为零，故如果有加速度，则加速度向上，故C、D错误；故选A【思路点拨】P静止，所以受力是平衡的，我们可以根据平衡条件来判断弹力和摩擦力的有无．判断物体的受力个数其实就是判断相互接触的物体间有无弹力或摩擦力的作用，处理时根据平衡条件进行判断即可．撤去MN，由牛顿第二定律求得加速度。

山东省枣庄三中2015届高三第一次学情调查(月考)数学(文)试题 Word版含解析

枣庄三中2015届高三第一次学情调查数学试题（文科）2014.10第Ⅰ卷（共50分）【题文】一、选择题：(本题共10个小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)山东省中学联盟网【题文】1．设集合{}1,2,3A =，{}4,5B =，{},,C x x b a a A b B ==-∈∈，则C 中元素的个数是( ) A ．3 B ．4 C ．5 D ． 6【知识点】集合及其运算A1【答案解析】B A={1，2，3}，B={4，5}，∵a ∈A ，b ∈B ，∴a=1，或a=2或a=3，b=4或b=5，则x=b-a=3，2，1，4，即B={3，2，1，4}．故选B ．【思路点拨】根据集合C 的元素关系确定集合C 即可．【题文】2．已知函数e ,0,()ln ,0,x x f x x x ⎧<=⎨>⎩则1[()]e f f =( )A ．1eB ．e -C ．eD ．1e -【知识点】指数函数对数函数B6 B7 【答案解析】A 因为1e >0,则f(1e )=-1<0,所以f(-1)= 1e -=1e故选A 【思路点拨】先确定x 的范围，是否符合函数关系再去求。

【题文】3．下列命题中，真命题是( ) A ．存在,e 0x x ∈≤R B ．1,1a b >>是1ab >的充分条件 C ．任意2,2x x x ∈>RD ．0a b +=的充要条件是1ab =-【知识点】命题及其关系、充分条件、必要条件A2【答案解析】B 对于A ，∵e x 0＞0恒成立，∴不存在x 0∈R ，使得e x 0≤0，即A 错误；对于C ，∃x=2，使得22=22，不满足2x ＞x 2，∴C 错误；对于B ，∵a ＞1＞0，b ＞1＞0， ∴ab ＞1，即a ＞1，b ＞1是ab ＞1的充分条件，故B 正确；对于D ，令a=b=0，不能推出ba=-1，即充分性不成立，故D 错误．综上所述，上述四个命题中是真命题的只有B ．故选B ．【思路点拨】对于A ，e x 0＞0恒成立，故可判断该选项的正误；对于B ，利用充分条件的概念可作出正误的判断；对于B ，利用充分条件的概念可作出正误的判断；对于C ，∃x=2，不满足2x ＞x 2，从而可知其正误；对于D ，可令a=b=0，作出其正误的判断．【题文】4. 下列函数中，在其定义域内既是奇函数又是减函数的是（）A.1y x =B. 1()2x y = C. y x = D.3y x =- 【知识点】函数的单调性函数的奇偶性B3 B4【答案解析】D 对于A ，是幂函数，在其定义域内既是奇函数，但不是减函数；对于B ，是指数函数，在其定义域内是减函数，但不是奇函数对于C ，是一次函数，在其定义域内是奇函数且是增函数；对于D ，是幂函数，在其定义域内既是奇函数又是减函数；综上知，D 满足题意,故选D ．【思路点拨】对于A ，是幂函数，在其定义域内既是奇函数，但不是奇函数；对于B ，是指数函数，在其定义域内是减函数，但不是奇函数．故可得结论对于C ，是一次函数，在其定义域内是奇函数且是增函数；对于D ，是幂函数，在其定义域内既是奇函数又是减函数；．【题文】5．若函数b bx x x f 33)(3+-=在()1,0内有极小值，则（）A. 0>bB. 1<bC.10<<bD. 21<b【知识点】导数的应用B12【答案解析】C 由题意得f′（x ）=3x 2-3b ，令f′（x ）=0，则x=±b又∵函数f （x ）=x 3-3bx+b 在区间（0，1）内有极小值，∴0＜b ＜1，∴b ∈（0，1），故答案为C ．【思路点拨】首先求出函数的导数，然后令导数为零，求出函数的极值，最后确定b 的范围．【题文】6.已知(),()f x g x 分别是定义在R 上的偶函数和奇函数，且32()()1f x g x x x -=++，则(1)(1)f g += ( )A ．－3B ．－1C ． 1D ．3 【知识点】函数的奇偶性与周期性B4【答案解析】C 由f （x ）-g （x ）=x 3+x 2+1，将所有x 替换成-x ，得f （-x ）-g （-x ）=-x 3+x 2+1，∵f （x ），g （x ）分别是定义在R 上的偶函数和奇函数，∴f （x ）=f （-x ），g （-x ）=-g （x ），即f （x ）+g （x ）=-x 3+x 2+1，再令x=1，得f （1）+g （1）=1．故答案为C ．【思路点拨】将原代数式中的x 替换成-x ，再结合着f （x ）和g （x ）的奇偶性可得f （x ）+g （x ），再令x=1即可．【题文】7.已知命题[]2:1,2,0,p x x a ∀∈-≥命题:,q x R ∃∈使2220x ax a ++-=，若命题“p 且q ”为真，则实数a 的取值范围是 ( )A ．}{|211a a a -<<>或 B ．}{|1a a ≥C ．}{|21a a -≤≤D ．}{|21a a a ≤-=或【知识点】命题及其关系A2【答案解析】D 命题p ：“∀x ∈[1，2]，x 2-a≥0”，a≤1；命题q ：“∃x ∈R”，使“x 2+2ax+2-a=0”，所以△=4a 2-4（2-a ）≥0，所以a≥1或a≤-2；命题P 且q 为真命题，两个都是真命题，11a 2a a ≤⎧⎨≥≤-⎩或当两个命题都是真命题时，解得{a|a≤-2或a=1}．所以所求a 的范围是{a|a≤-2且a=1}．故选D ．【思路点拨】求出命题p 与q 成立时，a 的范围，然后推出命题P 且q 是假命题的条件，推出结果．【题文】8. 已若当x ∈R 时，函数0()(||>=a a x f x 且1≠a ）满足)(x f ≤1，则函数)1(log +=x y a 的图像大致为( )【知识点】对数与对数函数B7【答案解析】C ∵函数f （x ）=a |x|（a ＞0且a≠1）满足f （x ）≤1，∴由|x|≥0，可得a |x|≤a 0=1，∴0＜a ＜1．故函数y=log a （x+1）在定义域（-1，+∞）上是减函数，且函数图象经过点（0，0），结合所给的选项，只有C 满足条件，故选C ．【思路点拨】由条件可得 0＜a ＜1，可得函数y=log a （x+1）在（-1，+∞）上是减函数，且函数图象经过点（0，0），结合所给的选项，得出结论．【题文】9．定义运算a b ad bc cd=-，若函数()123x f x xx -=-+在(,)m -∞上单调递减，则实数m 的取值范围是 A ．(2,)-+∞B ．[2,)-+∞C ．(,2)-∞-D ． (,2]-∞-【知识点】选修4-2 矩阵N2【答案解析】D 由题意可得函数()123x f x xx -=-+=（x-1）（x+3）-2（-x ）=x 2+4x-3的对称轴为x=-2，且函数f （x ）在（-∞，m ）上单调递减，故有m≤-2，故答案为D【思路点拨】由题意求函数的解析式，再根据二次函数的对称轴与区间端点m 的大小关系求得m 的范围．【题文】10.[]x 表示不超过x 的最大整数，例如[2.9]＝2，[－4.1]＝－5，已知[]()()f x x x x R =-∈，4()log (1)g x x =-，则函数()()()h x f x g x =-的零点个数是( )A ．2B ．3C ．4D ．5 【知识点】函数与方程B9 【答案解析】A 当0＜x ＜1时，[x]=0，则f （x ）=x-[x]=x ，当1≤x ＜2时，[x]=1，则f （x ）=x-[x]=x-1，当2≤x ＜3时，[x]=2，则f （x ）=x-[x]=x-2，当3≤x ＜4时，[x]=3，则f （x ）=x-[x]=x-3，当4≤x ＜5时，[x]=4，则f （x ）=x-[x]=x-4，当5≤x ＜6时，[x]=5，则f （x ）=x-[x]=x-5，此时f （x ）∈[0，1），而g （x ）log 4（x-1）≥1，即当n≤x ＜n+1，n≥6时，[x]=n ，则f （x ）=x-[x]=x-n ∈[0，1），而g （x ）log 4（x-1）≥1，由h （x ）=f （x ）-g （x ）=0得f （x ）=g （x ），分别作出函数f （x ）和g （x ）的图象如图：则两个函数图象有2个交点，故函数零点的个数为2个，故选A【思路点拨】由f （x+2）=f （x ），得到函数的周期是2，作出函数f （x ）和g （x ）的图象，利用数形结合即可得到结论．第Ⅱ卷（共100分）【题文】二、填空题：（本大题共5小题，每小题5分，共25分.请把答案填在答题纸的相应的横线上）.【题文】11．已知正实数11,,25,2aba b m m a b ==+=满足且,则m 的值为【知识点】对数与对数函数B7【答案解析】10 ∵正实数a ，b ，m ，满足2a =5b =m ，∴alg2=blg5=lgm ＞0，∴1a = lg 2lg m ，1b = lg 5lg m ．∴2= 11a b +=lg 2lg m +lg 5lg m =l lg m， ∴lgm=12，∴m=10．故答案为10．【思路点拨】正实数a ，b ，m ，满足2a =5b =m ，可得alg2=blg5=lgm ＞0，即可得出1a ，1b．【题文】12．163x y =-函数的值域是【知识点】函数及其表示B1【答案解析】[0，4） ∵3x ＞0，∴16-3x ＜16，∴0≤163x-＜4．故答案为 [0，4）【思路点拨】首先由指数函数的值域可得，3x 恒大于0，再用观察分析法求值域即可．【题文】13. 函数()(1)xf x x e =-⋅的单调递减区间 . 【知识点】函数的单调性与最值B3 【答案解析】（0，+∞） f′（x ）=[（1-x ）•e x ]′=-e x +（1-x ）•e x =-xe x ，令f′（x ）＜0得x ＞0，∴函数f （x ）的单调递减区间为（0，+∞）．故答案为（0，+∞）．【思路点拨】求导，令导数小于0，得x 的取值区间，即为f （x ）的单调减区间．【题文】14.已知函数()f x 是(,)-∞+∞上的奇函数,且()f x 的图象关于直线1x =对称,当[1,0]x ∈-时,()f x x =-，则(2013)(2014)f f += .【知识点】函数的奇偶性与周期性B4【答案解析】-1 ∵f （x ）的图象关于直线x=1对称，∴f （x ）=f （2-x ），又f （x ）是（-∞，+∞）上的奇函数，∴f （x ）=-f （x-2）， ∴f （x+4）=-f （x+2）=-[-f （x ）]=f （x ），即4为f （x ）的周期， ∴f （2013）=f （4×503+1）=f （1），f （2014）=f （4×503+2）=f （2），由x ∈[-1，0]时，f （x ）=-x ，得f （1）=-f （-1）=-1，由f （x ）=f （2-x ），得f （2）=f （0）=0，∴f （2013）+f （2014）=-1+0=-1，故答案为-1．【思路点拨】由f （x ）的图象关于直线x=1对称，得f （x ）=f （2-x ），又f （x ）是（-∞，+∞）上的奇函数，则f （x ）=-f （x-2），由此可推得函数的周期为4，借助周期性及已知表达式可求得答案．【题文】15.给出下列命题：①若)(x f y =是奇函数，则|)(|x f y =的图像关于y 轴对称；②若函数)(x f 对任意x R ∈满足1)4()(=+⋅x f x f ，则8是函数)(x f 的一个周期；③若03log 3log <<n m ，则10<<<n m ；④若||)(a x e x f -=在),1[+∞上是增函数，则1a ≤,其中正确命题的序号是 .【知识点】函数的单调性与最值函数的奇偶性与周期性B3 B4 【答案解析】①②④①若y=f （x ）是奇函数，则f （-x ）=-f （x ），∴|f （-x ）|=|-f （x ）|=|f （x ）|，即|f （x ）|为偶函数，∴图象关于y 轴对称；正确．②若函数f （x ）对任意x ∈R 满足f （x ）•f （x+4）=1，则f （x ）≠0，∴f （x ）•f （x+4）=f （x+4）•f （x+8）=1，即f （x+8）=f （x ），则8是函数f （x ）的一个周期；正确． ③若log m 3＜log n 3＜0，则3311log log m n<＜0，即log 3n ＜log 3m ＜0，即0＜n ＜m ＜1，∴③错误． ④设t=|x-a|，则函数y=e t 单调递增，t=|x-a|在[a ，+∞）上也单调递增，∴若f （x ）=e |x-a|在[1，+∞）上是增函数，则a≤1．正确．∴正确的是①②④．故答案为①②④．【思路点拨】①根据函数奇偶性的性质进行判断．②根据函数周期性的定义进行推导．③根据对数的运算法则进行计算．④根据复合函数的单调性进行判断．【题文】三、解答题：本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤【题文】16．（本小题满分12分）已知全集U=R ，集合[]231,0,22A y y x x x ⎧⎫==-+∈⎨⎬⎩⎭，{}21B x y x ==-。

广东省揭阳三中2015届高三数学上学期第一次月考试卷文(含解析)

广东省揭阳三中2015届高三上学期第一次月考数学试卷（文科）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设集合A={1，2}，则满足A∪B={1，2，3}的集合B的个数是（）A．1 B．3 C．4 D．82．（5分）设集合A={x|1≤x≤2}，B={y|1≤y≤4}，则下述对应法则f中，不能构成A到B 的映射的是（）A．f：x→y=x2B．f：x→y=3x﹣2 C．f：x→y=﹣x+4 D．f：x→y=4﹣x23．（5分）命题“∀x∈R，x2﹣2x+4≤0”的否定为（）A．∀x∈R，x2﹣2x+4≥0B．∃x∈R，x2﹣2x+4＞0C．∀x∉R，x2﹣2x+4≤0D．∃x∉R，x2﹣2x+4＞04．（5分）已知集合M={x|x＜3}，N={x|log2x＞1}，则M∩N=（）A．∅B．{x|0＜x＜3} C．{x|1＜x＜3} D．{x|2＜x＜3} 5．（5分）设命题p：函数y=sin2x的最小正周期为；命题q：函数y=cosx的图象关于直线对称．则下列判断正确的是（）A．p为真B．￢q为假C．p∧q为假D．p∨q为真6．（5分）下列函数中，在其定义域内既是奇函数又是减函数的是（）A．y=﹣x3，x∈R B．y=sinx，x∈R C．y=x，x∈R D．7．（5分）当0＜a＜b＜1时，下列不等式中正确的是（）A．＞（1﹣a）b B．（1+a）a＞（1+b）b C．（1﹣a）b＞D．（1﹣a）a＞（1﹣b）b8．（5分）为确保信息安全，信息需加密传输，发送方由明文→密文（加密），接受方由密文→明文（解密），已知加密规则为：明文a，b，c，d对应密文a+2b，2b+c，2c+3d，4d．例如明文1，2，3，4对应加密文5，7，18，16，当接受方收到密文14，9，23，28时，则解密得明文为（）A．7，6，1，4 B．6，4，1，7 C．4，6，1，7 D．1，6，4，79．（5分）函数f（x）=2x2﹣mx+3，当x∈D．（﹣∞，8]10．（5分）己知x∈，则方程2﹣|x|=cos2πx所有实数根的个数为（）A．2 B．3 C．4 D．5二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上.11．（5分）函数y=log2（x﹣1）的定义域是．12．（5分）函数f（x）对于任意实数x满足条件f（x+2）=，若f（1）=﹣5，则f （5）=．13．（5分）计算：=．14．（5分）设g（x）=，则g（g（））=．三、解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤. 15．（12分）已知U=R，A={x||x﹣3|＜2}，B={x|＞0}，求A∩B，C U（A∪B）．16．（12分）已知函数f（x）=，x∈R，（1）求f（x）+f（）的值；（2）计算f（1）+f（2）+…+f+f（）+f（）+…+f（）．17．（14分）设函数y=f（x）且lg（lgy）=lg（3x）+lg（3﹣x）．（Ⅰ）求f（x）的解析式及定义域．（Ⅱ）求f（x）的值域．18．（14分）已知函数f（x）=是奇函数．（1）求实数m的值；（2）若函数f（x）在区间上单调递增，求实数a的取值范围．19．（14分）函数的定义域为（0，1]（a为实数）．（Ⅰ）当a=﹣1时，求函数y=f（x）的值域；（Ⅱ）若函数y=f（x）在定义域上是减函数，求a的取值范围；（Ⅲ）求函数y=f（x）在x∈（0，1]上的最大值及最小值，并求出函数取最值时x的值．20．（14分）已知函数f（x）=ax2+bx+1（a，b为实数），x∈R，（1）若f（﹣1）=0，且函数f（x）的值域为时，g（x）=f（x）﹣kx是单调函数，求实数k 的取值范围；（3）设m＞0，n＜0，m+n＞0，a＞0且f（x）为偶函数，判断F（m）+F（n）能否大于零？广东省揭阳三中2015届高三上学期第一次月考数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）设集合A={1，2}，则满足A∪B={1，2，3}的集合B的个数是（）A．1 B．3 C．4 D．8考点：并集及其运算．分析：根据题意，分析可得，该问题可转化为求集合A={1，2}的子集个数问题，再由集合的元素数目与子集数目的关系可得答案．解答：解：A={1，2}，A∪B={1，2，3}，则集合B中必含有元素3，即此题可转化为求集合A={1，2}的子集个数问题，所以满足题目条件的集合B共有22=4个．故选择答案C．点评：本题考查了并集运算以及集合的子集个数问题，同时考查了等价转化思想．2．（5分）设集合A={x|1≤x≤2}，B={y|1≤y≤4}，则下述对应法则f中，不能构成A到B 的映射的是（）A．f：x→y=x2B．f：x→y=3x﹣2 C．f：x→y=﹣x+4 D．f：x→y=4﹣x2考点：映射．专题：应用题．分析：按照映射的定义，一个对应能构成映射的条件是，A中的每个元素在集合B中都有唯一的确定的一个元素与之对应．判断题中各个对应是否满足映射的定义，从而得到结论．解答：解：对于对应f：x→y=x2，当1≤x≤2 时，1≤x2≤4，在集合A={x|1≤x≤2}任取一个值x，在集合B={y|1≤y≤4}中都有唯一的一个y值与之对应，故A中的对应能构成映射．对于对应f：x→y=3x﹣2，当1≤x≤2 时，1≤3x﹣2≤4，在集合A={x|1≤x≤2}任取一个值x，在集合B={y|1≤y≤4}中都有唯一的一个y值与之对应，故B中的对应能构成映射．对于对应f：x→y=﹣x+4，当1≤x≤2时，2≤﹣x+4≤3，在集合A={x|1≤x≤2}任取一个值x，在集合B={y|1≤y≤4}中都有唯一的一个y值与之对应，故B中的对应能构成映射．对于对应f：x→y=4﹣x2 ，当x=2 时，y=0，显然y=0不在集合B中，不满足映射的定义，故D中的对应不能构成A到B的映射．故选D．点评：本题考查映射的定义，一个对应能构成映射时，必须使A中的每个元素在集合B中都有唯一的确定的一个元素与之对应．3．（5分）命题“∀x∈R，x2﹣2x+4≤0”的否定为（）A．∀x∈R，x2﹣2x+4≥0 B．∃x∈R，x2﹣2x+4＞0C．∀x∉R，x2﹣2x+4≤0D．∃x∉R，x2﹣2x+4＞0考点：全称命题；命题的否定．专题：计算题．分析：本题中的命题是一个全称命题，其否定是特称命题，依据全称命题的否定书写形式写出命题的否定即可．解答：解：∵命题“∀x∈R，x2﹣2x+4≤0”，∴命题的否定是“∃x∈R，x2﹣2x+4＞0”故选B．点评：本题考查命题的否定，解题的关键是掌握并理解命题否定的书写方法规则，全称命题的否定是特称命题，特称命题的否定是全称命题，书写时注意量词的变化．4．（5分）已知集合M={x|x＜3}，N={x|log2x＞1}，则M∩N=（）A．∅B．{x|0＜x＜3} C．{x|1＜x＜3} D．{x|2＜x＜3}考点：交集及其运算．分析：解出集合N，结合数轴求交集．解答：解：N={x|log2x＞1}={x|x＞2}，用数轴表示可得答案D故选D．点评：考查知识点有对数函数的单调性，集合的交集，本题比较容易5．（5分）设命题p：函数y=sin2x的最小正周期为；命题q：函数y=cosx的图象关于直线对称．则下列判断正确的是（）A．p为真B．￢q为假C．p∧q为假D．p∨q为真考点：复合命题的真假；三角函数的周期性及其求法；余弦函数的对称性．专题：三角函数的图像与性质；简易逻辑．分析：由题设条件可先判断出两个命题的真假，再根据复合命题真假的判断规则判断出选项中复合命题的真假即可得出正确选项．解答：解：由于函数y=sin2x的最小正周期为π，故命题p是假命题；函数y=cosx的图象关于直线x=kπ对称，k∈Z，故q是假命题．结合复合命题的判断规则知：￢q为真命题，p∧q 为假命题，p∨q为是假命题．故选C．点评：本题考查复合命题的真假判断，解题的关键是正确判断所涉及命题的真假及熟练掌握复合命题的真假判断规则，本题属于2015届高考常考题型也是对命题考查的常规题型，知识性强，难度不大．6．（5分）下列函数中，在其定义域内既是奇函数又是减函数的是（）A．y=﹣x3，x∈R B．y=sinx，x∈R C．y=x，x∈R D．考点：函数的图象与图象变化；奇函数．分析：根据基本函数的性质逐一对各个答案进行分析．解答：解：A在其定义域内既是奇函数又是减函数；B在其定义域内是奇函数但不是减函数；C在其定义域内既是奇函数又是增函数；D在其定义域内是非奇非偶函数，是减函数；故选A．点评：处理这种题目的关键是熟练掌握各种基本函数的图象和性质，其处理的方法是逐一分析各个函数，排除掉错误的答案．7．（5分）当0＜a＜b＜1时，下列不等式中正确的是（）A．＞（1﹣a）b B．（1+a）a＞（1+b）b C．（1﹣a）b＞D．（1﹣a）a＞（1﹣b）b考点：指数函数的单调性与特殊点．分析：根据指数的单调性，即当底数大于1时单调递增，当底数大于0小于1时单调递减，对选项逐一验证即可得到答案．解答：解析：∵0＜a＜1，∴0＜1﹣a＜1，y=（1﹣a）x为减函数，又∵0＜b＜1，∴＞b，b＞，∴＜（1﹣a）b，（1﹣a）b＜，∴A、C均错，又∵1＜1+a＜1+b，∴（1+a）a＜（1+b）a＜（1+b）b，∴B错．对于D，（1﹣a）a＞（1﹣a）b，而（1﹣a）b＞（1﹣b）b，∴（1﹣a）a＞（1﹣b）b．故选D点评：本题主要考查指数函数的单调性．属基础题．8．（5分）为确保信息安全，信息需加密传输，发送方由明文→密文（加密），接受方由密文→明文（解密），已知加密规则为：明文a，b，c，d对应密文a+2b，2b+c，2c+3d，4d．例如明文1，2，3，4对应加密文5，7，18，16，当接受方收到密文14，9，23，28时，则解密得明文为（）A．7，6，1，4 B．6，4，1，7 C．4，6，1，7 D．1，6，4，7考点：加密和数字签名的方法．专题：计算题．分析：利用接收方收到密文14，9，23，28及题目提供的加密规则，建立关于a，b，c，d 的方程组，从而可解得解密得到的明文．解答：解：设明文为a，b，c，d，∴4d=28，2c+3d=23，2b+c=9，a+2b=14，∴d=7，c=1，b=4，a=6，则解密得明文为6，4，1，7．故选B．点评：本题主要考查了加密和数字签名的方法，同时考查实际应用能力等数学基本能力，要加强新的信息与创新题，是个基础题．9．（5分）函数f（x）=2x2﹣mx+3，当x∈D．（﹣∞，8]考点：二次函数的性质．专题：计算题．分析：先求出函数f（x）=2x2﹣mx+3对应抛物线的对称轴，再由函数在上单调递增，则对称轴在区间的左侧求解．解答：解：函数f（x）=2x2﹣mx+3，∴其对称轴为：x=又∵函数在上单调递增∴≤﹣2，∴m≤﹣8．故选C．点评：本题主要考查二次函数的性质，涉及了二次函数的对称性和单调性，在研究二次函数单调性时，一定要明确开口方向和对称轴．10．（5分）己知x∈，则方程2﹣|x|=cos2πx所有实数根的个数为（）A．2 B．3 C．4 D．5考点：根的存在性及根的个数判断．专题：数形结合；函数的性质及应用．分析：在同一坐标系内作出函数f（x）=2﹣|x|，g（x）=cos2πx的图象，根据图象交点的个数，可得方程解的个数．解答：解：在同一坐标系内作出函数f（x）=2﹣|x|，g（x）=cos2πx的图象根据函数图象可知，图象交点的个数为5个∴方程2﹣|x|=cos2πx所有实数根的个数为5个故选D．点评：本题考查方程解的个数，考查函数图象的作法，考查数形结合的数学思想，属于中档题．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上.11．（5分）函数y=log2（x﹣1）的定义域是（1，+∞）．考点：对数函数的定义域．专题：计算题．分析：由函数的解析式知，令真数x﹣1＞0即可解出函数的定义域．解答：解：∵y=log2（x﹣1），∴x﹣1＞0，x＞1函数y=log2（x﹣1）的定义域是（1，+∞）故答案为（1，+∞）点评：本题考查求对数函数的定义域，熟练掌握对数函数的定义及性质是正确解答本题的关键．12．（5分）函数f（x）对于任意实数x满足条件f（x+2）=，若f（1）=﹣5，则f （5）=﹣5．考点：函数的周期性．专题：函数的性质及应用．分析：根据条件可得函数是周期为4的周期函数，然后利用函数的周期性即可得到结论．解答：解：∵f（x+2）=，∴f（x）≠0，且f（x+4）=f（x+2+2）=，即函数的周期为4．∵f（1）=﹣5，∴f（5）=f（1+4）=f（1）=﹣5．故答案为：﹣5；点评：本题主要考查函数值的计算，利用条件推出函数的周期性是解决本题的关键，要求熟练掌握函数周期性的应用．13．（5分）计算：=12．考点：有理数指数幂的化简求值．专题：规律型．分析：利用有理数指数幂的性质进行运算．解答：解：=．故答案为：12．点评：本题主要考查有理数指数幂的化简和求值，比较基础．14．（5分）设g（x）=，则g（g（））=．考点：对数的运算性质．专题：函数的性质及应用．分析：根据分段函数的解析式，先求出g（）的值，再求g（g（））的值．解答：解：∵g（x）=，∴g（）=ln=﹣ln2＜0，∴g（g（））=g（﹣ln2）=e﹣ln2==2﹣1=．故答案为：．点评：本题考查了求分段函数的函数值的问题，解题时应对自变量进行分析，是基础题．三、解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.15．（12分）已知U=R，A={x||x﹣3|＜2}，B={x|＞0}，求A∩B，C U（A∪B）．考点：交、并、补集的混合运算．专题：计算题．分析：根据绝对值的性质和不等式的解法分别解出集合A，B，再根据交集和并集、补集的定义进行求解；解答：解：∵U=R，A={x||x﹣3|＜2}，B={x|＞0}，∴A={x||x﹣3|＜2}={x|1＜x＜5}，∴A∩B={x|1＜x＜2或4＜x＜5}，∵A∪B=R，∴C U（A∪B）=∅；点评：此题主要考查不等式的解法，以及集合交、并、补的运算法则，是一道基础题；16．（12分）已知函数f（x）=，x∈R，（1）求f（x）+f（）的值；（2）计算f（1）+f（2）+…+f+f（）+f（）+…+f（）．考点：函数的值．专题：函数的性质及应用．分析：（1）由函数f（x）=，x∈R，能求出f（x）+f（）=+=1．（2）由f（x）+f（）=1，能求出f（1）+f（2）+…+f+f（）+f（）+…+f（）的值．解答：解：（1）∵函数f（x）=，x∈R，∴f（x）+f（）=+=1．（2）由（1）得：f（1）+f（2）+…+f+f（）+f（）+…+f（）==．点评：本题考查函数值的求法，解题时要认真审题，注意函数性质的合理运用．17．（14分）设函数y=f（x）且lg（lgy）=lg（3x）+lg（3﹣x）．（Ⅰ）求f（x）的解析式及定义域．（Ⅱ）求f（x）的值域．考点：对数函数图象与性质的综合应用．专题：综合题；函数的性质及应用．分析：（Ⅰ）利用对数的运算法则，结合对数式与指数式的互化，可得函数的解析式，利用真数大于0，可得函数的定义域；（Ⅱ）根据定义域，确定指数的范围，再利用指数函数的单调性，可求f（x）的值域．解答：解：（Ⅰ）∵lg（lgy）=lg（3x）+lg（3﹣x）．∴lg（lgy）=lg∴lgy=3x（3﹣x）∴y=103x（3﹣x）∵，∴0＜x＜3，即函数的定义域为（0，3）；（Ⅱ）令t=3x（3﹣x）=﹣3∵x∈（0，3），∴t∈（0，]∴10t∈∴函数的值域为．点评：本题考查对数的运算法则，考查函数的解析式与值域，正确运用对数的运算法则是关键．18．（14分）已知函数f（x）=是奇函数．（1）求实数m的值；（2）若函数f（x）在区间上单调递增，求实数a的取值范围．考点：奇偶性与单调性的综合．专题：综合题．分析：（1）根据函数f（x）为奇函数，设x＜0得到f（﹣x）=﹣f（x），进而的f（x）的解析式，求得m的值．（2）根据（1）中的解析式，可画出f（x）的图象，根据图象可知要使f（x）在上单调递增，则需a﹣2＞﹣1且a﹣2≤1，进而求得a的范围．解答：解：（1）设x＜0，则﹣x＞0，所以f（﹣x）=﹣（﹣x）2+2（﹣x）=﹣x2﹣2x，又f（x）为奇函数，所以f（﹣x）=﹣f（x），于是x＜0时，f（x）=x2+2x=x2+mx，所以m=2．（2）要使f（x）在上单调递增，结合f（x）的图象知所以1＜a≤3，故实数a的取值范围是（1，3]．点评：本题主要考查函数的单调性和奇偶性的综合运用．属基础题．19．（14分）函数的定义域为（0，1]（a为实数）．（Ⅰ）当a=﹣1时，求函数y=f（x）的值域；（Ⅱ）若函数y=f（x）在定义域上是减函数，求a的取值范围；（Ⅲ）求函数y=f（x）在x∈（0，1]上的最大值及最小值，并求出函数取最值时x的值．考点：利用导数求闭区间上函数的最值；函数的值域；函数的单调性与导数的关系．专题：综合题．分析：（I）将a的值代入函数解析式，利用基本不等式求出函数的值域．（II）求出导函数，令导函数大于等于0在定义域上恒成立，分离出a，构造函数，通过求函数的最小值，求出a的范围．（III）通过对a的讨论，判断出函数在（0，1）上的单调性，求出函数的最值．解答：解：（Ⅰ）显然函数y=f（x）的值域为；（Ⅱ）∵在定义域上恒成立而﹣2x2∈（﹣2，0）∴a≤﹣2（II）当a≥0时，函数y=f（x）在（0.1]上单调增，无最小值，当x=1时取得最大值2﹣a；由（2）得当a≤﹣2时，函数y=f（x）在（0.1]上单调减，无最大值，当x=1时取得最小值2﹣a；当﹣2＜a＜0时，函数y=f（x）在上单调减，在上单调增，无最大值，当时取得最小值．点评：求函数的单调性常借助导数，当导函数大于0对应的区间是函数的单调递增区间；当导函数小于0对应的区间是函数的单调递减区间．求含参数的函数的性质问题时，一般要对参数讨论．20．（14分）已知函数f（x）=ax2+bx+1（a，b为实数），x∈R，（1）若f（﹣1）=0，且函数f（x）的值域为时，g（x）=f（x）﹣kx是单调函数，求实数k 的取值范围；（3）设m＞0，n＜0，m+n＞0，a＞0且f（x）为偶函数，判断F（m）+F（n）能否大于零？考点：二次函数的性质．专题：综合题；压轴题．分析：（1）f（﹣1）=0⇒a﹣b+1=0，又值域为点评：本题是对二次函数性质的综合考查．其中（1）考查了二次函数解析式的求法．二次函数解析式的确定，应视具体问题，灵活的选用其形式，再根据题设条件列方程组，即运用待定系数法来求解．在具体问题中，常常会与图象的平移，对称，函数的周期性，奇偶性等知识有机的结合在一起．。

【名师解析】河南省南阳一中2015届高三上学期第一次月考数学理试题 Word版含解析

河南省南阳一中2015届高三第一次月考数学试题（理）【试卷综析】试题试卷结构稳定，考点分布合理，语言简洁，设问坡度平缓，整体难度适中. 注重基础. 纵观全卷，选择题、填空题比较平和，立足课本，思维量和运算量适当.内容丰富，考查了重点内容,渗透课改，平稳过渡.针对所复习的内容进行考查，是优秀的阶段性测试卷.一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）【题文】1．设U={1，2，3，4}，且M={x ∈U|2x ﹣5x+P=0}，若C U M={2，3}，则实数P 的值为（） A ．-4 B ．4 C ．-6D ．6【知识点】集合运算；一元二次方程的解. A1【答案解析】B 解析：因为U={1，2，3，4}，C U M={2，3}，所以M= {}1,4，所以 p= 144⨯=.故选B.【思路点拨】由已知条件得M= {}1,4，由韦达定理得p= 144⨯=. 【题文】2．“cos2α=﹣”是“cosα=45”的（） A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【知识点】充分条件；必要条件. A2 【答案解析】D 解析：由cos2α= 725-得2732cos 1cos 255αα-=-⇒=±；由cosα=45得27cos 22cos 125αα=-=.所以“cos2α=﹣”是“cosα=45”的既不充分也不必要条件，故选D.【思路点拨】通过判断命题：若“cos2α=﹣”则“cosα=45”；与命题：若“cosα=45”则“cos2α=﹣”.的真假得结论.【题文】3．已知向量,a b 满足1,4a b ==，且2a b ∙≥，则a 与b 的夹角的取值范围是（）A ．,6ππ⎡⎤⎢⎥⎣⎦ B ．0,3π⎛⎤ ⎥⎝⎦ C ．0,3π⎡⎤⎢⎥⎣⎦ D ．,3ππ⎡⎤⎢⎥⎣⎦【知识点】向量的数量积. F3【答案解析】C 解析：设a 与b 的夹角θ，则cos 14cos 2a b a b θθ⋅=⋅=⨯≥，所以1cos ,2θ≥所以0,3πθ⎡⎤∈⎢⎥⎣⎦.故选C. 【思路点拨】由向量数量积的定义，向量夹角的取值范围求解.【题文】4．已知{a n } 为等比数列，a 4+a 7=2，a 5a 6=﹣8，则a 1+a 10=（） A ．7 B ．5 C ．-5 D ．-7 【知识点】等比数列. D3【答案解析】D 解析：因为，a 5a 6=﹣8，所以478a a =-，又a 4+a 7=2，所以437224a q a =-⎧⇒=-⎨=⎩或4374122a q a =⎧⇒=-⎨=-⎩，所以a 1+a 10= 34737a a q q +=-，故选D.【思路点拨】由已知条件求得3q ，再由 a 1+a 10=3473a a q q+得结论. 【题文】5．已知,)(),cos ,(sin ),sin ,(cos b a x f x x b x x a ⋅===记要得到函数22cos sin y x x =-的图像，只需将函数()y f x =的图像（）A ．向左平移2π个单位长度 B ．向右平移2π个单位长度 C ．向左平移4π个单位长度D ．向右平移4π个单位长度【知识点】向量的数量积；函数sin()y A x ωϕ=+的图像. F3 C4【答案解析】C 解析：()2sin cos f x x x =sin 2x =，22cos sin cos2y x x x =-=sin 2sin 224x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭，故选C.【思路点拨】利用向量数量积的坐标运算，求得()sin 2f x x =，变形22cos sin y x x =-得sin 24y x π⎛⎫=+⎪⎝⎭，所以要得到函数22cos sin y x x =-的图像，只需将函数()y f x =的图像向左平移4π个单位长度. 【题文】6．已知ABC ∆中，4,AB AC BC ===，点P 为BC 边所在直线上的一个动点，则()AP AB AC ⋅+满足（）A ．最大值为16B ．最小值为4C ．为定值8D ．与P 的位置有关【知识点】向量的线性运算；向量的数量积. F1 F3【答案解析】C 解析：设线段BC 中点D,由已知得60,BAD CAD AD BC ∠=∠=⊥ 且2AD =,因为点P 在线段BC 上，所以AD BP ⊥,所以()()2AP AB AC AB BP AD ⋅+=+⋅22AB AD AD BP =⋅+⋅242cos6008=⨯⨯⨯+=.故选C.【思路点拨】设线段BC 中点D,由已知得60,BAD CAD AD BC ∠=∠=⊥且2AD =,因为点P 在线段BC 上，所以AD BP ⊥,所以()()2AP AB AC AB BP AD ⋅+=+⋅22AB AD AD BP =⋅+⋅242cos6008=⨯⨯⨯+=.【题文】7．已知函数1()lg ()2x f x x =-有两个零点21,x x ，则有（）A ．021<x xB ．121=x xC ．121>x xD ．1021<<x x【知识点】函数的零点. B9【答案解析】D 解析：设12x x <则()()120,1,1,x x ∈∈+∞，所以121211lg ,lg 22x x x x ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，两式相减得()211211lg 022x xx x ⎛⎫⎛⎫=-< ⎪ ⎪⎝⎭⎝⎭，所以1201x x <<，故选D.【思路点拨】通过画两函数1lg ,2xy x y ⎛⎫== ⎪⎝⎭的图像知，若12x x <则()()120,1,1,x x ∈∈+∞，由题意得121211lg ,lg 22x xx x ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，两式相减得()211211lg 022x xx x ⎛⎫⎛⎫=-< ⎪ ⎪⎝⎭⎝⎭，所以1201x x <<.【题文】8．若关于x 的不等式2－2x >|x －a| 至少有一个负数解，则a 的取值范围为（） A ．9,24⎡⎫-⎪⎢⎣⎭B ．5,24⎛⎫-⎪⎝⎭C ．7,24⎛⎫-⎪⎝⎭D ．7,33⎛⎫-⎪⎝⎭【知识点】函数与不等式. B8 E1【答案解析】A 解析：画出函数22,y x =-与y x a =-的图像，左右平移函数y x a =-的图像可知，从y x a =-图像左支过点（0,2）开始，向左平移到右支与函数22y x =-相切，这个过程中关于x 的不等式2－2x >|x －a| 至少有一个负数解，由直线y=x-a 与22y x =- 相切得94a =-，所以a 的取值范围为9,24⎡⎫-⎪⎢⎣⎭【思路点拨】由图像分析关于x 的不等式2－2x >|x －a| 至少有一个负数解的条件.【题文】9．设函数()f x 是定义在R 上的奇函数，且当0x ≥时，()f x 单调递减，若数列{}n a 是等差数列，且30a <，则()()()()()12345f a f a f a f a f a ++++的值（） A ．恒为负数 B ．恒为正数 C ．恒为0 D ．可正可负【知识点】函数的奇偶性，单调性；等差数列的性质. B3 B4 D2【答案解析】B 解析：因为函数()f x 是定义在R 上的奇函数，且当0x ≥时，()f x 单调递减，所以x<0时()f x >0，x>0时()f x <0，因为30a <，所以()30f a >，又因为15,a a 的中点是3a ，24,a a 的中点是3a ，所以()()()()15240,0f a f a f a f a +>+>，所以()()()()()12345f a f a f a f a f a ++++的值恒为正数，故选B.【思路点拨】任作一个在R 上单调递减的奇函数，由30a <，15,a a 关于3a 对称，24,a a 关于3a 对称得()30f a >，()()()()15240,0f a f a f a f a +>+>，所以 ()()()()()12345f a f a f a f a f a ++++的值恒为正数.【题文】10．在ABC ∆中，D 是BC 边上任意一点（D 与B ，C 不重合），且||||||||22DC BD AD AB ⋅+=，则ABC ∆一定是（）A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰直角三角形【知识点】余弦定理. C8【答案解析】C 解析：如图: 在ABD ∆中2222cos AD c BD c BD B =+-⋅,又DC=a-BD.代入已知等式得：()2222cos c c BD c BD B BD a BD =+-⋅+⋅-, 化简得cos 2a B c=，又222cos 2a c b B ac+-=，所以22222a c b aac c +-=，化简得b=c ，所以ABC ∆一定是等腰三角形，故选C. 【思路点拨】画出示意图在ABD ∆中由余弦定理表示2AD ,又DC=a-BD. 代入已知等式得cos 2a B c =,在ABC ∆中有余弦定理得222cos 2a c b B ac+-=，所以22222a c b aac c +-=，化简得b=c. 【题文】11．定义在R 上的可导函数()f x ，当(1,)x ∈+∞时，()()()f x f x xf x ''+<恒成立，(2)a f =，1(3)b f =, 1)c f =则a ，b ，c 的大小关系为（）【答案解析】A解析:构造函数()()1f x g x x =-，则()()()()()211f x x f x g x x '--'=-，因为()()()f x f x xf x ''+<，即()()()10f x x f x '-->在(1,)x ∈+∞时恒成立，所以()()1f xg x x =-是(1,)x ∈+∞的增函数，而()()2,3,a g b g c g ===23<<所以c<a<b ，故选A.【思路点拨】构造函数()()1f xg x x =-，利用此函数单调性确定a,b,c 的大小关系. 【题文】12．定义在R 上的奇函数f （x ），当x≥0时，，则关于x 的函数F （x ）=f （x ）﹣a （0＜a ＜1）的所有零点之和为（） A ．21a- Ｂ．21a-- Ｃ．12a -- Ｄ．12a --【知识点】函数的奇偶性；函数的零点． B4 B9【答案解析】D 解析：函数的零点共5个，设它们从小到大依次为：12345,,,,x x x x x ，其中12456,6x x x x +=-+=，3x 是方程()12log 1x a --=的解，所以312a x -=-，所以关于x 的函数F （x ）=f （x ）﹣a （0＜a ＜1）的所有零点之和为12a--，故选D.【思路点拨】由图像可以看到函数的零点共5个，它们的和为方程()12log 1x a --=的解.二、填空题（每题5分，共20分）【题文】13．⎰=>--baa b dx b x x a )())((【知识点】定积分. B13【答案解析】()28b a π-解析：设y =则()22224a b a b x y -+⎛⎫-+= ⎪⎝⎭，0y >，这是一个半圆，根据定积分的几何意义，所求积分为此半圆的面积，所以所求积分=()28b a π-.【思路点拨】被积函数的图像时半圆，根据定积分的几何意义，所求积分为此半圆的面积，所以所求积分=()28b a π-.【题文】14．函数)0(cos sin ≠-=ab x b x a y 的图像的一条对称轴为4π=x ,则以),(b a =为方向向量的直线的倾斜角为【知识点】两角和与差的三角函数；()sin y A x ωϕ=+的性质；平面向量. C5 C4 F1 【答案解析】34π 解析：)0(cos sin ≠-=ab xb x a y (),tan bx a ϕϕ=+=-，因为此函数图像的一条对称轴为4x π=，所以,424k k k Z πππϕπϕπ+=+⇒=+∈，所以tan tan 14b k aπϕπ⎛⎫=+==- ⎪⎝⎭ 1b a ⇒=-，所以以),(b a =为方向向量的直线的倾斜角为34π. 【思路点拨】根据已知条件求得b=-a ，所以点（a,b ）在直线y=-x 上，所以以),(b a a =为方向向量的直线的倾斜角为34π. 【题文】15．已知点A (1，－1)，B (3,0)，C (2,1)．若平面区域D 由所有满足AP →＝λAB →＋μAC →(1≤λ≤2,0≤μ≤1)的点P 组成，则D 的面积为_______．【知识点】平面向量基本定理；向量的坐标表示；向量的数量积. F2 F3【答案解析】3 解析：如图：延长AB 到D 使BD=AB,作BF 平行且等于AC,则点P 组成的图形是以BD 、BF为邻边的平行四边形，又cos cos FBD CAB ∠=∠()()(21,22,145AC AB AC AB⋅⋅===,所以3sin 5FBD ∠==,所以所求面积为： 23sin 35BD BF FBD ∠=⋅=.【思路点拨】画出满足AP →＝λAB →＋μAC →(1≤λ≤2,0≤μ≤1)的点P 组成的平面图形，求此平面图形的面积. 【题文】16．关于函数2()()1xf x x R x=∈+的如下结论：①()f x 是偶函数；②函数()f x 的值域是(2,2)-；③若12,x x ≠则一定有12()()f x f x ≠；④函数(1)f x +的图象关于直线1x =对称；其中正确结论的序号有＿＿＿＿。

安徽省蚌埠市第二中学2015届高三上学期第一次月考数学理试题 Word版含解析

安徽省蚌埠二中2015届高三第一次月考数学试卷（理科）参考答案与试题解析一、选择题（每小题5分，共50分）1．若集合A={x|y=2x}，集合，则A∩B=（）A．（0，+∞）B．（1，+∞）C．[0，+∞）D．（﹣∞，+∞）考点：函数的定义域及其求法；交集及其运算．分析：求出集合A中函数的定义域确定出A，求出集合B中函数的定义域确定出B，求出A与B的交集即可．解答：解：集合A中的函数y=2x，x∈R，即A=R，集合B中的函数y=，x≥0，即B=[0，+∞），则A∩B=[0，+∞）．故选C2．设a∈R，则“a=1”是“直线y=a2x+1与直线y=x﹣1平行”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．分析：结合直线平行的条件，利用充分条件和必要条件的定义进行判断．解答：解：若直线y=a2x+1与直线y=x﹣1平行，则a2=1，解得a=1或a=﹣1．所以“a=1”是“直线y=a2x+1与直线y=x﹣1平行”的充分不必要条件．故选A．3．已知复数z满足（3﹣4i）z=25，则z=（）A．﹣3﹣4i B．﹣3+4i C．3﹣4i D．3+4i考点：复数相等的充要条件．分析：由题意利用两个复数代数形式的乘除法，虚数单位i的幂运算性质，计算求得结果．解答：解：∵满足（3﹣4i）z=25，则z===3+4i，故选：D．4．下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行考点：命题的真假判断与应用；空间中直线与平面之间的位置关系．分析：利用直线与平面所成的角的定义，可排除A；利用面面平行的位置关系与点到平面的距离关系可排除B；利用线面平行的判定定理和性质定理可判断C正确；利用面面垂直的性质可排除D解答：解：A，若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面；排除A；B，若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，排除B；C，设平面α∩β=a，l∥α，l∥β，由线面平行的性质定理，在平面α内存在直线b∥l，在平面β内存在直线c∥l，所以由平行公理知b∥c，从而由线面平行的判定定理可证明b∥β，进而由线面平行的性质定理证明得b∥a，从而l∥a；故C正确；D，若两个平面都垂直于第三个平面，则这两个平面平行或相交，排除D；故选C5．设等比数列{a n}的前n项和为S n，若8a2+a5=0，则下列式子中数值不能确定的是（）A．B．C．D．考点：等比数列的性质．分析：根据已知的等式变形，利用等比数列的性质求出公比q的值，然后分别根据等比数列的通项公式及前n项和公式，即可找出四个选项中数值不能确定的选项．解答：解：由8a2+a5=0，得到=q3=﹣8，故选项A正确；解得：q=﹣2，则=q=﹣2，故选项C正确；则==，故选项B正确；而==，所以数值不能确定的是选项D．故选D6．若P（2，﹣1）为圆（x﹣1）2+y2=25的弦AB的中点，则直线AB的方程是（）A．x﹣y﹣3=0 B．2x+y﹣3=0 C．x+y﹣1=0 D．2x﹣y﹣5=0 考点：直线和圆的方程的应用；直线与圆相交的性质．分析：由圆心为O（1，0），由点P为弦的中点，则该点与圆心的连线垂直于直线AB求解其斜率，再由点斜式求得其方程．解答：解：已知圆心为O（1，0）根据题意：K op=k AB k OP=﹣1k AB=1，又直线AB过点P（2，﹣1），∴直线AB的方程是x﹣y﹣3=0故选A点评：本题主要考查直线与圆的位置关系及其方程的应用，主要涉及了弦的中点与圆心的连线与弦所在的直线垂直．7．如图，一个底面半径为R的圆柱被与其底面所成角为θ（00＜θ＜900）的平面所截，截面是一个椭圆．当θ为30°时，这个椭圆的离心率为（）A．B．C．D．考点：平面与圆柱面的截线．分析：利用已知条件，求出题意的长半轴，短半轴，然后求出半焦距，即可求出题意的离心率．解答：解：因为底面半径为R的圆柱被与底面成30°的平面所截，其截口是一个椭圆，则这个椭圆的短半轴为：R，长半轴为：=，∵a2=b2+c2，∴c=，∴椭圆的离心率为：e==．故选：A．点评：本题考查椭圆离心率的求法，注意椭圆的几何量与双曲线的几何量（a，b，c）关系的正确应用，考查计算能力．8．有红、蓝、黄、绿四种颜色的球各6个，每种颜色的6个球分别标有数字1、2、3、4、5、6，从中任取3个标号不同的球，这3个颜色互不相同且所标数字互不相邻的取法种数为（）A．80 B．84 C．96 D．104考点：计数原理的应用．分析：所标数字互不相邻的方法有4种，这3种颜色互不相同有C43A33种，根据分步计数原理，即可求出颜色互不相同且所标数字互不相邻的取法种数．解答：解：所标数字互不相邻的方法有：135，136，146，246，共4种方法．这3种颜色互不相同有C43A33=4×3×2×1=24种，∴这3种颜色互不相同且所标数字互不相邻的有4×24=96种．故选：C．点评：本题主要考查了排列组合，以及两个基本原理的应用，解题的关键是不遗漏不重复，属于中档题．9．函数：①y=x•sinx②y=x•cosx③y=x•|cosx|④y=x•2x的图象（部）如图所示，但顺序被打乱，则按照从左到右将图象对应的函数序号安排正确的一组是（）A．④①②③B．①④③②C．①④②③D．③④②①考点：正弦函数的图象；余弦函数的图象．分析：依据函数的性质与图象的图象对应来确定函数与图象之间的对应关系，对函数的解析式研究发现，四个函数中有一个是偶函数，有两个是奇函数，还有一个是指数型递增较快的函数，由这些特征接合图象上的某些特殊点判断即可．解答：解：研究发现①是一个偶函数，其图象关于y轴对称，故它对应第一个图象②③都是奇函数，但②在y轴的右侧图象在x轴上方与下方都存在，而③在y轴右侧图象只存在于x轴上方，故②对应第三个图象，③对应第四个图象，④与第二个图象对应，易判断．故按照从左到右与图象对应的函数序号①④②③故选C．点评：本题考点是正弦函数的图象，考查了函数图象及函数图象变化的特点，解决此类问题有借助两个方面的知识进行研究，一是函数的性质，二是函数值在某些点的符号即图象上某些特殊点在坐标系中的确切位置．10．已知函数f（x）是定义在R上的奇函数，当x＜0时，f（x）=e x（x+1），给出下列命题：①当x＞0时，f（x）=e x（1﹣x）；②f（x）＞0的解集为（﹣1，0）∪（1，+∞）；③函数f（x）有2个零点；④∀x1，x2∈R，都有|f（x1）﹣f（x2）|＜2，其中正确命题的个数是（）A．1 B．2C．3D．4考点：命题的真假判断与应用；奇偶性与单调性的综合．分析：逐个验证：①为函数对称区间的解析式的求解；②为不等式的求解，分段来解，然后去并集即可；③涉及函数的零点，分段来解即可，注意原点；④实际上是求函数的取值范围，综合利用导数和极值以及特殊点，画出函数的图象可得范围．解答：解：设x＞0，则﹣x＜0，故f（﹣x）=e﹣x（﹣x+1），又f（x）是定义在R上的奇函数，故f（﹣x）=﹣f（x）=e﹣x（﹣x+1），所以f（x）=e﹣x（x﹣1），故①错误；因为当x＜0时，由f（x）=e x（x+1）＞0，解得﹣1＜x＜0，当x＞0时，由f（x）=e﹣x（x ﹣1）＞0，解得x＞1，故f（x）＞0的解集为（﹣1，0）∪（1，+∞），故②正确；令e x（x+1）=0可解得x=﹣1，当e﹣x（x﹣1）=0时，可解得x=1，又函数f（x）是定义在R上的奇函数，故有f（0）=0，故函数的零点由3个，故③错误；④∀x1，x2∈R，都有|f（x1）﹣f（x2）|＜2，正确，因为当x＞0时f（x）=e﹣x（x﹣1），图象过点（1，0），又f′（x）=e﹣x（2﹣x），可知当0＜x＜2时，f′（x）＞0，当x＞2时，，f′（x）＜0，故函数在x=2处取到极大值f （2）=，且当x趋向于0时，函数值趋向于﹣1，当x趋向于+∞时，函数值趋向于0，由奇函数的图象关于原点对称可作出函数f（x）的图象，可得函数﹣1＜f（x）＜1，故有|f（x1）﹣f（x2）|＜2成立．综上可得正确的命题为②④，故选B点评：本题考查命题真假的判断，涉及函数性质的综合应用，属中档题．二、填空题（每小题5分，共25分）11．已知x，y满足，则z=2x+y的最大值为3．考点：简单线性规划．专题：计算题．分析：先根据约束条件画出可行域，再利用几何意义求最值，z=2x+y表示直线在y轴上的截距，只需求出可行域直线在y轴上的截距最大值即可．解答：解：，在坐标系中画出图象，三条线的交点分别是A（﹣1，﹣1），B（，），C（2，﹣1），在△ABC中满足z=2x+y的最大值是点C，代入得最大值等于3．故答案为：3．点评：本题只是直接考查线性规划问题，是一道较为简单的试题．近年来高考线性规划问题高考数学考试的热点，数形结合是数学思想的重要手段之一，体现了数形结合思想的应用．12．如果执行如图所示的程序图（判断条件k≤20？），那么输出的S=420．考点：程序框图．专题：算法和程序框图．分析：执行程序框图，分析程序框图的功能和意义，计算并输出S=2×（1+2+…+20）的值，不难计算为420．解答：解：执行程序框图，有k=1S=0满足条件k≤20，第1次执行循环体，有S=2，k=2满足条件k≤20，第2次执行循环体，有S=2+4，k=3满足条件k≤20，第3次执行循环体，有S=2+4+6，k=4…满足条件k≤20，第19次执行循环体，有S=2+4+..+38，k=20满足条件k≤20，第2次执行循环体，有S=2+4+…+40，k=21不满足条件k≤20，退出执行循环体，输出S的值根据程序框图的意义和功能，得S=2×（1+2+…+20）=420故答案为：420．点评：本题主要考察程序框图和算法，属于基础题．13．设（2x+1）5+（x﹣2）4=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a2=64．考点：二项式系数的性质．专题：二项式定理．分析：由题意可得，a2就是x2的系数，再根据二项式的展开式的通项公式可得x2的系数为+，计算求得结果．解答：解：由题意可得，a2就是x2的系数，再根据二项式的展开式的通项公式可得x2的系数为+=40+24=64，故答案为：64．点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于中档题．14．若方程log3（a﹣3x）+x﹣2=0有实根，则实数a的取值范围是[6，+∞）．考点：函数的零点．专题：函数的性质及应用．分析：由题意可得方程a=3x+32﹣x有解，即a值属于3x+32﹣x值的范围内，根据均值不等式求出实数a的取值范围．解答：解：由题意可得，方程2﹣x=log3（a﹣3x）有解，∵方程2﹣x=log3（a﹣3x）可化为32﹣x=a﹣3x，即方程a=3x+32﹣x有解．再根据基本不等式可得a=3x+32﹣x ≥2=6，故实数a的取值范围是[6，+∞），故答案为：[6，+∞）．点评：本题主要考查方程根的存在性及个数判断，利用基本不等式求函数的值域，体现了转化的数学思想，属于基础题．15．已知数列{a n}是各项均不为0的等差数列，S n为其前n项和，且满足a n2=S2n﹣1（n∈N+）．若不等式≤对任意的n∈N+恒成立，则实数λ的最大值为﹣21．考点：等差数列的性质．专题：等差数列与等比数列．分析：在已知递推式中分别取n=1，2，联立方程组求得首项和公差，求出等差数列的通项公式，进一步得到a n+1，代入不等式≤后分n为偶数和奇数变形，分离参数λ后分别利用基本不等式求最值和函数单调性求最值，取交集后得到λ的取值范围，则λ的最大值可求．解答：解：在a n2=S2n﹣1中，令n=1，n=2，得，即，解得a1=1，d=2，∴a n=a1+（n﹣1）d=1+2（n﹣1）=2n﹣1，a n+1=2n+1．①当n为偶数时，要使不等式≤恒成立，即需不等式恒成立，∵，等号在n=2时取得，∴此时λ需满足λ≤25；②当n为奇数时，要使不等式≤恒成立，即需不等式恒成立，∵随n的增大而增大，∴n=1时，取得最小值﹣6．则λ≤﹣6﹣15=﹣21．综合①、②可得λ的取值范围是λ≤﹣21．∴实数λ的最大值为﹣21．故答案为：﹣21．点评：本题考查数列递推式，考查了等差数列通项公式的求法，训练了利用基本不等式和函数单调性求函数的最值，体现了分类讨论的数学思想方法，是中档题．三、解答题（共75分）16．（12分）△ABC中角A，B，C的对边分别为a，b，c，且b2+c2﹣a2+bc=0，（1）求角A的大小；（2）若，求△ABC面积S△ABC的最大值．考点：余弦定理；三角形的面积公式．专题：计算题；解三角形．分析：（1）根据题中等式，利用余弦定理算出cosA=﹣，结合A为三角形的内角，可得A=；（2）利用基本不等式，算出bc≤1，当且仅当b=c=1时等号成立．由此结合正弦定理的面积公式，即可算出△ABC面积S△ABC的最大值．解答：解：（1）∵△ABC中，b2+c2﹣a2+bc=0，∴b2+c2﹣a2=﹣bc因此cosA===﹣∵A为三角形的内角，∴A=；（2）∵b2+c2﹣a2+bc=0，∴a2=b2+c2+bc=3，得b2+c2=﹣bc+3≥2bc解之得bc≤1，当且仅当b=c=1时等号成立∵△ABC面积S△ABC=bcsinA=bc∴当且仅当b=c=1时，△ABC面积S△ABC的最大值为．点评：本题给出三角形的边之间的平方关系，求角的大小并依此求三角形面积的最大值．着重考查了正余弦定理解三角形、运用基本不等式求最值等知识，属于中档题．17．（12分）数列{a n}的前n项和为S n，且a n是S n和1的等差中项，等差数列{b n}满足b1=a1，b4=S3．（Ⅰ）求数列{a n}、{b n}的通项公式；（Ⅱ）设c n=，数列{c n}的前n项和为T n，证明：T n＜．考点：数列与不等式的综合；数列的求和．专题：等差数列与等比数列．分析：（I）由已知条件得到S n=2a n﹣1，由此推导出数列{a n}是以a1=1为首项，2为公比的等比数列，从而得到，S n=2n﹣1，进而得到b1=a1=1，b4=1+3d=7，由此能求出{b n}的通项公式．（II）由c n=，得T n=，由此利用裂项求和法能证明．解答：（I）解：∵a n是S n和1的等差中项，∴S n=2a n﹣1，当n=1时，a1=S1=2a1﹣1，∴a1=1，当n≥2时，a n=S n﹣S n﹣1=（2a n﹣1）=2a n﹣2a n﹣1，∴a n=2a n﹣1，即，（3分）∴数列{a n}是以a1=1为首项，2为公比的等比数列，∴，S n=2n﹣1，设{b n}的公差为d，b1=a1=1，b4=1+3d=7，∴d=2，∴b n=1+（n﹣1）×2=2n﹣1．（6分）（II）证明：c n===，（7分）∴T n=，（9分）∵n∈N*，∴．（12分）点评：本题考查数列的通项公式的求法，考查数列前n项和的求法及不等式的证明，解题时要认真审题，注意裂项求和法的合理运用．18．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD是直角梯形，AB∥DC，AB⊥AD，平面PAD⊥平面ABCD，若AB=8，DC=2，AD=6，PA=4，∠PAD=45°，且．（Ⅰ）求证：PO⊥平面ABCD；（Ⅱ）设平面PAD与平面PBC所成二面角的大小为θ（0°＜θ≤90°），求cosθ的值．考点：与二面角有关的立体几何综合题；直线与平面垂直的判定．专题：空间角．分析：（Ⅰ）由已知条件利用余弦定理求出，从而得到PO⊥AD，由此能够证明PO⊥平面ABCD．（Ⅱ）过O作OE∥AB交BC于E，以O为坐标原点，分别以OA，OE，OP所在直线为x、y、z轴，建立空间直角坐标系O﹣xyz利用向量法能求出平面PAD与平面PBC所成二面角的大小的余弦值．解答：解：（Ⅰ）因为，，所以，…（1分）在△PAO中，由余弦定理PO2=PA2+AO2﹣2PA•AOcos∠PAO，得，…（3分）∴，∴PO2+AO2=PA2，…（4分）∴PO⊥AD，…又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PO⊂平面PAD，∴PO⊥平面ABCD．…（6分）（Ⅱ）如图，过O作OE∥AB交BC于E，则OA，OE，OP两两垂直，以O为坐标原点，分别以OA，OE，OP所在直线为x、y、z轴，建立空间直角坐标系O﹣xyz，…（7分）则O（0，0，0），，．…（8分）∴，=，…（9分）设平面PBC的一个法向量为=（x，y，z），由，得，即，取x=1，则，∴为平面PBC的一个法向量．…（11分）∵AB⊥平面PAD，∴为平面PAD的一个法向量．∴=，…（12分）∴．…（13分）点评：本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．19．（13分）某网站用“10分制”调查一社区人们的幸福度．现从调查人群中随机抽取16名，如图所示茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：（1）指出这组数据的众数和中位数；（2）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；（3）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．考点：离散型随机变量的期望与方差；众数、中位数、平均数．专题：概率与统计．分析：（1）根据所给的茎叶图看出16个数据，找出众数和中位数，中位数需要按照从小到大的顺序排列得到结论．（2）由题意知本题是一个古典概型，至多有1人是“极幸福”包括有一个人是极幸福和有零个人是极幸福，根据古典概型公式得到结果．（3）由于从该社区任选3人，记ξ表示抽到“极幸福”学生的人数，得到变量的可能取值是0、1、2、3，结合变量对应的事件，算出概率，写出分布列和期望．解答：解：（1）由茎叶图得到所有的数据从小到大排，8.6出现次数最多，∴众数：8.6；中位数：8.75；（2）设A i表示所取3人中有i个人是“极幸福”，至多有1人是“极幸福”记为事件A，则（3）ξ的可能取值为0、1、2、3.；；，ξ的分布列为ξ0 1 2 3P所以Eξ=．另解：ξ的可能取值为0、1、2、3．则，．ξ的分布列为ξ0 1 2 3P所以Eξ=．点评：本题是一个统计综合题，对于一组数据，通常要求的是这组数据的众数，中位数，平均数，题目分别表示一组数据的特征，这样的问题可以出现在选择题或填空题，考查最基本的知识点．20．（13分）分别过椭圆E：=1（a＞b＞0）左、右焦点F1、F2的动直线l1、l2相交于P点，与椭圆E分别交于A、B与C、D不同四点，直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4，且满足k1+k2=k3+k4，已知当l1与x轴重合时，|AB|=2，|CD|=．（1）求椭圆E的方程；（2）是否存在定点M，N，使得|PM|+|PN|为定值？若存在，求出M、N点坐标，若不存在，说明理由．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线中的最值与范围问题．分析：（1）由已知条件推导出|AB|=2a=2，|CD|=，由此能求出椭圆E的方程．（2）焦点F1、F2坐标分别为（﹣1，0），（1，0），当直线l1或l2斜率不存在时，P点坐标为（﹣1，0）或（1，0），当直线l1，l2斜率存在时，设斜率分别为m1，m2，设A（x1，y1），B（x2，y2），由，得，由此利用韦达定理结合题设条件能推导出存在点M，N其坐标分别为（0，﹣1）、（0，1），使得|PM|+|PN|为定值2．解答：解：（1）当l1与x轴重合时，k1+k2=k3+k4=0，即k3=﹣k4，∴l2垂直于x轴，得|AB|=2a=2，|CD|=，解得a=，b=，∴椭圆E的方程为．（2）焦点F1、F2坐标分别为（﹣1，0），（1，0），当直线l1或l2斜率不存在时，P点坐标为（﹣1，0）或（1，0），当直线l1，l2斜率存在时，设斜率分别为m1，m2，设A（x1，y1），B（x2，y2），由，得，∴，，===，同理k3+k4=，∵k1+k2=k3+k4，∴，即（m1m2+2）（m2﹣m1）=0，由题意知m1≠m2，∴m1m2+2=0，设P（x，y），则，即，x≠±1，由当直线l1或l2斜率不存在时，P点坐标为（﹣1，0）或（1，0）也满足，∴点P（x，y）点在椭圆上，∴存在点M，N其坐标分别为（0，﹣1）、（0，1），使得|PM|+|PN|为定值2．点评：本题考查椭圆方程的求法，考查是否存在定点M，N，使得|PM|+|PN|为定值的判断与证明，对数学思维的要求较高，有一定的探索性，解题时要注意函数与方程思想、等价转化思想的合理运用．21．（13分）已知函数φ（x）=lnx．（1）若曲线g（x）=φ（x）+﹣1在点（2，g（2））处的切线与直线3x+y﹣1=0平行，求a的值；（2）求证函数f（x）=φ（x）﹣在（0，+∞）上为单调增函数；（3）设m，n∈R+，且m≠n，求证：＜||．考点：利用导数求闭区间上函数的最值；利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．专题：证明题；导数的综合应用．分析：（1）先求出g（x）的导数g′（x），求出g′（2），根据条件得到g′（2）=﹣3，解出a的值；（2）可先求出f（x）的导数f′（x），并化简整理、因式分解，由条件x＞0，即可判断导数的符号，从而得证；（3）设m＞n＞0，应用分析法证明，要证原不等式成立，可以适当变形，只需证，然后构造函数h（x）=lnx﹣（x＞1），应用导数说明h（x）在（1，+∞）上是单调增函数，从而h（x）＞h（1）=0，即可得证．解答：解：（1）=（x＞0），（x ＞0），∵曲线在点（2，g（2））处的切线与直线3x+y﹣1=0平行，∴，解得a=14；（2）证明：═（x＞0），∴≥0，∴函数在（0，+∞）上为单调增函数；（3）不妨设m＞n＞0，则，要证＜||，即证，只需证，即证，只需证，设h（x）=lnx﹣（x＞1），由（2）得，h（x）在（1，+∞）上是单调增函数，∵x＞1，∴h（x）＞h（1）=0，即，即．∴不等式成立．点评：本题主要考查导数在函数中的应用：求单调区间、证明单调性以及不等式，考查应用导数求切线方程，以及构造函数解题的能力，是一道综合题．。

2015届银川一中高三上学期第一次月考理综解析版(2014.08)

宁夏银川一中2015届高三上学期第一次月考理综试题【试卷综析】本试卷是高三模拟试题，包含了高中物理相互作用、牛顿运动定理、以及选修3-3、3-4、3-5的全部内容，在考查问题上以基本定义、基本规律为主，注重个过程的分析，题型新颖，适合于高三一轮复习。

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

其中第Ⅱ卷第33～40题为选考题，其它题为必考题。

考生作答时，将答案写在答题卡上，在本试卷上答题无效。

第Ⅰ卷(共126分)二、选择题：本题共8小题，每小题6分，共48分.在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多个选项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分.【题文】14．2011年12月在上海举行的汽车展销会上，一辆汽车从静止开始匀加速运动，表中给出了某些时刻汽车的瞬时速度，根据表中的数据通过分析、以下结论不正确．．．的是 ( )A54 mC．汽车第8 s末的速度为24 m/s D．汽车运动第7 s内的位移为16 m 【知识点】匀变速直线运动的速度与时间的关系；匀变速直线运动的位移与时间的关系．A2 【答案解析】 D解析：从表格中看出，在1.0-6.0s内，汽车每秒速度增加3m/s，加速度为：a＝vt∆∆=3m/s2，所以：A、汽车的加速度为3m/s2，故A正确；B、根据x=12at2得汽车前6s内的位移为：x＝12×3×62m＝54m，故B正确；C、根据v=at得汽车第8s的速度为v=3×8=24m/s，故C正确；D、汽车第7s内的位移为：x=12×3×72−12×3×62m=392m，故D错误．故选：D【思路点拨】根据汽车在不同时刻所对应的速度，根据匀加速直线运动的速度时间关系可以求出汽车运动的加速度，由加速度可以求出汽车的速度及位移与时间的关系．根据汽车在不同时刻所对应原速度根据加速度的定义求出汽车的加速度，再由速度时间关系和位移时间关系求解是关键【题文】15．如图所示，质量为M的直角劈B放在水平面上，在劈的斜面上放一质量为m的物体A，用一沿斜面向上的力F作用于A上，使其沿斜面匀速上滑，在A上滑的过程中直角劈B相对地面始终静止，则关于地面对劈的摩擦力F f及支持力F N，下列说法正确的是A．F f向左，F N<Mg＋mg B．F f＝0，F N＝Mg＋mgC．F f向右，F N<Mg＋mg D．F f向左，F N＝Mg＋mg【知识点】摩擦力的判断与计算；牛顿第二定律．B4 B7【答案解析】 A解析：据题，物体A和直角劈B都处于平衡状态，将它们看成整体，现对整体进行受力情况：重力（M+m）g、力F、地面竖直向上的支持力N和摩擦力．由平衡条件得知，F有水平向右的分力，则地面对B的摩擦力f水平向左．且有：N+Fsinα=（M+m）g，则可知：N＜（M+m）g．所以f向左，N＜Mg+mg．故选：A【思路点拨】物体A匀速上滑，受力平衡，而直角劈B始终处于静止状态，受力也平衡，将它们作为整体进行研究，分析受力情况，由平衡条件求解地面对劈的摩擦力f及支持力N，本题解题技巧在于选择整体进行研究，应用整体法求解，比较简单，也可以采用隔离法进行处理．【题文】16．一质点沿x轴做直线运动，其v-t图像如图所示．质点在t＝0时位于x＝5 m 处，开始沿x轴正向运动．当t＝8 s时，质点在x轴上的位置为A．x＝3 m B．x＝8 m C．x＝9 m D．x＝14 m【知识点】匀变速直线运动的图像．A5【答案解析】 B解析：图象的“面积”大小等于位移大小，图象在时间轴上方“面积”表示的位移为正，图象在时间轴下方“面积”表示的位移为负，故8s时位移为：s=2(24)1(24)22⨯+⨯+-m＝3m，由于质点在t=0时位于x=5m处，故当t=8s时，质点在x轴上的位置为8m，故ACD错误，B正确．故选：B．【思路点拨】速度时间图象可读出速度的大小和方向，根据速度图象可分析物体的运动情况，确定何时物体离原点最远．图象的“面积”大小等于位移大小，图象在时间轴上方“面积”表示的位移为正，图象在时间轴下方“面积”表示的位移为负．本题抓住速度图象的“面积”等于位移是关键．能根据图象分析物体的运动情况，通过训练，培养基本的读图能力．【题文】17．科技馆里有一个展品，该展品放在暗处，顶部有一个不断均匀向下喷射水滴的装置，在频闪光源的照射下，可以看到水滴好像静止在空中固定的位置不动，如图所示．某同学为计算该装置喷射水滴的时间间隔，用最小刻度为毫米的刻度尺测量了空中几滴水滴间的距离，由此可计算出该装置喷射水滴的时间间隔为(g取10 m/s2) A．0.01 s B．0.02 s C．0.1 s D．0.2 s【知识点】自由落体运动．A3【答案解析】 C 解析：根据△y=gT2，知：0.1s==．故C正确，A、B、D 错误．故选C．【思路点拨】自由落体运动是匀变速直线运动，根据连续相等时间内的位移之差是一恒量求出喷射水滴的时间间隔．解决本题的关键掌握匀变速直线运动的推论，在连续相等时间内的位移之差是一恒量．【题文】18．三个共点力大小分别是F1、F2、F3，关于它们的合力F的大小，下列说法中正确的是 ( )A．F大小的取值范围一定是0≤F≤F1＋F2＋F3B．F至少比F1、F2、F3中的某一个大C．若F1∶F2∶F3＝3∶6∶8，只要适当调整它们之间的夹角，一定能使合力为零D．若F1∶F2∶F3＝3∶6∶2，只要适当调整它们之间的夹角，一定能使合力为零【知识点】力的合成．B3【答案解析】 C 解析：A、三个力的合力最小值不一定为零，三个力最大值等于三个力之和．故A错误．B、合力可能比三个力都大，也可能比三个力都小．故B错误．C、若F1：F2：F3=3：6：8，设F1=3F，则F2=6F，F3=8F，F1、F2的合力范围为[3F，9F]，8F在合力范围之内，三个力的合力能为零．故C正确．D、若F1：F2：F3=3：6：2，设F1=3F，则F2=6F，F3=2F，F1、F2的合力范围为[3F，9F]，2F 不在合力范围之内，三个力的合力不可能为零．故D错误．故选C．【思路点拨】当三个力的方向相同时，合力最大，三个力的合力不一定为零，当第三个力不在剩余两个力的合力范围内，合力不能为零．解决本题的关键掌握两个力的合力范围，从而会通过两个力的合力范围求三个力的合力范围．【题文】19．如图所示装置，两物体质量分别为m1，m2，不计一切摩擦、滑轮质量和滑轮的直径，若装置处于静止状态，则A.m1可以大于m2B.m1一定大于m2/2C.m2可能等于m1/2D.θ1一定等于θ 2【知识点】共点力平衡的条件及其应用；力的合成与分解的运用． B3 B7【答案解析】 AD解析：对m2分析可知，m2受拉力及本身的重力平衡，故绳子的拉力等于m2g；对滑轮分析，由于滑轮跨在绳子上，故两端绳子的拉力相等，它们的合力一定在角平分线上；由于它们的合力与m1的重力大小相等，方向相反，故合力竖直向上，故两边的绳子与竖直方向的夹角θ1和θ2相等；故D正确；由以上可知，两端绳子的拉力等于m2g，而它们的合力等于m1g，因互成角度的两分力与合力组成三角形，故可知2m2g＞m1g，故m2＞1 2m1，故A正确，B错误故选：AD．【思路点拨】对m2分析可知绳子的拉力大小，对滑轮分析，由于滑轮放在一根绳子上，绳子两端的张力相等，故可知两绳子和竖直方向上的夹角相等，由共点力的平衡关系可得出两质量的关系．本题要注意题目中隐含的信息，记住同一绳子各部分的张力相等，即可由几何关系得出夹角的关系；同时还要注意应用力的合成的一些结论．【题文】20．如图所示A、B两个运动物体的位移—时间图象，下述说法正确的是A．A、B两个物体开始时相距100m，同时相向运动B．B物体做匀速直线运动，速度大小为5m/sC．A、B两个物体运动8s时，在距A的出发点60m处相遇D．A物体在运动中停了6s【知识点】匀变速直线运动的图像；匀变速直线运动的位移与时间的关系．A2 A5 A6 A8 【答案解析】 ABC解析：A、根据图象，A、B两物体开始时相距100m，速度方向相反，是相向运动，故A正确；B、s-t图象的斜率表示速度，故B物体做匀速直线运动，速度大小为：v=601008--=-5m/s；故B正确；C、t=8s时有交点，表面A、B两物体运动8s时，在距A的出发点60m处相遇，故C正确；D、2s-6s，物体A位置坐标不变，保持静止，即停止了4s；故D错误；故选：ABC．【思路点拨】在位移图象中图象的斜率代表物体运动的速度；交点表示相遇．①处理图象问题要注意纵横坐标所代表的物理意义；②s-t的斜率代表物体运动的速度，纵坐标相同代表两物体相遇；③无论v-t图还是s-t图只能描绘直线运动．【题文】21．如图所示为位于水平面上的小车，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆的下端固定有质量为m的小球。

山东省德州市平原一中2015届高三上学期第一次月考数学(文)试卷Word版含解析

2014-2015学年山东省德州市平原一中高三（上）第一次月考数学试卷（文科）一、选择题：每小题5分．1．已知函数f（x）=lg（1﹣x）的定义域为M，函数的定义域为N，则M∩N=（）A．{x|x＜1且x≠0} B．{x|x≤1且x≠0} C．{x|x＞1} D．{x|x≤1}2．下列有关命题的说法正确的是（）A．命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”B．“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C．命题“∃x∈R，使得x2+x+1＜0”的否定是：“∀x∈R，均有x2+x+1＜0”D．命题“若x=y，则sinx=siny”的逆否命题为真命题3．已知a=log23，b=log46，c=log49，则（）A．a=b＜c B．a＜b＜c C．a=c＞b D．a＞c＞b4．函数f（x）=Asin（ωx+φ）（其中）的图象如图所示，为了得到g（x）=sin2x的图象，则只需将f（x）的图象（）A．向右平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向左平移个长度单位5．设函数f（x）=sin（wx+）+sin（wx﹣）（w＞0）的最小正周期为π，则（）A．f（x）在（0，）上单调递增B．f（x）在（0，）上单调递减C．f（x）在（0，）上单调递增D．f（x）在（0，）上单调递减6．已知函数，其图象相邻的两条对称轴方程为x=0与，则（）A．f（x）的最小正周期为2π，且在（0，π）上为单调递增函数B．f（x）的最小正周期为2π，且在（0，π）上为单调递减函数C．f（x）的最小正周期为π，且在上为单调递增函数D．f（x）的最小正周期为π，且在上为单调递减函数7．在△ABC中，，则sin∠BAC=（）A． B． C．D．8．已知平面向量=（1，﹣2），=（4，m），且⊥，则向量5﹣3=（）A．（﹣7，﹣16） B．（﹣7，﹣34） C．（﹣7，﹣4）D．（﹣7，14）9．平行四边形ABCD中，=（1，0），=（2，2），则等于（）A．4 B．﹣4 C．2 D．﹣210．O是△ABC所在的平面内的一点，且满足（﹣）•（+﹣2）=0，则△ABC的形状一定为（）A．正三角形 B．直角三角形C．等腰三角形D．斜三角形二、填空题：每小题5分．11．如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在（0，1），此时圆上一点P的位置在（0，0），圆在x轴上沿正向滚动．当圆滚动到圆心位于（2，1）时，的坐标为．12．设、是平面内两个不平行的向量，若与平行，则实数m= ．13．在直角三角形ABC中，∠ACB=90°，AC=BC=2，点P是斜边AB上的一个三等分点，则= ．14．已知向量，的夹角为120°，且||=1，||=2，则向量﹣在向量+方向上的投影是．15．已知，是夹角为的两个单位向量，=﹣2，=k+，若•=0，则实数k的值为．三、解答题（本大题共6小题，共75分，解答应写出文字说、证明过程或演算步骤）16．已知向量=（cosx，sinx），=（﹣cosx，cosx），=（﹣1，0）（1）若x=，求向量，的夹角；（2）当x∈[，]时，求函数f（x）=2•+1的最小值．17．已知=（cosα，sinα），=（cosβ，sinβ），0＜β＜α＜π．（1）若|﹣|=，求证：⊥；（2）设=（0，1），若+=，求α，β的值．18．已知函数f（x）=2．（Ⅰ）求函数f（x）的最大值，并写出f（x）取最大值时x的取值集合；（Ⅱ）已知△ABC中，角A，B，C的对边分别为a，b，c，若f（A）=，b+c=2，求实数a 的最小值．19．在△ABC中，a、b、c分别为内角A、B、C的对边，且a2=b2+c2+bc（Ⅰ）求A的大小；（Ⅱ）若sinB+sinC=1，试求内角B、C的大小．20．已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜）的图象过点（0，），最小正周期为，且最小值为﹣1．（1）求函数f（x）的解析式．（2）若x∈[，m]，f（x）的值域是[﹣1，﹣]，求m的取值范围．21．已知函数f（x）=（x﹣a）lnx，a∈R．（Ⅰ）当a=0时，求函数f（x）的极小值；（Ⅱ）若函数f（x）在（0，+∞）上为增函数，求a的取值范围．2014-2015学年山东省德州市平原一中高三（上）第一次月考数学试卷（文科）参考答案与试题解析一、选择题：每小题5分．1．已知函数f（x）=lg（1﹣x）的定义域为M，函数的定义域为N，则M∩N=（）A．{x|x＜1且x≠0} B．{x|x≤1且x≠0} C．{x|x＞1} D．{x|x≤1}考点：函数的定义域及其求法；交集及其运算．专题：函数的性质及应用．分析：由函数y=lgx的定义域是{x|x＞0}和y=的定义域是{x|x≠0}，即可求出答案．解答：解：∵1﹣x＞0，得x＜1，∴函数f（x）=lg（1﹣x）的定义域M={x|x＜1}．∵x≠0时，函数有意义，∴函数的定义域N={x|x≠0}．∴M∩N={x|x＜1}∩{x|x≠0}={x|x＜1，且x≠0}．故选A．点评：本题考查函数的定义域，充分理解函数y=lgx和y=的定义域是解决问题的关键．2．下列有关命题的说法正确的是（）A．命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”B．“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C．命题“∃x∈R，使得x2+x+1＜0”的否定是：“∀x∈R，均有x2+x+1＜0”D．命题“若x=y，则sinx=siny”的逆否命题为真命题考点：命题的否定；必要条件、充分条件与充要条件的判断．分析：对于A：因为否命题是条件和结果都做否定，即“若x2≠1，则x≠1”，故错误．对于B：因为x=﹣1⇒x2﹣5x﹣6=0，应为充分条件，故错误．对于C：因为命题的否定形式只否定结果，应为∀x∈R，均有x2+x+1≥0．故错误．由排除法即可得到答案．解答：解：对于A：命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”．因为否命题应为“若x2≠1，则x≠1”，故错误．对于B：“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件．因为x=﹣1⇒x2﹣5x﹣6=0，应为充分条件，故错误．对于C：命题“∃x∈R，使得x2+x+1＜0”的否定是：“∀x∈R，均有x2+x+1＜0”．因为命题的否定应为∀x∈R，均有x2+x+1≥0．故错误．由排除法得到D正确．故答案选择D．点评：此题主要考查命题的否定形式，以及必要条件、充分条件与充要条件的判断，对于命题的否命题和否定形式要注意区分，是易错点．3．已知a=log23，b=log46，c=log49，则（）A．a=b＜c B．a＜b＜c C．a=c＞b D．a＞c＞b考点：对数值大小的比较．专题：函数的性质及应用．分析：根据对数函数的性质和对数的换底公式，即可比较大小．解答：解：根据对数的换底公式可知log23=log49，∴a=c，∵函数y=log4x，为增函数，∴log46＜log49，即a=c＞b，故选：C．点评：本题主要考查函数值的大小比较，利用对数函数的单调性和对数的换底公式是解决本题的关键．4．函数f（x）=Asin（ωx+φ）（其中）的图象如图所示，为了得到g（x）=sin2x的图象，则只需将f（x）的图象（）A．向右平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向左平移个长度单位考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题；数形结合．分析：由已知中函数f（x）=Asin（ωx+φ）的图象，我们易分析出函数的周期、最值，进而求出函数f（x）=Asin（ωx+φ）的解析式，设出平移量a后，根据平移法则，我们可以构造一个关于平移量a的方程，解方程即可得到结论．解答：解：由已知中函数f（x）=Asin（ωx+φ）（其中）的图象，过（，0）点，（）点，易得：A=1，T=4（）=π，即ω=2即f（x）=sin（2x+φ），将（）点代入得：+φ=+2kπ，k∈Z又由∴φ=∴f（x）=sin（2x+），设将函数f（x）的图象向左平移a个单位得到函数g（x）=sin2x的图象，则2（x+a）+=2x解得a=﹣故将函数f（x）的图象向右平移个长度单位得到函数g（x）=sin2x的图象，故选A点评：本题考查的知识点是由函数f（x）=Asin（ωx+φ）的图象确定其中解析式，函数f （x）=Asin（ωx+φ）的图象变换，其中根据已知中函数f（x）=Asin（ωx+φ）的图象，求出函数f（x）=Asin（ωx+φ）的解析式，是解答本题的关键．5．设函数f（x）=sin（wx+）+sin（wx﹣）（w＞0）的最小正周期为π，则（）A．f（x）在（0，）上单调递增B．f（x）在（0，）上单调递减C．f（x）在（0，）上单调递增D．f（x）在（0，）上单调递减考点：三角函数中的恒等变换应用；三角函数的周期性及其求法．专题：计算题；三角函数的图像与性质．分析：利用两角和与两角差的正弦可化简得f（x）=﹣sinwx，依题意知w=2，利用正弦函数的单调性可得答案．解答：解：∵f（x）=sin（wx+）+sin（wx﹣）=﹣sinwx+coswx﹣sinwx﹣coswx=﹣sinwx，又f（x）的最小正周期为π，w＞0，∴w=2．∴f（x）=﹣sin2x，∵y=sin2x在[﹣，]上单调递增，∴f（x）=﹣sin2x在[﹣，]上单调递减，∴f（x）在（0，）上单调递减，故选：B．点评：本题考查三角函数中的恒等变换应用，着重考查两角和与两角差的正弦及正弦函数的单调性与周期性，属于中档题．6．已知函数，其图象相邻的两条对称轴方程为x=0与，则（）A．f（x）的最小正周期为2π，且在（0，π）上为单调递增函数B．f（x）的最小正周期为2π，且在（0，π）上为单调递减函数C．f（x）的最小正周期为π，且在上为单调递增函数D．f（x）的最小正周期为π，且在上为单调递减函数考点：两角和与差的正弦函数；三角函数的周期性及其求法；正弦函数的单调性．专题：三角函数的图像与性质．分析：利用两角和差的正弦公式化简函数的解析式为f（x）=2sin（ωx﹣），由题意可得=，解得ω的值，即可确定函数的解析式为f（x）=2sin（2x﹣），由此求得周期，由2kπ﹣≤2x﹣≤2kπ+，k∈z，求得x的范围，即可得到函数的增区间，从而得出结论．解答：解：∵函数=2[sin（ωx﹣cosωx]=2sin（ωx﹣），∴函数的周期为．再由函数图象相邻的两条对称轴方程为x=0与，可得=，解得ω=2，故f（x）=2sin（2x﹣）．故f（x）=2sin（2x﹣）的周期为=π．由 2kπ﹣≤2x﹣≤2kπ+，k∈z，可得kπ﹣≤x≤kπ+，故函数的增区间为[kπ﹣，kπ+]，k∈z，故函数在上为单调递增函数，故选C．点评：本题主要考查两角和差的正弦公式，正弦函数的图象、周期性及单调性，属于中档题．7．在△ABC中，，则sin∠BAC=（）A． B． C．D．考点：余弦定理；正弦定理．专题：解三角形．分析：由AB，BC及cos∠ABC的值，利用余弦定理求出AC的长，再由正弦定理即可求出sin∠BAC的值．解答：解：∵∠ABC=，AB=，BC=3，∴由余弦定理得：AC2=AB2+BC2﹣2AB•BC•cos∠ABC=2+9﹣6=5，∴AC=，则由正弦定理=得：sin∠BAC==．故选C点评：此题考查了正弦、余弦定理，熟练掌握正弦、余弦定理是解本题的关键．8．已知平面向量=（1，﹣2），=（4，m），且⊥，则向量5﹣3=（）A．（﹣7，﹣16） B．（﹣7，﹣34） C．（﹣7，﹣4）D．（﹣7，14）考点：数量积判断两个平面向量的垂直关系．专题：平面向量及应用．分析：利用向量垂直与数量积的关系即可得出．解答：解：∵，∴，解得m=2，∴=（5，﹣10）﹣（12，6）=（﹣7，﹣16）．故选A．点评：熟练掌握向量垂直与数量积的关系是解题的关键．9．平行四边形ABCD中，=（1，0），=（2，2），则等于（）A．4 B．﹣4 C．2 D．﹣2考点：平面向量数量积的运算．专题：平面向量及应用．分析：利用向量的运算法则和数量积的运算即可得出．解答：解：如图所示：由向量的加减可得：=（1，2）；====（0，2），∴==（1，2）•（0，2）=0+4=4．故选A．点评：熟练掌握向量的运算法则和数量积的运算是解题的关键．10．O是△ABC所在的平面内的一点，且满足（﹣）•（+﹣2）=0，则△ABC的形状一定为（）A．正三角形 B．直角三角形C．等腰三角形D．斜三角形考点：三角形的形状判断．专题：计算题．分析：利用向量的运算法则将等式中的向量用三角形的各边对应的向量表示，得到边的关系，得出三角形的形状．解答：解：∵====0，∴∴△ABC为等腰三角形．故选C点评：此题考查了三角形形状的判断，涉及的知识有平面向量的平行四边形法则，平面向量的数量积运算，向量模的计算，以及等腰三角形的判定方法，熟练掌握平面向量的数量积运算法则是解本题的关键．二、填空题：每小题5分．11．如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在（0，1），此时圆上一点P的位置在（0，0），圆在x轴上沿正向滚动．当圆滚动到圆心位于（2，1）时，的坐标为（2﹣sin2，1﹣cos2）．考点：圆的参数方程；平面向量坐标表示的应用．专题：平面向量及应用；坐标系和参数方程．分析：设滚动后圆的圆心为O'，切点为A，连接O'P．过O'作与x轴正方向平行的射线，交圆O'于B（3，1），设∠BO'P=θ，则根据圆的参数方程，得P的坐标为（2+cosθ，1+sinθ），再根据圆的圆心从（0，1）滚动到（2，1），算出θ=﹣2，结合三角函数的诱导公式，化简可得P的坐标为（2﹣sin2，1﹣cos2），即为向量的坐标．解答：解：设滚动后的圆的圆心为O'，切点为A（2，0），连接O'P，过O'作与x轴正方向平行的射线，交圆O'于B（3，1），设∠BO'P=θ∵⊙O'的方程为（x﹣2）2+（y﹣1）2=1，∴根据圆的参数方程，得P的坐标为（2+cosθ，1+sinθ），∵单位圆的圆心的初始位置在（0，1），圆滚动到圆心位于（2，1）∴∠AO'P=2，可得θ=﹣2可得cosθ=cos（﹣2）=﹣sin2，sinθ=sin（﹣2）=﹣cos2，代入上面所得的式子，得到P的坐标为（2﹣sin2，1﹣cos2）∴的坐标为（2﹣sin2，1﹣cos2）．故答案为：（2﹣sin2，1﹣cos2）点评：本题根据半径为1的圆的滚动，求一个向量的坐标，着重考查了圆的参数方程和平面向量的坐标表示的应用等知识点，属于中档题．12．设、是平面内两个不平行的向量，若与平行，则实数m= ﹣1 ．考点：平行向量与共线向量．专题：平面向量及应用．分析：利用向量共线定理和平面向量基本定理即可得出．解答：解：∵与平行，∴存在实数k使得，∴=，∵、是平面内两个不平行的向量，∴，解得m=k=﹣1．故答案为：﹣1．点评：本题考查了向量共线定理和平面向量基本定理，属于基础题．13．在直角三角形ABC中，∠ACB=90°，AC=BC=2，点P是斜边AB上的一个三等分点，则= 4 ．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由题意建立直角坐标系，可得及，的坐标，而原式可化为，代入化简可得答案．解答：解：由题意可建立如图所示的坐标系可得A（2，0）B（0，2），P（，）或P（，），故可得=（，）或（，），=（2，0），=（0，2），所以+=（2，0）+（0，2）=（2，2），故==（，）•（2，2）=4或=（，）•（2，2）=4，故答案为：4点评：本题考查平面向量的数量积的运算，建立坐标系是解决问题的关键，属基础题．14．已知向量，的夹角为120°，且||=1，||=2，则向量﹣在向量+方向上的投影是﹣．考点：平面向量数量积的含义与物理意义．专题：计算题；平面向量及应用．分析：利用求模运算得到，，进而得到向量﹣与向量+的夹角余弦，根据投影定义可得答案．解答：解：=1+2cos120°+4=3，所以，=1﹣2×1×2cos120°+4=7，所以，则cos＜，＞==，所以向量﹣在向量+方向上的投影是==﹣，故答案为：﹣．点评：本题考查平面向量数量积的含义及其物理意义，考查向量模的求解投影等概念，属基础题．15．已知，是夹角为的两个单位向量，=﹣2，=k+，若•=0，则实数k的值为．考点：平面向量数量积的运算．专题：平面向量及应用．分析：利用向量的数量积公式求出；利用向量的运算律求出，列出方程求出k．解答：解：∵是夹角为的两个单位向量∴∴==∵∴解得故答案为：点评：本题考查向量的数量积公式、考查向量的运算律、考查向量模的平方等于向量的平方．三、解答题（本大题共6小题，共75分，解答应写出文字说、证明过程或演算步骤）16．已知向量=（cosx，sinx），=（﹣cosx，cosx），=（﹣1，0）（1）若x=，求向量，的夹角；（2）当x∈[，]时，求函数f（x）=2•+1的最小值．考点：平面向量的综合题．专题：三角函数的求值；平面向量及应用．分析：（1）根据数量积条件下的夹角公式，将已知条件代入可求得两向量夹角的余弦值，再根据余弦函数的单调性及向量夹角的范围确定夹角；（2）通过利用三角变换先将f（x）=2•+1化简成一个角，一次，一种三角函数（正弦或余弦）的形式，再借助于换元思想研究该函数的最小值．解答：解：（1）当x=时，===又因为0≤π，∴=．（2）f（x）==2（﹣cos2x+sinxcosx）+1=2sinxcosx﹣（2cos2x﹣1）==sin2x﹣cos2x=sin（2x﹣）∵x∈[]，∴∈[]，故sin（）∈[﹣1，]，∴当，即x=时，f（x）=﹣．点评：本题是一道平面向量与三角函数的综合题，一般是先利用数量积的定义将所求表示成三角函数的形式，再借助于三角恒等变换将函数化简成形如y=Asin（ωx+θ）+C的形式，然后再求解．要注意计算准确．17．已知=（cosα，sinα），=（cosβ，sinβ），0＜β＜α＜π．（1）若|﹣|=，求证：⊥；（2）设=（0，1），若+=，求α，β的值．考点：平面向量数量积的运算；向量的模；同角三角函数间的基本关系；两角和与差的余弦函数；两角和与差的正弦函数．专题：平面向量及应用．分析：（1）由给出的向量的坐标，求出的坐标，由模等于列式得到cosαcosβ+sinαsinβ=0，由此得到结论；（2）由向量坐标的加法运算求出+，由+=（0，1）列式整理得到，结合给出的角的范围即可求得α，β的值．解答：解：（1）由=（cosα，sinα），=（cosβ，sinβ），则=（cosα﹣cosβ，sinα﹣sinβ），由=2﹣2（cosαcosβ+sinαsinβ）=2，得cosαcosβ+sinαsinβ=0．所以．即；（2）由得，①2+②2得：．因为0＜β＜α＜π，所以0＜α﹣β＜π．所以，，代入②得：．因为．所以．所以，．点评：本题考查了平面向量的数量积运算，考查了向量的模，考查了同角三角函数的基本关系式和两角和与差的三角函数，解答的关键是注意角的范围，是基础的运算题．18．已知函数f（x）=2．（Ⅰ）求函数f（x）的最大值，并写出f（x）取最大值时x的取值集合；（Ⅱ）已知△ABC中，角A，B，C的对边分别为a，b，c，若f（A）=，b+c=2，求实数a 的最小值．考点：余弦定理的应用；两角和与差的正弦函数；二倍角的余弦．专题：综合题；解三角形．分析：（Ⅰ）利用二倍角公式及辅助角公式，化简函数，即可求得函数的最大值，从而可得f（x）取最大值时x的取值集合；（Ⅱ）利用f（A）=sin（2A+）+1=，求得A，在△ABC中，根据余弦定理，利用b+c=2，及，即可求得实数a的最小值．解答：解：（Ⅰ）函数f（x）=2=（1+cos2x）﹣（sin2xcos﹣cos2xsin）=1+sin2x+=1+sin（2x+）．∴函数f（x）的最大值为2．要使f（x）取最大值，则sin（2x+）=1，∴2x+=2kπ+（k∈Z）∴x=kπ+（k∈Z）．故x的取值集合为{x|x=kπ+（k∈Z）}．（Ⅱ）由题意，f（A）=sin（2A+）+1=，化简得sin（2A+）=，∵A∈（0，π），∴2A+∈，∴2A+=，∴A=在△ABC中，根据余弦定理，得=（b+c）2﹣3bc．由b+c=2，知，即a2≥1．∴当b=c=1时，实数a取最小值1．点评：本题考查三角函数的化简，考查函数的最值，考查余弦定理的运用，考查基本不等式，综合性强．19．在△ABC中，a、b、c分别为内角A、B、C的对边，且a2=b2+c2+bc（Ⅰ）求A的大小；（Ⅱ）若sinB+sinC=1，试求内角B、C的大小．考点：余弦定理；两角和与差的正弦函数．专题：解三角形．分析：（Ⅰ）由a2=b2+c2+bc，利用余弦定理得a2=b2+c2﹣2bccosA，求得cosA的值，即可求得A的大小．（Ⅱ）由A的值求得B+C的值，利用两角和差的正弦公式求得 sin（B+）=1，从而求得B+的值，求得B的值，进而求得C的大小．解答：解：（Ⅰ）∵a2=b2+c2+bc，由余弦定理得a2=b2+c2﹣2bccosA，故cosA=，A=120°．（Ⅱ）∴B+C=，∵sinB+sinC=1，∴，∴，∴=1．又∵B为三角形内角，∴B+=，故B=C=．点评：本题主要考查余弦定理，两角和差的正弦、余弦公式的应用，根据三角函数的值求角，属于中档题．20．已知函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜）的图象过点（0，），最小正周期为，且最小值为﹣1．（1）求函数f（x）的解析式．（2）若x∈[，m]，f（x）的值域是[﹣1，﹣]，求m的取值范围．考点：函数y=Asin（ωx+φ）的图象变换．专题：计算题；三角函数的图像与性质．分析：（1）依题意，易求A=1，ω=3，由函数的图象过点（0，），0＜φ＜，可求得φ=，从而可得函数f（x）的解析式．（2）x∈[，m]⇒≤3x+≤3m+，依题意，利用余弦函数的性质可得π≤3m+≤，从而可求m的取值范围．解答：解：（1）由函数的最小值为﹣1，A＞0，得A=1，∵最小正周期为，∴ω==3，∴f（x）=cos（3x+φ），又函数的图象过点（0，），∴cosφ=，而0＜φ＜，∴φ=，∴f（x）=cos（3x+），（2）由x∈[，m]，可知≤3x+≤3m+，∵f（）=cos=﹣，且cosπ=﹣1，cos=﹣，由余弦定理的性质得：π≤3m+≤，∴≤m≤，即m∈[，]．点评：本题考查函数y=Asin（ωx+φ）确定函数解析式，着重考查余弦函数的单调性，考查解不等式的能力，属于中档题．21．已知函数f（x）=（x﹣a）lnx，a∈R．（Ⅰ）当a=0时，求函数f（x）的极小值；（Ⅱ）若函数f（x）在（0，+∞）上为增函数，求a的取值范围．考点：利用导数研究函数的极值；利用导数研究函数的单调性．专题：导数的综合应用．分析：（Ⅰ）当a=0时，可得函数f（x）的解析式，求导数，令导数为0，解出x的值，利用导函数值的正负来求其单调区间，进而求得其极小值；（Ⅱ）求导函数，由于函数f（x）在（0，+∞）上为增函数，转化为f'（x）≥0，对x∈（0，+∞）恒成立，分离参数，利用导数求g（x）=xlnx+x的最小值，即可求实数a的取值范围．解答：解：（Ⅰ）定义域（0，+∞）．当a=0时，f（x）=xlnx，f'（x）=lnx+1．令f'（x）=0，得．当时，f'（x）＜0，f（x）为减函数；当时，f'（x）＞0，f（x）为增函数．所以函数f（x）的极小值是．（Ⅱ）由已知得．因为函数f（x）在（0，+∞）是增函数，所以f'（x）≥0，对x∈（0，+∞）恒成立．由f'（x）≥0得，即xlnx+x≥a对x∈（0，+∞）恒成立．设g（x）=xlnx+x，要使“xlnx+x≥a对x∈（0，+∞）恒成立”，只要a≤g（x）min．因为g'（x）=lnx+2，令g'（x）=0得．当时，g'（x）＜0，g（x）为减函数；当时，g'（x）＞0，g（x）为增函数．所以g（x）在（0，+∞）上的最小值是．故函数f（x）在（0，+∞）是增函数时，实数a的取值范围是．点评：本题主要考查利用导数研究函数的极值以及函数的单调性，利用导数研究函数的单调性，求解函数的单调区间、极值、最值问题，是函数这一章最基本的知识，也是教学中的重点和难点，学生应熟练掌握．。

河南省开封市兰考三高2015届高三上学期第一次月考数学文试题 Word版含答案

侧视图2014-2015年高三第一次月考高三数学（文科）试题说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）满分150分，考试时间120分钟.第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．集合{}0,2,A a=，{}21,B a=，若{}0,1,2,4,16A B=，则a的值为A．0 B．1 C．2 D．42．设1z i=-（i是虚数单位），则2zz+=A．22i-B．22i+C．3i-D．3+3．下列说法中，正确的是A．命题“存在2,0x R x x∈->”的否定是“对任意2,x R x x∈-B．设,αβ为两个不同的平面，直线lα⊂，则“lβ⊥”是“αβ⊥” 成立的充分不必要条件.C．命题“若a b<，则22am bm<”的否命题是真命题.D．已知x R∈，则“1x>”是“2x>”的充分不必要条件.4．执行右面的框图，输出的结果s的值为A．3-B．2C．12-D．135．平面向量与的夹角为60°，1||),0,2(==，则|2|+A B．C．4 D．26．某三棱锥的三视图如图所示，该三棱锥的体积是A．83B．4 C．2 D．437．要得到函数sin24y xπ=-（）的图象，只要将函数sin2y x=的图象A．向左平移4π单位B．向右平移4π单位C．向右平移8π单位D．向左平移8π单位8．若直线2y x=上存在点(,)x y满足约束条件30230x yx yx a+-≤⎧⎪⎪--≤⎨⎪≥⎪⎩，则实数a的最大值为A ．-1B ．1C ．32D ．2 9．对数函数x y a log =(10≠>a a 且)与二次函数()x x a y --=21在同一坐标系内的图象可能是10．设函数()f x 的导函数为'()f x ，对任意x R ∈都有'()()f x f x >成立，则 A ．)3(ln 2)2(ln 3f f > B ．)3(ln 2)2(ln 3f f =C ．)3(ln 2)2(ln 3f f <D ．)3(ln 2)2(ln 3f f 与的大小不确定11. 函数1()ln 1f x x x =--在区间(),1k k +(k N ∈)上存在零点，则k 的值为 A ．0B ．2C ．0或1D ．0或212. 已知21F F 、分别是双曲线:C 12222=-by a x 的左、右焦点，若2F 关于渐近线的对称点恰落在以1F 为圆心，||1OF 为半径的圆上，则双曲线C 的离心率为 A ．3B ．3C ．2D ．2第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题 5分，共20分.13．若)2sin(3)6sin(αππα-=+，则=α2tan __________． 14．若直线l 是曲线31:13C y x x =++斜率最小的切线，则直线l 与圆2212x y +=的位置关系为 .15. 已知正项等比数列{a n }满足：a 7＝a 6＋2a 5，若存在两项a m ，a n 使得a m a n ＝4a 1，则1m ＋4n的最小值为 . 16. 定义:如果函数()y f x =在区间[],a b 上存在00()x a x b <<，满足0()()()f b f a f x b a-=-，则称0x 是函数()y f x =在区间[],a b 上的一个均值点.已知函数2()1f x x mx =-++在区间[]1,1-上存在均值点，则实数m 的取值范围是________.三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.17．设数列{}n a 满足12a =，248a a +=，且对任意*n N ∈，函数1212()()cos sin n n n n n f x a a a x a x a x ++++=-++⋅-⋅，满足'()02f π=.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若122n n n a b a =+（），求数列{}n b 的前n 项和n S .18. 有甲乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成已知在全部105人中随机抽取1人为优秀的概率为7. (Ⅰ)请完成上面的列联表； (Ⅱ)根据列联表的数据，若按95%的可靠性要求，能否认为“成绩与班级有关系” ; (Ⅲ)若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.参考公式: 22()()()()()n ad bc K a b c d a c b d -=++++参考数据：19. 如图，在平面四边形ABCD 中，已知45,90A C ∠=︒∠=︒，105,,ADC AB BD ∠=︒=现将四边形ABCD 沿BD 折起，使平面ABD ⊥平面BDC ，设点F 为棱AD 的中点. (1)求证:DC ⊥平面ABC; (2)求直线BF 与平面ACD 所成角的余弦值.20. 给定椭圆2222:1(0)y x C a b a b+=>>，称圆心在坐标原点O 的圆是椭圆C 的“伴随圆”. 若椭圆C 的一个焦点为20)F ，其短轴上的一个端点到2F (Ⅰ)求椭圆C 及其“伴随圆”的方程;(Ⅱ)若过点(0,)(0)P m m <的直线与椭圆C 只有一个公共点，且截椭圆C 的“伴随圆”所得的弦长为m 的值;(Ⅲ)过椭圆C 的“伴椭圆”上一动点Q 作直线12,l l ，使得12,l l 与椭圆C 都只有一个公共点，当直线12,l l 都有斜率时，试判断直线12,l l 的斜率之积是否为定值，并说明理由.21. 已知函数()()12ln 2(0)f x a x ax a x=-++≤. (Ⅰ)当0a =时，求()f x 的极值; (Ⅱ)当0a <时，讨论()f x 的单调性;(Ⅲ)若对任意的()[]123,2,,1,3,a x x ∈--∈恒有()()()12ln 32ln 3m a f x f x +->-成立，求实数m 的取值范围.D C B AFD C BA请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分. 22．选修4－1：几何证明选讲如图，直线AB 为圆的切线，切点为B ，点C 在圆上，ABC ∠的角平分线BE 交圆于点E ，DB 垂直BE 交圆于点D . （Ⅰ）证明：DB DC =；（Ⅱ）设圆的半径为1，BC =，延长CE 交AB 于点F ，求ΔBCF 外接圆的半径.23．选修4－4；极坐标与参数方程已知在平面直角坐标系xOy 中，直线l 过点P （1，-5），且倾斜角为3π，以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，半径为4的圆C 的圆心的极坐标为(4,)2π．（Ⅰ）写出直线l 的参数方程和圆C 的极坐标方程；（Ⅱ）试判定直线l 和圆C 的位置关系．24．选修4－5：不等式选讲已知函数()|21||2|f x x x a =-++，()3g x x =+. （Ⅰ）当2a =-时，求不等式()()f x g x <的解集；（Ⅱ）设1a >-，且当1[,)22a x ∈-时，()()f x g x ≤，求a 的取值范围高三数学（文科）一、选择题D B C A B B C B A C D D 二、填空题13.14. 相切 15. 32 16. (0,2)三、解答题17. 解:由1212()()cos -sin n n n n n f x a a a x a x a x ++++=-++⋅⋅1212--sin -cos n n n n n f x a a a a x a x ++++'=+⋅⋅（） 121'()--02n n n n f a a a a π+++=+= 所以,122n n n a a a ++=+ {}n a ∴是等差数列. 而12a = 34a = 1d = 2-111n a n n ∴=+⋅=+（）(2)111122121222n n n a n nb a n n +=+=++=++（）（）（） FED CB A111-22122121-2n n n n S ++=+（）（） 21=31-2n n n ++ 18. 解：(Ⅰ)(Ⅱ)根据列联表中的数据，得到22105(10302045) 6.109 3.84155503075k ⨯⨯-⨯=≈>⨯⨯⨯因此95%的把握认为“成绩与班级有关系”.(Ⅲ)设“抽到6或10号”为事件A ，先后两次抛掷一枚均匀的骰子，出现的点数为（x ，y ）. 所有的基本事件有（1，1）、（1，2）、（1，3）、……、（6，6），共36个. 事件A 包含的基本事件有：（1，5）、（2，4）、（3，3）、（4，2）、（5，1）（4，6）、（5，5）、（6、4），共8个82()369P A ∴==. 19. (1)证明:在图甲中∵AB BD =且45A ∠= ∴45ADB ∠= ,90ABD ∠= 即AB BD ⊥在图乙中,∵平面ABD ⊥平面BDC , 且平面ABD 平面BDC=BD∴AB ⊥底面BDC ,∴AB ⊥CD . 又90DCB∠=,∴DC ⊥BC ,且ABBC B=∴DC ⊥平面ABC(2)解:作BE⊥AC,垂足为E.由(1)知平面ABC⊥平面ACD,又平面ABC ⋂平面ACD=AC,∴BF ⊥平面ADC , ∴BFE ∠即为直线BF 与平面ACD 所成角. 设CD a =得AB=2,BD a BC =.∴BE =,BF =,FE =.∴cos BFE ∠==∴直线BF 与平面ACD .20. 解：（1）椭圆C 方程为：2213x y +=；椭圆C 的“伴随圆”方程为224x y +=；（2）设直线方程为：y kx m =+因为截椭圆C 的“伴随圆”所得弦长为.222(1)d m k ===+又2233x y y kx m ⎧+=⎨=+⎩ 得222(13)6330x k mkx m +++-= 22130k m ∆=+-= 24,2m m ∴==-（3）设00(,)Q x y ，直线00()y y k x x -=- 由（2）知2222001313()0k m k y kx +-=+--=即2220000(3)210k x x y k y -++-=2220120020121431y k k x y x k k -∴=+=-∴=-又为定值.21. 解: (1) 当0a =时,()()22121212ln ,(0).x f x x f x x x x x x-'=+=-=> ∴ ()f x 在10,2⎛⎫ ⎪⎝⎭上是减函数,在1,2⎛⎫+∞ ⎪⎝⎭上是增函数∴ ()f x 的极小值为122ln 22f ⎛⎫=- ⎪⎝⎭, 无极大值(2)()()()()2222221121212(0)ax a x ax x a f x a x x x x x +--+--'=-+==>① 当20a -<<时,()f x 在10,2⎛⎫ ⎪⎝⎭和1,a ⎛⎫-+∞ ⎪⎝⎭上是减函数,在11,2a ⎛⎫- ⎪⎝⎭上是增函数;② 当2a =-时,()f x 在()0,+∞上是减函数;③ 当2a <-时,()f x 在1,2⎛⎫+∞⎪⎝⎭和10,a ⎛⎫- ⎪⎝⎭上是减函数,在11,2a ⎛⎫- ⎪⎝⎭上是增函数(3) 当32a -<<-时,由(2)可知()f x 在[]1,3上是减函数,∴ ()()()()()1221342ln 33f x f x f f a a -≤-=-+- 由()()()12ln 32ln 3m a f x f x +->-对任意的()[]123,2,,1,3a x x ∈--∈恒成立,∴ ()()()12maxln 32ln 3m a f x f x +->-即()()2ln 32ln 342ln 33m a a a +->-+-对任意32a -<<-恒成立, 即243m a<-+对任意32a -<<-恒成立, 由于当32a -<<-时,132384339a -<-+<-, ∴ 133m ≤-22.解：（1）连接DE ，交BC 为G ，由弦切角定理得，ABE BCE ∠=∠，DB而,,ABE CBE CBE BCE BE CE ∠=∠∠=∠=故.又因为DB BE ⊥，所以DE 为直径，∠DCE=90°，由勾股定理可得DB=DC.（II ）由（1），CD E B D E ∠=∠，DB DC =，故DG 是BC的中垂线，所以2BG =，圆心为O ，连接BO ，则60BOG ∠=，ABE BCE CB∠=∠=∠，所以CF BF⊥，故外接圆半径为2. 24. 解：（I ）当2()a f x =-时，不等式<g(x)化为21223x x x -+---<0. 设函数y=21223x x x -+---，则15,212,1,236, 1.x x y x x x x ⎧-<⎪⎪⎪=--≤≤⎨⎪->⎪⎪⎩其图像如图从图像可知，当且仅当x (0,2)∈时，y<0，所以原不等式的解集是{}02x x <<；(II)当1[,),()1.22a x f x a ∈-=+不等式()()f x g x ≤化为13a x +≤+ 所以2x a ≥-对1[,)22a x ∈-都成立，故22aa -≥-，即43a ≤从而a 的取值范围是4(1,]3-。

重庆开县中学2015届高三第五期第一次月考(含解析)

开县中学高2015级第五期第一次月考历史试题一、选择题（每小题4分，共48分）1、关于西周灭亡的原因，司马迁认为是“烽火戏诸侯”；学者李峰在《西周的灭亡》一书中综合运用了考古发现、铭文和文献记录，同时又联系当时的地表形态特征，认为西周的衰落是由西周国家的基本统治结构决定的，其灭亡的外部重要原因主要是西北地区少数部族的侵袭。

你认为（）A、司马迁的观点属内因决定外因论，符合历史事实B、李峰的观点有考古发现及文献记录等为依据，比较可靠C、两人分别从不同角度探讨西周灭亡的原因，均为一家之言D、由于年代久远，两人的观点都是主观臆测，均不足为信【答案】B考点：商周时期的政治制度。

本题主要考查学生准确解读材料信息的能力。

通过材料可知司马迁认为西周的灭亡是外部的原因，所以A选项是错误的。

历史研究要讲究史实，这就要求通过考古发现，文献记载和史料记载等多种手段得出结论，所以材料中“某学者”的观点真实可靠。

所以答案选Ｂ。

2、“密折”一词始用于康熙朝，最初为一种特权，仅限于少数亲信官员等使用。

康熙五十一年前后，地方和中央人员才普遍获得奏折权。

雍正帝继位以后，又给予道员、知府、同知、副将一级的官员密上奏折的权力。

据统计，当时上密奏折的权力。

据统计，当时上密折的人数已达到1000人以上。

这表明（）A、清朝中央政府决策的开放性B、专制主义中央集权达到顶峰C、中央的政治权力进一步加强D、清朝加强了对人民的控制和镇压【答案】C考点：君主专制的强化。

本题考查获取材料信息、调用所学知识的能力，材料并没有反映出皇帝先接受地方官的建议再作出决策，故A项错误；专制主义达到顶峰的标志是清军机处的设立，故B 项错误；密上奏折表面上看是皇帝的恩惠，实际上皇帝通过此举可以进一步了解地方官的情况，以加强中央对地方的控制，故C项正确；D项在材料中没有体现，故排除。

3、《十二铜表法》规定：“出卖的物品纵使交付，非在买受人付清价款或提供担保以满足出卖人的要求后，其所有权并不移转。

宁夏银川一中2015届高三上学期第一次月考(含答案)

宁夏银川一中2015届高三上学期第一次月考英语试卷第Ⅰ卷本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部份。

考生做答时，将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码贴在答题卡的指定位置上。

2. 选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清晰。

3. 请按题号在各题的的答题区域(黑色线框)内作答，超出答题区域书写的答案无效。

4．保持卡面清洁，不折叠，不破损。

第一部分：听力（共两节，满分20分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节：（共5小题；第小题1分，满分5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳答案，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. ￡19.15.B. ￡9.15.C. ￡9.18. 答案是B。

1. What will the man probably do?A. Come in twenty minutesB. Have dinnerC. Go shopping2. What does the man mean?A. He went mountain climbing last year.B. He doesn’t want to go mountain climbing at all.C. He hasn’t traveled around the world yet.3. Why can Louise speak English well?A. Her family speak English.B. She spent her early years in America.C. She’s an American native.4. What does the woman mean?A. The man should wear his new shirt.B. This shirt needs to be washed first.C. This shirt is not suitable for today.5. What does the woman mean?A. The man will receive his order today.B. The man can call her again this afternoon.C. The man can come to pick it up if he wants.第二节（共15小题；每小题1分，满分15分）听下面5段对话或独白。

【名师解析】河南省南阳一中2015届高三上学期第一次月考英语试题 Word版含解析

南阳一中2012级高三秋期第一次月考英语试题【试卷综评】试卷以新课标为指导，从学什么，考什么的原则出发，遵循“题在书中”，既重基础又注重综合能力的提高。

本套试卷具有很好的区分度，即全面考查考生的基础知识与技能，又考查学生分析问题，解决问题的能力，测试效果较为明显。

阅读理解中的推理判断题，主旨大意题仍然是学生的薄弱环节，应重点练习。

做完型填空时，注意整体上把握文章大意。

书面表达以半开放式作文形式出现，即给出一定的提示内容，又要考生根据提示内容进行适当的发挥，从而有效考查考生的书面表达能力；总之，本次期中试卷难度适中，是一份质量较高的试卷。

温馨提示：1.本试卷满分150分= （阅读理解40分+完型20+语法填空15+单词拼写10+短文改错10+书面表达25分）×1.25分2.从21题开始根据题号涂卡。

第一部分：听力(略)第二部分：阅读理解（共2节，满分40分）第一节（共15小题；每小题2分，满分30分）（命题人：乾正潮）阅读下列短文，从每题所给的A、B、C和D中，选出最佳答案，并在答题卡上将该项涂黑。

【题文】AA group of 1309 passengers boarded the MS Balmoral on Sunday, in Southampton, England, on a voyage to retrace(重走) the path of the Titanic. The Titanic was the biggest ship in the world when it sailed on its ill-fated first voyage on April 10, 1912. Of the 2227 passengers and crew aboard, more than1500 died. The ship, which was headed for New York City, carried the rich and famous on its first voyage. It also carried immigrants who were seeking a better life in America.Relatives of people who sailed on the Titanic, historians, authors and people fascinated by the story of the unsinkable ship were on the Balmoral. They wanted to remember the Titanic and those who died on her first and last voyage.The Balmoral is following Titanic's original route from Southampton. First, the modern-day cruise liner docked（进港）in the port of Cherbourg, France, where the Titanic had picked up more passengers. On Monday afternoon, the Balmoral stops in Cobh, Ireland, the Titanic's last port of call before sailing to New York.The Balmoral then sailed the North Atlantic Ocean to the location where Titanic hit an iceberg . On Sunday, April 15, at 2：20 a. m. --- the time the Titanic went down---passengers andcrew held a memorial service. The next two days were spent in Halifax, Canada, where many victims of the sinking are buried. Then, the Balmoral will reach its final destination in New York City, where Titanic was supposed to dock—but never did.So far, several teams of divers have explored the site. They have recovered some items such as dishes and silverware and put them on public display. And more trips are planned to the wreckage in the future. The Titanic and its passengers and crew have been remembered in books, movies and TV programs. But there's a much more important contribution that Titanic gave us. After she sank, lawmakers and shipbuilders made ships safer. It took a terrible tragedy to make ship travel safer for all.21．We learn from the first paragraph that .A．about 700 passengers of the Titanic survived.B．the Titanic sank on its second voyage.C．less than 2000 passengers boarded the Titanic.D．all the passengers’ hopes of the Titanic lay in America.22．Which of the following shows the correct route of the Balmoral?a. Halifaxb. New York Cityc. Cobhd. Southamptone. CherbourgA．e-d-a-b-c B．d-e-c-a-b C．e-c-a-b-d D．d-c-e-a-b23．What might be the most important contribution of the Titanic?A．Its site attracts more exploring teams. B．It makes the later ships more secure.C．Some of its items are on public display. D．More trips are planned to its wreckage. 【答案】【知识点】C7社会生活类【文章综述】本文讲述了MS Balmoral 号的1,309乘客和船员们重走当年泰坦尼克号的路线，在泰坦尼克号当年沉没的地方举行了追悼会，来纪念死去的人们。

【名师解析】重庆市重庆一中2015届高三上学期第一次月考地理试题 Word版含解析

秘密★启用前2014年重庆一中高2015级高三上期第一次月考文科综合能力测试试题卷 2014.9【试卷综析】本试卷是高三年级月考文综试题，本试题考查的知识点有：地球、地图的基础知识，地球运动的意义，影响气候的形成因素，气候特点的对比，河流水文特征，板块分布，农业区位因素的对比，河流的综合开发，区域农业可持续发展，高新技术产业的区位因素，能源消费结构及意义等，该试题多以区域地理内容为载体，考查学生的定位、读图能力，体现了以基础知识和基本技能为载体，以能力测试为主导，在注重考查学科核心知识的同时，突出考查考纲要求的基本能力，重视学生科学素养的考查。

本试卷整体涉及知识点较多，难度中等，是一套不错的月考试题。

文科综合能力测试试题卷分为思想政治、历史、地理三个部分。

思想政治部分1至4页，历史部分5至8页，地理部分9至12页，共12页。

满分300分。

考试时间150分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3．答综合题时，必须使用0．5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

5．考试结束后，将试题卷和答题卡一并交回。

地理试题第一部分选择题一、选择题。

（本大题共12小题，每小题4分，共计48分。

在每小题列出的四个选项中，只有一项是最符合题目要求的。

多选、不选、错选均不得分。

）【题文】C4 E2 M1下图为沿23026'S 地形剖面示意图，读图回答25～27题。

25．与图中⑤地气候成因无关的是A .地形B .东南信风C .暖流D .东北信风26．有关图示地区说法正确的是A .⑤地位于②地的正东方向B .该剖面线穿过的地区地形以山地、高原为主C .④地所在国家的人口主要集中在其北部的平原地区D .甲、乙、丙三海域依次为印度洋、大西洋、太平洋安第斯山27．图中剖面线没有穿过的板块是A .亚欧板块B .印度洋板块C .太平洋板块D .美洲板块【知识点】本题组考查气候的形成、地球的形状、板块分布【答案解析】25.D 26. B 27.A 解析：25题，⑤地位于马达加斯加岛的东侧，受马达加斯加暖流、东南信风以及地形的抬升形成热带雨林气候，这里没有东北信风，故选D 。

【名师解析】河北省冀州中学2015届高三上学期第一次月考物理试题 Word版含解析

冀州中学高三第一次月考物理试题满分110分时间90分钟【试卷综析】本试卷是高三模拟试卷，包含了高中物理必修一、必修二、主要包含了匀变速运动规律、受力分析、牛顿第二定律、动能定理等，知识覆盖面广，知识点全面。

在题型上，和高考题一致，是份很好的试卷。

一．选择题（本题共20小题，每小题4分，共80分．1-16单选，17-20不定项选择）【题文】1．下面哪一组单位属于国际单位制的力学基本单位（）A ．m 、N 、kgB ．kg 、2m/s 、sC ．m 、kg 、sD ．2m/s 、kg 、N【知识点】力学单位制 C2 【答案解析】 C 解析：解：A 、其中的N 是导出单位，所以A 错误；B 、其中的m/s 2是导出单位，所以B 错误；C 、m 、kg 、s 分别是长度、质量、时间的单位，所以C 正确；D 、其中的N 是导出单位，所以D 错误．故选：C ．【思路点拨】国际单位制规定了七个基本物理量．分别为长度、质量、时间、热力学温度、电流、光强度、物质的量．它们的在国际单位制中的单位称为基本单位，而物理量之间的关系式推到出来的物理量的单位叫做导出单位．国际单位制规定了七个基本物理量，这七个基本物理量分别是谁，它们在国际单位制分别是谁，这都是需要学生自己记住的．【题文】2．如图，固定斜面，CD 段光滑，DE 段粗糙，A 、B 两物体叠放在一起从C 点由静止下滑，下滑过程中A 、B 保持相对静止，则（）A ．在CD 段时，A 受三个力作用B ．在DE 段时，A 可能受三个力作用C ．在DE 段时，A 受摩擦力方向一定沿斜面向上D ．整个下滑过程中，A 、B 均处于失重状态【知识点】共点力平衡的条件及其应用；物体的弹性和弹力．B1 B4 B7【答案解析】 C 解析：：A 、在CD 段，整体的加速度a=()gsin A B A Bm m m m θ++＝g sin θ，隔离对A 分析，有：m A gsin θ+f A =m A a ，解得f A =0，可知A 受重力和支持力两个力作用．故A 错误．B 、设DE 段物块与斜面间的动摩擦因数为μ，在DE 段，整体的加速度a=()gsin ()gsin A B A B A Bm m m m m m θμθ+-++=gsin θ-μgcos θ，隔离对A 分析，有：m A gsin θ+f A =m A a ，解得f A =-μm A gcos θ，方向沿斜面向上．若匀速运动，A 受到静摩擦力也是沿斜面向上，所以A 一定受三个力．故B 错误，C 正确．D 、整体下滑的过程中，CD 段加速度沿斜面向下，A 、B 均处于失重状态．在DE 段，可能做匀速直线运动，不处于失重状态．故D 错误．故选：C ．【思路点拨】根据牛顿第二定律求出整体的加速度，隔离对A 分析，判断B 对A 是否有摩擦力．本题考查了物体的受力分析，A 、B 保持相对静止，之间有无摩擦力是解决本题的突破口，本题通过整体隔离分析，运用牛顿第二定律求解．【题文】3．物体由静止开始做匀加速直线运动，经过8s ，改为匀减速直线运动，经过4s 停下。

河北省冀州中学2015届高三上学期第一次月考数学理试题 Word版含解析

冀州中学高三上学期第一次月考理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合{}0P y y =≥，PQ Q =，则集合Q 不可能是（）A ．∅B ．{}2,R y y x x =∈ C ．{}2,R xy y x =∈ D ．{}2log ,0y y x x => 【知识点】集合运算.【答案解析】D 解析：显然可能是A ,而B 中集合为{y|0y ≥},C 中集合为{y|y>0}， D 中集合为R,故选D.【思路点拨】逐个分析各选项得结论.2、设,a b R ∈，则“a b >”是“a a b b >”的 ( ) （A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件【知识点】充分条件；必要条件. 【答案解析】C 解析：0b a <≤时，有0b a b b a a b b a a b a ->-≥⎧⎪⇒->-⇒>⎨>≥⎪⎩成立，0b a <<时，有b b a a <成立，0b a ≤<时，有0b a ≤<，所以b b a a <成立；又0,0a b ≥≥时，22a a b b a b a b >⇔>⇒>成立，0,0a b ≥≤时，a a b b >为220a b +>，所以a,b 不同时为0，所以a>b 成立，0,0a b ≤≥时，a a b b >为220a b +<不成立，0,0a b ≤≤时，a a b b >为2222a b a b a b a b a b ->-⇔<⇔<⇒-<-⇒>成立.所以“a b >”是“aa bb >”的充要条件，故选C.【思路点拨】通过分析命题：若a b >，则a a b b >，与命题：若a a b b >，则a b >.的真假得正确选项.3、定义一种运算符号“”，两个实数a ，b 的“ab ”运算原理如图所示，若输人112cos3a π=，92tan 4b π=，则输出P ＝（） A 、4 B 、2 C 、0 D 、—2【知识点】算法与程序框图. L1【答案解析】A 解析：因为输入的a=1,b=2所以a b ≥不成立，所以 P=b(a+1)=22⨯=4，故选A.【思路点拨】由已知得输入的a,b 值依次为1,2，不满足a b ≥，所以输出P ＝4.【题文】4、已知向量,a b 的夹角为45︒，且1a =，210a b -=，则b =（）（A （B ）2 （C ）（D ）【知识点】平面向量的概念；平面向量的数量积. F1 F3 【答案解析】D 解析：由210a b -=得，()222224444cos4510a b a a b b b b -=-⋅+=-+=22260b b ⇒--=解得2b =-舍去，或32b =，故选 D. 【思路点拨】根据复数的模与数量积的关系求得结论.【题文】5、函数()122log 1xf x x =-的零点个数为（）（A ）1 （B ）2 （C ） 3 （D ）4【知识点】函数零点的意义. B9【答案解析】B 解析：由()22log 10xf x x =-=，得21log 2xx ⎛⎫= ⎪⎝⎭，画出两函数21log ,2xy x y ⎛⎫== ⎪⎝⎭得两图像交点个数即所求零点个数为2，故选 B.【思路点拨】根据函数零点的意义，利用图像求得零点个数.【题文】6、数列{}n a 共有12项，其中10a =，52a =，125a =，且11k k a a +-=1,2,3,,11k =，则满足这种条件的不同数列的个数为（）A.84B.168C.76D.152 【知识点】数列问题；计数原理. D1 J1【答案解析】A 解析：满足150,2a a ==且11k k a a +-=的数列前5项有4种情况，满足52a =，125a =，且11k k a a +-=的数列的第5至12项有16343121⨯+⨯+⨯=种，所以满足题设条件的不同数列的个数为42184⨯=个. 【思路点拨】由树图法求出满足题设条件的不同数列的个数.【题文】7、已知函数()21f x x =-+，()g x kx =. 若方程()()f x g x =有两个不相等的实根，则实数k 的取值范围是（） A 、10,2⎛⎫ ⎪⎝⎭ B 、1,12⎛⎫ ⎪⎝⎭C 、()1,2D 、()2,+∞ 【知识点】函数与方程. B9【答案解析】B 解析：画出函数()21f x x =-+的图像，当过原点的直线()g x kx = 由OA 逆时针旋转到与射线AB 平行时，方程()()f x g x =有两个不相等的实根，此时1,12k ⎛⎫∈ ⎪⎝⎭，故选B.【思路点拨】方程()()f x g x =有两个不相等的实根，即()21f x x =-+与()g x kx = 图像有两个不同交点.由图像得实数k 的取值范围.【题文】8、如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为（） A.14 B. 15 C. 16 D. 17【知识点】定积分与微积分基本定理；几何概型. B13 K3 【答案解析】C 解析：阴影部分的面积为)3122012110326x dx x x ⎛⎫=-= ⎪⎝⎭⎰，所以点P 恰好取自阴影部分的概率为：16. 【思路点拨】根据微积分基本定理与几何概型公式求解. 【题文】9、若函数()2sin f x x ω=(0)ω>的图像在(0,2)π上恰有一个极大值和一个极小值，则ω的取值范围是（）A ．3(,1]4B ．5(1,]4C ．34(,]45D ．35(,]44【知识点】函数()sin y A x ωϕ=+的图像与性质. C4【答案解析】D 解析：因为函数()2sin f x x ω=(0)ω>的图像在(0,2)π上恰有一个极大值和一个极小值，所以322354,524424ππωππω⎧⨯<⎪⎪⎛⎤⇒⎨⎥⎝⎦⎪⨯≥⎪⎩，故选D. 【思路点拨】根据条件数()2sin f x x ω=(0)ω>的图像在(0,2)π上恰有一个极大值和一个极小值，得关于ω的不等式组，解得ω的取值范围.【题文】10、已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为（）【知识点】几何体的三视图. G2【答案解析】C 解析：由三棱锥的俯视图与侧视图可知，此三棱锥的直观图如下，所以该三棱锥的正视图可能为C.故选C.【思路点拨】由三棱锥的俯视图与侧视图可得此三棱锥的直观图，从而得此三棱锥的的正视图的形状.【题文】11.已知双曲线12222=-by a x 的左右焦点分别为12F F 、，O 为双曲线的中心，P 是双曲线右支上的点，21F PF ∆的内切圆的圆心为I ，且圆I 与x 轴相切于点A ，过2F 作直线PI 的垂线，垂足为B ，若e 为双曲线的离心率，则 ( ) A . ||||OA e OB = B . ||||OB e OA = C . ||||OA OB = D . ||OA 与||OB 关系不定. 【知识点】双曲线及其几何性质. H6【答案解析】C 解析：如图：12122PF PF AF AF a OA a -=-=⇒=，延长2F B 交1PF 于C ，易得B 是线段2F C 的中点，又O 是线段12F F 的中点，所以OB 是12F F C ∆的中位线，所以OB=a ，故选 C.【思路点拨】画出图形，根据双曲线定义，内心性质，求得线段OA ，OB 的长即可. 【题文】12、设函数()f x 的导函数为()'f x ，对任意x ∈R 都有()()'f x f x >成立，则（）A . ()()3ln22ln3f f >B ．()()3ln22ln3f f =C . ()()3ln22ln3f f <D . ()3ln2f 与()2ln3f 的大小不确定【知识点】导数的应用. B12【答案解析】A 解析：设()()xf x h x e =，则2()()()()()0x x x xe f x e f x f x f x h x e e ''--'==< 在x ∈R 上恒成立，所以()()xf x h x e =是R 上的减函数，所以(ln 2)(ln 3)h h >，即 ln 2ln3(ln 2)(ln 3)3(ln 2)2(ln 3)f f f f e e>⇒>，故选 A. 【思路点拨】构造新函数()()xf x h x e=，利用已知条件判断其单调性，从而得正确选项. 第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）【题文】13、若复数z 满足24iz i =+，则在复平面内z 对应的点的坐标是 . 【知识点】复数运算. L4 【答案解析】(4，-2) 解析：()242442i ii z i i i i+⋅+===-⋅，所以在复平面内z 对应的点的坐标是(4，-2).【思路点拨】解已知复数方程得42z i =-，由此得复平面内z 对应的点的坐标. 【题文】14、已知7270127()x m a a x a x a x -=++++的展开式中4x 的系数是－35，则1237a a a a ++++= .【知识点】二项式定理. J3 【答案解析】1 解析：因为()717rr rr T C x m -+=-，所以()7743135rr r r m C m -=⎧=⎧⎪⇒⎨⎨=-=-⎩⎪⎩，所以当x=1时，012670a a a a a +++++=，当x=0时，01a =-，所以1237a a a a ++++=1.【思路点拨】根据二项式定理中的通项公式及已知求得m 值，再用赋值法求解.【题文】15、已知实数x ,y 满足条件0,0,1,x y x y x -⎧⎪+⎨⎪⎩≥≥≤则1()2x y -的最大值为．【知识点】简单的线性规划的应用. E5【答案解析】12 解析：画出可行域如图:令12x z y ⎛⎫=- ⎪⎝⎭，即12xy z ⎛⎫=+ ⎪⎝⎭，平移曲线12x y ⎛⎫= ⎪⎝⎭知，当曲线过点B （1，1）时z 最大，且最大值为111122⎛⎫-= ⎪⎝⎭.【思路点拨】画出可行域，令目标函数12x z y ⎛⎫=- ⎪⎝⎭，则12xy z ⎛⎫=+ ⎪⎝⎭，平移曲线12xy ⎛⎫= ⎪⎝⎭知，当曲线过可行域的顶点B （1，1）时z 最大，且最大值为111122⎛⎫-= ⎪⎝⎭.【题文】16、已知()111,P x y ，()222,P x y 是以原点O 为圆心的单位圆上的两点，12POP θ∠=（θ为钝角）．若3sin 45πθ⎛⎫+= ⎪⎝⎭，则1212x x y y +的值为．【知识点】向量数量积的坐标运算；两角和与差的三角函数. F2 C5【答案解析】解析：因为3sin 45πθ⎛⎫+= ⎪⎝⎭，所以sin cos θθ+=22sin cos 1θθ+=且θ为钝角，解得cos 10θ=-，所以1212x x y y +=1212cos cos 10OP OP OPOP θθ⋅=⋅==-. 【思路点拨】由已知等式得sin cos 5θθ+=，又22sin cos 1θθ+=且θ为钝角，解得cos θ=，所以1212x x y y +=1212cos cos OP OP OP OP θθ⋅=⋅==. 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）【题文】17、（本小题满分12分）已知△ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c ，且△ABC 的面积为cos S B = （1）若2c a =，求角A ，B ，C 的大小；（2)若a ＝2，且43A ππ≤≤，求边c 的取值范围．【知识点】解三角形. C8 【答案解析】(1),,632A B C πππ===；（2）1c ⎡⎤∈⎣⎦.解析：由三角形面积公式及已知得1sin cos ,2S ac B B ==化简得sin ,B B =即tan B =又0,B π<<故3B π=.………3分（1）由余弦定理得,22222222cos 423,b a c ac B a a a a =+-=+-=∴.b =∴::2a b c =,知,62A C ππ==………………………6分（2）由正弦定理得,sin sin a c A C =即sin 2sin ,sin sin a C Cc A A ==由2,3C A π=-得2222sin()2(sin cos cos sin )3331,sin sin A A A c A A πππ--===又由,43A ππ≤≤知1tan A ≤≤故1].c ∈ …………12分【思路点拨】（1）由面积公式及已知得3B π=,再由余弦定理及c=2a得b =，进而求得角A 、C. (2)由正弦定理及a=2得2sin sin C c A =，又23C A π=-，得1c =+.【题文】18.（本小题满分12分）某公司计划在迎春节联欢会中设一项抽奖活动：在一个不透明的口袋中装入外形一样号码分别为1，2，3，…，10的十个小球。

2015届高三10月月考成绩分析

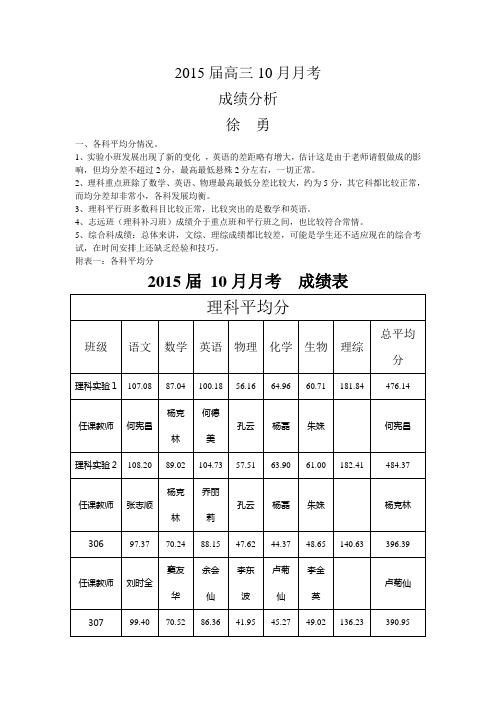
2015届高三10月月考
成绩分析
徐勇
一、各科平均分情况。

1、实验小班发展出现了新的变化，英语的差距略有增大，估计这是由于老师请假做成的影响，但均分差不超过2分，最高最低悬殊2分左右，一切正常。

2、理科重点班除了数学、英语、物理最高最低分差比较大，约为5分，其它科都比较正常，而均分差却非常小，各科发展均衡。

3、理科平行班多数科目比较正常，比较突出的是数学和英语。

4、志远班（理科补习班）成绩介于重点班和平行班之间，也比较符合常情。

5、综合科成绩：总体来讲，文综、理综成绩都比较差，可能是学生还不适应现在的综合考试，在时间安排上还缺乏经验和技巧。

附表一：各科平均分
2015届10月月考成绩表
二、总分分数段。

本表以2014年的高考录取线为段，分别统计各段的学生人数。

从统计结果来看，效果不太理想。

理科600分以上仅一人，与9月情况相同；一本线以上仅16人，比上次增加5人；二本线上84人，与9月相比下降了26人，三本以上101人，比前次少了138人，可见题目的难度对中间层次的学生影响比较大。

文科一本线以上1人，比上次有进步；二本线以上仅10人，比上月减少了9人，三本71人，比前次减少了9人。

2015届 10月月考成绩表
总分分数段
三、总分名次段。

将学生成绩排序后，再统计到各班，结果发现，年级前10名全部在实验小班；前50名有五名重点班学生闯入，比9月份多了3人；前100名有29人闯入；小班中，有25人掉出100名之外，比9月多了6人，有4人到了200名之外，比上次增加了2人。

2015届 10月月考成绩表
总分名次段。

各地2015届高三月考、联考、模拟试题分类汇编--语言表达1

各地2015届高三月考、联考、模拟试题分类汇编--语言表达1高三2010-10-20 19:38各地2015届高三月考、联考、模拟试题分类汇编--语言表达1安徽淮南二中2015届高三第一次月考19．当前，国家提出了家电下乡等惠民政策，网易对此进行了相关调查，下表是其中一项调查内容及结果。

阅读该表，完成下面题目。

（5分）在家电下乡活动中，哪些问题最受关注（票数3561）选项比例票数价格33．5% 1177品牌2．02% 72质量43．81% 1560服务7．5% 267补贴数额20．38% 726能耗 3.31% 118（1）根据上表，你得出什么结论。

答：（2）为了把这项惠民政策落到实处，请你给政府部门提一条建议。

答：参考答案：19．（1）在家电下乡活动中，民众最关心产品的质量、价格和政府补贴数额。

（3分）（2）政府职能部门要严把产品的质量关，不能让惠民政策成为坑民之举。

或政府部门制定补贴政策细则，补贴方法。

补贴数额要具体、透明。

（2分）安徽铜陵二中2015届高三第一次模拟17．下列各项中最适合填在横线上的一项是( )从这个意义上讲，我们希望孔子是灰色的。

或者说，我们愿意把他看作是灰色的。

但是，没有人会喜欢只有灰色的世界。

__________。

这也就是和谐。

(易中天《灰色的孔子和多彩的世界》)①这世界充满生命活力，姹紫嫣红，千姿百态，万类霜天竞自由。

②灰色也只有在和其他色彩搭配时，才能显示它的普适性，显示它的高贵和纯粹。

③也正因为有了思想的高贵纯粹，纷繁的世界才不至于俗不可耐。

④灰色提升着品位，而多彩保证了活力。

⑤因此，灰色的孔子又必须链接多彩的世界。

⑥正因为有了生活的五彩缤纷，理论的灰色才不显得死寂。

A．①⑥②⑤③④ B．②⑤①⑥③④C．②①⑤④⑥③ D．①②⑤④⑥③参考答案：17、答案：B解析：语句之间的衔接连贯，应该注意以下几点：话题一致，叙述角度一致，句式合理，陈述对象一致，感情色彩一致，前后照应，总提与分承照应，音节和谐，符合事理。

【名师解析】河南省南阳一中2015届高三上学期第一次月考物理试题 Word版含解析

【名师解析】河南省南阳一中2015届高三上学期第一次月考物理试题Word 版含解析【试卷综析】本试卷是高三模拟试卷，包含了高中物理必修一、必修二、选修3-1的电场内容、主要包含了匀变速运动规律、受力分析、牛顿第二定律、动能定理、机械能守恒、电场、等，知识覆盖面广，知识点全面。

题型难易适中，是份质量很高的试卷一、选择题（共48分，每题4分，其中1-8题为单选，9-12题为多选，多选题少选得2分，错选或多选不得分）（门道颖李志伟王森）【题文】1．某同学通过以下步骤测出了从一定高度落下的排球对地面的冲击力：将一张白纸铺在水平地面上，把排球在水里弄湿，然后让排球从规定的高度自由落下，并在白纸上留下球的水印。

再将印有水印的白纸铺在台秤上，将球放在纸上的水印中心，缓慢地向下压球，使排球与纸接触部分逐渐发生形变直至刚好遮住水印，记下此时台秤的示数即为冲击力的最大值。

下列物理学习或研究中用到的方法与该同学的方法相同的是：（）A ．建立“合力与分力”的概念B ．建立“点电荷”的概念C ．建立“电场强度”的概念D ．研究加速度与合力、质量的关系【知识点】力的合成．B3【答案解析】A 解析： A 、合力和分力是等效的，它们是等效替代的关系，所以A 正确．B 、点电荷是一种理想化的模型，是采用的理想化的方法，所以B 错误．C 、电场强度的定义是：试探电荷在电场中受到的电场力与试探电荷所带电量的比值．所以，建立“电场强度”的概念是采用了参考变量法，故B 错误；，所以C 错误．D 、研究加速度与合力、质量的关系的时候，是控制其中的一个量不变，从而得到其他两个物理量的关系，是采用的控制变量的方法，所以D 错误．故选A ．【思路点拨】通过白纸上的球的印迹，来确定球发生的形变的大小，从而可以把不容易测量的一次冲击力用球形变量的大小来表示出来，在通过台秤来测量相同的形变时受到的力的大小，这是用来等效替代的方法．在物理学中为了研究问题方便，经常采用很多的方法来分析问题，对于常用的物理方法一定要知道．【题文】2．下列说法中，正确的是：（）AE 与q 成反比B 与q 成反比C ．由可知，匀强电场中的任意两点、间的距离越大，则两点间的电势差也一定越大D ，其中电容器的电容与电容器两极板间电势差无关 I1 I2【答案解析】D 解析： A 、B 、电场场强与电势由场源决定，与检验电荷无关，则两种说法错误．C 、若匀强电场中的点a 、b 间的距离与电场线垂直，距离越大电势与不变．则C 错误;D 、 C=Q U是电容的定义式，采用比值法定义，C 表征了电容器容纳电荷本领的大小，由电容器本身性质决定，与U 、Q 无关，故D 正确．故选D【思路点拨】电场场强与电势由场源决定，与检验电荷无关，U ab =Ed 中的d 为沿场强方向的距离，电场强度与电势无定量关系．考查比值定义法的物理量，明确场强，电势的决定因素，简单ϕab U Ed =a bC U【题文】3．2013年6月13日，神舟十号与天宫一号成功实现自动交会对接。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

79 113 153
合计 257 304 373 460 546 643 749 854 979 1112 1242 1396 1556 1723 1879 2063 2228 2360 2472 2557 2754
仁怀市高三联考成绩段统计(文科)9月
>= >= >= >= >= >= >= >= >= >= >= >= 490 >= >= >= >= >= >= >= >= >=
17
岳敏
18
陈菊
19
陈菊
20
岳敏
21
刘小英
23
刘小英
级
地理
65.0 60.1 60.0 58.1 56.9 57.4
55.0
50.0 47.2 45.0
48.6
44.5
40.0
35.0
30.0
17
刘玉坤
18
刘玉坤
19
张春燕
20
王小龙
21
张春燕
23
王小龙
级
郑惠兰岳敏刘玉坤
宋双燕陈菊刘玉坤
曹桂菊陈菊张春燕
葛大燕葛大燕李红张常志张常志王彩丽司照雷王彩丽丁佳姬潘龙桂王运章丁佳姬李红范小亮潘龙桂司照雷周国霞
杨大才李映槐杨大才李映槐吴德勇余贵兵余贵兵潘小叶杨雷雷杨雷雷杨天贵胡明强祁仲秋潘小叶吴德勇祁仲秋杨天贵
胡勤
胡勤董仕梅董仕梅夏宇陈朝霞夏宇胡广勇胡广勇涂佳强陈霞吴光韦桑爱兰吴光韦涂佳强陈朝霞母先让
21.9
仁怀市高三联考成绩段统计(理科)9月
>=
一中酒高
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
>=
学校 600 590 580 570 560 550 540 530 520 510 500
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 2 0 0 6 0 0 9 0 0 14 0 0 16 0 0
2015届第二次月考分析
2015届高三年级组
2014年9月11日
陈宗涛胡勤
李红李映槐吴德勇李琼
夏宇王彩丽李勇潘龙桂陈霞刘德坤刘蕊美张金富赵云凤张榜燕周国霞
岳敏
宋双燕
杨荣智
母天庆
王运章
王小龙
班级 22 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
65.2
60.0 48.6 49.7 48.6 50.7 49.4 49.8 50.7 52.6 51.7 51.6 50.5 49.8
50.0
49.1
51.7
40.0
30.0
26.8
20.0
10.0
22 1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 级
宋琴曲李远艳赵云凤赵云凤刘蕊美李琼
总分 1 3 2 15 4 13 7 8 10 9 6 12 14 11 5 16 17
名次和 8 22 18 118 66 100 62 68 88 71 58 77 82 80 58 112 136
学科平均分名次统计(一中文科)
名次班级语文数学英语政治历史地理文综总分和 17 1 1 1 1 1 1 1 1 8
200
301 402 451 502 552 601 700 800 901 1001 1050
348 29 341 29 334. 29 5 317. 29 5 301 29 275 29 235. 29 5 193 29
文科总分名次段统计表
名次段前 30 分数线名 454.5 17 24 18 4 19 1 20 1 21 0 23 0 文科 30
前
前前
50
名
444
418 394
31
45 50
9
20 34
6
20 37
6
16 29
0
0 0
0
0 0
52
101 150
100 名 150 名
前
前前
200 名 370.5
250 名 342.5 300 名 298.5
53
53 53
50
67 72
51
60 69
41
59 67
1
3 10
4
8 29
200
250 300
学校 600 590 580 570 560 550 540 530 520 510 500
一中酒高茅高
480 470 460 450 440 430 420 410 400
0
0 0 0
0
0 0 0 0 >=
0
0 0 0 0 >=
0
0 0 0 0 >=
0
0 0 0 0 >=
0
0 0 0 0 >=
李琼沈晓川李远艳李琼陈丽君陈丽君刘蕊美陈丽君赵云凤李远艳刘蕊美
陈宗涛陈宗涛张金富敖洪进张榜燕李勇张丽红张丽红李勇张金富高平刘德坤高平张金富刘德坤张榜燕李勇何树元冉启才何树元熊明兵邬丽娟邬丽娟张永学罗军材周艳梅彭丽娟熊明兵罗军材彭丽娟冉启才冉启才周艳梅张永学宋琴曲李远艳赵云凤赵云凤刘蕊美李琼李琼沈晓川李远艳李琼陈丽君陈丽君刘蕊美陈丽君赵云凤李远艳刘蕊美
12.6
333.9 343.3
9.4
英语折算为135
语文 2014级 2015级差
数学
英语
政治
历史
地理
文综
总分
96.2 92.6
-3.7
45.7 67.8
22.1
64.2 50.2
-14.0
36.6 42.9
6.3
41.3 49.8
8.5
46.0 48.6
2.6
123.9 141.3
17.4
330.0 351.9
0
0 0 0 0 >=
0
0 0 0 0 >=
2
0 0 0 2 >=
4
0 0 0 4 >=
6
0 0 0 6 >=
7
0 0 0 7 >= 280 313 258 223 261
10
0 0 0 10 >=
15
0 0 0 15 >=
24
0 0 1 25 >=
37
0 0 1 38 >=
60
1 0 2 63 >=
79
3 0 2
97 117 135
7 0 3 10 2 5 16 3 7
四中
合计 0 >=
一中酒高茅高四中
84 107 134 161 >= >= >= > 0
学校 390 380 370 360 350 340 330 320 310 300 290 160 180 201 220 240 250 266 273 290 299 307 23 5 8 35 8 11 48 13 19 66 19 26 87 108 134 157 184 212 231 27 50 39 72 60 94 123 161 192
语文 1 3 2 16 8 13 9 4 15 12 7 11 6 5 10 14 17
学科平均分名次统计(一中理科) 数学英语物理化学生物理综 1 1 1 1 1 1 3 2 2 3 3 3 2 3 3 2 2 2 13 11 15 16 16 16 4 4 9 13 12 12 12 15 11 8 15 13 10 8 4 12 7 5 8 7 8 10 13 10 7 6 12 14 10 14 6 12 6 11 8 7 9 9 13 6 4 4 14 14 10 5 5 6 16 10 14 7 6 9 11 13 16 4 9 11 5 5 5 9 11 8 15 16 7 15 14 15 17 17 17 17 17 17
18
19 20 21 23
2
4 3 6 5
4
3 2 6 5
4
2 3 6 5
2
3 4 6 5
2
3 4 6 5
2
4 3 6 5
2
3 4 6 5
2
3 4 6 5
20
25 27 48 40
理科总分名次段统计表
名次段前 50 名分数线 471. 5 433. 5 415. 5 399. 5 377. 5 361. 5 355. 5 22 25 29 29 1 11 26 35 2 14 27 39 3 0 1 3 4 0 3 7 5 0 1 4 6 0 3 6 7 1 1 4 8 0 3 3 9 0 0 1 10 0 1 5 11 0 1 2 12 0 0 3 13 0 0 2 14 0 3 5 15 0 2 2 16 0 0 0 理科 51 101 150
0
9 >=
0