高考数学大二轮专题复习 第二编 专题整合突破 专题五 立体几何 第一讲 空间几何体的三视图、表面积与体积适
高考数学(理)二轮专题复习名师制作课件:专题五 第一讲 空间几何体
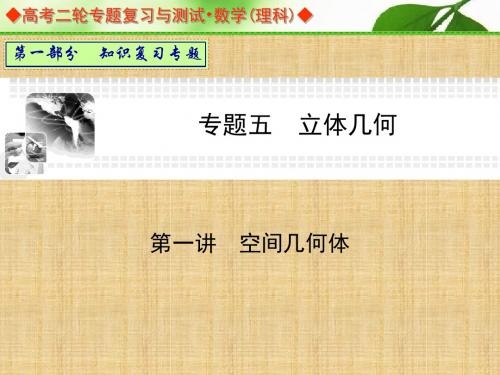
1.空间几何体的三视图包括__________ __________ 正(主)视图 、侧 (左)视图 俯视图 和___________ . 2.在三视图中,正(主)侧(左)一样________ ,正(主)俯 高 一样________ ,侧(左)俯一样________ . 长 宽
◆高考二轮专题复习与测试•数学(理科)◆
多面体与旋转体的表面积与体积的计算
1.多面体的表面积. 面积之和 . 多面体的表面积为各个面的___________ 2.旋转体的表面积. 2πr(r+L) ; (1)圆柱的表面积S=___________
πr(r+L) ; (2)圆锥的表面积S=___________
(3)圆台的表面积S=π(r′2+r2+r′L+rL);
◆高考二轮专题复习与测试•数学(理科)◆ 几何体 几何特征
有一个面是多边形,其余
图形
棱锥
多 面 体 棱台
各面都是有一个公共顶点 _______ 平行于 棱锥底面 的平面去截棱锥,
____________ 底面与截面 之间的部分,
叫做棱台
◆高考二轮专题复习与测试•数学(理科)◆
4 3 πR (4)球的体积V=________. 3
◆高考二轮专题复习与测试•数学(理科)◆
1.(2012年新课标全国卷)如图,网格纸上小正方形的边 长为1,粗线画出的是某几何体的三视图,则此几何体的体积 为( B )
A.6
B.9
C.12
D.18
◆高考二轮专题复习与测试•数学(理科)◆
2.(2012年江西卷)若一个几何体的三视图如图所示,则 此几何体的体积为( D )
◆高考二轮专题复习与测试•数学(理科)◆
跟踪训练
1.(2012年陕西卷)将正方形(如图1所示)截去两个三棱锥, 得到图2所示的几何体,则该几何体的左视图为( B )
2023版高考数学二轮总复习第2篇经典专题突破核心素养提升专题3立体几何第1讲空间几何体课件

5.(2022·全国乙卷)已知球 O 的半径为 1,四棱锥的顶点为 O,底面
的四个顶点均在球 O 的球面上,则当该四棱锥的体积最大时,其高为
A.13
B.12
(C )
C.
3 3
D.
2 2
【解析】 设该四棱锥底面为四边形 ABCD,四边形 ABCD 所在小 圆半径为 r,
设四边形 ABCD 对角线夹角为 α, 则 SABCD=12·AC·BD·sin α≤12·AC·BD≤12·2r·2r=2r2 (当且仅当四边形 ABCD 为正方形时等号成立)
在 Rt△ABC 中,AB= AC2+BC2= 2,则 AO1= 22,
在 Rt△AOO1 中,OO1= OA2-AO21 = 22,
故三棱锥
O-ABC
的体积为
V=13·S△ABC·OO1=13×12×1×1×
22=
2 12 .
故选 A.
3.(2021·全国新高考Ⅰ卷)已知圆锥的底面半径为 2,其侧面展开图
语,指的是一段类似隧道形状的几何体,如图,羡除ABCDEF中,底面
ABCD是正方形,EF∥平面ABCD,EF=2,其余棱长都为1,则这个几
何体的外接球的体积为
( B)
A. 32π
B.43π
C.8
3
2 π
D.4π
【解析】连接AC,BD交于点M,取EF中点O,
则 OM⊥面 ABCD, 取 BC 中点 G,连接 FG,作 GH⊥EF, 由题意可得 HF=12,FG= 23,则 HG= 22,
了一个“商功”的例子:今有刍童,下广二丈,袤三丈,上广三丈,袤
四丈,高三丈.问积几何?其意思是:今有上下底面皆为长方形的草垛 (如图所示),下底宽2丈,长3丈,上底宽3丈,长4丈,高3丈.问它的体 积是多少?该书提供的算法是:上底长的2倍与下底长的和与上底宽相 乘,同样下底长的2倍与上底长的和与下底宽相乘,将两次运算结果相 加,再乘以高,最后除以6.则这个问题中的刍童的体积为 ( B )
高考数学二轮复习 专题五 第1讲 空间几何体配套课件 理

2
答案 B
完整版ppt
ห้องสมุดไป่ตู้11
(2)(2013·四川)一个几何体的三视图如图所示,则该几 何体的直观图可以是( )
D
思维启迪 分析几何体的特征,从俯视图突破.
解析 由俯视图易知答案为D.
完整版ppt
12
空间几何体的三视图是从空间几何体的正面、左
面、上面用平行投影的方法得到的三个平面投影
图,因此在分析空间几何体的三视图问题时,先
解析 过M,N分别作两个垂直于底面的截面,将多面 体分割成一个三棱柱和两个四棱锥,
由正视图知三棱柱底面是等腰直角三角形,面积为
S1= 1×2×2=2,高为2,所以体积为V1=4, 2
两个四棱锥为全等四棱锥,棱锥的体积为
V1=2×1×2×1×2= 8,
3
3
所以多面体的体积为 V=83+4=230,选 D.
完整版ppt
6
4.空间几何体的两组常用公式
(1)柱体、锥体、台体的侧面积公式:
①S柱侧=ch(c为底面周长,h为高); ②S锥侧= ch′(c为底面周长,h′为斜高);
③S台侧= 1 (c+c′)h′(c′,c分别为上,下底面的 周长,h′12为斜高); ④S球表=42πR2(R为球的半径).
完整版ppt
完整版ppt
5
3.直观图的斜二测画法 空间几何体的直观图常用斜二测画法来画,其规则: (1)原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、 y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在 平面垂直. (2)原图形中平行于坐标轴的线段,直观图中仍分别平行于 坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变, 平行于y轴的线段长度在直观图中变为原来的一半.
高考理科数学大二轮复习课件专题五立体几何

D
典型例题分析与解答
01
02
03
04
05
例题1:在正方体 $ABCDA_1B_1C_1D_1$中,E 、F分别为棱$AA_1$、 $CC_1$的中点,则在空 间中与三条直线 $A_1D_1$、$EF$、 $CD$都相交的直线( )
A. 不存在 B. 有且只有两 条 C. 有且只有三条 D. 有无数多条
限时训练02ຫໍສະໝຸດ 03错题反思设定合理的答题时间,进行限时 训练,提高解题速度和应试能力 。
对错题进行反思和总结,找出错 误原因和解决方法,避免重复犯 错。
关注新题型,拓宽视野
关注高考动态
及时了解高考立体几何 的命题趋势和变化,把 握复习方向。
拓展新题型
适当拓展一些新题型和 新颖解法,拓宽解题思 路和方法。
台体体积计算: 1/3×(上底面积+下 底面积+√(上底面积 ×下底面积))×高。
锥体体积计算: 1/3×底面积×高。
球体性质及计算
球体性质
所有点到球心的距离都等于半径的几何体。
球体表面积计算
4πr^2,其中r为球体半径。
球体体积计算
4/3πr^3,其中r为球体半径。
03 空间向量在立体几何中应用
空间向量基本概念及运算
1 2
空间向量定义
空间向量是既有大小又有方向的量,可以用有向 线段表示。
空间向量运算
包括向量的加法、减法、数乘和数量积等运算, 满足相应的运算律。
3
空间向量基本定理
如果三个向量a、b、c不共面,那么对于空间中 的任意一个向量p,存在唯一的一组实数x、y、z ,使得p=xa+yb+zc。
人教A版2021届高考数学二轮复习讲义及题型归纳(拔高):立体几何第一章 空间直线、平面平行垂直

第一章空间直线、平面平行垂直一、考纲解读1.要理解空间直线和平面各种位置关系的定义.2.以立体几何的定义,公理和定理为出发点,认识和理解空间中线面平行的有关性质与判定,理解其判定定理与性质定理.二、命题趋势探究有关平行的问题是高考的必考内容,主要分为两大类:一类是空间线面关系的判定和推理;一类是几何量的计算,主要考查学生的空间想象能力,思维能力和解决问题的能力.平行关系是立体几何中的一种重要位置关系,在高考中,选择题、填空题几乎每年都考,难度一般为中档题,且常常以棱柱、棱锥为背景.(1)高考始终把直线与平面、平面与平面平行的判定与性质作为考查的重点,通常以棱柱、棱锥为背景设计命题.考查的方向是直线与平面、平面与平面的位置关系,结合平面几何有关知识考查.(2)以棱柱、棱锥为依托考查两平行平面的距离,可转化为点面距离,线面距离和两异面直线间的距离问题,通常是算、证结合,考查学生的渗透转化思想.三、知识点精讲(一).直线和平面平行1.定义直线与平面没有公共点,则称此直线l与平面α平行,记作l∥α2.判定方法(文字语言、图形语言、符号语言)(见表8-9)表8-93.性质定理(文字语言、图形语言、符号语言)(见表8-10) 表8-10(二).两个平面平行 1.定义没有公共点的两个平面叫作平行平面,用符号表示为:对于平面α和β,若αβφ=,则α∥β2.判定方法(文字语言、图形语言、符号语言)(见表8-11) 表8-113.性质定理(文字语言、图形语言、符号语言)(见表8-12) 表8-12b γ⎪=⎭线面平行”)面//面⇒线⊥面如果两个平面中有一个垂直于一条直线,那么另一个平面也垂直于这条直线//llαββα⎫⇒⊥⎬⊥⎭(三).线面垂直1.定义:如果一条直线和这个平面内的任意一条直线都垂直,那称这条直线和这个平面相互垂直.2.判定定理(文字语言、图形语言、符号语言)(见表1)表1文字语言图形语言符号语言判断定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直面⊥面⇒线⊥面两个平面垂直,则在一个平面内垂直于交线的直线与另一个平面垂直αββαβα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊥⊂=⋂⊥babba,a ba llb la b Pαα⊂⎫⎪⊥⎪⇒⊥⎬⊥⎪⎪=⎭__a平行与垂直的关系1一条直线与两平行平面中的一个平面垂直,则该直线与另一个平面也垂直βαβα⊥⇒⎭⎬⎫⊥aa//平行与垂直的关系2两平行直线中有一条与平面垂直,则另一条直线与该平面也垂直αα⊥⇒⎭⎬⎫⊥baba//3.性质定理(文字语言、图形语言、符号语言)(见表2)表2文字语言图形语言符号语言性质定理垂直于同一平面的两条直线平行babaa////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα文字语言图形语言符号语言垂直与平行的关系垂直于同一直线的两个平面平行βαβα//⇒⎭⎬⎫⊥⊥aa_α_b_aα_b_a_(四).斜线在平面内的射影 1.斜线的定义一条直线与一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和这个平面的交点叫做斜足. 2.射影的定义过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影.3.直线与平面所成的角平面内的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角.特别地,一条直线垂直于平面,我们说它们所成的角是直角;一条直线和平面平行,或在平面内,我们说它们所成的角是的角,故直线与平面所成的角的范围是.如图8-122所示,是平面的斜线,为斜足;是平面的垂线,为垂足;是在平面的射影,的大小即为直线与平面所成的角的大小.00,2π⎡⎤⎢⎥⎣⎦PA αA PO αO AO PA αPAO ∠PA α(五).平面与平面垂直 1.二面角的定义从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面;如图8-123所示,在二面角的棱上任取一点,以点为垂足,在半平面和内分别作垂直于棱的射线和,则射线和构成的叫做二面角的平面角,二面角的范围是.平面角是直角的二面角叫做直二面角.2.平面与平面垂直的定义如果两个相交平面的交线与第三个平面垂直,又这两个平面与第三个平面相交所得的两条交线互相垂直.(如图8-124所示,若,,且,,l αβ--l O O αβl OA OB OA OB AOB ∠[]0,πCD αβ=CD γ⊥AB αγ=BE βγ=,则)一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.3.判定定理(文字语言、图形语言、符号语言)文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面垂直βαβα⊥⇒⎭⎬⎫⊂⊥bb4.性质定理(文字语言、图形语言、符号语言)文字语言图形语言符号语言性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直αββαβα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊥⊂=⋂⊥babbaAB BE⊥αβ⊥___a四、思路小结(一).线线平行、线面平行、面面平行的转换如图0所示.(1) 证明直线与平面平行的常用方法:①利用定义,证明直线a 与平面α没有公共点,一般结合反证法证明;②利用线面平行的判定定理,即线线平行⇒线面平行.辅助线的作法为:平面外直线的端点进平面,同向进面,得平行四边形的对边,不同向进面,延长交于一点得平行于第三边的线段;③利用面面平行的性质定理,把面面平行转化成线面平行; (2) 证明面面平行的常用方法:①利用面面平行的定义,此法一般与反证法结合; ②利用面面平行的判定定理; ③利用两个平面垂直于同一条直线; ④证明两个平面同时平行于第三个平面.(3) 证明线线平行的常用方法:○1利用直线和平面平行的判定定理;○2利用平行公理; 性质 性质性质 判定判定判定 线∥面 线∥线面∥面图 0(二).证明空间中直线、平面的垂直关系线线线面面面 (1)证明线线垂直的方法 ①等腰三角形底边上的中线是高; ②勾股定理逆定理; ③菱形对角线互相垂直; ④直径所对的圆周角是直角; ⑤向量的数量积为零;⑥线面垂直的性质(); ⑦平行线垂直直线的传递性(∥). (2)证明线面垂直的方法 ①线面垂直的定义;②线面垂直的判定(); ③面面垂直的性质();平行线垂直平面的传递性(∥); ⑤面面垂直的性质().(3)证明面面垂直的方法 ①面面垂直的定义;②面面垂直的判定定理().⊥−−−−→←−−−−判定定理性质定理⊥−−−−→←−−−−判定定理性质定理⊥,a b a b αα⊥⊂⇒⊥,a c a ⊥b b c ⇒⊥,,,,a b a c c b b c P a ααα⊥⊥⊂⊂=⇒⊥,,,b a b a a αβαβαβ⊥=⊥⊂⇒⊥,a b α⊥a b α⇒⊥,,l l αγβγαβγ⊥⊥=⇒⊥,a a βααβ⊥⊂⇒⊥性质性质性质性质性质 判定判定 判定 判定 判定线∥面 线∥线面∥面线⊥面 线⊥线面⊥面图 3空间中的线面平行、垂直的位置关系结构图如图3所示,由图可知,线面垂直在所有关系中处于核心位置. 五、解答题题型总结 核心考点一:平行证明【例1】 如图所示,在正方体1111ABCD A B C D -中,E 是棱1DD 的中点.在棱11C D 上是否存在一点F ,使1B F ∥平面1A BE ?证明你的结论.原图:【解析】 在棱11C D 上存在点F ,使1B F ∥平面1A BE .且F 为11C D 的中点. 法一:分别取11C D 和CD 的中点F ,G ,连结EG ,BG ,1CD ,FG . 由四边形11A BCD 是平行四边形,有11D C A B ∥.又E ,G 分别为1D D ,CD 的中点,有1EG D C ∥,∴1EG A B ∥. 这说明1A 、B 、G 、E 共面,所以BG ⊂平面1A BE .BACD A 1B 1D 1C 1E E C 1D 1B 1A 1DCAB G F因四边形11C CDD 与11B BCC 皆为正方形,F ,G 分别为11C D 和CD 的中点, 所以11FG C C B B ∥∥,且11FG C C B B ==, ∴四边形1B BGF 是平行四边形,所以1B F BG ∥. 而1B F ⊄ 平面1A BE ,BG ⊂平面1A BE ,故1B F ∥平面1A BE .法二:连结1C D ,EF ,1AB ,且1AB 与1A B 交于点K ,连结EK , (要证线面平行转化为线线平行即1B F EK ∥) 由平行四边形11B C DA 有11B A C D ∥, 又,F E 为棱中点,有1EF C D ∥, ∴1EF B A ∥,∴1EF B K ∥,且1EF B K =. ∴1B F EK ∥,且1B F ⊄面1A BE ,EK ⊂面1A BE , ∴棱11C D 上存在中点F ,使得1B F ∥面1A BE .【例2】如图,已知正方体1111ABCD A B C D -中,E 、F 分别为AB 、BC 的中点,在棱1DD 上是否存在一点K ,使得AK ∥平面1EFD ?证明你的结论.原图:法一: K F ED 1C 1B 1A 1DCBAKFE DCBAD 1C 1B 1A 1EB延长AK 交11A D 于S ,连接CS 、AC .∴1CS D F ∥.另外,由E 、F 分别为AB 、BC 的中点,知EF AC ∥. ∵CSAC C =,∴面ACS ∥面1EFD∵AK ⊂面ACS ,∴AK ∥面1EFD. 法二:连接FQ ,平面1EFD 与面11BB C C 的交线即为FQ ,要想AK ∥面1EFD ,则只需AK FQ ∥即【例3】 如图,已知四棱锥B ACDE -的底面为直角梯形ACDE ,90BAC ACD ∠=∠=︒,60EAC ∠=︒,AB AC AE ==.在直线BC 上是否存在一点P ,使得DP ∥平面EAB ?请证明你的结论.原图:线段BC 的中点就是满足条件的点P . 证明如下:取AC 的中点M ,连结EM 、EC ,∵AE AC =且60EAC∠=︒,∴EAC △是正三角形,∴EM AC ⊥. 又∵ED AC ∥,∴ED FP ∥且ED FP =,四边形EFPD 是平行四边形. ∴DP EF ∥,而EF ⊂平面EAB ,DP ⊄平面EAB , ∴DP ∥平面EAB . 核心考点 :垂直证明【例1】在四棱锥S ABCD -中,底面ABCD 是正方形,SA ⊥底面ABCD ,SA AB =,点M 是SD 的中点,AN SC ⊥,且交SC 于点N ,证明:平面SAC ⊥平面AMN .BA CDEM NDCBA SMF PBA CDE● ∵SA ⊥底面ABCD ,CD ⊂平面ABCD ,∴SA CD ⊥;又∵CD AD ⊥,SA ⊂平面SAD ,AD ⊂平面SAD ,SA AD A =, ∴CD ⊥平面SAD .AM ⊂平面SAD ,∴CD AM ⊥.又∵SA AD AB ==,M 是SD 的中点, ∴AM SD ⊥;SD ⊂平面SCD ,CD ⊂平面SCD ,SD CD D =,∴AM ⊥平面SCD .SC ⊂平面SCD ,∴AM SC ⊥.又∵AN SC ⊥,AM 、AN ⊂平面AMN ,AM AN A =,∴SC ⊥平面AMN ,又∵SC ⊂平面SAC , ∴平面SAC ⊥平面AMN .【例2】如图,已知BCD △中,90BCD ∠=︒,1BC CD ==,AB ⊥平面BCD ,60ADB ∠=︒,E 、F分别是AC 、AD 上的动点,且()01AE AFAC ADλλ==<<. ⑴ 求证:不论λ为何值,总有平面BEF ⊥平面ABC ;⑵ 当λ为何值时,平面BEF ⊥平面ACD ?● ⑴ ∵AB ⊥平面BCD ,∴AB CD ⊥.∵CD BC ⊥,且AB BC B =,∴CD ⊥平面ABC .FEDCBA∴EF ⊥平面ABC .又∵EF ⊂平面BEF ,∴不论λ为何值,总有平面BEF ⊥平面ABC . ⑵ 由⑴知,BE EF ⊥,又平面BEF ⊥平面ACD , ∴BE ⊥平面ACD ,∴BE AC ⊥. ∵90BCD ∠=︒,1BC CD ==,60ADB ∠=︒【例3】在四棱锥S ABCD -中,底面ABCD 是正方形,SA ⊥底面ABCD ,SA AB =,点M 是SD 的中点,AN SC ⊥,且交SC 于点N ,证明:平面SAC ⊥平面AMN .【解析】∵SA ⊥底面ABCD ,CD ⊂平面ABCD , ∴SA CD ⊥;又∵CD AD ⊥,SA ⊂平面SAD ,AD ⊂平面SAD ,SA AD A =,M NDCBA S∴CD ⊥平面SAD .AM ⊂平面SAD ,∴CD AM ⊥.又∵SA AD AB ==,M 是SD 的中点, ∴AM SD ⊥;SD ⊂平面SCD ,CD ⊂平面SCD ,SD CD D =,∴AM ⊥平面SCD .SC ⊂平面SCD ,∴AM SC ⊥.又∵AN SC ⊥,AM 、AN ⊂平面AMN ,AM AN A =,∴SC ⊥平面AMN ,又∵SC ⊂平面SAC , ∴平面SAC ⊥平面AMN .【例4】如图,已知BCD △中,90BCD ∠=︒,1BC CD ==,AB ⊥平面BCD ,60ADB ∠=︒,E 、F分别是AC 、AD 上的动点,且()01AE AFAC ADλλ==<<. ⑴ 求证:不论λ为何值,总有平面BEF ⊥平面ABC ; ⑵ 当λ为何值时,平面BEF ⊥平面ACD ?⑴ ∵AB ⊥平面BCD ,∴AB CD ⊥.∵CD BC ⊥,且AB BC B =,∴CD ⊥平面ABC. ∴EF ⊥平面ABC .又∵EF ⊂平面BEF ,∴不论λ为何值,总有平面BEF ⊥平面ABC .FEDCBA⑵由⑴知,BE EF⊥,又平面BEF⊥平面ACD,∴BE⊥平面ACD,∴BE AC⊥.∵90==,60∠=︒ADBBC CDBCD∠=︒,1。
2023年高考数学二轮复习第二篇经典专题突破专题三立体几何第1讲空间几何体

第二篇 专题三 第1讲一、选择题1.如图,△A ′B ′C ′是水平放置的△ABC 的斜二测直观图,其中O ′C ′=O ′A ′=2O ′B ′,则以下说法正确的是( C )A .△ABC 是钝角三角形B .△ABC 是等腰三角形,但不是直角三角形 C .△ABC 是等腰直角三角形D .△ABC 是等边三角形【解析】根据题意,将△A ′B ′C ′还原成原图,如图,原图中,则有OC =OA =OB , 则△ABC 是等腰直角三角形; 故选C.2.如图,半径为R 的球的两个内接圆锥有公共的底面.若两个圆锥的体积之和为球的体积的38,则这两个圆锥的高之差的绝对值为( D )A .R2B .2R3C .4R3D .R【解析】设球的球心为O ,半径为R ,体积为V ,上面圆锥的高为h (h <R ),体积为V 1,下面圆锥的高为H (H >R ),体积为V 2,两个圆锥共用的底面的圆心为O 1,半径为r .由球和圆锥的对称性可知h +H =2R ,|OO 1|=H -R .∵V 1+V 2=38V ,∴13πr 2h +13πr 2H =38×43πR 3, ∴r 2(h +H )=32R 3.∵h +H =2R ,∴r =32R .∵OO 1垂直于圆锥的底面,∴OO 1垂直于底面的半径,由勾股定理可知R 2=r 2+|OO 1|2, ∴R 2=r 2+(H -R )2,∴H =32R ,∴h =12R ,则这两个圆锥的高之差的绝对值为R ,故选D.3.已知一个圆锥的侧面积是底面积的2倍,记该圆锥的内切球的表面积为S 1,外接球的表面积为S 2,则S 1S 2等于( C )A .12B .13C .14D .18【解析】如图,由已知圆锥侧面积是底面积的2倍,不妨设底面圆半径为r ,l 为底面圆周长,R 为母线长,则12lR =2πr 2, 即12·2π·r ·R =2πr 2, 解得R =2r ,故∠ADC =30°,则△DEF 为等边三角形, 设B 为△DEF 的重心,过B 作BC ⊥DF ,则DB 为圆锥的外接球半径,BC 为圆锥的内切球半径, 则BC BD =12,∴r 内r 外=12,故S 1S 2=14. 4.如图所示,在正方体ABCD -A 1B 1C 1D 1中,动点E 在BB 1上,动点F 在A 1C 1上,O 为底面ABCD 的中心,若BE =x ,A 1F =y ,则三棱锥O -AEF 的体积( B )A .与x ,y 都有关B .与x ,y 都无关C .与x 有关,与y 无关D .与y 有关,与x 无关【解析】由已知得V 三棱锥O -AEF =V 三棱锥E -OAF =13S △AOF ·h (h 为点E 到平面AOF 的距离).连接OC ,因为BB 1∥平面ACC 1A 1, 所以点E 到平面AOF 的距离为定值. 又AO ∥A 1C 1,OA 为定值, 点F 到直线AO 的距离也为定值, 所以△AOF 的面积是定值,所以三棱锥O -AEF 的体积与x ,y 都无关.5.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( C )A .2π3B .4π3C .5π3D .2π【解析】如图,过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径, 线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥, 该几何体的体积为V =V 圆柱-V圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3.6.如图,在三棱锥V -ABC 中,∠AVB =∠BVC =∠CVA =60°,VA =VB =VC ,若三棱锥V -ABC 的内切球O 的表面积为6π,则此三棱锥的体积为( D )A .63B .183C .62D .182【解析】连接VO ,并延长交底面ABC 于点E ,连接AE ,并延长交BC 于D ,∵在三棱锥V -ABC 中,∠AVB =∠BVC =∠CVA =60°,VA =VB =VC , ∴三棱锥V -ABC 是正四面体,∴E 是△ABC 的重心,∴VE ⊥平面ABC , ∵三棱锥V -ABC 的内切球O 的表面积为6π, ∴4πr 2=6π,解得球O 的半径r =OE =62, 设AB =a ,则AE =23AD =23a 2-⎝⎛⎭⎫a 22=3a 3,VE =a 2-⎝⎛⎭⎫3a 32=63a , ∴AO =VO =63a -62, ∵OE ⊥AE ,∴AE 2+OE 2=AO 2,∴⎝⎛⎭⎫3a 32+⎝⎛⎭⎫622=⎝⎛⎭⎫63a -622, 解得a =6,∴VE =63×6=26, ∴此三棱锥的体积为V =13S △ABC ·VE =13×12×6×6×sin 60×26=18 2.故选D.7.如图所示,某几何体由底面半径和高均为5的圆柱与半径为5的半球对接而成,在该封闭的几何体内部放入一个小圆柱体,且小圆柱体的上、下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为( B )A .2 000π9B .4 000π27C .81πD .128π【解析】小圆柱的高分为上、下两部分,上部分的高同大圆柱的高相等,为5,下部分深入底部半球内.设小圆柱下部分的高为h (0<h <5),底面半径为r (0<r <5).由于r ,h 和球的半径构成直角三角形,即r 2+h 2=52, 所以小圆柱的体积V =πr 2(h +5)=π(25-h 2)(h +5)(0<h <5),把V 看成是关于h 的函数,求导得V ′=-π(3h -5)(h +5). 当0<h <53时,V ′>0,V 单调递增;当53<h <5时,V ′<0,V 单调递减. 所以当h =53时,小圆柱的体积取得最大值.即V max =π⎝⎛⎭⎫25-259×⎝⎛⎭⎫53+5=4 000π27,故选B. 二、填空题8.如图,在正三棱柱ABC -A 1B 1C 1中,AB =4,AA 1=6.若E ,F 分别是棱BB 1,CC 1上的点,则三棱锥A -A 1EF 的体积是.【解析】因为在正三棱柱ABC -A 1B 1C 1中, AA 1∥BB 1,AA 1⊂平面AA 1C 1C ,BB 1⊄平面AA 1C 1C , 所以BB 1∥平面AA 1C 1C ,从而点E 到平面AA 1C 1C 的距离就是点B 到平面AA 1C 1C 的距离, 作BH ⊥AC ,垂足为点H ,由于△ABC 是正三角形且边长为4,所以BH =23,从而三棱锥A -A 1EF 的体积VA -A 1EF =VE -A 1AF =13S △A 1AF ·BH =13×12×6×4×23=8 3.9.已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为2. 【解析】如图,设B 1C 1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q , 连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形, ∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形, 则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心, 设截面圆的半径为r ,则r =R 2球 -D 1E 2=5-3= 2. 又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P =5,∴B 1P =D 1P 2-D 1B 21 =1, 同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点, ∴∠PEQ =π2,知PQ ︵的长为π2×2=2π2,即交线长为2π2.10.(2020·浙江)已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是__1__.【解析】如图,设圆锥的母线长为l ,底面半径为r ,则圆锥的侧面积S 侧=πrl =2π, 即r ·l =2.由于侧面展开图为半圆, 可知12πl 2=2π,可得l =2,因此r =1.11.在如图所示的斜截圆柱中,已知圆柱的底面直径为40 cm ,母线长最短50 cm ,最长80 cm ,则斜截圆柱的侧面面积S =__2 600π__cm 2.【解析】将题图所示的相同的两个几何体对接为圆柱,则圆柱的侧面展开图为矩形.由题意得所求侧面展开图的面积S =12×(π×40)×(50+80)=2 600π(cm 2).12.如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为1,P 为BC 的中点,过点A ,P ,C 1的平面截正方体所得的截面为M ,则截面M 的面积为2.【解析】如图,取A 1D 1,AD 的中点分别为F ,G . 连接AF ,AP ,PC 1,C 1F ,PG ,D 1G ,AC 1,PF . ∵F 为A 1D 1的中点,P 为BC 的中点,G 为AD 的中点,∴AF =FC 1=AP =PC 1=52,PG CD ,AF D 1G . 由题意可知CD C 1D 1,∴PG C 1D 1, ∴四边形C 1D 1GP 为平行四边形, ∴PC 1D 1G ,∴PC 1AF , ∴A ,P ,C 1,F 四点共面, ∴四边形APC 1F 为菱形. ∵AC 1=3,PF =2,过点A ,P ,C 1的平面截正方体所得的截面M 为菱形APC 1F ,∴截面M 的面积S =12AC 1·PF =12×3×2=62.三、解答题13.(2021·浙江高三期末)如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=5,BB 1=4,CC 1=3,求:(1)该几何体的体积; (2)该几何体的表面积.【解析】 (1)把几何体ABC -A 1B 1C 1补成直棱柱A 1B 1C 1-ADE , 如图,作C 作与底面平行的截面CMN ,则截得两个直棱柱,则AM =2,BN =BD =1,CE =2, S △A 1B 1C 1=12×2×2=2,V ADE -MNC =2×2=4,VMNC -A 1B 1C 1=2×3=6,所以VABC -A 1B 1C 1=6+4×12=8;(也可求出四棱锥C -ABNM 的体积为2)(2)A 1C 1=22,因此SABB 1A 1=12×(5+4)×2=9,SBB 1C 1C =12×(4+3)×2=7,SCC 1A 1A =12×(3+5)×22=82,又AC =22+(22)2=23, BC =22+12=5=AB ,等腰三角形ABC 的底边AC 上的高为h =(5)2-(3)2=2,S△ABC=12×23×2=6,所以所求表面积为S=2+6+9+7+82=18+82+ 6.。
【金版学案】高考数学(理)二轮专题复习课件:专题五 第一讲 空间几何体

___的三角形
平行于 用一个________棱
棱 锥底底面棱的锥面平,面与去截截面
台 ______________之
间的部分,叫做棱
Z主 干考点
梳理
以________的一边所在的
矩形 圆 直线为________,其余三 旋转轴 柱 边旋转形成的面所围成的
旋
旋转体叫做圆柱
转 体
圆 锥
直角三角形以的一条直角 ___边____________________ __所在的直线为旋转轴, 其余两边旋转形成的面所
G高 考热点 突破
规律方法
(1)求几何体体积问题,可以多
栏 目
链
接
角度、多方位地考虑问题.在求
三棱锥体积的过程中,等体积转
化法是常用的方法,转换底面的
原则是使其高易求,常把底面放
G高 考热点 突破
跟踪 训2.(练2014·江苏卷)设甲,乙两个圆柱的底面面积分别为 S1,
S2,体积为 V1,V2,若它们的侧面积相等且SS21=94,则VV12的值是
例1 下图是一个几何体的三视
图,根据图中数据,可得该几何体 栏
目
的表面积是( )
链 接
A.9π B.10π C.11π D.12π
G高 考热点 突破
思路点拨:本题可根据三视
图确定原几何体及其有关数据,
然解后由由三公式视求图得可表得面该积几.何 体 是
栏 目
析由一个底面半径为1,高为3的
链 接
圆柱及其上面的一个半径为1的
为( D)
栏 目 链 接
11 A. 2
B.5
9 C.2
D.4
Z主 干考点
梳理
3.(2014·大纲卷)正四棱锥的顶点都在同一球面上,
高考数学(理科,人教版)二轮专题整合突破复习课件专题五 第1讲 空间几何体(共35张PPT)

=
13 2
.故选 C.
4.(2013·福建,理 12)已知某一多面体内接于球构成一个简单组合 体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的 四边形是边长为 2 的正方形,则该球的表面积是 12π .
解析:由题意知该几何体是一个正方体内接于球构成的组合体, 球的直径 2r= 22 + 22 + 22 = 12,所以 r= 3,故该球的表面积为 S 2 球=4πr =4π×3=12π.
热点二
空间几何体的表面积与体积
【例 2】 已知某实心几何体的三视图如图所示(单位:cm),则该几
2 (96 + 8 π )cm 何体的表面积为 .
解析:由三视图可知,该几何体是由一个正方体和一个圆柱组成 的组合体,其表面积为 S 表=6×42+2π×4=96+8π(cm2).
规律方法 (1)求解几何体的表面积时要注意 S 表=S 侧+S 底. (2)求几何体的体积问题,可以多角度、多方位地考虑.对于规则 的几何体的体积,如求三棱锥的体积,采用等体积转化是常用的方法, 转化的原则是其高与底面积易求;对于不规则几何体的体积常用割 补法求解,即将不规则几何体转化为规则几何体,以易于求解. (3)对于给出几何体的三视图,求其体积或表面积的题目关键在 于要还原出空间几何体,并能根据三视图的有关数据和形状推断出 空间几何体的线面关系及相关数据,体积或表面积的求解套用对应 公式即可.
1 AF ·������△������������������ 3
2������������ ·������△������������������
=1∶24.
通过对近几年高考试题的分析可看出,空间几何体的命题形式 比较稳定,多为选择题或填空题,有时也出现在解答题的某一问中,题 目难度常为中低档题.考查的重点是直观图、 三视图、 面积与体积等 知识,此类问题多为考查三视图的还原问题,且常与空间几何体的表 面积、体积等问题交会,是每年的必考内容. 预计在新一年高考中: 对空间几何体的三视图的考查有难度加大的趋势,通过此类题 考查考生的空间想象能力;对表面积和体积的考查,常见形式为蕴涵 在两个几何体的“切”或“接”形态中,或以三视图为载体进行交会考 查,此内容还要注意强化几何体的核心——截面以及补形、 切割等数 学思想方法的训练.
2021年高考数学大二轮复习专题五空间几何5.1空间几何体练习
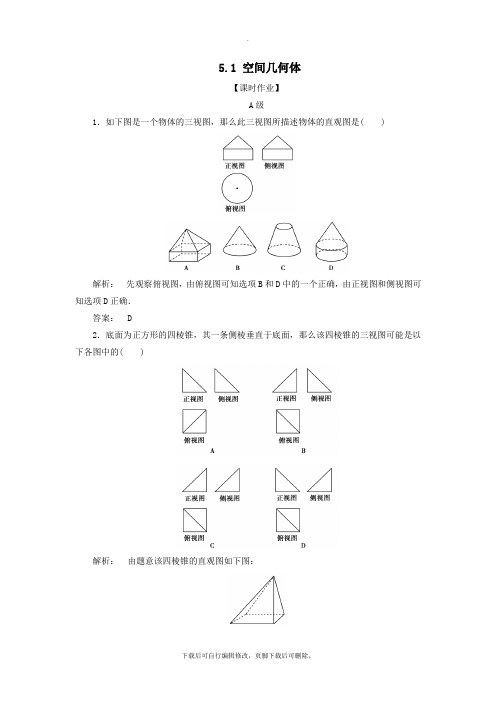
5.1 空间几何体【课时作业】A级1.如下图是一个物体的三视图,那么此三视图所描述物体的直观图是( )解析:先观察俯视图,由俯视图可知选项B和D中的一个正确,由正视图和侧视图可知选项D正确.答案: D2.底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图可能是以下各图中的( )解析:由题意该四棱锥的直观图如下图:那么其三视图如图:答案: C3.设一个球形西瓜,切下一刀后所得切面圆的半径为4,球心到切面圆心的距离为3,那么该西瓜的体积为( )A .100πB .2563πC.4003π D .5003π解析: 由题意知切面圆的半径r =4,球心到切面的距离d =3,所以球的半径R =r 2+d 2=42+32=5,故球的体积V =43πR 3=43π×53=5003π,即该西瓜的体积为5003π. 答案: D4.如图,水平放置的三棱柱的侧棱长为1,且侧棱AA 1⊥平面A 1B 1C 1,正视图是边长为1的正方形,俯视图为一个等边三角形,那么该三棱柱的侧视图面积为( )A .2 3B . 3 C.32D .1解析: 由直观图、正视图以及俯视图可知,侧视图是宽为32,长为1的长方形,所以面积S =32×1=32.应选C. 答案: C5.(2021·全国卷Ⅰ)圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,那么该圆柱的外表积为( )A .122πB .12πC .82πD .10π解析: 设圆柱的轴截面的边长为x ,那么由x 2=8,得x =22, ∴S 圆柱表=2S 底+S 侧=2×π×(2)2+2π×2×22=12π. 应选B. 答案: B6.(2021·福州市质量检测)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,那么该几何体的体积为( )A.π12+3 B .π12+6 C.π3+3 D .π3+6解析: 由三视图可知,该几何体是由直四棱柱与圆锥拼接而成的简单组合体,如下图.由题设得,V 四棱柱=12×(1+2)×2×1=3,V 圆锥=13π⎝ ⎛⎭⎪⎫122×1=π12,所以该几何体的体积V =V 四棱柱+V 圆锥=3+π12.应选A.答案: A7.(2021·武汉市局部学校调研)一个几何体的三视图如图,那么它的外表积为( )A .28B .24+2 5C .20+4 5D .20+2 5解析: 根据该几何体的三视图作出其直观图如下图,可以看出该几何体是一个底面是梯形的四棱柱.根据三视图给出的数据,可得该几何体中梯形的上底长为2,下底长为3,高为2,所以该几何体的外表积S =12×(2+3)×2×2+2×2+2×3+2×2+2×22+12=24+25,应选B.答案: B8.祖暅是南北朝时代的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,那么积不容异〞.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,那么满足祖暅原理的两个几何体为( )A .①②B .①③C .②④D .①④解析: 设截面与底面的距离为h ,那么①中截面内圆的半径为h ,那么截面圆环的面积为π(R 2-h 2);②中截面圆的半径为R -h ,那么截面圆的面积为π(R -h )2;③中截面圆的半径为R -h2,那么截面圆的面积为π⎝ ⎛⎭⎪⎫R -h 22;④中截面圆的半径为R 2-h 2,那么截面圆的面积为π(R 2-h 2).所以①④中截面的面积相等,故其体积相等,选D.答案: D9.(2021·昆明市高三摸底调研测试)古人采取“用臼春米〞的方法脱去稻谷的外壳,获得可供食用的大米,用于春米的“臼〞多用石头或木头制成.一个“臼〞的三视图如下图,那么凿去局部(看成一个简单的组合体)的体积为( )A .63πB .72πC .79πD .99π解析: 由三视图得凿去局部是圆柱与半球的组合体,其中圆柱的高为5,底面圆的半径为3,半球的半径为3,所以组合体的体积为32π×5+12×43π×33=63π,应选A.答案: A10.某几何体是直三棱柱与圆锥的组合体,其直观图和三视图如下图,正视图为正方形,其中俯视图中椭圆的离心率为( )A.12 B .24 C.22D .32解析: 依题意得,题中的直三棱柱的底面是等腰直角三角形,设其直角边长为a ,那么斜边长为2a ,圆锥的底面半径为22a 、母线长为a ,因此其俯视图中椭圆的长轴长为2a 、短轴长为a ,其离心率e =1-⎝⎛⎭⎪⎫a 2a 2=22,选C. 答案: C11.如图是一个几何体的三视图,其中正视图是边长为2的等边三角形,侧视图是直角边长分别为1和3的直角三角形,俯视图是半径为1的半圆,那么该几何体的内接三棱锥的体积的最大值为( )A.36 B .33 C.433D .3π3解析: 由三视图可知该几何体为半个圆锥,圆锥的母线长l =2,底面半径r =1,高h =l 2-r 2= 3.由半圆锥的直观图可得,当三棱锥的底面是斜边为半圆直径,高为半径的等腰直角三角形,棱锥的高为半圆锥的高时,其内接三棱锥的体积到达最大值,最大体积为V =16×2×1×3=33,应选B. 答案: B12.在棱长为3的正方体ABCD A 1B 1C 1D 1中,P 在线段BD 1上,且BP PD 1=12,M 为线段B 1C 1上的动点,那么三棱锥M PBC 的体积为( )A .1B .32C.92 D .与M 点的位置有关解析: ∵BP PD 1=12,∴点P 到平面BC 1的距离是D 1到平面BC 1距离的13,即为D 1C 13=1.M 为线段B 1C 1上的点,∴S △MBC =12×3×3=92,∴V M PBC =V P MBC =13×92×1=32.答案: B13.(2021·天津卷)如图,正方体ABCD A 1B 1C 1D 1的棱长为1,那么四棱锥A 1BB 1D 1D 的体积为________.解析: ∵正方体棱长为1, ∴矩形BB 1D 1D 的长和宽分别为1, 2.∵四棱锥A 1BB 1D 1D 的高是正方形A 1B 1C 1D 1对角线长的一半,即为22, ∴V 四棱锥A 1BB 1D 1D =13Sh =13×(1×2)×22=13.答案: 1314.(2021·江苏卷)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,那么V 1V 2的值是________.解析: 设圆柱内切球的半径为R ,那么由题设可得圆柱O 1O 2的底面圆的半径为R ,高为2R ,∴V 1V 2=πR 2·2R 43πR3=32. 答案: 3215.一个四棱锥的三视图如下图,其中侧视图为正三角形,那么该四棱锥的体积是________.解析: 由四棱锥的三视图可知,该四棱锥的直观图如图中四棱锥P ABCD 所示,底面ABCD 为边长为1的正方形,△PAD 是边长为1的等边三角形,作PO ⊥AD 于点O ,那么O 为AD 的中点,所以四棱锥的体积为V =13×1×1×32=36. 答案:3616.(2021·新疆自治区适应性检测)如图是一个四棱锥的三视图,其正视图与侧视图都是边长为23的正三角形,俯视图轮廓为正方形,那么此几何体的外接球的体积是________.解析: 根据三视图可知,该几何体是底面边长为23,斜高为23的正四棱锥S ABCD .其外接球的球心在正四棱锥的高上,设此四棱锥的底面中心为O ′,外接球球心为O ,连接SO ′,OB ,O ′B ,如图,设此四棱锥的外接球的半径为R ,那么根据正四棱锥的性质,易得SO ′=3,OO ′=3-R ,O ′B =6,可得(3-R )2+(6)2=R 2,解得R =52,故球的体积V =43πR 3=1256π.答案:1256π B 级1.(2021·兰州市诊断考试)刘徽?九章算术注?记载:“邪解立方,得两堑堵.邪解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.〞意即把一长方体沿对角面一分为二,这一样的两块叫堑堵,沿堑堵的一顶点与其相对的面的对角线剖开成两块,大的叫阳马,小的叫鳖臑,两者体积之比为定值2∶1,这一结论今称刘徽原理.如图是一个阳马的三视图,那么其外接球的体积为( )A.3πB .32πC .3πD .4π解析: 由三视图得阳马是一个四棱锥,如图中四棱锥P ABCD ,其中底面是边长为1的正方形,侧棱PA ⊥底面ABCD 且PA =1,所以PC =3,PC 是四棱锥P ABCD 的外接球的直径,所以此阳马的外接球的体积为4π3⎝ ⎛⎭⎪⎫323=32π,应选B.答案: B2.将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱的最大体积为( )A.π27 B .8π27C.π3D .2π9解析: 如下图,设圆柱的半径为r ,高为x ,体积为V ,由题意可得r 1=2-x2,所以x=2-2r ,所以圆柱的体积V =πr 2(2-2r )=2π(r 2-r 3)(0<r <1),设V (r )=2π(r 2-r 3)(0<r <1),那么V ′(r )=2π(2r -3r 2),由2π(2r -3r 2)=0得r =23,所以圆柱的最大体积V max =2π⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫232-⎝ ⎛⎭⎪⎫233=8π27.答案: B3.(2021·福建市第一学期高三期末考试)如图,在四棱锥E ABCD 中,AB ∥CD ,∠ABC =90°,CD =2AB =2CE =4,点F 为棱DE 的中点.(1)证明:AF ∥平面BCE ;(2)假设BC =4,∠BCE =120°,DE =25,求三棱锥B CEF 的体积.解析: (1)证明:如图,取CE 的中点M ,连接FM ,BM . 因为点F 为棱DE 的中点, 所以FM ∥CD 且FM =12CD =2,因为AB ∥CD ,且AB =2, 所以FM ∥AB 且FM =AB , 所以四边形ABMF 为平行四边形, 所以AF ∥BM ,因为AF ⊄平面BCE ,BM ⊂平面BCE , 所以AF ∥平面BCE .(2)因为AB ∥CD ,∠ABC =90°,所以CD ⊥BC . 因为CD =4,CE =2,DE =25,所以CD 2+CE 2=DE 2, 所以CD ⊥CE ,因为BC ∩CE =C ,BC ⊂平面BCE ,CE ⊂平面BCE , 所以CD ⊥平面BCE .因为点F 为棱DE 的中点,且CD =4, 所以点F 到平面BCE 的距离为2.S △BCE =12BC ·CE sin ∠BCE =12×4×2sin 120°=2 3.三棱锥B CEF 的体积V B CEF =V F BCE =13S △BCE ×2=13×23×2=433.4.右图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD =AD =2EC =2..下载后可自行编辑修改,页脚下载后可删除。
高考数学二轮复习考前专题五立体几何与空间向量第1讲空间几何体讲学案理(2021学年)

2018年高考数学二轮复习考前专题五立体几何与空间向量第1讲空间几何体讲学案理编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年高考数学二轮复习考前专题五立体几何与空间向量第1讲空间几何体讲学案理)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年高考数学二轮复习考前专题五立体几何与空间向量第1讲空间几何体讲学案理的全部内容。
第1讲空间几何体1。
以三视图为载体,考查空间几何体面积、体积的计算。
2.考查空间几何体的侧面展开图及简单的组合体问题.热点一三视图与直观图1.一个物体的三视图的排列规则俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图的宽度一样.即“长对正、高平齐、宽相等”.2.由三视图还原几何体的步骤一般先依据俯视图确定底面再利用正(主)视图与侧(左)视图确定几何体.例1(1)(2017届南昌模拟)一个四面体的顶点在空间直角坐标系O—xyz中的坐标分别是错误!,(1,0,1),错误!,错误!,绘制该四面体三视图时,按照如下图所示的方向画正(主)视图,则得到侧(左)视图可以为( )答案 B解析将四面体放在正方体中,得到如图四面体,得到如图的侧(左)视图,故选B.(2)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这块菜地的面积为________.答案 2+错误!解析如图,在直观图中,过点A作AE⊥BC,垂足为点E,则在Rt△ABE中,AB=1,∠ABE=45°,∴BE=错误!.而四边形AECD为矩形,AD=1,∴EC=AD=1,∴BC=BE+EC=22+1。
高考数学二轮复习专题五立体几何5.1空间几何体2

关闭
答案
-17-
规律总结
拓展演练
3.(2017全国Ⅰ,理7)某多面体的三视,正方形的边长为2,俯视图为
等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形
的面积之和为( )
关闭
A.10 B.12
C.14 D.16
由三视图可还原出几何体的直观图如图所示.该五面体中有两个侧 面是全等的直角梯形,且该直角梯形的上底长为 2,下底长为 4,高为 关闭
2B,则 S 梯=(2+4)×2÷2=6,所以这些梯形的面积之和为 12.
解析 答案
-18-
规律总结
拓展演练
4.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正
视图如图所示,则该三棱锥的体积是
.
关闭
由三棱锥的正视图知,三棱锥的高为 1,底面边长分别为 2 3,2,2,所以
底面三角形的高为 22-( 3)2=1,所以,三棱锥的体积为 V=13 ×
解析 答案
高频考点
-8-
命题热点一 命题热点二 命题热点三
题后反思1.求几何体体积问题,可以多角度、多方位地考虑问题. 在求三棱锥体积的过程中,等体积转化法是常用的方法,转换底面 的原则是使其高易求,常把底面放在已知几何体的某一面上.
2.求不规则几何体的体积,常用分割或补形的思想,将不规则几何 体变为规则几何体,易于求解.
【思考】 求解几何体的表面积及体积的常用技巧有哪些? 关闭
设圆例锥2《的九底章面算半术径》为是R我,高国为古h代. 内容极为丰富的数学名著,书中有
∵如米下堆问底题部:“今的有弧委长米为依8 垣尺内, 角,下周八尺,高五尺.问:积及为米几何?” ∴其 一14)意·,米思2堆π为R底=:“8部在,∴的屋R弧内=1长π墙6.为角8处尺堆,米放堆米的(如高图为,米5尺堆,问为米一堆个的圆体锥积的和四堆分放之的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题五立体几何第一讲空间几何体的三视图、表面积与体积适考素能特训理一、选择题1.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )答案D解析由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知侧视图为等腰三角形,且轮廓线为实线,故选D.2.[2016·重庆测试]某几何体的三视图如图所示,则该几何体的体积为( )A .23B .43C .53D .73答案 B 解析 依题意,题中的几何体是由一个直三棱柱与一个三棱锥所组成的,其中该直三棱柱的底面是一个直角三角形(腰长分别为1、2)、高为1;该三棱锥的底面是一个直角三角形(腰长分别为1、2)、高为1,因此该几何体的体积为12×2×1×1+13×12×2×1×1=43,选B .3.[2016·唐山统考]三棱锥P -ABC 中,PA⊥平面ABC 且PA =2,△ABC 是边长为3的等边三角形,则该三棱锥外接球的表面积为( )A .4π3B .4πC .8πD .20π答案 C解析 由题意得,此三棱锥外接球即为以△ABC 为底面、以PA 为高的正三棱柱的外接球,因为△ABC 的外接圆半径r =32×3×23=1,外接球球心到△ABC 的外接圆圆心的距离d =1,所以外接球的半径R =r 2+d 2=2,所以三棱锥外接球的表面积S =4πR 2=8π,故选C .4.[2016·武昌调研]某几何体的三视图如图所示,则该几何体的表面积为( )A .18+2πB .20+πC .20+π2D .16+π答案 B解析 由三视图可知,这个几何体是一个边长为2的正方体割去了相对边对应的两个半径为1、高为1的14圆柱体,其表面积相当于正方体五个面的面积与两个14圆柱的侧面积的和,即该几何体的表面积S =4×5+2×2π×1×1×14=20+π,故选B .5.[2016·陕西质检]某几何体的三视图如图所示,该几何体的体积为( )A .43B .52C .73D .3答案 A 解析 根据几何体的三视图,得该几何体是下部为直三棱柱,上部为三棱锥的组合体,如图所示.则该几何体的体积是V 几何体=V三棱柱+V三棱锥=12×2×1×1+13×12×2×1×1=43.故应选A .6.已知边长为1的等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C -AB -D 的余弦值为33,若A 、B 、C 、D 、E 在同一球面上,则此球的体积为( ) A .2π B .823π C .2πD .23π 答案 D解析 如图,取AB 的中点为M ,连接CM ,取DE 的中点为N ,连接MN ,CN ,可知∠CMN 即为二面角C -AB -D 的平面角,利用余弦定理可求CN =32=CM ,所以该几何体为正四棱锥,半径R =22,V =43πR 3=2π3,故选D .二、填空题7.[2016·广西南宁检测]设甲、乙两个圆柱的底面积分别为S 1、S 2,体积分别为V 1、V 2.若它们的侧面积相等且V 1V 2=32,则S 1S 2的值是________.答案 94解析 设甲、乙两个圆柱的底面半径分别为r 1,r 2,高分别为h 1,h 2,则有2πr 1h 1=2πr 2h 2,即r 1h 1=r 2h 2,又V 1V 2=πr 21h 1πr 22h 2,∴V 1V 2=r 1r 2,∴r 1r 2=32,则S 1S 2=⎝ ⎛⎭⎪⎫r 1r 22=94.8.[2016·山西太原一模]已知在直角梯形ABCD 中,AB⊥AD,CD⊥AD,AB =2AD =2CD =2,将直角梯形ABCD 沿AC 折叠成三棱锥D -ABC ,当三棱锥D -ABC 的体积取最大值时,其外接球的体积为________.答案 43π解析 当平面DAC⊥平面ABC 时,三棱锥D -ABC 的体积取最大值.此时易知BC⊥平面DAC ,∴BC⊥AD,又AD⊥DC,∴AD⊥平面BCD ,∴AD⊥BD,取AB 的中点O ,易得OA =OB =OC =OD =1,故O 为所求外接球的球心,故半径r =1,体积V =43πr 3=43π.9.[2016·云南玉溪一模]表面积为60π的球面上有四点S 、A 、B 、C ,且△ABC 是等边三角形,球心O 到平面ABC 的距离为3,若平面SAB⊥平面ABC ,则三棱锥S -ABC 体积的最大值为________.答案 27解析 设球O 的半径为R ,则有4πR 2=60π,解得R =15.由于平面SAB⊥平面ABC ,所以点S 在平面ABC 上的射影D 在AB 上,如图,当球心O 在三棱锥S -ABC 中,且D 为AB 的中点时,SD 最大,三棱锥S -ABC 的体积最大.设O′为等边三角形ABC 的中心,则OO′⊥平面ABC ,即有OO′∥SD.由于OC =15,OO′=3,则CO′=CO 2-OO′2=23,则DO′=3,则△ABC 是边长为6的等边三角形,则△ABC 的面积为12×6×33=9 3.在直角梯形SDO′O 中,作OM⊥SD 于M ,则OM =DO′=3,DM =OO′=3,∴SD=DM +MS =3+152-32=33,所以三棱锥S -ABC 体积的最大值为13×93×33=27.三、解答题10.[2016·达州一模]已知几何体A -BCED 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A -BCED 的体积为16.(1)求实数a 的值;(2)将直角三角形△ABD 绕斜边AD 旋转一周,求该旋转体的表面积.解 (1)由该几何体的三视图知AC⊥平面BCED ,且EC =BC =AC =4,BD =a ,体积V =13×4×+2=16,所以a =2.(2)在Rt △ABD 中,AB =42,BD =2,所以AD =6, 过点B 作AD 的垂线BH ,垂足为点H ,易得BH =423,该旋转体由两个同底的圆锥构成,圆锥底面半径为BH =423.所以圆锥底面周长为c =2π·423=82π3,两个圆锥的母线长分别为42和2,故该旋转体的表面积为S =12×82π3(2+42)=32π+82π3.11.[2016·河北五校联盟质检] 如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD ,Q 为AD 的中点,PA =PD =2,BC =12AD =1,CD=3,M 是棱PC 的中点.(1)求证:PA∥平面MQB ; (2)求三棱锥P -DQM 的体积.解 (1)证明:连接AC ,交BQ 于点N ,连接MN ,CQ ,∵BC∥AD 且BC =12AD ,即BC∥AQ,BC =AQ ,∴四边形BCQA 为平行四边形,且N 为AC 的中点,又点M 是棱PC 的中点,∴MN∥PA,又∵PA ⊄平面MQB ,MN ⊂平面MQB ,则PA∥平面MQB. (2)连接DM ,则V P -DQM =V M -PDQ , ∵平面PAD⊥底面ABCD ,CD⊥AD, ∴CD⊥平面PAD ,∴点M 到平面PAD 的距离为12CD ,∴V P -DQM =V M -PDQ =13S △PDQ ·12CD =13·12·QD·PQ·12CD =14.12.[2016·鹰潭二模]如图1所示,直角梯形ABCD ,∠ADC=90°,AB∥CD,AD =CD =12AB =2,点E 为AC 的中点,将△ACD 沿AC 折起,使折起后的平面ACD 与平面ABC 垂直(如图2),在图2所示的几何体D -ABC 中.(1)求证:BC⊥平面ACD ;(2)点F 在棱CD 上,且满足AD∥平面BEF ,求几何体F -BCE 的体积. 解 (1)证明:在图1中,由题意知,AC =BC =22, 所以AC 2+BC 2=AB 2,所以AC⊥BC因为E 为AC 的中点,连接DE ,则DE⊥AC, 又平面ADC⊥平面ABC ,且平面ADC∩平面ABC =AC ,DE ⊂平面ACD ,从而ED⊥平面ABC , 所以ED⊥BC又AC⊥BC,AC∩ED=E , 所以BC⊥平面ACD.(2)取DC 的中点F ,连接EF ,BF , 因为E 是AC 的中点,所以EF∥AD,又EF ⊂平面BEF ,AD ⊄平面BEF ,所以AD∥平面BEF , 由(1)知,DE 为三棱锥B -ACD 的高,因为三棱锥F -BCE 的高h =12DE =12×2=22,S △BCE =12S △ABC =12×12×22×22=2,所以三棱锥F -BCE 的体积为:V F -BCE =13S △BCE ·h=13×2×22=23.。
