上海市宝山区2014届高三上学期期末考试(一模)数学试题及答案
上海市宝山区2024届高三上学期期末教学质量监测(一模)数学试题 (2)

一、单选题二、多选题1. 如图所示,在数轴上表示的区间与下列不等式的解集相同的是()A.B.C.D.2. 已知为任意角,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知直线是圆的一条对称轴,则的最大值为( )A.B.C .1D.4. 高铁、扫码支付、共享单车、网购并称中国“新四大发明”,近日对全国100个城市的共享单车和扫码支付的使用人数进行大数据分析,其中共享单车使用的人数分别为,,,…,,它们的平均数为,方差为;其中扫码支付使用的人数分别为,,,…,,它们的平均数为,方差为,则,分别为( )A .,B.,C .,D .,5.已知集合,,则( )A.B.C.D.6. 已知定点及抛物线:,过点作直线与交于,两点,设抛物线的焦点为,则面积的最小值为( )A .2B .3C .4D .57. 设A,是轴上的两点,点的横坐标为2,且,若直线的方程为,则直线的方程是( ).A.B.C.D.8.若展开式中含项的系数为21,则实数的值为A .3B .-3C .2D .-29. 设,,分别为锐角三个内角,,的对边,且,则下列结论正确的是( )A.B.C.的取值范围是D .的取值范围是10. 若函数为函数的导函数,且对于任意实数,均有,且,则( )A .函数不可能为奇函数B .存在实数M,使得C .存在实数N,使得D .函数不存在零点11.在正方体中,点P满足,则()上海市宝山区2024届高三上学期期末教学质量监测(一模)数学试题 (2)上海市宝山区2024届高三上学期期末教学质量监测(一模)数学试题 (2)三、填空题四、解答题A .对于任意的正实数,三棱锥的体积始终不变B .对于任意的正实数,都有平面C .存在正实数,使得异面直线与所成的角为D .存在正实数,使得直线与平面所成的角为12. 下列说法正确的是( )A .已知,则函数B .已知,则函数的值域为C .已知,则函数的最小值为2D .已知,则.13.已知数列的前项和为,若,则______,______.14. 某学校共1000人参加数学测验,考试成绩近似服从正态分布,若,则估计成绩不及格(在90分以下)的学生人数为______.15. 在的二项式中,有且只有第五项的二项式系数最大,则_________.16.已知双曲线过点,且与的两个顶点连线的斜率之和为4.(1)求的方程;(2)过点的直线与双曲线交于,两点(异于点).设直线与轴垂直且交直线于点,若线段的中点为,证明:直线的斜率为定值,并求该定值.17. 已知双曲线:的右焦点为,直线:与的渐近线相交于点,,且的面积为.(1)求C 的标准方程;(2)过点F 作直线与C 的右支相交于M ,N 两点,若x 轴上的点G使得等式恒成立,求证:点的横坐标为.18. 已知函数,,a,,且曲线在处的切线方程为.(1)讨论函数的单调性;(2)若对任意,都有,求实数a 的取值范围.19.在平面直角坐标系中,设锐角的始边与轴的非负半轴重合,终边与单位圆交于点,将射线绕坐标原点按逆时针方向旋转后与单位圆交于点,记.(1)求函数的值域;(2)设的角、、所对的边分别为、、,若,且,,求.20. 某调查机构为了了解某产品年产量(吨)对价格(千元/吨)和利润的影响,对近五年该产品的年产量和价格统计如下表:(1)求关于的线性回归方程;(2)若每吨该产品的成本为千元,假设该产品可全部卖出,预测当年产量为多少时,年利润取到最大值?参考公式:,.21. 单板滑雪型池比赛是冬奥会比赛中的一个项目,进入决赛阶段的12名运动员按照预赛成绩由低到高的出场顺序轮流进行三次滑行,裁判员根据运动员的腾空高度、完成的动作难度和效果进行评分,最终取单次最高分作为比赛成绩.现有运动员甲、乙二人在2021赛季单板滑雪型池世界杯分站比赛成绩如下表:运动员甲的三次滑行成绩运动员乙的三次滑行成绩分站第1次第2次第3次第1次第2次第3次第1站80.2086.2084.0380.1188.400第2站92.8082.1386.3179.3281.2288.60第3站79.10087.5089.1075.3687.10第4站84.0289.5086.7175.1388.2081.01第5站80.0279.3686.0085.4087.0487.70假设甲、乙二人每次比赛成绩相互独立.(1)从上表5站中随机选取1站,求在该站运动员甲的成绩高于运动员乙的成绩的概率;(2)从上表5站中任意选取2站,用表示这2站中甲的成绩高于乙的成绩的站数,求的分布列和数学期望;(3)假如从甲、乙2人中推荐1人参加2022年北京冬奥会单板滑雪型池比赛,根据以上数据信息,你推荐谁参加,并说明理由.(注:方差,其中为,,…,的平均数)。
历年上海一模、二模专题汇编:矩阵与行列式【S】

高中数学上海市重点高中辅导讲义汇编学科:数学专题:矩阵行列式版本:学生用书姓名:年级:高二上海市各区县2016届高三上学期期末考试数学理试题汇编矩阵与行列式1、(宝山区2016届高三上学期期末)已知矩阵A =⎪⎪⎭⎫ ⎝⎛421y ,B =⎪⎪⎭⎫ ⎝⎛876x ,AB =⎪⎪⎭⎫⎝⎛50432219, 则x+y = .2、(崇明县2016届高三上学期期末)函数sin 2()1x f x =- cosx 的最小正周期是 .3、(宝山区2016届高三上学期期末)已知,0,>t ω函数xx x f ωωcos 1sin 3)(=的最小正周期为π2,将)(x f 的图像向左平移t 个单位,所得图像对应的函数为偶函数,则t 的最小值为 .4、(虹口区2016届高三上学期期末)行列式12cos()tan 25cos cot()x x x x ππ+-的最大值为______.5、(黄浦区2016届高三上学期期末)直线321x y=的一个方向向量可以是 .6、(嘉定区2016届高三上学期期末)已知31cos 75sin sin 75cos =︒-︒αα,则=+︒)230cos(α_______.7、(金山区2016届高三上学期期末)若线性方程组的增广矩阵为⎪⎪⎭⎫ ⎝⎛212332c c ,解为⎩⎨⎧==12y x , 则c 1–c 2= .8、(金山区2016届高三上学期期末)行列式dc b a (a 、b 、c 、d ∈{–1,1,2})所有可能的值中,最小值为 .9、(闵行区2016届高三上学期期末)函数()cos()sin sin()cos x xf x x xπ-=π+的最小正周期T = .10、(浦东新区2016届高三上学期期末)若复数z 满足1012ii z=-(i 为虚数单位),则z = . 11、(青浦区2016届高三上学期期末)方程组35604370x y x y ++=⎧⎨--=⎩的增广矩阵是____________.12、(松江区2016届高三上学期期末)行列式cos 20sin 20︒︒ sin 40cos 40︒︒的值是 .13、(徐汇区2016届高三上学期期末)若三条直线03=++y ax ,02=++y x 和012=+-y x 相交于一点,则行列式11221131-a的值为__________.14、(杨浦区2016届高三上学期期末)已知矩阵1012A ⎛⎫= ⎪-⎝⎭,2413B ⎛⎫= ⎪-⎝⎭,则=+B A _____________.15、(长宁区2016届高三上学期期末)关于x 的不等式的解集为.(1)求实数a ,b 的值; (2)若为纯虚数,求tan α的值.【例题解析】1. 【上海市十三校2013年高三调研考数学试卷(文科)】已知二元一次方程组的增广矩阵是421m m mm +⎛⎫⎪⎝⎭,若该方程组无解,则实数m 的值为___________.2. 【2013学年第一学期徐汇区学习能力诊断卷高三年级数学学科(文科)】计算:122423432⎛⎫⎛⎫⋅+ ⎪ ⎪⎝⎭⎝⎭= .3. 【黄浦区2013—2014学年度第一学期高三年级学业质量调研数学试卷(文科)】三阶行列式45sin 2cos 610sin ---x x x ()R x ∈中元素4的代数余子式的值记为()x f ,则函数()x f 的最小值为4. 【黄浦区2013—2014学年度第一学期高三年级学业质量调研数学试卷(文科)】各项都为正数的无穷等比数列{}na ,满足,,42t a m a ==且⎩⎨⎧==ty m x 是增广矩阵⎪⎪⎭⎫⎝⎛-2221103的线性方程组⎩⎨⎧=+=+2222111211c y a x a c y a x a 的解,则无穷等比数列{}na 各项和的数值是 _________.5. 【上海市杨浦区2013—2014学年度第一学期高三年级学业质量调研数学试卷(文科)】若行列式124012x -=,则x = .2014年高三二模汇编——矩阵、行列式1、(2014宝山四区文理1). 二阶行列式ii i ++-1101的值是 . (其中i 为虚数单位)2、(2014长宁二模文理7)对于任意),1()1,0(∞+∈ a ,函数)1(log 111)(--=x x f a 的反函数)(1x f -的图像经过的定点的坐标是______________.3、(2014奉贤二模理10)、已知函数cos ()sin x f x x=, 则方程()021cos =+⋅x x f 的解是________.4、(2014奉贤二模文10)、将函数cos ()sin x f x x=的图像向左平移m 个单位(0)m >,若所得图像对应的函数为偶函数, 则m 的最小值是________.5、(2014虹口二模5文6)、复数z 满足11z ii i=+,则复数z 的模等于_______________.7、(2014浦东二模文理3). 函数()31cos 4sin xx x f =的最大值为 .8、(2014松江三区二模文理7).函数()()sin cos cos 2sin cos sin x x x f x xx xπ+-=-的最小正周期T =____________.【课堂练习】1. 【上海市黄浦区2014届高三上学期期末考试(即一模)数学(理)试题】三阶行列式45sin 2cos 61sin ---xx x ()R x ∈中元素4的代数余子式的值记为()x f ,则函数()x f 的最小值为2. 【上海市十三校2013年高三调研考数学试卷(理科)】已知二元一次方程组的增广矩阵是421m m m m +⎛⎫⎪⎝⎭,若该方程组无解,则实数m 的值为___________.3. 【2013学年第一学期徐汇区学习能力诊断卷高三年级数学学科(理科)】计算:122423432⎛⎫⎛⎫⋅+ ⎪ ⎪⎝⎭⎝⎭= .4. 【上海市杨浦区2013—2014学年度第一学期高三年级学业质量调研数学试卷(理科)】若行列式124012x -=,则x = .5. 【上海市黄浦区2014届高三上学期期末考试(即一模)数学(理)试题】各项都为正数的无穷等比数列{}na ,满足,,42t a m a ==且⎩⎨⎧==ty mx 是增广矩阵⎪⎪⎭⎫⎝⎛-2221103的线性方程组⎩⎨⎧=+=+2222111211c y a x a c y a x a 的解,则无穷等比数列{}na 各项和的数值是 _________.上海市各区县2015届高三上学期期末考试数学理试题分类汇编矩阵与行列式一、填空题1、(宝山区20152、(宝山区2015届高三上期末)设矩阵241A x ⎛⎫= ⎪⎝⎭,2211B -⎛⎫= ⎪-⎝⎭,若BA =2412⎛⎫⎪--⎝⎭, 则x =3、(崇明县2015届高三上期末)已知线性方程组的增广矩阵为103210⎛⎫⎪⎝⎭,则其对应的方程组解为4、(奉贤区2015届高三上期末)已知⎪⎪⎭⎫⎝⎛-βαcos 200sin 为单位矩阵,且,2παβπ⎡⎤∈⎢⎥⎣⎦、,则tan()αβ+= 5、(虹口区2015届高三上期末)行列式()3sin tan 4cos tan()2x x x x ππ-+的最小值为6、(嘉定区2015届高三上期末)将函数xx x f 2sin 12cos 3)(=的图像向左平移m (0>m )个单位,所得图像对应的函数为偶函数,则m 的最小值为____________7、(金山区2015届高三上期末)当a >0,b >0且a+b =2时,行列式ba 11的值的最大值是8、(浦东区2015届高三上期末)已知一个关于y x ,的二元线性方程组的增广矩阵是⎪⎪⎭⎫ ⎝⎛-210211,则y x +=9、(松江区2015届高三上期末)若复数z 满足014=-zz ,则z 的值为10、(徐汇区2015届高三上期末)若全集U R =,不等式11111x x+≥-的解集为A ,则U A C =11、(杨浦区2015届高三上期末)设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,若30a b c a ba b c ++=+-,则角C =_______12、(黄浦区2015届高三上期末)若三阶行列式1302124121n m mn -+---中第1行第2列的元素3的代数余子式的值是15-,则|i |n m +(其中i 是虚数单位,R m n ∈、)的值是二、选择题 1、(浦东区2015届高三上期末)已知数列{}n a 的通项公式2,n a n n N *=∈,则5231234201220134345620142015a a a a a a a a a a a a a a a a ++++= ( )()A 16096-()B 16104- ()C 16112-()D 16120-。
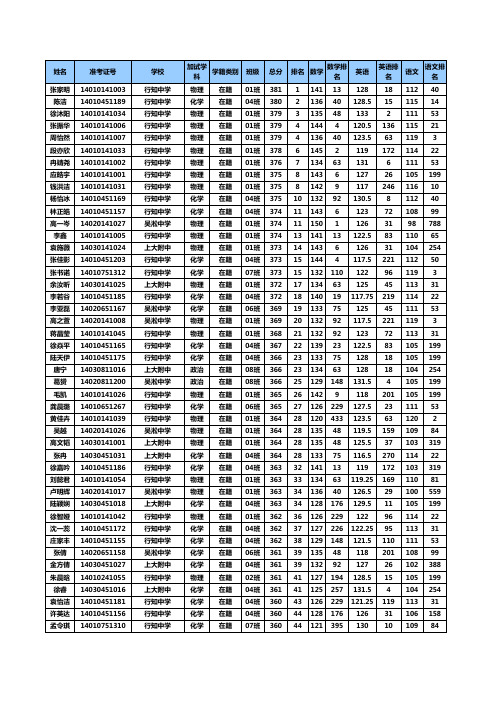
2014届上海市宝山区高三一模个人成绩
44 47 47 47 50 50 50 53 53 53 53 53 58 59 59 59 62 62 62 62 66 66 66 69 69 69 72 72 72 72 76 76 78 78 80 81 81 81 84 85 85 85 88 88 88
141 138 133 128 121 126 132 129 140 142 138 144 140 132 138 128 137 133 124 138 137 134 117 125 127 122 131 124 120 122 127 126 138 133 131 132 123 126 126 117 129 138 124 129 136
14030451006 14010141024 14010141035 14020651179 14010451174 14031021023 14090141001 14010141038 14010341108 14010341138 14020141040 14020651173 14020651180 14010141032 14010451180 14020141035 14010141009 14010141036 14010451188 14030451033 14010141011 14010451159 14030551021 14010451171 14030341024 14030451019 14010141046 14010451176 14030141037 14040502192 14010451154 14010451160 14020141031 14030141004 14150141027 14010141004 14010451199 14031021026 14010751307 14020821223 14030141031 14030451022 14010451178 14020141006 14020141025
2014年上海中考宝山区数学一模试卷附答案

2013学年宝山区第一学期期末考试九年级数学试卷(满分150分,考试时间100分钟)5.已知 D 、E 、F 分别为等腰△ ABC 边 BC 、CA 、AB 上的点,如果 AB = AC , BD =2 , CD =3 , CE =4 ,AE. FDE - B ,那么 AF 的长为()2A • 5. 5;B • 4. 5;C • 4;D • 3. 5.6.如图,梯形 ABCD 中,AD // BC , BF 丄 AD , CE 丄 AD ,且 点A 出发,沿折线AB — BC — CD 以每秒1个单位长的速度运动到点的面积为y ,则y 关于t 的函数图像大致是( )1.下列各式中,正确的是 ( )區 4 2 8 A . a a a ; B . 4 26a a a ;C . 4 216a a a ;2. 已知Rt △ ABC 中, .C =90;, 那么cosA 表示() 的值.BCB •BC C .AC A .-;;ACABBC3. 二次函数y - -(x -1)2- 3图像的顶点坐标是( )A • (-1,3);B . (1,3 );C . (-1,-3 );4.如图,在平行四边形 ABCD 中, 如果忒a , 7D4■* -1 那么a b 等于ACABD • (1,-3 ) •A • BD ;C • DB ;AC CA •9 . ,10.二次函数y =2x 3的图像开口方向11 .如图,二次函数 y=ax 2,bx 的图像开口向上,对称轴为直线 的值是 ___________ .12. ____________________________________________________ 抛物线y=(x ,2)2-3可以由抛物线 y =x 2 -3向 __________________ 13. 若a 与b 的方向相反,且 ? >|b ,则a +b 的方向与a 的方向 14. 如图已知△ ABC 中,D 为边AC 上一点,P 为边AB 上一点, ,AD = 6,当 AP 的长度为 ___________ 时厶ADP 和厶ABC 相似. 、选择题:(本大题共6题,每题4分,满分24分) D 停止.设运动时间为第秒题钛EFGDx=1,图像经过((平移)得到. AB =12, AC =817 .在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示),已知立杆 AB 的高度是6米,从侧面D 测到路况警示牌顶端 C 点和低端B 点的仰角分别是 60°和45。
上海市宝山区2014届高三英语上学期期末考试试题(上海市宝山一模)上海牛津版

宝山区2013学年第一学期期末高三年级英语学科质量监测试卷考生注意:1. 考试时间120分钟,试卷满分150分。
2. 本考试设试卷和答题纸两部分。
试卷分为第Ⅰ卷(第1—10页)和第Ⅱ卷(第10页),全卷共10页。
第I卷第1-16小题、第41-77小题采用多项选择题形式,答案必须涂写在答题纸相应位置,写在试卷上无效。
第I卷第17-40小题、第78-81小题和第II卷的试题,其答案必须写在答题纸相应位置,写在试卷上无效。
3.答题前,务必在答题纸上填写姓名、班级、学校和准考证号,并用铅笔在答题纸上正确涂写准考证号。
第I卷(共103分)Ⅰ. Listening ComprehensionSection A Short ConversationsDirections: In Section A, you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.1. A. A writer. B. A teacher. C. A reporter. D. A student.2. A. Husband and wife. B. Teacher and student.C. Boss and secretary.D. Doctor and nurse.3. A. At a science exhibition. B. Near an art museum.C. At a news conference.D. Near a paint store.4. A. Lock the door carefully. B. Open the door.C. Fix the lock himself.D. Call a repairman.5. A. Find a larger room. B. Sell the old table.C. Buy two bookshelves.D. Rearrange some furniture.6. A. The choice of courses. B. A day course.C. An evening course.D. Their work.7. A. She will not take any medicine.B. She hasn’t got a bad cold.C. She will take some medicine in a week.D. She will take some medicine at once.8. A. The woman is planning a trip to Austin.B. The woman hasn’t been to Austin before.C. The woman doesn’t like Austin.D. The woman has been to Austin before.9. A. It was a long lecture, but easy to understand.B. It was not as easy as she had expected.C. It was as difficult as she had expected.D. It was interesting and easy to follow.10. A. She felt it was tiring. B. She felt it was very nice.C. She felt it took less time.D. She thought it was expensive.Section B PassagesDirections: In Section B, you will hear two short passages, and you will be asked three questions on each of the passages. The passages will be read twice, but the questions will be spoken only once. When you hear a question, read the four possible answers on your paper and decide which one would be the best answer to the question you have heard.Questions 11 through 13 are based on the following passage.11. A. On Tuesday. B. On Wednesday. C. On Thursday. D. On Friday.12. A. There will be only multiple-choice questions.B. The exam will be both multiple-choice and essay questions.C. The exam will have an oral and a written section.D. There will be only essay questions.13. A. It will be easy to pass the exam.B. Students will be tested on all the material discussed in the class.C. The exam will cover topics from a variety of academic fields.D. Students must complete all parts of the exam.Questions 14 through 16 are based on the following passage.14. A. It helps reduce the cost for airlines.B. It is much cheaper for air travelers.C. It can use the computer to plan air travelling.D. It helps prevent passengers from losing their tickets.15. A. $60. B. $50. C. $70. D. $99.16. A. To attract travelers to take e-ticket flights.B. To punish those insisting on using paper tickets.C. To do much better than other airlines.D. To pay for the work to deal with lost tickets.Section C Longer ConversationsDirections: In Section C, you will hear two longer conversations. The conversations will be read twice. After you hear each conversation, you are required to fill in the numbered blanks with the information you have heard. Write your answers on your answer sheet.Blanks 17 through 20 are based on the following conversation.Blanks 21 through 24 are based on the following conversation.II. Grammar and VocabularySection ADirections: After reading the passages below, fill in the blanks to make the passages coherent and grammatically correct. For the blanks with a given word, fill in each blank with the proper form of the given word; for the other blanks, use one word that best fits each blank.( A )As a student, I get so many assignments every day. I have to stay up late in order to finish all my homework. I used to complain about all this pressure (25) school with my classmates. We did not appreciate our teachers for their hard work. We only (26) (know) that we got a lot of homework.After a few months, we did not complain about homework anymore (27) we knew that our teachers worked (28) (hard) than we did. We had no right to complain. Sometimes, we said, ―I didn’t go to bed until 12:00 o’clock last night. Now I just want to sleep.‖ Our teacher would answer us, ―I go to bed at 1:00 a.m. every day.‖ Since we knew how hard teachers work, we started to appreciate them. To give our thanks, we wrote a big card to the teachers (29) it was teachers’ day. When they got our card, they (30) (touch) because their students finally knew the teachers’ effort.After giving the card, I realized (31) powerful the sentence ―thank you‖ is. When we give our thanks to somebody, the world is full of love. I say ―thank you‖ to my friends, family, classmates, teachers, and even strangers. I like to see the smiles on their faces, so (32) (say) ―thank you‖ every day is the way I make the world a better place.( B )The year before last, a new superhero landed on Earth to live among humans. When people needed help, Thor became their defender and saved (33) world. People loved Thor and the actor who played him — Chris Hemsworth.Hemsworth was born in Melbourne, Australia, in 1983. His family moved between Melbourne and the Northern Territory. In the Northern Territory, Hemsworth’s parents worked on a cattle station. The work required the family (34) (live) two hours from the nearest big city. Since they had no TV, Hemsworth and his brothers learned to entertain (35) . They played outside, (36) (build) weapons and forts (堡垒). Later the family settled on Philip’s Island south of Melbourne (37) Hemsworth enjoyed surfing.In 2012, Hemsworth played Thor again in the film The Avengers. He was one of a group of superheroes (38) (assemble) to save planet Earth. That film earned $1 billion worldwide in just 19 days! He also starred in (39) is called Snow White and the Huntsman. Audiences (40) ____ seem to get enough of him! A second Thor film, Thor 2, is due out in 2013.Section BDirections: Complete the following passage by using the words in the box. Each word can only be used once. Note that there is one word more than you need.The next time you’re riding a subway or bus, pay attention to your fellow passengers. Chances are you’ll see plenty of them with their heads down, tapping the screens of their tablets or41 on their smartphones. While these folks may be making good use of their time by staying42 , their bodies are paying a heavy price for such convenience.As hand-held devices such as smartphones and tablets are becoming more common, users are reporting some new 43 problems. Florida chiropractor (脊椎按摩师) Dean Fishman began noticing an increased number of his patients 44 of neck and shoulder pain. He traced these 45 to the overuse of hand-held devices, specifically the action of bending the neck, and created the term ―Text Neck.‖ As if the painful symptoms weren’t bad enough, Fishman warns that an untreated case of Text Neck could lead to 46 spinal (脊柱的) damage. He founded the Text Neck Institute in an effort to treat and educate those suffering from Text Neck. Treatments offered there include chiropractic care, physical therapy, massage therapy and exercise planning.In order to avoid or reduce the possibility of getting Text Neck, use the following basic principles:●Avoid awkward positioning. Don’t strain (滥用) your neck, and stay aware of how your bodyis 47 in relation to the device.●Take frequent 48 when using any kind of mobile device.●When using a tablet, use a case that can back up the device at comfortable 49 angle.For those who 50 can’t take th eir eyes off their devices, there is an ironic twist –downloading a special app(应用程序)could help. Dr. Fishman has released an app called the Text Neck Indicator App, which measures the angle of your smartpphone. When the angle is appropriate, a green light appears in the upper corner of your screen. But when the angle puts you at risk for neck strain, the light turns red, obliging you to adjust your angle.III. Reading ComprehensionSection ADirections: For each blank in the following passage there are four words or phrases marked A, B, C and D. Fill in each blank with the word or phrase that best fits the context.More and more shoppers are buying things online these days, allowing them to avoid 51 salespeople and long lines at checkout counters. In spite of online convenience, 52 , there are some items — like clothes — that customers prefer to 53 before buying. In light of this, two companies are finding ways to modernize stores and 54 the gap between online and in-store retail (零售).A software company that also happens to sell designer jeans, Hointer has created a fast and painless shopping 55 for its customers.Shoppers walk into a Hointer store and select one of the many pairs of jeans 56 down from bars. Then they point their smartphones at the tag and 57 the Hointer app, after which they select the size and press ―try on.‖ The app then directs them to a specific dressing room.German-made robots bring out the 58 jeans and deliver them through a chute (斜槽) to the dressing room in about 30 seconds. Immediately after 59 pairs of jeans are dropped through another chute, the ―outbox,‖ they disappear from the list in the app.Purchases at Hointer are made with a swipe (刷卡) of a credit card. And interacting with a salesperson is optional! This allows Hointer to hire fewer people and focus on their ultimate goal: developing 60 that supports a retail revolution.Men’s clothing retailer Bonobos has 61 a more personalized shopping experience. Although it is —in fact —an online retailer, Bonobos has decided to open a handful of brick-and-mortar stores called Guideshops. Shoppers make a(n) 62 online before arriving at a Guideshop, where they receive one-on-one 63 from a fitting guide. Because these shops have limited inventories(存货), shoppers aren’t able to take home the outfits they select. But guides help shoppers make online purchases before they leave, after which the items will be 64 to customers in one or two days.While Hointer focuses on convenience, Bonobos Guideshops focus on customer service. But both efforts have one thing 65 : giving clothing retailers a new look for the 21st century.51. A. respectable B. considerate C. aggressive D. violent52. A. however B. therefore C. anyway D. moreover53. A. convince B. guarantee C. ensure D. examine54. A. break B. bridge C. shallow D. deepen55. A. experience B. mall C. direction D. principle56. A. hiding B. hanging C. storing D. labeling57. A. start B. upload C. save D. download58. A. desired B. well-designed C. promoted D. well-prepared59. A. qualified B. wanted C. chosen D. unwanted60. A. employment B. efficiency C. technology D. market61. A. come up with B. looked forward to C. looked up D. brought up62. A. decision B. appointment C. contribution D. impression63. A. contact B. instruction C. notice D. attention64. A. presented B. packaged C. delivered D. transferred65. A. in conclusion B. in common C. as usual D. in generalSection BDirections: Read the following three passages. Each passage is followed by several questions or unfinished statements. For each of them there are four choices marked A, B, C and D. Choose the one that fits best according to the information given in the passage you have just read.(A)Any snakebite can be dangerous if infection sets in. Some types of snake poison make the bite area swollen (肿胀的) or painful. Others cause bleeding or damage the heart’s nerves. Here are some especially dangerous snakes:The largest of all poisonous snakes, king cobras can reach 5.5 meters in length. Each king cobra bite contains enough poison to kill an elephant — or 20 people. But these big snakes usually avoid people. They live throughout India, southern China and Southeast Asia.A bite from Australia’s inland taipan, the world’s most poisonous snake, releases enough poison to kill 100 men. The good news is that people rarely come in contact with this snake, and atreatment for its poison exists.Russell’s viper lives throughout Asia, including India, southern China, and on the island of Taiwan. It prefers grassy fields but can be found in forests and urban areas. It bites more people and causes more deaths than any other poisonous snake.Though short, the common Indian krait packs a powerful punch (攻击) in its bite. Most often, it strikes people at night while they are sleeping. Since the bite causes little pain, victims are often not sure that they have been bitten until they begin to experience stomach cramps (痉挛). Without treatment, symptoms will worsen quickly and can lead to death.The black mamba, a native of Africa, is actually olive or grey in color. Only the inside of its mouth is black. When black mambas feel threatened by a human, they make a loud hissing sound to warn the person away. If the warning is ignored, the snake will attack the person repeatedly. And they can attack quickly, moving over the ground at speeds of up to 20 kilometers per hour.66. According to this article, what is a particular feature of the king cobra?A. Its seasonal changes.B. Its lack of movement.C. Its sense of hearing.D. Its remarkable size.67. According to this article, which of the following is known for its speed?A. The inland taipan.B. The black mamba.C. The Indian krait.D. The Russell’s viper.68. What does the article imply about the inland taipan?A. It was once believed to be extinct.B. A chance meeting with it could be fatal.C. Some people keep one as a pet.D. Very little is known about its behavior.69. In which magazine would you most likely find this article?A. Let’s Explore NatureB. Weekly Travel DigestC. Psychology MagazineD. Global Warning News(B)Basketball, baseball and soccer are classic sports that people will always enjoy. And yet we keep changing popular games like these in new ways to keep them fresh.This game is played in swimming pools withtwo teams of six players. Each player hasflippers (蛙鞋), a snorkel and a stick used forhitting a puck (圆盘). Each team earns pointsby hitting the puck into its underwater goal.Other team members must be ready to takethe puck when a team member goes up forair. That makes underwater hockey a trueteam sport.ChessboxingA sport can also be revised by mixing it withanother game. In chessboxing, two playerscompete on the chess board and in the ring.Though these sports may not be common, give them a look or even a try. 70. Why does the author think Underwater Hockey is a true team sport?A. Because all players in a team wear the same flippers and use a stick to hit a puck.B. Because each player in a team has to cooperate with other team members in the match.C. Because it is played underwater, the game is more dangerous than the sports played on land.D. Because each team earns points by hitting the puck into its underwater goal.71. In Chessboxing, the winner will be the one who _____.A. wins both in chess and in boxingB. defeats his opponent in chessC. wins in chess or in boxingD. can knock his opponent out of the boxing ringCycleballAnother fun game to watch, cycleball is likeindoor soccer on wheels. Each player rides aspecial bike designed for the game. Likesoccer, a team must put the ball in a goal.However, there is a catch . The ball can onlybe touched wit h the bikes’ wheels or theplayers’ heads. This game requires a lot ofpractice to learn the skills needed.BossaballThis exciting sport is part volleyball and partsoccer. But unlike both of those sports,players jump up and down throughout thegame. T hat’s because it’s played on aninflatable (可充气的) volleyball court with atrampoline on either side of the net. Oneplayer bounce on the trampoline while up tofour others stand around it. A team can touchthe ball six times before sending it backacross the net. Each player may touch theball once with arms or twice with other bodyparts.72. According to the article, at most how many players in all can take part in a Bossaball match?A. 4.B. 6.C. 8.D. 10.73. In Cycleball, the author mentions catch, whose meaning may be _____.A. sportB. skillC. ruleD. practice( C )Happiness can be described as a positive mood and a pleasant state of mind. According to recent polls(民意调查), sixty to seventy percent of Americans consider themselves to be moderately happy and one in twenty persons feels very unhappy. Psychologists have been studying the factors that contribute to happiness. It is not predictable, nor is a person in an apparently ideal situation necessarily happy. The ideal situation may have little to do with his actual feelings.A good education and income are usually considered necessary for happiness. Though both may contribute, they are only chief factors if the person is seriously undereducated or actually suffering from lack of physical needs.The rich are not likely to be happier than the middle-income group or even those with very low incomes. People with college educations are somewhat happier than those who did not graduate from high school, and it is believed that this is mainly because they have more opportunities to control their lives. Yet people with a high income and a college education may be less happy than those with the same income and no college education.Poor health does not rule out happiness except for the severely disabled or those in pain. Learning to cope with a health problem can contribute to happiness. Those who have good relationship with other family members are happier than those who live alone. Love has a higher correlation with happiness than any other factors.It should be noted that people quickly get used to what they have, and they are happiest when they feel they are increasing their level no matter where it stands at a given time.Children whose parents were happily married have happier childhoods, but are not necessarily happier adults.The best formula (准则) for happiness is to be able to develop AQ (Adversity Quotient that can be of great benefit when running into trouble), to have a personal involvement and commitment, and to develop self-confidence and self-esteem.74. It can be inferred from the passage that _____.A. happiness is neither predictable nor apparentB. a person in an apparently ideal situation must be happyC. the rich are not likely to be happier than the middle-income groupD. happiness is not necessarily connected to one’s situation in society75. According to the article, happiness is greatly dependent upon _____.A. a happy childhood in which one can do whatever he likesB. great wealth with which one can buy anythingC. a feeling that conditions are becoming for the betterD. a college degree that can help one achieve great success76. The letters AQ in the last paragraph most probably mean _____.A. ambition to defeat others in a severe competitionB. ability to overcome difficulty and get out of embarrassing situationC. methods of solving difficult problems and challenges in lifeD. attitudes towards severe competition especially in trouble77. The best title of this passage may be _____.A. What Does Happiness Consist inB. Happiness and UnhappinessC. Different Kinds of HappinessD. Causes of Happiness and UnhappinessSection CDirections: Read the passage carefully. Then answer the questions or complete the statements in the fewest possible words.Millions of personal computers across the world are running at this moment, but most are using just a fraction of their full capacity to process information. Imagine what could happen if the spare power of these millions of machines were used to solve global problems.The organization Charity Engine attempts to do just that. It enables researchers and companies to use the extra computing power of thousands of personal computers. These companies pay a usage fee that goes to carefully selected charities.The computersCharity Engine offers a free app that has the user’s computer do research as a background task. The program runs automatically, without direction from the user. Each computer works on a small chunk of a larger project and sends back its results. The results are combined to answer the researchers’ questions.The researchersCharity Engine mostly uses its computing power for companies doing scientific, medical or commercial research. For example, Rosetta@home attempts to help find cures for serious diseases by discovering the shapes of proteins. Another project, Einstein@Home, tests scientific theories. And another helps establishments in Africa such as universities search for ways to fight the spread of malaria.The CharitiesCharity Engine gives 50 percent of the profits from renting out computing power to various charities. Each organization it supports has a good reputation for working in an area of vital importance. Most of them seek to address the primary causes of poverty while bringing short-term relief. These include Oxfam, a network of organizations in 94 countries. Another is CARE International, one of the three largest international aid agencies, which works in 87 countries. Charity Engine also supports Doctors Without Borders, which supplies medical care, and WaterAid, which provides safe water and promotes hygiene(卫生) in developing countries. Another of its charities, Sightsavers, works to prevent and reverse blindness through medical treatments and provides training for the blind. Charity Engine helps many other organizations as well.An added bonusCharity Engine returns the other 50 percent of its earnings to the people who made it all possible. The app users are entered into draws. Chosen at random, the winners receive thousands of dollars in prizes!Thanks to Charity Engine, computing power that would have gone to waste is fighting poverty and bringing healing and hope.(Note: Answer the questions or complete the statements in NO MORE THAN TEN WORDS.)78. What does Charity Engine help companies do?___________________________________________________________________________.79. How does Charity Engine spend its earnings?___________________________________________________________________________.80. The computers selected by Charity Engine help researchers and companies through ________.81. According to the passage, besides many organizations, Charity Engine mostly supports _____.第II卷(共47分)I. TranslationDirections: Translate the following sentences into English, using the words given in the brackets.1. 部长的回答令所有在场的记者都很满意。
2014届上海市宝山区吴淞中学高三上学期第二次月考数学试题(2013.12)

第1页共8页
为等差数列的 {cn }的个数为
二、选择题(本大题满分 20 分)本大题共有 4 题,每题都给出代号为 A、B、C、D 的四个结 论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的括号内,选对得 4 分,不选、选错或者选出的代号超过一个(不论是否都写在括号内),一律得零分.
有 n 个首项都是 1 的等差数列,设第 m 个数列的第 k 项为
3.若函数
f
(x)
=
(2x
x
+1)( x
+
a)
为奇函数,则
a
=
4.函数 y = 2−x + 1(x > 0) 的反函数是 y =
5.棱长为 1 的正三棱柱 ABC − A1B1C1 中,异面直线 AB1 与 BC 所成角的大小为
6.在实数集 R 上定义运算 ⊗ : x ⊗ y = x(1 − y),若 (x − a) ⊗ (x + a) < 1对任意实数 x 都成
g(x) = 1 , g(0) = 0 2|x| − 1
,则方程
g(x) = log1 (x + 1)
2
的解的个数为
()
A.0 B.2 C.4
D.6
三、解答题(本大题满分 74 分)本大题共有 5 题,解答下列各题必须写出必要的步骤.
19.(本题满分 12 分,第(1)题 6 分、第(2)题 6 分)
(2)设直线 y = kx 与 C2 有公共点,求证 | k |> 1,进而证明原点不是“ C1 − C2 型点”;
上海市宝山区2014年中考一模(即期末)数学试题

2013学年宝山区第一学期期末考试九年级数学试卷 (2014.1.9)(满分150分,考试时间100分钟)一、选择题:(共6题,每题4分,满分24分) 1、下列各式中,正确的是( )A. 428a a a ⋅= B. 426a a a ⋅= C. 4216a a a ⋅= D. 422a a a ⋅= 2、已知Rt △ABC 中,090A ∠=,那么cos A 表示( )的值 A.BC AC B. BC AB C. AC BC D. ACAB3、二次函数2(1)3y x =--+图像的顶点坐标是( )A. (-1,3)B. (1,3)C. (-1,-3)D. (1,-3)4、如图,在平行四边形ABCD 中,如果,AB a AD b ==,那么a b + 等于( )A.BDB. ACC. DBD. CA5、已知D 、E 、F 分别为等腰△ABC 边BC 、CA 、AB 上的点,如果AB AC =,23BD CD ==,,342CE AE FDE B ==∠=∠,,,那么AF 的长为( )A.5.5B. 4.5C. 4D. 3.56、如图,梯形ABCD 中,AD ∥BC ,BF ⊥AD ,CE ⊥AD ,且AF=EF=ED=5, BF=12,动点G 从点A 出发,沿折现AB-BC-CD 以每秒1个单位长的速 度运动到点D 停止. 设运动时间为t 秒,△EFG 的面积为y ,则y 关于t 的函数图像大致是( )CAB第2题图第4题图DACB第5题图A BCF D E第6题图BACDF E二、填空题:(共12题,每题4分,满分48分) 7、计算(1)(1)a a +-的结果是______________.8、不等式组21111x x ->⎧⎨-<⎩的解集是______________.9、一元一次方程20x px q ++=的根的判别式是_________________. 10、二次函数223y x =+的图像开口方向__________________.11、如图,二次函数2y ax bx c =++的图像开口向上,对称轴为直线=1x ,图像经过(3, 0),则a b c -+的值是___________.12、抛物线2(2)3y x =+-可以由抛物线23y x =-向__________________(平移)得到.13、若a 与b 的方向相反,且a b > ,则a b + 的方向与a的方向_____________.14、如图已知△ABC 中,D 为边AC 上一点,P 为边AB 上一点,12AB =, 8,6A C A D ==,当AP 的长度为__________时△ADP 和△ABC 相似. 15、在△ABC 中,AB ∠∠、都是锐角,若31sin ,cos 22A B ==,则△ABC 的 形状为______________三角形. 16、某坡面的坡度为1:125,某车沿该坡面爬坡行进了__________米后,该车起始位置和终止位置两地所处的海拔高度上升了5米17、在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示),已知立杆AB 的高度是6米,从侧面D 测到路况警示牌顶端 C 点和低端B 点的仰角分别是60°和45°,则路况警示牌宽BC 的值 为_____________.18、如图,在平面直角坐标系中,Rt △OAB 的顶点A 的坐标为(9,0),3t a n3B O A ∠=,点C 的坐标为(2, 0),点P 为斜边OB 上的一个 动点,则PA+PC 的最小值为_______________.第11题图O yx 31第14题图ABCD地铁施工 绕道慢行CADB第18题图yxOBAPC三、(共8题,第19—22题每题8分;第23、24题每题10分;第25题12分;第26题14分,共78分)19、化简并求值:2112()24x x x -÷--,其中002cos 45tan 45x =- . (本题满分8分)20、已知一个二次函数的顶点A 的坐标为(1, 0),且图像经过点B (2, 3). (1)求这个二次函数的解析式.(2)设图像与y 轴的交点为C ,记=OA a ,试用a 表示OC OB -(直接写出答案)(本题4+4=8分)21、已知抛物线1l :223y x x =-++和抛物线2l :223y x x =+-相交于A 、B ,其中A 点的横坐标比B 点的横坐标大. (1)求A 、B 两点的坐标.(2)射线OA 与x 轴正方向所相交成的角的正弦值.(本题4+4=8分)22、如图已知:AD AB BDAE AC CE==,求证:=ABC ADE ∠∠. (本题满分8分)23、通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化. 类似的我们可以在等腰三角形中建立边角之间的联系. 我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad ). 如下图在△ABC 中,AB=AC ,顶角A 的正对记作sad A ,这时==BCsad A AB底边腰. 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的. 根据上述角的正对定义,解下列问题: (1)060=sad _____________; 090=sad ________________。
2014年上海市宝山区高考数学一模试卷含详解

2014年上海市宝山区高考数学一模试卷一、填空题(本大题满分56分)本大题共有14题每个空格填对得4分,否则一律得零分.1.(4分)已知复数3m+5+(1﹣m)i(i是虚数单位)对应的点在二、四象限的角平分线上,则实数m=.2.(4分)已知集合M={x|x2﹣2x≤0},N={x|},U=R,则图中阴影部分表示的集合是.3.(4分)函数y=3cosxcosx的最小正周期是.4.(4分)已知线性方程组的增广矩阵为,若该线性方程组无解,则a=.5.(4分)若函数y=f(x)的图象与y=ln﹣1的图象关于y=x对称,则f(x)=.6.(4分)函数y=f(x)的反函数f﹣1(x)=log(x﹣cos2),则方程f(x)=1的解是.7.(4分)阅读程序框图,运行相应的程序,当输入x的值为﹣25时,输出x的值为.8.(4分)已知复数z1满足(1+i)z1=﹣1+5i,z2=a﹣2﹣i,(a∈R),若,则a的取值范围是.9.(4分)若双曲线的渐近线方程为y=±3x,它的一个焦点与抛物线的焦点重合,则双曲线的标准方程为.10.(4分)()6的展开式中,常数项为.(用数字作答)11.(4分)多瑙河三角洲的一地点A位于北纬45°东经30°,大兴安岭地区的一地点B位于北纬45°东经120°,设地球的半径为R,则A,B两地之间的球面距离是.12.(4分)从正方体的六个面中任意选取3个面,其中有2个面不相邻的概率为.13.(4分)函数y=sinx+cosx,x∈[﹣,]的值域是.14.(4分)关于函数f(x)=给出下列四个命题:①当x>0时,y=f(x)单调递减且没有最值;②方程f(x)=kx+b(k≠0)一定有解;③如果方程f(x)=k有解,则解的个数一定是偶数;④y=f(x)是偶函数且有最小值.则其中真命题是.(只要写标题号)二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,选对得5分,否则一律得零分.15.(5分)设x为任意实数,则下列各式正确的是()A.tan(arctanx)=x B.arcsin(sinx)=xC.sin(arcsinx)=x D.cos(arccosx)=x16.(5分)设a和b都是非零实数,则不等式a>b和同时成立的充要条件是()A.a>b B.a>b>0C.a>0>b D.0>a>b 17.(5分)下列关于极限的计算,错误的是()A.==B.(++…+)=++…+=0+0+…+0=0C.(﹣n)===D.已知a n=,则== 18.(5分)记X(x y 1),T=,X′=,则方程XTX′=0表示的曲线只可能是()A.圆B.椭圆C.双曲线D.抛物线三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须写出必要步骤.19.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.(1)求四棱锥P﹣ABCD的体积;(2)求异面直线BM与PC所成角的大小(结果用反三角函数表示).20.(14分)在△ABC中,A,B,C所对的边分别为a,b,c,,,(1)求C;(2)若,求a,b,c.21.(14分)给定曲线Γ:(5﹣m)x2+(m﹣2)y2=8,(m∈R).(1)若曲线Γ是焦点为F1(﹣2,0),F2(2,0)的双曲线,求实数m的值;(2)当m=4时,记M是椭圆Γ上的动点,过椭圆长轴的端点A作AQ∥QM(O 为坐标原点),交椭圆于Q,交y轴于P,求的值.22.(16分)已知函数f(x)=ax2+ax和g(x)=x﹣a.其中a∈R且a≠0.(Ⅰ)若函数f(x)与g(x)的图象的一个公共点恰好在x轴上,求a的值;(Ⅱ)若函数f(x)与g(x)图象相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的a的值;如果没有,请说明理由.(Ⅲ)若p和q是方程f(x)﹣g(x)=0的两根,且满足,证明:当x∈(0,p)时,g(x)<f(x)<p﹣a.23.(18分)若数列{a n}的每一项都不等于零,且对于任意的n∈N*,都有=q (q为常数),则称数列{a n}为“类等比数列”.已知数列{b n}满足:b1=b(b>0),对于任意的n∈N*,都有b n•b n+1=﹣9×28﹣n.(1)求证:数列{b n}是“类等比数列”;(2)若{|b n|}是单调递减数列,求实数b的取值范围;(3)若b=2,求数列{b n}的前n项之积取最大值时n的值.2014年上海市宝山区高考数学一模试卷参考答案与试题解析一、填空题(本大题满分56分)本大题共有14题每个空格填对得4分,否则一律得零分.1.(4分)已知复数3m+5+(1﹣m)i(i是虚数单位)对应的点在二、四象限的角平分线上,则实数m=﹣3.【考点】A1:虚数单位i、复数.【专题】5N:数系的扩充和复数.【分析】根据复数的几何意义,求出对应的坐标,则对应的坐标满足方程y=﹣x 即可得到结论.【解答】解:复数3m+5+(1﹣m)i(i是虚数单位)对应的点的坐标为A(3m+5,1﹣m),∵A在二、四象限的角平分线y=﹣x上,∴1﹣m=﹣(3m+5),即2m=﹣6,解得m=﹣3,故答案为:﹣3【点评】本题主要考查复数的几何意义,根据复数和点的对应关系求出对应坐标是解决本题的关键,比较基础.2.(4分)已知集合M={x|x2﹣2x≤0},N={x|},U=R,则图中阴影部分表示的集合是(﹣∞,﹣3]∪(2,+∞).【考点】1J:Venn图表达集合的关系及运算.【专题】11:计算题.【分析】根据阴影部分的元素属于集合N,而不属于集合M,从而得出阴影部分对应集合是(C U M)∩N,通过集合运算求得即可.【解答】解:由阴影部分的元素属于集合N,而不属于集合M,M=[0,2],N=(﹣∞,﹣3]∪[1,+∞),∴C U M=(﹣∞,0)∪(2,+∞),阴影部分对应集合(C U M)∩N=(﹣∞,﹣3]∪(2,+∞).故答案为:(﹣∞,﹣3]∪(2,+∞).【点评】本题考查了Venn图表示集合关系及集合运算,进行集合运算要细心.3.(4分)函数y=3cosxcosx的最小正周期是π.【考点】H1:三角函数的周期性.【专题】56:三角函数的求值.【分析】函数解析式利用二倍角的正弦函数公式化为一个角的余弦函数,找出ω的值,代入周期公式即可求出最小正周期.【解答】解:y=3cosxcosx=3cos2x=(1+cos2x)=+cos2x,∵ω=2,∴最小正周期T==π.故答案为:π【点评】此题考查了三角函数的周期性及其求法,熟练掌握周期公式是解本题的关键.4.(4分)已知线性方程组的增广矩阵为,若该线性方程组无解,则a=2.【考点】OQ:系数矩阵的逆矩阵解方程组.【专题】11:计算题.【分析】将原方程组写成矩阵形式为Ax=b,其中A为3×3方阵,x为3个变量构成列向量,b为3个常数项构成列向量.而当它的系数矩阵D奇异时,或者说行列式D=0时,方程组有无数个解或无解.由此求得a值.【解答】解:系数矩阵D奇异时,或者说行列式D=0时,方程组有无数个解或无解.∴系数行列式D=0,即=0.解之得:a=2故答案为:2.【点评】本题主要考查系数矩阵的逆矩阵解方程组及克莱姆法则,克莱姆法则不仅仅适用于实数域,它在任何域上面都可以成立.5.(4分)若函数y=f(x)的图象与y=ln﹣1的图象关于y=x对称,则f(x)= e2x+2.【考点】4R:反函数.【专题】11:计算题;51:函数的性质及应用.【分析】利用反函数的定义通过解方程求出x的表达式,得到反函数y=f(x)的解析式.【解答】解:∵函数y=f(x)的图象与函数y=ln﹣1的图象关于直线y=x对称,由y=ln﹣1解得=e y+1,∴x=e2y+2,函数y=f(x)与函数y=lnx互为反函数,可得f(x)=e2x+2,故答案为:e2x+2.【点评】本题考查的知识点是函数的图象,函数解析式的求解及常用方法,其中根据同底的指数函数和对数函数互为反函数,得到函数y=f(x)的解析式,是解答本题的关键.6.(4分)函数y=f(x)的反函数f﹣1(x)=log(x﹣cos2),则方程f(x)=1的解是2.【考点】4R:反函数.【专题】51:函数的性质及应用.【分析】利用原函数与反函数的定义域与值域的对应关系,直接求解方程的解即可.【解答】解:∵原函数的定义域就是反函数的值域,原函数的值域就是反函数的定义域,∴f(x)=1的解就是求解反函数f﹣1(x)的值,∴f﹣1(x)=log(1﹣cos2)=log sin2=2,即f(x)=1的解为x=2.故答案为:2.【点评】本题考查原函数与反函数的对应关系,方程的解以及对数的运算性质,考查计算能力.7.(4分)阅读程序框图,运行相应的程序,当输入x的值为﹣25时,输出x的值为4.【考点】E7:循环结构.【专题】27:图表型.【分析】根据题意,按照程序框图的顺序进行执行,当|x|≤1时跳出循环,输出结果.【解答】解:当输入x=﹣25时,|x|>1,执行循环,x==4;|x|=4>1,执行循环,x==1,|x|=1,退出循环,输出的结果为x=3×1+1=4.故答案为:4.【点评】本题考查循环结构的程序框图,搞清程序框图的算法功能是解决本题的关键,按照程序框图的顺序进行执行求解,属于基础题.8.(4分)已知复数z1满足(1+i)z1=﹣1+5i,z2=a﹣2﹣i,(a∈R),若,则a的取值范围是(1,7).【考点】A8:复数的模.【专题】11:计算题.【分析】首先整理复数,把两个复数整理成最简形式,写出复数的共轭复数,做差,写出要用的向量的模,解不等式,求出a的范围.【解答】解:∵复数z1满足(1+i)z1=﹣1+5i,∴=2+3iz2=a﹣2﹣i,∴,∵,∴<,∴a2﹣8a﹣7<0,∴1<a<7故答案为:(1,7)【点评】本题考查复数的求模,在运算过程中注意复数的除法运算和复数的模长的表示,注意一元二次不等式的整理和求解集.9.(4分)若双曲线的渐近线方程为y=±3x,它的一个焦点与抛物线的焦点重合,则双曲线的标准方程为.【考点】K8:抛物线的性质;KB:双曲线的标准方程.【专题】11:计算题.【分析】先由双曲线的渐近线方程为y=±x,易得知=3,再由抛物线的焦点为(,0)可得双曲线中c=,最后根据双曲线的性质c2=a2+b2列方程组,解得a2、b2即可.【解答】解:由双曲线渐近线方程可知=3 ①因为抛物线的焦点为(,0),所以c=②又c2=a2+b2③联立①②③,解得a2=1,b2=9,所以双曲线的方程为.故答案为为.【点评】本题考查双曲线的标准方程,以及双曲线的简单性质的应用,确定c和a2的值,是解题的关键.10.(4分)()6的展开式中,常数项为15.(用数字作答)【考点】DA:二项式定理.【专题】11:计算题.【分析】本题是二项式展开式求项的问题,可由给出的式子求出通项表达式T r=+1(﹣1)r•,令x的次数为0即可.【解答】解:∵T r=(﹣1)r•,+1∴由6﹣3r=0得r=2,从而得常数项C6r=15,故答案为:15.【点评】本题考查二项式定理的基础知识与基本性质,二项式定理通常考查的内容有项、系数、和的运算等等,同时还会考查赋值法的数学思想,对这些知识要熟练地掌握,其在高考中的难度不大.11.(4分)多瑙河三角洲的一地点A位于北纬45°东经30°,大兴安岭地区的一地点B位于北纬45°东经120°,设地球的半径为R,则A,B两地之间的球面距离是.【考点】L*:球面距离及相关计算.【专题】5F:空间位置关系与距离.【分析】由已知中P和Q是地球上两点,A在北纬45°,东经30°,B在北纬45°,东经120°,A与B在同一纬度圈上,计算经度差,求出AB弦长,以及球心角,然后求出球面距离.【解答】解:地球表面上从A地(北纬45°,东经30°)到B地(北纬45°,西经120°)AB的纬圆半径是,经度差是90°,所以AB=R球心角是,A、B两地的球面距离是.故答案为:.【点评】本题考查球面距离及其它计算,考查空间想象能力,是基础题.其中计算出PQ弧对应的球心角是解答本题的关键.12.(4分)从正方体的六个面中任意选取3个面,其中有2个面不相邻的概率为.【考点】C6:等可能事件和等可能事件的概率.【专题】5I:概率与统计.【分析】所有的选法共有种,根据题意,使用间接法,首先分析从6个面中选取3个面的情况数目,再分析求出其中其中有2个面相邻,即8个角上3个相邻平面的情况数目,进而可得其中2个面不相邻的概率.【解答】解:所有的选法共有=20种,而其中有2个面相邻,即8个角上3个相邻平面,选法有8种,则满足条件的选法共有C63﹣8=12种,故其中2个面不相邻的概率是=,故答案为:.【点评】题考查组合的运用,等可能事件的概率,但涉及立体几何的知识,要求学生有较强的空间想象能力,属于中档题.13.(4分)函数y=sinx+cosx,x∈[﹣,]的值域是[﹣] .【考点】HW:三角函数的最值.【专题】57:三角函数的图像与性质.【分析】利用三角函数的辅助角公式将函数进行化简,利用三角函数的图象和性质即可得到结论.【解答】解:y=sinx+cosx=2sin(x+),若x∈[﹣,],则x+∈[﹣,],则﹣≤sin(x+)≤1,即≤2sin(x+)≤2,∴函数的值域为[﹣],故答案为:[﹣].【点评】本题主要考查三角函数的图象和性质,利用辅助角公式将函数进行化简是解决本题的关键.14.(4分)关于函数f(x)=给出下列四个命题:①当x>0时,y=f(x)单调递减且没有最值;②方程f(x)=kx+b(k≠0)一定有解;③如果方程f(x)=k有解,则解的个数一定是偶数;④y=f(x)是偶函数且有最小值.则其中真命题是②.(只要写标题号)【考点】3E:函数单调性的性质与判断;3K:函数奇偶性的性质与判断.【专题】51:函数的性质及应用.【分析】①x>0时,由x≠1知y=f(x)不具有单调性,判定命题错误;②函数f(x)=是偶函数,在x>0且k>0时,判定函数y=f(x)与y=kx在第一象限内有交点;由对称性知,x<0且k>0时,函数y=f(x)与y=kx 在第二象限内有交点;得方程f(x)=kx+b(k≠0)有解;③函数f(x)=是偶函数,且f(x)=0,举例说明k=0时,方程f(x)=k有1个解;④函数f(x)=是偶函数,画出函数的图象,即可判断结论是否正确.【解答】解:①当x>0时,y=f(x)==1+在区间(0,1)和(1,+∞)上分别是单调递减的函数,且无最值;∴命题①错误;②函数f(x)=是偶函数,当x>0时,y=f(x)==1+在区间(0,1)和(1,+∞)上分别是单调递减的函数;当k>0时,函数y=f(x)与y=kx在第一象限内一定有交点;由对称性知,当x<0且k>0时,函数y=f(x)与y=kx在第二象限内一定有交点;∴方程f(x)=kx+b(k≠0)一定有解;∴命题②正确;③∵函数f(x)=是偶函数,且f(x)=0当k=0时,函数y=f(x)与y=k的图象只有一个交点,∴方程f(x)=k的解的个数是奇数;∴命题③错误;④∵函数f(x)=是偶函数,x≠±1,x>0时,y=f(x)==1+在区间(0,1)和(1,+∞)上分别是单调递减的函数;由对称性知,x<0时,y=f(x)==1﹣在区间(﹣∞,﹣1)和(﹣1,0)上分别是单调递增的函数;如图所示,∴函数f(x)无最小值,命题④错误.故答案为:②.【点评】本题考查了含有绝对值的分式函数的图象与性质的问题,解题时应先去掉绝对值,化为分段函数,把分式函数分离常数,是易错题.二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,选对得5分,否则一律得零分.15.(5分)设x为任意实数,则下列各式正确的是()A.tan(arctanx)=x B.arcsin(sinx)=xC.sin(arcsinx)=x D.cos(arccosx)=x【考点】HV:反三角函数.【专题】56:三角函数的求值.【分析】根据反正切函数的定义,arctanx表示(﹣,)上正切值等于x的一个角,从而得出结论.【解答】解:根据反正切函数的定义,arctanx表示(﹣,)上正切值等于x的一个角,故有tan(arctanx)=x,故有A正确,故选:A.【点评】本题主要考查反三角函数的定义和性质,属于中档题.16.(5分)设a和b都是非零实数,则不等式a>b和同时成立的充要条件是()A.a>b B.a>b>0C.a>0>b D.0>a>b【考点】R3:不等式的基本性质.【专题】35:转化思想;49:综合法;59:不等式的解法及应用.【分析】根据不等式a>b和同时成立,可得把不等式a>b的两边同时除以ab,不等式变号,故有a>0>b.【解答】解:设a和b都是非零实数,∵不等式a>b和同时成立,∴把不等式a>b的两边同时除以ab,不等式变号为,∴a、b异号,∴a>0>b,故选:C.【点评】本题主要考查不等式的基本性质,属于基础题.17.(5分)下列关于极限的计算,错误的是()A.==B.(++…+)=++…+=0+0+…+0=0C.(﹣n)===D.已知a n=,则==【考点】6F:极限及其运算.【专题】21:阅读型;2A:探究型.【分析】题目中四个极限均为数列极限,A中分子分母最高次项次数相同,采用分子分母同时除以n2后求极限值;B和D需要先求和再取极限,C应先分子有理化,然后求极限.【解答】解:选项A求的是数列极限,采用分子分母同时除以n2后求极限值,正确;选项B应先求数列的前n项和,即,然后求得极限值为1,∴选项B错误;选项C是采用先分子有理化,然后分子分母同时除以n再取极限,正确;选项D是运用等比数列的求和公式先把奇数项和偶数项分别作和,然后求极限值,做法正确.故选:B.【点评】本题考查数列的极限及其求法,解答的关键是消去无穷大项,同时注意先化简再取极限,是基础题.18.(5分)记X(x y 1),T=,X′=,则方程XTX′=0表示的曲线只可能是()A.圆B.椭圆C.双曲线D.抛物线【考点】OY:三阶矩阵.【专题】17:选作题;5R:矩阵和变换.【分析】利用矩阵的乘法,可得方程XTX′=0,即可得出结论.【解答】解:∵X(x y 1),T=,X′=,∴方程XTX′=0为Ax2﹣Ay2+Dx+Ey+D+E+F=0,∴方程XTX′=0表示的曲线只可能是双曲线.故选:C.【点评】本题考查矩阵的乘法,考查学生的计算能力,比较基础.三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须写出必要步骤.19.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,PC与平面ABCD所成角的大小为arctan2,M为PA的中点.(1)求四棱锥P﹣ABCD的体积;(2)求异面直线BM与PC所成角的大小(结果用反三角函数表示).【考点】LF:棱柱、棱锥、棱台的体积;LM:异面直线及其所成的角.【专题】11:计算题.(1)先根据PA⊥平面ABCD以及PC与平面ABCD所成角的大小为arctan2,【分析】求出PA=4;再求出下底面面积即可求四棱锥P﹣ABCD的体积;(2)连接BD,交AC于点O,连接MO可得MO∥PC;所以∠BMO(或其补角)为异面直线BM与PC所成的角;然后在△BMO是直角三角形求得∠BMO即可.【解答】(本题满分(14分),第1小题(6分),第2小题8分)解:(1)连接AC,因为PA⊥平面ABCD,所以∠PCA为PC与平面ABCD所成的角…(2分)由已知,,而AC=2,所以PA=4.…(3分)底面积,…(4分)所以,四棱锥P﹣ABCD的体积.…(6分)(2)连接BD,交AC于点O,连接MO,因为M、O分别为PA、AC的中点,所以MO∥PC,所以∠BMO(或其补角)为异面直线BM与PC所成的角.…(8分)在△BMO中,,,,…(10分)(以下由余弦定理,或说明△BMO是直角三角形求得)或或.…(13分)所以,异面直线BM与PC所成角的大小为(或另外两个答案).…(14分)【点评】本题主要考查棱锥的体积计算以及异面直线及其所成的角.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.20.(14分)在△ABC中,A,B,C所对的边分别为a,b,c,,,(1)求C;(2)若,求a,b,c.【考点】9O:平面向量数量积的性质及其运算;HP:正弦定理.【专题】11:计算题.【分析】(1)先利用正弦定理把题设条件中的边转化成角的正弦,进而利用两角和的公式化简整理求的cotC的值,进而求得C.(2)根据求得ab的值,进而利用题设中和正弦定理联立方程组,求得a,b和c.【解答】解:(1)由得则有=得cotC=1即、(2)由推出;而,即得,则有解得.【点评】本题主要考查了正弦定理得应用.解题的关键是利用正弦定理解决三角形问题中的边,角问题.21.(14分)给定曲线Γ:(5﹣m)x2+(m﹣2)y2=8,(m∈R).(1)若曲线Γ是焦点为F1(﹣2,0),F2(2,0)的双曲线,求实数m的值;(2)当m=4时,记M是椭圆Γ上的动点,过椭圆长轴的端点A作AQ∥QM(O 为坐标原点),交椭圆于Q,交y轴于P,求的值.【考点】KH:直线与圆锥曲线的综合.【专题】5E:圆锥曲线中的最值与范围问题.【分析】(1)曲线Γ化为标准方程得,由此利用双曲线的简单性质能求出m的值.(2)当m=4时,曲线Γ:x2+2y2=8,此时A(﹣2,0),由,得:,由此利用韦达定理结合题设条件能求出的值.【解答】解:(1)∵曲线Γ:(5﹣m)x2+(m﹣2)y2=8,(m∈R),化简得,…(2分)由题意得,,且m<2,…(3分)又∵c=2,∴,解得m=﹣1,或m=4(舍)…(5分)∴m=﹣1.…(6分)(2)当m=4时,曲线Γ:x2+2y2=8,此时A(﹣2,0),…(7分)设直线OM方程为y=kx,由,得:,即,…(8分)∴OM2==x M2+(kx M)2=,…(10分)∵AQ∥OM,∴AQ方程为:y=k(x+2),于是P(o,2),AP==2•,…(11分)由,得:(1+2k2)x2+8k2x+16k2﹣8=0,从而AQ=•=.…(13分)∴==2.…(14分)【点评】本题考查双曲线中参数的求法,考查椭圆中线段比值的求法,综合性强,难度大,解题时要注意韦达定理的合理运用.22.(16分)已知函数f(x)=ax2+ax和g(x)=x﹣a.其中a∈R且a≠0.(Ⅰ)若函数f(x)与g(x)的图象的一个公共点恰好在x轴上,求a的值;(Ⅱ)若函数f(x)与g(x)图象相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的a的值;如果没有,请说明理由.(Ⅲ)若p和q是方程f(x)﹣g(x)=0的两根,且满足,证明:当x∈(0,p)时,g(x)<f(x)<p﹣a.【考点】3A:函数的图象与图象的变换;IT:点到直线的距离公式;R6:不等式的证明.【专题】15:综合题;16:压轴题.【分析】(1)若函数f(x)与g(x)的图象的一个公共点恰好在x轴上,说明函数f(x)与g(x)有共同的零点,即g(x)的零点也在函数f(x)的图象上,代入易求出a值.(2)若函数f(x)与g(x)图象相交于不同的两点A、B,则将直线方程代入抛物线方程后,对应的二次方程有两不等的实数根,再将△OAB的面积函数表示出来,根据函数的性质,易得最值及对应的a值.(3)综合零点的性质和不等式的性质,不难证明当x∈(0,p)时,g(x)<f (x)<p﹣a【解答】解:(Ⅰ)设函数g(x)图象与x轴的交点坐标为(a,0),又∵点(a,0)也在函数f(x)的图象上,∴a3+a2=0.而a≠0,∴a=﹣1(Ⅱ)依题意,f(x)=g(x),即ax2+ax=x﹣a,整理,得ax2+(a﹣1)x+a=0,①∵a≠0,函数f(x)与g(x)图象相交于不同的两点A、B,∴△>0,即△=(a﹣1)2﹣4a2=﹣3a2﹣2a+1=(3a﹣1)(﹣a﹣1)>0.∴﹣1<a<且a≠0.设A(x1,y1),B(x2,y2),且x1<x2,由①得,x1•x2=1>0,.设点o到直线g(x)=x﹣a的距离为d,则,.=∴S△OAB=.∵﹣1<a<且a≠0,∴当时,S△OAB 有最大值,S△OAB无最小值.(Ⅲ)由题意可知f(x)﹣g(x)=a(x﹣p)(x﹣q).∵,∴a(x﹣p)(x﹣q)>0,∴当x∈(0,p)时,f(x)﹣g(x)>0,即f(x)>g(x).又f(x)﹣(p﹣a)=a(x﹣p)(x﹣q)+x﹣a﹣(p﹣a)=(x﹣p)(ax﹣aq+1),x﹣p<0,且ax﹣aq+1>1﹣aq>0,∴f(x)﹣(p﹣a)<0,∴f(x)<p﹣a,综上可知,g(x)<f(x)<p﹣a.【点评】本题考查的主要知识点是函数零点的性质,即两个函数的图象的交点在x轴上,则说明两个函数有共同的零点,即一个函数的零点也在另一个函数的图象上,应该满足另一个函数的方程;若函数在(a,b)上有零点,则f(a)•f(b)<0.23.(18分)若数列{a n}的每一项都不等于零,且对于任意的n∈N*,都有=q(q为常数),则称数列{a n}为“类等比数列”.已知数列{b n}满足:b1=b(b>0),对于任意的n∈N*,都有b n•b n+1=﹣9×28﹣n.(1)求证:数列{b n}是“类等比数列”;(2)若{|b n|}是单调递减数列,求实数b的取值范围;(3)若b=2,求数列{b n}的前n项之积取最大值时n的值.【考点】8B:数列的应用;8E:数列的求和.【专题】15:综合题;54:等差数列与等比数列.【分析】(1)利用b n•b n+1=﹣9×28﹣n,再写一式,可得,即可得出结论;(2)确定数列{|b n|}的通项,根据{|b n|}递减,所以|b2k﹣1|>|b2k|>|b2k+1|,即可求出实数b的取值范围;(3)若b=2,分类讨论,利用T n取最大值时,n=4k(k∈N*),当n为奇数时,令|b n•b n+1|<1得,可得n≥13,即可求数列{b n}的前n项之积取最大值时n的值.【解答】(1)证明:因为b n•b n+1=﹣9×28﹣n,所以b n+1•b n+2=﹣9×27﹣n,所以,所以,数列{b n}是“类等比数列”.…(4分)(2)解:由b1=b,b1•b2=﹣9×27,得b2=﹣…(5分)所以b n=…(7分)因为{|b n|}递减,所以|b2k﹣1|>|b2k|>|b2k+1|,…(8分)解得:24<b<48.…(10分)(3)解:记数列{b n}的前n项之积为T n.当b=2时,b n=,由{b n}的通项公式可知.当n=4k﹣2或n=4k﹣1(k∈N*)时,T n<0,…(12分)又因为0<b4k<1,所以T4k+1=b4k+1T4k<T4k,+1因而T n取最大值时,n=4k(k∈N*)…(14分)当n为奇数时,令|b n•b n+1|<1得,所以n≥13,…(16分)因而|b1•b2|>1,…,|b11•b12|>1,|b13•b14|<1,|b15•b16|<1,…所以|T2|<|T4|<…|T12|,|T12|>|T14|>,….因而,当n=12时,T n取最大值.…(18分)【点评】本题考查新定义,考查数列的通项,考查数列{b n}的前n项之积,考查学生分析解决问题的能力,属于中档题.。
上海市宝山区2015届高三上学期期末质量监测数学试题 含解析

2014学年度质量管理考试数学试卷(满分150分,其中学业水平考试卷120分,附加题30分,完卷时间130分钟)2014。
12考试注意:1。
答卷前,考生务必将姓名、高考座位号、校验码等填写清楚. 2。
本试卷共有 32道试题,满分 150 分.考试时间 130分钟. 3。
请考生用钢笔或圆珠笔按要求在试卷相应位置上作答.一.(本大题满分 36 分)本大题共有 12 题,要求直接填写结果,每题填对3分,否则一律得 0 分. 1. 函数3tan y x =的周期是 . 【答案】π 【解析】试题分析:由πωπ==T 考点:正切函数的性质 2。
计算2413= .【答案】2考点:行列式的计算 3。
计算lim n →∞2123nn ++++= .【答案】21【解析】试题分析:212)1(lim 321lim 22=+=++++∞→∞→n n n n n n n考点:数列极限4。
二项式10(x 1)+展开式中,8x 的系数为 .【答案】45 【解析】试题分析:通项为rr r x C T -+=10101,令2=r ,88210345x x C T==,故8x 的系数为45考点:二项式定理5.设矩阵241A x ⎛⎫=⎪⎝⎭,2211B -⎛⎫= ⎪-⎝⎭,若BA =2412⎛⎫ ⎪--⎝⎭,则x = .【答案】2考点:矩阵的乘法 6.现有6位同学排成一排照相,其中甲、乙二人相邻的排法有种.【答案】240考点:排列7.若1cos()2πα+=-,322παπ<<,则sin α= .【答案】23- 【解析】试题分析:由已知21cos )cos(-=-=+ααπ,所以21cos =α,又παπ223<<,故23cos 1sin 2-=--=αα 考点:三角函数、诱导公式 8.若一个球的体积为π34,则它的表面积为__________.【答案】π12 【解析】试题分析:因ππ34343==RV ,所以3=R ,故ππ1242==R S考点:球的体积、表面积9.若函数sin(2)(0)y x ϕϕπ=+≤≤是R 上的偶函数,则ϕ的值是 . 【答案】2π考点:三角函数的性质10。
2014-2015学年上海市宝山区高三(上)期末数学模拟试卷

2014-2015学年上海市宝山区高三(上)期末数学模拟试卷试题解析一.(本大题满分36分)本大题共有12题,要求直接填写结果,每题填对3分,否则一律得0分.1.(3分)函数y=3tanx的周期是π.考点:三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:由条件根据y=Atan(ωx+φ)的周期等于T=,可得结论.解答:解:函数y=3tanx的周期为=π,故答案为:π.点评:本题主要考查三角函数的周期性及其求法,利用了y=Atan(ωx+φ)的周期等于T=,属于基础题.2.(3分)计算=2.考点:二阶矩阵.专题:计算题;矩阵和变换.分析:利用行列式的运算得,=2×3﹣1×4=2.解答:解:=2×3﹣1×4=2,故答案为:2.点评:本题考查了矩阵的运算,属于基础题.3.(3分)(2014•嘉定区三模)=.考点:极限及其运算.专题:导数的概念及应用;等差数列与等比数列.分析:利用等差数列的求和公式可得1+2+3+…+n=,然后即可求出其极限值.解答:解:==(+)=,故答案为:点评:本题主要考察极限及其运算.解题的关键是要掌握极限的实则运算法则和常用求极限的技巧!4.(3分)二项式(x+1)10展开式中,x8的系数为45.考点:二项式系数的性质.专题:二项式定理.分析:根据二项式(x+1)10展开式的通项公式,求出x8的系数是什么.解答:解:∵二项式(x+1)10展开式中,通项为T r+1=•x10﹣r•1r=•x10﹣r,令10﹣r=8,解得r=2,∴===45;即x8的系数是45.故答案为:45.点评:本题考查了二项式定理的应用问题,解题时应根据二项式展开式的通项公式进行计算,是基础题.5.(3分)设矩阵A=,B=,若BA=,则x=2.考点:矩阵与向量乘法的意义.专题:计算题;矩阵和变换.分析:由题意,根据矩阵运算求解.解答:解:∵A=,B=,BA=,∴4×2﹣2x=4;解得,x=2;故答案为:2.点评:本题考查了矩阵的运算,属于基础题.6.(3分)现有6位同学排成一排照相,其中甲、乙二人相邻的排法有240种.考点:计数原理的应用.专题:排列组合.分析:利用捆绑法,把甲乙二人捆绑在一起,看作一个复合元素,再和其他4人进行全排,问题得以解决解答:解:先把甲乙二人捆绑在一起,看作一个复合元素,再和其他4人进行全排,故有=240种,故答案为:240点评:本题主要考查了排列问题的中的相邻问题,利用捆绑法是关键,属于基础题7.(3分)若cos(π+α)=﹣,π<α<2π,则sinα=﹣.考点:运用诱导公式化简求值.专题:三角函数的求值.分析:利用诱导公式可知cosα=,又π<α<2π,利用同角三角函数间的关系式(平方关系)即可求得sinα的值.解答:解:∵cos(π+α)=﹣cosα=﹣,∴cosα=,又π<α<2π,∴sinα=﹣=﹣.故答案为:﹣.点评:本题考查诱导公式与同角三角函数间的关系式的应用,属于中档题.8.(3分)(2008•天津)若一个球的体积为,则它的表面积为12π.考点:球的体积和表面积.专题:计算题.分析:有球的体积,就可以利用公式得到半径,再求解其面积即可.解答:解:由得,所以S=4πR2=12π.点评:本题考查学生对公式的利用,是基础题.9.(3分)函数y=sin(2x+φ)(0≤φ≤π)是R上的偶函数,则φ的值是.考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:计算题.分析:根据函数y=sin(2x+φ)的图象特征,若它是偶函数,只需要x=0时,函数能取得最值.解答:解:函数y=sin(2x+ϕ)是R上的偶函数,就是x=0时函数取得最值,所以f(0)=±1即sinϕ=±1所以ϕ=kπ+(k∈Z),当且仅当取k=0时,得φ=,符合0≤φ≤π故答案为:点评:本题考查了正弦型函数的奇偶性,正弦函数的最值,是基础题.10.(3分)正四棱锥P﹣ABCD的所有棱长均相等,E是PC的中点,那么异面直线BE与PA所成的角的余弦值等于.考点:异面直线及其所成的角.专题:空间角.分析:根据异面直线所成角的定义先找出对应的平面角即可得到结论.解答:解:连结AC,BD相交于O,则O为AC的中点,∵E是PC的中点,∴OE是△PAC的中位线,则OE∥,则OE与BE所成的角即可异面直线BE与PA所成的角,设四棱锥的棱长为1,则OE==,OB=,BE=,则cos==,故答案为:点评:本题考查异面直线所成的角,作出角并能由三角形的知识求解是解决问题的关键,属中档题11.(3分)(2004•福建)直线x+2y=0被曲线x2+y2﹣6x﹣2y﹣15=0所截得的弦长等于4.考点:直线与圆的位置关系.专题:综合题;数形结合.分析:根据圆的方程找出圆心坐标和半径,过点A作AC⊥弦BD,可得C为BD的中点,根据勾股定理求出BC,即可求出弦长BD的长.解答:解:过点A作AC⊥弦BD,垂足为C,连接AB,可得C为BD的中点.由x2+y2﹣6x﹣2y﹣15=0,得(x﹣3)2+(y﹣1)2=25.知圆心A为(3,1),r=5.由点A(3,1)到直线x+2y=0的距离AC==.在直角三角形ABC中,AB=5,AC=,根据勾股定理可得BC===2,则弦长BD=2BC=4.故答案为:4点评:本题考查学生灵活运用垂径定理解决实际问题的能力,灵活运用点到直线的距离公式及勾股定理化简求值,会利用数形结合的数学思想解决数学问题,是一道综合题.12.(3分)已知函数f(x)=Asin(ωx+ϕ),(A>0,ω>0,0≤ϕ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+).考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:首先,根据所给函数的部分图象,得到振幅A=2,然后,根据周期得到ω的值,再将图象上的一个点代人,从而确定其解析式.解答:解:根据图象,得A=2,又∵T==,∴T=π,∴ω=2,将点(﹣,0)代人,得2sin(2x+ϕ)=0,∵0≤ϕ≤π,∴ϕ=,∴f(x)=2sin(2x+),故答案为:2sin(2x+)点评:本题重点考查了三角函数的图象与性质、特殊角的三角函数等知识,属于中档题.解题关键是熟悉所给函数的部分图象进行分析和求解.二.选择题(本大题满分36分)本大题共有12题,每题都给出四个结论,其中有且只有一个结论是正确的.考生必须把正确结论的代码写在题后的括号内,选对得3分,否则一律得0分.13.(3分)已知点P(tanα,cosα)在第三象限,则角α的终边在第几象限()A.第一象限B.第二象限C.第三象限D.第四象限考点:任意角的三角函数的定义.专题:计算题.分析:由题意,推导出,确定α的象限,然后取得结果.解答:解:∵P(tanα,cosα)在第三象限,∴,由tanα<0,得α在第二、四象限,由cosα<0,得α在第二、三象限∴α在第二象限.故选B点评:本题考查任意角的三角函数的定义,考查计算能力,是基础题.14.(3分)已知函数y=x a+b,x∈(0,+∞)是增函数,则()A.a>0,b是任意实数B.a<0,b是任意实数C.b>0,a是任意实数D.b<0,a是任意实数考点:指数函数的单调性与特殊点.专题:计算题;函数的性质及应用.分析:由幂函数的性质可知,a>0,b是任意实数.解答:解:∵函数y=x a+b,x∈(0,+∞)是增函数,∴a>0,b是任意实数,故选A.点评:本题考查了幂函数的单调性的判断,属于基础题.15.(3分)在△ABC中,若b=2asinB,则这个三角形中角A的值是()A.30°或60° B.45°或60° C.30°或120° D.30°或150°考点:正弦定理.专题:解三角形.分析:在△ABC中,利用正弦定理解得sinA=,从而求得A的值.解答:解:在△ABC中,若b=2asinB,则由正弦定理可得sinB=2sinAsinB,解得sinA=,∴A=30°或150°.故选D.点评:本题主要考查正弦定理的应用,根据三角函数的值求角,属于中档题.16.(3分)若log a3<log b3<0,则()A.0<a<b<1 B.0<b<a<1 C.a>b>1 D.b>a>1考点:对数函数的单调区间.专题:计算题;函数的性质及应用.分析:化log a3<log b3<0为log3b<log3a<0,利用函数的单调性求解.解答:解:∵log a3<log b3<0,∴<<0,即log3b<log3a<0,故0<b<a<1,故选B.点评:本题考查了对数的运算及对数函数单调性的利用,属于基础题.17.(3分)双曲线﹣=1的焦点到渐近线的距离为()A.2B. 2 C.D. 1考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:先根据双曲线方程求得焦点坐标和渐近线方程,进而利用点到直线的距离求得焦点到渐近线的距离.解答:解:双曲线﹣=1的焦点为(4,0)或(﹣4,0).渐近线方程为y=x或y=﹣x.由双曲线的对称性可知,任一焦点到任一渐近线的距离相等,d==2.故选A.点评:本题主要考查了双曲线的标准方程,双曲线的简单性质和点到直线的距离公式.考查了考生对双曲线标准方程的理解和灵活应用,属基础题.18.(3分)用数学归纳法证明等式1+3+5+…+(2n﹣1)=n2(n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到()A.1+3+5+…+(2k+1)=k2 B.1+3+5+…+(2k+1)=(k+1)2C.1+3+5+…+(2k+1)=(k+2)2 D.1+3+5+…+(2k+1)=(k+3)2考点:数学归纳法.专题:阅读型.分析:首先由题目假设n=k时等式成立,代入得到等式1+3+5+…+(2k﹣1)=k2.当n=k+1时等式左边=1+3+5++(2k﹣1)+(2k+1)由已知化简即可得到结果.解答:解:因为假设n=k时等式成立,即1+3+5+…+(2k﹣1)=k2当n=k+1时,等式左边=1+3+5+…+(2k﹣1)+(2k+1)=k2+(2k+1)=(k+1)2.故选B.点评:此题主要考查数学归纳法的概念问题,涵盖知识点少,属于基础性题目.需要同学们对概念理解记忆.19.(3分)设z=1+i(i是虚数单位),则复数+z2在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:利用复数代数形式的乘除运算化简求得对应点的坐标,则答案可求.解答:解:∵z=1+i,则复数+z2=,∴复数+z2在复平面上对应的点的坐标为(1,1),位于第一象限.故选:A.点评:本题考查了复数代数形式的乘除运算,考查了复数的等式表示法及其几何意义,是基础题.20.(3分)(2004•陕西)圆x2+y2﹣4x=0在点P(1,)处的切线方程为()A.x+y﹣2=0 B.x+y﹣4=0 C.x﹣y+4=0 D.x﹣y+2=0考点:圆的切线方程.专题:计算题.分析:本题考查的知识点为圆的切线方程.(1)我们可设出直线的点斜式方程,联立直线和圆的方程,根据一元二次方程根与图象交点间的关系,得到对应的方程有且只有一个实根,即△=0,求出k值后,进而求出直线方程.(2)由于点在圆上,我们也可以切线的性质定理,即此时切线与过切点的半径垂直,进行求出切线的方程.解答:解:法一:x2+y2﹣4x=0y=kx﹣k+⇒x2﹣4x+(kx﹣k+)2=0.该二次方程应有两相等实根,即△=0,解得k=.∴y﹣=(x﹣1),即x﹣y+2=0.法二:∵点(1,)在圆x2+y2﹣4x=0上,∴点P为切点,从而圆心与P的连线应与切线垂直.又∵圆心为(2,0),∴•k=﹣1.解得k=,∴切线方程为x﹣y+2=0.故选D点评:求过一定点的圆的切线方程,首先必须判断这点是否在圆上.若在圆上,则该点为切点,若点P(x0,y0)在圆(x﹣a)2+(y﹣b)2=r2(r>0)上,则过点P的切线方程为(x﹣a)(x0﹣a)+(y﹣b)(y0﹣b)=r2(r>0);若在圆外,切线应有两条.一般用“圆心到切线的距离等于半径长”来解较为简单.若求出的斜率只有一个,应找出过这一点与x轴垂直的另一条切线.21.(3分)“tanx=﹣1”是“x=﹣+2kπ(k∈Z)”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件考点:函数奇偶性的性质.专题:简易逻辑.分析:得出tan(=﹣+2kπ)=﹣1,“x=﹣+2kπ”是“tanx=﹣1”成立的充分条件;举反例tan=﹣1,推出“x=﹣+2kπ(k∈Z)”是“tanx=﹣1”成立的不必要条件.解答:解:tan(﹣+2kπ)=tan (﹣)=﹣1,所以充分;但反之不成立,如tan =﹣1.故选:B点评:本题主要考查了必要条件、充分条件与充要条件的判断.充分条件与必要条件是中学数学最重要的数学概念之一,要理解好其中的概念.22.(3分)(2013•福建)在四边形ABCD中,=(1,2),=(﹣4,2),则该四边形的面积为()A.B.C.5 D.10考点:向量在几何中的应用;三角形的面积公式;数量积判断两个平面向量的垂直关系.专题:计算题;平面向量及应用.分析:通过向量的数量积判断四边形的形状,然后求解四边形的面积即可.解答:解:因为在四边形ABCD中,,,=0,所以四边形ABCD的对角线互相垂直,又,,该四边形的面积:==5.故选C.点评:本题考查向量在几何中的应用,向量的数量积判断四边形的形状是解题的关键,考查分析问题解决问题的能力.23.(3分)(2006•天津)函数的反函数是()A.B.C.D.考点:反函数.分析:本题需要解决两个问题:一是如何解出x,二是如何获取反函数的定义域,求解x时,要注意x<0的条件,因为涉及2个解.解答:解:由解得,又∵原函数的值域是:y>2∴原函数的反函数是,故选D.点评:该题的求解有2个难点,一是解出x有两个,要根据x<0确定负值的一个,二是反函数的定义域要用原函数的值域确定,不是根据反函数的解析式去求.24.(3分)曲线y2=|x|+1的部分图象是()A.B.C.D.考点:曲线与方程.专题:函数的性质及应用.分析:分类讨论,去掉绝对值,化简函数的解析式,可得它的图象特征,结合所给的选项,得出结论.解答:解:当x≥0时,y2=x+1表示以(﹣1,0)为顶点的开口向右的抛物线.当x<0时,y2=﹣(x﹣1)表示以(1,0)为顶点的开口向左的抛物线,故选:C.点评:本题主要考查函数的图象特征,属于基础题.三、解答题(本大题满分48分)本大题共有5题,解答下列各题必须写出必要的步骤.25.(8分)解不等式组:.考点:其他不等式的解法.专题:不等式的解法及应用.分析:根据不等式的解法即可得到结论.解答:解:由|x﹣1|<3解得﹣2<x<4,由>1得﹣1=>0,解得3<x<5,所以,不等式解集为(3,4).点评:本题主要考查不等式组的求解,比较基础.26.(8分)如图,正四棱柱ABCD﹣A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan,求正四棱柱ABCD﹣A1B1C1D1的体积.考点:棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:由已知得AA1∥BB1,从而tan∠CB1B==,进而BB1=4,由此能求出正四棱柱ABCD﹣A1B1C1D1的体积.解答:解:∵正四棱柱ABCD﹣A1B1C1D1的底面边长AB=2,异面直线A1A与B1C所成角的大小为arctan,∴AA1∥BB1,∴∠CB1B为AA1、B1C所成的角,且tan∠CB1B==,…(4分)∵BC=AB=2,∴BB1=4,…(6分)∴正四棱柱ABCD﹣A1B1C1D1的体积V=Sh=22×4=16.…(8分)点评:本题考查正四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.27.(10分)已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点.(Ⅰ)求直线PF的方程;(Ⅱ)求△DAB的面积S范围;(Ⅲ)设,,求证λ+μ为定值.考点:直线的一般式方程;抛物线的应用.专题:计算题.分析:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),求出斜率用点斜式写出直线方程.(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2),用弦长公式求出线段AB的长,再由点到直线的距离公式求点D到直线AB的距离,用三角形面积公式表示出面积关于参数m的表达式,再根据m的取值范围求出面积的范围.(Ⅲ),,变化为坐标表示式,从中求出参数λ,μ用两点A,B的坐标表示的表达式,即可证明出两者之和为定值.解答:解:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),于是直线PF的斜率为,所以直线PF的方程为,即为mx+2y﹣m=0.(3分)(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2),由得m2x2﹣(2m2+16)x+m2=0,所以,x1x2=1.于是.点D到直线mx+2y﹣m=0的距离,所以.因为m∈R且m≠0,于是S>4,所以△DAB的面积S范围是(4,+∞).(9分)(Ⅲ)由(Ⅱ)及,,得(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,m﹣y1)=μ(x2+1,y2﹣m),于是,(x2≠±1).所以.所以λ+μ为定值0.(14分)点评:考查求直线方程、抛物线在的焦点弦弦长公式、点到直线的距离公式及向量中数乘向量的意义,涉及知识较多,综合性较强.28.(10分)已知函数f(x)=(x∈R).(1)写出函数y=f(x)的奇偶性;(2)当x>0时,是否存实数a,使v=f(x)的图象在函数g(x)=图象的下方,若存在,求α的取值范围;若不存在,说明理由.考点:函数恒成立问题;函数奇偶性的判断.专题:函数的性质及应用.分析:(1)当a=0时,f(x)=是奇函数;当a≠0时,函数f(x)=(x∈R),是非奇非偶函数.(2)若y=f(x)的图象在函数g(x)=图象的下方,则<,化简得a<+x恒成立,在求函数的最值.解答:解:(1)因为y=f(x)的定义域为R,所以:当a=0时,f(x)=是奇函数;当a≠0时,函数f(x)=(x∈R).是非奇非偶函数.(2)当x>0时,若y=f(x)的图象在函数g(x)=图象的下方,则<,化简得a<+x恒成立,因为x>0,∴即,所以,当a<4时,y=f(x)的图象都在函数g(x)=图象的下方.点评:本题主要考查函数的奇偶性,同时考查函数恒成立的问题,主要进行函数式子的恒等转化.29.(12分)已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为的直线交抛物线于点P2,再过P2作斜率为的直线交抛物线于点P3,﹣2<x<4,如此继续.一般地,过点3<x<5作斜率为的直线交抛物线于点P n+1,设点P n(x n,y n).(1)求x3﹣x1的值;(2)令b n=x2n+1﹣x2n﹣1,求证:数列{b n}是等比数列;(3)记P奇(x奇,y奇)为点列P1,P3,…,P2n﹣1,…的极限点,求点P奇的坐标.考点:数列与解析几何的综合.专题:计算题;等差数列与等比数列;圆锥曲线的定义、性质与方程.分析:(1)求出直线方程,联立抛物线方程,求出交点,即可得到;(2)设出两点点P n(x n,).P n+1(x n+1,),由直线的斜率公式,再由条件,运用等比数列的定义,即可得证;(3)运用累加法,求得x2n+1=+,再由数列极限的概念,即可得到点P奇的坐标.解答:(1)解:直线OP1的方程为y=x,由解得P1(4,4),直线P2P1的方程为y﹣4=(x﹣4),即y=x+2,由得P2(﹣2,1),直线P2P3的方程为y﹣1=(x+2),即y=x+,由解得,P3(3,),所以x3﹣x1=3﹣4=﹣1.(2)证明:因为设点P n(x n,).P n+1(x n+1,),由抛物线的方程和斜率公式得到,,所以x n+x n﹣1=,两式相减得x n+1﹣x n﹣1=﹣,用2n代换n得b n=x2n+1﹣x2n﹣1=﹣,由(1)知,当n=1时,上式成立,所以{b n}是等比数列,通项公式为b n=﹣;(3)解:由得,,,…,,以上各式相加得x2n+1=+,所以x奇=,y奇=x奇2=,即点P奇的坐标为(,).点评:本题考查联立直线方程和抛物线方程求交点,考查等比数列的定义和通项公式的求法,考查累加法求数列通项,及数列极限的运算,属于中档题.四、附加题(本大题满分30分)本大题共有3题,解答下列各题必须写出必要的步骤.30.(8分)有根木料长为6米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,问怎样利用木料,才能使光线通过的窗框面积最大(中间木档的面积可忽略不计).专题:函数的性质及应用.分析:求出窗框的高为3x,宽为.推出窗框的面积,利用二次函数的最值,求解即可.解答:解:如图设x,则竖木料总长=3x+4x=7x,三根横木料总长=6﹣7x,∴窗框的高为3x,宽为.…(2分)即窗框的面积y=3x•=﹣7x2+6x.(0<x<)…(5分)配方:y=﹣7(x﹣)2+(0<x<2 )…(7分)∴当x=米时,即上框架高为米、下框架为米、宽为1米时,光线通过窗框面积最大.…(8分)点评:本题考查二次函数的解析式的应用,考查分析问题解决问题的能力.31.(10分)(2008•辽宁)在平面直角坐标系xOy中,点P到两点,的距离之和等于4,设点P的轨迹为C.(Ⅰ)写出C的方程;(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时⊥?此时的值是多少?.考点:直线与圆锥曲线的综合问题.专题:综合题;压轴题;转化思想.分析:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是椭圆.从而写出其方程即可;(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时的值,从而解决问题.解答:解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以为焦点,长半轴为2的椭圆.它的短半轴,故曲线C的方程为.(4分)(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足消去y并整理得(k2+4)x2+2kx﹣3=0,故.(6分),即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,于是.所以时,x1x2+y1y2=0,故.(8分)当时,,.,而(x2﹣x1)2=(x2+x1)2﹣4x1x2=,所以.(12分)点评:本小题主要考查平面向量,椭圆的定义、标准方程及直线与椭圆位置关系等基础知识,考查综合运用解析几何知识解决问题的能力.设数列{a n}的首项a1为常数,且a n+1=3n﹣2a n(n∈N+).(1)证明:{a n﹣}是等比数列;(2)若a1=,{a n}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.(3)若{a n}是递增数列,求a1的取值范围.考点:等比关系的确定;数列的函数特性;等差数列的通项公式.专题:计算题;证明题;等差数列与等比数列;不等式的解法及应用.分析:(1)根据等比数列的定义,结合条件,即可得证;(2)由(1)求出数列{a n}的通项公式,再由等差数列的性质,得到方程,求出n,即可判断;(3)运用数列{a n}的通项公式,作差,再由n为偶数和奇数,通过数列的单调性,即可得到范围.解答:(1)证明:因为==﹣2,所以数列{a n﹣}是等比数列;(2)解:{a n﹣}是公比为﹣2,首项为a1﹣=的等比数列.通项公式为a n=+(a1﹣)(﹣2)n﹣1=+若{a n}中存在连续三项成等差数列,则必有2a n+1=a n+a n+2,即解得n=4,即a4,a5,a6成等差数列.(3)解:如果a n+1>a n成立,即>+(a1﹣)(﹣2)n﹣1对任意自然数均成立.化简得,当n为偶数时,因为是递减数列,所以p(n)max=p(2)=0,即a1>0;当n为奇数时,,因为是递增数列,所以q(n)min=q(1)=1,即a1<1;故a1的取值范围为(0,1).点评:本题考查数列的通项公式及等比数列的证明,考查等差数列的性质和已知数列的单调性,求参数的范围,考查运算能力,属于中档题和易错题.。
上海市宝山区2024届高三上学期期末教学质量监测(一模)数学试题(1)

一、单选题二、多选题1. 已知抛物线的焦点为,为坐标原点,为抛物线上两点,,且,则的斜率不可能是( )A.B.C.D.2. 如图,不共线的三个向量,,以圆心为起点,终点落在同一圆周上,且两两夹角相等,若,则()A.B.C.D.3.若,则A.B .2C.D.4. 复数满足方程,则( )A .2B.C.D .85. 已知函数f (x )是奇函数,当x >0时,f (x )=a x (a >0,a ≠1),且,则a 的值为( )A.B .3C .9D.6. 已知抛物线的焦点为F ,点P 在C 上,若点,则周长的最小值为( ).A .13B .12C .10D .87. 已知,分别为椭圆的左、右焦点,点是椭圆上位于第二象限内的点,延长交椭圆于点,若,且,则椭圆的离心率为A.B.C.D.8. 对于实数,“”是“”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件9. 已知,且,则( )A.的最大值为B .的最小值为9C.的最小值为D .的最大值为210. 如图,在棱长为1的正方体中,点M为线段上的动点(含端点),则( )上海市宝山区2024届高三上学期期末教学质量监测(一模)数学试题(1)上海市宝山区2024届高三上学期期末教学质量监测(一模)数学试题(1)三、填空题四、解答题A .存在点M ,使得平面B .存在点M ,使得∥平面C .不存在点M ,使得直线与平面所成的角为D .存在点M,使得平面与平面所成的锐角为11. 已知则可能满足的关系是()A.B.C.D.12.已知函数的定义域为,为奇函数,且对于任意,都有,则( )A.B.C .为偶函数D .为奇函数13. 是公差不为0的等差数列,是公比为正数的等比数列,,,,则数列的前项和等于__________.14. 已知、是方程的两根,并且、,则的值是______.15.的展开式中的系数为______(用数字做答).16. 已知函数.(1)若有两个极值点.求实数的取值范围.(2)在(1)的条件下,求证:.17. 如图所示,已知是边长为6的等边三角形,点M 、N 分别在,上,,O是线段的中点,将沿直线进行翻折,A 翻折到点P ,使得平面平面,如图所示.(1)求证:;(2)若,求点M到平面的距离.18. 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图如图.(1)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一年级中“体育良好”的学生人数;(2)为分析学生平时的体育活动情况,现从体育成绩在和的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在的概率.19. 如图,三棱柱-的底面是边长为2的等边三角形,底面,点分别是棱,上的点,且(Ⅰ)证明:平面平面;(II)若,求直线与平面所成角的正弦值.20. 为进一步完善公共出行方式,倡导“绿色出行”和“低碳生活”,淮南市建立了公共自行车服务系统,为了鼓励市民租用公共自行车出行,同时希望市民尽快还车,方便更多的市民使用,公共自行车按每次的租用时间进行缴费,具体缴费标准如下:①租用时间不超过1小时,免费;②超出一小时后每小时1元(不足一小时按一小时计算),一天24小时最高收费10元.某日甲、乙两人独立出行,各租用公共自行车一次,且两人租车时间都不会超过3小时,设甲、乙租用时间不超过一小时的概率分别是0.5,0.4;租用时间为1小时以上且不超过2小时的概率分别是0.2,0.4.(1)求甲比乙付费多的概率;(2)设甲、乙两人付费之差的绝对值为随机变量,求的分布列和数学期望.21. 已知函数,,为函数的导函数.(1)讨论函数的单调性;(2)当时,证明对任意的都成立.。
2014年上海市宝山区中考一模数学试卷(解析版)

11. (4 分)如图,二次函数 y=ax2+bx+c 的图象开口向上,对称轴为直线 x=1, 图象经过(3,0) ,则 a﹣b+c 的值是 .
12. (4 分)抛物线 y=(x+2)2﹣3 可以由抛物线 y=x2﹣3 向 得到. 13. (4 分)若 与 的方向相反,且| |>| |,则 的方向与 的方向
第 4 页(共 24 页)
(2)若 FG=1,AD=3,求 tan∠GFE 的值.
25. (12 分)如图,已知抛物线 y=﹣
+bx+4 与 x 轴相交于 A、B 两点,与 y
轴相交于点 C,若已知 B 点的坐标为 B(8,0) . (1)求抛物线的解析式及其对称轴方程; (2)连接 AC、BC,试判断△AOC 与△COB 是否相似?并说明理由; (3)M 为抛物线上 BC 之间的一点,N 为线段 BC 上的一点,若 MN∥y 轴,求 MN 的最大值; (4)在抛物线的对称轴上是否存在点 Q,使△ACQ 为等腰三角形?若存在,求 出符合条件的 Q 点坐标;若不存在,请说明理由.
,cosB= ,则△
16. (4 分)某坡面的坡度为 1:
,某车沿该坡面爬坡行进了
米后,该
车起始位置和终止位置两地所处的海拔高度上升了 5 米. 17. (4 分)在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如 图所示) ,已知立杆 AB 的高度是 6 米,从侧面 D 测到路况警示牌顶端 C 点和 低端 B 点的仰角分别是 60°和 45°,则路况警示牌宽 BC 的值为 .
18. (4 分)如图,在平面直角坐标系中,Rt△OAB 的顶点 A 的坐标为(9,0) , tan∠BOA= ,点 C 的坐标为(2,0) ,点 P 为斜边 OB 上的一个动点,则 .
2014-2015学年上海市宝山区高一(上)期末数学试卷和答案

2014-2015学年上海市宝山区高一(上)期末数学试卷一、填空题(本大题共有12题,满分36分)考生应在答题纸相应编号地空格内直接填写结果,每个空格填对得3分,否则一律得零分.1.(3,。
0分)函数y=log2(x-1)地定义域是.2.(3,00分)设全集U=R,集合S={x|xN-l},则[uS=.3.(3,00分)设关于x地函数y=(k -2)x+1是R上地增函数,则实数k地取值范围是.4.(3,00分)已知x=logy5,用含x地式子表示log?625,则log?625=.5.(3,00分)函数y=Jx(4-x)地最大值为.6.(3,00分)若函数f(x)=—^―-a是奇函数,则实数a地值为.3X+127.(3,00分)若不等式x-mx+n<0(m,n£R)地解集为(2,3),则m-n=.8.(3,00分)设a:OWxWl,P:mWxW2m+5,若a是0地充分条件,则实数m地取值范围是.9.(3,00分)设a,b均为正数,则函数f(x)=(a+b)x+ab地零点地最小22值为•10.(3,00分)给出下列命题:①直线x=a与函数y=f(x)地图象至少有两个公共点;②函数y=x「2在(0,+8)上是单调递减函数;③蓦函数地图象一定经过坐标原点;④函数f(x)=ax"(a〉0,a7^1)地图象恒过定点(2,1).⑤设函数y=f(x)存在反函数,且y=f(x)地图象过点(1,2),则函数y=f1(x) -1地图象一定过点(2,0).其中,真命题地序号为.211.(3,00分)设函数f(x)(xGR)满足|f(x)+(上匚)2|W1_,且|f(x)1+x23-(-^)2|WZ.则f(0)=•1+x2312.(3,00分)若F(x)=a*f(x)g(x)+b*[f(x)+g(x)]+c(a,b,c均为常数),则称F(x)是由函数f(x)与函数g(x)所确定地〃afb3c〃型函数.设函数fi(x)=x+l与函数f2(x)=x2-3x+6,若f(x)是由函数fi1(x)+1与函数f2(x)所确定地“1095”型函数,且实数m,n满足f(m)=lf(n)=6,则2m+n地值为.二、选择题(本大题共有4题,满分12分)每题有且只有一个正确答案,考生应在答题纸地相应编号上,将代表答案地小方格涂黑,选对得3分,否则一律得零分.13.(3,00分)"3>1"是“a>0”地()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件14.(3,00分)函数y=x+A(x>0)地递减区间为()xA.(0,4]B.[2,4]C.[2,+°°)D.(0,2]15.(3,00分)如图为函数f(x)=t+log a x地图象(a,t均为实常数),则下列结论正确地是()A.0<a<l,t<0B.0<a<l,t>0C.a>l,t<0D.a>l,t>016.(3,00分)设g(x)=|f(x+2m)-x|,f(t)为不超过实数t地最大整数,若函数g(x)存在最大值,则正实数m地最小值为()A.XB.X c.-L D.X161284三、解答题(本大题共有5题,满分52分)解答下列各题必须在答题纸相应编号地规定区域内写出必要地步骤.x2+3x-10<017.(8,00分)解不等式组:y+1—>1I x18.(8,00分)某“农家乐”接待中心有客房200间,每间日租金为40元,每天都客满.根据实际需要,该中心需提高租金.如果每间客房日租金每增加4元,客房出租就会减少10间.(不考虑其他因素)(1)设每间客房日租金提高4x元(xCW,x<20),记该中心客房地日租金总收入为y,试用x表示y;(2)在(1)地条件下,每间客房日租金为多少时,该中心客房地日租金总收入最高?19.(10,00分)已知f(x)=|x+a|(a>-2)地图象过点(2,1).(1)求实数a地值;(2)如图所示地平面直角坐标系中,每一个小方格地边长均为1.试在该坐标系中作出函数y=f(x没+a地简图,并写出(不需要证明)它地定义域、值域、f(x)奇偶性、单调区间.20.(12,00分)设函数f(x)=log m(1+mx)-log m(1-mx)(m>0,且m乂1).(1)判断f(x)地奇偶性;(2)当m=2时,解方程f(6x)=1;(3)如果f(u)=u-1,那么,函数g(x)=x2-ux地图象是否总在函数h(x) =ux-1地图象地上方?请说明理由.21.(14,00分)对于四个正数x,y,z,w,如果xw<yz,那么称(x,y)是(z,w)地“下位序对(1)对于2,3,7,11,试求(2,7)地“下位序对”;(2)设a,b,c,d均为正数,且(a,b)是(c,d)地“下位序对",试判断£,d 旦,地之间地大小关系;b b+d(3)设正整数n满足条件:对集合{t|0<t<2014)内地每个m£N+,总存在k £N,使得(m,2014)是(k,n)地“下位序对”,且(k,n)是(m+1,2015)地“下位序对求正整数n地最小值.2014-2015学年上海市宝山区高一(上)期末数学试卷参考答案与试题解析一、填空题(本大题共有12题,满分36分)考生应在答题纸相应编号地空格内直接填写结果,每个空格填对得3分,否则一律得零分.1.(3,00分)函数y=log2(x-1)地定义域是(1,+8).【解答】解:Vy=log2(x-1),.\x-l>0,x>l函数y=log2(x-1)地定义域是(1,+°°)故答案为(1,+8)2.(3,00分)设全集U=R,集合S={x|xN-l},贝l]「uS={x|xV-l}.【解答】解:..•全集U=R,集合S={x|xN-l},CuS={x|x<-1},故答案为:(x|x<-1}.3.(3,00分)设关于x地函数y=(k-2)x+l是R上地增函数,则实数k地取值范围是(2,+8).【解答】解:关于x地函数y=(k-2)x+1是R上地增函数所以:k-2>0解得:k>2所以实数k地取值范围为:(2,+8)故答案为:(2,+8)4.(3,00分)己知x=log75,用含x地式子表示log?625,则log7625=4x.【解答】解:Vx=log75,.•.log7625=lo g T54=4x,故答案为:4x.5.(3,00分)函数y=Jx(4-x)地最大值为2.【解答】解:函数*x(4-x)=J-x2+4x=V-(x-2)2+4函数地定义域{x0<x<4)所以:当x=2时,函数取最小值所以:ymin=2故答案为:26.(3,00分)若函数f(x)=—^—-a是奇函数,则实数a地值为1.3X+1【解答】解:因为奇函数f(x)=—2_-a地定义域是R,3X+1所以f(0)=W_-a=0,解得a=l,3°+l故答案为:1.7.(3,00分)若不等式x2-mx+n<0(m,n《R)地解集为(2,3),则m-n= -1.【解答】解:...不等式x2-mx+n<0(m,nGR)地解集为(2,3),.•.对应方程X2-mx+n=0地两个实数根2和3,由根与系数地关系,得Jnp2+3=5,寸i n=2X3=6‘m-n=5-6=-1.故答案为:-1.8.(3,00分)设a:OWxWl,P:mWxW2m+5,若a是。
上海市宝山区高三数学上学期期末模拟试卷带答案

2015年上海市宝山区高三数学上学期期末模拟试卷(带答案)2015年上海市宝山区高三数学上学期期末模拟试卷(带答案)一.(本大题满分36分)本大题共有12题,要求直接填写结果,每题填对3分,否则一律得0分.1.(3分)函数y=3tanx的周期是π.考点:三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:由条件根据y=Atan(ωx+φ)的周期等于T=,可得结论.解答:解:函数y=3tanx的周期为=π,故答案为:π.点评:本题主要考查三角函数的周期性及其求法,利用了y=Atan(ωx+φ)的周期等于T=,属于基础题.2.(3分)计算=2.考点:二阶矩阵.专题:计算题;矩阵和变换.分析:利用行列式的运算得,=2×3﹣1×4=2.解答:解:=2×3﹣1×4=2,故答案为:2.点评:本题考查了矩阵的运算,属于基础题.3.(3分)(2014嘉定区三模)=.考点:极限及其运算.专题:导数的概念及应用;等差数列与等比数列.分析:利用等差数列的求和公式可得1+2+3+…+n=,然后即可求出其极限值.解答:解:==(+)=,故答案为:点评:本题主要考察极限及其运算.解题的关键是要掌握极限的实则运算法则和常用求极限的技巧!4.(3分)二项式(x+1)10展开式中,x8的系数为45.考点:二项式系数的性质.专题:二项式定理.分析:根据二项式(x+1)10展开式的通项公式,求出x8的系数是什么.解答:解:∵二项式(x+1)10展开式中,通项为Tr+1=x10﹣r1r=x10﹣r,令10﹣r=8,解得r=2,∴===45;即x8的系数是45.故答案为:45.点评:本题考查了二项式定理的应用问题,解题时应根据二项式展开式的通项公式进行计算,是基础题.5.(3分)设矩阵A=,B=,若BA=,则x=2.考点:矩阵与向量乘法的意义.专题:计算题;矩阵和变换.分析:由题意,根据矩阵运算求解.解答:解:∵A=,B=,BA=,∴4×2﹣2x=4;解得,x=2;故答案为:2.点评:本题考查了矩阵的运算,属于基础题.6.(3分)现有6位同学排成一排照相,其中甲、乙二人相邻的排法有240种.考点:计数原理的应用.专题:排列组合.分析:利用捆绑法,把甲乙二人捆绑在一起,看作一个复合元素,再和其他4人进行全排,问题得以解决解答:解:先把甲乙二人捆绑在一起,看作一个复合元素,再和其他4人进行全排,故有=240种,故答案为:240点评:本题主要考查了排列问题的中的相邻问题,利用捆绑法是关键,属于基础题7.(3分)若cos(π+α)=﹣,π<α<2π,则sinα=﹣.考点:运用诱导公式化简求值.专题:三角函数的求值.分析:利用诱导公式可知cosα=,又π<α<2π,利用同角三角函数间的关系式(平方关系)即可求得sinα的值.解答:解:∵cos(π+α)=﹣cosα=﹣,∴cosα=,又π<α<2π,∴sinα=﹣=﹣.故答案为:﹣.点评:本题考查诱导公式与同角三角函数间的关系式的应用,属于中档题.8.(3分)(2008天津)若一个球的体积为,则它的表面积为12π.考点:球的体积和表面积.专题:计算题.分析:有球的体积,就可以利用公式得到半径,再求解其面积即可.解答:解:由得,所以S=4πR2=12π.点评:本题考查学生对公式的利用,是基础题.9.(3分)函数y=sin(2x+φ)(0≤φ≤π)是R上的偶函数,则φ的值是.考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:计算题.分析:根据函数y=sin(2x+φ)的图象特征,若它是偶函数,只需要x=0时,函数能取得最值.解答:解:函数y=sin(2x+ϕ)是R上的偶函数,就是x=0时函数取得最值,所以f(0)=±1即sinϕ=±1所以ϕ=kπ+(k∈Z),当且仅当取k=0时,得φ=,符合0≤φ≤π故答案为:点评:本题考查了正弦型函数的奇偶性,正弦函数的最值,是基础题.10.(3分)正四棱锥P﹣ABCD的所有棱长均相等,E是PC的中点,那么异面直线BE与PA所成的角的余弦值等于.考点:异面直线及其所成的角.专题:空间角.分析:根据异面直线所成角的定义先找出对应的平面角即可得到结论.解答:解:连结AC,BD相交于O,则O为AC的中点,∵E是PC的中点,∴OE是△PAC的中位线,则OE∥,则OE与BE所成的角即可异面直线BE与PA所成的角,设四棱锥的棱长为1,则OE==,OB=,BE=,则cos==,故答案为:点评:本题考查异面直线所成的角,作出角并能由三角形的知识求解是解决问题的关键,属中档题11.(3分)(2004福建)直线x+2y=0被曲线x2+y2﹣6x﹣2y﹣15=0所截得的弦长等于4.考点:直线与圆的位置关系.专题:综合题;数形结合.分析:根据圆的方程找出圆心坐标和半径,过点A作AC⊥弦BD,可得C为BD的中点,根据勾股定理求出BC,即可求出弦长BD的长.解答:解:过点A作AC⊥弦BD,垂足为C,连接AB,可得C为BD的中点.由x2+y2﹣6x﹣2y﹣15=0,得(x﹣3)2+(y﹣1)2=25.知圆心A为(3,1),r=5.由点A(3,1)到直线x+2y=0的距离AC==.在直角三角形ABC中,AB=5,AC=,根据勾股定理可得BC===2,则弦长BD=2BC=4.故答案为:4点评:本题考查学生灵活运用垂径定理解决实际问题的能力,灵活运用点到直线的距离公式及勾股定理化简求值,会利用数形结合的数学思想解决数学问题,是一道综合题.12.(3分)已知函数f(x)=Asin(ωx+ϕ),(A >0,ω>0,0≤ϕ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+).考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:首先,根据所给函数的部分图象,得到振幅A=2,然后,根据周期得到ω的值,再将图象上的一个点代人,从而确定其解析式.解答:解:根据图象,得A=2,又∵T==,∴T=π,∴ω=2,将点(﹣,0)代人,得2sin(2x+ϕ)=0,∵0≤ϕ≤π,∴ϕ=,∴f(x)=2sin(2x+),故答案为:2sin(2x+)点评:本题重点考查了三角函数的图象与性质、特殊角的三角函数等知识,属于中档题.解题关键是熟悉所给函数的部分图象进行分析和求解.二.选择题(本大题满分36分)本大题共有12题,每题都给出四个结论,其中有且只有一个结论是正确的.考生必须把正确结论的代码写在题后的括号内,选对得3分,否则一律得0分.13.(3分)已知点P(tanα,cosα)在第三象限,则角α的终边在第几象限()A.第一象限B.第二象限C.第三象限D.第四象限考点:任意角的三角函数的定义.专题:计算题.分析:由题意,推导出,确定α的象限,然后取得结果.解答:解:∵P(tanα,cosα)在第三象限,∴,由tanα<0,得α在第二、四象限,由cosα<0,得α在第二、三象限∴α在第二象限.故选B点评:本题考查任意角的三角函数的定义,考查计算能力,是基础题.14.(3分)已知函数y=xa+b,x∈(0,+∞)是增函数,则()A.a>0,b是任意实数B.a<0,b是任意实数C.b>0,a是任意实数D.b<0,a是任意实数考点:指数函数的单调性与特殊点.专题:计算题;函数的性质及应用.分析:由幂函数的性质可知,a>0,b是任意实数.解答:解:∵函数y=xa+b,x∈(0,+∞)是增函数,∴a>0,b是任意实数,故选A.点评:本题考查了幂函数的单调性的判断,属于基础题.15.(3分)在△ABC中,若b=2asinB,则这个三角形中角A的值是()A.30°或60°B.45°或60°C.30°或120°D.30°或150°考点:正弦定理.专题:解三角形.分析:在△ABC中,利用正弦定理解得sinA=,从而求得A的值.解答:解:在△ABC中,若b=2asinB,则由正弦定理可得sinB=2sinAsinB,解得sinA=,∴A=30°或150°.故选D.点评:本题主要考查正弦定理的应用,根据三角函数的值求角,属于中档题.16.(3分)若loga3<logb3<0,则()A.0<a<b<1B.0<b<a<1C.a>b>1D.b>a>1考点:对数函数的单调区间.专题:计算题;函数的性质及应用.分析:化loga3<logb3<0为log3b<log3a<0,利用函数的单调性求解.解答:解:∵loga3<logb3<0,∴<<0,即log3b<log3a<0,故0<b<a<1,故选B.点评:本题考查了对数的运算及对数函数单调性的利用,属于基础题.17.(3分)双曲线﹣=1的焦点到渐近线的距离为()A.2B.2C.D.1考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:先根据双曲线方程求得焦点坐标和渐近线方程,进而利用点到直线的距离求得焦点到渐近线的距离.解答:解:双曲线﹣=1的焦点为(4,0)或(﹣4,0).渐近线方程为y=x或y=﹣x.由双曲线的对称性可知,任一焦点到任一渐近线的距离相等,d==2.故选A.点评:本题主要考查了双曲线的标准方程,双曲线的简单性质和点到直线的距离公式.考查了考生对双曲线标准方程的理解和灵活应用,属基础题.18.(3分)用数学归纳法证明等式1+3+5+…+(2n﹣1)=n2(n∈N*)的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到()A.1+3+5+…+(2k+1)=k2B.1+3+5+…+(2k+1)=(k+1)2C.1+3+5+…+(2k+1)=(k+2)2D.1+3+5+…+(2k+1)=(k+3)2考点:数学归纳法.专题:阅读型.分析:首先由题目假设n=k时等式成立,代入得到等式1+3+5+…+(2k﹣1)=k2.当n=k+1时等式左边=1+3+5++(2k﹣1)+(2k+1)由已知化简即可得到结果.解答:解:因为假设n=k时等式成立,即1+3+5+…+(2k ﹣1)=k2当n=k+1时,等式左边=1+3+5+…+(2k﹣1)+(2k+1)=k2+(2k+1)=(k+1)2.故选B.点评:此题主要考查数学归纳法的概念问题,涵盖知识点少,属于基础性题目.需要同学们对概念理解记忆.19.(3分)设z=1+i(i是虚数单位),则复数+z2在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:利用复数代数形式的乘除运算化简求得对应点的坐标,则答案可求.解答:解:∵z=1+i,则复数+z2=,∴复数+z2在复平面上对应的点的坐标为(1,1),位于第一象限.故选:A.点评:本题考查了复数代数形式的乘除运算,考查了复数的等式表示法及其几何意义,是基础题.20.(3分)(2004陕西)圆x2+y2﹣4x=0在点P(1,)处的切线方程为()A.x+y﹣2=0B.x+y﹣4=0C.x﹣y+4=0D.x﹣y+2=0考点:圆的切线方程.专题:计算题.分析:本题考查的知识点为圆的切线方程.(1)我们可设出直线的点斜式方程,联立直线和圆的方程,根据一元二次方程根与图象交点间的关系,得到对应的方程有且只有一个实根,即△=0,求出k值后,进而求出直线方程.(2)由于点在圆上,我们也可以切线的性质定理,即此时切线与过切点的半径垂直,进行求出切线的方程.解答:解:法一:x2+y2﹣4x=0y=kx﹣k+⇒x2﹣4x+(kx﹣k+)2=0.该二次方程应有两相等实根,即△=0,解得k=.∴y﹣=(x﹣1),即x﹣y+2=0.法二:∵点(1,)在圆x2+y2﹣4x=0上,∴点P为切点,从而圆心与P的连线应与切线垂直.又∵圆心为(2,0),∴k=﹣1.解得k=,∴切线方程为x﹣y+2=0.故选D点评:求过一定点的圆的切线方程,首先必须判断这点是否在圆上.若在圆上,则该点为切点,若点P(x0,y0)在圆(x﹣a)2+(y﹣b)2=r2(r>0)上,则过点P的切线方程为(x﹣a)(x0﹣a)+(y﹣b)(y0﹣b)=r2(r >0);若在圆外,切线应有两条.一般用“圆心到切线的距离等于半径长”来解较为简单.若求出的斜率只有一个,应找出过这一点与x轴垂直的另一条切线.21.(3分)“tanx=﹣1”是“x=﹣+2kπ(k∈Z)”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件考点:函数奇偶性的性质.专题:简易逻辑.分析:得出tan(=﹣+2kπ)=﹣1,“x=﹣+2kπ”是“tanx=﹣1”成立的充分条件;举反例tan=﹣1,推出“x=﹣+2kπ(k∈Z)”是“tanx=﹣1”成立的不必要条件.解答:解:tan(﹣+2kπ)=tan(﹣)=﹣1,所以充分;但反之不成立,如tan=﹣1.故选:B点评:本题主要考查了必要条件、充分条件与充要条件的判断.充分条件与必要条件是中学数学最重要的数学概念之一,要理解好其中的概念.22.(3分)(2013福建)在四边形ABCD中,=(1,2),=(﹣4,2),则该四边形的面积为()A.B.C.5D.10考点:向量在几何中的应用;三角形的面积公式;数量积判断两个平面向量的垂直关系.专题:计算题;平面向量及应用.分析:通过向量的数量积判断四边形的形状,然后求解四边形的面积即可.解答:解:因为在四边形ABCD中,,,=0,所以四边形ABCD的对角线互相垂直,又,,该四边形的面积:==5.故选C.点评:本题考查向量在几何中的应用,向量的数量积判断四边形的形状是解题的关键,考查分析问题解决问题的能力.23.(3分)(2006天津)函数的反函数是()A.B.C.D.考点:反函数.分析:本题需要解决两个问题:一是如何解出x,二是如何获取反函数的定义域,求解x时,要注意x<0的条件,因为涉及2个解.解答:解:由解得,又∵原函数的值域是:y>2∴原函数的反函数是,故选D.点评:该题的求解有2个难点,一是解出x有两个,要根据x<0确定负值的一个,二是反函数的定义域要用原函数的值域确定,不是根据反函数的解析式去求.24.(3分)曲线y2=|x|+1的部分图象是()A.B.C.D.考点:曲线与方程.专题:函数的性质及应用.分析:分类讨论,去掉绝对值,化简函数的解析式,可得它的图象特征,结合所给的选项,得出结论.解答:解:当x≥0时,y2=x+1表示以(﹣1,0)为顶点的开口向右的抛物线.当x<0时,y2=﹣(x﹣1)表示以(1,0)为顶点的开口向左的抛物线,故选:C.点评:本题主要考查函数的图象特征,属于基础题.三、解答题(本大题满分48分)本大题共有5题,解答下列各题必须写出必要的步骤.25.(8分)解不等式组:.考点:其他不等式的解法.专题:不等式的解法及应用.分析:根据不等式的解法即可得到结论.解答:解:由|x﹣1|<3解得﹣2<x<4,由>1得﹣1=>0,解得3<x<5,所以,不等式解集为(3,4).点评:本题主要考查不等式组的求解,比较基础.26.(8分)如图,正四棱柱ABCD﹣A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成角的大小为arctan,求正四棱柱ABCD﹣A1B1C1D1的体积.考点:棱柱、棱锥、棱台的体积.专题:空间位置关系与距离.分析:由已知得AA1∥BB1,从而tan∠CB1B==,进而BB1=4,由此能求出正四棱柱ABCD﹣A1B1C1D1的体积.解答:解:∵正四棱柱ABCD﹣A1B1C1D1的底面边长AB=2,异面直线A1A与B1C所成角的大小为arctan,∴AA1∥BB1,∴∠CB1B为AA1、B1C所成的角,且tan∠CB1B==,…(4分)∵BC=AB=2,∴BB1=4,…(6分)∴正四棱柱ABCD﹣A1B1C1D1的体积V=Sh=22×4=16.…(8分)点评:本题考查正四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.27.(10分)已知点F为抛物线C:y2=4x的焦点,点P 是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点.(Ⅰ)求直线PF的方程;(Ⅱ)求△DAB的面积S范围;(Ⅲ)设,,求证λ+μ为定值.考点:直线的一般式方程;抛物线的应用.专题:计算题.分析:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),求出斜率用点斜式写出直线方程.(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2),用弦长公式求出线段AB的长,再由点到直线的距离公式求点D到直线AB的距离,用三角形面积公式表示出面积关于参数m的表达式,再根据m的取值范围求出面积的范围.(Ⅲ),,变化为坐标表示式,从中求出参数λ,μ用两点A,B的坐标表示的表达式,即可证明出两者之和为定值.解答:解:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),于是直线PF的斜率为,所以直线PF的方程为,即为mx+2y﹣m=0.(3分)(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2),由得m2x2﹣(2m2+16)x+m2=0,所以,x1x2=1.于是.点D到直线mx+2y﹣m=0的距离,所以.因为m∈R且m≠0,于是S>4,所以△DAB的面积S范围是(4,+∞).(9分)(Ⅲ)由(Ⅱ)及,,得(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,m﹣y1)=μ(x2+1,y2﹣m),于是,(x2≠±1).所以.所以λ+μ为定值0.(14分)点评:考查求直线方程、抛物线在的焦点弦弦长公式、点到直线的距离公式及向量中数乘向量的意义,涉及知识较多,综合性较强.28.(10分)已知函数f(x)=(x∈R).(1)写出函数y=f(x)的奇偶性;(2)当x>0时,是否存实数a,使v=f(x)的图象在函数g(x)=图象的下方,若存在,求α的取值范围;若不存在,说明理由.考点:函数恒成立问题;函数奇偶性的判断.专题:函数的性质及应用.分析:(1)当a=0时,f(x)=是奇函数;当a≠0时,函数f(x)=(x∈R),是非奇非偶函数.(2)若y=f(x)的图象在函数g(x)=图象的下方,则<,化简得a<+x恒成立,在求函数的最值.解答:解:(1)因为y=f(x)的定义域为R,所以:当a=0时,f(x)=是奇函数;当a≠0时,函数f(x)=(x∈R).是非奇非偶函数.(2)当x>0时,若y=f(x)的图象在函数g(x)=图象的下方,则<,化简得a<+x恒成立,因为x>0,∴即,所以,当a<4时,y=f(x)的图象都在函数g(x)=图象的下方.点评:本题主要考查函数的奇偶性,同时考查函数恒成立的问题,主要进行函数式子的恒等转化.29.(12分)已知抛物线x2=4y,过原点作斜率为1的直线交抛物线于第一象限内一点P1,又过点P1作斜率为的直线交抛物线于点P2,再过P2作斜率为的直线交抛物线于点P3,﹣2<x<4,如此继续.一般地,过点3<x<5作斜率为的直线交抛物线于点Pn+1,设点Pn(xn,yn).(1)求x3﹣x1的值;(2)令bn=x2n+1﹣x2n﹣1,求证:数列是等比数列;(3)记P奇(x奇,y奇)为点列P1,P3,…,P2n﹣1,…的极限点,求点P奇的坐标.考点:数列与解析几何的综合.专题:计算题;等差数列与等比数列;圆锥曲线的定义、性质与方程.分析:(1)求出直线方程,联立抛物线方程,求出交点,即可得到;(2)设出两点点Pn(xn,).Pn+1(xn+1,),由直线的斜率公式,再由条件,运用等比数列的定义,即可得证;(3)运用累加法,求得x2n+1=+,再由数列极限的概念,即可得到点P奇的坐标.解答:(1)解:直线OP1的方程为y=x,由解得P1(4,4),直线P2P1的方程为y﹣4=(x﹣4),即y=x+2,由得P2(﹣2,1),直线P2P3的方程为y﹣1=(x+2),即y=x+,由解得,P3(3,),所以x3﹣x1=3﹣4=﹣1.(2)证明:因为设点Pn(xn,).Pn+1(xn+1,),由抛物线的方程和斜率公式得到,,所以xn+xn﹣1=,两式相减得xn+1﹣xn﹣1=﹣,用2n代换n得bn=x2n+1﹣x2n﹣1=﹣,由(1)知,当n=1时,上式成立,所以是等比数列,通项公式为bn=﹣;(3)解:由得,,,…,,以上各式相加得x2n+1=+,所以x奇=,y奇=x奇2=,即点P奇的坐标为(,).点评:本题考查联立直线方程和抛物线方程求交点,考查等比数列的定义和通项公式的求法,考查累加法求数列通项,及数列极限的运算,属于中档题.四、附加题(本大题满分30分)本大题共有3题,解答下列各题必须写出必要的步骤.30.(8分)有根木料长为6米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,问怎样利用木料,才能使光线通过的窗框面积最大(中间木档的面积可忽略不计).专题:函数的性质及应用.分析:求出窗框的高为3x,宽为.推出窗框的面积,利用二次函数的最值,求解即可.解答:解:如图设x,则竖木料总长=3x+4x=7x,三根横木料总长=6﹣7x,∴窗框的高为3x,宽为.…(2分)即窗框的面积y=3x=﹣7x2+6x.(0<x<)…(5分)配方:y=﹣7(x﹣)2+(0<x<2)…(7分)∴当x=米时,即上框架高为米、下框架为米、宽为1米时,光线通过窗框面积最大.…(8分)点评:本题考查二次函数的解析式的应用,考查分析问题解决问题的能力.31.(10分)(2008辽宁)在平面直角坐标系xOy中,点P到两点,的距离之和等于4,设点P的轨迹为C.(Ⅰ)写出C的方程;(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时⊥?此时的值是多少?.考点:直线与圆锥曲线的综合问题.专题:综合题;压轴题;转化思想.分析:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是椭圆.从而写出其方程即可;(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时的值,从而解决问题.解答:解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以为焦点,长半轴为2的椭圆.它的短半轴,故曲线C的方程为.(4分)(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足消去y并整理得(k2+4)x2+2kx﹣3=0,故.(6分),即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,于是.所以时,x1x2+y1y2=0,故.(8分)当时,,.,而(x2﹣x1)2=(x2+x1)2﹣4x1x2=,所以.(12分)点评:本小题主要考查平面向量,椭圆的定义、标准方程及直线与椭圆位置关系等基础知识,考查综合运用解析几何知识解决问题的能力.设数列的首项a1为常数,且an+1=3n﹣2an(n∈N+).(1)证明:{an﹣}是等比数列;(2)若a1=,中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.(3)若是递增数列,求a1的取值范围.考点:等比关系的确定;数列的函数特性;等差数列的通项公式.专题:计算题;证明题;等差数列与等比数列;不等式的解法及应用.分析:(1)根据等比数列的定义,结合条件,即可得证;(2)由(1)求出数列的通项公式,再由等差数列的性质,得到方程,求出n,即可判断;(3)运用数列的通项公式,作差,再由n为偶数和奇数,通过数列的单调性,即可得到范围.解答:(1)证明:因为==﹣2,所以数列{an﹣}是等比数列;(2)解:{an﹣}是公比为﹣2,首项为a1﹣=的等比数列.通项公式为an=+(a1﹣)(﹣2)n﹣1=+若中存在连续三项成等差数列,则必有2an+1=an+an+2,即解得n=4,即a4,a5,a6成等差数列.(3)解:如果an+1>an成立,即>+(a1﹣)(﹣2)n﹣1对任意自然数均成立.化简得,当n为偶数时,因为是递减数列,所以p(n)max=p(2)=0,即a1>0;当n为奇数时,,因为是递增数列,所以q(n)min=q(1)=1,即a1<1;故a1的取值范围为(0,1).点评:本题考查数列的通项公式及等比数列的证明,考查等差数列的性质和已知数列的单调性,求参数的范围,考查运算能力,属于中档题和易错题.。
上海市宝山区2024届高三上学期期末教学质量监测(一模) 数学试题(含解析)

,则实数
a
的值为
.
8.若对于任意实数 x ,都有 x4 a0 a1 x 2 a2 x 22 a3 x 23 a4 x 24 ,则 a3
的值为
;
9.如图,在圆锥 S O 中, AC 为底面圆 O 的直径, SO OC 1 ,点 B 在底面圆周上, 且 AB BC .若 E 为线段 AB 上的动点,则 SEC 的周长最小值为
斜率分别为 k0、k1、k2 ,求证: k0 k1 k2 2 . 21.已知函数 f x ex x , g x ex x ,其中 e 为自然对数的底数.
(1)求函数 y f x 的图象在点 1, f 1 处的切线方程;
(2)设函数 F x af x g x , ①若 a e ,求函数 y F x 的单调区间,并写出函数 y F x m 有三个零点时实数 m
故答案为: 3 2 1
10. 5, 4, 2
【分析】根据题意,分别保证各科及格,再由得分效益最大求解. 【详解】首先保证各学科均及格,则思政、外语、专业课分别需要 3 周,4 周,2 周,还有 剩余复习时间 3 周,剩余时间复习一周思政可提高 7 分,复习外语可提高 3 分,复习专业课 可提高 15 分,故先安排一周复习专业课,剩余 2 周,若再复习专业课一周可提高 5 分,从 得分效益来看,先安排一周复习思政,剩一周再复习思政可提高 6 分,故安排复习思政, 综上,安排 5 周思政复习,4 周外语复习,2 周专业课复习,总分最高,
① 4∈ S ;②集合x x 3n 5, n N S .则下列选项中正确的是( )
A.①是真命题, ②是真命题;
B.①是真命题, ②是假命题
C.①是假命题, ②是真命题;
D.①是假命题, ②是假命题.
上海市宝山区2014届高三上学期期末考试物理试题

上海市宝山区2014届高三第一学期期末考试物理试题本试卷分第I卷(1—4页)和第II卷(5—8页)两部分。
全卷共8页。
满分150分。
考试时间120分钟。
第I卷(共56分)考生注意:1.答第1卷前,考生务必在试卷和答题卡上用黑色的钢笔或圆珠笔清楚填写姓名、班级、学校和准考证号,并用2B铅笔在答题卡上正确涂写准考证号。
2.第I卷(1—20题)由机器阅卷,答案必须全部涂写在答题卡上。
考生应将代表正确答案的小方格用2B铅笔涂黑。
注意试题题号和答题卡编号一一对应,不能错位。
答案需要更改时,必须将原选项用橡皮擦去,重新选择。
答案不能涂写在试卷上,涂写在试卷上一律不给分。
一.单项选择题1(共16分,每小题2分。
每小题只有一个正确选项,答案涂在答题卡上)1、下列物理量中,属于矢量的是A.质量 B.温度 C.磁通量 D.电场强度2、下列能中属于常规能的是A.太阳能 B.天然气 C.核能 D.潮汐能3、许多科学家在物理学发展过程中做出了重要贡献,下列叙述中符合物理学史实的是A.卡文迪许测出了万有引力常数B.安培最早发现了电流周围存在着磁场C.奥斯特发现了电流的磁效应,总结出了电磁感应定律D.伽利略通过理想斜面实验,总结出了惯性定律4、物体做竖直上抛运动时,在任意相同时间间隔内,速度的变化量A.大小相同、方向相同B.大小相同、方向不同C.大小不同、方向不同D.大小不同、方向相同5、一定质量的某种气体,其压强为P,热力学温度为T,下列说法中正确的是:A.P增大时,单位体积内气体分子数一定增大B.T减小时,单位体积内气体分子数一定增大C.P/T的比值增大时,单位体积内气体分子数一定增大D.P/T的比值增大时,单位体积内气体分子数可能增大,也可能减小6、在探究超重和失重规律时,某体重为G的同学站在一压力传感器上完成一次下蹲动作。
传感器和计算机相连,经计算机处理后得到压力F随时间t变化的图象,则下列图象中可能正确的是7、如图所示,由基本门电路组成的四个电路,其中能使小灯泡发光的是8、2013年12月2日,中国在西昌卫星发射中心用“长征三号乙”运载火箭,将嫦娥三号月球探测器成功送入太空。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宝山区2013学年第一学期期末
高三年级数学学科质量监测试
本试卷共有23道试题,满分150分,考试时间120分钟.
考生注意:
1.本试卷包括试题卷和答题纸两部分,答题纸另页,正反面.
2.在本试题卷上答题无效,必须在答题纸上的规定位置按照要求答题.
3.可使用符合规定的计算器答题.
一、填空题 (本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接写结果,每个空格填对得4分,否则一律得零分.
1.已知复数(是虚数单位)对应的点在二、四象限的角平分线上,则实数.
2.已知集合,,,则图中阴影部分表示的集合是.
3.函数的最小正周期是.
4.已知线性方程组的增广矩阵为,若该线性方程组无解,则.
5.若函数的图像与的图像关于对称,则_______. 6.函数的反函数,则方程的解是______.7.阅读程序框图,运行相应的程序,当输入的值为时,输出的值
为.
8.已知,则实数的取值范围是.
9.若双曲线的渐近线方程为,它的一个焦点与抛物线的焦点重合,则双曲线的标准方程为.
10.二项式展开式中的常数项为_________.
11.多瑙河三角洲的一地点位于北纬东经,大兴安岭地区的一地点位于北纬
东经,设地球半径为,则两地之间的球面距离是.12.从正方体的六个面中任意选取3个面,其中有2个面不相邻的概率
为.
13.函数的值域是 .
14.关于函数给出下列四个命题:
①当时,单调递减且没有最值;
②方程一定有解;
③如果方程有解,则解的个数一定是偶数;
④是偶函数且有最小值.则其中真命题是.(只要写标题号)
二、选择题 (本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在
答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.设为任意实数,则下列各式正确的是…………………………………()(A)(B)
(C)(D)
16.设和都是非零实数,则不等式和同时成立的充要条件是……()
(A)(B)(C)(D)
17.下列关于极限的计算,错误
..的是……………………………………………()
(A)==
(B)(++…+)=++…+=0+0+…+0=0
(C)(-n)===
(D)已知则=
18.记,,,则方程表示的曲线只可能是……………………………………………………()
(A)圆(B)椭圆(C)双曲线(D)抛物线
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须写出必要步骤.19.(本题满分12分)
如图,在四棱锥中,底面是边长为的菱形,,
平面,与平面所成角的大小为,为的中点.
求异面直线与所成角的大小(结果用反三角函数表示).
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
在△中,所对的边分别为,,.
(1)求;
(2)若,求,,.
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
给定曲线.
(1)若曲线是焦点为的双曲线,求实数的值;
(2)当时,记是椭圆上的动点,过椭圆长轴的端点作(为坐标原点),交椭圆于,交轴于,求的值.
22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分7分,第3
小题满分6分.
已知函数和,其中.
(1)若函数与图像的一个公共点恰好在x轴上,求的值;
(2)若函数与图像相交于不同的两点A、B,为坐标原点,试
问:△OAB的面积S有没有最值?如果有,求出最值及所对应的的值;如果没有,请说明理由.
(3)若和是方程的两根,且满足,证明:当时,.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3
小题满分8分.
若数列的每一项都不等于零,且对于任意的,都有(为
常数),则称数列为“类等比数列”.
已知数列满足:,对于任意的,都有.(1)求证:数列是“类等比数列”;
(2)若是单调递减数列,求实数的取值范围;
(3)若,求数列的前项之积取最大值时的值.
宝山区2013学年第一学期期末
高三年级数学监参考答案
2014.1.9
一、填空题
1、 2、∪ 3、 4、2; 5、 6、 7、4 8、(1,7)
9、 10、 11、 12、 13、 14. ②④
二、选择题ABCC
三、解答题
19、解:连结,因为平面,
所以为与平面所成的角………………………………………2分
由已知,,而,所以,.………4分连结,交于点,连结,
因为、分别为、的中点,所以∥,
所以(或其补角)为异面直线与所成的角.……………6分
在△中,,,,……………………9分
(以下由余弦定理,或说明△是直角三角形求得)
或或.………………………12分
所以,异面直线与所成角的大小为(或另外两个答案).
20、解:(1)由
得
……2分
则有=………4分得即.……………………………………………7分
(2)由推出
,
而,即得,………………………9分又(用其它边角关系等同)………………11分
则有
……………………………………………12分
解得
.…………………………………………………14分
21、解:(1)化简得………………………………………2分
由题意得,且…………………………………3分
又,所以解得,………………………5分
(舍)………………………………………………………………6分
(2)当时,曲线,此时,…………7分
设直线OM方程为,
由得:即……8分
………………10分因,则方程为:
于是,…11分
由得:
从而
=…………………………………………13分因此,……14分
22、解:(1)设函数图像与x轴的交点坐标为(,0),………1分
又∵点(,0)也在函数的图像上,∴.
而,∴.…………………………………………………3分
(2)依题意,,即,整理得,①
∵,函数与图像相交于不同的两点A、B,
∴△==.
∴且.…………………………………………………4分
设A(,),B(,),由①得,.
设点O到直线的距离为d,则,……………………5分
.………………………6分
∴=.……………8分
∵且,∴当时,有最大值,……………9分无最小值.…………………………………………………10分(3)由题意可知.…………………………11分
,∴,………………………………12分
∴当时,,即.…………………13分
又, (14)
分
∴,即.综上可知,.………………………………………16分23、解:(1)因为,所以,,所以,数列是“类等比数列”.…………………………………4分
(2)由得……………………………5分
所以…………………………………7分
因为递减,所以………………………………8分[或,对任意的正奇数n,成立。
]
解得:.……………………………………………………10分
(3)记数列的前项之积为.
当时,,由的通项公式可知.
当或,时,,………………………12分又因为,所以,
因而取最大值时,…………………………………………14分当n为奇数时,令得,所以,………16分
因而,,…,,,,…
所以,
或,由得,所以,即前12之积最大.
因而,当时,取最大值.…………………………………………18分。
