【教师版】小学奥数6-2-3 分数应用题(三).专项练习及答案解析
六年级奥数分数应用题经典例题加练习带答案

一.知识的回顾1.工厂原有职工128人,男工人数占总数的14,后来又调入男职工若干人,调入后男工人数占总人数的25,这时工厂共有职工人.【解析】在调入的前后,女职工人数保持不变.在调入前,女职工人数为1128(1)964⨯-=人,调入后女职工占总人数的23155-=,所以现在工厂共有职工3961605÷=人.2.有甲、乙两桶油,甲桶油的质量是乙桶的52倍,从甲桶中倒出5千克油给乙桶后,甲桶油的质量是乙桶的43倍,乙桶中原有油 千克. 【解析】 原来甲桶油的质量是两桶油总质量的55527=+,甲桶中倒出5千克后剩下的油的质量是两桶油总质量的44437=+,由于总质量不变,所以两桶油的总质量为545()3577÷-=千克,乙桶中原有油235107⨯=千克. 【例 2】 (1)某工厂二月份比元月份增产10%,三月份比二月份减产10%.问三月份比元月份增产了还是减产了?(2)一件商品先涨价15%,然后再降价15%,问现在的价格和原价格比较升高、降低还是不变?【解析】 (1)设二月份产量是1,所以元月份产量为:()1011+10%=11÷,三月份产量为:110%=0.9-,因为1011>0.9,所以三月份比元月份减产了(2)设商品的原价是1,涨价后为1+15%=1.15,降价15%为:()1.15115%=0.9775⨯-,现价和原价比较为:0.9775<1,所以价格比较后是价降低了。
【巩固】 把100个人分成四队,一队人数是二队人数的113倍,一队人数是三队人数的114倍,那么四队有多少个人?【解析】 方法一:设一队的人数是“1”,那么二队人数是:131134÷=,三队的人数是:141145÷=,345114520++=,因此,一、二、三队之和是:一队人数5120⨯,因为人数是整数,一队人数一定是20的整数倍,而三个队的人数之和是51⨯(某一整数), 因为这是100以内的数,这个整数只能是1.所以三个队共有51人,其中一、二、三队各有20,15,16人.而四队有:1005149-=(人).方法二:设二队有3份,则一队有4份;设三队有4份,则一队有5份.为统一一队所以设一队有[4,5]20=份,则二队有15份,三队有16份,所以三个队之和为15162051++=份,而四个队的份数之和必须是100的因数,因此四个队份数之和是100份,恰是一份一人,所以四队有1005149-=人(人).【例 3】 新光小学有音乐、美术和体育三个特长班,音乐班人数相当于另外两个班人数的25,美术班人数相当于另外两个班人数的37,体育班有58人,音乐班和美术班各有多少人?【解析】 条件可以化为:音乐班的人数是所有班人数的22527=+,美术班的学生人数是所有班人数的337310=+,所以体育班的人数是所有班人数的2329171070--=,所以所有班的人数为295814070÷=人,其中音乐班有2140407⨯=人,美术班有31404210⨯=人.【巩固】 甲、乙、丙三人共同加工一批零件,甲比乙多加工20个,丙加工零件数是乙加工零件数的45,甲加工零件数是乙、丙加工零件总数的56,则甲、丙加工的零件数分别为 个、 个.【解析】 把乙加工的零件数看作1,则丙加工的零件数为45,甲加工的零件数为453(1)562+⨯=,由于甲比乙多加工20个,所以乙加工了320(1)402÷-=个,甲、丙加工的零件数分别为340602⨯=个、440325⨯=个. 【例 4】 王先生、李先生、赵先生、杨先生四个人比年龄,王先生的年龄是另外三人年龄和的12,李先生的年龄是另外三人年龄和的13,赵先生的年龄是其他三人年龄和的14,杨先生26岁,你知道王先生多少岁吗?【解析】方法一:要求王先生的年龄,必须先要求出其他三人的年龄各是多少.而题目中出现了三个“另外三人”所包含的对象并不同,即三个单位“1”是不同的,这就是所说的单位“1”不统一,因此,解答此题的关键便是抓不变量,统一单位“1”.题中四个人的年龄总和是不变的,如果以四个人的年龄总和为单位“1”,则单位“1”就统一了.那么王先生的年龄就是四人年龄和的11123=+,李先生的年龄就是四人年龄和的11134=+,赵先生的年龄就是四人年龄和的11145=+(这些过程就是所谓的转化单位“1”).则杨先生的年龄就是四人年龄和的11113134560---=.由此便可求出四人的年龄和:111261*********⎛⎫÷---= ⎪+++⎝⎭(岁),王先生的年龄为:1120403⨯=(岁). 方法二:设王先生年龄是1份,则其他三人年龄和为2份,则四人年龄和为3份,同理设李先生年龄为1份,则四人年龄和为4份,设赵先生年龄为1份,则四人年龄和为5份,不管怎样四人年龄和应是相同的,但是现在四人年龄和分别是3份、4份、5份,它们的最小公倍数是60份,所以最后可以设四人年龄和为60份,则王先生的年龄就变为20份,李先生的年龄就变为15份,赵先生的年龄就变为12份,则杨先生的年龄为13份,恰好是26岁,所以1份是2岁,王先生年龄是20份所以就是40岁.【巩固】甲、乙、丙、丁四个筑路队共筑1200米长的一段公路,甲队筑的路是其他三个队的12,乙队筑的路是其他三个队的13,丙队筑的路是其他三个队的14,丁队筑了多少米?【解析】甲队筑的路是其他三个队的12,所以甲队筑的路占总公路长的11=1+23;乙队筑的路是其他三个队的13,所以乙队筑的路占总公路长的11=1+34; 丙队筑的路是其他三个队的14,所以丙队筑的路占总公路长的11=1+45,所以丁筑路为:11112001=260345⎛⎫⨯--- ⎪⎝⎭(米)【例 5】小刚给王奶奶运蜂窝煤,第一次运了全部的38,第二次运了50块,这时已运来的恰好是没运来的57.问还有多少块蜂窝煤没有运来?【解析】方法一:运完第一次后,还剩下58没运,再运来50块后,已运来的恰好是没运来的57,也就是说没运来的占全部的712,所以,第二次运来的50块占全部的:57181224-=,全部蜂窝煤有:150120024÷=(块),没运来的有:7120070012⨯=(块).方法二:根据题意可以设全部为8份,因为已运来的恰好是没运来的57,所以可以设全部为12份,为了统一全部的蜂窝煤,所以设全部的蜂窝煤共有[8,12]24=份,则已运来应是5241075⨯=+份,没运来的7241475⨯=+份,第一次运来9份,所以第二次运来是1091-=份恰好是50块,因此没运来的蜂窝煤有5014700⨯=(块).【巩固】 五(一)班原计划抽15的人参加大扫除,临时又有2个同学主动参加,实际参加扫除的人数是其余人数的13.原计划抽多少个同学参加大扫除?【解析】又有2个同学参加扫除后,实际参加扫除的人数与其余人数的比是1:3,实际参加人数比原计划多11113520-=+.即全班共有124020÷=(人).原计划抽14085⨯=(人)参加大扫除.【巩固】 某校学生参加大扫除的人数是未参加大扫除人数的14,后来又有20名同学参加大扫除,实际参加的人数是未参加人数的13,这个学校有多少人?【解析】 11204003141⎛⎫÷-=⎪++⎝⎭(人).【例 6】小莉和小刚分别有一些玻璃球,如果小莉给小刚24个,则小莉的玻璃球比小刚少73;如果小刚给小莉24个,则小刚的玻璃球比小莉少85,小莉和小刚原来共有玻璃球多少个?【解析】小莉给小刚24个时,小莉是小刚的74(=1一73),即两人球数和的114;小刚给小莉24个时,小莉是两人球数和的118(=5888-+),因此24+24是两人球数和的118-114=114.从而,和是(24+24) ÷114=132(个).【巩固】某班一次集会,请假人数是出席人数的91,中途又有一人请假离开,这样一来,请假人数是出席人数的223,那么,这个班共有多少人?【解析】因为总人数未变,以总人数作为”1”.原来请假人数占总人数的119+,现在请假人数占总人数的3322+,这个班共有:l÷(3322+-119+)=50(人).【例7】小明是从昨天开始看这本书的,昨天读完以后,小明已经读完的页数是还没读的页数19,他今天比昨天多读了14页,这时已经读完的页数是还没读的页数的13,问题是,这本书共有多少页?”【解析】首先,可以直接运算得出,第一天小明读了全书的11911019=+,而前二天小明一共读了全书的1131413=+,所以第二天比第一天多读的14页对应全书的111241020-⨯=。
【教师版】小学奥数6-2-6 溶液浓度问题(一).专项练习及答案解析
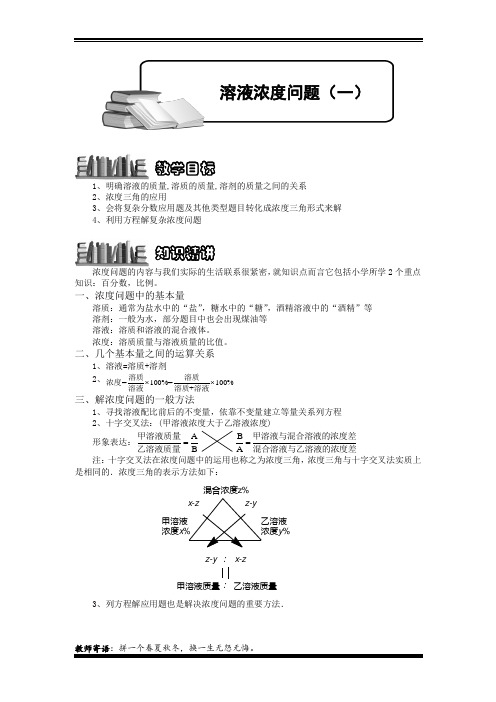
1、明确溶液的质量,溶质的质量,溶剂的质量之间的关系2、浓度三角的应用3、会将复杂分数应用题及其他类型题目转化成浓度三角形式来解4、利用方程解复杂浓度问题浓度问题的内容与我们实际的生活联系很紧密,就知识点而言它包括小学所学2个重点知识:百分数,比例。
一、浓度问题中的基本量溶质:通常为盐水中的“盐”,糖水中的“糖”,酒精溶液中的“酒精”等溶剂:一般为水,部分题目中也会出现煤油等溶液:溶质和溶液的混合液体。
浓度:溶质质量与溶液质量的比值。
二、几个基本量之间的运算关系1、溶液=溶质+溶剂2、=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液三、解浓度问题的一般方法1、寻找溶液配比前后的不变量,依靠不变量建立等量关系列方程2、十字交叉法:(甲溶液浓度大于乙溶液浓度)形象表达:AB =甲溶液质量乙溶液质量B A =甲溶液与混合溶液的浓度差混合溶液与乙溶液的浓度差注:十字交叉法在浓度问题中的运用也称之为浓度三角,浓度三角与十字交叉法实质上是相同的.浓度三角的表示方法如下:::乙溶液质量甲溶液质量z-y x-zy %浓度x 混合浓度z%3、列方程解应用题也是解决浓度问题的重要方法.知识精讲 教学目标溶液浓度问题(一)利用十字交叉即浓度三角进行解题(一)简单的溶液浓度问题【例1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到,那么这种溶液的食盐浓度为多少?【考点】溶液浓度问题【难度】2星【题型】解答【解析】两种配置溶液共含食盐40×15%+60×10%=12克,而溶液质量为40+60-50=50克,所以这种溶液的浓度为12÷50=24%.【答案】24%【巩固】一容器内有浓度为25%的糖水,若再加入20千克水,则糖水的浓度变为15%,问这个容器内原来含有糖多少千克?【考点】溶液浓度问题【难度】2星【题型】解答【解析】100100207.51525⎛⎫÷-=⎪⎝⎭。
小学奥数6-2-1 分数应用题(一).专项练习及答案解析

1. 分析题目确定单位“1”2. 准确找到量所对应的率,利用量÷对应率=单位“1”解题3. 抓住不变量,统一单位“1”一、知识点概述:分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系 例如:(1)a 是b 的几分之几,就把数b 看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1199÷=.二、怎样找准分数应用题中单位“1” (一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
(三)、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语,也不是部分数和总数的关系。
【教师版】小学奥数6-2-7 溶液浓度问题(二).专项练习及答案解析
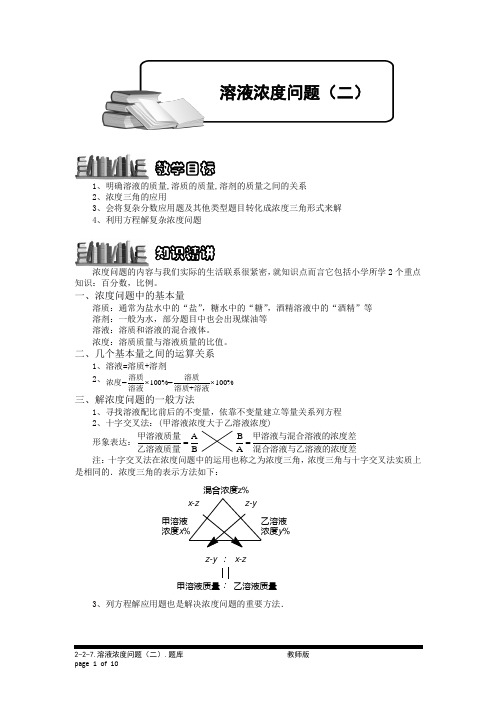
1、明确溶液的质量,溶质的质量,溶剂的质量之间的关系2、浓度三角的应用3、会将复杂分数应用题及其他类型题目转化成浓度三角形式来解4、利用方程解复杂浓度问题浓度问题的内容与我们实际的生活联系很紧密,就知识点而言它包括小学所学2个重点知识:百分数,比例。
一、浓度问题中的基本量溶质:通常为盐水中的“盐”,糖水中的“糖”,酒精溶液中的“酒精”等溶剂:一般为水,部分题目中也会出现煤油等溶液:溶质和溶液的混合液体。
浓度:溶质质量与溶液质量的比值。
二、几个基本量之间的运算关系 1、溶液=溶质+溶剂2、=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液三、解浓度问题的一般方法 1、寻找溶液配比前后的不变量,依靠不变量建立等量关系列方程2、十字交叉法:(甲溶液浓度大于乙溶液浓度)形象表达:A B =甲溶液质量乙溶液质量B A =甲溶液与混合溶液的浓度差混合溶液与乙溶液的浓度差注:十字交叉法在浓度问题中的运用也称之为浓度三角,浓度三角与十字交叉法实质上是相同的.浓度三角的表示方法如下:::乙溶液质量甲溶液质量z-y x-zy %浓度x 混合浓度z%3、列方程解应用题也是解决浓度问题的重要方法.知识精讲教学目标溶液浓度问题(二)模块一、利用十字交叉即浓度三角进行解题三种溶液混合多次【例 1】 有甲、乙、丙三个容器,容量为毫升.甲容器有浓度为40%的盐水400毫升;乙容器中有清水400 毫升;丙容器中有浓度为20%的盐水400毫升.先把甲、丙两容器中的盐水各一半倒入乙容器搅匀后,再把乙容器中的盐水200毫升倒入甲容器,200毫升倒入丙容器.这时甲、乙、丙容器中盐水的浓度各是多少?【考点】溶液浓度问题 【难度】4星 【题型】解答17.5%.小结:在做有关浓度的应用题时,为了弄清楚溶质质量、溶液质量的变化,尤其是变化多次的,常用列表的方法,使它们之间的关系一目了然.【答案】甲容器中盐水的浓度是27.5%,乙容器中浓度是15%,丙容器中浓度是17.5%【例 2】 在甲、乙、丙三缸酒精溶液中,纯酒精的含量分别占48%、62.5%和23,已知三缸酒精溶液总量是100千克,其中甲缸酒精溶液的量等于乙、丙两缸酒精溶液的总量.三缸溶液混合后,所含纯酒精的百分数将达56%.那么,丙缸中纯酒精的量是多少千克?【考点】溶液浓度问题 【难度】3星 【题型】解答【解析】 (法1)方程法.设丙缸酒精溶液的重量为x 千克,则乙缸为()50x -千克.根据纯酒精的量可列方程:()25048%5062.5%10056%3x x ⨯+-⨯+⨯=⨯, 解得18x =,所以丙缸中纯酒精的量是218123⨯=(千克). (法2)浓度三角法.由于甲缸酒精溶液为50千克,乙、丙两缸酒精溶液合起来也是50千克,所以如果将乙、丙两缸酒精溶液混合,得到的酒精溶液的浓度为56%248%64%⨯-=. 例题精讲那么乙、丙两缸酒精溶液的量之比为:()264%:64%62.5%32:183⎛⎫--= ⎪⎝⎭,而它们合起来共50千克,所以丙缸酒精溶液有1850183218⨯=+千克,丙缸中纯酒精的量是218123⨯=(千克). 【答案】12【例 3】 有A 、B 、C 三种盐水,按A 与B 数量之比为2:1混合,得到浓度为13%的盐水;按A 与B 数量之比为1:2混合,得到浓度为14%的盐水.如果A 、B 、C 数量之比为1:1:3,混合成的盐水浓度为10.2%,问盐水C 的浓度是多少?【考点】溶液浓度问题 【难度】3星 【题型】解答【解析】 A 与B 按数量之比为2:4混合时,浓度仍为14%,而这样的混合溶液也相当于A 与B 按数量之比为2:1混合后再混入三份B 盐水,则B 盐水浓度为()()14%613%34115%⨯-⨯÷-=.A 盐水的浓度为14%315%212%⨯-⨯=.再根据A 、B 、C 三种溶液混合的情况,那么C 盐水的浓度为: ()10.2%11312%115%138%⨯++-⨯-⨯÷=⎡⎤⎣⎦.【答案】8%【例 4】 已知三种混合物由三种成分A 、B 、C 组成,第一种仅含成分A 和B ,重量比为3:5;第二种只含成分B 和C ,重量比为1:2;第三种只含成分A 和C ,重量之比为2:3.以什么比例取这些混合物,才能使所得的混合物中A 、B 和C ,这三种成分的重量比为3:5:2?【考点】溶液浓度问题 【难度】4星 【题型】解答【解析】 注意到第一种混合物中A 、B 重量比与最终混合物的A 、B 重量比相同,均为3:5.所以,先将第二种、第三种混合物的A 、B 重量比调整到3:5,再将第二种、第三种混合物中A 、B 与第一种混合物中A 、B 视为单一物质D .最终配成():35:24:1D C =+=的物质; 第二种混合物不含A ,B 的含量为13,第三种混合物不含B ,A 的含量为25,所以237.55÷=倍第三种混合物含A 为3,15153÷=倍第二种混合物含B 为5, 即第二种、第三种混合物的重量比为2:1;于是此时含有C ,232129352145⨯+⨯=+, 即():29:452929:16C D =-=,而最终混合物中:1:429:116C D ==,所以第一种混合物的质量与后两种混合质量和之比为()11616:4520:9-=,所以三种混合物的重量比为20:6:3.【答案】20:6:3【例 5】 A 、B 、C 三个试管中各盛有10克、20克、30克水.把某种浓度的盐水10克倒入A 中,充分混合后从A 中取出10克倒入B 中,再充分混合后从B 中取出10克倒入C 中,最后得到的盐水的浓度是0.5%.问开始倒入试管A 中的盐水浓度是百分之几?【考点】溶液浓度问题 【难度】3星 【题型】解答 【解析】 整个过程中盐水浓度在下降.倒入A 中后,浓度变为原来的10110102=+;倒入B 中后,浓度变为A 中的10110203=+;倒入C 中后,浓度变为B 中的10110304=+.所以对于一开始倒入A 中的盐水浓度可以用倒推的方法,1110.5%12%432÷÷÷=,即一开始倒入A 中的盐水浓度为12%.【答案】12%【例6】有两种溶液,甲溶液的酒精浓度为10%,盐浓度为30%,乙溶液中的酒精浓度为50%,盐浓度为10%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度和盐浓度相等?【考点】溶液浓度问题【难度】3星【题型】解答【解析】一千克甲种溶液中含有酒精0.1千克,盐0.3千克,盐比酒精多0.2千克;而一千克乙种溶液中含有酒精0.5千克,盐0.1千克,盐比酒精少0.4千克.所以只需要0.5千克的乙种酒精将其与甲溶液混合后所得溶液中两种物质含量相等,即浓度相等.【答案】0.5【巩固】有两种溶液,甲溶液的酒精浓度为15%,盐浓度为10%,乙溶液中的酒精浓度为45%,盐浓度为5%.现在有甲溶液1千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【考点】溶液浓度问题【难度】3星【题型】解答【解析】可以这样来看,将溶液中的水剔出或者说蒸发掉,那么所得到的溶液就是盐溶在酒精中.(事实上这种情况不符合物理规律,但这只是假设).这时的处理后甲溶液盐浓度为10%(15%10%)0.4÷+=,÷+=,处理后乙溶液的盐浓度为5%(45%5%)0.1需要配置的溶液的盐浓度为1(13)0.25÷+=,由这些得出的条件使用十字交叉法得到两种处理后溶液的质量比应该为:--=。
小学奥数6-2-2 分数应用题(二).专项练习及答案解析(精品)

1. 分析题目确定单位“1”2. 准确找到量所对应的率,利用量÷对应率=单位“1”解题3.抓住不变量,统一单位“1”一、知识点概述:分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系 例如:(1)a 是b 的几分之几,就把数b 看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1199÷=.二、怎样找准分数应用题中单位“1” (一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
(三)、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语,也不是部分数和总数的关系。
(完整word版)小学六年级奥数专项:分数应用题

1 是原来总数的 3 。求现在书架上放着多少本书?
1 分析: 借出总数的 75%之后,还剩下 25%,又放上 60 本,这时架上的书是原来总数的 3 ,
这就可以找出 60 本书相当于故事书总数的几分之几了,问题也就可以求出来了。还可以画
找量率对应。如下图:
解答:( 1) 60 本书相当于故事书总数的几分之几?
1 ,或可注满乙容器及甲 2
14、有三堆棋子,每堆棋子一样多, 并且都只有黑白两种棋子。第一堆里的黑子数与第二堆
里的白子数一样多,第三堆里的黑子为全部黑子的
2 。把三堆棋子集中在一起,白子为全 5
部棋子的几分之几?
7
二、练习
1、一项工程,甲单独做 10 天完成,乙单独做 8 天完成,甲每天比乙少做(
13 公顷,稻
分析: 通过读题,将题目中的条件列成文字等式:
1
1
1
1
菜地的 2 +稻田的 3 =13 公顷+菜地的 3 +稻田的 2 =12 公顷
5
5
菜地的 6 +稻田的 6 =25 公顷
这就是说,菜地和稻田的
5 6 与 25 公顷相对应,因此可以求出两种地一共有多少公顷,
再求稻田有多少公顷。 解答: 两种地共有
1
1
总数的 8 + 16 本+总数的 2 - 8 本+余下的 67 本 =“单位 1”
将等式变形,量率分别放在等号的两边:
1
1
16 本- 8 本+余下的 67 本 =“单位 1”-总数的 8 -总数的 2
1 13 从上面的式子中可以看出, (67 - 8+16) 就是这批图书的 1- 8 - 2 = 8 ,因此列式为:
6
8、庆丰文具店运来的毛笔比钢笔多 店共运来多少万支笔?
绍兴市上虞区数学小学奥数系列6-2-1分数应用题专练3

绍兴市上虞区数学小学奥数系列6-2-1分数应用题专练3姓名:________ 班级:________ 成绩:________小朋友,带上你一段时间的学习成果,一起来做个自我检测吧,相信你一定是最棒的!一、分数应用题专练 (共23题;共99分)1. (5分) (2020六上·西安期末) 甲、乙、丙三个修路队合修一条45千米的公路,完工时甲队修了这条公路的,乙队和丙队所修公路长度之比为3:2,三个队各修了多少千米?2. (1分)中国文学家莫言,医学家屠呦呦都获得了诺贝尔奖。
屠呦呦获奖感言约有3500字,比莫言的获奖感言少了,莫言的获奖感言约有多少字?3. (5分)甲乙丙三人现在岁数的和是113岁,当甲的岁数是乙的岁数的一半时,丙是38岁,当乙的岁数是丙的岁数的一半时,甲是17岁,那么乙现在是多少岁?4. (5分) (2020五上·烟台期末) 水果店运来一批水果,其中香蕉360千克,菠萝的质量是香蕉的,橘子的质量比菠萝的少15千克。
水果店运来橘子多少千克?(先画线段图分析数量关系,再列式计算)5. (5分)抄一份书稿,一人抄,甲要12小时,乙要15小时。
两人合抄2小时后,剩下的由甲抄,还要几小时抄完?6. (5分)一盒饼干,连盒子共重500克,壮壮吃了这盒饼干的,剩下的饼干连盒子共重340克,饼干和盒子各重多少克?7. (5分)打字比赛。
(1)淘淘每分打多少个字?(2)壮壮每分打多少个字?8. (5分)(2018·长沙) 建造两座房子,其中第一座造价比第二座造价的3倍少32万元,而第二座房子的造价占两座房子总造价的,问第二座房子的造价是多少万元?9. (5分)看图列式计算。
(1)(2)10. (5分)小胖有一盒巧克力饼干,他第一天吃掉了全部的的七分之一;第二天吃了余下的六分之一;第三天吃了余下的五分之一;第四天吃了余下的四分之一;第五天吃了余下的三分之一;第六天吃了余下的二分之一;这时还剩下12块巧克力饼干,那么共有多少块巧克力饼干?11. (5分) (2018六上·福州期中) 有三包同样数量的糖果。
小学奥数分数问题50道详解(一)

小学奥数分数问题50道详解(一)
1. 分数是什么?
分数是用来表示一个整体被平均分成若干等分的数。
分数由一
个分子和一个分母组成,分子表示被平均分出来的等分的数量,分
母表示整体被平均分成的等分的数量。
2. 分数的基本运算
2.1 分数的加法
分数的加法就是将两个分数的分子相加,然后保持分母不变。
2.2 分数的减法
分数的减法可以通过将两个分数的分子相减,然后保持分母不
变来实现。
2.3 分数的乘法
分数的乘法可以通过将两个分数的分子相乘,分母相乘来实现。
2.4 分数的除法
分数的除法可以通过将一个分数的分子乘以另一个分数的倒数来实现。
3. 分数的化简
化简分数就是将分子和分母的公约数约去的过程。
如果一个分数的分子和分母没有公约数,那么这个分数就是最简分数。
4. 分数的比较
比较两个分数的大小可以通过找到它们的公共分母,然后比较它们的分子大小来实现。
5. 分数的转换
5.1 将分数转换为小数
将分数转换为小数可以通过将分子除以分母来实现。
5.2 将小数转换为分数
将小数转换为分数可以通过将小数的数字部分作为分子,小数的位数作为分母来实现。
6. 分数的运算技巧
6.1 分数的乘法技巧
当两个分数相乘时,如果它们的分子和分母都可以化简,可以
先化简分子和分母,再进行乘法运算。
6.2 分数的除法技巧
当两个分数相除时,可以先将除数和被除数都乘以同一个数,
使得被除数的分母变为1,然后再进行乘法运算。
以上是关于小学奥数分数问题的50道详解。
希望对你有帮助!。
小学奥数(分数应用题)

一、填空1、一辆汽车一共有66个座位,空车出发,第一站上一位乘客,第二站上两位乘客,第三站上三位乘客,以此类推,第()站后,车上坐满乘客。
2、李老师去买桌椅,他带的钱如果只卖桌子,恰好可以买40张,如果只买椅子,恰好可以买60把,那么李老师带的钱可以买()套桌椅。
3、甲数是已数3分之2的,已数是丙数的5分之4,甲,已,丙三个数的比是()4、一辆汽车从甲地开往已地,已行全长的5分子2,离中点还有8千米,甲、乙两地的距离()千米。
5、小明看一本书的7分子3,再看20页,已看页数与未看页数的比是4比3,这本书有()页。
6、一次数学竞赛,六(1)班选手中,男生的平均分是80分,女生的平均分是70分,全班选手的平均分是73分,该班选手中男、女生人数的比是()。
、、某商品打九折出售,可盈利215元,如果降价百分之20出售,要亏损125元,这件商品的进价是()元。
二、解答题1、一根铁丝长100米,第一次用去全长的5分子2,第二次用去余下的3分子1,第三次用去第一次的2分子1,还剩多少?2、加工一批零件,王师傅先加工了这批零件的7分子2,接着李师傅加工余下的5分子3,结果王师傅比李师傅少加工50个,这批零件共有多少个?3、果园有三种果树共280课,其中桃树棵树是苹果树的9分子7,苹果树是梨树的4分子3,三种果树各有多少棵?4、六年级三个班共有156人,其中六(1)班人数是六(2)班的7分子6,是六(3)班人数的13分子12,六年级三个班各有多少人?5、有两筐梨,乙筐的质量是甲筐5分子3,从甲筐中取出5千克放入乙筐后,乙筐的梨是甲筐的9分子7,甲、乙两筐梨共重多少千克?6、修一条路,已修是未修的3分子2,再修20米,已修的是未修的4分子3,这条路全长多少米?7、课外兴趣小组上学期男生占9分子5,这学期女生增加21人,男生就只占5分子2,这个小组现在有女生多少人?8、饲养场里有102只兔子,白兔只数的4分子3等于灰兔只数的3分子2,这个饲养场有白兔、灰兔各多少只?9、仓库里有大米和面粉共2000袋,大米运走5分子2,面粉运走10分子1后,仓库里剩下的大米和面粉正好相等,原来仓库里大米和面粉各有多少袋?10、甲桶油比乙桶油多3.6千克,如果从两桶中各取出1千克后,甲桶剩下的21分子2等于乙桶剩下的7分子1,甲桶里原有多少油?11、有甲、乙两桶油,葱甲桶中倒出3分子1给乙桶后,又从已桶中倒出5分子1给甲桶,这时两桶油各有24千克,原来两桶个有多少千克油?12、兄弟俩各有人民币若干元,哥哥拿出5分子1给弟弟后,弟弟又拿出4分子1给哥哥,这时他们各有90元,哥哥、弟弟原来各有多少元?13、六(1)班有54人,其中男生是全班的9分子5,本学期又转入几名男生,这时男生是全班的7分子4,本期转入几名男生?14、饲养场养兔280只,其中白兔占7分子5卖掉一些白兔后,白兔占5分子3,卖掉多少只白兔?15、光明小学六年级105人分成三个小组参加植树活动,已知第一小组和第二小组人数的比是2:3,第二小组人数是第三小组人数的5分子4,这三个小组各有多少人?16、甲、乙、丙三个数的平均数是165,其中甲是乙的6分子5,乙与丙的比是9:11,这三个数分别是多少?17、小明读一本故事书,已读页数和未读页数的比是1:5,如果再读30页,则已读页数和未读页数的比是3:5,这本书是多少页?18、甲乙两校原有图书本书的比是7:5,如果甲校给乙校650本,甲、乙两校图书本书的比是3:4,甲校原有图书多少本?19、箱子里有红、白两种玻璃球,红球与白球个数的比是3:2,每次从箱子里取出5个红球,6个白球,若干次后白球正好取完,红球还剩32个,箱子里原有两种球共多少个?20、书架上层与下层图书本书的比是4:5,若从上下两层各取走15本书,则上层书的本书与下层的比是7:10,原来两个书架各有多少本书?21一项工程,甲单独完成需要10天,乙单独完成需要12天,丙单独完成需要15天,现在三人共同完成这项工程,但甲中途提前撤出,结果用6天完成,甲只参与几天?22、一项工程,甲、乙合作5小时可完成,两队同时开工,中途甲停工2小时,因此经过6.5小时完工如果这项工程由甲单独做需要几小时?23、一项工程,甲单独做10天完成,乙单独做12天完成,这项工作先由甲做了几天,然后乙接着做,从开始到完工共用11小时,这项工作甲做了几天?24、一条公路,甲独修24天可以完成,乙独修30天可以完成,先由甲、乙两队合修4天,再由丙队参加一起修7天全部完成,如果甲、乙、丙三队同时开工一起修这条公路,几天可以完成?24、修一条公路,甲队独修要40天完成,乙队独修要24天完成,两队合修,同时从两端开工,结果在距中点750米处相遇,这段公路全长多少米?25、商店把货物按标价九折出售,还可以获利百分子20,若该商品的进价是210元,那么每件的标价应为多少元?26、王老板把一件衣服按八ude五折出售,还获利百分子27.5,已知这件衣服的进价是200元,这件衣服的标价是多少?27、某商品的进价是1509元,按商品的标价九折出售,利润率是百分子20,上坪的标价是多少?28、某商店同时出售两件服装,售价都是180元,其中一件盈利百字分子20,另一件亏损百分子20,就这两件服装而言,该商店时亏了还是赚了,亏或是赚多少?29、某商品按百分子20利润定价,然后按8.8折出售,共获利70元,这件商品的出售价是多少元?30、小明家养的鸡和鸭共有200只,如果将鸡卖掉20分子1,还比鸭多34只,小明家养的鸡和鸭各有多少只?31、商场里彩电和冰箱共350只,如果彩电卖出9分子1后,就比冰箱少10台,商场里彩电和冰箱各有多少台?32、学校有篮球和足球共21个,如果篮球再买来4分子3后,比足球多1个原来学校有篮球和足球各多少个?33、甲、乙、丙三人参加考试,共得260分,已知甲的分的3分子1,乙得分的4分子1与并得分的一半减去22分相等,那么丙的得分是多少?34、某校六年级原有两个班,将原一班的3分之1与原二班的4分子1组成新一班,将原一班的4分子1与原二班的3分子1组成新二班,余下的30人组成新三班,已知新一班人数比新二班的人数多百分之10,原一班有多少人。
小学奥数系列6-2-1分数应用题专练3及参考答案

小学奥数系列6-2-1分数应用题专练3一、分数应用题专练1. 新光小学有音乐、美术和体育三个特长班,音乐班人数相当于另外两个班人数的,美术班人数相当于另外两个班人数的,体育班有人,音乐班和美术班各有多少人?2.甲、乙、丙三人共同加工一批零件,甲比乙多加工20个,丙加工零件数是乙加工零件数的,甲加工零件数是乙、丙加工零件总数的,则甲、丙加工的零件数分别为________个、________个.3. 王先生、李先生、赵先生、杨先生四个人比年龄,王先生的年龄是另外三人年龄和的,李先生的年龄是另外三人年龄和的,赵先生的年龄是其他三人年龄和的,杨先生26岁,你知道王先生多少岁吗?4. 甲、乙、丙、丁四个筑路队共筑1200米长的一段公路,甲队筑的路是其他三个队的,乙队筑的路是其他三个队的,丙队筑的路是其他三个队的,丁队筑了多少米?5. 四只小猴吃桃,第一只小猴吃的是另外三只的总数的,第二只小猴吃的是另外三只吃的总数的,第三只小猴吃的是另外三只的总数的,第四只小猴将剩下的个桃全吃了.问四只小猴共吃了多少个桃?6. 兄弟四人去买电视,老大带的钱是另外三人的一半,老二带的钱是另外三人的,老三带的钱是另外三人总钱数的,老四带91元,兄弟四人一共带了多少钱?7. 小刚给王奶奶运蜂窝煤,第一次运了全部的,第二次运了块,这时已运来的恰好是没运来的.问还有多少块蜂窝煤没有运来?8. 五(一)班原计划抽的人参加大扫除,临时又有个同学主动参加,实际参加扫除的人数是其余人数的.原计划抽多少个同学参加大扫除?9. 某校学生参加大扫除的人数是未参加大扫除人数的,后来又有20名同学参加大扫除,实际参加的人数是未参加人数的,这个学校有多少人?10. 小莉和小刚分别有一些玻璃球,如果小莉给小刚24个,则小莉的玻璃球比小刚少;如果小刚给小莉24个,则小刚的玻璃球比小莉少,小莉和小刚原来共有玻璃球多少个?11. 某班一次集会,请假人数是出席人数的,中途又有一人请假离开,这样一来,请假人数是出席人数的,那么,这个班共有多少人?12. 小明是从昨天开始看这本书的,昨天读完以后,小明已经读完的页数是还没读的页数,他今天比昨天多读了页,这时已经读完的页数是还没读的页数的,问题是,这本书共有多少页?”13. 某校有学生人,其中女生的比男生的少人,那么男生比女生少多少人?14. 某校四年级原有两个班,现在要重新编为三个班,将原一班的与原二班的组成新一班,将原一班的与原二班的组成新二班,余下的人组成新三班.如果新一班的人数比新二班的人数多,那么原一班有多少人?15. 某工厂对一、二两个车间的职工进行重组,将原来的一车间人数的和二车间人数的分到一车间,将原来的一车间人数的和二车间人数的分到二车间,两个车间剩余的140人组成劳动服务公司,现在二车间人数比一车间人数多,现在一车间有________人,二车间有________人.16. 2008年第十三届“华罗庚金杯”少年数学邀请赛(小学组)决赛林林倒满一杯纯牛奶,第一次喝了,然后加入豆浆,将杯子斟满并搅拌均匀,第二次林林又喝了,继续用豆浆将杯子斟满并搅拌均匀,重复上述过程,那么第四次后,林林共喝了一杯纯牛奶总量的________(用分数表示)。
小学奥数6-2-3 分数应用题(三).专项练习及答案解析

1. 分析题目确定单位“1”2. 准确找到量所对应的率,利用量÷对应率=单位“1”解题3. 抓住不变量,统一单位“1”一、知识点概述:分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系例如:(1)a 是b 的几分之几,就把数b 看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1199÷=. 二、怎样找准分数应用题中单位“1” (一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
知识点拨教学目标分数应用题(三)解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
小学奥数与应用题——分数应用题

小学奥数与应用题——分数应用题小学奥数与应用题——分数应用题分数应用题一般有三种类型:1.求一个数a的几分之几是多少,即a乘以n除以m等于b;2.求一个数a是另一个数的b几分之几,即a除以b等于n除以m;3.已知一个数的几分之几是多少,求这个数,即b除以n 等于a除以m。
这三种分数应用题之间有联系,解题时要搞清楚它们之间的关系。
在解答分数应用题时,关键要通过分析数量关系,把每一道题中的某个量看作单位“1”,找出解题的数量关系式,再根据分数与除法的关系或一个数乘以分数的意义列式解答。
分数应用题在工农业生产和实际生活中应用十分广泛。
虽然这类应用题的变化很多,但只要认真去探索、去思考,也不难发现其中的解题规律。
1.基本类型在解答基本的分数应用题时,要抓住题目中的关键句进行分析。
首先明确单位“1”,如果单位“1”已知,用乘法计算;如果单位“1”未知,要先求出单位“1”,用除法或列方程计算;其次在列式时要考虑具体数量和分率之间的对应关系。
例如,在求一个中剩余多少油的问题中,如果已知一桶油的容量是4升,第一次用去11分之3,第二次用去34分之11,那么我们要先求出这桶油一共多少升,再求出还剩下多少升。
根据题意可以知道,一桶油的容量是4升,可以求出这桶油的总数是:4÷3/11=14(升)然后,我们可以先求出还剩这桶油的几分之几,即:1-11/34-5/12=5(升)答案是还剩下5升。
再例如,某工厂计划生产一批零件,第一次完成计划的1/4,第二次完成计划的13/27,第三次完成计划的超过计划的1/9,那么我们要求出计划生产零件的总数。
将“计划生产的零件个数”当作“1”,根据题意,我们首先要求出450个零件占计划任务的几分之内。
实际上“450个零件”可以分为两部分:一是完成剩下的任务1-13/27,二是超过部分“1/9”。
那么450个零件的对应分率就是:1-13/27+1/9=28/274计划生产零件的总数x可以用列方程的方法来解答:x/1=28/274x=1400答案是计划生产零件1400个。
小学奥数6-2-1 分数应用题(一).专项练习及答案解析

1. 分析题目确定单位“1”2. 准确找到量所对应的率,利用量÷对应率=单位“1”解题3. 抓住不变量,统一单位“1”一、知识点概述:分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系 例如:(1)a 是b 的几分之几,就把数b 看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1199÷=.二、怎样找准分数应用题中单位“1” (一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
(三)、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语,也不是部分数和总数的关系。
小学奥数6-2-3 分数应用题(三).专项练习及答案解析

1. 分析题目确定单位“1”2. 准确找到量所对应的率,利用量÷对应率=单位“1”解题3. 抓住不变量,统一单位“1”一、知识点概述:分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系例如:(1)a 是b 的几分之几,就把数b 看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1199÷=. 二、怎样找准分数应用题中单位“1” (一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
知识点拨教学目标分数应用题(三)解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
浙江省湖州市数学小学奥数系列6-2-1分数应用题专练3

浙江省湖州市数学小学奥数系列6-2-1分数应用题专练3姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、分数应用题专练 (共23题;共99分)1. (5分)菜园里西红柿获得丰收,收下全部的时,装满3筐还多24千克,收完其余部分时,又刚好装满6筐,求共收西红柿多少千克?2. (1分) (2018六上·山东月考) 甲乙两地相距504千米,一辆汽车从甲地开往乙地用6小时行了全程的,照这样计算,行驶全程用几小时?3. (5分) (2019六上·龙华) 一位科学家去世后,人们在他的墓碑上刻着:“他的童年占去一生的,接着是少年时代,又过了的时光,他找到了终身伴侣。
5年以后,婚姻之神赐给他一个儿子,可是儿子的命运不济,只活到父亲寿数的一半,就匆匆离去。
4年后,父亲也因悲伤过度而离开人世.”请问这位科学家活了多少岁?4. (5分)李红、黄强、张明三人共有108元,李红用自己钱数的,黄强用了自己钱数的,张明用自己钱数的,各买了一本相同的课外读物,那么三人原来各有多少钱?5. (5分)加工一批零件,甲、乙两人合作需15天完成。
现由甲、乙合作3天,再由乙单独做2天后,还剩这批零件的没完成。
若甲每天比乙多加工4个零件,就这批零件共有多少个?6. (5分)一件工程,甲、乙两人合作8天可以完成,乙、丙两人合作6天可以完成,丙、丁两人合作12天可以完成.那么甲、丁两人合作多少天可以完成?7. (5分) (2019六上·石林期中) 王大爷共养山羊和绵羊480只,绵羊只数是山羊的。
山羊和绵羊各多少只?8. (5分) (2016六上·台安月考) 脱式计算,能简算的要简算.12÷ ÷ ×(÷ )98÷(÷ )÷7+ × ( + ﹣)×12(﹣)× ÷9. (5分) (2019六上·龙华) 学校图书室新增故事书840本,是原有故事书的。
安徽省黄山市小学数学小学奥数系列6-2-1分数应用题专练3

安徽省黄山市小学数学小学奥数系列6-2-1分数应用题专练3姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、分数应用题专练 (共23题;共99分)1. (5分)一项工程,甲、乙合做15天完成,先由甲做5天,接着乙做3天,完成工作量的。
这项工程如果甲单独做要多少天完成?2. (1分)刚出生的格陵兰鲸的体重大约是2t,是成年格陵兰鲸体重的,成年格陵兰鲸的体重大约是多少吨?3. (5分) (2019六上·龙华) 菜场运来白菜吨,运来的黄瓜是白菜的,运来的黄瓜比萝卜少,运来的萝卜多少吨?4. (5分) (2020六上·西城期末) 无障碍设施建设体现了城市“以人为本”的建设理念.无障碍出入口应设计轮椅坡道,坡道的坡度要符合无障碍设施的设计要求,坡度指每段坡道的垂直高度与水平长度的比(如图).(1)一条轮椅坡道的坡度是1:16、水平长度是12.8m,这条轮椅坡道的垂直高度是多少米?(2)建设轮椅坡道有最大垂直高度的规定,坡度、最大垂直高度及水平长度的要求见如表.例如:当坡度是1:20时,垂直高度不能超过1.2m.坡度1:201:161:121:101:8最大垂直高度1.20.90.750.60.3/m水平长度/m2414.496 2.4如图是一条坡道的示意图,这条坡道是否符合轮椅坡道的选设要求?列式计算并说明理由.5. (5分) (2018六下·云南模拟) 爷爷家养白兔和灰兔共70只,其中灰兔的只数是白兔的。
爷爷家养白兔和灰兔各多少只?6. (5分) (2019六上·定西期末) 六年级学生分三组参加植树活动,甲组人数与植树总人数的比是7:24,如果从乙、丙两组各调4人到甲组,3个组人数刚好相等,那么六年级一共有学生多少人?7. (5分)(2018·浙江模拟) 小明打一篇文章,已打了900个字,还剩没有打完,这篇文章一共有多少字?8. (5分)一批零件,甲独做8天完成,乙独做12天完成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 分析题目确定单位“1”2. 准确找到量所对应的率,利用量÷对应率=单位“1”解题 3. 抓住不变量,统一单位“1”一、知识点概述:分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系 例如:(1)a 是b 的几分之几,就把数b 看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1199÷=.二、怎样找准分数应用题中单位“1” (一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
(三)、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语,也不是部分数和总数的关系。
知识点拨教学目标分数应用题(三)这类分数应用题的单位“1”比较难找。
需要将题目文字完善成我们熟悉的类似带“比”的文字,然后在分析。
例如:水结成冰后体积增加了,冰融化成水后,体积减少了。
完善后:水结成冰后体积增加了→“水结成冰后体积比原来增加了”→原来的水是单位“1”冰融化成水后,体积减少了→“冰融化成水后,体积比原来减少了”→原来的冰是单位“1”解题关键:要结合语文知识将题目简化的文字丰富后在分析单位“1”变化【例1】养殖专业户王老伯养了许多鸡鸭,鸡的只数是鸭的只数的114倍.鸭比鸡少几分之几?【考点】分数应用题【难度】1星【题型】解答【解析】方法一:把鸭看成单位“1”,那么鸡就是114,鸭比鸡少:111(11)1445-÷=(此时的单位“1”是鸡的只数).方法二:设鸭有4份,则鸡有5份,所以鸭比鸡少1 155÷=.【答案】1 5【巩固】某校男生比女生多37,女生比男生少几分之几?【考点】分数应用题【难度】1星【题型】解答【解析】方法一:男生比女生多37,则男生有310177+=,女生比男生少31037710÷=.方法二:设女生有7份,则男生有10份,所以女生比男生少3 31010÷=.【答案】3 10【例2】一炉铁水凝成铁块,其体积缩小了134,那么这个铁块又熔化成铁水(不计损耗),其中体积增加了几分之几?【考点】分数应用题【难度】1星【题型】解答【解析】方法一:设铁水的体积为1,则铁块为13313434-=.现在变回来,那么铁块的体积就要变为单位1,则铁水的体积就为333413433÷=,故体积增加了:341(1)13333-÷=.方法二:体积缩小是铁块比铁水缩小,所以可以设铁水为34份,则铁块为33份,铁块又熔化成铁水,体积增加是比铁块增加,所以用差的1份除以铁块的33份就是答案133.【答案】133例题精讲【巩固】水结成冰后体积增大它的110. 问:冰化成水后体积减少它的几分之几?【考点】分数应用题【难度】1星【题型】解答【解析】设水的体积是10份,则结成冰后体积为11份,冰化成水后比冰减少1 11111÷=.【答案】1 11【例3】磁悬浮列车的能耗很低。
它的每个座位的平均能耗是汽车的70%,而汽车每个座位的平均能耗是飞机的1021,则飞机每个座位的平均能耗是磁悬浮列车每个座位的平均能耗的________倍。
【考点】分数应用题【难度】2星【题型】解答【关键词】希望杯,六年级,二试【解析】磁悬浮列车每个座位的平均耗能是飞机每个座位的平均耗能的710110213⨯=,故飞机每个座位的平均能耗是磁悬浮列车每个座位的平均能耗的3倍。
【答案】3倍【例4】在下降的电梯中称重,显示的重量比实际体重减少17;在上升的电梯中称重,显示的重量比实际体重增加16.小明在下降的电梯中与小刚在上升的电梯中称得的体重相同,小明和小刚实际体重的比是.【考点】分数应用题【难度】2星【题型】解答【关键词】2008年,清华附中【解析】小明在下降的电梯中称得的体重为其实际体重的67,小刚在上升的电梯中称得的体重为其实际体重的76,而小明在下降的电梯中与小刚在上升的电梯中称得的体重相同,所以小明和小刚实际体重的比是:671:149:3676⎛⎫⎛⎫÷÷=⎪ ⎪⎝⎭⎝⎭.【答案】49:36【例5】学校阅览室里有36名学生在看书,其中女生占49,后来又有几名女生来看书,这时女生人数占所有看书人数的919.问后来又有几名女生来看书?【考点】分数应用题【难度】2星【题型】解答【解析】把总人数视为“1”,紧抓住男生人数不变进行解答.男生人数是436(1)209⨯-=人,后来阅览室的总人数是920(1)3819÷-=(名),后来有38362-=(名)女生进来.【答案】2名【巩固】工厂原有职工128人,男工人数占总数的14,后来又调入男职工若干人,调入后男工人数占总人数的25,这时工厂共有职工人.【关键词】2009年,五中,入学测试【解析】在调入的前后,女职工人数保持不变.在调入前,女职工人数为1128(1)964⨯-=人,调入后女职工占总人数的23155-=,所以现在工厂共有职工3961605÷=人.【答案】160人【巩固】学校派出60名选手参加2008年“华罗庚金杯小学数学邀请赛”,其中女选手占14.正式比赛时有几名女选手因故缺席,这样就使女选手人数变为参赛选手总数的211.正式参赛的女选手有多少名?【考点】分数应用题【难度】2星【题型】解答【解析】因为女选手人数有变化,男选手人数未变,所以抓住男选手人数不变求解.把总人数视为“1”,男选手人数是60×(1-14)=45(人),男选手人数占正式参赛选手总数的1-211,所以正式参赛选手总数是:45÷(1-211)=55(人),正式参赛的女选手人数是55×211=10(人)。
【答案】10人【巩固】某公司有15的职员参加新产品的开发工作,后来又有2名职工主动参加,这样参加新产品开发的职工人数是其余人数的13,原来有多少职工参加开发工作?【考点】分数应用题【难度】2星【题型】解答【解析】后来参加新产品开发的职工人数是总人数的11134=+,所以新加入的2个人占总人数的1114520-=,那么职工总人数为124020÷=人,原来参加开发的职工数是14085⨯=人.【答案】8人【例6】春天幼儿园中班小朋友的平均身高是115厘米,其中男孩比女孩多15,女孩的平均身高比男孩高10%,这个班男孩的平均身高是厘米。
【考点】分数应用题【难度】3星【题型】解答【关键词】希望杯,六年级,一试【解析】设男生有6人,女生有5人,则男生的平均身高为:115(56)[(110%)561]110⨯+÷+⨯+⨯=(厘米)【答案】110厘米【例7】有甲、乙两桶油,甲桶油的质量是乙桶的52倍,从甲桶中倒出5千克油给乙桶后,甲桶油的质量是乙桶的43倍,乙桶中原有油千克.【解析】 原来甲桶油的质量是两桶油总质量的55527=+,甲桶中倒出5千克后剩下的油的质量是两桶油总质量的44437=+,由于总质量不变,所以两桶油的总质量为545()3577÷-=千克,乙桶中原有油235107⨯=千克.【答案】10千克【例 8】 (1)某工厂二月份比元月份增产10%,三月份比二月份减产10%.问三月份比元月份增产了还是减产了?(2)一件商品先涨价15%,然后再降价15%,问现在的价格和原价格比较升高、降低还是不变?【考点】分数应用题 【难度】2星 【题型】解答【解析】 (1)设二月份产量是1,所以元月份产量为: ()1011+10%=11÷,三月份产量为:110%=0.9-,因为1011>0.9,所以三月份比元月份减产了(2)设商品的原价是1,涨价后为1+15%=1.15,降价15%为:()1.15115%=0.9775⨯-,现价和原价比较为:0.9775<1,所以价格比较后是价降低了。
【答案】(1)减产 (2)降低【巩固】 某工厂二月份比元月份增产110,三月份比二月份减产110.问三月份比元月份增产了还是减产了?【考点】分数应用题 【难度】2星 【题型】解答【解析】 工厂二月份比元月份增产110,将元月份产量看作1,则二月份产量为:1111(1)1010⨯+=,三月比二月减产110,则三月份产量为: 11199(1)11010100⨯-=<,所以三月份比元月份减产了.【答案】减产【巩固】 一件商品先涨价15,然后再降价15,问现在的价格和原价格比较升高、降低还是不变?【考点】分数应用题 【难度】2星 【题型】解答【解析】 111(1)(1)0.96155⨯+⨯-=<,所以现在的价格比原价降低了.【答案】降低【例 9】 某校三年级有学生240人,比四年级多14 ,比五年级少15.四年级、五年级各多少人?【考点】分数应用题 【难度】2星 【题型】解答 【解析】 比四年级,可以设四年级为4份,(一般情况下可设“比”、“是”、等词后面的实际量的份数为分数的分母),则三年级为5份恰有240人,所以一每份就是240548÷=,所以四年级就有48⨯4=192人,同理可设五年级有5份,则三年级有4份恰是240人,所以五年级就有300人.【答案】300人【巩固】 把100个人分成四队,一队人数是二队人数的113倍,一队人数是三队人数的114倍,那么四队有多少个人?【考点】分数应用题 【难度】2星 【题型】解答【解析】 方法一:设一队的人数是“1”,那么二队人数是:131134÷=,三队的人数是:141145÷=,345114520++=,因此,一、二、三队之和是:一队人数5120⨯,因为人数是整数,一队人数一定是20的整数倍,而三个队的人数之和是51⨯(某一整数), 因为这是100以内的数,这个整数只能是1.所以三个队共有51人,其中一、二、三队各有20,15,16人.而四队有:1005149-=(人).方法二:设二队有3份,则一队有4份;设三队有4份,则一队有5份.为统一一队所以设一队有[4,5]20=份,则二队有15份,三队有16份,所以三个队之和为15162051++=份,而四个队的份数之和必须是100的因数,因此四个队份数之和是100份,恰是一份一人,所以四队有1005149-=(人). 【答案】49人【例 10】 新光小学有音乐、美术和体育三个特长班,音乐班人数相当于另外两个班人数的25,美术班人数相当于另外两个班人数的37,体育班有58人,音乐班和美术班各有多少人?【考点】分数应用题 【难度】2星 【题型】解答【解析】 条件可以化为:音乐班的人数是所有班人数的22527=+,美术班的学生人数是所有班人数的337310=+,所以体育班的人数是所有班人数的2329171070--=,所以所有班的人数为295814070÷=人,其中音乐班有2140407⨯=人,美术班有31404210⨯=人.【答案】42人【巩固】 王先生、李先生、赵先生、杨先生四个人比年龄,王先生的年龄是另外三人年龄和的12,李先生的年龄是另外三人年龄和的13 ,赵先生的年龄是其他三人年龄和的14,杨先生26岁,你知道王先生多少岁吗? 【考点】分数应用题 【难度】2星 【题型】解答 【解析】 方法一:要求王先生的年龄,必须先要求出其他三人的年龄各是多少.而题目中出现了三个“另外三人”所包含的对象并不同,即三个单位“1”是不同的,这就是所说的单位“1”不统一,因此,解答此题的关键便是抓不变量,统一单位“1”.题中四个人的年龄总和是不变的,如果以四个人的年龄总和为单位“1”,则单位“1”就统一了.那么王先生的年龄就是四人年龄和的11123=+,李先生的年龄就是四人年龄和的11134=+,赵先生的年龄就是四人年龄和的11145=+(这些过程就是所谓的转化单位“1”).则杨先生的年龄就是四人年龄和的11113134560---=.由此便可求出四人的年龄和:111261*********⎛⎫÷---= ⎪+++⎝⎭(岁),王先生的年龄为:1120403⨯=(岁).方法二:设王先生年龄是1份,则其他三人年龄和为2份,则四人年龄和为3份,同理设李先生年龄为1份,则四人年龄和为4份,设赵先生年龄为1份,则四人年龄和为5份,不管怎样四人年龄和应是相同的,但是现在四人年龄和分别是3份、4份、5份,它们的最小公倍数是60份,所以最后可以设四人年龄和为60份,则王先生的年龄就变为20份,李先生的年龄就变为15份,赵先生的年龄就变为12份,则杨先生的年龄为13份,恰好是26岁,所以1份是2岁,王先生年龄是20份所以就是40岁. 【答案】40岁【巩固】 四只小猴吃桃,第一只小猴吃的是另外三只的总数的13,第二只小猴吃的是另外三只吃的总数的14,第三只小猴吃的是另外三只的总数的15,第四只小猴将剩下的46个桃全吃了.问四只小猴共吃了多少个桃?【考点】分数应用题 【难度】2星 【题型】解答【解析】 根据题意知前三只小猴分别吃了总数的14,15,16,所以四只小猴共吃了11146(1)120456÷---=(个)【答案】120个【巩固】 兄弟四人去买电视,老大带的钱是另外三人的一半,老二带的钱是另外三人的1/3,老三带的钱是另外三人总钱数的1/4,老四带91元,兄弟四人一共带了多少钱?【考点】分数应用题 【难度】2星 【题型】解答 【解析】 老大带的钱是另外三人的一半,也就说老大带的钱是一共带钱的1/3,同理老二带的钱是一共带钱的1/4,老三带的钱是一共带钱的1/5,所以老四带的钱是一共带钱的:1-1/3-1/4-1/5=13/60四人一共带的钱:91除以13/60=420(元)【答案】420元【例 11】 小刚给王奶奶运蜂窝煤,第一次运了全部的38,第二次运了50块,这时已运来的恰好是没运来的57.问还有多少块蜂窝煤没有运来?【考点】分数应用题 【难度】3星 【题型】解答 【关键词】迎春杯,决赛【解析】 方法一:运完第一次后,还剩下58没运,再运来50块后,已运来的恰好是没运来的57,也就是说没运来的占全部的712,所以,第二次运来的50块占全部的:57181224-=,全部蜂窝煤有:150120024÷=(块),没运来的有:7120070012⨯=(块).方法二:根据题意可以设全部为8份,因为已运来的恰好是没运来的57,所以可以设全部为12份,为了统一全部的蜂窝煤,所以设全部的蜂窝煤共有[8,12]24=份,则已运来应是5241075⨯=+份,没运来的7241475⨯=+份,第一次运来9份,所以第二次运来是1091-=份恰好是50块,因此没运来的蜂窝煤有5014700⨯=(块). 【答案】700块【巩固】 五(一)班原计划抽15的人参加大扫除,临时又有2个同学主动参加,实际参加扫除的人数是其余人数的13.原计划抽多少个同学参加大扫除?【考点】分数应用题 【难度】3星 【题型】解答 【解析】 又有2个同学参加扫除后,实际参加扫除的人数与其余人数的比是1:3,实际参加人数比原计划多11113520-=+.即全班共有124020÷=(人).原计划抽14085⨯=(人)参加大扫除.【答案】8人【巩固】 某校学生参加大扫除的人数是未参加大扫除人数的14,后来又有20名同学参加大扫除,实际参加的人数是未参加人数的13,这个学校有多少人?【考点】分数应用题 【难度】2星 【题型】解答【解析】 11204003141⎛⎫÷-= ⎪++⎝⎭(人).【答案】400人【例 12】 小莉和小刚分别有一些玻璃球,如果小莉给小刚24个,则小莉的玻璃球比小刚少37;如果小刚给小莉24个,则小刚的玻璃球比小莉少58,小莉和小刚原来共有玻璃球多少个?【考点】分数应用题 【难度】3星 【题型】解答【解析】 小莉给小刚24个时,小莉是小刚的47 (=1一37),即两人球数和的411;小刚给小莉24个时,小莉是两人球数和的811(=8885+-),因此24+24是两人球数和的811-411=411.从而,和是(24+24) ÷411=132(个). 【答案】132个【例 13】 某班一次集会,请假人数是出席人数的19,中途又有一人请假离开,这样一来,请假人数是出席人数的322,那么,这个班共有多少人?【考点】分数应用题 【难度】3星 【题型】解答【解析】 因为总人数未变,以总人数作为”1”.原来请假人数占总人数的119+,现在请假人数占总人数的3322+,这个班共有:l ÷(3322+-119+)=50(人).【答案】50人【巩固】 小明是从昨天开始看这本书的,昨天读完以后,小明已经读完的页数是还没读的页数19,他今天比昨天多读了14页,这时已经读完的页数是还没读的页数的13,问题是,这本书共有多少页?”【考点】分数应用题 【难度】3星 【题型】解答【解析】 首先,可以直接运算得出,第一天小明读了全书的11911019=+,而前二天小明一共读了全书的1131413=+,所以第二天比第一天多读的14页对应全书的111241020-⨯=。
