郑君里《信号与系统》(第3版)【教材精讲+考研真题解析】讲义第1章绪论【圣才出品】

合集下载

郑君里《信号与系统》(第3版)配套题库【考研真题+模拟试题】【圣才出品】

第 7 章离散时间系统的时域分析
一、填空题
1．周期分别为 3 和 5 的两个离散序列的卷积和的周期性为______。[北京航空航天大学
2007 研]
【答案】7
【解析】对于线性卷积，若一个周期为 M，另一个周期为 N，则卷积后周期为 M+N
－1，所以T T1 T2 1 3 5 1 7 。
2．某线性时不变（LTI）离散时间系统，若该系统的单位阶跃响应为
5 / 69
圣才电子书

十万种考研考证电子书、题库视频学习平台
Y z z 6z 1 8z 2 3z 3
根据时域卷积定理可得：
H
z
z
6 z 1 z
8z2 2 z1
3z 3
使用长除法可得：
H z 1 2z 1 3z 2
取逆变换可得：
h[n] n 2 n 1 3 n 2
圣才电子书十万种考研考证电子书、题库视频学习平台

yzs (0) 1, yzs (1) 1/ 2, yzs (2) 5/ 4, yzs (3) 13/ 8, yzs (4) 29 /16, yzs (5) 93/ 32 （2）零输入响应 yzi (n) 的递推方程可以化简为
由于
x[n] u[n 1] u[n] u[n 1] u[n 2]
u[n 1] u[n 1] u[n] u[n 2]
此式又可以写成：
x[n] n 1 2 n n 1 X z z 2 z 1
由题意可知：
yn x n*h n n 1 6 n 1 8 n 2 3 n 3
yzi (n) 0.5 yzi (n 1)
(n)
1 0
(n (n
0)
。当
0)

郑君里信号与系统讲义

1, t > 0 u (t ) = 0, t < 0
或
（1-11）
1, = u ( t ) 0, 1 2,
t >0 t<0 t =0
（1-12）
图 1-5 斜升函数 ☻ 符号函数：
图 1-6 单位阶跃函数
4
《信号与系统》讲义
第一章：绪论
1, t > 0 sgn ( t ) = −1, t < 0 或 1, t > 0 sgn ( t ) = −1, t < 0 0, t = 0 ☻ 门函数： G ( t ) = u ( t ) − u ( t − t0 ) , t0 > 0
☻ 采样函数：
= f ( t ) Sa = (t ) sin t t
（1-5）
注意与抽样信号定义上的差别！
- 0.2122
图 1-3 采样信号采样函数的性质（三点、三式）： ♦ 采样函数 Sa ( t ) 为偶函数，在 t 的正、负两方向振幅都逐渐衰减，当
±π , ±2π , , ± nπ 时，信号值为零。 t=
φ ( x)
《信号与系统》讲义
第一章：绪论
=
δ ( x − x0 ) /， f ′ ( x0 )
f ′ ( t0 ) δ ( t − t0 )
−1
φ ( x)
#证毕
即： = δ ( f (t ))
复合冲激函数的直观理解： ① δ ( f ( t ) ) = ∞ 的冲激位置在 f ( t ) =0，即在t 0 点；其余点为 0。 ② δ ( f ( t ) ) 的冲激强度不是 1，而是与 f ( t ) 的陡峭程度成反比。上述第②条可以通过广义极限逼近的冲激函数来理解：若 f ( t ) 在 t 0 邻域内缓变（斜率小），则 f ( t ) 的取值靠近 0，δ ( f ( t ) ) 的值就大；若 f ( t ) 在t 0 邻域内快变（斜率大），则 f ( t ) 的取值就远离 0， δ ( f ( t ) ) 的值就小；是反比关系。 ☻ 若光滑函数 f ( t ) 满足： f ( t ) |t =t1 , t2 , = 0 ，且 f ′ ( ti ) ≠ 0，∀i = 1, 2,... ，则：

郑君里《信号与系统》(第3版)(上册)(课后习题绪论)【圣才出品】

圣才电子书

（1） ut ut T sin 4π t ；
T
（2） ut 2ut T ut 2T sin 4π t 。
T
解：（1）信号 sin 4π t 的周期为 T ，截取信号 sin 4π t 在区间[0，T]上的波形如
T
2
T
图 1-5(a)所示。
（2）信号 sin 4π t 的周期为 T ，截取信号 sin 4π t 在区间[0，T]上的波形，在区
2
1-3 分别求下列各周期信号的周期 T：
（1） cos10t cos30t；
（2） e j10t ；
（3） 5sin8t2 ；
（4）
1n
ut
nT
ut
nT
T
n为正整数。
|
解：（1）分量 cos(10t) 的周期T1
2 10
5
，分量 cos(30t) 的周期T2
，两者的 15
最小公倍数是，所以此信号的周期T 。
eatu(t) 台eatu(t t0 ) eatu(t t0 ) ea(tt0 )u(t t0 )
eatu(t) ea(tt0 )u(t t0 )
（2）表达式（1-17）为
t
（f ）d
1
=
a
(1 eat ), (0
t
t0 )
1 a
(1
e at
)
1 a
1
e a (tt0 )
以上各式中 n 为正整数。
解：（1） eat sin(t) 时间、幅值均连续取值，故为连续时间信号（模拟信号）；
（2） enT 时间离散、幅值连续，故为离散时间信号（抽样信号）；
（3） cos(n ) 时间、幅值均离散，故为离散时间信号（数字信号）；

Chapter1-绪论

• 连续时间信号
– 模拟信号
• 时间和幅值都连续的信号。
– 阶梯信号
抽样信号
• 时间连续，幅值离散的信号。
2
• 离散时间信号
1
1
2
– 抽样信号
o
t
• 幅值具有无限精度的离散时间信号。
– 数字信号
3
• 幅值也被限定为某些离散值的离散时间信号。
10
典型确定性信号
• 1. f t Ket • 2. f t Asint
（连续、具有各阶连续导数）(t) 称为检验函数。
Ω上检验函数的全体记为 D（Ω）。
• 用检验函数定义冲激函数：
对于(x) D ，
若满足： f (t)，(t) f (t)(t)dt (0)
则：f (t) (t)称为冲激函数。
23
冲激函数的性质
• 根据个人定位按广度、深度分层次学习
– 理论性强、偏深（比照教材） – 内容有增减 – 顺序有调整
4
Chapter 1 绪论
• §1.1 信号与系统简述 • §1.2 信号分类与典型确定性信号 • §1.3 冲激函数、广义函数 • §1.4 信号分解 • §1.5 系统分类 • §1.6 线性系统
k
k
Sa kt
lim k
k
sin kt kt
k
●
2
k
k
(7) 采样函数平方逼近
t
sin2 kt
lim
k
kt2
(8) ？？逼近
t lim n
n 1 n2t 2
●
2
t
k
k
22
冲激函数的定义——之三
• 检验函数的通俗定义（描述性定义）：

信号与系统引论__郑君里_第1章_绪论ppt课件

u(t)
0 u(t)1
t0
0点
无
定1义
1
或
t0
2
O
t
2. 有延迟的单位阶跃信号
u(t t0 )
0 u(tt0) 1
3．复指数信号
f(t)Kset
( t )
Kteco stjKtesi nt
s j 为复数，称为复频率
, 均为实常数
的量 1/纲， s的为量 ra 纲 d为 /s
讨论
0, 0 直流信号 0, 0 等幅 0, 0 增长指数信号 0, 0 增幅振荡 0, 0 衰减指数信号 0, 0 衰减
二．几种典型确定性信号
1.指数信号
信号的表示
2.正弦信号
函数表达式 f t
波形
3.复指数信号(表达具有普遍意义)
4. 抽样信号(Sampling Signal) 5.钟形脉冲函数(高斯函数)
1．指数信号
f(t)Ket
l 0直流(常数)
0
f t
0
l 0指数衰减
l 0指数增长
④ sitn dtπ, sitn dtπ
⑤
0t
2
limSat()0
t
⑥
t
sit) n sc i π tn (π t
5．钟形脉冲函数(高斯函数)
f
(t
)

Ee
t

2
f t
E 0.78E
E e
O
t
2
在随机信号分析中占有重要地位。
1.3 信号的运算
f(t)f(2t)

信号与系统郑君里第三版_课件

f (t) f1(t) f2 (t)
信号的数乘运算是指某信号乘以一实常数K，它是
将原信号每一时刻的值都乘以K ，即
2020/3/6
f (t) Kf (t)
30
1.3.3 信号的反褶、时移、尺度变换运算
（1）反褶运算 f (t) f (t) f(t) 1
以 t = 0为轴反褶 f(-t)
f (0)
综合式（2）和式（4），可得出如下结论：冲激函数可以把冲激所在位置处的函数值抽取（筛选）出来。
2020/3/6
24
（2） (t) 是偶函数，即 (t) (t)
（3） t ( )d
0 t 0 1 t 0
u(t)
(t)
t
(
＋
E=1V －
C=1F
vc (t)
1
0
2

t
2020/3/6
例：图中假设S、E、C都是理
想元件（内阻为0），当 t = 0时 S闭合，求回路电流i（t）。
i(t) C dvC (t) dt
2 i(t)

1

0 2
0
t
i(t) (t)
(1)
0
t
演示 20
1. (t)的定义方法（1）用表达式定义
R(t) t, (t 0)
R(t)
R(t t0 ) t t0 , (t t0 )
R(t-t0)
1
1
0 2020/3/6
1
t
0
t0
t0+1 t 14
二、单位阶跃信号
u(t) 0, (t 0) 1, (t 0) u(t)

信号与系统(郑君里)复习要点

信号与系统复习书中最重要的三大变换几乎都有。

第一章信号与系统 1、信号的分类①连续信号和离散信号 ②周期信号和非周期信号连续周期信号f (t )满足f (t ) = f (t + m T )，离散周期信号f(k )满足f (k ) = f (k + m N )，m = 0,±1,±2,…两个周期信号x(t)，y(t)的周期分别为T 1和T 2，若其周期之比T 1/T 2为有理数，则其和信号x(t)+y(t)仍然是周期信号，其周期为T 1和T 2的最小公倍数。

③能量信号和功率信号 ④因果信号和反因果信号2、信号的基本运算（+ - × ÷） 2.1信号的（+ - × ÷）2.2信号的时间变换运算（反转、平移和尺度变换） 3、奇异信号3.1 单位冲激函数的性质f (t ) δ(t ) = f (0) δ(t ) ， f (t ) δ(t –a) = f (a) δ(t –a)例： 3.2序列δ(k )和ε(k ) f (k )δ(k ) = f (0)δ(k ) f (k )δ(k –k 0) = f (k 0)δ(k –k 0) 4、系统的分类与性质4.1连续系统和离散系统4.2 动态系统与即时系统 4.3 线性系统与非线性系统 ①线性性质 T [a f (·)] = a T [ f (·)](齐次性) T [ f 1(·)+ f 2(·)] = T[ f 1(·)]+T[ f 2(·)] （可加性）②当动态系统满足下列三个条件时该系统为线性系统：)0(d )()(f t t t f =⎰∞∞-δ)(d )()(a f t a t t f =-⎰∞∞-δ?d )()4sin(91=-⎰-t t t δπ)0('d )()('f t t f t -=⎰∞∞-δ)0()1(d )()()()(n n n f t t f t -=⎰∞∞-δ4)2(2])2[(d d d )(')2(0022=--=--=-==∞∞-⎰t t t t tt t t δ)(1||1)()()(t a a at n n n δδ⋅=)(||1)(t a at δδ=)(||1)(00a t t a t at -=-δδ)0()()(f k k f k =∑∞-∞=δy (·) = y f (·) + y x (·) = T[{ f (·) }, {0}]+ T[ {0}，{x (0)}] (可分解性) T[{a f (·) }, {0}] = a T[{ f (·) }, {0}]T[{f 1(t ) + f 2(t ) }, {0}] = T[{ f 1 (·) }, {0}] + T[{ f 2 (·) }, {0}](零状态线性)T[{0},{a x 1(0) +b x 2(0)} ]= aT[{0},{x 1(0)}] +bT[{0},{x 2(0)}](零输入线性) 4.4时不变系统与时变系统T[{0}，f (t - t d )] = y f (t - t d)(时不变性质)直观判断方法：若f (·)前出现变系数，或有反转、展缩变换，则系统为时变系统。

《信号与系统》郑君里教学课件讲义

（４）１９世纪末，人们研究用电磁波传送无线电信号。赫兹（Ｈ.Hertz）波波夫、马可尼等作出贡献。1901年马可尼成功地实现了横渡大西洋的无线电通信。
（5）光纤通信从此，传输电信号的通信方式得到广泛应用和迅速发展。如今：（１）卫星通信技术为基础“全球定位系统（Global Positioning System, 缩写为GPS）用无线电信号的传输，测定地球表面和周围空间任意目标的位置，其精度可达数十米之内。（２）个人通信技术：无论任何人在任何时候和任何地方都能够和世界上其他人进行通信。（３）“全球通信网”是信息网络技术的发展必然趋势。目前的综合业务数字网（Integrated Services Digital Network,缩写为ISDN),Internet或称因特网，以及其他各种信息网络技术为全球通信网奠定了基础。
信号与系统
郑君里
教学课件
1、教材：信号与系统郑君里杨为理应启珩编 2、信号与系统 Signals & Systems ALAN V.OPPENHEIM ALANS. WILLSKY 清华大学出版社（英文影印版）（中译本）刘树棠西安交通大学出版社 3、信号与系统例题分析及习题乐正友杨为理应启珩编 4、信号与系统习题集西北工业大学
5. 系统的分类
系统可分为物理系统与非物理系统，人工系统以及自然系统。物理系统：包括通信系统、电力系统、机械系统等；非物理系统：政治结构、经济组织、生产管理等；人工系统：计算机网、交通运输网、水利灌溉网以及交响乐队等；自然系统：小至原子核，大如太阳系，可以是无生命的，也可是有生命的（如动物的神经网络）。
4.信号、电路（网络）与系统的关系
离开了信号，电路与系统将失去意义。

郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解(1-2章)【圣才出品】

第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节，是整个信号与系统学习的基础。

本章介绍了有关信号与系统的基本概念和术语，给出几种典型的信号和系统的表现形式，讲述了各信号与系统的特点以及信号之间的运算和转换。

通过本章学习，读者应掌握：如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。

一、信号概述
1．信号的概念及分类（见表1-1-1）
表1-1-1信号的概念及分类
2．典型的连续信号（见表1-1-2）
表1-1-2典型的信号及表示形式
3．信号的运算（见表1-1-3）
表1-1-3信号的运算
4．阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号，许多复杂信号皆可由二者或二者的线性组合表示。

具体见表1-1-4及表1-1-5。

（1）单位阶跃信号u（t）
表1-1-4单位阶跃信号u（t）
（2）单位冲激信号δ（t）
表1-1-5单位冲激信号δ（t）表示形式及性质
5．信号的分解
一个一般信号根据不同类型可分解为以下几种分量，具体见表1-1-6。

表1-1-6信号的分解
二、系统
1．系统概念及分类（见表1-1-7）
表1-1-7系统的概念及分类
系统模型如下：
输入信号经过不同系统可得到不同输出信号，具体见表1-1-8。

表1-1-8不同系统特性
1.2课后习题详解
1-1分别判断图1-2-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？
（a）
（b）
（c）
（d）
（e）
（f）。

郑君里信号系统考研《信号与系统》考研真题与考研笔记

郑君里信号系统考研《信号与系统》考研真题与考研笔记第一部分考研真题精选一、选择题1下列信号属于功率信号的是（）。

[中国传媒大学2017研]A．e－tε（t）B．cos（2t）ε（t）C．te－tε（t）D．Sa（t）【答案】B查看答案【解析】如果信号f（t）的能量有界（0＜E＜∞，P＝0），称f（t）为能量有限信号，简称为能量信号。

如果信号f（t）的功率有界（0＜P＜∞，E＝∞），称f（t）为功率有限信号，简称为功率信号。

ACD三项的能量均为有限值，因此为能量信号。

B项，cos（2t）ε（t）是单边周期信号，因此能量无界，但是功率为有限值，因此B为功率信号。

2下列信号中，选项（）不是周期信号，其中m，n是整数。

[山东大学2019研]A．f（t）＝cos2t＋sin5tB．f（t）＝f（t＋mT）C．x（n）＝x（n＋mN）D．x（n）＝sin7n＋e iπn【答案】D查看答案【解析】A项，cos2t的周期为T1＝2π/2＝π，sin5t的周期为T2＝2π/5，由于T1/T2＝5/2，是有理数，因此为周期信号，且周期为T＝2T1＝5T2＝2π。

BC两项，一个连续信号满足f（t）＝f（t＋mT），m＝0，±1，±2，…，则称f （t）为连续周期信号，满足上式条件的最小的T值称为f（t）的周期。

一个离散信号f（k），若对所有的k均满足f（k）＝f（k＋mN），m＝0，±1，±2，…，则称f（k）为连续周期信号，满足上式条件的最小的N值称为f（k）的周期。

D项，sin7n的周期N1＝2π/7，e iπn的周期为N2＝2π/π＝2，N1/N2＝π/7为无理数，因此为非周期信号。

3下列关于单位冲激函数或单位样本函数的表达式，选项（）不正确。

[山东大学2019研]A．B．δ（t）*f（t）＝f（t）C．D．【答案】D查看答案【解析】冲激函数的极限形式的定义式应该为4下列叙述正确的有（）。

信号与系统考研电子讲义郑君里

12§1.2信号的描述，分类和典型示例(续）•指数信号和正弦信号•奇异信号–斜变信号–单位阶跃信号和符号函数–单位冲激和冲激偶信号正交信号•11(k 实指数信号1—(k 和s 都是实数)•若中的为0 , k 为实数βαj k +=β同时•0 , s ωσs +=ω若中的为,为实数j k则为实指数函数stke t x =)(正弦信号1—取周期复指数的实部•欧拉公式sin(cos()(0ωωφω+++=+t t et j •取实部则为正弦信号)()(00φφj =)cos()(0φω+t A t x 81.3§信号的运算（参考网站绪论的内容）Ee whu edu cn用Flash演示的动态过程§1.4阶跃信号与冲激信号一.奇异信号即本身、其导数或其积分有不连续点的函数。

1.斜变信号2.单位阶跃信号3.符号函数4.单位冲激5.冲激偶信号13信号加窗或取单边t t u t u e t t−−=−)]()([)(0f f(t)f()t（1）突然接入的直流电压（）2）突然接通又马上断开电源K负载r(t)r(t 3)r(t 1)r(t 2)r(t-3)-r(t-1)-r(t-2)f(t)1)]2()2()[1()(.101.38−−+−=−t u t u tt f a p 题2....)2()1()()(.+−+−+=t u t u t u t f b )]()([(sin )(.T t u t u t E t f c −−=πT二.单位冲激函数)(t dr )(t du δ=)(t u dt =)(t dt 1.定义:(p17—21))]()([1)(.lim ττδ−−+=t u t u t a 220ττ→)()(t t =δ1=∞dt t limfnn ∞→)(∫∞−fn0=t )(lim ∞→fnn 0≠t 用规则函数脉冲序列的极限来定义)(t Rt ut )(t)(tδtb.Dirac 定义:=)(t δ∫∞=1)(dt t δ00≠t 0=∞t c.利用冲激函数的抽样性∞)()()(00t f dt t t t f =−∫∞δ∞−∫∞−=)0()()(f dt t t f δ∞−)()()(.00t f dt t t t f a =−∫∞−δ1∞)()]([.00t t t t b −=−−δδ)()(.t aat c δδ=)()()()(.000t t t f t t t f d −=−δδt)()(.t dtt u e δ=)()(t u d =∫∞−ττδ+−)(t i c 由于冲激电流的出现，电容两端的电压可以突变；电感电流也可以突变。

郑君里《信号与系统》(第3版)【教材精讲+考研真题解析】讲义(1-6章)【圣才出品】

3 / 136
圣才电子书十万种考研考证电子书、题库视频学习平台

f t f (t nT ) n 0 , 1, 2 ,
b．非周期信号：在时间上不具有周而复始的特性。 ③连续信号与离散信号 a．连续信号：时间轴为连续时间变量； b．离散信号：时间轴为离散时间变量。 ④模拟信号、抽样信号、数字信号 a．模拟信号：时间幅度均连续的信号； b．抽样信号：时间离散，幅度连续的信号； c．数字信号：时间幅度均离散的信号。 3．信号的几种典型示例（1）指数信号： f (t) Keat , a R ；（2）正弦信号： f (t) K sin(t ) ；（3）复指数信号： f (t) Kest Ke( j)t ；（4）抽样信号： Sa(t) sin t ；

（2）积分
十万种考研考证电子书、题库视频学习平台
òt f t( )dt -¥
3．两信号相加或相乘
信号的相加、相乘与代数运算无异。
四、阶跃信号和冲激信号奇异信号是指函数本身有不连续点（跳变点）或其导数与积分有不连续点的信号，包括斜变、阶跃、冲激和冲激偶四种信号。 1．单位斜变信号
（2）反褶
f (t) f (t) ，把 f (t) 的波形以 t 0 为轴反褶过来。
（3）尺度变换
f (t) f (at) ( a 为正实系数)，若 a 1 ，则 f (t) 的波形沿时间轴被压缩；反之，则
被扩展。
2．微分和积分
（1）微分
f ¢(t) = d f (t) dt
5 / 136
圣才电子书
t （5）钟形信号(高斯函数)： f (t) Ee(t/ )2 。
4 / 136
圣才电子书十万种考研考证电子书、题库视频学习平台

郑君里《信号与系统》(第3版)(下册)配套题库【名校考研真题+课后习题+章节题库+模拟试题】

目　录第一部分　名校考研真题第7章　离散时间系统的时域分析第8章　z变换、离散时间系统的z域分析第9章　离散傅里叶变换以及其他离散正交变换第10章　模拟与数字滤波器第11章　反馈系统第12章　系统的状态变量分析第二部分　课后习题第7章　离散时间系统的时域分析第8章　z变换、离散时间系统的z域分析第9章　离散傅里叶变换以及其他离散正交变换第10章　模拟与数字滤波器第11章　反馈系统第12章　系统的状态变量分析第三部分　章节题库第7章　离散时间系统的时域分析第8章　z变换、离散时间系统的z域分析第9章　离散傅里叶变换以及其他离散正交变换第10章　模拟与数字滤波器第11章　反馈系统第12章　系统的状态变量分析第四部分　模拟试题第一部分　名校考研真题　说明：本部分从指定郑君里主编的《信号与系统》（第3版）为考研参考书目的名校历年考研真题中挑选最具代表性的部分，并对其进行了详细的解答。

所选考研真题既注重对基础知识的掌握，让学员具有扎实的专业基础；又对一些重难点部分（包括教材中未涉及到的知识点）进行详细阐释，以使学员不遗漏任何一个重要知识点。

第7章　离散时间系统的时域分析一、填空题1．周期分别为3和5的两个离散序列的卷积和的周期性为______。

[北京航空航天大学2007研]【答案】7【解析】对于线性卷积，若一个周期为M，另一个周期为N，则卷积后周期为M+N－1，所以。

2．某线性时不变（L TI）离散时间系统，若该系统的单位阶跃响应为则该系统的单位脉冲响应为______。

[北京交通大学研]【答案】【解析】本题考查离散时间系统的单位脉冲响应。

用表示单位阶跃响应，由于利用线性和时不变特性可得二、判断题一个离散时间信号实际上就是一组序列值的结合{x（n）}。

（）[南京大学2010研]【答案】√【解析】离散时间函数，只有在某些离散时给出函数值，只是在某些离散瞬时给出函数值。

因此，它是时间不连续的“序列”的。

三、选择题1．信号的周期是（）。

郑君里信号与系统考研总复习

E
1 Pn
Ts
s
s
E Fs ()
Ts

0
时域抽样等效于频域周期拓展
s
s

总结
是f(t)傅里叶
周期信号的傅立叶变换
级数的系数
n
F ( ) 2 Fn ( n0 )
n
周期信号的频谱是离散的
抽样信号的傅立叶变换
是抽样脉冲序列p(t) 傅里叶级数的系数
n
Fs ( ) PnF ( ns ) n
抽样（离散）信号的频谱是周期的
(二）奈奎斯特（Nyqist）抽样率 fs 和抽样间隔Ts
从前面的频谱图可以看出，从抽样信号重建原信号的必要条件：抽样频率大于等于原信号最高频率的2倍
s 2m or fs 2 fm
fs 2 fm
1.阶跃函数
Lu( t )
2.指数函数

0
1
estd
t

1 est 1 s 0 s
L eα t eα testd t
eα st

1
0
αs αs
3.单位冲激信号
0
σ α
L
t

0
t

estd
特解：rp (t )的函数形式与激励函数形式有关
)
解
方程双零法零零状输态入::利可用利卷用积经积典分法法求求解

变换域法: Z变换，在Z域求解微分方程

经典法:前面电路分析课里已经讨论过，但与(t)有关的问
题有待进一步解决—— h(t)；

考研专业课郑君里版《信号与系统》第一章补充习题——附带答案详解

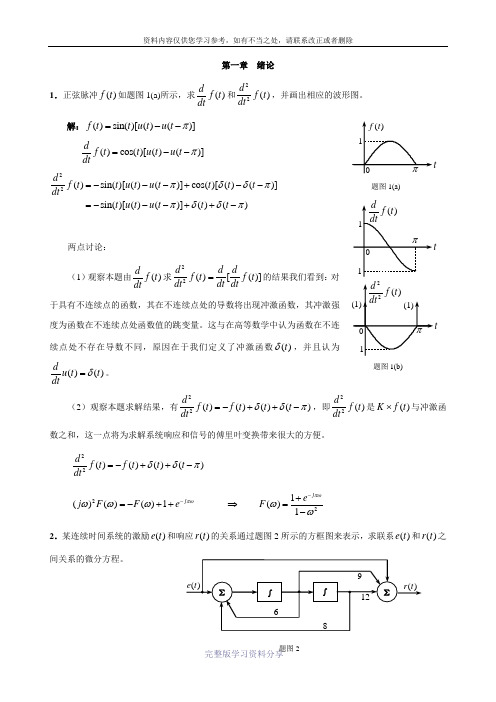
第一章绪论1．正弦脉冲()f t 如题图1(a)所示，求()df t dt和22()d f t dt ，并画出相应的波形图。

解：()sin()[()()]f t t u t u t π=--()cos()[()()]df t t u t u t dtπ=--22()sin()[()()]cos()[()()]sin()[()()]()()d f t t u t u t t t t dtt u t u t t t πδδππδδπ=---+--=---++-两点讨论：（1）观察本题由()df t dt求22()[()]d d d f t f t dt dt dt =的结果我们看到：对于具有不连续点的函数，其在不连续点处的导数将出现冲激函数，其冲激强度为函数在不连续点处函数值的跳变量。

这与在高等数学中认为函数在不连续点处不存在导数不同，原因在于我们定义了冲激函数()t δ，并且认为()()du t t dtδ=。

（2）观察本题求解结果，有22()()()()d f t f t t t dt δδπ=-++-，即22()d f t dt是()K f t ⨯与冲激函数之和，这一点将为求解系统响应和信号的傅里叶变换带来很大的方便。

22()()()()d f t f t t t dtδδπ=-++- 2()()()1j j F F eπωωωω-=-++ 21()1j e F πωωω-+⇒=-2．某连续时间系统的激励()e t 和响应()r t 的关系通过题图2所示的方框图来表示，求联系()e t 和()r t 之间关系的微分方程。

题图1(a)题图1(b)解：本题给出的方框图不是标准形式，无法直接写出微分方程。

除可用引入辅助函数()q t 的方法外，还可用以下方法求解。

()e t 到()r t 之间有一个直通环节，故1()()()r t r t e t =+，而1()r t 满足微分方程 21112()6()8()9()12()d d dr t r t r t e t e t dt dt dt++=--消去中间变量1()r t ，可得2222()6()8()()3()4()d d d dr t r t r t e t e t e t dt dt dt dt++=--3．判断下列系统是否为线性的、时不变的、因果的？（1）)()()(00t e b t r a t r dt d =+ （2）100)()()(b t e b t r a t r dtd+=+ （3）()2()()r t e t u t = （4）()cos[()]()r t e t u t = （5）)()(t e t r -= （6）)3()(t e t r = （7）τd τe t r t⎰∞-=)()( （8）τd τe t r t⎰∞-=5)()(（9）()()()n r t e t t nT δ∞=-∞=-∑解：（1）这是一个线性常系数微分方程，系统是线性的、时不变的、因果的。

信号与系统郑君里第一章绪论

信号与系统的应用领域举例
在工业自动控制上的应用电力系统中信息技术的应用在数据信号处理上的应用在生物医学领域中的应用在生物特征识别中的应用
在工业自动控制上的应用
工业控制与自动化 (电机调速) 例：炼铁高炉的给料电机带钢生产线的调速电机工具：
• 微分方程的时域求解 • 拉普拉斯变换 • 稳定性理论
信号波形表示——函数的图像如f(t)~t或F (j )~
应用现状与前景
信号与系统分析常见的应用有： (1)以某种特定的方式处理信号（信息）。经济预测是这方面的一个常见的例子，从过去的数据中预测出将来的趋势。（国家每年的GDP增长预测） (2)对污损信号的恢复。这种情况在背景噪声很强的语言通讯中会遇到。（星球间的信息传递和GPS） (3)在图像恢复和图像增晰方面的应用。（医学） (4)用来改变已知系统的性能。系统升级和设备改造。随着近代科学技术的发展，特别是大规模集成电路的出现，数字计算机的广泛应用，信息高速公路的建设，使信号与系统日益复杂，也促进了信号与系统理论研究的发展。
第一节信号与系统
背景知识与学科概况
信号与系统的概念出现在各种领域中，与其概念相关的思想和方法在各个领域中起着重要的作用。它的发展可以追溯到很多个世纪以前。例如：作为该领域的基本分析方法之一的傅里叶分析方法,其发展可追溯到从古代巴比伦人对天文学的研究。近些年的发展，这些概念和方法已经涉及到发射和接收机设计；计算机辅助图像和声音的采集恢复；工业生产与控制等领域中。所有这些方面的工作，已经对信号的表示、系统的分析和综合形成了一个完整的体系和一些强有力的数学工具。
生物特征识别
通过生物特征识别完成对人的识别；例子: