2014年中国第一届机器人旅游大赛
黄山学院2014年省双优生花名册
崔伊玲
女
安徽省合肥
新闻
本科
回
党员
2010-2011获校级“优秀团员”、“优秀学生干部”、“三好学生”;2010-2011获校一等专业奖学金;2011-2012获校“优秀青年”称号、“优秀学生干部”、“三好学生”;2012获“国家奖学金”;2012-2013获校三等专业奖学金。
51
孙玉
女
安徽省阜阳
41
黄俊知
男
皖金寨
酒店管理
本科
汉
党员
全国大学生英语竞赛三等奖;
2010—2011国家奖学金、校一等奖学金3次,三好学生3次,优秀学生干部1次,校“十佳青年”1次
42
杨阳
女
利辛县
建筑学
本科
汉
中共党员
2012年,获校第二届“十佳青年”。2013年,第五届“挑战杯”大学生课外学术科技竞赛校级一等奖、省级二等奖。获国家奖学金、国家励志奖学金2次、校三等奖学金、三好学生3次、优秀学生干部
32
秦静雅
女
皖砀山
旅游管理
本科
汉
党员
连续2年获国家励志奖学金。
2013年5月获校级优秀青年、
2011-2012年学年度获校二等奖学金,优秀班干,优秀团干。
2011-2012年度获“三好学生”
33
陈砺
男
皖安庆
旅游管理
本科
汉
党员
国家励志奖学金,优秀学生干部,校见义勇为嘉奖
34
黄佳乐
女
皖宣城
旅游管理
专科
汉
29
查婷婷
女
皖安庆
旅游管理
本科
汉
党员
2010-2011学年度:校“一等奖学金”、“三好学生”荣誉称号、“优秀团员”称号、“国家助学金”、2011-2012学年度:“国家励志奖学金”、校内“一等奖学金”、“三好学生”称号。2012-2013学年度:“国家助学金”。
第一届全国技能大赛世赛项目“机器人系统集成”全国机械行业选拔赛工作任务书(真题)

第⼀届全国技能⼤赛世赛项⽬“机器⼈系统集成”全国机械⾏业选拔赛⼯作任务书(真题)第⼀届全国技能⼤赛世赛项⽬“机器⼈系统集成”全国机械⾏业选拔赛⼯作任务书(真题)(备注:真题只展⽰竞赛形式和知识技能范围,最终竞赛内容将有不⼤于30%的变化)任务描述:因⽤户需求,公司对⼀套⼯业机器⼈主体的⾃动化设备进⾏改造,作为⼯程⼈员的您需根据任务和设备使⽤要求,进⾏机械模块的布局与安装、电⽓线路以及⽓动回路的安装,PLC与⼯业机器⼈编程与调试等⼯作,并编制⽤户⼿册。
(总分100分,时长300分钟)职业素养和安全⽂明要求(10分)本项⽬属于现场评分:所有竞赛选⼿,必须遵守安全⽂明⽣产制度,遵守与之有关系的各类技术规范;遵守机械和电⽓安全操作规程;遵守技术规程所规定的关于健康、安全、环境的纪律。
⼯作任务:任务1:设备零部件3D建模、布局设计、机械安装(15分)设备主要构成如图1所⽰图1 设备主要构成⽰意图(⼀)原料托盘、配料托盘、成品托盘、快换架的3D建模和绘图根据任务要求,对原料托盘、配料托盘、成品托盘、快换架实物(图2)进⾏测量,获得必要尺⼨。
选⼿需使⽤建模软件完成上述零部件的3D模型创建并⽣成零件⼯程图。
要求:1、图纸绘制准确,尺⼨标注满⾜机械设计规范及后续加⼯⼯艺要求,误差不⼤于0.5mm;2、创建快换架装配图,并标注相关必要尺⼨和必要信息;3、仔细观察快换架,⼿⼯测量所有零件,要求长度测量精度控制在±0.5mm以内。
测量尺⼨精确到⼀位⼩数。
在计算机中建⽴三维模型,最后⽣成所有零件的详细⼯艺图纸。
4、仔细观察原料托盘、配料托盘、成品托盘,⼿⼯测量所有零件,要求长度测量精度控制在±0.5mm以内。
测量尺⼨精确到⼀位⼩数。
在计算机中建⽴三维模型,最后⽣成所有零件的详细⼯艺图纸。
图2 机械模块⽰意图(⼆)⼯件的3D建模和绘图仔细观察⽩⾊圆柱体原料、不锈钢环配料(图3),⼿⼯测量所有零件,要求长度测量精度控制在±0.5mm以内。
机器人工作室社团材料汇总

公安技术学院机器人工作室2015年5月5日甘肃政法学院机器人工作室(Robotics Studio)是一个专门为爱好科技、积极创新的大学生成立的机器人创新实践工作室,由甘肃政法学院团委批准成立的团体。
一、机器人工作室简介开拓者工作室成立于2013年10月份,成员主要来自公安技术学院。
本工作室致力于为在校大学生打造一个集科技知识启蒙教育、创新思维拓展训练及创造能力开发培养为一体的实践创新平台,以期通过平台的各项活动促进教学改革、带动相关方向的学科建设,并不断培养和提升大学生的创新能力、动手能力、团队协作能力及独立分析并解决问题的能力。
工作室的日常事务性工作,包括以提高学生理论素养和实践能力为目标的理论设计和实际制作。
此外,工作室还组织成员参加一年一度的中国机器人大赛暨RoBoCup公开赛,以培养支撑竞赛、以竞赛促进培养,进一步调动大学生的积极性,使学生在整个竞赛活动的参与过程中,取得思维创新、动手实践等方面能力的长足进步。
成立之初,我校首支队伍就参加了2013年度中国机器人大赛,并在众多参赛队伍的激烈角逐下,取得“机器人探险游”子项目一等奖的成绩。
随着创新项目不断增加和工作经验的不断丰富,工作室已逐渐形成“帮、传、带、教”的学习形式和传承机制,即高年级学生帮助并带动低年级学生进行学习和研究,参与各类实际项目的执行,建立形成工作室技术梯度和人才梯度,为工作室今后的发展奠定坚实的基础。
二、机器人工作室的发展历史及现状分析甘肃政法学院开拓者工作室成立于2013年,最初的成员由我院参加2013年合肥机器人公开赛的队员组成,后在公安技术学院领导的大力支持下,成立了Robotics Studio工作室。
自成立以来,工作室获得了2013年中国机器人合肥公开赛一轻机器人旅游一等奖;2014年上海第一届机器人旅游大赛一轻一等奖、一重一等奖、二轻一等奖;在2014年第十届“博创杯”嵌入物联网设计大赛中,结合学科的移动安防监控系统,获得甘肃赛区二等奖;在2014年中国机器人大赛中,荣获一轻一等奖、一重一等奖、二轻特等奖。
《第一届全国大学生机械创新设计大赛决赛作品集》目录

《第一届全国大学生机械创新设计大赛决赛作品集》东北大区作品仿生机器蟹(哈尔滨工程大学)设计者:季宝锋刘德峰贾守波宋辉王刚指导教师:王立权陈东良刁彦飞螺旋传动管道机器人(哈尔滨工业大学)设计者:赵琦黄玉磊汪盛梁涛王玺唐能指导教师:宋宝玉焦映厚微定位仿生机器人(哈尔滨工业大学)设计者:侯磊石建军张乐敏乔遂龙周超王婷婷黎映相孙彬指导教师:邓宗全焦映厚孙立宁李满天基于并联机构和分布式控制系统的多功能机器人(哈尔滨工业大学)设计者:卢贤资刘明宇王祺刘强徐宇声刘祥雨周达顺指导教师:孙雅洲梁迎春焦映厚邓宗全轮足式机器人(长春理工大学)设计者:冯辉李荣张伙林刘国栋徐椿明兰宁荣大卓胡永宏刘洋周清指导教师:武秀东刘悦胡贞宋正勋机械式停水自闭水龙头(大连理工大学)设计者:于春宇孙灵俊指导教师:梁延德蚯蚓式爬行器(大连理工大学)设计者:王俊鹏李刚王宁全璐琳指导教师:梁延德圆柱凸轮数控铣削装置(东北大学)设计者:李兆维袁娜刘权利黄常舒指导教师:王仁德爬杆(绳)机器人(辽宁工程技术大学)设计者:梁文林许洪强李书新李再峰指导教师:何凡付治国新型大力钳(吉林大学)华北大区作品多功能齿动平口钳(北京化工大学)设计者:王建杨攀指导教师:王永涛微生物培养液自动抽取喷涂机(中国农业大学)设计者:徐结徐赫指导教师:张铁中爬杆管道两用机器人(北京航空航天大学)设计者:洪振军郑亮何帆杨亚涛周煊指导教师:范悦基于仿生的高适应性六足机器人(北京航空航天大学)设计者:吴文镜王剑薇过为贺仕伟孙明锋郑广强佟铁锋指导教师:王卫林仿生虫(北京航空航天大学)设计者:刘小明尹益平赵同钢赵鹏王云飞指导教师:张欣便携式助立器(北京工业大学)设计者:赵广宁冯伟周瑞洪毅张子祺赵敬元指导教师:王大康自行车防盗锁(北京科技大学)设计者:穆树亮指导教师:张少军无线遥控爬杆喷漆机器人(天津大学)设计者:卢鸿斌张莹李娜指导教师:杜玉明摩擦式电动翻谱台(天津大学)设计者:唐晓磊于滂倪宗悦农帅指导教师:车建明爬楼梯机器人(北京交通大学)设计者:张克涛温平李翔指导教师:方跃法房海蓉西北大区作品新型球形机器人(西安电子科技大学)设计者:沈宣江严军牛波甘运维林星陵侯俊利吴颖丁裕诚指导教师:李团结朱玉超杨小瑜新型纱线卷绕防叠试验机(西安思源职业学院)设计者:李阳李明牛科李京王栋雷辉指导教师:刘琦云方形区域喷灌龙头(西北工业大学)设计者:柏龙岳映章余朝举张彬李哲指导教师:葛文杰、 .环卫伴侣——多功能自走式环保清洁车(陕西科技大学)设计者:张江峰张大伟赵志明叶恒青苏源博魏军学兰晓青顾纪超指导教师:李思益张彩丽刘俊生军地两用全自动担架车的研制(第二炮兵工程学院)设计者:潘兴杰蒲鹏程黄伟伟余亮戴胜东指导教师:岳应娟熊磊周凯上下楼梯搬运器(新疆大学)设计者:谈建平宝英巴特王超努尔比亚贾殿锋指导教师:穆塔里夫阿赫迈德王湔油罐车注油自动控制系统(新疆大学)设计者:西克热木阿里木热孜万古丽肉孜古丽指导教师:伊里哈木穆合塔尔陈宏伟源源(球形机器人)(西安思源职业学院)设计者:孙华雷张晓峰唐怀丹焦荣指导教师:马维新新型揉搓式全自动洗衣机(陕西科技大学)设计者:屈菲张义盟张江峰叶恒青指导教师:贺炜王宁侠唐平智能型全开式窗户(兰州交通大学)设计者:王欣欣李伟岭指导教师:李万祥牛卫中华东大区作品新型立轴风力机(安徽工业大学)设计者:杜志高王睿孙自闽钟昌彬陈厚富陈伟军陈献张世勇刘肥李超指导教师:邱支振陈富强顾小林仿生机械——虫虫“小强”(浙江大学)设计者:胡军柯党田峰许正蓉指导教师:沈萌红三自由度微位移工作台(合肥工业大学)设计者:杨飞谢俊谢祖强张永斌汪念平指导教师:赵韩沈健仿生壁虎(浙江大学)设计者:张俊伍中宇刘炜焘指导教师:钱向勇汽车转向同步照明灯(哈尔滨工业大学威海分校)设计者:张连清刘纪涛肖阿阳时凯张立伟常青张洪勋林乐川指导教师:刘会英赵继俊王毅机器鱼尼莫(东南大学)设计者:王春健梁健付月明关鸿耀李明宋春峰赵薇张徐指导教师:王兴松许映秋自适应可翻转探测车(东南大学)设计者:徐侨荣胡彬彭竹云彭时林指导教师:王兴松许映秋液体流动阻尼式高楼逃生器(福州大学)设计者:叶强杨谊昌张国欣指导教师:叶仲和蓝兆辉刘开昌脉动式无级变速器(南昌大学)213设计者:杜小波郭立华叶震肖文鑫指导教师:黄兴元杨湘杰徐春水可折叠崎岖表面自适应障碍小车(上海交通大学)设‘计者:王玮彦袁君华丁琛瑜刘栩之李丰园指导教师:马培荪易拉罐空罐有偿回收装置(华东理工大学)设计者:巩彬彬指导教师:安琦中南大区作品行星轮式登月车(中国人民解放军国防科技大学)设计者:张佩柴世良周峰常伟陈坤指导教师:潘存云翁飞兵尚建忠健身洗衣机(华南理工大学)设计者:卢俊林世富指导教师:朱文坚智能洁地机器人(中南大学)设计者:汤展跃董惠柏指导教师:何竞飞机器昆虫步行机构(华南农业大学)设计者:董竹英魏浩华黄灿权黄章华指导教师:陈佳琦气动式龙眼去核机(华南农业大学)设计者:林楚帆张志辉陈嘉慧谢文彬许巨忠丁桂阳指导教师:谢海军吸附式蠕动探测维修机器人(海军工程大学)设计者:丰利军郜世杰张勇孟宇裴晶晶王菊花汪丹丹指导教师:江汉红摆盘式特种发动机(海军工程大学)设计者:王文斌张振有袁鹏胡照于振动指导教师:王德石仿生机械灵巧手(华中科技大学)设计者:赵信毅张庆春张布卿冯玮刘全国刘辉王政指导教师:吴昌林杨家军履带式水下铺设机(华中科技大学)设计者:张志甜黄海清牛毅徐天明指导教师:吴昌林两足行走机器人(湖南大学)设计者:王雄波姚凌云陈士剑吴占涛李丽冯长林汪祥指导教师:刘江南严贻满王虎符西南大区作品半球体螺旋槽数控研磨机(重庆大学)设计者:彭万彬李俊向拾文罗勇指导教师:袁绩乾陈国聪张济生带辅助环的楔铁式超越离合器(重庆工商大学)设计者:贺术祥陈雄陈敏指导教师:杜力环保型手推式草坪剪草机(昆明理工大学)设计者:胡永鹏李治威谭阳尤川宝何亮吴锋指导教师:谭蓉环卫保洁清扫自行车(西南科技大学)设计者:谭伟丰航驰指导教师:陈晓勇机械式自适应上下非等高台阶小车(成都电子机械高等专科学校) 设计者:甘保军刘维江磊洪小飞钟宁王超玉刘浪指导教师:胥宏宋呜霍平球形机器人运动机构(成都大学)设计者:李凯陈茂林杨杰李小林杨霞宋磊指导教师:董万福无级变速轮系操纵机构(重庆工学院)设计者:罗剑波杜潇指导教师:林昌华液压式无级变速器(西南交通大学)设计者:钱海挺郑家坤李小易李永生指导教师:刘桓龙潘惠龙谢进异形齿轮泵(四川工程职业技术学院)设计者:李雷胡茂林胡建国朱明军郑家兵郑立和指导教师:陈洪涛冷真龙周奎附录一批复附录二获奖名单。
2014年不容错过的148个比赛(竞赛)

2014年不容错过的148个比赛(竞赛)创意设计类(16个)1、霍普杯2014国际大学生建筑设计竞赛2、2014年“新人杯”全国大学生室内设计竞赛3、2014中国手绘艺术设计大赛4、2014全国大学生建筑设计方案竞赛5、2014第三届中国大学生设计大赛6、“中装杯”全国大学生空间与环境艺术设计大赛7、第六届全国大学生广告艺术大赛8、2014毕马威“我的未来,我做主”创意大赛9、2014搜房网“申远杯”大学生室内设计大赛10、2014年SUNRISE杯大学生建筑设计方案竞赛11、2014年“中兴捧月”校园赛事嘉年华12、2014年第四届奥雅设计之星大学生竞赛13、2014第五届现代汽车大学生广告大赛14、明日合伙人——2013华为手机创意天团招募季15、第四届“意彩石光”彩色宝石创意设计大赛16、2014年第四届设想未来大学生首饰创意设计大赛创新设计类(8个)1、“荣威·MG杯”中国大学生汽车设计大赛2、2014博世Thingking Ahead创新挑战赛3、2014第二届TI杯关爱健康医疗电子创意创新设计大赛4、第五届“工商银行杯”全国大学生银行产品创意设计大赛5、方兴杯第八届全国大学生房地产策划大赛6、2014国际青年创新大赛7、中国民生银行手机银行2014校园创新大赛8、UPDIS概念城市2014设计竞赛商业创业类(16个)1、联合利华中华闪亮未来商业精英挑战赛2、2014巴黎银行Ace-manager全球商业挑战赛3、2014宝洁精英挑战赛4、江苏省第四届大学生创新创意创业大赛5、第三届迪卡侬暑期大学生商业挑战赛6、2014年联想Yoga创意营销大赛7、2014年银联移动电子商务创意大赛8、第三届中国创新创业大赛9、2014年“中兴捧月”校园赛事嘉年华10、2014CIMA商业精英国际挑战赛11、首届福汇FXCM全国大学生外汇交易大赛12、2015欧莱雅校园市场策划大赛13、万达集团支持大学生就业创业十年计划14、“21世纪•路劲杯”互联网金融创新案例大赛15、第四届IMA校园管理会计案例大赛16、第11届中国最佳公共关系案例大赛绿色环保类(6个)1、施耐德电气"绿色城市"国际案例挑战赛2、“道达尔”第五届高校环保科技创意设计大赛3、2014根与芽大学生护鲨项目竞赛4、植物日记2014大学生环保微拍大赛5、2015全国大学生“生态创想‧绿色行动”环保大赛6、英特尔大连高校学生环保创意营销大赛公益创新类(6个)1、“创响新生代”2013康师傅创新挑战赛2、YESxBOP商业计划大赛3、第三届好丽友杯大学生公益梦想实践大赛4、2014年海航集团社会创新创投竞赛5、第三届EY安永大学生公益活动创新大赛6、全球社会企业创业大赛中国赛区学科技术类(20个)1、第十届全国周培源大学生力学竞赛2、第四届大学生HyperWorks仿真技术竞赛3、第四届全国财务新星财务方案设计大赛4、格力杯第八届中国制冷空调行业大学生科技竞赛5、“华大九天杯”大学生集成电路设计大赛6、第七届全国大学生网络商务创新应用大赛7、2014年全国大学生电子设计竞赛8、20134第十届博创杯全国大学生嵌入式物联网设计大赛9、2014年第八届全国大学生化工设计竞赛11、第五届“《英语世界》杯”翻译大赛12、第十二届“艾默生杯”空调与冷冻设计应用大赛13、2014年全国大学生西门子杯自动化挑战赛14、2014NI毕业设计竞赛15、2014ABB大学生创新大赛16、2014"AB杯"全国大学生自动化系统应用技术大赛17、2014年“中兴捧月”校园赛事嘉年华18、第三届AceBridge全国大学生行业研究大赛19、第五届"新东方杯"英语口语大赛20、第十届全国大学生“飞思卡尔”杯智能汽车竞赛人文艺术类(4个)1、第6届中国大学生现代摄影大赛2、第五届"校园行知客"挑战赛3、第十一届全国大学生一分钟影像大赛4、第8届大学生“企业社会责任”征文大赛IT互联网类(20个)1、微信公众平台创新大赛2、第三届“中国软件杯”大学生软件设计大赛3、2014年第七届“英特尔杯”全国大学生软件创新大赛4、第四届中国大学生服务外包创新创业大赛5、2014Astar百度之星程序设计大赛6、PowerLinux应用服务器定义未来挑战赛7、2014第三届中国云•移动互联网创新大奖赛8、2014年“中兴捧月”校园赛事嘉年华9、2014年第五届Android应用开发中国大学生挑战赛10、第三届阿里云开发者大赛11、第三届“Qrobot”杯全国机器人应用开发大赛12、第三届“T派-寻找腾讯校园CXO首席体验官”大赛13、大学生云OS应用开发大赛14、第二届中国大数据技术创新与创业大赛15、【创客时代•造起来】联想创客大赛16、人人网校园开发者大赛17、第二届QQ游戏全国大学生创意开发大赛18、第六届“蓝桥杯”全国软件和信息技术专业人才大赛19、第二届全国高校物联网应用创新大赛20、2014年"有道难题"网易创新大赛青年机遇类(6个)1、2014年春(秋)季黑苹果公益扶持计划2、全国大学生社会实践公益团队招募3、"西行寻梦"2014年全国高校"走向西部"社会服务项目小额资助4、MaD2015创不同年会——中国内地参加者实践学习计划5、世界未来能源峰会第三届中国学生团员招募6、第4届“见与行”暑期学校Gaze&Advance2015青年实践项目类(10个)1、2014年调研中国——大学生社会调查奖学金2、“青年中国行”大学生社会实践调研活动3、2014年度希望工程激励行动项目4、2014阿克苏诺贝尔中国大学生社会公益奖5、2014华硕大学生科普志愿者行动6、能源青年行2014暑期调研计划7、第六届CIDEG杯本科生暑期社会调研挑战赛8、第六届国际青年能源与气候变化峰会全球招募9、角落公益——中国大学生星火暖中华公益10、财经中国学子有责——中国大学生经济调研奖学金项目类(4个)1、2014百度奖学金计划2、2015瑞典全额奖学金挑战赛3、2014南都新闻奖学金4、2014南都营销奖学金高质量的国际商业比赛(竞赛)(32个)1、安永“明日商业领袖”案例大赛主办方:安永2、Emerging Market Competition主办方:瑞士瑞信银行3、Ace-manager competition主办方:法国巴黎银行4、埃森哲金融风险管理大赛主办方:埃森哲5、宝洁商业精英挑战赛主办方:宝洁6、壳牌Gourami全球商业挑战赛主办方:壳牌7、Unilever闪亮未来商业精英挑战赛主办方:联合利华8、毕马威商业案例分析主办方:毕马威9、IVEY可口可乐商业案例竞赛主办方:可口可乐10、壳牌大学生能源调研大赛主办方:壳牌四月初11、OVAL中日韩商业创意大赛主办方:OVAL12、贝恩杯咨询案例大赛主办方:贝恩公司13、SK商意擂台赛主办方:SK14、Credit Suisse HOLT Valuation Challenge 主办方:瑞士瑞信银行15、USB IBD Challenge(M&A)主办方:瑞士联合银行集团16、China Unionpay Creativity competition 主办方:中国银联17、Google online marketing challenge主办方:Google18、德勤税务精英挑战赛主办方:德勤19、JP Morgan Deal competition主办方:JP摩尔根20、花旗杯金融创新大赛主办方:花旗银行21、Credit Suisse Video competition主办方:瑞士瑞信银行22、现代汽车大学生汽车营销大赛主办方:现代23、stock pitching game主办方:富达国际投资24、morgan stanley code storm主办方:摩根士丹利25、CIMA Global business challenge主办方:特许管理会计师公会26、欧莱雅e-start在线商业挑战赛主办方:欧莱雅27、Citizen act CSR competition主办方:法国兴业银行28、欧莱雅校园市场策划大赛主办方:欧莱雅29、Schroders investment competition主办方:施罗德集团30、达能Trust game国际商业策划大赛主办方:达能31、CFA institute research challenge主办方:CFA institute32、Country pick主办方:CORDIAL共青团西北工业大学委员会、学生科协整理。
2014江苏省嬉戏谷杯PowerTech仿生机器人创意大赛竞赛规则

2014 江苏省嬉戏谷杯PowerTech仿生机器人创意大赛竞赛规则A.报名、报到规定有意参与2014PowerTech竞赛之队伍,须依下述说明完成报名与报到:一、报名资格PowerTech竞赛●所有参赛成员报名数据,经主办单位确认后不得再更改。
●严禁同一参赛者同时报名两个队伍参赛,经发现一律取消队伍参赛资格。
●请至活动网站下载报名表,并依报名表中『备注』之说明完整填写报名表。
●填妥后请于报名期间内,Email至活动信箱●报名表经工作人员确认无误后,将寄送报名成功信件至指导老师信箱。
●数据未完整及超过期限之报名表,恕不受理。
二、参赛证●竞赛报到时,工作人员将核对参赛人员资料。
●参赛者必须配戴有效之参赛证,方可进行报到及进入竞赛场地。
●竞赛过程(含制作时间与竞赛时间)无配戴或企图掩饰参赛证使之不易辨别者,须依工作人员引导离开现场。
B.工具使用规定C-1.除活动现场主办单位提供之热熔胶枪外,禁止自行携带或使用电动工具、气动工具。
C-2.本比赛可携带或使用市售夹具或自行设计制作之模具。
C-3.比赛现场主办单位备有热熔胶枪及胶条供参赛队伍黏合作品使用。
参赛队伍亦可自行携带安全性高之其他胶类用品供黏合用途,且安全须自行负责。
C-4.所有工具请小心使用,以确保安全并维持竞赛场地整洁。
C-5.为响应环保(减碳排放)教育,大会建议参赛队伍使用充电电池(工作电压在1.5V以下)。
C-6.活动中经工作人员或他人检举违反上述事项,经查证属实者一律取消参赛资格。
若对所携带之工具及材料规格有不清楚者,请于事前询问,并经主办单位竞赛评审委员会许可后方可带入会场。
C.创作竞赛规定D-1.选手及所属队伍违反以下规定的事项,取消参赛资格。
D-1-1.活动前未至报到处进行报到,私自进入场地者。
D-1-2.冒名顶替参赛者参与活动,经工作人员发现或他人检举者。
※请所有参赛者配带个人参赛证,于报到时出示查验。
D-1-3.制作或竞赛过程中,发生家长、指导教师或其他场外人士藉任何方式刻意指导之情事,经大会工作人员发现或其他人检举属实者。
第一届全国技能大赛竞赛项目

第一届全国技能大赛竞赛项目
(共86项)
一、世赛选拔项目(共63项)
(一)运输与物流(7项)
飞机维修、车身修理、汽车技术、汽车喷漆、重型车辆维修、货运代理、轨道车辆技术(新)
(二)结构与建筑技术(13项)
砌筑、家具制作、木工、混凝土建筑、电气装置、精细木工、园艺、油漆与装饰、抹灰与隔墙系统、管道与制暖、制冷与空调、瓷砖贴面、建筑信息建模(新)
(三)制造与工程技术(21项)
数控铁、数控车、建筑金属构造、电子技术、工业控制、工业机械、制造团队挑战赛、CAD机械设计、机电一体化、移动机器人、塑料模具工程、原型制作、焊接、水处理技术、化学实验室技术、增材制造(新)、工业设计技术(新)、工业4.0(新)、光电技术(新)、可再生能源(新)、机器人系统集成(新)(四)信息与通信技术(8项)
信息网络布线、网络系统管理、商务软件解决方案、印刷媒体技术、网站设计与开发、云计算、网络安全、移动应用开发(新)(五)创意艺术与时尚(6项)
时装技术、花艺、平面设计技术、珠宝加工、商品展示技术、3D数字游戏艺术
(六)社会及个人服务(8项)
烘焙、美容、糖艺/西点制作、烹饪(西餐)、美发、健康和社会照护、餐厅服务、酒店接待
二、国赛精选项目(共23项)
数控车、数控铳、电工、装配钳工、焊接、电子技术、CAD 机械设计、汽车维修、新能源汽车智能化技术、木工、砌筑、室内装饰设计、网络系统管理、物联网技术、信息网络布线、珠宝加工、时装技术、健康照护、餐厅服务、西式烹调、烘焙、茶艺、社会体育指导(健身)。
机器人竞赛项目

机器人竞赛项目一、国内目前举办的比较有影响力的机器人比赛1:中国青少年机器人竞赛(/)由中国科协举办,每年有不同省市科协承办,2001年举办第一届,至今已走过了9个年头.其所有竞赛项目,都为机器人项目,主要有:机器人创意比赛机器人基本技能比赛机器人足球比赛VEX机器人工程挑战赛FLL机器人工程挑战赛参赛学生按:小学,初中,高中各组别参赛.2:全国中小学电脑制作活动(/index.html)由教育部主办,各地电教馆负责承办。
机器人项目只是其中部分比赛项目。
证书含金量很高,全国赛机器人项目,每个项目只给前3名队伍,分别颁发一,二,三等奖证书。
自2003 年以来已经举办四届, 该赛事主要项目分为:FLL 机器人赛机器人足球机器人灭火(由广茂达公司承办)3:全国中小学信息技术创新实践活动()学生可以用机器人器材为载体,以小发明的项目参加。
此比赛影响力很大。
证书含金量也非常高。
4:中国机器人大赛暨Robocup 中国选拔赛()由中科院自动化学会主办, 该项赛事涵盖了大中小学, 自2003 年开始受到全国的瞩目。
5:“广茂达杯”中国智能机器人大赛开创于2000 年, 第七届“广茂达杯”中国智能机器人大赛于2006 年8 月在上海华东师范大学举行, 竞赛共设14 个项目, 包括:机器人灭火机器人足球机器人擂台赛机器人排雷创新项目展示机器人论文二、国际上公认的比较有影响的赛事主要包括以下几项赛事1:Robocup ( 机器人世界杯) ()每年一届, 包含大中小学, 主要以足球比赛为主, 是国际上公认的最高水准的机器人比赛。
目前, Robocup包括:电脑仿真比赛小型机器人赛中型机器人赛SONY 有腿机器人赛2:FLL ( First Lego League) 比赛()由美国的FIRST 和LEGO赞助举办, 一般要求在两分半钟完成九个项目。
3:FIRA 机器人足球赛()由国际机器人足球联合会(Federation ofInternational Robot soccer Association) 举办, 自1995 年以来每年在全球举行一次, 主要进行机器人足球项目赛事。
“机器人奥运游”比赛规则

“机器人奥运游”比赛规则一、竞赛目的、级别类型1、竞赛目的“机器人奥运游”竞赛项目要求参赛机器人在规定假期时间内,游历尽量多的景点,获得尽量多的得分,并在假期结束前回到出发地。
目的是引导参赛队研究、设计并制作具有优秀硬件与软件系统的移动机器人,逐步提高机器人的能力与智能。
1)系统规划与优化能力:在预定的时间内游历尽量多的景点,完成计划中的旅游活动,并回到出发地点。
是一种最优规划活动;有一定的系统规划与优化能力。
想得高分,就要游历尽量多的景点和难度高的景点,但存在来不及在规定的假期内回家的危险。
2)应变能力:有些可移动景点与路障的摆放数量与位置,在机器人放进出发区后,随机确定。
这在一定程度上可控制竞赛的难度,并使旅游路线有一定的不确定性。
未来,路线图也可以在赛前临时公布。
3)爬坡能力:桥型景点与天台景点的坡度要求机器人有较好的爬坡能力。
4)跨越门槛的能力:这对机器人都是重大考验。
5)快速性与稳定性:机器人在的整个旅游过程中,始终要在快速性与稳定性中间求得平衡,否则,难以取得好的成绩。
二、机器人外观与尺寸无具体限制,能适应旅游场地即可。
通常为四轮式。
a、传感器:在不违反规则和规范的情况下,对机器人传感器的类型和数量没有限制。
b、动力:请在每组比赛点名前为机器人充足电力。
在本组全部机器人完成比赛之前,不得充电。
c、其他:机器人不得伤害人、不应对场地等造成损坏。
三、场地、路线、环境1、场地比赛场地7m×10m,表面铺绿色地毯。
旅游道路的中心有宽度约24mm的引导线用以引导机器人,引导线为白色。
减速板表面上不铺地毯,涂灰色油漆。
比赛的起止区为一个500mm×500mm 的长方形区域。
连接该区域进出口处的是门廊计时装置(如图1-1)。
在门廊上会安装计时器,机器人经过门廊时,计时系统开始或停止计时。
图1-1500500100起止区域2、路线图机器人旅游路线由直道、弯道、环路和交叉路口等组成,任意两个交叉路口之间的距离不小于500mm 。
(必考题)初中数学八年级数学上册第一单元《勾股定理》测试(包含答案解析)(3)
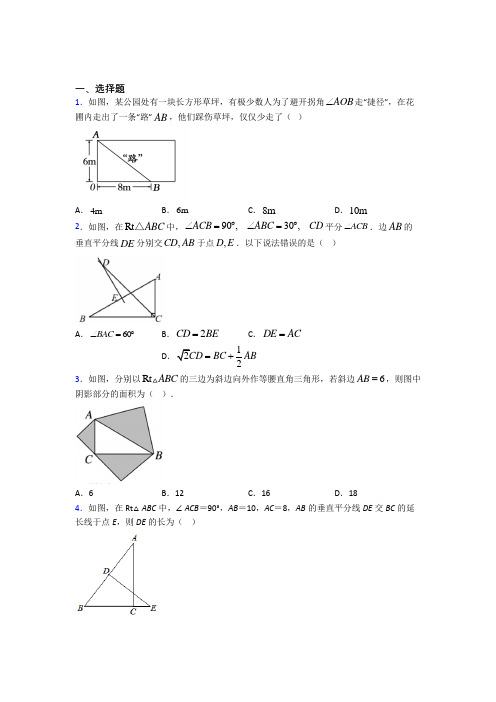
一、选择题1.如图,某公园处有一块长方形草坪,有极少数人为了避开拐角AOB ∠走“捷径”,在花圃内走出了一条“路”AB ,他们踩伤草坪,仅仅少走了( )A .4mB .6mC .8mD .10m 2.如图,在Rt ABC △中,90,30,ACB ABC CD ︒∠︒=∠=平分ACB ∠.边AB 的垂直平分线DE 分别交,CD AB 于点,D E .以下说法错误的是( )A .60BAC ∠=︒B .2CD BE =C .DE AC =D .122CD BC AB =+ 3.如图,分别以Rt ABC 的三边为斜边向外作等腰直角三角形,若斜边6AB =,则图中阴影部分的面积为( ).A .6B .12C .16D .184.如图,在Rt △ABC 中,∠ACB =90°,AB =10,AC =8,AB 的垂直平分线DE 交BC 的延长线于点E ,则DE 的长为( )A .103B .256C .203D .1545.如图,在△ABC 中,AB =6,AC =9,AD ⊥BC 于D ,M 为AD 上任一点,则MC 2-MB 2等于( )A .29B .32C .36D .456.如图,在Rt ABC ∆中,90,45,2B BCA AC ︒︒∠=∠==,点D 在BC 边上,将ABD ∆沿直线AD 翻折,点B 恰好落在AC 边上的点E 处,若点P 是直线AD 上的动点,连接,PE PC ,则PEC ∆的周长的最小值为( )A .22-B .2C .21+D .17.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地 送行二步与人齐,五尺人高曾记. 仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离AB 长度为1尺.将它往前水平推送10尺时,即A C '=10尺,则此时秋千的踏板离地距离A D '就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,则绳索OA 长为( )A .13.5尺B .14尺C .14.5尺D .15尺8.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC =2,BC =3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是( )A .413B .810C .41312+D .81012+ 9.如图,是一种饮料的包装盒,长、宽、高分别为4cm 、3cm 、12cm ,现有一长为16cm 的吸管插入到盒的底部,则吸管漏在盒外面的部分()h cm 的取值范围为( )A .34h <<B .34h ≤≤C .24h ≤≤D .4h = 10.为准备一次大型实景演出,某旅游区划定了边长为12m 的正方形演出区域,并在该区域画出4×4的网格以便演员定位(如图所示),其中O 为中心,A ,B ,C ,D 是某节目中演员的四个定位点.为增强演出效果,总策划决定在该节目演出过程中增开人工喷泉.喷头位于演出区域东侧,且在中轴线l 上与点O 相距14m 处.该喷泉喷出的水流落地半径最大为10m ,为避免演员被喷泉淋湿,需要调整的定位点的个数是( )A .1个B .2个C .3个D .4个11.若实数m 、n 满足340m n --=,且m 、n 恰好是Rt ABC △的两条边长,则第三条边长为( ).A .5B 7C .57D .以上都不对 12.2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a ,较短直角边为b ,则2()a b +的值为( )A .25B .19C .13D .169二、填空题13.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn ,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD 的距离为2寸,点C 和点D 距离门槛AB 都为1尺(1尺=10寸),则AB 的长是_____寸.14.如图,在三角形纸片ABC 中,∠ACB =90°,BC =6,AB =10,如果在AC 边上取一点E ,以BE 为折痕,使AB 的一部分与BC 重合,A 与BC 延长线上的点D 重合,那么CE 的长为________.15.如图,在Rt ABC △中,90C ∠=︒,点D 在BC 上,且12AC DC AB ==,若2AD =,则BD =___________.16.如图,在四边形ABCD 中,B D 90∠∠==︒,AD=CD ,AB+BC=8,则四边形ABCD 的面积是_________.17.如图,圆柱形容器中,高为1m,底面周长为4m,在容器内壁离容器底部0.4m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.6m与蚊子相对的点A 处,则壁虎捕捉蚊子的最短距离为______m(容器厚度忽略不计).18.如图,在Rt△ABC中,∠C=90°,AC=6、BC=8,CD⊥AB,则CD=___.19.一架5米长的梯子斜靠在一竖直的墙上,这时梯足距离墙脚3m,若梯子的顶端下滑1m,则梯足将滑动______.20.如图,在Rt△ABC中,∠C=90°,AB=5,则正方形ADEC与正方形BCFG的面积之和为_____.三、解答题21.如图,△ABC和△DCE都是等腰直角三角形,CA=CB,CD=CE,△DCE的顶点D在△ABC的斜边AB上(1)连结AE,求证:△ACE≌△BCD.(2)若BD=1,CD=3,求AD的长.22.如图,ABC中,∠C=90°,BC=5厘米,AB=55厘米,点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动,同时,点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动,P、Q两点运动几秒时,P、Q两点间的距离是210厘米?23.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?24.已知ABC的三个顶点的坐标分别为A(3,2)、B(﹣4,0)、C(0,2)(1)在下面的平面直角坐标系中分别描出A,B,C三点,并画出ABC;(2)求线段BC的长;(3)求ABC的面积.25.现代电视屏幕尺寸的设计,主要追求以下目标:一是更符合人体工程学要求(宽与长的比接近与0.618);二是设计适当的长宽比使屏幕的面积尽可能大现行的电视机屏幕有“宽屏”和“普屏”两种制式,宽屏的长宽比为16:9;普屏的长宽比为4:3.(1)哪种屏幕更适合人体工程学要求?请说明理由.(2)一般地,电视屏幕的“几寸”指的是这个屏幕的长方形的对角线长有多少英寸,1英寸2.54cm =,小明家想买80寸的宽屏..电视机(边框宽都为1cm ),并嵌入到墙中.则需要预留的长方形位置的长、宽各多少cm 33718.4≈,33.7 5.8≈)(3)在相同尺寸的电视机屏幕中,宽屏的屏幕面积大还是普屏的屏幕面积大?请说明理由.26.阅读下列材料并完成任务:中国古代三国时期吴国的数学家赵爽最早对勾股定理作出理论证明.他创制了一幅“勾股圆方图”(如图l),用数形结合的方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形ABCD 是由4个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为12ab ;中间的小正方形边长为b a -,面积为()2b a -.于是便得到式子:222+=a b c .赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中ABH ∆、BCG ∆、CDF ∆和DAE ∆是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD c =,DE a =,AE b =,取10c =,2b a -=.任务:(1)填空:正方形EFGH 的面积为______,四个直角三角形的面积和为______;(2)求()2a b +的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据勾股定理求出AB 即可.【详解】解:∵90AOB ∠=︒,∴22226810AO OB ++=(m ),6+8-10=4(m ),∴他们踩伤草坪,仅仅少走了4m ;故选:A .【点睛】本题考查勾股定理的应用,解题关键是熟练运用勾股定理求线段长.2.B解析:B【分析】利用直角三角形的性质、三角形内角和定理、勾股定理、全等三角形的判定与性质等知识对各选项的说法分别进行论证,即可得出结论.【详解】解:如图,连接BD 、AD ,过点D 作DM ⊥BC 于M ,DN ⊥CA 的延长线于N ,A 、在Rt ABC △中,90ACB ∠=︒,30ABC ∠=︒,∴60BAC ∠=︒.故此选项说法正确;B 、∵DM ⊥BC ,DN ⊥CA∴∠DNC =∠DMC =90°,∵CD 平分∠ACB ,∴∠DCN =∠DCM =45°.∴∠DCN =∠CDN =45°.∴CN=DN .则△CDN 是等腰直角三角形.同理可证:△CDM 也是等腰直角三角形,∴222DN CN DN +=.222DM CM DM +,∴DM=DN= CM=CN ,∠MDN =90°.∵DE 垂直平分AB ,∴BD=AD ,AB=2BE .∴Rt △BDM ≌△ADN ,∴∠BDM=∠AND .∴∠BDM+∠ADM =∠AND+∠ADM =∠MDN .∴∠ADB=90°.∴222BD AD +=. 即2.∵在Rt △AND 中,AD 是斜边,DN 是直角边,∴AD >DN 22DN .∴2BE >CD .故此选项说法错误.C 、∵BD=AD ,∠ADB=90°,∴△ABD 是等腰直角三角形.∴DE=12AB . 在Rt ABC △中,90ACB ∠=︒,30ABC ∠=︒, ∴AC=12AB . ∴DE=AC .故此选项说法正确.D 、∵Rt △BDM ≌△ADN ,∴BM=AN.∴CN=AC+AN=AC+BM=CM.∴BC=BM+CM=AC+2BM.∵CD=2CN,∴2CD=2CN=2AC+2BM=AC+2BM+AC.∵AC=12AB,∴2CD=12AB+BC.故此选项说法正确.故选:B.【点睛】本题属于三角形综合题,考查了直角三角形的性质,全等三角形的判定与性质,勾股定理等知识,难度较大,准确作出辅助线并灵活运用所学知识是解题的关键.3.D解析:D【分析】根据勾股定理和等腰直角三角形的面积公式,可以证明:以直角三角形的两条直角边为斜边的等腰直角三角形的面积和等于以斜边为斜边的等腰直角三角形的面积.则阴影部分的面积即为以斜边为斜边的等腰直角三角形的面积的2倍.【详解】解:在Rt△AHC中,AC2=AH2+HC2,AH=HC,∴AC2=2AH2,∴2,同理:22,在Rt△ABC中,AB2=AC2+BC2,AB=6,S阴影=S△AHC+S△BFC+S△AEB=12HC•AH+12CF•BF+12AE•BE,即22211112224222++=(AC2+BC2+AB2)14=(AB 2+AB 2) 12=AB 2 2162=⨯ 18=.故选:D .【点睛】本题考查了勾股定理的知识,难度适中,解题关键是运用勾股定理证明三个等腰直角三角形的面积之间的关系.4.C解析:C【分析】利用勾股定理求BC 的长度,连接AE ,然后设BE=AE=x ,结合勾股定理列方程求解.【详解】解:如图,∵Rt △ABC 中,∠ACB=90°,∴22221086BC AB AC =-=-=,∵DE 是AB 的垂直平分线,∴BD=12AB=5,∠EDB=90°,AE=BE 连接AE ,设AE=BE=x ,则CE=x-6在Rt △ACE 中,222(6)8x x -+=,解得:253x =∴BE=AE=253 在Rt △BDE 中,ED=22222520()533BE BD -=-=. 故选:C .【点睛】本题考查了勾股定理解直角三角形和线段垂直平分线的性质,掌握相关性质定理正确推理计算是解题关键.5.D解析:D【分析】在Rt △ABD 及Rt △ADC 中可分别表示出BD 2及CD 2,在Rt △BDM 及Rt △CDM 中分别将BD 2及CD 2的表示形式代入表示出BM 2和MC 2,然后作差即可得出结果.【详解】解:在Rt △ABD 和Rt △ADC 中,BD 2=AB 2−AD 2,CD 2=AC 2−AD 2,在Rt △BDM 和Rt △CDM 中,BM 2=BD 2+MD 2=AB 2−AD 2+MD 2,MC 2=CD 2+MD 2=AC 2−AD 2+MD 2,∴MC 2−MB 2=(AC 2−AD 2+MD 2)−(AB 2−AD 2+MD 2)=AC 2−AB 2=45.故选:D .【点睛】本题考查了勾股定理的知识,题目有一定的技巧性,比较新颖,解答本题需要认真观察,分别两次运用勾股定理求出MC 2和MB 2是本题的难点,重点还是在于勾股定理的熟练掌握.6.B解析:B【分析】连接BP ,根据已知条件求出AB=BC=1,由翻折得:BD=DE ,∠BDA=∠EDA ,AE=AB=1,1,证明△BDP ≌△EDP ,推出BP=EP ,当点P 与点D 重合时,即可求出PEC ∆的周长的最小值.【详解】连接BP ,在Rt ABC ∆中,90,45B BCA ︒∠=∠=︒,∴∠BAC=45BCA ∠=︒,AB=BC ,∴22222AB AC ===,∴AB=BC=1,由翻折得:BD=DE ,∠BDA=∠EDA ,AE=AB=1,∴1,在△BDP 和△EDP 中, BD ED BDP EDP DP DP =⎧⎪∠=∠⎨⎪=⎩,∴△BDP ≌△EDP ,∴BP=EP ,∴当点P 与点D 重合时,PE+PC=PB+PC=BC 的值最小,此时PEC ∆的周长最小, PEC ∆的周长的最小值为BC+CE=1+21-=2,故选:B ..【点睛】此题考查翻折的性质,勾股定理,全等三角形的判定及性质,解题的关键是根据翻折的性质证得△BDP ≌△EDP ,由此推出当点P 与点D 重合时PEC ∆的周长最小,合情推理科学论证.7.C解析:C【分析】设绳索有x 尺长,此时绳索长,向前推出的10尺,和秋千的上端为端点,垂直地面的线可构成直角三角形,根据勾股定理可求解.【详解】解:设绳索有x 尺长,则102+(x+1-5)2=x 2,解得:x=14.5.故绳索长14.5尺.故选:C .【点睛】本题考查勾股定理的应用,理解题意能力,关键是能构造出直角三角形,用勾股定理来解.8.D解析:D【分析】将CB 延长至点D ,使CB BD =,利用勾股定理求出AD 的长,即可求出结果.【详解】解:如图,将CB 延长至点D ,使CB BD =,∵2AC =,26CD BC ==,∴22436210AD AC CD +=+=2103AD BD +=+,一共有4个这样的长度,∴这个风车的外围周长是:()4210381012⨯+=+. 故选:D .【点睛】本题考查勾股定理,解题的关键是利用勾股定理求直角三角形边长.9.B解析:B【分析】根据题中已知条件,首先要考虑吸管放进杯里垂直于底面时露在杯口外的最长长度;最短时与底面对角线和高正好组成直角三角形,用勾股定理解答,进而求出露在杯口外的最短长度.【详解】①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16−12=4(cm ); ②露出部分最短时与底面对角线和高正好组成直角三角形,底面对角线长2234+,高为12cm ,由勾股定理可得:杯里面管长22512+=13cm ,则露在杯口外的长度最短为16−13=3(cm ),∴34h ≤≤故选:B .【点睛】本题考查了矩形中勾股定理的运用,解答此题的关键是要找出露在杯外面吸管最长和最短时,吸管在杯中所处的位置.10.B解析:B【分析】把此题转化成一个直角坐标系的问题,然后求各点坐标,最后利用勾股定理即可判断.【详解】设喷头在点P ,则A(6,0),B (3,0);C (3,3);D (4.5;1.5);P (14,0) 则AP=14-6=8m<10m ,故A 需调整;BP=14-3=11m>10m ,故B 不需调整;=,不需调整;=<10m ,故D 需调整;故选:B【点睛】此题考查了勾股定理的应用,根据坐标系找到相应点的坐标,根据勾股定理计算长度是解答此题的关键.11.C解析:C【分析】根据绝对值的非负性及算术平方根的非负性求出m=3,n=4,再分两种情况利用勾股定理求出第三边.【详解】∵30m -=,30m -≥≥,∴m-3=0,n-4=0,解得m=3,n=4,当3、4都是直角三角形的直角边长时,第三边长;当3是直角边长,4是斜边长时,第三边长=故选:C .【点睛】此题考查绝对值的非负性及算术平方根的非负性,勾股定理,根据绝对值的非负性及算术平方根的非负性求出m=3,n=4是解题的关键.注意:没有明确给出的是直角三角形直角边长还是斜边长时,应分情况求解第三边长.12.A解析:A 【分析】根据正方形的面积及直角边的关系,列出方程组,然后求解.【详解】解:由条件可得:22131131240a b ab a b ⎧+=⎪-⎪=⎨⎪>>⎪⎩, 解之得:32a b =⎧⎨=⎩. 所以2()25a b +=,【点睛】本题考查了正方形、直角三角形的性质及分析问题的推理能力和运算能力.二、填空题13.101【分析】取AB的中点O过D作DE⊥AB于E根据勾股定理解答即可得到结论【详解】解:取AB的中点O过D作DE⊥AB于E如图2所示:由题意得:OA=OB=AD=BC设OA=OB=AD=BC=r寸则解析:101【分析】取AB的中点O,过D作DE⊥AB于E,根据勾股定理解答即可得到结论.【详解】解:取AB的中点O,过D作DE⊥AB于E,如图2所示:由题意得:OA=OB=AD=BC,设OA=OB=AD=BC=r寸,则AB=2r(寸),DE=10寸,OE=12CD=1寸,∴AE=(r﹣1)寸,在Rt△ADE中,AE2+DE2=AD2,即(r﹣1)2+102=r2,解得:r=50.5,∴2r=101(寸),∴AB=101寸,故答案为:101【点睛】本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.14.3【分析】利用勾股定理可求出AC=8根据折叠的性质可得BD=ABDE=AE根据线段的和差关系可得CD的长设CE=x则DE=8-x利用勾股定理列方程求出x的值即可得答案【详解】∵∠ACB=90°BC=解析:3【分析】利用勾股定理可求出AC=8,根据折叠的性质可得BD=AB,DE=AE,根据线段的和差关系可得CD的长,设CE=x,则DE=8-x,利用勾股定理列方程求出x的值即可得答案.∵∠ACB =90°,BC =6,AB =10,∴,∵BE 为折痕,使AB 的一部分与BC 重合,A 与BC 延长线上的点D 重合,∴BD=AB=10,DE=AE ,∠DCE=90°,∴CD=BD-BC=10-6=4,设CE=x ,则DE=AE=AC-CE=8-x ,∴在Rt △DCE 中,DE 2=CE 2+CD 2,即(8-x )2=x 2+42,解得:x=3,∴CE=3,故答案为:3【点睛】本题考查了翻折变换的性质及勾股定理的应用,根据翻折前后的两个图形能够重合得到相等的线段并转化到一个直角三角形中,利用勾股定理列出方程是解此类题目的关键. 15.【分析】设在中利用勾股定理求出x 值即可得到AC 和CD 的长再求出AB 的长再用勾股定理求出BC 的长即可得到结果【详解】解:设∵∴即解得或(舍去)∴∵∴∴∴故答案是:【点睛】本题考查勾股定理解题的关键是掌1【分析】设AC DC x ==,在Rt ACD △中,利用勾股定理求出x 值,即可得到AC 和CD 的长,再求出AB 的长,再用勾股定理求出BC 的长,即可得到结果.【详解】解:设AC DC x ==,∵90C ∠=︒,∴222AC CD AD +=,即222x x +=,解得1x =或1-(舍去), ∴1AC DC ==, ∵12AC AB =, ∴2AB =,∴BC ===, ∴1BD BC CD =-=.1.【点睛】本题考查勾股定理,解题的关键是掌握利用勾股定理解直角三角形的方法.16.16【分析】求不规则四边形的面积可以转化为两个三角形的面积由题意可知:求出与的面积即为四边形ABCD 的面积【详解】连接AC ∵∴∴∵AB+BC=8∴∴∴故答案为:16【点睛】本题主要考查的是四边形面积解析:16【分析】求不规则四边形的面积,可以转化为两个三角形的面积,由题意B D 90∠∠==︒,可知:求出Rt ABC 与Rt ADC 的面积,即为四边形ABCD 的面积.【详解】连接AC ,∵B D 90∠∠==︒,∴222AB BC AC +=,222AD DC AC +=, ∴11=22ABC ADC ABCD S S S BC AB CD AD +=⋅+⋅四边形21122BC AB AD =⋅+ ()2221111=2224BC AB CD AB BC AB BC ⋅+=⋅++, ∵AB+BC=8, ∴222=64AB BC BC AB ++⨯,∴4464ABC ADCS S +=, ∴=16ABC ADC ABCD S SS +=四边形故答案为:16.【点睛】本题主要考查的是四边形面积的求解,三角形面积以及勾股定理,熟练运用三角形面积公式以及勾股定理是解答本题的关键.17.【分析】将容器侧面展开建立A 关于EC 的对称点A′根据两点之间线段最短可知A′B 的长度即为所求【详解】如图将容器侧面展开作A 关于EC 的对称点A′连接A′B 交EC 于F 则A′B 即为最短距离∵高为1m 底面周解析:234 5【分析】将容器侧面展开,建立A关于EC的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【详解】如图,将容器侧面展开,作A关于EC的对称点A′,连接A′B交EC于F,则A′B即为最短距离.∵高为1m,底面周长为4m,在容器内壁离容器底部0.4m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.6m与蚊子相对的点A处,∴A′D=42=2(m),BD=1+0.6-0.4=1.2(m),∴在直角△A′DB中,2222234A'D BD2 1.2+=+=,故答案是:2345.【点睛】本题考查了平面展开-最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.18.8【分析】根据勾股定理求得AB的长再根据三角形的面积公式得到关于CD 的方程解方程求得CD即可【详解】解:∵在Rt△ABC中∠C=90°AC=6BC=8∴AB=10∵S△ABC=×6×8=×10×CD解析:8【分析】根据勾股定理求得AB的长,再根据三角形的面积公式得到关于CD的方程,解方程求得CD即可.【详解】解:∵在Rt△ABC中,∠C=90°,AC=6,BC=8,∴AB=10,∵S △ABC =12×6×8=12×10×CD , ∴CD =4.8.故答案为:4.8.【点睛】本题考查了直角三角形中的面积的求解,解题的关键是熟知等面积法求线段的长度. 19.【分析】根据条件作出示意图根据勾股定理求解即可【详解】解:由题意可画图如下:在直角三角形ABO 中根据勾股定理可得如果梯子的顶度端下滑1米则在直角三角形中根据勾股定理得到:则梯子滑动的距离就是故答案为 解析:1m【分析】根据条件作出示意图,根据勾股定理求解即可.【详解】解:由题意可画图如下:在直角三角形ABO 中,根据勾股定理可得,22534OA =-=,如果梯子的顶度端下滑1米,则'413OA m =-=.在直角三角形''A B O 中,根据勾股定理得到:'4OB m =,则梯子滑动的距离就是'431OB OB m -=-=.故答案为:1m .【点睛】本题考查的知识点是勾股定理的应用,根据题目画出示意图是解此题的关键. 20.【分析】根据勾股定理正方形的面积公式计算即可【详解】在Rt △ACB 中AC2+BC2=AB2=25则正方形ADEC 与正方形BCFG 的面积之和=AC2+BC2=25故答案为:25【点睛】本题考查的是勾股解析:【分析】根据勾股定理、正方形的面积公式计算即可.【详解】在Rt △ACB 中,AC 2+BC 2=AB 2=25,则正方形ADEC 与正方形BCFG 的面积之和=AC 2+BC 2=25.故答案为:25.【点睛】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么a 2+b 2=c 2.三、解答题21.(1)见解析;(2)17AD =【分析】 (1)根据△ABC 和△DCE 都是等腰直角三角形可得DC CE =,BC CA =,再根据两个角的和可得BCD ACE ∠=∠,从而判断两个三角形全等;(2)根据△ACE ≌△BCD ,以及角的和可得DAE △为直角三角形,根据DCE 为等腰直角三角形,可求出DE 的长度,再根据勾股定理求出AD 的长度即可.【详解】(1)△ABC 和△DCE 都是等腰直角三角形∴90BCA DCE ∠=∠=,DC CE =,BC CA =∴BCD DCA DCA ACE ∠+∠=∠+∠∴BCD ACE ∠=∠,∴△ACE ≌△BCD (SAS );(2)△ACE ≌△BCD∴CBD CAE ∠=∠∴90CBD BAC CAE BAC ∠+∠=∠+∠=∴DAE △为直角三角形DCE 为等腰直角三角形∴22223332DE DC CE =+=+=△ACE ≌△BCD∴BD=AE=1∴2218117AD DE AE =-=-=【点睛】本题主要考查了三角形全等的性质、判定定理以及勾股定理得运用,熟练掌握全等三角形的性质和判定定理,熟练运用角和角之间的关系是解题的关键.22.2秒【分析】设P 、Q 两点运动x 秒时,P 、Q 两点间的距离是210厘米,先利用勾股定理求出AC 的长度,得到AP=2x 厘米,CQ=x 厘米,CP=(10﹣2x )厘米,再利用勾股定理得到(10﹣2x )2+x 2=(210)2求出x 的值.【详解】解:设P 、Q 两点运动x 秒时,P 、Q 两点间的距离是210厘米.在△ABC 中,∠C=90°,BC=5厘米,AB=55厘米,∴AC=2222(55)5AB BC -=-=10(厘米),∴AP=2x 厘米,CQ=x 厘米,CP=(10﹣2x )厘米,在Rt △CPQ 内有PC 2+CQ 2=PQ 2,∴(10﹣2x )2+x 2=(210)2,整理得:x 2﹣8x+12=0,解得:x=2或x=6,当x=6时,CP=10﹣2x=﹣2<0,∴x=6不合题意舍去.∴P 、Q 两点运动2秒时,P 、Q 两点间的距离是210厘米.【点睛】此题考查勾股定理,动点问题与几何图形,熟练掌握勾股定理的计算公式并运用解决问题是关键.23.132【解析】 试题分析:过点B 作BC ⊥AD 于C ,可以计算出AC 、BC 的长度,在直角△ABC 中根据勾股定理即可计算AB .试题过点B 作BC ⊥AD 于C ,所以AC=4﹣2+0.5=2.5m ,BC=4.5+1.5=6m ,在直角△ABC 中,AB 为斜边,则22225136()22AB BC AC =+=+=m,答:机器人从点A到点B之间的距离是132m.考点:勾股定理.24.(1)见解析;(2)25;(3)3【分析】(1)在平面直角坐标系中,描出A,B,C三点,然后顺次连接,即可画出△ABC;(2)由勾股定理来求线段BC的长度;(3)△ABC的底是BC的长度,高是点C的纵坐标,由三角形的面积公式进行解答.【详解】解:(1)如图所示;(2)在直角△BOC中,由勾股定理得到:BC=22OB OC+=2242+=25,即线段BC的长是25;(3)S△ABC=12AC×OC=12×3×2=3,即△ABC的面积是3.【点睛】本题考查了勾股定理,坐标与图形性质.勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.25.(1)宽屏更适合人体工程学要求,理由见解析;(2)需要预留的长方形位置的长为178cm,宽为101cm;(3)普屏的屏幕面积大,理由见解析【分析】(1)根据人体工程学要求求出宽与长的比与0.618比较大小即可(2)根据勾股定理先求出80寸的宽屏..电视机的长和宽,再分别加2即可(3)分别求出宽屏的屏幕面积和普屏的屏幕面积比较大小即可【详解】解:(1)宽屏更适合人体工程学要求,理由如下:∵宽屏的长宽比为16:9;∴宽屏的宽与长的比为9:16=0.5625;∴0.5625-0.618=-0.0555∵普屏的长宽比为4:3.∴普屏的宽与长的比为3:4=0.75∴0.75-0.618=0.132∴宽屏更适合人体工程学要求(2)∵宽屏的长宽比为16:9;∴设长为16xcm ,则宽为9xcm(x>0),∵电视机屏幕为80寸,∴(16x )2+(9x )2=(80 2.54)⨯2, ∴18.4x=80 2.54≈⨯∴x 11≈,∴长为16x=1611=176cm ⨯,宽为9x=911=99cm ⨯∴需要预留的长方形位置的长为:176+2=178cm,宽为:99+2=101cm(3)普屏的屏幕面积大,理由如下:设相同尺寸为a 寸,宽屏电视的长宽分别为16m 和9m ,普屏电视的长宽分别为4n 和3n∴222(16m)(9m)(2.54a)+=,222(4n)(3n)(2.54a)+= ∴2222.54a m 337=,222 2.54a n =25 ∴宽屏的屏幕面积=22214416m 9m 144m =2.54a 337⨯=⨯ 普屏的屏幕面积=222124n 3n 12n =2.54a 25⨯=⨯ ∵1441233725< ∴普屏的屏幕面积大【点睛】本题考查了勾股定理的应用以及长方形的面积,读懂题意,根据已知条件得出所需内容是解题的关键26.(1)4,96;(2)196.【分析】(1)根据题意得图中的四个直角三角形都全等,可得正方形EFGH 的边长为2,即可得正方形EFGH 的面积;再利用正方形ABCD 的面积-正方形EFGH 的面积即可得四个直角三角形的面积和;(2)易求得ab 的值,和a 2+b 2的值,根据完全平方公式即可求得(a+b )2的值,即可解题.【详解】(1)根据题意得,图中的四个直角三角形都全等,∴AB=c=10,AE-AH=b-a=2,∴正方形EFGH 的面积为22=4,正方形ABCD 的面积为102=100,∴四个直角三角形的面积和=正方形ABCD 的面积-正方形EFGH 的面积=100-4=96;(2)由(1)可知四个直角三角形的面积和为96,14962ab ∴⨯=,即296ab =. 222100a b c +==,()222210096196a b a b ab ∴+=++=+=. 【点睛】本题考查了完全平方公式的应用,考查了直角三角形中勾股定理的运用,求得ab 的值是解题的关键.。
Robocon机器人大赛历届比赛情况

印度·普内
哈尔滨工业大学代表中国参加国际赛。没有给任何对手任何的机 会,5场比赛都以相当稳定的18秒5的惊人成绩,干净漂亮地结束 了每一场比赛,稳健地走上了冠军领奖台,为中国实现“三连冠 ”。
日本·东京
电子科技大学代表中国队出征亚太区国际比赛,夺得冠军,实现 “四连冠”!
埃及·开罗
由于国际赛主办方的某些原因,泰国一队、泰国二队分别获得比 赛的冠亚军。
第5届
2006
1.比赛主题源于著名的吉隆坡标志性建筑--双子塔; 修建双子高 2.比赛的意图是以一组机器人用聚苯乙烯积木模仿建造双子塔 塔 及其周边建筑。首先建成双塔之一和两个“天桥”桥墩的参赛 队,实现了“竣工”,将获得胜利。
第6届
2007
1.比赛主题源于黄帝造指南车的故事,首次采用类似圆形的自 动区场地; 华夏之光 2.比赛要求参赛队操作代表皇帝的手动机器人与代表工匠的自 动机器人配合,把木块放到“战车”上并占有它。最先占有场 地中央的“战车”建成V字形“指南车”的参赛队获胜。
第1届
2002
第2届
2003
1.比赛以太空征服为主题,场上悬挂着多个篮筐,象征太空; 2.比赛的意图是将藤球射入9个篮筐内;每一个篮筐包含3个排 太空征服者 列成三角形的网袋,按照得分情况判定比赛的输赢;如某参赛 队将球射入包括中心篮筐3个网袋在内的所有篮筐,或者它的 得分比对手高时,该队将被视为获胜。
梅地亚影视中心
冠军:华中科技大学 亚军:国防科技大学 季军:哈尔滨工业大学 电子科技大学
哈尔滨工程大学
冠军:电子科技大学 亚军:国防科技大学 季军:华中科技大学 北京科技大学
冠军:电子科技大学 亚军:国防科技大学 国防科学技术大学 季军:哈尔滨工程大学 太原工业学院
机器人比赛简介

5.2 灭火竞赛 机器人灭火竞赛机器人灭火的想法是在1994年由美国三 一学院的JackMendelssohn教授首先提出的。比赛是在一 套模拟四室一厅住房内进行,要求参赛的机器人在最短的时 间内熄灭放置在任意一个房间中的蜡烛。参赛选手可以选择 不同的比赛模式,比如,在比赛场地方面可以选择设置斜坡 或家具障碍,在机器人的控制方面可选择声控和遥控,熄灭 蜡烛所用的时间最短,选择模式的难度最大,综合扣分最少 的选手为冠军。虽然比赛过程仅有短短几分甚至几秒钟的时 间,用来灭火的机器人体积也不超过3l立方厘米,但其中包 含了很高的科技含量。机器人装备了数据处理芯片、行走、 灭火装置以及火焰探测器、光敏探测器、声音探测器、红外 探测器和超声波探测器等各种仪器,这些设备使机器人好像 长了脑子、眼睛、耳朵和手脚,从而能够根据场地的不同情 况,智能性地完成避障、寻火、灭火等任务。目前,机器人 灭火比赛已成为全球最普及的智能机器人竞赛之一。
4、推动技术进步:机器人大赛对机器人技术及其相关学科领域的发展
起到了明显的推动作用,这在机器人足球系列比赛上体现得更加明显。 比如,机器人足球比赛对机器人的视觉功能要求非常高,只有机器人装 备的显卡性能越好,机器人的识别速度就越快,运动速度也就越快,这 样才能取得比赛的胜利,这就极大地促进了视觉技术的发展。在1996年, FIRA第一届比赛的时候,大部分参赛队所用显卡的工作频率是10桢/秒, 机器人的运动速度也仅在50厘米/秒;仅仅两年之后的FIRA第三届世界 杯时,显卡的频率就达到了60桢/秒,机器人的运动速度也相应提升到2 米/秒,技术指标翻了几倍之多。机器人大赛实际上是高技术的对抗赛, 从一个侧面反映了一个国家信息与自动化领域基础研究和高技术发展的 水平。机器人大赛使研究人员能够利用各种技术,获得更好的解决方案, 从而又反过来促进各个领域的发展,这也正是开展机器人大赛的深远意 义,同时也是机器人大赛的魅力所在。 5、促进学校教育:机器人足球系列比赛以推动技术进步为主要着眼点, 而其他综合性的比赛则更加侧重于教育意义。以FLL为例,FLL的每个 参赛队在每年的工程挑战赛主体公布之后,会有大约8个星期的时间来 做准备工作,具体包括分析竞赛题目、设计解决方案、用乐高的配件搭 建智能机器人模型、编写程序、反复不断的调试程序,优化程序和机器 人结构,使机器人能够完成挑战赛的任务。在这8个星期的时间里,孩 子们要想完成任务,就必须在互联网上搜集资料、向专家请教问题、到 图书馆查阅资料以及与其它伙伴交流、探讨问题等等,这同时也是一个 面对实际问题、解决困难、克服障碍的过程。因此,孩子们除了学到了 机器人相关知识之外,还能够在自尊心、沟通能力、动手能力等方面得 到一定的提高,而这也正是FLL以及其他机器人竞赛所要达到的目标之 一。
机器人游中国技术文档

中国第一届机器人旅游大赛设计创新竞赛技术报告参赛学校:______________________ 院/系/所/室/中心: ______________________ 机器人姓名:______________________ 领队老师:______________________ 指导老师:______________________学生队员信息表姓名专业年级手机中国第一届机器人旅游大赛组委会制二Ο一四年五摘要智能小车作为现代的新发明,是以后的发展方向,它可以按照预先设定的模式在一个环境里自动的运作,不需要人为的管理,可应用于科学勘探、危险作业等等的用途。
因此研究和开发智能小车控制系统具有十分重要的意义。
本设计是以中国机器人大赛暨RoboCup公开赛“机器人旅游”项目为背景,采用STM32F103ZET6作为主控芯片,设计制作了一款人型智能循迹小车。
本文采用总分的形式展开的,首先从整体设计上对小车做个简单的概述,再分别从小车的硬件结构和软件设计进行了详细的描述。
小车由底盘和人型上身构成,采用完整的两片半桥驱动芯片+极低内阻的N沟道MOSFET构造而成的电机驱动器,在灰度传感器、红外传感器以及触碰开关反馈信号的作用下,小车能够实现前进、后退、左转、右转等基本功能,可以自主识别路障,寻找最佳路径,并在到达景点处实现语音播报;人型上身由8个舵机构成,各关节可以自由活动,也为以后实践中完成任务提供了可能。
传感器将采集到的信号传给单片机进行处理,再由主控系统发出相应的控制信号给电机驱动,从而控制小车在预定的场地上实现自主识别路径,自主行进,自主触碰景点并且语言播报,最终完成“旅游”的任务。
关键词:STM32F103ZET6;智能循迹小车;传感器;电机驱动;舵机AbstractSmart car as a modern new invention is the future direction of development, in an environment where it can operate automatically at preset mode, without human management can be applied to the use of science exploration, dangerous jobs, etc.. Therefore, the research and development of intelligent car control system has great significance.The design is based on China Robot Competition and RoboCup Open "robot tourism" project as the background, using STM32F103ZET6 as the master chip, designed and manufactured a person intelligent tracking car. This paper takes the form of expanded score, first from the overall design of the car to be a simple overview, and then were small cars hardware architecture and software design are described in detail.Car from the chassis and humanoid upper body composition, using a complete two half-bridge driver IC + low resistance N-channel MOSFET drive motor constructed role in grayscale sensors, infrared sensors and touch switch feedback signal Next, the car can achieve forward, backward, turn left, turn right, and other basic functions, you can self-identify placement of barricades, find the best route and arrive at the voice broadcast attractions; humanoid upper body constituted by the eight servos, Each joint can move freely, but also for the future practice tasks possible. Sensors will be collected signal to the microcontroller for processing, and then issued by the main control system corresponding control signal to the motor driver to control the car to achieve self-recognition in a predetermined path venues, independent travel, attractions and self-touching language broadcaster, finalize the "Travel" task.Key Words:STM32F103ZET6;intelligent car;sensor;motor drive ;servos目录一、任务、背景和意义1.比赛研究背景1.1.项目的名称基于STM32开发平台的中国机器人旅游大赛之探险游1.2.国内的比赛情况机器人旅游竞赛项目起源于2004年的“机器人游北京”,及随后的“机器人游南京”、“机器人游江苏”、“机器人游中国”。
足球机器人历年比赛

目前全国有一百六十多所高校参加机器人比赛,以下是在这些高校中选出的八个(清华大学、中国科学技术大学、上海大学、国防科技大学、大连理工大学、浙江大学、东南大学和上海交通大学)最具代表性和成绩比较优异的大学参加足球机器人比赛的情况。
清华大学机器人实验室:自动化系控制理论所辖下有个机器人实验室,精密仪器系,计算机系也有但是不做硬件。
1998年在国内引入了Robocup仿真比赛。
2001年8月,第五届RoboCup世界杯赛在美国西雅图举行。
清华风神队获得冠军。
“广州理想杯2004中国足球机器人大赛”(2004年10月14-17日,广州)中荣获类人组最佳表演奖;主办:中国自动化学会机器人竞赛工作委员会、科技部高技术研究发展中心;“2005中国机器人大赛”(2005年7月28-30日,江苏常州)中荣获类人组项目比赛冠军,舞蹈组亚军;主办:中国自动化学会机器人竞赛工作委员会、科技部高技术研究发展中心“2004滨州机器人邀请赛”中荣获类人组表演奖,主办:中国自动化学会机器人竞赛工作委员会、山东滨州市人民政府。
中国科技大学1998年中国科技大学组建了国内第一支RoboCup仿真足球队。
1999年首届全国RoboCup仿真机器人足球赛在重庆举行。
中国科技大学夺得了冠军和亚军。
2000年中国科技大学的代表队首次参加RoboCup2000世界杯仿真组比赛中,在110个队的较量中闯入决赛,并夺得第九名的好成绩。
2001中国RoboCup2001仿真比赛随中国智能自动化学术年会于2001年8月13日-16日在昆明成功举行。
本次活动中共有来自清华大学、中国科技大学、浙江大学、上海大学等学校的12支仿真机器人足球队参加了比赛。
2001年8月,第五届RoboCup世界杯赛在美国西雅图举行。
清华风神队获得冠军。
中国科技大学蓝鹰队进入仿真组和四腿组八强。
2002年6月,日本福冈第六届RoboCup世界杯赛,清华大学蝉联仿真组冠军,北京理工大学获得亚军,中国科技大学进入仿真组和小型组前8名。
过山车项目及规则

2014全国赛——过山车项目及规则(定稿)一、适用学段中小学各年级,每个项目组由3名参赛选手组成。
二、项目描述用给定的材料设计和制作一个轨道,让一颗钢珠从轨道的顶部释放,然后使钢珠在重力的作用下下滑,直至轨道的末端。
在轨道上滑行时间越接近指定值越好。
三、项目规则A.轨道设计:(1)轨道的最高端为90cm,有一个5 cm长呈凹槽状的平台,用以放置钢珠;(2)轨道的最末端离底座平面2cm,需有收集器来收集钢珠;(3)轨道必须在竖直平面上有一个360度回旋;(4)轨道必须有一个断口,断口两个端点的垂直距离不超过5 cm,直线距离为10cm。
承接端可以利用规定的材料做一个设备以便于接住钢珠,该设备的最前沿即为承接端端点(见图);(5)轨道必须限制在一个长90cm、宽50cm、高90cm的立体范围内;(6)本次比赛钢珠运行的时间在10s-18s范围内,具体的指定值在搭建轨道时公布;(7)制作轨道的材料由参赛队自带,但必须是赛规定的材料。
规定材料为:ф4mm的塑料线材(用作轨道)、轨道夹、ф16mmPVC电线管、ф16mm三通接头、塑料棒、硬卡纸、ф3mm螺丝螺母、木质底座、其他连接材料等。
B.现场搭建:必须有一份完整的设计图纸和说明,并根据现场宣布的钢珠滑行时间修订设计数据,图纸上必须标有尺寸;工具和粘结材料自备。
钢珠自备,钢珠的直径为16mm;所有材料必须是原始的,既没有任何组装或已制成单体部件;搭建时间为3小时。
C.测试:(1)用手指轻推轨道顶端平台上的钢珠使其滑下;(2)在整个滑行过程中,不得再碰钢珠,以及不能施加任何能够引起钢珠改变运动状态的外力,否则该轮测试视作失败;(3)钢珠没能到达轨道末端就翻出轨道,则此轮测试视作失败;(4)如果钢珠在轨道上停止不动达3秒,则此轮测试视作失败;(5)允许进行三轮测试,取最好的一轮为比赛成绩;(6)一次测试完后可以对装置进行调整,但调整时间不能超过15分钟。
D.评分标准:(1)没有项目报告书不能参加比赛;(2)时间分:到达终点时,所用时间与规定时间之间的差值,以秒为单位,精确到小数后2位;此差值越小越好;(3)在时间分相同的情况下,以项目报告书的成绩排序。
技能大赛口号

技能大赛口号(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如规章制度、演讲致辞、合同协议、条据书信、活动方案、自我介绍、心得体会、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as rules and regulations, speeches, contract agreements, document letters, activity plans, self introductions, experiences, teaching materials, complete essays, other sample essays, and more. If you want to learn about different sample formats and writing methods, please stay tuned!技能大赛口号技能大赛口号14篇在现实生活或工作学习中,大家都看到过口号吧,口号是指挥一个团队共同行为的指令。
刘妙

2014年9月1日,参演的都市情感剧《良心》播出,饰演的“三好女儿”刘小娟 ;随后,主演的神话剧情 片《妈祖的传说》在央视六套播出,饰演乐善好施的妈祖娘娘 ;同年,参加天津卫视的社交生存真人秀《百万 粉丝》 。
刘妙
中国内地影视女演员
01 早年经历
03 社会活动
目录
02 演艺经历 04 人物评价
基本信息
刘妙,1987年10月21日出生于四川省成都市,毕业于重庆大学美视电影学院,中国内地影视女演员。 2 0 11 年 , 参 演 警 匪 剧 《 鹰 巢 之 预 备 警 官 》 , 从 而 正 式 进 入 演 艺 圈 。 2 0 1 4 年 , 主 演 的 神 话 剧 情 片 《 妈 祖 的 传 说》上映 。2015年,担任“熊猫保护爱心大使” 。2016年,获得第四届亚洲微电影节“金海棠奖”最佳新人 奖 。2017年,参演动作剧情片《擒贼先擒王》 。2022年,主演的革命人物传记电影《**小道》在中国大陆上映。
2022年4月22日,参演的革命人物传记片《**小道》上映,饰演遭遇困境却依然苦中作乐的**小女儿邓榕 ; 9月10日,参演的喜剧电影《暖暖的微笑》上映 ;11月,主演乡村振兴正能量题材电影《山那边的美好》 。
社会活动
社会活动
2 0 1 5 年 9 月 2 5 日 , 中 国 ·四 川 大 熊 猫 国 际 生 态 旅 游 节 暨 都 江 堰 首 届 大 熊 猫 生 态 旅 游 节 开 幕 式 在 都 江 堰 市 举 行 。 刘妙带领志愿者们宣读倡导大熊猫保护的《都江堰宣言》,并和张信哲、古亚鹏、阿斯根一同被授予“熊猫保护 爱心大使” 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年中国第一届机器人旅游大赛
“越野游”竞赛规则(室内地毯跑道1.0版)
一、竞赛类别
§1.1竞赛级别类型设置
二、机器人及报名要求
1、机器人由其教练操作启动和停止。
2、尺寸形状,要适应赛场地,不得伤害人,不得损坏场地与环境。
3、允许机器人在比赛中,为了降低重心等目的自动变形,但不得抛洒任何物体。
4、越野过程中,机器人可能会发生碰撞,要有相应的对策,但不允许恶意竞争。
5、参赛对象:在校学生为主研制的机器人。
三、场地、路线、环境
1、场地
室内地毯跑道运动场。
地毯与探险寻宝场地相同。
路途中摆放由密度板、塑料、布料、金属、沙、水等制成的特殊障碍设施。
不抢道比赛时,机器人沿白色引导线跑。
引导线宽度约23-26mm,两条引导线间距为500mm。
2、赛道/跑道
红色中心分隔线和场地边框线,线宽约23-26mm;也可以是200-600mm高宣传布,但底部和顶部各有一条30mm以上的肯定是红色。
机器人从起点出发后,沿赛道前行,然后围绕中心分隔线逆时针前进, 第2圈开始可抢跑道。
四、障碍
模仿野外环境,障碍的制作也不求精细,表现为尺寸有误差。
用普通密度板制作,表面为密度板原色。
1、双驼峰
为连续两个等腰三角条(峰高100mm,底边总长1200mm,宽度覆盖3个赛道)。
2、悬崖
高坡道,长600mm×高150mm;低坡道,长500mm×高125mm;悬崖间距30mm,底边总长1200mm(以后将适度增加高低差及间距),宽度覆盖3个赛道。
3、梯形山峰
四层梯形:第一层(底层),宽度覆盖3个赛道1500,,长1200mm;
第二层,宽度覆盖2.5个赛道,长1250mm;
第三层,宽度覆盖2.5个赛道,长750mm;
第四层,宽度覆盖0.5个赛道,长250mm。
各层厚度均为9mm。
4、波浪板
与探险寻宝游相同,此略。
五、竞赛程序、计时、排序
分组竞赛,每组1-3名机器人。
采用秒表计时。
1、初赛:各小组成绩混合排序,得出名次。
前50%机器人进入复赛。
2、复赛:各小组成绩混合排序,得出名次。
前9个机器人进入决赛。
3、决赛:各小组成绩混合排序,得出名次。
如时间相同,根据上一轮比赛成绩决定次序。
根据报名情况及赛场条件,实际赛场以报名后发布的为准。
六、其他
1、计划采用9mm 的中密度板制作(不包括波浪板)。
2、如与组委会规章不一致的,以组委会规章为准。
