坐标法面积、周长计算程序

合集下载

c++计算三角形面积海伦定理坐标

海伦定理是用来计算三角形面积的数学定理，它是由英国数学家海伦提出的，因此得名。

根据海伦定理，我们可以通过三角形的三条边长来计算其面积，而不需要知道三角形的高度。

这个定理在实际应用中非常有用，尤其是在计算机编程中。

在C++编程中，我们经常会遇到需要计算三角形面积的情况。

海伦定理为我们提供了一个简便的方法来实现这一计算。

下面，我将从简到繁地介绍C++中如何利用海伦定理来计算三角形面积。

一、海伦定理的原理和公式在介绍C++中的具体实现方法之前，我们需要先了解海伦定理的原理和公式。

海伦定理的公式如下：\[S = \sqrt{p(p-a)(p-b)(p-c)}\]其中，S代表三角形的面积，a、b、c分别代表三角形的三条边长，p 为半周长，计算公式如下：\[p = \frac{a + b + c}{2}\]海伦定理的原理是利用三角形的三条边长来计算其面积，而不需要借助三角形的高度。

这一点对于计算机编程而言非常实用，因为通常情况下我们只能直接获取三角形的三条边长。

二、C++实现海伦定理计算三角形面积在C++中，我们可以通过函数来实现利用海伦定理计算三角形面积的功能。

我们可以定义一个函数，命名为calcTriangleArea，该函数接受三个参数，分别代表三角形的三条边长。

函数的实现如下：```cpp#include <iostream>#include <cmath>using namespace std;double calcTriangleArea(double a, double b, double c) { double p = (a + b + c) / 2;double area = sqrt(p * (p - a) * (p - b) * (p - c));return area;}int m本人n() {double a, b, c;cout << "请输入三角形的三条边长：" << endl;cin >> a >> b >> c;double area = calcTriangleArea(a, b, c);cout << "三角形的面积为：" << area << endl;return 0;}```在上面的代码中，我们首先定义了calcTriangleArea函数，它接受三个double类型的参数a、b、c，并返回一个double类型的面积值。

测量CAD面积和长度的几种简单方法

测量CAD图面积与长度的简单办法测量Cad图纸中的面积与长度的方法很多，以下是根据自己多年的使用经验，总结出来的几种比较简单实用的方法，大家可根据个人的习惯，总结出更适合自己的测量方法。

一、图形面积和周长最省事的方法：1.测量闭合图形面积和周长简单而准确方法：如果要测量的是一个闭合的图形，只需要用鼠标左键点一下待测量闭合图形的任意一点，然后回车，面积和周长就都计算并显示出来了。

2.测量连续线段图形面积和周长简单的方法：如果要测量的是一个非闭合的连续线段图形可按以下方法测量：1)在命令行输入LI并回车；2)用鼠标左键点击需要测量的连续线段；3)回车后即可看到刚刚测量的，连续线段图形的面积与周长。

二、测量简单图形面积和周长的方法：如果要测量的是一个非闭合也非连续线段的矩形，可按以下步骤进行测量：1)对象捕捉置于开的状态；2)用鼠标点击工具栏中的矩形选项或在命令行输入rec回车；3)用鼠标点击待测矩形的一个角点；4)用鼠标点击待测矩形的对角点；5)用鼠标点击待测矩形的任一点（选取矩形框）；6)在命令行输入LI并回车，面积和周长就都计算并显示出来了。

三、测量复杂图形面积的方法：1.方法一：1)用鼠标点击工具栏中的多段线选项或在命令行输入PL并回车；2)用鼠标逐个点击待测图形的一个每一个角点，至最后一个非闭合角点；3)在命令行输入C并回车，令图形闭合；4)用鼠标点击待测图形的任一点（选取该图形）；5)在命令行输入LI并回车，面积和周长就都计算并显示出来了。

2.方法二：1)用鼠标点击工具栏中的区域图标选项或在命令行输入AREA并回车；2)用鼠标逐个点击待测图形的一个每一个角点，至最后一个闭合角点；3)直接回车后即可计算并显示出已测图形的面积和周长。

3.方法三：1)用鼠标点击标题栏中的工具选项；2)在下拉菜单中选中查询---面积；3)用鼠标逐个点击待测图形的一个每一个角点，至最后一个闭合角点；4)直接回车后即可计算并显示出已测图形的面积和周长。

CAD计算面积所有方法

CAD计算面积所有方法汇总CAD中关于测量面积的操作方法“查询”工具栏:“工具”菜单:查询面积命令行:area指定第一个角点或[对象(O)/添加(A)/减(S)]: 指定点(1) 或输入选项第一角点计算由指定点定义的面积和周长。

所有点必须都在一个与当前用户坐标系(UCS) 的XY 平面平行的平面上。

指定下一个角点或按ENTER 键全选: 指定点(2)继续指定点定义多边形,然后按ENTER 键完成周长定义。

如果不闭合这个多边形,AutoCAD 在计算该面积时假设从最后一点到第一点绘制了一条直线。

计算周长时,AutoCAD 加上这条闭合直线的长度。

对象计算选定对象的面积和周长。

可以计算圆、椭圆、样条曲线、多段线、多边形、面域和实体的面积。

注意二维实体(使用SOLID 命令创建)不报告面积。

选择对象:如果选择开放的多段线,AutoCAD 在计算面积时假设从最后一点到第一点绘制了一条直线。

然而计算周长时,AutoCAD 忽略此直线。

计算面积和周长(或长度)时将使用宽多段线的中心线。

添加打开“加”模式后,继续定义新区域时应保持总面积平衡。

“加”选项计算各个定义区域和对象的面积、周长,也计算所有定义区域和对象的总面积。

可以使用“减”选项从总面积中减去指定面积。

指定第一个角点或[对象(O)/减(S)]: 指定点(1) 或输入选项第一角点计算由指定点定义的面积和周长。

所有点必须都在一个与当前UCS 的XY 平面平行的平面上。

指定下一个角点或按ENTER 键全选(“加”模式): 指定点(2)指定点来定义多边形(3)。

按ENTER 键后AutoCAD 开始计算其面积和周长。

并且,打开“加”模式后,AutoCAD 将返回所有由选定点或选定对象定义的区域的总面积。

如果不闭合这个多边形,AutoCAD 在计算该面积时假设从最后一点到第一点绘制了一条直线。

计算周长时,AutoCAD 将加上这条闭合直线的长度。

对象计算选定对象的面积和周长。

三角形坐标求面积公式

三角形坐标求面积公式三角形是一个由三条线段组成的图形，它有三个顶点和三条边。

我们可以使用坐标来计算三角形的面积，其中每个顶点的坐标可以表示为(x,y)。

在本文中，我将介绍三个方法来计算三角形的面积：海伦公式、向量法和行列式法。

方法一：海伦公式海伦公式是一种计算三角形面积的常用方法，它使用三条边的长度来计算。

根据海伦公式，三角形的面积可以通过以下公式计算：s=(a+b+c)/2area = √(s × (s - a) × (s - b) × (s - c))其中，a、b和c分别代表三角形的三条边的长度，s是三角形的半周长。

例如，假设三角形的顶点坐标分别为A(x1,y1)，B(x2,y2)和C(x3,y3)，我们可以通过以下步骤计算三角形的面积：1.计算每条边的长度：a=√((x2-x1)²+(y2-y1)²)b=√((x3-x2)²+(y3-y2)²)c=√((x1-x3)²+(y1-y3)²)2.计算半周长：s=(a+b+c)/23.计算面积：area = √(s × (s - a) × (s - b) × (s - c))方法二：向量法向量法是另一种计算三角形面积的方法，它使用两个边的向量的叉积来计算。

在使用向量法之前，我们需要计算两个边的向量。

对于两个向量A(x1,y1)和B(x2,y2)，向量AB可以通过以下公式计算：AB=(x2-x1,y2-y1)使用向量法来计算三角形的面积时，我们可以按照以下步骤进行：1.计算两条边的向量：AB=(x2-x1,y2-y1)AC=(x3-x1,y3-y1)2.计算两个向量的叉积：cross_product = AB×AC = (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)3.计算面积：area = 0.5 * ，cross_product方法三：行列式法行列式法是另一种计算三角形面积的方法，它使用矩阵的行列式来计算。

二次函数的周长与面积(含最值问题)

【知识梳理】一．二次函数之周长因为平面直角坐标系中点的坐标的几何意义为点到轴的距离，即横平竖直的线段长，所以处理二次函数压轴题的核心思想即为斜线段转化为横平竖直的线段（“斜转直”）．“斜转直”的几种处理思路：①斜线段转化为横平或竖直的线段；②计算有关周长或面积的问题其本质一般也可转化为计算线段，所以同样可利用“斜转直”来处理；③出现斜放的角时，一般也可根据该角构建直角三角形，来实现“斜转直”．二．二次函数之面积割补求面积——铅垂法：12APB B A S PM x x =⋅⋅- 12APB B A S PM x x =⋅⋅- Tips ：①过动点作铅垂线；②铅垂线平行于y 轴或垂直于x 轴．二次函数之周长与面积（含最值问题）【经典例题】【例一】1．如图，在平面直角坐标系中，抛物线y =（x ﹣2）2与x 轴交于点A ，与y 轴交于点B ．过点B 作BC ∥x 轴，交抛物线于点C ，过点A 作AD ∥y 轴，交BC 于点D ，点P 在BC 下方的抛物线上（P 不与B ，C 重合），连结PC ，PD ，则△PCD 面积的最大值是．2．已知直线经过点A （0，2），B （2，0），点C 在抛物线2y x 的图象上，则使得ABC S =2的点有（）个．A ．4B ．3C ．2D ．1【例二】1.如图，抛物线2(3)3(0)y ax a x a=+++≠与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若126 5CC=，求m的值；（3）求△PBA面积的最大值以及此时点E的坐标．2.如图，二次函数()2302y ax x c a =-+≠的图象与x 轴交于A 、B 两点，与y 轴交于C 点，已知点A （-1，0），点C （0，-2）．（1）求抛物线的函数解析式；（2）在抛物线的对称轴上，是否存在点Q ，使△ACQ 周长最短？若不存在，请说明理由；若存在，求出点Q 的坐标．（3）若点M 是线段BC 下方的抛物线上的一个动点，求△BCM 面积的最大值以及此时点M 的坐标．3.如图，在平面直角坐标系中，二次函数214y x bx c =-++的图象与坐标轴交于A 、B 、C 三点，其中点A 的坐标为（0，8），点B 的坐标为（-4，0）．（1）求该二次函数的表达式及点C 的坐标；（2）点D 的坐标为（0，4），点F 为该二次函数在第一象限内图象上的动点，连接CD 、CF ，以CD 、CF 为邻边作平行四边形CDEF ，设平行四边形CDEF 的面积为S ．求S 的最大值.4.如图，抛物线2=-++与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C，对称轴与y x bx c抛物线交于点P，与直线BC交于点M，连接PB．（1）求抛物线的表达式；（2）抛物线上是否存在异于点P的一点Q，使△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．（3）在第一象限对称轴右侧的抛物线上是否存在一点R，使△RMP与△RMB的面积相等？若存在，求出点R的坐标；若不存在，请说明理由．【能力训练】1．如图，在平面直角坐标系中，抛物线24y x x c =-++与y 轴交于点A ，过点A 作AB ∥x 轴交抛物线于点B ，则以AB 为边的等边三角形ABC 的周长为．2．如图所示，在平面直角坐标系中，点A 是x 轴上一动点，过A 作AC x ⊥轴交抛物线222y x x =++于点C ，以AC 为边作等边ABC ∆，高AD 的最小值为．3．如图，P 是抛物线22y x x =-++在第一象限上的点，过点P 分别向x 轴和y 轴引垂线，垂足分别为A ，B ，则四边形OAPB 周长的最大值为．4．如图，抛物线223y x x =-++与x 轴交于A ，B 两点，它的对称轴与x 轴交于点N ，过顶点M 作ME y ⊥轴于点E ，连结BE 交MN 于点F ．（1）求F 的坐标．（2）求EMF ∆与BNF ∆的面积之和．5.如图，在平面直角坐标系中，点A ，B 在x 轴上，点C ，D 在y 轴上且OB =OC =3，OA =OD =1，抛物线2(0)y ax bx c a =++≠经过A ，B ，C 三点，直线AD 与抛物线交于另一点E ．（1）求这条抛物线的解析式；（2）若M 是直线AD 上方抛物线上的一个动点，求△AME 面积的最大值．（3）在抛物线上是否存在点G ，使得AEG S =3？如果存在，求出点G 的坐标；如果不存在，请说明理由．。

java 点位经纬度计算周长和面积

java 点位经纬度计算周长和面积Java是一种广泛应用于地理信息系统（GIS）和地理定位应用程序开发的编程语言。

在使用Java进行地理位置计算时，经纬度是常见的地理坐标系表示方式。

本文将介绍如何使用Java计算给定经纬度点位的周长和面积。

在计算点位的周长和面积之前，首先需要了解经纬度的表示方法。

经度（Longitude）是指地球表面某一点与本初子午线之间的夹角，取值范围为-180度到180度。

纬度（Latitude）是指地球表面某一点与赤道之间的夹角，取值范围为-90度到90度。

经纬度的表示方式通常为一个包含两个浮点数的二元组，例如（39.9075, 116.3972），其中39.9075是纬度，116.3972是经度。

要计算点位的周长和面积，可以使用地理坐标系中的球面三角法。

球面三角法是一种用于计算地球上两点间距离和角度的方法。

Java 中可以使用Math库中的方法来进行球面三角计算。

我们来计算给定多个点位的周长。

周长是指连接多个点位的线段总长度。

假设我们有四个点位：A（39.9075, 116.3972）、B（39.908, 116.3972）、C（39.908, 116.398）、D（39.9075, 116.398）。

我们可以按照点位的顺序依次计算相邻点位之间的距离，并将其累加起来即可得到周长。

代码如下：```javaimport java.util.ArrayList;public class CalculatePerimeter {public static void main(String[] args) {ArrayList<Point> points = new ArrayList<>();points.add(new Point(39.9075, 116.3972));points.add(new Point(39.908, 116.3972));points.add(new Point(39.908, 116.398));points.add(new Point(39.9075, 116.398));double perimeter = 0;for (int i = 0; i < points.size() - 1; i++) {Point p1 = points.get(i);Point p2 = points.get(i + 1);double distance = calculateDistance(p1, p2);perimeter += distance;}System.out.println("周长为：" + perimeter);}private static double calculateDistance(Point p1, Point p2) {double lat1 = Math.toRadians(titude);double lon1 = Math.toRadians(p1.longitude);double lat2 = Math.toRadians(titude);double lon2 = Math.toRadians(p2.longitude);double dlon = lon2 - lon1;double dlat = lat2 - lat1;double a = Math.sin(dlat / 2) * Math.sin(dlat / 2) +Math.cos(lat1) * Math.cos(lat2) *Math.sin(dlon / 2) * Math.sin(dlon / 2);double c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));double distance = 6371 * c * 1000; // 地球半径为6371公里，转换为米return distance;}static class Point {double latitude;double longitude;public Point(double latitude, double longitude) {titude = latitude;this.longitude = longitude;}}}```以上代码中，我们定义了一个Point类来表示点位的经纬度坐标。

线段的长度和面积的计算

线段的长度和面积的计算在几何学中，线段是由两个端点所确定的一条直线段，它是研究几何形状和测量的基础。

计算线段的长度和面积是几何学中的基本操作，它们在实际生活和工作中具有广泛的应用。

本文将介绍线段长度和面积的计算方法，并给出一些实际问题的例子。

一、线段长度的计算方法线段的长度是指线段上各点之间的距离，计算线段长度的方法有多种，常用的方法包括几何法和坐标法。

1. 几何法：对于两个已知端点的线段，我们可以使用勾股定理来计算其长度。

假设线段的两个端点分别为A(x1, y1)和B(x2, y2)，则线段的长度AB可以用以下公式表示：AB = √((x2 - x1)² + (y2 - y1)²)2. 坐标法：如果线段的两个端点在坐标系上已知，则可以通过计算两个点的坐标差来获取线段长度。

设线段的两个端点分别为A(x1, y1)和B(x2, y2)，则线段的长度AB可以用以下公式表示：AB = |x2 - x1| + |y2 - y1|二、线段面积的计算方法在线段的两个端点已知的情况下，我们可以根据线段长度来计算线段的面积。

线段的面积是指线段与坐标轴构成的矩形的面积，计算线段面积的方法如下。

1. 若线段平行于坐标轴，则由线段的长度可得到矩形的长和宽，进而计算出面积。

- 若线段平行于x轴，则矩形的长为线段的长度，宽为线段与x轴之间的垂直距离。

- 若线段平行于y轴，则矩形的长为线段的长度，宽为线段与y轴之间的垂直距离。

2. 若线段不平行于坐标轴，即线段倾斜，可以通过利用三角形的面积来计算线段面积。

- 假设线段的两个端点为A(x1, y1)和B(x2, y2)，则以A、B和原点构成的三角形的面积为线段的面积。

三、实际问题的例子线段长度和面积的计算方法在实际生活和工作中有广泛的应用，下面以几个例子来进行说明。

1. 圆的周长和面积：在计算圆的周长和面积时，可以利用半径与圆的周长、面积之间的关系来计算。

卡西欧5800程序集

第十四篇坐标法面积、周长计算1. 坐标法面积、周长计算程序(命名为ZBMJ)第1行：FreqOn:ClrStat:ClrMemory第2行：“N=1”: 1→N: “X=”?→C: “Y=”?→D: C→A:D→B:A→List X[1] :B→List Y[1]第3行：Lbl 0:“N=”:N+1→N◢“X=”?→E: “Y=”?→F:E→List X[N] :F→List Y[N]第4行：Pol(E-C,F-D+10^(-45)): I→G:J→H:L+G→L第5行：Pol(E-A,F-B+10^(-45)): E→C:F→D:N=2=>J?DMS◢第6行：“PMT=”: N=2=>0→I: L+I◢第7行：“ARE=”:S+GIsin(J-H)÷2→S:Abs(S)→List Freq[N]◢第8行：Goto 0N——取样点的顺序号PMT——多边形的周长ARE——多边形的面积X——对应点号N的取样点X坐标Y——对应点号N的取样点Y坐标以上为5800程序，在9860中程序如下第1行：ClrList:0→L:0→S:0→List 3[1]:0→List 4[1]第2行：“N=1”: 1→N: “X=”?→C: “Y=”?→D: C→A:D→B:A→List 1[1] :B→List 2[1]第3行：Lbl 0:“N=”:N+1→N◢“X=”?→E: “Y=”?→F:E→List 1[N] :F→List 2[N]第4行：Pol(E-C,F-D+10^(-45)) : List Ans[1]→G:List Ans[2]→H:L+G→L第5行：Pol(E-A,F-B+10^(-45)) : List Ans[1]→I:List Ans[2]→J: E→C:F→D:N=2=>J?DMS◢第6行：“PMT=”: N=2=>0→I: L+I→List 3[N]◢第7行：“ARE=”:S+GIsin(J-H)÷2→S:Abs S→List 4[N]◢第8行：Goto 02．计算实例：N=1 X = 940.5392 Y = 898.4861N=2 X = 1114.8811 Y = 996.4907 PMT=200.000 ARE=0 (29°20′31.54″) N=3 X = 1065.8788 Y = 1083.6617 PMT=523.607 ARE=10000N=4 X = 1338.2253 Y = 1007.3243 PMT=995.153 ARE=20000N=5 X = 1261.8880 Y = 734.9778 PMT=1226.241 ARE=70000N=6 X = 1212.8857 Y = 822.1488 PMT=1248.528 ARE=60000N=7 X = 1038.5438 Y = 724.1442 PMT=1365.686 ARE=800003. 说明：（1）动态显示结果：按照一定顺序（逆时针或顺时针均可）依次取样输入到计算器，可动态显示周长和面积，并可以随时停止，最后一次显示结果为最终结果。

三角形的周长和面积的计算公式

三角形的周长和面积的计算公式在几何学中，三角形是最基本的图形之一。

计算三角形的周长和面积是几何学中最常见的问题之一。

有多种方法可以用来计算三角形的周长和面积，下面将介绍其中两种常用的方法。

一、利用边长计算三角形的周长和面积假设三角形的三个边的长度分别为a、b、c，我们可以根据这些边长来计算三角形的周长和面积。

1. 计算周长：三角形的周长等于三个边长的和，即P = a + b + c。

2. 计算面积：我们可以使用海伦公式来计算三角形的面积，公式为：S = √(s(s - a)(s - b)(s - c))其中，s为三角形的半周长，计算公式为s = (a + b + c)/2。

二、利用坐标计算三角形的周长和面积除了使用边长计算三角形的周长和面积外，我们还可以使用三角形的顶点坐标来进行计算。

假设三角形的三个顶点坐标分别为(x1, y1)，(x2, y2)，(x3, y3)，我们可以根据这些顶点坐标来计算三角形的周长和面积。

1. 计算周长：我们可以使用两点之间的距离公式来计算三角形的周长。

首先计算出三个边的长度：a = √((x2 - x1)² + (y2 - y1)²)，b = √((x3 -x2)² + (y3 - y2)²)，c = √((x1 - x3)² + (y1 - y3)²)。

然后将三个边长相加即可得到三角形的周长P。

2. 计算面积：我们可以使用行列式的方法来计算三角形的面积，公式为：S = 0.5 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|其中，|x|表示取x的绝对值。

三、总结通过上述两种方法，我们可以准确地计算出任意三角形的周长和面积。

在实际应用中，对于已知边长的三角形，使用第一种方法计算较为简便；而对于已知顶点坐标的三角形，使用第二种方法则更为方便。

无论采用哪种方法，掌握计算三角形的周长和面积的公式对于几何学的学习和实际问题的解决都具有重要意义。

三角形的计算

三角形的计算三角形是几何学中基本的图形之一，它有着广泛的应用和计算方法。

在本文中，我们将深入探讨三角形的计算方法，包括计算三角形的面积、周长、角度等。

1. 三角形的面积计算三角形的面积计算是三角形计算中最基本的一部分。

常见的计算三角形面积的方法有以下几种：1.1 高乘以底除以2法对于任意三角形，我们可以通过计算三角形的底边长度和对应高的乘积，再除以2来求得三角形的面积。

公式如下：面积 = 0.5 * 底边长度 * 高1.2 海伦公式海伦公式适用于已知三边长度的情况下，通过半周长计算三角形的面积。

海伦公式的表达式如下：面积 = 根号(p * (p - a) * (p - b) * (p - c))其中，p是三角形的半周长，a、b、c分别是三角形的三条边长。

2. 三角形的周长计算三角形的周长计算是指计算三角形三条边的长度之和。

常用的周长计算方法有以下两种：2.1 边长求和法直接将三角形的三条边长相加即可求得三角形的周长。

2.2 点到点距离法如果三角形的三个顶点的坐标已知，我们可以通过计算各顶点之间的距离，然后将距离相加得到三角形的周长。

3. 三角形的角度计算三角形的角度计算是指计算三角形内部三个角的大小。

根据三角形的性质和已知条件，我们可以使用以下方法来计算三角形的角度：3.1 三角函数法对于已知三角形的三边长度或者已知一个角和两边的情况，我们可以使用正弦定理、余弦定理等三角函数来计算三角形的角度。

3.2 角平分线法如果三角形的内切圆圆心坐标已知，我们可以通过连接圆心和三个顶点，得到三角形的三条角平分线。

然后利用平分线的性质计算角度大小。

综上所述，三角形的计算涉及到面积、周长和角度三个方面。

通过各种计算方法，我们可以准确地得出三角形的相关参数。

在实际应用中，这些计算方法被广泛运用于建筑设计、地理测量、物理学等领域，为我们提供了重要的数学工具和基础。

掌握三角形的计算方法，对于进一步深入理解几何学和应用数学有着重要的意义。

CAD各种面积周长计算大全

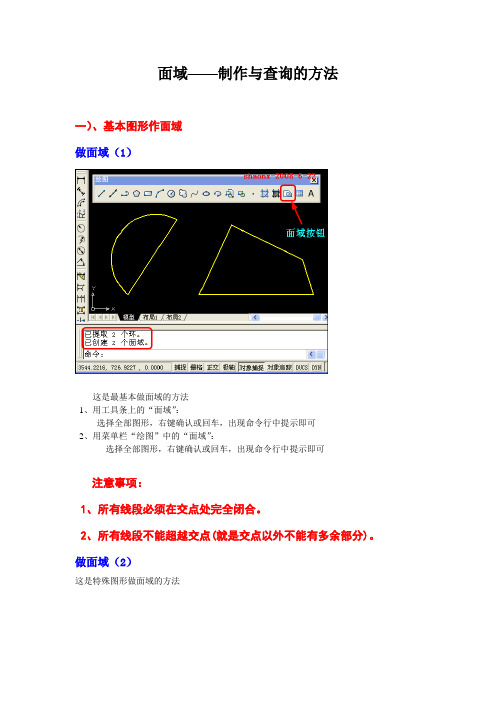
面域——制作与查询的方法一）、基本图形作面域做面域（1）这是最基本做面域的方法1、用工具条上的“面域”：选择全部图形，右键确认或回车，出现命令行中提示即可2、用菜单栏“绘图”中的“面域”：选择全部图形，右键确认或回车，出现命令行中提示即可注意事项：1、所有线段必须在交点处完全闭合。

2、所有线段不能超越交点(就是交点以外不能有多余部分)。

做面域（2）这是特殊图形做面域的方法如上图，求A、B的“面域”，用第一种方法就不行了具体做法如下：1、点击菜单栏的“绘图”，弹出下拉菜单：2、选择“边界”。

3、在对话框中，类型选“面域”，再点击“拾取点”。

4、在图形界面里点击A、B的内部后，所做成的面域与当前图层的颜色一致，同时，在命令行里也会出现已经做成面域的提示。

注意事项：所有线段必须在交点处完全闭合（二）、面域的操作（1）合并面域——就是将多个分散的面域合为一体如上图，如果要将A、B两个面域合并，可以使用菜单栏的“修改”→“实体编辑”→“并集”也可以使用“实体编辑”工具条中的“并集”命令具体操作如下：分别点选A、B两个面域右键确认或回车，两个面域即合为一体（2）扣除面域——就是从大面域中，扣除其他面域如上图，如果要将A面域中扣除B、C两个面域，可以使用菜单栏的“修改”→“实体编辑”→“差集”也可以使用“实体编辑”工具条中的“差集”命令具体操作如下：先点击A面域，右键确认或回车再分别点击B面域、C面域，右键确认或回车即可（三）、特殊情况的处理（1）一次做不成面域也许是CAD软件本身的缺陷，有时按常规做不成面域，如上图，在左下角这个狭长的区域作面域，应按照作面域的第二种方法，但提示：“找不到边界”等，无法做成面域，我的解决方法是：在区域内加辅助线条，如图中的红色线条，以缩小做面域的区域，如上图，加了1条辅助线条后，就可以做成2个面域，再合并，删除辅助线条，即做成1个面域。

（2）快速做成类似面域(封闭的多段线)大家知道，在CAD的三维操作时，如要拉升成实体，一定要将被拉升的对象做成面域，才可以拉升。

三角形的面积与周长计算让孩子使用不同方法计算三角形的面积和周长

三角形的面积与周长计算让孩子使用不同方法计算三角形的面积和周长三角形是几何学中的基本图形之一，它由三条边和三个角构成。

计算三角形的面积和周长是数学学习中的重要内容，让孩子使用不同的方法来计算三角形的面积和周长，可以培养他们的数学思维能力和推理能力。

本文将介绍几种常用的计算三角形面积和周长的方法，供孩子参考和学习。

一、计算三角形的面积在计算三角形的面积时，常用的方法有几何法和代数法。

1.1 几何法几何法是通过测量图形的边长或角度来计算面积的方法。

对于任意三角形ABC，可以使用以下方法计算其面积：（1）高度法：通过连接顶点A与底边BC上的某一点D，使AD与BC垂直相交，称AD为三角形ABC的高。

三角形的面积等于底边BC 长度与高AD长度的乘积的一半，即S = 0.5 × BC × AD。

（2）底边中位线法：通过连接底边BC的中点E与顶点A，使AE 为三角形ABC的中位线。

三角形的面积等于底边BC长度与中位线AE长度的乘积的一半，即S = 0.5 × BC × AE。

（3）三边长度法：若已知三角形ABC的三条边长分别为a、b、c，则可以使用海伦公式计算其面积。

海伦公式为S = √[s(s-a)(s-b)(s-c)]，其中s为三角形的半周长，即s = (a + b + c)/2。

1.2 代数法代数法是通过将三角形的面积转化为代数表达式，利用代数性质进行计算的方法。

对于任意三角形ABC，可以使用以下方法计算其面积：（1）矢量法：若已知三角形ABC的两条边的矢量表示为向量a和向量b，则三角形的面积等于向量a和向量b的叉积的一半的模长，即S = 0.5 × |a × b|。

（2）坐标法：若已知三角形ABC的三个顶点的坐标分别为A(x1,y1)，B(x2, y2)，C(x3, y3)，则可以使用行列式法计算其面积。

三角形的面积等于行列式的绝对值的一半，即S = 0.5 × |(x1y2 + x2y3 + x3y1 -x1y3 - x2y1 - x3y2)|。

平面图形的周长

公式推导：通过几何证明理解公式来源
公式简化：在特定情况下对公式进行简化处理
公式运用：掌握不同情况下公式的灵活运用
公式记忆技巧：采用口诀、联想等方法帮助记忆
0
0
0
0
1
2
3
4
特殊情况处理
圆形的周长计算：需要知道半径或直径，使用公式计算正方形的周长计算：知道边长，周长为4倍的边长特殊形状的周长计算：需要知道各边的长度，然后相加封闭图形的周长计算：需要知道各边的长度，然后相加
宽度
等边三角形周长公式： C = 3a，其中a为边
长
周长的几何意义
平面图形的周长是图形边界上所有点沿某一方向的总距离。周长是图形最外边界的长度，反映了图形的大小和形状。周长是图形所有边的长度之和，不考虑边的宽度。周长是图形边界上所有线段的长度之和。
04
平面图形周长的计算技巧
公式记忆与运用
周长是衡量图形大小的重要指标
周长相同的图形可以具有不同的面积
周长相同的图形不一定是同一种类型
计算方法
公式法：使用周长公式计ห้องสมุดไป่ตู้平面图形的周长
逐段计算法：将平面图形分割成若干个线段，分别计算每段的长度，然后相加得到周长
图形特性法：根据平面图形的特性，如平行四边形、三角形等，利用其特性计算周长
定性。
在建筑设计中，需要考虑平面图形的周长以确定合适的尺寸和比例，以实现
建筑的功能和美观。
周长的考虑可以帮助设计师更好地掌握建筑物的空间关系和布局，从而创造出更加舒适、美观和实用
的建筑。
在实际应用中，平面图形的周长可以通过测量、计算和绘图等方式来确定，以确保建筑设计的准确性

c++坐标系计算矩形面积

c++坐标系计算矩形面积矩形是二维平面上的一个几何图形，它由四条相互平行的边和四个顶点组成。

计算矩形的面积是数学问题中的一个基本操作。

在C++中，我们可以使用坐标系来计算矩形的面积。

一个矩形可以由两个对角顶点的坐标表示，左上角顶点和右下角顶点。

我们可以使用这两个顶点的坐标，通过计算两个顶点构成的长方形的边长，从而计算出矩形的面积。

下面是一个使用C++计算矩形面积的简单示例程序：```c++#include <iostream>using namespace std;int main() {float x1, y1, x2, y2, width, height, area;//读取左上角和右下角的顶点坐标cout << "请输入左上角顶点的x坐标: "; cin >> x1;cout << "请输入左上角顶点的y坐标: "; cin >> y1;cout << "请输入右下角顶点的x坐标: "; cin >> x2;cout << "请输入右下角顶点的y坐标: "; cin >> y2;//计算矩形的宽度和高度width = x2 - x1;height = y2 - y1;//计算矩形的面积area = width * height;//输出结果cout << "矩形的面积为: " << area << endl;return 0;}```这个程序首先要求用户输入矩形的两个对角顶点的坐标。

然后，程序计算矩形的宽度和高度，将它们相乘得到矩形的面积。

最后，程序输出计算得到的矩形的面积。

这个程序使用了变量`x1`、`y1`、`x2`、`y2`分别表示左上角和右下角顶点的x和y坐标。

初中数学如何计算三角形的周长和面积

初中数学如何计算三角形的周长和面积计算三角形的周长和面积是数学中常见的问题，下面将分别介绍这两种计算方法。

一、计算三角形的周长：三角形的周长是指三条边的长度之和。

计算三角形的周长的步骤如下：1. 确定三角形的三个顶点：首先，需要知道三角形的三个顶点的坐标。

2. 计算三个边的长度：通过使用两点之间的距离公式，可以计算出三角形的三个边的长度。

具体的公式为：d = √((x2 - x1)² + (y2 - y1)²)，其中(x1, y1)和(x2, y2)为两个顶点的坐标，d为两点之间的距离。

3. 求解周长：将三个边的长度相加即可得到三角形的周长。

二、计算三角形的面积：三角形的面积可以通过不同的公式计算，具体的公式取决于所给的信息。

下面介绍三种常见的计算方法：1. 根据边长计算面积：如果已知三角形的三个边的长度，可以使用海伦公式来计算三角形的面积。

具体的公式为：面积= √(s(s-a)(s-b)(s-c))，其中s为三角形的半周长，计算公式为：s = (a+b+c)/2，a、b、c分别为三角形的三个边的长度。

2. 根据底边和高计算面积：如果已知三角形的底边长度和对应的高，可以使用底边乘以高再除以2的方式计算三角形的面积。

具体的公式为：面积= (底边× 高) / 2。

3. 根据两边夹角和边长计算面积：如果已知两边夹角的度数和两边的长度，可以使用正弦函数计算三角形的面积。

具体的公式为：面积= (边1 × 边2 × sin(夹角)) / 2，其中边1和边2为两边的长度，夹角为两边之间的夹角的度数。

需要注意的是，对于非直角三角形，可以使用任意一种方法计算面积；而对于直角三角形，可以使用两条直角边的乘积再除以2的方式计算面积。

总结起来，计算三角形的周长可以通过计算三个边的长度之和得到。

计算三角形的面积可以根据所给的信息使用海伦公式、底边乘以高再除以2的方式或正弦函数计算。

闭合区域计算python

闭合区域计算python在Python中，有多种方法可以计算闭合区域的面积或周长。

下面将介绍两种常用的方法。

1. Shoelace公式（又称为高斯公式）：Shoelace公式可以用于计算任意简单多边形的面积。

该公式的基本思想是通过将多边形划分成若干个三角形，计算每个三角形的面积，然后将所有三角形的面积相加得到多边形的面积。

具体实现如下：def shoelace_formula(vertices):n = len(vertices)area = 0.0for i in range(n):j=(i+1)%narea += (vertices[i][0] * vertices[j][1] - vertices[j][0] * vertices[i][1])return abs(area) / 2.0```其中，`vertices`是一个包含多边形顶点坐标的列表，每个顶点坐标是一个二元组（x，y）。

2. Pythagorean Theorem（勾股定理）：当多边形是正多边形或矩形时，可以使用勾股定理来计算其周长。

对于正多边形，边长（s）和边数（n）之间的关系为：周长（C）=s*n。

对于矩形，给定长（l）和宽（w），周长（C）=2*（l+w）。

具体实现如下：def pythagorean_theorem(vertices):n = len(vertices)if n == 4: # 矩形l = abs(vertices[0][0] - vertices[1][0])w = abs(vertices[0][1] - vertices[3][1])return 2 * (l + w)else: # 正多边形s = abs(vertices[0][0] - vertices[1][0])return s * n```使用上述方法计算闭合区域的面积或周长时，需要注意顶点坐标的顺序。

对于多边形而言，顶点坐标顺序决定了多边形的朝向，会影响最终计算结果的正负。

凸包面积和周长的计算

凸包面积和周长的计算凸包是指包围一组点的最小凸多边形，它可以通过一系列点的坐标来确定。

凸包的面积和周长是凸包的两个重要指标，可以用来描述凸包的大小和形状。

一、凸包的面积计算凸包的面积可以通过计算凸包上所有边构成的三角形的面积之和来得到。

具体计算步骤如下：1. 首先，根据给定的一组点，确定凸包的顶点。

可以使用凸包算法如Graham扫描或Jarvis步进等方法来求解凸包的顶点。

2. 然后，通过连接凸包顶点的边，将凸包划分为一系列的三角形。

3. 接下来，计算每个三角形的面积。

可以使用海伦公式或矢量叉积等方法来计算三角形的面积。

4. 最后，将所有三角形的面积进行累加，即可得到凸包的面积。

凸包的面积计算可以用来衡量一组点的分布情况。

当凸包的面积较大时，说明点的分布比较离散；而当凸包的面积较小时，说明点的分布比较集中。

二、凸包的周长计算凸包的周长是指凸包边界上所有边的长度之和。

计算凸包的周长可以通过以下步骤实现：1. 根据给定的一组点，确定凸包的顶点。

2. 连接凸包顶点的边构成凸包的边界。

3. 遍历凸包的边界，计算每条边的长度。

4. 将所有边的长度进行累加，即可得到凸包的周长。

凸包的周长可以用来描述凸包的大小。

当凸包的周长较大时，说明凸包的形状比较复杂；而当凸包的周长较小时，说明凸包的形状比较简单。

凸包面积和周长的计算在计算几何和图形学中有着广泛的应用。

它们可以用来解决许多实际问题，比如计算地理区域的面积和周长、计算物体的外形和边界等。

总结起来，凸包的面积和周长是衡量凸包大小和形状的重要指标。

凸包的面积可以通过计算凸包上所有边构成的三角形的面积之和来得到，而凸包的周长是指凸包边界上所有边的长度之和。

凸包面积和周长的计算在计算几何和图形学中有着广泛的应用，可以用来解决许多实际问题。

通过对凸包面积和周长的计算，我们可以更好地理解和分析凸包的性质和特征，为后续的研究和应用提供参考依据。

坐标系中三角形面积的求法模型例谈

坐标系中三角形面积的求法模型例谈三角形的面积的计算是数学中一个重要的分支，它涉及到坐标系，面积的求法和多种数学模型，而且在实际应用中也很广泛。

本文以三角形面积的求法模型为例，剖析坐标系中三角形面积的求法。

一、坐标系中三角形面积的求法坐标系中三角形面积的求法可以分为两种：一种是狭义的三角形求面积模型，即根据三角形的三条边，利用三角函数来求解；另一种是广义的求面积模型，即利用坐标系的概念，将三角形的面积分解为多边形的面积。

1.义的三角形求面积模型狭义的三角形求面积模型是通过三角形的三条边来计算三角形面积的，它是利用三角函数求解，一般称为海伦公式。

它的表示形式如下：S=√[p(p-a)(p-b)(p-c)]其中，a、b、c分别代表三角形的三条边的长度，p为三角形的半周长，即p=（a+b+c）/2。

2.义的求面积模型广义的求面积模型是利用坐标系的概念，将三角形的面积分解为多边形的面积。

它的表达形式如下：S=1/2 ( ) ( )其中， ( , ) ( , )别为三角形顶点的坐标。

二、例谈1.义的三角形求面积模型例谈界定平面内一个三角形的三条边分别为a、b和c，其中的三条边是同角的，即三角形为等腰三角形，因此，此时，a=b=c，这时就称为等边三角形。

根据海伦公式，三角形的面积为：S =[p(p-a)(p-b)(p-c)] =3a^22.义的求面积模型例谈设三角形ABC的座标为：A (1,1)，B(3,2)，C(4,3)，则A、B、C三点的坐标分别为： (1,1)，(3,2)，(4,3) 。

根据广义的求面积模型，则三角形ABC的面积为：S=1/2 ( ) ( )=1/2（(1-3)×(1-2)+(-3-4)×(2-3)+(-4-1)×(3-1)）=1/2（(-2)×(-1)+(-7)×(-1)+(-5)×(2)）S=1/2 (2+7+10)= 8三、结论以上就是坐标系中三角形面积的求法模型的例谈。