第十四届“希望杯”四年级第二试试题含有答案
四年级希望杯奥数试卷【含答案】

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 17C. 20D. 214. 1千米等于多少米?A. 100米B. 1000米C. 10,000米D. 100,000米5. 下列哪个图形是三维图形?A. 正方形B. 圆形C. 立方体D. 三角形二、判断题(每题1分,共5分)1. 1+1=3 ()2. 长方形是一种特殊的正方形。
()3. 0是最小的自然数。
()4. 圆的周长等于直径的两倍。
()5. 任何数乘以0都等于0。
()三、填空题(每题1分,共5分)1. 1+2+3+4+5=_____2. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是____平方厘米。
3. 100的因数有____个。
4. 9是____的倍数。
5. 一个正方体的体积是27立方厘米,那么它的边长是____厘米。
四、简答题(每题2分,共10分)1. 请列举出前五个质数。
2. 请解释什么是因数和倍数。
3. 请简述平行四边形的特征。
4. 请解释什么是周长和面积。
5. 请列举出三种不同的三维图形。
五、应用题(每题2分,共10分)1. 一个长方形的长是8厘米,宽是4厘米,求它的周长和面积。
2. 一个数加上20后等于30,这个数是多少?3. 一个正方形的周长是24厘米,求它的边长。
4. 两个数相乘等于18,这两个数可能是什么?5. 一个立方体的体积是64立方厘米,求它的边长。
六、分析题(每题5分,共10分)1. 小明有10个苹果,他吃了一些后,还剩下6个苹果。
请问他吃了多少个苹果?2. 一个长方形的长是10厘米,宽是5厘米,求它的对角线长度。
七、实践操作题(每题5分,共10分)1. 请用纸和剪刀制作一个正方形。
2022年教学教材第14届希望杯四年级第2试模拟练习及参考答案配套精选卷

2021年小学第十五届“希望杯〞全国数学邀请赛四年级第2试试题一、填空题〔每题5分,共60分〕1、计算:1100÷25×4÷11=。
2、有15个数,它们的平均数是17,参加1个数后,平均数变成了2021参加的数是=。
3、设和是两个三位数,且a=b+1,b=c+2,×3+4=,那么=。
4、a+b=100,假设a除以3余数是2,b除以7余数是5,那么a×b的值最大是。
5、如图1所示,两个完全相同的等腰三角形中各有一个正方形,图乙中的正方形的面积是36平方厘米,那么图甲中的正方形的面积是平方厘米。
6、边长是2021方形的面积恰好等于边长是a和b的两个正方形打的面积的和,假设a和b都是自然数,那么a+b=。
7、今年是2021年,年份的数字之和是10,那么在本世纪内,数字和是10的所有年份的和是。
8、在纸上画2个圆,最多可得到2个交点,画3个圆,最多可得6个交点,那么,如果在纸上画10个圆,最多可得个交点。
9、小红带了面额是50元,202110元的人民币各5张,6张,7张,她买了230元的商品,那么有种付款的方式。
10、甲、乙、丙三个数的和是2021,甲比乙的2倍少3,乙比丙的3倍多2021甲是。
11、篮球比赛中,三分线外投中1球得3分,三分线内投中1球得2分,罚篮投中1球得1分,某球队在一次比赛中共投进32球,得65分,2分球的个数比3分球的个数的4倍多3个,那么这个球队在比赛中罚篮共投中________球。
12、在图2的算式中,A、B、C、D、E、F、G、H、I分别表示彼此不同的一位数。
那么“FIGAA〞表示的五位数是。
二、解答题〔每题15分,共60分〕每题都要写出推算过程。
13、甲、乙两人同时从A、B两地出发,相向而行,甲每分钟走70米,乙每分钟走60米,两人在距中点80米的地方相遇,求A、B两地之间的距离。
14、老师给学生分水果,准备了两种水果,其中橘子的个数是苹果个数的3倍多3个,每人分2个苹果,剩余6个苹果,每人分7个橘子,最后一人只能分到1个橘子,求学生的人数。
全国四年级希望杯数学竞赛全部试题与答案
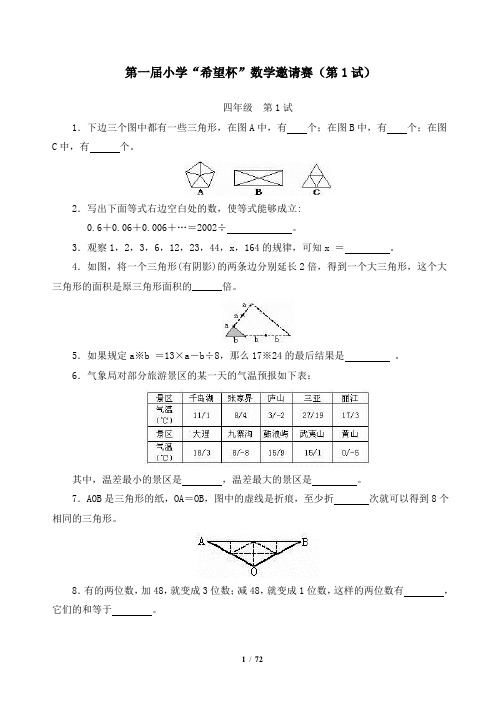
第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
【通用】全国四年级希望杯数学竞赛全部试题与答案
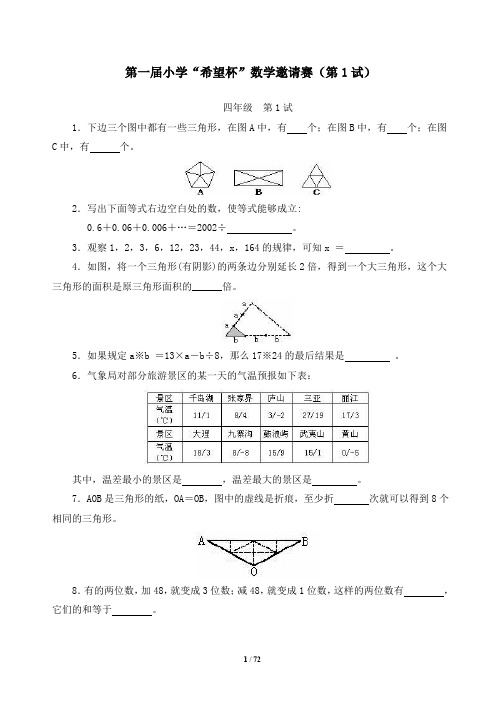
第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
全国四年级希望杯数学竞赛全部试题与答案

全国四年级希望杯数学竞赛全部试题与答案一、竞赛介绍“希望杯”是全国小学生奥数竞赛之一,自1996年创办以来,已经成为小学生数学竞赛中最有影响力的赛事之一。
本次比赛是面向四年级的“希望杯”数学竞赛,包含两个考试科目:数学(含应用题)和口算。
这个文档将介绍全部试题和答案。
二、数学试题试题一下列哪一个数是偶数?A. 1B. 3C. 5D. 2答案D. 2试题二根据下列算式,1 + 2 + 3 + 4 + 5 + 6 = ?A. 15B. 18C. 20D. 21答案D. 21试题三张三一周的零花钱是12元,他每天都要花1元,那么他一周之后还剩下多少钱?A. 5元B. 6元C. 7元D. 8元B. 6元试题四计算:(1 + 2 - 3)× 5A. 0B. 5C. 10D. 15答案B. 5试题五根据下列数字,找到其中的三个连续数字使它们的和最大。
{3, 6, 8, 2, 7, 1, 9, 0}A. 3, 6, 8B. 8, 2, 7C. 1, 9, 0D. 6, 8, 2答案B. 8, 2, 7三、口算试题试题一计算:1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10答案55试题二计算:9 × 5答案45计算:16 ÷ 4答案4试题四计算:47 - 23答案24试题五计算:200 ÷ 8答案25四、以上是全国四年级希望杯数学竞赛的全部试题和答案。
经过这次竞赛的练习,寻找方法和答案的过程不仅能够锻炼孩子们的思维能力和逻辑思维能力,同时也是对他们平时所学知识的一种回顾和检验。
希望这份文档能够对您有所帮助。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
四年级希望杯奥数试卷【含答案】

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 17C. 20D. 214. 1千克等于多少克?A. 100克B. 1000克C. 10,000克D. 1,000,000克5. 下列哪个图形是平行四边形?A. 正方形B. 长方形C. 三角形D. 圆形二、判断题(每题1分,共5分)1. 1+1=3 ()2. 长方形和正方形的周长都是边长的四倍。
()3. 9乘以9等于81。
()4. 0是最小的自然数。
()5. 圆的周长等于直径的两倍。
()三、填空题(每题1分,共5分)1. 一个正方形的边长是5厘米,那么它的面积是____平方厘米。
2. 1千克等于____克。
3. 2乘以2等于____。
4. 下列数字中,____是最大的偶数。
5. 下列图形中,____是唯一有曲线边的图形。
四、简答题(每题2分,共10分)1. 解释什么是质数。
2. 什么是平行四边形?3. 解释什么是周长。
4. 什么是面积?5. 什么是自然数?五、应用题(每题2分,共10分)1. 一个长方形的长是10厘米,宽是5厘米,求它的周长和面积。
2. 一个正方形的边长是6厘米,求它的周长和面积。
3. 一个圆形的半径是4厘米,求它的周长和面积。
4. 一个数字加上它的两倍等于15,求这个数字。
5. 一个数字减去5等于10,求这个数字。
六、分析题(每题5分,共10分)1. 小明有10个苹果,他吃了一半,然后又吃了一个,他还剩几个苹果?2. 一个长方形的长是8厘米,宽是4厘米,求它的对角线长度。
七、实践操作题(每题5分,共10分)1. 画一个边长为5厘米的正方形,并标出它的周长和面积。
2. 画一个半径为3厘米的圆形,并标出它的周长和面积。
全国四年级希望杯数学竞赛全部试题与答案

第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164规律,可知x =。
4.如图,将一个三角形(有阴影)两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
15.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影部分的面积是。
小学四年级希望杯历年数学竞赛试题和答案解析1_14届[最新[全套](完整版)]
]](https://img.taocdn.com/s3/m/f473ed0e0912a21614792942.png)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
2022希望杯夏令营4年级个人战试题及答案
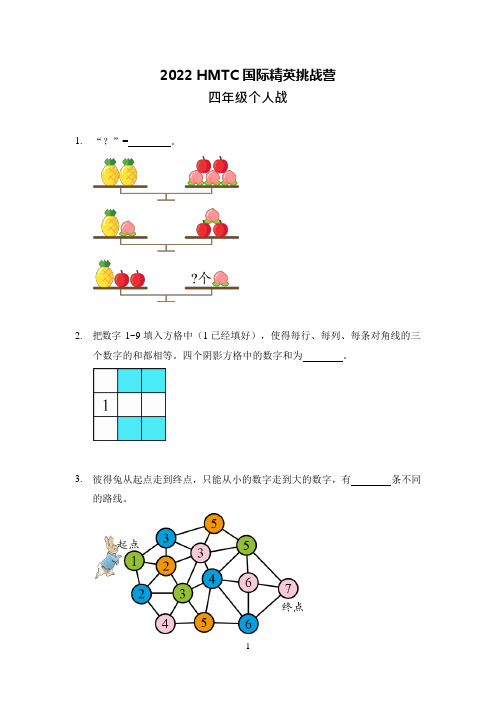
2022 HMTC 国际精英挑战营四年级个人战1. “?”= 。
2. 把数字1~9 填入方格中(1 已经填好),使得每行、每列、每条对角线的三个数字的和都相等。
四个阴影方格中的数字和为。
3. 彼得兔从起点走到终点,只能从小的数字走到大的数字,有条不同的路线。
4. 十二星座分为火象、土象、风象、水象四类象性,每一类象性都有3 个星座。
魔法学院有20 名学员,他们的星座如下表:现要选出8 名学员举行魔法比赛,要求每一类象性中选出2 个星座,一共有种不同的选法。
5. 计算:12÷( 3÷2) = 。
6. 把1~9 分别填入方框中,使得竖式成立,其中9 已经填好。
不同的填法有种。
7. 在5×5 的方格图中放棋子,每个方格内放1~2 枚棋子,黑格子放黑棋子,白格子放白棋子。
要求每行的白色棋子数量相同,每列的黑色棋子数量也相同。
一共有种不同的放棋子方法。
(棋盘不可旋转、翻转)8. 兔子镇有160 只兔子,其中49 只兔子喜欢吃萝卜,有15 只兔子既喜欢吃萝卜又喜欢吃白菜,有54 只兔子既不喜欢吃萝卜也不喜欢吃白菜。
那么,喜欢吃白菜的兔子有只。
9. 三只小猪搬砖造新房。
老大搬砖的数量是老二和老三搬砖总数的一半,老大和老二搬砖的总数是老三搬砖数量的3 倍,老二搬了100 块砖。
三只小猪一共搬了块砖。
10. 一个四位数的末位数字是2,如果把末位的2 移到首位,得到的新数比原来的数大180。
原来的数是。
11. 冰墩墩练习滑雪一周,其中后四天平均每天滑雪的长度比前三天平均每天滑雪的长度多4 千米,后三天平均每天滑雪的长度比前四天平均每天滑雪的长度多3 千米。
冰墩墩后三天滑雪的总长度比前三天滑雪的总长度多千米。
12. 黑恶魔从神塔偷了一颗时空宝石,然后沿直线向西逃跑。
黑恶魔跑了100 米时卫兵发现异常,从神塔出发以黑恶魔1.5 倍的速度追击。
在被追上的瞬间黑恶魔使用时空宝石的魔力转移到神塔东边的对称点上,然后向东逃跑。
小学四年级希望杯数学竞赛第一届至十一届全部试题与答案

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
全国四年级希望杯数学竞赛全部试题与答案

第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
××2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
15.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影部分的面积是。
2016年第14届希望杯4年级第2试模拟试题(1)-T版

2016年第14届小学“希望杯”全国数学邀请赛四年级第2试模拟试题(1)(时间:90分钟;满分120分)一、填空题。
(每小题5分,共60分) 1.计算:3333×3333+11111 = 。
【难度】:★★【考点】:积不变性质,乘法分配律 【答案】:11120000 【解析】: 3333×3333+11111 =9999×1111+11111 =(9999+1)×1111+10000 =10000×1111+10000 =11110000+10000 =111200002.计算:20162017×2015-20152015×2016= 。
【难度】:★★ 【考点】:重叠数 【答案】:2015 【解析】:20162017×2015-20152015×2016 =20162016×2015-20152015×2016+2015 =2016×10001×2015-2015×10001×2016+2015 =0+2015 =20153.如果a △b=a+b-6,a ☆b=2a+2b+ab 。
计算()[]84822÷☆☆△=。
【难度】:★★ 【考点】:定义新运算 【答案】:25 【解析】:2☆82△3632☆4200÷8=25=2×2+2×8+2×8 =2+36-6 =2×32+2×4+4×32=4+16+16 =32 =64+8+128=36 =2004.9个自然数从小到大排列,相邻两个数的差是2.其中最大的数与第二大的数之和是中间数的3倍,那么这9个自然数的和是。
【难度】:★★★【考点】:等差数列【答案】:126【解析】:把9个数从小到大依次排列、表示出来:①②③④⑤⑥⑦⑧⑨a a+2 a+4 a+6 a+8把中间数表示为a,则第二大的数为a+6,最大的数为a+8由此,题意可以翻译为:(a+8)+(a+6)=3×a 可以算出a=14和=中间数×项数=14×9=1265.在一次慈善义卖中,丹丹自制的蛋挞和布丁共卖了200个,收入479元。
第十四届小学“希望杯”全国数学邀请赛四年级第二试试题及答案解析

第十四届小学“希望杯”全国数学邀请赛四年级第2试试题解析一、解答题(每小题5分,共60分)1.计算:20162014201320152012201520132016⨯-⨯+⨯-⨯=______.【答案】1【考点】乘法分配律【解析】2016201420132016(2013201520122015)⨯-⨯-⨯-⨯=⨯---⨯2016(20142013)(20132012)2015=-20162015=12.60的不同约数(1除外)的个数是_____.【答案】11【考点】枚举法【解析】列举出60的约数,可以一对一对地找,60160=⨯,60320=⨯,=⨯,60230=⨯,所以60的约数有:1、2、3、4、5、=⨯,6061060415=⨯,605126、10、12、15、20、30、60,1除外共11个.3.今年丹丹4岁,丹丹的爸爸28岁,a年后,爸爸年龄是丹丹年龄的3倍,则a的值是_____.【答案】8【考点】年龄问题、差倍问题.【解析】无论今年还是a 年后,丹丹和爸爸的年龄差是不变的.a 年后年龄差为:28424-=(岁) a 年后丹丹年龄:()243112÷-=(岁) a 就为:1248-=(年).4. 已知a 比c 大2,则三位数自然数abc 与cba 的差是_____. 【答案】198 【考点】位值原理【解析】a 比c 大2,2a c -=,又10010abc a b c =++,10010cba c b a =++,2a c -=,abc cba- 10010(10010)a b c c b a =++-++100()()a c a c =---99()a c =- 992=⨯ 198=.5. 正方形A 的边长是10,若正方形B 、C 的边长都是自然数,且B 、C 的面积和等于A的面积,则B 和C 的边长的和是_____. 【答案】14 【考点】完全平方数【解析】B 、C 的面积和等于A 的面积,A 的面积1010100=⨯=,设B 的边长为b ,C 的边长为c ,所以22100b c +=,显然6,8b c ==或8,6b c ==, 所以B 的边长和C 的边长的和是6814+=.6. 已知9个数的平均数是9,如果把其中一个数改为9后,这9个数的平均数变为8,那么这个被改动的数是_____. 【答案】18 【考点】平均数【解析】原来的9个数的总和是9981⨯=,把其中一个数改为9后,9个数的总和是9872⨯=,所以被改动的数是(8172)918-+=.7. 如图1,水平相邻和竖直相邻的两个格点间的距离都是1,则图中阴影部分的面积是______.【答案】17 【考点】巧求面积【解析】两个格点间的距离都是1,所以每个小正方形的面积是111⨯=,通过平移得到阴影部分总共有17个小正方形,所以阴影部分的面积是17117⨯=.图18. 两个数的和是363,用较大的数除以较小的数,得商16余6,则这两个数中较大的数是_____. 【答案】342 【考点】和倍问题【解析】两个数的和是363,除数为1份,则被除数为16份还多6.16117+=所以17份的和应为:3636357-= 较小数为:()()363616121-÷+= 较大数为:36321342-=9. 如图2,阴影部分是一个边长为6厘米的正方形,在它的四周有四个长方形,若四个长方形的周长的和是92厘米,则四个长方形的面积的和是_____平方厘米.【答案】132 【考点】巧求面积【解析】已知正方形的边长是6,设每个长方形的另一条边分别为a b c d 、、、:四个长方形的周长的和是92厘米,即(6666)292a b c d +++++++⨯=,22a b c d +++=,图2四个长方形的面积等于a b c d+++6666=+++)6(a b c d=⨯6222=cm132()10.有一根长240厘米的木棒,先从左端开始每隔7厘米划一条线,再从右端开始每隔6厘米划一条线,并且从划线处截断木棒,则在所截得的小木棒中,长度是3厘米的木棒有_____根.【答案】12【考点】最小公倍数、周期问题【解析】由于从右端开始6厘米划一条线,刚好能将240厘米分成整数段,所以可以看成从左端每隔6厘米划一条线。
2016年希望杯初赛真题及解析(四年级)

4.
5.
6.
小书灯家长社区整理发布让家长无忧·让学习无忧 1 / 5
资料下载、家长交流、信息分享权威论坛:
【答案】667 【分析】题目中未明确说 4 个相同的数字必须是相邻的,52222 中已经有 4 个 2,所以 只要再将其中的 3 个 2 变成 5, 数中就有 4 个 5 了.又要求至少用了多少千瓦的 电,数字所在位数越低,所表示的数越小,所以这个数为 51555. 所以,至少用了 52222 51555=667 (千瓦)的电. 7. 已知碳素笔每支 1 元 8 角,笔记本每个 3 元 5 角,文具盒每个 4 元 2 角.晶晶买这 3 种 文具刚好用了 20 元,则她买了__________个笔记本. 【考点】应用题 【答案】4 【分析】根据题意,1 支碳素笔+1 个文具盒=1.8 元+4.2 元=6 元.即所买碳素笔和文具盒 的数量必须一样多. 当买 1 支碳素笔和 1 个文具盒时,所买笔记本 20 6 3.5 4 (个)刚好满足. 8. 已知碳素笔每支 1 元 8 角,笔记本每个 3 元 5 角,文具盒每个 4 元 2 角.晶晶买这 3 种 文具刚好用了 20 元,则她买了__________个笔记本. 【考点】差倍问题 【答案】144 【分析】根据商为 15,余数为 0,得:被除数÷除数=15. 即:被除数=15 除数,又被 除数-除数=2016,除数=差÷(倍数-1)= 2016 15 1 144 .
6 3 4 2 26
10. 已知 a、b、c 都是质数,若 a b b c 119 ,则 a b c ____________. 【考点】质数、奇偶性 【答案】14 【分析】 b a c 119 ,根据奇偶性可知: b、a c 均为奇质数,故 a、c 中必有 一个偶质数 2,又 119=7 17 , b 17 , a c 7 . a b c 7 17 24 . 11. 王华每星期二、六去学书法.已知 2016 年的元旦是星期五,那么在 2016 年 8 月,王华 学书法的天数是____________. 【考点】周期问题 【答案】9 天
2020年第十四届小学数学“梦想杯”全国数学邀请赛试卷(四年级第2试)

2016年第十四届小学“希望杯”全国数学邀请赛试卷(四年级第2试)一、填空题(每题5分,共60分).1.(5分)2016×2014﹣2013×2015+2012×2015﹣2013×2016=.2.(5分)60的不同约数(1除外)的个数是.3.(5分)今年丹丹4岁,丹丹的爸爸28岁,a年后爸爸年龄是丹丹年龄的3倍,则a的值是.4.(5分)已知a比c大2,则三位自然数与的差是.5.(5分)正方形A的边长的10,若正方形B,C的边长都是自然数,且B,C的面积和等于A的面积,则B和C的边长的和是.6.(5分)已知9个数的平均数是9,如果把其中一个数改为9后,这9个数的平均数变为8,那么这个被改动的数原来是.7.(5分)在下面的格点图中,水平相邻和竖直相邻的两个格点的距离都是1,则图中阴影部分的面积是.8.(5分)两个数的和是363,用较大的数除以较小的数,得商16余6,则这两个数中较大的是.9.(5分)如图,阴影部分是一个边长为6厘米的正方形,在它的四周有四个长方形,若四个长方形的周长的和是92厘米,则四个长方形的面积的和是平方厘米.10.(5分)有一根长240厘米的木棒,先从左端开始每隔7厘米划一条线,再从右端开始每隔6厘米划一条线,并且从划线处截断木棒,则在所截得的小木棒中,长度3厘米的木棒有根.11.(5分)在如图的9个方格中,每行、每列及每条对角线上三个数的和都相等,则x+y+a+b+c+d=.12.(5分)甲、乙两人分别从A、B两地同时出发,相向而行,4小时可相遇;若两人时速都增加3千米,则出发后3小时30分可相遇.A、B两地相距千米.二、解答题(每题15分,共60分).13.(15分)如图,用正方形a、b、c、d、e拼成一个长30厘米,宽22厘米的长方形,求正方形e的面积.14.(15分)有两块地,平均亩产粮食675千克,其中第一块地5亩,亩产粮食705千克.如果第二块地亩产粮食650千克,第二块地有多少亩?15.(15分)4个连续的自然数,从小到大依次是11的倍数、7的倍数、5的倍数、3的倍数,求这4个自然数的和最小值.16.(15分)有6个密封的盒子,分别装有红球、白球和黑球,每个盒子里只有一种颜色的球,且球的个数分别是15,16,18,19,20,31,已知黑球的个数是红球个数的2倍,白球只有1盒,问:(1)装有15个球的盒子里装的是什么颜色的球?(2)有多少个盒子装的是黑球?2016年第十四届小学“希望杯”全国数学邀请赛试卷(四年级第2试)参考答案与试题解析一、填空题(每题5分,共60分).1.(5分)2016×2014﹣2013×2015+2012×2015﹣2013×2016=1.【分析】根据乘法的分配律,提取公因数简算即可.【解答】解:2016×2014﹣2013×2015+2012×2015﹣2013×2016=2016×2014﹣2013×2016﹣2013×2015+2012×2015=2016×(2014﹣2013)﹣(2013﹣2012)×2015=2016×1﹣1×2015=2016﹣2015=1故答案为:1.【点评】本题考查了学生对整数四则混合运题目进行计算的能力.完成本题要注意分析式中数据,运用合适的简便方法计算.2.(5分)60的不同约数(1除外)的个数是11.【分析】先将60分解质因数,60=2×2×3×5,再写成标准式是22×3×5,再利用约数个数公式,约数个数=不同质因数指数加1然后再相乘,最后减去1,即得答案.【解答】60分解质因数60=2×2×3×5,再下称标准式是22×3×5,再利用约数个数公式,约数个数=不同质因数指数加1然后再相乘.60的不同约数(1除外)的个数是(2+1)×(1+1)×(1+1)﹣1=11个.答:答案是11个.【点评】约数个数公式的推导要用乘法原理,当然此题也可以用列举法求解.3.(5分)今年丹丹4岁,丹丹的爸爸28岁,a年后爸爸年龄是丹丹年龄的3倍,则a的值是8.【分析】根据“今年丹丹4岁,丹丹的爸爸28岁”,知道今年爸爸与丹丹相差28﹣4=24岁,再根据年龄差不会随时间的变化而改变,利用差倍公式,用24除以倍数差(3﹣1)即可求出当爸爸的年龄是丹丹年龄的3倍时丹丹的年龄,进而求出答案.【解答】解:年龄差:28﹣4=24(岁),丹丹的年龄:24÷(3﹣1)=24÷2=12(岁),12﹣4=8(年),所以,a的值是8.答:a年后爸爸年龄是丹丹年龄的3倍,则a的值是8.故答案为:8.【点评】关键是根据年龄差不会随时间的变化而改变,再根据差倍问题{差÷(倍数﹣1)=较小数,较小数×倍数=较大数,(或较小数+差=较大数)}与基本的数量关系解决问题.4.(5分)已知a比c大2,则三位自然数与的差是198.【分析】两个数字对调顺序的字母正好是a和c,而我们知道a﹣c=2.b在中间可以约掉.所以最终的差需要用a和c的差表示出来.【解答】解:=100a+10b+c﹣(100c+10b+a)=100a+10b+c﹣100c﹣10b﹣a=99a﹣99c=99(a﹣c)∵a﹣c=2∴99×2=198故答案为:198【点评】针对位值原理必须明白什么是完全拆分和不完全拆分.知道两数的差,我们就按照位值原理展开做差即可.5.(5分)正方形A的边长的10,若正方形B,C的边长都是自然数,且B,C的面积和等于A的面积,则B和C的边长的和是14.【分析】本题是说明两个正方形B和C的面积与A的面积相等,符合勾股定理,根据勾股定理a2+b2=c2即可求解.【解答】解:根据勾股定理a2+b2=c2得,其中一个正方形的边长是10,根据6,8,10是一组勾股数得.62+82=102满足条件.6+8=14,故答案为:14.【点评】本题考查对勾股定理的理解与运用,同时要掌握一些常见的勾股数组合,做题的时候比较快同时加强准确率.(3,4,5)(6,8,10,)(5,12,13)等6.(5分)已知9个数的平均数是9,如果把其中一个数改为9后,这9个数的平均数变为8,那么这个被改动的数原来是18.【分析】改动之前的总数是9×9=81,改动后的总数是8×9=72,前后相差9×9﹣8×9=9,说明这个数比原来减少了9,这个被改动的数原来是9+9=18;据此解答即可.【解答】解:9×9﹣8×9=81﹣72=99+9=18答:这个被改动的数原来是18.故答案为:18.【点评】此题考查了平均数的意义及求平均数的方法的拓展运用;知识点:总数量=平均数×总份数.7.(5分)在下面的格点图中,水平相邻和竖直相邻的两个格点的距离都是1,则图中阴影部分的面积是17.【分析】红色正方形的面积是3×3=9,每个外部的角的面积都是2×1÷2=1,8个一共是8,然后求整个的面积即可.【解答】解:3×3+2×1÷2×8=9+8科技新闻网:##科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料,我们是国内外最新的科技新闻网。
全国四年级希望杯数学竞赛全部试题与答案

第一届小学“盼望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式可以成立:0.6+0.06+0.006+…=2002÷。
3.视察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的倍。
5.假如规定a※b =13×a-b÷8,那么17※24的最终结果是。
6.气象局对局部旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.是三角形的纸,=,图中的虚线是折痕,至少折次就可以得到8个一样的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任教师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园教师给几组小挚友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小挚友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比拟小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
15.长方形被分成了4个小长方形,图4中的数字是它们每个的面积,阴影局部的面积是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四届小学“希望杯”全国数学邀请赛
四年级 第2试试题
2016年4月10日 上午9:00至11:00
一、填空题(每题5分,共60分)。
1、=⨯-⨯+⨯-⨯20162013201520122015201320142016 .
2、60的不同约数(1除外)的个数是 .
3、今年丹丹4岁,丹丹的爸爸28岁,a 年后爸爸年龄是丹丹年龄的3倍,则a 的值是 .
4、已知a 比c 大2,则三位自然数abc 与cba 的差是 .
5、正方形A 的边长的10,若正方形B ,C 的边长都是自然数,且B ,C 的面积和等于A 的面积,则 B 和C 的边长的和是 .
6、已知9个数的平均数是9,如果把其中一个数改为9后,这9个数的平均数变为8,那么这个被 改动的数原来是 ____ ____ .
7、在下面的格点图中,水平相邻和竖直相邻的两个格点的距离都是1,
则图中阴影部分的面积是 ________ .
8、两个数的和是363,用较大的数除以较小的数,得商16余6,则这两
个数中较大的是 _______ .
9、如图,阴影部分是一个边长为6厘米的正方形,在它的四周有四个
长方形,若四个长方形的周长的和是92厘米,则四个长方形的面积的
和是 平方厘米.
10、有一根长240厘米的木棒,先从左端开始每隔7厘米划一条线,再从右端开始每隔6厘米划一 条线,并且从划线处截断木棒,则在所截得的小木棒中,长度3厘米的木棒有 根.
11、在下图的9个方格中,每行、每列及每条对角线上三个数的和都相等,则=+++++d c b a y x . 12、甲、乙两人分别从A 、B 两地同时出发,相向而行,4小时可相遇;若两人时速都增加3千米,则出发后3小时30分可相遇。
A 、B 两地相距 千米.
二、解答题(每题15分,共60分)。
13、如图,用正方形a 、b 、c 、d 、e 拼成一个长30厘米,宽22厘米的长方形,求正方形e 的面 积.
14、有两块地,平均亩产粮食675千克,其中第一块地5亩,亩产粮食705千克。
如果第二块地亩产粮食650千克,第二块地有多少亩?
15、4个连续的自然数,从小到大一次是11的倍数、7的倍数、5的倍数、3的倍数,求这4个自然数的和最小值.
16、有6个密封的盒子,分别装有红球、白球和黑球,每个盒子里只有一种颜色的球,且球的个数分别是15,16,18,19,20,31,已知黑球的个数是红球个数的2倍,白球只有1盒,问:
(1)装有15个球的盒子里装的是什么颜色的球?
(2)有多少个盒子装的是黑球?
第十四届“希望杯”数学邀请赛四年级2试参考答案。
