材料科学基础相图
合集下载
材料科学基础第五章 材料的相结构及相图

电负性差ΔX<0.4时,易于形成固溶体。 如,Cu(1.9)-Ni(1.9),可无限互溶。
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
第一节 材料的相结构
THE PHASE STRUCTURE OF MATERIALS
固溶体
中间相
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
相:合金中具有同一聚集状态、同一晶体结构和性质 并以界面相互隔开的均匀组成部分。
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
3)电负性差因素
电负性:衡量原子吸引电子能力的参数,电负性越强,吸引 电子的能力越强。
电负性差ΔX>0.4时,易于形成较稳定的金属间化合物;
贵州师范大学
化学与材料科学学院
4)电子浓度因素
电子浓度:合金中各组成元素的价电子数总和与原子总数 的比值,记为e/a。
C电 合金中价电子数之和 原子数之和
例:合金含有摩尔分数为x、原子价为VB的溶质原子,溶剂 的原子价为VA,则合金的电子浓度为:
e V A 1 x V B x a
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
第一节 材料的相结构
THE PHASE STRUCTURE OF MATERIALS
固溶体
中间相
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
相:合金中具有同一聚集状态、同一晶体结构和性质 并以界面相互隔开的均匀组成部分。
SCHOOL OF CHEMISTRY AND MATERIAL SCIENCE OF GUIZHOU NORMAL UNIVERSITY
贵州师范大学
化学与材料科学学院
3)电负性差因素
电负性:衡量原子吸引电子能力的参数,电负性越强,吸引 电子的能力越强。
电负性差ΔX>0.4时,易于形成较稳定的金属间化合物;
贵州师范大学
化学与材料科学学院
4)电子浓度因素
电子浓度:合金中各组成元素的价电子数总和与原子总数 的比值,记为e/a。
C电 合金中价电子数之和 原子数之和
例:合金含有摩尔分数为x、原子价为VB的溶质原子,溶剂 的原子价为VA,则合金的电子浓度为:
e V A 1 x V B x a
《材料科学基础》课件——第五章相平衡与相图第一节第二节第三节第四节

相和相平衡
Байду номын сангаас四、自由度与相律
1、自由度:平衡系统中独立可变的因素
自由度数:独立可变的强度变量的最大数目
(强度变量与广度变量的区别)
2、相律:自然规律
在平衡系统中由于受平衡条件的制约,系统内
存在的相数有一定限制。 组元数 相数P≥1
吉布斯相律:不可为负数
f=c-p+n
外界影 响因素
通常外界影响因素只考虑T、P,所以f=c-p+2
• 掌握匀晶,包晶,共晶相图的特点,进而了解二元合金的一些平衡凝固,固 相转变的规律。
• 重点难点: • 二元系相图的建立,杠杆定律 • 包晶相图,共晶相图,共晶合金 • 相图分析,各种液固,固相转变的判断
材料的性能决定于内部的组织结构,而组织结构
又由基本的相所组成。
相:均匀而具有物理特性的部分,并和体系的其他 部分有明显界面。
晶型转变过程都是在恒温下进行,并伴随有体 积、密度的变化。 2、SiO2系统相图 α-石英与β-石英相变相当慢, β-石英常因冷却过快而被保留 到室温,在常压下,低于573℃
单元系相图
β-石英很稳定,所以自然界或低温时最常见的是 β-石英。晶型转变时,体积效应特别显著。 Al2O3、ZrO2也具有多晶型转变。 3、聚合物相图 (1)状态由分子间作用力决定,分子间约束力弱
共晶相图,平衡凝固,共晶合金,包晶相图,形成化合物的相图,含有双液 共存区的相图,熔晶相图等 ,二元相图的几何规律 ,单相,双相及三相共 存区,相图特征 ,二元系相图的分析,分析的方法与步骤,分析举例。
• 教学目的: • 学习相平衡与相图的基本知识,了解相图在材料科学学习中的重要性,学会
相图的使用。
材料科学基础2--第一章-相图4

相区
单相区:L, a, b 两相区: L+a, L+ b,a+b
相变线
TAE及TBE:初生(初晶)a及b析出线 即L→a, L→b
TAM及TBN:初生a及b结晶终了线 MF及NG: a及b溶解度变化线
即a→bII,b→aII MEN: 共晶线,即L→a+b
相变点
TA及TB:纯组元A、B的熔点 M及N:a及b的最大溶解度点 F及G:a及b室温溶解度点 E:共晶点,发生共晶反应的液相成分点
将支点由O移至N,则上式变为:
Wa(xa-xL)=W0(x0-xL) 将W0设为100%,则两相相对量分数为:
Wa
x0 xa
xL xL
100 %
将支点由O移至M,得到两相相对量分数为:
WL
xa xa
x0 xL
100 %
杠杆定律仅适用于平衡结晶条件。
WL 100 % Wa Wa 100 % WL
(1)组织形成过程 以x合金为例。 相组成物:a 组织组成物:
单相等轴a晶粒
(2)成分变化与相平衡
(a) 形核
T=T0时,固态核心成分位于温度水平线与 固相线的交点a0。
只有液相中某局部区域成分为a0时,才符合 结晶的浓度条件。
浓度起伏(成分起伏):
液相局部微区成分波动存在时起时伏、此 起彼伏的现象。
问题:假定合金分别冷却到1,2,3,4温度开始结晶,获得的组织特点有何不同?
(2)晶内偏析共晶
晶内偏析共晶: 端部固溶体合金非平衡结晶时出现共晶组织
的现象。 由于晶内偏析共晶数量较少,往往以离异
共晶形式存在。
两种情况促使离异共晶形成: ►靠近极限溶解度的端部固溶体的非平衡冷却 。 ►靠近极限溶解度的亚共晶合金的平衡冷却。 (3)次生相
单相区:L, a, b 两相区: L+a, L+ b,a+b
相变线
TAE及TBE:初生(初晶)a及b析出线 即L→a, L→b
TAM及TBN:初生a及b结晶终了线 MF及NG: a及b溶解度变化线
即a→bII,b→aII MEN: 共晶线,即L→a+b
相变点
TA及TB:纯组元A、B的熔点 M及N:a及b的最大溶解度点 F及G:a及b室温溶解度点 E:共晶点,发生共晶反应的液相成分点
将支点由O移至N,则上式变为:
Wa(xa-xL)=W0(x0-xL) 将W0设为100%,则两相相对量分数为:
Wa
x0 xa
xL xL
100 %
将支点由O移至M,得到两相相对量分数为:
WL
xa xa
x0 xL
100 %
杠杆定律仅适用于平衡结晶条件。
WL 100 % Wa Wa 100 % WL
(1)组织形成过程 以x合金为例。 相组成物:a 组织组成物:
单相等轴a晶粒
(2)成分变化与相平衡
(a) 形核
T=T0时,固态核心成分位于温度水平线与 固相线的交点a0。
只有液相中某局部区域成分为a0时,才符合 结晶的浓度条件。
浓度起伏(成分起伏):
液相局部微区成分波动存在时起时伏、此 起彼伏的现象。
问题:假定合金分别冷却到1,2,3,4温度开始结晶,获得的组织特点有何不同?
(2)晶内偏析共晶
晶内偏析共晶: 端部固溶体合金非平衡结晶时出现共晶组织
的现象。 由于晶内偏析共晶数量较少,往往以离异
共晶形式存在。
两种情况促使离异共晶形成: ►靠近极限溶解度的端部固溶体的非平衡冷却 。 ►靠近极限溶解度的亚共晶合金的平衡冷却。 (3)次生相
材料科学基础-第8章-三元相图

B
L
α C A B L1 S1 L+α L+α n L o L2
7
m
α S2
C
A
第五章 材料的变形与再结晶 L
4、变温截面(垂直截面)图 变温截面(垂直截面) (1)通过成分三角形顶点的截面
α
★ 位于该截面上的所有合金含另外两 顶点组元量之比w 相同。 顶点组元量之比wA/wC相同。 ★ 此图可反映合金在不同温度时所存 在相的种类; 在相的种类;
α
β
γ
L+α L+α+β、α+β+γ 一个四相平衡区:L+α 一个四相平衡区:L+α+β+γ
19
20
2、投影图
E1 A B
o
E E3 E2
C
合金o冷却过程中的相变: 合金o冷却过程中的相变:
L+α L+(α )+α→L+(α )+(α )+α L→ L+α→ L+(α+β)+α→L+(α+β+γ)+(α+β)+α→ )+(α )+α (α+β+γ)+(α+β)+α
A C L L+α α
α B
9
第五章 材料的变形与再结晶
5、投影图
L
α A B
C
10
第五章 材料的变形与再结晶
第二节 固态互不溶解的三元共晶相图
1、相图分析 每个侧面为组元固态下互不溶的二 元共晶相图。 三个共晶点。 元共晶相图。E1、E2、E3三个共晶点。 三个液相面: ★ 三个液相面: tAE1EE3tA、 tBE1EE2tB、 tCE2EE3tC。 三元四相共晶点E ★ 三元四相共晶点E:L→A+B+C ★ 重要的线: 重要的线: 三元三相共晶线E 三元三相共晶线E1E:L→A+B 三元三相共晶线E 三元三相共晶线E2E:L→B+C 三元三相共晶线E 三元三相共晶线E3E:L→A+C
L
α C A B L1 S1 L+α L+α n L o L2
7
m
α S2
C
A
第五章 材料的变形与再结晶 L
4、变温截面(垂直截面)图 变温截面(垂直截面) (1)通过成分三角形顶点的截面
α
★ 位于该截面上的所有合金含另外两 顶点组元量之比w 相同。 顶点组元量之比wA/wC相同。 ★ 此图可反映合金在不同温度时所存 在相的种类; 在相的种类;
α
β
γ
L+α L+α+β、α+β+γ 一个四相平衡区:L+α 一个四相平衡区:L+α+β+γ
19
20
2、投影图
E1 A B
o
E E3 E2
C
合金o冷却过程中的相变: 合金o冷却过程中的相变:
L+α L+(α )+α→L+(α )+(α )+α L→ L+α→ L+(α+β)+α→L+(α+β+γ)+(α+β)+α→ )+(α )+α (α+β+γ)+(α+β)+α
A C L L+α α
α B
9
第五章 材料的变形与再结晶
5、投影图
L
α A B
C
10
第五章 材料的变形与再结晶
第二节 固态互不溶解的三元共晶相图
1、相图分析 每个侧面为组元固态下互不溶的二 元共晶相图。 三个共晶点。 元共晶相图。E1、E2、E3三个共晶点。 三个液相面: ★ 三个液相面: tAE1EE3tA、 tBE1EE2tB、 tCE2EE3tC。 三元四相共晶点E ★ 三元四相共晶点E:L→A+B+C ★ 重要的线: 重要的线: 三元三相共晶线E 三元三相共晶线E1E:L→A+B 三元三相共晶线E 三元三相共晶线E2E:L→B+C 三元三相共晶线E 三元三相共晶线E3E:L→A+C
《材料科学基础教学课件》第一章-相图

在化学工业中的应用
化工过程控制
相图可以用来预测不同成分和温 度下的相态和物性,为化工过程 的控制提供依据,确保生产过程
的稳定性和安全性。
化学反应研究
相图可以用来研究化学反应过程中 物质的状态和性质变化,有助于深 入理解化学反应机理和反应条件的 选择。
分离技术应用
相图可以用来指导分离技术的选择 和应用,例如利用相图的溶解度曲 线进行萃取分离或结晶分离。
04
相图的应用
在材料科学中的应用
合金设计
相图是合金设计的基础,通过相 图可以确定合金的成分范围以及 各相的组成和性质,从而优化合 金的性能。
热处理工艺制定
利用相图可以确定合金在不同温 度下的相变过程,从而制定合理 的热处理工艺,优化材料的显微 组织和力学性能。
新材料研发
相图为新材料研发提供了理论指 导,通过研究不同成分和温度下 的相变规律,可以发现具有优异 性能的新型材料。
实验法是绘制相图最直接和可靠的方 法,但需要耗费大量的时间和资源。
实验法通常需要使用精密的实验仪器 和设备,如热分析仪、X射线衍射仪、 扫描电子显微镜等,以获得精确的数 据。
计算法
计算法是根据物质的分子或原 子模型,通过计算机模拟计算 物质之间的相平衡关系。
计算法可以快速地预测物质的 相平衡关系,但需要建立准确 的分子或原子模型,且对计算 资源的要求较高。
在冶金工业中的应用
钢铁冶金
01
钢铁冶金过程中涉及大量的相变和相分离,相图是指导钢铁冶
金工艺的重要工具,有助于优化炼钢和连铸连轧工艺。
有色金属冶金
02
在有色金属冶金中,相图可以用来确定合金的成分和温度范围,
优化熔炼、浇注和凝固工艺,提高产品的质量和性能。
材料科学基础第六讲-相图

温度降到3点时,合金III全部转化为β固 溶体。
3-4点时,为单相固溶体,不发生变化。 4点以下,将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应:L+α β II 包晶反应:L+ β γ III 包晶反应:L+ ε η IV 共析反应: β α + γ V 共析反应: γ α + δ VI 共析反应: δ α + ε VII 共析反应: ζ δ + ε VIII 包析反应: γ + ε ζ IX 包析反应: γ + ζ δ X 熔晶反应: γ ε + L XI 共晶反应: L η + θ
相律:表示在平衡条件下,系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时:F=C-P+1
J. Willard Gibbs
自由度:指平衡系统中可以独立改变的因素(如温度, 美国物理学家 压力,成分)等。纯金属的自由度最多一个,二元系 (1839-1903)
包晶转变区的特征是:反应相是液相和一个固相,其成分点位于水 平线的两端,所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
(一)含银量42.4%的铂银合金
当合金I自液态缓冷到1点时, 开始结晶出α相,与匀晶系 合金的结晶完全相同
当温度降到tD时,合金中 α 相的成分到P点,液相的成 分到C点。
应用相图时要注意的问题
连接线(等温线):两个平衡相成分点之间的连线
第三节 一元系相图
3-4点时,为单相固溶体,不发生变化。 4点以下,将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应:L+α β II 包晶反应:L+ β γ III 包晶反应:L+ ε η IV 共析反应: β α + γ V 共析反应: γ α + δ VI 共析反应: δ α + ε VII 共析反应: ζ δ + ε VIII 包析反应: γ + ε ζ IX 包析反应: γ + ζ δ X 熔晶反应: γ ε + L XI 共晶反应: L η + θ
相律:表示在平衡条件下,系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时:F=C-P+1
J. Willard Gibbs
自由度:指平衡系统中可以独立改变的因素(如温度, 美国物理学家 压力,成分)等。纯金属的自由度最多一个,二元系 (1839-1903)
包晶转变区的特征是:反应相是液相和一个固相,其成分点位于水 平线的两端,所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
(一)含银量42.4%的铂银合金
当合金I自液态缓冷到1点时, 开始结晶出α相,与匀晶系 合金的结晶完全相同
当温度降到tD时,合金中 α 相的成分到P点,液相的成 分到C点。
应用相图时要注意的问题
连接线(等温线):两个平衡相成分点之间的连线
第三节 一元系相图
材料科学基础-第4章相图

第四章
材料的相结构与相图
PHASE STRUCTURE AND PHASE DIAGRAM OF MATERIALS
材料的相结构 二元相图及其类型 复杂相图分析 相图的热力学基础 三元相图及其类型
THE END
第一节
材料的相结构
PHASE STRUCTURE OF MATERIALS
相 — 体系中成分、结构、性能相同且与 其他部分有界面隔开的均匀部分或 连续变化的部分 合金中的相
(4) 晶内偏析及其有害影响 晶内偏析—固溶体晶粒内部成分不均匀的 现象,也称枝晶偏析.枝干富含高熔点 组元,枝间富含低熔点组元. 偏析倾向:取决于 L/S 相线垂直距离 偏析程度:取决于 L/S 相线水平距离 有害影响
⎧ ⎨ ⎩
降低强度、塑性、韧性 降低抗腐蚀性能 加热时过早熔化
(5) 均匀化退火—将有晶内偏析的材料加热至 固相线以下100~200℃长期保温
E AB E AB
1 = ( E AA + E BB ) 2 1 > ( E AA + E BB ) 2 1 < ( E AA + EBB ) 2
无序 偏聚 有序
2) 有序固溶体(超结构) 能量条件 形成条件
E AB 1 < ( E AA + EBB ) 2
成分条件 A、B成一定比例 温度条件 低于一定温度
5) 具有匀晶相图的陶瓷系统
Mg2SiO4→(Mg,Fe)2SiO4→(Fe,Mg)2SiO4→Fe2SiO4
Mg2SiO4-Fe2SiO4 相图
Mg[CO3]-Fe[CO3], K[AlSi3O8]-Na[AlSi3O8] 其它: 菱镁矿 菱铁矿 钾长石 钠长石
2. 共晶相图及结晶分析 1) 相图分析
材料的相结构与相图
PHASE STRUCTURE AND PHASE DIAGRAM OF MATERIALS
材料的相结构 二元相图及其类型 复杂相图分析 相图的热力学基础 三元相图及其类型
THE END
第一节
材料的相结构
PHASE STRUCTURE OF MATERIALS
相 — 体系中成分、结构、性能相同且与 其他部分有界面隔开的均匀部分或 连续变化的部分 合金中的相
(4) 晶内偏析及其有害影响 晶内偏析—固溶体晶粒内部成分不均匀的 现象,也称枝晶偏析.枝干富含高熔点 组元,枝间富含低熔点组元. 偏析倾向:取决于 L/S 相线垂直距离 偏析程度:取决于 L/S 相线水平距离 有害影响
⎧ ⎨ ⎩
降低强度、塑性、韧性 降低抗腐蚀性能 加热时过早熔化
(5) 均匀化退火—将有晶内偏析的材料加热至 固相线以下100~200℃长期保温
E AB E AB
1 = ( E AA + E BB ) 2 1 > ( E AA + E BB ) 2 1 < ( E AA + EBB ) 2
无序 偏聚 有序
2) 有序固溶体(超结构) 能量条件 形成条件
E AB 1 < ( E AA + EBB ) 2
成分条件 A、B成一定比例 温度条件 低于一定温度
5) 具有匀晶相图的陶瓷系统
Mg2SiO4→(Mg,Fe)2SiO4→(Fe,Mg)2SiO4→Fe2SiO4
Mg2SiO4-Fe2SiO4 相图
Mg[CO3]-Fe[CO3], K[AlSi3O8]-Na[AlSi3O8] 其它: 菱镁矿 菱铁矿 钾长石 钠长石
2. 共晶相图及结晶分析 1) 相图分析
材料科学基础-第五章 材料的相结构及相图

相律在相图中的应用
C
2 二元系
P 1 2
3 1
f 2 1 0
3 2 1 0
含义
单相合金,成分和温度都可变 两相平衡,成分、相对量和温度 等因素中只有一个独立变量 三相平衡,三相的成分、相对 量及温度都确定 单相合金其中两个组元的含量 及温度三个因素均可变 两相平衡,两相的成分、数量 及温度中有两个独立变量 三相平衡,所有变量中只有 一个是独立变量 四相平衡所有因素都确定不变
结构简单的具有极高的硬度及熔点,是合金工具钢和硬 质合金的重要组成相。
I. 间隙化合物
间隙化合物和间隙固溶体的异同点
相同点: 非金属原子以间隙的方式进入晶格。
不同点: 间隙化合物:间隙化合物中的金属组元大多与自 身原来的结构类型不同 间隙固溶体:间隙固溶体中的金属组元仍保持自 身的晶格结构
I. 尺寸因素
II. 晶体结构因素 组元间晶体结构相同时,固溶度一般都较大,而且有可 能形成无限固溶体。若不同只能形成有限固溶体。
III. 电负性差因素
两元素间电负性差越小,越易形成固溶体,且形成的 固溶体的溶解度越大;随两元素间电负性差增大,固 溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体 2)ΔX>0.4~0.5,倾向于形成稳定的化合物
Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素 形成的金属化合物。 不遵守化合价规律,晶格类型随化合物电子浓度 而变化。 电子浓度为3/2时: 呈体心立方结构(b相); 电子浓度为21/13时:呈复杂立方结构(g相); 电子浓度为21/12时。呈密排六方结构(e相);
NaCl型 CaF2型 闪锌矿型 硫锌矿型 (面心立方) (面心立方) (立方ZnS) (六方ZnS)
材料科学基础三元相图

材料科学基础三元相图
一.三元相图的成分表示法:等腰三角形
材料科学基础三元相图
一.三元相图的成分表示法:直角坐标系
材料科学基础三元相图
3.浓度三角形中特殊线: 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算,四相平衡无从计算 1.两相平衡:杠杆定律
2.合金的凝固过程和组织
各点合金的组织
如表4-3(表中nmp区需修正) 如合金I:L→A 剩余液相交np于n1:L+A→M 至n2点,A消失,L→M 液相沿e1E:L→M+B 液相成分在E点:L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3.等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--:
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型, 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应,且靠近单变线 的为生成相
材料科学基础三元相图
3.三元相图分析法总结---四相平衡
x合金结晶:
L→A,L+A→M,L→M,L→M+C,L→M+B+C
y合金结晶: L→A,L+A→M,L+A→M+C,L→M+C,L→M+B+C 5.固相有固溶度时的包共晶 包共晶:Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2,c2c1为M+γ二元共晶结 束面投影
一.三元相图的成分表示法:等腰三角形
材料科学基础三元相图
一.三元相图的成分表示法:直角坐标系
材料科学基础三元相图
3.浓度三角形中特殊线: 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算,四相平衡无从计算 1.两相平衡:杠杆定律
2.合金的凝固过程和组织
各点合金的组织
如表4-3(表中nmp区需修正) 如合金I:L→A 剩余液相交np于n1:L+A→M 至n2点,A消失,L→M 液相沿e1E:L→M+B 液相成分在E点:L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3.等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--:
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型, 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应,且靠近单变线 的为生成相
材料科学基础三元相图
3.三元相图分析法总结---四相平衡
x合金结晶:
L→A,L+A→M,L→M,L→M+C,L→M+B+C
y合金结晶: L→A,L+A→M,L+A→M+C,L→M+C,L→M+B+C 5.固相有固溶度时的包共晶 包共晶:Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2,c2c1为M+γ二元共晶结 束面投影
材料科学基础 第五章 5.1-5.4相图

5.2.3 杠杆定律
设成份为 X的合金的总重量为1,液相的相对重量为 QL,其 成份为 X1,固相相对重量为Qα,其成份为X2,则 :
5.2.4 相图的类型和结构 根据组元的多少,可分为单元系、二元系、三元 系 …. 相图。
二元系相图的类型有:
① 液态无限溶解,固态无限溶解 -匀晶相图; ②液态无限溶解,固态有限溶解 -共晶相图和包晶
共晶组织:共晶转变产物。(是两相混合物)
共晶合金的特殊性质: ①比纯组元熔点低,简化了熔化和铸造的操作; ②共晶合金比纯金属有更好的流动性,其在凝固之 中防止了阻碍液体流动的枝晶形成,从而改善铸造 性能; ③恒温转变(无凝固温度范围)减少了铸造缺陷, 例如偏聚和缩孔; ④共晶凝固可获得多种形态的显微组织,尤其是规 则排列的层状或杆状共晶组织可能成为优异性能的 原位复合材料(in-situ composite )。
5.2.2 相律
相律(phase rule)是表示在平衡条件下,系统的自 由度数、组元数和相数之间的关系,是系统的平 衡条件的数学表达式。 相律数学表达式:f = C – P + 2 式中 P—平衡相数 C—体系的组元数 f—体系自由度(degrees of freedom) 数 2-温度和压力 自由度数 f:是指不影响体系平衡状态的独立可 变参数(温度、压力、浓度等)的数目。 在恒压下,相律表达式: f = C – P + 1
相律的应用
① 利用它可以确定系统中可能存在的最多平衡相数 单元系,因f ≥0,故 P≤1-0+1=2,平衡相最大为二个。 注意:这并不是说,单元系中能够出现的相数不能超过二 个,而是说,某一固定 T下,单元系中不同的相只能有两 个同时存在,而其它相则在别的条件下存在。
材料科学基础(Fe-C相图)

✓ 碳在中的溶解度曲线Biblioteka ✓ 记为Acm温度。Acm
✓ 低于此温度,奥
氏体中将析出
Fe3C , 称为二次渗碳体
Fe3CII。
(3) PQ线
✓ C在F中溶解度曲线。 ✓ 727℃时,碳在F中最
大解度为0.0218%; ✓ F从727℃冷却时会析
出极少量的渗碳体, 三次渗碳体Fe3CIII。 ✓ 室温下含<0.0008%C。
1899年英国人罗伯茨-奥斯汀(W.C.RobertsAusten)制定了第一张铁碳相图;1897年完成 初稿 , 1899年彻底完成。
洛兹本 (H.W.Bakhius Roozeboom)首先在合 金系统中应用吉布斯(Gibbs)相律修订铁碳相 图 ,1900年制定出较完整的铁碳平衡图。
相图的出现,是金属学发展的一个里程碑。
过共析钢球化退火:
球状P (球状Fe3C+F)
小结:
(5)共晶白口铁(C%≈4.3%)
组织转变
L→(L+Ld) →Ld→Ld′
用量热计法测定银铜合金的凝固点,并首先用冰点曲线表示 其实验成果。
1876年与J.洛基尔一起用光谱仪作定量分析,以辅助传统的 试金法。
1885年开始研究钢的强化,研究少量杂质对金的拉伸强度的 影响。奥斯汀采用Pt/(Pt-Rh)热电偶高温计,得以测定了 高熔点物质的冷却速度,创立共晶理论。用显微镜照相研究 金属的金相形貌。
3. 三个三相区:
(1)包晶转变: HJB线: (L+)→
发生在高温, 在随后的冷却过程中 组织还会变化。 此转变不作讨论。 (简化Fe-Fe3C相图)
(2)共晶转变: ECF线:
共晶组织 (+ Fe3C)为 莱氏体, Ld(Ledeburite)
材料科学基础 第5章 相图 5.2

§5-3 二元匀晶相图
二元匀晶(Isomorphous)相图
相图。
具有匀晶相图的二元合金系统有Cr-Mo, W-Mo等。
右图所示Cu-Ni相图是最常
见的二元匀晶相图,以此相图
为例进行讨论,其它匀晶相图
与此类似。
;
下面的一条曲线是固相线(Solid line),固相线以下的区域为
3、匀晶相图的特点
二组元在液态和固态都能够完全相互溶解,所有成分(Ni: 0~100%)的合金在固态只有一种晶体结构,相图中只有一个固相区。
因此,能够形成匀晶合金系的两种组元必须具有相同的晶体结构,相同的原子价,原子半径接近(相差不超过15%),相互不形成化合物。
材料科学基础-第五章-材料的相结构及相图-PPT

相图上为一条垂直线。
Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素
形成的金属化合物。
不遵守化合价规律,晶格类型随化合物电子浓度而
变化。
电子浓度为3/2时: 呈体心立方结构(b相);
电子浓度为21/13时:呈复杂立方结构(g相);
电子浓度为21/12时。呈密排六方结构(e相);
体。
III. 电负性差因素
IV. 两元素间电负性差越小,越易形成固溶体,且形
成的固溶体的溶解度越大;随两元素间电负性差
增大,固溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体
2)ΔX>0.4~0.5,倾向于形成稳定的化合物
IV. 电子浓度因素
V. 电子浓度的定义是合金中各组成元素的价电子数总
子的价电子数恰好使负离子具有稳定的电子层
结构。
金属元素与周期表中的ⅣA,ⅤA,ⅥA元素
形成正常价化合物。
有较高的硬度,脆性很大。
例如:Mg2Si、Mg2Sn、Mg2Pb、MgS、MnS等
(1)正常价化合物
正常价化合物的分子式只有AB,A2B或AB2两种。
常见类型:
NaCl型
CaF2型
Cu原子形成四面体(16个)。
每个镁原子有4个近邻镁原子和12个近邻铜原子;
每个铜原子有6个近邻的铜原子和6个近邻的镁原子
。
Cu
Mg
II. 拉弗斯(Laves)相
②MgZn2型:六方晶系。
Mg原子形成硫锌矿结构;Zn原子形成四面体。
每个Mg原子有4个近邻Mg原子和12个近邻Zn原
子。
每个Zn原子有6个近邻Zn原子和6个近邻Mg原子
Mg2Si
Mg—Si相图
(2)电子化合物
由ⅠB族或过渡金属元素与ⅡB,ⅢB,ⅣB族元素
形成的金属化合物。
不遵守化合价规律,晶格类型随化合物电子浓度而
变化。
电子浓度为3/2时: 呈体心立方结构(b相);
电子浓度为21/13时:呈复杂立方结构(g相);
电子浓度为21/12时。呈密排六方结构(e相);
体。
III. 电负性差因素
IV. 两元素间电负性差越小,越易形成固溶体,且形
成的固溶体的溶解度越大;随两元素间电负性差
增大,固溶度减小。
1)电负性差值ΔX<0.4~0.5时,有利于形成固溶体
2)ΔX>0.4~0.5,倾向于形成稳定的化合物
IV. 电子浓度因素
V. 电子浓度的定义是合金中各组成元素的价电子数总
子的价电子数恰好使负离子具有稳定的电子层
结构。
金属元素与周期表中的ⅣA,ⅤA,ⅥA元素
形成正常价化合物。
有较高的硬度,脆性很大。
例如:Mg2Si、Mg2Sn、Mg2Pb、MgS、MnS等
(1)正常价化合物
正常价化合物的分子式只有AB,A2B或AB2两种。
常见类型:
NaCl型
CaF2型
Cu原子形成四面体(16个)。
每个镁原子有4个近邻镁原子和12个近邻铜原子;
每个铜原子有6个近邻的铜原子和6个近邻的镁原子
。
Cu
Mg
II. 拉弗斯(Laves)相
②MgZn2型:六方晶系。
Mg原子形成硫锌矿结构;Zn原子形成四面体。
每个Mg原子有4个近邻Mg原子和12个近邻Zn原
子。
每个Zn原子有6个近邻Zn原子和6个近邻Mg原子
5 《材料科学基础》第五章 相平衡和相图

( p -T 图)
自由
一、水的相图
冰的熔融曲线 水的饱和蒸汽压曲线(蒸发曲线)
3个相区:
p=1, f=2 ,双变量系统(T、P) 3条界线: p=2 , f= 1,单变量系统(T或P) 1个无变量点(三相点):
T
p=3 , f=0 ,无变量系统
冰的饱和蒸汽压曲线(升华曲线)
??
注意:
•冰点和三相点O
第五章
第五章
§5.1
相平衡和相图
基本知识
§5.2
§5.3
单元系统
二元系统
§5.4
三元系统
§5.1
相平衡与相图的基本知识
一、相平衡的基本概念 二、相律 三、相平衡的研究方法
一、相平衡的基本概念
相平衡:是研究一个多组分(或单组分)多相系统中相的平
衡问题,即多相系统的平衡状态(包括相的个数、各相的状态、
二、二元凝聚系统相图的基本类型
三、复杂二元相图的分析步骤
四、二元系统专业相图
要求
一、二元系统相图的表示方法及杠杆规则
1、作为特种陶瓷的重要原料
由于7%~9%的体积效应,常加适量CaO或Y2O3稳定剂。
在>1500℃以上与四方型ZrO2形成立方晶型固溶体,称稳定
化立方ZrO2 。
2、熔点高(2680℃),作耐火材料 3、利用导氧导电性能,作氧敏传感器元件 4、利用体积效应,对陶瓷材料进行相变增韧。
增韧机理: 微裂纹增韧
实线部分: 四个单相区: 五条界线:
两个无变量点:
晶体的升华曲线(或延长线)与液体的蒸发曲线(或延长线) 的交点是该晶体的熔点。 两种晶型的升华曲线(或延长线)的交点是两种晶型的晶型转 变点。
材料科学基础 第四章 相图(3)
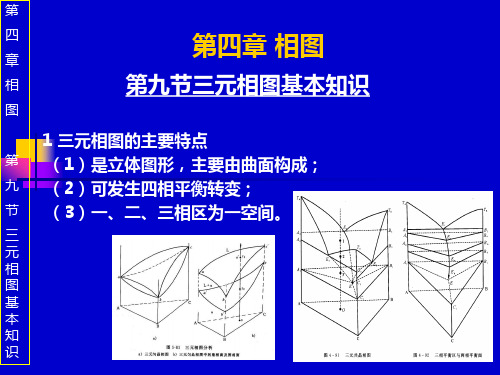
第 十 一 节 三 元 共 晶 相 图
25
第 四 章 相 图
第十一节 三元共晶相图
二 组元在固态有限溶解的共晶相图
(3)变温截面 ) 3个三相区 个三相区 共晶相图特征: 共晶相图特征:水平线 ;两相共晶区特征:曲边三角形。 两相共晶区特征:曲边三角形。 1个三相区 个三相区 应用:分析合金结晶过程,确定组织变化. 应用:分析合金结晶过程,确定组织变化 局限性:不能分析成分变化。 成分在单变量线上,不在垂直截面上) 局限性:不能分析成分变化。(成分在单变量线上,不在垂直截面上)
第十一节 三元共晶相图
一 组元在固态互不相溶的共晶相图 (1)相图分析 ) 熔点;二元共晶点;三元共晶点。 点:熔点;二元共晶点;三元共晶点。 两相共晶线 液相面交线 两相共晶面交线 液相单变量线
液相区与两相共晶面交线
第 十 一
线:EnE
节 三 元 共 晶 相 图
14
第 四 章 相 图 第 十 一 节 三 元 共 晶 相 图
第十一节 三元共晶相图
一 组元在固态互不相溶的共晶相图 (1)相图分析 ) 液相面 固相面 面: 两相共晶面 三相共晶面 两相区: 个 两相区:3个 单相区: 个 区: 单相区:4个 三相区: 个 三相区:4个 四相区: 个 四相区:1个
15
第 四 章 相 图 第 十 一 节 三 元 共 晶 相 图
第 十 一 节 三 元 共 晶 相 图
26
第 四 章 相 图
第十一节 三元共晶相图
二 组元在固态有限溶解的共晶相图 合金结晶过程分析; 合金结晶过程分析; 相组成物相对量计算(杠杆定律、重心定律) (4)投影图 相组成物相对量计算(杠杆定律、重心定律) ) 组织组成物相对量计算(杠杆定律、 组织组成物相对量计算(杠杆定律、重心定律)
材料科学基础材料的相结构与相图

第6页/共270页
共析钢:由F(铁素体相)+ Fe3C(渗碳体相)双相构成, 为双相合金。
第7页/共270页
4、合金的显微组织
在显微镜下,合金中各相的 形状、大小和分布所构成的综 合体称合金组织。
第8页/共270页
“相构成组织、组织决定性能”
第9页/共270页
例1:钢中的珠光体(P) 组织:
第65页/共270页
如果外界压力保持恒定(例如一个标 准大气压),那么单元系相图只要一个 温度轴来表示。 根据相律,在汽、水、冰的各单相区 内(f=1),温度可在一定范围内变动。 在熔点和沸点处,两相共存,f=0, 故温度不能变动,即相变为恒温过程。
第66页/共270页
在单元系中,除了可以出现气、 液、固三相之间的转变外,某些物 质还可能出现固态中的同素异构转 变。
第17页/共270页
2、溶解度(C):
固溶体在一定温度和压力下, 溶于溶质原子的极限浓度。 当溶质浓度小于溶解度时, 溶质浓度增加将导致固溶强化;
第18页/共270页
当溶质浓度大于溶解度时, 将析出第二相起作第二相强 化作用; 当析出的第二相非常细小时, 称弥散强化。
第19页/共270页
3、固溶体分类
第60页/共270页
在两相区,两相的质量比可以 用杠杆定律求得,即:
QL / Qα = bc/ab 即QL / Qα恰好与它们的杠杆 臂成反比关系。 杠杆定律只适用于两相区。
第61页/共270页
二、单元系相图
单元系相图:是通过几何图形描 述由单一组元构成的体系在不同温 度和压力条件下所可能存在的相及 多相的平衡。 现以水为例说明单元系相图的表 示和测定方法。
例2、合金渗碳体(Fe、
共析钢:由F(铁素体相)+ Fe3C(渗碳体相)双相构成, 为双相合金。
第7页/共270页
4、合金的显微组织
在显微镜下,合金中各相的 形状、大小和分布所构成的综 合体称合金组织。
第8页/共270页
“相构成组织、组织决定性能”
第9页/共270页
例1:钢中的珠光体(P) 组织:
第65页/共270页
如果外界压力保持恒定(例如一个标 准大气压),那么单元系相图只要一个 温度轴来表示。 根据相律,在汽、水、冰的各单相区 内(f=1),温度可在一定范围内变动。 在熔点和沸点处,两相共存,f=0, 故温度不能变动,即相变为恒温过程。
第66页/共270页
在单元系中,除了可以出现气、 液、固三相之间的转变外,某些物 质还可能出现固态中的同素异构转 变。
第17页/共270页
2、溶解度(C):
固溶体在一定温度和压力下, 溶于溶质原子的极限浓度。 当溶质浓度小于溶解度时, 溶质浓度增加将导致固溶强化;
第18页/共270页
当溶质浓度大于溶解度时, 将析出第二相起作第二相强 化作用; 当析出的第二相非常细小时, 称弥散强化。
第19页/共270页
3、固溶体分类
第60页/共270页
在两相区,两相的质量比可以 用杠杆定律求得,即:
QL / Qα = bc/ab 即QL / Qα恰好与它们的杠杆 臂成反比关系。 杠杆定律只适用于两相区。
第61页/共270页
二、单元系相图
单元系相图:是通过几何图形描 述由单一组元构成的体系在不同温 度和压力条件下所可能存在的相及 多相的平衡。 现以水为例说明单元系相图的表 示和测定方法。
例2、合金渗碳体(Fe、
材料科学基础课件第六章--相平衡与相图

F = C-P+n
自由 度数
独立组 元数
F = C-P+2
对凝聚态体系, 压力恒定或影响 较小,其相律为:
F = C-P+1
组元数C多,自 由度F大;相数P 多,自由度小
6.1.3 相平 衡研究方法
动态法
静态法 (淬冷法)
热分 析法
差热分 析法
T/℃
(1ቤተ መጻሕፍቲ ባይዱ 热分析法
1
2
3
原理:根据系统在冷却
ab c
100 80Bi 60Bi 20Bi 100 Bi 20Cd 40Cd 80Cd Cd
T/℃
ab c d e
t/s
Bi-Cd合金冷却曲线
546.15K
596.15K
L
L+Bi(s) ●
L+Cd(s)
20 40 Bi(s)+Cd(s) 80
0 Bi
WCd/%
100 Cd
Bi-Cd系统相图
液相线:由凝固开始温度连接起来的相界线 固相线:由凝固终结温度连接起来的相界线
元系统相图
P ●:熔点
■:转变点
2
L
●
Ⅱ
3
■
1
●
Ⅰ
O T0 T2 T1 T3
T
图 6-7 具有不可逆多晶转变的
单元系统相图
晶体I T3 晶体II
晶体Ⅰ 晶体Ⅱ 液相
(1) 晶体I、Ⅱ有稳定区 (2) 转变温度T3<T1 、T2(熔点)
T1 液 相 T2
(1)晶体Ⅱ无稳定区 (2)T3>T1、T2
6.2.2 单元系统专业相图
G
E
H
A+B
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章
相
图
4 四相平衡转变的类型
第
(1)共晶转变:L0 T αa+βb+γc;
九
(2)包晶转变:L0+αa+βb T γc;
节
(3)包共晶转变:L0+αa T βb+γc;
三
还有偏共晶、共析、包析、包共析转变等。
元
相
图
基
本
知
识
4
第 四
第九节 三元相图基本知识
章
相 5 共线法则与杠杆定律 图 (1)共线法则:在一定温度下,三元合金两相平衡时,合
10
第 四
第十节 三元匀晶相图
章
相 4 变温截面(垂直截面)
图
(1)做法:某一垂直平面与相图中各面的交线。
(2)二种常用变温截面
第
经平行于某条边的直线做垂直面获得;
十
经通过某一顶点的直线做垂直面获得。
节
(3)结晶过程分析
三
成分轴的两端不一定是纯组元;
元
注意: 液、固相线不一定相交;
匀
液、固相线不是成分变化线, 不能运用杠杆定律。
图 (1)做法:某一温度下的水平面与相图中各面的交线。
第 (2)截面图分析
十
3个相区:L, α, L+α;
节 三 元
2条相线:L1L2, S1S2(共轭曲线); 若干连接线:可作为计
匀
算相对量的杠杆(偏向
晶
低熔点组元;可用合金
相 图
成分点与顶点的连线近
似代替;过给定合金成
分点,只能有唯一的共
轭连线。)
晶
相
图
11
第 四
第十节 三元匀晶相图
章
相
图 5 投影图
第
(1)全方位投影图(匀晶相图不必要) 。
十
节
(2)等温线投影图:可确定合金结晶开始、结束温度。
三
元
匀
晶
相
图
2h 12
第 四
第十一节 三元共晶相图
章
相 一 组元在固态互不相溶的共晶相图
图
(1)相图分析
点:熔点;二元共晶点;三元共晶点。
第
两相共晶线
面:液相面、固相面;
第 区:L, α, L+α。
十
节
三 元 匀 晶 相 图
8
第 四
第十节 三元匀晶相图
章
相
图 2 三元固溶体合金的结晶规律
第
十
液相成分沿液相面、固相成分沿固相面,呈蝶形规律变化。
节 三
(立体图不实用)
元
匀 共轭线:平衡相成分点的连线。
晶
相
图
9
第 四
第十节 三元匀晶相图
章
相 3 等截温界面(水平截面)
第
两相共晶线
十
液相面交线
一 线:EnE 两相共晶面交线
节
液相单变量线
三
液相区与两相共晶面交线
元 共
固相单变量线
晶
相
图
20
第 四
第十一节 三元共晶相图
章
相 二 组元在固态有限溶解的共晶相图
图 (1)相图分析
液相面
第
固相面(组成)
十 面: 二相共晶面
一
三相共晶面
节
溶解度曲面:6个
三
两相区:6个
元 共
区: 单相区:4个
晶
三相区:4个
相 图
四相区:1个
21
第 四
第十一节 三元共晶相图
章
相 二 组元在固态有限溶解的共晶相图
图 (1)相图分析
第
十 一
节
三 元 共 晶 相 图
22
第 四
第十一节 三元共晶相图
章 二 组元在固态有限溶解的共晶相图
相 (2)等温截面
应用:可确定平衡相及其成分;可运用杠杆定律和重心定律。
第
相的成分给定,另一个相的成分点必然位于已知成分点连线 的延长线上。
九
(2)若两个平衡相的成分点已知,合金的成分点必然位于
节 两个已知成分点的连线上。
三
元
相
图
基
本
知
识
6
第 四
第九节 三元相图基本知识
章 6 重心法则
相
在一定温度下,三元合金三相平衡时,合金的成分点为三
图 个平衡相的成分点组成的三角形的质量重心。(由相率可知,
相
组织组成物的相对量。(杠杆定律与重心法则)
图
18
第 四
第十一节 三元共晶相图
章
相 一 组元在固态互不相溶的共晶相图
图
(5)典型合金室温组织
第
十 一
节
三 元 共 晶 相
图 4h 19
第 四
第十一节 三元共晶相图
章
相 二 组元在固态有限溶解的共晶相图
图 (1)相图分析
点:熔点;二元共晶点;三元共晶点。
十
液相面交线
一
节
线:EnE 两相共晶面交线
液相单变量线
三
元
液相区与两相共晶面交线
共
晶
相
图
13
第 四
第十一节 三元共晶相图
章
相
图 一 组元在固态互不相溶的共晶相图
第
(1)相图分析
十
一
节
液相面
三
固相面
元
共
面: 两相共晶面
晶
三相共晶面
相 图
两相区:3个
区: 单相区:4个
三相区:4个
四相区:1个
14
第 四
九
节
三
元
相
图
基
本
知
识
2
第 四
第九节 三元相图基本知识
章
相 3 成分三角形中特殊的点和线 图 (3)平行于某条边的直线:其上合金所含由此边对应顶点
所代表的组元的含量一定。
第 (4)通过某一顶点的直线:其上合金所含由另两个顶点所
九
代表的两组元的比值恒定。
节
三
元
相
图
基
本
知
识
3
第 四
第九节 三元相图基本知识
第十一节 三元共晶相图
章
相
图 一 组元在固态互不相溶的共晶相图
第
(1)相图分析
十
一
节
液相面
三
固相面
元
共
面: 两相共晶面
晶
三相共晶面
相 图
两相区:3个
区: 单相区:4个
三相区:4个
四相区:1个
15
第 四
第十一节 三元共晶相图
章
相 图
一 组元在固态互不相溶的共晶相图 (2)垂直截面图
第 十 一 节 三 元 共 晶 相 图
第
四
章
第九节 三元相图基本知识
相
图 2 成分表示法-成分三角形(等边、等腰、直角三角形)
第 (1)已知点确定成分;
九 节
(2)已知成分确定点。
三
元
相
图
基
本
知
识
1
第 四
第九节 三元相图基本知识
章
相
图
3 成分三角形中特殊的点和线
(1)三个顶点:代表三个纯组元;
第
(2)三个边上的点:二元系合金的成分点;
O点合金的室温组织 A+(A+C)+(A+B+C)
16
第 四
第十一节 三元共晶相图
章
相
图 一 组元在固态互不相溶的共晶相图
第
(3)水平截面图
十
一
节
三
元
共
晶
相
图
17
第 四
第十一节 三元共晶相图
章
相 一 组元在固态互不相溶的共晶相图
图
(4)投影图
第
十 一
节
三
元
共
晶 思考:分析O点合金的凝固过程,确定室温组织,计算室温
此时系统有一个自由度,温度一定时,三个平衡相的成分是
第 确定的。)
九
平衡相含量的计算:所计算
节
相的成分点、合金成分点和二者
三
元 连线的延长线与对边的交点组成
相 图
一个杠杆。合金成分点为支点。
基 本
计算方法同杠杆定律。
知
识
7
第 四
第十节 三元匀晶相图
章
相 1 相图分析 图 点:a, b, c-三个纯组元的熔点;
金的成分点和两个平衡相的成分点必然位
于成分三角形内的同一条直线上。
第
(由相率可知,此时系统有一个自由度,表示一个相的成
九
分可以独立改变,另一相的成分随之改变。)
节 (2)杠杆定律:用法与二元相同。三元相 Nhomakorabea图
基
本
知
识
5
第 四
第九节 三元相图基本知识
章
相 5 共线法则与杠杆定律
图 两条推论
(1)给定合金在一定温度下处于两相平衡时,若其中一个
