初中数学几何最值问题典型例题
(完整版)初中数学《几何最值问题》典型例题
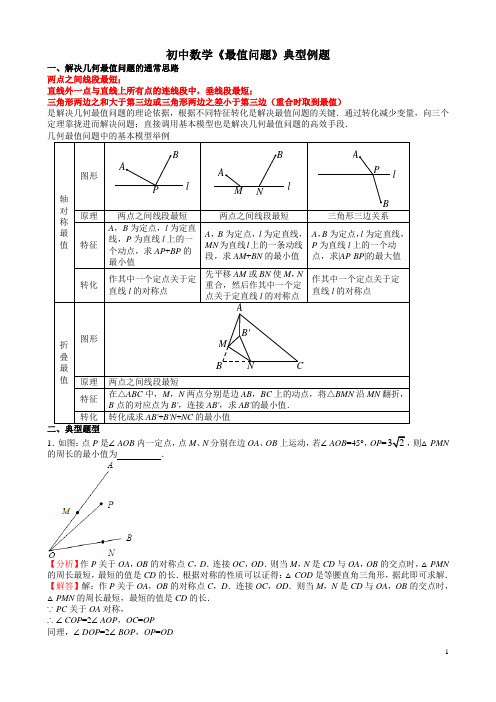
初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短;直线外一点与直线上所有点的连线段中,垂线段最短;三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段.轴对称最值图形lPBANM lBAAPBl 原理两点之间线段最短两点之间线段最短三角形三边关系特征A,B为定点,l为定直线,P为直线l上的一个动点,求AP+BP的最小值A,B为定点,l为定直线,MN为直线l上的一条动线段,求AM+BN的最小值A,B为定点,l为定直线,P为直线l上的一个动点,求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M,N重合,然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中,M,N两点分别是边AB,BC上的动点,将△BMN沿MN翻折,B点的对应点为B',连接AB',求AB'的最小值.转化转化成求AB'+B'N+NC的最小值1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△PMN 的周长的最小值为.【分析】作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN 的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.【解答】解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.∵PC关于OA对称,∴∠COP=2∠AOP,OC=OP同理,∠DOP=2∠BOP,OP=OD∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD.∴△COD是等腰直角三角形.则CD=2OC=2×32=6.【题后思考】本题考查了对称的性质,正确作出图形,理解△PMN周长最小的条件是解题的关键.2.如图,当四边形P ABN的周长最小时,a=.【分析】因为AB,PN的长度都是固定的,所以求出P A+NB的长度就行了.问题就是P A+NB什么时候最短.把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N点位置,此时P A+NB最短.设直线AB″的解析式为y=kx+b,待定系数法求直线解析式.即可求得a的值.【解答】解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,﹣1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),设直线AB″的解析式为y=kx+b,则123k bk b=+⎧⎨-=+⎩,解得k=4,b=﹣7.∴y=4x﹣7.当y=0时,x=74,即P(74,0),a=74.故答案填:74.【题后思考】考查关于X轴的对称点,两点之间线段最短等知识.3.如图,A 、B 两点在直线的两侧,点A 到直线的距离AM =4,点B 到直线的距离BN =1,且MN =4,P 为直线上的动点,|P A ﹣PB |的最大值为.D PB′N MA【分析】作点B 于直线l 的对称点B ′,则PB =PB ′因而|P A ﹣PB |=|P A ﹣PB ′|,则当A ,B ′、P 在一条直线上时,|P A ﹣PB |的值最大.根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值,进而求得|P A ﹣PB |的最大值.【解答】解:作点B 于直线l 的对称点B ′,连AB ′并延长交直线l 于P . ∴B ′N =BN =1,过D 点作B ′D ⊥AM , 利用勾股定理求出AB ′=5 ∴|P A ﹣PB |的最大值=5.【题后思考】本题考查了作图﹣轴对称变换,勾股定理等,熟知“两点之间线段最短”是解答此题的关键.4.动手操作:在矩形纸片ABCD 中,AB =3,AD =5.如图所示,折叠纸片,使点A 落在BC 边上的A ′处,折痕为PQ ,当点A ′在BC 边上移动时,折痕的端点P 、Q 也随之移动.若限定点P 、Q 分别在AB 、AD 边上移动,则点A ′在BC 边上可移动的最大距离为 .【分析】本题关键在于找到两个极端,即BA ′取最大或最小值时,点P 或Q 的位置.经实验不难发现,分别求出点P 与B 重合时,BA ′取最大值3和当点Q 与D 重合时,BA ′的最小值1.所以可求点A ′在BC 边上移动的最大距离为2.【解答】解:当点P 与B 重合时,BA ′取最大值是3, 当点Q 与D 重合时(如图),由勾股定理得A ′C =4,此时BA ′取最小值为1. 则点A ′在BC 边上移动的最大距离为3﹣1=2. 故答案为:2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象造成错误.5.如图,直角梯形纸片ABCD ,AD ⊥AB ,AB =8,AD =CD =4,点E 、F 分别在线段AB 、AD 上,将△AEF 沿EF 翻折,点A 的落点记为P .当P 落在直角梯形ABCD 内部时,PD 的最小值等于 .【分析】如图,经分析、探究,只有当直径EF最大,且点A落在BD上时,PD最小;根据勾股定理求出BD的长度,问题即可解决.【解答】解:如图,∵当点P落在梯形的内部时,∠P=∠A=90°,∴四边形PF AE是以EF为直径的圆内接四边形,∴只有当直径EF最大,且点A落在BD上时,PD最小,此时E与点B重合;由题意得:PE=AB=8,由勾股定理得:BD2=82+62=80,∴BD=45,∴PD=458 .【题后思考】该命题以直角梯形为载体,以翻折变换为方法,以考查全等三角形的判定及其性质的应用为核心构造而成;解题的关键是抓住图形在运动过程中的某一瞬间,动中求静,以静制动.6.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为.【分析】取AB的中点E,连接OD、OE、DE,根据直角三角形斜边上的中线等于斜边的一半可得OE=AB,利用勾股定理列式求出DE,然后根据三角形任意两边之和大于第三边可得OD过点E时最大.【解答】解:如图,取AB的中点E,连接OD、OE、DE,∵∠MON=90°,AB=2∴OE=AE=12AB=1,∵BC=1,四边形ABCD是矩形,∴AD,∴DE2,根据三角形的三边关系,OD<OE+DE,∴当OD过点E是最大,最大值为2+1.故答案为:2+1.【题后思考】本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,勾股定理,确定出OD过AB的中点时值最大是解题的关键.7.如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE,那么DE长的最小值是.【分析】设AC=x,BC=4﹣x,根据等腰直角三角形性质,得出CD=22x,CD′=22(4﹣x),根据勾股定理然后用配方法即可求解.【解答】解:设AC=x,BC=4﹣x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=22x,CD′=22(4﹣x),∵∠ACD=45°,∠BCD′=45°,∴∠DCE=90°,∴DE2=CD2+CE2=12x2+12(4﹣x)2=x2﹣4x+8=(x﹣2)2+4,∵根据二次函数的最值,∴当x取2时,DE取最小值,最小值为:4.故答案为:2.【题后思考】本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.8.如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK 的最小值为.【分析】根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连接P′Q与BD的交点即为所求的点K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值,然后求解即可.【解答】解:如图,∵AB=2,∠A=120°,∴点P′到CD的距离为2×33∴PK+QK3故答案为:3.【题后思考】本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.9.如图所示,正方形ABCD的边长为1,点P为边BC上的任意一点(可与B、C重合),分别过B、C、D作射线AP的垂线,垂足分别为B′、C′、D′,则BB′+CC′+DD′的取值范围是.【分析】首先连接AC,DP.由正方形ABCD的边长为1,即可得:S△ADP=12S正方形ABCD=12,S△ABP+S△ACP=S△ABC=12S正方形ABCD=12,继而可得12AP•(BB′+CC′+DD′)=1,又由1≤AP≤2,即可求得答案.【解答】解:连接AC,DP.∵四边形ABCD是正方形,正方形ABCD的边长为1,∴AB=CD,S正方形ABCD=1,∵S△ADP=12S正方形ABCD=12,S△ABP+S△ACP=S△ABC=12S正方形ABCD=12,∴S△ADP+S△ABP+S△ACP=1,∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•(BB′+CC′+DD′)=1,则BB′+CC′+DD′=2 AP,∵1≤AP≤2,∴当P当P与C重合时,有最小值2.∴2≤BB′+CC′+DD′≤2.故答案为:2≤BB′+CC′+DD′≤2.【题后思考】此题考查了正方形的性质、面积及等积变换问题.此题难度较大,解题的关键是连接AC,DP,根据题意得到S△ADP+S△ABP+S△ACP=1,继而得到BB′+CC′+DD′=2 AP.10.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A 和⊙B上的动点,则PE+PF的最小值是.【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值,进而求出即可.【解答】解:由题意可得出:当P与D重合时,E点在AD上,F在BD上,此时PE+PF最小,连接BD,∵菱形ABCD中,∠A=60°,∴AB=AD,则△ABD是等边三角形,∴BD=AB=AD=3,∵⊙A、⊙B的半径分别为2和1,∴PE=1,DF=2,∴PE+PF的最小值是3.故答案为:3.【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识,根据题意得出P点位置是解题关键.。
初中数学几何模型与最值问题09专题-一元二次方程在实际应用中的最值问题(含答案)

初中数学几何模型与最值问题专题9 一元二次方程在实际应用中的最值问题【应用呈现】1、 近年来,某县为发展教育事业,加大了对教育经费的投入,2009年投入6000万元,2011年投入8640万元.(1)求2009年至2011年该县投入教育经费的年平均增长率;(2)该县预计2012年投入教育经费不低于9500万元,若继续保持前两年的平均增长率,该目标能否实现?请通过计算说明理由.2、如图,要建造一个四边形花圃ABCD ,要求AD 边靠墙,CD ⊥AD ,AD ∥BC ,AB ∶CD =5∶4,且三边的总长为20 m .设AB 的长为5x m . (1)请求AD 的长;(用含字母x 的式子表示)(2)若该花圃的面积为50 m 2,且周长不大于30 m ,求AB 的长.【方法总结】一、一元二次方程判别式求解1、已知x 、y 为实数,且满足x y m ++=5,xy ym mx ++=3,求实数m 最大值与最小值。
2、已知m ,n 是关于x 的一元二次方程x 2﹣2tx +t 2﹣2t +4=0的两实数根,则(m +2)(n +2)的最小值是( ) A .7 B .11 C .12 D .16二、配方法求最值1、设a 、b 为实数,那么a ab b a b 222++--的最小值为_______。
2、将形状、大小完全相同的两个等腰三角形如图所示放置,点D 在AB 边上,△DEF 绕点D 旋转,腰DF 和底边DE 分别交△CAB 的两腰CA ,CB 于M ,N 两点,若CA =5,AB =6,AB =1:3,则MD +的最小值为 .三、 “夹逼法”求最值1、不等边三角形∆ABC 的两边上的高分别为4和12且第三边上的高为整数,那么此高的最大值可能为________。
1、国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路.某地区2017年底有贫困人口1万人,通过各方面的共同努力,2019年底该地区贫困人口减少到0.25万人,求该地区2017年底至2019年底贫困人口年平均下降的百分率.2、某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利50元.经调查发现:这种衬衫的售价每降低1元,平均每天能多售出2件,设每件衬衫降价x元.(1)降价后,每件衬衫的利润为元,平均每天的销量为件;(用含x的式子表示)(2)为了扩大销售,尽快滅少库存,商场决定采取降价措施,但需要平均每天盈利1600元,那么每件衬衫应降价多少元?3、2020年,我国脱贫攻坚在力度、广度、深度和精准度上都达到了新的水平,重庆市深度贫困地区脱贫进程明显加快,作风治理和能力建设初见成效,精准扶贫、精准脱贫取得突破性进展.为助力我市脱贫攻坚,某村村委会在网上直播销售该村优质农产品礼包,该村在今年1月份销售256包,2、3月该礼包十分畅销,销售量持续走高,在售价不变的基础上,3月份的销售量达到400包.(1)若设2、3这两个月销售量的月平均增长率为a%,求a的值;(2)若农产品礼包每包进价25元,原售价为每包40元,该村在今年4月进行降价促销,经调查发现,若该农产品礼包每包降价1元,销售量可增加5袋,当农产品礼包每包降价多少元时,这种农产品在4月份可获利4620元?4、某商场第一年销售某品牌手机5000部,如果每年的销售量比上年增长相同的百分率x,且第三年比第二年多销售了1200部,求x的值.5、某通讯公司规定:一名客户如果一个月的通话时间不超过A分钟,那么这个月这名客户只要交10元通话费;如果超过A分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟元交费.(Ⅰ)某名客户7月份通话90分钟,超过了规定的A分钟,则超过部分应交通话费元(用含A的代数式表示);(Ⅱ)下表表示某名客户8月份、9月份的通话情况和交费情况:月份通话时间/分钟通话费总数/元8月份80 259月份45 10根据上表的数据,求A的值.6、在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为9米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).(Ⅰ)根据题意填表;BC(m) 1 3 5 7矩形ABCD面积(m2)(Ⅱ)能够围成面积为100m2的矩形花园吗?如能说明围法,如不能,说明理由.专题9 一元二次方程在实际应用中的最值问题 答案【应用呈现】2、 近年来,某县为发展教育事业,加大了对教育经费的投入,2009年投入6000万元,2011年投入8640万元.(1)求2009年至2011年该县投入教育经费的年平均增长率;(2)该县预计2012年投入教育经费不低于9500万元,若继续保持前两年的平均增长率,该目标能否实现?请通过计算说明理由.【解析】(1)设每年平均增长的百分率为x . 60002)1(x +=8640,2)1(x +=1.44,∵1+x >0, ∴1+x =1.2, x =20%.答:每年平均增长的百分率为20%;(2)2012年该县教育经费为8640×(1+20%)=10368(万元)>9500万元. 故能实现目标.2、如图,要建造一个四边形花圃ABCD ,要求AD 边靠墙,CD ⊥AD ,AD ∥BC ,AB ∶CD =5∶4,且三边的总长为20 m .设AB 的长为5x m . (1)请求AD 的长;(用含字母x 的式子表示)(2)若该花圃的面积为50 m 2,且周长不大于30 m ,求AB 的长.【解析】(1)作BH ⊥AD 于点H ,则AH =3x ,由BC =DH =20-9x 得AD =20-6x (2)由2(20-9x )+3x +9x ≤30得x ≥53,由12[(20-9x )+(20-6x )]×4x =50得3x 2-8x +5=0,∴x 1=53,x 2=1(舍去),∴5x =253.答:AB 的长为253米 【方法总结】一、一元二次方程判别式求解1、已知x 、y 为实数,且满足x y m ++=5,xy ym mx ++=3,求实数m 最大值与最小值。
初中数学千题解——最值问题100题(详解版)

1.如图3.1所示,在Rt △ABC 中,∠A =30°,AB =4,点D 为边AB 的中点,点P 为边AC 上的动点,则PB +PD 的最小值为( )A.B.A.A.1.解 延长BC 至点'B ,使'BC B C =,连接'B P 、'B A ,如图4.1所示, ∴AC 垂直平分'BB ,∴'B A BA =,∴AC 平分'B AB ∠. ∵30CAB ︒∠=,∴'60B AB ︒∠=,∴'ABB ∆为等边三角形.∵点P 为AC 上一点,∴'PB PB =,∴''PB PD PB PD B D +=+≥,当且仅当'B 、P 、D 在同一直线上时,如图4.2所示,PB PD +取得最小值.在'Rt ADB ∆中,122AD AB ==,'60B AB ︒∠=,∴'tan 60B D AD ︒==故答案是C.思路点拨:这是典型的“将军饮马”型线段和最值问题,利用对称法将动线段构造至动点P 所在直线的两侧;根据“两点之间线段最短”找到最小值位置,利用勾股定理进行计算即可.拓展 若点D 为边AB 上任意一定点,则依旧可以根据勾股定理和60°特殊角计算'B D 的长度;若点D 是边AB 上的一动点,则'B D 将变为一条动线段,利用“垂线段最短”可确定最值位置还是在中点处.2.如图3.2所示,在矩形ABCD 中,AB =5,AD =3,动点P 满足13PAB ABCDS S矩形,则点P 到AB 两点距离之和P A +PB 的最小值为 .2.解 令点P 到AB 的距离为d .图3.1PCBD AD 图 4.2图 4.1ABCPB 'B 'PD CBAP ADBC图3.2∵111=35=5=5332PAB ABCD S S d ∆=⨯⨯矩形,∴2d =,∴点P 为到AB 距离为2的直线1l 、2l 上的点.直线1l 、2l 关于AB 对称,因此选其中一条进行计算.作点B 关于直线1l 的对称点'B ,连接'B C 、'B P 、'AB ,如图4.3所示, ∴''PA PB PA PB AB +=+≥,当且仅当A 、P 、'B 三点共线时取得最小值,如图4.4所示. 在'Rt ABB ∆中,5AB =,'24BB d ==,∴'AB =, 故PA PB +思路点拨:这是典型的“将军饮马”型线段和最值问题.根据题目中中给出的面积关系,可判断点P 的运动轨迹为直线(或称为“隐线”);利用轴对称的性质,构造对称点'B ,再运用线段公理获得不等式;根据勾股定理计算最值'AB .3.如图3.3所示,在矩形ABCD 中,AD =3,点E 为边AB 上一点,AE =1,平面内动点P 满足13PAB ABCDS S矩形,则DP EP 的最大值为 .3.解 令点P 到AB 的距离为d .∵13PAB ABCD S S ∆=矩形,∴2d =,∴点P 在到AB 距离为2的直线1l 、2l 上,如图4.5所示.作点E 关于直线1l 的对称点'E ,连接'E D 并延长交直线1l 于点P ,连接EP ,如图4.6所示, ∴'E P EP =.当点P 在直线1l 上时,''DP EP DP E P E D -=-≤,当且仅当D、'E 、P 三点共线时取得最大值图3.3B'E D =当点P 在直线2l 上时,DP EP ED -≤,当且仅当D 、E 、P 三点共线时取得最大值,如图4.7所示.在Rt △ADE 中,3AD =,1AE =,∴DE ==∴DP EP ED -≤=∴当点P 为DE 的延长线与直线2l思路点拨:解法如题2,需要找出满足条件的点P 所在的“隐线”,这里两条直线均要考虑(因为图形不对称).由于两边之差小于第三边,在共线时取得最大值,故遵循“同侧点直接延长,异侧点需对称后再延长”的规律,分别计算最大值并进行大小比较.特别说明 笔者认为这里的最大值只能取一个值.改编此题的目的是让大家不要忽略矩形外的“隐线”,毕竟题中叙述点P 时用的是“平面内”,而非“矩形内”. 4.已知222222y x xx x ,则y 的最小值为 .4.解 原式=+.建立平面直角坐标系,设(),0P x ,()1,1A ,()1,1B --,则AB 在x 轴的两侧,∴PA =PB ,∴y PA PB AB +=+≥,当A 、P 、B 三点共线时,y 值最小,∴min y AB ==思路点拨:若将式子看作函数,对于初中生来说解题难度较大.若换个角度,将每一个根式都看作是两点间的距离(距离公式是平面直角坐标系中的勾股定理),则将问题转化为我们熟悉的几何最值模型——两点之间线段最短. 5.已知22(3)9(1)4y x x ,则y 的最大值为 .5.解 原式=-.建立平面直角坐标系,设),0P x ,3,3A ,1,2B ,∴PA =PB =∴y PA PB AB -≤,当A 、P 、B 三点共线,即点P 在AB 延长线上时y值最大,∴max y AB ==. 思路点拨:阅读题目时需观察清楚“+”或“-”,切不可盲目下笔.本题与题4形式相似,解法相近,但是又有所不同.将代数式转化为平面直角坐标系中的两条线段的差;利用三边关系中的两边之差小于第三边,共线时取等找到最大值.6.如图3.4所示,在等腰Rt △ABC 中,∠BAC =90°,AB =AC ,BC =,点D 是边AB 上一动点,连接CD ,以AD 为直径的圆交CD 于点E ,则线段BE 长度的最小值为 .B解:连接AE ,取AC 得中点F ,连接EF ,如图4.8所示∵AD 是圆的直径 ∴∠AED =90° ∴∠AEC =90°∴EF =12AC =2∴点E 的轨迹为以点F 为圆心的圆弧(圆的定义) ∴BE ≥BF -EF当且仅当B 、E 、F 三点共线时等号成立,如图4.9所示 在Rt △ABF 中,AF =2,AB =4∴BF, ∴()min BE =BF -EF=-2BB思路点拨阅读题目时要找到三条关键信息:点E 为圆周上一点,AD 所对的圆周角是90°,∠DEC 是平角,连接AE 后就找到了定弦定角(或斜边上的中线),若一个角的度数和其所对的一条线段均为定值,则这个角的顶点的轨迹为圆(根据题目需求判断是否需要考虑两侧).因此判断出点E 的轨迹是圆(不是完整的圆,受限于点D 的运动范围).根据三角形的三边关系,知B 、E 、F 三点共线时BE 取得最小值.7.如图3.5所示,正方形ABCD 的边长是4,点E 是边AB 上一动点,连接CE ,过点B 作BG ⊥CE 于点G ,点P 时边AB 上另一动点,则PD +PG 的最小值为 .GP E DCBA解:取BC 得中点F ,连接GF ,作点D 关于AB 的对称点D ′,连接D ′P 、D ′A ,如图4.10所示.∴DP =D ′P∵∠BGC =90°,点F 为BC 的中点∴GF =12BC =2∵PD +PG =PD ′+PG ≥D ′G 又D ′G +GF ≥D ′F∴PD +PG +GF ≥D ′F -GF如图4.11所示,当且仅当D ′、P 、G 、F 四点共线时取得最小值.根据勾股定理得D ′F=∴PD +PG 的最小值为2FD'ABCDE P G GP EDCB AD'F思路点拨不难发现∠BGC =90°是个定角,因此点G 的轨迹为以BC 为直径的圆(部分),可以通过斜边上的中线构造长度不变的动线段,再利用三边关系求解.8.如图3.6所示,在矩形ABCD 中,AB =2,AD =3,点E 、F 分别为边AD 、DC 上的点,且EF =2,点G 为EF 的中点,点P 为边BC 上一动点,则P A +PG 的最小值为 .GP FED CB A解:作点A 关于BC 的对称点A ′,连接A ′B 、A ′P 、DG ,如图4.12所示∴P A ′=P A∴P A +PG =P A ′+PG ∵∠ADC =90°,EF =2∴DG =12EF =1∵P A ′+PG +DG ≥A ′D ∴P A ′+PG ≥A ′D -DG如图4.13所示,当且仅当A ′、P 、G 、D 四点共线时等号成立 根据勾股定理得 A ′D=5∴P A +PG 的最小值为4.A'AB C D EFP GGP FED CB AA'思路点拨与题7的已知条件是相似的,解法几乎一致,抓住核心条件,线段EF 始终不变,线段EF 所对的角为直角,因此斜边上的中线DG 始终不变,从而判断出点G 的轨迹图形为圆.利用轴对称的性质将线段和最小值问题转化为点到动点的距离最小值问题,再根据圆外一点到圆周上一点的距离最值求解.9.在平面直角坐标系中,A (3,0),B (a ,2),C (0,m ),D (n ,0),且m 2+n 2=4,若点E 为CD 的中点,则AB +BE 的最小值为( )A .3B .4C .5D .25 解:∵C (0,m ),D (n ,0),m 2+n 2=4,∴CD 2=4, ∴CD =2在Rt △COD 中,点E 为CD 的中点∴OE =1,即点E 在以O 为圆心,1为半径的圆上.作图4.14,连接OE ,过点A 作直线y =2的对称点A ′,连接A ′B 、A ′O ∴A ′(3,4)∴AB +BE =A ′B +BE =A ′B +BE +EO -EO ≥A ′O -EO如图4.15所示,当且仅当A ′、B 、E 、O 四点共线时等号成立.根据勾股定理得A ′O 5 ∴AB +BE 的最小值为4思路点拨根据两点之间的距离公式m 2+n 2=CD 2,得到CD 的长度;由已知条件判断出OE 为斜边上的中线,OE =12CD (定值);根据圆的定义可知点E 的轨迹是以坐标原点为圆心、12CD 为半径的圆;利用对称的性质将线段和的最值问题转化为圆外一点到圆周上一点的距离最值问题.10.如图3.7所示,AB =3,AC =2,以BC 为边向上构造等边三角形BCD ,则AD 的取值范围为 .DCBA解:以AB 为边向上作等边△ABE ,连接DE ,如图4.16所示∴AB =BE ,CB =BD ,∠ABC =∠EBD =60°-∠CBE 在△ABC 和△EBD 中 ,,,AB BE ABE EBD CB BD =⎧⎪=⎨⎪=⎩∠∠ ∴△ABC ≌△EBD (SAS ) ∴DE =AC =2∴点D 的轨迹是以点E 为圆心,2为半径的圆. ∴AE -ED ≤AD ≤AE +ED如图4.17和图4.18所示,当且仅当A 、E 、D 三点共线时取得最值 ∴1≤AD ≤5EBCDED BADCBE思路点拨这样理解AB =3,AC =2这个条件:固定一边AB ,∠CAB 可以自由变化,因此点C 的轨迹是以点A 为圆心、2为半径的圆.通过构造全等图形找出点D 的运动轨迹.利用圆外一点到圆周上的距离最值来解决问题.拓展 本题的解法较多,对于“定点+动点”的最值问题,探究动点的轨迹图形时直接的方法.11.如图3.8所示,AB =3,AC =2,以BC 为腰(点B 为直角顶点)向上构造等腰直角三角形BCD ,则AD 的取值范围为 ;解答:以AB 为腰做等腰直角△ABE (∠ABE =90°),连接DE ,如图4.19所示,∴AE =√2AB =3√2,∠ABC =∠EBD =90°-∠CBE , 在△ABC 和△EBD 中{AB =BE ∠ABC =∠EBD CB =BD图3.8DC图4.19C∴△ABC ≌△EBD (SAS ) ∴ED =AC =2∴点D 的轨迹为以点E 为圆心、2为半径的圆 ∴AE -ED ≤AD ≤AE +ED如图4.20和图4.21所示,当且仅当A ,E ,D 三点共线时取得最值,∴3√2-2≤AD ≤3√2+2思路点拨:解题方法基本同上题,也是通过构造全等图形找出点D 的运动轨迹上,再利用圆外一点到圆周上的距离最值来解决问题12. 如图3.9所示,AB =4,AC =2,以BC 为底边向上构造等腰直角三角形BCD ,则AD 的取值范围为 ,解答:以AB 为底边构造等腰直角△AEB (∠AEB =90°),连接DE ,如图4.22所示,图4.20图4.21C图3.9DBAC图4.22DBAC∴AE =√22AB =2√2,∠EBA =∠CBD =45°∵{ABEB =CBDB =√2∠ABC =∠EBD =45°-∠CBE ∴△ABC ∽△EBD∴DE =√22AC =√2∴点D 的轨迹为以点E 为圆心、√2 为半径的圆 AE -ED ≤AD ≤AE +ED如图4.23和图4.24所示,当A 、E 、D 三点共线时取得最值∴√2≤AD ≤3√2思路点拨:与前面两题不同的是,由于旋转中心不再是等腰三角形顶角的顶点,因此构造全等图形变成构造相似图形,从而找出点D 的运动轨迹,最后根据圆外一点到圆周上的距离最值来解决问题13. 如图3.10所示,AB =4,AC =2,以BC 为底边向上构造等腰直角三角形BCD ,连接AD 并延长至点P ,使AD =PD ,则PB 的取值范围为 ,图4.23BAC图4.24BAC解答:以AB 为底边构造等腰直角△AEB (∠AEB =90°),连接DE ,如图4.25所示,∴AE =√22AB =2√2,∠EBA =∠CBD =45°∵{AB EB=CBDB =√2∠ABC =∠EBD =45°-∠CBE∴△ABC ∽△EBD ∴DE =√22AC =√2∴点D 的轨迹为以点E 为圆心、√2 为半径的圆 延长AE 至点Q ,使AE =E Q ,连接P Q 、B Q , ∵AD =DP ,∴D Q=2DE =2√2如图4.23和图4.24所示,当A 、E 、D 三点共线时取得最值 ∵BE 垂直平分A Q ,∴AB =B Q ∵∠Q AB =45°,∴△AB Q 为等腰直角三角形,∴B Q=AB =4图3.10PA C图4.25AC∴B Q -P Q≤PB ≤B Q +P Q如图4.26和图4.27所示,当B 、P 、Q 三点共线时取得最值∴4-2 √2≤PB ≤4+2 √2思路点拨:注意到点P 的产生与中点有关,点P 的运动与点D “捆绑”在一起,故可通过构造中位线来判断点P 的运动轨迹,再利用圆外一点到圆周上的距离最值来解决问题14. 如图3.11所示,正六边形ABCDEF 的边长为2,两顶点A 、B 分别在x 轴和y 轴上运动,则顶点D 到坐标原点O 的距离的最大值和最小值的乘积为 ;解答:取AB 的中点G ,连接DG 、O G ,如图4.28所示,图4.26图4.27PAC图3.11∵∠A O B =∠x O y =90°,∴O G = 12AB =1,连接DB 、O D∴△DCB 为等腰三角形 ∵∠C =120°,∴∠DBC =30°,DB = √3DC =2 √3, ∴∠DBA =120°-30°=90°在Rt △DGB ,GB =1,∴DG =√DB 2+GB 2=√(2√3)2+12=√13∴DG -O G ≤O D ≤O G +DG当且仅当O 、G 、D 三点共线时取得最值D 、G 在点O 同侧时取得最大值,在点O 异侧时取最小值,如图4.29所示,∴√13-1≤O D ≤√13+1∴O D 的最大值和最小值乘积为(√13−1)(√13+1)=12图4.28图4.29思路点拨:这个是“墙角”型问题,类似于梯子在墙角滑动,将墙角变为平面直角坐标系,这样移动的范围能扩大到负方向;利用“墙角”产生的直角,以及AB 边长不变的特点,作出AB 的中点G ,利用斜边上的中线O G 和位置固定的两点D 、G 来构造两条大小不变、位置变化的线段O G 、DG ;利用两边之和与两边之差得到O D 的最大值和最小值;另辟蹊径:利用相对运动的知识,我们假设正六边形是不变的,坐标系可以绕着正六边形运动;利用∠A O B =90°,AB =2,判断出点O 的运动轨迹为一个圆,如图4.30所示,利用圆外一点到圆周上的距离最值解得O D 的最大值和最小值;读者可以自行计算验证15. 如图3.12所示,AB =4,点O 为AB 的中点,⊙O 的半径为1,点P 是⊙O 上一动点,△PBC 是以PB 为直角边的等腰直角三角形(点P 、B 、C 按逆时针方向排列),则AC 的取值范围为 ;解答:如图4.31所示,以O B 为腰向上构造等腰直角△O B Q ,连接O P 、C Q 、A Q ;图4.30O 2E图3.12CAB在等腰直角△O B Q 和等腰直角△BPC 中,CB BP =QBBO =√2,∠Q B O=45°, ∴∠CB Q=45°-∠Q BP =∠PB O ,∴△CB Q ∽△PB O ∴OPCQ =OBBQ =√22,∴C Q= √2 ∴点C 在以点Q 为圆心, √2为半径的圆上,∵OQ=O B =O A =2,∠QO B =90° ∴A Q= √AQ 2+OQ 2=2 √2 ∴A Q -Q C ≤AC ≤A Q +Q C如图4.32和图4.33所示,当且仅当A 、C 、Q 三点共线时取得最值,∴√2≤AC ≤3 √2思路点拨:由于△PBC 形状固定,两个动点P 、C 到点B 的距离之比始终不变,这是比较典型的位似旋转,也可理解为点P 、C “捆绑”旋转;旋转过程中,点C 的轨迹与点P 的轨迹图形相似,相似比为√2:1;利用相似找出动点C 轨迹的圆心,AC 的最值即定点A 到定圆上一动点的距离的最值16.如图3.13所示,⊙O 的半径为3,Rt △ABC 的顶点A 、B 在⊙O 上,∠B =90°,点C 在⊙O 内,且tan A =34.当点A 在圆上运动时,OC 的最小值为( )图4.31AB图4.32ABP 图4.33ABB.32D.53图3.13答案:连接OB,过点B向下作BD⊥OB,取BD=43OB,连接AD,如图4.34所示.∵∠CBA=∠OBD=90°,∴∠OBC=90°-∠OBA=∠DB A.∴CBAB=OBBD=34,∴△OCB∽△DAB,∴OCAD=34.∵AD≥OD-OAOA=2,当且仅当O、A、D三点共线时取得最值,∴OC=34AD≥34×2=32.图4.34思路点拨又是比较典型的位似旋转问题,我们利用相似的性质将OC的最值问题转化为AD的最值问题.通过旋转型相似构造Rt△OBD,其中∠OBD=90°,∠ODB=∠CAB,因此点D为定点.另外,由△OCB∽△DAB得到OC和AD之间的固定比例,从而可利用AD的最值求解OC的最值.AD的最值即为圆外一点到圆周上一点的距离最值.另辟蹊径根据直径所对的圆周角为90°,找到直径AD,而∠ACD=180°-∠ACB为定值,因此由定弦定角得出点C的轨迹为圆弧,可根据图4.35所示计算OC的最小值.图4.3517.如图3.14所示,在平面直角坐标系中,Q(3,4),点P是以Q为圆心、2为半径的⊙Q上一动点,A(1,0),B(-1,0),连接P A、PB,则P A2+PB2的最小值是___________.答案:连接OP 、QP 、OQ ,如图4.36所示.设P (x ,y ). 根据两点距离公式得∴P A 2=(x -1)2+y 2,PB 2=(x +1)2+y 2, ∴P A 2+PB 2=2x 2+2y 2+2=2(x 2+y 2)+2.∴OP OP 2=x 2+y 2,∴P A 2+PB 2=2OP 2+2,要求P A 2+PB 2的最小值,即求OP 2的最小值,也就是求OP 的最小值,∴OP ≥OQ -PQ , 如图4.37所示,当且仅当O 、P 、Q 三点共线时取得最值, ∴OP =5-2=3,∴P A 2+PB 2=2OP 2+2≥2×32+2=20.思路点拨根据P A 2+PB 2这样的形式,产生两个联想,一是勾股定理,二是坐标公式.要使用勾股定理,就得把P A 和PB 构造为两条直角边,在题图中难以实现,所以转而利用坐标公式表达,我们便发现P A 2+PB 2与OP 2的联系,而OP 的最小值即圆外一点到圆周上一点的距离最小值.弦外之音 我们会发现,虽然点P 在动,但OP 始终是△ABP 边AB 上的中线,且AB 是个定值,我们可以直接利用中线长公式得到P A 2+PB 2=2OP 2+24AB ,接下来的计算和上面是一致的.公式的应用有助于对思路的拓展,因此学有余力的同学可以自行推导中线长公式(仅用勾股定理即可).18.如图3.15所示,两块三角尺的直角顶点靠在一起,BC =3,EF =2,G 为DE 上一动点.将三角尺DEF 绕直角顶点F 旋转一周,在这个旋转过程中,B、G 两点的最小距离为___________.图3.15答案:在Rt △DEF 中,CE =2,∠CDE =30°,∴DF =DE =4. 如图4.38所示,当点G 与点D 重合时,CG max =DF =当CG ⊥DE 时,CG min =h =2DEFS DE⋅△CG当CG =3时,以C 为圆心、CG 为半径的圆恰好经过点B. 在△DEF 旋转的过程中,点G 会经过点B.因此,当BG 恰好重合时,BG 取得最小值为0.图4.38')思路点拨这是个“特别”的题,点G 是DE 上一动点,因此在转动的过程中,点G 的轨迹不是线而是面,这个面的形状为以点C 为圆心、分别以CG min 和CG max 为半径的同心圆环,点B 也在这个“面轨迹”中,因此BG 的最小值为0.19.如图3.16所示,在Rt △ABC 中,∠ABC =90°,∠ACB =30°,BC =△ADC 与△ABC 关于AC 对称,点E 、F 分别是边DC 、BC 上的任意一点,且DE =CF ,BE 、DF 相交于点P ,则CP 的最小值为()A.1 C.32D.2图3.16PEDBA答案:连接BD ,如图4.39所示.∵△ADC 与△ABC 关于AC 对称,∠ACB =30°,∴BC =CD ,∠BCD =60°, ∴△BDC 是等边三角形,∴BD =CD ,∠BDC =∠BCD =60°. 在△BDE 和△DCF 中,BD =CD ,∠BDC =∠BCD ,DE =CF , ∴△BDE ≌△DCF (SAS ),∴∠BED =∠DF C.∵∠BED +∠PEC =180°,∴∠PEC +∠DFC =180°, ∴∠DCF +∠EPF =∠DCF +∠BPD =180°. ∵∠DCF =60°,∴∠BPD =120°. ∵点P 在运动中保持∠BPD =120°,∴点P 的运动路径为以A 为圆心、AB 为半径的120°的弧.当C 、P 、A 三点共线时,CP 能取到最小值,如图4.40所示, ∴CP ≥AC -AP =2,即线段CP 的最小值为2.图4.40图4.39DABPE思路点拨需要熟悉等边三角形中的常见全等图形.因为点P 在运动中保持∠BPD =120°,BD 又是定长,所以点P 的路径是一段以点A 为圆心的弧,于是将CP 的最小值转化为圆外一点到圆上一点的距离最小值.20.如图3.17所示,sin O =35,长度为2的线段DE 在射线OA 上滑动,点C 在射线OB 上,且OC =5,则△CDE 周长的最小值为___________.图3.17EDCB A答案:过点C 作CC '∥DE 且CC '=DE ,连接C 'E ,如图4.41所示, ∴四边形CC 'ED 为平行四边形,∴C 'E =C D.作点C 关于OA 的对称点C ″,连接C ″E 、C ″D 、C ″C ,∴CE =C ″E , ∴CD +CE =C 'E +CE =C 'E +C '″E ≥C 'C ",当且仅当C '、E 、C "三点共线时取得最值,如图4.42所示. ∵CC "关于OA 对称,∴OA 垂直平分CC ", ∴CC "=2CF =2OC ·sin O =6.在Rt △CC 'C "中,C 'C "∴△CDE 周长的最小值为2.图4.42图4.41AEC″C'B CODA E DB COF C″C'思路点拨因为DE 为定值,所以△CDE 周长的最小值问题转变为CD +CE 的最小值问题.似“饮马”非“饮马”,注意观察,这是一定两动问题.利用平移将动线段DE “压缩”为一个动点;轴对称后根据两点之间线段最短找到最小值线段,再根据勾股定理计算即可解决问题.21、如图3.18所示,在矩形ABCD 中,AB=6,MN 在边AB 上运动,MN=3,AP=2,BQ=5,则PM+MN+NQ 的最小值是______________。
初中数学几何最值专题1:蚂蚁行程(最全修正版)

蚂蚁行程【例题精讲】例1、如图,一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是准备按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为40cm,A,B两点间的距离为30cm.若螳螂想吃掉B点处的小虫子,螳螂绕行的最短路程为cm。
解析提示:总结:例2、如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是。
解析提示:总结:例3、如图所示的圆锥底面半径OA=2cm,高PO=4cm,一只蚂蚁由A点出发绕侧面一周后回到A点处,则它爬行的最短路程为。
解析提示:总结:针对训练1、如图,已知圆柱的底面周长为6,高AB=3,小虫在圆柱表面爬行,从C点爬到对面的A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为.2、如图,有一圆柱,其高为14cm,它的底面周长为10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B 处的食物,其中B离上沿2cm,则蚂蚁经过的最短路程为.3、如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为。
4、如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为.5、如图,桌面上的正方体的棱长为2,B为一条棱的中点.已知蚂蚁沿正方体的表面从A点出发,到达B 点,则它运动的最短路程为()6、有一圆柱体油罐,已知油罐底面周长是12m,高AB是5m,要从点A处开始绕油罐一周建造房子,正好到达A点的正上方B处,问梯子最短有多长?7、(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G 处,求它爬行的最短路程.(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?8、李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题:(1)如图1,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处,那么蚂蚁需要爬行的最短路程的长是cm;(2)如图2,一个圆柱形食品盒,它的高为10cm,底面圆的周长为32cm.(先画出示意图,再写出解答过程)①点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物请求出蚂蚁需要爬行的最短路程;②将图2改为一个无盖的圆柱形食品盒,点C距离下底面3cm,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如图3).那么蚂蚁爬行的最短路程是多少?课堂精练1、如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为.2、如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是()m.3、如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?4、如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,P是BC上一点且PC=BC.一只蚂蚁从点A出发沿着圆柱的侧面爬行到点P,求爬行的最短路程是多少.。
完整)初中数学《几何最值问题》典型例题

完整)初中数学《几何最值问题》典型例题初中数学《最值问题》典型例题一、解决几何最值问题的通常思路解决几何最值问题的理论依据是:两点之间线段最短;直线外一点与直线上所有点的连线段中,垂线段最短;三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)。
根据不同特征转化是解决最值问题的关键。
通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段。
几何最值问题中的基本模型举例:1.三角形三边关系在三角形ABC中,M,N分别是边AB,BC上的动点,求AM+BN的最小值。
解析:先平移AM或BN使M,N重合,然后作其中一个定点关于定直线l的对称点。
2.图形对称在△ABC中,M,N两点分别是边AB,BC上的动点,将△XXX沿MN翻折,B点的对应点为B',连接AB',求AB'的最小值。
解析:转化成求AB'+B'N+NC的最小值。
二、典型题型1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△XXX的周长的最小值为.解析:作P关于OA,OB的对称点C,D,连接OC,OD。
则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长。
根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解。
解答:作P关于OA,OB的对称点C,D,连接OC,OD。
则当M,N是CD与OA,OB的交点时,△XXX的周长最短,最短的值是CD的长。
PC关于OA对称,∴∠COP=2∠AOP,OC=OP。
同理,∠DOP=2∠BOP,OP=OD。
COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD。
COD是等腰直角三角形。
则CD=2OC=2×32=64.分析】首先,把题目中的图形画出来,理清楚纸片折叠后的几何关系。
然后,可以利用勾股定理求出三角形的边长,再根据两点之间线段最短的原理,确定点A′在BC边上可移动的最大距离。
几何最值问题-2023年中考数学压轴题专项训练(全国通用)(解析版)

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图,在矩形ABCD 中,AB =8,AD =4,点E 是矩形ABCD 内部一动点,且∠BEC =90°,点P 是AB 边上一动点,连接PD 、PE ,则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹,利用“将军饮马”模型将PE 进行转化即可求解.【详解】解:如图,设点O 为BC 的中点,由题意可知,点E 在以BC 为直径的半圆O 上运动,作半圆O 关于AB 的对称图形(半圆O '),点E 的对称点为E 1,连接O 'E 1,则PE =PE 1,∴当点D 、P 、E 1、O '共线时,PD +PE 的值最小,最小值为DE 1的长,如图所示,在Rt △DCO '中,CD =8,CO '=6,∴DO '=82+62=10,又∵O 'E 1=2,∴DE 1=DO '-O 'E 1=8,即PD +PE 的最小值为8,故选:A .【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理,利用“将军饮马”模型将PE 进行转化时解题的关键.2(2023·安徽黄山·校考模拟预测)如图,在平面直角坐标系中,二次函数y =32x 2-32x -3的图象与x 轴交于点A ,C 两点,与y 轴交于点B ,对称轴与x 轴交于点D ,若P 为y 轴上的一个动点,连接PD ,则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,可求得∠ABO =30°,从而得出PE =12PB ,进而得出PD +12PB =PD +EP ,进一步得出结果.【详解】解:如图,作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,抛物线的对称轴为直线x =--322×32=12,∴OD =12,当x =0时,y =-3,∴OB =3,当y =0时,32x 2-32x -3=0,∴x 1=-1,x 2=2,∴A (-1,0),∴OA =1,∵tan ∠ABO =OA OB =13=33,∴∠ABO =30°,∴PE =12PB ,∴12PB +PD =PD +PE ≥DF ,当点P 在P 时,PD +PE 最小,最大值等于DF ,在Rt △ADF 中,∠DAF =90°-∠ABO =60°,AD =OD +PA =12+1=32,∴DF =AD ⋅sin ∠DAE =32×32-334,∴12PB +PD 最小=DF =334,故选:A .【点睛】本题以二次函数为背景,考查了二次函数与一元二次方程之间的关系,解直角三角形等知识,解决问题的关键是用三角函数构造12PB .3(2023秋·浙江金华·九年级统考期末)如图,正方形ABCD 的边长为4,点E 是正方形ABCD 内的动点,点P 是BC 边上的动点,且∠EAB =∠EBC .连结AE ,BE ,PD ,PE ,则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°,即可得点E 在以AB 为直径的半圆上移动,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,问题随之得解.【详解】解:∵四边形ABCD 是正方形,∴∠ABC =90°,∴∠ABE +∠EBC =90°,∵∠EAB =∠EBC ,∴∠EAB +∠EBA =90°,∴∠AEB =90°,∴点E 在以AB 为直径的半圆上移动,如图,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,E∵∠G =90°,FG =BG =AB =4,∴OG =6,OA =OB =OE =2,∴OF =FG 2+OG 2=213,∴EF =OF -OE =213-2,故PE +PD 的长度最小值为213-2,故选:A .【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理,正确的作出辅助线,得出点E 的运动路线是解题的关键.4(2022秋·安徽池州·九年级统考期末)如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,点P 为AC 边上的动点,过点P 作PD ⊥AB 于点D ,则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,点P 即为所求作的点,此时PB +PD 有最小值,连接AB ,根据对称性的性质,可知:BP =B P ,△ABC ≅△AB C ,根据S △ABB =S △ABC +S △AB C =2S △ABC ,即可求出PB +PD 的最小值.【详解】解:如下图,作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,连接AB ,点P 即为所求作的点,此时PB +PD 有最小值,根据对称性的性质,可知:BP =B P ,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,∴AB =AC 2+BC 2=5,根据对称性的性质,可知:△ABC ≅△AB C ,∴S △ABB =S △ABC +S △ABC =2S △ABC ,即12×AB ⋅B D =2×12BC ⋅AC ,∴5B D =24,∴B D =245,故选:B .【点睛】本题考查了轴对称一最短路线问题,解题的关键是掌握轴对称的性质.5(2023秋·甘肃定西·八年级校考期末)如图所示,在△ABC 中,∠ABC =68°,BD 平分∠ABC ,P 为线段BD 上一动点,Q 为 边AB 上一动点,当AP +PQ 的值最小时,∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ,连接PE ,证明△PBQ ≌△PBE SAS ,得出PE =PQ ,说明AP +PQ =AP +PE ,找出当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ 最小,过点A 作AE ⊥BC 于点E ,交BD 于点P ,根据三角形外角的性质可得答案.【详解】解:在BC 上截取BE =BQ ,连接PE ,如图:∵BD 平分∠ABC ,∠ABC =68°,∴∠ABD =∠CBD =12∠ABC =34°,∵BP =BP ,∴△PBQ ≌△PBE SAS ,∴PE =PQ ,∴AP +PQ =AP +PE ,∴当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ最小,过点A作AE ⊥BC 于点E ,交BD 于点P ,如图:∵∠AEB =90°,∠CBD =34°,∴∠APB =∠AEB +∠CBD =124°.故选:D .5【点睛】本题主要考查了角平分线的定义,三角形全等的判定和性质,垂线段最短,三角形内角和定理与三角形的外角的性质,解题的关键是找出使AP +PQ 最小时点P 的位置.6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图,E 为正方形ABCD 边AD 上一点,AE =1,DE =3,P 为对角线BD 上一个动点,则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点,根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长,求出EC 的长即可.【详解】连接EC ,交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长.∵AE =1,DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选:A【点睛】本题主要考查了正方形的性质和两点之间线段最短,这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称,连接BM 交AC 于N ′,N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可.【详解】∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,6连接BD ,BM 交AC 于N ′,连接DN ′,∴当B 、N 、M 共线时,DN +MN 有最小值,则BM 的长即为DN +MN 的最小值,∴AC 是线段BD 的垂直平分线,又∵CD =4,DM =1∴CM =CD -DM =4-1=3,在Rt △BCM 中,BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5.故选:D .【点睛】本题考查的是轴对称-最短路线问题及正方形的性质,先作出D 关于直线AC 的对称点,由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键.8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图,在平面直角坐标系中,二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点,与x 轴交于点C (3,0),若P 是x 轴上一动点,点D 的坐标为(0,-1),连接PD ,则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H ,根据2PD +PC =2PD +22PC =2PD +PJ ,求出DP +PJ 的最小值即可解决问题.【详解】解:连接BC ,过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H .∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0),∴b =2,∴二次函数的解析式为y =-x 2+2x +3,令y =0,-x 2+2x +3=0,解得x =-1或3,∴A (-1,0),令x =0,y =3,∴B (0,3),∴OB =OC =3,∵∠BOC =90°,∴∠OBC =∠OCB =45°,∵D(0,-1),∴OD =1,BD =4,∵DH ⊥BC ,∴∠DHB =90°,设DH =x ,则BH =x ,∵DH 2+BH 2=BD 2,7∴x =22,∴DH =22,∵PJ ⊥CB ,∴∠PJC =90°,∴PJ =22PC ,∴2PD +PC =2PD +22PC =2PD +PJ ,∵DP +PJ ≥DH ,∴DP +PJ ≥22,∴DP +PJ 的最小值为22,∴2PD +PC 的最小值为4.故选:A .【点睛】本题考查了二次函数的相关性质,以及等腰直角三角形的判定和性质,垂线段最短等知识,得到∠OBC =∠OCB =45°,PJ =22PC 是解题的关键.9(2022·山东泰安·统考中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的圆上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.810(2022·河南·校联考三模)如图1,正方形ABCD 中,点E 是BC 的中点,点P 是对角线AC 上的一个动点,设AP =x ,PB +PE =y ,当点P 从A 向点C 运动时,y 与x 的函数关系如图2所示,其中点M 是函数图象的最低点,则点M 的坐标是()A.42,35B.22,35C.35,22D.35,42【答案】A【分析】根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,从而确定正方形的边长为6,根据将军饮马河原理,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,利用相似三角形,计算AG 的长即为横坐标.【详解】如图,根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,∵点E 是BC 的中点,∴BC =6,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,∵四边形ABCD 是正方形,AB =6,∴CE ∥AD ,AC =62+62=62,DE =62+32=35,∴△CGE ∽△AGD ,∴CG AG =CE AD =12,∴AC AG=32,∴AG =42,故点M 的坐标为(42,35),故A 正确.故选:A .【点睛】本题考查了正方形的性质,三角形相似的判定和性质,函数图像信息的获取,将军饮马河原理,熟练掌握正方形的性质,灵活运用三角形相似,构造将军饮马河模型求解是解题的关键.2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图,矩形ABCD ,AB =4,BC =8,E 为AB 中点,F 为直线BC 上动点,B 、G 关于EF 对称,连接AG ,点P 为平面上的动点,满足∠APB =12∠AGB ,则DP 的最小值.【答案】210-22【分析】由题意可知,∠AGB =90°,可得∠APB =12∠AGB =45°,可知点P 在以AB 为弦,圆周角∠APB =45°的9圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧),设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,可知△AOB 为等腰直角三角形,求得OA =22AB =22=OP ,AQ =OQ =22OA =2,QD =AD -AQ =6,OD =OQ 2+QD 2=210,再由三角形三边关系可得:DP ≥OD -OP =210-22,当点P 在线段OD 上时去等号,即可求得DP 的最小值.【详解】解:∵B 、G 关于EF 对称,∴BH =GH ,且EF ⊥BG∵E 为AB 中点,则EH 为△ABG 的中位线,∴EH ∥AG ,∴∠AGB =90°,∵∠APB =12∠AGB ,即∠APB =12∠AGB =45°,∴点P 在以AB 为弦,圆周角∠APB =45°的圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧)设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,则OA =OB =OP ,∵∠APB =45°,∴∠AOB =90°,则△AOB 为等腰直角三角形,∴OA =22AB =22=OP ,又∵E 为AB 中点,∴OE ⊥AB ,OE =12AB =AE =BE ,又∵四边形ABCD 是矩形,∴∠BAD =90°,AD =BC =8,∴四边形AEOQ 是正方形,∴AQ =OQ =22OA =2,QD =AD -AQ =6,∴OD =OQ 2+QD 2=210,由三角形三边关系可得:DP ≥OD-OP =210-22,当点P 在线段OD 上时去等号,∴DP 的最小值为210-22,故答案为:210-22.【点睛】本题考查轴对称的性质,矩形的性质,隐形圆,三角形三边关系,正方形的判定及性质,等腰直角三角形的判定及性质,根据∠APB =12∠AGB =45°得知点P 在以AB 为弦,圆周角∠APB =45°的圆上是解决问题的关键.12(2023春·江苏连云港·八年级期中)如图,在边长为8的正方形ABCD 中,点G 是BC 边的中点,E 、F 分别是AD 和CD 边上的点,则四边形BEFG 周长的最小值为.【答案】2410【分析】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G ,根据两点之间线段最短即可解决问题.【详解】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G∵EB =EB ,FG =FG ,∴BE +EF +FG +BG =B E +EF +FG +BG ,∵EB +EF +FG ≥B G ,∴四边形BEFG 的周长的最小值=BG +B G ,∵正方形ABCD 的边长为8∴BG =4,BB =16,BG =12,∴B G =162+122=20,∴四边形BEFG 的周长的最小值为=4+20=24.故答案为:24.【点睛】本题考查轴对称求线段和的最短问题,正方形的性质,勾股定理,解题的关键是学会利用轴对称解决最短问题.13(2022·湖南湘潭·校考模拟预测)如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路AC <BD ,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM +PN 的距离最短,则最短距离是米.【答案】50【分析】作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,根据菱形的性质和勾股定理求出BC 长,即可得出答案.【详解】解:作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,∵四边形ABCD 是菱形,∴AC ⊥BD ,∠QBP =∠MBP ,即Q 在AB 上,∵MQ ⊥BD ,∴AC ∥MQ ,∴M 为BC 中点,∴Q 为AB 中点,∵N 为CD 中点,四边形ABCD 是菱形,∴BQ ∥CD ,BQ =CN ,∴四边形BQNC 是平行四边形,∴NQ =BC ,设AC 与BD 的交点为点O ,∵四边形ABCD 是菱形,∴AC ⊥BD,OC =12AC =30米,OB =12BD =40米,∴BC =OB 2+OC 2=50米,∴PM +PN 的最小值是50米.故答案为:50.11【点睛】本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P 的位置.14(2023春·江苏·九年级校考阶段练习)如图,正方形ABCD 的边长为4,⊙B 的半径为2,P 为⊙B 上的动点,则2PC -PD 的最大值是.【答案】2【分析】解法1,如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,连接PM 、DM ,推得2PC -PD=2PC -22PD =2PC -PM ,因为PC -PM ≤MC ,求出MC 即可求出答案.解法2:如图:连接BD 、BP 、PC ,在BD 上做点M ,使BM BP =24,连接MP ,证明△BMP ∼△BPD ,在BC 上做点N ,使BN BP=12,连接NP ,证明△BNP ∼△BPC ,接着推导出2PC -PD =22MN ,最后证明△BMN ∼△BCD ,即可求解.【详解】解法1如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,∴∠PDM =45,DM =PM =22PD ,∵四边形ABCD 正方形∴∠BDC =45°,DB DC=2又∵∠PDM =∠PDB +MDB ,∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ,DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为:2.解法2如图:连接BD 、BP 、PC根据题意正方形ABCD 的边长为4,⊙B 的半径为2∴BP =2,BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ,使BM BP=24,则BM =22,连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ,BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24,则PD =22PM ∵BP BC =24=12在BC 上做点N ,使BN BP=12,则BN =1,连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ,BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12,则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ,BM BC =224=28,BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为:2.【点睛】本题考查正方形的性质,相似三角形,勾股定理等知识,难度较大,熟悉以上知识点运用是解题关键.15(2023秋·广东广州·九年级统考期末)如图,四边形ABCD 中,AB ∥CD ,AC ⊥BC ,∠DAB =60°,AD =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则△MBC 面积的最小值为.【答案】63-4【分析】取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则OM +ME ≥OF ,通过计算得出当O ,M ,E 三点共线时,ME 有最小值,求出最小值即可.【详解】解:如图,取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则13OM +ME ≥OF ,∵AB ∥CD ,∠DAB =60°,AD =CD =4,∴∠ADC =120°,∵AD =CD ,∴∠DAC =30°,∴∠CAB =30°,∵AC ⊥BC ,∴∠ACB =90°∴∠B =90°-30°=60°,∴∠B =∠DAB ,∴四边形ABCD 为等腰梯形,∴BC =AD =4,∵∠AMD =90°,AD =4,OA =OD ,∴OM =12AD =2,∴点M 在以点O 为圆心,2为半径的圆上,∵AB ∥CD ,∴∠GCF =∠B =60°,∴∠DGO =∠CGF =30°,∵OF ⊥BC ,AC ⊥BC ,∴∠DOG =∠DAC =30°=∠DGO ,∴DG =DO =2,∴OG =2OD ⋅cos30°=23,GF =3,OF =33,∴ME ≥OF -OM =33-2,∴当O ,M ,E 三点共线时,ME 有最小值33-2,∴△MBC 面积的最小值为=12×4×33-2 =63-4.【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点,点M 位置的确定是解题关键.16(2023春·全国·八年级专题练习)如图,在等边△ABC 中,BD ⊥AC 于D ,AD =3cm .点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ,点M 为线段BD 上一动点,连接PM ,QM ,则PM +QM 的最小值为cm .【答案】5【分析】如图所示,作点P 关于BD 的对称点P ,且点P 在BC 上,则PM +QM =P M+QM ,当P ,M ,Q 在同一条直线上时,有最小值,证明四边形PP QA 是平行四边形,P Q =AP =AB -BP ,由此即可求解.【详解】解:如图所示,作点P 关于BD 的对称点P ,∵△ABC 是等边三角形,BD ⊥AC ,∴∠ABD =∠DBC =12∠ABC =12×60°=30°,14∴点P 在BC 上,∴P M =PM ,则PM +QM =P M +QM ,当P ,M ,Q 在同一条直线上时,有最小值,∵点P 关于BD 的对称点P ,∠ABD =∠DBC =30°,∴PP ⊥BM ,BP =BP =1cm ,∴∠BP P =60°,∴△BPP 是等边三角形,即∠BP P =∠C =60°,∴PP ∥AC ,且PP =AQ =1cm ,∴四边形PP QA 是平行四边形,∴P Q =AP =AB -BP ,在Rt △ABD 中,∠ABD =30°,AD =3,∴AB =2AD =2×3=6,∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5,故答案为:5.【点睛】本题主要考查动点与等边三角形,对称-最短路径,平行四边形的判定和性质的综合,理解并掌握等边三角形得性质,对称-最短路径的计算方法,平行四边形的判定和性质是解题的关键.17(2022秋·山东菏泽·九年级校考阶段练习)如图,在周长为12的菱形ABCD 中,DE =1,DF =2,若P 为对角线AC 上一动点,则EP +FP 的最小值为.【答案】3【分析】作F 点关于BD 的对称点F ,连接EF 交BD 于点P ,则PF =PF ,由两点之间线段最短可知当E 、P 、F 在一条直线上时,EP +FP 有最小值,然后求得EF 的长度即可.【详解】解:作F 点关于BD 的对称点F ,则PF =PF ,连接EF '交BD 于点P .∴EP +FP =EP +F P .由两点之间线段最短可知:当E 、P 、F '在一条直线上时,EP +FP 的值最小,此时EP +FP =EP +F P =EF .∵四边形ABCD 为菱形,周长为12,∴AB =BC =CD =DA =3,AB ∥CD ,∵AF =2,AE =1,∴DF =AE =1,∴四边形AEF D 是平行四边形,∴EF =AD =3.∴EP +FP 的最小值为3.故答案为:3.【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题,明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键.18(2023春·上海·八年级专题练习)如图,直线y =x +4与x 轴,y 轴分别交于A和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC +PD 的值最小时,点P 的坐标为.15【答案】(-1,0)【分析】直线y =x +4与x 轴,y 轴分别交于A 和B ,可求出点A ,B 的坐标,点C 、D 分别为线段AB 、OB 的中点,可求出点C 、D 的坐标,作点C 关于x 轴的对称点C ,连接C D 与x 轴的交点就是所求点P 的坐标.【详解】解:直线y =x +4与x 轴,y 轴分别交于A 和B ,∴当y =0,x =-4,即A (-4,0);当x =0,y =4,即B (0,4),∵点C 、D 分别为线段AB 、OB 的中点,∴C (-2,2),D (0,2),如图所示,过点C 关于x 轴的对称点C,∴C (-2,-2),∴直线C D 的解析式为:y =2x +2,当y =0,x =-1,即P (-1,0),故答案为:(-1,0).【点睛】本题主要考查一次函数与最短线段的综合,掌握对称中最短线段的解题方法是解题的关键.19(2023秋·黑龙江鸡西·九年级统考期末)如图,抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,在其对称轴上有一动点M ,连接MA ,MC ,AC ,则△MAC 周长的最小值是.【答案】32+10【分析】根据“将军饮马”模型,先求出A 1,0 ,B 3,0 ,C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,从而C △MAC =CA +CM +MA =CA +CM +MB ,AC =OA 2+OC 2=10,则△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,从而得到CB =OC 2+OB 2=32,即可得到答案.【详解】解:∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,16∴当y =0时,0=x 2-4x +3解得x =1或x =3,即A 1,0 ,B 3,0 ;当x =0时,y =3,即C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,即MA =MB ,∴C △MAC =CA +CM +MA =CA +CM +MB ,∵AC =OA 2+OC 2=10,∴△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,∵CB =OC 2+OB 2=32,∴△MAC 周长的最小值为CA +CB =32+10,故答案为:32+10.【点睛】本题考查动点最值问题与二次函数综合,涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识,熟练掌握动点最值的常见模型是解决问题的关键.20(2023秋·浙江温州·九年级校考期末)如图所示,∠ACB =60°,半径为2的圆O 内切于∠ACB.P 为圆O 上一动点,过点P 作PM 、PN 分别垂直于∠ACB 的两边,垂足为M 、N ,则PM +2PN 的取值范围为.【答案】6-23≤PM +2PN ≤6+23【分析】根据题意,本题属于动点最值问题-“阿氏圆”模型,首先作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示,通过代换,将PM +2PN 转化为PN +12PM =PN +HP =NH ,得到当MP 与⊙O 相切时,MF 取得最大值和最小值,分两种情况,作出图形,数形结合解直角三角形即可得到相应最值,进而得到取值范围.【详解】解:作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示:∵PM ⊥AC ,PN ⊥CB ,∴∠PMC =∠PNC =90°,∴∠MPN =360°-∠PMC -∠PNC -∠C =120°,∴∠MPH =180°-∠MPN =60°,∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ,∴PN +12PM =PN +HP =NH ,∵MF =NH ,∴当MP 与⊙O 相切时,MF 取得最大和最小,①连接OP ,OG ,OC ,如图1所示:可得:四边形OPMG 是正方形,∴MG =OP =2,在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG +GM =2+23,在Rt △CMF 中,MF =CM ⋅sin60°=3+3,∴HN =MF =3+3,即PM +2PN =212PM +PN =2HN =6+23;②连接OP ,OG ,OC ,如图2所示:可得:四边形OPMG 是正方形,17∴MG =OP =2,由上同理可知:在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG -GM =23-2,在Rt △CMF 中,MF =CM ⋅sin60°=3-3,∴HN =MF =3-3,即PM +2PN =212PM +PN =2HN =6-23,∴6-23≤PM +2PN ≤6+23.故答案为:6-23≤PM +2PN ≤6+23.【点睛】本题考查动点最值模型-“阿氏圆”,难度较大,掌握解决动点最值问题的方法,熟记相关几何知识,尤其是圆的相关知识是解决问题的关键.3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图,已知抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,交y 轴于点C .(1)求抛物线的解析式,连接BC ,并求出直线BC 的解析式;(2)请在抛物线的对称轴上找一点P ,使AP +PC 的值最小,此时点P 的坐标是;(3)点Q 在第一象限的抛物线上,连接CQ ,BQ ,求出△BCQ 面积的最大值.【答案】(1)y =-x 2+3x +4;y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ,B 4,0 两点,代入抛物线解析式,可得到抛物线解析式,从而得到C 0,4 ,再设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入,即可求解;(2)连接BC ,PB ,根据题意可得A 、B 关于抛物线的对称轴直线x =32对称,从而得到当P 在直线AB 上三点共线时,AP +CP 的值最小,把x =32代入直线BC 的解析式,即可求解;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,可得QD =-d 2+4d ,从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8,即可求解;【详解】(1)解:(1)∵抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,∴a -b +4=016a +4b +4=0,解得:a =-1b =3 ,18∴抛物线的解析式为y =-x 2+3x +4;∵抛物线与y 轴的交点为C ,∴C 0,4 ,设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入得:4k +b =0b =4 ,解得:k =-1b =4 ,∴直线BC 的解析式为y =-x +4;(2)如图,连接BC ,PB ,∵y =-x 2+3x +4=-x -32 2+74,∴抛物线的对称轴为直线x =32,根据题意得:A 、B 关于抛物线的对称轴直线x =32对称,∴AP =BP ,∴AP +CP =BP +CP ≥BC ,即当P 在直线AB 上时,AP +CP 的值最小,∴当x =32时,y =-32+4=52,∴P 32,52 ,故答案是:32,52 ;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,∴QD =-d 2+3d +4 --d +4 =-d 2+4d ,∵B 4,0 ,∴OB =4,∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8,当d =2时,S ΔBCQ 取最大值,最大值为8,∴△BCQ 的最大面积为8;【点睛】本题主要考查了二次函数的图像和性质,利用数形结合思想和分类讨论思想是解题的关键.22(2023秋·江苏淮安·八年级统考期末)如图1,直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,过点B 的直线交x 轴负半轴于点C -3,0 .(1)请直接写出直线BC 的关系式:(2)在直线BC 上是否存在点D,使得S △ABD =S △AOD 若存在,求出点D 坐标:若不存请说明理由;(3)如图2,D 11,0 ,P 为x 轴正半轴上的一动点,以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ,连接QA ,QD .请直接写出QB -QD 的最大值:.19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时,S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点,可求出点B 的坐标,再用待定系数法即可求解;(2)设D (a ,2a +6),分别用含a 的式子表示出出S △AOD ,S △ABD ,由此即可求解;(3)△BPQ 是等腰直角三角形,设P (m ,0)(m >0),可表示出QB ,再证Rt △BOP ≌Rt △PTQ (AAS ),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值,可求得点R 的坐标,根据勾股定理即可求解.【详解】(1)解:∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,令x =0,则y =6,∴B (0,6),且C -3,0 ,设直线BC 的解析式为y =kx +b ,∴b =6-3k +b =0,解得,k =2b =6 ,∴直线BC 的解析式为y =2x +6,故答案为:y =2x +6.(2)解:由(1)可知直线BC 的解析式为y =2x +6,直线AB 的解析式为y =-x +6,∴A (6,0),B (0,6),C (-3,0),∴OA =6,BO =6,OC =3,如图所示,点D 在直线BC 上,过点D 作DE ⊥x 轴于E ,∴设D (a ,2a +6),E (a ,0),∴S △ABC =12AC ·OB =12×(6+3)×6=27,S △ADC =12AC ·DE =12×(6+3)×a =92a ,S △AOD =12OA ·DE =12×6×a =3a ,∴S △ABD =S △ABC -S △ADC =27-92a ,若S △ABD =S △AOD ,则27-92a =3a ,当a >0时,27-92a =3a ,解得,a =185,即D 185,665 ;当a <0时,27+92a =-3a ,解得,a =-185,即D -185,-65 ;综上所述,当D 185,665 或D -185,-65时,S △ABD =S △AOD .(3)解:已知A (6,0),B (0,6),D (11,0),设P (m ,0)(m >0),∴在Rt △BOP 中,OB =6,OP =m ,∵△BPQ 是等腰直角三角形,∠BPQ =90°,∴BP =QP ;如图所示,过点Q 作QT ⊥x 轴于T ,20在Rt △BOP ,Rt △PTQ 中,∠BOP =∠PTQ =90°,∠BPO +∠QPA =∠QPA +∠PQT =90°,∴∠BPO =∠PQT ,∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP,∴Rt △BOP ≌Rt △PTQ (AAS ),∴OP =TQ =m ,OB =PT =6,∴AT =OP +PT -OA =m +6-6=m ,∴AT =QT ,且QT ⊥x 轴,∴△ATQ 是等腰直角三角形,∠QAT =45°,则点Q 的轨迹在射线AQ 上,如图所示,作点D 关于直线AQ 的对称点R,连接QR ,BR ,AR ,A (6,0),B (0,6),D (11,0),∵△ATQ 是等腰直角三角形,即∠QAT =45°,根据对称性质,∴∠QAR =45°,∴RA ⊥x 轴,且△DQA ≌△RQA ,∴AR =AD =11-6=5,则R (6,5),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值;∴由勾股定理得:BR =62+(6-5)2=37,故答案为:37.【点睛】本题主要考查一次函数,几何的综合,掌握待定系数法求解析式,将军饮马问题,等腰直角三角形的性质,勾股定理是解题的关键.23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中,∠B =60°.(1)如图1,若AC >BC ,CD 平分∠ACB 交AB 于点D ,且AD =3BD .证明:∠A =30°;(2)如图2,若AC <BC ,取AC 中点E ,将CE 绕点C 逆时针旋转60°至CF ,连接BF 并延长至G ,使BF =FG ,猜想线段AB 、BC 、CG 之间存在的数量关系,并证明你的猜想;(3)如图3,若AC =BC ,P 为平面内一点,将△ABP 沿直线AB 翻折至△ABQ ,当3AQ +2BQ +13CQ 取得最小值时,直接写出BPCQ的值.【答案】(1)见解析(2)BC =AB +CG ,理由见解析(3)213+33913【分析】(1)过点D 分别作BC ,AC 的垂线,垂足为E ,F ,易得DE =DF ,由∠B =60°,可得DE =DF =32BD ,由AD =3BD ,求得sin A =DE AD=12,可证得∠A =30°;(2)延长BA ,使得BH =BC ,连接EH ,CH ,易证△BCH 为等边三角形,进而可证△BCF ≌△HCE SAS ,可得BF =HE ,∠BFC =∠HEC ,可知∠AEH =∠CFG ,易证得△AEH ≌△CFG SAS ,可得AH =CG ,由BC =BH =AB +AH =AB +CG 可得结论;(3)由题意可知△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,可得CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,可知△ACQ ∽△MCN ,可得MN =32AQ ,由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ,N 都在线段BM 上时,3AQ +2BQ+13CQ 有最小值,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,可得CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,可证△CBR ∽△MBT ,得BR CR =BT MT ,设BC =a 由等边三角形的性质,可得CM =32a ,进而可得CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,结合BR CR=BTMT 可得:BQ +213CQ 313CQ =a +334a 34a ,可得BQ CQ =213+33913,由翻折可知,BP =BQ ,可求得BP CQ的值.【详解】(1)证明:过点D 分别作BC ,AC 的垂线,垂足为E ,F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,∴DE =DF ,又∵∠B =60°,∴DE =BD ⋅sin60°=32BD ,则DE =DF =32BD ,又∵AD =3BD ,∴sin A =DE AD =32BD3BD=12,∴∠A =30°;(2)BC =AB +CG ,理由如下:延长BA ,使得BH =BC ,连接EH ,CH ,∵∠ABC =60°,BH =BC ,∴△BCH 为等边三角形,∴CB =CH ,∠BCH =60°,∵CE 绕点C 逆时针旋转60°至CF ,∴CE =CF ,∠ECF =60°,则∠BCH -∠ACB =∠ECF -∠ACB ,∴∠ECH =∠FCB ,∴△BCF ≌△HCE SAS ,∴BF =HE ,∠BFC =∠HEC ,则∠AEH =∠CFG ,∵BF =FG ,∴BF =HE =FG ,又∵E 为AC 中点,∴AE =CE =CF ,∴△AEH ≌△CFG SAS ,∴AH =CG ,∴BC =BH =AB +AH =AB +CG ;(3)∵∠ABC =60°,AC =BC ,∴△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,则CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,∴sin ∠CQN =CN QN =313,cos ∠CQN =CQ QN =213,则∠ACM =∠QCN =90°,∴∠ACM -∠ACN =∠QCN -∠ACN ,则∠ACQ =∠MCN∴△ACQ ∽△MCN ,∴MN AQ =CM CA=32,即:MN =32AQ ,∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即:点Q ,N 都在线段BM 上时,3AQ +2BQ +13CQ 有最小值,如下图,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,则∠BRC =∠BTM =90°,CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,又∵∠CBR =∠MBT ,∴△CBR ∽△MBT ,∴BR CR=BT MT ,∵△ABC 是等边三角形,设BC =a ∴∠ACB =60°,AC =BC =a ,则CM =32a ,∵∠ACM =90°,∴∠MCT =30°,则CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,则由BR CR=BT MT 可得:BQ +213CQ 313CQ =a +334a34a ,整理得:133BQ CQ +23=4+333,得BQ CQ=213+33913,由翻折可知,BP =BQ ,∴BP CQ =BQ CQ=213+33913.【点睛】本题属于几何综合,考查了解直角三角形,等边三角形的判定及性质,全等三角形的判定及性质,相似三角形的判定及性质,旋转的性质以及费马点问题,掌握费马点问题的解决方法,添加辅助线构造全等三角形和相似三角形是解决问题的关键.24(2023春·江苏·八年级专题练习)定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB 、AC 上,AD =AE ,连接DE 、DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点,且连接PM 、PN .(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”.(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置,连接BD ,CE ,试判断PM 与PN 是否为“等垂线段”,并说明理由.(3)拓展延伸把△ADE 绕点A 在平面内自由旋转,若DE =2,BC =4,请直接写出PM 与PN 的积的最大值.。
初中数学最值问题典型例题(含答案分析)

考查知识点:1、“两点之间线段最短”(2、代数计算最值问题 问题原型:饮马问题造桥选址问题(完全平方公式 出题背景变式:角、三角形、菱形、矩形、正方形、梯形、 解题总思路:找点关于线的对称点实现“折”转“直” 几何基本模型: 条件 问题 方法 中考数学最值问题总结 ,“垂线段最短”,“点关于线对称”,“线段的平移”。
3、二次函数中最值问题) 配方求多项式取值 二次函数顶点)圆、坐标轴、抛物线等。
如下左图, A 、B 是直线I 同旁的两个定点.在直线I 上确定一点P ,使PA PB 的值最小. 作点 A 关于直线I 的对称点A ,连结AB 交I 于 点P ,则PA PB AB 的值最小 例1、如图,四边形 ABCD 是正方形,△ ABE 是等边三 角形,M 为对角线BD (不含B 点) 上任意一点,将 BM 绕点B 逆时针旋转60°得到BN ,连接 EN 、AM 、CM . (1) 求证:△ AMB ENB ; (2) ①当M 点在何处时,AM+CM 的值最小;②当 M 点在何处时,AM+BM+CM 的值最小,并说明理由;(3) 当AM+BM+CM 的最小值为 ■■ ■■■ I 时,求正方形的边长。
例2、如图13,抛物线y=ax2+ bx + c(a丰(的顶点为(1,4 ),交x轴于A B,交y轴于D, 其中B点的坐标为(3,0 )(1)求抛物线的解析式(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小•若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由•(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN// BD,交线段AD于点N,连接MD使厶DN WA BMD若存在,求出点T的坐标;若不存在,说明理由.例3、如图1,四边形AEFG与ABCD都是正方形,它们的边长分别为a,b(b >2a且点F在AD上(以下问题的结果可用a,b表示)(1) 求DBF;(2) 把正方形AEFG绕点A逆时针方向旋转45°得图2,求图2中的S^DBF;(3) 把正方形AEFG绕点A旋转任意角度,在旋转过程中DBF是否存在最大值,最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由。
初中数学的几何最值问题

1. 如图.∠MON=90°.矩形ABCD 的顶点A 、B 分别在边OM.ON 上.当B 在边ON 上运动时.A 随之在边OM 上运动.矩形ABCD 的形状保持不变.其中AB=2.BC=1.运动过程中.点D 到点O 的最大距离为【 】A .21+B .5C .1455 5D .522.在锐角三角形ABC 中.BC=24.∠ABC=45°.BD 平分∠ABC .M 、N分别是BD 、BC 上的动点.则CM+MN 的最小值是 。
3.如图.圆柱底面半径为2cm .高为9cm π.点A 、B 分别是圆柱两底面圆周上的点.且A 、B 在同一母线上.用一棉线从A 顺着圆柱侧面绕3圈到B.求棉线最短为 cm 。
4. 在△ABC 中.AB =5.AC =3.AD 是BC 边上的中线.则AD 的取值范围是 .5.如图.长方体的底面边长分别为2cm 和4cm .高为5cm .若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q 点.则蚂蚁爬行的最短路径长为【 】A.13cmB.12cmC.10cmD.8cm6.如图所示.在边长为2的正三角形ABC 中.E 、F 、G 分别为AB 、AC 、BC的中点.点P 为线段EF 上一个动点.连接BP 、GP.则△BPG 的周长的最小值是 .7.如图.菱形ABCD 中.AB=2.∠A=120°.点P.Q.K 分别为线段BC.CD.BD 上的任意一点.则PK+QK 的最小值为 A . 1 B .3 C . 2D .3+18. 如图.点A 的坐标为(-1.0).点B 在直线y x =上运动.当线段AB 最短时.点B 的坐标为【 】A.(0.0) B.(21-.21-) C.(22.22-) D.(22-.22-)9. 如图.△ABC中.∠BAC=60°.∠ABC=45°.AB=22.D是线段BC上的一个动点.以AD为直径画⊙O分别交AB.AC于E.F.连接EF.则线段EF长度的最小值为.10.已知梯形ABCD.AD∥BC.AB⊥BC.AD=1.AB=2.BC=3.问题1:如图1.P为AB边上的一点.以PD.PC为边作平行四边形PCQD.请问对角线PQ.DC的长能否相等.为什么?问题2:如图2.若P为AB边上一点.以PD.PC为边作平行四边形PCQD.请问对角线PQ的长是否存在最小值?如果存在.请求出最小值.如果不存在.请说明理由.问题3:若P为AB边上任意一点.延长PD到E.使DE=PD.再以PE.PC为边作平行四边形PCQE.请探究对角线PQ的长是否也存在最小值?如果存在.请求出最小值.如果不存在.请说明理由.问题4:如图3.若P为DC边上任意一点.延长PA到E.使AE=nPA(n为常数).以PE、PB为边作平行四边形PBQE.请探究对角线PQ的长是否也存在最小值?如果存在.请求出最小值.如果不存在.请说明理由.11. 如图所示.在菱形ABCD中.AB=4.∠BAD=120°.△AEF为正三角形.点E、F分别在菱形的边BC.CD上滑动.且E、F不与B.C.D重合.(1)证明不论E、F在BC.CD上如何滑动.总有BE=CF;(2)当点E、F在BC.CD上滑动时.分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变.求出这个定值;如果变化.求出最大(或最小)值.12. 如图.在△ABC中.点D、E分别在边BC、AC上.连接AD、DE.且∠1=∠B=∠C.(1)由题设条件.请写出三个正确结论:(要求不再添加其他字母和辅助线.找结论过程中添加的字母和辅助线不能出现在结论中.不必证明)答:结论一:;结论二:;结论三:.(2)若∠B=45°.BC=2.当点D在BC上运动时(点D不与B、C重合).①求CE的最大值;②若△ADE是等腰三角形.求此时BD的长.(注意:在第(2)的求解过程中.若有运用(1)中得出的结论.须加以证明)13.如图.等腰梯形ABCD中.AD∥BC.AD=AB=CD=2.∠C=60°.M是BC的中点.(1)求证:△MDC是等边三角形;(2)将△MDC绕点M旋转.当MD(即MD′)与AB交于一点E.MC(即MC′)同时与AD交于一点F时.点E.F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在.请说明理由;如果存在.请计算出△AEF周长的最小值.14.如图.⊙O的半径为2.点O到直线l的距离为3.点P是直线l上的一个动点.PQ切⊙O于点Q.则PQ的最小值为【】15.如图.在Rt△ABC中.∠C=90°.AB=10cm.AC:BC=4:3.点P从点A出发沿AB方向向点B 运动.速度为1cm/s.同时点Q从点B出发沿B→C→A方向向点A运动.速度为2cm/s.当一个运动点到达终点时.另一个运动点也随之停止运动.(1)求AC、BC的长;(2)设点P的运动时间为x(秒).△PBQ的面积为y(cm2).当△PBQ存在时.求y与x的函数关系式.并写出自变量x的取值范围;(3)当点Q在CA上运动.使PQ⊥AB时.以点B、P、Q为定点的三角形与△ABC是否相似.请说明理由;(4)当x=5秒时.在直线PQ上是否存在一点M.使△BCM得周长最小.若存在.求出最小周长.若不存在.请说明理由.16. 如图.圆柱形玻璃杯高为12cm、底面周长为18cm.在杯内离杯底4cm的点C处有一滴蜂蜜.此时一只蚂蚁正好在杯外壁.离杯上沿4cm与蜂蜜相对的点A处.则蚂蚁到达蜂蜜的最短距离为 cm.17. 如图.四边形ABCD中.∠BAD=120°.∠B=∠D=90°.在BC、CD上分别找一点M、N.使△AMN周长最小时.则∠AMN+∠ANM的度数为【】A.130° B.120° C.110° D.100°18. 点A、B均在由面积为1的相同小矩形组成的网格的格点上.建立平面直角坐标系如图所示.若P是x轴上使得-的值最大的点.Q是y轴上使得QA十QB的值最小PA PB⋅=.的点.则OP OQ19. 阅读材料:例:说明代数式 22x 1(x 3)4++-+的几何意义.并求它的最小值.解: 222222x 1(x 3) 4 (x 0)1(x 3)2++-+=-++-+.如图.建立平面直角坐标系.点P (x.0)是x 轴上一点.则22(x 0)1-+可以看成点P 与点A (0.1)的距离.22(x 3)2-+可以看成点P 与点B (3.2)的距离.所以原代数式的值可以看成线段PA 与PB 长度之和.它的最小值就是PA +PB 的最小值.设点A 关于x 轴的对称点为A′.则PA=PA′.因此.求PA +PB 的最小值.只需求PA′+PB 的最小值.而点A′、B 间的直线段距离最短.所以PA′+PB 的最小值为线段A′B 的长度.为此.构造直角三角形A′CB .因为A′C=3.CB=3.所以A′B=32.即原式的最小值为32。
初中数学的几何最值问题

1. 如图,∠MON=90°,矩形ABCD 的顶点A 、B 分别在边OM ,ON上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O的最大距离为【 】A .21+B .5C .1455 5D .522.在锐角三角形ABC 中,BC=24,∠ABC=45°,BD 平分∠ABC,M 、N 分别是BD 、BC 上的动点,则CM+MN 的最小值是 。
3.如图,圆柱底面半径为2cm ,高为9cm π,点A 、B 分别是圆柱两底面圆周上的点,且A 、B 在同一母线上,用一棉线从A 顺着圆柱侧面绕3圈到B ,求棉线最短为 cm 。
4. 在△ABC 中,AB =5,AC =3,AD 是BC 边上的中线,则AD 的取值范围是 .5.如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为【 】A.13cmB.12cmC.10cmD.8cm6.如图所示,在边长为2的正三角形ABC 中,E 、F 、G 分别为AB 、AC 、BC的中点,点P 为线段EF 上一个动点,连接BP 、GP ,则△BPG 的周长的最小值是 .7.如图,菱形ABCD 中,AB=2,∠A=120°,点P ,Q ,K 分别为线段BC ,CD ,BD 上的任意一点,则PK+QK 的最小值为 A . 1 B .3C . 2D .3+18. 如图,点A 的坐标为(-1,0),点B 在直线y x =上运动,当线段AB 最短时,点B 的坐标为【 】A.(0,0) B.(21-,21-) C.(22,22-) D.(22-,22-)9. 如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=22,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为.10.已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ 的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.问题4:如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.11. 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC.CD上滑动,且E、F不与B.C.D重合.(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.12. 如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C.(1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)答:结论一:;结论二:;结论三:.(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),①求CE的最大值;②若△ADE是等腰三角形,求此时BD的长.(注意:在第(2)的求解过程中,若有运用(1)中得出的结论,须加以证明)13.如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.(1)求证:△MDC是等边三角形;(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD 交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.14.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为【】15.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.(1)求AC、BC的长;(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;(3)当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC是否相似,请说明理由;(4)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由.16. 如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为cm.17. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为【】A.130° B.120° C.110° D.100°18. 点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得-的值最大的点,Q是y轴上使得QA十QB的值最PA PB⋅=.小的点,则OP OQ19. 阅读材料:例:说明代数式 22x 1(x 3)4++-+的几何意义,并求它的最小值. 解: 222222x 1(x 3) 4 (x 0)1(x 3)2++-+=-++-+,如图,建立平面直角坐标系,点P (x ,0)是x 轴上一点,则22(x 0)1-+可以看成点P 与点A (0,1)的距离,22(x 3)2-+可以看成点P 与点B (3,2)的距离,所以原代数式的值可以看成线段PA 与PB 长度之和,它的最小值就是PA +PB 的最小值.设点A 关于x 轴的对称点为A′,则PA=PA′,因此,求PA +PB 的最小值,只需求PA′+PB 的最小值,而点A′、B 间的直线段距离最短,所以PA′+PB 的最小值为线段A′B 的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B=32,即原式的最小值为32。
初中数学几何最值问题

初中数学几何最值问题公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]初中数学几何最值问题在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为几何最值问题.近年来,各地中考题常通过几何最值问题考查学生的实践操作能力、空间想象能力、分析问题和解决问题的能力.本文针对不同类型的几何最值问题作一总结与分析,希望对大家有所帮助.最值问题的解决方法通常有如下6大类:1.三角形的三边关系例1.如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是.2.两点间线段最短例2 如图2,圆柱底面半径为2cm,高为9 cm,点,A B分别是回柱两底面圆周上的点,且,A B在同一母线上,用一棉线从A顺着圆柱侧面绕3圈到B,求棉线长度最短为 .` 3.垂线段最短例3 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D在BC 上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是____________•4.利用轴对称例4.如上右图,矩形ABOC的顶点A的坐标为(﹣4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是()A.(0,)B.(0,)C.(0,2)D.(0,)例5 如图5,正方形ABCD,4AB=,E是BC的中点,点P是对角线AC上一动点,则PE PB+的最小值为 .5.利用二次函数例6在边长为2的等边三角形ABC中,P是BC边上任意一点,过点P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.(1)求证:不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;(2)当BP的长为何值时,四边形AMPN的面积最大,并求出最大值.6利用圆中直径是最长的弦例7.如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是.同步练习1.如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD 边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为___________.2.李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长。
初中数学几何最值专题39:定边定角之直角隐圆(最全修正版)
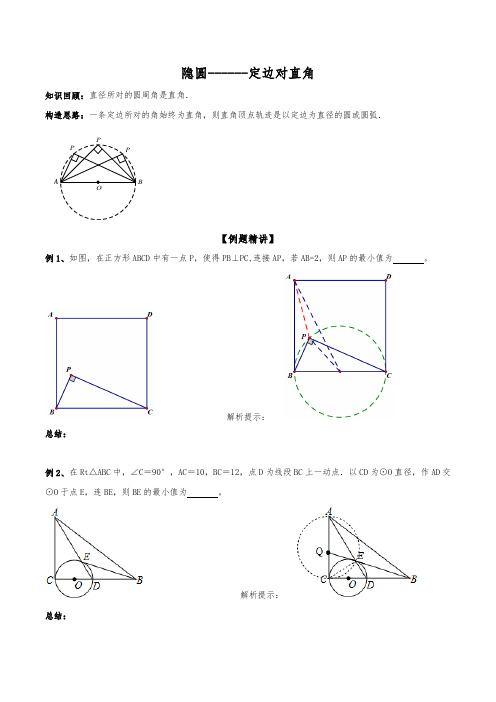
隐圆------定边对直角知识回顾:直径所对的圆周角是直角.构造思路:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.【例题精讲】解析提示:总结:例2、在Rt △ABC 中,∠C =90°,AC =10,BC =12,点D 为线段BC 上一动点.以CD 为⊙O 直径,作AD 交⊙O 于点E ,连BE ,则BE 的最小值为 。
解析提示:总结:A B例3、如图,在△ABC中,∠ABC=90°,AB=6,点P是AB边上的一个动点,以BP为直径的圆交CP于点Q,若线段AQ长度的最小值是3,则△ABC的面积为。
解析提示:总结:例4、如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一个动点,以CD为直径作圆O,连接BD交圆O于点E,则AE的最小值为。
解析提示:总结:例5、如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,当点E在⊙O的运动过程中,线段FG的长度的最小值为。
解析提示:总结:针对训练1、如图,△ABC 是边长为2的等边三角形,D 是边BC 上的动点,BE ⊥AD 于E ,则CE 的最小值为 。
2、已知正方形ABCD 边长为2,E 、F 分别是BC 、CD 上的动点,且满足BE=CF ,连接AE 、BF ,交点为P 点,则PD 的最小值为 。
3、如图,已知正方形ABCD 的边长为6,点E 是正方形内部一点,连接BE ,CE ,且∠ABE=∠BCE ,点P 是AB 边上一动点,连接PD ,PE ,则PD+PE 的长度最小值为 。
4、如图, AB 是半圆O 的直径,点C 在半圆O 上,AB=5,AC=4.D是弧BC 上的一个动点,连接AD ,过点C 作CE ⊥AD 于E ,连接BE .在点D 移动的过程中,BE 的最小值为 。
E FA B CDPB5、如图,AC =3,BC =5,且∠BAC =90°,D 为AC 上一动点,以AD 为直径作圆,连接BD 交圆于E 点,连CE ,则CE 的最小值为 。
初中数学几何最值问题(将军饮马、将军过河、费马点、隐圆、瓜豆、胡不归、阿氏圆)
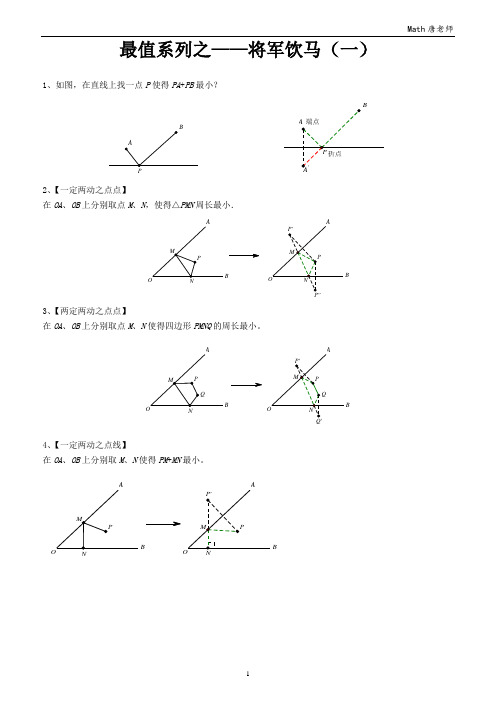
1、如图,在直线上找一点P使得PA+PB最小?2、【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B3、【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
BB4、【一定两动之点线】在OA、OB上分别取M、N使得PM+MN最小。
BB【将军过桥】1.已知将军在图中点A 处,现要过河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?2.已知A 、B 两点,MN 长度为定值,求确定M 、N 位置使得AM +MN +NB 值最小?军营河1.如图,在平面直角坐标系中,矩形ABCD 的顶点B 在原点,点A 、C 在坐标轴上,点D 的坐标为(6,4),E 为CD 的中点,点P 、Q 为BC 边上两个动点,且PQ =2,要使四边形APQE 的周长最小,则点P 的坐示应为______________.x2.如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值.AB CDEFM几何图形中的将军饮马正方形中的将军饮马1. 如图,正方形ABCD 的边长是4,M 在DC 上,且DM =1, N 是AC 边上的一动点,则△DMN 周长的最小值是___________.NMD CBA2.如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且AC :CB =1:3,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为( )A .(2,2)B .5(2,5)2C .8(3,8)3D .(3,3)3.如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( )PDCBAA .4B .5C .6D .7三角形中的将军饮马1.如图,在等边△ABC 中,AB =6, N 为AB 上一点且BN =2AN , BC 的高线AD 交BC 于点D ,M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________.A BCDMN2. 如图,在Rt △ABC 中,∠ACB =90°,AC =6.AB =12,AD 平分∠CAB ,点F 是AC 的中点,点E 是AD 上的动点,则CE +EF 的最小值为( )E AFCDBA .3B .4C .33D .233. 如图,在锐角三角形ABC 中,BC =4,∠ABC =60°, BD 平分∠ABC ,交AC 于点D ,M 、N 分别是BD ,BC 上的动点,则CM +MN 的最小值是( )NMDCBAA .3B .2C .23D .44.如图,△ABC 中,∠BAC =75°,∠ACB =60°,AC =4,则△ABC 的面积为_;点D ,点E ,点F 分别为BC ,AB ,AC 上的动点,连接DE ,EF ,FD ,则△DEF 的周长最小值为 .矩形、菱形中的将军饮马1. 如图,在菱形ABCD 中,AC=BD =6,E 是BC 的中点,P 、M 分别是AC 、AB 上的动点,连接PE 、PM ,则PE +PM 的最小值是( )EPDCBAMA .6 B.C.D .4.52.如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( )A .4(0,)3B .5(0,)3C .(0,2)D .10(0,)33.如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足13PAB ABCD S S ∆=矩形,则点P 到A 、B 两点距离之和PA +PB的最小值为( )DCBAPA. B.C.D4.如图,矩形ABCD 中,AB =10,BC =5,点E 、F 、G 、H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为( )H FGEDCB AA.B. C. D.特殊角的对称1. 如图,∠AOB =60°,点P 是∠AOB 内的定点且OPM 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )ABMOPNABC .6D .32. 如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为 .x3. 如图,已知正比例函数y =kx (k >0)的图像与x 轴相交所成的锐角为70°,定点A 的坐标为(0,4),P 为y 轴上的一个动点,M 、N 为函数y =kx (k >0)的图像上的两个动点,则AM +MP +PN 的最小值为____________.求两线段差的最大值问题基本图形解析:在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A-P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
初中数学几何最值问题

2 模型思想
2.1 建立方程模型 例4 已知△ XYZ是直角边长为1的等腰直角三角形( ∠Z=90 。),它的三
个顶点分别在等腰Rt△ ABC(∠ C=90。)的三边上. 求△ ABC直角边长的最大可能值.
精品
精品
精品
精品
几何最值问题
精品
1 几何变换
1.1 利用平移变换 例1 :已知点P在锐角△ABC的边上运动.试
确定点P的位置,使P A+PB+PC最小,并证 明你的结论. 解:当点P在锐角△ ABC最短边上的高的垂足 位置时, P A+PB+PC最小.
精品
精品Βιβλιοθήκη 精品【小结】利用旋转变换将“Y”字型线段组 转化为两定点之问的折线段,利用两点之间 线段最短确定在点共线的情形下取得最值.
初中数学《几何最值问题》典型例题

.
A 落在 BC 边上的 A′处, P、Q 分别在 AB、AD 边
【分析】 本题关键在于找到两个极端,即 BA′取最大或最小值时,点 P 或 Q 的位置.经实验不难发现,分 别求出点 P 与 B 重合时, BA′取最大值 3 和当点 Q 与 D 重合时, BA′的最小值 1.所以可求点 A′在 BC 边上 移动的最大距离为 2. 【解答】 解:当点 P 与 B 重合时, BA ′取最大值是 3, 当点 Q 与 D 重合时(如图) ,由勾股定理得 A′C=4 ,此时 BA ′取最小值为 1. 则点 A′在 BC 边上移动的最大距离为 3﹣ 1=2 . 故答案为: 2
.
3
【分析】 如图,经分析、探究,只有当直径 EF 最大,且点 A 落在 BD 上时, PD 最小;根据勾股定理求出 BD 的长度,问题即可解决. 【解答】 解:如图, ∵当点 P 落在梯形的内部时,∠ P=∠ A=90°, ∴四边形 PFAE 是以 EF 为直径的圆内接四边形, ∴只有当直径 EF 最大,且点 A 落在 BD 上时, PD 最小, 此时 E 与点 B 重合; 由题意得: PE =AB =8, 由勾股定理得: BD 2=82+62=80 ,
【题后思考】 本题考查了作图﹣轴对称变换,勾股定理等,熟知
“两点之间线段最短 ”是解答此题的关键.
4.动手操作:在矩形纸片 ABCD 中, AB=3, AD =5.如图所示,折叠纸片,使点
折痕为 PQ,当点 A′在 BC 边上移动时,折痕的端点 P、Q 也随之移动.若限定点
上移动,则点 A′在 BC 边上可移动的最大距离为
1
1
1
1
∵ S△ ADP = S 正方形 ABCD = , S△ABP+ S△ACP =S△ ABC= S 正方形 ABCD = ,
初中数学几何模型与最值问题11专题-二次函数在实际应用中的最值问题(含答案)

初中数学几何模型与最值问题专题11 二次函数在实际应用中的最值问题1、某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)求该种水果每次降价的百分率;(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?2、农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:(1)请你根据表中数据,用所学过一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)3、怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.(1)该店每天卖出这两种菜品共多少份;(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少.4、“五一”期间,恒大影城隆重开业,影城每天运营成本为1000元,试营业期间统计发现,影城每天售出的电影票张数y(张)与电影票售价x(元/张)之间满足一次函数:y=﹣4x+220(10≤x≤50,且x是整数),设影城每天的利润为w(元)(利润=票房收入﹣运营成本).(1)试求w与x之间的函数关系式;(2)影城将电影票售价定为多少元/张时,每天获利最大?最大利润是多少元?5、把函数21:23(0)C y ax ax a a =--≠的图象绕点(,0)P m 旋转180,得到新函数2C 的图象,我们称2C 是1C 关于点P 的相关函数.2C 的图象的对称轴与x 轴交点坐标为(,0)t .(1)填空:t 的值为 (用含m 的代数式表示) (2)若1a =-,当12x t ≤≤时,函数1C 的最大值为1y ,最小值为2y ,且121y y -=,求2C 的解析式; (3)当0m =时,2C 的图象与x 轴相交于,A B 两点(点A 在点B 的右侧).与y 轴相交于点D .把线段AD原点O 逆时针旋转90,得到它的对应线段''A D ,若线''A D 与2C 的图象有公共点,结合函数图象,求a 的取值范围.6、湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养天的总成本为万元;放养天的总成本为万元(总成本=放养总费用+收购成本).(1)设每天的放养费用是万元,收购成本为万元,求和的值;(2)设这批淡水鱼放养天后的质量为(),销售单价为元/.根据以往经验可知:与的函数关系为;与的函数关系如图所示.①分别求出当和时,与的函数关系式;①设将这批淡水鱼放养天后一次性出售所得利润为元,求当为何值时,最大?并求出最大值.(利润=销售总额-总成本)7、某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m.设饲养室为长为x(m),占地面积为.(1)如图,问饲养室为长x为多少时,占地面积y最大?(2)如图,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.8、铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:(1)求p与x的函数关系式;(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.9、2016年12月29日至31日,黔南州第十届旅游产业发展大会在“中国长寿之乡”﹣﹣罗甸县举行,从中寻找到商机的人不断涌现,促成了罗甸农民工返乡创业热潮,某“火龙果”经营户有A、B两种“火龙果”促销,若买2件A种“火龙果”和1件B种“火龙果”,共需120元;若买3件A种“火龙果”和2件B种“火龙果”,共需205元.(1)设A,B两种“火龙果”每件售价分别为a元、b元,求a、b的值;(2)B种“火龙果”每件的成本是40元,根据市场调查:若按(1)中求出的单价销售,该“火龙果”经营户每天销售B种“火龙果”100件;若销售单价每上涨1元,B种“火龙果”每天的销售量就减少5件.①求每天B种“火龙果”的销售利润y(元)与销售单价(x)元之间的函数关系?①求销售单价为多少元时,B种“火龙果”每天的销售利润最大,最大利润是多少?10、鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售为y个.(1)直接写出销售量y个与降价x元之间的函数关系式;(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?11、鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售为y个.(1)直接写出销售量y个与降价x元之间的函数关系式;(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?12、某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如下图所示:(1)求y与x的函数解析式(也称关系式);(2)求这一天销售西瓜获得的利润的最大值.13、我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量y(千克)与销售单价x(元)符合一次函数关系,如图所示.(1)求y与x之间的函数关系式,并写出自变量x的取值范围;(2)若在销售过程中每天还要支付其他费用450元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?专题11 二次函数在实际应用中的最值问题 答案1、某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)求该种水果每次降价的百分率;(2)从第一次降价的第1天算起,第x 天(x 为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x (天)的利润为y (元),求y 与x (1≤x <15)之间的函数关系式,并求出第几天时销售利润最大?(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元? 【解析】(1)设该种水果每次降价的百分率是x ,10(1﹣x )2=8.1,x =10%或x =190%(舍去). 答:该种水果每次降价的百分率是10%;(2)当1≤x <9时,第1次降价后的价格:10×(1﹣10%)=9,①y =(9﹣4.1)(80﹣3x )﹣(40+3x )=﹣17.7x +352,①﹣17.7<0,①y 随x 的增大而减小,①当x =1时,y 有最大值,y 大=﹣17.7×1+352=334.3(元); 当9≤x <15时,第2次降价后的价格:8.1元,①y =(8.1﹣4.1)(120﹣x )﹣(3x 2﹣64x +400)=﹣3x 2+60x +80=﹣3(x ﹣10)2+380,①﹣3<0,①当9≤x ≤10时,y 随x 的增大而增大,当10<x <15时,y 随x 的增大而减小,①当x =10时,y 有最大值,y 大=380(元).综上所述,y 与x (1≤x <15)之间的函数关系式为: 217.7352(19){ 36080(915)x x y x x x -+≤<=-++≤<,第10天时销售利润最大;(3)设第15天在第14天的价格基础上最多可降a 元,由题意得:380﹣127.5≤(4﹣a )(120﹣15)﹣(3×152﹣64×15+400),252.5≤105(4﹣a )﹣115,a ≤0.5. 答:第15天在第14天的价格基础上最多可降0.5元.2、农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p (千克)与销售价格x (元/千克)之间的关系,经过市场调查获得部分数据如下表:(1)请你根据表中数据,用所学过一次函数、二次函数、反比例函数的知识确定p 与x 之间的函数表达式 (2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?(3)若农经公司每销售1千克这种农产品需支出a 元(a >0)的相关费用,当40≤x ≤45时,农经公司的日获利的最大值为2430元,求a 的值.(日获利=日销售利润﹣日支出费用) 【解析】(1)假设P 与x 的一次函数关系,设函数关系式p kx b =+,则3060040300k b k b +=⎧⎨+=⎩,解得301500k b =-⎧⎨=⎩,①301500p x =-+,检验:当35,450x P ==,当45,150,x P ==当50,0x P ==,均符合一次函数解析式 ①所求的函数关系式301500p x =-+,(2)设日销售利润()()()3030150030w P x x x =-=-+-,即()223024004500030403000w x x x =-+-=--+,当40x =时,w 有最大值为3000元, 故这批农产口的销售价格定为40元,才能使日销售利润最大, (3)日获利()()()3030150030w p x a x x a =--=-+--, 即()()230240030150045000w x a x a =-++-+,对称轴这()2400301402302a x a +=-=+⨯-,若10a >,则当45x =时,w 有最大值,即22501502430w a =-<(不合题意), 若10a <,则当1402x a =+时,w 有最大值, 把1402x a =+代入,可得2130101004w a a ⎛⎫=-+ ⎪⎝⎭, 当2430w =时,21243030101004a a ⎛⎫=-+ ⎪⎝⎭,解得12a =,238a =(舍去), 综上所述,a 的值为2.3、怡然美食店的A 、B 两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元. (1)该店每天卖出这两种菜品共多少份;(2)该店为了增加利润,准备降低A 种菜品的售价,同时提高B 种菜品的售价,售卖时发现,A 种菜品售价每降0.5元可多卖1份;B 种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少. 【解析】(1)、设该店每天卖出A 、B 两种菜品分别为x 、y 份,根据题意得:()()2018112020141814280x y x y +=⎧⎪⎨-+-=⎪⎩,解得:2040x y =⎧⎨=⎩,答:该店每天卖出这两种菜品共60份;(2)、设A 种菜品售价降0.5a 元,即每天卖(20+a )份,总利润为w 元,因为两种菜品每天销售总份数不变,所以B 种菜品卖(40﹣a )份,每份售价提高0.5a 元. 则w=(20﹣14﹣0.5a )(20+a )+(18﹣14+0.5a )(40﹣a )=(6﹣0.5a )(20+a )+(4+0.5a )(40﹣a )=(﹣0.5a 2﹣4a +120)+(﹣0.5a 2+16a +160) =﹣a 2+12a +280=﹣(a ﹣6)2+316, 当a =6,w 最大,w=316答:这两种菜品每天的总利润最多是316元.4、“五一”期间,恒大影城隆重开业,影城每天运营成本为1000元,试营业期间统计发现,影城每天售出的电影票张数y (张)与电影票售价x (元/张)之间满足一次函数:y =﹣4x +220(10≤x ≤50,且x 是整数),设影城每天的利润为w (元)(利润=票房收入﹣运营成本). (1)试求w 与x 之间的函数关系式;(2)影城将电影票售价定为多少元/张时,每天获利最大?最大利润是多少元? 【解析】(1)根据题意,得:w =(﹣4x +220)x ﹣1000=﹣4x 2+220x ﹣1000;(2)①w =﹣4x 2+220x ﹣1000=﹣4(x ﹣27.5)2+2025,①当x =27或28时,w 取得最大值,最大值为2024,答:影城将电影票售价定为27或28元/张时,每天获利最大,最大利润是2024元.5、把函数21:23(0)C y ax ax a a =--≠的图象绕点(,0)P m 旋转180,得到新函数2C 的图象,我们称2C 是1C 关于点P 的相关函数.2C 的图象的对称轴与x 轴交点坐标为(,0)t .(1)填空:t 的值为 (用含m 的代数式表示) (2)若1a =-,当12x t ≤≤时,函数1C 的最大值为1y ,最小值为2y ,且121y y -=,求2C 的解析式; (3)当0m =时,2C 的图象与x 轴相交于,A B 两点(点A 在点B 的右侧).与y 轴相交于点D .把线段AD原点O 逆时针旋转90,得到它的对应线段''A D ,若线''A D 与2C 的图象有公共点,结合函数图象,求a 的取值范围.【解析】(1)221:23(1)4C y ax ax a a x a =--=--顶点(1,4)a -围绕点(,0)P m 旋转180180°的对称点为(21,4)m a -,2:(21)24C y a x m a =--++,函数的对称轴为:21x m =-,21t m =-,(2)1a =-时,21:(1)4C y x =--,①当112t ≤<时,12x =时,有最小值2154y =,x t =时,有最大值21(1)4y t =--+, 则21215(1)414y y t -=--+-=,无解; ①312t ≤≤时,1x =时,有最大值14y =,12x =时,有最小值22(1)4y t =--+,12114y y -=≠(舍去);①当32t >时,1x =时,有最大值14y =,x t =时,有最小值22(1)4y t =--+,212(1)1y y t -=-=,解得:0t =或2(舍去0),故222:(2)44C y x x x =--=-;(3)0m =,22:(1)4C y a x a =-++,点'',,,,A B D A D 的坐标分别为(1,0),(3,0),(0,3),(0,1),(3,0)a a --,当0a >时,a 越大,则OD 越大,则点'D 越靠左,当2C 过点'A 时,2(01)41y a a =-++=,解得:13a =, 当2C 过点'D 时,同理可得:1a =, 故:103a <≤或1a ≥; 当0a <时,当2C 过点'D 时,31a -=,解得:13a =-, 故:13a ≤-; 综上,故:103a <≤或1a ≥或13a ≤-.6、湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养天的总成本为万元;放养天的总成本为万元(总成本=放养总费用+收购成本).(1)设每天的放养费用是万元,收购成本为万元,求和的值; (2)设这批淡水鱼放养天后的质量为(),销售单价为元/.根据以往经验可知:与的函数关系为;与的函数关系如图所示. ①分别求出当和时,与的函数关系式;①设将这批淡水鱼放养天后一次性出售所得利润为元,求当为何值时,最大?并求出最大值.(利润=销售总额-总成本)【解析】(1)由题意得,解得答:a的值为0.04,b的值为30.(2)①当0≤t≤50时,设y与t的函数关系式为y=k1t+n1把点(0,15)和(50,25)的坐标分别代入y=k1t+n1,得解得①y与t的函数关系式为y=t+15当50<t≤100时,设y与t的函数关系式为y=k2t+n2把点(50,25)和(100,20)的坐标分别代入y=k2t+n2,得解得①y与t的函数关系式为y=t+30①由题意得,当0≤t≤50时,W=20000×(t+15)-(400t+300000)=3600t①3600>0,①当t=50时,W最大值=180000(元)当50<t≤100时,W=(100t+15000)(t+30)-(400t+300000)=-10t2+1100t+150000=-10(t-55)2+180250①-10<0,①当t=55时,W最大值=180250综上所述,当t为55天时,W最大,最大值为180250元.7、某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m.设饲养室为长为x(m),占地面积为.(1)如图,问饲养室为长x为多少时,占地面积y最大?(2)如图,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.【解析】(1)①=,①当x=25时,占地面积y最大;(2)=,①当x=26时,占地面积y最大.即当饲养室长为26m时,占地面积最大.①26-25=1≠2,①小敏的说法不正确.8、铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x 天(1≤x ≤15且x 为整数)时每盒成本为p 元,已知p 与x 之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y 盒,y 与x 之间的关系如下表所示:(1)求p 与x 的函数关系式;(2)若每天的销售利润为w 元,求w 与x 的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果. 【解析】(1)设p =kx +b (k ≠0),①第3天时,每盒成本为21元;第7天时,每盒成本为25元,①321725k b k b +=⎧⎨+=⎩,解得:118k b =⎧⎨=⎩,所以p =x +18;(2)1≤x ≤6时,w =10[50﹣(x +18)]=﹣10x +320,6<x ≤15时,w =[50﹣(x +18)](x +6)=﹣x 2+26x +192,所以,w 与x 的函数关系式为210320(16)26192(615)x x w x x x -+≤≤⎧=⎨-++<≤⎩, 当1≤x ≤6时,①﹣10<0,①w 随x 的增大而减小,①当x =1时,w 最大为﹣10+320=310,6<x ≤15时,w =﹣x 2+26x +192=﹣(x ﹣13)2+361,①当x =13时,w 最大为361, 综上所述,第13天时当天的销售利润最大,最大销售利润是361元;(3)w =325时,﹣x 2+26x +192=325,x 2﹣26x +133=0,解得x 1=7,x 2=19,所以,7≤x ≤13时,即第7、8、9、10、11、12、13天共7天销售利润不低于325元.9、2016年12月29日至31日,黔南州第十届旅游产业发展大会在“中国长寿之乡”﹣﹣罗甸县举行,从中寻找到商机的人不断涌现,促成了罗甸农民工返乡创业热潮,某“火龙果”经营户有A、B两种“火龙果”促销,若买2件A种“火龙果”和1件B种“火龙果”,共需120元;若买3件A种“火龙果”和2件B种“火龙果”,共需205元.(1)设A,B两种“火龙果”每件售价分别为a元、b元,求a、b的值;(2)B种“火龙果”每件的成本是40元,根据市场调查:若按(1)中求出的单价销售,该“火龙果”经营户每天销售B种“火龙果”100件;若销售单价每上涨1元,B种“火龙果”每天的销售量就减少5件.①求每天B种“火龙果”的销售利润y(元)与销售单价(x)元之间的函数关系?①求销售单价为多少元时,B种“火龙果”每天的销售利润最大,最大利润是多少?【解析】(1)根据题意得:2120{32205a ba b+=+=,解得:a=35,b=50;(2)①由题意得:y=(x﹣40)[100﹣5(x﹣50)]①y=﹣5x2+550x﹣14000;①①y=﹣5x2+550x﹣14000=﹣5(x﹣55)2+1125,①当x=55时,y最大=1125,①销售单价为55元时,B商品每天的销售利润最大,最大利润是1125元.10、鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售为y个.(1)直接写出销售量y个与降价x元之间的函数关系式;(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?【解析】(1)依题意有:y=10x+160;(2)依题意有:W=(80﹣50﹣x)(10x+160)=﹣10(x﹣7)2+5290,①-10<0且x为偶数,故当x=6或x=8时,即故当销售单价定为74或72元时,每周销售利润最大,最大利润是5280元;(3)依题意有:﹣10(x﹣7)2+5290≥5200,解得4≤x≤10,则200≤y≤260,200×50=10000(元).答:他至少要准备10000元进货成本.11、鄂州某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个,若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x元(x为偶数),每周销售为y个.(1)直接写出销售量y个与降价x元之间的函数关系式;(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?(3)若商户计划下周利润不低于5200元的情况下,他至少要准备多少元进货成本?【解析】(1)依题意有:y=10x+160;(2)依题意有:W=(80﹣50﹣x)(10x+160)=﹣10(x﹣7)2+5290,①-10<0且x为偶数,故当x=6或x=8时,即故当销售单价定为74或72元时,每周销售利润最大,最大利润是5280元;(3)依题意有:﹣10(x﹣7)2+5290≥5200,解得4≤x≤10,则200≤y≤260,200×50=10000(元).答:他至少要准备10000元进货成本.12、某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y (千克)与销售单价x (元/千克)的函数关系如下图所示:(1)求y 与x 的函数解析式(也称关系式);(2)求这一天销售西瓜获得的利润的最大值.【解析】(1)当6≤x ≤10时,由题意设y =kx +b (k =0),它的图象经过点(6,1000)与点(10,200), ①1000620010k b k b =+⎧⎨=+⎩ ,解得2002200k b =-⎧⎨=⎩, ①当6≤x ≤10时, y =-200x +2200,当10<x ≤12时,y =200,综上,y 与x 的函数解析式为()()20022006102001012x x y x ⎧-+≤≤⎪=⎨<≤⎪⎩ (2)设利润为w 元,当6≤x ≤10时,y =-200x +2200,w =(x -6)y =(x -6)(-200x +200)=-2002172x -()+1250, ①-200<0,6①x ≤10,当x =172时,w 有最大值,此时w=1250; 当10<x ≤12时,y =200,w =(x -6)y =200(x -6)=200x -1200,①200>0,①w =200x -1200随x 增大而增大,又①10<x ≤12,①当x =12时,w 最大,此时w=1200,1250>1200,①w 的最大值为1250,答:这一天销售西瓜获得利润的最大值为1250元.13、我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量y (千克)与销售单价x (元)符合一次函数关系,如图所示.(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围;(2)若在销售过程中每天还要支付其他费用450元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?【解析】(1)设一次函数关系式为(0)y kx b k =+≠由图象可得,当30x =时,140y =;50x =时,100y =①1403010050k b k b =+⎧⎨=+⎩,解得k 2b 200=-⎧⎨=⎩ ①y 与x 之间的关系式为2200(3060)y x x =-+≤≤.(2)设该公司日获利为W 元,由题意得2(30)(2200)4502(65)2000W x x x =--+-=--+①20a =-<;①抛物线开口向下;①对称轴65x =;①当65x <时,W 随着x 的增大而增大;①3060x ≤≤,①60x =时,W 有最大值;22(6065)200015=90W -⨯-+=最大值.即,销售单价为每千克60元时,日获利最大,最大获利为1950元.。
(完整word版)初中数学《几何最值问题》典型例题

初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短;直线外一点与直线上所有点的连线段中,垂线段最短;三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段.轴对称最值图形lPBANM lBAAPBl 原理两点之间线段最短两点之间线段最短三角形三边关系特征A,B为定点,l为定直线,P为直线l上的一个动点,求AP+BP的最小值A,B为定点,l为定直线,MN为直线l上的一条动线段,求AM+BN的最小值A,B为定点,l为定直线,P为直线l上的一个动点,求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M,N重合,然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中,M,N两点分别是边AB,BC上的动点,将△BMN沿MN翻折,B点的对应点为B',连接AB',求AB'的最小值.转化转化成求AB'+B'N+NC的最小值1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△PMN 的周长的最小值为.【分析】作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN 的周长最短,最短的值是CD的长.根据对称的性质可以证得:△COD是等腰直角三角形,据此即可求解.【解答】解:作P关于OA,OB的对称点C,D.连接OC,OD.则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.∵PC关于OA对称,∴∠COP=2∠AOP,OC=OP同理,∠DOP=2∠BOP,OP=OD∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD.∴△COD是等腰直角三角形.则CD=2OC=2×32=6.【题后思考】本题考查了对称的性质,正确作出图形,理解△PMN周长最小的条件是解题的关键.2.如图,当四边形P ABN的周长最小时,a=.【分析】因为AB,PN的长度都是固定的,所以求出P A+NB的长度就行了.问题就是P A+NB什么时候最短.把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N点位置,此时P A+NB最短.设直线AB″的解析式为y=kx+b,待定系数法求直线解析式.即可求得a的值.【解答】解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,﹣1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),设直线AB″的解析式为y=kx+b,则123k bk b=+⎧⎨-=+⎩,解得k=4,b=﹣7.∴y=4x﹣7.当y=0时,x=74,即P(74,0),a=74.故答案填:74.【题后思考】考查关于X轴的对称点,两点之间线段最短等知识.3.如图,A 、B 两点在直线的两侧,点A 到直线的距离AM =4,点B 到直线的距离BN =1,且MN =4,P 为直线上的动点,|P A ﹣PB |的最大值为.D PB′N MA【分析】作点B 于直线l 的对称点B ′,则PB =PB ′因而|P A ﹣PB |=|P A ﹣PB ′|,则当A ,B ′、P 在一条直线上时,|P A ﹣PB |的值最大.根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值,进而求得|P A ﹣PB |的最大值.【解答】解:作点B 于直线l 的对称点B ′,连AB ′并延长交直线l 于P . ∴B ′N =BN =1,过D 点作B ′D ⊥AM , 利用勾股定理求出AB ′=5 ∴|P A ﹣PB |的最大值=5.【题后思考】本题考查了作图﹣轴对称变换,勾股定理等,熟知“两点之间线段最短”是解答此题的关键.4.动手操作:在矩形纸片ABCD 中,AB =3,AD =5.如图所示,折叠纸片,使点A 落在BC 边上的A ′处,折痕为PQ ,当点A ′在BC 边上移动时,折痕的端点P 、Q 也随之移动.若限定点P 、Q 分别在AB 、AD 边上移动,则点A ′在BC 边上可移动的最大距离为 .【分析】本题关键在于找到两个极端,即BA ′取最大或最小值时,点P 或Q 的位置.经实验不难发现,分别求出点P 与B 重合时,BA ′取最大值3和当点Q 与D 重合时,BA ′的最小值1.所以可求点A ′在BC 边上移动的最大距离为2.【解答】解:当点P 与B 重合时,BA ′取最大值是3, 当点Q 与D 重合时(如图),由勾股定理得A ′C =4,此时BA ′取最小值为1. 则点A ′在BC 边上移动的最大距离为3﹣1=2. 故答案为:2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象造成错误.5.如图,直角梯形纸片ABCD ,AD ⊥AB ,AB =8,AD =CD =4,点E 、F 分别在线段AB 、AD 上,将△AEF 沿EF 翻折,点A 的落点记为P .当P 落在直角梯形ABCD 内部时,PD 的最小值等于 .【分析】如图,经分析、探究,只有当直径EF最大,且点A落在BD上时,PD最小;根据勾股定理求出BD的长度,问题即可解决.【解答】解:如图,∵当点P落在梯形的内部时,∠P=∠A=90°,∴四边形PF AE是以EF为直径的圆内接四边形,∴只有当直径EF最大,且点A落在BD上时,PD最小,此时E与点B重合;由题意得:PE=AB=8,由勾股定理得:BD2=82+62=80,∴BD=45,∴PD=458 .【题后思考】该命题以直角梯形为载体,以翻折变换为方法,以考查全等三角形的判定及其性质的应用为核心构造而成;解题的关键是抓住图形在运动过程中的某一瞬间,动中求静,以静制动.6.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为.【分析】取AB的中点E,连接OD、OE、DE,根据直角三角形斜边上的中线等于斜边的一半可得OE=AB,利用勾股定理列式求出DE,然后根据三角形任意两边之和大于第三边可得OD过点E时最大.【解答】解:如图,取AB的中点E,连接OD、OE、DE,∵∠MON=90°,AB=2∴OE=AE=12AB=1,∵BC=1,四边形ABCD是矩形,∴AD,∴DE2,根据三角形的三边关系,OD<OE+DE,∴当OD过点E是最大,最大值为2+1.故答案为:2+1.【题后思考】本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,勾股定理,确定出OD过AB的中点时值最大是解题的关键.7.如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE,那么DE长的最小值是.【分析】设AC=x,BC=4﹣x,根据等腰直角三角形性质,得出CD=22x,CD′=22(4﹣x),根据勾股定理然后用配方法即可求解.【解答】解:设AC=x,BC=4﹣x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=22x,CD′=22(4﹣x),∵∠ACD=45°,∠BCD′=45°,∴∠DCE=90°,∴DE2=CD2+CE2=12x2+12(4﹣x)2=x2﹣4x+8=(x﹣2)2+4,∵根据二次函数的最值,∴当x取2时,DE取最小值,最小值为:4.故答案为:2.【题后思考】本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.8.如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK 的最小值为.【分析】根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连接P′Q与BD的交点即为所求的点K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值,然后求解即可.【解答】解:如图,∵AB=2,∠A=120°,∴点P′到CD的距离为2×33∴PK+QK3故答案为:3.【题后思考】本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.9.如图所示,正方形ABCD的边长为1,点P为边BC上的任意一点(可与B、C重合),分别过B、C、D作射线AP的垂线,垂足分别为B′、C′、D′,则BB′+CC′+DD′的取值范围是.【分析】首先连接AC,DP.由正方形ABCD的边长为1,即可得:S△ADP=12S正方形ABCD=12,S△ABP+S△ACP=S△ABC=12S正方形ABCD=12,继而可得12AP•(BB′+CC′+DD′)=1,又由1≤AP≤2,即可求得答案.【解答】解:连接AC,DP.∵四边形ABCD是正方形,正方形ABCD的边长为1,∴AB=CD,S正方形ABCD=1,∵S△ADP=12S正方形ABCD=12,S△ABP+S△ACP=S△ABC=12S正方形ABCD=12,∴S△ADP+S△ABP+S△ACP=1,∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•(BB′+CC′+DD′)=1,则BB′+CC′+DD′=2 AP,∵1≤AP≤2,∴当P当P与C重合时,有最小值2.∴2≤BB′+CC′+DD′≤2.故答案为:2≤BB′+CC′+DD′≤2.【题后思考】此题考查了正方形的性质、面积及等积变换问题.此题难度较大,解题的关键是连接AC,DP,根据题意得到S△ADP+S△ABP+S△ACP=1,继而得到BB′+CC′+DD′=2 AP.10.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A 和⊙B上的动点,则PE+PF的最小值是.【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值,进而求出即可.【解答】解:由题意可得出:当P与D重合时,E点在AD上,F在BD上,此时PE+PF最小,连接BD,∵菱形ABCD中,∠A=60°,∴AB=AD,则△ABD是等边三角形,∴BD=AB=AD=3,∵⊙A、⊙B的半径分别为2和1,∴PE=1,DF=2,∴PE+PF的最小值是3.故答案为:3.【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识,根据题意得出P点位置是解题关键.。
初中数学几何模型与最值问题05专题-费马点中的对称模型与最值问题(含答案)

初中数学最值问题专题5 费马点中的对称模型与最值问题【专题说明】【例题】1、如图,在△ABC 中,△ACB =90°,AB =AC =1,P 是△ABC 内一点,求P A +PB +PC 的最小值.【分析】如图,以AD 为边构造等边△ACD ,连接BD ,BD 的长即为P A +PB +PC 的最小值.至于点P 的位置?这不重要!如何求BD ?考虑到△ABC 和△ACD 都是特殊的三角形,过点D 作DH △BA 交BA 的延长线于H 点,根据勾股定理,222BD BH DH =+即可得出结果.C2、如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.3、如图,P 是AOB ∠内一定点,点M ,N 分别在边OA ,OB 上运动,若30AOB ∠=︒,3OP =,则PMN的周长的最小值为___________.4、如图,点都在双曲线上,点,分别是轴,轴上的动点,则四边形周长的最小值为( )A .B .C .D .5、如图所示,30AOB ∠=,点P 为AOB ∠内一点,8OP =,点,M N 分别在,OA OB 上,求PMN ∆周长的最小值.ABCDME6、如图,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.(1)求直线AE的解析式;(2)点P为直线CE下方抛物线上的一点,连接P C,P E.当△P CE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是C P上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.7、已知,如图,二次函数()2230y ax ax a a =+-≠图象的顶点为H ,与x 轴交于A 、B 两点(B 点在A点右侧),点H 、B 关于直线l :y x =+对称.(1)求A 、B 两点的坐标,并证明点A 在直线l 上; (2)求二次函数解析式;(3)过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连结HN 、NM 、MK ,求HN +NM +MK 的最小值.专题5 费马点中的对称模型与最值问题 答案【专题说明】【例题】1、如图,在△ABC 中,△ACB =90°,AB =AC =1,P 是△ABC 内一点,求P A +PB +PC 的最小值.【分析】如图,以AD 为边构造等边△ACD ,连接BD ,BD 的长即为P A +PB +PC 的最小值.至于点P 的位置?这不重要!如何求BD ?考虑到△ABC 和△ACD 都是特殊的三角形,过点D 作DH △BA 交BA 的延长线于H 点,根据勾股定理,222BD BH DH =+即可得出结果.C2、如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.【分析】依然构造60°旋转,将三条折线段转化为一条直线段. 分别以AD 、AM 为边构造等边△ADF 、等边△AMG ,连接FG ,易证△AMD △△AGF ,△MD =GF △ME +MA +MD =ME +EG +GF过F 作FH △BC 交BC 于H 点,线段FH 的长即为所求的最小值.ABCDMEHFGE MDCBA3、如图,P 是AOB ∠内一定点,点M ,N 分别在边OA ,OB 上运动,若30AOB ∠=︒,3OP =,则PMN 的周长的最小值为___________.【解析】如图,作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△P MN 的周长最短,最短的值是CD 的长.△点P 关于OA 的对称点为C , △P M =CM ,O P=OC ,△COA =△P OA ; △点P 关于OB 的对称点为D , △P N =DN ,O P=OD ,△DOB =△P OB ,△OC =OD =O P=3,△COD =△COA +△P OA +△P OB +△DOB =2△P OA +2△P OB =2△AOB =60°, △△COD 是等边三角形, △CD =OC =OD =3.△△P MN 的周长的最小值=P M +MN +P N =CM +MN +DN ≥CD =3.4、如图,点都在双曲线上,点,分别是轴,轴上的动点,则四边形周长的最小值为()A.B.C.D.【解析】分别把点A(a,3)、B(b,1)代入双曲线y=得:a=1,b=3,则点A的坐标为(1,3)、B点坐标为(3,1),作A点关于y轴的对称点P,B点关于x轴的对称点Q,所以点P坐标为(﹣1,3),Q点坐标为(3,﹣1),连结P Q分别交x轴、y轴于C点、D点,此时四边形ABCD的周长最小,四边形ABCD周长=DA+DC+CB+AB=D P+DC+CQ+AB=P Q+AB==4+2=6,故选B.5、如图所示,30AOB ∠=,点P 为AOB ∠内一点,8OP =,点,M N 分别在,OA OB 上,求PMN ∆周长的最小值.【解析】如图,作P 关于OA 、OB 的对称点12P P 、,连结1OP 、2OP ,12PP 交OA 、OB 于M 、N ,此时PMN ∆周长最小,根据轴对称性质可知1PMPM =,2PN P N =,1212PMN PM MN P N PP ∴∆=++=,且1AOP AOP ∠=∠,2BOP BOP ∠=∠,12260POP AOB ∠=∠=︒,128OP OP OP ===,12PP O ∆为等边三角形,1218PP OP ==即PMN ∆周长的最小值为8.6、如图,在平面直角坐标系中,抛物线y =x 2﹣x ﹣与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,点E (4,n )在抛物线上.(1)求直线AE 的解析式;(2)点P 为直线CE 下方抛物线上的一点,连接P C ,P E .当△P CE 的面积最大时,连接CD ,CB ,点K是线段CB的中点,点M是C P上的一点,点N是CD上的一点,求KM+MN+NK的最小值;(3)点G是线段CE的中点,将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.【解析】(1)△y=x2﹣x﹣,△y=(x+1)(x﹣3).△A(﹣1,0),B(3,0).当x=4时,y=.△E(4,).设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:,解得:k=,b=.△直线AE的解析式为y=x+.(2)设直线CE的解析式为y=mx﹣,将点E的坐标代入得:4m﹣=,解得:m=.△直线CE的解析式为y=x﹣.过点P作P F△y轴,交CE与点F.设点P的坐标为(x,x2﹣x﹣),则点F(x,x﹣),则F P=(x﹣)﹣(x2﹣x﹣)=x2+x.△△E P C的面积=×(x2+x)×4=﹣x2+x.△当x=2时,△E P C的面积最大.△P(2,﹣).如图2所示:作点K关于CD和C P的对称点G、H,连接G、H交CD和C P与N、M.△K是CB的中点,△k(,﹣).△点H与点K关于C P对称,△点H的坐标为(,﹣).△点G与点K关于CD对称,△点G(0,0).△KM+MN+NK=MH+MN+GN.当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.△GH==3.△KM+MN+NK的最小值为3.(3)如图3所示:△y ′经过点D ,y ′的顶点为点F ,△点F (3,﹣).△点G 为CE 的中点,△G (2,).△FG =.△当FG =FQ 时,点Q (3,),Q ′(3,).当GF =GQ 时,点F 与点Q ″关于y =对称,△点Q ″(3,2).当QG =QF 时,设点Q 1的坐标为(3,a ).由两点间的距离公式可知:a +=,解得:a =﹣.△点Q 1的坐标为(3,﹣).综上所述,点Q 的坐标为(3,),Q ′(3,)或(3,2)或(3,﹣). 7、已知,如图,二次函数()2230y ax ax a a =+-≠图象的顶点为H ,与x 轴交于A 、B 两点(B 点在A=+对称.点右侧),点H、B关于直线l:y x(1)求A、B两点的坐标,并证明点A在直线l上;(2)求二次函数解析式;BK AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连结HN、NM、(3)过点B作直线//MK,求HN+NM+MK的最小值.【解析】(1)依题意,得ax2+2ax−3a=0(a≠0),两边都除以a得x2+2x−3=0,解得x1=−3,x2=1,△B点在A点右侧,△A点坐标为(−3,0),B点坐标为(1,0),答:A.B两点坐标分别是(−3,0),(1,0).证明:△直线l:y x+-=,△点A在直线l上.当x=−3时,y(3)0(2)△点H、B关于过A点的直线l:y x+对称,△AH=AB=4,过顶点H作HC△AB交AB于C点,则AC=12,2AB HC==△顶点H(1,-,代入二次函数解析式,解得a=,△二次函数解析式为2y x=,答:二次函数解析式为2y x=+.(3)直线AH的解析式为y=+,直线BK的解析式为y=-y xy⎧=⎪⎨⎪=-⎩,解得3xy=⎧⎪⎨=⎪⎩K),则BK=4,△点H、B关于直线AK对称,K,△HN+MN的最小值是MB,过K作KD△x轴于D,作点K关于直线AH的对称点Q,连接QK,交直线AH于E,则QM=MK,QE=EKAE△QK,△根据两点之间线段最短得出BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,△BK△AH,△△BKQ=△HEQ=90△,由勾股定理得QB8==△HN+NM+MK的最小值为8,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学几何最值问题典型例题TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短;直线外一点与直线上所有点的连线段中,垂线段最短;三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)是解决几何最值问题的理论依据,根据不同特征转化是解决最值问题的关键.通过转化减少变量,向三个定理靠拢进而解决问题;直接调用基本模型也是解决几何最值问题的高效手段.1.如图:点P 是∠AOB 内一定点,点M 、N 分别在边OA 、OB 上运动,若∠AOB =45°,OP =PMN 的周长的最小值为 .【分析】作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△PMN 的周长最短,最短的值是CD 的长.根据对称的性质可以证得:△COD 是等腰直角三角形,据此即可求解.【解答】解:作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△PMN 的周长最短,最短的值是CD 的长.∵PC 关于OA 对称,∴∠COP =2∠AOP ,OC =OP同理,∠DOP =2∠BOP ,OP =OD∴∠COD =∠COP +∠DOP =2(∠AOP +∠BOP )=2∠AOB =90°,OC =OD .∴△COD 是等腰直角三角形.则CD OC .【题后思考】本题考查了对称的性质,正确作出图形,理解△PMN 周长最小的条件是解题的关键.2.如图,当四边形PABN 的周长最小时,a = .【分析】因为AB,PN的长度都是固定的,所以求出PA+NB的长度就行了.问题就是PA+NB什么时候最短.把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N 点位置,此时PA+NB最短.设直线AB″的解析式为y=kx+b,待定系数法求直线解析式.即可求得a的值.【解答】解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,﹣1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),设直线AB″的解析式为y=kx+b,则123k bk b=+⎧⎨-=+⎩,解得k=4,b=﹣7.∴y=4x﹣7.当y=0时,x=74,即P(74,0),a=74.故答案填:74.【题后思考】考查关于X轴的对称点,两点之间线段最短等知识.3.如图,A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=1,且MN=4,P为直线上的动点,|PA﹣PB|的最大值为.【分析】作点B于直线l的对称点B′,则PB=PB′因而|PA﹣PB|=|PA﹣PB′|,则当A,B′、P在一条直线上时,|PA﹣PB|的值最大.根据平行线分线段定理即可求得PN和PM的值然后根据勾股定理求得PA、PB′的值,进而求得|PA﹣PB|的最大值.【解答】解:作点B于直线l的对称点B′,连AB′并延长交直线l于P.∴B′N=BN=1,过D点作B′D⊥AM,利用勾股定理求出AB′=5∴|PA﹣PB|的最大值=5.【题后思考】本题考查了作图﹣轴对称变换,勾股定理等,熟知“两点之间线段最短”是解答此题的关键.4.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为.【分析】本题关键在于找到两个极端,即BA′取最大或最小值时,点P或Q的位置.经实验不难发现,分别求出点P与B重合时,BA′取最大值3和当点Q与D重合时,BA′的最小值1.所以可求点A′在BC 边上移动的最大距离为2.【解答】解:当点P与B重合时,BA′取最大值是3,当点Q与D重合时(如图),由勾股定理得A′C=4,此时BA′取最小值为1.则点A′在BC边上移动的最大距离为3﹣1=2.故答案为:2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识,难度稍大,学生主要缺乏动手操作习惯,单凭想象造成错误.5.如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF 翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于.【分析】如图,经分析、探究,只有当直径EF最大,且点A落在BD上时,PD最小;根据勾股定理求出BD的长度,问题即可解决.【解答】解:如图,∵当点P落在梯形的内部时,∠P=∠A=90°,∴四边形PFAE是以EF为直径的圆内接四边形,∴只有当直径EF最大,且点A落在BD上时,PD最小,此时E与点B重合;由题意得:PE=AB=8,由勾股定理得:BD2=82+62=80,∴BD=45,∴PD=458.【题后思考】该命题以直角梯形为载体,以翻折变换为方法,以考查全等三角形的判定及其性质的应用为核心构造而成;解题的关键是抓住图形在运动过程中的某一瞬间,动中求静,以静制动.6.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM 上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为.【分析】取AB的中点E,连接OD、OE、DE,根据直角三角形斜边上的中线等于斜边的一半可得OE=AB,利用勾股定理列式求出DE,然后根据三角形任意两边之和大于第三边可得OD过点E时最大.【解答】解:如图,取AB的中点E,连接OD、OE、DE,∵∠MON=90°,AB=2∴OE=AE=12AB=1,∵BC=1,四边形ABCD是矩形,∴AD=BC=1,∴DE2根据三角形的三边关系,OD<OE+DE,∴当OD过点E2.2+1.【题后思考】本题考查了矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,勾股定理,确定出OD过AB的中点时值最大是解题的关键.7.如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是.【分析】设AC=x,BC=4﹣x,根据等腰直角三角形性质,得出CD=22x,CD′=22(4﹣x),根据勾股定理然后用配方法即可求解.【解答】解:设AC=x,BC=4﹣x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=22x,CD′=22(4﹣x),∵∠ACD=45°,∠BCD′=45°,∴∠DCE=90°,∴DE2=CD2+CE2=12x2+12(4﹣x)2=x2﹣4x+8=(x﹣2)2+4,∵根据二次函数的最值,∴当x取2时,DE取最小值,最小值为:4.故答案为:2.【题后思考】本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.8.如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK 的最小值为.【分析】根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连接P′Q与BD的交点即为所求的点K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值,然后求解即可.【解答】解:如图,∵AB=2,∠A=120°,∴点P′到CD的距离为33,∴PK+QK3【题后思考】本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.9.如图所示,正方形ABCD的边长为1,点P为边BC上的任意一点(可与B、C重合),分别过B、C、D 作射线AP的垂线,垂足分别为B′、C′、D′,则BB′+CC′+DD′的取值范围是.【分析】首先连接AC,DP.由正方形ABCD的边长为1,即可得:S△ADP=12S正方形ABCD=12,S△ABP+S△ACP=S△ABC=12S正方形ABCD=12,继而可得12AP(BB′+CC′+DD′)=1,又由1≤AP,即可求得答案.【解答】解:连接AC,DP.∵四边形ABCD是正方形,正方形ABCD的边长为1,∴AB=CD,S正方形ABCD=1,∵S△ADP=12S正方形ABCD=12,S△ABP+S△ACP=S△ABC=12S正方形ABCD=12,∴S△ADP+S△ABP+S△ACP=1,∴12APBB′+12APCC′+12APDD′=12AP(BB′+CC′+DD′)=1,则BB′+CC′+DD′=2 AP,∵1≤AP,∴当P与B重合时,有最大值2;当P与C.≤BB′+CC′+DD′≤2.≤BB′+CC′+DD′≤2.【题后思考】此题考查了正方形的性质、面积及等积变换问题.此题难度较大,解题的关键是连接AC,DP,根据题意得到S△ADP+S△ABP+S△ACP=1,继而得到BB′+CC′+DD′=2 AP.10.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A 和⊙B上的动点,则PE+PF的最小值是.【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值,进而求出即可.【解答】解:由题意可得出:当P与D重合时,E点在AD上,F在BD上,此时PE+PF最小,连接BD,∵菱形ABCD中,∠A=60°,∴AB=AD,则△ABD是等边三角形,∴BD=AB=AD=3,∵⊙A、⊙B的半径分别为2和1,∴PE=1,DF=2,∴PE+PF的最小值是3.故答案为:3.【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识,根据题意得出P点位置是解题关键.。
