《空间几何体》PPT精品课件人教B版1
合集下载
《空间几何体》PPT课件人教B版1

知识小结
简单几何体的结构特征
D1
C1
A1
B1
旋转体
由一个平面图形绕它 所在平面内的一条定 直线旋转所形成的封 闭几何体.
D
C
A
B
【全国百强校】内蒙古元宝山区平煤 高级中 学高中 数学人 教版必 修二同 步课件 :1.1空 间几何 体的结 构
【全国百强校】内蒙古元宝山区平煤 高级中 学高中 数学人 教版必 修二同 步课件 :1.1空 间几何 体的结 构 【全国百强校】内蒙古元宝山区平煤 高级中 学高中 数学人 教版必 修二同 步课件 :1.1空 间几何 体的结 构
棱柱
柱体 圆柱
棱锥
锥体
圆锥
台体 棱台
圆台
球体
【全国百强校】内蒙古元宝山区平煤 高级中 学高中 数学人 教版必 修二同 步课件 :1.1空 间几何 体的结 构
一、 棱柱的结构特征:
思考:具备哪些性质的几何体叫做棱柱?
A1
D1 B1
C1 A1
D A
C BA
C1
A1
B1 B1
E1 D1 C1
C A
BB
E CD
简单组合体的结构特征:
日常生活中常用到的日用品,比如:消毒液、 暖瓶、洗洁精等的主要几何结构特征是什么?
圆柱 圆台
圆柱
【全国百强校】内蒙古元宝山区平煤 高级中 学高中 数学人 教版必 修二同 步课件 :1.1空 间几何 体的结 构
【全国百强校】内蒙古元宝山区平煤 高级中 学高中 数学人 教版必 修二同 步课件 :1.1空 间几何 体的结 构
多面体
由若干个平面多边 形围成的几何体.
D1
C1
A1
B1
人教B版(2019)空间几何体PPT(新版)1

人教B版(2019)空间几何体PPT(新 版)1
6 13 +3 2 [如图,延长EF和A1B1相交于 M,连接AM交BB1于H,延长FE和A1D1相交于 N,连接AN交DD1于G,连接FH,EG,可得截面 五边形AHFEG.因为ABCD-A1B1C1D1是棱长为6的 正方体,且E,F分别是棱C1D1,B1C1的中点,所 以EF=3 2,AG=AH=2 13,EG=FH= 13, 截面的周长为AH+HF+EF+EG+AG=6 13 + 3 2.]
人教B版(2019)空间几何体PPT(新 版)1
人教B版(2019)空间几何体PPT(新 版)1
梯形的高为
252-
422=3 42,所以其面积为
2+ 2
2 2 ×3
4 2=98,
故选项 C 正确;连接 CG 交 EF 于点 H(图略),显然 H 不是 EF 的中
点,所以 C,G 到平面 AEF 的距离不相等,选项 D 不正确.]
在△O1DE中,DE=
人教B版(2019)空间几何体PPT(新 版)1
2π [如图,设△BCD的中心为点O1,球O 的半径为R,则A,O,O1三点共线.连接 O1D,O1E,OD,OE,则O1D= 3 ,AO1=
AD2-O1D2=3. 在Rt△OO1D中,R2=3+(3-R)2,即R=2,所以OO1=1.
人教B版(2019)空间几何体PPT(新 版)1
人教B版(2019)空间几何体PPT(新 版)1
人教B版(2019)空间几何体PPT(新 版)1
4.[多选]如图,正方体ABCD-A1B1C1D1的棱长为1,E,F,G分 别为BC,CC1,BB1的中点.则( )
A.直线D1D与直线AF垂直 B.直线A1G与平面AEF平行 C.平面AEF截正方体所得的截面面积为98 D.点C与点G到平面AEF的距离相等
人教新课标B版《空间几何体》PPT优质课件1
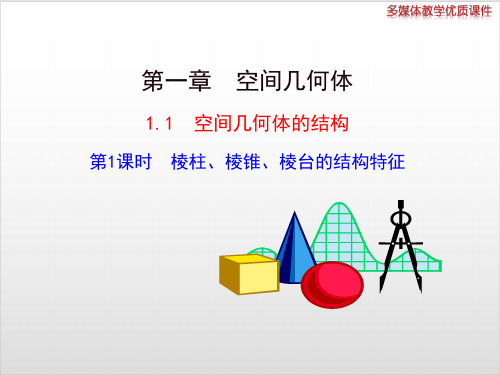
棱柱
棱锥
棱台
......
侧棱
侧棱
侧棱
侧面
侧面
侧面
人教新课标B版《空间几何体》PPT优 质课件1
底面 顶点
底面 顶点
底面 顶点
人教新课标B版《空间几何体》PPT优 质课件1
不论你在什么时候开始,重要的是开始 之后就不要停止。不论你在什么时候结束, 重要的是结束之后就不要悔恨。
人教新课标B版《空间几何体》PPT优 质课件1
人教新课标B版《空间几何体》PPT优 质课件1
人教新课标B版《空间几何体》PPT优 质课件1
【提升总结】 特殊的棱锥: 如果棱锥的底面为正多边形,且各侧面是全等的等腰 三角形,那么这样的棱锥称为正棱锥. 正棱锥各侧面底边上的高均相等,叫做正棱锥的斜高; 侧棱长等于底面边长的正三棱锥又称为正四面体.
底面
侧 面
顶点
侧 棱
底面
人教新课标B版《空间几何体》PPT优 质课件1
人教新课标B版《空间几何体》PPT优 质课件1
棱柱中,两个互相平行的面叫做棱柱的底面,简称底; 其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱 柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点. 底面是三角形、四边形、五边形……的棱柱分别叫做三 棱柱、四棱柱、五棱柱……我们用表示底面各顶点的字 母表示棱柱,如六棱柱ABCDEF-A′B′C′D′E′F′.
人教新课标B版《空间几何体》PPT优 质课件1
侧 面
人教新课标B版《空间几何体》PPT优 质课件1
底面
人教新课标B版《空间几何体》PPT优 质课件1
这个多边形面叫做棱锥的底面或底;有公共顶点的 各个三角形面叫做棱锥的侧面;各侧面的公共顶点 叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧 棱. 底面是三角形、四边形、五边形……的棱锥分别叫 做三棱锥、四棱锥、五棱锥……棱锥也用表示顶点 和底面各顶点的字母表示,如五棱锥S-ABCDE.
《空间几何体》ppt课件高中数学人教B版1

【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
b
a
c
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
正视图
c ba
俯视图
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
侧
正视图
三视图的形成
主 视 图
侧视图
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
俯视图
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
三视图的特点
长对正
高平齐
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
平行投影
思考2:我们把光由一点向外散射形成的 投影叫做中心投影,把在一束平行光线 照射下形成的投影叫做平行投影,那么 用灯泡照射物体和用手电筒照射物体形 成的投影分别是哪种投影?
思考3:用灯泡照射一个与投影面平行的 不透明物体,在投影面上形成的影子与 原物体的形状、大小有什么关系?当物 体与灯泡的距离发生变化时,影子的大 小会有什么不同?
宽相等
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
三视图的作图规则
主—俯:长对正 主—左:高平齐 主 左—俯:宽相等 视
图
左视图
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
俯视图
【全国百强校】福建省泉州第五中学 高中数 学必修 二课件 :1.2空 间几何 体的结 构
高中数学【人教B版】空间几何体ppt1

知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱 圆柱 棱锥 圆锥 棱台 圆台
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
8.简单组合体的结构特征
观察下图所示的几何体,说一说它们各由哪些 简单几何体组合而成?
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
做棱锥的侧面,各侧面的 侧棱 D
C
公共顶点叫做棱锥的顶点,
底面
相邻侧面的公共边叫做棱 A
B
锥的侧棱。
棱锥的表示
用表示顶点和底面各顶点的字母表示,如图所 示的棱锥表示为:“棱锥S—ABCD”
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
棱锥的分类:
按底面多边形的边数,可以分为三 棱锥、四棱锥、五棱锥、……
球的表示方法:用表示球 心的字母表示,如:“球O”
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
半径 O
球心
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
几何体的分类
柱体
锥体
台体
球
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
多面体
旋转体
高中数学【人教B版】空间几何体ppt1 【PPT 教研课 件】
定义:有两个面互相平行,其余各面都是 四边形,并且每相邻两个四边形的公共边
都互相平行,由这些面围成的几何体 叫做棱柱。
棱柱的有关概念
棱柱中,两个互相平行的面 叫棱柱的底面(简称底), 其余各面叫棱柱的侧面, 相邻侧面的公共边叫侧棱, 侧面与底面的公共顶点叫 棱柱的顶点。 特征:
人教B版(2019)空间几何体示范PPT1

③正三棱锥:底面是正三角形,侧面是三个全等的 等腰三角形.
S ④正四面体:每个面都是正三角形.
B
A
C
2.棱锥的结构特征 小结
正四面体
四面体
棱锥
正棱柱
三棱柱
正三棱柱
3.棱台的结构特征
(1)棱台的定义
①上下底面平行且相似 ②侧面均为梯形 ③侧棱延长线交于一点
上底面 侧棱 侧面 高
顶点 下底面
3.棱台的结构特征
1.棱柱的结构特征
(3)棱柱的分类 1、按侧棱与底面是否垂直可分为: 1) 侧棱不垂直于底的棱柱叫做斜棱柱.
人教B版( 2019) 空间几 何体示 范PPT1
人教B版( 2019) 空间几 何体示 范PPT1
1.棱柱的结构特征
(3)棱柱的分类
斜棱柱
棱
柱
直棱柱
一般的直棱柱 正棱柱
人教B版( 2019) 空间几 何体示 范PPT1
(2)棱台的表示
棱台可用表示上、下底面的字母来命名,如可以 记 作 棱 台ABCD-A’B’C’D’.
3.棱台的结构特征
(3)棱台的分类
①按底面多边形的边数分为三棱台、四 棱台、五棱台等;
3.棱台的结构特征
(3)棱台的分类
②正棱台:由正棱锥截得的棱台叫做正 棱台.
正四棱锥
正四棱台
练习:下图中 的几何体是 不是棱台? 为什么?
2 .用表示一条对角线端点的两个字母表示,
如:棱柱 AC1
D1 A1
C1
B1
A1
C1 A1 B1 B1
E1 D1 C1
D
C
C
E
A
BA
A
B
B
D C
S ④正四面体:每个面都是正三角形.
B
A
C
2.棱锥的结构特征 小结
正四面体
四面体
棱锥
正棱柱
三棱柱
正三棱柱
3.棱台的结构特征
(1)棱台的定义
①上下底面平行且相似 ②侧面均为梯形 ③侧棱延长线交于一点
上底面 侧棱 侧面 高
顶点 下底面
3.棱台的结构特征
1.棱柱的结构特征
(3)棱柱的分类 1、按侧棱与底面是否垂直可分为: 1) 侧棱不垂直于底的棱柱叫做斜棱柱.
人教B版( 2019) 空间几 何体示 范PPT1
人教B版( 2019) 空间几 何体示 范PPT1
1.棱柱的结构特征
(3)棱柱的分类
斜棱柱
棱
柱
直棱柱
一般的直棱柱 正棱柱
人教B版( 2019) 空间几 何体示 范PPT1
(2)棱台的表示
棱台可用表示上、下底面的字母来命名,如可以 记 作 棱 台ABCD-A’B’C’D’.
3.棱台的结构特征
(3)棱台的分类
①按底面多边形的边数分为三棱台、四 棱台、五棱台等;
3.棱台的结构特征
(3)棱台的分类
②正棱台:由正棱锥截得的棱台叫做正 棱台.
正四棱锥
正四棱台
练习:下图中 的几何体是 不是棱台? 为什么?
2 .用表示一条对角线端点的两个字母表示,
如:棱柱 AC1
D1 A1
C1
B1
A1
C1 A1 B1 B1
E1 D1 C1
D
C
C
E
A
BA
A
B
B
D C
人教B版(2019)空间几何体优质教学ppt1

课堂练习—棱柱的三视图
正视图
侧视图
俯
左
六棱柱
人教B版(2019)空间几何体优质教学 ppt1
俯视图
Hale Waihona Puke 人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱锥的三视图 俯
左
正三棱锥
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱锥的三视图 俯
左
正三棱锥 能看见的轮廓线和棱用实线表示,不能看见的轮廓 线和棱用虚线表示.
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱锥的三视图 俯
左
正四棱锥
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱台的三视图 俯
左
正四棱台
课堂练习—圆台的三视图 俯
三视图能反映物体真实的形状和长、宽、高.
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—基本几何体的三视图
上一节学习的棱柱、棱锥、棱台以及圆台 的三视图是怎样的?
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
斜投影
平 行 投 影
正投影
课程讲授—中心投影
光由一点向外散射形成的投影, 叫做中心投影.其投影线交于一点(投影中 心).
在中心投影中,如果改变物体与投射中 心或投影面之间的距离、位置,则其投影的 大小也随之改变.
人教B版(2019)空间几何体优质教学 ppt1
课程讲授—中心投影
正视图
侧视图
俯
左
六棱柱
人教B版(2019)空间几何体优质教学 ppt1
俯视图
Hale Waihona Puke 人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱锥的三视图 俯
左
正三棱锥
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱锥的三视图 俯
左
正三棱锥 能看见的轮廓线和棱用实线表示,不能看见的轮廓 线和棱用虚线表示.
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱锥的三视图 俯
左
正四棱锥
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—棱台的三视图 俯
左
正四棱台
课堂练习—圆台的三视图 俯
三视图能反映物体真实的形状和长、宽、高.
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
课堂练习—基本几何体的三视图
上一节学习的棱柱、棱锥、棱台以及圆台 的三视图是怎样的?
人教B版(2019)空间几何体优质教学 ppt1
人教B版(2019)空间几何体优质教学 ppt1
斜投影
平 行 投 影
正投影
课程讲授—中心投影
光由一点向外散射形成的投影, 叫做中心投影.其投影线交于一点(投影中 心).
在中心投影中,如果改变物体与投射中 心或投影面之间的距离、位置,则其投影的 大小也随之改变.
人教B版(2019)空间几何体优质教学 ppt1
课程讲授—中心投影
《空间几何体》高中数学ppt优质课件人教B版1

2.长方体的一个顶点上三条棱长分别是3,4,5,且它 的8个顶点都在同一球面上,则这个球的表面积是
(B)
A.25π B. 50π C. 125π D.都不对
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
小球的体积 等于它排开 液体的体积
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
割圆术 早在公元三世纪,我国数学家刘徽为推导圆的面 积公式而发明了“倍边法割圆术”.他用加倍的方式 不断增加圆内接正多边形的边数,使其面积与圆的面 积之差更小,即所谓“割之弥细,所失弥小”.这样 重复下去,就达到了“割之又割,以至于不可再割, 则与圆合体而无所失矣”.这是世界上最早的“极限” 思想.
•
8.特点就是这件事物不同于其他的地 方,每 种物品 都有自 己明显 的特点 ,比如 外形、 用途等 ,所以 ,如果 要想让 自己的 物品与 众不同 ,就一 定要抓 住它的 特点。
•
9.有的时候,我遇到的字只知道拼音 ,可不 知道它 的写法 ,我就 用音序 查字法 从字典 里寻出 它的芳 踪,有 时候看 到不会 读的字 ,我就 用部首 查字法 在字典 中找到 它的倩 影。
半径是R 的球的表面积:S = 4 R 2
球的表面积是大圆 面积的4倍
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
球的体积与表面积
1.球的体积公式: V = 4 R3. 3
(B)
A.25π B. 50π C. 125π D.都不对
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
小球的体积 等于它排开 液体的体积
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
割圆术 早在公元三世纪,我国数学家刘徽为推导圆的面 积公式而发明了“倍边法割圆术”.他用加倍的方式 不断增加圆内接正多边形的边数,使其面积与圆的面 积之差更小,即所谓“割之弥细,所失弥小”.这样 重复下去,就达到了“割之又割,以至于不可再割, 则与圆合体而无所失矣”.这是世界上最早的“极限” 思想.
•
8.特点就是这件事物不同于其他的地 方,每 种物品 都有自 己明显 的特点 ,比如 外形、 用途等 ,所以 ,如果 要想让 自己的 物品与 众不同 ,就一 定要抓 住它的 特点。
•
9.有的时候,我遇到的字只知道拼音 ,可不 知道它 的写法 ,我就 用音序 查字法 从字典 里寻出 它的芳 踪,有 时候看 到不会 读的字 ,我就 用部首 查字法 在字典 中找到 它的倩 影。
半径是R 的球的表面积:S = 4 R 2
球的表面积是大圆 面积的4倍
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
【 全 程 复 习 方略】 高中数 学多媒 体教学 优质课 件:第 一章 空 间 几何 体5
球的体积与表面积
1.球的体积公式: V = 4 R3. 3
人教新课标B版《空间几何体》PPT公开课课件1

2
体积不变.( ) (4)简单几何体的体积只与该几何体的底面积和高有关.( )
人教新课标B版《空间几何体》PPT公 开课课 件1
人教新课标B版《空间几何体》PPT公 开课课 件1
提示:(1)正确.多面体的表面积是几何体表面的面积,因此表 面积=侧面积+底面积.故此说法是正确的. (2)错误.只有直棱柱的侧面积才等于底面周长C与侧棱长l的乘 积,故此说法是错误的. (3)错误.因为圆柱的体积为πr2h,所以体积变为原来的. (4)正确.根据几何体的体积计算公式,可知该说法正确. 答案:(1)√ (2)× (3)× (4)√
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积
1.了解柱体、锥体、台体的表面积与体积公式. 2.掌握柱体、锥体、台体的体积的计算. 3.会利用表面积和体积公式解决一些简单的实际问题.
1.柱体的表面积 (1)棱柱的表面积:S表=__S_侧_+_2_S_底__. ①其中底面周长为C,高为h的直棱柱的侧面积: S侧=_C_h_; ②长、宽、高分别为a,b,c的长方体的表面积: S表=_2_(_a_b_+_a_c_+_b_c_)_; ③棱长为a的正方体的表面积:S表=_6_a_2.
4.柱体、锥体、台体的体积
(1)柱体的体积:V柱体=_S_h_(S表示柱体的底面面积,h表示柱
体的高). (2)锥体的体积:V锥体=__13 _S _h _(S表示锥体的底面面积,h表示
锥体的高). (3)台体的体积:V台体=_13__(S____S__S__S_)_h_(S′,S分别表示台体
的上、下底面面积,h表示台体的高).
人教新课标B版《空间几何体》PPT公 开课课 件1
人教新课标B版《空间几何体》PPT公 开课课 件1
体积不变.( ) (4)简单几何体的体积只与该几何体的底面积和高有关.( )
人教新课标B版《空间几何体》PPT公 开课课 件1
人教新课标B版《空间几何体》PPT公 开课课 件1
提示:(1)正确.多面体的表面积是几何体表面的面积,因此表 面积=侧面积+底面积.故此说法是正确的. (2)错误.只有直棱柱的侧面积才等于底面周长C与侧棱长l的乘 积,故此说法是错误的. (3)错误.因为圆柱的体积为πr2h,所以体积变为原来的. (4)正确.根据几何体的体积计算公式,可知该说法正确. 答案:(1)√ (2)× (3)× (4)√
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积
1.了解柱体、锥体、台体的表面积与体积公式. 2.掌握柱体、锥体、台体的体积的计算. 3.会利用表面积和体积公式解决一些简单的实际问题.
1.柱体的表面积 (1)棱柱的表面积:S表=__S_侧_+_2_S_底__. ①其中底面周长为C,高为h的直棱柱的侧面积: S侧=_C_h_; ②长、宽、高分别为a,b,c的长方体的表面积: S表=_2_(_a_b_+_a_c_+_b_c_)_; ③棱长为a的正方体的表面积:S表=_6_a_2.
4.柱体、锥体、台体的体积
(1)柱体的体积:V柱体=_S_h_(S表示柱体的底面面积,h表示柱
体的高). (2)锥体的体积:V锥体=__13 _S _h _(S表示锥体的底面面积,h表示
锥体的高). (3)台体的体积:V台体=_13__(S____S__S__S_)_h_(S′,S分别表示台体
的上、下底面面积,h表示台体的高).
人教新课标B版《空间几何体》PPT公 开课课 件1
人教新课标B版《空间几何体》PPT公 开课课 件1
《空间几何体》公开课ppt人教B版1

1.1空间几何体的结构
现代城市的建筑都是由各种各样的漂亮的几何体组成的.
(一)多面体
由若干个平面多边形围 成的空间图形叫做多面体。 多面体最少有____4____个面.
A
A
B
F
C
D
EB CD Nhomakorabea(1)围成多面体的各个多边形叫做
多面体的面
(2)两个面的公共边叫做多面体的棱
(3)棱与棱的公共点叫做多面体的顶点
柱、锥、台体的关系
圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什 么关系?
上底扩大
上底缩小
柱
台
锥
体
上底扩大
体
上底缩小
体
《 空 间 几 何 体》公 开课pp t人教B 版1
《 空 间 几 何 体》公 开课pp t人教B 版1
思考:下面的空间几何体是什么?
NBA
《 空 间 几 何 体》公 开课pp t人教B 版1
(4)平行于底面的截面
线
是与底面平行且半径不相
等的圆
A
(5)轴截面是等腰三角形.
《 空 间 几 何 体》公 开课pp t人教B 版1
顶点 S
轴
侧 面
O B
底面
《 空 间 几 何 体》公 开课pp t人教B 版1
几何体的分类
以下四种几何体分别是什么?
《 空 间 几 何 体》公 开课pp t人教B 版1
《 空 间 几 何 体》公 开课pp t人教B 版1
顶点 S
轴
侧 面
O B
底面
《 空 间 几 何 体》公 开课pp t人教B 版1
圆锥
以直角三角形的一条直角边所在直线
为旋转轴,其余两边旋转形成的曲面所围
现代城市的建筑都是由各种各样的漂亮的几何体组成的.
(一)多面体
由若干个平面多边形围 成的空间图形叫做多面体。 多面体最少有____4____个面.
A
A
B
F
C
D
EB CD Nhomakorabea(1)围成多面体的各个多边形叫做
多面体的面
(2)两个面的公共边叫做多面体的棱
(3)棱与棱的公共点叫做多面体的顶点
柱、锥、台体的关系
圆柱、圆锥、圆台之间呢?柱、锥、台体之间有什 么关系?
上底扩大
上底缩小
柱
台
锥
体
上底扩大
体
上底缩小
体
《 空 间 几 何 体》公 开课pp t人教B 版1
《 空 间 几 何 体》公 开课pp t人教B 版1
思考:下面的空间几何体是什么?
NBA
《 空 间 几 何 体》公 开课pp t人教B 版1
(4)平行于底面的截面
线
是与底面平行且半径不相
等的圆
A
(5)轴截面是等腰三角形.
《 空 间 几 何 体》公 开课pp t人教B 版1
顶点 S
轴
侧 面
O B
底面
《 空 间 几 何 体》公 开课pp t人教B 版1
几何体的分类
以下四种几何体分别是什么?
《 空 间 几 何 体》公 开课pp t人教B 版1
《 空 间 几 何 体》公 开课pp t人教B 版1
顶点 S
轴
侧 面
O B
底面
《 空 间 几 何 体》公 开课pp t人教B 版1
圆锥
以直角三角形的一条直角边所在直线
为旋转轴,其余两边旋转形成的曲面所围
空间几何体PPT精品课件人教B版1

空间几何体PPT精品课件人教B版1(精 品课件 )
空间几何体PPT精品课件人教B版1(精 品课件 )
1 画 轴 . 画 x 轴 , y 轴 , z 轴 , 三 轴 交 于 点 O , 使 x O y = 4 5 ,
x O z 9 0 .
Z
y
长4
宽3
O
x
高2
空间几何体PPT精品课件人教B版1(精 品课件 )
小结一下
1. 平面图形的斜二测画法的关键 与步骤; 2. 简单几何体的斜二测画法; 3. 简单组合体的斜二测画法; 4. 注意的几点.
空间几何体PPT精品课件人教B版1(精 品课件 )
空间几何体PPT精品课件人教B版1(精 品课件 )
练习1:下列说法是否正确? (1)水平放置的正方形的直观图可能是梯形. (×)
Z
D
Cy
长4
A D
B Q C
宽3
MO
Nx
高2
AP B
空间几何体PPT精品课件人教B版1(精 品课件 )
空间几何体PPT精品课件人教B版1(精 品课件 )
4成 图 .顺 次 连 接 A,B,C,D,并 加 以 整 理
去 掉 辅 助 线 ,将 被 遮 挡 住 的 部 分 改 为 虚 线 ,
就 可 得 到 长 方 体 的 直 观 图 .
(2)两条相交直线的直观图可能平行. (×)
(3)互相垂直的两条直线的直观图仍然互相垂直.
(×)
(4)等腰三角形的水平放置的直观图仍是等腰
三角形.
(×)
(5)水平放置的正三角形的直观图是一个底边长
不变,高为原三角形高的一半的三角形. (×)
空间几何体PPT精品课件人教B版1(精 品课件 )
空间几何体PPT精品课件人教B版1(精 品课件 )
1 画 轴 . 画 x 轴 , y 轴 , z 轴 , 三 轴 交 于 点 O , 使 x O y = 4 5 ,
x O z 9 0 .
Z
y
长4
宽3
O
x
高2
空间几何体PPT精品课件人教B版1(精 品课件 )
小结一下
1. 平面图形的斜二测画法的关键 与步骤; 2. 简单几何体的斜二测画法; 3. 简单组合体的斜二测画法; 4. 注意的几点.
空间几何体PPT精品课件人教B版1(精 品课件 )
空间几何体PPT精品课件人教B版1(精 品课件 )
练习1:下列说法是否正确? (1)水平放置的正方形的直观图可能是梯形. (×)
Z
D
Cy
长4
A D
B Q C
宽3
MO
Nx
高2
AP B
空间几何体PPT精品课件人教B版1(精 品课件 )
空间几何体PPT精品课件人教B版1(精 品课件 )
4成 图 .顺 次 连 接 A,B,C,D,并 加 以 整 理
去 掉 辅 助 线 ,将 被 遮 挡 住 的 部 分 改 为 虚 线 ,
就 可 得 到 长 方 体 的 直 观 图 .
(2)两条相交直线的直观图可能平行. (×)
(3)互相垂直的两条直线的直观图仍然互相垂直.
(×)
(4)等腰三角形的水平放置的直观图仍是等腰
三角形.
(×)
(5)水平放置的正三角形的直观图是一个底边长
不变,高为原三角形高的一半的三角形. (×)
空间几何体PPT精品课件人教B版1(精 品课件 )
人教新课标B版《空间几何体》PPT1

人教新课标B版《空间几何体》PPT1
C. 3
*
D. 都不对
人教新课标B版《空间几何体》PPT1
3、斜二侧画法中,位于平面直角坐标系
中的点M(4,4)在直观图中对应点是M‘,
则点M‘的找法是(
)
答案:在x‘o’y‘中,过点(4,0)和 y‘轴平行的直线与过(0,2)和x‘轴 平行的直线的交点即是.
人教新课标B版《空间几何体》PPT1
注:原图平行的线段直观图中仍然平行。
人教新课标B版《空间几何体》PPT1
*
人教新课标B版《空间几何体》PPT1
3、 利用斜二测画法画空间图形的直观图应 遵循的基本原则:
(1)在已知图形中取水平平面,取互相垂直的轴ox、oy, 再取oz轴,使∠xoy=450,且∠xoz=900 ;
(2)画直观图时,把它们画成对应的 o'x',o'y',o'z'
*
人教新课标B版《空间几何体》PPT1
人教新课标B版《空间几何体》PPT1
投影
中心投影 投影线交于一点 直观强、接近实物
平行投影 投影线平行
斜投影 不改变原 正投影 物形状
正视图
侧视图
三视图
俯视图
长对正、高平齐、宽相等
根据三视图,我们可以得 到一个精确的空间几何体
*
视图
直观图 斜二测画法
可以根 据直观 图的结 构想象 实物的 形象
轴,使 x ' o ' y ' 4 0 或 1 5 0 , x ' 3 o ' z ' 9 0 . 5 x ' o ' 0 y '所确定
的平面表示水平平面;
C. 3
*
D. 都不对
人教新课标B版《空间几何体》PPT1
3、斜二侧画法中,位于平面直角坐标系
中的点M(4,4)在直观图中对应点是M‘,
则点M‘的找法是(
)
答案:在x‘o’y‘中,过点(4,0)和 y‘轴平行的直线与过(0,2)和x‘轴 平行的直线的交点即是.
人教新课标B版《空间几何体》PPT1
注:原图平行的线段直观图中仍然平行。
人教新课标B版《空间几何体》PPT1
*
人教新课标B版《空间几何体》PPT1
3、 利用斜二测画法画空间图形的直观图应 遵循的基本原则:
(1)在已知图形中取水平平面,取互相垂直的轴ox、oy, 再取oz轴,使∠xoy=450,且∠xoz=900 ;
(2)画直观图时,把它们画成对应的 o'x',o'y',o'z'
*
人教新课标B版《空间几何体》PPT1
人教新课标B版《空间几何体》PPT1
投影
中心投影 投影线交于一点 直观强、接近实物
平行投影 投影线平行
斜投影 不改变原 正投影 物形状
正视图
侧视图
三视图
俯视图
长对正、高平齐、宽相等
根据三视图,我们可以得 到一个精确的空间几何体
*
视图
直观图 斜二测画法
可以根 据直观 图的结 构想象 实物的 形象
轴,使 x ' o ' y ' 4 0 或 1 5 0 , x ' 3 o ' z ' 9 0 . 5 x ' o ' 0 y '所确定
的平面表示水平平面;
《空间几何体》课件人教B版1

《空间几何体》课件人教B版1
思考:用一个平面去截一个球,截面是什么图形? 用一个截面去截
一个球,截面是圆 面。
O
球面被经过球心的平面截得的圆叫做大圆。 球面被不过球心的截面截得的圆叫球的小圆。
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
思考:设球的半径为R,截面圆半径为r,
球心与截面圆圆心的距离为d,则R、r、
圆台的结构特征
如何描述它们具有的共同结构特征?
用一个平行于圆锥
底面的平面去截圆锥,
底面与截面之间的部分
O’
是圆台.
O
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
圆台的结构特征
圆柱、圆锥可以
看作是由矩形或三角形
O’
绕其一边旋转而成,圆
台是否也可看成是某图
形绕轴旋转而成?
O
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
简单组合体
日常生活中我们常用到的日用品,比如:消毒液 、暖瓶、洗洁精等的主要几何结构特征是什么?
圆柱 圆台
圆柱
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主 要几何结构特征是什么?
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
思考:下面的空间几何体是什么?
NBA
《空间几何体》课件人教B版1
《空间几何体》课件人教B版1
思考:从旋转的角度分析,球是由什么图 形绕哪条直线旋转而成的?
以半圆的直径所在直线为旋转轴,半圆 面旋转一周形成的旋转体叫做球体,简 称球.
人教新课标B版《空间几何体》PPT精美课件1

定义 我们把一束平行
光线照射下形成的投
影,叫做平行投影.
平行投影的投影 线是平行的.
在平行投影中, 投影线正对着投影面
时,叫做正投影,否 则叫做斜投影.
投影面
光线
斜投影
投影线斜对 着投影面
正投影
对比三种投影
平行投影
(a)中心投影 (b)斜投影 (c)正投影
人教新课 标B版《 空间几 何体》 PPT精 美课件1
人教新课 标B版《 空间几 何体》 PPT精 美课件1
斜二测画法
由几何体的三视图可以得到几何体的直观图
z
正视图 侧视图
y′
A′
B′
o′
x′
y
俯视图
A
oB x
人教新课 标B版《 空间几 何体》 PPT精 美课件1
人教新课 标B版《 空间几 何体》 PPT精 美课件1
反思提高
思考题:如图ΔA’B’C’是水平放置的ΔABC的直 观图,则在ΔABC的三边及中线AD中,最长的线段 是( AC)
空间几何体的直观图
例1.画长、宽、高分别为4cm、3cm、2cm的长 方体ABCD-A′B′C′D′的直观图?
D′
z
C′
A′ D
y B′ Q
C
D′
A′ D
C′ B′
C
o
x
A
B
AP B
水平方向的矩形画成平行四边形的直观
图竖直方向(z轴)的线段长度不变
人教新课 标B版《 空间几 何体》 PPT精 美课件1
三视图的形成
光线从几何体的前面向后面正投影 所得的投影图称为“正视图”
正视图
俯视图
侧视图 光线从几何 体的左面向 右面正投影 所得的投影 图称为“侧 视图”
空间几何体PPT执教课件 人教B版1
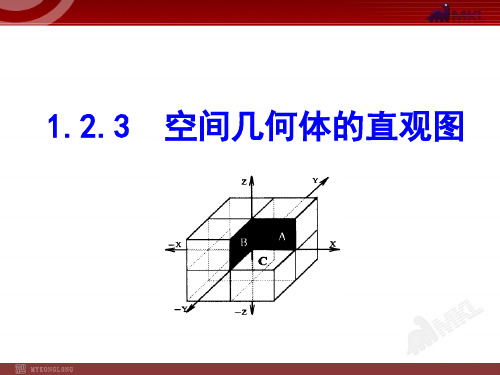
(3)连接A 'B ',C 'D ',D 'E ',F 'A ',并擦去辅助线x′轴和y′轴,便 获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F'.
y
F
A
ME
O
D
x
y
F M E
A
O
D x
B N C
B
NC
请你总结斜二测画法画水平放置的平面图形的方法步骤.
空间几何体PPT执教课件 人教B版1(精品课件)
空间几何体PPT执教课件 人教B版1(精品课件)
空间几何体PPT执教课件 人教B版1(精品课件)
(二) 空间几何体的直观图的画法
思考1:对于柱、锥、台等几何体的直观图,可用斜二测画法
或椭圆模板画出一个底面,我们能否再用一个坐标确定底面
外的点的位置?
Z
y
o
x
空间几何体PPT执教课件 人教B版1(精品课件)
A
B
y C
M
A
OBx
S
空间几何体PPT执教课件 人教B版1(精品课件)
C
A
B
空间几何体PPT执教课件 人教B版1(精品课件)
思考3:画棱柱、棱锥的直观图大致可分几个步骤进行?
画轴 → 画底面 → 画侧棱 → 成图
空间几何体PPT执教课件 人教B版1(精品课件)
空间几何体PPT执教课件 人教B版1(精品课件)
空间几何体PPT执教课件 人教B版1(精品课件)
2.一个四边形的直观图是边长为a的正方形,则原图形的面 积是 2 2 a 2 .
空间几何体PPT执教课件 人教B版1(精品课件)
空间几何体PPT教学课件人教B版1

【思考1】 : 对于柱、锥、台等几何体的直观图,可用斜二测 画法或椭圆模板画出一个底面,我们能否再用一 个坐标确定底面外的点的位置?
空间几何体PPT教学课件人教B版1(精 品课件 )
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
例2 用斜二测画法画长、宽、高分别是4 cm、3 cm、 2 cm的长方体ABCD-A′B′C′D′的直观图.
C . 画 与 直 角 坐 标 系 xOy 对 应 的 x′O′y′ 时 , ∠ x′O′y′可以画成 135°
D.在画直观图时,由于选轴的不同所画直观图可能不同
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
空间几何体PPT教学课件人教B版1(精 品课件 )
2.AB=2CD,AB∥x 轴,CD∥y 轴,已知在直观图中,
y
F ME
A
O
Dx
空间几何体PPT教学课件人教B版1(精 品课件 )
B
NC
F/
E/
A/
D/
B/
C/
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
【提升总结】 斜二测画法的步骤
(1)在已知图形中取互相垂直的x轴和y轴,两轴相交于点O.画 直观图时,把它们画成对应的x′轴与y′轴,两轴交于点O′, 且使∠x′o′y′=45°(或135°),它们确定的平面表示水 平面.
C
A
B
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
【思考3】 : 画棱柱、棱锥的直观图大致可分几个步骤进行?
画轴 → 画底面 → 画侧棱 → 成图
空间几何体PPT教学课件人教B版1(精 品课件 )
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
例2 用斜二测画法画长、宽、高分别是4 cm、3 cm、 2 cm的长方体ABCD-A′B′C′D′的直观图.
C . 画 与 直 角 坐 标 系 xOy 对 应 的 x′O′y′ 时 , ∠ x′O′y′可以画成 135°
D.在画直观图时,由于选轴的不同所画直观图可能不同
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
空间几何体PPT教学课件人教B版1(精 品课件 )
2.AB=2CD,AB∥x 轴,CD∥y 轴,已知在直观图中,
y
F ME
A
O
Dx
空间几何体PPT教学课件人教B版1(精 品课件 )
B
NC
F/
E/
A/
D/
B/
C/
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
【提升总结】 斜二测画法的步骤
(1)在已知图形中取互相垂直的x轴和y轴,两轴相交于点O.画 直观图时,把它们画成对应的x′轴与y′轴,两轴交于点O′, 且使∠x′o′y′=45°(或135°),它们确定的平面表示水 平面.
C
A
B
辉县市第二高级中学 李鑫平
空间几何体PPT教学课件人教B版1(精 品课件 )
【思考3】 : 画棱柱、棱锥的直观图大致可分几个步骤进行?
画轴 → 画底面 → 画侧棱 → 成图
人教新课标B版《空间几何体》优秀PPT1
•
1应该认识到,阅读是学校教育的重要 组成部 分,一 个孩子 如果在 十多年 的教育 历程中 没有养 成阅读 的习惯 、兴趣 和能力 ,一旦 离开校 园,很 可能把 书永远 丢弃在 一边, 这样的 结果一 定是我 们所有 的教育 工作者 不想看 到的。
•
2对教育来说,阅读是最基础的教学手 段,教 育里最 关键、 最重要 的基石 就是阅 读。
图
高 c平 齐
侧
c
视 图
b
思考
b
长对正
a
俯
视
a
图
b
同一个几何体的正视图、侧视图和俯视图在形状、大小 方面有何关系?
画图原则:正俯等长, 正侧等高,侧俯等宽.
人教新课标B版《空间几何体》优秀PP T1
人教新课标B版《空间几何体》优秀PP T1
画一画
例1.
正视图
变
式
侧 视
图
人教新课标B版《空间几何体》优秀PP T1
•
3但是现在,我们的教育在一定程度上 ,还不 够重视 阅读, 尤其是 延伸阅 读和课 外阅读 。
•
4. “山不在高,有仙则名。水不在深 ,有龙 则灵” 四句, 简洁有 力,类 比“斯 是陋室 ,惟吾 德馨” ,说明 陋室也 可借高 尚之士 散发芬 芳
•
5. 这是一篇托物言志的铭文,本文言 简义丰 、讲究 修辞。 文章骈 散结合 ,以骈 句为主 ,句式 整齐, 节奏分 明,音 韵和谐 。
•
12简·爱人生追求有两个基本旋律:富 有激情 、幻想 、反抗 和坚持 不懈的 精神; 对人间 自由幸 福的渴 望和对 更高精 神境界 的追求 。
人教新课标B版《空间几何体》优秀PP T1
复习:投影的概念和特征
人教新课标B版《空间几何体》PPT教学课件1

•
5. 这是一篇托物言志的铭文,本文言 简义丰 、讲究 修辞。 文章骈 散结合 ,以骈 句为主 ,句式 整齐, 节奏分 明,音 韵和谐 。
•
6.了解和名著有关的作家作品及相关 的诗句 、名言 、成语 和歇后 语等, 能按要 求向他 人推介 某部文 学名著 。
•
7.能够根据所提供的有关文学名著的 相关语 言信息 推断作 品的作 者、作 品的名 称和人 物形象 ,分析 人物形 象的性 格和作 品的思 想内容 并进行 简要评 价。
(rl rl)
人教新课 标B 版《空间几 何体》P P T 教学课件1
例2.如图,一个圆台形花盆盆口直径20cm,盆底直
径为15cm,底部渗水圆孔直径为1.5cm,盆壁长
15cm.为了美化花盆的外观,需要涂油漆.已知每平方
米用100毫升油漆,涂100个这样的花盆需要多少油漆
(取 3.14,结果精确到1毫升,可用计算器)?
P
根据台体的特征,如何求台体的体积? A
D
圆台(棱台)是由圆锥(棱锥)截成的
S
C
B
V 1 (S' S'S S )h
3
V
V大
V小
1 3
S(h
x)
1 3
S'x
A
1 [Sh (S S' )x] 3
h
D
S C
B
S' S
(h
x2 x)2
S'
x
x
S h x
S'h S S'
V 1 h[S (S S' ) 3
•
10保尔身上的人格特征或完美的精神 操守: 自我献 身的精 神、坚 定不移 的信念 、顽强 坚韧的 意志
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•
8.特点就是这件事物不同于其他的地 方,每 种物品 都有自 己明显 的特点 ,比如 外形、 用途等 ,所以 ,如果 要想让 自己的 物品与 众不同 ,就一 定要抓 住它的 特点。
•
9.有的时候,我遇到的字只知道拼音 ,可不 知道它 的写法 ,我就 用音序 查字法 从字典 里寻出 它的芳 踪,有 时候看 到不会 读的字 ,我就 用部首 查字法 在字典 中找到 它的倩 影。
2 圆柱、圆锥、圆台过轴的截 面(轴截面)分别是矩形、等腰
三角形、等腰梯形
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
圆柱、圆锥、圆台的关系
圆 柱
上底面变小 上底面扩大到
圆 台
上底面缩小到一个点 圆
上底面扩大
锥
与下底面相等
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
柱、锥、台、球的结构特征.gsp
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
圆: 在一个平面内,到定点的 距离等于定长的点的集合 O
球面: 在空间中,到定点的距
离等于定长的点的集合
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
4.下列表达不正确的是 (
B)
A 以矩形的一边所在直线为旋转轴,其余
三边旋转形成的曲面所围成的几何体叫圆柱
B 以直角三角形的一条边所在直线为旋转
轴,其余两边旋转形成的曲面围成的几何体
叫圆锥
C 以直角三角形的一条直角边所在直线为
旋转轴,其余两边旋转形成的曲面围成的几
何体叫圆锥
D 以等腰三角形的底边上的高所在直线为旋
连线是圆锥的母线;
(3)在圆台上下底面的圆周上各取一点,
则这两点的连线是圆台的母线;
(4)圆柱的任意两条母线所在的直线
是互相平行的。
其中正确的是( D )
A(1)(2)
B(2)(3)
C(1)(3)
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
D (2)(4)
[例1] 1.1 空间几何体的结构(2)PPT名师课件
转轴,其余各边旋转形成的曲面围成的几何
体叫圆锥
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
5、下列表达不正确的是( B )
A 用平行于圆锥底面的平面截圆锥, 截面和底面之间的部分是圆台
B 以直角梯形的一腰为旋转轴, 另一腰为母线的旋转面是圆台的侧面
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件 1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件 1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件 1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
•
6.抓住课文中的主要内容和重点句子 ,引导 学生从 “摇花 乐”中 体会到 作者对 童年生 活的和 对家乡 的怀念 之情。
Hale Waihona Puke •7.桂花是没有区别的,问题是母亲不 是在用 嗅觉区 分桂花 ,而是 用情感 在体味 它们。 一亲一 疏,感 觉自然 就泾渭 分明了 。从中 ,我们 不难看 出,家 乡在母 亲心中 的分量 。
2.一个矩形绕着一边的中垂线旋转 180度形成的封闭曲面所围成的几何体 是_圆_柱__
3、一个等腰三角形绕着底边上的 高所在的直线旋转180度形成的封闭曲 面所围成的几何体是_圆_锥
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
2. 说出下列图形绕虚线旋转一周,可 以形成怎样的几何体?
(1)
(2)
(3)
(4)
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
练习一 1、一个等腰梯形绕着两底边中点的
连线所在的直线旋转180度形成的封闭 曲面所围成的几何体是__圆__台__
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
C 圆柱、圆锥、圆台的底面都是圆. D 圆台的母线延长后与轴交于同一点
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
6、有下列命题:
(1)在圆柱的上下底面圆周上各取一点,
则这两点的连线是圆柱的母线;
(2)圆锥顶点与底面圆周上任意一点的
B
O
C
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
小结: 圆柱、圆锥、圆台、球的结构特征
课后练习 P8 练习 2 P10 习题 2
作业: 把一个圆锥截成圆台,截去的圆锥与圆
台的母线长比为2:1,圆台的上底面半径为 6cm,问下底面半径比上底面半径多多少?
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
旋转体
我们把由一个平面图形绕它所在 平面内的一条定直线旋转形成的 封闭几何体叫做旋转体。
圆柱
圆锥 球
圆台
圆柱与棱柱统
称为柱体。
圆台与棱台统
称为台体。
圆锥与棱锥统
称为锥体。
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
二 圆柱、圆锥、圆台的性质
1、底面都是圆 并且平行于底面的截面都是 圆
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
(2)
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件 1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
•
2.许地山这样说,也是这样做的,他 长大后 埋头苦 干,默 默奉献 ,成为 著名的 教授和 作家, 他也因 此取了 个笔名 叫落花 生,这 就是他 笔名的 由来。
•
3.在伟大庄严的教堂里,从彩色玻璃 窗透进 一股不 很明亮 的光线 ,沉重 的琴声 好像是 把人的 心都洗 淘了一 番似的 ,我感 到了我 自己的 渺小。
•
4.夕阳将下,余晖照映湖面,金光璀 璨,不 可名状 。一是 苏州光 福的石 壁,也 是太湖 的一角 ,更见 得静止 处,已 不是空 阔浩渺 的光景 。而即 小见大 ,可以 使人有 更多的 推想.
•
5.桃花源里景美人美,没有纷争。虽 然看似 一个似 有似无 ,亦真 亦幻的 所在, 但它是 陶渊明 心灵酿 出的一 杯美酒 ,是他 留给后 世美好 的向往.
把一个圆锥截成 圆台,已知圆台的上、
下底面半径的比是1:4,母线长为10cm,
求圆锥的母线长。
A
解:
设圆锥的母线长为 y ,则有
D
O E
(y-10):y= O D :O B1:4
4(y-10)=y
B
O
C
y 40 (cm) 3
答:圆锥的母线长为40 cm. 3
A
O
10cm D
E
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
1 . 1 空 间 几 何体的 结构(2 )PPT名 师课件
•
1.边塞诗的作者大多一些有切身边塞 生活经 历和军 旅生活 体验的 作家, 以亲历 的见闻 来写作 ;另一 些诗人 用乐府 旧题来 进行翻 新创作 。于是 ,乡村 便改变 成了另 一种模 样。正 是由于 村民们 的到来 ,那些 山山岭 岭、沟 沟坪坪 便也同 时有了 名字, 成为村 民们最 朴素的 方位标 识.
1.棱柱的定义:
有两个面互相平行,其余各面都是四边形,并 且每相邻两个四边形的公共边都互相平行,由 这些面所围成的几何体叫做棱柱。
2.棱锥的定义
有一个面是多边形,其余各面是有一个公共 顶点的三角形, 由这些面所围成的多面体叫
做棱锥。
3、棱台的概念:
用一个平行于棱锥底面的平面去截棱锥, 底面和截面之间的部分叫做棱台。
