初二上学期期中复习经典题有答案

合集下载

2024年全新八年级数学上册期中试卷及答案(人教版)

2024年全新八年级数学上册期中试卷及答案(人教版)一、选择题1. 若一个数的平方根是3，那么这个数是( )A. 9B. 9C. 3D. 3答案：A2. 下列哪个数是负数?( )A. 2B. 2C. 0D. 1/2答案：B3. 若一个数的三次方是27，那么这个数是( )A. 3B. 3C. 9D. 9答案：B4. 若一个数的绝对值是5，那么这个数可能是( )A. 5B. 5C. 0D. 1答案：A5. 下列哪个数是正数?( )A. 2B. 0C. 1/2D. 1/2答案：C二、填空题1. 若a的平方根是b，那么a的立方根是_________。

答案：b2. 若a的绝对值是5，那么a可能是_________。

答案：5或53. 若a的三次方是27，那么a的平方是_________。

答案：94. 若a的平方根是b，那么b的平方根是_________。

答案：a5. 若a的绝对值是5，那么a的平方是_________。

答案：25三、解答题1. 若一个数的平方根是4，求这个数。

解：设这个数为x，根据题意，有√x = 4。

解这个方程，得到x= 4^2 = 16。

所以这个数是16。

2. 若一个数的三次方是8，求这个数。

解：设这个数为y，根据题意，有y^3 = 8。

解这个方程，得到y = 2。

所以这个数是2。

3. 若一个数的绝对值是7，求这个数的平方。

解：设这个数为z，根据题意，有|z| = 7。

由于绝对值表示数的大小，不考虑正负，所以z可以是7或7。

无论z是正数还是负数，其平方都是49。

所以这个数的平方是49。

4. 若一个数的平方根是5，求这个数的立方。

解：设这个数为w，根据题意，有√w = 5。

解这个方程，得到w= 5^2 = 25。

求w的立方，得到w^3 = 25^3 = 15625。

所以这个数的立方是15625。

5. 若一个数的绝对值是3，求这个数的立方根。

解：设这个数为v，根据题意，有|v| = 3。

由于绝对值表示数的大小，不考虑正负，所以v可以是3或3。

八年级(上)期中数学试卷(含答案解析)

八年级（上）期中数学试卷一、选择题：（本题满分36分，每小题3分）1．以下列长度的三条线段为边，能组成三角形的是（）A．3，3，3 B．3，3，6 C．3，2，5 D．3，2，62．下列图案是几种名车的标志，在这几个图案中不是轴对称图形的是（）A． B． C． D．3．五边形的内角和是（）A．180°B．360°C．540°D．600°4．下列图形中有稳定性的是（）A．正方形B．直角三角形C．长方形D．平行四边形5．如图，△ABC中，BD是∠ABC的角平分线，DE∥BC，交AB于E，∠A=60°，∠BDC=95°，则∠BED的度数是（）A．35°B．70°C．110°D．130°6．已知：如图，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）A．∠A与∠D互为余角B．∠A=∠2C．△ABC≌△CED D．∠1=∠27．下列说法正确的是（）A．形状相同的两个三角形全等 B．面积相等的两个三角形全等C．完全重合的两个三角形全等 D．所有的等边三角形全等8．点M（1，2）关于x轴对称的点的坐标为（）A．（﹣1，﹣2）B．（﹣1，2）C．（1，﹣2）D．（2，﹣1）9．下列图形中对称轴最多的是（）A．等腰三角形B．正方形C．圆形 D．线段10．若等腰三角形的周长为26cm，一边为11cm，则腰长为（）A．11cm B．7.5cm C．11cm或7.5cm D．以上都不对11．如图：DE是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为（）厘米．A．16 B．18 C．26 D．2812．如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（）A．线段CD的中点B．OA与OB的中垂线的交点C．OA与CD的中垂线的交点D．CD与∠AOB的平分线的交点二、填空题（本题满分24分，每小题4分）13．如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=°．14．已知点P在线段AB的垂直平分线上，PA=6，则PB=．15．已知，如图，∠ACD=130°，∠A=∠B，那么∠A的度数是°．16．已知A（﹣1，﹣2）和B（1，3），将点A向平移个单位长度后得到的点与点B关于y轴对称．17．如图，AC=AD，BC=BD，则△ABC≌△；应用的判定方法是（简写）．18．如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带去配，这样做的数学依据是．三、解答题（本大题满分50分）19．如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程，说明△ABD≌△ACD的理由．∵AD平分∠BAC∴∠=∠（角平分线的定义）在△ABD和△ACD中∴△ABD≌△ACD．20．已知：如图，A、C、F、D在同一直线上，AF=DC，AB=DE，BC=EF，求证：△ABC≌△DEF．21．已知：如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE．22．已知：BE⊥CD，BE=DE，BC=DA，求证：△BEC≌△DAE．23．已知：如图，已知△ABC，分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2．24．如图，AC和BD相交于点O，且AB∥DC，OC=OD，求证：OA=OB．参考答案与试题解析一、选择题：（本题满分36分，每小题3分）1．以下列长度的三条线段为边，能组成三角形的是（）A．3，3，3 B．3，3，6 C．3，2，5 D．3，2，6【考点】三角形三边关系．【分析】三角形的三条边必须满足：任意两边之和＞第三边，任意两边之差＜第三边．【解答】解：A中，3+3＞3，能构成三角形；B中，3+3=6，不能构成三角形；C中，3+2=5，不能构成三角形；D中，3+2＜6，不能构成三角形．故选A．【点评】本题主要考查对三角形三边关系的理解应用．判断是否可以构成三角形，只要判断两个较小的数的和＜最大的数就可以．2．下列图案是几种名车的标志，在这几个图案中不是轴对称图形的是（）A． B． C． D．【考点】轴对称图形．【分析】根据轴对称图形的概念求解，如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．【解答】解：根据轴对称图形定义可知：A、不是轴对称图形，符合题意；B、是轴对称图形，不符合题意；C、是轴对称图形，不符合题意；D、是轴对称图形，不符合题意．故选A．【点评】掌握轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3．五边形的内角和是（）A．180°B．360°C．540°D．600°【考点】多边形内角与外角．【专题】常规题型．【分析】直接利用多边形的内角和公式进行计算即可．【解答】解：（5﹣2）•180°=540°．故选：C．【点评】本题主要考查了多边形的内角和定理，是基础题，熟记定理是解题的关键．4．下列图形中有稳定性的是（）A．正方形B．直角三角形C．长方形D．平行四边形【考点】三角形的稳定性．【分析】根据三角形具有稳定性可得答案．【解答】解：直角三角形有稳定性，故选：B．【点评】此题主要考查了三角形的稳定性，是需要识记的内容．5．如图，△ABC中，BD是∠ABC的角平分线，DE∥BC，交AB于E，∠A=60°，∠BDC=95°，则∠BED的度数是（）A．35°B．70°C．110°D．130°【考点】平行线的性质．【分析】由三角形的外角性质得出∠ABD=35°，由角平分线的定义求出∠ABC=2∠ABD=70°，再由平行线的性质得出同旁内角互补∠BED+∠ABC=180°，即可得出结果．【解答】解：∵∠BDC=∠A+∠ABD，∴∠ABD=95°﹣60°=35°，∵BD是∠ABC的角平分线，∴∠ABC=2∠ABD=70°，∵DE∥BC，∴∠BED+∠ABC=180°，∴∠BED=180°﹣70°=110°．故选C．【点评】本题考查了平行线的性质、三角形的外角性质；熟练掌握平行线的性质，运用三角形的外角性质求出∠ABD的度数是解决问题的关键．6．已知：如图，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）A．∠A与∠D互为余角B．∠A=∠2C．△ABC≌△CED D．∠1=∠2【考点】全等三角形的判定与性质．【分析】先根据角角边证明△ABC与△CED全等，再根据全等三角形对应边相等，全等三角形的对应角相等的性质对各选项判断后，利用排除法求解．【解答】解：∵AC⊥CD，∴∠1+∠2=90°，∵∠B=90°，∴∠1+∠A=90°，∴∠A=∠2，在△ABC和△CED中，，∴△ABC≌△CED（AAS），故B、C选项正确；∵∠2+∠D=90°，∴∠A+∠D=90°，故A选项正确；∵AC⊥CD，∴∠ACD=90°，∠1+∠2=90°，故D选项错误．故选D．【点评】本题主要考查全等三角形的性质，先证明三角形全等是解决本题的突破口，也是难点所在．做题时，要结合已知条件与全等的判定方法对选项逐一验证．7．下列说法正确的是（）A．形状相同的两个三角形全等 B．面积相等的两个三角形全等C．完全重合的两个三角形全等 D．所有的等边三角形全等【考点】全等图形．【分析】根据全等形的概念：能够完全重合的两个图形叫做全等形，以及全等三角形的判定定理可得答案．【解答】解：A、形状相同的两个三角形全等，说法错误，应该是形状相同且大小也相同的两个三角形全等；B、面积相等的两个三角形全等，说法错误；C、完全重合的两个三角形全等，说法正确；D、所有的等边三角形全等，说法错误；故选：C．【点评】此题主要考查了全等图形，关键是掌握全等形的概念．8．点M（1，2）关于x轴对称的点的坐标为（）A．（﹣1，﹣2）B．（﹣1，2）C．（1，﹣2）D．（2，﹣1）【考点】关于x轴、y轴对称的点的坐标．【分析】根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．【解答】解：点M（1，2）关于x轴对称的点的坐标为（1，﹣2），故选：C．【点评】解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．9．下列图形中对称轴最多的是（）A．等腰三角形B．正方形C．圆形 D．线段【考点】轴对称的性质．【分析】依据轴对称图形的概念，即在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，据此即可进行选择．【解答】解：A、因为等腰三角形分别沿底边的中线所在的直线对折，对折后的两部分都能完全重合，则等腰三角形是轴对称图形，底边的中线所在的直线就是对称轴，所以等腰三角形有1条对称轴；B、因为正方形沿对边的中线及其对角线所在的直线对折，对折后的两部分都能完全重合，则正方形是轴对称图形，对边的中线及其对角线所在的直线就是其对称轴，所以正方形有4条对称轴；C、因为圆沿任意一条直径所在的直线对折，对折后的两部分都能完全重合，则圆是轴对称图形，任意一条直径所在的直线就是圆的对称轴，所以说圆有无数条对称轴．D、线段是轴对称图形，有两条对称轴．故选：C．【点评】本题考查了轴对称图形的性质，解答此题的主要依据是：轴对称图形的定义及其对称轴的条数．10．若等腰三角形的周长为26cm，一边为11cm，则腰长为（）A．11cm B．7.5cm C．11cm或7.5cm D．以上都不对【考点】等腰三角形的性质．【分析】分边11cm是腰长与底边两种情况讨论求解．【解答】解：①11cm是腰长时，腰长为11cm，②11cm是底边时，腰长=（26﹣11）=7.5cm，所以，腰长是11cm或7.5cm．故选C．【点评】本题考查了等腰三角形的性质，难点在于要分情况讨论．11．如图：DE是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为（）厘米．A．16 B．18 C．26 D．28【考点】线段垂直平分线的性质．【分析】利用线段垂直平分线的性质得AE=CE，再等量代换即可求得三角形的周长．【解答】解：∵DE是△ABC中AC边的垂直平分线，∴AE=CE，∴AE+BE=CE+BE=10，∴△EBC的周长=BC+BE+CE=10厘米+8厘米=18厘米，故选B．【点评】本题考查了线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．12．如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（）A．线段CD的中点B．OA与OB的中垂线的交点C．OA与CD的中垂线的交点D．CD与∠AOB的平分线的交点【考点】角平分线的性质．【分析】利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交点．【解答】解：利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交P．故选D．【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质．做题时注意题目要求要满足两个条件①到角两边距离相等，②点在CD上，要同时满足．二、填空题（本题满分24分，每小题4分）13．如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=135°．【考点】全等三角形的判定与性质．【分析】观察图形可知∠1与∠3互余，∠2是直角的一半，利用这些关系可解此题．【解答】解：观察图形可知：△ABC≌△BDE，∴∠1=∠DBE，又∵∠DBE+∠3=90°，∴∠1+∠3=90°．∵∠2=45°，∴∠1+∠2+∠3=∠1+∠3+∠2=90°+45°=135°．故填135．【点评】此题综合考查角平分线，余角，要注意∠1与∠3互余，∠2是直角的一半，特别是观察图形的能力．14．已知点P在线段AB的垂直平分线上，PA=6，则PB=6．【考点】线段垂直平分线的性质．【分析】直接根据线段垂直平分线的性质进行解答即可．【解答】解：∵点P在线段AB的垂直平分线上，PA=6，∴PB=PA=6．故答案为：6．【点评】本题考查的是线段垂直平分线的性质，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．15．已知，如图，∠ACD=130°，∠A=∠B，那么∠A的度数是65°．【考点】三角形的外角性质．【分析】直接根据三角形内角与外角的性质解答即可．【解答】解：∵∠ACD是△ABC的外角，∴∠ACD=∠A+∠B，∵∠ACD=130°，∠A=∠B，∴∠A==65°．【点评】本题比较简单，考查的是三角形外角的性质，即三角形的外角等于不相邻的两个内角的和．16．已知A（﹣1，﹣2）和B（1，3），将点A向上平移5个单位长度后得到的点与点B关于y轴对称．【考点】关于x轴、y轴对称的点的坐标．【分析】熟悉：关于y轴对称的点，纵坐标相同，横坐标互为相反数；把一个点左右平移，则横坐标是左减右加，把一个点上下平移，则纵坐标是上加下减．【解答】解：根据平面直角坐标系中对称点的规律可知，点B关于y轴对称的点为（﹣1，3），又点A（﹣1，﹣2），所以将点A向上平移5个单位长度后得到的点（﹣1，3）．【点评】解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．平移时坐标变化规律：把一个点左右平移，则横坐标是左减右加，把一个点上下平移，则纵坐标是上加下减．17．如图，AC=AD，BC=BD，则△ABC≌△ABD；应用的判定方法是（简写）SSS．【考点】全等三角形的判定．【分析】此题不难，关键是找对对应点，即A对应A，B对应B，C对应D，即可．【解答】解：∵AC=AD，BC=BD，AB=AB（公共边），∴△ABC≌△ABD（SSS）．【点评】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，本题要用SSS．18．如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃．那么最省事的办法是带③去配，这样做的数学依据是两个角及它们的夹边对应相等的两个三角形全等．【考点】全等三角形的应用．【分析】已知三角形破损部分的边角，得到原来三角形的边角，根据三角形全等的判定方法，即可求解．【解答】解：第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃．故答案为：③；两个角及它们的夹边对应相等的两个三角形全等．【点评】此题主要考查了全等三角形的判定方法的开放性的题，要求学生将所学的知识运用于实际生活中，要认真观察图形，根据已知选择方法．三、解答题（本大题满分50分）19．如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程，说明△ABD≌△ACD的理由．∵AD平分∠BAC∴∠BAD=∠CAD（角平分线的定义）在△ABD和△ACD中∴△ABD≌△ACD SAS．【考点】全等三角形的判定；等腰三角形的性质．【专题】推理填空题．【分析】根据角平分线的定义及全等三角形的判定定理，填空即可．【解答】解：∵AD平分∠BAC∴∠BAD=∠CAD（角平分线的定义），在△ABD和△ACD中，，∴△ABD≌△ACD（SAS）．【点评】本题考查了全等三角形的判定，解答本题的关键是掌握全等三角形的判定定理及角平分线的定义．20．已知：如图，A、C、F、D在同一直线上，AF=DC，AB=DE，BC=EF，求证：△ABC≌△DEF．【考点】全等三角形的判定．【专题】证明题．【分析】首先根据AF=DC，可推得AF﹣CF=DC﹣CF，即AC=DF；再根据已知AB=DE，BC=EF，根据全等三角形全等的判定定理SSS即可证明△ABC≌△DEF．【解答】证明：∵AF=DC，∴AF﹣CF=DC﹣CF，即AC=DF；在△ABC和△DEF中∴△ABC≌△DEF（SSS）．【点评】本题考查了全等三角形全等的判定，熟练掌握各判定定理是解题的关键．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．21．已知：如图，点E、F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE．【考点】全等三角形的判定与性质．【专题】证明题．【分析】要证明AF=DE，可以证明它们所在的三角形全等，即证明△ABF≌△DEC，已知两边（由BE=CF得出BF=CE，AB=DC）及夹角（∠B=∠C），由SAS可以证明．【解答】证明：∵BE=CF，∴BE+EF=CF+EF，即BF=CE，又∵AB=DC，∠B=∠C，∴△ABF≌△DCE，∴AF=DE．【点评】本题考查了全等三角形的判定及性质；证明两边相等时，如果这两边不在同一个三角形中，通常是证明它们所在的三角形全等来证明它们相等，是一种很重要的方法．22．已知：BE⊥CD，BE=DE，BC=DA，求证：△BEC≌△DAE．【考点】全等三角形的判定．【专题】证明题．【分析】根据已知得出Rt△CEB和Rt△AED，利用HL定理得出即可．【解答】证明：∵BE⊥CD，∴∠CEB=∠AED=90°，∴在Rt△CEB和Rt△AED中，∴Rt△CEB≌Rt△AED（HL）．【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．23．已知：如图，已知△ABC，分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2．【考点】作图-轴对称变换．【分析】根据关于坐标轴对称的点的坐标特点画出图形即可．【解答】解：如图所示．【点评】本题考查的是作图﹣轴对称变换，熟知关于坐标轴对称的点的坐标特点是解答此题的关键．24．如图，AC和BD相交于点O，且AB∥DC，OC=OD，求证：OA=OB．【考点】等腰三角形的判定与性质；平行线的性质．【分析】根据OC=OD得，△ODC是等腰三角形；根据AB∥DC，得出对应角相等，求得△AOB是等腰三角形，证明最后结果．【解答】证明：∵OC=OD，∴△ODC是等腰三角形，∴∠C=∠D，又∵AB∥DC，∴∠A=∠C，∠B=∠D，∴∠A=∠B，∴△AOB是等腰三角形，∴OA=OB．【点评】本题主要考查了等腰三角形的判定和平行线的性质：两直线平行，内错角相等．。

湖南省长沙市2023-2024学年八年级上学期期中考试数学复习试卷(含答案)

湖南师范大学附属中学2023-2024学年度八年级上期期中考试数学试题一、选择题（共10小题，满分30分，每小题3分）1. 下列图形中，是轴对称图形的是（）A. B. C. D.2. 下列计算正确的是（）A. B.C. D.3. 下列能用完全平方公式进行因式分解的是（）A. B. C. D.4. 如图，实线内图形的面积可以用来验证下列的某个等式成立，该等式是（）A. B.C. D.5. 长方形的面积为，长为，则它的宽为（）A. B. C. D.6. 若，则的值为（）A. B. 6 C. D. 17. 下列式子，总能成立的是（）A. B.C. D.8. 计算的结果是（）A. B. C. D.9. 如图，A、B、C表示三个居民小区，为了居民生活的方便，现准备建一个生活超市，使它到这三个居民小区的距离相等，那么生活超市应建在（）A. AB，AC两边中线的交点处B. AB，AC两边高线的交点处C. 与这两个角的角平分线的交点处D. AB，AC两边的垂直平分线的交点处10. 如图所示的“三等分角仪”能三等分任意一个角. 这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O点转动. C点固定，，点D，E可在槽中滑动，若，则的度数是（）A. 65°B. 68°C. 66°D. 70°二、填空题（共6小题，满分18分，每小题3分）11. 分解因式：_________.12. 已知，，则的值为_________.13. 若，则代数式的值是_________.14. 等腰三角形有一个角是70°，则它的底角是_________.15. 如图，将一副三角尺按如图所示的方式叠放在一起，则图中的度数是_________.16. 如图，在中，，，，，AD是的平分线. 若P，Q分别是AD和AC上的动点，则的最小值是_________.三、解答题（共9小题，17，18，19每小题6分，20，21每小题8分，22，23每小题9分，24，25每小题10分. ）17. 计算：.18. 先化简，再求值：，其中.19. 如图，在中，，AB的垂直平分线MN交AC于点D，交AB于点E.，求的度数.20. 如图，在平面直角坐标系中，的顶点，，均在正方形网格的格点上.（1）画出关于x轴的对称图形，点的坐标为__________.（2）将沿x轴方向向左平移3个单位，向下平移2个单位后得到，直接写出顶点，，的坐标：_________，_________，_________.21. 如图，是等腰三角形，，点D是AB上一点，过点D作交BC于点E，交CA延长线于点F.（1）证明：是等腰三角形；（2）若，，，求EC的长.22. 将边长为x的小正方形和边长为y的大正方形按如图所示放置，其中点D 在边CE上.（1）若，且，求的值；（2）连接AG，EG，若，，求阴影部分的面积.23. 在中，，，.（1）求a的取值范围；（2）若为等腰三角形，求a的值与的周长.24. 如图1，在平面直角坐标系中，点A在x轴负半轴上，点B在y轴正半轴上，设，且.（1）请写出a和b的数量关系；（2）如图2，点D为AB的中点，点P为y轴负半轴上一点，以AP为边作等边三角形，连接DQ并延长交x轴于点M，若，求点M的坐标；（3）如图3，点C与点A关于y轴对称，点E为OC的中点，连接BE，过点B作，且，连接AF交BC于点P，过点F作轴交CB的延长线于点M，①求证：P为AF的中点；②求的值.图1 图2 图325. 定义：a，b，c为正整数，若，则称c为“完美勾股数”，a，b为c的“伴侣勾股数”. 如，则13是“完美勾股数”，5，12是13的“伴侣勾股数”. （1）数10________“完美勾股数”（填“是”或“不是”）；（2）已知的三边a，b，c满足. 求证：c是“完美勾股数”.（3）已知m，且，，，，c为“完美勾股数”，a，b为c的“伴侣勾股数”. 多项式有一个因式，求该多项式的另一个因式.八年级数学参考答案一、单项选择题（每小题3分，共30分）12345678910D D C C A A B D D B二、填空题（每小题3分，共18分）111213141516或三、解答题（本大题共9小题，第17、18、19题每小题6分，第20、21题每小题8分，第22、23题每小题9分，第24、25题每题10分，共72分）17.18. ，2解：当时，原式19.解：∵在中，，，的垂直平分线交于点，，，；20. （1）画图略，点的坐标为（2）.21. （1）证明见下. （2）4.解：（1），，，，，而，，，是等腰三角形；（2），，，，，是等边三角形，，.22. （1）2. （2）11.解：（1）；（2）阴影部分的面积为：，，.23. （1）（2）的周长为52.解：（1）由题意得：，故；（2）为等腰三角形，或，则或，，，的周长.24. （1）（2）（3）①证明见下②解：（1）∵点在轴负半轴上，，或，，，（2）连接，如图2所示：图2是等边三角形，，，，，为的中点，，，，，在和中，，，即，，为等边三角形，，；（3）①过点作轴交的延长线于点，如图3所示：图3则，，，在和中，，，由（1）可知，是等边三角形，∵点与点关于轴对称，又是的中点，，，在和中，为的中点.②又，，.25. （1）是；（2）证明如下；（3）（2）证明：是完美勾股数”（3）解：由题意得：又有一个因式为∴另一个因式为.。

人教版八年级上学期期中考试数学试卷及详细答案解析(共六套)

人教版八年级上学期期中考试数学试卷（一）一、选择题（每小题3分，共36分）1．下列图形中被虚线分成的两部分不是全等形的是（）A． B． C D．2．将一张矩形的纸对折，然后用笔尖在上面扎出“B”，再把它铺平，你可见到（）A．B．C．D．3．下列各式﹣2a，，， a2﹣ b2，，中，分式有（）A．1个B．2个C．3个D．4个4．如图，已知AB=AC，AD=AE，欲证△ABD≌△ACE，须补充的条件是（）A．∠B=∠C B．∠D=∠E C．∠1=∠2 D．∠CAD=∠DAC5．下面四个图形中，从几何图形的性质考虑，哪一个与其他三个不同？（）A．B．C．D．6．当△ABC和△DEF具备（）条件时，△ABC≌△DEF．A．所有的角对应相等B．三条边对应相等C．面积相等D．周长相等7．下列分式是最简分式的是（）A．B．C．D．8．若点O是△ABC三边垂直平分线的交点，则有（）A．OA=OB≠OC B．OB=OC≠OA C．OC=OA≠OB D．OA=OB=OC9．如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（）A．40°B．30°C．20°D．10°10．如图，把两个一样大的含30度的直角三角板，按如图方式拼在一起，其中等腰三角形有（）A．1个B．2个C．3个D．4个11．已知两个分式：A=﹣，B=，其中x≠3且x≠0，则A与B的关系是（）A．相等B．互为倒数C．互为相反数 D．不能确定12．如图，用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE，其作图依据是（）A．SAS B．SSS C．ASA D．AAS二、填空题（本大题共8小题，每小题3分，共计24分）13．已知=，则的值为．14．如图，在平面直角坐标系中，△AOB≌△COD，则点D的坐标是．15．分式，，﹣的最简公分母是．16．已知线段a，b，c，d成比例线段，且a=4，b=2，c=2，则d的长为．17．如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你再补充一个条件，使△ABC≌△DEF，你补充的条件是．18．已知点A（a﹣1，5）和点B（2，b﹣1）关于x轴成轴对称，则（a+b）2016= ．19．若x：y=1：3，且2y=3z，则的值是．20．如图，在四边形ABCD中，∠A=90°，AD=3，BC=5，对角线BD平分∠ABC，则△BCD的面积为．三、解答题（本大题满分60分）21．作图题小明不小心在一个三角形上撒一片墨水，请用尺规帮小明重新画一个三角形使它与原来的三角形完全相同．（保留作图痕迹，不写作法）22．已知﹣=4，求的值．23．如图所示，△DEF是等边三角形，且∠1=∠2=∠3，试问：△ABC是等边三角形吗？请说明理由．24．请你阅读下列计算过程，再回答所提出的问题：解：=（A）=（B）=x﹣3﹣3（x+1）（C）=﹣2x﹣6（D）（1）上述计算过程中，从哪一步开始出现错误：；（2）从B到C是否正确，若不正确，错误的原因是；（3）请你正确解答．25．如图，在△ABC中，BD=CD，∠1=∠2，小颖说：“AD⊥BC”，你认为她说的对吗？说明你的理由．26．计算：（1）÷（2）÷（﹣x﹣2）（3）（4）（1﹣）÷．27．已知△ABC的两条高AD，BE相交于点H，且AD=BD，试问：（1）∠DBH与∠DAC相等吗？说明理由．（2）BH与AC相等吗？说明理由．参考答案与试题解析一、选择题（每小题3分，共36分）1．下列图形中被虚线分成的两部分不是全等形的是（）A． B．C．D．【考点】K9：全等图形．【分析】根据全等形的概念进行判断即可．【解答】解：长方形被对角线分成的两部分是全等形；平行四边形被对角线分成的两部分是全等形；梯形被对角线分成的两部分不是全等形；圆被对角线分成的两部分是全等形，故选：C．2．将一张矩形的纸对折，然后用笔尖在上面扎出“B”，再把它铺平，你可见到（）A．B．C．D．【考点】P1：生活中的轴对称现象．【分析】认真观察图形，首先找出对称轴，根据轴对称图形的定义可知只有C 是符合要求的．【解答】解：观察选项可得：只有C是轴对称图形．故选：C．3．下列各式﹣2a，，， a2﹣b2，，中，分式有（）A．1个B．2个C．3个D．4个【考点】61：分式的定义．【分析】根据分式的定义，可得答案．【解答】解：，，，是分式，故选：D．4．如图，已知AB=AC，AD=AE，欲证△ABD≌△ACE，须补充的条件是（）A．∠B=∠C B．∠D=∠E C．∠1=∠2 D．∠CAD=∠DAC【考点】KB：全等三角形的判定．【分析】已知两边相等，要使两三角形全等必须添加这两边的夹角，即∠BAD=∠CAE，因为∠CAD是公共角，则当∠1=∠2时，即可得到△ABD≌△ACE．【解答】解：∵AB=AC，AD=AE，∠B=∠C不是已知两边的夹角，A不可以；∠D=∠E不是已知两边的夹角，B不可以；由∠1=∠2得∠BAD=∠CAE，符合SAS，可以为补充的条件；∠CAD=∠DAC不是已知两边的夹角，D不可以；故选C．5．下面四个图形中，从几何图形的性质考虑，哪一个与其他三个不同？（）A．B．C．D．【考点】P3：轴对称图形．【分析】根据轴对称图形的性质对各选项分析判断即可得解．【解答】解：A、是轴对称图形，B、不是轴对称图形，C、是轴对称图形，D、是轴对称图形，所以，B与其他三个不同．故选B．6．当△ABC和△DEF具备（）条件时，△ABC≌△DEF．A．所有的角对应相等B．三条边对应相等C．面积相等D．周长相等【考点】KB：全等三角形的判定．【分析】由SSS证明三角形全等即可．【解答】解：∵三条边对应相等的两个三角形全等，∴B选项正确；故选：B．7．下列分式是最简分式的是（）A．B．C．D．【考点】68：最简分式．【分析】根据最简分式的定义分别对每一项进行判断，即可得出答案．【解答】解：A、=，不是最简分式，故本选项错误；B、=，不是最简分式，故本选项错误；C、，是最简分式，故本选项正确；D、=，不是最简分式，故本选项错误；故选C．8．若点O是△ABC三边垂直平分线的交点，则有（）A．OA=OB≠OC B．OB=OC≠OA C．OC=OA≠OB D．OA=OB=OC【考点】KG：线段垂直平分线的性质．【分析】根据线段的垂直平分线的性质判断即可．【解答】解：∵点O是△ABC三边垂直平分线的交点，∴OA=OB，OA=OC，∴OA=OB=OC，故选：D．9．如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（）A．40°B．30°C．20°D．10°【考点】K7：三角形内角和定理；K8：三角形的外角性质；PB：翻折变换（折叠问题）．【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠A′DB=∠CA'D﹣∠B，又折叠前后图形的形状和大小不变，∠CA'D=∠A=50°，易求∠B=90°﹣∠A=40°，从而求出∠A′DB的度数．【解答】解：∵Rt△ABC中，∠ACB=90°，∠A=50°，∴∠B=90°﹣50°=40°，∵将其折叠，使点A落在边CB上A′处，折痕为CD，则∠CA'D=∠A，∵∠CA'D是△A'BD的外角，∴∠A′DB=∠CA'D﹣∠B=50°﹣40°=10°．故选：D．10．如图，把两个一样大的含30度的直角三角板，按如图方式拼在一起，其中等腰三角形有（）A．1个B．2个C．3个D．4个【考点】KI：等腰三角形的判定．【分析】由于图形是由两个一样大的含30°角的直角三角板按如图的方式拼在一起，故有AB=AE，AD=AC，∠B=∠E=30°，∠ACE=∠ADB=60°，则∠DAE=∠CAB=30°，所以得到等腰三角形△ABE，△ACD，△ACB，△ADE．【解答】解：根据题意△ABE，△ACD都是等腰三角形，又由已知∠ACE=∠ADB=60°，∴∠DAE=∠CAB=30°，已知∠B=∠E=30°，∴又得等腰三角形：△ACB，△ADE，所以等腰三角形4个．故选：D．11．已知两个分式：A=﹣，B=，其中x≠3且x≠0，则A与B的关系是（）A．相等B．互为倒数C．互为相反数 D．不能确定【考点】6B：分式的加减法．【分析】将两个分式化简即可判断．【解答】解：A===B故选（A）12．如图，用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE，其作图依据是（）A．SAS B．SSS C．ASA D．AAS【考点】N3：作图—复杂作图；KB：全等三角形的判定．【分析】直接利用基本作图方法结合全等三角形的判定方法得出答案．【解答】解：用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE，其作图依据是，在△DOM和△NCE中，，∴△DOM≌△NCE（SSS），∴∠DOM=∠NCE，∴CN∥OA．故选：B．二、填空题（本大题共8小题，每小题3分，共计24分）13．已知=，则的值为﹣．【考点】S1：比例的性质．【分析】根据两内项之积等于两外项之积可得x=3y，然后代入比例式进行计算即可得解．【解答】解：∵=，∴x=3y，∴==﹣．故答案为：﹣．14．如图，在平面直角坐标系中，△AOB≌△COD，则点D的坐标是（﹣2，0）．【考点】KA：全等三角形的性质；D5：坐标与图形性质．【分析】根据全等三角形对应边相等可得OD=OB，然后写出点D的坐标即可．【解答】解：∵△AOB≌△COD，∴OD=OB，∴点D的坐标是（﹣2，0）．故答案为：（﹣2，0）．15．分式，，﹣的最简公分母是36a4b2．【考点】69：最简公分母．【分析】找出系数的最小公倍数，字母的最高次幂，即可得出答案．【解答】解：分式，，﹣的最简公分母是36a4b2，故答案为36a4b2．16．已知线段a，b，c，d成比例线段，且a=4，b=2，c=2，则d的长为 1 ．【考点】S2：比例线段．【分析】根据四条线段成比例，列出比例式，再把a=4，b=2，c=2，代入计算即可．【解答】解：∵线段a、b、c、d是成比例线段，∴=，∵a=4，b=2，c=2，∴=，∴d=1．故答案为：1．17．如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你再补充一个条件，使△ABC≌△DEF，你补充的条件是FD=AC（答案不唯一）．【考点】KB：全等三角形的判定．【分析】已知△ABC与△DEF中有一组边与一组角相等，根据全等三角形的判定可知，只需要添加一组边或一组角即可全等．【解答】解：添加FD=AC，∵BF=EC，∴BF﹣CF=EC﹣CF∴BC=EF在△ABC与△DEF中，∴△ABC≌△DEF（SAS）故答案为：FD=AC（答案不唯一）18．已知点A（a﹣1，5）和点B（2，b﹣1）关于x轴成轴对称，则（a+b）2016= 1 ．【考点】P5：关于x轴、y轴对称的点的坐标．【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”列方程求出a、b的值，然后代入代数式进行计算即可得解．【解答】解：∵点A（a﹣1，5）和点B（2，b﹣1）关于x轴成轴对称，∴a﹣1=2，b﹣1=﹣5，解得a=3，b=﹣4，所以，（a+b）2016=（3﹣4）2016=1．故答案为：1．19．若x：y=1：3，且2y=3z，则的值是﹣5 ．【考点】64：分式的值．【分析】用含y的代数式表示x、z，代入分式，计算即可．【解答】解：∵x：y=1：3，2y=3z，∴x=y，z=y，∴==﹣5，故答案为：﹣5．20．如图，在四边形ABCD中，∠A=90°，AD=3，BC=5，对角线BD平分∠ABC，则△BCD的面积为7.5 ．【考点】KF：角平分线的性质．【分析】如图，过点D作DE⊥BC于点E．利用角平分的性质得到DE=AD=3，然后由三角形的面积公式来求△BCD的面积．【解答】解：如图，过点D作DE⊥BC于点E．∵∠A=90°，∴AD⊥AB．∴AD=DE=3．又∵BC=5，=BC•DE=×5×3=7.5．∴S△BCD故答案为：7.5．三、解答题（本大题满分60分）21．作图题小明不小心在一个三角形上撒一片墨水，请用尺规帮小明重新画一个三角形使它与原来的三角形完全相同．（保留作图痕迹，不写作法）【考点】N4：作图—应用与设计作图；KE：全等三角形的应用．【分析】先画出线段BA，然后从B，A两点，以线段BA为一边作∠A=∠E，∠F=∠B，两角另一边的交点就是就是第三点的位置，顺次连接即可．【解答】解：按尺规作图的要求，正确作出△ABC的图形：22．已知﹣=4，求的值．【考点】6D：分式的化简求值．【分析】先根据﹣=4求出ab与a﹣b之间的关系，再代入原式进行计算即可．【解答】解：∵﹣=4，∴=4，即a﹣b=﹣4ab，∴原式====6．23．如图所示，△DEF是等边三角形，且∠1=∠2=∠3，试问：△ABC是等边三角形吗？请说明理由．【考点】KM：等边三角形的判定与性质．【分析】由△DEF是等边三角形，得到∠DEF=60°，由邻补角的定义得到∠BEC=120°，得到∠BCE+∠2=120°，推出∠ACB=60°，于是得到结论．【解答】解：△ABC是等边三角形，理由：∵△DEF是等边三角形，∴∠DEF=60°，∴∠BEC=120°，∴∠BCE+∠2=120°，∵∠2=∠3，∴∠BCE+∠3=60°，∴∠ACB=60°，同理∠ABC=∠BAC=60°，∴△ABC是等边三角形．24．请你阅读下列计算过程，再回答所提出的问题：解：=（A）=（B）=x﹣3﹣3（x+1）（C）=﹣2x﹣6（D）（1）上述计算过程中，从哪一步开始出现错误： A ；（2）从B到C是否正确，若不正确，错误的原因是不能去分母；（3）请你正确解答．【考点】6B：分式的加减法．【分析】异分母分式相加减，先化为同分母分式，再加减．【解答】解：===，（1）故可知从A开始出现错误；（2）不正确，不能去分母；（3）===．25．如图，在△ABC中，BD=CD，∠1=∠2，小颖说：“AD⊥BC”，你认为她说的对吗？说明你的理由．【考点】KD：全等三角形的判定与性质．【分析】由BD=DC，可得∠DBC=∠DCB，点D在BC的垂直平分线，继而可得AB=BC，则可证得AD是BC的垂直平分线，即可得AD⊥BC．【解答】解：小颖说的对，理由如下：∵BD=DC，∴∠DBC=∠DCB，点D在BC的垂直平分线，∵∠1=∠2，∴∠ABC=∠ACB，∴AB=AC，∴点A在BC的垂直平分线，∴AD是BC的垂直平分线，即AD⊥BC．26．计算：（1）÷（2）÷（﹣x﹣2）（3）（4）（1﹣）÷．【考点】6C：分式的混合运算．【分析】根据因式分解和分式的基本性质即可进行化简运算．【解答】解：（1）原式=•﹣×=﹣==（2）原式=÷=﹣×=﹣（3）原式=﹣==（4）原式=÷=×a（a﹣1）=﹣a27．已知△ABC的两条高AD，BE相交于点H，且AD=BD，试问：（1）∠DBH与∠DAC相等吗？说明理由．（2）BH与AC相等吗？说明理由．【考点】KD：全等三角形的判定与性质．【分析】（1）相等．根据同角的余角相等即可证明．（2）相等．只要证明△BDH≌△ADC即可．【解答】解：（1）相等．理由如下：∵AD、BE是△ABC的高，∴∠ADB=∠AEB=90°，∴∠DBH+∠C=90°，∠DAC+∠C=90°，∠DBH=∠DAC．（2）相等．理由如下：在△BDH和△ADC中，，∴△BDH≌△ADC，∴BH=AC．人教版八年级上学期期中考试数学试卷（二）一、选择题（每小题3分，共24分）1．下列图形中，不是轴对称图形的是（）A．B．C．D．2．已知三角形两边长分别为3和8，则该三角形第三边的长可能是（）A．5 B．10 C．11 D．123．点P（4，5）关于x轴对称点的坐标是（）A．（﹣4，﹣5）B．（﹣4，5）C．（4，﹣5）D．（5，4）4．下列判断中错误的是（）A．有两角和其中一个角的对边对应相等的两个三角形全等B．有一边相等的两个等边三角形全等C．有两边和一角对应相等的两个三角形全等D．有两边和其中一边上的中线对应相等的两个三角形全等5．三角形中，若一个角等于其他两个角的差，则这个三角形是（）A．钝角三角形 B．直角三角形 C．锐角三角形 D．等腰三角形6．如图，△ABC中，∠C=70°，若沿图中虚线截去∠C，则∠1+∠2=（）A．360°B．250°C．180°D．140°7．如图，O是△ABC的∠ABC，∠ACB的平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若△ODE的周长为10厘米，那么BC的长为（）A．8cm B．9cm C．10cm D．11cm8．如图，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM．下列结论：①DF=DN；③AE=CN；③△DMN是等腰三角形；④∠BMD=45°，其中正确的结论个数是（）A．1个B．2个C．3个D．4个二、填空题（每小题3分，共21分）9．“三角形任意两边之和大于第三边”，得到这个结论的理由是．10．若正n边形的每个内角都等于150°，则n= ，其内角和为．11．如图，AD=AB，∠C=∠E，∠CDE=55°，则∠ABE= ．12．如图△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是．13．如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是．14．如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM 的周长最短为cm．15．在平面直角坐标系中，O为坐标原点，已知A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数为．三、解答题：（本大题共8个小题，满分75分）16．证明三角形内角和定理：三角形的三个内角的和等于180°．17．如图，点F、C在BE上，BF=CE，AB=DE，∠B=∠E．求证：∠A=∠D．18．如图，在△ABC中，∠C=∠ABC=2∠A，BD⊥AC于D，求∠DBC的度数．19．C、B、E三点在一直线上，AC⊥CB，DE⊥BE，∠ABD=90°，AB=BD，试证明AC+DE=CE．20．如图，三角形ABC中，AB=AC=2，∠B=15°，求AB边上的高．21．如图，在三角形ABC中，AD为中线，AB=4，AC=2，AD为整数，求AD的长．22．如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0），C（﹣1，0）．（1）将△ABC向右平移5个单位，再向下平移4个单位得△A1B1C1，图中画出△A 1B1C1，平移后点A的对应点A1的坐标是．（2）将△ABC沿x轴翻折△A2BC，图中画出△A2BC，翻折后点A对应点A2坐标是．（3）将△ABC向左平移2个单位，则△ABC扫过的面积为．23．如图①，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD，CE，BD和CE相交于点F，若△ABC不动，将△ADE绕点A任意旋转一个角度．（1）求证：△BAD≌△CAE．（2）如图①，若∠BAC=∠DAE=90°，判断线段BD与CE的关系，并说明理由；（3）如图②，若∠BAC=∠DAE=60°，求∠BFC的度数；（4）如图③，若∠BAC=∠DAE=α，直接写出∠BFC的度数（不需说明理由）参考答案与试题解析一、选择题（每小题3分，共24分）1．下列图形中，不是轴对称图形的是（）A．B．C．D．【考点】P3：轴对称图形．【分析】根据轴对称图形的概念对各个选项进行判断即可．【解答】解：A、是轴对称图形，A不合题意；B、不是轴对称图形，B符合题意；C、是轴对称图形，C不合题意；D、是轴对称图形，D不合题意；故选：B．2．已知三角形两边长分别为3和8，则该三角形第三边的长可能是（）A．5 B．10 C．11 D．12【考点】K6：三角形三边关系．【分析】根据三角形的第三边大于两边之差，而小于两边之和求得第三边的取值范围，再进一步选择．【解答】解：根据三角形的三边关系，得第三边大于：8﹣3=5，而小于：3+8=11．则此三角形的第三边可能是：10．故选：B．3．点P（4，5）关于x轴对称点的坐标是（）A．（﹣4，﹣5）B．（﹣4，5）C．（4，﹣5）D．（5，4）【考点】P5：关于x轴、y轴对称的点的坐标．【分析】利用关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，﹣y），进而得出答案．【解答】解：点P（4，5）关于x轴对称点的坐标是：（4，﹣5）．故选：C．4．下列判断中错误的是（）A．有两角和其中一个角的对边对应相等的两个三角形全等B．有一边相等的两个等边三角形全等C．有两边和一角对应相等的两个三角形全等D．有两边和其中一边上的中线对应相等的两个三角形全等【考点】KB：全等三角形的判定．【分析】全等三角形的判定定理有SAS，ASA，AAS，SSS，根据判定定理逐个判断即可．【解答】解：A、符合全等三角形的判定定理AAS，即能推出两三角形全等，故本选项错误；B、∵△ABC和△A′B′C′是等边三角形，∴AB=BC=AC，A′B′=B′C′=A′C′，∵AB=A′B′，∴AC=A′C′，BC=B′C′，即符合全等三角形的判定定理SSS，即能推出两三角形全等，故本选项错误；C、不符合全等三角形的判定定理，即不能推出两三角形全等，故本选项正确；D、如上图，∵AD、A′D′是三角形的中线，BC=B′C′，∴BD=B′D′，在△ABD和△A′B′D′中，，∴△ABD≌△A′B′D′（SSS），∴∠B=∠B′，在△ABC和△A′B′C′中，，∴△ABC≌△A′B′C′（SAS），故本选项错误；故选C．5．三角形中，若一个角等于其他两个角的差，则这个三角形是（）A．钝角三角形 B．直角三角形 C．锐角三角形 D．等腰三角形【考点】K7：三角形内角和定理．【分析】三角形三个内角之和是180°，三角形的一个角等于其它两个角的差，列出两个方程，即可求出答案．【解答】解：设三角形的三个角分别为：a°、b°、c°，则由题意得：，解得：a=90，故这个三角形是直角三角形．故选：B．6．如图，△ABC中，∠C=70°，若沿图中虚线截去∠C，则∠1+∠2=（）A．360°B．250°C．180°D．140°【考点】K7：三角形内角和定理；L3：多边形内角与外角．【分析】先利用三角形内角与外角的关系，得出∠1+∠2=∠C+（∠C+∠3+∠4），再根据三角形内角和定理即可得出结果．【解答】解：∵∠1、∠2是△CDE的外角，∴∠1=∠4+∠C，∠2=∠3+∠C，即∠1+∠2=∠C+（∠C+∠3+∠4）=70°+180°=250°．故选B．7．如图，O是△ABC的∠ABC，∠ACB的平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若△ODE的周长为10厘米，那么BC的长为（）A．8cm B．9cm C．10cm D．11cm【考点】KJ：等腰三角形的判定与性质．【分析】根据角平分线的定义以及平行线的性质，可以证得：∠OBD=∠BOD，则从而求解．依据等角对等边可以证得OD=BD，同理，OE=EC，即可证得BC=C△ODE【解答】解：∵BO是∠ACB的平分线，∴∠ABO=∠OBD，∵OD∥AB，∴∠ABO=∠BOD，∴∠OBD=∠BOD，∴OD=BD，同理，OE=EC，=10cm．BC=BD+DE+EC=OD+DE+OE=C△ODE故选C．8．如图，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM．下列结论：①DF=DN；③AE=CN；③△DMN是等腰三角形；④∠BMD=45°，其中正确的结论个数是（）A．1个B．2个C．3个D．4个【考点】KD：全等三角形的判定与性质；KF：角平分线的性质；KI：等腰三角形的判定；KW：等腰直角三角形；M6：圆内接四边形的性质．【分析】求出BD=AD，∠DBF=∠DAN，∠BDF=∠ADN，证△DFB≌△DAN，即可判断①，证△ABF≌△CAN，推出CN=AF=AE，即可判断②；根据A、B、D、M四点共圆求出∠ADM=22.5°，即可判断④，根据三角形外角性质求出∠DNM，求出∠MDN=∠DNM，即可判断③．【解答】解：∵∠BAC=90°，AC=AB，AD⊥BC，∴∠ABC=∠C=45°，AD=BD=CD，∠ADN=∠ADB=90°，∴∠BAD=45°=∠CAD，∵BE平分∠ABC，∴∠ABE=∠CBE=∠ABC=22.5°，∴∠BFD=∠AEB=90°﹣22.5°=67.5°，∴∠AFE=∠BFD=∠AEB=67.5°，∴AF=AE，∵M为EF的中点，∴AM⊥BE，∴∠AMF=∠AME=90°，∴∠DAN=90°﹣67.5°=22.5°=∠MBN，在△FBD和△NAD中∴△FBD≌△NAD，∴DF=DN，∴①正确；在△AFB和△△CNA中∴△AFB≌△CAN，∴AF=CN，∵AF=AE，∴AE=CN，∴②正确；∵∠ADB=∠AMB=90°，∴A、B、D、M四点共圆，∴∠ABM=∠ADM=22.5°，∴∠DMN=∠DAN+∠ADM=22.5°+22.5°=45°，∴④正确；∵∠DNA=∠C+∠CAN=45°+22.5°=67.5°，∴∠MDN=180°﹣45°﹣67.5°=67.5°=∠DNM，∴DM=MN，∴△DMN是等腰三角形，∴③正确；即正确的有4个，故选D．二、填空题（每小题3分，共21分）9．“三角形任意两边之和大于第三边”，得到这个结论的理由是两点之间线段最短．【考点】K6：三角形三边关系．【分析】三角形三边关系定理：三角形两边之和大于第三边，可以运用两点之间线段最短的性质进行判断．【解答】解：“三角形任意两边之和大于第三边”，得到这个结论的理由是：两点之间线段最短．故答案为：两点之间线段最短．10．若正n边形的每个内角都等于150°，则n= 12 ，其内角和为1800°．【考点】L3：多边形内角与外角．【分析】先根据多边形的内角和定理求出n，再根据多边形的内角和求出多边形的内角和即可．【解答】解：∵正n边形的每个内角都等于150°，∴=150°，解得，n=12，其内角和为（12﹣2）×180°=1800°．故答案为：12；1800°．11．如图，AD=AB，∠C=∠E，∠CDE=55°，则∠ABE= 125°．【考点】KD：全等三角形的判定与性质．【分析】在△ADC和△ABE中，由∠C=∠E，∠A=∠A和AD=AB证明△ADC≌△ABE，得到∠ADC=∠ABE，由∠CDE=55°，得到∠ADC=125°，即可求出∠ABE的度数．【解答】解：∵在△ADC和△ABE中，，∴△ADC≌△ABE（AAS），∴∠ADC=∠ABE，∵∠CDE=55°，∴∠ADC=125°，∴∠ABE=125°，故答案为125°．12．如图△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是5 ．【考点】KF：角平分线的性质；KQ：勾股定理．【分析】过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，再利用三角形的面积公式列式计算即可得解．【解答】解：如图，过点D作DE⊥AB于E，∵∠C=90°，AD平分∠BAC，∴DE=CD=2，∴△ABD的面积=AB•DE=×5×2=5．故答案为：5．13．如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是50°．【考点】KG：线段垂直平分线的性质；KH：等腰三角形的性质．【分析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD，根据等边对等角可得∠A=∠ABD，然后表示出∠ABC，再根据等腰三角形两底角相等可得∠C=∠ABC，然后根据三角形的内角和定理列出方程求解即可．【解答】解：∵MN是AB的垂直平分线，∴AD=BD，∴∠A=∠ABD，∵∠DBC=15°，∴∠ABC=∠A+15°，∵AB=AC，∴∠C=∠ABC=∠A+15°，∴∠A+∠A+15°+∠A+15°=180°，解得∠A=50°．故答案为：50°．14．如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM 的周长最短为8 cm．【考点】PA：轴对称﹣最短路线问题；KG：线段垂直平分线的性质；KH：等腰三角形的性质．【分析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．【解答】解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，=BC•AD=×4×AD=12，解得AD=6cm，∴S△ABC∵EF是线段AB的垂直平分线，∴点B关于直线EF的对称点为点A，∴AD的长为BM+MD的最小值，∴△BDM的周长最短=（BM+MD）+BD=AD+BC=6+×4=6+2=8cm．故答案为：8．15．在平面直角坐标系中，O为坐标原点，已知A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数为 4 ．【考点】KI：等腰三角形的判定；D5：坐标与图形性质．【分析】本题应该分情况讨论．以OA为腰或底分别讨论．当A是顶角顶点时，P 是以A为圆心，以OA为半径的圆与x轴的交点，共有1个，当O是顶角顶点时，P是以O为圆心，以OA为半径的圆与x轴的交点，有2个；P是OA的中垂线与x轴的交点，有1个，共有4个．【解答】解：（1）若AO作为腰时，有两种情况，当A是顶角顶点时，P是以A为圆心，以OA为半径的圆与x轴的交点，共有1个，当O是顶角顶点时，P是以O为圆心，以OA为半径的圆与x轴的交点，有2个；（2）若OA是底边时，P是OA的中垂线与x轴的交点，有1个．以上4个交点没有重合的．故符合条件的点有4个．故填：4．三、解答题：（本大题共8个小题，满分75分）16．证明三角形内角和定理：三角形的三个内角的和等于180°．【考点】K7：三角形内角和定理．【分析】先写出已知、求证，再画图，然后证明．过点A作EF∥BC，利用EF∥BC，可得∠1=∠B，∠2=∠C，而∠1+∠2+∠BAC=180°，利用等量代换可证∠BAC+∠B+∠C=180°．【解答】已知：△ABC，求证：∠BAC+∠B+∠C=180°，证明：过点A作EF∥BC，∵EF∥BC，∴∠1=∠B，∠2=∠C，∵∠1+∠2+∠BAC=180°，∴∠BAC+∠B+∠C=180°．即知三角形内角和等于180°．17．如图，点F、C在BE上，BF=CE，AB=DE，∠B=∠E．求证：∠A=∠D．【考点】KD：全等三角形的判定与性质．【分析】易证BC=EF，即可证明△ABC≌△DEF，可得∠A=∠D．即可解题．【解答】证明：∵BF=CE，∴BC=EF，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS），∴∠A=∠D．18．如图，在△ABC中，∠C=∠ABC=2∠A，BD⊥AC于D，求∠DBC的度数．【考点】K7：三角形内角和定理．【分析】根据三角形的内角和定理与∠C=∠ABC=2∠A，即可求得△ABC三个内角的度数，再根据直角三角形的两个锐角互余求得∠DBC的度数．【解答】解：∵∠C=∠ABC=2∠A，∴∠C+∠ABC+∠A=5∠A=180°，∴∠A=36°．∴∠C=∠ABC=2∠A=72°．∵BD⊥AC，∴∠DBC=90°﹣∠C=18°．19．C、B、E三点在一直线上，AC⊥CB，DE⊥BE，∠ABD=90°，AB=BD，试证明AC+DE=CE．【考点】KD：全等三角形的判定与性质．【分析】可证明△ABC≌△DBE，得到AC=BE DE=BC，即可证明AC+DE=CE．【解答】证明：∵∠ABD=90°，AC⊥CB，DE⊥BE，∴∠ABC+∠DBE=∠ABC+∠A，∴∠A=∠DBE；在△ABC与△DBE中，，∴△ABC≌△DBE（AAS），∴AC=BE，BC=DE，∴AC+DE=CE．20．如图，三角形ABC中，AB=AC=2，∠B=15°，求AB边上的高．【考点】KO：含30度角的直角三角形；KH：等腰三角形的性质．【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD的度数，然后根据30°角所对的直角边等于斜边的一半求解即可．【解答】解：过点C作BA的垂线，交BA的延长线于点D，解：∵∠B=∠ACB=15°，∴∠CAD=∠B+∠A CB=15°+15°=30°，∵AC=4cm，CD是AB边上的高，∴CD=AC=×2=1．∴AB边上的高是1．21．如图，在三角形ABC中，AD为中线，AB=4，AC=2，AD为整数，求AD的长．【考点】KD：全等三角形的判定与性质；K6：三角形三边关系．【分析】延长AD到E，使AD=DE，连接BE，证△ADC≌△EDB，推出AC=BE=2，在△ABE中，根据三角形三边关系定理得出AB﹣BE＜AE＜AB+BE，代入求出即可．【解答】解：延长AD到E，使AD=DE，连接BE，∵AD是BC边上的中线，∴BD=CD，在△ADC和△EDB中，，∴△ADC≌△EDB（SAS），∴AC=BE=2，在△ABE中，AB﹣BE＜AE＜AB+BE，∴4﹣2＜2AD＜4+2，∴1＜AD＜3，∵AD是整数，∴AD=2，22．如图，已知△ABC的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0），C（﹣1，0）．（1）将△ABC向右平移5个单位，再向下平移4个单位得△A1B1C1，图中画出△A 1B1C1，平移后点A的对应点A1的坐标是（3，﹣1）．（2）将△ABC沿x轴翻折△A2BC，图中画出△A2BC，翻折后点A对应点A2坐标是（﹣2，﹣3）．（3）将△ABC向左平移2个单位，则△ABC扫过的面积为13.5 ．【考点】P7：作图﹣轴对称变换；Q4：作图﹣平移变换．【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）利用关于x轴对称点的性质进而得出对应点位置；（3）利用平移的性质可得△ABC扫过的面积为△A′B′C′+平行四边形A′C′CA的面积．【解答】解：（1）如图所示：△A1B1C1，即为所求，平移后点A的对应点A1的坐标是：（3，﹣1）；故答案为：（3，﹣1）；（2）如图所示：△A2BC，即为所求，翻折后点A对应点A2坐标是：（﹣2，﹣3）；故答案为：（﹣2，﹣3）；（3）将△ABC向左平移2个单位，则△ABC扫过的面积为：S△A′B′C′+S平行四边形A′C′CA=×3×5+2×3=13.5．故答案为：13.5．23．如图①，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD，CE，BD和CE相交于点F，若△ABC不动，将△ADE绕点A任意旋转一个角度．（1）求证：△BAD≌△CAE．（2）如图①，若∠BAC=∠DAE=90°，判断线段BD与CE的关系，并说明理由；（3）如图②，若∠BAC=∠DAE=60°，求∠BFC的度数；（4）如图③，若∠BAC=∠DAE=α，直接写出∠BFC的度数（不需说明理由）【考点】KY：三角形综合题．【分析】（1）由等边三角形的性质得出AB=AC，AD=AE，∠BAC=∠EAD，从而得出∠BAD=∠CAE，即可得出△BAD≌△CAE．（2）判定BD与CE的关系，可以根据角的大小来判定．由∠BAC=∠DAE可得∠BAD=∠CAE，进而得△BAD≌△CAE，所以∠CBF+∠BCF=∠ABC+∠ACB．再由∠BAC=。

八年级(上)期中数学试卷附答案解析

八年级（上）期中数学试卷一、选择题（每小题3分，共30分）1．（3分）下列说法中错误的是（）A．一个三角形中至少有一个角不小于60°B．直角三角形只有一条高C．三角形的中线不可能在三角形外部D．三角形的中线把三角形分成面积相等的两部分2．（3分）下列说法，正确的有（）①七边形有14条对角线②外角和大于内角和的多边形只有三角形③若一个多边形的内角和与外角和的比是4：1，则它是九边形．A．0个 B．1个 C．2个 D．3个3．（3分）如图，已知AB∥CD，AB=CD，AE=FD，则图中的全等三角形有（）A．1对 B．2对 C．3对 D．4对4．（3分）如图，AB，CD表示两根长度相等的铁条，若O是AB，CD的中点，经测量AC=15cm，则容器的内径长为（）A．12cm B．13cm C．14cm D．15cm5．（3分）请你观察下面的四个图形，它们体现了中华民族的传统文化．对称现象无处不在，其中可以看作是轴对称图形的有（）A．4个 B．3个 C．2个 D．1个6．（3分）如图，△ABC是等边三角形，BD是中线，延长BC至E，使CE=CD．连接ED并延长和AB交于点F，若EF=12，则BD的长度是（）A．4 B．6 C．8 D．107．（3分）如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它的三条公路的距离相等，则可供选择的地址有（）A．一处B．二处C．三处D．四处8．（3分）如图，△ABC和△AB′C′关于直线l对称，下列结论：（1）∠ABC≌△AB′C′；（2）∠BAC′=∠B′AC；（3）l垂直平分CC′；（4）直线BC和B′C′的交点不一定在l上．其中正确的有（）A．4个 B．3个 C．2个 D．1个9．（3分）如图，∠1、∠2、∠3、∠4满足的关系是（）A．∠1+∠2=∠3+∠4 B．∠1+∠2=∠4﹣∠3 C．∠1+∠4=∠2+∠3 D．∠1+∠4=∠2﹣∠310．（3分）如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（）A．B．C．D．二、填空（每小题3分，共24分）11．（3分）（a﹣b）2•（b﹣a）5=．12．（3分）一副三角板，如图所示叠放在一起，则图中∠α的度数是．13．（3分）将一副三角尺如图所示叠放在一起，若AB=14cm，则阴影部分的面积是cm2．14．（3分）在△ABC中，∠BCA=90°，∠B=2∠A，CD⊥AB于D，若AB=10cm，则BD=cm．15．（3分）如图，AB=AC，BD=BC，若∠A=30°，则∠ABD的度数为．16．（3分）若一个等腰三角形的一个外角等于70°，则这个等腰三角形的顶角应该为．17．（3分）如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC=120°．以D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为．18．（3分）如图，AD是△ABC的角平分线，DE，DF分别是△BAD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（填序号）．三、解答题（共66分）19．（12分）如图所示，已知A（0，2），B（3，﹣2），C（4，2），请作出△ABC 关于直线AC对称的图形，并写出点B关于AC的对称点B′的坐标．20．（12分）已知如图，在△ABC中，∠ACB=90°，CE⊥AB于E，D为AB上一点，且AD=AC，AF平分∠CAE交CE于F．求证：FD∥BC．21．（12分）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板ADE如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE和EC有怎样的数量关系，并证明你的猜想．22．（8分）已知， +（4a﹣b﹣2）2=0，求代数式（﹣3ab2）2的值．23．（7分）先化简，再求值：3x（2x+1）﹣（2x+3）（x﹣5），其中x=﹣2．24．（15分）已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G．（1）求证：BF=AC；（2）求证：CE=BF；（3）CE与BG的大小关系如何？试证明你的结论．参考答案与试题解析一、选择题（每小题3分，共30分）1．（3分）下列说法中错误的是（）A．一个三角形中至少有一个角不小于60°B．直角三角形只有一条高C．三角形的中线不可能在三角形外部D．三角形的中线把三角形分成面积相等的两部分【解答】解：A、∵三角形的内角和等于180°，∴一个三角形中至少有一个角不少于60°，故本选项正确；B、直角三角形有三条高，故本选项错误；C、三角形的中线一定在三角形的内部，故本选项正确；D、三角形的中线把三角形的面积平均分成相等的两部分，故本选项正确．故选：B．2．（3分）下列说法，正确的有（）①七边形有14条对角线②外角和大于内角和的多边形只有三角形③若一个多边形的内角和与外角和的比是4：1，则它是九边形．A．0个 B．1个 C．2个 D．3个【解答】解：①7边形有=14条对角线，故正确；②外角和大于内角和的多边形只有三角形，故正确；③多边形外角和=360°，设这个多边形是n边形，根据题意得（n﹣2）•180°=360°×4，解得n=10．故错误．故选：C．3．（3分）如图，已知AB∥CD，AB=CD，AE=FD，则图中的全等三角形有（）A．1对 B．2对 C．3对 D．4对【解答】解：∵AB∥CD，∴∠A=∠D，∵AB=CD，AE=FD，∴△ABE≌△DCF（SAS），∴BE=CF，∠BEA=∠CFD，∴∠BEF=∠CFE，∵EF=FE，∴△BEF≌△CFE（SAS），∴BF=CE，∵AE=DF，∴AE+EF=DF+EF，即AF=DE，∴△ABF≌△CDE（SSS），∴全等三角形共有三对．故选：C．4．（3分）如图，AB，CD表示两根长度相等的铁条，若O是AB，CD的中点，经测量AC=15cm，则容器的内径长为（）A．12cm B．13cm C．14cm D．15cm【解答】解：∵O是AB，CD的中点，AB=CD，∴OA=OB=OD=OC，在△AOC和△BOD中，，∴△AOC≌△BOD，∴AC=BD=15cm，故选：D．5．（3分）请你观察下面的四个图形，它们体现了中华民族的传统文化．对称现象无处不在，其中可以看作是轴对称图形的有（）A．4个 B．3个 C．2个D．1个【解答】解：第一个图形是轴对称图形，第二个图形是轴对称图形，第三个图形是轴对称图形，第四个图形是轴对称图形，故选：A．6．（3分）如图，△ABC是等边三角形，BD是中线，延长BC至E，使CE=CD．连接ED并延长和AB交于点F，若EF=12，则BD的长度是（）A．4 B．6 C．8 D．10【解答】解：∵△ABC是等边三角形，∴∠A=∠ABC=∠ACB=60°，∵BD是中线，∴∠ABD=30°，∵CE=CD，∴∠CDE=∠E=30°，∴∠BFE=90°，∴BE=2BF，∵EF=12，∴BE2=BF2+EF2，即4BF2=BF2+144，解得BF=4，在Rt△BDF中，cos30°=，∴BD=BF÷cos30°=4÷=8．故选：C．7．（3分）如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它的三条公路的距离相等，则可供选择的地址有（）A．一处B．二处C．三处D．四处【解答】解：作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线，外角平分线相交于点P1、P2、P3，内角平分线相交于点P4，根据角平分线的性质可得到这4个点到三条公路的距离分别相等．故选D．8．（3分）如图，△ABC和△AB′C′关于直线l对称，下列结论：（1）∠ABC≌△AB′C′；（2）∠BAC′=∠B′AC；（3）l垂直平分CC′；（4）直线BC和B′C′的交点不一定在l上．其中正确的有（）A．4个 B．3个 C．2个 D．1个【解答】解：∵△ABC和△AB′C′关于直线L对称，∴（1）△ABC≌△AB′C′，正确；（2）∠B′AC=∠B′AC正确；（3）直线L一定垂直平分线段C C′，故本小题正确；（4）根据对应线段或其延长线的交点在对称轴上可知本小题错误；综上所述，正确的结论有3个．故选：B．9．（3分）如图，∠1、∠2、∠3、∠4满足的关系是（）A．∠1+∠2=∠3+∠4 B．∠1+∠2=∠4﹣∠3 C．∠1+∠4=∠2+∠3 D．∠1+∠4=∠2﹣∠3【解答】解：如图，由三角形外角的性质可得∠1+∠4=∠5，∠2=∠5+∠3，∴∠1+∠4=∠2﹣∠3，故选：D．10．（3分）如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（）A．B．C．D．【解答】解：按照题意，动手操作一下，可知展开后所得的图形是选项B．故选：B．二、填空（每小题3分，共24分）11．（3分）（a﹣b）2•（b﹣a）5=（b﹣a）7．【解答】解：原式=[﹣（b﹣a）]2•（b﹣a）5=（b﹣a）2•（b﹣a）5=（b﹣a）7故答案为：（b﹣a）712．（3分）一副三角板，如图所示叠放在一起，则图中∠α的度数是75°．【解答】解：如图，∠1=45°﹣30°=15°，∠α=90°﹣∠1=90°﹣15°=75°．故答案为：75°13．（3分）将一副三角尺如图所示叠放在一起，若AB=14cm，则阴影部分的面积是cm2．【解答】解：∵∠B=30°，∠ACB=90°，AB=14cm，∴AC=7cm．由题意可知BC∥ED，∴∠AFC=∠ADE=45°，∴AC=CF=7cm．=×7×7=（cm2）．故S△ACF故答案为：．14．（3分）在△ABC中，∠BCA=90°，∠B=2∠A，CD⊥AB于D，若AB=10cm，则BD= 2.5cm．【解答】解：在△ABC中，∠C=90°，∠B=2∠A，所以，∠A=30°，∠B=60°，BC=sin∠A×AB=×10=5cm；∵CD⊥AB∴∠B+∠BCD=∠A+∠B=90°即：∠BCD=∠A又∵∠CDB=∠ACB=90°∴△ACB∽△CDB∴=即：DB===2.5cm．15．（3分）如图，AB=AC，BD=BC，若∠A=30°，则∠ABD的度数为45°．【解答】解：∵AB=AC，∴∠C=∠ABC，∵BD=BC，∴∠C=∠CBD，∵∠A=30°，∴∠C=∠ABC=∠CBD=75°，∴∠CBD=30°，∴∠ABD=75°﹣30°=45°．故答案为45．16．（3分）若一个等腰三角形的一个外角等于70°，则这个等腰三角形的顶角应该为110°．【解答】解：等腰三角形一个外角为70°，那相邻的内角为110°三角形内角和为180°，如果这个内角为底角，内角和将超过180°，所以110°只可能是顶角．故答案为：110°．17．（3分）如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC=120°．以D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为6．【解答】解：∵△BDC是等腰三角形，且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB至F，使BF=CN，连接DF，在Rt△BDF和Rt△CND中，BF=CN，DB=DC∴△BDF≌△CND∴∠BDF=∠CDN，DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°，∠FDM=60°=∠MDN，DM为公共边∴△DMN≌△DMF，∴MN=MF∴△AMN的周长是：AM+AN+MN=AM+MB+BF+AN=AB+AC=6．18．（3分）如图，AD是△ABC的角平分线，DE，DF分别是△BAD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是②③④（填序号）．【解答】解：如果OA=OD，则四边形AEDF是矩形，没有说∠A=90°，不符合题意，故①错误；∵AD是△ABC的角平分线，∴∠EAD=∠FAD，在△AED和△AFD中，∴△AED≌△AFD（AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，故④正确；∵在△AEO和△AFO中，，∴△AEO≌△AFO（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，故②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，故③正确．综上可得：正确的是：②③④，故答案为：②③④．三、解答题（共66分）19．（12分）如图所示，已知A（0，2），B（3，﹣2），C（4，2），请作出△ABC 关于直线AC对称的图形，并写出点B关于AC的对称点B′的坐标．【解答】解：如图所示：点B′即为所求，∵A（0，2），B（3，﹣2），∴B点到AC的距离为4，则B′点到AC的距离也为4，且两点横坐标相等，∴B′（3，6）．20．（12分）已知如图，在△ABC中，∠ACB=90°，CE⊥AB于E，D为AB上一点，且AD=AC，AF平分∠CAE交CE于F．求证：FD∥BC．【解答】解：∵AF平分∠CAE，∴∠CAF=∠DAF在△CAF与△DAF中，∴△CAF≌△DAF（SAS）∴∠ACF=∠ADF∵∠ACB=∠CAE=90°，∴∠ACE+∠CAE=∠B+∠CAE=90°∴∠ACE=∠B，∴∠ADF=∠B∴FD∥BC21．（12分）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板ADE如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE和EC有怎样的数量关系，并证明你的猜想．【解答】解：数量关系为：BE=EC，位置关系是：BE⊥EC．证明如下：∵△AED是直角三角形，∠AED=90°，且有一个锐角是45°，∴∠EAD=∠EDA=45°，∴AE=DE，∵∠BAC=90°，∴∠EAB=∠EAD+∠BAC=45°+90°=135°，∠EDC=∠ADC﹣∠EDA=180°﹣45°=135°，∴∠EAB=∠EDC，∵D是AC的中点，∴AD=CD=AC，∵AC=2AB，∴AB=AD=DC，∵在△EAB和△EDC中，∴△EAB≌△EDC（SAS），∴EB=EC，且∠AEB=∠DEC，∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°，∴BE⊥EC．22．（8分）已知， +（4a﹣b﹣2）2=0，求代数式（﹣3ab2）2的值．【解答】解：∵+（4a﹣b﹣2）2=0，∴≥0，（4a﹣b﹣2）2≥0，∴，解得，∴（﹣3ab2）2=（﹣3×1×4）2=3623．（7分）先化简，再求值：3x（2x+1）﹣（2x+3）（x﹣5），其中x=﹣2．【解答】解：原式=6x2+3x﹣2x2+10x﹣3x+15=4x2+10x+15，当x=﹣2时，原式=16﹣20+15=11．24．（15分）已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G．（1）求证：BF=AC；（2）求证：CE=BF；（3）CE与BG的大小关系如何？试证明你的结论．【解答】（1）证明：∵CD⊥AB，∠ABC=45°，∴△BCD是等腰直角三角形．∴BD=CD．∵∠DBF=90°﹣∠BFD，∠DCA=90°﹣∠EFC，且∠BFD=∠EFC，∴∠DBF=∠DCA．在Rt△DFB和Rt△DAC中，∵∴Rt△DFB≌Rt△DAC（ASA）．∴BF=AC；（2）证明：∵BE平分∠ABC，∴∠ABE=∠CBE．在Rt△BEA和Rt△BEC中，∴Rt△BEA≌Rt△BEC（ASA）．∴CE=AE=AC．又由（1），知BF=AC，∴CE=AC=BF；（3）证明：∠ABC=45°，CD垂直AB于D，则CD=BD．H为BC中点，则DH⊥BC（等腰三角形“三线合一”）连接CG，则BG=CG，∠GCB=∠GBC=∠ABC=×45°=22.5°，∠EGC=45°．又∵BE垂直AC，故∠EGC=∠ECG=45°，CE=GE．∵△GEC是直角三角形，∴CE2+GE2=CG2，∵DH垂直平分BC，∴BG=CG，∴CE2+GE2=CG2=BG2；即2CE2=BG2，BG=CE，∴BG＞CE．21。

八年级上册期中测试卷及答案【含答案】

八年级上册期中测试卷及答案【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪种物质在空气中不支持燃烧？A. 氧气B. 二氧化碳C. 氮气D. 氢气2. 八进制数110转换为十进制数是？A. 72B. 64C. 88D. 963. 地球公转的方向是？A. 自西向东B. 自东向西C. 自南向北D. 自北向南4. 下列哪个国家不是联合国安理会常任理事国？A. 中国B. 法国C. 德国D. 英国5. 下列哪个不是我国的四大发明？A. 指南针B. 火药C. 印刷术D. 电脑二、判断题（每题1分，共5分）1. 长江是我国最长的河流。

（√）2. 1千米等于1000米。

（√）3. 地球围绕太阳转一圈需要365天。

（√）4. 鸟类是哺乳动物。

（×）5. 人类最早使用的工具是石器。

（√）三、填空题（每题1分，共5分）1. 我国的首都是______。

2. 地球上的淡水只占地球水体总量的______。

3. 人体最大的器官是______。

4. 现代计算机的电子器件主要采用______。

5. 八卦中，代表天的卦象是______。

四、简答题（每题2分，共10分）1. 请简述光合作用的过程。

2. 请解释牛顿第一定律。

3. 请简述抗日战争的时间。

4. 请解释欧姆定律。

5. 请简述工业革命的影响。

五、应用题（每题2分，共10分）1. 一个长方形的长是10厘米，宽是5厘米，求这个长方形的面积。

2. 小明有3个苹果，小红给了小明2个苹果，现在小明有多少个苹果？3. 一个正方形的边长是8厘米，求这个正方形的对角线长度。

4. 一辆汽车以60公里/小时的速度行驶，行驶了2小时，求汽车行驶的路程。

5. 一个班级有40名学生，其中有20名男生，求这个班级的女生人数。

六、分析题（每题5分，共10分）1. 请分析我国为什么要实行计划生育政策。

2. 请分析为什么说“失败是成功之母”。

七、实践操作题（每题5分，共10分）1. 请用所学的物理知识，解释如何用一个气压计测量大气压。

八年级物理上册期中考试(含答案)

八年级物理上册期中考试（含答案）(时间：60分钟分数：100分)班级：姓名：分数：一、选择题（每题2分，共30分）1、为保证司乘人员的安全，轿车上设有安全带未系提示系统．当乘客坐在座椅上时，座椅下的开关S1闭合，若未系安全带，则开关S2断开，仪表盘上的指示灯亮起；若系上安全带，则开关S2闭合，指示灯熄灭．下列设计最合理的电路图是（）A． B．B．C． D．2、若先在地球上，后在月球上分别用天平和弹簧测力计称量同一个物体，则会发现（）A．天平示数变大，弹簧测力计变大B．天平示数变小，弹簧测力计不变C．天平示数不变，弹簧测力计变大D．天平示数不变，弹簧测力计变小3、甲、乙两人站在一堵光滑的墙壁前，两人之间相距102m，且距离墙壁均为68m，如图所示，甲开了一枪后，乙先后听到两声枪响的时间间隔为（）（已知空气中声音的传播速度为340m/s）A．0.1s B．0.2s C．0.38s D．0.4s4、如图所示是甲和乙两种物质的质量与体积关系图象，分析图象可知（）A．若甲、乙的质量相等，则甲的体积较大B．若甲、乙的体积相等，则甲的质量较小C．乙物质的密度为0.5kg/m3D．甲、乙两种物质的密度之比为4：15、如图所示的物态变化实例中，由于液化形成的是（）A．立春时节冰化成的水B．白露时节草叶上的露珠C．大雪时节落在地上的雪D．冬至时节房檐上的冰挂6、甲、乙两辆汽车行驶在平直的公路上，甲车上的乘客看乙车在向北运动．乙车上的乘客看到甲车和树木都向南运动则以下说法中正确的是（）A．甲乙车可能都向南运动 B．甲乙两车可能都向北运动C．甲车向北运动乙车向南运动 D．甲车一定在向南运动，乙车向北运动7、如图所示，用手指压圆珠笔芯使它弯曲，同时手指感到疼痛，这个实验不能说明（）A．力的作用是相互的 B．力是物体对物体的作用C．力可以改变物体的形状 D．重力的方向竖直向下8、在平直轨道上行驶的火车中，放在车厢内小桌上的苹果相对于下列哪个物体是运动的（）A．这列火车的机车 B．坐在车厢椅子上的乘客C．从旁边走过的列车员 D．关着的车门9、生活中人们常常利用物体的惯性．下列描述正确的是（）A．标枪运动员通过助跑提高成绩，利用了运动员自身的惯性B．紧固锤头时撞击锤柄的下端，利用了锤柄的惯性C．拍打窗帘清除上面的浮灰，利用了窗帘的惯性D．将脸盆里的水泼出去，利用了水的惯性10、如图甲所示，水平地面上的一物体，受到方向不变的水平推力F的作用，F 的大小与时间t的关系和物体的速度v与时间t的关系如图乙所示，以下说法正确的是（）甲乙A．0～2秒，物体没有推动，是因为推力小于摩擦力B．2～4秒物体做匀速直线运动C．2～4秒物体受到的摩擦力是3ND．4～6秒，物体受到的摩擦力与水平推力是一对平衡力11、下列物体的受力分析，错误的是（）A．放在水平面上的木块 B．挂在天花板上的小球C．静止在斜面上的木块D．被细线拉住的氢气球12、用一段细铁丝做一个支架作为转动轴，把一根中间戳有小孔（没有戳穿）的饮料吸管放在转动轴上，吸管能在水平面内自由转动（如图所示）．用餐巾纸摩擦吸管使其带电，将带负电的橡胶棒靠近带电吸管的一端时，发现吸管被推开，下列说法正确的是（）A．吸管和橡胶棒带异种电荷B．吸管和餐巾纸摩擦后，两者带同种电荷C．吸管和餐巾纸摩擦时，吸管得电子带负电D．吸管和餐巾纸摩擦时，吸管失电子带负电13、2025年我国将实现宇航员登月计划，在月球上漫步的宇航员须借助无线电通讯设备才能进行交谈，其原因是（）A．月球上真空不能传声B．月球上只能传递超声波C．月球上声音传播速度快D．月球上宇航员声带无法振动发声14、如图是穿行在餐厅的机器人端着托盘送餐的情景．若认为机器人是静止的，则选择的参照物是（）A．地面B．托盘C．餐桌D．墙壁15、有四个容量均为200ml的瓶子，分别装满酱油、纯水、植物油和酒精，那么装的质量最多的是（ρ酱油＞ρ纯水＞ρ植物油＞ρ酒精）（）A．纯水B．酱油C．酒精D．植物油二、填空题（每题2分，共10分）1、常见的物质由分子组成，分子由_____组成；夏日荷花盛开飘来阵阵花香，这是________现象；清晨荷叶上的两颗露珠接触后成为了更大的一颗水珠，表明分子之间存在________力.2、如图所示，小明将一枚硬币放在碗底，眼睛在A处恰好看不到它，沿碗壁缓缓向碗中加水，小明在A处又能看到“硬币”．这是因为光从________斜射入________中时发生了________现象．3、一辆行驶的汽车车厢里挂着一个小球．当出现了如图所示的情景时，汽车在做________（选填“加速”、“匀速”或“减速’）运动．此时绳子对球的拉力和球受到的重力________（选填“是”、“不是”或“可能是”）一对平衡力．4、海南省正在开展社会文明大行动，规定汽车礼让行人．汽车不避让行人且冲过斑马线是很危险的，这是因为汽车具有________，在遇到紧急情况时刹车不易停住．汽车轮胎表面刻有深槽花纹，是为了________摩擦力（选填“增大”或“减小”）．5、如图所示，甲、乙两个完全相同的容器放在水平桌面上，分别盛有质量相同的不同液体，则液体对甲、乙两容器底部的压力F甲________F乙，甲、乙容器对水平桌面的压强p甲________p乙。

八年级上册数学期中测试题及答案

八年级上册数学期中测试题及答案一、选择题（每题3分，共30分）1. 下列哪个数不是实数？A. -3.14B. √2C. πD. i²2. 已知一个长方体的长、宽、高分别为8cm、6cm和5cm，其体积是多少立方厘米？A. 240B. 180C. 120D. 1003. 如果一个数的1/3加上2等于这个数本身，那么这个数是多少？A. 3B. 6C. -3D. -64. 下列哪个选项是二次根式？A. √3B. 3√2C. √16D. 4√55. 一个数的相反数是-5，那么这个数是：A. 5B. -5C. 1/5D. -1/56. 一个数的绝对值是8，那么这个数可能是：A. 8B. -8C. 8或-8D. 07. 下列哪个式子不是等式？A. 3x + 5 = 14B. 2y - 7 < 11C. 4z = 16D. 5w - 3 ≠ 28. 如果一个三角形的三个内角的度数之和是180度，那么这个三角形是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定9. 下列哪个选项是正确的不等式？A. 3 > 2 > 1B. 2 < 1 < 3C. 5 ≥ 5 ≥ 4D. 7 ≤ 6 ≤ 510. 一个数的平方根是3，那么这个数是：A. 6B. 9C. -9D. ±9二、填空题（每题4分，共20分）11. 一个数的立方是27，那么这个数是______。

12. 如果一个数除以-2的结果是3，那么这个数是______。

13. 一个长方体的长是10cm，宽是5cm，高是3cm，其表面积是______平方厘米。

14. 一个数的1/4加上3等于这个数的2倍，那么这个数是______。

15. 一个等腰三角形的两个底角相等，如果顶角是40度，那么底角是______度。

三、解答题（共50分）16. （10分）解方程组：\(\begin{cases} 2x + 3y = 11 \\ x - y = 2 \end{cases}\)17. （15分）已知一个长方体的长、宽、高分别是15cm、10cm和8cm，求其表面积和体积。

初二英语上上学期期中复习题附答案

初二英语上上学期期中复习题听力部分(共20分)I. 听句子,选择你所听到的句子中单词的反义词。

(5分)1. A. thin B. strong C. tall D. short2. A. cold B. happy C. warm D. hungry3. A. hard-working B. big C. small D. red4. A. small B. tall C. fat D. slim5. A. beautiful B. delicious C. safe D. thirstyII. 听句子, 判断你所听到的句子是否与所给句子的意思相一致。

如果一致写"S", 不一致写"D"。

(5分)1. There isn't anything else in the fridge.2. He often helps him to learn English.3. Lucy is shorter than Sandy.4. My father usually rides his bike to work.5. Shall we go to play football?III. 听短文,将文中所空的单词补充出来。

(10分)Sun Yue is a Chinese girl. She is from Beijing.She's 1 and 2 . She often helps me with my 3 4 . She has big eyes and short 5 hair. She's 6 . She's 7 than her mother now. Her 8 is basketball. She won a game yesterday evening. Sun Yue and I are good friends. We are always 9 the same clothes. So her clothes are like 10 .笔试部分(共80分)I. 词汇。

人教版八年级数学上学期期中考试复习测试题(含答案)

人教版八年级数学上学期期中考试复习测试题（含答案）一、选择题（本大题共 8 小题，每小题 3 分，共 24 分）1．在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）A． B． C． D．2．下列四组线段中，可以构成直角三角形的是（）A．4，5，6 B．2，3，4 C．5，12，13 D．6，7，83．到△ABC的三边距离相等的点是△ABC的（）A．三边中线的交点 B．三条角平分线的交点 C．三边上高的交点 D．三边垂直平分线的交点4.如图，一棵大树在一次强台风中于离地面10m处折断倒下，倒下部分的树梢到树的距离为24m,则这棵大树折断处到树顶的长度是（）A．10m B．15m C．26m D．30m5．如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF＝6，CF＝2，则AC的长度为（）A．6 B．7 C．8 D．9（第4题）（第5题）（第6题）（第7题）6．如图，已知∠ABC＝∠DCB，AC、BD交于点E，添加以下条件，不能判定△ABC≌△DCB的是（）A．AB＝DC B．BE＝CE C．AC＝DB D．∠A＝∠D7．如图，在△ABC中，∠ACB＝90°，∠B＝30°，AD平分∠BAC，E是AD中点，若BD＝9，则CE的长为（）A．3 B．3.5 C．4 D．4.58．在如图所示的3×3网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（）A．4个B．3个C．2个D．1个二、填空题（本大题共 10 小题，每小题 3 分，共 30 分)9.已知图中的两个三角形全等，则∠α的度数是°．10.如图，已知△ABC≌△ADE，若AB=7，AC=3，则BE的值为．（第9题）（第10题）（第13题）（第14题）11．已知一个等腰三角形的两边分别为5和10，则它的周长为．12.若一直角三角形两直角边长分别为6和8，则斜边长为．13．如图，在△ABC中，AB＝AC，D为BC中点，∠BAD＝35°，则∠B的度数为°. 14．如图，直线m∥n，以直线m上的点A为圆心，适当长为半径画弧，分别交直线m、n于点B，C，连接AB，BC．若∠1＝40°，则∠ABC＝°．15.如图，以直角△ABC的三边向外作正方形，其面积分别为S1，S2，S3，且S1=4，S2=8，则S3= ．（第15题）（第16题）（第17题）（第18题）16．如图，在△ABC中，ED∥BC，∠ABC和∠ACB的平分线分别交ED于点G、F，若BE＝3，CD＝4，ED＝5，则FG的长为．17．如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，S△ABC＝7，DE＝2，AB＝4，则AC长是．18．如图，在△ABC中，OA＝4，OB＝3，C点与A点关于直线OB对称，动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ＝∠BAO．当△PQB为等腰三角形时，OP的长度是．三、解答题（本大题共 10 小题，共 96 分）19.（8分）如图，已知点B、E、C、F在一条直线上，且AB＝DF，BE＝CF，∠B＝∠F．求证：△ABC≌△DFE．20.（8分）如图，△ABC中，DE，FG分别为AB、AC的垂直平分线，E、G分别为垂足，若△DAF的周长为16，求BC的长．21. （8分）如图，在8×8的正方形网格中，每个小正方形的边长都是1，已知△ABC的三个顶点均在格点上．（1）画出△ABC关于直线l对称的△A1B1C1；（2）在直线l上找一点P，使PA+PB的长最短；（3）△A1B1C1的面积为________．22.（8分）如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB于点E，DF⊥AC于点F．（1）求证：DE=DF；（2）如果S△A BC=14，AC=7，求DE的长．23.（10分）如图，在笔直的公路AB旁有一座山，为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处，已知点C与公路上的停靠站A的距离为15km，与公路上另一停靠站B的距离为20km，停靠站A、B之间的距离为25km，且CD⊥AB．（1）求修建的公路CD的长；（2）若公路CD修通后，一辆货车从C处经过D点到B处的路程是多少？24.（10分）如图，△ABC中，D是BC延长线上一点，满足CD＝AB，过点C作CE∥AB且CE＝BC，连接DE并延长，分别交AC、AB于点F、G．（1）求证：△ABC≌△DCE；（2）若∠B＝50°，∠D＝22°，求∠AFG的度数．25. （10分）如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，点E、F分别是BD和AC的中点，连接EF．（1）求证：EF⊥AC；（2）若BD＝26，EF＝5，求AC的长．26.（10分）如图，在等腰△ABC中，AB=AC，BC=5．点D为AC上一点，且BD=4，CD=3．（1）求证：BD⊥AC；（2）求AB的长．27. （12分）在△ABC中，∠ACB=90°，AC=BC，D是直线AB上一点（点D不与点A、B重合），连接DC并延长到E，使得CE=CD，过点E作EF⊥直线BC，交直线BC 于点F．（1）如图1，当点D为线段AB的上任意一点时，用等式表示线段EF、CF、AC的数量关系，并说明理由；（2）如图2，当点D为线段BA的延长线上一点时，依题意补全图2；（3）在（2）的条件下猜想线段EF、CF、AC的数量关系是否发生改变，若不变，请说明理由;若改变，写出它们的数量关系，并加以证明.28. （12分）如图，在等边△ABC中，AB＝9cm，点P从点C出发沿CB边向点B点以2cm/s的速度移动，点Q从B点出发沿BA边向A点以5cm/s速度移动．P、Q两点同时出发，它们移动的时间为t秒钟．（1）请用t的代数式表示BP和BQ的长度：BP＝，BQ＝．（2）若点Q在到达点A后继续沿三角形的边长向点C移动，同时点P也在继续移动，请问在点Q从点A到点C的运动过程中，t为何值时，直线PQ把△ABC的周长分成4：5两部分？（3）若P、Q两点都按顺时针方向沿△ABC三边运动，请问在它们第一次相遇前，t为何值时，点P、Q能与△ABC的一个顶点构成等边三角形？直接写出答案。

初二(上)数学期中复习训练题(含答案).docx

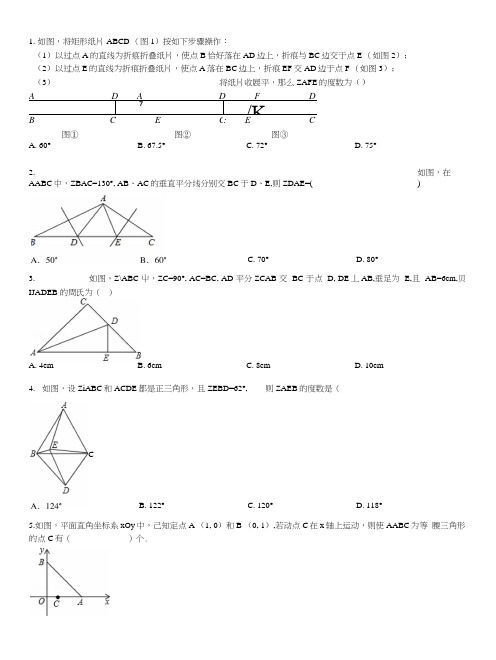
1.如图，将矩形纸片ABCD （图1）按如下步骤操作：（1）以过点A的直线为折痕折叠纸片，使点B恰好落在AD边上，折痕与BC边交于点E （如图2）；（2）以过点E的直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F （如图3）；（3）将纸片收展平，那么ZAFE的度数为（）A DA D F D 7/KB C E C: E C图①图②图③D. 75°2.如图，在AABC中，ZBAC=130°, AB、AC的垂直平分线分别交BC于D、E,则ZDAE=( )3.如图，Z\ABC 屮，ZC=90°, AC=BC, AD 平分ZCAB 交BC 于点D, DE丄AB,垂足为E,且AB=6cm,贝IJADEB 的周氏为（）A. 4cmB. 6cmC. 8cmD. 10cm5.如图，平面直角坐标系xOy中，己知定点A （1, 0）和B （0, 1）,若动点C在x轴上运动，则使AABC为等腰三角形的点C有（）个.C. 70°D. 80°4. 如图，设ZiABC和ACDE都是正三角形，且ZEBD=62°, 则ZAEB的度数是（B. 122°C. 120°D. 118°C7. 如图，在厶ABC 屮，AB 二AC, ZBAC=90°,直角ZEPF 的顶点P 是BC 的屮点，两边PE 、PF 分别交AB 、AC 于点E 、F,连接EF 交AP 于G.给出四个结论：①AE=CF ；②EF=AP ； @AEPF 是等腰直角三角形； ④ZAEP 二ZAGF.其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个8. 如图，AABC 是等腰直角三角形，ADEF 是一个含30。

角的直角三角形，将D 放在BC 的屮点上，转动ADEF, 设DE, DF 分另恢AC, BA 的延长线于E, G,则下列结论：① AG 二CE ② DG 二 DE③BG - AC=CE®S ABDG - S ACDE =^S AABC其中总是成立的是 ( )A.①②③B.①②③④C.②③④D.①②④9.如图，AABC 中，ZACB=90°, D 为AB ±任一点，过D 作AB 的垂线，分别交边AC 、BC 的延长线于E 、F 两点，ZBAC 、ZBFD 的平分线交于点1, AI 交DF 于点M, FI 交AC 于点N,连接BI.下列结论：①ZBAC=ZBFD ; ②ZENI=ZEMI ；③AI 丄FI ；④ZABI=ZFBI ；其中正确结论的个数是（）D. 4个6.如图，在Z\ABC 屮，ZBAC=90°, AD 丄BC 于D, BE 平分ZABC 交AD 于F,作EG 丄DC 于G,则下列结论其中正确结论的个数为（）10. 如图，RtAACB+, ZACB=90° , AABC 的角平分线AD 、BE 相交于点P,过P 作PF 丄AD 交BC 的延长线于点F, 交AC 于点H,则下列结论：①ZAPB=135° ；②BF=BA ；③PH=PD ；④连接CP, CP 平分ZACB,其中正确的是（） A.①②③B.①②④C.①③④D.①②③④11. 在ZXABC 中，ZB=2ZC, AD 丄BC 于D, AE 平分ZBAC,则下列结论:①AB+BD 二CD ；②S AABE ： S AAEC =AB ： AC ；③AC - AB=BE ；④ZB=4ZDAE 其屮正确的是（）12. 如图，在△八BC 中，ZABC=45° , AD, BE 分别为BC 、AC 边上的高,AD 、BE 相交于点P,下列结论： ①ZPCD 二45° ,②AE=EC, ®SAABP ： SAAPC=BD ： CD,④若 BP=2EC,则APDC 周长等于 AB 的长.正确的是13. 如图，C 为线段AE 上一动点（不与点A, E 重合），在AE 同侧分别作正三角形ABC 和正三角形CDE, AD 与BE 交于点0, AD 与BC 交于点P, BE 与CD 交于点Q,连接PQ.以下五个结论：①AD-BE ；②PQ 〃AE ；③AP 二BQ ；④DE 二DP ； ⑤ZA0B 二60° •其中正确的结论的个数是（）A. 2个B. 3个C. 4个D. 5个A.①②③④B.①③④C.②③④D.①②③A.①②B.①③C.①④D.①③④B DC ()14.如图：AABC 中，ZACB=90° , ZCAD二30° , AC=BC=AD, CE丄CD,且CE二CD,连接BD, DE, BE,则下列结论:@ZECA=165° ' @BE=BC；③AD丄BE；喑•其中正确的是＜)A.①②③B.①②④C.①③④D.①②③④15.如图，将30°的直角三角尺ABC绕直角顶点A逆吋针旋转到ADE的位置，使B点的对应点D落在BC边上，连接EB、EC,则下列结论：①ZDAC二ZDCA；②ED为AC的垂直平分线；③EB平分ZAED；④ED二2AB.其中正确的是（）A.①②③B.①②④C.②③④D.①②③④16.如图，AABC是等边三角形，F、G分别为AC和BC的中点，D在线段BG ±,连接DF,以DF为边在DF的右侧作等边ADFE, ED的延长线交AB于H,连接EC,则以下结论：①BF丄AC；②ZAHD+ZAFD二180°；③ZBCE=60°；④当D在线段BG上（不与G点重合）运动时，DOFC+CE.其中正确的是（）A.只有①③④B.只有①②④C.①②③④D.只有①②③E17.如图，AABC 中，AC二BC, ZACB=90° , AE 平分ZBAC 交BC 于E, BD丄AE 于D, DM丄AC 于连CD.下列结论: @AC+CE=AB；②CD冷楓③RAW。

初二上期中数学试卷及答案

一、选择题（每题4分，共20分）1. 下列各数中，绝对值最小的是（）A. -2B. -1C. 0D. 12. 已知a > 0，b < 0，则下列不等式中正确的是（）A. a > bB. a < bC. -a > -bD. -a < -b3. 下列代数式中，正确的是（）A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C. (a + b)^2 = a^2 - 2ab + b^2D. (a - b)^2 = a^2 + 2ab - b^24. 若x^2 - 5x + 6 = 0，则x的值为（）A. 2B. 3C. 2 或 3D. 无法确定5. 下列函数中，是二次函数的是（）A. y = x^2 + 2x + 1B. y = x^2 + 2C. y = 2x^2 - 4x + 3D. y = 2x + 3二、填空题（每题4分，共20分）6. 若a = 3，b = -2，则a^2 + b^2的值为______。

7. 分数2/3的倒数是______。

8. 若x = 4，则2x + 1的值为______。

9. 若a = -3，b = 2，则a^2 - b^2的值为______。

10. 下列方程中，方程x^2 - 5x + 6 = 0的解为______。

三、解答题（每题10分，共30分）11. 简化下列代数式：（1）(a + b)(a - b)（2）(a - b)^2 - (a + b)^2（3）(x - 1)(x + 1) - (x - 2)(x + 2)12. 解下列方程：（1）2x - 5 = 3x + 1（2）x^2 - 6x + 9 = 013. 已知二次函数y = ax^2 + bx + c（a ≠ 0），若a > 0，b < 0，c > 0，则函数的图像是（）A. 上升的抛物线B. 下降的抛物线C. 上升的直线D. 下降的直线四、应用题（每题10分，共20分）14. 小明骑自行车从A地到B地，若以每小时10公里的速度行驶，则全程需要3小时；若以每小时15公里的速度行驶，则全程需要2小时。

2023-2024学年八年级语文上学期期中试题及答案

2023-2024学年八年级语文上学期期中试题及答案2023-2024学年八年级语文上学期期中检测试题一、积累与运用(30分)1. 阅读下面语段，完成题目。

(每空1分，共4分)历史不可“穿越”，却能在文字中得以再现。

在《藤野先生》中，鲁迅满怀深情地回忆了给予他jiào huì的藤野先生;在《回忆我的母亲》中，朱德向我们展示了他那勤劳一生、宽厚rén cí的母亲;在《列夫·托尔斯泰》中，___B___。

在这千帆竞发___A___百舸争流的时代，我们更要认真阅读这些经典作品，了解别样的人生，丰富自己的生活体验。

(1)根据拼音在横线上用正楷写出相应的汉字。

期中考试有必要吗“减负”，不是单纯减少一次两次考试。

教育制度不作根本的改革，单单是喊一声口号，发一次号召，只是在作秀。

而教育制度的改革也绝对不是几年时间内能靠几个学校或是几个城市就可以完成的。

从我的切身体验来说，减负是一年年喊，教材却是一年比一年难。

翻翻孩子们的课本吧，往年初中的教学内容下放到小学五六年级，往年三四年级的内容则在一二年级开始学习。

“负”怎会减少?很多城市早在若干年前，就“取消”了所谓的期中考试，但代替它的，是每月一次或每学期两次的“月检测”。

之所以如此，正是检测手段必要性的体现，考试毕竟是当前时代背景下检验知识、了解差距的必要手段。

期中考试前的复习建议1、科目多怎么办?分清主次，安排时间，做必要的取舍。

将自己提升可能最大的学科，和之后中高考相关的学科，进行系统的复习，其他短时间不可能提高太多的学科，和中高考无关的学科，不要花费太多的时间，会导致最重要的学科没有系统复习。

2、文科重记忆，适合2人一组相互提问式的学习语文，英语，历史，地理，政治等需要背很多东西的学科，适合两个人互相提问背诵的方式学习，这样效率很高。

你自己会问对方一些你自己觉得不太背的下来的东西，两个人可以互相查缺补漏。

3、理科重逻辑，梳理逻辑框架，总结模型题型更重要。

人教版数学初二上学期期中试题与参考答案(2024年)

2024年人教版数学初二上学期期中复习试题(答案在后面)一、选择题（本大题有10小题，每小题3分，共30分）1、题目：已知一个长方形的长为8cm，宽为5cm，求该长方形的对角线长度。

A. 6cmB. 10cmC. 12cmD. 13cm2、题目：一个班级有学生40人，其中男生人数是女生人数的1.5倍，求该班级男生和女生的人数。

A. 男生30人，女生10人B. 男生25人，女生15人C. 男生35人，女生5人D. 男生20人，女生20人3、若一个矩形的长是宽的3倍，且其周长为48厘米，则该矩形的面积是多少平方厘米？A. 64B. 108C. 128D. 1444、已知直角三角形的两个锐角之比为1∶2，那么这两个锐角分别是多少度？A. 30°, 60°B. 45°, 45°C. 60°, 30°D. 以上都不正确5、一个长方形的长是10厘米，宽是5厘米，它的面积是（）A. 25平方厘米B. 50平方厘米C. 100平方厘米D. 200平方厘米6、一个正方形的周长是24厘米，那么它的边长是（）A. 2厘米B. 4厘米C. 6厘米D. 8厘米7、已知一个正方形的边长为(a)，如果它的边长增加到原来的1.5倍，则新正方形的面积与原正方形面积之比是多少？A.(1.5:1)B.(2.25:1)C.(3:1)D.(1.52:1)8、若一个等腰三角形的底角为(70∘)，则顶角的度数是多少？A.(40∘)B.(50∘)C.(60∘)D.(70∘)9、若直角三角形的两条直角边长分别为3和4，则斜边的长度是（）A. 5B. 7C. 8D. 10 10、一个长方形的长是10厘米，宽是8厘米，那么它的面积是（）A. 80平方厘米B. 90平方厘米C. 100平方厘米D. 120平方厘米二、填空题（本大题有5小题，每小题3分，共15分）1、若(x−3=7)，则(x=)______ 。

初二语文上学期期中复习试卷有答案

语文期中练习卷姓名一、积累运用共20分1．根据下面语段中的拼音写出相应的词语;2分阅读“爱国情怀”这一单元中的课文,倾听已届fēng zhúcán nián的海外游子的心声,体会被剥夺使用母语权利的亡国者的痛楚,品味着名科学家始终juànliàn着祖国的深情,领悟志士仁人面对山河破碎而壮志难酬的忧愤,感受古代外交家维护国家尊严、不辱使命的凛然正气……2．根据要求默写;8分①杜甫春望中,表达战乱中诗人思念离散亲人、盼望得到亲人音讯的千古名句是：“ , ;”②泊秦淮中表现在国运衰微的时候,官僚豪绅不以国事为念,反而聚集在酒楼中欣赏亡国之音的醉生梦死的生活的诗句是“ , ;”③陆游在十一月四日风雨大作中直接表现其爱国思想情怀的诗句是“, ;”③日有所思,夜有所梦,“ , ”就是着名爱国诗人陆游垂暮之年不忘收复失地、统一祖国的梦境,读来令人荡气回肠;④王勃在送杜少府之任蜀川一诗中歌颂友谊的千古名句是：“ , ;”⑤过零丁洋中直抒胸臆,表明作者文天祥以死明志的两句诗是：“,;”过零丁洋中作者用比喻来描写国家和个人的命运的句子是：“ , ;”⑥德高望重的李老师退休后仍然关心青年教师的成长,正如龚自珍在己亥杂诗中所说的“ , ;”⑦毛泽东在七律长征诗中,用夸张的修辞手法,反衬出红军战士敢于藐视并战胜一切困难的高大形象和伟大气魄的诗句是：“ , ;”⑧写出一句抒发爱国情怀的古诗：“ , ;”3．同学们课外收集了反映父母关爱子女的故事、谚语、格言、民谣、诗歌等,班级以“父母心”为话题组织了一次交流会,班主任、语文老师、部分学生家长也参加了这次会议,请你以主持人的身份设计一段开场白或一段结束语;文字限在100字以内;4分4．下面是某学生的作文片断,请按要求修改三处划线的语句;3分①每当站在祖国的地图前,使我油然而生无尽的遐想：祖国需要我们学好科学文化知识,②去开创那辽阔的大西北,③让塔克拉玛干沙漠改变模样；需要我们用勤劳的双手在大西南的横断山脉中,营造出一个个高峡平湖……第①处句子成分残缺,修改的方法是;第②处句子搭配不当,应修改为;第③处“改变模样”这一表述欠具体生动,宜改为;5．本学期,我们学习了长城专题,知道了长城在春秋战国时期就开始修筑了,明代也曾大规模地修建过长城,那你知道长城的一些知识吗3分①明长城东起,西至;②请写出与长城有关的一个人物、一个传说、一句俗语或诗句;人物传说俗语或诗句③你能用一个比喻句描述一下你心中的长城吗二、阅读理解共40分一14分甲晏子至,楚王赐晏子酒,酒酣,吏二缚一人诣王;王曰：“缚者何为者也”对曰：“齐人也,坐盗;”王视晏子曰：“齐人固善盗乎”晏于避席对曰：“婴闻之,橘生淮南则为橘,生于淮北则为枳,叶徒相似,其实味不同;所以然者何水土异也;今民生长于齐不盗,入楚则盗,得无楚之水土使民善盗耶”王笑回：“圣人非所与熙也,寡人反取病焉;”乙景公①之时,雨雪三日而不霁②;公被③狐白之裘,坐堂侧陛④;妻子入见,立有间;公曰：“怪哉雨雪三日而天不寒;”晏子对曰：“天不寒乎”公笑;晏子曰：“婴闻古之贤君,饱而知人之饥,温而知人之寒,逸而知人之劳;今君不知也;”公曰：“善;寡人闻命矣;”乃令出裘发粟以与饥寒者;孔子闻之曰：“晏子能明其所欲,景公能行其所善也;”节选自晏子春秋注①景公：齐国国君;②霁jì：天放晴;③被：同“披”;④陛：皇宫的台阶;6．用“／”标出下面句子朗读时应有的两处停顿;2分其实味不同7.解释下列加重的字;4分①吏二缚一人诣王②晏子避席对曰③晏子入见,立有间④逸而知人之劳8．用现代汉语翻译下列句子;4分①圣人非所与熙也,寡人反取病焉;译文：②乃令出裘发粟以与饥寒者;译文9．甲文中的“橘生淮南则为橘,生于淮北则为枳”现象说明了什么请简要回答;2分答：10．甲乙两文中的晏子、楚王、景公三人都有值得肯定的地方,请选其中两人,略作评析;2分答：二阅读人琴俱亡,完成下面四道题;王子猷、子敬俱病笃,而子敬先亡;子猷问左右：“何以都不闻消息此已丧矣;”语时了不悲;便索舆来奔丧,都不哭; 子敬素好琴,便径入坐灵床上,取子敬琴弹,弦既不调,掷地云：“子敬子敬,人琴俱亡;”因恸绝良久;月余亦卒;11、解释下列加点字在文中的意思;4分1何以都不闻消息2语时了不悲3子敬素好琴4因恸绝良久12、翻译下列句子;2分1语时了不悲;2取子敬琴弹,弦既不调;13、本文表现的是兄弟情;人们一般在形容兄弟之情深厚时,用人身上的某部位来打比方;你知道这个比方吗把它写出来;1分14、子猷“取子敬琴弹,弦既不调”,你认为这个“不调”说明了什么2分三阅读下列文段,完成习题;我说道：“爸爸,你走吧;”他往车外看了看说：“我买几个橘子去,你就在此地,不要走动;”我看那边月台的栅栏外有几个卖东西的等着顾客;走到那边月台,须穿过铁道,须跳下去又爬上去;父亲是一个胖子,走过去自然要费事些;我本来要去的,他不肯,只好让他去;我看见他戴着黑布大马褂,深青布棉袍,蹒跚地走到铁道旁,慢慢探身下去,尚不大难;可是他穿过铁道,要爬上那边月台,就不容易了;他用两手攀着上面,两脚再向上缩；显出努力的样子,这时我看见他的背影,我的眼泪很快地流下来了;我赶紧拭干了泪;怕他看见,也怕别人看见;我再向外看时,他已抱了朱红的橘子往回走了;过铁道时,他先将橘子散放在地上,自己慢慢爬下,再抱起橘子走;到这边时,我赶紧去搀他;他和我走到车上,将橘子一股脑儿放在我的皮大衣上,于是扑扑身上的泥土,心里很轻松似的;过一会说：“我走了,到那边来信”我望着他的背影混入来来往往的人里,再找不着了,我便进来坐下,我的眼泪又来了;15、写出能表明上文所写事情内容的小标题1分16、文中用哪些词语具体地写出父亲,“要爬上那边月台,就不容易了”2分17、父亲“心里很轻松似的”原因是什么2分18、“我赶紧拭干了泪”,“我赶紧去搀他”两句表现作者的心理活动是什么2分19、“我走了,到那边来信”“进去吧,里边没人”表达父亲怎样的内心活动和思想感情2分四11分①满天都是星光,火把也亮起来了;从山脚向上望,只见火把排成许多“之”字形,一直连到天上,跟星光接起来,分不出是火把还是星星;这真是我生平没见过的奇观;②大家都知道这座山是怎样的陡了,不由浑身紧张,前后呼喊起来,都想努一把力,好快些翻过山去;③“不要掉队呀”④“不要落后做乌龟呀”⑤“我们顶着天啦”⑥大家听了,哈哈地笑了起来;⑦在“之”字拐的路上一步一步地上去;向上看,火把在头顶上一点点排到天空；向下看,简直是绝壁,火把照着人的脸,就在脚底下;⑧走了半天,忽然前面又走不动了;传来的话说,前面又有一段路在峭壁上,马爬不上去;又等了一点多钟,传下命令来说,就在这里睡觉,明天一早登山;⑨就在这里睡觉怎么行呢下去到竹林里睡是不可能的;但就在路上睡么路只有一尺来宽,半夜里一个翻身不就骨碌下去了么而且路上的石头又非常不平,睡一晚准会疼死人;⑩但这是没有办法的,只得裹一条毯子,横着心躺下去;因为实在太疲倦,一会儿就酣然入梦了;节选自老山界20．选文第①⑦自然段两次提到了“火把”,说说它们在文中各自的作用是什么2分第①自然段：第⑦自然段：21．“这真是我生平没见过的奇观”一句表达作者什么心情句中的“奇观”指什么2分22．在艰难的爬山过程中不断传出红军的喊声笑声,从中可以看出什么2分23．文中哪些地方可以看出山陡山高,试举例说明;2分24．选文中人物的心理活动写得很传神,试举例分析心理活动的作用;2分五母亲的诗15分①母亲不是诗人,母亲不会写诗,但是今天,当我坐在宽敞明亮的写字楼里,打开电脑写这篇文章时,竟忽然觉得,母亲似乎写过一首诗——②十多年前,我上小学;冬天,家乡铺天盖地下了一场雪;风卷着雪花,狂暴地扫荡着田野村庄,摇撼着古树的躯干,把我家的门窗撞得哗啦啦地响;吃罢早饭,我背上书包上学去;打开房门,一股袭人的寒气迎面扑来,顿时让我打个寒噤;我赶紧把门撞上,哆哆嗦嗦地说：“哎呀,好吓人的风雪哟”母亲从里屋出来,见我缩头缩尾的样子,瞥我一眼,深情地说：“孩子,风雪吓人吗不,冬天的门就是风雪推开的呢;”说着她快步上前,哗地一声,房门大开,“走,我们上学去”③踏着洒满积雪的小路,母亲给我讲了许多有关季节的故事,而且全部和门有关;走到学校的时候,母亲有关季节的故事也讲完了,连缀起采,竟成了这么几句：“花朵把春天的门推开了／绿阴把夏天的门推开了／果实把秋天的门推开了／风雪把冬天的门推开了……”④说实话,我当时并不知道这是诗;但不知为何,母亲随口说的这些话,竟像母亲给我身上加的一件御寒的外衣,让我身子热乎乎的;从此,我天天念着它去上学,再不畏惧风霜雪雨;年年如母亲所说,飞雪送来了春,花朵盼来了夏,绿阴又迎来果实累累的秋……⑤岁月如流,人生如流,转眼十余年过去;我从大学毕业了,正赶上就业艰难,许多单位下岗分流;毫无门路的我,只得像一只无头小鸟似的在人才交流中心乱闯,结果半年过去后,依然没有找到一份工作;⑥那天,我又碰了一鼻子灰,悻悻地走出人才交流中心;抬头望,天空灰蒙蒙,弄得我的心情更加灰黯;既然城市容不下我,我便想到了回家去;于是,我搭上一辆便车,当天傍晚就来到乡下;⑦乡村的夜说来就来,不一会儿,四周就拉起了黑色的帷幕;我独立门前,仰望长空,星星闪烁;可在我看来,那些星星却像在对我眨着嘲笑的眼;我低头哀叹道：“唉,人倒霉连星星都生厌啊”然后咚地撞上房门,坐在屋内唉声叹气;⑧母亲从里屋出来,见我垂头丧气的样子,瞥我一眼,深情地说：“孩子,星星生厌吗不,黑夜的门就是星星推开的呢;”说着她快步上前,哗地一声,房门大开,“走,我们看星星去;”⑨坐在满天星斗的院坝,母亲给我讲了许多有关人生的故事,而且全都和门有关;天快亮的时候,母亲有关人生的故事也讲完了,连缀起来,竟成了这么几句：“星星把黑夜的门推开了／黑夜把坚韧的门推开了／坚韧把成功的门推开了／成功把生活的门推开了……”⑩说实话,我当时并不知道这是诗;但不知为何,母亲随口说的这些话,竟像母亲给我的心加了一件御寒的外衣,让我心里热乎乎的,我虽然未置一词,但是我却知道了自己应该怎样去做;16．文章写了母亲给“我”关心爱护的两件事,请用简洁的语言加以概括;2分①②17．第⑦自然段划线的句子属于描写,有什么作用3分18．第⑩自然段划线句子用了的修辞手法,说说此句的深刻含义;3分19．文中的母亲是一个怎样的人用简要的语言加以概括;2分20．你知道历史上有哪些有名的爱子故事吗请写两个来;2分相关链接日本动画片狐狸的故事里有这样一组镜头：狐狸的父母将断奶不久的小狐狸赶出了温暖的洞穴;惊慌失措的小狐狸恋着父母使劲地要往回跑,但是饱经沧桑的老狐狸却无情地厮打着驱赶着,不让其回“安乐窝”;如此一而再再而三,小狐狸最终无可奈何地走向了潜伏着危险,却又能任其施展才华的大千世界;21．父母如何教育孩子,不同的父母有不同的方法;看完故事,想想文中的母亲,结合自己的生活实际,谈谈你对如何教育子女这一问题的认识;3分1、阅读下面文字,把文中拼音所表示的汉字依次写在括号内;2分人会长大,花会枯wěi /垂挂下一季浓密期盼的感觉很长/一旦欢悦zh àn放的时刻真短/啊,在变幻的天空次第消失的云朵/曾经一切都在眼前,伸手可及/故乡和童年并chí在绿荫的梦中/时光以高速前行/夺走我亲情和不jiě事的年少;——选自席慕容时间2、古诗文默写;8分① ,大渡桥横铁索寒;②杜甫在春望一诗中写国都沦陷,山河依旧,春天来临却杂草丛生的诗句是：“, ”,从中表现了诗人忧国忧民的感情;③陆游在十一月四日风雨大作中直接表现其爱国思想情怀的诗句是“ , ;”④过零丁洋中直抒胸臆,表明作者文天祥以死明志的两句诗是：“ , ;”⑤落红不是无情物, ;3、请写出两句有关赞美亲情的诗句或名言;2分①②二运用共10分4、在下面的横线上补写一个与前面句式相同、语意连贯的句子;2分读沙漠,读出了它坦荡豪放的胸怀；读太阳,读出了它普照万物的无私；5,对下面的这段文字与标点进行修改不得超过．．．．6．处．,;4分1增补号： 3删除号： 4调位号：老作家巴金的随想录出版后,便引起了许多人的思考;这五本薄薄的小册子,誉为“说真话的大书”,由其是这位老人,在读了卢梭的“忏悔录”后,更是向世人发出了一个既严肃又深刻的问题：人们有没有勇气跪倒在自己面前;大概没有一个人敢保证,自己在以往从前的日子里能始终做到表里如一;哪一个人未曾说过假话呢哪一个国家没有因为种种原因而一渡走了弯路呢也恰恰是因此有了这一切,才有了勇于忏悔的国家和个人,才有了忏悔与反思后的腾飞;6、2008年北京奥运会吉祥物的征集活动已面向海内外,公开、公平地进行,力求征集和评选出能够代表中国,并为世界人民喜爱的吉祥物;请你向奥运会推荐一件吉;4分三综合性学习共4分7、阅读下面三则材料,请说出你的发现;材料一：几乎每一年,我们的中学生参加国际奥林匹克数学、物理、生物、信息学竞赛,都能够获得一块又一块金牌;一方面我们培养了一批又一批“金牌选手”与“读书高手”,而另一方面,我们却又缺乏世界级的大科学家;我们的学生在中学都行,而一到成年就不行了;奥赛金牌那么多,而诺贝尔奖我国至今没有人获得;材料二：在我们小学的课堂测试中曾发生过这样的事：老师出的题目是“冰融化后变成了”;有学生答案为“春天”被判错；老师说,答案应该是“水”;材料三：据报道：1998年高考的语文卷子在“战胜脆弱”的作文题中出现了大量雷同,竟有许多考生因为要战胜脆弱,便编造自己的父母亡故,然后在文中大谈自己是如何克服困难的;二、阅读理解共44分一阅读选文我的母亲,回答 8—12题;共14分,读的是“孟子见梁惠王”;到年底,父亲要“清算．．”我平日的功课;在夜里亲自听我背书,很严厉,桌上放着一根两指阔的竹板;我背向着他立着背书,背不出的时候,他提一个字,就叫我回转身来把手掌展放在桌上,他拿起这根竹板很重地打下来;我吃了这一下苦头,痛是血肉的身体所无法避免的感觉,当然失声地哭了,但是还要忍住哭,回过身去再背;不幸又有一处中断,背不下去；经他再提一字,再打一下;呜呜咽咽地背着那位前世冤家的“见梁惠王”的“孟子”我自己呜咽着背,同时听得见坐在旁边缝纫着的母亲也唏唏嘘嘘地泪如泉涌地哭着;我心里知道她见我被打,她也觉得好像刺心的痛苦,对我表着十二分的同情,但她却时时从呜咽着的、断断续续的声音里勉强说着“打得好”;她的饮泣吞声,为的是爱她的儿子；勉强硬着头皮说声“打得好”,为的是希望她的儿子上进;如今想起母亲见我被打,陪着我一同哭,那样的母爱,仍然使我感念着我的慈爱的母亲;背完了半本“梁惠王”,右手掌被打得发肿,有半寸高,偷向灯光中一照,通亮,好像满肚子装着已成熟的丝的蚕身一样;母亲含着泪抱我上床,轻轻把被窝盖上,向我额上吻了几吻;8、请结合上下文,说说“清算”一词在文中的含义和作用;2分9、文中描写母亲的语言只有3个字：“打得好”,请你揣摩出当时母亲说这句话的心情;2分10、选文在描写母亲的细节中,最使你感动的细节是哪一处试找出一例并写出让你感动的理由;3分11、母亲在作者童年的记忆中,只留下了几个闪光的片段,作者正是摄取这几个闪光的片段来塑造母亲形象的;每一位母亲对自己的儿女都充满了关心爱护,请你也用简洁的语言写出你所感受到的母爱中最动情的那一瞬间;3分12、结合上文,阅读胡适的我的母亲片段,对两位母亲的教育方法作出简要评价;4分母亲管束我最严,她是慈母兼任严父;但她从来不在别人面前骂我一句,打我一下;我做错了事,她只对我一望,我看见了她的严厉眼光,就吓住了;犯的事小,她等到第二天早晨我睡醒时才教训我;犯的事大,她等到晚上人静时,关了房门,先责备我,然后行罚,或罚跪,或拧我的肉,无论怎样重罚,总不许我哭出声音来;她教训儿子不是借此出气叫别人听的;17、解释下列句中加点的词语;2分①圣人非所与熙．也②齐人固．善盗乎③吾欲辱之,何以．也④晏子避席．．对曰18、用现代汉语写出下列句子的意思;4分①酒酣,吏二缚一人诣王;②橘生淮南则为橘,生于淮北则为枳,叶徒相似,其实味不同;19、楚国君臣采用了怎样的计谋来侮辱晏子的用自己的话回答 2分20、晏子的回答,体现了一个外交家的风范,请指出晏子外交语言的特点;4分三、写作40分22．家是什么是难舍的亲情,是温馨的集体,是亲爱的祖国;在这里,父亲用慈爱的伞为儿女撑起一方晴空,儿女用孝顺的心给父母奉上一缕慰藉；在这里,洋溢着浓浓的师生之情,伙伴之谊……请以“家”为话题,写一篇不少于500字的文章;参考答案：一、1．风烛残年眷恋2．①烽火连三月,家书抵万金;②商女不知亡国恨,隔江犹唱后庭花;③夜阑卧听风吹雨,铁马冰河入梦来;④海内存知己,天涯若比邻;⑤山河破碎风飘絮,身世浮沉雨打萍⑥落红不是无情物,化作春泥更护花;⑦五岭逶迤腾细浪,乌蒙磅礴走泥丸;⑧人生自古谁无死,留取丹心照汗青僵卧孤村不自哀,尚思为国戍轮台天下兴亡,匹夫有责等;3．略4．将“使”删去去开发那辽阔的大西北让塔克拉玛干沙漠重新披上绿装; 5．①鸭绿江嘉裕关②秦始皇、蒙恬等孟姜女哭长城不到长城非好汉等③示例：长城是我心中的彩虹;二、一6．其／实味／不同7．①捆绑②座位③一会儿④舒服安逸、安乐、安闲8．①品德高尚的人是不可以跟他戏弄开玩笑的,我反而自取耻辱自讨没趣了;②景公于是命令下属拿出衣服和粮食赐给挨饿受冻的百姓;9.环境影响成长水土异也;10．示例：①晏子机智善辩,具有民本思想和强烈的爱国热情;②楚王具有自知之明;③景公有着民本思想,从谏如流,且知错即改;二11．第①自然段写火把是为了说明它的“之”字形形状,火把跟星光相接,暗示路陡山高;第⑦自然段写火把,展示了“奇观”的细节,描写细致、生动;12．表达作者豪迈、喜悦的心情“火把排成许多‘之’字形,一直连到天上,跟星光接起来,分不出是火把还是星星”13．喊声笑声传达出了红军的英雄气概和乐观精神;14．如：只见火把排成许多“之”字形,一直连到天上,跟星光接起来,分不出是火把还是星星;15．如“横着心躺下去”,写出了红军战士不怕困难不怕苦的态度;三16．下雪时,母亲送我去上学；找不到工作时,母亲给我以鼓励;17．环境描写烘托我找不到工作时沮丧、郁闷的心理;18．比喻母亲教会我在挫折中学会坚强,在逆境中寻找希望,使我懂得了如何乐观地面对生活;19．母亲是一位乐观坚强,富有智慧,聪明能干,循循善诱或善于教育、激励孩子,富有爱心,富有诗意,朴实温柔的人;20．孟母三迁——让孩子有一个好的学习环境；曾子杀猪——教育孩子要讲信用;5.1总、竟2完全3弹琴4痛苦；极度悲伤6.1说话时完全不悲伤;2拿过子敬的琴来弹,几根弦的声音已经不协调了;7.手足情8.提示：“不调”既是写实际情况,也包含了“人琴俱亡”的凄凉;学生可根据自己的感觉来说,言之成理即可9.买橘送别10.用两手攀；两脚缩；身子微倾11.这种轻松的心情正是一种爱心,道出父亲不肯让“我”去,一定要自己去的道理：越是尽到做父亲的责任,心里越是感到踏实满足;为了照顾好儿子,什么灾祸、劳累,全都置之度外了;12.怕父亲看见自己流泪更不放心了；怕父亲劳累摔倒,体贴、心疼父亲;13.临别时父亲反复叮嘱,提醒,表现父亲对儿子的惦记,无微不至的体贴、关心的深挚的爱;1、萎、绽、驰、解2分,答对两个得1分;2、①金沙水拍云崖暖;②国破山河在,城春草木深;③僵卧孤村不自哀,尚思为国戍轮台;④人生自古谁无死,留取丹心照汗青;⑤化作春泥更护花;共8分;一句1分,有错该句不得分;3、参考示例：2分①谁言寸草心,报得三春晖; ——孟郊②天下无不是的父母,世间最难得者兄弟; ——程允升③遥知兄弟登高处,遍插茱萸少一人;——王维二共10分4、参考：读春雨,读出了它润物无声的柔情;读大海,读出了它气势磅礴的豪情;2分5、修改参考：1在“誉为‘真话的大书’”之前添上“被”2“由其”中的“由”改为“尤”3“忏悔录”改为忏悔录4“发出了一个既严肃又深刻的问题”中的“发出”改为“提出”;5删去“从前”或“以往”6“一渡”中的“渡”改为“度”7“因此”改为“因为”8“国家”与“个人”位置调换4分;改对1处给1分,给满4分为止;若有其他改法,只要正确合理亦可给分;6、不设统一答案,如“中国龙”、“熊猫”、“孙悟空”等,推荐理由只要言之有理即可;4分三4分7、我们的教育是老师喜欢用所谓的标准答案来衡量学生答题的对与错,结果是培养了学生的“考试能力”；削弱了学生的动手能力、实践能力想象力和创造力；造成好多学生不敢说真话、诉真情;4分;意思对即可;若有其他答案,只要合理,亦可酌情给分;二、共44分一共14分8、清算,列举全部罪恶或错误并做出相应的处理;使用“清算”一词,表现了父亲对子女学习上要求的严格和态度的严厉;2分,含义1分,作用1分9、母亲既疼爱儿子,又希望儿子上进,内心是矛盾痛苦的,话语既是违心的,又是出于对儿子的期待;意思对即可,只要能体会母亲矛盾的心情即可2分10、不设统一答案;如：“我自己呜咽着,同时听得见坐在旁边缝纫着的母亲也唏唏嘘嘘地泪如泉涌地哭着;”这个细节描写表现母亲对子女无限怜惜和疼爱之情;3分,举例得1分,说理由得2分;11、不设统一答案,内容只要能写出母爱让你感动的瞬间即可得2分,语言要求通顺,得1分;只要作答,一般不判0分;12、课文中的母亲和材料中的母亲都爱自己的孩子,但她们的教育方法有好的一面,也有不可取之处;课文中的母亲疼爱儿子,又希望儿子上进,并用自己的爱温暖孩子受伤的心,但面对丈夫的“棍棒”教育,虽然心疼却不能阻止2分；材料中的母亲教子严格,处罚孩子的目的是对孩子有所惩戒,在惩罚的过程中还很注意保护孩子的自尊心,但有时过于严厉了,体罚毕竟是不可取的;2分意思对即可三12分17、①同“嬉”,可玩笑; ②本来③用④离开座位,表示郑重;2分;答对两个给1分;意思对即可;18、①酒喝得正畅快的时候,两个小官吏捆绑着一个人到楚王面前;②橘树在淮河以南就成长为橘；在淮河以北就成了枳,两者只是叶子相似,它果实味道是不同的;4分;每小题2分;意思对即可;19、预先安排抓住齐人偷盗的情境,当晏子到来时,故意带到楚王面前,以此影射齐人都善偷,从而戏弄晏子;2分,意思对即可;。

数学八年级上册期中试卷及答案【含答案】

数学八年级上册期中试卷及答案【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 若 a > b，则下列哪个选项是正确的？A. a b > 0B. a + b > 0C. a × b > 0D. a ÷ b > 02. 下列哪个数是负数？A. -(-5)B. -|3|C. -(+2)D. -(-2)3. 若 a = 3，b = -2，则 a + b 的值为？A. 1B. 5C. -5D. -14. 下列哪个选项是正确的？A. 0 是正数B. 0 是负数C. 0 既不是正数也不是负数D. 0 是最小的自然数5. 下列哪个选项是正确的？A. 正数都大于 0B. 负数都小于 0C. 正数大于一切负数D. 0 大于一切负数二、判断题（每题1分，共5分）1. 两个负数相加，和一定是负数。

（）2. 两个正数相乘，积一定是正数。

（）3. 0 除以任何不为零的数都得零。

（）4. 任何正数都有两个平方根，这两个平方根互为相反数。

（）5. 负数都小于正数。

（）三、填空题（每题1分，共5分）1. 最大的负整数为______。

2. 如果 a > b，那么 a b = ______。

3. 如果 a < b，那么a ÷ b = ______。

4. 如果 a > 0，那么 -a = ______。

5. 如果 a < 0，那么 |a| = ______。

四、简答题（每题2分，共10分）1. 请简述有理数的概念。

2. 请简述相反数的概念。

3. 请简述绝对值的概念。

4. 请简述正数和负数的概念。

5. 请简述零的概念。

五、应用题（每题2分，共10分）1. 已知 a = 3，b = -2，求 a + b 的值。

2. 已知 a = -5，b = 4，求 a b 的值。

3. 已知 a = -3，b = -2，求a × b 的值。

4. 已知 a = 8，b = -4，求a ÷ b 的值。

八年级上学期期中考试测试卷(含答案)

八年级上学期期中考试测试卷（含答案）一．基础知识和综合运用(30分)1．默写古诗文中的名句。

(10分)(1 ) 树树皆秋色，______________________。

(《野望》)(2 ) 乱花渐欲迷人眼，__________________。

（《钱塘湖春行》）( 3) 庭中有奇树，_____________________。

（《庭中有奇树》)(4 )___________________，志在千里(《龟虽寿》)（5）柴门何萧条，___________________。

(《梁甫行》(6 ) 《记承天寺夜游》中描写月色如水，空明澄澈的句子是“____________________，____________________，__________________”(7 )《黄鹤楼》一诗中情景交融，抒发游子悲苦的思乡之情的诗句是：________________？____________ __。

2.阅读以下文字，完成第（1）--（5）题（8分）开学以来，语文学习的内容丰富多彩。

《消息二则》高屋建瓴，气势磅礴，是新闻作品中的瑰宝；《藤野先生》向我们讲述了那个特殊的年代里感人至深而又发人深省的往事；那清幽秀丽，雄奇险拨的《三峡》风光，令人不禁想做一次三峡之旅；《与朱元思书》以简练隽永的笔墨，描绘了一幅充满生机的大自然画卷，难道无不令我们向往吗?……（1）给文中加粗的字注音（2分）瓴（）隽（）（2）文中有一个错别字的词语是，这个词语的正确写法是（2分）（3）文中有一病句，改正后抄写在横线上（2分）（4）“隽永”的意思是：（1分）（5）本段文字运用的修辞方法有和（1分）3.名著知识填空（5分）《红星照耀中国》又名《》，是美国著名新闻记者（填写人名）写的一部纪实性作品，是世界上第一本忠实描绘红色中国的著作。

作者在书中写到的红军“大迁移”是指工农红军的，作者断定它是一场战略撤退，称赞它是一部，是现代史上的无与伦比的一次远征。

八年级数学(人教版)年级上册学期期中复习01(试题+答案版)及答案

八年级（上）人教版数学期中过关测试01学校：_____________班级：____________ 姓名：______________（时间：120分钟分值：120分）一、选择题（共10小题，每小题3分，共30分）1．下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）A．B．C．D．2．如图，已知点A、D、C、F在同一条直线上，AB＝DE，BC＝EF，要使△ABC≌△DEF，还需要添加一个条件是（）A．∠BCA＝∠F B．∠B＝∠E C．BC∥EF D．∠A＝∠EDF3．三条公路将A、B、C三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是（）A．三条高线的交点B．三条中线的交点C．三条角平分线的交点D．三边垂直平分线的交点4．如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是（）A．∠B＝∠C B．AD⊥BC C．AD平分∠BAC D．AB＝2BD5．一个多边形的每一个外角都等于45°，那么这个多边形的内角和为（）A．1260°B．1080°C．1620°D．360°6．某同学把一块三角形的玻璃打碎了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（）A．带①去B．带②去C．带③去D．带①②③去7．空调安装在墙上时，一般都会采用如图的方法固定，这种方法应用的几何原理是（）A．两点确定一条直线B．两点之间线段最短C．三角形的稳定性D．垂线段最短8．以下是四位同学在钝角三角形ABC中画BC边上的高，其中画法正确的是（）A．B．C．D．9．如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若∠BAC＝102°，则∠EAF为（）A．38°B．40°C．24°D．44°10．如图，在△ABC中，已知点D，E，F分别为BC，AD，EC的中点，且S＝12cm2，则阴影部分面△ABC积S＝（）cm2．A．1B．2C．3D．4二、填空题（共5小题，每小题3分，共15分）11．已知等腰三角形一腰上的高与另一腰的夹角为50°，则等腰三角形的顶角度数为．12．一个三角形的三边为2、4、x，另一个三角形的三边为y、2、6，若这两个三角形全等，则x+y ＝．13．若一个三角形的三条高所在直线的交点在三角形外部，此三角形是三角形．14．如图所示，∠A＝∠E，AC⊥BE，AB＝EF，BE＝18，CF＝8，则AC＝．15．如图，△ABC中，∠A＝75°，∠B＝65°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，则∠2的度数是．三、解答题（共8小题，共75分）16．（8分）如果一个多边形的内角和是外角和的3倍还多180°，那么这个多边形的边数是多少？17．（8分）如图，在平面直角坐标系中，A（2，4），B（3，1），C（﹣2，﹣1）．（1）在图中作出△ABC关于x轴的对称图形△A1B1C1，并写出点A1，B1，C1的坐标；（2）求△ABC的面积．18．（9分）已知：如图，∠A＝∠D＝90°，AC＝BD．求证：AB＝CD．19．（9分）如图，在△ABC中，∠B＝26°，∠BAC＝30°，过点A作BC边上的高，交BC的延长线于点D，CE平分∠ACD，交AD于点E．求∠AEC的度数．20．（10分）已知：如图，∠A＝∠D＝90°，点E、F在线段BC上，DE与AF交于点O，且AB＝CD，BE ＝CF．求证：△OEF是等腰三角形．21．（10分）如图，点P是∠AOB外的一点，点Q与P关于OA对称，点R与P关于OB对称，直线QR 分别交OA、OB于点M、N，若PM＝PN＝4，MN＝5．（1）求线段QM、QN的长；（2）求线段QR的长．22．（10分）如图所示，已知△ABD≌△CFD，AD⊥BC于D．（1）求证：CE⊥AB；（2）已知BC＝7，AD＝5，求AF的长．23．（11分）如图，在四边形ABCD中，AD∥BC，点E为对角线BD上一点，∠A＝∠BEC，且AD＝BE．（1）求证：△ABD≌△ECB．（2）若∠BDC＝70°．求∠ADB的度数．参考答案一、选择题12345678910DBCDBCCBCC二、填空题11．40°或140°12．1013．钝角14．1015．60°三、解答题16．解：设这个多边形的边数为n ，根据题意，得（n ﹣2）•180＝360×3+180，解得：n ＝9．即这个多边形的边数是9．17．解：（1）如图所示：△A 1B 1C 1即为所求，A 1（2，﹣4），B 1（3，﹣1），C 1（﹣2，1）．（2）S △ABC ＝5×5―12×4×5―12×1×3―12×2×5=172．18．证明：连接BC ，∵∠A＝∠D＝90°，∴△ABC和△DCB都是直角三角形．在Rt△ABC和Rt△DCB中，BC=CBAC=DB，∴Rt△ABC≌Rt△DCB（HL）．∴AB＝CD．19．解：∵∠B＝26°，∠BAC＝30°，∴∠ACD＝56°，∵CE平分∠ACD，∴∠ACE＝∠ECD＝28°，∵AD⊥BD，∴∠CDE＝90°，∴∠AEC＝∠ECD+∠D＝118°．20．证明：∵BE＝CF，∴BE+EF＝CF+EF，即BF＝CE，在Rt△ABF和Rt△DCE中，AB=DC BF=CE，∴Rt△ABF≌Rt△DCE（HL）∴∠AFB＝∠DEC，∴OE＝OF，∴△OEF是等腰三角形．21．解：（1）∵P，Q关于OA对称，∴OA垂直平分线段PQ，∴MQ＝MP＝4，∵MN＝5，∴QN＝MN﹣MQ＝5﹣4＝1．（2）∵P，R关于OB对称，∴OB垂直平分线段PR，∴NR＝NP＝4，∴QR＝QN+NR＝1+4＝5．22．（1）证明：∵△ABD≌△CFD，∴∠BAD＝∠DCF，又∵∠AFE＝∠CFD，∴∠AEF＝∠CDF＝90°，∴CE⊥AB；（2）解：∵△ABD≌△CFD，∴BD＝DF，∵BC＝7，AD＝DC＝5，∴BD＝BC﹣CD＝2，∴AF＝AD﹣DF＝5﹣2＝3．23．证明：（1）∵AD∥BC，∴∠ADB＝∠CBE，在△ABD和△ECB中，∠A=∠BEC AD=BE∠ADB=∠CBE，∴△ABD≌△ECB（ASA）；（2）∵△ABD≌△ECB，∴BD＝BC，∴∠BDC＝∠BCD＝70°，∴∠DBC＝40°，∴∠ADB＝∠CBD＝40°．八年级（上）人教版数学期中过关测试01参考答案一、选择题12345678910DBCDBCCBCC二、填空题11．40°或140°12．1013．钝角14．1015．60°三、解答题16．解：设这个多边形的边数为n ，根据题意，得（n ﹣2）•180＝360×3+180，解得：n ＝9．即这个多边形的边数是9．17．解：（1）如图所示：△A 1B 1C 1即为所求，A 1（2，﹣4），B 1（3，﹣1），C 1（﹣2，1）．（2）S △ABC ＝5×5―12×4×5―12×1×3―12×2×5=172．18．证明：连接BC ，∵∠A＝∠D＝90°，∴△ABC和△DCB都是直角三角形．在Rt△ABC和Rt△DCB中，BC=CBAC=DB，∴Rt△ABC≌Rt△DCB（HL）．∴AB＝CD．19．解：∵∠B＝26°，∠BAC＝30°，∴∠ACD＝56°，∵CE平分∠ACD，∴∠ACE＝∠ECD＝28°，∵AD⊥BD，∴∠CDE＝90°，∴∠AEC＝∠ECD+∠D＝118°．20．证明：∵BE＝CF，∴BE+EF＝CF+EF，即BF＝CE，在Rt△ABF和Rt△DCE中，AB=DC BF=CE，∴Rt△ABF≌Rt△DCE（HL）∴∠AFB＝∠DEC，∴OE＝OF，∴△OEF是等腰三角形．21．解：（1）∵P，Q关于OA对称，∴OA垂直平分线段PQ，∴MQ＝MP＝4，∵MN＝5，∴QN＝MN﹣MQ＝5﹣4＝1．（2）∵P，R关于OB对称，∴OB垂直平分线段PR，∴NR＝NP＝4，∴QR＝QN+NR＝1+4＝5．22．（1）证明：∵△ABD≌△CFD，∴∠BAD＝∠DCF，又∵∠AFE＝∠CFD，∴∠AEF＝∠CDF＝90°，∴CE⊥AB；（2）解：∵△ABD≌△CFD，∴BD＝DF，∵BC＝7，AD＝DC＝5，∴BD＝BC﹣CD＝2，∴AF＝AD﹣DF＝5﹣2＝3．23．证明：（1）∵AD∥BC，∴∠ADB＝∠CBE，在△ABD和△ECB中，∠A=∠BEC AD=BE∠ADB=∠CBE，∴△ABD≌△ECB（ASA）；（2）∵△ABD≌△ECB，∴BD＝BC，∴∠BDC＝∠BCD＝70°，∴∠DBC＝40°，∴∠ADB＝∠CBD＝40°．。

初二期中测试题及答案

初二期中测试题及答案一、选择题（每题2分，共20分）1. 下列哪个选项是正确的？A. 地球是宇宙的中心B. 地球围绕太阳公转C. 月球是地球的卫星D. 太阳是地球的卫星答案：B2. 以下哪个朝代是中国历史上第一个统一的封建王朝？A. 商朝B. 周朝C. 秦朝D. 汉朝答案：C3. 以下哪个选项是光合作用的产物？A. 氧气B. 二氧化碳C. 水D. 葡萄糖答案：A4. 以下哪个是化学变化？A. 铁生锈B. 冰融化C. 切割木材D. 蒸馏水答案：A5. 以下哪个是英语中的第一人称单数？A. IB. YouC. HeD. They答案：A6. 以下哪个是二次函数的一般形式？A. y = ax^2 + bx + cB. y = ax + bC. y = ax^3 + bx^2 + cx + dD. y = a/x答案：A7. 以下哪个是《三国演义》中的人物？A. 刘备B. 关羽C. 张飞D. 以上都是答案：D8. 以下哪个是人体最大的淋巴器官？A. 扁桃体B. 胸腺C. 脾脏D. 淋巴结答案：C9. 以下哪个是法国的首都？A. 伦敦B. 柏林C. 巴黎D. 罗马答案：C10. 以下哪个是联合国的创始会员国之一？A. 中国B. 俄罗斯C. 美国D. 以上都是答案：D二、填空题（每题2分，共20分）1. 地球的赤道周长大约是________千米。

答案：400752. 世界上最长的河流是________。

答案：尼罗河3. 化学元素周期表中，氧元素的原子序数是________。

答案：84. 牛顿的第二定律公式是________。

答案：F = ma5. 英语中，“图书馆”的单词是________。

答案：library6. 圆周率π的近似值是________。

答案：3.141597. 世界上最大的沙漠是________。

答案：撒哈拉沙漠8. 人体中最大的细胞是________。

答案：卵细胞9. 法国的国庆日是每年的________月________日。