平行四边形-拔高(9页)
平行四边形拔高练习

平⾏四边形拔⾼练习专题⼀平⾏四边形1.若A 、B 、C 三点不共线,则以其为顶点的平⾏四边形共有()个2.⼀个平⾏四边形的两条邻边的长分别是4cm 和5cm ,它们的夹⾓是30°,这个平⾏四边形的⾯积是().3.⼀个四边形的边长依次是a 、b 、c 、d 且,则这个四边形的形状为 .若,判定以a 、b 、c 、d 为边的四边形的形状为4.平⾏四边形ABCD 中,AB=5cm, BC=3cm, ∠D 与∠C 的平分线分别交AB 于F,E, EF=5. 如图,⼝ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上翻折,点A 正好落在CD 上的点F ,若△FDE 的周长为8,△FCB 的周长为22,则FC 的长为 .6.如图所⽰,在形状为平⾏四边形的⼀块地ABCD 中,有⼀条⼩折路EFG .?现在想把它改为经过点E 的直路,要求⼩路两侧⼟地的⾯积都不变,?请在图中画出改动后的⼩路.7.如图,为公园的⼀块草坪,其四⾓上各有⼀棵树,现园林⼯⼈想使这个草坪的⾯积扩⼤⼀倍,⼜要四棵树不动,并使扩⼤后的草坪为平⾏四边形,试问这个想法能否实现,若能请你设计出草图.8. 如图,在矩形ABCD 中,AB=3,AD=4,点P 在AD 上,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE+PF 等于()8. 如图所⽰,在平⾏四边形ABCD 中,∠ABC=60°,且AB=BC ,∠MAN=60°.请探索BM ,DN 与AB 的数量关系,并证明你的结论.9.如图:平⾏四边形ABCD ,在AB 的延长线上截取BE =AB ,BF =BD ,连结CE 、DF 交于G 点,试说明:CD =CG 。
10.如图将矩形纸⽚ABCD 沿AE 折叠,使点B 落在直⾓梯形AECD 的中位线FG 上,若则AE 的长为()44444a bcdabcd +++=bd ac d c b a 222222+=+++11.如图,将边长为8㎝的正⽅形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是()12.如图,矩形中,过对⾓线交点作交于则的长是()13.将矩形纸⽚ABCD按如图所⽰的⽅式折叠,AE、EF为折痕,∠BAE=30°,AB=,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为().14.如图,在矩形中,动点从点出发,沿→→→⽅向运动⾄点处停⽌.设点R运动的路程为,的⾯积为,如果关于的函数图象如图2所⽰,则当时,点R应运动到()15.如图,在平⾏四边形ABCD中,以AC为斜边作Rt△ACE,⼜∠BED=90°,则四边形ABCD 是矩形.试说明理由.16.如图,四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD?的中点,那么MN⊥BD 成⽴吗?试说明理由.17.如图矩形中,延长到,使,是中点.求证:.18.如图所⽰,在直⾓坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对⾓线的交点P的坐标为(52,1)⑴写出B、C、D三点的坐标;⑵若在线段AB上有⼀点若在AB上有⼀点E(⼆分之三,0),过E点的直线将矩形ABCD的⾯积分为相等的两部分,求直线的解析式;⑶若过C点的直线将矩形ABCD的⾯积分为4:3两部分,并与y轴交于点M,求M点的坐标.ABCD35AB BC==,.O OE AC⊥AD E,AE3MNPQ R N N P Q M Mx MNR△y y x9x=ABCD CB E CE AC=F AE BF DF⊥l1.如图,菱形OABC 的⼀边OA 在x 轴上,将菱形OABC 绕原点O 顺时针旋转75°⾄OA ′B ′C ′的位置,若C=120°,则点B′的坐标为()2.如图是⼀个利⽤四边形的不稳定性制作的菱形晾⾐架.已知其中每个菱形的边长为20cm ,墙上悬挂晾⾐架的两个铁钉A 、B 之间的距离为20cm ,则∠1等于()A 、90°B 、60°C 、45°D 、30°3.如图,点P 是边长为1的菱形ABCD 对⾓线AC 上的⼀个动点,点M 、N 分别是AB 、BC 边上的中点,MP+NP 的最⼩值是()4.已知:如图,C 是线段BD 上⼀点,△ABC 和△ECD 都是等边三⾓形,R 、F 、G 、H 分别是四边形ABDE 各边的中点,求证:四边形RFGH 是菱形。
平行四边形综合训练拔高题.doc

平行四边形综合训练拔高题一.选择题(共15小题)1.如图,?ABCD中,A C.BD 为对角线,BC=3,BC边上的高为2,则阴影部分的面积为()A.3 B.6 C.12 D.242.已知平行四边形一边长为10,一条对角线长为6,则它的另一条对角线α的取值范围为()A.4<α<16 B.14<α<26C.12<α<20 D.以上答案都不正确3.在?ABCD中,AB=3,BC=4,当?ABCD的面积最大时,下列结论正确的有()①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④4.某地需要开辟一条隧道,隧道AB 的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE的长为1100m,则隧道AB的长度为()A.3300m B.2200m C.1100m D.550m5.如图,在矩形ABCD中,P、R 分别是BC和DC上的点,E、F 分别是AP和RP的中点,当点P在BC上从点B向点C移动,而点R不动时,下列结论正确的是()A.线段EF的长逐渐增长B.线段EF的长逐渐减小C.线段EF的长始终不变D.线段EF的长与点P 的位置有关6.如图,DE是△ABC的中位线,且△ADE的周长为20,则△ABC的周长为()A.30 B.40 C.50 D.无法计算7.如图是一个由 5 张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为()A.4S1 B.4S2 C.4S2+ S3 D.3S1+4S38.如图,?ABCD的对角线A C、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= B C,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB?AC;③OB=AB;④OE= BC,成立的个数有()A.1 个B.2 个C.3 个D.4 个9.如图,在平行四边形ABCD中,A E⊥BC于E,AF⊥CD于F,若AE=4,AF=6,平行四边形ABCD的周长为40.则平行四边形ABCD的面积为()A.24 B.36 C.40 D.4810.如图所示,?ABCD中,两条对角线AC、BD 相交于点O,AF⊥BD 于F,CE ⊥BD于E,则图中全等三角形的对数共有()A.5 对B.6 对C.7 对D.8 对11.若?ABCD的对称中心在坐标原点,AD∥x 轴,若A 的坐标为(﹣1,2),则点C的坐标为()A.(1,﹣2)B.(2,﹣1)C.(1,﹣3)D.(2,﹣3)12.如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°13.如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于()A.2 B.3 C.4 D.614.在面积为15 的平行四边形ABCD中,过点A 作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为()A.11+ B.11﹣C.11+ 或11﹣D.11+ 或1+15.如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为()A.13 B.17 C.20 D.26二.解答题(共 6 小题)16.如图,已知 B E∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.17.在?ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.(1)如图1,若∠ADC=9°0,G是EF的中点,连接AG、C G.①求证:BE=BF.②请判断△AGC的形状,并说明理由;(2)如图2,若∠ADC=6°0,将线段FB绕点F顺时针旋转60°至FG,连接AG、C G.那么△AGC又是怎样的形状.(直接写出结论不必证明)18.在平行四边形ABCD中,对角线BD⊥B C,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.若平行四边形ABCD的面积为,求AG的长.。
平行四边形画高(课堂PPT)

2
长方形
正方形 平行四边形
梯形
3
❖❖它两有组几对条边边分?别边平有行什的么四特边点形?,是平行 有四几边个形角. ?是什么样的角?
❖平行四边形有四条边,对边平行且相 等,有四个角, 对角相等.
4
做一做,想一想。
平行四边形容易变形,具有不稳定性。
5
想一想:长方形、正方形是平行四边形 吗?
A
底
D
高
B
底
C
判断下面的红色线段是平行四边形的底 和高吗?是的话,哪条是底,哪条是高?
高
底 (1)
高 底
(2)
×
(3)
×
(4) 底2
高 1 高2
×
(5)
×
(6)
底1 (7)
16
1、判断:
(1)两组对边分别平行的图形是平行四边形。 (X) (2)平行四边形的两组对边分别平行且相等。 (√ ) (3)长方形、正方形都是特殊的平行四边形。 (√ )
高
底
从平行四边形一条边上的一点到对 边引一条垂线,这点和垂足之间的线段 叫做平行四边形的高。
这条对边叫做平行四边形的底。
11
平行四边形高的画法 高 底
步骤:
1. 找一条边做底 2. 找对边一个点 3.利用学具对准
点和线 4.画高:用虚线 5.写上底和高
12
高 底
13
高 高
底 底
14
思考:平行四边形有几条高?
长方形正方形平行四边形梯形长方形正方形对边相等且平行四个角是直角四条边都相等对边平行四个角是直角正方形我们可以用图来表示四边形之间的关系101112平行四边形高的画法找对边一个点4
北师大版九年级数学上册 第一章 特殊的平行四边形 培优、拔高专题讲义专题训练

19、如图所示,点 坐标为 藰 ڹ,点 坐标为 藰 ڹ藰 ,动点 从点 开始沿 以每秒 个单位长
度的速度向点 移动,动点 从点 开始沿 以每秒 藰 个单位长度的速度向点 移动.如果 、
分别从 、 同时出发,用 (秒)表示移动的时间 ڹ藰 ,那么,
当 为何值时,四边形
第 2 页 共 11 页
(Ⅰ)求证:四边形 PBQD 是平行四边形; (Ⅱ)若 AD=6cm,AB=4cm,点 P 从点 A 出发,以 1cm/s 的速度向点 D 运动(不与点 D 重合),设点 P 运 动的时间为 ts,请用含 t 的代数式表示 PD 的长,并求出当 t 为何值时四边形 PBD 是菱形,并求出此时菱 形的周长.
以矩形 A1B1C1D1 的中点为顶点作菱形 A2B2C2D2 ,……,如此下去,得到四边形 A2019B C D 2019 2019 2019 的面积用
含 a,b 的代数式表示为
。
3、如图所示,正方形 ABCD 的面积为 12,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角
线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为
北师大版九年级数学上册 第一章 特殊的平行四边形 培优、拔高专题讲义及练习 1、已知,R△ABC 中,∠C=90°,AC=3,BC=4,P 为 AB 上任意一点,PF⊥AC 于 F,PE⊥BC 于 E,则 EF 的最 小值是___________.
2、如图,菱形 ABCD 的对角线长分别为 a、b,以菱形 ABCD 各边的中点为顶点作矩形 A1B1C1D1 ,然后再
沿着
y
轴向上平移
2 3
个单位交
x
轴于点
M ,交直线 l1 于点 N ,求 NMF 的面积.
特殊平行四边形拔高复习

第一章特殊平行四边形拔高复习一特殊平行四边形知识汇总矩形1如定义:有一个角是直角的平行四边形叫做矩形2.性质:(1)矩形的四个角都是直角亠(2)矩形的对角线相等(3)具备平行四边形的性质3.判定:(1 )有一个角是直角的平行四边形是矩形(定义)(2)对角线相等的平行四边形是矩形(3)有三个角是直角的四边形是矩形養形1如定义:有一组邻边相等的平行四边形叫做菱形厶•性质:(1)菱形的四条边都相等(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角a (3)具备平行四边形的性质丄3.判定:(1)一组邻边相等的平行四边形是菱形亠(2)对角线互相垂直的平行四边形是菱形(3)四边相等的四边形是菱形正方形1.定义:有一组邻边相等且有一个角是直角的平行四边形是正方形鼻2 •性质:(I )边:两组对边分别平行;四条边都相等;相邻边互相垂直亠(2 )内角:四个角都是90°;(3)对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;鼻(4)对称性:既是中心对称图形,乂是轴对称图形(有四条对称轴)。
(5)形状:正方形也属于长方形的一种。
6(.)正方形具有平行四边形、菱形、矩形的一切性质。
3.判定:(1)对角线相等的菱形是正方形。
鼻(2)有一个角为直角的菱形是正方形。
鼻(3)对角线互相垂直的矩形是正方形。
(4)一组邻边相等的矩形是正方形。
鼻(5)-组邻边相等且有一个角是直角的平行四边形是正方形。
(6)对角线互相垂直且相等的平行四边形是正方形。
人(7)对角线互相垂直,平分且相等的四边形是正方形。
•(8)一组邻边相等,有三个角是直角的四边形是正方形。
(9)既是菱形乂是矩形的四边形是正方形。
二专题整合与拔高专题一特殊四边形的综合应用1、(2013・白银)如图,在△ ABC中,D是BC边上的一点,E是AD的中点,过A点作BC 的平行线交CE 的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;(2)当厶ABC满足什么条件时,四边形AFB D是矩形?并说明理由.考点:矩形的判定;全等三角形的判左与性质.专题:证明题.分析:(1)根据两直线平行,内错角相等求出Z AFE=zDCE,然后利用“角角边”证明A AEF和ADEC全等,根拯全等三角形对应边相等可得A F=CD,再利用等量代换即可得证;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知Z ADB=90\由等腰三角形三线合—的性质可知必须是AB=AC.解答:解:(1 )BD=CD.理由如下:T AFII BC.・•. Z AFE=z DCE»•••E是AD的中点,AE = DE,r ZxOT=ZDCEAEF 和厶DEC 屮「上AEF二ZDEC •AE=DE・・・△AEF更△ DEC (A AS),.•・AF =CD,・・• AF= B D ,・・・BD = C D;(2)当A ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:V AFII BD, AF=BD>四边形AF BD是平行四边形,・・• A B=AC, BD=C D,/. Z ADB=9 0\/. -AFBD是矩形.点评:本题考査了矩形的判曲全等三角形的判定与性质,平行四边形的判曲是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.2、(13年山东靑岛、2 1 )已知:如图,在矩形A B CD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点(1 )求证:AA BM^ADCM(2)判断四边形MENF是什么特殊四边形,并证明你的结论:(3)当AD:AB= ____________ 时,四边形MEN F是正方形(只写结论,不需证明)解析:(U)因为四边形A BCD是矩形,所以,ZA=ZD=90c,人M DAB=DC,又MA二HD,所以CM⑵四边形MEN F是菱形;理由:因为CE=EM/CN=NB,所以,FN〃MB,同理可得:EN〃MC, 所以,四边形MENF为平行四边形,又厶ABM^AD CM・:平行四边形畑'胪是菱形(3)2: 13.( 2 012珠海,1 8 , 7分)如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A8CD,(此时,点B,落在对角线AC上,点/V落在CD的延长线上),A8交AD于点E, 连结AA'、CE.求证:(1 )AA DA f ^ACI) E;(2 )直线CE是线段AA,的垂直平分线.【解析】(1)由题设可得AD二DC, ZADA' =ZCDE=90° > DA'二DE.•••△ADA' ^ACDE.(2)证CE是ZACA'的角平分线,由等腰三角形的“三线合一”可得CE是线段AA,的垂直平分线.【答案】(1)由正方形的性质及旋转,得AD=DC, ZADC=90° , A C二A' C, ZDA' E=45° , ZADA Z =ZCD E=90° , A ZD EA r =ZDA r E=4 5 ° . ADA,二DE.•••△ADA' ^ACDE・(2)由正方形的性质及旋转,得CD=CB r , ZCB f E=ZC D E=90 ° ,CE二CE,ARtACB r E ^Rt ACD E ••:心2 C, /.直线CE是线段AA'的垂直平分线.【点评】本题要求综合应用正方形的性质,旋转变换,三角形全等的判左,等腰三角形的“三线合一S 线段垂直平分线的判左等知识解决问题,是一道证线段垂直平分线的典型范例.专题二构造特殊四边形解决问1 •如图?RtA ABC 中,ZC=90。
八级数学平行四边形的性质和判定拔高教案

学生: ______________ 名思教育个性化辅导教案班主任: ____________ 日期: ________________ 时段: _____________________二、平行四边形的性质1、 (边)平行四边形的对边平行且相等.例如:如图①所示,在 ABCD 中,ABCD ,ADBC . 由上述性质可得,夹在两条平行线间的平行线段相等.如图2,直线l i II, CD 是夹在直线l i , 12间的平行线段,则四边形 ABCD 是平行四边形,故ABCD .2、 (角)平行四边形的对角相等,邻角互补.例如:如图①所示,在ABCD 中, Z ABC = Z CDA ,/BAD =Z BCD . ABC + /BAD = 180 ° , A BC + /BCD = 180 ° , B CD +/CDA = 180 ° , BAD + ZCDA = 180 ° .3、 (对角线)平行四边形的对角线互相平分.例如:如图①所示,在ABCD 中, OA = OC , OB = OD .图① 图② 图③4、 经过平行四边形对角线的交点的直线被对边截得的两条线段相等,并且该直线平分平行四边形的面积.例如:如图③所示,在 ABCD 中,EF 经过对角 线的交点0,与AD 和BC 分别交于点E , F ,则0E = OF , 且 S 四边形ABFE = S 四边形EFCD【例2] ABCD 的周长为30 cm ,它的对角线AC 和BD 交于0,且△AOB 的 周长比△ BOC 的周长大5 cm ,求AB , AD 的长.三、平行四边形的判定两组对边分别平行的四边形叫做平行四边形. 两组对边分别相等的四边形是平行四边形. 一组对边平行且相等的四边形是平行四边形 两组对角分别相等的四边形是平行四边形.5、 方法五(对角线):对角线互相平分的四边形是平行四边形.6、 注意:(1)判定方法可作为“画平行四边形”的依据; (2) 一组对边平行,另一组对边相等的四边形不一定是平行四边形.【例3 ]已知,如图,在四边形 ABCD 中,AC 与BD 相交于点O , AB //CD ,AO = CO .四边形ABCD 是平行四边形,请说明理由.四、三角形的中位线1、定义:连接三角形两边中点的线段叫做三角形的中位线.2、 性质:三角形两边中点连线平行于第三边,并且等于第三边的一半.3、 注意:(1) 一个三角形有三条中位线,每条中位线与第三边都有相应的位置关系和数量 关系;(2) 三角形的中位线不同于三角形的中线, 三角形的中位线是连接两边中点的线 段,而三角形的中线是连接三角形一边的中点和这边所对顶点的线段.【例4]如图所示,在△ ABC 中,点D , E 、F 分别是AB , BC , CA 的中点1、 方法一(边)2、 方法二(边) 3、 方法三若△ABC的周长为10 cm,则8EF的周长是______________ cm.五、两条平行线间的距离1、定义:两条平行线中,一条直线上任意一点到另一直线的距离,叫做这两条平行线间的距离.如图所示,a//b,点A在直线a上,过A点作AC丄b,垂足为C,则线段AC 的长是点A到直线b的距离,也是两条平行线a, b之间的距离.2、规律:(1)如图,过直线a上点B作BD丄b,垂足为D,则线段BD的长也是两条平行线a, b之间的距离.于是由平行四边形的性质可知平行线的又一个性质:平行线间的距离处处相等.(2)两条平行线之间的距离是指垂线段的长度,当两条平行线的位置确定时,它们之间的距离也随之确定,它不随垂线段的位置的改变而改变,是一个定值.【例5】如图所示,如果l i //|2,那么z\ABC的面积与A DBC的面积相等吗由此你还能得出哪些结论六、平行四边形性质的应用平行四边形性质的应用非常广泛,可以利用它说明线段相等、证明线段平行、求角的度数、求线段的长度、求图形的周长、求图形的面积等.【例6】如图,ABCD的对角线相交于点0,过0作直线EF,并与线段AB, CD的反向延长线交于E, F, 0E与0F是否相等,阐述你的理由.七、平行四边形的判定的应用1、判定平行四边形的一般思路:①考虑对边关系:证明两组对边分别平行;或两组对边分别相等;或一组对边平行且相等;②考虑对角关系:证明两组对角分别相等;③考虑对角线关系:证明两条对角线互相平分.【例7】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)关系:① AD //BC,②AB = CD,③/A =Z C,④/B+ ZC= 180 ° .已知:在四边形ABCD中, ________ , _____ ;求证:四边形ABCD是平行四边形.八、平行四边形的性质和判定的综合应用1、平行四边形的性质和判定的应用主要有以下几种情况:(1) 直接运用平行四边形的性质解决某些问题,如求角的度数、线段的长、证明角相等或互补、证明线段相等或倍分关系;(2) 判定一个四边形为平行四边形,从而得到两角相等、两直线平行等;(3) 综合运用:先判定一个四边形是平行四边形,然后再用平行四边形的性质去解决某些问题;或先运用平行四边形的性质得到线段平行、角相等等,再判定一个四边形是平行四边形.校长签字:_____________。
人教版八年级数学下《平行四边形的性质》拔高练习

《平行四边形的性质》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)如图,在▱ABCD中,对角线AC、BD相交于O,α=60°.若AB=OD=2,则▱ABCD的面积是()A.8B.C.2D.42.(5分)如图,在▱ABCD中,连接AC,∠ABC=∠CAD=45°,AB=,则BC的长是()A.B.2C.2D.43.(5分)如图,▱ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E 点,CF平分∠BCD交AD于F点,则EF的长为()A.1cm B.2cm C.3cm D.4cm4.(5分)如图,在▱ABCD中AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2:3,▱ABCD的周长为40,则AB的长为()A.8B.9C.12D.155.(5分)如图,在平行四边形ABCD中,BC=7,CE平分∠BCD交AD边于点E ,且AE =3,则AB 的长为( )A .5B .4C .3D .二、填空题( 本大题共5小题,共25.0分)6.(5分)如图,在平行四边形ABCD 中,已知点E 在边BC 上,∠BAE =∠DAC ,AB =7,AD =10,则CE = .7.(5分)如图,平行四边形ABCD 的周长为20,对角线AC 的长为5,则△ABC的周长为 .8.(5分)如图,在平行四边形ABCD 中,BC =10,AC =8,BD =14,△AOD的周长是 .9.(5分)如图,在▱ABCD 中,E 、F 分别是AB 、DC 边上的点,AF 与DE 交于点P ,BF 与CE 交于点Q ,若S △APD =20cm 2,S △BQC =30cm 2,则图中阴影部分的面积为 cm 2.10.(5分)如图,平行四边形ABCD 中,AB =5,BC =3,∠ADC 与∠BCD 的平分线分别交AB 于F ,E ,则EF = .三、解答题(本大题共5小题,共50.0分)11.(10分)如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.(1)求平行四边形ABCD的面积S;(2)求证:∠EMC=2∠AEM.12.(10分)如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.(1)若BM=4,MC=3,AC=,求AM的长度;(2)若∠ACB=45°,求证:AN+AF=EF.13.(10分)如图,在平行四边形中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,BE=2,DF=3,求AB,BC的长及平行四边形ABCD的面积?14.(10分)如图,平行四边形ABCD的对角线AC、BD相交于点O,且AC=10,BD=16,AB=6,求△OCD的周长.15.(10分)如图,在平行四边形ABCD中,AB=10,AD=8,AC⊥BC.求BC,CD,AC,OA的长,以及平行四边形ABCD的面积.《平行四边形的性质》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)如图,在▱ABCD中,对角线AC、BD相交于O,α=60°.若AB=OD=2,则▱ABCD的面积是()A.8B.C.2D.4【分析】根据等边三角形的判定得出△DOC是等边三角形,再根据平行四边形的性质和的面积公式即可求解.【解答】解:∵在▱ABCD中,∴AB=DC,∵α=60°.AB=OD=2,∴△DOC是等边三角形,∴△DOC的面积=,∴▱ABCD的面积=4△DOC的面积=4,故选:D.【点评】本题考查了平行四边形的性质和面积,解此题的关键是熟练掌握平行四边形的性质.2.(5分)如图,在▱ABCD中,连接AC,∠ABC=∠CAD=45°,AB=,则BC的长是()A.B.2C.2D.4【分析】根据平行四边形的性质可得出CD=AB=、∠D=∠CAD=45°,由等角对等边可得出AC=CD=,再利用勾股定理即可求出BC的长度.【解答】解:∵四边形ABCD是平行四边形,∴CD=AB=,BC=AD,∠D=∠ABC=∠CAD=45°,∴AC=CD=,∠ACD=90°,即△ACD是等腰直角三角形,∴BC=AD==2.故选:B.【点评】本题考查了平行四边形的性质、等腰三角形的性质以及勾股定理,根据平行四边形的性质结合∠ABC=∠CAD=45°,找出△ACD是等腰直角三角形是解题的关键.3.(5分)如图,▱ABCD中,AB=3cm,BC=5cm,BE平分∠ABC交AD于E 点,CF平分∠BCD交AD于F点,则EF的长为()A.1cm B.2cm C.3cm D.4cm【分析】根据平行四边形的性质可知∠AEB=∠EBC,又因为BE平分∠ABC,所以∠ABE=∠EBC,则∠ABE=∠AEB,则AB=AE=3,同理可证FD=3,继而可求得EF=AE+DE﹣AD.【解答】解:∵四边形ABCD是平行四边形,∴∠AEB=∠EBC,AD=BC=5cm,∵BE平分∠ABC,∴∠ABE=∠EBC,则∠ABE=∠AEB,∴AB=AE=3cm,同理可证:DF=DC=AB=3cm,则EF=AE+FD﹣AD=3+3﹣5=1cm.故选:A.【点评】本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.4.(5分)如图,在▱ABCD中AE⊥BC,垂足为E,AF⊥CD,垂足为F,若AE:AF=2:3,▱ABCD的周长为40,则AB的长为()A.8B.9C.12D.15【分析】根据平行四边形的对边相等,可知一组邻边的和就是其周长的一半.根据平行四边形的面积,可知平行四边形的一组邻边的比和它的高成反比.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∴BC+CD=40÷2=20,根据平行四边形的面积公式,得BC:CD=AF:AE=3:2.∴BC=12,CD=8,∴AB=CD=8,故选:A.【点评】本题主要考查了平行四边形的性质,平行四边形的一组邻边的和等于周长的一半,平行四边形的一组邻边的比和它的高的比成反比.5.(5分)如图,在平行四边形ABCD中,BC=7,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为()A.5B.4C.3D.【分析】利用平行四边形的性质以及角平分线的性质得出∠DEC=∠DCE,进而得出DE=DC=AB求出即可.【解答】解:∵在▱ABCD中,CE平分∠BCD交AD于点E,∴∠DEC=∠ECB,∠DCE=∠BCE,AB=DC,∴∠DEC=∠DCE,∴DE=DC=AB,∵AD=BC=7,AE=3,∴DE=DC=AB=4.故选:B.【点评】此题主要考查了平行四边形的性质以及角平分线的性质,得出DE=DC =AB是解题关键.二、填空题(本大题共5小题,共25.0分)6.(5分)如图,在平行四边形ABCD中,已知点E在边BC上,∠BAE=∠DAC,AB=7,AD=10,则CE= 5.1.【分析】由▱ABCD的性质及∠BAE=∠DAC可得∠BAE=∠BCA,进而可判定△BAE∽△BCA,可得,可BE的长,即可得CE的长.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC=10,∴∠DAC=∠BCA,又∵∠BAE=∠DAC,∴∠BAE=∠BCA,∵∠B=∠B,∴△BAE∽△BCA,∴,∵AB=7,BC=10,∴BE=4.9,∴EC=5.1.故答案为:5.1.【点评】本题主要考查相似三角形的判定及性质、平行四边形的性质,根据平行四边形的性质得到∠BAE=∠BCA是判定三角形相似的前提,熟练运用相似形的性质是解题的关键.7.(5分)如图,平行四边形ABCD 的周长为20,对角线AC 的长为5,则△ABC 的周长为 15 .【分析】因为ABCD 是平行四边形,由题意得AB +BC =10,而AC 知道,那么△ABC 的周长就可求出.【解答】解:∵平行四边形中对边相等,∴AB +BC =20÷2=10,∴△ABC 的周长=AB +BC +AC =10+5=15.故答案为:15.【点评】本题考查了平行四边形的性质,三角形的周长等知识,灵活应用性质是解题的关键.8.(5分)如图,在平行四边形ABCD 中,BC =10,AC =8,BD =14,△AOD的周长是 21 .【分析】根据平行四边形的性质可得AD =BC =10,AO =CO =AC =4,BO =DO =BD =7,即可求△AOD 的周长.【解答】解:∵四边形ABCD 是平行四边形∴AD =BC =10,AO =CO =AC =4,BO =DO =BD =7∴△AOD 的周长=AD +AO +DO =21故答案为21【点评】本题考查了平行四边形的性质,熟练运用平行四边形的性质解决问题是本题的关键.9.(5分)如图,在▱ABCD 中,E 、F 分别是AB 、DC 边上的点,AF 与DE 交于点P ,BF 与CE 交于点Q ,若S △APD =20cm 2,S △BQC =30cm 2,则图中阴影部分的面积为 50 cm 2.【分析】连接E 、F 两点,由三角形的面积公式我们可以推出S △EFC =S △BCQ ,S △EFD =S △ADF ,所以S △EFG =S △BCQ ,S △EFP =S △ADP ,因此可以推出阴影部分的面积就是S △APD +S △BQC .【解答】解:连接E 、F 两点,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴△EFC 的FC 边上的高与△BCF 的FC 边上的高相等,∴S △EFC =S △BCF ,∴S △EFQ =S △BCQ ,同理:S △EFD =S △ADF ,∴S △EFP =S △ADP ,∵S △APD =20cm 2,S △BQC =30cm 2,∴S 四边形EPFQ =50cm 2,故答案为:50.【点评】本题主要考查了平行四边形的性质,题目综合性较强,主要考查了平行四边形的性质,解答此题关键是作出辅助线,找出同底等高的三角形.10.(5分)如图,平行四边形ABCD 中,AB =5,BC =3,∠ADC 与∠BCD 的平分线分别交AB 于F ,E ,则EF = 1 .【分析】由题意可得AD =AF =3,BC =BE =3,即可求EF 的长.【解答】解:∵四边形ABCD是平行四边形∴DC∥BA,AD=BC=3∵DF平分∠ADC∴∠ADF=∠CDF∵DC∥AB∴∠CDF=∠DF A∴∠ADF=∠AFD∴AD=AF=3同理可得BE=BC=3∵EF=AF+BE﹣AB∴EF=3+3﹣5=1故答案为:1【点评】本题考查了平行四边形的性质,熟练运用平行四边形的性质是本题的关键.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.(1)求平行四边形ABCD的面积S;(2)求证:∠EMC=2∠AEM.【分析】(1)利用平行四边形的性质以及直角三角形的性质得出CE的长,进而得出答案;(2)利用全等三角形的判定得出△AEM≌△DNM(ASA),根据全等三角形的性质得到EM=MN,根据直角三角形的性质得到MN=MC,根据等腰三角形和三角形的外角的性质即可得到结论.【解答】(1)解:∵M为AD的中点,AM=2AE=4,∴AD=2AM=8.在▱ABCD的面积中,BC=CD=8,又∵CE⊥AB,∴∠BEC=90°,∵∠BCE=30°,∴BE=BC=4,∴AB=6,CE=4,∴▱ABCD的面积为:AB×CE=6×4=24;(2)证明:延长EM,CD交于点N,连接CM.∵在▱ABCD中,AB∥CD,∴∠AEM=∠N,在△AEM和△DNM中∵,∴△AEM≌△DNM(ASA),∴EM=MN,又∵AB∥CD,CE⊥AB,∴CE⊥CD,∴CM是Rt△ECN斜边的中线,∴MN=MC,∴∠N=∠MCN,∴∠EMC=2∠N=2∠AEM.【点评】此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质等知识,熟练应用平行四边形的性质是解题关键.12.(10分)如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.(1)若BM=4,MC=3,AC=,求AM的长度;(2)若∠ACB=45°,求证:AN+AF=EF.【分析】(1)如图1中,连接AE,在Rt△ACE中,求出AE,再在Rt△AEM中求出AM即可;(2)如图,连接AE,作EH⊥AF于F,EG⊥DC交DC的延长线于E.由Rt △EHA≌Rt△EGC(HL),推出AH=CG,由Rt△EHF≌Rt△EGF(HL),推出FH=FG,由△AON≌△COF(ASA),推出AN=CF,推出AN+AF=FC+AF =FG﹣CG+FH+AH=2FH,由EF=FH,即可解决问题;【解答】(1)解:如图1中,连接AE.∵AB=AM,BE=EM,∴AE⊥BM,在Rt△ACE中,∵AC=,EC=EM+CM=5,∴AE==,在Rt△AEM中,AM==.(2)如图,连接AE,作EH⊥AF于F,EG⊥DC交DC的延长线于E.∵∠AEC=∠AFC=90°,∴∠AEC+∠AFC=90°,∴A,E,C,F四点共圆,∴∠AFE=∠ACE=45°,∴∠EF A=∠EFG=45°,∵EH⊥F A,EG⊥FG,∴EH=EG,∵∠ACE=∠EAC=45°,∴AE=EC,∴Rt△EHA≌Rt△EGC(HL),∴AH=CG,∵EF=EF,EH=EG,∴Rt△EHF≌Rt△EGF(HL),∴FH=FG,∵AB∥CD,∴∠OAN=∠OCF,∵∠AON=∠COF,OA=OC,∴△AON≌△COF(ASA),∴AN=CF,∴AN+AF=FC+AF=FG﹣CG+FH+AH=2FH,∵EF=FH,∴AN+AF=EF.【点评】本题考查平行四边形的性质、全等三角形的判定和性质、四点共圆、角平分线的性质定理、等腰直角三角形的判定和性质的等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.13.(10分)如图,在平行四边形中,AE⊥BC于E,AF⊥CD于F,∠EAF=60°,BE=2,DF=3,求AB,BC的长及平行四边形ABCD的面积?【分析】根据AE⊥BC于E,AF⊥CD于F,∠EAF=60°,可以得到∠C的度数,由四边形ABCD是平行四边形可以得到∠B、∠D的度数,然后根据解直角三角形的相关知识可以求得AB、BC的长,根据特殊角的三角函数可以求得AE的长,由平行四边形的面积等于底乘以高,可以求得四边形ABCD的面积.【解答】解:∵AE⊥BC于E,AF⊥CD于F,∴∠AEC=∠AFC=90∵∠EAF=60°,∴∠C=360﹣∠AEC﹣∠AFC﹣∠EAF=120,∴∠B=60°∴∠BAE=30°,∴AB=2BE=4;cm.∵∠D=∠B=60°,∴∠DAF=30°.∴AD=2DF=6cm.∴BC=AD=6cm在Rt△ADF中,AF==3(cm),∴ABCD的面积=CD•AF=4×3=12(cm2).【点评】本题考查平行四边形的性质、平行四边形的面积,30°角所对的直角边和斜边的关系,解题的关键是明确题意,找出所求问题需要的条件.利用数形结合的思想解答问题.14.(10分)如图,平行四边形ABCD的对角线AC、BD相交于点O,且AC=10,BD=16,AB=6,求△OCD的周长.【分析】根据平行四边形的性质即可解决问题;【解答】解:∵四边形ABCD是平行四边形,∴AB=CD=6,OA=OC=5,OB=OD=8,∴△OCD的周长=6+5+8=19.【点评】本题考查平行四边形的性质、三角形的周长等知识,解题的关键是熟练掌握平行四边形的性质,属于中考基础题.15.(10分)如图,在平行四边形ABCD中,AB=10,AD=8,AC⊥BC.求BC,CD,AC,OA的长,以及平行四边形ABCD的面积.【分析】根据平行四边形的性质得到AD=BC=8,OA=OC=AC,根据勾股定理求出AC的长,根据平行四边形的面积公式即可求出平行四边形ABCD 的面积.【解答】解:∵AC⊥BC,∴∠ACB=90°,∵四边形ABCD是平行四边形,∴AD=BC=8,AB=CD=10,OA=OC=AC,∵AB=10,BC=8,由勾股定理得:AC==6,∴OA=3;∴▱ABCD的面积是BC×AC=8×6=48.答:BC=8,CD=10,AC=6,OA=3,▱ABCD的面积是48.【点评】本题主要考查对平行四边形的性质,勾股定理等知识点的理解和掌握,能求出AC的长度是解此题的关键.。
平行四边形专题(拔高)

平行四边形专题1.如图,在周长为20cm的平行四边形ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD 于E,求△ABE的周长.2.平行四边形两条边的对角线的长分别是x,y一边是12,则x,y的值可能是()A.8,14B.10,14C.18,20D.10,383.如图所示,在平行四边形ABCD中,∠ABC的平分线交AD于E,且AE=2,DE=1,平行四边形ABCD的周长是()4.如图,点P是平行四边形ABCD内一点,已知S△PAB=7,S△PAD=4,那么S△PAC等于()5.如图所示,在?ABCD中,AB>BC,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于F 点,连接EF.(1)延长DE交AB于M点,则图中与线段EM一定相等的线段有哪几条?说明理由;(不再另外添加字母和辅助线)(2)EF、BC与AB之间有怎样的数量关系?为什么?(3)如果将条件“AB>BC”改为“AB<BC”,其它条件不变,EF、BC与AB的关系又如何?请画出图形并证明你的结论.6.如图,在平行四边形内有一点E满足ED⊥AD于D,∠EBC=∠EDC,∠ECB=45。
,请在图中找出与BE相等的一条线段,并予以证明。
7.已知:如图,在ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF、EG、AG,∠1=∠2。
(l)若CF=2,AE=3,求BE的长;(2)求证:。
8.如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.(1)求证:∠BEN=∠BGN.(2)求的值.(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.。
专题19 平行四边形、矩形、菱形--拔高题

专题19 平行四边形、矩形、菱形阅读与思考平行四边形、矩形、菱形的性质定理与判定定理是从对边、对角、对角线三个方面探讨的,矩形、菱形都是特殊的平行四边形,矩形的特殊性由一个直角所体现,菱形的特殊性是由邻边相等来体现,因此它们除兼有平行四边形的一般性质外,还有特有的性质;反过来,判定一个四边形为矩形或菱形,也就需要更多的条件.连对角线后平行四边形、矩形、菱形就与特殊三角形联系在一起,所以讨论平行四边形、矩形、菱形相关问题时,常用到特殊三角形性质、全等三角形法;另一方面,又要善于在四边形的背景下思考问题,运用平行四边形、矩形、菱形的丰富性质为解题服务,常常是判定定理与性质定理的综合运用.熟悉以下基本图形:例题与求解【例l】如图,矩形ABCD的对角线相交于O,AE平分∠BAD,交BC于E,∠CAE=15°,那么∠BOE=________.D(“祖冲之杯”邀请赛试题)解题思路:从发现矩形内含的特殊三角形入手.【例2】下面有四个命题:①一组对边相等且一组对角相等的四边形是平行四边形;②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所连结的对角线平分另一条对角线的四边形是平行四边形;④一组对角相等且这一组对角的顶点所连结的对角线被另一条对角线平分的四边形是平行四边形;其中,正确的命题的个数是( ) B. 2 C. 3 (全国初中数学联赛试题)解题思路:从四边形边、角、对角线三类元素任意选取两类,任意组合就产生许多判定平行四边形的命题,关键在于对假命题能突破正规的、标准位置的图形构造反例否定.【例3】如图,菱形ABCD 的边长为2,BD =2,E ,F 分别是边AD ,CD 上的两个动点且满足AE +CF =2.(1)判断△BEF 的形状,并说明理由; (2)设△BEF 的面积为S ,求S 的取值范围.DACB(烟台中考试题)解题思路:对于(1)由数量关系发现图形特征;对于(2),只需求出BE 的取值范围.【例4】如图,设P 为等腰直角三角形ACB 斜边AB 上任意一点,PE ⊥AC 于点E ,PF ⊥BC 于点F ,PG ⊥EF 于点G ,延长GP 并在春延长线上取一点D ,使得PD =PC .求证:BC ⊥BD ,BC =BD .AB(全国初中数学联赛试题)解题思路:只需证明△CPB ≌△DPB ,关键是利用特殊三角形、特殊四边形的性质.【例5】在□A BCD 中,∠BAD 的平分线交直线BC 于点E ,交直线DC 的延长线于点F .图3图2图1DFC(1)在图1中证明CE =CF ;(2)若∠ABC =90°,G 是EF 的中点(如图2),直接写出∠BDG 的度数;(3)若∠ABC =120°,FG ∥CE ,FG =CE ,分别连结DB ,DG (如图3),求∠BDG 的度数.(北京市中考试题)解题思路:对于(1),由角平分线加平行线的条件可推出图中有3个等腰三角形; 对于(2),用测量的方法可得∠BDG =45°,进而想到等腰直角三角形,连CG ,BD ,只需证明△BGC ≌△DGF ,这对解决(3),有不同的解题思路. 对于(3)【例6】如图,△ABC 中,∠C =90°,点M 在BC 上,且BM =AC ,点N 在AC 上,且AN =MC ,AM 与BN 相交于点P . 求证:∠BPM =45°.NMB(浙江省竞赛试题)解题思路:条件给出的是线段的等量关系,求证的却是角度等式,由于条件中有直角和相等的线段,因此,可想到等腰直角三角形,解题的关键是平移AN 或AC ,即作ME ⊥AN ,ME =AN ,构造平行四边形.,能力训练A 级1. 如图,□ABCD 中,BE ⊥CD ,BF ⊥AD ,垂足分别为E 、F ,若CE =2,DF =1,∠EBF =60°,则□ABCD 的面积为________.第1题A2. 如图,□ABCD 的对角线相交于点O ,且AD ≠CD ,过点O 作OM ⊥AC ,交AD 于点M ,若△CDM 周长为a ,那么□ABCD 的周长为 ________.第2题MB(浙江省中考试题)3. 如图,在Rt△ABC 中,∠B =90°,∠BAC =78°,过C 作CF ∥AB ,连结AF 与BC 相交于G ,若GF =2AC ,则∠BAG 的大小是________.第3题FA(“希望杯”竞赛试题)4. 如图,在菱形ABCD 中,∠B =∠EAF =60°,∠BAE =20°,则∠CEF 的大小是________.第4题BDC(“希望杯”邀请赛试题)5. 四边形的四条边长分别是a ,b ,c ,d ,其中a ,c 为对边,且满足222222a b c d ab cd +++=+,则这个四边形一定是( )A.两组角分别相等的四边形B. 平行四边形C. 对角线互相垂直的四边形D. 对角线相等的四边形6.现有以下四个命题:①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③有一个角为直角且对角线互相平分的四边形为矩形;④菱形的对角线的平方和等于边长的平方的4倍.其中,正确的命题有( )A. ①②B.③④C. ③D. ①②③④7. 如图,在矩形ABCD 中,AB =1,AD AF 平分∠DAB ,过点C 作CE ⊥BD 于E ,延长AF ,EC 交于点H ,下列结论中:①AF =FH ;②BO =BF ;③CA =CH ;④BE =3ED .正确的是( )A. ②③B.③④C. ①②④D. ②③④HB(齐齐哈尔中考试题)8. 如图,矩形ABCD 的长为a ,宽为b ,如果12341(S S )2S S ==+,则4S =( )A.38abB. 34abC. 23abD. 12ab第8题AB E F(“缙云杯”竞赛试题)9. 已知四边形ABCD ,现有条件:①AB ∥DC ;②AB =DC ;③AD ∥BC ;④AD =BC ;⑤∠A=∠C ;⑥∠B =∠D .从中取两个条件加以组合,能推出四边形ABCD 是平行四边形的有哪几种情形请具体写出这些组合.(江苏省竞赛试题)10. 如图,△ABC 为等边三角形,D 、F 分别是BC 、AB 上的点,且CD =BF , 以AD 为边作等边△ADE .(1)求证:△ACD ≌△CBF ;(2)当D 在线段BC 上何处时,四边形CDEF 为平行四边形,且∠DEF =30°,证明你的结论.EACD(江苏省南通市中考试题)11. 如图,在Rt△ABC 中,AB =AC ,∠A =90°,点D 为BC 上任一点,DF ⊥AC 于F ,DE ⊥AC 于E ,M 为BC 中点,试判断△MEF 是什么形状的三角形,并证明你的结论.MBCD(河南省中考试题)12. 如图,△ABC 中,AB =3,AC =4,BC =5,△ABD ,△ACE ,△BCF 都是等边三角形,求四边形AEFD 的面积.E(山东省竞赛试题)B 级1. 如图,已知ABCD 是平行四边形,E 在AC 上,AE =2EC ,F 在AB 上,BF =2AF ,如果△BEF 的面积为22cm ,则□ABCD 的面积是________.第1题B(“希望杯”竞赛试题)2. 如图,已知P 为矩形ABCD 内一点,PA =3,PD =4,PC =5,则PB =________.第2题BC(山东省竞赛试题)3. 如图,在矩形ABCD 中,AB =6cm ,BC =8cm ,现将矩形折叠,使B 点与D 点重合,则折痕EF 长为________.第3题F B C(武汉市竞赛试题)4. 如图,在矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,使点D 落在点D '处,CD '交AB 于点F ,则重叠部分△AFC 的面积为 ________.第4题AB(山东省竞赛试题)5. 如图,在矩形ABCD 中,已知AD =12,AB =5,P 是AD 边上任意一点,PE ⊥BD 于E ,PF ⊥AC 于F ,那么PE +PF 的值为________.第5题C(全国初中数学联赛试题)6. 如图,菱形ABCD 的边长为4 cm ,且∠ABC =60°,E 是BC 的中点,P 点在BD 上,则PE+PC 的最小值为________.第6题EDB(“希望杯”邀请赛试题)7. 如图,△ABC 的周长为24,M 是AB 的中点,MC =MA =5,则△ABC 的面积是( )A. 30B. 24C.16第7题BC(全国初中数学联赛试题)8. 如图,□ABCD 中,∠ABC =75°,AF ⊥BC 于F ,AF 交BD 于E ,若DE =2AB ,则∠AED的大小是( )A. 60°B. 65° ° °第8题B9. 如图,已知∠A =∠B ,1AA ,1PP ,1BB 均垂直于11A B ,1AA =17,1PP=16,1BB =20,11A B =12,则AP+PB 的值为( )A. 15B.14C. 13第9题B A1P 1(全国初中数学联赛试题)10. 如图1,△ABC 是直角三角形,∠C =90°,现将△ABC 补成矩形,使△ABC 的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可画出两个:矩形ACBD 和矩形AEFB (如图2).图1图3EDBACB解答问题:(1)设图2中矩形ACBD 和矩形AEFB 的面积分别为1S ,2S ,则1S ________2S (填“>”、“=”或“<”).(2)如图3,△ABC 是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出________个,利用图3画出来.(3)如图4,△ABC 是锐角三角形且三边满足BC >AC >AB ,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出________个,利用图4画出来.(4)在(3)中所画出的矩形中,哪一个的周长最小为什么图4ABC(陕西中考试题)11.四边形ABCD 中,AB =BC =CD =DA ,∠BAD =120°,M 为BC 上一点,N 为CD 上一点.求证:若△AMN 有一个内角等于60°,则△AMN 为等边三角形.12. 如图,六边形ABCDEF 中,AB ∥DE ,BC ∥EF ,CD ∥AF ,对边之差BC -EF =ED -AB=AF -CD >0.求证:该六边形的各角相等.EB(全俄数学奥林匹克试题)。
特殊平行四边形拔高题含答案
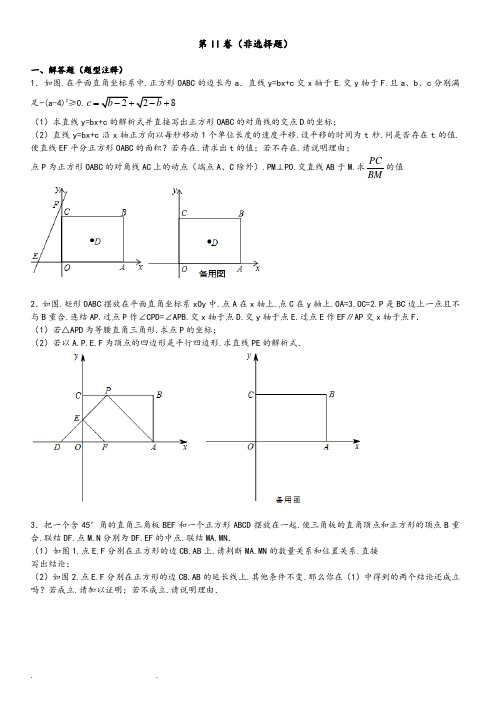
第II 卷(非选择题)一、解答题(题型注释)1.如图.在平面直角坐标系中.正方形OABC 的边长为a .直线y=bx+c 交x 轴于E.交y 轴于F.且a 、b 、c 分别满足-(a-4)2≥0.228c b b =-+-+(1)求直线y=bx+c 的解析式并直接写出正方形OABC 的对角线的交点D 的坐标;(2)直线y=bx+c 沿x 轴正方向以每秒移动1个单位长度的速度平移.设平移的时间为t 秒.问是否存在t 的值.使直线EF 平分正方形OABC 的面积?若存在.请求出t 的值;若不存在.请说明理由; 点P 为正方形OABC 的对角线AC 上的动点(端点A 、C 除外).PM ⊥PO.交直线AB 于M.求PCBM的值2.如图.矩形OABC 摆放在平面直角坐标系xOy 中.点A 在x 轴上.点C 在y 轴上.OA=3.OC=2.P 是BC 边上一点且不与B 重合.连结AP.过点P 作∠CPD=∠APB.交x 轴于点D.交y 轴于点E.过点E 作EF ∥AP 交x 轴于点F . (1)若△APD 为等腰直角三角形.求点P 的坐标;(2)若以A.P.E.F 为顶点的四边形是平行四边形.求直线PE 的解析式.3.把一个含45°角的直角三角板BEF 和一个正方形ABCD 摆放在一起.使三角板的直角顶点和正方形的顶点B 重合.联结DF.点M.N 分别为DF.EF 的中点.联结MA.MN .(1)如图1.点E.F 分别在正方形的边CB.AB 上.请判断MA.MN 的数量关系和位置关系.直接 写出结论;(2)如图2.点E.F 分别在正方形的边CB.AB 的延长线上.其他条件不变.那么你在(1)中得到的两个结论还成立吗?若成立.请加以证明;若不成立.请说明理由.BFNME CDA FCBEMNAD图1 图24.如图.已知正方形ABCD.AC 、BD 相交于点O.E 为AC 上一点.AH ⊥EB 交EB 于点H.AH 交BD 于点F . (1)若点E 在图1的位置.判断OE 与OF 的数量关系.并证明你的结论;(2)若点E 在AC 的延长线上.请在图2中按题目要求补全图形.判断OE 与OF 的数量关系.并证明你的结论.5.已知一个矩形纸片OACB.将该纸片放置在平面直角坐标系中.点A (11.0).点B (0.6).点P 为BC 边上的动点(点P 不与点B 、C 重合).经过点O 、P 折叠该纸片.得点B′和折痕OP .设BP=t .(Ⅰ)如图①.当∠BOP=30°时.求点P 的坐标;(Ⅱ)如图②.经过点P 再次折叠纸片.使点C 落在直线PB′上.得点C′和折痕PQ.若AQ=m.试用含有t 的式子表示m ;(Ⅲ)在(Ⅱ)的条件下.当点C′恰好落在边OA 上时.求点P 的坐标(直接写出结果即可). 6.阅读下列材料:已知:如图1.在Rt △ABC 中.∠C=90°.AC=4.BC=3.P 为AC 边上的一动点.以PB.PA 为边构造□APBQ .求对角线PQ 的最小值及此时APAC的值是多少.在解决这个问题时.小明联想到在学习平行线间的距离时所了解的知识:端点分别在两条平行线上的所有线段中.垂直于平行线的线段最短.进而.小明构造出了如图2的辅助线.并求得PQ的最小值为3.参考小明的做法.解决以下问题:(1)继续完成阅读材料中的问题:当PQ的长度最小时.APAC= ;(2)如图3.延长PA到点E.使AE=nPA(n为大于0的常数).以PE.PB为边作□PBQE.那么对角线PQ的最小值为.此时APAC= ;(3)如图4.如果P为AB边上的一动点.延长PA到点E.使AE=nPA(n为大于0的常数).以PE.PC为边作□PCQE.那么对角线PQ的最小值为.此时APAC= .7.在图1、图2、图3、图4中.点P在线段BC上移动(不与B、C重合).M在BC的延长线上.(1)如图1.△ABC和△APE均为正三角形.连接CE.①求证:△ABP≌△ACE.②∠ECM的度数为°.(2)①如图2.若四边形ABCD和四边形APEF均为正方形.连接CE.则∠ECM的度数为°.②如图3.若五边形ABCDF和五边形APEGH均为正五边形.连接CE.则∠ECM的度数为°.(3)如图4.n边形ABC…和n边形APE…均为正n边形.连接CE.请你探索并猜想∠ECM的度数与正多边形边数n 的数量关系(用含n的式子表示∠ECM的度数).并利用图4(放大后的局部图形)证明你的结论.8.已知O是坐标原点.点A的坐标是(5.0).点B是y轴正半轴上一动点.以OB.OA为边作矩形OBCA.点E.H分别在边BC和边OA上.将△BOE沿着OE对折.使点B落在OC上的F点处.将△ACH沿着CH对折.使点A落在OC上的G 点处。
平行四边形拔高练习

平行四边形拔高练习.平行四边形专题一三点不共线,则以其为顶点的平行C1.若A、B、)个四边形共有(4cm2.一个平行四边形的两条邻边的长分别是2222?2ac?2?c?dabd?b这个平行四边形的5cm和,它们的夹角是30°,.)面积是(、c、一个四边形的边长依次是3.a、b,d且 .则这个四边形的形状为,判定以a若、b、c、4444abcd?b??ac?d4d为边的四边形的形状为4.平行四边形ABCD中,AB=5cm, BC=3cm, ∠D与∠C的平分线分别交AB于F,E, EF= 5. 如图,口ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,则FC的长为 .6.如图所示,在形状为平行四边形的一块地ABCD中,有一条小折路EFG.?现在想把它改为经过点E的直路,要求小路两侧土地的面积都不变,?请在图中画出改动后的小路.7.如图,为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面并又要四棵树不动,积扩大一倍,试使扩大后的草坪为平行四边形,若能请你设,问这个想法能否实现.计出草图在P,AD=4,点8. 如图,在矩形ABCD中,AB=3 上,AD )等于,则PE+PF (PFPE⊥AC于E,⊥BD于F中,∠ABCD8. 如图所示,在平行四边形,BM,∠MAN=60°.请探索ABC=60°,且AB=BC 与AB的数量关系,并证明你的结论.DN的AB9.如图:平行四边形ABCD,在连结BD,==延长线上截取BEAB,BF 点,试说明:CD=。
CGGDFCE、交于落B折叠,使点AE沿ABCD如图将矩形纸片10.,则AB=在直角梯形AECD的中位线FG上,若3AE的长为()11.如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F 处,折痕为MN,则线段CN的长是()12.如图,矩形中,过对角线交点OABCD.53,BC?AB?作交于则的长是(),EACOE?AEAD13.将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=,折叠后,3点C落在AD边上的C处,并且点B落在EC 边11上的B处.则BC的长为().114.如图,在矩形中,动点从点出发,沿N MNPQR→→→方向运动至点处停止.设点R 运N QMPM动的路程为,的面积为,如果关于的MNR△xxyy函数图象如图2所示,则当时,点R 应运动9x?到()以中,ABCD在平行四边形,如图15.则四边形又∠BED=90°,为斜边作Rt△ACE,AC..试说明理由ABCD是矩形ABC=ABCD中,∠16.如图,四边形BD?N分别是AC、、∠ADC=90°,M成立吗?试说那么MN⊥BD的中点,明理由.是,到17.如图矩形中,延长,使FEACABCDCE?CB中点.求证:.DFBF?AE如图所示,在直角坐标系中,18.,(1的顶点,A的坐标为ABCD矩形的坐标为P0),对角线的交点5 ,(1) 2.、D三点的坐标;写出⑴ B、C⑵若在线段AB上有一点若在AB上有一点E(二分之三,0),过E点的直线将矩形ABCD的面积分为相等的两部分,求直线的解析式;⑶若过C点的直线将矩形ABCD的面积分为4:l3两部分,并与y轴交于点M,求M点的坐标.1.如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,OB=2,∠C=120°,则点B′的坐3为()2.如图是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20cm,墙上悬挂晾衣架的两个铁钉A、B之间的距离为20cm,则∠1等于()A、90°B、60°C、45°D、30°3.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M、N分别是AB、BC 边上的中点,MP+NP的最小值是()4.已知:如图,C是线段BD上都是等边ECDABC和△一点,△分别是四HG、R、F、三角形,各边的中点,求证:边形ABDE RFGH是菱形。
《平行四边形》PPT课件共(25张PPT)

观察下面的图形是平行四边形吗?
是
是
不是
是
不是
不是 不是
不是
是
1.
1
练习五
2
3
(2、3、5 )是长方形,( 2 )是正方 形,( 123456)是平行四边形.
说一说你是怎ቤተ መጻሕፍቲ ባይዱ辨认长方形和正方形 的.
补充习题
1.从下面各图中找出所有正方形、长方形和 ⑩《行路难》中运用典故,借此表明自己对从政还有所期待的诗句:闲来垂钓碧溪上,忽复乘舟梦日边。
前面我们已经学了生命的珍贵与独特,每个人都是独一无二的,我们都应该为自己的生命喝彩,用心的呵护生命,并且努力地让自己的生命绽放出精彩的光芒。有人说,生命如此
宝贵,守住生命,我们才能感受四季的冷暖变化,体验生活的千姿百态,追求人生幸福的种种可能。
(一)《北冥有鱼》
⑩《行路难》中运用典故,借此表明自己对从政还有所期待的诗句:闲来垂钓碧溪上,忽复乘舟梦日边。
平行四边形。 明月几时有? 把酒问青天。 不知天上宫阙, 今夕是何年。
【主旨】这首咏月怀亲词运用形象的描绘和 浪漫主义的想象,紧紧围绕中秋之月展开描写、抒情和议论。上片极写词人在“天上”“人间”的徘徊、矛盾,下片对月怀人,心情由郁结到
心胸开阔,把自己对兄弟的感情升华到探索人生的乐观与不幸的哲理高度。表达了词人乐观旷达的人生态度和对生活的美好祝愿以及无限热爱情。
人思念家乡和亲人情感的自然流露。 颈联承上启下,自然过渡。诗人由望月怀乡自然引出对弟弟的思念,绵绵愁思中夹杂着对生离死别的焦虑和不安,语气分外沉痛,写是伤心折
肠,令人不忍卒读,同时也概括了安史之乱中人民饱经忧患丧乱的普遍遭遇。
(1)认识维护身体健康的重要意义。
( 1)个正方形
【素材】《平行四边形》拔高训练(人教版)

四边形拔高训练题一.解答题(共39小题)1.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC (或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)2.如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.(1)依题意补全图形;(2)求证:∠ABE=∠CBE;(3)设AB=2,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为多少?3.如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.(1)试探究BE与BF的数量关系,并证明你的结论;(2)求EF的最大值与最小值.4.如图,在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合)且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.(1)求证:△APQ≌△QCE;(2)求∠QAE的度数;(3)设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.5.已知四边形ABCD是矩形,连接AC,点E是边CB延长线上一点,CA=CE,连接AE,F是线段AE的中点,(1)如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;(2)如图2,连接BD交AC于O,连接DF分别交AB、AC于G、H,连接GC,若∠FDB=30°,S四边形GBOH=,求线段GC的长.6.如图,菱形ABCD中,∠ABC=60°,有一度数为60°的∠MAN绕点A旋转.(1)如图①,若∠MAN的两边AM,AN分别交BC,CD于点E,F,则线段CE,DF的大小关系如何?请证明你的结论;(2)如图②,若∠MAN的两边AM,AN分别交BC,CD的延长线于点E,F,则线段CE,DF 还有(1)中的结论吗?请说明你的理由.7.如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,求证:∠FCN=45°;(3)请问在AB边上是否存在一点Q,使得四边形DQEF是平行四边形?若存在,请证明;若不存在,请说明理由.8.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?9.如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.(1)证明:BE=AG;(2)E位于什么位置时,∠AEF=∠CEB?说明理由.10.如图1,图2,正方形ABCD的边长为1,P是对角线BD上一动点,连接AP、CP,过P 作PN⊥AP交射线CD与点N.(1)求证:AP=CP.(2)①若点N在边CD上,如图1,判断△APN的形状,并说明理由;②若点N在边CD的延长线上,如图2,①中的结论还成立吗?(不需要证明).(3)若N为边CD的中点,求BP的长.11.如图,已知正方形ABCD,点P为射线BA上的一点(不和点A,B重合),过P作PE⊥CP,且CP=PE,过E作EF∥CD交射线BD于F点,EC交直线BD于G点.(1)求证:EF=AB;(2)请探究BF,DG和CD这三条线段之间的数量关系,并证明你的结论.12.如图,直线MN经过正方形ABCD的一个顶点A,过点B作BE⊥MN于点E,过点C作CF ⊥MN于点F,当直线MN经过点D(如图1)时,易证:AF+CF=2BE.当直线MN不经过点D时,线段AF、CF、BE又有怎样的数量关系?请直接写出你的猜想,并选择图(2)、图(3)中的一种情况给予证明.13.如图,在正方形ABCD中,点P为AD边上一点,PC的垂直平分线交PC于E交CB的延长线于F,连接PF交AB于G,连接CG.(1)如图1,求证:GC平分∠PGB;(2)如图2连接AN,试判断线段PC与AN的数量关系,并给予证明.14.如图,在正方形ABCD中,P是对角线AC上的一动点(包括点A、点C),点E在直线BC 上,且PE=PB.(1)求证:△BCP≌△DCP;(2)连接DE,求证:△DPE为等腰直角三角形;(3)若AB=,点P在AC上运动过程中,求出△DPE面积的最大值和最小值.15.如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且AB=2FB,求FG的长;(2)求证:AE+BF=AF.16.如图所示,已知E是边长为1的正方形ABCD对角线BD上一动点,点E从B点向D点运动(与B、D不重合),过点E作直线GH平行于BC,交AB于点G,交CD于点H,EF⊥AE于点E,交CD(或CD的延长线)于点F.(1)如图(1),求证:△AGE≌△EHF;(2)点E在运动的过程中(图(1)、图(2)),四边形AFHG的面积是否发生变化?请说明理由.17.如图,AC为正方形ABCD的一条对角线,点E为DA边延长线上的一点,连接BE,在BE 上取一点F,使BF=BC,过点B作BK⊥BE于B,交AC于点K,连接CF,交AB于点H,交BK 于点G.(1)求证:BH=BG;(2)求证:BE=BG+AE.18.如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF 交于点H,连接DH交AC于点O.(1)求证:△ABF≌△CAE;(2)HD平分∠AHC吗?为什么?19.(1)如图1,已知矩形ABCD中,点E是BC上的一动点,过点E作EF⊥BD于点F,EG ⊥AC于点G,CH⊥BD于点H,试证明CH=EF+EG;(2)若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,则EF、EG、CH三者之间具有怎样的数量关系,直接写出你的猜想;(3)如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC,连接CL,点E是CL上任一点,EF⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想;(4)观察图1、图2、图3的特性,请你根据这一特性构造一个图形,使它仍然具有EF、EG、CH这样的线段的关系,并满足(1)或(2)的结论,写出相关题设的条件和结论.20.如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并猜测∠FCN的度数,并说明理由.21.如图,在矩形ABCD中,AB=4,AD=2,E、F分别是AB、CD上的点,且BE=DF,连接BF、DE.(1)求证:四边形DEBF是平行四边形;(2)当AE的长为多少时,四边形DEBF是菱形?(3)在(2)的基础上,若点P是对角线AC上的一个动点,请在图中用直尺在边AC上作出点P,使得PB+PE的值最小,并求出这个最小值.22.如图,正方形ABCD,BE⊥ED,连接BD,CE.(1)求证:∠EBD=∠ECD;(2)设EB,EC交AD于F,G两点,若AF=2FG,探究线段CG与DG之间的数量关系并证明.23.在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.(1)写出点C的坐标;(2)求证:MD=MN;(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明.24.如图,正方形AOCD中,点B是OC上任意一点,以AB为边作正方形ABEF.①连接DF,求证:∠ADF=90°;②连接CE,猜想∠ECM的度数,并证明你的结论;③设点B在线段OC上运动,OB=x,正方形AOCD的面积为16,正方形ABEF的面积为y,试求y与x的函数关系式,并写出x的取值范围.25.如图,已知▱ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.(1)试说明DE=BC;(2)试问AB与DG+FC之间有何数量关系?写出你的结论,并说明理由.26.在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM垂直DE延长线于点M.(1)求证:GA=GB;(2)若AH=CH,求证:AG=BM.27.在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一动点,以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,求证:BC⊥CF;(2)如图2,当点D在线段BC延长线上时,请探究线段CF,BC,CD之间的关系;(3)如图3,在(1)的条件下,若BC=2,CF交DE于点P,连接AP,求△ACP的面积的最大值.28.如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.(1)若BF=BD=,求BE的长;(2)若∠ADE=2∠BFE,求证:FH=HE+HD.29.正方形ABCD中,E、F分别为边BC、DC上的点,若∠BAE=30°,∠DAF=15°.(1)试猜想EF、BE、DF之间的数量关系,并证明;(2)若正方形的边长为,求△AEF的面积;(3)若连接BD,交AE于M、交AF于N,请探究线段BM、MN、DN之间的数量关系,并给出证明.30.如图1,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45度.则有结论EF=BE+FD 成立;(1)如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请说明理由.(2)若将(1)中的条件改为:如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并证明.31.已知:如图1.四边形ABCD是菱形,AB=6,∠B=∠MAN=60°.绕顶点A逆时针旋转∠MAN,边AM与射线BC相交于点E(点E与点B不重合),边AN与射线CD相交于点F.(1)当点E在线段BC上时,求证:BE=CF;(2)设BE=x,△ADF的面积为y.当点E在线段BC上时,求y与x之间的函数关系式,写出函数的定义域;(3)连接BD,如果以A、B、F、D为顶点的四边形是平行四边形,求线段BE的长.32.菱形ABCD中,∠B=60°,一块三角板的60°角的顶点绕点A转动,两边分别交BC、CD 于点E、F.(1)说明△ABC、△ACD都是等边三角形.(2)判断△AEF的形状,说明理由?(3)如果AB=2,写出△CEF的周长的最小值.33.如图1,在正方形ABCD中,点E、F分别是BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE;②AF⊥DE.(不需要证明).(1)如图2,若点E、F不是正方形ABCD的边的中点,但满足CE=DF,则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)(2)如图3,若点E、F分别在正方形ABCD的边CB的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.34.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为时,求正方形的边长.35.在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足分别为E、F,如图①.(1)请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?若点P在DC的延长线上,如图②,那么这三条线段的长度之间又具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别直接写出结论;(2)就(1)中的三个结论选择一个加以证明.36.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.37.如图,正方形ABCD的对角线AC、BD相交于O.(1)(图1)若E为AC上一点,过A作AG⊥EB于G,AG、BD交于F,求证:OE=OF;(2)(图2)若E为AC延长线上一点,AG⊥EB交EB的延长线于G,AG的延长线交DB的延长线于F,其他条件不变,OE=OF还成立吗?若成立,请予以证明;若不成立,请说明理由.38.已知点E是边长为2的正方形ABCD的AB边的延长线上一点,P为边AB上的一个动点(不与A、B重合),直线PF⊥PD,∠EBC的平分线与PF交于点Q.(1)如图1,当P为AB的中点时,求PD的长,并比较PD与PQ长的大小;(2)如图2,在点P运动过程中,PD与PQ长的大小关系会发生变化吗?为什么?(3)设PB=x,△BPQ和△PAD的面积分别是S1、S2,又y=,试求y与x之间的函数关系式,并判断y随PB的变化而怎样变化?39.如图,在正方形ABCD中.(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?2018年01月10日626****8110的初中数学组卷参考答案与试题解析一.解答题(共39小题)1.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC (或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:AH=AB ;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论)【分析】(1)由三角形全等可以证明AH=AB,(2)延长CB至E,使BE=DN,证明△AEM≌△ANM,能得到AH=AB,(3)分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,然后分别延长BM和DN交于点C,得正方形ABCE,设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,解得x.【解答】解:(1)如图①AH=AB.(2)数量关系成立.如图②,延长CB至E,使BE=DN.∵ABCD是正方形,∴AB=AD,∠D=∠ABE=90°,在Rt△AEB和Rt△AND中,,∴Rt△AEB≌Rt△AND,∴AE=AN,∠EAB=∠NAD,∴∠EAM=∠NAM=45°,在△AEM和△ANM中,,∴△AEM≌△ANM.∴S△AEM=S△ANM,EM=MN,∵AB、AH是△AEM和△ANM对应边上的高,∴AB=AH.(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,∴BM=2,DN=3,∠B=∠D=∠BAD=90°.分别延长BM和DN交于点C,得正方形ABCD,由(2)可知,AH=AB=BC=CD=AD.设AH=x,则MC=x﹣2,NC=x﹣3,在Rt△MCN中,由勾股定理,得MN2=MC2+NC2∴52=(x﹣2)2+(x﹣3)2(6分)解得x1=6,x2=﹣1.(不符合题意,舍去)∴AH=6.【点评】本题主要考查正方形的性质和三角形全等的判断,难度中等.2.如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN,连接AN,CN,取AN的中点E,连接BE,AC,交于F点.(1)依题意补全图形;(2)求证:∠ABE=∠CBE;(3)设AB=2,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为多少?【分析】(1)依照题意补全图形即可;(2)连接CE,只要证明△ABE≌△CBE即可.(3)找出EN所扫过的图形为四边形DFCN.根据正方形以及等腰直角三角形的性质可得出BD∥CN,由此得出四边形DFCN为梯形,再由AB=2,可算出线段CF、DF、CN的长度,利用梯形的面积公式即可得出结论.【解答】解:(1)依题意补全图形,如图1所示.(2)证明:连接CE,如图2所示.∵四边形ABCD是正方形,∴∠BCD=90°,AB=BC,∴∠ACB=∠ACD=∠BCD=45°,∵∠CMN=90°,CM=MN,∴∠MCN=45°,∴∠ACN=∠ACD+∠MCN=90°.∵在Rt△ACN中,点E是AN中点,∴AE=CE=AN.∵AE=CE,AB=CB,BE=BE,∴△ABE≌△CBE,∴∠ABE=∠CBE.∴点B,E在AC的垂直平分线上,(3)在点M沿着线段CD从点C运动到点D的过程中,线段EN所扫过的图形为四边形DFCN.∵∠BDC=45°,∠DCN=45°,∴BD∥CN,∴四边形DFCN为梯形.∵AB=1,∴CF=DF=BD=,CN=CD=2,∴S梯形DFCN=(DF+CN)•CF=(+2)×=3.故答案为:3.【点评】本题考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、平行线的性质以及梯形的面积公式,解题的关键是正确寻找全等三角形解决问题,学会利用特殊位置解决实际问题,属于中考压轴题.3.如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.(1)试探究BE与BF的数量关系,并证明你的结论;(2)求EF的最大值与最小值.【分析】(1)由在边长为4的菱形ABCD中,BD=4,易得△ABD、△CBD都是边长为4的正三角形,继而证得△BDE≌△BCF(SAS),则可证得结论;(2)由△BDE≌△BCF,易证得△BEF是正三角形,继而可得当动点E运动到点D或点A时,BE的最大,当BE⊥AD,即E为AD的中点时,BE的最小.【解答】解:(1)BE=BF,证明如下:∵四边形ABCD是边长为4的菱形,BD=4,∴△ABD、△CBD都是边长为4的正三角形,∵AE+CF=4,∴CF=4﹣AE=AD﹣AE=DE,又∵BD=BC=4,∠BDE=∠C=60°,在△BDE和△BCF中,,∴△BDE≌△BCF(SAS),∴BE=BF;(2)∵△BDE≌△BCF,∴∠EBD=∠FBC,∴∠EBD+∠DBF=∠FBC+∠DBF,∴∠EBF=∠DBC=60°,又∵BE=BF,∴△BEF是正三角形,∴EF=BE=BF,当动点E运动到点D或点A时,BE的最大值为4,当BE⊥AD,即E为AD的中点时,BE的最小值为,∵EF=BE,∴EF的最大值为4,最小值为.【点评】此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.注意证得△BDE≌△BCF是解此题的关键.4.如图,在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合)且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.(1)求证:△APQ≌△QCE;(2)求∠QAE的度数;(3)设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.【分析】(1)判断出△PBQ是等腰直角三角形,然后求出∠APQ=∠QCE=135°,再根据同角的余角相等求出∠PAQ=∠CQE,再求出AP=CQ,然后利用“角边角”证明即可;(2)根据全等三角形对应边相等可得AQ=EQ,判断出△AQE是等腰直角三角形,再根据等腰直角三角形的性质解答;(3)把△ABQ绕点A逆时针旋转90°得到△ADG,求出∠GAF=45°,从而得到∠GAF=∠QAF,再利用“边角边”证明△AQF和△AGF全等,根据全等三角形对应边相等可得QF=GF,再根据两直线平行,同位角相等求出∠CQF=45°,然求出CQ=CF,分别用x表示出CQ、CF、QF,利用勾股定理列式表示出QF,然后列出方程求出x,再求出△AGF的面积,即为△AQF的面积.【解答】(1)证明:在正方形ABCD中,∠B=90°,AB=BC,∵BP=BQ,∴△PBQ是等腰直角三角形,AP=CQ,∴∠BPQ=45°,∵CE为正方形外角的平分线,∴∠APQ=∠QCE=135°,∵AQ⊥QE,∴∠CQE+∠AQB=90°,又∵∠PAQ+∠AQB=90°,∴∠PAQ=∠CQE,在△APQ和△QCE中,,∴△APQ≌△QCE(ASA);(2)解:∵△APQ≌△QCE,∴AQ=EQ,∵AQ⊥QE,∴△AQE是等腰直角三角形,∴∠QAE=45°;(3)解:如图,把△ABQ绕点A逆时针旋转90°得到△ADG,则AQ=AG,BQ=DG,∠BAQ=∠DAG,∵∠QAE=45°,∴∠GAF=45°,∴∠GAF=∠QAF,在△AQF和△AGF中,,∴△AQF≌△AGF(SAS),∴QF=GF,∵QF∥CE,∴∠CQF=45°,∴△CQF是等腰直角三角形,∴CQ=CF,∵BQ=x,∴CQ=CF=2﹣x,∴DF=2﹣(2﹣x)=x,∴QF=GF=2x,在Rt△CQF中,CQ2+CF2=QF2,即(2﹣x)2+(2﹣x)2=(2x)2,解得x=2﹣2,∴△AGF的面积=×2(2﹣2)×2=4﹣4,即△AQF的面积为4﹣4.【点评】本题考查了正方形的性质,全等三角形的判定与性质,旋转的性质,等腰直角三角形的判定与性质,勾股定理的应用,难点在于(3)作辅助线构造成全等三角形并利用勾股定理列出方程.5.已知四边形ABCD是矩形,连接AC,点E是边CB延长线上一点,CA=CE,连接AE,F是线段AE的中点,(1)如图1,当AD=DC时,连接CF交AB于M,求证:BM=BE;(2)如图2,连接BD交AC于O,连接DF分别交AB、AC于G、H,连接GC,若∠FDB=30°,S四边形GBOH=,求线段GC的长.【分析】(1)如图1,根据等腰三角形的三线合一得CF⊥AE,则∠AF C=90°,证明△AEB≌△CMB,可得BE=BM;(2)如图2,作辅助线构建三角形全等,先证明△AMF≌△EBF,得FM=BF,AM=BE,再证明△DMB是等腰三角形,由三线合一得:DF平分∠BDM,根据∠FDB=30°得△BDM是等边三角形;由此△ACE为等边三角形,△OHD为直角三角形,设未知数:OH=x,根据S四边形GBOH=S△DGB ﹣S△OHD,列方程得出结论.【解答】证明:(1)如图1,∵AC=EC,F是AE的中点,∴CF⊥AE,∴∠AFC=90°,∵四边形ABCD是矩形,AD=DC,∴矩形ABCD为正方形,∴AB=BC,∠ABC=90°,∴∠AFC=∠ABC,∵∠AMF=∠BMC,∴∠EAB=∠MCB,∵∠ABE=∠ABC=90°,∴△AEB≌△CMB,∴BE=BM;(2)如图2,连接BF并延长交直线AD于M,∵F是AE的中点,∴AF=EF,∵四边形ABCD是矩形,∴AD∥BC,AC=BD,∴∠M=∠FBE,∵∠AFM=∠EFB,∴△AMF≌△EBF,∴FM=BF,AM=BE,∵AD=BC,∴AD+AM=BC+BE,即DM=CE,∵AC=CE,∴EC=DM=AC=BD,∴△DMB是等腰三角形,∵F是BM的中点,∴DF平分∠BDM,∵∠BDF=30°,∴∠BDM=60°,∴△BDM是等边三角形,∴∠M=60°,在Rt△BCD中,∠BDC=90°﹣60°=30°,∴∠DBC=60°,∵OB=OC,∴∠DBC=∠OCB=60°,∴△ACE为等边三角形,在△OHD中,∠HOD=∠BOC=60°,∴∠OHD=90°,设OH=x,则OD=2x,BD=4x,BC=2x,∴DH=x,AH=x,DC=AB=2x,Rt△ABC中,∠ACE=60°,∴∠BAC=30°,∴cos30°=,AG==,∴BG=AB﹣AG=2x﹣=,∴S四边形GBOH=S△DGB﹣S△OHD,=BG•AD﹣OH•DH,=••2x﹣•x•x=,解得:x2=9,x=±3,∴BC=2x=6,BG=×3=4,由勾股定理得:CG===2.【点评】本题考查了矩形的性质和全等三角形的性质和判定,又考查了等边三角形和30°的直角三角形的性质,设未知数,表示边的长度,根据直角三角形中30°角所对的直角边是斜边的一半得出其它边长,与三角函数和勾股定理相结合,分别表示出△DGB和△OHD各边的长,为列方程作铺垫,从而使问题得以解决.6.如图,菱形ABCD中,∠ABC=60°,有一度数为60°的∠MAN绕点A旋转.(1)如图①,若∠MAN的两边AM,AN分别交BC,CD于点E,F,则线段CE,DF的大小关系如何?请证明你的结论;(2)如图②,若∠MAN的两边AM,AN分别交BC,CD的延长线于点E,F,则线段CE,DF还有(1)中的结论吗?请说明你的理由.【分析】(1)猜想:CE=DF,连接AC,易得△ABC、△ACD为正三角形,根据等边三角形的性质,利用ASA即可判定△AEC≌△AFD,因为全等三角形的对应边相等,所以CE=DF.(2)结论CE=DF仍然成立,同(1)类似可得△ACE≌△ADF(AAS),从而不难求得结论.【解答】解:(1)猜想:CE=DF.(1分)如图①,连接AC,∵菱形ABCD中,∠ABC=60°,∴△ABC、△ACD为正三角形.∵AC=AD,∠ACE=∠ADF=60°,∠CAE=∠DAF=60°﹣∠CAF,∴△AEC≌△AFD(ASA).(4分)∴CE=DF.(1分)(2)结论CE=DF仍然成立.(1分)如图②,连接AC∵菱形ABCD中,∠ABC=60°,∴△ABC、△ACD为正三角形.∵AC=AD,∠ACB=∠ADC=60°,∴∠ACE=∠ADF=120°.∵∠CAE=∠DAF=60°﹣∠DAE,∴△ACE≌△ADF(AAS).(2分)∴CE=DF.(1分)【点评】此题主要考查学生对全等三角形的判定及性质等知识点的综合运用.7.如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,求证:∠FCN=45°;(3)请问在AB边上是否存在一点Q,使得四边形DQEF是平行四边形?若存在,请证明;若不存在,请说明理由.【分析】(1)根据同角的余角相等得∠DAG=∠BAE,再根据“SAS”证得△ADG≌△ABE;(2)过F作BN的垂线,设垂足为H,首先证△ABE、△EHF全等,然后得AB=EH,BE=FH;然后根据AB=BC=EH,即BE+EC=EC+CH,得到CH=BE=FH,即可得证.(3)在AB上取AQ=BE,连接QD,首先证△DAQ、△ABE、△ADG三个三角形全等,易证得AG、QD平行且相等,又由于AG、EF平行且相等,所以QD、EF平行且相等,即可得证.【解答】证明:(1)连接DG∵四边形ABCD和四边形AEFG是正方形,∴DA=BA,EA=GA,∴∠BAD=∠EAG=90°,∴∠DAG=∠BAE,∴△ADG≌△ABE;(2)过F作BN的垂线,设垂足为H,∵∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,∴∠BAE=∠HEF,∵AE=EF,∴△ABE≌△EHF,∴AB=EH,BE=FH,∴AB=BC=EH,∴BE+EC=EC+CH,∴CH=BE=FH,∴∠FCN=45°;(3)在AB上取AQ=BE,连接QD,∵AB=AD,∴△DAQ≌△ABE,∵△ABE≌△EHF,∴△DAQ≌△ABE≌△ADG,∴∠GAD=∠ADQ,∴AG、QD平行且相等,又∵AG、EF平行且相等,∴QD、EF平行且相等,∴四边形DQEF是平行四边形.∴在AB边上存在一点Q,使得四边形DQEF是平行四边形.【点评】考查全等三角形的判定及平行四边形的判定,难度较大.8.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?【分析】(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.【解答】(1)证明:在正方形ABCD中,∵,∴△CBE≌△CDF(SAS).∴CE=CF.(2)解:GE=BE+GD成立.理由是:∵由(1)得:△CBE≌△CDF,∴∠BCE=∠DCF,∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.∵,∴△ECG≌△FCG(SAS).∴GE=GF.∴GE=DF+GD=BE+GD.【点评】本题主要考查证两条线段相等往往转化为证明这两条线段所在三角形全等的思想,在第二问中也是考查了通过全等找出和GE相等的线段,从而证出关系是不是成立.9.如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.(1)证明:BE=AG;(2)E位于什么位置时,∠AEF=∠CEB?说明理由.【分析】(1)要证明AG=BE,只要证明三角形ABG和EBC全等即可.两三角形中已知的条件有一组直角,AB=BC,只要再得出一组对应角相等即可.我们发现∠1和∠2都是∠3的余角因此∠1=∠2,这样就构成了两三角形全等的条件ASA,因此两三角形全等.(2)要求E位于什么位置时,∠AEF=∠CEB,我们先看若两角相等能得出什么.若∠AEF=∠CEB,由(1)中的全等三角形我们可得出∠AGF=∠CEB,因此∠AEF=∠AGF,三角形GFA 和AEF中,有一条公共边,∠DAC=∠CAB=45°,因此两三角形全等,那么AG=AE,由(1)知AG=BE,因此AE=BE,那么只有AE=BE时,∠AEF=∠CEB.【解答】(1)证明:∵四边形ABCD是正方形,∴∠ABC=90°,∴∠1+∠3=90°.∵BG⊥CE,∴∠BOC=90°.∴∠2+∠3=90°.∴∠1=∠2.在△GAB和△EBC中,∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2,∴△GAB≌△EBC(ASA).∴AG=BE.(2)解:当点E位于线段AB中点时,∠AEF=∠CEB.理由如下:当点E位于线段AB中点时,AE=BE;由(1)知,AG=BE,∴AG=AE;∵四边形ABCD是正方形,∴∠GAF=∠EAF=45°;又∵AF=AF,∴△GAF≌△EAF(SAS);∴∠AGF=∠AEF;由(1)知,△GAB≌△EBC;∴∠AGF=∠CEB;∴∠AEF=∠CEB.【点评】本题考查了全等三角形的判定,正方形的性质等知识点,利用全等三角形来得出线段相等是这类题的常用方法.10.如图1,图2,正方形ABCD的边长为1,P是对角线BD上一动点,连接AP、CP,过P 作PN⊥AP交射线CD与点N.(1)求证:AP=CP.(2)①若点N在边CD上,如图1,判断△APN的形状,并说明理由;②若点N在边CD的延长线上,如图2,①中的结论还成立吗?(不需要证明).(3)若N为边CD的中点,求BP的长.【分析】(1)根据正方形的性质可得AD=CD,∠ADB=∠CDB=45°,然后利用“边角边”证明△ADP和△CDP全等,根据全等三角形对应边相等证明即可;(2)①根据四边形的内角和定理求出∠DAP+∠DNP=180°,再根据邻补角的定义可得∠DNP+∠PNC=180°,从而得到∠DAP=∠PNC,再根据全等三角形对应角相等可得∠DAP=∠DCP,然后求出∠DCP=∠PNC,再根据等角对等边可得PN=CP,然后根据等腰直角三角形的定义解答;②同理求出AP=CP,∠DAP=∠DCP,再根据三角形的内角和定理求出∠DAP=∠N,然后求出∠N=∠DCP,根据等角对等边可得PN=CP,从而得解;(3)过点P作EF∥BC分别交AB、CD于E、F,可得四边形EBCF是矩形,EF⊥AB,EF⊥CD,根据矩形的对边相等可得BE=CF,再根据线段中点的定义和等腰三角形三线合一的性质求出CF,然后根据△BEP是等腰直角三角形解答.【解答】解:(1)∵四边形ABCD是正方形,∴AD=CD,∠ADB=∠CDB=45°,在△ADP和△CDP中,,∴△ADP≌△CDP(SAS),∴AP=CP;(2)①△APN是等腰直角三角形.理由如下:在正方形ABCD中,∠ADC=90°,∵PN⊥AP,∴∠APN=90°,∴∠DAP+∠DNP=180°,∵∠PNC+∠DNP=180°,∴∠PNC=∠DAP,∵△ADP≌△CDP,∴∠DCP=∠DAP,∴∠PNC=∠DCP,∴PN=PC,又∵AP=PC,∵AP=PN,∴△APN是等腰直角三角形;②①中得结论仍然成立.理由如下:同理可得AP=CP,∠DAP=∠DCP,∵AP⊥PN,AD⊥DN,∴∠DAP=∠N,∴∠N=∠DCP,∴PN=PC,又∵AP=PC,∵AP=PN,∴△APN是等腰直角三角形;(3)过P作EF∥BC分别交AB、CD于E、F,可得四边形EBCF是矩形,EF⊥AB,EF⊥CD,∴BE=CF,∵PN=PC,PF⊥CD,∴CF=NF=CN,∵N是CD的中点,∴CN=CD=,∴BE=CF=CN=×=,在正方形ABCD中,∠ABD=45°,∴△BEP是等腰直角三角形,∴PE=BE=,∴BP===.【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,等腰直角三角形的判定与性质,勾股定理,熟记各性质是解题的关键,难点在于(2)根据四边形的内角和定理和邻补角的定义求出相等的角.11.如图,已知正方形ABCD,点P为射线BA上的一点(不和点A,B重合),过P作PE⊥CP,且CP=PE,过E作EF∥CD交射线BD于F点,EC交直线BD于G点.(1)求证:EF=AB;(2)请探究BF,DG和CD这三条线段之间的数量关系,并证明你的结论.【分析】(1)过点E作EM⊥AB,交BA的延长线于点M,连结AE,根据同角的余角相等求出∠BPC=∠MEP,然后利用“角角边”证明△BPC和△MEP全等,根据全等三角形对应边相等可得BP=ME,BC=MP,然后求出AM=BP,从而得到AM=ME,判断出∠MAE=45°,从而得到∠MAE=∠ABD,然后根据同位角相等,两直线平行求出AE∥BD,再根据平行四边形的定义求出四边形ABFE是平行四边形,然后根据平行四边形的对边相等证明即可;(2)①分点P在线段AB上时,利用“角角边”证明△EGF和△CGD全等,根据全等三角形对应边相等可得FG=DG,再根据等腰直角三角形的性质解答即可;②点P在射线BA上时,同理可求.【解答】(1)证明:过点E作EM⊥AB,交BA的延长线于点M,连结AE,∵PE⊥CP,∴∠EPM+∠BPC=∠EPM,∵EM⊥AB,∴∠EPM+∠MEP=90°,∴∠BPC=∠MEP,∵四边形ABCD是正方形,∴∠ABC=90°,AB=BC,∠ABD=∠CBD=45°,AB∥CD,∴∠ABC=∠M=90°,在△BPC和△MEP中,,∴△BPC≌△MEP(AAS),∴BP=ME,BC=MP,∴AB=MP,∴AM=BP,。
特殊平行四边形拔高题含答案

第II 卷(非选择题)一、解答题(题型注释)1.如图,在平而直角坐标系中,正方形OABC 的边长为乩 直线y=bx+c 交x 轴于E,交y 轴于F,且a. b. c 分别满足-(a~4)*^0, c = Jb — 2 +』2 — b +8(1)求直线y=bx+c 的解析式并直接写出正方形OABC 的对角线的交点D 的坐标;<2)直线y=bx+c 沿x 轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t 秒,问是否存在t 的值, 使直线EF 平分正方形OABC 的而积?若存在,请求出t 的值;若不存在,谙说明理由;PC 点P 为正方形。
賦的对角线AC 上的动点(端点A 、C 除外),PM±PO,交直线AB 于*求而2.如图,矩形OABC 摆放在平而直角坐标系xOy 中,点A 在x 轴上,点C 在y 轴上,0A 二3, 0C=2, P 是BC 边上一 点且不与B 重合,连结AP,过点P 作ZCPD 二ZAPB,交x 轴于点D,交y 轴于点E,过点E 作EF 〃AP 交x 轴于点F.(1)若AAPD 为等腰直角三角形,求点P 的坐标; (2) 若以A, P, E, F 为顶点的四边形是平行四边形,求直线PE 的解析式.3.把一个含45°角的直角三角板BEF 和一个正方形ABCD 摆放在一起,使三角板的直角顶点和正方形的顶点B 重 合,联结DF,点M, N 分别为DF, EF 的中点,联结MA, MN.(1)如图1,点E, F 分别在正方形的边CB, AB 上,请判断MA, MN 的数量关系和位置关系,直接 写出结论: (2) 如图2,点E, F 分别在正方形的边CB, AB 的延长线上,其他条件不变,那么你在(1)中得到的两个结论 还成立吗?若成立,请加以证明:若不成立,请说明理由.的值备用图备用国A D图1 图24.如图,已知正方形ABCD, AC、BD相交于点0, E为AC上一点,AH丄EB交EB于点H, AH交BD于点F.(1)若点E在图1的位置,判断0E与0F的数量关系,并证明你的结论:(2)若点E在AC的延长线上,请在图2中按题目要求补全图形,判断0E与0F的数量关系,并证明你的结论.5.已知一个矩形纸片OACB,将该纸片放置在平而直角坐标系中,点A (11, 0),点B (0, 6),点P为BC边上的动点(点P不与点B. C重合),经过点0、P折叠该纸片,得点B'和折痕0P.设BP二t・(I)如图⑪当ZB0P二30°时,求点P的坐标;(II)如图②,经过点P再次折叠纸片,使点C落在直线PB'上,得点C'和折痕PQ,若AQ二m,试用含有t的式子表不m:(III)在(II)的条件下,当点C'恰好落在边0A上时,求点P的坐标(直接写岀结果即可).6 •阅读下列材料:已知:如图1,在RtAABC中,ZC=90% AC=4, BC=3, P为AC边上的一动点,以PB, PA为边构造D APBQ,求对AD角线PQ的最小值及此时—的值是多少.AC(3)如图4,如果P 为AB 边上的一动点,延长PA 到点E,使AE=nPA (n 为大于0的常数),以PE, PC 为边作D PCQE,AD那么对角线PQ 的最小值为_,此时—=_・AC7.在图1.图2.图3、图4中,点P 在线段BC 上移动(不与B 、C 重合),M 在BC 的延长线上.(1)如图1, AABC 和AAPE 均为正三角形,连接CE.①求证:AABP^AACE.②ZECM 的度数为 _________ ・(2) ___________________________________________________________________________________________________________ ①如图2,若四边图2在解决这个问题时,小明联想到在学习平行线间的距离时所了解的知识:端点分别在两条平行线上的所有线段中, 垂直于平行线的线段最短.进而,小明构造出了如图2的辅助线,并求得PQ 的最小值为3.参考小明的做法,解 决以下问题:(1)(2) 值为 AD继续完成阅读材料中的问题:当PQ 的长度最小时,—=_: AC如图3,延长PA 到点E,使AE=nPA (n 为大于0的常数).以PE, PB 为边作口PBQE,那么对角线PQ 的最小Ap O图4形ABCD和四边形APEF均为正方形,连接CE.则ZECM的度数为 ____________________________________ ° .②如图3,若五边形ABCDF和五边形APEGH均为正五边形,连接CE.则ZECM的度数为 _______________ ° .(3)如图4, n边形ABC…和n边形APE…均为正n边形,连接CE,请你探索并猜想ZECM的度数与正多边形边数n 的数量关系(用含n的式子表示ZECH的度数),并利用图4 (放大后的局部图形)证明你的结论.B PC M B P C B P C M图图8.已知0是坐标原点,点A的坐标是(5, 0),点B是y轴正半轴上一动点,以OB, 0A为边作矩形0BCA,点E,H分别在边BC和边0A±,将ABOE沿着0E对折,使点B落在0C上的F点处,将AACH沿着CH对折,使点A落在0C 上的G点处。
八年级数学——平行四边形的性质和判定拔高教案

名思教育个性化辅导教案学生: 学科: 教师: 班主任: 日期: 时段: 课题教学目标重难点透视知识点剖析序号知识点预估时间掌握情况123教学内容第一部分:知识点梳理一、平行四边形的定义1、定义:两组对边分别平行的四边形叫做平行四边形.2、表示方法:平行四边形用符号“”表示.平行四边形ABCD记作“ABCD”,读作“平行四边形ABCD”.3、平行四边形的基本元素:边、角、对角线.4、平行四边形的定义的作用:平行四边形的定义既是性质,又是判定方法.(1)由定义可知平行四边形的两组对边分别平行;(2)由定义可知只要四边形中有两组对边分别平行,那么这个四边形就是平行四边形.【例1】对于平行四边形ABCD,AC与BD相交于点O,下列说法正确的是( ).A.平行四边形ABCD表示为“ACDB”B.平行四边形ABCD表示为“ABCD”C.AD∥BC,AB∥CDD.对角线为AC,BO二、平行四边形的性质1、(边)平行四边形的对边平行且相等.例如:如图①所示,在ABCD中,AB CD,AD BC.由上述性质可得,夹在两条平行线间的平行线段相等.如图2,直线l1∥l2.AB,CD是夹在直线l1,l2间的平行线段,则四边形ABCD是平行四边形,故AB CD.2、(角)平行四边形的对角相等,邻角互补.例如:如图①所示,在ABCD 中,∠ABC=∠CDA,∠BAD=∠BCD.∠ABC+∠BAD=180°,∠ABC+∠BCD=180°,∠BCD+∠CDA=180°,∠BAD+∠CDA=180°.3、(对角线)平行四边形的对角线互相平分.例如:如图①所示,在ABCD 中,OA=OC,OB=OD.图①图②图③4、经过平行四边形对角线的交点的直线被对边截得的两条线段相等,并且该直线平分平行四边形的面积.例如:如图③所示,在ABCD中,EF经过对角线的交点O,与AD和BC分别交于点E,F,则OE=OF,且S四边形ABFE=S四边形EFCD【例2】ABCD的周长为30 cm,它的对角线AC和BD交于O,且△AOB的周长比△BOC的周长大5 cm,求AB,AD的长.三、平行四边形的判定1、方法一(边):两组对边分别平行的四边形叫做平行四边形.2、方法二(边):两组对边分别相等的四边形是平行四边形.3、方法三(边):一组对边平行且相等的四边形是平行四边形4、方法四(角):两组对角分别相等的四边形是平行四边形.5、方法五(对角线):对角线互相平分的四边形是平行四边形.6、注意:(1)判定方法可作为“画平行四边形”的依据;(2)一组对边平行,另一组对边相等的四边形不一定是平行四边形.【例3】已知,如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.四边形ABCD是平行四边形,请说明理由.四、三角形的中位线1、定义:连接三角形两边中点的线段叫做三角形的中位线.2、性质:三角形两边中点连线平行于第三边,并且等于第三边的一半.3、注意:(1)一个三角形有三条中位线,每条中位线与第三边都有相应的位置关系和数量关系;(2)三角形的中位线不同于三角形的中线,三角形的中位线是连接两边中点的线段,而三角形的中线是连接三角形一边的中点和这边所对顶点的线段.【例4】如图所示,在△ABC中,点D,E,F分别是AB,BC,CA的中点,若△ABC 的周长为10 cm,则△DEF的周长是__________cm.五、两条平行线间的距离1、定义:两条平行线中,一条直线上任意一点到另一直线的距离,叫做这两条平行线间的距离.如图所示,a∥b,点A在直线a上,过A点作AC⊥b,垂足为C,则线段AC的长是点A到直线b的距离,也是两条平行线a,b之间的距离.2、规律:(1)如图,过直线a上点B作BD⊥b,垂足为D,则线段BD的长也是两条平行线a,b之间的距离.于是由平行四边形的性质可知平行线的又一个性质:平行线间的距离处处相等.(2)两条平行线之间的距离是指垂线段的长度,当两条平行线的位置确定时,它们之间的距离也随之确定,它不随垂线段的位置的改变而改变,是一个定值.【例5】如图所示,如果l1∥l2,那么△ABC的面积与△DBC的面积相等吗?由此你还能得出哪些结论?六、平行四边形性质的应用平行四边形性质的应用非常广泛,可以利用它说明线段相等、证明线段平行、求角的度数、求线段的长度、求图形的周长、求图形的面积等.【例6】如图,ABCD的对角线相交于点O,过O作直线EF,并与线段AB,CD 的反向延长线交于E,F,OE与OF是否相等,阐述你的理由.七、平行四边形的判定的应用1、判定平行四边形的一般思路:①考虑对边关系:证明两组对边分别平行;或两组对边分别相等;或一组对边平行且相等;②考虑对角关系:证明两组对角分别相等;③考虑对角线关系:证明两条对角线互相平分.【例7】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.已知:在四边形ABCD中,_______,_______;求证:四边形ABCD是平行四边形.八、平行四边形的性质和判定的综合应用1、平行四边形的性质和判定的应用主要有以下几种情况:(1)直接运用平行四边形的性质解决某些问题,如求角的度数、线段的长、证明角相等或互补、证明线段相等或倍分关系;(2)判定一个四边形为平行四边形,从而得到两角相等、两直线平行等;(3)综合运用:先判定一个四边形是平行四边形,然后再用平行四边形的性质去解决某些问题;或先运用平行四边形的性质得到线段平行、角相等等,再判定一个四边形是平行四边形.【例8】如图所示,在ABCD中,E,F分别是AD,BC上的点,且AE=CF,AF 与BE交于G,DF与CE交于H,连接EF,GH,试问EF与GH是否互相平分?为什么?九、三角形的中位线性质的应用1、常见三角形的中位线的性质的应用:①线段间的位置关系②线段间的数量关系③几何求值(计算角度、求线段的长度)④证明(证明线段相等或不等、证明线段的倍分关系、证明两角相等)⑤作图,且能解决生活实际问题.2、解题技巧:应用三角形中位线定理解决问题时,已知条件中往往给出两个中点,若已知条件只给出一个中点,必须要证明另一个点也是中点,才能运用此定理.【例9】在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( ).A.9.5 B.10.5 C.11 D.15.5十、平行四边形的性质探究题1、解题技巧:平行四边形的探究型问题,关键是根据平行四边形的性质和判定,构造出平行四边形.【例10】如图,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D,E,F分别在AC,AB,BC上,试探索PD+PE+PF与a的关系.十一、平行四边形的判定的探究题1、运动型问题的解题技巧:运动变化题,这类题的解决技巧是把“运动”的“静止”下来,以静制动,同时注意不同的情况.【例11】如图所示,已知在四边形ABCD中,AD∥BC(AD>BC),BC=6 cm,点P从A点以1 cm/s的速度向D点出发,同时点Q从C点以2 cm/s的速度向B点出发,设运动时间为t 秒,问t为何值时,四边形ABQP是平行四边形?平行四边形性质和判定练习题1、如图, AECF的对角线相交于点O,DB经过点O,分别与AE、CF交于BD.求证:四边形ABCD是平行四边形.2、如图,四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.3、已知:如图,在△ABC中,∠BAC=90°,DE、DF 是△ABC的中位线,连接EF、AD.求证:EF=AD.课堂总结课后作业:课堂反馈:学生签字:校长签字: ___________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GFEDCBA四边形 平行四边形1.如图,在□ABCD 中,AE =EB ,AF =2,则FC 等于_____.2.如图①,将一块斜边长为12cm ,∠B=60°的直角三角板 ABC ,绕点C 沿逆时针方向旋转90°到△A′B′C′的 位置,再沿CB 向右平移,使点B′刚好落在斜边AB 上, 那么此三角板向右平移的距离是 。
3.如图,在□ABCD 中,分别以AB 、AD 为边向外 作等边△ABE 、△ADF ,延长CB 交AE 于点G ,点G 在点A 、E 之间,连结CG 、CF ,则以下四个结论一定正确的是( )①△CDF ≌△EBC ②∠CDF =∠EAF ③△ECF 是等边三角形 ④CG ⊥AEA .只有①②B .只有①②③C .只有③④D .①②③④4.如图③,△ABC 中,∠C=90°,点M 在BC 上,且BM=AC ,点N 在AC上,且AN=MC,AM与BN相交于点P,求证:∠BPM=45°。
FA E BCDDACB5.如图,已知四边形ABCD 的对角线AC 、BD 交于点P ,过点P 作直线,交AD 于E 点、交BC 于F 点。
若PE=PF ,且AP+AE=CP+CF 。
证明:四边形ABCD 是平行四边形。
6.将一副三角尺如图拼接:含30°角的三角尺(△ABC )的长直角边与含45°角的三角尺(△ACD )的斜边恰好重合.已知AB =2,P 是AC 上的一个动点. (1)当点P 运动到∠ABC 的平分线上时,连接DP ,求DP 的长; (2)当点P 在运动过程中出现PD =BC 时,求此时∠PDA 的度数;(3)当点P 运动到什么位置时,以D ,P ,B ,Q 为顶点的平行四边形的顶点Q 恰好在边BC 上?求出此时□DPBQ 的面积.菱形1.如图,已知菱形ABCD 的一个内角,对角线 AC 、BD 相交于点O ,点E 在AB 上,且,则= 度.2. 如图,菱形ABCD 中,∠B =60°,AB =2㎝,E 、F 分别是BC 、CD 的中点,连结AE 、EF 、AF ,则△AEF 的周长为( ) A .㎝ B .㎝C .㎝D .3㎝3︒=∠80BAD BO BE =EOA ∠3233343.如图,P 是菱形ABCD 对角线BD 上一点,PE⊥AB 于点E ,PE =4cm ,则点P 到BC 的距离是_____cm.4.已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF . (1)求证:BE = DF ;(2)连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.5.在平行四边形ABCD 中,AC 、BD 交于点O ,过点O 作直线EF 、GH ,分别交平行四边形的四条边于E 、G 、F 、H 四点,连结EG 、GF 、FH 、HE . (1)如图①,试判断四边形EGFH 的形状,并说明理由;(2)如图②,当EF ⊥GH 时,四边形EGFH 的形状是 ;(3)如图③,在(2)的条件下,若AC =BD ,四边形EGFH 的形状是 ; (4)如图④,在(3)的条件下,若AC ⊥BD ,试判断四边形EGFH 的形状,并说明理由.HG F E O D C B A 图① H G F E O D C B A 图② A B CD OEFGH 图③ A B C D O E F G H 图④矩形1.矩形ABCD 中,E 、F 、M 为AB 、BC 、CD 边上的点, 且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM 的长为( ) A .5 B . C .6 D .2.如图,点P 是矩形ABCD 的边AD 的一个动点,矩形的两条边AB 、BC 的长分别为3和4,那么点P 到矩形的两条对角线AC 和BD 的距离之和是( )A .B .C .D .不确定3.如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,∠BEG>60°,现沿直线EG 将纸片折叠,使点B 落在纸片上的点H 处,连接AH ,则与∠BEG 相等的角的个数为( )A .4B .3C .2D .14.如图,矩形ABCD 中,AB =8cm ,BC =4cm ,E 是 DC 的中点,BF =BC ,则四边形DBFE 的面积为.5.如图矩形纸片ABCD ,AB =5cm ,CD 上有一点E ,ED =2cm ,AD 上有一点P ,PD =3cm ,过P 作PF⊥AD 交BC 于F ,将纸片折叠,使P 点与E 点重合,折痕与PF 交于Q 点,则PQ 的长是______cm.6.小明尝试着将矩形纸片ABCD (如图①,AD >CD )沿过A 点的直线折叠,使得B 点落在AD 边上的点F 处,折痕为AE (如图②);再沿过D 点的直线折叠,使得C 点落在DA 边上的点N 处,E 点落在AE 边上的点M 处,折痕为DG (如图③).如果第二次折叠后,M 点正好在∠NDG 的平分线上,那么矩形ABCD 长与宽的比值为 .252612565245412cm BAGCDHEAB CDM N A ' B '7.如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN(点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.(提示:在直角三角形中,斜边的中线等于斜边的一半)正方形1.如图,已知正方形的边长为3,为边上一点, .以点为中心,把△顺时针旋转,得△,连接,则的长等于 . 2. 四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的处,点A 对应点为, 且=3,则AM 的长是( ) (相似三角形,对应边成比例) A .1.5 B .2 C .2.25 D .2.5ABCD E CD 1DE =A ADE 90︒ABE 'EE 'EE 'B 'A 'C B '图1B① ②③A DE 'A PEDCB3.已知:如图,在正方形外取一点, 连接,,.过点作的垂线交 于点.若,① △≌△;② ②点到直线 ③;④⑤其中正确结论的序号是( )A .①③④ B.①②⑤ C.③④⑤ D.①③⑤4.正方形、正方形和正方形的位置如图所示,点在线段上,正方形 的边长为4,则的面积为( ) A .10 B .12 C .14 D .16 5.正方形ABCD 中,点O 是对角线DB 的中点,点P 是DB 所在直线上的一个动点,PE ⊥BC 于E ,PF ⊥DC 于F .(1)当点P 与点O 重合时(如图①),猜测AP 与EF 的数量及位置关系,并证明你的结论;(2)当点P 在线段DB 上 (不与点D 、O 、B 重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;(3)当点P 在DB 的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.ABCD E AE BE DE A AE ED P 1AE AP ==PB APD AEB B AE EB ED ⊥1APD APB S S ∆∆+=4ABCD S =正方形ABCD BEFG RKPF G DK BEFG DEK ∆梯形1.如图.梯形ABCD 中,AD∥BC、AB =CD ,AC 丄BD 于点O ,∠BAC=60°,若BC =6,则此梯形的面积为( )2.如图,在直角梯形ABCD 中,AD ∥BC ,BC AB ⊥,2=AD ,4=BC ,点E 在AB 边上,且CE 平分BCD ∠,DE 平分ADC ∠,则点E 到CD 的距离为 .3.如图,在梯形ABCD 中,AB ∥CD ,对角线AC 、BD 交于点O ,则s △AOD = s △BOC .(填“>”、“=”或“<”)4. 如图,梯形ABCD 中,AD ∥BC , 点E 在BC 上,AE =BE ,点F 是CD 的中点,且AF ⊥AB ,若AD =2.7,AF =4,AB =6,则CE 的长为A .2 2B .23-1C .2.5D .2.35. 如图,已知梯形ABCD 的中位线为EF ,且△AEF 的面积为6cm 2,则梯形ABCD的面积为( ) A .12 cm 2 B .18 cm 2C .24 cm 2D .30 cm 2ABCD FA DB C E F6. 在一块形状为直角梯形的草坪中,修建了一条由 A→M→N→C 的小路(M 、N 分别是AB 、CD 中点). 极少数同学为了走“捷径”,沿线段AC 行走,破坏了 草坪,实际上他们仅少走了( ) A. 7米 B. 6米 C. 5米 D. 4米7. 如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD = 2,将腰CD 以D 为中心逆时针旋转90°至DE ,连接AE 、CE ,△ADE 的面积为3,则BC 的长为 .8. 如图,梯形ABCD 中,AD ∥BC ,EF 是梯形的中位线,对角线AC 交EF 于G ,若BC =10cm ,EF =8cm ,则GF 的长等于 cm .9. 如图,在等腰梯形ABCD 中,AC ⊥BD ,AC =6cm ,则等腰梯形ABCD 的面积为_____cm .10. 如图,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时的长为__________.11.如图,在直角梯形ABCD 中,AD ∥BC ,,AD = 6,BC = 8,,点M 是BC的中点.点P 从点M 出发沿MB 以每秒1个单位长的速度向点B 匀速运动,到达点B 后立刻以原速度沿BM 返回;点Q 从点M 出发以每秒1个单位长的速度在射线MC 上匀速运动.在点P ,Q 的运动过程中,以PQ 为边作等边三角形EPQ ,使它与梯形ABCD 在射线BC 的同侧.点P ,Q 同时出发,当点P 返回到点M 时停止运动,点Q 也随之停止.设点P ,Q 运动的时间是t 秒(t >0).(1)设PQ 的长为y ,在点P 从点M 向点B 运动的过程中,写出y 与t 之间的函数关系式(不必写t 的取值范围).(2)当BP = 1时,求△EPQ 与梯形ABCD 重叠部分的面积.(3)随着时间t 的变化,线段AD 会有一部分被△EPQ 覆盖,被覆盖线段的290B ∠=︒33=ABGF E D CBA (第8题)A BC DP长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接..写出t 的取值范围;若不能,请说明理由.12.如图,在梯形ABCD 中,AD ∥BC,E 是BC 的中点,AD=5,BC=12,,∠C=,点P 是BC 边上一动点,设PB 长为x.(1)当x 的值为 时,以点P 、A 、D 、E 为顶点的四边形为直角梯形.(2)当x 的值为 时,以点P 、A 、D 、E 为顶点的四边形为平行网边形. (3)点P 在BC 边上运动的过程中,以点P 、A 、D 、E 为顶点的四边形能否构成菱形?试说明理由.045BPQ(备用图)。
