2,冲击荷载下混凝土本构模型及损伤延迟指标的参数研究

合集下载

混凝土静力与动力损伤本构模型研究进展述评

混凝土静力与动力损伤本构模型研究进展述评混凝土静力损伤本构模型主要研究混凝土在长期外力作用下所产生的损伤。

该模型是通过研究混凝土的各种物理、力学性质和损伤特性，建立混凝土的本构模型，以预测混凝土在外力作用下的力学响应。

静力损伤本构模型的研究重点在于如何描述混凝土在长期力学载荷下的损伤累积效应。

常见的静力损伤本构模型有Kachanov-Rabotnov模型、Modified-Kachanov-Rabotnov模型和Nakamura模型等。

这些模型均是基于破裂力学理论和实验结果建立的，在工程领域得到广泛应用。

总体上说，混凝土静力损伤本构模型和混凝土动力损伤本构模型的研究都是为了更好地预测和模拟混凝土在不同载荷作用下的力学响应，进而更好地评估和控制工程结构的损伤和破坏。

这些模型的研究，对于提高工程结构的安全可靠性和延长使用寿命具有重要意义。

目前这些混凝土损伤本构模型仍面临一些挑战和亟待解决的问题。

现有的模型大多基于理论推导和实验数据，缺少考虑材料微结构和内部缺陷对混凝土力学响应的影响以及不同外界环境条件下混凝土力学响应的变化规律。

今后需要进一步深入研究混凝土的微观结构和内部缺陷对力学响应的影响，在此基础上修正和完善损伤本构模型，提高其适用性和准确性。

由于混凝土在不同工程结构中的应用要求和环境条件存在巨大差异，因此需要基于工程实际情况进行本构模型的有效性验证和改进。

应进一步推广高性能混凝土等新型材料的应用，探索建立适合其力学响应特性的新型损伤本构模型，为未来工程结构的设计和施工提供更好的支持。

混凝土材料具有一定的弹性和塑性。

在外界力学载荷作用下，会产生不同程度的损伤和变形。

特别是超出材料界限时，混凝土会失去刚性，变得越来越脆弱。

在进行混凝土损伤本构模型研究时，对于混凝土的断裂特性和损伤行为的研究也非常重要。

静力损伤本构模型是针对混凝土在长期外力作用下所产生的损伤进行研究的。

这种损伤模式主要是由于混凝土在受力过程中会出现隐蔽的微裂缝，从而导致材料的内部结构发生改变。

强冲击荷载作用下混凝土材料动态本构模型

第29卷第3期2008年9月固体力学学报C H IN ESE J OU RNAL O F SOL ID M EC HAN ICSVol.29No.3September2008强冲击荷载作用下混凝土材料动态本构模型3刘海峰1,233　宁建国1(1北京理工大学爆炸科学与技术国家重点实验室,北京,100081)(2宁夏大学土木与水利工程学院,银川,750021)摘　要　基于混凝土强冲击荷载作用下的实验研究,以修正Ottosen四参数破坏准则为流动法则,引入损伤,构造了一个塑性与损伤相耦合的动态本构模型用于描述混凝土材料的冲击特性.在该模型中,考虑了引起混凝土材料弱化的两种不同的损伤机制:拉伸损伤和压缩损伤.其中,拉伸损伤是由微裂纹的张开和扩展引起的,通过拉伸应变来控制;压缩损伤相关于微空洞体积分数比的演化,并通过微空洞塌陷引起的压缩应变来控制,由此压缩损伤和拉伸损伤就完全耦合了.通过模型计算模拟结果与实验结果比较发现,随着冲击速度的提高,混凝土的峰值应力显著增加,即混凝土材料的承载能力增大,同时混凝土内部产生显著的塑性变形.模拟曲线与实验曲线拟合良好,因而可以用该模型模拟混凝土材料在强冲击荷载下的动态特性.关键词　混凝土,轻气炮,冲击特性,动态本构模型0　引言混凝土是目前工业与民用建筑中最常用的结构工程材料,已经被广泛地应用于高层建筑物,长跨桥,大坝,水电站,隧道和码头等.这些混凝土结构在其工作过程中除了承受正常的设计载荷外,往往还要承受诸如爆炸,冲击和撞击等动载荷.为了更好地设计和分析这些混凝土结构,必须对混凝土材料在冲击载荷作用下的力学性能及其本构特性进行研究.目前,人们对混凝土材料的动态力学性能已经有了比较深刻的认识和研究,对其动态本构特性也做了许多研究工作.Wat stein[1]利用落锤装置进行了混凝土材料的动态力学性能实验,由于落锤本身的惯性,所测得的实验结果很难确保是材料动态性能的真实反应;Bischoff[2]和胡时胜等[3]利用SHPB 压杆对混凝土的动态力学性能进行了实验研究;商霖等[4,5]利用SH PB压杆和轻气炮动力实验装置分别对混凝土材料和钢筋混凝土材料在冲击荷载作用下的力学性能进行了系统深入的研究.混凝土材料动态本构模型是研究其在爆炸或冲击荷载作用下损伤破坏机理,应力波的传播规律和衰减规律,结构破坏效应等的理论基础.基于对混凝土材料变形机理的分析,混凝土材料动态本构模型分为粘塑性本构模型[6,7]和损伤型本构模型[8,9],但由于缺乏对混凝土材料在冲击荷载作用下破坏机理的全面认识,因此至今仍未有一种大家普遍接受的本构模型.为了更好地描述冲击荷载作用下混凝土材料的动态响应特性,商霖等[4,5]在理想各向同性的粘弹性本构关系的基础上,引入损伤,分别建立混凝土材料和钢筋混凝土材料的动态本构模型,但没有将定义的损伤与材料的微观损伤机制联系起来;宁建国等[10]提出了一个塑性与损伤相耦合的动态本构模型,在该模型中,认为拉伸损伤是由微裂纹的张开和扩展引起的;压缩损伤由微孔洞的塌陷引起,通过混凝土材料的塑性体应变控制,但并没有将这两种损伤有效的耦合起来.本文基于损伤与塑性耦合理论,以修正的Otto sen四参数破坏准则为屈服法则,引入损伤,构造了一个动态本构模型用于描述混凝土材料的冲击特性,利用该模型对混凝土材料在强冲击荷载作用下的冲击特性进行数值模拟,并将该模型的预测曲线与宁建国等[10]提出的本构模型的预测曲线及实验结果进行比较,结果表明:模型预示结果无论在变形趋势上,还是数值精度上都与实验结果符合得很好.3 33国家自然科学基金项目(10625208,10572024)资助.2007209225收到第1稿,2008204204收到修改稿.通信作者. Tel:010*********, E2mail:liuhaifeng1557@.1　本构模型建立1.1　本构关系在小应变的前提下,遵循应变分解假定,将应变的增量可以分解为弹性部分和塑性部分,即εij = εe ij + εpij (1)弹性变形与应力之间满足弹性关系εe ij =M ij kl σkl (2)式中,M ij kl 为柔度张量,假设弹性和塑性之间不存在耦合,则M ij kl 为常张量.M ij kl =12G I ij kl +19Kδijδkl σkl (3)其中,G 和K 为材料的剪切模量和体积模量,与材料的杨氏模量E ,泊松比ν满足下列关系G =E/2(1+ν),　K =E/3(1-2ν) I ij kl 为特殊等同张量I ij kl =I ij kl -δij δkl /3,　I ij kl =(δik δjl +δjkδil )/2将上述表达式代入式(3)得到以ν,E 表示的柔度张量　M ij kl =1E 12(1+ν)(δik δjl +δil δjk )-νδijδkl (4)将式(4)代入式(2),并两边对时间求导得 εeij =1E 12(1+ν)(δik δjl +δil δjk )-νδij δkl σkl(5)将式(5)代入式(1)得 εij =1E 12(1+ν)(δik δjl +δil δjk )-νδij δkl σkl + εpij (6)塑性应变率由下式控制εpij =γ〈<(F )〉5F σij(7)式中,γ为流变系数,F 为屈服函数,采用修正后Ottosen 屈服准则;函数<(F )=(e F -1)m 1,其中m 1为常数;函数〈x 〉定义如下〈x 〉=0,x ≤0x ,x >0将式(7)代入式(6)得 εij =1E 12(1+ν)(δik δjl +δil δjk )-νδij δkl σkl + γ〈<(F )〉5Fσij(8)1.2　Otto sen 屈服法则及其修正Ottosen [11]于1977年研究混凝土材料时提出了如下的四参数破坏准则F (σij )=AJ 2f 2c+λJ 2f c +B I 1f c -1=0(9)其中,f c 为在准静态情况下混凝土的单轴抗压强度;A 和B 为常数;λ=λcos (3θ)>0,其中θ为应力角θ=13arccos 33J 32J 3/22I 1,J 2和J 3分别为应力张量第一不变量,应力偏量第二不变量和第三不变量 I 1=σkk ,　J 2=12s ij s ij J 3=13s ij s jk s ki ,　s ij =σij -13σkkδij 函数δij 由下式定义δij =0,i ≠j 1,i =j根据等边三角形的薄膜比拟法则,可以得到偏平面λ的表达式为λ=1γ=k 1cos arccos k 2cos (3θ)/3, co s (3θ)≥0k 1cos π/3-arcco s -k 2co s (3θ), co s (3θ)<0其中,k 1为尺寸因子,k 2为形状因子,其数值由λt (θ=0)和λc (θ=π/3)来确定.Otto sen 模型中的四个参数k 1,k 2,A 和B 由混凝土的单轴抗拉强度,单轴抗压强度,双轴等压强度和三轴等压强度的数据确定.取双轴等压强度f b c =1.16f c (Kupfer 等)[12];三轴强度ξ/f c =-5和r/f c =4(Balmer 和Richart [13,14]).当f 0=f t /f c 取不同数值时,各参数的变化如表1所示.表1　Ottosen 模型参数表Table 1　Parameter table of Ottosen modelf 0=f t /f cABk 1k 2λt λc λc /λt 0.081.80764.096214.48630.991414.47257.78340.53780.101.27593.196211.73650.980111.71096.53150.55770.120.92182.59699.91100.96479.87205.69790.5772在Ottosen 法则中:当A =0,λ为常数时,Otto 2sen 准则退化为经典Drucker 2Prager 准则;当A =B =0,λ为常数时,Ottosen 准则退化为von Mises 准则;λ为常数时,和Hsieh 2Chen 混凝土弹塑性硬化模型非常相似.同时由于该模型与他人实验数据拟合很好,因此得到广泛应用.・232・固　体　力　学　学　报 2008年借鉴Lemaitre 等[15]提出的三轴等效应力概念,用等效屈服应力Y d 替代式(9)中的f c ,得到如下修正后的Otto sen 屈服法则F (σij )=AJ 2Y 2d+λJ 2Y d +B I 1Y d -1=0(10)等效屈服应力Y d 定义如下Y d =σeq R 1/2ν(11)其中,σeq 为等效应力,σeq =3/2s ij s ij ;R ν为三轴函数,用于揭示静水压力对塑性变形的影响,可以表示如下R ν=23(1+ν)+3(1-2ν)P σeq2(12)冲击荷载作用下,在一维应力条件下σeq 等于动态应力强度σd ,由大量实验研究可知[16218],混凝土材料在高应变率下单轴抗压强度σd 和准静态情况下的单轴抗压强度f c 具有如下关系σd =f c f ( ε)(13)其中,f (ε)为应变率相关函数,目前常见的有幂数型和对数型[16218],本文采用如下形式f ( ε)=H 1(log ε)2+H 2log ε+H 3其中,H 1,H 2和H 3为常数,由实验数据拟合得到.将式(13)代入式(11)得到Y d =23(1+ν)σ2d +3(1-2ν)P 2(14)其中,P 为相应于动态应力强度σd 时的静水压力.2　损伤的引入混凝土各组成部分之间力学性能相差很大,而且内部存在大量的微裂纹和微空洞缺陷.在外荷载的作用下,由于微裂纹和微空洞缺陷的存在,使混凝土的力学性能产生弱化效应,为了表征这种弱化效应,把材料某种程度的弱化定义为损伤D.Lemait re [19,20]应变等价性原理:损伤材料(D ≠0)在有效应力作用下产生的应变与同种材料无损(D =0)时发生的应变等价.根据这一原理,受损材料(D ≠0)应力2应变本构关系可以从无损材料(D =0)的本构方程来导出,只要用损伤后的有效应力来取代无损材料本构关系中的名义应力.即通常所谓的Cauchy 应力σij =σij1-D(15)其中, σij 为有效应力,σij 为名义应力,D 为损伤因子,0≤D ≤1,当D =0时,表示材料无损伤,D =1时,表示材料完全丧失承载能力.用式(15)中 σij 替代式(8)中σij ,得到包含损伤的混凝土本构关系εij1E 12(1+ν)(δik δjl +δil δjk )-νδij δkl ・ σkl (1-D )+σkl D(1-D )2+γ〈<(F 1)〉5F 15σij (16)其中F 1(σij )=AJ 2(1-D )2Y 2d +λJ 2(1-D )Y d +BI 1(1-D )Y d-1由于混凝土内部存在大量的微裂纹和微空洞缺陷,因此损伤D 由两部分引起.一部分是由于混凝土内部微裂纹的张开和扩展引起的,通过拉伸应变来控制,设由于微裂纹引起的损伤部分为D t ;另一部分是由于混凝土内部的微空洞引起的,通过压缩应变来控制,设由于微空洞引起的损伤部分为D c .因此损伤D 为这两部分耦合,为简单计算,设损伤D 为D t 和D c 的线性组合,即D =αD t +(1-α)D c ,α为权重系数,0≤α≤1,α=0表示损伤D 完全由微空洞缺陷引起,α=1,表示损伤D 全部是由微裂纹的张开和扩展引起的.2.1　微裂纹损伤变量的描述2.1.1　微裂纹损伤的定义混凝土内部存在大量随机分布的微裂纹,其大小和尺寸各不相同,在动态和冲击载荷作用下,这些微裂纹被激活,形成应力释放区,并产生累积损伤,导致材料强度和刚度的劣化,并最终开裂破坏.假设这些微裂纹符合理想微裂纹体系统条件,定义宏观损伤D t 为含裂纹材料中单位体积内微裂纹所占的比例,且损伤是不可逆,则D t =V d V=V -V sV, D t ≥0(17)其中,V 是含损伤材料的体积,V s 是体积V 内无损伤部分的体积,V d 是体积V 中微裂纹所占体积.设含微裂纹代表性体积单元内单位体积微裂纹密度分布函数为n,则n d v 表示t 时刻体积在v 2v +d v 范围内的微裂纹数.因此损伤D t 可以表示如下D t =∫∞nv d v (18)其中,v 为单个微裂纹的特征体积,n (a,t )是理想微裂纹体系统中的数密度分布函数,满足下列演化方程5n 5t +5(n a )5t=n N(19)・332・第3期刘海峰等:　强冲击荷载作用下混凝土材料动态本构模型其中,n N为微裂纹的成核率密度, a为微裂纹的扩展速率,对于理想微裂纹系统n N=n N(a,σ(t)), a= a(a,σ(t))对式(18)求导得D t=( D t)g+( D t)n(D t)g=∫∞0n v d v (D t)n=∫∞0n N v d v (20)式(20)表明,损伤变量D t的变化是由裂纹线性尺度的长大和成核两个部分引起的.2.1.2　微裂纹的扩展微裂纹的成核过程是一个随机过程,并用成核率密度n N来描述,其大小与应力状态及微裂纹的尺寸有关,借鉴白以龙[21]给出的如下成核密度表达式　n N=K th σtσth-1aa thm-1exp-aa thm(21)其中,K th,m和a th为材料常数,与材料的性质有关, a为微裂纹的尺寸,σth是微裂纹成核的阈值应力,只有应力σt>σth微裂纹成核,并且扩展,否则保持不变,上述参数均可以通过实验来确定.σt是混凝土内部引起微裂纹损伤演化的拉伸应力,与混凝土外部作用荷载σ不相同,但具有某种函数关系.为简单计算,采用σt=k|σ|,其中k为应力转化因子,表征材料内部微损伤对其内部场的影响.对于压缩情况,k <1;对于拉伸情况k>1,具体取值参见Ortiz 等[22,23]的工作.根据文献[24]裂纹失稳脆性断裂临界条件,可以得到微裂纹损伤演化发展的阈值应力σth=K IC/Yπa th,Y是形状系数,与试件几何形状,载荷条件和裂纹大小,位置等有关系,本文取Y=1;K IC 是材料的断裂韧度,表示材料抵抗裂纹失稳扩展能力的物理量,可以由实验确定.假设混凝土材料内微裂纹是钱币状,则单个微裂纹的特征体积可以表示如下[25]v=βa3(22)其中,β是几何因子,依赖于微裂纹的形状和尺寸.将式(22),(21)代入式(20)第三式得到由于微裂纹成核引起损伤的增加为 (D t)n=3K th σtσth-1・∫∞0a a th m-1exp-a a th mβ2a5d a 当m=1时,上式简化为(D t)n=360K thβ2a6thσtσth-1由于a th为10-3m量级,因此可以忽略微裂纹成核引起的损伤增加,只考虑混凝土原有微裂纹长大引起的损伤增加.王道荣[26]在I型裂纹扩展研究的基础上,提出了如下微裂纹扩展速率的计算公式aa=1-ν22λ1Eπ(σ2t-σ2th)C R(23)其中,λ1为材料单位表面能;C R为瑞利波波速,由下式确定C R=0.862+1.14ν1+νE2(1+ν)ρ其中,ρ为材料密度.其它参数同前.将式(23)代入式(20)第二式得(D t)g=∫∞03nβa3 a a d v= 3(1-ν2)2λ1Eπ(σ2t-σ2th)C R D t(24)代入式(20)第一式得D t=3(1-ν2)2λ1Eπ(σ2t-σ2th)C R D t(25)积分得　D t=D t0exp3(1-ν2)2λ1Eπ(σ2t-σ2th)C R(t-t0)(26)其中,D t0是混凝土材料初始损伤值,t0是裂纹扩展的初始时间.2.2　微空洞损伤变量的描述2.2.1　微空洞损伤变量的定义混凝土内部随机分布了大量的微空洞.在爆炸或冲击荷载作用下,随着微空洞的塌陷,混凝土材料压缩密实,体积模量也相应增大,由此出现了损伤为负值的情况,把这种损伤为负值的损伤称为负损伤D c.假设这些微空洞的分布是均匀的,并以其体积百分比f3(表示为材料孔隙度δ与密度ρ的乘积)作为表征材料内部损伤的度量D c=f3=δρ2.2.2　微空洞损伤演化方程G r jeu等[27]根据质量守恒定律推出了微空洞的演化方程,认为微空洞的演化由材料的体积应变控制.微空洞的扩展方程表示为f3=(1-f3) εkk(27)利用以上演化方程,可得到微空洞体积百分比f3的・432・固　体　力　学　学　报 2008年表示形式f3=1-(1-f30)e-εkk(28)其中,f30(=δ0ρ0)是初始微空洞体积百分比,δ0是混凝土材料的初始孔隙度,ρ0是混凝土材料的初始密度.3　模型参数的确定选用一级轻气炮动力实验装置在200m/s2500 m/s速度范围内冲击混凝土圆柱形靶板,靶板试件应变率响应范围达到了104s-12105s-1,横向约束围压应力范围在1GPa21.5GPa之间.研究中,共做了7发弹体冲击靶板的实验,其中3发实验取到了比较满意的实验信号.飞片和靶板采用同质材料,其原料配比和物理参数见表2和表3.飞片直径为75 mm,厚度为5mm,靶板由5块相同的圆盘形试件组成,试件直径为70mm,厚度为5mm,在圆盘形试件之间安装双螺旋形锰铜压阻传感器(共3个,分别对应于测试点No1,No2,No3),用于记录冲击信号.为了分析方便,取其加载段应变率平均值为实验响应应变率,实验可近似看作是恒应变率的.图12图3为不同冲击速度下混凝土材料应力应变曲线,并与本文提出的本构模型进行了比较,模型参数见表4.表2　混凝土试件组份材料配合比Table2　Composition of concrete specimens组份水泥粉煤灰硅灰砂子水HSG A E 配比/g3005020540100 2.5 2.5表3　混凝土物理参数表Table3　Parameter table of concrete杨氏模量E/GPa 泊松比ν材料密度ρ/kg・m23孔隙度δ0/cm3・g-1410.223500.041表4中,参数k1,k2,A和B由混凝土的单轴拉伸、单轴压缩实验,结合表1确定;参数H1,H2和H3通过对实验数据拟合得到;断裂韧度K IC和λ1取自断裂力学手册;针对不同的加载情况,裂纹成核尺度a th的量级约取为1mm;由于没有相应的微观测试方法,参考文献[28]中岩石材料,混凝土材料初始损伤值D t0的具体取值见表4;参数k可以通过在裂纹・532・第3期刘海峰等:　强冲击荷载作用下混凝土材料动态本构模型扩展阈值应力σth与混凝土材料弹性极限σs之间建立关系,将其粗略求得;屈服参数m1,γ和α通过利用试凑法不断拟合逼近已有实验结果得到.表4　模型参数表Table4　Table of model parameter for concrete屈服参数材料参数m1γλ1/MJ・m-210.010.08状态参数A B k1k21.27593.196211.73650.9801损伤参数K IC/MPa・m k D t0a th/m0.90.40.070.001拟合参数H1H2H3α0.1340.1351.2960.8图12图3为不同冲击速度下混凝土靶板内部在不同的测试点(测试点分别为No1,No2,No3)位置处的模型预测曲线与实验测试曲线的比较,从图中可以看出,模型预示结果无论在变形趋势上,还是数值精度上都与实验结果符合得很好.同时将本文提出的本构模型预测曲线与宁建国等[10]提出的本构模型预测曲线进行了比较,发现本文提出的本构模型预测曲线与实验结果拟合较好.通过对图12图3不同靶板内同一测点处(如测点No1或No2或No3)在不同冲击速度下应力应变曲线的比较发现,随着冲击速度的提高,混凝土的承载能力显著增加,即图中峰值应力增大,相应的峰值应变亦显著增加,即混凝土材料的塑性变形增大.这主要是两方面的原因,一方面由于混凝土材料是率相关材料,受到应变率效应的影响,另一方面由于静水压力相关性的影响,横向的约束压力限制了混凝土材料裂纹的发展.4　结论混凝土材料在冲击荷载作用下的响应是一个非常复杂的过程,不仅涉及了材料内部微结构损伤缺陷的演化发展,而且还涉及了材料应变率敏感效应影响.进行混凝土材料特性研究的时候,不可能将所有的因素都考虑进去,因此必须根据混凝土材料在冲击荷载作用下的宏观现象作了一些假设,以此简化计算.本文基于损伤与塑性耦合理论,以修正Otto sen 四参数破坏准则为屈服法则,引入损伤,发展了一个动态本构模型用于描述混凝土材料的冲击特性,在该模型中,考虑了引起混凝土材料弱化的两种不同的损伤机制:拉伸损伤和压缩损伤.其中,拉伸损伤是由微裂纹的张开和扩展引起的,通过拉伸应变来控制;压缩损伤相关于微空洞体积分数比的演化,并通过微空洞塌陷引起的压缩应变来控制,将总的损伤看成是这两种损伤的线性组合,由此压缩损伤和拉伸损伤就完全耦合了.宏观上,假设混凝土材料是一个均匀连续体;而从细观角度来看,混凝土材料内部则存在了大量随机分布的微裂纹和微空洞等损伤缺陷.假设微裂纹是均匀分布,且符合理想微裂纹体系统条件,定义含裂纹材料中单位体积内微裂纹所占的比例来表征微裂纹损伤所引起的混凝土材料宏观力学性能的劣化.基于裂纹扩展模型,微裂纹被激活、成核并扩展.当累积裂纹达到某一阈值时,混凝土材料发生粉碎性破坏.同时需要考虑微空洞的演化发展,且随着微空洞的塌陷,混凝土材料压缩密实.利用该模型对混凝土材料在强冲击荷载作用下的冲击特性进行数值模拟,并将该模型的预测曲线与宁建国等[10]提出的本构模型的预测曲线及实验结果进行比较,结果表明:该模型预示结果无论在变形趋势上,还是数值精度上都与实验结果符合得更好.因此,可以用该模型模拟混凝土材料在强冲击荷载下的动态特性.参考文献[1]　Watstein D.Effect of strain rate on the compressivestrength and elastic properties of concrete[J].Journalof American Concrete Institute,1953,49(8):7292744.[2]　Bischoff P pressive behavior of concrete athigh strain rates[J].Material and Structure,1991,144(24):4252450.[3]　胡时胜,王道荣,刘剑飞.混凝土材料动态力学性能实验研究[J].工程力学,2001,18(5):1152118.(Hu SS,Wang D R,Liu J F.Experimental study of dynamic・632・固　体　力　学　学　报 2008年mechanical behavior of concrete[J].Engineering Me2chanics,2001,18(5):1152118.(in Chinese))[4]　商霖,宁建国.强冲击载荷下混凝土动态本构关系[J].工程力学,2005,22(2):1162119.(Shang L,NingJ G.Dynamic constitutive relationship of concretesubjected to shock loading[J].Engineering mechan2ics,2005,22(2):1162119.(in Chinese))[5]　商霖,宁建国,孙远翔.强冲击载荷作用下钢筋混凝土本构关系的研究[J].固体力学学报,2005,26(2):1752181.(Shang L,Ning J G,Sun Y X.The constitu2tive relationship of reinforced concrete subjected toshock loading[J].Acta Mechanics Solida Sinica,2005,26:1752181.(in Chinese))[6]　Perzyna P.Fundamental problems in visco2plasticity[J].Advances in Applied Mechanics,1966,9:2432377.[7]　李兆霞.一个综合模糊裂纹和损失的混凝土应变软化本构模型[J].固体力学学报,1995,16(1):22230.(LiZ X.A viscoplastic model combined damage andsmeared crack for softening of concrete[J].Acta Me2chanics Solida Sinica,1995,16:22230.(in Chinese)) [8]　Krajcinovic D,Silva M.Statistical aspects of the con2tinuous damage mechanics[J].International Journal ofSolids and Structures,1982,18:5512562.[9]　Dube J F.Rate dependent damage model for concretein dynamics[J].Journal of Engineering Mechanics,1996,122:9392947.[10]　宁建国,商霖,孙远翔.混凝土材料冲击特性的研究[J].力学学报,2006,38(2):1992208.(Ning J G,Shang L,Sun Y X.Investigation on impacting behav2ior of concrete[J].Chinese Journal of Theoretical andApplied Mechanics,2006,38(2):1992208.(in Chi2nese))[11]　Ottosen N S.A failure criterion for concrete[J].Jour2nal of Engineering Mechanics,1977,103:5272535. [12]　Kupfer H,Hilsdorf H K,Rusch H.Behavior of con2crete under biaxial stresses[J].Journal of AmericanConcrete Institute,1969,66:6562666.[13]　Richart F E,Brandtzaeg A,Brown R L.A study of thefailure of concrete under combined compressive stres2ses[Z].Bulletin No.185,Urbana:University of Illi2nois,Engineering Experiment Station,1928.[14]　Balmer G G.Shearing strength of concrete under hightriaxial stress computation of Mohrs envelope ascurve[R].Report No.SP223,Washington D C:Struc2tural Research Laboratory,1949.[15]　Lemaitre J,Chaboche J L.Aspect phenomenologiquede la rupture par endommagement[J].Journal deMecanique Applique,1978,2(3):3172365.[16]　Abrams D A.Effect of rate of application of load onthe compressive strength of concrete[J].Journal ofAmerican Society for Testing Materials,1917,17:3642377.[17]　Bischoff P H,Perry S H.Impact behavior of plainconcrete in uniaxial compression[J].Journal of Engi2neering Mechanics,1995,121(6):6852693.[18]　Tang T X,Malvern L E,J enkins D A.Dynamic com2pressive testing of concrete and mortar[J].Journal ofEngineering Mechanics,1984,1:6632666.[19]　Lemaitre J.Application of damage concepts to predictcreep fatigue failure[J].Journal of Engineering Mate2rials and Technology,1979,101(1):2022209.[20]　勒迈特J.损伤力学教程[M].北京:科学出版社,1996.(Lemaitre J.A Course on Damage Mechanics[M].Beijing:Science press,1996.(in Chinese)) [21]　白以龙.冲击载荷下材料的损伤和破坏[C]//王礼立,余同希,李永池.冲击动力学进展.安徽:中国科学技术大学出版社,1992:34257.(Bai Y L.Damage andbreakage of material subjected to impact loading[C]//Wang L L,Yu T X,Li Y C.Devolvement of dy2namic mechanic.Anhui:press of University of Scienceand Technology of China,1992:34257.(in Chinese)) [22]　Ortiz M,Popov E P.A physical model of the inelasti2city of concrete[J].Proceeding of the Royal Society,London,Series A,Mathematical and Physical Sci2ences,1982,383:1012125.[23]　Ortiz M,Popov E P.Plain concrete as a compositematerial[J].Mechanics of Material,1982,1:1392150.[24]　王铎.断裂力学[M].哈尔滨:哈尔滨工业大学出版社,1989.(Wang D.Fracture Mechanics[M].Harbin:Harbin institute of technology press,1989.(in Chi2nese))[25]　Mura T.Micromechanics of defects in solids[M].Dordrecht:Martinus Nijhoff publisher,1987. [26]　王道荣.高速侵彻现象的工程分析方法和数值模拟研究[D].安徽:中国科学技术大学,2002.(Wang D R.Research on numerical simulation and engineering a2nalysis methods of penetration phenomenon at highspeed[D].Anhui:University of Science and Technol2ogy of China,2002.(in Chinese))[27]　G r jeu M,Michel J C,Suquet P.A micromechanicalapproach of damage in viscoplastic materials by evolu2tion in size,shape and distribution of voids[J].Com2puter Methods in Applied Mechanics and Engineer2・732・第3期刘海峰等:　强冲击荷载作用下混凝土材料动态本构模型ing ,2000,183:2232246.[28]　Taylor L M ,Chen E P.Kuszmaul J S.Micro 2crackinduced damage accumulation in brittle rock underdynamic loading[J ].Journal of Computer Methods in Applied Mechanics and Engineering ,1986,55:3012332.CONSTITUTIVE MODE L OF CONCRETESUBJECTED TO INTENSE IMPACT LOADINGHaifeng Liu 1,2 Jianguo Ning 1(1S tate Key L aboratory of Ex plosive S cience and Technolog y ,B ei j ing I nstitute of Technolog y ,B ei j ing ,100081)(2Civil and hy d raulic Engineering De partment of N ing x ia Universit y ,Yinchuan ,750021)Abstract Based on t he damage and Ottosen failure criterion ,a constit utive model is developed to in 2vestigate t he mechanical behavior of concrete subjected to intense impact loading.Different damage mecha 2nisms such as tensile and comp ressive damage are considered in t his model.Suppose t he tensile damage con 2t rolled by t he tensile st rain is caused by micro 2cracks opening and st retching ,t he compressive damage con 2t rolled by comp ressive st rain is about t he evolutio n of micro 2voids.So t he tensile damage and compressive damage are coupling.Experimental result s indicate t hat wit h t he increase of impact velocity ,t he bearing ca 2pacity and plastic deformation of concrete enhance greatly.A comparison between model p rediction and ex 2perimental result s shows t hat bot h of t hem agree well wit h each ot her.So t he model can be used to simu 2late t he dynamic mechanical behavior of concrete.K ey w ords concrete ,light gas gun ,impact behavior ,dynamic constit utive model・832・固　体　力　学　学　报 2008年。

混凝土弹塑性损伤本构模型研究

混凝土弹塑性损伤本构模型研究一、概述混凝土作为一种广泛应用于土木工程领域的重要建筑材料，其力学行为的研究对于工程结构的设计、施工和维护至关重要。

弹塑性损伤本构模型作为描述混凝土材料在复杂应力状态下力学行为的重要工具，近年来受到了广泛关注。

该模型能够综合考虑混凝土的弹性、塑性变形以及损伤演化等多个方面，为工程结构的非线性分析和损伤评估提供了有效的理论支持。

本文旨在深入研究混凝土弹塑性损伤本构模型的理论框架、数值实现及其在工程中的应用。

我们将对混凝土弹塑性损伤本构模型的基本理论进行梳理，包括模型的建立、参数的确定以及损伤演化方程的推导等方面。

通过数值模拟和试验验证相结合的方法，对模型的准确性和适用性进行评估。

我们将探讨该模型在土木工程结构非线性分析、损伤评估以及加固修复等方面的实际应用，为工程实践提供有益的参考和指导。

通过本文的研究，我们期望能够为混凝土弹塑性损伤本构模型的理论发展和工程应用提供新的思路和方法，推动土木工程领域相关技术的创新和发展。

1. 研究背景：介绍混凝土作为一种广泛应用的建筑材料，在土木工程中的重要性。

混凝土，作为土木工程领域中使用最广泛的建筑材料之一，其性能与行为对结构的整体安全性、经济性和耐久性具有至关重要的影响。

由于其独特的物理和力学性能，混凝土在桥梁、大坝、高层建筑、地下结构等各类土木工程设施中发挥着不可替代的作用。

随着工程技术的不断进步和建筑需求的日益增长，对混凝土材料性能的理解和应用要求也越来越高。

混凝土是一种非均质、多相复合材料，其力学行为表现出明显的弹塑性特性，并且在受力过程中可能产生损伤累积，进而影响其长期性能。

建立能够准确描述混凝土弹塑性损伤行为的本构模型，对于准确预测混凝土结构的受力性能、优化设计方案以及保障结构安全具有重要的理论和实际意义。

近年来，随着计算力学和材料科学的快速发展，对混凝土弹塑性损伤本构模型的研究已成为土木工程领域的研究热点之一。

通过对混凝土材料在复杂应力状态下的力学行为进行深入研究，建立更加精细和准确的本构模型，有助于提升对混凝土结构性能的认识，推动土木工程技术的进步与发展。

钢筋混凝土柱冲击数值模拟方法与关键参数的研究

钢筋混凝土柱冲击数值模拟方法与关键参数的研究发表时间：2019-06-20T17:07:12.847Z 来源：《防护工程》2019年第6期作者：祁立斌[导读] 本文采用LS-DYNA软件建立车-柱撞击有限元模型，对比验证所采用的材料模型和接触方式。

西安市市政建设（集团）有限公司摘要：钢筋混凝土柱在服役过程中，除遭受地震作用外，还可能遭受冲击荷载作用，例如建筑物遭受车辆撞击作用。

本文采用LS-DYNA软件建立车-柱撞击有限元模型，对比验证所采用的材料模型和接触方式。

研究表明：采用MAT_145#混凝土模型和MAT_3#能够较好反映冲击荷载作用下钢筋混凝土柱的动力响应和损伤分布，能够模拟出与试验结果比较吻合的剪切破坏状态，验证了数值模型的可靠性。

1. 绪论钢筋混凝土柱服役过程中，除遭受地震作用外，还可能遭受冲击荷载作用，例如建筑物遭受车辆撞击作用[1，2]。

钢筋混凝土柱的抗冲击性能研究是个十分复杂的动态过程，涉及到混凝土、钢材等材料非线性、接触非线性以及构件的大变形。

然而，受限于现有动力试验技术的发展、实验室场地条件的限制以及高昂的试验费用，难以采用试验手段对型钢混凝土柱在冲击荷载作用下的动力特性进行精细化的分析。

鉴于此，本文采用LS-DYNA有限元软件对车-柱撞击数值分析中所涉及的材料模型参数，接触碰撞参数和其他关键技术等进行验证与分析，建议一种分析此类问题的合理的有限元模型参数。

2. 材料模型2.1 混凝土本文采用SCHWER_MURRAY_CAP_MODEL（MAT_145#）[3]模型模拟混凝土材料。

MAT_145#为连续盖帽模型，能够反映碰撞冲击过程中混凝土材料的动力特性，包括达到峰值强度前的应变强化、达到峰值强度后的应变软化以及应变率效应，适用于在冲击问题中模拟土体、混凝土和岩石等岩土材料。

混凝土为水泥、砂、石和水等组成的工程复合材料，其在受力之前内部就存在微裂缝和微孔洞，这些微孔洞在静水压力作用下开始破坏并被压实，这在宏观上表现为混凝土材料不可恢复的塑性体积变形。

混凝土损伤本构模型

混凝土损伤本构模型混凝土作为一种重要的建筑材料，在建筑结构中具有重要的作用。

然而，由于外界环境和使用条件的不断变化，混凝土在使用过程中可能会受到损伤，这些损伤可能会导致结构的不安全性。

因此，混凝土损伤本构模型的研究对于建筑结构的安全性具有重要的意义。

混凝土损伤本构模型是指用于描述混凝土材料在受到外部荷载作用后产生的损伤行为的数学模型。

通过研究混凝土在受损状态下的力学性能，可以为工程结构的设计和评估提供重要的依据。

本文将对混凝土损伤本构模型的发展历史、基本原理、研究现状及其应用进行综述，并探讨该领域的未来发展方向。

一、混凝土损伤本构模型的发展历史混凝土损伤本构模型的研究始于上世纪60年代。

最早提出的混凝土损伤本构模型是由Scheel和Lubbock于1961年提出的弹塑性损伤理论。

随后，梁奇等学者在1978年提出了一种考虑混凝土受损状态的本构模型，这为混凝土损伤本构模型的研究奠定了基础。

随着研究的不断深入，人们对混凝土损伤本构模型的要求也越来越高，例如考虑温度、湿度等耐久性因素对混凝土材料的影响。

在本构模型的建立方面，人们不仅关注其数学表达形式，更加重视其实际工程应用的可靠性和有效性。

混凝土损伤本构模型的研究发展历程为混凝土损伤本构模型的研究奠定了基础，同时也为今后的研究提供了重要的借鉴。

二、混凝土损伤本构模型的基本原理混凝土损伤本构模型的基本原理是通过描述混凝土在受到外部荷载作用后产生的损伤和变形过程，从而建立相应的数学模型。

其核心是将损伤参数引入材料的本构关系中，以描述材料在损伤过程中的力学性能。

混凝土损伤本构模型一般包括两方面的内容，即损伤模型和本构模型。

损伤模型用于描述混凝土在受到外部荷载作用后产生的损伤行为，通常采用损伤变量或者损伤指标来描述损伤程度。

本构模型则用于描述混凝土在不同损伤状态下的应力-应变关系，通常采用应力-应变关系的修正形式来描述材料的非线性和损伤效应。

混凝土损伤本构模型的基本原理是将损伤参数引入材料的本构关系中，以描述材料在损伤过程中的力学性能。

基于理想无损状态的混凝土弹塑性损伤本构模型研究及应用共3篇

基于理想无损状态的混凝土弹塑性损伤本构模型研究及应用共3篇基于理想无损状态的混凝土弹塑性损伤本构模型研究及应用1混凝土作为一种广泛应用于工程中的重要材料，在承受外力和环境作用下容易发生损伤。

因此，混凝土的损伤行为研究已经成为一个热门的研究领域。

其中，弹塑性损伤是混凝土损伤中较为复杂的一种。

为了更好地研究混凝土弹塑性损伤本构模型，本文将介绍基于理想无损状态的混凝土弹塑性损伤本构模型研究及应用。

1. 弹塑性本构模型概述弹塑性本构模型是研究材料承受外力后弹性和塑性响应的数学模型。

在混凝土中，弹性和塑性响应在不同阶段起到了不同的作用。

弹性阶段通常是指材料在外力作用下的瞬时变形，而塑性阶段则指材料在外力作用下发生的几乎恒定的变形。

因此，混凝土弹塑性损伤本构模型可以描述由于外力作用导致的混凝土弹性阶段和塑性阶段的响应，以及这些响应与混凝土发生损伤之间的关系。

2. 理想无损状态混凝土在初始时存在一个理想无损状态，即没有受到任何外力或环境作用。

在理想无损状态下，混凝土的本构特性可以被准确地描述，为进一步研究混凝土的弹塑性损伤本构模型提供了有力的基础。

3. 混凝土弹塑性损伤本构模型混凝土弹塑性损伤本构模型主要分为两类：基于连续损伤理论的本构模型和基于分离损伤理论的本构模型。

前者认为损伤是一个连续的过程，而后者则是将损伤分为不同的阶段，每个阶段具有不同的损伤特征。

本文主要介绍基于连续损伤理论的混凝土弹塑性损伤本构模型。

该模型将混凝土的本构响应视为弹性响应和塑性响应之和，并通过引入损伤变量来描述损伤发生的过程。

具体而言，混凝土的应变张量可以表示为：ε = εe + εp + εd其中，εe表示混凝土的弹性应变，εp表示混凝土的塑性应变，εd 表示混凝土的损伤应变。

根据连续损伤理论，损伤可以用损伤变量D 来描述，即：D = 1 - (1 - εd/εf)n其中，εf是混凝土的最大应变，n是连续损伤理论中的材料参数。

假设混凝土在最大应变处完全破坏，则D=1。

爆炸冲击作用下三种混凝土本构模型对比研究

爆炸冲击作用下三种混凝土本构模型对比研究
杜闯;宋帅;张江鹏
【期刊名称】《兵器装备工程学报》
【年(卷),期】2022(43)11
【摘要】数值模拟是结构抗爆领域研究的重要方法,数值模拟效果在很大程度上取决于动态本构模型的选择。

本文对混凝土主要的3种动态本构模型:HJC、RHT和K&C进行分析,针对不同模型的关键参数、优缺点进行了评述。

采用3种不同动态本构模型模拟了文献中的钢筋混凝土板爆炸试验,对比分析了不同本构模型的模拟结果,为进一步完善抗爆数值模拟提供参考。

分析结果表明:在爆炸冲击工况下,RHT 和K&C在本构理论的表达上相对全面,HJC对破坏形态和最大挠度的描述更接近试验。

【总页数】8页(P49-56)
【作者】杜闯;宋帅;张江鹏
【作者单位】河北工业大学土木与交通学院;河南省特种防护材料重点实验室【正文语种】中文
【中图分类】O383
【相关文献】
1.爆炸冲击载荷作用下双层钢板混凝土板与钢筋混凝土板动态响应对比研究
2.爆炸冲击载荷作用下钢筋混凝土介质裂纹扩展速度的实验研究
3.HJC和K&C混凝土模型在爆炸荷载
作用下的对比研究4.4种车辆模型作用下T形刚构桥冲击系数对比研究5.强冲击载荷作用下钢筋混凝土本构关系的研究
因版权原因，仅展示原文概要，查看原文内容请购买。

不同损伤模型下超高性能混凝土SHPB试验数值模拟对比

２０２２４ＢＡＢ２１４０６６)
作者简介:任亮(１９８０—) ꎬ男ꎬ博士ꎬ主要从事ＵＨＰＣ构件抗震与抗冲击等方面研究ꎮ
Copyright©博看网. All Rights Reserved.
第４期
任亮等:不同损伤模型下超高性能混凝土ＳＨＰＢ试验数值模拟对比
６６１
２. ＮａｔｉｏｎａｌＥｘｐｅｒｉｍｅｎｔａｌＴｅａｃｈｉｎｇＤｅｍｏｎｓｔｒａｔｉｏｎＣｅｎｔｅｒｏｆＣｉｖｉｌＥｎｇｉｎｅｅｒｉｎｇꎬ ＥａｓｔＣｈｉｎａＪｉａｏｔｏｎｇＵｎｉｖｅｒｓｉｔｙꎬ
基于
动态破坏进程ꎮ
ＵＨＰＣ单轴和三轴压缩试验数据ꎬ 校准了
中关键参数的取值ꎬ分析了ＵＨＰＣ梁在低速
１基于ＵＨＰＣ材料的损伤模型
参数确定
落锤冲击下的动力性能ꎮ 贾鹏程等 [１０] 进一
１. １ＫＣＣ模型参数确定
Ｃｏｎｔｉｎｕｏｕｓ￣Ｓｕｒｆａｃｅ￣Ｃａｐ( ＣＳＣ) 冲击损伤模型
ＣｏｍｐａｒｉｓｏｎｏｎＮｕｍｅｒｉｃａｌＳｉｍｕｌａｔｉｏｎｏｆＳＨＰＢ
ＴｅｓｔｆｏｒＵｌｔｒａ￣ｈｉｇｈＰｅｒｆｏｒｍａｎｃｅＣｏｎｃｒｅｔｅ
ｕｎｄｅｒＤｉｆｆｅｒｅｎｔＤａｍａｇｅＭｏｄｅｌｓ
ＲＥＮＬｉａｎｇ１ꎬ２ ꎬ ＺＨＥＮＧＳｈｅｎｇｐｅｉ１ ꎬ ＣＡＩＡｎｇｌｉｎ３ ꎬ ＧＵＯＺｈｏｎｇｚｈａｏ１ ꎬ ＹＵ
步指出ＣＳＣ模型对ＵＨＰＣ梁出现的剪胀效
ＫＣＣ模型通过定义三个独立的剪切破坏
应描述较差ꎮ
面来控制混凝土类材料处理复杂应力条件下
的非线性行为[１１] ꎬ应用线性插值函数考虑当
虽然应用上述三种损伤模型目前已实现

混凝土动力损伤本构模型研究进展述评

混凝土动力损伤本构模型研究进展述评一、概述混凝土作为一种广泛应用于土木工程领域的建筑材料，其性能表现直接关系到工程结构的安全与稳定性。

随着科技的不断进步和工程需求的日益增长，对混凝土材料性能的研究也日益深入。

混凝土在动力荷载作用下的损伤机制和本构模型研究尤为重要。

本文旨在概述混凝土动力损伤本构模型的研究进展，探讨相关领域的研究成果和发展趋势。

混凝土在受到地震、爆炸等动力荷载作用时，会产生复杂的应力波传播、裂缝扩展和损伤累积等现象。

这些现象对混凝土结构的整体性能产生显著影响。

建立准确的混凝土动力损伤本构模型对于预测结构在动力荷载作用下的响应和破坏过程具有重要意义。

随着计算力学、材料科学等领域的交叉融合，混凝土动力损伤本构模型的研究取得了长足的进步。

从最初的弹性模型、塑性模型，到后来的损伤力学模型、粘弹塑性模型等，模型的复杂性和准确性不断提高，能够更好地描述混凝土材料的非线性行为。

混凝土动力损伤本构模型的研究仍面临诸多挑战。

如混凝土材料的复杂性和不确定性、动力荷载的多样性和复杂性、试验数据的缺乏等，都是制约模型发展的关键因素。

未来的研究应更加关注混凝土材料的细观机制、多尺度建模、智能化建模等方面，以提高模型的预测精度和适用性。

随着人工智能、大数据等技术的快速发展，混凝土动力损伤本构模型的研究也将迎来新的发展机遇。

通过对大量试验数据的挖掘和分析，建立数据驱动的混凝土本构模型，将有望为混凝土结构的性能评估和防灾减灾提供有力支持。

1.1 研究背景和意义混凝土作为现代建筑中最常用的建筑材料之一，其性能的好坏直接关系到建筑物的安全性和稳定性。

在地震、爆炸等动力荷载作用下，混凝土会发生损伤甚至破坏，对人们的生命财产安全造成极大的威胁。

对混凝土的动力损伤机理及其本构模型进行研究，对于提高建筑物的抗震、抗爆等能力，保障人们的生命财产安全具有重要意义。

随着科技的进步和研究的深入，混凝土动力损伤本构模型的研究逐渐受到广泛关注。

混凝土动态计算本构新模型

混凝土动态计算本构新模型一、本文概述混凝土作为一种广泛应用的建筑材料，其力学性能和动态行为一直是土木工程和材料科学领域的研究重点。

随着工程结构向着大型化、复杂化、动态化的方向发展，对混凝土材料在动态荷载作用下的力学行为理解提出了更高的要求。

传统的混凝土本构模型，虽然在静态或准静态条件下能够提供较为准确的预测，但在高应变率、强冲击等动态环境下，其适用性往往受到限制。

发展新型的混凝土动态计算本构模型，对于准确评估混凝土结构的动态性能、优化设计方案以及提高工程安全性具有重要的理论价值和现实意义。

本文旨在介绍一种新型的混凝土动态计算本构模型，该模型综合考虑了混凝土材料的非线性、应变率效应、损伤演化以及多轴应力状态等因素，旨在更准确地描述混凝土在动态荷载作用下的力学行为。

通过引入先进的本构理论、结合实验结果和数值分析，本文详细阐述了新模型的建立过程、关键参数的确定方法以及模型的验证与应用。

希望本文能够为相关领域的研究人员提供新的思路和方法，推动混凝土动态力学性能的深入研究和发展。

二、混凝土动态力学特性混凝土作为一种广泛应用于土木工程中的材料，其动态力学特性一直是研究者们关注的重点。

动态力学特性描述的是混凝土在受到快速或冲击载荷作用下的力学响应，这与混凝土在静载作用下的表现有显著的不同。

在动态加载条件下，混凝土展现出更高的强度和更脆的破坏模式。

这是因为快速加载导致混凝土内部微裂缝的扩展速度加快，进而引发更多的裂缝产生和扩展。

动态加载还导致混凝土的应变率敏感性增强，即随着加载速率的增加，混凝土的强度也会随之提高。

为了准确描述混凝土的动态力学特性，研究者们提出了多种动态本构模型。

这些模型通常基于混凝土的应力-应变关系，并考虑了应变率、温度等因素的影响。

一些模型还尝试引入损伤因子来描述混凝土在加载过程中的损伤演化。

现有的动态本构模型仍存在一些问题和挑战。

例如，一些模型在描述高应变率下的混凝土行为时可能存在误差；另一些模型则可能过于复杂，不利于工程应用。

混凝土塑性—损伤本构模型研究

混凝土塑性—损伤本构模型的研究背景和意义
混凝土塑性—损伤本构模型的研究旨在描述混凝土在受力过程中塑性变形和损伤发展的内在规律，为结构设计和施工提供理论支持。由于混凝土材料的复杂性和多层次性，其本构关系一直是一个研究热点。建立更为精确、可靠的混凝土塑性—损伤本构模型对于提高结构安全性、优化设计方案具有重要意义。
研究方法：混凝土塑性—损伤本构模型的建立、参数估计、验证方法等
研究混凝土塑性—损伤本构模型通常涉及理论建模、数值计算和实验验证三个环节。首先，基于对混凝土材料行为的深入理解，结合相关理论和假设建立本构模型。然后，利用数值计算方法对模型进行求解，并通过实验手段对模型进行验证和调整。
在建立模型的过程中，需要充分考虑混凝土的多层次结构和应力—应变关系。同时，参数估计也是重要的一环，需要通过大量实验数据和使用合适的数据拟合方法来确定模型参数。此外，为了验证模型的准确性，通常需要将模型计算结果与实验结果进行对比，分析误差和模型的适用范围。
2、模型的优缺点：现有的混凝土塑性—损伤本构模型具有较高的预测能力和精度，能够为工程设计和施工提供较为准确的指导。然而，这些模型往往较为复杂，需要耗费大量计算资源和时间，对于工程应用带来一定挑战。此外，模型的适用性和可靠性还需要通过更多的实验验证和研究来完善和改进。
3、实际应用前景：随着计算机技术和数值计算方法的不断发展，混凝土塑性—损伤本构模型在工程实践中的应用前景越来越广阔。未来研究可以针对模型的简化、参数优化和自适应调整等方面进行深入研究，提高模型的易用性和精度，进一步拓展其应用范围。同时，结合智能化、信息化技术，可以实现混凝土结构全生命周期的智能化健康监测和管理，为工程实践提供更为全面和精准的支持。
感谢观看

冲击荷载下钢筋混凝土梁的性能及损伤评估

冲击荷载下钢筋混凝土梁的性能及损伤评估赵武超;钱江;张文娜【摘要】基于落锤冲击试验,通过数值模拟研究钢筋混凝土梁在冲击荷载下的抗冲击性能和损伤机理.针对冲击荷载局部效应明显和持时短暂等特点,提出基于截面损伤因子的损伤评估方法;采用参数分析方法研究了箍筋间距、边界条件、冲头形状和面积以及冲击位置对钢筋混凝土梁的动态响应和损伤程度的影响.结果表明:基于截面的损伤评估方法能够比较直观地描述梁体损伤沿长度方向的分布;端部的固支约束可以有效地改变钢筋混凝土梁的耗能机制,并能提高梁的抗冲击承载潜力;冲击位置会直接影响梁体的裂缝分布和破坏模式;碰撞接触面积和冲头形状也对梁的损伤分布具有一定的影响.【期刊名称】《爆炸与冲击》【年(卷),期】2019(039)001【总页数】12页(P108-119)【关键词】钢筋混凝土梁;冲击荷载;动态响应;耗能机制;损伤评估【作者】赵武超;钱江;张文娜【作者单位】同济大学土木工程防灾国家重点实验室,上海200092;同济大学土木工程防灾国家重点实验室,上海200092;同济大学土木工程防灾国家重点实验室,上海200092【正文语种】中文【中图分类】O342随着恐怖袭击、偶然撞击事故的不断增加，结构的抗冲击性能在防护工程、结构工程乃至国防工程中备受关注。

由于混凝土材料的广泛应用和冲击荷载的复杂性，钢筋混凝土结构的抗冲击性能研究一直是工程防灾减灾领域的重要课题之一。

国内外很多学者对钢筋混凝土构件的动态抗冲击性能进行了一系列试验和数值研究。

Loedolf[1]采用前端带有缓冲器的水平摆锤来研究在硬碰撞情况下钢筋混凝土柱的动态响应和破坏模式。

Fujikake等[2]对不同配筋率的钢筋混凝土梁进行了落锤冲击试验，并建立了预测构件冲击响应的双自由度弹簧-质量模型。

Saatci等[3]通过落锤试验研究了钢筋混凝土梁的抗剪机制对其抗撞性能的影响。

赵德博等[4]采用落锤冲击试验对钢筋混凝土梁的抗冲击性能和研究方法进行了讨论。

水泥固化土本构模型的损伤规律研究

水泥土无侧限抗压强度的损伤规律张树彬1 郭秀娟2 王清3（1吉林省经济管理干部学院 130012 2吉林建筑工程学院 130021 3吉林大学建设工程学院130026）摘要：水泥土地基因其施工工艺简单、价格低廉而被广泛应用。

采用5%、10%、15%水泥掺入量加固不同地域软土，通过无侧限抗压强度试验结果表现为慢性损伤规律性，根据弹塑性损伤规律建立数学模型，经检验其拟合效果良好。

关键词：水泥土；无侧限抗压强度；损伤规律0 概述水泥土是由水泥、土、外掺剂和水按一定配合比混合搅拌，经一系列物理、化学反应所形成一种混合胶凝材料，是介于土与混凝土材料之间的一种介质，为一种复杂多相体系而且具有不均匀性。

因而，可将弹塑性损伤原理引入水泥土中，以建立水泥土弹塑性本构模型及水泥土演变方程。

20世纪60年代以剑桥模型为代表的弹塑性模型标志着人们在土力学特性认识的第一次飞跃，土体结构性数学模型的建立意味人们在深化土体力学特性认识上完成了第二次飞跃。

近年我国学者童小东、熊传详等探讨水泥土弹塑性损伤本构模型[1,2]。

本试验根据水泥掺入比为5%、10%、15%不同地域软土水泥土的无侧限抗压强度影响效果[4]，探讨水泥土组分抗压强度损伤效果的规律性，并对损伤效果进行了模拟验证。

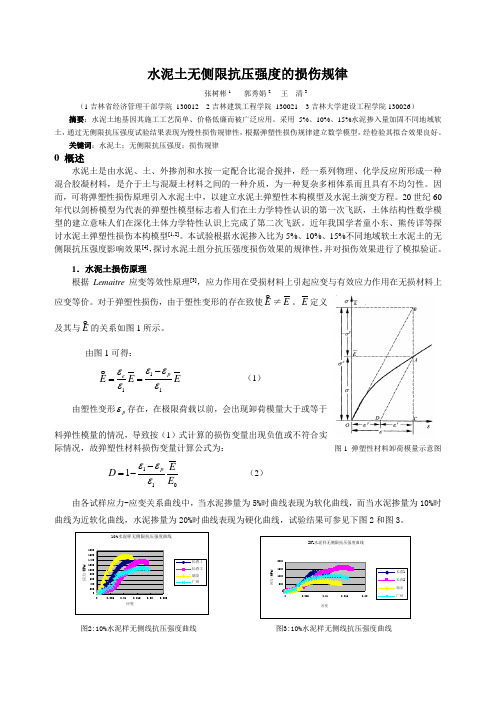
1．水泥土损伤原理根据Lemaitre 应变等效性原理[3]，应力作用在受损材料上引起应变与有效应力作用在无损材料上应变等价。

对于弹塑性损伤，由于塑性变形的存在致使 E ≠E 。

E 定义及其与 E的关系如图1所示。

由图1可得：111pe EE E εεεεε-== （1）由塑性变形p ε存在，在极限荷载以前，会出现卸荷模量大于或等于材料弹性模量的情况，导致按（1）式计算的损伤变量出现负值或不符合实际情况，故弹塑性材料损伤变量计算公式为：图1 弹塑性材料卸荷模量示意图1101p ED E εεε-=-（2）由各试样应力-应变关系曲线中，当水泥掺量为5%时曲线表现为软化曲线，而当水泥掺量为10%时曲线为近软化曲线，水泥掺量为20%时曲线表现为硬化曲线，试验结果可参见下图2和图3。

混凝土HJC本构模型参数的研究

混凝土HJC本构模型参数的研究一、本文概述Overview of this article混凝土作为一种广泛应用的建筑材料，其力学性能和本构关系的准确描述对于工程设计和结构安全至关重要。

随着科学技术的进步和工程实践的发展，对混凝土本构模型的研究日益深入。

其中，HJC （Holmquist-Johnson-Cook）本构模型作为一种能够描述混凝土在高应变率、高压力和大变形条件下的力学行为的模型，受到了广泛关注。

Concrete, as a widely used building material, accurate description of its mechanical properties and constitutive relationships is crucial for engineering design and structural safety. With the progress of science and technology and the development of engineering practice, research on concrete constitutive models is becoming increasingly in-depth. Among them, the HJC (Holmquist Johnson Cook) constitutive model has received widespread attention as a model that can describe the mechanical behavior of concrete under high strain rate, high pressure, and large deformation conditions.本文旨在研究混凝土HJC本构模型的参数，通过对现有文献的综述和实验数据的分析，探讨各参数对混凝土力学性能的影响规律，为工程实践中混凝土结构的准确模拟和分析提供理论支持。

混凝土多轴强度和本构特性实验研究钢筋混凝土结构精品课程首页

• 基于准静态本构模型的修正
•
动态、冲击载荷作用下，影响混凝土材料力学特性
的因素很多，主要有材料的应变率敏感效应和静水压力相
关性，这两个影响因素相互耦合很难在实验中完全别离。
其中混凝土材料应变率敏感效应的研究一直都得到了研究
者们的重视和关注，也取得了很大的成果[5],[6],[7] 。由
此，我们可以通过对一些已有混凝土材料准静态本构模型
等缺陷的演化开展而引起的。内部拉伸应力作用下，混凝
土材料表现出一种脆性特性，其损伤演化标志就是微裂纹
的开裂开展。随着微裂纹的扩展，混凝土材料强度和刚度
逐渐损伤弱化，并表现为一种各向异性响应，同时伴随有
裂纹之间的摩擦和滑移效应。压缩载荷作用下，混凝土材
• ε2----表示双轴受压时 σ2方向的压应变，
• ε0----表示单轴受压时的压应变。
• ε1/ε0为横坐标，
• ε2/ε0为纵坐标，将双轴受压碾压混凝土的变形绘于图3中。
• 图3 碾压混凝土双轴受压变形曲线
• 结论:
• 从图3可以看出，双轴受压时碾压混凝土的极限应变值大大高于单轴受压时的极限应变值，并随着应力比α的增大而增大。
纹的损伤演化开展会诱导材料的各向异性。随后，人们又开展了细观统计型模型，其认为，随机裂纹的演化开展不
会诱导材料的各向异性。不管是细观还是唯象的，这些模
型都包含了一些相同的根本组成元素，所采用的根本方法也有类似之处。
• 基于塑性与损伤耦合的本构模型[28]，[29]，[30]，[31]
•
混凝土材料非弹性应变是由材料内部微裂纹和微空洞
•
• 基于粘弹性理论的本构模型[15]，[16]，[17]
•

混凝土损伤本构模型

混凝土损伤本构模型混凝土是一种复杂的材料，受外界力学作用时会产生各种不同的损伤状态。

为了深入了解混凝土的力学行为，需要研究混凝土损伤本构模型。

混凝土损伤本构模型是描述混凝土力学性能的数学模型。

它是基于混凝土的材料特性和损伤特性所建立的模型。

在混凝土力学行为中，应力状态通常被描述为三轴压缩状态。

混凝土在这种状态下的力学性能与单轴压缩状态下不同。

在单轴压缩状态下，混凝土的应变增加速度随应力增加而慢慢减缓，即发生了应变硬化现象。

而在三轴压缩状态下，混凝土往往表现出应变软化现象，随着应力的增加，混凝土的应变增加速度会逐渐变快。

混凝土损伤本构模型的基本假设是混凝土存在破坏史。

这种史包括由初次受力到完全破坏的一系列阶段。

实际上，混凝土在受力过程中会产生多种损伤形式，如微裂纹、毛细裂纹、宏观裂缝等。

而混凝土损伤本构模型的主要任务就是将这些损伤形式数学化，从而形成能够描述混凝土损伤状态的数学表达式。

目前，常见的混凝土损伤本构模型通常包括：微观本构模型、弹塑性本构模型和连续损伤本构模型等。

其中，连续损伤本构模型是最常用的一种。

连续损伤本构模型是一种基于力学守恒原理的损伤本构模型。

它基于连续体力学理论的基础上，将损伤分为两个部分：体积损伤和刚度损伤。

其中，体积损伤是由体积收缩引起的，而刚度损伤是由裂缝形成和扩展引起的。

在连续损伤本构模型中，混凝土受力时，当应力达到一定值时，混凝土会产生微小裂缝，这些微小裂缝会不断扩展。

当这些裂缝扩展到一定程度时，混凝土会发生刚度损失。

通过描述裂缝的扩展过程，可以建立混凝土损伤本构模型。

总之，混凝土损伤本构模型是现代建筑工程领域中不可缺少的一种力学模型。

通过对混凝土损伤的数学表达，可以更准确地描述混凝土的力学行为，提高工程设计的可靠性和安全性。

冲击荷载下钢-混凝土格栅坝动力性能分析及试验研究

冲击荷载下钢-混凝土格栅坝动力性能分析及试验研究摘要：钢-混凝土格栅坝是一种常用于水利工程的防洪设施，其在面对冲击荷载时的动力性能对于保障其安全稳定运行至关重要。

本文通过对冲击荷载下钢-混凝土格栅坝的动力性能进行分析，并进行相应的试验研究，旨在深入了解其动力响应规律，为格栅坝的设计与工程实践提供理论依据。

关键词：钢-混凝土格栅坝，冲击荷载，动力性能，试验研究一、引言钢-混凝土格栅坝作为常见的防洪设施之一，具有良好的抗洪能力和水流引导性能，广泛应用于河流、水库等水利工程中。

在一些特殊情况下，如暴雨、山洪等极端天气条件下，格栅坝常常要面临冲击荷载的挑战。

因此，对钢-混凝土格栅坝在冲击荷载下的动力性能进行深入研究，有助于提高格栅坝的设计与施工质量，确保其安全可靠运行。

二、冲击荷载下格栅坝的动力性能分析1. 冲击荷载对格栅坝的作用机理冲击荷载是指大量水体在力的作用下，瞬间作用于格栅坝上的荷载。

这种荷载对于格栅坝的动态响应产生了显著影响。

当冲击荷载作用于格栅坝上时，格栅坝内部会产生一系列动力响应，如振动、变形等，这对于格栅坝的稳定性和安全性均有重要影响。

2. 动力响应的分析方法针对格栅坝在冲击荷载下的动力响应，可以采用有限元分析方法进行模拟与分析。

通过建立合理的有限元模型，考虑材料本构关系、边界条件等因素，可以较准确地预测格栅坝在不同冲击荷载下的动力响应情况。

此外，还可以进行物理模型试验，对格栅坝的动态响应进行实际测量与观察。

三、试验研究及结果分析本文在实验室中搭建了一台模拟格栅坝的试验装置，并选取了几组不同冲击荷载条件下的试验参数，对格栅坝的动力性能进行了测试与分析。

试验结果表明，在冲击荷载作用下，格栅坝产生了明显的振动响应，并且振幅随着冲击荷载的增加而增大。

此外，格栅坝的变形也随着冲击荷载的增加而增大，但变形程度较小，不会影响格栅坝的结构稳定性。

四、讨论与建议在冲击荷载下，钢-混凝土格栅坝的动力性能分析与试验研究对于优化其设计与施工具有重要意义。

受侧向冲击的混凝土墩柱本构模型对比

受侧向冲击的混凝土墩柱本构模型对比杨帅;魏明晖;方从启【摘要】By modeling of ANSYS and explicit dynamical analysis of LS-DYNA, we simulate the concrete pier columns to lateral impact mass, apply four types of concrete constitutive model on the simulation, such as Johnson Holmquist concrete constitutive model, brittle damage constitutive model, continuous surface cap constitutive model, concrete damage model, etc, and test the accuracy of the simulation calculation by the system energy. The numerical simulation value is compared with the experiment results to further validate the accuracy of the simulation calculation. The concrete constitutive models are compared with prediction accuracy, prediction speed and parameter number.%采用ANSYS 建模和LS-DYNA显式动力分析的方式,分别使用HJC、脆性损伤、盖帽和混凝土损伤等4种混凝土本构模型,对钢筋混凝土墩柱的侧向冲击过程进行仿真.从系统能量的角度验证数值计算的正确性;并将冲击过程中的冲击物块加速度和钢筋应变的历时值与试验值进行对比,进一步证实仿真计算的正确性.从各本构模型的计算结果、模拟所耗费的计算时间以及所需的参数数量等方面进行对比.【期刊名称】《水运工程》【年(卷),期】2017(000)012【总页数】6页(P198-203)【关键词】墩柱;混凝土本构;冲击;HJC本构;脆性损伤本构;盖帽本构;混凝土损伤本构【作者】杨帅;魏明晖;方从启【作者单位】中交四航工程研究院有限公司, 广东广州510230;河海大学力学与材料学院, 江苏南京210098;中交四航工程研究院有限公司, 广东广州510230;上海交通大学船舶海洋与建筑工程学院, 上海200240【正文语种】中文【中图分类】TU375;U656我国海域辽阔，大规模的基础建设主要集中于沿海地区。

混凝土损伤本构理论研究综述

第30卷第3期水利水电科技进展2010年6月V ol.30N o.3Advances in Science and T echnology of Water Res ources Jun.2010　基金项目:国家自然科学重点基金(90510017);水利部公益专项(200701004)作者简介:何建涛(1981—),男,陕西蒲城人,博士研究生,从事水工结构抗震研究。

E 2mail :hejt2004@ DOI :10.3880/j.issn.1006Ο7647.2010.03.022混凝土损伤本构理论研究综述何建涛,马怀发,陈厚群(中国水利水电科学研究院工程抗震研究中心,北京　100048)摘要:首先论述混凝土本构模型研究的重要性,并说明损伤力学理论较适于构建混凝土本构模型;然后对损伤变量的定义、损伤演化方程的确定、损伤本构模型的建立以及如何考虑不可恢复变形与率效应进行较为详细的论述;最后就混凝土损伤本构模型的发展方向提出了看法。

关键词:混凝土本构模型;损伤力学;率效应;综述中图分类号:T V431 文献标识码:A 文章编号:1006Ο7647(2010)03Ο0089Ο06R esearch review on concrete d am age constitutive theory//HE Jian 2tao ,M A Huai 2fa ,CHE N H ou 2qun (Earthquake Engineering Research Center ,China Institute o f Water Resources and Hydropower Research ,Beijing 100048,China )Abstract :First ,the im portance of researches on concrete constitutive m odels was presented.The theory of damage mechanics was shown to be suitable for the establishment of concrete constitutive m odels.Then ,the definition of damage variables ,the determination of damage ev olution equations ,the establishment of concrete constitutive m odels as well as how to consider the irreversible deformation and strain rate effect were discussed.Finally ,s ome opinions about the development direction of concrete damage constitutive m odels were proposed.K ey w ords :concrete constitutive m odel ;damage mechanics ;strain rate effect ;review 混凝土由于具有抗压强度高、耐久性好、适应性强、能够和钢筋较好地共同工作等优点,在很多领域得到了广泛应用。

混凝土损伤模型综述

混凝土损伤模型综述:：本文系统地综述了混凝土损伤研究的概况, 分析了各个有代表意义的混凝土损伤本构模型基础之上,对比研究了各个模型的特点及各自适用范围，并对有待进一步研究的问题进行了讨论。

关键词：混凝土，本构模型，损伤1 前言混凝土作为重要的建筑材料已有百余年的历史，当前广泛应用于各个领域本构模型，当然，在土木工程和采矿工程中也是必不可少的，在结构工程等混凝土更为广泛应用的研究领域，人们已经对混凝土的力学特性进行了广泛的研究本构模型，但是对混凝土损伤与断裂过程中的裂纹扩展以及损伤与断裂机制等基本问题，还需要进一步的研究。

随着结构形式由单纯的一般房屋建筑结构扩展到重力式海洋平台、高拱坝、核电站混凝土保护层和大跨度混凝土桥梁等复杂结构,结构的工作环境和荷载作用也变得更加复杂,导致许多新的工程和力学现象不断地出现,使得对混凝土破坏理论的研究必须向更深的层次发展,以适应工程实际的需要。

在混凝土的损伤研究中,大量学者针对具体工程情况提出了各种不同的损伤本构模型,但是由于适用条件的特殊性及所建立模型的复杂化,很少有一种能够有明确的物理意义、表达简单、便于工程师接受的一般损伤本构关系式。

从物理意义来看损伤力学是比较适合用来描述混凝土材料的本构关系的。

本文基于对损伤本构模型的思考,结合有待进一步研究的问题,对一些有代表性的损伤模型进行了综述。

2 混凝土损伤本构模型2.1 混凝土各向同性弹性损伤模型2.1.1 Loland 损伤模型该模型为单轴拉伸模型. 假设材料为弹性各向同性,损伤也是各向同性的,该模型的定义简单,适用于混凝土受拉情况,所得到的应力-应变曲线和所采用的试验结果较符合论文服务。

但是有效应力在第二阶段假定为一常数,得到的应力- 应变是线性关系,这是值得商榷的。

2.1.2 Mazars 损伤模型该模型的特点:假定峰值应力前应力- 应变关系为直线,因此无初始损伤或损伤不发展,在单轴受拉、受压情况下与试验吻合较好,但是在多轴应力条件下误差较大。