matlab最优化计算问题概论 PPT课件
matlab教程ppt(完整版)

控制流语句
使用条件语句(如if-else)和 循环语句(如for)来控制程序 流程。
变量定义
使用赋值语句定义变量,例如 `a = 5`。
矩阵运算
使用矩阵进行数学运算,如加 法、减法、乘法和除法等。
函数编写
创建自定义函数来执行特定任 务。
02
MATLAB编程语言基础
变量与数据类型
变量命名规则
数据类型转换
编辑器是一个文本编辑器 ,用于编写和编辑 MATLAB脚本和函数。
工具箱窗口提供了一系列 用于特定任务的工具和功 能,如数据可视化、信号 处理等。
工作空间窗口显示当前工 作区中的变量,可以查看 和修改变量的值。
MATLAB基本操作
数据类型
MATLAB支持多种数据类型, 如数值型、字符型和逻辑型等 。
04
MATLAB数值计算
数值计算基础
01
02
03
数值类型
介绍MATLAB中的数值类 型,包括双精度、单精度 、复数等。
变量赋值
讲解如何给变量赋值,包 括标量、向量和矩阵。
运算符
介绍基本的算术运算符、 关系运算符和逻辑运算符 及其优先级。
数值计算函数
数学函数
列举常用的数学函数,如 三角函数、指数函数、对 数函数等。
矩阵的函数运算
总结词:MATLAB提供了许多内置函 数,可以对矩阵进行各种复杂的运算
。
详细描述
矩阵求逆:使用 `inv` 函数求矩阵的 逆。
特征值和特征向量:使用 `eig` 函数 计算矩阵的特征值和特征向量。
行列式值:使用 `det` 函数计算矩阵 的行列式值。
矩阵分解:使用 `factor` 和 `expm` 等函数对矩阵进行分解和计算指数。
matlab教程ppt(完整版)

汇报人:可编辑
2023-12-24
目录
• MATLAB基础 • MATLAB编程 • MATLAB矩阵运算 • MATLAB数值计算 • MATLAB可视化 • MATLAB应用实例
01
CATALOGUE
MATLAB基础
MATLAB简介
MATLAB定义
MATLAB应用领域
菜单栏
包括文件、编辑、查看、主页 、应用程序等菜单项。
命令窗口
用于输入MATLAB命令并显示 结果。
MATLAB主界面
包括命令窗口、当前目录窗口 、工作空间窗口、历史命令窗 口等。
工具栏
包括常用工具栏和自定义工具 栏。
工作空间窗口
显示当前工作区中的变量。
MATLAB基本操作
变量定义
使用变量名和赋值符号(=)定义变 量。
详细描述
直接输入:在 MATLAB中,可以直 接通过输入矩阵的元 素来创建矩阵。例如 ,`A = [1, 2, 3; 4, 5, 6; 7, 8, 9]`。
使用函数创建: MATLAB提供了多种 函数来创建特殊类型 的矩阵,如`eye(n)`创 建n阶单位矩阵, `diag(v)`创建由向量v 的元素构成的对角矩 阵。
使用bar函数绘制柱状图 ,可以自定义柱子的宽
度、颜色和标签。
使用pie函数绘制饼图, 可以自定义饼块的比例
和颜色。
三维绘图
01
02
03
04
三维线图
使用plot3函数绘制三维线图 ,可以展示三维空间中的数据
点。
三维曲面图
使用surf函数绘制三维曲面图 ,可以展示三维空间中的曲面
。
三维等高线图
matlab软件培训讲稿2_优化计算13页
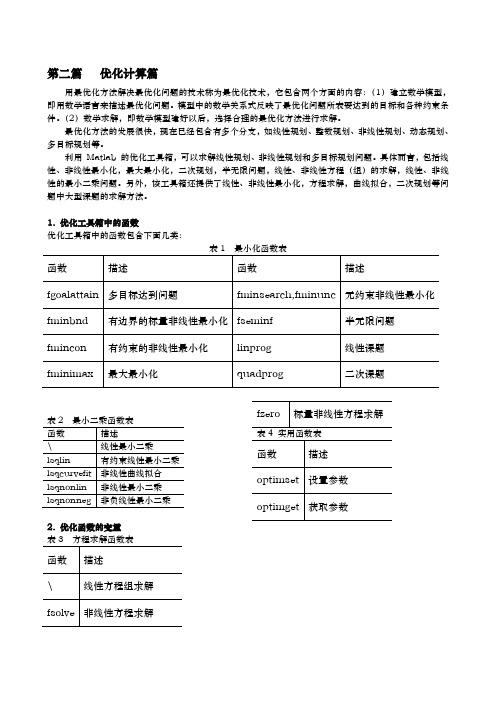
第二篇优化计算篇用最优化方法解决最优化问题的技术称为最优化技术,它包含两个方面的内容:(1)建立数学模型,即用数学语言来描述最优化问题。
模型中的数学关系式反映了最优化问题所表要达到的目标和各种约束条件。
(2)数学求解,即数学模型建好以后,选择合理的最优化方法进行求解。
最优化方法的发展很快,现在已经包含有多个分支,如线性规划、整数规划、非线性规划、动态规划、多目标规划等。
利用Matlab 的优化工具箱,可以求解线性规划、非线性规划和多目标规划问题。
具体而言,包括线性、非线性最小化,最大最小化,二次规划,半无限问题,线性、非线性方程(组)的求解,线性、非线性的最小二乘问题。
另外,该工具箱还提供了线性、非线性最小化,方程求解,曲线拟合,二次规划等问题中大型课题的求解方法。
1. 优化工具箱中的函数优化工具箱中的函数包含下面几类:2. 优化函数的变量下面两个表描述工具箱中优化函数的输入输出变量:3. 参数设置利用optimset 函数,可以创建和编辑参数结构;利用optimget 函数,可以获得options 优化参数。
3.1 optimget函数利用该函数获得options 优化参数,其语法结构如下:●val=optimget(options,’param’)返回优化参数options 中指定的参数的值。
●val=optimget(options,’param’,default)若options 结构参数中没有定义指定参数,则返回默认值。
3.2 optimset函数利用该函数创建或编辑优化选项参数结构,其语法结构如下: ● options=optimset(‘param1’,values1,’param2’,value2,…) 创建一个称为 options 的优化选项参数,其中指定的参数具有指定值。
● options=optimset()创建一个选项结构,其中所有的元素被设置为 [](默认值)。
● options=optimset(potimfun)创建一个含有所有参数名和与优化函数 optimfun 相关的默认值的选项结构 options 。
优化问题的MATLAB求解课件

MATLAB简介
MATLAB是一种高级编程语言和交互 式环境,主要用于数值计算、数据分 析和可视化。
它广泛应用于工程、科学、技术和数 学领域,支持多种编程范式,包括面 向对象编程。
MATLAB编程基础
MATLAB使用类似于数学表达式的语 法,支持多种数据类型,包括数组、 矩阵和结构体。
程序流程控制结构包括条件语句、循 环语句和开关语句等。
05
非线性规划问题求解
非线性规划问题概述
1
非线性规划问题是在满足一定约束条件下,寻找 一组变量使得某个目标函数达到最小或最大的问 题。
2
约束条件可以是等式或不等式,目标函数是非线 性函数。
3
非线性规划问题在许多领域都有广泛应用,如机 器学习、数据挖掘、金融、工程等。
MATLAB求解非线性规划问题
此外,MATLAB优化工具 箱还可以用于图像处理、 信号处理等领域。
在生物医学领域, MATLAB优化工具箱可用 于药物研发、疾病预测等 。
04
线性规划问题求解
线性规划问题概述
线性规划问题是在满足一组线性约束条件下,寻 找线性函数的最大或最小值的问题。
线性规划问题通常用于解决资源分配、生产计划 、运输和分配等问题。
整数规划问题实例
问题描述
以最小化总成本为例,考虑一个 生产计划问题,其中包含多个产 品、多个资源、多个工艺流程和 多个约束条件。
数学模型
使用线性整数规划模型描述该问 题,包括决策变量、目标函数和 约束条件。
求解过程
使用MATLAB的优化工具箱进行 求解,并分析求解结果。
感谢您的观看
THANKS
这些函数使用户能够通过 调用函数并传递参数来定
义和解决优化问题。
精通MATLAB最优化计算一书的MATLAB优化工具箱课件

精通MATLAB最优化计算一书的MATLAB优化工具箱课件
智能优化算法(ga求解器)
优化工具箱中的智能优化算法包括遗传算法(ga)和模拟退火算法(simulannealbnd),MATLAB中的ga求解器功能非常强大,既能求解无约束优化问题,也能求解约束优化问题,而且约束条件可以是非线性的,但是simulannealbnd求解器只能求解无约束优化问题。 在Solver下拉选框中选择ga; 在适应函数栏输入@(x)x^4-3*x^3+x^2-2; 变量个数输入1,其余参数默认; 单击Start按钮运行。
精通MAI优化工具应用实例
例5-1 fminunc求解器应用实例。 例5-2 fminsearch求解器应用实例。 例5-3 fmincon求解器应用实例。 例5-4 lsqnonlin求解器应用实例。 例5-5 linprog求解器应用实例。 例5-6 ga求解器应用实例。
精通MATLAB最优化计算一书的MATLAB优化工具箱课件
5.4 小结
本章全面介绍了优化工具箱函数的功能、语法,以及GUI优化工具的使用及实例,GUI优化工具是进行MATLAB最优化计算的最简洁、最容易掌握的工具,后面的章节还会对常用的工具箱的函数进行详细讲述,并辅以实例。 通过本章读者不仅对MATLAB优化工具箱函数的强大功能有一个初步了解,还为后面更具体的介绍及应用打下基础。
精通MATLAB最优化计算一书的MATLAB优化工具箱课件
5.3.2 GUI优化工具的界面
GUI优化工具的界面主要分为三大块: 左边为优化问题的描述及计算结果显示(Problem Setup and Results); 中间为优化选项的设置(Options); 右边为帮助(Quick Reference)。 为了界面的简洁,可以单击右上角的“<<”按钮将帮助隐藏起来。
ppt第十二章用MATLAB解最优控制问题及应用实例

Y (t ) U (t ) 为 m 维控制向量, X (t ) 为 n 维状态向量, 其中, l 为维输出向量。
l
寻找最优控制,使下面的性能指标最小
1 T 1 tf T J (u ) e (t f ) Pe (t f ) e (t )Q(t )e(t ) U T (t ) R(t )U (t ) dt 2 2 t0
的调用格式为: [Ac,Bc,Cc,Dc,Tc,Kc]=ctrbf(A,B,C) 在MATLAB的控制系统工具箱中提供了obsvf()函 数。该函数可以求出系统的可观测阶梯变换,该函 数的调用格式为: [Ao,Bo,Co,Do,To,Ko]=obsvf(A,B,C)
5, 系统的时域分析
对于系统的阶跃响应,控制系统工具箱中给出了
第十二章 用MATLAB解最 优控制问题及应用实例
第十二章 用MATLAB解最优 控制问题及应用实例
12.1 12.2 MATLAB工具简介 用MATLAB解线性二次型最优控制问题
12.3
12.4
用MATLAB解最优控制问题应用实例
小结
MATLAB是集数值运算、符号运算及图形处理 等强大功能于一体的科学计算语言。作为强大的 科学计算平台,它几乎能满足所有的计算需求。 MATLAB具有编程方便、操作简单、可视化界面、 优良的仿真图形环境、丰富的多学科工具箱等优 点,尤其是在自动控制领域中MATLAB显示出更为 强大的功能。
采用care函数的优点在于可以设置P的终值 条件,例如我们可以在下面的程序中设置P的终值 条件为[0.2;0.2]。 [P,E,K,RR]=care(A,B,Q,R,[0.2;0.2],eye(size(A))) 采用lqr()函数不能设置代数黎卡提方程的 边界条件。
第11章 MATLAB 优化问题的求解实例解析PPT课件

【例11-13】利用目标规划方法重新求解【例11-1】。
• 解:首先设置目标函数相应的目标函数值向量[-950,-50],编写如下语 句:
• A=[1,1;1.25,0.75;0,1];b=[200;200;150]; • goal=[-950,-50]; • weight=abs(goal); • x0=[50,50]; • lb=[0 0];ub=[inf,inf]; • options=optimset('GoalsExactAchieve',2); % 设置独立变量数 • f=@(x)[-4*x(1)-5*x(2),-x(1)]; % 定义函数表达式 • [x,fval]=fgoalattain(f,x0,goal,weight,A,b,[],[],lb,ub,[],options) % 求解目
运行结果: x=
0.6667 1.3333 fval =-8.2222
【例11-10】求解下面一维情形的半无限优化
问题。 0
Semi-infinite constraints
min f(x)(x10.5)2(x20.5)2(x30.5)2
K-11(x,1)sin(1x1)cos(1x2)10100(150)2sin(1x3)x3 1 xs.t.K-22(x,2)sin(2x2)cos(2x1)10100(250)2sin(2x3)x3 1
最优值:-3.0498 最优值:-0.064936 最 优 值 :3.5925
最 优 值 :3.7766
2 1
-2
0 -1
-1
最 优 值 :-6.5511
-1
MATLAB多目标优化计算 ppt课件

6.1 函数fgoalattain
三、例题
(4) M文件运算结果 (5) 优化结果处理
Optimization terminated successfully:
Search direction less than 2*options.
xopt =
1.0e+003 *
dd1
0.1000
1.2269
Ld
ceq=[];
[x,fval,exitflag,output, grad,hessian]= fgoalattain(@fun,x0,goal,w,A,b,Apept课q件,beq,Lb,Ub,’Nlc’,options,P1,P92…)
6.1 函数fgoalattain
三、例题
(3)编制优化设计的M文件
等式约束
g1(X) x1 0
边 界 约 束 g2(X) x1 1 0 变量x1的上下限
g3(X) x2 0
g4 (X) ppxt课2件 1 0
变量x2的上下限
16
6.2 函数fminimax
三、例题
(2)编制优化设计的M文件
%矩形截面梁两目标优化设计的目标函数文件
function f=JXL_2mb_MB(x) f(1)=x(1)*x(2); f(2)=-x(1)*x(2)^2/6;
目标函数文件名 初始点
附加参数 设置优化选项参数
各分目标期望值 各分目标权重 线性不等式约束的常数向量
无定义时以空矩阵 符号“[ ]”代替
非线性约束条件的函数名 设计变量的下界和上界
线性等式约束的常数向量
线性不等式约束的系数矩阵
ppt课件
线性等式约束的系数4矩阵
6.1 函数fgoalattain
MATLAB课件第七章 最优化计算方法

以fun702为文件名保存此函数文件。 在命令窗口输入: x0=[-2;4]; x=fminunc('fun702',x0) 结果显示:
f=
-1.0000 x=
Matlab程序: ch702.m
1.0000 1.0000
即极小值为-1,是x1=1,x2=1时取得。
【例 3】 解非线性方程组
x1 2 x 2 1 0 ( x1 2 ) 2 ( x 2 0 .5 ) 2 1 0
max f 3x1 x 2 x 3 x 1 2 x 2 x 3 11 4 x 1 x 2 2 x 3 3 2 x1 x 3 1 x 0 , i 1, 2 , 3 i
s .t .
解:考虑到linprog函数只解决形如
【例 4】 求解约束非线性规划:
max s .t . e
e
x1
x1
x 2 (3 e
2
2
x1
x2 )
(初值为[1;1])
2
x2
3
首先将问题转化为matlab要求的格式;即求出 fun,A,b,Aeq,Beq,X0,Lb,Ub
解:首先建立一个m文件fun7041.m
function y=fun7041(x) y=-exp(x(1))*x(2)^2*(3-exp(x(1))-x(2)^2);
k 1
k
k
k
由此得到下一个点 4) 检验新得到的点
x
k
P
k
k
k 1
是否满足精度要求的最
优解。
如果是,则结束运算;
否则,令 k k 1, 返回 ( 2 ) 继续迭代
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 模型表达 max f 6x1 8x2 s.t. 8x1 4x2 300 3x1 4x2 100 2x1 9x2 200 x1 0, x2 0
最优化问题的典型实例
❖ 分派问题
▪ 假设某个项目有4项连续的任务构成,即完成了任务1才能开始任务2,完成了 任务2之后才能开始任务3,以此类推。并且规定由项目组中的甲乙丙丁四名成 员每人完成且仅完成其中的一项任务,四个项目组成员分别完成四项任务的时 间如表所示,应该如何分配这些任务,即让哪个成员去完成哪个任务,可以使 得花费的总时间最短
• 金融投资中,如何选择和设计证券组合或者投资项目组合,以便在可以接受的风险限 度内获得尽可能大的投资回报?
• 机械设计中,如何在满足工作条件、裁荷和工艺要求,并在强度、刚度、寿命、尺寸 范围及其
• 针对化学过程如何设计控制方案,才能既优化其性能,又能保证其鲁棒性? • 在电力分配中,由N个火力发电厂组成一个供电网,要求输出总负荷为S,该如何分
最优化问题的数学描述
❖ 最优化问题的数学模型
▪ 由各例子可以看出,最优化问题涉及的领域非常广泛,形式也千变万化,各自 有不同的机理和解决方法,但是它们却可以用统一的数学形式表达,简单的说, 均可以转化为最小(或最大)化一个n维变量x的实函数f(x),其中对变量含有 多种约束。一般情况下,最优化问题的数学模型可以表达如下: min f (x) s.t. hi (x) 0 i 1, 2, p, p n gj (x) 0 j 1, 2, m
最优化问题的解决方案
❖ 解决方案的步骤
▪ 提出需要进行最优化的问题,确定研究问题的范围,并为问题的解决准备一些 先决条件,例如与问题相关的数据和资料
▪ 建立能够反映上述实际情况的最优化问题的数学模型,确定设计变量、目标函 数和有关约束条件
▪ 对建立的数学模型进行分析和修正,选择合适的优化算法 ▪ 运用合适的软件编写优化算法程序,对最优化模型进行求解 ▪ 如果是理论问题,对优化结果进行分析和比较,总结规律;如果是实际问题,
• 生产A可获利8x1(千元),生产B可获利8x2(千元),故目标函数为 f 6x1 8x2 优化设计的目标就是使得函数f最大化
• 煤的消耗总量应该小于300吨 8x1 4x2 300 • 电力资源的消耗不得高于其供应量100千瓦 3x1 4x2 100 • 劳动力时间的消耗不得高于300工作日 2x1 9x2 200 • 每种产品数量满足非负限制 x1 0, x2 0
▪ 混合解法
• 混合解法即是结合了上述两种方法,例如以梯度法为代表的一类解法,这类解法往 往是解析法和数值算法相结合的一种方法
▪ 其他优化方法
• 诸如以网络图为基础的图论方法和近代发展起来的各种智能优化算法如遗传算法、 神经网络方法、蚁群算法、禁忌搜索、粒子群算法等等。
本章重点回顾
❖ 最优化问题和最优化方法的定义 ❖ 最优化问题的建模方法,即如何确定最优化问题的设计变量、目标函数和
▪ 根据约束条件的类型分类
• 有无约束——无约束优化问题和约束优化问题 • 约束类型——线性规划、二次规划、整数规划、0-1规划、非线性规划等
▪ 根据最优化问题的解分类
• 如果最优化问题的解不随时间变化,则称其为静态最优化问题或参数最优化问题 • 如果最优化问题的解随时间而变,则称其为动态最优化问题
44
Eij xij
i 1j 1
最优化问题的典型实例
❖ 分派问题
▪ 问题分析
• 每个人只能完成一项任务 x11 x12 x13 x14 1 x21 x22 x23 x24 1 x31 x32 x33 x34 1 x41 x42 x43 x44 1
每项工作有且仅有一人去完成 x11 x21 x31 x41 1 x12 x22 x32 x42 1 x13 x23 x33 x43 1 x14 x24 x34 x44 1
约束条件,能够用数学语言描述简单的最优化问题; ❖ 最优化问题的分类 ❖ 一些最优化问题的解法
将所获得的最优解应用到实际问题中进行验证和实施,再进行理论分析
❖ 解决方案的关键问题
▪ 数学模型的建立 ▪ 优化算法的编制
最优化问题的解决方案
❖ 优化问题的求解方法
▪ 解析法
• 对于最优化数学模型中的目标函数和约束条件,如果其具有明确的数学解析表达式, 则一般可以按照函数求极值的必要条件,用导数方法或者变分法等数学分析的手段 求出其解析解,然后按照问题的实际物理意义确定问题的最优解。
成员
甲 乙 丙 丁
时间
任务1 (天)
20 22 21 22
任务2 (天)
12 15 13 16
任务3 (天)
33 29 31 32
任务4 (天)
26 23 24 23
最优化问题的典型实例
❖ 分派问题
▪ 问题分析 • 设计变量 xij
1 当指派第i个成员去完成第j个任务时 0 当不指派第i个成员去完成第j个任务时
最优化问题的典型实例
❖ 投资决策问题
▪ 问题分析
• 我们可以设定该问题的目标是要在选择相应投资项目之后使得投资收益率最大,对
于某项目我们是投资还是不投资,于是我们令设计变量为xi(i=1,2,…n),其中当我们
决定投资第i个项目时,xi=1,当我们决定不投资第i个项目时,xi=0 n
n
• 目标为投资收益率最大,故目标函数应为总收益和总投资的比值 f
资源
活动
生产产品A (吨)
生产产品B 资源的供应
(吨)
量
煤(吨)
8
电力(千瓦) 3
工作日
2
利润(千元) 6
4
300
4
100
9
200
8
—
最优化问题的典型实例
❖ 资源利用问题
▪ 问题分析
• 设x1和x2分别代表产品A、B计划数(单位:吨),f表示利润(单位:千元),则问 题就是确定A、B的生产数量x1和x2,既可以充分利用资源,又可以使利润最大化
配每个发电厂的发电量,在满足各电厂发电量约束的条件下使得总的生产消耗为最小?
▪ 数学描述
• 上述各类问题资源的最优利用问题,所有类似的这种课题统称为最优化问题,研究解 决这些问题的科学一般就总称之为最优化理论和方法,用数学语言描述的话,最优化 方法就是在给定的约束条件下,如何在某种范围内选取一些决策变量的取值,使得一 个或者多个既定目标达到最优状态(极大、极小或者某种妥协状态)的一门学科。
▪ 由于军事上的需要产生了运筹学 ▪ 线性规划,非线性规划 ,动态规划
❖ 现代优化方法
▪ 遗传算法 ▪ 神经网络 ▪ 模拟退火
最优化问题的典型实例
❖ 资源利用问题
▪ 某工厂生产A、B两种产品,制造1吨A产品需要耗煤8吨,耗电3千瓦,耗时2个 工作日;制造1吨B产品需要耗煤4吨,用电4千瓦,耗时9个工作日。已知制造1 吨产品A和B分别可以获利6000元和8000元。现在该厂原料有煤300吨,电100 千瓦,如果需要在200工作日内生产这两种产品并达到利润最大,应当如何安 排A和B的生产数量
▪ 数值解法
• 如果目标函数或者约束条件较为复杂,或者并没有明确的数学解析表达式,抑或是 以现有的解析方法和手段无法求取解析解的优化问题,我们可以用数值解法来解决, 在现在计算机高速发展的时代,数值算法则显示出了其优越性。其基本的思想就是 用搜索的方法经过一系列的迭代,使得产生的这些序列能够逐步逼近问题的最优解, 数值解法常常需要经验或者试验,同时结果也需要通过实际问题的验证才是有效的。
其中xij为0-1变量,i代表项目组成员的序号,j代表任务的序号,则: x11、x12、x13、x14分别代表指派甲完成任务1、任务2、任务3、任务4 x21、x22、x23、x24分别代表指派乙完成任务1、任务2、任务3、任务4 x31、x32、x33、x34分别代表指派丙完成任务1、任务2、任务3、任务4 x41、x42、x43、x44分别代表指派丁完成任务1、任务2、任务3、任务4
❖ 最优化问题的三要素
▪ 设计变量 ▪ 目标函数 ▪ 约束条件
最优化问题的数学描述
❖ 最优化问题分类
▪ 根据设计变量的特征分类
• 按照设计变量的维数进行分类——一维优化问题,n维优化问题 • 根据设计变量的取值进行分类——离散最优化和连续最优化
▪ 根据目标函数的类型分类
• 只有一个目标的优化问题称为单目标优化问题 • 存在两个或者两个以上目标函数的优化问题,称为多目标优化问题
最优化理论和方法的产生和发展
❖ 一些古老的方法
▪ 黄金分割法 ▪ 阿基米德证明:如果给定平面几何图形的周长,则在各种图形中,圆所包围的
面积为最大。
❖ 古典最优化方法——精确的分析方法
▪ 理论基础的建立——牛顿和莱布尼茨在他们所创建的微积分理论 ▪ 有约束的最优化问题 ▪ 变分法
❖ 最优化理论和方法
• 该问题的目标就是选择一种合适的一对一的组合,使得最后所花费的时间总和最小。 根据上述假设,我们可以得到目标函数,即所花费的总时间为:
f 20x11 12x12 33x13 26x14 22x21 15x22 29x23 23x24
21x31 13x32 31x33 24x34 22x41 16x42 32x43 23x44
▪ 数学模型
44
min f
Eij xij
i 1j 1
4
s.t.
xij 1 (i 1, 2, 3, 4)
j1
4
xij
i1
1 (j
1, 2, 3, 4)
xij 0 或 1
最优化问题的典型实例
❖ 投资决策问题
▪ 某企业有n个项目可供选择投资,并且至少要对其中一个项目投资。已知该企 业拥有总资金A元,投资于第i(i=1,2,…n)个项目需花资金ai元,并预计可收益 bi元。试选择最佳投资方案。
