2019年中考数学专题复习小练习专题14几何初步知识三角形多边形
2019中考数学试题分类考点训练及中考冲刺集训-三角形-试题及解析

11.三角形(时间:45分钟共16题答对____题正确率_______%)命题点1 三角形三边关系1.(2019•淮安)下列长度的3根小木棒不能搭成三角形的是()A.2cm,3cm,4cm B.1cm,2cm,3cmC.3cm,4cm,5cm D.4cm,5cm,6cm2.(2019•扬州)已知n是正整数,若一个三角形的3边长分别是n+2、n+8、3n,则满足条件的n 的值有()A.4个B.5个C.6个D.7个3.(2019•自贡)已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为()A.7 B.8 C.9 D.10命题点2 三角形内角和及外角4.(2019•绍兴)如图,墙上钉着三根木条a,b,C,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是()A.5°B.10°C.30°D.70°5.(2019•青岛)如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为()A.35°B.40°C.45°D.50°6.(2019•杭州)在△ABC中,若一个内角等于另外两个内角的差,则()A.必有一个内角等于30°B.必有一个内角等于45°C.必有一个内角等于60°D.必有一个内角等于90°7.(2019•眉山)如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠C的度数是()A.50°B.60°C.70°D.80°8.(2019•枣庄)将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是()A .45°B .60°C .75°D .85°命题点3 三角形的高、中线、角平分线9.(2019·达州)如图,在Rt△ABC 中.△ACB =90°,AC =2,BC =3.(1)尺规作图:不写作法,保留作图痕迹。
中考数学复习《多边形》专项提升训练(附答案)

中考数学复习《多边形》专项提升训练(附答案) 学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列说法中,正确的是( )A.直线有两个端点B.射线有两个端点C.有六边相等的多边形叫做正六边形D.有公共端点的两条射线组成的图形叫做角2.如图,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是( )A.7B.8C.9D.103.有下列说法:①由许多条线段连接而成的图形叫做多边形;②多边形的边数是不小于4的自然数;③从一个多边形(边数为n)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成(n-2)个三角形;其中正确的结论有( )A.1个B.2个C.3个D.4个4.一个多边形的外角中,钝角的个数不可能是( )A.1个B.2个C.3个D.4个5.若一个正多边形的一个外角是36°,则这个正多边形的边数是( )A.10B.9C.8D.66.如图,小华从A点出发,沿直线前进10米后左转24,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )A.140米B.150米C.160米D.240米7.如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2 的度数是( )A.15°B.25°C.30°D.45°8.如果仅用一种多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )A.正三角形B.正四边形C.正六边形D.正八边形9.用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第n个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )A.n2+4n+2B.6n+1C..n2+3n+3D.2n+410.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是( )A.222B.280C.286D.292二、填空题11.形状、大小完全相同的三角形________(填“能”或“不能”)铺满地面;形状、大小完全相同的四边形________(填“能”或“不能”)铺满地面.12.如果一个多边形的各个外角都是40°,那么这个多边形的内角和是.13.一个多边形有44条对角线,那么这个多边形内角和是__________.14.如图是由射线AB、BC、CD、DE、EA组成的图形,∠1+∠2+∠3+∠4+∠5=.15.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=_____度.16.两个完全相同的正五边形都有一边在直线上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB= .三、解答题17.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.18.若两个多边形的边数之比为1:2,两个多边形的内角和之和为1440°,求这两个多边形的边数.19.一个多边形的内角和比四边形的内角和多540°并且这个多边形的各个内角都相等,这个多边形的每个内角等于几度?20.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.21.如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.(1)若∠F=80,则∠ABC+∠BCD=;∠E=;(2)探索∠E与∠F有怎样的数量关系,并说明理由;(3)给四边形ABCD添加一个条件,使得∠E=∠F所添加的条件为.22.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠BCD=124°,∠DEF=80°.(1)观察直线AB与直线DE的位置关系,你能得出什么结论并说明理由;(2)试求∠AFE的度数.23.探索问题:(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请你用学过的知识予以证明;(2)如图②﹣1,则∠A+∠B+∠C+∠D+∠E=°;如图②﹣2,则∠A+∠B+∠C+∠D+∠E=°;如图②﹣3,则∠A+∠B+∠C+∠D+∠E=°;(3)如图③,下图是一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F =°.参考答案1.D2.B.3.A4.D5.A6.B.7.A8.D9.B10.D11.答案为:能,能.12.答案为:1260°.13.答案为:1 620°14.答案为:360°.15.答案为:360.16.答案为:108°.17.解:设这个多边形的边数是n依题意得(n﹣2)×180°=3×360°﹣180°,n﹣2=6﹣1,n=7. ∴这个多边形的边数是7.18.解:设这两个多边形的边数分别为n、2n,依题意得180(n﹣2)+180(2n﹣2)=1440540n﹣720=1440540n=2160n=4所以这两个多边形的边数分别为4和8所以这两个多边形的内角和分别为:180°×(4﹣2)=360°和180°×(8﹣2)=1080°19.解:设这个多边形的边数为n则有(n﹣2)•180°=360°+540°解得n=7.∵这个多边形的每个内角都相等∴它每一个内角的度数为900°÷7=20.解:连接AF.∵在△AOF和△COD中,∠AOF=∠COD∴∠C+∠D=∠OAF+∠AFD∴∠A+∠B+∠C+∠D+∠E+∠F=∠OAF+∠OFA+∠CFE+∠OAB+∠E+∠F=∠BAF+∠AFE+∠E+∠B=360°.21.解:(1)∵∠F=80∴∠FBC+∠BCF=180°﹣∠F=100°.∵∠ABC、∠BCD的角平分线交于点F∴∠ABC=2∠FBC,∠BCD=2∠BCF∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=200°;∵四边形ABCD的内角和为360°∴∠BAD+∠CDA=360°﹣(∠ABC+∠BCD)=160°.∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E∴∠DAE=12∠BAD,∠ADE=12∠CDA∴∠DAE+∠ADE=12∠BAD+12∠CDA=12(∠BAD+∠CDA)=80°∴∠E=180°﹣(∠DAE+∠ADE)=100°;(2)∠E+∠F=180°.理由如下:∵∠BAD+∠CDA+∠ABC+∠BCD=360°∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E∠ABC、∠BCD的角平分线交于点F∴∠DAE+∠ADE+∠FBC+∠BCF=180°∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°∴∠E+∠F=360°﹣(∠DAE+∠ADE+∠FBC+∠BCF)=180°;(3)AB∥CD.故答案为200°;100°;AB∥CD.22.解:(1)AB∥DE.理由如下:延长AF、DE相交于点G∵CD∥AF∴∠CDE+∠G=180°.∵∠CDE=∠BAF∴∠BAF+∠G=180°∴AB∥DE;(2)延长BC、ED相交于点H.∵AB⊥BC∴∠B=90°.∵AB∥DE∴∠H+∠B=180°∴∠H=90°.∵∠BCD=124°∴∠DCH=56°∴∠CDH=34°∴∠G=∠CDH=34°.∵∠DEF=80°∴∠EFG=80°﹣34°=46°∴∠AFE=180°﹣∠EFG=180°﹣46°=134°.23.解:(1)如图①,∠BOC=∠B+∠C+∠A.(2)如图②,∠A+∠B+∠C+∠D+∠E=180°.如图③根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D∵∠1+∠2+∠E=180°∴x=∠A+∠B+∠C+∠D+∠E=180°.如图④,延长EA交CD于点F,EA和BC交于点G根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B ∵∠GFC+∠FGC+∠C=180°∴x=∠A+∠B+∠C+∠D+∠E=180°.(3)如图⑤,∵∠BOD=70°∴∠A+∠C+∠E=70°∴∠B+∠D+∠F=70°∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.。
2019年中考数学专题复习:三角形

2019年中考数学专题复习:三角形“2019年中考数学专题复习:三角形”,更多20XX中考复习指导等信息,请及时关注中考网!2019年中考数学专题复习:三角形1、相似多边形定义1:形状相同的图形叫做相似图形。
定义2:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形。
相似多边形对应边的比叫做相似比。
性质相似多边形的对应角相等,对应边成比例。
2、相似三角形的判定定义:三个角分别相等,三条边成比例的两个三角形相似。
定理:平行线分线段成比例定理两条直线被一组平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
判定1:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
判定2:三边成比例的两个三角形相似。
判定3:两边成比例且夹角相等的两个三角形相似。
判定4:两角分别相等的两个三角形相似。
3、相似三角形的性质相似三角形的对应角相等,对应边成比例;相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比;相似三角形对应线段的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方。
4、位似图形定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心。
这时的相似比又叫位似比。
1、了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割。
2、通过具体实例认识图形的相似。
了解相似多边形和相似比。
3、掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例。
4、了解相似三角形的判定定理:两角分别相等的两个三角形相似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似。
5、了解相似三角形的性质定理:相似三角形对应线段的比等于相似比;面积比等于相似比的平方。
6、了解图形的位似,知道利用位似可以将一个图形放大或缩小。
2019年北京中考数学习题精选:三角形(含多边形及其内角和)

一、选择题1.(2018北京市朝阳区初二年级第一学期期末)画△ABC的高BE,以下画图正确的是A B C D答案:D2.(2018北京市丰台区初二期末)如图所示,△ABC中AC边上的高线是A.线段DA B.线段BAC.线段BC D.线段BD答案:D3.(2018北京市怀柔区初二期末)为估计池塘两岸A,B间的距离,小明的办法是在地面上取一点O,连接OA,OB,测得OB=15.1m,OA=25.6m.这样小明估算出A,B间的距离不会大于A.26m B.38m C.40m D.41m答案:D4.(2018北京市平谷区初二期末)用直角三角板,作△ABC的高,下列作法正确的是A B C D 答案:D5.(2018北京延庆区八年级第一学区期末) 如图,将ABC △放在正方形网格图中(图中每个小正方形的边长均为1),点A ,B ,C 恰好在网格图中的格点上,那么ABC △中BC 边上的高是A.B. C.D.答案:A6、(2018北京房山区二模)如图,在△ABC 中,过点B 作PB ⊥BC 于B ,交AC 于P ,过点C 作CQ ⊥AB ,交AB 延长线于Q ,则△ABC 的高是 A .线段PB B .线段BC C .线段CQ D .线段AQ答案:C7.(2018北京西城区九年级统一测试)如果一个正多边形的内角和等于720︒,那么该正多边形的一个外角等于( ). A .45︒ B .60︒ C .72︒ D .90︒答案:B8.(2018北京延庆区初三统一练习)利用尺规作图,作△ABC 边上的高AD ,正确的是 答案:B9.(2018北京平谷区中考统一练习)一个正多边形的每个内角的度数都等于相邻外角的度数,则该正多边形的边数是ABCDABC DABC DABDA B . C .D .A .3B .4C .6D .12 答案B10.(2018北京市大兴区检测)已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是A. 3B. 4 C .5 D . 6 答案D11.(2018北京海淀区第二学期练习)若正多边形的一个外角是120°,则该正多边形的边数是 A.6 B. 5 C. 4 D.3 答案D12.(2018北京门头沟区初三综合练习)如图所示,有一条线段是ABC (AB >AC )的中线,该线段是13.(2018北京海淀区第二学期练习)用三角板作ABC △的边BC 上的高,下列三角板的摆放位置正确的是A B D答案A二、填空题 14.(2018北京延庆区初三统一练习)右图是一个正五边形,则∠1的度数是 . 答案:72°15、(2018北京丰台区二模)正六边形每个内角的度数是 .答案:120°1C BAA ABC ACABCBCCC B B C C16.(2018北京昌平区初二年级期末)小龙平时爱观察也喜欢动脑,他看到路边的建筑和电线架等,发现了一个现象:一切需要稳固的物品都是由三角形这个图形构成的,当时他就思考,数学王国中不仅只有三角形,为何偏偏用三角形稳固它们呢?请你用所学的数学知识解释这一现象的依据为 . 答案:三角形具有稳定性17.(2018北京市朝阳区初二年级第一学期期末)如图,点D 是线段AB 上一点,90CAB ADE ABF ∠=∠=∠=︒,AC BD =,AD BF =,AB DE =.若AEB α∠=,则CEF ∠= .(用含α的式子表示)答案:900-α18、(2018北京市海淀区八年级期末)如图,在四边形ABCD 中,∠A =90°,∠D =40°,则∠B +∠C 为 .答案:230° 19、(2018北京市怀柔区初二期末)三角形的三个内角的度数比是1:1:2.则最大内角的度数是____________. 答案:90°20、.(2018北京市怀柔区初二期末)如图,△ABC 中,BC 边所在直线上的高是线段____________.G E DC B A答案:AD21.(2018北京市门头沟区八年级期末)2017年11月5日19时45分,我国在西昌卫星发射中心用长征三号乙运载火箭,以“一箭双星”的方式成功发射第二十四、二十五颗北斗导航卫星.这两颗卫星属于中圆地球轨道卫星,是我国北斗三号第一、二 颗组网卫星,开启了北斗卫星导航系统全球 组网的新时代.如图所示,在发射运载火箭时,运载火箭 的发射架被焊接成了许多的三角形,这样做的原因是: . 答案:略22. (2018北京市顺义区八年级期末)已知:ABC ∆中,AB AC =,30B A ∠-∠=︒,则A ∠= .答案:40︒23.(2018北京市顺义区八年级期末)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 度.答案:7524.(2018北京市顺义区八年级期末)已知: 如图,ABC △中,45ABC ∠=, H 是高AD 和BE 的交点,12AD =,17BC =,则线段BH 的长为 .答案:13 25.(2018北京石景山区初三毕业考试)若正多边形的一个外角是45°,则该正多边形的边数是_______. 答案:八26、(2018北京昌平区二模)10.如图,∠1是五边形ABCDE 的一个外角.若∠1=60°, 则∠A +∠B +∠C +∠D 的度数为_________.HE CDBA答案:420°27.(2018北京东城区一模)若多边形的内角和为其外角和的3倍,则该多边形的边数为________________. 答案8 三、解答题28.(2018北京延庆区初三统一练习)如图,在△ABC 中,AD 平分∠BAC 交BC 于点D ,过点D 作DE ∥AB 交AC 于点E . 求证:AE=DE . 证明:∵AD 平分∠BAC∴∠BAD =∠DAE , ∵DE ∥AB∴∠BAD =∠ADE ……3分 ∴∠DAE =∠ADE ……4分 ∴AE =DE ……5分29.(2018北京市朝阳区一模)如图,BD 是△ABC 的角平分线,DE //BC 交AB 于点E .(1)求证:BE=DE ;(2)若AB=BC =10,求DE 的长.解(1)证明:∵BD 是△ABC 的角平分线,∴∠EBD =∠CBD . ∵DE //BC ,∴∠EDB =∠CBD . ∴∠EDB =∠EBD .∴BE=DE . ……………………………………………………2分EA(2)解:∵AB=BC ,BD 是△ABC 的角平分线,∴AD =DC . ………………………………………………………… 3分 ∵DE //BC ,∴1==DCAD EBAE .……………………………………………………… 4分∴521==AB BE .∴5=DE . ………………………………………………………5分30. (2018北京市朝阳区综合练习(一))如图,在△ACB 中,AC =BC ,AD 为△ACB 的高线,CE 为△ACB 的中线.求证:∠DAB =∠ACE.∴∠CAB =∠B ,CE ⊥AB . ………………………………………2分 ∴∠CAB +∠ACE =90°. …………………………………………3分 ∵AD 为△ACB 的高线, ∴∠D =90°.∴∠DAB +∠B =90°. ………………………………………4分∴∠DAB =∠ACE . …………………………………………………5分31.(2018北京门头沟区初三综合练习)如图,在△ABC 中,AD 是BC 边上的高,BE 平分∠ABC 交AC 边于E ,∠BAC =60°,∠ABE =25°. 求∠DAC 的度数. 解 ∵BE 平分∠ABC ,∴∠ABC =2∠ABE =2×25°=50°, ………2分 ∵AD 是BC 边上的高,∴∠BAD =90°﹣∠ABC =90°﹣50°=40°, …………4分 ∴∠DAC =∠BAC ﹣∠BAD =60°﹣40°=20° ………………5分32.(2018北京通州区一模)B答案:33.(2018北京市大兴区检测)如图,在△ABC中,AB=AC,点D,点E 分别是BC,AC上一点,且DE⊥AD. 若∠BAD=55°,∠B=50°,求∠DEC的度数.解:∵AB=AC,∴∠B=∠C.∵∠B=50°,∴∠C =50°.……………………1分∴∠BAC=180°-50°-50°=80°.…………………………………………………2分∵∠BAD=55°,∴∠DAE=25°.…………………………………………………………………3分∵DE⊥AD,∴∠ADE=90°.…………………………………………………………………4分∴∠DEC=∠DAE +∠ADE=115°.………………………………………………5分 34.(2018北京东城区一模) 如图,在△ABC 中,∠BAC =90°,AD ⊥BC 于点D . BF 平分∠ABC 交AD 于点E ,交AC 于点F . 求证:AE =AF .证明: ∵∠BAC =90°,∴∠FBA +∠AFB =90°. -------------------1分 ∵AD ⊥BC ,∴∠DBE +∠DEB =90°.---------------- 2分 ∵BE 平分∠ABC ,∴∠DBE =∠FBA . -------------------3分∴∠AFB =∠DEB . -------------------4分 ∵∠DEB =∠FEA , ∴∠AFB =∠FEA .∴AE =AF . -------------------5分35.(2018北京市朝阳区初二年级第一学期期末)已知:如图,点D ,E 在ABC ∆的边BC 上,AB AC =,AD AE =.求证:BD CE =.证明:过点A 作AH BC ⊥于点H . ………………………………………………1分 ∵AB AC =,AD AE =,∴HB HC =,HD HE =. ……………………………………………3分 ∴HB HD HC HE -=-.即BD CE =. ……………………………………………………5分 36.(2018北京市朝阳区初二年级第一学期期末)在等边ABC ∆外作射线AD ,使得AD 和AC 在直线AB 的两侧,BAD α∠=(0180α︒<<︒),点B 关于直线AD 的对称点为P ,连接PB ,PC . (1)依题意补全图1;(2)在图1中,求BPC ∆的度数;ECBA(3)直接写出使得PBC ∆是等腰三角形的α的值.解:(1)补全的图形如图所示.………………………………1分(2)解:连接AP ,如图.由点B 关于直线AD 的对称点为P ,可得AD 垂直平分PB . ∴AP AB =. ∴PAD BAD ∠=∠.∵ABC ∆是等边三角形, ∴AB AC =,60BAC ∠=︒.∴AP AC =. ………………………………………………………………2分 ∴APC ACP ∠=∠.∴在APC ∆中,22180APC PAD BAC ∠+∠+∠=︒. ∴60APC PAD ∠+∠=︒.∴30BPC ∠=︒. …………………………………………………………3分 (3)30︒,75︒,120︒,165︒.……………………………………………7分 37.(2018北京市东城区初二期末)如图,在△ABC 中,AB =AC ,AD ⊥于点D ,AM 是△ABC 的外角∠CAE 的平分线. (1)求证:AM ∥BC ;(2)若DN 平分∠ADC 交AM 于点N ,判断△ADN 的形状并说明理由.CBA备用图图1DCBAPDCB APD CAAB C P AB C PB解:(1)∵AB =AC ,AD ⊥BC ,∴∠BAD =∠CAD =12BAC ∠.…………… 1分 ∵AM 平分∠EAC ,∴∠EAM =∠MAC=12EAC ∠.…………… 2分 ∴∠MAD =∠MAC +∠DAC =1122EAC BAC ∠+∠=1180902⨯︒=︒。
2019年中考数学几何知识点详解与专项练习精选汇编

2019年中考数学几何知识点详解与专项练习精选汇编各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢2014 几何知识点详解与专项练习精选汇编2014中考几何一轮复习:三角形的有关概念下载2014中考几何一轮复习:全等三角形下载2014中考几何一轮复习:等腰三角形下载2014中考几何一轮复习:直角三角形下载2014中考几何一轮复习:角平分线、垂直平分线下载2014中考几何一轮复习:平行四边形下载2014中考几何一轮复习:矩形、菱形下载2014中考几何一轮复习:正方形下载2014中考几何一轮复习:梯形下载2014中考几何一轮复习:三角形、梯形中位线下载2014中考几何一轮复习:锐角三角函数下载2014中考几何一轮复习:解直角三角形下载2014中考几何一轮复习:三角函数的综合运用下载2014中考几何一轮复习:比例线段下载2014中考几何一轮复习:相似三角形下载2014中考几何一轮复习:相似三角形下载2014中考几何一轮复习:相似形的综合运用下载2014中考几何一轮复习:相似形的综合运用下载2014中考几何一轮复习:圆的有关概念和性质下载2014中考几何一轮复习:垂径定理下载2014中考几何一轮复习:切线的判定和性质下载2014中考几何一轮复习:与圆有关的角下载2014中考几何一轮复习:圆中成比例的线段下载2014中考几何一轮复习:圆与圆下载2014中考几何一轮复习:圆与圆下载2014中考几何一轮复习:正多边形与圆下载#p#分页标题#e#相关阅读:2014年数学学习方法分类解析汇总2014年数学学习方法:浅谈平面几何中矛盾的转换下载2014年数学学习方法:四边形的性质与判定上一篇:2014年数学中考复习备考计划下一篇:2014中考数学选择题专项练习十六标签:中考数学阅读一轮复习垂径定理各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢。
初三数学中考复习三角形专项复习练习含解析

初三数学中考复习三角形专项复习练习含解析1. 如图,图中以AB为边的三角形的个数共有( B )A.1个B.2个C.3个D.4个2. 如图所示,∠BAC的对边是( C )A.BD B.DC C.BC D.AD3. 若△ABC三条边分别为m,n,p,且|m-n|+(n-p)2=0,则那个三角形为( B )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形4. 如图,D为AC上一点,AD=DC,E为BC上一点,BE=EC,则下列说法不正确的是( D )A.DE是△BDC的中线B.BD是△ABC的中线C.D为AC中点,E为BC中点D.∠C的对边是DE5. 如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( A )A.40°B.45°C.80°D.85°6. 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E.则下列说法不正确的是( C )A.AC是△ABC的高B.DE是△BCD的高C.DE是△ABE的高D.AD是△ACD的高7. 若△ABC和△DEF全等,A和E,B和D分别是对应顶点,则下列结论错误的是( A )A.BC=EF B.∠B=∠D C.∠C=∠F D.AC=EF 8.如图,在△ABC与△DEF中,给出以下六个条件:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F.以其中三个条件作为已知,不能判定△ABC与△DEF全等的是( D )A.①②⑤B.①②③C.①④⑥D.②③④,第7题图),第8题图),第10题图)9.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( A ) A.80°B.100°C.60°D.45°10.已知三角形两边的长分别是3和8,则此三角形的周长取值范畴是( C )A.3<C<8 B.5<C<11 C.16<C<22 D.11<C<1 611.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC 的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S △BEF,且S△ABC=12,则S△ADF-S△BEF等于( B )A.1 B.2 C.3 D.412.假如一个三角形中任意两个内角的和大于第三个内角,那个三角形是__锐角__三角形.13. 如图,已知△ABC的面积是36 cm2,BD=4 cm,DC=8 cm,则阴影部分的面积是__12__cm2.14. 如图,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是__50°__.15.如图,点A在线段ED上,AC=CD,BC=CE,∠1=∠2,假如AB=7,AD=5,那么AE=__2__.16. 你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的过程中,两人上升的最大高度AA′,BB′的数量关系是___相等____.17. 等腰三角形的周长为20 cm,其中一边长为6 cm,则另两边长分别为_____6cm,8cm或7cm,7cm ____.18. 如图,在△ABC中,AD⊥BC,垂足为D,E为BD上的一点,E G∥AD,分别交AB和CA的延长线于点F,G,∠AFG=∠G.(1)试说明△ABD≌△ACD;(2)若∠B=40°,求∠G和∠FAG的大小.解:(1)由ASA可证△ABD≌△ACD(2)∠G=50°,∠FAG=80°19.如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD,延长使DF=BD,过F点作AB的平行线段MF,连接MD并延长,在其延长线上取一点E,使DE=DM,在E点开工就能使A,C,E成一条直线,你明白其中的道理吗?解:∵BD=DF,DE=DM,∠BDE=∠FDM,∴△BDE≌△FDM,故∠BEM=∠DMF,∴BE∥MF,又∵AB∥MF,依照过直线外一点有且只有一条直线与已知直线平行,∴A,C,E在一条直线上20.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图①所示放置,使得一直角边重合,连接BD,CE.(1)试说明:BD=CE;(2)延长BD交CE于点F,求∠BFC的度数;(3)若如图②放置,上面的结论还成立吗?请简单说明理由.解:(1)易得△ADB≌△AEC(SAS),∴BD=CE(2)∵△ADB≌△AEC,∴∠DBA=∠ECA,∴∠BFC=180°-∠AC E-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°(3)同样成立,BD=CE且∠BFC=90°.理由∵△ABC,△ADE是等腰直角三角形,∴AB=AC,AD=AE,且∠BAC=∠EAD,∴∠BAD=∠C AE,∴△ADB≌△AEC,∴BD=CE,∠ABF=∠ACF,∴∠BFC=∠BA C=90°。
中考数学专题复习小训练专题14几何初步知识三角形多边形

中考数学专题复习小训练专题14几何初步知识三角形多边形凡读书......须要读得字字响亮,不可误一字,不可少一字,不可多一字,不可倒一字,不可牵强暗记,只是要多诵数遍,自然上口,久远不忘。
古人云,读书百遍,其义自见。
谓读得熟,则不待解说,自晓其义也。
余尝谓,读书有三到,谓心到,眼到,口到。
1.2022·滨州有一个角为75°,则它的余角的度数为()A.285°B.105°C.75°D.15°2.2022·宿迁如图Z14-1,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是()图Z14-1A.80°B.85°C.95°D.100°3.2022·常德已知三角形的两边长分别是3和7,则此三角形第三边的长可能是()A.1B.2C.8D.114.2022·长沙一个三角形三个内角的度数之比为1∶2∶3,则这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形5.2022·大庆将正方体的表面沿某些棱剪开,得到如图Z14-2所示的平面图形,则原正方体中与“创”字所在的面相对的面上所标的汉字是()图Z14-2A.庆B.力C.大D.魅6.2022·菏泽如图Z14-3,直线a∥b,含45°角的三角尺的两个顶点分别落在直线a,b上,若∠1=30°,则∠2的度数是()图Z14-3邴原少孤,数岁时,过书舍而泣。
师曰:童子何泣?原曰:孤者易伤,贫者易感。
夫书者,凡得学者,有亲也。
一则愿其不孤,二则羡其得学,中心伤感,故泣耳。
师恻然曰:欲书可耳原曰:无钱资。
师曰:童子苟有志吾徒相教不求资也。
1/2凡读书......须要读得字字响亮,不可误一字,不可少一字,不可多一字,不可倒一字,不可牵强暗记,只是要多诵数遍,自然上口,久远不忘。
中考数学专题复习 三角形与多边形

第四章 三角形
第2节 三角形与多边形
上一页 返回导航 下一页
课标导航
·理解三角形及其内角、外角、中线、高线、角平分线等概念,会按照边长的 关系和角的大小对三角形进行分类,了解三角形的稳定性.
·探索并证明三角形的内角和定理.掌握它的推论.证明三角形的任意两边之 和大于第三边.
·了解三角形重心的概念. ·探索并证明三角形的中位线定理. ·了解多边形的定义,多边形的定点、边、内角、外角、对角线等概念;探索 并掌握多边形内角和与外角和公式.
∴BF=2BT=2 3.
∵∠A F E =120°,∠A F B =∠A B F =30°,
∴∠B F E =90°.
∴S
△PE
F=
S
△B EF
=1·E 2
F
·BF
=1×2×2 2
3=2
外心 三角形三边垂直平分线的交点,外心到各顶点的距离相等.
上一页 返回导航 下一页
3.(1)下列说法错误的是( D ) A.三角形的内心是三角形内切圆的圆心 B.三角形的外心是三角形外接圆的圆心 C.三角形的重心到每个顶点的距离等于它到对边中点距离的 2 倍 D.等腰三角形的四心重合
上一页 返回导航 下一页
上一页 返回导航 下一页
2.(1)如图,在△ABC 中,AE 是中线,AD 是∠BAC 的角平分线,AF ⊥BC 于点 F,∠B=30°,∠C=50°.
①BE= EC ; ②∠BAD= 50 °; ③∠DAF= 10 °; ④S△AEC = S△ABE.(填“>”“<”或“=”)
上一页 返回导航 下一页
AD×BC×14.
上一页 返回导航 下一页
顶点连中点,倍长造全等 点 D 是 BC 的中点,延长 AD 到 E,使 AD=DE,则有 点 D 为 BC 的中点,延长 ED △ACD≌△EBD,AC∥BE. 到点 F,使 DF=ED,连接 CF,则有△BED≌△CFD.
2019年中考总复习几何与图形模块之《多边形与平行四边形》复习
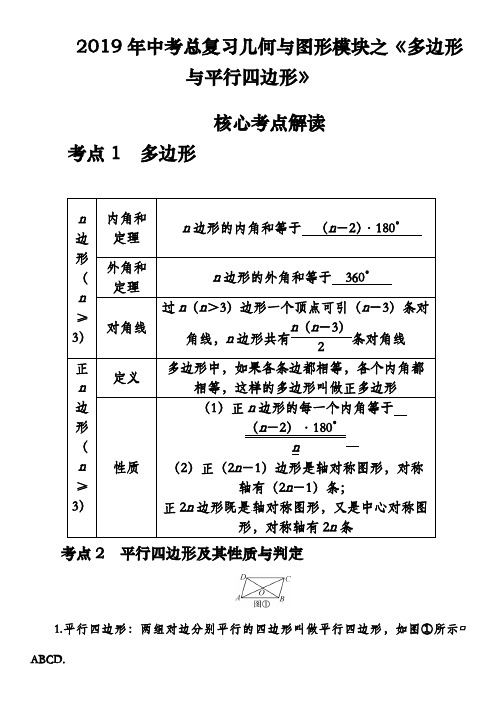
2019年中考总复习几何与图形模块之《多边形与平行四边形》核心考点解读考点1 多边形n边形(n≥3) 内角和 定理 n 边形的内角和等于 (n -2)·180°外角和 定理n 边形的外角和等于 360°对角线过n (n >3)边形一个顶点可引(n -3)条对角线,n 边形共有n (n -3)2条对角线正n边 形(n≥3)定义多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形 性质(1)正n 边形的每一个内角等于(n -2)·180°n(2)正(2n -1)边形是轴对称图形,对称轴有(2n -1)条;正2n 边形既是轴对称图形,又是中心对称图形,对称轴有2n 条考点2 平行四边形及其性质与判定1.平行四边形:两组对边分别平行的四边形叫做平行四边形,如图①所示▱ABCD.2.平行四边形的性质文字描述字母表示(参考图①) (1)对边 平行且相等AB CD AD BC (2)对角 相等∠DAB =∠DCB ,∠ADC =∠ABC(3)对角线 互相平分 OA =OC ,OB =OD(4)平行四边形是中心对称图形,对称中心是两条对角线的交点 3.平行四边形的判定文字描述字母表示(参考图①)(1)两组对边分别平行的四边形是平行四边形⎭⎪⎬⎪⎫AB ∥CD ,AD ∥BC ⇒四边形ABCD 是平行四边形(2)两组对边分别相等的四边形是平行四边形⎭⎪⎬⎪⎫AB =CD ,AD =BC ⇒四边形ABCD 是平行四边形(3)一组对边平行且相等的四边形是平行四边形⎭⎪⎬⎪⎫AB ∥CD ,AB =CD 或⎭⎪⎬⎪⎫AD ∥BC AD =BC ⇒四边形ABCD 是平行四边形(4)两组对角分别相等的四边形是平行四边形⎭⎪⎬⎪⎫∠DAB =∠DCB ,∠ADC =∠ABC⇒四边形ABCD 是平行四边形(5)两条对角线互相平分的四边形是平行四边形⎭⎪⎬⎪⎫OA =OC ,OB =OD⇒四边形ABCD 是平行四边形核心考点解读多边形的内角和与外角和例1 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 8 . 【解析】任何多边形的外角和是360°,即这个多边形的内角和是3×360°.设多边形的边数为n ,根据n 边形的内角和是(n -2)·180°,得(n -2)·180=3×360,解得n =8. 则这个多边形的边数是8.【点评】已知多边形的内角和求边数,可以转化为方程的问题来解决. 平行四边形的性质与判定例2 如图,在△ABC 中,∠ACB =90°,∠CAB =30°,以线段AB 为边向外作等边△ABD ,点E 是线段AB 的中点,连接CE 并延长交线段AD 于点F.(1)求证:四边形BCFD 为平行四边形; (2)若AB =6,求平行四边形BCFD 的面积.【解析】(1)在Rt △ABC 中,E 为AB 的中点,则CE =BE =12AB ,得到∠BCE=∠EBC =60°.证得△AEF ≌△BEC ,可得∠AFE =∠BCE =60°,又∠D =60°,得∠AFE =∠D =60°,所以FC ∥BD.又由于∠BAD =∠ABC =60°,可推出四边形BCFD 是平行四边形;(2)在Rt △ABC 中,求出BC ,AC 即可解决问题.【解答】(1)证明:在△ABC 中,∠ACB =90°,∠CAB =30°,∴∠ABC =60°.在等边△ABD 中,∠BAD =60°, ∴∠BAD =∠ABC =60°,∴AD ∥BC. ∵E 为AB 的中点,∴AE =BE.又∵∠AEF =∠BEC ,∴△AEF ≌△BEC (ASA ), ∴∠AFE =∠BCE.在△ABC 中,∠ACB =90°,E 为AB 的中点, ∴CE =12AB ,BE =12AB ,∴CE =BE ,∴∠BCE =∠EBC =60°=∠AFE.又∵∠D =60°,∴∠AFE =∠D =60°,∴FC ∥BD. 又∵AD ∥BC ,即FD ∥BC , ∴四边形BCFD 是平行四边形;(2)解:∵∠CAB =30°,∠BAD =60°, ∴∠CAD =90°,即CA ⊥AD.在Rt △ABC 中,∵∠BAC =30°,AB =6, ∴BC =12AB =3,AC =3BC =33,∴S 平行四边形BCFD =3×33=9 3.,强化训练1.(2018·北京中考)若正多边形的一个外角是60°,则该正多边形的内角和为( )A.360°B.540°C.720°D.900°2.(2016·来宾中考)如果一个正多边形的一个外角为30°,那么这个正多边形的边数是()A.6B.11C.12D.183.(2018·宁波中考)如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为()A.50°B.40°C.30°D.20°4.(2018·黔南中考)如图,在▱ABCD中,已知AC=4cm,若△ACD的周长为13 cm,则▱ABCD的周长为()A.26 cmB.24 cmC.20 cmD.18 cm5.如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D,E分别是BC,AD的中点,AF∥BC交CE的延长线于F.则四边形AFBD的面积为.6.(2018·百色中考适应性演练)在平行四边形ABCD中,已知E,F,G,H分别是AB,BC,CD,DA上的点,且BE=DG,∠BFE=∠DHG.求证:(1)△BEF≌△DGH;(2)四边形EFGH为平行四边形.证明:强化训练答案1.(2018·北京中考)若正多边形的一个外角是60°,则该正多边形的内角和为(C)A.360°B.540°C.720°D.900°2.(2016·来宾中考)如果一个正多边形的一个外角为30°,那么这个正多边形的边数是(C)A.6B.11C.12D.183.(2018·宁波中考)如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为(B)A.50°B.40°C.30°D.20°,(第3题图)4.(2018·黔南中考)如图,在▱ABCD中,已知AC=4 cm,若△ACD的周长为13 cm,则▱ABCD的周长为(D)A.26 cmB.24 cmC.20 cmD.18 cm(第4题图)5.如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D,E分别是BC,AD的中点,AF ∥BC交CE的延长线于F.则四边形AFBD的面积为12 W.6.(2018·百色中考适应性演练)在平行四边形ABCD中,已知E,F,G,H分别是AB,BC,CD,DA上的点,且BE=DG,∠BFE=∠DHG.求证:(1)△BEF≌△DGH;(2)四边形EFGH 为平行四边形.证明:(1)∵四边形ABCD 是平行四边形, ∴∠B =∠D.在△BEF 和△DGH 中,∵⎩⎪⎨⎪⎧∠BFE =∠DHG ,∠B =∠D ,BE =DG ,∴△BEF ≌△DGH (AAS ); (2)∵四边形ABCD 是平行四边形, ∴AD =BC ,AB =DC ,∠A =∠C.由(1)得△BEF ≌△DGH ,∴BF =DH ,EF =GH. 又∵BE =DG ,∴AH =CF ,AE =CG. 在△AEH 和△CGF 中, ∵⎩⎪⎨⎪⎧AE =CG ,∠A =∠C ,AH =CF ,∴△AEH ≌△CGF (SAS ),∴EH =GF.又∵EF =GH ,∴四边形EFGH 是平行四边形.。
全国通用中考数学复习第四单元图形的初步认识与三角形第14讲三角形的基础知识练习(2021年整理)

(全国通用版)2019年中考数学复习第四单元图形的初步认识与三角形第14讲三角形的基础知识练习编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((全国通用版)2019年中考数学复习第四单元图形的初步认识与三角形第14讲三角形的基础知识练习)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(全国通用版)2019年中考数学复习第四单元图形的初步认识与三角形第14讲三角形的基础知识练习的全部内容。
第14讲三角形的基础知识重难点三角形中角度的相关计算(2018·眉山)将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是(C)A.45°B.60°C.75°D.85°【思路点拨】由直角三角板中各内角度数,结合三角形内角和定理可求得∠1,即∠2的大小,再由三角形外角的性质可求得∠α的度数.错误!求解三角形中有关的角度时,若已知角和待求角可以转化为一个三角形的内角之间或内、外角之间的关系问题,则可以直接利用三角形内角和或外角性质求解.【变式训练1】(2018·黄石)如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=(A)A.75° B.80°C.85° D.90°【变式训练2】(2018·株洲)如图,直线l1,l2被直线l3所截,且l1∥l2,过l1上的点A作AB⊥l3交l3于点B,其中∠1<30°,则下列一定正确的是(D)A.∠2>120° B.∠3<60° C.∠4-∠3>90° D.2∠3>∠4【变式训练3】(2017·泰州)将一副三角板如图叠放,则图中∠α的度数为15°.考点1三角形的高、中线、角平分线1.(2018·贵阳)如图,在△ABC中有四条线段DE,BE,EF,FG,其中一条线段是△ABC的中线,则该线段是(B)A.线段DE B.线段BE C.线段EF D.线段FG2.(2017·泰州)三角形的重心是(A)A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边的垂直平分线的交点D.三角形三条内角平分线的交点考点2三角形的中位线3.(2018·南京)如图,在△ABC中,用直尺和圆规作AB,AC的垂直平分线,分别交AB,AC于点D,E连接DE.若BC=10 cm,则DE=5cm.4.如图,在△ABC中,点D,E,F分别是边AB,BC,CA上的中点,且AB=6 cm,AC=8 cm,则四边形ADEF的周长等于14cm。
三角形与多边形几何-中考复习专题(第十四讲)

第14讲三角形和多边形1.了解等腰三角形、等边三角形、直角三角形的概念,会识别这三种图形;理解等腰三角形、等边三角形、直角三角形的性质和判定.2. 能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题.3. 会运用等腰三角形、等边三角形、直角三角形的知识解决有关问题.知识要点一、三角形的概念及其性质1.三角形的内角和外角(1)三角形的内角和等于180°.(2)三角形的任意一个外角等于和它不相邻的两个内角之和;三角形的一个外角大于任何一个和它不相邻的内角.2.三角形三边之间的关系三角形任意两边之和大于第三边,任意两边之差小于第三边.3.三角形内角与对边对应关系在同一个三角形内,大边对大角,大角对大边;在同一三角形中,等边对等角,等角对等边.4.三角形具有稳定性.5.三角形中的四条特殊的线段是:高线、角平分线、中线、中位线.要点诠释:(1)三角形的中位线:连结三角形两边中点的线段是三角形的中位线.(2)中位线定理:三角形的中位线平行于第三边且等于第三边的一半.二、特殊三角形考点1 等腰三角形1、有两条边相等的三角形叫做等腰三角形.性质:(1)具有三角形的一切性质;(2)两底角相等(等边对等角);(3)顶角的平分线,底边中线,底边上的高互相重合(三线合一);(4)等边三角形的各角都相等,且都等于60°.要点诠释:等边三角形中高线,中线,角平分线三线合一,共有三条.2、判定:(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);(2)三个角都相等的三角形是等边三角形;(3)有一个角为60°的等腰三角形是等边三角形.要点诠释:(1)腰、底、顶角、底角是等腰三角形特有的概念;(2)等边三角形是特殊的等腰三角形.考点二、直角三角形1、直角三角形:有一个角是直角的三角形叫做直角三角形.2、性质:(1)直角三角形中两锐角互余;(2)直角三角形中,30°锐角所对的直角边等于斜边的一半; (3)在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°;(4)勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方;(5)勾股定理逆定理:如果三角形的三边长a ,b ,c 满足a2+b2=c2,那么这个三角形是直角三角形;(6)直角三角形中,斜边上的中线等于斜边的一半.要点诠释:(1)直角三角形中,SRt △ABC=21ch=21ab ,其中a 、b 为两直角边,c 为斜边,h 为斜边上的高; (2)圆内接三角形,当一条边为直径时,该三角形是直角三角形.3.判定:(1)两内角互余的三角形是直角三角形;(2)一条边上的中线等于该边的一半,则这条边所对的角是直角,这个三角形是直角三角形;(3)如果三角形两边的平方和等于第三边的平方,则这个三角形是直角三角形,第三边为斜边.典型例题例1、如图点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,以OC为边作等边三角形OCD,连AC、AD.(1)当α=150°时,试判断△AOD的形状,并说明理由;(2)探究:当a为多少度时,△AOD是等腰三角形?例2、已知: 如图, 菱形ABCD中, E、F分别是CB、CD上的点,BE=DF.(1)求证:AE=AF. (2)若AE垂直平分BC,AF垂直平分CD,求证:△AEF为等边三角形.例3、如图,△ABC中,CF⊥AB,垂足为F,M为BC的中点,E为AC上一点,且ME=MF.(1)求证:BE⊥AC;(2)若∠A=50°,求∠FME的度数.例4、如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE 于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.例5、如图①,△ABC 中.AB=AC ,P 为底边BC 上一点,PE ⊥AB ,PF ⊥AC ,CH ⊥AB ,垂足分别为E 、F 、H .易证PE+PF=CH .证明过程如下:如图①,连接AP .∵PE⊥AB,PF⊥AC,CH⊥AB,∴ABP S △=12AB•PE,ACP S △=12AC•PF,ABC S △=12AB•CH. 又∵ABP ACP ABC S S S +=△△△,∴12AB•PE+12AC•PF=12AB•CH.∵AB=AC,∴PE+PF=CH.(1)如图②,P 为BC 延长线上的点时,其它条件不变,PE 、PF 、CH 又有怎样的数量关系?请写出你的猜想,并加以证明:(2)填空:若∠A=30°,△ABC 的面积为49,点P 在直线BC 上,且P 到直线AC 的距离为PF ,当PF=3时,则AB 边上的高CH=______.点P 到AB 边的距离PE=________.例6、在△ABC中,AC=BC,,点D为AC的中点.(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连结CF,过点F作,交直线AB于点H.判断FH与FC的数量关系并加以证明.(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.1、把腰长为1的等腰直角三角形折叠两次后,得到的一个小三角形的周长是________.2、如图,△ABC为等边三角形,延长BC到D,延长BA到E,使AE=BD,连接CE、DE. 求证:CE=DE.3、以等腰三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,……,如此作下去,若OA=OB=1,则第n个等腰直角三角形的面积S n=________.4、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=CDBC; ②S⊿ABC+S⊿CDE≥S⊿ACE ; ③BM⊥DM;④BM=DM.正确结论的个数是()A.1个 B.2个 C.3个 D.4个课堂练习MECA1、有一段火车路线,含这段铁路的首尾两站在内共有5个车站(如图),图中共有几条线段?在这段线路上往返行车,需印制几种车票(每种车票要印出上车站与下车站)?2、如图,点A、B、C在直线l上,则图中共有______条线段.3、三角形三边长分别是6,2a﹣2,8,则a的取值范围是()A.1<a<2 B.<a<2 C.2<a<8 D.1<a<44、已知a,b,c为△ABC的三条边,化简得_________.5、下列命题:(1)等边三角形也是等腰三角形;(2)三角形的外角等于两个内角的和;(3)三角形中最大的内角不能小于60°;(4)锐角三角形中,任意两内角之和必大于90°,其中错误的个数是( )A.0 个B.1个C.2个D.3个课后练习1、一个多边形的内角和是900∘,这个多边形的边数是( )A. 10B. 9C. 8D. 72、如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角。
2019年中考数学知识点:多边形

2019年中考数学知识点:多边形各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢新一轮复习备考周期正式开始,为各位初三考生整理了各学科的复习攻略,主要包括中考必考点、中考常考知识点、各科复习方法、考试答题技巧等内容,帮助各位考生梳理知识脉络,理清做题思路,希望各位考生可以在考试中取得优异成绩!下面是《数学知识点:多边形》,仅供参考!多边形1、多边形:由一些线段首尾顺次连结组成的图形,叫做多边形。
2、多边形的边:组成多边形的各条线段叫做多边形的边。
3、多边形的顶点:多边形每相邻两边的公共端点叫做多边形的顶点。
4、多边形的对角线:连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
5、多边形的周长:多边形各边的长度和叫做多边形的周长。
6、凸多边形:把多边形的任何一条边向两方延长,如果多边形的其他各边都在延长线所得直线的问旁,这样的多边形叫凸多边形。
说明:一个多边形至少要有三条边,有三条边的叫做三角形;有四条边的叫做四边形;有几条边的叫做几边形。
今后所说的多边形,如果不特别声明,都是指凸多边形。
7、多边形的角:多边形相邻两边所组成的角叫做多边形的内角,简称多边形的角。
8、多边形的外角:多边形的角的一边与另一边的反向延长线所组成的角叫做多边形的外角。
注意:多边形的外角也就是与它有公共顶点的内角的邻补角。
9、n边形的对角线共有条。
说明:利用上述公式,可以由一个多边形的边数计算出它的对角线的条数,也可以由一个多边形的对角线的条数求出它的边数。
10、多边形内角和定理:n边形内角和等于180°。
11、多边形内角和定理的推论:n 边形的外角和等于360°。
说明:多边形的外角和是一个常数,利用它解决有关计算题比利用多边形内角和公式及对角线求法公式简单。
无论用哪个公式解决有关计算,都要与解方程联系起来,掌握计算方法。
各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢。
2019中考数学专题复习小练习专题14几何初步知识三角形多边形

最新】2019年中考数学专题复习小练习专题14 几何初步知识三角形多边1. 2018郴州如图Z— 14—1,直线a, b被直线c所截,下列条件中,不能判定a// b的是()图Z—14—1A. / 2= Z 4B. / 1+/4= 180 °C. / 5= / 4D. / 1 = / 32. 2018东营下列图形,根据AB// CD能得到/ 1 = / 2的是()图Z- 14 —23. 2018达州已知:如图Z- 14—3, AB// CD, / 1= 45° / 3= 80° 则/2 的度数为()图Z—14—3A. 30°B. 35°C. 40°D. 45°4. 2018长沙下列长度的三条线段,能组成三角形的是()A. 4 cm, 5 cm, 9cm B. 8 cm, 8 cm, 15 cmC. 5 cm, 5 cm, 10 cmD. 6 cm, 7 cm, 14 cm5. 2018杭州若线段AM , AN分别是△ ABC的BC边上的高和中线,则()A. AM>ANB. AM>ANC. AM<AND. AM K AN6. 2018潍坊把一副三角尺放在同一水平桌面上,摆放成如图Z- 14 —4所示的形状,使两个直角顶点重合,两条斜边平行,则 /1的度数是()图Z—14—4A.45° B.60°C.75° D.82.5 °7. 2018上海通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2 条,那么该多边形的内角和是__________________ 度.8. 2018泰州已知三角形两边的长分别为1, 5,第三边长为整数,则第三边的长为________ .9. 2018北京用一组a, b, c的值说明命题若a v b,则ac v be”是错误的,这组值可以是a= ___________ , b = ________ , c= _________ .详解详析1 . D2.B3.B4.B5.D6.C7.5408.59.答案不唯一,如1 , 2,-1一、选择题.下列属于相对脆弱的自然生态系统的是.绿洲荒漠交界带.水土流失严重区.地质灾害易发区.高寒带生态系统解析:选D相对脆弱的自然生态系统常见的有海岛生态系统、干旱区生态系统和高寒带生态系统等。
2019年中考数学总复习 第4章 图形的初步认识与三角形、四边形 第4节 多边形与平行四边形(精练)试题

第四节多边形与平行四边形1.(湘西中考)下列说法错误的是( D)A.对角线互相平分的四边形是平行四边形B.两组对边分别相等的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.一组对边相等,另一组对边平行的四边形是平行四边形2.(2019乌鲁木齐中考)如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( C)A.4 B.5 C.6 D.73.(河北中考)如图,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是( B)A.7 B.8 C.9 D.10(第3题图)(第4题图)4.(宁夏中考)在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于__2__.5.(2019通辽中考)在平行四边形ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F.若AD=11,EF=5,则AB=__8或3__.6.(2019汇川升学二模)如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处,若AD=2,BC=3,则EF的长为.7.(梅州中考)如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S △BCF=__4__.(第7题图)(第8题图)8.(2019十堰中考)如图,在▱ABCD 中,AB =213 cm ,AD =4 cm ,AC ⊥BC ,则△DBC 比△ABC 的周长长__4__cm .9.(2019原创)如图,▱ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上折叠,使点A 正好与CD 上的F 点重合,若△FDE 的周长为16,△FCB 的周长为28,则FC 的长为( C )A .4B .5C .6D .710.(2019南充中考)如图,在▱ABCD 中,过对角线BD 上一点P 作EF∥BC,GH ∥AB ,且CG =2BG ,S △BPG =1,则S ▱AEPH =__4__.(第10题图)(第11题图)11.(2019西宁中考)如图,将▱ABCD 沿EF 对折,使点A 落在点C 处,若∠A=60°,AD =4,AB =8,则AE 的长为__285__.12.(东营中考)如图,在Rt △ABC 中,∠B =90°,AB =4,BC>AB ,点D 在BC 上,以AC 为对角线的平行四边形ADCE 中,DE 的最小值是__4__.(第12题图)(第13题图)13.(2019齐齐哈尔中考)如图,在等腰三角形纸片ABC 中,AB =AC =10,BC =12,沿底边BC 上的高AD 剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是.14.(2019武汉中考)如图,在▱ABCD 中,∠D =100°,∠DAB 的平分线AE 交DC 于点E ,连接BE.若AE =AB ,则∠EBC 的度数为__30°__.(第14题图)(第15题图)15.(2019连云港中考)如图,在▱ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,若∠EAF=56°,则∠B=__56°__.16.(2019福建中考)两个完全相同的正五边形都有一边在直线l 上,且有一个公共顶点O ,其摆放方式如图所示,则∠AOB=__108__°.(第16题图)(第17题图)17.(2019邵阳中考)如图所示的正六边形ABCDEF ,连接FD ,则∠FDC 的大小为__90°__.18.(2019益阳中考)如图,在▱ABCD 中,AE ⊥BD 于E ,CF ⊥BD 于F ,连接AF ,CE.求证:AF =CE. 证明:∵四边形ABCD 是平行四边形, ∴AB =CD ,AB ∥CD , ∴∠ABE =∠CDF. 又∵AE⊥BD,CF ⊥BD , ∴∠AEB =∠CFD=90°, AE ∥CF ,在△ABE 和△CDF 中, ⎩⎪⎨⎪⎧∠ABE=∠CDF,∠AEB =∠CFD,AB =CD ,∴△ABE ≌△CDF(AAS ), ∴AE =CF , ∵AE ∥CF ,∴四边形AECF 是平行四边形,∴AF =CE.19.(鄂州中考)如图,▱ABCD 中,BD 是它的一条对角线,过A ,C 两点作AE⊥BD,CF ⊥BD ,垂足分别为E ,F ,延长AE ,CF 分别交CD ,AB 于M ,N.(1)求证:四边形CMAN 是平行四边形. (2)已知DE =4,FN =3,求BN 的长. 解:(1)∵四边形ABCD 是平行四边形, ∴CD ∥AB , ∵AM ⊥BD ,CN ⊥BD , ∴A M∥CN,又∵CM∥AN, ∴四边形AMCN 是平行四边形;(2)∵四边形AMCN 是平行四边形, ∴CM =AN ,∵四边形ABCD 是平行四边形, ∴CD =AB ,CD ∥AB ,∴DM =BN ,∠MDE =∠NBF,在△MDE 和△NBF 中, ⎩⎪⎨⎪⎧∠MDE=∠NBF,∠DEM =∠BFN=90°,DM =BN , ∴△MDE ≌△NBF ,∴ME =NF =3,在Rt △DME 中, ∵∠DEM =90°,DE =4,ME =3, ∴DM =DE 2+ME 2=32+42=5, ∴BN =DM =5.20.如图①,在△OAB 中,∠OAB =90°,∠AOB =30°,OB =8,以OB 为边,在△OAB 外作等边△OBC,D 是OB 的中点,连接AD 并延长交OC 于点E.(1)求证:四边形ABCE 是平行四边形;(2)如图②,将图①中的四边形ABCO 折叠,使点C 与点A 重合,折痕为FG ,求OG 的长. 解:(1)∵在Rt △OAB 中,D 为OB 的中点, ∴AD =12OB ,OD =BD =12OB ,DO =DA ,∴∠DAO =∠DOA=30°, ∴∠EOA =∠DOC+∠DOA =90°,∴∠AEO=60°,又∵△OBC为等边三角形,∴∠BCO=∠AEO=60°,∴BC∥AE,∵∠BAO=∠COA=90°,∴CO∥AB,∴四边形ABCE是平行四边形;(2)在Rt△OAB中,OA=OB·cos30°=43,在Rt△AOG中,设OG=x,则AG=CG=8-x,根据勾股定理得x2+(43)2=(8-x)2,解得x=1.即OG=1.。
2019年中考数学真题分类汇编—三角形初步知识

三角形初步知识一、选择题1. ( 山东省枣庄市,4,3分)如图,在△ABC 中,AB =AC ,∠A =30°,E 为BC 延长线上一点,∠ABC 与∠AC E 的平分线相交于点D ,则∠D 等于()A .15°B .17.5°C .20°D .22.5°A B D C E【答案】A .【逐步提示】本题考查了三角形的一个外角等于不相邻的两个内角的和的性质,解题的关键是找出角与角之间的联系.根据角平分线的性质可以得到∠ABC 与∠DBE 、∠ACE 与∠DCE 的关系,再结合∠DCE -∠DBE =∠D ,∠ACE -∠ABC =∠A ,即可找出∠D 与∠A 的关系.【详细解答】解:∵∠ABC 与∠ACE 的平分线相交于点D ,∴∠DBE =∠ABC ,∠DCE =∠ACE ,又∵∠1212DCE -∠DBE =∠D ,∠ACE -∠ABC =∠A ,∴∠D =∠A =×30°=15° ,故选择A .1212【解后反思】本题解题的关键是:找到已知角平分线的条件中所涉及的角,与已知角和要求的角之间的联系,从而正确求解.在求角度问题时,常常要用到三角形内角和等于180°,或三角形外角等于不相邻的两个内角的和的性质,在求角度问题时有时应用外角的性质进行运算更简单便捷.【关键词】角的平分线 ;三角形的外角和;整体思想2. (四川达州,8,3分)如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中的一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;.根据以上操作,若要得到100个小三角形,则需要操作的次数是A.25B.33C.34D.50第8题图【答案】B【逐步提示】本题考查了规律探索型问题以及方程思想,解题的关键是要能通过特殊情况归纳出一般规律.解题思路是:设需要操作的次数为n,根据图形探索规律,用含n的代数式表示出n次操作得到的三角形的个数,然后列出方程即可求解.【详细解答】解:设要得到100个小三角形需要操作的次数为n,根据题意得,3n+1=100,解得n=33.故选择B.【解后反思】1.规律探索问题是指由几个特殊的结论,通过类比、猜想、推理等一系列的数学思维活动,探求一般性的规律.解题时,要善于分析给出的材料信息,理清题目的条件与结论之间的联系,通过观察、实验、比较、归纳,作出符合一定规律与事实的推测性猜想,并能验证规律的合理性、正确性,一般有如下两种类型:(1)与数、式有关的规律探索:利用已有的一些已知数或算式之间的关系,预测问题的变化趋势,进而猜想、归纳出一般性的规律.(2)与图形有关的规律探索:从一些特殊的图形变化中发现不变的因素或按规律变化的因素,即从图形的变化特点寻求规律,并推广到一般情况.2.方程思想是一种重要的数学思想,所谓方程思想是指从分析问题的数量关系入手,将问题中的已知量和未知量之间的数量关系,通过适当设元建立方程(组),然后通过解方程(组)使问题得到解决的思维方式.【关键词】规律探索型问题;方程与函数思想3.(四川省广安市,8,3分)下列说法:①三角形的三条高一定都在三角形内;②有一个角是直角的四边形是矩形;③有一组邻边相等的平行四边形是菱形;④两边及一角对应相等的两个三角形全等;⑤一组对边平行,另一组对边相等的四边形是平行四边形.其中正确的个数有()A.1个B.2个C.3个D.4个【答案】A【逐步提示】本题考查了三角形的中线、高线、角平分线的概念,矩形的判定,菱形的判定,全等三角形的判定,平行四边形的判定等,解题的关键是掌握这些概念、定理等.因为直角三角形与钝角三角形的三条高不都在三角形内,故①错;至少有三个角是直角的四边形是才是矩形,故②错;③是菱形的定义,正确;满足④的条件时有可能形成“边边角”的情况,故错误;等腰梯形满足“一组对边平行,另一组对边相等”,但它不是平行四边形,故⑤错误.【详细解答】解:只有③正确,故选择A.【解后反思】要理解三角形“三线”的概念,掌握三角形、平行四边形、矩形、菱形的判定方法,这是正确解题的基础.能画图举反例,以排除不符合条件情形,也是解这类题的基本功,要多思考,勤积累.类似的问题还有:判断下列说法是否正确:(1)一组对边相等且一组对角相等的四边形是平行四边形.解:错误.如图1,作△ABC,使AB=AC,在BC上取一点D(D点不与B、C重合且BD≠CD),连接AD.再以A为顶点,AD为一边,作∠EAD,使∠EAD=∠ADC,且AE=DC,连接DE.由上述画图方法,可知△ADC≌△DAE(SAS).所以DE=AC=AB,∠AED=∠C=∠B.即四边形ABCD有一组对边相等(DE=AB)、一组对角相等(∠AED=∠B),但却不是平行四边形(另一组对边AE和BD不平行也不相等).(2)一组对边相等,且一条对角线平分另一条对角线的四边形是平行四边形.解:错误.如图2,画两条相交直线,交点为O,在其中一条直线上截取OA=OC,分别过A、C两点向另一条直线作垂线,垂足分别为E、F.在线段OF上取一点D(D点不与O、F重合),连接CD.再在线段OE的延长线上取一点B,使EB=FD,连接AB.由上述画图方法,易知△COF≌△AOE(AAS),则CF=AE,由“SAS”可判定△CFD≌△AEB,则CD=AB.连接AD、BC,则四边形ABCD满足条件,却不是平行四边形.(3)一组对角相等,且连接这一组对角的顶点的对角线被另一条对角线平分的四边形是平行四边形.解:错误.如图,画一个“筝形”ABCD,其中AB=AD,BC=DC且AO≠OC,则该“筝形”满足条件,但它不是平行四边形.【关键词】中线、高线、角平分线;矩形的判定;菱形的判定;全等三角形的判定;平行四边形的判定4. (四川乐山,3,3分)如图2,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A= ( ).A .35°B .95°C .85°D .75°A B C DE图235°60°【答案】C .【逐步提示】CE 是∠ACD 的平分线,并且是△ABC 的外角,根据“三角形的外角等于和它不相邻的两个内角的和”求解.【详细解答】解:∵CE 是∠ACD 的平分线,∴∠ACD=60°×2=120°,又∵∠ACD 是△ABC 的外角,∴∠ACD=∠A+∠B ,∴∠A =∠ACD-∠B=120°-35°=85°,故选择C .【解后反思】三角形的外角等于和它不相邻的两个内角的和.求一个角的度数:(1)当问题以三角形为背景时,可利用三角形的内角和定理和推论解决;(2)当问题中含有平行线时,可利用平行线的性质将其转化为其它角;即“两直线平行可得:同位角相等、内错角相等、同旁内角互补”根据角平分线的性质求相应角的角度.【关键词】三角形的内角和;角的平分线二、填空题1. ( 四川省广安市,12,3分)如图,直线l 1∥l 2,若∠1=130°,∠2=60°,则∠3=___________.123l 1l 2第12题图【答案】70°【逐步提示】本题考查了平行线的性质、三角形的外角定理、对顶角性质等,解题的关键是掌握这些性质.如图,由“两直线平行,内错角相等”可得∠4=∠1.由三角形外角定理,可得∠4=∠2+∠5,由对顶角相等,可得∠5=∠3,综合以上结论,可得∠3=∠1-∠2.【详细解答】解:∵l 1∥l 2,∴∠4=∠1.∵∠4=∠2+∠5,∠5=∠3,∴∠4=∠2+∠3.∴∠1=∠2+∠3.∴∠3=∠1-∠2=130°-60°=70°.故答案为70°.【解后反思】有关平行线的求角问题,常常要利用平行线的性质、三角形内角和或外角定理、对顶角性质实现角的转化,使所求的角与已知角从间接联系变为直接联系,从而得解.相关知积为:(1)平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.(2)三角形的内角和等于180°;三角形的一个外角等于和它不相邻的两个内角和.(3)对顶角相等.【关键词】 平行线的性质;三角形的外角定理;对顶角性质2. ( 四川省内江市,26,12分)问题引入:(1)如图①,在△ABC 中,点O 是∠ABC 和∠ACB 平分线的交点,若∠A =α,则∠BOC =____________(用α表示); 如图②,∠CBO =∠ABC ,∠BCO =∠ACB ,∠A =α,则∠BOC =____________(用α表1313示).拓展研究:(2)如图③,∠CBO =∠DBC ,∠BCO =∠ECB ,∠A =α,猜想∠BOC =____________(用α表示),并1313说明理由.(3)BO 、CO 分别是△ABC 的外角∠DBC 、∠ECB 的n 等分线,它们交于点O ,∠CBO =∠DBC ,∠BCO 1n =∠ECB ,∠A =α,请猜想∠BOC =____________ .1n③②①EAB AA B C C 【逐步提示】本题属于规律探究题,要求学生根据题意,结合图形,从探究的角度出发,利用三角形内角和、邻补角的定义、角平分线的定义等知识,分别求出∠BOC .(1)如图①,利用三角形内角和证得∠BOC =90°+∠α.;如图②,同理证得∠BOC =120°+∠α;1212(2)如图③,利用三角形内角和与邻补角的定义证得∠BOC =120°-∠α;13(3)同理,证得∠BOC =.1180-n nα-⋅∠ ()【详细解答】解:(1)如图①,在△ABC 中,∵点O 是∠ABC 和∠ACB 平分线的交点, ∴∠CBO =∠ABC ,∠BCO =∠ACB .1212∵∠A =α,∴∠BOC =180°-(∠ABC +∠ACB )12=180°-(180°-∠A )12=180°-(180°-∠α)12=180°-90°+∠α12=90°+∠α.12如图②,∵∠CBO =∠ABC ,∠BCO =∠ACB ,∠A =α,1313∴∠BOC =180°-(∠ABC +∠ACB )13=180°-(180°-∠A )13=180°-(180°-∠α)13=180°-60°+∠α12=120°+∠α.12故答案为90°+∠α,120°+∠α.1212(2)如图③,∵∠CBO =∠DBC ,∠BCO =∠ECB ,∠A =α,1313∴∠BOC =180°-(∠DBC +∠ECB )13=180°-[360°-(∠ABC +∠ACB )]13=180°-[360°-(180°-∠A )]13=180°-(180°+∠α)13=180°-60°-∠α13=120°-∠α.13故答案为120°-∠α.13(3)∵∠CBO =∠DBC ,∠BCO =∠ECB ,∠A =α,1n 1n∴∠BOC =180°-(∠DBC +∠ECB )1n=180°- [360°-(∠ABC +∠ACB )]1n=180°- [360°-(180°-∠A )]1n=180°-(180°+∠α)1n =×180°-∠α.1n n -1n =1180-n nα-⋅∠ ()故答案为. 1180-n nα-⋅∠ ()【解后反思】通过解题我们得到关于三角形内、外角等分线有如下规律:规律1:BO 、CO 分别是△ABC 的∠ABC 、∠ACB 的n 等分线,它们交于点O ,∠CBO =∠ABC ,∠BCO =1n ∠ACB ,∠A =α,则∠BOC =;1n1180+n n α-⋅∠ ()规律2:BO 、CO 分别是△ABC 的外角∠DBC 、∠ECB 的n 等分线,它们交于点O ,∠CBO =∠DBC ,∠1nBCO =∠ECB ,∠A =α,则∠BOC =.1n1180-n n α-⋅∠ ()【关键词】 三角形的内角和;规律探索;邻补角;角的平分线。
多边形性质+几何小题--2019中考真题汇编(教师版)

001(2019•北京)正十边形的外角和为()A.180°B.360°C.720°D.1440°解:因为任意多边形的外角和都等于360°,所以正十边形的外角和等于360°,.故选:B.002(2019•福建)已知正多边形的一个外角为36°,则该正多边形的边数为()A.12 B.10 C.8 D.6解:360°÷36°=10,所以这个正多边形是正十边形.故选:B.003(2019•白银)如图,足球图片正中的黑色正五边形的内角和是()A.180°B.360°C.540°D.720°解:黑色正五边形的内角和为:(5﹣2)×180°=540°,故选:C.004(2019•海南)如图,⊙O与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧所对的圆心角∠BOD的大小为144度.解:∵五边形ABCDE是正五边形,∴∠E=∠A108°.∵AB、DE与⊙O相切,∴∠OBA=∠ODE=90°,∴∠BOD=(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,故答案为:144.005(2019•河北)下列图形为正多边形的是()A.B.C.D.解:正五边形五个角相等,五条边都相等,故选:D.006(2019•陕西)若正六边形的边长为3,则其较长的一条对角线长为6.解:如图所示为正六边形最长的三条对角线,由正六边形性质可知,△AOB,△COD为两个边长相等的等边三角形,∴AD=2AB=6,故答案为6.007(2019•上海)如图,在正边形ABCDEF中,设,,那么向量用向量、表示为2.解:连接CF.∵多边形ABCDEF是正六边形,AB∥CF,CF=2BA,∴2,∵,∴2,故答案为2.008(2019•云南)一个十二边形的内角和等于()A.2160°B.2080°C.1980°D.1800°解:十二边形的内角和等于:(12﹣2)•180°=1800°;故选:D.009(2019•新疆)五边形的内角和为540度.解:五边形的内角和为(5﹣2)×180°=540°.故答案为:540.010(2019•广东)一个多边形的内角和是1080°,这个多边形的边数是8.解:设多边形边数有x条,由题意得:180(x﹣2)=1080,解得:x=8,故答案为:8.011(2019•河池)如图,在正六边形ABCDEF中,AC=2,则它的边长是()A.1 B.C.D.2解:如图,过点B作BG⊥AC于点G.正六边形ABCDEF中,每个内角为(6﹣2)×180°÷6=120°,∴∠ABC=120°,∠BAC=∠BCA=30°,∴AG AC,∴GB=1,AB=2,即边长为2.故选:D.012(2019•柳州)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为5.解:如图所示,连接OB、OC,过O作OE⊥BC,设此正方形的边长为a,∵OE⊥BC,∴OE=BE,即a=5.故答案为:5.013(2019•梧州)正九边形的一个内角的度数是()A.108°B.120°C.135°D.140°解:该正九边形内角和=180°×(9﹣2)=1260°,则每个内角的度数.故选:D.014(2019•辽阳)已知正多边形的一个外角是72°,则这个正多边形的边数是5.解:这个正多边形的边数:360°÷72°=5.故答案为:5015(2019•湖州)如图,已知正五边形ABCDE内接于⊙O,连结BD,则∠ABD的度数是()A.60°B.70°C.72°D.144°解:∵五边形ABCDE为正五边形,∴∠ABC=∠C108°,∵CD=CB,∴∠CBD36°,∴∠ABD=∠ABC﹣∠CBD=72°,故选:C.016(2019•衢州)如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为()A.1 B.C.D.2解:边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸带宽度,所以原来的纸带宽度2.故选:C.017(2019•咸宁)若正多边形的内角和是540°,则该正多边形的一个外角为()A.45°B.60°C.72°D.90°解:∵正多边形的内角和是540°,∴多边形的边数为540°÷180°+2=5,∵多边形的外角和都是360°,∴多边形的每个外角=360÷5=72°.故选:C.018(2019•孝感)刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正十二边形的面积S1来近似估计⊙O的面积S,设⊙O的半径为1,则S﹣S1=0.14.解:∵⊙O的半径为1,∴⊙O的面积S=3.14,∴圆的内接正十二边形的中心角为30°,∴过A作AC⊥OB,∴AC OA,∴圆的内接正十二边形的面积S1=1213,∴则S﹣S1=0.14,故答案为:0.14.019(2019•湘西州)已知一个多边形的内角和是1080°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形解:设所求多边形边数为n,则(n﹣2)•180°=1080°,解得n=8.故选:D.020(2019•益阳)若一个多边形的内角和与外角和之和是900°,则该多边形的边数是5.解:∵多边形的内角和与外角和的总和为900°,多边形的外角和是360°,∴多边形的内角和是900﹣360=540°,∴多边形的边数是:540°÷180°+2=3+2=5.故答案为:5.021(2019•岳阳)若一个多边形的内角和等于它的外角和,则这个多边形的边数为4.解:设多边形的边数为n,则(n﹣2)×180°=360°,解得:n=4,故答案为:4.022(2019•株洲)如图所示,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P,且∠ABP=60°,则∠APB=66度.解:∵五边形ABCDE为正五边形,∴∠EAB=108度,∵AP是∠EAB的角平分线,∴∠P AB=54度,∵∠ABP=60°,∴∠APB=180°﹣60°﹣54°=66°.故答案为:66.023(2019•淮安)若一个多边形的内角和是540°,则该多边形的边数是5.解:设这个多边形的边数是n,则(n﹣2)•180°=540°,解得n=5,故答案为:5.024(2019•泰州)八边形的内角和为1080°.解:(8﹣2)•180°=6×180°=1080°.故答案为:1080°.025(2019•宿迁)如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是()A.6πB.62πC.6πD.62π解:6个月牙形的面积之和=3π﹣(22π﹣62)=6π,故选:A.026(2019•徐州)如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD=30°.解:连接OB、OC,多边形的每个外角相等,且其和为360°,据此可得多边形的边数为:,∴∠AOB,∴∠AOD=40°×3=120°.∴∠OAD.故答案为:30°027(2019•扬州)如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边,若AB是⊙O的内接正n边形的一边,则n=15.解:连接BO,∵AC是⊙O内接正六边形的一边,∴∠AOC=360°÷6=60°,∵BC是⊙O内接正十边形的一边,∴∠BOC=360°÷10=36°,∴∠AOB=∠AOC﹣∠BOC=60°﹣36°=24°,∴n=360°÷24°=15;故答案为:15.028(2019•滨州)若正六边形的内切圆半径为2,则其外接圆半径为.解:如图,连接OA、OB,作OG⊥AB于G;则OG=2,∵六边形ABCDEF正六边形,∴△OAB是等边三角形,∴∠OAB=60°,∴OA,∴正六边形的内切圆半径为2,则其外接圆半径为.故答案为:.029(2019•济宁)如图,该硬币边缘镌刻的正九边形每个内角的度数是140°.解:该正九边形内角和=180°×(9﹣2)=1260°,则每个内角的度数140°.故答案为:140°.030(2019•青岛)如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是54°.解:连接AD,∵AF是⊙O的直径,∴∠ADF=90°,∵五边形ABCDE是⊙O的内接正五边形,∴∠ABC=∠C=108°,∴∠ABD=72°,∴∠F=∠ABD=72°,∴∠F AD=18°,∴∠CDF=∠DAF=18°,∴∠BDF=36°+18°=54°,故答案为:54.031(2019•枣庄)用一条宽度相等的足够长的纸条打一个结(如图1所示),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中,∠BAC=36度.解:∵∠ABC108°,△ABC是等腰三角形,∴∠BAC=∠BCA=36度.032(2019•成都)如图,正五边形ABCDE内接于⊙O,P为上的一点(点P不与点D重合),则∠CPD的度数为()A.30°B.36°C.60°D.72°解:如图,连接OC,OD.∵ABCDE是正五边形,∴∠COD72°,∴∠CPD∠COD=36°,故选:B.033(2019•广安)如图,正五边形ABCDE中,对角线AC与BE相交于点F,则∠AFE=72度.解:∵五边形ABCDE是正五边形,∴∠EAB=∠ABC,∵BA=BC,∴∠BAC=∠BCA=36°,同理∠ABE=36°,∴∠AFE=∠ABF+∠BAF=36°+36°=72°.故答案为:72034(2019•南充)如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=15度.解:∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,在正六边形ABEFGH中,∵AB=AH,∠BAH=120°,∴AH=AD,∠HAD=360°﹣90°﹣120°=150°,∴∠ADH=∠AHD(180°﹣150°)=15°,故答案为:15.035(2019•雅安)如图,已知⊙O的内接六边形ABCDEF的边心距OM=2,则该圆的内接正三角形ACE的面积为()A.2 B.4 C.6D.4解:如图所示,连接OC、OB,过O作ON⊥CE于N,∵多边形ABCDEF是正六边形,∴∠COB=60°,∵OC=OB,∴△COB是等边三角形,∴∠OCM=60°,∴OM=OC•sin∠OCM,∴OC(cm).∵∠OCN=30°,∴ON OC,CN=2,∴CE=2CN=4,∴该圆的内接正三角形ACE的面积=34,故选:D.036(2019•宜宾)如图,六边形ABCDEF的内角都相等,AD∥BC,则∠DAB=60°.解:在六边形ABCDEF中,(6﹣2)×180°=720°,120°,∴∠B=120°,∵AD∥BC,∴∠DAB=180°﹣∠B=60°,故答案为:60°.037(2019•资阳)若正多边形的一个外角是60°,则这个正多边形的内角和是720°.解:该正多边形的边数为:360°÷60°=6,该正多边形的内角和为:(6﹣2)×180°=720°.故答案为:720°.038(2019•自贡)图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看作正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近()A.B.C.D.解:连接AC,设正方形的边长为a,∵四边形ABCD是正方形,∴∠B=90°,∴AC为圆的直径,∴AC AB a,则正方形桌面与翻折成的圆形桌面的面积之比为:,故选:C.039(2019•自贡)如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则cos(α+β)=.解:给图中各点标上字母,连接DE,如图所示.在△ABC中,∠ABC=120°,BA=BC,∴∠α=30°.同理,可得出:∠CDE=∠CED=30°=∠α.又∵∠AEC=60°,∴∠AED=∠AEC+∠CED=90°.设等边三角形的边长为a,则AE=2a,DE=2×sin60°•a a,∴AD a,∴cos(α+β).故答案为:.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题14 几何初步知识、三角形、多边形
1.2018·郴州如图Z-14-1,直线a,b被直线c所截,下列条件中,不能判定a∥b 的是( )
图Z-14-1
A.∠2=∠4 B.∠1+∠4=180°
C.∠5=∠4 D.∠1=∠3
2.2018·东营下列图形,根据AB∥CD能得到∠1=∠2的是( )
图Z-14-2
3.2018·达州已知:如图Z-14-3,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
图Z-14-3
A.30° B.35°
C.40° D.45°
4.2018·长沙下列长度的三条线段,能组成三角形的是( )
A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cm
C.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm
5.2018·杭州若线段AM,AN分别是△ABC的BC边上的高和中线,则( )
A.AM>AN B.AM≥AN
C.AM<AN D.AM≤AN
6.2018·潍坊把一副三角尺放在同一水平桌面上,摆放成如图Z-14-4所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
图Z-14-4
A.45° B.60°
C.75° D.82.5°
7.2018·上海通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是________度.
8.2018·泰州已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为________.
9.2018·北京用一组a,b,c的值说明命题“若a<b,则ac<bc”是错误的,这组值可以是a=________,b=________,c=________.
详解详析1.D 2.B 3.B 4.B 5.D 6.C7.540 8.5 9.答案不唯一,如1,2,-1。
