八年级数学上册第四章数据分析4.5.1方差同步练习2(新版)青岛版
八年级数学上册第四章数据分析4-5-2方差同步练习1新版青岛版 (2)

4.5.2 方差1. 甲、乙两学生在一年里,学科平均分相等,但它们的方差不相等,正确评价他们的学习情况是()A. 因为他们平均分相等,所以学习水平一样B. 成绩虽然一样,方差较大的,说明潜力大,学习态度踏实C. 表面上看这两个学生平均成绩一样,但方差小的学习成绩较稳定D. 平均分相等,方差不等,说明学习水平不一样,方差较小的同学学习较稳定2. 为了判定八年级(1)、(2)两班学生口语测试成绩哪个班比较整齐,通常需要知道两组成绩的()A. 平均数B. 方差C. 众数D. 中位数3. 一组数据的方差一定是()A. 正数B. 任意实数C. 负数D. 非负数4.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计这两人中的新手是.5.跳远运动员李刚对训练效果进行测试,6次跳远的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9(单位:m),这6次成绩的平均数为7.8,方差为.如果李刚再跳两次,成绩分别为7.7,7.9.则李刚这8次跳远成绩的方差.(填“变大”“不变”或“变小”)6.甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷):甲经计算,=10,=10,试根据这组数据估计种水稻品种的产量比较稳定.7.如图所示是甲、乙两人在一次射击比赛中击中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数所在圆环被击中所得的环数),每人射击了6次.(1)请用列表法将他俩的射击成绩统计出来.(2)请你用学过的统计知识,对他俩的这次射击情况进行比较.8.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.甲、乙射击成绩统计表甲、乙射击成绩折线图(1)请补全上述图表(请直接在表中填空和补全折线图).(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?。
八年级数学上册第四章数据分析4.1平均数与加权平均数练习2青岛版(2021年整理)

八年级数学上册第四章数据分析4.1 平均数与加权平均数同步练习2 (新版)青岛版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(八年级数学上册第四章数据分析4.1 平均数与加权平均数同步练习2 (新版)青岛版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为八年级数学上册第四章数据分析4.1 平均数与加权平均数同步练习2 (新版)青岛版的全部内容。
平均数与加权平均数一、选择题1.小明记录了今年一月份某五天的最低温度(单位:℃):1,2,0,—1,—2,这五天的最低温度的平均值是( )A.1℃B.2℃ C。
0℃ D.-1℃2。
(易错题)小红记录了一周中连续5天的最低气温,并整理成下表.由于一个数据不小心被墨迹污染,请你算一算这个数据是( )星期一二三四五平均气温最低气温1618191818。
2(℃)A。
21 B。
18.2 C。
19 D。
203。
随着时代的发展,许多人开始注重精神的享受,应运而生的便是旅游的兴起.有人对南山旅游人数做了10天统计,结果有3天是每天800人,有2天是每天1200人,有5天是每天700人,那么这10天平均每天的旅游人数是( )A.830人B.850人C.900人 D。
800人4.在今年的助残募捐活动中,我市某中学九年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是( )A.20元 B。
15元 C。
12元 D.10元二、填空题5.一组数据中有3个7,4个11和3个9,那么它们的平均数是______.6.某组学生进行“引体向上”测试,有2名学生做了8次,其余4名学生分别做了10次、7次、6次、9次,那么这组学生的平均成绩为______次,在平均成绩之上的有______人.7.某校一次歌咏比赛中,7位评委给8年级(1)班的歌曲打分如下:9。
初中数学青岛版八年级上册第4章 数据分析4.5方差-章节测试习题(3)

章节测试题1.【题文】申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1)(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.【答案】(1)选择平均数,A店的日营业额的平均值是2.5百万元,B店的日营业额的平均值是2.5百万元;(2)A组新数据的方差约为1.0,B组新数据的方差约为0.6;(3)答案见解析.【分析】(1)在数据差别不是很大的情况下评价平均水平一般采用平均数;(2)分别用每一个数据减去其平均数,得到新数据后计算其方差后比较即可;(3)用今年的数据大体反映明年的数据即可.【解答】解:(1)选择平均数.A店的日营业额的平均值是×(1+1.6+3.5+4+2.7+2.5+2.2)=2.5(百万元),B店的日营业额的平均值是×(1.9+1.9+2.7+3.8+3.2+2.1+1.9)=2.5(百万元).(2)0.6,1.9,0.5,-1.3,-0.2,-0.3;B组数据的新数为0,0.8,1.1,-0.6,-1.1,-0.2,∴A组新数据的平均数x A=×(0.6+1.9+0.5-1.3-0.2-0.3)=0.2(百万元),B组新数据的平均数x B=×(0+0.8+1.1-0.6-1.1-0.2)=0(百万元).∴A组新数据的方差s=×[(0.2-0.6)2+(0.2-1.9)2+(0.2-0.5)2+(0.2+1.3)2+(0.2+0.2)2+(0.2+0.3)2]≈1.0,B组新数据的方差s=×(02+0.82+1.12+0.62+1.12+0.22)≈0.6.这两个方差的大小反映了A,B两家餐饮店相邻两天的日营业额的变化情况,并且B餐饮店相邻两天的日营业额的变化情况比较小.(3)观察今年黄金周的数据发现今年的3号、4号、5号营业额较高,故明年的3号、4号、5号营业额可能较高.方法总结:本题考查了算术平均数和方差的计算,算术平均数的计算公式是:,方差的计算公式为:,根据公式求解即可.2.【题文】某农民在自己家承包的甲、乙两片荒山上各栽了200棵苹果树,成活率均为96%,现已挂果.他随意从甲山采摘了4棵树上的苹果,称得质量(单位:千克)分别为36,40,48,36;从乙山采摘了4棵树上的苹果,称得质量(单位:千克)分别为50,36,40,34,将这两组数据组成一个样本,回答下列问题:(1)样本容量是多少?(2)样本平均数是多少?并估算出甲、乙两山苹果的总产量;(3)甲、乙两山哪个山上的苹果长势较整齐?【答案】(1)样本容量为8;(2)甲、乙两山苹果的总产量约为15 360千克;(3)甲山上的苹果长势较整齐.【分析】(1)根据样本容量的定义即可解决问题;(2)求出样本平均数,用样本估计总体的思想解决问题即可;(3)比较方差的大小,即可判断.【解答】解:(1)样本容量为 .(2) .甲、乙两山苹果的总产量约为400×40×96%=15360(千克).(3)∵ ,∴ .∵ ,∴ .∴, ∴甲山上的苹果长势较整齐.3.【答题】能够刻画一组数据离散程度的统计量是()A. 平均数B. 众数C. 中位数D. 方差【答案】D【分析】本题考查了方差.【解答】由于方差反映数据的波动情况,∴能够刻画一组数据离散程度的统计量是方差,选D.4.【答题】在方差的计算公式s=[(x-20)+(x-20)+…+(x-20)]中,数字10和20分别表示的意义可以是()A. 数据的个数和方差B. 平均数和数据的个数C. 数据的个数和平均数D. 数据组的方差和平均数【答案】C【分析】本题考查了方差.【解答】10位于分数的分母上,根据方差的计算公式可知,10表明样本数据的个数,也就是样本容量为10,数字20为样本数据的平均数,即样本的均值.选C.5.【答题】一组数据8,0,2,,4的方差等于()A. 15B. 16C. 17D. 18【答案】B【分析】本题考查了方差.【解答】数据8、0、2、−4、4的平均数,方差,选B.6.【答题】甲、乙两组数据,它们都是由n个数据组成,甲组数据的方差是0.4,乙组数据的方差是0.2,那么下列关于甲乙两组数据波动说法正确的是().A. 甲的波动小B. 乙的波动小C. 甲、乙的波动相同D. 甲、乙的波动的大小无法比较【答案】B【分析】本题考查了方差.【解答】∵s甲2=0.4,s乙2=0.2,方差小的为乙,∴本题中成绩比较稳定的是乙,乙的波动小,选B.7.【答题】方差反映了一组数据的波动大小.有两组数据,甲组数据:-1,-1,0,1,2;乙组数据:-1,-1,0,1,1,它们的方差分别记为和,则() A. = B. >C. <D. 无法比较【答案】B【分析】本题考查了方差.【解答】,,∵s甲2=[(−1−0.2)2+(−1−0.2)2+(0−0.2)2+(1−0.2)2+(2−0.2)2]=1.224,s乙2=[(−1−0)2+(−1−0)2+(0−0)2+(1−0)2+(1−0)2]=0.8,∴s甲2>s乙2,选B.8.【答题】两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学成绩哪一位更稳定,通常还需要比较他们成绩的()A. 众数B. 中位数C. 方差D. 以上都不对【答案】C【分析】本题考查了方差.【解答】根据方差的意义:是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.故要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生三级蛙跳测试成绩的方差.由于方差能反映数据的稳定性,需要比较这两名学生三级蛙跳成绩的方差.选C.9.【答题】如果一组数据x1,x2,…,x n的方差是3,则另一组数据x1+5,x2+5,…,x n+5的方差是()A. 3B. 8C. 9D. 14【答案】A【分析】本题考查了方差.【解答】设数据x1,x2,…,x n的平均数设为a,则数据x1+5,x2+5,…,x n+5的平均数为a+5,根据方差公式:s2[(x1-a)2+(x2-a)2+…+(x n-a)2]=3.则s2{[(x1+5)-(a+5)]2+[(x2+5)-(a+5)]2+…+(x n+5)-(a+5)]}2=[(x1-a)2+(x2-a)2+…+(x n-a)2]=3.选A.10.【答题】已知甲、乙两组数据的平均数相等,若甲组数据的方差=0.055,乙组数据的方差=0.105,则______组数据波动较大.【答案】乙【分析】本题考查了方差.【解答】∵s甲2<s乙2,∴乙组数据波动较大.故答案为:乙.11.【答题】两个小组进行定点投篮对抗赛,每组6名组员,每人投10次.两组组员进球数的统计结果如下:组别6名组员的进球数平均数甲组8 5 3 1 1 0 3乙组 5 4 3 3 2 1 3则组员投篮水平较整齐的小组是______组.【答案】乙【分析】本题考查了方差.【解答】甲的方差=[(8-3)2+(5-3)2+(3-3)2+(1-3)2+(1-3)2+(0-3)2]÷6≈7.7,乙的方差=[(5-3)2+(4-3)2+(3-3)2+(3-3)2+(2-3)2+(1-3)2]÷6≈1.7,由于乙的方差较小,∴整齐的是乙组.故答案为:乙.12.【答题】某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差______(填“变小”“不变”或“变大”).【答案】变大【分析】本题考查了方差.【解答】∵减少木工2名,增加电工、瓦工各1名,∴这组数据的平均数不变,但是每个数据减去平均数后平方和增大,则该工程队员工月工资的方差变大.故答案为:变大.13.【答题】甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为______(填>或<).【答案】>【分析】本题考查了方差.【解答】观察平均气温统计图可知:乙地的平均气温比较稳定,波动小,则乙地的日平均气温的方差小,故>,故答案为:>.14.【题文】甲、乙两个样本的相关信息如下:样本甲数据:1,6,2,3;样本乙方差:=3.4.(1)计算样本甲的方差;(2)试判断哪个样本波动大.【答案】见解答.【分析】本题考查了方差.【解答】(1)∵样本甲的平均数是,∴样本甲的方差是:=[(1-3)2+(6-3)2+(2-3)2+(3-3)2]=3.5.(2)∵=3.5,=3.4,∴>,∴样本甲的波动大.15.【题文】要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.(1)已求得甲的平均成绩为8环,求乙的平均成绩;(2)观察图形,直接写出甲,乙这10次射击成绩的方差,哪个大;(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选______参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选______参赛更合适.【答案】见解答.【分析】本题考查了平均数、方差.【解答】(1)乙的平均成绩是:(8+9+8+8+7+8+9+8+8+7)÷10=8(环).(2)根据图象可知:甲的波动大于乙的波动,则>,(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选乙参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选甲参赛更合适.。
青岛版八年级数学上册第四章数据分析同步练习(共20套)

青岛版八年级数学上册第四章数据分析同步练习(共20套)1.1加权平均数.某次考试,5名学生的平均分是83,除学生甲外,其余4名学生的平均分是80,则学生甲的得分是__________。
.某校几名学生参加今年全国初中数学竞赛,其中8名男同学的平均成绩为85分,4名女同学的平均成绩为76分,则该校12名同学的平均成绩为_________。
.已知一跳高运动员在1次大型运动会上成绩的平均数为2.35米,若选派参加亚运会,可以预料,他的成绩大约为______米。
.经随机调查某校初三30名学生每天完成家庭作业时间为3小时,由可估计该校家庭作业约为___________小时。
从甲、乙、丙三个厂家生产的同一产品中,各抽出8件产品,对其使用寿命进行跟踪调查,结果如下:甲:3,4,5,6,8,8,8,10乙:4,6,6,6,8,9,12,13丙:3,3,4,7,9,10,11,12试计算三个厂这三批灯泡的平均寿命并比较哪个厂生产的产品寿命最长。
参考答案.95.82.2.35.3乙2中位数已知一组数据的中位数为80,可知这组数据中大于或小于这个中位数的数据各占,中位数有个。
一次英语口语测试中,20名学生的得分如下:0,80,100,60,80,70,90,50,80,70,80,70,90,80,90,80,70,90,60,80。
这次英语口试中学生得分的中位数是。
已知一组数据:x1=4,x2=5,x3=6,x4=7,它们出现的次数依次为2,3,2,1,则这组数据的中位数为,平均数为。
学校体育节前一位同学在进行投掷训练中,投了20次标枪,其中3次投了45米,8次投了45.8米,7次投了45.4米,1次投了46.1米,1次犯规,求这位同学每次投掷标枪党的米数的中位数和平均数。
在一次环保知识竞赛中,某班50名同学得分情况如下:0分,2人;60分,3人;70分,6人;80分,14人;90分,15人;100分,5人;110分,4人;120分,1人。
八年级数学上册 第四章 数据分析 4.5.2 方差同步练习2 (新版)青岛版

方差一、选择题 1.数据-2,-1,0,1,2的方差是( ) A.0 B.2 C.2 D.4 2.一次数学测试,某小组五名同学的成绩、成绩的方差、平均成绩如下表所示(有两个数据被遮盖),那么被遮盖的两个数据依次是( )甲 乙 丙 丁 戊 方差 平均成绩 得分 81 79 ■ 80 82 ■ 80A.80,2B.80,2C.78,2D.78,23.某市测得一周的PM2.5的日均值(单位:微克/立方米)如下:31、30、34、35、36、34、31.对这组数据下列说法正确的是( )A.众数是35B.中位数是34C.平均数是35D.方差是64.一组数据-1,0,3,5,x 的极差是7,那么x 的值可能有( ).A.1个B.2个C.4个D.6个5.已知样本数据1,2,4,3,5,下列说法不正确的是( ).A.平均数是3B.中位数是4C.极差是4D.方差是2 二、填空题6.一组数据100,97,99,103,101中,极差是______,方差是______.7.数据1,3,2,5和x 的平均数是3,则这组数据的方差是______.8.一个样本的方差1212s [(x 1-3)2+(x 2-3)2+…+(x n -3)2],则样本容量是______,样本平均数是______.三、解答题9.甲、乙两组数据如下:甲组:10 9 11 8 12 13 10 7;乙组:7 8 9 10 11 12 11 12.分别计算出这两组数据的极差和方差,并说明哪一组数据波动较小.10.为检测一批橡胶制品的弹性,现抽取15条皮筋的抗拉伸程度的数据(单位:牛):5 4 4 4 5 7 3 3 5 56 6 3 6 6(1)这批橡胶制品的抗拉伸程度的极差为______牛;(2)若生产产品的抗拉伸程度的波动方差大于 1.3,这家工厂就应对机器进行检修,现在这家工厂是否应检修生产设备?通过计算说明.11.为迎接“外研社杯”全国英语演讲大赛.某市举行优秀学生选拔赛,学校为了迎接比赛,特组织学生进行英语口语比赛训练,把20名学生分成甲、乙两个小组,训练测试成绩如下(单位:分):甲组:76,90,84,86,87,86,81,82,83,85;乙组:82,84,85,89,79,91,89,80,79,74.根据学过的知识判断哪个小组学生的成绩比较整齐.12.已知甲、乙两位同学11次测验成绩如图所示(单位:分):(1)他们的平均成绩分别是多少?(2)他们的测验成绩的方差是多少?(3)现要从中选出一人参加比赛,历届比赛表明,成绩达到98分以上才能进入决赛,你认为应选谁参加这次比赛,为什么?(4)分析两名同学的成绩各有何特点?并对两名同学各提一条学习建议参考答案1.C 解析∵数据-2,-1,0,1,2的平均数是x=(-2-1+0+1+2)÷5=0,∴数据-2,-1,0,1,2的方差是s2=15[(-2)2+(-1)2+02+12+22]=2.故选C.2.C 解析由表可知丙的成绩为80×5-(81+79+80+82)=78,方差s2=15[(81-80)2+(79-80)2+(78-80)2+(80-80)2+(82-80)2]=2.3.B 解析这组数中,31与34出现的次数最多,都是两次,故众数为31与34;把这7个数由小到大排序后,排在最中间的数是34;故中位数是34,平均数为x=313034353634317++++++=33;方差s2=[(31-33)2+(30-33)2+(34-33)2+(35-33)2+(36-33)2+(34-33)2+(31-33)2]= 327.故选B.4.B.5.B.6.6;4.7.2.8.12;3.9.甲组的极差是6,方差是3.5;乙组的极差是5,方差是3;说明乙组的波动较小.10.(1)4;(2)方差约是1.5,大于1.3,说明应该对机器进行检修.11.解:x甲=110(76+90+84+86+87+86+81+82+83+85)=84(分),x乙=110(82+84+85+89+79+91+89+80+79+74)=83.2(分),∴2s甲=110×[(76-84)2+(90-84)2+…+(85-4)2]=13.2,2 s 乙=110×[(82-83.2)2+(84-83.2)2+…+(74-83.2)2]=26.36.∵2s甲<2s乙,∴甲组学生的成绩比较整齐.12.分析:对于(1)(2)根据定义及统计图中给出的数据计算即可;对于(3)应选成成绩达到98分以上的次数多的选手参加比赛;(4)根据上面的计算结果提出建议即可.解:(1)x甲=111×(99+100+100+95+93+90+98+100+93+90+98)=96,x乙=111×(98+99+96+94+95+92+92+98+96+99+97)=96.即甲的平均成绩是96分,乙的平均成绩是96分.(2)2s甲=111[(99-96)2+(100-96)2+…+(98-96)2]≈14.18,2 s 乙=111[(98-96)2+(99-96)2+…+(97-96)2]≈5.82.即甲的方差是14.18,乙的方差是5.82.(3)选甲.因为11次测验中甲有4次测验成绩超过98分,而乙只有2次超过98分.(4)由(2)(3)知乙的成绩稳定,甲的成绩波动较大,但是甲的高分率较高,有潜力.建议:甲在今后的学习中应使成绩保持稳定,乙在今后的学习中应不断努力,提高高分率.。
八年级数学上册第四章数据分析4.5.2方差同步练习3新版青岛版
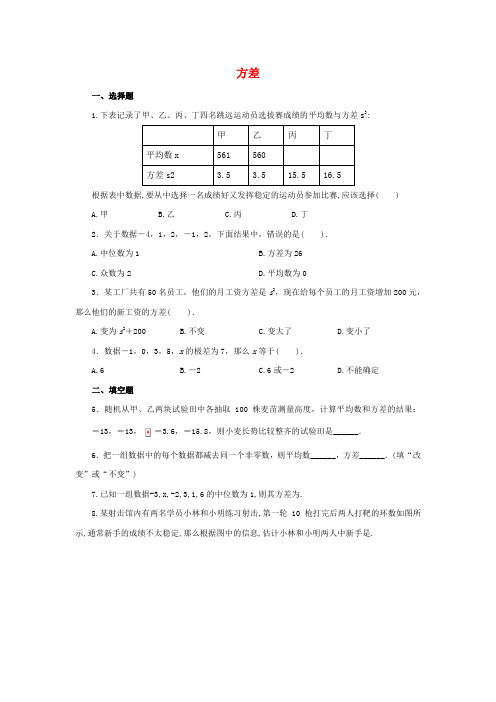
方差一、选择题1.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2:根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )A.甲B.乙C.丙D.丁2.关于数据-4,1,2,-1,2,下面结果中,错误的是( ).A.中位数为1B.方差为26C.众数为2D.平均数为03.某工厂共有50名员工,他们的月工资方差是s2,现在给每个员工的月工资增加200元,那么他们的新工资的方差( ).A.变为s2+200B.不变C.变大了D.变小了4.数据-1,0,3,5,x的极差为7,那么x等于( ).A.6B.-2C.6或-2D.不能确定二、填空题5.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果:=13,=13,=3.6,=15.8,则小麦长势比较整齐的试验田是______.6.把一组数据中的每个数据都减去同一个非零数,则平均数______,方差______.(填“改变”或“不变”)7.已知一组数据-3,x,-2,3,1,6的中位数为1,则其方差为.8.某射击馆内有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是.9.(探究题)已知x1,x2,x3的方差是2,则数据2x1+3,2x2 +3,2x3+3的方差是____.三、解答题10.甲、乙两个组各10名同学进行英语口语会话测试,每个人测试5次,每个同学合格的次数分别如下:甲组:4 1 2 2 1 3 3 1 2 1;乙组:4 3 0 2 1 3 3 0 1 3.(1)如果合格3次以上(含3次)为及格标准,请你说明哪个小组的及格率高;(2)请你比较两个小组口语会话的合格次数谁比较稳定.11.已知一个样本:78,79,76, 81, 75, 78, 74, 72, 79, 80, 76, 77, 75, 75,73,74,72,75,76,77.(1)计算这组数据的极差;(2)将该组数据适当分组,作出频数分布表和频数分布直方图.12.某研究性学习小组,为了了解本校七年级学生一天中做家庭作业所用的时间(时间以整数记,单位:分),对本校的七年级学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成条形统计图(如图所示),请结合统计图中提供的信息,解答下列问题:(1)这个研究性学习小组抽取的样本容量是多少?(2)在被调查的学生中,一天做家庭作业所用的时间超过120分钟的人数占被调查学生总人数的百分之几?(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段?参考答案1.A 解析∵甲的方差是3.5,乙的方差是3.5,丙的方差是15.5,丁的方差是16.5,∵===.∴发挥稳定的运动员应从甲和乙中选拔.∵甲的成绩的平均数是561,乙的成绩的平均数是560,∴成绩好的应是甲.∴要选择-名成绩好又发挥稳定的运动员参加比赛,应该选甲.故选A.2.B.3.B.4.C.5.甲.6.改变;不变.7.9 解析除x外把这组数据从小到大排序得-3,-2,1,3,6,因中位数是1,故有-3,-2,x,1,3,6,或-3,-2,1,x,3,6两种情况,因此=1,解得x=1,平均数==1,方差s2==9,故答案为9.8.小林解析从统计图可以看出小明的成绩波动小,稳定;小林的成绩波动大,不稳定,可知新手是小林.9.810.(1)甲组及格率是30%,乙组及格率是50%,乙组及格率高;(2)=2,=2,=1,=1.8,甲组更稳定.11.解:(1)9.(2)略.12.解:(1)3+4+6+8+9=30,所以这个研究性学习小组抽取的样本容量是30.(2)(9+8+4)÷30×100%=70%,故被调查的学生中,一天做家庭作业所用的时间超过120分钟的人数占被调查学生总人数的70%.(3)中位数落在了120. 5~150.5分这个时间段内.。
八年级数学上册第四章数据分析4-5-1方差同步练习1新版青岛版 (2)

4.5.1 方差
1.甲、乙、丙、丁四位选手各射击10次,每人平均成绩都是9.3环,方差如下表:
则这四人中成绩发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁
2.数据4,2,6的中位数和方差分别是( )
A.2,
B.4,4
C.4,
D.4,
3.已知样本x1,x2,x3,…,x n的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2x n+3的方差是( )
A.1
B.2
C.3
D. 4
4. 若的平均数为x,方差为S2,则样本x1+x,x2+x,x3+x的平均数是,方差是。
5. 甲、乙两种水稻,经统计甲水稻的株高方差是2.0,乙水稻的株高方差是1.8,可估计水稻比水稻长的整齐。
6. 已知x1,x2,x3的方差是2,则数据2x1+3,2x2+3,2x3+3的方差是。
7. 若1,2,3,a的平均数是3,又4,5,a,b的平均数是5,则样本0,1,2,3,4,a,b的方差是。
8.英语老实在班级搞了英语听力对比试验,现对甲、乙两个试验组各10名同学进行英语听力测验,各测5次,每组同学合格的次数分别如下:
甲:4,1,2,2,1,3,3,1,2,1
乙:4,3,0,2,1,3,3,0,1,3
(1)如果合格3次以上(含3次)作为及格标准,请说明哪一组的及格率高;
(2)请你比较哪个小组的英语听力的合格次数比较稳定。
参考答案
1.B
2.C
3.D
4.2x S2
5. 乙甲
6. 8
7. 4
8. (1)甲30%乙50%(2)甲比较稳定。
【新】八年级数学上册第四章数据分析4.5.1方差同步练习2新版青岛版

方差一、选择题1.某校有21名同学参加某项比赛,预赛成绩各不相同,要取前10名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的 ( )A.最高分 B.中位数C.极差 D.平均数2.为了了解某校学生的课外阅读情况,随机抽查了10名学生周阅读用时数,结果如下表:则关于这10名学生周阅读所用时间,下列说法正确的是( )A.中位数是6.5B.众数是12C.平均数是3.9D.方差是63.在2015年的中考中,某校6名学生的体育成绩统计图如图,则这组数据的众数、中位数、方差依次是( )A.18,18,1B.18,17,5.3C..18,18,3D.18,17,5.1二、填空题4.已知一组数据1,2,0,-1,x,1的平均数是1,则这组数据的极差为______.5.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是______.6.为了从甲、乙两名同学中选拔一人参加电脑知识竞赛,在相同条件下,对他们的电脑知识进行了10次测验,成绩如下:(单位:分)回答下列问题:(1)甲同学成绩的众数是 分,乙同学成绩的中位数是 分;(2)若甲同学成绩的平均数为x 甲,乙同学成绩的平均数为x 乙,则x 甲与x 乙的大小关系是 ;(3)经计算知:222=13.2=26.36,s s s 甲乙甲, 2s 乙,这表明 .(用简明的文字语言表述)三、解答题7.星期天上午,茱萸湾动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如下表所示: 甲队.乙队:(1)根据上述数据完成下表:(2)根据前面的统计分析,回答下列问题:①能代表甲队游客一般年龄的统计数据是_____________________; ②平均数能较好地反映乙队游客的年龄特征吗?为什么?8.为了解某品牌A ,B 两种型号冰箱的销售状况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成如下的统计表:(1)完成下表(结果精确到0.1):(2)请你根据七个月的销售情况在图中绘制成折线统计图,并依据折线图的变化趋势,对专卖店今后的进货情况提出建议(字数控制在20~50字).9.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和如图所示的统计图: 甲、乙射击成绩统计表甲、乙射击成绩折线图(1)请补全上述图表(直接在表中填空和补全折线图);(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?10.一次学科测验,学生得分均为整数,满分为10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次测验中甲、乙两组学生成绩分布的条形统计图如图所示.(1)请补全下面的统计表:(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出三条支持乙组学生观点的理由.参考答案1.B2.D 解析由题意可知,由小到大排序后第5、6名学生的周阅读用时数都是5小时,故中位数是5;周阅读用时数是5小时的学生最多,有4人,故众数是5;平均数x=3445281210⨯+⨯+⨯+=6;s2=[(6-4)2×3+(6-5)2×4+(6-8)2×2+(6-12)2]=6,故选D.3.A 解析由统计图可知6名学生的成绩为17,17,18,18,18,20,易看出众数是18,中位数是18,平均数x=(17×2+18×3+20×1)÷6=18,方差s2=16[(17-18)2×2+(18-18)2×3+(20-18)2]=1.4.4.5.8.6.(1)86;83(2)x甲>x乙(3)<;甲同学成绩比乙同学成绩稳定解析(1)甲同学的10次成绩中,86分出现了2次,出现的次数最多,所以甲同学成绩的众数是86分;将乙同学的10次成绩按从小到大的顺序排列,中间的两个数是82,84,所以乙同学成绩的中位数是82842+=83.(2)x甲=7684908681878682858310+++++++++=84,x乙=8284858979809189747910+++++++++=83.2.所以x甲>x乙.点拨:本题是-道统计知识的综合性题目,考查了众数、中位数、平均数、方差的概念,它们从不同的角度反映了数据的变化趋势,通过表中信息培养分析判断能力,体现了统计思想.7.(1)(2)①平均数;②不能;方差太大.8.(1)A型:平均数 14;方差4.3(约);B型:中位数 15.(2)略.9.分析:从折线图上读取甲、乙每次射击的成绩,再进行平均数、中位数、方差的计算,然后根据求得的信息补全图表并解答所求问题.解:(1)根据折线统计图得乙的射击成绩并按从小到大的顺序排列为2,4,6,7,7,8,8,9,9,10,则平均数为2467788991010+++++++++=7,中位数为782+=7.5,方差为110×[(2-7)2+(4-7)2+(6-7)2+(7-7)2+(7-7)2+(8-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4;由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩由小到大排列为5,6,6,6,7,7,7,8,9,9,中位数为7,方差为110×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:甲、乙射击成绩统计表甲、乙射击成绩折线图(2)甲胜出.理由:两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差.(3)若希望乙胜出,应规定命中9环与10环的次数多的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.10.思路建立(1)从条形图中读取所反映的信息即可找到中位数,再根据获得的信息计算乙组的平均分.(2)只要根据图表信息回答正确即可(答案不唯一).(1)甲组:中位数为7;乙组:平均分为7,中位数为7 解析每组分别有12人,甲组3分的1人,6分的3人,7分的4人,8分、9分的都2人,中位数是7分.乙组5分的2人,6人的1人,7分的5人,8分的3人,9分的1人,平均分为112(5×2+6+7×5+8×3+9)=7(分),中位数也是7分.(2)解:(答案不唯一)①因为乙组学生的平均成绩高于甲组学生的平均成绩,所以乙组学生的成绩好于甲组;②因为甲、乙两组学生成绩的平均分相差不大,而乙组学生成绩的方差小于甲组学生成绩的方差,说明乙组学生成绩的波动比甲组小,所以乙组学生的成绩好于甲组;③因为乙组学生的最低分高于甲组学生的最低分,所以乙组学生的成绩好于甲组.。
八年级数学上册第四章数据分析4.1平均数与加权平均数同步练习2新版青岛版word版本

均匀数与加权均匀数一、选择题1. 小明记录了今年一月份某五天的最低温度( 单位 : ℃ ):1,2,0,-1,-2,这五天的最低温度的均匀值是( )A.1 ℃℃℃℃2.(易错题) 小红记录了一周中连续 5 天的最低气温, 并整理成下表. 因为一个数据不当心被墨迹污染, 请你算一算这个数据是()礼拜一二三四五均匀气温最低气温( ℃ )161819183.跟着时代的发展, 好多人开始侧重精神的享受, 应运而生的即是旅行的流行 . 有人对南山旅行人数做了 10 天统计 , 结果有 3 天是每日 800 人, 有 2 天是每日 1200 人 , 有 5 天是每日 70 0 人 , 那么这 10 天均匀每日的旅行人数是( )A.830 人人C.900 人人4. 在今年的助残募捐活动中, 我市某中学九年级(1) 班的同学组织献爱心捐款活动,班长依据第一组12 名同学的捐款状况绘制成以下列图的条形统计图. 依据图中供给的信息, 第一组同学捐款金额的均匀数是( )A.20 元元元元二、填空题5.一组数据中有 3 个 7, 4 个 11 和 3 个 9,那么它们的均匀数是______.6.某组学生进行“引体向上”测试,有 2 名学生做了8 次,其他 4 名学生分别做了10 次、7 次、6 次、9 次,那么这组学生的均匀成绩为______ 次,在均匀成绩之上的有______人.7.某校一次歌唱竞赛中,7 位评委给8 年级 (1) 班的歌曲打分以下:9.65 ,9.70 ,9.68 ,9.75 , 9.72 ,9.65 ,9.78 ,去掉一个最高分,再去掉一个最低分,计算均匀分为该班最后得分,则 8 年级 (1) 班最后得分是 ______分.8. 某学校举行演讲竞赛 ,5 位评委对某选手打分以下:(单位 : 分 )9.5,9.4,9.4,9.5,9.2,则这个选手的均匀分为分 .9.( 教材习题变式 ) 某市广播电视局欲招聘播音员一名, 对 A、B 两名候选人进行了两项测试 , 两人的两项测试成绩以下表所示. 依据实质需要 , 广播电视局将面试、综合知识测试的得分按 3:2 的比率计算两人的总成绩, 那么 ______( 填 A 或 B) 将被录取 .测试成绩测试项目A B面试9095综合知识测试8580三、解答题10.甲、乙两支仪仗队队员的身高( 单位:厘米 ) 以下:甲队: 178 177179 178177 178 177 179 178179;乙队: 178 179 176 178 180 178 176 178 177 180.(1)将下表填完好:身高(厘米)176177178179180甲队(人数)340乙队(人数)211(2)甲队队员身高的均匀数为 ______厘米,乙队队员身高的均匀数为______厘米;(3)你以为哪支仪仗队更为整齐 ?简要说明原由.11.小明和小颖本学期数学平常成绩、期中成绩、期末成绩分别以下:平常期中期末小明859092小颖908388若是学期总评按平常成绩、期中成绩、期末成绩各占1∶ 3∶ 6 的比率来计算,那么小明和小颖的学期总评成绩谁较高?参照答案120121. C 分析 x50 ,应选 C.2. D 分析设被墨迹污染了的数据为 x,则有 (16+18+19+18+x) ÷5=18. 2 解得 x=20,应选 D.3.A 分析运用加权均匀数公式计算可得,x 80031200270055830 (人),应选 A.4. D分析由题意,得(6 ×5+4×10+2×25) ÷12=10 ( 元 ) ,应选 D.5. 9.2. 6.8;2. 7 .9.70 .8.解析先求出这组数据的和,而后用这个和除以这组数据的个数,(9.5+9.4+9.4+9.5+9.2)÷5=9.4 ,即这个选手均匀分为9.4 分.9. B分析 A 的成绩为903 85 2=88( 分),5B 的成绩为903852=89( 分 ) ,因此 B 将被录取 .510. (1) 略; (2)178 , 178; (3) 甲队,原由略.11.小明。
2020-2021【名校提分专用】八年级数学上册第四章数据分析4.5.1方差同步练习2新版青岛版

方差一、选择题1.某校有21名同学参加某项比赛,预赛成绩各不相同,要取前10名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )A.最高分 B.中位数C.极差 D.平均数2.为了了解某校学生的课外阅读情况,随机抽查了10名学生周阅读用时数,结果如下表:周阅读用时数(小时) 4 5 8 12学生人数(人) 3 4 2 1则关于这10名学生周阅读所用时间,下列说法正确的是( )A.中位数是6.5B.众数是12C.平均数是3.9D.方差是63.在2015年的中考中,某校6名学生的体育成绩统计图如图,则这组数据的众数、中位数、方差依次是( )A.18,18,1B.18,17,5.3C..18,18,3D.18,17,5.1二、填空题4.已知一组数据1,2,0,-1,x,1的平均数是1,则这组数据的极差为______.5.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是______.6.为了从甲、乙两名同学中选拔一人参加电脑知识竞赛,在相同条件下,对他们的电脑知识进行了10次测验,成绩如下:(单位:分)甲同学76 84 90 86 81 87 86 82 85 83乙同学 82 84 85 89 79 80 91 89 74 79回答下列问题:(1)甲同学成绩的众数是 分,乙同学成绩的中位数是 分;(2)若甲同学成绩的平均数为x 甲,乙同学成绩的平均数为x 乙,则x 甲与x 乙的大小关系是 ;(3)经计算知:222=13.2=26.36,s s s 甲乙甲, 2s 乙,这表明 .(用简明的文字语言表述)三、解答题7.星期天上午,茱萸湾动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如下表所示:甲队.年龄 13 14 15 16 17 人数 21412乙队:年龄 3 4 5 6 54 57 人数 122311(1)根据上述数据完成下表:平均数 中位数 众数 方差 甲队游客年龄 15 15 乙队游客年龄15411.4(2)根据前面的统计分析,回答下列问题:①能代表甲队游客一般年龄的统计数据是_____________________; ②平均数能较好地反映乙队游客的年龄特征吗?为什么?8.为了解某品牌A ,B 两种型号冰箱的销售状况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成如下的统计表:月份1月 2月 3月 4月 5月 6月 7月 A 型销售量/台 10 14 17 16 13 14 14 B 型销售量/台6101415161720(1)完成下表(结果精确到0.1):平均数中位数方差A型销售量14B型销售量14 18.6(2)请你根据七个月的销售情况在图中绘制成折线统计图,并依据折线图的变化趋势,对专卖店今后的进货情况提出建议(字数控制在20~50字).9.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和如图所示的统计图: 甲、乙射击成绩统计表平均数中位数方差命中10环的次数甲7 0乙 1甲、乙射击成绩折线图(1)请补全上述图表(直接在表中填空和补全折线图);(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?10.一次学科测验,学生得分均为整数,满分为10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次测验中甲、乙两组学生成绩分布的条形统计图如图所示.(1)请补全下面的统计表:平均数方差中位数合格率优秀率甲组 6.9 2.4 91.7% 16.7%乙组 1.3 83.3% 8.3%(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出三条支持乙组学生观点的理由.参考答案1.B2.D 解析由题意可知,由小到大排序后第5、6名学生的周阅读用时数都是5小时,故中位数是5;周阅读用时数是5小时的学生最多,有4人,故众数是5;平均数x=3445281210⨯+⨯+⨯+=6;s2=[(6-4)2×3+(6-5)2×4+(6-8)2×2+(6-12)2]=6,故选D.3.A 解析由统计图可知6名学生的成绩为17,17,18,18,18,20,易看出众数是18,中位数是18,平均数x=(17×2+18×3+20×1)÷6=18,方差s2=16[(17-18)2×2+(18-18)2×3+(20-18)2]=1.4.4.5.8.6.(1)86;83(2)x甲>x乙(3)<;甲同学成绩比乙同学成绩稳定解析(1)甲同学的10次成绩中,86分出现了2次,出现的次数最多,所以甲同学成绩的众数是86分;将乙同学的10次成绩按从小到大的顺序排列,中间的两个数是82,84,所以乙同学成绩的中位数是82842+=83.(2)x甲=7684908681878682858310+++++++++=84,x乙=8284858979809189747910+++++++++=83.2.所以x甲>x乙.点拨:本题是-道统计知识的综合性题目,考查了众数、中位数、平均数、方差的概念,它们从不同的角度反映了数据的变化趋势,通过表中信息培养分析判断能力,体现了统计思想.7.(1)(2)①平均数;②不能;方差太大.8.(1)A型:平均数 14;方差4.3(约);B型:中位数 15.(2)略.9.分析:从折线图上读取甲、乙每次射击的成绩,再进行平均数、中位数、方差的计算,然后根据求得的信息补全图表并解答所求问题.解:(1)根据折线统计图得乙的射击成绩并按从小到大的顺序排列为2,4,6,7,7,8,8,9,9,10,则平均数为2467788991010+++++++++=7,中位数为782+=7.5,方差为110×[(2-7)2+(4-7)2+(6-7)2+(7-7)2+(7-7)2+(8-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4;由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩由小到大排列为5,6,6,6,7,7,7,8,9,9,中位数为7,方差为110×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:甲、乙射击成绩统计表平均数中位数方差命中10环的次数甲7 7 1.6 0乙7 7.5 5.4 1甲、乙射击成绩折线图(2)甲胜出.理由:两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差.(3)若希望乙胜出,应规定命中9环与10环的次数多的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.10.思路建立(1)从条形图中读取所反映的信息即可找到中位数,再根据获得的信息计算乙组的平均分.(2)只要根据图表信息回答正确即可(答案不唯一).(1)甲组:中位数为7;乙组:平均分为7,中位数为7 解析每组分别有12人,甲组3分的1人,6分的3人,7分的4人,8分、9分的都2人,中位数是7分.乙组5分的2人,6人的1人,7分的5人,8分的3人,9分的1人,平均分为112(5×2+6+7×5+8×3+9)=7(分),中位数也是7分.(2)解:(答案不唯一)①因为乙组学生的平均成绩高于甲组学生的平均成绩,所以乙组学生的成绩好于甲组;②因为甲、乙两组学生成绩的平均分相差不大,而乙组学生成绩的方差小于甲组学生成绩的方差,说明乙组学生成绩的波动比甲组小,所以乙组学生的成绩好于甲组;③因为乙组学生的最低分高于甲组学生的最低分,所以乙组学生的成绩好于甲组.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差
一、选择题
1.某校有21名同学参加某项比赛,预赛成绩各不相同,要取前10名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
A.最高分 B.中位数
C.极差 D.平均数
2.为了了解某校学生的课外阅读情况,随机抽查了10名学生周阅读用时数,结果如下表:
则关于这10名学生周阅读所用时间,下列说法正确的是( )
A.中位数是6.5
B.众数是12
C.平均数是3.9
D.方差是6
3.在2015年的中考中,某校6名学生的体育成绩统计图如图,则这组数据的众数、中位数、方差依次是( )
A.18,18,1
B.18,17,5.3
C..18,18,3
D.18,17,5.1
二、填空题
4.已知一组数据1,2,0,-1,x,1的平均数是1,则这组数据的极差为______.5.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是______.
6.为了从甲、乙两名同学中选拔一人参加电脑知识竞赛,在相同条件下,对他们的电脑知识进行了10次测验,成绩如下:(单位:分)
回答下列问题:
(1)甲同学成绩的众数是 分,乙同学成绩的中位数是 分;
(2)若甲同学成绩的平均数为x 甲,乙同学成绩的平均数为x 乙,则x 甲与x 乙的大小关系是 ;
(3)经计算知:222
=13.2=26.36,s s s 甲乙甲
, 2s 乙,这表明 .(用简明的文字语言表述)
三、解答题
7.星期天上午,茱萸湾动物园熊猫馆来了甲、乙两队游客,两队游客的年龄如下表所示:
甲队.
乙队:
(1)根据上述数据完成下表:
(2)根据前面的统计分析,回答下列问题:
①能代表甲队游客一般年龄的统计数据是_____________________; ②平均数能较好地反映乙队游客的年龄特征吗?为什么?
8.为了解某品牌A ,B 两种型号冰箱的销售状况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成如下的统计表:
(1)完成下表(结果精确到0.1):
(2)请你根据七个月的销售情况在图中绘制成折线统计图,并依据折线图的变化趋势,对专卖店今后的进货情况提出建议(字数控制在20~50字).
9.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和如图所示的统计图: 甲、乙射击成绩统计表
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
10.一次学科测验,学生得分均为整数,满分为10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次测验中甲、乙两组学生成绩分布的条形统计图如图所示.
(1)请补全下面的统计表:
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出三条支持乙组学生观点的理由.
参考答案
1.B
2.D 解析由题意可知,由小到大排序后第5、6名学生的周阅读用时数都是5小时,故中位数是5;周阅读用时数是5小时的学生最多,有4人,故众数是5;平均数
x=34452812
10
⨯+⨯+⨯+
=6;s2=[(6-4)2×3+(6-5)2×4+(6-8)2×2+(6-12)2]=6,故
选D.
3.A 解析由统计图可知6名学生的成绩为17,17,18,18,18,20,易看出众数是
18,中位数是18,平均数x=(17×2+18×3+20×1)÷6=18,方差s2=1
6
[(17-18)2×2+
(18-18)2×3+(20-18)2]=1.
4.4.
5.8.
6.(1)86;83
(2)x甲>x乙
(3)<;甲同学成绩比乙同学成绩稳定
解析(1)甲同学的10次成绩中,86分出现了2次,出现的次数最多,所以甲同学成绩的众数是86分;将乙同学的10次成绩按从小到大的顺序排列,中间的两个数是82,84,
所以乙同学成绩的中位数是8284
2
+
=83.
(2)x甲=76849086818786828583
10
+++++++++
=84,
x乙=82848589798091897479
10
+++++++++
=83.2.
所以x甲>x乙.
点拨:本题是-道统计知识的综合性题目,考查了众数、中位数、平均数、方差的概念,它们从不同的角度反映了数据的变化趋势,通过表中信息培养分析判断能力,体现了统计思想.
7.(1)
(2)①平均数;②不能;方差太大.
8.(1)A型:平均数 14;方差4.3(约);B型:中位数 15.
(2)略.
9.分析:从折线图上读取甲、乙每次射击的成绩,再进行平均数、中位数、方差的计算,然后根据求得的信息补全图表并解答所求问题.
解:(1)根据折线统计图得乙的射击成绩并按从小到大的顺序排列为2,4,6,7,7,
8,8,9,9,10,则平均数为24677889910
10
+++++++++
=7,中位数为
78
2
+
=7.5,方
差为
1
10
×[(2-7)2+(4-7)2+(6-7)2+(7-7)2+(7-7)2+(8-7)2+(8-7)2+(9-7)2+(9-7)
2+(10-7)2]=5.4;由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩由小到大排列为5,6,6,6,7,7,7,
8,9,9,中位数为7,方差为
1
10
×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)
2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:
甲、乙射击成绩统计表
甲、乙射击成绩折线图
(2)甲胜出.理由:两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差.
(3)若希望乙胜出,应规定命中9环与10环的次数多的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.
10.思路建立(1)从条形图中读取所反映的信息即可找到中位数,再根据获得的信息计算乙组的平均分.(2)只要根据图表信息回答正确即可(答案不唯一).
(1)甲组:中位数为7;乙组:平均分为7,中位数为7 解析每组分别有12人,甲组3分的1人,6分的3人,7分的4人,8分、9分的都2人,中位数是7分.乙组5分的
2人,6人的1人,7分的5人,8分的3人,9分的1人,平均分为
1
12
(5×2+6+7×5+8×3+9)
=7(分),中位数也是7分.
(2)解:(答案不唯一)
①因为乙组学生的平均成绩高于甲组学生的平均成绩,所以乙组学生的成绩好于甲组;
②因为甲、乙两组学生成绩的平均分相差不大,而乙组学生成绩的方差小于甲组学生成绩的方差,说明乙组学生成绩的波动比甲组小,所以乙组学生的成绩好于甲组;③因为乙组学生的最低分高于甲组学生的最低分,所以乙组学生的成绩好于甲组.。
