最新青岛版八年级数学上册全册完整课件
合集下载
青岛版数学八年级上册全册优质课件【完整版】

追问:当满足三个条件时,△ABC 与△A′B′C′ 全等吗?满足三个条件时,又分为几种情况呢?
三个条件
① 三边 ② 三角 ③ 两边一角 ④ 两角一边
动手操作,验证猜想
先任意画出一个△ABC,再画出一个△A′B′C′,使
A′B′=AB,B′C′=BC,A′C′=AC。把画好的△A′B′C′剪下,
放到△ABC 上,它们全等吗?
画法: (1)画线段B′C′=BC;
(2)分别以B′、C′为圆心,BA、BC 为半径画弧,两
弧交于点A′;
(3)连接线段A′B′,A′C′。
动脑思考,得出结论
思考:作图的结果反映了什么规律?你能用文字语 言和符号语言概括吗?
边边边公理: 三边对应相等的两个三角形全等。简写为“边边 边”或“SSS”。
动脑思考,得出结论
用符号语言表达:
在△ABC 与 △ A′B′C′中,
AB =A′B′,
∵ AC =A′C′,
B
BC =B′C′,
∴ △ABC ≌△A′B′C′ (SSS)。
判断两个三角形全等的推理 过程,叫做证明三角形全等。 B′
A
C A′
C′
应用所学,例题解析
例1 如图,有一个三角形钢架,AB =AC ,AD 是
谢谢
怎样判定三角形全等
创设情境,导入新知
已知△ABC ≌△ A′B′C′,找出其中相等的边与
角:
A
A′
B
AB =A′B′ ∠A =∠A′
C B′
BC =B′C′ ∠B =∠B′
C′
AC =A′C′ ∠C =∠C′
思考:满足这六个条件可以保证△ABC≌△A′B′C′吗?
动脑思考,分类辨析
青岛版初中八年级上册 第一章 全等三角形 1.1全等三角形(2) 课件

• 2.若整张的报纸与半张报纸相
似,则整张报纸的长与宽的比是
(
)
图形 A
图形 B
图形 C
如果图形A与图形B相似,图形B与图形C相似, 那么图形A与图形C相似。
图形的放大
两个图形相似
图形的缩小
相似图形的关系
两个图形相似,其中一个图形可以看 作由另一个图形放大或缩小得到。
小练习
ABDF
相似多边形 两个相似的平面图形之间有什么关系呢? 为什么有些图形是相似的,而有些不是呢? 相似图形有什么主要特征呢?
例题 (1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC 的长.
解:(1)∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,
A
∠DFE=∠C,∠D=∠EFC,
E
AE EF DF AD
EB BC FC EF
∵AD=3,EF=4,代入 EF AD B
青岛版八年级数学上册 第1章全等三角形
1.1 全等三角形
学习目标
学习目标
• 了解相似形的概念,知道相似形与全等形 的关系 • 经历相似多边形概念的形成过程 ,了解相 似多边形及相似比的含义 •能根据相似多边形的定义解决简单的问题
请观察下面几组图片
你从几组图片发现了什么?
它们的大小不一定相等,形状相同.
相似比与叙述的顺序有关。
题型1 判断多边形相似
例题 一块长 3m,宽1.5m的矩形黑板,镶其外
围矩的 形木 相质 似边 吗宽?为7什.5么cm?。边框内外边缘A 所组成的
D
解: ∵ 矩形的每个内角都等于90o.
E
HH
∴ ∠A =∠E = 90°,∠B =∠F = 90° FF
【青岛版】八年级数学上册(全书)课件省优PPT(共422张)

∵△ABC≌△DEF(〕 ∴∠A =∠D, ∠B =∠E, ∠C =∠F(全等三角形的对应角相等〕
请填空
公共点 A
D
1、假设△AOC≌△BOD ,ACBຫໍສະໝຸດ D∠A= ∠B公共角C
O B
A
2、假设
CE
E
D
△ABD≌△AC∠ECEA,BD= ,
B
C
3、假设 ∠BDA= CD
△ABC≌△CDA∠,DACAB =
E
A D
B
⑴△ ABC ≌△ DEC ⑵对应边是 AC与DC ,AB与DE ,BC与EC ⑶对应角是 ∠A与∠D、∠B与∠E、∠ACB与∠DCE
一个三角形经过平移、 翻折、旋转 ,前后的图 形全等 .常见的图形有:
AD
B E CF
平移
A
A
D
D
B
翻折
C
B EC
旋转
判断题 1〕√全等三角形的对应边相等 ,对应角相等 . 〔〕 2〕全等三角形的周长相等 ,面积也相等 . 〔 〕 3〕√ 面积相等的三角形是全等三角形 . 〔 〕 4〕周长相等的三角形是全等三角形 . 〔 X 〕
A
D
∠BAC=
公共边
B
C
在以以下图中 , △ABO≌△ACO,BO和 CO , AB和AC是对应边.
用等式的形式表示出三组对应边和三组 对应角 .
A
O
B
C
在以以下图中 , △ABO≌△DCO,A和D , B和C是对应顶点.用等式的形式表示出三 组对应边和三组对应角 .
A
D
O
B
C
在图中 ,△ABC≌△DEF ,∠A和 ∠D , ∠B和∠E是对应角 ,试找出它们的 对应边和另一组对应角.
最新青岛版八年级上册数学精品课件第1章 全等三角形

知识点 已知两角及其夹边作三角形
如图所示的是举世闻名的三星堆考古中挖掘出的一个三角形 残缺玉片的示意图,工作人员想制作该玉片模型,则利用图中哪些 数据就可制成符合规格的三角形玉片模型?可利用∠A,∠B,AB已知, 结合ASA进而可得全等三角形.
知识点 已知两角及其夹边作三角形
注意所作两个角必须在射线的同侧,否则,两个角的终边没有 交点,即找不到三角形的第三个顶点.
知识点 三角形全等的判定方法2——角边角
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图 中标有①,②,③,④的四块),他想去配一块与原来一样大小的玻璃, 又想只带一块碎片去,他通过仔细考虑后,发现只带第①块玻璃即 可.原来沿着第①块玻璃碎片的两边延长,就可以得到一个完整的 三角形,这个新三角形与原来的三角形依据“ASA”可以判定是全 等三角形.
知识点 三角形全等的判定方法4——边边边
如图所示,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将 仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角 的两边上,过点A,C画一条射线AE,AE就是∠PAQ的平分线.此角平分仪 的画图原理是:根据仪器结构,依据三角形全等的判定方法“SSS”可得 △ABC≌△ADC,这样就有∠QAE=∠PAE.
第1章 全等三角形
1.1 全等三角形
知识点 全等形
如图所示,用复印机复印东西时,用同一个原件复印出来的文件 放在一起能完全重合,是全等形.
知识点 全等形
1.裁剪全等形物品. 2.判定是否为全等形.
知识点 全等三角形
如图所示,用一副七巧板拼成了一只狐狸的图案.七 巧板是一种古老的中国传统智力玩具,顾名思义,是由七 块板组成的,有一块正方形,一块平行四边形,五块三角形, 其中有两组全等三角形.七块板可拼成许多图形(1600种 以上),例如:三角形、平行四边形、不规则多边形,玩家 也可以把它拼成人物、动物、桥、房、塔等.
青岛版八年级数学上册比和比例课件

课本96页 练习 第1,2题 课本100页 习题3.6 第1题
例2 甲是边长为a的正方形,中间有一个边长为b的
正方形喷水池,草坪乙是长为c,宽为a-b的长 方形,求甲、乙两块草坪的面积的比。
解
草坪甲的面积是 a2 b2,草坪乙的面积是 ca b
a2 b2 a ba b a b
ca b ca b
c
所以甲、乙两块草坪的面积的比是
a
c
b
.
1.八年级一班有学生42名,如果男、女生人数
八年级一班男、女生人数的比为m:n,你知道 m:n的含义吗?
两个数a与b(b≠0)相除,叫做a与b的比。
记作:a : b或 a b
其中,a叫做比的前项,b叫做比的后项。
1.比的前项与后项是有顺序的;如 a 和 b 不同。
注 ba 2.符号a:b和 a 都读作“a比b”,可以利用分式的基本
性质把
a
b 化简。
(2)50x :15 50x = 10x
15 3
或10x : 3
例1
八年级一班有学生a名,如果男、女生人数
的比是m:n,那么该班女生有多少名?
解
因为男、女生人数的比是m:n,
所以女生人数为该班学生总数的
m
n
n
.
于是
a
n mn
man(n 名)
所以该班女生有 an 名。
mn
如图,时代中学的校园有两块草坪,草坪
是3:2,所以储蓄款项占总数的 2 2 . 32 5
于是 2800 2 1120元
5
所以,小亮家每月储蓄1120元。
1.两个数a与b(b≠0)相除,叫做a与b的比。
记作:a : b或 a b
青岛版(五四制)八年级上册数学课件1.2.1全等三角形的判定——边角边

2.边角边公理的应用中所用到的数学方法: 证明线段(或角相等)证明线转段化(或角)所在的两个 三角形全等.
用公理证明两个三角形全等需注 意 1.证明两个三角形全等所需的条件应按对应边、对应角、 对应边顺序书写. 2.公理中所出现的边与角必须在所证明的两个三角形中. 3.公理中涉及的角必须是两边的夹角.
灿若寒星
灿若寒星
灿若寒星
问题:如图有一池塘。要测池塘两端A、B的距离,可无 法直接达到,因此这两点的距离无法直接量出。你能想 出办法来吗?
在平地上取一个可直接到达A和 B的点C,连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
A
连结ED,
那么量出DE的长,就是A、B的距离.
为什么?
D
_A_E__=_A_D__(已知)
∠A=∠A(公共角) A
E
B
__A_C_=_A__B_(已知)
∴△AEC≌△ADB()SAS
灿若寒星
例1 已知:如图,AC=AD,∠CAB=∠DAB.
求证:△ACB≌△ADB.
C
证明:
△ACB≌△ADB A
B
这两个条件够吗?
还要什么条件呢?
还要一条边
D
灿若寒星
灿若寒星
B
连结ED,
A
那么量出DE的长,就是A、B的距离.
你知道为什么吗?
C
D E 灿若寒星
灿若寒星
边角边公理
有两边和它们的夹角对应相等的 两个三角形全等.
可以简写成“边角边”或“SAS” S——边A——角
灿若寒星
试一试
在下列图中找出全等三角形,并把它们用符号写出来.
30º
Ⅰ
Ⅱ
ⅣⅣ ⅢⅢ
用公理证明两个三角形全等需注 意 1.证明两个三角形全等所需的条件应按对应边、对应角、 对应边顺序书写. 2.公理中所出现的边与角必须在所证明的两个三角形中. 3.公理中涉及的角必须是两边的夹角.
灿若寒星
灿若寒星
灿若寒星
问题:如图有一池塘。要测池塘两端A、B的距离,可无 法直接达到,因此这两点的距离无法直接量出。你能想 出办法来吗?
在平地上取一个可直接到达A和 B的点C,连结AC并延长至D使CD=CA
延长BC并延长至E使CE=CB
A
连结ED,
那么量出DE的长,就是A、B的距离.
为什么?
D
_A_E__=_A_D__(已知)
∠A=∠A(公共角) A
E
B
__A_C_=_A__B_(已知)
∴△AEC≌△ADB()SAS
灿若寒星
例1 已知:如图,AC=AD,∠CAB=∠DAB.
求证:△ACB≌△ADB.
C
证明:
△ACB≌△ADB A
B
这两个条件够吗?
还要什么条件呢?
还要一条边
D
灿若寒星
灿若寒星
B
连结ED,
A
那么量出DE的长,就是A、B的距离.
你知道为什么吗?
C
D E 灿若寒星
灿若寒星
边角边公理
有两边和它们的夹角对应相等的 两个三角形全等.
可以简写成“边角边”或“SAS” S——边A——角
灿若寒星
试一试
在下列图中找出全等三角形,并把它们用符号写出来.
30º
Ⅰ
Ⅱ
ⅣⅣ ⅢⅢ
最新青岛版八年级数学上册全套PPT课件

A1 C1
BC=B1C1.
B
C
B1
C1
性质:全等三角形的对应边相等,对应角相等。
例1.如图,已知△ABC △FED,
那么AC∥FD吗?为什么?
解:ABC FED(已知)
B
F
C
42
13 D
E
1 2(全等三角形的对应角相等) A
1 3 180 (平角的定义)
2 4 180
一池塘两端A、B的距离。设计了如下方案: 如图,先在平地上取一个可直接到达A、B的 点C,再连结AC、BC并分别延长AC至D,使 DC=AC,EC=BC,最后测得DE的距离即为AB 的长.你认为这种方法是否可行?
A
B
·C
E
D
两边和它们的夹角对应相等的两个三角
形全等,简写成“边角边”或“SAS”
课
堂
能利用角边角条件说明你的结论吗? A
理由:因为 ∠A+∠B+∠C=180o
∠D+∠E+∠F=180o 又因为 ∠A=∠D, ∠B=∠E
C
所以 ∠C=∠F
在△ABC和△DEF中
B
D
根据ASA,
E
F
所以 △ABC≌△DEF (ASA)
判定方法3
两角分别相等且其中一组等角的对边也
相等的两个三角形全等。
(简写“角角边”或“AAS”)
ABC DEF
温馨提示:记两个三角形全等时,通常把表 示对应顶点的字母写在对应位置上,这样有 利于解题!
知识点三:全等三角形的性质
观察下图中的两个三角形,哪些边分别对应相等,哪些
角分别对应相等? A
A1
B
AAB=A1B1,. C AC=A1C1,
青岛版八年级上册课件 1.1 全等三角形(共20张PPT)

•
3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021
全等三角形
表示:△ ABC≌△DEF A
D
对应顶点写在对应位置上
F
B
C
E
对应元素
对应顶点 A D B E C F 对应边 AB与DE BC与EF AC与DF 对应角 ∠A与∠D ∠B与∠E ∠C与∠F
全等三角形对应边相等,对应角相等。
试一试 找出下列各图全等三角形中的对应边和对应角
AD
A
B E CF
•
10、阅读一切好书如同和过去最杰出 的人谈 话。05:14:5205:14:5205:148/14/2021 5:14:52 AM
•
11、一个好的教师,是一个懂得心理 学和教 育学的 人。21.8.1405:14:5205:14Aug-2114- Aug-21
•
12、要记住,你不仅是教课的教师, 也是学 生的教 育者, 生活的 导师和 道德的 引路人 。05:14:5205:14:5205:14Satur day, August 14, 2021
(4)如图,已知△ AOC ≌ △BOD 求证:AC∥BD
•
17、儿童是中心,教育的措施便围绕 他们而 组织起 来。上 午5时14分52秒 上午5时14分05:14:5221.8.14
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四
最新青岛版初二数学上册第一章 全等三角形 全单元课件
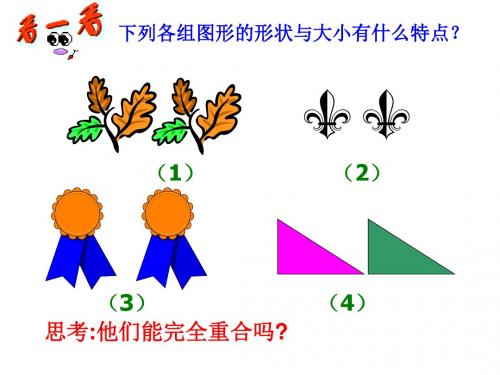
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3) 思考:他们能完全重合吗?
(4)
1.了解全等形及全等三角形的概念; 2.理解全等三角形的性质,会寻找全等三角形的对应顶点、 对应边、对应角; 3.运用全等三角形的性质既能解决简单的问题,也 能解决综合性的问题;
预习并尝试解决以下问题
1. 什么是全等形?全等形有哪些特征? 2.什么是全等三角形? 什么是全等三角形的对应顶点、对应边、对应角? 3.全等三角形如何表示?
说出上面两个全等三角形的对应顶点,对应边和对应角。
练一练 1.已知△ABC≌△DEF,写出相等的线段和相等的角。 A E F B C D
AB=DE,BC=EF,AC=DF; ∠A=∠D,∠B=∠E,∠C=∠F.
例1 如图,已知△ADC≌△CBA, 写出图中相等的边、相等的角。 B 解 ∵ △ADC≌△CBA
(全等三角形的对应角相等)
例2 如图,已知△ABC≌△DCB, AB=7,BD=5,∠A=60°,求线段 DC、AC和∠D. 解 ∵ △ABC≌△DCB ∴ DC=AB=7,AC=BD=5; B
D
A
C
(全等三角形的对应边相等)
∴ ∠D=∠A=60°.
(全等三角形的对应角相等)
练一练
4.如图,已知△ABC≌△DBE, AB=8,BE=6,∠C=55°, 求线段DB、BC和∠BED. D 解 ∵ △ABC≌△DCB ∴ DB=AB=8,BC=BE=6; (全等三角形的对应边相等) E
A
4cm
D
3cm
M
B
N
C
动不如
动
提高1:请指出下列全等三角形的对应边和对应角
如上图,△ ABD ≌ △CDB,则AB= CD ; ∠CDB ; AD= C ;BD= DB ; ∠ABD= ∠C B ∠DBC ; ∠A= ∠ADB= ;
(1)
(2)
(3) 思考:他们能完全重合吗?
(4)
1.了解全等形及全等三角形的概念; 2.理解全等三角形的性质,会寻找全等三角形的对应顶点、 对应边、对应角; 3.运用全等三角形的性质既能解决简单的问题,也 能解决综合性的问题;
预习并尝试解决以下问题
1. 什么是全等形?全等形有哪些特征? 2.什么是全等三角形? 什么是全等三角形的对应顶点、对应边、对应角? 3.全等三角形如何表示?
说出上面两个全等三角形的对应顶点,对应边和对应角。
练一练 1.已知△ABC≌△DEF,写出相等的线段和相等的角。 A E F B C D
AB=DE,BC=EF,AC=DF; ∠A=∠D,∠B=∠E,∠C=∠F.
例1 如图,已知△ADC≌△CBA, 写出图中相等的边、相等的角。 B 解 ∵ △ADC≌△CBA
(全等三角形的对应角相等)
例2 如图,已知△ABC≌△DCB, AB=7,BD=5,∠A=60°,求线段 DC、AC和∠D. 解 ∵ △ABC≌△DCB ∴ DC=AB=7,AC=BD=5; B
D
A
C
(全等三角形的对应边相等)
∴ ∠D=∠A=60°.
(全等三角形的对应角相等)
练一练
4.如图,已知△ABC≌△DBE, AB=8,BE=6,∠C=55°, 求线段DB、BC和∠BED. D 解 ∵ △ABC≌△DCB ∴ DB=AB=8,BC=BE=6; (全等三角形的对应边相等) E
A
4cm
D
3cm
M
B
N
C
动不如
动
提高1:请指出下列全等三角形的对应边和对应角
如上图,△ ABD ≌ △CDB,则AB= CD ; ∠CDB ; AD= C ;BD= DB ; ∠ABD= ∠C B ∠DBC ; ∠A= ∠ADB= ;
青岛版八年级数学上册《全等三角形》课件(共26张PPT)

∴∠F=∠C=25°
EF=BC=6cm
பைடு நூலகம்
E
F
DF=AC=4cm
D
拓展训练共提高
(4)如右图,已知△ABD≌△ACE,
且∠C=45°,AC = 8,AE = 5,则 ∠B = 45° , DC = 3 .
8D
C
5
A
5
E
B
寻找对应边、对应角的规律
在全等三角形中,一般是:
1.有公共边,则公共边为对应边 2.有公共角,则公共角为对应角
(对顶角为对应角) 3.最大边与最大边(最小边与最小边) 为 对应边;最大角与最大角(最小角与最小角) 为对应角
4.对应角的对边为对应边; 对应边的对角为对应角。 5.根据书写规范,按照对应 顶点找对应边或对应角。
随堂练习
2、如图:△AOD≌△BOC,写出其中相等的角
D
C
解:∠A=∠B
∠D=∠C
∠EAC=∠BAC=180°- 30°-85°=65°
开动你的脑筋,你一定行!
2.如图,已知△ AOC ≌ △BOD 求证:AC∥BD
随堂练习
3、如,△ABC≌△DEF,∠C=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度?
A 解:
∵△DEF≌△ABC
B
C
∵△ABC≌△DEF(已知) ∴AB=DE, AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等)
请填空
公共点 A
D
1、若△AOC≌△BOD,AC= BD
∠A= ∠B
O
公共角C
A
2、若△ABD≌△ACE,BD=CE, E
新青岛版八年级数学上册《全等三角形》优课件

找另一边 (SSS)
已 知 两 边
找夹角 (SAS)
变式1、如图所示:已知∠B=∠C,请你添加一个条件————,使得
△ABE≌△ACD
∠A为公共角
思路
A
找夹边(ASA) 已 知 两 角
找对边(AAS)
D
E
B
C
变式2:如图所示,AB=AD,∠E=∠C 要想使△ABC≌△ADE可以添加的条件是 依据是
OA=OC
∠AOB= ∠COD
A
OB=OD
∴ △ABO≌△CDO (SAS)
∴ ∠A= ∠C
∴ DC∥AB
C O
B
基础练习--3
如图,已知AB=AD,AC=AE,∠1=∠2,
求证:BC=DE
A
12
EC
请同学们注 意书写格式 哦!
B
D
拓展与提高
如图5,已知:AB=CD,AD=CB,O为AC任一点, 过O作直线分别交AB、CD的延长线于F、E,求证: ∠E=∠F.
提示:由条件易证△ABC≌△CDA 从而得知 ∠BAC=∠DCA ,即:AB∥CD.
合作交流
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全
等三角形?请任选一对给予证明。
E
答: △ABF≌△DEC
A
F
C
D
△ABC≌△DEF △CBF≌△FEC
B
练2
1、结合题中条件和结论,选择恰当方法。 2、全等是说明线段或角相等的重要方法之一。 说明时注意:
①观察结论中的线段或角,在哪两个可能全等的三角形中。
②分析已有条件,欠缺条件,选择判定方法。 ③公共边,公共角以及对顶角一般都是题中隐含的条件。
青岛版八年级上册 1.1全等三角形 (共23张PPT)

角分别对应相等? A
A1
B
AAB=A1B1,. C AC=A1C1,
∠A=∠A1,
B∠B=∠B1,
∠C1=∠C1.
A1 C1
BC=B1C1.
结B论:全等三角形的C对应边相等,对B1应角相等。 C1
请填空
公共点 A
D
1、若△AOC≌△BOD,AC= BD
∠A= ∠B
O
公共角C
A
2、若△ABD≌△ACE,BD=CE, E
D A
B
CE
则AC边的对应边为 CA
C F (3)已知△ABC≌△DEF, 则AB边的对应边为 DE
∠C的对应角为 ∠F
D
随堂练习
1、如图:△ABC≌△AEC, ∠B=30°, ∠ACB=85°,
求出△AEC各内角的度数.
A
E
解:∵△AEC≌△ABC
∴∠E=∠B=30° B
C
∠ACE=∠ACB=85°
• 能够完全重合的图形叫做全等图形 • 能够重合的两个三角形叫做全等三角形 • 你能够找出生活中的一些全等图形吗?
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/8/142021/8/14Saturday, August 14, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/8/142021/8/142021/8/148/14/2021 5:12:11 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/8/142021/8/142021/8/14Aug-2114-Aug-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/8/142021/8/142021/8/14Saturday, August 14, 2021
青岛版八年级数学上册《线段的垂直平分线》PPT教学课件

EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分
线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上
的点;④若EA=EB,则过点E的直线垂直平分线段AB.其
中正确的个数有( C) A.1个 B.2个 C.3个
D.4个
M
2.如图,NM是线段AB的垂直平分线,下列说
法正确的有: ①②③.
=
CAC+BC
=
12+7=19.
A D C
第十五页,共十七页。
3.如图,如果△ACD的周长为18cm,△ABC的 周长为28cm, DE是BC的垂直平分线,根据这 些条件,你可以求出哪条线段的长? 【解析】 (1)△ACD的周长=AD +CD+AC=18cm; (2)△ABC的周长=AB+AC+BC=28cm; (3)由DE是BC的垂直平分线得:BD=CD;所以AD+CD= AD+BD=AB. (4)综上可得BC=10cm.
第十一页,共十七页。
2.如图,△ABC中,边AB,BC的垂直
A
平分线交于点P.
(1)求证:PA=PB=PC.
P
(2)点P是否也在边AC的垂直平分线
上呢?由此你能得出什么结论? B
C
结论:三角形三条边的垂直平分线相交于一点,这个点 到三角形三个顶点的距离相等.
第十二页,共十七页。
通过本课时的学习,需要我们:
①AB⊥MN,②AD=DB, ③MN⊥AB,
A
D
B
④MD=DN,⑤AB是MN的垂直平分线
N
第七页,共十七页。
问题思考:既然轴对称图形的对称轴是任何
一对对称点所连线段的垂直平分线,那么轴对称 图形的对称轴如何来作呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 全等三角形
最新青岛版八年级数学上册全册完 整课件
1.1 全等三角形
最新青岛版八年级数学上册全册完 整课件
1.2 怎样判定三角形全等
最新青岛版八年级数学上册全册完 整课件
1.3 尺规作图
最新青岛版八年级数学上册全册 完整课件目录
0002页 0054页 0095页 0117页 0145页 0160页 0194页 0210页 0268页 0295页 0315页 0337页 0368页 0389页 0432页 0517页 0566页
第1章 全等三角形 1.2 怎样判定三角形全等 第2章 图形的轴对称 2.2 轴对称的基本性质 2.4 线段的垂直平分线 2.6 等腰三角形 3.1 分式的基本性质 3.3 分式的乘法与除法 3.5 分式的加法与减法 3.7 可化为一元一次方程的分式方程 4.1 加权平均数 4.3 众数 4.5 方差 第5章 几何证明初步 5.2 为什么要证明 5.4 平行线的性质定理和判定定理 5.6 几何证明举例
最新青岛版八年级数学上册全册完 整课件
第2章 图形的轴对称
最新青岛版八年级数学上册全册完 整课件
2.1 图形的轴对称
最新青岛版八年级数学上册全册完 整课件
2.2 轴对称的基本性质
最新青岛版八年级数学上册全册完 整课件
2.3 轴对称图形
最新青岛版八年级数学上册全册完 整课件
2.4 线段的垂直平分线
最新青岛版八年级数学上册全册完 整课件
