2.5 第1课时 等比数列的前n项和
2020版新学优数学同步人教A必修五课件:2.5 第1课时 等比数列的前n项和

1
a1=2,a6=16,则
.
解析:①由公式可得
②由
.
3×(1-45 )
S5=
=1
1-4
023.
1
a1=2,a6=16,得 q=2,
1
63
2-16×2
故 S6=
1-2
答案:①1 023=2. Nhomakorabea63
②2
第七页,编辑于星期日:一点 二十八分。
课前篇自主预习
二、错位相减法求数列的和
1.思考:推导等比数列前n项和公式的方法称为错位相减法,这种方法还适合
和一个等比数列的各项相乘得到的数列,可以采用错位相减法求和.
第十六页,编辑于星期日:一点 二十八分。
课堂篇探究学习
探究一
1
2
探究二
思维辨析
5
8
2-1
,①
2
2-1
3
4
当堂检测
解:设 Sn= + + +…+
1
1 3
5
则2Sn=4 + 8 + 16+…+ +1 ,②
2
1
1 2 2
2
2
①-②,得2Sn=2 + 4 + 8 + 16+…+
1 (1-1 )
1 -
(n≥2).当 n=1 时,S1=a1=
,也满足上式.于是 Sn=
1-
1-
1-
1 (1- )
(q≠1).
1-
=
第四页,编辑于星期日:一点 二十八分。
课前篇自主预习
4.填空:
等比数列的前n项和公式
2.5.1等比数列前n项和公式(第1课时)

若q=1,则 S3=3 a1 , S 6 6a1 , S 9 9a1 由 a1 0可得S3 S 6 2S 9,与题设矛盾
q 1 a1 (1 q ) a1 (1 q ) 2a1 (1 q ) 1 q 1 q 1 q
3 6 9
整理,得q3+q6=2q9
各个格子里的麦粒数依次是:
1, 2, 22, 23, 24, 25,…,263,
发明者要求的麦粒总数就是: 1+ 2+22+23+24+25+…+263.
通项: an=2n-1
前n项和:Sn
等比数列的求和
引入新课
1 2 2 2
2 3
2
4
263
这一格放 的麦粒可 以堆成一 座山!!!
263
分析:由于每格的麦粒数都是前一格的2倍, 共有64格每格所放的麦粒数依次为:
1, 2, 2 , 2 ,, 2 .
它是以1为首项公比是2的等比数列, 麦粒的总数为:
2
3
63
S64 1 2 2 2 2 .
2 3 63
S64 1 2 2 2 2 的方法 . (1) ,就 2 3 63 是错位相 2S64 2(1 2 2 2 2 ). 减法 ! 2 3 63 64 (2) 即2S64 2 2 2 2 2 .
1 243
.
已知等比数列an 中,
练习1.
2或-3
1 a1 2 , S3 14.则q
a3 8或18 2 a1 1, a4 216 则 q -6 , S4 185
a1、q、n、a n、sn
第二章 2.5 第1课时 等比数列前n项和公式

§2.5等比数列的前n项和第1课时等比数列前n项和公式学习目标1.掌握等比数列的前n项和公式及公式证明思路.2.会用等比数列的前n项和公式解决有关等比数列的一些简单问题.知识点一等比数列的前n项和公式知识点二 错位相减法1.推导等比数列前n 项和的方法叫错位相减法.2.该方法一般适用于求一个等差数列与一个等比数列对应项积的前n 项和,即若{b n }是公差d ≠0的等差数列,{c n }是公比q ≠1的等比数列,求数列{b n ·c n }的前n 项和S n 时,也可以用这种方法.思考 如果S n =a 1+a 2q +a 3q 2+…+a n q n -1,其中{a n }是公差为d 的等差数列,q ≠1.两边同乘以q ,再两式相减会怎样?知识点三 使用等比数列求和公式时注意事项(1)一定不要忽略q =1的情况;(2)知道首项a 1、公比q 和项数n ,可以用S n =a 1(1-q n )1-q ;知道首尾两项a 1,a n 和q ,可以用S n =a 1-a n q 1-q; (3)在通项公式和前n 项和公式中共出现了五个量:a 1,n ,q ,a n ,S n .知道其中任意三个,可求其余两个.1.在等比数列{a n }中,a 1=b ,公比为q ,则前3项和为b (1-q 3)1-q.( ) 2.求数列{n ·2n }的前n 项和可用错位相减法.( )3.a 1(1-q n )1-q =a 1(q n -1)q -1.( ) 4.等比数列前n 项和S n 不可能为0.( )题型一 等比数列前n 项和公式的直接应用例1 求下列等比数列前8项的和:(1)12,14,18,…; (2)a 1=27,a 9=1243,q <0.反思感悟 求等比数列前n 项和,要确定首项、公比或首项、末项、公比,应特别注意q =1是否成立. 跟踪训练1 (1)求数列{(-1)n +2}的前100项的和;(2)在14与78之间插入n 个数,组成所有项的和为778的等比数列,求此数列的项数.题型二 前n 项和公式的综合利用例2在等比数列{a n}中,a1=2,S3=6,求a3和q.反思与感悟 (1)a n =a 1qn -1,S n =a 1(1-q n )1-q ⎝⎛⎭⎪⎫或S n =a 1-a n q 1-q 两公式共有5个量.解题时,有几个未知量,就应列几个方程求解. (2)当q =1时,等比数列是常数列,所以S n =na 1;当q ≠1时,等比数列的前n 项和S n 有两个公式.当已知a 1,q 与n 时,用S n =a 1(1-q n )1-q 比较方便;当已知a 1,q 与a n 时,用S n =a 1-a n q 1-q比较方便. 跟踪训练2 已知等比数列{a n }是递增数列,S n 是{a n }的前n 项和.若a 1,a 3是方程x 2-5x +4=0的两个根,则S 6= .题型三 利用错位相减法求数列的前n 项和例3 求数列⎩⎨⎧⎭⎬⎫n 2n 的前n 项和.反思感悟 一般地,如果数列{a n }是等差数列,{b n }是公比不为1的等比数列,求数列{a n b n }的前n 项和时,可采用错位相减法.跟踪训练3 求和:S n =x +2x 2+3x 3+…+nx n (x ≠0).分期付款模型典例小华准备购买一部售价为5 000元的手机,采用分期付款方式,并在一年内将款全部付清.商家提出的付款方式为:购买2个月后第1次付款,再过2个月后第2次付款,…,购买12个月后第6次付款,每次付款金额相同,约定月利率为0.8%,每月利息按复利计算,求小华每期付款金额是多少.(参考数据:1.00812≈1.10)[素养评析]本题考查数学建模素养,现在购房、购车越来越多采用分期付款方式,但有关方不一定都会计算,所以建立一个老少皆宜的模型来套用是必要的,在建立模型过程中,要把制约因素抽象为符号表示,并通过前若干项探索规律,抓住这些量之间的关系建立关系式.1.等比数列1,x,x2,x3,…的前n项和S n等于()A.1-x n1-xB.1-x n -11-xC.⎩⎪⎨⎪⎧ 1-x n 1-x ,x ≠1且x ≠0n ,x =1D.⎩⎪⎨⎪⎧1-x n -11-x ,x ≠1且x ≠0n ,x =1 2.设等比数列{a n }的公比q =2,前n 项和为S n ,则S 4a 2等于( ) A .2 B .4 C.152 D.1723.等比数列{a n }的各项都是正数,若a 1=81,a 5=16,则它的前5项的和是( )A .179B .211C .243D .2754.某厂去年产值为a ,计划在5年内每年比上一年产值增长10%,从今年起5年内,该厂的总产值为 .5.已知数列{a n }的前n 项和为S n ,且a n =n ·2n ,则S n = .1.在等比数列的通项公式和前n 项和公式中,共涉及五个量:a 1,a n ,n ,q ,S n ,其中首项a 1和公比q 为基本量,且“知三求二”.2.前n 项和公式的应用中,注意前n 项和公式要分类讨论,即当q ≠1和q =1时是不同的公式形式,不可忽略q =1的情况.3.一般地,如果数列{a n }是等差数列,{b n }是等比数列且公比为q ,求数列{a n ·b n }的前n 项和时,可采用错位相减法求和.一、选择题1.等比数列{a n }中,a 1=2,a 2=1,则S 100等于( )A .4-2100B .4+2100C .4-2-98D .4-2-1002.在等比数列{a n }中,已知a 1=3,a n =48,S n =93,则n 的值为( )A .4B .5C .6D .73.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则S 5S 2等于( )A .11B .5C .-8D .-114.已知数列{a n }是等差数列,若a 2+2,a 4+4,a 6+6构成等比数列,则数列{a n }的公差d 等于() A .1 B .-1C .2D .-25.设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2=3a 2+2,S 4=3a 4+2,则a 1等于( )A .-2B .-1 C.12 D.236.已知数列{a n }满足3a n +1+a n =0,a 2=-43,则{a n }的前10项和等于 ( ) A .-6(1-3-10) B.19(1-3-10) C .3(1-3-10) D .3(1+3-10)7.一弹球从100米高处自由落下,每次着地后又跳回到原来高度的一半再落下,则第10次着地时所经过的路程和是(结果保留到个位)( )A .300米B .299米C .199米D .166米二、填空题8.设等比数列{a n }的前n 项和为S n ,若a 1=1,S 6=4S 3,则a 4= .9.数列a 1,a 2-a 1,a 3-a 2,…,a n -a n -1,…是首项为1,公比为2的等比数列,那么a n = .10.已知正项数列{a n }满足a 2n +1-6a 2n =a n +1a n .若a 1=2,则数列{a n }的前n 项和S n = . 11.设等比数列{a n }的前n 项和为S n ,若S 3+S 6=2S 9,则数列的公比q = .三、解答题12.(2018·绵阳检测)在等比数列{a n }中,a 2-a 1=2,且2a 2为3a 1和a 3的等差中项,求数列{a n }的首项、公比及前n 项和.13.设数列{a n }满足a 1+3a 2+32a 3+…+3n -1a n =n 3,n ∈N *. (1)求数列{a n }的通项公式;(2)设b n =n a n,求数列{b n }的前n 项和S n .14.在等比数列{a n }中,对任意n ∈N *,a 1+a 2+…+a n =2n -1,则a 21+a 22+…+a 2n 等于() A .(2n -1)2 B.(2n -1)23 C .4n -1 D.4n -1315.已知等差数列{a n }满足a 2=0,a 6+a 8=-10.(1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和.。
高中数学 第二章 数列 2.5 等比数列的前n项和 第1课时 等比数列前n项和的求解练习(含解析)新

第1课时 等比数列前n 项和的求解A 级 基础巩固一、选择题1.设{a n }是公比为正数的等比数列,若a 1=1,a 5=16,则数列{a n }前7项的和为() A .63 B .64 C .127 D .128解析:设数列{a n }的公比为q (q >0),则有a 5=a 1q 4=16,所以q =2,数列的前7项和为S 7=a 1(1-q 7)1-q =1-271-2=127.答案:C2.设在等比数列{a n }中,公比q =2,前n 项和为S n ,则S 4a 3的值为() A.154B.152C.74D.72解析:根据等比数列的公式,得S 4a 3=a 1(1-q 4)(1-q )·a 1q 2=(1-q 4)(1-q )q 2=1-24(1-2)×22=154. 答案:A3.一座七层的塔,每层所点的灯的盏数都等于上面一层的2倍,一共点381盏灯,则底层所点灯的盏数是()A .190B .191C .192D .193解析:设最下面一层灯的盏数为a 1,则公比q =12,n =7,由a 1⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫1271-12=381,解得a 1=192.答案:C4.已知数列{a n }满足3a n +1+a n =0,a 2=-43,则{a n }的前10项和等于()A .-6(1-3-10) B.19(1-3-10)C .3(1-3-10) D .3(1+3-10)解析:因为3a n +1+a n =0,a 2=-43≠0,所以a n ≠0,所以a n +1a n =-13,所以数列{a n }是以-13为公比的等比数列.因为a 2=-43,所以a 1=4,所以S 10=4⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-13101-⎝ ⎛⎭⎪⎫-13=3(1-3-10).答案:C5.已知S n 是等比数列{a n }的前n 项和,若存在m ∈N *,满足S 2m S m =9,a 2m a m =5m +1m -1,则数列{a n }的公比为()A .-2B .2C .-3D .3解析:设数列{a n }的公比为q ,若q =1,则S 2mS m=2,与题中条件矛盾,故q ≠1. 因为S 2m S m =a 1(1-q 2m )1-q a 1(1-q m)1-q =q m +1=9,所以q m=8. 所以a 2m a m =a 1q 2m -1a 1q m -1=q m =8=5m +1m -1,所以m =3,所以q 3=8, 所以q =2. 答案:B 二、填空题6.在等比数列{a n }中,公比q =2,前99项的和S 99=30,则a 3+a 6+a 9+…+a 99=________.解析:因为S 99=30,即a 1(299-1)=30,数列a 3,a 6,a 9,…,a 99也成等比数列且公比为8,所以a 3+a 6+a 9+…a 99=4a 1(1-833)1-8=4a 1(299-1)7=47×30=1207.答案:12077.对于数列{a n },定义数列{a n +1-a n }为数列{a n }的“差数列”,若a 1=1,{a n }的“差数列”的通项公式为a n +1-a n =2n,则数列{a n }的前n 项和S n =________.解析:因为a n +1-a n =2n ,应用累加法可得a n =2n-1, 所以S n =a 1+a 2+a 3+…+a n =2+22+23+ (2)-n=2(1-2n)1-2-n=2n +1-n -2.答案:2n +1-n -28.(2016·某某卷)设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1=________,S 5=________.解析:a 1+a 2=4,a 2=2a 1+1⇒a 1=1,a 2=3,再由a n +1=2S n +1,a n =2S n -1+1(n ≥2)⇒a n +1-a n =2a n ⇒a n +1=3a n (n ≥2),又a 2=3a 1, 所以a n +1=3a n (n ≥1),S 5=1-351-3=121.答案:1121 三、解答题9.在等比数列{a n }中,a 2=3,a 5=81. (1)求a n 及其前n 项和S n ; (2)设b n =1+log 3a n ,求数列⎩⎨⎧⎭⎬⎫1b n ·b n +1的前10项和T 10.解:(1)设{a n }的公比为q ,依题意得⎩⎪⎨⎪⎧a 1q =3,a 1q 4=81,解得⎩⎪⎨⎪⎧a 1=1,q =3.因此,a n =3n -1,S n =1(1-3n )1-3=3n-12.(2)由(1)知b n =1+log 3a n =1+(n -1)=n , 则1b n b n +1=1n (n +1)=1n -1n +1,所以T 10=11×2+12×3+…+110×11=1-12+12-13+…+110-111=1-111=1011.10.数列{a n }满足a 1=1,na n +1=(n +1)a n +n (n +1),n ∈N *. (1)证明:数列⎩⎨⎧⎭⎬⎫a n n 是等差数列;(2)设b n =3n·a n ,求数列{b n }的前n 项和S n . (1)证明:由已知可得a n +1n +1=a nn+1, 即a n +1n +1-a nn=1,所以⎩⎨⎧⎭⎬⎫a n n 是以a 11=1为首项,1为公差的等差数列.(2)解:由(1)得a nn=1+(n -1)·1=n , 所以a n =n 2.从而b n =n ·3n.S n =1×31+2×32+3×33+…+n ·3n ,①3S n =1×32+2×33+…+(n -1)·3n +n ·3n +1.②① —②得,-2S n =31+32+…+3n -n ·3n +1=3·(1-3n)1-3-n ·3n +1=(1-2n )·3n +1-32.所以S n =(2n -1)·3n +1+34.B 级 能力提升1.在等比数列{a n }中,a 1+a 2+…+a n =2n -1(n ∈N *),则a 21+a 22+…+a 2n 等于() A .(2n -1)2B.13(2n -1)2C .4n-1 D.13(4n -1)解析:a 1+a 2+…+a n =2n-1,即S n =2n-1,则S n -1=2n -1-1(n ≥2),则a n =2n -2n -1=2n -1(n ≥2),又a 1=1也符合上式,所以a n =2n -1,a 2n =4n -1,所以a 21+a 22+…+a 2n =13(4n -1).答案:D2.等比数列{a n }的前n 项和为S n ,若a 1+a 2+a 3+a 4=1,a 5+a 6+a 7+a 8=2,S n =15,则该数列的项数n =________.解析:a 5+a 6+a 7+a 8a 1+a 2+a 3+a 4=(a 1+a 2+a 3+a 4)q 4a 1+a 2+a 3+a 4=q 4=2.因为a 1+a 2+a 3+a 4=a 1(1-q 4)1-q =a 1(1-2)1-q =-a 11-q =1,所以a 11-q =-1.所以S n =a 1(1-q n )1-q=q n-1=15,所以q n=16,即(q 4)n4=24,所以n4=4,所以n =16.答案:163.已知等比数列{a n }的各项均为正数,且a 1+2a 2=5,4a 23=a 2a 6. (1)求数列{a n }的通项公式;(2)若数列{b n }满足b 1=2,且b n +1=b n +a n ,求数列{b n }的通项公式; (3)设=a nb n b n +1,求数列{}的前n 项和T n . 解:(1)设等比数列{a n }的公比为q ,由4a 23=a 2a 6得4a 23=a 24,所以q 2=4,由条件可知q >0,故q =2,由a 1+2a 2=5得a 1+2a 1q =5,所以a 1=1,故数列{a n }的通项公式为a n =2n -1.(2)由b n +1=b n +a n 得b n +1-b n =2n -1,故b 2-b 1=20,b 3-b 2=21,……,b n -b n -1=2n -2(n ≥2),以上n -1个等式相加得b n -b 1=1+21+…+2n -2=1·(1-2n -1)1-2=2n -1-1,由b 1=2,所以b n =2n -1+1(n ≥2).当n =1时,符合上式,故b n =2n -1+1(n ∈N *).(3)=a nb n b n +1=b n +1-b n b n b n +1=1b n -1b n +1, 所以T n =c 1+c 2+…+=⎝ ⎛⎭⎪⎫1b 1-1b 2+⎝ ⎛⎭⎪⎫1b 2-1b 3+…+⎝ ⎛⎭⎪⎫1b n -1b n +1=1b 1-1b n +1=12-12n +1.。
《2.5 等比数列的前n项和》 课件 1-优质公开课-人教A版必修5精品

1.19≈2.36 1.110≈2.60 1.111≈2.85
1.00499≈1.04 1.004910≈1.05 1.004911≈1.06
解:(1)今年学生人数为b人,则10年后学生人数为b(1+4.9‰)10≈1.05b, 由题设可知,1年后的设备为 a×(1+10%)-x=1.1a-x, 2年后的设备为 (1.1a-x)×(1+10%)-x=1.12a-1.1x-x=1.12a-x(1+1.1),…, 10年后的设备为
题型三 等比数列的综合应用
【例3】 (12分) (2012年高考陕西卷)设{an}是公比不为1的等比数列,其前 n项和为Sn,且a5,a3,a4成等差数列. (1)求数列{an}的公比; (2)证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
名师导引: (1)由a5,a3,a4成等差数列,列方程求解; (2)利用求和公式,等差中项证明. (1)解:设数列{an}的公比为q(q≠0,q≠1). 由a5,a3,a4成等差数列, 得2a3=a5+a4,……………………………………………………2分 即2a1q2=a1q4+a1q3.………………………………………………4分 由a1≠0,q≠0得,q2+q-2=0, 解得q1=-2,q2=1(舍去), 所以q=-2.………………………………………………………6分
法二 对任意 k∈N+,2Sk= 2a1(1 qk ) , 1 q
Sk+2+Sk+1= a1(1 qk 2 ) + a1(1 qk 1) = a1(2 qk 2 qk 1) ,
1 q
1 q
1 q
高中数学人教A版必修五优化练习:第二章 2.5 第1课时 等比数列的前n项和公式 含解析

[课时作业] [A 组 基础巩固]1.等比数列{a n }中,a n =2n ,则它的前n 项和S n =( ) A .2n -1 B .2n -2 C .2n +1-1D .2n +1-2解析:a 1=2,q =2, ∴S n =2×(1-2n )1-2=2n +1-2.答案:D2.在等比数列{a n }中,若a 1=1,a 4=18,则该数列的前10项和S 10=( )A .2-128B .2-129C .2-1210D .2-1211解析:设等比数列{a n }的公比为q ,由a 1=1,a 4=18,得q 3=18,解得q =12,于是S 10=a 1(1-q 10)1-q =1-(12)101-12=2-129.答案:B3.等比数列{a n }中,已知前4项之和为1,前8项和为17,则此等比数列的公比q 为( ) A .2 B .-2 C .2或-2D .2或-1解析:S 4=a 1·(1-q 4)1-q =1,①S 8=a 1·(1-q 8)1-q =17,②②÷①得1+q 4=17,q 4=16. q =±2. 答案:C4.已知数列{a n }为等比数列,S n 是它的前n 项和,若a 2·a 3=2a 1,且a 4与2a 7的等差中项为54,则S 5=( ) A .35 B .33 C .31D .29 解析:设数列{a n }的公比为q ,∵a 2·a 3=a 21·q 3=a 1·a 4=2a 1, ∴a 4=2.又∵a 4+2a 7=a 4+2a 4q 3=2+4q 3=2×54,∴q =12.∴a 1=a 4q 3=16.S 5=a 1·(1-q 5)1-q =31.答案:C5.等比数列{a n }中,a 3=3S 2+2,a 4=3S 3+2,则公比q 等于( ) A .2 B.12 C .4D.14解析:a 3=3S 2+2,a 4=3S 3+2,等式两边分别相减得a 4-a 3=3a 3,即a 4=4a 3,∴q =4. 答案:C6.若数列{a n }满足a 1=1,a n +1=2a n ,n =1,2,3,…,则a 1+a 2+…+a n =________. 解析:由a n +1a n =2,∴{a n }是以a 1=1,q =2的等比数列,故S n =1×(1-2n )1-2=2n-1.答案:2n -17.等比数列{a n }的前n 项和为S n ,已知S 1,2S 2,3S 3成等差数列,则{a n }的公比为________. 解析:∵S 1,2S 2,3S 3成等差数列,∴4S 2=S 1+3S 3, 即4(a 1+a 1q )=a 1+3(a 1+a 1q +a 1q 2), ∴4(1+q )=1+3(1+q +q 2),解之得q =13.答案:138.等比数列的前n 项和S n =m ·3n +2,则m =________. 解析:设等比数列为{a n },则 a 1=S 1=3m +2,S 2=a 1+a 2=9m +2⇒a 2=6m , S 3=a 1+a 2+a 3=27m +2⇒a 3=18m , 又a 22=a 1·a 3⇒(6m ) 2=(3m +2)·18m ⇒m =-2或m =0(舍去).∴m =-2. 答案:-29.在等差数列{a n }中,a 4=10,且a 3,a 6,a 10成等比数列,求数列{a n }前20项的和S 20. 解析:设数列{a n }的公差为d ,则a 3=a 4-d =10-d ,a 6=a 4+2d =10+2d ,a 10=a 4+6d =10+6d , 由a 3,a 6,a 10成等比数列,得a 3a 10=a 26, 即(10-d )(10+6d )=(10+2d )2.整理,得10d 2-10d =0.解得d =0或d =1. 当d =0时,S 20=20a 4=200;当d =1时,a 1=a 4-3d =10-3×1=7, 于是S 20=20a 1+20×192d =20×7+190=330.10.已知数列{a n }的前n 项和S n =2n -n 2,a n =log 5b n ,其中b n >0,求数列{b n }的前n 项和T n .解析:当n ≥2时,a n =S n -S n -1 =(2n -n 2)-[2(n -1)-(n -1)2] =-2n +3,当n =1时,a 1=S 1=2×1-12=1也适合上式, ∴{a n }的通项公式a n =-2n +3(n ∈N *). 又a n =log 5b n , ∴log 5b n =-2n +3, 于是b n =5-2n +3,b n +1=5-2n +1,∴b n +1b n =5-2n +15-2n +3=5-2=125. 因此{b n }是公比为125的等比数列,且b 1=5-2+3=5,于是{b n }的前n 项和T n =5⎣⎡⎦⎤1-⎝⎛⎭⎫125n 1-125=12524⎣⎡⎦⎤1-⎝⎛⎭⎫125n .[B 组 能力提升]1.已知等比数列{a n }的前n 项和S n =2n -1,则a 21+a 22+…+a 2n 等于( )A .(2n -1)2 B.13(2n -1) C .4n -1D.13(4n -1) 解析:根据前n 项和S n =2n -1,可求出a n =2n -1,由等比数列的性质可得{a 2n }仍为等比数列,且首项为a 21,公比为q 2,∴a 21+a 22+…+a 2n =1+22+24+…+22n -2=13(4n -1). 答案:D2.设S n 是等比数列{a n }的前n 项和,若S 4S 2=3,则S 6S 4=( )A .2 B.73 C.310D .1或2解析:设S 2=k ,则S 4=3k ,由数列{a n }为等比数列(易知数列{a n }的公比q ≠-1),得S 2,S 4-S 2,S 6-S 4为等比数列,又S 2=k ,S 4-S 2=2k ,∴S 6-S 4=4k ,∴S 6=7k ,∴S 6S 4=7k 3k =73,故选B. 答案:B3.已知数列{a n }是递增的等比数列,a 1+a 4=9,a 2a 3=8,则数列{a n }的前n 项和等于________.解析:由题意,⎩⎪⎨⎪⎧a 1+a 4=9a 2·a 3=a 1·a 4=8,解得a 1=1,a 4=8或者a 1=8,a 4=1,而数列{a n }是递增的等比数列,所以a 1=1,a 4=8,即q 3=a 4a 1=8,所以q =2,因而数列{a n }的前n 项和S n=a 1(1-q n )1-q =1-2n 1-2=2n -1.答案:2n -14.设数列{a n }(n =1,2,3,…)的前n 项和S n 满足S n +a 1=2a n ,且a 1,a 2+1,a 3成等差数列,则a 1+a 5=________.解析:由S n +a 1=2a n ,得a n =S n -S n -1=2a n -2a n -1(n ≥2),即a n =2a n -1(n ≥2).从而a 2=2a 1,a 3=2a 2=4a 1.又因为a 1,a 2+1,a 3成等差数列,所以a 1+a 3=2(a 2+1),所以a 1+4a 1=2(2a 1+1),解得a 1=2,所以数列{a n }是首项为2,公比为2的等比数列,故a n =2n ,所以a 1+a 5=2+25=34. 答案:345.(2016·高考全国Ⅲ卷)已知数列{a n }的前n 项和S n =1+λa n ,其中λ≠0. (1)证明{a n }是等比数列,并求其通项公式; (2)若S 5=3132,求λ.解析:(1)证明:由题意得a 1=S 1=1+λa 1, 故λ≠1,a 1=11-λ,a 1≠0.由S n =1+λa n ,S n +1=1+λa n +1得a n +1=λa n +1-λa n ,即a n +1(λ-1)=λa n .由a 1≠0,λ≠0得a n ≠0,所以a n +1a n =λλ-1.因此{a n }是首项为11-λ,公比为λλ-1的等比数列,于是a n =11-λ⎝⎛⎭⎫λλ-1n -1.(2)由(1)得S n =1-⎝⎛⎭⎫λλ-1n .由S 5=3132得1-⎝⎛⎭⎫λλ-15=3132,即⎝⎛⎭⎫λλ-15=132. 解得λ=-1.6.设{a n }是公比大于1的等比数列,S n 为数列{a n }的前n 项和.已知S 3=7,且a 1+3,3a 2,a 3+4构成等差数列. (1)求数列{a n }的通项;(2)令b n =ln a 3n +1,n =1,2,…,求数列{b n }的前n 项和T n . 解析:(1)由已知得⎩⎪⎨⎪⎧a 1+a 2+a 3=7,(a 1+3)+(a 3+4)2=3a 2,解得a 2=2.设数列{a n }的公比为q ,由a 2=2,可得a 1=2q ,a 3=2q ,又S 3=7,可知2q +2+2q =7,即2q 2-5q +2=0.解得q 1=2,q 2=12.由题意得q >1,∴q =2,∴a 1=1. 故数列{a n }的通项为a n =2n -1.(2)由于b n =ln a 3n +1,n =1,2,…, 由(1)得a 3n +1=23n ,∴b n =ln 23n =3n ln 2. 又b n +1-b n =3ln 2,∴{b n }是等差数列, ∴T n =b 1+b 2+…+b n =n (b 1+b n )2=3n (n +1)2·ln 2.故T n =3n (n +1)2ln 2.。
高中数学第二章数列2.5等比数列的前n项和第1课时等比数列的前n项和aa高二数学

• 『规律总结(zǒngjié)』 在等比数列{an}的五个量a1,q,an,n,Sn 中,a1,q是最基本的元素,当条件与结论间的联系不明显时 ,均可以用a1,q列方程组求解.
第十六页,共五十页。
〔跟踪练习1〕 (2015·重庆文,16)已知等差数列{an}满足a3=2,前3项和S3=92. (1)求{an}的通项公式; (2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
!果真是这样吗?我们一起来帮他算一算.
第六页,共五十页。
• 1.等比数列(děnɡ bǐ shù liè)的前n项和公式
已知量 公式
首项、公比与项数
Sn=__a_1_n1_a-_1 _q_n_q=1 ___1_-__q____q≠1
首项、末项与公比 Sn=__a_1-_n_aa_1 _nq_q=1
第三十一页,共五十页。
(2)由(1),得bn=an+k及{bn}是公比为2的等比数列,得 Tn=b111--22n=b1(2n-1), 由bn=an+k得Tn=Sn+nk,∴Sn=b1(2n-1)-nk. ∵S6=T4,S5=-9, ∴6331bb11- -65kk= =1-5b91,, 解得k=8.
新课标导学
数学
必修5 ·人教A版
第一页,共五十页。
第二章
数列(shùliè)
等比数列 的前 项和 2.5
(děnɡ bǐ shù liè)
n
课时 第1
(kèshí)
等比数列的前n项和
第二页,共五十页。
1
自主预习学案
2
互动探究学案
3
课时作业学案
第三页,共五十页。
自主预习(yùxí)学案
2019-2020人教A版数学必修5第2章 2.5 第1课时 等比数列的前n项和
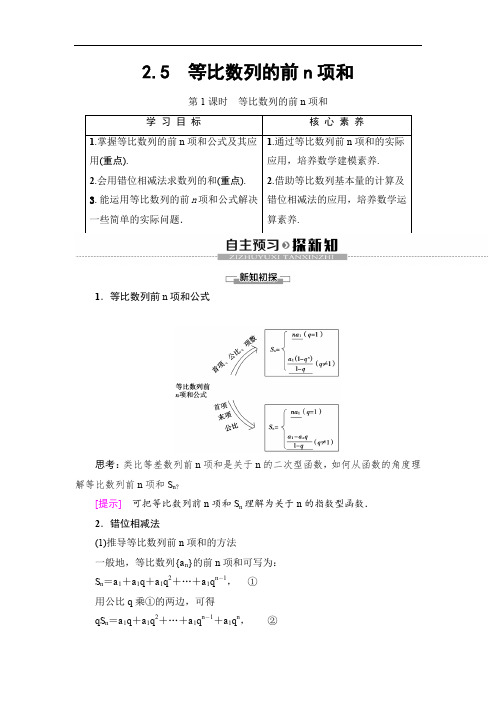
2.5 等比数列的前n 项和第1课时 等比数列的前n 项和1.等比数列前n 项和公式思考:类比等差数列前n 项和是关于n 的二次型函数,如何从函数的角度理解等比数列前n 项和S n ?[提示] 可把等比数列前n 项和S n 理解为关于n 的指数型函数. 2.错位相减法(1)推导等比数列前n 项和的方法一般地,等比数列{a n }的前n 项和可写为: S n =a 1+a 1q +a 1q 2+…+a 1q n -1, ① 用公比q 乘①的两边,可得 qS n =a 1q +a 1q 2+…+a 1q n -1+a 1q n ,②由①-②,得(1-q )S n =a 1-a 1q n , 整理得S n =a 1(1-q n )1-q(q ≠1).(2)我们把上述方法叫错位相减法,一般适用于数列{a n ·b n }前n 项和的求解,其中{a n }为等差数列,{b n }为等比数列,且q ≠1.思考:等比数列的前n 项和公式的推导还有其他的方法吗?[提示] 根据等比数列的定义,有:a 2a 1=a 3a 2=a 4a 3=…=a n a n -1=q ,再由合比定理,则得a 2+a 3+a 4+…+a na 1+a 2+a 3+…+a n -1=q ,即S n -a 1S n -a n=q ,进而可求S n .1.等比数列1,x ,x 2,x 3,…(x ≠0)的前n 项和S n 为( ) A .1-x n 1-xB .1-x n -11-xC .⎩⎨⎧1-x n1-x (x ≠1),n (x =1)D .⎩⎨⎧1-x n -11-x (x ≠1),n (x =1)C [当x =1时,数列为常数列,又a 1=1,所以S n =n . 当x ≠1时,q =x ,S n =a 1(1-x n )1-x =1-x n1-x.]2.等比数列{a n }中,a 1=1,q =2,则S 5=________. 31 [S 5=a 1(1-q 5)1-q =1-251-2=31.]3.数列12,24,38,416,…的前10项的和S 10=________. 509256[S 10=12+24+38+…+929+10210, 则12S 10=14+28+…+9210+10211.两式相减得,12S 10=12+14+18+…+1210-10211=12⎣⎢⎢⎡⎦⎥⎥⎤1-⎝ ⎛⎭⎪⎫12101-12-10211,所以S 10=509256.]4.某厂去年产值为a ,计划在5年内每年比上一年的产值增长10%,从今年起5年内,该厂的总产值为________.11(1.15-1)a [去年产值为a ,从今年起5年内各年的产值分别为1.1a ,1.12a ,1.13a ,1.14a ,1.15a .所以1.1a +1.12a +1.13a +1.14a +1.15a =a ·1.1-1.161-1.1=11(1.15-1)a.]n (1)S 2=30,S 3=155,求S n ; (2)a 1+a 3=10,a 4+a 6=54,求S 5;(3)a 1+a n =66,a 2a n -1=128,S n =126,求q . [解] (1)由题意知 ⎩⎨⎧a 1(1+q )=30,a 1(1+q +q 2)=155, 解得⎩⎨⎧a 1=5,q =5或⎩⎪⎨⎪⎧a 1=180,q =-56.从而S n =14×5n +1-54或S n =1 080×⎣⎢⎢⎡⎦⎥⎥⎤1-⎝ ⎛⎭⎪⎫-56n 11. (2)法一:由题意知⎩⎪⎨⎪⎧a 1+a 1q 2=10,a 1q 3+a 1q 5=54,解得⎩⎪⎨⎪⎧a 1=8,q =12,从而S 5=a 1(1-q 5)1-q =312. 法二:由(a 1+a 3)q 3=a 4+a 6, 得q 3=18,从而q =12. 又a 1+a 3=a 1(1+q 2)=10,所以a 1=8,从而S 5=a 1(1-q 5)1-q =312.(3)因为a 2a n -1=a 1a n =128,所以a 1,a n 是方程x 2-66x +128=0的两根. 从而⎩⎨⎧a 1=2,a n =64或⎩⎨⎧a n =2,a 1=64.又S n =a 1-a n q 1-q=126,所以q 为2或12.1.在等比数列 {a n }的五个量a 1,q ,a n ,n ,S n 中,已知其中的三个量,通过列方程组,就能求出另外两个量,这是方程思想与整体思想在数列中的具体应用.2.在解决与前n 项和有关的问题时,首先要对公比q =1或q ≠1进行判断,若两种情况都有可能,则要分类讨论.1.在等比数列{a n }中.(1)若a 1=2,a n =162,S n =112,求n 和q ; (2)已知S 4=1,S 8=17,求a n .[解] (1)由S n =a 1-a n q 1-q 得112=2-162q1-q ,∴q =-2,又由a n =a 1q n -1得162=2(-2)n -1,∴n =5.(2)若q =1,则S 8=2S 4,不合题意,∴q ≠1, ∴S 4=a 1(1-q 4)1-q=1,S 8=a 1(1-q 8)1-q=17,两式相除得1-q 81-q 4=17=1+q 4,∴q =2或q =-2,∴a 1=115或a 1=-15,∴a n =115·2n -1或-15·(-2)n -1.从借贷后第二个月开始等额还贷,分6个月付清,试问每月应支付多少元?(1.016≈1.061,1.015≈1.051)思路探究:解决等额还贷问题关键要明白以下两点:(1)所谓复利计息,即把上期的本利和作为下一期本金,在计算时每一期本金的数额是不同的,复利的计算公式为S =P (1+r )n ,其中P 代表本金,n 代表存期,r 代表利率,S 代表本利和.(2)从还贷之月起,每月还贷金额是构成等比数列还是等差数列,首项是什么,公比或公差是多少.[解] 法一:设每个月还贷a 元,第1个月后欠款为a 0元,以后第n 个月还贷a 元后,还剩下欠款a n 元(1≤n ≤6),则a 0=10 000,a 1=1.01a 0-a , a 2=1.01a 1-a =1.012a 0-(1+1.01)a , …a 6=1.01a 5-a =…=1.016a 0-[1+1.01+…+1.015]a . 由题意,可知a 6=0,即1.016a 0-[1+1.01+…+1.015]a =0, a =1.016×1021.016-1.∵1.016≈1.061,∴a =1.061×1021.061-1≈1 739.故每月应支付1 739元.法二:一方面,借款10 000元,将此借款以相同的条件存储6个月,则它的本利和为S 1=104(1+0.01)6=104×(1.01)6(元).另一方面,设每个月还贷a 元,分6个月还清,到贷款还清时,其本利和为 S 2=a (1+0.01)5+a (1+0.01)4+…+a=a [(1+0.01)6-1]1.01-1=a [1.016-1]×102(元).由S 1=S 2,得a =1.016×1021.016-1.以下解法同法一,得a ≈1 739,故每月应支付1 739元.解数列应用题的具体方法步骤(1)认真审题,准确理解题意,达到如下要求:①明确问题属于哪类应用问题,即明确是等差数列问题还是等比数列问题,还是含有递推关系的数列问题?是求a n ,还是求S n ?特别要注意准确弄清项数是多少.②弄清题目中主要的已知事项.(2)抓住数量关系,联想数学知识和数学方法,恰当引入参数变量,将文字语言翻译成数学语言,将数量关系用数学式子表达.(3)将实际问题抽象为数学问题,将已知与所求联系起来,列出满足题意的数学关系式.2.一个热气球在第一分钟上升了25 m 的高度,在以后的每一分钟里,它上升的高度都是它在前一分钟里上升高度的80%. 这个热气球上升的高度能超过125 m 吗?[解] 用a n 表示热气球在第n 分钟上升的高度, 由题意,得a n +1=45a n ,因此,数列{a n }是首项a 1=25,公比q =45的等比数列.热气球在前n 分钟内上升的总高度为S n =a 1+a 2+…+a n =a 1(1-q n )1-q =25×⎣⎢⎢⎡⎦⎥⎥⎤1-⎝ ⎛⎭⎪⎫45n 1-45=125×[1-(45)n]<125. 故这个热气球上升的高度不可能超过125 m.1.对于S 64=1+2+4+8+…+262+263,用2乘以等式的两边可得2S 64=2+4+8+…+262+263+264,对这两个式子作怎样的运算能解出S 64?[提示] 比较两式易知,两式相减能消去同类项,解出S 64,即S 64=1-2641-2=264-1.2.由项数相等的等差数列{n }与等比数列{2n }相应项的积构成新的数列{n ·2n }是等比数列吗?是等差数列吗?该数列的前n 项和S n 的表达式是什么?[提示] 由等差数列及等比数列的定义可知数列{n ·2n }既不是等差数列,也不是等比数列.该数列的前n 项和S n 的表达式为S n =1·21+2·22+3·23+…+n ·2n .3.在等式 S n =1·21+2·22+3·23+…+n ·2n 两边同乘以数列{2n }的公比后,该等式的变形形式是什么?认真观察两式的结构特征,你能将求S n 的问题转化为等比数列的前n 项和问题吗?[提示] 在等式S n =1·21+2·22+3·23+…+n ·2n ,① 两边同乘以{2n }的公比可变形为2S n =1·22+2·23+3·24+…+(n -1)·2n +n ·2n +1,② ②-①得:S n =-1·21-22-23-24-…-2n +n ·2n +1 =-(21+22+23+…+2n )+n ·2n +1.此时可把求S n 的问题转化为求等比数列{2n }的前n 项和问题.我们把这种求由一个等差数列{an }和一个等比数列{b n }相应项的积构成的数列{a n b n }前n 项和的方法叫错位相减法.【例3】 已知等比数列{a n }满足:a 1=12,a 1,a 2,a 3-18成等差数列,公比q ∈(0,1),(1)求数列{a n }的通项公式;(2)设b n =na n ,求数列{b n }的前n 项和S n .思路探究:(1)根据a 1,a 2,a 3-18成等差数列求得公比q ,写出通项公式; (2)由b n =na n 可知利用错位相减法求和. [解] (1)设等比数列{a n }的公比为q ,a 1=12,因为a 1,a 2,a 3-18成等差数列,所以2a 2=a 1+a 3-18, 即得4q 2-8q +3=0, 解得q =12或q =32,又因为q ∈(0,1),所以q =12, 所以a n =12·⎝ ⎛⎭⎪⎫12n -1=12n .(2)根据题意得b n =na n =n2n , S n =12+222+323+…+n 2n , ① 12S n =122+223+324+…+n 2n +1, ②作差得12S n =12+122+123+…+12n -n 2n +1,S n =2-(n +2)⎝ ⎛⎭⎪⎫12n.1.本题中设c n =na n,求数列{c n }的前n 项和S n ′.[解] 由题意知c n =n ·2n ,所以S n ′=1×21+2×22+3×23+…+(n -2)×2n -2+(n -1)×2n -1+n ·2n , 2S n ′=1×22+2×23+3×24+…+(n -2)×2n -1+(n -1)×2n +n ·2n +1, 两式相减得:-S n ′=1×21+22+23+24+…+2n -1+2n -n ·2n +1=2(1-2n )1-2-n ·2n +1=(1-n )·2n +1-2,所以S n ′=(n -1)·2n +1+2.2.本题中设d n =(2n -1)a n ,求数列{d n }的前n 项和T n . [解] 由题意可得:T n =1×12+3×122+…+(2n -1)×12n ,12T n =1×122+3×123+…+(2n -3)×12n +(2n -1)×12n +1, 两式相减得12T n =1×12+2×122+…+2×12n -(2n -1)×12n +1=12+12×1-12n -11-12-(2n -1)×12n +1=32-12n -1-2n -12n +1,所以T n =3-42n -2n -12n =3-2n +32n.错位相减法的适用题目及注意事项(1)适用范围:它主要适用于{a n }是等差数列,{b n }是等比数列,求数列{a n b n }的前n 项和.(2)注意事项:①利用“错位相减法”时,在写出S n 与qS n 的表达式时,应注意使两式错对齐,以便于作差,正确写出(1-q )S n 的表达式.②利用此法时要注意讨论公比q 是否等于1的情况.1.在等比数列的通项公式和前n 项和公式中,共涉及五个量:a 1,a n ,n ,q ,S n ,其中首项a 1和公比q 为基本量,且“知三求二”.2.前n 项和公式的应用中,注意前n 项和公式要分类讨论,即当q ≠1和q =1时是不同的公式形式,不可忽略q =1的情况.3.一般地,如果数列{a n }是等差数列,{b n }是等比数列且公比为q ,求数列{a n ·b n }的前n 项和时,可采用错位相减法求和.1.判断正误(1)求等比数列{a n }的前n 项和时可直接套用公式S n =a 1(1-q n )1-q 来求.( )(2)若首项为a 的数列既是等差数列又是等比数列,则其前n 项和为S n =na .( )(3)若某数列的前n 项和公式为S n =-aq n +a (a ≠0,q ≠0且q ≠1,n ∈N *),则此数列一定是等比数列.( )[答案] (1)× (2)√ (3)√[提示] (1)错误.在求等比数列前n 项和时,首先应看公比q 是否为1,若q ≠1,可直接套用,否则应讨论求和.(2)正确.若数列既是等差数列,又是等比数列,则是非零常数列,所以前n 项和为S n =na .(3)正确.根据等比数列前n 项和公式S n =a 1(1-q n )1-q (q ≠0且q ≠1)变形为S n =a 11-q -a 11-q q n (q ≠0且q ≠1),若令a =a 11-q,则和式可变形为S n =a -aq n .2.已知等比数列{a n }的首项a 1=3,公比q =2,则S 5等于( ) A .93 B .-93 C .45 D .-45 A [S 5=a 1(1-q 5)1-q =3(1-25)1-2=93.]3.在公比为整数的等比数列{a n }中,如果a 1+a 4=18,a 2+a 3=12,则这个数列的前8项之和S 8=________.510 [a 1+a 4=a 1(1+q 3)=18,a 2+a 3=a 1(q +q 2)=12,两式联立解得q =2或12,而q 为整数,所以q =2,a 1=2,代入公式求得S 8=2(1-28)1-2=510.]4.求和:12+34+58+716+…+2n -12n .[解] 设S n =12+34+58+716+…+2n -12n=12+322+523+724+…+2n -32n -1+2n -12n ,① 则12S n =122+323+524+…+2n -32n +2n -12n +1.② ①-②,得12S n =12+222+223+224+…+22n -2n -12n +1 =12+12+122+…+12n -1-2n -12n +1 =12+12-12n -1×121-12-2n -12n +1=32-12n -1-2n -12n +1=32-2n +32n +1,∴S n =3-2n +32n .。
2.5 §1等比数列的前n项和

2.5 等比数列的前n项和第一课时教学目标1.掌握等比数列前n项和公式的推导方法.2.会用等比数列前n项和公式解决一些简单问题.知识回顾1.等比数列的定义及数学表达式:2.等比数列的通项公式:3.等比数列的性质:知识探究探究(一)等比数列前n项和公式的推导问题导思:对于数列1,2,22,23,…,2n,…问题1:该数列的首项和公比分别是多少?问题2:该数列的前n项和S n怎样表示呢?问题3:观察求和的式子,相邻两项有什么特征?怎样把某一项变成它的后一项?问题4:那么该数列2S n的表达式如何?问题5:S n与2S n的表达式中有许多相同项,你有什么办法消去这些相同项?所得结论如何?探究新知:等比数列{a n}的首项为a1,公比为q,如何求它的前n项和S n呢?问题1:等比数列的前n项和S n怎样表示呢?问题2:前n项和S n采用什么方法,怎样化简呢?问题3:观察求和的式子,相邻两项有什么特征?怎样把某一项变成它的后一项?问题4:需要构造另一个式子,而要达到消项的目的,就须使两式具有相同的项,如何构造式子?问题5:为了消项,接下来将这两个式子怎么样?思考:你还有其他方法去推导等比数列前n项和公式吗?1.等比数列的前n 项和S n =⎩⎪⎨⎪⎧na 1(q =1)a 1(1-q n )1-q(q ≠1)思考1:根据求和公式,要求一个等比数列的前n 项和,一般要先求出哪些量?思考2:能否将S n 和用a 1, q ,a n 来表示?思考3:q ≠1时,应该怎样选用哪个公式?探究(二)错位相减法求和问题 教材中推导等比数列前n 项和的方法叫错位相减法.这种求和方法是我们应该掌握的重要方法之一,这种方法的适用范围可以拓展到一个等差数列{a n }与一个等比数列{b n }对应项之积构成的新数列求和.下面是利用错位相减法求数列{n2n }前n 项和的步骤和过程,请你补充完整.设S n =12+222+323+…+n2n∴12S n =_______________________________ ∴S n -12S n =_______________________________即12S n =__________________=__________________ ∴S n =__________________=__________________小结:典例讲练例1.设数列{a n }是等比数列,其前n 项和为S n ,且S 3=3a 3,求公比q 的值.例2.设等比数列{a n }的前n 项和为S n ,若S 3+S 6=2S 9,求数列的公比q .变式:在等比数列{a n }中,a 1+a n =66,a 3a n -2=128,S n =126,求n 和q .例4.求和:1×21+2×22+3×23+…+n ·2n =______________.例5.求数列1,3a ,5a 2,7a 3,…,(2n -1)·a n -1的前n 项和.课堂小结:这节课我们主要学习了什么? 首项、末项与公比 S n =⎩⎪⎨⎪⎧na 1q =a 1-qa n1-qq2.两种方法:错位相减、解方程推导等比数列前n 项和的方法叫错位相减法.一般适用于求一个等差数列与一个等比数列对应项积的前n 项和.3.三种数学思想:类比、方程、分类讨论 课后作业1.已知数列{a n }满足3a n +1+a n =0,a 2=34-,则{a n }的前10项和等于( ) A.()-10-61-3B.()-1011-39C.()-1031-3D.()-1031+32.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则( ) A.11 B.5 C.-8D.-113.已知{a n }是首项为1的等比数列,S n 是{a n }的前n 项和,且,则数列的前5项和为( ) A.或5 B.或5 C. D.52S S =369s s =1n a ⎧⎫⎨⎬⎩⎭158311631161584.已知数列{a n }的前n 项和为S n ,a 1=1,S n =2a n +1,,则S n =( )A. 2n -1B.⎝⎛⎭⎫32n -1C.⎝⎛⎭⎫23n -1D.12n -15.已知等比数列{a n }为递增数列,若a 1>0,且2(a n +a n +2)=5a n +1,则数列{a n }的公比q = _______.6.等比数列{a n }的前n 项和为S n ,公比不为1.若a 1=1,则对任意的n ∈N *,都有a n +2+a n +1-2a n =0,则S 5=________.7.在等比数列{a n }中,已知a 1+a 2+…+a n =2n -1,则a 12+a 22+…+a n 2等于________.8.已知等比数列{a n }的公比为q =-12. (1)若a 3=41,求数列{a n }的前n 项和; (Ⅱ)证明:对任意k ∈N +,a k ,a k +2,a k +1成等差数列.9.已知等差数列{a n }前三项的和为-3,前三项的积为8.(Ⅰ)求等差数列{a n }的通项公式;(Ⅱ)若a 2,a 3,a 1成等比数列,求数列{|a n |}的前n 项和.2.5 等比数列的前n 项和第一课时教学目标1.掌握等比数列前n 项和公式的推导方法.2.会用等比数列前n 项和公式解决一些简单问题. 知识回顾1.等比数列的定义及数学表达式:如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q 表示(q ≠0).数学符号表述:a n +1a n=q (q 为常数,q ≠0,n ∈N *)2.等比数列的通项公式:a n =a 1·q n -1(n ∈N *)或a n =a m ·q n -m . 3.等比数列的性质:在等比数列{a n }中,若m+n=p+q (m ,n ,p ,q ∈N *),则a m ·a n =a p ·a q . 推论1:若m+n =2p ,则a m ·a n =a p 2.推论2:若{a n }是有穷数列,则与首末两项等距离的两项积相等,且等于首末两项之积,即a 1a n =a 2a n -1=….知识探究探究(一)等比数列前n 项和公式的推导问题导思:对于数列1,2,22,23,…,2n ,…问题1:该数列的首项和公比分别是多少?【提示】首项为1,公比为2.问题2:该数列的前n 项和S n 怎样表示呢?【提示】数列的前n 项和S n =1+2+22+…+2n -1①问题3:观察求和的式子,相邻两项有什么特征?怎样把某一项变成它的后一项?【提示】后项=前项×公比。
高中数学第二章数列25等比数列的前n项和第1课时等比数列前n项和的求解课件新人教A版必修

另一方面,设每个月还贷 a 元,分 6 个月还清,到贷 款还清时,其本利和为
S2=a(1+0.01)5+a(1+0.01)4+…+a=
a[(1+1.001.0-1)1 6-1]=a(1.016-1)×102(元). 由 S1=S2,得 a=11.0.0116×6-1102. 因为 1.016≈1.061,所以 a=11.0.06611×-1102≈1 739. 故每月应支付 1 739 元.
=12+121-1-1212n-1-22nn-+11 =32-22nn++13, 所以 Sn=3-2n2+n 3. 答案:3-2n2+n 3
类型 1 等比数列求和公式的基本运算 [典例 1] 在等比数列{an}中: (1)S2=30,S3=155,求 Sn; (2)a1+a3=10,a4+a6=54,求 S5; (3)a1+an=66,a2an-1=128,Sn=126,求 q. 解:(1)由题意知aa11((11++qq)+=q2)30=,155,
[变式训练] 在等比数列{an}中:
(1)若 a1= 2,an=16 2,Sn=11 2,求 n 和 q; (2)已知 S4=1,S8=17,求 an.
解:(1)由 Sn=a11--aqnq得 112=Βιβλιοθήκη 2-16 1-q2q,
所以 q=-2,
又由 an=a1qn-1 得 16 2= 2(-2)n-1, 所以 n=5.
又 Sn=a11--aqnq=126, 所以 q 为 2 或12. 归纳升华 1.在等比数列{an}的五个量 a1,q,an,n,Sn 中, 已知其中的三个量,就能求出另两个量,这是方程思想 与整体思想在数列中的具体应用. 2.在解决与前 n 项和有关的问题时,首先要判断公 比 q 是否等于 1,若两种情况都有可能,则要分类讨论.
高中数学第二章数列2.5等比数列的前n项和第一课时等比数列的前n项和练习(含解析)新人教A版必修5

高中数学第二章数列2.5等比数列的前n项和第一课时等比数列的前n项和练习(含解析)新人教A版必修51.等比数列{a n}的各项都是正数,若a1=81,a5=16,则它的前5项和是( B )(A)179 (B)211 (C)248 (D)275解析:由16=81×q4,q>0得q=,所以S5==211.故选B.2.在等比数列{a n}中,若a4,a8是方程x2-4x+3=0的两根,则a6的值是( A )(A)(B)-(C)±(D)±3解析:依题意得,a4+a8=4,a4a8=3,故a4>0,a8>0,因此a6>0(注:在一个实数等比数列中,奇数项的符号相同,偶数项的符号相同),a6==.故选A.3.等比数列{a n}的前n项和为S n,已知S3=a2+10a1,a5=9,则a1等于( C )(A)(B)-(C)(D)-解析:设等比数列{a n}的公比为q,由S3=a2+10a1得a1+a2+a3=a2+10a1,即a3=9a1,所以q2=9,又a5=a1q4=9,所以a1=.故选C.4.等比数列{a n}中,a3=3S2+2,a4=3S3+2,则公比q等于( C )(A)2 (B)(C)4 (D)解析:因为a3=3S2+2,a4=3S3+2,所以a4-a3=3(S3-S2)=3a3,即a4=4a3,所以q==4,故选C.5.等比数列{a n}的前n项和S n=3n-a,则实数a的值为( B )(A)0 (B)1 (C)3 (D)不存在解析:法一当n≥2时,a n=S n-S n-1=3n-3n-1=2·3n-1,==3.又a1=S1=3-a,a2=2×3=6,则=.因为{a n}是等比数列,所以=3,得a=1.故选B.法二由等比数列前n项和公式知,3n系数1与-a互为相反数,即-a=-1,则a=1.故选B.6.在14与之间插入n个数组成等比数列,若各项和为,则数列的项数为( B )(A)4 (B)5 (C)6 (D)7解析:设公比为q,由等比数列的前n项和公式及通项公式得解之,得则数列的项数为5.故选B.7.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为“有一个人走378里路,第一天健步行走,从第二天起脚痛,每天走的路程为前一天的一半,走了6天后到达目的地.”则该人最后一天走的路程为( C )(A)24里(B)12里(C)6里(D)3里解析:记每天走的路程里数为{a n},易知{a n}是公比q=的等比数列,S6=378,S6==378,所以a1=192,所以a6=192×=6,故选C.8.设S n为等比数列{a n}的前n项和,若a1=1,且3S1,2S2,S3成等差数列,则a n= .解析:由3S1,2S2,S3成等差数列知,4S2=3S1+S3,可得a3=3a2,所以公比q=3,故等比数列通项a n=a1q n-1=3n-1.答案:3n-19.在等比数列{a n}中,已知a1+a2+a3=1,a4+a5+a6=-2,则该数列的前15项和S15= .解析:记b1=a1+a2+a3,b2=a4+a5+a6,…,b5=a13+a14+a15,依题意{b n}构成等比数列,其首项b1=1,公比为q==-2,则{b n}的前5项和即为{a n}的前15项和S15==11.答案:1110.在等比数列{a n}中,公比q=,且log2a1+log2a2+…+log2a10=55,则a1+a2+…+a10= .解析:据题意知log2(·q1+2+…+9)=log2(·q45)=55,即=2100.又a n>0,所以a1=210,所以S10=211-2.答案:211-211.已知等比数列前20项和是21,前30项和是49,则前10项和是.解析:由S10,S20-S10,S30-S20成等比数列,所以(S20-S10)2=S10·(S30-S20),即(21-S10)2=S10(49-21).所以S10=7或S10=63.答案:7或6312.已知数列{a n} 的前n项和为S n,a1=1,S n=2a n+1,求S n的值.解:因为S n=2a n+1,所以n≥2时,S n-1=2a n.因为a n=S n-S n-1=2a n+1-2a n,所以3a n=2a n+1,所以=.又因为S1=2a2,所以a2=,所以=,所以{a n}从第二项起是以为公比的等比数列.所以S n=a1+a2+a3+…+a n=1+=()n-1.13.知{a n}是等差数列,满足a1=3,a4=12,数列{b n}满足b1=4,b4=20,且{b n-a n}为等比数列.(1)求数列{a n}和{b n}的通项公式;(2)求数列{b n}的前n项和.解:(1)设等差数列{a n}的公差为d,由题意得d===3,所以a n=a1+(n-1)d=3n(n=1,2,…).设等比数列{b n-a n}的公比为q,由题意得q3===8,解得q=2.所以b n-a n=(b1-a1)q n-1=2n-1.从而b n=3n+2n-1(n=1,2,…).(2)由(1)知b n=3n+2n-1(n=1,2,…).数列{3n}的前n项和为n(n+1),数列{2n-1}的前n项和为=2n-1.所以数列{b n}的前n项和为n(n+1)+2n-1.14.已知数列{a n}满足a1=1,a n+1=3a n+1.(1)求证是等比数列,并求{a n}的通项公式;(2)求证++…+<.证明:(1)由a n+1=3a n+1得a n+1+=3(a n+).又a1+=,所以是首项为,公比为3的等比数列.所以a n+=,因此{a n}的通项公式为a n=.(2)由(1)知=.因为当n≥1时,3n-1≥2×3n-1,所以≤.于是++…+≤1++…+=(1-)<.所以++…+<.15.数列{a n}中,已知对任意n∈N*,a1+a2+a3+…+a n=3n-1,则+++…+等于( B )(A)(3n-1)2(B)(9n-1)(C)9n-1 (D)(3n-1)解析:因为a1+a2+…+a n=3n-1,n∈N*,n≥2时,a1+a2+…+a n-1=3n-1-1,所以当n≥2时,a n=3n-3n-1=2·3n-1,又n=1时,a1=2适合上式,所以a n=2·3n-1,故数列{}是首项为4,公比为9的等比数列.因此++…+==(9n-1).故选B.16.已知S n是等比数列{a n}的前n项和,若存在m∈N*,满足=9,=,则数列{a n}的公比为( B )(A)-2 (B)2 (C)-3 (D)3解析:设公比为q,若q=1,则=2,与题中条件矛盾,故q≠1.因为==q m+1=9,所以q m=8.所以==q m=8=,所以m=3,所以q3=8,所以q=2.故选B.17.设各项都是正数的等比数列{a n},S n为前n项和且S10=10,S30=70,那么S40= .解析:依题意,知数列{a n}的公比q≠-1,数列S10,S20-S10,S30-S20,S40-S30成等比数列,因此有(S20-S10)2=S10(S30-S20),即(S20-10)2=10(70-S20),故S20=-20或S20=30;又S20>0,因此S20=30,S20-S10=20,S30-S20=40,故S40-S30=80,S40=150.答案:15018.已知等差数列{a n}的首项a1=1,公差d>0,且第2项,第5项,第14项分别是等比数列{b n}的第2项,第3项,第4项.(1)求数列{a n}与{b n}的通项公式;(2)设数列{c n}对于任意n∈N*均有+++…+=a n+1成立,求c1+c2+c3+…+c2 015+c2 016的值. 解:(1)依题意得b2=a2=a1+d,b3=a5=a1+4d,b4=a14=a1+13d,由等比中项得(1+4d)2=(1+d)(1+13d),解得d=2或d=0(舍去),因此a n=1+2(n-1)=2n-1,b2=3,b3=9,b4=27,故数列{b n}是首项为1,公比为3的等比数列.因此b n=3n-1.(2)因为+++…+=a n+1,所以当n≥2时,+++…+=a n,两式作差得=a n+1-a n=d,又d=2,故c n=2×3n-1,又=a2,所以c1=3,因此数列c n=。
第一部分 第二章 2.5 第一课时 等比数列的前n项和

等比数列前 n 项和的重要性质
(1)等比数列{an}的前 n 项和 Sn,满足 Sn,S2n-Sn,S3n -S2n, 4n-S3n, S …成等比数列(其中 Sn, 2n-Sn, 3n-S2n, S S … 均不为 0),这一性质可直接应用. S偶 (2)等比数列的项数是偶数时, =q; S奇 S奇-a1 等比数列的项数是奇数时, =q. S偶
理解教材新知
2.5 第 二 章 数 列 等 比 数 列 的 前 第一 课时 把握热点考向 考点一
考点二 考点三
等比
n
项 和
数列
的前n 项和 应用创新演练
返回
返回
返回
已知等比数列{an},公比为q,Sn是其前n项的和,则 Sn=a1+a2+…+an=a1+a1q+a1q2+…+a1qn-1. 问题1:若q=1,则Sn与an有何关系? 提示:Sn=na1.
na1q=1, a11-qn Sn= q≠1 1-q
首项a1,末项an与公比q
na1q=1, Sn= a1-anq 1-q q≠1
公式
返回
1.当公比 q=1 时,等比数列{an}是常数列,各项均 相等,所以 Sn=na1. 2.当公比 q≠1 时,等比数列{an}的前 n 项和 Sn 有 a11-qn 两个计算公式,当已知 a1,q 与 n 时利用 计算 1-q a1-anq 较方便;当已知 a1,an 与 q 时,用 较好. 1-q
n
返回
又∵2
n-1
96 = 3 =32,∴n=6.
Байду номын сангаас
a1-anq 法二:由公式 Sn= 及已知条件得 1-q a1-96×2 189= ,解得 a1=3,又由 an=a1·n-1, q 1-2 得 96=3·n-1,解得 n=6. 2
第2章2.5第1课时

课 时 作 业
课 堂 互 动 探 究
新课标 ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修5
易 错 易 误 辨 析 当 堂 双 基 达 标
设等比数列{an}的前 n 项和为 Sn,已知 a2=6,6a1+a3=30. 求 an 和 Sn.
+
这两个等式的右边有何相同点?若用②式减去①式,会有 什么结果?
【提示】 两个等式的右边除首项与末项不同外,其余各
项均相同,若用②式减去①式会把这些相同的项全部消掉,求 得 Sn=2n 1-1.
+
课 时 作 业
课 堂 互 动 探 究
菜 单
教 师 备 课 资 源
新课标 ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
当 堂 双 基 达 标
课 时 作 业
课 堂 互 动 探 究
菜 单
教 师 备 课 资 源
新课标 ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修5
易 错 易 误 辨 析 当 堂 双 基 达 标
●教学建议 基于本节课为公式推导课, 应着重采用探究式教学方法. 在 教学中以学生的分组讨论和自主探究为主,辅之以启发性的问 题诱导点拨,充分体现学生是主体,教师服务于学生的思路.
课 时 作 业
课 堂 互 动 探 究
菜 单
教 师 备 课 资 源
新课标 ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修5
易 错 易 误 辨 析
等比数列的前 n 项和公式
2.5.1 等比数列的前n项和

4 q 3
4
③
解得:q
4 3
.
代入③得:n=5.
解法2 Q a 1 a n q 1 .
a1 qa n 1q
4 3
又 an 9 16 q
n1
9
16
q
Sn
16 9 1q
781 144
解得:q
.
16 9
q
n1
作业
课本61页A组1—6
a 1 (1 q )
n
代入等比数列前n 项和公式
得 5000(1 1 . 1 )
n
Sn
1 q
n
1 1 .1
30000
整理得 1 . 1
1 .6
两边取对数得
用计算器算得
n lg 1 . 1 lg 1 . 6
n lg 1 . 6 lg 1 . 1 0 . 20 0 . 041 5(年 )
他真的花不了几个钱吗?
分析:由于每一个钉子的价钱都是前一个钉子的
2 3 23
2倍,共有24个钉子, 每个钉子的价钱依 次为:
1, 2 , 2
, 2 ,L
,2
.
它是以1为首项,公比是2的等比数列.
买24个钉子要花的钱为: (单位:分)
S 24 1 2 2 2 L 2 .
2 3 23
例题
【例1】 求“卖马的故事”中要买24个钉子的价钱
S 24 1 2 2 L 2
2
23
〔解〕 S 2 4 1 2 2 2 L 2 2 3
1 2
24
1 2
2
课时作业32:2.5 第1课时 等比数列前n项和公式

§2.5 等比数列的前n 项和 第1课时 等比数列前n 项和公式1.在等比数列{a n }中,a 1=2,a 2=1,则S 100等于( ) A .4-2100 B .4+2100 C .4-2-98D .4-2-100答案 C 解析 q =a 2a 1=12.S 100=a 1(1-q 100)1-q=2⎣⎡⎦⎤1-⎝⎛⎭⎫121001-12=4(1-2-100)=4-2-98.2.已知在等比数列{a n }中,a n =2×3n -1,则由此数列的偶数项所组成的新数列的前n 项和S n 的值为( ) A .3n -1 B .3()3n -1 C.9n -14D.3()9n -14答案 D解析 ∵a n =2×3n -1,则数列{a n }是以2为首项,3为公比的等比数列,由此数列的偶数项所组成的新数列是以6为首项,以9为公比的等比数列,则前n 项和为S n =6()1-9n 1-9=3()9n -14.3.设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则S 5S 2等于( )A .11B .5C .-8D .-11 答案 D解析 由8a 2+a 5=0得8a 1q +a 1q 4=0,∵a 1≠0,q ≠0,∴q =-2,则S 5S 2=a 1(1+25)a 1(1-22)=-11.4.一弹球从100米高处自由落下,每次着地后又跳回到原来高度的一半再落下,则第10次着地时所经过的路程和是(结果保留到个位)( ) A .300米 B .299米 C .199米 D .166米答案 A解析 小球10次着地共经过的路程为100+100+50+…+100×⎝⎛⎭⎫128=2993964≈300(米). 5.设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2=3a 2+2,S 4=3a 4+2,则a 1等于( ) A .-2 B .-1 C.12 D.23答案 B解析 由S 2=3a 2+2,S 4=3a 4+2,得a 3+a 4=3a 4-3a 2,即q +q 2=3q 2-3,解得q =-1(舍去)或q =32,将q =32代入S 2=3a 2+2中得a 1+32a 1=3×32a 1+2,解得a 1=-1.6.记S n 为等比数列{a n }的前n 项和.若a 1=13,a 24=a 6,则S 5=________. 答案1213解析 设等比数列{a n }的公比为q ,因为a 24=a 6,所以(a 1q 3)2=a 1q 5,所以a 1q =1,又a 1=13,所以q =3,所以S 5=a 1(1-q 5)1-q =13×(1-35)1-3=1213.7.已知S n 为等比数列{a n }的前n 项和,S n =93,a n =48,公比q =2,则项数n =________,a 1=________. 答案 5 3解析 由S n =93,a n =48,公比q =2,得⎩⎪⎨⎪⎧ a 1(2n -1)=93,a 1·2n -1=48,解得⎩⎪⎨⎪⎧a 1=3,n =5. 8.设等比数列{a n }的前n 项和为S n ,若S 3+S 6=2S 9,则数列的公比q =________.答案 -342解析 当q =1时,S n =na 1,S 3+S 6=3a 1+6a 1=9a 1=S 9≠2S 9;当q ≠1时,a 1(1-q 3)1-q +a 1(1-q 6)1-q =2×a 1(1-q 9)1-q ,得2-q 3-q 6=2-2q 9, ∴2q 9-q 6-q 3=0,解得q 3=-12或q 3=1(舍去)或q 3=0(舍去),∴q =3-12=-342. 9.在等比数列{a n }中,a 2-a 1=2,且2a 2为3a 1和a 3的等差中项,求数列{a n }的首项、公比及前n 项和.解 设数列{a n }的公比为q (q ≠0).由已知可得⎩⎪⎨⎪⎧a 1q -a 1=2,4a 1q =3a 1+a 1q 2,所以⎩⎪⎨⎪⎧a 1(q -1)=2, ①q 2-4q +3=0, ②解②得q =3或q =1. 由于a 1(q -1)=2,因此q =1不符合题意,应舍去. 故公比q =3,首项a 1=1.所以数列{a n }的前n 项和S n =a 1(1-q n )1-q =1×(1-3n )1-3=3n -12(n ∈N *).10.设数列{a n }满足a 1+3a 2+32a 3+…+3n -1a n =n 3,n ∈N *.(1)求数列{a n }的通项公式;(2)设b n =na n ,求数列{b n }的前n 项和S n .解 (1)∵a 1+3a 2+32a 3+…+3n -1a n =n 3,∴a 1+3a 2+32a 3+…+3n -2a n -1=n -13(n ≥2),两式相减得3n -1a n =n 3-n -13=13(n ≥2),∴a n =13n (n ≥2).验证当n =1时,a 1=13也满足上式,故a n =13n (n ∈N *).(2)∵b n =na n=n ·3n ,∴S n =1×3+2×32+3×33+…+n ·3n ,①①×3,得3S n =1×32+2×33+3×34+…+n ·3n +1,② 由①-②,得-2S n =3+32+33+…+3n -n ·3n +1, 即-2S n =3-3n +11-3-n ·3n +1,∴S n =2n -14·3n +1+34(n ∈N *).11.在等比数列{a n }中,a 1=4,q =5,则使S n >107的最小正整数n 的值是( ) A .11 B .10 C .12 D .9答案 A解析 由题意可知在等比数列{a n }中,a 1=4,q =5, ∴S n =4·(1-5n )1-5=5n-1.∵S n >107,∴5n -1>107,∴n >10.01,∵n 为正整数,∴n ≥11,故n 的最小值为11.12.已知等比数列{a n }的前n 项和为S n ,a 4-a 1=78,S 3=39.设b n =log 3a n ,那么数列{b n }的前10项和为( ) A .log 371 B.692 C .50 D .55答案 D解析 设等比数列{a n }的公比为q ,由a 4-a 1=78,S 3=39,得⎩⎪⎨⎪⎧a 1q 3-a 1=78,a 1+a 1q +a 1q 2=39,两式作比得q -1=2,即q =3,∴a 1(33-1)=78,则a 1=3,∴a n =a 1q n -1=3·3n -1=3n ,∴b n =log 3a n =log 33n =n ,则数列{b n }的前10项和为1+2+3+…+10=(1+10)×102=55.13.已知正项数列{a n }满足a 2n +1-6a 2n =a n +1a n .若a 1=2,则数列{a n }的前n 项和S n =________. 答案 3n -1,n ∈N *解析 ∵a 2n +1-6a 2n =a n +1a n ,∴(a n +1-3a n )(a n +1+2a n )=0. ∵a n >0,∴a n +1=3a n . 又a 1=2,∴{a n }是首项为2,公比为3的等比数列, ∴S n =2(1-3n )1-3=3n-1,n ∈N *.14.已知数列{a n }的前n 项和为S n ,a 1=1,2S n =a n +1-1,则S n =________. 答案 3n -12解析 当n =1时,则有2S 1=a 2-1, ∴a 2=2S 1+1=2a 1+1=3;当n ≥2时,由2S n =a n +1-1得出2S n -1=a n -1,上述两式相减得2a n =a n +1-a n ,∴a n +1=3a n ,得a n +1a n =3且a 2a 1=3,所以数列{a n }是以1为首项,以3为公比的等比数列,则a n =1×3n -1=3n -1,a n +1=3n , 那么2S n =a n +1-1=3n-1,因此,S n =3n -12.15.在等比数列{a n }中,对任意n ∈N *,a 1+a 2+…+a n =2n -1,则a 21+a 22+…+a 2n 等于( )A .(2n-1)2B.(2n -1)23 C .4n-1 D.4n -13答案 D解析 ∵a 1+a 2+…+a n =2n -1,∴a 1=21-1=1. ∵a 1+a 2=1+a 2=22-1=3,∴a 2=2,∴{a n }的公比为2.∴{a 2n }的公比为4,首项为a 21=1. ∴a 21+a 22+…+a 2n =a 21(1-4n )1-4=4n-13.16.已知等差数列{a n }满足a 2=0,a 6+a 8=-10. (1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和.解 (1)设等差数列{a n }的公差为d ,由已知条件可得⎩⎪⎨⎪⎧ a 1+d =0,2a 1+12d =-10,解得⎩⎪⎨⎪⎧a 1=1,d =-1.故数列{a n }的通项公式为a n =2-n ,n ∈N *.(2)设数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和为S n ,即S n =a 1+a 22+…+a n2n -1,①S n 2=a 12+a 24+…+a n -12n -1+a n 2n .② 所以,当n >1时,①-②得 S n2=a 1+a 2-a 12+…+a n -a n -12n -1-a n 2n =1-⎝⎛⎭⎫12+14+…+12n -1-2-n 2n=1-⎝⎛⎭⎫1-12n -1-2-n 2n =n 2n .所以S n =n2n -1,当n =1时也成立.综上所述,数列⎩⎨⎧⎭⎬⎫a n 2n -1的前n 项和S n =n2n -1,n ∈N *.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.五个量n,a1,q,an,Sn中,解决“知三求二” 问题.
【即时练习】 等比数列1,a,a2,a3,…的前n项和为(
a 1- an- 1 A. 1+ 1- a an+1- 1 C. a- 1 1- an B. 1- a D.以上皆错
)
【解析】选 D.要考虑到公比为1的情况,此时Sn = n.
5.(2014·福建高考)在等比数列{an}中, a2 = 3 , a5=81. (1)求 an. (2)设 bn=log3an,求数列{bn}的前 n 项和 Sn.
【解析】(1)设{an}的公比为 q,依题意得
a 1 q = 3 , a 1 = 1 , 4 解得 a1q =81, q=3.
1.掌握等比数列的前n项和公式.(重点)
2.掌握前n项和公式的推导方法.(重点)
3.对前n项和公式能进行简单应用.(难点)
探究:等比数列的前n项和公式 S1=a1
S2=a1+a2=a1+a1q
=a1(1+q)
S3=a1+a2+a3=a1+a1q +a1q2
=a1(1+q+q2) S4=a1+a2+a3+a4=a1+a1q+a1q2+a1q3 =a1(1+q+q2+q3)
观察:
S2
a1 (1 q )(1 q ) 1 q
2
a1 (1 q 2 ) 1 q
S3
a1 (1 q q )(1 q ) 1 q
a1 (1 q ) 1 q
3
a1 (1 q n ) 猜想得:S n ( q 1) 1 q
Sn= a1+a1q+a1q2+a1q3+„+a1qn-2+a1qn-1 qSn= a1q+a1q2+a1q3+„+a1qn-2+a1qn-1 +a1qn ①-②得: Sn(1-q)=a1-a1qn
① ②
a1 (1 q ) . 当q≠1时,S n 1 q
n
, q 1 na1 等比数列{an}的前n项和 S n a1 (1 q n ) 1 q . q 1
有了上述公式,就可以解决开头提出的问题了, 问题1:a1=1,q=2,n=64.可得:
1 (1-2 64 ) 64 =2 -1(粒 )=18 446 744 073 709 551 615( 粒) S64= 1-2
1 5 n+ 1 从而 Sn= ×5 - 或 Sn= 4 4
11
.
1.数列{2n-1}的前99项和为 ( C )
A.2100-1
C.299-1
B.1-2100
D.1-299
【解析】选 C.a1=1,q=2, 1×1-299 ∴S99= =299-1. 1- 2
2.若等比数列{an}的前3项的和为13,首项为1,则 3或-4 . 其公比为__________
估计千粒麦子的质量约为40g,那么麦粒的总质量超
过了7 000亿吨,因此,国王不能实现他的诺言.
等比数列的前n项和公式
, q 1 na1 S n a1 (1 q n ) 1 q . q 1
1.注意q=1与q≠1两种情形
a1 ( 1 q n ) a1 a n q Sn 2.q≠1时, 1 q 1 q
2.5 等比数列的前n项和 第1课时 等比数列的前n项和
传说在很久以前,古印度舍罕王在宫廷单调
的生活中,发现了64格棋(也就是现在的国际象 棋)的有趣和奥妙, 决定要重赏发明人— —他的宰相西萨•班• 达依尔,让他随意选 择奖品.
宰相要求的赏赐是:在棋盘的第一格内赏他一 粒麦子,第二格内赏他两粒麦子,第三格内赏他 四粒麦子„„依此 ? 类推,每一格上的 麦子数都是前一格 的两倍,国王一听, 几粒麦子,加起来 也不过一小袋,他 就答应了宰相的要 求.实际上国王能 满足宰相的要求吗?
1-q3 【解析】 由题知 = 13,1 + q + q2 = 13, q2 + q 1-q -12=0,所以 q=3 或 q=-4. 答案:3 或-4
3. (2015· 全国卷Ⅰ) 数列 an 中 a1 2, an 1 2an , S n 为 an 的 前 n 项和,若 S n 126 ,则 n= .
例 求下列等比数列前8项的和: 1 1 1 (1) , , , . 2 4 8 1 (2)a1=27,a 9= ,q < 0. 243 1 1 解 : 1因为a1 = ,q = ,n = 8, 2 2 8 8 1 1 1 1 1- 1- 8 2 2 2 2 1 255 所以S8 = = = 1- = . 1 1 2 256 12 2
公 比
等 比 数 列 前 n 项 和
适用公式
q=1
Sn na1 (a1 0)
a1 1 q n 1 q
Sn
(a1 0,q 0)
q≠1
a1 a n q Sn (a1 0,q 0) 1 q
勤奋可以弥补聪明的不足,但聪明无法弥 补懒惰的缺陷。
因此,an=3
n- 1
.
(2)因为 bn=log3an=n-1, 所以数列{bn}为等差数列,其前 n 项和 Sn=
n ( b1+ bn) n - n
2 = 2
2
.
Sn = a1 + a2 + 鬃 ? an
错位相减法
二
知 三 求
通项 公式
a1 , q, n an , S n
求和 公式
等比数列的前n项和公式
【变式练习】 在等比数列{an}中,S2=30,S3=155,求Sn;
a11+q=30, 解:(1)由题意知 2 a11+q+q =155, a1=5, 解得 q=5
பைடு நூலகம்
a =180, 1 或 5 q=- , 6 1
5 n 080×1--6
1 1 8 2 由a = 27,a = ,可得 =27× q , 1 9 243 243 又由q < 0,可得 1 q=- , 3 1 8 27 1- - 3 1 640 于是当n = 8时,S8 = = . 81 1 1- - 3
【解析】∵ a1 2, an 1 2an ,∴数列 an 是首项为 2,公比为 2 的等比数列,
2(1 2n ) n Sn 126 ∴ ,∴ 2 1 2
64 ,∴n=6.
答案:6
4.2+(2+22)+(2+22+23)+„+(2+22+23+„+210) 212-24 =__________.
