过渡教材(学案)
高中生物选修1(新教材)精品学案1:4-1-免疫系统的组成和功能 人教版

免疫系统的组成和功能〖学习目标〗1.举例说明免疫细胞、免疫器官和免疫活性物质等是免疫调节的结构与物质基础。
2.概述人体的免疫包括生来就有的非特异性免疫和后天获得的特异性免疫。
〖学习过程〗一、免疫系统的组成1.免疫器官(1)组成:主要由组织构成,并借助于相互联系。
(2)5种免疫器官的比较(3) 是免疫细胞产生并发育成熟的地方;是免疫细胞集中分布的场所。
2.免疫细胞(1)概念:执行功能的细胞,包括各种类型的白细胞。
(2)来源:来自。
(3)三种免疫细胞的比较②树突状细胞:分布于皮肤、消化道、呼吸道等很多内,成熟时具有,具有强大的功能。
③巨噬细胞:几乎分布于机体的各种组织中,具有功能。
(4)抗原呈递细胞:包括。
(5)抗原:能引发的物质。
3.免疫活性物质(1)概念:由产生的、并发挥作用的物质。
(2)代表①抗体:机体产生的专门应对抗原的。
②溶菌酶。
③细胞因子:由淋巴细胞分泌,包括、干扰素、肿瘤坏死因子等。
二、免疫系统的功能1.人体的三道防线(1)第一道防线:皮肤、黏膜等。
(2)第二道防线:体液中的和等。
第一道防线和第二道防线参与非特异性免疫。
非特异性免疫的来源和特点是:①来源:机体在长期过程中遗传下来的,人人生来就有的防御功能。
②特点:不针对某一类特定的,而是对多种都有防御作用。
(3)第三道防线:机体在个体发育过程中与接触后获得的,主要针对特定的起作用,因而具有性,叫作免疫。
2.免疫系统的功能(1) :机体排除外来的一种免疫防护作用。
这是免疫系统最基本的功能。
(2) :是指机体,进行自身调节,维持内环境稳态的功能。
(3) :是指机体,防止肿瘤发生的功能。
探究:1.艾滋病人因左脚被铁钉扎伤后感染了破伤风。
该患者治疗破伤风的时间比正常人要长,原因是?2.免疫活性物质均是由免疫细胞产生的吗?试举例说明。
3.溶菌酶杀菌一定为第二道防线吗?为什么?重点归纳:1.免疫系统的组成2.免疫细胞的起源和分化3.抗原与抗体的区别1.B细胞分化成熟的部位是()A.骨髓B.胸腺C.淋巴结D.扁桃体2.人体的主要免疫器官包括()A.肝脏、淋巴结、脾B.胸腺、脾、淋巴结C.心脏、肺、胰腺D.胸腺、胃腺、唾液腺3.人的胃液能杀灭所吃食物中90%的病原体,这种免疫机能属于人体的()A.第一道防线B.第二道防线C.第三道防线D.第四道防线4.(多选)以下内容属于免疫系统的基本功能的是()A.免疫防御B.免疫自稳C.免疫监视D.免疫效应5.如图是人体防御外界病原体侵染的三道免疫防线的示意图,其中①~⑦表示免疫细胞,⑧和⑨表示免疫活性物质。
新教材 人教A版高中数学选择性必修第一册全册优秀学案(知识点考点汇总及配套习题,含解析)

人教A版高中数学选择性必修第一册全册学案第一章空间向量与立体几何........................................................................................................ - 2 -1.1空间向量及其运算......................................................................................................... - 2 -1.1.1空间向量及其线性运算...................................................................................... - 2 -1.1.2空间向量的数量积运算.................................................................................... - 16 -1.2空间向量基本定理....................................................................................................... - 29 -1.3空间向量及其运算的坐标表示................................................................................... - 38 -1.3.1空间直角坐标系................................................................................................ - 38 -1.3.2空间运算的坐标表示........................................................................................ - 46 -1.4空间向量的应用 .......................................................................................................... - 59 -1.4.1用空间向量研究直线、平面的位置关系........................................................ - 59 -第1课时空间向量与平行关系........................................................................ - 59 -第2课时空间向量与垂直关系........................................................................ - 69 -1.4.2用空量研究距离、夹角问题............................................................................ - 79 -章末总结 ............................................................................................................................... - 97 - 第二章直线和圆的方程............................................................................................................ - 113 -2.1直线的倾斜角与斜率................................................................................................. - 113 -2.1.1倾斜角与斜率 ................................................................................................. - 113 -2.1.2两条直线平行和垂直的判定.......................................................................... - 121 -2.2直线的方程 ................................................................................................................ - 131 -2.2.1直线点斜式方程.............................................................................................. - 131 -2.2.2直线的两点式方程.......................................................................................... - 137 -2.2.3直线的一般式方程.......................................................................................... - 145 -2.3直线的交点坐标与距离公式..................................................................................... - 154 -2.3.1两条直线的交点坐标...................................................................................... - 154 -2.3.2两点间的距离公式.......................................................................................... - 154 -2.3.3点到直线的距离公式...................................................................................... - 163 -2.3.4两条平行直线间的距离.................................................................................. - 163 -2.4圆的方程 .................................................................................................................... - 171 -2.4.1圆的标准方程 ................................................................................................. - 171 -2.4.2圆的一般方程 ................................................................................................. - 180 -2.5直线与圆、圆与圆的位置关系................................................................................. - 188 -2.5.1直线与圆的位置关系...................................................................................... - 188 -2.5.2圆与圆的位置关系.......................................................................................... - 199 -章末复习 ............................................................................................................................. - 208 - 第三章圆锥曲线的方程............................................................................................................ - 222 -3.1椭圆 ............................................................................................................................ - 222 -3.1.1椭圆及其标准方程.......................................................................................... - 222 -3.1.2椭圆的简单几何性质...................................................................................... - 234 -第1课时椭圆的简单几何性质...................................................................... - 234 -第2课时椭圆的标准方程及性质的应用...................................................... - 244 -3.2双曲线 ........................................................................................................................ - 256 -3.2.1双曲线及其标准方程...................................................................................... - 256 -3.2.2双曲线的简单几何性质.................................................................................. - 267 -3.3抛物线 ........................................................................................................................ - 281 -3.3.1抛物线及其标准方程...................................................................................... - 281 -3.3.2抛物线的简单几何性质.................................................................................. - 291 -章末复习 ............................................................................................................................. - 303 - 全书复习 ..................................................................................................................................... - 316 -第一章空间向量与立体几何1.1空间向量及其运算1.1.1空间向量及其线性运算学习目标核心素养1.理解空间向量的概念.(难点)2.掌握空间向量的线性运算.(重点)3.掌握共线向量定理、共面向量定理及推论的应用.(重点、难点) 1.通过空间向量有关概念的学习,培养学生的数学抽象核心素养.2.借助向量的线性运算、共线向量及共面向量的学习,提升学生的直观想象和逻辑推理的核心素养.国庆期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观赏黄浦江,然后抵达东方明珠(B)游玩,如图1,游客的实际位移是什么?可以用什么数学概念来表示这个过程?图1图2如果游客还要登上东方明珠顶端(D)俯瞰上海美丽的夜景,如图2,那么他实际发生的位移是什么?又如何表示呢?1.空间向量(1)定义:在空间,具有大小和方向的量叫做空间向量. (2)长度或模:空间向量的大小. (3)表示方法:①几何表示法:空间向量用有向线段表示;②字母表示法:用字母a ,b ,c ,…表示;若向量a 的起点是A ,终点是B ,也可记作:AB →,其模记为|a |或|AB →|.2.几类常见的空间向量名称方向 模 记法 零向量任意 0 0 单位向量任意 1 相反向量相反 相等 a 的相反向量:-a AB →的相反向量:BA → 相等向量 相同 相等 a =b3.(1)向量的加法、减法空间向量的运算 加法 OB →=OA →+OC →=a +b减法 CA →=OA →-OC →=a -b 加法运算律 ①交换律:a +b =b +a②结合律:(a +b )+c =a +(b +c )①定义:实数λ与空间向量a 的乘积λa 仍然是一个向量,称为向量的数乘运算.当λ>0时,λa 与向量a 方向相同;当λ<0时,λa 与向量a 方向相反;当λ=0时,λa =0;λa 的长度是a 的长度的|λ|倍.②运算律a .结合律:λ(μa )=μ(λa )=(λμ)a .b .分配律:(λ+μ)a =λa +μa ,λ(a +b )=λa +λb .思考:向量运算的结果与向量起点的选择有关系吗?[提示] 没有关系.4.共线向量(1)定义:表示若干空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量. (2)方向向量:在直线l 上取非零向量a ,与向量a 平行的非零向量称为直线l 的方向向量.规定:零向量与任意向量平行,即对任意向量a ,都有0∥a .(3)共线向量定理:对于空间任意两个向量a ,b (b ≠0),a ∥b 的充要条件是存在实数λ使a =λb .(4)如图,O 是直线l 上一点,在直线l 上取非零向量a ,则对于直线l 上任意一点P ,由数乘向量定义及向量共线的充要条件可知,存在实数λ,使得OP →=λa .5.共面向量(1)定义:平行于同一个平面的向量叫做共面向量. (2)共面向量定理:若两个向量a ,b 不共线,则向量p 与向量a ,b 共面的充要条件是存在唯一的有序实数对(x ,y ),使p =x a +y b .(3)空间一点P 位于平面ABC 内的充要条件:存在有序实数对(x ,y ), 使AP →=xAB →+yAC →或对空间任意一点O ,有OP →=OA →+xAB →+yAC →.思考:(1)空间中任意两个向量一定是共面向量吗?(2)若空间任意一点O 和不共线的三点A ,B ,C ,满足OP →=13OA →+13OB →+13OC →,则点P 与点A ,B ,C 是否共面?[提示] (1)空间中任意两个向量都可以平移到同一个平面内,成为同一个平面的两个向量,因此一定是共面向量.(2)由OP →=13OA →+13OB →+13OC →得OP →-OA →=13(OB →-OA →)+13(OC →-OA →)即AP →=13AB →+13AC →,因此点P 与点A ,B ,C 共面.1.思考辨析(正确的打“√”,错误的打“×”)(1)空间向量a ,b ,c ,若a ∥b ,b ∥c ,则a ∥c .( ) (2)相等向量一定是共线向量.( ) (3)三个空间向量一定是共面向量.( ) (4)零向量没有方向.( )[提示] (1)× 若b =0时,a 与c 不一定平行.(2)√ 相等向量一定共线,但共线不一定相等.(3)× 空间两个向量一定是共面向量,但三个空间向量可能是共面的,也可以是不共面的.(4)× 零向量有方向,它的方向是任意的.2.如图所示,在四棱柱ABCD -A 1B 1C 1D 1所有的棱中,可作为直线A 1B 1的方向向量的有( )A .1个B .2个C .3个D .4个D [共四条AB ,A 1B 1,CD ,C 1D 1.]3.点C 在线段AB 上,且|AB |=5,|BC |=3,AB →=λBC →,则λ=________. -53 [因为C 在线段AB 上,所以AB →与BC →方向相反,又因|AB |=5,|BC |=3,故λ=-53.]4.在三棱锥A -BCD 中,若△BCD 是正三角形,E 为其中心,则AB →+12BC →-32DE →-AD →化简的结果为________.0 [延长DE 交边BC 于点F ,连接AF ,则有AB →+12BC →=AF →,32DE →+AD →=AD→+DF →=AF →,故AB →+12BC →-32DE →-AD →=0.]空间向量的有关概念①若|a |=|b |,则a =b 或a =-b ;②若向量a 是向量b 的相反向量,则|a |=|b |;③在正方体ABCD -A 1B 1C 1D 1中,AC →=A 1C 1→;④若空间向量m ,n ,p 满足m =n ,n =p ,则m =p .其中正确命题的序号是________.(2)如图所示,在平行六面体ABCD -A ′B ′C ′D ′中,顶点连接的向量中,与向量AA ′→相等的向量有________;与向量A ′B ′→相反的向量有________.(要求写出所有适合条件的向量)(1)②③④ (2)BB ′→,CC ′→,DD ′→ B ′A ′→,BA →,CD →,C ′D ′→ [(1)对于①,向量a 与b 的方向不一定相同或相反,故①错;对于②,根据相反向量的定义知|a |=|b |,故②正确;对于③,根据相等向量的定义知,AC →=A 1C 1→,故③正确;对于④,根据相等向量的定义知正确.(2)根据相等向量的定义知,与向量AA ′→相等的向量有BB ′→,CC ′→,DD ′→.与向量A ′B ′→相反的向量有B ′A ′→,BA →,CD →,C ′D ′→.]解答空间向量有关概念问题的关键点及注意点(1)关键点:紧紧抓住向量的两个要素,即大小和方向.(2)注意点:注意一些特殊向量的特性.①零向量不是没有方向,而是它的方向是任意的,且与任何向量都共线,这一点说明了共线向量不具备传递性.②单位向量方向虽然不一定相同,但它们的长度都是1.③两个向量模相等,不一定是相等向量;反之,若两个向量相等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相反,则它们为相反向量. [跟进训练]1.下列关于空间向量的命题中,正确命题的个数是( )①长度相等、方向相同的两个向量是相等向量;②平行且模相等的两个向量是相等向量;③若a ≠b ,则|a |≠|b |;④两个向量相等,则它们的起点与终点相同.A .0B .1C .2D .3B [根据向量的定义,知长度相等、方向相同的两个向量是相等向量,①正确;平行且模相等的两个向量可能是相等向量,也可能是相反向量,②不正确;当a =-b 时,也有|a |=|b |,③不正确;只要模相等、方向相同,两个向量就是相等向量,与向量的起点与终点无关,④不正确.综上可知只有①正确,故选B.]空间向量的线性运算 1111为向量AC 1→的有( )①(AB →+BC →)+CC 1→;②(AA 1→+A 1D 1→)+D 1C 1→;③(AB →+BB 1→)+B 1C 1→;④(AA 1→+A 1B 1→)+B 1C 1→.A .1个B .2个C .3个D .4个(2)已知正四棱锥P -ABCD ,O 是正方形ABCD 的中心,Q 是CD 的中点,求下列各式中x ,y ,z 的值.①OQ →=PQ →+yPC →+zP A →;②P A →=xPO →+yPQ →+PD →.[思路探究] (1)合理根据向量的三角形和平行四边形法则,以及在平行六面体中,体对角线向量等于从同一起点出发的三条棱向量的和.如AC 1→=AB →+AD →+AA 1→.(2)根据数乘向量及三角形或平行四边形法则求解.(1)D [对于①,(AB →+BC →)+CC 1→=AC →+CC 1→=AC 1→;对于②,(AA 1→+A 1D 1→)+D 1C 1→=AD 1→+D 1C 1→=AC 1→;对于③,(AB →+BB 1→)+B 1C 1→=AB 1→+B 1C 1→=AC 1→;对于④,(AA 1→+A 1B 1→)+B 1C 1→=AB 1→+B 1C 1→=AC 1→.](2)[解] ①如图,∵OQ →=PQ →-PO →=PQ →-12(P A →+PC →)=PQ →-12PC →-12P A →,∴y =z =-12.②∵O 为AC 的中点,Q 为CD 的中点,∴P A →+PC →=2PO →,PC →+PD →=2PQ →,∴P A →=2PO →-PC →,PC →=2PQ →-PD →,∴P A →=2PO →-2PQ →+PD →,∴x =2,y =-2.1.空间向量加法、减法运算的两个技巧(1)巧用相反向量:向量减法的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.(2)巧用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得运算结果.2.利用数乘运算进行向量表示的技巧(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质. [跟进训练] 2.已知空间四边形ABCD ,连接AC ,BD ,设M ,G 分别是BC ,CD 的中点,则MG →-AB →+AD →等于( )A .32DB → B .3MG →C .3GM →D .2MG →B [MG →-AB →+AD →=MG →-(AB →-AD →)=MG →-DB →=MG →+BD →=MG →+2MG →=3MG →.]共线问题【例3】 (1)设e 1,e 2是空间两个不共线的向量,已知AB =e 1+k e 2,BC =5e 1+4e 2,DC →=-e 1-2e 2,且A ,B ,D 三点共线,实数k =________.(2)如图所示,已知四边形ABCD ,ABEF 都是平行四边形且不共面,M ,N 分别是AC ,BF 的中点,判断CE →与MN →是否共线.[思路探究] (1)根据向量共线的充要条件求解.(2)根据数乘向量及三角形法则,把MN →表示成λCE →的形式,再根据向量共线的充要条件求解.(1)1 [AD →=AB →+BC →+CD →=(e 1+k e 2)+(5e 1+4e 2)+(e 1+2e 2)=7e 1+(k +6)e 2. 设AD →=λAB →,则7e 1+(k +6)e 2=λ(e 1+k e 2),所以⎩⎨⎧ λ=7λk =k +6,解得k =1.] (2)[解] 法一:因为M ,N 分别是AC ,BF 的中点,且四边形ABCD ,四边形ABEF 都是平行四边形,所以MN →=MA →+AF →+FN →=12CA →+AF →+12FB →.又因为MN →=MC →+CE →+EB →+BN →=-12CA →+CE →-AF →-12FB →,以上两式相加得CE →=2MN →,所以CE →∥MN →,即CE →与MN →共线.法二:因为四边形ABEF 为平行四边形,所以连接AE 时,AE 必过点N . ∴CE →=AE →-AC →=2AN →-2AM →=2(AN →-AM →)=2MN →.所以CE →∥MN →,即CE →与MN →共线.证明空间三点共线的三种思路对于空间三点P ,A ,B 可通过证明下列结论来证明三点共线.(1)存在实数λ,使P A →=λPB →成立.(2)对空间任一点O ,有OP →=OA →+tAB →(t ∈R ).(3)对空间任一点O ,有OP →=xOA →+yOB →(x +y =1).[跟进训练]3.如图,在正方体ABCD -A 1B 1C 1D 1中,E 在A 1D 1上,且A 1E →=2ED 1→,F 在对角线A 1C 上,且A 1F →=23FC →.求证:E ,F ,B 三点共线.[证明] 设AB →=a ,AD →=b ,AA 1→=c , 因为A 1E →=2ED 1→,A 1F →=23FC →, 所以A 1E →=23A 1D 1→,A 1F →=25A 1C →, 所以A 1E →=23AD →=23b ,A 1F →=25(AC →-AA 1→)=25(AB →+AD →-AA 1→)=25a +25b -25c ,所以EF →=A 1F →-A 1E →=25a -415b -25c =25⎝ ⎛⎭⎪⎫a -23b -c .又EB →=EA 1→+A 1A →+AB →=-23b -c +a =a -23b -c , 所以EF →=25EB →,所以E ,F ,B 三点共线.向量共面问题1.什么样的向量算是共面向量?[提示] 能够平移到同一个平面内的向量称为共面向量. 2.能说明P ,A ,B ,C 四点共面的结论有哪些? [提示] (1)存在有序实数对(x ,y ),使得AP →=xAB →+yAC →.(2)空间一点P 在平面ABC 内的充要条件是存在有序实数组(x ,y ,z )使得OP →=xOA →+yOB →+zOC →(其中x +y +z =1).(3)四点中任意两点的方向向量与另外两点的方向向量共线,如P A →∥BC →.3.已知向量a ,b ,c 不共面,且p =3a +2b +c ,m =a -b +c ,n =a +b -c ,试判断p ,m ,n 是否共面.[提示] 设p =x m +y n ,即3a +2b +c =x (a -b +c )+ y (a +b -c )=(x +y )a +(-x +y )b +(x -y )c .因为a ,b ,c 不共面,所以⎩⎨⎧x +y =3,-x +y =2,x -y =1,而此方程组无解,所以p 不能用m ,n 表示,即p ,m ,n 不共面.【例4】 已知A ,B ,C 三点不共线,O 为平面ABC 外一点,若点M 满足OM →=13OA →+13OB →+13OC →.(1)判断MA →,MB →,MC →三个向量是否共面; (2)判断M 是否在平面ABC 内.[思路探究] (1)根据向量共面的充要条件,即判断是否MA →=xMB →+yMC →;(2)根据(1)的结论,也可以利用OM →=xOA →+yOB →+zOC →中x +y +z 是否等于1.[解] (1)∵OA →+OB →+OC →=3OM →, ∴OA →-OM →=(OM →-OB →)+(OM →-OC →), ∴MA →=BM →+CM →=-MB →-MC →, ∴向量MA →,MB →,MC →共面.(2)由(1)知向量MA →,MB →,MC →共面,而它们有共同的起点M ,且A ,B ,C 三点不共线,∴M ,A ,B ,C 共面,即M 在平面ABC 内.1.[变条件]若把本例中条件“OM →=13OA →+13OB →+13OC →”改为“OA →+2OB →=6OP →-3OC →”,点P 是否与点A 、B 、C 共面.[解] ∵3OP →-3OC →=OA →+2OB →-3OP →=(OA →-OP →)+(2OB →-2OP →),∴3CP →=P A →+2PB →,即P A →=-2PB →-3PC →.根据共面向量定理的推论知:点P 与点A ,B ,C 共面.2.[变条件]若把本例条件变成“OP →+OC →=4OA →-OB →”,点P 是否与点A 、B 、C 共面.[解] 设OP →=OA →+xAB →+yAC →(x ,y ∈R ),则 OA →+xAB →+yAC →+OC →=4OA →-OB →,∴OA →+x (OB →-OA →)+y (OC →-OA →)+OC →=4OA →-OB →, ∴(1-x -y -4)OA →+(1+x )OB →+(1+y )OC →=0,由题意知OA →,OB →,OC →均为非零向量,所以x ,y 满足:⎩⎨⎧1-x -y -4=0,1+x =0,1+y =0,显然此方程组无解,故点P 与点A ,B ,C 不共面.3.[变解法]上面两个母题探究,还可以用什么方法判断? [解] (1)由题意知,OP →=16OA →+13OB →+12OC . ∵16+13+12=1,∴点P 与点A 、B 、C 共面. (2)∵OP →=4OA →-OB →-OC →,而4-1-1=2≠1. ∴点P 与点A 、B 、C 不共面.解决向量共面的策略(1)若已知点P 在平面ABC 内,则有AP →=xAB →+yAC →或OP →=xOA →+yOB →+zOC →(x +y +z =1),然后利用指定向量表示出已知向量,用待定系数法求出参数.(2)证明三个向量共面(或四点共面),需利用共面向量定理,证明过程中要灵活进行向量的分解与合成,将其中一个向量用另外两个向量来表示.1.一些特殊向量的特性(1)零向量不是没有方向,而是它的方向是任意的. (2)单位向量方向虽然不一定相同,但它们的长度都是1.(3)两个向量模相等,不一定是相等向量,反之,若两个向量相等,则它们不仅模相等,方向也相同.若两个向量模相等,方向相反,则它们为相反向量.2.OP →=OA →+xAB →+yAC →称为空间平面ABC 的向量表达式.由此可知空间中任意平面由空间一点及两个不共线向量唯一确定.3.证明(或判断)A ,B ,C 三点共线时,只需证明存在实数λ,使AB →=λBC →(或AB →=λAC →)即可,也可用“对空间任意一点O ,有OC →=tOA →+(1-t )OB →”来证明A ,B ,C 三点共线.4.空间一点P 位于平面MAB 内的充要条件是存在有序实数对(x ,y ),使MP →=xMA →+yMB →,满足这个关系式的点都在平面MAB 内;反之,平面MAB 内的任一点都满足这个关系式.这个充要条件常用于证明四点共面.5.直线的方向向量是指与直线平行或共线的非零向量,一条直线的方向向量有无穷多个,它们的方向相同或相反.6.向量p 与向量a ,b 共面的充要条件是在a 与b 不共线的前提下才成立的,若a 与b 共线,则不成立.1.下列条件中使M 与A ,B ,C 一定共面的是( ) A .OM →=2OA →-OB →-OC → B .OM →=15OA →+13OB →+12OC → C .MA →+MB →+MC →=0 D .OM →+OA →+OB →+OC →=0C [由MA →+MB →+MC →=0得MA →=-MB →-MC →,故M ,A ,B ,C 共面.] 2.已知正方体ABCD -A 1B 1C 1D 1,若点F 是侧面CD 1的中心,且AF →=AD →+mAB→-nAA 1→,则m ,n 的值分别为( )A .12,-12 B .-12,-12 C .-12,12D .12,12A [由于AF →=AD →+DF →=AD →+12(DC →+DD 1→)=AD →+12AB →+12AA 1→,所以m =12,n =-12,故答案为A.]3.化简:12(a +2b -3c )+5⎝ ⎛⎭⎪⎫23a -12b +23c -3(a -2b +c )=________. 56a +92b -76c [原式=12a +b -32c +103a -52b +103c -3a +6b -3c =⎝ ⎛⎭⎪⎫12+103-3a +⎝ ⎛⎭⎪⎫1-52+6b +⎝ ⎛⎭⎪⎫-32+103-3c =56a +92b -76c .] 4.给出下列四个命题:①方向相反的两个向量是相反向量;②若a ,b 满足|a |>|b |且a ,b 同向,则a >b ; ③不相等的两个空间向量的模必不相等; ④对于任何向量a ,b ,必有|a +b |≤|a |+|b |. 其中正确命题的序号为________.④ [对于①,长度相等且方向相反的两个向量是相反向量,故①错;对于②,向量是不能比较大小的,故不正确;对于③,不相等的两个空间向量的模也可以相等,故③错;只有④正确.]5.设两非零向量e 1,e 2不共线,且k e 1+e 2与e 1+k e 2共线,求k 的值. [解] ∵两非零向量e 1,e 2不共线,且k e 1+e 2与e 1+k e 2共线,∴k e 1+e 2=t (e 1+k e 2),则(k -t )e 1+(1-tk )e 2=0.∵非零向量e 1,e 2不共线,∴k -t =0,1-kt =0,解得k =±1.1.1.2 空间向量的数量积运算学习 目 标核心 素 养1.掌握空间向量夹角的概念及表示方法.2.掌握空间向量的数量积的定义、性质、运算律及计算方法.(重点)3.掌握投影向量的概念.(重点)4.能用向量的数量积解决立体几何问题.(难点)1.通过学习空间向量的数量积运算,培养学生数学运算的核心素养.2.借助投影向量概念的学习,培养学生直观想象和逻辑推理的核心素养.3.借助利用空间向量数量积证明垂直关系、求夹角和距离运算,提升学生的逻辑推理和数学运算核心素养.已知两个非零向量a 与b ,在空间任取一点O ,作OA →=a ,OB →=b ,则∠AOB =θ叫做向量a 与b 的夹角.如果a 与b 的夹角为90°,则称a 与b 垂直,记作a ⊥b .已知两个非零向量a 与b ,它们的夹角为θ,把a ·b =|a ||b |cos θ叫做a 与b 的数量积(或内积)类比探究一下:两个空间向量的夹角以及它们的数量积能否像平面向量那样来定义呢?1.空间向量的夹角 (1)夹角的定义已知两个非零向量a ,b ,在空间任取一点O ,作OA →=a ,OB →=b ,则∠AOB 叫做向量a ,b 的夹角,记作〈a ,b 〉.(2)夹角的范围空间任意两个向量的夹角θ的取值范围是[0,π].特别地,当θ=0时,两向量同向共线;当θ=π时,两向量反向共线,所以若a ∥b ,则〈a ,b 〉=0或π;当〈a ,b 〉=π2时,两向量垂直,记作a ⊥b .2.空间向量的数量积(1)定义:已知两个非零向量a ,b ,则|a ||b |cos 〈a ,b 〉叫做a ,b 的数量积,记作a ·b .即a ·b =|a ||b |cos 〈a ,b 〉.规定:零向量与任何向量的数量积为0. (2)常用结论(a ,b 为非零向量) ①a ⊥b ⇔a ·b =0.②a ·a =|a ||a |cos 〈a ,a 〉=|a |2. ③cos 〈a ,b 〉=a ·b|a ||b |. (3)数量积的运算律(2)若a ·b >0,则〈a ,b 〉一定是锐角吗?[提示] (1)若a ·b =0,则不一定有a ⊥b ,也可能a =0或b =0.(2)当〈a ,b 〉=0时,也有a ·b >0,故当a ·b >0时,〈a ·b 〉不一定是锐角. 3.投影向量 (1)投影向量在空间,向量a 向向量b 投影,可以先将它们平移到同一个平面内,进而利用平面上向量的投影,得到与向量b 共线的向量c ,c =|a |cos 〈a ,b 〉b|b |,则向量c 称为向量a 在向量b 上的投影向量,同理向量b 在向量a 上的投影向量是|b |cos 〈a ,b 〉a|a |.(2)向量a 在平面β上的投影向量向量a 向平面β投影,就是分别由向量a 的起点A 和终点B 作平面β的垂线,垂足分别为A ′,B ′,得到向量A ′B ′→,则向量A ′B ′→称为向量a 在平面β上的投影向量.这时,向量a,A ′B ′→的夹角就是向量a 所在直线与平面β所成的角.[提醒] (1)两个向量的数量积是数量,而不是向量,它可以是正数、负数或零; (2)向量数量积的运算不满足消去律、作商和乘法的结合律 ,即a ·b =a ·c ⇒b =c ,a ·b =k ⇒b =k a ,(a ·b )·c =a ·(b·c )都不成立.1.思考辨析(正确的打“√”,错误的打“×”) (1)对于非零向量a ,b ,〈a ,b 〉与〈a ,-b 〉相等. ( ) (2)对于任意向量a ,b ,c ,都有(a ·b )c =a (b ·c ). ( ) (3)若a ·b =b ·c ,且b ≠0,则a =c . ( ) (4)(3a +2b )·(3a -2b )=9|a |2-4|b |2. ( )[提示] (1)× (2)× (3)× (4)√2.(教材P 8练习T 1改编)在正三棱柱ABC -A 1B 1C 1中,若AB =BB 1,则AB 1与BC 1所成角的余弦值为( )A .38B .14C .34D .18B [令底面边长为1,则高也为1,AB 1→=AB →+BB 1→,BC 1→=B C →+CC 1→,∴AB 1→·BC 1→=(AB →+BB 1→)·(BC →+CC 1→)=AB →·BC →+BB 1→·CC 1→=1×1×cos 120°+12=12,又|AB 1→|=|BC 1→|= 2.∴cos 〈AB 1,BC 1〉=122×2=14.故选B.]3.已知a =3p -2q ,b =p +q ,p 和q 是相互垂直的单位向量,则a·b =( ) A .1 B .2 C .3 D .4 A [由题意知,p·q =0,p 2=q 2=1.所以a ·b =(3p -2q )·(p +q )=3p 2+p ·q -2q 2=3-2=1.]4.设a ⊥b ,〈a ,c 〉=π3,〈b ,c 〉=π6,且|a |=1,|b |=2,|c |=3,则向量a +b +c 的模是________.17+63 [因为|a +b +c |2=(a +b +c )2=|a |2+|b |2+|c |2+2(a ·b +a ·c +b ·c )=1+4+9+2⎝ ⎛⎭⎪⎫0+1×3×12+2×3×32=17+63,所以|a +b +c |=17+6 3.]空间向量数量积的运算【例1】 (1)如图,三棱锥A -BCD 中,AB =AC =AD =2,∠BAD =90°,∠BAC=60°,则AB →·CD →等于( )A .-2B .2C .-2 3D .2 3(2)在四面体OABC 中,棱OA ,OB ,OC 两两垂直,且OA =1,OB =2,OC =3,G 为△ABC 的重心,求OG →·(OA →+OB →+OC →)的值.(1)A [∵CD →=AD →-AC →,∴AB →·CD →=AB →·(AD →-AC →)=AB →·AD →-AB →·AC →=0-2×2×cos 60°=-2.](2)[解] OG →=OA →+AG →=OA →+13(AB →+AC →) =OA →+13[(OB →-OA →)+(OC →-OA →)] =13OB →+13OC →+13OA →.∴OG →·(OA →+OB →+OC →)=⎝ ⎛⎭⎪⎫13OB →+13OC →+13OA →·(OA →+OB →+OC →)=13OB →2+13OC →2+13OA →2 =13×22+13×32+13×12=143.在几何体中求空间向量的数量积的步骤(1)首先将各向量分解成已知模和夹角的向量的组合形式.(2)利用向量的运算律将数量积展开,转化成已知模和夹角的向量的数量积. (3)根据向量的方向,正确求出向量的夹角及向量的模. (4)代入公式a·b =|a ||b |cos 〈a ,b 〉求解.[跟进训练]1.在长方体ABCD -A 1B 1C 1D 1中,AB =AA 1=2,AD =4,E 为侧面AA 1B 1B 的中心,F 为A 1D 1的中点,求下列向量的数量积:(1)BC →·ED 1→;(2)BF →·AB 1→.[解] 如图,设AB →=a ,AD →=b ,AA 1→=c ,则|a |=|c |=2,|b |=4,a·b =b·c =c·a =0.(1)BC →·ED 1→=BC →·(EA 1→+A 1D 1→)=b ·12(c -a )+b =|b |2=42=16.(2)BF →·AB 1→=(BA 1→+A 1F →)·(AB →+AA 1→)=c -a +12b ·(a +c )=|c |2-|a |2=22-22=0.利用数量积证明空间垂直关系=OC ,M ,N 分别是OA ,BC 的中点,G 是MN 的中点,求证:OG ⊥BC .[思路探究] 首先把向量OG →和BC →均用OA →、OB →、OC →表示出来,通过证明OG →·BC →=0来证得OG ⊥BC .[证明] 连接ON ,设∠AOB =∠BOC =∠AOC =θ,又设OA →=a ,OB →=b ,OC →=c , 则|a |=|b |=|c |. 又OG →=12(OM →+ON →) =12⎣⎢⎡⎦⎥⎤12OA →+12(OB →+OC →) =14(a +b +c ),BC →=c -b . ∴OG →·BC →=14(a +b +c )·(c -b ) =14(a ·c -a ·b +b ·c -b 2+c 2-b ·c ) =14(|a |2·cos θ-|a |2·cos θ-|a |2+|a |2)=0. ∴OG →⊥BC →,即OG ⊥BC .用向量法证明垂直关系的步骤 (1)把几何问题转化为向量问题; (2)用已知向量表示所证向量;(3)结合数量积公式和运算律证明数量积为0; (4)将向量问题回归到几何问题.[跟进训练]2.如图,四棱锥P -ABCD 中,底面ABCD 为平行四边形,∠DAB =60°,AB =2AD ,PD ⊥底面ABCD .证明:P A ⊥BD .[证明] 由底面ABCD 为平行四边形,∠DAB =60°,AB =2AD 知,DA ⊥BD ,则BD →·DA →=0.由PD ⊥底面ABCD 知,PD ⊥BD ,则BD →·PD →=0.又P A →=PD →+DA →,∴P A →·BD →=(PD →+DA →)·BD →=PD →·BD →+DA →·BD →=0,即P A ⊥BD .夹角问题夹角〈a ,b 〉为( )A .30°B .45°C .60°D .以上都不对(2)如图,在空间四边形OABC 中,OA =8,AB =6,AC =4,BC =5,∠OAC =45°,∠OAB =60°,求异面直线OA 与BC 的夹角的余弦值.[思路探究] (1)根据题意,构造△ABC ,使AB →=c ,AC →=b ,BC →=a ,根据△ABC 三边之长,利用余弦定理求出向量a 与b 之间的夹角即可.(2)求异面直线OA 与BC 所成的角,首先来求OA →与BC →的夹角,但要注意异面直线所成角的范围是⎝ ⎛⎦⎥⎤0,π2,而向量夹角的取值范围为[0,π],注意角度的转化.(1)D [∵a +b +c =0,|a |=2,|b |=3,|c |=4, ∴以这三个向量首尾相连组成△ABC ;令AB →=c ,AC →=b ,BC →=a ,则△ABC 三边之长分别为BC =2,CA =3,AB =4; 由余弦定理,得:cos ∠BCA =BC 2+CA 2-AB 22BC ·CA =22+32-422×2×3=-14, 又向量BC →和CA →是首尾相连,∴这两个向量的夹角是180°-∠BCA , ∴cos 〈a ,b 〉=14,即向量a 与b 之间的夹角〈a ,b 〉不是特殊角.](2)[解] ∵BC →=AC →-AB →,∴OA →·BC →=OA →·AC →-OA →·AB →=|OA →|·|AC →|·cos 〈OA →,AC →〉-|OA →|·|AB →|·cos 〈OA →,AB →〉=8×4×cos 135°-8×6×cos 120° =24-16 2.∴cos 〈OA →,BC →〉=OA →·BC →|OA →|·|BC →|=24-1628×5=3-225,∴异面直线OA 与BC 的夹角的余弦值为3-225.利用向量数量积求夹角问题的思路(1)求两个向量的夹角有两种方法:①结合图形,平移向量,利用空间向量夹角的定义来求,但要注意向量夹角的范围;②先求a ·b ,再利用公式cos 〈a ,b 〉=a ·b|a ||b |求出cos 〈a ,b 〉的值,最后确定〈a ,b 〉的值.(2)求两条异面直线所成的角,步骤如下:①根据题设条件在所求的异面直线上取两个向量(即直线的方向向量); ②将异面直线所成角的问题转化为向量夹角问题; ③利用数量积求向量夹角的余弦值或角的大小;④异面直线所成的角为锐角或直角,利用向量数量积求向量夹角的余弦值时应将余弦值加上绝对值,从而求出异面直线所成的角的大小.[跟进训练]3.如图,在正方体ABCD -A 1B 1C 1D 1中,求BC 1→与AC →夹角的大小.[解] 不妨设正方体的棱长为1,则BC 1→·AC →=(BC →+CC 1→)·(AB →+BC →) =(AD →+AA 1→)·(AB →+AD →)=AD →·AB →+AD →2+AA 1→·AB →+AA 1→·AD → =0+AD 2→+0+0=AD 2→=1, 又∵|BC 1→|=2,|AC →|=2,∴cos 〈BC 1→,AC →〉=BC 1→·AC →|BC 1→||AC →|=12×2=12.∵〈BC 1→,AC →〉∈[0,π],∴〈BC 1→,AC →〉=π3. 即BC 1→与AC →夹角的大小为π3.距离问题1.用数量积解决的距离问题一般有哪几种? [提示] 线段长度即点点距、点线距、点面距. 2.求模的大小常用哪些公式?[提示] 由公式|a |=a ·a 可以推广为|a ±b |=(a ±b )2=a 2±2a ·b +b 2.3.如图,已知线段AB ⊥平面α,BC ⊂α,CD ⊥BC ,DF ⊥平面α,且∠DCF =30°,D 与A 在平面α的同侧,若AB =BC =CD =2,试求A ,D 两点间的距离.[提示] ∵AD →=AB →+BC →+CD →,∴|AD →|2=(AB →+BC →+CD →)2=|AB →|2+|BC →|2+|CD →|2+2AB →·BC →+2AB →·CD +2BC →·CD →=12+2(2·2·cos 90°+2·2·cos 120°+2·2·cos 90°)=8,∴|AD →|=22,即A ,D 两点间的距离为2 2.【例4】 如图所示,在平行四边形ABCD 中,AB =AC =1,∠ACD =90°,沿着它的对角线AC 将△ACD 折起,使AB 与CD 成60°角,求此时B ,D 间的距离.[思路探究] BD →=BA →+AC →+CD →―→|BD →|2 注意对〈BA →,CD →〉的讨论,再求出B ,D 间距离.[解] ∵∠ACD =90°,∴AC →·CD =0,同理可得AC →·BA →=0.∵AB 与CD 成60°角,∴〈BA →,CD →〉=60°或〈BA →,CD →〉=120°.又BD →=BA →+AC →+CD →,∴|BD →|2=|BA →|2+|AC →|2+|CD →|2+2BA →·AC →+2BA →·CD →+2AC →·CD →=3+2×1×1×cos 〈BA →,CD →〉.∴当〈BA →,CD →〉=60°时,|BD →|2=4,此时B ,D 间的距离为2;当〈BA →,CD →〉=120°时,|BD →|2=2,此时B ,D 间的距离为 2.求两点间的距离或线段长的方法(1)将相应线段用向量表示,通过向量运算来求对应向量的模.(2)因为a ·a =|a |2,所以|a |=a·a ,这是利用向量解决距离问题的基本公式.另外,该公式还可以推广为|a ±b |=(a ±b )2=a 2±2a ·b +b 2.(3)可用|a ·e |=|a ||cos θ|(e 为单位向量,θ为a ,e 的夹角)来求一个向量在另一个向量所在直线上的投影.[跟进训练]4.如图所示,在平面角为120°的二面角α-AB -β中,AC ⊂α,BD ⊂β,且AC ⊥AB ,BD ⊥AB ,垂足分别为A ,B .已知AC =AB =BD =6,求线段CD 的长.[解] ∵AC ⊥AB ,BD ⊥AB ,∴CA →·AB →=0,BD →·AB →=0.∵二面角α-AB -β的平面角为120°,∴〈CA →,BD →〉=180°-120°=60°. ∴CD →2=(CA →+AB →+BD →)2=CA →2+AB →2+BD →2+2CA →·AB →+2CA →·BD →+2BD →·AB →=3×62+2×62×cos 60°=144,∴CD =12.1.空间两向量的数量积与平面向量的数量积类似,由于数量积不满足结合律,因此在进行数量积运算时,一次、二次式与实数运算相同,运算公式也相同,三次及以上必须按式中的运算顺序依次进行运算.2.空间向量数量积运算的两种方法(1)利用定义:利用a ·b =|a ||b |cos 〈a ,b 〉并结合运算律进行计算.(2)利用图形:计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.3.在几何体中求空间向量数量积的步骤(1)首先将各向量分解成已知模和夹角的向量的组合形式.(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积. (3)代入a ·b =|a ||b |cos 〈a ,b 〉求解.4.空间向量中求两向量夹角与平面向量中的求法完全相同,都是应用公式cos 〈a ,b 〉=a·b |a |·|b |,解题的关键就是求a ·b 和|a |、|b |.求模时注意|a |2=a ·a 的应用.1.如图,空间四边形ABCD 的每条边和对角线的长都等于1,E ,F ,G 分别是AB ,AD ,DC 的中点,则FG →·AB →=( )A .34B .14C .12D .32B [由题意可得FG →=12AC →,∴FG →·AB →=12×1×1×cos 60°=14.]2.已知两异面直线的方向向量分别为a ,b ,且|a |=|b |=1,a·b =-12,则两直线的夹角为( )A .30°B .60°C .120°D .150°B [设向量a ,b 的夹角为θ,则cos θ=a·b|a ||b |=-12,所以θ=120°,则两个方向向量对应的直线的夹角为180°-120°=60°.]3.在空间四边形ABCD 中,AB →·CD →+BC →·AD →+CA →·BD →=________. 0 [原式=AB →·CD →+BC →·AD →+CA →·(AD →-AB →) =AB →·(CD →-CA →)+AD →·(BC →+CA →) =AB →·AD →+AD →·BA →=0.]4.如图所示,在一个直二面角α-AB -β的棱上有两点A ,B ,AC ,BD 分别是这个二面角的两个面内垂直于AB 的线段,且AB =4,AC =6,BD =8,则CD 的长为________.229 [∵CD →=CA →+AB →+BD →=AB →-AC →+BD →, ∴CD →2=(AB →-AC →+BD →)2=AB →2+AC →2+BD →2-2AB →·AC →+2AB →·BD →-2AC →·BD →=16+36+64=116, ∴|CD →|=229.]5.如图,已知空间四边形ABCD 的每条边和对角线的长都等于a ,点M ,N 分别是边AB ,CD 的中点.(1)求证:MN 为AB 和CD 的公垂线; (2)求MN 的长;(3)求异面直线AN 与MC 所成角的余弦值. [解] 设AB →=p ,AC →=q ,AD →=r .由题意,可知|p |=|q|=|r|=a ,且p ,q ,r 三向量两两夹角均为60°. (1)证明:MN →=AN →-AM →=12(AC →+AD →)-12AB → =12(q +r -p ), ∴MN →·AB →=12(q +r -p )·p =12(q ·p +r ·p -p 2)=12(a 2·cos 60°+a 2·cos 60°-a 2)=0 ∴MN ⊥AB ,同理可证MN ⊥CD . ∴MN 为AB 与CD 的公垂线. (2)由(1)可知MN →=12(q +r -p ),∴|MN →|2=(MN →)2=14(q +r -p )2=14[q 2+r 2+p 2+2(q ·r -q·p -r ·p )]=14(a 2+a 2+a 2+2⎝ ⎛⎭⎪⎫a 22-a 22-a 22]=14×2a 2=a 22.∴|MN →|=22a , ∴MN 的长度为22a .(3)设向量AN →与MC →的夹角为θ,∵AN →=12(AC →+AD →)=12(q +r ),MC →=AC →-AM →=q -12p , ∴AN →·MC →=12(q +r )·⎝ ⎛⎭⎪⎫q -12p =12⎝ ⎛⎭⎪⎫q 2-12q ·p +r·q -12r ·p =12⎝ ⎛⎭⎪⎫a 2-12a 2·cos 60°+a 2cos 60°-12a 2·cos 60° =12⎝ ⎛⎭⎪⎫a 2-a 24+a 22-a 24=a 22. 又∵|AN →|=|MC →|=32a ,∴AN →·MC →=|AN →|·|MC →|·cos θ=32a·32a ·cos θ=a 22. ∴cos θ=23.∴向量AN →与MC →的夹角的余弦值为23. 从而异面直线AN 与MC 所成角的余弦值为23.1.2 空间向量基本定理学 习 目 标核 心 素 养1.了解空间向量基本定理及其意义.2.掌握空间向量的正交分解.(难点)3.掌握在简单问题中运用空间三个不共面的向量作为基底表示其他向量的方法.(重点)1.通过基底概念的学习,培养学生数学抽象的核心素养.2.借助基底的判断及应用,提升逻辑推理、直观想象及数学运算的核心素养.(1)共面向量定理:如果两个向量a 、b 不共线,则向量p 与向量a 、b 共面的充要条件是存在实数对(x ,y ),使得p =x a +y b .(2)共面向量定理的推论:空间一点P 在平面MAB 内的充要条件是存在有序实数对(x ,y ),使得MP →=xMA →+yMB →,或对于空间任意一定点O ,有OP →=xOM →+yOA →+zOB →(x +y +z =1).今天我们将对平面向量基本定理加以推广,应用上面的几个公式我们可以解决与四点共面有关的问题,得出空间向量基本定理.1.空间向量基本定理如果三个向量a ,b ,c 不共面,那么对任意一个空间向量p ,存在唯一的有序实数组(x ,y ,z ),使得p =x a +y b +z c .。
高中生物选修1(新教材)精品学案4:2-3-1-兴奋在神经纤维上的传导 人教版

第3节第1课时兴奋在神经纤维上的传导〖学习目标〗1.描述静息电位和动作电位的形成。
2.简述兴奋在神经纤维上的传导。
〖学习内容〗兴奋在神经纤维上的传导1.在神经系统中,兴奋是以的形式沿着神经纤维传导的,这种电信号也叫。
2.神经冲动在神经纤维上的过程。
(1)神经冲动的产生(2)神经冲动的传导兴奋部位与未兴奋部位之间:形成。
局部电流方向:膜内由部位→部位,膜外由部位→部位3.特点兴奋在神经纤维上的传导方向是向的。
〖课后检测〗1.下列对于神经兴奋的叙述,错误的是()A.反射弧中的感受器和效应器必须在同一部位B.神经细胞兴奋时细胞膜对Na+通透性增大C.兴奋部位细胞膜两侧的电位表现为膜内为正、膜外为负D.细胞膜内外K+、Na+分布不均匀是神经纤维兴奋传导的基础2.神经细胞兴奋时,细胞内外K+和Na+的分布特征是()A.细胞外的K+和Na+浓度均高于细胞内的B.细胞外的K+和Na+浓度均低于细胞内的C.细胞外的K+浓度高于细胞内的,Na+相反D.细胞外的K+浓度低于细胞内的,Na+相反3.为探究神经元动作电位与钠离子浓度的关系,研究人员把从青蛙体内分离出的神经元,分别放入正常海水和低钠海水中,测定神经元受到刺激后的电位变化,结果如图。
下列叙述错误的是()A.低钠海水除了钠离子浓度外,其他应与正常海水一致B.神经元动作电位的幅度与细胞外钠离子的浓度有关C.用高钠海水重复该实验,动作电位的幅度不会上升D.降低细胞外钠离子浓度会延缓动作电位峰电位的产生▁▃▅▇█参 *考 *答 *案█▇▅▃▁1.电信号神经冲动2.传导(1)K+外流内负外正Na+内流内正外负内负外正内正外负局部电流(2)局部电流兴奋未兴奋未兴奋兴奋3.双向〖课后检测〗1.〖〖答案〗〗A〖〖解析〗〗效应器与感受器可能分布在同一部位,也可能不在同一部位,如寒冷刺激时,感受器分布于皮肤等位置,而效应器是骨骼肌、皮肤血管、立毛肌等,A错误;当神经纤维的某一部位受到刺激产生兴奋时,细胞膜对钠离子通透性增加,Na+内流,B正确;兴奋部位,细胞膜对钠离子通透性增加,Na+内流,细胞膜两侧的电位表现为膜内为正、膜外为负,C正确;K+主要存在于细胞内,Na+主要存在于细胞外,细胞膜内外K+、Na+分布不均匀是神经纤维兴奋传导的基础,D正确。
新教材人教版高中英语选择性必修第三册全册书2022新高考一轮复习学案(知识点考点汇总及配套习题)

人教版选择性必修第三册复习学案Unit 1Art ....................................................................................................................... - 1 - Unit 2Healthy Lifestyle ............................................................................................... - 21 - Unit 3Environmental Protection................................................................................. - 39 - Unit 4Adversity and Courage...................................................................................... - 54 - Unit 5Poems ............................................................................................................... - 70 -Unit 1Art主题语境:人与社会(艺术与艺术欣赏)【话题词汇】1.sculpture n. 雕塑;雕刻2.statue n. 塑像;雕像3.Chinese landscape painting 中国山水画4.watercolor painting 水彩画5.oil painting 油画6.portrait n. 肖像画7.figure n. 画像8.carve n. & v. 雕刻9.gallery n. 画廊10.exhibition n. 展览;展览品11.display n.& v t. 展示;陈列12.design n.& v. 图案;设计13.draft n. 草稿;草图14.sketch n. 草图;素描15.shade n. 暗影16.inspiration n. 灵感;启发17.insight n. 洞察力18.technique n. 技巧19.masterpiece n. 杰作20.admire v. 钦佩;赞美21.reflect v. 反映;反射22.represent v. 代表;象征;体现23.unique adj. 独特的24.creative adj. 有创造性的25.abstract adj. 抽象的;深奥的26.extraordinary adj. 非凡的27.vivid adj. 生动的28.visual adj. 视觉的29.valuable adj. 有价值的30.precious adj. 宝贵的;珍贵的【话题短语】1.true to life 逼真2.take pictures (photos)/take a picture (photo) 拍照3.works of art 艺术品4.works appreciation 作品欣赏5.abstract art 抽象艺术6.make comments on 对……作评论7.Beijing Opera 京剧8.be designed for... 为……而设计9.be faced with 面对,面临10.be open to 向……开放11.be shaped like... 形状像……12.on exhibition/display/show 在展出13.enjoy great popularity 广受欢迎14.queue up/stand in line 排队15.range from...to... 范围从……到……16.sense of beauty 美感17.show up 出现18.go through many difficulties 经历许多困难19.widen one's horizons 开阔某人的眼界【话题佳句】1.I'm writing to invite you to see the exhibition of Chinese paper-cutting art, which is a Chinese folk art with a long history.我写信邀请你参观中国剪纸艺术展。
2020版历史新教材人教必修一同步学案:第26课中华人民共和国成立和向社会主义的过渡和答案

知识点一中华人民共和国的成立1.中国人民政治协商会议第一届全体会议(1)1949年9月,中国人民政治协商会议第一届全体会议在北平中南海怀仁堂隆重开幕。
来自党派、区域、军队、团体等界别的代表参加了会议。
(2)毛泽东在全体会议上致开幕词,大会一致决定采用“中华人民共和国”的国名,通过了《中国人民政治协商会议共同纲领》等几个重要文件。
(3)大会选举了中央人民政府委员会,毛泽东为主席,朱德、刘少奇、宋庆龄、李济深、张澜、高岗为副主席。
2.开国大典(1)1949年10月1日,中央人民政府举行第一次会议,决议接受《中国人民政治协商会议共同纲领》为施政方针。
(2)政府主席、副主席和委员就职,任命周恩来为政务院总理兼外交部部长,中央人民政府宣告成立。
下午3时,在天安门广场举行了盛大的开国大典。
3.中华人民共和国成立的意义(1)中华人民共和国的成立,结束了帝国主义、封建主义和官僚资本主义长期压迫和剥削中国各族人民的历史,人民真正成为国家的主人。
(2)从根本上改变了中国社会的发展方向,为实现由新民主主义向社会主义过渡创造了前提条件。
(3)中华民族开始以崭新的姿态自立于世界民族之林,中国历史进入新纪元。
[学习聚焦]中华人民共和国的成立,开启了中华民族伟大复兴的历史新纪元。
中国人民政治协商会议是中国共产党领导的以工农联盟为基础的人民民主统一战线的组织形式。
《中国人民政治协商会议共同纲领》包括序言和总纲、政权机关、军事制度、经济政策、文化教育政策、民族政策、外交政策,是新中国的建国纲领,具有临时宪法的作用。
1949年10月1日,中华人民共和国开国大典在北京隆重举行。
毛泽东站在天安门城楼上,向全世界庄严宣告:“中华人民共和国中央人民政府今天成立了!”中华人民共和国的成立,开辟了中国历史新纪元。
知识点二人民政权的巩固1.新中国面临的严峻形势(1)新中国成立时,国民党残余军队还盘踞在华南、西南地区。
人民解放军仍在进行人民解放战争的后期作战,肃清土匪和一切反革命武装。
高一升高二衔接教材高二预科班数学精品课程二十讲(教学案):第十八讲 不等式及其性质同步提升训练

第十八讲不等式及其性质一、选择题(每题4分,共40分)1.若a ,b ,c ∈R ,a >b ,则下列不等式成立的是( )A.1a <1b B .a 2>b 2C.a c 2+1>bc 2+1D .a |c |>b |c | 2.已知a 、b 为非零实数,且a <b ,则下列命题成立的是( )A .a 2<b 2B .a 2b <ab 2C.1ab 2<1a 2bD.b a <ab3.若x ∈(e-1,1),a =ln x ,b =2ln x ,c =ln 3x ,则( )A .a <b <cB .c <a <bC .b <a <cD .b <c <a4.若a >0且a ≠1,M =log a (a 3+1),N =log a (a 2+1),则M ,N 的大小关系为( )A .M <NB .M ≤NC .M >ND .M ≥N5.若a >b >c 且a +b +c =0,则下列不等式中正确的是( )A .ab >acB .ac >bcC .a |b |>c |b |D .a 2>b 2>c 2 6.若1<a 1<b1,则下列结论中不正确的是( ) A .log b a > log a b B .│log b a +log a b │>2C .(log a b )2<1 D .│log b a │+ │ log a b │>│ log b a + log a b │7.设a>0,b>0,则不等式-b<x1<a 等价于( ) A .-b 1< x <0或0<x<a 1 B .-a 1<x<b 1C .x<-a 1或x>b 1D .x<-b 1或x>a18.设全集U =R ,A ={x|x 2-5x -6>0},B ={x||x -5|<a}(a 是常数),且11∈B ,则( ) A .(U A)∩B =RB .A ∪(U B)=RC .(U A)∪(U B)=RD .A ∪B =R9.下列各对不等式中同解的是( )A .72<x 与 x x x +<+72 B .0)1(2>+x 与01≠+xC .13>-x 与13>-xD .33)1(x x >+与xx 111<+ 10.若122+x ≤()142x -,则函数2x y =的值域是() A .1[,2)8B .1[,2]8C .1(,]8-∞D .[2,)+∞二、填空题(每题5分,共20分)11.若1≤a ≤5,-1≤b ≤2,则a -b 的取值范围是________.12.若x ∈R ,则x1+x 2与12的大小关系为________.13.以下结论:(1)a>b ⇒│a │>b ;(2)a>b ⇒a 2>b 2;(3)│a │>b ⇒a>b ;(4)a>│b │⇒a>b ,其中正确结论的序号是___________________.14.已知-2π≤α<β≤2π,则2βα-的范围为. 三、解答题(6小题,共60分)15.(本题10分)设a >b >0,试比较a 2-b 2a 2+b 2与a -ba +b的大小.16.(本题10分)设f (x )=1+log x 3,g (x )=2log x 2,其中x >0且x ≠1,试比较f (x )与g (x )的大小.17.(本题10分)设f(x)=3ax 2+2bx+c ,若a+b+c=0,f(0)>0,f(1)>0 求证:(1)a>0,-2<ab<-1 (2)函数f(x)在(0,1)内有零点.18.(本题10分)解不等式(1)2(23)log (3)0x x -->(2)2232142-<---<-x x19.(本题10分)不等式049)1(220822<+++++-m x m mx x x 的解集为R ,求实数m 的取值范围。
2019-2020年新教材突破人教版物理必修第一册学案:第三章+阶段回顾(第4~5节)及答案

阶段回顾(第4~5节)易错点一合力与分力的关系理解不到位1.(多选)如图所示,一件重为G的行李,被轻绳OA和OB吊在空中,拉力分别为F1、F2。
下列说法正确的是()A.F1、F2的合力是GB.F1、F2的合力是FC.行李对轻绳OA的拉力方向与F1方向相反,大小相等D.行李受到重力G、OA绳拉力F1、OB绳拉力F2,还有F共四个力答案BC解析在受力分析中,分力和合力不能同时看作物体所受的力,行李受到竖直向下的重力G、OA绳拉力F1、OB绳拉力F2三个力的作用,D错误;F1、F2的合力是F,A错误,B正确;行李对轻绳OA的拉力与F1是一对作用力和反作用力,等大反向,C正确。
2.如图所示,物体放在倾角为θ的粗糙斜面上静止不动,把物体所受的重力G分解为F1、F2,下列说法正确的是()A.F2是物体受到的下滑力,F1是斜面受到的压力B.F2是使物体有下滑趋势的力,F1是使物体压紧斜面的力C.物体受到的摩擦力等于G cosθ,与F2等大反向D.若只减小斜面的倾角θ,两个分力F1、F2均减小答案 B解析物体受重力、支持力与摩擦力作用处于静止状态。
根据平衡条件可知,物体受到的摩擦力大小等于G sinθ,与F2等大反向,C错误;F1、F2是重力的两个分力,实际不存在,不是物体受到的力,A错误;F2的作用效果是使物体下滑,F1的作用效果是使物体压紧斜面,B正确;若只减小斜面的倾角θ,分力F1=G cosθ增大,分力F2=G sinθ减小,D错误。
易错点二不会根据力的作用效果分解力3.如图所示,被轻绳系住静止在光滑斜面上的小球,若按力的实际作用效果来分解,小球受到的重力G的两个分力方向分别是图中的()A.1和4 B.2和4C.3和4 D.3和2答案 C解析小球的重力产生两个作用效果,一是使绳子拉伸,二是使斜面受压,这两个分力方向分别是3和4,C正确,A、B、D错误。
易错点三绳的“活结”与“死结”模型认识不清4.如图甲所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为m1的物体,∠ACB=30°;图乙所示的轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向成30°角,轻杆的G点用细绳GF拉住一个质量为m2的物体,重力加速度为g,则下列说法正确的是()A.图甲中BC对滑轮的作用力为m1g 2B.图乙中HG杆受到绳的作用力为m2gC.细绳AC段的拉力F AC与细绳EG段的拉力F EG之比为m1∶m2D.细绳AC段的拉力F AC与细绳EG段的拉力F EG之比为m1∶2m2答案 D解析图甲中绳跨过滑轮,与滑轮接触的点是“动点”,也称为“活结”,绳上拉力大小处处相等,两段绳的拉力都是m1g,互成120°角,因此合力的大小是m1g,故BC对滑轮的作用力大小也是m1g(方向与竖直方向成60°角斜向右上方),A错误;图乙中绳与杆的端点连在一起,杆的端点与绳接触的点是“静点”,也称为“死结”,两段绳上的拉力不一定相等,此时,杆对G点的弹力方向沿杆,由力的平衡条件可得HG杆受到绳的作用力为3m2g,B错误;图乙中F EG sin30°=m2g,得F EG=2m2g,故F ACF EG=m12m2,C错误,D正确。
高中生物选修1(新教材)优质学案2-1-神经调节的结构基础 人教版

第1节神经调节的结构基础〖学习目标〗 1.阐述神经系统的基本结构。
2.阐明自主神经系统的作用特点及意义。
3.说明组成神经系统的细胞的结构特点。
〖素养要求〗 1.生命观念:基于对神经系统是一个信息网络的理解,认同信息流在生命活动中具有重要作用。
2.科学思维:归纳比较内脏运动神经的作用特点。
一、神经系统的基本结构1.中枢神经系统(1)脑的组成及功能(2)脊髓①位置:位于椎管内。
②功能:是脑与躯干、内脏之间的联系通路,调节运动的低级中枢。
(3)神经中枢在中枢神经系统内,大量神经细胞聚集在一起,形成许多不同的神经中枢,分别负责调控某一特定的生理功能。
2.外周神经系统(1)脑神经(共12对)①分布:主要分布在头面部。
②功能:负责管理头面部的感觉和运动。
(2)脊神经(共31对)①分布:主要分布在躯干、四肢。
②功能:负责管理躯干、四肢的感觉和运动。
(3)传入神经和传出神经①脑神经和脊神经都含有传入神经和传出神经。
②传出神经又分为支配躯体运动的神经(躯体运动神经)和支配内脏器官的神经(内脏运动神经)。
③功能:传入神经将接受到的信息传递到中枢神经系统;传出神经将中枢神经系统发出的指令信息传输到相应器官,从而使机体对刺激作出反应。
3.自主神经系统(1)概念:支配内脏、血管和腺体的传出神经,它们的活动不受意识支配,称为自主神经系统。
(2)分类①交感神经a.人体处于兴奋状态时,交感神经活动占优势。
b.表现为心跳加快,支气管扩张等。
②副交感神经a.人体处于安静状态时,副交感神经活动占优势。
b.表现为心跳减慢,支气管收缩等。
(3)意义①使机体对外界刺激作出更精确的反应。
②使机体更好地适应环境的变化。
判断正误(1)脑属于中枢神经系统,脊髓属于外周神经系统()(2)人交感神经活动占据优势时,会出现心跳加快、胃肠蠕动和消化腺分泌活动加强的现象()(3)中枢神经系统就是神经中枢()(4)交感神经使内脏器官的活动加强,副交感神经使内脏器官的活动减弱()(5)绝大多数内脏器官同时受到交感神经和副交感神经的双重支配,两者的作用往往相同()〖答案〗(1)×(2)×(3)×(4)×(5)×特别提醒中枢神经系统和神经中枢的区别(1)中枢神经系统包括脑和脊髓,它接受全身各处传入的信息,经它整合加工后成为协调运动的指令信息,或者储存在中枢神经系统内成为学习、记忆的基础。
高中生物选修1(新教材)精品学案1:2-4-神经系统的分级调节 人教版
神经系统的分级调节〖学习目标〗分析位于脊髓的低级神经中枢和脑中相应的高级神经中枢相互联系、相互协调,共同调控器官和系统的活动,维持机体的稳态。
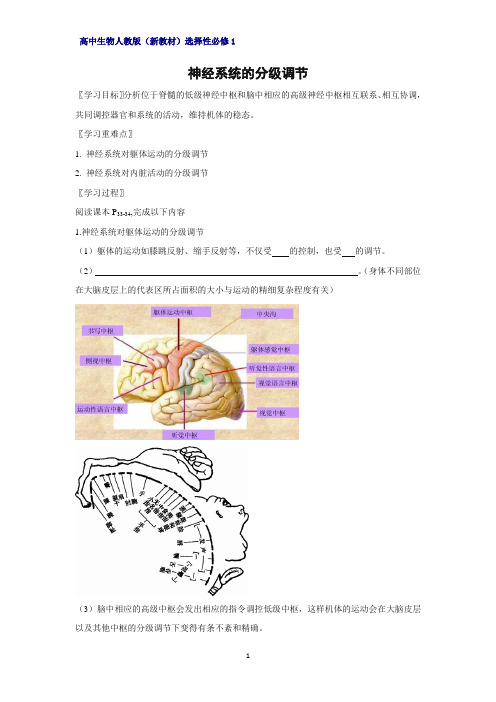
〖学习重难点〗1. 神经系统对躯体运动的分级调节2. 神经系统对内脏活动的分级调节〖学习过程〗阅读课本P33-34,完成以下内容1.神经系统对躯体运动的分级调节(1)躯体的运动如膝跳反射、缩手反射等,不仅受的控制,也受的调节。
(2)。
(身体不同部位在大脑皮层上的代表区所占面积的大小与运动的精细复杂程度有关)(3)脑中相应的高级中枢会发出相应的指令调控低级中枢,这样机体的运动会在大脑皮层以及其他中枢的分级调节下变得有条不紊和精确。
2. 神经系统对内脏活动的分级调节(以排尿反射为例)排尿不仅受的控制,也受的调控。
①脊髓对膀胱的控制是由自主神经系统支配的。
神经兴奋,膀胱,排尿反射发生。
②人之所以能有意识地控制排尿,是因为可对脊髓进行调控。
〖知识结构〗神经系统的分级调节概念图〖课堂作业〗1.做膝跳反射实验时,若实验前告诉受试者,在其有思想准备的情况下,膝跳反射可能表现得会弱一些,原因是()A.反射弧发生变化B.传出神经受阻C.感受器受到抑制D.高级中枢对低级中枢有调节作用2.下列关于神经系统的分级调节的叙述,正确的是()A.中枢神经系统中的不同神经中枢分别负责调控某一特定的生理功能B.脑干中有许多维持生命活动必要的中枢,还与生物节律的控制有关C.饮酒过量的人表现为语无伦次,与此生理功能相对应的结构是小脑D.成年人有意识地“憋尿”,说明排尿活动只受高级中枢的调控3.人体各部位的感觉与运动机能在大脑皮层体觉区与运动区中有它的代表区。
下列关于人大脑皮层功能的叙述,正确的是()A. 一侧手指传入神经上的神经冲动,可传到对侧大脑皮层中央后回中间部B. 一侧大脑皮层中央前回底部受损,会使对侧下肢的运动功能出现障碍C. 头面部肌肉的代表区,在运动区呈倒置排列即口部在上、眼部在下D. 分辨精细的部位如手,在体觉区所占的面积比躯干的小4.人体排尿是一种复杂的反射活动,下图为排尿反射过程。
(2019版新教材)人教版高中化学必修第一册全册学案(知识点详解及配套习题)
2019版新教材高中化学必修第一册全册学案物质的分类胶体[明确学习目标] 1.学会物质分类方法,会从不同角度对物质进行分类。
2.了解同素异形体。
3.能够根据分散质粒子的大小对分散系分类。
4.会制备Fe(OH)3胶体,会鉴别胶体与溶液。
学生自主学习根据物质的组成和性质分类1.同素异形体(1)由□01同一种元素形成的几种性质不同的单质叫做该元素的同素异形体。
(2)同素异形体的物理性质不同,化学性质不同。
(3)举例:O2与□02O3;红磷与白磷;金刚石、□03石墨与C60互为同素异形体。
2.根据物质的组成分类(1)交叉分类法①含义:根据不同的分类标准,对同一事物进行多种分类的一种分类方法。
②举例:Ⅱ.某些盐的交叉分类(2)树状分类法①含义:对同类事物按照某些属性进行再分类的分类法。
②举例:3.根据物质的性质分类(1)根据物质的性质对物质进行分类是化学上常用的分类方法。
(2)举例:根据性质对氧化物进行分类分散系及其分类1.分散系(1)概念:□01把一种(或多种)物质以粒子形式分散到另一种(或多种)物质中所形成的混合物。
(2)组成(3)分类 ①分散质和分散剂各有固、液、气三种状态,以其状态为分类标准共分为□049种分散系。
②分散系按照分散质粒子直径大小分类2.胶体的制备和特征(1)Fe(OH)3胶体的制备制备原理:FeCl 3+3H 2O=====△Fe(OH)3(胶体)+3HCl具体操作:往烧杯中注入40 mL 蒸馏水,将烧杯中的蒸馏水加热至沸腾,向沸水中逐滴加入5~6滴□08FeCl 3饱和溶液,继续煮沸至溶液呈□09红褐色,停止加热。
(2)胶体的特性——丁达尔效应当平行光束通过胶体时,可以看到□10一条光亮的“通路”,这是由于胶体粒子对光线□11散射形成的,叫做丁达尔效应,可用来区分胶体和□12溶液。
1.在科学研究中分类法的意义何在?提示:运用分类法对物质进行科学的分类,然后分门别类地研究它们的组成、结构、性质和用途,就能够发现物质及其变化的规律,把握物质的本质属性和内在联系。
高中生物选修1(新教材)精品学案1:5-1-2-生长素的生理作用 人教版

第1节第2时生长素的生理作用〖学习目标〗理解生长素的生理作用。
〖学习内容〗生长素的生理作用1.作用方式与细胞内某种蛋白质——生长素特异性结合,引发细胞内一系列信号转导过程,进而诱导特定,从而产生效应。
2.生理作用(1)细胞水平上:促进、诱导等。
(2)器官水平上:影响器官的。
3.特点(1)一般情况下,生长素在浓度较低时生长,在浓度过高时则会生长。
(2)①图中生长素对同一器官的作用:生长素在一定浓度范围内植物器官生长,超过该范围则植物器官的生长。
②同一浓度的生长素作用于不同器官引起的生理效应也不同,这是因为不同的器官对生长素的敏感程度,曲线体现了根、芽、茎的敏感程度为。
③曲线在三点生长素的促进效果最佳,A2、B2、C2三点对应的生长素浓度对根、芽、茎的作用分别是。
(3)实例:顶端优势不同器官敏感度不同:根芽茎不同细胞成熟度敏感度不同:幼嫩细胞衰老细胞不同物种敏感度不同:双子叶植物单子叶植物〖课堂练习〗1、植物生长素对植物的新陈代谢、生长发育等生命活动起着重要的调节作用,其特点是()A.只能抑制植物生长B.只能促进植物生长C.高浓度时促进生长,低浓度时抑制生长D.高浓度时抑制生长,低浓度时促进生长2、下图表示不同浓度生长素对芽生长的影响。
当植物表现出顶端优势时,顶芽和最靠近顶芽的侧芽所含生长素的浓度分别为()A.a和b B.b和aC.b和c D.c和b3、下图表示生长素对植物某营养器官生长的影响,“低浓度促进生长、高浓度抑制生长”一句中,高浓度、低浓度分别指()A.大于a的浓度、小于a的浓度B.大于c的浓度、小于c的浓度C.大于b的浓度、小于b的浓度D.大于a的浓度、小于c的浓度4、下列关于植物茎的负向重力性和根的向重力性的叙述,正确的是()A.在根部“3→4”的运输需要消耗A TPB.生长素对2处和6处的作用相同C.两种现象说明根对生长素的敏感性高于茎D.两种现象均能体现生长素作用的两重性5、将一盆栽植物横放于地面,则其水平方向的茎近地侧生长素浓度变化的曲线为(图中虚线表示对茎生长既不促进也不抑制的生长素浓度)(D)A B C D▁ ▃ ▅ ▇ █ 参 *考 *答 *案█ ▇ ▅ ▃ ▁1.受体基因的表达2.(1)细胞伸长生长细胞分化(2) 生长、发育3.(1)促进抑制(2)①促进抑制②不同根>芽>茎。
初高中化学衔接教学案及初高中衔接教材

初高中化学衔接教学案·第一讲物质的组成和分类关键词:宏观组成,微观组成与结构,关于组成与结构的化学用语,分类思想,分类方法,分类标准(依据)与示例,分类应用一、物质的组成与结构所有的物质都是由最基本的成份“化学元素”组成。
虽然物质种类繁多(达3千多万种),但组成这些物质的化学元素只有100多种(现行元素周期表中排有112种元素)。
这些元素又以分子、原子或离子等微观粒子(简称“微粒”或“粒子”)形态存在于自然界,按不同的方式构成了千变万化的宏观物质世界。
1.元素概念。
【课堂练习】(1)写出1-18号元素名称、符号(2)元素符号的意义(3)H、H2、H+、H-的共同点是什么?2.原子。
它由和构成。
原子核由和构成,带正电荷,不带电,核内所有电荷总数称为“核电荷数”,同种元素可能有多种原子,但这些原子的核电荷数相同,属于同类原子。
把不同元素按核电荷数由小到大排序,所得序号数称为“原子序数”,即原子序数= 核电荷数;核外电子带负电荷,其负电荷总数等于核电荷数,故原子呈电中性。
思考:如何理解“原子是化学变化中的最小粒子”?原子核外电子按能量高低分层排布,离核越近能量越,越稳定,离核越远,能量越越不稳定。
最外层电子能量最,故化学变化中通常内层电子不发生变化,改变的往往是最外层电子(最外层电子也称为“价电子”)。
【课堂练习】(1)原子核外电子分层排布规律:①每层最多排个电子;②最外层不超过个电子,次外层不超过个电子,倒数第三层不超过电子。
③当最外层电子达到个时,达到稳定结构。
(2)画出下列元素的原子结构示意图:①氢原子②氧原子③硅原子④氯原子⑤钾原子⑥镁原子⑦氦原子⑧氩原子(3)电子式:在元素符号周围用小黑点“·”或小叉叉“×”表示原子最外层电子的式子叫“电子式”。
请写出下列原子的电子式:①氢原子②钙原子③铝原子④碳原子⑤氮原子⑥氧原子⑦氯原子3.离子(1)某些原子通过得、失电子生成简单阴、阳离子,又称单核离子,如Na+、Cl-等;复杂离子又称多核离子,如OH-、SO42-、NH4+、CO32-等等,它们是多个原子通过共价键结合而成的带电荷的原子团,相对比较稳定,常常作为一个整体参与化学反应。
(2019版新教材)人教版高中化学必修第一册全册学案(知识点详解及配套习题)

2019版新教材高中化学必修第一册全册学案物质的分类胶体[明确学习目标] 1.学会物质分类方法,会从不同角度对物质进行分类。
2.了解同素异形体。
3.能够根据分散质粒子的大小对分散系分类。
4.会制备Fe(OH)3胶体,会鉴别胶体与溶液。
学生自主学习根据物质的组成和性质分类1.同素异形体(1)由□01同一种元素形成的几种性质不同的单质叫做该元素的同素异形体。
(2)同素异形体的物理性质不同,化学性质不同。
(3)举例:O2与□02O3;红磷与白磷;金刚石、□03石墨与C60互为同素异形体。
2.根据物质的组成分类(1)交叉分类法①含义:根据不同的分类标准,对同一事物进行多种分类的一种分类方法。
②举例:Ⅱ.某些盐的交叉分类(2)树状分类法①含义:对同类事物按照某些属性进行再分类的分类法。
②举例:3.根据物质的性质分类(1)根据物质的性质对物质进行分类是化学上常用的分类方法。
(2)举例:根据性质对氧化物进行分类分散系及其分类1.分散系(1)概念:□01把一种(或多种)物质以粒子形式分散到另一种(或多种)物质中所形成的混合物。
(2)组成(3)分类 ①分散质和分散剂各有固、液、气三种状态,以其状态为分类标准共分为□049种分散系。
②分散系按照分散质粒子直径大小分类2.胶体的制备和特征(1)Fe(OH)3胶体的制备制备原理:FeCl 3+3H 2O=====△Fe(OH)3(胶体)+3HCl具体操作:往烧杯中注入40 mL 蒸馏水,将烧杯中的蒸馏水加热至沸腾,向沸水中逐滴加入5~6滴□08FeCl 3饱和溶液,继续煮沸至溶液呈□09红褐色,停止加热。
(2)胶体的特性——丁达尔效应当平行光束通过胶体时,可以看到□10一条光亮的“通路”,这是由于胶体粒子对光线□11散射形成的,叫做丁达尔效应,可用来区分胶体和□12溶液。
1.在科学研究中分类法的意义何在?提示:运用分类法对物质进行科学的分类,然后分门别类地研究它们的组成、结构、性质和用途,就能够发现物质及其变化的规律,把握物质的本质属性和内在联系。
高中生物选修1(新教材)优质学案3-3-1-体液调节与神经调节的比较和体温调节 人教版

第3节神经调节与体液调节的关系第1课时体液调节与神经调节的比较和体温调节〖学习目标〗 1.举例说明体液调节除激素外,其他体液成分参与的稳态调节。
2.概括比较体液调节和神经调节的特点。
3.以体温调节为例,概括神经调节和体液调节的关系。
〖素养要求〗 1.生命观念:结合体温调节的过程深化稳态与平衡观。
2.科学思维:构建体温调节的概念模型。
一、体液调节与神经调节的比较1.体液调节(1)概念:激素等化学物质,通过体液传送的方式对生命活动进行调节。
(2)主要内容:激素调节。
(3)其他化学物质:组胺、某些气体分子(如NO、CO等)以及一些代谢产物(如CO2)。
(4)范围①一些低等动物只有体液调节。
②在人和高等动物体内,体液调节和神经调节都是机体调节生命活动的重要方式。
2.体液调节和神经调节的比较比较项目神经调节体液调节作用途径反射弧体液运输反应速度迅速较缓慢作用范围准确、比较局限较广泛作用时间短暂比较长判断正误(1)体液调节就是激素调节()(2)在紧张恐惧时,人体肾上腺素会在短时间内分泌增加,这一过程属于神经调节()(3)肾上腺素随体液运输作用于人体,人表现为呼吸频率加快,心跳加速等,这一过程属于体液调节()(4)当恐惧因素消除后,心率一般不会立马恢复至安静水平,原因是体液调节反应较缓慢()(5)体液调节作用范围较广泛、作用时间较短()(6)某些低等动物只有体液调节,没有神经调节()〖答案〗(1)×(2)√(3)√(4)×(5)×(6)√特别提醒体液调节≠激素调节。
体液调节的研究对象不仅包括激素,还包括参与机体生命活动调节的其他调节因子,而激素调节的研究对象只有激素。
血液中CO2增多引起呼吸频率加快,请分析该过程的调节机制。
〖提示〗血液中CO2增多,高浓度的CO2随体液运输,可有效刺激呼吸中枢,呼吸中枢活动加强,呼吸加深加快,肺的通气量增大,从而加快对CO2的清除,此过程是由体液和神经共同调节的。
人教版(新教材)高中生物选修1优质学案2 5 人脑的高级功能

第5节人脑的高级功能〖学习目标〗 1.简述人类的语言功能与大脑皮层言语区的关系。
2.简要说明人类记忆的过程及记忆与学习的关系。
3.简述情绪是人脑的高级功能之一。
〖素养要求〗 1.生命观念:调整自己的情绪,积极、健康地享受美好生活。
2.科学思维:运用学习和记忆规律提高学习效率。
一、语言功能1.大脑的功能(1)感知外部世界。
(2)控制机体的反射活动。
(3)具有语言、学习和记忆等方面的高级功能。
2.语言功能(1)语言功能是人脑特有的高级功能。
(2)言语区(示意图)判断正误(1)人脑的言语区的H区受损后看不懂文字()(2)语言功能是人脑特有的高级功能,大多数人由大脑皮层的右半球主导()(3)V区受损,看不见文字()〖答案〗(1)×(2)×(3)×1.残奥会闭幕式上,中国残疾人艺术团表演的舞蹈得到一致好评。
这些聋哑人要准确理解指导老师的“手语”表达的含义,主要依靠哪些中枢?〖提示〗视觉中枢和语言中枢。
2.思考下列现象可能与哪些中枢受损有关。
①某患者听不见别人的讲话。
②某患者能听见但听不懂别人的谈话。
③某患者看不见。
④某患者能看见但看不懂文字的含义。
〖提示〗①听觉中枢;②大脑皮层的H区;③视觉中枢;④大脑皮层的V区。
核心归纳言语区的分区及损伤症中枢名称别名受损后的病症病症的症状书写性语言写中枢书写中枢(W区)失写症病人可听懂别人的谈话和看懂文字,也会讲话,手部运动正常,但失去书写、绘图能力运动性语言中枢说话中枢(S区)运动性失语症病人可以看懂文字,也能听懂别人讲话,但自己却不会讲话听觉性语言中枢听话中枢(H区)听觉性失语症病人能讲话、书写,也能看懂文字,能听懂别人发音,但不懂其含义,病人可以模仿别人说话,但往往是答非所问视觉性语言中枢阅读中枢(V区)失读症病人的视觉无障碍,但看不懂文字的含义,即不能阅读1.如图是人的大脑皮层(左半球侧面)示意图。
若S区受损伤,患者会出现()A.不能书写B.不能讲话C.看不懂文字D.听不懂说话〖答案〗 B2.某人的大脑某个部位受到损伤,但能用语言表达自己的思想,也能听懂别人的谈话,却读不懂报刊上的新闻。
新教材2023版高中语文古诗词诵读念奴娇过洞庭学案部编版必修下册

念奴娇·过洞庭知人论世一、创作背景人们比较熟悉辛弃疾与苏轼之间的继承和发展关系,但却较少有人注意张孝祥在苏、辛之间所起到的过渡性作用。
张孝祥实际上是南宋豪放词派重要的奠基人之一。
这首《念奴娇》就是张孝祥被广泛传诵的代表作。
宋孝宗乾道二年(1166年),张孝祥因受政敌谗害而被免职。
他从桂林北归,途经洞庭湖,即景生情,写下这首词。
二、白话译文洞庭湖与青草湖相连,浩瀚无垠,在这个中秋将至的时候,没有一丝风过的痕迹。
是玉的世界,还是琼的原野?三万顷明镜般的湖水,载着我一叶细小的扁舟。
皎洁的明月和灿烂的银河,在这浩瀚的玉镜中映出她们的芳姿,水面上下一片明亮澄澈。
体会着万物的空明,却不知如何道出,与君分享。
感怀这一轮孤光自照的明月啊,多少年徘徊于岭海之间,胸襟仍像冰雪一样透明。
而此刻的我,正披着萧瑟幽冷的须发和衣袂,平静地泛舟在这广阔浩淼的苍溟之中。
让我捧尽西江清澈的江水,细细地斟在北斗星做成的酒勺中,请天地万象统统来做我的宾客。
我尽情地拍打着我的船舷,独自放声高歌啊,怎能记得此时是何年!欣赏领悟一、整体赏析这首中秋词是作者泛舟洞庭湖时即景抒怀之作。
开篇直说地点与时间,然后写湖面、小舟、月亮、银河。
此时作者想起岭南一年的官宦生涯,感到自己无所作为而有所愧疚。
而且想到人生苦短不免心酸,不过由于自己坚持正道,又使他稍感安慰。
他要用北斗做酒勺,舀尽长江做酒浆痛饮。
全词格调昂奋,一波三折。
“洞庭春草”指的是洞庭湖加上与之相连的春草湖,点出地点,题目是“过洞庭”,词一开头就紧扣题目。
“近中秋”点出时间,秋天天高气爽,“月到中秋分外明”,秋月对于生活在农业社会与大自然息息相关的古代文人来说,当是别有意味。
“风色”二字值得注意,风有风向、强弱,从来没有听说过风有色彩,其实张孝祥用“风色”是有所本的,李白《庐山谣》“登高壮观天地间,大江茫茫去不还。
黄云万里动风色,白波九道流雪山”说的是黄云万里改变了风的色彩;张孝祥的“更无一点风色”说的是洞庭青草湖上,万里无云,水波不兴,不仅没有风,而且连风的影子都没有,这种表达方式富有新意,增添了一分诗意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 乘法公式、因式分解重点:和(差)的立方公式,立方和(差)公式及应用,十字相乘法,分组分解法,试根法 难点:公式的灵活运用,因式分解教学过程: 一、 乘法公式 回顾初中常用的乘法公式:平方差公式=-22b a ______________________ 完全平方公式=+2)(b a ______________________(从项的角度变化)那三数和的平方公式呢?=++2)(c b a ______________________ (从指数的角度变化)看看和与差的立方公式是什么?如=+3)(b a ______________________ 能用学过的公式推导吗?(平方―――立方) 那=-3)(b a ______________________ ▲符号的记忆,和――差 从代换的角度看问:能推导立方和、立方差公式吗?即( )( )=33b a ±▲符号的记忆,系数的区别例1:(1))1)(1)(1)(1(22+++--+x x x x x x(2)已知,012=-+x x 求证:x x x 68)1()1(33-=--+▲注意观察结构特征,及整体的把握。
二、因式分解:将一个多项式化成几个整式的积的形式,与乘法运算是互逆变形。
初中学过的方法有:提取公因式法,公式法(平方差、完全平方、立方和、立方差等) (1)十字相乘法试分解因式:=++232x x ________________要将二次三项式x 2 + px + q 因式分解,就需要找到两个数a 、b ,使它们的积等于常数项q ,和等于一次项系数p , 满足这两个条件便可以进行如下因式分解,即x 2+ px + q = x 2+(a + b)x + ab = (x + a)(x + b).用十字交叉线表示a +b (交叉相乘后相加)若二次项的系数不为1呢?)0(2≠++a c bx ax ,如:3722+-x x =____________整理:对于二次三项式ax 2+bx+c (a ≠0),如果二次项系数a 可以分解成两个因数之积,即a=a 1a 2,常数项c 可以分解成两个因数之积,即c=c 1c 2,把a 1,a 2,c 1,c 2排列如下:a 1 +c 1a 2 +c 2a 1c 2 + a 2c 1 = a 1c 2 + a 2c 1按斜线交叉相乘,再相加,得到a 1c 2+a 2c 1,若它正好等于二次三项式ax 2+bx+c 的一次项系数b ,即a 1c 2+a 2c 1=b ,那么二次三项式就可以分解为两个因式a 1x+c 1与a 2x+c 2之积,即 ax 2+bx+c=(a 1x+c 1)(a 2x+c 2)。
〔按行写分解后的因式〕 十字相乘法关键:(1)____________;(2)________________;(3)_________________________例2:因式分解:(1)322-+x x (2)5762++-x x(3)22865y xy x -+ (4)2)322)((----y x y x(2)分组分解法:____________________________________ 分解yn ym xn xm +++,观察;得:▲如何适当分组是关键(尝试,结构),分组的原则,目的是什么?分组后可以提取公因式,或;利用公式练习:因式分解(1)x x x 33923+++ (2)224)1(4y xy x +-+(3)433-+x x归纳:如何选择适当的方法将下列各式分解因式(1)652-+x x ; (2)652+-x x ; (3)652++x x ;(4)652--x x (5)2223a ax x -+; (6)2233xy y x y x +--;(7)b a ab b a +-+-2222 (8)646-a ;(9)a x a x ++-)1(2第二节 二次函数及其最值重点:二次函数的三种表示形式,韦达定理,给定区间的最值问题 难点:给定区间的最值问题一、韦达定理(二次方程根与系数之间的关系)二次方程)0(02≠=++a c bx ax 的两根为21,x x ,则_________,__________2121==+x x x x作用:(1)已知方程,得出根与系数的关系(2)已知两数21,x x ,构造出以两数为根的一元二次方程(系数为1):________________________ 例1:21,x x 是方程05322=--x x 的两根,不解方程,求下列代数式的值; ①2221x x + ②||21x x - ③3231x x +二、二次函数的三种形式(1) 一般式:__________________(2) 顶点式:__________________,其中顶点坐标为_____________练:求下列函数的最值。
(1)542+-=x x y (2)8632-+=x x y (3)4322+--=x x y除了上述两种表示方法外,我们还可以借助图像与x 轴的交点,得出另一种表示方法;函数)0(2≠++=a c bx ax y 的图像与x 轴公共点的横坐标就是方程02=++c bx ax 的根,那它根的情况由谁决定 ,(判别式),当方程有两根21,x x 时,由韦达定理可知ac x x ab x x =-=+2121,,所以_______________________________________2=++=c bx ax y ,这是二次函数的交点式。
(3)交点式:________________________▲根据题目所给条件,适当选择三种形式。
例2:分别求下列一元二次函数的解析式。
(1) 已知二次函数的图象过点(-3,0),(1,0),且顶点到x 轴的距离等于2;(2) 已知二次函数的对称轴为x =1,最大值为15,图象与x 轴有两个交点,其横坐标的立方和为17;三、二次函数在给定范围内的最值问题例3、已知函数322+--=x x y ,当自变量x 在下列取值范围内时,分别求函数的最大值或最小值,并求当函数取最大(小)值时所对应的自变量x 的值: (1)2-≤x ; (2)2≤x ; (3)12≤≤-x ; (4)30≤≤x1、 已知某二次函数的图象的顶点为A (2,18),它与x 轴两个交点之间的距离为6,求此二次函数的解析式。
2、 如图,用长为18m 的篱笆(虚线部分),(1) 设矩形的一边为x (m ),面积为y (2m ),求y 关于x 式,并写出自变量x 的取值范围;(2) 当x 为何值时,所围苗圃的面积最大,最大面积是多少第三节比例关系,性质及其应用教学过程:4个非零数a ,b ,c ,d 成比例,即d c b a ::=,也可写成dc b a =,其中a ,d 叫做比例外项,b ,c 叫做比例内项,d 叫做a ,b ,c 的第四比例项。
特别的当比例内项相等时,即c b b a ::=,(或cb b a =),此时b 叫做ac 的比例中项。
一、比例的性质 1、 基本性质 __________⇔=dc ba ,比例的两个外项的乘积等于两个内项的乘积。
特别地,____________⇔=c b b a2、 更比性质 当abcd 0≠时,⇔⇔⇔⇔=________________________________dc b a比例式有多种变形形式:内项和外项可以相应的交换位置(注意是对应位置,即交叉相乘相等出现的式子是一样的)3、合比性质_____________⇒=d c b a 证明:__________________4、等比性质________________________)0(⇒≠+++===n d b nm dc b a(证明:__________________________________________________________)例1:(1)已知83=-bb a ,求证:811=ba(2)已知)0(≠±=d b dc ba ,求证:db d b ca c a -+=-+(3)已知,4,3=++===f d b fe dc ba 求e c a ++的值。
二、 比例性质的应用 (一)平行线等分线段定理____________________________________________________推论:___________________________________________________例2:已知三角形ABC 中,AD 是角平行线,求证:ACAB DCBD =▲三角形内角平分线性质定理: _____________________________________________练习:已知在∆ABC 中,AD 是角平分线,AB =5cm ,AC =4cm ,BC =7cm ,则BD=_____cm.1、根据下列各式,求b a :的值。
(1)83=+bb a (2)75=-ab a2、已知,2===fe dc ba 则fd be c a 3232+-+-=_______________。
3、已知在△ABC 中,AB =6,BC =8,AC =7,MN//AC ,分别交AB ,BC 于点M ,N ,且AM =BN ,求MN 的长。
4、已知AD 是△ABC 的角平分线,BH ⊥AD ,垂足为H ,CK ⊥AD ,垂足为K ,求证:DKDH ACAB =第四节一、Rt∆的射影定理及其应用①Rt∆ABC中,CD是斜边AB上的高,图中线段AC、BC、AD、BD、CD之间有些怎样的关系呢?(比如等量关系、大小关系、比例关系等)让学生探究得出以下结论(1)____________;(2)____________________(3)________________;(4)________________ 其中(1)(2)(3②引入射影的概念(引垂直)(1)点在直线上的正射影(2)线段在直线上的正射影③射影定理:_____________________________________________________④射影定理的应用:求Rt∆的边长、面积等有关量,研究相似、比例式的问题练习:圆O上一点C在直径AB上的射影为D,AD=2,DB=8,求CD、AC和BC的长。
例1:∆ABC中,顶点C在AB边上的射影为D,且DBADCD⋅=2,求证:∆ABC是直角三角形。
二、常见的轨迹(1)到两定点距离相等的点的轨迹是____________________________________(2)到一个定点的距离等于定长的点的轨迹是____________________________________(3)与一条直线的距离等于定长的点的轨迹是____________________________________(4)与两条平行直线距离相等的点的轨迹是____________________________________(5)与相交两直线距离相等的点的轨迹是____________________________________(6)与已知线段两端点所连线段相互垂直的点的轨迹是____________________________________三、三角形的“心”(结合图形)(1)内心―――_________的圆心―――圆心到_________的距离相等――-三条_________的交点(2)外心―――_________的圆心――-圆心到_________的距离相等―――三条_________的交点可得▲Rt△的外心就是_________,锐角三角形的外心在_________,而钝角三角形的外心在_________(3)重心―――_________的交点―――重心的性质________________________(4)垂心―――-_________的交点Rt△的垂心就是_________,锐角三角形的垂心在_________,而钝角三角形的垂心在_________要求:清楚上述“四心”对应的性质,从形的角度理解和记忆,并能运用性质解题问:等腰三角形的四心有何特殊?__________________那等边三角形呢?_______________________________例2:(1)已知直角三角形的斜边长为c,两直角边长分别为a,b,则内切圆的半径为r=____________ (2)在△ABC中,AB=AC=5,BC=6,求:①△ABC内切圆的半径;②外接圆的半径。
