一元多项式的加减求导运算算法(数据结构算法)
数据结构课程设计-一元多项式的加法、减法、乘法的实现

一、设计题目一元多项式的加法、减法、乘法的实现。
二、主要内容设有一元多项式A m(x)和B n(x).A m(x)=A0+A1x1+A2x2+A3x3+… +A m x mB n(x)=B0+B1x1+B2x2+B3x3+… +B n x n请实现求M(x)= A m(x)+B n(x)、M(x)= A m(x)-B n(x)和M(x)= A m(x)×B n(x)。
要求:1) 首先判定多项式是否稀疏2) 采用动态存储结构实现;3) 结果M(x)中无重复阶项和无零系数项;4) 要求输出结果的升幂和降幂两种排列情况三、具体要求及应提交的材料1.每个同学以自己的学号和姓名建一个文件夹,如:“312009*********张三”。
里面应包括:学生按照课程设计的具体要求所开发的所有源程序(应该放到一个文件夹中)、任务书和课程设计说明书的电子文档。
2.打印的课程设计说明书(注意:在封面后夹入打印的“任务书”以后再装订)。
四、主要技术路线提示为把多个小功能结合成一个完整的小软件,需使用“菜单设计”技术(可以是控制台方式下的命令行形式,若能做成图形方式则更好)。
五、进度安排共计两周时间,建议进度安排如下:选题,应该在上机实验之前完成需求分析、概要设计可分配4学时完成详细设计可分配4学时调试和分析可分配10学时。
2学时的机动,可用于答辩及按教师要求修改课程设计说明书。
注:只用课内上机时间一般不能完成设计任务,所以需要学生自行安排时间做补充。
六、推荐参考资料(不少于3篇)[1]苏仕华等编著,数据结构课程设计,机械工业出版社,2007[2]严蔚敏等编著,数据结构(C语言版),清华大学出版社,2003[3]严蔚敏等编著,数据结构题集(C语言版),清华大学出版社,2003指导教师签名日期年月日系主任审核日期年月日摘要分析了matlab,mathmatic,maple等数学软件对一元多项式的计算过程,步骤后。
由于这些软件比较大功能齐全,但是实用性不强。
一元多项式的加法数据结构

一元多项式的加法数据结构一元多项式是数学中常见的一种代数表达式形式,由多个单项式按照一定的规则相加而成。
在计算机科学中,为了方便对一元多项式进行处理,需要定义一种合适的数据结构来表示和操作一元多项式的加法运算。
一元多项式的加法数据结构可以使用链表来实现。
每个节点表示一个单项式,包含两个成员变量:系数和指数。
系数表示单项式的系数,指数表示单项式的指数。
通过将多个单项式的系数和指数组织成一个链表,即可表示一个一元多项式。
在链表中,每个节点按照指数从小到大的顺序排列。
这样可以方便进行多项式的加法运算。
当两个一元多项式相加时,只需按照指数的大小依次比较两个链表中的节点,并根据指数的大小关系进行相应的操作。
具体的加法算法如下:1. 创建一个新的链表作为结果链表。
2. 初始化两个指针分别指向两个原始链表的头节点。
3. 循环比较两个链表中的节点,直到其中一个链表遍历完为止。
4. 比较当前节点的指数大小关系:- 如果两个节点的指数相等,将它们的系数相加,并将结果添加到结果链表中。
- 如果第一个链表中的节点指数较小,将第一个链表的节点添加到结果链表中,并将指针指向下一个节点。
- 如果第二个链表中的节点指数较小,将第二个链表的节点添加到结果链表中,并将指针指向下一个节点。
5. 当其中一个链表遍历完后,将另一个链表中剩余的节点依次添加到结果链表中。
6. 返回结果链表作为两个一元多项式相加的结果。
通过上述算法,可以实现对一元多项式的加法运算。
这种链表结构的一元多项式加法数据结构具有以下优点:- 灵活性:可以表示任意长度的一元多项式,不受固定数组长度的限制。
- 高效性:在添加节点和遍历节点时,时间复杂度为O(n),其中n 为一元多项式的项数。
- 可扩展性:可以方便地扩展其他操作,如乘法、求导等。
除了链表结构,还可以使用数组等数据结构来表示一元多项式的加法。
不同的数据结构适用于不同的应用场景。
链表结构适合于插入和删除操作较多的情况,而数组结构适合于随机访问和内存占用较小的情况。
一元多项式的计算问题-数据结构与算法课程设计报告

合肥学院计算机科学与技术系课程设计报告2009 ~2010 学年第 2 学期课程数据结构与算法课程设计名称一元多项式的计算问题学生姓名周维学号**********专业班级08计科(2)指导教师王昆仑教授2010年6月题目:(一元多项式的计算问题)要求能够按照指数降序排列建立并输出一元多项式;能够完成两个一元多项式的相加、相减,并将结果输入。
一、问题分析和任务定义1.问题分析本程序关键点是如何将输入的两个多项式相加、相减操作。
①如何将输入的一元多项式按指数的降序排列②如何确定要输入的多项式的项数;③如何将输入的两个一元多项式显示出来。
④如何将输入的两个一元多项式进行相加操作。
⑤如何将输入的两个一元多项式进行相减操作。
本程序是通过链表实现一元多项式的相加减操作。
2、任务定义此程序需要完成如下的要求:将多项式按照指数降序排列建立并输出,将两个一元多项式进行相加、相减操作,并将结果输入。
a:输入多项式的项数并建立多项式;b:输出多项式,输出形式分别为浮点和整数序列,序列按指数升序排列;c:多项式a和b相加,建立多项式a+b;d:多项式a和b相减,建立多项式a-b。
e:多项式的输出。
二、数据结构的选择和概要设计:(1)数据结构的选用A:基于链表中的节点可以动态生成的特点,以及链表可以灵活的添加或删除节点的数据结构,为了实现任意多项式的加法,减法,因此选择单链表的结构体,它有一个系数,指数,下一个指针3个元属;例如,图1中的两个线性链表分别表示一元多项式和一元多项式。
从图中可见,每个结点表示多项式中的一项。
图1 多项式表的单链存储结构B:本设计使用了以下数据结构:t ypedef struct {float coef; //系数int expn; //指数} ElemType;typedef struct LNode{ElemType data;struct LNode *next;}LNode;C:设计本程序需用到九个模块,用到以下九个子函数如下:1、void Menu()//建立菜单2、LNode *InitList() // 创建链表3、void ChaLNode(LNode *L,ElemType x)//插入链表4、LNode *AddPolyn(LNode *A,LNode *B)//多项式相加5、void Invert(LNode *L)//逆序输出链表6、void Print(LNode *L)//输出多项式7、main()//主程序模块调用链一元多项式的各种基本操作模块。
一元多项式计算(数据结构课程设计)

一元多项式计算(数据结构课程设计)一、系统设计1、算法思想根据一元多项式相加的运算规则:对于两个一元多项式中所有指数相同的项,对应指数相加(减),若其和(差)不为零,则构成“和(差)多项式”中的一项;对于两个一元多项式中所有指数不相同的项,则分别写到“和(差)多项式”中去。
因为多项式指数最高项以及项数是不确定的,因此采用线性链表的存储结构便于实现一元多项式的运算。
为了节省空间,我采用两个链表分别存放多项式a 和多项式b,对于最后计算所得的多项式则利用多项式a进行存储。
主要用到了单链表的插入和删除操作。
(1)一元多项式加法运算它从两个多项式的头部开始,两个多项式的某一项都不为空时,如果指数相等的话,系数就应该相加;相加的和不为零的话,用头插法建立一个新的节点。
P 的指数小于q的指数的话就应该复制q的节点到多项式中。
P的指数大于q的指数的话,就应该复制p节点到多项式中。
当第二个多项式空,第一个多项式不为空时,将第一个多项式用新节点产生。
当第一个多项式空,第二个多项式不为空时,将第二个多项式用新节点产生。
(2)一元多项式的减法运算它从两个多项式的头部开始,两个多项式的某一项都不为空时,如果指数相等的话,系数就相减;相加的和不为零的话,用头插法建立一个新的节点。
p的指数小于q的指数的话,就应该复制q的节点到多项式中。
P的指数大于q的指数的话就应该复制p的节点到多项式中,并且建立的节点的系数为原来的相反数;当第二个多项式空,第一个多项式不为空时,将第一个多项式用新节点产生。
当第一个多项式空,第二个多项式不为空时,将第二个多项式用新节点产生,并且建立的节点的系数为原来的相反数。
2、概要设计(1)主函数流程图:(注:a代表第一个一元二次方程,b代表第二个一元二次方程)(2)一元多项式计算算法用类C语言表示:Typedef struct00{ //项的表示,多项式的项作为LinkList的数据元素Float coef;//细数Int expn;//指数}term,ElemType;//两个类型名:term用于本ADT,ElemType为LinkList的数据对象名Typedef LinkList polynomial://用带表头的节点的有序链表表示多项式//基本操作的函数原型说明Void CreatePolyn(polynomail&P);//输入n的系数和指数,建立表示一元多项式的有序链表P 销毁一元多项式P Void DestroyPolyn(polynomailP);销毁一元多项式PvoidPrintPoly(polynomail P);//打印输入一元多项式PIntPolynLength(polynnomail P);//返回一元多项式P中的项数void CreatPolyn(polynomail&Pa.polunomail&Pb);//完成多项式相加运算,即:Pa=Pa+Pb,并贤惠一元多项式Pb voidSubtractPolyn(polunomail&Papolunomail&Pb);//完成多项式相减运算,即:Pa=Pa-Pb,并销毁一元多项式Pb//基本操作的算法描述Int cmp(tem a,temp b);//依a的指数值<(或=)(或>b的住数值,分别返回-1、0和+1Void CreatePolyn(polynomail&P,int m){//输入m项的系数和指数,建立表示一元多项式的有序链表PInitList(P);h=GetHead(P);E.coef=0.0; e.expn=-1;S erCurElem(h,e);//设置头结点的数据元素For (i=1;i<=m;++i){ //依次输入m个非零项Scanf(e.coef,e.epn);If(!LocateElem(P,e,q,(*cmp)())){//当前链表中不存在该指数项If(MakeNode(s,e))InsFirst(q,s);//生成节点并插入链表}}}//CreatPolun二、详细设计1、算法实现(1)输入一元多项式函数:void shuchu(pnode *head){pnode *p;int one_time=1;p=head;while(p!=NULL) /*如果不为空*/{if(one_time==1){if(p->zhishu==0) /*如果指数为0的话,直接输出系数*/printf("%5.2f",p->xishu); /*如果系数是正的话前面就要加+号*/else if(p->xishu==1||p->xishu==-1)printf("X^%d",p->zhishu); /*如果系数是1的话就直接输出+x*//*如果系数是-1的话就直接输出-x号*/else if(p->xishu>0) /*如果系数是大于0的话就输出+系数x^指数的形式*/ printf("%5.2fX^%d",p->xishu,p->zhishu);else if(p->xishu<0) /*如果系数是小于0的话就输出系数x^指数的形式*/ printf("%5.2fX^%d",p->xishu,p->zhishu);one_time=0;}else{if(p->zhishu==0) /*如果指数为0的话,直接输出系数*/{if(p->xishu>0)printf("+%5.2f",p->xishu); /*如果系数是正的话前面就要加+号*/}else if(p->xishu==1) /*如果系数是1的话就直接输出+x号*/printf("+X^%d",p->zhishu);else if(p->xishu==-1) /*如果系数是-1的话就直接输出-x号*/printf("X^%d",p->zhishu);else if(p->xishu>0) /*如果系数是大于0的话就输出+系数x^指数的形式*/ printf("+%5.2fX^%d",p->xishu,p->zhishu);else if(p->xishu<0) /*如果系数是小于0的话就输出系数x^指数的形式*/printf("%5.2fX^%d",p->xishu,p->zhishu);}p=p->next; /*指向下一个指针*/}printf("\n");}(2)加法函数/*两个多项式的加法运算*/pnode * add(pnode *heada,pnode *headb){pnode *headc,*p,*q,*s,*r; /*headc为头指针,r,s为临时指针,p指向第1个多项式并向右移动,q指向第2个多项式并向右移动*/float x; /*x为系数的求和*/p=heada; /*指向第一个多项式的头*/q=headb; /*指向第二个多项式的头*/headc=(pnode *)malloc(sizeof(pnode)); /*开辟空间*/r=headc;while(p!=NULL&&q!=NULL) /*2个多项式的某一项都不为空时*/{if(p->zhishu==q->zhishu) /*指数相等的话*/{x=p->xishu+q->xishu; /*系数就应该相加*/if(x!=0) /*相加的和不为0的话*/{s=(pnode *)malloc(sizeof(pnode)); /*用头插法建立一个新的节点*/s->xishu=x;s->zhishu=p->zhishu;r->next=s;r=s;}q=q->next;p=p->next; /*2个多项式都向右移*/}else if(p->zhishu<q->zhishu) /*p的系数小于q的系数的话,就应该复制q节点到多项式中*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=q->xishu;s->zhishu=q->zhishu;r->next=s;r=s;q=q->next; /*q向右移动*/}else/*p的系数大于q的系数的话,就应该复制p节点到多项式中*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next; /*p向右移动*/}}/*当第2个多项式空,第1个数不为空时,将第一个数剩下的全用新节点产生*/ while(p!=NULL){s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next;}/*当第1个多项式空,第1个数不为空时,将第2个数剩下的全用新节点产生*/ while(q!=NULL){s=(pnode *)malloc(sizeof(pnode));s->xishu=q->xishu;s->zhishu=q->zhishu;r->next=s;r=s;q=q->next;}r->next=NULL; /*最后指向空*/headc=headc->next; /*第一个头没有用到*/return headc; /*返回头接点*/}(3)减法函数/*两个多项式的加法运算*/pnode * add(pnode *heada,pnode *headb){pnode *headc,*p,*q,*s,*r; /*headc为头指针,r,s为临时指针,p指向第1个多项式并向右移动,q指向第2个多项式并向右移动*/float x; /*x为系数的求和*/p=heada; /*指向第一个多项式的头*/q=headb; /*指向第二个多项式的头*/headc=(pnode *)malloc(sizeof(pnode)); /*开辟空间*/r=headc;while(p!=NULL&&q!=NULL) /*2个多项式的某一项都不为空时*/{if(p->zhishu==q->zhishu) /*指数相等的话*/{x=p->xishu+q->xishu; /*系数就应该相加*/if(x!=0) /*相加的和不为0的话*/{s=(pnode *)malloc(sizeof(pnode)); /*用头插法建立一个新的节点*/s->xishu=x;s->zhishu=p->zhishu;r->next=s;r=s;}q=q->next;p=p->next; /*2个多项式都向右移*/}else if(p->zhishu<q->zhishu) /*p的系数小于q的系数的话,就应该复制q节点到多项式中*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=q->xishu;s->zhishu=q->zhishu;r->next=s;r=s;q=q->next; /*q向右移动*/}else/*p的系数大于q的系数的话,就应该复制p节点到多项式中*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next; /*p向右移动*/}}/*当第2个多项式空,第1个数不为空时,将第一个数剩下的全用新节点产生*/ while(p!=NULL){s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next;}/*当第1个多项式空,第1个数不为空时,将第2个数剩下的全用新节点产生*/ while(q!=NULL){s=(pnode *)malloc(sizeof(pnode));s->xishu=q->xishu;s->zhishu=q->zhishu;r->next=s;r=s;q=q->next;}r->next=NULL; /*最后指向空*/headc=headc->next; /*第一个头没有用到*/return headc; /*返回头接点*/}2、程序代码/*一元多项式计算*//*程序功能:能够按照指数降序排列建立并输出多项式;能够完成两个多项式的相加、相减,并将结果输出;*//*提示:输入完一元多项式之后,输入“0 0”结束本一元多项式的输入*//*注意:系数只精确到百分位,最大系数只能为999.99,指数为整数.如果需要输入更大的系数,可以对程序中5.2%f进行相应的修改*/#include<stdio.h>#include<malloc.h>#include<stdlib.h>#include<conio.h>/*建立结构体*/typedef struct pnode{float xishu; /*系数*/int zhishu; /*指数*/struct pnode *next; /*下一个指针*/}pnode;/*用头插法生成一个多项式,系数和指数输入0时退出输入*/pnode * creat()int m;float n;pnode *head,*rear,*s; /*head为头指针,rear和s为临时指针*/ head=(pnode *)malloc(sizeof(pnode));rear=head; /*指向头*/scanf("%f",&n); /*系数*/scanf("%d",&m); /*输入指数*/while(n!=0) /*输入0退出*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=n;s->zhishu=m;s->next=NULL;rear->next=s; /*头插法*/rear=s;scanf("%f",&n); /*输入系数*/scanf("%d",&m); /*输入指数*/}head=head->next; /*第一个头没有用到*/return head;}/*调整多项式*/void tiaozhen(pnode *head){pnode *p,*q,*t;float temp;p=head;while(p!=NULL){q=p;t=q->next;while(t!=NULL){if(t->zhishu>q->zhishu)q=t;t=t->next;}temp=p->xishu;p->xishu=q->xishu;q->xishu=temp;temp=p->zhishu;p->zhishu=q->zhishu;q->zhishu=temp;p=p->next;}/*显示一个多项式*/void shuchu(pnode *head){pnode *p;int one_time=1;p=head;while(p!=NULL) /*如果不为空*/{if(one_time==1){if(p->zhishu==0) /*如果指数为0的话,直接输出系数*/printf("%5.2f",p->xishu); /*如果系数是正的话前面就要加+号*/else if(p->xishu==1||p->xishu==-1)printf("X^%d",p->zhishu); /*如果系数是1的话就直接输出+x*//*如果系数是-1的话就直接输出-x号*/else if(p->xishu>0) /*如果系数是大于0的话就输出+系数x^指数的形式*/ printf("%5.2fX^%d",p->xishu,p->zhishu);else if(p->xishu<0) /*如果系数是小于0的话就输出系数x^指数的形式*/ printf("%5.2fX^%d",p->xishu,p->zhishu);one_time=0;}else{if(p->zhishu==0) /*如果指数为0的话,直接输出系数*/{if(p->xishu>0)printf("+%5.2f",p->xishu); /*如果系数是正的话前面就要加+号*/}else if(p->xishu==1) /*如果系数是1的话就直接输出+x号*/printf("+X^%d",p->zhishu);else if(p->xishu==-1) /*如果系数是-1的话就直接输出-x号*/printf("X^%d",p->zhishu);else if(p->xishu>0) /*如果系数是大于0的话就输出+系数x^指数的形式*/ printf("+%5.2fX^%d",p->xishu,p->zhishu);else if(p->xishu<0) /*如果系数是小于0的话就输出系数x^指数的形式*/ printf("%5.2fX^%d",p->xishu,p->zhishu);}p=p->next; /*指向下一个指针*/}printf("\n");/*两个多项式的加法运算*/pnode * add(pnode *heada,pnode *headb){pnode *headc,*p,*q,*s,*r; /*headc为头指针,r,s为临时指针,p指向第1个多项式并向右移动,q指向第2个多项式并向右移动*/float x; /*x为系数的求和*/p=heada; /*指向第一个多项式的头*/q=headb; /*指向第二个多项式的头*/headc=(pnode *)malloc(sizeof(pnode)); /*开辟空间*/r=headc;while(p!=NULL&&q!=NULL) /*2个多项式的某一项都不为空时*/{if(p->zhishu==q->zhishu) /*指数相等的话*/{x=p->xishu+q->xishu; /*系数就应该相加*/if(x!=0) /*相加的和不为0的话*/{s=(pnode *)malloc(sizeof(pnode)); /*用头插法建立一个新的节点*/s->xishu=x;s->zhishu=p->zhishu;r->next=s;r=s;}q=q->next;p=p->next; /*2个多项式都向右移*/}else if(p->zhishu<q->zhishu) /*p的系数小于q的系数的话,就应该复制q节点到多项式中*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=q->xishu;s->zhishu=q->zhishu;r->next=s;r=s;q=q->next; /*q向右移动*/}else/*p的系数大于q的系数的话,就应该复制p节点到多项式中*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next; /*p向右移动*/}}/*当第2个多项式空,第1个数不为空时,将第一个数剩下的全用新节点产生*/ while(p!=NULL){s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next;}/*当第1个多项式空,第1个数不为空时,将第2个数剩下的全用新节点产生*/ while(q!=NULL){s=(pnode *)malloc(sizeof(pnode));s->xishu=q->xishu;s->zhishu=q->zhishu;r->next=s;r=s;q=q->next;}r->next=NULL; /*最后指向空*/headc=headc->next; /*第一个头没有用到*/return headc; /*返回头接点*/}/*两个多项式的减法运算*/pnode * sub(pnode *heada,pnode *headb){pnode *headc,*p,*q,*s,*r;float x; /*x为系数相减*/p=heada; /*指向第一个多项式的头*/q=headb; /*指向第二个多项式的头*/headc=(pnode *)malloc(sizeof(pnode)); /*开辟空间*/r=headc;while(p!=NULL&&q!=NULL) /*两个多项式的某一项都不为空时*/{if(p->zhishu==q->zhishu) /*指数相等的话*/{x=p->xishu-q->xishu; /*系数相减*/if(x!=0) /*相减的差不为0的话*/{s=(pnode *)malloc(sizeof(pnode)); /*用头插法建立一个新的节点*/s->xishu=x;s->zhishu=p->zhishu;r->next=s;r=s;}q=q->next;p=p->next; /*2个多项式都向右移*/}else if(p->zhishu<q->zhishu) /*p的系数小于q的系数的话*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=-q->xishu; /*建立的节点的系数为原来的相反数*/s->zhishu=q->zhishu;r->next=s;r=s;q=q->next;}else{s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next; /*p向右移动*/}}while(p!=NULL) /*当第2个多项式空,第1个数不为空时,将第一个数剩下的全用新节点产生*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=p->xishu;s->zhishu=p->zhishu;r->next=s;r=s;p=p->next;}while(q!=NULL) /*当第1个多项式空,第1个数不为空时,将第2个数剩下的全用新节点产生*/{s=(pnode *)malloc(sizeof(pnode));s->xishu=-q->xishu; /*建立的节点的系数为原来的相反数*/ s->zhishu=q->zhishu;r->next=s;r=s;q=q->next;}r->next=NULL; /*最后指向空*/headc=headc->next; /*第一个头没有用到*/return headc; /*返回头接点*/}void add_main(){pnode * a,*b,*c;printf("\n输入第一个一元多项式:\n系数指数\n");a=creat();tiaozhen(a);printf("\n输入第二个一元多项式:\n系数指数\n");b=creat();tiaozhen(b);c=add(a,b);printf("第一个一元多项式如下:");shuchu(a);printf("第二个一元多项式如下:");shuchu(b);printf("两式相加如下:");shuchu(c);}void sub_main(){pnode * a,*b,*c;printf("\n输入第一个一元多项式:\n系数指数\n");a=creat();tiaozhen(a);printf("\n输入第二个一元多项式:\n系数指数\n");b=creat();tiaozhen(b);c=sub(a,b);printf("第一个一元多项式如下:");shuchu(a);printf("第二个一元多项式如下:");shuchu(b);printf("两式相减如下:");shuchu(c);}void open(){printf("\n****************************************************\n");printf(" 功能项: * 1 两个一元多项式相加;2 两个一元多项式相减;0 退出*\n");printf("****************************************************\n\n请选择操作: ");}void main(){int choose;open();while(choose!=0){scanf("%d",&choose);getchar();switch(choose){case 0:return;case 1:printf("\n 两个一元多项式相加\n");add_main();choose=-1;open();break;case 2:printf("\n 两个一元多项式相减\n");sub_main();choose=-1;open();break;default:printf("没有该选项!请重新选择操作!\n\n");open();}}}三、测试方案及结果1、测试方案在Visual C++ 6.0环境中调试运行。
数据结构 线性结 一元多项式的加法乘法实现

求解思路
1.多项式表示 2. 程序框架 3. 读多项式 4. 加法实现 5. 乘法实现 6. 多项式输出
多项式的表示
仅表示非零项
数组: 编程简单、调试容易
需要事先确定数组大小
一种比较好的实现方法是: 动态数组
链表:
动态性强 编程略为复杂、调试比较困难
while (t1 && t2) {
if (t1->expon == t2->expon) {
…..
}
else if (t1->expon > t2->expon) {
……
}
else {
……
}
}
while (t1) {
return 0; }
如何读入多项式
Polynomial ReadPoly() {
…… scanf("%d", &N); …… while ( N-- ) {
scanf("%d %d", &c, &e); Attach(c, e, &Rear); } ….. return P; }
4 3 4 -5 2 6 1 -2 0
两种处理方法: 1. Rear初值为NULL
在Attach函数中根据Rear是 否为NULL做不同处理
Attach
ce
Rear (当前结果表达式尾项指针)
Rear
如何读入多项式
Polynomial ReadPoly() {
…… scanf("%d", &N); …… while ( N-- ) {
多项式的乘积: (a+b)(c+d) = ac+ad+bc+bd
c语言数据结构实现——一元多项式的基本运算

文章标题:深入理解C语言中的数据结构实现——一元多项式的基本运算在C语言中,数据结构是非常重要的一个概念,它为我们处理各种复杂的数据提供了便利。
其中,一元多项式的基本运算是数据结构中的一个重要内容,它涉及到多种数据结构的操作和算法,是我们学习C 语言中数据结构的一个重要入口。
在本文中,我们将深入探讨C语言中一元多项式的基本运算,帮助读者更深入地理解这一重要的概念。
一、一元多项式的表示方式在C语言中,一元多项式可以使用数组来表示。
每个数组元素对应一个项,数组的下标对应每一项的次数,数组的值对应该项的系数。
一个一元多项式可以表示为:```cfloat polynomial[10] = {0, 1, 2, 0, 4}; // 表示多项式 1 + 2x + 4x^4 ```二、一元多项式的基本运算1. 一元多项式的加法有两个多项式 A 和 B,它们分别表示为 `float polynomialA[10]` 和`float polynomialB[10]`,那么它们的加法运算可以表示为:```cfor (int i = 0; i < 10; i++) {polynomialC[i] = polynomialA[i] + polynomialB[i];}```2. 一元多项式的减法一元多项式的减法是指将两个多项式相减得到一个新的多项式。
与加法类似,多项式 A 和 B 的减法运算可以表示为:```cfor (int i = 0; i < 10; i++) {polynomialC[i] = polynomialA[i] - polynomialB[i];}```3. 一元多项式的乘法式 A 和 B 的乘法运算可以表示为:```cfor (int i = 0; i < 10; i++) {for (int j = 0; j < 10; j++) {polynomialC[i+j] += polynomialA[i] * polynomialB[j];}}```4. 一元多项式的除法一元多项式的除法涉及到较为复杂的算法,需要考虑余数和商的处理。
数据结构一元多项式的运算

数据结构一元多项式的运算正文:1. 引言本文档旨在介绍数据结构中一元多项式的运算方法。
一元多项式是指在一个变量上的多项式,其中每一项由一个系数和一个指数组成。
我们将会讨论一元多项式的表示、存储和基本运算,包括多项式的加法、减法、乘法和求导等操作。
2. 一元多项式的表示和存储2.1 一元多项式的定义一元多项式是指在一个变量x上的多项式,每一项由一个系数和一个指数组成,例如:2x^3 - 5x^2 + 3x + 1.其中,2、-5、3和1分别是系数,3、2、1和0分别是指数。
2.2 一元多项式的表示方法一元多项式可以使用数组、链表或其他数据结构来表示。
在本文中,我们选择使用数组来表示一元多项式。
数组的索引代表指数,数组的元素代表系数。
例如,多项式 2x^3 - 5x^2 + 3x + 1 可以表示为 [1, 3, -5, 2]。
2.3 一元多项式的存储结构为了表示一元多项式,我们可以使用一个数组来存储多项式的系数。
数组的长度应该比多项式的最高指数大1.数组的索引代表指数,数组的元素代表系数。
例如,数组 [1, 3, -5, 2] 表示的多项式 2x^3 - 5x^2 + 3x + 1 中,索引0对应指数为3的项,索引1对应指数为2的项,以此类推。
3. 一元多项式的基本运算3.1 一元多项式的加法一元多项式的加法是指将两个多项式相加,并合并同类项。
具体操作如下:- 将两个多项式的系数相加,并将结果存储在一个新的多项式中。
- 遍历新的多项式,将相邻的相同指数的项合并。
3.2 一元多项式的减法一元多项式的减法是指将一个多项式减去另一个多项式,并合并同类项。
具体操作如下:- 将两个多项式的系数相减,并将结果存储在一个新的多项式中。
- 遍历新的多项式,将相邻的相同指数的项合并。
3.3 一元多项式的乘法一元多项式的乘法是指将两个多项式相乘,并合并同类项。
具体操作如下:- 遍历一个多项式的每一项,与另一个多项式的每一项相乘。
c语言数据结构实现——一元多项式的基本运算

c语言数据结构实现——一元多项式的基本运算在C语言中,一元多项式的表示与运算是常见的数据结构操作之一。
一元多项式由一系列具有相同变量的单项式组成,每个单项式由系数和指数组成。
本文将介绍如何使用C语言实现一元多项式的基本运算,包括多项式的创建、求和、差、乘积等操作。
首先,我们需要定义一个结构体来表示单项式。
每个单项式由一个系数和一个指数组成,我们可以将其定义如下:```cstruct term{float coefficient; // 系数int exponent; // 指数};typedef struct term Term;```接下来,我们可以定义一个结构体来表示一元多项式。
一元多项式由一系列单项式组成,可以使用一个动态数组来存储这些单项式。
```cstruct polynomial{Term* terms; // 单项式数组int num_terms; // 单项式数量};typedef struct polynomial Polynomial;```现在,我们可以开始实现一元多项式的基本运算了。
1. 创建一元多项式要创建一元多项式,我们需要输入每个单项式的系数和指数。
我们可以使用动态内存分配来创建一个适应输入的单项式数组。
```cPolynomial create_polynomial(){Polynomial poly;printf("请输入多项式的项数:");scanf("%d", &poly.num_terms);poly.terms = (Term*)malloc(poly.num_terms * sizeof(Term));for(int i = 0; i < poly.num_terms; i++){printf("请输入第%d个单项式的系数和指数:", i+1);scanf("%f %d", &poly.terms[i].coefficient, &poly.terms[i].exponent);}return poly;}```2. 求两个一元多项式的和两个一元多项式的和等于对应指数相同的单项式系数相加的结果。
数据结构课程设计一元多项式的加减法运算

武汉理工大学华夏学院课程设计报告书课程名称:数据结构与算法分析题目:用C语言实现一元多项式的加减法运算系名:信息工程系专业班级:物联网工程1122班姓名:隋明超学号: 10213312201 指导教师:司晓梅2014年 1 月 3 日武汉理工大学华夏学院信息工程系课程设计任务书课程名称:数据结构与算法分析指导教师:司晓梅班级名称:物联网1121-2 开课系、教研室:信息系计算机一、课程设计目的与任务《数据结构》课程设计是为训练学生的数据组织能力和提高程序设计能力而设置的增强实践能力的课程。
目的:学习数据结构课程,旨在使学生学会分析研究数据对象的特性,学会数据的组织方法,以便选择合适的数据的逻辑结构和存储结构以及相应操作,把现实世界中的问题转换为计算机内部的表示和处理,这就是一个良好的程序设计技能训练的过程。
提高学生的程序设计能力、掌握基本知识、基本技能,提高算法设计质量与程序设计素质的培养就是本门课程的课程设计的目的。
任务:根据题目要求,完成算法设计与程序实现,并按规定写出课程设计报告。
二、课程设计的内容与基本要求设计题目:用C语言实现一元多项式的加减法计算〔问题描述〕输入并建立两个多项式并输出多项式设计一个程序:对两个多项式进行加、减法运算,建立一个新多项式并输出。
〔实现提示〕:选择单链表存储多项式具体要完成的任务是:A. 编制完成上述问题的C语言程序、进行程序调试并能得出正确的运行结果。
B. 写出规范的课程设计报告书;三、课程设计步骤及时间进度和场地安排时间:本课程设计安排在第18周地点:现代教育中心具体时间安排如下:第一天:布置题目,确定任务、查找相关资料第二天~第四天:功能分析,编写程序,调试程序、运行系统;第五天上午:撰写设计报告;第五天下午:程序验收、答辩。
四、课程设计考核及评分标准课程设计考核将综合考虑学生的系统设计方案、运行结果、课程设计报告书的质量、态度、考勤、答辩情况等各因素。
数据结构一元多项式的运算

数据结构一元多项式的运算第一章引言在计算机科学中,数据结构是研究非原子数据对象的组织、存储和管理的科学和技术。
一元多项式是代数中的基本概念之一,它在计算机科学中有着广泛的应用。
本文将介绍一元多项式的运算,包括多项式的表示、加法、减法、乘法等操作。
第二章多项式的表示1.稀疏数组表示法稀疏数组表示法是一种常用的多项式表示方法。
它通过一个数组来存储多项式中非零项的指数和系数。
数组的下标表示项的指数,数组元素表示项的系数。
对于没有出现的指数,数组元素为零。
2.链表表示法链表表示法是另一种常用的多项式表示方法。
每个节点包含项的指数和系数,并通过指针串接成链表。
链表的节点可以按照指数的升序或降序排列。
第三章多项式的加法多项式的加法是指将两个多项式相加得到一个新的多项式。
具体操作如下:1.根据多项式的表示方法,分别遍历两个多项式的非零项。
2.比较当前项的指数大小,如果两个指数相等,则将系数相加得到新的系数,并将结果加入结果多项式中。
3.如果一个多项式的指数大于另一个多项式的指数,则将该项加入结果多项式中。
4.重复以上操作,直到遍历完所有的非零项。
第四章多项式的减法多项式的减法是指将两个多项式相减得到一个新的多项式。
具体操作如下:1.根据多项式的表示方法,分别遍历被减数和减数的非零项。
2.比较当前项的指数大小,如果两个指数相等,则将被减数的系数减去减数的系数得到新的系数,并将结果加入结果多项式中。
3.如果被减数的指数大于减数的指数,则将该项加入结果多项式中,并将被减数的系数变为相反数。
4.重复以上操作,直到遍历完所有的非零项。
第五章多项式的乘法多项式的乘法是指将两个多项式相乘得到一个新的多项式。
具体操作如下:1.创建一个结果多项式,将其初始化为零多项式。
2.根据多项式的表示方法,分别遍历两个多项式的非零项。
3.将两个项的系数相乘得到新的系数,并将两个项的指数相加得到新的指数。
4.将新的系数和指数合并为一个项,并将该项加入结果多项式中。
数据结构实验-一元多项式的加法运算

一元多项式加法一、实验目的通过实现多项式加法,对链表有更深入的了解二、实验内容问题描述:设计一个一元稀疏多项式简单的加法计算器实现要求:一元稀疏多项式简单计算器的基本功能是:(1)输入并建立多项式:1785937)(x x x x A +++=;879228)(x x x x B -+=(2)输出多项式(3)多项式A 和B 相加,建立多项式C =A +B ,并输出相加的结果多项式C(4)选作:多项式A 和B 相减,建立多项式C =A -B ,并输出相减的结果多项式D 方法说明:(1)多项式的输入与存储用带表头结点的单链表存储多项式,链表中的每个节点分别存储多项式各项的系数和指数,即每从键盘输入多项式的一对数(系数,指数),可对应建立链表的一个结点。
每个节点的结构为:建立两个链表,其中pa 和pb 分别为它们的头指针:pb结果链表Pa(或者是Pc)Pc(2)多项式数据类型的定义struct tagNode{float coef;int exp;struct tagNode *next;typedef struct tagNode Node;typedef struct tagNode* pNode;(3)主要算法①创建两个链表,分别存放多项式1和多项式2,这两个链表中的节点是按指数降序或者升序排列的②多项式相加,下面给出多项式相加的部分实现/*下面的函数实现两个多项式的相加,要相加的链表分别由pa和pb指向(其中,pa,pb都是分配了空间的头结点)。
相加的结果直接由pa指向的链表保存,即是在pa链表中添加或删除(当系数因为相加为0的情况下)一些结点,构成结果。
相加的链表中指数按从小到大的顺序排列好的,是升序链表。
*/void add_poly(Node *pa,Node *pb){Node *p=pa->pNext;//链表1,将来的结果也放在此Node *q=pb->pNext;//链表2Node *pre=pa;Node *u;//临时用float x;while (p!=NULL && q!=NULL)//当两个链表都不为空{if (p->exp<q->exp)//比较链表1跟链表2当前节点的指数大小,链表1也是存放结果的地方{pre=p;p=p->pNext;//p指向要比较的下一个结点。
一元多项式的计算,数据结构程序设计图形界面

一元多项式的计算,数据结构程序设计图形界面
对于一元多项式的计算,可以使用链表来存储每一项的系数和指数,然后进行加减乘除等运算。
具体实现的步骤如下:
1. 定义一个多项式节点的结构体,包含两个成员:系数和指数。
2. 定义一个链表结构体,包含两个成员:头节点和尾节点。
3. 实现链表的初始化函数、插入节点函数、删除节点函数、遍历链表函数等基本操作。
4. 实现多项式加法、减法、乘法、除法等运算函数。
对于加减法,可以遍历两个链表,依次将相同指数的项相加或相减;对于乘法,可以使用两个for循环遍历两个链表,将每一项相乘并按照指数相加;对于除法,可以使用辗转相除法,将被除数一部分一部分地减去除数,直到余数小于除数为止,每一部分的商可视为一项。
对于数据结构程序设计图形界面,可以使用Qt等UI框架来实现。
可以使用布局管理器来设计UI界面,使用信号与槽机制来处理用户的操作输入,将用户输入的参数传递给多项式计算函数,最终将计算结果显示在UI界面上。
数据结构一元多项式的运算-无删减范文

数据结构一元多项式的运算数据结构一元多项式的运算简介一元多项式是数学中常见的概念,用于表示一个变量的多项式表达式。
在计算机科学中,经常需要对一元多项式进行各种运算,如加法、减法、乘法等。
为了实现这些运算,可以使用数据结构来存储和操作一元多项式。
本文将介绍一元多项式的数据结构和常见的运算方法,并给出相应的代码示例。
数据结构一元多项式可以用链表来表示。
每个节点包含两个部分:系数(coefficient)和指数(exponent)。
系数表示该项的权重,指数表示该项的幂次。
链表的每个节点按照指数的升序排列。
以下是一个一元多项式的链表表示的示例:```markdown1.2x^2 + 3.7x^4 - 0.5x^3 -2.1x^1 + 4.0``````markdownNode 1: coefficient=1.2, exponent=2Node 2: coefficient=3.7, exponent=4Node 3: coefficient=-0.5, exponent=3Node 4: coefficient=-2.1, exponent=1Node 5: coefficient=4.0, exponent=0```运算方法加法运算两个一元多项式相加可以按照如下步骤进行:1. 遍历两个链表的节点,分别取出当前节点的系数和指数。
2. 如果两个节点的指数相等,将系数相加,并将其作为结果链表的节点。
3. 如果两个节点的指数不相等,将指数较小的节点插入结果链表,并继续遍历指数较大的节点。
4. 当其中一个链表遍历完后,直接将另一个链表的节点插入结果链表。
以下是加法运算的代码示例:```pythondef addPolynomials(p1, p2):result = Nonetl = Nonewhile p1 is not None and p2 is not None:if p1.exponent == p2.exponent:coef_sum = p1.coefficient + p2.coefficient if coef_sum != 0:node = Node(coef_sum, p1.exponent)if result is None:result = tl = nodeelse:tl.next = nodetl = nodep1 = p1.nextp2 = p2.nextelif p1.exponent > p2.exponent:node = Node(p1.coefficient, p1.exponent) if result is None:result = tl = nodeelse:tl.next = nodetl = nodep1 = p1.nextelse:node = Node(p2.coefficient, p2.exponent) if result is None:result = tl = nodeelse:tl.next = nodetl = nodep2 = p2.nextwhile p1 is not None:node = Node(p1.coefficient, p1.exponent)if result is None:result = tl = nodeelse:tl.next = nodetl = nodep1 = p1.nextwhile p2 is not None:node = Node(p2.coefficient, p2.exponent) if result is None:result = tl = nodeelse:tl.next = nodetl = nodep2 = p2.nextreturn result```减法运算减法运算可以看作加法运算的特殊情况,即将第二个多项式的系数取负数,再进行加法运算。
数据结构和算法-一元多项式运算算法(加法)

数据结构和算法-⼀元多项式运算算法(加法)算法名称:⼀元多项式算法算法介绍:加法运算:将具有与相同幂项的系数相加即可得到合并后的多项式。
若某个幂项只存在于⼀个多项式中,则直接合并到结果中举例利⽤代码实现这⾥主要使⽤了链表,通过3个函数来进⾏操作。
分别是Inpu函数,Add运算函数,打印函数。
代码:1. /*采⽤链表的⽅式*/2. #include<stdio.h>3. #include<stdlib.h>4. #include<limits.h>5. typedef struct polyn //定义多项式的结构6. {7.8. float coef; //系数项9. int expn; //指数10. struct polyn *next; //指向下⼀项11. }POLYN,*pPOLYN;12. void PolynInput(pPOLYN *p) //输⼊⼀元多项式13. {14. int i,min=INT_MIN; //INT_MIN是int型的最⼩数15. pPOLYN p1,p2; //分别表⽰2个多项式的指针16. if(!(*p=(POLYN *)malloc(sizeof(POLYN)))) //为头结点分配内存17. {18.19. printf("内存分配失败 \n");20. exit(0);21. }22. (*p)->coef=0; //设置头结点的系数为023. printf("输⼊该多项式的项数:");24. scanf("%d",&((*p)->expn));25. (*p)->next=NULL;26. for(i=0;i<(*p)->expn;i++) //输⼊多项式各项27. {28. if(!(p1=(pPOLYN)malloc(sizeof(POLYN)))) //分配⼀个多项式的内存29. {30. printf("内存分配失败: \n");31. exit(0);32. }33. printf("第%d项系数:",i+1);34. scanf("%f",&(p1->coef));35. do{36. printf("第%d项指数:",i+1);37. scanf("%d",&(p1->expn));38. if(p1->expn<min)39. printf("\n前项=指数值不能⼩于前⼀项指数值%d!\n重新输⼊\n",(*p)->next->expn);40. }while(p1->expn<min);41. min=p1->expn;42. p1->next=(*p)->next;43. (*p)->next=p1;44. }45. p1=(*p)->next; //合并多项式中指数值相同的项46. while(p1)47. {48. p2=p1->next; //取下⼀节点49. while(p2 && p2->expn==p1->expn) //若节点有效,节点与q节点的指数相同50. {51. p1->coef+=p2->coef; //累加系数52. p1->next=p2->next; //删除r指向的节点53. free(p2);54. p2=p1->next;56. }57. p1=p1->next;58. }59. }60. void PolynPrint(pPOLYN p) //输出多项式61. {62. pPOLYN p1;63. int i;64. printf("\n\n计算后的多项式共有%d项 \n",p->expn);65. p1=p->next;66. i=1;67. while(p1)68. {69. printf("第%d项,系数:%g,指数:%d\n",i++,p1->coef,p1->expn);70. p1=p1->next;71. }72. printf("\n");73. }74. void PolynAdd(pPOLYN pa,pPOLYN pb) //多项式相加pa=pa+pb75. {76.77. pPOLYN pa1,pb1,pc1,p;78. pa1=pa->next; //指向被加链表的第⼀个有效项79. pb1=pb->next; //指向加链表的第⼀个有效项80. pc1=pa; //指向被加链表81. pc1->next=NULL;82. pa->expn=0; //清空多项式项⽬数据83. while(pa1 && pb1) //两个多项式都未结束84. {85.86. if(pa1->expn > pb1->expn) //如果pa1指数⼤于pb187. {88. pc1->next=pa1; //将pa1指数加⼊结果链表中89. pc1=pa1;90. pa1=pa1->next; //处理pa1中的下⼀项91. pc1->next=NULL;92.93. }else if(pa1->expn < pb1->expn) //pa1的指数⼩于pb1的指数94. {95. pc1->next=pb1; //将pb1指数加⼊结果链表中96. pc1=pb1;97. pb1=pb1->next; //处理pb1的下⼀项98. pc1->next=NULL;99. }else { //pa1指数等于pb1指数,进⾏系统相加100. pa1->coef+=pb1->coef; //累加素数101. if(pa1->coef!=0) //若系数不为0102. {103. pc1->next=pa1; //将相加结果添加到结果链表中104. pc1=pa1;105. pa1=pa1->next; //处理pa1的下⼀项106. pc1->next=NULL;107. p=pb1;108. pb1=pb1->next; //处理pb1的下⼀项109. free(p);110. }111. else{ //系数为0,则不记录该项112. p=pa1; //⽤p指向pa1中的该项113. pa1=pa1->next; //链表中删除该项114. free(p); //释放该项所占⽤内存115. p=pb1; //⽤临时指针指向pb1中的该项116. pb1=pa1->next; //链表中删除该项117. free(p); //释放该项所占⽤内存118. pa->expn--; //后⾯要进⾏累加操作,此处先减119. }120. }121. pa-pa->expn++; //累加⼀个结果项122. }123. if(pa1) //若pa1中还有项124. {125. pc1->next=pa1; //将pa1中的项添加到结果链表中126. while(pa1)127. {128.129. pa->expn++;130. pa1=pa1->next;131. }132. }133. if(pb1) //若pb1中还有项134. {135.136. pc1->next=pb1; //将pb1中的项添加到结果链表中137. while(pb1)138. {140. pb1=pb1->next;141. }142. }143. free(pb); //释放pb头链所占的内存空间144. }145. int main()146. {147. pPOLYN pa=NULL,pb=NULL; //指向多项式链表的指针148. printf("输⼊第⼀个多项式数据:\n");149. PolynInput(&pa); //调⽤函数输⼊⼀个多项式150. printf("\n输⼊第⼆个多项式数据:\n");151. PolynInput(&pb); //调⽤函数,输⼊另⼀个多项式152. PolynAdd(pa,pb); //调⽤多项式相加函数153. printf("\n两个多项式之和为:");154. PolynPrint(pa); //输出运算得到的多项式155. getch();156. return 0;157. }附件列表。
一元多项式的加减求导运算算法(数据结构算法)

if(expo1==0)
{
i=1;
cout<<coef1;
}
else if(expo1==1)
{
i=1;
if(coef1==1)
cout<<"X";
else if(coef1==-1)
cout<<"-X";
else
cout<<coef1<<"X";
}
else
{
i=1;
if(coef1==1) cout<<"XA"<<expo1;
temp=h;
h->next =NULL;〃头结点
cout<<"多项式"<<o<<"的项数:";cin»num;
for(i nt i=1;i<=nu m;i++)
{
cout<<"请输入第"<<i<<"项"<<endl; cout<<"系数:";
cin> >coef1;
cout<<"指数:";
cin> >expo1; data=new polyno de; data->coef=coef1;
(2)计算多项式A与B的和,即建立多项式A+B
(3)按照指数升序次序,输出多项式AB、A+B
(4)计算多项式A与B的差,即建立多项式A-B;
(5)计算多项式A的导函数A,。
一元多项式的加法减法乘法和求导

一元多项式的加法、减法、乘法和求导一、【实验构思(Conceive)】(10%)(本部分应包括:描述实验实现的基本思路,包括所用到的离散数学、工程数学、程序设计、算法等相关知识)1、一元稀疏多项式的加法、减法、乘法和求导法则:假设:f(x) = 3 x^8 + 9 x^5g(x) = 7 x^9 + 3 x则:f(x) + g(x) = 7 x^9 + 3 x^8 + 9 x^5 + 3 xf(x) - g(x) = -7 x^9 + 3 x^8 + 9 x^5 - 3 xf(x) * g(x) = 21 x^17 + 63 x^14 + 9 x^9 + 27 x^6f'(x) = 24 x^7 + 45 x^42、基本思路:首先定义一个结构体,其中定义一元多项式中的两个参数:系数和指数和链表中结点的指针域;然后一一罗列每个在主程序中用到的函数,并一一实现;最后在主程序中主要完成用户的输入和相关函数的调用。
二、【实验设计(Design)】(20%)void insert(PLOYList *head,PLOYList *input)//查找位置插入新链节的函数,且让输入的多项式呈降序排列PLOYList *creat(char ch)//输入多项式PLOYList *add(PLOYList *head,PLOYList *pre)//多项式相加,head为第一个多项式建立的链表表头,pre为第二个多项式建立的链表表头PLOYList *sub(PLOYList *head,PLOYList *pre)//多项式相减PLOYList *mul(PLOYList *head,PLOYList *pre)//多项式相乘PLOYList *der(PLOYList *head)//多项式求导void print(PLOYList *fun)//输出多项式,fun指要输出的多项式链表的表头void start()//用户选择界面主程序:void main(){PLOYList *f,*g,*pf,*hf,*p;int sign=-1;start();while(sign!=0){scanf("%d",&sign);switch(sign){case 0:break;case 1://多项式相加{printf(" 你选择的操作是多项式相加:\n");printf(" 请输入第一个多项式f(x):");f=creat('f');printf(" 第一个多项式为:f(x)=");print(f);printf(" 请输入第二个多项式g(x):");g=creat('g');printf(" 第二个多项式为:g(x)=");print(g);printf(" 结果为:F(x)=f(x)+g(x)=");f=add(f,g);print(f);printf("\n\n");printf(" 继续请选择相应操作,退出请按0. ");break;}case 2://多项式相减{printf(" 你选择的操作是多项式相减:\n");printf(" 请输入第一个多项式f(x):");f=creat('f');printf(" 第一个多项式为:f(x)=");print(f);printf(" 请输入第二个多项式g(x):");g=creat('g');printf(" 第二个多项式为:g(x)=");print(g);printf(" 结果为:F(x)=f(x)-g(x)=");f=sub(f,g);print(f);printf("\n\n");printf(" 继续请选择相应操作,退出请按0. ");break;}case 3://多项式相乘{printf(" 你选择的操作是多项式相乘:\n");printf(" 请输入第一个多项式f(x):");f=creat('f');printf(" 第一个多项式为:f(x)=");print(f);printf(" 请输入第二个多项式g(x):");g=creat('g');printf(" 第二个多项式为:g(x)=");print(g);printf(" 结果为:F(x)=f(x) * g(x)=");pf=mul(f,g);print(pf);printf("\n\n");printf(" 继续请选择相应操作,退出请按0. ");break;}case 4://多项式求导{printf("您选择的是对一个一元多项式求导:\n");printf("请输入一个一元多项式:");f = creat('f');printf("这个多项式为:f(x)= ");print(f);printf("求导结果为:F(x)=f'(x)= ");f=der(f);print(f);printf("\n\n");printf(" 继续请选择相应操作,退出请按0. ");break;}case 5://帮助用户理解输入规则{printf("---------------------------帮助------------------------------\n");printf(" \n");printf(" 1.输入时只输入多项式的系数与指数\n");printf(" 2.输入多项式形式:系数1 指数1 系数2 指数2 …… ,以0 0 结束\n");printf(" 3.例如输入\"1 1 2 2 0 0\" 表示\"1*X^1+2*X^2\" \n");printf(" \n");printf("---------------------------帮助------------------------------\n");printf("\n\n");break;}default:{printf( "看完帮助信息后请重新选择操作\n");break;}}//swith}//while}//void三、【实现描述(Implement)】(30%)1.插入函数,用来对根据用户输入的项建立的单个结点进行排序,使其按照指数降序排列,此函数也可以用在多项式的加减法里,因为加减法实质上也是插入的过程。
数据结构一元多项式的运算

数据结构一元多项式的运算在计算机科学和数学领域中,数据结构一元多项式的运算具有重要的地位。
一元多项式是指形如$P(x) = a_n x^n + a_{n-1} x^{n-1} +\cdots + a_1 x + a_0$ 的表达式,其中$a_i$ 是系数,$x$ 是变量,$n$ 是多项式的次数。
要有效地处理一元多项式,需要选择合适的数据结构来存储它们,并设计相应的算法来进行各种运算,如加法、减法、乘法和除法等。
常见的数据结构用于表示一元多项式有两种:顺序存储结构和链式存储结构。
顺序存储结构通常使用数组来存储多项式的系数。
可以将系数按照多项式的次数从高到低依次存放在数组的相应位置。
这种方式简单直观,但存在一些局限性。
例如,如果多项式的次数很高,但大部分系数为零,会浪费大量的存储空间。
而且,对于多项式的插入和删除操作,效率也比较低。
相比之下,链式存储结构更加灵活。
每个节点可以存储一个系数和对应的指数,然后通过指针将这些节点连接起来。
这样可以有效地节省存储空间,并且对于多项式的动态修改操作更加方便。
接下来,让我们详细探讨一下一元多项式的加法运算。
假设我们有两个一元多项式$P(x) = 3x^3 + 2x^2 5x + 1$ 和$Q(x) = 2x^3 4x^2 + 6x 3$ 。
要进行加法运算,我们需要将相同次数的项的系数相加。
首先,比较两个多项式的最高次数。
在这个例子中,都是 3 次。
然后,从高次项开始逐次相加。
对于 3 次项,系数分别为 3 和 2,相加得到 5,所以相加后的多项式的 3 次项系数为 5。
对于 2 次项,系数分别为 2 和-4,相加得到-2。
依此类推,最后得到相加后的多项式为$5x^3 2x^2 + x 2$ 。
在实现加法运算的算法时,需要考虑两个多项式的长度可能不同的情况。
可以使用两个指针分别遍历两个多项式,当其中一个指针到达末尾时,将另一个多项式剩余的项直接添加到结果多项式中。
一元多项式的加减求导运算算法(数据结构算法)
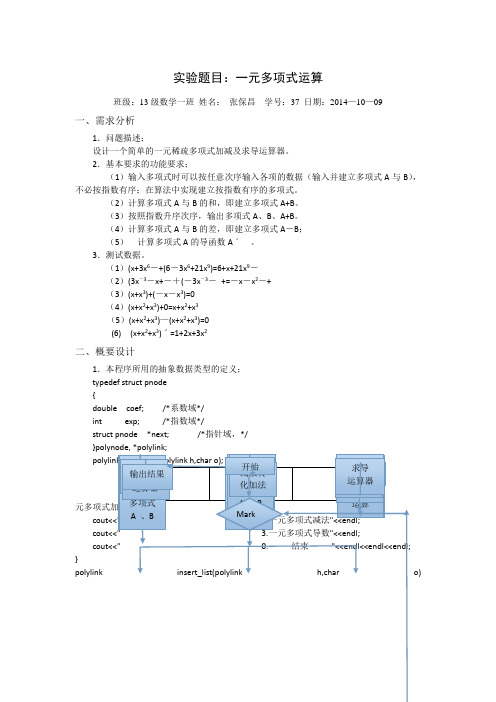
实验题目:一元多项式运算班级:13级数学一班姓名:张保昌学号:37 日期:2014—10—09一、需求分析1.问题描述;设计一个简单的一元稀疏多项式加减及求导运算器。
2.基本要求的功能要求;(1)输入多项式时可以按任意次序输入各项的数据(输入并建立多项式A与B),不必按指数有序;在算法中实现建立按指数有序的多项式。
(2)计算多项式A与B的和,即建立多项式A+B。
(3)按照指数升序次序,输出多项式A、B、A+B。
(4)计算多项式A与B的差,即建立多项式A-B;(5)计算多项式A的导函数Aˊ。
3.测试数据。
(1)(x+3x6-+(6-3x6+21x9)=6+x+21x9-(2)(3x-3-x+-+(―3x―3-+=-x-x2-+(3)(x+x3)+(―x―x3)=0(4)(x+x2+x3)+0=x+x2+x3(5)(x+x2+x3)—(x+x2+x3)=0(6) (x+x2+x3)ˊ=1+2x+3x2二、概要设计1.本程序所用的抽象数据类型的定义;typedef struct pnode{double coef; /*系数域*/int exp; /*指数域*/struct pnode *next; /*指针域,*/}polylink o)元多项式加法"<<endl;cout<<" 2.一元多项式减法"<<endl;cout<<" 3.一元多项式导数"<<endl;cout<<" 0. 结束"<<endl<<endl<<endl; }polylink insert_list(polylink h,char o)//输入多项式{h=new polynode;double coef1;int num,expo1;polylink temp;polynode *data;temp=h;h->next =NULL;//头结点cout<<"多项式"<<o<<"的项数: ";cin>>num;for(int i=1;i<=num;i++){cout<<"请输入第"<<i<<"项"<<endl;cout<<"系数:";cin>>coef1;cout<<"指数:";cin>>expo1;data=new polynode;data->coef=coef1;data->exp =expo1;data->next =NULL;temp->next =data;temp=data;}return h;}polylink simply_list(polylink h)//初步化简,系数无0,无重复指数{polylink p,q,r,k;p=h->next ;if(!p)return h;//空表while(p){k=p;q=k->next ;while(q){if(q->exp==p->exp ){r=q;q=q->next ;p->coef +=r->coef ;k->next =r->next ;delete r;}else{q=q->next ;k=k->next;}}p=p->next ;}k=h;q=h->next ;while(q){if( q ->coef==0){r=q;q=q->next ;k->next =r->next ;delete r;}else{q=q->next ;k=k->next ;}}return h;}void list_display(polylink h,char o)//显示{polylink p;double coef1;int expo1,i=0;p=h->next ;if(!p){cout<<"多项式"<<o<<" : 0 "<<endl;}elsecout<<"多项式"<<o<<" : ";while(p){coef1=p->coef ;expo1=p->exp ;if(i==0){if(expo1==0){i=1;cout<<coef1;}else if(expo1==1){i=1;if(coef1==1)cout<<"X";else if(coef1==-1)cout<<"-X";elsecout<<coef1<<"X";}else{i=1;if(coef1==1)cout<<"X^"<<expo1;else if(coef1==-1)cout<<"-X^"<<expo1;elsecout<<coef1<<"X^"<<expo1;}}else{if(expo1==1){if(coef1==1)cout<<"+X";else if(coef1==-1)cout<<"-X";else if(coef1>0)cout<<"+"<<coef1<<"X";elsecout<<coef1<<"X";}else{if(coef1==-1)cout<<"-X^"<<expo1;else if(coef1==1)cout<<"+X^"<<expo1;else if(coef1>0)cout<<"+"<<coef1<<"X^"<<expo1;elsecout<<coef1<<"X^"<<expo1;}}p=p->next ;}cout<<endl;}polylink order_list(polylink h)//升序排列{polynode temp;polylink p,q,r;p=h->next;if(!p)return h;while(p->next){q=p->next ;r=p;while(q){if(q->exp <r->exp )r=q;q=q->next ;}=r->coef ;=r->exp ;r->coef =p->coef ;r->exp =p->exp ;p->coef = ;p->exp = ;p=p->next ;}return h;}polylink add(polylink ha,polylink hb)//加法{polylink a;a=ha;while(a->next )a=a->next ;a->next =hb->next ;delete hb;ha=simply_list(ha);ha=order_list(ha);return ha;}polylink opposite(polylink b){polylink hb;hb=b->next;while(hb){hb->coef =(-1)*hb->coef;hb=hb->next ;}return b;}polylink derivative(polylink a)//求导{polylink ha;ha=a->next ;while(ha){ha->coef *=ha->exp ;ha->exp --;ha=ha->next ;}return a;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验题目:一元多项式运算班级:13级数学一班姓名:张保昌学号:37 日期:2014—10—09一、需求分析1.问题描述;设计一个简单的一元稀疏多项式加减及求导运算器。
2.基本要求的功能要求;(1)输入多项式时可以按任意次序输入各项的数据(输入并建立多项式A与B),不必按指数有序;在算法中实现建立按指数有序的多项式。
(2)计算多项式A与B的和,即建立多项式A+B。
(3)按照指数升序次序,输出多项式A、B、A+B。
(4)计算多项式A与B的差,即建立多项式A-B;(5)计算多项式A的导函数Aˊ。
3.测试数据。
(1)(x+3x6-+(6-3x6+21x9)=6+x+21x9-(2)(3x-3-x+-+(―3x―3- +=-x-x2-+(3)(x+x3)+(―x―x3)=0(4)(x+x2+x3)+0=x+x2+x3(5)(x+x2+x3)—(x+x2+x3)=0(6) (x+x2+x3)ˊ=1+2x+3x2二、概要设计1.本程序所用的抽象数据类型的定义;typedef struct pnode{double coef; /*系数域*/int exp; /*指数域*/struct pnode *next; /*指针域,*/}polynode, *polylink;}polylink o)元多项式加法"<<endl;cout<<" 2.一元多项式减法"<<endl;cout<<" 3.一元多项式导数"<<endl;cout<<" 0. 结束 "<<endl<<endl<<endl; }polylink insert_list(polylink h,char o)//输入多项式{h=new polynode;double coef1;int num,expo1;polylink temp;polynode *data;temp=h;h->next =NULL;//头结点cout<<"多项式"<<o<<"的项数 : ";cin>>num;for(int i=1;i<=num;i++){cout<<"请输入第"<<i<<"项"<<endl;cout<<"系数 :";cin>>coef1;cout<<"指数 :";cin>>expo1;data=new polynode;data->coef=coef1;data->exp =expo1;data->next =NULL;temp->next =data;temp=data;}return h;}polylink simply_list(polylink h)//初步化简,系数无0,无重复指数{polylink p,q,r,k;p=h->next ;if(!p)return h;//空表while(p){k=p;q=k->next ;while(q){if(q->exp==p->exp ){r=q;q=q->next ;p->coef +=r->coef ;k->next =r->next ;delete r;}else{q=q->next ;k=k->next;}}p=p->next ;}k=h;q=h->next ;while(q){if( q ->coef==0){r=q;q=q->next ;k->next =r->next ;delete r;}else{q=q->next ;k=k->next ;}}return h;}void list_display(polylink h,char o)//显示{polylink p;double coef1;int expo1,i=0;p=h->next ;if(!p){cout<<"多项式"<<o<<" : 0 "<<endl;}elsecout<<"多项式"<<o<<" : ";while(p){coef1=p->coef ;expo1=p->exp ;if(i==0){if(expo1==0){i=1;cout<<coef1;}else if(expo1==1){i=1;if(coef1==1)cout<<"X";else if(coef1==-1)cout<<"-X";elsecout<<coef1<<"X";}else{i=1;if(coef1==1)cout<<"X^"<<expo1;else if(coef1==-1)cout<<"-X^"<<expo1;elsecout<<coef1<<"X^"<<expo1;}}else{if(expo1==1){if(coef1==1)cout<<"+X";else if(coef1==-1)cout<<"-X";else if(coef1>0)cout<<"+"<<coef1<<"X";elsecout<<coef1<<"X";}else{if(coef1==-1)cout<<"-X^"<<expo1;else if(coef1==1)cout<<"+X^"<<expo1;else if(coef1>0)cout<<"+"<<coef1<<"X^"<<expo1;elsecout<<coef1<<"X^"<<expo1;}}p=p->next ;}cout<<endl;}polylink order_list(polylink h)//升序排列{polynode temp;polylink p,q,r;p=h->next;if(!p)return h;while(p->next){q=p->next ;r=p;while(q){if(q->exp <r->exp )r=q;q=q->next ;}=r->coef ;=r->exp ;r->coef =p->coef ;r->exp =p->exp ;p->coef = ;p->exp = ;p=p->next ;}return h;}polylink add(polylink ha,polylink hb)//加法{polylink a;a=ha;while(a->next )a=a->next ;a->next =hb->next ;delete hb;ha=simply_list(ha);ha=order_list(ha);return ha;}polylink opposite(polylink b){polylink hb;hb=b->next;while(hb){hb->coef =(-1)*hb->coef;hb=hb->next ;}return b;}polylink derivative(polylink a)//求导{polylink ha;ha=a->next ;while(ha){ha->coef *=ha->exp ;ha->exp --;ha=ha->next ;}return a;}。
