07S005125_徐谦_QRD-LSL算法自适应均的衡器实验
RLS自适应均衡算法及其应用

RLS自适应均衡算法及其应用首先,让我们了解一下自适应均衡的背景。
在通信系统中,信号可能会受到噪声、多径衰落等干扰,导致信号质量的下降。
为了提高信道的可靠性和传输质量,我们需要一种方式来解决这些问题。
自适应均衡器就是一种能够根据实际信道特性调整其参数,以最大程度地减小干扰并恢复信号的算法。
在RLS自适应均衡算法中,我们使用了递归最小二乘(Recursive Least Squares, RLS)方法来调整均衡器的参数。
RLS算法根据当前输入信号的特性和预测误差,不断地更新均衡器的系数。
这种算法通过最小化预测误差的平方和来找到最优的均衡器参数。
其优点是具有快速收敛速度和较好的稳定性。
RLS算法主要有两个重要的步骤:预测和系数更新。
在预测步骤中,我们使用均衡器的当前系数对输入信号进行预测,得到预测值。
在系数更新步骤中,我们通过比较预测值和实际值之间的误差,来计算均衡器的系数调整量。
系数的更新是通过迭代计算得到的,即每次更新使用上一次更新得到的结果。
这样可以不断地调整均衡器的参数,以适应信道的变化。
RLS自适应均衡算法可以应用于各种通信系统中。
例如,在无线通信系统中,RLS算法可以用于解决多径衰落的问题。
多径衰落会导致信号在传输过程中受到不同路径的衰减,造成信号畸变。
通过使用RLS算法,我们可以根据当前信道的特性来调整均衡器的参数,并实现信号的恢复。
另外,在语音处理中,RLS自适应均衡算法也有广泛的应用。
通过使用RLS算法,我们可以对语音信号进行优化和增强。
例如,在语音通信中,可以使用RLS算法降噪和减少回音,提高语音信号的质量。
在音频设备中,也可以使用RLS算法来提高音频的清晰度和质量。
总结一下,RLS自适应均衡算法是一种可以通过自适应调整均衡器系数来恢复信号或增强信号的算法。
通过递归最小二乘方法,RLS算法可以根据当前信道的特性来调整均衡器的参数,并实现信号的恢复。
RLS算法在无线通信系统和语音处理中有广泛的应用,并已经取得了显著的效果。
RLS和LMS自适应算法分析

RLS和LMS自适应算法分析RLS(Recursive Least Squares)和LMS(Least Mean Square)是两种常用的自适应滤波算法,用于实时信号处理和系统辨识。
本文将对这两种算法进行详细的分析。
1.RLS算法:RLS算法是一种基于权值的算法,用于实时估计系统的参数。
其基本思想是通过最小化误差平方和,更新滤波器的权值。
具体算法步骤如下:a.初始化滤波器权值和协方差矩阵。
b.输入新的观测值,并计算滤波器输出。
c.根据观测值和滤波器输出的误差,更新滤波器的权值和协方差矩阵。
d.重复步骤b和步骤c,直到滤波器收敛。
RLS算法的优点是收敛速度快,能够较快地适应系统的变化。
同时,由于使用了协方差矩阵更新权值,能够更好地抑制噪声。
2.LMS算法:LMS算法是一种基于梯度下降的算法,也是一种最小均方误差(Mean Square Error,MSE)的自适应算法。
具体算法步骤如下:a.初始化滤波器权值。
b.输入新的观测值,并计算滤波器输出。
c.根据观测值和滤波器输出的误差,更新滤波器的权值。
d.重复步骤b和步骤c,直到滤波器收敛。
LMS算法的优点是计算简单,实现容易。
然而,由于是一种基于梯度下降的算法,其收敛速度相对较慢,并且对于高维信号处理时存在着性能损失的问题。
3.RLS算法与LMS算法的比较:a.计算复杂度:RLS算法的计算复杂度较高,需要对协方差矩阵进行计算和更新,而LMS算法的计算复杂度较低,只需要进行简单的权值更新。
b.收敛速度:RLS算法的收敛速度较快,能够较快地适应变化的系统;而LMS算法的收敛速度相对较慢。
c.稳定性:RLS算法对于数据的不确定性比较敏感,误差的扩散效应较小;而LMS算法存在着误差累积的问题。
根据相关应用需求,选择合适的自适应算法。
如果需要较快地适应系统的变化,并能较好地抑制噪声,可以选择RLS算法;而如果需要计算简单、实现容易,且对于系统的适应速度要求较低,可以选择LMS算法。
LMS法自适应均衡器实验
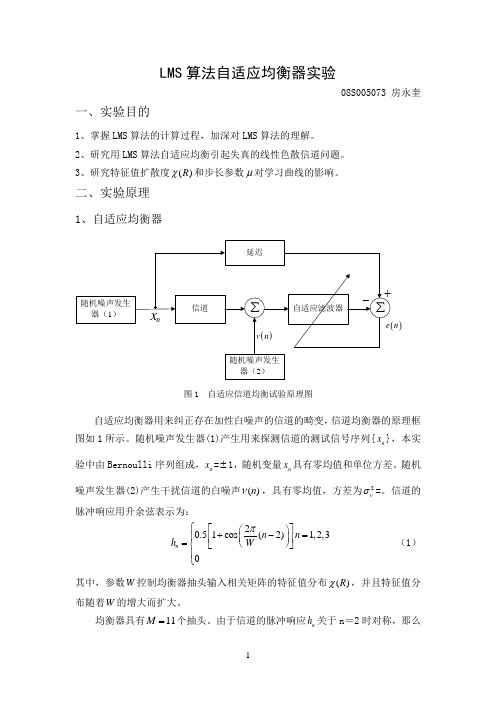
LMS 算法自适应均衡器实验08S005073 房永奎一、实验目的1、掌握LMS 算法的计算过程,加深对LMS 算法的理解。
2、研究用LMS 算法自适应均衡引起失真的线性色散信道问题。
3、研究特征值扩散度()R χ和步长参数μ对学习曲线的影响。
二、实验原理1、自适应均衡器)n图1 自适应信道均衡试验原理图自适应均衡器用来纠正存在加性白噪声的信道的畸变,信道均衡器的原理框图如1所示。
随机噪声发生器(1)产生用来探测信道的测试信号序列{n x },本实验中由Bernoulli 序列组成,n x =±1,随机变量n x 具有零均值和单位方差。
随机噪声发生器(2)产生干扰信道的白噪声()n ν,具有零均值,方差为2νσ=。
信道的脉冲响应用升余弦表示为:20.51cos (2)1,2,30n n n h W π⎧⎡⎤⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩(1) 其中,参数W 控制均衡器抽头输入相关矩阵的特征值分布()R χ,并且特征值分布随着W 的增大而扩大。
均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于n =2时对称,那么均衡器的最优抽头权值on ω在5n =时对称。
因此,信道的输入n x 被延时了257∆=+=个样值,以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时∆,LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
2、均衡器输入相关矩阵在时刻n ,均衡器第1个抽头的输入为()()()31k k u n h x n k v n ==-+∑ (2)其中所有参数均为实数。
因此,均衡器输入的11个抽头(),(1),,(10)u n u n u n --的自相关矩阵R 为一个对称的1111⨯矩阵。
此外,因为脉冲响应n h 仅在1,2,3n =时为非零,且噪声过程()v n 是零均值、方差为2v σ的白噪声,因此相关矩阵R 是主对角线的,有以下特殊结构所示:()()()()()()()()()()()()()()()012001012021010021000000r r r r r r r r r r r r r r r ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦R (3) 其中()22221230v r h h h σ=+++ (4)()12231r h h h h =+ (5)()132r h h = (6)其中方差20.001v σ=。
基于混沌序列和噪声敏感度的自适应盲检测水印算法

基于混沌序列和噪声敏感度的自适应盲检测水印算法
徐飞;薛胜军;滕璇
【期刊名称】《计算机应用研究》
【年(卷),期】2008(25)9
【摘要】提出了一种新的自适应盲检测水印算法.首先混沌序列经过细胞自动机和平滑处理,然后生成水印比特,最后根据噪声敏感度系数自适应地嵌入原始图像的中频系数中,并且提供了一套盲检测方法.实验证明,算法在保证图像具有良好感知透明性的同时,还对一些常见攻击方式(如高斯噪声、中值滤波、JPEG压缩和剪切等)具有很好的鲁棒性.
【总页数】3页(P2816-2818)
【作者】徐飞;薛胜军;滕璇
【作者单位】武汉理工大学,计算机科学与技术学院,武汉,430063;武汉理工大学,计算机科学与技术学院,武汉,430063;武汉理工大学,计算机科学与技术学院,武
汉,430063
【正文语种】中文
【中图分类】TP309
【相关文献】
1.基于高斯随机序列的彩色图像盲检测水印算法 [J], 赵春晖;孙建军;朱海峰
2.自适应的基于混沌序列的数字水印算法 [J], 成亚萍;傅德胜;季赛
3.基于ANFIS的倒谱域盲检测混沌音频水印算法 [J], 管先念;王炳和
4.基于自适应神经网络模糊系统的混沌音频水印盲检测 [J], 王炳和;管先念;吕明
5.基于混沌序列的自适应嵌入水印算法 [J], 张二锋;赵玉霞
因版权原因,仅展示原文概要,查看原文内容请购买。
基于LMS算法的自适应线性均衡器设计

基于LMS算法的自适应线性均衡器设计自适应线性均衡器(Adaptive Linear Equalizer)是一种用于解决通信系统中信号传输过程中引起的衰落、多径干扰和色散等问题的数字信号处理技术。
其中,最常用的算法就是最小均方算法(LMS算法)。
本文将对基于LMS算法的自适应线性均衡器设计进行详细探讨,以便进一步理解该技术的原理和应用。
自适应线性均衡器的设计目标就是使得接收到的信号尽可能接近发送信号。
在传输过程中,信号可能受到多径干扰、噪声和失真等因素的影响。
自适应线性均衡器的任务就是根据接收信号的特征自动调整其内部权值,以最小化输出信号与原始信号之间的误差。
LMS算法是一种基于梯度下降的迭代算法,它通过最小化均方(Mean Square Error,MSE)误差来更新权值。
LMS算法的基本思想是根据误差信号的梯度来调整权值,从而最小化误差。
在自适应线性均衡器中,LMS算法的实现需要以下步骤:1.定义输入信号和目标信号:将输入信号表示为x(n),目标信号(即发送信号)表示为d(n)。
2.初始化权值向量:将权值向量w(n)初始化为一个较小的初值,通常为零。
3.计算估计输出:根据当前权值向量,计算自适应线性均衡器的估计输出y(n)。
4.计算误差信号:将估计输出与目标信号进行比较,计算误差信号e(n)。
5.更新权值向量:根据误差信号的梯度计算出权值的变化量,并将其加到当前的权值向量上,得到新的权值向量。
6.重复步骤3到步骤5,直到收敛或达到预设的迭代次数。
自适应线性均衡器的设计中,一些关键问题需要考虑:1.学习率:学习率决定了权值的更新速度,过大的学习率可能导致不稳定性,而过小的学习率则会导致收敛速度过慢。
因此,需要根据实际情况选择合适的学习率。
2.初始权值:初始权值的选择可能会影响算法的收敛速度和性能。
通常可以将初始权值设置为零或一个随机小值,然后通过迭代调整权值。
3.触发更新:权值的更新可以在每个符号周期内进行,也可以在每个数据块周期内进行。
RLS自适应均衡算法及其应用

RLS自适应均衡算法及其应用
在信号处理中,自适应均衡算法的主要目标是通过调整滤波器的系数
来消除信号传输中的失真和衰减。
该算法利用当前和过去的输入数据来预
测滤波器系数的最佳值,并将其用于信号分析、信道均衡和等应用中。
RLS自适应均衡算法通过最小化预测误差的平方和来确定滤波器系数。
算法的主要步骤包括初始化滤波器的系数和协方差矩阵,然后进行迭代计算,包括计算增益矩阵、误差信号、估计误差和更新滤波器系数。
随着迭
代次数的增加,滤波器系数收敛到最佳值。
1.具有较快的收敛速度和较好的跟踪性能;
2.对于信号的任何统计特性都是最优的;
3.可以处理非线性系统。
在通信系统中,RLS自适应均衡算法被广泛应用于消除信号传输中的
多径干扰,提高信号的质量和可靠性。
具体应用包括:
1.无线通信系统中的信道均衡:通过自适应均衡算法,可以对信号在
多径信道中的干扰进行估计和补偿,从而提高接收信号的质量。
2.降噪和滤波:自适应均衡算法可以应用于降低信号中的噪声和滤除
不需要的频率分量,从而提高信号的清晰度。
3.系统辨识和模型适应:通过使用自适应均衡算法,可以实时地对信
号的系统特性进行建模和辨识,从而提高系统的鲁棒性和适应性。
4.通信信道的均衡和均化:自适应均衡算法可以用于对通信信道进行
均衡和均化处理,从而提高信道的跨学科性能。
总之,RLS自适应均衡算法是一种优秀的信号处理工具,广泛应用于
通信系统和信号处理领域。
它具有快速收敛、最优性能和适应性强等特点,并在信号传输的失真和干扰消除中发挥着重要作用。
SIGNAL STRENGTH DETECTOR

专利内容由知识产权出版社提供
专利名称:SIGNAL STRENGTH DETECTOR 发明人:XU, Jie 申请号:US2020/02614 7 申请日:202004 01 公开号:WO2020/172688A2 公开日:20200827 专利附图:
摘要:The disclosure relates to technology for signal strength detection. An apparatus for detecting signal strength is disclosed. The apparatus comprises a differential sensor stage having an input and an output, a differential reference stage having an input and an output, a capacitor stage configured to couple an input signal to
Hale Waihona Puke the input of the differential sensor stage, a biasing circuit configured to bias the differential sensor stage and the differential reference stage. The apparatus has a differential output between the output of the differential sensor stage and the output of the differential reference stage. The differential output is configured to provide a signal indicative of strength of the input signal.
一种基于小波变换去噪的自动泊车高精度测评方法[发明专利]
![一种基于小波变换去噪的自动泊车高精度测评方法[发明专利]](https://img.taocdn.com/s3/m/81f6421042323968011ca300a6c30c225901f073.png)
专利名称:一种基于小波变换去噪的自动泊车高精度测评方法专利类型:发明专利
发明人:徐启敏,宋剑,李旭
申请号:CN202210035381.1
申请日:20220112
公开号:CN114252277A
公开日:
20220329
专利内容由知识产权出版社提供
摘要:本发明公开了一种基于小波变换去噪的自动泊车高精度测评方法,该方法需要在被测车辆上安装一套高性能组合导航系统采集测评所需车辆运动参数,同时需要测量车辆尺寸、泊车位尺寸等基础参数信息。
此外,对于测量噪声较大的横摆角速度和侧向加速度数据,采用小波变换去噪方法提高测量精度。
本发明对自动泊车的完成度和过程稳定性两方面进行定量测评,包括:车辆纵轴线与泊车位内侧边线的夹角、泊车完成时车辆侧边前后端与泊车侧边线的距离、车尾与后车位线的距离等。
本发明与自动泊车的实现原理和技术无关,从第三方的角度开展测评,测评结果准确可靠。
申请人:东南大学
地址:210096 江苏省南京市玄武区四牌楼2号
国籍:CN
代理机构:南京众联专利代理有限公司
代理人:张天哲
更多信息请下载全文后查看。
自适应步幅卷积的细粒度图像识别方法及系统[发明专利]
![自适应步幅卷积的细粒度图像识别方法及系统[发明专利]](https://img.taocdn.com/s3/m/34eac0c0534de518964bcf84b9d528ea81c72f02.png)
专利名称:自适应步幅卷积的细粒度图像识别方法及系统专利类型:发明专利
发明人:董翔宇,朱涛,刘之奎,徐斓瑛,容圣海,李腾,廖军,罗沙,谢佳,李卫国,黄道均,王子磊,周正,张俊杰,王刘芳,李
冀,刘鑫,朱元付,常文婧
申请号:CN202111508103.5
申请日:20211210
公开号:CN114359711A
公开日:
20220415
专利内容由知识产权出版社提供
摘要:本发明提供一种自适应步幅卷积的细粒度图像识别方法及系统,属于图像识别技术领域。
所述识别方法包括:将待分类图像输入注意力图提取器中以得到具有突出判别区域的注意力图,其中,所述注意力图提取器包括卷积神经网络、特征图重塑模块和三线性乘积模块,所述卷积神经网络用于根据所述待分类图像生成对应的特征图,所述特征图重塑模块用于将所述特征图重塑成矩阵,所述三线性乘积模块用于根据所述矩阵生成所述注意力图;采用步幅向量生成器根据所述注意力图生成用于表示卷积核分别沿着x轴和y轴方向上扫描的步幅向量;采用动态步幅卷积模块根据所述步幅向量对所述特征图进行滑窗计算以得到所述识别结果。
该识别方法及系统能够提高图像识别的准确性。
申请人:国网安徽省电力有限公司超高压分公司,中国科学技术大学先进技术研究院,国家电网有限公司
地址:231131 安徽省合肥市包河区桐城南路397号
国籍:CN
代理机构:北京润平知识产权代理有限公司
代理人:肖冰滨
更多信息请下载全文后查看。
基于归一化LMS算法自适应均衡器的Simulink实现

基于归一化LMS算法自适应均衡器的Simulink实现
顾海燕;陈黎平
【期刊名称】《数据采集与处理》
【年(卷),期】2006(021)B12
【摘要】为了克服硬件实现归一化LMS算法自适应均衡器的缺点,构造了数据传输系统中采用归一化LMS算法自适应均衡器的Simulink仿真模型。
首先介绍了归一化LMS算法,给出基于归一化LMS算法自适应均衡器的建模过程,最后研究了抽头输入向量相关矩阵的特征值和步长参数对该自适应均衡器性能的影响。
仿真结果同时验证了该模型的正确性和Simulink作为仿真工具的有效性。
【总页数】4页(P15-18)
【作者】顾海燕;陈黎平
【作者单位】上海交通大学电子信息与电气工程学院,上海200240
【正文语种】中文
【中图分类】TN911.5
【相关文献】
1.基于LMS算法的自适应均衡器的MATLAB实现 [J], 尹丽丽;吴跃东
2.采用FPGA实现基于LMS算法的自适应均衡器的设计研究 [J], 金健;陈涛
3.基于归一化LMS算法自适应均衡器的Simulink实现 [J], 顾海燕;陈黎平
4.自适应均衡器的LMS算法实现及其仿真 [J], 张雅彬;王融丽;刘昕
5.Normalzed LMS算法自适应均衡器设计与仿真实现 [J], 黄波
因版权原因,仅展示原文概要,查看原文内容请购买。
基于载噪比与差错感知的自适应分层协同防碰撞算法

基于载噪比与差错感知的自适应分层协同防碰撞算法史苇杭;周岩;林楠【摘要】针对射频识别(RFID)系统中多阅读器与多标签之间的数据碰撞问题,基于载噪比和差错感知,提出一种自适应分层协同防碰撞算法.分析RFID标签和阅读器的物理和电气属性,设计适用于多种应用场景的载噪比和差错感知分析模型.基于误码率和丢包率的变化规律,结合物理层和网络层的跨层设计,构建分层协同控制架构,解决多阅读器与多标签之间的数据容易发生碰撞的问题.实验结果表明,该算法在碰撞概率、标签识别率和阅读器寻呼次数等方面的性能均优于二叉树防碰撞算法.【期刊名称】《计算机工程》【年(卷),期】2016(042)008【总页数】5页(P24-27,33)【关键词】射频识别系统;载噪比;差错感知;分层协同设计;多标签;多阅读器;防碰撞【作者】史苇杭;周岩;林楠【作者单位】郑州大学软件技术学院,郑州450002;河南工程学院计算机学院,郑州451191;郑州大学软件技术学院,郑州450002【正文语种】中文【中图分类】TP319近年来,射频识别(Radio Frequency Identification,RFID)技术[1-2]已经在多种领域得到广泛运用,例如图书馆[3]、农产品物流[4]等。
然而,影响RFID系统工作效率和数据可靠性的主要问题是:多应用业务中多标签与多阅读器之间的数据无法相互确认,导致数据错误或延迟,发生数据碰撞。
因此,如何使得多应用业务中多标签与多阅读器识别有序且识别率高,同时确保数据的完整性和信息的可信度,并且在应用业务、阅读器和标签之间建立合理映射体系,成为RFID系统应用亟需解决的问题。
文献[5]通过将锁位后退与锁位寻呼相结合,提出基于二叉树的RFID防碰撞算法。
文献[6]通过将多目标并行识别与动态位隙标签分类相结合,研究一种支持独立成分分析和动态位隙分组的多标签防碰撞算法。
为了解决大量数据标签的识别问题,文献[7]结合分组限制响应和标签规模,提出一种具有高识别率的防碰撞算法。
单矢量时反自适应多通道误差反馈的判决反馈均衡技术

单矢量时反自适应多通道误差反馈的判决反馈均衡技术生雪莉;阮业武;殷敬伟;韩笑【摘要】针对复杂的海洋环境噪声和水声信道多途效应导致误差反馈DFE均衡器在水声通信中的均衡性能受到严重的限制问题,本文利用信号矢量场和噪声矢量场的相干性差异和矢量水听器振速通道具有偶极子指向性的物理特性,建立单矢量自适应多通道误差反馈DFE均衡器进行抗噪声;利用时间反转镜的空-时聚焦特性进行抑制信道多途干扰.实验结果表明:所提算法不仅保留了误差反馈DFE均衡器的优点,且其抗噪声干扰与信道多途干扰的能力更强,在水声通信中稳定性更好、均衡后误码率更低.【期刊名称】《哈尔滨工程大学学报》【年(卷),期】2018(039)012【总页数】9页(P1894-1901,2016)【关键词】水声通信;信道均衡;判决反馈均衡技术;矢量水听器;多通道误差反馈的判决反馈均衡器;时间反转镜技术;自适应算法【作者】生雪莉;阮业武;殷敬伟;韩笑【作者单位】哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001;哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001;北京系统工程研究院水声对抗技术重点实验室,北京100000;哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001;哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001;哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001;哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001;北京系统工程研究院水声对抗技术重点实验室,北京100000;哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001;哈尔滨工程大学水声技术重点实验室,黑龙江哈尔滨150001【正文语种】中文【中图分类】TN929.3近年来水声通信成为了无线通信中一个比较热门的研究方向。
而海洋信道是一个多途效应严重、可利用带宽有限、海洋环境噪声大、不均匀介质折射、衰落严重、快速时变和多普勒效应严重的复杂信道,可以说是无线信道中最为复杂的一种信道[1]。
一种快速最优自适应频率校准电路

一种快速最优自适应频率校准电路
徐卫林;朱潮勇;于越;周茜;李海鸥
【期刊名称】《微电子学与计算机》
【年(卷),期】2018(35)4
【摘要】提出一种快速最优自适应频率校准电路,应用于卫星导航接收机的宽带频率合成器中.该自适应频率校准电路通过共用频率合成器中多模分频器的分频码,快速定位到多频带压控振荡器的理想目标频带,并进行反馈校准,搜索出目标频点的上下两条实际目标频带,并分别与之比较偏差,选择距离最近的目标频带.该自适应频率校准电路采用数模混合电路设计,模拟部分以减小搜索步长,数字部分以提高校准算法的准确性和减少搜索步数.基于0.18μm CMOS工艺的混合信号仿真验证表明,相对于传统的频率校准电路,提出的快速最优自适应频率校准电路可以实现更短的锁定时间,并选取最优频带,从而有利于频率合成器的环路稳定和相位噪声优化.
【总页数】6页(P108-113)
【关键词】自适应;频率校准;快速;数模混合;最优算法
【作者】徐卫林;朱潮勇;于越;周茜;李海鸥
【作者单位】广西精密导航技术与应用重点实验室,桂林电子科技大学,广西桂林541004
【正文语种】中文
【中图分类】TN402
【相关文献】
1.一种二级快速自适应最优层叠滤波算法 [J], 赵春晖;孙莉;崔颖
2.一种频率自适应采样电路 [J], 吕翔;付祥波;张虹
3.一种快速自适应最优小波包基搜索算法 [J], 李姣军;李恒;苏理云;李刚
4.一种快速高分辨率的VCO频率校准技术 [J], 蔡青松;杨中;贾晓云;乔树山;樊晓华
5.一种频率自适应欠采样电路的设计及FPGA实现 [J], 裴永浩;苏淑靖
因版权原因,仅展示原文概要,查看原文内容请购买。
用于自适应天线的稳健的RLS算法

用于自适应天线的稳健的RLS算法
吴启晖;王金龙;沈良;任国春
【期刊名称】《电子学报》
【年(卷),期】2002(030)006
【摘要】抗干扰通信是电子战的重要组成部分,自适应天线不仅具有很强的抗干扰能力而且可以与其它通信抗干扰技术相兼容.自适应算法是自适应天线的核心.本文把应用数学学科研究的热门方法之一"稳健估计(RE)"应用于RLS算法中,得到稳健的RLS算法(RRLS),理论分析与计算机模拟结果都证明了RRLS算法基本保持了RLS算法的优点,同时在抗突出值干扰方面,优于RLS算法,提高了RLS算法的稳健性.
【总页数】3页(P893-895)
【作者】吴启晖;王金龙;沈良;任国春
【作者单位】解放军理工大学通信工程学院,江苏南京,210016;解放军理工大学通信工程学院,江苏南京,210016;解放军理工大学通信工程学院,江苏南京,210016;解放军理工大学通信工程学院,江苏南京,210016
【正文语种】中文
【中图分类】TN914
【相关文献】
1.用于自适应数字波束形成的稳健子阵异步RLS算法 [J], 刘军;金荣洪;范瑜;耿军平
2.基于DTW和RLS算法的数字稳健识别 [J], 黄邦奉
3.基于逆QRD-RLS算法的自适应天线阵结构设计 [J], 周妮;陈龙
4.用于移动通信的自适应天线 [J], M.Barrett;R.Amott;董钧良;徐乃英
5.用于家庭VHF—FM接收的自适应天线系统 [J], 沙济彰
因版权原因,仅展示原文概要,查看原文内容请购买。
基于DDLMS算法的信道均衡器的FPGA实现

基于DDLMS算法的信道均衡器的FPGA实现
白勇博;陈自力;祁栋升
【期刊名称】《无线电工程》
【年(卷),期】2011(041)002
【摘要】无线通信系统中均衡技术是改善信道特性解决码间干扰的有效方法.从分析判决引导最小均方误差算法(DDLMS)算法出发,研究了其在信道均衡技术上的应用,并通过Matlab仿真和软件(Xilinx System Generator for DSP)开发软件在FPGA上实现了一个基于DDLMS算法的基带均衡器.从仿真测试结果可以看出,实现的信道均衡器能够达到消除码间干扰的效果.
【总页数】3页(P10-12)
【作者】白勇博;陈自力;祁栋升
【作者单位】军械工程学院,河北,石家庄,050003;军械工程学院,河北,石家
庄,050003;军械工程学院,河北,石家庄,050003
【正文语种】中文
【中图分类】TN911.5
【相关文献】
1.采用FPGA实现基于LMS算法的自适应均衡器的设计研究 [J], 金健;陈涛
2.基于DD-LLMS算法的盲自适应判决反馈均衡器 [J], 刘锋
3.基于LMS算法的光纤信道自适应均衡器的研究 [J], 王敬辉;刘剑飞;王蒙军;曾祥烨
4.基于归一化LMS算法自适应均衡器的Simulink实现 [J], 顾海燕;陈黎平
5.基于LMS算法的均衡器仿真实现 [J], 黄李健
因版权原因,仅展示原文概要,查看原文内容请购买。
RLS自适应算法基本原理

稳态剩余均方误差 ex (n ) lim (n) min
n
随着迭代时间增长,跟踪能力越来越好
RLS算法性能分析
RLS算法的特点
1、RLS算法对非平稳信号的适应性好。
2、RLS算法收敛速度快,估计精度高稳定性好。 3、遗忘因子越大,越不易遗忘,效果越好。 4、RLS算法计算复杂度高,不利于实时性出理。
在线更新
RLS算法基本原理
• 所谓自适应实现是指利用前一时刻获得的滤 波器参数,根据估计误差自动调节现时刻的 参数,使得某个代价函数达到最小,从而实 现最优滤波。
J (n) E{| (n) | } E{| d (n) w u(n) | }
2 H 2
• 下降算法:最广泛使用的自适应算法 自适应梯度算法(LMS) 自适应高斯-牛顿算法(RLS)
可取滤波器的实际输入d*(i)作为期望响应d(i)。 将误差代入代价函数得到加权误差平方和的完整表达式
J (n) | d (i) w (n) * u(i) |
ni H i 0
n
2
RLS算法基本原理
• 抽头权向量取的是n时刻的w(n)而不是i时 刻的w(i). • i<=n时刻,
更新权向量: (n) w(n 1) k (n)e* (n) w 1 更新 P(n) [ P(n 1) k (n)u H (n ) P(n - 1)]
RLS算法基本原理
希望相关矩阵初始值R(0)在R(n)中占很小的 比重,因此设R(0)=σI。σ一般取0.001。
R ( n) n i u (i )u H (i )
引入遗忘因子作用是离n时刻近的误差附较大权重, 离n时刻远的误差赋较小权重,确保在过去某一段时 间的观测数据被“遗忘”,从而使滤波器可以工作在 非 平稳状态下。) d (i) wH (n)u(i) (i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H a r b i n I n s t i t u t e o f T e c h n o l o g y
自适应信号处理(实验)
课程名称:自适应信号处理
设计题目:QRD-LSL算法自适应均衡器实验
院系:电子与信息技术研究院
班级:信息二班
设计者:徐谦
学号:07S005125
指导教师:邹斌
设计时间:2008年4月23日
哈尔滨工业大学
QRD-LSL 算法自适应均衡器实验
07S005125 徐谦
一、实验目的
1、研究QRD-LSL 算法用于有失真线性信道的自适应均衡问题。
2、比较QRD-LSL 算法和RLS 算法学习曲线。
二、实验原理
1、自适应均衡器
)
n
图1 自适应均衡试验框图
如图1所示,系统中使用两个独立的随机数发生器,一个用n x 来表示,用来测试信道。
另一个用()n ν来表示,用来模拟接收器中加性白噪声的影响。
序列n x 是n x =1±的Bernoulli
序列,随机变量n x 具有零均值和单位方差。
第二个序列()n ν具有零均值,其方差2
v σ由实
验中需要的信噪比决定。
均衡器有11个抽头。
信道的冲激响应定义为
20.51cos (2)1,2,30n n n h W π⎧⎡⎤⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩
(1) 其中,W 控制幅度失真的大小,因此也控制信道产生的特征值扩散度()R χ。
将延迟7个样值之后的信道输入n x 作为均衡器的期望响应。
2、自适应均衡器实验参数
加权因子:=1λ 预测阶数:10M =
均衡器抽头数:111M += 归一化参数:0.004δ=
表1中列出:(1)自相关函数(),0,1,2r l l =的值;(2)最小特征值min λ,最大特征值
max λ,特征值扩散度()max min /χλλ=R 。
3、QRD-LSL 算法信号流图
图2 QRD-LSL 滤波器算法信号流图
三、程序流程图
图3 基于QRD-LSL算法自适应均衡试验程序流程图
四、实验内容及结果分析
1、学习曲线
图4给出当信道参数取四种不同值( 2.93.13.3W =、、和3.5)时,QRD-LSL 算法的学习曲线。
通过对最终预测阶数10M =进行200次独立的试验,再对最后的先验估计误差(即更新项)()1M n ξ+的平均值取集平均,得到每一条曲线。
为了计算()1M n ξ+,我们对
1m M =+利用
()()()()
()
1/2
1/2
m m m m m e n n n n n εγξγ==
(2)
可以得到:
()()
()
111/2
1M M M n n n εξγ+++=
(3) 其中()1M n ε+为角度归一化联合过程估计误差的最终值,()1M n γ+为相关的变换因子。
对于每一个特征值扩散度,一旦初始化完成,QRD-LSL 算法与RLS 算法的学习曲线的路径实际是相同的。
这一关系通过比较图4和图5中的曲线很容易验证(在这两种情况下,都采用双精度算法,这样有限精度效应可以忽略)。
0204060
80100120140160180
200
10
-3
10
-2
10
-1
10
10
1
迭代次数 n
均方误差
图4 自适应均衡实验中的QRD-LSL 算法学习曲线
需要注意的是,当计算图4中曲线时,在初始化阶段,计算更新项()1M n ξ+时不考虑变换因子()1M n γ+固有的瞬态变化的影响。
204060
80100120140160180
200
10
-3
10
-2
10
-1
100
10
1
迭代次数 n
集平均平方误差
W=2.9W=3.3W=3.1
图5 四种不同特征值扩散度情况下RLS 算法的学习曲线(=0.004δ,=1.0λ)
2、变换因子
在图6中,我们示出了四种变换因子()1M n γ+的集平均(对于最后一级)与迭代次数之间的关系,它对应前面指定的四种不同的特征值扩散度()R χ。
图中画出的曲线通过对
()1M n γ+进行200次独立试验并取集平均获得。
值得注意的是,在初始瞬态结束后,变换因
子的集平均()m n γE ⎡⎤⎣⎦随时间的变化规律遵循以下所谓的逆定理(已被逼近证实)。
()1m m
n n
γE ≈-
⎡⎤⎣⎦ 对于1,2,,1m M =+ 和d n m ≥ (4) 这一方程提供了对图6所示实验计算曲线的良好拟合,特别是当n 比预测阶数1m M =+大很多的情况下,可以检验拟合结果的正确性。
同样需要注意的是,当10n ≥时,实验得到的
变换因子()1M n γ+曲线对均衡器输入相关矩阵特征值扩散度的变化不敏感。
20
40
60
80100120140
160
180
200
迭代次数 n
集平均变换系数
图6 变换因子()1m n γ+对于不同特征值扩散度的集平均
3、脉冲响应
在图7中,我们画出经500n =次迭代后自适应均衡器脉冲响应对四个特征值扩散度中每一个的集平均结果。
如前,实验中集平均通过200次独立试验得到。
对于所有实际情况,QRD-LSL 算法的结果很难与信道脉冲响应相应理论值区分。
迭代次数 n
(a )W=2.9,()R χ=6.0782 (b )W=3.1,()R χ=11.1238
0123
45678910
迭代次数 n
迭代次数 n
(c )W=3.3,()R χ=21.7132 (d )W=3.5,()R χ=46.8216 图7 不同特征值分布情况下自适应均衡器的集平均脉冲响应
迭代次数 n。
