苏科版八年级上册数学 第2章 轴对称复习讲义(解析版)
数学八年级苏科版(上册)第二章轴对称图形电子课件

苏科八年级 上册
【探究活动2】 观察下面图形,它们有什么共同特点?
苏科八年级 上册
【探究活动2】
把一个图形沿一条直线折叠,如果直 线两旁的部分能互相重合,那么这个图形叫 _轴__对__称__图__形___._
苏科八年级 上册
【探究活动2】
联系实际,你能举出一个轴对称图形的 实例吗?
你能正确地完成课本P41页第1题的练习吗?
l
l
AO ●
A′
●
●
苏科八年级 上册
l
12
A●
o
● A′
∵ 把纸沿折痕 l 折叠时,点A、A′重合,
∴ 线段OA、OA′重合, ∴ O是AA′的中点. ∵ ∠1=∠2 且 ∠1+∠2=180°, ∴ ∠1=∠2=90°. ∴ l 垂直且平分AA′.
苏科八年级 上册
【归纳概括】
垂直并且平分一条线段的直线,叫做这条线 段的垂直平分线.
苏科八年级 上册
【归纳总结】
问题1: 根据课本图形2-1和2-4进行比较,轴对 称与轴对称图形之间有什么区别吗?
苏科八年级 上册
【归纳总结】
问题2: 如果把一个轴对称图形沿对称轴分成两 个图形,那么这两个图形成轴对称吗?如果把两个 成轴对称的图形看成一个整体,它是一个轴对称图 形吗?
苏科八年级 上册 【归纳总结】
【活动四】 小明取一张纸,用小针在纸上扎出“4”,然后
将纸放在镜子前. ((11))图你中能两画个出“镜4”子有所什在么直关线系l的?位置吗?
方方法法((21))
l
●A
E●
C●
● D H●
●F
●B
G●
苏科八年级 上册
(2)图中点A、B、C、D的对称点分
2-5 等腰三角形的轴对称性2021-2022学年八年级数学上册讲义(苏科版)(解析版)

第2章轴对称图形2.5 等腰三角形的轴对称性课程标准课标解读1. 掌握等腰三角形的性质,并能利用它证明两个角相等、两条线段相等以及两条直线垂直.2. 掌握等腰三角形的判定定理.3. 熟练运用等腰三角形的判定定理与性质定理进行推理和计算.1.理解等腰三角形是轴对称图形2.掌握等边对等角的性质3.掌握“三线合一”的性质知识点01 等腰三角形的定义有两条边相等的三角形,叫做等腰三角形,其中相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.如图所示,在△ABC中,AB=AC,则它叫等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C 是底角.【微点拨】等腰直角三角形的两个底角相等,且都等于45°.等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角).∠A=180°-2∠B,∠B=∠C= .1802A︒-∠目标导航知识精讲【即学即练1】1.已知等腰三角形的一边长5cm ,另一边长10cm ,则它的周长是( ) A .20cm B .25cmC .20cm 或25cmD .无法确定【答案】B 【分析】题目给出等腰三角形有两条边长为5cm 和10cm ,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形. 【详解】 解:分两种情况:当腰为5时,5+5=10,所以不能构成三角形;当腰为10时,5+10>10,所以能构成三角形,周长是:10+10+5=25cm . 故选:B .知识点02 等腰三角形的性质1.等腰三角形的性质性质1:等腰三角形的两个底角相等(简称“等边对等角”).性质2:等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(简称“三线合一”). 2.等腰三角形的性质的作用性质1证明同一个三角形中的两角相等.是证明角相等的一个重要依据. 性质2用来证明线段相等,角相等,垂直关系等. 3.等腰三角形是轴对称图形等腰三角形底边上的高(顶角平分线或底边上的中线)所在直线是它的对称轴,通常情况只有一条对称轴. 【即学即练2】2.如图,ABC 面积为9,BP 平分ABC ∠,AP BP ⊥于点P ,连结CP ,则BPC △的面积为( )A .5B .4.5C .4D .3.5【答案】B 【分析】延长AP 交BC 于E ,根据已知条件证得△ABP△△EBP ,根据全等三角形的性质得到AP=PE ,得出S△ABP=S△EBP ,S△ACP=S△ECP ,推出S△PBC=12S△ABC . 【详解】解:延长AP 交BC 于E ,△BP 平分△ABC , △△ABP=△EBP , △AP△BP ,△△APB=△EPB=90°, 在△ABP 和△EBP 中,ABP EBP BP BPAPB EPB ∠=∠⎧⎪=⎨⎪∠=∠⎩, △△ABP△△EBP (ASA ), △AP=PE ,△S△ABP=S△EBP ,S△ACP=S△ECP , △S△PBC=12S△ABC=12×9=4.5, 故选:B .知识点03 等腰三角形的判定1. 对应顶点,对应边,对应角定义如果一个三角形中有两个角相等,那么这两个角所对的边也相等(简称“等角对等边”). 【微点拨】等腰三角形的判定是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.【即学即练3】3.如图,ABC 中,,BF CF 分别平分ABC ∠和ACB ∠,过点F 作//DE BC 交AB于点D ,交AC 于点E ,那么下列结论:△DFB DBF ∠=∠;△ECF EFC ∠=∠;△ADE 的周长等于BFC △的周长;△1902BFC A ∠=︒+∠.其中正确的有( )A .△△B .△△△C .△△△D .△△△【答案】C 【分析】△根据平分线的性质、平行线的性质,借助于等量代换可求出DBF DFB ∠=∠;△同理可得△的结论;△用特殊值法,当ABC ∆为等边三角形时,连接AF ,根据等边三角形的性质,角平分线定义和等腰三角形的判定便可得出BF AF CF ==,进而得BF CF AC +>,便可得出;ADE ∆的周长不等于BFC ∆的周长;△利用两次三角形的内角和,以及平分线的性质,进行等量代换,可求的BFC ∠和BAC ∠之间的关系式. 【详解】 解:△BF 是ABC ∠的角平分线,ABF CBF ∴∠=∠,又//DE BC ,CBF DFB ∴∠=∠,DBF DFB ∴∠=∠,故△正确;△同理ECF EFC ∠=∠,故△正确;△假设ABC ∆为等边三角形,则AB AB BC ==,如图,连接AF ,D BF D FB ∠=∠,ECF EFC ∠=∠,BD DF ∴=,EF EC =,ADE ∴∆的周长AD DF EF AE AD BD AE EC AB AC =+++=+++=+, F 是ABC ∠,ACB ∠的平分线的交点∴第三条平分线必过其点,即AF 平分BAC ∠, ABC ∆为等边三角形,60BAC BCA ABC ∴∠=∠=∠=︒, 30FAB FBA FAC FCA ∴∠=∠=∠=∠=︒, FA FB FC ∴==, FA FC AC +>, FB FC AC ∴+>,FB FC BC BC AC ∴++>+, FB FC BC AB AC ∴++>+,即BFC ∆的周长AD E >∆的周长,故△错误;△在ABC ∆中,180BAC ABC ACB ∠+∠+∠=︒⋯(1), 在BFC ∆中180CFB FBC FCB ∠+∠+∠=︒, 即1118022CFB ABC ACB ∠+∠+∠=︒⋯(2),(2)2⨯-(1)得1902BFC BAC ∠=︒+∠,故△正确;故选C .考法01 等腰三角形的性质性质1:等腰三角形的两个底角相等(简称“等边对等角”).性质2:等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(简称“三线合一”).【典例1】如图所示,OB 平分,CBA OC ∠平分ACB ∠,且//BC MN ,设18,16,12AB BC AC ===,则AMN 的周长为( )A .30B .33C .36D .39【答案】A 【分析】能力拓展根据BO 平分△CBA ,CO 平分△ACB ,且MN△BC ,可得出MO=MB ,NO=NC ,所以三角形AMN 的周长是AB+AC . 【详解】解:△BO 平分△CBA ,CO 平分△ACB , △△MBO=△OBC ,△OCN=△OCB , △MN△BC ,△△MOB=△OBC ,△NOC=△OCB , △△MBO=△MOB ,△NOC=△NCO , △MO=MB ,NO=NC , △AB=18,AC=12,△△AMN 的周长=AM+MN+AN=AB+AC=18+12=30. 故选:A .考法02 等腰三角形的判定判定方法:在同一三角形中,有两条边相等的三角形是等腰三角形在同一三角形中,有两个角相等的三角形是等腰三角形(简称:在同一三角形中,等角对等边) 【典例2】如图,C 为线段AB 上一动点(不与点A ,B 重合),在AB 同侧分别作等边ACD △和等边,BCE AE 与BD 交于点F ,AE 与CD 交于点G ,BD 与CE 交于点H ,连接GH .以下四个结论:△EAB BDC ∠=∠;△CGH 为等边三角形;△60FGH FHG ∠+∠=︒;△AC DH =.其中正确的是( )A .△△△B .△△△C .△△△D .△△△△【答案】A 【分析】根据等边三角形的性质可以得出△ACE△△DCB ,就可以得出△CAE =△CDB ,通过证明△ACG△△DCH 就可以得出CG =CH ,AG=DH ,可以得出△GCH 是等边三角形,再判断AC 与DH 的大小关系,求出△DFG=△GCA=60°,利用外角定理即可得到60FGH FHG ∠+∠=︒. 【详解】△△ACD 和△BCE 是等边三角形,△AD =AC =CD ,CE =CB =BE ,△ACD =△BCE =60°. △△ACB =180°, △△DCE =60°. △△DCE =△BCE .△△ACD +△DCE =△BCE +△DCE , △△ACE =△DCB .在△ACE 和△DCB 中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,△△ACE△△DCB (SAS ), △CAE CDB ∠=∠即EAB BDC ∠=∠,△正确;在△ACG 和△DCH 中,60ACG DCH AC DC CAG CDH ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,△△ACG△△DCH (ASA ), △GC=HC,AG=DH 又△GCH=60°,△CGH 为等边三角形,△正确; 又AC≠AG ,△DH≠AC ,△错误;△△GAC+△ACG+△AGC=180°,△GDF+△DFG+△DGF=180° 又△AGC=△DGF ,△GAC=△GDF △△DFG=△ACG=60°又△DFG=FGH FHG ∠+∠, △60FGH FHG ∠+∠=︒,△正确; 故选A .题组A 基础过关练1.若等腰三角形的周长为26cm ,一边为6cm ,则腰长为( )分层提分A.6cm B.10cm C.10cm或6cm D.以上都不对【答案】B【分析】题中给出了周长和一边长,而没有指明这边是否为腰长,则应该分两种情况进行分析求解.【详解】解:△当6cm为腰长时,则腰长为6cm,底边=26-6-6=14cm,因为14>6+6,所以不能构成三角形;△当6cm为底边时,则腰长=(26-6)÷2=10cm,因为6-6<10<6+6,所以能构成三角形;故腰长为10cm.故答案为:B.2.等腰三角形的两边长分别为4cm,8cm,则该三角形的周长为()A.16cm B.20cm C.16cm或20cm D.以上都不对【答案】B【分析】根据题意得出两种情况,根据三角形的三边关系定理看看能否组成三角形,再求出周长即可.【详解】解:当等腰三角形的三边长是4cm,4cm,8cm时,4+4=8,不符合三角形的三边关系定理,此时不能组成三角形;当等腰三角形的三边长是4 cm,8 cm,8 cm时,符合三角形的三边关系定理,此时能组成三角形,三角形的周长是4+8+8=20(cm),所以该三角形的周长是20 cm,故选:B.3.下列关于等边三角形的性质的叙述中,错误的是()A.是等腰三角形B.三个角都相等C.三条边都相等D.只有一条对称轴【答案】D【分析】利用等边三角形的性质依次分析即可得出答案.【详解】解:A、等边三角形也是等腰三角形,原说法正确,故此选项不合题意;B、等边三角形三个角都相等,原说法正确,故此选项不合题意;C、等边三角形三条边都相等,原说法正确,故此选项不合题意;D 、等边三角形有3条对称轴,原说法错误,故此选项符合题意; 故选:D .4.已知直角三角形中30°角所对的直角边为4cm ,则斜边的长为( ) A .8 cm B .6 cmC .4 cmD .2 cm【答案】A 【分析】根据30°角所对的直角边等于斜边的一半可求得斜边长. 【详解】解:△直角三角形中30°角所对的直角边为4cm , △斜边长为8cm . 故选:A .5.已知ABC ∆中,3,60,AC AB C ==∠=︒则ABC ∆的周长等于( )A B .3 C .6 D .9【答案】D 【分析】判断ABC 为等边三角形即可求出其周长. 【详解】根据题意可知ABC 为等边三角形, △ABC 的三条边相等且等于3, △ABC 的周长为33=9⨯. 故选:D .6.如果等腰三角形的两边长分别为7cm 和3cm .那么它的第三边的长是( ) A .3cm B .4cmC .7cmD .3cm 或7cm【答案】C 【分析】根据等腰三角形腰的情况分类讨论,然后根据三角形的三边关系即可得出结论. 【详解】解:若7cm 为等腰三角形的腰长, △3+7>7△3cm 、7cm 、7cm 能构成三角形,故符合题意; 若3cm 为等腰三角形的腰长, △3+3<7△3cm 、3cm 、7cm 不能构成三角形,故不符合题意; 综上:它的第三边的长是7cm 故选C .7.若等腰三角形的一个角为100︒,则它一腰上的高与底边的夹角是( ) A .50︒ B .40︒C .10︒D .80︒【答案】A 【分析】根据题意先画出图形,由题意可知等腰三角形的顶角为100°,根据等腰三角形的性质得出=40B ACB ∠=∠︒,由CD BD ⊥,可得90B BCD ∠+∠=︒,则BCD ∠可得.【详解】 如图:△等腰三角形的一个角为100°,△等腰三角形的顶角为100°,即100BAC ∠=︒, △△ABC 是等腰三角形, △AB=AC ,△=40B ACB ∠=∠︒, △CD BD ⊥, △90D ∠=︒, △90B BCD ∠+∠=︒,△90904050BCD B ∠=︒-∠=︒-︒=︒, 故选:A .题组B 能力提升练1.下列命题的逆命题是真命题的是( ) A .同位角相等,两直线平行 B .等边三角形是锐角三角形 C .若两个角是直角,则它们相等 D .全等三角形的对应角相等【答案】A 【分析】先写出逆命题,再根据平行线的性质、等边三角形的定义、全等三角形的判定逐项判断即可得. 【详解】A 、逆命题:两直线平行,同位角相等, 此逆命题是真命题,此项符合题意;B 、逆命题:锐角三角形是等边三角形, 此逆命题是假命题,此项不符题意;C 、逆命题:若两个角相等,则它们是直角, 此逆命题是假命题,此项不符题意;D 、逆命题:三个角分别对应相等的两个三角形是全等三角形, 此逆命题是假命题,此项不符题意; 故选:A .2.已知等边ABC 的边长为3,点E 在直线AB 上,点D 在直线CB 上,且ED EC =,若6AE =,则CD 的长为( ) A .6 B .9C .3或6D .3或9【答案】D 【分析】△E 在线段AB 的延长线上时,过E 点作EF CD ⊥于F ,△当E 在线段AB 的延长线时,过E 点作EF CD ⊥于F ,根据等边三角形的性质求出BE 长和60ABC ∠=︒,解直角三角形求出BF ,求出CF ,即可求出答案. 【详解】解:点E 在直线AB 上,6AE =,点E 位置有两种情况: △E 在线段AB 的延长线上时,过E 点作EF CD ⊥于F ,ABC ∆是等边三角形,ABC ∆的边长为3,6AE =,633BE ∴=-=,60ABC∠=︒,60EBF ∴∠=︒,30BEF ∴∠=︒,1322BF BE ∴==, 39322CF ∴=+=, ED EC =,CF DF ∴=,9292CD ∴=⨯=;△如图2,当E 在线段AB 的延长线时,过E 点作EF CD ⊥于F ,ABC ∆是等边三角形,ABC ∆的边长为3,6AE =,639BE ∴=+=,60ABC∠=︒,60EBF ∴∠=︒,30BEF ∴∠=︒,1922BF AE ∴==, 93322CF ∴=-=, ED EC =,CF DF ∴=,3232CD ∴=⨯=;C=或3,即9故选:D.3.下列命题是假命题的是()A.线段垂直平分线上的点到线段两端的距离相等B.三角形的一个外角等于与它不相邻的两个内角的和C.有一个外角是120°的等腰三角形是等边三角形D.有两边和一角对应相等的两个三角形全等【答案】D【分析】根据垂直平分线的性质、三角形外角的定义、等边三角形的判定定理、全等三角形的判定定理依次判断即可.【详解】解:线段垂直平分线上的点到线段两端的距离相等,所以A选项为真命题,不符合题意;三角形的外角等于与它不相邻的两个内角的和,所以B选项为真命题,不符合题意;有一个外角是120°的等腰三角形,与它相邻的内角等于60°,是等边三角形,所以C选项为真命题,不符合题意;有两边和其夹角对应相等的两个三角形全等,所以D选项为假命题,符合题意;故选:D.4.下列命题中,假命题是()A.直角三角形的两个锐角互余B.等腰三角形的两底角相等C.面积相等的两个三角形全等D.有一个角是60︒的等腰三角形是等边三角形【答案】C【分析】根据直角三角形的性质、等腰三角形的性质、全等三角形的概念、等边三角形的判定定理判断即可.【详解】解:A、直角三角形的两个锐角互余,本选项说法是真命题;B、等腰三角形的两底角相等,本选项说法是真命题;C、面积相等的两个三角形不一定全等,本选项说法是假命题;D、有一个角是60°的等腰三角形是等边三角形,本选项说法是真命题;故选:C.5.等腰ABC中,过点B的直线BD分ABC为两个等腰三角形,则顶角为_____度.【答案】36°或1807或90°或108°【分析】根据题意分四种情况画出图形,结合等腰三角形的性质进行求解.【详解】解:△ABC中,AB=AC,若AD=BD,BC=BD,△△A=△ABD,△BDC=△C,则△C=△BDC=2△A,△△A+△ABC+△C=△A+2△A+2△A=180°,△△A=36°;若AD=BD,BC=CD,△△A=△ABD,△CBD=△CDB,则△CDB=2△A,△△A+△ABC+△C=△A+△A+2△A+3△A=180°,△△A=1807︒;若AD=BD ,AD=CD , △△B=△C=△BAD=△CAD , △△BAC+△ABC+△C=180°, △△BAD=△CAD=45°, △△BAC=90°;若AD=BD ,AC=CD ,△△B=△BAD ,△CAD=△CDA ,则△CDA=2△BAD ,△C=180°-2△CAD=180°-4△BAD , △△B=△C ,△△BAD=180°-4△BAD , △△BAD=36°,△△BAC=3△BAD=108°;故答案为:36°或1807︒或90°或108°. 6.已知在ABC 中,16C ∠=︒且为最小的内角,过顶点B 的一条直线把这个三角形分割成两个等腰三角形,则B∠=_______︒【答案】123°或132°或90°或48°【分析】根据题意作图,结合等腰三角形的性质分情况讨论即可求解.【详解】解:如图,若BC=CD,AD=BD,由题意可得:△DBC=△BDC=(180°-△C)÷2=82°,△△ABD=△BAD=12△BDC=41°,△△ABC=△ABD+△DBC=123°,△△ADB=180°-82°=98°,则在BC=CD的前提下只有AD=BD;如图,若CD=BD,AB=BD,由题意可得:△DBC=△C=16°,△△ADB=2△C=32°,△△A=△ADB=32°,△ABD=180°-△A-△ADB=116°,△△ABC=△ABD+△DBC=132°,符合最小的内角为△C=16°,如图,若BD=CD,AB=AD,则△C=△DBC=16°,△△ADB=△ABD=2△C=32°,△△A=180°-2×32°=116°,△△ABC=△ABD+△DBC=48°;如图,若BD=CD,AD=BD,△△ADB=2△C=2△DBC=32°,△△A=△ABD=(180°-32°)÷2=74°,△△ABC=△ABD+△DBC=90°;若BD=BC,则△C=△CDB=16°,△△ADB=180°-△CDB=164°,则只能满足AD=BD,△△A=12△CDB=8°,即△A<△C,不满足;综上:△ABC 的度数为123°或132°或90°或48°. 故答案为:123°或132°或90°或48°.7.如图,在四边形ABDE 中,C 是BD 的中点,3AB =,4BD =,5DE =,若120ACE ∠=︒,则线段AE 的最大值为___________.【答案】10 【分析】作B 关于AC 的对称点F ,D 关于EC 的对称点G ,连接AF ,FC ,CG ,EG ,FG .根据两点之间线段最短解决问题即可. 【详解】解:作B 关于AC 的对称点F ,D 关于EC 的对称点G ,连接AF ,FC ,CG ,EG ,FG ,如图所示:△C 是BD 边的中点, △CB=CD=12BD=2, △点B 、点F 关于AC 对称,△CF=CB=2,AF=AB=3,△BCA=△FCA . 同理CD=CG=2,ED=EG=5,△DCE=△GCE , △CG=CF=2, △△ACE=120°,△△BCA+△DCE=180°-120°=60°. △△FCA+△GCE=60°. △△FCG=60°.△△FGC 是等边三角形. △FG=2,△AE≤AF+FG+EG=3+2+5=10,△当A 、F 、G 、E 共线时,AE 的值最大2,最大值为10, 故答案为:10.题组C 培优拔尖练1.如图,在等腰ABC 中,AB AC =,120BAC ∠=︒,AD BC ⊥于点D ,点P 是CA 延长线上一点,点O 在AD 延长线上,OP OB =,下面的结论:△30APO OBD ∠-∠=︒;△BPO △是正三角形;△AB AP AO -=;△2BOC AOBP S S =四边形△,其中正确的个数是( )A .1个B .2个C .3个D .4个【答案】C 【分析】由题意易得OB=OC ,则有△OBD=△OCD ,△APO=△OCP ,进而根据角的关系可证△,然后可得△PBO=△PBA+△APO ,由三角形内角和可得△OPB=60°,可判断△,在AB 上找一点E ,使AE=AP ,连接PE ,延长AO ,在AO 的延长线上找一点F ,使AF=AB ,连接BF ,由此可得AP=PE=AE ,△APE=60°,进而可证△BPE△△OPA ,然后根据全等三角形的性质可判断△,最后根据等积法及三角形全等的性质与判定可判断△. 【详解】解:△AB AC =,AD BC ⊥,120BAC ∠=︒, △BD=DC ,△ACB=△ABC=30°, △OB=OC , △△OBD=△OCD , △OB=OP , △OC=OP , △△APO=△OCP ,△△OCP -△OCB=△ACB=30°,△30APO OBD ∠-∠=︒,故△正确; △OP=OB , △△OPB=△PBO ,△△PBO=△PBA+△ABD+△OBC=△PBA+30°+△APO -30°, △△PBO=△PBA+△APO ,△在△ABC 中,△BAC+△ABC+△ACB=180°,即△OPB+△APO+△PBA+△ABC+△ACB=180°, △2△OPB+60°=180°, △△OPB=60°,△△BPO 是正三角形,故△正确;在AB 上找一点E ,使AE=AP ,连接PE ,如图所示:△△PAE=60°,△△PAE 是等边三角形, △AP=PE=AE ,△APE=60°,△△BPE=△APB -△APE ,△OPA=△APB -△BPO , △△BPE=△OPA , △OP=BP ,△△BPE△△OPA (SAS ), △BE=AO , △AB -BE=AE , △AB -OA=AP ,△AB AP AO -=,故△正确;延长AO ,在AO 的延长线上找一点F ,使AF=AB ,连接BF , △△ABF 是等边三角形, △△ABF=60°,△△ABO+△OBF=60°,△ABO+△PBA=60°, △△PBA=△OBF ,△PB=OB ,AB=BF , △△APB△△FOB (SAS ), △AOBP S S =四边形△ABF ,如要证2BOC AOBP S S =四边形△,需证12OD AD =,由题意无法证明12OD AD =,故△错误; 所以正确的个数有3个; 故选:C .2.如图,在Rt ABC ∆中,90BAC ∠=︒,45C ∠=︒,AD BC ⊥于点D ,ABC ∠的平分线分别交AC 、AD 于E 、F 两点,M 为EF 的中点,AM 的延长线交BC 于点N ,连接EN ,下列结论:△AFE ∆为等腰三角形;△DF DN =;△AN BF =;△EN NC ⊥.其中正确的结论有( )A .1个B .2个C .3个D .4个【答案】D 【分析】△由等腰直角三角形的性质得△BAD=△CAD=△C=45°,再根据三角形外角性质可得到△AEF=△AFE ,可判断△AEF 为等腰三角形,于是可对△进行判断;求出BD=AD ,△DBF=△DAN ,△BDF=△ADN ,证△DFB△△DAN ,即可判断△△;连接EN ,只要证明△ABE△△NBE ,即可推出△ENB=△EAB=90°,由此可知判断△. 【详解】解:△等腰Rt△ABC 中,△BAC=90°,AD△BC , △△BAD=△CAD=△C=45°,BD=AD , △BE 平分△ABC , △△ABE=△CBE=12△ABC=22.5°, △△AEF=△CBE+△C=22.5°+45°=67.5°, △AFE=△FBA+△BAF=22.5°+45°=67.5°, △△AEF=△AFE ,△AF=AE ,即△AEF 为等腰三角形,所以△正确;△M 为EF 的中点, △AM△BE ,△△AMF=△AME=90°,△△DAN=90°−67.5°=22.5°=△MBN , 在△FBD 和△NAD 中FBD NAD BD ADBDF ADN ∠=∠⎧⎪=⎨⎪∠=∠⎩, △△FBD△△NAD (ASA ),△DF=DN ,AN=BF ,所以△△正确; △AM△EF ,△△BMA=△BMN=90°, △BM=BM ,△MBA=△MBN , △△MBA△△MBN , △AM=MN ,△BE 垂直平分线段AN , △AB=BN ,EA=EN , △BE=BE , △△ABE△△NBE , △△ENB=△EAB=90°, △EN△NC ,故△正确, 故选:D .3.如图,在Rt△ABC 中,△BAC =90°,AB =AC ,BF 平分△ABC ,过点C 作CF △BF 于F 点,过A 作AD △BF 于D 点.AC 与BF 交于E 点,下列四个结论:△BE =2CF ;△AD =DF ;△AD +DE =12BE ;△AB +BC =2AE .其中正确结论的序号是( )A .只有△△△B .只有△△C .只有△△△D .只有△△【答案】A 【分析】适当做辅助线,构建三角形.延长CF 并交BA 延长线于H△证明△ABE△△ACH ,得到BE=CH ,又可证CH=2CF ,故可得BE =2CF△若要得到AD =DF ,则需要证明△ADF 为等腰直角三角形,需要证明△DAF 为45°即可 △过E 作EM AF ⊥交AF 于点M ,证明△EMF 为等腰直角三角形,EM MF =12AD DE AM EM AM MF AF CF BE +=+=+===△过E 作EN BC ⊥于点N ,证明2AE AE EN AE EC AC =+<+=,得到22AB BC AE BC AE +>+>,即可证明△错误. 【详解】△延长BA 、CF ,交于点H ,△,BF CH CBF HBF ⊥∠=∠ △BCH H ∠=∠ △BC BH = △2CH CF =△90ABE AEB ∠+∠=︒ 90FCE FEC ∠+∠=︒ AEB FEC ∠=∠ △ABF ACF ∠=∠△90BAF CAH ∠=∠=︒ AB AC = △BAE CAH ≌ △,2BE CH BE CF ==△由△知,F 为CH 中点,又CAH 为直角三角形 故12AF CH CF HF === △H FAH ∠=∠△,45BC BH HBC =∠=︒ △67.5H FAH ∠=∠=︒ △90HAC ∠=︒ △22.5FAC ∠=︒ 又BF 为HBC ∠的平分线 △22.5HBF ∠=︒ △67.5BAD ∠=︒△9067.522.5CAD ∠=︒-︒=︒45FAD FAC DAC ∠=∠+∠=︒在RT ADF 中,45DAF DFA ∠=∠=︒ △AD DF =△过E 作EM AF ⊥交AF 于点M ,由△知,CA 为△DAF 的平分线△,DE EM AD AM == △EMF 为等腰直角三角形 △EM MF =△12AD DE AM EM AM MF AF CF BE +=+=+=== △过E 作EN BC ⊥于点N ,可知AE EN =在RT ENC 中,EN EC <△2AE AE EN AE EC AC =+<+= 即2AE AC <,而AC AB = △2AE AB <故22AB BC AE BC AE +>+>△2AB BC AE +≠,故△错误,本题答案选A.4.如图,AD 为等腰△ABC 的高,其中△ACB =50°,AC =BC ,E ,F 分别为线段AD ,AC 上的动点,且 AE =CF , 当 BF +CE 取最小值时,△AFB 的度数为( )A .75°B .90°C .95°D .105°【答案】C 【分析】先构造△CFH 全等于△AEC ,得到△BCH 是等腰直角三角形且FH=CE ,当FH+BF 最小时,即是BF+CE 最小时,此时求出△AFB 的度数即可. 【详解】解:如图,作CH△BC ,且CH=BC ,连接HB ,交AC 于F ,此时△BCH 是等腰直角三角形且FH+BF 最小,△AC=BC ,△CH=AC,△△HCB=90°,AD△BC,△AD//CH,△△ACB=50°,△△ACH=△CAE=40°,△△CFH△△AEC,△FH=CE,△FH+BF=CE+BF最小,此时△AFB=△ACB+△HBC=50°+45°=95°.故选:C.5.如图,在△ABC中,AD为△BAC的平分线,BM△AD,垂足为M,且AB=5,BM=2,AC=9,则△ABC与△C 的关系为()A.△ABC=2△C B.△ABC=52△C C.14△ABC=△C D.△ABC=3△C【答案】D【分析】延长BM到E,证明△ABF△△AEM,利用线段长度推出△BCE是等腰三角形,再根据角度转换求出即可.【详解】证明:延长BM,交AC于E,△AD平分△BAC,BM△AD,△△BAM=△EAM ,△AMB=△AME 又△AM=AM , △△ABM△△AEM ,△BM=ME ,AE=AB ,△AEB=△ABE, △BE=BM+ME=4,AE=AB=5, △CE=AC -AE=9-5=4, △CE=BE ,△△BCE 是等腰三角形, △△EBC=△C ,又△△ABE=△AEB=△C+△EBC. △△ABE=2△C ,△△ABC=△ABE+△EBC=3△C. 故选D.6.如图在ABC 中,ABC ∠和ACB ∠的平分线交于点G ,过点G 作//EF BC 交AB 于E ,交AC 于F ,过点G 作GD AC ⊥于D ,下列四个结论:其中正确的结论有( )个. △EF BE CF =+;△90BGC A ∠=︒+∠;△点G 到ABC 各边的距离相等; △设GD m =,AE AF n +=,则AEF S mn =△;△AEF 的周长等于+AB AC 的和.A .1B .2C .3D .4【答案】C 【分析】△根据△ABC 和△ACB 的平分线相交于点G 可得出△EBG=△CBG ,△BCG=△FCG ,再由EF△BC 可知△CBG=△EGB ,△BCG=△CGF ,故可得出BE=EG ,GF=CF ,由此可得出结论;△先根据角平分线的性质得出△GBC+△GCB=12(△ABC+△ACB ),再由三角形内角和定理即可得出结论;△根据三角形角平分线的性质即可得出结论;△连接AG ,由三角形的面积公式即可得出结论;△根据BE=EG ,GF=CF ,进行等量代换可得结论.【详解】解:△△△ABC和△ACB的平分线相交于点G,△△EBG=△CBG,△BCG=△FCG.△EF△BC,△△CBG=△EGB,△BCG=△CGF,△△EBG=△EGB,△FCG=△CGF,△BE=EG,GF=CF,△EF=EG+GF=BE+CF,故△正确;△△△ABC和△ACB的平分线相交于点G,△△GBC+△GCB=12(△ABC+△ACB)=12(180°-△A),△△BGC=180°-(△GBC+△GCB)=180°-12(180°-△A)=90°+12△A,故△错误;△△△ABC和△ACB的平分线相交于点G,△点G也在△BAC的平分线上,△点G到△ABC各边的距离相等,故△正确;△连接AG,作GM△AB于M,如图所示:△点G是△ABC的角平分线的交点,GD=m,AE+AF=n,△GD=GM=m,△S△AEF=12AE•GM+12AF•GD=12(AE+AF)•GD=12nm,故△错误.△△BE=EG,GF=CF,△AE+AF+EF=AE+AF+EG+FG=AE+AF+BE+CF=AB+AC,即△AEF的周长等于AB+AC的和,故△正确,故选:C.7.如图,等腰ABC的底边BC长为4cm,面积为216cm,腰AC的垂直平分线EF交AC于点E,交AB 于点F,D为BC的中点,M为直线EF上的动点.则CDM周长的最小值为()A.6cm B.8cm C.9cm D.10cm【答案】D【分析】连接AD,AM,由于△ABC是等腰三角形,点D是BC边的中点,故AD△BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AC的垂直平分线可知,点A关于直线EF的对称点为点C,MA=MC,推出MC+DM=MA+DM≥AD,故AD的长为BM+MD的最小值,由此即可得出结论.【详解】解:连接AD,MA.△△ABC是等腰三角形,点D是BC边的中点,△AD△BC,△S△ABC=12BC•AD=12×4×AD=16,解得AD=8 cm,△EF是线段AC的垂直平分线,△MA=MC,△MC+DM=MA+DM≥AD,△AD的长为CM+MD的最小值,△△CDM的周长最短=(CM+MD)+CD=AD+12BC=8+12×4=10(cm).故选:D.。
苏科版八年级上册数学 第2章 轴对称复习

第二章轴对称图形复习教学目标:1:了解轴对称图形和两个图形成轴对称的概念,知道轴对称图形和两个图形成轴对称的区别与联系.2:理解线段垂直平分线的性质和判定.3:掌握等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“三线合一”). 4:掌握直角三角形的性质教学重、难点:1:线段垂直平分线的性质2:等腰三角形与直角三角形的判定和性质.轴对称与轴对称图形题型1:轴对称图形1、下列图形中,是.轴对称图形的为()ABC D2、如图1,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离相等?角与线段的轴对称性题型2:角与线段1、到三角形的三个顶点距离相等的点是()A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三条边的垂直平分线的交点2、如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°, ∠BAD=60°,则△ABC是__________ 三角形.3、如图,在△ABC中,∠C = 90°,AD平分∠BAC,且CD = 5,则点D到AB的距离为 .4、如图8,△ABC中,AB=AC,∠A=50°,AB的垂直平分线交AC于D,∠DBC的度数_______.等腰三角形轴对称性题型3:等腰三角形和直角三角形1、等腰三角形的一个外角等于100°,则与它不相邻的两个内角的度数分别为()A.40° 40°B.80° 20°C.50° 50°D.50° 50°或80° 20°2、若等腰三角形的周长为26,一边为11,则腰长为().A.11B.7.5C.11或7.5D.以上都不对3 、已知:如图,在△ABC中,D是BC上的点,AD=AB,E,F分别是AC,BD的中点,AC=6,EF=__________________例题讲解例1、下列图形中对称轴最多的是( ) .A.等腰三角形B.正方形C.圆D.线段例2、如图,在△ABC中,∠C=50°按图中虚线将∠C剪去后,∠1+∠2=________________°.例3、如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12,则图中阴影部分的面积为___________.例4、如图3,△ABC中,∠BAC=120°,若DE、FG分别垂直平分AB、AC,△AEF的周长为10cm,求∠EAF的度数及BC的长.1、等腰三角形两边长分别是3和6,则该三角形的周长为____________ .2、若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是().A.75°或15°B.75°C.15°D.75°和30°3、如图,D,E,F分别是等边△ABC各边上的点,且AD=BE=CF,则△DEF的形状是()A.等边三角形B.腰和底边不相等的等腰三角形C.直角三角形D.不等边三角形7、已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4,BC=______________.4、已知:如图,在△ABC中,AB=AC,BD平分∠ABC,E是底边BC的延长线上的一点,且CD=CE.(1)求证:△BDE是等腰三角形.(2)若∠A=36°,求∠ADE的度数.思考:如图,△ABC中,AB=AC=13,BC=10,AD是BC上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为_________1、如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠ABC=________ 度.2、如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为()厘米.A.16 B.18 C.26 D.283、如图,△ABC中,AB=AC,D在BC上,∠BAD=30°,在AC上取点E,使AE=AD,∠EDC=______________度.5、如图,△ABC为正三角形,D为边BA延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.:3、如图1,在△ABC中,BO平分∠ABC,CO平分∠ACB,过点O作DE∥BC,交AB于点D,交AC与点D,交AC于点E.(1)试找出图中的等腰三角形,并说明理由;(2)若BD=4、CE=3,求DE的长;(3)若AB=12、AC=9,求△ADE的周长;(4)若将原题中平行线DE的方向改变,如图2,OD∥AB,OE∥AC,BC=16,你能得出什么结论呢?。
苏科版八年级数学上册第二章轴对称图形等腰三角形的轴对称性课件(共20张)

(1).等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴。
(2).对称性
重合的线段
重合的角
=
=
=
=ห้องสมุดไป่ตู้
=
=
AB AC
BD CD
AD AD
∠B ∠C
∠BAD ∠CAD
∠ADB ∠ADC
(3).根据上面的操作,你有什么发现呢?
80°, 20°
(3).如果等腰三角形一个角为80°,它的另外两个角为 _____________________ .
80°, 20°或 50°, 50°
比一比,看谁做得快
14或16
(4).已知等腰三角形的两边长分别是4和6,则它的周长是________.
(5).已知等腰三角形的两边长分别是3和7,则它的周长是________ .
3
1
2
4
︶
︵
︶
︶
解: DE∥AF 在△ABC中 ∵ AB=AC ,AF⊥BC ∴ ∠BAF = ∠ CAF (三线合一) ∵ AD=AE ∴ ∠ADE = ∠AED ∵∠BAC是△ADE的外角, ∴ ∠ BAC = ∠ADE +∠AED =2∠AED . ∵ ∠ BAC = ∠BAF + ∠ CAF = 2∠CAF ∴ ∠AED = ∠CAF ∴ DE∥AF
选做题:已知:如图,∠A=∠D=90°,AB=CD,AC与BD相交于点F,E是BC的中点. 求证:∠BFE=∠CFE.
谢谢
勤奋是你生命的密码,能译出你一部壮丽的史诗。
=
=
=
AB AC
BD CD
AD AD
∠B ∠C
∠BAD ∠CAD
∠ADB ∠ADC
苏科版八年级上册数学第二章 轴对称图形含答案(满分必备)

苏科版八年级上册数学第二章轴对称图形含答案一、单选题(共15题,共计45分)1、下列命题是真命题的是().A.有两条边、一个角相等的两个三角形全等。
B.等腰三角形的对称轴是底边上的中线。
C.全等三角形对应边上的中线相等。
D.有一个角是60°的三角形是等边三角形。
2、如图所示,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为()A.15°B.30°C.45°D.60°3、有一张平行四边形纸片ABCD,已知,按如图所示的方法折叠两次,则的度数等于()A.55°B.50°C.45°D.40°4、到△ABC三个顶点距离相等的点是△ABC的()A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三条垂直平分线的交点5、在下列汽车标志中,既是轴对称图形,又是中心对称图形的是()A. B. C. D.6、如图,在△ABC中,AB>AC,分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=7,AC=5,则△ACD的周长为()A.2B.12C.17D.197、剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为()A. B. C. D.8、△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道()A.△ABC的周长B.△AFH的周长C.四边形FBGH的周长D.四边形ADEC的周长9、如图,C、D在以线段AB为直径的⊙O上,若CA=CD,且∠ACD=40°,则∠CAB=()A.10°B.20°C.30°D.40°10、已知AB=8cm,小红在作线段AB的垂直平分线时操作如下:分别以A和B 为圆心,5cm的长为半径画弧,两弧相交于C、D,则直线CD即为所求,根据此种作图方法所得到的四边形ADBC的面积是()A.12cm 2B.24cm 2C.36cm 2D.48cm 211、如图,AB∥CD,AB=AC,∠1=40°,则∠ACE的度数为()A.80°B.100°C.120°D.160°12、如图,把一矩形纸片OABC放入平面直角坐标系xoy中,使OA,OC分别落在x轴、y轴上,现将纸片OABC沿OB折叠,折叠后点A落在点A'的位置,若OA=1,OB=2,则点A'的坐标为()A. B. C.() D.()13、将AD与BC两边平行的纸条ABCD按如图所示折叠,则∠1的度数为()A.72°B.45°C.56°D.60°14、如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=BF;④AE=BG.其中正确的个数是()A.1个B.2个C.3个D.4个15、如图,等边的边长为3,点D在边上,,线段在边上运动,,有下列结论:① 与可能相等;② 与可能相似;③四边形面积的最大值为;④四边形周长的最小值为.其中,正确结论的序号为()A.①④B.②④C.①③D.②③二、填空题(共10题,共计30分)16、某同学从平面镜里看到镜子对面的电子钟的示数如图所示,这时的实际时间是________.17、如图,在△ABC中,已知∠B=∠C,则可判定AB=AC的依据是________;18、如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为________.19、在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则折痕CE的长为________.20、已知点在直线上,点在直线上,与关于y轴对称.则和的交点坐标为________.21、如图,矩形纸片ABCD,AD=2AB=4,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为________.22、如图,BE⊥AC,垂足为D,且AD=CD,BD=ED.若∠ABC=54°,则∠E=________°.23、如图,△ABC中,已知AB=5,AC=4,AD平分∠BAC交BC于D,DE⊥AC交AC于点E,若DE=2,则△ABC的面积为________.24、如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB=________.25、把一张长方形纸条按如图方式折叠,若∠1=40°,则∠2的度数是________.三、解答题(共5题,共计25分)26、如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.27、如图,在长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿AF折叠,使点D落在BC上的点E处.求BE及CF的长.28、作图题:(要求保留作图痕迹,不写作法)(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);(2)连结BE,若AC=10,AB=6,求△ABE的周长.29、如图,在中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数.30、如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:BC =3AD.参考答案一、单选题(共15题,共计45分)1、C2、D3、B4、D5、A6、B7、D8、A9、B10、B11、B12、B13、C14、C15、D二、填空题(共10题,共计30分)16、17、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)28、。
最新苏科版八年级数学上册 轴对称的性质(含解析)
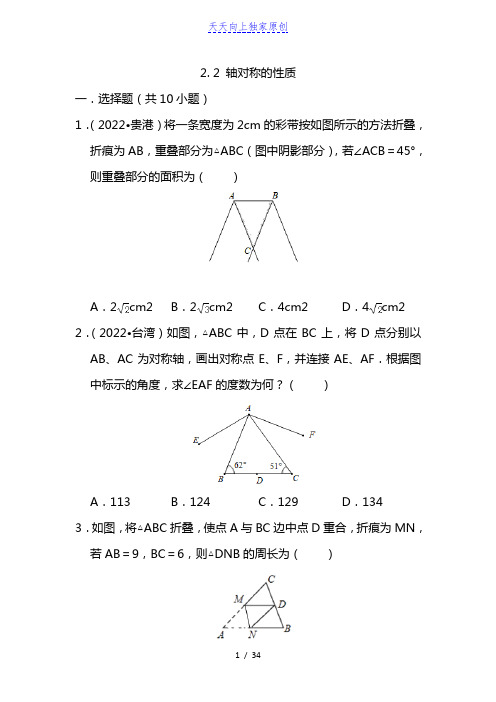
2. 2 轴对称的性质一.选择题(共10小题)1.(2022•贵港)将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC(图中阴影部分),若∠ACB=45°,则重叠部分的面积为()A.2cm2 B.2cm2 C.4cm2 D.4cm2 2.(2022•台湾)如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,求∠EAF的度数为何?()A.113 B.124 C.129 D.134 3.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为()A.12 B.13 C.14 D.15 4.(2018•湖州)如图,已知在△ABC中,∠BAC>90°,点D为BC 的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是()A.AE=EF B.AB=2DEC.△ADF和△ADE的面积相等D.△ADE和△FDE的面积相等5.(2018•天津)如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是()A.AD=BD B.AE=AC C.ED+EB=DB D.AE+CB =AB6.(2018•临安区)如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿左图中的虚线剪开,拼成如图的一座“小别墅”,则图中阴影部分的面积是()A.2 B.4 C.8 D.10 7.(2022•重庆)如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC',DC′与AB交于点E,连结AC',若AD=AC′=2,BD=3,则点D到BC′的距离为()A.B.C.D.8.(2022•重庆)如图,在△ABC中,∠ABC=45°,AB=3,AD⊥BC于点D,BE⊥AC于点E,AE=1.连接DE,将△AED沿直线AE翻折至△ABC所在的平面内,得△AEF,连接DF.过点D作DG⊥DE交BE于点G.则四边形DFEG的周长为()A.8 B.4C.2+4 D.3+2 9.(2018•青羊区自主招生)如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则△B′DE的面积为()A.B.C.D.10.(2022•内江)如图,将△ABC沿着过BC的中点D的直线折叠,使点B落在AC边上的B1处,称为第一次操作,折痕DE到AC 的距离为h1;还原纸片后,再将△BDE沿着过BD的中点D1的直线折叠,使点B落在DE边上的B2处,称为第二次操作,折痕D1E1到AC的距离记为h2;按上述方法不断操作下去……经过第n次操作后得到折痕Dn﹣1En﹣1,到AC的距离记为hn.若h1=1,则hn的值为()A.1+B.1+C.2﹣D.2﹣二.填空题(共6小题)11.(2022•江西)如图,在△ABC中,点D是BC上的点,∠BAD =∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=°.12.(2022•吉林)如图,在四边形ABCD中,AB=10,BD⊥AD.若将△BCD沿BD折叠,点C与边AB的中点E恰好重合,则四边形BCDE的周长为.13.(2022•西藏)如图,把一张长为4,宽为2的矩形纸片,沿对角线折叠,则重叠部分的面积为.14.(2018•乌鲁木齐)如图,在Rt△ABC中,∠C=90°,BC=2,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F 为直角三角形,则AE的长为.15.(2022•越秀区校级二模)如图,将△ABC沿DE折叠,使点A 与BC边的中点F重合,下列结论中:①EF=AB;②∠BAF=∠CAF;③S四边形ADFE=AF×DE;④∠BDF+∠FEC=2∠BAC,正确的是(填序号)16.(2022•兴庆区校级一模)如图,将△ABC折叠,使点A与BC 边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为.三.解答题(共4小题)17.(2022•湘潭)如图,将△ABC沿着AC边翻折,得到△ADC,且AB∥CD.(1)判断四边形ABCD的形状,并说明理由;(2)若AC=16,BC=10,求四边形ABCD的面积.18.(2018•长春)图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM、ON的端点均在格点上.在图①、图②给定的网格中以OM、ON为邻边各画一个四边形,使第四个顶点在格点上.要求:(1)所画的两个四边形均是轴对称图形.(2)所画的两个四边形不全等.19.(2017•安徽)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.(2)画出△DEF关于直线l对称的三角形.(3)填空:∠C+∠E=.20.如图所示,每个小正方形的边长为1,△ABC,△DEF的顶点都在小正方形的顶点处.(1)将△ABC平移,使点A平移到点F,点B,C的对应点分别是点B',C',画出△FB'C';(2)画出△DEF关于DF所在直线对称的△DE'F;(3)直接写出四边形B'C'FE'的面积是.答案与解析一.选择题(共10小题)1.(2022•贵港)将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC(图中阴影部分),若∠ACB=45°,则重叠部分的面积为()A.2cm2 B.2cm2 C.4cm2 D.4cm2 【分析】过B作BD⊥AC于D,则∠BDC=90°,依据勾股定理即可得出BC的长,进而得到重叠部分的面积.【解答】解:如图,过B作BD⊥AC于D,则∠BDC=90°,∵∠ACB=45°,∴∠CBD=45°,∴BD=CD=2cm,∴Rt△BCD中,BC==2(cm),∴重叠部分的面积为×2×2=2(cm),故选:A.【点评】本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.2.(2022•台湾)如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,求∠EAF的度数为何?()A.113 B.124 C.129 D.134【分析】连接AD,利用轴对称的性质解答即可.【解答】解:连接AD,∵D点分别以AB、AC为对称轴,画出对称点E、F,∴∠EAB=∠BAD,∠FAC=∠CAD,∵∠B=62°,∠C=51°,∴∠BAC=∠BAD+∠DAC=180°﹣62°﹣51°=67°,∴∠EAF=2∠BAC=134°,故选:D.【点评】此题考查轴对称的性质,关键是利用轴对称的性质解答.3.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为()A.12 B.13 C.14 D.15【分析】由D为BC中点知BD=3,再由折叠性质得ND=NA,从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD 可得答案.【解答】解:∵D为BC的中点,且BC=6,∴BD=BC=3,由折叠性质知NA=ND,则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,故选:A.【点评】本题主要考查翻折变换,解题的关键是掌握翻折变换的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.4.(2018•湖州)如图,已知在△ABC中,∠BAC>90°,点D为BC 的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是()A.AE=EF B.AB=2DEC.△ADF和△ADE的面积相等D.△ADE和△FDE的面积相等【分析】先判断出△BFC是直角三角形,再利用三角形的外角判断出A正确,进而判断出AE=CE,得出DE是△ABC的中位线判断出B正确,利用等式的性质判断出D正确.【解答】解:如图,连接CF,∵点D是BC中点,∴BD=CD,由折叠知,∠ACB=∠DFE,CD=DF,∴BD=CD=DF,∴△BFC是直角三角形,∴∠BFC=90°,∵BD=DF,∴∠B=∠BFD,∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE,∴AE=EF,故A正确,由折叠知,EF=CE,∴AE=CE,∵BD=CD,∴DE是△ABC的中位线,∴AB=2DE,故B正确,∵AE=CE,∴S△ADE=S△CDE,由折叠知,△CDE≌△FDE,∴S△CDE=S△FDE,∴S△ADE=S△FDE,故D正确,当AD=AC时,△ADF和△ADE的面积相等∴C选项不一定正确,故选:C.【点评】此题主要考查了折叠的性质,直角三角形的判定和性质,三角形的中位线定理,作出辅助线是解本题的关键.5.(2018•天津)如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是()A.AD=BD B.AE=AC C.ED+EB=DB D.AE+CB =AB【分析】先根据图形翻折变换的性质得出BE=BC,根据线段的和差,可得AE+BE=AB,根据等量代换,可得答案.【解答】解:∵△BDE由△BDC翻折而成,∴BE=BC.∵AE+BE=AB,∴AE+CB=AB,故D正确,故选:D.【点评】本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.6.(2018•临安区)如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿左图中的虚线剪开,拼成如图的一座“小别墅”,则图中阴影部分的面积是()A.2 B.4 C.8 D.10【分析】本题考查空间想象能力.【解答】解:阴影部分由一个等腰直角三角形和一个直角梯形组成,由第一个图形可知:阴影部分的两部分可构成正方形的四分之一,正方形的面积=4×4=16,∴图中阴影部分的面积是16÷4=4.故选:B.【点评】解决本题的关键是得到阴影部分的组成与原正方形面积之间的关系.7.(2022•重庆)如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC',DC′与AB交于点E,连结AC',若AD=AC′=2,BD=3,则点D到BC′的距离为()A.B.C.D.【分析】连接CC',交BD于点M,过点D作DH⊥BC'于点H,由翻折知,△BDC≌△BDC',BD垂直平分CC',证△ADC'为等边三角形,利用解直角三角形求出DM=1,C'M=DM=,BM=2,在Rt△BMC'中,利用勾股定理求出BC'的长,在△BDC'中利用面积法求出DH的长.【解答】解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,∵AD=AC′=2,D是AC边上的中点,∴DC=AD=2,由翻折知,△BDC≌△BDC',BD垂直平分CC',∴DC=DC'=2,BC=BC',CM=C'M,∴AD=AC′=DC'=2,∴△ADC'为等边三角形,∴∠ADC'=∠AC'D=∠C'AC=60°,∵DC=DC',∴∠DCC'=∠DC'C=×60°=30°,在Rt△C'DM中,∠DC'C=30°,DC'=2,∴DM=1,C'M=DM=,∴BM=BD﹣DM=3﹣1=2,在Rt△BMC'中,BC'===,∵S△BDC'=BC'•DH=BD•CM,∴DH=3×,∴DH=,故选:B.【点评】本题考查了轴对称的性质,解直角三角形,勾股定理等,解题关键是会通过面积法求线段的长度.8.(2022•重庆)如图,在△ABC中,∠ABC=45°,AB=3,AD⊥BC于点D,BE⊥AC于点E,AE=1.连接DE,将△AED沿直线AE翻折至△ABC所在的平面内,得△AEF,连接DF.过点D作DG⊥DE交BE于点G.则四边形DFEG的周长为()A.8 B.4C.2+4 D.3+2 【分析】先证△BDG≌△ADE,得出AE=BG=1,再证△DGE与△EDF 是等腰直角三角形,在直角△AEB中利用勾股定理求出BE的长,进一步求出GE的长,可通过解直角三角形分别求出GD,DE,EF,DF的长,即可求出四边形DFEG的周长.【解答】解:∵∠ABC=45°,AD⊥BC于点D,∴∠BAD=90°﹣∠ABC=45°,∴△ABD是等腰直角三角形,∴AD=BD,∵BE⊥AC,∴∠GBD+∠C=90°,∵∠EAD+∠C=90°,∴∠GBD=∠EAD,∵∠ADB=∠EDG=90°,∴∠ADB﹣∠ADG=∠EDG﹣∠ADG,即∠BDG=∠ADE,∴△BDG≌△ADE(ASA),∴BG=AE=1,DG=DE,∵∠EDG=90°,∴△EDG为等腰直角三角形,∴∠AED=∠AEB+∠DEG=90°+45°=135°,∵△AED沿直线AE翻折得△AEF,∴△AED≌△AEF,∴∠AED=∠AEF=135°,ED=EF,∴∠DEF=360°﹣∠AED﹣∠AEF=90°,∴△DEF为等腰直角三角形,∴EF=DE=DG,在Rt△AEB中,BE===2,∴GE=BE﹣BG=2﹣1,在Rt△DGE中,DG=GE=2﹣,∴EF=DE=2﹣,在Rt△DEF中,DF=DE=2﹣1,∴四边形DFEG的周长为:GD+EF+GE+DF=2(2﹣)+2(2﹣1)=3+2,故选:D.【点评】本题考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,勾股定理,解直角三角形等,解题关键是能够灵活运用等腰直角三角形的判定与性质.9.(2018•青羊区自主招生)如图,Rt△ABC中,∠ACB=90°,AC =3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则△B′DE的面积为()A.B.C.D.【分析】根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,Rt△ABC中根据勾股定理求得AB=5,进而证得△ABC∽△DB′F,由三角形相似的性质即可求得B′F的长,通过证明△ACE∽△ABC,可得AE=DE=,即可求解.【解答】解:连接B'E,∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB=5,根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,AE=DE ∴B′D=BC﹣CD=4﹣3=1,∵∠B′DF=∠CDE,∴∠A=∠B′DF,∵∠B=∠B′,∴△ABC∽△DB′F,∴∴=,∴B′F=,∵∠A=∠A,∠ACB=∠AEC=90°∴△ACE∽△ABC∴∴AE=∴DE=∴△B′DE的面积=×DE×B'F=故选:B.【点评】此题主要考查了翻折变换,勾股定理的应用,三角形相似判定和性质的等,根据折叠的性质求得相等的角是本题的关键.10.(2022•内江)如图,将△ABC沿着过BC的中点D的直线折叠,使点B落在AC边上的B1处,称为第一次操作,折痕DE到AC的距离为h1;还原纸片后,再将△BDE沿着过BD的中点D1的直线折叠,使点B落在DE边上的B2处,称为第二次操作,折痕D1E1到AC的距离记为h2;按上述方法不断操作下去……经过第n次操作后得到折痕Dn﹣1En﹣1,到AC的距离记为hn.若h1=1,则hn的值为()A.1+B.1+C.2﹣D.2﹣【分析】根据相似三角形的性质,对应高的比对于相似比,得出h2=,依次得出h3、h4、h5、……hn,再对hn进行计算变形即可.【解答】解:∵D是BC的中点,折痕DE到AC的距离为h1∴点B到DE的距离=h1=1,∵D1是BD的中点,折痕D1E1到AC的距离记为h2,∴D1E1到AC的距离h2=h1+点B到D1E1的距离=1+h1=1+,同理:h3=h2+h1=1++,h4=h3+h1=1+++……hn=1++++…+=2﹣故选:C.【点评】考查图形变化规律的问题,首先根据变化求出第一个、第二个、第三个……发现规律得出一般性的结论.二.填空题(共6小题)11.(2022•江西)如图,在△ABC中,点D是BC上的点,∠BAD =∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=20 °.【分析】根据三角形内角和和翻折的性质解答即可.【解答】解:∵∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,∴∠ADC=40°+40°=80°,∠ADE=∠ADB=180°﹣40°﹣40°=100°,∴∠CDE=100°﹣80°=20°,故答案为:20【点评】此题考查翻折的性质,关键是根据三角形内角和和翻折的性质解答.12.(2022•吉林)如图,在四边形ABCD中,AB=10,BD⊥AD.若将△BCD沿BD折叠,点C与边AB的中点E恰好重合,则四边形BCDE的周长为20 .【分析】根据直角三角形斜边上中线的性质,即可得到DE=BE=AB=5,再根据折叠的性质,即可得到四边形BCDE的周长为5×4=20.【解答】解:∵BD⊥AD,点E是AB的中点,∴DE=BE=AB=5,由折叠可得,CB=BE,CD=ED,∴四边形BCDE的周长为5×4=20,故答案为:20.【点评】本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.13.(2022•西藏)如图,把一张长为4,宽为2的矩形纸片,沿对角线折叠,则重叠部分的面积为 2.5 .【分析】设BF长为x,则CF=x,FD=4﹣x,在直角三角形CDF 中,利用勾股定理可求出x,继而利用三角形面积公式进行计算求解.【解答】解:设BF长为x,则FD=4﹣x,∵∠ACB=∠BCE=∠CBD,∴△BCF为等腰三角形,BF=CF=x,在Rt△CDF中,(4﹣x)2+22=x2,解得:x=2.5,∴BF=2.5,∴S△BFC=BF×CD=×2.5×2=2.5.即重叠部分面积为2.5.故答案为:2.5.【点评】此题考查了图形的折叠变换,能够根据折叠的性质和勾股定理求出BF的长是解答此题的关键.14.(2018•乌鲁木齐)如图,在Rt△ABC中,∠C=90°,BC=2,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F 为直角三角形,则AE的长为3或.【分析】利用三角函数的定义得到∠B=30°,AB=4,再利用折叠的性质得DB=DC=,EB′=EB,∠DB′E=∠B=30°,设AE=x,则BE=4﹣x,EB′=4﹣x,讨论:当∠AFB′=90°时,则∴BF=cos30°=,则EF=﹣(4﹣x)=x﹣,于是在Rt△B′EF中利用EB′=2EF得到4﹣x=2(x﹣),解方程求出x得到此时AE 的长;若B′不落在C点处,作EH⊥AB′于H,连接AD,如图,证明Rt△ADB′≌Rt△ADC得到AB′=AC=2,再计算出∠EB′H=60°,则B′H=(4﹣x),EH=(4﹣x),接着利用勾股定理得到(4﹣x)2+[(4﹣x)+2]2=x2,方程求出x得到此时AE的长.【解答】解:∵∠C=90°,BC=2,AC=2,∴tanB===,∴∠B=30°,∴AB=2AC=4,∵点D是BC的中点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F∴DB=DC=,EB′=EB,∠DB′E=∠B=30°,设AE=x,则BE=4﹣x,EB′=4﹣x,当∠AFB′=90°时,在Rt△BDF中,cosB=,∴BF=cos30°=,∴EF=﹣(4﹣x)=x﹣,在Rt△B′EF中,∵∠EB′F=30°,∴EB′=2EF,即4﹣x=2(x﹣),解得x=3,此时AE为3;若B′不落在C点处,作EH⊥AB′于H,连接AD,如图,∵DC=DB′,AD=AD,∴Rt△ADB′≌Rt△ADC,∴AB′=AC=2,∵∠AB′E=∠AB′F+∠EB′F=90°+30°=120°,∴∠EB′H=60°,在Rt△EHB′中,B′H=B′E=(4﹣x),EH=B′H=(4﹣x),在Rt△AEH中,∵EH2+AH2=AE2,∴(4﹣x)2+[(4﹣x)+2]2=x2,解得x=,此时AE为.综上所述,AE的长为3或.故答案为3或.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了含30度的直角三角形三边的关系和勾股定理.15.(2022•越秀区校级二模)如图,将△ABC沿DE折叠,使点A 与BC边的中点F重合,下列结论中:①EF=AB;②∠BAF=∠CAF;③S四边形ADFE=AF×DE;④∠BDF+∠FEC=2∠BAC,正确的是③④(填序号)【分析】根据翻折变换的性质可得AE=EF,AF⊥DE,∠ADE=∠EDF,∠AED=∠DEF,根据平行线的性质和等腰三角形三线合一的性质判断只有AB=AC时①②正确;根据对角线互相垂直的四边形的面积等于对角线乘积的一半可得S四边形ADFE=AF•DE,判断出③正确;根据翻折的性质和平角的定义表示出∠ADE和∠AED,然后利用三角形的内角和定理列式整理即可得到∠BDF+∠FEC=2∠BAC,判断出④正确.【解答】解:∵△ABC沿DE折叠点A与BC边的中点F重合,∴AE=EF,AF⊥DE,∠ADE=∠EDF,∠AED=∠DEF,只有AB=AC时,∠BAF=∠CAF=∠AFE,EF∥AB,故①②错误;∵AF⊥DE,∴S四边形ADFE=AF•DE,故③正确;由翻折的性质得,∠ADE=(180°﹣∠BDF),∠AED=(180°﹣∠FEC),在△ADE中,∠ADE+∠AED+∠BAC=180°,∴(180°﹣∠BDF)+(180°﹣∠FEC)+∠BAC=180°,整理得,∠BDF+∠FEC=2∠BAC,故④正确.综上所述,正确的是③④共2个.故答案为:③④.【点评】本题考查了翻折变换的性质,主要利用了平行线判定,等腰三角形三线合一的性质,三角形的内角和定理,熟记各性质并准确识图是解题的关键.16.(2022•兴庆区校级一模)如图,将△ABC折叠,使点A与BC 边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为12 .【分析】由D为BC中点知BD=3,再由折叠性质得ND=NA,从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD 可得答案.【解答】解:∵D为BC的中点,且BC=6,∴BD=BC=3,由折叠性质知NA=ND,则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,故答案为:12.【点评】本题主要考查翻折变换,解题的关键是掌握翻折变换的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.三.解答题(共4小题)17.(2022•湘潭)如图,将△ABC沿着AC边翻折,得到△ADC,且AB∥CD.(1)判断四边形ABCD的形状,并说明理由;(2)若AC=16,BC=10,求四边形ABCD的面积.【分析】(1)由折叠的性质得出AB=AD,BC=CD,∠BAC=∠DAC,∠BCA=∠DCA,由平行线的性质得出∠BAC=∠DAC,得出∠BAC=∠DAC=∠BCA=∠DCA,证出AD∥BC,AB=AD=BC=CD,即可得出结论;(2)连接BD交AC于O,由菱形的性质得出AC⊥BD,OA=OB=AC=8,OB=OD,由勾股定理求出OB==6,得出BD=2OB=12,由菱形面积公式即可得出答案.【解答】解:(1)四边形ABCD是菱形;理由如下:∵△ABC沿着AC边翻折,得到△ADC,∴AB=AD,BC=CD,∠BAC=∠DAC,∠BCA=∠DCA,∵AB∥CD,∴∠BAC=∠DAC,∴∠BAC=∠DAC=∠BCA=∠DCA,∴AD∥BC,AB=AD=BC=CD,∴四边形ABCD是菱形;(2)连接BD交AC于O,如图所示:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=AC=8,OB=OD,∴OB===6,∴BD=2OB=12,∴四边形ABCD的面积=AC×BD=×16×12=96.【点评】本题考查了翻折变换的性质、菱形的判定与性质、平行线的性质、勾股定理等知识;熟练掌握翻折变换的性质,证明四边形ABCD是菱形是解题的关键.18.(2018•长春)图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM、ON的端点均在格点上.在图①、图②给定的网格中以OM、ON为邻边各画一个四边形,使第四个顶点在格点上.要求:(1)所画的两个四边形均是轴对称图形.(2)所画的两个四边形不全等.【分析】利用轴对称图形性质,以及全等四边形的定义判断即可.【解答】解:如图所示:【点评】此题考查了作图﹣轴对称变换,以及全等三角形的判定,熟练掌握各自的性质是解本题的关键.19.(2017•安徽)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.(2)画出△DEF关于直线l对称的三角形.(3)填空:∠C+∠E=45°.【分析】(1)将点A、B、C分别右移2个单位、下移2个单位得到其对应点,顺次连接即可得;(2)分别作出点D、E、F关于直线l的对称点,顺次连接即可得;(3)连接A′F′,利用勾股定理逆定理证△A′C′F′为等腰直角三角形即可得.【解答】解:(1)△A′B′C′即为所求;(2)△D′E′F′即为所求;(3)如图,连接A′F′,∵△ABC≌△A′B′C′、△DEF≌△D′E′F′,∴∠C+∠E=∠A′C′B′+∠D′E′F′=∠A′C′F′,∵A′C′==、A′F′==,C′F′==,∴A′C′2+A′F′2=5+5=10=C′F′2,∴△A′C′F′为等腰直角三角形,∴∠C+∠E=∠A′C′F′=45°,故答案为:45°.【点评】本题主要考查作图﹣平移变换、轴对称变换,熟练掌握平移变换、轴对称变换及勾股定理逆定理是解题的关键.20.如图所示,每个小正方形的边长为1,△ABC,△DEF的顶点都在小正方形的顶点处.(1)将△ABC平移,使点A平移到点F,点B,C的对应点分别是点B',C',画出△FB'C';(2)画出△DEF关于DF所在直线对称的△DE'F;(3)直接写出四边形B'C'FE'的面积是8 .【分析】(1)分别作出B,C的对应点B′,C′即可.(2)作出点E的对称点E′即可.(3)利用分割法求四边形的面积即可.【解答】解:(1)△FB'C'如图所示.(2)△DE'F如图所示.(3)四边形B'C'FE'的面积=4×4﹣×2×3﹣×2×3﹣×1×4=8.故答案为8.【点评】本题考查﹣轴对称变换,平移变换,四边形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.。
八年级数学上册 第二章 轴对称作图知识点与同步训练(含解析)苏科版

轴对称作图几何图形都可以看作由点组成,只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形;对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.反射问题是轴对称中常出现的一种题型,此类问题实质就是图形的对称变换,部分题目还会涉及光线反射等一些实际的应用折叠问题是轴对称中常出现的一种题型,此类问题的折痕其实就是对称轴,解决方案常运用轴对称图形的“对应边相等、对应角相等”,“对应点的连线被对称轴垂直平分”等性质,辅以动手操作,有针对性地添加辅助线来解决问题。
重难点:轴对称作图问题反射问题,折叠问题考点:轴对称作图问题,反射问题,折叠问题易错点:①对称轴是一条直线,②作图需虚线,③折叠前后的对应关系题模一:轴对称的作图问题例3.1.1已知线段AB和''A B轴对称,求画出对称轴l.B'A'BA【答案】见解析【解析】连接'AA,作'AA的中垂线即为对称轴l.例3.1.2如图,由四个小正方形组成的田字格中,ABC∆的顶点都是小正方形的顶点.在田字格上画与ABC∆成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含ABC 本身)共有( )个. C BAA . 1B . 2C . 3D . 4【答案】B【解析】 由轴对称的性质可得.题模二:反射问题例3.2.1 如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )A . 4次B . 5次C . 6次D . 7次【答案】B【解析】 B例3.2.2 在平面直角坐标系xOy 中,矩形OABC 如图放置,动点P 从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P 第2次碰到矩形的边时,点P 的坐标为 ;当点P 第6次碰到矩形的边时,点P 的坐标为 ;当点P 第xx 次碰到矩形的边时,点P 的坐标为____________.【答案】 (7,4),(0,3),(1,4)【解析】 本题考查找规律问题,观察计算可得,坐标循环周期为6次。
苏科版八年级上册数学 第二章轴对称图形 小结与思考 教案

轴对称图形复习课学习目标1、回顾和整理本章所学知识,用自己喜欢的方式进行总结和归纳,构建本章知识结构框架,使所学知识系统化。
2、进一步巩固和掌握轴对称性质和简单的轴对称图形-----线段、角、等腰三角形、等边三角形、等腰梯形的性质,并能运用这些性质解决问题。
学习重点:轴对称图形的性质,以及运用于解题教学难点:有条理地表达,熟练地运用已知结论解决问题学习过程一、知识点网络轴对称一个图形沿着某一条直线折叠,如果它能够与另一个图形______,那么就说这两个图形成轴对称。
这条直线就是______.两个图形中的对应点叫做 .轴对称图形一个图形沿着某条直线对折,如果直线两旁的部分能够完全_____ ,那么就称这个图形是轴对称图形。
轴对称与轴对称图形之间有什么区别?又有什么联系?轴对称的性质1、关于轴对称的图形全等。
2、如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线。
3、轴对称图形中,两条成轴对称的线段的“走向”只有两种可能:互相平行或它们所在直线的交点在对称轴上。
设计轴对称图案图案的对称不但要求图形对称外,有时颜色也“对称”。
线段的对称轴线段是轴对称图形,它有两条对称轴:它的垂直平分线与它本身所在的直线。
线段垂直平分线的性质线段的垂直平分线上的点到线段两端的距离相等线段垂直平分线的判定到线段两端距离相等的点,在这条线段的垂直平分线上。
角的对称轴角是轴对称图形,角平分线所在直线是它的对称轴。
角平分线的性质角平分线上的点到角的两边距离相等。
角平分线的判定角的内部到角的两边距离相等的点,在这个角的平分线上。
二、专题复习专题一 轴对称的性质【例1】如图(1)所示,△ABC 和△A ′B ′C ′关于直线MN 对称,△A ″B ″C ″和△A ′B ′C ′关于直线EF 对称. (1)画直线EF 。
(2)用全等符号写出与△ABC 全等的三角形。
(3)连接AA ′,CC ′,AA ′与直线MN 有什么位置关系?AA ′与CC ′有什么位置关系?专题二 线段的轴对称性【例2】如图,在△ABC 中, ∠ACB=900,AB 的垂直平分线交BC 于E,垂足为D,∠CAE:∠EAB=2:1,则∠B=___ .ABCABCABC图M NECB专题三 角的轴对称性如图:在中,∠B=90°,BC=18cm ,AD 是角平分线,且BD :CD=1:2,则点D 到AC 的距离是______cm.三、课堂小结本节课重点复习了以下知识点和应用 1、轴对称的概念、性质和应用。
苏科版八年级数学上册第二章 轴对称 总复习

轴对称总复习【知识梳理】1、轴对称图形相对一个图形的对称而言;轴对称是关于直线对称的两个图形而言。
2、轴对称的性质:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连的线段的垂直平分线;3、线段的垂直平分线:①性质定理:②判定定理:拓展:三角形三条边的垂直平分线的交点到三个顶点....的距离相等4、角的角平分线:①性质定理:②判定定理:拓展:三角形三个角的角平分线的交点到三条边...的距离相等。
5、等腰三角形:①性质定理:等边对等角;三线合一。
②判断定理:等角对等边。
6、等边三角形:①性质定理:拓展:等边三角形每条边都能运用三线合一....这性质。
②判断定理:⑴三条边都相等的三角形是等边三角形;⑵三个角都相等的三角形是等边三角形;有两个角是60°的三角形是等边三角形;⑶有一个角是60°的等腰三角形是等边三角形。
7、直角三角形推论:⑴直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半。
⑵直角三角形中,斜边上的中线等于斜边的一半。
拓展:直角三角形常用面积法...求斜边上的高。
【例题精讲】题型一:线段的轴对称例1:如图,在△ABC中,DE是AC的垂直平分线.(1)若AC=6,△ABD的周长是13,则△ABC的周长是_______;(2)若△ABC的周长是30,△ABD的周长是25,则AC=_______.变式:如图,在△ABC中,边AB、AC的垂直平分线分别交BC于点E、点D.(1)若BC=8,则△ADE的周长是_______;(2) 若∠BAC=110°,那么∠EAD=______(3) 若∠EAD=100°,那么∠BAC=______题型二:角的轴对称例2:如图,在△ABC中,∠C=90°,AD平分∠BAC.(1)若CD=5,则点D到AB的距离为.(2) 若BD:DC=3:2,点D到AB的距离为6,则BC的长是.变式:如图,OP平分∠AOB,PA OA,PB OB,垂足分别为A、B.下列结论中,不一定成立的是( )A.PA=PB B.PO平分∠APBC.OA=OB D.AB垂直平分OP题型三:作图题例3:请你先在图的BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.例4:如图,求作点P,使点P同时满足:①PA=PB;②到直线m,n的距离相等.题型四:等腰三角形例5:(1)等腰三角形的一边长为5,另一边长为11,则该等腰三角形的周长为(2)等腰三角形的两边长分别为4、5.则该等腰三角形的周长为(3)已知等腰三角形的一个外角为100°,则这个等腰三角形的顶角为__________.(4)等腰△ABC中,若∠A=30°,则∠B=变式:(1)如图①,在Rt△ABC中,若AB=AC,AD=AE,∠BAD=40°,则∠EDC=_______.(2)如图②,∠ACB=90°,E、F为AB上的点,AE=AC,BC=BF,则∠ECF=___ __.(3)如图③,AB=AC=DC,且BD=AD,则∠B=___ __.例6:如图,∠ABC、∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.试说明BD+EC=DE.例7:如图,已知AB=AC,AD=AE.求证:BD=CE.题型五:等边三角形例8:(1)如图①,在等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE=____.(2)如图②,正方形ABCD,△EAD为等边三角形,则∠EBC=_______.(3)如图③,已知等边△ABC,AC=AD,且AC⊥AD,垂足为A,则∠BEC=_______.例9:如图,C为线段AE上一动点(点C不与点A、E重合),在AE的同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.下列五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°,其中恒成立的有__________(填序号).例10:如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连接AE.求证:AE∥BC.题型六:等边三角形例11:(1)在Rt△ABC中,∠C=90°,CD是斜边AB的中线,且CD=4 cm,则AB=_______.(2)在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则AC=_______.(3)在Rt△ABC中,∠C=90°,AC=8,BC=6,则AB边上的高CD= .例12:如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.【课堂练习】1.画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.(1)尺规作图(不写作法,保留作图痕迹):作∠AOB的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连接OE、CF、DF.(2)在所画图中,①线段OE与CD之间有怎样的数量关系,并说明理由.②求证:△CDF为等腰直角三角形2.如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1 .(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)(2)若已经摆放了3根小棒,则θ1 =___________,θ2 =__________,θ3=__________;(用含θ的式子表示)(3)若只能摆放4根小棒,求θ的范围.3.如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_______.4.若直角三角形斜边上的高和中线分别为10 cm、12 cm,则它的面积为__________cm2.5.如图,某市把一块形状为直角三角形的废地开辟为生物园,∠ACB=90o.AC=80 m.BC=60m.(1)若入口E在边AB上,且与A、B距离相等,求从人口E到出口C的最短路线的长;(2)若线段CD是一条水渠,且点D在AB边上,已知水渠造价约为10元/m,则点D在距点A多远处,此水渠的造价最低?最低造价是多少?1、Be honest rather clever 20.7.157.15.202017:4817:48:50Jul-2017:482、By reading we enrich the mind; by conversation we polish it.二〇二〇年七月十五日2020年7月15日星期三3、All things are difficult before they areeasy.17:487.15.202017:487.15.202017:4817:48:507.15.202017:487.15.20204、By other's faults, wise men correct theirown.7.15.20207.15.202017:4817:4817:48:5017:48:505、Our destiny offers not the cup of despair, but the chalice of opportunity. So let us seize it, not in fear, but in gladness. Wednesday, July 15, 2020July 20Wednesday, July 15, 20207/15/20206、I have no trouble being taken seriously as a woman and a diplomat [in Ghana].。
苏科版八年级数学上册2.1 轴对称与轴对称图形(含解析)

2.1 轴对称与轴对称图形一.选择题(共10小题)1.(2019•北京)下列倡导节约的图案中,是轴对称图形的是()A.B.C.D.2.(2019•徐州)下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是()A.B.C.D.3.(2019•东营)下列图形中,是轴对称图形的是()A.B.C.D.4.(2019•泰安)下列图形:是轴对称图形且有两条对称轴的是()A.①②B.②③C.②④D.③④5.(2019•泰州)如图图形中的轴对称图形是()A.B.C.D.6.(2018•资阳)下列图形具有两条对称轴的是()A.等边三角形B.平行四边形C.矩形D.正方形7.(2018•苏州)下列四个图案中,不是轴对称图案的是()A.B.C.D.8.(2018•河北)图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线()A.l1B.l2C.l3D.l4 9.(2018•无锡)下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有()A.1个B.2个C.3个D.4个10.(2018•重庆)下列图形中一定是轴对称图形的是()A.直角三角形B.四边形C.平行四边形D.矩形二.填空题(共6小题)11.在平面镜里看到背后墙上,电子钟示数如图所示,这时的时间应是.12.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有种.13.(2019•滨湖区一模)给出下列4种图形:①线段,②等腰三角形,③平行四边形,④圆.其中,不一定是轴对称图形的是(填写序号).14.(2019•海安县一模)在等腰三角形、平行四边形、矩形、菱形、正方形、正六边形、圆这7种图形中,一定是轴对称图形的共有种.15.(2018•和平区二模)如图,在正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,点E、F、P、Q分别在边AB、BC、CD、AD上,点M、N在边HG 上,且组成的图形为轴对称图形,则正方形ABCD的面积为.16.弹子盘为长方形ABCD,四角有洞,弹子从A出发,路线与小正方形的边成45°角,撞到边界即反弹(如图所示).AB=4,AD=3,弹子最后落入B洞.那么,当AB=9,AD=8时,弹子最后落入洞,在落入洞之前,撞击BC边次.三.解答题(共4小题)17.(2018秋•徐州期末)在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.18.仔细观察下列图案,并按规律在横线上画出合适的图案.19.(2018秋•张家港市校级期末)如图,DA、CB是平面镜前同一发光点S发出的经平面镜反射后的反射光线,请通过画图确定发光点S的位置,并将光路图补充完整.20.(2018秋•相城区期中)画图:试画出下列正多边形的所有对称轴,并完成表格,正多边形的边数3 4 5 6 7…对称轴的条数…根据上表,猜想正n边形有条对称轴.答案与解析一.选择题(共10小题)1.(2019•北京)下列倡导节约的图案中,是轴对称图形的是()A.B.C.D.【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,根据轴对称图形的概念求解.【解答】解:A、不是轴对称图形,故此选项错误;B、不是轴对称图形,故此选项错误;C、是轴对称图形,故此选项正确;D、不是轴对称图形,故此选项错误.故选:C.【点评】此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.(2019•徐州)下图均由正六边形与两条对角线所组成,其中不是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念求解可得.【解答】解:不是轴对称图形,故选:D.【点评】本题主要考查轴对称图形,解题的关键是掌握轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.3.(2019•东营)下列图形中,是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念对各选项分析判断即可得解.【解答】解:A、不是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、是轴对称图形,故本选项正确.故选:D.【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.4.(2019•泰安)下列图形:是轴对称图形且有两条对称轴的是()A.①②B.②③C.②④D.③④【分析】根据轴对称图形的概念分别确定出对称轴的条数,从而得解.【解答】解:①是轴对称图形且有两条对称轴,故本选项正确;②是轴对称图形且有两条对称轴,故本选项正确;③是轴对称图形且有4条对称轴,故本选项错误;④不是轴对称图形,故本选项错误.故选:A.【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.5.(2019•泰州)如图图形中的轴对称图形是()A.B.C.D.【分析】根据轴对称图形的概念判断即可.【解答】解:A、不是轴对称图形;B、是轴对称图形;C、不是轴对称图形;D、不是轴对称图形;故选:B.【点评】本题考查的是轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.6.(2018•资阳)下列图形具有两条对称轴的是()A.等边三角形B.平行四边形C.矩形D.正方形【分析】根据轴对称及对称轴的定义,结合所给图形即可作出判断.【解答】解:A、等边三角形由3条对称轴,故本选项错误;B、平行四边形无对称轴,故本选项错误;C、矩形有2条对称轴,故本选项正确;D、正方形有4条对称轴,故本选项错误;故选:C.【点评】本题考查了轴对称图形及对称轴的定义,常见的轴对称图形有:等腰三角形,矩形,正方形,等腰梯形,圆等等.7.(2018•苏州)下列四个图案中,不是轴对称图案的是()A.B.C.D.【分析】根据轴对称的概念对各选项分析判断利用排除法求解.【解答】解:A、是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项正确;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选:B.【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.8.(2018•河北)图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线()A.l1B.l2C.l3D.l4【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:该图形的对称轴是直线l3,故选:C.【点评】此题主要考查了轴对称图形,关键是掌握轴对称图形的定义.9.(2018•无锡)下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有()A.1个B.2个C.3个D.4个【分析】直接利用轴对称图形的性质画出对称轴得出答案.【解答】解:如图所示:直线l即为各图形的对称轴.,故选:D.【点评】此题主要考查了轴对称图形,正确把握轴对称图形的定义是解题关键.10.(2018•重庆)下列图形中一定是轴对称图形的是()A.直角三角形B.四边形C.平行四边形D.矩形【分析】根据轴对称图形的概念对各选项分析判断即可得解.【解答】解:A、不是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、是轴对称图形,故本选项正确.故选:D.【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.二.填空题(共6小题)11.在平面镜里看到背后墙上,电子钟示数如图所示,这时的时间应是21:05.【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.【解答】解:由图分析可得题中所给的“20:15”与“21:05”成轴对称,这时的时间应是21:05.故答案为:21:05.【点评】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.12.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有4种.【分析】结合图象根据轴对称图形的概念求解即可.【解答】解:根据轴对称图形的概念可知,一共有四种涂法,如下图所示:.故答案为:4.【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.13.(2019•滨湖区一模)给出下列4种图形:①线段,②等腰三角形,③平行四边形,④圆.其中,不一定是轴对称图形的是③(填写序号).【分析】直接利用轴对称图形的概念分析得出答案.【解答】解:①线段,②等腰三角形,③平行四边形,④圆.其中,不一定是轴对称图形的是③.故答案为:③.【点评】此题主要考查了轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.14.(2019•海安县一模)在等腰三角形、平行四边形、矩形、菱形、正方形、正六边形、圆这7种图形中,一定是轴对称图形的共有6种.【分析】直接利用轴对称图形的定义分析得出答案.【解答】解:等腰三角形、平行四边形、矩形、菱形、正方形、正六边形、圆这7种图形中,一定是轴对称图形的共有等腰三角形、矩形、菱形、正方形、正六边形、圆6种.故答案为:6.【点评】此题主要考查了轴对称图形的定义,正确把握定义是解题关键.15.(2018•和平区二模)如图,在正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,点E、F、P、Q分别在边AB、BC、CD、AD上,点M、N在边HG 上,且组成的图形为轴对称图形,则正方形ABCD的面积为+.【分析】连接BD,交PQ于R,交HG于S,交EF于K,依据轴对称图形的性质,即可得到BD的长,进而得到正方形ABCD的面积.【解答】解:如图,连接BD,交PQ于R,交HG于S,交EF于K,∵正方形ABCD中,有面积为4的正方形EFGH和面积为2的正方形PQMN,∴EH=EF=2,MQ=QP=,又∵组成的图形为轴对称图形,∴BD为对称轴,∴△BEF、△DPQ为等腰直角三角形,四边形EKSH、四边形MSRQ为矩形,∴EK=BK=EF=1,DR=QR=PQ=,KN=EH=2,RS=MQ=,∴BD=1+2++=3+,∴正方形ABCD的面积=BD2=×(3+)2=+,故答案为:+.【点评】本题主要考查了轴对称图形,轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.16.弹子盘为长方形ABCD,四角有洞,弹子从A出发,路线与小正方形的边成45°角,撞到边界即反弹(如图所示).AB=4,AD=3,弹子最后落入B洞.那么,当AB=9,AD=8时,弹子最后落入D洞,在落入洞之前,撞击BC边4次.【分析】根据当AB=4,AD=3时的例图及弹子的运行规律:每一条运行轨迹都是一个正方形的对角线,画出图形,即可得出结论.【解答】解:当AB=9,AD=8时,弹子的弹射路径如图所示:∴弹子最后落入D洞,在落入洞之前,撞击BC边4次.故答案为:D,4.【点评】此题考查了生活中的轴对称现象,读懂题意,根据题意总结出弹子的运行规律,画出图形是解题的关键.三.解答题(共4小题)17.(2018秋•徐州期末)在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.【分析】直接利用轴对称图形的性质得出符合题意的答案.【解答】解:如图所示:.【点评】此题主要考查了轴对称图形的性质,正确把握轴对称图形的性质是解题关键.18.仔细观察下列图案,并按规律在横线上画出合适的图案.【分析】观察图形规律,可得空白处应该为字母E和它的轴对称图形,作出图形即可.【解答】解:如图所示:.【点评】本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.19.(2018秋•张家港市校级期末)如图,DA、CB是平面镜前同一发光点S发出的经平面镜反射后的反射光线,请通过画图确定发光点S的位置,并将光路图补充完整.【分析】作出BC和AD的入射光线,相交处即为点S所在位置.【解答】解:【点评】用到的知识点为:入射角等于反射角;两条入射光线的交点处是点光源所在处.20.(2018秋•相城区期中)画图:试画出下列正多边形的所有对称轴,并完成表格,正多边形的边数3 4 5 6 7…对称轴的条数…根据上表,猜想正n边形有n条对称轴.【分析】轴对称就是一个图形的一部分,沿着一条直线对折,能够和另一部分重合,这样的图形就是轴对称图形,这条直线就是对称轴,依据定义即可求解.【解答】解:如图,故填3,4,5,6,7,n.【点评】正确理解轴对称图形的定义是解决本题的关键,本题是一个基础题.。
苏科版八年级上册数学 第2章 轴对称 总复习讲义(无参考解析)

轴对称总复习【知识梳理】知识点1、轴对称定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形关于对称,也称这两个图形成,这条直线叫做,两个图形中的对应点叫做.知识点2、轴对称图形定义:,那么称这个图形是轴对称图形,这条直线就是对称轴。
知识点3、线段的垂直平分线(重点)1.定义:垂直并且平分一条线段的直线,叫做这条直线的,也叫中垂线。
2.线段的垂直平分线必须满足两个条件:①;②.3.轴对称的性质(1)关于某条直线成轴对称的两个图形全等.(2)对称轴是对应点所连线段的垂直平分线.知识点4、成轴对称的图形的画法画一个图形关于某条直线对称的图形,其步骤为:①首先要确定哪条直线是对称轴;②然后在已知图形中找特殊点,过此点作对称轴的垂线段并延长一倍,即得到对称点;③顺次连接对称点。
知识点5、线段的轴对称性(重点、难点)线段是轴对称图形,它的对称轴有条,分别是.线段垂直平分线的性质:.线段垂直平分线的判定:.知识点6、线段的垂直平分线的作法(重点)用尺规作线段AB的垂直平分线的方法:1.分别以A、B为圆心,为半径画弧,两弧相交于点C、D.2.过C、D两点作直线.直线CD就是线段AB的垂直平分线.画图,理由如下:知识点7、角的轴对称性(重点、难点)角是轴对称图形,它的对称轴有条,对称轴是.角平分线的性质:.角平分线的判定:.知识点8、角的平分线的作法用尺规作∠AOB 的平分线的方法:1.以点O为圆心,任意长为半径画弧,分别交射线OA、OB 于点D、E.2.分别以D、E两点为圆心,为半径画弧,两弧在∠AOB的内部交于点C.3.画射线OC.则射线OC就是∠AOB的平分线,画图,理由如下:知识点9、等腰三角形的性质及判定(重点、难点)1.等腰三角形是轴对称图形,有条对称轴,是它的对称轴.2.等腰三角形的性质定理:(简称“等边对等角”) .3.等腰三角形的互相重合(简称“三线合一”).4.如果一个三角形中有两个角相等,那么(简称“等角对等边”) .知识点10、等边三角形的性质及判定(难点)1.定义:叫做等边三角形,等边三角形也称为正三角形.2.等边三角形的性质( 1 )等边三角形是轴对称图形,且有对称轴.( 2 )等边三角形的三个内角,并且每一个角都等于.3.等边三角形的判定(l )的三角形是等边三角形.( 2 )的三角形是等边三角形.( 3 )的等腰三角形是等边三角形.知识点11、直角三角形斜边上的中线的性质定理(重点)1.直角三角形斜边上的.2.如果在直角三角形中有一个锐角为30°,那么.【例题精讲】例1、如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是()A.1 B.2 C.3 D.4例2、如图,△ABC为等边三角形,以AC为直角边作等腰直角三角形ACD,∠ACD=90°,则∠CBD=°.例3、已知直角三角形斜边长为10cm,周长为22cm,则此直角三角形的面积为.例4、(1)如图(1),在△ABC,AB=AC,O为△ABC内一点,且OB=OC,求证:直线AO垂直平分BC.以下是小明的证题思路,请补全框图中的分析过程.(2)如图(2),在△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.请你只用无刻度的直尺画出BC边的垂直平分线(不写画法,保留画图痕迹).(3)如图(3),在五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,请你只用无刻度的直尺画出CD 边的垂直平分线,并说明理由.例5、(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE=;(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).【课堂练习】1、如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC=°.2、如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为()3、如图,BD是△ABC的角平分线,DE⊥AB于点E.△ABC的面积为20,AB=12,BC=8,则DE的长为.4、探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC (点B、C除外)上运动时,试猜想并探究∠BAD与∠CDE的数量关系;(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.5、如图所示,有一块直角三角形纸片,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.1cm B.1.5cm C.2cm D.3cm6、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是EC、DB的中点.求证:MN⊥BD.。
苏科版八年级上册数学第2章 轴对称的作图

A.12
B.13
C.25
D.37
【点拨】如图,连接C′C,交AB于E,延长交A′B′于D,连接 CB′,CA′, ∵点A关于BC边的对称点为A′,点B关于AC 边的对称点为B′,点C关于AB边的对称点为C′, ∴AC=A′C,BC=B′C,∠ACB= ∠A′CB′,AB垂直平分CC′,∴△ABC≌△A′B′C(SAS), ∴S△ABC=S△A′B′C,∠A=∠AA′B′, AB=A′B′,∴AB∥A′B′,∴CD⊥A′B′.
苏科版八年级上
第2章轴对称图形
2.2.2 轴对称的作图
习题链接
温馨提示:点击 进入讲评
1 2 3 4长为1的小等边三角形构成的网格,网格图中 1
有3个小等边三角形已涂上阴影.请在余下的空白小等边 三角形中,选取一个涂上阴影,使得4个阴影小等边三角 形组成一个轴对称图形.
定的网格中,按下列要求画图:
(1)在图①中,画一条不与AB重合的线段MN,使MN与AB
关于某条直线对称,且M、N为格点.
解:(答案不唯一)如图①,MN即为所求;
(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC 关于某条直线对称,且P、Q为格点.
解:如图②, PQ即为所求;
(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条 直线对称,且D、E、F为格点.
解:如图③,△DEF即为所求.
已知:如图,方格图中每个小正方形的边长为1, 8 点A、B、C、M、N都在格点上.
(1)画出△ABC关于直线MN对称的△A1B1C1.
解:如图所示.
(2)在直线MN上找一点P,使|PB-PA|最大,在图形上 画出点P的位置,并直接写出|PB-PA|的最大值.
苏科初中数学八上 轴对称讲义

轴对称重难点易错点解析题面:下列选项正确的是( )A.轴对称图形和两个图形成轴对称的含义是一样的B.若两个图形全等,则它们一定关于某条直线对称C.两个成轴对称的图形对应点到对称轴的距离相等D.等腰三角形只有一条对称轴轴对称 vs. 成轴对称两个成轴对称的图形对应点到对称轴的距离相等几类典型问题:坐标系中的轴对称、将军饮马、折叠问题、设计图案金题精讲题一题面:如图:将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为 .D1DA EC1B C题二题面:某学校要在校园内一块正方形的园地上种植四种不同的植物,对该正方形的设计要求如下:(1)四种植物各自所占的图形必须全等;(2)最终图形必须为轴对称图形.某同学按照要求设计出了如下两种方案,请你再设计两种不同的种植方案.思维拓展题面:小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是从左至右第_____个.讲义参考答案重难点易错点解析答案:C金题精讲题一答案:20°题二答案:略思维拓展答案:49.1 单项式乘单项式力.教学重点:理解单项式相乘的法则,会进行单项式的乘法运算.教学难点:能运用单项式乘以单项式的法则解决实际问题.【情景创设】用6个边长为a 的小正方体拼成一个长方体,并用不同的方法表示你所拼出来的长方体的体积,从不同的表示方法中,你能发现些什么? (1)体积的表示方法;(2)面对你的侧面积的表示方法. 探索新知让学生在交流的基础上思考下列问题:(1)体积的表示方法:①3a ·2a ·a =________________=6a 3,②3a ·2a ·b =________________=6a 2b .侧面积的表示方法:3a ·2a =________________=6a 2. (2)从不同的表示中你发现了什么? (3)通过下面两个计算我们来进一步的探讨:(2a 2b )(3ab 2)=[2 ×3]•(a 2•a )(b •b 2)=6a 3b3系数相乘 相同字母 相同字母(4ab 2)(5b )=[4×5]•(b 2• b )•a =20ab 3系数相乘 相同字母 只在一个单项式中出现的字母你能告诉大家你算出的结果吗?你是怎样来思考的呢? 通过探索得到单项式乘单项式的计算法则: (1)将它们的系数相乘; (2)相同字母的幂相乘;(3)只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.【展示交流】例 1 计算:① -13a 2·(-6ab ); ② 6x 2·(-2x 2y ).注:教师强调格式规范,板书过程.(通过计算引导学生发现单项式与单项式相乘时,一找系数,二找相同字母的幂,三找只在一个单项式里出现的字母.) 练习1: 判断正误:(1)3x 3·(-2x 2)=5x 3; (2)3a 2·4a 2=12a 2; (3)3b 3·8b 3=24b 9;(4)-3x ·2xy =6x 2y ; (5)3ab +3ab =9a 2b 2. 练习2:课本练一练 第1、2题.例 2 计算:(1)(2x )3·(-3xy 2); (2)(-2a 2b )·(-a 2)·14bc .注:遇到乘方形式先用积的乘方公式展开,然后转化为单项式乘以单项式的形式,再根据今天所学内容计算. 练习3:计算:(1)(a 2)2·(-2ab ); (2)-8a 2b ·(-a 3b 2) ·14b 2 ;(3)(-5an +1b ) ·(-2a )2;(4)[-2(x -y )2]2·(y -x )3.【盘点收获】【课后作业】 补充习题和同步练习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴对称总复习
【知识梳理】
轴对称与轴对称图形的区别和联系
区别:轴对称是指两个图形之间的形状与位置关系,•成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.
联系:1:都是折叠重合2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形,反之亦然。
【例题精讲】
例1:如图,阴影部分是由5个大小相同的小正方形组成的图形,请分别在图中方格内涂两个小正方形,使涂后所得阴影部分图形是轴对称图形.
解:如图所示:
例2:如图,如下图均为2×2的正方形网格,每个小正方形的边长均为1.请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上,且位置不同的三角形.
解:
巩固练习
1.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,请在下面所给的格纸中一一
画出所有符合条件的三角形.(所给的六个格纸未必全用)
解:与△ABC成轴对称且也以格点为顶点的三角形有5个,
分别为△BCD,△BFH,△BCF,△GEH,△AEG.
2.如图,在4×3正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形.
解:如图所示,答案不唯一,参见下图.
知识点四(线段、角的轴对称性)
【知识梳理】
线段的轴对称性
(1)线段是轴对称图形,线段的垂直平分线是它的对称轴。
(2)线段垂直平分线的性质与判定
性质定理:线段的垂直平分线上的点到线段两段的距离相等。
判定定理:到线段两段距离相等的点在这条线段的垂直平分
线上。
注:线段的垂直平分线及线段自身所在的直线都是线段的
对称轴。
角的对称性
(1)角是轴对称图形,角平分线所在的直线是它的对称轴。
(2)角平分线的性质与判定
性质定理:角平分线上的点到角两边的距离相等。
判定定理:角的内部到角两边距离相等的点在角的平分线上。
注:“距离”指垂直到直线的线段长度。
【例题精讲】
例1:如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC 于点F,且BC=4,DE=2,则△BCD的面积是.
解:∵CD平分∠ACB交AB于点D,
∴∠DCE=∠DCF,
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,
在△DEC和△DFC中,
∠DCE=∠DCF
∠DEC=∠DFC
CD=CD
(AAS)
∴△DEC≌△DFC,
∴DF=DE=2,
∴S△B C D=BC×DF÷2
=4×2÷2
=4
答:△BCD的面积是4.
故答案为:4.
例2:如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E 点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
解:∵DE是AB的垂直平分线,
∴AE=BE;
∵△ABC的周长=AB+AC+BC,△EBC的周长=BE+EC+BC=AE+EC+BC=AC+BC,
∴△ABC的周长-△EBC的周长=AB,
∴AB=40-24=16(cm).
故答案为:16.
例3:如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是cm.
解:∵△ABC中,DE是AC的中垂线,
∴AD=CD,AE=CE=AC=3cm,
∴△ABD得周长=AB+AD+BD=AB+BC=13 ①
则△ABC的周长为AB+BC+AC=AB+BC+6 ②
把②代入①得△ABC的周长=13+6=19cm
故答案为:19.
解:①∵DM、EN分别垂直平分AB和AC,
∴AD=BD,AE=EC,
∴∠B=∠BAD,∠C=∠EAC(等边对等角),
∵∠BAC=∠DAE+∠BAD+∠CAE,∴∠BAC=∠DAE+∠B+∠C;
又∵∠BAC+∠B+∠C=180°,∠DAE=50°,
∴∠BAC=115°;
②∵△ADE的周长为19cm,∴AD+AE+DE=19cm,
由②知,AD=BD,AE=EC,
∴BD+DE+EC=19,即BC=19cm.
故答案为:115,19.
巩固练习
1.直线l1、l2、l3表示三条两两相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,则可供选择的地址有处.
解:∵中转站要到三条公路的距离都相等,
∴货物中转站必须是三条相交直线所组成的三角形的内角或外角平分线的交点,而外角平分线有3个交点,内角平分线有一个交点,
∴货物中转站可以供选择的地址有4个.
故答案为:4.
2.已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是度.
解:过点E作EF⊥AD,
∵DE平分∠ADC,且E是BC的中点,
∴CE=EB=EF,
又∵∠B=90°,且AE=AE,
∴△ABE≌△AFE,
∴∠EAB=∠EAF.
又∵∠CED=35°,∠C=90°,
∴∠CDE=90°-35°=55°,
∴∠CDA=110°,
∵∠B=∠C=90°,
∴DC∥AB,
∴∠CDA+∠DAB=180°,
∴∠DAB=70°,
∴∠EAB=35°.
故答案为:35.
3.如图:在△ABC中,∠C=90°AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
说明:(1)CF=EB.
(2)AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
∵在Rt△DCF和Rt△DEB中,
BD=DF;
DC=DE;
,
∴Rt△CDF≌Rt△EBD(HL).
∴CF=EB;
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,
∵
CD=DE
AD=AD
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
4.如图,在△ABC中,直线ON是AB的垂直平分线,OA=OC.求证:点O在BC的垂直平分线上.
解:连接OB,
∵直线ON是AB的垂直平分线,
∴OA=OB,
∵OA=OC,
∴OB=OC,
∴点O在BC的垂直平分线上.
【课堂练习】
1、在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有个.
解:如图所示,有3个使之成为轴对称图形.
故答案为:3.
2、开车时,从后视镜中看到后面一辆汽车车牌号的后四位数是“”,则该车号牌的后四位应该是.
解:由图分析可得题中所给的“”与“9087”成轴对称.
故答案为:9087
3、在下列的图形上补一个小正方形,使它成为一个轴对称图形,并画出对称轴
解:
解:∵AB=AC,∠A=40°,
∴∠C=∠ABC=70°,
∵AB的垂直平分线MN交AC于D,∴AD=BD,
∴∠A=∠ABD=40°,
∴∠DBC=30°.
故答案为30°.
5、如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC 于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
解:(1)证明:∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°-40°)÷2=70°
∴∠DBC=∠ABC-∠ABD=70°-40°=30°;
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AE=12,
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.
6、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ED=EC,即△CDE为等腰三角形,
∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,
∴△OED≌△OEC(AAS),
∴OC=OD;
(3)在△DOE和△COE中,
∵
OC=OD
∠EOC=∠BOE
OE=OE
,
∴△DOE≌△COE,
∴DE=CE,
∴OE是线段CD的垂直平分线.。
