六年级下数学_比和比例专题复习
(完整版)小学六年级_比和比例知识点梳理
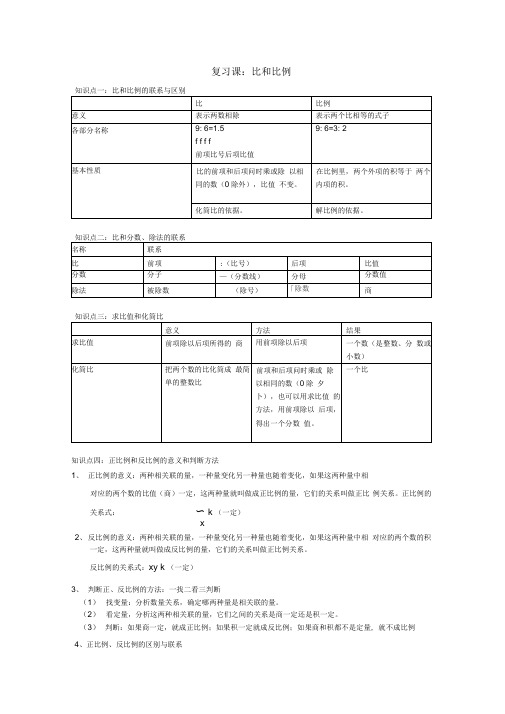
复习课:比和比例知识点四:正比例和反比例的意义和判断方法1、正比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
正比例的关系式:〜 k (一定)x2、反比例的意义:两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系。
反比例的关系式:xy k (一定)3、判断正、反比例的方法:一找二看三判断(1)找变量:分析数量关系,确定哪两种量是相关联的量。
(2)看定量,分析这两种相关联的量,它们之间的关系是商一定还是积一定。
(3)判断:如果商一定,就成正比例;如果积一定就成反比例;如果商和积都不是定量, 就不成比例4、正比例、反比例的区别与联系知识点五:用比例知识解决问题1、按比例分配问题(1)按比例分配应用题:把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题。
(2)解题方法一般方法:把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法:把比看做分得的分数,先求出各部分的总分数,然后再用“总量总份数=平均每份的量(归一)",再用"一份的量各部分量所对应的份数”,求出各部分的量。
用比例知识解答:首先设未知量为。
再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式,再解比例求出X。
2、用正、反比例知识解答应用题的步骤(1)分析数量关系。
判断成什么比例。
(2)找等量关系。
如果成正比例,则按等比找等量关系式;如果成反比例,则按等积找等量关系式。
(3)解比例式。
设未知数为X,并代入等量关系式,得正比例式或反比例式。
(4)解比例。
(5)检验并写出答语。
精讲典型题例题1填空(1)一项工程,甲单独做要4天,乙单独做要5天完成,甲和乙的工作效率比是(): ()(2)把2米:4厘米化成最简单的整数比是(),比值是()。
六年级下学期数学比及比例整理复习

比例的基本性质包括合比性质、等比性质以及反 比性质。
03 比例的应用问题解决方法
解决比例的应用问题通常需要找到问题中的比例 关系,然后利用比例的性质进行求解。
比例尺与相似图形
01
02
03
04
05
比例尺的定义
比例尺的种类
相似图形的定义
相似图形的性质
比例尺与相似图 形的关系
比例尺是表示实际距离与 图上距离之间的比例关系 的尺子。
错题分析与纠正
错题1
分析
纠正
小明做了一道题“某校男、女 生人数的比是5:3,女生人数比 男生少40人。该校男、女生各 有多少人?”他设男生人数为x ,列出的方程是5x-3x=40,解 得x=20。因此他得出男生有 20人,女生有20-40=-20人。
小明的错误在于没有正确理解 题目中的比例关系。他设男生 人数为x是正确的,但是应该将 女生人数设为3/5x,而不是直 接减去40。正确的方程应该是 x-3/5x=40。
比的表示方法
比可以用分数、小数或百分数来表示。例如,3:4可以 表示为3/4,0.75或75%。
比的性质与运算规则
比的性质
比具有传递性、反身性和等比性质。传递性指如果a:b=c:d且b、d不为0,则a:c=b:d;反身性 指任何数a(a≠0)与自身的比都等于1;等比性质指如果a:b=c:d,那么a+c:b+d=(a+b):(c+d) 。
比例尺分为数字比例尺和 线段比例尺两种。
相似图形是指形状相同但 大小不一定相同的图形。
相似图形的对应角相等, 对应边成比例。
在绘制地图或设计图纸时 ,常常需要用到相似图形 和比例尺的知识,通过相 似图形的性质和比例尺的 换算,可以准确地表示出 实际物体的大小和形状。
六年级下册数学期末专项复习三——比和比例(含答案)

六年级下册数学期末专项复习三——比和比例时间:60分钟满分:100分题号一二三四五六总分得分一、填空。
(每空1分,共17分)1.在人体素描画中,一般身高是头长的7倍,头长与身高的比是( )。
2.20:( )=( )÷20==( )%=( )成3.写出比值是0.4的两个比( )和( ),用这两个比组成比例是( )。
4.一个比的前项是9,如果前项增加18,要使比值不变,那么后项就该( )或( )。
5.如果a=b×(a,b均是不为零的自然数),那么a:b=( )。
(填最简整数比)6.下图是洗手池打开下水道的开口后,排水量变化情况图,下水道口打开40秒时排水量是( )L,这个下水道排水口打开的时间与排水量成( )比例关系。
7.一架飞机,能在空中连续飞行9小时,平均每小时飞行740km。
若每小时飞行925km,则这架飞机最多飞出( )小时就应该降落。
8.一杯牛奶,喝去后用果汁加满,又喝去,再用果汁加满,这时杯子里果汁和牛奶的体积比是( )。
9.如下图所示,身高1.5m的王华站在大树旁边,测得她的影子长2.4m,测得大树落在地面上的影子长3.2m,落在墙上的影子高0.5m,这棵大树实际高( )m。
10.自行车的前齿轮共有100个齿,后齿轮有30个齿,如果前齿轮转5圈,那么后齿轮转( )圈。
二、判断。
(5分)1.谚语“春分秋分,昼夜平分”是指在春分和秋分时昼夜时间比是1:1。
()2.等边三角形中,周长和边长成正比例关系。
()3.在一个比例中,如果两个内项的积是1,那么两个外项一定互为倒数。
()4.百分数可以看作比的后项是100的特殊形式的比。
()5.线段比例尺改写成数值比例尺是1:15000000。
()三、选择。
(10分)1.已知a和b是两个相关联的量,并且7:a=b:9,那么a与b( )。
A.成正比例关系B.成反比例关系C.不成比例关系D.无法确定2.有一个比是4:3,如果它的前项加上16,要使比值不变,比的后项要( )。
六年级数学《比和比例》知识点

六年级数学《比和比例》知识点一、比的意义和性质1、比的意义两个数相除又叫做两个数的比。
2、比的性质比的前项和后项同时乘上或者除以相同的数(0除外),比值不变。
3、比的应用通过比可以应用一些问题。
二、比例的意义和性质1、比例的意义表示两个比相等的式子叫做比例。
2、比例的性质在一个比例中,组成比例的两个数,叫做比例的项。
在一比例里,两外项的积等于两内项的积。
这叫做比例的基本性质。
3、解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。
这个求未知项的过程,叫做解比例。
三、正比例和反比例1、成正比例的量如果两种量是相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
2、成反比例的量如果两种量是相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。
3、正比例和反比例的判断方法判断两种量是否成正比例或反比例的方法:一是看这两种相关联的量中相对应的两个数的比值是否一定;二是看这两种量中相对应的两个数的积是否一定。
比的意义:两个量的关系可以用比来表示,我们通常称之为“比”。
定义:在两个量的比中,我们把数量放在前面,单位“1”放在后面,我们称之为前项,后项。
比与除法、分数的关系:比的前项相当于被除数或分子,后项相当于除数或分母,比值相当于商或分数值。
比的性质:比的前项和后项同时乘上或者除以相同的数(0除外),比值不变。
比例的意义:表示两个比相等的式子叫做比例。
组成比例的四个数叫做比例的项。
两外两项叫做内项,中间两项叫做外项。
如果中间的两项是两个相同的数,这样的比例叫做对称比例。
比例尺的意义:我们把图上距离和实际距离的比叫做比例尺。
我们把比例尺分为放大比例尺和缩小比例尺两种。
缩小比例尺的计算方法:已知实际距离求图上距离,根据公式计算即可;已知图上距离求实际距离根据公式计算即可。
六年级下数学比和比例专题复习

比和比例1、两个数相除,又叫做这两个数的比,“:”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项,前项除以后项所得的商叫做比值。
比的后项不能为0。
2、分数的基本性质:分数的分子和分母同时乘以或者除以相同的数(0除外),分数的大小不变。
乘积是1的两个数互为倒数。
1的倒数是1,0没有倒数。
3、商不变的规律:在除法里,被除数和除数同时扩大或者同时缩小相同的倍(0除外),商不变。
4、比的基本性质:比的前项和后项同时乘以或者除以相同的数(0除外),它们的比值不变。
5、小数的性质:在小数的末尾添上零或者去掉零小数的大小不变。
6、公因数只有1的两个数叫做互质数。
最简整数比:比的前项和后项是互质数。
7、比的化简:用商不变的性质、分数的基本性质或比的基本性质来化简。
8、比例:①表示两个比相等的式子叫做比例。
如:(3:4=9:12)。
比例有四个项,分别是两个内项和两个外项。
在3:4=9:12中,其中3与12叫做比例的外项,4与9叫做比例的内项。
比例的四个数均不能为0。
9、比例的基本性质:在一个比例中,两个外项的积等于两个内项的积。
10、比、比例、比例尺、百分数的后面不能带单位。
一.填空1、=3:()=()÷15=()成=()%2、112:的比值是(),把它化为最简的整数比是()3、比例4:9=20:45写成分数形式是(),根据比例的基本性质写成乘法形式是()4、18的约数有(),选出其中四个数组成一个比例是()5、在比例尺1:2000000的地图上,图上1厘米表示实际距离()千米。
6、在一个比例中,两个内项互为倒数,一个外项是25,另一个外项是()7.甲数除以乙数的商是4,甲数与乙数的最简整数比是()8、我国<<国旗法>>规定,国旗的长和宽的比是3:2,学校的国旗宽是128厘米,长应该是( )厘米。
9、三角形底一定,它的高和面积成()比例。
10、用、 6、 30、 1这四个数组成两个比例式是()和()11、某厂男职工人数是女职工的23,女职工与男职工的人数比是()12、两个正方体的棱长比是3:4,它们的体积比是()13、如果3a=2b,那么a:b=():()14、从A地到B地,甲用12分钟,乙用8分钟,甲乙的速度比是( )15、小圆的半径是2厘米,大圆的半径是3厘米,小圆和大圆的周长比是(),面积比是()16、甲乙两数之比是3:4,它们的和是,则甲数是(),乙数是()17、一个比8:15,如果后项增加60,要使比值不变,比的前项应该增加()18、在比例尺是1200的学校平面图上,量得教室的长8厘米,宽6厘米,教室实际面积是()19、男生人数比女生人数少20%,男生人数与女生人数的比是():()20、甲数的13等于乙数的25,甲数与乙数的比是()二、判断1、圆柱的底面积一定,它的高与体积成正比例。
六年级数学下册总复习《比和比例》
0
40
80
120千米
2、在比例尺是1∶4000000的地图上量 得甲、乙两地的距离是35cm,若把这 两地画在比例尺是1:7000000的地图 上,应画多少长?
3、在一副比例尺1:5000000 的地图上,甲、乙两城间的 距离是2.4cm,一列火车每小 时72千米的速度从甲城开往 乙城,共要几小时?
分 子 6
分 分数的基本性质 数 分数的分母和分子同 值 时乘以或除以相同的 2 数(0除外),比值不变。
三、求比值和化简比 举例 求 比 = 4÷ 值 = 10
2 : 4 5 9 3 5 10 2 3 10 × 5 =5 9 2 =3
一般方法
结果
:
根据比值的意义, 是一个商,可 用前项除以后项。 以是整数、小 所得的商如果是分 数或分数,但 数,不能是假分数。不能是假分数。
轻松学数学 快乐在海卫
例2
(1) X︰( 2 × 5
5 1 )= : 9 10 1 9
(2)(10+5)χ=10×30
(3) 2.3︰X=(9.6 - 4.5)︰10.2
按比例分配是把一个量按一定的比来分配. 解题方法: (1)根据比,得出各部分占总量的几分之 几,即先求出总份数,然后求出各部分量占 总量的几分之几,最后按照求一个数的几分 之几是多少的解题方法,求出各部分的量。 (2)根据比,求出总份数,然后用总 数量 除以总份数, 求出另一份是多少,再用一份 的量乘各部分的份数求得各部分的量。
性质 应用 0.9:0.6=9:(6)=3:(2)
例如:
1. 0.9︰0.6 =(0.9×10)︰(0.6×10) = 9 ︰6 =(9÷3)︰(6÷3) = 3 ︰2 2. 5 ︰6 = 20︰24
六年级下册数学知识点解析:比和比例

次火车自北京西站开往安庆西站,行驶至全程的511再向前56千米处所用时间比提速前减少了60分钟,而到达安庆西站比提速前早了2小时.问北京西站、安庆西站两地相距多少千米两地相距多少千米? ?【分析与解】设北京西站、安庆西站相距多少千米?设北京西站、安庆西站相距多少千米?(511x+56)x+56)::x=60x=60::120120,即,即,即((511x+56)x+56)::x=1x=1::2,即x=1011x+112x+112,解得,解得x=1232x=1232.. 即北京西站、安庆西站两地相距即北京西站、安庆西站两地相距1232千米,千米,3.两座房屋A 和B 各被分成两个单元.若干只猫和狗住在其中.已知:各被分成两个单元.若干只猫和狗住在其中.已知:A A 房第一单元内猫的比率房第一单元内猫的比率((即住在该单元内猫的数目与住在该单元内猫狗总数之比在该单元内猫的数目与住在该单元内猫狗总数之比))大于B 房第一单元内猫的比率;并且A 房第二单元内猫的比率也大于B 房第二单元内猫的比率.试问是否整座房屋A 内猫的比率必定大于整座房屋B 内猫的比率的比率? ?【分析与解】 如下表给出的反例指出:如下表给出的反例指出:如下表给出的反例指出:对所提出问题的回答应该是否定的.对所提出问题的回答应该是否定的.对所提出问题的回答应该是否定的.表中具体写出了各个表中具体写出了各个单元及整座房屋中的宠物情况和猫占宠物总数的比率.单元及整座房屋中的宠物情况和猫占宠物总数的比率. 小升初数学知识点解析:比和比例两个数相除又叫做两个数的比.两个数相除又叫做两个数的比.一、比和比例的性质性质1:若a: b=c a: b=c::d ,则,则(a + c)(a + c)(a + c)::(b + d)= a (b + d)= a::b=c b=c::d ;性质2:若a: b=c a: b=c::d ,则,则(a - c)(a - c)(a - c)::(b - d)= a (b - d)= a::b=c b=c::d ;性质3:若a: b=c a: b=c::d ,则,则(a +x c)(a +x c)(a +x c)::(b +x d)=a (b +x d)=a::b=c b=c::d ;(x 为常数)性质4:若a: b=c a: b=c::d ,则a ×d ×d = = = b×b×b×c c ;(即外项积等于内项积即外项积等于内项积) )正比例:如果a ÷b=k(k 为常数为常数)),则称a 、b 成正比;成正比;反比例:如果a ×b=k(k 为常数为常数)),则称a 、b 成反比.成反比.二、比和比例在行程问题中的体现在行程问题中,因为有在行程问题中,因为有速度速度=路程时间,所以:,所以: 当一组物体行走速度相等,那么行走的路程比等于对应时间的反比;当一组物体行走速度相等,那么行走的路程比等于对应时间的反比;当一组物体行走路程相等,那么行走的速度比等于对应时间的反比;当一组物体行走路程相等,那么行走的速度比等于对应时间的反比;当一组物体行走时间相等,那么行走的速度比等于对应路程的正比.当一组物体行走时间相等,那么行走的速度比等于对应路程的正比.1.A 和B 两个数的比是8:5,每一数都减少34后,后,A A 是B 的2倍,试求这两个数.倍,试求这两个数.【分析与解】方法一:设A 为8x 8x,则,则B 为5x 5x,于是有,于是有,于是有(8x-34):(5x-34)=2(8x-34):(5x-34)=2(8x-34):(5x-34)=2::1,x=17x=17,所以,所以A 为136136,,B 为8585.. 方法二:因为减少的数相同,所以前后A A 、、B 的差不变,开始时差占3份,后来差占1份且与B 一样多,也就是说减少的3434,占开始的,占开始的3-1=2份,所以开始的1份为34÷2=17,所以A 为17×8=136,B 为17×5=85.17×5=85.2.近年来.近年来火车火车大提速,大提速,142714274.家禽场里鸡、鸭、鹅三种家禽中公篱与母篱数量之比是2:3,已知鸡、鸭、鹅数量之比是8:7:5,公鸡、母鸡数量之比是1:3,公鸭、母鸭数量之比是3:4.试求公鹅、母鹅的数量比..试求公鹅、母鹅的数量比.【分析与解】 公鸡占家禽场家禽总数的公鸡占家禽场家禽总数的公鸡占家禽场家禽总数的 =21124615:(3544)45:46:(3544)46:47.333345´´+´´=´´+´´=8118751310´=+++,母鸡占总数的310; 公鸭占总数的8338753420´=+++,母鸭占总数的420; 公鹅占总数的213332102020-+=+(),母鹅占总数的234232102020-+=+(),公鹅、母鹅数量之比【分析与解】70cm 的杆子产生影子的长度为175cm;所以影子的长度与杆子的长度比为:所以影子的长度与杆子的长度比为:175175175::70=2.5倍.为322020::3:2.5.在古巴比伦的在古巴比伦的金字塔金字塔旁,旁,其朝西下降的阶梯旁其朝西下降的阶梯旁6m 的地方树立有1根走子,其影子的其影子的前端前端正好到达阶梯的第3阶(箭头箭头)).另外,此时树立l 根长70cm 自杆子,其影子的长度为175cm 175cm,设阶梯各阶的高度,设阶梯各阶的高度与深度都是50cm 50cm,求柱子的高度为多少?,求柱子的高度为多少? 于是,影子的长度为6+1.5+1.6+1.5+1.5×25×25×2.5=11.25.5=11.25.5=11.25,所以杆子的长度为,所以杆子的长度为11.11.25÷225÷225÷2.5=4.5m .5=4.5m .5=4.5m..6.已知三种.已知三种混合物混合物由三种成分A 、B 、C 组成,第一种仅含成分A 和B ,重量比为3:5;第二种只含成分B 和C ,重量比为I :2;第三种只含成分A 和C ,重量之比为2:3.以什么.以什么比例比例取这些混合物,才能使所得的混合物中A ,B 和C ,这三种成分的重量比为3:5:2 ?【分析与解】注意到第一种混合物种A 、B 重量比与最终混合物的A 、B 重量比相同,均为3:5.5.所以,所以,k=65. 标准的时钟每隔56511分钟重合一次.分钟重合一次. 假设经历了假设经历了x 分钟.分钟. 于是,甲钟每隔于是,甲钟每隔52460651124605´´´-分钟重合一次,甲钟重合了246052460´-´×x 次;次; 同理,乙钟重合了同理,乙钟重合了246052460´+´×x 次;次; 于是,需要乙钟比甲钟多重合于是,需要乙钟比甲钟多重合于是,需要乙钟比甲钟多重合 246052460´+´×x-246052460´-´×x=102460´×x=10; 所以,所以,x=24x=24x=24×60;×60;×60; 所以要经历24×60×65511分钟,则为5246065 51165246011´´=´天.于是为65天510(24)10()1111´=天.后来,由一队工人23与二队工人13组成新一队,其余的工人组成新二队.其余的工人组成新二队.两支新队又同时分别接受两项工作量与条件完全相同的工程,两支新队又同时分别接受两项工作量与条件完全相同的工程,两支新队又同时分别接受两项工作量与条件完全相同的工程,结果新二队结果新二队先将第二种、第三种先将第二种、第三种混合物混合物的A 、B 重量比调整到重量比调整到 3 3 3::5,再将第二种、第三种混合物中A 、B 与第一种混合物中A 、B 视为单一物质视为单一物质. .第二种混合物不含第二种混合物不含A ,第三种混合物不含B ,所以1.5倍第三种混合物含A 为3,5倍第二种混合物含B 为5,即第二种、第三种混合物的重量比为5:1.51.5..于是此时含有于是此时含有C 为5×2+15×2+1..5×3=145×3=14.5.5.5,在最终混合物中,在最终混合物中C 的含量为3A 3A//5B 含量的2倍.有14.14.5÷25÷25÷2-1=6.25-1=6.25-1=6.25,所以含有第一种混合物,所以含有第一种混合物6.256.25..即第一、二、三这三种混合物的即第一、二、三这三种混合物的比例比例为6.256.25::5:1.5=251.5=25::2020::6.7.现有男、女职工共1100人,其中全体男工和全体女工可用同样人,其中全体男工和全体女工可用同样天数天数完成同样的工作;若将男工人数和女工人数对调一下,则全体男25天完成的工作,全体女工需36天才能完成,问:男、女工各多少人女工各多少人? ?【分析与解】 直接设出男、女工人数,然后在通过直接设出男、女工人数,然后在通过直接设出男、女工人数,然后在通过方程方程求解,过程会比较繁琐.求解,过程会比较繁琐.设开始男工为“1”,此时女工为“设开始男工为“1”,此时女工为“k k ”,有1名男工相当k 名女工.男工、女工人数对调以后,则男工为“男工为“k k ”,相当于女工“,相当于女工“k k 2”,女工为“I”.,女工为“I”.有k 2:1=361=36::2525,所以,所以于是,开始有男工数为11k+×1100=500人,女工600人.人.8.有甲乙两个钟,甲每天比.有甲乙两个钟,甲每天比标准时间标准时间慢5分钟,而乙每天比标准时间快5分钟,在3月15日的日的零点零点零分的时候两钟正好对准.若已知在某一时刻,乙钟和甲钟时针与分针都分别重合,且在从3月15日开始到这个时候,乙钟时针与分针重合的次数比甲钟多10次,那么这个时候的标准时间是多少次,那么这个时候的标准时间是多少? ?【分析与解】 小时106(60)541111´=分钟.分钟.9.一队和二队两个.一队和二队两个施工施工队的人数之比为3:4,每人工作效率之比为5:4,两队同时分别接受两项工作量与条件完全相同的工程,结果二队比一队早完工96÷147=282´´´´282×4645天.天.144:(282×:(282×4645)=(144×45):(282×46))=(144×45):(282×46)=540。
六年级比和比例复习知识点及典型例题

比和比例知识点:比比例意义两个数相除,又叫做两个数的比。
表示两个比相等的式子,叫做比例。
各部分名称举例:0.9 : 0.6 =1.5名称:前项后项比值举例:5 : 6 = 20 : 24名称:外项基本性质比的前项或后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个外项的积等于两个内项的积。
2、按比分配的实际应用:例:一辆货车和一列客车同时从相距135km的两地相向而行,经过1.5小时相遇。
已知货车和客车的速度比是7:8,求货车行驶速度。
135÷1.5×=423、比例综合应用:例:在一幅比例尺为1:4000000的中国地图上,量得浙江湖州到山东日照的图书距离为15cm。
陈老师早上6:00从湖州出发开车去日照旅游,下午2:00到达目的地。
途中陈老师开车的平均速度是多少?75练一练:1、北京到济南高速公路距离大约为430km,北京到天津大约为120km。
一辆汽车从北京出发开往济南,当行驶到天津时用了1.5小时。
按照这个速度,北京到济南全程需要多少小时?5.3752、刘大伯家养鸡、鸭、鹅共1800只,这三种家禽的只数比是5:3:1.刘大伯家养鸡、鸭、鹅各多少只?内项3、为创建海华公司,张、王、李三人分别投资100万元、120万元和80万元。
在他们三人的共同努力下,到年末,公司共盈利60万元,你认为该如何合理分配这笔钱,每人分别得多少?4、在比例尺是1:3000000的地图上,量得A、B两城之间的距离是2.4厘米。
在A、B两城之间有一中途停靠站C,A、B两城到C站的距离比是7:5。
一辆汽车从B城到C站共用了0.6小时,求这辆汽车的速度。
5、甲乙两人分别从相距255千米的两地同时出发相向而行,已知甲乙速度比为10:7,两人相遇时各行了多少千米?6、小淘气看一本科技书,第一天看了全书的,第二天看了42页,这时看了的页数与剩下的页数比是2:5,这本科技书一共有多少页?7、某车间生产了甲、乙、丙三种配套机件共1280只,其中甲乙两种机件只数的比是3∶2,丙种机件比甲种多80只,丙种机件生产了多少只?8、把长35厘米的圆柱体按3∶2截成了一长一短两个小圆柱体后,表面积总和增加了30平方厘米。
六年级下册数学专题-比和比例

知识点一:认识比1、两个数相除又叫两个数的比,任何两个相关数量的比都可以抽象为两个数的比。
知识点二:比、除法、分数的关系2、比、除法、分数之间的联系:知识点三:比值的计算方法3、计算方法:求两个数的比的比值,就是用比的前项除以后项。
4、比和比值的区别:(1)比表示的是两个数的一种关系;比值是一个数值; (2)比可以写成bab a 或:的形式;比值可以是分数、小数或整数。
知识点四:比的基本性质5、比的前项、后项同时乘或除以相同的数(0除外),比值不变。
这叫做比的基本性质。
知识点五:化简比6、如果比的前项和后项都是整数,化简时可直接把比的前项和后项同时除以它们的最大公因数。
比 前项 比号 后项 比值 除法 被除数 除号 除数 商 分数 分子分数线分母分数值比和比例知识归纳提示:在以后解决问题或计算时,求两个数或几个数的比,如果没有特殊要求,一般要求出最简单的整数比。
知识点六:比例的意义7、比例的意义:表示两个比相等的式子叫做比例。
比例中有两个内项和两个外项。
拓展:比和比例的联系:比例是由比组成的。
比和比例的区别:(1)意义不同,比表示两个数相除的关系;比例表示两个比相等的关系 (2)形式不同,比由两项组成,比例由四项组成。
知识点七:比例的基本性质8、在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
如果用字母表示比例的四个项,d c b a ::=,那么比例的基本性质可以表示成c b d a ⨯=⨯。
拓展:(1)根据比例的基本性质,可以判断两个比能否组成比例。
(2)组成比例的4个数最多可以组成8个不同的比例。
(3)根据比例的基本性质,已知比例中的任意三项,就可以求出第四项。
知识点八:解比例9、根据比例的基本性质,把两个外项和两个内项分别相乘,将比例式改写成c b d a ⨯=⨯的形式,再解方程求出x 的值。
【例1】 比的意义:一辆汽车3小时行驶了150千米,这辆汽车行驶的路程和时间的比是多少?比值是多少?比值表示什么?【练习】甲3小时走15千米,乙4小时走24千米。
小学六年级的的比和比例知识点复习.doc

比和比例知识点1、基本概念( 1)两个数 相除 ,又叫做这两个数的 比,“ ∶ ”是 比号 ,比号前面的数叫做比的 前项 ,比号后面的数叫做比的 后项 ,前项除以后项所得的商叫做 比值 。
比的后项不能为0。
( 2)分数的基本性质∶ 分数的分子和分母同时乘以或者除以相同的数(0 除外),分数的大小不变。
乘积是 1 的两个数互为 倒数 。
1 的倒数是 1, 0 没有倒数。
( 3)商不变的规律∶在除法里,被除数和除数同时扩大或者同时缩小相同的倍(0 除外),商不变。
( 4)比的基本性质 ∶比的前项和后项同时乘以或者除以相同的数(0 除外),它们的比值不变。
( 5)小数的性质∶ 在小数的末尾添上零或者去掉零小数的大小不变。
( 6)公因数只有1 的两个数叫做 互质数 。
如( 5 和 7,7 和 9)最简整数比 ∶比的前项和后项是互质数。
( 7)比的化简 ∶用商不变的性质、分数的基本性质或比的基本性质来化简。
化简比的方 法整数比比的前项和后项同时除以它们最大公因数(也可以一步一步的除)如, 18:6= ( 18÷ 6):( 6÷6) =3:1 或 18:6= ( 18÷ 2):( 6÷ 2) =9:3= (9÷ 3):(3÷ 3) =3:1小数比先把比的前项和后项同时乘以10、 100⋯⋯,变成整数比;再把整数比化成最简比如, 0.25:1.5= (0.25 × 100):( 1.5 × 100) =25:150=1:6分数比先把比的前项和后项同时乘以它们分母的最小公倍数,变成整数比;再把整数比化成最简比 如, 5 : 3 =( 5 × 24):( 3× 24)=20:96 8 6 8混合比先把混合比变成小数比或分数比(如果比中的分数不能化成有限小数的,一般化为分数比) ,再变成整数比,最后把整数比化成最简比如, 5:0.3 中的 5不能化成有限小数,所以把5:0.3 先化为分数比。
六年级下册数学总复习-比和比例:第 1 课时 比和比例的基本知识-通用版

9.判断下面生活中的实例是否成比例,如果成比例,成什 么比例?
(1)用煤的天数一定,每天用煤量与总用煤量。 ( 成正比例 )
(2)一本书的页数一定,已看的页数与未看的页数。 ( 不成比例 )
(3)把一张 100 元的人民币分别换成同一种面值的零钱,面 值和张数。 ( 成反比例 )
8 3.4.5、7.5、 1 和 3 这四个数可以组成比例。 ( √ )
2 10 4.因为 C=πd,所以π和 d 成反比例关系。 ( ✕ )
5.相关联的两种量不成正比例关系就成反比例关系。 ( ✕ )
三、选择。(每小题 3 分,共 18 分)
1.下面各比中,比值最大的是( C )。
A.3∶2
B.4∶3
第一组、第二组收集到的瓶子数量的比是 4∶3=8∶6; 第二组、第三组收集到的瓶子数量的比是 6∶5; 所以第一组、第二组、第三组收集到的瓶子数量的比是 8∶6∶5。
D.正方形的周长和边长成正比例关系
四、计算。(38 分)
1.求下面各比的比值。(8 分)
3 ∶6= 1
4
8
3∶ 9 =5 4 20 3
2.4∶0.16=15 2 时∶12 分=2 5
2.把下面各比化成最简整数比。(12 分)
2 ∶ 8 =3∶4 5 15 1.4∶3.5=2∶5
200g∶ 2 kg=1∶2 5
=7y(x、y 均不为 0)可以得出 x∶y=( 7∶5 )。
3. 5 ∶2.5 的比值是( 1 ),如果后项除以 4,要使比值
4
2
不变,前项应( 除以 4 );如果前项除以 4,后项不变,比值是
六年级下册数学 比和比例复习【精编】

比和比例比和比例一.错题回顾1、从甲地到乙地的实际距离是560千米,在一幅地图上量得它们间的距离是14厘米,这幅地图的比例尺是( )。
2、一个圆锥的体积是7.63m ,高是7.6m ,它的底面积是( )2m 。
3、在一幅1:8000000的地图上量得甲乙两地的距离是6厘米。
一辆汽车上午十时以90千米/时的速度从甲地开往乙地,到达乙地时( )时( )分。
1、若a 与b 成正比例关系(a 、b ≠0),则下面等式中错误的是( ) A 、2a=3b B 、ab =2 C 、5.1=baD 、a=4b二.内容讲解知识点:填空题型1. 学校食堂买来一批大米,第一周用去25%,第二周用去35%,这时用去和剩下的大米数量的最简比是( )。
2.一个等腰三角形的一个底角与顶角度数的比是4:1,它的底角是( )°,顶角是( )°。
3. 如图,E 为平行四边形AD 的一点,已知线段AE 与ED 的比是1:2,阴影部分的面积是12cm ²,那么平行四边形的面积是( )cm ²。
4.已知a ÷b =0.6,那么a 与b 成( )比例关系,a 与b 的最简比是( )。
5.如图③,已知阴影部分占大圆面积的51,占小圆面积的41,那么大圆与小圆面积的最简比是( : )。
③6.甲车间原有人数是乙车间的45,从甲车间抽调80人到乙车间后,甲乙两车间的人数之比是1:2.甲车间原有( )人。
7.( )÷56=87=56:( )=( )%=( )(填小数) 8.一套衣服原价600元,现在降价 20%,现价与原价的最简整数比是( ),比值是( )。
9.在一幅1:600000的地图上量得李村到张村的距离是7厘米,那么实际距离是( )千米;在另一幅地图上,量得李村和张村相隔21厘米,则这幅地图的比例尺是( )。
知识点:选择题型1.从东城到西城,甲车要用5小时,乙车要用4小时。
甲乙两车速度的比是( ) A.5:4 B.4:5 C.9:4 D.9:52.一个三角形三个角的度数的比是3:4:5,这是一个( )三角形。
数学人教版六年级下册整理与复习-比和比例

比例
意义
各部分 名称
基本 性质
二、先在下表中写出比和比例的一些知识,再举例 说明。
比
比例
意义 两个数相除又叫两个 表示两个比相等的式
数的比。
子叫做比例。
各部分 名称
基本 性质
3 ∶ 2 = 1.5 前项 后项 比值
比号
比的前项和后项同时 乘或者同时除以相同 的数(0除外),比值 不变。
3 ∶ 2 = 9 ∶6
求实际距离
人教版数学六年级下册
整理和复习
1.数与代数 比和ቤተ መጻሕፍቲ ባይዱ例
一、梳理旧知,探寻联系
比 比和比例
比例
比的意义 比的基本性质
比、分数和除法的关系
比的应用
比例的意义和基本性质
正、反比例 比例的应用
正反比例的意义、图象
判断两个相关联的量 是否成正比例或反比例
二、先在下表中写出比和比例的一些知识,再举例 说明。
比
三、比、分数、除法的关系
联系 各部分名称
例子
分数 分子 分数线- 分母 分数值
除法 被除数 除号÷ 除数 比 前项 比号∶ 后项
商 比值
5 8
5÷8 5∶8
①你们看出来它们之间的联系了吗?谁相当于谁呢? ②比的基本性质、分数的基本性质、商不变的规律之 间有什么联系?
四、试一试
化简比: 2∶ 2 3
六、按比分配的意义
3.水是由氢和氧按1:8的质量比化合而成的,5.4kg的 水含氢和氧各多少?
氢:5.4× 1 =0.6(千克)
81
氧:5.4× 8 =4.8(千克)
81
答:5.4kg的水含氢0.6千克,含氧4.8千克。
六、按比分配的意义
六年级下比和比例整理与复习

六年级下比和比例整理与复习在六年级下册的数学学习中,比和比例是非常重要的知识点。
它们不仅在数学学科中有着广泛的应用,还与我们的日常生活息息相关。
现在,让我们一起来对这部分知识进行整理和复习,加深对它们的理解和掌握。
一、比的认识比,表示两个数相除的关系。
例如,3∶5 可以读作“三比五”,其中3 是前项,5 是后项,“∶”是比号。
比的基本性质:比的前项和后项同时乘或除以相同的数(0 除外),比值不变。
利用比的基本性质,可以将比化简为最简整数比。
例如,将 12∶18 化简,先找出 12 和 18 的最大公因数是 6,然后将前项和后项同时除以 6,得到 2∶3。
二、比例的认识比例,表示两个比相等的式子。
例如,3∶4 = 9∶12 就是一个比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项,中间的两项叫做比例的内项。
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
利用比例的基本性质,可以解比例。
比如,解比例 2∶x = 4∶8,根据比例的基本性质可得 4x = 2×8,4x = 16,x = 4。
三、比和比例的联系与区别联系:比例是由两个比值相等的比组成的。
区别:1、意义不同:比表示两个数相除,比例表示两个比相等。
2、项数不同:比有两项,前项和后项;比例有四项,两个内项和两个外项。
3、基本性质不同:比的基本性质是比的前项和后项同时乘或除以相同的数(0 除外),比值不变;比例的基本性质是在比例里,两个外项的积等于两个内项的积。
四、正比例和反比例1、正比例两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
例如,汽车行驶的速度一定,行驶的路程和时间成正比例关系。
因为路程÷时间=速度(一定)。
2、反比例两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
六年级数学:比和比例总复习
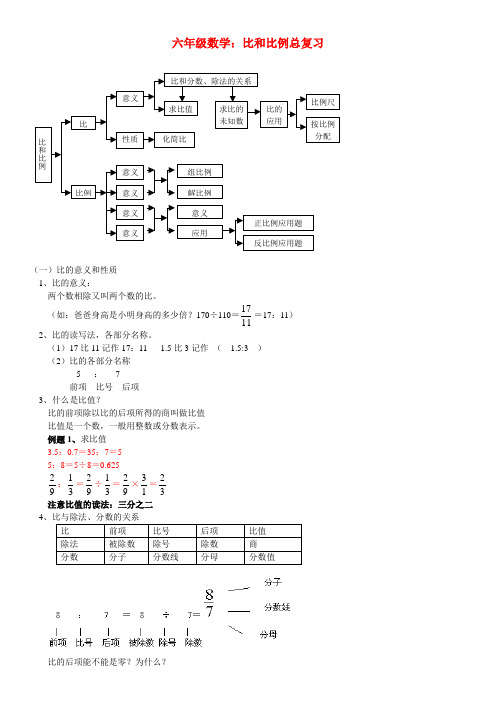
六年级数学:比和比例总复习(一)比的意义和性质 1、比的意义:两个数相除又叫两个数的比。
(如:爸爸身高是小明身高的多少倍?170÷110=1117=17:11) 2、比的读写法,各部分名称。
(1)17比11记作17:11 1.5比3记作 ( 1.5:3 )(2)比的各部分名称5 : 7 前项 比号 后项 3、什么是比值?比的前项除以比的后项所得的商叫做比值比值是一个数,一般用整数或分数表示。
例题1、求比值3.5:0.7=35:7=55:8=5÷8=0.62592:31=92÷31=92×13=32 注意比值的读法:三分之二 4比的后项能不能是零?为什么?小结:因为除法中除数不能为0,分数中分母不能为0,所以比的后项也不能是零。
例题2、求下面比的未知项。
x :3=0.21 120:x =24解:x =3×0.21 解: x =120÷24 x =0.63 x =5 根据什么可以求出比的未知项?5、比的基本性质: 比的前项和后项同时乘以或除以一个相同的数 (零除外),比值不变。
为什么“零除外”?6、化简比:应用比的基本性质,可以把比化成和它相等的最简单的整数比。
把比化成最简单的整数比,叫做化简比。
例题3、化简比(1)63:9=963=17 (2)7.5:2.5=75:25=3:1想一想:把整数比、小数比或分数比化成最简单的整数比的一般方法是什么? ①整数比写成分数后约分后得最简比。
②小数比先化成整数比,再化简。
③分数比先同乘分母的最小公倍数化成整数比,再化简。
例4、填空:( )÷4=()9=0.75=( ):20=( )%(3)÷4=()129=0.75=( 15):20=(75 )% 注意:熟练掌握除法、分数、小数、比、百分数之间的关系,整体观察把握公用条件。
(二)按比分配例5、六年级三个班共有150人,一班人数、二班人数和三班的人数比是6:5:4,这三个班各有多少人? 6+5+4=15150×156=60(人) 150×155=50(人)150×154=40(人)答:一班有60人,二班有50人,三班有40人。
六年级下学期数学比和比例整理复习

比 意义 。
两个数相除又叫做两个数的比。
比例
表示两个比相等 的式子叫做比例。。
各部 分
名称
90 : 60 = 1.5
前项 比号 后项
比值
9:6 = 3:2
内项 外项
基本 性质
比的前项和后项同时乘或同时 除以相同的数(0除外),比值 不变。
在比例里,两个内项的积 等于两个外项的积。。
2、比和分数、除法有什么关系?
):
7)甲数和乙数的比是3:5,甲数占乙数的-3 ,乙数占
甲乙两数总数的-85 。
5
8)3x=4y,(x、y都不为0),x和 y的比是( 4):(3 )
9)两个数的比值是4,前项和后项同时扩大3倍,比值 是( 不变)。
1)两和正方形的边长的比是3:5,它们面积的比是( D 长的比是( B )。
A:1:3 B: 3:5 C:1:25 D:9:25
20 1
)
比
在工农业生产和日常生活 中,常常需要把一个数量 按照一定的比来进行分配。 这种分配方法通常叫做按 比例分配。
按比例分配的解题思路:
①根据比先求出总份数。 ②求出每份是多少。 ③求出各部分的量。 ④答题并检验。
①根据比先求出总份数。 ②求出各部分数占总数的几分之 几。 ③运用分数乘法列式计算,求出 各部分的量。
(2)说出下面各比例尺的具体意义.
①比例尺1:3000000表示(
)。
表示图上距离1厘米相当于实际距离3000000厘米。
②比例尺20:1表示(
)。
表示图上距离20厘米相当于实际距离1厘米。
③比例尺0 30 60km表示(
)。
表示图上距离1厘米相当于实际距离30千米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比和比例 一。
填空
1、0.6=3:( )=( )÷15=( )成=( )%
、112
: 0.75的比值是( ),把它化为最简的整数比是( ) 、比例4:9=20:45写成分数形式是( ),根据比例的基本性质写成乘法 形式是( ) 、18的约数有( ),选出其中四个数组成一个比例是( ) 、在比例尺1:2000000的地图上,图上1厘米表示实际距离( )千米。
、在一个比例中,两个内项互为倒数,一个外项是25 ,另一个外项是( ) 甲数除以乙数的商是4,甲数与乙数的最简整数比是( ) 、我国<<国旗法>>规定,国旗的长和宽的比是3:2,学校的国旗宽是128厘米, 长应该是( )厘米。
、三角形底一定,它的高和面积成( )比例。
、用0.2 、 6、 30、 1这四个数组成两个比例式是( )和( ) 、某厂男职工人数是女职工的23 ,女职工与男职工的人数比是( ) 、两个正方体的棱长比是3:4,它们的体积比是( ) 、如果3a=2b ,那么a :b=( ):( ) 、从A 地到B 地,甲用12分钟,乙用8分钟,甲乙的速度比是( ) 、小圆的半径是2厘米,大圆的半径是3厘米,小圆和大圆的周长比是( ), 面积比是( ) 、甲乙两数之比是3:4,它们的和是1.4,则甲数是( ),乙数是( ) 、一个比8:15,如果后项增加60,要使比值不变,比的前项应该增加( ) 、在比例尺是1200 的学校平面图上,量得教室的长8厘米,宽6厘米,教室实 际面积是( ) 、男生人数比女生人数少20%,男生人数与女生人数的比是( ):( ) 、甲数的13 等于乙数的25 ,甲数与乙数的比是( ) 二、判断 、圆柱的底面积一定,它的高与体积成正比例 。
( )
2、圆周率是圆的直径与周长的比值。
( )
3、把16:2化作最简的整数比是8。
( )
4、如果Y=5X ,则x 与y 成正比例。
( ) 5、一个非0的自然数与它的倒数成反比。
( )
三、选择题
1、能与1.6:1.2组成比例的是 ( )
A、1.2:1.6 B、25
:0.3 C、3:4 2、一克的盐放入49克的水中,盐和盐水的比是 ( )
A、1:49 B、1:48 C、1:50
3、x ×13 =y ×15
时,x :y =( ) A、13 :15
B、5:3 C、3:5 4、一本书已看总页数的60%,没看页数与总页数的比是 ( )
A、2:3 B、3:5 C、2:5
5、花生的出油率一定,花生的质量和榨出的油的质量( )
A、成正比例 B、成反比例 C、不成比例
四、计算
1、化简比
1.5:3.5 115
:1.8 9分:0.4小时
2、求出比值
3.75:112 1.35:2.4 213 :312
3、解比例
0.499.8 =16x 7:x=4.8:9.6 x:34 =12:18
五、解决问题
1、房产博览会上,某楼盘的模型是按照1:500的比例尺制作的,该楼盘1号楼模型高7厘米,它的实际高度是多少?
2、兰州到乌鲁木齐的铁路长约1900千米,在比例尺是1:40000000的地图上,它的长是多少?
3、修一条长12千米的公路,开工3天修了1.5千米。
照这样计算,修完这条路还要多少天?
4、专业户刘大伯家养鸡、鸭、鹅共1800只,这三种家禽的只数比是5:3:1。
刘大伯家养鸡、鸭、鹅各多少只?
5、把一批书按4:5:6的比例分给甲、乙、丙三个班,已知甲班比丙班少分到24本,三个班各分到多少本书?
6、亮亮家造了新房,准备用边长是0.4米的正方形地砖装饰客厅地面,这样需要180块,装修老师建议改用边长0.6米的正方形地砖铺地。
请你算一算需要多少块?
六、数学思考
一艘轮船以每小时40千米的速度从甲港开往乙港,行了全程的20% 后,又行驶了1小时,这时未行路程与已行路程的比是3:1。
甲乙两港相距多少千米?。
