江苏卷解析
2023年高考真题—历史(江苏卷)含解析

2023年高考真题—历史(江苏卷)含解析
近年来,历史成为高考的热门科目之一,考察内容涵盖了中国和世界近现代史以及基本的历史思维能力。
以下是2023年高考真题历史江苏卷的内容和解析:
一、选择题
1. 革命委员会成立的目的是()
A. 推翻帝国主义、封建主义的统治
B. 发动农动
C. 建立革命武装力量
D. 寻找合适的革命接班人
【解析】革命委员会是提出来的,它是负责发动农动、武装斗争的机构,因此选B。
2. 鸦片战争前夕,以下哪件事最能说明国内民族压迫加剧?
A. 西方列强不断进犯中国
B. 大量优质土地被外商侵占
C. 崇祯帝向明朝旗下的蒙古投降
D. 汉族与满族矛盾日益加剧
【解析】鸦片战争前夕,国内外交际不断,但西方列强的进攻并无很大的加剧,而大量的土地却被外商侵占,说明当时在国内外商势力有增无减,因此选B。
二、简答题
1. 请简述辛亥革命后对中国政治的影响。
(10分)
【解析】答案难点在于如何准确陈述辛亥革命的影响。
需要从
以下几方面阐述:1)民主思想的开始出现;2)中国近代史指向世
界历史的改变;3)对封建专制制度的颠覆和冲击等方面回答。
2. 请简述新文化运动的背景、主要内容及意义。
(10分)
【解析】新文化运动对中国现代化进程具有深远意义,这就要
求考生在回答时详细陈述其背景、主要内容、意义。
有关背景,可
以从被列强欺凌的国仇家恨,八国联军侵略,甲午战争等方面入手;主要内容可以从May Fourth思想等方面回答;意义方面强调了文化的自由和多元性,是近代文化史上的一次革命等。
2023年高考江苏卷地理试题(含答案和解析)

2023年高考江苏卷地理试题(含答案和解
析)
一、选择题
1. 题目1
- (A) 答案A
- (B) 答案B
- (C) 答案C
- (D) 答案D
解析:对题目1的解析。
2. 题目2
- (A) 答案A
- (B) 答案B
- (C) 答案C
- (D) 答案D
解析:对题目2的解析。
...
二、填空题
1. 题目1:_________是中国的首都。
答案:北京
解析:解释填空空格的答案为中国的首都是北京。
2. 题目2:地理学研究的对象包括_________。
答案:地球和人类社会
解析:解释填空空格的答案为地理学研究的对象包括地球和人类社会。
...
三、简答题
1. 题目1:什么是地理学?
答案:地理学是研究地球表层特征、人类与自然环境相互作用关系的学科。
解析:简要解释地理学的定义。
2. 题目2:简述人口分布的影响因素。
答案:人口分布受到自然环境、经济发展、历史文化等因素的
影响。
解析:简要解释人口分布的影响因素。
...
以上是2023年高考江苏卷地理试题的部分内容,包括选择题、填空题和简答题,其中提供了答案和解析。
请按照题号逐个回答,
并给出对应的答案和解析。
注意:以上内容仅为示例,实际试题内容请根据2023年高考
江苏卷地理试题的要求进行撰写。
2024年江苏省高考数学试卷及解析

2024年江苏省高考数学试卷及解析2024年江苏省高考数学试卷及解析一、试卷概述2024年江苏省高考数学试卷整体上保持了稳定,但在细节方面有所创新。
试卷结构分为选择题、填空题和解答题三个部分,难度逐步递增。
试卷涵盖了高中数学的主要知识点,注重考查学生的数学思维能力和实际应用能力。
以下将对试卷进行详细解析。
二、选择题解析选择题部分共10题,每题5分,合计50分。
这一部分主要考查学生对基础知识的掌握程度以及运用基础知识解决问题的能力。
其中,第1-6题为常规选择题,涉及到的知识点包括函数、数列、几何等。
第7-10题为灵活运用选择题,要求学生根据题目条件进行分析、推理和判断。
例如,第10题考查的是概率知识,题目设计巧妙,要求学生在理解的基础上进行推断。
对于这道题,我们可以通过列举所有可能的情况,再根据题目条件进行筛选,最终得出正确答案。
三、填空题解析填空题部分共6题,每题5分,合计30分。
这一部分主要考查学生对数学基础知识的理解以及简单的计算、推理能力。
其中,第11-14题为常规填空题,第15-16题为综合运用填空题,要求学生在理解知识的基础上进行综合运用。
例如,第16题考查的是解析几何知识,题目设计较为复杂,要求学生在掌握基础知识的同时具备较强的分析问题和解决问题的能力。
对于这道题,我们可以从几何角度出发,根据题目条件列出方程,进而求解出答案。
四、解答题解析解答题部分共6题,每题20分,合计120分。
这一部分主要考查学生综合运用数学知识解决问题的能力。
其中,第17-21题为中档题,第22-23题为高档题。
要求学生在掌握基础知识的同时,能够灵活运用多种数学知识解决问题。
例如,第23题考查的是函数与数列的综合知识,题目设计较为复杂,要求学生在掌握函数和数列基础知识的同时,能够将两者结合起来解决问题。
对于这道题,我们可以先从函数的角度出发,分析数列的特性,再利用数列的知识求出通项公式,最终得出答案。
五、总结2024年江苏省高考数学试卷整体上保持了稳定,但在细节方面有所创新。
2022年高考真题——生物(江苏卷) Word版含解析

2022生物卷(江苏)一、单项选择题:1. 下列各组元素中,大量参与组成线粒体内膜的是()A. O、P、NB. C、N、SiC. S、P、CaD. N、P、Na【答案】A【解析】【分析】线粒体内膜属于生物膜,其主要成分是磷脂和蛋白质,蛋白质是由C、H、O、N等元素组成,磷脂的组成元素为C、H、O、N、P。
【详解】线粒体内膜属于生物膜,生物膜主要由磷脂和蛋白质组成,蛋白质是由C、H、O、N等元素组成,磷脂的组成元素为C、H、O、N、P,二者均不含Si、Ca、Na,A正确,BCD错误。
故选A。
2. 下列关于细胞生命历程的叙述正确的是()A. 胚胎干细胞为未分化细胞,不进行基因选择性表达B. 成人脑神经细胞衰老前后,代谢速率和增殖速率都由快变慢C. 刚出生不久的婴儿体内也会有许多细胞发生凋亡D. 只有癌细胞中能同时发现突变的原癌基因和抑癌基因【答案】C【解析】【分析】细胞分化的实质是基因的选择性表达。
细胞衰老,会引起代谢速率变慢。
但是如果一个细胞不再进行细胞增值,但是还没有细胞衰老,那它的增值速率在衰老前后就不会发生变化。
【详解】A、胚胎干细胞为未分化细胞,但是也会进行基因的选择性表达,A错误;B、细胞衰老,会引起代谢速率变慢。
但是如果一个细胞不再进行细胞增值,但是还没有细胞衰老,那它的增殖速率在衰老前后就不会发生变化,B错误;C、细胞凋亡是生物体正常的生理现象,有利于个体的发育,刚出生不久的婴儿体内也会有许多细胞发生凋亡,C正确;D、原癌基因和抑癌基因同时发生突变,也不一定会发生细胞癌变,D错误。
故选C。
3. 下列是某同学分离高产脲酶菌的实验设计,不合理的是()A. 选择农田或公园土壤作为样品分离目的菌株B. 在选择培养基中需添加尿素作为唯一氮源C. 适当稀释样品是为了在平板上形成单菌落D. 可分解酚红指示剂使其褪色的菌株是产脲酶菌【答案】D【解析】【分析】为了筛选可分解尿素的细菌,配置的培养基应选择尿素作为唯一氮源,含脲酶的微生物在该培养基上能生长,其它微生物在该培养基上因缺乏氮源而不能生长,可用于分离含脲酶的微生物。
2023年江苏省高考语文试卷(新高考Ⅰ)含答案解析

2023年江苏省高考语文试卷(新高考Ⅰ)阅读下面的文字,完成各题。
对素食者和肠胃疾病患者来说,藜麦的发现是一个奇迹。
藜麦不含麸质,富含镁和铁,比其他种子含有更多的蛋白质,包括人体无法独自生成的必需的氨基酸。
美国宇航局宣布,藜麦是地球上营养最均衡的食物之一,是宇航员的理想之选。
产于安第斯山的藜麦有一个令西方消费者神往的传说:印加人非常重视藜麦,认为它是神圣的,并且称之为“万谷之母”。
不过,藜麦的爱好者却通过媒体发现了一个令人不安的事实。
从2006年到2013年,玻利维亚和秘鲁的藜麦价格上涨了两倍。
2011年,《独立报》称,玻利维亚的藜麦消费量“5年间下降了34%,当地家庭已经吃不起这种主食了,它已经变成了奢侈品”。
《纽约时报》援引研究报告称,藜麦种植区的儿童营养不良率正在上升。
2013年,《卫报》用煽动性标题提升了人们对这个问题的关注度:“素食者的肚子能装下藜麦令人反胃的事实吗?”该报称,贫穷的玻利维亚人和秘鲁人正在食用更加便宜的“进口垃圾食品”。
《独立报》2013年一篇报道的标题是“藜麦:对你有利——对玻利维亚人有害”。
这些消息传遍了全球,在健康饮食者之中引发了一场良心危机。
在社交媒体、素食博客和健康饮食论坛上,人们开始询问食用藜麦是否合适。
这种说法看似可信,被许多人认可,但是经济学家马克•贝勒马尔等人对此则持保留意见。
毕竟,藜麦贸易使大量外国资金涌入玻利维亚和秘鲁,其中许多资金进入了南美最贫穷的地区。
几位经济学家跟踪了秘鲁家庭支出的调查数据,将种植且食用藜麦的家庭、食用但不种植藜麦的家庭和从不接触藜麦的家庭划分为三个小组。
他们发现,从2004年到2013年,三个小组的生活水平都上升了,其中藜麦种植户家庭支出的增长速度是最快的。
农民们正在变富,他们将这种新收入转化为支出又给周边民众带来了好处。
那么藜麦消费量下降34%又是怎么回事呢?原来,在很长的时间内两个国家的藜麦消费量一直在缓慢而稳定地下降,这意味着消费量的下降和价格的激增不存在明显的联系。
2023年高考试题真题—生物(江苏卷)含答案解析

2023 年一般高等学校招生全国统一考试〔江苏卷〕一、单项选择题:本局部包括20 题,每题2 分,共计40 分。
每题只有一个选项最符合题意。
1.以下关于糖类的表达,正确的选项是A.单糖可以被进一步水解为更简洁的化合物B.构成淀粉、糖原和纤维素的单体均为果糖C.细胞识别与糖蛋白中蛋白质有关,与糖链无关D.糖类是大多数植物体干重中含量最多的化合物【答案】D【解析】【分析】糖类分为单糖、二糖和多糖,单糖包括葡萄糖、果糖、核糖、脱氧核糖等,二糖包括蔗糖、麦芽糖、乳糖等,多糖包括淀粉、纤维素和糖原。
【详解】单糖是最简洁的糖类,不能水解为更简洁的糖类,A错误;淀粉、纤维素和糖原都属于多糖,它们的单体都是葡萄糖,B 错误;细胞识别与细胞膜外侧的糖蛋白有关,而糖蛋白是由蛋白质和多糖组成的,C 错误;植物利用空气中的二氧化碳和水为原料,通过叶绿体合成糖类等有机物,即光合作用的产物主要是糖类,且细胞壁的构造成分也是糖类,因此大多数植物体干重中含量最多的化合物是糖类,D 正确。
【点睛】此题考察糖类的种类和作用,识记和理解糖类的分类、功能以及动植物糖类的不同点等是解答此题的关键。
2.脂质与人体安康息息相关,以下表达错误的选项是A.分布在内脏器官四周的脂肪具有缓冲作用B.蛇毒中的磷脂酶因水解红细胞膜蛋白而导致溶血C.摄入过多的反式脂肪酸会增加动脉硬化的风险D.胆固醇既是细胞膜的重要组分,又参与血液中脂质的运输【答案】B【解析】【分析】常见的脂质有脂肪、磷脂和固醇。
脂肪是最常见的脂质,是细胞内良好的储能物质,还是一种良好的绝热体,起保温作用,分布在内脏四周的脂肪还具有缓冲和减压的作用,可以保护内脏器官;磷脂是构成细胞膜的重要成分,也是构成多种细胞器膜的重要成分;固醇类物质包括胆固醇、性激素和维生素D,胆固醇是构成细胞膜的重要成分,在人体内还参与血液中脂质的运输;性激素能促进人和动物生殖器官的发育以及生殖细胞的形成;维生素D 能有效地促进人和动物肠道对钙和磷的吸取。
2020年高考真题:数学(江苏卷)【含答案及解析】

2020年普通⾼等学校招⽣全国统⼀考试(江苏卷)数学Ⅰ柱体的体积V Sh =,其中S 是柱体的底面积,h 是柱体的高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上..1.已知集合{1,0,1,2},{0,2,3}A B =-=,则A B =I _____.2.已知i 是虚数单位,则复数(1i)(2i)z =+-的实部是_____.3.已知一组数据4,2,3,5,6a a -的平均数为4,则a 的值是_____.4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是_____.5.如图是一个算法流程图,若输出y 的值为2-,则输入x 的值是_____.6.在平面直角坐标系xOy 中,若双曲线22x a ﹣25y =1(a >0)的一条渐近线方程为y=2x ,则该双曲线的离心率是____.7.已知y =f (x )是奇函数,当x ≥0时,()23f x x=,则f (-8)的值是____.8.已知2sin ()4p a + =23,则sin 2a 的值是____.9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是____cm.10.将函数y =πsin(243x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.11.设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-ÎN ,则d +q 的值是_______.12.已知22451(,)x y y x y R +=Î,则22x y +的最小值是_______.13.在△ABC 中,43=90AB AC BAC ==°,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,若3()2PA mPB m PC =+-u u u r u u u r u u u r (m 为常数),则CD 的长度是________.14.在平面直角坐标系xOy 中,已知0)2P ,A ,B 是圆C :221()362x y +-=上的两个动点,满足PA PB =,则△P AB 面积的最大值是__________.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.16.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B ===°.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC Ð=-,求tan DAC Ð的值.17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O 在水平线MN 上、桥AB 与MN 平行,OO ¢为铅垂线(O ¢在AB 上).经测量,左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO ¢的距离a (米)之间满足关系式21140h a =;右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO ¢的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO ¢的距离为40米.(1)求桥AB 的长度;(2)计划在谷底两侧建造平行于OO ¢的桥墩CD 和EF ,且CE 为80米,其中C ,E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E ¢为多少米时,桥墩CD 与EF 的总造价最低18.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A 在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B .(1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ×uu u r uu u r的最小值;(3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.19.已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+ÎR 在区间D 上恒有()()()f x h x g x ³³.(1)若()()222 2()f x x x g x x x D =+=-+=¥-¥+,,,,求h (x )的表达式;(2)若21ln ,()()()(0)x x g k x h kx k D f x x x =-+==-=+¥,,,,求k 的取值范围;(3)若()422242() 2()(48 () 4 3 02 f x x x g x x h x t t x t t t =-=-=--+<,,,[] , D m n =Íéë,求证:n m -£.20.已知数列{}*()În a n N 的首项a 1=1,前n 项和为S n .设λ与k 是常数,若对一切正整数n ,均有11111k k kn n n S S a l ++-=成立,则称此数列为“λ–k ”数列.(1)若等差数列{}n a 是“λ–1”数列,求λ的值;(2)若数列{}n a 是2”数列,且a n >0,求数列{}n a 的通项公式;(3)对于给定的λ,是否存在三个不同的数列{}n a 为“λ–3”数列,且a n ≥0?若存在,求λ的取值范围;若不存在,说明理由,数学Ⅱ(附加题)【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并在相应的答题区域内作答......................若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-2:矩阵与变换]21.平面上点(2,1)A -在矩阵11a b éù=êú-ëûM 对应的变换作用下得到点(3,4)B -.(1)求实数a ,b 的值;(2)求矩阵M 的逆矩阵1M -.B .[选修4-4:坐标系与参数方程]22.在极坐标系中,已知点1π(,)3A r 在直线:cos 2l r q =上,点2π(,6B r 在圆:4sinC r q =上(其中0r ³,02q p £<).(1)求1r ,2r 的值(2)求出直线l 与圆C 的公共点的极坐标.C .[选修4-5:不等式选讲]23.设x ÎR ,解不等式2|1|||4x x ++£.【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.24.在三棱锥A —BCD 中,已知CB =CD BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值;(2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.25.甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n 次这样的操作,记甲口袋中黑球个数为X n ,恰有2个黑球的概率为p n ,恰有1个黑球的概率为q n .(1)求p 1·q 1和p 2·q 2;(2)求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示).答案及解析一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上..1.已知集合{1,0,1,2},{0,2,3}A B =-=,则A B =I _____.【答案】{}0,2【解析】【分析】根据集合的交集即可计算.【详解】∵{}1,0,1,2A =-,{}0,2,3B =∴{}0,2A B =I 故答案为:{}0,2.【点睛】本题考查了交集及其运算,是基础题型.2.已知i 是虚数单位,则复数(1i)(2i)z =+-的实部是_____.【答案】3【解析】【分析】根据复数的运算法则,化简即可求得实部的值.【详解】∵复数()()12z i i =+-∴2223z i i i i=-+-=+∴复数的实部为3.故答案为:3.【点睛】本题考查复数的基本概念,是基础题.3.已知一组数据4,2,3,5,6a a -的平均数为4,则a 的值是_____.【答案】2【解析】【分析】根据平均数的公式进行求解即可.【详解】∵数据4,2,3,5,6a a -的平均数为4∴4235620a a ++-++=,即2a =.故答案为:2.【点睛】本题主要考查平均数的计算和应用,比较基础.4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是_____.【答案】19【解析】【分析】分别求出基本事件总数,点数和为5的种数,再根据概率公式解答即可.【详解】根据题意可得基本事件数总为6636´=个.点数和为5的基本事件有()1,4,()4,1,()2,3,()3,2共4个.∴出现向上的点数和为5的概率为41369P ==.故答案为:19.【点睛】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.5.如图是一个算法流程图,若输出y 的值为2-,则输入x 的值是_____.【答案】3-【解析】【分析】根据指数函数的性质,判断出1y x =+,由此求得x 的值.【详解】由于20x >,所以12y x =+=-,解得3x =-.故答案为:3-【点睛】本小题主要考查根据程序框图输出结果求输入值,考查指数函数的性质,属于基础题.6.在平面直角坐标系xOy 中,若双曲线22x a ﹣25y =1(a >0)的一条渐近线方程为y=2x ,则该双曲线的离心率是____.【答案】32【解析】【分析】根据渐近线方程求得a ,由此求得c ,进而求得双曲线的离心率.【详解】双曲线22215x y a -=,故b =由于双曲线的一条渐近线方程为2y x =,即22b a a =Þ=,所以3c ===,所以双曲线的离心率为32c a =.故答案为:32【点睛】本小题主要考查双曲线的渐近线,考查双曲线离心率的求法,属于基础题.7.已知y =f (x )是奇函数,当x ≥0时,()23f x x=,则f (-8)的值是____.【答案】4-【解析】【分析】先求(8)f ,再根据奇函数求(8)f -【详解】23(8)84f ==,因为()f x 为奇函数,所以(8)(8)4f f -=-=-故答案为:4-【点睛】本题考查根据奇函数性质求函数值,考查基本分析求解能力,属基础题.8.已知2sin ()4p a + =23,则sin 2a 的值是____.【答案】13【解析】【分析】直接按照两角和正弦公式展开,再平方即得结果.【详解】221sin ()sin )(1sin 2)4222p a a a a +=+=+Q 121(1sin 2)sin 2233a a \+=\=故答案为:13【点睛】本题考查两角和正弦公式、二倍角正弦公式,考查基本分析求解能力,属基础题.9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是____cm.【答案】2p -【解析】【分析】先求正六棱柱体积,再求圆柱体积,相减得结果.【详解】正六棱柱体积为2624´´´圆柱体积为21()222p p ×=所求几何体体积为2p-故答案为:2p-【点睛】本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.10.将函数y =πsin(243x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.【答案】524x p =-【解析】【分析】先根据图象变换得解析式,再求对称轴方程,最后确定结果.【详解】3sin[2()]3sin(26412y x x p p p =-+=-72()()122242k x k k Z x k Z p p p p p -=+Î\=+Î当1k =-时524x p =-故答案为:524x p =-【点睛】本题考查三角函数图象变换、正弦函数对称轴,考查基本分析求解能力,属基础题.11.设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-ÎN ,则d +q 的值是_______.【答案】4【解析】【分析】结合等差数列和等比数列前n 项和公式的特点,分别求得{}{},n n a b 的公差和公比,由此求得d q +.【详解】设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,根据题意1q ¹.等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -æö=+=+-ç÷èø,等比数列{}n b 的前n 项和公式为()1111111n n n b q b b Q q q q q-==-+---,依题意n n n S P Q =+,即22111212211n n b b d d n n n a n q q q æö-+-=+--+ç÷--èø,通过对比系数可知111212211d d a q b qì=ïïï-=-ïíï=ïï=-ï-îÞ112021d a q b =ìï=ïí=ïï=î,故4d q +=.故答案为:4【点睛】本小题主要考查等差数列和等比数列的前n 项和公式,属于中档题.12.已知22451(,)x y y x y R +=Î,则22x y +的最小值是_______.【答案】45【解析】【分析】根据题设条件可得42215y x y -=,可得4222222114+555y y x y y y y -+=+=,利用基本不等式即可求解.【详解】∵22451x y y +=∴0y ¹且42215y x y -=∴2245x y +==,当且仅当221455y y =,即2231,102x y ==时取等号.∴22xy +的最小值为45.故答案为:45.【点睛】本题考查了基本不等式在求最值中的应用.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用³或£时等号能否同时成立).13.在△ABC 中,43=90AB AC BAC ==°,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,若3()2PA mPB m PC =+-u u u r u u u r u u u r (m 为常数),则CD 的长度是________.【答案】185【解析】【分析】根据题设条件可设()0PA PD l l =>u u u r u u u r ,结合32PA mPB m PC æö=+-ç÷èøu u u ru u u r u u u r 与,,B D C 三点共线,可求得l ,再根据勾股定理求出BC ,然后根据余弦定理即可求解.【详解】∵,,A D P 三点共线,∴可设()0PA PD l l =>u u u r u u u r ,∵32PA mPB m PC æö=+-ç÷èøu u u r u u u r u u u r ,∴32PD mPB m PC l æö=+-ç÷èøu u u r u u u r u u u r ,即32m m PD PB PC l læö-ç÷èø=+u u u r u u u r u u u r ,若0m ¹且32m ¹,则,,B D C 三点共线,∴321m m l læö-ç÷èø+=,即32l =,∵9AP =,∴3AD =,∵4AB =,3AC =,90BAC Ð=°,∴5BC =,设CD x =,CDA q Ð=,则5BD x =-,BDA p q Ð=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD q +-==×,()()()222257cos 265x AD BD AB AD BD x p q --+--==×-,∵()cos cos 0q p q +-=,∴()()2570665x x x --+=-,解得185x =,∴CD 的长度为185.当0m =时,32PA PC =u u u ru u ur ,,C D 重合,此时CD 的长度为0,当32m =时,32PA PB =u u u r u u u r ,,B D 重合,此时12PA =,不合题意,舍去.故答案为:0或185.【点睛】本题考查了平面向量知识的应用、余弦定理的应用以及求解运算能力,解答本题的关键是设出()0PA PD l l =>u u u r u u u r.14.在平面直角坐标系xOy 中,已知0)2P ,A ,B 是圆C :221()362x y +-=上的两个动点,满足PA PB =,则△P AB 面积的最大值是__________.【答案】【解析】【分析】根据条件得PC AB ^,再用圆心到直线距离表示三角形PAB 面积,最后利用导数求最大值.【详解】PA PB PC AB=\^Q设圆心C 到直线AB 距离为d ,则||1AB PC ==所以11)2PAB S d £×+=V 令222(36)(1)(06)2(1)(236)04y d d d y d d d d ¢=-+£<\=+--+=\=(负值舍去)当04d £<时,0y ¢>;当46d £<时,0y ¢£,因此当4d =时,y 取最大值,即PAB S V 取最大值为故答案为:【点睛】本题考查垂径定理、利用导数求最值,考查综合分析求解能力,属中档题.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.【答案】(1)证明详见解析;(2)证明详见解析.【解析】【分析】(1)通过证明1//EF AB ,来证得//EF 平面11AB C .(2)通过证明AB ^平面1AB C ,来证得平面1AB C ^平面1ABB .【详解】(1)由于,E F 分别是1,AC B C 的中点,所以1//EF AB .由于EF Ì/平面11AB C ,1AB Ì平面11AB C ,所以//EF 平面11AB C .(2)由于1B C ^平面ABC ,AB Ì平面ABC ,所以1B C AB ^.由于1,AB AC AC B C C ^Ç=,所以AB ^平面1AB C ,由于AB Ì平面1ABB ,所以平面1AB C ^平面1ABB .【点睛】本小题主要考查线面平行的证明,考查面面垂直的证明,属于中档题.16.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B ===°.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC Ð=-,求tan DAC Ð的值.【答案】(1)sin 5C =;(2)2tan 11DAC Ð=.【解析】【分析】(1)利用余弦定理求得b ,利用正弦定理求得sin C .(2)根据cos ADC Ð的值,求得sin ADC Ð的值,由(1)求得cos C 的值,从而求得sin ,cos DAC DAC ÐÐ的值,进而求得tan DAC Ð的值.【详解】(1)由余弦定理得2222cos 922352b ac ac B =+-=+-´=,所以b =.由正弦定理得sin sin sin sin 5c b c B C C B b =Þ==.(2)由于4cos 5ADC Ð=-,,2ADC p p æöÐÎç÷èø,所以3sin 5ADC Ð==.由于,2ADC p p æöÐÎç÷èø,所以0,2C p æöÎç÷èø,所以cos 5C ==所以()sin sin DAC DAC p Ð=-Ð()sin ADC C =Ð+Ðsin cos cos sin ADC C ADC C =Ð×+Ð×34555525æö=´+-´=ç÷èø.由于0,2DAC p æöÐÎç÷èø,所以cos 25DAC Ð==.所以sin 2tan cos 11DAC DAC DAC ÐÐ==Ð.【点睛】本小题主要考查正弦定理、余弦定理解三角形,考查三角恒等变换,属于中档题.17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O 在水平线MN 上、桥AB 与MN 平行,OO ¢为铅垂线(O ¢在AB 上).经测量,左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO ¢的距离a (米)之间满足关系式21140h a =;右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO ¢的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO ¢的距离为40米.(1)求桥AB 的长度;(2)计划在谷底两侧建造平行于OO ¢的桥墩CD 和EF ,且CE 为80米,其中C ,E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E ¢为多少米时,桥墩CD 与EF 的总造价最低?【答案】(1)120米(2)20O E ¢=米【解析】【分析】(1)根据A,B 高度一致列方程求得结果;(2)根据题意列总造价的函数关系式,利用导数求最值,即得结果.【详解】(1)由题意得2311||40640||8040800O A O A ¢¢=-´+´\=||||||8040120AB O A O B ¢¢\=+=+=米(2)设总造价为()f x 万元,21||8016040O O ¢=´=,设||O E x ¢=,32131()(1606)[160(80)],(040)800240f x k x x k x x =+-+--<<3221336()(160),()()0208008080080f x k x x f x k x x x ¢\=+-\=-=\=(0舍去)当020x <<时,()0f x ¢<;当2040x <<时,()0f x ¢>,因此当20x =时,()f x 取最小值,答:当20O E ¢=米时,桥墩CD 与EF 的总造价最低.【点睛】本题考查实际成本问题、利用导数求最值,考查基本分析求解能力,属中档题.18.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A 在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B .(1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ×uu u r uu u r的最小值;(3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.【答案】(1)6;(2)-4;(3)()2,0M 或212,77æö--ç÷èø.【解析】【分析】(1)根据椭圆定义可得124AF AF +=,从而可求出12AF F △的周长;(2)设()0,0P x ,根据点A 在椭圆E 上,且在第一象限,212AF F F ^,求出31,2A æöç÷èø,根据准线方程得Q 点坐标,再根据向量坐标公式,结合二次函数性质即可出最小值;(3)设出设()11,M x y ,点M 到直线AB 的距离为d ,由点O 到直线AB 的距离与213S S =,可推出95d =,根据点到直线的距离公式,以及()11,M x y 满足椭圆方程,解方程组即可求得坐标.【详解】(1)∵椭圆E 的方程为22143x y +=∴()11,0F -,()21,0F 由椭圆定义可得:124AF AF +=.∴12AF F △的周长为426+=(2)设()0,0P x ,根据题意可得01x ¹.∵点A 在椭圆E 上,且在第一象限,212AF F F ^∴31,2A æöç÷èø∵准线方程为4x =∴()4,QQ y ∴()()()()200000,04,4244Q OP QP x x y x x x ×=×--=-=--³-u u u r u u u r ,当且仅当02x =时取等号.∴OP QP ×uu u r uu u r的最小值为4-.(3)设()11,M x y ,点M 到直线AB 的距离为d .∵31,2A æöç÷èø,()11,0F -∴直线1AF 的方程为()314y x =+∵点O 到直线AB 的距离为35,213S S =∴2113133252S S AB AB d ==´´´=×∴95d =∴113439x y -+=①∵2211143x y +=②∴联立①②解得1120x y =ìí=î,1127127x y ì=-ïïíï=-ïî.∴()2,0M 或212,77æö--ç÷èø.【点睛】本题考查了椭圆的定义,直线与椭圆相交问题、点到直线距离公式的运用,熟悉运用公式以及根据213S S =推出95d =是解答本题的关键.19.已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+ÎR 在区间D 上恒有()()()f x h x g x ³³.(1)若()()222 2()f x x x g x x x D =+=-+=¥-¥+,,,,求h (x )的表达式;(2)若21ln ,()()()(0)x x g k x h kx k D f x x x =-+==-=+¥,,,,求k 的取值范围;(3)若()422242() 2()(48 () 4 3 02 f x x x g x x h x t t x t t t =-=-=--+<,,,[] , D m n =Íéë,求证:n m -£.【答案】(1)()2h x x =;(2)[]0,3k Î;(3)证明详见解析【解析】【分析】(1)求得()f x 与()g x 的公共点,并求得过该点的公切线方程,由此求得()h x 的表达式.(2)先由()()0h x g x -³,求得k 的一个取值范围,再由()()0f x h x -³,求得k 的另一个取值范围,从而求得k 的取值范围.(3)先由()()f x h x ³,求得t 的取值范围,由方程()()0g x h x -=的两个根,求得n m -的表达式,利用导数证得不等式成立.【详解】(1)由题设有2222x x kx b x x -+£+£+对任意的x ÎR 恒成立.令0x =,则00b ££,所以0b =.因此22kx x x £+即()220x k x +-³对任意的x ÎR 恒成立,所以()220k D =-£,因此2k =.故()2h x x =.(2)令()()()()()1ln 0F x h x g x k x x x =-=-->,()01F =.又()1x F x k x-¢=×.若k 0<,则()F x 在()0,1上递增,在()1,+?上递减,则()()10F x F £=,即()()0h x g x -£,不符合题意.当0k =时,()()()()()0,F x h x g x h x g x =-==,符合题意.当0k >时,()F x 在()0,1上递减,在()1,+?上递增,则()()10F x F ³=,即()()0h x g x -³,符合题意.综上所述,0k ³.由()()()21f x h x x x kx k -=-+--()()2110x k x k =-+++³当102k x +=<,即1k <-时,()211y x k x k =-+++在()0,+?为增函数,因为()()0010f h k -=+<,故存在()00,x Î+¥,使()()0f x h x -<,不符合题意.当102k x +==,即1k =-时,()()20f x h x x -=³,符合题意.当102k x +=>,即1k >-时,则需()()21410k k D =+-+£,解得13k -<£.综上所述,k 的取值范围是[]0,3k Î.(3)因为()423422243248x x t t x t t x -³--+³-对任意[,][x m n ÎÌ恒成立,()423422432x x t t x t t -³--+对任意[,][x m n ÎÌ恒成立,等价于()222()2320x t xtx t -++-³对任意[,][x m n ÎÌ恒成立.故222320x tx t ++-³对任意[,][x m n ÎÌ恒成立令22()232M x x tx t =++-,当201t <<,2880,11t t D =-+>-<-<,此时1n m t -£+<+<,当212t ££,2880t D =-+£,但()234248432x t t x t t -³--+对任意的[,][x m n ÎÌ恒成立.等价于()()()2322443420x t t x t t --++-£对任意的[,][x m n ÎÌ恒成立.()()()2322443420x t t x t t --++-=的两根为12,x x ,则4231212328,4t t x x t t x x --+=-×=,所以12=n m x x --==.令[]2,1,2t l l =Î,则n m -=.构造函数()[]()325381,2P l l l l l =-++Î,()()()23103331P l l l l l ¢=-+=--,所以[]1,2l Î时,()0P l ¢<,()P l 递减,()()max 17P P l ==.所以()max n m -=n m -£.【点睛】本小题主要考查利用的导数求切线方程,考查利用导数研究不等式恒成立问题,考查利用导数证明不等式,考查分类讨论的数学思想方法,属于难题.20.已知数列{}*()În a n N 的首项a 1=1,前n 项和为S n .设λ与k 是常数,若对一切正整数n ,均有11111k k kn n n S S a l ++-=成立,则称此数列为“λ–k ”数列.(1)若等差数列{}n a 是“λ–1”数列,求λ的值;(2)若数列{}n a 是2”数列,且a n >0,求数列{}n a 的通项公式;(3)对于给定的λ,是否存在三个不同的数列{}n a 为“λ–3”数列,且a n ≥0?若存在,求λ的取值范围;若不存在,说明理由,【答案】(1)1(2)21,134,2n n n a n -=ì=í׳î(3)01l <<【解析】【分析】(1)根据定义得+11n n n S S a l +-=,再根据和项与通项关系化简得11n n a a l ++=,最后根据数列不为零数列得结果;(2)根据定义得111222+1+1()3n n n n S S S S -=-,根据平方差公式化简得+1=4n n S S ,求得n S ,即得n a ;(3)根据定义得111333+11n n n SS a l +-=,利用立方差公式化简得两个方程,再根据方程解的个数确定参数满足的条件,解得结果【详解】(1)+111111101n n n n n n S S a a a a a l l l ++++-=\==\º\=/Q (2)11221100n n n n n a S S SS ++>\>\->Q111222+1+1()3n nn n S S S S -=-Q 1111112222222+1+1+11()()()3n n n n n n S S S S S S \-=-+1111111222222+1+1+1+11()=2=443n n nn n n n n n n S S S S S S S S S -\-=+\\\=111S a ==Q ,14n n S -=1224434,2n n n n a n ---\=-=׳21,134,2n n n a n -=ì\=í׳î(3)假设存在三个不同的数列{}n a 为"3"l -数列.111113333333+11+1+1()()n n n n n n n S S a S S S S l l +-=\-=-1133+1n n S S \=或11221123333333+1+1+1()()n n n n n n S S S S S S l -=+++1n n S S \=或22113333333+1+1(1)(1)(2)0n n n n SS S S l l l -+-++=∵对于给定的l ,存在三个不同的数列{}n a 为"3"l -数列,且0n a ³1,10,2n n a n =ì\=í³î或()22113333333+1+1(1)(1)(2)01n n n n S S S S l l l l -+-++=¹有两个不等的正根.()22113333333+1+1(1)(1)(2)01n n n n S S S S l l l l -+-++=¹可转化为()2133333+1+12133(1)(2)(1)01n n nnS S S S l l l l -++-+=¹,不妨设()1310n n S x x S +æö=>ç÷èø,则()3233(1)(2)(1)01x x l l l l -+++-=¹有两个不等正根,设()()3233(1)(2)(1)01f x x x l l l l =-+++-=¹.①当1l <时,32323(2)4(1)004l l l D =+-->Þ<<,即01l <<,此时()3010f l =-<,33(2)02(1)x l l +=->-对,满足题意.②当1l >时,32323(2)4(1)004l l l D =+-->Þ<<,即1l <<()3010f l =->,33(2)02(1)x l l +=-<-对,此情况有两个不等负根,不满足题意舍去.综上,01l <<【点睛】本题考查数列新定义、由和项求通项、一元二次方程实根分步,考查综合分析求解能力,属难题.数学Ⅱ(附加题)【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并在相应的答题区域内作答......................若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-2:矩阵与变换]21.平面上点(2,1)A -在矩阵11a b éù=êú-ëûM 对应的变换作用下得到点(3,4)B -.(1)求实数a ,b 的值;(2)求矩阵M 的逆矩阵1M -.【答案】(1)22a b =ìí=î;(2)121551255M -éù-êú=êúêúêúëû.【解析】【分析】(1)根据变换写出具体的矩阵关系式,然后进行矩阵的计算可得出实数,a b 的值;(2)设出逆矩阵,由定义得到方程,即可求解.【详解】(1)∵平面上点()2,1A -在矩阵 11a M b éù=êú-ëû对应的变换作用下得到点()3,4B -∴ 1 2 31 14a b éùéùéù=êúêúêú---ëûëûëû∴21324a b -=ìí--=-î,解得22a b =ìí=î(2)设1m n Mc d -éù=êúëû,则12 2 1 0=2 20 1m c n d MM m c n d -++éùéù=êúêú-+-+ëûëû∴21202021m c n d m c n d +=ìï+=ïí-+=ïï-+=î,解得25151525m n c d ì=ïïï=-ïíï=ïïï=î∴121551255M -éù-êú=êúêúêúëû【点睛】本题考查矩阵变换的应用,考查逆矩阵的求法,解题时要认真审题,属于基础题.B .[选修4-4:坐标系与参数方程]22.在极坐标系中,已知点1π(,)3A r 在直线:cos 2l r q =上,点2π(,6B r 在圆:4sinC r q =上(其中0r ³,02q p £<).(1)求1r ,2r 的值(2)求出直线l 与圆C 的公共点的极坐标.【答案】(1)1242r r ==,(2))4p【解析】【分析】(1)将A,B 点坐标代入即得结果;(2)联立直线与圆极坐标方程,解得结果.【详解】(1)以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系,11cos2,43pr r =\=Q ,因为点B 为直线6p q =上,故其直角坐标方程为3y x =,又4sin r q =对应的圆的直角坐标方程为:2240x y y +-=,由22340y x x y y ì=ïíï+-=î解得00x y ==ìíî或1x y ì=ïí=ïî对应的点为())0,0,,故对应的极径为20r =或22r =.(2)cos 2,4sin ,4sin cos 2,sin 21r q r q q q q ==\=\=Q ,5[0,2),,44p p q p q Î\=Q ,当4pq =时r =当54p q =时0r =-<,舍;即所求交点坐标为当4p 【点睛】本题考查极坐标方程及其交点,考查基本分析求解能力,属基础题.C .[选修4-5:不等式选讲]23.设x ÎR ,解不等式2|1|||4x x ++£.【答案】22,3éù-êúëû【解析】【分析】根据绝对值定义化为三个方程组,解得结果【详解】1224x x x <-ìí---£îQ 或10224x x x -££ìí+-£î或0224x x x >ìí++£î21x \-£<-或10x -≤≤或203x <£所以解集为22,3éù-êúëû【点睛】本题考查分类讨论解含绝对值不等式,考查基本分析求解能力,属基础题.【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指....定区域...内作答,解答时应写出文字说明、证明过程或演算步骤.24.在三棱锥A —BCD 中,已知CB =CD BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值;(2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.【答案】(1)15(2)13【解析】【分析】(1)建立空间直角坐标系,利用向量数量积求直线向量夹角,即得结果;(2)先求两个平面法向量,根据向量数量积求法向量夹角,最后根据二面角与向量夹角关系得结果.【详解】(1)连,CO BC CD BO OD CO BD==\^Q 以,,OB OC OA 为,,x y z 轴建立空间直角坐标系,则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -\(1,0,2),(1,1,1)cos ,15AB DE AB DE \=-=\<>==-uu u r uu u r uu u r uuu r 从而直线AB 与DE所成角的余弦值为15(2)设平面DEC 一个法向量为1(,,),n x y z =u r11200(1,2,0),00x y n DC DC x y z n DE ì+=×=ìï=\íí++=×=ïîîu v u u u vu uu v u v uu u vQ 令112,1(2,1,1)y x z n =\=-=\=-u r设平面DEF 一个法向量为2111(,,),n x y z =u u r 11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ìì+=×=ïï=+=+=\íí×=ïîï++=îu u v u u u v u uu v u u u v u u u v u u u v uu u v u uv u u u v Q 令111272,5(2,7,5)y x z n =-\==\=-u ur12cos ,n n \<>==u r u u r因此sin 13q ==【点睛】本题考查利用向量求线线角与二面角,考查基本分析求解能力,属中档题.25.甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n 次这样的操作,记甲口袋中黑球个数为X n ,恰有2个黑球的概率为p n ,恰有1个黑球的概率为q n .(1)求p 1·q 1和p 2·q 2;(2)求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示).【答案】(1)112212716,,332727p q p q ====;;(2)()111222+33n n n n p q p q --+=+【解析】【分析】(1)直接根据操作,根据古典概型概率公式可得结果;(2)根据操作,依次求n n p q ,,即得递推关系,构造等比数列求得2n n p q +,最后根据数学期望公式求结果.【详解】(1)11131232,333333p q ´´====´´,211131211227++3333333927p p q ´´=´´=´´=´´,211231122222516+0+3333333927q p q ´´+´=´´+=´´=´´(2)1111131212++333339n n n n n p p q p q ----´´=´´=´´,111112*********+(1)+33333393n n n n n n q p q p q q -----´´+´´=´´+--´=-´´´,因此112122+333n n n n p q p q --+=+,从而11111212(2+),21(2+1)333n n n n n n n n p q p q p q p q ----+=+\+-=-,即1111121(2+1),2133n n n n n n p q p q p q -+-=-\+=+.又n X 的分布列为nX 012P1n np q --n q np 故1()213n n n nE X p q =+=+.【点睛】本题考查古典概型概率、概率中递推关系、构造法求数列通项、数学期望公式,考查综合分析求解能力,属难题.。
2023年高考化学真题完全解读(江苏卷)

2023年高考真题完全解读(江苏卷)2023年江苏高考化学卷在传承“宽基础、厚实践、重能力”风格中有发展,平稳中蕴新意。
试卷考查的知识内容基础、全面而不失新颖与创新,化学试卷保持了以往的命题风格,在化学基础知识中融合对考生学习方法和思维能力的考查、关注对考生学科素养的培养与提高。
整体呈现据标立本、紧密联系生产生活实际、紧跟学科前沿的风格,融合考查学生的化学学科必备知识、基本技能和学科核心素养,化学试题突出能力立意、突出学科特点、突出核心素养、突出创新能力的鲜明特色,有利于发挥高考的导向功能,有利于推进化学新课程教学改革。
试题主要特点如下:一、立足基础,考查主干知识试题突出了对中学化学核心基础知识、基本技能、基本观点和基本方法的考查。
考查学生对基础知识的掌握,对基本概念的理解。
掌握元素基础知识是能力提升的前提和保障,试卷中考查内容涵盖高中化学重要的元素化合物知识、基本概念与理论、化学基础实验技能和化学计算,覆盖了《考试大纲》中所要求掌握基础知识的90%以上。
部分试题命制素材直接源于教材,如第3题考查课本中学生熟悉的NH 4+的电子式、NO 2-中N 元素的化合价、N 2分子中存在N ≡N 键、H 2O 为非极性分子;第6题考查实验室制取Cl 2的实验原理及装置;第4题的微粒半径大小的比较、电离能变化规律、晶体类型判断;第8题氮及其化合物的转化过程中的变化、融合在工业流程分析及实验室制备少量NH 3原理。
对核心主干知识不仅仅是体现在记忆层面,还将考查对其的在具体问题解决过程中的理解和应用水平。
第10题是以金属硫化物(M x S y )催化反应为载体,考查反应的ΔS 、平衡常数、氧化还原反应、化学平衡等核心主干知识;第11题聚焦一些重要元素及其化合物间的转化,探究0.1mol·L -1 FeSO 4溶液的性质;第16题实验室模拟“镁法工业烟气脱硫”并制备MgSO 4·H 2O ,融合在工业流程分析、反应原理综合、实验及探究试题中进行考查,考查了调整溶液pH 对对物质转化行为的影响,以获得目标产物的思路方法。
(2022年)高考化学真题试卷(江苏卷)带答案解析

2022 年高考化学真题试卷〔江苏卷〕一、单项选择题〔共 10 题;共 20 分〕1. 糖类是人体所需的重要养分物质。
淀粉分子中不含的元素是〔〕【答案】 C【考点】多糖的性质和用途【解析】【解答】淀粉的化学式为(C 6H 10O 5)n , 故淀粉中含有碳元素、氢元素和氧元素,不含有氮元素,C 符合题意; 故答案为:C【分析】依据淀粉的化学式确定淀粉中所含和不含的元素。
2. 反响 NH 4Cl+NaNO 2=NaCl+N 2↑+2H 2O 放热且产生气体,可用于冬天石油开采。
以下表示反响中相关微粒的化学用语正确的选项是〔 〕【答案】 D【考点】原子中的数量关系,电子式、化学式或化学符号及名称的综合3. 以下有关物质的性质与用途具有对应关系的是〔 〕【答案】 BA. 氢B. 碳C. 氮D. 氧A. 中子数为 18 的氯原子: 18Cl 17B. N 2 的构造式:N=NC. Na +的构造示意图:D. H 2O 的电子式:【解析】【解答】A 、中子数为 18 的氯原子,其质量数=质子数+中子数=17+18=35,因此该原子的表示方 法为:35C l 17, A 不符合题意;B 、N 2 的构造式为 N≡N ,B 不符合题意;C 、Na 的最外层电子数为11,失去一个电子后形成Na+,其离子构造示意图为 , C 不符合题意;D 、H 2O 中存在两个氢氧共价键,其电子式为 故答案为:D, D 符合题意;【分析】A 、标在元素符号左上角的数字表示的是质量数,质量数=质子数+中子数; B 、N 2 分子中存在 N≡N ;C 、Na +是在 Na 原子的根底上失去最外层一个电子形成的;D 、H 2O 中存在着氢氧共价键;A. NH 4HCO 3 受热易分解,可用作化肥 C. SO 2 具有氧化性,可用于纸浆漂白B. 稀硫酸具有酸性,可用于除去铁锈 D. Al 2O 3 具有两性,可用于电解冶炼铝3 42 44 3 3 434 33【考点】镁、铝的重要化合物,化肥、农药及其合理利用,二氧化硫的漂白作用【解析】【解答】A 、NH4HCO 3 中含有氮元素,可作氮肥,做氮肥与其受热易分解的性质无关,A 不符合题意;B 、铁锈的主要成分是 Fe 2O 3 , 属于金属氧化物,金属氧化物能与酸反响,二者具有对应关系,B 符合题意;C 、SO 2 漂白纸浆的过程,是与纸浆中的有色物质发生化合反响形成无色物质,过程中没有涉及氧化复原反响,不表达 SO 2 的氧化性,该过程表达了 SO 2 的漂白性,C 不符合题意;D 、Al 2O 3 具有两性,既能与强酸溶液反响,也能与强碱溶液反响,该性质与电解冶炼铝的用途无关,D 不符合题意; 故答案为:B【分析】A 、受热易分解与做化肥无关; B 、金属氧化物能与酸反响;C 、SO 2 漂白纸浆表达了 SO 2 的漂白性;D 、Al 2O 3 具有两性,既能与强酸溶液反响,也能与强碱溶液反响; 4.室温下,以下各组离子在指定溶液中能大量共存的是〔 〕 A. 0.1 mol·L −1NaOH 溶液:Na +、K +、 CO 2− B. 0.1 mol·L −1FeCl 2 溶液:K +、Mg 2+、 SO 2− 、 AlO − 、 MnO − C. 0.1 mol·L −1K 2CO 3 溶液:Na +、Ba 2+、Cl −、OH −D. 0.1 mol·L −1H 2SO 4 溶液:K +、 NH + 、 NO − 、 HSO − 【答案】 A 【考点】离子共存【解析】【解答】A 、溶液中各离子相互间不形成难溶物〔或微溶物〕、不形成弱电解质、不形成易挥发性物质、不发生络合反响和氧化复原反响,可大量共存,A 符合题意;B 、溶液中的 MnO -具有氧化性,Fe 2+具有复原性,二者可发生氧化复原反响,不行大量共存,B 不符合题意;C 、溶液中的 Ba 2+能与 CO 2-形成 BaCO 3沉淀,不行大量共存,C 不符合题意; D 、溶液中 NO -在酸性条件下具有氧化性,能将HSO -氧化成 SO 2- , 同时H +能与 HSO -反响生成 SO 和33432H 2O ,不行大量共存,D 不符合题意; 故答案为:A【分析】A 、溶液中各离子相互间不发生反响; B 、MnO -具有氧化性,可将 Fe 2+氧化;C 、Ba 2+能与 CO 2-形成 BaCO 沉淀;D 、H +能与 HSO 3-反响形成 SO 2 和 H 2O ,NO 3-在酸性条件下具有氧化性; 5.以下试验操作能到达试验目的的是〔 〕A. 用经水潮湿的 pH 试纸测量溶液的 pHB. 将 4.0 g NaOH 固体置于 100 mL 容量瓶中,加水至刻度,配制1.000 mol·L −1NaOH 溶液C. 用装置甲蒸干 AlCl 3 溶液制无水 AlCl 3 固体D. 用装置乙除去试验室所制乙烯中的少量SO 2 【答案】 D【考点】溶液酸碱性的推断及相关计算,二氧化硫的性质,蒸发和结晶、重结晶,配制肯定物质的量浓度的溶液【解析】【解答】A 、测溶液的 pH 值时,应用枯燥干净的玻璃棒蘸取待测液滴在pH 试纸上,显色后与标准比色卡比照,得出溶液的pH 值;假设pH 试纸润湿,则相当于对溶液进展了稀释操作,对于酸性溶液,会使得结果偏大,对于碱性溶液,会的结果偏小,对于中性溶液,则无影响,A 不符合题意;B 、配制肯定物质的量浓度的溶液时,应先将固体在烧杯中溶解,恢复至室温后,再转移到容量瓶中, 不行在容量瓶内进展溶解操作,B 不符合题意;C 、AlCl 3 在水中易水解,产生 Al(OH)3 和具有挥发性的 HCl ,直接加热蒸发 AlCl 3 溶液,最终得到的是Al(OH)3 , 欲得到 AlCl 3 晶体,应在 HCl 气流中加热蒸发,以抑制 AlCl 3 的水解,C 不符合题意;D 、SO 2 能与NaOH 溶液反响,乙烯不能,故将混合气体通过NaOH 溶液,可除去乙烯中混有的SO 2 , D符合题意; 故答案为:D【分析】A 、依据测溶液 pH 的试验操作分析; B 、不能在容量瓶内进展溶解;C 、AlCl 3 在水中易水解,产生 Al(OH)3 和具有挥发性的 HCl ;D 、SO 2 能与 NaOH 溶液反响,乙烯不能;6. 以下有关化学反响的表达正确的选项是〔 〕【答案】 C【考点】氯气的试验室制法,硝酸的化学性质,二氧化硫的性质,钠的化学性质【解析】【解答】A 、常温下,浓硝酸能使铁钝化,稀硝酸不能使铁钝化,A 不符合题意; B 、试验室制取 Cl 2 所用的试剂为 MnO 2 和浓盐酸,MnO 2 与稀盐酸不反响,B 不符合题意; C 、氨水过量,则 SO 2 反响,反响生成(NH 4)2SO 3 , C 符合题意;D 、室温下,Na 与空气中的O 2 反响生成 Na 2O ,在加热条件下, 反响生成 Na 2O 2 , D 不符合题意; 故答案为:C【分析】A 、常温下,浓硝酸能使铁钝化;A. Fe 在稀硝酸中发生钝化C. SO 2 与过量氨水反响生成(NH 4)2SO 3 B. MnO 2 和稀盐酸反响制取 Cl 2D. 室温下 Na 与空气中O 2 反响制取 Na 2O 2A. 原子半径:r (W)> r (Z)> r (Y)> r (X)B. 由X 、Y 组成的化合物是离子化合物C. Z 的最高价氧化物对应水化物的酸性比W 的强D. W 的简洁气态氢化物的热稳定性比X 的强 32 2 2223B 、依据试验室制取 Cl 2 的原理分析;C 、氨水过量,则 SO 2 少量,反响生成 SO 2-;D 、室温下, Na 与O 2 反响生成 Na 2O ;7. 以下指定反响的离子方程式正确的选项是〔 〕A. 室温下用稀 NaOH 溶液吸取 Cl :Cl +2OH −=ClO −+Cl −+H OB. 用铝粉和 NaOH 溶液反响制取少量H :Al+2OH −= AlO − +H ↑ 2 22 C. 室温下用稀 HNO溶解铜:Cu+2NO − +2H +=Cu 2++2NO ↑+H O33 2 2D. 向 Na 2SiO 3 溶液中滴加稀盐酸:Na 2SiO 3+2H +=H 2SiO 3↓+2Na + 【答案】 A【考点】离子方程式的书写【解析】【解答】A 、Cl 2 与 NaOH 溶液反响生成 NaCl 、NaClO 和H 2O ,该反响的离子方程式为: Cl 2+2OH −=ClO −+Cl −+H 2O ,A 符合题意;B 、Al 与 NaOH 溶液反响的离子方程式为:2Al+2OH -+2H 2O=2AlO -+3H ↑,B 不符合题意;C 、铜与稀硝酸反响的离子方程式为:3Cu+8H ++2NO -=3Cu 2++2NO↑+4H O ,C 不符合题意;32D 、盐酸与 Na 2SiO 3 溶液反响的离子方程式为:SiO 2-+2H +=H 2SiO 3↓,D 不符合题意; 故答案为:A【分析】A 、Cl 2 与 NaOH 溶液反响生成 NaCl 、NaClO 和 H 2O ; B 、不满足电荷守恒; C 、左右两边电荷不守恒;D 、Na 2SiO 3 是可溶性盐,在离子方程式中可以拆解成离子形式;8. 短周期主族元素X 、Y 、Z 、W 的原子序数依次增大,X 是地壳中含量最多的元素,Y 原子的最外层有2 个电子,Z 的单质晶体是应用最广泛的半导体材料,W 与X 位于同一主族。
2023年江苏卷地理高考真题及答案解析
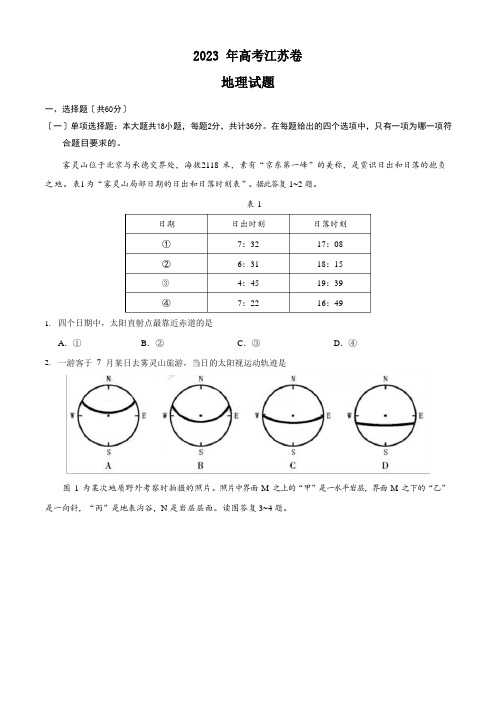
2023 年高考江苏卷地理试题一、选择题〔共60分〕〔一〕单项选择题:本大题共18小题,每题2分,共计36分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
雾灵山位于北京与承德交界处,海拔2118 米,素有“京东第一峰”的美称,是赏识日出和日落的抱负之地。
表l 为“雾灵山局部日期的日出和日落时刻表”。
据此答复1~2 题。
表1日期日出时刻日落时刻①7:32 17:08②6:31 18:15③4:45 19:39④7:22 16:491.四个日期中,太阳直射点最靠近赤道的是A.①B.②C.③D.④2.一游客于7 月某日去雾灵山旅游,当日的太阳视运动轨迹是图1 为某次地质野外考察时拍摄的照片。
照片中界面M 之上的“甲”是一水平岩层,界面M 之下的“乙”是一向斜,“丙”是地表沟谷,N是岩层层面。
读图答复3~4题。
3.界面M 反映的地质含义不同于N 的是A.沉积物变化4.该区域B.古气候变化C.古环境变化D.构造运动变化A.甲抬升前持续承受沉积C.乙形成后经受长期侵蚀B.乙形成时代晚于甲岩层D.丙是背斜受侵蚀的结果图2 为“某地地形与甲地建筑物布局示意图”。
读图答复5~6 题。
5.与乙地相比,将建筑物布局在甲地主要考虑的因素是A.地形B.水源C.植被D.坡向6.与甲地地形平坦方式相符的剖面是图3 为“某月19 日18 时澳大利亚海平面等压线分布图”。
读图答复7~8 题。
7.该月最可能是A.3 月8.此时,澳大利亚A.①地天高云淡C.③地南风暴雨B.6 月C.8 月D.10 月B.②地干热风大D.④地北风炎热图4 为“我国某城市不同年份各年龄段人口数量占比图”。
读图答复9~10 题。
9.与2023 年相比,2023 年该城市A.人口总数削减B.老龄化加剧C.平均年龄减小D.劳动力增多10.影响该城市人口年龄构造变化的主要因素是A.自然增长B.医疗水平C.机械增长D.生育观念城市不透水面是指阻挡水分下渗到土壤的城市人工地面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014江苏卷答案解析21.【考点】考察状语从句连词辨析【答案】A【解析】本题考察的是状语从句的连词辨析。
Though尽管;as随着,因为;since自从,既然;unless除非,如果…不…;句意:尽管历史不能改变,但是为了面对未来我们还是要从历史中学会教训。
根据句意可知上下文之间存在着转折关系,所以使用though表示让步和转折。
故A。
22.【考点】考察定语从句【答案】D【解析】本题定语从句的先行词是work,后面的定语从句a good impression is a must的句子结构很完整,所以使用关系副词在句中做状语,同时也引导起这个定语从句。
句意:在日常交流中这本书书帮助了很多,尤其是在需要有良好印象的工作之中。
AC两项都是关系代词在句中不能做状语,when的先行词通常都是指时间的名词。
故D正确。
【试题延伸】where引导定语从句时,是表示地点或者抽象意义“在…方面”,本身在从句部分充当地点状语。
并且有些时候一些词会很抽象的用作地点,比如,case,stage,position,state,activity,business,occasion,situation,point,work等,但也要视情况而定。
23.【考点】考察时态【答案】C【解析】句意:—你对即将在南京举行的青奥会了解多少?—很好,媒体以多种形式对青奥会举行了报道。
根据本句中的well,可知后者对青奥会很了解。
这主要是因为媒体多种形式的报道,本句使用现在完成时体现出过去所发生的事情对现在的影响。
故C正确。
24.【考点】考察介词短语辨析【答案】C【解析】in place有序,在适当的位置;in order井井有条;in shape健康的,状态良好的;in fashion流行的,时尚的;句意:为了保持健康,每天早晨Tom总去慢跑,也经常做引体向上。
根据句意可知Tom锻炼的目的是为了保持健康。
故C正确。
25.【考点】考察动词词义辨析【答案】A【解析】Chase追求,追逐;register登记,注册;offer提供;compensate补偿,赔偿;句意:来自大学里的优秀毕业生收到大公司的追逐。
根据句意说明A正确。
26.【考点】考察名词性从句【答案】B【解析】本题考察的是名词性从句中的表语从句。
表语从句通常都是放在系动词be的后面,说明主语的情况。
本句中的what引导起宾语从句,并在宾语从句里放在made me的后面做宾语补足语。
句意:—真乱啊!你总说这么懒!—我不应该受到责备。
是你让我成为这样的。
That在表语从句中不能做成分,how在句中做状语。
Who指人,通常都做主语。
故B正确。
27.【考点】考察名词词义辨析【答案】A【解析】A象征;标志;符号;记号;代表人物;B肖像;identity身份;statue雕像,塑像;句意:虽然两年前就已遭软禁,她在去年的选举中仍然是势力强大的代表人物。
故A正确。
28.【考点】考察形容词词义辨析。
【答案】B【解析】Rigid僵硬的,死板的;sure确信的,肯定的,有把握的;perfect完美一的;fair 公平的;句意:“幸福,“可以肯定的是,不是个静态简单的定义。
根据句意说明B项符合。
29.【考点】考察非谓语动词用法【答案】D【解析】本题较难,a lively question-and-answer session followed是一个完整的句子,本题的两部分之间缺少连词,所以逗号前面的不能是句子,只能是一个独立主格结构。
名词his lecture与动词give之间构成被动关系,所以使用过去分词表示被动,排除B项。
A项表示正在进行,C项不定式表示将要进行。
都符合语义,D项having been done在做状语的时候相当于done。
本句的独立主格结构His lecture having been given相当于After his lecture had been given。
句意:他的演讲结束后,将是一个现场问答部分。
故D正确。
30.【考点】考察动词短语辨析【答案】B【解析】本题考察的是动词pay及put的短语辨析。
Pay back偿还;报复;报答;偿付;pay off 付清;(付清工资后)解雇;(努力)得到回报;put away收拾,整理,放在一边,不管不顾;put off推迟;句意:—爸爸,我认为Oliver并不是这份工作的合适人选。
—我明白的,我马上就去付清他的工资,解雇他。
根据句意本句中的pay off表示(付清工资后)解雇。
故B。
31.【考点】考察情态动词词义辨析【答案】C【解析】本题考察的是情态动词的特殊意义。
Might也许;would会,过去常常做某事;should 应该,竟然;could能够;句意:让我难过的是,如此贫穷的他们竟然给我带来了食物。
根据句意可知本句中的should表示“竟然”。
故C正确。
【试题延伸】在平时的学习中既要注意情态动词的基本含义,也要注意情态动词的特殊意义,如must偏偏,非得;should竟然;mustn’t禁止,千万不能;等等。
情态动词Shall用于所有人称,表示命令,警告,允诺;以及法律规定中要做的事情。
32.【考点】考察副词词义辨析【答案】D【解析】Also也;just只不过,仅仅;nevertheless 然而,不过;otherwise要不然;另外;句意:星期天我不能去接你了,另外我还会很忙。
故D正确。
33.【考点】考察动词词义辨析【答案】D【解析】本题考察的是以字母r开始的动词词义辨析。
Remember记得;remind提醒,使…想起…;recover康复;recall回忆;句意:相传端午节是为了让我们想起屈原的精神。
B项应该使用remind sb of sth使某人想起某事。
根据句意说明D正确。
34.【考点】考察代词词义辨析【答案】C【解析】Something某些事情,重要人物;anything任何事情,一些事情;everything一切;nothing没有东西;没有事情;无关紧要的东西;句意:优秀的家庭对她的成员们来说意味着许多,但并不是一切。
根据句意可知本句使用everything一切符合上下文含义。
故C正确。
35.【考点】考察交际用语【答案】A【解析】本题考察的是交际用语。
Dear me天哪!(表示惊讶)Hi,there嗨,你好;Thank goodness 谢天谢地;Come on加油;得了吧!句意:—天哪!有人让实验室的门开着。
—不要看着我!不是我干的。
根据句意可知前者对于实验室的门还开着很惊讶。
故选择A项。
第二节完形填空(共20小题,每小题1分,满分20分)【考点】考察人生哲理类完型填空【文章大意】人生中最重要的是要拥有自己。
有了自信,我们就可以做到我们想做的任何事情。
本文以大师戴尔•卡耐基的成功故事告诉我们信心的重要性。
36.【答案】D 【试题解析】考察动词词义辨析。
A承认;B填充,装满;C提供;D认识到;认出;戴尔•卡耐基从密苏里的一个默默无闻的农场里走出来成为一名国际大师,是因为他找到一个方法来满足人们共同的需要。
这个需要是1906年他在StateTeachers College学习的时候意识到的。
本句是一个强调句型,强调的是recognize的宾语need。
37. 【答案】B 【试题解析】考察名词词义辨析及上下文串联。
A任务;工作;B教育;C优势;D指导;为了得到教育,戴尔•卡耐基与很多困难在做斗争。
根据下文叙述可知他为了求得教育,他克服了很多困难。
38. 【答案】B 【试题解析】考察名词辨析及语境理解。
A培训;B寄宿膳食;C教育;D设备;他的父亲没有钱付他的大学寄宿膳食的钱,他不得不骑马12英里去上学。
39. 【答案】A 【试题解析】考察介词辨析。
A在…之间;B在…期间;C超过;越过;C通过;他的很多学习都是在农场到学校途中进行的,因为他在上学的路上要花很多时间。
40. 【答案】C 【试题解析】考察连词辨析及上下文串联。
A当…时;然而,尽管;B当…时;C因为;D尽管;因为他没有时间也没有衣服,所以他没有参加各种学校的活动。
上下文之间存在着因果关系,所以使用because。
41. 【答案】D 【试题解析】考察名词辨析及上下文串联。
A允许,许可证;B兴趣;C才干;D 服装;因为他没有时间也没有衣服,所以他没有参加各种学校的活动。
ABC三项与句意不相符。
42. 【答案】B 【试题解析】考察固定搭配。
Try on试穿;try for申请;他申请参加足球队,但是教练拒绝了他,说他太体重太轻了。
43. 【答案】A 【试题解析】A轻的;淡的;B灵活的;C乐观的;D外向的;BCD三项和教练拒绝队员没有联系,如果队员过于瘦弱,不适合足球这项剧烈运动,教练的拒绝是有理由的。
44. 【答案】C 【试题解析】A赢得;B实现;C形成,发展;D获得;在这段时间里,卡耐基慢蛮难第形成了一种自卑感。
通常都使用develop表示养成,形成一种性格。
故C正确。
45. 【答案】A 【试题解析】考察动词词义辨析及语境理解。
A阻止;B保护;C挽救;D使…免受;他妈妈知道这种自卑感会阻止他发展自身的潜力。
本句中的prevent sb from doing sth 阻止某人做某事,这个结构符合上下文含义。
46. 【答案】A 【试题解析】考察动词词义辨析及语法。
A建议;B要求;C请求;D坚持要求,坚持认为;他的妈妈建议他参加辩论队,认为辩论队里的演讲的练习会给与他所需要的认可和信心。
根据句意说明A项正确,而且在join前面省略了should,这是一个虚拟语气。
47. 【答案】B 【试题解析】考察名词词义辨析及上下文串联。
A出席;B练习;C耐心;D潜力;;他的妈妈建议他参加辩论队,认为辩论队里的演讲的练习会给与他所需要的认可和信心。
故B正确。
48. 【答案】C 【试题解析】考察副词词义辨析及上下文串联。
A有希望地;B当然;C最后;D 自然地;卡耐基采纳了妈妈的建议,多次努力以后,最后终于成功了。
根据after several attempts可知C项正确。
49. 【答案】D 【试题解析】考察词义辨析。
A关键的;B破坏的;C基本的;D转折的;turning point转折点。
这件事情证明是他人生的转折点。
从此他走了上成功之路。
50. 【答案】D 【试题解析】考察名词词义辨析及上下文串联。
A进步;B经历,经验;C能力,技能;D自信;在很多人面前发表演讲帮助他得到了他所需要的信心。
之前他曾经一度很自卑,现在演讲让他重新获得自信。
51. 【答案】C 【试题解析】考察上下文串联。
A骑马;B足球;C演讲;D农艺;到他大四的时候,他赢得了演讲方面所有的最高荣誉。
有很多学生都来向他寻求指导,接着在他的指导之下,他们也相继赢得了比赛。
