九年级数学_25.2_用列举法求概率(课件人教版.ppt)
合集下载
人教版九年级数学上册优质课课件《25.2列表法求概率》

拓广探索
• 在围棋盒中有x颗黑色棋子 和y颗白色棋子,从盒中随 机地取出一个棋子,如果它 是黑色棋子的概率是3/8, 写出表示x和y关系的表达 式.如果往盒中再放进10颗 黑色棋子,则取得颗黑色棋 子的概率为1/2,求x和y的 值.
小结
拓展
从表面上看,随机现象的每一次观察结果都是偶 然的,但多次观察某个随机现象,立即可以发现: 在大量的偶然之中存在着必然的规律.
本题中元音字母: A E I 辅音字母: B C D H
• 例题选讲 • 甲乙两个同学做“石头、剪刀、布”的 游戏,在一个回合中两人能分出胜负的 概率是多少? • 分析:(1)一个回合:那么是几次等 可能试验?树形图应该画几级?(甲、 乙独立出拳的,应该算两次) • (2)每一个级别里应该画几条树枝? (每个试验的结果有几种可能性)
用列表法求概率时应注意各种结果出现的 可能性必须相同. 用列表格法的优缺点及局限性. 有放回还是无放回的问题
要学会建立适当的数学模型
小结
拓展
回 味 无 穷
用树状图或表格表示概率
1、利用树状图或表格可以清晰地表示出某 个事件发生的所有可能出现的结果;从而较 方便地求出某些事件发生的概率.
2 根据不同的情况选择恰当的方法表示某个事 件发生的所有可能结果。 3.当试验包含两步时,列表法比较方便,当然, 此时也可以用树形图法,当试验在三步或三 步以上时,用树形图法方便.
.“手心手背”是同学们中间广为流传的游戏, 游戏时甲、乙、丙三方每次做“手心”“手背” 两种手势中的一种,规定:⑴出现三个相同手 势不分胜负须继续比赛;⑵出现一个“手心” 和或一个“手背”和两个“手心”时,则一种 手势者为胜,两种相同手势者为负。 假定甲、乙、丙三人每次都是等可能地做这 两种手势,那么,甲、乙、丙三位同学胜的 概率是否一样?这个游戏对三方是否公平? 若公平,请说明理由,若不公平,如何修改 游戏规则才能使游戏对三方都公平?
人教版数学九上25.2 用列举法求概率(精品课件共2课时52页)

3
于4为事件B. () = 16
第1次
第2次
1
2
3
4
1
2
3
4
(1,1)
(2,1)
(3,1)
(4,1)
(1,2)
(2,2 )
(3,2)
(4,2)
(1,3)
15
5
2.一个不透明的袋中有四个完全相同的小球,把它们分别标号为
1,2,3,4.随机地摸取一个小球然后放回,再随机地摸出一个小球.
求下列事件的概率:
(1)两次取出的小球标号相同;
(2)两次取出的小球标号和等于4.
解:(1)记两次取出的小球标号
4
1
相同为事件A. () = 16 = 4
(2)记两次取出的小球标号和等
一共有结果
4种
一正一反的结果 2种
2
1
P(老师赢) = = .
4
2
2
1
P(学生赢)= = .
4
2
两面一样的结果 2种
答:因为P(老师赢) = P(学生赢),
所以这个游戏公平.
“同时掷两枚质地均匀的硬币”与“先后两次掷
一枚硬币”,这两种试验的所有可能结果一样吗?
第一次 第二次 所有可能的结果
(正,正)
的m种结果)求事件发生的概率的方法,我们称为直接列举法.
注意:(1)为保证结果不重不漏,直接列举时,要有一定的顺序性.
(2)用列举法求概率的前提条件有两个:
①所有可能出现的结果是有限个;
②每个结果出现的可能性相等.
(3)所求概率是一个准确数,一般用分数表示.
新知探究 跟踪训练
例1 若我们把十位上的数字比个位和百位上数字都小的三位数称
于4为事件B. () = 16
第1次
第2次
1
2
3
4
1
2
3
4
(1,1)
(2,1)
(3,1)
(4,1)
(1,2)
(2,2 )
(3,2)
(4,2)
(1,3)
15
5
2.一个不透明的袋中有四个完全相同的小球,把它们分别标号为
1,2,3,4.随机地摸取一个小球然后放回,再随机地摸出一个小球.
求下列事件的概率:
(1)两次取出的小球标号相同;
(2)两次取出的小球标号和等于4.
解:(1)记两次取出的小球标号
4
1
相同为事件A. () = 16 = 4
(2)记两次取出的小球标号和等
一共有结果
4种
一正一反的结果 2种
2
1
P(老师赢) = = .
4
2
2
1
P(学生赢)= = .
4
2
两面一样的结果 2种
答:因为P(老师赢) = P(学生赢),
所以这个游戏公平.
“同时掷两枚质地均匀的硬币”与“先后两次掷
一枚硬币”,这两种试验的所有可能结果一样吗?
第一次 第二次 所有可能的结果
(正,正)
的m种结果)求事件发生的概率的方法,我们称为直接列举法.
注意:(1)为保证结果不重不漏,直接列举时,要有一定的顺序性.
(2)用列举法求概率的前提条件有两个:
①所有可能出现的结果是有限个;
②每个结果出现的可能性相等.
(3)所求概率是一个准确数,一般用分数表示.
新知探究 跟踪训练
例1 若我们把十位上的数字比个位和百位上数字都小的三位数称
人教版九年级数学上册25.2 用列举法求概率课件(共42张PPT)

过程与方法
理解 的结果,其中A包含m种)的意义,并能解决 一些实际问题。探究用特殊方法 “列举法” 求概率的简便方法,然后应用这种方法解决 一些实际问题。
P(A) = m (在一次试验中有n种可能 n
教学目标
情感态度与价值观
通过丰富的数学活动,交流成功的经 验,体验数学活动充满着探索和创造,体 验数学方法的多样性灵活性,提高解题能 力。
3 1 = 6 2
(3)点数大于2且小于5有2种可能,即点数 为 3, 4,
P(点数大于2且小于5)=
2 1 = 6 3
例2:掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上; (3)一枚硬币正面朝上,一枚硬币反面朝上。
解:我们把掷两枚硬币所能产生的结果全部 列举出来,它们是:正正,正反,反正,反 反。所有的结果共有4个,并且这4个节结果 出现的可能性相等。 (1)所有的结果中,满足两枚硬币全部正面 朝上(记为事件A)的结果只有一个,即“正 1 正”,所以P(A)=
6
(1)以上两个试验有什么共同的特点? 一次试验中,可能出现的结果有限个。一 次试验中,各种结果发生的可能性相等。 (2)对于上述所说的试验,如何求事件的概率? 一般地,如果在一次试验中,有n种可 能的结果,并且它们发生的可能性都相等, 事件A包含其中的m种结果,那么事件A发生 m 的概率为 . P A =
(2)满足两个骰子的点数之和是9(记为事 件B)的结果有4个,则
4 1 P( B) = = 9 36
(3)满足至少有一个骰子的点数为2(记为 事件C)的结果有11个,则
P(C)=
11 36
想一想
“同时掷两枚硬币”,与“先后两次掷 一枚硬币”,这两种试验的所有可能结果 一样吗?
人教版九年级数学上册《用列举法求概率》概率初步PPT精品教学课件

板书设计
把两枚骰子分别记为第1枚和第2枚,这样就可以用下面的方形表格列举出
所有可能出现的结果.
解决问题
两枚骰子分别记为第1枚和第2枚,所有可能的结果列表如下:
(1)满足两枚骰子点数相同(记为事件A)的结果有6个
6
1
(表中斜体加粗部分),所以P(A)= 36 = 6.
(2)满足两枚骰子的和是9(记为事件B)的结果有4个
2.如图所示的扇形图给出的是地球上海洋、陆地的表面积约占地球表面积的
百分比. 若宇宙中有一块陨石落在地球上,则它落在海洋中的概率是
%.
达标检测
1.“同吋掷两枚质地均匀的骰子,至少有一枚骰子的点数是3”的概率为
(
)
1
A.
3
11
B.
36
5
C.
12
1
D.
4
2.不透明的袋子中装有红球1个、绿球1个、白球2个,这些球除颜色外无
出场,由于人为指定出场顺序不合规,要重新抽签确定出场顺序,则抽签后三个
运动员出场顺序都发生变化的概率是
.
达标检测
5.一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,
2
3
其中红球1个,若从中随机摸出一个球,这个球是白球的概率为 .
(1)求袋子中白球的个数;
(2)随机摸出一个球后放回并搅匀,再随机摸出一个球,请用画树状图
5
,全是辅音字母的结果有两个,
12
2
1
即BCH,BDH,所以P(三个辅音)= = .
12
6
P(一个元音)=
练习巩固
1.经过某十字路口的汽车,可能直行,也可能左转或右转. 如果这三种可能
人教版九年级上册25.2 用列举法求概率 (共45张PPT)

答案:7/18.
概率与函数综合 点M(x,y)可以在数字-1,0,1,2中任意选取.试求 (1)点M在第二象限内的概率. (2)点M不在直线y=-2x+3上的概率.
答案:(1)1/4;(2)7/8.
电流通过的概率
已知电流在一定时间段内正常通过电子元件 的概率是0.5,分别在一定时间段内,A、B之间和C、D之 间电流能够正常通过的概率.
练习
2. 有6张看上去无差别的卡片,上面分别写着1,2,3,4,5, 6. 随机抽取1张后,放回并混在一起,再随机抽取1张,那么 第二次取出的数字能够整除第一次取出的数字的概率是多少?
练习 某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意 拿一件衬衫和一条长裤,求正好是一套白色的概率______.
答案:甲获胜的概率是1/4, 乙获胜的概率是3/4,不公平.
练习 先后抛掷三枚均匀的硬币,至少出现一次正面的概率_____.
答案:7/8.
练习 有两把不同的锁和三把钥匙,其中两把钥匙恰好能分别打开这 两把锁,第三把钥匙不能打开这两把锁.任意取一把钥匙去开 任意一把锁,一次打开锁的概率是多少?
答案:1/3.
答案:1/2.
练习——是否放回 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早 上起床没看清随便穿了两只就去上学,问小明正好穿的是相同 的一双袜子的概率是多少?
答案:1/3.
练习——是否放回 在6张卡片上分别写有1~6的整数,随机的抽取一张后放回,再 随机的抽取一张,那么,第一次取出的数字能够整除第2次取出 的数字的概率是多少?
A AA AA A B B B BB B C CD DE E C C D DE E HI HI HI HI H I HI
(1)P(1个元音)
概率与函数综合 点M(x,y)可以在数字-1,0,1,2中任意选取.试求 (1)点M在第二象限内的概率. (2)点M不在直线y=-2x+3上的概率.
答案:(1)1/4;(2)7/8.
电流通过的概率
已知电流在一定时间段内正常通过电子元件 的概率是0.5,分别在一定时间段内,A、B之间和C、D之 间电流能够正常通过的概率.
练习
2. 有6张看上去无差别的卡片,上面分别写着1,2,3,4,5, 6. 随机抽取1张后,放回并混在一起,再随机抽取1张,那么 第二次取出的数字能够整除第一次取出的数字的概率是多少?
练习 某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意 拿一件衬衫和一条长裤,求正好是一套白色的概率______.
答案:甲获胜的概率是1/4, 乙获胜的概率是3/4,不公平.
练习 先后抛掷三枚均匀的硬币,至少出现一次正面的概率_____.
答案:7/8.
练习 有两把不同的锁和三把钥匙,其中两把钥匙恰好能分别打开这 两把锁,第三把钥匙不能打开这两把锁.任意取一把钥匙去开 任意一把锁,一次打开锁的概率是多少?
答案:1/3.
答案:1/2.
练习——是否放回 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早 上起床没看清随便穿了两只就去上学,问小明正好穿的是相同 的一双袜子的概率是多少?
答案:1/3.
练习——是否放回 在6张卡片上分别写有1~6的整数,随机的抽取一张后放回,再 随机的抽取一张,那么,第一次取出的数字能够整除第2次取出 的数字的概率是多少?
A AA AA A B B B BB B C CD DE E C C D DE E HI HI HI HI H I HI
(1)P(1个元音)
九年级数学上册 第二十五章 概率初步 25.2 用列举法求概率教学课件 (新版)新人教版.pptx

21
四、强化训练
18
二、新课讲解
红,红; 红,黑; 黑,红 黑,黑. 画树状图 ;
列表
列举
第一次抽出 一张牌
红牌
黑牌
第二次抽出 一张牌
红牌 黑牌 红牌
黑牌
第一次抽 第二次抽 出一张牌 出一张牌
红牌 黑牌
红牌 黑牌 红牌 黑牌
19
二、新课讲解
可能产生的结果共4个。每种出现的可
能性相等。各为 1
4
1 。即概率都为 4
解:两枚骰子分别记为第一枚和第二枚,可以用表 格列举出所有可能的结果.
10
二、新课讲解
一 二
1
1 (1,1)
2
(2,1)
3
(3,1)
4
(4,1)
5(5,1)Fra bibliotek6(6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
11
P(C)=
36
13
二、新课讲解
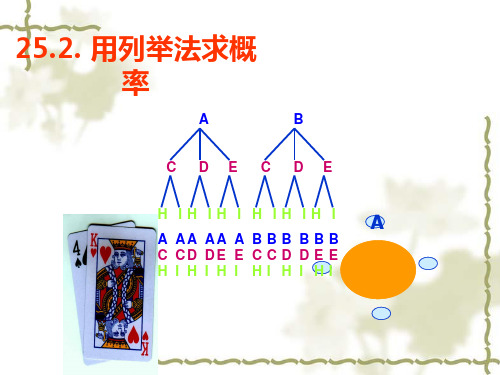
例3 甲口袋中装有2个相同的小球,它们分别写有字母A 和B;乙口袋中装有3个相同的小球,它们分别写有字母C、 D和E;丙口袋中装有2个相同的小球,它们分别写有字母 H和I,从3个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个,2个和3个元音字 母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少?
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
四、强化训练
18
二、新课讲解
红,红; 红,黑; 黑,红 黑,黑. 画树状图 ;
列表
列举
第一次抽出 一张牌
红牌
黑牌
第二次抽出 一张牌
红牌 黑牌 红牌
黑牌
第一次抽 第二次抽 出一张牌 出一张牌
红牌 黑牌
红牌 黑牌 红牌 黑牌
19
二、新课讲解
可能产生的结果共4个。每种出现的可
能性相等。各为 1
4
1 。即概率都为 4
解:两枚骰子分别记为第一枚和第二枚,可以用表 格列举出所有可能的结果.
10
二、新课讲解
一 二
1
1 (1,1)
2
(2,1)
3
(3,1)
4
(4,1)
5(5,1)Fra bibliotek6(6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
11
P(C)=
36
13
二、新课讲解
例3 甲口袋中装有2个相同的小球,它们分别写有字母A 和B;乙口袋中装有3个相同的小球,它们分别写有字母C、 D和E;丙口袋中装有2个相同的小球,它们分别写有字母 H和I,从3个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个,2个和3个元音字 母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少?
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
人教版数学九年级上册25.2用列举法求概率(共48张PPT)

在一次试验中,如果可能出现的结果只有有限个, 且各种结果出现的可能性大小相等,那么我们可以通过 列举试验结果的方法,求出随机事件发生的概率,这种 求概率的方法叫列举法.
1 、创设情景,发现新知
每次选择2名同学分别拨动A、B两个转盘上的 指针,使之产生旋转,指针停止后所指数字较 大的一方为获胜者,(若箭头恰好停留在分界 线上,则重转一次)。 作为游戏者,你会选择哪个装置呢?
5
6
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
解:由表中可以看出,在两堆牌中分别取一张,它可 能出现的结果有36个,它们出现的可能性相等 但满足两张牌的数字之积为奇数(记为事件,1)(5,3)(5,5) 这9种情况,所以
学习重难点
1、一般地,如果在一次试验中,有几种可能的 结果,并且它们发生的可能性都 相等,事件A包含其中的。种结果,那么事件A发 生的概率为P(A)= ,以及运用它 解决实际间题. 2、通过实验理解P(A)= 并应用它解决一些具体题 目
回答下列问题,并说明理由. (1)掷一枚硬币,正面向上的概率是_______; (2)袋子中装有 5 个红球,3 个绿球,这些球除了 颜色外都相同,从袋子中随机摸出一个球,它是红色的 概率为________; (3)掷一个骰子,观察向上一面的点数,点数大 于 4 的概率为______.
你能求出小亮得分的概率吗?
用表格表示
红桃 黑桃
1
2
3
4
5
6
1
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2
3 4
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
人教版九年级上25.2 用列举法求概率(2)PPT教学课件

5,7(两个转盘除表面数字不同外,其他完
全相同)。每次选择2名同学分别拨动A、B两
个转盘上的指针,使之产生旋转,指针停止
后所指数字较大的一1 方为获胜者,负者则表
演一个节目(若箭头恰好停留在分界线4 上,
8
7
则重转一次)。作6为游戏者,你会选5 择哪个
装置呢?并请说明理由。 A
2020/12/09
图2 联欢晚会游戏转盘
2020/12/09
7
PPT精品课件
谢谢观看
Thank You For Watching
8
所得结果没有影响。
21~6的整数,随机的抽取一张后放 回,再随机的抽取一张,那么,第 一次取出的数字能够整除第2次 取出的数字的概率是多少?
问:我们以前做的题目可以用列表法吗?
2020/12/09
6
练习2:一天晚上小伟帮助妈妈 清洗两个只有颜色不同的有盖 茶杯,此时突然停电了,小伟 只好把杯盖和茶杯随即地搭配 在一起,求颜色搭配正确和颜 色搭配错误的概率各是多少? (P153第4题)
25.2. 用列举法求概率(2)
2020/12/09
Waiyuxuexiao
Liudeguang
1
2006.10.17
复习引入
等可能性事件(古典概形)的两个特征: 1.出现的结果有限多个; 2.各结果发生的可能性相等;
等可能性事件的概率-------列举法
2020/12/09
2
复习:
已知一纸箱中装有5个只有颜色不 同的球,其中2个白球,3个红球。
B
4
例1、同时掷两个质地均匀的骰子,计算 下列事件的概率: (1)两个骰子的点数相同 (2)两个骰子点数之和是9 (3)至少有一个骰子的点数为2
《用列举法求概率》九年级初三数学上册PPT课件

2.两次结果点数的和是9,
6
36
1.满足条件的可能有6种,P(两次结果点数相同)=
2.满足条件的可能有4种,P(两次结果点数和为9)=
3.至少有一次结果的点数为2。
=
4
36
=
3.满足条件的可能有11种,P(至少一次结果点数为2)=
解:通过题意可以画出如下树状图,可能出现的36种结果,并且它们出现的概率是相同的。
时间:20XX
3.满足条件的可能有2种,即“正反”“反正”
P(两枚硬币正面和反面朝上各一枚)=
2 1
=
4 2
观察这两个问题,抛掷方法改变后,
试验产生的结果一样吗?
情景引入
观察这两个问题,抛掷方法改变后,得到的结果一样吗?为什么?
把一枚质地均匀的骰子投两次,观察向上一面的点数,求下列事件的概率.
1.两次结果的点数相同,
时间:20XX
前言
学习目标
1.用列举法(包括列表、画树状图)计算简单事件发生的概率。
2.能画“两级”树状图求简单事件概率。
3.通过观察列举法的结果是否重复和遗漏。
重点难点
重点:能够运用列表法和树状图法计算简单事件发生的概率。
难点:不重复不遗漏的列出所有可能的情况。
情景引入
【分析】在一次试验中,如果可能出现的结果
I H
I
H
I H
I H
I
A A A A A A B B B B B B
C C D D E E C C D D E E
H I H I H I H I H I H I
① ② ① ② ② ③ 辅 ① 辅 ① ① ②
1
2)全是辅音有2种可能,P(1个元音)=6
6
36
1.满足条件的可能有6种,P(两次结果点数相同)=
2.满足条件的可能有4种,P(两次结果点数和为9)=
3.至少有一次结果的点数为2。
=
4
36
=
3.满足条件的可能有11种,P(至少一次结果点数为2)=
解:通过题意可以画出如下树状图,可能出现的36种结果,并且它们出现的概率是相同的。
时间:20XX
3.满足条件的可能有2种,即“正反”“反正”
P(两枚硬币正面和反面朝上各一枚)=
2 1
=
4 2
观察这两个问题,抛掷方法改变后,
试验产生的结果一样吗?
情景引入
观察这两个问题,抛掷方法改变后,得到的结果一样吗?为什么?
把一枚质地均匀的骰子投两次,观察向上一面的点数,求下列事件的概率.
1.两次结果的点数相同,
时间:20XX
前言
学习目标
1.用列举法(包括列表、画树状图)计算简单事件发生的概率。
2.能画“两级”树状图求简单事件概率。
3.通过观察列举法的结果是否重复和遗漏。
重点难点
重点:能够运用列表法和树状图法计算简单事件发生的概率。
难点:不重复不遗漏的列出所有可能的情况。
情景引入
【分析】在一次试验中,如果可能出现的结果
I H
I
H
I H
I H
I
A A A A A A B B B B B B
C C D D E E C C D D E E
H I H I H I H I H I H I
① ② ① ② ② ③ 辅 ① 辅 ① ① ②
1
2)全是辅音有2种可能,P(1个元音)=6
人教版九年级上 25.2用列举法求概率(2)(15张ppt)

2、列表时要注意顺序、括号及逗号的正 确使用。
(1)点数为2; (2)点数为奇数; (3)点数大于2小于5.
解:(1)点数为2有1种可能,因此P(点数为2)= 1 ; 6
(2)点数为奇数有3种可能,即点数为1,3,5, 因此P(点数为奇数)= 1 ;
2
(3)点数大于2且小于5有2种可能,即点数为3,4, 因此 P(点数大于2且小于5)= 1 .
解:一共有7种等可能的结果.
(1)指向红色有3种结果, P(指向红色)=__73___;
(2)指向红色或黄色一共有5种
5
等可能的结果,P( 指向红或黄)=__7___; (3)不指向红色有4种等可能的结果
4
P( 不指向红色)= ___7___.
例4、同时掷两个质地均匀的骰子,计算 下列事件的概率: (1)两个骰子的点数相同 (2)两个骰子点数之和是9 (3)至少有一个骰子的点数为2
(2)如果随机取出一个球是白球的概 率为1/6,则应往纸箱内加放几个红 球?
2. 为活跃联欢晚会的气氛,组织者设计了
以下转盘游戏:A、B两个带指针的转盘分别
被分成三个面积相等的扇形,转盘A上的数字
分别是1,6,8,转盘B上的数字分别是4,5,
7(两个转盘除表面数字不同外,其他完全相
同)。每次选择2名同学分别拨动A、B两个转
• 25.2. 用列举法求概率(2)
学习目标
1.理解一个事件概率的意义. 2.会在具体情境中求出一个事件的概率.(重点) 3.会进行简单的概率计算及应用.(难点)
复习引入
等可能性事件(古典概形)的两个特征: 1.出现的结果有限多个; 2.各结果发生的可能性相等;
等可能性事件的概率-------列举法
(1)点数为2; (2)点数为奇数; (3)点数大于2小于5.
解:(1)点数为2有1种可能,因此P(点数为2)= 1 ; 6
(2)点数为奇数有3种可能,即点数为1,3,5, 因此P(点数为奇数)= 1 ;
2
(3)点数大于2且小于5有2种可能,即点数为3,4, 因此 P(点数大于2且小于5)= 1 .
解:一共有7种等可能的结果.
(1)指向红色有3种结果, P(指向红色)=__73___;
(2)指向红色或黄色一共有5种
5
等可能的结果,P( 指向红或黄)=__7___; (3)不指向红色有4种等可能的结果
4
P( 不指向红色)= ___7___.
例4、同时掷两个质地均匀的骰子,计算 下列事件的概率: (1)两个骰子的点数相同 (2)两个骰子点数之和是9 (3)至少有一个骰子的点数为2
(2)如果随机取出一个球是白球的概 率为1/6,则应往纸箱内加放几个红 球?
2. 为活跃联欢晚会的气氛,组织者设计了
以下转盘游戏:A、B两个带指针的转盘分别
被分成三个面积相等的扇形,转盘A上的数字
分别是1,6,8,转盘B上的数字分别是4,5,
7(两个转盘除表面数字不同外,其他完全相
同)。每次选择2名同学分别拨动A、B两个转
• 25.2. 用列举法求概率(2)
学习目标
1.理解一个事件概率的意义. 2.会在具体情境中求出一个事件的概率.(重点) 3.会进行简单的概率计算及应用.(难点)
复习引入
等可能性事件(古典概形)的两个特征: 1.出现的结果有限多个; 2.各结果发生的可能性相等;
等可能性事件的概率-------列举法
人教版数学九上25.2《用列举法求概率》(第1课时)PPT课件

C. 2
D.2
9
3
3
9
【解析】选A.∵上下午各选一个馆共9种选法。∴小明恰好
上午选中台湾馆,下午选中法国馆这两个场馆的概率是 1 .
9
4.从一幅充分均匀混合的扑克牌中,随机抽取一张,
抽到大王的概率是(
6的概率是( 2 ( 13 ). 27
54
1
),抽到牌面数字是
54
),抽到黑桃的概率是
5.四张形状、大小、质地相同的卡片上分别画上圆、 平行四边形、等边三角形、正方形,然后反扣在桌面 上,洗匀后随机抽取一张,抽到轴对称图形的概率是 ( 0.75 ),抽到中心对称图形的概率是( 0.75 ). 6. 某班文艺委员小芳收集了班上同学喜爱传唱的七 首歌曲,作为课前三分钟唱歌曲目:歌唱祖国,我和 我的祖国,五星红旗,相信自己,隐形的翅膀,超越 梦想,校园的早晨,她随机从中抽取一支歌,抽到 “相信自己”这首歌的概率是( 1 ).
【解析】(1)掷得点数为2或4或6(记为事件A)有3种 结果,因此P(A) 3 1 ;
62 (2)小明前五次都没掷得点数2,可他第六次掷得点
数仍然可能为1,2,3,4,5,6,共6种.他第六次掷 得点数2(记为事件B)有1种结果,因此P(B)= 1 .
6
例题
【例2】如图:是一个转盘,转盘分成7个相同的扇形, 颜色分为红、黄、绿三种,指针固定,转动转盘后任 其自由停止,某个扇形会停在指针所指的位置,(指 针指向交线时,当作指向右边的扇形)求下列事件的 概率: (1)指向红色; (2)指向红色或黄色;
62
跟踪训练
掷1个质地均匀的正方体骰子,观察向上一面的点数. (1)求掷得点数为2或4或6的概率; (2)小明在做掷骰子的试验时,前五次都没掷得 点数2,求他第六次掷得点数2的概率.
人教版数学九年级上册《用列举法求概率》ppt课件
(6,6)
123456 1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1) 2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2) 3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3) 4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4) 5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
个小方格,标号为 3,在3的周围的 正方形中有3个地 雷,我们把他的去
域遇记到为地A雷区的,概A区 外率记为为7/B7区2,,,下 一A由区步于还小3是王/8B应大区该?于踩在 7/72,
例2:掷两枚硬币,求下列事件的概率:
(1)两枚硬币全部正面朝上。
(2)两枚硬币全部反面朝上。
(3)一枚硬币正面朝上,一枚反面朝上。
的可能?他们的概 率各是多少?
古典概型的特点
1.可能出现的结果只有有限多 个; 可能2.各性结事果件出的现概的率可可能以性用相列等举;法 而求得。
列举法就是把要数的对 象一一列举出来分析求 解的方法.
例1、如图:计算
解:A区有8格3个雷,机扫雷游戏,在 遇雷的概率为 9×9个小方格中,
3B小 还/区8方有,有1格09,-×39=-79个=7地2雷个,随地只小机雷有王埋,开1个藏每始地着 个 随雷1小 机,0方 踩个,格 一
例4、甲口袋中装有2个相同的小 球,它们分别写有字母A和B; 乙口袋中装有3个相同的小球,它 们分别写有字母C、D和E;丙口袋 中装有2个相同的小球,它们分别 写有字母H和I。从3个口袋中各随 机地取出1个小球。
(1)取出的3个小球上恰好有1个、 2个和3个元音字母的概率分别是 多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作 P139-140
业
1、2样才算公平 ?
用表格表示
红桃 黑桃
1
2
3
4
5
6
1
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2
3 4
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
★ 用列表法求概率 列表法是指用表格的形式反映试验(随机事件)发生的各种情况出 现 的次数和方式,以及某一事件发生的可能的次数和方式,从而求出 概 注:当一次试验涉及两个因数,且可能出现的结果较多时,为了不 率的方法。 从复、不遗漏地列出所有可能得结果,通常用列表法,即一个因素 作为行标,一个因素作为列标。
三、巩固练习
(一) 完成下列选择题 (1) 从长10cm、7cm、5cm、3cm的四条线段中,任选三条,能 组成三角形的概率是( C )
1 A、 4 1 B、 3 1 C、 2 3 D、 4
(2) 要从小强、小红、和小华三人中随机选两人作为旗手,,则 小强和小红同时入选的概率是( B)
2 A、 3 1 B、 3 1 C、 2 1 D、 6
小亮
P(A)=
满足两张牌的数字之积为偶数(记为事件B),有36-9=27种情况,
1 9 36 4
27 36
小明
P(B)=
=
3 4
因为 ,即P(B)>P(A)。这个游戏规则 不公平,所以,我如果是小亮,我不愿意接受这个游戏规则。
27 9 36 大于 36
课堂小结
本节课你学到了什么? 还有什么困惑吗?
(4)、抛掷一枚质地均匀的硬币向上一面 相等 2 有_____ 种可能的结果。它们的可能性 ____, 1 由此能得到“正面向上”的概率为 2 _________. (5)、不透明的袋子中装有5个红球、3个 绿球,这些球出了颜色外无其他差别,从袋 子中随机摸出一个球,“摸出红球”和“摸 5 3 8 8 出绿球”的概率 分别为__________、_______.
5
6
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
解:由表中可以看出,在两堆牌中分别取一张,它可 能出现的结果有36个,它们出现的可能性相等 但满足两张牌的数字之积为奇数(记为事件A) 的有(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5) 这9种情况,所以
25.2. 用列举法求概率
一、自主学习
(一)、完成下列填空: 1、概率的定义:一般地,对于一个随机事件A, 可能性大小的数值 我们把刻画其发生_________________, 称为 随机事件A发生的概率。 2、等可能性事件的两个特征: (1)、每一次试验中,可能出现的结果 有限 只有________ 个。 (2)、每一次试验中,各种结果出现的 相等 可能性_______. 3、一般地,如果在一次试验中,有n种 可能的结果,并且可能性都相等,事件A包含其中的m种结果, m 那么事件A发生的概率,P(A)=________ n 1 当A为必然事件时,P(A)=_______. 1 0 当A为不可能事件时,P(A)=———
例2 同时掷两个质地均匀的骰子, 计算下列事件的概率: (1)两个骰子的点数相同 (2)两个骰子点数 之和是9 (3)至少有一个骰子的点数 2
提问:将题中的“同时掷两个骰子”改为 “把一个骰子掷两次”,所得的结果 有变化吗?
(没有变化)
小结
用列举法求概率的步骤: (1) 将实验(随机事件)发生的所有结 果n种可能列出来; (2) 找到所求事件A发生的结果m种可能; m (3) 套入公式P(A)= n 计算
(3) 寒假即将来临,小明和小亮要从甲乙丙三个社区中随机选取 一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实 践活动的概率为( B )
1 A、 2 1 B、 3 1 C、 6 1 D、 9
(二)
完成课本P138
练习 1题
思考:
小明和小亮做扑克游戏,桌面上放有两 堆牌,分别是红桃和黑桃的1,2,3,4,5,6, 小明建议:”我从红桃中抽取一张牌,你从 黑桃中取一张,当两张牌数字之积为奇 数时,你得1分,为偶数我得1分,先得 到10分的获胜”。如果你是小亮,你愿 意接受这个游戏的规则吗?
二、合作探究
怎样用列举法求概率 列举法---- 在一次试验中,通过列举试验结果的方法
例1 同时抛掷两枚质地均匀的硬币,求下列事件的概率: (1)、两枚硬币全部正面向上 ; (2)、两枚硬币全部反面向上; (3)、一枚硬币正面向上、一枚硬币反面向上。 思考:“同时抛掷两枚质地均匀的硬币”与“先后 两次抛掷一枚质地均匀的硬币”,这两种 试验的所有可能结果一样吗? (一样)
