圆柱与圆锥典型及易错题型
北师大版数学六年级(下册)圆柱与圆锥经典易错题型

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.将一根长16分米的圆柱形钢材截成三段较短的圆柱形,其表面积增加了24 平方分米,这根钢材原来的体积是多少?【答案】解:24÷4=6(平方分米)16×6=96(立方分米)答:这根钢材原来的体积是96立方分米。
【解析】【分析】将一根圆柱形钢材截成三段,增加了四个底面积,据此求出圆柱形钢材的底面积,再用底面积乘高即可求出这根钢材的体积。
2.一个圆锥形沙堆,底面周长是31.4米,高是1.2米.每立方米黄沙重2吨,这堆黄沙重多少吨?【答案】解:底面半径:31.4÷(2×3.14)=31.4÷6.28=5(米)这堆沙子的总重量: ×3.14×52×1.2×2=3.14×25×0.4×2=78.5×0.4×2=31.4×2=62.8(吨)答:这堆黄沙重62.8吨。
【解析】【分析】用底面周长除以圆周率的2倍即可求出底面半径。
根据圆锥的体积公式计算出沙子的体积,再乘每立方米沙子的重量即可求出总重量。
3.如图,一个内直径是20cm的纯净水水桶里装有纯净水,水的高度是22cm.将水桶倒放时,空余部分的高度是3cm,无水部分是圆柱形.这个纯净水水桶的容积是多少升?【答案】解:3.14×(20÷2)2×22+3.14×(20÷2)2×3=3.14×100×(22+3)=3.14×100×25=7850(立方厘米)7850立方厘米=7.85升答:这个纯净水水桶的容积是7.85升。
【解析】【分析】水桶的容积包括水的体积和空余部分的体积,根据圆柱的体积公式分别计算后再相加即可求出水桶的容积。
4.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.【答案】解:3.14×(20÷2)2×2.24+314=3.14×100×2.24+314=703.36+314=1017.36(立方厘米),1017.36 ÷(3.14×92)=1017.36×3÷254.34=3052.08÷254.34=12(厘米),答:铅锤的高是12厘米。
圆柱和圆锥易错题

一、圆柱和圆锥的关系1、一个圆柱和一个圆锥等底等高,如果圆柱的体积是18立方厘米,那么圆锥的体积是()立方厘米:如果圆锥的体积是18立方厘米,那么圆柱的体积是()立方厘米。
2、(判断)一个圆锥的高是6厘米,如果一个圆柱和它等底等体积,那么圆柱的高是18厘米。
()3、24个完全相同的圆锥形实心铁块,可以熔铸成()个与它等底等高的圆柱形实心铁块。
4、一个圆柱与一个圆锥的体积和高分别相等,如果圆锥的底面积是15dm2,那么圆柱的底面积是()5、一个圆柱与一个圆锥的底面积之比是1:4,高之比是2:3,它们的体积之比是()。
6、如果一个圆锥的体积是一个圆柱体积的13,那么这个圆柱和这个圆锥一定等底等高。
()二、削去1、有一根棱长是6分米的正方体木料,如果将它削成一个最大的圆柱,那么圆柱的体积是()立方分米;如果将它削成一个最大的圆锥,那么圆锥的体积是()立方分米。
2、有等底等高的圆锥形和圆柱形容器各1个,将圆柱形容器内装满水后,再倒入圆锥形容器中,当圆柱形容器内的水全部倒完时,溢出了90.6毫升水,这时圆锥形容器内有()毫升水。
3、把一个正方体木块加工成一个最大的圆柱,正方体与圆柱的体积比是()4、一个棱长为4分米的正方体木块,削成一个最大的圆柱形木块,体积减少()立方分米。
5、把一个底面半径为3dm,高为ldm的圆柱形木块,削去()dm3才能削成一个最大的圆锥。
6、把一个棱长为6cm的正方体木块加工成一个最大的圆锥,这个圆锥的体积是()dm3。
三、旋转得到的立体图形1、把右图中的直角三角形以任意一条直角边为轴快速旋转一周,得到的立体图形是(),它的体积最大是()立方厘米。
2、把一个长4厘米,宽3厘米的长方形绕它的一条边旋转一周,得到圆柱体,当圆柱的体积最大时,它的侧面积是()平方厘米。
3、如图,直角三角形绕直角边(虚线)旋转一周后得到的立体图形是(),它的体积是()立方厘米。
4、如图,阴影部分旋转一周得到的立体图形的体积是多少?(单位:cm)5、一个长方形的长是4cm,宽是3cm,以这个长方形的长为轴旋转一周,得到的立体图形是(),这个立体图形的表面积是()cm2,体积是()cm3四、体积转化和体积增减(如果半径和高未知,就用方程)1、有一根底面直径是4分米,高是6分米的圆柱形钢坯,把它熔铸成一个底面直径为12米的圆锥形配件。
小升初必备:圆柱与圆锥典型及易错题型分析

小升初必备:圆柱与圆锥典型及易错题型分析圆柱与圆锥典型及易错题型(一)关于圆锥与圆柱相互之间的关系:1.若圆锥与圆柱等底等高,则它们的体积不等(圆锥的体积是圆柱的三分之一);2.若圆锥与圆柱等底等体积,则它们的高不等(圆锥的高是圆柱的3倍);3.若圆锥与圆柱等高等体积,则它们的底不等(圆锥的底面积是圆柱的3倍)。
练:1、一个圆柱和一个圆锥等底等高,它们的体积和是24立方分米,那么圆柱的体积是_________立方分米.2、一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是()立方分米。
A12B36C4D8(二)、关于圆柱、圆锥的典型实际问题:1.实质求圆柱的侧面积:通风管(如圆柱形烟囱)压路机1、做一根长1米,底面周长是2分米的圆柱形通风管,需要铁皮多少平方分米?(管壁厚度忽略不计)2.求的滚轮转动一周所压过的路面面积就是求圆柱(滚轮)的侧面积;(所压过的路面面积=圆柱(滚轮)的侧面积×转动速度×时间)1、压路机的滚筒是个圆柱,它的宽是3米,滚筒横截面半径是1米,那么滚筒转一周可压路面多少平方米?如果压路机的滚筒每分钟转10周,那么5分钟可以行驶多少米?3.求无盖的圆柱形表面积。
1、求圆柱形水桶能装水多少升,是求它的();做一节圆柱形通风管要多少铁皮,是求它的()A.侧面积B.表面积C.体积D.容积2、一个圆柱形儿童游泳池底面半径是4米,深0.5米.在它的四周和池底抹上水泥,每平方米需要水泥10千克,一共用水泥多少千克?3、一个无盖的圆柱形铁皮水桶,高50厘米,底面直径30厘米,做这个水桶约莫需用几何铁皮? (得数保留整数)4、做一个无盖的圆柱形鱼缸,底面半径3dm,高5dm。
(1)做这个鱼缸至少要几何平方分米?(得数保留整十平方分米)(2)这个鱼缸能装几何千克水?(1升水重1千克)5、圆柱的体积求底面积或高时,要用体积除以底面积或高,圆锥的体积求底面积或高时,要先乘以3再除以底面积或高。
【数学】北师大版数学六年级(下册)圆柱与圆锥经典易错题型

【数学】北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.计算下面圆柱的表面积和体积,圆锥的体积。
(1)(2)【答案】(1)解:表面积:3.14×52×2+3.14×5×2×13=157+408.2=565.2(cm2)体积:3.14×52×13=1020.5(dm3)(2) ×3.14×82×15= ×3.14×64×15=1004.8(cm3)【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式计算即可;(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
2.在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米.每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)【答案】解:圆锥的体积: ×[3.14×(4÷2)2]×1.5= ×1.5×12.56=6.28(立方米)这堆沙的吨数:1.7×6.28=10.676(吨)≈11(吨)答:这堆沙约重11吨。
【解析】【分析】这堆沙大约的重量=这堆沙的体积×每立方米大约的重量,其中这堆沙的体积=圆锥的体积=πr2h,得数要保留整数,就是把得出的数的十分位上的数进行“四舍五入”即可。
3.圆柱的底面半径和高都是2厘米,把它浸入一个均匀水槽内的水中,量得水位上升了4厘米.再把一个底面直径为6厘米的圆锥浸入水中,水位又上升了 4.5厘米.求圆锥的高.【答案】解:3.14×22×2÷4=3.14×4×2÷4=6.28(平方厘米)6.28×4.5×3÷[3.14×(6÷2)2]=3.14×27÷[3.14×9]=3(厘米)答:圆锥的高是3厘米。
北师大版数学六年级(下册)圆柱与圆锥经典易错题型

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。
(1)做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)(2)如果烟囱中充满废气,一节烟囱中最多可以容纳废气多少立方米?【答案】(1)解:40cm=0.4m3.14×0.4×2.5=3.14(m2)答:做一节烟囱一共需要铁皮3.14平方米。
(2)解:3.14×(0.4÷2)2×2.5=0.314(m3)答:一节烟囱中最多可以容纳废气0.314立方米。
【解析】【分析】1cm=0.01m,(1)做一节烟囱一共需要铁皮的平方米数=这节烟囱横截面的周长×长,其中这节烟囱横截面的周长=横截面的半径×2×π;(2)一节烟囱中最多可以容纳废气的立方米数=这节烟囱的容积=πr2h。
据此代入数据作答即可。
2.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.【答案】解:3.14×(20÷2)2×2.24+314=3.14×100×2.24+314=703.36+314=1017.36(立方厘米),1017.36 ÷(3.14×92)=1017.36×3÷254.34=3052.08÷254.34=12(厘米),答:铅锤的高是12厘米。
【解析】【分析】根据题意可知,先求出圆锥形铅锥的体积,用圆柱形玻璃杯上面的空白部分的体积+溢出的水的体积=圆锥形铅锥的体积,然后用圆锥形铅锥的体积÷÷铅锥的底面积=铅锥的高,据此列式解答.3.工地上有一个圆锥形的沙堆,高是1.5米,底面半径是6米,每立方米的沙约重1.7吨。
北师大版数学六年级(下册)圆柱与圆锥经典易错题型

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.一个底面半径为12厘米的圆柱形杯中装有水,手里浸泡了一个底面直径是12厘米,高是18厘米的圆锥体铁块,当铁块从杯中取山来时,杯中的水面会下降多少厘米??【答案】解: ×3.14×(12÷2)2×18÷(3.14×122)= ×3.14×36×18÷(3.14×144)=1.5(厘米)答:桶内的水将下降1.5厘米。
【解析】【分析】水面下降部分水的体积就是圆锥的体积,根据圆锥的体积公式先计算出圆锥体铁块的体积,也就是水面下降部分水的体积。
用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。
2.一个圆锥体形的沙堆,底面周长是25.12米,高1.8米,用这堆沙在8米宽的公路上铺5厘米厚的路面,能铺多少米?【答案】解:5厘米=0.05米沙堆的底面半径:25.12÷(2×3.14)=25.12÷6.28=4(米)沙堆的体积: ×3.14×42×1.8=3.14×16×0.6=3.14×9.6=30.144(立方米)所铺沙子的长度:30.144÷(8×0.05)=30.144÷0.4=75.36(米).答:能铺75.36米。
【解析】【分析】根据1米=100厘米,先将厘米化成米,除以进率100,然后求出沙堆的底面半径,用公式:C÷2π=r,要求沙堆的体积,用公式:V=πr2h,最后用沙堆的体积÷(公路的宽×铺沙的厚度)=铺沙的长度,据此列式解答.3.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm。
把瓶口塞紧后使其瓶口向下倒立,这时酒深25cm。
求酒瓶的容积。
【答案】解:3.14×(10÷2)2×[15+(30-25)]=1570(cm3)答:酒瓶的容积是1570 cm3。
北师大版数学六年级(下册)圆柱与圆锥经典易错题型

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.工厂要生产一节烟囱,烟囱长2.5m,横截面是直径为40cm的圆。
(1)做一节烟囱一共需要铁皮多少平方米?(接头处忽略不计)(2)如果烟囱中充满废气,一节烟囱中最多可以容纳废气多少立方米?【答案】(1)解:40cm=0.4m3.14×0.4×2.5=3.14(m2)答:做一节烟囱一共需要铁皮3.14平方米。
(2)解:3.14×(0.4÷2)2×2.5=0.314(m3)答:一节烟囱中最多可以容纳废气0.314立方米。
【解析】【分析】1cm=0.01m,(1)做一节烟囱一共需要铁皮的平方米数=这节烟囱横截面的周长×长,其中这节烟囱横截面的周长=横截面的半径×2×π;(2)一节烟囱中最多可以容纳废气的立方米数=这节烟囱的容积=πr2h。
据此代入数据作答即可。
2.计算下面圆柱的表面积和体积,圆锥的体积。
(1)(2)【答案】(1)解:表面积:3.14×52×2+3.14×5×2×13=157+408.2=565.2(cm2)体积:3.14×52×13=1020.5(dm3)(2) ×3.14×82×15= ×3.14×64×15=1004.8(cm3)【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式计算即可;(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
3.我们熟悉的圆柱、长方体、正方体等立体的图形都称作直柱体,如图所示的三棱柱也是直柱体。
(1)通过比较,请你说说这类立体图形有什么样的共同特征呢?(至少写出3点)(2)我们已经学过圆柱、长方体、正方体的体积计算方法,请你大胆猜测一下,三棱柱的体积如何计算?若这个三棱柱的底面是一个直角三角形,两条直角边分别为2cm、3cm,高为5cm,请你计算出它的体积。
圆柱与圆锥易错题目(1)

圆柱与圆锥易错题目(1)一、圆柱与圆锥1.看图计算.(1)求圆柱的表面积(单位:dm)(2)求零件的体积(单位:cm)【答案】(1)解:3.14×10×20+3.14×(10÷2)2×2=628+3.14×25×2=628+157=785(平方分米)答:圆柱的表面积是785平方分米。
(2)解: ×3.14×(2÷2)2×3+3.14×(2÷2)2×4= ×3.14×1×3+3.14×1×4=3.14+12.56=15.7(立方厘米)答:零件的体积是15.7立方厘米。
【解析】【分析】(1)圆柱的表面积是两个底面积加上一个侧面积,根据圆面积公式计算出底面积,用底面周长乘高求出侧面积;(2)圆柱的体积=底面积×高,圆锥的体积=底面积×高×,根据公式计算,用圆柱的体积加上圆锥的体积就是总体积。
2.计算圆锥的体积。
【答案】解:3.14×2²×15×=3.14×4×5=62.8(dm³)【解析】【分析】圆锥的体积=底面积×高×,根据圆锥的体积公式计算体积即可。
3.一根圆柱形木材长20分米,把它截成3段,表面积增加了12.56平方分米。
这根木材体积是多少立方米?【答案】解:12.56÷4×20=62.8(立方分米)=0.0628(立方米)答:这根木材体积是0.0628立方米。
【解析】【分析】将圆柱形木材截成3段,增加了4个底面积,用增加的表面积除以4即可求出圆柱的底面积,然后用底面积乘高即可求出这根圆柱形木材的体积。
4.将一根底面直径是20厘米,长1米的圆木沿着直径劈成相等的两半。
每半块木头的表面积和体积是多少?【答案】解:1米=100厘米,表面积:3.14×(20÷2)2+[3.14×20×100]÷2+20×100=5454(平方厘米)体积:3.14×(20÷2)2×100÷2=15700(立方厘米)答:每半块木头的表面积是5454平方厘米,体积是15700立方厘米。
北师大版数学六年级(下册)圆柱与圆锥经典易错题型
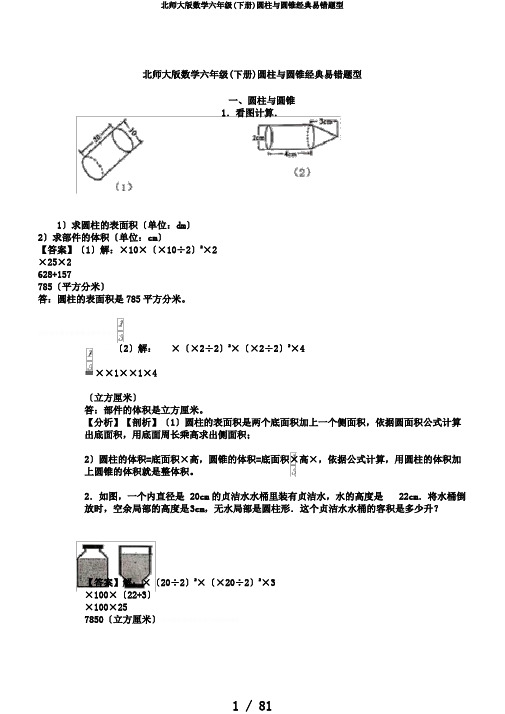
北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.看图计算.1〕求圆柱的表面积〔单位:dm〕2〕求部件的体积〔单位:cm〕【答案】〔1〕解:×10×〔×10÷2〕2×2×25×2628+157785〔平方分米〕答:圆柱的表面积是785平方分米。
〔2〕解:×〔×2÷2〕2×〔×2÷2〕2×4=××1××1×4〔立方厘米〕答:部件的体积是立方厘米。
【分析】【剖析】〔1〕圆柱的表面积是两个底面积加上一个侧面积,依据圆面积公式计算出底面积,用底面周长乘高求出侧面积;2〕圆柱的体积=底面积×高,圆锥的体积=底面积×高×,依据公式计算,用圆柱的体积加上圆锥的体积就是整体积。
2.如图,一个内直径是 20cm的贞洁水水桶里装有贞洁水,水的高度是22cm.将水桶倒放时,空余局部的高度是3cm,无水局部是圆柱形.这个贞洁水水桶的容积是多少升?【答案】解:×〔20÷2〕2×〔×20÷2〕2×3×100×〔22+3〕×100×257850〔立方厘米〕7850立方厘米=升答:这个贞洁水水桶的容积是升。
【分析】【剖析】水桶的容积包含水的体积和空余局部的体积,依据圆柱的体积公式分别计算后再相加即可求出水桶的容积。
3.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,杯中水面距杯口厘9厘米的圆锥形铅锤完整浸入水中,水会溢出314立方厘米.求铅锤米.假定将一个半径为的高.【答案】解:×〔20÷2〕2×2.24+314×100×2.24+314703.36+314〔立方厘米〕,2〕÷〔×9×3÷÷12〔厘米〕,答:铅锤的高是12厘米。
【数学】北师大版数学六年级(下册)圆柱与圆锥经典易错题型
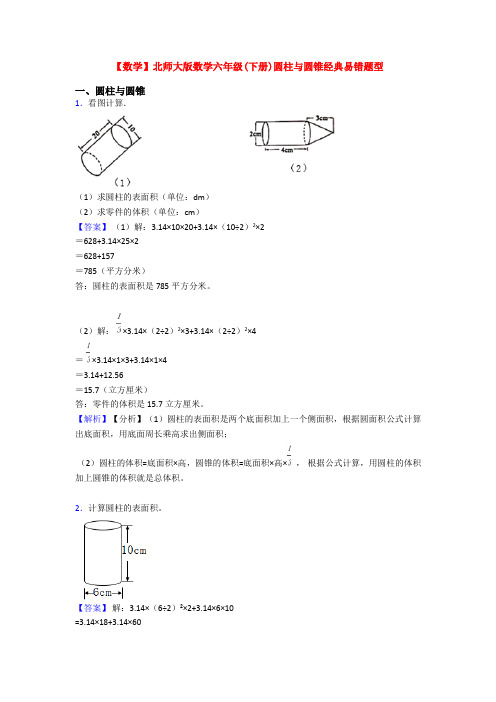
【数学】北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.看图计算.(1)求圆柱的表面积(单位:dm)(2)求零件的体积(单位:cm)【答案】(1)解:3.14×10×20+3.14×(10÷2)2×2=628+3.14×25×2=628+157=785(平方分米)答:圆柱的表面积是785平方分米。
(2)解: ×3.14×(2÷2)2×3+3.14×(2÷2)2×4= ×3.14×1×3+3.14×1×4=3.14+12.56=15.7(立方厘米)答:零件的体积是15.7立方厘米。
【解析】【分析】(1)圆柱的表面积是两个底面积加上一个侧面积,根据圆面积公式计算出底面积,用底面周长乘高求出侧面积;(2)圆柱的体积=底面积×高,圆锥的体积=底面积×高×,根据公式计算,用圆柱的体积加上圆锥的体积就是总体积。
2.计算圆柱的表面积。
【答案】解:3.14×(6÷2)²×2+3.14×6×10=3.14×18+3.14×60=56.52+188.4=244.92(cm³)【解析】【分析】圆柱的表面积是两个底面积加上侧面积,根据圆面积公式计算底面积,用底面周长乘高求出侧面积。
3.工地上有一个圆锥形的沙堆,高是1.5米,底面半径是6米,每立方米的沙约重1.7吨。
这堆沙约重多少吨?(得数保留整吨数)【答案】解:3.14×6²×1.5××1.7=3.14×18×1.7=56.52×1.7≈96(吨)答:这堆沙约重96吨。
六年级圆柱与圆锥易错题

六年级圆柱与圆锥易错题
以下是一些六年级圆柱与圆锥的易错题:
1. 一个圆柱体和一个圆锥体的底面积相等、体积也相等,圆锥的高是27厘米,圆柱的高是多少厘米.
2. 一个圆柱体和一个圆锥体的底面积和体积都相等,圆锥的高是18厘米,圆柱的高是多少厘米.
3. 一个圆柱体和一个圆锥体的底面积相等、体积不相等,圆锥的体积是圆柱的(1/3),圆锥的高是27厘米,圆柱的高是多少厘米.
4. 一个圆柱体和一个圆锥体的底面积相等、高相等,它们的体积之和是144立方厘米,圆锥的体积是多少立方厘米.
5. 圆锥体的底面积不变,高增加(1/5),则体积增加多少
6. 圆柱体与一个圆锥体的底面积相等、高也相等,圆柱的体积是3立方分米,圆锥的体积是多少立方分米.
7. 圆柱体与一个圆锥体的底面积和体积都相等,圆锥的高是9分米,圆柱的高是多少分米.
8. 一个圆柱体和一个圆锥体的底面积和体积都相等,圆锥的高是24厘米,圆柱的高是多少厘米.
9. 一个圆柱体和一个圆锥体的底面积相等、高不相等,圆柱的体积是圆锥的(3/5),圆锥的高是27厘米,圆柱的高是多少厘米.
10. 一个圆柱体和一个圆锥体的底面积和体积都相等,已知圆锥的高是18
厘米,则圆柱的高是多少厘米.
这些题目需要学生仔细理解并应用圆柱和圆锥的体积公式(V=πr^2h)以
及相关的数学知识。
如果他们在这方面有困难,可能需要更多的练习和解释。
六年级圆柱圆锥易错题精选

六年级圆柱圆锥易错题精选圆柱圆锥易错题1.用一张长30厘米,宽18厘米的长方形纸,围成一个圆柱,这个圆柱体的侧面积是()平方厘米。
解:首先,我们需要知道圆柱的侧面积公式为2πrh,其中r为底面半径,h为圆柱的高。
由于题目没有给出高,我们需要先求出底面半径。
根据长方形纸的长度和宽度,可以得到圆柱的底面周长为2(30+18)=96厘米,即2πr=96,解得r=48/π。
再根据圆柱的高为18厘米,代入公式2πrh,即可得到圆柱体的侧面积为2π×48/π×18=1728平方厘米。
2.一个圆柱的侧面展开是正方形,当圆柱的高是15分米时,圆柱的底面周长是()分米。
解:根据题意,圆柱的侧面展开是正方形,说明圆柱的高等于底面周长。
因此,底面周长为15分米。
3.等底等高的圆柱和圆锥。
圆柱的体积是36立方厘米,圆锥的体积是()立方厘米;圆锥的体积是36立方厘米圆柱体积比圆锥大()立方厘米。
解:由于圆柱和圆锥等底等高,它们的底面积相等。
设它们的底面积为S,圆柱的高为h,圆锥的高为H,则圆柱的体积为V1=S×h=36,圆锥的体积为V2=1/3×S×H。
将V1代入可得S×h=36,带入V2可得V2=1/3×S×(3h)=1/3×36×3h=36h。
因此,圆锥的体积为36h立方厘米,圆柱的体积比圆锥大36-36h立方厘米。
如果圆锥的体积是36立方厘米,则圆柱的体积比圆锥大0立方厘米,圆锥的体积为1立方厘米。
4.把一个底面直径和高都是6分米的圆柱的,底面分成若干等份,再切开拼成一个长方体。
这个长方体的长是()分米,宽是()分米,高是()分米,体积是()立方分米。
解:首先,我们需要知道圆柱的底面积为πr²,其中r为底面半径。
由于底面直径为6分米,即r=3分米。
将底面分成n等份,则每份的弧长为2πr/n,每份的面积为πr²/n。
圆柱与圆锥典型及易错题型

圆柱与圆锥典型及易错题型一、圆柱与圆锥1.一个圆锥体形的沙堆,底面周长是25.12米,高1.8米,用这堆沙在8米宽的公路上铺5厘米厚的路面,能铺多少米?【答案】解:5厘米= 0.05米沙堆的底面半径:25.12+ (2x3.14)=25.12+6.28=4 (米)1沙堆的体积:x3.14x42x1.8 = 3.14x16x0.6 = 3.14x9.6 = 30.144 (立方米)所铺沙子的长度:30.144+ (8x0.05)=30.144+0.4 = 75.36 (米).答:能铺75.36米。
【解析】【分析】根据1米=100厘米,先将厘米化成米,除以进率100,然后求出沙堆的1底面半径,用公式:C+2n=r,要求沙堆的体积,用公式:V= nr2h,最后用沙堆的体积+ (公路的宽x铺沙的厚度)=铺沙的长度,据此列式解答.2.工地上有一个圆锥形的沙堆,高是1.5 米,底面半径是6 米,每立方米的沙约重1.7 吨。
这堆沙约重多少吨?(得数保留整吨数)【答案】解:3.14x62x1.5x x1.7=3.14x18x1.7=56.52x1.7,96 (吨)答:这堆沙约重96吨。
1【解析】【分析】圆锥的体积=底面积x高x ,先计算圆锥的体积,再乘每立方米沙的重量即可求出总重量。
3.如下图,爷爷的水杯中部有一圈装饰,是悦悦怕烫伤爷爷的手特意贴上的。
这条装饰圈宽5cm,装饰圈的面积是多少cm2?【答案】解:3.14x6x5 = 94.2 (cm2)答:装饰圈的面积是94.2cm2。
【解析】【分析】解:装饰圈的面积就是高5cm的圆柱的侧面积,用底面周长乘5即可求出装饰圈的面积。
4.一个圆柱体容器的底面直径是16 厘米,容器中盛有10 厘米深的水,现在把一个圆锥形铁块浸没到水中,水面上升了3厘米,圆锥形铁块的体积是多少立方厘米?【答案】解:3.14x (16“)2x3= 3.14x64x3= 200.96x3= 602.88 (立方厘米)答:圆锥形铁块体积是602.88立方厘米。
人教版数学6年级下册 第3单元(圆柱和圆锥)易错题三(含答案)

第3单元圆柱与圆锥-易错题-人教版易错点大集合易错点一:圆柱的表面积典例把一个圆柱体的侧面展开得到一个正方形,这个圆柱体的底面周长是10厘米,高是多少厘米,侧面积是多少平方厘米.跟踪训练1.将一个边长为5分米的正方形纸片卷成圆柱筒,这个圆柱的侧面积是多少平方分米.2.用铁皮制成一个高是5分米,底面周长是12.56分米的圆柱形水桶(没有盖),至少需要多少平方米铁皮?答:至少需要多0.7536平方米铁皮.3.一个圆柱底面半径是4分米,圆柱侧面积是62.8平方分米,这个圆柱的表面积是多少?4.一个圆柱体,底面半径是7厘米,表面积是1406.72平方厘米.这个圆柱的高是多少?5.圆柱侧面展开是一个正方形,已知圆柱的底面积是10平方厘米,则圆柱的侧面积是多少平方厘米?易错点二:圆柱的体积典例将一根长4米的圆柱形木料锯成3段,表面积增加了60平方分米。
这根木料的体积多少立方分米。
跟踪训练1.把一个棱长是6分米的正方体木块,削成一个最大的圆柱体,这个圆柱体的体积是多少立方分米。
2.把一个底面直径是20厘米的圆柱沿直径竖直切成两半,表面积比原来增加了400平方厘米,原来这个圆柱的底面积是多少,体积是多少。
3.一个长5cm、宽4cm的长方形纸,以这个长方形的长边为轴旋转一周,得到的立体图形是什么图形,它的体积是多少cm3。
4.一个圆柱底面半径是5cm,高是8cm,这个圆柱的侧面积是多少cm2,表面积是多少cm2,体积是多少cm3。
5.一个圆柱体油桶的体积是192dm3,底面积是16dm2,它的高是多少dm。
易错点三:圆锥的体积典例直角三角形的两条直角边分别是3厘米,4厘米。
若以其中一条直角边所在的直线为轴旋转一周,得到一个体积最大的圆锥,这个圆锥的体积是多少立方厘米。
跟踪训练1.一个圆锥形沙堆,高1.2m,底面直径是6m,这堆沙子的体积是多少m3。
2.一个圆锥的底面半径是3cm,高是4cm,它的体积是多少cm3。
苏教版小学数学六年级下册圆柱圆锥易错题

苏教版小学数学六年级下册圆柱圆锥易错题一、圆柱与圆锥1.看图计算.(1)求圆柱的表面积(单位:dm)(2)求零件的体积(单位:cm)【答案】(1)解:3.14×10×20+3.14×(10÷2)2×2=628+3.14×25×2=628+157=785(平方分米)答:圆柱的表面积是785平方分米。
(2)解: ×3.14×(2÷2)2×3+3.14×(2÷2)2×4= ×3.14×1×3+3.14×1×4=3.14+12.56=15.7(立方厘米)答:零件的体积是15.7立方厘米。
【解析】【分析】(1)圆柱的表面积是两个底面积加上一个侧面积,根据圆面积公式计算出底面积,用底面周长乘高求出侧面积;(2)圆柱的体积=底面积×高,圆锥的体积=底面积×高×,根据公式计算,用圆柱的体积加上圆锥的体积就是总体积。
2.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.【答案】解:3.14×(20÷2)2×2.24+314=3.14×100×2.24+314=703.36+314=1017.36(立方厘米),1017.36 ÷(3.14×92)=1017.36×3÷254.34=3052.08÷254.34=12(厘米),答:铅锤的高是12厘米。
【解析】【分析】根据题意可知,先求出圆锥形铅锥的体积,用圆柱形玻璃杯上面的空白部分的体积+溢出的水的体积=圆锥形铅锥的体积,然后用圆锥形铅锥的体积÷÷铅锥的底面积=铅锥的高,据此列式解答.3.将一根底面直径是20厘米,长1米的圆木沿着直径劈成相等的两半。
圆柱与圆锥典型及易错题型

圆柱与圆锥典型及易错题型一、圆柱与圆锥1.如图,这是用塑料薄膜覆盖的蔬菜大棚,长15米,横截面是一个直径为2米的半圆。
大棚内的空间有多大?【答案】解:3.14×(2÷2)2×15÷2=23.55(立方米)答:大棚内的空间有23.55立方米。
【解析】【分析】观察图可知,大棚的形状是一个圆柱的一半,要求大棚内的空间大小,用圆柱的体积÷2=大棚内的空间大小,据此列式解答.2.计算圆锥的体积。
【答案】解:3.14×2²×15×=3.14×4×5=62.8(dm³)【解析】【分析】圆锥的体积=底面积×高×,根据圆锥的体积公式计算体积即可。
3.我们熟悉的圆柱、长方体、正方体等立体的图形都称作直柱体,如图所示的三棱柱也是直柱体。
(1)通过比较,请你说说这类立体图形有什么样的共同特征呢?(至少写出3点)(2)我们已经学过圆柱、长方体、正方体的体积计算方法,请你大胆猜测一下,三棱柱的体积如何计算?若这个三棱柱的底面是一个直角三角形,两条直角边分别为2cm、3cm,高为5cm,请你计算出它的体积。
【答案】(1)答:①上下两个底面的大小和形状完全相同,并且它们相互平行。
②侧面与底面垂直,两个底面之间的距离就是直柱体的高。
③直柱体的侧面展开图是长方形。
④当底面周长与高相等时,侧面展开图是正方形。
(2)答:我们学过的长方体,正方体和圆柱体的体积都可以用“底面积×高”来计算.因为三棱柱也是直柱体,所以我精测,三棱柱的体积计算方法也可以用“底面积x高”来计算。
三棱柱的体积:2×3÷2×5=15cm3【解析】【分析】(1)根据每种直柱体的特征总结出它们共同的特征即可,例如:①它们的上下两个底面的大小和形状完全相同,并且它们相互平行;②它们的侧面与底面垂直,两个底面之间的距离就是直柱体的高;③它们的侧面展开图是长方形;④当底面周长与高相等时,侧面展开图是正方形;(2)长方体、正方体的体积都可以用“底面积×高”来计算,而三棱柱也是直柱体,所以三棱柱的体积也可以用“底面积×高”来计算,直角三角形的面积等于两条直角边乘积的一半,据此作答即可。
圆柱圆锥12种易错题型

圆柱圆锥12种易错题型
以下是一些与圆柱和圆锥相关的易错题型:
1. 计算圆柱或圆锥的体积时,忘记将高度和半径或直径的单位统一换算。
2. 混淆圆柱的体积公式和表面积公式,或者混淆圆锥的体积公式和表面积公式。
3. 在计算圆柱或圆锥的体积时,未正确平方或立方半径或直径的值。
4. 错误地将圆柱的底面面积与圆柱的侧面积相加来求圆柱的表面积。
5. 错误地将圆柱的表面积与圆柱的体积相加来求圆柱的总表面积。
6. 忽略圆锥的底面积,在计算圆锥的表面积时只考虑侧面积。
7. 错误地将圆锥的表面积与圆锥的体积相加来求圆锥的总表面积。
8. 混淆圆柱和圆锥的形状,例如将一个圆锥误认为是圆柱。
9. 在解决与圆锥相关的问题时,未将斜高或母线的长度考虑在内。
10. 未正确使用三角函数来计算圆锥的斜高或母线的长度。
11. 在计算圆锥的体积时,未正确将半径或直径的平方乘以高度再乘以π。
12. 忽略圆柱或圆锥的单位问题,在计算结果中缺少单位。
请注意,这只是一些常见的易错题型,根据具体的问题和知识点可能会有其他的易错点。
在解答题目时,请仔细阅读题目要求,理清思路,避免粗心导致的错误。
【精品】北师大版数学六年级(下册)圆柱与圆锥经典易错题型

【精品】北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.一个底面半径为12厘米的圆柱形杯中装有水,手里浸泡了一个底面直径是12厘米,高是18厘米的圆锥体铁块,当铁块从杯中取山来时,杯中的水面会下降多少厘米??【答案】解: ×3.14×(12÷2)2×18÷(3.14×122)= ×3.14×36×18÷(3.14×144)=1.5(厘米)答:桶内的水将下降1.5厘米。
【解析】【分析】水面下降部分水的体积就是圆锥的体积,根据圆锥的体积公式先计算出圆锥体铁块的体积,也就是水面下降部分水的体积。
用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。
2.一个圆锥体形的沙堆,底面周长是25.12米,高1.8米,用这堆沙在8米宽的公路上铺5厘米厚的路面,能铺多少米?【答案】解:5厘米=0.05米沙堆的底面半径:25.12÷(2×3.14)=25.12÷6.28=4(米)沙堆的体积: ×3.14×42×1.8=3.14×16×0.6=3.14×9.6=30.144(立方米)所铺沙子的长度:30.144÷(8×0.05)=30.144÷0.4=75.36(米).答:能铺75.36米。
【解析】【分析】根据1米=100厘米,先将厘米化成米,除以进率100,然后求出沙堆的底面半径,用公式:C÷2π=r,要求沙堆的体积,用公式:V=πr2h,最后用沙堆的体积÷(公路的宽×铺沙的厚度)=铺沙的长度,据此列式解答.3.计算下面圆柱的表面积和体积,圆锥的体积。
(1)(2)【答案】(1)解:表面积:3.14×52×2+3.14×5×2×13=157+408.2=565.2(cm2)体积:3.14×52×13=1020.5(dm3)(2) ×3.14×82×15= ×3.14×64×15=1004.8(cm3)【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式计算即可;(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
北师大版数学六年级(下册)圆柱与圆锥经典易错题型

北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.一个底面半径为12厘米的圆柱形杯中装有水,手里浸泡了一个底面直径是12厘米,高是18厘米的圆锥体铁块,当铁块从杯中取山来时,杯中的水面会下降多少厘米??【答案】解: ×3.14×(12÷2)2×18÷(3.14×122)= ×3.14×36×18÷(3.14×144)=1.5(厘米)答:桶内的水将下降1.5厘米。
【解析】【分析】水面下降部分水的体积就是圆锥的体积,根据圆锥的体积公式先计算出圆锥体铁块的体积,也就是水面下降部分水的体积。
用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。
2.一个圆柱形的汽油桶,底面半径是2分米,高是5分米,做这个桶至少要用多少平方分米的铁皮?它的容积是多少升?【答案】解:3.14×22×2+3.14×2×2×5=3.14×4×2+3.14×4×5=25.12+62.8=87.92(dm2)3.14×22×5=62.8(dm3)62.8dm3=62.8L答:做这个桶至少要用87.92平方分米的铁皮。
它的容积是62.8升。
【解析】【分析】需要铁皮的面积就是油桶的表面积,用底面积的2倍加上侧面积就是表面积,圆柱的侧面积=底面周长×高;圆柱的容积=底面积×高,根据公式计算即可。
3.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm。
把瓶口塞紧后使其瓶口向下倒立,这时酒深25cm。
求酒瓶的容积。
【答案】解:3.14×(10÷2)2×[15+(30-25)]=1570(cm3)答:酒瓶的容积是1570 cm3。
【解析】【分析】酒瓶的容积相当于高15厘米的圆柱形酒的体积,和高是(30-25)厘米的圆柱形空气的体积,把这两部分体积相加就是酒瓶的容积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱与圆锥典型及易错题型一、圆柱与圆锥1.一个圆锥体形的沙堆,底面周长是25.12米,高1.8米,用这堆沙在8米宽的公路上铺5厘米厚的路面,能铺多少米?【答案】解:5厘米=0.05米沙堆的底面半径:25.12÷(2×3.14)=25.12÷6.28=4(米)沙堆的体积: ×3.14×42×1.8=3.14×16×0.6=3.14×9.6=30.144(立方米)所铺沙子的长度:30.144÷(8×0.05)=30.144÷0.4=75.36(米).答:能铺75.36米。
【解析】【分析】根据1米=100厘米,先将厘米化成米,除以进率100,然后求出沙堆的底面半径,用公式:C÷2π=r,要求沙堆的体积,用公式:V=πr2h,最后用沙堆的体积÷(公路的宽×铺沙的厚度)=铺沙的长度,据此列式解答.2.工地上有一个圆锥形的沙堆,高是1.5米,底面半径是6米,每立方米的沙约重1.7吨。
这堆沙约重多少吨?(得数保留整吨数)【答案】解:3.14×6²×1.5××1.7=3.14×18×1.7=56.52×1.7≈96(吨)答:这堆沙约重96吨。
【解析】【分析】圆锥的体积=底面积×高×,先计算圆锥的体积,再乘每立方米沙的重量即可求出总重量。
3.如下图,爷爷的水杯中部有一圈装饰,是悦悦怕烫伤爷爷的手特意贴上的。
这条装饰圈宽5cm,装饰圈的面积是多少cm2?【答案】解:3.14×6×5=94.2(cm²)答:装饰圈的面积是94.2cm2。
【解析】【分析】解:装饰圈的面积就是高5cm的圆柱的侧面积,用底面周长乘5即可求出装饰圈的面积。
4.一个圆柱体容器的底面直径是16厘米,容器中盛有10厘米深的水,现在把一个圆锥形铁块浸没到水中,水面上升了3厘米,圆锥形铁块的体积是多少立方厘米?【答案】解:3.14×(16÷2)2×3=3.14×64×3=200.96×3=602.88(立方厘米)答:圆锥形铁块体积是602.88立方厘米。
【解析】【分析】水面上升部分水的体积就是圆锥的体积,因此用圆柱的底面积乘水面上升的高度即可求出圆锥的体积。
5.求下图(单位:厘米)钢管的体积。
【答案】解:10÷2=5(厘米);8÷2=4(厘米);3.14×(52-42)×100=3.14×(25-16)×100=3.14×9×100=28.26×100=2826(立方厘米).【解析】【分析】根据题意可知,这根钢管的体积=底面积×高,底面是一个圆环,根据圆环的面积S=π(R2-r2),据此先求出底面积,然后乘钢管的长度,即可得到这根钢管的体积,据此列式解答.6.一个圆锥形的沙堆,高1.2米,沿着它的外边缘走一圈是18.84米,如果每立方米沙重1.6吨,这堆沙重多少吨?【答案】 18.84÷3.14÷2=6÷2=3(米)×3.14×32×1.2×1.6=×3.14×9×1.2×1.6=3.14×3×1.2×1.6=9.42×1.2×1.6=11.304×1.6=18.0864(吨)答:这堆沙重18.0864吨.【解析】【分析】已知圆锥的底面周长,求底面半径,用C÷π÷2=r,然后用公式:V=πr2h 求出圆锥沙堆的体积,最后用每立方米沙的质量×圆锥沙堆的体积=这堆沙的质量,据此列式解答.7.如图,有一个圆柱形的零件,高是10cm,底面直径是6cm,零件的一端有一个圆柱形的孔,圆柱形孔的直径是4cm,孔深5cm,如果将这个零件接触空气的部分涂上防锈漆,一共需涂多少平方厘米?【答案】解:3.14×6×10+3.14×(6÷2)2×2+3.14×4×5=307.72(平方厘米)答:一共需涂307.72平方厘米。
【解析】【分析】涂防锈漆的面是圆柱形孔的侧面和一个底面;故根据圆柱的侧面积公式:S=πdh和圆柱的底面积公式即圆的面积公式:S=πr²,求出这两个面积;最后求和。
8.一个圆柱体的蓄水池,从里面量底面周长31.4米,深2米,在它的内壁与底面抹上水泥。
(1)抹水泥的面积是多少平方米?(2)蓄水池能蓄多少吨水?(每立方米水约重1.1吨)【答案】(1)31.4×2=62.8(平方米),31.4÷2÷3.14=15.7÷3.14=5(米)3.14×52+62.8=3.14×25+62.8=78.5+62.8=141.3(平方米)答:抹水泥的面积是141.3平方米。
(2)3.14×52×2×1.1=3.14×25×2×1.1=78.5×2×1.1=157×1.1=172.7(吨)答:蓄水池能蓄水172.7吨。
【解析】【分析】(1)已知圆柱的底面周长,用底面周长÷2÷3.14=底面半径,然后用圆柱的侧面积+底面积=抹水泥的面积,据此列式解答;(2)要求蓄水池能蓄水多少吨,先求出圆柱的体积,然后乘每立方米水的质量即可得到,据此列式解答。
9.在一个底面半径为10厘米的圆柱形杯里装满水,水里放了一个底面半径为5厘米的圆锥形铅锤,当铅锤从水中完全取出后,杯里的水面下降了0.5厘米,这个铅锤的体积是多少?【答案】 3.14×102×0.5=157(立方厘米)答:这个铅锤的体积是157立方厘米。
【解析】【分析】根据题意得出这个铅锤的体积等于,底面半径为10厘米,高为0.5厘米圆柱的体积,根据圆柱的体积=底面积×高即可解答。
10.如图,用彩带捆扎一个圆柱形礼盒,打结处用了35厘米长的彩带,礼盒的底面周长是94.2厘米,高是10厘米,求一共用了多长的彩带?【答案】解:94.2÷3.14×8+10×8+35=240+80+35=355(厘米)答:一共用了355厘米的彩带。
【解析】【分析】根据题意可知,先求出这个圆柱的底面直径,用圆柱的底面周长÷π=底面直径,观察图可知,彩带的长度=底面直径的长度×8+圆柱的高×8+打结部分的长度,据此列式解答.11.一个圆锥形小麦堆,底面半径是2米,高是1.5米。
如果每立方米小麦重0.75吨,那么这堆小麦一共重多少吨?【答案】解:×3.14×22×1.5×0.75=×3.14×4×1.5×0.75=3.14×4×0.5×0.75=12.56×0.5×0.75=6.28×0.75=4.71(吨)答:这堆小麦一共重4.71吨.【解析】【分析】根据题意可知,先求出圆锥形麦堆的体积,用公式:V= πr2h,然后用体积×每立方米小麦的质量=这堆小麦的总质量,据此列式解答12.做一个底面直径是4分米,高是5分米的圆柱形铁皮油桶,(1)做这个铁皮油桶,至少要用铁皮多少平方分米?(得数用进一法保留整平方分米)(2)这个油桶里装了的油,这些油重多少千克?(每升油重0.85千克,得数保留整千克数)【答案】(1)解:3.14×4×5+3.14×(4÷2)2×2=62.8+3.14×4×2=62.8+25.12=87.92≈88(平方分米)答:至少要用铁皮88平方分米。
(2)解:3.14×(4÷2)2×5=3.14×4×5=62.8(立方分米)62.8立方分米=62.8升0.85×62.8× =42.794≈43(千克)答:这个油桶能装油43千克。
【解析】【分析】(1)根据圆面积公式计算底面积,用底面周长乘高求出侧面积,用底面积的2倍加上侧面积就是需要铁皮的面积;(2)用底面积乘高求出油桶的容积,然后用油桶的容积乘每升油的重量求出装满油的总重量,用总重量乘即可求出装油的重量。
13.一个圆柱形的木料,底面直径是6dm,长2m。
(1)这根木料的表面积是________dm2,体积是________dm2。
(2)如果将它截成4段,这些木料的表面积比原木料增加了________。
(结果保留两位小数)【答案】(1)433.32;565.2(2)169.56dm2【解析】【解答】解:这根木料的底面半径是6÷2=3dm;2m=20dm;(1)这根木料的表面积是6×3.14×20+3×3×3.14×2=433.32dm2,体积是3×3×3.14×20=565.2dm3;(2)如果将它截成4段,就相当于把这个圆柱的表面积增加2×3=6个圆的面积,即6×3×3×3.14=169.56dm2。
故答案为:(1)433.32;565.2;(2)169.56dm2。
【分析】圆柱的底面半径=圆柱的底面直径÷2;(1)木料的表面积=木料的侧面积+木料的底面积×2,其中木料的侧面积=木料的底面周长×木料的长,木料的底面周长=木料的底面直径×π,木料的底面积=木料的底面半径2×π;(2)把一个圆柱截成4段,就是把这个圆柱切了3次,每切一次就增加2个底面,所以木料增加的表面积=切的次数×2×木料的底面积。
14.(1)求圆柱的表面积和体积。
(2)求下面图形的体积。
【答案】(1)解:表面积: 3.14×4×6+3.14× ×2=75.36+25.12=100.48(cm2)体积: 3.14× ×6=3.14×4×6=75.36(cm3)(2)解:3.14× ×6- ×3.14× ×3=3.14×6- ×3.14×3=3.14×(6-1)=15.7(立方分米)【解析】【解答】(1)表面积: 3.14×4×6+3.14×()2×2 =12.56×6+3.14×4×2=75.36+25.12=100.48(cm2)体积:3.14×()2×6=3.14×4×6=12.56×6=75.36(cm3)(2)3.14×()2×6-×3.14×()2×3=3.14×6-×3.14×3=3.14×(6-1)=3.14×5=15.7(立方分米)【分析】(1)已知圆柱的底面直径和高,求圆柱的表面积,用公式:S=πdh+π()2×2,据此列式计算;要求圆柱的体积,用公式:V=π()2h,据此列式计算。
