第5章 光的偏振-1
(张三慧教材)波动与光学Y第5章光的偏振

9
10
3. 偏振棱镜
11
*5.5 圆偏振光和椭圆偏振光
1. 波片
从单轴晶体切下来的薄片, 其表面与晶体的光轴平行。
12
( n n )d o e
2 n n ) d o e ( o e
1 波片 4
半波片
(n n o e)d 4
/2
2 2 2 2
2
18
d 2 2 I I sin 2 sin n n 2 1 0 e
当
时, K K 0 , 1 , 2
2
I2 0 , 出现消光现象,
当 2 K1
4
2 1 , I 2 达到极大。 时, s in
1. 偏振光的获得
14
1) 线偏振光:
从自然光获得线偏振光,用起偏器、波片、 玻片堆、偏振片、尼科耳棱镜等。 2) 椭圆偏振光: 自然光通过起偏器和一个波片即可。 2. 检验偏振光 设入射光有以下五种:
自然光、部分偏振光、线偏振光、圆偏振光、椭圆偏振光。
第一步
令入射光通过偏振片I , 改变 I 的透振方向,观 察透射光强变化。 强度无变化 a. 令入射光依次通过
第五章
5.1 光的偏振状态
光波的横波性
光的偏振
1
偏振态
1 线偏振光
平面偏振
振动平面
(完全)线偏振光
2 自然光
无穷多个振幅相等,振动方向任意,彼此间没有固定 的相位关系的光振动的组合,称为自然光。
2 2 I A A x ix x
2
2 2 I A A y y iy
第五章光的偏振

第五章 光的偏振§1 光的横波性及偏振态一、偏振现象日常生活中可发现光的许多偏振现象。
如:电视接收天线方向与电磁振动方向一致时,信号最清晰,而不是与传播方向一致时;又如:超快开关,利用光波偏振的电光效应,可制成s 910-的高速开关;量糖汁,利用偏振光在糖溶液中振动面的旋转,测量糖溶液的浓度。
干涉和衍射揭示光的波动性,但波有给、横波之分,干涉、衍射并不能体现这种区别。
二、偏振定义横波纵波:区别:横波有偏振,纵波无偏振波的偏振:振动方向相对于传播方向不对称例:机械波横波(1)能通过 (2)不能通过纵波:装置无论怎样摆置,均能通过可看出:纵波的振动方向对传播方向有对称性;横波的振动方向对传播方向没有对称性;例:光学实验,两块偏振片P 1、P 2;21p p 透光 21p p ⊥ 消光光发生类似的偏振现象,光是横波电矢量与光的传播方向垂直但在与传播方向垂直的二维空间里电矢量可以有各种不同的振动状态(称为偏振态) 如:(用一块偏振片)从普通光源出来的光,通过P 1,有光,(转动P 1)。
而从P 1出来的光射入P 2,(转动P 2,有时有光,某位置又无关),说明普通光源的光与从P 1出来的光的偏振态是不同。
有五种偏振状态:自然光(非偏振奋光),平面偏振光(线编光)部分偏振光、圆偏光,椭圆偏光。
三、偏振态1、平面偏振光(线偏光)只包含一种振动方向的光,即振动方向只限于某一确定方向,平偏光的数学表达式(一般)yky t A E :y x ky t A E :x y y x x )cos( )cos( -=-=ωω方向方向 而对于任意方向振动的平偏光,可将此振动分解,用两个位相相同,振方互相垂直的光波迭加来描述,其与x 轴夹角为θ。
θθωsin ,cos )cos()(A A A A ky t y A x A y E x E E y x y x y x ==-+=+=)cos()(ky t y A x A E y x --=ω2、自然光实验:普通光源,转动偏振片,都有光,且光强一样。
物理光学第五章-光偏振
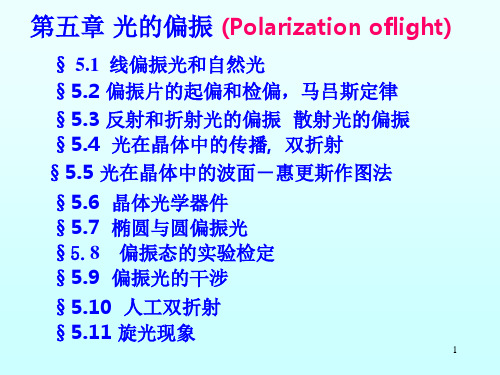
在 i1=0o 和 i1=90o 的两种情况:
Ap1 As1 cos(i1 i2 )
Ap1 As1 cos(i1 i2 )
Ap1 As1 Ap1 As1
Ap1 As1 Ap1 As1
合成后的反射光仍然是自然光。
其它角度入射: cos(i1 i2) cos(i1 i2)
Ap1 As1 Ap1 As1
Ax aix, Ay aiy
没有优势方向
自然光的分解
一束自然光可分解为两束振 动方向相互垂直的、等幅的、 不相干的线偏振光。
Ax Ay
I 0 Ax2 Ay2 I x I y
Ix
Iy
I0 2
自然光的表示法:
4
部分偏振光
部分偏振光的分解
部分偏振光可分解为两束振动方向相互垂直的、 不等幅的、不相干的线偏振光。
22
§5.4 光在晶体中的传播, 双折射
一、双折射现象
1 双折射 玻璃
自然光
自然光
晶体(方解石)
e o
Caco3
o光:ordinary light
e•
e光:extraordinary light
•o
23
2.寻常光和非寻常光
自然光
n1
i
n2
(各向异
re
性媒质) ro
e光 o光
o光 : 遵从折射定律
2
——消光
9
例1. 已知 MM'NN ' LL' 以角速度 转动
自然光入射强度为 I自
求:出射光 I ? 频率=?Imax ?
t
解: I 1
I自 2
M
L N'
I2 I1 cos2 t I自 cos2 t
第五章光的偏振

三. 椭圆与圆偏振光的检偏
用四分之一波片和偏振片P可区分出自然
光和圆偏振光或部分偏振光和椭圆偏振光
自然光 圆偏振光
四 自然光 分 之 一 线偏振光 波 片
偏 振
线偏振光
I不变
片
( 转
线偏振光
I变, 有消光
动
)
以入射光方向为轴
部分 部分偏振光 四 偏振光
分 之 椭圆偏振光 一 线偏振光 波 片
偏 振
sin re
e光折射线也不一定在入射面内。
3. 晶体的光轴
当光在晶体内沿某个特殊方向传播时不发生 双折射,该方向称为晶体的光轴。
例如,方解石晶体(冰洲石)
102° A
• 光轴是一特殊的方向,凡平 光轴 行于此方向的直线均为光轴。
B
单轴晶体:只有一个光轴的晶体
双轴晶体:有两个光轴的晶体
4. 主平面和主截面 主平面:晶体中光的传播方向与晶体 光轴构成的平面。
e
ne
c
e
n0 ,ne称为晶体的主折射率
光轴
正晶体 : ne> no
vet
(e< o) vot 负晶体 : ne<
子波源
no
(e>o)
正晶体 (vo > ve)
vet
光轴
vot vet
子波源 负晶体 (vo < ve )
三. 单轴晶体中光传播的惠更斯作图法(e>o)
光轴 线偏振光
电气石晶片
y x
分子型
入射 电磁波
z
z
线栅起偏器
• 偏振片的起偏 P
非偏振光I0
···
二. 马吕斯定律
高中物理第5章光的干涉衍射偏振第1节光的干涉托马斯杨素材鲁科版选修3-4(new)

托马斯·杨——人物简介托马斯·杨,英国医生兼物理学家,光的波动说的奠基人之一.1773年6月13日托马斯·杨生于英国萨默塞特郡的米菲尔顿一个富裕的贵格会教徒的家庭,是十个孩子中的老大。
从小就有神童之称,兴趣十分广泛,两岁就学会了看书,十四岁时用拉丁文写过一篇自传,就在当时他已掌握了多种语言。
在杨成年后,他对职业的选择受到了他叔父的影响,他的叔父是一位卓越的医生,杨在家庭同意下转到了医学方面.在十九岁时,他进入伦敦的圣巴塞罗缪医学院学医,21岁时,即以他的第一篇关于眼睛的调节机理的医学论文成为英国皇家学会会员。
为了进一步深造,他到爱丁堡和剑桥继续学习,后来又到德国哥廷根去留学继续研究医学。
在那里,他受到一些德国自然哲学家的影响,开始怀疑起光的微粒说。
1797年回到英国,进入剑桥的伊曼纽尔学院继续攻读医学,1799年杨在剑桥大学完成了学习。
那时,他的叔父已经去世,去世时留给他一笔巨大遗产,包括房屋、书籍、艺术品和一万英镑现款。
这笔巨大遗产使他在经济上完全独立,帮助他度过了一生。
1801年托马斯·杨进行了著名的杨氏干涉实验,为光的波动说的复兴奠定了基础。
1803年,杨已是知名的物理学家了,被聘为伦敦皇家学院自然哲学教授。
1802年他被选为皇家学会的外事秘书,他担任这个职务一直到他去世。
1818年他被任命为《航海天文历》的主持人,做了不少工作以改进实用天文学和航海援助工作。
1829年5月10日托马斯·杨在伦敦逝世。
终年五十六岁。
尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
第五章光的偏振椭圆偏振光与圆偏振光

14
C X
(5)如果1/4波片的厚度为:
2
3 4
5 4
3 2
正椭圆偏振光
7 4
2
10
二. 椭圆偏振光和圆偏振光的获得
由前面的学习知道,要获得椭圆(或圆)偏振光, 首先必须先有两束同频率、振动方向相互垂直,且有确 定的相位关系,并沿同一方向传播的线偏振光。 这可以让一束线偏振光通过波片来实现。
4)当Δφ 取除±kπ 以及±(2k+1)π/2且Ax=Ay之外的值,光
矢量E的矢端的轨迹是一个椭圆。椭圆偏振光也有右旋和左 旋之分。
正椭圆偏振光。长、短轴分别与X、Y轴重合。
1
当 0<< 时,为右旋椭圆偏振光; 当 << 2 时,为左旋椭圆偏振光; ( 2 k 1) 且 A x A y 时, 是 特别地,当 2
把一个起偏器透振方向与1/4波片的光轴成450 组成的器件,称为圆偏振器或圆起偏器。
17
总结:
偏振态
E x Ax cos(t kz) E y Ay cos(t kz )
当Δφ 取不同值时,光振动有不同的状态,这就是光的 偏振态。 光的偏振态有:圆偏振,椭圆偏振,线偏振,自然光 和部分偏振光。前3种可以说是纯偏振态。
E 2Ex E y E 0 A A Ax A y
2 x 2 x
第五章 光的偏振

101052, 7808
A
光轴
A
D
D
B
B
C
C
29
注意:光轴仅标志一定的方向, A
并不特指某条直线。
D
单轴晶体:
只有一个光轴的晶体。如方 B
解石(碳酸钙、冰有两个光轴的晶体。如云母、 硫磺、黄玉等。
30
⒉ 主截面:
包含晶体光轴和给定光线的平面
3. o,e光的性质 实验表明:
第五章 光的偏振
Chap.5 Polarization of Light
1
主要内容
5.1 自然光与偏振光 5.2 线偏振光与部分偏振光 5.3 光通过单轴晶体时的双折射现象 5.4 光在晶体中的波面 5.5 光在晶体中的传播方向 5.6 偏振器件
2
5.7 椭圆偏振光和圆偏振光 5.8 偏振态的实验检验 5.9 偏振光的干涉
由折射定律 sin i0 n2 sin r0 n1
n2 r0
和布儒斯特定律
tg i0
sin i0 cos i0
n2 n1
20
sin i0 sin i0 sin r0 cos i0
sin r0 cos i0
sin
2
i0
r0
2
i0
i0
r0
2
即反射线与折射线垂直。
i0 i0
n1
n2
r0
证毕
I1
I2
P2
P2
P1 A1
A2 A
13
垂直分量 A 不能通过P2 , 平行分量 A2 可通过 P2 。
P2
P1 A1
A2 A1 cos
A2
由于光强与光振幅平方成正比, A
第5章 光的偏振

§5-1 自然光与偏振光*(1课时) §5-2 线偏振光与部分偏振光*(1课时) §5-3 光通过单轴晶体时的双折射现象*(1课时) §5-4 光在晶体中的波面(0.5课时) §5-5 光在晶体中的传播方向(0.5课时) §5-6 偏振器件(1课时) §5-7 椭圆偏振光和圆偏振光*(1.5课时) §5-8 偏振态的实验检验*(0.5课时) §5 复习课(1课时)
起偏振角
i10
n1 n2
i2
tan i10
n2 n1
i10称为布儒斯特角或起偏振角
布儒斯特(1781-1868)
i10
空气
n空气
玻璃
n玻璃
i2
i2
空气
n空气
玻璃
n玻璃
i10
tan i10
n2 n1
1.5 1
1.5
tan i10
n2 n1
1 1.5
co t i10
空气→玻璃 玻璃→空气
i10 i10
第五章 光的偏振
Chap.5 Polarlization of Light
偏振现象是横波区别于纵波的一个最明显标志。
光的偏振有五种可能的状态:自然光、线偏振光、 部分偏振光、椭圆偏振光和圆偏振光。
自然界的大多数光源发出的光是自然光,是非偏 振的。
如何从自然光获得偏振光以及如何鉴别自然光和 各种偏振光。
B光强不变 B光强变化
无消光 有消光
A为自然光 A为部分偏振光
A为线偏振光
3.马吕斯定律(Mulus Law)
P
I
I ?
检偏器
A1 Acos I A12 A2 cos2 I cos2
光强为 I 的线偏振光通过检偏器 后,透射光的光强为
第五章_光的偏振

(3)若入射光为自然光,转动检偏器透射的光 强无变化。
39
例题5.2 P312
通过偏振片观察一束部分偏振光。当偏振片 由对应透射光强最大的位置转过60º 时,其光强减 为一半,试求这束部分偏振光中的自然光和线偏 振光的强度之比以及光束的偏振度。 解:部分偏振光相当于自然光和线偏振光的叠加。 设自然光的强度为In, 线偏振光的强度为Ip,则部 分偏振光的强度为In+Ip。 当偏振片处于使透射光强最大的位置时,其中的 线偏振光通过偏振片后的强度仍为Ip,而自然光透 过的强度为In /2。则透过的总光强为:
向 传播方
E
·
面 振 动 面对光的传播方向看
2
光是横波,光的振动方向应始终与光的传 播方向垂直.但是,在垂直于光的传播方向的平 面内, 光矢量还可以有不同的振动状态,我们 称在垂直于光传播方向的二维平面内,光矢量 的振动状态叫做光波的偏振态.
光波按偏振态来划分,可分为五种:
(1)自然光;(2)部分偏振光;(3)线偏振光; (4)圆偏振光;(5)椭圆偏振光。 也可以是以上几种偏振状态的组合。
16
rp
A' p1 Ap1
tg (i1 i2 ) , tg (i1 i2 )
A's1 sin( i1 i2 ) rs , As1 sin( i1 i2 )
A' p1 Ap1
tg (i1 i2 ) sin( i1 i2 ) cos(i1 i2 ) tg (i1 i2 ) sin( i1 i2 ) cos(i1 i2 )
A' p1 A's1
《光学教程》第五版 姚启钧 第五章 光的偏振

2
,I
2
0
——
消光
例5-2 假定在两个静止的、理想的、正交的起偏器之间有另 一个理想的起偏器以角速度w旋转,试证透射光的强度满足
下列关系式: I I1 1 cos 4t
8
★例5-3设一水晶棱镜的顶角A为60度,光轴与棱镜主截面垂 直,钠光以最小偏向角的方向在棱镜中折射,用焦距为0.5m 的透镜聚焦,no=1.54425,ne=1.5536,试求o光和e光两谱线的间 隔为多少?
第五章 光的偏振
物理科学与技术学院
•5.1 偏振光与自然光、偏振度 •5.2 由反射和折射获得偏振光 布儒斯特定律 •5.3 单轴晶体的双折射现象 •5.4 用波面的概念解释双折射现象 •5.5 偏振棱镜和偏振片 马吕斯定律 •5.6 椭圆偏振光与圆偏振光 波片 •5.7 偏振态的实验检验 •5.8 偏振光的干涉 •5.9 光弹性效应和电光效应 •5.10 线偏振光沿晶体光轴传播时振动面的旋转
有一块玻璃浸于水中,如光从玻璃面反射也为完全偏振光,试
求水面与玻璃面之间的夹角。
解:
i0 i1 90
tan i1
n空气 n水
1 1.33
tan i2
n玻 n水
1.5 1.33
i1 365620 i2 482616
i2 i1 112956
光轴B
n()为e光的折射率
{单轴晶体:方解石、石英 双轴晶体:云毋、硫磺、黄玉
5.3.3 主截面
主截面
晶体光轴与晶体表面法线构成的平面叫主截面
法线
102°A 78°
经过每一点有三个主截面 注意与课本定义的差别
B
第五章光的偏振

第五章光的偏振(Polarization of light)●学习目的通过本章的学习使得学生了解光通过各向异性介质时所产生的偏振现象,初步掌握自然光、线偏振光、椭圆偏振光的检测方法。
●内容提要1、阐明惠更斯作图法,说明光在晶体中的传播规律;2、介绍布儒斯特定律和马吕斯定律;3、阐明自然光、线偏振光、椭圆偏振光的概念和检测方法;4、介绍1/4波片的功用;5、讨论光在各向异性介质中的传播情况。
●重点1、偏振光的检测方法;2、光在晶体中的传播行为。
●难点1、偏振光的检测方法;2、各向异性介质光的传播行为。
●计划学时计划授课时间10学时●教学方式及教学手段课堂集中式授课,采用多媒体教学。
●参考书目1、《光学》第二版章志鸣等编著,高等教育出版社,第七章2、《光学。
近代物理》陈熙谋编著,北京大学出版社,第四章第一节 自然光与偏振光一、光的偏振性1、纵波:波的振动方向和波的传播方向相同的波称为纵波。
2、横波:波的振动方向和波的传播方向相互垂直的波称为纵波。
3、偏振:波的振动方向相对于传播方向的不对称性称为偏振。
只有横波才有偏振现象。
4、振动面:电矢量和光的传播方向所构成的平面称为偏振光的振动面。
二、自然光和偏振光(natural light )1、偏振光的种类● 平面偏振光:光在传播过程中电矢量的振动只限于某一平面内,则这种光称为平面偏振光。
● 线偏振光:(linearly polarized light )光在传播过程中电矢量在传播方向垂直的平面上的投影为一条直线,则这种光称为线偏振光。
线偏振光的表示法:● 部分偏振光(partially polarized light )彼此无固定相位关系、振动方向任意、不同方向上振幅不同的大量光振动的组合称部分偏振光。
部分偏振光可分解为两束振动方向相互垂直、不等幅、不相干的线偏振光。
▲部分偏振光的表示:迎着光的传播方向看· · · ·· 光振动垂直板面光振动平行板面圆偏振光和椭圆偏振光光矢量按一定频率在垂直传播方向的平面内旋转(左旋或右旋),其矢端轨迹是圆的称圆偏振光(circularly polarized light );其矢端轨迹是椭圆的称椭圆偏振光(ellipticly polarized light )。
光学测试技术-第5章-偏振光分析法测量

武汉大学 电子信息学院
11
§5.1 偏振光分析法基本原理
可见,转动检偏器使β=φ/2,便能产生消光现象。即: 入射到试样上的线偏光振动方向与试样快轴方向成45°经 试样后变为椭圆偏振光,该椭圆偏振光再经过1/4波片,若 椭圆的长短轴分别与波片的快慢轴平行,则从波片出射的 将是线偏光,且振动方向与原来的线偏光振动方向之间的 夹角与被测试样双折射相位差成简单的线性关系。
垂直,则等倾线是暗十字;
武汉大学 电子信息学院
6
§5.1 偏振光分析法基本原理
等倾线与波长及待测样品的位相差无关。 φ=2nπ时也将出现消光现象,即试样上所有双折射光程差为波
长整数倍的点也将形成暗条纹,这种暗条纹被称为等色线。 等色线是双折射光程差相等的点的轨迹,其分布与被测点的应
力双折射分布有关。如果使用白光光源,则等色条纹也将呈现 不同颜色。 平面偏光仪可以同时产生等倾条纹和等色条纹,其中等倾条纹 反映了主方向的分布信息,等色条纹则反映双折射相位差的分 布。在分析中需要对它们进行分离并分别加以测量。
I I0 [1- cos(2 - )]
2
武汉大学 电子信息学院
14
§5.1 偏振光分析法基本原理
I I0 [1- cos(2 - )]
2
武汉大学 电子信息学院
15
§5.2 光学玻璃应力双折射测量
一、光学玻璃应力产生的原因 光学玻璃由高温熔炼而成。玻璃毛坯在退火冷却的过程中,
中心和边缘部分存在温差,导致玻璃各处受力不均匀而产生应力。 应力的存在使玻璃从各向同性变成各向异性,直接破坏了光学材 料的光学均匀性,对成像系统的像质有直接的影响,因此是光学 材料必须控制和检测的参量。 二、应力与双折射之间的关系
第5章 光的偏振
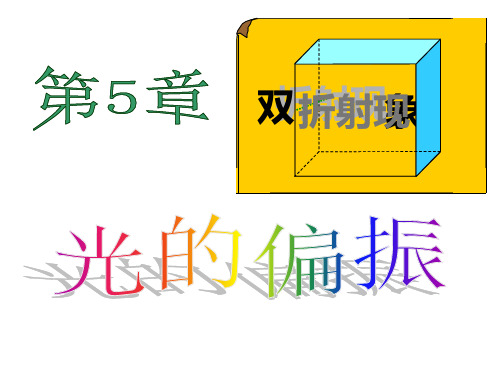
纸面
双 折
光 光
射
方解石 晶体
3. 晶体的光轴
当光在晶体内沿某个特殊方向传播时不发 生双折射,该方向称为晶体的光轴。
例如,方解石晶体
102° A
• 光轴是一特殊的方向,凡平 光轴 行于此方向的直线均为光轴。
单轴晶体:只有一个光轴的晶体
B
双轴晶体:有两个光轴的晶体
4. 主平面和主截面
主平面:晶体中光的传播方向与晶体 光轴构成的平面。
这两 个成分所占的比例。
解:设该光束中线偏振光的强度为I01,自然光的强
度为I02,则
I0 I01 I02
由马吕斯定律,该光束通过偏振片后光强为:
I max
I01
I
1 2
I0
I
2
0
1
c
os2 1
2
I min
1 2
I
I02
02
且 Imax=5Imin
I01
1 2
I02
5 2
I02
得
I01 2I02
自然光
i0
偏振光
部分偏振光 (近于偏振)
例题 一束自然光以某一角射到平面玻璃板上,反射 光恰为线偏振光,且折射光的折射角为320,求:
(1) 自然光的入射角; (2) 玻璃的折射率;
解:(1) 反射光为线偏振光时,反射光与折射光垂
直 r i 90
0
i 90 r 58 0
Hale Waihona Puke (2)tan i0
纸面
双
折 射
光 光
方解石 晶体
当方解石晶体旋转时, o光不动,e光围绕o光旋转
纸面
双
折 射
第五章光的偏振线偏振光和部分偏振光

tani10 n2 n1
其中利用了折射定律, 2.布儒斯特定律(1815年)
当入射角 i1 达到某一角 i10 时,且有
反射光中只有光振动垂直于入射面的线偏振光,但折射 光仍为部分偏振光,这一规律称之为布儒斯特定律。 i i
10
10
i10 称为布儒斯特角或起偏角。 推论:反射光线与透射光线垂直
反射光能否成为线偏振光呢?
由菲涅耳公式:
rp
0
A ' p1 Ap 1
tan(i1 i2 ) , tan(i1 i2 )
当
i1 i2 90
时,
分母为无穷大,
rp 0,
由于Ap1 0,则必有
A' p1 0
A's1 sin(i1 i2 ) rs , As1 sin(i1 i2 )
i2
n1 n2
注意: 1.当入射角为布儒斯特角(起偏角) i10时,折射光是 偏振化程度最强部分偏振光,但并非线偏振光. 2.虽然反射光是垂直于入射面的线偏振光,但反射 光中的垂直分量只占入射光中全部垂直分量15%,即 反射偏振光非常微弱. 推论:根据光的可逆性,当入射光以 i 2 角从 n2 介质入射于界面时,此 i 2 角即为布儒斯特角 .
I I0 cos
2
注意两点:
①入射光必须是线偏振光,不是自然光; ②是与cos2α正比,而不是与cosα正比。
证明:
ON1表示入射线偏振光的振动方向,ON2表示检偏器的透 光轴方向,两者的夹角为α.入射线偏振光的光矢量振幅为 E0,将此光矢量沿ON2及垂直于ON2的方向分解为两个分 量,它们的大小分别为E0cos α和E0sin α,其中只有平行于 检偏器透光轴方向ON2的分量可以透过检偏器.由于光强和 振幅的平方成正比,所以透过检偏器的透射光强I和入射 线偏振光的光强I0之比为
现代光学基础课件:光学教程第5章-光的偏振

自然光 入射
线偏振 光出射
E∥光轴:
吸收很少 通过较多
E⊥光轴: 吸收较多 通过很少
1mm厚的电气石晶体可把垂直于光轴振动的光矢量全部吸收!
二、人造偏振片:
透明聚乙烯醇片,强烈吸收某一方向上的光振动,透射光成 为线偏振光。
透振方向:允许通过光矢量振动的方向。 透振方向
三、马吕斯定律 Law of Mulus 偏振片可作 起偏器:使自然光变成线偏振光
检偏器:鉴别自然光、线偏振光、部分偏振光
1、自然光通过起偏器的情形 若入射光为 I0,有出射光:
I
1 2
I0
2、设:P1 为起偏器, P2 为检偏器,通过P1 的光强为I,振幅
为A,求通过P2 的光强为Iθ
P1 和 P2 透振方向平行时: P1 和 P2 透振方向成θ角时: P1 和 P2 透振方向垂直时:
i
i
部分偏振光可视为一个平面偏振光和一个自然光的混合
部分偏振光的图示法:
··· · ·
//占优
········
⊥占优
偏振度
定义:
P0
P Imax I min I max I min
Imax:强度最大方向光强 Imin:强度最小方向光强
偏振度最小,自然光
0 P 1 部分偏振光
P 1
偏振度最大,线偏振光
▲ 自然光 natural (普通光源发光)
在垂直于光传播方向的平面内, 光振动在各个方向的几率相 同,没有那一个方向占更大优势.我们称这种光为自然光.
y
x
Ax Aix Ay Aiy
i
i
把自然光中所有方向的振动都投影到相互垂直的两个方向上,这
华中科技大学 工程光学第五章 光的偏振和晶体光学基础

Brewster
David Brewster (1781-1868), Scottish physicist, professor of physics at St. Amdrews College. Initially a minister in the Church of Scotland, Brewster became interested in optics, found the angle named after him, contributed also the dichroism, absorption spectra, and stereo-photography, invented the kaleidoscope, and wrote a book about it. 39
which regulate the polarization of light by
reflection from transparent bodies.”
40
Malus
Etienne Louis Malus (1775-1812), French army officer and engineer. One evening in 1808 while standing near a window in his home in Paris, Malus was looking through a crystal of Iceland spar at he setting sun reflected in the windows across the street. As he turned the crystal about the line of sight, the two image of the sun seen through the crystal became alternately darker and brighter, changing every 90o of rotation. After this accidental observation Malus followed it up quickly by more solid experimental work and concluded that the light by reflection on the glass, became polarized.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
均不一定相同
乱!
普通光源发光:
在人们观察的时间内有无穷次的 发光按统计的观点人们观察到的 将是:在垂直传播方向的平面内 各个方向的光振动全有 Y
X
Z
各个振动方向的强度相等
是各个振动 的无规混杂
自然光
5
三、自然光与偏振光
线偏振光(Linearly polarized beam)
光振动矢量只在一个方向振动
i i
把自然光中所有方向的振动都投影到相互垂直的两个方向上,这两 个方向上的平均振幅相等。
自然光可分解成两个
{
相互垂直 振幅相等
无固定位相关系
}
的线偏振光
自然光的图示法:
7
部分偏振光
振动方向随机变化,某一方向振幅最大(振动占优势),与其垂直方向 振幅最小。
y Ay Ax x
Ax Aix Ay Aiy
振动面:光振动矢量与光的传播方向构成的平面 线偏振光的图示法:
振动面与屏幕垂直
屏幕即为振动面
普通光源:一个原子的一次发光一定是偏振光,不同次发 光无规律 激光器:可以实现偏振光发射
6
自然光(普通光源发光) 平均效果:任何方向上均有相同的平均振幅和能量,没有哪个方向
的振动占优势
y x
Ax Aix Ay Aiy
在玻璃片下表面仍为布 儒斯特角入射
i1 tan 1 (n1 / n2 )
16
•玻璃 n2=1.5 , 布儒斯特角
n2 tg i0 n1
光矢量垂直于入射 面的线偏振光反射
i0 56.3
•水 n2=1.33 ,
i0
i0
r0
i0 53.1
玻璃片堆
玻璃堆可产生较强的反射偏振光。
光矢量平行于入射 面的线偏振光透射0来自I0自然光P1
I
P2
P3
证明:如图所示,在 t 时刻
I1 I0 /2, I 2 I1cos2 I 0cos 2 sin 2 2 I I 2 cos 2 2
P3
P2
2
P1
25
I0
自然光
I1
I2
I
P1
2
P2
P3
I 0cos sin I 0 sin 2 I 2 8 I 0 (1 cos4 ) 16 I 0 (1 cos4 t ) 16
吸收很少 E // 光轴: 通过较多 吸收较多 E 光轴:
通过很少
1mm 厚的电气石晶体可把垂直于光轴振动的光矢量全部吸收!
10
二、人造偏振片
延伸并加碘的聚乙烯醇片,强烈 吸收某一方向上的光振动,透射 光成为线偏振光。 透振方向:允许通过光矢量振动 的方向。
优点:造价低廉;面积大,通光孔径大;轻便。
与各向同性介质一样!
32
33
单轴晶体(Uniaxial crystal)
只有一个光轴方向: 方解石(冰洲石)、石英(Quartz)、红宝石 人工拉制单轴晶体、APD(磷酸二氢氨)、铌酸锂(LiNiO3)
双轴晶体(Biaxial crystal)
有两个光轴方向:
云母(Mica)、蓝宝石(Sapphire)、黄玉
晶体的主截面:包含晶体光轴与界面法线的平面 入射光线在主截面内的特殊情况下:o光和e光的主平面 与晶体的主截面重合—我们讨论的情况 4. 光线入射面 包含入射光线与界面法线的平面。
36
5. o光和e光的振动方向 o光和e光都是线偏振光,其振动方向如何?
用检偏器检验知:
o光的振动垂直o光的主平面 e光的振动在e光的主平面内
17
薄膜偏振分光棱镜
n2 起偏振角—布儒斯特角 tani0 n1
单波长分光棱镜
18
四、马吕斯定律 (Law of Mulus)
人物介绍:马吕斯
马吕斯 ( Etienne Louis Malus 17751812 )法国物理学家及军事工程师。出 生于巴黎,1796年毕业于巴黎工艺学院, 曾在工程兵部队中任职。1808年起在巴 黎工艺学院工作。1810年被选为巴黎科 学院院士,曾获得过伦敦皇家学会奖章。
第5章 光的偏振 Polarization of Light
§5.1 自然光与偏振光(了解) §5.2 线偏振光和部分偏振光(掌握) §5.3 光通过单轴晶体时的双折射现象(掌握) §5.4 光在晶体中的波面(了解) §5.5 光在晶体中的传播方向(掌握) §5.6 偏振器件(了解) §5.7 椭圆偏振光和圆偏振光(掌握) §5.8 偏振态的实验检验(掌握) §5.9 偏振光的干涉(掌握) §5.10 磁光效应和旋光效应(了解)
I10 I1 cos 2 30 2
I 20 I2 cos 2 60 2
I10 1 I 20 3
27
§5.3 晶体中的双折射
一、晶体的双折射现象
方解石晶体 实物照片 方解石晶体
纸面
折射现象 双 折射现
1.双折射现象 用眼睛观看发光点,会看到 两个像点,透过方解石晶体, 纸面上的字成了双字。
37
入射光线在主平面内时,两条光线的主截面就是主平面 o光的振动垂直主截面 e光的振动在主截面内 两光偏振方向垂直
n1 sin i ne sin ie n1 sin i no sin io
38
不服从折射定律
服从折射定律
5. o光和e光的相对光强 设入射光强为I,振幅为A
2、线偏振光垂直入射
A p
tan(i1 i2 ) Ap tan(i1 i2 )
一般入射角 i1 (0,90除外),反射光和透射光均为部分 偏振光
14
2. 特殊情况 (布儒斯特定律Brewster’s Law)
自然光
线偏振光
n1
i10 i2
A p Ap
2
i2
部分偏振光
n2
费 涅 耳 公 式
1
Ax
入射 的自然光 光强为I0
从P1出射线偏振光光 强为 I = I0 /2
Ax = Ay
该偏振片可从自然光中取得线偏振光所以称为起偏器
20
起偏
将自然光转变成偏振光的过程。
P1
检偏
检测偏振光的过程。
P1
P2
21
2. 线偏振光通过起偏器的情形
过P1 的线偏振 光光强为 I
P1
P2
P1
θ
P2
缺点:带有选择性吸收,使透射的偏振光略带颜色。
11
形象说明偏振片的原理
透振方向
12
13
三、反射光的偏振态 (熟练运用结论)
1. 一般情况 自然光分解成: S波:光矢量垂直于入射面 P波:光矢量平行于入射面 由菲涅耳公式(P30 1.5节):
As sin(i1 i2 ) As sin(i1 i2 )
2 2
P3
P2
2
P1
26
例 有两个偏振片,一个用作起偏器,一个用作检偏器,当 它们的偏振化方向之间的夹角为 30° 时,一束单色自然光 穿过它们,出射光强为 I1 ; 当它们的偏振化方向之间的夹 角为 60° 时,另一束单色自然光穿过它们,出射光强为 I2 ,且I1 = I2,求两束单色自然光的强度之比。 解: 设第一束光的强度为I10,第二束光的强度为I20 ,它们 透过起偏片后,强度减半,根据马吕斯定律
tan(i1 i2 ) 0 tan(i1 i2 )
反射光为光矢量垂直于入射面的完全偏振光
透射光为部分偏振光
n2 i10 称为起偏振角—布儒斯特角 tani10 n1
15
3. 用玻璃片堆获得线偏振光
在玻璃片上表面用布儒 斯特角入射
i0 tan1 (n2 / n1 ) i0 i2 2
从实用的角度看,首先必须解决两大问题: 1. 如何判断光源的偏振态,偏振光的检验 2. 如何从普通光源中取得偏振光 利用反射和折射 利用二向色性 利用晶体的双折射 起偏振器:用某种方式从 自然光中获得偏振光的光 学元件
9
§5.2 线偏振光与部分偏振光
一、二向色性与偏振片
二向色性:某些各向异性晶体 对不同方向光振动具有选择吸 收的性质 天然晶体中,电气石(六角形 片状)具有最强的二向色性
P1
A
P2
A// A cos
从P2 出射光强为 Iθ= A//2= I cos2θ
A A sin
θ
马吕斯定律 I I cos2
22
I0
I1
I2
P1
马吕斯定律 讨论:
1.当
P2
1 2 I 2 I1cos I 0 cos 2
2
0 或
时, I 2 I1
29
当方解石晶体旋转时,o光不动,e光围绕o光旋转 方解石 晶体
纸面 双 折 射
光 光
30
3. o光和e光的偏振态 均为线偏振光 用检偏器检验 o光和e光
振动方向垂直(条件见后)
问题:(1)e光在晶体内的传播方向? (2) o光和e光的偏振方向
31
二、光轴、主平面与主截面
1. 光轴(特殊方向) 实验中改变入射光的方向,发现在晶体中存在特殊方向, 光在晶体中沿这个方向传播时不发生双折射,该特殊方向称 为晶体的光轴 注意:在晶体内光轴是一个方向 实验上怎么操作呢?令入射表面垂直光轴,光线沿光轴方向 入射,光线在晶体内部传播不发生双折射。
3 时, I 2 0 2.当 或 2 2
23
立体电影
24
例(P267 5.4) 有三个偏振片堆叠在一起,第一块与第三块的偏 振片化方向相互垂直,第二块和第一块的偏振化方向相互平行, 然后第二块偏振片以恒定的角速度 绕光传播的方向旋转,设 入射自然光的光强为 I0。试证明:此自然光通过这一系统后, 出射光的光强为 I I (1 cos4t )/16
