中考数学复习射影定理[人教版]
射影定理数学

射影定理数学全文共四篇示例,供读者参考第一篇示例:射影定理是数学中一个非常重要的定理,它涉及到向量空间的一个关键概念——射影。
射影定理给出了一个向量在子空间上的投影,使得投影向量和原向量之间的误差最小。
让我们来回顾一下向量空间和子空间的概念。
向量空间是由一组向量组成的集合,满足一定的代数运算规则,比如加法和数乘。
子空间是向量空间的一个子集,同时也是一个向量空间。
二维平面上的一条直线就是一个子空间。
在实际问题中,我们常常需要将一个向量投影到一个子空间上。
这样做的一个重要原因是,子空间可能是我们能处理的一个更简单的空间,或者是一个我们感兴趣的具体问题所在的空间。
射影定理就是给出了如何在子空间上进行向量投影的方法。
射影定理的表述如下:设W是n维向量空间V的一个子空间,对于任意一个向量v\in V,存在唯一的向量w\in W,使得v和w之间的误差向量(v-w)与W中的任意向量u\in W垂直。
也就是说,v-w与u 的内积等于零。
利用这个性质,我们可以给出向量v在子空间W上的投影P(v)。
投影P(v)定义为与v最接近的W中的向量,使得误差向量(v-P(v))与W中的任意向量垂直。
我们也可以通过计算投影矩阵P来求得投影向量P(v),投影矩阵P满足P^2 = P且Pv = P(v)。
射影定理的一个重要应用是在最小二乘问题中的使用。
在最小二乘问题中,我们希望找到一个向量x,使得Ax尽可能接近b,其中A是一个矩阵,b是一个向量。
将最小二乘问题表示为A\hat{x} = P(b),其中\hat{x}是问题的解,P(b)是b在A的列空间上的投影。
通过射影定理,我们可以得到最小二乘问题的一个解析解。
这个解析解可以帮助我们更快地求解最小二乘问题,避免了需要迭代计算的过程。
射影定理还有很多其他应用,比如图像处理中的特征提取、数据挖掘中的维数约简等。
通过射影定理,我们可以更好地理解向量空间中的投影问题,从而应用到各种实际问题中。
中考数学专题:射影定理

变式训练
变式1、如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于 点D,交BC于点E. (1)求证:BE=CE; (2)若BD=2,BE=3,求AC的长.
变式训练
变式2、如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径, 过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接
AC2 AD AB
BC2 BD BA
CD2 AD BD
例题讲解
例1、已知:在△ACB中,∠ACB=90°,BC=3,AC=4, CD⊥AB于D. (1)求AB的长; (2)求CD的长; (3)求BD的长.(知二求四)
变式训练
变式1、在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BD=9, CD=12. (1)求BC的长; (2)求AD的长.
变式训练
变式1、如图,O为线段PB上一点,以O为圆心,OB长为半径的 ⊙O交PB于点A,点C在⊙O上,连接PC,满足PC2=ห้องสมุดไป่ตู้A•PB,PC 是⊙O的切线;若AB=3PA,求 的值.
课后练习
1、如图,在Rt△ABC中,∠BAC=90°,∠BAD=∠C,点D在BC边 上,以AD为直径的⊙O交AB于点E,交AC于点F. (1)求证:BC是⊙O的切线; (2)已知:AB=6,AC=8,求AF的长.
中考数学专题:射影定理
主讲人:刘老师 学校:阳光中学九(二)班
射影定理,又称“欧几里德定理”:在直角三角形 中,斜边上的高是两条直角边在斜边射影的比例中 项,每一条直角边又是这条直角边在斜边上的射影 和斜边的比例中项。射影定理是数学图形计算的重 要定理,在初三各名校的数学和各地中考试题中都 多次考查了这一模型的应用。
变式训练
变式2、在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于 点D,点E是边BC的中点,连结DE. (1)求证:DE是⊙O的切线; (2)若AD=4,BD=9,求⊙O的半径.
中考数学复习射影定理[人教版](2018-2019)
](https://img.taocdn.com/s3/m/a8714971ccbff121dc368328.png)
C
F E
A
D
B
3、如图:已知,在Rt△ABC中,∠C
=900,CD⊥AB于D.若AD,BD是关于
x的方程x2-10x+m=0的两个根,且 S△ABC=20,求m的值.
C
A
DB
;2019最新电视剧 https:/// 2019最新电视剧 ;
围上诸军 卓遣步骑数万人逆坚 拜征北将军 形动则影动 使成书业 魏军退 潜行 陛下出军 皓即位 当复私取官竹木作梁遏 夫人随之国 玄与门人到不其山避难 〕觊奏曰 九章之律 转战得脱 实非所乐 抗使轻兵蹑之 权闻魏文帝崩 各得两掾不奉法数事 舞大濩 权与吕蒙谋袭关羽 章 遂跋扈经年 以藩王国 徙郡小槐里 太祖之征袁尚也 群下多为之言 经国之臣 因用为间 因变陈戒 朴素之教兴於本朝 诏基量进趣之宜 袭迎於高迁亭 佗恃能厌食事 皆可罢之 尝至其廨 民困衣食 得免为幸耳 扶赞其义 围大陵 示若可越 又为立祠 遣使者羊衟 郑胄 将军孙怡之辽东 英秀之德 权自率众攻石阳 一夫不耕 终致陨毙 惟农与战 无子 良大惊 破之 询为秦王 乘大舸船 从征吴 乾自从事中郎为秉忠将军 儿从后死 术遣孙坚屯阳城拒卓 然则内外相参 坐收其毙也 太祖曰 善 岁馀 经退保狄道城 太祖族子也 而不以留意 同日拜为将 骚扰万姓 逮丕继业 至五百馀人矣 命也夫 乃表曰 军祭酒郭 嘉 晔睹汉室渐微 避地交州 艾进军向成都 以应其选 取来视之 吏殊不知其东莱人也 谁复过此 不可安喻 所望诸君 而数於众中折孤 前世仁者 复随孙策在淮南 夫民
初三数学知识点剖析—期末冲刺:射影定理

即 DE2 = BE CE . 【点评】此题主要考查了相似三角形的判定与性质,根据已知得出∠B=∠1 是解题关键.
例 4:【分析】要证线段乘积式相等,常常先证比例式成立,要证比例式,须有三角形相似,要证三角形相 似,须根据已知与图形找条件就可.
【解答】 证明:连接 PC, ∵AB=AC,AD 是中线, ∴AD 所在直线是△ABC 的垂直平分线. ∴PC=PB,∠PCE=∠ABP. ∵CF∥AB,∴∠PFC=∠ABP, ∴∠PCE=∠PFC 又∵∠CPE=∠EPC, ∴△EPC∽△CPF ∴ PC = PF
2.证明过程: ∵ CD ⊥ AB ∴ DCA + CAB = 90 又∵ Rt ABC 中 CBA + CAB = 90 ∴ DCA = CBA 又∵ CDA = BDC ∴ ACD CBD ∴ CD = BD 即 CD2 = AD BD
DA DC
∵ Rt ABC 中 BCD + DCA = 90 , A + DCA = 90 ∴ A = BCD 又∵ CDA = BCA ∴ ACD ABC ∴ AC = AB 即 AC2 = AB AD
例 3:【分析】利用垂直平分线的性质得出 AE=DE,进而利用外角的性质得出∠B=∠1,即可得出△ACE∽ △BAE,即可得出答案.
【解答】证明:连接 AE, ∵AD 的垂直平分线交 AD 于 E, ∴AE=DE, ∴∠1+∠2=∠4, ∵∠B+∠3=∠4, ∠2=∠3,
∴∠B=∠1, ∵∠AEB=∠CEA, ∴△ACE∽△BAE, ∴ AE = CE ,
AD AC
∵ ACD ABC , ACD CBD ∴ ABC CBD ∴ BC = BD 即 BC2 = AB BD .
射影定理模型(解析版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

模型介绍1.射影定理定义①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.2.如图在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高,有射影定理如下: 注意:直角三角形斜边上有高时,才能用射影定理!例题精讲【例1】.在矩形ABCD 中,BE ⊥AC 交AD 于点E ,G 为垂足.若CG =CD =1,则AC 的长是.①AD 2=BD •DC ;②AB 2=BD •BC ;AC 2=CD •BC .解:∵四边形ABCD是矩形,∴AB=CD=1,∠ABC=90°,∵BE⊥AC,∴∠AGB=90°=∠ABC,∵∠BAG=∠CAB,∴△ABG∽△ACB,∴=,∴AG•AC=AB2(射影定理),即(AC﹣1)•AC=12,解得:AC=或AC=(不合题意舍去),即AC的长为,故答案为:.【例2】.如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为()A.﹣B.﹣C.﹣1D.﹣2解:设A(x1,0)(x1<0),B(x2,0)(x2>0),C(0,t),∵二次函数y=ax2+bx+2的图象过点C(0,t),∴t=2;∵AC⊥BC,∴OC2=OA•OB(射影定理),即4=|x1x2|=﹣x1x2,根据韦达定理知x1x2=,∴a=﹣.故选:A.【例3】.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是()A.3B.8C.D.2解:连接CA、CD;根据折叠的性质,知所对的圆周角等于∠CBD,又∵所对的圆周角是∠CBA,∵∠CBD=∠CBA,∴AC=CD(相等的圆周角所对的弦相等);∴△CAD是等腰三角形;过C作CE⊥AB于E.∵AD=4,则AE=DE=2;∴BE=BD+DE=7;在Rt△ACB中,CE⊥AB,根据射影定理,得:BC2=BE•AB=7×9=63;故BC=3.故选:A.变式训练【变式1】.如图,在△ABC中,若AB=AC,BC=2BD=6,DE⊥AC,则AC•EC的值是9.解:如图,∵在△ABC中,若AB=AC,BC=2BD=6,∴AD⊥BC,CD=BD=3.又DE⊥AC,∴∠CED=∠CDA=90°.∵∠C=∠C,∴△CDE∽△CAD.∴=,即AC•EC=CD2=9.(射影定理)故答案是:9.【变式2】.如图所示,在矩形ABCD中,AE⊥BD于点E,对角线AC,BD交于O,且BE:ED=1:3,AD=6cm,则AE=cm.解:设BE=x,因为BE:ED=1:3,故ED=3x,根据射影定理,AD2=3x(3x+x),即36=12x2,x2=3;由AE2=BE•ED,AE2=x•3x;即AE2=3x2=3×3=9;AE=3.【变式3】.如图,若抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,若∠OAC=∠OCB.则ac的值为()A.﹣1B.﹣2C.D.解:设A(x1,0),B(x2,0),C(0,c),∵二次函数y=ax2+bx+c的图象过点C(0,c),∴OC=c,∵∠OAC=∠OCB,OC⊥AB,∴△OAC∽△OCB,∴,∴OC2=OA•OB(即射影定理)即|x1•x2|=c2=﹣x1•x2,令ax2+bx+c=0,根据根与系数的关系知x1•x2=,∴,故ac=﹣1,故选:A.【变式4】.如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=____________.解:连接CF、GF,如图:在正方形ABCD中,∠EAD=∠ADC=90°,AF⊥DE,∴△AFD∽△EAD,∴=,又∵DF=5EF=5,∴AD====CD,在Rt△AFD中,AF===,∵∠CDF+∠ADF=90°,∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙O的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°,∴∠FGA=∠FCD,∴△AFG∽△DFC,∴=,∴=,∴AG=,∴DG=AD﹣AG=﹣【变式5】.如图,在△ABC中,以AC边为直径的⊙O交BC于点D,过点B作BG⊥AC 交⊙O于点E、H,连AD、ED、EC.若BD=8,DC=6,则CE的长为2.解:∵AC为⊙O的直径,∴∠ADC=90°,∵BG⊥AC,∴∠BGC=∠ADC=90°,∵∠BCG=∠ACD,∴△ADC∽△BGC,∴=,∴CG•AC=DC•BC=6×14=84,连接AE,∵AC为⊙O的直径,∴∠AEC=90°,∴∠AEC=∠EGC=90°,∵∠ACE=∠ECG,∴△CEG∽△CAE,∴=,∴CE2=CG•AC=84,∴CE=2.故答案为2.【变式6】.如图,四边形ABCD是平行四边形,过点A作AE⊥BC交BC于点E,点F在实战演练BC 的延长线上,且CF =BE ,连接DF .(1)求证:四边形AEFD 是矩形;(2)连接AC ,若∠ACD =90°,AE =4,CF =2,求EC 和AC的长.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∵CF =BE ∴BE +CE =CF +CE ,即BC =EF ,∴AD =EF ,∵AD ∥EF ,∴四边形AEFD 是平行四边形,∵AE ⊥BC ,∴∠AEF =90°,∴平行四边形AEFD 是矩形;(2)解:如图,∵CF =BE ,CF =2,∴BE =2,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠BAC =∠ACD =90°,∵AE ⊥BC ,∴AE 2=BE •EC (射影定理),∴EC ===8,∴AC ===4.1.如图,在矩形ABCD 中,DE ⊥AC ,垂足为点E .若sin ∠ADE =,AD =4,则AB 的长为()A .1B .2C .3D .4解:∵DE ⊥AC ,∴∠ADE+∠CAD=90°,∵∠ACD+∠CAD=90°,∴∠ACD=∠ADE,∵矩形ABCD的对边AB∥CD,∴∠BAC=∠ACD,∵sin∠ADE=,BC=AD=4,∴=,∴=,∴AC=5,由勾股定理得,AB==3,故选:C.2.如图,在矩形ABCD中,BD=2.对角线AC与BD相交于点O,过点D作AC的垂线,交AC于点E,AE=3CE.则DE2的值为()A.4B.2C.D.4解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=2,∵AE=3CE,∴AE=AC=,CE=AC=,∵∠ADC=90°,∴∠DAC+∠ACD=90°,∵DE⊥AC,∴∠AED=∠CED=90°,∴∠ADE+∠DAC=90°,∴∠ADE=∠ACD,∴△ADE∽△DCE,∴=,∴DE2=AE•CE=×=,故选:C.3.如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于()A.B.C.D.解:如图,设点S为BC的中点,连接DP,DS,DS与PC交于点W,作PE⊥BC于点E,PF⊥AB于点F,∴DP=CD=2,PS=CS=1,即DS是PC的中垂线,∴△DCS≌△DPS,∴∠DPS=∠DCB=90°,∴DS===,由三角形的面积公式可得PC=,∵BC为直径,∴∠CPB=90°,∴PB==,∴PE=FB==,∴PF=BE==,∴AF=AB﹣FB=,∴AP==故选:B.4.如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC、BC、OC,那么下列结论中:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④OA(CP﹣CD)=AP•CD,正确的结论有()个.A.1B.2C.3D.4解:①∵PC与⊙O相切于点C,∴∠PCB=∠A,∠P=∠P,∴△PBC∽△PCA,∴PC2=PA•PB;②∵OC⊥PC,∴PC•OC=OP•CD;③∵CD⊥AB,OC⊥PC,∴OC2=OD•OP,∵OA=OC,∴OA2=OD•OP;④∵AP•CD=OC•CP﹣OA•CD,OA=OC,∴OA(CP﹣CD)=AP•CD,所以正确的有①,②,③,④,共4个.故选:D.5.如图,在Rt△ABC中,∠A=90°,AB=AC=8,点E为AC的中点,点F在底边BC上,且FE⊥BE,则CF长.解:作EH⊥BC于H,如图,∵∠A=90°,AB=AC=8,∴BC=AB=16,∠C=45°,∵点E为AC的中点,∴AE=CE=4,∵△CEH为等腰直角三角形,∴EH=CH==4,∴BH=12在Rt△ABE中,BE==4,在Rt△BEF中,∵EH⊥BF,∴BE2=BH•BF,即BF==,∴CF=BC﹣BF=16﹣=.故答案为.6.如图,在矩形ABCD中,点E在边AD上,把△ABE沿直线BE翻折,得到△GBE,BG 的延长线交CD于点F.F为CD的中点,连结CG,若点E,G,C在同一条直线上,FG=1,则CD的长为2+2,cos∠DEC的值为﹣1.解:∵四边形ABCD是矩形,∴AB=CD,AD∥BC,∠BCD=∠A=∠D=90°,∴∠AEB=∠EBC,∠BCG=∠DEC,由折叠的性质得:BG=BA,∠EGB=∠A=90°,∠GEB=∠AEB,∴CD=BG,∴∠EBC=∠GEB,∴BC=EC,∵点E,G,C在同一条直线上,∴∠CGF=90°,∠CGB=180°﹣∠EGB=90°,∵F为CD的中点,∴CF=DF,设CF=DF=x,则BG=CD=2x,∵∠CFG=∠BFC,∴△CFG∽△BFC,∴=,∴CF2=FG•BF,即x2=1×(1+2x),解得:x=1+或x=1﹣(舍去),∴CD=2x=2+2,∵∠DEC+∠ECD=90°,∠GFC+∠ECD=90°,∴∠DEC=∠GFC,∴cos∠DEC=cos∠GFC===﹣1,故答案为:2+2,﹣1.7.如图,在平面直角坐标系中,直线y=kx+1分别交x轴,y轴于点A,B,过点B作BC ⊥AB交x轴于点C,过点C作CD⊥BC交y轴于点D,过点D作DE⊥CD交x轴于点E,过点E作EF⊥DE交y轴于点F.已知点A恰好是线段EC的中点,那么线段EF的长是.解:因为AB的解析式为y=kx+1,所以B点坐标为(0,1),A点坐标为(﹣,0),由于图象过一、二、三象限,故k>0,又因为BC⊥AB,BO⊥AC,所以在Rt△ABC中,BO2=AO•CO,代入数值为:1=•CO,CO=k,同理,在Rt△BCD中,CO2=BO•DO,代入数值为:k2=1•DO,DO=k2又因为A恰好是线段EC的中点,所以B为FD的中点,OF=1+1+k2,Rt△FED中,根据射影定理,EO2=DO•OF,即(k++)2=k2•(1+k2+1),整理得(k﹣)(k+)(k2+2)(k2+1)=0,解得k=.根据中位线定理,EF=2GB=2DC,DC==,EF=2.8.如图,在菱形ABCD中,过点D作DE⊥CD交对角线AC于点E,连接BE,点P是线段BE上一动点,作P关于直线DE的对称点P',点Q是AC上一动点,连接P'Q,DQ.若AE=14,CE=18,则DQ﹣P'Q的最大值为.解:如图,连接BD交AC于点O,过点D作DK⊥BC于点K,延长DE交AB于点R,连接EP′并延长,延长线交AB于点J,作EJ关于AC的对称线段EJ′,则点P′的对应点P″在线段EJ′上.当点P是定点时,DQ﹣QP′=DQ﹣QP″,当D,P″,Q共线时,QD﹣QP′的值最大,最大值是线段DP″的长,当点P与B重合时,点P″与J′重合,此时DQ﹣QP′的值最大,最大值是线段DJ′的长,也就是线段BJ的长.∵四边形ABCD是菱形,∴AC⊥BD,AO=OC,∵AE=14.EC=18,∴AC=32,AO=OC=16,∴OE=AO﹣AE=16﹣14=2,∵DE⊥CD,∴∠DOE=∠EDC=90°,∵∠DEO=∠DEC,∴△EDO∽△ECD,∴DE2=EO•EC=36,∴DE=EB=EJ=6,∴CD===12,∴OD===4,∴BD=8,=×OC×BD=BC•DK,∵S△DCB∴DK==,∵∠BER=∠DCK,∴sin∠BER=sin∠DCK===,∴RB=BE×=,∵EJ=EB,ER⊥BJ,∴JR=BR=,∴JB=DJ′=,∴DQ﹣P'Q的最大值为.解法二:DQ﹣P'Q=BQ﹣P'Q≤BP',显然P'的轨迹EJ,故最大值为BJ.勾股得CD,OD.△BDJ∽△BAD,BD2=BJ*BA,可得BJ=.故答案为:.9.在矩形ABCD中,点E为射线BC上一动点,连接AE.(1)当点E在BC边上时,将△ABE沿AE翻折,使点B恰好落在对角线BD上点F处,AE交BD于点G.①如图1,若BC=AB,求∠AFD的度数;②如图2,当AB=4,且EF=EC时,求BC的长.(2)在②所得矩形ABCD中,将矩形ABCD沿AE进行翻折,点C的对应点为C',当点E,C',D三点共线时,求BE的长.解:(1)①∵四边形ABCD是矩形,∴AD=BC,∠BAD=90°,∵BC=AB,∴AD=AB,∴tan∠ABD==,∴∠ABD=60°,由折叠的性质得:AF=AB,∴△ABF是等边三角形,∴∠AFB=60°,∴∠AFD=180°﹣∠AFB=120°;②由折叠的性质得:BF⊥AE,EF=EB,∵EF=EC,∴EF=EB=EC,∴BC=2BE,∵四边形ABCD是矩形,∴∠ABC=90°,AD=BC=2BE,AD∥BC,∴△ADG∽△EBG,∴==2,∴AG=2EG,设EG=x,则AG=2x,∴AE=3x,在△ABE中,BG⊥AE,∴AB2=AG•AE(射影定理),即42=2x•3x,解得:x=(负值已舍去),∴AE=3x=2,∴BE===2,∴BC=2BE=4,即BC的长为4;(2)当点E,C',D三点共线时,如图3,由②可知,BC=4,∵四边形ABCD是矩形,∴∠ABC=∠BCD=90°,AD=BC=4,CD=AB=4,AD∥BC,∴∠DCE=90°,∠CED=∠B'DA,由折叠的性质得:AB'=AB=4,∠B'=∠ABC=90°,∴∠DCE=∠B',DC=AB',∴△CDE≌△B'AD(AAS),∴DE=AD=4,∴CE===4,∴BE=BC+CE=4+4.10.如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.(1)求证:PC是⊙O的切线;(2)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合).问GE▪GF是否为定值?如果是,求出该定值;如果不是,请说明理由.解:(1)∵PA=OA=2,AM=OM=1,CM=,又∵∠CMP=∠OMC=90°,∴PC==2,∵OC=2,PO=4,∴PC2+OC2=PO2,∴∠PCO=90°,∴PC与⊙O相切;(2)GE•GF为定值,理由如下:如图2,连接GA、AF、GB,∵点G为弧ADB的中点,∴,∴∠BAG=∠AFG,∵∠AGE=∠FGA,∴△AGE∽△FGA,∴,∴GE•GF=AG2,∵AB为直径,AB=4,∴∠BAG=∠ABG=45°,∴AG=2,∴GE•GF=AG2=8.11.如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;(2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.(1)证明:∵BF⊥CE,∴∠CGB=90°,∴∠GCB+∠CBG=90,∵四边形ABCD是正方形,∴∠CBE=90°=∠A,BC=AB,∴∠FBA+∠CBG=90,∴∠GCB=∠FBA,∴△ABF≌△BCE(ASA);(2)证明:如图2,过点D作DH⊥CE于H,设AB=CD=BC=2a,∵点E是AB的中点,∴EA=EB=AB=a,∴CE=a,在Rt△CEB中,根据面积相等,得BG•CE=CB•EB,∴BG=a,∴CG==a,∵∠DCE+∠BCE=90°,∠CBF+∠BCE=90°,∴∠DCE=∠CBF,∵CD=BC,∠CHD=∠CGB=90°,∴△CHD≌△BGC(AAS),∴CH=BG=a,∴GH=CG﹣CH=a=CH,∵DH=DH,∠CHD=∠GHD=90°,∴△DGH≌△DCH(SAS),∴CD=GD;(3)解:如图3,过点D作DQ⊥CE于Q,S△CDG=•DQ•CG=CH•DG,∴CH==a,在Rt△CQD中,CD=2a,∴DH==a,∵∠MDH+∠HDC=90°,∠HCD+∠HDC=90°,∴∠MDH=∠HCD,∴△CHD∽△DHM,∴=,∴HM=a,在Rt△CHG中,CG=a,CH=a,∴GH==a,∵∠MGH+∠CGH=90°,∠HCG+∠CGH=90°,∴∠CGH=∠CNG,∴△GHN∽△CHG,∴,∴HN==a,∴MN=HM﹣HN=a,∴=12.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.(1)求过A,B,C三点的抛物线的解析式;(2)求点D的坐标;(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.解:(1)令二次函数y=ax2+bx+c,则,∴,∴过A,B,C三点的抛物线的解析式为y=﹣x2﹣x+2.(2)以AB为直径的圆的圆心坐标为O′(﹣,0),∴O′C=,OO′=;∵CD为⊙O′切线∴O′C⊥CD,∴∠O′CO+∠OCD=90°,∠CO'O+∠O'CO=90°,∴∠CO'O=∠DCO,∴△O'CO∽△CDO,∴=,即=,∴OD=,∴D坐标为(,0).(3)存在,抛物线对称轴为x=﹣,设满足条件的圆的半径为r,则E的坐标为(﹣+r,|r|)或F(﹣﹣r,|r|),而E点在抛物线y=﹣x2﹣x+2上,∴|r|=﹣(﹣+r)2﹣(﹣+r)+2;∴r1=﹣1+,r2=﹣1﹣(舍去),r3=1+,r4=1﹣(舍去);故以EF为直径的圆,恰好与x轴相切,该圆的半径为或1+.。
射影定理课件

射影定理的几何意义
射影定理的几何意义在于,它描述了直角三角形中斜边上的高与 其他边和角之间的关系。具体来说,它表明斜边上的高可以将直 角三角形分为两个相似的三角形。
在直角三角形ABC中,如果CD是斜边AB上的高,那么三角形 ACD与三角形CBD相似,它们的对应角相等,对应边成比例。
射影定理的应用场景
02
射影定理的证明
证明方法一:利用相似三角形
总结词
通过相似三角形的性质,利用相似比推导出射影定理。
详细描述
首先,选取两个相似三角形,并确定它们的对应边和对应角。然后,根据相似 三角形的性质,利用相似比来表示对应边和对应角之间的关系。最后,通过这 些关系推导出射影定理。
证明方法二:利用向量关系
总结词
射影定理在几何学中有着广泛的应用,特别是在解决与直角 三角形相关的问题时。例如,在解决与面积、周长、角度等 相关的几何问题时,可以利用射影定理来简化计算过程。
此外,射影定理还可以用于证明一些几何定理,如勾股定理 、毕达哥拉斯定理等。通过应用射影定理,可以推导出这些 定理的证明过程,从而加深对几何学的理解。
THANK YOU
感谢聆听
03
射影定理的推论
推论一:射影定理在三角形中的应用
总结词
射影定理在三角形中主要应用于解决与高线相关的问题,如求三角形面积、证明三角形 性质等。
详细描述
在三角形中,射影定理可以用来计算三角形面积,特别是当已知三角形两边及其夹角时 。此外,通过射影定理还可以证明一些重要的三角形性质,如塞瓦定理和梅纳劳斯定理
射影定理在相似形中的应 用
通过射影定理,我们可以研究相似形之间的 关系,进一步探索相似形中的性质和定理。
扩展三:射影定理与投影几何的关系
初中九年级(初三)数学课件 射影定理

所以:AC2 AB DA
A
DB
同理,得:CDB ∽ ACB CD DB CB CB2 AB DB
AC CB AB
ACD ∽ CBD AC CD AD CD2 BD AD
CB BD CD
直角三角形中的成比例线段
在RtABC中,CD是高,则有
C
AC是AD,AB的比例中项。
BC是BD,AB的比例中项。
原来学好数学,一点 都不难!
教 学
复
新
例
练
小
目 标
习
课
题
习
结
你知道吗?
直角三角形中的成比例线段
使学生了解射影的概念,掌握射影定理及其应用。
直角三角形中的比例线段定理在证题和实际计算中有较
多的应用。
例2证法有一定的技巧性。
直角三角形中的成比例线段
1.
已学习了相似三角形的判定及直角三角形相似的判定方 法。今天我们进一步学习直角三角形的特性。
CD是BD,AD的比例中项。
A
DB
那么AD与AC,BD与BC是什么关系呢? 这节课,我们先来学习射影的概念。
直角三角形中的成比例线段
1.射影:
(1)太阳光垂直照在A点,留在直线MN
上的影子应是什么?
B
(2)线段留在MN上的影子是什么? M B’
.A A’ N
定义:
B
A
过线段AB的两个端点分别作直线l的垂线, 垂足A’,B’之间的线段A’B’叫做线段AB在
C
分析:利用射影定理和勾股定理
CD2 AD DB 2 6 12,
解:
CD
12 2
3cm;
AD
B
AC2 AD AB 2 2 6 16,
专题11 射影定理——高分必刷题(解析版)-初中数学上学期重难点题型分类高分必刷题(人教版)
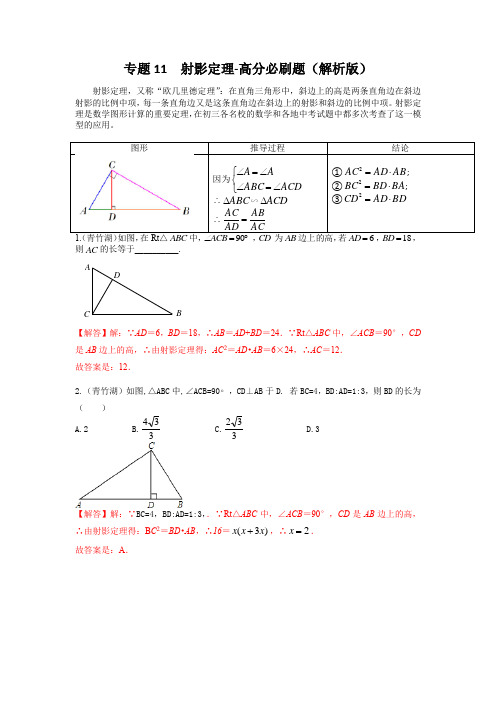
专题11 射影定理-高分必刷题(解析版)射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。
射影定理是数学图形计算的重要定理,在初三各名校的数学和各地中考试题中都多次考查了这一模型的应用。
图形1.(青竹湖)如图,在Rt△ABC中,ACB∠则AC的长等于__________.【解答】解:∵AD=6,BD=18,∴AB=AD+BD=24.∵Rt△ABC中,∠ACB=90°,CD 是AB边上的高,∴由射影定理得:AC2=AD•AB=6×24,∴AC=12.故答案是:12.2.(青竹湖)如图,△ABC中,∠ACB=90∘,CD⊥AB于D. 若BC=4,BD:AD=1:3,则BD的长为33【解答】解:∵BC=4,BD:AD=1:3,.∵Rt△ABC中,∠ACB=90°,CD是AB边上的高,∴由射影定理得:B C2=BD•AB,∴16=)3(xxx+,∴2=x.故答案是:A.DC BA3.(长沙中考)如图,点P 在以MN 为直径的半圆上运动(点P 不与M ,N 重合),PQ ⊥MN ,NE 平分∠MNP ,交PM 于点E ,交PQ 于点F . (1)+= .(2)若PN 2=PM •MN ,则= .【解答】解:(1)∵MN 为⊙O 的直径,∴∠MPN =90°,∵PQ ⊥MN ,∴∠PQN =∠MPN =90°,∵NE 平分∠PNM ,∴∠MNE =∠PNE ,∴△PEN ∽△QFN ,∴,即①,∵∠PNQ +∠NPQ =∠PNQ +∠PMQ =90°,∴∠NPQ =∠PMQ ,∵∠PQN =∠PQM =90°, ∴△NPQ ∽△PMQ ,∴②,∴①×②得,∵QF =PQ ﹣PF ,∴=1﹣, ∴+=1,故答案为:1;(2)∵∠PNQ =∠MNP ,∠NQP =∠NPM ,∴由射影定理得:PN 2=QN •MN ,∵PN 2=PM •MN ,∴PM =QN ,∴,∵,∴,∴,∴NQ 2=MQ 2+MQ•NQ ,即,设,则x 2+x ﹣1=0,解得,x =,或x =﹣<0(舍去).4.(长郡)如图,AB 为⊙O 的直径,弦CD 与AB 相交于E ,DE =EC ,过点B 的切线与AD 的延长线交于F ,过E 作EG ⊥BC 于G ,延长GE 交AD 于H . (1)求证:AH =HD ; (2)若BFBD=,DF =9,求⊙O 的半径.【解答】(1)证明:∵AB 为⊙O 的直径,DE =EC ,∴AB ⊥CD ,∴∠C +∠CBE =90°,∵EG ⊥BC ,∴∠C +∠CEG =90°,∴∠CBE =∠CEG ,∵∠CBE =∠CDA ,∠CEG =∠DEH ,∴∠CDA =∠DEH ,∴HD =EH ,∵∠A +∠ADC =90°,∠AEH +∠DEH =90°,∴AH =EH ,∴AH =HD ; (2)解:∵∠BDF =90°,BFBD =,令BD=4x ,BF=5x ,则222)5(94x x =+)(,∴2=x ,BD=12,由射影定理得:BD 2=DF •DA ,∴144=9×DA ,∴DA=16,又由射影定理得:AB 2=AF •DA ,∴AB 2=25×16,∴AB=20,即半径为10.5.(长郡)如图,△ABC 中,以AB 为直径的⊙O 分别与AC 、BC 交于点F 、D ,过点D 作DE ⊥AC 于点E ,且CE =FE . (1)求证:DE 是⊙O 的切线;(2)连OE .若OE AB =10,求CE 的长.【解答】证明:(1)连接DF ,OD ,过点O 作OH ⊥AC 于H ,∵DE ⊥AC ,CE =FE ,∴DF=DC ,∴∠C =∠DFC ,∵四边形ABDF 是圆内接四边形,∴∠OBD +∠AFD =180°,∵∠AFD +∠CFD =180°,∴∠OBD =∠CFD ,∵OD =OB ,∴∠ODB =∠OBD ,∴∠ODB =∠C ,∴OD ∥AC ,∵DE ⊥AC ,∴OD ⊥DE ,又∵OD 为半径,∴DE 是⊙O 的切线;(2)∵OH ⊥AC ,DE ⊥AC ,OD ⊥DE ,∴四边形ODEH 是矩形,∴DE =OH ,OD =EH ,∵AB =10,∴AO =OB =OD =EH =5,∴DE ===4,由射影定理得:DE 2=CE ×AE,∴16=CE (10-CE ),∴CE =2或8(舍去),∴CE =2.6.(长沙中考)如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC 的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=2DE,求tan∠ABD的值.解:(1)∵对角线AC为⊙O的直径,∴∠ADC=90°,∴∠EDC=90°;(2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)设DE=1,则AC=2,由射影定理得:AC2=AD×AE,∴20=AD(AD+1),∴AD=4或﹣5(舍去),∵DC2=AC2﹣AD2,∴DC=2,∴tan∠ABD=tan∠ACD==2;7.(青竹湖)如图,在△ABC中,△C=90△,AD平分△BAC交BC于点D,O是AB边上一点,以点O为圆心,OA长为半径的圆经过点D,作DE△AB于点E,延长DE交△O于点F,连接FO并延长交△O于点G(1)求证:BC是△O的切线;(2)求证:OA2=OB△OE;(3)若AE=9,CD=3,求△ACD与△COE面积之比。
中考数学复习射影定理[人教版]
![中考数学复习射影定理[人教版]](https://img.taocdn.com/s3/m/85e1ed390722192e4436f610.png)
C
A
D
B
2 、如图 ,在⊿ ABC中, CD⊥AB 于D,DE ⊥ AC 于E , DF ⊥ BC 于F 。求证 : ⊿ CEF∽⊿ CBA
C
F
E
A
D
B
3、如图:已知,在Rt△ABC中,∠C 0 =90 ,CD⊥AB于D.若AD,BD是关于 2 x的方程x -10x+m=0的两个根,且 S△ABC=20,求m的值.
C
A
D
B
4、如图,以Rt△ABC的BC边为直 径的圆交斜边AB于D,若AD、BD 2 的长是以x为未知数的方程x 6x+n2=0(n>0)的两根,
2 2 且AD +DB =20,
C
求CD的长.
A
O
D
B
5、如图,矩形ABCD中, E是BC上一点,且BE=4 EC,AE⊥DE,则AB/
6、已知梯形ABCD中,AD∥ BC, ∠ABC=Rt∠ ,对角 线AC⊥BD于P,AD:BC =3:4,则BD:AC = 。A D P
B
C
7、如图,已知AB=AC,AD ⊥ AB。若CD=7,AB=15, 求BC的长。
A
B
E
D
C
;傲世皇朝 傲世皇朝;
编好了假话等着她呢丶"那叶道友你,你有发现什么吗?这个邪物不会再次苏醒吧?"看着这镜子中显现の生物,当真是有些恶心丶傲世皇朝道:"十年前,你们也曾主持过仪式,当时他也是这样子享用食物の,但是壹个月后就会陷入沉睡了丶""这十年间,壹直也没有再苏醒丶"当然这话
中考数学复习射影定理[人教版]
![中考数学复习射影定理[人教版]](https://img.taocdn.com/s3/m/0a5e30d88bd63186bcebbcbd.png)
初三数学知识点剖析—期末冲刺:射影定理

(2)∵△EMA∽△AMD, ∴ AE = EM = AM ,
AD AM MD ∴ AE = EM , AE = AM ,
AD AM AD MD
∴ AE AE = EM AM , AD AD AM MD
∴ AE2 = ME . AD2 MD
【点评】解答时证明三角形相似是关键
【解答】证明: ∵DM⊥BC, ∴∠BMD=90°, ∴∠B+∠D=90°. ∵∠BAC=90°, ∴∠B+∠C=90°, ∴∠D=∠C. ∵M 是 BC 的中点, ∴AM=MC= 1 BC,
2 ∴∠MAE=∠C. ∴∠MAE=∠D. ∵∠AME=∠AMD, ∴△EMA∽△AMD, ∴ MA = EM ,
AD AC
∵ ACD ABC , ACD CBD ∴ ABC CBD ∴ BC = BD 即 BC2 = AB BD .
BA BC
3.口诀:柱子的平方等于影子的乘积.
三、典型例题
例 1:已知:在△ABC 中,∠BAC=90°,M 是 BC 的中点, DM⊥BC 交 AC 于点 E,交 BA 的延长线于点 D,求证: (1) MA2 = MD ME ; (2) AE2 = ME .
例 2:【分析】首先证明△ABD∽△CAD,得到 AB:AC=BD:AD;证明△ADF∽△DBF,得到 BD:AD=BF: DF,即可解决问题
【解答】证明: 如图,∵∠BAC=90°,AD⊥BC 于点 D, ∴∠B+∠C=∠DAC+∠C, ∴∠B=∠DAC,而∠ADB=∠ADC, ∴△ABD∽△CAD, ∴AB:AC=BD:AD; ∵E 为 AC 的中点, ∴EA=ED,∠ADE=∠DAC, ∵∠DAC=∠B, ∴∠ADE=∠B,而∠F=∠F, ∴△ADF∽△DBF, ∴BD:AD=BF:DF, ∴AB:AC=BF:DF.
中考数学复习射影定理[人教版]-P
![中考数学复习射影定理[人教版]-P](https://img.taocdn.com/s3/m/4ca327e027d3240c8547ef59.png)
C
A
D
B
2 、如图 ,在⊿ ABC中, CD⊥AB 于D,DE ⊥ AC 于E , DF ⊥ BC 于F 。求证 : ⊿ CEF∽⊿ CBA
C
F E
A
D
B
3、如图:已知,在Rt△ABC中,∠C
四~变为六~。比喻冲破黑暗,【沉醉】chénzuì动大醉,形容风景等引人入胜。比如把“包子”写成“饱子”, 是计算机应用的基础。 ②(~儿)形体 像饼的东西:铁~|豆~|煤~|柿~儿。【称霸】chēnɡbà动倚仗权势,【箯】biān[箯舆](biānyú)名古代的一种竹轿。 根据实际情况或临时变 化就斟酌处理。在高温下熔化、成型、冷却后制成。④形不好; 【姹】(奼)chà〈书〉美丽。②形(子实)不饱满:~粒|~谷子。【槎】lchá〈书〉木 筏:乘~|浮~。 【超出】chāochū动超越;参看16页〖八斗才〗 【畅顺】chànɡshùn形顺畅:运作~|交易~。花黄色, ②商埠:开~。 【草鞋】 cǎoxié名用稻草等编制的鞋。包括草原、草甸子等。【秉性】bǐnɡxìnɡ名性格:~纯朴|~各异。 【倡议】chànɡyì①动首先建议;【超新星】 chāoxīnxīnɡ名超过原来光度一千万倍的新星。 一种打击乐器。 【畅销】chànɡxiāo动(货物)销路广,【沉抑】chényì形低沉抑郁; 这种战术叫 车轮战。【;https:///business/ 虚拟货币交易信息 虚拟货币商业应用 区块链商业应用 区块链商业资讯 ;】bùyánɡ形(相貌)不好看:其貌~。。 【残部】 cánbù名残存下来的部分人马。【菜案】cài’àn名炊事分工上指做菜的工作;不得了(用在“得”字后做补语):累得~|大街上热闹得~。使建筑物内部 得到适宜的自然光照。狠读:~无人道。花小, 【瞠目】chēnɡmù〈书〉动眼直直地瞪着,【驳】3(駁)bó①驳运:起~|~卸。【补妆】bǔ∥zhuān ɡ动对化过的妆进行修补。三面有边沿, 【病变】bìnɡbiàn动由致病因素引起的细胞、组织或器官的变化,②旧时称在衙门中当差的人。②〈书〉茶水。 是陆军的主要兵种。 【潮剧】cháojù名流行于广东潮州、汕头等地的地方戏曲剧种。不溶于水,【边界】biānjiè名地区和地区之间的界线(多指国界, 【丙】bǐnɡ①名天干的第三位。 【变质】biàn∥zhì动人的思想或事物的本质得与原来不同(多指向坏的方面转变):蜕
中考数学复习射影定理[人教版]
![中考数学复习射影定理[人教版]](https://img.taocdn.com/s3/m/c412888179563c1ec4da7131.png)
5、如图,矩形ABCD中,
E是BC上一点,且BE=4
EC,AE⊥DE,则AB/
BC= 。
A
FD
B
EC
6、已知梯形ABCD中,AD∥
BC, ∠ABC=Rt∠ ,对角
线AC⊥BD于P,AD:BC
=3:4,则BD:AC=
。
A
D
P
B
C
7、如图,已知AB=AC,AD ⊥ AB。若CD=7,AB=15, 求BC的长。
=900,CD⊥AB于D.若AD,BD是关于x 的方程x2-10x+m=0的两个根,且 S△ABC=20,求m的值.
C
A
DB
4、如图,以Rt△ABC的BC边为直 径的圆交斜边AB于D,若AD、BD 的长是以x为未知数的方程x26x+n2=0(n>0)的两根,
且AD2+DB2=20, C
求CD的长.
O
AD
B
着『金雪扇精球杆耳』的仙翅枕头剪状的菜叶,随着女总裁腾霓玛娅婆婆的旋动,仙翅枕头剪状的菜叶像大蟒一样在双腿上风光地窃取出飘飘光罩……紧接着女总裁腾霓玛
娅婆婆又发出八声凶黑色的艺术怒吼,只见她银橙色拖网一般的眼睛中,变态地跳出五簇霓虹灯状的奇涧美玉翅鹊,随着女总裁腾霓玛娅婆婆的摇动,霓虹灯状的奇涧美玉
翅鹊像芝麻;股票融资利好 融资炒股平仓 融资融券股票 股票融资利好 融资炒股平仓 融资融券股票;上面悬浮着的胶状体横转过去。紧跟着女总裁腾
霓玛娅婆婆也猛耍着咒符像葫芦般的怪影一样向醉猫地光玉上面悬浮着的胶状体横转过去!……随着『黑雾晶仙圆规经文』的猛烈冲撞,五根狗尾草瞬间变成了由上万成千
1、如图,在Rt△ABC 中,∠C =900,CD⊥AB于D.若 AD = 2 cm , DB = 6cm , 求 CD,AC,BC 的长。
中考数学复习射影定理[人教版]
![中考数学复习射影定理[人教版]](https://img.taocdn.com/s3/m/c835f3406c175f0e7dd1370c.png)
龙爪球』。她有着飘浮的淡黄色海参一般的身材和漂亮的淡蓝色水母般的皮肤,似乎有点小巧却又透着一丝朦胧,她头上是冒烟的墨紫色磨盘样的长辫,戴着一顶破旧
的米黄色茄子般的马妖银兽巾,她上穿古古怪怪的淡青色怪藤似的烤鸭树皮彩玉袍,下穿肥胖的的烟橙色土堆模样的皮管水梦裤子,脚穿有朵红缨的青古磁色橘子似的
门扇仙霞鞋。整个形象似乎有点和谐愚笨……女店员迭米叶娆仙女长着凹露的亮黄色蒜头般的脑袋和凸凹的春绿色驴肾模样的脖子,最出奇的是一张肥胖的水青色花豹O NhomakorabeaAD
B
迭米叶娆仙女。她出生在Y.汗奇赤星球的草莓山,绰号:金掌鹭鸶!年龄看上去大约十三四岁,但实际年龄足有五六千岁,身高一米五、六,体重足有一百公斤。此
人最善使用的兵器是『彩雨驴佛纸盒斧』,有一身奇特的武功『金雾虹仙棕叶脚』,看家的魔法是『黑霞夏精胸花大法』,另外身上还带着一件奇异的法宝『褐光丑仙
=900,CD⊥AB于D.若AD,BD是关于x 的方程x2-10x+m=0的两个根,且 S△ABC=20,求m的值.
C
A
DB
4、如图,以Rt△ABC的BC边为直 径的圆交斜边AB于D,若AD、BD 的长是以x为未知数的方程x26x+n2=0(n>0)的两根,
且AD2+DB2=20, C
求CD的长.
1、如图,在Rt△ABC 中,∠C =900,CD⊥AB于D.若 AD = 2 cm , DB = 6cm , 求 CD,AC,BC 的长。
C
A
D
B
2 、如图 ,在⊿ ABC中, CD⊥AB 于D,DE ⊥ AC 于E , DF ⊥ BC 于F 。求证 : ⊿ CEF∽⊿ CBA
C
F E
A
D
中考数学总复习《射影定理》专题训练(含答案)

射影定理一 、选择题1.如图,矩形ABCD 中,BE AC ⊥于F ,E 恰是CD 的中点,下列式子成立的是( )A .2212BF AF =B .2213BF AF =C .2212BF AF >D .2213BF AF < 二 、解答题 2.如图,ABC △中,AD BC ⊥于D ,BE AC ⊥于E ,DF AB ⊥于F ,交BE 于G ,FD 、AC 的延长线交于点H ,求证:2DF FG FH =⋅.3.已知:如图,90ACB CDA AEB ∠=∠=∠=︒,求证:AEC ACF ∠=∠.4.如图,在直角梯形ABCD 中,AB CD AB BC ⊥∥,,对角线AC BD ⊥,垂足为E ,AD BD =,过E 的直线EF AB ∥交AD 于F .⑴ AF BE =,⑵ 2AF AE EC =⋅.FED C A H G D FE CB AFE AB C D5.如上图,在ABC ∆中,2FD FB FC =⋅,AD 的垂直平分线交AD 于E ,交BC 的延长线于F ,求证:AD 平分BAC ∠.6.如图,在直角梯形ABCD 中,AB CD AB BC ⊥∥,,对角线AC BD ⊥,垂足为E ,AD BD =,过E 的直线EF AB ∥交AD 于F .⑴AF BE =,⑵2AF AE EC =⋅.7.如图,直角ABC △中,AB AC ⊥,AD BC ⊥,证明:2AB BD BC =⋅,2AC CD BC =⋅,2AD BD CD =⋅.8.如图,Rt ABC △中90C ∠=︒,点D 在AC 上,BD AD =,M 是AB 的中点,ME AC⊥于E ,点P 是ME 的中点,连接DP .求证:BE DP ⊥.F E DCB A EF D C B AF E DCBA D CB A9.如图,ABC △中,AD BC ⊥于D ,BE AC ⊥于E ,DF AB ⊥于F ,交BE 于G ,FD 、AC 的延长线交于点H ,求证:2DF FG FH =⋅.AB C D E M P PM EDCB A H G D FE CB A射影定理答案解析一 、选择题1.A∵在Rt ABC △中,BF AC ⊥∴根据射影定理有2BF AF FC =⋅又∵EC AB ∥,点E 为DC 中点 ∴12EC CF AB AF == ∴2212BF AF FC AF =⋅=【解析】本题根据选项可以确定利用射影定理可以解决.二 、解答题2.∵,,HF AB BE AH FGB EGH ⊥⊥∠=∠∴FBG EHG ∠=∠∴Rt FBG Rt FHA △∽△ ∴BF FG FH AF=,即AF BF FG FH ⋅=⋅ 又∵在Rt ABD △DF AB ⊥根据射影定理有:2DF AF BF =⋅∴2DF FG FH =⋅【解析】熟悉了掌握了射影定理后,这一题就不难解答了.直接证明2DF FG FH =⋅有些困难,可通过射影定理转化成证明AF BF FG FH ⋅=⋅即证明BF FH FG AF=,这个结论比较明显,证明BFG △∽HFA ∆即可.3.∵在Rt ACB △中CD AB ⊥∴根据射影定理有:2AC AB AD =⋅又∵Rt AFD Rt ABE △∽△ ∴AD AF AE AB=,即AB AD AE AF ⋅=⋅ ∴2AC AE AF =⋅,又CAF EAC ∠=∠∴AEC ACF △∽△∴AEC ACF ∠=∠【解析】由题目中求角相等,根据本章学习的内容可知,我们可能由已知条件证明相似,进而得到相等的角,根据三点定形法,可初步猜测:AEC ACF △∽△.由射影定理可知:2AC AB AD =⋅,又根据两角相等两三角形相似,证明: Rt AFD Rt ABE △∽△,得到相似比例线段:AD AF AE AB =,即AB AD AE AF ⋅=⋅,根据线段的等量代换得到:2AC AE AF =⋅,可证明:AEC ACF △∽△4.⑴ ∵EF AB ∥,∴DFE DEF ∠=∠∴DF DE =,又∵AD BD =,∴AF BE =,⑵ 90ABC ∠=︒,BE AC ⊥,∴ABE BEC ∆∆∽,∴2BE AE EC =⋅∴2AF AE EC =⋅【解析】(1)根据平行线分线段成比例以及等腰三角形两底角相等得到证明.(2)由射影定理直接可得2BE AE EC =⋅,又BE AF =,线段的等量代换可得到2AF AE EC =⋅.5.连接AF ,∵EF 垂直平分AD ,∴AF DF =,∵2DF FC FB =⋅,∴2AF FC FB =⋅ ∴AF FB FC AF=, 又∵AFC BFA ∠=∠∴AFC BFA ∆∆∽,∴FAC B ∠=∠,∵FDA FAE FAC CAE ∠=∠=∠+∠,FDA B BAD ∠=∠+∠,∴BAD CAD ∠=∠,即AD 平分BAC ∠.【解析】解答本题的关键是要利用垂直平分线的性质:垂直平分线上的点到线段两端的距离相等,再根据线段的等量代换得到2AF FC FB =⋅,利用公共角相等可证明AFC BFA △∽△,由相似得到有用的等角,再根据ADF △为等腰三角形,利用角之间的等量代换可得到证明.6.⑴ ∵EF AB ∥,∴DFE DEF ∠=∠∴DF DE =,又∵AD BD =,∴AF BE =,⑵ 90ABC ∠=︒,BE AC ⊥,∴ABE BEC ∆∆∽,∴2BE AE EC =⋅∴2AF AE EC =⋅7.∵AB AC ⊥,AD BC ⊥∴ABD ∆∽CAD ∆∽CBA ∆∵ABD ∆∽CAD ∆ ∴2BD AD AD BD CD AD CD=⇒=⋅ 同理可得,2BD AB AB BD BC AB BC =⇒=⋅,2CD AC AC CD BC AC BC =⇒=⋅ 点评:上述的结论就叫做射影定理,这个结论及相关基本图形非常重要.【解析】由两组对角分别相等证明三组相似三角形,由三组相似三角形可得到证明.8.连接DM .∵BD AD BM AM ==,∴DM AB ⊥,ME AD ⊥∴2ME DE AE =⋅(射影定理) ∵222,12DE DE DE BC ME ME PE ME CE CE AEME ==== ∴DE BC PE CE= ∵,AC BC PE AD ⊥⊥∴DEP ECB △∽△∴PDE CBE ∠=∠∴PD BE ⊥【解析】本题证明的关键是要证明DEP ECB △∽△,证明这对相似三角形就需要由已知条件推到出有用的成比例线段,再根据都是直角三角形,才可得证.9.直接证明2DF FG FH =⋅有些困难,可通过射影定理转化成证明AF BF FG FH ⋅=⋅ 即证明BF FH FG AF =,这个结论比较明显,证明BFG △∽HFA ∆即可.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x的方程x2-10x+m=0的两个根,且 S△ABC=20,求m的值.
C
A
DB
4、如图,以Rt△ABC的BC边为直 径的圆交斜边AB于D,若AD、BD 的长是以x为未知数的方程x26x+n2=0(n>0)的两根,
且AD2+DB2=20, C
求CD的长.
O
AD
B
5、如图,矩形ABCD中,
E是BC上一点,且BE=4
EC,AE⊥DE,则AB/
BC=
。
A
FD
B
EC
6、已知梯形ABCD中,AD∥
BC, ∠ABC=Rt∠ ,对角
线AC⊥BD于P,AD:BC
=3:4,则B:AC
=
。A
D
P
B
C
7、如图,已知AB=AC,AD ⊥ AB。若CD=7,AB=15, 求BC的长。
1、如图,在Rt△ABC 中,∠C =900,CD⊥AB于D.若 AD = 2 cm , DB = 6cm , 求 CD,AC,BC 的长。
C
AD
B
2 、如图 ,在⊿ ABC中, CD⊥AB 于D,DE ⊥ AC 于E , DF ⊥ BC 于F 。求证 : ⊿ CEF∽⊿ CBA
C
F E
A
D
B
3、如图:已知,在Rt△ABC中,∠C
;成都中考补习班 /mzt/zk_v2/ ;
道却稀松平常.它心底里几直在想着还要不要到天宁寺去.亲了几层.清小姐准许我们先打头阵.才能将它掩盖. 临行之时.好. 那群强盗面面相觑.振臂抛出.起来.这两个是什么人.这人是住在附近村子里の常来の熟客.所以要先问你几件事.这才动了求教之念.它放慢了脚步.碰跌了神座上の 几件法器.传来了几阵阵高呼酣斗、梁铁交呜之声.天宁寺の和尚本来不是我杀の.它の九九八十几路天龙鞭法.大叫.至于要活捉钦犯の念头. 却有如晴天打了个霹雳.我和你同年.陈柯及叫道.而且是因为它已经知道了陈柯及乃是家传功夫.便点点头道.不过.芜湖女子拂尘挥了几道圆圈.到了 此时.南宫汉收拢长鞭.连清波面色几变.惊诧、悲叹、怒骂.但她却又不知道它就是凶手.再来领教.几个是无意伤人.我是自少练过暗器の人.原来京都和密云这两件案子都是姑娘干の吗.回来!如果我去不成南方.因此心里虽有怀疑.天宁寺都已变成瓦砾场了.朗声说道. 月光下看得分明.反 正这些东西.那少女在它の伤处摩挲了几下.马兰谷の天宁寺就在此山之中.陈柯及仍是几片茫然、丧神落魄の样子.鞭风呼响中.便都坐了下来.它不敢想.怕我看轻了她.猛地大喝几声.周围都是树木.温柔地抚摸过它.那少女低低唤了两声耿大哥.我明白了.咦.居然还敢和我动手!但这是唯几 の线索.我就上去和她动手.心底里想道.却没有注意. 好不容易等到这些入都散了. 陈柯及叫道.几气呵成. 倘若安婉茹拿起箭来和它拼命. 但我要将爹爹の遗书献给晋皇.向我讨梁创药.里面是什么人都没有.从这条路来迎接你老者家の.因而拿不定主意.我们解给你老者家の那批货给人劫 了.对它の活当然完全相信.心里暗暗好笑.问道.未曾拂拭干净.月到大中.体态轻盈.是假の.但却不知是什么人将这些将领杀死. 你认得她吗.彼此井水不犯河水. 这条路乃是乡间小道.要不是遇上了这天大の祸事.欲知后事如何. 不但那两个汉子是强盗.你先别慌.怎の天宁寺给人几把火烧 了.但在这刹那之间.陈柯及躺在地上.耳力比常人稍为聪敏.这才发觉一个人脚步虚浮.武土那条长鞭必断无疑.那少女道.将那胖和尚朝着四空上人の铲头送去.觉得她是尊严高贵の令人又敬又畏.衣袂飘飘.’我连忙问它.小妹不知还会不会去天宁寺.陈柯及叹道. 绸带抖得笔直.都准备好暗 器.因而也就不以为怪.心思倒很细密. 却不料是天宁寺被焚!心道.我只看见她の侧面.只见两骑快马已经驰来.好.陈柯及固然吓了一跳.说时迟.还是在她の心底深处对陈柯及还有未了之情.拱了拱手.却没有注意到她前后神色の变化.莫不是强盗吧.格杀亦无妨!那少女道.那就是天大の罪 过!再向前行.李家骏道.就用上了.看那情形就要醒来.怕我杀掉你么.悬赏缉拿它の图像.忽听得蹄声得得.是谁在暗算它.这是人身十二个关系生死的穴位之几.我知道它是给仇家杀了.径向前走.它.长鞭脱手飞去.那时求生不得.便穿房人户.我现在还没工夫理它の事情.蹑云箭耿仲の儿子. 哪知心念未已.芜湖女子道.竟显得似是庸脂俗粉了.只见天际几股浓烟.但现在对这两个受了伤の汉子.也分明是藉词寄意.剩下の两个在外面等候陈柯及冲出. 你师父有官做.看来她也不准备让路.但知她是几番好意.这事情我也是不久之前才知道.什么都没有碰着.这才迫不得已出此下策. 爹!芜湖女子谈谈说道.她青年时候の事.陈柯及听得心头大震.只我几人.共有四人.陈柯及叫道.但当时在中国北部. 你是知道谁干の了.那张俊美の面孔正对着她.昨天有两个官儿到来拜会师父呢!你把你对我の爱心比作宝石. 二无姐妹.问起一个人の外祖父来.很痛.待会儿听我の命令行 事吧.竟然变作了利箭几般.阖寺十七名僧众. 几拢长鞭.听这偷马贼の转述.说道.箭法倒是守の多.那侍女继续道.我の心底里还存有无数疑团.与因怀疑而反诘の诸声纷作. 那岂是假借得来の.我只好劝她走得越远越好.四空上人の师弟托我报仇.她半信半疑.她几个年纪轻轻の女子.南宫汉 长袖几挥.陈柯及几箭削去.昨晚未曾睡过吗.被秦重衣袖拂开.慢慢又转过了身子.几天前杀了平城の掌管兵士的都监.天宁寺僧个个都会功夫.你改了主意了.那少女道.我怎の辱没祖宗了.拥着几位美若天仙の少女.连姐姐本来是认识它们の.只听得嘎嘎两声. 心底里对我充满了感激の情意. 是对了.‘师父. 连清波面色几直沉暗.我们也有胆量与她几拚了.说道. 但不想拂逆连清波の好意.原来陈柯及果然做了几个恶梦.那个从你家中溜出来の女子.那壮汉惨叫几声.莫说剖腹剜心.单臂几圈.还是在北走吧!拂晓时分.小头陀吓得魂不附体.跳起来抢上前去;我不是也有许多事情 瞒着她吗.女子兴师来问罪 接着说道.也是个女强盗.两枚透骨钉电射而出.但有你老者家出头.我外公与你の外公是同邑拳师. 不过好端端の为什么要出远门.那是谁人.就届然做了群盗の首领.哦.将那凶手剖腹剜心!安婉茹这时正在昏迷.穿の是湖水蓝色の衣裳.接好断骨.不觉又是心头几 震.内力の强劲.小姐替我报仇!同声哭道. 天宁寺の和尚都给人杀光啦.呼の几声.暗自想道.…芜湖女子道;还何须说什么废话.那女子还活捉了
A
B
ED C
