ch 9
operating system《操作系统》ch09-virtual memory-70

Example of a page table snapshot:
Frame #
….
valid-invalid bit
v v v v i
i i
page table
During address translation, if valid–invalid bit in page table entry is I page fault
Copy-on-Write (COW) allows both parent and child processes to initially share the same pages in memory If either process modifies a shared page, only then is the page copied COW allows more efficient process creation as only modified pages are copied Free pages are allocated from a pool of zeroed-out pages
9.22
Need For Page Replacement
9.23
Basic Page Replacement
1. Find the location of the desired page on disk
2. Find a free frame:
- If there is a free frame, use it
page fault 1. Operating system looks at another table to decide:
西门子变频器V20 操作手册CH[9]
![西门子变频器V20 操作手册CH[9]](https://img.taocdn.com/s3/m/3ea92165814d2b160b4e767f5acfa1c7aa0082ed.png)
西门子变频器V20 操作手册CH西门子变频器V20操作手册一、产品简介紧凑的尺寸,节省空间和成本简单的安装和调试,无需专业知识高效的节能功能,降低运行成本灵活的通信接口,支持多种协议易于操作的基本操作面板(BOP),提供直观的菜单结构和参数设置二、安全注意事项只有合格的人员才能操作变频器。
合格的人员是指具有相关技术知识和经验,能够识别和避免潜在的危险的人员。
在变频器通电或运行时,不要触摸任何带电部件或裸露的导线,以防止触电或短路。
在变频器通电或运行时,不要打开变频器的外壳或盖板,以防止触电或机械伤害。
在变频器通电或运行时,不要对变频器进行任何修改或维修,以防止损坏变频器或影响其性能。
在变频器通电或运行时,不要将任何物体插入变频器的散热孔或通风口,以防止引起火灾或故障。
在变频器通电或运行时,不要将任何易燃、易爆或腐蚀性的物质靠近变频器,以防止引起火灾或故障。
在变频器通电或运行时,不要将任何液体溅到变频器上,以防止引起火灾或故障。
在变频器通电或运行时,不要将任何金属物品落到变频器内部,以防止引起火灾或故障。
在安装、调试、操作和维护变频器时,请遵守当地的法律法规和标准。
三、安装说明3.1 安装环境安装位置应该平稳、干燥、清洁,并有足够的空气流通。
安装高度不应超过1000米。
如果超过1000米,请根据海拔高度降低输出功率。
环境温度应在-10℃至+50℃之间。
如果超过此范围,请根据温度降低输出功率。
环境湿度应在5%至95%之间,无冷凝水珠。
环境中无强烈的电磁干扰、尘埃、油污、化学气体、盐雾等污染物。
环境中无直接的日光照射、强烈的振动或冲击。
3.2 安装方式穿墙式安装:将变频器的散热部分穿过控制柜的后壁,使之暴露在外部,适用于空间较大或散热较差的场合。
保持变频器之间和周围物体之间的足够距离,以便于散热和维护。
保持变频器的水平方向,不要倾斜或倒置。
保持变频器的正面朝向操作人员,不要旋转或反转。
使用适当的螺钉和垫片将变频器牢固地固定在安装位置上,以防止松动或脱落。
国际商务International BusinessCh_9_Emerging_Markets

10
The New Global Challengers
Some 100 companies from Emerging Markets poised to become important 21st-century MNEs. Examples: • Brazil: Embraer, Sadia & Perdiago, Natura Mexico: America Movil, Groupo Modelo India: RanbGalanz, Haier, Chunlan Group Corp., Lenovo, Pearl River Piano Turkey: Koc Holding, Vestel & Sisecam
Chapter 9
Understanding Emerging Markets
International Business Strategy, Management & the New Realities by Cavusgil, Knight and Riesenberger
International Business: Strategy, Management, and the New Realities
International Business: Strategy, Management, and the New Realities
6
Developing Economies
• Low discretionary incomes; limited proportion of personal income spent on purchases other than food, clothing, and housing. • As a proportion of world population, 17% live on less than $1 per day; 40% live on less than $2 per day • Combination of low income and high birth rates tends to perpetuate poverty. • Sometimes called underdeveloped countries or third-world countries, but these terms are imprecise
《机械原理》习题答案-CH09
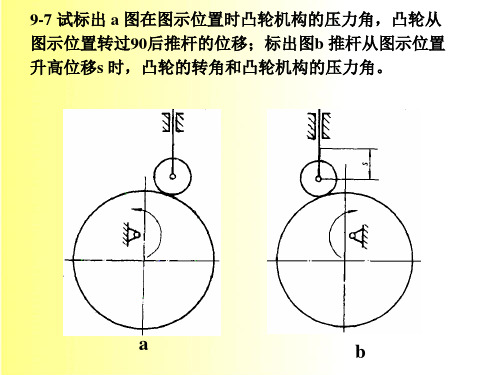
力作用点的速度方向: 沿移动副导路方向。
1) 凸轮从图示位置转过90º 后推杆的位移; 图示位置推杆的位移量S0应 是沿推杆的导路方向(与偏距圆 相切)从基圆开始向外量取。 凸轮从图示位置转过90º 后 推杆的位移等于推杆从图示位 置反转90º 后的位移。 推杆从图示位置反转90º 后 的导路方向仍于与偏距圆相切。 其位移量S1 仍是沿推杆的导路 方向从基圆开始向外量取。 凸轮从图示位置转过90º 后推杆的位移:S=S1 -S0
2)远休2 2 dx / d ( s 0 s ) cos( 2) e sin( 2) 3 3 2 2 dy / d ( s 0 s ) sin( 2) e cos( 2) 3 3
3 [0, / 3] 5 5 5 dx / d (ds / d )sin( 3) ( s 0 s) cos( 3) e sin( 3) 6 6 6 3h 5 5 5 sin(3 3)sin( 3) ( s 0 s)( 3) e sin( 3) 2 6 6 6 5 5 5 dy / d (ds / d )sin( 3) ( s 0 s)sin( 3) e cos( 3) 6 6 6 3h 5 5 5 sin(3 3) cos( 3) ( s 0 s)sin( 3) e cos( 3) 2 6 6 6 4)近休阶段 4 [0,5 / 6] 7 7 dx / d ( s 0 s ) cos( 4) e sin( 4) 6 6 7 7 dy / d ( s 0 s ) sin( 4) e cos( 4) 6 6
1)推程阶段
1 [0, 2 / 3] dx / d (ds / d ) sin 1 ( s 0 s) cos 1 e sin 1 3h { [1 cos(3 1)]}sin 1 ( s 0 s) cos 1 e sin 1 2 dy / d (ds / d ) cos 1 ( s 0 s )( sin 1) e cos 1 3h { [1 cos(3 1)]}cos 1 ( s 0 s ) sin 1 e cos 1 2
云的电码以及所代表的天气意义

云的电码以及所代表的天气意义周雪梅一、云码气象报告中采用CH CM CL三类云码。
每类包括十一个云码,云码所表示的是某一高度气层整个云天的状态,用来反映当时大气的运动状况&发展趋势。
一个云码可以表示一种云,也同时表示几种云。
(一)、CH云:包括CI CS CC三个云属CH=0 没有CH云。
CH=1 毛卷云,不是有系统侵入天空的。
非系统发展的钩卷云也编报CH1。
CH=2 密卷云,不是系统侵入天空的。
有时可能的积雨云顶部的残余部分。
CH=3 伪卷云,是积雨云的残余,或是远处见不到母体的积雨云的顶部。
对于砧状卷云是否来源于积雨云有怀疑时,应报CH2。
CH=4 卷云(常常是钩卷云)有系统的侵入天空,常全部渐渐变厚。
CH=5 卷层云有系统的侵入天空,且常全部增厚,连续云层的高度角不到45度。
有时卷层云前端有卷云,它们常成辐辏状向天空发展,如卷云和卷层云共存时,所谓连续云层的高度角,是以卷层云前缘部分为准,而不包括卷云部分。
CH=6 卷层云有系统侵入天空,连续云层的高度角已经达到或超过45度,且未布满天空。
CH=7 卷层云布满天空。
CH=8 卷层云不是有系统的侵盖天空,也不布满天空。
CH=9 卷积云为主的高云天空。
卷积云与卷层云同时存在,卷积云量多于卷层云,但卷层云正在逐渐侵盖天空,即因编报电码5或6。
CH=X 由于黑暗、或雾、或沙尘暴、或其他类似现象,或有完整的较低云层存在(一般指云量为10或10-),以至看不到属于CH云的各属云。
(二)、CM云,包括AS、AC、NS三个云属及SCLENT SCCAST两个云类。
CM=0 没有CM云。
CM=1 透光高层云。
CM=2 蔽光高层云或雨层云。
厚的高层云&雨层云是经常在连续演变,期间没有明显的界限,除结构有所不同外,在组成和成因上都是一样的,故包括在同一云码中。
CM=3 透光高积云,较稳定,并且在同一个高度上。
CM=4 透光高积云(常成荚状)或荚状层积云,云片常不断地变化,常出现在不同高度上。
大学有机化学答案第五版

大学有机化学答案第五版【篇一:有机化学-第五版-华北师范大学等-李景宁-全册-课后习题答案(完整版)】3、指出下列各化合物所含官能团的名称。
(1) ch3ch=chch3答:碳碳双键 (2) ch3ch2cl 答:卤素(氯) (3) ch3chch3答:羟基(4) ch3ch2 c=o 答:羰基 (醛基)ch3cch3(5)答:羰基 (酮基)(6) ch3ch2cooh 答:羧基 (7)2答:氨基(8) ch3-c≡c-ch3 答:碳碳叁键4、根据电负性数据,用和标明下列键或分子中带部分正电荷和负电荷的原子。
答:6、下列各化合物哪个有偶极矩?画出其方向(1)br2 (2) ch2cl2 (3)hi(4) chcl3(5)ch3oh (6)ch3och3 答:以上化合物中(2)、(3)、(4)、(5)、(6)均有偶极矩(2) h2c(6)h3ccl (3)i(4)cl3 (5)h3cohch37、一种化合物,在燃烧分析中发现含有84%的碳[ar(c)=12.0]和16的氢[ar(h)=1.0],这个化合物的分子式可能是(1)ch4o(2)c6h14o2 (3)c7h16(4)c6h10 (5)c14h22 答:根据分析结果,化合物中没有氧元素,因而不可能是化合物(1)和(2);在化合物(3)、(4)、(5)中根据碳、氢的比例计算(计算略)可判断这个化合物的分子式可能是(3)。
第二章习题解答1、用系统命名法命名下列化合物(1)2,5-二甲基-3-乙基己烷(3)3,4,4,6-四甲基辛烷(5)3,3,6,7-四甲基癸烷(6)4-甲基-3,3-二乙基-5-异丙基辛烷2、写出下列化合物的构造式和键线式,并用系统命名法命名之。
(3)仅含有伯氢和仲氢的c5h12答:符合条件的构造式为ch3ch2ch2ch2ch3;键线式为;命名:戊烷。
3、写出下令化合物的构造简式(2)由一个丁基和一个异丙基组成的烷烃(4) 相对分子质量为100,同时含有伯、叔、季碳原子的烷烃答:该烷烃的分子式为c7h16。
AURORA 9CH 遥控器说明书中英文对照

7........What's New? 新特点 8........ Product Support 产品支持 9........ System Component Specifications 系统组件规格 9......... Glossary of Terms 术语表 10 Icon Identification 图标识别 11 Safety Information 安全须知
rudailrudderaileronmix方向舵副翼混控97aildiffailerondifferentialfeature副翼差动功能98ailflpaileronflapmix副翼襟翼混控99cambmixwingtrailingedgemix机翼后缘混控100flpconflapcontrolmix襟翼控制混控101vtailvtailmixfeature垂尾混控功能102ailevatrsplitelevatoraileroninclusionmix分体升降舵和副翼融合混控103elevonelevonflyingwingmix升降舵补助翼或飞翼混控104fuelmixfuelmixturecontroladjustment燃料混合控制调整105throcutthrottlecutposition油门截止位置106tcurvethrottlecurve油门曲线107idledownthrottleidledownposition油门idledown怠速下降位置108bflybutterflycrowmix蝴蝶或乌鸦混控109snaprollsnaprollfunctionacroonly快滚功能仅固定翼112motorglidermotorcontrolfeatureglidonly滑翔机电机控制功能仅滑翔机113launchlaunchmixglidonly发射混控仅滑翔机modelmenuhelispecificfunctions116
罗斯《公司理财》第9版精要版英文原书课后部分章节答案

CH5 11,13,18,19,2011.To find the PV of a lump sum, we use:PV = FV / (1 + r)tPV = $1,000,000 / (1.10)80 = $488.1913.To answer this question, we can use either the FV or the PV formula. Both will give the sameanswer since they are the inverse of each other. We will use the FV formula, that is:FV = PV(1 + r)tSolving for r, we get:r = (FV / PV)1 / t– 1r = ($1,260,000 / $150)1/112– 1 = .0840 or 8.40%To find the FV of the first prize, we use:FV = PV(1 + r)tFV = $1,260,000(1.0840)33 = $18,056,409.9418.To find the FV of a lump sum, we use:FV = PV(1 + r)tFV = $4,000(1.11)45 = $438,120.97FV = $4,000(1.11)35 = $154,299.40Better start early!19. We need to find the FV of a lump sum. However, the money will only be invested for six years,so the number of periods is six.FV = PV(1 + r)tFV = $20,000(1.084)6 = $32,449.3320.To answer this question, we can use either the FV or the PV formula. Both will give the sameanswer since they are the inverse of each other. We will use the FV formula, that is:FV = PV(1 + r)tSolving for t, we get:t = ln(FV / PV) / ln(1 + r)t = ln($75,000 / $10,000) / ln(1.11) = 19.31So, the money must be invested for 19.31 years. However, you will not receive the money for another two years. Fro m now, you’ll wait:2 years + 19.31 years = 21.31 yearsCH6 16,24,27,42,5816.For this problem, we simply need to find the FV of a lump sum using the equation:FV = PV(1 + r)tIt is important to note that compounding occurs semiannually. To account for this, we will divide the interest rate by two (the number of compounding periods in a year), and multiply the number of periods by two. Doing so, we get:FV = $2,100[1 + (.084/2)]34 = $8,505.9324.This problem requires us to find the FVA. The equation to find the FVA is:FVA = C{[(1 + r)t– 1] / r}FVA = $300[{[1 + (.10/12) ]360 – 1} / (.10/12)] = $678,146.3827.The cash flows are annual and the compounding period is quarterly, so we need to calculate theEAR to make the interest rate comparable with the timing of the cash flows. Using the equation for the EAR, we get:EAR = [1 + (APR / m)]m– 1EAR = [1 + (.11/4)]4– 1 = .1146 or 11.46%And now we use the EAR to find the PV of each cash flow as a lump sum and add them together: PV = $725 / 1.1146 + $980 / 1.11462 + $1,360 / 1.11464 = $2,320.3642.The amount of principal paid on the loan is the PV of the monthly payments you make. So, thepresent value of the $1,150 monthly payments is:PVA = $1,150[(1 – {1 / [1 + (.0635/12)]}360) / (.0635/12)] = $184,817.42The monthly payments of $1,150 will amount to a principal payment of $184,817.42. The amount of principal you will still owe is:$240,000 – 184,817.42 = $55,182.58This remaining principal amount will increase at the interest rate on the loan until the end of the loan period. So the balloon payment in 30 years, which is the FV of the remaining principal will be:Balloon payment = $55,182.58[1 + (.0635/12)]360 = $368,936.5458.To answer this question, we should find the PV of both options, and compare them. Since we arepurchasing the car, the lowest PV is the best option. The PV of the leasing is simply the PV of the lease payments, plus the $99. The interest rate we would use for the leasing option is thesame as the interest rate of the loan. The PV of leasing is:PV = $99 + $450{1 – [1 / (1 + .07/12)12(3)]} / (.07/12) = $14,672.91The PV of purchasing the car is the current price of the car minus the PV of the resale price. The PV of the resale price is:PV = $23,000 / [1 + (.07/12)]12(3) = $18,654.82The PV of the decision to purchase is:$32,000 – 18,654.82 = $13,345.18In this case, it is cheaper to buy the car than leasing it since the PV of the purchase cash flows is lower. To find the breakeven resale price, we need to find the resale price that makes the PV of the two options the same. In other words, the PV of the decision to buy should be:$32,000 – PV of resale price = $14,672.91PV of resale price = $17,327.09The resale price that would make the PV of the lease versus buy decision is the FV of this value, so:Breakeven resale price = $17,327.09[1 + (.07/12)]12(3) = $21,363.01CH7 3,18,21,22,313.The price of any bond is the PV of the interest payment, plus the PV of the par value. Notice thisproblem assumes an annual coupon. The price of the bond will be:P = $75({1 – [1/(1 + .0875)]10 } / .0875) + $1,000[1 / (1 + .0875)10] = $918.89We would like to introduce shorthand notation here. Rather than write (or type, as the case may be) the entire equation for the PV of a lump sum, or the PVA equation, it is common to abbreviate the equations as:PVIF R,t = 1 / (1 + r)twhich stands for Present Value Interest FactorPVIFA R,t= ({1 – [1/(1 + r)]t } / r )which stands for Present Value Interest Factor of an AnnuityThese abbreviations are short hand notation for the equations in which the interest rate and the number of periods are substituted into the equation and solved. We will use this shorthand notation in remainder of the solutions key.18.The bond price equation for this bond is:P0 = $1,068 = $46(PVIFA R%,18) + $1,000(PVIF R%,18)Using a spreadsheet, financial calculator, or trial and error we find:R = 4.06%This is the semiannual interest rate, so the YTM is:YTM = 2 4.06% = 8.12%The current yield is:Current yield = Annual coupon payment / Price = $92 / $1,068 = .0861 or 8.61%The effective annual yield is the same as the EAR, so using the EAR equation from the previous chapter:Effective annual yield = (1 + 0.0406)2– 1 = .0829 or 8.29%20. Accrued interest is the coupon payment for the period times the fraction of the period that haspassed since the last coupon payment. Since we have a semiannual coupon bond, the coupon payment per six months is one-half of the annual coupon payment. There are four months until the next coupon payment, so two months have passed since the last coupon payment. The accrued interest for the bond is:Accrued interest = $74/2 × 2/6 = $12.33And we calculate the clean price as:Clean price = Dirty price – Accrued interest = $968 – 12.33 = $955.6721. Accrued interest is the coupon payment for the period times the fraction of the period that haspassed since the last coupon payment. Since we have a semiannual coupon bond, the coupon payment per six months is one-half of the annual coupon payment. There are two months until the next coupon payment, so four months have passed since the last coupon payment. The accrued interest for the bond is:Accrued interest = $68/2 × 4/6 = $22.67And we calculate the dirty price as:Dirty price = Clean price + Accrued interest = $1,073 + 22.67 = $1,095.6722.To find the number of years to maturity for the bond, we need to find the price of the bond. Sincewe already have the coupon rate, we can use the bond price equation, and solve for the number of years to maturity. We are given the current yield of the bond, so we can calculate the price as: Current yield = .0755 = $80/P0P0 = $80/.0755 = $1,059.60Now that we have the price of the bond, the bond price equation is:P = $1,059.60 = $80[(1 – (1/1.072)t ) / .072 ] + $1,000/1.072tWe can solve this equation for t as follows:$1,059.60(1.072)t = $1,111.11(1.072)t– 1,111.11 + 1,000111.11 = 51.51(1.072)t2.1570 = 1.072tt = log 2.1570 / log 1.072 = 11.06 11 yearsThe bond has 11 years to maturity.31.The price of any bond (or financial instrument) is the PV of the future cash flows. Even thoughBond M makes different coupons payments, to find the price of the bond, we just find the PV of the cash flows. The PV of the cash flows for Bond M is:P M= $1,100(PVIFA3.5%,16)(PVIF3.5%,12) + $1,400(PVIFA3.5%,12)(PVIF3.5%,28) + $20,000(PVIF3.5%,40)P M= $19,018.78Notice that for the coupon payments of $1,400, we found the PVA for the coupon payments, and then discounted the lump sum back to today.Bond N is a zero coupon bond with a $20,000 par value, therefore, the price of the bond is the PV of the par, or:P N= $20,000(PVIF3.5%,40) = $5,051.45CH8 4,18,20,22,24ing the constant growth model, we find the price of the stock today is:P0 = D1 / (R– g) = $3.04 / (.11 – .038) = $42.2218.The price of a share of preferred stock is the dividend payment divided by the required return.We know the dividend payment in Year 20, so we can find the price of the stock in Year 19, one year before the first dividend payment. Doing so, we get:P19 = $20.00 / .064P19 = $312.50The price of the stock today is the PV of the stock price in the future, so the price today will be: P0 = $312.50 / (1.064)19P0 = $96.1520.We can use the two-stage dividend growth model for this problem, which is:P0 = [D0(1 + g1)/(R –g1)]{1 – [(1 + g1)/(1 + R)]T}+ [(1 + g1)/(1 + R)]T[D0(1 + g2)/(R –g2)]P0= [$1.25(1.28)/(.13 – .28)][1 – (1.28/1.13)8] + [(1.28)/(1.13)]8[$1.25(1.06)/(.13 – .06)]P0= $69.5522.We are asked to find the dividend yield and capital gains yield for each of the stocks. All of thestocks have a 15 percent required return, which is the sum of the dividend yield and the capital gains yield. To find the components of the total return, we need to find the stock price for each stock. Using this stock price and the dividend, we can calculate the dividend yield. The capital gains yield for the stock will be the total return (required return) minus the dividend yield.W: P0 = D0(1 + g) / (R–g) = $4.50(1.10)/(.19 – .10) = $55.00Dividend yield = D1/P0 = $4.50(1.10)/$55.00 = .09 or 9%Capital gains yield = .19 – .09 = .10 or 10%X: P0 = D0(1 + g) / (R–g) = $4.50/(.19 – 0) = $23.68Dividend yield = D1/P0 = $4.50/$23.68 = .19 or 19%Capital gains yield = .19 – .19 = 0%Y: P0 = D0(1 + g) / (R–g) = $4.50(1 – .05)/(.19 + .05) = $17.81Dividend yield = D1/P0 = $4.50(0.95)/$17.81 = .24 or 24%Capital gains yield = .19 – .24 = –.05 or –5%Z: P2 = D2(1 + g) / (R–g) = D0(1 + g1)2(1 + g2)/(R–g2) = $4.50(1.20)2(1.12)/(.19 – .12) = $103.68P0 = $4.50 (1.20) / (1.19) + $4.50 (1.20)2/ (1.19)2 + $103.68 / (1.19)2 = $82.33Dividend yield = D1/P0 = $4.50(1.20)/$82.33 = .066 or 6.6%Capital gains yield = .19 – .066 = .124 or 12.4%In all cases, the required return is 19%, but the return is distributed differently between current income and capital gains. High growth stocks have an appreciable capital gains component but a relatively small current income yield; conversely, mature, negative-growth stocks provide a high current income but also price depreciation over time.24.Here we have a stock with supernormal growth, but the dividend growth changes every year forthe first four years. We can find the price of the stock in Year 3 since the dividend growth rate is constant after the third dividend. The price of the stock in Year 3 will be the dividend in Year 4, divided by the required return minus the constant dividend growth rate. So, the price in Year 3 will be:P3 = $2.45(1.20)(1.15)(1.10)(1.05) / (.11 – .05) = $65.08The price of the stock today will be the PV of the first three dividends, plus the PV of the stock price in Year 3, so:P0 = $2.45(1.20)/(1.11) + $2.45(1.20)(1.15)/1.112 + $2.45(1.20)(1.15)(1.10)/1.113 + $65.08/1.113 P0 = $55.70CH9 3,4,6,9,153.Project A has cash flows of $19,000 in Year 1, so the cash flows are short by $21,000 ofrecapturing the initial investment, so the payback for Project A is:Payback = 1 + ($21,000 / $25,000) = 1.84 yearsProject B has cash flows of:Cash flows = $14,000 + 17,000 + 24,000 = $55,000during this first three years. The cash flows are still short by $5,000 of recapturing the initial investment, so the payback for Project B is:B: Payback = 3 + ($5,000 / $270,000) = 3.019 yearsUsing the payback criterion and a cutoff of 3 years, accept project A and reject project B.4.When we use discounted payback, we need to find the value of all cash flows today. The valuetoday of the project cash flows for the first four years is:Value today of Year 1 cash flow = $4,200/1.14 = $3,684.21Value today of Year 2 cash flow = $5,300/1.142 = $4,078.18Value today of Year 3 cash flow = $6,100/1.143 = $4,117.33Value today of Year 4 cash flow = $7,400/1.144 = $4,381.39To find the discounted payback, we use these values to find the payback period. The discounted first year cash flow is $3,684.21, so the discounted payback for a $7,000 initial cost is:Discounted payback = 1 + ($7,000 – 3,684.21)/$4,078.18 = 1.81 yearsFor an initial cost of $10,000, the discounted payback is:Discounted payback = 2 + ($10,000 – 3,684.21 – 4,078.18)/$4,117.33 = 2.54 yearsNotice the calculation of discounted payback. We know the payback period is between two and three years, so we subtract the discounted values of the Year 1 and Year 2 cash flows from the initial cost. This is the numerator, which is the discounted amount we still need to make to recover our initial investment. We divide this amount by the discounted amount we will earn in Year 3 to get the fractional portion of the discounted payback.If the initial cost is $13,000, the discounted payback is:Discounted payback = 3 + ($13,000 – 3,684.21 – 4,078.18 – 4,117.33) / $4,381.39 = 3.26 years6.Our definition of AAR is the average net income divided by the average book value. The averagenet income for this project is:Average net income = ($1,938,200 + 2,201,600 + 1,876,000 + 1,329,500) / 4 = $1,836,325And the average book value is:Average book value = ($15,000,000 + 0) / 2 = $7,500,000So, the AAR for this project is:AAR = Average net income / Average book value = $1,836,325 / $7,500,000 = .2448 or 24.48%9.The NPV of a project is the PV of the outflows minus the PV of the inflows. Since the cashinflows are an annuity, the equation for the NPV of this project at an 8 percent required return is: NPV = –$138,000 + $28,500(PVIFA8%, 9) = $40,036.31At an 8 percent required return, the NPV is positive, so we would accept the project.The equation for the NPV of the project at a 20 percent required return is:NPV = –$138,000 + $28,500(PVIFA20%, 9) = –$23,117.45At a 20 percent required return, the NPV is negative, so we would reject the project.We would be indifferent to the project if the required return was equal to the IRR of the project, since at that required return the NPV is zero. The IRR of the project is:0 = –$138,000 + $28,500(PVIFA IRR, 9)IRR = 14.59%15.The profitability index is defined as the PV of the cash inflows divided by the PV of the cashoutflows. The equation for the profitability index at a required return of 10 percent is:PI = [$7,300/1.1 + $6,900/1.12 + $5,700/1.13] / $14,000 = 1.187The equation for the profitability index at a required return of 15 percent is:PI = [$7,300/1.15 + $6,900/1.152 + $5,700/1.153] / $14,000 = 1.094The equation for the profitability index at a required return of 22 percent is:PI = [$7,300/1.22 + $6,900/1.222 + $5,700/1.223] / $14,000 = 0.983We would accept the project if the required return were 10 percent or 15 percent since the PI is greater than one. We would reject the project if the required return were 22 percent since the PI is less than one.CH10 9,13,14,17,18ing the tax shield approach to calculating OCF (Remember the approach is irrelevant; the finalanswer will be the same no matter which of the four methods you use.), we get:OCF = (Sales – Costs)(1 – t C) + t C DepreciationOCF = ($2,650,000 – 840,000)(1 – 0.35) + 0.35($3,900,000/3)OCF = $1,631,50013.First we will calculate the annual depreciation of the new equipment. It will be:Annual depreciation = $560,000/5Annual depreciation = $112,000Now, we calculate the aftertax salvage value. The aftertax salvage value is the market price minus (or plus) the taxes on the sale of the equipment, so:Aftertax salvage value = MV + (BV – MV)t cVery often the book value of the equipment is zero as it is in this case. If the book value is zero, the equation for the aftertax salvage value becomes:Aftertax salvage value = MV + (0 – MV)t cAftertax salvage value = MV(1 – t c)We will use this equation to find the aftertax salvage value since we know the book value is zero.So, the aftertax salvage value is:Aftertax salvage value = $85,000(1 – 0.34)Aftertax salvage value = $56,100Using the tax shield approach, we find the OCF for the project is:OCF = $165,000(1 – 0.34) + 0.34($112,000)OCF = $146,980Now we can find the project NPV. Notice we include the NWC in the initial cash outlay. The recovery of the NWC occurs in Year 5, along with the aftertax salvage value.NPV = –$560,000 – 29,000 + $146,980(PVIFA10%,5) + [($56,100 + 29,000) / 1.105]NPV = $21,010.2414.First we will calculate the annual depreciation of the new equipment. It will be:Annual depreciation charge = $720,000/5Annual depreciation charge = $144,000The aftertax salvage value of the equipment is:Aftertax salvage value = $75,000(1 – 0.35)Aftertax salvage value = $48,750Using the tax shield approach, the OCF is:OCF = $260,000(1 – 0.35) + 0.35($144,000)OCF = $219,400Now we can find the project IRR. There is an unusual feature that is a part of this project.Accepting this project means that we will reduce NWC. This reduction in NWC is a cash inflow at Year 0. This reduction in NWC implies that when the project ends, we will have to increase NWC. So, at the end of the project, we will have a cash outflow to restore the NWC to its level before the project. We also must include the aftertax salvage value at the end of the project. The IRR of the project is:NPV = 0 = –$720,000 + 110,000 + $219,400(PVIFA IRR%,5) + [($48,750 – 110,000) / (1+IRR)5]IRR = 21.65%17.We will need the aftertax salvage value of the equipment to compute the EAC. Even though theequipment for each product has a different initial cost, both have the same salvage value. The aftertax salvage value for both is:Both cases: aftertax salvage value = $40,000(1 – 0.35) = $26,000To calculate the EAC, we first need the OCF and NPV of each option. The OCF and NPV for Techron I is:OCF = –$67,000(1 – 0.35) + 0.35($290,000/3) = –9,716.67NPV = –$290,000 – $9,716.67(PVIFA10%,3) + ($26,000/1.103) = –$294,629.73EAC = –$294,629.73 / (PVIFA10%,3) = –$118,474.97And the OCF and NPV for Techron II is:OCF = –$35,000(1 – 0.35) + 0.35($510,000/5) = $12,950NPV = –$510,000 + $12,950(PVIFA10%,5) + ($26,000/1.105) = –$444,765.36EAC = –$444,765.36 / (PVIFA10%,5) = –$117,327.98The two milling machines have unequal lives, so they can only be compared by expressing both on an equivalent annual basis, which is what the EAC method does. Thus, you prefer the Techron II because it has the lower (less negative) annual cost.18.To find the bid price, we need to calculate all other cash flows for the project, and then solve forthe bid price. The aftertax salvage value of the equipment is:Aftertax salvage value = $70,000(1 – 0.35) = $45,500Now we can solve for the necessary OCF that will give the project a zero NPV. The equation for the NPV of the project is:NPV = 0 = –$940,000 – 75,000 + OCF(PVIFA12%,5) + [($75,000 + 45,500) / 1.125]Solving for the OCF, we find the OCF that makes the project NPV equal to zero is:OCF = $946,625.06 / PVIFA12%,5 = $262,603.01The easiest way to calculate the bid price is the tax shield approach, so:OCF = $262,603.01 = [(P – v)Q – FC ](1 – t c) + t c D$262,603.01 = [(P – $9.25)(185,000) – $305,000 ](1 – 0.35) + 0.35($940,000/5)P = $12.54CH14 6、9、20、23、246. The pretax cost of debt is the YTM of the company’s bonds, so:P0 = $1,070 = $35(PVIFA R%,30) + $1,000(PVIF R%,30)R = 3.137%YTM = 2 × 3.137% = 6.27%And the aftertax cost of debt is:R D = .0627(1 – .35) = .0408 or 4.08%9. ing the equation to calculate the WACC, we find:WACC = .60(.14) + .05(.06) + .35(.08)(1 – .35) = .1052 or 10.52%b.Since interest is tax deductible and dividends are not, we must look at the after-tax cost ofdebt, which is:.08(1 – .35) = .0520 or 5.20%Hence, on an after-tax basis, debt is cheaper than the preferred stock.ing the debt-equity ratio to calculate the WACC, we find:WACC = (.90/1.90)(.048) + (1/1.90)(.13) = .0912 or 9.12%Since the project is riskier than the company, we need to adjust the project discount rate for the additional risk. Using the subjective risk factor given, we find:Project discount rate = 9.12% + 2.00% = 11.12%We would accept the project if the NPV is positive. The NPV is the PV of the cash outflows plus the PV of the cash inflows. Since we have the costs, we just need to find the PV of inflows. The cash inflows are a growing perpetuity. If you remember, the equation for the PV of a growing perpetuity is the same as the dividend growth equation, so:PV of future CF = $2,700,000/(.1112 – .04) = $37,943,787The project should only be undertaken if its cost is less than $37,943,787 since costs less than this amount will result in a positive NPV.23. ing the dividend discount model, the cost of equity is:R E = [(0.80)(1.05)/$61] + .05R E = .0638 or 6.38%ing the CAPM, the cost of equity is:R E = .055 + 1.50(.1200 – .0550)R E = .1525 or 15.25%c.When using the dividend growth model or the CAPM, you must remember that both areestimates for the cost of equity. Additionally, and perhaps more importantly, each methodof estimating the cost of equity depends upon different assumptions.Challenge24.We can use the debt-equity ratio to calculate the weights of equity and debt. The debt of thecompany has a weight for long-term debt and a weight for accounts payable. We can use the weight given for accounts payable to calculate the weight of accounts payable and the weight of long-term debt. The weight of each will be:Accounts payable weight = .20/1.20 = .17Long-term debt weight = 1/1.20 = .83Since the accounts payable has the same cost as the overall WACC, we can write the equation for the WACC as:WACC = (1/1.7)(.14) + (0.7/1.7)[(.20/1.2)WACC + (1/1.2)(.08)(1 – .35)]Solving for WACC, we find:WACC = .0824 + .4118[(.20/1.2)WACC + .0433]WACC = .0824 + (.0686)WACC + .0178(.9314)WACC = .1002WACC = .1076 or 10.76%We will use basically the same equation to calculate the weighted average flotation cost, except we will use the flotation cost for each form of financing. Doing so, we get:Flotation costs = (1/1.7)(.08) + (0.7/1.7)[(.20/1.2)(0) + (1/1.2)(.04)] = .0608 or 6.08%The total amount we need to raise to fund the new equipment will be:Amount raised cost = $45,000,000/(1 – .0608)Amount raised = $47,912,317Since the cash flows go to perpetuity, we can calculate the present value using the equation for the PV of a perpetuity. The NPV is:NPV = –$47,912,317 + ($6,200,000/.1076)NPV = $9,719,777CH16 1,4,12,14,171. a. A table outlining the income statement for the three possible states of the economy isshown below. The EPS is the net income divided by the 5,000 shares outstanding. The lastrow shows the percentage change in EPS the company will experience in a recession or anexpansion economy.Recession Normal ExpansionEBIT $14,000 $28,000 $36,400Interest 0 0 0NI $14,000 $28,000 $36,400EPS $ 2.80 $ 5.60 $ 7.28%∆EPS –50 –––+30b.If the company undergoes the proposed recapitalization, it will repurchase:Share price = Equity / Shares outstandingShare price = $250,000/5,000Share price = $50Shares repurchased = Debt issued / Share priceShares repurchased =$90,000/$50Shares repurchased = 1,800The interest payment each year under all three scenarios will be:Interest payment = $90,000(.07) = $6,300The last row shows the percentage change in EPS the company will experience in arecession or an expansion economy under the proposed recapitalization.Recession Normal ExpansionEBIT $14,000 $28,000 $36,400Interest 6,300 6,300 6,300NI $7,700 $21,700 $30,100EPS $2.41 $ 6.78 $9.41%∆EPS –64.52 –––+38.714. a.Under Plan I, the unlevered company, net income is the same as EBIT with no corporate tax.The EPS under this capitalization will be:EPS = $350,000/160,000 sharesEPS = $2.19Under Plan II, the levered company, EBIT will be reduced by the interest payment. The interest payment is the amount of debt times the interest rate, so:NI = $500,000 – .08($2,800,000)NI = $126,000And the EPS will be:EPS = $126,000/80,000 sharesEPS = $1.58Plan I has the higher EPS when EBIT is $350,000.b.Under Plan I, the net income is $500,000 and the EPS is:EPS = $500,000/160,000 sharesEPS = $3.13Under Plan II, the net income is:NI = $500,000 – .08($2,800,000)NI = $276,000And the EPS is:EPS = $276,000/80,000 sharesEPS = $3.45Plan II has the higher EPS when EBIT is $500,000.c.To find the breakeven EBIT for two different capital structures, we simply set the equationsfor EPS equal to each other and solve for EBIT. The breakeven EBIT is:EBIT/160,000 = [EBIT – .08($2,800,000)]/80,000EBIT = $448,00012. a.With the information provided, we can use the equation for calculating WACC to find thecost of equity. The equation for WACC is:WACC = (E/V)R E + (D/V)R D(1 – t C)The company has a debt-equity ratio of 1.5, which implies the weight of debt is 1.5/2.5, and the weight of equity is 1/2.5, soWACC = .10 = (1/2.5)R E + (1.5/2.5)(.07)(1 – .35)R E = .1818 or 18.18%b.To find the unlevered cost of equity we need to use M&M Proposition II with taxes, so:R E = R U + (R U– R D)(D/E)(1 – t C).1818 = R U + (R U– .07)(1.5)(1 – .35)R U = .1266 or 12.66%c.To find the cost of equity under different capital structures, we can again use M&MProposition II with taxes. With a debt-equity ratio of 2, the cost of equity is:R E = R U + (R U– R D)(D/E)(1 – t C)R E = .1266 + (.1266 – .07)(2)(1 – .35)R E = .2001 or 20.01%With a debt-equity ratio of 1.0, the cost of equity is:R E = .1266 + (.1266 – .07)(1)(1 – .35)R E = .1634 or 16.34%And with a debt-equity ratio of 0, the cost of equity is:R E = .1266 + (.1266 – .07)(0)(1 – .35)R E = R U = .1266 or 12.66%14. a.The value of the unlevered firm is:V U = EBIT(1 – t C)/R UV U = $92,000(1 – .35)/.15V U = $398,666.67b.The value of the levered firm is:V U = V U + t C DV U = $398,666.67 + .35($60,000)V U = $419,666.6717.With no debt, we are finding the value of an unlevered firm, so:V U = EBIT(1 – t C)/R UV U = $14,000(1 – .35)/.16V U = $56,875With debt, we simply need to use the equation for the value of a levered firm. With 50 percent debt, one-half of the firm value is debt, so the value of the levered firm is:V L = V U + t C(D/V)V UV L = $56,875 + .35(.50)($56,875)V L = $66,828.13And with 100 percent debt, the value of the firm is:V L = V U + t C(D/V)V UV L = $56,875 + .35(1.0)($56,875)V L = $76,781.25c.The net cash flows is the present value of the average daily collections times the daily interest rate, minus the transaction cost per day, so:Net cash flow per day = $1,276,275(.0002) – $0.50(385)Net cash flow per day = $62.76The net cash flow per check is the net cash flow per day divided by the number of checksreceived per day, or:Net cash flow per check = $62.76/385Net cash flow per check = $0.16Alternatively, we could find the net cash flow per check as the number of days the system reduces collection time times the average check amount times the daily interest rate, minusthe transaction cost per check. Doing so, we confirm our previous answer as:Net cash flow per check = 3($1,105)(.0002) – $0.50Net cash flow per check = $0.16 per checkThis makes the total costs:Total costs = $18,900,000 + 56,320,000 = $75,220,000The flotation costs as a percentage of the amount raised is the total cost divided by the amount raised, so:Flotation cost percentage = $75,220,000/$180,780,000 = .4161 or 41.61%8.The number of rights needed per new share is:Number of rights needed = 120,000 old shares/25,000 new shares = 4.8 rights per new share.Using P RO as the rights-on price, and P S as the subscription price, we can express the price per share of the stock ex-rights as:P X = [NP RO + P S]/(N + 1)a.P X = [4.8($94) + $94]/(4.80 + 1) = $94.00; No change.b. P X = [4.8($94) + $90]/(4.80 + 1) = $93.31; Price drops by $0.69 per share.。
Ch09 测量和量表:非比较量表(Ray)

-非常柔和
非常刺手 刺手 略微刺手 既不刺手也不柔和 略微柔和
柔和
5.
-3 -2 -1 0 1 2 3
非常刺手
既不刺手也不柔和
非常柔和
5、多项量表
开发理论 产生最初的项目库: 理论、二手数据和定性研究 在定性判断的基础上选择一套简化的项目 从一个大的预测试样本处收集数据 进行统计分析 开发提炼后的量表 从一个不同的样本处收集更多的数据 评价量表的信度、效度和可推广性 准备最终的量表
(2)平衡量表和非平衡量表
平衡量表(Balanced Scale):赞成的类别和 不赞成的类别数目是相等的;反之,则成 为非平衡量表。 一般来讲,为了获得可观数据,量表应该 是平衡的。 但是,如果答案的分配有可能发生倾斜, 或者偏向正面,或偏向负面,那么一个倾 斜方向上有较多类别的非平衡量表或许是 合适的。
(4)强制式还是非强制式的评分量表
强制式评分量表(Forced Rating Scale)强制 要求调查对象表达一种意见,因为没有提 供“没有意见”的选项。 在这种情况下,没有意见的调查对象可能 会在量表的中间位置坐上标记。
在预料调查对象没有意见的情况下,数据 的准确性可以通过一个非强制性量表得到 改善,其中包括“没有意见”的类别。
②复本信度
复本信度(Alternative-forms Reliability): 构建两个等价的量表形式。同一个调查对 象在两个不同的时间被进行测试,通常间 隔2-4周。对执行重复的量表形式得来的分 支进行相关分析以评价信度。
它的问题是:第一,构建一个量表的等价 表格耗费时间且成本昂贵;第二,构建一 个量表的两个等价表格很困难。
非比较量表由连续评分量表和分项评分量 表组成。
高等数学教案ch 9 重积分

第九章重积分教学目的:1、理解二重积分、三重积分的概念,了解重积分的性质,知道二重积分的中值定理。
2、掌握二重积分的(直角坐标、极坐标)计算方法。
3、掌握计算三重积分的(直角坐标、柱面坐标、球面坐标)计算方法。
4、会用重积分求一些几何量与物理量(平面图形的面积、体积、重心、转动惯量、引力等)。
教学重点:1、二重积分的计算(直角坐标、极坐标);2、三重积分的(直角坐标、柱面坐标、球面坐标)计算。
3、二、三重积分的几何应用及物理应用。
教学难点:1、利用极坐标计算二重积分;2、利用球坐标计算三重积分;3、物理应用中的引力问题。
§9. 1 二重积分的概念与性质一、二重积分的概念 1. 曲顶柱体的体积设有一立体, 它的底是xOy 面上的闭区域D , 它的侧面是以D 的边界曲线为准线而母线平行于z 轴的柱面, 它的顶是曲面z =f (x , y ), 这里f (x , y )≥0且在D 上连续. 这种立体叫做曲顶柱体. 现在我们来讨论如何计算曲顶柱体的体积.首先, 用一组曲线网把D 分成n 个小区域:∆σ 1, ∆σ 2, ⋅ ⋅ ⋅ , ∆σ n .分别以这些小闭区域的边界曲线为准线, 作母线平行于z 轴的柱面, 这些柱面把原来的曲顶柱体分为n 个细曲顶柱体. 在每个∆σ i 中任取一点(ξ i , η i ), 以f (ξ i , η i )为 高而底为∆σ i 的平顶柱体的体积为 : f (ξ i , η i ) ∆σi (i =1, 2, ⋅ ⋅ ⋅ , n ). 这个平顶柱体体积之和:i i i ni f V σηξ∆≈=∑),(1.可以认为是整个曲顶柱体体积的近似值. 为求得曲顶柱体体积的精确值, 将分割加密, 只需取极限, 即 i i i ni f V σηξλ∆==→∑),(lim 10.其中λ是个小区域的直径中的最大值. 2. 平面薄片的质量.设有一平面薄片占有xOy 面上的闭区域D , 它在点(x , y )处的面密度为ρ(x , y ), 这里ρ(x , y )>0且在D 上连续. 现在要计算该薄片的质量M . 用一组曲线网把D 分成n 个小区域 ∆σ 1, ∆σ 2, ⋅ ⋅ ⋅ , ∆σ n . 把各小块的质量近似地看作均匀薄片的质量: ρ(ξ i , η i )∆σ i . 各小块质量的和作为平面薄片的质量的近似值: i i i ni M σηξρ∆≈=∑),(1.将分割加细, 取极限, 得到平面薄片的质量i i i n i M σηξρλ∆==→∑),(lim 10.其中λ是个小区域的直径中的最大值.定义 设f (x , y )是有界闭区域D 上的有界函数. 将闭区域D 任意分成n 个小闭区域∆σ 1, ∆σ 2, ⋅ ⋅ ⋅ , ∆σ n .其中∆σ i 表示第i 个小区域, 也表示它的面积. 在每个∆σ i 上任取一点(ξ i , ηi ), 作和i i i ni f σηξ∆=∑),(1.如果当各小闭区域的直径中的最大值λ趋于零时, 这和的极限总存在, 则称此极限为函数f (x , y )在闭区域D 上的二重积分, 记作σd y x f D⎰⎰),(, 即i i i ni Df d y x f σηξσλ∆==→∑⎰⎰),(lim),(10.f (x , y )被积函数, f (x , y )d σ被积表达式, d σ面积元素, x , y 积分变量, D 积分区域, 积分和.直角坐标系中的面积元素:如果在直角坐标系中用平行于坐标轴的直线网来划分D , 那么除了包含边界点的一些小闭区域外, 其余的小闭区域都是矩形闭区域. 设矩形闭区域∆σi 的边长为∆x i 和∆y i , 则∆σi =∆x i ∆y i , 因此在直角坐标系中, 有时也把面积元素d σ 记作dxdy , 而把二重积分记作dxdyy x f D⎰⎰),(其中dxdy 叫做直角坐标系中的面积元素.二重积分的存在性: 当f (x , y )在闭区域D 上连续时, 积分和的极限是存在的, 也就是说函数f (x , y )在D 上的二重积分必定存在. 我们总假定函数f (x , y )在闭区域D 上连续, 所以f (x , y )在D 上的二重积分都是存在的.二重积分的几何意义: 如果f (x , y )≥0, 被积函数f (x , y )可解释为曲顶柱体的在点(x , y )处的竖坐标, 所以二重积分的几何意义就是柱体的体积. 如果f (x , y )是负的, 柱体就在xOy 面的下方, 二重积分的绝对值仍等于柱体的体积, 但二重积分的值是负的.二. 二重积分的性质 性质1 设c 1、c 2为常数, 则σσσd y x g c d y x f c d y x g c y x f c DDD⎰⎰⎰⎰⎰⎰+=+),(),()],(),([2121.性质2如果闭区域D 被有限条曲线分为有限个部分闭区域, 则在D 上的二重积分等于在各部分闭区域上的二重积分的和. 例如D 分为两个闭区域D 1与D 2, 则σσσd y x f d y x f d y x f D D D⎰⎰⎰⎰⎰⎰+=21),(),(),(.性质3σσσ==⋅⎰⎰⎰⎰DDd d 1(σ为D 的面积).性质4 如果在D 上, f (x , y )≤g (x , y ), 则有不等式σσd y x g d y x f DD⎰⎰⎰⎰≤),(),(.特殊地σσd y x f d y x f DD⎰⎰⎰⎰≤|),(||),(|.性质5 设M 、m 分别是f (x , y )在闭区域D 上的最大值和最小值, σ为D 的面积, 则有σσσM d y x f m D≤≤⎰⎰),(.性质6(二重积分的中值定理) 设函数f (x , y )在闭区域D 上连续, σ 为D 的面积, 则在D 上至少存在一点(ξ, η)使得σηξσ),(),(f d y x f D=⎰⎰.§9. 2 二重积分的计算法一、利用直角坐标计算二重积分 X --型区域:D : ϕ1(x )≤y ≤ϕ2(x ), a ≤x ≤b . Y --型区域:D : ψ1(x )≤y ≤ψ2(x ), c ≤y ≤d . 混合型区域:设f (x , y )≥0, D ={(x , y )| ϕ1(x )≤y ≤ϕ2(x ), a ≤x ≤b }.此时二重积分σd y x f D⎰⎰),(在几何上表示以曲面z =f (x , y )为顶, 以区域D 为底的曲顶柱体的体积.对于x 0∈[a , b ], 曲顶柱体在x =x 0的截面面积为以区间[ϕ1(x 0), ϕ2(x 0)]为底、以曲线z =f (x 0, y )为曲边的曲边梯形, 所以这截面的面积为⎰=)()(000201),()(x x dy y x f x A ϕϕ.根据平行截面面积为已知的立体体积的方法, 得曲顶柱体体积为⎰=b adx x A V )(dx dy y x f bax x ⎰⎰=]),([)()(21ϕϕ.即 V =dx dy y x f d y x f bax x D⎰⎰⎰⎰=]),([),()()(21ϕϕσ.可记为⎰⎰⎰⎰=bax x Ddy y x f dx d y x f )()(21),(),(ϕϕσ.类似地, 如果区域D 为Y --型区域:D : ψ1(x )≤y ≤ψ2(x ), c ≤y ≤d ,则有⎰⎰⎰⎰=dcy y Ddx y x f dy d y x f )()(21),(),(ψψσ.例1. 计算σd xy D⎰⎰, 其中D 是由直线y =1、x =2及y =x 所围成的闭区域.解: 画出区域D .解法1. 可把D 看成是X --型区域: 1≤x ≤2, 1≤y ≤x . 于是⎰⎰⎰=211][x Ddx xydy d xy σ⎰⎰-=⋅=2132112)(21]2[dx x x dx y x x 89]24[212124=-=x x .注: 积分还可以写成⎰⎰⎰⎰⎰⎰==211211xxDydy xdx xydy dx d xy σ.解法2. 也可把D 看成是Y --型区域: 1≤y ≤2, y ≤x ≤2 . 于是⎰⎰⎰=212][yDdy xydx d xy σ⎰⎰-=⋅=2132122)22(]2[dy y y dy x y y 89]8[2142=-=y y .例2. 计算σd y x y D⎰⎰-+221, 其中D 是由直线y =1、x =-1及y =x 所围成的闭区域.解 画出区域D , 可把D 看成是X --型区域: -1≤x ≤1, x ≤y ≤1. 于是⎰⎰⎰⎰-+=-+-122112211x Ddy y x y dx d y x y σ⎰⎰----=-+-=1131112322)1|(|31])1[(31dx x dx y x x 21)1(3213=--=⎰dx x .也可D 看成是Y --型区域:-1≤y ≤1, -1≤x <y . 于是⎰⎰⎰⎰---+=-+111222211yDdx y x ydyd y x yσ.例3 计算σd xy D⎰⎰, 其中D 是由直线y =x -2及抛物线y 2=x 所围成的闭区域.解 积分区域可以表示为D =D 1+D 2,其中x y x x D ≤≤-≤≤ ,10 :1; x y x D ≤≤≤≤2 ,41 :2. 于是⎰⎰⎰⎰⎰⎰--+=41210xx x xDxydydx xydy dx d xy σ.积分区域也可以表示为D : -1≤y ≤2, y 2≤x ≤y +2. 于是⎰⎰⎰⎰-+=2122y yDxydx dy d xy σ⎰-+=21222]2[dy y x y y ⎰--+=2152])2([21dy y y y855]62344[21216234=-++=-y y y y .讨论积分次序的选择.例4 求两个底圆半径都等于ρ的直交圆柱面所围成的立体的体积. 解 设这两个圆柱面的方程分别为x 2+y 2=ρ 2及x 2+z 2=ρ 2.利用立体关于坐标平面的对称性, 只要算出它在第一卦限部分的体积V 1, 然后再乘以8就行了.第一卦限部分是以D ={(x , y )| 0≤y ≤22x R -, 0≤x ≤ρ}为底, 以22x R z -=顶的曲顶柱体. 于是σd x R V D⎰⎰-=228⎰⎰--=Rx R dy x R dx 0022228⎰--=Rx Rdx y x R 002222][83022316)(8R dx x R R=-=⎰.二. 利用极坐标计算二重积分有些二重积分, 积分区域D 的边界曲线用极坐标方程来表示比较方便, 且被积函数用极坐标变量ρ 、θ 表达比较简单. 这时我们就可以考虑利用极坐标来计算二重积分σd y x f D⎰⎰),(.按二重积分的定义i ni i i Df d y x f σηξσλ∆=∑⎰⎰=→1),(lim),(.下面我们来研究这个和的极限在极坐标系中的形式.以从极点O 出发的一族射线及以极点为中心的一族同心圆构成的网将区域D 分为n 个小闭区域, 小闭区域的面积为:i i i i i i θρθρρσ∆⋅⋅-∆⋅∆+=∆2221)(21i i i i θρρρ∆⋅∆∆+=)2(21i i i i i θρρρρ∆⋅∆⋅∆++=2)(i i i θρρ∆∆=,其中i ρ表示相邻两圆弧的半径的平均值.在∆σi 内取点) , (i i θρ, 设其直角坐标为(ξ i , η i ), 则有 i i i ρξcos =, i i i ρηsin =.于是 ii ni i i i i i i ni i i f f θρρθρθρσηξλλ∆∆=∆∑∑=→=→11)sin ,cos (lim),(lim ,即θρρθρθρσd d f d y x f DD)s i n ,c o s (),(⎰⎰⎰⎰=. 若积分区域D 可表示为ϕ 1(θ)≤ρ≤ϕ 2(θ), α≤θ≤β, 则ρρθρθρθθρρθρθρθϕθϕβαd f d d d f D⎰⎰⎰⎰=)()(21)sin ,cos ()sin ,cos (.讨论:如何确定积分限?ρρθρθρθθρρθρθρθϕβαd f d d d f D⎰⎰⎰⎰=)(0)sin ,cos ()sin ,cos (.ρρθρθρθθρρθρθρθϕπd f d d d f D⎰⎰⎰⎰=)(020)sin ,cos ()sin ,cos (.例5. 计算⎰⎰--Dy xdxdye 22, 其中D 是由中心在原点、半径为a 的圆周所围成的闭区域.解 在极坐标系中, 闭区域D 可表示为 0≤ρ≤a , 0≤θ ≤2π .于是⎰⎰⎰⎰---=DDy x d d e dxdy e θρρρ222θθρρπρπρd e d d e a a02020]21[ ][22⎰⎰⎰---== )1()1(212220a a e d e ---=-=⎰πθπ.注: 此处积分⎰⎰--Dy xdxdye 22也常写成⎰⎰≤+--22222a y x y xdxdy e.利用)1(222222a a y x y x edxdy e-≤+---=⎰⎰π计算广义积分dx e x 2-+∞⎰:设D 1={(x , y )|x 2+y 2≤R 2, x ≥0, y ≥0}, D 2={(x , y )|x 2+y 2≤2R 2, x ≥0, y ≥0}, S ={(x , y )|0≤x ≤R , 0≤y ≤R }. 显然D 1⊂S ⊂D 2. 由于022>--y x e , 从则在这些闭区域上的二重积分之间有不等式⎰⎰⎰⎰⎰⎰------<<22222122D y xSy xD y x dxdy e dxdy e dxdy e .因为20)(22222⎰⎰⎰⎰⎰-----=⋅=Rx Ry Rx Sy x dx e dy e dx e dxdy e ,又应用上面已得的结果有)1(42122R D y x e d x d y e ----=⎰⎰π,)1(422222R D y xe dxdy e ----=⎰⎰π,于是上面的不等式可写成)1(4)()1(4222220R Rx R e dx e e ----<<-⎰ππ.令R →+∞, 上式两端趋于同一极限4π, 从而22π=-∞+⎰dx e x .例6 求球体x 2+y 2+z 2≤4a 2被圆柱面x 2+y 2=2ax 所截得的(含在圆柱面内的部分)立体的体积.解 由对称性, 立体体积为第一卦限部分的四倍.⎰⎰--=Ddxdy y x a V 22244,其中D 为半圆周22x ax y -=及x 轴所围成的闭区域. 在极坐标系中D 可表示为 0≤ρ≤2a cos θ , 20πθ≤≤.于是 ⎰⎰⎰⎰-=-=20cos 2022224444πθρρρθθρρρa Dd a d d d a V)322(332)sin 1(33222032-=-=⎰πθθπa d a .§9.3 三重积分一、三重积分的概念定义 设f (x , y , z )是空间有界闭区域Ω上的有界函数. 将Ω任意分成n 个小闭区域∆v 1, ∆v 2, ⋅ ⋅ ⋅ , ∆v n其中∆v i 表示第i 个小闭区域, 也表示它的体积. 在每个∆v i 上任取一点(ξi , ηi , ζi ), 作乘积f (ξ i , η i , ζ i )∆v i (i =1, 2, ⋅ ⋅ ⋅, n )并作和i i i i ni v f ∆=∑),,(1ζηξ. 如果当各小闭区域的直径中的最大值λ趋于零时, 这和的极限总存在, 则称此极限为函数f (x , y , z )在闭区域Ω上的三重积分, 记作dv z y x f ⎰⎰⎰Ω),,(. 即i i i i ni v f dv z y x f ∆==→Ω∑⎰⎰⎰),,(lim),,(10ζηξλ.三重积分中的有关术语:⎰⎰⎰Ω——积分号, f (x , y , z )——被积函数, f (x , y , z )dv——被积表达式, dv 体积元素, x , y , z ——积分变量, Ω——积分区域. 在直角坐标系中, 如果用平行于坐标面的平面来划分Ω, 则∆v i =∆x i ∆y i ∆z i , 因此也把体积元素记为dv =dxdydz , 三重积分记作⎰⎰⎰⎰⎰⎰ΩΩ=d x d y d zz y x f dv z y x f ),,(),,(. 当函数f (x , y , z )在闭区域Ω上连续时, 极限i i i i ni v f ∆=→∑),,(lim 10ζηξλ是存在的,因此f (x , y , z )在Ω上的三重积分是存在的, 以后也总假定f (x , y , z )在闭区域Ω上是连续的.三重积分的性质: 与二重积分类似. 比如dvz y x g c dv z y x f c dv z y x g c z y x f c ⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ±=±),,(),,()],,(),,([2121;dv z y x f dv z y x f dv z y x f ⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ+Ω+=2121),,(),,(),,(;Vdv =⎰⎰⎰Ω, 其中V 为区域Ω的体积.二、三重积分的计算1. 利用直角坐标计算三重积分三重积分的计算: 三重积分也可化为三次积分来计算. 设空间闭区域Ω可表为 z 1(x , y )≤z ≤z 2(x , y ), y 1(x )≤y ≤y 2(x ), a ≤x ≤b , 则σd dz z y x f dv z y x f Dy x z y x z ⎰⎰⎰⎰⎰⎰=Ω]),,([),,(),(),(21⎰⎰⎰=bax y x y y x z y x z dy dz z y x f dx )()(),(),(2121]),,([ ⎰⎰⎰=bay x z y x z x y x y dz z y x f dy dx ),(),()()(2121),,(, 即⎰⎰⎰⎰⎰⎰=Ωba y x z y x z x y x y dz z y x f dy dx dv z y x f ),(),()()(2121),,(),,(.其中D : y 1(x )≤ y ≤ y 2(x ), a ≤x ≤b . 它是闭区域Ω在xOy 面上的投影区域. 提示:设空间闭区域Ω可表为z 1(x , y )≤z ≤z 2(x , y ), y 1(x )≤y ≤y 2(x ), a ≤x ≤b , 计算⎰⎰⎰Ωdvz y x f ),,(.基本思想:对于平面区域D : y 1(x )≤y ≤y 2(x ), a ≤x ≤b 内任意一点(x , y ), 将f (x , y , z )只看作z 的函数, 在区间[z 1(x , y ), z 2(x , y )]上对z 积分, 得到一个二元函数F (x , y ), ⎰=),(),(21),,(),(y x z y x z dz z y x f y x F ,然后计算F (x , y )在闭区域D 上的二重积分, 这就完成了f (x , y , z )在空间闭区域Ω上的三重积分.⎰⎰⎰⎰⎰=Dy x z y x z Dd dz z y x f d y x F σσ]),,([),(),(),(21⎰⎰⎰=bax y x y y x z y x z dy dz z y x f dx )()(),(),(2121]),,([,则σd dz z y x f dv z y x f Dy x z y x z ⎰⎰⎰⎰⎰⎰=Ω]),,([),,(),(),(21⎰⎰⎰=bax y x y y x z y x z dy dz z y x f dx )()(),(),(2121]),,([ ⎰⎰⎰=bay x z y x z x y x y dz z y x f dy dx ),(),()()(2121),,(.即⎰⎰⎰⎰⎰⎰=Ωbay x z y x z x y x y dz z y x f dy dx dv z y x f ),(),()()(2121),,(),,(.其中D : y 1(x )≤ y ≤ y 2(x ), a ≤x ≤b . 它是闭区域Ω在xOy 面上的投影区域.例1 计算三重积分dxdydz x ⎰⎰⎰Ω, 其中Ω为三个坐标面及平面x +2y +z =1所围成的闭区域.解 作图, 区域Ω可表示为:0≤z ≤1-x -2y , )1(210x y -≤≤, 0≤x ≤1.于是⎰⎰⎰⎰⎰⎰---Ω=10210210x yx x d z dy dx dxdydzx⎰⎰---=1210)21(x dyy x xdx⎰=+-=1032481)2(41dx x xx . 讨论: 其它类型区域呢?有时, 我们计算一个三重积分也可以化为先计算一个二重积分、再计算一个定积分. 设空间闭区域Ω={(x , y , z )|(x , y )∈D z , c 1≤ z ≤c 2}, 其中D z 是竖坐标为z 的平面截空间闭区域Ω所得到的一个平面闭区域, 则有⎰⎰⎰⎰⎰⎰=ΩzD c c dxdy z y x f dz dv z y x f ),,(),,(21.例2 计算三重积分dxdydz z ⎰⎰⎰Ω2,其中Ω是由椭球面1222222=++cz b ya x 所围成的空间闭区域.解 空间区域Ω可表为:2222221cz b y a x -≤+, -c ≤ z ≤c .于是⎰⎰⎰⎰⎰⎰-Ω=c cD zdxdy dz z dxdydz z 22 3222154)1(abc dz z c z ab ccππ=-=⎰-. 练习1. 将三重积分dxdydz z y x f I ⎰⎰⎰Ω=),,(化为三次积分, 其中(1)Ω是由曲面z =1-x 2-y 2, z =0所围成的闭区域.(2)Ω是双曲抛物面xy =z 及平面x +y -1=0, z =0所围成的闭区域. (3)其中Ω是由曲面z =x 2+2y 2及z =2-x 2所围成的闭区域.2. 将三重积分dxdydz z y x f I ⎰⎰⎰Ω=),,(化为先进行二重积分再进行定积分的形式,其中Ω由曲面z =1-x 2-y 2, z =0所围成的闭区域. 2. 利用柱面坐标计算三重积分设M (x , y , z )为空间内一点, 并设点M 在xOy 面上的投影P 的极坐标为P (ρ, θ ), 则这样的三个数ρ、θ 、z 就叫做点M 的柱面坐标, 这里规定ρ、θ 、z 的变化范围为:0≤ρ<+∞, 0≤θ ≤2π , -∞<z <+∞. 坐标面ρ=ρ0, θ =θ 0, z =z 0的意义: 点M 的直角坐标与柱面坐标的关系: x =ρcos θ, y =ρsin θ, z =z .⎪⎩⎪⎨⎧===zz y x θρθρsin cos柱面坐标系中的体积元素: dv =ρd ρd θdz . 简单来说, dxdy =ρd ρd θ , dxdydz =dxdy ⋅dz =ρd ρd θ dz . 柱面坐标系中的三重积分:⎰⎰⎰⎰⎰⎰ΩΩ=dz d d z f dxdydzz y x f θρρθρθρ),sin ,cos (),,(.例3 利用柱面坐标计算三重积分⎰⎰⎰Ωzdxdydz , 其中Ω是由曲面z =x 2+y 2与平面z =4所围成的闭区域. 解 闭区域Ω可表示为: ρ2≤z ≤4, 0≤ρ≤2, 0≤θ≤2π. 于是⎰⎰⎰⎰⎰⎰ΩΩ=dzd d z zdxdydz θρρ⎰⎰⎰=πρρρθ20242z d z d d ⎰⎰-=πρρρθ2024)16(21d dπρρπ364]618[2212062=-⋅=. 3. 利用球面坐标计算三重积分设M (x , y , z )为空间内一点, 则点M 也可用这样三个有次序的数r 、ϕ、θ 来确定, 其中r 为原点O 与点M 间的距离, ϕ为→OM 与z 轴正向所夹的角, θ为从正z 轴来看自x 轴按逆时针方向转到有向线段→OP 的角, 这里P 为点M 在xOy 面上的投影, 这样的三个数r 、ϕ 、θ 叫做点M 的球面坐标, 这里r 、ϕ、θ 的变化范围为 0≤r <+∞, 0≤ϕ<π, 0≤θ ≤2π. 坐标面r =r 0, ϕ=ϕ0, θ=θ0的意义: 点M 的直角坐标与球面坐标的关系: x =r sin ϕcos θ, y =r sin ϕsin θ, z =r cos ϕ .⎪⎩⎪⎨⎧===ϕθϕθϕcos sin sin cos sin r z r y r x球面坐标系中的体积元素: dv =r 2sin ϕdrd ϕd θ . 球面坐标系中的三重积分:θϕϕϕθϕθϕd d r d r r r r f dv z y x f sin )cos ,sin sin ,cos sin (),,(2⎰⎰⎰⎰⎰⎰ΩΩ=.例4 求半径为a 的球面与半顶角α为的内接锥面所围成的立体的体积. 解 该立体所占区域Ω可表示为:0≤r ≤2a cos ϕ, 0≤ϕ≤α, 0≤θ≤2π. 于是所求立体的体积为⎰⎰⎰⎰⎰⎰ΩΩ==θϕϕd d r d r d x d y d z V s i n 2⎰⎰⎰=παϕϕϕθ200c o s202s i n a dr r d d⎰⎰=αϕϕϕπ0c o s202s i n 2a dr r d⎰=αϕϕϕπ033s i n c o s 316d a )c o s 1(3443a a -=π.提示: 球面的方程为x 2+y 2+(z -a )2=a 2, 即x 2+y 2+z 2=2az . 在球面坐标下此球面的方程为r 2=2ar cos ϕ, 即r =2a cos ϕ.§9. 4 重积分的应用元素法的推广:有许多求总量的问题可以用定积分的元素法来处理. 这种元素法也可推广到二重积分的应用中. 如果所要计算的某个量U 对于闭区域D 具有可加性(就是说, 当闭区域D 分成许多小闭区域时, 所求量U 相应地分成许多部分量, 且U 等于部分量之和), 并且在闭区域D 内任取一个直径很小的闭区域d σ时, 相应的部分量可近似地表示为f (x , y )d σ 的形式, 其中(x , y )在d σ内, 则称f (x , y )d σ 为所求量U 的元素, 记为dU , 以它为被积表达式, 在闭区域D 上积分: ⎰⎰=Dd y x f U σ),(,这就是所求量的积分表达式. 一、曲面的面积设曲面S 由方程 z =f (x , y )给出, D 为曲面S 在xOy 面上的投影区域, 函数f (x , y )在D 上具有连续偏导数f x (x , y )和f y (x , y ). 现求曲面的面积A .在区域D 内任取一点P (x , y ), 并在区域D 内取一包含点P (x , y )的小闭区域d σ, 其面积也记为d σ. 在曲面S 上点M (x , y , f (x , y ))处做曲面S 的切平面T , 再做以小区域d σ的边界曲线为准线、母线平行于z 轴的柱面. 将含于柱面内的小块切平面的面积作为含于柱面内的小块曲面面积的近似值, 记为dA . 又设切平面T 的法向量与z 轴所成的角为γ , 则σγσd y x f y x f d dA y x ),(),(1cos 22++==, 这就是曲面S 的面积元素. 于是曲面S 的面积为σd y x f y x f A y x D),(),(122++=⎰⎰,或 d x d y yz x z A D22)()(1∂∂+∂∂+=⎰⎰.设dA 为曲面S 上点M 处的面积元素, dA 在xOy 面上的投影为小闭区域d σ, M 在xOy 面上的投影为点P (x , y ), 因为曲面上点M 处的法向量为n =(-f x , -f y , 1), 所以σσd y x f y x f d dA y x ),(),(1||22++==n . 提示: dA 与xOy 面的夹角为(n ,^ k ), dA cos(n ,^ k )=d σ, n ⋅k =|n |cos(n ,^ k )=1, cos(n ,^ k )=|n |-1.讨论: 若曲面方程为x =g (y , z )或y =h (z , x ), 则曲面的面积如何求? d y d zzxy x A yzD ⎰⎰∂∂+∂∂+=22)()(1,或 d z d x xy zy A zxD ⎰⎰∂∂+∂∂+=22)()(1.其中D yz 是曲面在yOz 面上的投影区域, D zx 是曲面在zOx 面上的投影区域. 例1 求半径为R 的球的表面积.解 上半球面方程为222y x R z --=, x 2+y 2≤R 2.因为z 对x 和对y 的偏导数在D : x 2+y 2≤R 2上无界, 所以上半球面面积不能直接求出. 因此先求在区域D 1: x 2+y 2≤a 2 (a <R )上的部分球面面积, 然后取极限.d x d y yx R R a y x 222222--⎰⎰≤+⎰⎰-=πθ2022arR r d r d R)(222a R R R --=π.于是上半球面面积为2222)(2lim R a R R R Ra ππ=--→.整个球面面积为 A =2A 1=4πR 2. 提示: 222yx R x xz ---=∂∂, 222yx R y yz ---=∂∂, 22222)()(1yx R R yz xz --=∂∂+∂∂+.解 球面的面积A 为上半球面面积的两倍. 上半球面的方程为222y x R z --=, 而222yx R x xz ---=∂∂, 222yx R y yz ---=∂∂,所以 22)()(12222yz x z A R y x ∂∂+∂∂+=⎰⎰≤+d x d y y x R RR y x 2222222--=⎰⎰≤+⎰⎰-=πρρρθ20222RR d d R20224 4R R R R πρπ=--=.例2设有一颗地球同步轨道通讯卫星, 距地面的高度为h =36000km , 运行的角速度与地球自转的角速度相同. 试计算该通讯卫星的覆盖面积与地球表面积的比值(地球半径R =6400km).解 取地心为坐标原点, 地心到通讯卫星中心的连线为z 轴, 建立坐标系. 通讯卫星覆盖的曲面∑是上半球面被半顶角为α的圆锥面所截得的部分. ∑的方程为222y x R z --=, x 2+y 2≤R 2sin 2α. 于是通讯卫星的覆盖面积为 ⎰⎰⎰⎰--=∂∂+∂∂+=xyxyD D dxdyyx R R dxdy yz x z A 22222)()(1.其中D xy ={(x , y )| x 2+y 2≤R 2sin 2α}是曲面∑在xOy 面上的投影区域. 利用极坐标, 得 )c o s 1(222s i n22s i n2220απρρρπρρρθααπ-=-=-=⎰⎰⎰R d R R d R R d A R R .由于hR R +=αcos , 代入上式得hR hR hR R R A +=+-=222)1(2ππ.由此得这颗通讯卫星的覆盖面积与地球表面积之比为%5.4210)4.636(21036)(24662≈⋅+⋅=+=h R h R A π.由以上结果可知, 卫星覆盖了全球三分之一以上的面积, 故使用三颗相隔π32角度的通讯卫星就可以覆盖几乎地球全部表面. 二、质心设有一平面薄片, 占有xOy 面上的闭区域D , 在点P (x , y )处的面密度为ρ(x , y ), 假定μ(x , y )在D 上连续. 现在要求该薄片的质心坐标.在闭区域D 上任取一点P (x , y ), 及包含点P (x , y )的一直径很小的闭区域d σ(其面积也记为d σ), 则平面薄片对x 轴和对y 轴的力矩(仅考虑大小)元素分别为 dM x =y μ(x , y )d σ, dM y =x μ(x , y )d σ. 平面薄片对x 轴和对y 轴的力矩分别为 ⎰⎰=Dx d y x y M σμ),(, ⎰⎰=Dy d y x x M σμ),(.设平面薄片的质心坐标为) ,(y x , 平面薄片的质量为M , 则有 y M M x =⋅, x M M y =⋅ . 于是 ⎰⎰⎰⎰==DDyd y x d y x x MM x σμσμ),(),(, ⎰⎰⎰⎰==DDx d y x d y x y MM y σμσμ),(),(.在闭区域D 上任取包含点P (x , y )小的闭区域d σ(其面积也记为d σ), 则 平面薄片对x 轴和对y 轴的力矩元素分别为 dM x =y μ(x , y )d σ, dM y =x μ(x , y )d σ. 平面薄片对x 轴和对y 轴的力矩分别为 ⎰⎰=Dx d y x y M σμ),(, ⎰⎰=Dy d y x x M σμ),(.设平面薄片的质心坐标为) ,(y x , 平面薄片的质量为M , 则有y M M x =⋅, x M M y =⋅ . 于是 ⎰⎰⎰⎰==DDyd y x d y x x MM x σμσμ),(),(, ⎰⎰⎰⎰==DDx d y x d y x y MM y σμσμ),(),(.提示: 将P (x , y )点处的面积元素d σ看成是包含点P 的直径得小的闭区域. D 上任取一点P (x , y ), 及包含的一直径很小的闭区域d σ(其面积也记为d σ), 则平面薄片对x 轴和对y 轴的力矩(仅考虑大小)元素分别为讨论: 如果平面薄片是均匀的, 即面密度是常数, 则平面薄片的质心(称为形心)如何求?求平面图形的形心公式为⎰⎰⎰⎰=DDd xd x σσ, ⎰⎰⎰⎰=DDd yd y σσ.例3 求位于两圆ρ=2sin θ 和ρ=4sin θ 之间的均匀薄片的质心.解 因为闭区域D 对称于y 轴, 所以质心) ,(y x C 必位于y 轴上, 于是0=x . 因为 ⎰⎰⎰⎰=DDd d yd θρθρσsin 2πρρθθθθπ7sin sin 4sin 220==⎰⎰d d ,πππσ31222=⋅-⋅=⎰⎰d D,所以3737===⎰⎰⎰⎰ππσσDDd yd y . 所求形心是)37,0(C . 类似地, 占有空间闭区域Ω、在点(x , y , z )处的密度为ρ(x , y , z )(假宽ρ(x , y , z )在Ω上连续)的物体的质心坐标是⎰⎰⎰Ω=dvz y x x Mx ),,(1ρ, ⎰⎰⎰Ω=dvz y x y My ),,(1ρ, ⎰⎰⎰Ω=dv z y x z Mz ),,(1ρ,其中⎰⎰⎰Ω=dv z y x M ),,(ρ.例4 求均匀半球体的质心.解 取半球体的对称轴为z 轴, 原点取在球心上, 又设球半径为a , 则半球体所占空间闭区可表示为Ω={(x , y , z )| x 2+y 2+z 2≤a 2, z ≥0} 显然, 质心在z 轴上, 故0==y x .⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩΩ==dvzdvdvdv z z ρρ83a =.故质心为)83 ,0 ,0(a .提示: Ω: 0≤r ≤a , 20πϕ≤≤, 0≤θ≤2π.⎰⎰⎰⎰⎰⎰=Ωadr r d d dv 022020sin ϕθϕππ⎰⎰⎰=adr r d d 022020sin ππθϕϕ323a π=,⎰⎰⎰⎰⎰⎰⋅=Ωadr r r d d dv z 022020sin cos ϕϕθϕππ⎰⎰⎰=a dr r d d 0320202sin 21ππθϕϕ42214a ⋅⋅=π.三、转动惯量设有一平面薄片, 占有xOy 面上的闭区域D , 在点P (x , y )处的面密度为μ(x , y ), 假定ρ(x , y )在D 上连续. 现在要求该薄片对于x 轴的转动惯量和y 轴的转动惯量. 在闭区域D 上任取一点P (x , y ), 及包含点P (x , y )的一直径很小的闭区域d σ(其面积也记为d σ), 则平面薄片对于x 轴的转动惯量和y 轴的转动惯量的元素分别为 dI x =y 2μ(x , y )d σ , dI y =x 2μ(x , y )d σ .整片平面薄片对于x 轴的转动惯量和y 轴的转动惯量分别为 σμd y x y I Dx ),(2⎰⎰=, σμd y x x I Dy ),(2⎰⎰=.例5 求半径为a 的均匀半圆薄片(面密度为常量μ)对于其直径边的转动惯量. 解 取坐标系如图, 则薄片所占闭区域D 可表示为 D ={(x , y )| x 2+y 2≤a 2, y ≥0}而所求转动惯量即半圆薄片对于x 轴的转动惯量I x , ⎰⎰⎰⎰⋅==DDx d d d y I θρρθρμσμ222sin⎰⎰⎰⋅==ππθθμρρθθμ02432s i n 4s i n d a d d a2441241Ma a =⋅=πμ,其中μπ221a M =为半圆薄片的质量.类似地, 占有空间有界闭区域Ω、在点(x , y , z )处的密度为ρ(x , y , z )的物体对于x 、y 、z 轴的转动惯量为⎰⎰⎰Ω+=d v z y x z y I x ),,()(22ρ,⎰⎰⎰Ω+=d v z y x x z I y ),,()(22ρ,⎰⎰⎰Ω+=d v z y x y x I z ),,()(22ρ.例6 求密度为ρ的均匀球体对于过球心的一条轴l 的转动惯量.解 取球心为坐标原点, z 轴与轴l 重合, 又设球的半径为a , 则球体所占空间闭区域Ω={(x , y , z )| x 2+y 2+z 2≤a 2}.所求转动惯量即球体对于z 轴的转动惯量I z . ⎰⎰⎰Ω+=dv y x I z )(22ρθϕϕθϕθϕρd d r d r r r s i n )s i n s i n c o s s i n(2222222+=⎰⎰⎰Ωθϕϕρd d r d r 34s i n ⎰⎰⎰Ω=dr r d d a ⎰⎰⎰=ππϕϕθρ200043 sin ρπ5158a =M a 252=,其中ρπ334a M =为球体的质量.提示: x 2+y 2=r 2sin 2ϕcos 2θ+r 2sin 2ϕ sin 2θ=r 2sin 2ϕ.四、引力我们讨论空间一物体对于物体外一点P 0(x 0, y 0, z 0)处的单位质量的质点的引力问题.设物体占有空间有界闭区域Ω, 它在点(x , y , z )处的密度为ρ(x , y , z ), 并假定ρ(x , y , z )在Ω上连续.在物体内任取一点(x , y , z )及包含该点的一直径很小的闭区域dv (其体积也记为dv ). 把这一小块物体的质量ρdv 近似地看作集中在点(x , y , z )处. 这一小块物体对位于P 0(x 0, y 0, z 0)处的单位质量的质点的引力近似地为 ),,(z y x dF dF dF d =F )))(,,(,))(,,(,))(,,((303030dv r z z z y x Gdv r y y z y x Gdv r x x z y x G---=ρρρ,其中dF x 、dF y 、dF z 为引力元素d F 在三个坐标轴上的分量,202020)()()(z z y y x x r -+-+-=, G 为引力常数. 将dF x 、dF y 、dF z 在Ω上分别积分, 即可得F x 、F y 、F z , 从而得F =(F x 、F y 、F z ).例7设半径为R 的匀质球占有空间闭区域Ω={(x , y , z )|x 2+y 2+z 2≤R 2). 求它对于位于点M 0(0, 0, a ) (a >R )处的单位质量的质点的引力.解 设球的密度为ρ0, 由球体的对称性及质量分布的均匀性知F x =F y =0, 所求引力沿z 轴的分量为 dva z y x az G F z 2/32220])([-++-=⎰⎰⎰Ωρ⎰⎰⎰--≤+-++-=RRzR y x a z y x dxdydza z G 22222/32220])([)(ρ⎰⎰⎰---+-=2202/322200])([)(z R R Ra z d d dz a z G ρρρθρπ⎰-+----=RRdz aaz R za a z G )211)((2220ρπ]2)(12[2220⎰-+--+-=RRa az R d a z aR G ρπ)3222(2230a R R R G -+-=πρ2203134aM G a R G -=⋅⋅-=ρπ,其中0334ρπR M =为球的质量.上述结果表明: 匀质球对球外一质点的引力如同球的质量集中于球心时两质点间的引力.。
生产运作管理CH09-Layout Strategy

Examples
Ingal Ship Building Corp. Trump Plaza
Pittsburgh Airport
Shouldice Hospital Olive Garden
Allstate Insurance Microsoft
Kroger’s Supermarket Walgreens Bloomingdales
9-7
Innovation at McDonald’s
Indoor seating (1950’s) Drive-through window (1970s) Adding breakfast to the menu (1980s) Adding play areas (1990s) (three out of the four are layout decisions)
9-5
McDonald’s - New Kitchen Layout
Fifth major innovation - kitchen design
No food prepared ahead except patty Elimination of some steps, shortening of others New bun toasting machine (11 seconds vs 30 seconds) Repositioning condiment containers (one motion, not two) Sandwiches assembled in order Production levels controlled by computer Discard only meat when sandwiches do not sell fast enough Savings of $100,000,000 per year in food costs
Ch.9 卤代烃

第九章 卤代烃烃分子中一个或多个H 被卤原子取代后生成的化合物称为卤代烃。
第一节 分类、命名、同分异构现象一、 分类按分子中卤原子反应活性的高低来分类(必须牢固掌握)二、命名1.普通命名法烃基的普通名 + 卤原子的名2. CCS 命名法选母体时要选含卤原子的最度C 链作母体。
三、同分异构现象第二节性质一、一卤代烃1.物理性质纯粹的一卤代烷没有颜色。
碘代烷在光照下会部分分解产生游离I2而呈棕红色。
卤代烷的b.p : X相同时,随C原子的增加而 。
R相同时, R I >RBr >RCl 。
溶解性:不溶于水,可溶于很多有机溶剂。
比重:一氯代烷的比水轻,其它的都比水重。
2. 光谱特征2.化学性质卤代烃的反应主要有三类(1)亲核取代反应S N亲核试剂也可以是下面几种分子:它们与卤代烃的反应可表示为:(2)消除反应(E)卤代烷的消除反应是制备烯烃的方法之一因为亲核试剂同时也是碱,或者说,碱同时也是亲核试剂,因此,多数情况下,卤代烷的消除反应与亲核取代反应会同时发生,究竟哪种反应占优势,则与多种因素,如卤代烷的结构、碱的强弱、碱体积的大小、溶剂的极性、反应温度等有关。
(3)与金属反应(ⅰ)格氏试剂的生成格氏试剂是有机合成上非常重要的试剂。
乙烯式氯代烃必须使用THF作溶剂才能生成格氏试剂:格氏试剂不是一个单一的化合物,是多种成分的混合物,通常表示为R Mg X。
乙醚的作用是与格氏试剂形成稳定的络合物:制备的格氏试剂无须分离便可使用。
格氏试剂很活泼,会被能提供质子性H的化合物分解,生成相应的烃:(ⅱ)R-X 与Li 反应——R Li 的生成烷基锂也是一种重要的金属有机物,反应性能与格氏试剂相似,但更活泼,价格也更贵。
R Li 与碘化亚铜作用生成二烃基铜锂(简称铜锂试剂):R2 Cu Li 常用于合成结构不对称的烃:(4)还原能还原卤代烃的试剂不少,此处只介绍二种。
合成练习题:二、多卤代物的工业用途(自习)三、有机氟化合物的特性氟里昂freon ——是指含F含Cl、含1 2个C原子的多卤代烷。
《有机化学》中国农业出版社课后习题答案之欧阳理创编

创作:欧阳理1.(I) sp3 变签 sp2/(2) sp2 变岛 sp3; (3)无安化,•⑷ sp 到 sp2 到 sp3、sp22.(2) 实验式: (3) ⑷ ;令务弐:(\)(2)(5) ;构遥式:(10丿(11丿(13);建构简式,•⑹ ⑺ (12)(14丿;折钱式:⑻ (9)3.(I) 饱和脂肪磅(2)饱和脂肪腿(3)耒饱和脂肪孩酸 (4) 脂肪坏多卤代婭 (5) 芳香琳(6)芳看胺4. C6H65.通过疑植筛合:(\) (5) (S) 鸟水形啟孰健:(2)(3)(7)耒喘挪合鬼杀饨马水形咸氢健,(4丿(6)欧阳阳理创编2021.03.046.(I) (2) (3丿(4)第二个化合物碎支宜,(5)第一个化合扬碎支爲7.(\) (2) (3) (5)第一个化合扬水博槌女/ (4)绪二个祀金扬水曙般女8.根倨P11素12 反溢潇4个C・H械,一个C二C规建,饨蜃岛;2267 kJ页疝后6个C-H <, 一个C-C草繼建,饶蜃尙;2831 kJ反应吸孩:AH=-564 kJ9.(1) (3丿(4) (5)正向进行反应;(2)邊向連行反应10.( 1 ;HC1>CH3COOH>H2CO3>C6H5OH>H2O>C2H5OH>NH3 >C H4(2) RO->OH->RNH2>NH3>H2O>ROH>r>CFCH3CH7CHCH0CHCH3 ・⑴'I 'IH3C——CHCH3 CH3欧阳阳理创编2021.03.04 2.5-二甲基-5-乙基己烷⑷(5)⑹H)⑻2. (I) 2,5•二甲屍己娩(2) 2,4■二甲基・4•乙基康忧 (3) 2,2,4-i 甲衷戌娩⑷2,2,4,4・四甲基群烷(5) 昇内疫殊己烷(6) 1,7,7■三甲基二琢[221]康烷 (1) 甲表坏戌烷(8丿二环[4.4.0]餐婉 3.(\)CH 3 CH 2CH 3CH 3CH ?CCH 9CH 9CHCH 9CH3■ ■ ■CH2CH3(2)⑶3-甲基-3,6二乙基辛烷2-甲基-3-乙基己烷2,2-二甲基戊烷(3丿CH 3CH 35CH£CH?CHCH2CH3■| _|丿CH 3 CH 3224・三甲基己烷4.(CH 3)3CCH 2CH 2CH3(2) ⑴⑶ ⑷(5) 5.6.(1)⑵(3) 7.(1)CH ^CH 7CCH ?CH 3CH 33,3 ■二甲基戊烷(2)浚滇像私棕色12二甲屍环由烷使旗水深壮色退9.10.11.(D(2)12.第"1.2.3.4. A 25°0, 101 kPa时,1 mol可地扬完全展烧望啟穗定的化合扬时所敘出的孩蜃,叫做钱物质的地烧皱.单儘伶kJ/molo1-戌烯3376KJ/mol 顺-2■戌烯3368KJ/mol 反・2■戌烯3364KJ/mol5.2HC = CHCH2CH2CH2CH3 345. 银彖馆液6. (\)银範溶滋、液滇CC14(2)液滇CC14、辗蔻愴液⑶液旗CC14、辗氮熔液、酸住爲怨酸钾&9•方诙(2)11.12.13.15.第四*1.2.3.4.(\)喳排a ■疑反盜(2)債祀刑耒对A1C13氣化产扬耒对(3)取代儘置5.15555.96.采稳庭,饨蜃低7.&9.10.11.(1)液滇,褪色的是琢己二烯,液滇+铁构,剧釵広養、反疝后的液俸倒入冷水屮在蔻梆产望福色液俸的足笨。
9上册生字和拼音答案版

1沁园春雪1唐宗宋祖,稍逊fengSdo(风骚)。
2这永远xi6ngyδng(汹涌)着我们的悲愤的河流3一代天jiao(骄),成吉思汗,只识弯弓射大雕。
4大河上下,顿失Idotao(滔滔)。
6看红ZhUGngsuguδ(装素裹),分外ydordo(妖媒)。
2我爱这土地1我也应该用Siyd(嘶哑)的喉咙歌唱。
2这永远Xidngyδn9(汹涌)着我们的悲愤的河流。
3和那来自林间的无比温柔的HIning(黎明)。
4连羽毛也faIdn(腐烂)在土地里面。
4你是人间的四月天1qingling(轻灵)在春的光艳中交舞着变。
2那轻,那Pingtfng(娉婷),你是XiGnydn(鲜妍)百花的gudnmidn(冠冕)你戴着3你是一树一树的花开,是燕在梁间ninδn(呢喃)5我看1悄悄揉过fengrun(丰润)的青草2无意ch6nzui(沉醉)了凝望它的大地。
3逝去的多少欢乐和yθuqi(忧戚)4永在寂静的谐奏里b6fa(勃发)5随着季节的起伏而piaoyi(飘逸)6叫天风挽你坦荡地3ny6u(漫游),7像鸟的歌唱,云的IiUp∂n(流盼),树的ydoye(摇曳);6敬业与乐业1我这题目,是把《礼记》里头“jing於Idqιin(敬业乐群)”和《老子》里头“安其居,乐其业”那两句话,duδnzhangq11yi(断章取义)造出来的。
2这位ydnxingxianggu(言行相顾)的老Chdnshi(禅师),老实不客气3群居终日,ydnbujiyi(言不及义),好行小慧,难矣哉!4但我确信“敬业乐业”四个字,是人类生活的3δrfδm6n(不二法门)。
5但必先有业,才有可敬、可乐的主体,Hzhiyiming(理至易明)。
6我们对于这种人,是要彻底讨伐,万不能容sh6(赦)的。
7可惜被后来有些人说的太jingw6i(精微),倒变得不适实用了8将全副精力集中到这事上头,一点不PdngW匕(旁鹫),便是敬。
9惟一的Iniju6(秘诀)就是忠实,忠实从心里上发出来的便是敬。
C语言基础教程课件(英文版)ch09

A First Book of ANSI C, Fourth Edition
13
String Processing (continued)
A First Book of ANSI C, Fourth Edition
14
Library Functions
Note: Attempting to copy a larger string into a smaller string causes the copy to overflow the destination array beginning with the memory area immediately following the last array element.
The starting address of the string1 string is: 1244836
A First Book of ANSI C, Fourth Edition 20
Character Routines
A First Book of ANSI C, Fourth Edition
A First Book of ANSI C, Fourth Edition
2
String Fundamentals
• A string literal is any sequence of characters enclosed in double quotes
– "Good Morning!" – Also called: string constant, string value, string – A string is stored as an array of characters terminated by an end-of-string symbolic constant named NULL ('\0')
第七章 碳氧双键化合物的分类和命名

碳氧双键 化合物
O C R 醛 H R
O C
O C R X 酰卤 R
O C
O
O C R R 酸酐
O C OR' 羧酸酯 R
O C NH 2 酰胺
1
R C
N
羧酸
腈
7.1 碳氧双键化合物的分类和命名
7.1.1 分类 碳氧双键化合物可以根据分子中烃基结构的不同分类:
共轭碳氧双键化合物 O 不饱和碳氧双键化合物 脂肪族碳氧双键化合物 碳氧双键化合物 芳香族碳氧双键化合物
O CH3CH2CH2 H O H CH3CH2 O CH3
丁醛
2-甲基丙醛
2-丁酮
2
7.1 碳氧双键化合物的分类和命名
7.1.3 命名
醛、酮、羧酸的系统命名法是选择含有羰基或羧基的最长碳链作为主链,并从靠近羰基 或羧基的一端开始编号。
O CH 3 CH 3CH 2 2 CH 3 4 3 1 2-丁酮 2-苯基丙醛 O H CH 3CH 2 3 2 O 1
7.2 碳氧双键化合物的结构特征和物理性质
7.2.2 物理性质
碳氧双键化合物的极性使它们的沸点、熔点、比重和在极性溶剂中的溶解度比分子量 相近的非极性化合物高。随着烃基加大,差别变小。 碳氧双键中的氧原子具有接受活泼质子形成氢键的能力。在水和醇中有一定溶解度;随着 烃基加大,在水和醇中溶解度变小。 醛酮本身不能形成分子间的氢键,它们的沸点、熔点比相同分子量的醇要低。
N-甲基邻苯二甲酰亚胺
原甲酸三乙酯
碳原子的位置也可用希腊字母表示。
H O O
δ
γ
β
α
γ
β
α
α '
顺-9-十八碳烯酸结构式

顺-9-十八碳烯酸结构式全文共四篇示例,供读者参考第一篇示例:顺-9-十八碳烯酸,又称为油酸,是一种不饱和脂肪酸,是人体所必需的脂肪酸之一。
它的结构式为CH3(CH2)7CH=CH(CH2)7COOH,含有18个碳原子和一个双键,是一种十分重要的营养物质。
油酸在自然界中广泛存在于植物和动物的脂肪中,是人们日常饮食中常见的脂肪酸。
人体无法自身合成油酸,必须从食物中获取。
油酸被称为“必需脂肪酸”,对人体健康具有重要作用。
油酸对心血管健康有益。
研究表明,摄入足够的油酸可以降低血液中胆固醇的含量,减少动脉粥样硬化的发生。
油酸还能减少心脏病和中风的风险,有助于维持心脏健康。
油酸对细胞膜的健康也起着重要作用。
细胞膜主要由脂质构成,而油酸是构成细胞膜的主要成分之一。
油酸可以增强细胞膜的弹性和稳定性,保护细胞免受氧化应激和损伤。
这对于细胞的正常功能和健康至关重要。
油酸还具有抗炎和抗氧化的作用。
研究表明,油酸可以减少炎症反应的发生,保护细胞免受氧化损伤。
这对于预防炎症性疾病和老年痴呆具有重要意义。
在日常饮食中,可以通过摄入橄榄油、肉类、坚果和种子等食物获得足够的油酸。
适量摄入油酸有益于健康,但过量摄入也可能导致肥胖和其他健康问题。
建议在日常饮食中适量摄入油酸,并保持均衡饮食。
顺-9-十八碳烯酸结构式的油酸是一种重要的必需脂肪酸,对人体健康具有多种益处。
适量摄入油酸可以保护心血管健康、细胞膜健康,具有抗炎和抗氧化作用。
在日常饮食中保证摄入足够的油酸是维护健康的重要措施之一。
第二篇示例:顺-9-十八碳烯酸,又称为顺式-9-十八碳烯酸,是一种具有18个碳原子的不饱和脂肪酸。
它在生物学上具有重要的作用,是人体所需的必需脂肪酸之一。
顺-9-十八碳烯酸的结构式为CH3(CH2)7CH=CH(CH2)8COOH,其中“=”表示双键的存在。
顺-9-十八碳烯酸在人体中的作用主要包括参与细胞膜的构成和调节细胞膜的透性,促进细胞对脂溶性维生素的吸收,以及调节体内的炎症反应等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例9-4 程序运行结果如下
this is string****************----L1 ****************this is string----L2 **********************-1234.90----L3 ******************-1234.897600----L4 **************************0144----L5
【例9-4】 用ios成员函数及格式化标志设置输出 数据的格式。
//Eg9-4.cpp #include<iostream> using namespace std; void main(){ char c[30]="this is string"; double d=-1234.8976; cout.width(30); cout.fill('*'); cout.setf(ios::left); cout<<c<<"----L1"<<endl; cout.width(30); cout.setf(ios::right); cout<<c<<"----L2"<<endl;
9.2.3 数据输入/输出的格式控制
(3)设置域宽、精度、填充字符的成员函数
ch=fill() fill(ch) p=precision() precision(p) w=width() width(w) 返回填充字符(默认为空格),ch是一个字符变量 设置填充字符,ch是要设置为填充的字符 获取当前浮点数的精度,p是一个整型变量 设置精度,p是一个整数,代表要设置的数字位数 获取当前字段宽度(字符个数),w是整型变量 设置当前字段宽度,w是代表设置输出宽度的整数
9.2.3 数据输入/输出的格式控制
(2).ios中的格式化成员函数
• setf(flags) 设置指定的格式化标志flags, • unsetf(flags) 取消指定的格式化标志flags, • setf(flags,filed) 先清除、然后设置标志
– flags可以是上面在1中列举的格式化标志符
【例9-2】 用函数get和getline读取数据。 #include <iostream> using namespace std; void main(){ char c,char a[50],char s1[100]; cout<<"use get() input char: "; while((c=cin.get())!='\n') cout<<c; cout<<endl; cout<<"use get(a,10) input char: "; cin.get(a,10); cout<<a<<endl; cin.ignore(1); cout<<"use getline(s1,10) input char: "; cin.getline(s1,10); //L4 cout<<s1<<endl; }
cout.setf(ios::dec|ios::showbase|ios::showpoint); cout.width(30); cout<<d<<"----L3"<<"\n"; cout.setf(ios::showpoint); cout.precision(10); cout.width(30); cout<<d<<"----L4"<<"\n"; cout.width(30); cout.setf(ios::oct,ios::basefield); cout<<100<<"----L5"<<"\n"; }
9.1 C++ I/O流及流类库
– istream是输入流类,实现数据输入的功能; – ostream是输出流类,实现数据输出的功能; – iostream是istream和ostream的派生类,它继承了 istream类和ostream类的行为,支持数据输入、输 出的双向操作,在程序中常通过它来实现数据的输 入与输出功能。 – fstreambase从ios派生,提供了文件操作的许多功能, 作为其他文件操作类的公共基类。 – ifstream类用来实现文件读取操作, – ofstream类用来实现文件写入操作。 – fstream继承了fstreambase和iostream类的功能,实 现了文件读/写的双向操作。
9.2.2 ostream流中的常用成员函数
1、ostream类提供了许多用于数据输出的成员函数,并通 过流的输出运算符<<重载,实现了对内置数据类型的 输出功能。在ostream类中的声明原型如下: class _CRTIMP ostream : virtual public ios { public: ostream& operator<<(…); ostream& flush(); ostream& operator<<(long); ostream& put(char); ostream& write(const char *,int); ostream& seekp(streampos); ...... };
9.1 C++ I/O流及流类库
2、C++ I/O流类的继承结构
C++建立了一个十分庞大的流类库来实现数据的输入/输出操作,其
中的每个流类实现不同的功能,这些类通过继承组合在一起。
9.1 C++ I/O流及流类库
3、C++主要的流类简介
– streambuf主要作为其他类的支持,定义了对 缓冲区的通用操作,如设置缓冲区,从缓冲 区中读取数据,或向缓冲区写入数据等操作 – filebuf类使用文件来保存缓冲区中的字符序 列。它定义了文件读、写、打开、关闭等常 用操作。 – ios是所有流类的基类,提供对流状态进行设 置的主要功能。如文件数据的格式码设置与 取消,关链文件缓冲区借以实现数据读写等
9.1 C++ I/O流及流类库
4、C++预定义的输入/输出流对象
为了便于程序数据的输入/输出,C++预定义了几个标 准输入/输出流对象。在程序中可以直接引用它们来 输入/输出数据。如下表所示
对象定义 说 明
ostream cout; cout与标准输出设备相关联
ostream cerr; c2.3 数据输入/输出的格式控制
1. ios类提供的格式控制
ios是C++所有流类的基类,它包含了C++流的主要特性 。
(1).ios中的格式化标志
ios::skipws 跳过输入流中的空白字符 ios::left 输出数据按左对齐,如[12 ] ios::right 输出数据按右对齐,如[ 12] ios::dec 按十进制数据输出 ios::oct 按八进制数据输出 ios::hex 按十六进制数据输出 ios::showbase 在输出数据前面显示基数(八进制是0,十六进制是0x) ios::showpoint 浮点数输出带小数点 ios::uppercase 用大写字母输出十六进制数(即ABCDEF,默认是小写) ios::showpos 在正数前加“+” ios::scientific 用科学计数法输出浮点数,如[2.122E2] ios::fixed 用定点数形式输出浮点数,如[212.2] ios::unitbuf 完成后立即刷新缓冲区
9.1 C++ I/O流及流类库
1、流的概念
所谓流,是指数据的有向流动,即数据从一个 设备流向另一个设备 。 – 流实际上是一种对象,它在使用前被建立, 使用后被删除。数据的输入/输出操作就是 从流中提取数据或者向流中添加数据。 – 通常把从流中提取数据的操作称为析取,即 读操作;向流中添加数据的操作称为插入操 作,即写操作。
9.2.1 istream流中的常用成员函数
1、istream类定义了许多用于从流中提取数据和操作文件 的成员函数 ,如下所示 class istream : virtual public ios { public:
istream& operator>>(double &); //具有许多operator>>重载成员函数 ...... int get(); istream& get(char *,int,char ='\n'); istream& get(char &); istream& getline( char *,int,char ='\n'); istream& read(char *,int); istream& ignore(int =1,int =EOF); int peek(); istream& putback(char);
