MatLab练习题-程序设计完成
MATLAB编程练习(含答案很好的)

001双峰曲线图:z=peaks(40);mesh(z);surf(z)002解方程:A=[3,4,-2;6,2,-3;45,5,4];>> B=[14;4;23];>> root=inv(A)*B003傅里叶变换load mtlb ;subplot(2,1,1);plot(mtlb);>> title('原始语音信息');>> y=fft(mtlb);>> subplot(2,1,2);>> yy=abs(y);>> plot(yy);>> title('傅里叶变换')004输入函数:a=input('How many apples\n','s')005输出函数a=[1 2 3 4 ;5 6 7 8;12 23 34 45;34 435 23 34]a =1 2 3 45 6 7 812 23 34 4534 435 23 34disp(a)a =1 2 3 45 6 7 812 23 34 4534 435 23 34b=input('how many people\n' ,'s')how many peopletwo peopleb =two people>> disp(b)two people>>006求一元二次方程的根a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/(2*a)x1 =-1.0000 + 1.4142i>> x2=(-b-d)/(2*a)x2 =-1.0000 - 1.4142i007求矩阵的相乘、转置、存盘、读入数据A=[1 3 5 ;2 4 6;-1 0 -2;-3 0 0];>> B=[-1 3;-2 2;2 1];>> C=A*BC =3 142 20-3 -53 -9>> C=C'C =3 2 -3 314 20 -5 -9>> save mydat C>> clear>> load mydat C008编写数学计算公式:A=2.1;B=-4.5;C=6;D=3.5;E=-5;K=atan(((2*pi*A)+E/(2*pi*B*C))/D) K =1.3121009A=[1 0 -1;2 4 1;-2 0 5];>> B=[0 -1 0;2 1 3;1 1 2];>> H=2*A+BH =2 -1 -26 9 5-3 1 12>> M=A^2-3*BM =3 3 -62 13 -2-15 -3 21>> Y=A*BY =-1 -2 -29 3 145 7 10>> R=B*AR =-2 -4 -1-2 4 14-1 4 10>> E=A.*BE =0 0 04 4 3-2 0 10>> W=A\BW =0.3333 -1.3333 0.66670.2500 1.0000 0.25000.3333 -0.3333 0.6667 >> P=A/BP =-2.0000 3.0000 -5.0000-5.0000 3.0000 -4.00007.0000 -9.0000 16.0000>> Z=A.\BWarning: Divide by zero.Z =0 -Inf 01.0000 0.2500 3.0000-0.5000 Inf 0.4000>> D=A./BWarning: Divide by zero.D =Inf 0 -Inf1.0000 4.0000 0.3333-2.0000 0 2.5000010a=4.96;b=8.11;>> M=exp(a+b)/log10(a+b)M =4.2507e+005011求三角形面积:a=9.6;b=13.7;c=19.4;>> s=(a+b+c)/2;>> area=sqrt(s*(s-a)*(s-b)*(s-c))area =61.1739012逻辑运算A=[-1 0 -6 8;-9 4 0 12.3;0 0 -5.1 -2;0 -23 0 -7]; >> B=A(:,1:2)B =-1 0-9 40 00 -23>> C=A(1:2,:)C =-1.0000 0 -6.0000 8.0000 -9.0000 4.0000 0 12.3000>> D=B'D =-1 -9 0 00 4 0 -23>> A*Bans =1.0000 -184.0000-27.0000 -266.90000 46.0000 207.0000 69.0000>> C<Dans =0 0 1 01 0 0 0>> C&Dans =1 0 0 00 1 0 1>> C|Dans =1 1 1 11 1 0 1>> ~C|~Dans =0 1 1 11 0 1 0013矩阵运算练习:A=[8 9 5;36 -7 11;21 -8 5]A =8 9 536 -7 1121 -8 5>> BB =-1 3 -22 0 3-3 1 9>> RT=A*BRT =-5 29 56-83 119 6-52 68 -21>> QW=A.*BQW =-8 27 -1072 0 33-63 -8 45>> ER=A^3ER =6272 3342 294415714 -856 52608142 -1906 2390 >> BF=A.^3BF =512 729 12546656 -343 13319261 -512 125 >> A/Bans =3.13414.9634 -0.4024-1.2561 12.5244 -3.2317-1.9878 6.4512 -2.0366>> EKV=B\AEKV =10.7195 -1.2683 3.52449.4756 1.5854 3.71954.8537 -1.4878 1.3171>> KDK=[A,B]KDK =8 9 5 -1 3 -236 -7 11 2 0 321 -8 5 -3 1 9 >> ERI=[A;B]ERI =8 9 536 -7 1121 -8 5-1 3 -22 0 3-3 1 9014一般函数的调用:A=[2 34 88 390 848 939];>> S=sum(A)S =2301>> min(A)ans =2>> EE=mean(A)EE =383.5000>> QQ=std(A)QQ =419.3794>> AO=sort(A)AO =2 34 88 390 848 939 >> yr=norm(A)yr =1.3273e+003>> RT=prod(A)RT =1.8583e+012>> gradient(A)ans =32.0000 43.0000 178.0000 380.0000 274.5000 91.0000 >> max(A)ans =939>> median(A)ans =239>> diff(A)ans =32 54 302 458 91>> length(A)ans =6>> sum(A)ans =2301>> cov(A)ans =1.7588e+005>>015矩阵变换:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> tril(A)ans =34 0 08 34 034 55 2>> triu(A)ans =34 44 230 34 230 0 2>> diag(A)ans =34342norm(A)ans =94.5106>> rank(A)ans =3>> det(A)ans =-23462>> trace(A)ans =70>> null(A)ans =Empty matrix: 3-by-0>> eig(A)ans =80.158712.7671-22.9257>> poly(A)ans =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> logm(A)Warning: Principal matrix logarithm is not defined for A with nonpositive real eigenvalues. A non-principal matrixlogarithm is returned.> In funm at 153In logm at 27ans =3.1909 + 0.1314i 1.2707 + 0.1437i 0.5011 - 0.2538i0.4648 + 0.4974i 3.3955 + 0.5438i 0.1504 - 0.9608i0.2935 - 1.2769i 0.8069 - 1.3960i 3.4768 + 2.4663i>> fumn(A)Undefined command/function 'fumn'.>> inv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> cond(A)ans =8.5072>> chol(A)Error using ==> cholMatrix must be positive definite.>> lu(A)ans =34.0000 44.0000 23.00000.2353 23.6471 17.58821.0000 0.4652 -29.1816>> pinv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> svd(A)ans =94.510622.345611.1095>> expm(A)ans =1.0e+034 *2.1897 4.3968 1.93821.31542.6412 1.16431.8782 3.7712 1.6625>> sqrtm(A)ans =5.2379 + 0.2003i 3.4795 + 0.2190i 1.8946 - 0.3869i0.5241 + 0.7581i 5.1429 + 0.8288i 2.0575 - 1.4644i3.0084 - 1.9461i4.7123 - 2.1276i 2.1454 + 3.7589i >>016多项式的计算:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> P=poly(A)P =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> PPA=poly2str(P,'X')PPA =X^3 - 70 X^2 - 1107 X + 23462017多项式的运算:p=[2 6 8 3];w=[32 56 0 2];>> m=conv(p,w)m =64 304 592 548 180 16 6 >> [q,r]=deconv(w,p)q =16r =0 -40 -128 -46>> dp=polyder(w)dp =96 112 0>> [num,den]=polyder(w,p)num =80 512 724 312 -16den =4 24 68 108 100 48 9>> b=polyfit(p,w,4)Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 74b =-0.6704 9.2037 -32.2593 0 98.1333>> r=roots(p)r =-1.2119 + 1.0652i-1.2119 - 1.0652i-0.5761018求多项式的商和余p=conv([1 0 2],conv([1 4],[1 1]))p =1 5 6 10 8>> q=[1 0 1 1]q =1 0 1 1>> [w,m]=deconv(p,q)w =1 5m =0 0 5 4 3>> cq=w;cr=m;>> disp([cr,poly2str(m,'x')])5 x^2 + 4 x + 3>> disp([cq,poly2str(w,'x')])x + 5019将分式分解a=[1 5 6];b=[1];>> [r,p,k]=residue(b,a)r =-1.00001.0000p =-3.0000-2.0000k =[]020计算多项式:a=[1 2 3;4 5 6;7 8 9];>> p=[3 0 2 3];>> q=[2 3];>> x=2;>> r=roots(p)r =0.3911 + 1.0609i0.3911 - 1.0609i-0.7822>> p1=conv(p,q)p1 =6 9 4 12 9>> p2=poly(a)p2 =1.0000 -15.0000 -18.0000 -0.0000 >> p3=polyder(p)p3 =9 0 2>> p4=polyval(p,x)p4 =31021求除式和余项:[q,r]=deconv(conv([1 0 2],[1 4]),[1 1 1])022字符串的书写格式:s='student's =student>> name='mary';>> s1=[name s]s1 =marystudent>> s3=[name blanks(3);s]s3 =marystudent>>023交换两个数:clearclca=[1 2 3 4 5];b=[6 7 8 9 10];c=a;a=b;b=c;ab24If语句n=input('enter a number,n=');if n<10nend025 if 双分支结构a=input('enter a number ,a=');b=input('enter a number ,b=');if a>bmax=a;elsemax=b;endmax026三个数按照由大到小的顺序排列:A=15;B=24;C=45;if A<BT=A;A=B;B=T;elseif A<CT=A;A=C;C=T;elseif B<CT=B;B=C;C=T;endABC027建立一个收费优惠系统:price=input('please jinput the price : price=') switch fix(price/100)case[0,1]rate =0;case[2,3,4]rate =3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100;endprice=price*(1-rate)028:while循环语句i=0;s=0;while i<=1212s=s+i;i=i+1;ends029,用for循环体语句:sum=0;for i=1:1.5:100;sum=sum+i;endsum030循环的嵌套s=0;for i=1:1:6;for j=1:1:8;s=s+i^j;end;end;s031continue 语句的使用:for i=100:120;if rem(i,7)~=0;continue;end;iend032x=input ('输入X的值x=')if x<1y=x^2;elseif x>1&x<2y=x^2-1;elsey=x^2-2*x+1;endy033求阶乘的累加和sum=0;temp=1;for n=1:10;temp=temp*n;sum=sum+temp;endsum034对角线元素之和sum=0;a=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]; for i=1:4;sum=sum+a(i,i);endsum035用拟合点绘图A=[12 15.3 16 18 25];B=[50 80 118 125 150.8];plot(A,B)036绘制正玄曲线:x=0:0.05:4*pi;y=sin(x);plot(x,y)037绘制向量x=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18] plot(x)x=[0 0.2 0.5 0.7 0.6 0.7 1.2 1.5 1.6 1.9 2.3]plot(x)x=0:0.2:2*piy=sin(x)plot(x,y,'m:p')038在正弦函数上加标注:t=0:0.05:2*pi;plot(t,sin(t))set(gca,'xtick',[0 1.4 3.14 56.28])xlabel('t(deg)')ylabel('magnitude(v)')title('this is a example ()\rightarrow 2\pi')text(3.14,sin(3.14),'\leftarrow this zero for\pi')039添加线条标注x=0:0.2:12;plot(x,sin(x),'-',x,1.5*cos(x),':');legend('First','Second',1)040使用hold on 函数x=0:0.2:12;plot(x,sin(x),'-');hold onplot(x,1.5*cos(x),':');041一界面多幅图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)')subplot(222);plot(x,y2);title('cos(x)')subplot(223);plot(x,y3);title('sin(2x)')subplot(224);plot(x,y4);title('cos(2x)')042染色效果图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)');fill(x,y1,'r') subplot(222);plot(x,y2);title('cos(x)');fill(x,y2,'b') subplot(223);plot(x,y3);title('sin(2x)');fill(x,y3,'k') subplot(224);plot(x,y4);title('cos(2x)');fill(x,y4,'g')043特殊坐标图clcy=[0,0.55,2.5,6.1,8.5,12.1,14.6,17,20,22,22.1] subplot(221);plot(y);title('线性坐标图');subplot(222);semilogx(y);title('x轴对数坐标图');subplot(223);semilogx(y);title('y轴对数坐标图');subplot(224);loglog(y);title('双对数坐标图')t=0:0.01:2*pi;r=2*cos(2*(t-pi/8));polar(t,r)044特殊函数绘图:fplot('cos(tan(pi*x))',[-0.4,1.4])fplot('sin(exp(pi*x))',[-0.4,1.4])045饼形图与条形图:x=[8 20 36 24 12];subplot(221);pie(x,[1 0 0 0 1]);title('饼图');subplot(222);bar(x,'group');title('垂直条形图');subplot(223);bar(x,'stack');title('累加值为纵坐标的垂直条形图'); subplot(224);barh(x,'group');title('水平条形图');046梯形图与正弦函数x=0:0.1:10;y=sin(x);subplot(121);stairs(x);subplot(122);stairs(x,y);047概率图x=randn(1,1000);y=-2:0.1:2;hist(x,y)048向量图:x=[-2+3j,3+4j,1-7j];subplot(121);compass(x);rea=[-2 3 1];imag=[3 4 -7];subplot(122);feather(rea,imag);049绘制三维曲线图:z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)x=-10:0.5:10;y=-8:0.5:8;[x,y]=meshgrid(x,y);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2); subplot(221);mesh(x,y,z);title('普通一维网格曲面');subplot(222);meshc(x,y,z);title('带等高线的三维网格曲面'); subplot(223);meshz(x,y,z);title('带底座的三维网格曲面'); subplot(224);surf(x,y,z);title('充填颜色的三维网格面')050 带网格二维图x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);plot(x,y1,'r+-',x,y2,'k*:')grid onxlabel('Independent Variable x') ylabel('Dependent Variable y1&y2') text(1.5,0.5,'cos(x)')051各种统计图y=[18 5 28 17;24 12 36 14;15 6 30 9]; subplot(221);bar(y)x=[4,6,8];subplot(222);bar3(x,y)subplot(223);bar(x,y,'grouped') subplot(224);bar(x,y,'stack')052曲面图x=-2:0.4:2;y=-1:0.2:1;[x,y]=meshgrid(x,y);z=sqrt(4-x.^2/9-y.^2/4); surf(x,y,z)grid on053创建符号矩阵e=[1 3 5;2 4 6;7 9 11];m=sym(e)符号表达式的计算问题因式分解:syms xf=factor(x^3-1)s=sym('sin(a+b)'); expand(s)syms x tf=x*(x*(x-8)+6)*t; collect(f)syms xf=sin(x)^2+cos(x)^2; simplify(f)syms xs=(4*x^2+8*x+3)/(2*x+1); simplify(s)通分syms x yf=x/y-y/x;[m,n]=numden(f)嵌套重写syms xf=x^4+3*x^3-7*x^2+12; horner(f)054求极限syms x a;limit(exp(-x),x,0,'left')求导数syms xdiff(x^9+x^6)diff(x^9+x^6,4)055求不定积分与定积分syms x ys=(4-3*x^2)^2;int(s)int(x/(x+y),x)int(x^2/(x+2),x,1,3) double(ans)056函数的变换:syms x ty=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)057求解方程syms a b c xs=a*x^2+b*x+c;solve(s)syms x y zs1=2*x^2+y^2-3*z-4;s2=y+z-3;s3=x-2*y-3*z;[x,y,z]=solve(s1,s2,s3)058求微分方程:y=dsolve('Dy-(t^2+y^2)/t^2/2','t')059求级数和syms x ksymsum(k)symsum(k^2-3,0,10)symsum(x^k/k,k,1,inf)060泰勒展开式syms xs=(1-x+x^2)/(1+x+x^2);taylor(s)taylor(s,9)taylor(s,x,12)taylor(s,x,12,5)061练习syms x a;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)syms xs=x*cos(x);diff(s)diff(s,2)diff(s,12)syms xs1=x^4/(1+x^2);int(s1)s2=3*x^2-x+1int(s2,0,2)syms x y zs1=5*x+6*y+7*z-16;s2=4*x-5*y+z-7;s3=x+y+2*z-2;[x,y,z]=solve(s1,s2,s3)syms x yy=dsolve('Dy=exp(2*x-y)','x')y=dsolve('Dy=exp(2*x-y)','y(0)=0','x')n=sym('n');s=symsum(1/n^2,n,1,inf)x=sym('x');f=sqrt(1-2*x+x^3)-(1-3*x+x^2)^(1/3);taylor(f,6)062求于矩阵相关的值a=[2 2 -1 1;4 3 -1 2;8 5 -3 4;3 3 -2 2]adet=det(a)atrace=trace(a)anorm=norm(a)acond=cond(a)arank=rank(a)eiga=eig(a)063矩阵计算A=[0.1389 0.6038 0.0153 0.9318;0.2028 0.2772 0.7468 0.4660;0.1987 0.1988 0.4451 0.4186]B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)064求根及求代数式的值P=[4 -3 2 5];x=roots(P)x=[3 3.6];F=polyval(P,x)065多项式的和差积商运算:f=[1 2 -4 3 -1]g=[1 0 1]g1=[0 0 1 0 1]f+g1f-g1conv(f,g)[q,r]=deconv(f,g)polyder(f)066各种插值运算:X=0:0.1:pi/2;Y=sin(X);interp1(X,Y,pi/4)interp1(X,Y,pi/4,'nearest')interp1(X,Y,pi/4,'spline')interp1(X,Y,pi/4,'cubic')067曲线的拟合:X=0:0.1:2*pi;Y=cos(X);[p,s]=polyfit(X,Y,4)plot(X,Y,'K*',X,polyval(p,X),'r-')068求函数的最值与0点x=2:0.1:2;[x,y]=fminbnd('x.^3-2*x+1',-1,1) [x,y]=fzero('x.^3-2*x+1',1)069求多项式的表达式、值、及图像y=[1 3 5 7 19]t=poly(y)x=-4:0.5:8yx=polyval(t,x)plot(x,yx)070数据的拟合与绘图x=0:0.1:2*pi;y=sin(x);p=polyfit(x,y,5);y1=polyval(p,x)plot(x,y,'b',x,y1,'r')071求代数式的极限:syms xf=sym('log(1+2*x)/sin(3*x)');b=limit(f,x,0)072求导数与微分syms xf=sym('x/(cos(x))^2');y1=diff(f)y2=int(f,0,1)078划分网格函数[x,y]=meshgrid(-2:0.01:2,-3:0.01:5); t=x.*exp(-x.^2-y.^2);[px,py]=gradient(t,0.05,0.1);td=sqrt(px.^2+py.^2);subplot(221)imagesc(t)subplot(222)imagesc(td)colormap('gray')079求多次多项方程组的解:syms x1 x2 a ;eq1=sym('x1^2+x2=a')eq2=sym('x1-a*x2=0')[x1 x2]=solve(eq1,eq2,x1,x2)v=solve(eq1,eq2)v.x1v.x2an1=x1(1),an2=x1(2)an3=x2(1),an4=x2(2)080求解微分方程:[y]=dsolve('Dy=-y^2+6*y','y(0)=1','x')s=dsolve('Dy=-y^2+6*y','y(0)=1','x')[u]=dsolve('Du=-u^2+6*u','u(0)=1')w=dsolve('Du=-u^2+6*u','z')[u,w]=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z') v=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z')081各种显现隐含函数绘图:f=sym('x^2+1')subplot(221)ezplot(f,[-2,2])subplot(222)ezplot('y^2-x^6-1',[-2,2],[0,10])x=sym('cos(t)')y=sym('sin(t)')subplot(223)ezplot(x,y)z=sym('t^2')subplot(224)ezplot3(x,y,z,[0,8*pi])082极坐标图:r=sym('4*sin(3*x)')ezpolar(r,[0,6*pi])083多函数在一个坐标系内:x=0:0.1:8;y1=sin(x);subplot(221)plot(x,y1)subplot(222)plot(x,y1,x,y2)w=[2 3;3 1;4 6]subplot(223)plot(w)q=[4 6:3 5:1 2]subplot(224)plot(w,q)084调整刻度图像:x=0:0.1:10;y1=sin(x);y2=exp(x);y3=exp(x).*sin(x);subplot(221)plot(x,y2)subplot(222)loglog(x,y2)subplot(223)plotyy(x,y1,x,y2)085等高线等图形,三维图:t=0:pi/50:10*pi;subplot(2,3,1)plot3(t.*sin(t),t.*cos(t),t.^2) grid on[x,y]=meshgrid([-2:0.1:2])z=x.*exp(-x.^2-y.^2)subplot(2,3,2)plot3(x,y,z)box offsubplot(2,3,3)meshz(x,y,z)subplot(2,3,4)surf(x,y,z)contour(x,y,z)subplot(2,3,6)surf(x,y,z)subplot(2,3,5)contour(x,y,z)box offsubplot(2,3,6)contour3(x,y,z)axis off086统计图Y=[5 2 1;8 7 3;9 8 6;5 5 5;4 3 2]subplot(221)bar(Y)box offsubplot(222)bar3(Y)subplot(223)barh(Y)subplot(224)bar3h(Y)087面积图Y=[5 1 2;8 3 7;9 6 8;5 5 5;4 2 3];subplot(221)area(Y)grid onset(gca,'Layer','top','XTick',1:5)sales=[51.6 82.4 90.8 59.1 47.0];x=90:94;profits=[19.3 34.2 61.4 50.5 29.4];subplot(222)area(x,sales,'facecolor',[0.5 0.9 0.6], 'edgecolor','b','linewidth',2) hold onarea(x,profits,'facecolor',[0.9 0.85 0.7], 'edgecolor','y','linewidth',2) hold offset(gca,'Xtick',[90:94])set(gca,'layer','top')gtext('\leftarrow 销售量') gtext('利润')gtext('费用')xlabel('年','fontsize',14)088函数的插值:x=0:2*pi;y=sin(x);xi=0:0.1:8;yi1=interp1(x,y,xi,'linear')yi2=interp1(x,y,xi,'nearest') yi3=interp1(x,y,xi,'spline')yi4=interp1(x,y,xi,'cublic')p=polyfit(x,y,3)yy=polyval(p,xi)subplot(3,2,1)plot(x,y,'o')subplot(3,2,2)plot(x,y,'o',xi,yy)subplot(3,2,3)plot(x,y,'o',xi,yi1)subplot(3,2,4)plot(x,y,'o',xi,yi2)subplot(3,2,5)plot(x,y,'o',xi,yi3)subplot(3,2,6)plot(x,y,'o',xi,yi4)089二维插值计算:[x,y]=meshgrid(-3:0.5:3);z=peaks(x,y);[xi,yi]=meshgrid(-3:0.1:3); zi=interp2(x,y,z,xi,yi,'spline') plot3(x,y,z)hold onmesh(xi,yi,zi+15)hold offaxis tight090函数表达式;function f=exlin(x)if x<0f=-1;elseif x<1f=x;elseif x<2f=2-x;elsef=0;end091:硬循环语句:n=5;for i=1:nfor j=1:nif i==ja(i,j)=2;elsea(i,j)=0;endendendwhile 循环语句:n=1;while prod(1:n)<99^99;n=n+1endn:092 switch开关语句a=input('a=?')switch acase 1disp('It is raning') case 0disp('It do not know')case -1disp('It is not ranging')otherwisedisp('It is raning ?')end093画曲面函数:x1=linspace(-3,3,30)y1=linspace(-3,13,34)[x,y]=meshgrid(x1,y1);z=x.^4+3*x.^2-2*x+6-2*y.*x.^2+y.^2-2*y; surf(x,y,z)。
matlab简单编程21个题目及答案
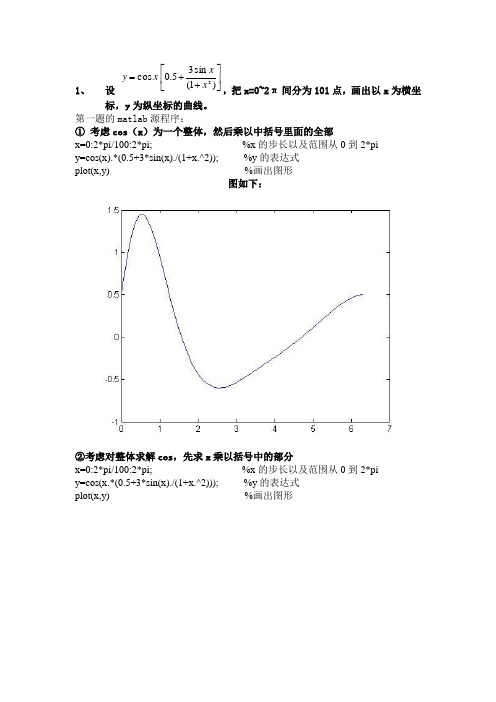
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
MATLAB编程练习.doc

编程训练实例1.你玩过牌吗?把13张牌反过来(背面朝上)按一定的顺序排列,先把你已经排好的牌第一张取出放在这叠牌的最底层,拿出第二张放在桌面上,然后将第三张取出又放在最底层,取出第四张放在桌子上……直到游戏结束,你依次取出放在桌子上的牌刚好为K,Q,J,10,9,8,7,6,5,4,3,2,A。
问你一开始时这13张牌的顺序是怎样的?请你用MATLAB编程解决这个问题?请把程序附上。
%调用格式为chengxufunction chengxua={1,13};k=2;j=1;b={'K','Q','J','10','9','8','7','6','5','4','3','2','A'};%for c=1:4for i=1:13if mod(i,2)~=0a{i}=b{j};j=j+1;endendfor i=2:2:13if mod(i,4)~=0a{i}=b{j};j=j+1;endendfor i=4:4:13if mod(i,8)~=0a{i}=b{j};j=j+1;endenda{8}=b{13};a或function f=card()a=1:13;i=1;for j=1:13n=numel(a); %目前的片数;numle为元数的个数。
a(n+1)=a(1); %在多少张里面取第一张。
a(1)=[]; %将上面取出的第一张牌所在空格剪掉。
b(i)=a(1); %翻出来时桌面上亮出来的牌。
i=i+1;a(1)=[];%随着i自增,取出现的空格为空。
(即删除)。
endc={'K','Q','J','10','9','8','7','6','5','4','3','2','A'};%因为10占两位,故用单元d=cell(1,13);%由BC对应的数,将C中字符型的牌放入由B决定对应的D中。
Matlab上机实验答案

Matlab上机实验答案实验一MATLAB运算基础1. 先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。
>> z1=2*sin(85*pi/180)/(1+exp(2))z1 =0.2375>> x=[2 1+2i;-0.45 5];>> z2=1/2*log(x+sqrt(1+x^2))z2 =0.7114 - 0.0253i 0.8968 + 0.3658i0.2139 + 0.9343i 1.1541 - 0.0044i2.9,,2.9,3.0>> a=-3.0:0.1:3.0;>> z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2) (>> z33=(exp(0.3*a)-exp(-0.3*a))/2.*sin(a+0.3)+log((0.3+a)/2)可以验证z3==z33,是否都为1)z3 =Columns 1 through 50.7388 + 3.1416i 0.7696 + 3.1416i 0.7871 + 3.1416i 0.7913 + 3.1416i 0.7822 + 3.1416iColumns 6 through 100.7602 + 3.1416i 0.7254 + 3.1416i 0.6784 + 3.1416i 0.6196 + 3.1416i 0.5496 + 3.1416iColumns 11 through 150.4688 + 3.1416i 0.3780 + 3.1416i 0.2775 + 3.1416i 0.1680 + 3.1416i 0.0497 + 3.1416iColumns 16 through 20-0.0771 + 3.1416i -0.2124 + 3.1416i -0.3566 + 3.1416i -0.5104 + 3.1416i -0.6752 + 3.1416iColumns 21 through 25-0.8536 + 3.1416i -1.0497 + 3.1416i -1.2701 + 3.1416i -1.5271 + 3.1416i -1.8436 + 3.1416iColumns 26 through 30-2.2727 + 3.1416i -2.9837 + 3.1416i -37.0245 + 0.0000i -3.0017 + 0.0000i -2.3085 + 0.0000iColumns 31 through 35-1.8971 + 0.0000i -1.5978 + 0.0000i -1.3575 + 0.0000i -1.1531 + 0.0000i -0.9723 + 0.0000iColumns 36 through 40-0.8083 + 0.0000i -0.6567 + 0.0000i -0.5151 + 0.0000i -0.3819 + 0.0000i -0.2561 + 0.0000iColumns 41 through 45-0.1374 + 0.0000i -0.0255 + 0.0000i 0.0792 + 0.0000i 0.1766 + 0.0000i 0.2663 + 0.0000iColumns 46 through 500.3478 + 0.0000i 0.4206 + 0.0000i 0.4841 + 0.0000i 0.5379 + 0.0000i 0.5815 + 0.0000iColumns 51 through 550.6145 + 0.0000i 0.6366 + 0.0000i 0.6474 + 0.0000i 0.6470 + 0.0000i 0.6351 + 0.0000iColumns 56 through 600.6119 + 0.0000i 0.5777 + 0.0000i 0.5327 + 0.0000i 0.4774 + 0.0000i 0.4126 + 0.0000iColumn 610.3388 + 0.0000i(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.5 >> t=0:0.5:2.5; >>z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3).*(t.^2-2.*t+1)z4 =0 0.2500 0 1.2500 1.0000 2.2500 2. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵) (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2]>> A=[12 34 -4;34 7 87;3 65 7];>> B=[1 3 -1; 2 0 3;3 -2 7];>> A+6*Bans =18 52 -1046 7 10521 53 49>> I=eye(3);>> A-B+Ians =12 31 -332 8 840 67 1(2)>> A*Bans =68 44 62309 -72 596154 -5 241>> A.*Bans =12 102 468 0 2619 -130 49(3)>> A^3ans =37226 233824 48604247370 149188 60076678688 454142 118820 >> A.^3ans =1728 39304 -6439304 343 65850327 274625 343 (4)>> A/Bans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000>> B\Aans =109.4000 -131.2000 322.8000-53.0000 85.0000 -171.0000-61.6000 89.8000 -186.2000(5)>> [A,B]ans =12 34 -4 1 3 -134 7 87 2 0 33 65 7 3 -2 7 >> [A([1,3],:);B^2]ans =12 34 -43 65 74 5 111 0 1920 -5 403. 设有矩阵A和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
matlab简单编程21个题目及答案

1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
MATLAB程序设计期末复习题集

第1章 MATLAB系统环境一、选择题1.最初的MATLAB核心程序是采用()语言编写的。
A.FORTRAN B.C C.BASIC D.PASCAL2.2016年3月发布的MATLAB版本的编号为()。
A.MATLAB 2016Ra B.MATLAB R2016aC.MATLAB 2016Rb D.MATLAB R2016b3.下列选项中能反应MATLAB特点的是()。
A.算法最优 B.不需要写程序C.程序执行效率高 D.编程效率高4.当在命令行窗口执行命令时,如果不想立即在命令行窗口中输出结果,可以在命令后加上()。
A.冒号(:) B.逗号(,) C.分号(;) D.百分号(%)5.如果要重新执行以前输入的命令,可以使用()。
A.左移光标键(←) B.右移光标键(→)C.下移光标键(↓) D.上移光标键(↑)6.MATLAB命令行窗口中提示用户输入命令的符号是()。
A.> B.>> C.>>> D.>>>>7.plot(x,y)是一条()命令。
A.打印 B.输出 C.绘图 D.描点8.以下两个命令行的区别是()。
>> x=5,y=x+10>> x=5,y=x+10;A.第一个命令行同时显示x和y的值,第二个命令行只显示x的值B.第一个命令行同时显示x和y的值,第二个命令行只显示y的值C.第一个命令行只显示x的值,第二个命令行同时显示x和y的值D.第一个命令行只显示y的值,第二个命令行同时显示x和y的值9.下列命令行中,输出结果与其他3项不同的是()。
A.>> 10+20+... B.>> ...30 10+20+30C.>> 10+20+30%5 D.>> %10+20+3010.下列选项中,不是MATLAB帮助命令的是()。
A.lookfor B.lookfor –all C.search D.help二、填空题1.MATLAB一词来自的缩写。
matlab设计gui程序例题

近年来,MATLAB在科学计算和工程领域中的应用变得越来越广泛。
其中,GUI(Graphical User Interface)程序设计作为MATLAB的一个重要应用领域,对于帮助用户更直观地理解和使用MATLAB具有重要意义。
本文将以MATLAB设计GUI程序为主题,探讨其原理、实现方法和实际例题,并对其进行深入解析和探讨。
1. GUI程序设计的基本原理在MATLAB中,GUI程序设计主要通过图形用户界面工具包(GUIDE)来实现。
GUIDE工具包提供了一系列可以直观拖放的元素,包括按钮、文本框、下拉菜单等,用户可以通过拖拉这些元素的方式来设计出自己理想的界面。
MATLAB还提供了丰富的回调函数,用户可以将不同控件的回调函数与自定义函数进行绑定,实现交互式的操作。
2. GUI程序设计的实现方法为了更深入地理解GUI程序设计,我们可以以一个简单的例子来说明其实现方法。
假设我们需要设计一个简单的温度转换器,用户可以输入摄氏温度,然后通过点击按钮来实现摄氏温度到华氏温度的转换。
我们可以通过GUIDE工具包来设计界面,添加一个文本框用于输入摄氏温度,一个按钮用于触发转换操作,以及一个用于显示结果的文本框。
我们可以在回调函数中编写转换的过程,当用户点击按钮时,根据用户输入的摄氏温度进行计算,并将结果显示在结果文本框中。
3. 实际例题:温度转换器GUI程序设计现在,让我们按照上面的思路来实际设计一个温度转换器的GUI程序。
我们打开MATLAB并新建一个GUI程序,接着使用GUIDE工具包来设计界面,按照前文描述的方法添加文本框、按钮和结果文本框。
我们为按钮添加点击事件的回调函数,编写摄氏温度到华氏温度的转换算法,并将结果显示在结果文本框中。
我们保存并运行程序,测试其功能和效果。
4. 总结与思考通过上述例题的实际操作,我们更深入地理解了MATLAB的GUI程序设计原理和实现方法。
GUI程序设计能够帮助我们更直观地操作MATLAB,提高使用效率和便利性。
matlab编程经典例题

例3-3 求一元二次方程ax2 +bx+c=0的根。 程序如下: a=input('a=?'); b=input('b=?'); c=input('c=?'); d=b*b-4*a*c; x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
(2) 双分支if语句: if 条件 语句组1 else 语句组2 end 当条件成立时,执行语句组1,否则执行语 句组2,语句组1或语句组2执行后,再执行 if语句的后继语句。
例3-4 计算分段函数的值。 程序如下: x=input('请输入x的值:'); if x<=0 y= (x+sqrt(pi))/exp(2); else y=log(x+sqrt(1+x*x))/2; end Y
(3) 多分支if语句: if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else 语句组n end 语句用于实现多分支选择结构。
例3-5 输入一个字符,若为大写字母,则输出其 对应的小写字母;若为小写字母,则输出其对应 的大写字母;若为数字字符则输出其对应的数值, 若为其他字符则原样输出。 c=input('请输入一个字符','s'); if c>='A' & c<='Z' disp(setstr(abs(c)+abs('a')-abs('A'))); elseif c>='a'& c<='z' disp(setstr(abs(c)- abs('a')+abs('A'))); elseif c>='0'& c<='9' disp(abs(c)-abs('0')); else disp(c); end
matlab基础练习题(带答案)

matlab基础练习题(带答案)Matlab 基础练习题常量、变量、表达式1、 MATLAB 中,下⾯哪些变量名是合法的?()(A )_num (B )num_ (C )num- (D )-num 2、在MA TLAB 中,要给出⼀个复数z 的模,应该使⽤()函数。
(A )mod(z) (B )abs(z) (C )double(z) (D )angle(z) 3、下⾯属于MATLAB 的预定义特殊变量的是?()(A )eps (B )none (C )zero (D )exp4、判断:在MA TLAB 的内存⼯作区中,存放⼀个英⽂字符 'a' 需要占⽤1个字节,存放⼀个中⽂字符‘啊’需要占⽤2个字节。
(错,都是2个字节)5、判断:MA TLAB 中,i 和j (对)6、判断:MA TLAB 中,pi 代表圆周率,它等于3.14。
(错,后⾯还有很多位⼩数)7、在MA TLAB 中,若想计算的51)3.0sin(21+=πy 值,那么应该在MA TLAB 的指令窗中输⼊的MA TLAB 指令是__y1=2*sin(0.3*pi)/(1+sqrt(5))_。
8、在MA TLAB 中,a = 1,b = i ,则a 占_8__个字节,b 占_16_个字节,c 占________字节。
9、在MA TLAB 中,inf 的含义是__⽆穷⼤__,nan 的含义是__⾮数(结果不定)___。
数组1、在MA TLAB 中,X 是⼀个⼀维数值数组,现在要把数组X 中的所有元素按原来次序的逆序排列输出,应该使⽤下⾯的()指令。
(A )X[end:1] (B )X[end:-1:1] (C )X (end:-1:1) (D )X(end:1) 2、在MA TLAB 中,A 是⼀个字⼆维数组,要获取A 的⾏数和列数,应该使⽤的MATLAB的命令是()。
(A )class(A) (B )sizeof(A) (C )size(A) (D )isa(A)3、在MATLAB 中,⽤指令x=1:9⽣成数组x 。
matlab练习

《数学实验》在线习题1一、单项选择题(将选择答案写在答题纸上,每小题2分共20分)1.在MA TLAB 命令窗口中键入命令,Vname=prod(7:9)/prod(1:3),可计算组合数!6!3!939⨯=C ,如果省略了变量名Vname ,MA TLAB 表现计算结果将用下面的哪一变量名做缺省变量名AA )ans ;B )pi ;C )NaN ;D )eps2.宝石切割问题中,石料左右长度、前后长度、上下高度分别为a 1、a 2、a 3,即a 1×a 2×a 3(cm 3),而精品尺寸为b 1×b 2×b 3(cm 3)。
操作时,同向切割连续两次再旋转刀具。
某一切割方案的切割面积依次为:2a 1a 2→ 2a 1b 3 → 2b 2b 3,则这一切割方案为BA )左右→前后→上下;B )上下→前后→左右;C )前后→上下→左右;D )前后→ 左右→上下 3.机场指挥塔位置:北纬30度35.343分,东经104度2.441分,在MA TLAB 中用变量B=[30 35.343]表达纬度,L=[104 2.441]表达经度。
将数据转化为以度为单位的实数,下面正确的语句是A ) =B(1)+B(2)/60,Q=L(1)+L(2); B) P = 60*B(1) + B(2),Q=60*L(1)+L(2) C ) P = B(1) + B(2)/60,Q=L(1)+L(2)/60; D) P=B(1)+B(2),Q=L(1)+ L(2);。
4.用MA TLAB 随机产生60个1到365之间的正整数,应该使用下面的哪一条命令AA ) fix(365*rand(1,60));B )1+fix(366*rand(1,60));C )1+fix(364*rand(1,60));D )1+fix(365*rand(1,60))5.用A 、B 、C 表示三角形的三条边,用MA TLAB 表示条件“任意两条边之和大于第三条边”的逻辑表达式应该用下面哪一行语句AA ) A+B>C | A+C>B | B+C>A ; B ) A+B>=C | A+C>=B | B+C>=A ; C ) A+B>=C&A+C>=B&B+C>=A ;D ) A+B>C & A+C>B & B+C>A ; 6.在MA TLAB 命令窗口中,键入命令syms x ; y=int(6*x^4)。
08-09-1MATLAB程序设计A卷

3.Plot the 3Dmeshfigureand3Dsurface figureof the function
(1)nand exist in Workspace of Matlab. It is no any limit;
(2)nand are unknown variables. Please inputxby keyboard one by one, and give amarkof end the data input. Examinees can use loop statement and length() function and input() function, but cannot use mean() function, std() function, and var() function directly(可以使用循环语句和length()函数、input()函数等进行编程,但不能直接使用mean()、std()和var()等函数).
in the range of and ,respectively.
四.综合编程题(每小题11分,共22分)
1. Write a function program to compute the following function
and call this function program to compute the value of in main program or command window, there, shows thefactorial(阶乘) of .
数学实验matlab练习题

2015-2016数学实验练习题一、选择题1.清除Matlab工作空间(wordspace)变量的命令是(B )A. clcB. clearC. clfD.delete2. 清除当前屏幕上显示的所有内容,但不清除工作空间中的数据的命令是( A )A. clcB. clearC. clfD.delete3. 用来清除图形的命令( C )A. clcB. clearC. clfD.delete4. 在MATLAB程序中,使命令行不显示运算结果的符号是( A )A. ;B. %C. #D. &5. 在MATLAB程序中,可以将某行表示为注释行的符号是( B )A. ;B. %C. #D. &6.在循环结构中跳出循环,执行循环后面代码的命令为 ( B )A. returnB. breakC. continueD. Keyboard7.在循环结构中跳出循环,但继续下次循环的命令为( C )A. returnB. breakC. continueD. Keyboard8. MATLAB中用于声明全局变量的关键字是( C )A. infB. symsC. globalD. function9. 用户可以通过下面哪项获得指令的使用说明( A )A. helpB. loadC. demoD. lookfor10.在MATLAB命令窗口中键入命令S=zoros(3);可生成一个三行三列的零矩阵,如果省略了变量名S,MATLAB表现计算结果将用下面的哪一变量名做缺省变量名( A )A. ans;B. pi;C. NaN;D. Eps.11. 9/0的结果是( B )A. NAN;B. Inf;C. eps;D. 012.在MATLAB中程序或语句的执行结果都可以用不同格式显示,将数据结果显示为分数形式,用下面哪一条命令语句( D )A. format long;B. format long e;C. format bank;D. fromat rat13. 下列MATLAB命令中是构造1行3列的(-1,1)均匀分布随机矩阵的命令的是(D)A. randn(1,3);B. rand(1,3);C. ones(3);D. 以上都不对14. 产生四维元素都为1矩阵的语句为( A )A. ones(4)B. eye(4)C. zeros(4)D. rand(4)15. 用round 函数对数组[2.48 6.39 3.93 8.52]取整,结果为 ( C )A. [2 6 3 8]B. [2 6 4 8]C. [2 6 4 9]D. [3 7 4 9]16. y=dsolve(‘Dy=1/(1+x^2)-2*y^2’,’y(0)=0’,’x ’); ezplot(y)的功能是( A )A. 求微分方程特解并绘图;B. 解代数方程;C. 求定积分;D.求微分方程通解.17. MATLAB 命令roots([1,0,0,-1])的功能是 ( D )A. 产生向量[1,0,0,1];B. 求方程310x 的根;C. 求多项式31x的值; D. 求方程310x 的根。
实验4答案 Matlab程序设计1

实验4 Matlab 程序设计1实验目的:1、 掌握建立和执行M 文件的方法;2、 掌握实现选择结构的方法;3、 掌握实现循环结构的方法。
实验内容:1. 从键盘输入一个4位整数,按如下规则加密后输出。
加密规则:每位数字都加上7,然后用和除以10的余数取代该数字;再把第一位与第三位交换,第二位与第四位交换。
a = input('请输入一个四位整数:');a1 = fix(a/1000);a2 = rem(fix(a/100),10);a3 = rem(rem(fix(a/10),100),10);a4 = rem(a,10);a1 = rem(a1+7,10)a2 = rem(a2+7,10)a3 = rem(a3+7,10)a4 = rem(a4+7,10)b1 = a1;a1 = a3;a3 = b1;b2 = a2;a2 = a4;a4 = b2;b = a1*1000+a2*100+a3*10+a42. 求分段函数的值。
,x x x x y x x x x x x x ⎧+- <≠-⎪=-+ ≤<≠≠⎨⎪-- ⎩2226035605231且且及其他用if 语句实现,分别输出x=-5,-3,0,1,2,2.5,3,5时的y 值。
x = input(请输入X 的值:');if x <0 & x~=-3y = x.*x +x-6;elseif x>=0 & x<5 & x~=2 & x~=3y = x.*x-5*x+6;elsey = x.*x-x-1;endy3.输入一个百分制成绩,要求输出成绩等级A、B、C、D、E,其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和swich语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
山东大学《matlab程序设计》期末作业

《Matlab 程序设计》 期末作业学院: 专业: 班级:学号: 姓名: 成绩:一 、 简答题(每题10分,共50分)1、假设有两个矩阵A 和B ,请用这两个矩阵说明Matlab 数值计算中的“左除”与“右除”有什么区别?2、脚本M 文件与函数M 文件的主要区别是什么?3、设矩阵A=[1 4 3 9;5 30 12 42;2 18 32 15],试编程找出A 中所有大于或等于5的元素,并把这些元素组成一个列向量,并计算出这些元素的总和(注意附上标注说明)4、利用Matlab 编写程序求取335lim 21x x x →∞++和120()t t dt -⎰,并对求取结果进行分子和分母的提取(注意附上标注说明)。
5、利用Matlab 编写程序求微分方程x e y y y x 2cos 52=+'-''的通解。
二、 综合题(每题20分,共40分)1、在同一张图上分别画出两组坐标)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图和折线图。
要求只能利用plot 命令进行绘制,X 坐标范围[0,105] ,Y 坐标范围[0,1450]。
2、已知学生的名字和百分制分数。
编写相应的程序要求输入所有学生的百分制分数后,一次性判断每个学生的成绩分别是“满分”、“优秀”、“良好”、“及格”还是“不及格”,并要求最后用单元数组按行分别输出每个学生的名字、分数和成绩判断结果。
学生姓名 Jack Marry Peter Rose Tom成 绩 72 83 56 94 100判断标准:满分(100),优秀(90-99),良好(80-89),及格(60-79),不及格(<60)三、 论述题(共10分)浅谈一下Fortran 、matlab 、maple 和mathematic 这四种计算语言的特点和区别。
MATLAB考核期末(含答案)

一、微分方程求解。
(15分)设1)(8)(4)(2)(2233=+++t y dt t dy dt t y d dt t y d ,0)0(=y ,1)0(=dtdy ,0)0(22=dt y d 用ode45方法求微分方程的解。
要求: 1)仿真时间t=30秒2)结果绘制在一张图中,包括t y -曲线,一阶t y -'曲线,二阶t y -''曲线,三阶t y -'''曲线3)用图例命令分别说明四条曲线为“t y -”,“t y -'”,“t y -''” ,“t y -'''” 4)定义横坐标为“时间”,纵坐标为“输出”,图形标题名称为“微分方程的解”解:系统方程为 1)(8)(4)(2)(2233=+++t y dt t dy dt t y d dt t y d , 这是一个单变量三阶常微分方程。
将上式写成一个一阶方程组的形式,这是函数ode45调用规定的格式。
令:y y =)1()1()2(∙∙==y y y)2()1()3(∙∙∙∙∙===y y y y⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∙∙∙)2(4)3(2)1(81)3()2()3()2()1(y y y y y y y y函数文件程序:function ydot=myfun1(t,y)ydot=[y(2);y(3);1-8*y(1)-2*y(3)-4*y(2)];主文件程序: t=[0 30]; y0=[0;1;0];[tt,yy]=ode45(@myfun1,t,y0);y=(1-yy(:,3)-2*yy(:,2)-4*yy(:,1))/8;plot(tt,y,'r',tt,yy(:,1),'k',tt,yy(:,2),'-g',tt,yy(:,3),'-.b'); legend('y-t','y ˊ-t','y ˊˊ-t','y ˊˊˊ-t') title('微分方程的解') xlabel('时间') ylabel('输出')运行程序后输出图形如下:二、数值计算,编程完成以下各题(共20分,每小题5分)1、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3, 5]的图形,求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m inf .解:程序如下x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; plot(x,y);fn='(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5'; [xmin,fmin]=fminbnd(fn,3,5) hold onplot(xmin,fmin,'r*'); Xlabel('x') Ylabel('f(x)')经过运行后得到的图像截图如下:运行后的最小值点m in x =4.6051,m in f = -8.3383e+003。
MATLAB编程练习.doc

编程训练实例1.你玩过牌吗?把13张牌反过来(背面朝上)按一定的顺序排列,先把你已经排好的牌第一张取出放在这叠牌的最底层,拿出第二张放在桌面上,然后将第三张取出又放在最底层,取出第四张放在桌子上……直到游戏结束,你依次取出放在桌子上的牌刚好为K,Q,J,10,9,8,7,6,5,4,3,2,A。
问你一开始时这13张牌的顺序是怎样的?请你用MATLAB编程解决这个问题?请把程序附上。
%调用格式为chengxufunction chengxua={1,13};k=2;j=1;b={'K','Q','J','10','9','8','7','6','5','4','3','2','A'};%for c=1:4for i=1:13if mod(i,2)~=0a{i}=b{j};j=j+1;endendfor i=2:2:13if mod(i,4)~=0a{i}=b{j};j=j+1;endendfor i=4:4:13if mod(i,8)~=0a{i}=b{j};j=j+1;endenda{8}=b{13};a或function f=card()a=1:13;i=1;for j=1:13n=numel(a); %目前的片数;numle为元数的个数。
a(n+1)=a(1); %在多少张里面取第一张。
a(1)=[]; %将上面取出的第一张牌所在空格剪掉。
b(i)=a(1); %翻出来时桌面上亮出来的牌。
i=i+1;a(1)=[];%随着i自增,取出现的空格为空。
(即删除)。
endc={'K','Q','J','10','9','8','7','6','5','4','3','2','A'};%因为10占两位,故用单元d=cell(1,13);%由BC对应的数,将C中字符型的牌放入由B决定对应的D中。
数学建模Matlab上机实训题目

数学建模Matlab上机实训题目一、矩阵及数组操作:1.利用基本矩阵产生3×3和15×8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机矩阵([-1,1]之间)、正态分布矩阵(均值为1,方差为4)。
2.利用fix及rand函数生成[0,10]上的均匀分布的10×10的整数随机矩阵a,然后统计a中大于等于5的元素个数。
3.在给定的矩阵中删除含有整行内容全为0的行,删除整列内容全为0的列。
二、绘图:4.在同一图形窗口画出下列两条曲线图像:y1=2x+5;y2=x^2-3x+1,并且用legend标注。
5.画出下列函数的曲面及等高线:z=x^2+y^2+sin(xy).三、程序设计:6.编写程序计算(x在[-3,3],间隔0.01)7.有一列分数序列:求前15项的和。
8.用至少三种方法编写函数实现求任意整数n的阶乘。
9*.将任意偶数m写成两个素数p1、p2的和(试着写出所有的m=p1+p2的可能形式)。
10*.是否任意3的倍数m可以写成两个素数p1、p2、p3的和(试着写出所有的m=p1+p2+p3 的可能形式)?四、数据处理与拟合初步:分别采用y=c1+c2e^(-t)和y=d1+d2te^(-t)进行拟合,并画出拟合曲线进行对比。
12.计算下列定积分:13.微分方程组当t=0时,x1(0)=1,x2(0)=-0.5,求微分方程t在[0,25]上的解,并画出相空间轨道图像。
14.设通过测量得到时间t与变量y的数据:t=[0 0.3 0.8 1.1 1.6 2.3];y=[0.5 0.82 1.14 1.25 1.35 1.41];分别采用多项式:y=a0+a1t+a2t2和指数函数y=b0+b1e-t+b2te-t进行拟合,并计算均方误差、画出拟合效果图进行比较。
15.V an der Pol(范德堡)方程是典型的二阶非线性方程之一:y”-u(1-y^2)y’+y=0,y(0)=2,y‘(0)=0;其中u>0为标量。
成人自考本科2021年MATLAB题库应用设计题

2021年MATLAB题库习题:1.求分段函数的值。
2 6 x0x-32 5 0x52x xy xx⎧+-<≠⎪⎨=-≤<⎪⎩且其他;要求x的取值范围为[-10,10]步长为2,得到相对应的y的值.2.编写MATLAB程序,在同一图形窗口中绘制y1和y2两条曲线,并对图形坐标轴进行控制。
3.求解以下线性方程组,要求写出程序代码和运行结果2x1- 3x2+ x3+2x4=8x1+3x2+ x4=6x1- x2+ x3+8x4=17x1+ x2-2x3+2x4=54.打印出所有的水仙花数。
所谓“水仙花数”,是指一个三位数,其各位数字立方之和等于该数本身。
5.给定一个多输入一多输出系统G(s)=,使用MATLAB表示该传递函数。
6.编写一程序,计算:已知在一个笼子里有鸡与兔共30只,共有爪100个,试问其中鸡有多少只?兔有多少只?7.已知>>B=[1+2i,13+10i,4+3i;12+2i,4+7i,5+14i;7+9i,10+3i,14+5i],若>>B1=B`,>>B2=B`.>>B3=conj(B`),列出B1,B2,B3的表达式8.若一离散型MIMO传递函数为:, 其采样周期为0.5s,建立系统的传递函数模型。
9.某离散系统的传递函数为,采样时间T=1s,写出求解此系统的单位阶跃响应曲线的程序代码。
10.已知两状态空间方程描述的系统进行并联连接,其中状态系数矩阵为,,,,求此并联系统的状态空间模型。
11.输入矩阵a= [1 2 3;4 5 6;7 8 9](1)使用全下标方式取出元素“3”,使用单下标方式取出元素“8”,取出后两行子矩阵块,使用逻辑矩阵方式取出[1 3;7 9](2)使用全下标方式给第一二行的第三列分别赋值为30,60,使用单下标方式把第二列元素赋值为20,50,80,使用全元素方式把矩阵按行的顺序赋值为1,2,312.在同一个窗口中建立4个子图,在子图中分别绘制sin(x)、cos(x)、sin(2x)、cos(2x)曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MatLab 练习题(4)-程序设计
学号: 班级: 姓名: 注意: 1,请按要求作题,直接输入答案,并保存文件.
2,仔细填写 “学生信息”.
3,把此word 文档的文件名更名为你的 “学号第*次”.上传至http ://10.1.9.91. 例: “MatLab 练习册.doc ” ——-> “200504101第四次作业.doc ” )
1, 编辑函数文件hanshu.m,该函数是
32()33f x x x x =--+,并用它来计算(0.34)f 、(3)f 、(6.87)f 、2(3)(2)(4)f f f --
答案:(填写程序语句和结果)
函数文件:
hanshu.m
function f=hanshu(x)
f=x^3-3*x^2-x+3;
程序:
hanshu(0.34)
hanshu(3)
hanshu(6.87)
hanshu(3)-hanshu(2)*[hanshu(-4)]^2
ans =
2.3525
ans =
ans =
178.7820
ans =
33075
2,编程求一个四位数abca ,使2
(51)abca c =+。
答案:(填写程序语句和结果)
程序:
for a=1:9
for b=0:9
for c=0:9
if a*1000+b*100+c*10+a==(5*c+1)^2
x=a*1000+b*100+c*10+a
end
end
end
end
x
结果:
x =
1681
3利用二分法编程求方程 03323=+--x x x 在[0,3]内的根.
答案: (填写程序语句和结果)
程序:
a=0;
b=3;
x=a:b;
f =@(x)x^3-3*x^2-x+3;
c=(a+b)./2;
while abs(b-a)>1e-6
if f(c)*f(b)<0
a=c;
else
b=c;
end
c=(a+b)./2;
x=c;
end
x
结果:
x =
1.0000
*4, 利用二分法编程求方程 tan(x)-x-0.5=0 在[0,1.5]内的根.
答案:(填写程序语句和结果)
a=0;
b=1.5;
x=a:b;
f =@(x)tan(x)-x-0.5;
c=(a+b)./2;
while abs(b-a)>1e-6
if f(c)*f(b)<0
a=c;
else
b=c;
end
c=(a+b)./2;
x=c;
end
x
结果x =
0.9750
5,列出所有的水仙花数, 水仙花数是一个三位数,其各位数字立方和等于该数本身. 例如: 333351153++=
答案:(填写程序语句和结果)
程序:
for a=1:9
for b=0:9
for c=0:9
if a*100+b*10+c==a^3+b^3+c^3
x=a*100+b*10+c
end
end
end
end
结果:
x =
153
x =
370
x =
371
x =
407
x =
407
*6, 利用 Λ+-+-≈71513114π
公式求π的近似值,直到误差小于610- 答案: (填写程序语句和结果)
程序:
s=0;
k=1;
while 1/(2*k-1)>10^(-6)
s=s+(-1)^(k+1)/(2*k-1);
k=k+1;
end
s1=4*s
s1 =
3.1492
7,写出小于5000的、立方的末四位是8888的所有自然数的程序
答案: (填写程序语句和结果)
程序:
for a=0:5000
if rem(a^3,10000)==8888
a
end
end
结果:
a =
1942
a =
4442
8,先思考如何用推理的方法(1)求Fibonacc数列中第2007个数除以6 的余数(2)若将Fibonacc数列按如下方式分组:(1)、(1,2)、(3,5,8)、(13,21,34,55)、……问2007组数的和除以6的余数是几?然后再用matlab 编程验证你的结果。
答案: (填写你的思考过程和你的结果以及matlab程序语句)
分析:斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、34……
注意:
0是第0项,不是第一项。
这个数列从第二项开始,每一项都等于前两项之和。
(分析参考网上)(1)程序:
a(1)=1;
a=1;
for i=3:2007
k=i-1;
j=i-2;
a(i)=a(k)+a(j);
end
rem(a(2007),6)
结果:
ans =
NaN
a(2007)
ans =
Inf
9*,应用
11
11......
2!!
e
n
≈++++
近似求e之值,要求误差小于6
10-
程序:n=1;
m=1;
while 1/n>10^(-6);
for c=c+1;
n=n*c;
m=m+1/n;
end
m1=m;
end
m1
结果:
m1 =
2.7385
10,定义一个函数shjiech计算双阶乘,要求对输入的一个整数N,该函数能立即计算出其双阶乘。
并用它来计算200!!
答案: (填写程序语句和结果)
程序:
function jiech=shjiech(n)
if rem(n,2)==0
as=2:2:n;
else as=1:2:n;
end
jiech=prod(as);
结果:
shjiech(200)
ans =
1.1831e+188
11,定义多元函数
22
22()
(,)()x y
f x y x y e-+
=+,并用它来计算(2,3)
f-、(3,4)
f、
(0,0)
f,并画出它的图形。
答案: (填写程序语句和结果)
程序:
function m=f(x,y)
m=(x^2+y^2)*exp(-x^2-y^2)
结果:
f(-2,3)
f(3,4)
f(0,0
ans =
2.9384e-005
ans =
3.4720e-010
ans
作图程序:
x=-4:0.05:4;y=x;
[X,Y]=meshgrid(x,y);
Z=(X.^2+Y.^2)*exp(-X.^2-Y.^2);
mesh(X,Y,Z)
图:
*12,编写函数文件SQRT.m 迭代公式是11()2n n n a x x x +=+,误差小于10-6。
答案: (填写程序语句和结果)
程序:
function genhaoa=sqrt1(a)
x0=1;
x1=1/2*(x0+a/x0);
while abs(x1-x0)>10^(-6)
x0=x1;
x1=1/2*(x0+a/x0);
end
genhaoa=x1。
