雷达脉冲压缩matlab
二相编码脉冲压缩matlab代码

二相编码脉冲压缩matlab代码脉冲压缩是一种雷达技术,它通过发送一个较宽的脉冲并在接收时压缩该脉冲来提高雷达的分辨率。
二相编码脉冲压缩是其中的一种实现方式,它使用一个二相编码信号来发送和接收脉冲。
以下是一个简单的MATLAB 代码示例,用于模拟二相编码脉冲压缩的过程。
请注意,这只是一个基本的示例,实际的实现可能会更复杂。
matlab复制代码% 参数设置fc = 10e9; % 载波频率 (GHz)fc_bin = 100e6; % 编码信号频率 (Hz)t_bin = 1/fc_bin; % 编码信号周期t_pulse = 10*t_bin; % 脉冲宽度t_total = 100*t_bin; % 总时间% 生成二相编码信号N_bin = round(t_total/t_bin); % 编码信号周期数code = randi([0,1], N_bin, 1); % 二相编码信号code = double(code); % 转换为双精度% 生成载波信号carrier = cos(2*pi*fc*(0:N_bin-1)*t_bin); % 生成载波信号% 二相编码脉冲压缩compressed_pulse = conv(carrier, code, 'same'); % 进行脉冲压缩compressed_pulse = compressed_pulse(N_bin/2+1:end); % 去除重复部分% 绘制结果figure;subplot(2,1,1);plot(carrier);title('载波信号');xlabel('时间 (s)');ylabel('幅度');subplot(2,1,2);plot(compressed_pulse);title('压缩脉冲');xlabel('时间 (s)');ylabel('幅度');这段代码首先设置了参数,包括载波频率、编码信号频率、脉冲宽度和总时间。
相位编码脉冲压缩信号的 matlab 实现

相位编码脉冲压缩(Phase-Coded Pulse Compression)是一种雷达信号处理技术,可以用于提高雷达系统的性能。
下面是一个简单的MATLAB 实现示例:```matlab定义参数N = 1024; 信号长度fc = 100e6; 载波频率fs = 500e6; 采样频率t = (0:N-1)/fs; 时间向量生成相位编码信号phase_code = exp(1i*2*pi*(0:N-1)/N); 相位编码序列signal = cos(2*pi*fc*t + phase_code); 相位编码脉冲信号进行匹配滤波filter = fliplr(conj(phase_code)); 匹配滤波器compressed_signal = signal.*filter; 压缩信号绘制结果subplot(2,1,1); plot(t,abs(compressed_signal)); title('压缩信号时域');subplot(2,1,2); freqz(filter,1,N,fs); title('匹配滤波器频率响应');```在上面的代码中,首先定义了信号的长度、载波频率和采样频率等参数。
然后生成一个长度为`N` 的相位编码序列`phase_code`,并使用该序列生成相位编码脉冲信号`signal`。
接着,通过翻转和取共轭操作得到匹配滤波器`filter`,将信号与滤波器进行乘法运算得到压缩信号`compressed_signal`。
最后,绘制压缩信号的时域表示和匹配滤波器的频率响应。
需要注意的是,这只是一个简单的示例,实际的相位编码脉冲压缩信号处理可能需要更复杂的算法和技术。
Matlab在雷达信号处理和雷达成像中的应用

Matlab在雷达信号处理和雷达成像中的应用随着科技的不断发展,雷达技术在军事、航空、天文等领域扮演着非常重要的角色。
而在雷达的研究和应用中,数据的处理和成像是至关重要的环节。
Matlab作为一款强大的数学软件,被广泛应用于雷达信号处理和雷达成像的领域。
本文将探讨Matlab在雷达信号处理和雷达成像中的具体应用。
一、雷达信号处理1. 信号预处理雷达接收到的信号常常受到多种干扰,例如噪声、杂波等。
Matlab提供了丰富的信号预处理函数和工具箱,可以对雷达信号进行滤波、降噪、去除杂波等操作。
其中,滤波操作可以通过FIR、IIR滤波器实现,而降噪操作可以通过小波分析等方法实现。
Matlab的强大计算能力和可视化功能使得信号预处理更加高效准确。
2. 目标检测雷达信号中的目标通常表现为一些特征突出的信号,例如脉冲幅度、脉冲宽度等。
通过对这些特征进行分析和处理,可以实现雷达信号中目标的检测和定位。
Matlab提供了一系列的目标检测算法和函数,如常用的卡尔曼滤波、最小二乘法等。
通过对雷达信号进行预处理和目标检测,可以提高雷达系统的性能和准确度。
3. 距离测量雷达系统通过测量目标与雷达之间的回波时间来实现距离的测量。
Matlab提供了丰富的信号处理函数和工具,可以实现对回波信号的采样、分析和测量。
通过对回波信号进行FFT、相关分析等处理,可以精确地测量目标与雷达之间的距离。
二、雷达成像1. 合成孔径雷达成像合成孔径雷达(SAR)是一种基于合成孔径技术的雷达成像方法,可以利用雷达的运动和信号处理来实现高分辨率的雷达图像。
Matlab提供了完善的SAR成像算法和工具箱,可以实现SAR数据的处理、成像和评估。
通过对SAR数据进行范围压缩、方位压缩和图像重建,可以获得高质量的SAR图像。
2. 多普勒处理雷达在接收回波信号时,目标的运动会引起回波频率的改变,这被称为多普勒效应。
多普勒处理是雷达成像的重要环节之一。
Matlab提供了多普勒处理的算法和函数,例如多普勒频谱分析和多普勒滤波等。
雷达线性调频信号(LFM)脉冲压缩

西南科技大学课程设计报告课程名称:设计名称:雷达线性调频信号的脉冲压缩处理姓名:学号:班级:指导教师:起止日期: 2010.12.25-----2011.1.5学生班级:学生姓名:学号:设计名称:雷达线性调频信号的脉冲压缩处理起止日期: 2010、12、25——2011、1、03 指导教师:课程设计学生日志课程设计评语表雷达线性调频信号的脉冲压缩处理一、 设计目的和意义掌握雷达测距的工作原理,掌握匹配滤波器的工作原理及其白噪声背景下的匹配滤波的设计,线性调频信号是大时宽频宽积信号;其突出特点是匹配滤波器对回波的多普勒频移不敏感以及更好的低截获概率特性。
LFM 信号在脉冲压缩体制雷达中广泛应用;利用线性调频信号具有大带宽、长脉冲的特点,宽脉冲发射已提高发射的平均功率保证足够的作用距离;而接受时采用相应的脉冲压缩算法获得窄脉冲已提高距离分辨率,较好的解决了雷达作用距离和距离分辨率之间的矛盾;。
而利用脉冲压缩技术除了可以改善雷达系统的分辨力和检测能力,还增强了抗干扰能力、灵活性,能满足雷达多功能、多模式的需要。
二、 设计原理 1、匹配滤波器原理:在输入为确知加白噪声的情况下,所得输出信噪比最大的线性滤波器就是匹配滤波器,设一线性滤波器的输入信号为)(t x : )()()(t n t s t x +=其中:)(t s 为确知信号,)(t n 为均值为零的平稳白噪声,其功率谱密度为2/No 。
设线性滤波器系统的冲击响应为)(t h ,其频率响应为)(ωH ,其输出响应:)()()(t n t s t y o o += 输入信号能量:∞<=⎰∞∞-dt t s s E )()(2输入、输出信号频谱函数: dt e t s S t j ⎰∞∞--=ωω)()()()()(ωωωS H S o =ωωωπωωd e S H t s tj o ⎰∞-=)()(21)( 输出噪声的平均功率:ωωωπωωπd P H d P t n E n n o o ⎰⎰∞∞-∞∞-==)()(21)(21)]([22)()()(21)()(2122ωωωπωωπωωd P H d e S H SNR n t j o o ⎰⎰∞∞-∞∞-=利用Schwarz 不等式得:ωωωπd P S SNR n o ⎰∞∞-≤)()(212上式取等号时,滤波器输出功率信噪比o SNR 最大取等号条件:otj n eP S H ωωωαω-=)()()(* 当滤波器输入功率谱密度是2/)(o n N P =ω的白噪声时,MF 的系统函数为: ,)()(*o t j e kS H ωωω-=oN k α2=k 为常数1,)(*ωS 为输入函数频谱的复共轭,)()(*ωω-=S S ,也是滤波器的传输函数)(ωH 。
脉冲压缩相参积累matlab

脉冲压缩相参积累Matlab算法是一种用于信号处理和雷达技术中的算法,它能够通过相参积累技术将雷达信号进行压缩,从而提高信噪比以及增强雷达系统的性能。
在本文中,我们将深入探讨脉冲压缩相参积累Matlab算法的原理、应用和优势,并共享个人观点和理解。
一、脉冲压缩相参积累Matlab算法的原理脉冲压缩相参积累Matlab算法的原理基于相参技术和信号处理原理。
在雷达系统中,接收到的信号包含了来自目标的回波信号以及来自噪声的干扰信号,而脉冲压缩相参积累算法能够通过相参技术将回波信号进行累积,从而增强目标信号的幅度,减小干扰噪声的影响,提高信噪比。
Matlab作为一种功能强大的数学工具,能够实现脉冲压缩相参积累算法,为雷达系统提供有效的信号处理解决方案。
二、脉冲压缩相参积累Matlab算法的应用脉冲压缩相参积累Matlab算法在雷达系统中有着广泛的应用。
通过该算法,雷达系统能够实现对目标信号的有效提取和增强,减小了噪声的影响,从而提高了雷达系统的性能。
脉冲压缩相参积累Matlab算法还可以应用于医学成像、通信系统等领域,为信号处理和数据分析提供了强大的工具支持。
三、脉冲压缩相参积累Matlab算法的优势相较于传统的信号处理技术,脉冲压缩相参积累Matlab算法具有以下优势:能够有效提高目标信号的信噪比,提高信号的分辨率和探测性能;能够减小噪声对系统性能的影响,增强了系统的稳定性和可靠性;Matlab作为一种高效的数学工具,能够实现算法的快速开发和验证,为工程应用提供了便利。
个人观点和理解脉冲压缩相参积累Matlab算法作为一种高效的信号处理算法,在雷达技术和其他领域都具有非常重要的应用价值。
通过对算法原理的深入理解和工程实践的应用,我认为这一算法能够为信号处理和系统性能优化提供有力支持,有望在未来得到更广泛的应用和推广。
总结和回顾在本文中,我们对脉冲压缩相参积累Matlab算法进行了深入的探讨。
首先介绍了算法的原理,然后探讨了其在雷达系统中的应用和优势,最后共享了个人观点。
基于MATLAB的脉冲压缩技术

基于MATLAB的脉冲压缩技术周春明;杨丹【摘要】文章以线性调频Chirp信号为例,给出了一种基于MATLAB软件的脉冲压缩技术的仿真研究方法.该方法能够得到窗函数类型、脉冲压缩参数如时宽T和带宽B对脉冲压缩的影响效果,研究中利用MATLAB软件搭建匹配滤波器系统模型,分别在改变窗函数类型、发射信号的时宽T、带宽B的条件下对Chirp信号进行脉冲压缩处理的仿真,得出3组脉压后信号的主瓣峰值、主瓣宽度以及旁瓣峰值的特征效果图.结果表明,脉冲压缩后主瓣高度随时宽T的增大而增高;一定范围内带宽B越大主瓣越窄;加窗函数削弱了旁瓣能量,但同时降低了主瓣峰值,加宽了主瓣宽度.脉冲压缩技术为提高医疗领域的图像分辨率和探测深度提供了巨大的助力,同时脉冲压缩技术的日益成熟将为其他领域带来全新的技术革新.【期刊名称】《辽东学院学报(自然科学版)》【年(卷),期】2019(026)003【总页数】5页(P199-203)【关键词】时宽T;带宽B;Chirp信号;脉冲压缩【作者】周春明;杨丹【作者单位】辽东学院机械电子工程学院,辽宁丹东 118003;丹东百特仪器有限公司,辽宁丹东 118000【正文语种】中文【中图分类】TP311脉冲压缩的理论及技术研究普遍应用于雷达领域中,主要用于距离的探测和目标辨认。
Newhouse于1974年将脉冲压缩技术引入到了B型超声诊断仪[1]。
脉冲压缩技术可以很好地解决影响B型超声诊断仪图像效果的图像分辨率和探测深度之间的矛盾[2]。
脉冲压缩后信号的主瓣高度决定了探测深度,主瓣宽度和旁瓣决定了图像分辨率,它们是表征脉压效果的重要特征[3]。
脉冲压缩技术的引进不仅可以提高图像分辨率和探测深度,还将增加系统的信噪比,进而提高B超仪的诊断效果。
因此本文的研究将间接的对医学的发展和人们的生活质量产生不同程度的影响。
本文以线性调频Chirp信号的脉冲压缩处理为例,介绍基于MATLAB软件的脉冲压缩技术的研究与仿真方法。
Matlab中的雷达信号处理方法介绍

Matlab中的雷达信号处理方法介绍概述:雷达是一种利用电磁波来探测和跟踪目标的无线电设备。
它通过发射射频脉冲并接收返回的回波,然后利用信号处理方法来提取有关目标的信息。
在雷达系统中,信号处理是至关重要的一环,它能够帮助提高信号的质量、准确性和可靠性。
在本文中,我们将介绍一些在Matlab中常用的雷达信号处理方法。
1. 数据预处理雷达接收到的信号常常受到多种因素的干扰,如杂波、多径等,这些干扰会对信号质量造成影响。
因此,在进行信号处理之前,首先需要对接收到的信号进行预处理。
在Matlab中,我们可以使用数字滤波器来去除杂波,并采用信号增强技术来改善信号质量。
2. 脉冲压缩脉冲压缩是一种常用的雷达信号处理方法,它可以帮助我们提高雷达系统的分辨率和探测能力。
脉冲压缩的基本原理是通过改变脉冲信号的频谱特性,使得目标反射信号的时间延迟可以在距离域中得到良好的分辨。
在Matlab中,我们可以使用一些常见的脉冲压缩算法,如Matched Filter和Stretch Processing等。
3. 目标检测雷达系统的一个重要任务是检测目标的存在,并对目标进行跟踪。
在Matlab中,我们可以使用多种方法来实现目标检测,如CFAR(Constant False Alarm Rate)和Pulse Integration等。
CFAR方法是一种常用的自适应检测算法,它可以根据环境背景来自动调整检测门限,从而实现对目标的可靠检测。
4. 目标跟踪目标跟踪是在雷达系统中实现目标随时间变化的位置和速度的估计。
在Matlab 中,我们可以使用Kalman滤波器或粒子滤波器等方法来实现目标跟踪。
这些方法可以根据目标的动态模型和观测数据来估计目标的状态,并提供与目标相关的参数,如位置、速度和加速度等。
5. 雷达成像雷达成像是一种将雷达回波信号转换为图像形式的方法。
它可以提供目标的空间分布信息,并帮助我们对目标进行更详细的分析和判断。
(完整word版)雷达信号处理的MATLAB仿真

11目录1. 设计的基本骤 (1)1.1 雷达信号的产生 (1)1.2 噪声和杂波的产生 (1)2. 信号处理系统的仿真 (1)2.1 正交解调模块 (2)2.2 脉冲压缩模块 (2)2.3 回波积累模块 (2)2.4 恒虚警处理(CFAR)模块 (4)结论 (11)1 设计的基本骤雷达是通过发射电磁信号,再从接收信号中检测目标回波来探测目标的。
再接收信号中,不但有目标回波,也会有噪声(天地噪声,接收机噪声);地面、海面和气象环境(如云雨)等散射产生的杂波信号;以及各种干扰信号(如工业干扰,广播电磁干扰和人为干扰)等。
所以,雷达探测目标是在十分复杂的信号背景下进行的,雷达需要通过信号处理来检测目标,并提取目标的各种信息,如距离、角度、运动速度、目标形状和性质等。
图3-6 设计原理图2 信号处理系统的仿真雷达信号处理的目的是消除不需要的信号(如杂波)及干扰,提取或加强由目标所产生的回波信号。
雷达信号处理的功能有很多,不同的雷达采用的功能也有所不同,本文是对某脉冲压缩雷达的信号处理部分进行仿真。
一个典型的脉冲压缩雷达的信号处理部分主要由A/D 采样、正交解调、脉冲压缩、视频积累、恒虚警处理等功能组成。
因此,脉冲压缩雷达信号处理的仿真模型.2.1 正交解调模块雷达中频信号在进行脉冲压缩之前,需要先转换成零中频的I、Q 两路正交信号。
中频信号可表示为:0()()cos(2())IF f t A t f t t πϕ=+ (3.2)式(3.2)中, f 0 为载波频率。
令:00()()cos 2()sin 2IF f t I t f t Q t f t ππ=- (3.3)则00()()cos 2()sin 2IF f t I t f t Q t f t ππ=- (3.4)在仿真中,所有信号都是用离散时间序列表示的,设采样周期为T ,则中频信号为f IF (rT ) ,同样,复本振信号采样后的信号为f local =exp(−j ω 0rT ) (3.5)则数字化后的中频信号和复本振信号相乘解调后,通过低通滤波器后得到的基带信号fBB (r ) 为:11000{()cos()}(){()sin()}()N N BB IF IF n nf f r n r n T h n j f r n r n T h n ωω--==-----∑∑ (3.6)式(3.6)中, h (n ) 是积累长度为N 的低通滤波器的脉冲响应。
雷达线性调频信号(LFM)脉冲压缩

西南科技大学课程设计报告课程名称:设计名称:雷达线性调频信号的脉冲压缩处理姓名:学号:班级:指导教师:起止日期: 2010.12.25-----2011.1.5学生班级:学生姓名:学号:设计名称:雷达线性调频信号的脉冲压缩处理起止日期: 2010、12、25——2011、1、03 指导教师:课程设计学生日志课程设计评语表雷达线性调频信号的脉冲压缩处理一、 设计目的和意义掌握雷达测距的工作原理,掌握匹配滤波器的工作原理及其白噪声背景下的匹配滤波的设计,线性调频信号是大时宽频宽积信号;其突出特点是匹配滤波器对回波的多普勒频移不敏感以及更好的低截获概率特性。
LFM 信号在脉冲压缩体制雷达中广泛应用;利用线性调频信号具有大带宽、长脉冲的特点,宽脉冲发射已提高发射的平均功率保证足够的作用距离;而接受时采用相应的脉冲压缩算法获得窄脉冲已提高距离分辨率,较好的解决了雷达作用距离和距离分辨率之间的矛盾;。
而利用脉冲压缩技术除了可以改善雷达系统的分辨力和检测能力,还增强了抗干扰能力、灵活性,能满足雷达多功能、多模式的需要。
二、 设计原理 1、匹配滤波器原理:在输入为确知加白噪声的情况下,所得输出信噪比最大的线性滤波器就是匹配滤波器,设一线性滤波器的输入信号为)(t x : )()()(t n t s t x +=其中:)(t s 为确知信号,)(t n 为均值为零的平稳白噪声,其功率谱密度为2/No 。
设线性滤波器系统的冲击响应为)(t h ,其频率响应为)(ωH ,其输出响应:)()()(t n t s t y o o += 输入信号能量:∞<=⎰∞∞-dt t s s E )()(2输入、输出信号频谱函数: dt e t s S t j ⎰∞∞--=ωω)()()()()(ωωωS H S o =ωωωπωωd e S H t s tj o ⎰∞-=)()(21)( 输出噪声的平均功率:ωωωπωωπd P H d P t n E n n o o ⎰⎰∞∞-∞∞-==)()(21)(21)]([22)()()(21)()(2122ωωωπωωπωωd P H d e S H SNR n t j o o ⎰⎰∞∞-∞∞-=利用Schwarz 不等式得:ωωωπd P S SNR n o ⎰∞∞-≤)()(212上式取等号时,滤波器输出功率信噪比o SNR 最大取等号条件:otj n eP S H ωωωαω-=)()()(* 当滤波器输入功率谱密度是2/)(o n N P =ω的白噪声时,MF 的系统函数为: ,)()(*o t j e kS H ωωω-=oN k α2=k 为常数1,)(*ωS 为输入函数频谱的复共轭,)()(*ωω-=S S ,也是滤波器的传输函数)(ωH 。
大作业雷达线性调频脉冲紧缩的原理及其MATLAB仿真(DOC)
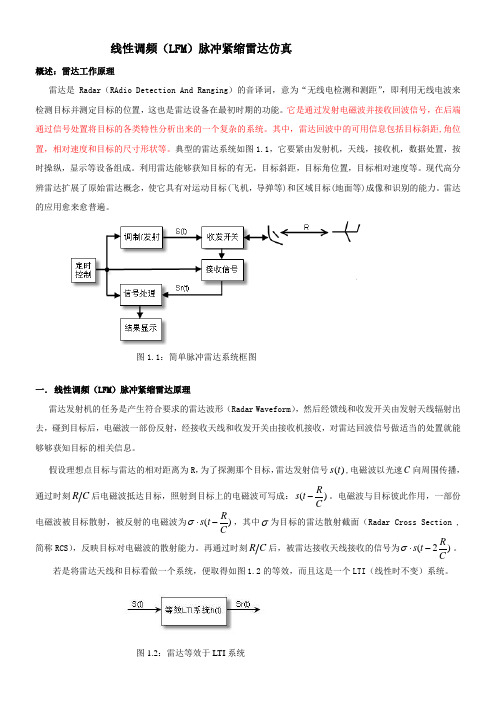
线性调频(LFM )脉冲紧缩雷达仿真概述:雷达工作原理雷达是Radar (RAdio Detection And Ranging )的音译词,意为“无线电检测和测距”,即利用无线电波来检测目标并测定目标的位置,这也是雷达设备在最初时期的功能。
它是通过发射电磁波并接收回波信号,在后端通过信号处置将目标的各类特性分析出来的一个复杂的系统。
其中,雷达回波中的可用信息包括目标斜距,角位置,相对速度和目标的尺寸形状等。
典型的雷达系统如图1.1,它要紧由发射机,天线,接收机,数据处置,按时操纵,显示等设备组成。
利用雷达能够获知目标的有无,目标斜距,目标角位置,目标相对速度等。
现代高分辨雷达扩展了原始雷达概念,使它具有对运动目标(飞机,导弹等)和区域目标(地面等)成像和识别的能力。
雷达的应用愈来愈普遍。
图1.1:简单脉冲雷达系统框图一. 线性调频(LFM )脉冲紧缩雷达原理雷达发射机的任务是产生符合要求的雷达波形(Radar Waveform ),然后经馈线和收发开关由发射天线辐射出去,碰到目标后,电磁波一部份反射,经接收天线和收发开关由接收机接收,对雷达回波信号做适当的处置就能够够获知目标的相关信息。
假设理想点目标与雷达的相对距离为R ,为了探测那个目标,雷达发射信号()s t ,电磁波以光速C 向周围传播,通过时刻R C 后电磁波抵达目标,照射到目标上的电磁波可写成:()Rs t C-。
电磁波与目标彼此作用,一部份电磁波被目标散射,被反射的电磁波为()Rs t Cσ⋅-,其中σ为目标的雷达散射截面(Radar Cross Section ,简称RCS ),反映目标对电磁波的散射能力。
再通过时刻R C 后,被雷达接收天线接收的信号为(2)Rs t Cσ⋅-。
若是将雷达天线和目标看做一个系统,便取得如图1.2的等效,而且这是一个LTI (线性时不变)系统。
图1.2:雷达等效于LTI 系统等效LTI系统的冲击响应可写成:1()()Miii h t t σδτ==-∑ (1.1)M 表示目标的个数,i σ是目标散射特性,i τ是光速在雷达与目标之间来回一次的时刻,2ii R cτ=(1.2) 式中,i R 为第i 个目标与雷达的相对距离。
matlab脉冲压缩二维频域升采样代码

MATLAB脉冲压缩是一种常用的雷达信号处理技术,它可以有效地提高雷达系统的目标分辨能力和信噪比,从而对目标进行更精确的检测和跟踪。
本文将介绍如何利用MATLAB编写脉冲压缩二维频域升采样代码,以实现对雷达信号的高效处理。
一、脉冲压缩概述脉冲压缩是通过波形压缩技术来提高雷达系统的性能。
其基本原理是通过对雷达返回信号进行处理,使得目标回波的峰值增强,从而提高目标的探测和测距精度。
脉压信号通常是一种带调制的脉冲信号,经过处理后可以得到更窄的主瓣和更低的旁瓣,从而提高了信号的分辨率和抗干扰能力。
二、二维频域升采样二维频域升采样是一种常见的信号处理方法,它可以通过增加信号的采样率来提高信号的分辨能力和抗混叠能力。
对于雷达信号的脉冲压缩处理,可以采用二维频域升采样来进一步提高信号处理的效果。
三、MATLAB代码实现在MATLAB中,可以利用信号处理工具箱中的函数来实现脉冲压缩和二维频域升采样的处理。
需要对原始雷达信号进行脉冲压缩处理,然后利用二维FFT变换对信号进行频域升采样处理。
下面是一个简单的MATLAB代码示例:```matlab读取原始雷达信号raw_signal = load('radar_signal.mat');脉冲压缩处理compressed_signal = matched_filter(raw_signal, pulse);二维FFT变换fft_signal = fft2pressed_signal, M, N);频域升采样处理upsampled_signal = ifft2(fft_signal, M_up, N_up);```在上面的代码中,加载了原始的雷达信号数据,并且进行了脉冲压缩处理。
然后利用MATLAB中的fft2函数对信号进行二维FFT变换,得到频域表示的信号。
最后通过ifft2函数对频域信号进行升采样处理,得到了经过二维频域处理的雷达信号。
四、结果分析经过脉冲压缩和二维频域升采样处理后的雷达信号,其分辨能力和抗混叠能力得到了显著提高。
雷达信号处理的MATLAB仿真

1.1
现代雷达信号处理需要面对各种应用需求和复杂雷达工作环境,因此需要研究各种先进技术来提高雷达从回波信号中提取目标信息的能力,研究内容包括杂波和干扰抑制技术、脉冲个信号相参积累技术、阵列信号处理技术、目标检测技术、目标特征信息提取和识别技术、信号处理系统设计技术等。
1.1.1
早期的雷达,主要的功能是发现目标和测定目标的空间位置,所以信号处理功能相对简单,在噪声背景下目标检测目标回波是其主要的任务。位提高雷达在噪声背景下发现目标的能力,视频信号积累和恒虚警(CFAR)检测技术得到了快速的发展。通过视频信号积累可以提高目标回波的信号噪声比(SNR),提高雷达在噪声背景下对目标的发现能力,通过恒虚警的检测可以使雷达八只较高的发现目标的能力的同时,使发生虚警(由于噪声引起,事实上没有目标)的概率大为降低。
雷达脉冲压缩matlab仿真

雷达发射线性调频信号,载频10GHz,线性调频信号带宽10MHz,脉宽5us,采样率自设,两目标距离雷达5000米和5020米(1)模拟两个目标的回波,并进行脉冲压缩(匹配滤波),验证脉冲压缩对改善雷达距离分辨力的作用(2)调整两个目标的间距从1米到20米,观察结果得出结论。
①源代码:clear all;close all;fc=10e9;%载频B=10e6;%带宽fs=2*fc;%采样率T=5*10^-6;%雷达脉宽t=0:1/fs:10*T;s1=5000;%目标1距离s2=5020;%目标2距离c=3e8;%光速t1=2*s1/c;%雷达波从目标1回波的延时t2=2*s2/c;%雷达波从目标2回波的延时u=B/T;st=rectpuls(t,T).*exp(j*2*pi*(fc*t+u*t.^2));%发射信号sr1=rectpuls((t-t1),T).*exp(j*2*pi*(fc*(t-t1)+u*(t-t1).^2));%目标1的回波sr2=rectpuls((t-t2),T).*exp(j*2*pi*(fc*(t-t2)+u*(t-t2).^2));%目标2的回波sr=sr1+sr2;%两目标总的回波figure(1);plot(real(sr));%未压缩回波title('未压缩回波');axis([6*10^5,7.4*10^5,-2,2]);F=fftshift(fft(sr));%进行脉冲压缩Ft=F.*conj(F);f=ifft(Ft);figure(2);plot(fftshift(abs(f)));%压缩回波title('压缩回波');axis([4.9*10^5,5.1*10^5,0,2*10^5]);②运行结果:改变相对距离为1米,运行结果如下:两目标不可分辨,直到两目标相对距离为13米时,目标可清晰分辨,如下:结论:当目标的相对距离较近时,目标的未压缩回波已不能分辨出两目标的位置,这时使用脉冲压缩可以增加雷达的分辨力,但其能力也是有限的,当两目标的相对距离太近时,即使脉冲压缩也不能分辨,即脉冲压缩不能使脉宽无限小。
线性调频脉冲雷达信号matlab仿真

二〇一年十月课题小论文题目:线性调频(LFM )脉冲压缩雷达仿真学院:专业:学生姓名:刘斌学号:年级:指导教师:线性调频(LFM )脉冲压缩雷达仿真一.雷达工作原理雷达是Radar (RAdio Detection And Ranging )的音译词,意为“无线电检测和测距”,即利用无线电波来检测目标并测定目标的位置,这也是雷达设备在最初阶段的功能。
典型的雷达系统如图1.1,它主要由发射机,天线,接收机,数据处理,定时控制,显示等设备组成。
利用雷达可以获知目标的有无,目标斜距,目标角位置,目标相对速度等。
现代高分辨雷达扩展了原始雷达概念,使它具有对运动目标(飞机,导弹等)和区域目标(地面等)成像和识别的能力。
雷达的应用越来越广泛。
图1.1:简单脉冲雷达系统框图雷达发射机的任务是产生符合要求的雷达波形(Radar Waveform ),然后经馈线和收发开关由发射天线辐射出去,遇到目标后,电磁波一部分反射,经接收天线和收发开关由接收机接收,对雷达回波信号做适当的处理就可以获知目标的相关信息。
假设理想点目标与雷达的相对距离为R ,为了探测这个目标,雷达发射信号()s t ,电磁波以光速C 向四周传播,经过时间R 后电磁波到达目标,照射到目标上的电磁波可写成:()Rs t C -。
电磁波与目标相互作用,一部分电磁波被目标散射,被反射的电磁波为()Rs t Cσ⋅-,其中σ为目标的雷达散射截面(Radar Cross Section ,简称RCS ),反映目标对电磁波的散射能力。
再经过时间R 后,被雷达接收天线接收的信号为(2)Rs t C σ⋅-。
如果将雷达天线和目标看作一个系统,便得到如图1.2的等效,而且这是一个LTI (线性时不变)系统。
图1.2:雷达等效于LTI 系统等效LTI 系统的冲击响应可写成:1()()Mi i i h t t σδτ==-∑(1.1)M 表示目标的个数,i σ是目标散射特性,i τ是光速在雷达与目标之间往返一次的时间,2i i R cτ=(1.2)式中,i R 为第i 个目标与雷达的相对距离。
dechirp处理matlab 代码

一、引言dechirp处理是一种在信号处理中常用的方法,它可以用于降低雷达和通信系统中的脉冲压缩信号的带宽。
在Matlab代码中,我们可以使用dechirp函数来进行处理,以实现信号的脉冲压缩和处理。
本文将详细介绍dechirp处理的原理、Matlab代码的编写和使用方法。
二、dechirp处理的原理在雷达和通信系统中,脉冲压缩是一种用于提高系统分辨率的重要技术。
脉冲压缩信号的带宽较宽,需要经过处理才能得到高分辨率的测量结果。
而dechirp处理就是一种常用的带通滤波技术,它通过对信号进行频率扫描和去调制处理,将信号的带宽降低,从而实现脉冲压缩的效果。
在Matlab中,可以使用dechirp函数来实现对信号的处理和压缩。
三、Matlab代码的编写在Matlab中,使用dechirp函数可以很方便地对信号进行脉冲压缩处理。
下面是一个简单的Matlab代码示例:```matlab生成脉冲压缩信号fs = 1000; 采样频率t = 0:1/fs:1-1/fs; 生成时间数组f0 = 50; 起始频率f1 = 150; 终止频率t1 = 1; 持续时间x = chirp(t, f0, t1, f1, 'linear');生成脉冲压缩滤波器fstart = 2*(f1 - f0); 滤波器起始频率fstop = 0; 滤波器终止频率y = dechirp(x, fstart, fs, fstop);显示结果subplot(2,1,1);plot(t, x);title('原始信号');subplot(2,1,2);plot(t, abs(y));title('脉冲压缩后的信号');```上面的代码首先生成了一个线性调频信号,然后使用dechirp函数进行脉冲压缩处理,最终通过subplot函数将原始信号和处理后的结果进行了显示。
四、使用方法使用dechirp处理时,需要指定输入信号、起始频率、采样频率和终止频率这几个关键参数。
雷达线性调频信号(LFM)脉冲压缩

西南科技大学课程设计报告课程名称:设计名称:雷达线性调频信号的脉冲压缩处理姓名:学号:班级:指导教师:起止日期: 2010.12.25-----2011.1.5学生班级:学生姓名:学号:设计名称:雷达线性调频信号的脉冲压缩处理起止日期: 2010、12、25——2011、1、03 指导教师:课程设计学生日志课程设计评语表雷达线性调频信号的脉冲压缩处理一、 设计目的和意义掌握雷达测距的工作原理,掌握匹配滤波器的工作原理及其白噪声背景下的匹配滤波的设计,线性调频信号是大时宽频宽积信号;其突出特点是匹配滤波器对回波的多普勒频移不敏感以及更好的低截获概率特性。
LFM 信号在脉冲压缩体制雷达中广泛应用;利用线性调频信号具有大带宽、长脉冲的特点,宽脉冲发射已提高发射的平均功率保证足够的作用距离;而接受时采用相应的脉冲压缩算法获得窄脉冲已提高距离分辨率,较好的解决了雷达作用距离和距离分辨率之间的矛盾;。
而利用脉冲压缩技术除了可以改善雷达系统的分辨力和检测能力,还增强了抗干扰能力、灵活性,能满足雷达多功能、多模式的需要。
二、 设计原理 1、匹配滤波器原理:在输入为确知加白噪声的情况下,所得输出信噪比最大的线性滤波器就是匹配滤波器,设一线性滤波器的输入信号为)(t x : )()()(t n t s t x +=其中:)(t s 为确知信号,)(t n 为均值为零的平稳白噪声,其功率谱密度为2/No 。
设线性滤波器系统的冲击响应为)(t h ,其频率响应为)(ωH ,其输出响应:)()()(t n t s t y o o += 输入信号能量:∞<=⎰∞∞-dt t s s E )()(2输入、输出信号频谱函数: dt e t s S t j ⎰∞∞--=ωω)()()()()(ωωωS H S o =ωωωπωωd e S H t s tj o ⎰∞-=)()(21)( 输出噪声的平均功率:ωωωπωωπd P H d P t n E n n o o ⎰⎰∞∞-∞∞-==)()(21)(21)]([22)()()(21)()(2122ωωωπωωπωωd P H d e S H SNR n t j o o ⎰⎰∞∞-∞∞-=利用Schwarz 不等式得:ωωωπd P S SNR n o ⎰∞∞-≤)()(212上式取等号时,滤波器输出功率信噪比o SNR 最大取等号条件:otj n eP S H ωωωαω-=)()()(* 当滤波器输入功率谱密度是2/)(o n N P =ω的白噪声时,MF 的系统函数为: ,)()(*o t j e kS H ωωω-=oN k α2=k 为常数1,)(*ωS 为输入函数频谱的复共轭,)()(*ωω-=S S ,也是滤波器的传输函数)(ωH 。
大作业-雷达线性调频脉冲压缩地原理及其MATLAB仿真

线性调频(LFM)脉冲压缩雷达仿真概述:雷达工作原理雷达是Radar(RAdio Detection And Ranging)的音译词,意为“无线电检测和测距”,即利用无线电波来检测目标并测定目标的位置,这也是雷达设备在最初阶段的功能。
它是通过发射电磁波并接收回波信号,在后端经过信号处理将目标的各种特性分析出来的一个复杂的系统。
其中,雷达回波中的可用信息包括目标斜距,角位置,相对速度以及目标的尺寸形状等。
典型的雷达系统如图1.1,它主要由发射机,天线,接收机,数据处理,定时控制,显示等设备组成。
利用雷达可以获知目标的有无,目标斜距,目标角位置,目标相对速度等。
现代高分辨雷达扩展了原始雷达概念,使它具有对运动目标(飞机,导弹等)和区域目标(地面等)成像和识别的能力。
雷达的应用越来越广泛。
图1.1:简单脉冲雷达系统框图一.线性调频(LFM)脉冲压缩雷达原理雷达发射机的任务是产生符合要求的雷达波形(Radar Waveform),然后经馈线和收发开关由发射天线辐射出去,遇到目标后,电磁波一部分反射,经接收天线和收发开关由接收机接收,对雷达回波信号做适当的处理就可以获知目标的相关信息。
s t,电磁波假设理想点目标与雷达的相对距离为R,为了探测这个目标,雷达发射信号()以光速C 向四周传播,经过时间R C 后电磁波到达目标,照射到目标上的电磁波可写成:()Rs t C -。
电磁波与目标相互作用,一部分电磁波被目标散射,被反射的电磁波为()Rs t Cσ⋅-,其中σ为目标的雷达散射截面(Radar Cross Section ,简称RCS ),反映目标对电磁波的散射能力。
再经过时间R C 后,被雷达接收天线接收的信号为(2)Rs t C σ⋅-。
如果将雷达天线和目标看作一个系统,便得到如图1.2的等效,而且这是一个LTI (线性时不变)系统。
图1.2:雷达等效于LTI 系统等效LTI 系统的冲击响应可写成: 1()()Miii h t t σδτ==-∑ (1.1)M 表示目标的个数,i σ是目标散射特性,i τ是光速在雷达与目标之间往返一次的时间,2ii R cτ=(1.2) 式中,i R 为第i 个目标与雷达的相对距离。
matlab 雷达信号处理流程

matlab 雷达信号处理流程雷达信号处理是指对雷达接收到的信号进行分析和处理的过程。
其主要目的是提取出目标的信息,并进行目标检测、跟踪和识别。
雷达信号处理的流程一般包括以下几个步骤:1.接收信号的预处理:雷达接收到的信号往往带有噪声和干扰,需要进行预处理来提高信号的质量。
这包括去除噪声、干扰和杂波,并进行信号增强。
2.脉冲压缩:雷达信号在传播过程中会因为距离的增加而发生衰减,为了提高信号的分辨率和灵敏度,需要对信号进行脉冲压缩。
常用的压缩方式包括线性调频脉冲压缩和非线性调频脉冲压缩。
3.目标检测:目标检测是指从雷达接收到的信号中识别出目标的存在。
这需要对信号进行特征提取,并使用适当的检测算法来检测目标。
常用的目标检测算法包括CFAR(恒虚警率)检测和匹配滤波器等。
4.目标跟踪:目标跟踪是指在连续的雷达扫描中,对已经检测到的目标进行跟踪和预测。
常用的跟踪算法包括卡尔曼滤波器和粒子滤波器等。
5.目标识别:目标识别是指对已经检测和跟踪到的目标进行分类和识别。
这需要对目标进行特征提取,并使用合适的分类算法来进行识别。
常用的目标识别算法包括基于特征的方法和神经网络方法等。
6.告警和决策:在对目标进行识别之后,需要根据识别结果进行告警和决策。
这包括判断目标的威胁程度、判断是否需要采取行动等。
以上是一般雷达信号处理的主要流程。
不同的雷达系统和应用场景可能会有所不同,但总体上都会包括以上几个步骤。
通过对雷达信号进行处理,可以提高雷达系统的性能和可靠性,并广泛应用于军事、民用以及科学研究等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
雷达脉冲压缩摘要:脉冲压缩雷达能同时提高雷达的作用距离和距离分辨率。
这种体制采用宽脉冲发射以提高发射的平均功率,保证足够大的作用距离;而接受时采用相应的脉冲压缩算法获得窄脉冲,以提高距离分辨率,较好的解决雷达作用距离与距离分辨率之间的矛盾。
关键词:脉冲压缩;匹配滤波;matlab1、雷达工作原理雷达是Radar (Radio Detection And Ranging )的音译词,意为“无线电检测和测距”,即利用无线电波来检测目标并测定目标的位置,这也是雷达设备在最初阶段的功能[1]。
典型的雷达系统如图1.1,它主要由发射机,天线,接收机,数据处理,定时控制,显示等设备组成。
利用雷达可以获知目标的有无,目标斜距,目标角位置,目标相对速度等。
现代高分辨雷达扩展了原始雷达概念,使它具有对运动目标(飞机,导弹等)和区域目标(地面等)成像和识别的能力。
雷达的应用越来越广泛。
图1.1 简单脉冲雷达系统框图雷达发射机的任务是产生符合要求的雷达波形(Radar Waveform ),然后经馈线和收发开关由发射天线辐射出去,遇到目标后,电磁波一部分反射,经接收天线和收发开关由接收机接收,对雷达回波信号做适当的处理就可以获知目标的相关信息。
假设理想点目标与雷达的相对距离为R ,为了探测这个目标,雷达发射信号()s t ,电磁波以光速C 向四周传播,经过时间R 后电磁波到达目标,照射到目标上的电磁波可写成:()Rs t C -。
电磁波与目标相互作用,一部分电磁波被目标散射,被反射的电磁波为()Rs t Cσ⋅-,其中σ为目标的雷达散射截面(Radar Cross Section ,简称RCS ),反映目标对电磁波的散射能力[2]。
再经过时间R 后,被雷达接收天线接收的信号为(2)Rs t C σ⋅-。
如果将雷达天线和目标看作一个系统,便得到如图1.2的等效,而且这是一个LTI (线性时不变)系统。
图1.2 雷达等效于LTI 系统等效LTI 系统的冲击响应可写成: 1()()Miii h t t σδτ==-∑ (1.1)M 表示目标的个数,i σ是目标散射特性,i τ是光速在雷达与目标之间往返一次的时间,2ii R cτ=(1.2) 式中,i R 为第i 个目标与雷达的相对距离。
雷达发射信号()s t 经过该LTI 系统,得输出信号(即雷达的回波信号)()r s t :11()()*()()*()()M Mr i i i i i i s t s t h t s t t s t σδτστ====-=-∑∑ (1.3)图1.3 雷达回波信号处理()s t 的匹配滤波器()r h t 为:*()()r h t s t =- (1.4)于是, *()()*()()*()*()o r r s t s t h t s t s t h t ==- (1.5)对上式进行傅立叶变换:*2()()()()|()|()o S jw S jw S jw H jw S jw H jw = = (1.6)如果选取合适的()s t ,使它的幅频特性|()|S jw 为常数,那么1.6式可写为:()()o S jw kH jw = (1.7) 其傅立叶反变换为: 1()()()Mo iii s t kh t kt σδτ===-∑ (1.8)()o s t 中包含目标的特征信息i τ和i σ。
从 ()o s t 中可以得到目标的个数M 和每个目标相对雷达的距离: 2i icR τ=(1.9) 这也是线性调频(LFM )脉冲压缩雷达的工作原理。
2、线性调频(LFM )信号脉冲压缩雷达能同时提高雷达的作用距离和距离分辨率。
这种体制采用宽脉冲发射以提高发射的平均功率,保证足够大的作用距离;而接受时采用相应的脉冲压缩算法获得窄脉冲,以提高距离分辨率,较好的解决雷达作用距离与距离分辨率之间的矛盾。
脉冲压缩雷达最常见的调制信号是线性调频(Linear Frequency Modulation )信号,接收时采用匹配滤波器(Matched Filter )压缩脉冲。
LFM 信号(也称Chirp 信号)的数学表达式为:22()2()()c K j f t t t s t rect Te π+= (2.1)式中c f 为载波频率,()t rect T为矩形信号,11()0,t t rect TT elsewise⎧ , ≤⎪=⎨⎪ ⎩(2.2) BK T=,是调频斜率,于是,信号的瞬时频率为()22c T T f Kt t + -≤≤,如图 2.1图2.1 典型的chirp 信号(a )up-chirp(K>0)(b )down-chirp(K<0)将2.1式中的up-chirp 信号重写为:2()()c j f ts t S t e π= (2.3)式中,2()()j Kt t S t rect e Tπ= (2.4)是信号s(t)的复包络。
由傅立叶变换性质,S(t)与s(t)具有相同的幅频特性,只是中心频率不同而以,因此,Matlab 仿真时,只需考虑S(t)[3]。
3、FM 脉冲的匹配滤波信号()s t 的匹配滤波器的时域脉冲响应为:*0()()h t s t t =- (3.1)0t 是使滤波器物理可实现所附加的时延。
理论分析时,可令0t =0,重写3.1式,*()()h t s t =- (3.2)将2.1式代入3.2式得:22()()c j f t j Kt th t rect ee Tππ-=⨯ (3.3 )图3.1:LFM 信号的匹配滤波如图3.1,()s t 经过系统()h t 得输出信号()o s t ,2222()()()()*()()()()()()()c c o j f u j f t u j Ku j K t u s t s t h t s u h t u du h u s t u du u t u e rect e e rect e du T T ππππ∞∞-∞-∞∞----∞= =- =-- =⨯ ⎰⎰⎰当0t T ≤≤时,22222022222()2sin ()T T c c j Kt j Ktu t j Ktu T j f t j Kt T j f ts t e e due ee t j Kt K T t t eKtπππππππππ---==⨯--- =⎰(3.4)当0T t -≤≤时,22222022222()2sin ()T T c c t j Kt j Ktu j KtuT j f t j Kt T j f ts t e e dut e e ej Kt K T t t eKtπππππππππ+---=+ =⨯--+ =⎰(3.5)合并3.4和3.5两式:20sin (1)()()2c j f t tKT tt T s t Trect e KTt Tπππ-= (3.6) 3.6式即为LFM 脉冲信号经匹配滤波器得输出,它是一固定载频c f 的信号。
当t T ≤时,包络近似为辛克(sinc )函数。
0()()()()()22t tS t TSa KTt rect TSa Bt rect T Tππ== (3.7)图3.2:匹配滤波的输出信号如图3.2,当Bt ππ=±时,1t B =±为其第一零点坐标;当2Bt ππ=±时,12t B =±,习惯上,将此时的脉冲宽度定义为压缩脉冲宽度。
1122B B τ=⨯= (3.8) LFM 信号的压缩前脉冲宽度T 和压缩后的脉冲宽度τ之比通常称为压缩比D , TD TB τ== (3.9)3.9式表明,压缩比也就是LFM 信号的时宽频宽积。
4、matlab 程序与结果分析 (1)主要程序:x(:,1:n) = 0.;y(1:n) = 0.; replica(1:n) = 0.;replica = exp(i * pi * (b/taup) .* t.^2);for j = 1:1:nmb range = smb_range(j) ;x(j,:) = smb_rcs(j) .*exp(-i*2*pi*f0*2*range/c).* exp(i * pi * (b/taup) .* (t +(2*range/c)).^2) ; y = x(j,:) + y; endrfft = fft(replica,nfft); yfft = fft(y,nfft);out= abs(ifft((rfft .* conj(yfft)))) ./ (nfft);s = taup * c /2; Npoints = ceil(rrec * nfft /s);dist =linspace(0, rrec, Npoints);(2)运行结果雷达信号对三个目标进行探测,本设计中,分辨出相邻两点目标的最小距离是1.5米。
故当两点距离小于1.5米时,雷达将分辨不出,即视为一点。
5、结论脉冲压缩雷达既保持了窄脉冲的高距离分辨力,又能获得宽脉冲的强检测能力。
脉冲压缩技术是大时宽带宽乘积信号经过匹配滤波器实现的, 不同的信号形式有不同的压缩性能, 其中线性调频脉冲信号的诸多优点使其称为脉冲压缩信号的首选,它也是最早、应用最广泛的脉冲压缩信号。
脉冲压缩技术能在雷达发射功率受限的情况下, 提高目标的探测距离, 并且保持很高的分辨力, 是雷达反隐身、多目标分辨、抗干扰的重要手段, 在目前的雷达信号系统中有着广泛的应用。
6、参考文献[1]丁鹭飞,耿富录·雷达原理(第三版)·西安:西安电子科技大学出版社,2006.[2]楼顺天,姚若玉,沈俊霞·MATLAB程序设计语言·西安:西安电子科技大学西电出版社,2007.[3]元春,苏广州,米红·宽带雷达信号产生技术[M]·北京:国防工业出版社,2002.附录:nmb = 4; %目标个数3个rrec =200; %测量目标最远距离b = 100e6; %调频信号带宽smb_range = [10,30,40,100]; %三点目标的距离最小分辨距离为s=c/2b=1.5m smb_rcs = [1 1 1 2]; %三点目标的横截面积taup = 0.005e-3; %信号持续脉宽f0 = 5.6e9; % 载频频率c = 3e8; % 信号传播的速度,即光速fs = 2*b; % 采样的频率sampling_interval = 1/fs;n = fix(taup/sampling_interval); %总共点数(取整)nfft =n % 采样点数freqlimit = 0.5*fs;freq = linspace(-freqlimit,freqlimit,n); % 频率采样间隔= fs/n = 1/taup;t = linspace(-taup/2,taup/2,n); %相邻点时间间隔x(:,1:n) = 0.; % x为矩阵y(1:n) = 0.;replica(1:n) = 0.;replica = exp(i * pi * (b/taup) .* t.^2); %基带线性调频信号for j = 1:1:nmb %矩阵方法将接收信号叠加range = smb_range(j) ;x(j,:) = smb_rcs(j) .*exp(-i*2*pi*f0*2*range/c).* exp(i * pi * (b/taup) .* (t +(2*range/c)).^2) ; %接收信号y = x(j,:) + y; %信号叠加endrfft = fft(replica,nfft);yfft = fft(y,nfft);out= abs(ifft((rfft .* conj(yfft)))) ./ (nfft);s = taup * c /2; Npoints = ceil(rrec * nfft /s);dist =linspace(0, rrec, Npoints);%图片显示:figuresubplot(311)plot(t,real(replica));axis tight;xlabel('Range in meters');ylabel('Amplitude in dB');title('线性调频信号');subplot(312)plot(t,real(y));axis tight;xlabel('Range in meters');ylabel('Amplitude in dB');title('压缩前雷达回波');subplot(313)plot(dist, out(1:Npoints))xlabel ('Target relative position in meters')ylabel ('压缩后雷达回波') grid。
