SPSS-相关性和回归分析(一元线性方程)案例解析
SPSS相关性和回归分析一元线性方程案例解析

将“居民总储蓄”和“居民总消费”两个变量移入“变量”框内,在“相关系数”栏目中选择“Pearson",(Pearson是一种简单相关系数分析和计算的方法,如果需要进行进一步分析,需要借助“多远线性回归”分析)在“显著性检验”中选择“双侧检验”并且勾选“标记显著性相关”点击确定,得到如下结果:
2:从anvoa b的检验结果来看(其实这是一个“回归模型的方差分析表)F的统计量为:29.057,P值显示为0.000,拒绝模型整体不显著的假设,证明模型整体是显著的
3:从“系数a”这个表可以看出“回归系数,回归系数的标准差,回归系数的T显著性检验等,回归系数常量为:2878.518,但是SIG为:0.452,常数项不显著,回归系数为:0.954,相对的sig为:0.000,具备显著性,由于在“anvoa b”表中提到了模型整体是“显著”的
SPSS-相关性和回归分析(一元线性方物和人都不是以个体存在的,它们都被复杂的关系链所围绕着,具有一定的相关性,也会具备一定的因果关系,(比如:父母和子女,不仅具备相关性,而且还具备因果关系,因为有了父亲和母亲,才有了儿子或女儿),但不是所有相关联的事物都具备因果关系。
所以一元线性方程为:居民总消费=2878.518+0.954*居民总储蓄
其中在“样本数据统计”中,随即误差一般叫“残差”:
从结果分析来看,可以简单的认为:居民总储蓄每增加1亿,那居民总消费将会增加0.954亿
提示:对于回归参数的估计,一般采用的是“最小二乘估计法”原则即为:“残差平方和最小“
点击“分析”--回归----线性”结果如下所示:
将“因变量”和“自变量”分别拖入框内(如上图所示)从上图可以看出:“自变量”指“居民总储蓄”, "因变量”是指“居民总消费”
相关分析和回归分析SPSS实现

相关分析与回归分析一、试验目标与要求本试验项目的目的是学习并使用SPSS 软件进行相关分析与回归分析,具体包括:(1) 皮尔逊pearson 简单相关系数的计算与分析(2) 学会在SPSS 上实现一元及多元回归模型的计算与检验。
(3) 学会回归模型的散点图与样本方程图形。
(4) 学会对所计算结果进行统计分析说明。
(5) 要求试验前,了解回归分析的如下内容。
♦ 参数α、β的估计♦ 回归模型的检验方法:回归系数β的显著性检验(t -检验);回归方程显著性检验(F -检验)。
二、试验原理1.相关分析的统计学原理相关分析使用某个指标来表明现象之间相互依存关系的密切程度。
用来测度简单线性相关关系的系数是Pearson 简单相关系数。
2.回归分析的统计学原理相关关系不等于因果关系,要明确因果关系必须借助于回归分析。
回归分析是研究两个变量或多个变量之间因果关系的统计方法。
其基本思想是,在相关分析的基础上,对具有相关关系的两个或多个变量之间数量变化的一般关系进行测定,确立一个合适的数据模型,以便从一个已知量推断另一个未知量。
回归分析的主要任务就是根据样本数据估计参数,建立回归模型,对参数与模型进行检验与判断,并进行预测等。
线性回归数学模型如下:i ik k i i i x x x y εββββ+++++= 22110在模型中,回归系数是未知的,可以在已有样本的基础上,使用最小二乘法对回归系数进行估计,得到如下的样本回归函数:iik k i i i e x x x y +++++=ββββˆˆˆˆ22110 回归模型中的参数估计出来之后,还必须对其进行检验。
如果通过检验发现模型有缺陷,则必须回到模型的设定阶段或参数估计阶段,重新选择被解释变量与解释变量及其函数形式,或者对数据进行加工整理之后再次估计参数。
回归模型的检验包括一级检验与二级检验。
一级检验又叫统计学检验,它是利用统计学的抽样理论来检验样本回归方程的可靠性,具体又可以分为拟与优度评价与显著性检验;二级检验又称为经济计量学检验,它是对线性回归模型的假定条件能否得到满足进行检验,具体包括序列相关检验、异方差检验等。
利用spss进行一元回归分析.

“描述性”复选框:
“部分相关和偏相关性”复选框:
• 显示自变量间的相关、部分相关和偏相关系数。
“共线性诊断”复选框:
• 给出一些用于共线性诊断的统计量,如特征根(Eigenvalues)、方差 膨胀因子(VIF)等。
以上各项在默认情况下只有“估计”和“模型拟合度”复选框被选中。
【绘制】按钮
“模型拟合度”复选框:
“R方变化”复选框:
• 模型拟合过程中进入、退出的变量的列表,以及一些有关拟合优度的检 验:R,R2和调整的R2, 标准误及方差分析表。 • 显示模型拟合过程中R2、F值和p值的改变情况。 • 提供一些变量描述,如有效例数、均数、标准差等,同时还给出一个自 变量间的相关矩阵。
Case2目的: 分析平均气温和降雨量之间的数量关系
Case2习题要求: 做散点图,查看两因素之间是否线性相关 如果线性相关,接着做线性回归分析,揭示其数量关系 对回归方程做显著性检验,写出结论
Case2:气温&降雨量
给这个例子的目的是,看大家是否真的理解做散点图的意 义 当散点图都不呈现线性关系,那有多少同学接着就做了一 元线性回归?根本就没有在脑子里思考一下它究竟是不是 一元线性关系。 希望大家在以后的软件学习中,要问自己做每一步操作的 意义何在,不要机械的不思考的动手 Case3:大家用case1的数据,分析一下年蒸发量与纬度 的关系。
用于选择需要绘制的回归分析诊断或预测图。
• 可绘制的有标准化残差的直方图和正态分布图,应变量、预测值 和各自变量残差间两两的散点图等。
【保存】按钮
许多时候我们需要将回归分析的结果存储起来,然后用得到的残差、 预测值等做进一步的分析,保存按钮就是用来存储中间结果的。
相关分析和回归分析SPSS实现

相关分析和回归分析SPSS实现SPSS(统计包统计分析软件)是一种广泛使用的数据分析工具,在相关分析和回归分析方面具有强大的功能。
本文将介绍如何使用SPSS进行相关分析和回归分析。
相关分析(Correlation Analysis)用于探索两个或多个变量之间的关系。
在SPSS中,可以通过如下步骤进行相关分析:1.打开SPSS软件并导入数据集。
2.选择“分析”菜单,然后选择“相关”子菜单。
3.在“相关”对话框中,选择将要分析的变量,然后单击“箭头”将其添加到“变量”框中。
4.选择相关系数的计算方法(如皮尔逊相关系数、斯皮尔曼等级相关系数)。
5.单击“确定”按钮,SPSS将计算相关系数并将结果显示在输出窗口中。
回归分析(Regression Analysis)用于建立一个预测模型,来预测因变量在自变量影响下的变化。
在SPSS中,可以通过如下步骤进行回归分析:1.打开SPSS软件并导入数据集。
2.选择“分析”菜单,然后选择“回归”子菜单。
3.在“回归”对话框中,选择要分析的因变量和自变量,然后单击“箭头”将其添加到“因变量”和“自变量”框中。
4.选择回归模型的方法(如线性回归、多项式回归等)。
5.单击“统计”按钮,选择要计算的统计量(如参数估计、拟合优度等)。
6.单击“确定”按钮,SPSS将计算回归模型并将结果显示在输出窗口中。
在分析结果中,相关分析会显示相关系数的数值和统计显著性水平,以评估变量之间的关系强度和统计显著性。
回归分析会显示回归系数的数值和显著性水平,以评估自变量对因变量的影响。
值得注意的是,相关分析和回归分析在使用前需要考虑数据的要求和前提条件。
例如,相关分析要求变量间的关系是线性的,回归分析要求自变量与因变量之间存在一定的关联关系。
总结起来,SPSS提供了强大的功能和工具,便于进行相关分析和回归分析。
通过上述步骤,用户可以轻松地完成数据分析和结果呈现。
然而,分析结果的解释和应用需要结合具体的研究背景和目的进行综合考虑。
相关分析和一元线性回归分析SPSS报告

用下面的数据做相关分析和一元线性回归分析:选用普通高等学校毕业生数和高等学校发表科技论文数量做相关分析和一元线性回归分析。
一、相关分析1.作散点图普通高等学校毕业生数和高等学校发表科技论文数量的相关图从散点图可以看出:普通高等学校毕业生数和高等学校发表科技论文数量的相关性很大。
2.求普通高等学校毕业生数和高等学校发表科技论文数量的相关系数把要求的两个相关变量移至变量中,因为都是定距数据,选择相关系数中的Pearson,点击确定,可以得到下面的结果:Correlations普通高等学校毕业生数(万人) 高等学校发表科技论文数量(篇)普通高等学校毕业生数(万人) Pearson Correlation 1 .998**Sig. (2-tailed) .000N 14 14高等学校发表科技论文数量(篇) Pearson Correlation .998** 1 Sig. (2-tailed) .000N 14 14**. Correlation is significant at the level (2-tailed).两相关变量的Pearson相关系数=,表示呈高度正相关;相关系数检验对应的概率P值=,小于显着性水平,应拒绝原假设(两变量之间不具有相关性),即毕业生人数好发表科技论文数之间的相关性显着。
3.求两变量之间的相关性选择相关系数中的全部,点击确定:Correlations(万人) (篇)Kendall's tau_b (万人) Correlation Coefficient **Sig. (2-tailed) . .N 14 14(篇) Correlation Coefficient **Sig. (2-tailed) . .N 14 14Spearman's rho (万人) Correlation Coefficient **Sig. (2-tailed) . .N 14 14(篇) Correlation Coefficient **Sig. (2-tailed) . .N 14 14**. Correlation is significant at the level (2-tailed).注解:两相关变量(毕业生数和发表论文数)的Kendall相关系数=,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显着。
SPSS相关性和回归分析一元线性方程案例解析

其中在“样本数据统计”中,随即误差一般叫“残差”:
从结果分析来看,可以简单的认为:居民总储蓄每增加1亿,那居民总消费将会增加0.954亿
提示:对于回归参数的估计,一般采用的是“最小二乘估计法”原则即为:“残差平方和最小“
1:点击“分析”—相关—双变量,进入如下界面:
将“居民总储蓄”和“居民总消费”两个变量移入“变量”框内,在“相关系数”栏目中选择“Pearson",(Pearson是一种简单相关系数分析和计算的方法,如果需要进行进一步分析,需要借助“多远线性回归”分析)在“显著性检验”中选择“双侧检验”并且勾选“标记显著性相关”点击确定,得到如下结果:
从以上结果,可以看出“Pearson"的相关性为0.821,(可以认为是“两者的相关系数为0.821)属于“正相关关系”同时“显著性(双侧)结果为0.000,由于0.000<0.01,所以具备显著性,得出:“居民总储蓄”和“居民总消费”具备相关性,有关联。
既然具备相关性,那么我们将进一步做分析,建立回归分析,并且构建“一元线性方程”,如下所示:
2:从anvoa b的检验结果来看(其实这是一个“回归模型的方差分析表)F的统计量为:29.057,P值显示为0.000,拒绝模型整体不显著的假设,证明模型整体是显著的
3:从“系数a”这个表可以看出“回归系数,回归系数的标准差,回归系数的T显著性检验等,回归系数常量为:2878.518,但是SIG为:0.452,常数项不显著,回归系数为:0.954,相对的sig为:0.000,具备显著性,由于在“anvoa b”表中提到了模型整体是“显著”的
SPSS-相关性和回归分析(一元线性方程)案例解析
SPSS实现一元线性回归分析实例

SPSS实现一元线性回归分析实例2009-12-14 15:311、准备原始数据。
为研究某一大都市报开设周日版的可行性,获得了34种报纸的平日和周日的发行量信息(以千为单位)。
数据如图1所示。
SPSS17.0图12、判断是否存在线性关系。
制作直观散点图:(1)SPSS:菜单Analyze/Regression/linear Regression,如图2所示:图2 (2)打开对话框如图3图3图3中,Dependent是因变量,Independent是自变量,分别将左栏中的sunday选入因变量,daily选入自变量,newspaper作为标识标签选入case labels.(3)点击图3对话框中的plots按钮,如图4所示:图4将因变量DEPENTENT 选入Y:,自变量 ZPRED 选入X: continue 返回上级对话框。
单击主对话框OK.便生成散点图如图5所示:图5从以上散点图可看出,二者变量之间关系趋势呈线性关系。
2、回归方程菜单Analyze/Regression/linear Regression,在图3对话框的右边单击statistics如图6所示:图6regression coefficient回归系数,estimates估计值,confidence intervals level:95%置信区间,model fit拟合模型。
点击continue返回主对话框,单击OK.结果如图7、图8所示:图7图7中第一个图是变量的输入与输出,从图下的提示可知所有变量均输入与输出,没有遗漏。
图7中的第二图是模型总和R值,R平方值,R调整后的平方值,及标准误。
图8图8中第一图为方差统计图,包括回归平方和,自由度,方程检验F值及P值。
图8第二图为回归参数图,从图中可知,constant为回归方程截距,即13.836,回归系数为1.340,标准误分别为:35.804和0.071,及t检验值和95%的置信区间的最大值和最小值。
用spss做一元线性回归分析
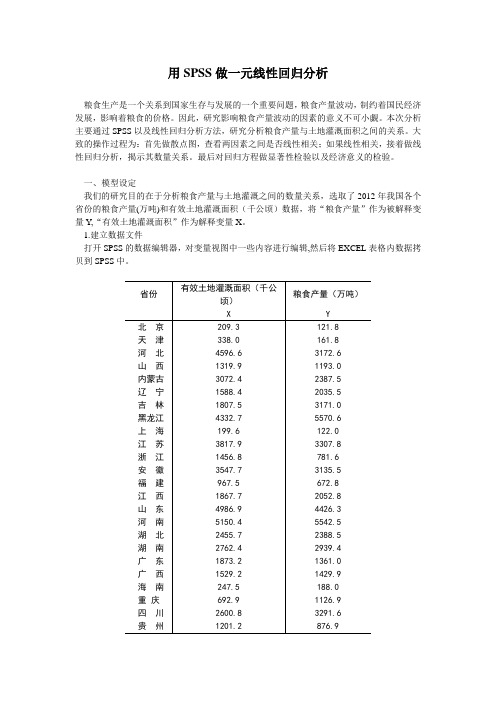
用SPSS做一元线性回归分析粮食生产是一个关系到国家生存与发展的一个重要问题,粮食产量波动,制约着国民经济发展,影响着粮食的价格。
因此,研究影响粮食产量波动的因素的意义不可小觑。
本次分析主要通过SPSS以及线性回归分析方法,研究分析粮食产量与土地灌溉面积之间的关系。
大致的操作过程为:首先做散点图,查看两因素之间是否线性相关;如果线性相关,接着做线性回归分析,揭示其数量关系。
最后对回归方程做显著性检验以及经济意义的检验。
一、模型设定我们的研究目的在于分析粮食产量与土地灌溉之间的数量关系,选取了2012年我国各个省份的粮食产量(万吨)和有效土地灌溉面积(千公顷)数据,将“粮食产量”作为被解释变量Y,“有效土地灌溉面积”作为解释变量X。
1.建立数据文件打开SPSS的数据编辑器,对变量视图中一些内容进行编辑,然后将EXCEL表格内数据拷贝到SPSS中。
云南1634.2 1673.6西藏245.3 93.7陕西1274.3 1194.7甘肃1291.8 1014.6青海251.7 103.4宁夏477.6 359.0新疆3884.6 1224.7表一2.画散点图从菜单上依次点选:图形—旧对话框—散点/点状,定义简单分布,设置Y为粮食产量,X 为有效土地灌溉面积,点击确定,即可出现下面的散点图。
图一由散点图发现,粮食产量与有效土地灌溉面积之间线性相关。
所以建立如下线性模型:二、线性回归分析从菜单上依次点选:分析—回归—线性,出现线性回归对话框。
在主对话框中设置因变量为“粮食产量”,自变量为“有效土地灌溉面积”,“方法”选择默认的“进入”,即自变量一次全部进入的方法。
然后,单击右侧“保存”(注意:在“保存”中被选中的项目,都将在数据编辑窗口显示),在出现的界面中勾选95%的置信区间单值,未标准化残差。
最后,关于“统计量”,在默认情况下有“估计”和“模型拟合度”复选框被选中,再勾选“R方变化”复选框。
上述操作完成后,单击确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS-相关性和回归分析(一元线性方程)案例解析
2011-09-06 12:56
第一步:我们先来分析“居民总储蓄”和“居民总消费”是否具备相关性(采用SPSS 19版本)
1:点击“分析”—相关—双变量,进入如下界面:
将“居民总储蓄”和“居民总消费”两个变量移入“变量”框内,在“相关系数”栏目中选择“Pearson",(Pearson是一种简单相关系数分析和计算的方法,如果需要进行进一步分析,需要借助“多远线性回归”分析)在“显著性检验”中选择“双侧检验”并且勾选“标记显著性相关”点击确定,得到如下结果:
从以上结果,可以看出“Pearson"的相关性为0.821,(可以认为是“两者的相关系数为0.821)属于“正相关关系”同时“显著性(双侧)结果为0.000,由于0.000<0.01,所以具备显著性,得出:“居民总储蓄”和“居民总消费”具备相关性,有关联。
既然具备相关性,那么我们将进一步做分析, 建立回归分析,并且构建“一元线性方程”,如下所示:
点击“分析”--回归----线性” 结果如下所示:
将“因变量”和“自变量”分别拖入框内(如上图所示)从上图可以看出:“自变量”指“居民总储蓄” , "因变量”是指“居民总消费”
点击“统计量”进入如下界面:
在“回归系数”中选择“估计” 在右边选择“模型拟合度” 在残差下面选择“Durbin-watson(u), 点击继续按钮
再点击“绘制图”在“标准化残差图”下面选择“正太概率分布图”选项
再点击“保存”按钮,在残差下面选择“未标准化”(数据的标准化,方法有很多,这里不介绍啦)
得到如下结果:
结果分析如下:
1:从模型汇总b 中可以看出“模型拟合度”为0.675,调整后的“模型拟合度”为0.652,就说明“居民总消费”的情况都可以用该模型解释,拟合度相对较高
2:从anvoa b的检验结果来看(其实这是一个“回归模型的方差分析表)F 的统计量为:29.057,P值显示为0.000,拒绝模型整体不显著的假设,证明模型整体是显著的
3:从“系数a”这个表可以看出“回归系数,回归系数的标准差,回归系数的T显著性检验等,回归系数常量为:2878.518,但是SIG为:0.452,常数项不显著,回归系数为:0.954,相对的sig为:0.000,具备显著性,由于在“anvoa b”表中提到了模型整体是“显著”的
所以一元线性方程为:居民总消费=2878.518+0.954*居民总储蓄
其中在“样本数据统计”中,随即误差一般叫“残差” :
从结果分析来看,可以简单的认为:居民总储蓄每增加1亿,那居民总消费将会增加0.954亿
提示:对于回归参数的估计,一般采用的是“最小二乘估计法”原则即为:“残差平方和最小“。
