2012高考冲刺-数学1
2012高考数学押题卷全国卷(一)

A. (3,5)
B.
⎛ ⎜⎝
1 2
,
+∞
⎞ ⎟⎠
C. (−1, 2)
D.
⎛ ⎜⎝
1 3
,1⎞⎟⎠
⎧1, x > 0
7. 已知符号函数 sgn(x) = ⎨⎪0, x = 0 ,则函数 f (x) = sgn (ln x) − ln2 x 的零点个数为( ).
⎪⎩−1, x < 0
A. 4
B. 3
C. 2
B. 2
3
C.
2
2
D.
3
班级
密
学校
《洞穿高考数学解答题核心考点》配套密押试卷 第 1 页,共 8 页
《洞穿高考数学解答题核心考点》配套密押试卷 第 2 页,共 8 页
密封线内不得答题
∫ 10.
设函数 f (x) = ax2 + c (a ≠ 0) ,若
1
f (x)dx =
0
f (x0 ) , 0 - x0 -1,则 x0 的值为(
24.(本小题满分 10 分)选修 4—5:不等式选讲
设函数 f (x) = x − a + 3x ,其中 a > 0 . (1)当 a = 1时,求不等式 f (x) . 3x + 2 的解集;
{ } (2)若不等式 f (x) - 0 的解集为 x x -�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
2012年高考前汇境一中数学理试题(校内试题) 数学理

i=12 s=1DOs = s * ii = i -1 LOOP UNTIL 条 件PRINT s END (第7题)程序2012年高考前汇境一中数学理试题(校内试题)(满分:150分,考试时间:120分钟)第I 卷(选择题,共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}2,1,0,1,2A =--,集合{}|||B x Z x a =∈≤,则满足 的实数可以取的一个值为( )A .0B .1C .2D .32.若复数)2)((i i a z ++=(a ∈R )是纯虚数,则实数的值为 ( )A .5.0B .1-C .D .0 3. 如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )A .36π B .12π C .33π D .433π 4.若将函数x y 2sin =的图像平移后得到函数)42sin(π+=x y 的图像,则下面说法正确的是 ( )A .向右平移8πB. 向左平移8πC. 向左平移4πD.向右平移4π5. 已知点O 、、不在同一条直线上,点为该平面上一点,且BA OA OP +=22,则( )A .点P 在线段AB 上 B .点P 在线段AB 的反向延长线上C .点P 在线段AB 的延长线上D .点P 不在直线AB 上6.在等差数列}{n a 中,21232a a +=,则1532a a +的值是( ) A. 24 B. 48 C. 96 D. 无法确定7.如果下面的程序执行后输出的结果是11880,那么在程序UNTIL 后面的条件应为( )A .10<i B. 10i <= C. 9<=i D. 9<i8.已知直线和平面,那么//a α的一个充分条件是 ( )A .存在一条直线b ,//a b 且b α⊂B .存在一条直线b ,a b ⊥且b α⊥C .存在一个平面β,a β⊂且//αβD .存在一个平面β,β//a 且//αβ9.已知动点P 到两个定点)0,1(),0,1(21F F -的距离之和为)1(32≥λλ,则点P 轨迹的离心率的取值范围为( ) A .3[,1)3B .33(,]32C .3(0,]3D .3(,1)210.如果有穷数列m a a a a ,...,,,321(为正整数)满足1121,...,,a a a a a a m m m ===-.即),...,2,1(1m i a a i m i ==+-,我们称其为“对称数列“例如,数列,,5,,与数列8,,,,,8都是“对称数列”.设}{n b 是项数为),1(2*N m m m ∈>的“对称数列”,并使得,,22,32,…,12-m 依次为该数列中连续的前项,则数列}{n b 的前2010项和2010S 可以是⑴201021- ⑵100622- (3)122201021---+m m 其中正确命题的个数为 ( ) A .0 B .1 C .2 D .3⊂≠A B正视图 俯视图 侧视图2009~2010学年第一学期高三期末考数学试题 第1页 共4页第II 卷(非选择题,共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案写在答题卡的相应位置上 11.求曲线2,x y x y ==所围成图形的面积 。
2012年高考数学一轮复习资料 第1讲 走进高考综合概述.doc

第一部分:2011全国统一考试数学(江苏卷)一.填空题(14题,每题5分,满分70分)1、已知集合A={-1,1,2,4},B={-1,0,2},则A ⋂B=_________ 简析:A ⋂B={-1,2}2、函数f(x)=log 5(2x+1)的单调增区间是__________简析:由2x+1>0,知x>-12;所以,增区间为(-12,+∞) 3、设复数z 满足i(z+1)=-3+2i (i 是虚数单位),则z 的实部是_________简析:由已知,z=-3+2ii -1=1+3i ,所经z 的实部是14、根据如图所示的伪代码,当输入a,b 分别为2,3时,最后输出的m 的值是________ 简析:由伪代码知,这是比较a,b 大小并输出大者的一段程序,故最后输出的m 值是35、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______ 简析:从四个不同数中一次取两个数共有6种取法,其中一个数是另一个的2倍只有12,24两种,故其概率为136、某老师从星期一到星期五收到的信件数分别是10,6,8,5,6,则该组数据的方差s 2_____简析:5天收到信件数的平均数为10+6+8+5+65=7,所以,该组数据方差s 2=32+12+12+22+125=1657、已知tan(x+π4)=2,则tanx tan2x的值为__________简析:由tan(x+π4)=2解得tanx=13,所以,tanx tan2x = tanx 2tanx 1-tan 2x=1-tan 2x 2=498、在平面直角坐标系xOy 中,过坐标原点的一条直线与函数f(x)=2x的图象交于P 、Q 两点,则线段PQ 长的最小值是________简析:法一——数形结合,在同一坐标系中作出简图,观察知,过原点的直线为y=x 时,被y=2x的图象截得的弦PQ 长最短,此时,PQ=4; 法二——转化求解,设过原点直线方程为y=kx (k>0),联立⎩⎪⎨⎪⎧y=kxy=2x ,解得⎩⎪⎨⎪⎧x=2k y=2k 或⎩⎪⎨⎪⎧x=-2k y=-2k, 不妨设P(2k ,2k),由对称性知,|PQ|=2|OP|=22k +2k ≥224=4,当且仅当2k=2k ,即k=1时等号成立;9、函数f(x)=Asin(ωx+ϕ) (A,ω,ϕ是常数,A>0,ω>0)的部分图象如图所示,则f(0)=_______简析:观察图象知,A=2,T 4=7π12-π3=π4,f(π3)=0;由T=π=2πω,得ω=2;由f(π3)=2sin(2π3+ϕ)=0,知2π3+ϕ=k π (k ∈Z),取k=1得ϕ=π3;Read a,bIf a>b Then m ←a Else m ←bEnd If Print m所以,f(x)=2sin(2x+π3),所以,f(0)=2sin π3=6210、已知e 1,e 2是夹角为2π3的两个单位向量,a =e 1-2e 2,b =k e 1+e 2,若a ·b =0,则实数k的值为_____简析:由已知,有(e 1-2e 2)·(k e 1+e 2)=0,注意到e 1,e 2是夹角为2π3的两个单位向量,整理得,k -2+(1-2k)cos 2π3=0,即4k=5,k=5411、已知实数a ≠0,函数f(x)=⎩⎨⎧2x+a , x<1-x -2a ,x ≥1,若f(1-a)=f(1+a),则a 的值为________简析:分段函数,分段考虑。
2012高考数学冲刺 不等式

不等式 知识点总结精华考试内容:不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式. 考试要求:(1)理解不等式的性质及其证明.(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.(3)掌握分析法、综合法、比较法证明简单的不等式. (4)掌握简单不等式的解法.(5)理解不等式│a │-│b │≤│a+b │≤│a │+│b │不 等 式 知识要点三.不等式、线性规划、算法1.掌握课本上的几个不等式性质,注意使用条件,另外需要特别注意: ①若0ab >,b a >,则11ab>.即不等式两边同号时,不等式两边取倒数,不等号方向要改变.②如果对不等式两边同时乘以一个代数式,要注意它的正负号,如果正负号未定,要注意分类讨论.③取倒数:0a b <<⇔011ab>>;0a b >>⇔011ab<<;如112x-<<,等价于110x-<<或102x <<2.掌握几类不等式(一元一次、二次、绝对值不等式、简单的指数、对数不等式)的解法,尤其注意用分类讨论的思想解含参数的不等式;勿忘数轴标根法,零点分区间法.3.掌握重要不等式,(1)均值不等式:若0,>b a ,2211a b a b++≥(当且仅当b a =时取等号)使用条件:“一正二定三相等 ”, 常用的方法为:拆、凑、平方等; (2),,a b c R ∈,222a b c ab bc ca ++≥++(当且仅当a b c ==时,取等号); (3)公式注意变形如:22222()ab a b ++≥,22()a b ab +≤;若0,0a b m >>>,则b b m aa m++<(真分数的性质);4.证明不等式常用方法:⑴比较法:作差比较:0A B A B -≤⇔≤.注意:若两个正数作差比较有困难,可以通过它们的平方差来比较大小;⑵综合法:由因导果;⑶分析法:执果索因.基本步骤:要证…需证…,只需证…; ⑷反证法:正难则反;⑸放缩法:将不等式一侧适当的放大或缩小以达证题目的.放缩法的方法有:①添加或舍去一些项,||a >n >.②将分子或分母放大(或缩小)③利用基本不等式,如:(1)2n n ++<.④利用常用结论:0111-=<;2211111111(1)(1)1kk k kkk kk k++---=<<=-(程度大);0322111111211()kkk k --+<=-(程度小);⑹换元法:减少不等式中变量,以使问题化难为易,化繁为简,常用的换元有三角换元、代数换元.如:知222x y a +=,可设cos ,sin x a y a θθ==;22221xy ab+=,可设cos ,sin x a y b θθ==;6.(1)一元二次不等式ax bx c a 200++>≠()或ax bx c a 200++<≠⇒()分a >0及a <0情况分别解之,如设0a >,12,x x 是方程20ax bx c ++=的两实根,且12x x <,则其解集如下表:如解关于x 的不等式:01)1(2<++-x a ax 。
2012年高考数学冲刺复习资料

2012年高考数学冲刺复习资料(共分五大专题)专题一:三角与向量的交汇题型分析及解题策略【命题趋向】三角函数与平面的向量的综合主要体现为交汇型,在高考中,主要出现在解答题的第一个试题位置上,其难度中等偏下,分值一般为12分,交汇性主要体现在:三角函数恒等变换公式、性质与图象与平面的向量的数量积及平面向量的平行、垂直、夹角及模之间都有着不同程度的交汇,在高考中是一个热点.如08年安徽理科第5题(5分),考查三角函数的对称性与向量平移、08年山东文第8题理第15题(5分)考查两角和与差与向量垂直、08福建文理第17题(12分)考查三角函数的求值与向量积、07的天津文理第15题(4分)考查正余弦定理与向量数量积等.根据2012年考纲预计在2012年高考中解答题仍会涉及三角函数的基本恒等变换公式、诱导公式的运用、三角函数的图像和性质、向量的数量积、共线(平行)与垂直的充要条件条件.主要考查题型:(1)考查纯三角函数函数知识,即一般先通过三角恒等变换公式化简三角函数式,再求三角函数的值或研究三角函数的图象及性质;(2)考查三角函数与向量的交汇,一般是先利用向量知识建立三角函数关系式,再利用三角函数知识求解;(3)考查三角函数知识与解三角形的交汇,也就是将三角变换公式与正余弦定理交织在一起.【考试要求】1.理解任意角的正弦、余弦、正切的定义.掌握同角三角函数的基本关系式.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.2.掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式.3.能正确运用三角公式进行简单三角函数式的化简、求值和恒等式证明.4.理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx φ)的简图,理解A,ω,φ的物理意义.5.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.6.掌握向量的加法和减法.掌握实数与向量的积,理解两个向量共线的充要条件.7.了解平面向量的基本定理.理解平面向量的坐标的概念,掌握平面向量的坐标运算.8.掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.9.掌握平面两点间的距离公式以及线段的定比分点和中点坐标公式,并且能熟练运用.掌握平移公式.【考点透视】向量具有代数运算性与几何直观性的“双重身份”,即可以象数一样满足“运算性质”进行代数形式的运算,又可以利用它的几何意义进行几何形式的变换.而三角函数是以“角”为自变量的函数,函数值体现为实数,因此平面向量与三角函数在“角”之间存在着密切的联系.同时在平面向量与三角函数的交汇处设计考题,其形式多样,解法灵活,极富思维性和挑战性.主要专题二:函数与导数的交汇题型分析及解题策略【命题趋向】函数的观点和方法既贯穿了高中代数的全过程,又是学习高等数学的基础,是高考数学中极为重要的内容,纵观全国及各自主命题省市近三年的高考试题,函数与导数在选择、填空、解答三种题型中每年都有试题,分值26分左右,如08年福建文11题理12题(5分)为容易题,考查函数与导函数图象之间的关系、08年江苏14题(5分)为容易题,考查函数值恒成立与导数研究单调性、08年北京文17题(12分)为中档题考查函数单调性、奇偶性与导数的交汇、08年湖北理20题(12分)为中档题,考查利用导数解决函数应用题、08年辽宁理22题(12分)为中档题,考查函数利用导数确定函数极值与单调性问题等.预测2012年关于函数与导数的命题趋势,仍然是难易结合,既有基本题也有综合题,函数与导数的交汇的考查既有基本题也有综合题,基本题以考查基本概念与运算为主,考查函数的基础知识及函数性质及图象为主,同时考查导数的相关知识,知识载体主要是三次函数、指数函数与对数函数综合题.主要题型:(1)利用导数研究函数的单调性、极值与最值问题;(2)考查以函数为载体的实际应用题,主要是首先建立所求量的目标函数,再利用导数进行求解.【考试要求】1.了解函数的单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法.2.了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数.3.掌握有理指数幂的运算性质.掌握指数函数的概念、图象和性质.4.掌握对数的运算性质;掌握对数函数的概念、图像和性质.5.能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.6.了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念.7.熟记基本导数公式(c,xm(m为有理数),sinx,cosx,ex,ax,lnx,logax的导数);掌握两个函数和、差、积、商的求导法则.了解复合函数的求导法则,会求某些简单函数的导数.8.理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值.【考点透视】高考对导数的考查主要以工具的方式进行命题,充分与函数相结合.其主要考点:(1)考查利用导数研究函数的性质(单调性、极值与最值);(2)考查原函数与导函数之间的关系;(3)考查利用导数与函数相结合的实际应用题.从题型及考查难度上来看主要有以下几个特点:①以填空题、选择题考查导数的概念、求函数的导数、求单调区间、求函数的极值与最值;②与导数的几何意义相结合的函数综合题,利用导数求解函数的单调性或求单调区间、最值或极值,属于中档题;③利用导数求实际应用问题中最值,为中档偏难题.【典例分析】题型一导函数与原函数图象之间的关系如果原函数定义域内可导,则原函数的图象f(x)与其导函数f¢(x)的图象有密切的关系:1.导函数f¢(x)在x轴上、下方图象与原函数图象上升、下降的对应关系:(1)若导函数f¢(x)在区间D上恒有f¢(x)>0,则f(x)在区间D上为增函数,由此进一步得到导函数f¢(x)图象在x轴上方的图象对应的区间D为原函数图象中的上升区间D;(2)若导函数f¢(x)在区间D上恒有f¢(x)<0,则f(x)在区间D上为减函数,由此进一步得到导函数f¢(x)图象在x轴下方的图象对应的区间为原函数图象中的下降区间.2.导函数f¢(x)图象的零点与原函数图象的极值点对应关系:导函数f¢(x)图象的零点是原函数的极值点.如果在零点的左侧为正,右侧为负,则导函数的零点为原函数的极大值点;如果在零点的左侧为负,右侧为正,则导函数的零点为原函数的极小值点.题型二利用导数求解函数的单调性问题若f(x)在某区间上可导,则由f¢(x)>0(f¢(x)<0)可推出f(x)为增(减)函数,但反之则不一定,如:函数f(x)=x3在R上递增,而f¢(x)≥0.f(x)在区间D内单调递增(减)的充要条件是f¢(x0)≥0(≤0),且f¢(x)在(a,b)的任意子区间上都不恒为零.利用导数求解函数单调性的主要题型:(1)根据函数解析式,求函数的单调区间;(2)根据函数的单调性函数求解参数问题;(3)求解与函数单调性相关的其它问题,如函数图象的零点、不等式恒成立等问题.题型三求函数的极值问题极值点的导数一定为0,但导数为0的点不一定是极值点,同时不可导的点可能是极值点.因此函数的极值点只能在导数为0的点或不可导的点产生.利用导数求函数的极值主要题型:(1)根据函数解析式求极值;(2)根据函数的极值求解参数问题.解答时要注意准确应用利用导数求极值的原理求解题型四求解函数的最值问题函数在闭区间上的最值是比较所有极值点与端点的函数值所得结果,因此函数在闭区间[a,b]上的端点函数值一定不是极值,但它可能是函数的最值.同时,函数的极值不一定是函数的最值,最值也不一定是极值.另外求解函数的最值问题,还可以直接结合函数的单调性来求解.利用导数求解函数最值问题的主要题型:(1)根据函数的解析式求函数的最大值;(2)根据函数在一个区间上的最值情况求解参数问题.题型五导数与数学建模的问题此类试题主要是利用函数、不等式与导数相结合设计实际应用问题,旨在考查考生在数学应用方面阅读、理解陈述的材料,能综合应用所学数学知识、思想和方法解决实际问题的能力,这是高考中的一个热点.专题三:数列与不等式的交汇题型分析及解题策略【命题趋向】数列与不等式交汇主要以压轴题的形式出现,试题还可能涉及到与导数、函数等知识综合一起考查.主要考查知识重点和热点是数列的通项公式、前n项和公式以及二者之间的关系、等差数列和等比数列、归纳与猜想、数学归纳法、比较大小、不等式证明、参数取值范围的探求,在不等式的证明中要注意放缩法的应用.此类题型主要考查学生对知识的灵活变通、融合与迁移,考查学生数学视野的广度和进一步学习数学的潜能.近年来加强了对递推数列考查的力度,这点应当引起我们高度的重视.如08年北京文20题(12分)中档偏上,考查数列与不等式恒成立条件下的参数问题、08年湖北理21题(12分)为中档偏上,考查数列与不等式交汇的探索性问题、08年江西理19题(12分)中等难度,考查数列求和与不等式的交汇、08年全国卷Ⅰ理22(12分)压轴题,难说大,考查数学归纳法与不等式的交汇,等等.预计在2012年高考中,比较新颖的数列与不等式选择题或填空题一定会出现.数列解答题的命题热点是与不等式交汇,呈现递推关系的综合性试题.其中,以函数与数列、不等式为命题载体,有着高等数学背景的数列与不等式的交汇试题是未来高考命题的一个新的亮点,而命题的冷门则是数列与不等式综合的应用性解答题.【考试要求】1.理解数列的概念,了解数列通项公式的意义,了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.2.理解等差数列的概念.掌握等差数列的通项公式与前n项和公式,并能解决简单的实际问题.3.理解等比数列的概念,掌握等比数列的通项公式与前n项和公式,并能解决简单的实际问题。
资料复习参考高考数学冲刺复习1

改革开放的三十多年, 我国经济得到了巨大的发展, 已经从依赖资源、廉价劳动力的时代进入知识经济时代。
知识经济条件下, 创新将成为经济增长的根本所在。
何以创新? 人力资源管理成为关键。
公司若要在竞争的社会中立于不败之地, 必须把人才资源放在第一位, 只有有效、合理、科高考数学冲刺复习资料专题一: 三角与向量的交汇题型分析及解题策略【典例分析】题型一 三角函数平移与向量平移的综合三角函数与平面向量中都涉及到平移问题, 虽然平移在两个知识系统中讲法不尽相同, 但它们实质是一样的, 它们都统一于同一坐标系的变化前后的两个图象中.解答平移问题主要注意两个方面的确定: (1)平移的方向;(2)平移的单位.这两个方面就是体现为在平移过程中对应的向量坐标.【例1】 把函数y =sin2x 的图象按向量 =(- , -3)平移后, 得到函数y =Asin(ωx +()(A >0, ω>0, |(|= )的图象, 则(和B 的值依次为题型二 三角函数与平面向量平行(共线)的综合此题型的解答一般是从向量平行(共线)条件入手, 将向量问题转化为三角问题, 然后再利用三角函数的相关知识再对三角式进行化简, 或结合三角函数的图象与民性质进行求解.此类试题综合性相对较强, 有利于考查学生的基础掌握情况, 因此在高考中常有考查.【例2】 已知A 、B 、C 为三个锐角, 且A +B +C =π.若向量 =(2-2sinA, cosA +sinA)与向量 =(cosA -sinA, 1+sinA)是共线向量.(Ⅰ)求角A ;(Ⅱ)求函数y =2sin 2B +cos C -3B 2的最大值.题型三 三角函数与平面向量垂直的综合此题型在高考中是一个热点问题, 解答时与题型二的解法差不多, 也是首先利用向量垂直的充要条件将向量问题转化为三角问题, 再利用三角函数的相关知识进行求解.此类题型解答主要体现函数与方程的思想、转化的思想等.【例3】 已知向量 =(3sin α,cos α), =(2sin α, 5sin α-4cos α), α∈( , 2π), 且 ⊥ .(Ⅰ)求tanα的值;(Ⅱ)求cos( + )的值.【例3】 已知向量 =(cos α,sin α), =(cos β,sin β), | - |= .(Ⅰ)求cos(α-β)的值;(Ⅱ)若- <β<0<α< , 且sin β=- , 求sin α的值.题型五 三角函数与平面向量数量积的综合此类题型主要表现为两种综合方式: (1)三角函数与向量的积直接联系;(2)利用三角函数与向量的夹角交汇, 达到与数量积的综合.解答时也主要是利用向量首先进行转化, 再利用三角函数知识求解.【例5】 设函数f(x)= · .其中向量 =(m, cosx), =(1+sinx, 1), x ∈R, 且f( )=2.(Ⅰ)求实数m 的值;(Ⅱ)求函数f(x)的最小值.六、解斜三角形与向量的综合在三角形的正弦定理与余弦定理在教材中是利用向量知识来推导的, 说明正弦定理、余弦定理与向量有着密切的联系.解斜三角形与向量的综合主要体现为以三角形的角对应的三角函数值为向量的坐标, 要求根据向量的关系解答相关的问题.【例6】已知角A.B.C为△ABC的三个内角, 其对边分别为a、b、c, 若=(-cos , sin ), =(cos , sin ), a=2 , 且·=.(Ⅰ)若△ABC的面积S=, 求b+c的值.(Ⅱ)求b+c的取值范围.【专题训练】一、选择题1. 已知=(cos40(, sin40(), =(cos20(, sin20(), 则·=__________3. 已知△ABC中, =, =, 若·<0, 则△ABC是__________4. 设=( ,sin(), =(cos(, ), 且∥, 则锐角(为__________6.已知向量=(6, -4), =(0, 2), =+( , 若C点在函数y=sin x的图象上,实数(=()A. B. C. - D. -8.设0≤θ≤2π时, 已知两个向量=(cosθ, sinθ), =(2+sinθ, 2-cosθ), 则向量长度的最大值是__________ ()A. B. C. 3 D. 29.若向量=(cos(,sin(), =(cos(,sin(), 则与一定满足()A. 与的夹角等于(-(B. ⊥C. ∥D. ( +)⊥( -)10. 已知向量=(cos25(,sin25(), =(sin20(,cos20(), 若t是实数, 且=+t , 则| |的最小值为__________11. O是平面上一定点, A.B.C是该平面上不共线的3个点, 一动点P满足: =+(( +), (∈(0,+∞), 则直线AP一定通过△ABC的__________12. 对于非零向量我们可以用它与直角坐标轴的夹角(,((0≤(≤(,0≤(≤()来表示它的方向, 称(,(为非零向量的方向角, 称cos(,cos(为向量的方向余弦, 则cos2(+cos2(=__________13. 已知向量=(sin(, 2cos(), =( ,-).若∥, 则sin2(的值为____________.14. 已知在△OAB(O为原点)中, =(2cos(, 2sin(), =(5cos(, 5sin(), 若·=-5, 则S△AOB的值为_____________.15.将函数f(x)=tan(2x+)+1按向量a平移得到奇函数g(x), 要使|a|最小, 则a=____________.16. 已知向量=(1, 1)向量与向量夹角为, 且·=-1.则向量=__________.三、解答题17. 在△ABC中, 角A.B.C的对边分别为a、b、c, 若·=·=k(k∈R).(Ⅰ)判断△ABC的形状;(Ⅱ)若c=, 求k的值.18. 已知向量=(sinA,cosA), =( ,-1), ·=1, 且为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.19. 在△ABC中, A.B.C所对边的长分别为a、b、c, 已知向量=(1, 2sinA), =(sinA, 1+cosA), 满足∥, b +c=a.(Ⅰ)求A的大小;(Ⅱ)求sin(B+)的值.20. 已知A.B.C的坐标分别为A(4, 0), B(0, 4), C(3cosα, 3sinα).(Ⅰ)若α∈(-π, 0), 且| |=| |, 求角α的大小;(Ⅱ)若⊥, 求的值.21. △ABC的角A.B.C的对边分别为a、b、c, =(2b-c, a), =(cosA, -cosC), 且⊥.(Ⅰ)求角A的大小;(Ⅱ)当y=2sin2B+sin(2B+)取最大值时, 求角的大小.22. 已知=(cosx+sinx, sinx), =(cosx-sinx, 2cosx),(Ⅰ)求证: 向量与向量不可能平行;(Ⅱ)若f(x)=·, 且x∈[-, ]时, 求函数f(x)的最大值及最小值.专题二: 函数与导数的交汇题型分析及解题策略【典例分析】题型一导函数与原函数图象之间的关系【例1】如果函数y=f(x)的图象如右图, 那么导函数y=f((x)的图象可能是()【例2】设f((x)是函数f(x)的导函数, y=f((x)的图象如图所示, 则y=f(x)的图象最有可能是()题型二利用导数求解函数的单调性问题若f(x)在某区间上可导, 则由f((x)>0(f((x)<0)可推出f(x)为增(减)函数, 但反之则不一定, 如: 函数f(x)=x3在R上递增, 而f((x)≥0.f(x)在区间D内单调递增(减)的充要条件是f((x0)≥0(≤0), 且f((x)在(a, b)的任意子区间上都不恒为零.利用导数求解函数单调性的主要题型: (1)根据函数解析式, 求函数的单调区间;(2)根据函数的单调性函数求解参数问题;(3)求解与函数单调性相关的其它问题, 如函数图象的零点、不等式恒成立等问题.【例3】(08全国高考)已知函数f(x)=x3+ax2+x+1, a∈R.(Ⅰ)讨论函数f(x)的单调区间;(Ⅱ)设函数f(x)在区间(-, -)内是减函数, 求a的取值范围.题型三求函数的极值问题【例4】(08·四川)设x=1和x=2是函数f(x)=x5+ax3+bx+1的两个极值点.(Ⅰ)求a和b的值;(Ⅱ)略.【例5】(08陕西高考)已知函数f(x)=(c>0, 且c≠1, k∈R)恰有一个极大值点和一个极小值点, 其中一个是x=-c. (Ⅰ)求函数f(x)的另一个极值点;(Ⅱ)求函数f(x)的极大值M和极小值m, 并求M-m≥1时k的取值范围.题型四求解函数的最值问题【例6】(08浙江高考)已知a是实数, 函数f(x)=x2(x-a).(Ⅰ)略;(Ⅱ)求f(x)在区间[0, 2]上的最大值.题型五导数与数学建模的问题【例7】(08·湖北)水库的蓄水量随时间而变化, 现用表示时间, 以月为单位, 年初为起点, 根据历年数据, 某水库的蓄水量(单位: 亿立方米)关于t的近似函数关系式为V(t)=,(Ⅰ)该水库的蓄求量小于50的时期称为枯水期.以i-1<t<i表示第1月份(i=1, 2, …, 12),同一年内哪几个月份是枯水期?(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).【例8】(2006年福建卷)统计表明, 某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: y= x2-x+8 (0<x≤120).已知甲、乙两地相距100千米.(Ⅰ)当汽车以40千米/小时的速度匀速行驶时, 从甲地到乙地要耗油多少升?(Ⅱ)当汽车以多大的速度匀速行驶时, 从甲地到乙地耗油最少?最少为多少升?【专题训练】一、填空题1. 函数f(x)=x3+ax2+3x-9, 已知f(x)有两个极值点x1, x2, 则x1·x2=__________.2. 函数f(x)= x3+ax+1在(-∞, -1)上为增函数, 在(-1, 1)上为减函数, 则f(1)为__________.3. 函数f(x)=x3-3ax-a在(0, 1)内有最小值, 则a的取值范围为__________.4. 已知函数f(x)=x2(ax+b)(a, b∈R)在x=2时有极值, 其图象在点(1, (1))处的切线与直线3x+y=0平行,则函数f(x)的单调减区间为__________.6. 设函数f(x)=sin(ωx+)-1(ω>0)的导数f((x)的最大值为3, 则f(x)的图象的一条对称轴的方程是__________.7.函数f(x)的定义域为开区间(a, b), 导函数f((x)在(a, b)内的图象如下图所示.则函数f(x)在开区间(a, b)内有极小值点__________. ()A.1个B.2个C.3个D.4个13. 右图是一个三次多项式函数f(x)的导函数f((x)的图象,则当x=______时, 函数取得最小值.14. 已知函数f(x)=x3-x2+2x+1, 且x1, x2是f(x)的两个极值点, 0<x1<1<x2<3, 则a的取值范围_________.15.已知函数f(x)=x3+bx2+cx+d在区间[-1, 2]上是减函数, 那么b+c最大值为___________. 16. 曲线y=2x4上的点到直线y=-x-1的距离的最小值为____________.三、解答题17. 设函数f(x)=2x3-3(a-1)x2+1, 其中a≥1.(Ⅰ)求f(x)的单调区间;(Ⅱ)讨论f(x)的极值.18. 已知定义在R上的函数f(x)=x2(ax-3), 其中a为常数.(Ⅰ)若x=1是函数f(x)的一个极值点, 求a的值;(Ⅱ)若函数f(x)在区间(-1, 0)上是增函数, 求a的取值范围.19. 已知函数f(x)=x3+bx2+ax+d的图象过点P(0, 2), 且在点M(-1, f(-1))处的切线方程为6x-y+7=0.(Ⅰ)求函数y=f(x)的解析式;(Ⅱ)求函数y=f(x)的单调区间.20. 设函数f(x)=(x+1)ln(x+1), 若对所有的x≥0, 都有f(x)≥ax成立, 求实数a的取值范围.21. 已知函数f(x)=-x2+8x, g(x)=6lnx+m.(Ⅰ)求f(x)在区间[t, t+1]上的最大值h(t);(Ⅱ)是否存在实数m, 使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在, 求出m的取值范围;, 若不存在, 说明理由。
2012高考文科数学冲刺题及答案

2012届高三下学期4月冲刺题文科数学本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页,满分150分。
考试用时120分钟。
参考公式:柱体的体积公式:,其中表示柱体的底面积,表示柱体的高.圆柱的侧面积公式:,其中c是圆柱的底面周长,是圆柱的母线长.球的体积公式V=, 其中R是球的半径.球的表面积公式:S=4π,其中R是球的半径.用最小二乘法求线性回归方程系数公式 .如果事件互斥,那么.第I卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,,则为()A. B. C.{-1,0,1} D.2.若复数是实数,则的值为()A. B.3 C.0 D.3.曲线C:y = x2 + x 在 x = 1 处的切线与直线ax-y+1= 0互相垂直,则实数a的值为()A. B.-3 C. D.-4.已知变量x,y满足的最大值为()A.5 B.6 C.7 D.85.如图是一个几何体的三视图,则此三视图所描述几何体的表面积为()A.B.20C.D.286.下列命题中:①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.②若p为:,则为:.③命题“”的否命题是“”.④命题“若则q”的逆否命题是“若p,则”.其中正确结论的个数是()A.1 B.2 C.3 D.47.双曲线的离心率为,则它的渐近线方程是()A. B. C. D.8.将函数的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移个单位,所得函数的最小正周期为()A.π B.2π C.4π D.8π9.数列的前n项和;(n∈N*);则数列的前50项和为()A.49 B.50 C.99 D.10010.中,三边之比,则最大角的余弦值等于()A. B. C. D.11.数列中,如果数列是等差数列,则()A.B.C.D.12.已知,若在上恒成立,则实数的取值范围是()A. B. C. D.第Ⅱ卷(非选择题共90分)二、填空题:(本大题共4小题,每小题4分,共16分。
2012高考理科数学冲刺题及答案

{}{}1|,02|2-==<-=x y x N x x x M =)(N C M R I {|01}x x <<{|02}x x <<{|1}x x <∅1z i i=-2012高考理科数学冲刺题及答案 理 科 数 学本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页,满分150分。
考试用时120分钟。
参考公式:柱体的体积公式:v sh =,其中s 表示柱体的底面积,h 表示柱体的高. 圆柱的侧面积公式:s cl =,其中c 是圆柱的底面周长,l 是圆柱的母线长.球的体积公式V=34R 3π, 其中R 是球的半径. 球的表面积公式:S=4πR 2,其中R 是球的半径. 用最小二乘法求线性回来方程系数公式1221ˆˆˆ,ni ii nii x y nx ybay bx xnx==-⋅==--∑∑ . 如果事件A B 、互斥,那么()()()P A B P A P B +=+. 第I 卷 (选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知实数集R , ,则( )A .B .C .D .2.i 为虚数单位,则复数的虚部是 ( )A .2iB .2i -C .2D .—23.设随机变量ξ服从正态分布()3,4N ,若()()232P a P a ξξ<-=>+,则a 的值为A .73B .53C .5D .32(20)()2cos (0)2x x f x x x π+-≤<⎧⎪=⎨≤≤⎪⎩4.已知函数()()32120f x x ax x a a=++>,则()2f 的最小值为 ( ) A .32 B .16 C .288a a++D .1128a a++5.设a 、b 是两条不同直线,α、β是两个不同平面,则下列命题错误的是 ( )A .若a α⊥,//b α,则a b ⊥B .若a α⊥,//b a ,b β⊂,则αβ⊥C .若a α⊥,b β⊥,//αβ,则//a bD .若//a α,//a β,则//αβ6.若把函数3y x sinx =-的图象向右平移m (m >0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是 ( )A .3πB .23πC .6πD .56π 7.如图,若程序框图输出的S 是126,则判定框①中应为 ( )A .?5≤nB .?6≤nC .?7≤nD .?8≤n8.ABC ∆的外接圆的圆心为O ,半径为1,2AO AB AC =+u u u r u u u r u u u r且OA AB =u u u r u u u r ,则向量BA u u u r在向量BC u u u r 方向上的投影为() A .21 B .23 C .21- D .23-9.已知数列{}n a 满足*331log 1log ()n n a a n ++=∈N 且2469a a a ++=,则15793log ()a a a ++ 的值是( )A .5-B .51-C .5D .5122221(0,0)x y a b a b -=>>c bx ax x x f +++=2213)(2310.函数 的图象与x 轴所围成的封闭图形的面积 ( )A .3B .72 C .92D . 411 ,过左焦点F1作斜率为33的直线交双曲线的右支于点P ,且y 轴平分线段F1P ,则双曲线的离心率是 ( )A .2B .51+C .3D .23+12.已知21x x 、分不是函数 的两个极值点,且)1,0(1∈x ,)2,1(2∈x ,则12--a b 的取值范畴是( )A .)41,(-∞Y ),1(+∞ B . )41,1(-- C . )2,41( D . )1,41( 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分,将答案填在题后的横线上.)13.关于x 的二项式41(2)x x -展开式中的常数项是 。
2012年高考数学冲刺复习精练一
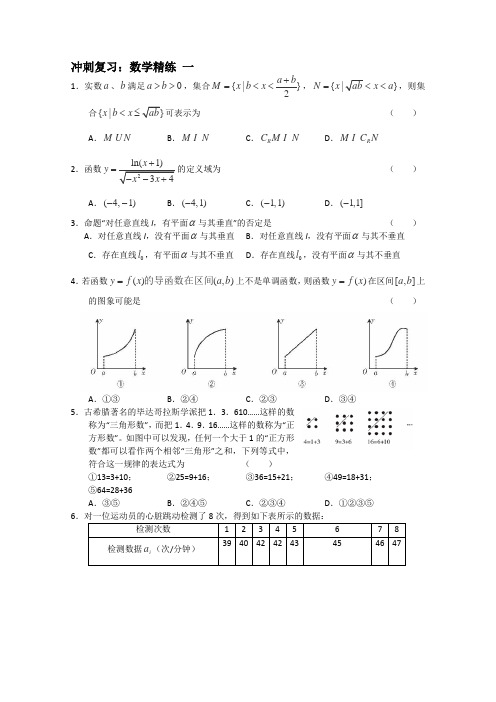
冲刺复习:数学精练 一1.实数a 、b 满足0a b >>,集合{|}2a bM x b x +=<<,{|}N x x a =<<,则集合{|x b x <≤可表示为( )A .MNB .MN C .R C M N D .R M C N2.函数y =的定义域为( )A .(4,1)--B .(4,1)-C .(1,1)-D .(1,1]-3.命题“对任意直线l ,有平面α与其垂直”的否定是 ( ) A .对任意直线l ,没有平面α与其垂直 B .对任意直线l ,没有平面α与其不垂直C .存在直线0l ,有平面α与其不垂直D .存在直线0l ,没有平面α与其不垂直4.若函数()(,)y f x a b =的导函数在区间上不是单调函数,则函数()y f x =在区间[,]a b 上的图象可能是( )A .①③B .②④C .②③D .③④ 5.古希腊著名的毕达哥拉斯学派把1.3.610……这样的数称为“三角形数”,而把1.4.9.16……这样的数称为“正方形数”。
如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为 ( ) ①13=3+10; ②25=9+16; ③36=15+21; ④49=18+31; ⑤64=28+36 A .③⑤ B .②④⑤ C .②③④ D .①②③⑤ 6上述数据的统计分析中,一部分计算见如右图所示的程序框图(其中a是这8个数据的平均数),则输出的的值是()A.6 B.7C.8 D.567.正三棱锥底面边长为a,侧棱与底面成角为60°,过底面一边作一截面使其与底面成30°的二面角,则此截面的面积为()A.34a2B.33a2C.13a2D.38a28.甲、乙、丙三人值周一至周六的班,每人值两天班,若甲不值周一.乙不值周六,则可排出不同的值班表数为()A.12 B.42 C.6 D.909.设,x y满足约束条件360,20,0,0,x yx yx y--≤⎧⎪-+≥⎨⎪≥≥⎩若目标函数(0,z ax by a b=+>>0)的最大值为12,则23a b+的最小值为()A.256B.83C.113D.410.已知2b是1一a和1+a的等比中项,则a+4b的取值范围是()A.⎥⎦⎤⎝⎛∞-45,B.(一∞,45)C.⎥⎦⎤⎝⎛-451,D.(一1,45)11.设G是ABC∆的重心,且0)sin35()sin40()sin56(=++GCCGBBGAA,则角B的大小为()A.45°B.60°C.30°D.15°12.设点P是双曲线22221(,0)x ya ba b-=>>与圆2222x y a b+=+在第一象限的交点F1,F2分别是双曲线的左.右焦点,且12||2||PF PF=,则双曲线的离心率为()ABCD参考答案1.D;2.C;3.D;4.D;5.A;6.B;7.D;8.B;9.A;10.C;11.B;12.A。
2012年高考数学冲刺复习:数学精练48.pdf

【学习目标】 1、学会运用欧姆定律、串并联电路电流、电压、电阻的特点解电表示数变化类型题。
2、培养系统解题的能力和逻辑推理能力。
【重点难点】 运用欧姆定律、串并联电路电流、电压、电阻的特点解电表示数变化类型题。
【课前预习】 串联电路的电流、电压、电阻的特点 分类 特点串联电路并联电路电流特点电压特点电阻特点一个比例分压关系分流关系【新知导学】 如图所示电路中,开关S闭合后,当滑动变阻器的滑片P向右移动时,各电表的示数如何变化? 一般步: (1)拆除电表,认清电路,明确电表测量对象。
(2)根据滑片P的移动方向,判断电路中电阻的变化。
(3)判断电路中电流的变化,电压的变化。
分析:电阻R、 R1和电流表 联,电压表V1测 两端电压,电压表V2测 两端电压,当滑片P向右移,R1的阻值变 ,使电路中电流变 ,电流表示数变 ,根据串联分压,电阻变大分压变大,所以电阻R1分得电压变 ,电阻R分得电压变 ,电压表V2示数变 ,V1示数变 。
注:串联电路中,电压的变化可用串联分压来判断,电阻变大,分压变大,另一电阻的分压会减小(适用于一定值电阻与变阻器串联)。
【典型例题】 (一)滑动变阻器类 问题1. 如图1,当滑动变阻器的滑片P向上移动 时,则( ) A.电流表的示数变小,电压表的示数变小. B.电流表的示数变大,电压表的示数变大. C.电流表的示数变大,电压表的示数不变. D.电流表的示数变小,电压表的示数变大. 问题2. 如图2所示,电源电压保持不变,当滑动变阻器的滑片P向右移动时,则( ) A.电压表的示数变小,电流表的示数变大 B.电压表的示数变大,电流表的示数变小. C.电压表、电流表的示数均变大. D.电压表、电流表的示数均变小. 问题3 在如图3所示的电路中,电源电压不变当变阻器的滑片P向右移动时,则( ) A.电流表Al的示数减小,A的示数减小. B.电流表Al的示数不变,A的示数减小. C.电流表Al的示数不变,A的示数增大. D.电流表Al的示数减小,A的示数不变. (二)开 关 类 问题1: 如图4,电源电压不变,当开关S闭合时,电流表A1的示数将 , 电流A的示数 。
2012年普通高等学校招生全国统一考试数学冲刺卷(1)(浙江卷) 新人教A版

2012年普通高等学校招生全国统一考试(某某卷)冲刺卷一数 学(理科)本试卷分选择题和非选择题两部分。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)1.答题前,考生务必将自己的某某、准备考证号用黑色字迹的签字笔或钢笔分别填写在试卷个答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:如果事件A , B 互斥, 那么棱柱的体积公式P (A +B )=P (A )+P (B )V =Sh如果事件A , B 相互独立, 那么 其中S 表示棱柱的底面积, h 表示棱柱的高P (A ·B )=P (A )·P (B )棱锥的体积公式如果事件A 在一次试验中发生的概率是p , 那么nV =31Sh次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积, h 表示棱锥的高P n (k )=C k n p k (1-p )n -k(k = 0,1,2,…, n ) 球的表面积公式棱台的体积公式S = 4πR 2)2211(31S S S S h V ++=球的体积公式其中S 1, S 2分别表示棱台的上、下底面积, V =34πR 3h 表示棱台的高 其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知()⎩⎨⎧≤+>=0),1(02x x f x x x f ,则()()22-+f f 的值为A .6B .5C .4D .2 2.“6πα=”是“212cos =α”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件3.下列命题中错误..的是 A .如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β B .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β C .如果平面α⊥平面γ,平面β⊥平面γ,l αβ⋂=,那么l ⊥平面γ D .如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β4.阅读下面的程序框图,若使输出的结果不大于37,则输入的整数i 的最大值为 A .4 B .5 C .6 D .75.已知双曲线13622=-y x 的左右焦点分别为F 1,F 2, 点M 在双曲线上且M F 1⊥x 轴,则F 1到直线F 2M 的 距离为 A .563B .665 C .56D .656.设a 是抛掷一枚质地均匀的骰子得到的点数,则方程022=++ax x 有两个不相等的实数根的概率为 A .32 B .31C .21D .1257.已知圆C :03242222=-++++m m y mx y x ,若过点(1,2-)可作圆的切线有两条,则实数m 的取值X 围是(第4题图)A .()⎪⎭⎫ ⎝⎛+∞⋃-∞-,231,B .(1-,4) C .⎪⎭⎫ ⎝⎛4,23D .⎪⎭⎫ ⎝⎛-23,18.某电台现录制好10首曲目,其中美声唱法2首,民族唱法4首,通俗唱法4首.拟分两期播出,每期播放其中5首,要求三种唱法每期都有,通俗唱法曲目不得相邻,且第一期的最后一首曲目必须是美声唱法. 则不同的编排方法种数为 A .40320B .80640C .35712D .714249.设函数()4sin(21)f x x x =+-,则在下列区间中函数()f x 不.存在零点的是 A .[]4,2--B .[]2,0-C .[]0,2D .[]2,410.,P Q 是两个定点,点M 为平面内的动点,且MP MQλ=(0λ>且1λ≠),点M 的轨迹围成的平面区域的面积为S ,设()S f λ=(0λ>且1λ≠)则以下判断正确的是 A .)(λf 在)1,0(上是增函数,在),(∞+1上是减函数 B .)(λf 在)1,0(上是减函数,在),(∞+1上是减函数 C .)(λf 在)1,0(上是增函数,在),(∞+1上是增函数 D .)(λf 在)1,0(上是减函数,在),(∞+1上是增函数非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分。
2012年高考数学冲刺复习:数学精练12.pdf

【教学目标】 【教学重点】 理解含蓄深沉的语言。
【教学难点】 认识生命的本质,养成积极进取的生活态度。
【教学课时】 两课时。
【教学过程】 第一课时 一、导入新课 地球养育着无数生命,可是置身于生机勃勃的大千世界中,不少人却常常感觉不到他的不平凡,更感觉不到生命这朴实的形式下面蕴藏着的丰富哲理。
下面,我们就来看一看世纪老人冰心是怎样以散文的形式揭示这一人生哲理的。
今天,我们要学习的是世纪老人冰心写的一篇关于生命的优美散文──《谈生命》。
二、预习课文 1、收集冰心的有关资料(建议学生从生平、思想、成就、作品等方面进行专题收集); 2、自读课文,勾划不认识、不理解的字词,查工具书,给这些字注音、解释; 三、检查预习 1、 提问有关冰心的文学常识。
2、 生字:注音并朗读。
云翳(yì) 岩(chán) 羞怯(qiè) 休憩(qì) 骄奢(shē) 心魂惊骇(hài) 荫庇(yìn) 枭鸟(xiāo) 芳馨(xīn) 朔风(shuò) 丛莽(mǎng) 2、解释: 骄奢:骄狂专横; 岩:⑴一种陡而隆起的岩石,如悬崖或崖、孤立突出的岩石;⑵参差不齐的岩石海岸,尤指给航行造成威胁的。
本文应为⑴项。
怡悦:喜悦;高兴。
云翳:中医病名。
眼球角膜疾病后所遗留的一层薄若云雾状翳障。
一泻千里:⑴指江河水势奔流直下;⑵比喻文笔奔放畅达。
心平气和:⑴指思想或精神平静没有不安或压抑的感情;⑵指抑制或重新克制住了自己的感情;平静下来。
休憩:休息。
绯红:深红色。
卑微:⑴指地位低下而渺小出身卑微的人;⑵衰微。
四、整体感悟 1、初读课文,把握内容大意。
思考:本文围绕生命谈了些什么内容? 鼓励学生大胆发表自己阅读后的认识与体会,只要言之成理即可。
提示:这篇文章用“一江春水”和“一棵小树”为喻,形象地描述了生命的历程,揭示了生命的本质,表达了珍爱生命思想感情和奋发向上的生活态度。
2012年高考数学临考突击专项训练系列:选择 13.pdf

答案:如图所示 7.在探究“串联电路电压的规律”实验中: (1)要用电压表测灯L2两端的电压,连接电路如图甲所示.图中只有一根导线连错了,请你在连错的导线上划“×”,并用铅笔画线表示导线将电路连接正确. (2)改正电路后,闭合开关.如图乙所示,电压表的示数为______V,若电源电压为3 V,则灯L1两端的电压是______V. 【解析】(1)由题图可知电压表与灯L1串联,是错误的.要用电压表测L2两端的电压,应使电压表与灯L2并联. (2)改正后,两灯串联,电压表选用的是小量程,分度值是0.1 V,所以示数是1.2 V,即U2=1.2 V,而电源电压U=3 V,所以U1=U-U2=3V-1.2 V=1.8 V. 答案:(1) (2)1.2 1.8 智能提升作业 基础梳理.知识点睛 各部分电路两端的电压之 和U=U1+U2 相等 总电 压 U=U1=U2 若n个用电器串联,则:U=U1+U2+…+Un;若n个用电器并联,则:U=U1=U2=…=Un. 要点归纳.诱思探究 实验探究:探究串联电路电压的规律 1.实验器材:两节干电池、导线若干、开关、不同规格的小灯泡若干、电压表. 2.实验步骤: (1)电路图(如图) (2)分别把电压表并联在如图所示的电路的A、B两点,B、C两点,A、C两点,并记下电压表示数. (3)换上另外四只不同规格的小灯泡,重复两次实验. (4)实验记录数据如下: (5)分析实验数据知:A、C两点间的电压总等于A、B间电压和B、C间电压之和. 实验序号 A、B间电压U1/V B、C间电压U2/V A、C间电压U/V 1 1.2 1.8 3 2 1.0 2.0 3 3 0.8 2.2 3 3.实验结论:串联电路中总电压等于各部分电路两端的电压之和. 1.连接电路时,开关处于断开状态还是闭合状态? 提示:断开状态. 2.采用不同规格的小灯泡多次测量的目的是什么? 提示:(1)对于规格相同的小灯泡,无论串联还是并联,两小灯泡两端电压都相同,无法得出实验结论. (2)避免偶然性,使实验结论具有普遍性. 3.实验中,如何选择电压表的量程? 提示:所选量程略大于电源电压且指针偏转角度不要太小. 4.若把电压表串联在电路中,小灯泡是否发光?此时电压表的示数是多少? 提示:因电压表本身电阻很大,故电路中电流几乎为零,小灯泡几乎不发光,此时电压表的示数近似等于电源电压. 5.当A、B或B、C之间被短路时,电压表测出A、C两点之间的电压大小有何特点? 提示:当小灯泡被短路时,电压表始终测电源电压,电压表的示数始终不变. 6.若探究并联电路电压的规律,如何设计实验电路图? 提示:分别测出小灯泡两端电压和两小灯泡并联后两端电压. 7.说出并联电路电压规律. 提示:并联电路中各支路两端电压都等于电源电压. 易错剖析.举一反三 不能将电压表正确接入电路 【典例】在探究串联电路的电压关系时,某同学使用的电路如图所示,他先用电压表正确地测量了灯L2两端的电压,为了测量灯L1两端的电压,他想将电压表接A点的那一段导线改接到电路中的C点,而保持接电压表B点的导线不动.对这种做法的正确性以及理由,三位同学进行如下的讨论:①甲同学:这种做法不正确,因为电压表正、负接线柱接反了;②乙同学:这种做法不正确,因为灯L1两端的电压值超出电压表的量程;③丙同学:这种做法正确,A点改接到C点时,电压表与灯L1是并联的.他们的讨论正确的有 A.① B.①② C.② D.③ 【易错答案】B、C、D 【纠错剖析】 选项 易错角度 纠错剖析 B、C 错误地认为L1两端的电压值超出电压表的量程 电源由两节干电池串联组成,故电源电压为3 V,L1与L2串联,则L1两端的电压一定小于3 V,因此L1两端的电压值不会超出电压表的量程 D 错误地认为只要电压表与灯L1并联即可测量灯L1的电压,忽视了电压表正负接线柱的正确接法 A点改接到C点时,电压表正负接线柱接反,指针反转,会损坏电压表 【正确答案】选A.连接A点导线与电压表负接线柱连接,改接C点后,正负接线柱接反,会损坏电压表,故①说法正确,故选A. 课时训练.基础达标 1.在探究串、并联电路电压的规律实验中,不需要的实验器材是( ) A.电源 B.小灯泡 C.电流表 D.电压表 【解析】选C.探究串、并联电路电压规律,需测量不同小灯泡两端电压和总电压,不需测量电路中的电流值,故不需要的实验器材是电流表. 2.如图所示,将电压表先后并联在AB处、BC处、AC处,当开关S闭合后,电压表读数最大时,是接在( ) A.AC处 B.AB处 C.BC处 D.三处一样大 【解析】选A.灯泡L1、L2串联,串联电路两端的总电压等于各部分电路两端的电压之和.将电压表先后并联在AB处、BC处、AC处,分别测量的是灯泡L1两端的电压U1、灯泡L2两端的电压U2,电源电压U,而U=U1+U2,故接AC处电压表读数最大. 3.小亮家的卫生间按如图所示的电 路安装了照明灯和换气扇,它们( ) A.只能各自独立工作,而不能同时工作 B.只能同时工作,而不能各自独立工作 C.工作时,两端的电压一定相等 D.工作时,通过的电流一定相等 【解析】选C.照明灯和换气扇是并列连接在一起的,故二者是并联的,因此,二者能够独立工作,开关同时闭合时,也能同时工作,故A、B都是错误的;在并联电路中,各支路两端的电压都等于电源电压,故C是正确的;只有在串联电路中,电流才一定相等,故D是错误的. 4.若将20只相同的小灯泡串联接在220 V的电路中,每只小 灯泡两端的电压为_______V,若将20只相同的小灯泡并联 在110 V的电路中,每只小灯泡两端的电压为_______V. 【解析】串联电路的总电压等于各用电器两端电压之和, 20只灯泡相同,则每只灯泡两端电压相同,即 并联电路各支路两端的电压相等,都等于电 源电压,故并联时,每只小灯泡两端的电压为110 V. 答案:11 110 5.如图所示,当S1闭合、S2断开 时,电压表示数为2.5 V;当S1 断开、S2闭合时,电压表示数为 6 V.灯L1两端的电压为_______V, 灯L2两端的电压为_______V,电 源电压为_______V. 【解析】灯L1与L2串联,当S1闭合、S2断开时,电压表并联在L1的两端,测L1的电压,U1=2.5 V;当S1断开、S2闭合时,电压表并联在电源两端,测电源电压,也就是灯L1、L2串联后的总电压U,由U=U1+U2可知,灯L2两端的电压U2=U-U1=6 V-2.5 V=3.5 V. 答案:2.5 3.5 6 6.将图中的元件用笔画线连接起来,要求两节干电池串联,电灯L1与L2串联,电压表V1测L1两端的电压,V2测L2两端的电压. 【解析】电源为两节干电池串联,则总电压为3 V,故电压表V1和V2均应选用“-”和“3”两接线柱;连接电路时,先将除电压表之外的元件依次连接,连接好后,最后根据电压表的测量要求,将电压表分别与被测的用电器并联,同时要注意正负接线柱的正确接法;连接时,接线点必须在接线柱上,导线不能交叉. 一、串联电路电压的规律 1.内容:串联电路中总电压等于_________________________. 2.公式:____________. 1.内容:并联电路各支路两端的电压_____,并且等于____ ___. 2.公式:___________.。
2012年高考数学临考突击专项训练系列:选择 23.pdf

例题3:一个定值电阻与一个滑动变阻器串联后接在电源上,用电压表测得定值电阻两端的电压是6伏,又用电流表测得通过定值电阻的电流是0.3安,求这个定值电阻的阻值。
解:已知U=6伏,I=0.3安 = =20欧 答:阻值是20欧。
㈢已知电流、电压,求电阻 车床照明灯的电压是36V,它正常工作时灯丝的电阻是32Ω。
求通过灯丝的电流。
R=32Ω I=? U=36V 已知: U=36V R=32Ω 求: I=? 答:车床照明灯正常工作时,通过灯丝的电流约为1.13A. 解: I=U R 36V 32Ω=≈ 1.13A 在如图所示的电路中,调节滑动变阻器 R’,使灯泡正常发光,用电流表测得通过它的电流值是0.6A。
已知该灯泡正常发光时的电阻是20Ω,求灯泡两端的电压。
已知: R=20Ω,求: 解: U=? U=I×R=0.6A×20Ω 两端的电压是12V。
=12V 答: R=20Ω A R′ I=0.6A I=0.6A 某同学用一只电流表和灯泡串联,测得它正常发光时的电流是0.18A,再用电压表测得灯泡两端的电压是220V,试计算灯丝正常发光时的电阻值。
答: 已知: 求: 解: U=220V, I=0.18A R=? 灯丝正常发光时的电阻值为1222Ω R=U I 220V 0.18A==1222Ω A V 如何测量一个待测电阻(或小灯泡)的阻值? 1、请画出测量的电路图; 2、列出所需器材; 3、写出测量步骤。
伏安法测电阻 1.有甲乙两导体,甲导体的电阻是2Ω,两端电压是2V;乙导体的电阻是4Ω,两端电压是8V。
某学生计算甲导体中的电流I甲时,列出: 课堂练习 I甲=U R 8V 2Ω =4A = 试指出以上计算过程错在何处?并用正确的方法计算出甲乙两导体中通过的电流值。
误将乙导体两端的电压作为甲导体两端的电压。
答: 正解: I甲=U甲 R甲 2V 2Ω =1A = I乙=U乙 R乙 8V 4Ω =2A = 2.加在某一电阻器两端的电压为5V时,通过它的电流是0.5 A,则该电阻器的电阻应是多大?如果两端的电压增加到20V,此时这个电阻器的电阻值是多大?通过它的电流是多大? U2=20V R=? I2=? I1=0.5A R U1=5V 已知: 已知: U1=5V,I1=0.5A 求:R=? 解: U1 I1 5V 0.5AR==10Ω=U2=20V,R=10 Ω 解: 求:I2=? R U2 10 Ω 20V=I2==2A 3、某电流表的电阻约为0.1Ω,它的量程是0.6A,如将这个电流表直接连接到2V的蓄电池的两极上,会产生什么后果? 德国物理学家欧姆用 的方法研究了电流与电压和电阻的关系,得到导体中的电流跟导体两端的电压成 ,跟导体的电阻成 。
2012年普通高等学校招生全国统一考试数学冲刺卷 Ⅰ 理(浙江卷)

2012年普通高等学校招生全国统一考试冲刺卷Ⅰ数学理科(某某卷)本试卷分选择题和非选择题两部分。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)1.答题前,考生务必将自己的某某、准备考证号用黑色字迹的签字笔或钢笔分别填写在试卷个答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:如果事件A , B 互斥, 那么棱柱的体积公式P (A +B )=P (A )+P (B )V =Sh如果事件A , B 相互独立, 那么 其中S 表示棱柱的底面积, h 表示棱柱的高P (A ·B )=P (A )·P (B ) 棱锥的体积公式如果事件A 在一次试验中发生的概率是p , 那么nV =31Sh次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积, h 表示棱锥的高P n (k )=C k n p k (1-p )n -k(k = 0,1,2,…, n ) 球的表面积公式棱台的体积公式S = 4πR 2)2211(31S S S S h V ++=球的体积公式其中S 1, S 2分别表示棱台的上、下底面积, V =34πR 3h 表示棱台的高 其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)集合}2{},,,{},2,3{=⋂==N M b a N M a若,则M∪N=(A){0,1,2}(B){0,1,3}(C){0,2,3}(D){1,2,3}(2)下列命题中的假命题是(A) ∀x R ∈,120x -> (B)∀*x N ∈,2(1)0x ->(C) ∃x R ∈,lg 1x < (D) ∃x R ∈,tan 2x = (3)设复数z 满足zi21+=i ,则 z =(A)—2+i(B)—2—i(C) 2+i(D) 2—i (4)数列1111424816,8,16,32,,的前n 项和为(A) 1221n n +--- (B) 2223n n +---(C) 1221n n +-+-(D) 11221n n +----(5)设13log 2a =,12log 3b =,0.312c ⎛⎫= ⎪⎝⎭,则(A) a <b <c(B) a <c <b(C) b <c <a(D) b <a <c(6)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且2,32cos -=⋅=CB AC C 且则,26=+b a c 等于(A) 5(B) 13(C) 4 (D)17(7)0,65,31=•∠=∠==OC OB AOB C AOB 外且在点π,设实数n m , 满足OB n OA m OC +=,则等于nm(A)—2 (B) 2 (C) 3 (D) —3(8)设双曲线22221x y a b-=的一条渐近线与抛物线21y x =+只有一个公共点,则双曲线的离心率为 (A)54(B)5(C)2(9) 10)31(xx -的展开式中含x 的正整数指数幂的项数是 (A) 2 (B) 0 (C) 6(D) 4(10)将一颗骰子投掷两次,第一次出现的点数记为a ,第二次出现的点数记为b ,设两条直线l 1:ax +b y =2,l 2:x +2y =2平行的概率为P 1,相交的概率为P 2,试问点(P 1,P 2)与直线l 2:x +2y =2的位置关系是(A)P 在直线l 2的右下方 (B)P 在l 2直线的左下方 (C)P 在直线l 2的右上方(D)P 在直线l 2上非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分. (11) 右边程序框图输出的结果为▲. (12)在ABC ∆中,已知D 是AB 边上一点,若12,3AD DB CD CA CB λ==+,则λ等于▲.(13)已知函数)(x f 是R 上的偶函数,且在(0,+∞)上有f '(x )> 0,若f (-1)= 0,那么关于x 的不等式x f (x )的解集是▲.(14)如图,是某几何体的三视图,其中正视图是腰长为a 2形俯视图是半径为a 的半圆,则该几何体的表面积是▲.(15)过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=则椭圆的离心率为▲.(16)具有性质1f x ⎛⎫-⎪⎝⎭=()f x -的函数,我们称其为满足“倒负”变换的函数,下列函数:(1)y =x -1x ; (2)y =x +1x; (3)y =0101)11x x x x x⎧⎪⎪⎨⎪⎪⎩(<<)(=-(>), 其中不满足“倒负”变换的函数是▲. (17)设f 1(x )=21+x ,f n +1(x )=f 1[f n (x )],且a n =f n (0)-1f n (0)+2,则a 2011等于▲.三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. (18)(本题满分14 分)如图,在平面直角坐标系xOy 中,以x 轴为始边作两个锐角,αβ,它们的终边分别与单位圆交于,A B 两点.已知,A B (1)求tan()αβ+的值; (2)求2αβ+的值.(19)(本题满分14分)各项均为正数的数列{}n a 中,n S a ,11=是数列{}n a 的前n 项和,对任意*∈N n ,有)(222R p p pa pa S n n n ∈-+=; (1)求常数p 的值; (2)求数列{}n a 的通项公式;(3)记n nn n S b 234⋅+=,求数列{}n b 的前n 项和n T(20)(本题满分14分)如图,四棱锥P —ABCD 中,底面ABCD 为矩形,PD ⊥底面ABCD ,AD=PD =1,AB =2a ,(a >0),E 、F 分别CD 、PB 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年高考冲刺数学强化训练
上海南汇中学 王海平
2012年5月15日星期二(高考倒数第22天)
集合与简易逻辑
1. 例1.集合R x x y y M ∈==,2,R x x y y N ∈+-==,12,则=N M
例2.集合{}R x x y y x M ∈==,),(2,{}
R x x y y x N ∈+-==,1),(2
,=N M
例3.集合()(){}R M ∈+==λλ,4,32,1,集合()(){}
R N ∈+==λλ,5,43,2,则=N M
2.研究集合必须注意集合元素的特征,即集合元素的三性:确定性、互异性、无序性。
例4.已知集合{},,lg()A x xy xy =,集合{}y x B ,||,0=,且B A =,则=+y x
3.集合的性质:① 任何一个集合P 都是它本身的子集,记为P P ⊆。
② 空集是任何集合P 的子集,记为P ⊆∅。
③ 空集是任何非空集合P 的真子集,记为P ≠
⊂∅。
注意:若条件为B A ⊆,在讨论的时候不要遗忘了∅=A 的情况。
例5.集合}012|{2
=--=x ax x A ,如果∅=+
R A ,实数a 的取值范围
集合的运算:
④ ()()C B A C B A =、()()C B A C B A =; ()()()U U U C A B C A C B = 、()()()U U U C A B C A C B = 。
⑤ ∅=⇔⊆⇔⊆⇔=⇔=B C A A C B C B A B B A A B A U U U 。
⑥ 对于含有n 个元素的有限集合M ,其子集、真子集、非空子集、非空真子集的个数依次为:n
2、
12-n 、12-n 、22-n 。
例6.满足条件{}{}5,4,3,2,12,1⊆⊂≠
A 的集合A 共有 个。
4.研究集合之间的关系,当判断不清时,建议通过“具体化...”的思想进行研究。
例7.已知{}N k k x x M ∈+==,12,{}
N k k x x N ∈±==,14,则N M _____。
5.补集思想....
常运用于解决否定型或正面较复杂的有关问题。
例8.设函数()()1222422+----=p p x p x x f 在区间[]1,1-上至少存在一个实数C ,使()0>c f ,求实数p 的取值范围
6.命题是表达判断的语句。
判断正确的叫做真命题;判断错误的叫做假命题。
① 命题的四种形式及其内在联系: 原命题:如果α,那么β;
逆命题:如果β,那么α; 否命题:如果α,那么; 逆否命题:如果β,那么α;
② 等价命题:对于甲、乙两个命题,如果从命题甲可以推出命题乙,同时从命题乙也可以推出命题甲,既“甲⇔乙”,那么这样的两个命题叫做等价命题。
③ 互为逆否命题一定是等价命题,但等价命题不一定是互为逆否命题。
④ 当某个命题直接考虑有困难时,可通过它的逆否命题来考虑。
例9.“βαs i n s i n ≠”是“βα≠”的 条件。
⑤ 注意命题“如果α,那么β”的否定与它的否命题的区别:
命题“如果α,那么β”的否定是“如果α,那么”;否命题是“如果α,那么”。
*例10.“若a 和b 都是偶数,则b a +是偶数”的否命题是 否定是
7.常见结论的否定形式:
8在判断“充要条件”的过程中,应注意步骤性:
首先必须区分谁是条件、谁是结论,然后由推导关系判断结果。
【参考答案】§集合与简单逻辑 1.[]1,0
2. ⎪⎭
⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛21,22,21,22 3. (){}2,2--
4. 2-
5. 0≤a
6. 7
7. N M ≠
⊂ 8. ⎪⎭
⎫ ⎝⎛
-23,3
9. 充分非必要条件
10. 否命题是“若a 和b 不都是偶数,则b a +是奇数”;否定是“若a 和b 都是偶数,则b a +是奇数”。
