山东省英雄山中学09-10学年高一数学上期中考试试卷人教版必修一

合集下载

(完整版)人教版高一上学期必修1数学期中测试题含答案,推荐文档

10.A
11.A 提示： f 3 f 2 f 1 f 0， f 2 f 0.414， f 2 f 1
由于函数 f (x) 在 R 上为偶函数，且在区间[1,0] 上为递增，于是区间[0,1] 上为递减。
为单调递增。
y
loga
x 单调递减。
6.C。7.C
8.A
提示：由 x log2 3 1得 x
lg 2 lg 3
log 3
2 ，于是 3x
9x
2 22
6。
9.B 提示：函数 y f (x 1) 中的 x 1应满足1 x 1 2 0 x 1，故
y f (x 1) 的定义域为0,1。
20．（本题满分 12 分）已知 f (x) loga (1 x)(a 0, a 1) 。（1）求 f (x) 得定义域；（2）求使 f (x) 0 成立的 x 的取值范围。
21．（本题满分 12 分）我国是水资源匮乏的国家为鼓励节约用水，某市打算出台一项水费政策措施，规定：每一季度每人用水量不超过 5 吨时，每吨水费收基本价 1．3 元；若超过 5 吨而不超过 6 吨时，超过部分水费加收 200%；若超过 6 吨而不超过 7 吨时，超过部分的水费加收 400%，如果某
2 3
,
Hale Waihona Puke 4．已知 f (x6 ) log2 x ，则 f (8) （）
4
A.
3
B. 8
C. 18
1
D.
2
5．当 0＜a＜1 时，在同一坐标系中，函数 y ax 与 y loga x 的图象是( )
6、若函数 y (a2 3a 3) a x 是指数函数，则有
（
）
A、 a 1或a 2 B、 a 1

人教版高一数学上学期期中考试试题(含两套,附答案)

人教版高一数学上学期期中考试试题（含两套，附答案）考试时间：120分钟满分：150分一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请将正确的答案填涂在答题卡上.1. 已知集合{}6,5,4,3,2,1=U ，{}5,3,2=M ,{}6,4=N ,则=N M C U)(（） A.{}46， B.{}146，， C.∅ D.{}23456，，，， 2.以下各组两个函数是相同函数的是（） A ()(),f x g x ==B.()()2,25f x g x x ==-C.)(12)(),(12)(Z n n n g Z n n n f ∈+=∈-=D.12)(|1|)(2+-=-=x x x g x x f ，3.已知点M 在幂函数()f x 的图象上，则()f x 的表达式为（） A.12()f x x = B.12()f x x -= C.2()f x x = D.2()f x x -=4. 函数⎪⎩⎪⎨⎧≥<-=-)1(2)1(21)(x x xx f x ，((2))f f -=（）A.21 B.41C.2D.4 5.函数()2ln f x x x=-的零点所在的大致区间的（） A.()1,2 B.()2,3 C.(),3e D.(),e +∞ 6.函数xxee xf --=)(是（）A.奇函数，且在(,)-∞+∞上是增函数B.奇函数，且在(,)-∞+∞上是减函数C.偶函数，且在(,)-∞+∞上是增函数D.偶函数，且在(,)-∞+∞上是减函数 7.对于函数()f x ，在使()f x m ≤恒成立的式子中，常数m 的最小值称为函数()f x 的“上界值”，则函数33()33x x f x -=+的“上界值”为（）A.2B.－2C.1D.－18.已知1.01.1=x ，1.19.0=y ，34log 32=z ，则（） A.z y x >> B.z x y >> C.x z y >> D.y z x >>9.函数()()2212f x x a x =+-+在(]4,∞-上是减函数，则实数a 的取值范围是（） A.3a ≤- B.3a ≥- C.5a ≥ D.3a ≥10.已知2211)(xx x f -+=，则)(x f 不满足．．．的关系是（） A.)()(x f x f =- B.)()1(x f xf = C.)()1(x f x f -= D.)()1(x f xf -=-11.已知函数324)(2---=xx x f ，若2)1(->-x f ，则实数x 的取值范围是（） A.[]3,1- B.[]2,2- C.()()+∞∞-,20, D.()2,0 12.如图一直角墙角，两边的长度尺足够长，P 处有一棵树与两墙的距离分别是am 、4m ，其中012a <<，不考虑树的粗细，现在想用16m 长的篱笆，借助墙角围成一个矩形的花圃ABCD ，设此矩形花圃的最大面积为S ，若将这棵树围在花圃内，则函数()S f a =（单位2m ）的图象大致是（）二、填空题（本大题共4小题，每小题5分，共20分）13.已知集合{}2|230A x x x =--=，{}|0B x x a =-=，若B A ⊂≠，则实数a 的值构成的集合是．14.2()lg(45)f x x x =--+的单调递增区间为． 15.已知函数)(x f )10(2≠>=-a a ax ，经过定点)1,(m ，则函数x m y =的反函数是．16.若函数()x f 同时满足：①对于定义域上的任意x ，恒有()()0=-+x f x f ；②对于定义域上的任意21,x x ，当21x x ≠时，恒有()()02121<--x x x f x f ，则称函数()x f 为“理想函数”。

山东省泰安英雄山中学2009届高三年级第一次复习检测数学文科卷人教版

山东省泰安英雄山中学2009届高三年级第一次复习检测数学文科卷第Ⅰ卷一、选择题（本大题共12小题，每题，5分，共60分） 1．设集合""""},30|{},01|{B m A m x x B x xx A ∈∈<<=<-=是那么的（）A ．充分不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 2．若命题p B A x p ⌝∈则 :是（）A ．B x A x ∉∉且 B ．B x A x ∉∉或C ．B A x ∉D ．B A x ∈3．已知函数)1(+=x f y 的图象过点（3，2），则函数)(x f 的图象关于x 轴的对称图形一定过点（）A ．（2，－2）B ．（2，2）C ．（－4，2）D ．（4，－2）4．如果奇函数)(x f 在区间)0](,[>>a b b a 上是增函数，且最小值为m ，那么)(x f 在区间],[a b --上是（）A ．增函数且最小值为mB ．增函数且最大值为－mC ．减函数且最小值为mD ．减函数且最大值为－m5．定义M N N M B x A x x B A -==∉∈=-是若且},6,3,2{},5,4,3,2,1{},|{等于（） A ．M B ．N C ．{1，4，5} D ．{6}6．与函数)12lg(1.0-=x y 的图象相同的函数解析式是（）A ．)21(12>-=x x y B ．121-=x yC ．)21(121>-=x x y D ．|121|-=x y 7．对一切实数x ，不等式01||2≥++x a x 恒成立，则实数a 的取值范围是（）A ．]2,(--∞B ．[－2，2]C ．),2[+∞-D ．),0[+∞8．把函数)(x f y =的图像沿x 轴向右平移2个单位，所得的图像为C ，C 关于x 轴对称的图像为y=2x 的图像，则)(x f y =的函数表达式为（）A ．22+=x yB ．22+-=x yC ．22--=x yD ．)2(log 2+-=x y9．设奇函数),0()(+∞在x f 上为增函数，且的则不等式0)()(,0)1(<--=xx f x f f 解集为（）A ．),1()0,1(+∞-B ．)1,0()1,( --∞C ．),1()1,(+∞--∞D ．)1,0()0,1( -10．当]2,0[∈x 时，函数23)1(4)(2=--+=x x a ax x f 在时取得最大值，则a 的取值范围是（）A ．],21[+∞-B ．),0[+∞C ．),1[+∞D ．),32[+∞11．已知),(1,log 1,4)13()(+∞-∞⎩⎨⎧><+-=是x x x a x a x f a 上是减函数，那么a 的取值范围是（）A ．（0，1）B ．)31,0(C ．)1,71[D ．)31,71[12．国家规定个人稿费纳税办法是：不超过800元的不纳税；超过800元而不超过4000元的按超过800元部分的14%纳税；超过400元的按全部稿酬的11%纳税。

人教版新教材高中数学高一上学期期中考试数学试卷(共三套)

人教版新教材高中数学高一上学期期中考试数学试卷（一）一、选择题（共12小题）1．命题“0x R ∃∈，2450x x ++>”的否定是（）A ．0x R ∃∈，2450x x ++>B ．0x R ∃∈，2450x x ++≤C ．x R ∀∈，2450x x ++>D ．x R ∀∈，2450x x ++≤2x 的取值范围是（） A ．1≥x B ．2x ≠ C ．1x > D ．1≥x 且2x ≠3．若a >b >0，c <d <0，则一定有（）A ．a c >b dB ．a c b cD ．a d C ．P Q =D ．不确定5．若1m n >>，a =，()1lg lg 2b m n =+，lg 2m n c +⎛⎫= ⎪⎝⎭，则（） A ．a b c <时，不等式11x a x +≥-恒成立，则实数a 的取值范围是（） A ．(],2-∞ B ．[)2,+∞ C ．[)3,+∞ D ．(],3-∞7．一元二次方程220x bx +-=中，若0b <，则这个方程根的情况是（）A ．有两个正根B ．有一正根一负根且正根的绝对值大C ．有两个负根D ．有一正根一负根且负根的绝对值大8．不等式22412ax x a x ++>-对一切x ∈R 恒成立，则实数a 的取值范围是（）A ．2a >B ．2a <-C ．22a -<<D ．2a < 9．已知函数21,0(),0x x f x x x +≥⎧=⎨<⎩，则[(2)]f f -的值为（） A ．1 B ．2C ．4D ．5 10．若函数()f x 满足(32)98f x x +=+，则()f x 的解析式是（）A ．()98f x x =+B ．()=32f x x +C ．()=34f x x --D ．()=32f x x +或()=34f x x --11．已知函数22,(1)()(21)36,(1)x ax x f x a x a x ⎧-+≤=⎨--+>⎩，若()f x 在(),-∞+∞上是增函数，则实数a 的取值范围是（）A ．1,12⎛⎤ ⎥⎝⎦B ．1,2⎛⎫+∞ ⎪⎝⎭C ．[1,)+∞D ．[]1,212．已知函数2()23f x x ax =-+，且其对称轴为1x =，则以下关系正确的是（）A ．(3)(2)(7)f f f -<，0y >，且28x y xy +=，则x y +的最小值是________．16．已知函数()f x =的定义域为R ，则a 的取值范围为_______ .17．已知函数()151x m f x =-+是奇函数，则实数m 的值为________. 18．已知函数()f x 是定义在R 上的奇函数，当0x ≥时，()()1f x x x =+，则0x <时，()f x = ________.三．解析题（共6小题）19．已知函数()218f x ax bx =++，()0f x >的解集为()3,2-．（1）求()f x 的解析式；（2）当1x >-时，求()211f x y x -=+的最大值． 20．已知关于x 的不等式2260kx x k -+<；（1）若不等式的解集为()2,3，求实数k 的值；（2）若0k >，且不等式对一切23x <<都成立，求实数k 的取值范围．21．已知函数2()23=++f x x ax ，[]4,6x ∈-．（1）当2a =-时，求()f x 的最值；（2）求实数a 的取值范围，使()y f x =在区间[]4,6-上是单调函数；22．已知函数()[)22,1,x x a f x x x++=∈+∞．（1）当12a =时，求函数()f x 的最小值；（2）若对任意[)1,x ∈+∞，()0f x >恒成立，试求实数a 的取值范围．23．已知函数()21x b f x x +=-是定义域()1,1-上的奇函数. （1）确定()f x 的解析式；（2）用定义证明：()f x 在区间()1,1-上是减函数；（3）解不等式()()10f t f t -+<.24．已知()()2227m f x m m x -=--是幂函数，且在()0,∞+上单调递增．（1）求m 的值；（2）求函数()()()211g x f x a x =--+在区间[]2,4上的最小值()h a ．【答案解析】二．选择题（共12小题）1．命题“0x R ∃∈，2450x x ++>”的否定是（）A ．0x R ∃∈，2450x x ++>B ．0x R ∃∈，2450x x ++≤C ．x R ∀∈，2450x x ++>D ．x R ∀∈，2450x x ++≤ 【答案】D【解析】命题“0x R ∃∈，2450x x ++>”的否定是：x R ∀∈，2450x x ++≤故选D2x 的取值范围是（） A ．1≥xB ．2x ≠C ．1x >D ．1≥x 且2x ≠【答案】D【解析】解：根据题意，得1020x x -≥⎧⎨-≠⎩，解得1≥x 且2x ≠. 故选：D.3．若a >b >0，c <d <0，则一定有（）A ．a c >b dB ．a c bc D ．ad －d >0，∴110d c>>--，又a >b >0，∴a b d c >--，∴a b d c <.故选：D.方法2：令a ＝3，b ＝2，c ＝－3，d ＝－2.则a c ＝－1，b d＝－1，排除选项A ，B. 又a d ＝－32，b c ＝－23，∴a b d c <，排除选项C. 故选：D.4．若实数x ，y ，z 满足1212y x y y z y-<<-⎧⎨-<<-⎩，记2P xy yz xz y =+++，2Q x y z =++，则P 与Q 的大小关系是（）A ．P Q C ．P Q =D ．不确定【答案】A【解析】 ()22P Q xy yz xz y x y z =--+++++()()()2111xz y x z y =+-++-- ()()111x y z y =+-+--因为1212y x y y z y -<<-⎧⎨-<<-⎩，所以()10,1x y +-∈，()10,1z y +-∈，所以()()()110,1x y z y +-+-∈，所以110P Q -<-=，即P Q <故选：A5．若1m n >>，a ，()1lg lg 2b m n =+，lg 2m n c +⎛⎫= ⎪⎝⎭，则（） A ． a b c <>，所以lg lg 0m n >>，则()1lg lg 2b m n =+≥，因为lg lg m n >，所以等号不成立，即()1lg lg 2b m n a =+>=，因为2m n +>()1lg lg lg 22m n c m n b +⎛⎫=>=+= ⎪⎝⎭，所以a b c <<，故选:A.6．当1x >时，不等式11x a x +≥-恒成立，则实数a 的取值范围是（） A ．(],2-∞B ．[)2,+∞C ．[)3,+∞D ．(],3-∞ 【答案】D【解析】因为当1x >时，不等式11x a x +≥-恒成立，又111121311x x x x +=-++≥+=--，当且仅当2x =时取等号，所以11`x x +-的最小值等于3， 3a ∴≤则实数a 的取值范围为](3-∞，故选：D7．一元二次方程220x bx +-=中，若0b <，则这个方程根的情况是（）A ．有两个正根B ．有一正根一负根且正根的绝对值大C ．有两个负根D ．有一正根一负根且负根的绝对值大【答案】B【解析】由220x bx +-=，可知()2241280b b ∆=-⨯⨯-=+>，所以方程有两个不相等的实数根.设方程220x bx +-=的两个根为c ，d ，则c d b +=-，2cd =-，由2cd =-得方程的两个根为一正一负，排除Ａ，Ｃ由c d b +=-和0b <可知方程的两个根中，正数根的绝对值大于负数根的绝对值，Ｂ正确故选：B.8．不等式22412ax x a x ++>-对一切x ∈R 恒成立，则实数a 的取值范围是（）A ．2a >B ．2a <-C ．22a -<<D ．2a <【答案】A【解析】不等式22412ax x a x ++>-对一切x ∈R 恒成立，即()22410a x x a +++->对一切x ∈R 恒成立，若20a +=，显然不恒成立.若20a +≠，则200a +>⎧⎨∆<⎩，即()()20164210a a a +>⎧⎨-+-<⎩，解得2a >. 故选：A9．已知函数21,0(),0x x f x x x +≥⎧=⎨<⎩，则[(2)]f f -的值为（） A ．1B ．2C ．4D ．5 【答案】D【解析】因为函数21,0(),0x x f x x x +≥⎧=⎨<⎩，则(2)=4f -，又(4)=5f ，所以[(2)]=5f f -故选：D.10．若函数()f x 满足(32)98f x x +=+，则()f x 的解析式是（）A ．()98f x x =+B ．()=32f x x +C ．()=34f x x --D ．()=32f x x +或()=34f x x --【答案】B【解析】设232,3t t x x -=+∴=，所以2()983(2+8=323t f t t t -=⨯+=-+）所以()=32f x x +.故选：B.11．已知函数22,(1)()(21)36,(1)x ax x f x a x a x ⎧-+≤=⎨--+>⎩，若()f x 在(),-∞+∞上是增函数，则实数a 的取值范围是（）A ．1,12⎛⎤ ⎥⎝⎦B ．1,2⎛⎫+∞ ⎪⎝⎭C ．[1,)+∞D ．[]1,2【答案】D【解析】因为函数22,(1)()(21)36,(1)x ax x f x a x a x ⎧-+≤=⎨--+>⎩，在(),-∞+∞上是增函数，所以1210122136a a a a a ≥⎧⎪->⎨⎪-+≤--+⎩，解得12a ≤≤，故选：D12．已知函数2()23f x x ax =-+，且其对称轴为1x =，则以下关系正确的是（）A ．(3)(2)(7)f f f -<<B ．(3)(2)(7)f f f -=<C ．(2)(3)(7)f f f <-<D ．(2)(7)(3)f f f <<-【答案】C【解析】解：根据题意，函数2()25f x x ax =-+，其对称轴为1x =，其开口向上， ()f x 在[1，)+∞上单调递增，()()35f f -=，则有()()()2(3)57f f f f <-=<；故选：C ．三．填空题（共6小题）13．已知集合A ＝{x |x <a }，B ＝{x |1<x <2}，A ∪(∁R B )＝R ，则实数a 的取值范围是________．【答案】{a |a ≥2}【解析】∵B ＝{x |1<x <2}，∴∁R B ＝{x |x ≤1或x ≥2}．又∵A ∪(∁R B )＝R ，A ＝{x |x <a }．观察∁R B 与A 在数轴上表示的区间，如图所示：可得当a ≥2时，A ∪(∁R B )＝R.故答案为{a |a ≥2}14．已知14x y -<+<，23x y <-<，则32x y +的取值范围是________. 【答案】323,22⎛⎫- ⎪⎝⎭【解析】设()()32+=++-x y m x y n x y ，则32m n m n +=⎧⎨-=⎩，∴5212m n ⎧=⎪⎪⎨⎪=⎪⎩即()()513222+=++-x y x y x y ，又∵14x y -<+<，23x y <-<， ∴()551022x y -<+<，()13122x y <-<， ∴()()351232222x y x y -<++-<，即3233222x y -<+< ，∴32x y +的取值范围为323,22⎛⎫- ⎪⎝⎭. 故答案为：323,22⎛⎫- ⎪⎝⎭15．已知0x >，0y >，且28x y xy +=，则x y +的最小值是________．【答案】18【解析】解：因为0x >，0y >，且28x y xy +=，所以281y x +=，所以28()x y x y y x ⎛⎫+=++ ⎪⎝⎭ 2882x y y x=+++1018≥+= 当且仅当28x y y x =，即12,6x y ==取等号，所以x y +的最小值为18，故答案为：1816．已知函数()f x =的定义域为R ，则a 的取值范围为_____ .【答案】[]0,1【解析】由于函数()f x =的定义域为R ，∴不等式2210ax ax ++≥对任意的x ∈R 恒成立，当0a =时，10≥恒成立，即0a =符合题意；当0a ≠时，则20440a a a >⎧⎨∆=-≤⎩，得001a a >⎧⎨≤≤⎩，解得01a <≤.综上，a 的取值范围是[]0,1. 故答案为：[]0,1. 17．已知函数()151xmf x =-+是奇函数，则实数m 的值为________. 【答案】2 【解析】因为()f x 是奇函数，所以(0)102mf =-=，解得2m =， 2m =时，51()15151x x xm f x -=-=++，满足()()f x f x -=-，是奇函数，故答案为：2．18．已知函数()f x 是定义在R 上的奇函数，当0x ≥时，()()1f x x x =+，则0x <时，()f x = ________. 【答案】()1x x - 【解析】当0x <时，0x -> ()()1f x x x ∴-=--()f x 为奇函数 ()()()1f x f x x x ∴=--=- 本题正确结果：()1x x - 三．解析题（共6小题）19．已知函数()218f x ax bx =++，()0f x >的解集为()3,2-．（1）求()f x 的解析式；（2）当1x >-时，求()211f x y x -=+的最大值．【答案】（1）()23318f x x x =--+；（2）max 3y =-.【解析】（1）因为函数()218f x ax bx =++，()0f x >的解集为()3,2-，那么方程2180ax bx ++=的两个根是3-，2，且0a <，由韦达定理有3213183326b a ab a ⎧-+=-=-⎪=-⎧⎪⇒⎨⎨=-⎩⎪-⋅=-=⎪⎩，所以()23318f x x x =--+．（2）()()221113331331111f x x x x x y x x x x x -++---⎛⎫===-⋅=-+ ⎪++++⎝⎭()13111x x ⎡⎤=-++-⎢⎥+⎣⎦，由1x >-，则：根据均值不等式有：1121x x ++≥+，当且仅当 111x x +=+，即0x =时取等号， ∴当0x =时，max 3y =-．20．已知关于x 的不等式2260kx x k -+<；（1）若不等式的解集为()2,3，求实数k 的值；（2）若0k >，且不等式对一切23x <<都成立，求实数k 的取值范围．【答案】（1）25k =（2）20,5⎛⎤⎥⎝⎦【解析】（1）不等式2260kx x k -+<的解集为()2,32∴和3是方程2260kx x k -+=的两根且0k >由根与系数的关系得：223k+=，解得：25k =（2）令()226f x kx x k =-+，则原问题等价于()()2030f f ⎧≤⎪⎨≤⎪⎩即44609660k k k k -+≤⎧⎨-+≤⎩，解得：25k ≤又0k >∴实数k 的取值范围是20,5⎛⎤⎥⎝⎦21．已知函数2()23=++f x x ax ，[]4,6x ∈-．（1）当2a =-时，求()f x 的最值；（2）求实数a 的取值范围，使()y f x =在区间[]4,6-上是单调函数；【答案】（1）最小值是1-，最大值是35.；（2）6a -或4a . 【解析】解：（1）当2a =-时，22()43(2)1f x x x x =-+=--，由于[]4,6x ∈-，()f x ∴在[]4,2-上单调递减，在[]2,6上单调递增，()f x ∴的最小值是()21f =-，又(4)35,(6)15f f -==，故()f x 的最大值是35.（2）由于函数()f x 的图像开口向上，对称轴是x a =-，所以要使()f x 在[]4,6-上是单调函数，应有4a --或6a -，即6a -或4a .22．已知函数()[)22,1,x x a f x x x++=∈+∞．（1）当12a =时，求函数()f x 的最小值；（2）若对任意[)1,x ∈+∞，()0f x >恒成立，试求实数a 的取值范围．【答案】（1）72（2）3a >- 【解析】（1）当12a =时，()122f x x x =++，∵()f x 在区间[)1,+∞上为增函数，∴由对勾函数的性质知函数()f x 在区间[)1,+∞上的最小值为()712f =.（2）在区间[)1,+∞上，()220x x af x x++=>恒成立220x x a ⇔++>恒成立．设22y x x a =++，[)1,x ∈+∞，因为()222+a=11y x x x a =+++-在[)1,+∞上递增，∴当1x =时，min 3y a =+，于是，当且仅当min 30y a =+>时，函数()0f x >恒成立，故3a >-.23．已知函数()21x bf x x +=-是定义域()1,1-上的奇函数. （1）确定()f x 的解析式；（2）用定义证明：()f x 在区间()1,1-上是减函数；（3）解不等式()()10f t f t -+<. 【答案】（1）()21x f x x =-；（2）证明见解析；（3）1,12⎛⎫⎪⎝⎭. 【解析】（1）由于函数()21x bf x x +=-是定义域()1,1-上的奇函数，则()()f x f x -=-，即()2211x bx b x x -++=-+-+，化简得0b =，因此，()21xf x x =-；（2）任取1x 、()21,1x ∈-，且12x x <，即1211x x -<<<，则()()()()()()()()()()()()2212212112121222221211221211111111111x x x x x x x x x x f x f x x x x x x x x x ----+-=-==---+-+--，1211x x -<<<，210x x ∴->，1210x x +>，110x -<，110x +>，210x -<，210x +>.()()120f x f x ∴->，()()12f x f x ∴>，因此，函数()y f x =在区间()1,1-上是减函数；（3）由（2）可知，函数()y f x =是定义域为()1,1-的减函数，且为奇函数，由()()10f t f t -+<得()()()1f t f t f t -<-=-，所以111111t t t t ->-⎧⎪-<-<⎨⎪-<<⎩，解得112t <<. 因此，不等式()()10f t f t -+<的解集为1,12⎛⎫⎪⎝⎭.24．已知()()2227m f x m m x -=--是幂函数，且在()0,∞+上单调递增．（1）求m 的值；（2）求函数()()()211g x f x a x =--+在区间[]2,4上的最小值()h a ．【答案】（1）4 （2）当52a <时， ()()274h a g a ==-；当5922a ≤≤时，()()22121124a a g h a --⎛⎫==-+ ⎪⎝⎭，当92a >时， ()()4218h a g a ==-．【解析】（1）()()2227m f x m m x -=--是幂函数，∴2271m m --=，解得4m =或2m =-；又()f x 在()0,∞+上单调递增， ∴20m ->， ∴m 的值为4；（2）函数()()()()2211211g x f x a x x a x =--+=--+，当52a <时，()g x 在区间[]2,4上单调递增，最小值为()()274h a g a ==-；当5922a ≤≤时，()g x 在区间[]2,4上先减后增，最小值为()()22121124a a g h a --⎛⎫==-+ ⎪⎝⎭，当92a >时，()g x 在区间[]2,4上单调递减，最小值为()()4218h a g a ==-．人教版新教材高中数学高一上学期期中考试数学试卷（二）一、选择题（共12小题）1．有下列四个命题，其中真命题是（）． A ．n ∀∈R ，2n n ≥B ．n ∃∈R ，m ∀∈R ，m n m ⋅=C ．n ∀∈R ，m ∃∈R ，2m n <D ．n ∀∈R ，2n n <2． 22530x x --<的一个必要不充分条件是（）A ．132x -<22，则a b >B ．若a b >，则11a b< C ．若a b >，c d >，则a c b d ->- D ．若a b >，c d <，则a b c d> 4．下列不等式中，正确的是（） A ．a ＋4a≥4 B ．a 2＋b 2≥4abC ≥2a b+ D ．x 2＋23x 5．已知2x >-，8y >-，8082x y x -=++，则x y +的最小值为（） A ．2B ．4C ．8D ．146．已知m ，0n >，4121m n +=+，则m n +的最小值为（） A ．72B ．7C ．8D ．47．不等式10xx-≥的解集为（） A ．[0，1]B ．（0，1]C ．（﹣∞，0]∪[1，+∞）D ．（﹣∞，0）∪[1，+∞）8．已知11232f x x ⎛⎫-=+ ⎪⎝⎭，()8f m =，则m 等于（）A ．14- B ．14C ．32D ．32-9．已知定义在R 上的奇函数()f x 满足：当0x ≥时，()3f x x =，若不等式()()242f t f m mt ->+对任意实数t 恒成立，则实数m 的取值范围是（） A．(,-∞ B．()C ．()(),02,-∞+∞D．(),-∞⋃+∞10．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（） A ．y ＝x 2+2xB ．y ＝x 3C ．y ＝lnxD ．y ＝x 211．已知函数321()(1)m f x m m x -=--是幂函数，对任意的12,(0,)x x ∈+∞且12x x ≠，满足1212()()0f x f x x x ->-，若,,0a b R a b ∈+<，则()()f a f b +的值（） A ．恒大于0 B ．恒小于0 C ．等于0 D ．无法判断12．已知()f x 是定义在[]1,1-上的奇函数，对任意的[]12,1,1x x ∈-，均有()()()()21210x x f x f x --≥．当[]0,1x ∈时，()25x f f x ⎛⎫= ⎪⎝⎭，()()11f x f x =--，则 2902913143152016201620162016f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-+-++-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（） A ．112-B ．6-C ．132-D ．254-四．填空题（共6小题）13．已知条件2:340p x x --；条件22:690q x x m -+-≤，若q ￢是p ￢的充分不必要条件，则实数m 的取值范围是__________． 14．已知0,0a b >>，且1ab =，则11822a b a b+++的最小值为_________． 15．已知正实数a ，b 满足36a b +=，则1412a b+++的最小值为______．16．若222x x a x x a +++--≥对x ∈R 恒成立，则实数a 的取值范围为______.17．已知函数()2(1)mf x m m x =--是幂函数，且()f x 在(0,)+∞上单调递增，则实数m =________.18．已知()f x 是定义域为(),-∞+∞的奇函数，满足()()11f x f x -=+，若()12f =，则()()()()1232020f f f f ++++=________.三．解析题（共6小题）19．已知函数()|31||1|f x x x =-++．（1）解不等式()2f x ；（2）记函数()()2|1|g x f x x =++的值域为M ，若t M ∈，求44t t+的最小值． 20．设:p 实数x 满足22430x ax a -+<，:q 实数x 满足31x -<. （1）若1a =，且p q ∧为真，求实数x 的取值范围；（2）若其中0a >且p ⌝是q ⌝的充分不必要条件，求实数a 的取值范围. 21．已知函数()f x 对任意x 满足：3()(2)4f x f x x --=，二次函数()g x 满足：(2)()4g x g x x +-=且()14g =-．（1）求()f x ，()g x 的解析式；（2）若[,]x m n ∈时，恒有()()f x g x ≥成立，求n m -的最大值．22．已知函数23f x x x =-（）．（1）对任意0x R f x m ∈-≥，（）恒成立，求实数m 的取值范围：（2）函数()g x kx k =-，设函数()()()F x f x g x =-，若函数()y F x =有且只有两个零点，求实数k 的取值范围．23．已知函数()f x 是定义在[]1,1-上，若对于任意[],1,1x y ∈-，都有()()()f x y f x f y +=+且0x >时，有()0f x >.（1）证明：()f x 在[]1,1-上为奇函数，且为单调递增函数；（2）解不等式1(1)()02f x f x ++>；24．已知函数()4mf x x x=-，且()43f =.（1）求m 的值；（2）证明()f x 的奇偶性；（3）判断()f x 在()0,∞+上的单调性，并给予证明.【答案解析】一、选择题（共12小题）1．有下列四个命题，其中真命题是（）． A ．n ∀∈R ，2n n ≥B ．n ∃∈R ，m ∀∈R ，m n m ⋅=C ．n ∀∈R ，m ∃∈R ，2m n <D ．n ∀∈R ，2n n <【答案】B 【解析】对于选项A ，令12n =，则2111242⎛⎫=< ⎪⎝⎭，故A 错；对于选项B ，令1n =，则m ∀∈R ，1⋅=m m 显然成立，故B 正确；对于选项C ，令1n =-，则21<-m 显然无解，故C 错；对于选项D ，令1n =-，则2(1)1-<-显然不成立，故D 错. 故选B2． 22530x x --<的一个必要不充分条件是（）A ．132x -<22，则a b >B ．若a b >，则11a b< C ．若a b >，c d >，则a c b d ->- D ．若a b >，c d <，则a b c d> 【答案】A 【解析】对于选项A ，若ac bc >22，所以20c >，则a b >，所以该选项正确；对于选项B ，11b aa b ab--=符号不能确定，所以该选项错误；对于选项C ，设1,0,1,3,2,3a b c d a c b d ===-=--=-=，所以a c b d -<-，所以该选项错误；对于选项D ，设0,1,2,1,0,1,a b a b a b c d c d c d==-=-=-==∴<，所以该选项错误；故选：A4．下列不等式中，正确的是（） A ．a ＋4a≥4 B ．a 2＋b 2≥4abC ≥2a b+ D ．x 2＋23x 【答案】D 【解析】a ＜0，则a ＋4a≥4不成立，故A 错； a ＝1，b ＝1，a 2＋b 2＜4ab ，故B 错，a ＝4，b ＝16＜2a b+，故C 错；由基本不等式得x 2＋23x ≥=D 项正确. 故选：D.5．已知2x >-，8y >-，8082x y x -=++，则x y +的最小值为（） A ．2 B ．4C ．8D ．14【答案】C 【解析】解：因为8082x y x -=++，所以822082x y x +--=++，即82182y x +=++，因为2x >-，8y >-，所以20x +>，80y +>，所以()8282x y x y y x ⎛⎫+=++ ⎪++⎝⎭ ()()82281082x y y x ⎛⎫⎡⎤=+++-+ ⎪⎣⎦++⎝⎭()()822882x y y x ++=+++8==当且仅当()()822882x y y x ++=++即4x =，4y =时取等号，故选：C6．已知m ，0n >，4121m n +=+，则m n +的最小值为（） A ．72B ．7C ．8D ．4【答案】A 【解析】 ∵m ，0n >，4121m n+=+， ∴()()4111411911554122122n m m n m n m n m n +⎛⎫⎛⎫++=+++⨯=++≥+= ⎪ ⎪++⎝⎭⎝⎭，当且仅当411n m m n +=+且4121m n +=+，即2m =，32n =时取等号，故m n +的最小值72. 故选：A.7．不等式10xx-≥的解集为（） A ．[0，1]B ．（0，1]C ．（﹣∞，0]∪[1，+∞）D ．（﹣∞，0）∪[1，+∞）【答案】B 【解析】根据题意，1100(1)0x x x x x x--≥⇒≤⇒-≤且0x ≠，解得01x <≤，即不等式的解集为（0，1]，故选：B8．已知11232f x x ⎛⎫-=+ ⎪⎝⎭，()8f m =，则m 等于（） A ．14-B ．14C ．32 D ．32-【答案】B 【解析】解：设112x t -=，则22x t =+，()47f t t ∴=+，()478f m m ∴=+=，解得14m =．故选：B ．9．已知定义在R 上的奇函数()f x 满足：当0x ≥时，()3f x x =，若不等式()()242f t f m mt ->+对任意实数t 恒成立，则实数m 的取值范围是（）A ．(,-∞ B ．()C ．()(),02,-∞+∞D ．(),-∞⋃+∞【答案】A 【解析】由于函数()y f x =为R 上的奇函数，则()()f x f x =--. 当0x <时，0x ->，则()()()33f x f x x x =--=--=.所以，对任意的x ∈R ，()3f x x =，则函数()y f x =为R 上的增函数.由()()242f t f m mt ->+可得224mt m t +<-，即2420mt t m ++<，由题意可知，不等式2420mt t m ++<对任意的实数t 恒成立. ①当0m =时，则有40t <，在t R ∈不恒成立；②当0m ≠时，则(2,1680m m m <⎧⇒∈-∞⎨∆=-<⎩. 综上所述，实数m的取值范围是(,-∞. 故选：A ．10．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（） A ．y ＝x 2+2x B ．y ＝x 3 C ．y ＝lnx D ．y ＝x 2【答案】D 【解析】A 选项：y ＝x 2+2x 是非奇非偶函数所以，所以不是偶函数，不合题意；B 选项：y ＝x 3是奇函数，不合题意；C 选项：y ＝lnx 是非奇非偶函数，所以不是偶函数，不合题意；D 选项：y ＝x 2既是偶函数又在区间（0，+∞）上单调递增. 故选：D11．已知函数321()(1)m f x m m x -=--是幂函数，对任意的12,(0,)x x ∈+∞且12x x ≠，满足1212()()0f x f x x x ->-，若,,0a b R a b ∈+<，则()()f a f b +的值（）A ．恒大于0B ．恒小于0C ．等于0D ．无法判断【答案】B 【解析】由题可知：函数321()(1)m f x m m x -=--是幂函数则21=12--⇒=m m m 或1m =- 又对任意的12,(0,)x x ∈+∞且12x x ≠，满足1212()()0f x f x x x ->-所以函数()f x 为(0,)+∞的增函数，故2m =所以()7=f x x ，又()()f x f x -=-，所以()f x 为R 单调递增的奇函数由0a b +<，则a b <-，所以()()()<-=-f a f b f b 则()()0f a f b +< 故选：B12．已知()f x 是定义在[]1,1-上的奇函数，对任意的[]12,1,1x x ∈-，均有()()()()21210x x f x f x --≥．当[]0,1x ∈时，()25x f f x ⎛⎫=⎪⎝⎭，()()11f x f x =--，则 2902913143152016201620162016f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-+-++-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（） A ．112-B ．6-C ．132-D ．254-【答案】C 【解析】由f （x ）=1-f （1-x ），得 f （1）=1，令12x =，则1122f =（）， ∵当x ∈[0，1]时，25x f f x =（）（）， ∴152x f f x =（）（），即1111111111115222525410224f f f f f f ⎛⎫====== ⎪⎝⎭（）（），（），（）（）， 1290125201610＜＜， ∵对任意的x 1，x 2∈[-1，1]，均有（x 2-x 1）（f （x 2）-f （x 1））≥0290120164f ∴=（），同理29131431512016201620164f f f =⋯=-==（）（）（）． ∵f （x ）是奇函数，∴2902913143152016201620162016f f f f -+-+⋯+-+-（）（）（）（） 29029131431513[]20162016201620162f f f f =--++⋯++=-（）（）（）（），故选：C ．五．填空题（共6小题）13．已知条件2:340p x x --；条件22:690q x x m -+-≤，若q ￢是p ￢的充分不必要条件，则实数m 的取值范围是__________．【答案】4m ≥或4m ≤- 【解析】∵条件2:340p x x --；∴:14p x -≤，∴:4p x ⌝>或1x <-， ∵条件22:690q x x m -+-，，∴:3q x m ⌝>+或x 3m <-，若q ￢是p ￢的充分不必要条件，则31434m m m ⎧--⎪⇒≥⎨+⎪⎩，解得：4m ≥或4m ≤-故答案为4m ≥或4m ≤-14．已知0,0a b >>，且1ab =，则11822a b a b+++的最小值为_________．【答案】4 【解析】0,0,0a b a b >>∴+>，1ab =,11882222ab ab a b a b a b a b∴++=++++842a b a b +=+≥=+，当且仅当a b +=4时取等号，结合1ab =,解得22a b =-=+，或22a b =+=. 故答案为：415．已知正实数a ，b 满足36a b +=，则1412a b+++的最小值为______．【答案】1313+ 【解析】正实数a ，b ，即0a >，0b >；36a b +=，13(2)13a b ∴+++=则13(2)11313a b +++=，那么：14(12a b+++13(2)4(1)3(2))()1()131313(2)13(1)a b a b b a +++++=++++121213+⨯=当且仅当2(1)2)a b +=+时，即取等号．∴1412a b +++的最小值为：1313+，故答案为：1313+． 16．若222x x a x x a +++--≥对x ∈R 恒成立，则实数a 的取值范围为______.【答案】2a ≥ 【解析】因为222x x a x x a +++--≥对x ∈R 恒成立，当20x x a --≥时，222221x x a x x a x x +++--=≥∴≥或1x ≤-恒成立，因此22(1)(1)02110a a a ⎧----≤∴≥⎨--≤⎩；当20x x a --<时，222221x x a x x a x a x a +++--=+≥∴≥-恒成立，因此2(1)(1)02112a a a a a ⎧----≥⎪∴≥⎨-<⎪⎩；综上：2a ≥ 故答案为：2a ≥17．已知函数()2(1)mf x m m x =--是幂函数，且()f x 在(0,)+∞上单调递增，则实数m =________.【答案】2 【解析】由题意，函数()2(1)mf x m m x =--是幂函数，可得211m m --=，即220m m --=，解得2m =或1m =-，当2m =时，函数()2f x x =，此时()f x 在(0,)+∞上单调递增，符合题意；当1m =-时，函数()1f x x -=，此时()f x 在(0,)+∞上单调递减，不符合题意，故答案为：2.18．已知()f x 是定义域为(),-∞+∞的奇函数，满足()()11f x f x -=+，若()12f =，则()()()()1232020f f f f ++++=________.【答案】0. 【解析】因为()f x 是定义域为(,)-∞+∞的奇函数，所以()()f x f x -=-且()00f = 又(1)(1)f x =f +x -所以()()()()()21111f x f x f x f x f x ⎡⎤⎡⎤+=++=-+=-=-⎣⎦⎣⎦ 所以()()()()()4222f x f x f x f x f x ⎡⎤⎡⎤+=++=-+=--=⎣⎦⎣⎦ 所以函数()f x 的周期为4，又因为()12f =、()00f =，在(1)(1)f x =f +x -中，令1x =，可得：()()200f f ==在(1)(1)f x =f +x -中，令2x =，可得：()()()3112f f f =-=-=- 在(1)(1)f x =f +x -中，令3x =，可得：()()()4220f f f =-=-= 所以()()()()2020(3)(2020)1234505004(1)(2)f f f f +f f f f +++=⨯+++=⨯=⎡⎤⎣⎦ 故答案为：0.三．解析题（共6小题）19．已知函数()|31||1|f x x x =-++．（1）解不等式()2f x ；（2）记函数()()2|1|g x f x x =++的值域为M ，若t M ∈，求44t t +的最小值．【答案】（1）1|02x x ⎧⎫≤≤⎨⎬⎩⎭；（2）17. 【解析】解：（1）依题意，得4,1,1()22,1,314,.3x x f x x x x x ⎧⎪-≤-⎪⎪=-+-<<⎨⎪⎪≥⎪⎩于是1()242x f x x ≤-⎧≤⇔⎨-≤⎩或113222x x ⎧-<<⎪⎨⎪-+≤⎩或1342x x ⎧≥⎪⎨⎪≤⎩，解得102x ≤≤.即不等式()2f x ≤的解集为1|02x x ⎧⎫≤≤⎨⎬⎩⎭. （2）证明：()|31|3|1||31(33)|4g x x x x x =-++≥--+=，当且仅当(31)(33)0x x -+≤时，取等号，所以[4,)M =+∞. 则44y t t=+在[4,)+∞单调递增，所以4114444174t t t t ⎛⎫⎛⎫+=+≥⨯+= ⎪ ⎪⎝⎭⎝⎭.所以44t t +的最小值为17. 20．设:p 实数x 满足22430x ax a -+<，:q 实数x 满足31x -<. （1）若1a =，且p q ∧为真，求实数x 的取值范围；（2）若其中0a >且p ⌝是q ⌝的充分不必要条件，求实数a 的取值范围. 【答案】（1）{}|23x x <<（2）423a ≤≤【解析】对于q ：由31x -<得131x -<-<，解24x <<（1）当1a =时，对于p ：()()243310x x x x -+=--<，解得13x <<，由于p q∧为真，所以,p q 都为真命题，所以2413x x <<⎧⎨<<⎩解得23x <<，所以实数x 的取值范围是{}|23x x <<.（2）当0a >时，对于p ：()()224303x ax a x a x a =---+<，解得3a x a <<.由于p ⌝是q ⌝的充分不必要条件，所以p 是q 的必要不充分条件，所以234a a ≤⎧⎨≥⎩，解得423a ≤≤.所以实数a 的取值范围是423a ≤≤.21．已知函数()f x 对任意x 满足：3()(2)4f x f x x --=，二次函数()g x 满足：(2)()4g x g x x +-=且()14g =-．（1）求()f x ，()g x 的解析式；（2）若[,]x m n ∈时，恒有()()f x g x ≥成立，求n m -的最大值．【答案】（1）求()1f x x =+，2()23g x x x =--；（2）n m -的最大值5. 【解析】（1）()()324f x f x x --=①，用2x -代替上式中的x ，得()()3284f x f x x --=-②，联立①②，可得()1f x x =+；设()2g x ax bx c =++，所以()()()()222224g x g x a x b x c ax bx c x +-=++++---=，即4424ax a b x ++=所以44420a ab =⎧⎨+=⎩，解得1a =，2b =-，又()14g =-，得3c =-，所以2()23g x x x =--. （2）令()()f x g x ≥，即2123x x x +--≥2340x x --≤解得14x -≤≤所以当[]1,4x ∈-时，()()f x g x ≥若要求[,]x m n ∈时，恒有()()f x g x ≥成立，可得()415n m -≤--=，即n m -的最大值是5.22．已知函数23f x x x =-（）．（1）对任意0x R f x m ∈-≥，（）恒成立，求实数m 的取值范围：（2）函数()g x kx k =-，设函数()()()F x f x g x =-，若函数()y F x =有且只有两个零点，求实数k 的取值范围．【答案】（1）94⎛⎫-∞- ⎪⎝⎭，；（2）()()01-∞⋃+∞，，. 【解析】解：（1）23f x x x =-（）的定义域为R ， 22()3()3()（-）f x x x x x f x =---=-=，故函数()y f x =关于y 轴对称，当0x >时，23（）f x x x =-，当32x =时，min 39()()24f x f ==-，对任意,()0x R f x m ∈-≥恒成立，即有min ()m f x ≤，故实数m 的取值范围为94-∞-（，）．（2）显然1x =不是函数()()()F x f x g x =-的零点．故函数()()()F x f x g x =-有且只有两个零点．y k ⇔=与23||()1x x h x x -=-的图象有两个交点．当0x ≥时，223||3()11x x x xh x x x --==--， 222223(23)(1)(3)23()()01(1)(1)x x x x x x x x h x x x x ------+''===>---恒成立，故函数()y h x =在(0,1)单调递增，在(1,)+∞单调递增，且当(0,1)x ∈时，1x →时，函数()h x →+∞，当(1,)x ∈+∞时，1x →时，函数()h x →-∞，x →+∞时，函数()h x →+∞，当0x <时，223||3()11x x x xh x x x -+==--， 2222223(23)(1)(3)23(3)(1)()()1(1)(1)(1)x x x x x x x x x x h x x x x x ++--+---+''====---- 令()0h x '=，因为0x <，故解得1x =-，当(,1)x ∈-∞-时， ()0h x '>，故在(,1)-∞-单调递增，当(1,0)x ∈-时， ()0h x '<，故在(1,0)-单调递减，函数()y h x =的图像如图所示，根据图象可得，实数k 的取值范围为01-∞+∞（，）（，）．23．已知函数()f x 是定义在[]1,1-上，若对于任意[],1,1x y ∈-，都有()()()f x y f x f y +=+且0x >时，有()0f x >.（1）证明：()f x 在[]1,1-上为奇函数，且为单调递增函数；（2）解不等式1(1)()02f x f x ++>；【答案】（1）证明见解析；（2）2,03x ⎛⎤∈- ⎥⎝⎦. 【解析】（1）证明：令0x y ==有(0)0f =，令y x =-，()()()f x x f x f x -=+-，即0(0)()()f f x f x ==+-，所以()f x 是奇函数. 又令1211x x ，则()()21f x f x -=()()()2121f x f x f x x +-=-，又当0x >时，有()0f x >，210x x ->， ∴()210f x x ->，即()()210f x f x ->， ∴()f x 在定义域[]1,1-上为单调递增函数；（2）∵()f x 在[]1,1-上为单调递增的奇函数，有1(1)()02f x f x ++>，则1(1)()2f x f x +>-，∴1111112112x x x x ⎧⎪-≤+≤⎪⎪-≤-≤⎨⎪⎪+>-⎪⎩，即202223x x x ⎧⎪-≤≤⎪-≤≤⎨⎪⎪>-⎩，2,03x ⎛⎤∈- ⎥⎝⎦，解得不等式的解集为2,03x ⎛⎤∈- ⎥⎝⎦.24．已知函数()4mf x x x=-，且()43f =. （1）求m 的值；（2）证明()f x 的奇偶性；（3）判断()f x 在()0,∞+上的单调性，并给予证明.【答案】（1）1m =；（2）奇函数，证明见解析；（3）单调增函数，证明见解析. 【解析】（1）()4444134m m f =-=-=，解得1m =；（2）因为()4f x x x=-，定义域为{}0x x ≠，关于原点对称，又()()44f x x x f x x x ⎛⎫-=--=--=- ⎪-⎝⎭，因此，函数()y f x =为奇函数；（3）设120x x >>，则()()()12121212214444f x f x x x x x x x x x ⎛⎫⎛⎫-=---=-+- ⎪ ⎪⎝⎭⎝⎭()()()1212121212441x x x x x x x x x x -⎛⎫=-+=-+ ⎪⎝⎭，因为120x x >>，所以120x x ->，所以()()12f x f x >，因此，函数()y f x =在()0,∞+上为单调增函数.人教版新教材高中数学高一上学期期中考试数学试卷（三）一、选择题（共12小题） 1．已知R a ∈，则“1a >”是“11a<”的（） A ．充分非必要条件 B ．必要非充分条件 C ．充要条件D ．既非充分又非必要条件2．若a ＞b ，则下列各式中正确的是（） A ．ac ＞bcB ．ac 2＞bc 2C ．a +c 2＞b +c 2D ．11a b＜3．设m =，n =p =，则m ，n ，p 的大小顺序为（） A ．m p n >>B ．p n m >>C ．n m p >>D ．m n p >>4．已知0,0x y >>，且142x y +=，242mx y m +>+恒成立，则实数m 的取值围是（）A ．(8,0)-B ．C ．(9,1)-D ．(8,1)-5．若函数()()22422x x f x x x -+=>-在x a =处取最小值，则a =（）A ．1B ．2C ．4D ．66．已知关于x 的不等式()()110ax x -+<的解集是1(,1),2⎛⎫-∞-⋃-+∞ ⎪⎝⎭，则a 等于（）A ．2B ．2-C ．12- D ．127．已知命题“∃x 0∈R ，20014(2)04x a x +-+≤”是假命题，则实数a 的取值范围为（） A ．(－∞，0) B ．[0，4] C ．[4，＋∞) D ．(0，4)8．将函数()212x f x x x -=-的图象向左平移1个单位长度，得到函数()g x 的图象，则函数()g x 的图象大致是（）A ．B ．C ．D ．9．如果2()(2)1f x ax a x =--+在区间1,2⎛⎤-∞ ⎥⎝⎦上为减函数，则a 的取值（）A ．(0,1]B ．[0,1)C ．[0,1]D ．(0,1)10．已知定义在R 上的奇函数()y f x =，当0x ≥时，22()f x x a a =--，若对任意实数x 有()()f x a f x -≤成立，则正数a 的取值范围为（）A ．)1,4⎡+∞⎢⎣ B ．)1,2⎡+∞⎢⎣ C ．(10,4⎤⎥⎦D ．(10,2⎤⎥⎦11．已知321()(1)1x f x x x +=+--，若(2018)f a =，则(2016)f -=（） A ．a -B ．2a -C ．4a -D ．1a -12．已知,a b ∈R ，不等式22122x ax bx x ++<++在x ∈R 上恒成立，则（） A ．0a ，0b >且1a b +=，则311a b++的最小值为____________. 16．已知二次不等式220ax x b ++>的解集为1x x a ⎧⎫≠-⎨⎬⎩⎭，且a b >，则22a b a b +-的最小值为__________. 17．当2x ≠时，则42y x x =+-的值域是____________ 18．若不等式组22202(52)50x x x k x k ⎧-->⎨+++<⎩的整数解只有－2，则k 的取值范围是________．三．解析题（共6小题）19．已知集合{}2|2A x x -=≤≤，集合{}|1B x x =>. （1）求()R C B A ⋂；（2）设集合{}|6M x a x a =<<+，且A M M ⋃=，求实数a 的取值范围. 20．已知0a >，0b >. （1）若1a b +=，求14a b+的最小值；（2≥21．已知函数2()2f x ax bx a =+-+．（1）若关于x 的不等式()0f x >的解集是(1,3)-，求实数,a b 的值；（2）若2,0b a =>，解关于x 的不等式()0f x >． 22．已知函数2()1(0)f x x ax a =++>.（1）若()f x 的值域为[0,)+∞，求关于x 的方程()4f x =的解；（2）当2a =时，函数22()[()]2()1g x f x mf x m =-+-在[2,1]-上有三个零点，求m 的取值范围. 23．求函数解析式（1）已知()f x 是一次函数，且满足3(1)2(1)217.f x f x x +--=+求()f x ．（2）已知()f x 满足12()()3f x f x x+=，求()f x ．24．定义在非零实数集上的函数()f x 对任意非零实数,x y 满足:()()()f xy f x f y =+,且当01x <<时()0f x <.(1)求(1)f -及(1)f 的值； (2)求证:()f x 是偶函数；(3)解不等式：21(2)02f f x ⎛⎫+-≤ ⎪⎝⎭.【答案解析】一、选择题（共12小题） 1．已知R a ∈，则“1a >”是“11a<”的（） A ．充分非必要条件 B ．必要非充分条件 C ．充要条件D ．既非充分又非必要条件。

山东省高一上学期期中考试数学试卷-附带答案

山东省高一上学期期中考试数学试卷-附带答案学校:___________班级：___________姓名：___________考号：___________本试卷共4页，22题，全卷满分150分。

考试用时120分钟。

注意事项：1.答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一.单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合A={x|x ＜0}，B={x|﹣x 2－x +2＞0}，则C R A ∩B=（）A.{x|0＜x ＜1}B.{x|0≤x ＜1}C.{x|﹣2＜x ＜0}D.{x|1＜x ＜2} 2.已知函数f(x)=(m 2－m －1)x m 为幂函数，则m 为（） A.﹣1或2 B.2 C.﹣1 D.1 3.若函数f(x)的定义域为［-1，2]，则函数y=2√x+1的定义域为（）A.（﹣√3，2]B.[0，√3]C.(﹣1，2]D.(﹣1，√3] 4.已知a ，b ，c 均为实数，则（）A.若a>b ，则ac 2>bc 2B.若a<b<0．则b a >abC.若a>6且1a >1b ，则b<0<a D.若a0，√3－x >0．则命题p 的否定是（）A.∀x>0，√3－x ≤0B.∃x>0，3－x ≤0C.∃x>0，√3－x ≤0D.∀x ≤0，√3－x ≤0 6.已知函数f(x)=x+√x +1．其定义城为M ，值域为N ．则"x ∈M"是"x ∈N"的条件（）． A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要7.已知函数f(x)是定义在R 上的奇函数，当x ≥0时，f(x)=12(lx －a 2l+|x －2a 2l －3a 2)．若∀x ∈R ，f(x －a)<f(x)，则实数a 的取值范围为（）A.[﹣16，16] B.[0，16] C.[﹣13，13] D.(0，16)8.不等式x 2+2axy+4y 2≥0对于∀x ∈[2，3]，∀y ∈[2，9］恒成立，则a 的取值范围是（） A.[-2，+∞) B.[-5，+∞) C.[﹣133，+∞) D.[-1，+∞)二．多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．9.已知函数f(x)={x 2－2x +1，x ≤1﹣x +1，x ＞1，下列说法正确的是（）A.函数f(x)是减函数B.∀a ∈R ，f(a 2)>f(a －1)C.若f(a －4)>f(3a)，则a 的取值范围是（﹣2，+∞)D.在区间［1，2］上的最大值为0 10.已知a ，b 是两个正实数，满足a+b=1，则（）A.√a +√b 的最小值为1B.√a +√b 的最大值为√2C.a 2+b 2的最小值为12 D.a 2+b 2的最大值为1 11.已知函数f(x)=ax 2－3x+4，若任意x 1，x 2∈[﹣1，+∞）且x 1≠x 2：都有f （x 1）－f （x 2）x 1－x 2<﹣1，则实数a 的值可以是（）A.﹣1B.﹣12 C.0 D.1212.已知函数f(x)的定义域为R ，f(x －1）为奇函数，f(3x －2）为偶函数，则（） A.f(13)=0 B.f(1)=0 C.f(4)=0 D.f(3)=0 三.填空题：本题共4小题，每小题5分，共20分． 13.已知函数f （x ）={2x +1x ,x ＜0x 2－3x +1，x ≥0，则f （f （2））= .14.写出3x －1>0的一个必要不充分条件是 . 15.关于x 的不等式11－x≥2x 的解集为 .16.设函数f(x)的定义域为R ，满足f(x+1)=3f(x)，且当x ∈(0，1］时，f(x)=x(x －1)．若对任意x∈(-∞，m]，都有f(x)≥﹣2，则m 的取值范围是 .四．解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤。

2023-2024学年山东省泰安市英雄山中学高一(上)期中数学试卷【答案版】

2023-2024学年山东省泰安市英雄山中学高一（上）期中数学试卷一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求。

1．命题“∀x ＜0，x 3﹣x 2+1≤0”的否定是（）A ．∃x ＜0，x 3﹣x 2+1≥0B ．∃x ＜0，x 3﹣x 2+1＞0C ．∃x ≥0，x 3﹣x 2+1≤0D ．∀x ≥0，x 3﹣x 2+1＞02．已知集合A ＝{x |﹣1≤x ≤1}，B ＝{x |3x ＜1}，则A ∩B ＝（）A ．[﹣1，0）B ．[﹣1，0]C ．（﹣1，1）D ．[0，1）3．设集合M ＝{x |0＜x ≤3}，N ＝{x |0＜x ≤2}，那么“a ∈M ”是“a ∈N ”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．下列函数中，是奇函数，又在定义域内为减函数的是（）A ．y ＝（12）xB ．y =1xC ．y ＝﹣x 3D ．y ＝x 25．函数f （x ）=2x +2−x x 的图象大致为（）A ．B ．C ．D ．6．若奇函数f （x ）在[1，3]上是增函数，且有最小值7，则它在[﹣3，﹣1]上（）A ．是减函数，有最小值﹣7B ．是增函数，有最小值﹣7C ．是减函数，有最大值﹣7D ．是增函数，有最大值﹣77．已知幂函数f(x)=mx m−12满足条件f （3﹣a ）＞f （a ），则实数a 的取值范围是（）A ．[0，1）B ．[0，32)C ．[0，32]D ．[0，3]8．若函数f(x)={(5a −4)x +7a −3，(x ＜1)(2a −1)x ，(x ≥1)在（﹣∞，+∞）上单调递减，则实数a 的取值范围为（）A ．[35，45)B ．[35，1]C ．(35，45)D ．(12，45)二、选择题：本题共4小题，每小题5分，共20分。

在每小题给出的选项中，有多项符合题目要求。

山东省泰安英雄山中学2009届高三年级第一次复习检测数学理科卷

山东省泰安英雄山中学2009届高三年级第一次复习检测数学理科卷第Ⅰ卷一、选择题（本大题共12小题，每题，5分，共60分） 1．设集合""""},30|{},01|{B m A m x x B x xx A ∈∈<<=<-=是那么的（）A ．充分不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件2．已知函数)1(+=x f y 的图象过点（3，2），则函数)(x f 的图象关于x 轴的对称图形一定过点（）A ．（2，－2）B ．（2，2）C ．（－4，2）D ．（4，－2）3．如果奇函数)(x f 在区间)0](,[>>a b b a 上是增函数，且最小值为m ，那么)(x f 在区间],[a b --上是（）A ．增函数且最小值为mB ．增函数且最大值为－mC ．减函数且最小值为mD ．减函数且最大值为－m4．与函数)12lg(1.0-=x y 的图象相同的函数解析式是（）A ．21(12>-=x x y B ．121-=x yC ．21(121>-=x x y D ．|121|-=x y 5．对一切实数x ，不等式01||2≥++x a x 恒成立，则实数a 的取值范围是（）A ．]2,(--∞B ．[－2，2]C ．),2[+∞-D ．),0[+∞6．已知函数)12(+=x f y 是定义在R 上的奇函数，函数)(x g y =的图象与函数)(x g y =的图象关于直线x y =对称，则)()(x g x g -+的值为（）A ．2B ．0C ．1D ．不确定7．把函数)(x f y =的图像沿x 轴向右平移2个单位，所得的图像为C ，C 关于x 轴对称的图像为y=2x 的图像，则)(x f y =的函数表达式为（）A ．22+=x y B ．22+-=x yC ．22--=x yD ．)2(log 2+-=x y8．当,10时<<- B ．b a b a )1()1(+>-C ．bba a 1)1()1(->-D ．b a b a )1()1(->-9．设奇函数),0()(+∞在x f 上为增函数，且的则不等式0)()(,0)1(<--=xx f x f f 解集为（）A ．),1()0,1(+∞-B ．)1,0()1,( --∞C ．),1()1,(+∞--∞D ．)1,0()0,1( -10．当]2,0[∈x 时，函数23)1(4)(2=--+=x x a ax x f 在时取得最大值，则a 的取值范围是（）A ．],21[+∞-B ．),0[+∞C ．),1[+∞D ．),32[+∞11．已知),(1,log 1,4)13()(+∞-∞⎩⎨⎧><+-=是x x x a x a x f a 上是减函数，那么a 的取值范围是（）A ．（0，1）B ．31,0(C ．)1,71[D ．)31,71[12．某种电热水器的水箱盛满水是200升，加热到一定温度，即可用来洗浴。

(整理版)第一学期期中试卷高一数学

~ 度第一学期期中试卷高一数学第一卷客观卷〔共36分〕一、选择题〔每题3分，共36分，每题的四个选项中，只有一项为哪项符合题目要求的〕 1．集合A =｛x | x ( x -1) = 0｝，那么A ．0∈AB ． 1∉AC ． -1∈AD ． 0∉A 2．集合M={(x,y)|x+y=2}, N={(x,y)|x-y=4},那么M ∩N 为A ．x=3,y=-1B ．(3,-1)C ． {3 ,-1}D ．{(3,-1)} 3．以下函数中，与函数y = x ( x ≥0 ) 是同一函数的一个为A ． y． y2C ． yD ． y =2x x4．函数21,0(),0x x f x x x +≥⎧=⎨<⎩，那么f 〔-2〕的值为A ．1B ．2C ．4D ．55．函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数，那么a 的取值范围是A ．a ≥3B ．a ≤－3C ．a ≤5D ．a ≥－36．函数f 〔x 〕=|x |和g 〔x 〕=x 〔2－x 〕的递增区间依次是A ．〔－∞，0]，〔－∞，1]B ．〔－∞，0]，［1，+∞)C ．［0，+∞)，〔－∞，1]D ．［0，+∞〕，［1，+∞〕7．设集合A ＝{x|－5≤x ＜1＝，B ＝{x|x ≤2}，那么A B ＝ A ．{x|－5≤x ＜1＝ B ．{x|－5≤x ≤2} C ．{x|x ＜1＝ D ．{x|x ≤2}8．函数xx f 1)(=，那么)1(-x f 的图像大致是x〔A 〕〔B 〕〔C 〕〔D 〕 9．图中的曲线是log a y x =(0,1)a a >≠的图象，a 的值为2，43，310，15，那么相应曲线1234,,,C C C C 的a 依次为 A ．2，43，15，310 B ．2，43，310，15C ．15，310，43，2D ．43，2，310，1510．函数y=log 2x-123-x 的定义域是A ．〔32，1〕⋃〔1，+∞〕B ．〔21，1〕⋃〔1，+∞〕 C ．〔32，+∞〕 D ．〔21，+∞〕11．函数lg(1)lg(1)y x x =-++的图象关于A ．直线0x =B ．直线0y =对称C ．点(0,0)对称D ．点(1,1)对称12．假设4log 3log 32⋅=P ，5lg 2lg +=Q ，0e M =，1ln =N ，那么正确的选项是0 x C 1C 2 C 4C 3 1yA Q P =B ． M Q =C ． N M =D ．P N =第II 卷主观卷〔共64分〕二、填空题：(本大题共4小题，每题4分，总分值16分；把答案填在横线上)13．化简1416()81-的值为．14．函数(1)x y a a =>的定义域是[1,1]-，且最大值与最小值的差为1，那么a = ．15．集合{1,2},{,},a A B a b ==假设1{}2A B =,那么A B = ．16．设236ab==，那么11a b+的值为．三、解答题：(本大题共5小题,共48分．)． 17．〔8分〕非空集合2{|0}Ax x ax b ，2{|8150}Bx x x ，且A B ⊆．求：〔1〕写出集合B 所有的子集；〔2〕求ab 的值．18．〔8分〕求以下函数的定义域：〔1〕y 〔2〕xx y +++=31)5(log 219．〔8分〕函数1()f x xx．〔1〕求f (x ) 的定义域；〔2〕用单调性定义证明函数1()f x xx在(0,)+∞上单调递增．20．〔8分〕函数)(x f 是定义在R 上的奇函数，且当0>x 时，x x x f -=2)(．〔1〕计算)0(f ，)1(-f ；〔2〕当0<x 时，求)(x f 的解析式．21．〔8分〕函数2()log (41)xf x ax ．假设函数()f x 是R 上的偶函数，求：实数a 的值；22．〔8分〕函数()log (1)log (3),(01).a a f x x x a =-++<<〔1〕求函数()f x 的定义域；〔2〕假设函数()f x 的最小值为2-，求实数a 的值．。

(word版)高一数学期中考试测试题(必修一含答案)

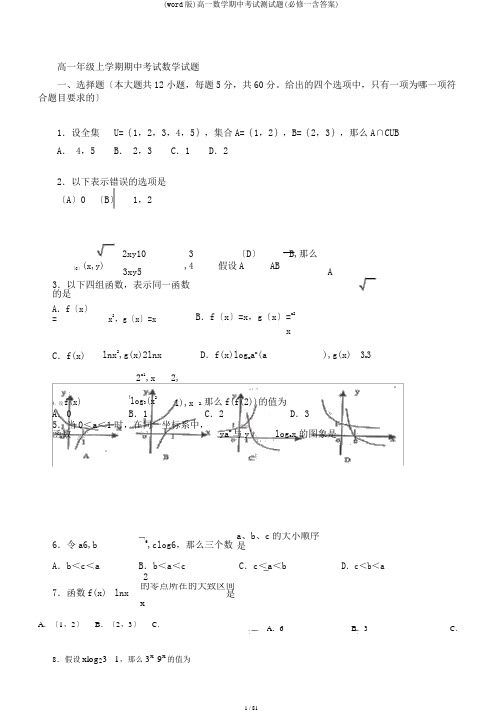
高一年级上学期期中考试数学试题一、选择题〔本大题共12小题，每题5分，共60分。

给出的四个选项中，只有一项为哪一项符合题目要求的〕1．设全集U=｛1，2，3，4，5｝，集合A=｛1，2｝，B=｛2，3｝，那么A∩C UBA． 4，5 B． 2，3 C．1 D．22．以下表示错误的选项是〔A〕0 〔B〕1，2〔C〕(x,y)2xy103,4〔D〕假设AB,那么ABA 3xy53．以下四组函数，表示同一函数的是A．f〔x〕=x2，g〔x〕=x B．f〔x〕=x，g〔x〕=x2xC．f(x)lnx2,g(x)2lnx D．f(x)log a a x(a),g(x)3x34．设f(x)2x1,x2,{log3(x21),x 2.那么f(f(2))的值为A．0B．1C．2D．35．当0＜a＜1时，在同一坐标系中，函数ya x与y log a x的图象是6．令a6,b6,clog6，那么三个数a、b、c的大小顺序是A．b＜c＜a B．b＜a＜c C．c＜a＜b D．c＜b＜a7．函数f(x)lnx2的零点所在的大致区间是xA．〔1，2〕B．〔2，3〕C．8．假设xlog231，那么3x9x的值为A．6B．3C．1,1和〔3，4〕 D ． e,e51D ．2 29．假设函数y=f x的定义域为1,2，那么y f(x1)的定义域为〔〕A．2,3B．0,1C．1,0D．3,2 10．f(x)是偶函数，当x＜0时，f(x)x(x1)，那么当x＞0时，f(x)A．x(x1)B．x(x1)C x(x1)D．x(x1)11．设f(x)(x R)为偶函数，且f(x)在0,上是增函数，那么f(2)、f()、f(3)的大小顺序是A．f()f(3)f(2)B．C．f()f f(2)D．f()f(2)f(3) f()f(2)f(3)12函数f(x)的图象是连续不断的，x与f(x)的对应关系见下表，那么函数f(x)在区间[1,6]上的零点至少有X123456 Y(A)2(B)3(C)4(D)5第二卷(非选择题共90分)二、填空题(本大题共4小题，每题4分，共16分。

((新人教版))必修一高一数学第一学期期中考试试卷(K12教育文档)

((新人教版))必修一高一数学第一学期期中考试试卷(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（((新人教版))必修一高一数学第一学期期中考试试卷(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为((新人教版))必修一高一数学第一学期期中考试试卷(word版可编辑修改)的全部内容。

必修一高一数学第一学期期中考试试卷试卷满分：150分考试时间:120分钟第Ⅰ卷(选择题,共60分）一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求的。

）1．已知集合{1,2,3,4}A =，那么A 的真子集的个数是（）A 、15B 、16C 、3D 、42．若()f x =(3)f = （）A 、10B 、4C 、D 、2 3。

不等式（x ＋1）(2－x ）＞0的解集为 ( ）A 、{|12}x x x <->或B 、{|21}x x x <->或C 、{|21}x x -<<D 、{|12}x x -<<4．下列各组函数中，表示同一函数的是（）A 、0,1x y y == B 、11,12+-=-=x x y x yC 、33,x y x y ==D 、()2,x y x y ==5．函数)3(-=x f y 的定义域为[4,7］，则)(2x f y =的定义域为A 、（1，4）B ［1，2]C 、)2,1()1,2(⋃--D 、 ]2,1[]1,2[⋃-- 6．若:f A B →能构成映射，下列说法正确的有（ )（1）A 中的任一元素在B 中必须有像且唯一；（2）B 中的多个元素可以在A 中有相同的原像;（3）B 中的元素可以在A 中无原像；（4）像的集合就是集合B .A 、1个B 、2个C 、3个D 、4个7．若函数2()2(1)2f x x a x =+-+在区间(,4)-∞上是减函数,则实数a 的取值范围是A、3a≤-B、3a≥-C、5a≤D、3a≥8．定义域为R的函数y=f(x）的值域为[a，b]，则函数y=f（x＋a）的值域为（ ) A．［2a，a＋b] B．[a，b］C．[0,b－a］D．［－a,a＋b］9．下列所给4个图象中，与所给3件事吻合最好的顺序为（）(1)我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；(2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间;（3)我出发后，心情轻松,缓缓行进，后来为了赶时间开始加速。

人教版高一数学上学期期中检测试卷(含答案)

人教版高一数学上学期期中检测试卷（含答案）一、选择题1. 已知集合A ={1,2}，B ={x|−1<x <2}，则A ∩B =( )A.{0}B.{1}C.{1,2}D.{0,1,2}2. 命题“∀x ∈N ，x 2+x >0”的否定是( )A.∀x ∉N ，x 2+x <0B.∀x ∈N ，x 2+x ≤0C.∃x ∈N ，x 2+x <0D.∃x ∈N ，x 2+x ≤03. 设f (x )={x +3, x ≥0,1, x <0,则f(f (−1))=( ) A.4 B.3 C.2 D.14. 若a >b ，则下列不等式成立的是（）A.a 2>b 2B.a 3>b 3C.2a−b <1D.1a <1b5. 已知p:|x|>1，q:x >1，则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6. 函数y =1+x|x|的图象大致是( ) A. B. C. D.7. 函数f (x )是定义在R 上的奇函数， x >0时f (x )=x 2−3x ，则不等式f (x )<0的解集是( )A.(0,3)B.(3,+∞)C.(−∞,−3)∪(0,3)D.(−3,0)∪(3,+∞)8. 已知m ， n ∈R ，且有2m +2n =2m+n ，则m +n +1+2m+n 的最小值是( )A.6B.7C.8D.9二、多选题9.已知集合A ={1, 16, 4x}，B ={1, x 2}，若B ⊆A ，则x 可能取值有( )A.0B.−4C.1D.410.以下说法正确的有( )A.实数x>y>0是1x <1y成立的充要条件B.不等式ab≤(a+b2)2对a，b∈R恒成立C.命题“∃x∈R，x2+x+1≥0”的否定是“∀x∈R，x2+x+1<0"D.若1x +1y=1，则x+y的最小值是411.已知a，b，c为实数，且a>b>0，则下列不等式正确的是()A.1a <1bB.ac2>bc2C.ba<abD.a2>ab>b212.已知f(x)是定义在R上的奇函数，且f(x)的图象关于直线x=1对称，当0≤x≤1时，f(x)=x，关于函数g(x)=|f(x)|+f(|x|)，下列说法正确的是()A.g(x)为偶函数B.g(x)在(−1,0)上单调递增C.方程g(x)=0在[0,4]上恰有三个实根D.g(x)的最大值为2三、填空题13.函数y=a x−2020+1(a>0且a≠1）的图象必经过定点________.14.若函数y=mx2+x+2在[3,+∞)上是减函数，则m的取值范围是________.15.函数f(x)的定义域为(0, 3)，则函数y=f(x+1)x−1的定义域是________．16.若x,y是正数，且x+2y=1，则xy的最大值为________，1x +xy的最小值为________.四、解答题17.已知函数f(x)=√4−x+√x+3的定义域为集合A．(1)求集合A；(2)若集合B={x∈N|0<x<3}，求A∩B并写出它的所有子集．18.已知命题p：∀x∈[1, 2]，x2−a≥0，命题q：∃x∈R，x2+2ax+2−a=0．若命题p与q都是真命题，求实数a的取值范围．19.已知函数f(x)是定义在R上的偶函数，且当x≤0时，f(x)=x2+2x．(1)现已画出函数f(x)在y轴左侧的图像，如图所示，请补出完整函数f(x)的图像，并根据图像写出函数f(x)的增区间；(2)写出函数f(x)的解析式和值域.20.已知函数f(x)=x+m，且此函数图象过点(1, 5)．x(1)求f(x)的解析式；(2)讨论函数f(x)在[2, +∞)上的单调性？并证明你的结论．(3)求函数f(x)在区间[2, 4]上的最小值和最大值．21.如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B点在AM上，D 点在AN上，且对角线MN过C点，已知AB=3米，AD=4米.(1)要使矩形AMPN的面积大于50平方米，则DN的长应在什么范围？(2)当AN的长为多少米时，矩形花坛AMPN的面积最小？并求出最小值．22.定义在非零实数集上的函数f(x)对任意非零实数x，y满足：f(xy)=f(x)+f(y)，且当0<x<1时，f(x)<0．(1)求f(−1)及f(1)的值；(2)求证：f(x)是偶函数；)≤0．(3)解不等式：f(2)+f(x2−12参考答案:一、1-4 BDAB 5-8 BBCB二、9.A,B10.B,C11.A,C,D12.A,D三、13.(2020,2)14.m≤−1615.{x|−1<x<2且x≠1}16.18,1+2√2四、17.解：(1)∵ 函数f(x)=√4−x+√x+3，∵ 函数的定义域为：{4−x≥0，x+3>0，解得−3<x≤4，∵ 集合A={x|−3<x≤4}.(2)∵ 集合B={x∈N|0<x<3}={1, 2}，集合A={x|−3<x≤4}，∵ A∩B={1, 2}，∵ A∩B的所有子集为：⌀，{1}，{2}，{1, 2}．18.解：根据题意，命题p：∀x∈[1, 2]，x2−a≥0，若命题p为真，必有a≤(x2)min=1，即a≤1；对于命题q，∃x∈R，x2+2ax+2−a=0，若命题q为真，即方程x2+2ax+2−a=0有解，则有Δ=4a2−4(2−a)≥0，解可得：a≥1或a≤−2.若命题p与q都是真命题，即{a≤1,a≥1或a≤−2,则有a≤−2或a=1.故a的取值范围为{a|a≤−2或a=1}．19.解：(1)函数图像如图所示：f(x)的递增区间是(−1, 0)，(1, +∞)．(2)∵x ≤0时，f(x)=x 2+2x ,令x >0, 则−x <0,故f(−x)=x 2−2x ,∵ 函数f(x)为偶函数，∵ f(x)=f(−x)，∴当x >0时，f(x)=x 2−2x .∵ f(x)={x 2+2x ，x ≤0，x 2−2x ，x >0，值域为：{y|y ≥−1}．20.解：(1)∵ 函数图象过点(1, 5)．得1+m =5，解得m =4,∵ f(x)=x +4x .(2)函数f(x)在[2, +∞)上的单调递增，证明如下：∀x 1，x 2∈[2,+∞)，且x 1<x 2，f (x 1)−f (x 2)=x 1+4x 1−x 2−4x 2 =(x 1−x 2)+4(x 2−x 1)x 1x 2=(x 1−x 2)(x 1x 2−4)x 1x 2，∵ x 1，x 2∈[2,+∞)且x 1<x 2，∵ x 1−x 2<0，x 1x 2>4， x 1x 2>0，∵ f (x 1)−f (x 2)<0，即f (x 1)<f (x 2)，∵ f (x )在[2,+∞)上单调递增.(3)由f(x)在[2, +∞)上单调递增，可知函数f(x)在区间[2, 4]上也单调递增，当x =2时，函数取得最小值4，当x =4时，函数取得最大值5．21.解：(1) 设DN 的长为x (x >0)米，则AN =x +4米． ∵ DN AN =DC AM ， ∵ AM =3(x+4)x ， ∵ S AMPN =AN ⋅AM =3(x+4)2x ，由矩形AMPN 的面积大于50得： 3(x+4)2x >50，又x >0，得： 3x 2−26x +48>0，解得： 0<x <83或x >6，即DN 长的取值范围为： (0,83)∪(6,+∞). (2)由(1)得，矩形花坛AMPN 的面积为：y =3(x +4)2x =3x 2+24x +48x =3x +48x+24 ≥2√3x ⋅48x +24=48，当且仅当3x =48x ，即x =4时，矩形花坛AMPN 的面积取得最小值48，故DN 的长为4米时，矩形AMPN 的面积最小，最小值为48平方米．22.解：(1)在f(xy)=f(x)+f(y)中，令x =y =1，则f(1)=f(1)+f(1)，∵ f(1)=0，再令x =y =−1，则f(1)=f(−1)+f(−1)，∵ f(−1)=0.(2)在f(xy)=f(x)+f(y)中，令y =−1，则f(−x)=f(x)+f(−1)=f(x)，∵ f(−x)=f(x)，∵ f(x)为偶函数.(3)任取x 1，x 2∈(0, +∞)，且x 1<x 2，∵ 0<x 1x 2<1，∵ f(x1x 2)<0， ∵ f(x 1)=f(x 2⋅x 1x 2)=f(x 2)+f(x1x 2)<f(x 2)，∵ f(x)在(0, +∞)是增函数， ∵ f(x)在(−∞, 0)是减函数， ∵ f(2)+f(x 2−12)=f(2x 2−1)≤0=f(1)=f(−1)，∵ {2x 2−1<0，2x 2−1≥−1，或{2x 2−1>0，2x 2−1≤1，解得−√22<x <√22或−1≤x <−√22或√22<x ≤1， ∵ 不等式的解集为[−1, −√22)∪(−√22, √22)∪(√22, 1].。