第九届希望杯5年级初赛试题(可以A4打印效果好).docx

合集下载

第九届小学“希望杯”全国数学邀请赛五年级第1试 .doc

数学试题（四）同学们注意：本试题共27个小题，满分150分，考试时间120分钟一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将各小题所选答案的标号填入题后的表格内.1.下列计算正确的是( )A．B．C．D.2.下列图形中不是轴对称图形的是（）A B C D3.如果三角形的两边长分别为3和5，则第三边长可以是（）A．1 B．2 C．4D．84.下列事件是必然事件的是（）A．从一副扑克牌中任意抽出一张牌，花色是红桃.B．打开电视，正在播放《新闻联播》.C．在平面内，度量一个三角形的内角度数，其和为360°.D．今天是星期六，明天就是星期日.5.化简的结果是（）A．-2B．±2C．2D．46.将一张正方形纸片按图①、图②所示的方式依次对折后，再沿图③中的虚线剪裁，最后将图④中的纸片打开铺平，所得到的图案是（）A．B．C．D．7.如下图，∥，则∠1的度数为（）A.B.C. D.8.一只小狗在如上图所示的大小完全相同的方砖上走来走去，最终停在阴影方砖上的概率是（）A．B．C．D．9.观察下列图形它们是按一定的规律排列的，依照此规律，第8个图形的“★”有（）A．24个B．27个C．30个D．33个10.小刚徒步到同学家取自行车，在同学家逗留几分钟后他骑车上学，设他从家出发后所用的时间为(分钟)，所走的路程为(米），则与的函数图象大致是（）A B C D11.如右图，在△ABC中，AB=AC，点D在BC上，且∠BAD=∠DAC=30°，点E在AC上，且AD=AE，则∠EDC的度数为（）A．10°B．15°C．20°D．30°12.已知则的值为（）A．-4B．-1 C．2 D．7二、填空题：（本大题共6个小题，每小题4分，共24分）在每个小题中，请将每小题的正确答案填在上面表格内．13.第十五届中国重庆汽车工业展于2013年6月13日在重庆国际博览中心圆满结束，据统计，7天时间45万人次先后观展，100余厂商卖出17600辆车，将数17600用科学记数法表示为 .14.已知等腰三角形的一个内角为75o，则其顶角为 .15.已知，, 则 = .16.计算：= .17.如上图，△ABC中，∠C=，AC=BC，AD是△ABC的角平分线，DE⊥AB于E，若AB=6，则△DEB的周长为.18.如上图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠MAN的度数为 .三、解答题：（本大题3个小题，每小题6分，共18分）解答时必须给出必要的演算过程或推理步骤．19.计算：20.化简：21.已知线段和如图所示，求作△ABC使BC=，AC=2，∠C=.要求：用尺规作图，画图必须用铅笔，不要求写作法，但要保留作图痕迹.四、解答题：（本大题3个小题，第22题8分，第23、24题10分，共28分）解答时必须给出必要的演算过程或推理步骤．22.在△ABC中，D是BC边上的中点，F、E分别是AD及其延长线上的点，CF∥BE．求证：CF=BE．23.先化简，再求值：，其中满足：.24.为全面推进素质教育，重庆一中积极开展“体育选修”活动，结合我校实际，决定开设A：篮球，B：乒乓球，C：羽毛球，D：健美操，E：田径5种活动项目，为了解初一学生最喜欢哪一种活动项目，从2000名学生中随机抽取了部分学生进行调查，并将调查结果绘制了两幅不完整的统计图:（1）参加调查的人数共有人；在扇形统计图中，表示“C”的扇形的圆心角为度；（2）补全条形统计图，并计算扇形统计图中的；（3）学校决定下学期从A、B、C、D、E这5种活动项目中选取一种作为全校课外活动必修科目，选中健美操的概率是多少？四、解答题（本大题3个小题，第25、26题10分，第27题12分，共32分）解答时必须给出必要的演算过程或推理步骤．25.已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向外作等边△ABD和等边△ACE．（1）如图1，连接线段BE、CD．求证：△AB E≌△A DC；（2）如图2，连接DE交AB于点F．求证：F为DE中点．26.“龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．(1)填空：折线OABC表示赛跑过程中的路程与时间的关系，线段OD表示赛跑过程中的路程与时间的关系．赛跑的全程是米．(2)兔子在起初每分钟跑多少米？乌龟每分钟爬多少米？(3)乌龟用了多少分钟追上了正在睡觉的兔子？(4)兔子醒来，以48千米/时的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你算算兔子中间停下睡觉用了多少分钟？27.已知两个全等的等腰直角△ABC、△DEF，其中∠ACB=∠DFE=90°，E为AB中点，线段DE，EF分别交线段CA，CB（或它们所在直线）于M、N．（1）如图l所示放置，当线段EF经过△ABC的顶点C时，点N与点C重合，线段DE 交AC于M，求证：AM=MC；（2）如图2所示放置，当线段EF与线段BC边交于N点，线段DE与线段AC交于M 点，连MN，EC，请探究AM，MN，CN之间的等量关系，并说明理由；（3）如图3所示放置，当线段EF与BC延长线交于N点，线段DE与线段AC交于M 点，连MN，EC，请猜想AM，MN，CN之间的等量关系，不必说明理由．数学试题答案（四）一、选择题：二、填空题：题号 1 2 3 4 5 6 7 8 9 答案 D C C D A B C B A 题号10 11 12 13 14 15 16 17 18 答案 B B C 1.76×104 75° 3 2 6 60°三、解答题：19、解：原式=……………………………………… 5分=…………………………………………………………6分20、解：原式= …………………………………… 2分=…………………………………………………………6分21、画图正确5分，结论1分.22、证明：∵D是BC边上的中点，∴BD=CD，∵CF∥BE，∴∠E=∠CFD，∠DBE=∠FCD………………………………………3分在△DEB和△DFC中，…………………………………………………… 6分∴△BDE≌△CFD(AAS)……………………………………………… 7分∴CF=BE．…………………………………………………………… 8分23、解：原式=……………3分=………………………4分=…………………………………………………………6分∵∴………………………………………………………8分∴原式==…………………………………………10分24、解：（1）300 ……………………………………………………………………1分108°……………………………………………………………………3分（2）补全图形（活动C有90人，标数据）…………………………………4分∵∴m=20………………………………………………………………………6分(3)共有5种等可能的结果，分别是：A、B、C、D、E，选中健美操可能出现的结果有1种. ……………………………………7分∴……………………………………………………………10分25、证明：：(1)∵△ABD和△ACE是等边三角形，∴AB=AD，AC=AE，∠DAB=∠EAC=60°，∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，在△ABE和△ADC中，∴△ABE≌△ADC （SAS）…………………………………………………………………4分(2)如图，作DG∥AE，交AB于点G，由∠EAC=60°，∠CAB=30°得：∠FAE=∠EAC+∠CAB=90°，∴∠DGF=∠FAE=90°，又∵∠ACB=90°，∠CAB=30°，∴∠ABC=60°，又∵△ABD为等边三角形，∠DBG=60°，DB=AB，∴∠DBG=∠ABC=60°，在△DGB和△ACB中，∴△DGB≌△ACB（AAS）…………………………………………………………………7分∴DG=AC，∵△AEC为等边三角形，∴AE=AC，∴DG=AE，在△DGF和△EAF中，∴△DGF≌△EAF（AAS）………………………………………………………………9分∴DF=EF，即F为DE中点．……………………………………………………………10分26、解：（1）兔子，乌龟，1500；…………………………………………………………3分（2）结合图象得出：兔子在起初每分钟跑700米…………………………………………………4分1500÷30=50（米）∴乌龟每分钟爬50米．………………………………………………………5分（3）700÷50=14（分钟）乌龟用了14分钟追上了正在睡觉的兔子．…………………………………7分（4）∵48千米=48000米∴48000÷60=800（米/分）……………………………………………………8分（1500-700）÷800=1（分钟）30+0.5-1×2=28.5（分钟）兔子中间停下睡觉用了28.5分钟．…………………………………………10分27、解：（1）∵AC=BC，E为AB中点，∴CE⊥AB，∠ACE=∠BCE=∴∠AEC=90°，∴∠A=∠ACE=45°，∴AE=CE，∵DF=EF，∠DFE=90°，∴∠FED=45°，∴∠FED=又∵AE=CE，∴AM=MC；……………………………………………………………………3分（2）AM=MN+CN，理由如下：……………………………………………………4分在AM截取AH，使得AH=CN，连接BH，由（1）知AE=CE，∠A=∠BCE=45°∵在△AHE与△CNE中：∴△AHE≌△CNE（SAS）……………………………………………………6分∴HE=NE，∠AEH=∠CEN，∴∠HEM=∠AEC-∠AEH-MEC=∠AEC-∠CEN-MEC=∠AEC-∠MEF=90°-45°=45°，∴∠HEM=∠NEM=45∵在△HEM与△NEM中：∴△HEM≌△NEM（SAS）…………………………………………………9分∴HM=MN，∴AM=AH+HM=CN+MN；即AM=MN+CN …………………………………………………………10分（3）猜得：MN=AM+CN…………………………………………………………12分。

希望杯第一届至第十届五年级试题与答案

10．三个武术队进行擂台赛，每队派 6 名选手，先由两队各出 1 名选手上擂台比武，负者下台，不再上台，胜者继续同其它队的一位选手比武，负者下台，和胜者不同队的双一位选手上台……继续下去。当有两个队的选手全部被击败时，余下的队即获胜。这时最少要进行_____场比武。
1 6
11．两种饮水器若干个，一种容量 12 升水，另一种容量 15 升水。153 升水恰好装满这些饮水器，其中 15 升容量的_____个。
14．小光前天登录到数理天地网站，他在首页看到"您是通过什么方式知道本网站的？" 调查，他查看了投票结果，发现投票总人数是 500 人，"杂志"项的投票率是 68%。当他昨天再次登录数理天地网站时，发现"杂志"项的投票率上升到 72%，则当时的投票总人数至少是_____ 。
的四位数是
。
8． a ， b ， c 都是质数，并且 a ＋ b ＝33， b ＋ c ＝44， c ＋ d ＝66，那么 d ＝
，
BA
9．如果A◆B＝ A B ，那么1◆2－2◆3－3◆4－…－2002◆2003－2003◆2004＝
。
10．用1－8这八个自然数中的四个组成四位数，从个位到千位的的数字依次增大，且任意两个数字的
1．计算
_______ 。
2．将 1、2、3、4、5、6 分别填在右图中的每个方格内，使折叠成的正方体中对面数字的和相等。
3．在纸上画 5 条直线，最多可有_______ 个交点。
4．气象局对部分旅游景区的某一天的气温预报如下表：
景区
千岛湖张家界庐山三亚丽江大理九寨沟鼓浪屿
气温(℃) 11/1
算英语，平均分是91分。小永三门功课的平均成绩是

五年级希望杯初赛试题

五年级希望杯初赛试题五年级希望杯初赛试题希望杯是重要的奥林匹克赛事，下面就是小编为您收集整理的五年级希望杯初赛试题的相关文章，希望可以帮到您，如果你觉得不错的话可以分享给更多小伙伴哦！五年级希望杯初赛试题1、5.45×24×0.2－3.45×4.8=（）2、200－199＋198－197＋······＋4－3＋2－1=（）3、一列火车全长215米，每秒行驶25米，要经过长960米的大桥，全车通过需要（）秒。

4、甲乙两个数的和是70，甲比乙多16，甲乙两数的积是（）。

5、林地里有桃树、梨树和苹果树共200棵，桃树是梨树的3倍，苹果树是桃树的`2倍，苹果树有（）棵。

6、有一批水果，每箱放30个则多20个；每箱放35个则少10个。

这批水果至少有（）个。

7、在一个长20分米，宽15分米的长方体容器中，有20分米深的水。

现在在水中沉入一个棱长30厘米的正方体铁块，这时容器中水深（）分米。

8、东城区仓库，第一天运出所有粮食的一半多2吨，第二天又运出余下的一半少0.8吨，第三天运出6吨粮食后，还有4吨。

仓库中原来共存粮食（）吨。

9、甲乙两车分别同时从A、B两地出发，甲车每小时行55千米，乙车每小时行45千米，两车在离中点25千米处相遇。

两地相距（）千米。

10、一个正方体的高增加3分米，就变成了一个长方体，且表面积比原来增加了60平方分米，原来正方体的体积是（）立方分米。

11、一个棱长为6厘米的正方体木块，如果把它锯成棱长为2厘米的正方体若干块，表面积增加（）平方厘米。

12、5100除以一个三位数，余数是95，这个三位数最大是（）。

13、有一个长方形，如果长减少4米，宽减少2米，面积就比原来减少44平方米，且剩下部分正好是一个正方形，这个正方形的周长是（）米。

14、两数相除商是4，余数是17，被除数、除数、商和余数的和是673，被除数是（）。

2011年第九届小学“希望杯”全国数学邀请赛五年级第1试+答案

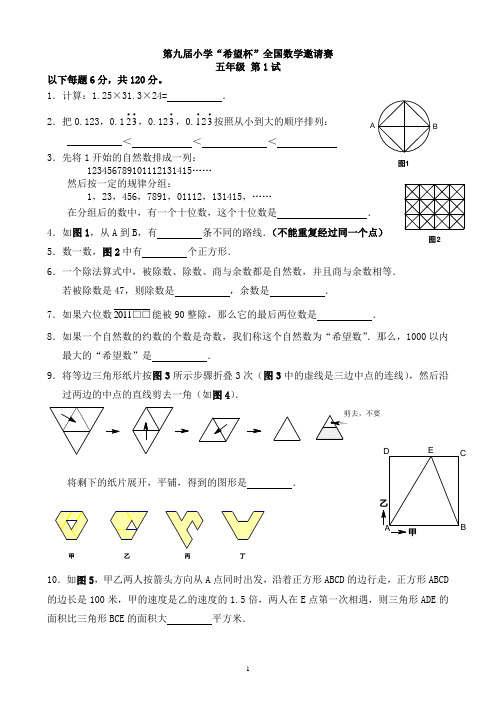
乙甲E D CBA丁丙乙甲第九届小学“希望杯”全国数学邀请赛五年级第1试以下每题6分，共120分。

1．计算：1.25×31.3×24= ．2．把0.123，0.1∙∙32，0.12∙3，0.∙12∙3按照从小到大的顺序排列：___________＜＜＜3．先将1开始的自然数排成一列：123456789101112131415……然后按一定的规律分组：1，23，456，7891，01112，131415，……在分组后的数中，有一个十位数，这个十位数是．4．如图1，从A 到B ，有条不同的路线．（不能重复经过同一个点）5．数一数，图2中有个正方形．6．一个除法算式中，被除数、除数、商与余数都是自然数，并且商与余数相等．若被除数是47，则除数是，余数是．7．如果六位数□□2011能被90整除，那么它的最后两位数是．8．如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”．那么，1000以内最大的“希望数”是．9．将等边三角形纸片按图3所示步骤折叠3次（图3中的虚线是三边中点的连线），然后沿过两边的中点的直线剪去一角（如图4）．将剩下的纸片展开，平铺，得到的图形是．10．如图5，甲乙两人按箭头方向从A 点同时出发，沿着正方形ABCD 的边行走，正方形ABCD 的边长是100米，甲的速度是乙的速度的1.5倍，两人在E 点第一次相遇，则三角形ADE 的面积比三角形BCE 的面积大平方米．图1BA 图211．星期天早晨，哥哥和弟弟去练习跑步．哥哥每分钟跑110米，弟弟每分钟跑80米．弟弟比哥哥多跑了半小时，结果比哥哥多跑了900米．那么哥哥跑了米．12．小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元．那么笔记本每个元，笔每支元．13．数学家维纳是控制论的创始人．在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄．维纳的回答很有趣，他说：“我的年龄的立方是以个四位数，年龄的四次方是一个六位数，这两个数刚好把0~9这10个数字全都用上了，不重也不漏．”那么，维纳这一年岁．（注：数a的立方等于a×a×a，数a的四次方等于a×a×a×a）14．鸡与兔共100只，鸡的脚比兔的脚多26只．那么，鸡有只．15．小松鼠储藏了一些松果过冬．小松鼠原计划每天吃6个松果，实际每天比原计划多吃2个，结果提前5天吃完了松果．小松鼠一共储藏了个松果．16．商店对某种饮料推出“第二杯半价”的促销办法．那么，若买两杯这种饮料，相当于在原价的基础上打折．17．A、B、C、D四人进行围棋比赛，每人都要与其他三人各赛一盘．比赛在两张棋盘上同时进行，每人每天只赛一盘．第一天A与C比赛，第二天C与D比赛，第三天B与比赛．18．有白球和红球共300个，纸盒100个．每个纸盒里都放3个球，其中放1个白球的纸盒有27个，放2个或3个红球的纸盒共有42个，放3个白球和3个红球的纸盒数量相同．那么，白球共有个．19．用长5厘米、宽4厘米、高3厘米的长方体木块叠成一个最大的正方体，至少需要个这样的长方体木块．20．如图6，梯形ABCD的上底AD长12厘米，高BD长18厘米，BE=2DE，则下底BC长厘米．DAECB。

2011年第九届希望杯五年级初赛试题及讲解

2011年第九届希望杯五年级数学初赛试题及讲解1、计算：1.25×31.3×242、把0.123，0.1，0.12，0.按照从小到大的顺序排列：﹤﹤﹤3、先将从1开始的自然数排成一列：123456789101112131415……然后按一定的规律分组：1，23，456，7891，01112，131415，……在分组后的数中有一个十位数，这个十位数是。

4、如图1，从A到B，有条不同的路线。

（不能重复经过同一个点）5、数一数，图2中有个正方形。

6、在一个除法算式中，被除数、除数、商与余数都是自然数，并且商与余数相等。

若被除数是47，则除数是，余数是。

7、如果六位数能被90整除，那么它的最后两位数是。

8、如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”。

那么1000以内的最大的“希望数”是。

9、将等边三角形纸片按图3所示步骤折叠3次（图3中的虚线是三边的中点的连线），然后沿过两边的中点的直线减去一个角（如图4）将剩下的纸片展开，平铺，得到的图形是。

10. 如图5，甲、乙两人按箭头方向从A点同时出发，沿着正方形ABCD的边行走，正方形ABCD的边长是100米，甲的速度是乙的速度的1.5倍，两人在E点第一次相遇，则三角形ADE的面积比三角形BCE的面积大__________平方米。

11、星期天早晨，哥哥和弟弟去练习跑步。

哥哥每分钟跑110米，弟弟每分钟跑80米。

弟弟比哥哥多跑了半小时。

结果比哥哥多跑了900米。

那么哥哥跑了米。

12、小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元。

那么，笔记本每个元，笔每支元。

13、数学家维纳是控制论的创始人。

在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄。

维纳的回答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0～9这10个数字全都用上了，不重也不漏。

第九届希望杯五年级试题word版

第九届小学“希望杯”全国数学邀请赛五年级第2试一、填空题（每小题5分，共60分）1.计算：0.15÷2.2×56＝。

2.15+115+1115+……+1111111115＝。

3.一个自然数除以3，得余数2，用所得的商除以4，得余数3.若用这个自然数除以6，得余数。

4.数一数，图1中共有个长方形。

5.有一些自然数（0除外）既是平方数，又是立方数（注：平方数可以写成两个相同自然数的乘积，立方数可以写成三个相同的自然数的乘积）。

如：1＝1×1＝1×1×1，64＝8×8＝4×4×4.那么，1000以内的自然数中，这样的数有个。

6.有一个自然数，它的最小的两个约数的差是4，最大的两个约数的差是308，则这个自然数是。

7.如图2，先将4黑1白共5个棋子放在一个圆圈上，然后在同色的两子之间放入一个白子，在异色的两子之间放入一个黑子，再将原来的5个棋子拿掉。

如此不断操作下去，圆圈上的5个棋子中最多有个白子。

8.甲、乙两人分别从A、B两地同时相向而行，甲的速度是乙的速度的3倍。

经过60分钟，两人相遇。

然后，甲的速度减为原速的一半，乙的速度不变，两人各自继续前行。

那么，当甲到达B地后，再经过分钟，乙到达A地。

9.如图3，将一个棱长为1米的正方体木块分别沿长、宽、高三个方向锯开1,2,3次，得到24个长方体木块。

这24快长方体木块的表面积的和是平方米。

10.小丽和小明的桶中原来各装有3千克和5千克水。

如果把小丽桶里的水向小明的桶里倒，装满小明的桶后，小丽则剩半桶水；如果把小明桶里的水向小丽的桶里倒，装满小丽的桶后，小明则剩3/4桶水。

问小丽的桶最多可以装千克水，小明的桶最多可以装千克水。

11.将1---2011的奇数排成一列，然后按每组1,2,3,2,1,2,3,2,1，…个数的规律分组如下（每个括号为一组）：（1）,（3,5）,（7,9,11）,（13,15）,（17）,（19,21）,（23,25,27）,(29,31),（33），…则最后一个括号内的各数之和是。

五年级希望杯数学竞赛题目

五年级希望杯数学竞赛题目一、题目与解析。

1. 计算：0.125×0.25×0.5×64- 解析：- 把64分解成8×4×2。

- 原式=(0.125×8)×(0.25×4)×(0.5×2)。

- 因为0.125×8 = 1，0.25×4=1，0.5×2 = 1。

- 所以结果为1×1×1 = 1。

2. 计算：(1.25+1.25+1.25+1.25)×25×8- 解析：- 括号里1.25+1.25+1.25+1.25 = 1.25×4。

- 原式=(1.25×4)×25×8。

- 根据乘法交换律和结合律，先算4×25 = 100，1.25×8 = 10。

- 结果为100×10 = 1000。

3. 一个数除以5余3，除以6余4，除以7余5。

这个数最小是多少？- 解析：- 这个数加上2就能被5、6、7整除。

- 5、6、7的最小公倍数为5×6×7=210。

- 所以这个数最小是210 - 2 = 208。

4. 有一个自然数，用它分别去除63，90，130都有余数，三个余数的和为25。

这三个余数中最大的一个是多少？- 解析：- 设这个自然数为x，设除63的余数为a，除90的余数为b，除130的余数为c。

- 则63 = k_1x + a，90=k_2x + b，130 = k_3x + c。

- 已知a + b + c = 25。

- 那么63+90 + 130-(a + b + c)=(k_1 + k_2 + k_3)x。

- 即63+90+130 - 25=(k_1 + k_2 + k_3)x。

- 计算得258=(k_1 + k_2 + k_3)x。

- 把258分解因数：258 = 2×3×43。

第九届新希望杯五年级初赛A卷

第九届“新希望杯”全国数学大赛五年级试题(A 卷)一、填空题(每小题8分，共80分)1、计算：()()=+÷⨯-102.34.56.78.9 。

2、解方程：()[]65432=⨯-÷+x ，=x 。

3、如图，转盘被均匀分成了8个区域，上面分别写着1、2、3、4、5、6、7、8，转动转盘一次，指针所指区域(若指针指在边界则重新转动一次)的数字是质数的可能性为。

4、从7月1日起，某地居民阶梯电价按照居民每月用电量分为三档。

第一档为0—180度，0.57元/度；第二档为超过180度但不超过400度的部分，0.62元/度；第三档为超过400度的部分，0.87元/度。

如王同学家11月份用电200度，电费为180×0.57＋(200—180)×0.62＝115元。

如果王同学家12月份的电费为263.36元，那么王同学家12月份的用电量为度。

5、对两位数进行一次操作是指：将这个两位数的两个数字相乘，如果乘积是个两位数，就写下这个乘积；如果乘积是个一位数，就在这个乘积的前面添上2。

如对67连续进行3次操作依次得到：67→42→28→16。

那么对39连续进行1230次操作后得到的两位数是。

6、如图，在8×8的方格纸中，每个小方格的面积为1，则“风车”的面积为。

7、多位数2013123123123个…123 除以11所得的余数是。

8、参加2012年“新希望杯”北京夏令营的代表队共有80支，其中来自湖北的代表队比来自武汉的代表队的3倍多1支，已知来自湖北但不是来自武汉的代表队共有35支，那么不是来自湖北的代表队共有支。

9、如图，摆第1个“小屋子”需7颗棋子，摆第2个“小屋子”需13颗棋子，摆第3个“小屋子”需19颗棋子，……照这样摆下去，摆第30个“小屋子”需颗棋子。

第4个第3个第2个第1个10、纸上写着一列自然数1、2、……、1228、1229、1230。

2011年第九届希望杯五年级初赛试题及讲解

2011年第九届希望杯五年级初赛试题及讲解<i>真题及详细讲解</i>1、计算：1.25×31.3×242、把0.123，0.1，0.12，0.按照从小到大的顺序排列：3、先将从1开始的自然数排成一列：***-********-********** 然后按一定的规律分组：1，23，456，7891，01112，*****，在分组后的数中有一个十位数，这个十位数是。

4、如图1，从A到B，有条不同的路线。

（不能重复经过同一个点）5、数一数，图2中有个正方形。

6、在一个除法算式中，被除数、除数、商与余数都是自然数，并且商与余数相等。

若被除数是47，则除数是，余数是。

7、如果六位数能被90整除，那么它的最后两位数是。

8、如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”。

那么1000以内的最大的“希望数”是。

11、星期天早晨，哥哥和弟弟去练习跑步。

哥哥每分钟跑110米，弟弟每分钟跑80米。

弟弟比哥哥多跑了半小时。

结果比哥哥多跑了900米。

那么哥哥跑了米。

12、小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元。

那么，笔记本每个元，笔每支元。

13、数学家维纳是控制论的创始人。

在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄。

维纳的回答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0～9这10个数字全都用上了，不重也不漏。

【免费下载】第九届希望杯五年级数学初赛试题及讲解

2011年第九届希望杯五年级数学初赛试题及讲解1、计算：1.25×31.3×242、把0.123，0.1，0.12，0.按照从小到大的顺序排列：﹤ ﹤ ﹤ 3、先将从1开始的自然数排成一列：123456789101112131415……然后按一定的规律分组：1，23，456，7891，01112，131415，……在分组后的数中有一个十位数，这个十位数是。

4、如图1，从A 到B ，有条不同的路线。

（不能重复经过同一个点）5、数一数，图2中有个正方形。

6、在一个除法算式中，被除数、除数、商与余数都是自然数，并且商与余数相等。

若被除数是47，则除数是，余数是。

7、如果六位数能被90整除，那么它的最后两位数是。

8、如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”。

那么1000以内的最大的“希望数”是。

术架等及系，然来避免9、将等边三角形纸片按图3所示步骤折叠3次（图3中的虚线是三边的中点的连线），然后沿过两边的中点的直线减去一个角（如图4）将剩下的纸片展开，平铺，得到的图形是。

10. 如图5，甲、乙两人按箭头方向从A 点同时出发，沿着正方形ABCD 的边行走，正方形ABCD 的边长是100米，甲的速度是乙的速度的1.5倍，两人在E 点第一次相遇，则三角形ADE 的面积比三角形BCE 的面积大__________平方米。

11、星期天早晨，哥哥和弟弟去练习跑步。

哥哥每分钟跑110米，弟弟每分钟跑80米。

弟弟比哥哥多跑了半小时。

结果比哥哥多跑了900米。

那么哥哥跑了米。

12、小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差0.4元，如果再买2个笔记本则还差2元。

那么，笔记本每个元，笔每支元。

13、数学家维纳是控制论的创始人。

在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄。

维纳的回答很有趣，他说：“我的年龄的立方是一个四位数，年龄的四次方是一个六位数，这两个数刚好把0～9这10个数字全都用上了，不重也不漏。

第9-11届希望杯数学竞赛五年级二试试题含答案.docx

笫九届小学“希望杯”全国数学邀请赛五年级第2试一、填空题（每小题5分，共60分）1> 计算：0・ 15 —2.1X56二___________ o2、15 + 115 + 11154- ........... +1111111115= ___________ o3、一个自然数除以3,得余数2,用所得的商除以4,得余数3。

若用这个自然数除以6,得余数_________________ o4、数一数，图1中共有5、有一些自然数（0除外）既是平方数（可写成两个相同的自然数的乘积），又是立方数（可写成三个相同的自然数的乘积）。

女口：1 = 1X1=1X1X1, 64 = 8X8二4X4X4。

那么在1000 以内的自然数中，这样的数有_____________ 个。

6、有一个自然数，它的最小的两个约数的差是4,最大的两个约数的差是308,则这个自然数是 ________________ o7、如图2,先将4黑1白共5个棋子放在一个圆圈上，然后在同色的两了之间放入一个白了，在异色的两子之间放入一个黑子，再将原来的5个棋子拿掉。

如此不断操作下去，圆圈上的5个棋子中最多有 __________ 个白子。

8、屮、乙两人分别从A、B两地同时相向而行，屮的速度是乙的速度的3倍，经过60分钟，两人相遇。

然后，甲的速度减为原速的一半，乙的速度不变，两人各自继续前行。

那么，当甲到达B地后，再经过__________ 分钟，乙到达______ A地。

9、如图3,将一个棱长为1米的正方体木块分别沿长、宽、高三个方向锯开1, 2, 3次，得到24个长方体木块。

这24块长方体木块的表面积的和是________________ 平方米。

(18)10 •如图4,小丽和小明的桶中原来各装有3千克和5千克水。

根据图中的信息可知，小丽的桶最多可以装____________ 千克水，小明的桶最多可以装_____________ 千克水。

2011年第九届希望杯5年培训题(1-100)

2011年五年级赛前集训题（一）1、计算：11.725－8.17＋5.275＋6.83 = 。

2、计算：2×（18.5－3.15）＋6.6÷（0.75－0.2）=______。

3、计算：201×2011.2011－201.1×2010.201 =______。

4、计算：0.＋0.＋0.＋0.＋0.＋0.＋0.＋0.＋0.=_______。

5、不用计算试比较下面两个乘积的大小：（填表示大小关系的符号）1234567×8765432_____2345678×7654321.7、已知两个数相邻自然数的乘积是1111122222，那么这两个数是和。

8、在方框中填上适当的数使等式成立：9.716－[81.9－(3.77＋15.4)÷□]×1.2=0。

9、把＋，－，×，÷四个运算符号分别填入下面等式的○内，使等式成立（每个运算符号只能使用一次）：（13○7○11）○（15○6）=1010、定义新运算符※，它的运算规则是：x※y=x×y－x÷y,按此规则计算4※2.5= ，2.5※4= 。

11、将分数化为小数后，小数点后面第2011位上的数字是______，从小数点后第1位到第2011位的所有数字之和是。

12、3种图形○，□，△排列规律如下：○□□△△△○□□△△△○□□△△△…那么从左到右排列的第2011个图形是_____,前2011个图形中○共有____个。

2011年五年级赛前集训题（二）13、观察一下的一串算式：第1个算式：1＋2，第2个算式：3＋4＋5，第3个算式：6＋7＋8＋9，….可推知第100个算式的计算结果是。

14、2011×2011×…×2011的末两位数是______。

2011个201115、一张长方形纸片上有2011个点，加上4个顶点共有2015个点，并且这2015个点中任意3个点都不在同一条直线上。

第九届小学希望杯数学竞赛五年级一试试题及答案

第九届小学希望杯数学竞赛五年级一试试题及答案一、选择题（每题2分，共40分）1.下面哪一个数是2的倍数？A. 15B. 12C. 9D. 62.求10+20的结果是多少？A. 30B. 25C. 40D. 153.45÷5=？A. 9B. 8C. 7D. 64.如果一个四边形的长是7cm，宽是4cm，那么它的面积是多少？A. 21cm²B. 28cm²C. 16cm²D. 32cm²5.下面哪一个数字是奇数？A. 12B. 8C. 7D. 166.如果一个数加上8等于25，那么这个数是多少？A. 17B. 18C. 15D. 207.一个三角形的底是6cm，高是3cm，那么它的面积是多少？A. 9cm²B. 12cm²C. 15cm²D. 18cm²8.如果一个数减去4等于10，那么这个数是多少？A. 14B. 11C. 15D. 169.27÷3=？A. 9B. 8C. 7D. 610.在1-50中，个位数为7的数字有几个？A. 4B. 5C. 6D. 711.8×5=？A. 40B. 35C. 45D. 3012.54÷9=？A. 6B. 7C. 8D. 913.如果一个长方形的长是5cm，宽是3cm，那么它的周长是多少？A. 10cmB. 12cmC. 16cmD. 14cm14.下面哪一个数字是偶数？A. 13B. 18C. 25D. 3115.求45-21的结果是多少？A. 24B. 26C. 20D. 2216.如果一个数减去5等于8，那么这个数是多少？A. 13B. 12C. 11D. 1417.一个正方形的边长是4cm，那么它的面积是多少？A. 12cm²B. 16cm²C. 8cm²D. 20cm²18.如果3个苹果共卖给两个人，每人分多少个？A. 1B. 2C. 3D. 419.在1-100中，十位数为2的数字有几个？A. 9B. 10C. 11D. 1220.9×6=？A. 45B. 54C. 36D. 63二、填空题（共20分）1.计算：20+15=______2.计算：36÷6=______3.一个矩形的长是8cm，宽是4cm，周长是______cm。

第届小学希望杯全国数学邀请赛五年级第试

第届小学希望杯全国数学邀请赛五年级第试The Standardization Office was revised on the afternoon of December 13, 2020第九届小学希望杯全国数学邀请赛五年级第1试以下每题6分，共120分．1．计算：××24= ．2．把，••32，•3，•1•3按照从小到大的顺序排列：___________＜＜＜3．先将1开始的自然数排成一列：……然后按一定的规律分组：1，23，456，7891，01112，131415，……在分组后的数中，有一个十位数，这个十位数是．4．如图1，从A 到B ，有条不同的路线．（不能重复经过同一个点）5．数一数，图2中有个正方形．6．一个除法算式中，被除数、除数、商与余数都是自然数，并且商与余数相等．若被除数是47，则除数是，余数是．7．如果六位数□□2011能被90整除，那么它的最后两位数是．8．如果一个自然数的约数的个数是奇数，我们称这个自然数为“希望数”．那么，1000以内最大的“希望数”是．9．将等边三角形纸片按图3所示步骤折叠3次（图3中的虚线是三边中点的连线），然后沿过两边的中点的直线剪去一角（如图4）．图1B A 图2图3 图4将剩下的纸片展开，平铺，得到的图形是．丁丙乙甲10．如图5，甲乙两人按箭头方向从A点同时出发，沿着正方形ABCD 的边行走，正方形ABCD的边长是100米，甲的速度是乙的速度的倍，两人在E点第一次相遇，则三角形ADE的面积比三角形BCE的面积大平方米．11．星期天早晨，哥哥和弟弟去练习跑步．哥哥每分钟跑110米，弟弟每分钟跑80米．弟弟比哥哥多跑了半小时，结果比哥哥多跑了900米．那么哥哥跑了米．12．小明带了30元钱去买文具，买了3个笔记本和5支笔，剩余的钱，如果再买2支笔还差元，如果再买2个笔记本则还差2元．那么笔记本每个元，笔每支元．13．数学家维纳是控制论的创始人．在他获得哈佛大学博士学位的授予仪式上，有人看他一脸稚气的样子，好奇地询问他的年龄．维纳的回答很有趣，他说：“我的年龄的立方是以个四位数，年龄的四次方是一个六位数，这两个数刚好把0~9这10个数字全都用上了，不重也不漏．”那么，维纳这一年岁．（注：数a的立方等于a×a×a，数a 的四次方等于a×a×a×a）14．鸡与兔共100只，鸡的脚比兔的脚多26只．那么，鸡有只．甲ED CBA15．小松鼠储藏了一些松果过冬．小松鼠原计划每天吃6个松果，实际每天比原计划多吃2个，结果提前5天吃完了松果．小松鼠一共储藏了个松果．16．商店对某种饮料推出“第二杯半价”的促销办法．那么，若买两杯这种饮料，相当于在原价的基础上打折．17．A、B、C、D四人进行围棋比赛，每人都要与其他三人各赛一盘．比赛在两张棋盘上同时进行，每人每天只赛一盘．第一天A与C比赛，第二天C与D比赛，第三天B与比赛．18．有白球和红球共300个，纸盒100个．每个纸盒里都放3个球，其中放1个白球的纸盒有27个，放2个或3个红球的纸盒共有42个，放3个白球和3个红球的纸盒数量相同．那么，白球共有个．19．用长5厘米、宽4厘米、高3厘米的长方体木块叠成一个最大的正方体，至少需要个这样的长方体木块．20．如图6，梯形ABCD的上底AD长12厘米，高BD长18厘米，BE=2DE，则下底BC长厘米．DAECB。

第九届希望杯5年级初赛试题(可以A4打印效果好).docx

第九届小学“希望杯”全国数学邀请赛 五年级 第1试 .doc

希望杯第一届至第十届五年级试题与答案

五年级希望杯初赛试题

2011年第九届小学“希望杯”全国数学邀请赛五年级第1试+答案

2011年第九届希望杯五年级初赛试题及讲解

第九届希望杯五年级试题word版

五年级希望杯数学竞赛题目

第九届新希望杯五年级初赛A卷

2011年第九届希望杯五年级初赛试题及讲解

【免费下载】第九届希望杯五年级数学初赛试题及讲解

第9-11届希望杯数学竞赛五年级二试试题含答案.docx

2011年第九届希望杯5年培训题(1-100)

第九届小学希望杯数学竞赛五年级一试试题及答案

第届小学希望杯全国数学邀请赛五年级第试

第九届小学“希望杯”全国数学邀请赛五年级第1试 .doc